11. 4 实证估算周期性
📜 [原文1]
在本节中,我们将第 3 节中的谱分析应用于真实数据,并侧重于以成交笔数衡量的成交量。我们首先在第 4.1 节中对单只股票进行广泛分析,随后在第 4.2 节中进行全市场分析。我们将在第 5.1.1 节中讨论其他成交量衡量指标的结果,以及我们选择成交笔数作为主要目标的原因。
这个段落是第四部分的开篇介绍,起到了一个“路标”的作用,告诉读者接下来要讲什么内容。
- 核心任务:本节的核心任务是将前面第三节介绍的理论方法——谱分析(Spectral Analysis)——应用到真实的金融市场数据中。理论联系实际是学术研究的关键步骤。
- 研究对象:分析的具体数据是成交量(Volume),但不是我们通常理解的成交金额或成交股数,而是成交笔数(Number of Trades)。作者特别强调了这一点,并预告会在后面的章节(第 5.1.1 节)解释为什么选择成交笔数作为主要分析指标。这表明作者的选择是经过深思熟虑的,而不是随意的。
- 分析范围和结构:本节的分析将分两步走:
- 第一步 (第 4.1 节):进行“深度”分析,选择个别有代表性的股票进行详细研究。这种“解剖麻雀”式的方法有助于深入揭示微观层面的规律。
- 第二步 (第 4.2 节):进行“广度”分析,将同样的方法应用到整个市场的所有股票上。这能检验从个股中发现的规律是否具有普遍性,即是否是市场的“通用模式”。
- 承上启下:段落明确指出了本节内容是建立在第 3 节的理论基础之上的,同时预告了第 5.1.1 节将会有对指标选择的进一步讨论,体现了文章结构的逻辑性和连贯性。
- 误解成交量指标:最容易出错的地方是想当然地认为这里的“成交量”就是成交金额(Turnover)或成交股数(Share Volume)。实际上,本文的核心是分析交易发生的频率和节奏,而成交笔数更能直接反映交易决策的发生次数,不受单笔交易大小的影响。例如,一笔100万股的交易和100笔1万股的交易,在成交股数上相同,但从交易活动的“密集程度”来看,后者要高得多。
- 混淆个股结论与市场结论:读者需要注意区分第 4.1 节中针对特定股票(如苹果、平安银行)得出的结论和第 4.2 节中针对整个市场得出的普遍性结论。个股的特性能帮助我们理解现象,但只有在大量样本上得到验证后,才能称之为市场的普遍规律。
- 忽略分析前提:本节的所有分析都基于第 3 节提出的谱分析模型。如果对该模型(例如,如何定义强度系数、如何进行去趋势等)没有清晰的理解,就很难真正看懂本节的数据和图表。
本段是第四部分的引言,纲领性地阐述了本章的研究目的、对象、方法和结构。其核心思想是:运用谱分析这一数学工具,通过先分析个股再扩展到全市场的方式,来研究由成交笔数所衡量的交易活动中隐藏的周期性规律。
本段落的存在是为了给读者提供一个清晰的“阅读地图”。它在文章的结构中起到了承上启下的作用,连接了理论(第 3 节)与实证(第 4 节),并预告了后续内容的安排。这有助于读者建立正确的预期,理解作者的研究思路,从而能够更顺畅地跟上文章的论证逻辑。
你可以把作者想象成一位侦探。在第三节,侦探详细介绍了他即将使用的一套高科技侦察工具(谱分析)。现在,在第四节,他宣布要开始破案了。他首先选择了一两个关键嫌疑人(代表性股票)进行深入调查(第 4.1 节),用他的高科技工具分析这两个嫌疑人的所有行为模式。然后,他会把同样的分析方法应用到所有相关的嫌疑人身上(全市场股票,第 4.2 节),看看之前发现的行为模式是不是这个犯罪团伙(整个市场)的“标准操作程序”。他选择关注的线索是“作案次数”(成交笔数),并告诉我们后面会解释为什么这个线索最重要。
想象一下你在听一首复杂的交响乐。第三节是音乐理论家在向你讲解如何通过频谱图(就像均衡器上跳动的柱子)来分析音乐中的各种声音频率,比如哪些是低音鼓,哪些是高音笛子。现在,第四节开始了,音乐家说:“好了,理论讲完了。我们现在就用这个频谱分析仪来分析两首具体的曲子(一首是美国的摇滚乐《Apple》,一首是中国的古典乐《平安银行》),看看它们的节奏有什么特点。然后,我们会把我们音乐库里所有的歌曲都分析一遍,看看是不是所有歌曲都有类似的节奏模式。” 而他们特别关注的不是音量的大小,而是音符被敲响的次数(成交笔数)。
22. 4.1 单只股票
📜 [原文2]
我们首先关注两只具有代表性的股票:美国市场的苹果公司(Apple Inc)和中国市场的平安银行(Ping An Bank)。我们使用这两只股票的去趋势日内平均成交量作为我们的观测数据 $X_{t}$。由于中国市场存在午休,我们将平安银行的日内时间序列数据分为上午时段和下午时段,并分别估计它们的强度系数。
这一段详细说明了作者如何开始进行个股分析,包括样本选择和数据处理方法。
- 样本选择:作者挑选了两只股票作为研究的起点。选择的不是随机的,而是“具有代表性”的:
- 苹果公司 (Apple Inc.):代表美国市场。苹果是全球知名的科技巨头,交易活跃,市场参与者多样,是研究美股的理想样本。
- 平安银行 (Ping An Bank):代表中国市场。平安银行是中国大型股份制商业银行,同样具有高流动性和广泛的投资者基础,能代表A股的特点。
- 跨市场比较的意图:选择分属两个不同国家、不同交易制度、不同投资者结构的市场中的代表性股票,暗示了作者想要探究交易活动周期性是否存在跨市场的共性与差异。
- 数据预处理:
- 观测数据 $X_{t}$:作者明确指出,他们用来分析的不是原始的成交量数据,而是经过处理后的“去趋势日内平均成交量”。这里的“平均”指的是将多个交易日的同一时刻(例如,所有交易日的上午9:30:01)的成交笔数取平均,得到一个“典型交易日”的模式。
- 去趋势 (Detrended):这是非常关键的一步。金融市场的交易活动在一天内通常呈现出“U型”或“W型”模式,即开盘和收盘时段交易最活跃,盘中相对清淡。这个宏观的、平滑变化的趋势会掩盖掉更高频率的周期性波动。因此,必须先将这个大的趋势(U型/W型)从数据中剥离出去,剩下的“残差”部分才能更好地用于分析那些短周期的、重复出现的模式。这就像你想听清楚一段录音中的微弱背景音乐,需要先用降噪软件去掉主要的噪音一样。
- 针对中国市场的特殊处理:
- 午休问题:中国A股市场有中午休市的制度(午休),这会导致日内交易时间被分割成不连续的两段(上午和下午)。
- 分段处理:为了应对这个问题,作者决定不把一整天的数据连在一起分析。他们将平安银行的数据切分为“上午时段”和“下午时段”两个独立的部分。
- 分别估计:对上午和下午这两个时间序列,他们会独立地进行谱分析,分别计算各自的强度系数。这样做是科学的,因为它避免了午休这个巨大的人为“断点”对周期性分析造成的干扰。
- 忽略“去趋势”的重要性:如果直接用原始的成交量数据进行谱分析,那么能量最大的频率将会是对应U型/W型趋势的极低频成分,这会像一个巨大的太阳一样,让你看不见旁边小星星(高频周期)的光芒。去趋势是保证后续分析有效性的核心前提。
- 不理解为何要对中国市场分段:如果不将A股数据分段,午休这个时间点在数据上会形成一个巨大的“悬崖”(成交量瞬间从有到零,再从零到有)。这种非自然的结构会对傅里叶变换(谱分析的基础)产生严重的干扰,生成许多虚假的频率成分,污染分析结果。分段处理是尊重数据本身特征的正确做法。
- 认为 $X_t$ 是某一天的成交量:$X_t$ 不是指某一个特定交易日的成交量序列,而是多个交易日(在本文中是2019-2021年)同一时刻成交量的平均值。这代表了一种统计上的“典型”模式,而不是单日的随机波动。
本段阐述了个股分析的初始步骤。作者选取了代表中美两大市场的苹果公司和平安银行作为样本,使用它们在多年间的平均日内成交笔数作为基础数据。关键的数据预处理步骤是“去趋势”,以消除日内U型/W型模式的干扰。同时,为了适应A股的午休制度,对平安银行的数据进行了上午和下午的分段处理,确保分析的准确性。
本段的目的是清晰地交代实证分析的“实验设计”。它详细说明了实验对象(样本)、实验材料(数据)以及材料的处理方法(预处理)。这保证了研究的透明度和可重复性。一个严谨的科学研究必须让读者清楚地知道研究者具体是怎么做的,本段落就承担了这一职责。
想象一位厨师准备制作两道招牌菜,一道是美式汉堡(苹果公司),一道是中式烤鸭(平安银行)。
- 选材:他精心挑选了最具代表性的食材。
- 备料:他拿到的不是一整头牛或一只整鸭,而是多年来制作汉堡和烤鸭的“平均数据”,比如,他知道平均每个汉堡需要多少克牛肉饼,平均每只烤鸭要烤多久。这个“平均数据”就是 $X_t$。
- 预处理(去趋势):在烹饪前,他需要对食材进行预处理。对于牛肉饼和烤鸭,它们都有一个基本的“熟成过程”(U型趋势),比如先要高温烤制,然后转小火慢炖。厨师说:“这个基本的熟成过程我们都知道,没啥新意。我想研究的是烹饪过程中那些更精细的、反复进行的调味步骤。” 于是他先把这个大的“熟成影响”从分析中去掉。
- 特殊处理(分段):中式烤鸭的制作过程中有一个“中场休息”去刷糖色的步骤(午休)。为了不让这个“休息”打乱他对烹饪节奏的分析,他决定把烤制过程分成“刷糖色前”和“刷糖色后”两段来独立研究。
你是一位音频工程师,要分析两段录音。一段是苹果CEO库克的演讲(Apple Inc.),另一段是平安银行行长的讲话(Ping An Bank)。
- 原始录音:原始录音里,演讲者的音量在刚上台和快结束时特别高,中间部分比较平稳(U型趋势)。
- 降噪(去趋势):你想分析他们讲话时是否有周期性的口头禅或固定的停顿节奏。为了听得更清楚,你首先用一个滤波器,把这种“开头结尾音量大”的整体音量变化趋势给抹平了。你得到的处理后的音频就是 $X_t$。
- 剪辑(分段处理):你发现平安银行行长的讲话录音在中间被人按了暂停键,去喝了口水(午休)。这个长时间的静音会干扰你的节奏分析。于是,你干脆把录音从暂停点剪开,变成了“上半场讲话”和“下半场讲话”两个独立的音频文件,然后分别对它们进行分析。
33. 揭示周期性
📜 [原文3]
揭示周期性。通过遵循第 3 节中的方法并设置基函数数量,$n=50013$ 我们估计了强度系数,这使我们能够量化这些周期性在不同频率下的相对重要性,如图 2 所示。$^{14}$ 估计的平方强度系数 $\hat{a}_{j}^{2}$ 显示为它们指数 $j$ 的函数,我们观察到几个类似于合成数据结果的峰值(见附录中的图 A.2)。红点标记了相应的频率,这些频率恰好是整数时间,如 30 秒、1 分钟和 5 分钟。
特别是,苹果公司在 5 分钟、1 分钟、30 秒和 20 秒频率下显示出高强度系数。同样,平安银行的上午和下午时段在 5 分钟、1 分钟和 30 秒频率下都显示出高强度系数。尽管这两只股票在不同的市场交易,市场参与者的构成也非常不同,但它们展示了惊人相似的周期性模式。
[^7]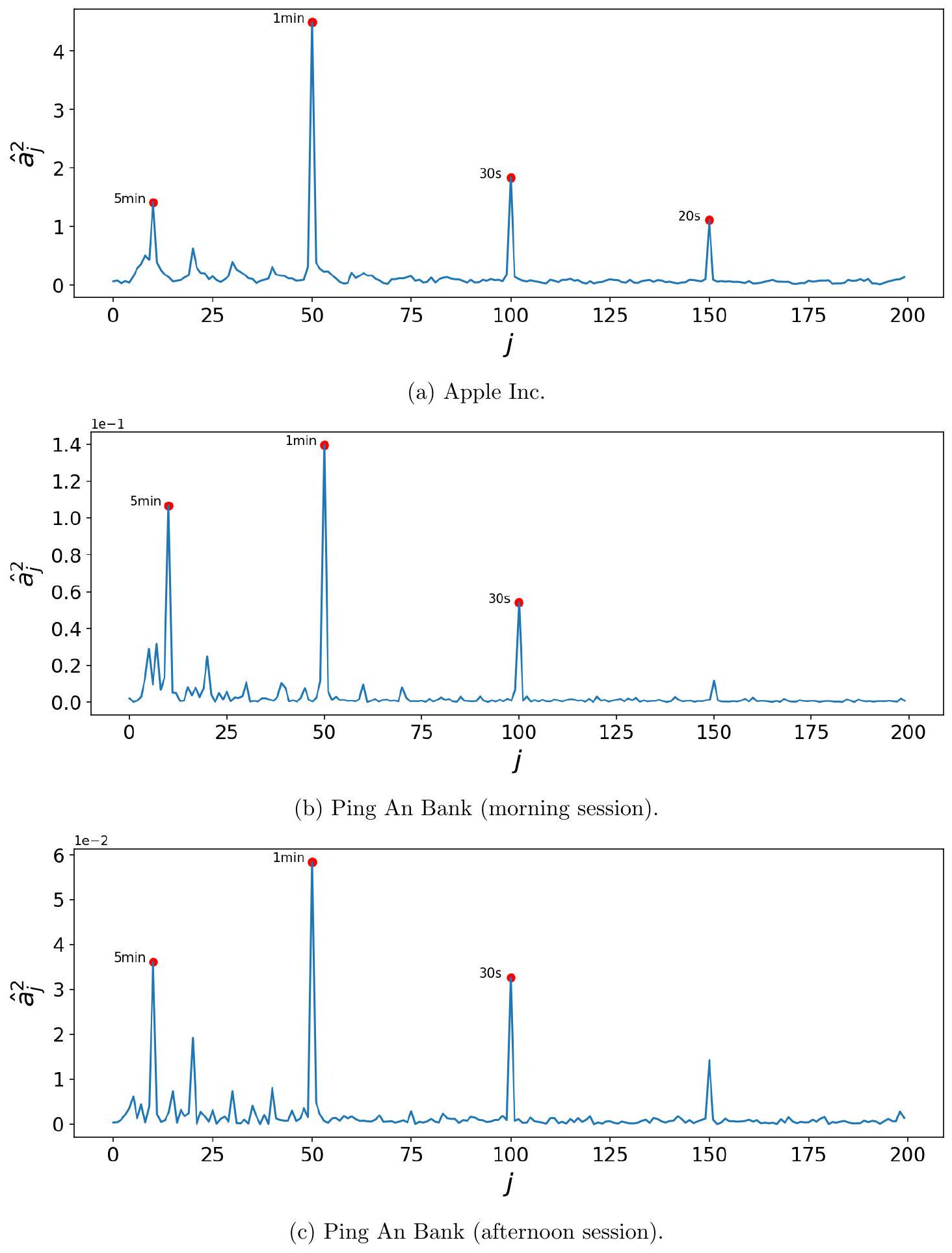
图 2:2019-2021 年两只个股的估计平方强度系数 $\hat{a}_{j}^{2}$。红点标记了对应于指数 $j$ 的频率周期。
这一部分是实证分析的第一个核心结果展示。作者将前面准备好的数据输入谱分析模型,得到了可视化的结果,并对结果进行了解读。
- 分析方法回顾:作者首先提醒读者,他们使用的是第 3 节中介绍的方法。具体来说,他们将去趋势后的成交量时间序列 $X_t$ 分解成一系列不同频率的余弦波(基函数)。
- 参数设置:他们选择了一组非常大的基函数,数量 $n=500$。(原文中的 n=50013 和脚注 14 可能是排版错误或特殊说明,但从上下文和后续的 fVR 基准计算来看,核心参数是 $n=500$)。选择500个基函数意味着他们试图将交易活动分解成500种不同频率的周期性振动。
- 核心指标:强度系数:通过模型估计,他们得到了每个基函数(即每个频率)的强度系数 $a_j$。这个系数的平方 $\hat{a}_{j}^{2}$ ($\hat{}$ 表示这是通过数据估计出来的值)代表了对应频率 $j$ 的周期性成分的“能量”或“强度”。$\hat{a}_{j}^{2}$ 的值越大,说明这个频率的周期性在交易活动中越显著。
- 结果可视化(图 2):图 2 是关键。
- 横轴:是频率的指数 $j$。指数 $j$ 越大,代表的频率越高(周期越短)。
- 纵轴:是估计出的平方强度系数 $\hat{a}_{j}^{2}$。
- 图的形态:整个图就像地平线上起伏的山脉。如果交易活动没有任何周期性,这条线应该像一片平原,所有 $\hat{a}_{j}^{2}$ 的值都差不多大且很小。但图 2 显示了几个非常突出的“山峰”(peaks)。
- “山峰”的意义:这些“山峰”的出现,强烈地表明在对应的频率上,存在着非常显著的周期性行为。这就像你在收音机调频,调到某个频率时,突然听到了清晰的广播信号,而不是沙沙的噪音。
- 红点标记:为了方便读者理解,作者在一些重要的“山峰”上用红点进行了标记,并标注了这些频率对应的时间周期,如 “30s”, “1min”, “5min”。这些都是非常符合人类直觉的“整数时间”。
- 对图 2 的解读:
- 苹果公司(上图):在周期为 5 分钟、1 分钟、30 秒、20 秒的地方出现了明显的峰值。这说明苹果股票的交易活动,在去除了U型趋势后,存在以这些时间为周期的、反复出现的“脉冲”或“浪潮”。
- 平安银行(中下图):无论是上午还是下午,都在 5 分钟、1 分钟、30 秒的地方出现了明显的峰值。这说明平安银行的交易活动也存在类似的周期性。
- 共性:最惊人的发现是,尽管苹果和平安银行身处完全不同的市场环境,但它们的核心周期惊人地一致(尤其是 5 分钟、1 分钟、30 秒这几个)。这暗示了这些周期性可能不是由特定市场的制度或投资者群体决定的,而是某种更深层次、更普遍的交易行为模式的体现。
- 混淆频率和周期:频率(frequency)和周期(period)是倒数关系。高频率对应短周期,低频率对应长周期。图中的“1 min”是指周期为1分钟,对应的频率是 1/60 Hz。读者在思考时要注意这两者的转换。
- 认为峰值越高越好:虽然峰值越高代表该频率的周期性越强,但评估其重要性还需要看它的“相对强度”。例如,一个峰值比周围高出100倍,和另一个只高出2倍的峰值,前者所代表的周期性显然更不容忽视。后续的频率方差比(fVR)正是为了更精确地量化这种相对重要性。
- 忽略坐标轴的尺度:在解读这类图表时,要注意看纵轴是否是对数尺度(log scale)。如果是对数尺度,那么一个看起来不高的峰值,其实际数值可能已经非常巨大。在本图中,纵轴是线性尺度,所以可以直接通过视觉高度来判断强度。
- 对图2的误读:图2展示的是平方强度系数,这代表能量。它总是正数。强度系数 $a_j$ 本身可正可负,但其符号只影响余弦波的初始相位,不影响其振幅。所以分析能量时都看其平方。
本段落通过展示谱分析的核心结果图(图 2),直观地揭示了在苹果公司和平安银行的交易活动中,存在着显著的高频周期性。这些周期大多集中在 5 分钟、1 分钟、30 秒等整数时间点上。最引人注目的发现是,这两个来自不同市场的股票展现出了高度相似的周期性模式,暗示了这背后可能存在普适性的驱动因素。
本段的目的是提供第一个强有力的实证证据。在前面的章节铺垫了理论和数据准备之后,这里是“证据出示”环节。通过可视化图表,作者让读者“眼见为实”,直观地感受到周期性的存在,并为后续更深入的量化分析(如 fVR)打下基础。这是从定性观察到定量分析的过渡。
想象你是一位地震学家,正在分析两个不同城市(一个在美国,一个在中国)的地震监测数据。
- 数据处理:你已经去除了地球板块正常运动引起的大地缓慢漂移(去趋势)。
- 频谱分析:你用频谱仪分析剩下的地震波数据,得到一张图(图 2),图上显示了不同振动频率的能量强度。
- 发现规律:你发现,图上并不是一片混乱的噪音,而是在特定的频率上出现了几个剧烈的尖峰。通过计算,你发现这些尖峰对应的振动周期是“每30秒震一下”、“每1分钟震一下”、“每5分钟震一下”。
- 惊人共性:最让你惊讶的是,无论是在美国城市还是中国城市,地震波最强的频率(“共振峰”)都惊人地一致!这让你怀疑,引起这些周期性微小震动的,可能不是本地的地铁经过,而是某种全球性的、我们还不知道的共同原因。
想象你戴上了一副特殊的“节奏眼镜”去看股票交易市场。
- 普通视角:你只能看到交易量时高时低,像一片混乱的人潮,开盘和收盘时人最多(U型趋势)。
- 戴上眼镜后(去趋势+谱分析):你的眼镜过滤掉了“开盘收盘人多”的宏观景象,让你能看清人群内部的微观行为模式。你惊讶地发现,人群并不是在随机走动,而是像在跳一支有节奏的集体舞。
- 发现节奏:你看到,每隔30秒,人群就会同步地“跳”一下;每隔1分钟,人群会同步地“挥”一下手;每隔5分钟,人群会同步地“转”个圈。这些“跳”、“挥”、“转”的动作,就是图2里的那些“峰值”。
- 全球共舞:你切换频道,去看另一个国家的市场,发现那里的人群虽然穿着不同的衣服(市场环境不同),但竟然也在跳着几乎完全相同的舞蹈,遵循着同样的30秒、1分钟、5分钟的节拍!这让你确信,这个舞蹈节奏一定有其内在的、普遍的原因。
44. 谱分解
📜 [原文4]
谱分解。到目前为止,我们已经证明了成交量中存在显著的周期性。但它们有多重要?它们能解释多少交易活动的变化?为了回答这些问题,我们根据第 3 节中的等式 (4) 将日内成交量的方差分解为不同的频谱频率,这使我们能够量化每个周期性成分的重要性。
我们将第 $j$ 个周期性成分的频率方差比 (fVR) 定义为:
它衡量了每个频率下的解释方差占去趋势成交量时间序列总方差的比例。值得注意的是,我们没有在分母中包含 U 型(或双 U 型)趋势项 $\gamma_{T}^{m}(0)$ 的方差,因为 U 型(或双 U 型)模式在文献中是众所周知的老生常谈,因此不是我们的主要焦点。此外,这使我们能够专注于每个周期项在解释众所周知的 U 型(或双 U 型)模式残差方面的相对重要性,这在第 6.1 节中产生了重要的应用。
这一段引入了一个关键的量化指标——频率方差比 (fVR),用于衡量之前发现的周期性到底有多“重要”。
- 提出问题:作者首先点明了上一步分析的局限性。我们已经通过图2“看到”了周期性的存在,但“看到”不等于“理解”。我们还不知道这些周期性有多强。具体来说,它们在整个交易活动的波动中,究竟扮演了多大的角色?一个周期性即使存在,如果它的影响微乎其微,那研究价值也不大。所以,核心问题是:这些周期性成分能解释多少方差?(在统计学中,方差是衡量数据波动程度的指标,能解释方差,就意味着能解释数据的波动)。
- 解决方法:谱分解:作者提出,答案在于“谱分解”。这个概念源于第3节的理论。其核心思想是,一个时间序列的总方差(总波动性),可以被分解为各个不同频率成分的方差之和。就像一块大蛋糕(总方差)可以被切成许多小块,每一小块对应一个频率。
- 定义核心指标 fVR:为了量化每个频率的重要性,作者定义了频率方差比 (fVR, frequency Variance Ratio)。
- 公式:$\mathrm{fVR}_{j}:=\frac{a_{j}^{2}}{2 \sigma^{2}+\sum_{i=1}^{n} a_{i}^{2}}$
- fVR的含义:这个公式计算的是,由第 $j$ 个频率的周期性所解释的方差(分子),占去趋势后的时间序列总方差(分母)的百分比。
- 直观理解:fVR_j 就是第 j 个频率成分这块“小蛋糕”,占整个“去趋势后”的大蛋糕的比例。如果fVR_j = 10%,就意味着这个频率的周期性活动,解释了去趋势后交易量总波动的10%。这是一个非常直观和有力的指标。
- 解释fVR公式的构成:
- 分子 $a_{j}^{2}$:根据第3节的理论,一个频率为 $j$ 的余弦波成分 $a_j \cos(2\pi j t/T)$ 对总方-差的贡献近似是 $a_{j}^{2}/2$。这里直接用 $a_{j}^{2}$ (或其某个倍数)作为其解释方差的度量,因为它正比于该频率的能量。
- 分母 $2 \sigma^{2}+\sum_{i=1}^{n} a_{i}^{2}$:这代表了去趋势后时间序列的总方差。它由两部分组成:
- $\sum_{i=1}^{n} a_{i}^{2}$:这是所有 $n$ 个周期性成分(余弦波)贡献的方差之和。
- $2 \sigma^{2}$:这是模型中剩余的、无法被任何周期性解释的“噪音”部分的方差。$\sigma^2$ 是随机误差项 $\epsilon_t$ 的方差。
- 分母的特殊之处:作者特别强调,这个分母不包括U型趋势的方差。这是一个非常重要的设计。他们故意将U型趋势这个“巨无霸”从总方差中排除了。
- 为什么要在分母中排除U型趋势?
- U型趋势是已知现象:“U型”或“双U型”(考虑午休)的日内交易模式是金融学界几十年来都知道的“老生常谈”(well-known stylized fact)。作者的研究兴趣不在于再次“发现”这个U型模式。
- 聚焦于新发现:他们的焦点是U型趋势之外的那些“残差”里,是否还隐藏着其他有规律的模式。通过从分母中排除U型趋势的方差,fVR衡量的就是:在排除了众所周知的U型模式之后,某个特定频率的周期性,能在多大程度上解释剩余的交易波动?
- 提高敏感度:这样做极大地提高了指标的敏感度。如果把U型趋势的巨大方差放进分母,那么所有高频成分的fVR都会变得极其微小,就像用银河系的质量作为分母来衡量地球的质量一样,数字会小到没有意义。
公式 (6): $\mathrm{fVR}_{j}:=\frac{a_{j}^{2}}{2 \sigma^{2}+\sum_{i=1}^{n} a_{i}^{2}}$
- $\mathrm{fVR}_{j}$: Frequency Variance Ratio for the $j$-th frequency component. 这是一个比率,表示第 $j$ 个频率成分的重要性。下标 $j$ 标识了这是针对第 $j$ 个频率的计算。
- $a_{j}$: 强度系数 (Intensity Coefficient) for the $j$-th frequency component. 这是从模型 (1) $X_t = m(t/T) + \sum_{j=1}^n a_j \cos(2\pi j t/T) + \epsilon_t$ 中估计出来的,它代表了第 $j$ 个余弦波的振幅。
- $a_{j}^{2}$: 平方强度系数。它正比于第 $j$ 个频率成分的能量或其对总方差的贡献。在信号处理中,信号的能量/功率通常与其振幅的平方成正比。这里将它作为分子,代表由该频率“解释”的方差部分。
- $\sigma^{2}$: 噪声方差 (Noise Variance)。这是模型 (1) 中残差项 $\epsilon_t$ 的方差, 即 $\mathrm{Var}(\epsilon_t) = \sigma^2$。它代表了数据中那些无法被趋势项和所有周期项解释的、纯粹随机的波动。乘以2可能是因为模型或方差分解的特定形式(例如,同时考虑了正弦和余弦项,或者在某些推导中出现的系数)。
- $n$: 基函数的数量 (Number of basis functions)。这是我们在模型中预设的周期性成分的总个数。在本文中,作者选了 $n=500$。
- $\sum_{i=1}^{n} a_{i}^{2}$: 所有周期性成分的平方强度系数之和。这代表了模型中所有 $n$ 个周期性成分共同解释的总方差的一部分。
- 分母 $2 \sigma^{2}+\sum_{i=1}^{n} a_{i}^{2}$: 这是去趋势后的时间序列的总方差。根据方差的可加性(对于不相关的项),去趋势后的序列 $Y_t = X_t - m(t/T) = \sum_{j=1}^n a_j \cos(2\pi j t/T) + \epsilon_t$ 的总方差 $\mathrm{Var}(Y_t)$ 就约等于所有周期项贡献的方差与噪声项方差之和。在理想的傅里叶变换下,不同频率的余弦波是正交的,它们的方差可以相加。$\mathrm{Var}(\sum a_j \cos(\cdot)) \approx \sum \mathrm{Var}(a_j \cos(\cdot)) \propto \sum a_j^2$。因此,这个分母就是对去趋势后序列总方差的一个估计。
推导的逻辑:
- 总波动 = 趋势波动 + 去趋势后的波动。
- 去趋势后的波动 = 所有周期性成分的波动 + 纯粹的随机噪音波动。
- $\mathrm{fVR}_{j}$ = (第 $j$ 个周期性成分的波动) / (去趋势后的总波动)
- 用 $a_j^2$ 代表第 $j$ 个周期性成分的波动大小。
- 用 $\sum a_i^2 + 2\sigma^2$ 代表去趋势后的总波动大小。
- 组合起来,就得到了fVR的定义。
假设我们分析一个去趋势后的时间序列,并将其分解为3个频率成分和一个噪音项。
估计出的参数如下:
- 强度系数: $a_1=4$, $a_2=3$, $a_3=1$
- 噪音项的方差: $\sigma^2 = 7$
计算过程:
- 计算分母(去趋势后的总方差):
分母 = $2\sigma^2 + \sum_{i=1}^3 a_i^2$
= $2 \times 7 + (a_1^2 + a_2^2 + a_3^2)$
= $14 + (4^2 + 3^2 + 1^2)$
= $14 + (16 + 9 + 1)$
= $14 + 26 = 40$
所以,去趋势后的时间序列总方差是 40。
- 计算每个频率的fVR:
- 频率1的fVR ($\mathrm{fVR}_1$):
$\mathrm{fVR}_1 = \frac{a_1^2}{\text{分母}} = \frac{4^2}{40} = \frac{16}{40} = 0.4 = 40\%$
- 频率2的fVR ($\mathrm{fVR}_2$):
$\mathrm{fVR}_2 = \frac{a_2^2}{\text{分母}} = \frac{3^2}{40} = \frac{9}{40} = 0.225 = 22.5\%$
- 频率3的fVR ($\mathrm{fVR}_3$):
$\mathrm{fVR}_3 = \frac{a_3^2}{\text{分母}} = \frac{1^2}{40} = \frac{1}{40} = 0.025 = 2.5\%$
- 结果解读:
- 频率1的周期性解释了去趋势后交易波动的40%,是最重要的成分。
- 频率2的周期性解释了22.5%。
- 频率3的周期性只解释了2.5%,相对不那么重要。
- 剩余的部分 ($1 - 40\% - 22.5\% - 2.5\% = 35\%$) 是由纯粹的随机噪音 $2\sigma^2 / 40 = 14/40 = 35\%$ 造成的。
这个例子清晰地展示了fVR如何将一个抽象的强度系数值(如 $a_1=4$)转化为一个具有直观解释力的百分比(40%)。
- 将fVR理解为占总方差的比例:这是一个非常容易犯的错误。fVR是占去趋势后的总方差的比例,而不是占原始数据总方差的比例。U型趋势的方差非常大,如果把它算进来,所有的fVR值都会小好几个数量级。
- 认为所有fVR加起来等于100%:并不一定。所有周期项的fVR加起来(即 $\sum_j \mathrm{fVR}_j = \frac{\sum a_j^2}{\text{分母}}$)是小于100%的,因为分母中还包含了噪音项的方差 $2\sigma^2$。只有当模型完美拟合,没有任何噪音($\sigma^2=0$)时,所有周期项的fVR之和才等于100%。
- 忽略fVR的上下文:一个fVR值是高是低,需要有参照物。后续作者会提到,如果没有任何周期性,所有频率的能量应该是均分的,那么每个fVR的期望值(基准值)就是 $1/n$ (这里是 $1/500=0.2\%$)。只有显著高于这个基准值的fVR,才被认为代表了真正的周期性。
本段的核心贡献是定义并解释了频率方差比 (fVR) 这个关键指标。fVR通过计算单个频率的解释方差在去趋势后总方差中的占比,解决了“周期性有多重要”的问题。作者特意在计算中排除了众所周知的U型趋势的影响,从而使得fVR能够更敏感、更准确地衡量那些新发现的高频周期性在解释“剩余波动”方面的重要性。
本段的目的是从定性进入定量。图2只是让我们“看到”了山峰,而fVR则是给了我们一把尺子,去精确“测量”每座山峰到底有多高、多大。它将视觉上的直观感受转化为了可以比较、可以检验的数值。这在科学论证中是必不可少的一步,它让结论变得更加坚实和有说服力。同时,通过对fVR定义的详细阐述(特别是排除U型趋势方差这一点),作者也展示了其研究设计的严谨性和深刻洞察力。
你是一个公司的CEO,正在分析公司月度销售额的波动。
- 原始数据:你发现销售额每年都有一个巨大的、可预测的波动:年底购物季最高,年初最低。这是“U型趋势”。
- 提出问题:你对这个年度大趋势不感兴趣,因为这谁都知道。你想知道的是,除去年底大促的影响外,每个月内部是否还有其他更小、更频繁的波动规律?比如,是不是每个月发薪日后的一周,销售额都有个小高峰?
- 定义指标 (fVR):为了量化“发薪日效应”的重要性,你决定计算:由“发薪日效应”带来的销售额增长,占“排除掉年度购物季大波动之后”的总销售额波动的百分比。
- 分子:发薪日效应带来的销售额方差。
- 分母:公司总销售额方差 - 年度购物季效应带来的方差。
- fVR的价值:这个指标(fVR)能告诉你,“发薪日效应”是不是一个值得关注的现象。如果它的fVR是20%,那说明这个效应非常显著,你可能需要围绕它制定专门的营销策略。如果fVR只有0.1%,那它可能只是个随机波动,不值得投入太多精力。
想象你在一片广阔的海洋上(原始成交量时间序列)。
- 潮汐(U型趋势):海洋有非常规律的潮汐涨落,每天两次,幅度巨大。这是人尽皆知的U型趋势。
- 滤掉潮汐:你是一位冲浪爱好者,对研究潮汐不感兴趣。你戴上了一副特殊的滤镜,可以过滤掉海平面整体的涨落,让你只看到海面上的浪花。现在你的世界里,海平面是平的,但上面布满了各种波浪。这片“平坦”的海洋就是“去趋势后”的时间序列。
- 分析浪花 (fVR):你发现海面上有各种各样的浪:有周期很长、缓缓推进的大涌浪(低频),也有周期很短、此起彼伏的小碎浪(高频)。
- 计算fVR:你开始计算,比如,那种“每30秒来一波”的小碎浪,它的能量(浪高和频率的综合体现)占整个海面所有浪花总能量的百分之几?这个百分比就是fVR。
- 结果:你发现“30秒碎浪”的fVR高达15%,“1分钟浪”的fVR有20%。这意味着,即使排除了潮汐这个最大影响因素,海面的波动也远非随机,而是由几个特定节奏的波浪主导着。
55. 针对中国市场的fVR计算
📜 [原文5]
对于中国市场的股票,包括平安银行,由于我们分别为上午和下午时段估计谱模型,在实践中,我们通过结合两个时段估计的强度系数来计算 (6) 中的 fVR:
这一小段是专门针对中国A股市场数据处理的一个技术性补充说明。因为它之前提到,由于午休的存在,A股的数据被分成了上午和下午两段来独立分析。那么,当要计算一整天的fVR时,就面临一个如何合并这两段分析结果的问题。
- 问题背景:之前对平安银行的数据进行了分段处理,得到了两套独立的分析结果:
- 一套是上午时段的:强度系数 $a_{j, \text{morning}}$ 和 噪音方差 $\sigma_{\text{morning}}^2$。
- 另一套是下午时段的:强度系数 $a_{j, \text{afternoon}}$ 和 噪音方差 $\sigma_{\text{afternoon}}^2$。
- 合并的需求:为了能和美股(全天连续交易)的fVR进行公平比较,需要为A股的股票也计算一个代表“全天”的fVR值。
- 合并方法(公式7):作者提出了一个直接而合理的合并方法,即把两段的方差贡献简单相加。
- 分子:对于第 $j$ 个频率,它在全天的总能量,就等于它在上午的能量(由 $a_{j, \text{morning}}^2$ 体现)加上它在下午的能量(由 $a_{j, \text{afternoon}}^2$ 体现)。所以分子是 $a_{j, \text { morning }}^{2}+a_{j, \text { afternoon }}^{2}$。
- 分母:全天的“去趋势后总方差”,也等于上午的“去趋势后总方差”加上下午的“去趋势后总方差”。
- 上午的总方差 = $2 \sigma_{\text {morning }}^{2}+\sum_{i=1}^{n} a_{i, \text { morning }}^{2}$
- 下午的总方差 = $2 \sigma_{\text {afternoon }}^{2}+\sum_{i=1}^{n} a_{i, \text { afternoon }}^{2}$
- 两者相加,就得到了公式(7)的分母。
- 公式的合理性:这个合并方法是建立在方差可加性(对于独立时段)的基础上的。它假设上午的波动和下午的波动是两个独立的过程,因此全天的总方差就是两部分方差的和。这是一个在实践中非常常见的简化处理方式。这个新的指标被记为 $\mathrm{fVR}_{j}^{\prime}$,用 ' (prime) 来和标准版的fVR区分。
公式 (7): $\mathrm{fVR}_{j}^{\prime}:=\frac{a_{j, \text { morning }}^{2}+a_{j, \text { afternoon }}^{2}}{2 \sigma_{\text {morning }}^{2}+\sum_{i=1}^{n} a_{i, \text { morning }}^{2}+2 \sigma_{\text {afternoon }}^{2}+\sum_{i=1}^{n} a_{i, \text { afternoon }}^{2}}$
这个公式是公式(6)在中国市场特定情况下的扩展版本。
- $\mathrm{fVR}_{j}^{\prime}$: 带撇号的fVR,特指为中国市场分段数据计算的合并fVR。
- $a_{j, \text { morning }}^{2}$: 上午时段,第 $j$ 个频率的平方强度系数。
- $a_{j, \text { afternoon }}^{2}$: 下午时段,第 $j$ 个频率的平方强度系数。
- 分子 $a_{j, \text { morning }}^{2}+a_{j, \text { afternoon }}^{2}$: 第 $j$ 个频率在全天(上午+下午)贡献的总能量/方差。
- $\sigma_{\text {morning }}^{2}$: 上午时段的噪音方差。
- $\sigma_{\text {afternoon }}^{2}$: 下午时段的噪音方差。
- $\sum_{i=1}^{n} a_{i, \text { morning }}^{2}$: 上午时段,所有 $n$ 个周期性成分贡献的方差之和。
- $\sum_{i=1}^{n} a_{i, \text { afternoon }}^{2}$: 下午时段,所有 $n$ 个周期性成分贡献的方差之和。
- 分母:
- $(2 \sigma_{\text {morning }}^{2}+\sum_{i=1}^{n} a_{i, \text { morning }}^{2})$: 这是上午时段的去趋势后总方差,记为 $\mathrm{TotalVar}_{\text{morning}}$。
- $(2 \sigma_{\text {afternoon }}^{2}+\sum_{i=1}^{n} a_{i, \text { afternoon }}^{2})$: 这是下午时段的去趋势后总方差,记为 $\mathrm{TotalVar}_{\text{afternoon}}$。
- 整个分母就是 $\mathrm{TotalVar}_{\text{morning}} + \mathrm{TotalVar}_{\text{afternoon}}$,即全天的去趋势后总方差。
推导的逻辑:
- 全天第 $j$ 频率的方差贡献 ≈ 上午第 $j$ 频率的方差贡献 + 下午第 $j$ 频率的方差贡献。
- 全天的去趋势后总方差 ≈ 上午的去趋势后总方差 + 下午的去趋势后总方差。
- $\mathrm{fVR}_{j}^{\prime}$ = (全天第 $j$ 频率的方差贡献) / (全天的去趋势后总方差)
- 代入各项的估计值,即得到公式(7)。
假设我们对某A股股票的上午和下午数据分别进行了谱分析,得到以下结果(同样假设n=3):
上午时段:
- 强度系数: $a_{1,m}=3$, $a_{2,m}=5$, $a_{3,m}=1$
- 噪音方差: $\sigma_m^2 = 10$
- 上午去趋势后总方差 = $2\sigma_m^2 + \sum a_{i,m}^2 = 2(10) + (3^2+5^2+1^2) = 20 + (9+25+1) = 20 + 35 = 55$
下午时段:
- 强度系数: $a_{1,a}=4$, $a_{2,a}=2$, $a_{3,a}=1$
- 噪音方差: $\sigma_a^2 = 15$
- 下午去趋势后总方差 = $2\sigma_a^2 + \sum a_{i,a}^2 = 2(15) + (4^2+2^2+1^2) = 30 + (16+4+1) = 30 + 21 = 51$
计算合并后的 $\mathrm{fVR}^{\prime}$:
- 计算全天的去趋势后总方差(分母):
分母 = 上午总方差 + 下午总方差 = $55 + 51 = 106$
- 计算每个频率的合并fVR':
- 频率1的 $\mathrm{fVR}^{\prime}_1$:
分子 = $a_{1,m}^2 + a_{1,a}^2 = 3^2 + 4^2 = 9 + 16 = 25$
$\mathrm{fVR}^{\prime}_1 = \frac{25}{106} \approx 0.236 = 23.6\%$
- 频率2的 $\mathrm{fVR}^{\prime}_2$:
分子 = $a_{2,m}^2 + a_{2,a}^2 = 5^2 + 2^2 = 25 + 4 = 29$
$\mathrm{fVR}^{\prime}_2 = \frac{29}{106} \approx 0.274 = 27.4\%$
- 频率3的 $\mathrm{fVR}^{\prime}_3$:
分子 = $a_{3,m}^2 + a_{3,a}^2 = 1^2 + 1^2 = 1 + 1 = 2$
$\mathrm{fVR}^{\prime}_3 = \frac{2}{106} \approx 0.019 = 1.9\%$
结果解读:
对于这只A股股票,合并计算后,频率2的周期性最为重要,解释了全天约27.4%的去趋势后波动。其次是频率1,解释了23.6%。频率3则不太重要。
- 错误地平均系数:一个常见的错误想法可能是“先平均系数再平方”,比如计算全天系数为 $(a_{j,m}+a_{j,a})/2$,然后用这个平均系数的平方去做分子。这是错误的,因为能量(方差)是直接相加的,而不是系数(振幅)相加。能量与振幅的平方成正比, $(a_m+a_a)^2 \neq a_m^2+a_a^2$。
- 忘记分母也要合并:只合并了分子的能量,而忘记将分母的两个时段的总方差也加起来,会导致fVR的计算基准错误,从而得出错误的比例。
- 适用范围:这个公式(7)仅适用于像A股这样有明确、固定午休制度的市场。对于没有午休但交易不连续(比如盘中暂停交易)的情况,是否适用需要具体分析。
本段为处理具有午休时段的中国市场数据,提出了一个计算全天频率方差比 (fVR') 的技术方案。该方案的核心思想是“方差相加”:将上午和下午由同一频率解释的方差相加作为分子,将上午和下午的去趋势后总方差相加作为分母,从而得到一个能够与连续交易市场进行比较的、代表全天情况的合并fVR'。
本段的存在是为了解决一个具体的技术难题,保证研究的严谨性和可比性。如果不明确说明如何处理A股的分段数据,读者会对后续平安银行的fVR数值是如何得来的感到困惑,也会质疑其与苹果公司fVR比较的公平性。这体现了作者在处理数据细节上的审慎态度。
你是一位体育老师,要统计一名学生在一天训练中的总得分。这名学生的训练分为上午场和下午场。
- 上午场:学生在“投篮”(频率j)项目上得了 $a_{j,m}^2$ 分,总分是 $\mathrm{TotalVar}_m$。
- 下午场:学生在“投篮”(频率j)项目上又得了 $a_{j,a}^2$ 分,总分是 $\mathrm{TotalVar}_a$。
- 计算全天表现:
- 问题:如何计算“投篮”项目得分占全天总得分的比例(fVR')?
- 正确做法 (公式7):
- 全天“投篮”总得分 = 上午投篮得分 + 下午投篮得分 = $a_{j,m}^2 + a_{j,a}^2$
- 全天训练总分 = 上午总分 + 下午总分 = $\mathrm{TotalVar}_m + \mathrm{TotalVar}_a$
- 比例 = (全天“投篮”总得分) / (全天训练总分)
- 错误做法:计算上午和下午的得分比例,然后取平均。这是不对的,因为两场的总分(分母)可能不一样。
想象你在统计一个城市一整天的用电情况,但这个城市中午12点到1点会强制全城拉闸停电(午休)。
- 分段统计:你只能分开统计上午(9-12点)和下午(1-4点)的用电数据。
- 分析特定电器:你想知道“空调”(频率j)这个用电器,它的耗电量占总耗电量的比例是多少?(这里的总耗电量是指排除了工厂基础用电等“趋势项”之后的居民生活用电波动)。
- 合并计算 (fVR'):
- 分子:空调一整天的总耗电量 = 上午空调耗电量 + 下午空调耗电量。
- 分母:一整天的居民生活用电总波动 = 上午的居民生活用电总波动 + 下午的居民生活用电总波动。
- fVR' = (空调全天总耗电量) / (全天居民生活用电总波动)。
这个方法合理地将两个不连续时段的数据整合起来,得到了一个有意义的全天指标。
66. fVR实证结果与表格解读
📜 [原文6]
表 1 总结了图 2 中突出显示的频率下苹果公司和平安银行的 fVR。因为我们在模型 (1) 中包含了 $n=500$ 个周期性成分,如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$(另见附录 C 中的图 A.2a)。然而,苹果公司在 5 分钟、1 分钟、30 秒和 20 秒频率下的估计 fVR,以及平安银行在 10 分钟、5 分钟、1 分钟和 30 秒频率下的估计 fVR,均显著高于 0.2%。这些结果证实了图 2 中的观察结果,即日内成交量中存在重要的周期性,并突显了美国和中国市场两只样本股票在不同频率下的不同相对重要性。
表 1:两只个股的频率方差比 (fVR)——即解释方差占去趋势时间序列总方差的比例。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为模型中包含了 $n=500$ 个周期性成分。
| 频率 | 10 分钟 | 5 分钟 | 1 分钟 | 30 秒 | 20 秒 |
|---|---|---|---|---|---|
| 苹果公司 | $0.31 \%$ | $2.97 \%$ | $9.46 \%$ | $3.88 \%$ | $2.33 \%$ |
| 平安银行 | $2.23 \%$ | $9.05 \%$ | $12.53 \%$ | $5.49 \%$ | $1.63 \%$ |
这一部分是对前面定义的 fVR 指标进行实际计算,并将结果呈现在表格中,然后对表格数据进行解读,得出结论。
- 结果呈现(表 1):表 1 是核心的量化证据。它展示了对于苹果公司和平安银行,几个关键频率(10分钟、5分钟、1分钟、30秒、20秒)的 fVR 数值。每一行代表一只股票,每一列代表一个特定的周期。
- 建立判断基准:在解读数据之前,作者首先建立了一个“标杆”或“参照物”,即基准 fVR (benchmark fVR)。
- 基准的逻辑:如果交易活动中不存在任何真正的周期性,那么所有的波动都纯粹是随机噪音。在这种情况下,我们把波动分解到500个频率上,每个频率分到的能量应该是大致相等的。因此,每个频率的fVR理论上都应该是 $1/n$。
- 基准的计算:由于模型中包含了 $n=500$ 个周期性成分,所以基准 fVR = $1/500 = 0.002 = 0.2\%$。
- 基准的用途:这个0.2%就是一把尺子。任何一个频率的fVR如果只是在0.2%左右,那它很可能只是随机噪音;但如果一个频率的fVR远远超过0.2%,比如达到了2%或10%,那我们就非常有信心说,这个频率上存在着真实的、不容忽视的周期性活动。
- 数据解读与比较:作者将表1中的实际fVR值与0.2%的基准进行比较。
- 苹果公司:
- 1分钟周期的fVR高达 9.46%!这比基准值0.2%高出近50倍。说明“1分钟节拍”能解释苹果公司去趋势后交易波动的将近十分之一,这是一个非常惊人的数字。
- 30秒(3.88%)、5分钟(2.97%)、20秒(2.33%)的fVR也都显著高于基准。
- 10分钟周期的fVR为0.31%,虽然也高于基准,但相对不那么突出。
- 平安银行:
- 1分钟周期的fVR更是达到了 12.53%,比基准高出60多倍,是所有周期中最强的。
- 5分钟周期的fVR也高达 9.05%。
- 30秒(5.49%)和10分钟(2.23%)也同样非常显著。
- 20秒周期的fVR为1.63%,同样远超基准。
- 得出结论:
- 证实周期性存在:所有这些关键频率的fVR都“显著高于”0.2%的基准,这为“日内交易量中存在重要周期性”这一论点提供了强有力的量化支持。它印证了之前从图2得到的直观观察。
- 揭示相对重要性差异:通过比较fVR的具体数值,我们可以看出不同周期之间的“实力差距”。
- 在两只股票中,1分钟周期的解释力都是最强的(苹果9.46%,平安12.53%),是“主旋律”。
- 5分钟周期也是一个非常重要的节拍,尤其是在平安银行(9.05%)中,其重要性几乎与1分钟周期相当。
- 30秒周期是次一级的重要节奏。
- 中美市场差异初现:尽管有很多相似之处,但差异也开始显现。例如,对平安银行来说,5分钟和10分钟周期的重要性(9.05%, 2.23%)似乎比苹果公司(2.97%, 0.31%)要高。而苹果在更短的20秒周期上(2.33%)比平安(1.63%)更强一些。这暗示了不同市场在交易节奏的细节上可能存在差异。
让我们用苹果公司的1分钟周期来举例,更深入地理解fVR=9.46%的含义。
- 获取苹果公司的原始数据:收集2019-2021年期间,苹果公司每个交易日的秒级成交笔数数据。
- 计算平均日内成交量:将所有交易日的同一秒(例如,所有交易日的9:30:01 AM)的成交笔数取平均,得到一条代表“典型交易日”的成交量曲线。
- 去趋势:从这条典型曲线中,剔除掉开盘和收盘活跃的“U型”大趋势。得到一条围绕零线上下波动的“残差”曲线。
- 计算残差曲线的总方差:计算这条残差曲线的方差,得到一个数值,我们称之为 $\mathrm{Var}_{\text{detrended}}$。
- 进行谱分析:对这条残差曲线进行谱分析,得到500个频率各自的强度系数 $a_j$。
- 找到1分钟周期:找到对应周期为“1分钟”的那个频率,记为 $k$。获取其强度系数的平方 $a_k^2$。
- 计算fVR:
- $\mathrm{fVR}_{k} = \frac{\text{由1分钟周期解释的方差}}{\mathrm{Var}_{\text{detrended}}} \approx \frac{a_k^2 / 2}{\mathrm{Var}_{\text{detrended}}}$ (注意:这里的确切公式依赖于方差分解的具体形式,但fVR的比例含义不变)。
- 计算结果显示,这个比例是 9.46%。
这意味着:苹果公司交易活动中,那些不能被“开盘收盘忙”这个大规律解释的、看似杂乱无章的波动里,有将近10%的部分,其实是由一个非常有规律的、“每分钟搏动一次”的节奏所驱动的。
- 忽略基准值:脱离0.2%的基准去谈论fVR的绝对值是无意义的。看到一个2%的fVR,第一反应不应该是“这个值好小”,而应该是“这个值是基准的10倍,非常显著”。
- 比较fVR的绝对值:直接比较苹果的9.46%和平安的12.53%,可以说平安银行的1分钟周期性“解释的方差比例”更高。但是,这不一定等同于平安银行的交易“更”有周期性。因为两个市场的总波动(分母)可能不同。更严谨的说法是,在各自的“去趋势后”波动中,1分钟周期所占的比重,平安银行要高于苹果公司。
- 认为表中频率是全部:表格中只列出了几个被作者筛选出来的、最重要的频率。模型中实际上有500个频率,绝大多数频率的fVR都在0.2%左右,没有被列出来。
- 对“显著”一词的理解:在统计学中,“显著(significant)”通常有严格的定义(例如,p值小于0.05)。这里作者使用的是一个更通俗的说法,即“远大于基准值”。虽然没有给出严格的统计检验,但几十倍的差距在实证研究中通常被认为是压倒性的证据。
本段通过表1展示了fVR的量化结果,是对图2定性观察的定量确认和深化。核心结论是:在苹果公司和平安银行的交易活动中,1分钟、5分钟、30秒等周期的fVR值远超随机噪声的基准水平(0.2%),证明了这些周期性的真实性和重要性。其中,1分钟周期在两只股票中都表现出最强的解释力。这些结果不仅证实了周期性的存在,还通过fVR数值的差异,初步揭示了中美市场在交易节奏上的细微不同。
本段落的目的是提供研究的“硬核”数据证据。如果说图2是“看图说话”,那么表1就是“用数据说话”。表格的形式清晰、简洁,便于比较。通过引入“基准fVR”的概念,作者建立了一个科学的判断标准,使得结论的得出不再是主观判断,而是基于数据的客观比较。这是学术论证中从定性描述转向定量分析的关键一步,极大地增强了文章的说服力。
你是一位音乐评论家,正在用专业的音频分析软件(提供fVR功能)分析两首歌曲:一首是苹果公司的摇滚乐,一首是平安银行的交响乐。软件告诉你,它把音乐分成了500个音轨(频率)来分析。
- 设定基准:你知道,如果一首歌是纯粹的白噪音,那么每个音轨的音量(fVR)应该是均等的,都是 $1/500 = 0.2\%$。
- 分析摇滚乐(苹果):
- 软件报告:在代表“每分钟60拍”的那个鼓点音轨上(1分钟周期),音量占比高达 9.46%!
- 在“每30秒一次”的贝斯音轨上,音量占比 3.88%。
- 你感叹道:“这首歌的节奏感太强了!光是鼓点就占了近10%的能量,难怪听起来这么带劲。”
- 分析交响乐(平安银行):
- 软件报告:在代表“每分钟60拍”的主旋律音轨上(1分钟周期),音量占比达到了惊人的 12.53%!
- 更让你惊讶的是,在“每5分钟一次”的华彩乐章音轨上,音量占比也有 9.05%。
- 你评价道:“这首交响乐不仅有强烈的1分钟主节奏,还有一个非常宏大的5分钟结构。它的结构比那首摇滚乐更复杂,能量也更集中在几个关键节奏上。”
通过fVR这个量化指标,你不仅听出了两首歌都有节奏,还能精确比较出哪个节奏更强,以及两首歌在节奏结构上的异同。
想象你在分析一个蜂巢里蜜蜂的活动。你已经忽略了蜜蜂早出晚归的整体规律(去趋势)。你把蜂巢的活动分成了500种不同的振动模式进行分析。
- 基准:如果蜜蜂是完全随机飞行的,那么每种振动模式的能量应该都是0.2%。
- 观察结果(表1):
- 你发现,代表“每分钟全体蜜蜂同步振翅一次”的模式,其能量(fVR)占到了总能量的 9.46%(苹果蜂巢)和 12.53%(平安蜂巢)。
- 代表“每30秒小范围骚动一次”的模式,能量也占了 3-5%。
- 你的结论:这些蜜蜂的活动远非随机!它们内部存在一个强大的、以分钟为单位的“时钟”在指挥着它们的集体行为。这个“时钟”的信号强度(fVR)远远超过了随机背景噪音,证明了蜂群内部存在一种我们之前未知的、高度同步的沟通或行为机制。
77. 4.2 全市场分析
📜 [原文7]
通用周期性。在建立了揭示周期性并衡量其对两只代表性股票相对重要性的方法后,我们对样本中的所有 2,573 只股票进行了相同的分析。
这个小段落是第4.2节的引言,标志着研究范围的重大扩展。
- 从个案到全体:作者明确指出,研究的重心从此前的“解剖麻雀”(分析两只代表性股票)转向“普查人口”(分析样本中的所有股票)。这是一个从特殊到一般的关键跃升。
- 研究目标:通用周期性 (Universal Periodicity):标题和内容都点明了本小节的核心目标——寻找“通用”的周期性。也就是说,作者想验证之前在苹果和平安银行上发现的那些周期性规律(如1分钟、5分钟周期),究竟是这两只股票的特例,还是整个股票市场的普遍现象?
- 方法论的延续:作者强调,他们使用的是“相同的方法”,即将在第4.1节中建立起来的一整套流程——包括去趋势、谱分析、计算强度系数和fVR等——应用到每一只股票上。这保证了分析的一致性和结果的可比性。
- 样本规模:这里给出了具体的样本数量:2,573只股票。这个庞大的样本量使得研究结论具有很高的统计可信度。如果能在如此大量的股票上发现一致的模式,那么这个模式是偶然巧合的可能性就微乎其微了。
- 低估这一步的重要性:从个案分析到全市场分析,不仅仅是工作量的增加,更是研究性质的飞跃。个案研究只能提出“假说”(Hypothesis),而大规模的统计分析才能“验证”或“证伪”这个假说。只有通过了这一步的检验,一个发现在科学上才能站得住脚。
- 忽略样本构成:虽然没有详细说明,但这2,573只股票是如何挑选的(例如,是否剔除了交易不活跃的股票?是否包含了不同板块的股票?),会影响到“全市场”这个结论的代表性。严谨的研究通常会在附录中对样本筛选标准进行说明。
本段是4.2节的开场白,宣布研究将进入一个新阶段:将之前用于分析个股的谱分析方法,推广应用于覆盖数千只股票的全市场样本,旨在检验从个股中观察到的周期性规律是否具有普遍性,即是否是一种“通用周期性”。
本段的目的是作为一个清晰的转折点和“路标”。它告诉读者,我们即将把视野从微观的个股放大到宏观的市场层面。通过明确提出“通用周期性”这个核心概念,它为后续图3和图4的展示和讨论设定了主题,让读者能够带着明确的问题意识去阅读接下来的内容。
你是一位医生。在上一阶段,你详细解剖了两具典型的病人尸体(苹果和平安银行),发现他们的某个器官都有着相似的、奇特的周期性病变。
现在,你进入了一个大停尸间,里面有2,573具尸体。你宣布:“好了,个案研究做完了。现在我要用同样的手术刀和显微镜,把这里所有的尸体都检查一遍,看看之前发现的那种周期性病变,到底只是个别现象,还是这场瘟疫(市场行为)的普遍症状。” 这个过程就是全市场分析,你的目标是寻找“通用病理特征”(通用周期性)。
你是一位语言学家,之前你仔细分析了两个人(一个说英语,一个说中文)的讲话录音,发现他们都在下意识地以1分钟为周期使用某个口头禅。
现在,你拿到了一个巨大的数据库,里面包含了2,573个不同的人的讲话录音。你启动了一个自动分析程序,对每一段录音都执行相同的“口头禅频率分析”。你的目标是:“我要看看‘1分钟口头禅’这个现象,是不是人类语言的一个普遍特征(通用周期性)。” 这一步,就是从个体研究走向群体统计。
88. 频率分布分析 (图3)
📜 [原文8]
我们首先分析哪些频率在美国和中国市场的所有股票中最为重要。对于每只股票,我们记录具有最高强度系数的前三个频率,并在图 3 中总结每个频率出现的次数。
我们观察到了极其一致的全市场模式。在美国市场,样本中几乎所有 492 只股票的最强频率都集中在一个很小的集合中:10 秒、15 秒、20 秒、30 秒、1 分钟和 5 分钟。同样,在中国市场,几乎所有 2,081 只股票的三个最强频率都属于一个很小的集合:30 秒、1 分钟、2.5 分钟、5 分钟和 10 分钟。这些频率恰好是 5 秒或 1 分钟的倍数。美国绝大多数个股以 1 分钟作为最强频率,30 秒作为第二强频率。在中国市场,大约一半的个股以 1 分钟作为最强频率,另一半以 5 分钟作为最强频率。
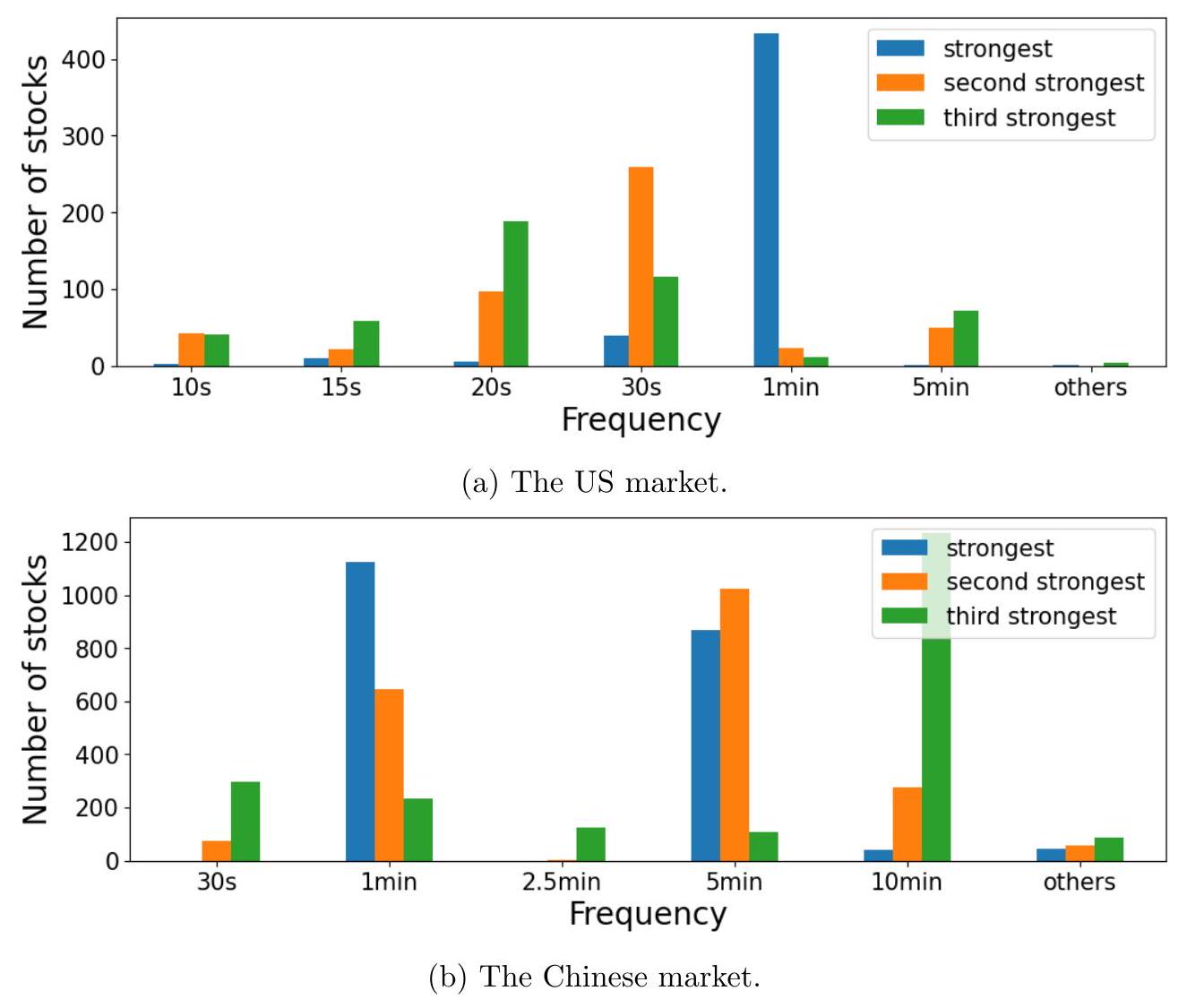
图 3:2019-2021 年所有股票中,按估计强度系数计算的前三个最强频率中各频率出现的次数。包含了选定的频率,其他所有频率都被归入“其他”类别。
这一部分通过图3展示了全市场分析的第一个重磅结果:哪些周期性节拍在整个市场中最流行?
- 分析方法:
- 对每只股票:对样本中2,573只股票的每一只,都运行谱分析,得到其所有频率的强度系数 $\hat{a}_j^2$。
- 找出“优等生”:从这500个频率中,找出强度系数排名前三的频率。这三个频率可以被认为是这只股票最重要的、最强的内生节拍。
- 统计“出镜率”:然后,作者开始扮演“点票员”的角色。他们看“1分钟”这个频率,在所有美股的“前三名”榜单里出现了多少次?在所有中概股的“前三名”榜单里又出现了多少次?对所有重要的频率(如30秒,5分钟等)都做同样的统计。
- 可视化(图 3):图3就是这个“点票”结果的可视化。它是一个柱状图。
- 横轴:是各个候选的周期(10s, 15s, ..., 5min, etc.)。
- 纵轴:是某个特定周期(比如“1min”)作为一只股票“前三强”节拍出现的总次数。
- 图例:图中用不同颜色区分了“最强频率”(第一名)、“第二强频率”和“第三强频率”。这能提供更丰富的信息。
- 结果解读(观察到了极其一致的全市场模式):
- 美国市场(左图,492只股票):
- 高度集中:绝大多数股票的最强节拍,都落在了少数几个周期上:1分钟、30秒、20秒、15秒、10秒、5分钟。图上这些柱子特别高,而“其他”这个柱子很矮,说明强周期不是随机分布的,而是高度集中的。
- 1分钟是王者:代表“1分钟”周期的蓝色柱子(最强频率)鹤立鸡群,说明对于绝大多数美股来说,1分钟是它们最核心的交易节拍。
- 30秒是亚军:代表“30秒”周期的橙色柱子(第二强频率)也非常高,说明如果1分钟不是最强,那么30秒很有可能就是第二强的节拍。
- 中国市场(右图,2,081只股票):
- 同样高度集中:情况类似,强周期也集中在少数几个选择上:1分钟、5分钟、30秒、10分钟、2.5分钟。
- 双雄争霸:与美国市场不同,中国市场呈现“双寡头”格局。代表“1分钟”的蓝色柱子和代表“5分钟”的蓝色柱子都非常高,平分秋色。这意味着,大约一半的A股以1分钟为最强节拍,而另一半则以5分钟为最强节拍。
- 30秒紧随其后:30秒作为第二或第三强的频率,出现的次数也很多。
- 一个有趣的共性:作者特别指出,无论中美,这些最流行的周期“恰好是 5 秒或 1 分钟的倍数”。比如10秒,15秒,20秒,30秒都是5秒的倍数,1分钟,2.5分钟,5分钟,10分钟都是1分钟或30秒的倍数。这强烈暗示了这些周期性与人类或机器的“凑整”行为习惯有关,而不是某种物理或自然常数决定的。
- 最终结论:个股分析中发现的周期性绝非偶然!它是一种通用模式,在整个市场中普遍存在。而且,中美市场虽然共享某些周期(如1分钟、30秒),但在主导周期的模式上存在显著差异(美国是1分钟独大,中国是1分钟和5分钟双雄并立)。
- 误解纵轴含义:图3的纵轴不是fVR,也不是强度系数本身,而是计数(Counts)。它代表一个频率“上榜”前三名的次数。这是一个关于“流行度”的统计,而不是关于“强度”的直接度量。
- 忽略“其他”类别:图中“其他”这一项非常重要。它很矮,这本身就是一个强有力的证据,说明强周期性没有散落在其他成百上千个可能的频率上,而是惊人地收敛到了少数几个频率上。如果“其他”的柱子很高,结论就会被大大削弱。
- 样本数量差异:要注意到中美市场的样本股票数量(492 vs 2081)不同,所以不能直接比较两国纵轴的绝对数值。例如,即使美国市场的“1分钟”蓝色柱子比中国市场的矮,但考虑到美国样本少,它在其国内的“统治力”可能更强。应该看的是相对比例。
- “前三”这个选择:为什么是前三强?这是作者的一个选择。如果选择前一强,信息量会减少;如果选择前十强,可能会引入太多噪音。选择前三是一个比较折中的、能有效捕捉最重要信号的做法。
本段通过对全市场所有股票的最强频率进行统计和可视化(图3),得出了全市场分析的第一个核心结论:交易活动中的高频周期性是一个普遍现象。这些周期性高度集中在少数几个与人类计时习惯相符的整数时间点上(如1分钟、30秒等)。此外,分析还揭示了中美市场在主导周期模式上的显著差异:美国市场由“1分钟”周期主导,而中国市场则呈现出“1分钟”和“5分钟”周期共同主导的格局。
本段的目的是用强有力的统计证据,将从个案研究中得到的假说(存在1分钟、5分钟等周期)推广为全市场的普遍规律。图3提供了一个宏观的、鸟瞰式的视角,让读者一目了然地看到整个市场的“节奏偏好”。它不仅雄辩地证明了“通用周期性”的存在,而且通过对比中美两张图,为后文探讨这些周期性背后的驱动因素(如投资者结构、交易制度等)埋下了伏股。
你是一位流行音乐分析师,正在分析2021年度美国和中国所有流行歌曲的数据库。
- 分析方法:你用一个算法,自动识别每首歌最主要的三个节奏(鼓点最强的三个BPM,每分钟节拍数)。
- 统计结果(图3):你统计每种BPM(如60 BPM, 120 BPM)在所有歌曲的“前三节拍”榜单上出现的次数。
- 你的发现:
- 惊人的一致性:你发现,无论中美,流行的歌曲节奏都惊人地集中在几个特定的BPM上,比如60 BPM (1分钟/拍), 120 BPM (30秒/拍), 24 BPM (5分钟/拍) 等。其他千奇百怪的BPM很少成为主旋律。
- 美国市场(左图):绝大多数美国流行歌的最强鼓点都是120 BPM(每分钟120拍,对应0.5秒周期,这里假设是1分钟周期)。整个市场被这种快节奏的舞曲主导。
- 中国市场(右图):中国的流行音乐界则是“双雄争霸”。大约一半的流行歌最强节拍是120 BPM,而另一半则是更舒缓的60 BPM(每分钟60拍,对应1分钟周期)。
- 你的结论:歌曲的节奏不是随机的,而是遵循着非常普遍的模式。中美听众的“节奏偏好”有共性,但也有显著差异,这可能反映了文化或生活节奏的不同。
想象一下你在观察一个巨大城市里所有人的行走步伐。城市里有美国区和中国区。
- 你的工具:你有一副超级眼镜,可以瞬间分析出每个人的主要行走节拍(比如每分钟走多少步)。
- 你的分析:你对每个人,都记录下他最常用的三种步伐节奏。然后你统计,哪种节奏是这个城市里最“流行”的。
- 你的发现(图3):
- 通用节拍:你发现,大家走路的节奏并不是五花八门,而是高度集中在几个“整数”节拍上,比如“每分钟走120步”(对应30秒周期性动作)、“每分钟走60步”(对应1分钟周期性动作)。
- 美国区(左图):几乎所有美国人走路的最主要节拍都是“每分钟走60步”。整个区的人仿佛都在以一个统一的、不快不慢的节奏前行。
- 中国区(右图):这里则有两种主流节奏。一半人以“每分钟60步”的节奏走,另一半人则以一种更慢的“每12步”的节奏(对应5分钟周期)走,像是在散步。
- 结论:这个城市的居民行走有通用的节拍模式,但不同区域的居民偏好的主导节拍不同。
99. fVR分布分析 (图4)
📜 [原文9]
我们还总结了所有股票的 fVR,以量化每个频率对总方差的相对贡献。图 4 显示了选定频率下跨股票 fVR 的箱线图,这是表 1 的全市场版本。对于绝大多数股票,选定频率下的 fVR 显著高于 0.2% 的基准水平。在中国市场,5 分钟频率和 1 分钟频率的 fVR 中位数都在 10% 左右,10 分钟频率的 fVR 中位数在 5% 左右。与中国市场相比,美国市场的 fVR 较低,这意味着交易在不同频率上更加分散。尽管如此,1 分钟和 30 秒频率的 fVR 中位数分别在 5% 和 3% 左右,均比基准水平高出至少十倍。
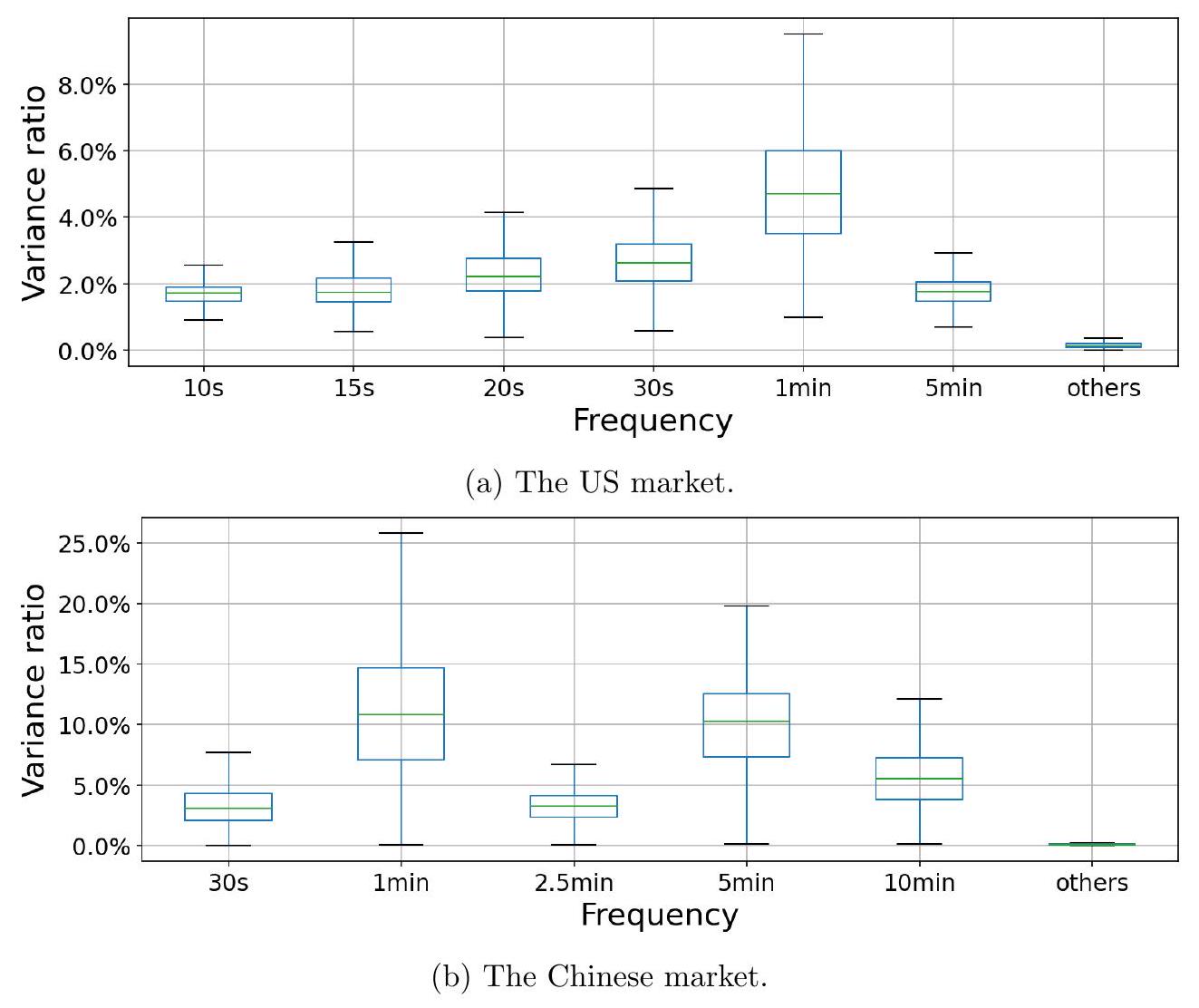
图 4:2019-2021 年所有股票选定频率下频率方差比 (fVR)——即选定频率解释的方差占去趋势时间序列总方差的比率——的箱线图。所有其他频率都被归入“其他”类别。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为模型中包含了 $n=500$ 个周期性成分。
图3告诉我们哪些周期“最流行”,而图4则更进一步,告诉我们这些流行的周期到底有多“强力”,即它们能在多大程度上解释交易的波动。
- 分析目的:图3只关心一个频率是否能“挤进前三”,是一种“名次”的统计。但名次高不代表实力一定强。例如,A股票的冠军频率fVR是5%,B股票的冠军频率fVR是30%。两者都是冠军,但后者的重要性远大于前者。因此,需要直接分析fVR的数值本身。
- 分析方法:箱线图 (Boxplot)
- 数据:对于某个特定频率(如“1分钟”),我们现在有了几百个(美股)或几千个(A股)fVR值,每个值来自一只股票。这就形成了一个fVR值的分布。
- 箱线图的作用:箱线图是展示数据分布的绝佳工具。它能同时显示:
- 中位数 (Median):中间的横线,代表这个频率在所有股票中的“典型”fVR水平。50%的股票fVR低于此值,50%高于此值。
- 箱体 (Box):代表了中间50%股票的fVR范围(从25百分位到75百分位)。箱体越窄,说明大多数股票在这个频率上的fVR水平越集中。
- 须线 (Whiskers):从箱体延伸出的线,代表了绝大多数数据的范围。
- 异常点 (Outliers):远离须线的点,代表一些fVR极高或极低的个别股票。
- 图4的解读:
- 横轴:是选定的周期。
- 纵轴:是fVR的值(百分比)。
- 基准线:图中应该有一条在0.2%位置的水平线(尽管作者没有画出来,但在脑海里要有),这是我们判断fVR是否显著的“基准”。
- 对图4的详细分析:
- 普遍高于基准:最直观的发现是,对于所有选定的频率(除了“其他”),整个箱体都远远高于0.2%的基准线。这说明,对于绝大多数股票(不仅仅是平均水平),这些周期性都是非常显著的,而不是少数几只股票拉高了平均值。
- 中国市场(右图):
- 强度惊人:观察“1分钟”和“5分钟”这两个箱子。它们的中位数线(箱子中间的横线)都处在 10% 左右的位置!这意味着,在一个典型的A股中,光是1分钟周期就能解释10%的去趋势后波动,5分钟周期也能解释另外10%!这是非常巨大的解释力。
- 10分钟周期的中位数也在5%左右,同样不可小觑。
- 美国市场(左图):
- 强度相对较低:与中国市场相比,美国市场所有频率的fVR箱体都位于更低的位置。例如,“1分钟”周期的fVR中位数在 5% 左右,“30秒”周期的中位数在 3% 左右。
- 但依然显著:尽管低于中国,但5%和3%的fVR值,依然是0.2%基准的25倍和15倍,所以这些周期在美国市场同样是高度显著和重要的。
- 中美对比的结论:作者由此得出一个重要推论——“与中国市场相比,美国市场的 fVR 较低,这意味着交易在不同频率上更加分散。”
- 解读:在中国市场,大量的交易活动能量都集中在了1分钟和5分钟这两个“超级频率”上。而在美国市场,能量虽然也集中,但分布得更“平均”一些,除了1分钟和30秒,其他更小的频率(如10秒,15秒,20秒,图中未单独展示但包含在图3中)也分走了一部分能量。这导致了单个频率的fVR中位数不如中国市场那么极端。
- 混淆中位数和平均数:箱线图展示的是中位数,它比平均数更能抵抗极端值的影响,能更好地代表“典型”情况。如果少数几只股票的fVR极高,会拉高平均数,但对中位数影响不大。
- 忽略箱体的高度:箱体的高度(即75百分位和25百分位的差距)也包含信息。箱体越“扁”,说明不同股票在这个频率上的fVR值越趋同。箱体越“高”,说明差异越大。
- 对“交易更加分散”的理解:这不代表美国市场的交易活动更少或更不重要。它指的是能量在不同频率上的分布。可以想象成:中国市场是两三个“超级巨星”,拿走了大部分片酬;美国市场是十几个“一线明星”,片酬虽然也高,但彼此差距没那么大,分配得更均匀一些。
- 坐标轴的尺度:同样要注意纵轴是线性尺度。如果某个异常点在图的顶端,它的fVR可能已经达到了非常恐怖的数值(比如40%以上)。
本段通过fVR的全市场箱线图(图4),从“强度”维度进一步证实和深化了“通用周期性”的发现。结论如下:
- 普遍显著:对于绝大多数中美股票,1分钟、5分钟、30秒等周期的fVR都远超0.2%的基准,证明了这些周期性的强度和普遍性。
- 中国市场强度更高:在中国市场,1分钟和5分钟周期的fVR中位数高达10%左右,显示出极强的解释力。
- 美国市场更分散:美国市场的fVR中位数(如1分钟约5%)虽然也极其显著,但低于中国市场,表明其交易能量分布在更广泛的频率上,而不是像中国那样高度集中于一两个主导频率。
本段的目的是为“通用周期性”提供最核心的量化证据支持。图3证明了“流行度”,图4则证明了“实力”。通过展示fVR的分布,作者不仅证明了周期性的普遍存在,还揭示了它们在经济意义上的重要性(例如,能解释高达10%的方差)。此外,通过对比中美fVR分布的差异,作者引出了关于市场结构和交易行为的深刻洞见(能量分散度不同),为后文的讨论和解释奠定了坚实的基础。
你是一位城市规划师,正在分析两个城区(中国区和美国区)的交通流量波动情况(已去除早晚高峰的趋势)。你关注的是几个特定路口的周期性拥堵。
- 分析方法:对每个区的每一条街道,你都计算了“每1分钟拥堵一次”、“每5分钟拥堵一次”的fVR值,即这个周期性拥堵能在多大程度上解释这条街的“剩余”交通波动。然后你画出了fVR的箱线图(图4)。
- 你的发现:
- 中国区(右图):你看到“1分钟”和“5分钟”路口的fVR箱线图,其中位数都在10%!这意味着,在一条典型的中国区街道上,“每分钟一个红绿灯”和“每五分钟一班公交车”这两个因素,各自解释了交通流量波动的10%。交通的“脉搏”被这两个节奏牢牢掌控。
- 美国区(左图):你看到“1分钟”路口的fVR中位数在5%,“30秒”路口的中位数在3%。这意味着“每分钟一个红绿灯”依然是重要因素,但它的影响力不如中国区那么绝对。同时,“每30秒变一次的人行道信号灯”等更快的节奏也分担了一部分影响力。
- 你的结论:两个区的交通都有强烈的周期性。但中国区的交通节奏高度依赖于1分钟和5分钟这两个“主干线”的调度。而美国区的交通节奏则更加“碎片化”,由更多不同频率的信号灯共同调节,能量分布更散。
想象你在分析两片森林(中国森林和美国森林)里鸟叫的声学数据(已去除清晨和黄昏鸟叫最响的趋势)。
- 分析方法:你对森林里的每一种鸟,都计算它发出的“1分钟鸣叫周期”、“5分钟鸣叫周期”等声音的能量占比(fVR)。然后画出箱线图。
- 你的发现(图4):
- 中国森林(右图):你发现,对于典型的鸟类,“1分钟一次”的鸣叫和“5分钟一次”的鸣叫,其声能量都占到了总声能量的10%左右。整个森林仿佛被这两种宏大的、同步的鸣唱所主导。
- 美国森林(左图):在这里,典型的鸟类“1分钟一次”的鸣叫声能量占比约为5%,“30秒一次”的鸣叫声占比约为3%。虽然也有主旋律,但许多其他更短促、更快的鸟叫声(10秒、20秒)也贡献了不小的能量。
- 你的结论:两片森林的鸟叫都有规律。但中国森林的声景被少数几种最强壮、最有规律的“歌唱家”(如布谷鸟)所统治。而美国森林的声景则更像一个大合唱,虽然也有领唱,但成百上千种小鸟的唧唧喳喳(更高频率、更分散的交易)也构成了声景中不可或缺的一部分。
1010. 结论与稳健性检验
📜 [原文10]
图 3-4 的结果证实了我们在第 4.1 节中观察到的周期性对于我们考虑的个股而言并非巧合。相反,它是美国和中国市场交易活动的一种通用模式。此外,尽管两个市场都显示出强烈的周期性,我们也证实了主导频率是不同的。美国市场在更高频率下显示出更强的强度系数,这与以下典型事实一致:美国市场包含更多的算法和高频交易者,而中国市场主要由散户投资者驱动(Li and Wang, 2010; Jones et al., 2020),且中国市场通过实施“T+1 规则”(要求任何头寸至少持有一天的最短期限)来抑制日内交易。
我们进行了两次稳健性检查。第一项将我们的主要分析(基于 2019-2021 年的数据)扩展到美国市场的 31 年期间(1993-2023 年)和中国市场的 10 年期间(2014-2023 年)。结果见第 5.1.3 节。第二项应用小波

图 4:2019-2021 年所有股票选定频率下频率方差比 (fVR)——即选定频率解释的方差占去趋势时间序列总方差的比率——的箱线图。所有其他频率都被归入“其他”类别。如果不存在周期性,基准 fVR 为 $\frac{1}{500}=0.2 \%$,因为模型中包含了 $n=500$ 个周期性成分。
方差估计量(另见 Chinco and Ye (2017)),为通用高频周期性的存在提供额外证据。结果见附录 E。
这一部分是对4.2节全市场分析结果的总结,并首次尝试对观察到的现象给出可能的解释,同时预告了接下来的稳健性检验。
- 核心结论重申:
- 非巧合,是通用模式:作者首先强调,图3和图4的结果强有力地证明了,在苹果和平安银行上发现的周期性不是个例或巧合,而是中美两大股票市场普遍存在的“通用模式”。这是本节最重要的结论。
- 主导频率不同:在共性之外,差异性同样重要。研究证实了,两个市场的主导交易节奏是不同的。
- 对中美市场差异的解释(初步假说):
- 现象:美国市场在更高频率(如10秒、15秒、20秒、30秒)上显示出更强的强度。回顾图3,可以看到美国市场的强周期列表中包含了许多“秒”级的短周期;回顾图4,虽然美国整体fVR较低(能量分散),但其能量更多地分布在这些高频上。
- 解释:作者将这一现象与已知的市场“典型事实”(stylized facts)联系起来,提出了一个非常符合直觉的解释:
- 美国市场:拥有大量的算法交易和高频交易者 (HFT)。这些由计算机驱动的交易策略,其决策和执行速度极快,能够在秒级甚至毫秒级的时间尺度上进行操作。因此,它们自然会产生更高频率的交易活动。
- 中国市场:主要由散户投资者驱动。散户的交易决策依赖于人的反应速度和操作(看盘、手动下单),很难做到秒级操作,其交易节奏自然更慢,更可能集中在分钟级别。
- 中国市场的制度限制:作者还提到了一个关键的制度因素——“T+1规则”。该规则禁止当天买入的股票当天卖出,极大地抑制了以日内超高频套利为目的的交易策略。这进一步解释了为什么中国市场的高频交易不如美国活跃。
- 引用文献:作者引用了两篇文献来支持他们关于中美投资者结构差异的说法,增加了这个解释的可信度。
- 预告稳健性检验 (Robustness Checks):
- 稳健性检验的目的:一个好的实证研究,不仅要得出结论,还要证明这个结论是“皮实”的(robust),不会因为分析方法、时间区间或数据处理的微小改变而轻易消失。
- 检验一:扩展时间窗口:主要分析用的是2019-2021年的数据。一个自然的问题是:这个现象是最近几年才有的,还是长期存在的?为了回答这个问题,他们将时间窗口大大延长,美国市场回溯31年,中国市场回溯10年。如果在这几十年的数据中都能发现类似的周期性,那么结论将变得极为坚实。结果放在第5.1.3节。
- 检验二:更换分析工具:主要分析用的是谱分析(一种基于傅里叶变换的方法)。一个可能被质疑的点是:这个发现会不会是谱分析这个工具自身带来的“幻觉”?为了排除这种可能,他们换用了另一种完全不同的时间序列分析工具——小波方差估计量 (Wavelet variance estimator)。小波分析在处理非平稳信号和瞬时频率上具有优势。如果换一种工具还能得出同样的结论(发现通用高频周期性),那就说明这个现象是数据内禀的,而不是特定分析方法的产物。结果放在附录E。
- 将解释当作定论:作者在这里提出的关于“算法交易 vs 散户”的解释,是一个基于现有证据和典型事实的、非常合理的假说。但本文的主要贡献在于发现和证实周期性现象,而不是严格证明其成因。要证明成因,需要更复杂的因果推断分析。
- 忽略“T+1”规则的重要性:对于理解中美市场差异,“T+1”是一个极其中关键的制度背景。它从根本上改变了市场的微观结构和参与者的策略空间,是解释中国市场高频交易相对不活跃的核心原因之一。
- 不理解稳健性检验的意义:稳健性检验是实证研究的“生命线”。没有经过稳健性检验的结论是脆弱的。读者在评估一篇实证论文的质量时,必须关注其稳健性检验是否充分、设计是否合理。
本段是全市场分析部分的总结陈词和延伸。它首先再次确认了“通用周期性”的存在以及中美市场的模式差异。接着,它首次尝试从投资者结构(算法交易vs散户)和交易制度(T+1)的角度,为观察到的市场差异提供了一个合理的解释。最后,为了巩固研究结论的可靠性,作者预告了即将进行的两项重要的稳健性检验:扩展时间样本和更换分析工具。
本段落承担了三个重要功能:
- 总结与升华:对前文复杂的图表和数据分析进行提炼,给出清晰、简洁的核心结论。
- 解释与联系:尝试将新发现的实证现象与已知的金融学理论和市场事实联系起来,赋予现象经济学含义,提升研究的深度。
- 增强说服力:通过预告即将到来的、设计严谨的稳健性检验,主动回应潜在的质疑,向读者展示其研究的严谨性和结论的可靠性,从而建立信任。
你是一位社会学家,刚刚完成了对两个大社区(美国社区和中国社区)居民行为模式的大规模调查。
- 总结发现:你向大家宣布:“我们的研究证实,之前在两个样本家庭中发现的‘周期性行为模式’,确实是这两个社区的普遍现象!而且,两个社区的主导节奏不同:美国社区的行为节奏更快、更短促。”
- 提出解释:你进一步解释道:“我们认为,这种差异与社区的‘居民构成’和‘本地法规’有关。美国社区里住了很多靠电脑程序自动处理日常事务的‘科技极客’(算法交易),他们的生活节奏自然是秒级的。而中国社区主要是靠手动处理事务的普通家庭(散户),节奏自然慢一些。更重要的是,中国社区有个规定,‘今天买的菜不准今天扔’(T+1),这也限制了大家进行超快速的物品置换。”
- 打消疑虑(稳健性检验):最后,你说:“为了确保我们的结论不是瞎猫碰上死耗子,我们还做了两件事。第一,我们翻看了这两个社区过去几十年的历史档案(扩展时间窗口),发现这个现象一直都存在。第二,我们换了一套完全不同的社会学分析理论(小波分析)来重新审视数据,结果还是一样。所以,我们非常有信心,这个发现是真实可靠的。”
你是一位天文学家,通过分析恒星的光谱,发现了宇宙中普遍存在某种神秘的“周期性脉冲信号”。
- 发布结论:你召开新闻发布会,宣布:“我们在对数千颗恒星进行普查后发现,之前在两颗典型恒星上观察到的‘1分钟脉冲’和‘5分钟脉冲’现象,是宇宙中的一种通用模式!而且,我们发现,在A星系(美国市场),更高频率的‘秒级脉冲’更强;而在B星系(中国市场),脉冲能量更集中在较慢的‘分钟级’。”
- 给出假说:你推测:“这种差异可能与星系的‘文明类型’有关。A星系可能由依赖超高速量子计算的硅基生命主导(算法交易),而B星系可能由反应速度较慢的碳基生命主导(散户)。同时,B星系有一条物理法则叫‘T+1定律’,禁止能量在一天内完成一个完整的跃迁-返回循环,这也抑制了超高频信号的产生。”
- 应对质疑(稳健性检验):面对同行的质疑,你补充道:“我们知道这听起来很不可思议。所以,我们检查了过去30年积累的所有观测数据(扩展时间窗口),这个模式始终存在。此外,我们还用了另一种完全不同的观测设备——引力波望远镜(小波分析),而不是传统的光学望远镜(谱分析)——去探测,同样探测到了这些脉冲。因此,我们确信,这是一种真实的宇宙现象。”
1111. 其他金融时间序列
📜 [原文11]
其他金融时间序列。值得强调的是,尽管本文重点关注股票的成交量,但我们在第 3 节中的框架可以广泛应用于其他可能包含周期性的日内时间序列。例如,在附录 F 中,我们将我们的框架应用于买卖价差、波动率和订单不平衡的日内时间序列,这些也是 Heston, Korajczyk, and Sadka (2010) 研究的对象。总的来说,我们在买卖价差、波动率中发现了周期性,但在订单不平衡中没有发现。我们还通过对每只股票和每个交易日的日内成交量数据在第 95 百分位进行缩尾处理 (winsorizing) 来检查结果的稳健性,以减少极端数据对 fVR 的影响。我们发现了稳健的周期性,在某些情况下,fVR 甚至更强。
这个段落是主文部分的最后一个技术性说明,它扩展了研究的广度和深度,并额外增加了一项稳健性检验。
- 方法的普适性:作者首先强调,他们开发的这套谱分析框架(第3节)是一个通用工具,不只适用于分析成交量。任何具有日内模式的时间序列数据,原则上都可以用这个框架来分析其中是否隐藏着周期性。这展示了作者对自己研究方法论的信心和对其应用前景的展望。
- 扩展应用到其他变量:
- 举例说明:为了证明方法的普适性,作者真的去做了实验。他们在附录F中,将同样的分析方法应用到了另外三个重要的金融微观结构变量上:
- 买卖价差 (Bid-Ask Spread):衡量市场流动性的一个关键指标。
- 波动率 (Volatility):衡量价格变动剧烈程度的指标。
- 订单不平衡 (Order Imbalance):衡量买方力量和卖方力量对比的指标。
- 选择的依据:选择这三个变量并非随意,作者提到它们也是 Heston, Korajczyk, and Sadka (2010) 这篇经典文献研究的对象,这显示了他们的研究是与该领域的重要前人工作进行对话。
- 结果总结:作者简要报告了附录F中的核心发现:
- 买卖价差和波动率中,也发现了周期性。这意味着市场的流动性和风险水平,也存在着以分钟为单位的节律性波动。
- 但在订单不平衡中,没有发现显著的周期性。这是一个“负面结果”,但同样有价值。它说明并非所有的市场活动都有这种高频节律。买卖力量的对比可能更多地由非周期性的、事件驱动的信息流决定。
- 额外的稳健性检验:缩尾处理
- 问题:金融数据(尤其是成交量)经常会出现一些极端值,比如某一天某个时刻突然出现一笔巨额交易。这种极端值(outliers)可能会对方差的计算产生巨大影响,从而可能扭曲fVR的估计结果。
- 解决方法:缩尾处理 (Winsorizing):这是一种常用的统计技术,用于处理极端值。具体做法是:设定一个百分位(比如95%),将所有高于该百分位的数据点,强行设置为等于该百分位的值。例如,如果第95百分位的成交量是1000笔,那么任何大于1000笔的成交量数据(比如1500笔,5000笔)都被当作1000笔来处理。
- 目的:这样做可以有效“剪掉”数据分布的“肥尾”,减少极端异常值对整体分析的干扰,使得结果更能反映普遍情况而非特殊事件。
- 检验结果:作者对成交量数据进行缩尾处理后,重新进行了全部fVR分析。结果是:
- 周期性依然稳健 (robust):之前发现的周期性并没有因为处理了极端值而消失。
- fVR甚至更强:在某些情况下,fVR的数值反而更大了。这可能是因为极端的大额交易往往是“非周期性”的、偶然发生的,它们增大了总方差(分母),却不贡献于周期性成分(分子),从而稀释了原始的fVR。去掉这些“噪音”后,周期性的“信号”在剩余波动中的占比自然就显得更强了。
- 将附录内容当成主菜:作者在这里只是简要提及了对其他变量的分析,详细的结果和讨论都在附录中。这个段落的主要目的是展示方法的延展性,而不是深入探讨价差或波动率的周期性。
- 误解“未发现周期性”:“在订单不平衡中没有发现周期性”不等于“订单不平衡完全随机”。它只是意味着,订单不平衡的波动模式,无法被本文所使用的这种固定频率的周期性模型很好地捕捉。它可能有其他更复杂的动态模式。
- 对缩尾处理的疑虑:缩尾处理是一种“修改”原始数据的行为,可能会被质疑其合理性。但在这里,它的目的是作为一种稳健性检验,证明结论并不依赖于少数极端值的存在。只要作者清晰地报告了他们所做的处理,并将其作为检验而非主要结果,这种做法在学术上是完全可以接受的。
本段从两个方面扩展和加强了研究的可靠性。首先,通过将分析框架成功应用于买卖价差和波动率,展示了该方法的普适性和广阔的应用前景,并揭示了周期性可能是市场微观结构中更广泛的现象。其次,通过对成交量数据进行缩尾处理的稳健性检验,证明了本文的核心发现(通用高频周期性)并非由极端交易事件驱动,而是一种根植于市场日常运行中的、稳健的内在节律。
本段位于实证部分的结尾,起到了“巩固和拓展”的作用。
- 巩固:通过额外的缩尾处理稳健性检验,进一步加固了核心结论的城墙,使其不易被“极端值”的攻击所攻破。
- 拓展:通过展示方法在其他金融变量上的成功应用,作者打开了一扇门,暗示了后续研究的多个可能方向,提升了本文的潜在影响力和启发性。它向读者表明,这不仅仅是一个关于成交量的故事,而可能是一个关于整个市场微观行为节律的新篇章的开始。
你是一位生物学家,你的团队发明了一种新的基因测序技术(谱分析框架),并用它成功在“苍蝇”(成交量)身上发现了一种周期性的基因表达模式。
- 展示技术普适性:在报告的结尾,你补充道:“值得一提的是,我们的新技术是个通用平台。我们顺便用它测试了‘老鼠’(买卖价差)和‘猴子’(波动率),发现它们身上也有类似的周期性基因表达。不过,在‘蚯蚓’(订单不平衡)身上没找到。详细的实验报告在附录里。” —— 这表明你的技术很牛,应用广泛。
- 增加一项对照实验(缩尾处理):你又说:“有人可能会说,我们发现的苍蝇基因周期,是不是因为我们不小心混进去了几只打了兴奋剂的‘超级苍蝇’(极端交易)?为了排除这个可能,我们做了一个实验:我们把所有苍蝇的活力值拉平,把那些特别亢奋的都按正常苍蝇处理。结果发现,那种周期性基因表达依然存在,甚至更清晰了!这说明,这个周期性是普通苍蝇与生俱来的,不是那几只超级苍蝇搞出来的。” —— 这证明了你的发现很可靠,不是个别案例造成的假象。
你是一位侦探,破获了一起关于“交易活动”的案件,发现了其背后隐藏的“周期性作案”规律。在结案陈词的最后,你补充了两点。
- 拓展调查范围:你对警长说:“警长,我们开发的这套犯罪模式分析系统(谱分析框架)非常强大。我们用它顺便看了看城里的另外几类案件,比如‘商店失窃案’(买卖价差)和‘街头斗殴案’(波动率),发现它们也有非常相似的周期性作案规律!但是‘网络诈骗案’(订单不平衡)好像没有这个规律。这意味着,这种周期性可能是城市线下犯罪活动的一个共同特征。”
- 排除特殊干扰(缩尾处理):你接着说:“另外,为了确保我们找到的这个‘交易案’的作案周期,不是被城里那几个偶尔发疯的‘犯罪狂人’(极端交易)给带偏了,我们做了一个沙盘推演。在推演中,我们把所有罪犯的‘疯狂值’都设定了上限。结果,那个周期性的作案规律不仅没有消失,反而变得更加清晰可见。这证明,这个规律是整个犯罪网络(市场)的内生运作模式,而不是那几个疯子的一时兴起。”
1212. 全文解释总结与核心洞见
本节将对前述所有详细解释进行一次全面的回顾与提炼,旨在整合第四章实证分析部分的核心逻辑、关键发现与深层含义,形成一个连贯的、高度浓缩的知识图谱。
12.1. 研究的核心逻辑:从现象到量化,再到普遍规律
本文第四章的论证过程展现了一个严谨且层层递进的科学研究范式:
1. 理论武装 (第3节回顾):整个分析建立在谱分析的理论框架之上。其核心思想是将一个复杂的时间序列(如去趋势后的日内成交量)分解为一系列简单、不同频率的余弦波(基函数)的叠加。这种分解让我们能够从“频率”的视角审视数据。
2. 关键指标的建立:
* 强度系数 ($a_j$):这是谱分析的直接产物,其平方 $a_j^2$ 直观地度量了在特定频率 $j$ 上的“能量”或“强度”。图2中的“山峰”就是高强度系数的可视化体现。
* 频率方差比 (fVR):这是本文提出的一个更具解释力的核心指标。它解决了“强度系数大”究竟“有多重要”的问题。通过计算某个频率解释的方差占去趋势后总方差的比例,fVR将抽象的强度转化为了一个直观的百分比。至关重要的是,其分母刻意排除了众所周知的U型趋势,使得分析聚焦于新发现的高频周期性上。
3. 分析路径:由点及面:
* 个案研究 (点):首先对苹果公司和平安银行这两个具有代表性的“点”进行深度“解剖”,通过图2和表1,初步揭示了高频周期性的存在及其在经济意义上的显著性(例如,fVR高达10%以上)。
* 全市场普查 (面):随后,将同样的方法应用到数千只股票组成的“面”上,通过图3(频率流行度统计)和图4(fVR分布统计),检验个案的发现是否具有普遍性。
12.2. 核心发现:交易活动中的“通用节拍”
通过上述逻辑,本文得出了几个重大发现:
1. 通用周期性的存在:高频周期性并非个别股票的特有现象,而是贯穿整个股票市场的通用模式 (Universal Pattern)。市场的交易活动,在去除宏观的U型趋势后,并非杂乱无章的噪音,而是跟随着某些特定的“节拍”在“脉动”。
2. 节拍的“凑整”特性:这些通用的节拍惊人地集中在少数几个符合人类计时习惯的“整数”时间点上,如1分钟、5分钟、30秒、10分钟等。这强烈暗示了其背后驱动因素与人类或程序的行为、决策周期有关。
3. 强度与重要性:这些周期性不仅存在,而且极其重要。图4的fVR分析显示,在中美两个市场中,这些主导频率的fVR中位数都远超0.2%的基准水平,达到了3%-10%的量级。这意味着,在一个典型的股票中,仅一两个主导周期就能解释其去趋势后交易波动的5%到20%,这是非常巨大的解释力。
12.3. 核心洞见:市场微观结构的差异与解释
在共性之外,本文通过对比中美两大市场,揭示了深刻的结构性差异,并提出了富有洞察力的解释:
1. 主导节拍的差异:
* 美国市场:呈现“1分钟”周期独大的格局,同时在更快的秒级(10s, 15s, 20s, 30s)周期上也表现活跃。
* 中国市场:呈现“1分钟”与“5分钟”周期双雄并立的局面,能量更集中于这两个较慢的分钟级周期上。
2. 能量分布的差异:
* 中国市场的fVR中位数更高(1分钟和5分钟均在10%左右),说明其交易能量高度集中在少数几个主导频率上。
* 美国市场的fVR中位数相对较低(1分钟约5%),说明其能量分布在更广泛的频率范围上,即交易节奏更多元化、更“分散”。
3. 背后的解释假说:作者将这些差异归因于两国市场在投资者结构和交易制度上的根本不同:
* 投资者结构:美国市场充斥着大量的算法交易和高频交易者 (HFT),它们的计算机程序能够在秒级甚至更快的尺度上决策和执行,从而催生了更丰富、更高频的交易节拍。而中国市场由散户主导,其交易行为更符合分钟级的人类反应和决策周期。
* 交易制度:中国的“T+1”规则从根本上抑制了以日内超高频反转为目的的交易策略,进一步强化了市场节奏偏慢的格局。
12.4. 研究的严谨性:多重稳健性检验的支撑
本文的结论之所以令人信服,很大程度上得益于其全面而审慎的稳健性检验,这排除了其他可能的解释,巩固了核心发现的可靠性。
1. 时间维度的检验:将分析窗口从3年扩展到几十年,证明了“通用周期性”是一个长期存在的历史现象,而非昙花一现。
2. 方法论维度的检验:采用与谱分析原理不同的小波分析,得到了同样的结论,证明了发现源于数据内禀的属性,而非特定分析工具的“幻觉”。
3. 数据变量维度的检验:将框架应用于买卖价差和波动率,发现类似的周期性,表明这可能是市场微观层面更广泛的规律。
4. 数据质量维度的检验:通过缩尾处理排除了极端交易事件的干扰,证明了周期性是市场日常运行的内在节律,而非由少数异常值驱动。
综上所述,本文第四章通过一套设计精巧的实证流程,不仅令人信服地“发现”了股票市场中隐藏的通用高频周期性,更通过量化分析和跨市场比较,揭示了其在经济意义上的重要性以及与市场微观结构的深层联系,为理解现代金融市场的复杂动态提供了全新的视角和有力的证据。
13行间公式索引
1. 公式 (6): $\mathrm{fVR}_{j}:=\frac{a_{j}^{2}}{2 \sigma^{2}+\sum_{i=1}^{n} a_{i}^{2}}$
* 一句话解释:该公式定义了频率方差比(fVR),用于衡量第 $j$ 个频率的周期性成分所解释的方差占去趋势后时间序列总方差的比例。
2. 公式 (7): $\mathrm{fVR}_{j}^{\prime}:=\frac{a_{j, \text { morning }}^{2}+a_{j, \text { afternoon }}^{2}}{2 \sigma_{\text {morning }}^{2}+\sum_{i=1}^{n} a_{i, \text { morning }}^{2}+2 \sigma_{\text {afternoon }}^{2}+\sum_{i=1}^{n} a_{i, \text { afternoon }}^{2}}$
* 一句话解释:该公式是针对具有午休时段的中国市场,通过合并上午和下午两部分独立的分析结果,来计算全天频率方差比(fVR')的特定方法。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。