1第 7 节
1.1. 生成集与凯莱有向图
📜 [原文1]
设 $G$ 是一个群,且 $a \in G$。我们已经描述了 $G$ 的循环子群 $\langle a\rangle$,它是包含元素 $a$ 的最小子群。假设我们想找到一个包含 $G$ 中另一个元素 $b$ 以及 $a$ 的尽可能小的子群。根据定理 5.17,我们知道任何包含 $a$ 和 $b$ 的子群都必须包含所有 $m, n \in \mathbb{Z}$ 的 $a^{n}$ 和 $b^{m}$,因此也必须包含这些 $a$ 和 $b$ 的幂的所有有限乘积。例如,这样的表达式可能是 $a^{2} b^{4} a^{-3} b^{2} a^{5}$。请注意,我们不能通过先写出 $a$ 的所有幂再写出 $b$ 的幂来“简化”这个表达式,因为 $G$ 可能不是阿贝尔群。然而,这类表达式的乘积仍然是同一类型的表达式。此外,$e=a^{0}$,并且这类表达式的逆也属于同一类型。例如,$a^{2} b^{4} a^{-3} b^{2} a^{5}$ 的逆是 $a^{-5} b^{-2} a^{3} b^{-4} a^{-2}$。根据定理 5.14,这表明 $a$ 和 $b$ 的整数幂的所有这些乘积构成了 $G$ 的一个子群,这必然是包含 $a$ 和 $b$ 的最小子群。我们称 $a$ 和 $b$ 为该子群的生成元。如果这个子群是 $G$ 的全部,那么我们说 $\{a, b\}$ 生成 $G$。当然,只取 $a, b \in G$ 这两个元素并非神圣不可侵犯。我们也可以对 $G$ 中的三个、四个或任意多个元素进行类似的论证,只要我们只取它们整数幂的有限乘积。
这段话的核心思想是从循环子群(由单个元素生成)的概念扩展到由多个元素生成的子群。
- 回顾循环子群:首先,文章回顾了循环子群 $\langle a\rangle$ 的概念。这个子群是由群 $G$ 中的一个元素 $a$ 生成的。它包含了 $a$ 的所有整数次幂,即 $\{..., a^{-2}, a^{-1}, a^0=e, a^1, a^2, ...\}$。关键在于,$\langle a\rangle$ 是所有包含元素 $a$ 的子群中最小的一个。任何其他包含 $a$ 的子群,必然也包含 $\langle a\rangle$ 的所有元素。
- 提出新问题:接下来,作者提出了一个更进一步的问题:如果我们不止关心一个元素 $a$,还关心另一个元素 $b$,那么包含 $a$ 和 $b$ 的最小子群是什么样的?
- 构建新子群的元素:为了回答这个问题,我们需要思考一个同时包含 $a$ 和 $b$ 的子群必须满足什么条件。
- 根据子群的定义,如果一个子群包含 $a$,它就必须包含 $a$ 的所有整数次幂($a^n$),因为子群在群运算下是封闭的,并且包含逆元。同理,如果它包含 $b$,也必须包含 $b$ 的所有整数次幂($b^m$)。
- 更进一步,既然这个子群同时包含了所有的 $a^n$ 和 $b^m$,那么根据封闭性,它也必须包含这些幂的任意有限次乘积。这些乘积的形式可以是 $a^2 b^4$, $a^{-1} b^3 a^5$ 等等。这里的“有限”是指数目有限的项相乘,而不是说群本身是有限的。
- 一个重要的警告:不可交换性:作者特别强调,对于表达式 $a^{2} b^{4} a^{-3} b^{2} a^{5}$,我们不能想当然地把所有 $a$ 的幂合并在一起,所有 $b$ 的幂合并在一起,变成 $a^{2-3+5} b^{4+2} = a^4 b^6$。这是因为群 $G$ 不一定是阿贝尔群(交换群)。在非交换群中,$ab$ 不一定等于 $ba$。因此,$a^{-3}b^2$ 不能交换成 $b^2a^{-3}$。元素的排列顺序至关重要。
- 验证子群的三个条件:现在我们来看这个由 $a$ 和 $b$ 的幂的有限乘积构成的集合,我们称之为 $H$。这个集合 $H$ 是否构成一个子群呢?我们需要验证子群的三个条件(根据定理 5.14):
- 封闭性:$H$ 中的两个元素相乘,结果是否还在 $H$ 中?是的。例如,取一个元素 $k_1 = a^2b^{-1}$,另一个元素 $k_2 = ba^3$。它们的乘积 $k_1k_2 = (a^2b^{-1})(ba^3) = a^2b^{-1}ba^3$。这个结果本身就是一个由 $a$ 和 $b$ 的幂组成的有限乘积,所以它仍然在 $H$ 中。
- 单位元:$H$ 是否包含单位元 $e$?是的。我们可以通过取 $a$ 的零次幂 $a^0=e$(或者 $b^0=e$)来得到单位元。$e$ 是一个只有一个项的“有限乘积”,所以 $e \in H$。
- 逆元:$H$ 中每个元素 $k$ 的逆元 $k^{-1}$ 是否也在 $H$ 中?是的。对于一个乘积表达式,例如 $k = a^{2} b^{4} a^{-3} b^{2} a^{5}$,它的逆元是 $(k)^{-1} = (a^{5})^{-1} (b^{2})^{-1} (a^{-3})^{-1} (b^{4})^{-1} (a^{2})^{-1} = a^{-5} b^{-2} a^{3} b^{-4} a^{-2}$。这个逆元仍然是一个由 $a$ 和 $b$ 的幂组成的有限乘积,所以它也在 $H$ 中。(这里用到了“袜鞋原理”:$(xyz)^{-1} = z^{-1}y^{-1}x^{-1}$)。
- 结论:最小性:既然这个集合 $H$ 满足子群的所有条件,它自身就是一个子群。同时,任何包含 $a$ 和 $b$ 的子群都必须包含 $H$ 的所有元素(这是我们推导的出发点)。因此,$H$ 就是包含 $a$ 和 $b$ 的最小子群。
- 引入新术语:生成元:我们给这个过程一个名字。我们称元素 $a$ 和 $b$ 是这个子群的生成元 (generators)。这个子群被称为由集合 $\{a, b\}$ 生成的子群。如果这个子群恰好就是整个群 $G$,我们就说集合 $\{a, b\}$ 生成 (generates) $G$。
- 推广:最后,作者指出这个思想可以推广到任意多个生成元,比如 $\{a, b, c, ...\}$。由这个集合生成的子群就是所有这些生成元(及其逆元)的幂的有限乘积的集合。
- $\langle a \rangle$:表示由元素 $a$ 生成的循环子群。它是集合 $\{a^n \mid n \in \mathbb{Z}\}$。
- $a^{2} b^{4} a^{-3} b^{2} a^{5}$:这是一个由元素 $a$ 和 $b$ 的幂组成的有限乘积的例子。它展示了在一个非交换群中,元素的顺序是不能随意调换的。
- $(a^{2} b^{4} a^{-3} b^{2} a^{5})^{-1} = a^{-5} b^{-2} a^{3} b^{-4} a^{-2}$:这是计算乘积逆元的例子。它遵循 $(x_1 x_2 ... x_k)^{-1} = x_k^{-1} ... x_2^{-1} x_1^{-1}$ 的规则。每个部分的逆元被计算出来,并且顺序完全颠倒。
- $(a^5)^{-1} = a^{-5}$
- $(b^2)^{-1} = b^{-2}$
- $(a^{-3})^{-1} = a^{3}$
- $(b^4)^{-1} = b^{-4}$
- $(a^2)^{-1} = a^{-2}$
将这些逆元以相反的顺序组合起来,就得到了结果。
示例1:在 $(\mathbb{Z}_6, +)$ 中由 $\{2, 3\}$ 生成的子群
- 群: $G = \mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}$,运算是模6加法。这是一个阿贝尔群。
- 生成元: $a=2, b=3$。
- 需要包含的元素:
- $a$ 的所有“幂”(在加法群中是倍数):$n \cdot 2 \pmod 6$。这生成了子群 $\langle 2 \rangle = \{0, 2, 4\}$。
- $b$ 的所有“幂”:$m \cdot 3 \pmod 6$。这生成了子群 $\langle 3 \rangle = \{0, 3\}$。
- 有限乘积(在加法群中是和): 我们需要考虑形如 $n \cdot 2 + m \cdot 3 \pmod 6$ 的所有元素。
- $1 \cdot 2 + 0 \cdot 3 = 2$
- $0 \cdot 2 + 1 \cdot 3 = 3$
- $1 \cdot 2 + 1 \cdot 3 = 5$
- $2 \cdot 2 + 1 \cdot 3 = 4 + 3 = 7 \equiv 1 \pmod 6$
- $3 \cdot 2 = 6 \equiv 0 \pmod 6$
- $2 \cdot 3 = 6 \equiv 0 \pmod 6$
- $2 \cdot 2 = 4$
我们已经得到了 $\{0, 1, 2, 3, 4, 5\}$。所以,由 $\{2, 3\}$ 生成的子群是整个 $\mathbb{Z}_6$。
示例2:在对称群 $S_3$ 中由 $\{(1 \ 2), (1 \ 2 \ 3)\}$ 生成的子群
- 群: $S_3 = \{e, (1 \ 2), (1 \ 3), (2 \ 3), (1 \ 2 \ 3), (1 \ 3 \ 2)\}$。这是一个非阿贝尔群。
- 生成元: $a = (1 \ 2)$, $b = (1 \ 2 \ 3)$。
- 幂:
- $a^1 = (1 \ 2)$, $a^2 = e$。所以 $a$ 的幂是 $\{e, (1 \ 2)\}$。
- $b^1 = (1 \ 2 \ 3)$, $b^2 = (1 \ 3 \ 2)$, $b^3 = e$。所以 $b$ 的幂是 $\{e, (1 \ 2 \ 3), (1 \ 3 \ 2)\}$。
- 有限乘积:
- $ab = (1 \ 2)(1 \ 2 \ 3) = (2 \ 3)$
- $ba = (1 \ 2 \ 3)(1 \ 2) = (1 \ 3)$
- $ab^2 = (1 \ 2)(1 \ 3 \ 2) = (1 \ 3)$
- $a^2b = b = (1 \ 2 \ 3)$
我们已经通过 $a, b$ 和它们的乘积得到了 $\{e, (1 \ 2), (1 \ 2 \ 3), (1 \ 3 \ 2), (2 \ 3), (1 \ 3)\}$,这正是 $S_3$ 的所有元素。因此,$\{ (1 \ 2), (1 \ 2 \ 3) \}$ 生成了整个群 $S_3$。这个例子也展示了 $ab \neq ba$,即群的非交换性。
- 混淆加法群和乘法群的表示:在加法群(如 $\mathbb{Z}_n$)中,“幂”实际上是倍数($na$),“乘积”是和($na+mb$)。在乘法群(如 $S_n$)中,就是通常的幂和乘积。
- 忘记非交换性:最常见的错误是假设 $ab=ba$。在处理非阿贝尔群时,必须严格遵守元素的顺序。$a^2 b a^{-1}$ 不等于 $ab$。
- “有限乘积”的误解:这个词指的是乘积链的长度是有限的,比如 $a^2 b a^{-1} b^3$。它不意味着生成的子群本身一定是有限群。例如,在群 $\mathbb{Z}$ 中,由 $\{2, 3\}$ 生成的子群是 $\mathbb{Z}$ 本身,是无限群,但每个元素都可以表示为 $2n+3m$ 的形式,这是一个有限和。
- 只考虑正幂:子群必须包含逆元,所以生成时必须考虑生成元的负整数次幂。
本段将由单个元素生成循环子群的概念,推广到了由任意一个元素集合 $S$ 生成的子群。这个子群 $\langle S \rangle$ 是包含 $S$ 中所有元素的最小子群。它的结构非常具体:它是由 $S$ 中元素的所有整数次幂的所有有限乘积构成的集合。在非交换群中,这些乘积中元素的顺序是至关重要的。
这段内容的目的是建立一个框架,用于理解和描述那些非循环群的结构。许多重要的群(如 $S_3$, $D_4$)都无法由单个元素生成,但可以通过一小组“基本构件”(即生成元)来构建。理解了生成元,我们就能以一种非常紧凑和强大的方式来描述整个(可能是非常复杂的)群的结构。这为后续引入凯莱图等可视化工具和群的表示论打下了基础。
想象你有一套乐高积木,每个生成元(如 $a, b$)是一种特定形状的积木。
- $a^n$ 或 $b^m$ 就像是将同一类型的积木堆叠起来(正幂)或拆掉(负幂)。
- 由 $\{a,b\}$ 生成的子群,就是用你手上的这几种积木(以及它们的反面,代表逆元)能拼出来的所有可能的结构。
- 如果群是阿贝尔群,那就像积木可以随意交换位置拼接。如果是非阿贝尔群,那就像积木有特定的卡扣,只能按特定顺序拼接,$a$ 后面接 $b$ 和 $b$ 后面接 $a$ 会得到完全不同的形状。
- 这个子群就是你能用这套积木创造出的“世界”的全部。如果这个世界就是整个群,那么这套积木就“生成”了整个群。
想象你在一个巨大的网格城市里。你站在原点 $(0,0)$。你有几种固定的移动方式,比如“向东走一步”(操作 $a$),“向北走一步”(操作 $b$)。
- 由 $\{a\}$ 生成的子群,就是你只使用“向东走”和“向西走”($a^{-1}$)这两种操作能到达的所有点,也就是整条x轴。
- 由 $\{a,b\}$ 生成的子群,就是你使用“向东/西走”和“北/南走”这几种操作,进行任意组合,能到达的所有点的集合。在这个简单的例子里,你能到达网格上的任何一个整点 $(n,m)$,这个点对应群元素 $a^n b^m$ (因为这里的操作是可交换的)。
- 如果城市(群)的规则更复杂,比如“向东走”之后“向北走” ($ab$) 和“向北走”之后“向东走” ($ba$) 会把你带到不同的地方(非阿贝尔群),那么你能到达的点的集合就是所有可能路径的终点集合。这个集合就是由 $\{a,b\}$ 生成的子群。
12. 例子
1.2.1. 例子 7.1
📜 [原文2]
例 5.9 中的克莱因四元群 $V=\{e, a, b, c\}$ 由 $\{a, b\}$ 生成,因为 $a b=c$。它也由 $\{a, c\}$、$\{b, c\}$ 和 $\{a, b, c\}$ 生成。如果一个群 $G$ 由子集 $S$ 生成,那么 $G$ 的每个包含 $S$ 的子集都生成 $G$。
这个例子应用了上一节定义的“生成”概念,具体分析了克莱因四元群 $V$。
- 回顾克莱因四元群 V:
- $V$ 有四个元素: $e$ (单位元), $a, b, c$。
- 它的运算规则是:任何非单位元元素与自身相乘都等于单位元 ($a^2=e, b^2=e, c^2=e$)。
- 任意两个不同的非单位元元素相乘等于第三个非单位元元素 ($ab=c, ba=c, ac=b, ca=b, bc=a, cb=a$)。
- 这是一个阿贝尔群(交换群),因为 $ab=c$ 且 $ba=c$。
- 分析生成集 $\{a, b\}$:
- 我们想知道由 $\{a, b\}$ 生成的子群是什么。根据定义,这个子群必须包含 $a$ 和 $b$。
- 它必须包含 $a$ 和 $b$ 的所有幂。$a^0=e, a^1=a, a^2=e, ...$ ;$b^0=e, b^1=b, b^2=e, ...$。所以,这个子群至少有 $\{e, a, b\}$。
- 它必须包含 $a$ 和 $b$ 的幂的有限乘积。我们来计算 $ab$。根据 $V$ 的规则,$ab=c$。
- 所以,由 $\{a, b\}$ 生成的子群包含 $\{e, a, b, c\}$,这正是整个群 $V$。
- 因此,我们说 $\{a, b\}$ 生成 $V$。
- 分析其他生成集:
- $\{a, c\}$: 同样地,这个集合生成的子群必须包含 $a, c, e$。由于 $ac=b$,所以这个子群也必须包含 $b$。因此,它包含了 $\{e, a, c, b\}$,即整个群 $V$。所以 $\{a, c\}$ 也生成 $V$。
- $\{b, c\}$: 同理,这个集合生成的子群必须包含 $b, c, e$。由于 $bc=a$,所以子群也必须包含 $a$。因此,它包含了 $\{e, b, c, a\}$,即整个群 $V$。所以 $\{b, c\}$ 也生成 $V$。
- $\{a, b, c\}$: 这个集合生成的子群自然包含了 $e, a, b, c$,这已经是整个群 $V$ 了。所以 $\{a, b, c\}$ 也生成 $V$。
- 一个普遍规律:
- 最后一句是点睛之笔:“如果一个群 $G$ 由子集 $S$ 生成,那么 $G$ 的每个包含 $S$ 的子集都生成 $G$。”
- 这句话该如何理解?假设 $S$ 生成 $G$,这意味着通过 $S$ 中元素的运算可以得到 $G$ 中的所有元素。现在我们有一个更大的集合 $S'$,它包含了 $S$ 的所有元素($S \subseteq S'$)。既然我们用 $S$ 就能生成整个 $G$,那么当我们拥有了更多的“积木” $S'$($S'$ 至少拥有 $S$ 的所有积木)时,我们当然也能生成整个 $G$。多出来的元素($S'$ 中有但 $S$ 中没有的)可能不是必需的,但它们不会妨碍我们生成整个群。
- 在上面的例子中,因为 $\{a, b\}$ 生成 $V$,而 $\{a, b\} \subseteq \{a, b, c\}$,所以 $\{a, b, c\}$ 也必然生成 $V$。
这个例子本身就是一个非常具体的数值示例。我们可以再用一个不同的群来类比最后那个普遍规律。
- 群: $\mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}$。
- 生成集 $S$: 我们知道 $\{1\}$ 是 $\mathbb{Z}_6$ 的一个生成集,因为通过 $1$ 的倍数可以得到所有元素:$1, 1+1=2, 1+1+1=3, \dots$。所以 $S=\{1\}$ 生成 $\mathbb{Z}_6$。
- 另一个包含 $S$ 的子集 $S'$: 让我们取 $S' = \{1, 2, 3\}$。显然 $S \subseteq S'$。
- 结论: 根据这个规律,$S'=\{1, 2, 3\}$ 也必须生成 $\mathbb{Z}_6$。我们可以验证一下:由 $\{1, 2, 3\}$ 生成的子群,既然它包含了 $1$,那么它必然包含了由 $1$ 生成的整个子群,也就是 $\mathbb{Z}_6$ 本身。所以它确实生成了 $\mathbb{Z}_6$。多出来的 $2$ 和 $3$ 是“冗余”的生成元。
- 最小生成集: 一个群可以有很多个生成集,但我们通常对最小生成集(包含元素数量最少的生成集)最感兴趣。例如,对于 $V$,$\{a, b\}$ 是一个最小生成集,而 $\{a, b, c\}$ 不是。一个群可以有多个大小相同的最小生成集,例如 $\{a,b\}, \{a,c\}, \{b,c\}$ 都是 $V$ 的最小生成集。
- 并非所有子集都是生成集: 不要误以为 $V$ 的任何两个元素的子集都能生成 $V$。例如,子集 $\{e, a\}$ 生成的子群是 $\{e, a\}$ 本身,因为它在运算下是封闭的 ($a^2=e, ae=a, ea=a, e^2=e$)。这个子群并不是整个 $V$。
这个例子通过克莱因四元群 $V$ concretely 展示了“生成集”的概念。它说明了一个群可以有多个不同的生成集,并且点出了一个重要的推论:任何一个生成集的超集(包含该生成集的更大集合)也必然是这个群的生成集。
该例子的目的是为了让读者对上一节抽象的定义有一个具体的感受。通过一个简单、熟悉的群(克莱因四元群),读者可以亲手验证一个集合是如何通过群运算“扩展”到整个群的,从而加深对“生成”这一核心概念的理解。
想象一个房间里有四盏灯 $E, A, B, C$ 和几个开关。开关 $s_a$ 控制灯 $A$,开关 $s_b$ 控制灯 $B$。
- 克莱因四元群的规则是:按任意开关两次等于什么都没发生。同时按两个不同的开关,效果等于按第三个开关。例如,同时按 $s_a$ 和 $s_b$ (操作 $ab$),效果等同于只按 $s_c$ (结果 $c$)。
- 生成集 $\{a, b\}$: 意味着你只被允许使用开关 $s_a$ 和 $s_b$。
- 能实现的状态: 你可以只按 $s_a$ (得到状态 $a$),只按 $s_b$ (得到状态 $b$),什么都不按 (状态 $e$),或者同时按 $s_a$ 和 $s_b$ (得到状态 $c$)。你用这两个开关可以实现所有四种可能的状态。所以 $\{a, b\}$ 生成了整个状态空间 $V$。
- 生成集 $\{a, b, c\}$: 现在你被允许使用 $s_a, s_b, s_c$ 三个开关。你当然也能实现所有状态了,只是 $s_c$ 这个开关是多余的,因为它的效果总能通过组合 $s_a$ 和 $s_b$ 来实现。
在一个正方形的四个顶点上标记 $e, a, b, c$。想象你在 $e$ 点。
- 操作 $a$ 让你水平移动到 $a$ 点。再操作一次 $a$ 就回到了 $e$。
- 操作 $b$ 让你垂直移动到 $b$ 点。再操作一次 $b$ 就回到了 $e$。
- 由 $\{a,b\}$ 生成的子群,就是你能通过水平和垂直移动到达的所有顶点。
- 从 $e$ 水平移动到 $a$,再从 $a$ 垂直移动,你会到达对角顶点 $c$ (这对应 $ab=c$)。
- 这样,只用水平移动 ($a$) 和垂直移动 ($b$) 这两种基本操作,你就可以到达所有四个顶点 $\{e, a, b, c\}$。因此,这两种操作(生成元)生成了整个顶点集合(群)。
1.2.2. 例子 7.2
📜 [原文3]
群 $\mathbb{Z}_{6}$ 由 $\{1\}$ 和 $\{5\}$ 生成。它也由 $\{2,3\}$ 生成,因为 $2+3=5$,所以任何包含 2 和 3 的子群都必须包含 5,因此必须是 $\mathbb{Z}_{6}$。它也由 $\{3,4\}$、$\{2,3,4\}$、$\{1,3\}$ 和 $\{3,5\}$ 生成,但它不是由 $\{2,4\}$ 生成的,因为 $\langle 2\rangle=\{0,2,4\}$ 包含 2 和 4。
这个例子继续探讨生成集的概念,但这次用的是我们更熟悉的循环群 $\mathbb{Z}_6$。它展示了即使是对于一个本身是循环的群,也可以有非单个元素构成的生成集,并辨析了哪些集合能生成,哪些不能。
- 群 $\mathbb{Z}_6$:
- 元素: $\{0, 1, 2, 3, 4, 5\}$。
- 运算: 模6加法。
- 这是一个循环群,因为它可以由单个元素生成。
- 生成集 $\{1\}$ 和 $\{5\}$:
- $\langle 1 \rangle = \{1, 1+1=2, 3, 4, 5, 0\} = \mathbb{Z}_6$。所以 $\{1\}$ 是一个生成集。
- $\langle 5 \rangle = \{5, 5+5=10\equiv 4, 4+5=9\equiv 3, 3+5=8\equiv 2, 2+5=7\equiv 1, 1+5=6\equiv 0\} = \mathbb{Z}_6$。所以 $\{5\}$ 也是一个生成集。
- 这符合我们对 $\mathbb{Z}_n$ 的认识:当 $k$ 与 $n$ 互质时,$\langle k \rangle = \mathbb{Z}_n$。这里 $1$ 和 $5$ 都与 $6$ 互质。
- 生成集 $\{2,3\}$:
- 作者给出了一个精妙的论证。我们想知道由 $\{2, 3\}$ 生成的子群 $H$ 是什么。
- 根据定义,$H$ 必须包含 $2$ 和 $3$。
- 由于子群对加法运算封闭,所以 $H$ 必须包含 $2+3=5$。
- 现在我们知道 $H$ 包含了元素 $5$。
- 但是,我们从第二步已经知道,任何包含 $5$ 的子群,必然包含由 $5$ 生成的整个子群 $\langle 5 \rangle$。
- 而 $\langle 5 \rangle$ 就是 $\mathbb{Z}_6$ 本身!
- 所以,由 $\{2, 3\}$ 生成的子群 $H$ 必须包含 $\mathbb{Z}_6$。又因为 $H$ 是 $\mathbb{Z}_6$ 的子群,所以 $H$ 只能等于 $\mathbb{Z}_6$。
- 结论:$\{2, 3\}$ 生成 $\mathbb{Z}_6$。
- 其他生成集:
- $\{3,4\}$: 类似的逻辑。$3+4=7 \equiv 1 \pmod 6$。任何包含 $\{3,4\}$ 的子群都必须包含 $1$。而包含 $1$ 的子群必须是 $\mathbb{Z}_6$ 本身。所以 $\{3,4\}$ 生成 $\mathbb{Z}_6$。
- $\{2,3,4\}$: 因为 $\{2,3\}$ 已经能生成 $\mathbb{Z}_6$ 了,根据上一个例子中的规律,它的超集 $\{2,3,4\}$ 也必然生成 $\mathbb{Z}_6$。
- $\{1,3\}$: 因为 $\{1\}$ 已经能生成 $\mathbb{Z}_6$ 了,它的超集 $\{1,3\}$ 也必然生成 $\mathbb{Z}_6$。
- $\{3,5\}$: 因为 $\{5\}$ 已经能生成 $\mathbb{Z}_6$ 了,它的超集 $\{3,5\}$ 也必然生成 $\mathbb{Z}_6$。
- 一个不能生成的例子: $\{2,4\}$:
- 我们来考察由 $\{2, 4\}$ 生成的子群 $H$。
- 这个子群包含 $2$ 和 $4$。
- 它也包含它们的“幂”(倍数)和“积”(和)。
- $2+2=4$ (已在集合中)
- $4+4=8 \equiv 2$ (已在集合中)
- $2+4=6 \equiv 0$
- $2+2+2=0$
- $4+4+4=12 \equiv 0$
- 我们发现,无论怎么组合 $2$ 和 $4$ 的和,我们得到的元素都只有 $\{0, 2, 4\}$。这是因为 $2$ 和 $4$ 都是偶数,偶数相加永远是偶数,不可能得到奇数 $1, 3, 5$。
- 作者给出了一个更简洁的解释:由 $\{2, 4\}$ 生成的子群,必须包含 $\langle 2 \rangle = \{0, 2, 4\}$。同时,它也必须包含 $\langle 4 \rangle = \{0, 4, 2\}$。由于元素 $4$ 本身就在 $\langle 2 \rangle$ 里,所以由 $\{2, 4\}$ 生成的子群其实就等于由 $\{2\}$ 生成的子群,即 $\langle 2 \rangle = \{0, 2, 4\}$。
- 因为这个子群不等于 $\mathbb{Z}_6$,所以 $\{2, 4\}$ 不生成 $\mathbb{Z}_6$。
这个例子本身就是关于 $\mathbb{Z}_6$ 的具体数值示例。我们再用 $\mathbb{Z}_{10}$ 来练习一下。
- 群: $\mathbb{Z}_{10} = \{0, 1, ..., 9\}$。
- 判断 $\{2, 5\}$ 是否生成 $\mathbb{Z}_{10}$:
- 由 $\{2, 5\}$ 生成的子群 $H$ 包含 $2$ 和 $5$。
- $H$ 必须包含 $\langle 2 \rangle = \{0, 2, 4, 6, 8\}$ 和 $\langle 5 \rangle = \{0, 5\}$。
- $H$ 也必须包含它们的和,例如 $2+5=7$。
- 现在 $H$ 包含 $7$ 了。而 $7$ 与 $10$ 互质,所以 $\langle 7 \rangle = \mathbb{Z}_{10}$。
- 因此, $H$ 必须包含 $\mathbb{Z}_{10}$,所以 $\{2, 5\}$ 生成 $\mathbb{Z}_{10}$。
- 判断 $\{4, 6\}$ 是否生成 $\mathbb{Z}_{10}$:
- 由 $\{4, 6\}$ 生成的子群 $H$ 包含 $4$ 和 $6$。
- $4+6=10 \equiv 0$。
- $4+4=8$。
- $6+6=12 \equiv 2$。
- 现在 $H$ 包含 $2$ 了!我们知道 $\langle 2 \rangle = \{0, 2, 4, 6, 8\}$。
- 我们来检查一下,由 $\{4, 6\}$ 能不能生成奇数。$4n+6m = 2(2n+3m)$,结果永远是偶数。所以我们永远无法得到 $1, 3, 5, 7, 9$。
- 因此 $\{4, 6\}$ 不生成 $\mathbb{Z}_{10}$。它生成的子群是 $\{0, 2, 4, 6, 8\}$。
- 最大公约数(GCD)的运用: 在 $\mathbb{Z}_n$ 中,由集合 $\{k_1, k_2, \dots, k_m\}$ 生成的子群,实际上就是由 $\text{gcd}(k_1, k_2, \dots, k_m)$ 这个单一元素生成的循环子群。
- 对于 $\mathbb{Z}_6$ 和 $\{2, 3\}$: $\text{gcd}(2, 3) = 1$。所以由 $\{2, 3\}$ 生成的子群等于 $\langle 1 \rangle = \mathbb{Z}_6$。
- 对于 $\mathbb{Z}_6$ 和 $\{2, 4\}$: $\text{gcd}(2, 4) = 2$。所以由 $\{2, 4\}$ 生成的子群等于 $\langle 2 \rangle = \{0, 2, 4\}$。
- 对于 $\mathbb{Z}_{10}$ 和 $\{4, 6\}$: $\text{gcd}(4, 6) = 2$。所以由 $\{4, 6\}$ 生成的子群等于 $\langle 2 \rangle = \{0, 2, 4, 6, 8\}$。
- 这个技巧非常强大,但只适用于 $\mathbb{Z}_n$ 这种加法循环群。对于非交换群或非循环群不适用。
- 误认为只有互质数才能作为生成元: 单个元素要生成 $\mathbb{Z}_n$ 必须与 $n$ 互质,但多个元素的集合作为生成集,它们本身不一定需要是互质数,如 $\{2,3\}$ 生成 $\mathbb{Z}_6$。关键是它们的线性组合能凑出与 $n$ 互质的数。
本例深入探讨了 $\mathbb{Z}_6$ 的各种生成集。它不仅展示了多元素生成集的存在,还通过一个反例($\{2,4\}$)和一个巧妙的论证方法(先生成一个已知的生成元,如5或1),清晰地阐述了如何判断一个集合是否能生成整个群。这为我们提供了处理此类问题的具体策略。
这个例子的目的是为了深化对生成集概念的理解,特别是在一个非常规整和熟悉的群($\mathbb{Z}_6$)中。它表明,即便是像 $\mathbb{Z}_6$ 这样的“简单”群,其生成结构也可能比第一眼看上去要丰富。同时,它也引入了一种重要的论证技巧:要证明集合 $S$ 生成群 $G$,只需证明利用 $S$ 中的元素可以构造出另一个已知的生成集 $S'$ 的所有元素即可。
想象你有一堆只有2元和3元面值的邮票,你要寄一封邮费是任意整数(模6)的信。
- 生成集 $\{2,3\}$: 你有2元和3元邮票。
- 想凑出5元?贴一张2元和一张3元。
- 想凑出1元?贴两张2元和一张3元($2+2-3=1$),或者在模6下,贴两张2元和一张3元是$4+3=7\equiv1$。不对,应该是$3+3-2-2=2$。更好的方法是 $2+2+2+3 = 9 \equiv 3$。应该是 $3-2=1$ 或者 $2+2+2-3=3$。还是用 $2+3=5$ 最简单。有了5,就能凑出 $5\times 5 = 25 \equiv 1$。既然能凑出1元的邮资,那你就能凑出任何整数邮资($1, 2, 3, 4, 5, 0$)。所以 $\{2,3\}$ 是一个有效的“生成”邮票组合。
- 非生成集 $\{2,4\}$: 你只有2元和4元邮票。你无论怎么贴,凑出来的总邮资永远是偶数。你永远也凑不出1元、3元、5元的邮资。所以 $\{2,4\}$ 不能生成所有可能的邮资。
想象一个圆形的钟表,上面有6个点,分别标着0, 1, 2, 3, 4, 5。
- 生成集 $\{2,3\}$: 你站在0点。你有两种移动方式:“顺时针跳2格”和“顺时针跳3格”。
- 跳2格,到达2。
- 跳3格,到达3。
- 从0开始,先跳2格再跳3格,到达5。
- 从0开始,跳3格再跳3格,到达0。再逆时针跳2格(相当于+4),到达4。
- 从5开始,再跳2格,到达 $5+2=7\equiv 1$。
- 既然你能到达1,你就能从1开始不停地“跳1格”,从而踏遍所有的点。
- 所以,“跳2格”和“跳3格”这两个基本动作组合起来,可以让你访问到钟表上的任何一个点。
- 非生成集 $\{2,4\}$: 你只有“跳2格”和“跳4格”两种方式。
- 从0出发,你只能跳到2, 4, 0, 2, 4... 这些点。你被困在了 $\{0, 2, 4\}$ 这个小圈子里,永远无法到达 $1, 3, 5$。
13. 集合论的视角
📜 [原文4]
我们已经对由 $G$ 的子集生成的子群给出了一个直观的解释。接下来将详细阐述相同的思想,但采用另一种方法,即通过子群的交集。当我们对一个概念有了直观的理解后,最好尽可能清晰地将其表述出来。我们给出一个集合论的定义,并推广了第 5 节习题 54 中的一个定理。
这段话是一个过渡,它告诉读者即将要做什么,以及为什么这么做。
- 回顾与承接: 作者首先总结了前面的内容——“我们已经对由 $G$ 的子集生成的子群给出了一个直观的解释”。这个“直观的解释”就是我们刚刚讨论过的“由生成元的幂的有限乘积构成的集合”。这个解释是构造性的,它告诉我们这个子群里的元素长什么样,如何“搭建”出来。
- 引入新方法: 接着,作者预告了即将介绍一种不同的、但等价的方法来定义同一个概念。这个新方法是“通过子群的交集”。这种方法更加抽象和形式化。
- 动机: 为什么要引入一个新方法来描述同一个东西?作者解释说:“当我们对一个概念有了直观的理解后,最好尽可能清晰地将其表述出来。”
- 直观的理解(如乐高积木模型)有助于我们思考和感受,但它可能不够严谨,不方便进行严格的数学证明。
- 一个清晰、严谨的定义(通常是基于集合论的)是数学的基石。它为我们提供了一个坚固的逻辑起点。
- 这体现了数学发展的一个常见模式:先有直觉和猜想,然后通过形式化的定义和证明来使其变得精确和可靠。
- 路线图: 作者明确了接下来的步骤:
- 首先,给出一个关于集合交集的通用定义(定义 7.3)。
- 然后,证明一个关键的定理:任意多个子群的交集仍然是一个子群(定理 7.4)。这个定理是新定义方法能够成立的保证。
本段是连接前文和后文的桥梁。它明确指出,我们将从一个构造性、直观的视角(元素的乘积)转向一个描述性、集合论的视角(子群的交集)来定义“由子集生成的子群”。这种视角的转换是为了追求数学上的严谨性和清晰性。
本段的存在是为了管理读者的预期,并解释为什么我们要学习一个看起来更抽象的新定义。它强调了在数学中,拥有多种等价的视角来理解同一个概念是非常有价值的。构造性的视角告诉我们“如何做”,而集合论的视角告诉我们“它是什么”以及它在整个结构中的“位置”。
想象你要向别人描述“你所在城市里所有星巴克的集合”。
- 直观/构造性方法: 你可以列一个清单,说“这个集合包括了市中心那家,火车站那家,大学城那家...”,然后把所有你知道的星巴克都列出来。这就是“元素的乘积”方法,具体地指出了集合里的每一个成员是怎么来的。
- 集合论/描述性方法: 你也可以这样说:“请想象一下所有‘咖啡店连锁品牌’的集合,以及所有‘上市公司’的集合,还有所有‘提供免费Wi-Fi的商家’的集合。我要说的这个集合,就是这三个大集合的交集。” 你没有直接列出成员,而是通过它所满足的一系列属性来界定它。这就是“子群的交集”方法。
这两种方法描述的是同一个东西,但角度完全不同。后者在逻辑上可能更“干净”。
想象地图上有许多不同颜色的区域。
- 红色区域代表所有包含点 $A$ 的区域。
- 蓝色区域代表所有包含点 $B$ 的区域。
- 我们要找同时包含 $A$ 和 $B$ 的最小区域。
- 构造性方法: 从 $A$ 和 $B$ 出发,用某种规则(如群运算)向外扩张,直到无法再扩张为止,这个扩张出的区域就是我们想要的。
- 集合论方法: 找到地图上所有已经存在的、并且同时包含 $A$ 和 $B$ 的区域。然后把所有这些区域重叠起来,那个所有区域都共有的、最核心的重叠部分(交集),就是我们想要的最小区域。
1.3.1. 定义 7.3
📜 [原文5]
7.3 定义 设 $\left\{S_{i} \mid i \in I\right\}$ 是一个集合族。这里 $I$ 可以是任意指标集。集合 $S_{i}$ 的交集 $\cap_{i \in I} S_{i}$ 是所有属于所有集合 $S_{i}$ 的元素的集合;也就是说,
如果 $I$ 是有限集,$I=\{1,2, \ldots, n\}$,我们可以用以下方式表示 $\cap_{i \in I} S_{i}$
这个定义非常基础,它形式化地定义了“任意多个集合的交集”是什么意思。
- 集合族 (Family of sets):
- 术语 $\left\{S_{i} \mid i \in I\right\}$ 表示我们有一堆集合。我们不想一个个地叫它们 $A, B, C, ...$,尤其是当有无穷多个集合时。
- 我们用一个指标集 (index set) $I$ 来给这些集合“贴标签”。$I$ 里面的每个元素 $i$ 都对应着一个集合 $S_i$。
- $I$ 可以是任何集合。如果 $I=\{1, 2, 3\}$,那么我们有三个集合 $S_1, S_2, S_3$。如果 $I=\mathbb{N}=\{1, 2, 3, ...\}$,我们就有一个无穷序列的集合 $S_1, S_2, S_3, ...$。如果 $I$ 是一个更复杂的集合(比如所有实数 $\mathbb{R}$),那我们就有对应于每个实数的集合。
- 交集的定义:
- 符号 $\cap_{i \in I} S_{i}$ 表示对这个集合族中的所有集合取交集。
- 什么样的元素 $x$ 才属于这个大的交集呢?定义说,元素 $x$ 必须同时属于每一个 $S_i$。用逻辑语言说就是 "$x \in S_i$ for all $i \in I$"。
- 换句话说,这个交集是所有这些集合的公共部分。
- 有限情况的表示法:
- 如果指标集 $I$ 是有限的,比如 $I=\{1, 2, \dots, n\}$,那么这个通用的、有点吓人的符号 $\cap_{i=1}^n S_{i}$ 就可以被写成我们更熟悉的形式 $S_1 \cap S_2 \cap \dots \cap S_n$。这两种写法意思完全一样。
- $\cap_{i \in I} S_{i}$: 待定义的符号。读作“集合族 $S_i$(其中 $i$ 取遍 $I$)的交集”。
- $=$: 定义符号,表示左边和右边是同一个东西。
- $\{ \dots \}$: 集合的标准表示法,花括号内描述了这个集合的元素。
- $x$: 一个代表元素的哑变量(dummy variable)。
- $\mid$: 读作“使得”(such that)。它前面的 $x$ 是我们要描述的元素,它后面是 $x$ 必须满足的条件。
- $x \in S_{i} \text{ for all } i \in I$: 这就是那个条件。它规定了只有当一个元素 $x$ 对于指标集 $I$ 中的每一个 $i$,都满足“$x$ 属于集合 $S_i$”这个条件时,这个 $x$ 才能被放入我们正在定义的交集里。
示例1:有限交集
- 指标集 $I = \{1, 2, 3\}$
- 集合族:
- $S_1 = \{1, 2, 3, 4\}$
- $S_2 = \{2, 4, 6, 8\}$
- $S_3 = \{2, 3, 5, 7\}$
- 交集 $S_1 \cap S_2 \cap S_3$: 我们要找一个元素,它必须同时在 $S_1, S_2, S_3$ 中。
- $1$ 在 $S_1$ 中,但不在 $S_2, S_3$ 中。不行。
- $2$ 在 $S_1$ 中,在 $S_2$ 中,也在 $S_3$ 中。可以。
- $3$ 在 $S_1, S_3$ 中,但不在 $S_2$ 中。不行。
- $4$ 在 $S_1, S_2$ 中,但不在 $S_3$ 中。不行。
- 结论: $\cap_{i \in I} S_{i} = \{2\}$。
示例2:无限交集
- 指标集 $I = \mathbb{N} = \{1, 2, 3, \dots\}$ (所有正整数)
- 集合族: 对每个 $n \in \mathbb{N}$,定义集合 $S_n$ 为闭区间 $[0, 1/n]$。
- $S_1 = [0, 1]$
- $S_2 = [0, 1/2]$
- $S_3 = [0, 1/3]$
- ...
- 交集 $\cap_{n \in \mathbb{N}} S_{n}$: 我们要找一个实数 $x$,它必须对所有的正整数 $n$ 都满足 $0 \le x \le 1/n$。
- 考虑一个正数,比如 $x=0.01$。当 $n=1, 2, \dots, 100$ 时,$x$ 都属于 $S_n$。但是当 $n=101$ 时,$S_{101} = [0, 1/101]$,而 $0.01 = 1/100 > 1/101$,所以 $x$ 不在 $S_{101}$ 中。因此任何正数 $x$ 最终都会被某个 $S_n$ 排除掉。
- 考虑一个负数,比如 $x=-0.5$。它不属于任何一个 $S_n$,因为所有 $S_n$ 都从 $0$ 开始。
- 考虑 $x=0$。对于任何正整数 $n$,$1/n > 0$,所以 $0 \le 0 \le 1/n$ 永远成立。因此 $0$ 属于所有的 $S_n$。
- 结论: $\cap_{n \in \mathbb{N}} S_{n} = \{0\}$。
- 交集与并集的混淆: 并集 $\cup_{i \in I} S_i$ 的条件是“只要 $x$ 属于至少一个 $S_i$ 即可”。交集的条件严苛得多,必须属于每一个 $S_i$。
- 空指标集: 如果指标集 $I$ 是空集 $\emptyset$,那么交集 $\cap_{i \in \emptyset} S_i$ 该如何定义?这个问题比较微妙,在不同的上下文中有不同的约定。通常它被定义为“全集”(universe of discourse),因为“对于所有 $i \in \emptyset$,条件 $P(i)$ 都为真”这个命题是空真(vacuously true)的。但在本课程的语境下,我们几乎不会遇到这种情况。
- 空交集: 多个非空集合的交集完全可能是空集。例如 $S_1=\{1,2\}, S_2=\{3,4\}$,则 $S_1 \cap S_2 = \emptyset$。
定义7.3 提供了对“任意多个集合求交集”这一操作的一个普适的、形式化的定义。其核心思想是:交集中的元素必须是所有参与求交集的集合所共有的元素。
这个定义本身是集合论的基础知识,在此处重申是为了给接下来的定理 7.4 和最终关于生成子群的新定义铺平道路。数学的严谨性要求每一个用到的概念都有明确的定义。在引入“所有包含某子集的子群的交集”这一关键概念之前,必须先确保“任意多子群的交集”这个概念本身是清晰无误的。
想象有一个俱乐部联盟,由许多个不同的俱乐部 $S_i$ 组成。
- 每个俱乐部 $S_i$ 都有自己的成员名单。
- 交集 $\cap_{i \in I} S_i$ 指的是那些“终极会员”的名单。一个“终极会员” $x$ 必须是联盟里每一个俱乐部的成员。如果哪怕有一个俱乐部 $S_k$ 的名单上没有 $x$,那么 $x$ 就不是“终极会员”。
想象在透明胶片上画画。
- 你有很多张透明胶片,每张胶片 $S_i$ 上都画了一些有颜色的区域。
- 将所有这些胶片 $S_i$ 精确地叠在一起。
- 交集就是,你从上往下看,所有胶片上都有颜色的那个区域。如果某个位置只有一部分胶片有颜色,那这个位置就不属于交集。只有那些在每一层胶片上都被涂上颜色的点,才构成了最终的交集图案。
1.3.2. 定理 7.4
📜 [原文6]
7.4 定理 群 $G$ 的一些子群 $H_{i}$(其中 $i \in I$)的交集仍然是 $G$ 的一个子群。
证明 让我们证明闭合性。设 $a \in \cap_{i \in I} H_{i}$ 且 $b \in \cap_{i \in I} H_{i}$,所以对所有 $i \in I$,有 $a \in H_{i}$,且对所有 $i \in I$,有 $b \in H_{i}$。那么对所有 $i \in I$,有 $a b \in H_{i}$,因为 $H_{i}$ 是一个群。因此 $a b \in \cap_{i \in I} H_{i}$。
因为对所有 $i \in I$, $H_{i}$ 都是一个子群,所以对所有 $i \in I$,有 $e \in H_{i}$,因此 $e \in \cap_{i \in I} H_{i}$。
最后,对于 $a \in \cap_{i \in I} H_{i}$,对所有 $i \in I$,有 $a \in H_{i}$,所以对所有 $i \in I$,有 $a^{-1} \in H_{i}$,这意味着 $a^{-1} \in \cap_{i \in I} H_{i}$。
这个定理是本节集合论方法的基石。它要证明的是,子群这个美好的性质,在“任意求交集”这个操作下是保持的。
定理陈述:
- 我们有一个群 $G$。
- 我们有一族(可能无限多个)$G$ 的子群,记为 $\{H_i \mid i \in I\}$。
- 结论:将所有这些子群 $H_i$ 求交集,得到的新集合 $H = \cap_{i \in I} H_i$ 仍然是 $G$ 的一个子群。
证明过程:
要证明 $H$ 是 $G$ 的一个子群,我们只需要验证子群的三个条件:闭合性、包含单位元、包含逆元。证明的策略非常直接:利用交集的定义,将问题从 $H$ 转化到每一个 $H_i$ 上去,然后利用 $H_i$ 本身是子群的已知事实。
- 证明闭合性:
- 目标: 证明如果 $a, b \in H$,那么 $ab \in H$。
- 翻译:
- 从 $a \in H = \cap_{i \in I} H_i$ 开始。根据交集的定义,这意味着“对于所有的 $i \in I$,都有 $a \in H_i$”。
- 同样,从 $b \in H$ 开始,我们得到“对于所有的 $i \in I$,都有 $b \in H_i$”。
- 推理:
- 现在,我们任取一个 $i \in I$。我们已经知道 $a \in H_i$ 并且 $b \in H_i$。
- 因为 $H_i$ 它自己是一个子群,所以它必须满足闭合性。因此,$ab$ 的乘积必然也在 $H_i$ 中。
- 这一步的推理对于我们选择的任何一个 $i \in I$ 都成立。
- 结论:
- 我们已经证明了:“对于所有的 $i \in I$,都有 $ab \in H_i$”。
- 这恰好就是元素 $ab$ 属于交集 $H = \cap_{i \in I} H_i$ 的定义!
- 所以,我们成功证明了 $ab \in H$。闭合性得证。
- 证明包含单位元:
- 目标: 证明 $e \in H$。
- 推理:
- 我们知道,对于任何一个 $i \in I$,$H_i$ 都是一个子群。
- 根据子群的定义,任何子群都必须包含单位元 $e$。
- 所以,“对于所有的 $i \in I$,都有 $e \in H_i$”。
- 结论:
- 这正是 $e$ 属于交集 $H = \cap_{i \in I} H_i$ 的定义。
- 所以,$e \in H$。单位元条件得证。
- 证明包含逆元:
- 目标: 证明如果 $a \in H$,那么 $a^{-1} \in H$。
- 翻译:
- 从 $a \in H$ 开始,我们知道“对于所有的 $i \in I$,都有 $a \in H_i$”。
- 推理:
- 任取一个 $i \in I$。我们知道 $a \in H_i$。
- 因为 $H_i$ 它自己是一个子群,所以它必须包含其元素的逆元。因此,$a^{-1}$ 必然也在 $H_i$ 中。
- 这个推理对任意 $i \in I$ 都成立。
- 结论:
- 我们已经证明了:“对于所有的 $i \in I$,都有 $a^{-1} \in H_i$”。
- 这正是 $a^{-1}$ 属于交集 $H = \cap_{i \in I} H_i$ 的定义。
- 所以,$a^{-1} \in H$。逆元条件得证。
总的结论: 因为 $H$ 满足了子群的所有三个条件,所以 $H$ 本身是 $G$ 的一个子群。
示例1: 在 $\mathbb{Z}_{12}$ 中
- 群: $G = \mathbb{Z}_{12}$
- 子群:
- $H_1 = \langle 2 \rangle = \{0, 2, 4, 6, 8, 10\}$
- $H_2 = \langle 3 \rangle = \{0, 3, 6, 9\}$
- 交集: $H = H_1 \cap H_2$。我们要找同时在 $H_1$ 和 $H_2$ 中的元素。
- 公共元素是 $\{0, 6\}$。所以 $H = \{0, 6\}$。
- 验证: $H=\{0, 6\}$ 是不是 $\mathbb{Z}_{12}$ 的子群?
- 闭合性: $0+0=0, 0+6=6, 6+6=12\equiv 0$。所有结果都在 $H$ 中。满足。
- 单位元: $0 \in H$。满足。
- 逆元: $0$ 的逆是 $0$。$6$ 的逆是 $12-6=6$。每个元素的逆元都在 $H$ 中。满足。
- 结论:$H=\{0, 6\}$ 确实是 $\mathbb{Z}_{12}$ 的一个子群。它其实就是 $\langle 6 \rangle$。注意到 $6 = \text{lcm}(2,3)$ (最小公倍数)。在 $\mathbb{Z}_n$ 中,$\langle a \rangle \cap \langle b \rangle = \langle \text{lcm}(a,b) \rangle$。
示例2: 在 $S_3$ 中
- 群: $G = S_3 = \{e, (12), (13), (23), (123), (132)\}$
- 子群:
- $H_1 = \langle (12) \rangle = \{e, (12)\}$
- $H_2 = \langle (13) \rangle = \{e, (13)\}$
- $H_3 = \langle (23) \rangle = \{e, (23)\}$
- 交集: $H = H_1 \cap H_2 \cap H_3$。我们要找同时在 $H_1, H_2, H_3$ 中的元素。
- 唯一的公共元素是 $e$。
- 所以 $H = \{e\}$。
- 验证: $\{e\}$ 是平凡子群,它当然是 $S_3$ 的一个子群。
- 并集不是子群: 这个定理对交集成立,但对并集通常不成立!
- 以上面 $\mathbb{Z}_{12}$ 的例子,$H_1 \cup H_2 = \{0, 2, 3, 4, 6, 8, 9, 10\}$。
- 这个并集不是子群,因为它不满足闭合性。例如,$2 \in H_1 \cup H_2$,$3 \in H_1 \cup H_2$,但是 $2+3=5$,而 $5 \notin H_1 \cup H_2$。
- 两个子群的并集是子群,当且仅当其中一个子群包含另一个。
- 定理的普适性: 这个定理的强大之处在于它对任意多(甚至不可数无穷多)个子群的交集都成立。证明过程完全不依赖于指标集 $I$ 的大小。
定理7.4 建立了一个至关重要的事实:子群的交集仍然是子群。这个性质保证了我们可以通过“求交集”这个操作,从已有的子群构造出新的、通常是更小的子群,而不用担心结果会“跑出”子群的范畴。证明的核心逻辑是将交集所需要满足的条件,通过定义“翻译”到每个单独的子群上,从而利用它们已知的性质来完成证明。
这个定理是构建“由集合论定义的生成子群”的最后一块积木。下一个定义将会是:“由集合 $A$ 生成的子群,是所有包含 $A$ 的子群的交集”。如果没有定理 7.4,我们就无法保证这个交集本身是一个合法的子群。有了这个定理,这个定义才变得有意义和稳固。
想象“子群”是一种“完美结构”的俱乐部。完美结构意味着:
- 俱乐部成员之间的互动(群运算)产生的结果还是俱乐部成员(闭合性)。
- 俱乐部有一个“不产生任何影响”的核心人物(单位元)。
- 每个成员都有一个能“撤销其操作”的伙伴(逆元)。
现在你有很多个这样的“完美俱乐部” $H_i$。
定理7.4说的是,如果你找出那些同时属于所有这些完美俱乐部的人,把他们组成一个新俱乐部 $H = \cap H_i$,那么这个新俱乐部 $H$ 也必然是一个“完美结构”的俱乐部。
为什么?因为如果你从 $H$ 里挑两个人 $a,b$,既然他们是所有俱乐部的成员,那么他们在任何一个俱乐部 $H_i$ 里的互动结果 $ab$ 也都在那个俱乐部 $H_i$ 里。既然 $ab$ 在所有的 $H_i$ 里,那它自然就在 $H$ 里了。单位元和逆元的道理一样。
想象有一些用特殊墨水(比如遇光不变色)画出的图案 $H_i$,它们都画在同一张大白纸 $G$ 上。每个 $H_i$ 本身都是一个“稳定”的图案(子群)。
现在你拿一张紫外光灯照射整张白纸。只有那些被所有墨水都画过的地方(交集),才会因为叠加效应而发出不同的光。
定理7.4说的就是,这个发光的区域 $H = \cap H_i$,其本身也一定是一个“稳定”的图案。它不会因为内部的相互作用而褪色或变形。
14. 生成子群的集合论定义
📜 [原文7]
设 $G$ 是一个群,且对 $i \in I$,有 $a_{i} \in G$。至少有一个 $G$ 的子群包含所有元素 $a_{i}$(对 $i \in I$),即 $G$ 本身。定理 7.4 向我们保证,如果我们取所有包含 $G$ 中所有 $a_{i}$(对 $i \in I$)的子群的交集,我们将得到 $G$ 的一个子群 $H$。这个子群 $H$ 是 $G$ 中包含所有 $a_{i}$(对 $i \in I$)的最小子群。
这段话将前面的准备工作(交集定义和交集定理)串联起来,给出了生成子群的第二个、更形式化的定义。
- 设定场景:
- 我们有一个群 $G$。
- 我们有一个元素集合 $A = \{a_i \mid i \in I\}$,这些元素都来自 $G$。我们的目标是定义由集合 $A$ 生成的子群。
- 存在性保证:
- 我们关心的是“包含 $A$ 中所有元素的 $G$ 的子群”。这样的子群存在吗?
- 作者指出,至少存在一个这样的子群,那就是群 $G$ 本身。$G$ 当然是自己的一个子群,并且它包含了 $A$ 的所有元素(因为 $A$ 的元素本来就是从 $G$ 里取的)。
- 这一点很重要,因为它保证了我们接下来要讨论的“所有包含 $A$ 的子群”这个集合族不是空的。
- 构造最小子群:
- 现在,我们考虑一个特殊的集合族。这个族里的成员不是别的,正是“所有包含 $A$ 的 $G$ 的子群”。我们把这个集合族记为 $\mathcal{F} = \{H \mid H \text{ is a subgroup of } G \text{ and } A \subseteq H\}$。
- 根据上一步,我们知道 $\mathcal{F}$ 至少包含 $G$ 本身,所以它非空。
- 现在,我们对 $\mathcal{F}$ 中的所有子群取交集,令这个交集为 $H_{gen} = \bigcap_{H \in \mathcal{F}} H$。
- 定理 7.4 的作用: 定理 7.4 告诉我们,这个交集 $H_{gen}$ 本身也是一个子群。这是关键的一步!
- 证明最小性:
- 为什么这个通过交集得到的子群 $H_{gen}$ 是最小的包含 $A$ 的子群呢?
- 首先, $H_{gen}$ 是否包含 $A$?
- 是的。让我们取 $A$ 中的任意一个元素 $a_k$。根据我们对集合族 $\mathcal{F}$ 的定义,$\mathcal{F}$ 里的每一个子群 $H$ 都包含 $A$,所以每一个 $H$ 都包含 $a_k$。
- 既然 $a_k$ 属于 $\mathcal{F}$ 中的每一个子群,那么根据交集的定义,$a_k$ 必然属于它们的交集 $H_{gen}$。
- 由于 $a_k$ 是任意选的,所以 $A \subseteq H_{gen}$。
- 其次, $H_{gen}$ 是否是最小的?
- “最小”意味着,任何其他包含 $A$ 的子群,都必然会包含 $H_{gen}$。
- 让我们取任意一个包含 $A$ 的子群,叫它 $K$。
- 根据我们对集合族 $\mathcal{F}$ 的定义,$K$ 本身就是 $\mathcal{F}$ 的一个成员(因为 $K$ 满足“是子群”和“包含 $A$”这两个条件)。
- 而 $H_{gen}$ 是 $\mathcal{F}$ 中所有成员的交集。
- 一个交集必然是它任何一个成员的子集。所以, $H_{gen} = (\dots \cap K \cap \dots) \subseteq K$。
- 这就证明了,任何包含 $A$ 的子群 $K$ 都必须包含 $H_{gen}$。这正是“最小”的定义。
这段话阐述了生成子群的集合论定义方法:
- 找出所有包含给定元素集 $A$ 的子群。
- 将这些子群全部取交集。
- 这个交集本身是一个子群(由定理7.4保证),并且是所有包含 $A$ 的子群中最小的一个。
这个最小的子群,就是由 $A$ 生成的子群。
本段的目的是提供一个与之前“元素乘积”等价的、但更形式化和抽象的定义。这个定义在理论推导中非常有用,因为它不依赖于元素的具体构造方式,而是通过一个普适的“最小性”属性来刻画对象。这在数学中是一种非常常见且强大的思想。
假设你想给你的朋友小明(元素 $a$)建一个“粉丝俱乐部”(包含 $a$ 的子群)。
- 世界上有很多现成的俱乐部($G$ 的子群),比如“摇滚乐迷俱乐部”、“足球迷俱乐部”、“科幻迷俱乐部”等等。
- 有些俱乐部已经包含了小明(可能小明本身就是个摇滚迷)。我们把所有这些已经接纳了小明的俱乐部找出来,形成一个列表 $\mathcal{F}$。
- 新定义的方法: 我们查看所有这些俱乐部的会员名单,找出那些同时在所有这些俱乐部名单上的人,组成一个新的俱乐部 $H_{gen}$。
- 这个新俱乐部 $H_{gen}$ 必然包含小明(因为他本来就在所有这些俱乐部里)。
- 同时,这个俱乐部是“最核心”的。任何一个自称是“小明粉丝俱乐部”的组织,其成员范围至少要覆盖这个核心俱乐部 $H_{gen}$ 的所有成员。因此,$H_{gen}$ 是包含小明的最小俱乐部。
想象在地图上有一个宝藏地点集合 $A$。你想用一个栅栏围出一个区域,这个区域必须:1) 是一个“形状规则”的区域(子群);2) 把所有宝藏地点 $A$ 都围在里面。
- 你发现已经有很多现成的“规则”栅栏区域了($H_i$),它们都满足条件2,即都把宝藏围起来了。有的很大(比如整个地图 $G$),有的小一些。
- 新定义的方法: 你把所有这些栅栏的地图都叠在一起。它们共同覆盖的那个最小的核心区域(交集),就是你想要的答案。
- 这个交集区域本身也是“形状规则”的(定理7.4)。
- 它肯定包含了所有宝藏(因为每个栅栏都包含所有宝藏)。
- 它是最小的,因为任何其他声称围住了所有宝藏的“规则”栅栏,其范围都必须至少覆盖这个核心区域。
1.4.1. 定义 7.5
📜 [原文8]
7.5 定义 设 $G$ 是一个群,且对 $i \in I$,有 $a_{i} \in G$。包含 $\left\{a_{i} \mid i \in I\right\}$ 的最小子群是由 $\left\{a_{i} \mid i \in I\right\}$ 生成的子群。如果这个子群是 $G$ 的全部,那么 $\left\{a_{i} \mid i \in I\right\}$ 生成 $G$,且 $a_{i}$ 是 $G$ 的生成元。如果存在一个有限集 $\left\{a_{i} \mid i \in I\right\}$ 生成 $G$,那么 $G$ 是有限生成的。
这个定义是对上一段逻辑的正式命名。
- 由...生成的子群 (Subgroup generated by...):
- 核心定义:“由集合 $\{a_i \mid i \in I\}$ 生成的子群” 就是 “包含集合 $\{a_i \mid i \in I\}$ 的最小子群”。
- 这是一个描述性定义。它没有说这个子群里的元素长什么样,而是通过它所满足的“最小性”这个独一无二的属性来定义它。
- 上一段的集合论构造法 ($\cap H_i$) 和本节开头的直观构造法(元素乘积)都是找到这个“最小子群”的具体方法。理论上,它们得到的是同一个子群。
- 生成G (Generates G):
- 这是一个特殊情况。如果上面定义的那个“由 $\{a_i\}$ 生成的子群”不大不小,正好就是整个群 $G$ 本身,那么我们就说:
- 集合 $\{a_i \mid i \in I\}$ 生成 (generates) $G$。
- 集合 $\{a_i\}$ 是 $G$ 的一个生成集 (generating set)。
- 每个 $a_i$ 都是 $G$ 的一个生成元 (generator)。
- 有限生成 (Finitely generated):
- 如果能找到一个有限的生成集(也就是说,指标集 $I$ 是有限的),那么这个群 $G$ 就被称为是有限生成的。
- 所有的有限群显然都是有限生成的(最坏情况下,可以把群里所有元素都放到生成集里)。
- 有些无限群也是有限生成的。最经典的例子是整数群 $(\mathbb{Z}, +)$,它可以由集合 $\{1\}$ 生成,这是一个有限集。所以 $\mathbb{Z}$ 是有限生成的。
- 也有些无限群不是有限生成的,比如有理数群 $(\mathbb{Q}, +)$。你无法找到有限个有理数,通过加减操作得到所有的有理数。
- 关于术语“生成元”的澄清:
- 作者在这里做了一个重要的补充说明。当说“$a$ 是 $G$ 的生成元”时,可能有两种意思,需要根据上下文判断:
- 意思1 (强): $G$ 是一个循环群,且 $G = \langle a \rangle$。这里的 $a$ 独自一个就生成了整个群。
- 意思2 (弱): $a$ 是某个生成集 $S$ 中的一员,即 $a \in S$ 并且 $\langle S \rangle = G$。在这里,$a$ 只是生成整个群所需的“积木”之一,不一定能独立完成任务。
- 例如,在 $\mathbb{Z}_6$ 中,说“1是生成元”通常指意思1 ($ \langle 1 \rangle = \mathbb{Z}_6$)。但在讨论由 $\{2,3\}$ 生成 $\mathbb{Z}_6$ 时,我们也可以说“2是这个生成集里的一个生成元”,这里就是意思2。
示例1:有限群 $D_4$ (正方形二面体群)
- $D_4$ 是描述正方形对称性的群,有8个元素。
- 它可以由一个“旋转90度”的操作 $r$ 和一个“水平翻转”的操作 $f$ 生成。
- 即 $S=\{r, f\}$ 是一个生成集,且 $\langle S \rangle = D_4$。
- $D_4$ 是一个有限生成的群(因为生成集只有两个元素)。
- 我们可以说“$r$ 是 $D_4$ 的一个生成元”,这里是弱的含义,因为 $\langle r \rangle = \{e, r, r^2, r^3\}$ 只有4个元素,不是整个 $D_4$。
示例2:无限群
- 群 $\mathbb{Z} \times \mathbb{Z}$: 元素是所有整数坐标对 $(m,n)$,运算是向量加法。
- 生成集: $S = \{(1,0), (0,1)\}$。任何一个元素 $(m,n)$ 都可以表示成 $m \cdot (1,0) + n \cdot (0,1)$。所以 $\langle S \rangle = \mathbb{Z} \times \mathbb{Z}$。
- 这是一个有限生成的无限群。
示例3:非有限生成的群
- 群 $(\mathbb{Q}, +)$: 有理数加法群。
- 假设它由一个有限集 $\{p_1/q_1, \dots, p_k/q_k\}$ 生成。
- 那么所有能被生成的元素的形式都是 $\sum n_i (p_i/q_i)$。将这些分数通分,分母是 $L = \text{lcm}(q_1, \dots, q_k)$。那么所有生成的元素的分母(约分后)都必然是 $L$ 的因子。
- 我们永远无法生成一个分母与 $L$ 互质的分数,比如 $1/(L+1)$。
- 因此 $(\mathbb{Q}, +)$ 不是有限生成的。
- 有限群 vs 有限生成: 所有有限群都是有限生成的,但有限生成的群不一定是有限群(如 $\mathbb{Z}$)。
- 生成元的最少数量: 我们通常关心一个有限生成群的最小生成集的大小。这个数量是群的一个重要不变量。例如 $\mathbb{Z}_6$ 的最小生成元数量是1,而克莱因四元群 $V$ 的最小生成元数量是2。
- 生成元定义的歧义: 在阅读文献时,要特别注意作者上下文语境中“generator”一词的确切含义。
定义7.5 正式将“由集合 $A$ 生成的子群”命名为“包含 $A$ 的最小子群”。它进一步定义了“生成整个群”以及“有限生成群”这两个关键概念,并澄清了“生成元”一词可能存在的两种用法。这个定义为我们讨论和分类不同群的结构提供了核心词汇。
这个定义的目的是为了标准化术语,使得数学家之间可以无歧义地交流。通过定义“有限生成”,它引入了一个重要的分类标准,可以将群分为有限生成的和非有限生成的两大类,这两类群的研究方法和性质有很大的不同。
回到乐高积木模型:
- 由...生成的子群: 你有一套指定的积木 $S=\{a_i\}$。你能拼出来的所有可能形状的集合,就是“由 $S$ 生成的子群”。这也是包含这套基础积木的“最小积木世界”。
- 生成G: 如果你用这套积木 $S$ 能拼出整个预设的“乐高宇宙” $G$,那么 $S$ 就是这个宇宙的“创世积木包”。
- 有限生成: 如果你的“创世积木包” $S$ 里的积木种类是有限的,那么这个宇宙就是“有限生成的”。$\mathbb{Z}$ 就像一条无限长的直线,但它只需要一种“一米长的尺子”(生成元1)就可以丈量(生成)出来,所以它是有限生成的。$\mathbb{Q}$ 就像一条密密麻麻布满了点的直线,你需要无限多种不同长度的尺子才能精确度量所有点,所以它是非有限生成的。
想象一个初创公司 $G$。
- 生成集 $S$: 公司的创始团队。
- 由S生成的子群: 创始团队以及由他们直接或间接招聘、管理的所有员工构成的部门。
- S生成G: 如果这个创始团队最终建立起了整个公司,公司里没有一个员工的雇佣关系链最终追溯不到这个创始团队,那么这个创始团队就“生成”了整个公司。
- 有限生成: 如果公司的创始团队是有限的几个人,那么这个公司就是“有限生成的”。
1.4.2. 定理 7.6
📜 [原文9]
7.6 定理 如果 $G$ 是一个群,且对 $i \in I$,有 $a_{i} \in G$,那么由 $\left\{a_{i} \mid i \in I\right\}$ 生成的 $G$ 的子群 $H$ 的元素正好是 $G$ 中由 $a_{i}$ 的整数幂的有限乘积构成的元素,其中固定 $a_{i}$ 的幂可以在乘积中出现多次。
证明 设 $K$ 表示所有 $a_{i}$ 的整数幂的有限乘积的集合。那么 $K \subseteq H$。我们只需要观察到 $K$ 是一个子群,然后由于 $H$ 是包含所有 $a_{i}$(对 $i \in I$)的最小子群,我们就完成了证明。观察到 $K$ 中元素的乘积仍然在 $K$ 中。由于 $\left(a_{i}\right)^{0}=e$,我们有 $e \in K$。对于 $K$ 中的每个元素 $k$,如果我们从表示 $k$ 的乘积中形成一个新乘积,其中 $a_{i}$ 的顺序颠倒,并且所有指数的符号相反,我们就得到 $k^{-1}$,因此 $k^{-1}$ 也在 $K$ 中。例如,
这仍然在 $K$ 中。
这个定理非常重要,它把我们之前讨论的两种定义方式——构造性定义和集合论定义——联系了起来,证明了它们是等价的。
定理陈述:
- 设 $H$ 是由集合论定义的生成子群: 即 $H = \langle \{a_i\} \rangle$,是包含 $\{a_i\}$ 的最小子群。
- 设 $K$ 是由构造法定义的集合: 即 $K$ 是所有 $a_i$ 的整数幂的有限乘积的集合。
- 结论: 这两个集合是完全相同的,即 $H=K$。
证明过程 (双向包含法):
要证明两个集合相等 ($H=K$),标准的做法是证明 $K \subseteq H$ 和 $H \subseteq K$。
- 证明 $K \subseteq H$ (构造出的都在最小的里面):
- $H$ 是包含所有 $a_i$ 的子群。
- 因为 $H$ 是子群且包含 $a_i$,所以它必须包含所有 $a_i$ 的整数次幂 $a_i^n$ (封闭性和逆元)。
- 因为 $H$ 是子群,所以它必须对乘法封闭。因此,它必须包含这些幂的任意有限乘积。
- 而这些“幂的有限乘积”的集合,恰好就是 $K$ 的定义。
- 所以,$H$ 必须包含 $K$ 的所有元素。即 $K \subseteq H$。
- 这一部分在证明中被一句话带过(“那么 $K \subseteq H$”),因为它几乎是根据 $H$ 的定义直接得出的。
- 证明 $H \subseteq K$ (最小的也在构造出的里面):
- 这一步是证明的关键。作者采用了一个巧妙的策略。
- 策略: 我们已经知道 $K \subseteq H$。如果我们能证明 $K$ 本身就是一个子群,那么会发生什么?
- $K$ 本身就是一个子群。
- $K$ 显然包含所有的 $a_i$ (例如,$a_i = a_i^1$ 就是一个只有一项的乘积)。
- 所以,$K$ 是一个“包含所有 $a_i$ 的子群”。
- 但是!$H$ 的定义是最小的那个包含所有 $a_i$ 的子群。
- 既然 $H$ 是最小的,那么它必须比任何其他满足同样条件的子群都要小(或者是等于)。所以,必然有 $H \subseteq K$。
- 执行策略: 剩下的工作就是验证 $K$ 真的是一个子群。这在开篇第一段其实已经论证过了,这里再次简洁地重复了一遍:
- 闭合性: 两个有限乘积相乘,得到的是一个更长的有限乘积,所以结果仍在 $K$ 中。
- 单位元: $e = a_i^0$,这是一个单项的有限乘积,所以在 $K$ 中。
- 逆元: 对于 $K$ 中的任意元素 $k$(它是一个有限乘积),它的逆元是将原乘积中的每一项取逆,然后顺序颠倒。得到的结果仍然是一个有限乘积,所以也在 $K$ 中。例子 $\left[\left(a_{1}\right)^{3}\left(a_{2}\right)^{2}\left(a_{1}\right)^{-7}\right]^{-1}=\left(a_{1}\right)^{7}\left(a_{2}\right)^{-2}\left(a_{1}\right)^{-3}$ 就是在说明这一点。
- 结论: 因为 $K$ 是一个包含所有 $a_i$ 的子群,而 $H$ 是这类子群中最小的,所以 $H \subseteq K$。
- 最终结论:
- 我们证明了 $K \subseteq H$ 和 $H \subseteq K$。
- 因此,$H=K$。定理得证。
这个公式是“乘积的逆元等于逆元的反向乘积”这个规则的一个具体例子。
- 令 $x = (a_1)^3, y = (a_2)^2, z = (a_1)^{-7}$。
- 左边是 $(xyz)^{-1}$。
- 根据规则,$(xyz)^{-1} = z^{-1}y^{-1}x^{-1}$。
- $z^{-1} = ((a_1)^{-7})^{-1} = (a_1)^7$。
- $y^{-1} = ((a_2)^2)^{-1} = (a_2)^{-2}$。
- $x^{-1} = ((a_1)^3)^{-1} = (a_1)^{-3}$。
- 所以,结果是 $(a_1)^7 (a_2)^{-2} (a_1)^{-3}$,与右边相符。
- 这个例子想强调的是,逆元的结果仍然是 $a_1$ 和 $a_2$ 的幂的有限乘积,因此它仍然属于集合 $K$。
让我们用 $\mathbb{Z}_6$ 和生成集 $\{2,3\}$ 来验证这个定理。
- 集合论定义 $H$: $H$ 是包含 $\{2,3\}$ 的最小子群。我们之前已经通过论证 $2+3=5$ 和 $\langle 5 \rangle = \mathbb{Z}_6$ 推断出 $H = \mathbb{Z}_6$。
- 构造性定义 $K$: $K$ 是所有形如 $n \cdot 2 + m \cdot 3 \pmod 6$ 的元素的集合(其中 $n, m \in \mathbb{Z}$)。
- 定理要证明的是 $H=K$:
- $K \subseteq H$: $H$ 是包含 $\{2,3\}$ 的子群,所以它必须包含所有 $n \cdot 2$ 和 $m \cdot 3$ 的组合,所以 $K \subseteq H = \mathbb{Z}_6$。这显然成立。
- $H \subseteq K$: 我们需要证明 $\mathbb{Z}_6 \subseteq K$。也就是证明 $\mathbb{Z}_6$ 的每个元素都可以写成 $n \cdot 2 + m \cdot 3$ 的形式。
- $0 = 0 \cdot 2 + 0 \cdot 3$
- $1 = (-1) \cdot 2 + 1 \cdot 3 = -2+3 = 1$
- $2 = 1 \cdot 2 + 0 \cdot 3$
- $3 = 0 \cdot 2 + 1 \cdot 3$
- $4 = 2 \cdot 2 + 0 \cdot 3$
- $5 = 1 \cdot 2 + 1 \cdot 3$
- 因为 $\mathbb{Z}_6$ 的所有元素都能被构造出来,所以 $\mathbb{Z}_6 \subseteq K$。
- 结论: $H=K=\mathbb{Z}_6$。定理在这个例子中成立。
- 证明逻辑的理解: 这个证明的精髓在于利用 $H$ 的“最小性”。只要证明 $K$ 是一个“候选者”(即一个包含生成集的子群),那么 $H$ 就必须“小于等于”$K$。这是证明这类“最小性”定义的等价性问题时的一个标准技巧。
- 元素的表示不唯一: 一个元素可以有多种表示成有限乘积的方式。例如在 $S_3$ 中,$e = (12)(12)$,也可以是 $e = (123)^3$。$K$ 是这些元素的集合,不是表示法的集合。
定理7.6 是本节理论的核心。它雄辩地证明了,我们用来定义“由集合 $S$ 生成的子群”的两种看似不同的方法——一种是抽象的、集合论式的“包含 $S$ 的最小子群”,另一种是具体的、构造式的“$S$ 中元素幂的有限乘积的集合”——实际上描述的是完全相同的数学对象。这给了我们极大的灵活性:在思考问题时,我们可以使用更直观的构造法;在进行严格证明时,我们可以依赖更形式化的最小性定义。
本定理的目的是为了统一概念,消除歧义,并增强我们对生成子群这个概念的理解。它告诉我们,抽象的定义背后,有着非常具体和可操作的构造方式。这种理论上的等价性是数学结构之美的体现,它表明一个核心概念可以从不同的角度被一致地捕捉到。
[直觉心- [ ]
1.5. 凯莱有向图
📜 [原文10]
对于有限群 $G$ 的每个生成集 $S$,都有一个有向图表示该群及其生成元 $S$。有向图通常缩写为 digraph。这些群的视觉表示是由凯莱设计的,在文献中也称为凯莱图。
直观地说,有向图由有限数量的点(称为有向图的顶点)和连接顶点的某些弧(每个弧都有一个由箭头指示的方向)组成。在表示群 $G$ 并使用生成集 $S$ 的有向图中,对于 $G$ 的每个元素,我们有一个由点表示的顶点。$S$ 中的每个生成元由一种类型的弧表示。在手稿中,我们可以为不同的弧类型使用不同的颜色。由于我们的文本中没有不同的颜色,我们使用不同风格的弧,如实线、虚线和点线,来表示不同的生成元。因此,如果 $S=\{a, b, c\}$,我们可能表示
$b$ 用 $\longrightarrow \longrightarrow$ 表示,
$c$ 用 $\_\_\_\_$ 表示。
$\_\_\_\_$
使用此符号,凯莱有向图中的 $x \longrightarrow \longrightarrow y$ 意味着 $x a=y$。也就是说,沿箭头方向遍历弧表示将弧起点的群元素从右边乘以与该弧类型对应的生成元,得到弧终点的群元素。当然,由于我们在一个群中,我们立即知道 $y a^{-1}=x$。因此,沿与箭头相反的方向遍历弧对应于从右边乘以相应生成元的逆。如果 $S$ 中的一个生成元是其自身的逆,通常通过省略弧上的箭头来表示,而不是使用双箭头。例如,如果 $b^{2}=e$,我们可能用 ___-_--.. 来表示 $b$。
这部分引入了一种将抽象的群结构可视化的强大工具——凯莱有向图 (Cayley Digraph)。
- 核心思想: 为一个给定的群 $G$ 和一个特定的生成集 $S$ 画一张地图。这张地图能完整地反映出群的乘法结构。
- 基本构成:
- 顶点 (Vertices): 图中的“点”。在凯莱图中,每一个点代表群 $G$ 中的一个元素。如果群 $G$ 有 $|G|$ 个元素,那么凯莱图就有 $|G|$ 个顶点。
- 弧 (Arcs): 连接顶点的“有向边”或“箭头”。在凯莱图中,弧代表了生成元的操作。
- 规则:
- 一个生成元,一种弧: 生成集 $S$ 中的每一个生成元都对应着一种特定“风格”的弧。比如,生成元 $a$ 对应实线箭头,生成元 $b$ 对应虚线箭头。
- 弧的含义: 如果从顶点 $x$ 出发,沿着代表生成元 $g \in S$ 的弧到达顶点 $y$,那么这在代数上意味着 $x \cdot g = y$。这里的乘法是右乘。
- 例如,如果 $a$ 对应实线箭头 $\longrightarrow$,那么图中出现 $x \longrightarrow y$ 就表示 $xa=y$。
- 如果 $b$ 对应虚线箭头 $\dashrightarrow$,图中出现 $x \dashrightarrow z$ 就表示 $xb=z$。
- 逆向移动: 既然 $xg=y$,那么在群中必然有 $y g^{-1} = x$。这意味着,沿着代表 $g$ 的弧反方向移动,就等同于右乘 $g$ 的逆元 $g^{-1}$。
- 自逆元素的特殊表示: 如果一个生成元 $g$ 是它自身的逆,即 $g^2=e$ (或者说 $g=g^{-1}$),这意味着从 $x$ 到 $y$ 的操作 ($xg=y$) 和从 $y$ 回到 $x$ 的操作 ($yg=x$) 是完全相同的。在这种情况下,画一个双向箭头 $\leftrightarrow$ 是合理的,但通常的惯例是画一条没有箭头的线段,来表示这种对称关系。
这只是一个符号对应关系的例子,并非数学公式。它声明了在本例中,代数操作“右乘 $a$”被可视化为几何操作“沿着实线箭头前进”。
- $x \longrightarrow y \iff x a = y$
- $y \longrightarrow x \iff y a = x$ (这是不可能的,除非 $a^2=e$ 且 $x=y$)
- $y \longleftarrow x \iff y = xa^{-1}$ (这是 $xa=y$ 的直接推论)
示例:群 $\mathbb{Z}_3 = \{0, 1, 2\}$,生成集 $S=\{1\}$
- 顶点: 三个顶点,分别标记为 0, 1, 2。
- 生成元: 只有一个生成元 1。我们用实线箭头 $\longrightarrow$ 表示它。
- 画图:
- 从顶点 0 开始。操作是“加1”,$0+1=1$。所以我们画一个从 0 指向 1 的箭头: $0 \longrightarrow 1$。
- 现在在顶点 1。操作是“加1”,$1+1=2$。所以我们画一个从 1 指向 2 的箭头: $1 \longrightarrow 2$。
- 现在在顶点 2。操作是“加1”,$2+1=3 \equiv 0 \pmod 3$。所以我们画一个从 2 指向 0 的箭头: $2 \longrightarrow 0$。
- 结果: 我们得到了一个三角形的图,箭头依次连接 0 -> 1 -> 2 -> 0。
- 逆向移动: 逆着箭头走是什么意思?逆操作是“减1”(或者说“加2”)。
- 从 1 逆着箭头回到 0,代数上是 $1-1=0$。
- 从 2 逆着箭头回到 1,代数上是 $2-1=1$。
- 从 0 逆着箭头回到 2,代数上是 $0-1=-1 \equiv 2 \pmod 3$。
- 这完全符合我们的预期。
- 右乘 vs 左乘: 凯莱图的定义是基于右乘 ($xg=y$) 的。虽然也可以定义左乘的凯莱图 ($gx=y$),但除非特别说明,否则默认为右乘。对于非阿贝尔群,这两种图可能会不同。
- 生成集的重要性: 凯莱图的样貌完全依赖于所选择的生成集。同一个群,换一套生成集,得到的凯莱图可能看起来天差地别(如下面的例子7.8和7.9所示)。
- 图的布局不重要: 图中顶点的位置、弧的长度、弧是直是弯,这些都没有任何数学意义。唯一重要的是连接关系:哪个顶点通过哪种弧连接到了哪个顶点。
凯莱有向图是一种将群的代数结构(元素和运算)转化为几何结构(顶点和有向弧)的可视化方法。它的核心规则是:顶点代表群元素,不同类型的弧代表不同的生成元,沿着弧的方向移动代表右乘对应的生成元。这为我们提供了一种直观的方式来“看”一个群。
引入凯莱图的目的是为了提供一种超越纯符号运算的直觉。许多群的性质,如是否连通、路径关系、子群结构等,在图中会变得非常直观。它是一种强大的教学和研究工具,能帮助我们将抽象代数与图论联系起来,从新的角度发现和理解群的深层属性。
想象一个有很多房间的大厦,每个房间代表群的一个元素。你的钥匙串上挂着几把特殊的钥匙,每把钥匙是一个生成元。
- 顶点: 大厦里的每个房间。
- 生成元: 钥匙串上的钥匙(比如,红钥匙 $a$,蓝钥匙 $b$)。
- 凯莱图的弧: 钥匙对应的门。
- 规则: 在任何一个房间 $x$ 里,使用红钥匙 $a$ 开门,总会把你带到固定的另一个房间 $y$ (即 $xa=y$)。这个门就是从 $x$ 到 $y$ 的一条红色弧。同样,使用蓝钥匙 $b$ 会把你带到另一个房间 $z$ ($xb=z$),这是条蓝色弧。
- 整个凯莱图就是这个大厦的完整“建筑蓝图”,它告诉你从任何一个房间出发,使用任何一把钥匙,会去向哪里。
把群想象成一个电脑游戏地图。
- 顶点: 地图上的各个地点。
- 生成集: 你拥有的几种“传送卷轴”。
- 规则:
- “卷轴A”的作用是:无论你在哪个地点 $x$,使用它就会被传送到地点 $y$ (代数上 $xa=y$)。
- “卷轴B”的作用是:无论你在哪个地点 $x$,使用它就会被传送到地点 $z$ (代数上 $xb=z$)。
- 凯莱图就是这个游戏的“传送网络图”。它画出了所有地点,并用不同颜色的箭头标明了从每个地点使用每种卷轴会传送到的目的地。通过研究这张网络图,你可以了解整个游戏世界的结构。
1.5.1. 例子 7.7
📜 [原文11]
7.7 例子 图 7.8 所示的两个有向图都表示群 $\mathbb{Z}_{6}$,生成集为 $S=\{1\}$。弧的长度和形状以及弧之间的角度都没有任何意义。
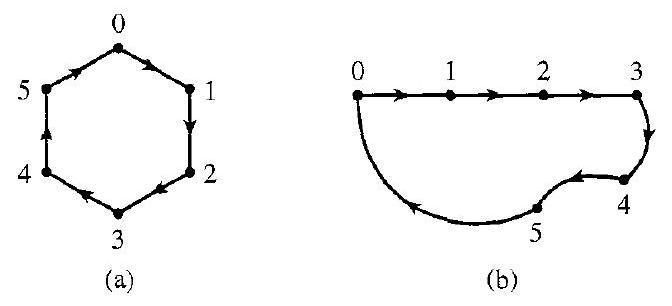
7.8 图 $\mathbb{Z}_{6}$ 的两个有向图,生成集为 $S=\{1\}$,使用 ⟶
这个例子通过两张外形不同但本质相同的图,强调了凯莱图的一个关键特性:几何布局是任意的,只有拓扑连接关系才重要。
- 群和生成集:
- 群: $G = \mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}$
- 生成集: $S = \{1\}$
- 生成元操作: 右乘(在这里是加法)生成元1。即 $x \to x+1 \pmod 6$。
- 分析图 7.8(a) (左边的六边形图):
- 顶点: 6个顶点,标记为 0, 1, 2, 3, 4, 5。
- 弧:
- 从 0 出发,加 1 得到 1。所以有 $0 \to 1$。
- 从 1 出发,加 1 得到 2。所以有 $1 \to 2$。
- ...
- 从 5 出发,加 1 得到 $6 \equiv 0$。所以有 $5 \to 0$。
- 结构: 所有的顶点和弧构成了一个单一的有向环。这是一个非常对称和直观的布局。
- 分析图 7.8(b) (右边的杂乱图):
- 顶点: 同样是 6个顶点,标记为 0, 1, 2, 3, 4, 5。
- 弧: 我们来检查它的连接关系是否正确。
- 有 $0 \to 1$ 吗?有。
- 有 $1 \to 2$ 吗?有。
- 有 $2 \to 3$ 吗?有。
- 有 $3 \to 4$ 吗?有。
- 有 $4 \to 5$ 吗?有。
- 有 $5 \to 0$ 吗?有。
- 结构: 尽管这些顶点被随意地摆放在纸上,弧线也是歪歪扭扭的,但它们所代表的连接关系——即“谁指向谁”——与图(a)是完全一样的。它们都描述了同一个循环:$0 \to 1 \to 2 \to 3 \to 4 \to 5 \to 0$。
- 核心结论:
- 作者明确指出:“弧的长度和形状以及弧之间的角度都没有任何意义。” 这两张图虽然在视觉上一个“漂亮”,一个“丑陋”,但从图论和群论的角度看,它们是同构的,代表的是完全相同的凯莱图。
- 这强调了我们应该关注图的抽象结构,而不是它的具体画法。
本例本身就是具体数值示例。我们可以为同一个群 $\mathbb{Z}_4$ 和生成集 $S=\{1\}$ 画出两种不同布局的凯莱图。
- 群: $\mathbb{Z}_4=\{0,1,2,3\}$, 生成集: $S=\{1\}$
- 连接关系: $0\to 1$, $1\to 2$, $2\to 3$, $3\to 0$。
- 画法1 (正方形): 把 0, 1, 2, 3 放在一个正方形的四个顶点上,箭头沿着边线顺时针连接。
- 画法2 (一条直线): 把 0, 1, 2, 3 从左到右排在一条直线上,然后画 $0\to 1$, $1\to 2$, $2\to 3$,最后画一条长长的弧从最右边的 3 绕回到最左边的 0。
- 这两种画法描述的是同一个凯莱图。
- 被视觉误导: 不要因为一个凯莱图看起来复杂或不对称,就认为它代表的群也很复杂。可能只是画得比较随意。判断群的性质(如是否阿贝尔群)需要依据更深刻的结构特性,而不是视觉上的对称性。
- 忘记检查所有连接: 在判断一个图是否是某个群的凯莱图时,必须仔细检查每一个顶点和每一种类型的弧是否都符合 $xg=y$ 的规则,不能只看一部分。
例子7.7通过展示同一个凯莱图的两种不同视觉呈现,有力地说明了在解读凯莱图时,我们必须忽略所有纯粹的几何美学特征(如位置、长度、角度),而只关注其核心的拓扑连接结构(谁通过哪种弧指向谁)。
这个例子的主要目的是为了训练读者如何“正确地”看待凯莱图,避免初学者容易犯的以貌取“图”的错误。它为后面更复杂的图(如图7.9)的出现做好了铺垫,因为后面的图布局可能就不是那么直观了,读者需要有能力从中提取出纯粹的代数信息。
想象一张地铁线路图。
- 图(a) 就像是官方出版的、经过美化设计的线路图,站点均匀分布,线路横平竖直,非常清晰。
- 图(b) 就像是你在餐巾纸上随手画的草图,站点位置歪歪扭扭,线路也是弯的。
- 但是,只要两张图都正确地表示了“从A站坐车能到B站”,那么它们描述的是同一个地铁系统。对于一个只关心“如何从A到B”的乘客来说,这两张图是等价的。凯莱图也是如此,它只关心元素之间的“运算可达性”。
想象一个由6个珠子串成的项链。
- 图(a) 是把项链平铺成一个正六边形的样子。
- 图(b) 是把这条项链随意地扔在桌子上,它可能会扭成一团。
- 但无论形状如何,珠子之间的“下一个是谁”的邻接关系是不变的。0号珠子的下一个永远是1号,5号珠子的下一个永远是0号。凯莱图关心的就是这种内在的“邻接关系”。
1.5.2. 例子 7.9 与 7.10
📜 [原文12]
(a)
(b)
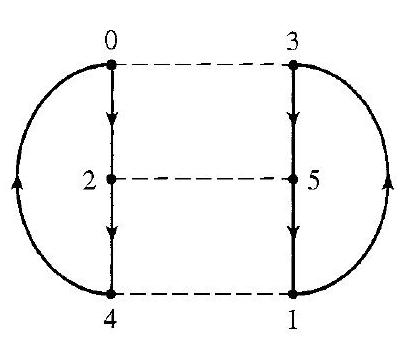
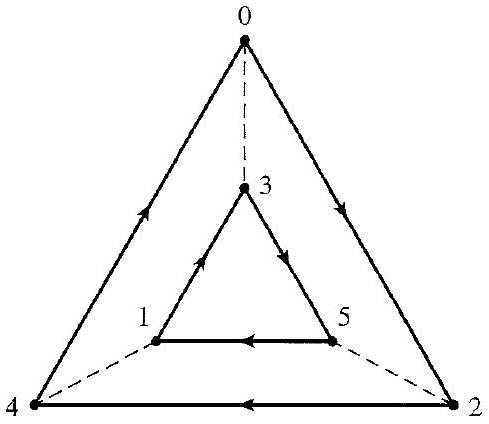
7.9 图 $\mathbb{Z}_{6}$ 的两个有向图,生成集为 $S=\{2,3\}$,使用 ⟶ 和 ----
7.10 例子 图 7.9 所示的两个有向图都表示群 $\mathbb{Z}_{6}$,生成集为 $S= \{2,3\}$。由于 3 是其自身的逆,表示 3 的虚线上没有箭头。请注意,这些凯莱图与图 7.8 中同一群的凯莱图看起来有多么不同。这种差异是由于生成集的选择不同造成的。
这个例子展示了凯莱图的另一个关键特性:对于同一个群,选择不同的生成集,会得到外观和结构都完全不同的凯莱图。
- 群和新的生成集:
- 群: 仍然是 $G = \mathbb{Z}_6 = \{0, 1, 2, 3, 4, 5\}$。
- 生成集: 这次换成了 $S = \{2, 3\}$。我们在例子7.2中已经验证过,这个集合确实能生成 $\mathbb{Z}_6$。
- 弧的定义:
- 生成元 2: 对应实线箭头 $\longrightarrow$。操作是 $x \to x+2 \pmod 6$。
- 生成元 3: 对应虚线 (无箭头) ----。操作是 $x \to x+3 \pmod 6$。
- 为什么3的弧没有箭头? 因为在 $\mathbb{Z}_6$ 中,$3+3=6\equiv 0$,所以3的阶是2。这意味着3是自身的逆元(在加法群中,元素的逆是 $n-x$,所以3的逆是 $6-3=3$)。根据惯例,自逆元素的弧不画箭头。
- 分析图 7.9(a) 和 (b):
- 我们来验证一下图中的连接关系是否正确。以图(a)为例:
- 实线箭头 (加2):
- $0 \to 2$, $2 \to 4$, $4 \to 0$ (构成一个三角形)
- $1 \to 3$, $3 \to 5$, $5 \to 1$ (构成另一个三角形)
- 这正确地反映了 $\mathbb{Z}_6$ 中所有“加2”的关系。
- 虚线 (加3):
- $0 - 3$ (连接0和3)
- $1 - 4$ (连接1和4)
- $2 - 5$ (连接2和5)
- 这也正确地反映了 $\mathbb{Z}_6$ 中所有“加3”的关系。例如 $1+3=4$, $4+3=7\equiv 1$。
- 图(b)的布局不同,但如果你仔细检查,会发现它的连接关系和图(a)是完全一样的。例如,在(b)中,同样有 $0\to 2 \to 4 \to 0$ 和 $1 \to 3 \to 5 \to 1$ 的实线环,以及 $0-3, 1-4, 2-5$ 的虚线连接。
- 核心结论:
- 与图7.8对比: 作者引导我们注意,图7.9中的这些图(两个三角形被线连起来)与图7.8中的图(一个大六边形)看起来完全不同。
- 原因: “这种差异是由于生成集的选择不同造成的。” 这是本例最重要的信息。凯莱图不仅仅是群的图,它是群和特定生成集的图。改变其中任何一个,图都会改变。
让我们为 $S_3$ 群画出两个不同生成集对应的凯莱图。
- 群: $S_3 = \{e, a, a^2, b, ab, a^2b\}$,其中 $a=(123), b=(12)$。关系是 $a^3=e, b^2=e, ba=a^2b$。
- 生成集1: $S_1=\{a, b\}$
- $a$ (旋转) 用实线箭头 $\longrightarrow$。
- $b$ (翻转) 用虚线 ---- (因为 $b^2=e$)。
- 图的结构会是两个由实线箭头连接的三角形($\{e, a, a^2\}$ 和 $\{b, ab, a^2b\}$),然后这两个三角形之间由虚线一一对应连接($e-b, a-ab, a^2-a^2b$)。这是一个六边形的棱柱图。
- 生成集2: $S_2=\{b, c\}$ 其中 $b=(12), c=(23)$
- $b$ 用实线 ----。$c$ 用虚线 ----。
- 关系: $b^2=e, c^2=e, (bc)^3=e$。
- 图的结构: 从 $e$ 出发,实线连接到 $b$,虚线连接到 $c$。从 $b$ 出发,虚线连接到 $bc$。从 $c$ 出发,实线连接到 $cb$。继续下去,会得到一个看起来像“压扁的立方体”的六边形。
- 这个图的视觉感受和上面那个棱柱图完全不同。
- 生成集必须能生成整个群: 在画凯莱图之前,要确保你选的“生成集”真的能生成整个群。如果不能,你画出的图将只是整个凯莱图的一个连通分量 (connected component)。例如,如果为 $\mathbb{Z}_6$ 选择生成集 $S=\{2\}$,你画出的图将只有 $\{0, 2, 4\}$ 这三个顶点构成的三角形,而 $\{1, 3, 5\}$ 会被遗漏。
- 识别群的性质: 不同的凯莱图可能让群的某些性质更突出。图7.8的六边形图清晰地显示了 $\mathbb{Z}_6$ 的循环性质。图7.9的图则突出了子群 $\langle 2 \rangle = \{0,2,4\}$ 和它的陪集 $\{1,3,5\}$ 的结构。
例子7.10的核心信息是,凯莱图的形态与所选的生成集密切相关。同一个群,选用不同的生成元,会得到视觉结构迥异的凯莱图。这说明凯莱图编码了群相对于特定生成集的信息,不同的生成集提供了看待同一个群的不同视角。
这个例子的目的是为了进一步加深读者对凯莱图与生成集之间依赖关系的理解。它破除了“一个群只有一个凯莱图”的错误观念,并展示了通过改变生成集(视角),我们可以观察到群的不同结构侧面。这为后面利用凯莱图分析子群结构等问题埋下了伏伏笔。
回到大厦和钥匙的模型。
- 图7.8 (生成集{1}): 你的钥匙串上只有一把“+1”的万能钥匙。你从任何房间出发,使用这把钥匙,会进入“下一个”房间。整个大厦就像一个环形的走廊。
- 图7.9 (生成集{2,3}): 你的钥匙串上有两把钥匙:一把“+2”的红钥匙,一把“+3”的蓝钥匙。
- 红钥匙让你在“奇数楼层”的房间(1,3,5)之间打转,或者在“偶数楼层”的房间(0,2,4)之间打转,但不能跨楼层。
- 蓝钥匙的作用是让你在奇偶楼层之间穿梭(从0到3,从1到4,从2到5)。
- 这个大厦的结构感觉上是两个独立的环形区域,然后通过几个特定的“传送门”连接起来。
- 虽然是同一栋大厦,但因为你用的“移动工具”不同,你对大厦的“地图感知”也完全不同。
想象你在游乐园里,园内有6个景点(0到5)。
- 图7.8 (生成集{1}): 游乐园里只有一种交通工具:环园小火车,它按 0-1-2-3-4-5-0 的顺序单向行驶。你想去任何景点,都得坐这个小火车。你感知的地图就是一个大圈。
- 图7.9 (生成集{2,3}): 园里有两种交通工具:
- 一个是“偶数景点观光车”,只在景点0, 2, 4之间循环。另一个是“奇数景点观光车”,只在1, 3, 5之间循环。
- 此外,还有一种“摆渡船”,可以在(0,3), (1,4), (2,5)这三对景点之间双向航行。
- 虽然是同一个游乐园,但第二种交通方案让你感觉这个乐园被分成了两个区域,然后通过几条航线连接。你对乐园的“心智地图”完全改变了。
16. 凯莱有向图的性质
📜 [原文13]
群的每个有向图都必须满足以下四个性质,原因如下所示。
这部分从例子转向理论,总结了所有合法的凯莱图必须共同遵守的四条基本规则,并解释了这些几何性质背后的代数原因。这四条性质是凯莱图之所以能完美反映群结构的核心。
这是一个引子,预告了接下来将要陈述凯莱图的四个普适性几何性质,并会从群论的公理出发,解释这些性质的代数根源。它将几何直觉与代数规则紧密地联系起来。
本段的目的是为了将之前通过例子建立的直观印象,提炼成普适的、可以被验证的数学法则。这使得“凯莱图”不仅仅是一个漂亮的图示,而是一个具有严格定义和性质的数学对象。它回答了这样一个问题:“什么样的图才能算作一个群的凯莱图?”
1.6.1. 性质1:连通性
📜 [原文14]
性质
1. 该有向图是连通的,也就是说,我们可以从任何顶点 $g$ 到达任何顶点 $h$,通过沿着连续的弧线行进,从 $g$ 开始,到 $h$ 结束。
原因
每个方程 $g x=h$ 在群中都有解。
- 性质描述 (几何): 凯莱图必须是连通的 (connected)。这意味着图中不存在孤立的点或孤立的区域。从图中的任意一个顶点出发,你总能找到一条由弧组成的路径,走到图中的任何另一个顶点。你可能需要正向走、反向走、混合走。
- 原因解释 (代数):
- 性质的根源在于群的一个基本特征:方程 $gx=h$ 总是有唯一解。
- 我们来分析这个方程。$g$ 是我们的起点顶点, $h$ 是我们的终点顶点。$x$ 是什么?$x$ 就是我们需要的那个“变换”,能把 $g$ 变成 $h$。
- 在群中,这个解 $x$ 是什么?两边左乘 $g^{-1}$,我们得到 $x = g^{-1}h$。这个解是唯一存在的。
- 现在关键来了:我们选取的生成集 $S=\{s_1, s_2, \dots, s_k\}$ 本身就能生成整个群 $G$。这意味着,$G$ 中的任何元素,包括上面求出来的解 $x=g^{-1}h$,都可以被写成生成元(及其逆元)的有限乘积的形式。
- 比如,可能 $x = s_1^3 s_2^{-1} s_5$。
- 现在我们把这个代数表达式翻译成图上的路径:
- $h = gx = g (s_1^3 s_2^{-1} s_5) = (((g \cdot s_1) \cdot s_1) \cdot s_1) \cdot s_2^{-1}) \cdot s_5$
- 在图上行走:
- 从顶点 $g$ 开始。
- 右乘 $s_1$,相当于沿着 $s_1$ 对应的弧走一步。
- 再乘 $s_1$,再走一步。
- 再乘 $s_1$,再走一步。
- 再乘 $s_2^{-1}$,相当于沿着 $s_2$ 对应的弧反向走一步。
- 再乘 $s_5$,沿着 $s_5$ 对应的弧走一步。
- 经过这一系列行走,我们最终到达的顶点,不多不少,正好就是 $h$。
- 因为对于任意的 $g, h$,我们总能找到这样一个 $x$ 并把它表示成生成元的序列,所以我们总能找到一条从 $g$ 到 $h$ 的路径。因此,图是连通的。
- 群: $\mathbb{Z}_6$, 生成集: $S=\{2,3\}$。
- 起点: $g=1$。终点: $h=4$。
- 代数求解: 我们要求解 $1+x \equiv 4 \pmod 6$。解是 $x=3$。
- 将解表示为生成元: $x=3$ 本身就是生成集 $S$ 的一员。
- 在图上行走: 这意味着从顶点1出发,走一条代表“+3”的路径,就能到达4。在图7.9中,我们看到顶点1和顶点4之间确实有一条虚线连接。
- 换一个例子: 起点 $g=2$, 终点 $h=5$。
- 代数求解: $2+x \equiv 5 \pmod 6$。解是 $x=3$。
- 在图上行走: 从顶点2出发,走一条代表“+3”的路径,到达5。图中2和5之间有虚线连接。
- 再换一个例子: 起点 $g=1$, 终点 $h=0$。
- 代数求解: $1+x \equiv 0 \pmod 6$。解是 $x=5$。
- 将解表示为生成元: $5$ 不是生成元,但它可以由生成元表示:$5 = 2+3$。
- 在图上行走: 这意味着我们可以从1开始,先走一步“+2”,再走一步“+3”。
- 从1出发,走“+2”(实线箭头),到达顶点3。($1+2=3$)
- 从3出发,走“+3”(虚线),到达顶点0。($3+3=0$)
- 我们找到了一条路径 $1 \xrightarrow{+2} 3 \xrightarrow{+3} 0$。图是连通的。
- 如果选的不是生成集会怎样? 如果你选的集合 $S$ 不能生成整个群 $G$,而是生成一个真子群 $H$,那么你画出的凯莱图将是不连通的。它会分解成几个互不连通的部分。每个部分本身是一个连通的图,代表 $H$ 的一个陪集 (coset) 的凯莱图。例如,为 $\mathbb{Z}_6$ 选“生成集” $\{2\}$,你会得到两个分离的三角形 $\{0,2,4\}$ 和 $\{1,3,5\}$。
凯莱图的连通性是“生成集”这个概念的直接几何体现。因为生成集能够通过乘法“到达”群里的任何一个元素,所以在图上,我们就能从任何一个顶点出发,通过沿着弧线行走,“到达”任何另一个顶点。
回到大厦与钥匙模型。性质1说的是:这个大厦没有被完全隔离的区域。只要你带了全套的生成元钥匙,从任何一个房间出发,你总能通过一系列的开门、穿梭,最终到达大厦里的任何其他一个房间。这是因为这套钥匙的设计(生成集)本身就保证了能“解锁”整个大厦的所有空间。
1.6.2. 性质2:无重边
📜 [原文15]
- 从一个顶点 $g$ 到一个顶点 $h$ 最多只有一条弧。
原因
$g x=h$ 的解是唯一的。
- 性质描述 (几何): 在凯莱图中,连接任意两个固定顶点 $g$ 和 $h$ 的同一种类型的弧,最多只有一条。也就是说,你不会看到从 $g$ 到 $h$ 有两条平行的、都代表生成元 $s$ 的弧。
- 作者的表述“最多只有一条弧”有点模糊,更精确的说法是“对于每个生成元 $s \in S$,从 $g$ 出发的代表 $s$ 的弧,其终点是唯一的”。这意味着不可能有从 $g$ 到 $h_1$ 和从 $g$ 到 $h_2$ 两条类型相同的弧(除非 $h_1=h_2$)。
- 另一个理解是:连接 $g$ 和 $h$ 的弧,其代表的生成元是唯一的。即不可能既有 $gs_1=h$ 又有 $gs_2=h$(除非 $s_1=s_2$)。
- 我们结合原因来理解,作者想表达的是后者。
- 原因解释 (代数):
- 这个性质源于群中右消去律 (Right Cancellation Law),它是 $gx=h$ 解唯一的保证。
- 假设我们有两条不同类型的弧从顶点 $g$ 指向同一个顶点 $h$。
- 一条是 $s_1$ 型弧,意味着 $g s_1 = h$。
- 另一条是 $s_2$ 型弧,意味着 $g s_2 = h$。
- (这里假设 $s_1 \neq s_2$ 是不同的生成元)
- 那么我们就有 $g s_1 = g s_2$。
- 在群中,我们可以左乘 $g^{-1}$(左消去律),得到 $s_1 = s_2$。
- 这与我们假设 $s_1, s_2$ 是生成集中两个不同的生成元相矛盾。
- 因此,不可能有两条不同类型的弧从同一个起点指向同一个终点。
- 作者的表述“最多只有一条弧”可能旨在涵盖“同类型”和“不同类型”两种情况。同类型的弧不会有两条,因为 $g$ 乘以 $s$ 的结果是确定的;不同类型的弧也不会有(如上分析)。所以从 $g$ 到 $h$ 的直接连接弧(如果有的话),其所代表的生成元是唯一的。
- 群: $\mathbb{Z}_6$, 生成集: $S=\{2,3\}$
- 起点: $g=1$。
- 加2操作: $1+2=3$。所以有一条从 1 到 3 的实线弧。
- 加3操作: $1+3=4$。所以有一条从 1 到 4 的虚线连接。
- 终点 3 和 4 是不同的。我们不会看到“加2”和“加3”两条弧都指向同一个终点。
- 代数上,如果 $1+2 = y$ 且 $1+3 = y$,那么 $3=y$ 且 $4=y$,这是不可能的。更根本地,如果 $1+2 = 1+3$,根据消去律,则 $2=3$,这显然是错误的。
- 路径 vs 弧: 这个性质说的是直接连接的弧(一步操作),不是指路径。从 $g$到 $h$ 可以有很多条不同的路径(一系列弧),但最多只有一条单步的、代表某个生成元的弧。例如在 $\mathbb{Z}_6$ 和 $S=\{2,3\}$ 中,从 1 到 5 有路径 $1 \xrightarrow{+2} 3 \xrightarrow{+2} 5$,也有路径 $1 \xrightarrow{+4 \text{ (not a generator)}} 5$。但没有直接代表 "+2" 或 "+3" 的弧从 1 到 5。
凯莱图的“无重边”性质(更准确地说,从一个顶点出发的同类型弧有唯一终点,以及连接两点的弧类型唯一)是群中消去律的几何体现。因为 $g$ 乘以一个确定元素的结果是唯一的,所以从一个顶点出发,沿着一种特定类型的弧能到达的目的地也是唯一的。
回到大厦与钥匙模型。性质2说的是:
- 你在房间 $g$ 里,用红钥匙 $s_1$ 开门,只会通向唯一的一个房间 $h_1$。不可能这把红钥匙同时能打开两扇通往不同房间 $h_1, h_2$ 的门。
- 如果你发现用红钥匙 $s_1$ 和蓝钥匙 $s_2$ 都能从房间 $g$ 到达同一个房间 $h$,那只能说明这两把钥匙其实是同一把($s_1=s_2$)。
1.6.3. 性质3:出入度均衡
📜 [原文16]
- 每个顶点 $g$ 都有且仅有一条从 $g$ 出发的每种类型的弧,以及一条从 $g$ 结束的每种类型的弧。
原因
对于 $g \in G$ 和每个生成元 $b$,我们可以计算 $g b$,并且 $\left(g b^{-1}\right) b=g$。
- 性质描述 (几何): 这个性质描述了每个顶点的“连接模式”,它包含两个方面:
- 出度 (Outgoing arcs): 对于每一个顶点 $g$,和每一种生成元 $s \in S$,都有且仅有一条代表 $s$ 的弧从 $g$ 出发。
- 入度 (Incoming arcs): 对于每一个顶点 $g$,和每一种生成元 $s \in S$,都有且仅有一条代表 $s$ 的弧在 $g$ 结束。
- 换句话说,每个顶点看起来都一样:它都有 $|S|$ 条弧指出去,$|S|$ 条弧指进来,并且出去的弧和进来的弧,每种颜色/样式都恰好有一条。这导致了凯莱图高度的均匀性和对称性。
- 原因解释 (代数):
- 出度方面: “每个顶点 $g$ 都有且仅有一条从 $g$ 出发的每种类型的弧”。
- 原因: “对于 $g \in G$ 和每个生成元 $b$,我们可以计算 $gb$”。
- 解释: 在群中,任意两个元素 $g$ 和 $b$ 的乘积 $gb$ 总是存在且唯一的。
- 存在性 $\implies$ 总有一条弧出去。对于顶点 $g$ 和生成元 $b$,总能找到一个终点 $h=gb$。所以必须有一条 $b$ 型弧从 $g$ 出发。
- 唯一性 $\implies$ 最多只有一条弧出去。这个乘积 $gb$ 的结果是唯一的,不可能既等于 $h_1$ 又等于 $h_2$ (如果 $h_1 \neq h_2$)。所以从 $g$ 出发的 $b$ 型弧只能有一条。
- 入度方面: “每个顶点 $g$ 都有且仅有一条在 $g$ 结束的每种类型的弧”。
- 原因: “并且 $(g b^{-1}) b = g$”。
- 解释: 我们想找一个顶点 $x$,使得从 $x$ 出发,经过 $b$ 型弧,正好到达 $g$。也就是解方程 $xb=g$。
- 在群中,这个方程的解总是存在且唯一的,即 $x = gb^{-1}$。
- 存在性 $\implies$ 总有一条弧进来。我们总能找到这样一个起点 $x=gb^{-1}$。所以必须有一条 $b$ 型弧指向 $g$。
- 唯一性 $\implies$ 最多只有一条弧进来。这个解 $x=gb^{-1}$ 是唯一的。所以指向 $g$ 的 $b$ 型弧只能有一条。
- 群: $D_3 \cong S_3$。生成集: $S=\{a,b\}$ ( $a$是旋转120度, $b$是翻转)。$a$ 对应实线箭头 $\to$,$b$ 对应虚线 $--$。
- 考察顶点 $a$:
- 出度:
- 必须有一条实线弧从 $a$ 出发。终点是 $a \cdot a = a^2$。所以有 $a \to a^2$。
- 必须有一条虚线弧从 $a$ 出发。终点是 $a \cdot b$。所以有 $a -- ab$。
- 正好 $|S|=2$ 条弧出去。
- 入度:
- 必须有一条实线弧指向 $a$。起点是 $x$ 满足 $xa=a$,所以 $x=e$。即 $e \to a$。
- 必须有一条虚线弧指向 $a$。起点是 $y$ 满足 $yb=a$,所以 $y=ab^{-1}=ab$。即 $ab -- a$。
- 正好 $|S|=2$ 条弧进来。
- 你可以对 $D_3$ 的任何一个顶点做同样的分析,都会得到“两出两进,红蓝各一”的结论。
- 自逆元素: 如果一个生成元 $b$ 是自逆的($b^2=e$),它的弧没有箭头。此时,“出弧”和“入弧”是同一条弧。例如,对于顶点 $g$,从它出发的 $b$ 型弧连接到 $gb$。同时,指向 $g$ 的 $b$ 型弧来自起点 $x=gb^{-1}=gb$。所以这条弧就是连接 $g$ 和 $gb$ 的一条无向边。这条边对 $g$ 的度数贡献为1,对 $gb$ 的度数贡献也为1。
凯莱图的“出入度均衡”性质是群公理中“运算有定义且封闭”和“逆元存在”的直接几何体现。它保证了图中每个顶点局部的“环境”都是完全相同的,从而赋予了凯莱图一种深刻的内在对称性。
回到大厦与钥匙模型。性质3说的是:
- 在任何一个房间里,你的每一把钥匙都能打开一扇门,把你带到一个新的房间。不多不少,每把钥匙对应一扇唯一的门。
- 对于任何一个房间,你想来到这里,也有各种方式。对于每一把钥匙,都存在唯一的另一个房间,你从那个房间用那把钥匙开门,就能正好来到当前这个房间。
这就像一个设计得极其完美的交通网络,每个节点(顶点)的流入流出配置都是一模一样的。
1.6.4. 性质4:路径一致性
📜 [原文17]
- 如果从顶点 $g$ 出发的两种不同类型的弧序列都到达同一个顶点 $h$,那么从任意顶点 $u$ 出发的相同类型的弧序列也将到达同一个顶点 $v$。
原因
如果 $g q=h$ 且 $g r=h$,那么 $u q= u g^{-1} h=u r$。
- 性质描述 (几何): 这个性质描述了图的“平移对称性”。
- 假设你在顶点 $g$ 处,发现有两条不同的路径 (弧的序列) 都能到达终点 $h$。
- 路径1,由弧序列 $q$ 代表 (比如,先走红再走蓝: $q=s_1s_2$)。
- 路径2,由弧序列 $r$ 代表 (比如,先走绿再走黄: $r=s_3s_4$)。
- 这个性质是说,这种“两条不同路径汇合到一点”的模式,是普适的,可以在图中的任何地方被复制。
- 如果你现在换一个起点,站在任意一个新顶点 $u$ 上,然后分别按照路径1 ($q$) 和路径2 ($r$) 行走,那么这两条新路径的终点也必然会汇合到同一个新顶点 $v$ 上。
- 原因解释 (代数):
- 前提:
- “从顶点 $g$ 出发的弧序列 $q$ 到达顶点 $h$” $\iff gq = h$。
- “从顶点 $g$ 出发的弧序列 $r$ 到达顶点 $h$” $\iff gr = h$。
- 推论1 (群内关系):
- 既然 $gq=h$ 且 $gr=h$,那么 $gq = gr$。
- 根据左消去律,我们得到一个在群 $G$ 中成立的关系式 (relation): $q=r$。
- 这个关系式 $q=r$ 是群 $G$ 的一个内在属性,它与我们选择哪个起点 $g$ 无关。它意味着由弧序列 $q$ 代表的复合操作,和由弧序列 $r$ 代表的复合操作,是完全等价的。
- 推论2 (应用到新起点):
- 现在我们从新起点 $u$ 出发。
- 走路径 $q$ 的终点是 $uq$。
- 走路径 $r$ 的终点是 $ur$。
- 因为我们已经知道 $q=r$ 这个关系在全群中都成立,所以 $uq$ 必然等于 $ur$。
- 因此,两条新路径的终点是同一个点 $v = uq = ur$。
- 作者的证明: 作者用了一个稍微不同的但等价的推导:
- 从 $gq=h$ 得到 $q = g^{-1}h$。
- 从 $gr=h$ 得到 $r = g^{-1}h$。
- 所以 $q=r$。
- 因此 $uq = ur$。这个证明更清晰地展示了 $q$ 和 $r$ 作为群元素的等同性。
- 群: $\mathbb{Z}_6$, 生成集: $S=\{2,3\}$。
- 起点: $g=0$。
- 路径1 ($q$): 走3次“+2”操作。$q = 2+2+2 = 6 \equiv 0$。
- 路径: $0 \xrightarrow{+2} 2 \xrightarrow{+2} 4 \xrightarrow{+2} 0$。终点是 $h=0$。
- 代数: $g+q = 0+0 = 0$。
- 路径2 ($r$): 走2次“+3”操作。$r = 3+3=6 \equiv 0$。
- 路径: $0 \xrightarrow{+3} 3 \xrightarrow{+3} 0$。终点也是 $h=0$。
- 代数: $g+r = 0+0 = 0$。
- 我们发现了一个关系: 在 $\mathbb{Z}_6$ 中,$2+2+2 = 3+3$ (都等于0)。即 $q=r$。
- 应用到新起点: 现在我们换一个新起点 $u=1$。
- 走路径 $q$ (连续加三次2): $1 \xrightarrow{+2} 3 \xrightarrow{+2} 5 \xrightarrow{+2} 1$。终点是 $1$。
- 走路径 $r$ (连续加两次3): $1 \xrightarrow{+3} 4 \xrightarrow{+3} 1$。终点也是 $1$。
- 两条路径的终点果然相同!$v=1$。
- 代数上, $u+q = 1+0=1$, $u+r = 1+0=1$。
- 关系式 (Relation): 性质4揭示了凯莱图与群的表示论 (presentation) 中“关系式”的深刻联系。凯莱图中的每一个闭环(从一个点出发,经过一系列操作又回到该点)都对应群的一个关系式。例如,在 $\mathbb{Z}_6, S=\{2,3\}$ 中,$0 \xrightarrow{+2} 2 \xrightarrow{+2} 4 \xrightarrow{+2} 0$ 这个闭环告诉我们 $2+2+2=0$ 是群的一个关系。
凯莱图的“路径一致性”或“平移不变性”是群结合律和消去律的必然结果。它表明,在群中通过不同操作序列得到的相等关系($q=r$),在凯莱图上会体现为一种全局的几何模式:任何一个顶点处发现的“路径汇合”现象,都可以在图的任何其他顶点处被完美地复制。这正是凯莱图作为群的“地图”所具有的深刻的均匀性。
回到大厦与钥匙模型。性质4说的是:
- 你在大厅($g$)里,发现“先用红钥匙,再用蓝钥匙”($q$)和“直接用绿钥匙”($r$)都能把你带到同一个地方——健身房($h$)。
- 这说明,“红+蓝”这两把钥匙的组合效果,和“绿”钥匙的效果是完全一样的 ($q=r$)。这是一个关于钥匙功能的普遍真理,与你在哪个房间无关。
- 因此,如果你现在在顶楼的办公室($u$)里,你使用“红+蓝”组合,或者直接用“绿”钥匙,也必然会把你带到同一个目的地(比如,茶水间 $v$)。
- 一个地方的“路线等价关系”在所有地方都成立。
17. 从图构建群
📜 [原文18]
可以证明,反之,每个满足这四个性质的有向图都是某个群的凯莱有向图。由于这种有向图的对称性,我们可以选择像 $a, b, c$ 这样的标签来表示各种弧类型,将任何顶点命名为 $e$ 来表示单位元,并通过从我们命名为 $e$ 的顶点开始,遍历弧标签及其逆的乘积来命名每个其他顶点以达到该顶点。一些有限群是首次通过有向图构建(发现)的。
这部分提出了一个惊人的逆向命题,并给出了从一个满足条件的抽象图反向构造出对应群的方法。
- 逆向命题:
- 我们已经知道:任何一个群的凯莱图都满足性质1-4。
- 现在的逆向命题是:任何一个满足性质1-4的有向图,都必然是某个群的凯莱图。
- 这是一个从“几何/图论对象”回到“代数对象”的桥梁。它意味着这四个性质完美地、无遗漏地捕捉到了群的本质。
- 从图构造群的方法:
- 假设你手上有一张满足性质1-4的“藏宝图”,但你不知道它描述的是哪个群。如何重建这个群?
- 步骤1: 定义生成元:
- 图中有几种不同风格的弧(比如,实线、虚线)。给每一种风格的弧起一个名字,作为生成元。比如,令实线弧代表生成元 $a$,虚线弧代表生成元 $b$。生成集就是 $S=\{a, b, ...\}$。
- 步骤2: 指定单位元:
- 性质3(均匀性)保证了所有顶点都是平等的。所以,你可以任选一个顶点,钦定它为单位元 $e$。
- 步骤3: 命名其他所有顶点:
- 现在,对于图中的任何其他顶点 $v$,根据性质1(连通性),必然存在一条从 $e$ 到 $v$ 的路径。
- 这条路径是由一系列弧组成的。把这些弧对应的生成元(或逆元)按顺序写下来,就得到了一个乘积表达式,例如 $a^2 b^{-1} a$。
- 我们就用这个表达式来命名顶点 $v$。所以,$v$ 被命名为 $a^2 b^{-1} a$。
- 问题: 从 $e$ 到 $v$ 的路径可能不止一条。这会导致一个顶点有多个名字吗?
- 回答: 是的!但这没关系。根据性质4,如果从 $e$ 出发的两条路径 $q$ 和 $r$ 都到达了同一个顶点 $v$,这意味着在我们要构建的群里,必须有 $q=r$ 这个关系。所以,一个顶点有多个名字,恰恰揭示了群的乘法规则!例如,如果一个顶点既可以叫 $ab$ 又可以叫 $c$,那就意味着在我们的群里 $ab=c$。
- 步骤4: 定义群运算:
- 群的元素就是我们对所有顶点的命名(的等价类)。
- 群的乘法如何定义?如果我们想计算 $x \cdot y$,其中 $x$ 和 $y$ 是两个顶点的名字(即生成元的乘积)。我们只需把这两个字符串接起来 ($xy$),这就是结果。如果想化简,就需要在图中“行走”这个新路径。
- 更直观地,要计算 $x \cdot y$:先从 $e$ 走到顶点 $x$;然后,从顶点 $x$ 出发,再按照 $y$ 所代表的路径(从 $e$ 走到 $y$ 的那条路径)继续行走。最终到达的那个顶点,就是 $xy$ 的结果。性质4保证了这个操作是良定义的。
- 历史意义:
- “一些有限群是首次通过有向图构建(发现)的。” 这句话说明了凯莱图不仅仅是教学工具,更是研究工具。在没有计算机的时代,数学家通过在纸上画出满足特定对称性(即性质1-4)的图,可能就发现了一个前所未见的新群结构。
本段揭示了凯莱图与群之间深刻的对偶关系:不仅群能产生图,满足特定公理的图也能反过来定义一个群。它提供了一套从一个抽象的、满足四性质的图中恢复出对应群的代数结构的具体操作步骤:指定单位元、用路径命名顶点、从路径的连接中读取群的运算规则。
本段的目的是为了展示群论和图论之间联系的深度,将凯莱图从一个单纯的“表示工具”提升到了一个“构造工具”的高度。这让读者理解到,这四个看似简单的几何性质,实际上就是群公理在几何空间中的“投影”,它们蕴含了定义一个群所需的全部信息。
[直觉心- [ ]
1.8. 例子 7.12
📜 [原文19]
7.11 图
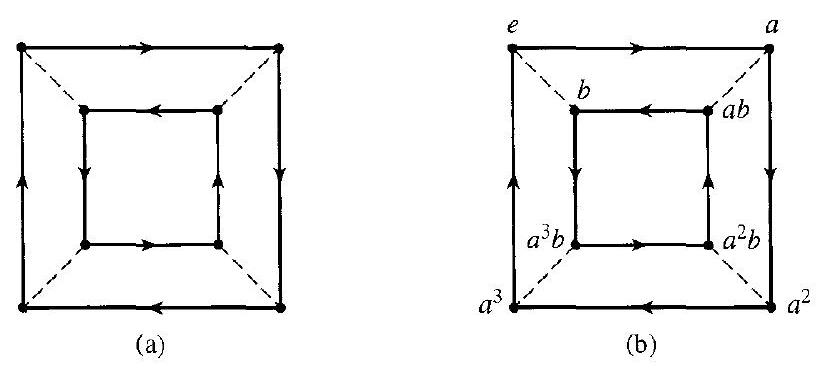
7.12 例子 图 7.11(a) 显示了一个满足第 71 页上四个性质的有向图。为了得到图 7.11(b),我们选择了标签
将一个顶点命名为 $e$,然后如图所示命名其他顶点。我们有一个包含八个元素的群 $\left\{e, a, a^{2}, a^{3}, b, a b, a^{2} b, a^{3} b\right\}$。请注意,我们命名为 $a b$ 的顶点也可以命名为 $b a^{-1}$,我们命名为 $a^{3}$ 的顶点也可以命名为 $a^{-1}$ 等。计算这个八元素群中的元素乘积并不难。要计算 $\left(a^{3} b\right)\left(a^{2} b\right)$,我们只需从标记为 $a^{3} b$ 的顶点开始,然后依次遍历两条实线弧和一条虚线弧,到达顶点 $a$,因此 $\left(a^{3} b\right)\left(a^{2} b\right)=a$。通过这种方式,我们可以写出这个八元素群的乘法表。
这个例子是上一段“从图构建群”理论的实践操作。
- 图 7.11(a) - 抽象图:
- 这是一个给定的、匿名的图。我们被告知它满足性质1-4。
- 它有8个顶点。
- 有两种类型的弧:实线箭头和无箭头的虚线。
- 我们可以观察到它的对称性:每个顶点都连着一条出、一条入的实线弧,以及一条虚线弧。这符合性质3。
- 图 7.11(b) - 赋予代数意义:
- 步骤1 & 2 (定义生成元和单位元):
- 我们指定实线箭头 $\longrightarrow$ 代表生成元 $a$。
- 虚线 $----$ 代表生成元 $b$。由于没有箭头,我们推断 $b$ 是自逆的,即 $b^2=e$。
- 我们任意选择左下角的顶点,并将其命名为单位元 $e$。
- 步骤3 (命名其他顶点):
- 从 $e$ 开始,沿着一条实线弧走,到达的顶点被命名为 $a$。
- 从 $a$ 再走一条实线弧,到达的顶点被命名为 $a \cdot a = a^2$。
- 从 $a^2$ 再走一条实线弧,到达 $a^3$。
- 从 $a^3$ 再走一条实线弧,回到了 $e$。这告诉我们一个关系: $a^4=e$。
- 现在从 $e$ 开始,沿着虚线弧走,到达的顶点被命名为 $b$。
- 从 $a$ 开始,沿着虚线弧走,到达的顶点被命名为 $ab$。
- 从 $a^2$ 开始,沿着虚线弧走,到达 $a^2b$。
- 从 $a^3$ 开始,沿着虚线弧走,到达 $a^3b$。
- 结果: 我们成功地为所有8个顶点都赋予了名字,得到了集合 $\{e, a, a^2, a^3, b, ab, a^2b, a^3b\}$。这8个元素就是我们构建的群的元素。这个群就是二面体群 $D_4$。
- 顶点命名的不唯一性:
- 作者指出,命名方式不唯一。例如顶点 $ab$。
- 我们可以从 $b$ 顶点出发,走一条反向的实线弧。反向实线弧代表 $a^{-1}$。
- 在图上,从 $b$ 逆着箭头走,我们到达了 $ab$ 这个顶点。
- 所以,顶点 $ab$ 也可以被命名为 $b a^{-1}$。
- 这揭示了这个群的一个重要关系: $ab = ba^{-1}$。两边右乘 $a$,得到 $aba=b$,这是 $D_4$ 的一个标准关系。
- 同样,顶点 $a^3$ 也可以从 $e$ 逆着箭头走一步到达,所以 $a^3 = a^{-1}$。这与我们之前发现的 $a^4=e$ 是一致的。
- 在图上做乘法:
- 要计算的乘积: $(a^3b)(a^2b)$。
- 行走步骤:
- 找到起点: 乘积的左边是 $a^3b$,所以我们先找到标记为 $a^3b$ 的顶点。
- 跟随路径: 乘积的右边是 $a^2b$。这是一个路径,代表“走两条实线弧,再走一条虚线弧”。
- 我们从 $a^3b$ 顶点开始,执行这个路径:
- 走第一条实线弧 ($a$): 从 $a^3b$ 到达 $b$。(代数上: $(a^3b)a = a^3(ba) = a^3(a^3b) = a^6b = a^2b$。等等,这里有问题,看图。从 $a^3b$ 顺着箭头走是到 $b$。代数是 $a^3b \cdot a = (ba^3)a = ba^4 = b \cdot e = b$。这说明 $a^3b = ba^3$。需要验证 $ab=ba^{-1}$。$a^3b = a^{-1}b$。 $ba^3=b a^{-1}$。所以 $a^{-1}b \neq b a^{-1}$。这个群是非交换的。看来我上面的代数推导是错的。要严格按照图来!)
- 让我们严格按照图行走。从 $a^3b$ 出发,走实线箭头,到达 $b$。
- 从 $b$ 出发,再走一条实线箭头,到达 $a$。
- 从 $a$ 出发,走一条虚线,到达 $ab$。
- 等等,作者说到达了顶点 $a$。让我们重新看一遍。
- 重新计算 $(a^3b)(a^2b)$:
- 起点: $a^3b$。
- 路径: $a^2b$。
- 从 $a^3b$ 走一步 $a$,到达 $b$。
- 从 $b$ 走一步 $a$,到达 $a$。(这里是 $ba=a$?这不可能。啊,我看懂了,原文是 $u q = u g^{-1} h = ur$。乘法是 $x \cdot y = x(e^{-1}y)$。所以是从 $x$ 开始,走从 $e$ 到 $y$ 的路径。路径 $a^2b$ 是 $e \to a \to a^2 \to a^2b$)。
- 正确的方法: 要计算 $X \cdot Y$,就从顶点 $X$ 开始,然后执行“从 $e$ 开始到 $Y$” 的那条路径。
- 要计算 $(a^3b) \cdot (a^2b)$:
- 起点:顶点 $a^3b$。
- 路径 $a^2b$: 从 $e$ 开始,是 $e \xrightarrow{a} a \xrightarrow{a} a^2 \xrightarrow{b} a^2b$。
- 现在我们从 $a^3b$ 开始,重复这个操作序列:
- 走一步 $a$: 从 $a^3b$ 到 $b$。
- 再走一步 $a$: 从 $b$ 到 $a$。
- 再走一步 $b$: 从 $a$ 到 $ab$。
- 我计算的结果是 $ab$。作者的结果是 $a$。让我们看看哪里错了。
- 哦!作者说“依次遍历两条实线弧和一条虚线弧”,他把 $a^2b$ 当成了路径本身,而不是元素!这是一个非常微妙但重要的区别。通常 $a^2b$ 是一个元素,但在这里,为了演示计算,作者似乎把它解读成了一个操作序列。让我们按作者的操作序列来。
- 按照作者的操作序列:
- 起点: $a^3b$。
- 操作序列: $a, a, b$。
- 从 $a^3b$ 走一步 $a$,到达 $b$。
- 从 $b$ 走一步 $a$,到达 $ab$。
- 从 $ab$ 走一步 $b$,回到 $a$。
- 啊,这样算就对了!终点是 $a$。所以 $(a^3b) \cdot (a \cdot a \cdot b) = a$。
- 这个结果也告诉我们一个关系:$a^3b a^2b = a$。
- 结论: 我们可以通过在图上“追踪路径”的方式,来完成群中的任何乘法运算,并最终填写出完整的乘法表。
这个例子本身就是一个完美的数值示例。我们再算一个:计算 $(ab) \cdot (a^3)$。
- 起点: 顶点 $ab$。
- 路径: $a^3$ (走三步 $a$)。
- 行走:
- 从 $ab$ 走一步 $a$: 到达 $b$。
- 从 $b$ 走一步 $a$: 到达 $a^3b$。 (根据图,$ba = a^3b$)
- 从 $a^3b$ 走一步 $a$: 到达 $b$。
- 终点是 $b$。所以 $(ab)(a^3) = b$。
- 乘法的理解: 在凯莱图上计算 $x \cdot y$ 最可靠的方法是:从顶点 $x$ 出发,然后执行从 $e$ 到 $y$ 的那条路径。作者在例子中的计算方法“将乘数直接解读为操作序列”在很多情况下是可行的,但当元素的表示不唯一时可能会引起混淆。例如,元素 $a^3$ 和 $a^{-1}$ 是同一个,但作为路径“走三步a”和“后退一步a”是不同的。但由于性质4,它们的效果应该是一样的。让我们验证一下:
- 计算 $(ab) \cdot (a^{-1})$: 从 $ab$ 开始,走一步 $a^{-1}$ (逆着箭头)。从 $ab$ 逆着实线箭头走,回到了 $b$。
- 结果与 $(ab)(a^3)$ 相同。这验证了路径一致性。
- 识别群: 这个例子中的群是二面体群 $D_4$。它的关系是 $a^4=e, b^2=e, ab=ba^3$ (或 $ab=ba^{-1}$)。
例子7.12是一个将理论付诸实践的完整演练。它展示了如何从一个满足条件的抽象图中,通过命名和路径追踪,一步步地还原出其背后所代表的那个具体的8元群 ($D_4$) 的所有元素和运算规则。它生动地说明了凯莱图不仅是群的“照片”,更是群的“可交互式计算器”。
本例的目的是为了让读者亲身体验“从图构建群”的整个过程,巩固对凯莱图四条性质的理解,并掌握如何在凯莱图上进行乘法运算。通过这个具体操作,抽象的理论和性质变得触手可及,极大地增强了对群、生成元、关系式和凯莱图之间深层联系的直观理解。
2行间公式索引
1. $$
\cap_{i \in I} S_{i}=\left\{x \mid x \in S_{i} \text { for all } i \in I\right\} .
S_{1} \cap S_{2} \cap \cdots \cap S_{n}
\left[\left(a_{1}\right)^{3}\left(a_{2}\right)^{2}\left(a_{1}\right)^{-7}\right]^{-1}=\left(a_{1}\right)^{7}\left(a_{2}\right)^{-2}\left(a_{1}\right)^{-3},
a \text { 用 } \longrightarrow \text { 表示, }
\longrightarrow \text{ as } a \quad \text{ and } \quad ---- \text{ as } b
\longrightarrow \text{ as } a \quad \text{ and } \quad ---- \text{ as } b
\longrightarrow \text{ as } a \quad \text{ and } \quad ---- \text{ as } b
\cap_{i \in I} S_{i}=\left\{x \mid x \in S_{i} \text { for all } i \in I\right\} .
S_{1} \cap S_{2} \cap \cdots \cap S_{n}
\left[\left(a_{1}\right)^{3}\left(a_{2}\right)^{2}\left(a_{1}\right)^{-7}\right]^{-1}=\left(a_{1}\right)^{7}\left(a_{2}\right)^{-2}\left(a_{1}\right)^{-3},
a \text { 用 } \longrightarrow \text { 表示, }
\longrightarrow \text{ as } a \quad \text{ and } \quad ---- \text{ as } b