11. 二面体群 (Dihedral Groups)
1.1 二面体群的引入
11.1 几何对称性的群
📜 [原文1]
群的一个重要例子家族是其元素为几何对象的对称的群。最简单的子类是当几何对象为正平面图形时。
这段话是二面体群学习的开篇,它为我们引入了一个非常直观和重要的群的例子来源:几何对象的对称性。
- 群 (Group):首先,回忆一下群是一个数学结构,它包含一个集合和在这个集合上的一个二元运算,这个运算满足一些特定的规则(封闭性、结合律、有单位元、有逆元)。我们之前可能接触过数字组成的群,比如整数加法群 $(\mathbb{Z}, +)$。
- 几何对象的对称 (Symmetry of a Geometric Object):现在,作者告诉我们,群的元素不一定非得是数字,它们也可以是“动作”或“变换”。这里的“对称”就是一个动作。什么样的动作算是对称呢?就是一个你对一个几何图形(比如一个正方形)进行一番操作后,它看起来跟没动过一样。比如,你把一个正方形旋转90度,它仍然占据着完全相同的空间,看起来和原来一模一样。这个“旋转90度”的动作就是一个对称操作。
- 对称的集合构成群:关键思想是,所有这些对称操作的集合,再加上“接连进行操作”这个二元运算(称为运算复合),可以构成一个群。比如,先旋转90度,再旋转180度,效果等于一次性旋转270度。这个新的操作(旋转270度)也必须是这个对称集合里的一员(封闭性)。
- 正平面图形 (Regular Planar Figures):为了让问题简化,我们从最简单的几何对象开始研究,也就是二维平面上的正多边形,例如正三角形、正方形、正五边形等。这些图形的对称性最容易分析,它们对应的群就是我们即将要学习的二面体群。
本段没有公式。
- 示例1:正方形的对称
想象一个放在桌面上的正方形卡片。
- 旋转对称:你可以把它顺时针旋转90度、180度、270度,它看起来都和原来一样。旋转360度(或0度)也算,这是“不动”操作。这些都是旋转对称。
- 翻转对称:你可以沿着水平中线、垂直中线,或者两条对角线把它翻过来,它也和原来一样。这些都是翻转对称。
- 所有这些操作(4个旋转 + 4个翻转)的集合,就构成了正方形的对称群,我们后面会学到它叫 $D_8$。
- 示例2:等边三角形的对称
想象一个等边三角形卡片。
- 旋转对称:你可以把它顺时针旋转120度、240度。旋转360度(或0度)也算。
- 翻转对称:你可以沿着三条顶点到对边中点的连线(高线)进行翻转。
- 所有这些操作(3个旋转 + 3个翻转)的集合,构成了等边三角形的对称群,也就是 $D_6$。
- 对称是动作,不是图形本身:群的元素是“旋转”、“翻转”这些刚体运动,而不是顶点或者边。
- “看起来一样”的严格定义:指的是图形在变换后,其占据的空间范围和原来完全重合。每个顶点都移动到了之前某个顶点的位置上。
- 不是所有图形都有很多对称:一个不规则的四边形可能除了“不动”之外没有任何对称操作。我们从正多边形入手正是因为它们具有丰富的、规律的对称性。
本段引入了从几何对称角度来理解群的概念。它指出,一个正多边形的所有对称操作(即那些让图形看起来不变的刚体运动)的集合,在“连续操作”(运算复合)下,会形成一个群。
这一段的目的是为二面体群的定义铺平道路。它通过一个具体、直观的例子(几何对称)来引入一类新的、重要的群,使得抽象的群论概念与现实世界中的几何直觉联系起来。
想象你手里有一块正多边形的木板,还有一个和它完全一样的模具(或者在纸上画出它的轮廓)。你把木板拿起来,在空中随意旋转、翻转,然后再放回模具里。只要它能完美地放回去,你刚才做的这一整套动作就构成了一个对称操作。这个对称群就是所有能让木板完美归位的操作方法的集合。
盯着一个正方形。闭上眼睛,让别人把它旋转一个角度或者翻转一下。你睁开眼睛,如果看不出任何变化,那么别人做的就是一个对称操作。二面体群就是研究所有这些“看不出变化”的操作的集合。
11.2 二面体群的定义与阶
📜 [原文2]
对于每个 $n \in \mathbb{Z}^{+}, n \geq 3$,令 $D_{2 n}$ 为正 $n$ 边形的对称集,其中对称是 $n$ 边形的任何刚体运动,这种运动可以通过取 $n$ 边形的一个副本,在三维空间中以任何方式移动此副本,然后将该副本放回原始 $n$ 边形上使其完全覆盖它来实现。更精确地,我们可以通过首先选择 $n$ 个顶点的标记来描述这些对称,例如如下图所示。
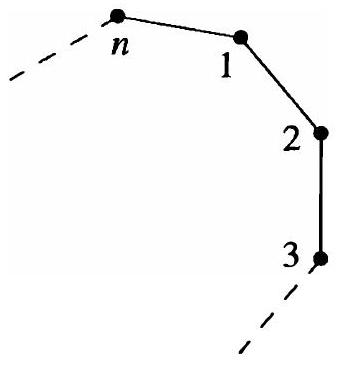
然后,每个对称 $s$ 可以通过对应的 $\{1,2,3, \ldots, n\}$ 上的置换 $\sigma$ 唯一描述,其中如果对称 $s$ 将顶点 $i$ 放到原来顶点 $j$ 所在的位置,则 $\sigma$ 是将 $i$ 映射到 $j$ 的置换。例如,如果 $s$ 是一个绕 $n$ 边形中心顺时针旋转 $2 \pi / n$ 弧度的旋转,则 $\sigma$ 是将 $i$ 映射到 $i+1,1 \leq i \leq n-1$ 的置换,且 $\sigma(n)=1$。现在将 $D_{2 n}$ 变成一个群,通过定义 $s, t \in D_{2 n}$ 的 $st$ 为首先对 $n$ 边形应用 $t$ 然后应用 $s$ 得到的对称(注意我们将对称视为 $n$ 边形上的函数,因此 $st$ 只是函数复合——像往常一样从右到左阅读)。如果 $s, t$ 分别在顶点上实现置换 $\sigma, \tau$,则 $st$ 实现 $\sigma \circ \tau$。 $D_{2 n}$ 上的二元运算是结合的,因为函数复合是结合的。 $D_{2 n}$ 的单位元是恒等对称(它使所有顶点保持不变),表示为 $1$,而 $s \in D_{2 n}$ 的逆元是对称,它反转 $s$ 的所有刚体运动(因此如果 $s$ 实现置换 $\sigma$ 在顶点上, $s^{-1}$ 实现 $\sigma^{-1}$)。在下一段中我们展示
因此 $D_{2 n}$ 称为阶为 $2 n$ 的二面体群。在某些文献中,此群记为 $D_{n}$;然而, $D_{2 n}$(其中下标表示群的阶而不是顶点的数量)在群论文献中更常见。
这段话给出了二面体群 $D_{2n}$ 的严格定义,并解释了为什么它是一个群。
- 定义 $D_{2n}$:
- 对象:一个正 $n$ 边形,其中 $n \geq 3$(三角形、四边形等,两边形和一边形无法构成平面图形)。
- 元素: $D_{2n}$ 的元素是这个正 $n$ 边形的所有对称操作。
- 对称的定义 (刚体运动):一个对称操作是一个刚体运动。这意味着在运动过程中,图形本身不能被弯曲、拉伸或压缩,任意两点间的距离保持不变。就像把一个硬纸板模型拿起来移动一样。最终,移动后的图形必须完美地覆盖原来的位置。
- 用置换来描述对称:
- 为了精确地描述一个对称操作,我们给 $n$ 个顶点编号,从 1 到 $n$。
- 一个对称操作会使顶点发生移动。原来在位置 $i$ 的顶点,经过操作后,会跑到原来位置 $j$ 的地方。
- 我们可以用一个置换 (permutation) $\sigma$ 来记录这个变化:$\sigma(i) = j$。置换本质上是一个从集合 $\{1, 2, ..., n\}$ 到其自身的一一映射。
- 每个不同的对称操作都对应一个唯一的顶点置换。因此,我们可以把研究对称操作转化为研究这些置换。
- 例子:对于一个正 $n$ 边形,顺时针旋转 $2\pi/n$ 弧度(即转过一个顶点的角度)。顶点1跑到顶点2的位置,顶点2跑到顶点3的位置,...,顶点 $n$ 跑回顶点1的位置。对应的置换 $\sigma$就是:$\sigma(1)=2, \sigma(2)=3, ..., \sigma(n-1)=n, \sigma(n)=1$。
- 群的结构:
- 二元运算 (Binary Operation):定义为运算复合 (composition)。$st$ 的意思“先做 $t$ 操作,再做 $s$ 操作”。这和函数复合 $f(g(x))$ 的顺序 $g$ first, $f$ second 是一致的,所以要从右往左读。因为做完 $t$ 和 $s$ 之后,图形仍然是对称的,所以这个运算是封闭的。
- 结合律 (Associativity):$(st)u = s(tu)$。这可以直接从函数复合的结合律继承而来。先做 $u$,再做 $t$,再做 $s$ 的最终结果,和你先计算“$t$ 之后是 $u$”的结果 ($tu$) 再进行 $s$ 操作,或者先计算“$s$ 之后是 $t$”的结果 ($st$) 再进行 $u$ 操作,是一样的。
- 单位元 (Identity Element):就是“什么都不做”的操作,称为恒等对称,记为 $1$。它让所有顶点都保持在原位。
- 逆元 (Inverse Element):对于任何一个对称操作 $s$,总存在一个逆操作 $s^{-1}$,它能“撤销” $s$ 的效果。比如,如果 $s$ 是顺时针旋转90度,那么 $s^{-1}$ 就是逆时针旋转90度(或者顺时针旋转270度)。连续进行 $s$ 和 $s^{-1}$ 操作,就等于什么都没做。
- 群的阶 (Order of a Group):
- 阶指的是群中元素的个数,记为 $|G|$。
- 作者在这里预告,后面会证明正 $n$ 边形的对称操作总共有 $2n$ 个。
- 因此,这个群的阶是 $2n$,记为 $|D_{2n}|$。下标 $2n$ 直接表示了群的阶。
- 符号约定:
- 本书采用 $D_{2n}$ 的记法,强调其阶为 $2n$。
- 有些书会记为 $D_n$,用下标 $n$ 代表 $n$ 边形。在使用不同教材时需要注意这个区别。例如,正方形的对称群,本书中是 $D_8$,在其他书中可能是 $D_4$。
- $D_{2n}$:表示正 $n$ 边形的二面体群。下标 $2n$ 是一个符号约定,代表这个群的阶。
- $|\cdot|$:这个竖线符号在这里表示集合的基数(cardinality),也就是集合中元素的数量。当应用于一个群时,它表示群的阶。
- $2n$:一个代数表达式,表示两倍的 $n$。
- 推导:这在当前段落是一个结论的陈述,而非推导。其推导过程在下一段中给出。它断言:对于一个有 $n$ 个顶点的正多边形,总共有 $2n$ 种不同的刚体运动可以使其自身重合。
- 示例1:$D_6$ (正三角形, $n=3$)
- $n=3$,所以群的阶是 $|D_{2\cdot3}| = |D_6| = 6$。
- 顶点标记:给正三角形的三个顶点标记为1, 2, 3。
- 对称操作:
- 恒等操作 (单位元):不动。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}$。
- 旋转120度 ($r$):顶点1->2, 2->3, 3->1。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}$。
- 旋转240度 ($r^2$):顶点1->3, 3->2, 2->1。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}$。
- 沿顶点1的高线翻转 ($s_1$):顶点1不动, 2和3互换。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}$。
- 沿顶点2的高线翻转 ($s_2$):顶点2不动, 1和3互换。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$。
- 沿顶点3的高线翻转 ($s_3$):顶点3不动, 1和2互换。置换为 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$。
- 运算复合:我们来计算 $r \cdot s_1$(先翻转 $s_1$,再旋转 $r$)。
- 初始状态:(1, 2, 3)
- 应用 $s_1$(2,3互换):(1, 3, 2)
- 应用 $r$(1->2, 2->3, 3->1):(2, 1, 3)
- 最终结果是 (2, 1, 3)。我们看原始的 (1, 2, 3) 是如何变化的:顶点1到了位置2,顶点2到了位置1,顶点3到了位置3。
- 这对应的置换是 $\begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix}$,这正是 $s_3$ 操作。所以 $r s_1 = s_3$。
- 运算顺序:$st$ 是先 $t$ 后 $s$。这是函数复合的标准,但和我们从左到右的阅读习惯相反,非常容易搞错。
- $D_{2n}$ vs $D_n$:一定要注意你正在阅读的文献使用的是哪种约定。本书用 $D_{2n}$,下标是阶。
- $n \ge 3$ 的限制:$n=1$ 或 $n=2$ 无法在平面上构成一个“多边形”,无法形成有意义的翻转。一个线段($n=2$)的对称群只有两个元素:不动和旋转180度,它的结构比较退化,通常不包含在二面体群的一般讨论中。
- 刚体运动:“在三维空间中移动”这个描述很重要。翻转一个平面的多边形,必须将它“抬起”到第三维空间,才能翻过来再放下。
本段给出了二面体群 $D_{2n}$ 的形式化定义。它是一个由正 $n$ 边形的所有对称操作(刚体运动)构成的集合,其二元运算是运算复合。通过将对称操作与顶点置换相关联,我们可以精确地描述和计算这些操作。该群的阶(元素总数)为 $2n$。
本段的目的是建立二面体群的严格数学框架。它不仅定义了研究对象($D_{2n}$),还确认了它满足群的所有公理(封闭性、结合律、单位元、逆元),从而证明它确实是一个群。这为后续深入分析其结构(如计算其阶、寻找生成元和关系)奠定了基础。
[直觉心-智模型]
将二面体群 $D_{2n}$ 想象成一个“操作手册”。这本手册描述了所有能让一个正 $n$ 边形“完美归位”的动作。手册的每一页是一个动作(比如“顺时针旋转90度”)。手册还告诉你如何“组合”两个动作(比如“先做A,再做B,效果等同于C”)。这个手册里的所有内容,就是一个完整的数学系统——一个群。
想象你有一把万能钥匙和一个有 $n$ 个齿的锁。这把锁的特殊之处在于,钥匙插进去转动(旋转)或者翻个面再插进去(翻转),只要能打开锁,这个钥匙的操作就是一个对称。$D_{2n}$ 就是这把万能钥匙所有可能开锁的动作的集合。
11.3 计算二面体群的阶
📜 [原文3]
为了找到阶 $\left|D_{2 n}\right|$,观察到给定任何顶点 $i$,存在一个将顶点 $1$ 送入位置 $i$ 的对称。由于顶点 $2$ 与顶点 $1$ 相邻,顶点 $2$ 必须落在位置 $i+1$ 或 $i-1$(其中 $n+1$ 是 $1$,$1-1$ 是 $n$,即顶点的整数标签以模 $n$ 方式读取)。此外,通过在第一次对称之后进行一次关于通过顶点 $i$ 和 $n$ 边形中心的线的反射,可以看到顶点 $2$ 可以通过某个对称发送到位置 $i+1$ 或 $i-1$。因此,有序顶点对 $1,2$ 在应用对称后有 $n \cdot 2$ 个可能的位置。由于对称是刚体运动,可以看到一旦有序顶点对 $1,2$ 的位置被指定,对称对所有剩余顶点的作用就完全确定了。因此正 $n$ 边形恰好有 $2 n$ 个对称。我们还可以明确地展示 $2 n$ 个对称。这些对称是绕中心旋转 $2 \pi i / n$ 弧度的 $n$ 个旋转,$0 \leq i \leq n-1$,以及通过 $n$ 条对称轴的 $n$ 个反射(如果 $n$ 为奇数,每条对称轴都通过一个顶点和对边的中点;如果 $n$ 为偶数,则有 $n/2$ 条对称轴通过两个相对的顶点,另有 $n/2$ 条对称轴垂直平分两条相对的边)。例如,如果 $n=4$ 且我们在 $x, y$ 平面原点处绘制一个正方形,则对称轴是
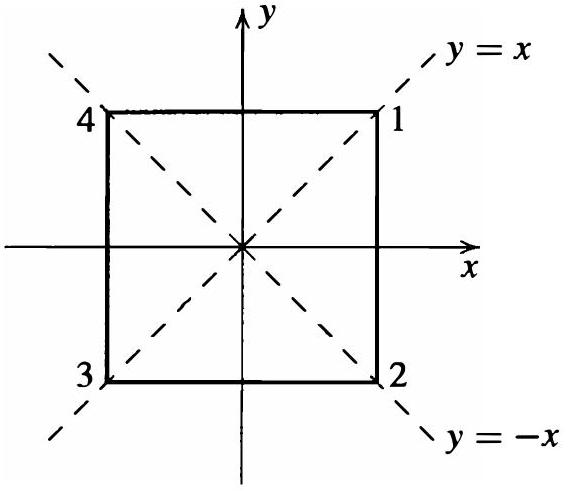
直线 $x=0$( $y$ 轴), $y=0$( $x$ 轴), $y=x$ 和 $y=-x$(注意通过原点的“反射”不是反射而是一个 $\pi$ 弧度的旋转)。
这段话用两种方法来证明 $|D_{2n}| = 2n$。
方法一:基于顶点位置的计数论证
- 确定一个顶点的最终位置:我们来追踪顶点1的去向。通过旋转,我们可以把顶点1移动到任意一个顶点的位置上(从位置1到位置n,共 $n$ 种选择)。例如,想把顶点1移动到位置 $i$,只需将整个多边形旋转 $(i-1) \cdot (2\pi/n)$ 弧度即可。所以,顶点1的最终位置有 $n$ 种可能性。
- 确定相邻顶点的最终位置:现在,我们来看顶点2。因为对称是刚体运动,它必须保持顶点之间的邻接关系。顶点2原来是顶点1的邻居。当顶点1被移动到位置 $i$ 后,顶点2必须移动到位置 $i$ 的邻居那里。位置 $i$ 有两个邻居:位置 $i+1$ 和位置 $i-1$。(这里的加减法是在模 $n$ 的意义下,即 $n+1$ 就是 $1$,$1-1$ 就是 $n$)。所以,顶点2的最终位置只有 $2$ 种可能性。
- 组合可能性:
- 顶点1的去向有 $n$ 种选择。
- 对于每一种顶点1的去向,顶点2的去向有 $2$ 种选择。
- 所以,有序顶点对 (1, 2) 的最终位置组合有 $n \times 2 = 2n$ 种。
- 唯一确定性:一旦我们固定了相邻两个顶点(如1和2)的最终位置,整个多边形就被“钉死”了。因为所有其他顶点与1和2的相对位置是固定的(刚体运动保持距离和角度),所以所有其他顶点的最终位置也随之唯一确定。
- 结论:由于有序顶点对 (1, 2) 有 $2n$ 种可能的最终位置,并且每一种位置组合都唯一地对应一个对称操作,所以总共有 $2n$ 个对称操作。因此,群的阶是 $2n$。
方法二:直接枚举所有对称操作
- 旋转 (Rotations):
- 我们可以将正 $n$ 边形绕其中心旋转。
- 旋转的角度必须是 $2\pi/n$ 的整数倍,才能使图形重合。
- 这些旋转是:旋转 $0 \cdot (2\pi/n)$ (不动), $1 \cdot (2\pi/n)$, $2 \cdot (2\pi/n)$, ..., $(n-1) \cdot (2\pi/n)$。
- 旋转 $n \cdot (2\pi/n) = 2\pi$ 就等于旋转0度,回到了起点。
- 所以,总共有 $n$ 个不同的旋转操作。
- 反射 (Reflections) / 翻转:
- 我们还可以通过对称轴来翻转多边形。
- 总共有 $n$ 条这样的对称轴。
- 当 $n$ 是奇数时 (如正三角形, $n=3$):每条对称轴都从一个顶点出发,连接到对边的中点。有 $n$ 个顶点,所以有 $n$ 条这样的轴。
- 当 $n$ 是偶数时 (如正方形, $n=4$):有两种对称轴。
- 一种是连接一对相对的顶点。有 $n/2$ 对相对顶点,所以有 $n/2$ 条这样的轴。
- 另一种是连接一对相对的边的中点。有 $n/2$ 对相对的边,所以有 $n/2$ 条这样的轴。
- 总计 $n/2 + n/2 = n$ 条轴。
- 所以,无论 $n$ 是奇是偶,总有 $n$ 个不同的翻转操作。
- 结论:
- $n$ 个旋转 + $n$ 个翻转 = $2n$ 个对称操作。
- 这两种操作是完全不同的(没有一个旋转可以等同于一个翻转),并且已经包含了所有可能性。
- 所以,群的阶是 $2n$。
关于正方形对称轴的例子:
对于一个中心在原点的正方形($n=4$),它的四个顶点可以设为 $(1,1), (-1,1), (-1,-1), (1,-1)$。
- $x=0$ ($y$轴) 和 $y=0$ ($x$轴) 是连接对边中点的对称轴。
- $y=x$ 和 $y=-x$ 是连接相对顶点的对称轴。
- 这总共是4条对称轴,对应4个翻转操作。
- 注意:“通过原点的反射” (point reflection),即 $(x,y) \to (-x, -y)$,在二维平面上它等价于绕原点旋转180度($\pi$弧度),所以它是一个旋转操作,而不是我们这里讨论的轴对称反射。
本段没有新的公式,主要是对上一段 $|D_{2n}|=2n$ 的证明。
- 示例1:正五边形 ($n=5$, 奇数)
- 计数法:顶点1可以去5个位置中的任意一个。确定后,顶点2可以去相邻的2个位置。所以总共有 $5 \times 2 = 10$ 个对称操作。$|D_{10}|=10$。
- 枚举法:
- 旋转:旋转 $0^\circ, 72^\circ, 144^\circ, 216^\circ, 288^\circ$。共5个。
- 翻转:5条对称轴,每条都从一个顶点连接到对边的中点。共5个。
- 总计 $5+5=10$ 个。
- 示例2:正六边形 ($n=6$, 偶数)
- 计数法:顶点1可以去6个位置中的任意一个。确定后,顶点2可以去相邻的2个位置。所以总共有 $6 \times 2 = 12$ 个对称操作。$|D_{12}|=12$。
- 枚举法:
- 旋转:旋转 $0^\circ, 60^\circ, 120^\circ, 180^\circ, 240^\circ, 300^\circ$。共6个。
- 翻转:
- 连接相对顶点的轴有 $6/2 = 3$ 条。
- 连接相对边中点的轴有 $6/2 = 3$ 条。
- 总共有 $3+3=6$ 条对称轴,对应6个翻转。
- 总计 $6+6=12$ 个。
- 混淆两种计数方法:第一种方法是抽象的、基于组合的论证。第二种是具体的、基于几何构造的论证。两者殊途同归。
- 偶数 $n$ 的对称轴:初学者容易只想到连接顶点的对称轴,而忘记了连接边中点的轴。
- 旋转与反射的区分:要清楚地认识到旋转操作保持了顶点的原始顺序(比如顺时针1-2-3-..),而反射操作会逆转这个顺序(变成逆时针1-2-3-..)。因此,任何旋转都不可能是一个反射。
- 关于“通过原点的反射”:在二维情况下,中心对称等价于旋转180度。但在三维空间中,点反射(inversion)是一个独立的操作,它不等同于任何旋转。由于我们这里考虑的是平面图形在三维空间中的刚体运动,所以上下文很重要,这里的“反射”特指轴对称。
本段通过两种不同的方法——“顶点位置计数”和“直接枚举旋转与反射”——清晰地证明了正 $n$ 边形的对称群 $D_{2n}$ 的阶(元素个数)恰好为 $2n$。
本段的目的是为二面体群最重要的一个基本属性——它的阶——提供一个坚实的证明。确定群的阶是理解一个有限群结构的第一步,也是最基本的一步。
想象你在定制一把有 $n$ 个齿的钥匙。
- 首先,你要决定钥匙上的第一个标记(比如一个红点,对应顶点1)要对准锁上的哪个孔($n$ 种选择)。
- 然后,你要决定这个标记旁边的第二个标记(蓝点,对应顶点2)是在第一个孔的顺时针邻居还是逆时针邻居($2$ 种选择)。
- 一旦这两步做完,这把钥匙剩下的所有齿的位置都定死了。
- 所以,总共的钥匙样式就是 $n \times 2 = 2n$ 种。每一种样式就对应 $D_{2n}$ 里的一个元素。
拿一张正方形纸片,标上顶点1, 2, 3, 4。
- 把顶点1放到右下角(原来4的位置)。你可以直接把纸片顺时针转90度,这样2就到了左下角(原来3的位置)。
- 或者,你可以先把纸片沿垂直中线翻转,1到了左上角(原来2的位置),然后再顺时针转90度,1就到了右下角(原来4的位置),但这次2到了右上角(原来1的位置)。
- 这展示了,对于顶点1的同一种最终位置(右下角),顶点2可以有两种不同的最终位置(左下角或右上角),这对应了两种不同的对称操作。
1.2 二面体群的代数结构
12.1 生成元 $r$ 和 $s$
📜 [原文4]
由于二面体群将作为整个文本中的一个例子被广泛使用,我们固定一些符号并提及一些计算,这些计算将简化未来的计算并有助于将 $D_{2 n}$ 视为一个抽象群(而不是在每个实例中都回到几何设置)。将一个正 $n$ 边形固定在 $x, y$ 平面的原点,并按顺时针方向将顶点从 $1$ 到 $n$ 连续标记。令 $r$ 为绕原点顺时针旋转 $2 \pi / n$ 弧度的旋转。令 $s$ 为关于通过顶点 $1$ 和原点的对称轴的反射(我们对每个 $n$ 使用相同的字母,但上下文总是会使 $n$ 清楚)。
这段话的目的是从具体的几何描述过渡到更抽象的代数描述。几何直觉虽然好,但每次都去想怎么旋转翻转太麻烦了。我们希望能找到几个“基本操作”,通过组合它们来得到所有的对称操作。
- 目标:为了方便计算和理论分析,我们需要一套代数工具来描述 $D_{2n}$,而不仅仅是依赖几何图形。
- 标准化设置:
- 把正 $n$ 边形放在二维坐标系的中心。
- 按顺时针方向给顶点编号 1, 2, ..., $n$。这是一个重要的约定。
- 定义基本操作 (生成元):
- $r$ (rotation):定义为“最小单位”的顺时针旋转。也就是旋转 $2\pi/n$ 弧度($360/n$ 度),刚好让一个顶点移动到下一个顶点的位置。
- $s$ (symmetry/reflection):定义为一个特定的反射(翻转)。为了统一,我们选择“穿过顶点1和中心的对称轴”进行翻转。
- 核心思想:作者接下来将要说明,仅仅使用 $r$ 和 $s$ 这两个操作,通过反复组合(比如 $r, r^2, s, sr, rs, srs, ...$),就能够表示出 $D_{2n}$ 中的所有 $2n$ 个元素。因此,$r$ 和 $s$ 被称为生成元 (generators)。
本段没有公式,主要是符号定义。
- $r$: 代表最小单位的顺时针旋转 ($2\pi/n$ 弧度)。
- $s$: 代表沿穿过顶点1和中心的轴的反射。
- 示例1:$D_8$ (正方形, $n=4$)
- 顶点:顺时针标记为1, 2, 3, 4。假设顶点1在右上角。
- $r$:顺时针旋转 $360/4 = 90$ 度。效果:1->2, 2->3, 3->4, 4->1。
- $s$:沿穿过顶点1和中心的轴(即对角线 $y=x$)进行反射。效果:1和3不动,2和4互换。
- 示例2:$D_6$ (正三角形, $n=3$)
- 顶点:顺时针标记为1, 2, 3。假设顶点1在顶部。
- $r$:顺时针旋转 $360/3 = 120$ 度。效果:1->2, 2->3, 3->1。
- $s$:沿穿过顶点1和中心的轴(即顶点1的高线)进行反射。效果:1不动,2和3互换。
- 标记方向:本文约定是顺时针标记。如果换成逆时针,某些公式(如 $rs=sr^{-1}$)的形式可能会改变。
- $s$ 的选择:我们选择了穿过顶点1的轴。选择任何一个其他的反射作为生成元 $s$ 也能生成整个群,但得到的关系式可能会不同,尽管底层的群结构是一样的。选择一个固定的 $s$ 是为了标准化。
- 上下文中的 $n$:符号 $r$ 和 $s$ 的具体含义取决于 $n$。在 $D_8$ 中,$r$ 是旋转90度;在 $D_6$ 中,$r$ 是旋转120度。在讨论时要清楚上下文是哪个二面体群。
本段为二面体群 $D_{2n}$ 选定了两个特殊的元素作为生成元:$r$ (最小单位顺时针旋转) 和 $s$ (过顶点1的反射)。这为后续将 $D_{2n}$ 的几何描述转化为代数描述奠定了基础。
本段的目的是引入生成元的概念,这是从具体例子走向抽象代数结构的关键一步。通过少数几个生成元和它们之间的关系,我们可以完全捕捉一个群的结构,而无需再依赖其原始定义(如几何图形)。这极大地简化了分析和计算。
想象你在玩一套乐高积木。你有一大堆各式各样的积木块($D_{2n}$ 的所有元素)。现在你发现,其实只需要两种最基本的积木块($r$ 和 $s$),通过不同的方式拼接它们,就能搭出所有其他的积木块。$r$ 和 $s$ 就是你的“基础积木”,即生成元。
想象你在控制一个在圆形轨道上运动的机器人。
- $r$ 是一个按钮,按一下,机器人就顺时针走到下一个站点。
- $s$ 是另一个按钮,按一下,机器人的左右方向会颠倒(比如它之前是面向轨道外侧,按了 $s$ 后就面向轨道内侧),同时它的位置会关于“起点站”(顶点1)对称地跳到另一边。
- $D_{2n}$ 就是你可以通过按这两个按钮的不同组合,让机器人到达的所有可能状态的集合。
12.2 生成元的基本性质
📜 [原文5]
我们将以下计算的细节留作练习(在很大程度上我们将使用 $D_{6}$ 和 $D_{8}$,因此读者可能希望先对 $n=3$ 和 $n=4$ 尝试这些练习):
(1) $1, r, r^{2}, \ldots, r^{n-1}$ 都是不同的,并且 $r^{n}=1$,所以 $|r|=n$。
(2) $|s|=2$。
(3) 对于任何 $i$, $s \neq r^{i}$。
(4) 对于所有 $0 \leq i, j \leq n-1$ 且 $i \neq j$, $s r^{i} \neq s r^{j}$,所以
也就是说,每个元素可以唯一地写成 $s^{k} r^{i}$ 的形式,其中 $k=0$ 或 $1$ 且 $0 \leq i \leq n-1$。
这部分列出了生成元 $r$ 和 $s$ 的五个基本性质,这些性质是理解 $D_{2n}$ 代数结构的核心。
(1) 关于 $r$ 的性质
- $r, r^2, ..., r^{n-1}$ 都不同:$r^i$ 表示连续进行 $i$ 次最小单位旋转。只要 $i < n$,旋转的总角度 $i \cdot (2\pi/n)$ 就小于 $2\pi$,所以每次得到的顶点排列都不同。
- $r^n = 1$:连续进行 $n$ 次最小单位旋转,总共旋转了 $n \cdot (2\pi/n) = 2\pi$ 弧度,也就是360度。这等价于“不动”操作,也就是单位元 $1$。
- $|r|=n$:一个元素的阶 (order of an element) 被定义为使 $g^k=1$ 的最小正整数 $k$。因为 $r^n=1$ 并且所有小于 $n$ 的正整数次幂都不等于 $1$,所以 $r$ 的阶是 $n$。这 $n$ 个旋转操作 $1, r, ..., r^{n-1}$ 构成了一个 $n$ 阶的循环子群。
(2) 关于 $s$ 的性质
- $|s|=2$:$s$ 是一个反射。对一个图形进行一次反射,它会翻转过去。再进行一次相同的反射,它会翻转回来,回到原始状态。所以,$s^2 = s \cdot s = 1$。因为 $s$ 本身不是单位元1,所以 $s$ 的阶是2。
(3) 旋转与反射的区别
- $s \neq r^i$:任何一个反射操作都不可能等同于一个旋转操作。一个直观的理解是:拿一张标有 1, 2, 3, ... 顺时针顺序的纸片。无论你怎么旋转,顶点的顺时针顺序 1->2->3->... 是不会改变的。但是只要你做一次反射,这个顺序就会被逆转,变成逆时针的 1->n->n-1->...。因为它们对顶点顺序的影响本质不同,所以它们不可能是同一个操作。
(4) 列出所有元素
- $sr^i \neq sr^j$:这个性质说的是,用 $s$ 左乘不同的旋转,会得到不同的结果。我们可以用消去律来证明:假设 $sr^i = sr^j$。因为 $s$ 有逆元 $s^{-1}$ (就是 $s$ 本身),我们可以在等式两边同时左乘 $s^{-1}$:$s^{-1}(sr^i) = s^{-1}(sr^j)$,得到 $(s^{-1}s)r^i = (s^{-1}s)r^j$,即 $1 \cdot r^i = 1 \cdot r^j$,也就是 $r^i=r^j$。但这与我们假设的 $i \neq j$ 和性质(1)中 $r^i$ 互不相同矛盾。所以假设不成立,$sr^i \neq sr^j$。
- 列出 $D_{2n}$ 的所有元素:
- 我们已经知道有 $n$ 个不同的旋转:$\{1, r, r^2, ..., r^{n-1}\}$。
- 我们现在构造另外 $n$ 个元素:$\{s, sr, sr^2, ..., sr^{n-1}\}$。根据上面的证明,这 $n$ 个元素也互不相同。
- 根据性质(3),后面这组元素(都是反射)和前面那组元素(都是旋转)没有交集。
- 这样,我们总共找到了 $n + n = 2n$ 个不同的元素。
- 因为我们已经知道 $|D_{2n}|=2n$,所以这 $2n$ 个元素就是 $D_{2n}$ 的全部。
- 唯一表示:这个列表 $\{s^k r^i | k \in \{0,1\}, 0 \le i < n\}$ 不仅包含了所有元素,而且每个元素的表示法是唯一的。这为 $D_{2n}$ 中的元素提供了一个“标准型”。任何一个元素都可以被写成 “一个可选的翻转,后跟一个旋转” 的形式。
- $D_{2n}$: 二面体群
- $\{...\}$: 集合的表示法,里面列出了所有的元素。
- $1, r, \ldots, r^{n-1}$: 这是由旋转生成的 $n$ 个元素。$1$ 就是 $r^0$。
- $s, sr, \ldots, sr^{n-1}$: 这是另外 $n$ 个元素,它们都是反射。每个元素都是先进行一个旋转 $r^i$,然后再进行一次反射 $s$。
- 推导: 这个公式是性质(1), (3), (4)的直接逻辑结论。我们构造了两个不相交的、各有 $n$ 个元素的集合,它们的并集大小为 $2n$,正好等于 $|D_{2n}|$,因此这个并集就是 $D_{2n}$ 本身。
- 示例: $D_8$ (正方形, $n=4$)
- $|r|=4$: $r$ 是旋转90度。$r^2$ 是180度, $r^3$ 是270度, $r^4$ 是360度(即 $1$)。
- $|s|=2$: $s$ 是沿对角线翻转。翻两次等于没翻。
- $s \neq r^i$: 翻转改变了顶点的时针顺序,旋转不改变。
- 元素列表:
- 旋转 (4个):
- $1 = r^0$: 不动
- $r$: 旋转90度
- $r^2$: 旋转180度
- $r^3$: 旋转270度
- 反射 (4个):
- $s$: 沿对角线y=x翻转
- $sr$: 先转90度,再沿y=x翻转。这是一个沿y轴的翻转。
- $sr^2$: 先转180度,再沿y=x翻转。这是一个沿对角线y=-x的翻转。
- $sr^3$: 先转270度,再沿y=x翻转。这是一个沿x轴的翻转。
- 我们找到了4个旋转和4个反射,总共8个元素,它们构成了 $D_8$。
- 唯一表示: 任何一个元素都可以写成 $s^k r^i$ ($k \in \{0,1\}, i \in \{0,1,2,3\}$)。比如,沿y轴的翻转,它的标准型是 $sr$。
- 元素的阶 vs 群的阶: $|r|=n$ 指的是元素 $r$ 的阶,即 $r$ 需要自乘 $n$ 次才变回单位元。$|D_{2n}|=2n$ 指的是群 $D_{2n}$ 的阶,即群中元素的总数。
- $sr^i$ 是什么: 这是一个复合操作,从右向左执行,先旋转 $r^i$,再翻转 $s$。
- $sr^i$ 是反射: 一个旋转($r^i$)和一个反射($s$)的复合总是一个反射。两个旋转的复合是旋转,两个反射的复合是旋转。
本段通过分析生成元 $r$ 和 $s$ 的性质,得出了 $D_{2n}$ 的一个重要结构性结论:$D_{2n}$ 由 $n$ 个旋转 $\{r^i\}$ 和 $n$ 个反射 $\{sr^i\}$ 构成。这不仅再次确认了群的阶是 $2n$,还为群中的每一个元素提供了一种唯一的“标准型”表示法 ($s^k r^i$)。
本段的目的是将 $D_{2n}$ 的所有元素用生成元 $r$ 和 $s$ 系统地表示出来。这使得我们可以脱离几何图形,完全在代数的框架内讨论 $D_{2n}$ 的元素。这是建立 $D_{2n}$ 乘法表和关系式的基础。
$D_{2n}$ 的世界被分成了两个“国度”:
- 旋转国度: 这里有 $n$ 个居民 $(1, r, ..., r^{n-1})$。他们都是“保序族”,保持顶点的顺时针次序。这个国度自己就是一个小王国(循环子群)。
- 反射国度: 这里也有 $n$ 个居民 $(s, sr, ..., sr^{n-1})$。他们都是“逆序族”,会颠倒顶点的顺时针次序。
操作 $s$ 就像一张“签证”,可以让你从旋转国度跨入反射国度。从 $r^i$ 跨过去,就变成了 $sr^i$。
想象一个有 $n$ 个站点的环形单轨列车。
- 旋转 $r^i$ 就是让列车顺时针前进 $i$ 站。列车本身朝向不变。
- 反射 $s$ 操作就像是把列车从轨道上吊起来,翻个面,再放到关于“1号站”对称的位置上。
- $sr^i$ 就是列车先顺时针跑 $i$ 站,然后被吊起来翻个面,放到对称位置。
- $D_{2n}$ 的所有元素就是列车所有可能的最终状态(位置和朝向)。
12.3 关键关系式 $rs = sr^{-1}$
📜 [原文6]
(5) $r s=s r^{-1}$。[首先计算 $s$ 在 $\{1,2, \ldots, n\}$ 上实现什么置换,然后分别计算此方程的两边对顶点 $1$ 和 $2$ 的作用。]这尤其表明 $r$ 和 $s$ 不可交换,因此 $D_{2 n}$ 是非阿贝尔群。
(6) 对于所有 $0 \leq i \leq n$, $r^{i} s=s r^{-i}$。[通过对 $i$ 进行归纳,并使用 $r^{i+1} s=r\left(r^{i} s\right)$ 以及前面的计算。]这表明如何将 $s$ 与 $r$ 的幂交换。
这部分揭示了 $r$ 和 $s$ 之间最重要的互动规则,这个规则是 $D_{2n}$ 非阿贝尔性的根源。
(5) 基本关系 $rs = sr^{-1}$
- 含义: 这个等式被称为交换关系 (commutation relation)。它说明 $r$ 和 $s$ 是不可交换的($rs \neq sr$)。它提供了一个规则,告诉我们如果想把 $s$ 从 $r$ 的右边移到左边,代价是需要把 $r$ 变成它的逆元 $r^{-1}$。
- 证明思路: 要证明两个对称操作相等,我们只需证明它们对所有顶点的作用是相同的。因为对称是刚体运动,我们其实只需证明它们对两个相邻顶点(如1和2)的作用相同即可。
- $s$ 的置换: $s$ 是沿通过顶点1的轴翻转。顶点1不动。顶点2移动到顶点 $n$ 的位置,顶点3到 $n-1$,...,通常,顶点 $i$ 移动到 $n-i+2$ 的位置(模n)。特别地,$s(1)=1, s(2)=n, s(n)=2$。
- $r^{-1}$ 的置换: $r$ 是顺时针旋转,则 $r^{-1}$ 是逆时针旋转 $2\pi/n$。所以 $r^{-1}(i) = i-1$ (模n)。
- 计算左边 $rs$ 对顶点1的作用: $(rs)(1) = r(s(1)) = r(1) = 2$。
- 计算右边 $sr^{-1}$ 对顶点1的作用: $(sr^{-1})(1) = s(r^{-1}(1)) = s(n) = 2$。
- 两者对顶点1的作用相同。
- 计算左边 $rs$ 对顶点2的作用: $(rs)(2) = r(s(2)) = r(n) = 1$。
- 计算右边 $sr^{-1}$ 对顶点2的作用: $(sr^{-1})(2) = s(r^{-1}(2)) = s(1) = 1$。
- 两者对顶点2的作用也相同。
- 由于 $rs$ 和 $sr^{-1}$ 对相邻顶点1和2的作用完全一样,它们必然是同一个对称操作。
- 非阿贝尔性 (Non-Abelian):因为 $r^{-1} \neq r$ (除非 $r^2=1$, 即 $n=2$,但这被排除了),所以 $rs = sr^{-1} \neq sr$。一个群中只要存在一对元素不可交换,该群就是非阿贝尔群。因此,所有 $D_{2n}$ (for $n \ge 3$) 都是非阿贝尔群。
(6) 推广关系 $r^i s = sr^{-i}$
- 含义: 这个关系将(5)推广到 $r$ 的任意次幂。它提供了一个通用的“交换 $s$ 和 $r$ 的幂”的法则。
- 证明思路 (数学归纳法):
- 基础步骤 (Base Case): 当 $i=1$ 时,$r^1s = sr^{-1}$,这正是性质(5),已证明成立。
- 归纳假设 (Inductive Hypothesis): 假设对于某个 $k \ge 1$,$r^k s = sr^{-k}$ 成立。
- 归纳步骤 (Inductive Step): 我们需要证明 $r^{k+1}s = sr^{-(k+1)}$。
- $r^{k+1}s = r(r^k s)$ (根据幂的定义和结合律)
- $= r(sr^{-k})$ (根据归纳假设)
- $= (rs)r^{-k}$ (结合律)
- $= (sr^{-1})r^{-k}$ (根据基础步骤(5))
- $= s(r^{-1}r^{-k})$ (结合律)
- $= sr^{-(k+1)}$ (根据幂的法则)
- 证明完成。这个关系对所有正整数 $i$ 都成立。(对于 $i=0$,$r^0s=1s=s$ and $sr^{-0}=s1=s$,也成立)。
本段没有新的大型行间公式,主要是关系式。
- $rs = sr^{-1}$: $r$ 和 $s$ 的基本交换关系。
- $r^{-1}$: 元素 $r$ 的逆元。因为 $r^n=1$, 所以 $r \cdot r^{n-1} = 1$,因此 $r^{-1}=r^{n-1}$。这个逆元代表逆时针旋转 $2\pi/n$。
- $r^i s = sr^{-i}$: 推广的交换关系。注意指数 $i$ 变成了 $-i$。
- 示例: $D_8$ (正方形, $n=4$)
- $r$ 是顺时针转90度, $s$ 是沿过1,3的对角线翻转。$r^{-1} = r^3$ 是转270度。
- 验证 $rs=sr^{-1}$ ($sr^3$):
- $rs$: 先翻转 $s$ (2,4互换),顶点序列 (1,2,3,4) -> (1,4,3,2)。再旋转 $r$ (所有顶点顺时针移一格),(1,4,3,2) -> (2,1,4,3)。
- $sr^3$: 先旋转 $r^3$ (转270度),(1,2,3,4) -> (4,1,2,3)。再翻转 $s$ (2,4互换),(4,1,2,3) -> (2,1,4,3)。
- 两者最终效果都是 (2,1,4,3),所以 $rs=sr^3$ 在 $D_8$ 中成立。
- 验证 $r^2s = sr^{-2}$ ($sr^2$):
- $r^2s$: 先翻转 $s$ (2,4互换) -> (1,4,3,2)。再转180度 $r^2$ -> (3,2,1,4)。
- $sr^2$: 先转180度 $r^2$ -> (3,4,1,2)。再翻转 $s$ (2,4互换) -> (3,2,1,4)。
- 两者相等。注意这里 $r^2=r^{-2}$ 因为 $r^4=1$。
- 忘记逆元: 在交换 $s$ 和 $r$ 时,最常见的错误就是直接写 $rs=sr$,而忘记了 $r$ 必须变成 $r^{-1}$。
- $r^{-i}$ 的计算: $r^{-i}$ 就是 $(r^i)^{-1}$,也等于 $(r^{-1})^i$。在计算时,它等于 $r^{n-i}$。
- 结合律的使用: 在推导 $r^{i+1}s$ 时,我们频繁地使用了结合律来重新组合括号,例如 $r(sr^{-k}) = (rs)r^{-k}$。这是群运算的基本功。
本段建立了描述 $D_{2n}$ 代数结构的核心关系:$rs=sr^{-1}$ 及其推广 $r^is=sr^{-i}$。这个关系捕捉了旋转和反射相互作用的本质,并证明了 $D_{2n}$ (for $n\ge 3$) 都是非阿贝尔群。
本段的目的是提供一个计算工具。有了这个“交换法则”,我们就可以处理任何由 $r$ 和 $s$ 组成的表达式了。无论 $r$ 和 $s$ 如何混合,我们总能通过反复应用这个法则,把所有的 $s$ 都移动到表达式的左边(或者右边),从而把任意一个元素都化简成 $s^k r^i$ 的标准形式。
想象 $r$ 和 $s$ 是两个操作杆。
- 拉动 $r$ 杆,平台顺时针转一格。
- 拉动 $s$ 杆,平台翻转。
- $rs=sr^{-1}$ 这个规则告诉你:【先拉 $r$ 再拉 $s$】的效果,等同于【先拉动一个“反向 $r$”杆(让平台逆时针转一格),再拉 $s$】。这个规则不是对称的,体现了操作的顺序很重要。
拿一张正方形纸片,顶点1,2,3,4顺时针排列。
- $rs$: 先翻转 (1,4,3,2),再旋转 (2,1,4,3)。
- $sr$: 先旋转 (4,1,2,3),再翻转 (2,1,4,3)。
咦,在这个例子中 $rs$ 和 $sr$ 的结果相同了?让我们重新检查。
- $s$ (沿1-3对角线翻转): $s(1)=1, s(2)=4, s(3)=3, s(4)=2$。
- $r$ (顺时针转90度): $r(1)=2, r(2)=3, r(3)=4, r(4)=1$。
- $rs$: $r(s(1,2,3,4)) = r(1,4,3,2) = (2,1,4,3)$。
- $sr$: $s(r(1,2,3,4)) = s(2,3,4,1) = (4,3,2,1)$。
- (2,1,4,3) 和 (4,3,2,1) 是不同的置换。rs 将 (1,2,3,4) 变成 (2,1,4,3),而 sr 将 (1,2,3,4) 变成 (4,3,2,1)。
- 现在来检查 sr^{-1}。$r^{-1}=r^3$ (转270度)。$r^{-1}(1,2,3,4) = (4,1,2,3)$。
- $sr^{-1}$: $s(r^{-1}(1,2,3,4)) = s(4,1,2,3) = (2,1,4,3)$。
- 结果表明,$rs=(2,1,4,3)$ 和 $sr^{-1}=(2,1,4,3)$ 是相同的,而 $sr=(4,3,2,1)$ 是不同的。这就直观地验证了 $rs=sr^{-1}$ 并且 $rs \neq sr$。
12.4 利用关系式进行计算
📜 [原文7]
完成这些计算后,我们现在观察到 $D_{2 n}$ 的完整乘法表可以用 $r$ 和 $s$ 单独表示,也就是说, $D_{2 n}$ 的所有元素都有一个(唯一)的 $s^{k} r^{i}$ 形式的表示,其中 $k=0$ 或 $1$ 且 $0 \leq i \leq n-1$,并且这种形式的两个元素的任何乘积都可以使用“关系”(1)、(2) 和 (6) 简化为另一种相同形式(所有指数都以模 $n$ 方式简化)。例如,如果 $n=12$,
这段话总结了前面所有工作的成果:我们现在拥有一个完整的代数系统来描述 $D_{2n}$。
- 代数系统的组成部分:
- 元素 (标准型): 所有元素都可以唯一地写成 $s^k r^i$ 的形式 ($k \in \{0,1\}, i \in \{0, ..., n-1\}$)。
- 运算规则 (关系式):
- $r^n = 1$ (旋转的循环性)
- $s^2 = 1$ (反射的对合性)
- $r^i s = sr^{-i}$ (交换法则)
- 系统的完备性:这三条规则足够用来计算任意两个元素的乘积,并将结果化简回标准型。这意味着我们不再需要回到几何图形,就可以完成群中的所有运算。
- $D_{12}$ ($n=12$) 的例子分析:
- 问题: 计算 $(sr^9)(sr^6)$。这是一个反射乘以另一个反射。我们预期结果会是一个旋转。
- 步骤1: $(sr^9)(sr^6) = s(r^9s)r^6$
- 这里使用了结合律,把括号重新组合,目的是为了让 $r^9$ 和 $s$ 相遇。
- 步骤2: $s(r^9s)r^6 = s(sr^{-9})r^6$
- 这里使用了关键的交换关系 (6): $r^is = sr^{-i}$。把 $r^9s$ 换成了 $sr^{-9}$。
- 步骤3: $s(sr^{-9})r^6 = s^2 r^{-9}r^6 = s^2 r^{-9+6}$
- 再次使用结合律和指数律。我们让两个 $s$ 和两个 $r$ 的幂分别相遇。
- 步骤4: $s^2 r^{-9+6} = 1 \cdot r^{-3} = r^{-3}$
- 使用了关系(2) $s^2=1$。
- 步骤5: $r^{-3} = r^{12-3} = r^9$
- 最后一步,将指数化为 $0$ 到 $n-1$ (即 $0$ 到 $11$) 之间。指数是在模 $n$ (这里是模12) 的意义下计算的。$-3 \equiv 9 \pmod{12}$。
- 结论: $(sr^9)(sr^6) = r^9$。两个反射的乘积确实是一个旋转。
- $(sr^9)(sr^6)$: 两个 $D_{24}$ ($n=12$) 中元素的乘积。它们都是反射。
- $s(r^9 s)r^6$: 应用结合律,准备处理中间的 $r^9s$ 部分。
- $s(s r^{-9})r^6$: 应用交换关系 $r^is = sr^{-i}$ (其中 $i=9$)。
- $s^2 r^{-9+6}$: 再次应用结合律,并使用指数律 $r^a r^b = r^{a+b}$。
- $r^{-3}$: 应用关系 $s^2=1$。
- $r^9$: 将指数化为标准范围。在模12的算术中,$-3$ 和 $9$ 是等价的,因为 $-3+12=9$。最终结果 $r^9$ 是一个旋转,且是标准形式。
- 示例1: $D_8$ ($n=4$) 中计算 $(sr)(sr^3)$
- $(sr)(sr^3) = s(rs)r^3$ (结合律)
- $= s(sr^{-1})r^3$ (交换关系 $rs=sr^{-1}$)
- $= s^2 r^{-1} r^3$ (结合律)
- $= 1 \cdot r^{-1+3}$ ($s^2=1$ 和指数律)
- $= r^2$。
- 结果是一个旋转 $r^2$ (转180度)。
- 示例2: $D_6$ ($n=3$) 中计算 $(sr^2)(r)$
- $(sr^2)(r) = s(r^2 r)$ (结合律)
- $= s r^3$ (指数律)
- $= s \cdot 1$ (关系 $r^3=1$)
- $= s$。
- 结果是一个反射 $s$。
- 指数的模运算: 在进行指数加减后,切记要将结果对 $n$ 取模,使其落在 $[0, n-1]$ 的范围内。例如,在 $D_8$ 中,$r^5 = r^{4+1} = r^4 r^1 = 1 \cdot r = r$。$r^{-2} = r^{4-2} = r^2$。
- 死记硬背 vs 理解: 不要只记住 $rs=sr^{-1}$,要理解它的作用是“移动 $s$ 并改变 $r$ 的指数符号”。
- 运算顺序: 严格遵守从左到右的计算顺序,除非有括号。在化简过程中,灵活运用结合律是关键。
本段展示了如何仅使用三个核心关系 ($r^n=1, s^2=1, r^is=sr^{-i}$) 来完成二面体群中的任何乘法运算。这标志着我们已经成功地将 $D_{2n}$ 从一个几何对象完全转化为一个抽象的代数系统,所有的运算都可以在符号层面完成。
本段的目的是展示这套代数系统的“威力”和“完备性”。通过一个具体的计算例子,它向读者证明,我们已经掌握了在 $D_{2n}$ 中进行纯代数计算所需的一切工具。这为后面引入更抽象的“生成元与关系” (presentations) 概念提供了动机和范例。
这套系统就像一种“代数语法”。
- 名词: $s^k r^i$ (标准形式的元素)
- 语法规则:
- $r$ 的指数超过 $n-1$ 就绕回0 ($r^n=1$)
- $s$ 出现两次就抵消 ($s^2=1$)
- $s$ 跑到 $r^i$ 的左边时,$r^i$ 要变号 ($r^is=sr^{-i}$)
任何一个由 $r, s$ 组成的“句子”(表达式),都可以通过这些语法规则,整理成一个标准的“名词”。
想象你在玩一个只有三个按钮的计算器。
- 按钮 "R": 显示的数字加1。
- 按钮 "S": 显示的数字取负号。
- 按钮 "RESET": 当数字达到 $n$ 时自动或手动归零。当 S 被按两次时,负号消失。
计算 $(sr^9)(sr^6)$ 在 $D_{12}$ 中就像:
S -> 屏幕显示 -
R (9次) -> 屏幕显示 -9
S -> 屏幕显示 9 (负负得正)
R (6次) -> 屏幕显示 15
RESET (模12) -> 15 mod 12 = 3。
哦,这个想象有点问题。让我们换一个。
把 $s$ 看作一个“反转”开关,把 $r$ 看作一个“旋转”齿轮。
sr^9: 齿轮在“反转”状态,并转了9格。
sr^6: 齿轮在“反转”状态,并转了6格。
$(sr^9)(sr^6)$:
- 执行 sr^6: 开启“反转”开关,转6格。
- 接着执行 sr^9: 再次开启“反转”开关 (开关回到“正常”状态),然后在这个“正常”状态下转9格。
等等,这个模型也不对,因为它预设了可交换性。
正确的模型必须体现 $r^9s = sr^{-9}$。
想象 $s$ 是一个镜子。
- $(sr^9)(sr^6)$: 先做 $sr^6$: 旋转6格,然后照镜子。
- 再做 $sr^9$: 对刚才镜子里的像,再旋转9格,然后再照镜子。
- $s(r^9(s(r^6(\text{obj})))) = s r^9 s r^6 (\text{obj})$
- $s (r^9 s) r^6 (\text{obj}) = s (s r^{-9}) r^6 (\text{obj}) = s^2 r^{-9} r^6 (\text{obj}) = r^{-3} (\text{obj}) = r^9 (\text{obj})$。
这个过程需要严格的符号操作,直观想象反而容易出错。这恰恰说明了代数系统的价值:它提供了一个不会犯错的、机械的计算程序。
1.3 生成元和关系 (Generators and Relations)
13.1 生成元和关系的泛化概念
📜 [原文8]
使用二面体群的生成元 $r$ 和 $s$ 提供了一种简单而简洁的在 $D_{2 n}$ 中进行计算的方法。我们也可以类似地为任意群引入生成元和关系的概念。尽早拥有这些概念(在正式论证之前)是有用的,因为它们提供了描述许多群和在其上进行计算的简单方法。生成元将在第 2.4 节中更详细地讨论,这两个概念将在第 6.3 节中引入自由群概念时得到严格处理。
这段话是一个承上启下的引言。
- 承上:它回顾了我们刚刚对 $D_{2n}$ 所做的工作——通过生成元 ($r, s$) 和它们满足的关系 ($r^n=1, s^2=1, rs=sr^{-1}$) 来描述和计算这个群。这种方法被评价为“简单而简洁”。
- 启下:它提出,这种“用生成元和关系来描述群”的思想,并不仅仅适用于二面体群,而是一种可以推广到任意群的强大方法。
- 学习路线图:作者坦诚地告诉我们,这里的介绍是非正式的、启发性的。这些概念的严格数学定义将在后续章节中给出:
- 生成元 (Generators) 会在 2.4 节详细讨论。
- 关系 (Relations) 和整个展示 (Presentation) 理论的严格基础,则需要等到 6.3 节学习了自由群 (Free Groups) 之后才能建立。
- 提前引入的目的:为什么现在就要引入一个不严格的概念?因为这个工具非常有用。它让我们能用一种非常紧凑的方式来“定义”和“操作”很多不同的群,即使我们还没有学完所有背后的理论。这是一种“先学会用,再理解原理”的教学策略。
本段没有公式。
- 整数加法群 $(\mathbb{Z}, +)$:这个群是无限群。我们可以说它是由 $\{1\}$ 生成的。因为任何一个正整数 $k$ 都可以通过 $1+1+...+1$ (k次) 得到,任何一个负整数 $-k$ 都可以通过 $(-1)+(-1)+...+(-1)$ (k次) 得到,0就是空和。所以 $\mathbb{Z} = \langle 1 \rangle$。
- 模4整数加法群 $(\mathbb{Z}_4, +)$:元素是 $\{0,1,2,3\}$。这个群也是由 $\{1\}$ 生成的:$1$, $1+1=2$, $1+1+1=3$, $1+1+1+1=4\equiv0$。它满足的关系是 $1^4=0$ (在加法群里,幂次表示连加,单位元是0),可以写成 $4 \cdot 1 = 0$。
- 非正式 vs 不正确: 这里引入的概念是非正式的,意味着缺乏严格的定义和证明,但这并不意味着它们是错误的。它们是基于直觉和例子的,而严格的理论将在后面补充。
- 并非所有群都有简洁的表示: 虽然这个方法很强大,但并不是每个群都能找到一个简单、漂亮的“生成元和关系”展示。
本段将二面体群的学习经验进行升华,预告了群的生成元和关系这一普遍性概念,并说明了先非正式地引入它是为了实用性,其严格理论将在后续章节中展开。
本段的目的是进行一次概念上的飞跃。它告诉读者,我们刚刚对 $D_{2n}$ 做的分析,不仅仅是一个孤立的案例研究,而是一种具有普遍意义的描述群的方法的第一个实例。这为读者建立了一个“纲要”式的认识,让他们对未来的学习内容有一个预期。
我们之前为 $D_{2n}$ 制作了一个“操作手册”。现在我们意识到,我们可以为许多不同的“机器”(群)都编写类似的操作手册。每本手册都只包含两部分:
- 基本零件清单 (List of basic parts) -> 生成元集 (Set of generators)
- 组装规则 (Assembly rules) -> 关系集 (Set of relations)
只要有了这两样东西,原则上我们就能构建和理解整台机器。
想象你在学习一种新的语言。
- 生成元就像是这种语言的字母表。
- 关系就像是这种语言的基本拼写规则或语法规则(比如 q 后面必须跟 u)。
只要掌握了字母表和基本规则,你就可以拼出这种语言里的所有单词(群的所有元素),并且知道如何将单词组合成有意义的句子(群的运算)。
13.2 生成元集、关系和展示的定义
📜 [原文9]
群 $G$ 的元素子集 $S$ 具有这样的性质: $G$ 的每个元素都可以写成 $S$ 的元素及其逆元的(有限)乘积,这被称为 $G$ 的生成元集。我们将通过写 $G=\langle S\rangle$ 来表示这一点,并说 $G$ 由 $S$ 生成或 $S$ 生成 $G$。例如,整数 $1$ 是整数加法群 $\mathbb{Z}$ 的一个生成元,因为每个整数都是有限个 $+1$ 和 $-1$ 的和,所以 $\mathbb{Z}=\langle 1\rangle$。根据 $D_{2 n}$ 的性质 (4),集合 $S=\{r, s\}$ 是 $D_{2 n}$ 的一个生成元集,所以 $D_{2 n}=\langle r, s\rangle$。我们稍后将看到,在有限群 $G$ 中,如果 $G$ 的每个元素都是 $S$ 中元素的有限乘积(即不需要包含 $S$ 中元素的逆元),则集合 $S$ 生成 $G$。
一般群 $G$ 中生成元满足的任何方程都称为 $G$ 中的关系。因此在 $D_{2 n}$ 中我们有关系: $r^{n}=1, s^{2}=1$ 和 $r s=s r^{-1}$。此外,在 $D_{2 n}$ 中,这三个关系具有附加性质,即群元素之间的任何其他关系都可以从这三个关系中导出(这并非显而易见;它源于我们可以仅使用这三个关系来精确确定两个群元素何时相等)。
一般来说,如果某个群 $G$ 由子集 $S$ 生成,并且存在一些关系集合,例如 $R_{1}, R_{2}, \ldots, R_{m}$(这里每个 $R_{i}$ 是 $S \cup\{1\}$ 中元素的方程),使得 $S$ 中元素之间的任何关系都可以从这些关系中推导出来,我们将这些生成元和关系称为 $G$ 的展示,并写为
这段话给出了生成元集、关系和展示的非正式定义。
- 生成元集 (Generating Set)
- 定义: 群 $G$ 的一个子集 $S$ 如果能“表示”出 $G$ 中所有的元素,那么 $S$ 就是一个生成元集。
- “表示”的严格含义: $G$ 中的任意一个元素 $g$,都可以被写成 $S$ 中的元素(比如 $s_1, s_2, ...$)以及它们的逆元($s_1^{-1}, s_2^{-1}, ...$)的有限次乘积。例如,$g = s_1 s_2^{-1} s_1 s_3 ...$。
- 符号: $G = \langle S \rangle$ 读作 “$G$ is generated by $S$”(G由S生成)。
- 例子:
- $\mathbb{Z} = \langle 1 \rangle$。因为任何整数都可以由 $1$ 和它的逆元 $-1$ 相加(加法群里的“乘积”)得到。
- $D_{2n} = \langle r, s \rangle$。我们已经看到,所有元素都能写成 $s^k r^i$ 的形式,这显然是 $r, s$ 的乘积。
- 有限群的特殊情况: 对于有限群,我们不需要特意包括逆元。因为如果一个元素 $g$ 的阶是 $k$ (即 $g^k=1$),那么它的逆元 $g^{-1}$ 就等于 $g^{k-1}$,而 $g^{k-1}$ 本身就是 $g$ 的乘积。所以,在有限群中,只要能用 $S$ 中元素的乘积表示所有元素就行了。
- 关系 (Relation)
- 定义: 一个关系是在生成元之间成立的一个方程。任何一个把生成元组合起来最终等于单位元的表达式,都是一个关系。例如,在 $D_{2n}$ 中,$r^n=1$ 是一个关系,$s^2=1$ 是一个关系。$rs=sr^{-1}$ 也可以改写成 $rsr s^{-1}=1$ (右乘$s^{-1}$)或者 $s^{-1}rsr=1$ (左乘$s^{-1}$,右乘$r$), 也是一个关系。
- $D_{2n}$ 中的关系: $r^n=1$, $s^2=1$, $rs=sr^{-1}$ 是我们找到的三个重要关系。
- 展示 (Presentation)
- 定义: 一个群的展示由两部分组成:一个生成元集 $S$,和一个“完备”的关系集 $\{R_1, R_2, ..., R_m\}$。
- “完备”的含义: 这个关系集必须足够强大,以至于群中所有其他的关系都能通过代数推导从它们得出。用另一种方式说,这组关系完全定义了群的乘法结构。任何两个用生成元表示的词 (word),如果它们在群里代表同一个元素,那么我们一定能用这些关系来证明它们相等。
- 符号: $G = \langle S \mid R_1, ..., R_m \rangle$。竖线 | 分隔了生成元和关系。
- 这个定义的微妙之处: “所有其他关系都能被推导出来”这个条件,在没有自由群理论的情况下是很难验证的。目前我们只能直观理解为:这组关系“足够了”,不多也不少,正好能定义清楚这个群。
- $G$: 我们要定义的群。
- $\langle \ldots \mid \ldots \rangle$: 这是群的展示的 표준符号。
- $S$: 竖线左边,是生成元的集合。例如 $S = \{r, s\}$。
- $R_1, R_2, \ldots, R_m$: 竖线右边,是定义群结构的关系列表。这些通常是形如“某个表达式=1”的方程。
- 示例1: $\mathbb{Z}_n$ (模n整数加法群)
- 生成元集: $S=\{x\}$ (我们可以让 $x$ 对应于 $1$)。
- 关系: $x^n=1$ (在加法群里,这表示 $n \cdot x = 0$)。
- 展示: $\mathbb{Z}_n = \langle x \mid x^n=1 \rangle$。这是一个 $n$ 阶循环群的展示。
- 示例2: Klein四元群 $V_4$
- 这是一个4阶阿贝尔群,可以想成是两个开关,每个开关有开/关两种状态。
- 生成元集: $S=\{a, b\}$ (a是第一个开关,b是第二个开关)。
- 关系:
- $a^2=1$ (按两次a等于没按)。
- $b^2=1$ (按两次b等于没按)。
- $ab=ba$ (按a和按b的顺序无所谓),这个关系可以写成 $aba^{-1}b^{-1}=1$。
- 展示: $V_4 = \langle a, b \mid a^2=1, b^2=1, ab=ba \rangle$。
- 生成元集不唯一: 一个群可以有多个不同的生成元集。例如 $D_6$ 可以由 $\{r, s\}$ 生成,也可以由两个反射 $\{s, sr\}$ 生成。
- 关系集不唯一: 对应于不同的生成元集,关系集也会不同。即使对于同一个生成元集,也可能有多组等价的“完备”关系集。
- “最小”生成元集: 我们通常希望能找到尽可能少的生成元来生成整个群。但定义本身不要求生成元集是最小的。
- “展示”的陷阱: 给定一个展示,要判断它定义的群到底是什么样子(阶是多少?是不是阿贝尔群?甚至是不是平凡群?)可能非常困难。这个问题被称为“字问题 (word problem)”,在一般情况下是不可解的。
本段形式化(虽然仍非严格)地定义了群的生成元集、关系和展示这三个核心概念。生成元集是群的“基本构件”,关系是“组装规则”,而展示则是这两者的结合,它提供了一种用纯代数方式来定义一个群的强大工具。
本段的目的是为读者提供一套用抽象代数语言描述群的词汇和语法。通过将具体的群(如 $D_{2n}$)抽象成一个展示 $\langle S \mid R \rangle$,我们可以专注于其内在的代数结构,而不必再关心它最初的定义(比如几何、矩阵等)。这使得不同来源的群可以被放在同一个框架下进行比较和研究。
群的展示 $\langle S \mid R \rangle$ 就像一份“分子结构图”。
- 生成元 $S$: 是构成这种分子的“原子”种类(比如碳原子、氢原子)。
- 关系 $R$: 是原子之间如何“成键”的规则(比如碳原子有4个键,氢原子有1个键,某些键角是固定的)。
通过这份结构图,理论上你可以推导出这种分子的一切化学和物理性质(群的所有代数性质)。
想象你在用一套指令来编程一个机器人。
- 生成元 $S$: 是机器人能懂的基本指令集(如 MOVE_FORWARD, TURN_LEFT)。
- 关系 $R$: 是指令序列的等价规则。例如,TURN_LEFT 四次等于什么都不做(L*4 = IDLE),或者 MOVE_FORWARD 再 MOVE_BACKWARD 也等于什么都不做(F B = IDLE)。
- 展示 $\langle S \mid R \rangle$ 就是这份完整的指令集和等价规则说明书。任何复杂的程序(群元素)最终都可以通过这些规则化简。
13.3 二面体群的展示
📜 [原文10]
二面体群 $D_{2 n}$ 的一个展示(使用上述生成元和关系)是
我们将看到,使用此展示来描述 $D_{2 n}$(而不是总是回到原始几何描述)将大大简化对这些群的操作。
这段话正式给出了二面体群 $D_{2n}$ 的标准展示。
- 展示的构成:
- 生成元: $\langle r, s \mid ... \rangle$ 的左半部分,表明我们用 $r$ 和 $s$ 这两个元素来生成整个群。
- 关系: $\langle ... \mid r^n=s^2=1, rs=sr^{-1} \rangle$ 的右半部分,列出了定义这个群结构的三个核心规则。
- $r^n=1$: 旋转 $n$ 次回到原点。
- $s^2=1$: 反射两次回到原状。
- $rs=sr^{-1}$: 旋转和反射的交换关系。
- 展示的意义: 这个简洁的公式 (1.1) 完全捕捉了二面体群 $D_{2n}$ 的所有结构信息。我们断言,任何在 $D_{2n}$ 中成立的其他关系(比如我们之前计算的 $(sr^9)(sr^6)=r^9$ 在 $D_{12}$ 中),都可以从这三个基本关系代数推导出来。
- 实用价值: 作者强调,从现在开始,我们应该更多地把 $D_{2n}$ 看作是由这个展示定义的抽象群,而不是总去想正n边形的几何图像。这样做可以简化操作和证明,让我们专注于其代数性质。
- $D_{2n}$: 二面体群。
- $=$: 这里的等号表示“可以由...来展示”。
- $\langle r, s \mid \ldots \rangle$: 表示由生成元 $r$ 和 $s$ 展示的群。
- $r^n=s^2=1$: 这是写在一个等式里的两个关系的简写,意思是 $r^n=1$ 并且 $s^2=1$。
- $rs=sr^{-1}$: 第三个关系,也是最关键的交换关系。
- 示例1: $D_6$ (正三角形)
- 展示: $D_6 = \langle r, s \mid r^3=1, s^2=1, rs=sr^{-1} \rangle$。
- 在这个群里,$r^{-1}=r^2$。所以交换关系也可以写成 $rs=sr^2$。
- 群的元素 (6个): $\{1, r, r^2, s, sr, sr^2\}$。
- 示例2: $D_8$ (正方形)
- 展示: $D_8 = \langle r, s \mid r^4=1, s^2=1, rs=sr^{-1} \rangle$。
- 在这个群里,$r^{-1}=r^3$。所以交换关系是 $rs=sr^3$。
- 群的元素 (8个): $\{1, r, r^2, r^3, s, sr, sr^2, sr^3\}$。
- 这只是一个展示: 重要的是要记住,一个群可以有不同的展示。例如,对于 $D_{2n}$,我们可以选择不同的生成元,比如两个反射 $a=s$ 和 $b=sr$。那么对应的关系就会变成 $a^2=1, b^2=1, (ab)^n=1$ (这在练习7中提到)。虽然看起来很不一样,但它们定义的是同一个群。
- 从展示到群: 我们是从一个已知的群 ($D_{2n}$的几何定义) 提炼出了这个展示。反过来,从一个抽象的展示出发,要确定它到底描述了一个怎样的群,则要困难得多,下一节会讨论这个问题。
本段给出了二面体群 $D_{2n}$ 的标准代数展示 $\langle r, s \mid r^n=s^2=1, rs=sr^{-1} \rangle$。这个展示是研究二面体群代数性质的出发点和核心工具。
本段的目的是提供一个“最终答案”式的总结。在详细分析了 $D_{2n}$ 的几何和代数性质后,本段用一个非常简洁、优美的群展示公式,将所有这些性质打包在一起。这不仅是一个总结,也是未来分析的起点。
这个展示公式就是二面体群的“基因序列”。
- r, s: 仅有的两种“碱基”。
- r^n=1, s^2=1, rs=sr^{-1}: 碱基配对和组合的规则。
这个基因序列包含了构建出完整“生物体”($D_{2n}$群)所需的所有信息。
想象你在为一个游戏设计一个角色的技能系统。
- 生成元: 角色有两个基本技能:r (冲刺) 和 s (闪避)。
- 关系:
- r^n=1: 连续冲刺 n 次会让你回到起点。
- s^2=1: 连续闪避两次等于没动。
- rs=sr^{-1}: “冲刺后闪避”的效果等于“先做一个反向冲刺(比如后撤),然后再闪避”。
这个展示就是角色的核心技能机制说明书。所有花哨的连招(群元素)都是由这两个基本技能按规则组合而成的。
13.4 展示的微妙之处:塌缩
📜 [原文11]
展示提供了一种描述许多群的简单方法,但需要考虑一些微妙之处。其中之一是,在任意展示中,判断群的两个元素(用给定生成元表示)何时相等可能很困难(甚至不可能)。因此,可能无法清楚地知道所展示群的阶是多少,甚至该群是有限的还是无限的!例如,可以证明 $\left\langle x_{1}, y_{1} \mid x_{1}^{2}=y_{1}^{2}=\left(x_{1} y_{1}\right)^{2}=1\right\rangle$ 是一个阶为 $4$ 的群的展示,而 $\left(x_{2}, y_{2} \mid x_{2}^{3}=y_{2}^{3}=\left(x_{2} y_{2}\right)^{3}=1\right)$ 是一个无限群的展示(参见练习)。
另一个微妙之处是,即使在相当简单的展示中,也可能发生一些“塌缩”(collapse),因为关系以某种不明显的方式交织在一起,即可能存在未在展示中明确给出的“隐藏”或隐式关系,而是指定关系的结果。这种塌缩使得通常难以确定所展示群大小的下限。例如,假设人们模仿 $D_{2 n}$ 的展示,试图通过定义来创建另一个群:
“交换关系” $x y=y x^{2}$ 确定了如何交换 $y$ 和 $x$(即如何将 $y$ 从 $x$ 的右侧“移动”到左侧),因此就像在群 $D_{2 n}$ 中一样,这个群中的每个元素都可以写成 $y^{k} x^{i}$ 的形式,其中 $y$ 的所有幂都在左侧,$x$ 的所有幂都在右侧。此外,根据前两个关系,任何 $x$ 和 $y$ 的幂都可以简化,使得 $i$ 介于 $0$ 和 $n-1$ 之间,$k$ 是 $0$ 或 $1$。人们可能因此认为 $X_{2 n}$ 再次是一个阶为 $2 n$ 的群。事实并非如此,因为在这个群中存在一个“隐藏关系”,它是从关系 $x=x y^{2}$(因为 $y^{2}=1$)通过反复应用交换关系和结合律将 $y$ 移动到左侧而获得的:
由于 $x^{4}=x$,根据消去律, $X_{2 n}$ 中 $x^{3}=1$,并且根据上述讨论, $X_{2 n}$ 对于任何 $n$ 的阶至多为 $6$。甚至可能发生更多的塌缩,具体取决于 $n$ 的值(参见练习)。
这段话揭示了使用群展示时一个非常重要的“陷阱”:塌缩 (collapse)。
- 展示的困难性:
- 字问题 (Word Problem): 给定一个展示和两个由生成元组成的字符串(“字”),如何判断它们是否代表同一个群元素?这在一般情况下是无法判定的。
- 阶的问题: 给定一个展示,如何确定这个群的阶?它可能是有限的,也可能是无限的。这也很难判断。
- 例子:
- $\langle x_1, y_1 \mid x_1^2=y_1^2=(x_1y_1)^2=1 \rangle$ 定义了一个4阶群 (实际上是$D_4$,即$V_4$ Klein四元群)。
- $\langle x_2, y_2 \mid x_2^3=y_2^3=(x_2y_2)^3=1 \rangle$ 看起来很相似,但它定义的却是一个无限群。这说明微小的关系变化可以导致结构的天壤之别。
- 塌缩 (Collapse):
- 定义: 塌缩是指从给定的关系出发,通过代数推导,可以得出一个或多个没有在原始关系列表中明确写出的、更强的“隐藏关系”。
- 后果: 这些隐藏关系会强制一些原本看起来不同的元素变得相等,从而使得群的实际阶远小于我们最初根据标准型数量(如 $2n$)所预估的上限。群“塌缩”成了一个比预期更小的群。
- 难以确定下限: 因为我们不知道会存在哪些隐藏关系,所以很难对群的阶给出一个有效的下限。我们只能通过标准型给出一个上限。
- $X_{2n}$ 的例子:
- 展示: $X_{2n} = \langle x, y \mid x^n=1, y^2=1, xy=yx^2 \rangle$。
- 初步分析 (错误的): 这个展示看起来和 $D_{2n}$ 的非常像。$x$ 像是 $r$,$y$ 像是 $s$。交换关系是 $xy=yx^2$。我们也可以把所有元素写成 $y^k x^i$ 的形式 ($k \in \{0,1\}, i \in \{0,...,n-1\}$)。这样看来,似乎有 $2n$ 个元素。
- 发现隐藏关系: 作者展示了一个绝妙的推导,来寻找隐藏关系。
- 起点:$x=x \cdot 1 = x y^2$ (因为 $y^2=1$ 是一个给定的关系)。
- $x = (xy)y$ (结合律)
- $= (yx^2)y$ (应用交换关系 $xy=yx^2$)
- $= (yx)(xy)$ (结合律)
- $= (yx)(yx^2)$ (再次应用交换关系)
- $= y(xy)x^2$ (结合律)
- $= y(yx^2)x^2$ (再次应用交换关系)
- $= y^2 x^2 x^2 = y^2 x^4$ (结合律和指数律)
- $= 1 \cdot x^4 = x^4$ (应用关系 $y^2=1$)
- 推导结论: 我们从 $x$ 出发,经过一系列合法的代数变换,得到了 $x^4$。所以,在 $X_{2n}$ 这个群里,必须有 $x = x^4$。
- 应用消去律: 在群里,如果 $x=x^4$,我们可以两边同乘以 $x^{-1}$,得到 $1 = x^3$。
- 群的塌缩: 我们推导出了一个新的、隐藏的关系 $x^3=1$!这意味着 $x$ 的阶最多是3。无论原始的 $n$ 是多少(比如 $n=100$),$x$ 的幂次都会在 $x^0, x^1, x^2$ 之间循环。
- 新的阶上限: 由于 $x$ 的不同幂最多只有3个 ($1, x, x^2$),而 $y$ 的不同幂最多有2个 ($1, y$),所以群 $X_{2n}$ 的元素总数最多是 $2 \times 3 = 6$ 个。它从一个看似 $2n$ 阶的群塌缩到了一个最多6阶的群。
这个展示定义了一个新的群 $X_{2n}$,它模仿了 $D_{2n}$ 的展示,但改变了交换关系。
这一长串推导是寻找隐藏关系的关键。每一步都只用了结合律和给定的三个关系。它最终揭示了 $x=x^4$,从而导出 $x^3=1$ 这个隐藏关系。
- $X_{10}$ ($n=5$):
- 展示: $\langle x, y \mid x^5=1, y^2=1, xy=yx^2 \rangle$。
- 我们天真地以为它有 $2 \times 5 = 10$ 个元素。
- 但我们推导出了隐藏关系 $x^3=1$。
- 现在我们同时拥有 $x^5=1$ 和 $x^3=1$。
- $x=x^1 = x^{5-2\cdot2}$... 不,应该用裴蜀定理。$\text{gcd}(5,3)=1$。存在整数 $a,b$ 使得 $5a+3b=1$。例如 $5(2)+3(-3)=1$。
- 所以 $x^1 = x^{10-9} = x^{5 \cdot 2} x^{3 \cdot (-3)} = (x^5)^2 (x^3)^{-3} = 1^2 \cdot 1^{-3} = 1$。
- 我们推导出了 $x=1$!这是更强的隐藏关系。
- 如果 $x=1$,那么展示变成了 $\langle 1, y \mid 1=1, y^2=1, 1y=y1 \rangle$。这只剩下了 $\langle y \mid y^2=1 \rangle$,这是一个2阶群 $\{1, y\}$。
- 所以 $X_{10}$ 实际上塌缩成了一个2阶群。
- 想当然: 看到一个展示,千万不要凭第一印象去猜测它的阶。必须警惕塌缩的可能性。
- 推导的技巧性: 发现隐藏关系的推导过程通常很有技巧性,没有固定的算法。上面那个从 $x=xy^2$ 出发的推导就是天才的一笔。
- 展示不等于群: 一个展示是群的一个“蓝图”。不同的蓝图可能因为内部规则的矛盾或冗余,最终建成同一个建筑,甚至是建成一个“茅草屋”(平凡群)。
本段通过例子警告我们,群的展示是一个微妙的工具。由于可能存在由给定关系代数推导出的“隐藏关系”,一个展示所定义的群可能会“塌缩”成比预期小得多的群。因此,从一个展示反向推断群的真实结构(特别是其阶)是一件困难且需要谨慎的事情。
本段的目的是给读者“泼一盆冷水”,防止他们对群展示这个工具过于乐观和滥用。它通过具体的例子,展示了从一个看似合理的展示出发,可能会得到意想不到的、退化的结果。这强调了“为已知群寻找展示”和“分析未知展示所定义的群”是两个难度完全不同的问题。
群的展示就像一套法律系统。
- 生成元: 是系统中的基本行动者或实体。
- 关系: 是明确颁布的法律条文。
- 隐藏关系: 是由大法官们通过解释现有法律条文而推导出的“判例法”。
- 塌缩: 某个判例法可能会产生巨大影响,使得很多原本以为合法的行为(不同的群元素)被宣布为非法或等同于其他行为,从而大大压缩了公民的“合法行为空间”(群的阶变小了)。
想象你在玩一个用规则生成的折纸游戏。
- 生成元: “向里折”、“向外折”。
- 关系: 一些基本的折叠规则,比如“向里折两次再展开等于没折”。
- 塌缩: 你按照规则折了一通,结果发现整张纸被折成了一个无限小的点,或者变成了一个简单的三角形,而不是你想象中的复杂飞船。这就是因为规则之间发生了意想不到的相互作用,导致结构塌缩了。
13.5 塌缩到平凡群的例子
📜 [原文12]
作为另一个例子,考虑展示
在这种情况下,很容易猜测 $Y$ 是一个阶为 $12$ 的群,但再次存在额外的隐式关系。实际上,这个群 $Y$ 退化为阶为 $1$ 的平凡群,即 $u$ 和 $v$ 满足附加关系 $u=1$ 和 $v=1$(练习中概述了证明)。
这种塌缩不会发生在 $D_{2 n}$ 的展示中,因为我们通过独立的(几何)方法表明存在一个阶为 $2 n$ 的群,其生成元为 $r$ 和 $s$,并满足 (1) 中的关系。结果是,一个仅具有这些关系的群的阶必须至少为 $2 n$。另一方面,很容易看出(使用与上述 $X_{2 n}$ 相同类型的论证以及交换关系 $r s=s r^{-1}$),任何由 (1) 中的生成元和关系定义的群的阶至多为 $2 n$。因此,具有展示 (1) 的群的阶恰好为 $2 n$,并且该群确实是正 $n$ 边形的对称群。
我们对于展示 (1) 的额外信息是存在一个已知阶的群满足此信息。相比之下,我们对任何满足 (2) 或 (3) 中关系的群都没有独立的知识。如果没有这种独立的“下限”信息,我们甚至可能无法确定给定的展示是否仅描述了平凡群,如 (3) 中所示。
虽然在一般情况下,通过展示来规定群时必须格外小心,但对已知群使用展示是一个强大的概念和计算工具。关于展示的额外结果,包括更详细的例子,出现在第 6.3 节中。
这段话通过一个更极端的例子,并与 $D_{2n}$ 的情况对比,深刻总结了群展示的理论要点。
- 极端塌缩的例子 ($Y$):
- 展示: $Y = \langle u, v \mid u^4=1, v^3=1, uv=v^2u^2 \rangle$。
- 天真的猜测: 基于 $u$ 的幂有4种 ($1,u,u^2,u^3$),$v$ 的幂有3种 ($1,v,v^2$),我们可能会猜测这个群的阶是 $4 \times 3 = 12$。
- 实际结果: 作者指出,这个群会完全塌缩。通过一系列推导(在练习中),可以从给定的关系中证明 $u=1$ 和 $v=1$。
- 平凡群: 如果所有的生成元都等于单位元,那么由它们生成的群里就只有一个元素——单位元本身。这就是平凡群 (trivial group)。
- 这个例子说明塌缩可以是灾难性的,把一个看似复杂的结构变成最简单的结构。
- 为什么 $D_{2n}$ 的展示没有塌缩:
- 这是一个非常关键的论证。我们是如何确定 $D_{2n} = \langle r, s \mid r^n=1, s^2=1, rs=sr^{-1} \rangle$ 的阶恰好是 $2n$ 的?
- 论证分两步 (三明治法则):
- 下限 (Lower Bound): 我们从一个具体的、已知的对象——正 $n$ 边形的对称群——出发。我们用几何方法证明了这个群的阶就是 $2n$。我们还验证了这个群里的旋转 $r$ 和反射 $s$ 确实满足这三个关系。这就证明了:存在一个阶为 $2n$ 的群满足这些关系。因此,由这些关系定义的抽象群的阶至少是 $2n$。它不可能塌缩成比 $2n$ 更小的群,否则就会与我们找到的那个几何实例相矛盾。
- 上限 (Upper Bound): 我们从展示本身出发。利用交换关系 $rs=sr^{-1}$,我们可以把任何由 $r, s$ 组成的字符串都化简成 $s^k r^i$ 的标准形式,其中 $k \in \{0,1\}, i \in \{0, ..., n-1\}$。这表明,由这个展示定义的群,其元素个数至多是 $2 \times n = 2n$ 个。
- 结论: 既然这个群的阶至少是 $2n$,又至多是 $2n$,那么它的阶就恰好是 $2n$。
- 关键区别:
- 对于 $D_{2n}$ 的展示 (1.1),我们有一个“外部保证”——一个来自几何的、阶为 $2n$ 的实例。
- 对于 $X_{2n}$ 的展示 (1.2) 和 $Y$ 的展示 (1.3),我们没有这样的外部信息。我们只是凭空写下了一些关系。没有这个“下限保证”,我们完全无法排除塌缩的可能性。
- 总结与展望:
- 结论: 直接通过一个展示来定义和分析一个未知的群是危险的,需要非常小心。
- 正确用法: 反过来,为一个已知的、具体的群(如对称群、矩阵群)找到一个展示,是一个非常有用的方法,它可以提炼出群的代数本质,并成为一个强大的计算工具。
- 预告: 更多关于展示的理论和例子将在 6.3 节中给出。
解释:这个公式声明了二面体群 $D_{2n}$(正 $n$ 边形的对称群)的阶(元素的总数)为 $2n$。
- $$ D_{2 n}=\left\{1, r, r^{2}, \ldots, r^{n-1}, s, s r, s r^{2}, \ldots, s r^{n-1}\right\} $$
解释:这个公式列出了二面体群 $D_{2n}$ 的所有 $2n$ 个元素,它们由 $n$ 个旋转 ($r^i$) 和 $n$ 个反射 ($sr^i$) 组成。
- $$ \left(s r^{9}\right)\left(s r^{6}\right)=s\left(r^{9} s\right) r^{6}=s\left(s r^{-9}\right) r^{6}=s^{2} r^{-9+6}=r^{-3}=r^{9} . $$
解释:这是一个在 $D_{24}$ ($n=12$) 中进行群运算的例子,展示了如何使用关系式将两个元素的乘积化简为标准形式。
- $$ G=\left\langle S \mid R_{1}, R_{2}, \ldots, R_{m}\right\rangle . $$
解释:这是群的展示的通用符号,表示群 $G$ 由生成元集 $S$ 和关系集 $\{R_i\}$ 所定义。
- $$ D_{2 n}=\left\langle r, s \mid r^{n}=s^{2}=1, r s=s r^{-1}\right\rangle . \tag{1.1} $$
解释:这是二面体群 $D_{2n}$ 的标准代数展示,用两个生成元 $r,s$ 和三个核心关系完全定义了该群的结构。
- $$ X_{2 n}=\left\langle x, y \mid x^{n}=y^{2}=1, x y=y x^{2}\right\rangle . \tag{1.2} $$
解释:这个公式定义了一个新的群 $X_{2n}$,作为例子来说明群展示可能因为隐藏关系而发生“塌缩”。
- $$ \begin{aligned} x & =x y^{2}=(x y) y=\left(y x^{2}\right) y=(y x)(x y)=(y x)\left(y x^{2}\right) \\ & =y(x y) x^{2}=y\left(y x^{2}\right) x^{2}=y^{2} x^{4}=x^{4} \end{aligned} $$
解释:这是一系列详细的代数推导,用于从群 $X_{2n}$ 的展示中揭示其隐藏关系 $x=x^4$ (并由此得出 $x^3=1$)。
- $$ Y=\left\langle u, v \mid u^{4}=v^{3}=1, u v=v^{2} u^{2}\right\rangle . \tag{1.3} $$
解释:这个公式定义了另一个群 $Y$,作为一个更极端的例子,它看起来像一个12阶群,但实际上会塌缩成只有1个元素的平凡群。
14.5 练习题 14-18
📜 [原文13]
- 找到 $\mathbb{Z}$ 的一个生成元集。
- 找到 $\mathbb{Z} / n \mathbb{Z}$ 的一个生成元集和关系。
- 证明群 $\left\langle x_{1}, y_{1} \mid x_{1}^{2}=y_{1}^{2}=\left(x_{1} y_{1}\right)^{2}=1\right\rangle$ 是二面体群 $D_{4}$(其中 $x_{1}$ 可以替换为字母 $r$,$y_{1}$ 可以替换为 $s$)。[证明最后一个关系与 $x_{1} y_{1}=y_{1} x_{1}^{-1}$ 相同。]
- 令 $X_{2 n}$ 为展示 (1.2) 中显示的群。
(a) 证明如果 $n=3 k$,则 $X_{2 n}$ 的阶为 $6$,并且当 $x$ 替换为 $r$ 且 $y$ 替换为 $s$ 时,它具有与 $D_{6}$ 相同的生成元和关系。
(b) 证明如果 $(3, n)=1$,则 $x$ 满足附加关系: $x=1$。在这种情况下,推断 $X_{2 n}$ 的阶为 $2$。 [使用事实 $x^{n}=1$ 和 $x^{3}=1$。]
- 令 $Y$ 为展示 (1.3) 中显示的群。
(a) 证明 $v^{2}=v^{-1}$。[使用关系: $v^{3}=1$。]
(b) 证明 $v$ 与 $u^{3}$ 交换。[证明 $v^{2} u^{3} v=u^{3}$,方法是将左侧写成 $\left(v^{2} u^{2}\right)(u v)$ 并使用关系将其简化为右侧。然后使用 (a) 部分。]
(c) 证明 $v$ 与 $u$ 交换。[证明 $u^{9}=u$,然后使用 (b) 部分。]
(d) 证明 $u v=1$。[使用 (c) 部分和最后一个关系。]
(e) 证明 $u=1$,推断 $v=1$,并得出结论 $Y=1$。[使用 (d) 部分和方程 $u^{4} v^{3}=1$。]
练习 14: $\mathbb{Z}$ 的生成元
- 目标: 找到能生成整数加法群 $(\mathbb{Z}, +)$ 的集合。
- 解答:
- 一个可能的生成元集是 $\{1\}$。因为任何正整数 $k$ 都可以表示为 $k$ 个 $1$ 相加,任何负整数 $-k$ 都可以表示为 $k$ 个 $-1$(即 $1$ 的逆元)相加,而 $0$ 可以视为空和。因此 $\mathbb{Z} = \langle 1 \rangle$。
- 同理,$\{-1\}$ 也是一个生成元集。
- 另一个例子是 $\{2, 3\}$。因为 $2$ 和 $3$ 的最大公约数是 $1$,根据裴蜀定理,存在整数 $a, b$ 使得 $2a+3b=1$(例如,$2(-1)+3(1)=1$)。既然可以通过 $2$ 和 $3$ 的线性组合得到 $1$,那么也就能得到所有整数。
练习 15: $\mathbb{Z} / n \mathbb{Z}$ 的展示
- 目标: 找到模 $n$ 整数加法群 $(\mathbb{Z}_n, +)$ 的一个生成元集和关系。这个群在乘法群语境下记为 $\mathbb{Z}_n$。
- 解答: $\mathbb{Z}_n$ 是一个循环群。
- 生成元集: 我们可以选择 $\{[1]\}$ 作为生成元集,其中 $[1]$ 是 $1$ 所在的同余类。
- 关系: 在加法群中,运算是加法,单位元是 $[0]$。生成元 $[1]$ 与自身相加 $n$ 次会得到 $[n]$,也就是 $[0]$。在书写展示时,我们习惯使用乘法符号,将群记为 $C_n$,生成元记为 $x$,单位元记为 $1$。此时,加法运算对应乘法运算,$[1]$ 对应 $x$,$n \cdot [1] = [0]$ 对应 $x^n=1$。
- 展示: $\langle x \mid x^n=1 \rangle$。
练习 16: 证明 $\left\langle x, y \mid x^{2}=y^{2}=(x y)^{2}=1\right\rangle$ 是 $D_{4}$
- 理解 $D_4$: 在本书的约定中,$D_{2n}$ 的下标是群的阶。所以 $D_4$ 是 $n=2$ 的情况,即 $D_{2 \cdot 2}$。它的展示是 $\langle r, s \mid r^2=1, s^2=1, rs=sr^{-1} \rangle$。因为 $r^2=1$,所以 $r=r^{-1}$。因此交换关系变为 $rs=sr$。这说明 $D_4$ 是一个4阶阿贝尔群,其中所有非单位元元素的阶都是2。这个群通常被称为 Klein 四元群 ($V_4$)。
- 目标: 证明 $\langle x, y \mid x^2=y^2=(xy)^2=1 \rangle$ 和 $D_4$ 的展示是等价的。
- 证明: 我们需要证明给定的关系蕴含了可交换关系 $xy=yx$。
- 从关系 $(xy)^2=1$ 开始,即 $xyxy=1$。
- 在等式右边乘以 $y$:$xyxy \cdot y = 1 \cdot y \implies xyx(y^2) = y$。
- 使用关系 $y^2=1$:$xyx(1) = y \implies xyx=y$。
- 在等式右边乘以 $x$:$xyx \cdot x = yx \implies xy(x^2)=yx$。
- 使用关系 $x^2=1$:$xy(1)=yx \implies xy=yx$。
- 结论: 我们已经从 $\langle x, y \mid x^2=y^2=(xy)^2=1 \rangle$ 推导出了 $xy=yx$。因此,这个展示等价于 $\langle x, y \mid x^2=1, y^2=1, xy=yx \rangle$。这与我们上面分析的 $D_4$ 的展示 $\langle r, s \mid r^2=1, s^2=1, rs=sr \rangle$ 在结构上是完全相同的(只需将 $x$ 对应于 $r$,$y$ 对应于 $s$)。
练习 17: 分析 $X_{2n}$
- 回顾: 群的展示为 $X_{2n} = \langle x, y \mid x^n=1, y^2=1, xy=yx^2 \rangle$。在正文中,我们已经推导出了一个通用的隐藏关系 $x^3=1$。
- (a) 当 $n=3k$ (n是3的倍数):
- 分析关系: 我们有两个关于 $x$ 的关系:$x^n=1$ (即 $x^{3k}=1$) 和 $x^3=1$。
- $x^3=1$ 这个关系更强。它可以推导出 $x^{3k}=(x^3)^k = 1^k = 1$。这意味着当 $n$ 是3的倍数时,给定的关系 $x^n=1$ 是由隐藏关系 $x^3=1$ 蕴含的,所以它是一个冗余关系。
- 等价展示: 因此,$X_{2n}$ 的展示等价于 $\langle x, y \mid x^3=1, y^2=1, xy=yx^2 \rangle$。
- 与 $D_6$ 比较: $D_6$ 的标准展示是 $\langle r, s \mid r^3=1, s^2=1, rs=sr^{-1} \rangle$。在 $D_6$ 中,因为 $r^3=1$,所以 $r^{-1}=r^2$。因此 $D_6$ 的交换关系可以写成 $rs=sr^2$。
- 结论: $X_{2n}$ (当 $n=3k$) 的展示与 $D_6$ 的展示在结构上完全相同($x \leftrightarrow r, y \leftrightarrow s$)。因此,$X_{2n}$ 同构于 $D_6$,其阶为6。
- (b) 当 $\text{gcd}(3, n)=1$ (n与3互质):
- 分析关系: 我们同时拥有两个关系:$x^n=1$ 和 $x^3=1$。
- 根据裴蜀定理,因为 $n$ 和 $3$ 互质,所以存在整数 $a,b$ 使得 $an+b(3)=1$。
- 现在我们来计算 $x^1$:
$x^1 = x^{an+3b} = x^{an} \cdot x^{3b} = (x^n)^a \cdot (x^3)^b$。
- 使用这两个关系 $x^n=1$ 和 $x^3=1$:
$x^1 = (1)^a \cdot (1)^b = 1 \cdot 1 = 1$。
- 新的隐藏关系: 我们推导出了一个更强的隐藏关系 $x=1$。
- 群的塌缩: 将 $x=1$ 代入 $X_{2n}$ 的展示,它变成了 $\langle 1, y \mid 1^n=1, y^2=1, 1y=y1^2 \rangle$。这些关系都变成了无意义的 $1=1$ 或 $y=y$。唯一剩下的有效关系是 $y^2=1$。
- 结论: 这个展示简化为了 $\langle y \mid y^2=1 \rangle$。这是一个由单个2阶元素生成的群,即2阶循环群 $\{1, y\}$。因此,在这种情况下,$X_{2n}$ 塌缩成了一个阶为2的群。
练习 18: 证明 $Y=1$
- 回顾: 群的展示为 $Y = \langle u, v \mid u^4=1, v^3=1, uv=v^2u^2 \rangle$。
- (a) 证明 $v^2=v^{-1}$:
- 从关系 $v^3=1$ 开始。
- 在等式两边同时右乘 $v^{-1}$:$v^3 v^{-1} = 1 \cdot v^{-1}$。
- $v^2 = v^{-1}$。证明完毕。
- (b)-(e) 的整体证明思路: 与其严格按照每个子问题的提示(特别是(c)中证明 $u^9=u$ 的提示非常困难),我们采用一条更直接的路径来证明 $u=1, v=1$。这条路径同样只使用给定的关系。
- 推导新的隐藏关系 $u^2=v^2$:
- 从交换关系 $uv=v^2u^2$ 开始。
- 两边左乘 $v^{-1}$: $v^{-1}uv = v^{-1}v^2u^2 = vu^2$。我们得到第一个有用的式子:$v^{-1}uv = vu^2$。
- 回到 $uv=v^2u^2$,两边右乘 $v^{-1}$: $u = v^2u^2v^{-1}$。
- 现在我们计算 $vu$:
- 使用关系 $v^3=1$:$vu = (1)u^2v^{-1} = u^2v^{-1}$。我们得到第二个有用的式子:$vu = u^2v^{-1}$。
- 现在我们有两个关于 $vu$ 的表达式。将第二个代入第一个的右侧:
- 这个方向似乎复杂了。让我们尝试另一条路。我们已经有 $v^{-1}uv = vu^2$。现在把这个结果代入它自身。
- 让我们试试一个新策略。从 $uv=v^2u^2$ 和 $vu=u^2v^{-1}$ 出发。
- 我们有 $u^2=vu$。将 $vu = u^2v^{-1}$ 代入:$u^2 = u^2v^{-1}$。
- 两边左乘 $(u^2)^{-1}$,我们得到 $1=v^{-1}$。
- 如果 $v^{-1}=1$,那么 $v=1$。
- 等等,推导有误! $u^2=vu$ 是从 $v(v^2u^2)=v(uv)$ 推出的,左边是 $v^3u^2=u^2$,右边是 $vu$。所以 $u^2=vu$ 是正确的。
- 然后 $u^2 = u^2 v^{-1}$ 也是正确的。
- 然后 $(u^2)^{-1} u^2 = (u^2)^{-1} u^2 v^{-1}$,得到 $1 = 1 \cdot v^{-1}$,即 $v^{-1}=1$。这个推导是正确的!
- 所以我们得到了隐藏关系 $v=1$。
- 证明 $u=1$:
- 将我们刚刚推导出的 $v=1$ 代入到原始交换关系 $uv=v^2u^2$ 中。
- $u(1) = (1)^2 u^2 \implies u = u^2$。
- 在群中,如果 $u=u^2$,我们可以两边右乘 $u^{-1}$ (只要u不是单位元)。$u u^{-1} = u^2 u^{-1} \implies 1 = u$。
- 所以我们又推导出了 $u=1$。
- 结论:
- 我们从展示 $Y=\left\langle u, v \mid u^{4}=v^{3}=1, u v=v^{2} u^{2}\right\rangle$ 出发,通过纯代数推导,证明了其生成元必须满足 $u=1$ 和 $v=1$。
- 这意味着由这个展示定义的群中,唯一的元素就是单位元。
- 因此,$Y$ 塌缩成了阶为1的平凡群,即 $Y=1$。
2行间公式索引
1.
解释:这个公式声明了二面体群 $D_{2n}$(正 $n$ 边形的对称群)的阶(元素的总数)为 $2n$。
2.
解释:这个公式列出了二面体群 $D_{2n}$ 的所有 $2n$ 个元素,它们由 $n$ 个旋转 ($r^i$) 和 $n$ 个反射 ($sr^i$) 组成。
3.
解释:这是一个在 $D_{24}$ ($n=12$) 中进行群运算的例子,展示了如何使用关系式将两个元素的乘积化简为标准形式。
4.
解释:这是群的展示的通用符号,表示群 $G$ 由生成元集 $S$ 和关系集 $\{R_i\}$ 所定义。
5.
解释:这是二面体群 $D_{2n}$ 的标准代数展示,用两个生成元 $r,s$ 和三个核心关系完全定义了该群的结构。
6.
解释:这个公式定义了一个新的群 $X_{2n}$,作为例子来说明群展示可能因为隐藏关系而发生“塌缩”。
7.
解释:这是一系列详细的代数推导,用于从群 $X_{2n}$ 的展示中揭示其隐藏关系 $x=x^4$ (并由此得出 $x^3=1$)。
8.
解释:这个公式定义了另一个群 $Y$,作为一个更极端的例子,它看起来像一个12阶群,但实际上会塌缩成只有1个元素的平凡群。