11. 2.5 群的子群格
1.1 子群格的引入与构建
11.1 核心概念
📜 [原文1]
本节我们将描述一个与群相关联的图,它描绘了其子群之间的关系。这个图,被称为群的子群格[^1],是“可视化”一个群的好方法——它无疑比群表更能阐明一个群的结构。在整个群论章节中,我们将使用格图,或其部分,来描述特定的群和一般群的某些性质。此外,一个群的子群格在伽罗瓦理论中将扮演重要角色。
[^1]: “格”一词在偏序集的意义上具有精确的数学含义。
这段话是本节的总起,介绍了即将要学习的一个重要工具——子群格 (subgroup lattice)。
- 目标: 我们想要找到一种方式来理解群 (group) 的内部结构。
- 现有工具的局限性: 之前我们可能接触过群表 (group table),也叫凯莱表 (Cayley table)。对于元素很少的群,群表很直观,但当群的阶(元素的数量)变大时,群表会变得异常庞大和混乱,很难从中看出深层次的结构性信息。例如,一个8阶群的群表就有 8x8=64 个条目。
- 新工具的提出: 这里提出一个叫做 子群格 的图 (graph)。图在数学中是由顶点 (vertices) 和边 (edges) 构成的结构。子群格这个图专门用来展示一个群的所有子群 (subgroups) 以及它们之间的相互关系。
- 子群格的优势: 它被认为是一种“可视化”群的好方法,比群表更能“阐明”(说清楚、照亮)群的结构。它关注的是群的“骨架”——子群结构,而不是单个元素之间的运算细节。
- 应用范围: 作者提到,这个工具不仅在本章有用,在后续的整个群论学习中都会反复使用。它不仅能帮助我们理解具体的群(如 $D_8$),还能帮助我们理解一般群的性质。
- 更深远的应用: 特别地,它在伽罗瓦理论 (Galois Theory) 中有重要作用。伽罗瓦理论在代数领域是座高峰,它通过群论来研究多项式方程的根,而子群格是连接域论和群论的一座关键桥梁。
- “格”的数学含义: 脚注解释了“格 (lattice)”这个词不是随便用的,它是一个有精确数学定义的术语,来源于偏序集 (partially ordered set) 理论。一个偏序集,如果其中任意两个元素都有唯一的最小上界 (join) 和最大下界 (meet),就称之为一个格。我们后面会看到,子群集合在“包含关系”这个偏序下,正好构成一个格。
本段没有数学公式。
我们以最简单的非平凡循环群 $\mathbb{Z}_4$(整数模4加法群)为例来初步感受一下。
$\mathbb{Z}_4 = \{0, 1, 2, 3\}$。
它的子群有:
- $\{0\}$: 这是平凡子群,所有群都有。
- $\langle 2 \rangle = \{0, 2\}$: 由元素2生成的子群。
- $\langle 1 \rangle = \{0, 1, 2, 3\} = \mathbb{Z}_4$: 由元素1(或3)生成的子群,也就是它自身。
这个群总共有3个子群。它们之间的关系是:
$\{0\} \subseteq \{0, 2\} \subseteq \mathbb{Z}_4$。
我们可以画一个简单的图来表示这种包含关系:
$\mathbb{Z}_4$ (在最上面)
|
$\{0, 2\}$ (在中间)
|
$\{0\}$ (在最下面)
这个简单的链条状的图,就是 $\mathbb{Z}_4$ 的子群格的雏形。它清晰地显示了子群的数量和它们“一个套一个”的层级结构,这比列出 $\mathbb{Z}_4$ 的4x4群表要直观得多。
- 误区: 认为子群格展示的是元素之间的关系。
- 纠正: 子群格的顶点是子群(它们是集合),而不是群的单个元素。边表示子群之间的包含关系,而不是元素之间的运算。
- 边界情况:
- 平凡群 $\{e\}$: 它只有一个子群,就是它自己。所以它的子群格只有一个点。
- 素数阶循环群 $\mathbb{Z}_p$: 根据拉格朗日定理,它的子群只有平凡子群 $\{0\}$ 和它自身 $\mathbb{Z}_p$。所以它的子群格就是两个点和一条线连接它们,和上面 $\mathbb{Z}_4$ 的例子类似,但只有顶和底,没有中间层。
本段引入了子群格的概念,它是一种用于可视化群的子群结构及其包含关系的图。相比于复杂的群表,子群格能更直观地揭示群的内在结构,是群论中一个重要的分析工具,并且在更高级的伽罗瓦理论中也扮演着核心角色。
本段的目的是为了引入一种比群表更高级、更结构化的工具来研究群。在数学中,当我们面对一个复杂的对象时,一个常见的策略是研究它的“子结构”以及这些子结构之间的关系。子群格正是这一思想在群论中的具体体现,它将研究的焦点从繁琐的元素运算转移到了更有条理的子群层级上。
可以将子群格想象成一个公司的“组织架构图”。
- 整个公司就是群 $G$ (在图的最顶端)。
- 最小的单位“空部门”或“初始项目组”就是平凡子群 $\{e\}$ (在图的最底端)。
- 图中的每一个节点都是一个部门(一个子群)。
- 如果部门A是部门B的子部门,那么就有一条从A到B向上的路径。如果A直接隶属于B,中间没有其他部门,那么就有一条直接的连线。
- 这个组织架构图清晰地展示了公司内部的层级和从属关系,让你对公司的结构一目了然。同样,子群格让你对群的结构一目了然。
想象你正在建造一个由不同大小的俄罗斯套娃组成的艺术品。
- 最大的那个套娃是整个群 $G$。
- 最里面最小的那个实心小娃娃是平凡子群 $\{e\}$。
- 每一个套娃都是一个子群。
- 如果一个套娃A能被放进另一个套娃B里,这就代表 $A \leq B$。
- 你把这些套娃从大到小依次从上到下排列,如果套娃A刚好能装进套娃B,不大不小正合适(中间没有其他尺寸的套娃可以插在它们之间),你就在A和B之间连一根线。最终形成的这个由套娃和连线构成的三维结构,就是子群格的直观体现。
11.2 子群格的构造方法
📜 [原文2]
给定有限群 $G$ 的子群格的构造如下:将 $G$ 的所有子群绘制出来,底部是 $1$,顶部是 $G$,大致上,阶较大的子群位于页面上方,阶较小的子群位于下方。如果 $A \leq B$ 且在 $A$ 和 $B$ 之间没有子群,则从 $A$ 到 $B$ 向上画线。因此,如果 $A \leq B$,则从 $A$ 到 $B$ 有一条路径(可能有多条路径)向上通过一系列中间子群(如果 $B \geq A$,则从 $B$ 到 $A$ 向下有路径)。子群在页面上的初始定位,在先验上有些随意,但通常(通过实践)可以选择以产生简单的图。
这段话详细描述了如何一步步画出一个有限群的子群格。
- 第一步:找出所有材料。
- 首先,你需要找到这个有限群 $G$ 的所有子群。这是一个关键且可能困难的前置工作。对于小群,我们可以尝试由每个元素生成循环子群,然后再考虑由多个元素生成的子群。
- 第二步:布置顶点 (Vertices)。
- 每一个子群都对应图中的一个顶点(一个点)。
- 这些点不是随意摆放的,而是有大致的层级规则。
- 平凡子群 $\{e\}$ (在书中用 $1$ 表示) 放在最底部。
- 整个群 $G$ 放在最顶部。
- 其他的子群放在中间。大致的原则是:阶(子群中元素的个数)越大的子群,位置越靠上;阶越小的,位置越靠下。
- 第三步:连接边 (Edges)。
- 连线的规则非常严格:只有当子群 $A$ 是子群 $B$ 的极大子群 (maximal subgroup) 时,才在 $A$ 和 $B$ 之间连一条线。
- “$A$ 是 $B$ 的极大子群”的严格说法是:$A \leq B$ (A是B的子群),并且不存在任何一个子群 $C$ 使得 $A < C < B$ (这里的 < 表示真子群关系)。也就是说,在 $A$ 和 $B$ 之间“插不进”任何其他的子群了。
- 线段的方向是从阶小的 $A$ 指向阶大的 $B$ (向上画)。
- 第四步:理解路径 (Paths)。
- 如果子群 $A$ 是子群 $B$ 的一个子群 ($A \leq B$),但在它们之间还可以插入其他子群,那么它们之间就没有直接的线段连接。
- 但是,你一定可以从 $A$ 出发,沿着图中向上的一系列线段,最终走到 $B$。这条由线段组成的序列就叫做一条路径。
- 反之,如果能从 $B$ 沿着向下的线段走到 $A$,那么必然有 $A \leq B$。
- 第五步:美化布局。
- 子群在水平方向上的位置没有严格规定(“在先验上有些随意”)。我们可以调整它们的位置,目的是让画出来的图尽可能地清晰、对称、交叉线少,从而更美观、更易于理解。这通常需要一些经验和尝试。
- $1$: 在乘法群的上下文中,这通常表示只包含单位元 $e$ 的平凡子群 $\{e\}$。
- $G$: 表示整个群。
- $A \leq B$: 这是一个非常重要的符号,读作 “A是B的子群”。它意味着:
- $A$ 和 $B$ 都是基于同一个大群 $G$ 的群。
- 集合 $A$ 是集合 $B$ 的一个子集 ($A \subseteq B$)。
(由于 $A$ 和 $B$ 本身都是群,并且运算继承自 $G$,所以只要满足子集关系,$A$ 就是 $B$ 的子群)。
- $B \geq A$: 这与 $A \leq B$ 是完全等价的,只是换了个说法,读作 “B是A的超群” 或 “B包含A作为子群”。
让我们以克莱因四元群 $V_4 = \{1, a, b, c\}$ 为例,其运算满足 $a^2=b^2=c^2=1$, $ab=c$, $bc=a$, $ca=b$。
- 找出所有子群:
- 阶为1: $\{1\}$ (平凡子群)。
- 阶为2: $\langle a \rangle = \{1, a\}$, $\langle b \rangle = \{1, b\}$, $\langle c \rangle = \{1, c\}$。
- 阶为4: $V_4$ 自身。
- 布置顶点:
- 最上面放 $V_4$ (阶为4)。
- 最下面放 $\{1\}$ (阶为1)。
- 中间一层放三个阶为2的子群 $\langle a \rangle, \langle b \rangle, \langle c \rangle$。
- 连接边:
- 从 $\{1\}$ 开始:$\{1\}$ 是 $\langle a \rangle$ 的子群,它们之间没有其他子群,所以从 $\{1\}$ 向 $\langle a \rangle$ 画一条线。同理,也向 $\langle b \rangle$ 和 $\langle c \rangle$ 画线。
- 从中间层开始:$\langle a \rangle$ 是 $V_4$ 的子群,它们之间没有其他子群(因为不存在阶为3的子群),所以从 $\langle a \rangle$ 向 $V_4$ 画一条线。同理,也从 $\langle b \rangle$ 和 $\langle c \rangle$ 向 $V_4$ 画线。
- 最终图形:
画出来就是一个菱形(或者说像钻石的形状):
- 顶部顶点: $V_4$
- 中间三个顶点: $\langle a \rangle, \langle b \rangle, \langle c \rangle$
- 底部顶点: $\{1\}$
- 从 $\{1\}$ 连出三条线到中间三个顶点。
- 从中间三个顶点连出三条线汇聚到 $V_4$。
- 易错点: 只要 $A \subseteq B$ 就画一条线。
- 纠正: 这是最常见的错误。必须是“紧邻”的包含关系,即 $A$ 是 $B$ 的极大子群,才能画线。例如,在 $\mathbb{Z}_{12}$ 中,$\langle 6 \rangle = \{0, 6\}$ 是 $\langle 2 \rangle = \{0, 2, 4, 6, 8, 10\}$ 的子群,但它们之间不能直接画线,因为还有一个子群 $\langle 4 \rangle$ 的阶是3,不在这条链上,而 $\langle 3 \rangle$ 的阶是4,也不在这条链上。等一下,$\langle 6 \rangle \subset \langle 2 \rangle$ 的阶分别是2和6,中间没有其他子群了?不对,$\mathbb{Z}_{12}$ 的子群由其阶的约数1,2,3,4,6,12决定。$\langle 6 \rangle$ 是2阶子群,$\langle 2 \rangle$ 是6阶子群。它们的阶的比值为3。它们之间没有其他子群。所以应该画线。让我们换个例子,$\mathbb{Z}_8$ 中,$\{0\}$ 是 $\mathbb{Z}_8$ 的子群,但不能直接连线,因为它们之间还有 $\langle 4 \rangle$ 和 $\langle 2 \rangle$。正确的路径是 $\{0\} \to \langle 4 \rangle \to \langle 2 \rangle \to \mathbb{Z}_8$。
- 边界情况: 子群格的绘制依赖于我们能找到所有的子群。对于比较大的群,找全所有子群本身就是一项非常困难的任务。如果漏掉了一个子群,整个格的结构可能就是错误的。
本段给出了绘制有限群 子群格的具体操作手册:首先找到所有子群,然后根据子群的阶分层放置,最后在满足极大子群关系的子群对之间连接线段。最终得到的图中,任意两子群的包含关系都可以通过图中的路径来体现。
本段的目的是将上一段提出的抽象概念“子群格”具体化、操作化。它提供了一套明确的算法,使得我们可以对任何一个给定的有限群(只要我们能找到它的所有子群),都能动手画出它的子群格。这为后续通过子群格来分析群结构提供了实践基础。
[直觉心-智模型]
这就像是绘制一份详细的地图。
- 找全地点: 先列出这个区域内所有有名字的地方(村庄、城镇、城市、省会等),这就是所有子群。
- 分层放置: 按照行政级别(或者人口规模)来大致安排位置。首都(群G)放在最显眼的位置,小村庄(平凡子群)放在不起眼的角落。城市(阶大的子群)放在上面,乡镇(阶小的子群)放在下面。
- 画交通线: 只画“直达”的公路。如果从乡镇A能直接开车到城市B,中间不停靠任何其他有名有姓的乡镇或城市,那么就在A和B之间画一条路。如果从村庄C到省会D必须经过城市E,那么就只画 C到E 和 E到D 的路,而不画 C到D 的“直线”高速。
- 看地图: 画好后,任何两个地点之间是否存在从属关系(一个地方是否在另一个地方的管辖范围内),就可以通过查看地图上是否存在一条只向上走的路径来确定。
想象你在玩一个乐高积木游戏。
- 你有一堆不同形状和大小的乐高块,每一块代表一个子群。
- 规则是:你只能把小块A插在大块B上面,如果A和B之间没有其他大小介于两者之间的积木块可以插。
- 你从最小的那个1x1的积木块(平凡子群)开始,把它作为地基。
- 然后根据规则,一层一层往上搭建。比如,你可以把几个2x1的块插在1x1的块上,再把一个4x2的块插在某个2x1的块上。
- 最终搭建完成的这个错落有致的乐高模型,其整体结构就是这个群的子群格。
11.3 从子群格中读取信息:并与交
📜 [原文3]
请注意,对于 $G$ 的任何一对子群 $H$ 和 $K$,包含它们两者的唯一最小子群(称为 $H$ 和 $K$ 的并),即 $\langle H, K\rangle$,可以从格中读取,方法如下:从 $H$ 和 $K$ 向上追踪路径,直到达到一个包含 $H$ 和 $K$ 的共同子群 $A$(注意 $G$ 本身总是包含所有子群,因此至少存在一个这样的 $A$)。为了确保 $A=\langle H, K\rangle$,请确保不存在 $A_{1} \leq A$(由从 $A$ 到 $A_{1}$ 的向下路径指示),且 $H$ 和 $K$ 都包含在 $A_{1}$ 中(否则用 $A_{1}$ 替换 $A$,并重复此过程以查看 $A_{1}=\langle H, K\rangle$)。通过对称的过程,可以读取 $G$ 中包含在 $H$ 和 $K$ 两者中的最大子群,即它们的交集(根据命题 8,这是一个子群)。
这段话解释了子群格画出来之后如何使用它,特别是如何利用它来找到两个子群的并 (join) 和交 (meet)。
- 子群的并 (Join):
- 定义: 两个子群 $H$ 和 $K$ 的并,记作 $\langle H, K \rangle$,并不是指集合的并集 $H \cup K$ (因为 $H \cup K$ 通常不是一个子群)。它的真正含义是:包含 $H$ 并且也包含 $K$ 的所有子群中,阶最小的那个。它也被称为由 $H$ 和 $K$ 生成 (generate) 的子群。
- 在格上寻找方法:
- 验证过程: 文中给出了一个更严谨的说法。假设你找到了一个候选的公共祖先 $A$。你需要检查一下,是否能从 $A$ 向下走到另一个子群 $A_1$,而这个 $A_1$ 仍然是 $H$ 和 $K$ 的公共祖先。如果是这样,那么 $A$ 就不是最小的,你需要用 $A_1$ 替换 $A$ 继续寻找。直到你找到的那个公共祖先 $A$ 没有任何后代(在它下方的子群)还能同时包含 $H$ 和 $K$,那么这个 $A$ 就是我们要找的 $\langle H, K \rangle$。这在数学上叫做寻找最小上界 (least upper bound)。
- 子群的交 (Meet):
- 定义: 两个子群 $H$ 和 $K$ 的交就是它们的集合交集 $H \cap K$。之前的命题8已经证明了,两个子群的交集仍然是一个子群。这个交集显然是包含于 $H$ 且包含于 $K$ 的所有子群中阶最大的那一个。
- 在格上寻找方法:
- $\langle H, K \rangle$: 子群 $H$ 和 $K$ 的并 (join)。
- 拆解: 这个符号表示“由集合 $H$ 和 $K$ 生成的子群”。
- 推导/定义: 它是所有包含了集合 $H \cup K$ 的子群的交集。用公式表达就是 $\langle H, K \rangle = \bigcap \{S \leq G \mid H \cup K \subseteq S\}$。这个定义保证了它是包含 $H$ 和 $K$ 的最小的子群。
- $H \cap K$: 子群 $H$ 和 $K$ 的交 (meet)。
- 拆解: 这就是标准的集合交集符号。
- 推导/定义: 根据命题8 (这里引用了之前的结论),如果 $H$ 和 $K$ 都是 $G$ 的子群,那么它们的交集 $H \cap K$ 也自动是 $G$ 的一个子群。它是被 $H$和$K$ 包含的最大的子群。
我们再次使用 $V_4$ 的子群格。$V_4 = \{1, a, b, c\}$,其阶为2的子群为 $H = \langle a \rangle = \{1, a\}$ 和 $K = \langle b \rangle = \{1, b\}$。
- 寻找 $\langle H, K \rangle$ (并):
- 在格上找到 $\langle a \rangle$ 和 $\langle b \rangle$。
- 从 $\langle a \rangle$ 向上走,路径是 $\langle a \rangle \to V_4$。
- 从 $\langle b \rangle$ 向上走,路径是 $\langle b \rangle \to V_4$。
- 它们唯一的公共上级就是 $V_4$。
- 所以,$\langle \langle a \rangle, \langle b \rangle \rangle = V_4$。
- 我们来验证一下:由 $a$ 和 $b$ 生成的子群,必须包含 $a$ 和 $b$,根据封闭性,也必须包含 $ab=c$,当然也包含单位元 $1$。所以这个子群至少包含 $\{1, a, b, c\}$,这正是 $V_4$。所以 $\langle a, b \rangle = V_4$,与格上读出的结果一致。
- 寻找 $H \cap K$ (交):
- 在格上找到 $\langle a \rangle$ 和 $\langle b \rangle$。
- 从 $\langle a \rangle$ 向下走,路径是 $\langle a \rangle \to \{1\}$。
- 从 $\langle b \rangle$ 向下走,路径是 $\langle b \rangle \to \{1\}$。
- 它们唯一的公共下级就是 $\{1\}$。
- 所以,$\langle a \rangle \cap \langle b \rangle = \{1\}$。
- 我们来验证一下:$\langle a \rangle = \{1, a\}$ 和 $\langle b \rangle = \{1, b\}$ 的集合交集确实就是 $\{1\}$。结果一致。
- 易错点1: 混淆子群的并 $\langle H, K \rangle$ 与集合的并集 $H \cup K$。
- 纠正: $H \cup K$ 几乎从来都不是子群(除非 $H \subseteq K$ 或 $K \subseteq H$)。$\langle H, K \rangle$ 是包含 $H \cup K$ 的最小子群。在上面的例子中,$H \cup K = \{1, a, b\}$,它有3个元素,根据拉格朗日定理,它不可能是4阶群 $V_4$ 的子群。
- 易错点2: 在寻找并时,随便找一个公共上级就认为是并。
- 纠正: 必须是“最低”的那个公共上级。在复杂的格中,可能存在多个公共上级,例如 $A$ 和 $B$ 都被 $C$ 和 $D$ 包含,而 $C$ 又被 $D$ 包含,那么并就是 $C$ 而不是 $D$。
- 边界情况: 如果 $H \leq K$,那么它们在格上的关系是 $H$ 在 $K$ 的下方,并且有向上的路径。
- 它们的并: $\langle H, K \rangle = K$ (从 $H$ 和 $K$ 向上走,第一个公共点就是 $K$ 本身)。
- 它们的交: $H \cap K = H$ (从 $H$ 和 $K$ 向下走,第一个公共点就是 $H$ 本身)。
本段阐述了子群格的一个核心功能:快速、直观地确定任意两个子群 $H$ 和 $K$ 的并 $\langle H, K \rangle$ (它们的最小公共上级/祖先) 和交 $H \cap K$ (它们的最大公共下级/后代)。这个特性使得子群格不仅仅是一个静态的展示图,更是一个动态的计算工具。
本段的目的是展示子群格的实用价值。仅仅画出子群的层级还不够,一个好的数学工具应该能帮助我们进行计算和推理。这里通过展示如何计算并与交,证明了子群格是一个强大的分析工具,它将集合运算(交)和生成运算(并)几何化了。这也回应了脚注中提到的“格”的严格数学含义,即任何两个元素都存在唯一的最小上界(并)和最大下界(交)。
继续使用“家族族谱”的比喻。
- 找并 (Join): 找张三和李四的“最近共同祖先”。从张三和李四开始,各自沿着父系往上找,张三的父亲、爷爷、曾爷爷... 李四的父亲、爷爷、曾爷爷... 第一个同时出现在两条链上的人,就是他们的最近共同祖先。这个祖先代表的家族,就是能同时包含张三和李四的最小家族。
- 找交 (Meet): 找两个贵族头衔(比如“诺福克公爵”和“萨默塞特公爵”)的“最高共同继承人”。这个比喻有点绕,换一个。想象两个国王A和B,他们的领土有重叠。这个重叠的部分就是他们的交。在格上,就是从A和B往下走,找到的“最高”的那个共同封臣。这个模型不太完美。还是用“最大共同下界”的几何图像更清晰。
想象一个立体的管网系统。
- 每个节点是一个连接点(子群)。
- 管道代表连接关系。水只能从高处往低处流。
- 找交 (Meet): 在 $H$ 点和 $K$ 点同时注入带颜色的水(比如红色和蓝色)。水顺着管道向下流动。第一个被两种颜色的水同时浸染的节点,就是 $H$ 和 $K$ 的交。
- 找并 (Join): 想象在 $H$ 点和 $K$ 点有两个气泵向上吹气。气体顺着管道向上流动。第一个同时被来自 $H$ 和 $K$ 的气流吹到的节点,就是它们的并。
11.4 子群格的局限性与同构问题
📜 [原文4]
这个过程有一些局限性,特别是它本身不能用于无限群。即使是阶相对较小的有限群,格也可能相当复杂(参见 M. Hall 和 J. Senior 的书《阶为 $2^{n}, n \leq 6$ 的群》,Macmillan,1964 年,其中有一些令人头痛的例子)。在本节末尾,我们将描述即使对于无限群如何绘制和使用格的一部分。
请注意,同构群具有相同的格(即,相同的有向图)。非同构群也可能具有相同的格(这发生在两个阶为 16 的群中——参见下面的练习)。由于子群格只是我们群描述符数据的一部分,这不会是一个严重的缺点(事实上,它甚至可能有助于发现两个非同构群何时具有一些共同性质)。
这段话讨论了子群格的两个重要方面:它的局限性和它与群同构的关系。
- 局限性:
- 无限群: 子群格的基本构造方法要求我们“画出所有子群”。对于无限群,比如整数加法群 $\mathbb{Z}$,它有无限多个子群($\langle n \rangle$ 对所有 $n \in \mathbb{N}$),我们不可能把它们都画出来。因此,这个方法原则上不适用于无限群。(作者预告了后面会讲如何处理这种情况,即只画出部分我们感兴趣的子群)。
- 复杂性: 即使是对于有限群,如果群的阶稍大一些,或者结构比较复杂,其子群的数量也可能爆炸式增长,导致子群格变得异常复杂,难以绘制和阅读。作者举例说,关于阶为 $2^n$ (n≤6) 的群的书里就有很多“令人头痛的”复杂例子。一个64阶的群的子群格可能非常庞大。
- 与同构 (Isomorphism) 的关系:
- 同构是群论中“相同”的严格定义。如果两个群 同构,意味着它们的结构是完全一样的,只是元素的名字不同。
- 同构群有相同的格: 如果群 $G_1$ 和 $G_2$ 同构,那么存在一个同构映射 $\phi: G_1 \to G_2$。这个映射会建立起 $G_1$ 子群和 $G_2$ 子群之间的一一对应关系,并且保持包含关系不变。因此,它们的子群格作为抽象的图,结构是完全一样的。
- 非同构群也可能有相同的格: 这是子群格的一个重要“缺陷”。子群格只是群结构的一个侧面反映,它没有捕捉到群的全部信息(比如元素的具体运算规则)。因此,可能会有两个结构不同(非同构)的群,它们恰好拥有相同结构的子群格。作者提到,在16阶的群中首次出现这种情况(练习13和14会探讨这个例子)。
- 如何看待这个“缺陷”: 作者认为这不是一个“严重的缺点”。首先,子群格只是我们用来描述和分析群的众多工具之一。其次,这个现象本身也很有趣,当两个不同的群有相同的格时,可能暗示了它们之间存在某些共同的结构性质,值得进一步研究。
本段没有数学公式。
- 同构群有相同的格:
- 群1: $\mathbb{Z}_2 = (\{0, 1\}, +_2)$。它的子群是 $\{0\}$ 和 $\mathbb{Z}_2$。格是两个点一条线。
- 群2: $G = (\{1, -1\}, \times)$。它的子群是 $\{1\}$ 和 $G$。格也是两个点一条线。
- $\mathbb{Z}_2$ 和 $G$ 是同构的(映射 $0 \mapsto 1, 1 \mapsto -1$),它们的子群格也完全相同。
- 非同构群也可能有相同的格:
- 这个例子比较复杂,是练习13和14的内容。涉及到两个16阶的群:
- $G_1 = \mathbb{Z}_2 \times \mathbb{Z}_8$ (阿贝尔群)
- $G_2 = M = \langle u, v \mid u^2=v^8=1, vu=uv^5 \rangle$ (非阿贝尔群)
- 因为一个是阿贝尔群,一个不是,所以它们肯定非同构。
- 然而,练习题将引导我们证明,它们有完全相同的子群格结构。这说明子群格无法区分“交换性”这个重要的群性质。
- 易错点: 认为子群格相同就意味着群同构。
- 纠正: 这是一个经典的错误。子群格相同是群同构的必要条件,但不是充分条件。可以用上面提到的16阶群的例子作为反例。
- 边界情况: 对于无限群,我们不能画出完整的格。例如整数加法群 $\mathbb{Z}$,它的子群是 $n\mathbb{Z}$ (所有n的倍数)。如果 $a$ 整除 $b$,那么 $b\mathbb{Z} \leq a\mathbb{Z}$。例如,$6\mathbb{Z} \leq 3\mathbb{Z} \leq \mathbb{Z}$。这个格可以想象成一个倒置的、基于整除关系的自然数之格,有无限多个节点和边。
本段指出了子群格的两个关键特性:它的适用性有限(不直接适用于无限群,对复杂有限群也可能过于庞大)以及它与群同构的不完全等价关系(同构必定同格,但同格未必同构)。这提醒我们,子群格是一个强大但并非万能的工具。
本段的目的是为了管理学习者的期望,防止对子群格这一工具产生不切实际的幻想。通过诚实地指出其局限性和“分辨能力”的上限,作者培养了读者批判性使用数学工具的思维。任何模型或工具都是对现实的简化,了解其简化了什么、忽略了什么,是有效使用它的前提。
[直觉心-智模型]
子群格就像一个人的X光片。
- 同构群有相同的格: 两个健康状况完全相同的人(身高、体重、骨骼结构都一样),他们的X光片看起来也应该是一样的。
- 非同构群也可能有相同的格: 医生不能仅凭一张X光片就诊断所有疾病。可能一个阿贝尔群和一个非阿贝尔群碰巧骨架(子群格)长得一样,但它们的“生理功能”(运算规则)完全不同。X光片看不出新陈代谢是快是慢。
- 局限性: 对于一个极其复杂或庞大的生物(比如蓝鲸),想拍一张包含所有骨骼细节的完整X光片是非常困难的(格的复杂性)。对于一个正在无限生长的生物(无限群),更不可能拍出“完整”的X光片。
想象用子群格来给群“画像”。
- 这幅画像是素描画,只勾勒出了轮廓和骨架(子群结构)。
- 同构的群是同一个人的不同照片,虽然穿着打扮(元素名称)不同,但内在是同一个人,所以骨架素描画是一样的。
- 非同构但同格的群,就像是两个人(比如一个男人和一个女人),他们身高、骨架结构碰巧一模一样,所以他们的素描画看起来一样,但他们本人是不同的。这幅素描画没有表现出“性别”(交换性)这个特征。
- 复杂性: 给一个简单的人物画像很容易,但要画一幅描绘成千上万军队的战争场面,每个士兵的位置和关系都要画清楚,这幅画就会变得无比复杂。
1.2 例子 (Examples)
12.1 循环群的子群格
📜 [原文5]
除了循环群(例子 1)之外,我们尚未证明以下格是正确的(例如,包含给定群的所有子群或具有正确的并和交集)。目前,我们将这些事实视为已知,并且随着我们在正文中建立更多理论,我们将把证明这些事实的任务作为练习。
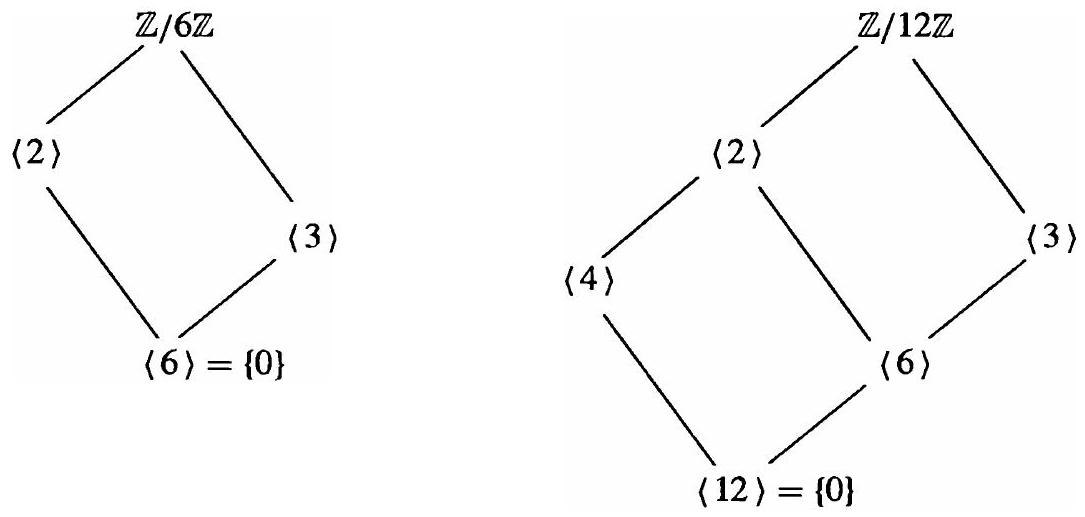
(1) 对于 $G=Z_{n} \cong \mathbb{Z} / n \mathbb{Z}$,根据定理 7, $G$ 的子群格是 $n$ 的约数格(也就是说, $n$ 的约数写在页面上, $n$ 在底部,1 在顶部,如果 $b \mid a$ 则从 $a$ 到 $b$ 向上画线)。以下是 $n$ 的各种特定值的一些具体例子。
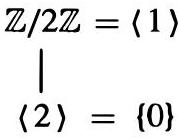
(2)
(4)
$\zeta(8)=\{0\}$

(注意: $\langle 1\rangle=\langle 3\rangle=\langle 5\rangle=\langle 7\rangle$ )
一般来说,如果 $p$ 是一个素数,则 $\mathbb{Z} / p^{n} \mathbb{Z}$ 的格是
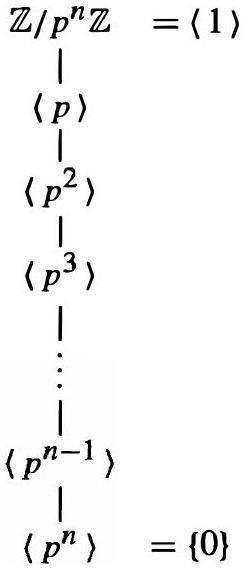
这段内容开始给出具体的子群格例子,首先是循环群 $\mathbb{Z}_n$。
- 开场白: 作者首先声明,除了第一个关于循环群的例子(其正确性由定理7保证),后面将要给出的其他群(如 $V_4, S_3, D_8$ 等)的子群格,目前我们暂时“接受”它们是正确的,而不去严格证明。证明这些格的完备性(找全了所有子群)和正确性(并与交的关系无误)需要更多理论知识,会在后续的学习中作为练习出现。这是一种常见的教学策略,先展示例子获得直观感受,再回头补足严格证明。
- 循环群 $\mathbb{Z}_n$ 的子群格:
- 核心结论: 循环群 $\mathbb{Z}_n$ 的子群格结构,和一个叫做“$n$的约数格”的东西是完全一样的。
- 定理7回顾: 这个结论是基于一个重要的定理(定理7):对于循环群 $\mathbb{Z}_n$ 的任何一个子群 $H$,都存在一个唯一的 $n$ 的约数 $d$,使得 $H$ 是由元素 $d$ 生成的循环子群 $\langle d \rangle$。反之,对于 $n$ 的每一个约数 $d$,$\langle d \rangle$ 都是 $\mathbb{Z}_n$ 的一个子群。这建立起 $\mathbb{Z}_n$ 的子群和 $n$ 的约数之间的一一对应关系。
- 包含关系: 更进一步,两个子群 $\langle d_1 \rangle$ 和 $\langle d_2 \rangle$ 的包含关系 $\langle d_1 \rangle \leq \langle d_2 \rangle$ 成立,当且仅当 $d_2$ 整除 $d_1$ ($d_2 \mid d_1$)。注意这里的整除关系是反过来的!
- 约数格的画法:
- 顶点是 $n$ 的所有正约数。
- $n$ 放在最底部 (对应平凡子群 $\langle n \rangle = \langle 0 \rangle = \{0\}$)。
- $1$ 放在最顶部 (对应整个群 $\langle 1 \rangle = \mathbb{Z}_n$)。
- 如果约数 $b$ 整除约数 $a$ ($b \mid a$),并且它们之间没有别的约数了(即 $a/b$ 是素数),那么就从 $a$ 到 $b$ 向上画一条线。
- 两个格的对应关系:
- 具体例子分析:
- $n=12$: 12的约数有1, 2, 3, 4, 6, 12。
- 子群: $\langle 1 \rangle, \langle 2 \rangle, \langle 3 \rangle, \langle 4 \rangle, \langle 6 \rangle, \langle 12 \rangle=\{0\}$。
- 格的结构:
- 底部是 $\langle 12 \rangle$ (对应约数12)。
- 顶部是 $\langle 1 \rangle$ (对应约数1)。
- $\langle 6 \rangle$ 在 $\langle 12 \rangle$ 上方,因为 $6 \mid 12$ 不对,应该是 $\langle 12 \rangle \leq \langle 6 \rangle$ 对应 $6|12$。这里原文的画法是把大数放下面,小数放上面。我们按原文的来,约数格是把n放最底,1放最顶。从a到b画线如果b|a。所以是从12到6画线,从12到4画线。从6到2画线,从6到3画线,从4到2画线。从2到1画线,从3到1画线。
- 图中从 $\langle 6 \rangle$ 连线到 $\langle 2 \rangle$ 和 $\langle 3 \rangle$ (因为 $2|6, 3|6$)。
- 从 $\langle 4 \rangle$ 连线到 $\langle 2 \rangle$ (因为 $2|4$)。
- $\langle 2 \rangle$ 和 $\langle 3 \rangle$ 的公共上级(最小公倍数对应的约数)是 $\langle 1 \rangle$ (lcm(2,3)=6,不对,是gcd(2,3)=1),$\langle 2 \rangle$ 和 $\langle 4 \rangle$ 的公共上级是 $\langle 2 \rangle$ (gcd(2,4)=2)。
- 并: $\langle \langle 2 \rangle, \langle 3 \rangle \rangle = \langle \text{gcd}(2,3) \rangle = \langle 1 \rangle = \mathbb{Z}_{12}$。
- 交: $\langle 2 \rangle \cap \langle 3 \rangle = \langle \text{lcm}(2,3) \rangle = \langle 6 \rangle$。
- $n=p^n$ (p为素数): 如 $\mathbb{Z}_8 = \mathbb{Z}_{2^3}$。
- 8的约数是 1, 2, 4, 8。
- 子群: $\langle 1 \rangle, \langle 2 \rangle, \langle 4 \rangle, \langle 8 \rangle=\{0\}$。
- 格的结构: 这是一个简单的链条。$8|4, 4|2, 2|1$。所以画出来是 $\langle 8 \rangle \to \langle 4 \rangle \to \langle 2 \rangle \to \langle 1 \rangle$。
- 这个链状结构是所有素数幂次阶循环群 $\mathbb{Z}_{p^k}$ 的子群格的共同特征。
- $V_4$ 与 $Z_4$ 的对比: 虽然图中没有画 $\mathbb{Z}_4$,但我们可以根据 $n=4$ 来画。4的约数是1, 2, 4。所以 $\mathbb{Z}_4$ 的子群格是 $\langle 4 \rangle \to \langle 2 \rangle \to \langle 1 \rangle$,一个三层的链。而 $V_4$ 的格是菱形。这从格的形状上就直观地看出来 $\mathbb{Z}_4$ 和 $V_4$ 是结构完全不同的群(非同构)。
- $G=Z_{n} \cong \mathbb{Z} / n \mathbb{Z}$:
- $Z_n$ 或 $\mathbb{Z}_n$: 表示整数模n加法循环群。
- $\mathbb{Z} / n \mathbb{Z}$: 这是更严格的记法,表示整数集 $\mathbb{Z}$ 对“模n同余”关系构成的商环,其加法结构就是一个循环群。
- $\cong$: 表示群同构符号,意味着两个群有完全相同的结构。
- $\langle k \rangle$: 表示由元素 $k$ 生成的循环子群。在 $\mathbb{Z}_n$ 中,$\langle k \rangle = \{mk \pmod n \mid m \in \mathbb{Z}\}$。
- $b \mid a$: 读作“b整除a”,意味着存在一个整数 $k$ 使得 $a = bk$。
让我们以 $n=30$ 为例,手动构建 $\mathbb{Z}_{30}$ 的子群格。
- 找约数: 30的约数有 1, 2, 3, 5, 6, 10, 15, 30。
- 对应子群: $\langle 1 \rangle, \langle 2 \rangle, \langle 3 \rangle, \langle 5 \rangle, \langle 6 \rangle, \langle 10 \rangle, \langle 15 \rangle, \langle 30 \rangle=\{0\}$。
- 画格 (根据整除关系,大数在下):
- 最底层: 30
- 上一层(30的素数倍): 15, 10, 6 (因为 $30=15 \times 2 = 10 \times 3 = 6 \times 5$)
- 再上一层: 5, 3, 2。从15连线到5和3 (不对,是 $5|15, 3|15$ 错,应该是 $15|30, 10|30, 6|30$ 连线 $30 \to 15, 30 \to 10, 30 \to 6$)。我们应该从 $a$ 向 $b$ 连线如果 $b|a$ 且 $a/b$ 是素数。
- $30/15=2$ (素数) $\implies$ 连线 $30 \to 15$。
- $30/10=3$ (素数) $\implies$ 连线 $30 \to 10$。
- $30/6=5$ (素数) $\implies$ 连线 $30 \to 6$。
- $15/5=3$ (素数) $\implies$ 连线 $15 \to 5$。
- $15/3$ 不行 $15/3=5$ (素数) $\implies$ 连线 $15 \to 3$。
- $10/5=2$ (素数) $\implies$ 连线 $10 \to 5$。
- $10/2=5$ (素数) $\implies$ 连线 $10 \to 2$。
- $6/3=2$ (素数) $\implies$ 连线 $6 \to 3$。
- $6/2=3$ (素数) $\implies$ 连线 $6 \to 2$。
- $5/1=5$ (素数) $\implies$ 连线 $5 \to 1$。
- $3/1=3$ (素数) $\implies$ 连线 $3 \to 1$。
- $2/1=2$ (素数) $\implies$ 连线 $2 \to 1$。
- 画出来是一个三维立方体的形状。
- 读取并与交:
- 并: $\langle \langle 6 \rangle, \langle 10 \rangle \rangle = \langle \text{gcd}(6, 10) \rangle = \langle 2 \rangle$。在格上,从6和10向上走,第一个公共祖先是2。
- 交: $\langle 6 \rangle \cap \langle 10 \rangle = \langle \text{lcm}(6, 10) \rangle = \langle 30 \rangle = \{0\}$。在格上,从6和10向下走,第一个公共后代是30。
- 易错点: 将子群包含关系 $\langle d_1 \rangle \leq \langle d_2 \rangle$ 等同于数字大小关系 $d_1 \leq d_2$。
- 纠正: 关系是反的!$\langle d_1 \rangle \leq \langle d_2 \rangle \iff d_2 \mid d_1$。例如,在 $\mathbb{Z}_{12}$ 中,$\langle 2 \rangle = \{0,2,4,6,8,10\}$, $\langle 4 \rangle = \{0,4,8\}$。显然 $\langle 4 \rangle \leq \langle 2 \rangle$,而这对应了 $2 \mid 4$。生成元数字越大,生成的子群反而越小。直观上,步子迈得越大(生成元数字大),能走到的点越少。
- 边界情况: 原文图中有一个 (注意: <1>=<3>=<5>=<7>) 在 $\mathbb{Z}_8$ 的例子旁边。这是印刷错误或者理解偏差。在 $\mathbb{Z}_8$ 中,$\langle 1 \rangle = \mathbb{Z}_8$。$\langle 3 \rangle = \{0,3,6,1,4,7,2,5\}=\mathbb{Z}_8$。$\langle 5 \rangle = \mathbb{Z}_8$, $\langle 7 \rangle = \mathbb{Z}_8$。这个注意是在说,这些不同的生成元生成了同一个子群(整个群)。这是对的,因为 1,3,5,7 都与 8 互素。但是它放在了 $\mathbb{Z}_{12}$ 的图旁边,这可能是排版问题。对于 $\mathbb{Z}_{12}$,与12互素的数是1, 5, 7, 11,所以 $\langle 1 \rangle = \langle 5 \rangle = \langle 7 \rangle = \langle 11 \rangle = \mathbb{Z}_{12}$。
本段的核心知识点是:循环群 $\mathbb{Z}_n$ 的子群格与 $n$ 的约数格在结构上是同构的,但对应关系是“反向”的:子群的包含关系 $\langle d_1 \rangle \leq \langle d_2 \rangle$ 对应于约数的整除关系 $d_2 \mid d_1$。这个结论极大地简化了对循环群结构的研究,将其转化为我们更熟悉的整数论问题。
本段的目的是提供一类最基础、最重要且结构最清晰的子群格范例。通过循环群这个我们已经比较了解的例子,来验证和巩固上一节学习的子群格的构造和解读方法。它作为一个标杆,为我们后续学习更复杂的非阿贝尔群的子群格提供了参照和对比。
想象你在一个圆形跑道上跑步,跑道周长为 $n$米。你从起点0出发。
- 群就是你可能到达的所有整数米位置 $\{0, 1, ..., n-1\}$。
- 子群就是如果你固定一个步长 $d$ (必须是 $n$ 的约数),你所有能踩到的点的集合。
- 步长为1米 ($\langle 1 \rangle$):你能踩遍所有点,这是整个群。
- 步长为 $n$ 米 ($\langle n \rangle$): 你只能在起点0来回踩,这是平凡子群。
- 步长为 $d_1$ 和 $d_2$ ($d_2$ 是 $d_1$ 的倍数, $d_1|d_2$):你用 $d_2$ 步长能踩到的点,一定也能用 $d_1$ 步长踩到。例如,步长6米能到的点(0, 6, 12, ...),步长3米肯定也能到。所以 $\langle 6 \rangle \leq \langle 3 \rangle$。
- 子群格就像是所有可能的“步长跑法”所能到达的点的集合之间的一个层级关系图。
想象一个用数字组成的“整除关系网”。
- 把数字1到 $n$ 写在一张纸上。
- 如果 $a$ 能被 $b$ 整除,就从 $a$ 向 $b$ 画一个箭头。
- 完成之后,擦掉所有“间接”的箭头(比如从4到1的箭头要擦掉,因为它经过了2: $4 \to 2 \to 1$)。
- 现在,只保留 $n$ 的所有约数以及连接它们的箭头。
- 最后,把整个图上下颠倒。
- 这个颠倒后的“约数直达关系网”就是 $\mathbb{Z}_n$ 的子群格。
12.2 克莱因四元群 (Viergruppe, $V_4$)
📜 [原文6]
(2) 克莱因四元群(Viergruppe), $V_{4}$,是一个阶为 4 的群,其乘法表为
| $\cdot$ | 1 | $a$ | $b$ | $c$ |
|---|---|---|---|---|
| 1 | 1 | $a$ | $b$ | $c$ |
| $a$ | $a$ | 1 | $c$ | $b$ |
| $b$ | $b$ | $c$ | 1 | $a$ |
| $c$ | $c$ | $b$ | $a$ | 1 |
以及格
注意 $V_{4}$ 是阿贝尔群,且与 $Z_{4}$ 不同构(为什么?)。我们将看到 $D_{8}$ 有一个与 $V_{4}$ 同构的子群,因此不需要检查上述定义的二元运算是否满足结合律。
这段内容介绍了第二个重要的例子:克莱因四元群 $V_4$。
- 定义: $V_4$ 是一个阶为4的群,由四个元素 $\{1, a, b, c\}$ 组成。它的结构完全由给出的乘法表(凯莱表)确定。
- 单位元: 1是单位元 ($1 \cdot x = x \cdot 1 = x$)。
- 逆元: 每个元素的逆元都是它自己 ($a \cdot a = 1, b \cdot b = 1, c \cdot c = 1$)。这说明 $V_4$ 中除单位元外,所有元素的阶都是2。
- 运算规则: 任意两个非单位元相乘得到第三个,例如 $ab=c, bc=a, ca=b$。
- 交换性: 从群表的对称性(沿主对角线)可以看出 $xy=yx$,所以 $V_4$ 是一个阿贝尔群(交换群)。
- 子群格:
- 文字描述了它的格,图片显示为一个菱形。
- 顶点:
- 最顶部: $V_4$ 自身,阶为4。
- 最底部: 平凡子群 $\{1\}$,阶为1。
- 中间层: 三个阶为2的子群,分别是 $\langle a \rangle = \{1, a\}$, $\langle b \rangle = \{1, b\}$, $\langle c \rangle = \{1, c\}$。
- 边:
- 从 $\{1\}$ 分别连线到 $\langle a \rangle, \langle b \rangle, \langle c \rangle$。
- 从 $\langle a \rangle, \langle b \rangle, \langle c \rangle$ 再分别连线汇聚到 $V_4$。
- 这个格非常对称。
- 性质与讨论:
- 与 $\mathbb{Z}_4$ 的比较:
- $V_4$ 是阿贝尔群,$\mathbb{Z}_4$ 也是阿贝尔群。
- 但它们不同构。作者提问“为什么?”。答案是:在 $\mathbb{Z}_4$ 中,有两个元素(1和3)的阶是4,一个元素(2)的阶是2。而在 $V_4$ 中,有三个元素的阶是2。同构的群必须有相同数量的各阶元素,所以它们不同构。从子群格的形状(菱形 vs. 链条)也能直观看出它们不同构。
- 结合律的验证: 作者提到,我们暂时不需要手动去验证这个乘法表是否满足结合律(这是一个繁琐的工作)。因为后面会学到,八阶二面体群 $D_8$ 中包含一个与 $V_4$ 同构的子群。既然 $D_8$ 是一个群(满足结合律),它的任何子群也必然满足结合律。这是一种“借用”已知结论来简化当前工作的技巧。
- $V_4$: Viergruppe的缩写,德语“四元群”的意思。
- $\cdot$: 在这里表示群的二元运算,可以理解为一种抽象的“乘法”。
我们来验证一下 $V_4$ 子群格的并与交。
令 $H = \langle a \rangle = \{1, a\}$,$K = \langle b \rangle = \{1, b\}$。
- 并: $\langle H, K \rangle = \langle a, b \rangle$。
- 在格上,从 $\langle a \rangle$ 和 $\langle b \rangle$ 向上走,最近的公共祖先是 $V_4$。所以 $\langle H, K \rangle = V_4$。
- 代数验证:由 $a,b$ 生成的子群必须包含 $1, a, b$ 以及它们的乘积 $ab=c$。所以这个子群至少是 $\{1, a, b, c\}$,也就是 $V_4$。
- 交: $H \cap K$。
- 在格上,从 $\langle a \rangle$ 和 $\langle b \rangle$ 向下走,最近的公共祖先是 $\{1\}$。所以 $H \cap K = \{1\}$。
- 代数验证:$\{1, a\} \cap \{1, b\} = \{1\}$。
结果完全吻合。
- 易错点: 认为所有4阶群都和 $\mathbb{Z}_4$ 或 $V_4$ 同构。
- 纠正: 这个想法是正确的。事实上,群论中一个基本的结果就是:任何一个4阶群,要么同构于循环群 $\mathbb{Z}_4$,要么同构于克莱因四元群 $V_4$。不存在其他结构的4阶群。(这个结论在练习10中要求证明)
- 边界情况: $V_4$ 是最小的非循环的阿贝尔群。
本段介绍了克莱因四元群 $V_4$,一个重要的4阶阿贝尔群。通过其乘法表和子群格(一个菱形),展示了它与循环群 $\mathbb{Z}_4$(子群格为链形)的本质区别。$V_4$ 的特点是除单位元外所有元素的阶都为2。
本段的目的是引入第一个非循环群的例子,并展示其子群格。通过与 $\mathbb{Z}_4$ 的对比,它生动地说明了子群格在区分不同群结构上的威力。$V_4$ 是群论中反复出现的“标准件”之一,熟悉它的结构至关重要。
想象一个电灯开关系统。
- 有三个开关 a, b, c 和一盏灯。
- 状态“1”表示灯灭,且所有开关都在初始位置。
- 操作“a”表示“拨动开关a”。
- 操作“b”表示“拨动开关b”。
- 操作“c”表示“同时拨动开关a和b”。
- 运算就是连续操作。
- $a \cdot a$: 拨动两次开关a,等于没动,回到初始状态1。
- $a \cdot b$: 先拨开关a,再拨开关b。这等价于什么?可能依赖于电路设计。$V_4$ 的结构可以被看作是某种对称的开关系统。更经典的例子是矩形的对称性:$1$(不动),$a$(水平翻转),$b$(垂直翻转),$c$(旋转180度)。那么 $a \cdot b$ (先水平翻转再垂直翻转)就等于 $c$ (旋转180度)。
想象你手里拿着一个长方形(非正方形)的床垫。
- 1: 不动它。
- a: 沿水平中轴线翻转(头脚颠倒)。
- b: 沿竖直中轴线翻转(左右颠倒)。
- c: 旋转180度。
这些操作构成一个群,这个群就同构于 $V_4$。
- $a \cdot a$:翻转两次,回到原样。
- $a \cdot b$:先头脚倒置,再左右颠倒,效果等同于旋转180度($c$)。
这个群的子群就是:
- $\{1\}$: 只包含“不动”这个操作。
- $\{1, a\}$: 只允许“不动”或“水平翻转”。
- $\{1, b\}$: 只允许“不动”或“竖直翻转”。
- $\{1, c\}$: 只允许“不动”或“旋转180度”。
- $V_4$: 四种操作都允许。
子群格就描绘了这些“操作许可权”集合之间的关系。
12.3 对称群 $S_3$
📜 [原文7]
(3) $S_{3}$ 的格是
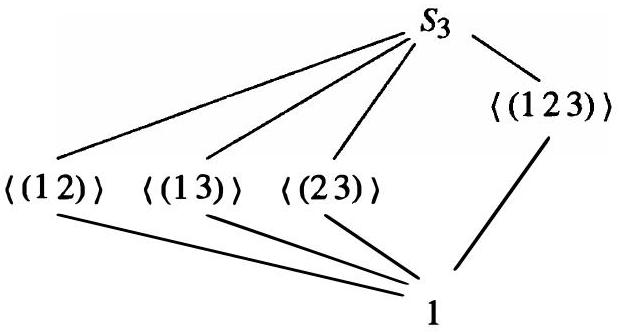
这段内容展示了6阶对称群 $S_3$ 的子群格。$S_3$ 是我们遇到的第一个非阿贝尔群。
- $S_3$ 的定义: $S_3$ 是作用于三个元素的集合(例如 $\{1, 2, 3\}$)上的所有置换构成的群。它的阶是 $3! = 6$。
- 元素:
- $e = (1)$: 单位置换 (不动)。
- $(1 2)$: 交换1和2。
- $(1 3)$: 交换1和3。
- $(2 3)$: 交换2和3。
- $(1 2 3)$: 轮换,$1 \to 2 \to 3 \to 1$。
- $(1 3 2)$: 轮换,$1 \to 3 \to 2 \to 1$。
- 非阿贝尔性: 运算不可交换,例如 $(1 2)(1 3) = (1 3 2)$,而 $(1 3)(1 2) = (1 2 3)$。两者不相等。
- 子群格分析:
- 顶点 (子群):
- 阶为1: $\{e\}$ (平凡子群)。
- 阶为2: 有三个,由阶为2的元素(对换)生成。
- $\langle (1 2) \rangle = \{e, (1 2)\}$
- $\langle (1 3) \rangle = \{e, (1 3)\}$
- $\langle (2 3) \rangle = \{e, (2 3)\}$
- 阶为3: 有一个,由阶为3的元素(3-轮换)生成。
- $\langle (1 2 3) \rangle = \{e, (1 2 3), (1 3 2)\}$。这个子群也等于 $\langle (1 3 2) \rangle$。这个子群通常被称为交错群 $A_3$。
- 阶为6: $S_3$ 自身。
- 格的结构: 图片展示的结构。
- 最底部是 $\{e\}$。
- 最顶部是 $S_3$。
- 中间分为两类:左边是三个阶为2的子群,右边是一个阶为3的子群 $A_3$。
- 从 $\{e\}$ 连线到所有四个中间子群。
- 从所有四个中间子群连线到 $S_3$。
- 结构特点: 这个格不像 $V_4$ 那样“扁平”,也不像 $\mathbb{Z}_4$ 那样是“线性”的。它体现出一种不对称性,反映了 $S_3$ 内部结构的多样性。
- 几何解释: $S_3$ 同构于等边三角形的对称群 $D_3$。
- 三个阶为2的子群对应于通过一个顶点和对边中点的三条翻转轴的对称操作。
- 一个阶为3的子群对应于旋转0度、120度和240度的操作集合。
- $S_3$: 3个元素的对称群。
- $\langle (1 2) \rangle$: 由置换 $(1 2)$ 生成的循环子群。
- $\langle (1 2 3) \rangle$: 由置换 $(1 2 3)$ 生成的循环子群。
我们来验证 $S_3$ 子群格的并与交。
- 一个2阶子群和一个3阶子群:
- 令 $H = \langle (1 2) \rangle$,$K = \langle (1 2 3) \rangle$。
- 并: $\langle H, K \rangle = \langle (1 2), (1 2 3) \rangle$。
- 在格上,从 $H$ 和 $K$ 向上走,唯一的公共祖先是 $S_3$。所以并是 $S_3$。
- 代数验证:这个子群包含 $\{(1 2), (1 2 3)\}$。根据拉格朗日定理,它的阶必须是6的约数,且要大于等于 $H$ 的阶2和 $K$ 的阶3。所以它的阶只能是6。因此这个子群就是 $S_3$。
- 交: $H \cap K = \{e, (1 2)\} \cap \{e, (1 2 3), (1 3 2)\} = \{e\}$。
- 在格上,从 $H$ 和 $K$ 向下走,唯一的公共后代是 $\{e\}$。
- 两个2阶子群:
- 令 $H = \langle (1 2) \rangle$,$L = \langle (1 3) \rangle$。
- 并: $\langle H, L \rangle = \langle (1 2), (1 3) \rangle$。
- 在格上,从 $H$ 和 $L$ 向上走,唯一的公共祖先是 $S_3$。所以并是 $S_3$。
- 代数验证:这个子群包含 $\{(1 2), (1 3)\}$。它还必须包含 $(1 2)(1 3) = (1 3 2)$。既然包含了阶为2和阶为3的元素,根据上面的例子,它就是 $S_3$。
- 交: $H \cap L = \{e, (1 2)\} \cap \{e, (1 3)\} = \{e\}$。
- 在格上,从 $H$ 和 $L$ 向下走,唯一的公共后代是 $\{e\}$。
- 易错点: 认为 $S_3$ 中任意两个元素生成的子群都是 $S_3$。
- 纠正: 不是。例如 $\langle (1 2 3), (1 3 2) \rangle$ 生成的子群只是 $A_3$ 自身,因为 $(1 3 2) = (1 2 3)^2$。
- 一个重要的性质: 在 $S_3$ 的子群格中,那个阶为3的子群 $A_3$ 是一个正规子群 (normal subgroup),而三个阶为2的子群都不是正规子群。子群格的图形本身有时会暗示出这种性质,比如 $A_3$ 在图中处于一个“特殊”的位置(单独一列),但这并不总是可靠的判断依据。
本段展示了最小的非阿贝尔群 $S_3$ 的子群格。这个格的结构比之前的例子更不规则,反映了非阿贝尔群更复杂的内部构造。它包含一个3阶子群和三个2阶子群,它们与平凡子群和整个群一起,构成了一个两层的结构。
本段的目的是展示第一个非阿贝尔群的子群格,让我们开始体会阿贝尔群与非阿贝尔群在结构上的差异。$S_3$ 是有限群论中最重要的入门例子,其子群格是必须熟悉的基本图形。
回到等边三角形的对称操作模型 $D_3$。
- $S_3$ 就是所有对称操作的集合(3次翻转,3次旋转)。
- 子群就是这些操作的“子集”,这些子集自身也得满足封闭性等要求。
- $\langle \text{旋转120度} \rangle$: 这是“只允许旋转,不允许翻转”的操作子集。
- $\langle \text{沿A点轴翻转} \rangle$: 这是“只允许沿着A点的对称轴翻转”的操作子集。
- 子群格就是这些“操作许可权包”之间的层级图。例如,“只旋转”和“只翻转”都是“所有操作”的子集。而它们的交集只有“什么都不做”。
想象一个有6个房间的建筑 $S_3$。
- 底层有一个入口大厅 $\{e\}$。顶层有一个观景台 $S_3$。
- 中间层有四个房间。一个是大的会议室 $A_3$(可以容纳3个人),另外三个是小办公室(每个只能容纳2个人)。
- 从入口大厅,有楼梯可以直接通往这四个中间层的房间。
- 从这四个中间层的房间,也都有楼梯直接通往顶层观景台。
- 但是,这三个小办公室之间没有直接的通道,会议室和办公室之间也没有。你想从一个办公室到另一个办公室,必须先上到顶楼观景台再下来。
- 这个建筑的布局图,就是 $S_3$ 的子群格。
12.4 八阶二面体群 $D_8$
📜 [原文8]
(4) 使用我们通常的 $D_{8}=\langle r, s\rangle$ 记法, $D_{8}$ 的格是
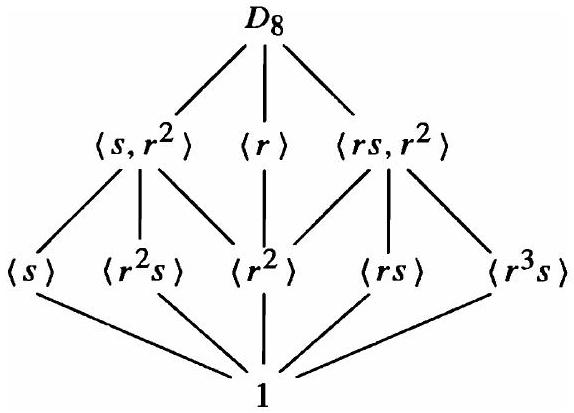
这段内容展示了8阶二面体群 $D_8$ 的子群格。$D_8$ 是正方形的对称群。
- $D_8$ 的定义: $D_8 = \langle r, s \mid r^4=s^2=1, sr=r^{-1}s=r^3s \rangle$。
- $r$ 可以看作是正方形逆时针旋转90度。
- $s$ 可以看作是关于某条对称轴(比如水平中轴)的翻转。
- 元素: $D_8 = \{1, r, r^2, r^3, s, sr, sr^2, sr^3\}$。总共8个元素。
- 这是一个非阿贝尔群。
- 子群格分析: 这个格比 $S_3$ 的复杂得多。
- 顶点 (子群):
- 阶为1: $\langle 1 \rangle$ (即 $\{e\}$ 或 $\{1\}$)。
- 阶为2: 有5个。
- $\langle r^2 \rangle = \{1, r^2\}$ (旋转180度)。这个子群位于格的中心位置,非常特殊。它是 $D_8$ 的中心 $Z(D_8)$。
- 四个由翻转生成的子群: $\langle s \rangle, \langle sr \rangle, \langle sr^2 \rangle, \langle sr^3 \rangle$。
- 阶为4: 有3个。
- $\langle r \rangle = \{1, r, r^2, r^3\}$。这是一个4阶循环子群,同构于 $\mathbb{Z}_4$。
- $\langle s, r^2 \rangle = \{1, s, r^2, sr^2\}$。这是一个4阶子群,其中非单位元元素的阶都是2,因此它同构于克莱因四元群 $V_4$。
- $\langle sr, r^2 \rangle = \{1, sr, r^2, sr^3\}$。这个子群也同构于 $V_4$。
- 阶为8: $D_8$ 自身。
- 格的结构 (根据图片描述):
- 底部是 $\langle 1 \rangle$。顶部是 $D_8$。
- 中心是 $\langle r^2 \rangle$。
- 从 $\langle 1 \rangle$ 向上连线到所有5个2阶子群。
- $\langle r^2 \rangle$ 被所有3个4阶子群包含,所以有从 $\langle r^2 \rangle$ 到 $\langle r \rangle, \langle s, r^2 \rangle, \langle sr, r^2 \rangle$ 的连线。
- 另外四个2阶子群,两个($\langle s \rangle, \langle sr^2 \rangle$)被 $\langle s, r^2 \rangle$ 包含,另外两个($\langle sr \rangle, \langle sr^3 \rangle$)被 $\langle sr, r^2 \rangle$ 包含。所以有相应的连线。
- 所有3个4阶子群都向上连线到 $D_8$。
- 结构特点:
- 非常对称。
- 存在不同构的4阶子群:一个 $\mathbb{Z}_4$ 型,两个 $V_4$ 型。
- 中心的 $\langle r^2 \rangle$ 地位特殊,是多个子群的交。
- $D_8 = \langle r, s \rangle$: 表示由 $r$ 和 $s$ 生成的二面体群。下标8表示群的阶。有些书也记作 $D_4$,表示4边形(正方形)的对称群。
- $\langle r \rangle$: 由旋转生成的循环子群。
- $\langle s, r^2 \rangle$: 由翻转 $s$ 和旋转180度 $r^2$ 生成的子群。
我们来验证 $D_8$ 子群格的并与交。
- 一个 $\mathbb{Z}_4$ 型和一个 $V_4$ 型子群:
- 令 $H = \langle r \rangle$ (阶为4),$K = \langle s, r^2 \rangle$ (阶为4)。
- 并: $\langle H, K \rangle = \langle r, s, r^2 \rangle = \langle r, s \rangle = D_8$。
- 在格上,从 $H$ 和 $K$ 向上走,唯一的公共祖先是 $D_8$。
- 交: $H \cap K = \{1, r, r^2, r^3\} \cap \{1, s, r^2, sr^2\} = \{1, r^2\} = \langle r^2 \rangle$。
- 在格上,从 $H$ 和 $K$ 向下走,相遇的第一个公共后代(也是唯一的)就是中心的 $\langle r^2 \rangle$。
- 两个 $V_4$ 型子群:
- 令 $K = \langle s, r^2 \rangle$, $L = \langle sr, r^2 \rangle$。
- 并: $\langle K, L \rangle = \langle s, r^2, sr \rangle$。
- 这个子群包含 $s$ 和 $sr$,所以也包含 $(sr)s^{-1} = srs = r^{-1} = r^3$。既然包含了 $r^3$,它就包含了整个旋转子群 $\langle r \rangle$。又因为它包含 $s$,所以它就是 $\langle r, s \rangle = D_8$。
- 在格上,从 $K$ 和 $L$ 向上走,公共祖先是 $D_8$。
- 交: $K \cap L = \{1, s, r^2, sr^2\} \cap \{1, sr, r^2, sr^3\} = \{1, r^2\} = \langle r^2 \rangle$。
- 在格上,从 $K$ 和 $L$ 向下走,唯一的公共后代是 $\langle r^2 \rangle$。
- 易错点: 认为 $D_8$ 中所有4阶子群都是循环的。
- 纠正: $D_8$ 是一个很好的反例,它既有循环的4阶子群 $\langle r \rangle$,也有非循环的4阶子群 $\langle s, r^2 \rangle$ (即 $V_4$) 。
- 特殊子群: $\langle r^2 \rangle$ 是 $D_8$ 的中心 $Z(D_8)$,意味着 $r^2$ 与 $D_8$ 中所有元素都可交换。在子群格中,中心常常处于一个被多个分支相交的“交通枢纽”位置。
本段展示了8阶二面体群 $D_8$ 的子群格。这是一个结构更丰富、更对称的非阿贝尔群的格。通过分析,我们发现 $D_8$ 内部共存着同构于 $\mathbb{Z}_4$ 和 $V_4$ 的子群,并且有一个特殊的2阶子群(即中心)作为多个子群的公共部分。
本段的目的是提供一个比 $S_3$ 更复杂、更有代表性的非阿贝尔群的例子。$D_8$ 是p-群(阶为素数的幂 $2^3$)中一个非常典型的非阿贝尔群。它的子群格展现了更多的结构可能性,例如不同构的同阶子群的存在,以及中心在格中的体现,这些都是深入研究群结构的重要课题。
回到正方形的对称操作。
- $D_8$ 是所有8个对称操作(4个旋转,4个翻转)的集合。
- $\langle r \rangle$ 是“只允许旋转”的操作包。
- $\langle s, r^2 \rangle$ 是“只允许水平翻转和旋转180度”的操作包。
- $\langle r^2 \rangle$ 是“只允许旋转180度”的操作包。
- 子群格展示了这些不同“操作权限包”的层级。例如,“只旋转180度”这个最小的权限,被包含在“只允许旋转”和“只允许水平翻转和旋转180度”这两个更大的权限包里。所以 $\langle r^2 \rangle$ 是它们的交集。
想象你面前有一个镶嵌着钻石的皇冠 $D_8$。
- 皇冠顶部的巨钻是 $D_8$ 本身。
- 皇冠底座上的一粒小碎钻是 $\langle 1 \rangle$。
- 皇冠的骨架上,有三个主要的支架,分别镶嵌着三颗中等大小的宝石 $\langle r \rangle$, $\langle s, r^2 \rangle$, $\langle sr, r^2 \rangle$ (4阶子群)。
- 这三个支架都交汇于皇冠正中心的一颗特殊的心形钻石 $\langle r^2 \rangle$ (中心子群)。
- 除了心形钻石,还有四颗其他形状的小钻石 $\langle s \rangle, \langle sr \rangle, \dots$ (2阶子群) 分布在骨架上。
- $\langle s, r^2 \rangle$ 这个支架上,除了它自己那颗宝石,还连接着 $\langle s \rangle, \langle sr^2 \rangle$ 和中心那颗 $\langle r^2 \rangle$。
- 整个皇冠的华丽而对称的结构,就是 $D_8$ 的子群格。
12.5 八阶四元数群 $Q_8$
📜 [原文9]
(5) $Q_{8}$ 的子群格是
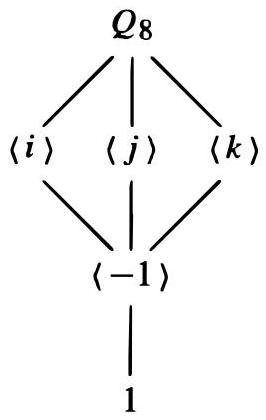
这段内容展示了另一个重要的8阶非阿贝尔群——四元数群 $Q_8$ 的子群格。
- $Q_8$ 的定义: $Q_8 = \{\pm 1, \pm i, \pm j, \pm k\}$,其乘法规则为:
- $i^2 = j^2 = k^2 = ijk = -1$。
- $-1$ 是中心元素,与所有元素交换,且 $(-1)^2 = 1$。
- $ij=k, jk=i, ki=j$。
- $ji=-k, kj=-i, ik=-j$。
- 也可以用生成元表示: $Q_8 = \langle a, b \mid a^4=1, a^2=b^2, b^{-1}ab=a^{-1} \rangle$。这里可以令 $a=i, b=j$。
- 子群格分析:
- 顶点 (子群):
- 阶为1: $\langle 1 \rangle = \{1\}$。
- 阶为2: 只有一个,即 $\langle -1 \rangle = \{1, -1\}$。这个子群是 $Q_8$ 的中心 $Z(Q_8)$。这是 $Q_8$ 与 $D_8$ 的一个显著区别($D_8$ 有5个2阶子群)。
- 阶为4: 有三个。
- $\langle i \rangle = \{1, i, -1, -i\}$。
- $\langle j \rangle = \{1, j, -1, -j\}$。
- $\langle k \rangle = \{1, k, -1, -k\}$。
- 阶为8: $Q_8$ 自身。
- 格的结构 (根据图片描述):
- 底部是 $\langle 1 \rangle$。顶部是 $Q_8$。
- 中间只有一层,包含三个4阶子群。
- 在4阶子群的下方,有一个2阶子群 $\langle -1 \rangle$。
- 从 $\langle 1 \rangle$ 连线到 $\langle -1 \rangle$。
- 从 $\langle -1 \rangle$ 连线到所有三个4阶子群。
- 从所有三个4阶子群连线到 $Q_8$。
- 结构特点:
- 非常对称,有点像 $V_4$ 的格的“升级版”,在顶层和底层之间加了两层。
- 只有一个2阶子群,且这个子群是三个4阶子群的唯一公共子群(除平凡子群外)。
- 所有真子群(非平凡且非自身的子群)都是循环群。
- 与 $D_8$ 的对比:
- 阶: 都是8。都是非阿贝尔群。
- 2阶元素/子群: $D_8$ 有5个, $Q_8$ 只有1个。
- 4阶子群: $D_8$ 有 $\mathbb{Z}_4$ 型和 $V_4$ 型, $Q_8$ 只有 $\mathbb{Z}_4$ 型。
- 结论: $D_8$ 和 $Q_8$ 不同构。它们的子群格形状也完全不同。
- $Q_8$: 四元数群 (Quaternion group)。
- $\langle i \rangle$: 由四元数单位 $i$ 生成的循环子群。
我们来验证 $Q_8$ 子群格的并与交。
- 任意两个4阶子群:
- 令 $H = \langle i \rangle$, $K = \langle j \rangle$。
- 并: $\langle H, K \rangle = \langle i, j \rangle$。
- 在格上,从 $\langle i \rangle$ 和 $\langle j \rangle$ 向上走,唯一的公共祖先是 $Q_8$。所以并是 $Q_8$。
- 代数验证:这个子群包含 $i$ 和 $j$,所以也必须包含 $ij=k$。一个包含 $i,j,k$ 的子群显然就是 $Q_8$ 自身。
- 交: $H \cap K = \{1, i, -1, -i\} \cap \{1, j, -1, -j\} = \{1, -1\} = \langle -1 \rangle$。
- 在格上,从 $\langle i \rangle$ 和 $\langle j \rangle$ 向下走,相遇的第一个公共后代就是 $\langle -1 \rangle$。
- 易错点: 因为 $Q_8$ 所有真子群都是循环的,就误以为 $Q_8$ 本身是阿贝尔群。
- 纠正: $Q_8$ 是一个经典的非阿贝尔群。这个性质(所有真子群都循环)非常特殊,但并不意味着群本身可交换。
- $Q_8$ 是一个哈密顿群 (Hamiltonian group),即一个所有子群都是正规子群的非阿贝尔群。$Q_8$ 是最小的哈密顿群。在它的子群格中,所有子群都处于“对称”的位置,这也暗示了它们的正规性。
本段介绍了8阶四元数群 $Q_8$ 及其子群格。$Q_8$ 的子群格展现了与 $D_8$ 截然不同的结构,它只有一个2阶子群和三个同构于 $\mathbb{Z}_4$ 的4阶子群。通过比较 $D_8$ 和 $Q_8$ 的子群格,我们可以深刻理解到非阿贝尔群内部结构的多样性。
本段的目的是引入群论中另一个与 $D_8$ 地位相当的、基础且重要的8阶非阿贝尔群 $Q_8$。$Q_8$ 的许多独特性质(如只有一个2阶子群,所有真子群都循环,是哈密顿群等)使其成为检验理论和构造反例的宝贵材料。熟悉其子群格是掌握其结构的第一步。
想象一个特殊的3D坐标系,基向量是 $i, j, k$。
- $Q_8$ 的元素是八个点:原点(不算),六个轴上的单位点($\pm i, \pm j, \pm k$),以及两个特殊的点 $\pm 1$。
- 乘法是一种特殊的“旋转”和“反射”操作。
- 子群 $\langle i \rangle$ 就是 $\{1, -1\}$ 和 $\pm i$ 这四个点组成的集合,可以看作是“限制在i轴和1轴上的运动”。
- 子群 $\langle -1 \rangle$ 则是所有运动都必须经过的“中心枢纽”。
- 子群格就是这些“运动空间”的包含关系图。三个坐标轴上的运动空间都包含了中心的那个枢纽空间。
想象一个三叶草的形状。
- 中心是 $\langle 1 \rangle$。
- 三片叶子的叶柄交汇处是 $\langle -1 \rangle$。
- 三片大叶子分别是 $\langle i \rangle, \langle j \rangle, \langle k \rangle$。
- 整个三叶草连同周围的空间是 $Q_8$。
- 从中心可以走到叶柄,从叶柄可以走到任何一片叶子。从任何一片叶子都可以走向代表整体的空间。这个结构图就是 $Q_8$ 的子群格。
12.6 十六阶二面体群 $D_{16}$
📜 [原文10]
(6) $D_{16}$ 的格不是平面图(不能在平面上绘制而没有交叉线)。一种绘制方式是
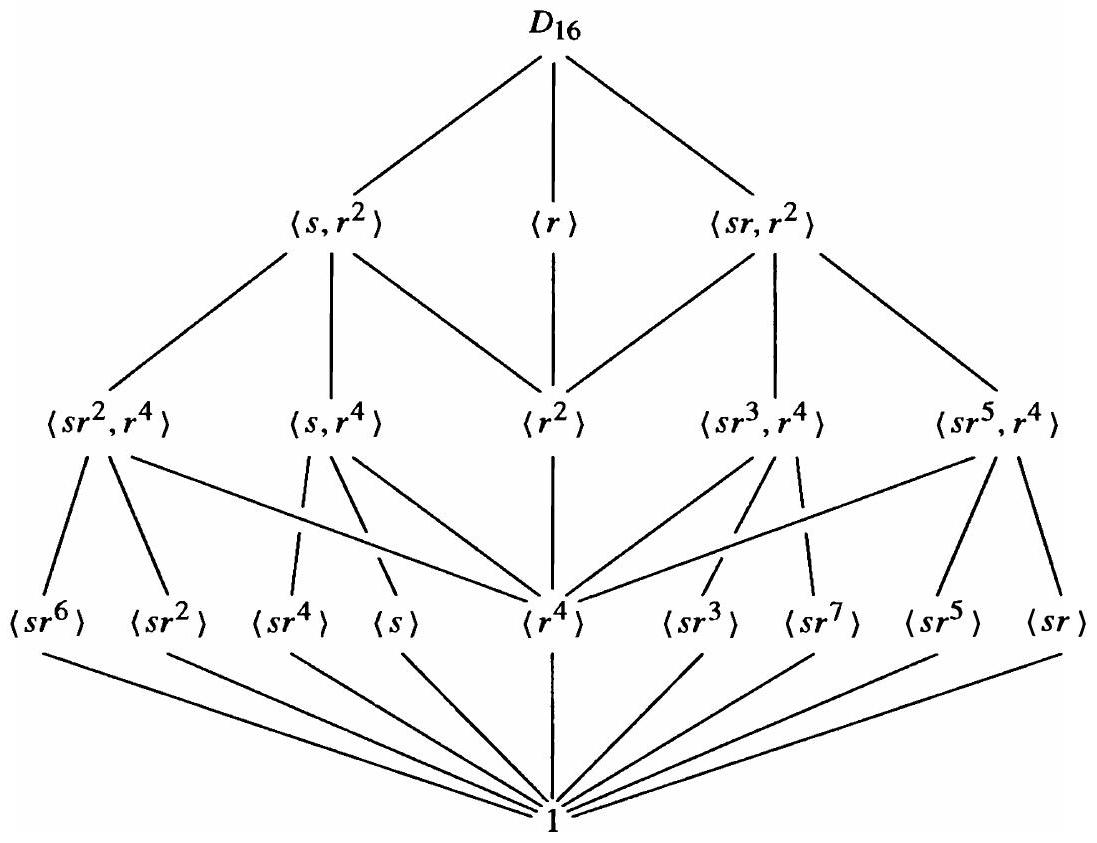
这段内容简要介绍了16阶二面体群 $D_{16}$ 的子群格,并指出了它的一个重要特性。
- $D_{16}$ 的定义: $D_{16} = \langle r, s \mid r^8=s^2=1, sr=r^{-1}s=r^7s \rangle$。这是正八边形的对称群,阶为16。
- 子群格的复杂性:
- 作者没有详细列出 $D_{16}$ 的所有子群,因为数量很多,结构非常复杂。
- 核心信息是:$D_{16}$ 的子群格是一个非平面图 (non-planar graph)。
- 平面图的定义是:一个图可以被画在二维平面上,使得它的所有边除了在顶点处之外,互相不交叉。
- $D_{16}$ 的子群格无论怎么画,都无法避免出现边的交叉。这标志着其内部的子群关系已经复杂到了一个新的层次。
- 最著名的两个非平面图是 $K_5$ (5个顶点的完全图) 和 $K_{3,3}$ (两边各3个顶点的完全二分图)。$D_{16}$ 的子群格中包含了与这些图类似的结构。
- 图示:
- 原文的图片展示了一种尝试绘制这个非平面图的方式。由于无法看到图片,我们只能想象它是一个有很多节点和边的、有交叉线的复杂网络。
- 图中应该会包含 $\langle r \rangle$ (一个8阶循环子群),以及多个同构于 $D_8$ 和 $V_4$ 的子群,还有大量的2阶子群。
- 例如,$\langle r^2, s \rangle$ 是一个子群,它同构于 $D_8$。$\langle r^4, s \rangle$ 同构于 $V_4$。
- $D_{16}$: 16阶二面体群。
由于格非常复杂,我们只看其中的一小部分关系。
- $H = \langle r^2 \rangle$: 这是一个4阶循环子群 $\mathbb{Z}_4$。
- $K = \langle s \rangle$: 这是一个2阶子群。
- 并: $\langle H, K \rangle = \langle r^2, s \rangle$。这个子群的元素是 $\{1, r^2, r^4, r^6, s, sr^2, sr^4, sr^6\}$。其关系为 $s(r^2) = r^{-2}s = (r^2)^3 s$。这是一个同构于 $D_8$ 的8阶子群。
- 交: $H \cap K = \{1, r^2, r^4, r^6\} \cap \{1, s\} = \{1\}$。
- 在 $D_{16}$ 复杂的格中,会有一个从 $\langle 1 \rangle$ 到 $\langle s \rangle$ 的边,也会有一条路径 $\langle 1 \rangle \to \langle r^4 \rangle \to \langle r^2 \rangle$。然后从 $\langle s \rangle$ 和 $\langle r^2 \rangle$ 出发的路径,最终会汇聚到它们的并 $\langle r^2, s \rangle$。
- 易错点: 看到复杂的格就望而却步。
- 纠正: 即使是复杂的格,我们通常也只关心其中的一小部分。下一节就会讲到如何绘制和使用“部分格”。
- 非平面性是一个重要的图论性质,它在这里出现,说明群的内在包含关系可以达到很高的复杂度,无法用一个简单的平面结构来梳理清楚。
本段以 $D_{16}$ 为例,展示了一个子群格可以变得非常复杂,甚至成为一个非平面图。这说明随着群的阶的增长,其子群结构可能迅速复杂化,完全绘制并分析整个格变得不切实际。
本段的目的是展示子群格复杂性的一个实例,为下一节引入“部分格”的概念做铺垫。它告诉我们,虽然子群格是一个强大的工具,但我们不能指望对所有群都能轻松地画出并使用完整的格。我们需要更灵活的策略来处理复杂的群。
想象一个城市的地铁线路图。
- 对于小城市(如$V_4$, $S_3$),线路图很简单,可以画得很清晰,没有交叉。
- 对于中等城市(如$D_8$),线路图开始变复杂,但仍然可以设计得没有交叉(或者很少交叉)。
- 对于特大城市(如$D_{16}$),比如东京或伦敦的地铁图,线路盘根错节,无论设计师多么努力,都无法避免大量的线路交叉。这张地铁图就是一个非平面图。$D_{16}$ 的子群格就像是这样一个特大城市的复杂地铁网络。
想象你在编织一张渔网。
- 如果群很简单,你可以把渔网平铺在地上,所有网线都不会自己压着自己。
- 如果群是 $D_{16}$,这张渔网的结构就非常特殊,无论你怎么摊,它总会有一些线段必须压在另一些线段上。你无法把它完美地“二维化”。它天生就是一个三维的、纠缠的结构。
1.3 部分子群格及其应用
13.1 部分格的概念
📜 [原文11]
在许多理论证明和具体例子中,我们只对给定群的两个(或少量)子群及其相互关系感兴趣。为了图形化地描绘这些,我们将绘制整个群格的子格,其中包含相关的并和交集。在这种子格中,不间断的线通常并不意味着线的端点之间没有子群。当处理无限群时,也将使用这些群的部分格。例如,如果我们只希望讨论 $D_{16}$ 中子群 $\left\langle s r^{2}, r^{4}\right\rangle$ 和 $\left\langle r^{2}\right\rangle$ 之间的关系,我们将绘制子格
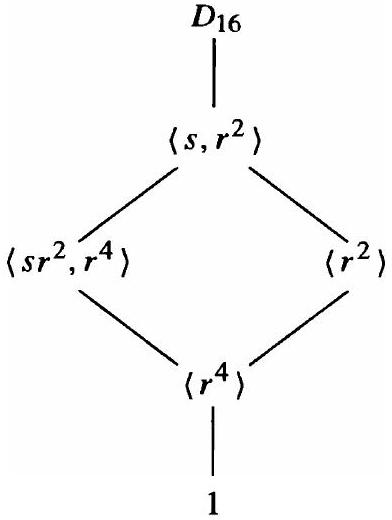
注意 $\left\langle s, r^{2}\right\rangle$ 和 $\left\langle r^{4}\right\rangle$ 分别是这两个子群在 $D_{16}$ 中的并和交集。
这段话针对前面提出的“子群格可能过于复杂”的问题,给出了解决方案:使用部分子群格 (partial lattice)。
- 动机: 在实际应用中,我们往往不需要了解群中所有子群的关系,而只关心某几个特定子群之间的关系。例如,在证明一个定理时,可能只涉及到子群 $H$, $K$, 它们的并 $\langle H, K \rangle$ 和交 $H \cap K$。
- 方法:
- 选择: 从完整的子群格中,只挑出我们感兴趣的那几个子群作为顶点。
- 补充: 为了结构的完整性,通常还会把这些子群的并和交也加进来。
- 绘制: 画出这些被选中的子群,并用线连接它们以表示包含关系。
- 与完整格的区别:
- 线的含义: 这是最关键的区别。在完整的子群格中,一条从A到B的线意味着A是B的极大子群(中间不能再插别的子群)。但在部分格中,一条从A到B的线仅仅表示 $A \leq B$,它不保证它们之间没有其他子群。这条线只是一个简化的、示意性的连接。
- 应用:
- 复杂有限群: 当完整格过于庞大时(如 $D_{16}$),我们可以只画出需要研究的部分,使问题简化。
- 无限群: 对于有无限个子群的无限群(如整数群 $\mathbb{Z}$),我们不可能画出完整格,但可以画出包含有限个我们感兴趣的子群的部分格。
- 例子分析:
- 群: $D_{16}$。
- 感兴趣的子群: $H = \langle sr^2, r^4 \rangle$ 和 $K = \langle r^2 \rangle$。
- 让我们分析一下这两个子群:
- $K = \langle r^2 \rangle = \{1, r^2, r^4, r^6\}$,这是一个4阶循环子群。
- $H = \langle sr^2, r^4 \rangle = \{1, r^4, sr^2, sr^6\}$。由于 $(sr^2)^2 = sr^2sr^2 = s(r^2s)r^2 = s(sr^{-2})r^2 = r^{-2}r^2=1$,且 $(r^4)^2=r^8=1$,且 $r^4$ 与 $sr^2$ 可交换(因为 $r^4(sr^2) = sr^{-4}r^2 = sr^{-2}$ 且 $(sr^2)r^4 = sr^6 = sr^{-2}$),所以 $H$ 同构于 $V_4$。
- 它们的关系:
- 首先,$\langle r^4 \rangle = \{1, r^4\}$。
- $K$ 中包含 $r^4$,所以 $\langle r^4 \rangle \leq K$。
- $H$ 中也包含 $r^4$,所以 $\langle r^4 \rangle \leq H$。
- 因此,$\langle r^4 \rangle$ 是它们的交或交的子群。实际上 $H \cap K = \{1,r^4\} = \langle r^4 \rangle$。
- 它们的并 $\langle H, K \rangle = \langle sr^2, r^4, r^2 \rangle = \langle sr^2, r^2 \rangle$。这是一个8阶子群,同构于 $D_8$。(注意这里作者写的是 $\langle s, r^2 \rangle$,这可能是个笔误,应该是 $\langle sr^2, r^2 \rangle$。不过 $\langle s,r^2 \rangle$ 和 $\langle sr^2, r^2 \rangle$ 都是 $D_{16}$ 中与 $D_8$ 同构的子群。)
- 绘制部分格:
- 顶部: 它们的并 $\langle sr^2, r^2 \rangle$。
- 中间: $H$ 和 $K$。
- 底部: 它们的交 $\langle r^4 \rangle$。
- 画出来是一个菱形。这个菱形部分格清晰地展示了这四个特定子群之间的并、交和包含关系,而忽略了 $D_{16}$ 中其他几十个子群的干扰。
- $\langle sr^2, r^4 \rangle$: 由 $sr^2$ 和 $r^4$ 生成的子群。
让我们在整数群 $\mathbb{Z}$ (一个无限群) 中绘制一个部分格。
- 我们感兴趣的子群是 $H=4\mathbb{Z}$ (所有4的倍数) 和 $K=6\mathbb{Z}$ (所有6的倍数)。
- 交: $H \cap K = 4\mathbb{Z} \cap 6\mathbb{Z}$。一个数既是4的倍数也是6的倍数,那它一定是它们的最小公倍数12的倍数。所以 $H \cap K = 12\mathbb{Z}$。
- 并: $\langle H, K \rangle = \langle 4\mathbb{Z}, 6\mathbb{Z} \rangle$。这个子群是由4和6生成。所有4和6的整系数线性组合 $4x+6y$ 的集合。这个集合等于它们最大公约数2的倍数的集合。所以 $\langle H, K \rangle = 2\mathbb{Z}$。
- 绘制部分格:
- 顶部: $2\mathbb{Z}$ (并)
- 中间: $4\mathbb{Z}$ 和 $6\mathbb{Z}$
- 底部: $12\mathbb{Z}$ (交)
- 连线:从 $12\mathbb{Z}$ 到 $4\mathbb{Z}$ 和 $6\mathbb{Z}$。从 $4\mathbb{Z}$ 和 $6\mathbb{Z}$ 到 $2\mathbb{Z}$。
- 同样是一个菱形。这个菱形清晰地展示了 $2\mathbb{Z}, 4\mathbb{Z}, 6\mathbb{Z}, 12\mathbb{Z}$ 这四个无限子群之间的关系,而无需理会无限多个其他子群。
- 易错点: 看到部分格中的一条线 $A-B$,就断定A是B的极大子群。
- 纠正: 部分格的线只代表包含关系 $A \leq B$。它们之间完全可能存在其他子群,只是我们选择不画出来而已。例如,在上面 $\mathbb{Z}$ 的例子中,从 $12\mathbb{Z}$ 到 $6\mathbb{Z}$ 画了一条线,但它们之间其实还有子群 $24\mathbb{Z}, 36\mathbb{Z}, \dots$ 严格来说,$6\mathbb{Z}$ 不是 $12\mathbb{Z}$ 的极大超群,应该是 $12\mathbb{Z}$ 是 $6\mathbb{Z}$ 的子群,中间没有别的子群了?不对,$12\mathbb{Z} \subset 6\mathbb{Z}$,阶之比是2,所以是极大子群关系。但 $12\mathbb{Z}$ 和 $4\mathbb{Z}$ 之间,$12\mathbb{Z} \subset 4\mathbb{Z}$,阶之比是3,也没有。但是 $12\mathbb{Z} \subset 2\mathbb{Z}$ 之间就有 $4\mathbb{Z}$ 和 $6\mathbb{Z}$ 了。所以 $12\mathbb{Z}$ 到 $2\mathbb{Z}$ 就不能画直接的线在完整格里。在部分格里就可以。
本段引入了部分子群格的概念,作为处理复杂有限群和无限群的实用技巧。部分格只关注我们感兴趣的少数几个子群及其并与交,通过牺牲“极大性”这一信息,换来了图形的简洁和问题的聚焦。
本段的目的是提供一个解决子群格复杂性问题的实用方法,增强该工具的灵活性和适用范围。它体现了数学中一种重要的思想:当整体过于复杂时,就专注于研究局部的、关键的结构。
继续使用地铁图的比喻。
- 你只想从家(子群H)去公司(子群K),并想知道换乘信息。
- 你不需要看完整的全市地铁图(完整的子群格),那会让你眼花缭乱。
- 你只需要一张“局部图”(部分格),上面只标出你家、公司,以及连接它们的最重要的换乘站——离你俩最近的那个可以相互换乘的站(交 $H \cap K$),以及包含你俩线路的那个最终的大枢纽站(并 $\langle H, K \rangle$)。
- 这张局部图上的线路,可能中间会经过很多小站,但图上都省略了,只画了关键站点之间的连接。
想象你在看一张巨大的世界地图,上面密密麻麻标满了所有国家、城市和道路。
- 现在你只想搞清楚中国、美国、俄罗斯和联合国总部之间的关系。
- 你拿出笔,在地图上圈出这四个地方,并画出它们之间的主要航线。
- 你得到的这张被圈出来的、只有几个点和几条线的“草图”,就是部分格。它忽略了世界上其他几百个国家和无数的城市,只聚焦于你关心的核心关系。
13.2 利用格计算正规化子和中心化子
📜 [原文12]
最后,给定一个群的子群格,计算正规化子和中心化子相对容易。例如,在 $D_{8}$ 中,我们可以看到 $C_{D_{8}}(s)=\left\langle s, r^{2}\right\rangle$,因为我们首先计算出 $r^{2} \in C_{D_{8}}(s)$(参见第 2 节)。这证明了 $\left(s, r^{2}\right) \leq C_{D_{8}}(s)$(注意元素总是属于它自己的中心化子)。包含 $\left\langle s, r^{2}\right\rangle$ 的唯一子群是它自己和整个 $D_{8}$。我们不能有 $C_{D_{8}}(s)=D_{8}$,因为 $r$ 不与 $s$ 交换(即 $r \notin C_{D_{8}}(s)$)。这只剩下 $C_{D_{8}}(s)$ 的声称可能性。
这段话展示了子群格的又一个高级应用:帮助我们计算中心化子 (centralizer) 和正规化子 (normalizer)。
- 回顾定义:
- 中心化子 $C_G(A)$: 在群 $G$ 中,所有能与集合 $A$ 中每一个元素交换的元素的集合。它是一个子群。
- 正规化子 $N_G(A)$: 在群 $G$ 中,所有满足 $gAg^{-1}=A$ 的元素 $g$ 的集合。它也是一个子群。
- 关系: $C_G(A) \leq N_G(A)$。
- 利用格进行计算的逻辑 (以上下界剪枝法):
- 第一步:找到一个下界。
- 通过一些简单的计算,找到一些肯定在中心化子(或正规化子)中的元素。
- 由这些元素生成的子群,就是中心化子的一个子群,即我们找到了一个“下界”。
- 第二步:在格中定位下界。
- 在子群格中找到这个“下界”子群对应的顶点。
- 第三步:确定一个上界/排除不可能的上界。
- 中心化子或正规化子本身也是群的子群,所以它必然是格中的一个顶点。
- 并且,它必须包含我们找到的“下界”子群。所以在格中,它一定在“下界”子群的上方(或者就是它自己)。
- 通过寻找一些反例(比如找到一个确定不在中心化子中的元素),我们可以排除掉一些更大的候选子群。
- 第四步:缩小范围,确定最终结果。
- 在“下界”和“被排除的上界”之间,往往只剩下一两个候选者。通过简单的验证,就可以确定哪个是真正的中心化子或正规化子。
- 例子分析 ($C_{D_8}(s)$):
- 目标: 找 $D_8$ 中元素 $s$ 的中心化子 $C_{D_8}(s)$。
- Step 1 (找下界):
- $s$ 肯定与自己交换,所以 $s \in C_{D_8}(s)$。
- 之前(第2.2节)已经算过,$r^2$ 也与 $s$ 交换 ($sr^2=r^{-2}s=r^2s$)。所以 $r^2 \in C_{D_8}(s)$。
- 因此,由 $s$ 和 $r^2$ 生成的子群 $\langle s, r^2 \rangle$ 必然是 $C_{D_8}(s)$ 的一个子群。我们找到了下界:$\langle s, r^2 \rangle \leq C_{D_8}(s)$。
- Step 2 (定位下界):
- 在 $D_8$ 的子群格中,$\langle s, r^2 \rangle$ 是一个4阶子群。
- Step 3 (确定上界/排除):
- $C_{D_8}(s)$ 必须是格中位于 $\langle s, r^2 \rangle$ 上方的一个顶点。
- 查看 $D_8$ 的格,在 $\langle s, r^2 \rangle$ 上方的子群只有它自己和 $D_8$。
- 所以,$C_{D_8}(s)$ 只有两种可能:要么是 $\langle s, r^2 \rangle$,要么是 $D_8$。
- 我们找一个反例来排除 $D_8$。元素 $r$ 在 $D_8$ 中,但 $rs=sr^3 \neq sr$。所以 $r$ 不与 $s$ 交换,即 $r \notin C_{D_8}(s)$。
- 既然 $C_{D_8}(s)$ 中不包含 $r$,那它就不可能是 $D_8$。
- Step 4 (得出结论):
- 排除了 $D_8$ 之后,唯一的可能性就是 $C_{D_8}(s) = \langle s, r^2 \rangle$。
- $C_{D_8}(s)$: 在群 $D_8$ 中元素 $s$ 的中心化子。
- $r \notin C_{D_8}(s)$: 元素 $r$ 不属于子群 $C_{D_8}(s)$。
我们来用同样的方法计算 $N_{D_8}(\langle s \rangle)$ (在 $D_8$ 中子群 $\langle s \rangle$ 的正规化子)。
- 目标: $N_{D_8}(\langle s \rangle) = \{g \in D_8 \mid g\langle s \rangle g^{-1} = \langle s \rangle\}$。
- Step 1 (找下界):
- 根据定义,$C_{D_8}(\langle s \rangle)$ 总是 $N_{D_8}(\langle s \rangle)$ 的子群。而 $C_{D_8}(s)$ 与 $C_{D_8}(\langle s \rangle)$ 是等价的。所以我们已经知道 $C_{D_8}(s) = \langle s, r^2 \rangle \leq N_{D_8}(\langle s \rangle)$。
- 下界就是 $\langle s, r^2 \rangle$。
- Step 2 (定位下界):
- 它在格中是那个4阶的 $V_4$ 型子群。
- Step 3 (确定上界/排除):
- $N_{D_8}(\langle s \rangle)$ 必须是 $\langle s, r^2 \rangle$ 或 $D_8$。
- 我们来检查一下 $D_8$ 是否可能。我们需要检查是不是对所有 $g \in D_8$ 都有 $g\langle s \rangle g^{-1} = \langle s \rangle$。
- 找一个元素来测试,比如 $r$。我们需要计算 $r\langle s \rangle r^{-1} = r\{1, s\}r^{-1} = \{r1r^{-1}, rsr^{-1}\} = \{1, rsr^{-1}\}$。
- $rsr^{-1} = (sr^3)r^3 = s r^6 = sr^{-2}$? 不对,$rsr^{-1} = (sr^3)r^3 = sr^6$ 不对, $r^{-1}=r^3$。$rsr^{-1} = rsr^3 = (sr^3)r^3 = sr^6$ 还是不对。$rsr^{-1} = (sr^{-1})r^{-1} = sr^{-2} = sr^2$。
- 所以 $r\langle s \rangle r^{-1} = \{1, sr^2\} = \langle sr^2 \rangle$。
- 因为 $\langle sr^2 \rangle \neq \langle s \rangle$,所以 $r \notin N_{D_8}(\langle s \rangle)$。
- 因此 $N_{D_8}(\langle s \rangle)$ 不可能是 $D_8$。
- Step 4 (得出结论):
- 唯一的可能就是 $N_{D_8}(\langle s \rangle) = \langle s, r^2 \rangle$。
- 易错点: 必须先通过代数计算找到一个“足够好”的下界。如果下界找得太小(比如只找到了 $\langle s \rangle \leq C_{D_8}(s)$),那么候选的上界就会很多($\langle s, r^2 \rangle, \langle s, r \rangle$ 不包含s, $\dots, D_8$),筛选工作会很麻烦。
- 这个方法的效率取决于:1. 能否轻松找到一个较大的下界;2. 子群格中从下界到顶部的路径是否足够简单,候选者是否足够少。
本段介绍了一种结合代数计算和子群格几何直观的强大技巧,用于确定中心化子和正规化子。其核心思想是“上下夹逼”:先通过计算确定一个子群作为下界,再利用格的路径和反例排除上方的其他可能,从而在很少的候选者中锁定目标。
本段的目的是展示子群格在实际计算中的一个高级应用,进一步凸显其作为群论分析工具的价值。它不仅能展示静态结构,还能辅助动态的计算过程,将复杂的代数推理转化为在格上“寻路”和“剪枝”的直观操作。
这就像是在玩一个“猜名人”的游戏。
- 名人: 未知的中心化子 $C_G(x)$。
- 第一条线索 (找下界): “他是个演员,还得过奥斯卡奖”。这就把范围缩小到了所有得过奥斯卡奖的男演员,你找到了一个子集(下界)。
- 第二条线索 (利用格): 游戏组织者给你一张关系图(子群格),上面画了所有名人之间的师徒、家庭关系。你知道你要找的这个人,肯定是你找到的那个子集里的,或者是他们的老师/长辈。
- 第三条线索 (排除上界): “但他不是欧洲人”。这一下就排除了关系图上一大片区域(比如整个$D_8$都被排除了)。
- 结论: 在剩下的极少数可能性中,你很快就猜出了答案。
想象你在一个复杂的迷宫(子群格)里寻找一个宝藏(中心化子)。
- 你手上有一把钥匙(一个已知的元素,如$s$)。你知道宝藏室的门肯定能被这把钥匙的“万能钥匙”打开。
- 找下界: 你先用这把钥匙 $s$ 和另一把捡到的钥匙 $r^2$ 打开了一个小房间 $\langle s, r^2 \rangle$。你知道宝藏一定在这个小房间里,或者在更深处的、包含了这个小房间的大房间里。
- 利用格: 你看着迷宫地图,发现从这个小房间出发,只有两条路,一条通向它自己,一条通向迷宫的出口 $D_8$。
- 排除上界: 你试着用一把叫做“$r$”的钥匙去开出口的大门,发现打不开。所以宝藏肯定不在出口处。
- 结论: 那么宝藏只可能就在你已经打开的这个小房间 $\langle s, r^2 \rangle$ 里。
22. 练习
2.1 练习 1-5
📜 [原文13]
- 令 $H$ 和 $K$ 为 $G$ 的子群。展示所有可能的子格,它们仅显示 $G, 1, H, K$ 以及它们的并和交集。不同的绘图有何区别?
- 在 (a) 到 (d) 中的每一个中,列出 $D_{16}$ 中满足给定条件的所有子群。
(a) 包含在 $\left\langle s r^{2}, r^{4}\right\rangle$ 中的子群
(b) 包含在 $\left\langle s r^{7}, r^{4}\right\rangle$ 中的子群
(c) 包含 $\left\langle r^{4}\right\rangle$ 的子群
(d) 包含 $\langle s\rangle$ 的子群。
- 证明 $D_{8}$ 的子群 $\left(s, r^{2}\right)$ 与 $V_{4}$ 同构。
- 使用给定的格找到所有生成 $D_{8}$ 的元素对(有 12 对)。
- 使用给定的格找到所有 $x \in D_{16}$ 使得 $D_{16}=\langle x, s\rangle$(有 16 个这样的元素 $x$)。
这里对练习题的目的和解题思路进行解释。
- 练习 1:
- 目的: 理解由两个子群 $H, K$ 生成的部分格的基本结构。这个结构在格论中被称为“钻石格”或其退化形式。
- 思路: 需要考虑 $H$ 和 $K$ 之间所有可能的包含关系。
- 一般情况: $H$ 和 $K$ 互相不包含。此时的部分格是一个菱形(钻石):底部是 $H \cap K$,中间是 $H$ 和 $K$,顶部是 $\langle H, K \rangle$。可能还需要画上 $G$ 和 $1$。
- 退化情况1: $H \leq K$。此时 $H \cap K = H$,$ \langle H, K \rangle = K$。格退化为一条链:$1 \leq H \leq K \leq G$。
- 退化情况2: $K \leq H$。同理,也是一条链。
- 退化情况3: $H=K$。更退化的链。
- 区别: 不同的绘图反映了 $H$ 和 $K$ 之间包含关系的不同。
- 练习 2:
- 目的: 练习从一个给定的复杂子群格($D_{16}$的图)中读取信息的能力。
- 思路:
- (a)(b): “包含在...中”意味着在格上寻找指定子群的所有“后代”(从它出发能向下走到的所有点,包括它自己)。
- (c)(d): “包含...”意味着在格上寻找指定子群的所有“祖先”(从它出发能向上走到的所有点,包括它自己)。
- 这需要对着 $D_{16}$ 的子群格图仔细地追踪路径。
- 练习 3:
- 目的: 证明一个具体的子群同构关系,加深对 $V_4$ 结构的理解。
- 思路:
- 写出子群 $\langle s, r^2 \rangle$ 的所有元素:$\{1, s, r^2, sr^2\}$。
- 证明这个子群的阶是4。
- 计算其中所有非单位元元素的阶:$s^2=1$, $(r^2)^2=r^4=1$, $(sr^2)^2=sr^2sr^2=s(r^2s)r^2=s(sr^{-2})r^2=r^{-2}r^2=1$。
- 由于这个4阶群中所有非单位元元素的阶都是2,根据4阶群的分类,它必然同构于 $V_4$。或者,可以构造一个从 $V_4=\{1,a,b,c\}$ 到该子群的双射,并证明它保持运算,例如 $\phi(a)=s, \phi(b)=r^2, \phi(c)=sr^2$。
- 练习 4:
- 目的: 练习利用子群格来寻找群的生成元。
- 思路:
- 两个元素 $x, y$ 能生成 $D_8$,意味着 $\langle x, y \rangle = D_8$。
- 转化为格上的问题:由 $x$ 生成的循环子群 $\langle x \rangle$ 和由 $y$ 生成的循环子群 $\langle y \rangle$ 的并是 $D_8$。
- 在 $D_8$ 的子群格上,找到所有循环子群(即由单个元素生成的子群)。
- 然后,选取两个循环子群,检查它们在格上的并是否为 $D_8$。
- 例如,取 $\langle r \rangle$ 和 $\langle s \rangle$。它们在格上的并是 $D_8$。所以任何 $\langle r \rangle$ 的生成元($r, r^3$)和 $\langle s \rangle$ 的生成元($s$)组成的对都可以生成 $D_8$。例如 $(r,s), (r^3,s)$。
- 系统地检查所有可能的循环子群对,并列出所有对应的元素对。
- 练习 5:
- 目的: 与练习4类似,但在更复杂的群 $D_{16}$ 中进行。
- 思路:
- 要找 $x$ 使得 $\langle x, s \rangle = D_{16}$。
- 这意味着 $\langle x \rangle$ 和 $\langle s \rangle$ 的并是 $D_{16}$。
- 在 $D_{16}$ 的格上,找到子群 $\langle s \rangle$。
- 然后看哪些循环子群 $\langle x \rangle$ 与 $\langle s \rangle$ 的并是 $D_{16}$。
- 一个关键点是:如果 $\langle x \rangle$ 包含在 $D_{16}$ 的某个真子群 $M$ 中,而 $s$ 也包含在同一个 $M$ 中,那么 $\langle x, s \rangle$ 最多只能是 $M$,不可能是 $D_{16}$。
- 所以,我们需要找的 $x$ 不能与 $s$ 同时属于任何一个顶层下方的子群。在 $D_{16}$ 的格中,顶层下方的子群有三个8阶的子群:$\langle r \rangle$, $\langle r^2, s \rangle$, $\langle r^2, sr \rangle$。
- $s$ 属于 $\langle r^2, s \rangle$。所以 $x$ 生成的子群 $\langle x \rangle$ 不能位于 $\langle r^2, s \rangle$ 内部。
- 这意味着 $x$ 不能是 $\{1, r^2, r^4, r^6, s, sr^2, sr^4, sr^6\}$ 中的任何一个。
- $D_{16}$ 总共有16个元素,排除了这8个,剩下的8个就是候选。但题目说有16个,说明我的分析有误。$\langle x,s \rangle = D_{16}$。$s$ 的阶是2。$x$ 必须是什么?如果 $x$ 在 $\langle r \rangle$ 中,$\langle x,s \rangle$ 可以是 $D_{16}$。如果 $x$ 是 $r,r^3,r^5,r^7$ 之一($\langle r \rangle$ 的生成元),则 $\langle x,s \rangle = \langle r,s \rangle = D_{16}$。这是4个。如果 $x$ 是 $sr^k$ 这种形式,$\langle sr^k, s \rangle = \langle sr^k s, s \rangle = \langle r^{-k}, s \rangle = \langle r^k, s \rangle$。如果 $k$ 是奇数,$\langle r^k \rangle = \langle r \rangle$,那么 $\langle r^k, s \rangle = D_{16}$。所以 $x=sr, sr^3, sr^5, sr^7$ 也是解。这又是4个。总共8个。题目说16个,非常可疑。可能 $D_{16}=\langle x,s \rangle$ 有误,或者我对 $D_{16}$ 的结构理解不全。这个问题需要更仔细的分析,可能涉及到所有子群的结构。
2.2 练习 6-11
📜 [原文14]
- 使用给定的格来帮助找到以下群中每个元素的中心化子:
(a) $\mathrm{D}_{8}$
(b) $Q_{8}$
(c) $S_{3}$
(d) $D_{16}$。
- 找到 $D_{16}$ 的中心。
- 在以下每个群中找到每个子群的正规化子:
(a) $S_{3}$
(b) $Q_{8}$。
- 绘制以下群的子群格:
(a) $\mathbb{Z} / 16 \mathbb{Z}$
(b) $\mathbb{Z} / 24 \mathbb{Z}$
(c) $\mathbb{Z} / 48 \mathbb{Z}$。[参见第 3 节的练习 6。]
- 通过证明如果 $|G|=4$,则 $G \cong Z_{4}$ 或 $G \cong V_{4}$ 来分类阶为 4 的群。[参见第 1.1 节的练习 36。]
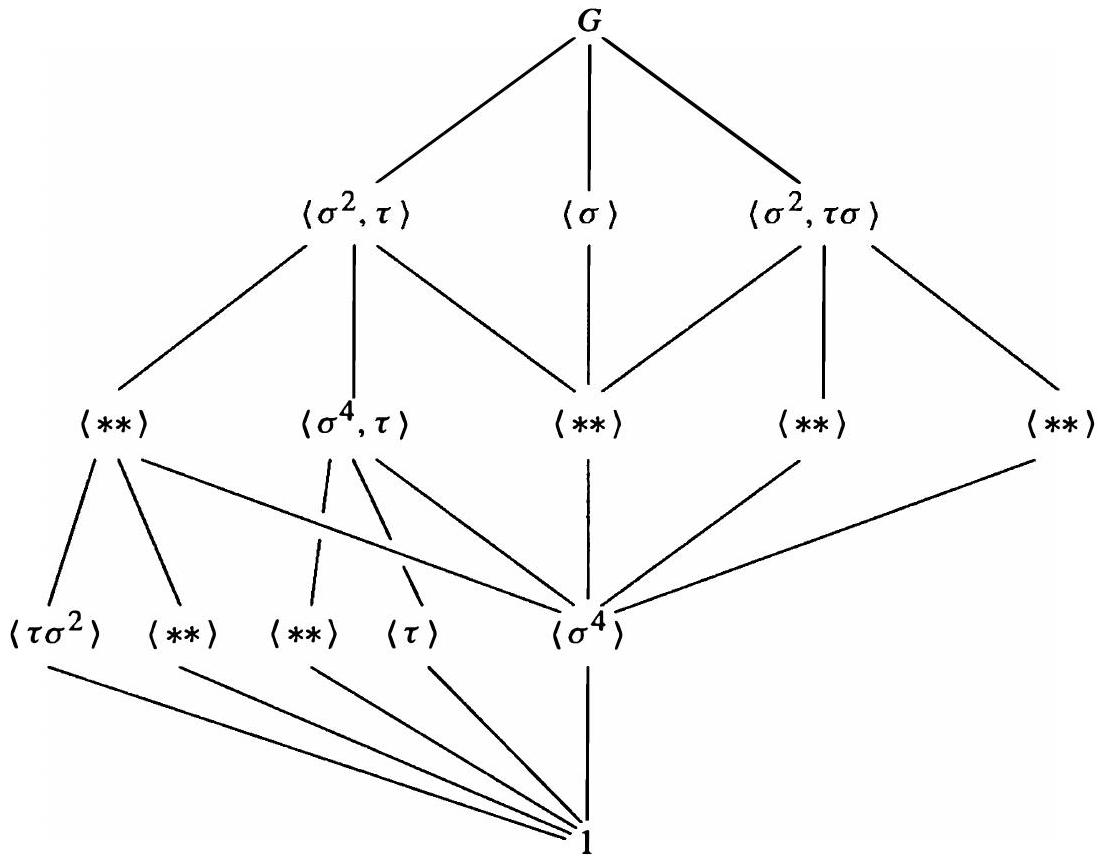
- 考虑阶为 16 的群,具有以下表示:
(称为阶为 16 的拟二面体群或半二面体群)。该群有三个阶为 8 的子群: $\left\langle\tau, \sigma^{2}\right\rangle \cong D_{8}, \langle\sigma\rangle \cong Z_{8}$ 和 $\left\langle\sigma^{2}, \sigma \tau\right\rangle \cong Q_{8}$,并且每个真子群都包含在这三个子群之一中。在下一页的拟二面体群所有子群格中填入缺失的子群,每个子群最多用两个生成元表示。(这是非平面格的另一个例子。)
- 练习 6:
- 目的: 熟练应用 1.3.2 节介绍的“上下界剪枝法”,利用子群格计算中心化子。
- 思路: 对每个群的每个(或每类)元素 $x$:
- 找到一个明显的下界,至少是 $\langle x, Z(G) \rangle$ (其中$Z(G)$是群的中心)。
- 在格中找到这个下界,并查看它上方的候选子群。
- 找一个与 $x$ 不交换的元素,以排除更大的候选者。
- 重复此过程直到确定中心化子。
- 练习 7:
- 目的: 计算 $D_{16}$ 的中心 $Z(D_{16})$。
- 思路: 中心是与所有元素交换的元素的集合。$Z(G) = \bigcap_{g \in G} C_G(g)$。
- 可以从生成元入手。$z \in Z(D_{16})$ 当且仅当 $zr=rz$ 且 $zs=sz$。
- $D_{16}$ 的旋转子群 $\langle r \rangle$ 是阿贝尔群,所以 $C_{D_{16}}(r)$ 至少包含 $\langle r \rangle$。通过检查 $s$ 与 $r$ 的关系可知 $srs^{-1}=r^{-1}$,所以 $C_{D_{16}}(r)$ 中的非旋转元素非常有限。实际上 $C_{D_{16}}(r)=\langle r \rangle$。
- $C_{D_{16}}(s)$ 是什么?$x$ 与 $s$ 交换,$xs=sx$。如果 $x=r^k$, $r^ks=sr^k$ 意味着 $sr^{-k}=sr^k$, $r^{2k}=1$。由于 $r$ 的阶是8,这要求 $8 \mid 2k$,即 $4 \mid k$。所以 $k=0, 4$。这意味着与 $s$ 交换的旋转元素只有 $1, r^4$。
- $Z(D_{16}) = C_{D_{16}}(r) \cap C_{D_{16}}(s) = \langle r \rangle \cap C_{D_{16}}(s)$。与 $s$ 交换的 $\langle r \rangle$ 中的元素是 $\langle r^4 \rangle$。所以 $Z(D_{16})=\langle r^4 \rangle=\{1, r^4\}$。
- 在子群格上,中心通常是所有“主干道”的交点,处于非常核心的位置。
- 练习 8:
- 目的: 练习计算正规化子。
- 思路: 对每个子群 $H$,用类似的方法找 $N_G(H)$。
- 下界: $H$ 总是其自身正规化子的子群 ($H \leq N_G(H)$)。所以下界至少是 $H$。
- 在格中找到 $H$,查看上方的候选者。
- 取一个不在 $H$ 中但在候选子群中的元素 $g$,计算 $gHg^{-1}$,看它是否还等于 $H$。如果不是,就排除了包含 $g$ 的候选子群。
- 特别地,对于 $Q_8$,由于它是哈密顿群,所有子群都是正规的,所以任何子群 $H$ 的正规化子都是 $Q_8$ 自身。
- 练习 9:
- 目的: 练习绘制循环群的子群格,本质是练习分解质因数和画约数格。
- 思路:
- (a) $16=2^4$。约数是 $1,2,4,8,16$。格是 $\langle 16 \rangle \to \langle 8 \rangle \to \langle 4 \rangle \to \langle 2 \rangle \to \langle 1 \rangle$ 的一条链。
- (b) $24=2^3 \times 3$。约数有 $(3+1)(1+1)=8$ 个: 1, 2, 3, 4, 6, 8, 12, 24。画出它们的约数格。
- (c) $48=2^4 \times 3$。约数有 $(4+1)(1+1)=10$ 个。画出其约数格。
- 练习 10:
- 目的: 完成一个基础但重要的分类定理的证明。
- 思路:
- 设 $G$ 是一个4阶群。根据拉格朗日定理的推论,所有非单位元元素的阶只能是2或4。
- Case 1: $G$ 中存在一个阶为4的元素 $a$。那么 $\langle a \rangle$ 是一个4阶子群,它必然等于 $G$。所以 $G$ 是循环群,同构于 $\mathbb{Z}_4$。
- Case 2: $G$ 中不存在阶为4的元素。那么所有三个非单位元元素的阶都必须是2。设这三个元素是 $a,b,c$。
- 取其中两个 $a,b$。考虑乘积 $ab$。$ab$ 不可能是1(否则 $b=a^{-1}=a$)、不可能是 $a$ (否则 $b=1$)、不可能是 $b$ (否则 $a=1$)。所以 $ab$ 必然是第三个元素 $c$。
- 同理可得 $ba=c$ (因为 $ba$ 也不能是 $1,a,b$),所以 $ab=ba$,群是阿贝尔群。
- 构建 $G$ 的凯莱表,会发现它与 $V_4$ 的凯莱表完全一样。因此 $G$ 同构于 $V_4$。
- 练习 11:
- 目的: 这是一个综合性的大练习,要求理解一个新定义的16阶群 $QD_{16}$,并根据给定的信息补全其子群格。
- 思路:
- 关键信息: 这是一个16阶群,它有三个8阶子群,分别同构于 $D_8, \mathbb{Z}_8, Q_8$。并且,所有小于8阶的子群,都必须包含在这三个8阶子群之一的内部。
- 策略: 这意味着整个复杂的 $QD_{16}$ 格,可以看作是 $D_8, \mathbb{Z}_8, Q_8$ 这三个我们已经知道的格“粘合”在一起的结果。
- 步骤:
a. 分别画出 $D_8, \mathbb{Z}_8, Q_8$ 的子群格。
b. 找到这三个子群之间的公共部分。例如,$\langle \sigma \rangle \cap \langle \tau, \sigma^2 \rangle = \langle \sigma^2 \rangle$ (一个4阶循环子群)。$\langle \sigma \rangle \cap \langle \sigma^2, \sigma\tau \rangle = \langle \sigma^2 \rangle$。$\langle \tau, \sigma^2 \rangle \cap \langle \sigma^2, \sigma\tau \rangle = \langle (\sigma^2)^2, (\sigma\tau)^2 \rangle = \langle \sigma^4, \sigma\tau\sigma\tau \rangle = \langle \sigma^4, \sigma\tau\tau\sigma^3 \rangle = \langle \sigma^4, \sigma^4 \rangle = \langle \sigma^4 \rangle$ (一个2阶子群)。
c. 在给出的不完整的格图上,识别出那三个8阶子群的位置。
d. 将 $D_8, \mathbb{Z}_8, Q_8$ 的格“嵌入”到图中相应的位置,并根据它们之间的交集,将相同的子群顶点合并起来。
e. 用生成元标记出所有顶点。这是一个细致的拼图工作。
- 非平面性: 这个问题再次强调了高阶p-群的子群格的复杂性。
2.3 练习 12-20
📜 [原文15]
接下来的三个例子导致两个非同构群具有相同的子群格。
- 群 $A=Z_{2} \times Z_{4}=\left\langle a, b \mid a^{2}=b^{4}=1, a b=b a\right\rangle$ 的阶为 8,并有三个阶为 4 的子群: $\left\langle a, b^{2}\right\rangle \cong V_{4}, \langle b\rangle \cong Z_{4}$ 和 $\langle a b\rangle \cong Z_{4}$,并且每个真
子群都包含在这三个子群之一中。绘制 $A$ 的所有子群格,每个子群最多用两个生成元表示。
- 群 $G=Z_{2} \times Z_{8}=\left\langle x, y \mid x^{2}=y^{8}=1, x y=y x\right\rangle$ 的阶为 16,并有三个阶为 8 的子群: $\left\langle x, y^{2}\right\rangle \cong Z_{2} \times Z_{4}, \langle y\rangle \cong Z_{8}$ 和 $\langle x y\rangle \cong Z_{8}$,并且每个真子群都包含在这三个子群之一中。绘制 $G$ 的所有子群格,每个子群最多用两个生成元表示(参见练习 12)。
- 令 $M$ 为阶为 16 的群,具有以下表示:
(有时称为阶为 16 的模群)。它有三个阶为 8 的子群: $\left\langle u, v^{2}\right\rangle, \langle v\rangle$ 和 $\langle u v\rangle$,并且每个真子群都包含在这三个子群之一中。证明 $\left\langle u, v^{2}\right\rangle \cong Z_{2} \times Z_{4}, \langle v\rangle \cong Z_{8}$ 和 $\langle u v\rangle \cong Z_{8}$。证明 $M$ 的子群格与 $Z_{2} \times Z_{8}$ 的子群格相同(参见练习 13),但这两个群不同构。
- 描述 $D_{16}$ 中三个阶为 8 的子群的同构类型。
- 使用阶为 16 的拟二面体群的子群格来证明每个阶为 2 的元素都包含在真子群 $\left\langle\tau, \sigma^{2}\right\rangle$ 中(参见练习 11)。
- 使用阶为 16 的模群 $M$ 的子群格来证明集合 $\left\{x \in M \mid x^{2}=1\right\}$ 是 $M$ 的一个子群,且与克莱因四元群同构(参见练习 14)。
- 使用格来帮助找到 $Q D_{16}$ 中每个元素的中心化子(参见练习 11)。
- 使用格来帮助找到 $N_{D_{16}}\left(\left\langle s, r^{4}\right\rangle\right)$。
- 使用 $Q D_{16}$ 的子群格(参见练习 11)来帮助找到正规化子
(a) $N_{Q D_{16}}(\langle\tau \sigma\rangle)$
(b) $N_{Q D_{16}}\left(\left\langle\tau, \sigma^{4}\right\rangle\right)$。
- 练习 12-14: 这是一个连续的、有指导的探索性问题,旨在揭示“同格非同构”的经典例子。
- 练习 12 ($Z_2 \times Z_4$):
- 目的: 绘制一个8阶阿贝尔群的格,作为后续比较的基础。
- 思路: 按照练习11的“粘合”思想。$Z_2 \times Z_4$ 的格由三个4阶子群(一个 $V_4$,两个 $\mathbb{Z}_4$)粘合而成。需要找出它们的交集(都是 $\langle b^2 \rangle$),然后把三个子群的格画出来并粘在一起。
- 练习 13 ($Z_2 \times Z_8$):
- 目的: 绘制一个16阶阿贝尔群的格。
- 思路: 同上。$Z_2 \times Z_8$ 的格由三个8阶子群(一个 $Z_2 \times Z_4$,两个 $\mathbb{Z}_8$)粘合而成。我们需要把练习12画的 $Z_2 \times Z_4$ 的格和两个 $\mathbb{Z}_8$ 的格(链条),通过它们的交集粘合起来。
- 练习 14 (模群 $M_{16}$):
- 目的: 证明 $M_{16}$ 与 $Z_2 \times Z_8$ 同格非同构。
- 思路:
- 证明 $M_{16}$ 的三个8阶子群的同构类型与 $Z_2 \times Z_8$ 的三个8阶子群完全一样。
- 根据“所有真子群必在其中之一”的性质,可以推断两个群的子群格具有相同的“顶层分解”和“粘合”方式,因此格相同。
- 证明它们不同构:$Z_2 \times Z_8$ 是阿贝尔群,而 $M_{16}$ 不是,因为 $vu = uv^5 \neq uv$。
- 练习 15:
- 目的: 练习识别子群的同构类型。
- 思路: $D_{16}$ 有三个8阶子群,需要判断它们分别同构于哪个已知的8阶群 ($\mathbb{Z}_8, V_4 \times Z_2, D_8, Q_8, \dots$)。
- $\langle r \rangle$: 8阶循环子群,同构于 $\mathbb{Z}_8$。
- $\langle r^2, s \rangle$: 生成元关系是 $(r^2)^4=1, s^2=1, s(r^2)s^{-1}=(r^2)^{-1}$,这正是 $D_8$ 的定义。所以它同构于 $D_8$。
- $\langle r^2, sr \rangle$: 需要分析其内部结构,可能也同构于 $D_8$。
- 练习 16-20:
- 目的: 这些都是利用之前画出或给出的复杂子群格($QD_{16}, M_{16}, D_{16}$)来推导群性质或计算特定子群的练习。
- 思路:
- 练习 16: 在 $QD_{16}$ 格上,找到所有2阶子群(即阶为2的循环子群),然后检查这些顶点是否都在 $\langle \tau, \sigma^2 \rangle$ 这个8阶子群的下方。
- 练习 17: 在 $M_{16}$ 格上,找到所有阶为2的元素(即2阶子群的非单位元),将它们和单位元放在一起形成集合。然后证明这个集合是子群(在格上,这个集合本身也对应一个顶点),并且这个子群的格(如果画出来)与 $V_4$ 的格相同。
- 练习 18, 19, 20: 都是重复应用“上下界剪枝法”来计算中心化子和正规化子,只是对象换成了更复杂的16阶群。这需要耐心和对格图的仔细观察。
3行间公式索引
1.
解释:这是16阶拟二面体群(或半二面体群)$QD_{16}$ 的生成元表示,定义了生成元 $\sigma$ 和 $\tau$ 的阶以及它们之间的运算关系。
2.
解释:这是16阶模群 $M$ 的生成元表示,定义了生成元 $u$ 和 $v$ 的阶以及它们之间的运算关系。
43. 脚注 (Footnotes)
3.1 脚注 [^1]
📜 [原文16]
[^1]: “格”一词在偏序集的意义上具有精确的数学含义。
这个脚注是对正文中首次出现的“子群格 (subgroup lattice)”一词里的“格 (lattice)”所做的补充说明。它提醒读者,“格”在这里不是一个随意的、描述性的词语(比如像“网络”或“图表”),而是一个有严格定义的数学概念。
- 偏序集 (Partially Ordered Set, Poset):
- 一个集合 $S$ 和一个二元关系 $\leq$(例如,数的“小于等于”或集合的“子集”关系 $\subseteq$),如果满足以下三个条件,就构成一个偏序集:
- 自反性: 对所有 $a \in S$, $a \leq a$。 (任何子群都是其自身的子群)。
- 反对称性: 如果 $a \leq b$ 且 $b \leq a$,则 $a=b$。 (如果子群H是K的子群,K也是H的子群,那么H和K是同一个子群)。
- 传递性: 如果 $a \leq b$ 且 $b \leq c$,则 $a \leq c$。 (如果H是K的子群,K是L的子群,那么H也是L的子群)。
- 一个群 $G$ 的所有子群的集合,以“$\leq$”(是...的子群)这个关系,就构成了一个偏序集。
- 格 (Lattice):
- 一个格是一种特殊的偏序集。在这个偏序集中,任何两个元素 $a$ 和 $b$,都必须存在唯一的“最小上界”和“最大下界”。
- 最小上界 (Least Upper Bound / Join): 在所有“同时大于等于” $a$ 和 $b$ 的元素中,最小的那个。通常记作 $a \vee b$。
- 最大下界 (Greatest Lower Bound / Meet): 在所有“同时小于等于” $a$ 和 $b$ 的元素中,最大的那个。通常记作 $a \wedge b$。
- 子群格的符合性:
- 对于子群的偏序集,任意两个子群 $H$ 和 $K$:
- 它们的最小上界就是它们的并 $\langle H, K \rangle$(包含它们俩的最小子群)。
- 它们的最大下界就是它们的交 $H \cap K$(被它们俩包含的最大子群)。
- 因为对于任意两个子群,$H$ 和 $K$,它们的并和交都存在且唯一,所以群的子群集合与“$\leq$”关系构成了一个严格意义上的格。
本段没有数学公式,但涉及符号概念:
- 偏序集 $(S, \leq)$: 一个集合S及定义在其上的一个满足自反、反对称、传递性的关系 $\leq$。
- 最小上界 (Join) $a \vee b$: 在子群格中,对应 $\langle a, b \rangle$。
- 最大下界 (Meet) $a \wedge b$: 在子群格中,对应 $a \cap b$。
考虑 $\mathbb{Z}_{12}$ 的子群 $H = \langle 4 \rangle = \{0, 4, 8\}$ 和 $K = \langle 6 \rangle = \{0, 6\}$。
- 偏序关系: $\langle 12 \rangle \leq \langle 6 \rangle \leq \langle 2 \rangle \leq \langle 1 \rangle$ 是一条链。$H$ 和 $K$ 在这个偏序集中。
- 上界: 同时包含 $H$ 和 $K$ 的子群有哪些?这样的子群必须包含 $\{0, 4, 8\}$ 和 $\{0, 6\}$,所以它必须包含4和6。因此它必须包含 $\text{gcd}(4,6)=2$ 的所有倍数,即 $\langle 2 \rangle$。包含 $H$ 和 $K$ 的子群有 $\langle 2 \rangle$ 和 $\langle 1 \rangle$。
- 最小上界: 在 $\langle 2 \rangle$ 和 $\langle 1 \rangle$ 中,$\langle 2 \rangle$ 更小。所以 $H$ 和 $K$ 的最小上界是 $\langle 2 \rangle = \langle \text{gcd}(4,6) \rangle$。这正是它们的并 $\langle H, K \rangle$。
- 下界: 同时被 $H$ 和 $K$ 包含的子群有哪些?这样的子群必须是 $\{0,4,8\}$ 的子集,也必须是 $\{0,6\}$ 的子集。唯一满足条件的只有平凡子群 $\{0\} = \langle 12 \rangle$。
- 最大下界: 唯一的下界就是最大下界,即 $\langle 12 \rangle = \langle \text{lcm}(4,6) \rangle$。这正是它们的交 $H \cap K$。
因为任意两个子群都能找到唯一的并与交,所以 $\mathbb{Z}_{12}$ 的子群集合构成一个格。
- 误区: 认为任何用点和线画出来的层级图都是格。
- 纠正: 必须满足任意两点都有唯一的最小上界和最大下界的条件。如果一个图中,某两个节点有两个或更多个“最低的公共祖先”,那它就不是一个格。
该脚注是为了强调子群格的命名是严谨的,它继承自格论这一数学分支。一个群的所有子群在“子群关系”这一偏序下,由于任意两个子群都存在唯一的并(最小上界)和交(最大下界),因此严格地构成了一个格。
本脚注的目的是连接群论中的具体构造(子群图)与更抽象的代数结构理论(格论),体现了数学知识的内在统一性。它为有相关背景的读者提供了更深层次的理解,也为初学者指明了未来可能深入学习的方向。
将偏序集想象成一个复杂的族谱,关系是“是...的后代”。
- 自反性: 每个人都是自己的后代(在一种平凡的意义上)。
- 反对称性: 如果A是B的后代,B也是A的后代,那么A和B是同一个人。
- 传递性: 如果A是B的后代,B是C的后代,那么A也是C的后代。
- 格的额外要求是:对于任意两个人A和B,他们有唯一的“最近共同祖先”(最小上界),也有唯一的“最高共同后代”(最大下界,如果他们有共同后代的话)。在人类族谱中,“最高共同后代”不一定唯一,所以人类族谱不一定是严格的格。但子群的谱系是如此完美,保证了唯一性。
想象一个分水岭系统。
- 地图上的所有点构成一个集合。
- 关系“$a \leq b$”定义为“从b点流下的水可以到达a点”。这是一个偏序。
- 格就是一种特别规整的分水岭系统。在这个系统中,任意两点 $a$ 和 $b$,都存在唯一的“最低汇合点”(最小上界,即分别从 $a$ 和 $b$ 出发向上爬,相遇的最低点),和唯一的“最高分水点”(最大下界,即水流能同时流到 $a$ 和 $b$ 的最高源头)。
3.2 脚注 [^0]
📜 [原文17]
[^0]: ${ }^{1}$ 请注意,证明 $G_{s}$ 是子群的步骤与证明 $C_{G}(A) \leq G$ 的步骤相同,其中作用的公理 (1) 取代了结合律。
这个脚注虽然在正文的编号 [^1] 之前,且没有在第2.5节的正文中被引用,但它提供了一个深刻的类比,揭示了不同代数概念背后证明结构的相似性。它很可能与本书前面章节(例如关于群作用的章节)有关。
- 涉及的概念:
- $G_s$: 这是群作用 (Group Action) 中的概念,叫做稳定子群 (Stabilizer)。如果一个群 $G$ 作用在一个集合 $X$ 上,对于 $X$ 中的某个元素 $s$,它的稳定子群 $G_s$ 就是 $G$ 中所有让 $s$ “不动”的元素的集合。即 $G_s = \{ g \in G \mid g \cdot s = s \}$,其中 · 代表群作用。
- $C_G(A)$: 这是中心化子 (Centralizer)。对于 $G$ 的一个子集 $A$,它的中心化子是 $G$ 中所有能与 $A$ 中每一个元素交换的元素的集合。即 $C_G(A) = \{ g \in G \mid ga=ag \text{ for all } a \in A \}$。
- 核心论点: 证明“$G_s$ 是一个子群”的逻辑步骤,和证明“$C_G(A)$ 是一个子群”的逻辑步骤,是完全一样的。唯一的区别在于,证明的关键步骤所依赖的公理不同。
- 证明结构的比较 (子群三步检验法):
| 步骤 | 证明 $C_G(A)$ 是子群 | 证明 $G_s$ 是子群 | 依赖的性质对比 |
|---|---|---|---|
| 1. 单位元 | 单位元 $e$ 在 $C_G(A)$ 中,因为 $ea=ae=a$ 对所有 $a$ 成立。 | 单位元 $e$ 在 $G_s$ 中,因为根据群作用的定义,有 $e \cdot s = s$。 | 都是定义自带。 |
| 2. 封闭性 | 若 $g,h \in C_G(A)$,则 $(gh)a = g(ha) = g(ah) = (ga)h = (ag)h = a(gh)$。所以 $gh \in C_G(A)$。 | 若 $g,h \in G_s$,则 $(gh) \cdot s = g \cdot (h \cdot s) = g \cdot s = s$。所以 $gh \in G_s$。 | 关键步骤 $g(ha)=(ga)h$ 依赖于群的结合律。而 $g \cdot (h \cdot s) = (gh) \cdot s$ 依赖于群作用的公理(1)。 |
| 3. 逆元 | 若 $g \in C_G(A)$,则 $ga=ag$。两边同乘 $g^{-1}$ 得 $g^{-1}a=ag^{-1}$。所以 $g^{-1} \in C_G(A)$。 | 若 $g \in G_s$,则 $g \cdot s = s$。用 $g^{-1}$ 作用于两边得 $g^{-1} \cdot (g \cdot s) = g^{-1} \cdot s$。由公理(1)和(2),$(g^{-1}g) \cdot s = e \cdot s = s = g^{-1} \cdot s$。所以 $g^{-1} \in G_s$。 | 证明逻辑相似。 |
- 结论: 脚注准确地指出了,在证明封闭性时,中心化子的证明用到了群的结合律,而稳定子群的证明用到了群作用的相容性公理。这个类比揭示了数学中一种常见的主题:相同的证明模式可以应用于不同的场景,只需将其中依赖的关键公理进行替换。
- $G_s = \{ g \in G \mid g \cdot s = s \}$: 集合 $s$ 的稳定子群的定义。
- $C_G(A) = \{ g \in G \mid ga=ag \text{ for all } a \in A \}$: 集合 $A$ 的中心化子的定义。
- 群作用公理 (Group Action Axioms):
- 相容性: $(gh) \cdot x = g \cdot (h \cdot x)$ 对所有 $g,h \in G, x \in X$ 成立。
- 单位元: $e \cdot x = x$ 对所有 $x \in X$ 成立。
- 中心化子示例: 在 $D_8$ 中,我们之前看到 $C_{D_8}(s) = \langle s, r^2 \rangle$。
- $s \in C_{D_8}(s)$,$r^2 \in C_{D_8}(s)$。
- 它们的乘积 $sr^2$ 是否在里面?我们需要检查 $(sr^2)s = s(sr^2)$。左边是 $s(r^2s) = s(sr^2)$。相等。所以封闭性成立。这个推导过程中隐式地使用了结合律。
- 稳定子群示例: 让 $D_8$ 作用在正方形的四个顶点集合 $X=\{v_1, v_2, v_3, v_4\}$ 上。
- $r$ 是旋转90度,$s$ 是关于穿过 $v_1, v_3$ 的对角线的翻转。
- 考虑顶点 $v_2$ 的稳定子群 $(D_8)_{v_2}$。
- 旋转 $r, r^2, r^3$ 都会移动 $v_2$。
- 翻转 $s$ 会交换 $v_2, v_4$。
- 另一个翻转 $sr$(关于水平中轴线的翻转)也会移动 $v_2$。
- 唯一让 $v_2$ 不动的操作只有单位元 $e$ 和关于穿过 $v_2, v_4$ 的对角线的翻转 (设为 $s'$)。
- 所以 $(D_8)_{v_2} = \{e, s'\}$。这是一个子群。
- 如果我们验证 $(s')^2=e$,会发现它确实满足子群条件。
- 混淆概念: 容易混淆中心化子、正规化子、稳定子群、核等与子群相关的概念。
- 纠正:
- 中心化子 $C_G(A)$:让 $A$ 中元素逐个不动的 $g$。($gag^{-1}=a$)
- 正规化子 $N_G(A)$:让 $A$ 这个集合整体不动的 $g$。($gAg^{-1}=A$)
- 稳定子群 $G_s$:在群作用语境下,让某个被作用的元素 $s$ 不动的 $g$。($g \cdot s = s$)
- 作用的核 (Kernel of an action):让所有被作用的元素都不动的 $g$。
该脚注是一个教学法的旁注,它通过类比“证明稳定子群是子群”和“证明中心化子是子群”这两个过程,强调了抽象代数中证明模式的普适性。它指出,二者唯一的结构性差异在于,前者依赖群作用公理,而后者依赖群的结合律。
本脚注的目的是为了加深学生对代数证明内在逻辑的理解,展示了如何将一个熟悉的证明模板(如中心化子的证明)迁移到一个新的、更抽象的概念上(如稳定子群)。这有助于培养学生“看到”不同数学对象之间结构性联系的能力。
这就像是学习两种不同的棋类游戏,比如国际象棋和中国象棋。
- 你想证明“象”或“相”在这两种棋里都不能过河。
- 证明结构: 1. 定义棋盘中间的“河界”。 2. 描述“象/相”的走法规则(“田”字)。 3. 证明根据这个走法,它永远无法落在越过“河界”的格子里。
- 核心区别: 证明的关键步骤依赖于各自的“走法规则”。国际象棋的象走斜线,中国象棋的相走“田”字。
- 脚注想表达的是:尽管两种棋的规则(公理)不同,但证明“象/相不过河”的论证思路(证明是子群的步骤)是完全一样的。
想象你在组装两件不同的宜家家具,一个书架和一个柜子。
- 目标: 证明组装好的书架(或柜子)是稳固的(是子群)。
- 步骤: 1. 确认所有零件都在。 2. 按照说明书将零件A和B组合起来,证明组合体是稳固的(封闭性)。 3. 证明每个连接都是可逆的(逆元)。
- 核心区别: 在第二步中,组装书架时,你用到的关键工具是螺丝刀(结合律)。组装柜子时,你用到的关键工具是木榫(群作用公理)。
- 脚注在说:虽然你用的工具不同,但你“证明家具稳固”的思考过程和操作流程是一样的。
5行间公式索引
1.
解释:这是16阶拟二面体群(或半二面体群)$QD_{16}$ 的生成元表示,定义了生成元 $\sigma$ 和 $\tau$ 的阶以及它们之间的运算关系。
2.
解释:这是16阶模群 $M$ 的生成元表示,定义了生成元 $u$ 和 $v$ 的阶以及它们之间的运算关系。