1直积群 (Direct Product Group)
1.1 直积群的定义
📜 [原文1]
令 $G, G^{\prime}$ 为两个群。直积集 $G \times G^{\prime}$,即由 $G$ 中的元素 $a$ 和 $G^{\prime}$ 中的元素 $a^{\prime}$ 组成的对 $(a, a^{\prime})$ 的集合,可以通过分量乘法构成一个群——也就是说,对的乘法由以下规则定义:
对 $(1,1)$ 是单位元,$\left(a, a^{\prime}\right)$ 的逆元是 $\left(a^{-1}, a^{\prime-1}\right)$。 $G \times G^{\prime}$ 中的结合律遵循于它在 $G$ 和 $G^{\prime}$ 中成立的事实。
以这种方式获得的群称为 $G$ 和 $G^{\prime}$ 的直积,并表示为 $G \times G^{\prime}$。它以一种简单的方式与两个因子 $G$ 和 $G^{\prime}$ 相关,我们可以通过一些同态来总结这种关系。
这段话的核心思想是:如何用两个已知的群,像搭积木一样,构造出一个新的、更大的群。这个新的群被称为直积群。
- 原材料:首先,我们需要两个群,我们称之为 $G$ 和 $G^{\prime}$。每个群都有自己的元素和自己的运算规则。
- 构造新集合:我们构造一个新的集合,记作 $G \times G^{\prime}$。这个集合里的元素很特别,它们不是单个的数字或符号,而是一个个的“有序对”(ordered pair),写作 $(a, a^{\prime})$。这个有序对的第一个部分 $a$ 必须是来自第一个群 $G$ 的元素,第二个部分 $a^{\prime}$ 必须是来自第二个群 $G^{\prime}$ 的元素。这个过程就像从两个篮子里(一个装满了 $G$ 的元素,一个装满了 $G^{\prime}$ 的元素)各取一个元素配对。
- 定义新运算:光有元素的集合还不够,要成为一个群,必须定义元素之间的运算。这里的运算规则非常直观,叫做分量乘法 (component-wise multiplication)。也就是说,要计算两个有序对 $(a, a^{\prime})$ 和 $(b, b^{\prime})$ 的乘积,我们只需要把它们对应位置的元素分别相乘即可。第一个分量 $a$ 和 $b$ 在群 $G$ 中相乘,得到 $ab$;第二个分量 $a^{\prime}$ 和 $b^{\prime}$ 在群 $G^{\prime}$ 中相乘,得到 $a^{\prime}b^{\prime}$。最后把这两个结果组成一个新的有序对 $(ab, a^{\prime}b^{\prime})$。
- 验证群的公理:为了确认我们这样构造出来的新结构确实是一个群,我们需要检查它是否满足群的四个基本条件:
- 封闭性 (Closure):由于 $a, b$ 都在 $G$ 中,根据 $G$ 的封闭性,$ab$ 也必然在 $G$ 中。同理,$a^{\prime}b^{\prime}$ 也必然在 $G^{\prime}$ 中。因此,它们的乘积 $(ab, a^{\prime}b^{\prime})$ 仍然是一个符合格式的有序对,所以这个新结构在分量乘法下是封闭的。
- 单位元 (Identity Element):一个群必须有一个单位元,任何元素乘以它都等于自身。在直积群中,这个单位元就是 $(1, 1)$。这里的第一个 $1$ 是群 $G$ 的单位元,第二个 $1$ 是群 $G^{\prime}$ 的单位元。我们可以验证:$(a, a^{\prime}) \cdot (1, 1) = (a \cdot 1, a^{\prime} \cdot 1) = (a, a^{\prime})$。
- 逆元 (Inverse Element):对于群中的任意一个元素,都必须存在一个逆元,使得它与逆元的乘积等于单位元。对于直积群中的任意元素 $(a, a^{\prime})$,它的逆元就是 $(a^{-1}, a^{\prime-1})$。这里的 $a^{-1}$ 是 $a$ 在群 $G$ 中的逆元,$a^{\prime-1}$ 是 $a^{\prime}$ 在群 $G^{\prime}$ 中的逆元。验证一下:$(a, a^{\prime}) \cdot (a^{-1}, a^{\prime-1}) = (a \cdot a^{-1}, a^{\prime} \cdot a^{\prime-1}) = (1, 1)$。
- 结合律 (Associativity):运算必须满足结合律,即 $(x \cdot y) \cdot z = x \cdot (y \cdot z)$。对于直积群中的三个元素 $(a, a^{\prime})$, $(b, b^{\prime})$, $(c, c^{\prime})$,我们有:
- 命名:这个通过分量乘法构造出来的群 $G \times G^{\prime}$,就叫做 $G$ 和 $G^{\prime}$ 的直积。$G$ 和 $G^{\prime}$ 被称为直积的因子 (factors)。
- $\left(a, a^{\prime}\right)$: 这是直积群 $G \times G^{\prime}$ 中的一个元素。它是一个有序对,其中 $a \in G$ ( $a$ 是群 $G$ 中的一个元素),$a^{\prime} \in G^{\prime}$ ( $a^{\prime}$ 是群 $G^{\prime}$ 中的一个元素)。
- $\left(b, b^{\prime}\right)$: 这是直积群 $G \times G^{\prime}$ 中的另一个元素。其中 $b \in G$,$b^{\prime} \in G^{\prime}$。
- $\cdot$: 这个点号代表直积群 $G \times G^{\prime}$ 中定义的运算。
- $=$: 等于号表示运算的结果。
- $\left(a b, a^{\prime} b^{\prime}\right)$: 这是运算的结果,也是一个有序对。
- $ab$: 这是 $a$ 和 $b$ 在群 $G$ 中进行运算的结果。注意,这里的乘法是 $G$ 内部的运算。
- $a^{\prime} b^{\prime}$: 这是 $a^{\prime}$ 和 $b^{\prime}$ 在群 $G^{\prime}$ 中进行运算的结果。注意,这里的乘法是 $G^{\prime}$ 内部的运算。
这个公式的核心是分量式 (component-wise) 的运算。就像向量加法一样,对应位置的元素进行各自的运算,然后组合成新的结果。
示例 1:整数加法群的直积
- 令 $G = (\mathbb{Z}, +)$,即整数加法群。元素是所有整数,运算是普通加法。单位元是 $0$,一个元素 $n$ 的逆元是 $-n$。
- 令 $G^{\prime} = (\mathbb{Z}, +)$,也是整数加法群。
- 我们来构造直积群 $\mathbb{Z} \times \mathbb{Z}$。
- 元素:形如 $(m, n)$ 的有序对,其中 $m, n$ 都是整数。例如 $(2, 3)$, $(-1, 5)$, $(0, 0)$。
- 运算:分量加法。例如,计算 $(2, 3) + (-1, 5)$:
$(2, 3) + (-1, 5) = (2 + (-1), 3 + 5) = (1, 8)$。
- 单位元:$(0, 0)$,因为 $(m, n) + (0, 0) = (m+0, n+0) = (m, n)$。
- 逆元:元素 $(m, n)$ 的逆元是 $(-m, -n)$,因为 $(m, n) + (-m, -n) = (m-m, n-n) = (0, 0)$。
- 这个直积群 $\mathbb{Z} \times \mathbb{Z}$ 在几何上可以看作是二维平面上所有整数坐标点构成的集合,运算是向量加法。
示例 2:循环群的直积
- 令 $G = C_2 = (\{0, 1\}, +_2)$,即2阶循环群,运算是模2加法。$0+0=0, 0+1=1, 1+0=1, 1+1=0$。单位元是 $0$。
- 令 $G^{\prime} = C_3 = (\{0, 1, 2\}, +_3)$,即3阶循环群,运算是模3加法。单位元是 $0$。
- 我们来构造直积群 $C_2 \times C_3$。
- 元素:集合是 $\{(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)\}$。这个群一共有 $2 \times 3 = 6$ 个元素。
- 运算:分量模加法。例如,计算 $(1, 2) + (1, 1)$:
$(1, 2) + (1, 1) = (1 +_2 1, 2 +_3 1) = (0, 0)$。
- 单位元:$(0, 0)$。
- 逆元:元素 $(1, 2)$ 的逆元是 $(1, 1)$,因为它们的和是单位元 $(0, 0)$。
- 混淆运算:最常见的错误是混淆不同群的运算。在计算 $(ab, a^{\prime}b^{\prime})$ 时,$ab$ 的运算是在 $G$ 中进行的,$a^{\prime}b^{\prime}$ 的运算是在 $G^{\prime}$ 中进行的。如果 $G$ 是加法群,$G^{\prime}$ 是乘法群,那么运算形式可能是 $(a+b, a^{\prime} \cdot b^{\prime})$。
- 元素的阶:直积群中一个元素 $(a, a^{\prime})$ 的阶 (order) 是使得 $(a, a^{\prime})^k = (a^k, (a^{\prime})^k)$ 等于单位元 $(1, 1)$ 的最小正整数 $k$。这要求 $a^k=1$ 且 $(a^{\prime})^k=1$ 同时成立。因此,$k$ 必须是 $a$ 的阶和 $a^{\prime}$ 的阶的最小公倍数。即 $\text{ord}(a, a^{\prime}) = \text{lcm}(\text{ord}(a), \text{ord}(a^{\prime}))$。
- 交换律:即使 $G$ 和 $G^{\prime}$ 都是阿贝尔群(交换群),这并不意味着直积群中的任意两个元素都可以随意交换分量。例如,在 $\mathbb{Z} \times \mathbb{Z}$ 中,$(a, b) + (c, d) = (a+c, b+d) = (c+a, d+b) = (c, d) + (a, b)$,所以 $\mathbb{Z} \times \mathbb{Z}$ 是阿贝尔群。但如果 $G$ 或 $G^{\prime}$ 中有一个不是阿贝尔群,那么 $G \times G^{\prime}$ 也不是阿贝尔群。
- 集合与群:$G \times G^{\prime}$ 首先是一个笛卡尔积集合 (Cartesian product set),只有在为其定义了合适的分量乘法并满足群公理后,才成为一个直积群。
直积是一种从已有群构造新群的基本方法。它将两个群 $G$ 和 $G^{\prime}$ 的元素配对形成有序对 $(a, a^{\prime})$,并定义了一种自然的分量乘法。这个新群 $G \times G^{\prime}$ 的结构很大程度上继承了其因子群 $G$ 和 $G^{\prime}$ 的性质,但又是一个更复杂的独立实体。
直积的概念主要服务于两个目的:
- 构造 (Construction):它提供了一种系统性的方法来创造出更复杂、更多样的群的例子。这对于研究群的分类和性质至关重要。
- 分解 (Decomposition):反过来看,如果一个复杂的群 $G$ 能够被分解,即证明它同构于某个直积群 $H \times K$,那么我们就可以通过研究更简单的群 $H$ 和 $K$ 来理解 $G$ 的结构。这是一种化繁为简的强大分析工具。
想象一个控制面板上有两个独立的旋钮。第一个旋钮有 $|G|$ 个档位,对应群 $G$ 的所有元素。第二个旋钮有 $|G^{\prime}|$ 个档位,对应群 $G^{\prime}$ 的所有元素。
- 直积群的一个元素:就是两个旋钮的当前状态组合,例如“(旋钮1在 $a$ 档, 旋钮2在 $a^{\prime}$ 档)”,即 $(a, a^{\prime})$。
- 直积群的运算:就是分别拨动两个旋钮。如果你想执行操作 $(b, b^{\prime})$,你就把第一个旋钮从当前档位 $a$ 按照 $G$ 的规则拨动 $b$ 的量,到达 $ab$ 档;同时把第二个旋钮从当前档位 $a^{\prime}$ 按照 $G^{\prime}$ 的规则拨动 $b^{\prime}$ 的量,到达 $a^{\prime}b^{\prime}$ 档。最终两个旋钮的状态就是 $(ab, a^{\prime}b^{\prime})$。
这两个旋钮的操作是完全独立的,互不影响,这正是直积的核心特征。
- 二维坐标系:如果 $G = \mathbb{R}$(实数加法群),$G^{\prime} = \mathbb{R}$,那么直积群 $\mathbb{R} \times \mathbb{R}$ 就是我们熟悉的二维笛卡尔平面。一个元素 $(x, y)$ 就是平面上的一个点。群的运算 $(x_1, y_1) + (x_2, y_2) = (x_1+x_2, y_1+y_2)$ 就是向量的平行四边形法则。
- 圆环面 (Torus):如果 $G = C_n$ (n阶循环群,可想象为钟表的n个点),$G^{\prime} = C_m$,那么直积群 $C_n \times C_m$ 可以想象成一个圆环面(甜甜圈的表面)。一个维度的运动是在一个圆上循环($n$ 个位置),另一个维度的运动是在另一个垂直的圆上循环($m$ 个位置)。$C_n \times C_m$ 的一个元素就对应圆环面上的一个网格点。
1.2 直积群与因子群的关系
📜 [原文2]
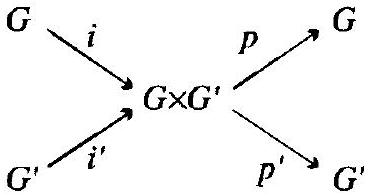
它们定义为 $i(x)=(x, 1), i^{\prime}\left(x^{\prime}\right)=\left(1, x^{\prime}\right), \quad p\left(x, x^{\prime}\right)=x, \quad p^{\prime}\left(x, x^{\prime}\right)=x^{\prime}$。内射同态 $i$ 和 $i^{\prime}$ 可用于将 $G$ 和 $G^{\prime}$ 分别与其像,即 $G \times G^{\prime}$ 的子群 $G \times 1$ 和 $1 \times G^{\prime}$ 进行识别。映射 $p$ 和 $p^{\prime}$ 是满射, $p$ 的核是 $1 \times G^{\prime}$, $p^{\prime}$ 的核是 $G \times 1$。这些是投影。
这段话描述了直积群 $G \times G^{\prime}$ 和其原始的因子群 $G, G^{\prime}$ 之间存在的四种标准联系方式。这些联系都是通过群同态(保持群结构的映射)来建立的。
- 从因子群到直积群 (内射/嵌入):
- 映射 i: 我们如何把群 $G$ “放进”直积群 $G \times G^{\prime}$ 中?我们可以定义一个映射 $i: G \to G \times G^{\prime}$,它把 $G$ 中的任意一个元素 $x$ 变成直积群中的 $(x, 1)$。这里的 $1$ 是 $G^{\prime}$ 的单位元。这个映射是同态,因为 $i(xy) = (xy, 1) = (x, 1)(y, 1) = i(x)i(y)$。它也是内射(一对一)的,因为如果 $i(x_1) = i(x_2)$,那么 $(x_1, 1) = (x_2, 1)$,这意味着 $x_1 = x_2$。
- 映射 i': 同样地,我们可以定义一个映射 $i': G' \to G \times G'$,它把 $G'$ 中的任意一个元素 $x'$ 变成直积群中的 $(1, x')$。这里的 $1$ 是 $G$ 的单位元。这个映射也是一个内射同态。
- 识别 (Identification): 通过这两个内射同态,我们可以在直积群 $G \times G'$ 内部找到两个特殊的子群:
- $i(G) = \{(x, 1) | x \in G\}$,记作 $G \times 1$。这个子群的结构和原始的 $G$ 完全一样(同构)。
- $i'(G') = \{(1, x') | x' \in G'\}$,记作 $1 \times G'$。这个子群的结构和原始的 $G'$ 完全一样(同构)。
- 因此,我们可以把 $G$ 和 $G'$ 看作是“嵌入”在 $G \times G'$ 内部的两个特殊子群。
- 从直积群到因子群 (满射/投影):
- 映射 p: 我们如何从直积群的一个元素 $(x, x')$ 中“提取”出属于 $G$ 的部分?我们定义一个映射 $p: G \times G' \to G$,它把 $(x, x')$ 直接映射到它的第一个分量 $x$。这个映射被称为投影 (projection)。它是同态,因为 $p((a, a')(b, b')) = p(ab, a'b') = ab = p(a, a')p(b, b')$。它也是满射(映上)的,因为对于 $G$ 中的任何一个元素 $x$,我们总能在 $G \times G'$ 中找到一个元素(比如 $(x, 1)$)映射到它。
- 映射 p': 类似地,我们定义另一个投影 $p': G \times G' \to G'$,它把 $(x, x')$ 映射到它的第二个分量 $x'$。这个映射也是一个满射同态。
- 核 (Kernel): 同态的核是指被映射到目标群单位元的所有源群元素的集合。
- $p$ 的核 $\text{ker}(p)$:我们需要找到所有被 $p$ 映射到 $G$ 的单位元 $1_G$ 的元素 $(x, x')$。即 $p(x, x') = x = 1_G$。满足这个条件的元素形如 $(1_G, x')$,其中 $x'$ 可以是 $G'$ 中的任何元素。这个集合正是我们前面提到的子群 $1 \times G'$。
- $p'$ 的核 $\text{ker}(p')$:我们需要找到所有被 $p'$ 映射到 $G'$ 的单位元 $1_{G'}$ 的元素 $(x, x')$。即 $p'(x, x') = x' = 1_{G'}$。满足这个条件的元素形如 $(x, 1_{G'})$,这个集合正是子群 $G \times 1$。
- $i(x)=(x, 1)$:
- $i$: 内射 (injection) 或嵌入 (embedding) 映射。
- $x$: 输入,是群 $G$ 的一个元素。
- $(x, 1)$: 输出,是直积群 $G \times G'$ 的一个元素,第二个分量固定为 $G'$ 的单位元。
- $i^{\prime}\left(x^{\prime}\right)=\left(1, x^{\prime}\right)$:
- $i'$: 另一个内射映射。
- $x'$: 输入,是群 $G'$ 的一个元素。
- $(1, x')$: 输出,是直积群 $G \times G'$ 的一个元素,第一个分量固定为 $G$ 的单位元。
- $p\left(x, x^{\prime}\right)=x$:
- $p$: 投影 (projection) 映射。
- $(x, x')$: 输入,是直积群的一个元素。
- $x$: 输出,是群 $G$ 的一个元素,即输入的第一个分量。
- $p^{\prime}\left(x, x^{\prime}\right)=x^{\prime}$:
- $p'$: 另一个投影映射。
- $(x, x')$: 输入,是直积群的一个元素。
- $x'$: 输出,是群 $G'$ 的一个元素,即输入的第二个分量。
图示解释:
那个交换图表达了这些映射之间的关系。
```
i'
G' ---> G x G'
<---
p'
^ |
| |
p v i
G <---- G x G'
```
- 从 $G$ 出发,通过 $i$ 映射到 $G \times G'$,再通过 $p$ 投影回来,就回到了 $G$ 本身 ($p(i(x)) = p(x, 1) = x$)。这说明 $p$ 是 $i$ 的一个“左逆”。
- 从 $G$ 出发,通过 $i$ 映射到 $G \times G'$,再通过 $p'$ 投影到 $G'$,结果是 $p'(i(x)) = p'(x, 1) = 1_{G'}$ (G'的单位元)。这说明 $G$ 的像完全落在 $p'$ 的核里。
- 类似的关系对 $G', i', p'$ 和 $p$ 也成立。
示例:$C_2 \times C_3$
- 群: $C_2 = \{0, 1\}$, $C_3 = \{0, 1, 2\}$, $C_2 \times C_3 = \{(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)\}$。
- 内射 i: $i: C_2 \to C_2 \times C_3$
- $i(0) = (0, 0)$
- $i(1) = (1, 0)$
- $i$ 的像 (image) 是 $C_2 \times \{0\} = \{(0,0), (1,0)\}$,这个子群与 $C_2$ 同构。
- 内射 i': $i': C_3 \to C_2 \times C_3$
- $i'(0) = (0, 0)$
- $i'(1) = (0, 1)$
- $i'(2) = (0, 2)$
- $i'$ 的像是 $\{0\} \times C_3 = \{(0,0), (0,1), (0,2)\}$,这个子群与 $C_3$ 同构。
- 投影 p: $p: C_2 \times C_3 \to C_2$
- $p(0,0)=0, p(0,1)=0, p(0,2)=0$
- $p(1,0)=1, p(1,1)=1, p(1,2)=1$
- 这个映射是满射的,因为 $0$ 和 $1$ 都被映射到了。
- $p$ 的核是所有被映射到 $C_2$ 的单位元 $0$ 的元素集合:$\{(0,0), (0,1), (0,2)\}$,这正是 $\{0\} \times C_3$。
- 投影 p': $p': C_2 \times C_3 \to C_3$
- $p'(0,0)=0, p'(1,0)=0$
- $p'(0,1)=1, p'(1,1)=1$
- $p'(0,2)=2, p'(1,2)=2$
- 这个映射是满射的。
- $p'$ 的核是所有被映射到 $C_3$ 的单位元 $0$ 的元素集合:$\{(0,0), (1,0)\}$,这正是 $C_2 \times \{0\}$。
- 像 vs. 群本身: 严格来说,$G$ 和 $G \times 1$ 是两个不同的集合,但因为它们作为群的结构完全一样(同构),我们常常为了方便而“识别”它们,把它们看作是同一个东西。这是一种常见的数学上的“滥用符号”,但能大大简化讨论。
- 核是正规子群: 一个重要的事实是,任何同态的核都是一个正规子群。因此,$G \times 1$ 和 $1 \times G'$ 都是 $G \times G'$ 的正规子群。这一点在后面的命题中会用到。
直积群 $G \times G'$ 内部包含了两个与其因子群 $G$ 和 $G'$ 同构的子群 $G \times 1$ 和 $1 \times G'$。同时,$G \times G'$ 又可以被“压回”到它的因子群 $G$ 和 $G'$,这个过程就是投影。内射(嵌入)和投影(满射)这两种同态,构成了直积群和其因子群之间最基本的联系。
这段话的目的是建立直积群这个新构造与我们已知的因子群之间的明确数学关系。它告诉我们,直积群并没有完全“忘记”它的来源,而是以子群和商群的形式保留了 $G$ 和 $G'$ 的全部信息。这些同态($i, i', p, p'$)就像是翻译官,让我们可以在直积群的语境下讨论 $G$ 和 $G'$,或者反过来。
再次使用二维坐标系的例子,令直积群为 $G = \mathbb{R} \times \mathbb{R}$(平面)。
- 子群 $G \times 1$ 就是 $\mathbb{R} \times \{0\}$,即平面上的 x-轴。x-轴本身就是一条直线,它的结构和 $\mathbb{R}$ 完全一样。
- 子群 $1 \times G'$ 就是 $\{0\} \times \mathbb{R}$,即平面上的 y-轴。y-轴也和 $\mathbb{R}$ 结构一样。
- 投影 $p: \mathbb{R} \times \mathbb{R} \to \mathbb{R}$, $p(x, y) = x$,就像是把平面上任意一个点 $(x, y)$ 的灯光垂直投射到 x-轴上,只看它的 x-坐标。
- 投影 $p': \mathbb{R} \times \mathbb{R} \to \mathbb{R}$, $p'(x, y) = y$,就像是把点 $(x, y)$ 的灯光水平投射到 y-轴上,只看它的 y-坐标。
- $p$ 的核是所有投影到 x-轴原点($x=0$)的点,即所有形如 $(0, y)$ 的点,这正是 y-轴。
想象一个长方体。
- 长方体本身可以看作是三个区间(代表三个群)的直积。
- 内射:x-轴上的一条边可以看作是第一个区间群的“嵌入”。
- 投影:将整个长方体压扁到 xy-平面上,就得到了一个矩形(两个群的直积),这就是一个投影操作。这个操作的核,即所有被压到原点的点,就是垂直于 xy-平面的 z-轴上的那条边。
2将群分解为直积
2.1 分解的愿望与一个例子
📜 [原文3]
将给定的群 $G$ 分解为直积显然是可取的,也就是说,找到群 $H$ 和 $H^{\prime}$,使得 $G$ 同构于直积 $H \times H^{\prime}$。群 $H$ 和 $H^{\prime}$ 将更简单,并且 $H \times H^{\prime}$ 与其因子之间的关系很容易理解。一个群是直积的情况很少见,但偶尔也会发生。
例如,6阶循环群可以分解,这相当令人惊讶:6阶循环群 $C_{6}$ 同构于2阶循环群和3阶循环群的直积 $C_{2} \times C_{3}$。为了说明这一点,假设 $C_{2}=\langle y\rangle$ 和 $C_{3}=\langle z\rangle$,其中 $y^{2}=1$ 和 $z^{3}=1$,并令 $x$ 表示直积群 $C_{2} \times C_{3}$ 的元素 $(y, z)$。使得 $x^{k}=\left(y^{k}, z^{k}\right)$ 是单位元 $(1,1)$ 的最小正整数 $k$ 是 $k=6$。所以 $x$ 的阶是 6。由于 $C_{2} \times C_{3}$ 的阶也是 6,它等于循环群 $\langle x\rangle$。 $x$ 的幂依次为
$\square$
- 分解的目标:这段话首先提出了一个重要目标——分解群。就像将一个大整数分解成质因数乘积(例如 $12 = 2^2 \times 3$)可以帮助我们理解这个数的性质一样,如果我们能将一个复杂的群 $G$ 分解成两个更小的、更简单的群 $H$ 和 $H'$ 的直积,即证明 $G \cong H \times H'$($G$ 同构于 $H \times H'$),那么我们对 $G$ 的理解就会深刻得多。因为 $H$ 和 $H'$ 更简单,而且我们已经知道直积是如何运作的。
- 稀有但重要:作者提醒我们,并不是所有的群都能被这样漂亮地分解。这就像不是所有整数都是合数一样(素数就不能再分解)。能够被分解成直积的群是比较特殊的,但一旦遇到,这就是一个非常重要的性质。
- 令人惊讶的例子:$C_6$ 的分解
- 问题:我们来看一个具体的群,6阶循环群 $C_6$。它能被分解吗?
- 猜测:$C_6$ 的阶是 6,而 $6=2 \times 3$。那么,$C_6$ 是否和 $C_2 \times C_3$ 有关呢?
- 证明思路:要证明 $C_6 \cong C_2 \times C_3$,我们需要证明 $C_2 \times C_3$ 本身就是一个6阶循环群。如果能做到这一点,因为所有同阶的循环群都是同构的,所以命题就得证。
- 执行证明:
- 首先,构建直积群 $C_2 \times C_3$。设 $C_2$ 的生成元是 $y$ ($y^2=1$),$C_3$ 的生成元是 $z$ ($z^3=1$)。(注意:原文为了通用性用了乘法表示,如果用加法群 $C_2=\{0,1\}, C_3=\{0,1,2\}$,则 $y=1, z=1$,单位元是 $(0,0)$)。我们继续沿用原文的乘法表示,单位元分别是 $1$。
- $C_2 \times C_3$ 的阶是 $|C_2| \times |C_3| = 2 \times 3 = 6$。
- 为了证明它是循环群,我们只需要在其中找到一个6阶的元素即可。如果找到了,这个元素生成的循环子群的阶也是6,就会占满整个群。
- 我们来考察元素 $x = (y, z)$。我们来计算它的阶。
- $x^k = (y, z)^k = (y^k, z^k)$。要使 $x^k$ 成为单位元 $(1, 1)$,必须同时满足 $y^k = 1$ (在 $C_2$ 中) 和 $z^k = 1$ (在 $C_3$ 中)。
- $y$ 的阶是 2,所以 $y^k=1$ 意味着 $k$ 必须是 2 的倍数。
- $z$ 的阶是 3,所以 $z^k=1$ 意味着 $k$ 必须是 3 的倍数。
- 要同时满足这两个条件, $k$ 必须是 2 和 3 的公倍数。我们要找最小的正整数 $k$,所以 $k$ 就是 2 和 3 的最小公倍数,即 $\text{lcm}(2, 3) = 6$。
- 因此,元素 $x = (y, z)$ 的阶是 6。
- 我们在一个6阶群 ($C_2 \times C_3$) 中找到了一个6阶的元素 ($(y, z)$)。这意味着这个元素可以生成整个群。
- 所以,$C_2 \times C_3$ 是一个由 $(y, z)$ 生成的6阶循环群。
- 结论:因为 $C_6$ 和 $C_2 \times C_3$ 都是6阶循环群,所以它们必然同构,即 $C_6 \cong C_2 \times C_3$。
- $x$ 的幂:
为了直观感受,文章列出了 $x=(y,z)$ 的所有幂次:
- $x^0 = (y^0, z^0) = (1, 1)$ (用加法表示是 $(0,0)$)
- $x^1 = (y^1, z^1) = (y, z)$ (用加法表示是 $(1,1)$)
- $x^2 = (y^2, z^2) = (1, z^2)$ (用加法表示是 $(0,2)$)
- $x^3 = (y^3, z^3) = (y, 1)$ (用加法表示是 $(1,0)$,因为 $y^3=y$)
- $x^4 = (y^4, z^4) = (1, z)$ (用加法表示是 $(0,1)$,因为 $z^4=z$)
- $x^5 = (y^5, z^5) = (y, z^2)$ (用加法表示是 $(1,2)$)
- $x^6 = (y^6, z^6) = (1, 1)$ (用加法表示是 $(0,0)$),回到单位元。
这 6 个元素各不相同,正好是 $C_2 \times C_3$ 的所有元素。
这是一个元素列表,展示了由元素 $(y, z)$ 生成的循环群的所有成员。
- $(1,1)$: 这是 $x^0$ 或 $x^6$,是单位元。
- $(y, z)$: 这是 $x^1$。
- $(1, z^2)$: 这是 $x^2 = (y^2, z^2)$。因为 $y \in C_2$,所以 $y^2=1$。
- $(y, 1)$: 这是 $x^3 = (y^3, z^3)$。因为 $y^3 = y^2 \cdot y = 1 \cdot y = y$,且 $z \in C_3$,所以 $z^3 = 1$。
- $(1, z)$: 这是 $x^4 = (y^4, z^4)$。因为 $y^4 = (y^2)^2 = 1^2 = 1$,且 $z^4 = z^3 \cdot z = 1 \cdot z = z$。
- $(y, z^2)$: 这是 $x^5 = (y^5, z^5)$。因为 $y^5=y$, $z^5=z^2$。
示例 1:$C_6$ 的分解 (已在上面详细解释)
- $G = C_6 = \{0, 1, 2, 3, 4, 5\}$ (模6加法)。这是一个6阶循环群。
- $H = C_2 = \{0, 1\}$ (模2加法)。
- $K = C_3 = \{0, 1, 2\}$ (模3加法)。
- 直积群 $C_2 \times C_3$ 是一个6阶循环群,因为它包含6阶元素 $(1, 1)$。
- 因此 $C_6 \cong C_2 \times C_3$。
- 我们可以建立一个具体的同构映射 $\phi: C_6 \to C_2 \times C_3$,定义为 $\phi(k) = (k \pmod 2, k \pmod 3)$。
- $\phi(0) = (0, 0)$
- $\phi(1) = (1, 1)$
- $\phi(2) = (0, 2)$
- $\phi(3) = (1, 0)$
- $\phi(4) = (0, 1)$
- $\phi(5) = (1, 2)$
这个映射是一一对应的,并且保持运算(中国剩余定理的群论形式)。
示例 2:$C_{10}$ 的分解
- $G = C_{10}$,阶为 $10 = 2 \times 5$。因为 2 和 5 互素。
- 我们可以推断 $C_{10} \cong C_2 \times C_5$。
- 证明:在 $C_2 \times C_5$ 中考虑元素 $(1, 1)$(使用加法表示)。
- 它的阶是 $\text{lcm}(\text{ord}(1 \text{ in } C_2), \text{ord}(1 \text{ in } C_5)) = \text{lcm}(2, 5) = 10$。
- 我们在一个10阶群 ($C_2 \times C_5$) 中找到了一个10阶元素。
- 所以 $C_2 \times C_5$ 是一个10阶循环群。
- 因此 $C_{10} \cong C_2 \times C_5$。
- 并非所有阶都可以分解:$C_4$ 的阶是 $4 = 2 \times 2$。但是 $C_4 \not\cong C_2 \times C_2$。为什么?因为 $C_4$ 中有4阶的元素(生成元),而在 $C_2 \times C_2$ 中,任何一个元素 $(a, b)$ 的阶是 $\text{lcm}(\text{ord}(a), \text{ord}(b))$。由于 $a,b$ 的阶最大是2,所以 $(a,b)$ 的阶最大也是2。$C_2 \times C_2$ 中根本没有4阶元素。因此它们不可能是同构的。
- 分解的条件:这个例子暗示了一个重要规律,即 $C_{rs} \cong C_r \times C_s$ 的关键在于 $r$ 和 $s$ 互素 (relatively prime),即它们的最大公约数是1。
分解群是群论中的一个核心任务,它能帮助我们将复杂问题简化。一个重要的例子是循环群的分解:一个rs阶的循环群 $C_{rs}$ 可以被分解成 $C_r \times C_s$,当且仅当 $r$ 和 $s$ 互素。这个例子通过构造一个生成元,证明了 $C_2 \times C_3$ 确实是一个6阶循环群,从而与 $C_6$ 同构。
本段的目的是通过一个具体且有点出人意料的例子 ($C_6$ 的分解),来展示群的分解这一想法的威力和可行性。它不仅阐述了分解的愿望,还实际操作了一遍,为后面更具一般性的结论(命题2.11.3)做铺垫,并引出了一个关键问题:什么时候一个群可以被分解成直积?
想象一个有6个位置的旋转罗盘 ($C_6$)。你每次可以转1格、2格...
再想象一个只有两个状态的开关(上下,$C_2$)和一个有三个档位的旋钮(高中低,$C_3$)。
$C_6 \cong C_2 \times C_3$ 的意思是:罗盘的6个位置状态,可以和“开关状态-旋钮档位”的 $2 \times 3 = 6$ 种组合状态一一对应,并且你在罗盘上转一下,等价于在另一边对开关和旋钮进行一次对应的操作。例如,罗盘转一格,可能对应于“把开翻成关,同时把旋钮调到下一档”。这个对应关系是精确且无损的。
想象一条长度为6的线段,上面的整点是 $\{0, 1, 2, 3, 4, 5\}$ ($C_6$)。
再想象一个 $2 \times 3$ 的网格 ($C_2 \times C_3$)。
$C_6 \cong C_2 \times C_3$ 意味着你可以把这条线段“盘起来”,精确地覆盖到这个 $2 \times 3$ 网格的所有点上,并且线段上的“加1”操作(向前走一步)对应于网格上的一种特定移动方式(比如向右下方移动,并且在边界处“循环”)。这个例子中的移动方式就是 $(k \pmod 2, k \pmod 3)$。
2.2 循环群分解的普遍规律
📜 [原文4]
对于阶为 $rs$ 的循环群,只要整数 $r$ 和 $s$ 没有公因子,就有类似的陈述。
命题 2.11.3 令 $r$ 和 $s$ 为互素整数。阶为 $rs$ 的循环群同构于阶为 $r$ 的循环群和阶为 $s$ 的循环群的直积。$\square$
这段话将前面 $C_6$ 的例子推广成一个普遍的定理。
- 前提条件:这个命题的核心前提是 $r$ 和 $s$ 是互素整数 (coprime integers),也就是说,它们的最大公约数 $\text{gcd}(r, s) = 1$。
- 命题内容:如果上述条件成立,那么一个阶为 $rs$ 的循环群 (记作 $C_{rs}$) 就一定和阶为 $r$ 的循环群 ($C_r$) 与阶为 $s$ 的循环群 ($C_s$) 的直积 ($C_r \times C_s$) 是同构的。
- $C_{rs} \cong C_r \times C_s \iff \text{gcd}(r, s) = 1$
- 证明思路 (与 $C_6$ 例子完全相同):
- 我们想证明 $C_{rs}$ 和 $C_r \times C_s$ 是同构的。
- $C_{rs}$ 是一个阶为 $rs$ 的循环群。
- 直积群 $C_r \times C_s$ 的阶是 $|C_r| \times |C_s| = r \times s = rs$。
- 所以,这两个群的阶是相同的。
- 根据群论基本定理,如果我们可以证明 $C_r \times C_s$ 也是一个循环群,那么由于两个同阶的循环群必然同构,命题就得证了。
- 要证明 $C_r \times C_s$ 是循环群,我们只需要在里面找到一个阶为 $rs$ 的元素。
- 设 $C_r$ 的生成元是 $y$(阶为 $r$),$C_s$ 的生成元是 $z$(阶为 $s$)。我们来考察直积群中的元素 $x = (y, z)$。
- 元素 $x$ 的阶是使得 $x^k = (y^k, z^k) = (\text{单位元}, \text{单位元})$ 成立的最小正整数 $k$。
- 这要求 $k$ 既是 $r$ 的倍数,又是 $s$ 的倍数。所以 $k$ 是 $r$ 和 $s$ 的公倍数。
- 我们找的是最小的 $k$,所以 $k = \text{lcm}(r, s)$ (最小公倍数)。
- 这里用到了一个关键的数论知识:对于任意两个正整数 $r, s$,有 $\text{lcm}(r, s) \times \text{gcd}(r, s) = r \times s$。
- 因为命题的条件是 $r, s$ 互素,所以 $\text{gcd}(r, s) = 1$。
- 因此,$k = \text{lcm}(r, s) = (r \times s) / \text{gcd}(r, s) = rs / 1 = rs$。
- 我们找到了一个阶为 $rs$ 的元素 $x = (y, z)$。
- 在一个阶为 $rs$ 的群 ($C_r \times C_s$) 中找到了一个阶为 $rs$ 的元素,这证明了 $C_r \times C_s$ 是一个循环群。
- 证毕。
示例 1 (互素):
- $r=3, s=5$。它们互素。
- 命题预测:$C_{15} \cong C_3 \times C_5$。
- 验证:在 $C_3 \times C_5$ 中,元素 $(1, 1)$ 的阶是 $\text{lcm}(3, 5) = 15$。所以 $C_3 \times C_5$ 是15阶循环群。结论正确。
示例 2 (不互素):
- $r=2, s=4$。它们不互素,$\text{gcd}(2, 4) = 2$。
- 命题不适用。我们来看看 $C_8$ 和 $C_2 \times C_4$ 是否同构。
- $C_8$ 是8阶循环群,它有8阶的元素。
- 在 $C_2 \times C_4$ 中,任意元素 $(a, b)$ 的阶是 $\text{lcm}(\text{ord}(a), \text{ord}(b))$。
- $a \in C_2$,所以 $\text{ord}(a)$ 只能是 1 或 2。
- $b \in C_4$,所以 $\text{ord}(b)$ 只能是 1, 2, 或 4。
- 那么 $\text{lcm}(\text{ord}(a), \text{ord}(b))$ 的最大可能值是 $\text{lcm}(2, 4) = 4$。
- $C_2 \times C_4$ 中所有元素的阶最大只能是 4。它没有8阶的元素。
- 因此,$C_2 \times C_4$ 不是循环群,它不可能和 $C_8$ 同构。
- 充要条件:这个命题实际上是一个充要条件,即 $C_{rs} \cong C_r \times C_s$ 当且仅当 $\text{gcd}(r, s) = 1$。原文只强调了充分性(互素 $\implies$ 同构),但反过来也成立。如果它们不互素,直积群就不是循环群,因而不能和循环群 $C_{rs}$ 同构。
- 推广到多个因子:这个命题可以推广。$C_{n_1 n_2 \dots n_k} \cong C_{n_1} \times C_{n_2} \times \dots \times C_{n_k}$ 当且仅当这些整数 $n_1, n_2, \dots, n_k$ 两两互素。例如,$C_{30} \cong C_2 \times C_3 \times C_5$。
- 中国剩余定理 (Chinese Remainder Theorem):这个命题是中国剩余定理在群论中的一个直接体现。一个关于整数 $x \pmod{rs}$ 的问题,可以分解为两个独立的问题 $x \pmod r$ 和 $x \pmod s$ 来解决,当 $r, s$ 互素时,解是唯一对应的。
命题 2.11.3 给出了循环群可以被分解为更小的循环群的直积的精确条件:当且仅当阶的各个因子相互互素。这是群论中一个非常基本和重要的结构性定理。
这个命题的目的是将前面例子的观察提升为一般性的数学真理。它为有限循环群的结构提供了一个完整的分解图景,使得任何有限循环群都可以被看作是若干个素数幂阶的循环群的直积(例如 $C_{12} \cong C_4 \times C_3$, 因为 $12=4 \times 3$ 且 $\text{gcd}(4,3)=1$)。这是有限阿贝尔群基本定理的一个特例。
想象两个齿轮,一个有 $r$ 个齿,一个有 $s$ 个齿。它们啮合在一起转动。
- 互素:如果 $r, s$ 互素,比如 3 和 5。你给两个齿轮都做上标记,让它们从标记对标记的位置开始转。它们需要转动 $\text{lcm}(3, 5) = 15$ 次(大齿轮转3圈,小齿轮转5圈)才能再次回到标记对标记的状态。这个系统完整地遍历了 $3 \times 5 = 15$ 个组合状态,构成了一个“大循环”。这就像 $C_{15} \cong C_3 \times C_5$。
- 不互素:如果 $r, s$ 不互素,比如 4 和 6 ($\text{gcd}=2$)。它们只需要转动 $\text{lcm}(4, 6) = 12$ 次就能回到初始状态,而不是 $4 \times 6 = 24$ 次。这个系统无法遍历所有24个可能的组合状态,它只在一个大小为12的子循环里运动。这就像 $C_4 \times C_6$ 不是一个24阶循环群。
想象在电脑屏幕上画一个 $r \times s$ 的像素网格。从左上角 $(0, 0)$ 开始,你每次移动 "向右下角一步",即从 $(x, y)$ 移动到 $((x+1) \pmod r, (y+1) \pmod s)$。
- 如果 $r, s$ 互素,你的移动轨迹会不重复地经过网格上的每一个像素点,最终在第 $rs$ 步回到起点。这形成了一个覆盖整个空间的大循环。
- 如果 $r, s$ 不互素,你的移动轨迹会在回到起点之前,只访问所有像素点的一部分。例如 $4 \times 6$ 的网格,你会在12步后回到起点,只访问了12个点,还有12个点你永远也访问不到。
2.3 反例:C4的不可分解性
📜 [原文5]
另一方面,4阶循环群不同构于两个2阶循环群的直积。$C_{2} \times C_{2}$ 的每个元素的阶都是 1 或 2,而4阶循环群包含两个4阶元素。
这段话是命题 2.11.3 的一个关键反例,用来说明互素这个条件是绝对必要的。
- 要考察的对象:4阶循环群 $C_4$。它的阶是 $4 = 2 \times 2$。这里的因子是 $r=2, s=2$。
- 检查条件:$r=2, s=2$ 并不是互素的,因为它们的最大公约数 $\text{gcd}(2, 2) = 2 \neq 1$。
- 命题的预测:由于条件不满足,命题 2.11.3 不保证 $C_4$ 和 $C_2 \times C_2$ 同构。这段话的目的是证明它们确实不同构。
- 证明方法:寻找结构上的本质不同。要证明两个群不同构,最常用的方法是找到一个群拥有的、但另一个群不具备的、在同构映射下应该保持不变的性质。元素的阶的分布情况就是一个这样的关键性质。
- 分析 $C_4$:
- $C_4 = \{0, 1, 2, 3\}$ (模4加法)。
- 我们来检查每个元素的阶:
- $\text{ord}(0) = 1$ (单位元)。
- $\text{ord}(1) = 4$ (因为 $1+1=2, 1+1+1=3, 1+1+1+1=0$)。这是一个4阶元素。
- $\text{ord}(2) = 2$ (因为 $2+2=4 \equiv 0$)。这是一个2阶元素。
- $\text{ord}(3) = 4$ (因为 $3+3=6 \equiv 2, 3+3+3=9 \equiv 1, 3+3+3+3=12 \equiv 0$)。这是一个4阶元素。
- 结论:$C_4$ 拥有4阶元素(事实上是两个)。
- 分析 $C_2 \times C_2$:
- $C_2 \times C_2 = \{(0,0), (0,1), (1,0), (1,1)\}$ (分量模2加法)。
- 我们来检查每个元素的阶:
- $\text{ord}(0,0) = 1$ (单位元)。
- $\text{ord}(0,1) = \text{lcm}(\text{ord}(0), \text{ord}(1)) = \text{lcm}(1, 2) = 2$。
- $\text{ord}(1,0) = \text{lcm}(\text{ord}(1), \text{ord}(0)) = \text{lcm}(2, 1) = 2$。
- $\text{ord}(1,1) = \text{lcm}(\text{ord}(1), \text{ord}(1)) = \text{lcm}(2, 2) = 2$。
- 结论:$C_2 \times C_2$ 中,除了单位元,所有元素的阶都是 2。它根本没有4阶元素。
- 得出最终结论:
- $C_4$ 有4阶元素。
- $C_2 \times C_2$ 没有4阶元素。
- 如果存在一个同构映射 $\phi: C_4 \to C_2 \times C_2$,它必须保持元素的阶。也就是说,如果 $g \in C_4$ 的阶是 4,那么 $\phi(g)$ 在 $C_2 \times C_2$ 中的阶也必须是 4。
- 但 $C_2 \times C_2$ 中没有4阶元素,所以这样的同构映射不可能存在。
- 因此,$C_4$ 和 $C_2 \times C_2$ 不是同构的。
- $C_4$: 就像一个正方形的四个顶点,你只能沿着边按一个方向走,必须走4步才能回到起点。
- $C_2 \times C_2$: 想象一个矩形的四个顶点。你站在任何一个非起始的顶点,走一步(根据这个顶点的属性,比如“横着走”或“斜着走”)就能回到起点。这个群有时被称为克莱因四元群 (Klein four-group)。
- 同阶不一定同构:这是群论初学者最容易犯的错误之一。$C_4$ 和 $C_2 \times C_2$ 的阶都是4,但它们的内部结构完全不同。阶相同只是同构的必要条件,远非充分条件。
- 关注元素阶的分布:比较两个群是否同构时,不能只看群的阶,而要看它们各自拥有多少个1阶元素,多少个2阶元素,多少个3阶元素……这个“元素阶的清单”如果不一样,两个群就一定不同构。
本段通过对比 $C_4$ 和 $C_2 \times C_2$ 中元素阶的分布,清晰地证明了它们虽然同阶,但结构不同,因此不同构。这强有力地说明了命题 2.11.3 中“互素”条件的不可或缺性。
本段的目的是提供一个具体的反例,以加深对命题 2.11.3 的理解。它通过展示一个失败的分解案例,从反面强调了成功的分解(如 $C_6$)背后的深刻数学原理。这有助于学习者建立更稳固、更具辨析性的知识体系。
- $C_4$ 就像一个单行道环岛,你必须绕一整圈才能回来。
- $C_2 \times C_2$ 就像一个十字路口,你从任何一个方向过来,下一步就是穿过路口,再下一步就又回来了(假设对称)。或者想象你有两个电灯开关,控制一盏灯。无论当前是什么状态,你拨动任何一个开关,灯的状态改变;再拨动一下同一个开关,灯的状态又变回来。任何操作,重复两次就回到了原点。
- $C_4$: 一根有4个珠子的手链,珠子编号0,1,2,3。从1号珠子出发,你只能顺着走到2,再到3,再到0,最后才能回到1。这是一个长度为4的旅程。
- $C_2 \times C_2$: 想象一张纸,对折一次,再对折一次,然后展开。纸上有四个区域。你可以把“穿过水平折痕”看作一个操作,$x$;把“穿过垂直折痕”看作另一个操作,$y$。从任何一个区域出发,执行两次 $x$ 操作就会回到原区域。执行两次 $y$ 操作也会回到原区域。执行 $xy$ 操作(穿过水平再穿过垂直)等于 $yx$ 操作(穿过垂直再穿过水平)。这个系统里,任何操作的阶都是2。
3识别直积的条件
3.1 乘法映射及其性质
📜 [原文6]
下一个命题描述了直积群。
命题 2.11.4 令 $H$ 和 $K$ 是群 $G$ 的子群,并令 $f: H \times K \rightarrow G$ 为乘法映射,定义为 $f(h, k)=h k$。它的像是集合 $H K=\{h k \mid h \in H, k \in K\}$。
(a) $f$ 是内射当且仅当 $H \cap K=\{1\}$。
(b) $f$ 是从直积群 $H \times K$ 到 $G$ 的同态当且仅当 $K$ 的元素与 $H$ 的元素可交换:$h k=k h$。
(c) 如果 $H$ 是 $G$ 的正规子群,那么 $H K$ 是 $G$ 的子群。
(d) $f$ 是从直积群 $H \times K$ 到 $G$ 的同构当且仅当 $H \cap K=\{1\}$,$H K=G$,并且 $H$ 和 $K$ 都是 $G$ 的正规子群。
这个命题非常重要,它回答了一个核心问题:假设我们有一个大群 $G$ 和它的两个子群 $H, K$,在什么条件下,我们可以说 $G$ 就等价于(同构于)$H$ 和 $K$ 的直积?这个命题从一个叫做“乘法映射”的工具入手,一步步建立起判定条件。
核心工具:乘法映射 f
- 我们不再从外部构造直积,而是反过来,从 $G$ 内部出发。
- 我们取子群 $H$ 和 $K$ 构造一个直积群 $H \times K$ (这是一个外部的、辅助的群)。
- 定义一个映射 $f: H \times K \to G$,它的作用是把有序对 $(h, k)$ 映射到 $G$ 中的元素 $h \cdot k$ (这里的乘法是 $G$ 中的乘法)。这个 $f$ 就叫乘法映射。
- $f$ 的像,也就是所有 $hk$ 形式的元素的集合,被记为 $HK$。
命题的四个部分,层层递进:
(a) 何时 $f$ 是内射 (一对一)?
- 内容:$f$ 是内射的,当且仅当 $H$ 和 $K$ 的交集里只有一个元素,就是单位元 $1$。即 $H \cap K = \{1\}$。
- 解释:
- ($\Rightarrow$) 如果 $H \cap K$ 里有另一个非单位元元素 $x$,那么 $x \in H$ 且 $x \in K$。同时 $x^{-1} \in H$。考虑 $f(x^{-1}, x) = x^{-1}x = 1$。再考虑 $f(1, 1) = 1 \cdot 1 = 1$。我们找到了两个不同的输入 $(x^{-1}, x)$ 和 $(1, 1)$,它们都映射到了同一个输出 $1$。所以 $f$ 不是内射的。
- ($\Leftarrow$) 如果 $H \cap K = \{1\}$,假设 $f(h_1, k_1) = f(h_2, k_2)$,即 $h_1k_1 = h_2k_2$。我们可以变形这个等式:$h_2^{-1}h_1 = k_2k_1^{-1}$。等式左边 ($h_2^{-1}h_1$) 是 $H$ 中的元素,右边 ($k_2k_1^{-1}$) 是 $K$ 中的元素。由于这个元素同时在 $H$ 和 $K$ 中,它必定属于它们的交集 $H \cap K$。而我们假设交集只有单位元 $\{1\}$。所以 $h_2^{-1}h_1 = 1$ 且 $k_2k_1^{-1} = 1$。这立即导出 $h_1=h_2$ 和 $k_1=k_2$。因此,输入 $(h_1, k_1)$ 和 $(h_2, k_2)$ 必须是相同的。所以 $f$ 是内射的。
- 小结(a):$H, K$ “除了单位元之外没有公共部分”是保证 $G$ 中的每个元素最多只能有一种 "$hk$" 写法的关键。
(b) 何时 $f$ 是同态 (保持结构)?
- 内容:$f$ 是一个群同态,当且仅当 $H$ 中的任意元素都与 $K$ 中的任意元素可交换 (commute),即对所有 $h \in H, k \in K$,都有 $hk=kh$。
- 解释:
- 要成为同态,必须满足 $f(\text{op}_1) = f(\text{op}_2)$,即 $f((h_1,k_1) \cdot_{H \times K} (h_2,k_2)) = f(h_1,k_1) \cdot_G f(h_2,k_2)$。
- 左边:$f((h_1h_2, k_1k_2)) = (h_1h_2)(k_1k_2)$。
- 右边:$(h_1k_1)(h_2k_2)$。
- 要让 $h_1h_2k_1k_2 = h_1k_1h_2k_2$ 对所有的 $h_1, h_2 \in H, k_1, k_2 \in K$ 都成立,通过消去 $h_1$ 和 $k_2$,我们发现这等价于 $h_2k_1 = k_1h_2$ 对所有 $h_2 \in H, k_1 \in K$ 成立。
- 小结(b):$H$ 和 $K$ 的元素必须能够“和平相处”(互相交换),乘法映射 $f$ 才能成为一个同态。否则,运算顺序的改变会导致结果不同,结构就被破坏了。
(c) 何时 $HK$ 是一个子群?
- 内容:如果 $H$ 是 $G$ 的一个正规子群,那么集合 $HK$ 自身就构成 $G$ 的一个子群。(对称地,如果 $K$ 是正规子群,结论也成立)。
- 解释:
- 要证明 $HK$ 是子群,需要验证封闭性和逆元。
- 关键步骤:证明 $HK=KH$。因为 $H$ 是正规子群,对于任何 $k \in K$,我们有 $kH = Hk$(左陪集等于右陪集)。所以 $KH = \bigcup_{k \in K} kH = \bigcup_{k \in K} Hk = HK$。
- 封闭性:任取两个 $HK$ 中的元素 $h_1k_1$ 和 $h_2k_2$。它们的积是 $(h_1k_1)(h_2k_2) = h_1(k_1h_2)k_2$。因为 $k_1h_2 \in k_1H = Hk_1$,所以 $k_1h_2$ 可以写成某个 $h'k_1$ 的形式。但更简单的方法是利用 $HK=KH$:$(HK)(HK) = H(KH)K = H(HK)K = (HH)(KK) = HK$。所以 $HK$ 对乘法封闭。
- 逆元:任取 $hk \in HK$。它的逆元是 $(hk)^{-1}=k^{-1}h^{-1}$。由于 $k^{-1} \in K, h^{-1} \in H$,所以 $k^{-1}h^{-1} \in KH$。因为我们已经证明了 $KH=HK$,所以逆元也在 $HK$ 中。
- 小结(c):只要有一个子群是正规的,它们的乘积集合 $HK$ 就是一个良定义的子群。
(d) 何时 $f$ 是同构 (完美的结构等价)?
- 内容:$f$ 是一个同构,当且仅当满足以下三个条件:
- $H \cap K = \{1\}$ ($f$ 是内射,来自(a))
- $HK = G$ ($f$ 是满射,即 $f$ 的像覆盖整个 $G$)
- $H$ 和 $K$ 都是 $G$ 的正规子群。
- 解释:
- 同构 = 内射 + 满射 + 同态。
- $f$ 内射 $\iff H \cap K = \{1\}$ (来自 a)。
- $f$ 满射 $\iff HK = G$ (根据 $f$ 的像的定义)。
- $f$ 同态 $\iff hk=kh$ (来自 b)。
- 所以,初看起来,条件应该是 (1) $H \cap K=\{1\}$, (2) $HK=G$, (3) $H, K$ 元素互相交换。
- 命题(d)的巧妙之处在于,它用“$H, K$ 都是正规子群”这个条件替换了“元素互相交换”。它断言,在(1)和(2)成立的前提下,“$H, K$ 都是正规的”与“$H, K$ 元素互相交换”是等价的。
- 证明这个等价性:
- ($\Rightarrow$) 假设 $H,K$ 都是正规子群。我们要证明 $hk=kh$。考虑交换子 $hkh^{-1}k^{-1}$。
- 可以写成 $(hkh^{-1})k^{-1}$。因为 $K$ 是正规子群,$hkh^{-1} \in K$,所以 $(hkh^{-1})k^{-1} \in K$。
- 也可以写成 $h(kh^{-1}k^{-1})$。因为 $H$ 是正规子群,$kh^{-1}k^{-1} \in H$,所以 $h(kh^{-1}k^{-1}) \in H$。
- 所以交换子 $hkh^{-1}k^{-1}$ 同时属于 $H$ 和 $K$,即属于 $H \cap K$。
- 因为 $H \cap K = \{1\}$,所以 $hkh^{-1}k^{-1} = 1$。
- 变形得到 $hk = kh$。
- ($\Leftarrow$) 假设 $H,K$ 元素互相交换。我们要证明它们是正规的。以 $H$ 为例,要证对任意 $g \in G$,有 $gHg^{-1}=H$。因为 $HK=G$,所以 $g$ 可以写成 $g=h_0k_0$ 的形式。
- $gHg^{-1} = (h_0k_0)H(h_0k_0)^{-1} = h_0k_0Hk_0^{-1}h_0^{-1}$。
- 因为 $H$ 的元素和 $K$ 的元素可交换,所以 $k_0Hk_0^{-1} = H$ (即 $k_0h k_0^{-1} = h k_0 k_0^{-1} = h \in H$)。
- 所以 $gHg^{-1} = h_0Hh_0^{-1}$。因为 $H$ 是子群,$h_0 \in H$,所以 $h_0Hh_0^{-1}=H$。
- 因此 $H$ 是正规子群。同理可证 $K$ 也是正规子群。
- 小结(d):这是整个命题的高潮。它给出了一个群 $G$ 能被“内部”分解成子群 $H, K$ 的直积的充要条件。这三个条件(交集为{1},并集为G,两者都正规)比检查元素交换律要更容易操作,因为“正规性”是群论里一个更结构化的概念。
- 正规性 vs 交换性: 单个子群 $H$ 是正规的,不意味着 $H$ 的元素和 $K$ 的元素可交换。但如果 $H$ 和 $K$ 都是正规的,且交集为{1},它们就一定可交换。
- HK vs H×K: $H \times K$ 是一个外部构造的、元素是有序对的群。$HK$ 是 $G$ 的一个子集(在(c,d)条件下是子群),元素是 $G$ 自己的元素。命题(d)说的就是,在特定条件下,群 $HK$(也就是 $G$)和群 $H \times K$ 的结构是一模一样的。
- 半直积 (Semidirect Product):如果命题(d)的条件中,只要求一个子群(比如 $H$)是正规的,而另一个不是,那么 $G$ 可能同构于一种更复杂的结构,叫做半直积 $H \rtimes K$。这超出了本章范围,但说明了每个条件的重要性。
命题 2.11.4 是一个诊断工具。它提供了一套完整的标准,用于判断一个给定的群 $G$ 是否可以被看作是其两个子群 $H$ 和 $K$ 的“内部直积”。这套标准包括:$H, K$ 应该只在单位元处相交,它们的乘积应该能覆盖整个群 $G$,并且它们都应该是 $G$ 中的正规子群。
这个命题将直积从一个外部构造工具,转变为一个内部结构分析工具。之前我们是“用 $H,K$ 建造 $H \times K$”,现在我们是“在 $G$ 里面寻找 $H,K$,来诊断 $G$ 是否是 $H \times K$”。这使得我们能够分析和分解已经存在的群,是群论结构分析的核心定理之一。
想象一个公司 $G$。
- $H$ 和 $K$ 是两个部门。
- 条件1:$H \cap K = \{1\}$。两个部门没有兼职人员,除了大老板(单位元)谁也不属于。这样职责清晰。
- 条件2:$HK = G$。公司里任何一项任务(元素 $g$),都可以分解成一个H部门的任务($h$)和一个K部门的任务($k$)的组合来完成。
- 条件3:$H, K$ 都正规。这意味着两个部门的地位是平等的,且它们的运作不受公司其他部分的影响。比如,你让全公司的人($g$)来监督H部门的工作流程($gHg^{-1}$),流程还是H部门自己的流程($H$)。K部门同理。这种强大的独立性,最终导致了两个部门的工作可以完全解耦,互不干扰($hk=kh$)。
- 当这三个条件满足时,这个公司 $G$ 的整体运作模式,就等价于两个完全独立运营的公司 $H$ 和 $K$ 的简单组合。要了解 $G$,只需要分别了解 $H$ 和 $K$ 就行了。
回到二维平面 $\mathbb{R}^2$。
- $G = \mathbb{R}^2$ (向量加法群)。
- $H$ 是 x-轴,即 $\{(x, 0) | x \in \mathbb{R}\}$。
- $K$ 是 y-轴,即 $\{(0, y) | y \in \mathbb{R}\}$。
- 我们来验证命题 2.11.4(d) 的条件:
- $H \cap K = \{(0,0)\}$。x-轴和y-轴只在原点相交。满足。
- $H+K = \mathbb{R}^2$。平面上任何一个向量 $(x,y)$ 都可以写成一个x-轴向量 $(x,0)$ 和一个y-轴向量 $(0,y)$ 的和。满足。
- $H, K$ 都是 $\mathbb{R}^2$ 的正规子群。因为 $\mathbb{R}^2$ 是阿贝尔群,任何子群都是正规的。满足。
- 所有条件都满足,因此命题告诉我们 $\mathbb{R}^2 \cong H \times K$。这和我们最初把 $\mathbb{R}^2$ 定义为 $\mathbb{R} \times \mathbb{R}$ 是完全一致的。这个例子展示了命题如何从内部结构反推出直积形式。
3.2 一个非同态的双射例子
📜 [原文7]
值得注意的是,乘法映射可能是双射,尽管它不是群同态。例如,当 $G=S_{3}$,并使用通常的表示法, $H=\langle x\rangle$ 和 $K=\langle y\rangle$ 时,就会发生这种情况。
这部分给出了一个重要的警示:即使乘法映射 $f(h,k)=hk$ 既是内射又是满射(即双射),它也不一定是一个群同态。这意味着,即使集合 $H \times K$ 和群 $G$ 的元素可以一一对应,它们的运算结构也可能完全不同。
- 背景设定:
- 群 $G = S_3$,即3个元素的置换群,它的阶是 $3! = 6$。
- $S_3$ 的元素通常表示为 $\{1, x, x^2, y, yx, yx^2\}$,其中 $x$ 是一个3-循环(如 (1 2 3)),满足 $x^3=1$;$y$ 是一个对换(如 (1 2)),满足 $y^2=1$。并且它们不交换:$xy = yx^2 \neq yx$。
- 子群选择:
- $H = \langle x \rangle = \{1, x, x^2\}$。这是一个3阶循环子群。
- $K = \langle y \rangle = \{1, y\}$。这是一个2阶循环子群。
- 分析乘法映射 $f: H \times K \to S_3$:
- 内射性 (Injectivity):根据命题 2.11.4(a),我们需要检查 $H \cap K$。
- $H=\{1, (123), (132)\}$
- $K=\{1, (12)\}$
- 它们的交集 $H \cap K = \{1\}$。
- 因此,$f$ 是内射的。这意味着从 $H \times K$ 映射过来的6个元素都是不同的。
- 满射性 (Surjectivity):我们需要检查 $HK=S_3$。
- 集合 $H \times K$ 有 $|H| \times |K| = 3 \times 2 = 6$ 个元素。
- 因为 $f$ 是内射的,它会把这6个不同的输入映射到 $S_3$ 中6个不同的输出。
- 由于 $S_3$ 总共也只有6个元素,所以 $f$ 的像必然覆盖了整个 $S_3$。即 $HK=S_3$。
- 因此,$f$ 是满射的。
- 双射性 (Bijectivity):因为 $f$ 既是内射又是满射,所以它是一个双射。这意味着作为集合,$H \times K$ 和 $S_3$ 的元素之间存在一个一一对应关系。
- 同态性 (Homomorphism):根据命题 2.11.4(b),我们需要检查 $H$ 和 $K$ 的元素是否可交换。
- 取 $h=x \in H$, $k=y \in K$。
- $hk = xy$。
- $kh = yx$。
- 我们知道在 $S_3$ 中,$xy \neq yx$。
- 所以,$H$ 和 $K$ 的元素不是普遍可交换的。
- 因此,$f$ 不是一个群同态。
- 结论:尽管存在一个从集合 $H \times K$ 到 $S_3$ 的一一对应,但这个对应关系不保持群的运算结构。因此,$S_3$ 不同构于直积群 $H \times K$。由于 $H \cong C_3, K \cong C_2$,这实际上是说 $S_3 \not\cong C_3 \times C_2$。
- $H \times K = \{ (1,1), (1,y), (x,1), (x,y), (x^2,1), (x^2,y) \}$
- $S_3 = \{ 1, y, x, xy, x^2, x^2y \}$ (这是 $hk$ 的结果)
- $f$ 将两者一一对应。例如 $f(x,y)=xy$。
- 让我们来验证非同态性:
- 在 $H \times K$ 中运算:$(x,1) \cdot (1,y) = (x \cdot 1, 1 \cdot y) = (x,y)$。
- 通过 $f$ 映射到 $S_3$:$f(x,y) = xy$。
- 这是路径1:先在 $H \times K$ 中运算,再映射。
- 现在走路径2:先分别映射,再在 $S_3$ 中运算。
- $f(x,1) = x \cdot 1 = x$。
- $f(1,y) = 1 \cdot y = y$。
- 两者在 $S_3$ 中相乘:$x \cdot y = xy$。
- 咦?这个例子 $f((x,1)(1,y)) = f(x,1)f(1,y)$ 居然成立了!看来需要找一个不成立的例子。
- 让我们换一对元素:在 $H \times K$ 中运算 $(1,y) \cdot (x,1) = (1 \cdot x, y \cdot 1) = (x,y)$。
- 再走路径2:
- $f(1,y) = y$。
- $f(x,1) = x$。
- 两者在 $S_3$ 中相乘:$y \cdot x = yx$。
- 比较两条路径的结果:$xy \neq yx$。
- 所以 $f((1,y)(x,1)) \neq f(1,y)f(x,1)$。同态性质被破坏。
- 双射不等于同构:这是最关键的警示。在群论(以及其他代数结构中),结构的保持(同态)远比元素的一一对应(双射)重要。
- $S_3$ vs $C_6$:$S_3$ 和 $C_6$ (即 $C_2 \times C_3$) 的阶都是6。但 $S_3$ 是非阿贝尔群,而 $C_6$ 是阿贝尔群,所以它们不可能同构。这个例子从乘法映射的角度解释了为什么 $S_3$ 不能被分解成 $C_3$ 和 $C_2$ 的直积。
本段通过 $S_3$ 的例子,生动地展示了命题 2.11.4(d) 中正规性(或等价的交换性)条件的重要性。仅仅满足内射和满射条件,只能保证元素数量上匹配,但不能保证运算规则匹配。
这个例子的目的是作为一个“反例”或“边界情况”,用来强调同构的严格性。它防止读者在看到乘法映射是双射后,就草率地得出群同构的结论。它迫使我们必须回头检查同态属性,也就是检查元素是否可交换,或者更结构化地,检查子群是否正规。
想象你有两套完全不同的乐高积木,$H$ 和 $K$。$H$ 有3块,$K$ 有2块。你可以把它们配对,组成 $3 \times 2 = 6$ 种组合 $(h, k)$。这构成了集合 $H \times K$。
现在有一个模型 $G$(比如 $S_3$),它也是由6块积木组成的。
你发现,你可以用 $H, K$ 的每一对积木 $(h,k)$ 焊接起来 ($hk$),恰好能造出模型 $G$ 的每一块积木,不多不少(这就是双射)。
但是,$G$ 这个模型有自己的组合规则($S_3$的乘法表)。而你在 $H \times K$ 世界里的组合规则是“H的归H,K的归K,各玩各的”(分量乘法)。
这个例子说明,即使你可以用原材料拼出最终模型,最终模型的内在组合规则,可能和你原材料的组合规则是完全不兼容的。
你有红、黄、蓝三种颜色的颜料($H$),和“亮光”、“哑光”两种调料($K$)。你可以混合出 $3 \times 2=6$ 种不同的漆($HK=G=S_3$)。
但是,在 $H \times K$ 的世界里,操作是独立的:“把红色换成黄色”和“把亮光换成哑光”是两个不相干的操作,先后顺序无所谓。
但在 $S_3$ 的世界里,操作的顺序至关重要。比如“先旋转再翻转”和“先翻转再旋转”得到的结果是不同的。
因此,虽然漆的种类可以一一对应,但调制它们的操作流程(群结构)是无法对应的。
3.3 命题2.11.4的证明
📜 [原文8]
证明。(a) 如果 $H \cap K$ 包含一个元素 $x \neq 1$,那么 $x^{-1}$ 在 $H$ 中,并且 $f\left(x^{-1}, x\right)=1=f(1,1)$,所以 $f$ 不是内射。假设 $H \cap K=\{1\}$。令 $\left(h_{1}, k_{1}\right)$ 和 $\left(h_{2}, k_{2}\right)$ 为 $H \times K$ 的元素,使得 $h_{1} k_{1}=h_{2} k_{2}$。我们将此方程两边左乘 $h_{1}^{-1}$,右乘 $k_{2}^{-1}$,得到 $k_{1} k_{2}^{-1}=h_{1}^{-1} h_{2}$。左边是 $K$ 的一个元素,右边是 $H$ 的一个元素。由于 $H \cap K=\{1\}$,所以 $k_{1} k_{2}^{-1}=h_{1}^{-1} h_{2}=1$。因此 $k_{1}=k_{2}, h_{1}=h_{2}$,并且 $\left(h_{1}, k_{1}\right)=\left(h_{2}, k_{2}\right)$。
(b) 令 $\left(h_{1}, k_{1}\right)$ 和 $\left(h_{2}, k_{2}\right)$ 为直积群 $H \times K$ 的元素。这些元素在直积群 $H \times K$ 中的直积是 $\left(h_{1} h_{2}, k_{1} k_{2}\right)$,并且 $f\left(h_{1} h_{2}, k_{1} k_{2}\right)=h_{1} h_{2} k_{1} k_{2}$,而 $f\left(h_{1}, k_{1}\right) f\left(h_{2}, k_{2}\right)=h_{1} k_{1} h_{2} k_{2}$。这些元素相等当且仅当 $h_{2} k_{1}=k_{1} h_{2}$。
(c) 假设 $H$ 是一个正规子群。我们注意到 $K H$ 是 $K$ 中 $k$ 的左陪集 $k H$ 的并集,并且 $H K$ 是右陪集 $H k$ 的并集。由于 $H$ 是正规的, $k H=H k$,因此 $H K=K H$。$H K$ 在乘法下的封闭性随之而来,因为 $H K H K=H H K K=H K$。此外, $(h k)^{-1}=k^{-1} h^{-1}$ 在 $K H=H K$ 中。这证明了 $H K$ 在逆元下的封闭性。
(d) 假设 $H$ 和 $K$ 满足给定的条件。那么 $f$ 既是内射又是满射,所以它是双射。根据 (b),它是一个同构当且仅当对于所有 $H$ 中的 $h$ 和 $K$ 中的 $k$,有 $h k=k h$。考虑交换子 $\left(h k h^{-1}\right) k^{-1}=h\left(k h^{-1} k^{-1}\right)$。由于 $K$ 是正规的,左边在 $K$ 中,由于 $H$ 是正规的,右边在 $H$ 中。由于 $H \cap K=\{1\}$,$h k h^{-1} k^{-1}=1$,所以 $h k=k h$。反之,如果 $f$ 是一个同构,则可以在同构群 $H \times K$ 中而不是在 $G$ 中验证所列出的条件。$\square$
这部分是命题 2.11.4 的正式数学证明,它将我们之前通过解释和例子建立起来的直觉,用严格的逻辑语言表述出来。
(a) 内射性证明
- 目标:证明 "$f$ 内射 $\iff H \cap K = \{1\}$"。
- ($\Leftarrow$) 方向 (证明 "如果 $H \cap K = \{1\}$,那么 $f$ 内射")
- 假设 $H \cap K = \{1\}$。
- 要证 $f$ 内射,我们假设 $f(h_1, k_1) = f(h_2, k_2)$,目标是推出 $(h_1, k_1) = (h_2, k_2)$。
- $h_1k_1 = h_2k_2$。这是一个在群 $G$ 中的等式。
- 通过代数变形,把 $H$ 的元素都移到一边,$K$ 的元素都移到另一边:两边左乘 $h_2^{-1}$,右乘 $k_1^{-1}$,得到 $h_2^{-1}h_1 = k_2k_1^{-1}$。(注意:原文的推导是左乘 $h_1^{-1}$ 右乘 $k_2^{-1
,得到 $k_{1} k_{2}^{-1}=h_{1}^{-1} h_{2}$。
- 核心论证:等式左边的 $k_1k_2^{-1}$,因为 $k_1, k_2 \in K$ 且 $K$ 是子群,所以它一定是 $K$ 的元素。等式右边的 $h_1^{-1}h_2$,因为 $h_1, h_2 \in H$ 且 $H$ 是子群,所以它一定是 $H$ 的元素。
- 现在我们有一个元素,它既在 $H$ 里,又在 $K$ 里。这意味着它必须属于它们的交集 $H \cap K$。
- 根据我们的初始假设,$H \cap K = \{1\}$。所以这个元素只能是单位元 $1$。
- 因此,$h_1^{-1}h_2 = 1$ (推出 $h_1=h_2$) 且 $k_1k_2^{-1} = 1$ (推出 $k_1=k_2$)。(注意,原文这里的小代数变形 $k_1k_2^{-1}=h_1^{-1}h_2$ 和我之前解释的 $h_2^{-1}h_1=k_2k_1^{-1}$ 只是代数操作顺序不同,本质和结论完全一样)。
- 我们成功证明了 $h_1=h_2$ 和 $k_1=k_2$,这意味着输入 $(h_1, k_1)$ 和 $(h_2, k_2)$ 是同一个。
- 证毕,$f$ 是内射的。
- ($\Rightarrow$) 方向 (证明 "如果 $f$ 内射,那么 $H \cap K = \{1\}$")
- 假设 $f$ 是内射的。
- 我们要证明 $H \cap K = \{1\}$。我们用反证法,假设交集里有一个非单位元的元素 $x$,即 $x \in H, x \in K$ 且 $x \neq 1$。
- 因为 $x \in H$,那么它的逆元 $x^{-1}$ 也一定在 $H$ 里。
- 考虑两个不同的输入:$(x^{-1}, x)$ 和 $(1, 1)$。它们是不同的,因为 $x \neq 1$。
- 计算它们在 $f$ 下的像:
- $f(x^{-1}, x) = x^{-1}x = 1$。
- $f(1, 1) = 1 \cdot 1 = 1$。
- 我们找到了两个不同的输入,却得到了相同的输出。这与 $f$ 是内射的假设相矛盾。
- 因此,我们最初的假设(存在非单位元 $x$)是错误的。
- 结论:$H \cap K$ 中不可能有非单位元的元素,所以 $H \cap K = \{1\}$。
(b) 同态性证明
- 目标:证明 "$f$ 是同态 $\iff hk=kh$ 对所有 $h \in H, k \in K$ 成立"。
- 根据同态的定义, $f$ 是同态意味着对于 $H \times K$ 中的任意两个元素 $(h_1, k_1)$ 和 $(h_2, k_2)$,都必须满足 $f((h_1, k_1) \cdot (h_2, k_2)) = f(h_1, k_1) \cdot f(h_2, k_2)$。
- 计算等式左边 (先在源群运算,再映射):
- 在直积群 $H \times K$ 中运算:$(h_1, k_1) \cdot (h_2, k_2) = (h_1h_2, k_1k_2)$。
- 应用映射 $f$:$f(h_1h_2, k_1k_2) = (h_1h_2)(k_1k_2)$。
- 计算等式右边 (先映射,再在目标群运算):
- 分别应用映射 $f$:$f(h_1, k_1) = h_1k_1$,$f(h_2, k_2) = h_2k_2$。
- 在群 $G$ 中运算:$(h_1k_1)(h_2k_2)$。
- 建立等价关系:
- 在群中,我们可以消去等式两边的相同元素。左边消去 $h_1$,右边消去 $k_2$:
- 因为 $h_2$ 和 $k_1$ 是 $H$ 和 $K$ 中的任意元素,所以这个条件就等价于“$H$ 中的任意元素都与 $K$ 中的任意元素可交换”。
(c) HK 是子群的证明
- 目标:证明如果 $H$ 是正规子群,那么 $HK$ 是 $G$ 的一个子群。
- 关键引理:$HK = KH$
- $HK$ 的定义是 $\{hk \mid h \in H, k \in K\}$。它是所有右陪集 $Hk$ 的并集。
- $KH$ 的定义是 $\{kh \mid k \in K, h \in H\}$。它是所有左陪集 $kH$ 的并集(针对 $K$ 中的元素 $k$)。
- $H$ 是正规子群的定义是:对于 $G$ 中任何元素 $g$,都有 $gH=Hg$。这个性质对于 $K$ 中的元素 $k$ 自然也成立,即 $kH=Hk$ for all $k \in K$。
- 因此,$KH = \bigcup_{k \in K} kH = \bigcup_{k \in K} Hk = HK$。
- 验证子群公理:
- 封闭性:取 $HK$ 中任意两个元素 $x_1, x_2$。$x_1=h_1k_1, x_2=h_2k_2$。
- 它们的积为 $x_1x_2 = (h_1k_1)(h_2k_2) = h_1(k_1h_2)k_2$。
- 利用刚才的引理:$(HK)(HK) = H(KH)K$。因为 $KH=HK$,所以这等于 $H(HK)K$。
- 利用结合律,变为 $(HH)(KK)$。
- 因为 $H, K$ 都是子群,它们对自身的运算是封闭的,所以 $HH=H, KK=K$。
- 最终得到 $(HK)(HK)=HK$。这表明任意两个 $HK$ 中元素的乘积仍然在 $HK$ 中。封闭性得证。
- 逆元:取 $HK$ 中任意一个元素 $x=hk$。
- 它的逆元是 $x^{-1} = (hk)^{-1} = k^{-1}h^{-1}$ (袜子-鞋子原理)。
- $k^{-1} \in K$, $h^{-1} \in H$。所以 $k^{-1}h^{-1}$ 是 $KH$ 中的一个元素。
- 因为 $KH=HK$,所以这个逆元也一定在 $HK$ 中。逆元封闭性得证。
- 结论:$HK$ 满足封闭性和逆元条件,因此是 $G$ 的一个子群。
(d) 同构条件证明
- 目标:证明 "$f$ 是同构 $\iff H \cap K=\{1\}, HK=G, \text{ and } H, K \text{ are normal in } G$"。
- ($\Leftarrow$) 方向 (假设三个条件成立,证明 f 是同构)
- 内射性:条件 $H \cap K=\{1\}$ 根据 (a) 的证明,直接保证了 $f$ 是内射的。
- 满射性:条件 $HK=G$ 根据乘法映射 $f$ 的像的定义,直接保证了 $f$ 是满射的。
- 双射性:由于 $f$ 既内射又满射,所以 $f$ 是一个双射。
- 同态性:现在我们需要证明 $f$ 是同态。根据 (b) 的证明,这等价于证明 $hk=kh$ 对所有 $h \in H, k \in K$ 成立。
- 证明 $hk=kh$:
- 考虑交换子元素 $c = hkh^{-1}k^{-1}$。
- 从 $K$ 的角度看: $c = (hkh^{-1})k^{-1}$。因为 $K$ 是正规子群,所以对于任意的 $h \in G$,都有 $hKh^{-1}=K$。这意味着 $hkh^{-1}$ 是 $K$ 中的一个元素。既然 $hkh^{-1} \in K$ 且 $k^{-1} \in K$,那么它们的乘积 $c$ 也必然在 $K$ 中。
- 从 $H$ 的角度看: $c = h(kh^{-1}k^{-1})$。因为 $H$ 是正规子群,所以对于任意的 $k \in G$,都有 $kHk^{-1}=H$。这意味着 $kh^{-1}k^{-1}$ 是 $H$ 中的一个元素。既然 $h \in H$ 且 $kh^{-1}k^{-1} \in H$,那么它们的乘积 $c$ 也必然在 $H$ 中。
- 得出结论: 元素 $c$ 同时属于 $H$ 和 $K$,所以它必须在它们的交集 $H \cap K$ 中。
- 根据条件 $H \cap K=\{1\}$,我们得出 $c=1$。
- $hkh^{-1}k^{-1}=1 \implies hkh^{-1}=k \implies hk=kh$。
- 同态性得证。因为 $f$ 是内射、满射、同态的,所以 $f$ 是一个同构。
- ($\Rightarrow$) 方向 (假设 f 是同构,证明三个条件成立)
- $f$ 同构 $\implies f$ 内射 $\implies H \cap K = \{1\}$ (根据a)。
- $f$ 同构 $\implies f$ 满射 $\implies HK=G$。
- $f$ 同构 $\implies f$ 同态 $\implies hk=kh$ 对所有 $h \in H, k \in K$ 成立 (根据b)。
- 现在我们只需要从 $hk=kh$ (以及其他两个条件) 推出 $H, K$ 是正规子群。
- 证明 $H$ 是正规的:
- 要证 $H$ 正规,需证对任意 $g \in G$,有 $gHg^{-1}=H$。
- 因为 $HK=G$,所以任意 $g$ 都可以写成 $g=h_0k_0$ 的形式,其中 $h_0 \in H, k_0 \in K$。
- $gHg^{-1} = (h_0k_0)H(h_0k_0)^{-1} = h_0k_0Hk_0^{-1}h_0^{-1}$。
- 因为 $H, K$ 的元素可交换,所以对于任意 $h' \in H$,有 $k_0h'k_0^{-1} = h'k_0k_0^{-1} = h'$。这意味着 $k_0Hk_0^{-1}=H$。
- 代入上式,得到 $gHg^{-1} = h_0Hh_0^{-1}$。
- 因为 $h_0 \in H$ 且 $H$ 是一个子群,所以 $h_0H=H$ 且 $Hh_0^{-1}=H$。因此 $h_0Hh_0^{-1}=H$。
- 结论: $gHg^{-1}=H$。$H$ 是正规子群。
- 证明 $K$ 是正规的:证明过程完全对称,只需交换 $H, K$ 的角色即可。
- 最后的说明: "反之,如果 $f$ 是一个同构,则可以在同构群 $H \times K$ 中而不是在 $G$ 中验证所列出的条件。" 这句话有些绕。它的意思是,如果 G 同构于 $H \times K$ (这里的 $H,K$ 是抽象的群),那么 $G$ 内部一定可以找到两个子群 $H' \cong H$ 和 $K' \cong K$,使得 $H', K'$ 满足命题(d)的三个条件。这是因为在直积群 $H \times K$ 中,子群 $H \times \{1\}$ 和 $\{1\} \times K$ 就完美地满足这三个条件。同构会把这个漂亮的结构原封不动地搬到 $G$ 里面。
44阶群的分类 (Classification of Groups of Order 4)
📜 [原文9]
我们使用此命题来分类4阶群:
命题 2.11.5 4阶群有两种同构类,即4阶循环群 $C_{4}$ 的同构类和克莱因四元群的同构类,克莱因四元群同构于两个2阶群的直积 $C_{2} \times C_{2}$。
这部分是前面理论知识的一次精彩应用。目标是找出所有可能的、本质上不同的4阶群有多少种。结论是只有两种。
- 分类问题:在数学中,“分类”一个对象意味着列出所有可能的、不同构的该对象的清单。这里我们要分类所有阶为4的群。
- 拉格朗日定理的应用:根据拉格朗日定理,群中任何元素的阶都必须整除群的阶。对于一个4阶群 $G$,其任何元素的阶只可能是1, 2, 或 4。
- 分类策略:按元素的最大阶数讨论。这是一个非常有效的方法。一个4阶群,它里面阶最大的元素的阶是多少?只有两种可能:要么是4,要么是2。
- 情况 1:群 $G$ 中包含一个4阶元素。
- 假设 $G$ 中有一个元素 $g$,其阶 $\text{ord}(g)=4$。
- 考虑由 $g$ 生成的循环子群 $\langle g \rangle = \{1, g, g^2, g^3\}$。
- 这个子群的阶是4。
- 由于这个子群 $\langle g \rangle$ 包含在 $G$ 中,并且它们的阶都是4,所以这个子群就是 $G$ 本身,即 $G = \langle g \rangle$。
- 这说明 $G$ 是一个4阶循环群。
- 所有4阶循环群都是同构的,我们通常用 $C_4$ 来代表这一类。
- 所以,第一种可能性就是 $C_4$。
- 情况 2:群 $G$ 中不包含4阶元素。
- 在这种情况下,所有非单位元的元素的阶都只能是2。(因为阶必须整除4,又不能是4,只能是2)。
- 这意味着对于 $G$ 中任何非单位元的元素 $x$,都有 $x^2 = 1$,这等价于 $x = x^{-1}$ (每个元素都是自身的逆元)。
- 证明 $G$ 是阿贝尔群:取 $G$ 中任意两个元素 $x, y$。
- 它们的乘积 $xy$ 也是 $G$ 中的一个元素。所以 $(xy)$ 的阶也必然是2(除非 $xy=1$)。
- $(xy)^2 = 1 \implies (xy)(xy)=1$。
- 在这个等式两边左乘 $x$(即 $x^{-1}$),得到 $x(xyxy)=x \cdot 1 \implies (xx)yxy = x \implies 1 \cdot yxy = x \implies yxy = x$。
- 再在两边右乘 $y$(即 $y^{-1}$),得到 $yxyy = xy \implies yx \cdot 1 = xy \implies yx = xy$。
- 由于 $x,y$ 是任意的,所以 $G$ 中所有元素都可交换,$G$ 是一个阿贝尔群。
- 应用命题 2.11.4(d):我们想把 $G$ 分解成直积。
- 因为 $G$ 是阿贝尔群,它的任何子群都是正规子群。这使得命题 2.11.4(d) 的第三个条件($H,K$都正规)自动满足。
- 我们来寻找合适的子群 $H$ 和 $K$。
- 在 $G$ 中任取一个非单位元的元素 $x$。令 $H = \langle x \rangle = \{1, x\}$。这是一个2阶循环子群。
- 由于 $|G|=4, |H|=2$,还存在元素不在 $H$ 中。任取一个 $y \in G$ 且 $y \notin H$。令 $K = \langle y \rangle = \{1, y\}$。这也是一个2阶循环子群。
- 现在我们来验证命题 2.11.4(d) 的另外两个条件:
- $H \cap K = \{1\}$:因为 $y \notin H$,所以 $y \neq x$ 且 $y \neq 1$。所以 $H$ 和 $K$ 除了单位元 1 之外没有公共元素。条件满足。
- $HK=G$:我们已经知道 $H$ 是正规的,所以 $HK$ 是一个子群。它的阶是 $|HK| = \frac{|H||K|}{|H \cap K|} = \frac{2 \times 2}{1} = 4$。一个阶为4的子群包含在一个阶为4的群 $G$ 中,它只能是 $G$ 本身。所以 $HK=G$。条件满足。
- 得出结论:所有三个条件都满足,因此 $G \cong H \times K$。
- 因为 $H \cong C_2$,$K \cong C_2$,所以 $G \cong C_2 \times C_2$。
- 所以,第二种可能性就是 $C_2 \times C_2$。这个群通常被称为克莱因四元群 (Klein four-group)。
- 最终分类:由于以上两种情况覆盖了所有可能性,任何4阶群要么同构于 $C_4$,要么同构于 $C_2 \times C_2$。不存在第三种本质不同的4阶群。
示例 1:4阶循环群 $C_4$
- 元素: $\{0, 1, 2, 3\}$
- 运算: 模4加法
- 元素阶分布:
- $\text{ord}(0) = 1$ (1个)
- $\text{ord}(2) = 2$ (1个)
- $\text{ord}(1) = 4, \text{ord}(3) = 4$ (2个)
示例 2:克莱因四元群 $V_4 \cong C_2 \times C_2$
- 元素: $\{(0,0), (0,1), (1,0), (1,1)\}$
- 运算: 分量模2加法
- 元素阶分布:
- $\text{ord}(0,0) = 1$ (1个)
- $\text{ord}(0,1)=2, \text{ord}(1,0)=2, \text{ord}(1,1)=2$ (3个)
- 几何模型: 对称群 of a rectangle (not a square). 元素是:单位操作,水平翻转,垂直翻转,旋转180度。
- 关键分支:证明的关键在于,一旦确定群里没有4阶元素,就能推出所有非单位元元素都是2阶,进而推出群是阿贝尔群。这个逻辑链不能断。
- 不要混淆:$C_4$ 和 $C_2 \times C_2$ 都是4阶阿贝尔群,但它们不同构。区分它们的最好方法就是看元素阶的分布:$C_4$ 有4阶元素,而 $C_2 \times C_2$ 没有。
命题 2.11.5 是群论中一个基础的分类结果。它利用拉格朗日定理和刚刚建立的关于直积分解的命题 2.11.4,完美地证明了4阶群只有两种本质不同的结构。这个证明过程本身就是如何运用抽象理论解决具体问题的典范。
本段的目的是展示理论的威力。前面的命题 2.11.4 看起来非常抽象,而本段用它作为关键工具,解决了一个非常具体和根本的问题:世界上到底有几种4阶群?这让学习者体会到抽象代数理论的价值和力量。
想象你有4个一模一样的球,你想把它们串成一个圈,使得这个圈具有群的结构。你有几种方法?
- 方法1 ($C_4$): 把4个球串成一个简单的圈。任何一个球都可以作为起点"1",下一个是"2",再下一个是"3",最后一个是"0"。这是一个“单行道”,必须走4步才能回到起点。
- 方法2 ($C_2 \times C_2$): 想象你站在一个房间的中心,墙上有“前、后、左、右”四个位置。你可以定义操作,比如“前后交换”,“左右交换”。你会发现任何操作做两次都会回到原状,而且先“前后交换”再“左右交换”,和你先“左右交换”再“前后交换”结果一样。这是一个完全不同的结构。
这个命题告诉你,除了这两种方式,你不可能再发明出第三种具有群结构的4球游戏。
- $C_4$: 一个正方形的旋转对称群。包括旋转0, 90, 180, 270度。这是一个循环群。
- $C_2 \times C_2$: 一个长方形的对称群。包括旋转0度,旋转180度,沿水平中轴线翻转,沿垂直中轴线翻转。这不是一个循环群,因为没有任何一个操作可以生成所有其他操作。
5行间公式索引
1.
解释: 此公式定义了直积群 $G \times G^{\prime}$ 中的分量乘法运算规则。
2.
解释: 此列表展示了由元素 $(y, z)$ 在直积群 $C_2 \times C_3$ 中生成的所有六个元素,证明了 $C_2 \times C_3$ 是一个6阶循环群。