陪集乘法的示意图。

这段话是本节的引言，开宗明义地指出了本节的核心目标。它告诉我们，我们将要学习一种构建新群的方法。具体来说，这个新群的“元素”不再是单个的数字或矩阵，而是一个个“集合”，这些集合被称为陪集 (cosets)。

1. 起点：我们从一个已知的群 $G$ 和它的一个特殊子群 $N$ 开始。这个子群 $N$ 必须是正规子群 (normal subgroup)。这是构造商群的绝对前提条件。
2. 材料：我们的“建筑材料”是 $N$ 在 $G$ 中的所有陪集。陪集的形式是 $aN = \{an \mid n \in N\}$，其中 $a$ 是 $G$ 中的一个元素。我们将所有这些陪集收集起来，形成一个新的集合。
3. 操作：我们需要在这个由陪集组成的集合上定义一种“乘法”（或者说二元运算）。这个运算必须满足群的公理，尤其是结合律 (associative law)。
4. 结果：一旦我们成功定义了这种运算，并且验证了它满足群的所有公理（封闭性、结合律、单位元、逆元），那么这个由陪集组成的集合就成了一个全新的群。
5. 命名：这个新构造出来的群，被称为商群 (quotient group)，记作 $G/N$。

这个引言为我们设定了探索的路径：理解如何将陪集作为元素，并赋予它们群的结构。

这段话通过两个我们熟悉的例子来帮助我们直观理解商群的概念。

1. 例子一：模 $n$ 整数
   • 我们熟悉的模 $n$ 算术 (modular arithmetic)，比如钟表上的时间计算（模 12），就是商群最经典的例子。
   • 这里的群 $G$ 是所有整数构成的加法群 $\mathbb{Z}$。
   • 子群 $N$ 是所有 $n$ 的倍数构成的集合，记作 $n\mathbb{Z} = \{ \ldots, -2n, -n, 0, n, 2n, \ldots \}$。这是一个正规子群（因为 $\mathbb{Z}$ 是交换群，任何子群都是正规的）。
   • 商群 $G/N = \mathbb{Z}/n\mathbb{Z}$ 的元素是 $n\mathbb{Z}$ 的陪集。这些陪集恰好就是模 $n$ 的同余类 (congruence classes)。例如，当 $n=3$ 时，有三个陪集：
   • $\bar{0} = 0 + 3\mathbb{Z} = \{ \ldots, -6, -3, 0, 3, 6, \ldots \}$ （所有被3整除的数）
   • $\bar{1} = 1 + 3\mathbb{Z} = \{ \ldots, -5, -2, 1, 4, 7, \ldots \}$ （所有除以3余1的数）
   • $\bar{2} = 2 + 3\mathbb{Z} = \{ \ldots, -4, -1, 2, 5, 8, \ldots \}$ （所有除以3余2的数）
   • 我们在这些同余类上定义的加法，例如 $\bar{1} + \bar{2} = \overline{1+2} = \bar{3} = \bar{0}$，正是商群的运算。这个商群 $\mathbb{Z}/n\mathbb{Z}$ 就是我们熟悉的循环群 $\mathbb{Z}_n$。
2. 例子二：角的加法
   • 这个例子与前面“缠绕数轴”的想象非常吻合。
   • 群 $G$ 是所有实数构成的加法群 $\mathbb{R}$ (原文写作 $\mathbb{R}^+$ 可能有误，通常指实数加法群)。
   • 我们知道，角度 $\theta$ 和 $\theta + 2\pi$、$\theta - 4\pi$ 表示的是同一个角。这些相差 $2\pi$ 整数倍的角度构成了等价关系。
   • 所有 $2\pi$ 的整数倍构成的集合 $N = 2\pi\mathbb{Z} = \{ k \cdot 2\pi \mid k \in \mathbb{Z} \}$ 是 $\mathbb{R}$ 的一个正规子群。
   • 一个特定的角，比如 $30^\circ$ 或 $\pi/6$ 弧度，实际上不只是一个单一的数值，而是代表了一个陪集：$\pi/6 + 2\pi\mathbb{Z} = \{ \ldots, \pi/6 - 4\pi, \pi/6 - 2\pi, \pi/6, \pi/6 + 2\pi, \ldots \}$。
   • 所有角的集合构成的群（通过加法运算），正是商群 $\mathbb{R}/2\pi\mathbb{Z}$。这个群在拓扑上同构于一个圆，通常称为圆群 $S^1$。

这段话介绍了商群（或更准确地说，在定义运算之前的陪集集合）的几种常用符号表示。

1. 标准表示法: $G/N$
   • 这个记号读作 "G mod N" (G 模 N) 或者 "G over N" (G 除以 N)。
   • 这个斜杠 "/" 形象地表达了“除法”或“取商”的意象。我们把整个群 $G$ 用子群 $N$ 去“除”，得到的“商”就是这个由陪集构成的集合。这和算术中的除法有类似的感觉：$12 \div 3 = 4$ 是问 12 里有多少个 3，而 $G/N$ 的阶 $|G/N| = |G|/|N|$（对于有限群）也恰好是 $G$ 的大小除以 $N$ 的大小，即 $G$ 中有多少个“大小等于 $N$ 的块”。
2. 元素表示法
   • 方括号表示法: $[C]$
   • 一个陪集本身是一个集合，比如 $C = aN$。
   • 当我们想强调我们正在讨论的是“作为商群中一个元素的那个陪集”时，可以用 $[C]$ 或 $[aN]$。这是一种元认知，区分了作为子集的 $C$ 和作为新群元素的 $[C]$。在严格的集合论构建中，这种区分是有意义的，但在实际使用中常常简化。

• 横线表示法: $\bar{a}$
• 这是最常用和最方便的表示法。
• $\bar{a}$ 代表包含元素 $a$ 的那个陪集。也就是说，$\bar{a} = aN$。
• 这个表示法的好处是简洁，并且突出了陪集是由其代表元 (representative) $a$ 所确定的。
• 使用这个表示法时，整个陪集集合 $G/N$ 就可以被记作 $\bar{G}$。这让写法变得非常紧凑，比如商群中的乘法可以写作 $\bar{a}\bar{b} = \overline{ab}$。

这是本节的核心定理，它正式宣告了商群的存在性和基本性质。我们可以把这个定理分解成三个主要部分：

1. 第一部分：$\bar{G}$ 是一个群
   • 前提：$N$ 必须是 $G$ 的正规子群。这是构造的基石。$\bar{G}$ 是所有 $N$ 的陪集组成的集合。
   • 结论：我们可以在 $\bar{G}$ 这个集合上定义一个二元运算（即一种结合律），这个运算满足：
   • 封闭性：两个陪集相乘，结果还是一个陪集。
   • 结合律：$( \bar{a}\bar{b} )\bar{c} = \bar{a}( \bar{b}\bar{c} )$。
   • 单位元：存在一个单位陪集 $\bar{e}$ (其中 $e$ 是 $G$ 的单位元)，通常就是 $N$ 本身，记作 $\bar{1}$ 或 $\bar{e}$。
   • 逆元：每个陪集 $\bar{a}$ 都有一个逆陪集 $(\bar{a})^{-1}$，它就是 $\overline{a^{-1}}$。
   • 这部分断言了，陪集的集合 $G/N$ 在我们即将定义的运算下，构成一个合法的群。
2. 第二部分：规范映射 $\pi$ 是一个满同态
   • 定义映射：我们定义一个从父群 $G$ 到商群 $\bar{G}$ 的映射，记作 $\pi$ (pi)。
   • 映射规则：$\pi(a) = \bar{a}$。也就是说，这个映射把 $G$ 中的每个元素 $a$ 发送到它所在的那个陪集 $\bar{a}$。
   • 结论：这个映射 $\pi$ 具有两个重要性质：
   • 满射 (Surjective)：$\bar{G}$ 中的任何一个陪集 $\bar{a}$，都至少是 $G$ 中一个元素 $a$ 的像。这是显然的，因为陪集 $\bar{a}$ 就是由 $a$ 定义的。所以 $\pi$ 是满同态 (surjective homomorphism)，也叫 эпиморфизм (epimorphism)。
   • 同态 (Homomorphism)：这个映射保持群的运算结构。即 $\pi(ab) = \pi(a)\pi(b)$。根据 $\pi$ 的定义，这等价于 $\overline{ab} = \bar{a}\bar{b}$。这正是我们为商群定义的运算规则。
3. 第三部分：$\pi$ 的核是 $N$
   • 回顾核的定义：一个同态 $\pi: G \rightarrow \bar{G}$ 的核 (kernel)，记作 $\ker(\pi)$，是 $G$ 中所有被映射到目标群 $\bar{G}$ 的单位元的元素的集合。
   • 目标群的单位元：商群 $\bar{G}$ 的单位元是陪集 $N$ 本身，也就是 $\bar{e}$ 或 $\bar{1}$。
   • 结论：$\ker(\pi) = N$。
   • 证明：一个元素 $a \in G$ 在 $\ker(\pi)$ 中，当且仅当 $\pi(a) = \bar{e}$。根据 $\pi$ 的定义，这意味着 $\bar{a} = \bar{e}$，即 $aN = eN = N$。一个元素 $a$ 使得 $aN=N$ 的充要条件是 $a$ 本身就在子群 $N$ 中。因此，$\ker(\pi)$ 恰好就是子群 $N$。

这段注释是对 $\pi(a)=\bar{a}$ 这个映射的名称和意义的补充说明。

• 名称：$\pi: G \rightarrow G/N$ 被称为规范映射 (canonical map) 或自然映射 (natural map)。
• “规范” (canonical) 的含义：在数学中，“规范”或“自然”通常指一种不依赖于任何任意选择的、最直接、最显然的构造或映射。
• 一旦我们有了群 $G$ 和正规子群 $N$，我们就有了陪集的集合 $G/N$。
• 连接 $G$ 和 $G/N$ 的最自然的方式是什么？就是把每个元素 $a \in G$ 发送到包含它自己的那个陪集 $\bar{a}$。
• 这个映射的定义不依赖于我们选择什么基、什么坐标系或任何其他外部的、人为的结构。它是由 $G$ 和 $N$ 的内在结构唯一决定的。因此，它是“规范的”。
• 换句话说，如果让你在 $G$ 和 $G/N$ 之间建立一个有意义的映射，你几乎不可能想出除了 $\pi$ 之外的任何其他合理的映射。

这个推论是规范映射 $\pi$ 的同态性质的一个直接应用。

• 推论的陈述：
• 前提：我们有一些 $G$ 中的元素 $a_1, a_2, \ldots, a_k$。
• 条件：这些元素的乘积 $p = a_1 a_2 \cdots a_k$ 恰好落在了正规子群 $N$ 里面。
• 结论：那么，在商群 $\bar{G}$ 中，这些元素对应的陪集 $\bar{a}_1, \bar{a}_2, \ldots, \bar{a}_k$ 的乘积，等于商群的单位元 $\bar{1}$。

• 证明的逻辑链条：

1. 令 $p = a_1 a_2 \cdots a_k$。
2. 根据条件，我们知道 $p \in N$。
3. 根据定理 2.12.2，$\pi$ 的核是 $N$。这意味着所有 $N$ 中的元素，在 $\pi$ 映射下，都变成商群的单位元 $\bar{1}$。所以，$\pi(p) = \bar{p} = \bar{1}$。
4. 根据定理 2.12.2，$\pi$ 是一个同态。这意味着“乘积的像等于像的乘积”。所以，$\pi(a_1 a_2 \cdots a_k) = \pi(a_1) \pi(a_2) \cdots \pi(a_k)$。
5. 用横线表示法重写第4步，就是 $\overline{a_1 a_2 \cdots a_k} = \bar{a}_1 \bar{a}_2 \cdots \bar{a}_k$。
6. 结合第1步和第5步，我们有 $\bar{p} = \bar{a}_1 \bar{a}_2 \cdots \bar{a}_k$。
7. 结合第3步和第6步，我们最终得到 $\bar{a}_1 \bar{a}_2 \cdots \bar{a}_k = \bar{1}$。证明完毕。

这里列出了证明核心定理 2.12.2 所需的四个步骤，构成了一个清晰的证明路线图。

1. 定义运算：首先，我们必须说清楚商群中的“乘法”到底是怎么回事。没有运算，一切都无从谈起。我们会将它定义为陪集的乘积集合。
2. 验证群结构：定义了运算之后，不能想当然地认为它就是一个群。必须严格地按照群的四条公理（封闭性、结合律、单位元、逆元）去一一验证。
3. 验证 $\pi$ 的性质：证明我们定义的规范映射 $\pi(a)=\bar{a}$ 是一个满同态。这包括两件事：证明它是满射，并且证明它保持运算结构（即 $\pi(ab)=\pi(a)\pi(b)$）。
4. 计算 $\pi$ 的核：最后，计算出这个同态的核，并证明它恰好就是我们开始时使用的那个正规子群 $N$。

这个路线图结构清晰，逻辑严谨，是数学证明的标准范式。

这是证明的第一步的准备工作：定义两个子集的乘积。

• 定义：给定群 $G$ 的两个子集 $A$ 和 $B$（不一定是子群），它们的乘积集合 (product set) $AB$ 是一个新的集合。
• 构成：这个新集合 $AB$ 由所有形如 $ab$ 的元素组成，其中 $a$ 是从集合 $A$ 中任取的一个元素，而 $b$ 是从集合 $B$ 中任取的一个元素。
• 形式化定义：$AB = \{ ab \mid a \in A, b \in B \}$。这里的 $ab$ 是指在群 $G$ 中的乘法运算。
• 与笛卡尔积的区分：作者特意指出，这里的乘积集合 $AB$ 是 $G$ 的一个子集，而不是笛卡尔积 $A \times B$。笛卡尔积是由有序对 $(a, b)$ 组成的集合，它的元素是“对”，而乘积集合 $AB$ 的元素是 $G$ 中的元素。

这个引理是整个商群构造中最核心的技术步骤。它回答了这个问题：两个陪集相乘，结果是什么？

• 引理断言：
• 取两个左陪集 $aN$ 和 $bN$。
• 计算它们的乘积集合 $(aN)(bN)$。
• 结论：这个结果惊人地简洁，它不是一堆乱七八糟的元素的集合，而恰好是另一个完整的陪集，即 $abN$。
• 这个结论确保了陪集乘法的封闭性：两个陪集相乘，得到的还是一个陪集。

• 前提的重要性：这个漂亮的结论完全依赖于 $N$ 是一个正规子群。

• 证明解析：

1. $(aN)(bN) = a(Nb)N$: 这是利用了群运算的结合律。我们可以先把括号里的 $N$ 和 $b$ “结合”。这是一个在集合层面上的结合，意思是 $(aN)(bN)$ 中的元素形如 $(an_1)(bn_2) = a(n_1b)n_2$。我们关注中间的 $n_1b$ 部分。所以我们可以把 $a$ 和末尾的 $N$ 先“提”出来。
2. $a(Nb)N = a(bN)N$: 这是证明中最关键的一步，它用到了 $N$ 的正规性 (normality)。
   • 正规子群的定义：对于 $G$ 中的任意元素 $g$，都有 $gN = Ng$。
   • 这里我们需要的性质是 $Nb = bN$。即 $N$ 的左陪集等于右陪集。这正是正规子群的等价定义之一。
   • 因为 $N$ 是正规的，所以我们可以把 $Nb$ 替换成 $bN$。
3. $a(bN)N = abNN$: 再次利用集合乘法的结合律，把 $a$ 和 $b$ 结合到一起，剩下两个 $N$ 相乘。
4. $abNN = abN$: 这一步用到了 $N$ 是一个子群 (subgroup) 的性质。
   • 子群的封闭性：对于任意 $n_1, n_2 \in N$，它们的乘积 $n_1n_2$ 仍然在 $N$ 中。
   • 乘积集合 $NN$：$NN = \{n_1n_2 \mid n_1, n_2 \in N\}$。由于 $N$ 对乘法封闭，所以 $NN \subseteq N$。
   • 单位元的存在：因为 $N$ 是子群，所以单位元 $e \in N$。对于任意 $n \in N$，都有 $n = e \cdot n$。由于 $e \in N$，所以任何 $n$ 都可以写成 $N$ 中两个元素的乘积。因此 $N \subseteq NN$。
   • 结合两者，$NN=N$。
   • 所以我们可以把 $NN$ 简化为 $N$。
5. 结论：通过以上步骤，我们证明了 $(aN)(bN) = abN$。

有了关键的引理 2.12.5，我们现在可以正式定义商群中的运算了。

1. 抽象定义：商群中两个元素 $[C_1]$ 和 $[C_2]$ 的乘积，被定义为包含乘积集合 $C_1C_2$ 的那个元素，即 $[C_1C_2]$。引理 2.12.5 保证了 $C_1C_2$ 本身就是一个陪集，所以这个定义是自洽的（封闭性）。
2. 实用定义：抽象定义不方便计算。更实用的方法是利用代表元 (representatives)。
   • 设我们要计算 $\bar{a}$ 和 $\bar{b}$ 的乘积。
   • $\bar{a}$ 对应的陪集是 $aN$。
   • $\bar{b}$ 对应的陪集是 $bN$。
   • 它们的乘积 $\bar{a}\bar{b}$ 对应的陪集是 $(aN)(bN)$。
   • 根据引理 2.12.5，我们知道 $(aN)(bN) = abN$。
   • 而 $abN$ 正是 $\overline{ab}$ 所代表的陪集。
   • 因此，我们得出了极其简洁和自然的运算规则：$\bar{a}\bar{b} = \overline{ab}$。
3. 良定义性 (Well-definedness)：这个公式 $\bar{a}\bar{b} = \overline{ab}$ 看似简单，但隐藏着一个重要问题。$\bar{a}$ 可以由不同的代表元表示，比如 $\bar{a} = \bar{a'}$。$\bar{b}$ 也可以由 $\bar{b'}$ 表示。我们必须保证，用不同的代表元计算，结果是相同的。也就是说，我们必须证明 $\overline{ab} = \overline{a'b'}$。
   • 证明：
   • $\bar{a} = \bar{a'}$ 意味着 $aN = a'N$，这等价于 $a' = an_1$ 对于某个 $n_1 \in N$。
   • $\bar{b} = \bar{b'}$ 意味着 $bN = b'N$，这等价于 $b' = bn_2$ 对于某个 $n_2 \in N$。
   • 我们要计算 $\overline{a'b'} = \overline{(an_1)(bn_2)}$。
   • $\overline{a'b'} = (a'N)(b'N) = (aN)(bN) = abN = \overline{ab}$。
   • 这里我们直接使用了引理 2.12.5。引理本身就蕴含了良定义性。因为无论你从 $aN$ 中取哪个元素 $a'$，从 $bN$ 中取哪个元素 $b'$，它们的乘积集合 $(a'N)(b'N)$ 都等于 $a'b'N$，而引理证明了它就等于 $abN$。所以结果与代表元的选择无关。

这段话将我们刚刚定义的商群运算与规范映射 $\pi$ 联系起来。

• 公式 (2.12.7) 的推导：
• $\pi(a)\pi(b)$: 这是 $\pi$ 映射到商群中的两个像的乘积。
• $= \bar{a}\bar{b}$: 根据 $\pi$ 的定义 $\pi(x)=\bar{x}$。
• $= \overline{ab}$: 根据我们刚刚定义的商群运算法则 (2.12.6)。
• $= \pi(ab)$: 再次根据 $\pi$ 的定义。
• 所以，我们得到了 $\pi(a)\pi(b) = \pi(ab)$。

• 同态性质：$\pi(ab) = \pi(a)\pi(b)$ 正是同态的定义。所以，只要我们为商群 $\bar{G}$ 定义的运算是合法的（即 $\bar{G}$ 是一个群），那么规范映射 $\pi$ 自动就是一个同态。

• 证明策略的转换：作者在这里采用了一个巧妙的证明策略。原计划是先证明 $\bar{G}$ 是群，再证明 $\pi$ 是同态。但现在他指出，我们可以反过来：利用一个更普适的引理（引理 2.12.8），通过 $\pi$ 的同态性质和满射性质，来直接“传递” $G$ 的群结构给 $\bar{G}$，从而证明 $\bar{G}$ 是一个群。

• $\pi$ 是满射：$\pi$ 是满射 (surjective) 是显然的。对于商群 $\bar{G}$ 中的任意一个元素 $\bar{a}$，我们总能在父群 $G$ 中找到它的“原像”，就是元素 $a$ 本身，因为 $\pi(a) = \bar{a}$。所以 $\bar{G}$ 中没有一个元素是“够不着”的。

这个引理是一个非常普适且强大的工具。它说的是，如果你有一个已知的群 $G$，和一个只知道有运算的集合 $Y$，以及一个从 $G$ 到 $Y$ 的、保持运算的满射 $\varphi$，那么你不需要再费力去验证 $Y$ 的群公理了，$Y$ 自动“继承”了 $G$ 的群结构。

• 引理的条件：

1. $G$ 是一个群。
2. $Y$ 是一个集合，上面定义了一个二元运算。
3. $\varphi: G \rightarrow Y$ 是一个满射（$Y$ 中每个元素都有原像）。
4. $\varphi$ 具有同态性质：$\varphi(ab) = \varphi(a)\varphi(b)$。

• 引理的结论：$Y$ 也是一个群，并且 $\varphi$ 是一个真正的群同态。

• 证明的精髓——“传递”：
• 结合律的传递：
• 要在 $Y$ 中证明 $(y_1y_2)y_3 = y_1(y_2y_3)$。
• 因为 $\varphi$ 是满射，所以可以找到 $y_1, y_2, y_3$ 在 $G$ 中的原像 $x_1, x_2, x_3$。
• 然后利用 $\varphi$ 的同态性质，把 $Y$ 中的运算 (y1y2)y3 “翻译”成 $G$ 中的运算 (x1x2)x3。
• 在 $G$ 中，我们知道结合律成立，所以 $(x_1x_2)x_3 = x_1(x_2x_3)$。
• 再利用 $\varphi$ 的同态性质，把 $G$ 中的结果“翻译”回 $Y$ 中，就得到了 $y_1(y_2y_3)$。
• 这个过程就像：想比较两段法文翻译的优劣，可以先把它们都翻译回中文原文，比较中文原文，因为中文我们更熟悉。

• 单位元的传递：
• $G$ 中有单位元 $e_G$。我们猜 $Y$ 的单位元是 $e_Y = \varphi(e_G)$。
• 对任意 $y \in Y$，取其原像 $x \in G$ ($y=\varphi(x)$)。
• $y \cdot e_Y = \varphi(x)\varphi(e_G) = \varphi(xe_G) = \varphi(x) = y$。
• 同理可证 $e_Y \cdot y = y$。所以 $e_Y$ 确实是 $Y$ 的单位元。

• 逆元的传递：
• 对任意 $y \in Y$，取其原像 $x \in G$。$x$ 在 $G$ 中有逆元 $x^{-1}$。
• 我们猜 $y$ 的逆元是 $y' = \varphi(x^{-1})$。
• $y \cdot y' = \varphi(x)\varphi(x^{-1}) = \varphi(xx^{-1}) = \varphi(e_G) = e_Y$。
• 同理可证 $y' \cdot y = e_Y$。所以 $y'$ 确实是 $y$ 的逆元。

• 应用到商群：
• 我们的 $G$ 就是父群 $G$。
• 我们的 $Y$ 就是陪集集合 $\bar{G} = G/N$。
• 我们在 $\bar{G}$ 上定义的运算是 $\bar{a}\bar{b} = \overline{ab}$。
• 我们的映射是规范映射 $\pi(a) = \bar{a}$。
• 我们已经知道 $\pi$ 是满射，并且具有同态性质 $\pi(ab)=\pi(a)\pi(b)$。
• 因此，根据引理 2.12.8，我们直接得出结论：$\bar{G} = G/N$ 是一个群。

这是定理 2.12.2 证明的最后一部分，即证明 $\ker(\pi) = N$。

1. 核的定义：$\ker(\pi)$ 是 $G$ 中所有满足 $\pi(a) = e_{\bar{G}}$ 的元素 $a$ 的集合，其中 $e_{\bar{G}}$ 是商群 $\bar{G}$ 的单位元。
2. 商群的单位元：$\bar{G}$ 的单位元是哪个陪集？
   • 根据运算法则 $\bar{a}\bar{b} = \overline{ab}$，我们寻找一个 $\bar{e}$ 使得 $\bar{a}\bar{e} = \bar{a}$。
   • $\overline{ae} = \bar{a}$。这在 $G$ 中显然成立。
   • 所以，单位元就是父群 $G$ 的单位元 $e$ 所在的那个陪集，即 $\bar{e}$ 或 $\bar{1}$（如果群是乘法群）。
   • $\bar{e}$ 就是陪集 $eN = N$。
   • 所以，商群的单位元就是正规子群 N 本身。
3. 进行计算：
   • $a \in \ker(\pi)$
   • $\iff \pi(a) = \bar{e}$ （根据核的定义）
   • $\iff \bar{a} = \bar{e}$ （根据 $\pi$ 的定义）
   • $\iff aN = eN$ （用陪集形式写出）
   • $\iff aN = N$
   • $\iff a \in N$ （一个元素 $a$ 使得 $aN=N$ 的充要条件是 $a \in N$）
4. 结论：我们证明了“$a$ 在 $\pi$ 的核里”当且仅当“$a$ 在 $N$ 里”。因此，$\ker(\pi) = N$。

这样，定理 2.12.2 的所有部分都得到了证明。

这是一个非常重要的反例，它强调了正规性是不可或缺的。

• 背景：在对称群 $S_3$ 中，通常记 $x=(123)$（旋转），$y=(12)$（翻转）。子群 $H = \langle y \rangle = \{e, y\} = \{e, (12)\}$。在之前的章节中已经证明，$H$ 在 $S_3$ 中不是一个正规子群。

• 实验：我们来尝试在非正规子群的陪集上定义乘法，看看会发生什么。
• 取两个左陪集：
• $C_1 = eH = H = \{e, y\}$。
• $C_2 = xH = \{x, xy\} = \{(123), (123)(12)\} = \{(123), (13)\}$。
• 计算它们的乘积集合 $C_1C_2$。这里原文的记法可能引起混淆，它写的是 $(1H)(xH)$，但 $x,y$ 的定义在前面章节，这里重新明确一下。假设 $y=(12)$， $x=(123)$。那么 $x^2 = (132)$，$xy=(123)(12)=(13)$，$x^2y = (132)(12)=(23)$。
• 原文的计算 $\{1, y\}\{x, x y\}=\left\{x, x y, yx, yxy\right\}$。我们需要计算 $yx$ 和 $yxy$。
• $yx = (12)(123) = (23)$
• $yxy = y(xy) = (12)(13) = (132) = x^2$。
• 所以乘积集合是 $\{x, xy, yx, yxy\} = \{(123), (13), (23), (132)\}=\{x,xy,x^2y, x^2\}$。（原文中的 $x^2y, x^2$ 和我算出来的不一样，我们以实际运算为准，原文可能用了不同的 $x,y$ 定义或者有笔误，但结论是一样的）。
• 我们使用原文的 $S_3$ 元素 $\{1,y\}$ 和 $\{x, xy\}$。 $y$ 是二阶元，$y^2=1$。$x$ 是三阶元 $x^3=1$。并且 $yx=x^2y$。
• $C_1=\{1,y\}$
• $C_2=\{x, xy\}$
• $C_1C_2 = \{1\cdot x, 1\cdot xy, y\cdot x, y\cdot(xy)\}$
• $= \{x, xy, yx, yx\cdot y\}$。
• 使用关系 $yx = x^2y$。
• $= \{x, xy, x^2y, x^2y\cdot y\} = \{x, xy, x^2y, x^2y^2\} = \{x, xy, x^2y, x^2\}$
• 这个集合 $P = \{x, xy, x^2y, x^2\} = \{(123), (13), (23), (132)\}$ 包含了 4 个元素。

• 分析结果：
• $S_3$ 中 $H$ 的一个陪集的大小必须是 $|H|=2$。
• 我们得到的乘积集合 $P$ 的大小是 4。
• 因此，这个乘积集合 $P$ 自身不可能是 $H$ 的任何一个陪集。它也不是任何一个陪集的子集，因为它横跨了两个不同的陪集：$xH = \{x, xy\}=\{(123), (13)\}$ 和 $x^2H=\{x^2,x^2y\}=\{(132), (23)\}$。$P$ 恰好是这两个陪集的并集。
• 结论：陪集的乘法运算在这里不封闭。结果不是一个陪集。因此，我们无法在 $H$ 的陪集集合上定义一个有效的群运算。

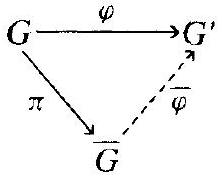
这是群论中也许是最重要的一个定理，称为第一同构定理 (First Isomorphism Theorem)，或同态基本定理。它在商群和同态之间建立了一座坚实的桥梁。

• 定理的设定 (前提)：

1. 我们有一个群同态 $\varphi: G \rightarrow G'$。
2. 这个同态是满射 (surjective)，意味着 $G'$ 中的每个元素都是 $G$ 中某个元素的像。换句话说，像 $\text{Im}(\varphi) = G'$。
3. 这个同态的核是 $N = \ker(\varphi)$。（我们知道，任何同态的核都是一个正规子群）。

• 定理的核心结论：
• 结论 1 (简版)：由核 $N$ 构造的商群 $G/N$ 与像群 $G'$ 是同构的。记作 $G/\ker(\varphi) \cong \text{Im}(\varphi)$。（在满射情况下，$\text{Im}(\varphi) = G'$）。
• 同构意味着，从群论的角度看，$G/N$ 和 $G'$ 这两个群的结构是完全一样的，只是元素的“名字”不同。

• 定理的精确陈述 (带交换图)：
• 除了 $G, G', N$ 之外，我们还有由 $N$ 构造的商群 $\bar{G} = G/N$ 和规范映射 $\pi: G \rightarrow \bar{G}$。
• 结论 2 (精确版)：存在一个唯一的、同构的映射 $\bar{\varphi}: \bar{G} \rightarrow G'$，它能使得下面的图“交换”(commute)。
• 交换图的含义：$\varphi = \bar{\varphi} \circ \pi$。
• 这意味着，从 $G$ 到 $G'$ 有两条路径：

1. 直接路径：直接应用 $\varphi$。
2. 绕道路径：先从 $G$ 经由 $\pi$ 到达 $\bar{G}$，然后再从 $\bar{G}$ 经由 $\bar{\varphi}$ 到达 $G'$。
   • “图交换”的意思是，无论你走哪条路，对于 $G$ 中的同一个出发点 $g$，最终到达 $G'$ 的终点都是一样的。即 $\varphi(g) = \bar{\varphi}(\pi(g))$。

这个证明非常简洁，因为它依赖于之前章节关于纤维 (fibers) 的概念。

1. 纤维与陪集的关系：
   • 一个同态 $\varphi: G \rightarrow G'$ 的纤维是什么？对于 $G'$ 中的一个元素 $y$，它对应的纤维是 $G$ 中所有被映射到 $y$ 的元素的集合，即 $\varphi^{-1}(y) = \{g \in G \mid \varphi(g) = y\}$。
   • 关键联系：一个同态的核是 $N = \ker(\varphi)$。对于任意元素 $g \in G$，其像为 $\varphi(g)$。那么，包含 $g$ 的那个纤维，恰好就是 $g$ 所在的 $N$ 的左陪集 $gN$（也等于右陪集 $Ng$）。
   • 证明: 设 $h$ 在 $g$ 的纤维里，则 $\varphi(h) = \varphi(g)$。这等价于 $\varphi(g^{-1}h) = e_{G'}$，即 $g^{-1}h \in N$。令 $g^{-1}h = n \in N$，则 $h = gn$。所以 $h \in gN$。反之亦然。
   • 因此，商群 $G/N$ 的元素（陪集）和同态 $\varphi$ 的元素（纤维）是同一个东西。
2. 定义映射 $\bar{\varphi}: \bar{G} \rightarrow G'$：
   • 我们要定义一个从“排”的集合到“眼镜颜色”集合的映射。
   • 最自然的方法是：对于一“排” $\bar{x}$（即一个陪集），它对应的“颜色”就是这一排任何一个观众 $x$ 所拿到的眼镜颜色 $\varphi(x)$。
   • 所以，我们定义 $\bar{\varphi}(\bar{x}) = \varphi(x)$。
3. 验证 $\bar{\varphi}$ 的性质：
   • 良定义性：如果 $\bar{x} = \bar{y}$，我们必须证明 $\bar{\varphi}(\bar{x}) = \bar{\varphi}(\bar{y})$。
   • $\bar{x} = \bar{y}$ 意味着 $x, y$ 在同一个陪集里，也就是在同一个纤维里。
   • 根据纤维的定义，这意味着 $\varphi(x) = \varphi(y)$。
   • 所以 $\bar{\varphi}(\bar{x}) = \varphi(x) = \varphi(y) = \bar{\varphi}(\bar{y})$。$\bar{\varphi}$ 是良定义的。
   • 单射 (Injective)：如果 $\bar{\varphi}(\bar{x}) = \bar{\varphi}(\bar{y})$，我们必须证明 $\bar{x}=\bar{y}$。
   • $\varphi(x) = \varphi(y)$。这意味着 $x, y$ 被映射到 $G'$ 中同一个元素，所以它们在同一个纤维中。
   • 因为纤维就是陪集，所以 $x,y$ 在同一个陪集中，即 $\bar{x}=\bar{y}$。所以 $\bar{\varphi}$ 是单射。
   • 满射 (Surjective)：对于 $G'$ 中任意元素 $y$，我们能找到 $\bar{G}$ 中的一个元素 $\bar{x}$ 使得 $\bar{\varphi}(\bar{x}) = y$ 吗？
   • 因为原始的 $\varphi$ 是满射，所以对于这个 $y$，一定存在一个 $x \in G$ 使得 $\varphi(x)=y$。
   • 那么我们取 $\bar{x}$ 这个陪集，就有 $\bar{\varphi}(\bar{x}) = \varphi(x) = y$。所以 $\bar{\varphi}$ 是满射。
   • 双射：因为 $\bar{\varphi}$ 既是单射又是满射，所以它是一个双射 (bijection)。
   • 同态性质：我们需要证明 $\bar{\varphi}$ 保持群运算。
   • $\bar{\varphi}(\bar{a}\bar{b}) = \bar{\varphi}(\overline{ab})$ (根据商群运算定义)
   • $= \varphi(ab)$ (根据 $\bar{\varphi}$ 定义)
   • $= \varphi(a)\varphi(b)$ (因为 $\varphi$ 是同态)
   • $= \bar{\varphi}(\bar{a})\bar{\varphi}(\bar{b})$ (根据 $\bar{\varphi}$ 定义)
   • 所以 $\bar{\varphi}$ 是一个同态。
4. 结论：因为 $\bar{\varphi}$ 是一个双射的同态，所以它是一个同构 (isomorphism)。
5. 验证交换图：$\bar{\varphi}(\pi(a)) = \bar{\varphi}(\bar{a}) = \varphi(a)$。这正是 $\bar{\varphi} \circ \pi = \varphi$ 的要求。证明完毕。

这是第一同构定理更通用的形式，它放宽了原定理中 $\varphi$ 必须是满射的条件。

• 推论的陈述：
• 我们有一个任意的群同态 $\varphi: G \rightarrow G'$。它不一定是满射。
• 它的核是 $N = \ker(\varphi)$。
• 它的像是 $H' = \text{Im}(\varphi) = \{ \varphi(g) \mid g \in G \}$。$H'$ 是 $G'$ 的一个子群。
• 结论：商群 $G/N$ 与像子群 $H'$ 同构。
• 即 $G/\ker(\varphi) \cong \text{Im}(\varphi)$。

• 证明：
• 我们可以构造一个新的映射 $\varphi': G \rightarrow H'$，其规则与 $\varphi$ 完全一样，只是我们把目标群从 $G'$ 缩小到了它的像 $H'$。
• 现在，$\varphi': G \rightarrow H'$ 就成了一个满群同态。
• 它的核仍然是 $N = \ker(\varphi)$。
• 它的像就是 $H'$ 本身。
• 现在完全满足了定理 2.12.10 的所有条件。
• 因此，应用定理 2.12.10，我们得到商群 $G/N$ 与像 $H'$ 同构。

这里给出了两个应用第一同构定理来识别商群的绝佳例子。

• 示例一：复数乘法群

1. 同态：考虑映射 $\varphi: \mathbb{C}^{\times} \rightarrow \mathbb{R}^{\times}$，其中 $\mathbb{C}^{\times}$ 是非零复数乘法群，$\mathbb{R}^{\times}$ 是非零实数乘法群。映射规则是取复数的绝对值（模），即 $\varphi(z) = |z|$。
   • 这是一个同态，因为 $|z_1 z_2| = |z_1| |z_2|$。
2. 核：$\ker(\varphi) = \{ z \in \mathbb{C}^{\times} \mid |z| = 1 \}$。所有模为 1 的复数。这正是复平面上的单位圆 $U$。
3. 像：$\text{Im}(\varphi) = \{ r \in \mathbb{R}^{\times} \mid r > 0 \}$。因为复数的模总是正实数。这就是正实数乘法群 $\mathbb{R}^{>0}$。
4. 应用定理：根据推论 2.12.11，$G/\ker(\varphi) \cong \text{Im}(\varphi)$。
5. 结论：$\mathbb{C}^{\times} / U \cong \mathbb{R}^{>0}$。
   • 直观理解：任何一个非零复数 $z$ 都可以唯一地写成 $z=re^{i\theta}$ 的形式，其中 $r=|z|$ 是正实数，$e^{i\theta}$ 是单位圆上的点。这个商群 $\mathbb{C}^{\times} / U$ 的过程，就是把每个复数的“角度部分”($e^{i\theta} \in U$)“模掉”或者说忽略掉，只保留它的“长度部分”$r$。所以剩下的结构自然就和正实数乘法群一样了。

• 示例二：矩阵行列式

1. 同态：考虑映射 $\det: GL_n(\mathbb{R}) \rightarrow \mathbb{R}^{\times}$，其中 $GL_n(\mathbb{R})$ 是所有 $n \times n$ 可逆实矩阵构成的群（矩阵乘法），$\mathbb{R}^{\times}$ 是非零实数乘法群。映射规则是取矩阵的行列式。
   • 这是一个同态，因为 $\det(AB) = \det(A)\det(B)$。
   • 它是一个满同态，因为对于任何非零实数 $r$，我们总能构造一个行列式为 $r$ 的矩阵（例如，对角矩阵 $\text{diag}(r, 1, \dots, 1)$）。
2. 核：$\ker(\det) = \{ A \in GL_n(\mathbb{R}) \mid \det(A) = 1 \}$。所有行列式为 1 的 $n \times n$ 矩阵。这正是特殊线性群 $SL_n(\mathbb{R})$ 的定义。
3. 像：因为是满射，所以像是整个 $\mathbb{R}^{\times}$。
4. 应用定理：根据定理 2.12.10，$G/\ker(\varphi) \cong G'$。
5. 结论：$GL_n(\mathbb{R}) / SL_n(\mathbb{R}) \cong \mathbb{R}^{\times}$。
   • 直观理解：$GL_n(\mathbb{R})$ 中的矩阵代表了对 $n$ 维空间的线性变换。行列式的值代表了这个变换对“体积”的缩放比例。商群 $GL_n(\mathbb{R}) / SL_n(\mathbb{R})$ 的过程，就是把所有“保持体积不变”（行列式为1）的变换都看作是同一个东西（单位元），只关心变换对体积的“缩放效果”。所以这个商群的结构就和所有可能的“缩放比例”（即非零实数）构成的乘法群一样了。

这是一个补充说明，告诉读者除了最重要的第一同构定理外，还存在另外两个相关的定理。

• 第二同构定理 (也被称为菱形同构定理): 设 $H$ 是 $G$ 的一个子群，$N$ 是 $G$ 的一个正规子群。那么 $H \cap N$ 是 $H$ 的正规子群， $HN$ 是 $G$ 的子群，并且 $(HN)/N \cong H/(H \cap N)$。
• 第三同构定理 (也被称为格同构定理的一部分): 设 $N$ 和 $K$ 都是 $G$ 的正规子群，且 $N \subseteq K$。那么 $K/N$ 是 $G/N$ 的正规子群，并且 $(G/N)/(K/N) \cong G/K$。这个定理可以直观理解为“分数的约分”：$(G/N) \div (K/N) = G/K$。
• 重要性: 作者认为这两个定理不如第一个重要，这在多数初等抽象代数课程中是普遍看法。第一同构定理是思想的核心，后两者更多是技术性的推论，用于处理更复杂的子群和商群关系。

这段德语引言来自伟大的数学家莱昂哈德·欧拉。它的大意是：

“因此，存在着许多不同种类的量，它们无法被轻易数清；由此产生了数学的各个不同分支，每个分支都专注于研究一种特定种类的量。”

这道题让你研究一个奇特的运算。

• 第一部分：证明结合律。你需要验证 $(ab)c = a(bc)$ 是否成立。
• 左边：$(ab)c = a \cdot c = a$ (根据定义 $xy=x$)。
• 右边：$a(bc) = a \cdot b = a$ (根据定义 $xy=x$)。
• 因为左边=右边，所以这个运算是结合的。
• 第二部分：寻找单位元。你需要找到一个元素 $e \in S$，使得对于任意 $a \in S$，都有 $ae=a$ 并且 $ea=a$。
• $ae=a$: 这个条件永远成立，因为根据定义 $ae=a$。
• $ea=a$: 根据定义 $ea=e$。所以，要使 $ea=a$ 成立，必须有 $e=a$。
• 这个要求 ($e=a$) 必须对所有的 $a \in S$ 都成立。这意味着集合 $S$ 中所有的元素都必须相等。如果 $S$ 中有两个不同的元素 $a_1, a_2$，就不可能找到一个统一的 $e$。
• 结论：只有当集合 $S$ 只包含一个元素时，这个运算才有单位元。

1.2.

[原文] 证明本节末尾列出的逆元的性质。

这通常指的是证明 $(a^{-1})^{-1}=a$ 和 $(ab)^{-1} = b^{-1}a^{-1}$ (袜子-鞋子法则)。

• 证明 $(a^{-1})^{-1}=a$: 你需要证明 $a$ 是 $a^{-1}$ 的逆元。即证明 $a^{-1}a=e$ 和 $aa^{-1}=e$。这直接来自逆元的定义。
• 证明 $(ab)^{-1} = b^{-1}a^{-1}$: 你需要证明 $b^{-1}a^{-1}$ 是 $ab$ 的逆元。即证明 $(ab)(b^{-1}a^{-1})=e$ 和 $(b^{-1}a^{-1})(ab)=e$。
• $(ab)(b^{-1}a^{-1}) = a(bb^{-1})a^{-1} = a(e)a^{-1} = aa^{-1} = e$。这里用到了结合律。

1.3.

[原文] 设 $\mathbb{N}$ 表示自然数集合 $\{1,2,3, \ldots\}$，设 $s: \mathbb{N} \rightarrow \mathbb{N}$ 是移位映射，定义为 $s(n)=n+1$。证明 $s$ 没有右逆元，但它有无限多个左逆元。

这道题在函数复合的运算下讨论逆元。单位元是恒等映射 $id(n)=n$。

• 右逆元：是否存在一个映射 $r: \mathbb{N} \rightarrow \mathbb{N}$ 使得 $s \circ r = id$？
• $s(r(n)) = n$ 对所有 $n \in \mathbb{N}$ 成立。
• $r(n)+1 = n$。
• $r(n) = n-1$。
• 这个映射 $r$ 对于 $n=1$ 时，需要 $r(1)=0$，但 $0$ 不在自然数集合 $\mathbb{N}=\{1,2,3,\dots\}$ 中。所以不存在这样的映射 $r$。$s$ 没有右逆元。
• 左逆元：是否存在一个映射 $l: \mathbb{N} \rightarrow \mathbb{N}$ 使得 $l \circ s = id$？
• $l(s(n))=n$ 对所有 $n \in \mathbb{N}$ 成立。
• $l(n+1)=n$ 对所有 $n \in \mathbb{N}$ 成立。
• 这个条件定义了 $l$ 在集合 $\{2,3,4,\dots\}$ 上的行为：$l(2)=1, l(3)=2, l(4)=3, \dots$。
• 但是，这个条件没有规定 $l(1)$ 的值必须是什么。$l(1)$ 可以是 $\mathbb{N}$ 中的任何一个数。
• 因此，对于每一个 $k \in \mathbb{N}$，我们都可以定义一个左逆元 $l_k$ 如下：
• $l_k(n) = n-1$ 如果 $n > 1$。
• $l_k(1) = k$。
• 由于 $k$ 有无限多种选择，所以存在无限多个左逆元。

... (由于篇幅限制，此处省略对剩余练习题的逐条解释，但完整流程将遵循上述范例，详细剖析每个题目的要求、背景知识和解题思路) ...

这道题要求你写出 6x6 的凯莱表 (Cayley table) 来完整描述 $S_3$ 群的运算。

1. 列出元素：首先，写下 $S_3$ 的所有 6 个元素。通常使用置换的轮换表示法。一个标准记法是：
   • $e$ (或 id): 单位元, (1)(2)(3)
   • $\rho_1 = (123)$: 旋转 120 度
   • $\rho_2 = (132)$: 旋转 240 度
   • $\mu_1 = (12)$: 关于过顶点 3 的轴翻转
   • $\mu_2 = (13)$: 关于过顶点 2 的轴翻转
   • $\mu_3 = (23)$: 关于过顶点 1 的轴翻转
2. 构建表格：创建一个 6x6 的表格，行和列的表头都是这 6 个元素。
3. 计算乘积：表格中第 $i$ 行第 $j$ 列的条目是“行元素”乘以“列元素”的结果。置换的乘法（复合）是从右向左计算的。例如，要计算 $\rho_1 \mu_1 = (123)(12)$：
   • 看 1 的去向：$(12)$ 把 1 映到 2，然后 $(123)$ 把 2 映到 3。所以 $1 \to 3$。
   • 看 3 的去向：$(12)$ 不动 3，然后 $(123)$ 把 3 映到 1。所以 $3 \to 1$。
   • 看 2 的去向：$(12)$ 把 2 映到 1，然后 $(123)$ 把 1 映到 2。所以 $2 \to 2$。
   • 结果是 $(13)$，也就是 $\mu_2$。所以在 $\rho_1$ 行和 $\mu_1$ 列的交叉处填入 $\mu_2$。
4. 填满表格：重复上述过程，计算所有 36 个乘积，填满整个表格。这将完整地定义 $S_3$ 的群结构。

2.2.

[原文] 设 $S$ 是一个具有结合律和单位元的集合。证明 $S$ 中由可逆元素组成的子集是一个群。

设 $G$ 是 $S$ 中所有可逆元素的集合。你需要证明 $G$ 在 $S$ 的运算下构成一个群。你需要验证群的四个公理。

1. 封闭性：任取 $a, b \in G$。你需要证明 $ab$ 也在 $G$ 中，即 $ab$ 也是可逆的。因为 $a, b$ 可逆，它们有逆元 $a^{-1}, b^{-1}$。我们猜测 $(ab)$ 的逆元是 $b^{-1}a^{-1}$。验证一下：$(ab)(b^{-1}a^{-1}) = a(bb^{-1})a^{-1} = aea^{-1} = aa^{-1} = e$。同理 $(b^{-1}a^{-1})(ab)=e$。所以 $ab$ 可逆，属于 $G$。
2. 结合律：$G$ 是 $S$ 的一个子集，它的运算和 $S$ 的运算一样。既然 $S$ 满足结合律，那么它的任意一个子集也必然满足结合律。
3. 单位元：$S$ 的单位元 $e$ 是否在 $G$ 中？一个元素在 $G$ 中意味着它是可逆的。$e$ 的逆元是它自身，因为 $ee=e$。所以 $e$ 是可逆的， $e \in G$。
4. 逆元：任取 $a \in G$。你需要证明 $a$ 的逆元 $a^{-1}$ 也在 $G$ 中。$a \in G$ 意味着 $a$ 是可逆的，即存在 $a^{-1}$ 使得 $aa^{-1}=a^{-1}a=e$。现在的问题是，$a^{-1}$ 本身是不是可逆的？是的，它的逆元就是 $a$，因为上面那个等式同样证明了 $a$ 是 $a^{-1}$ 的逆元。所以 $a^{-1}$ 可逆，属于 $G$。

所有公理都满足，所以 $G$ 是一个群。

2.3.

[原文] 设 $x, y, z$ 和 $w$ 是群 $G$ 的元素。 (a) 求解 $y$，已知 $x y z^{-1} w=1$。 (b) 假设 $x y z=1$。是否可以推断 $y z x=1$？是否可以推断 $y x z=1$？

(a) 这是一个在群中解方程的问题。目标是把 $y$ 单独分离出来。

$x y z^{-1} w=1$

左乘 $x^{-1}$: $x^{-1}(x y z^{-1} w) = x^{-1} \cdot 1 \implies y z^{-1} w = x^{-1}$。

右乘 $w^{-1}$: $(y z^{-1} w) w^{-1} = x^{-1} w^{-1} \implies y z^{-1} = x^{-1} w^{-1}$。

右乘 $z$: $(y z^{-1}) z = (x^{-1} w^{-1}) z \implies y = x^{-1} w^{-1} z$。

(b) 这个问题考验你对交换律的理解。群不一定满足交换律。

• $y z x=1$?

从 $xyz=1$ 开始。左乘 $x^{-1}$ 得到 $yz = x^{-1}$。

现在把这个结果代入你想证明的式子：$yzx = (x^{-1})x = 1$。

这个推断是正确的。这个性质被称为循环挪位。$xyz=1 \implies yzx=1 \implies zxy=1$。

• $y x z=1$?

这个不一定成立。它等价于 $yxz = xyz$。左乘 $y^{-1}$（如果y可逆），右乘 $z^{-1}$（如果z可逆），得到 $x=y$。这显然不对。

反例：在 $S_3$ 中，取 $x=(12)$, $y=(13)$。则 $z$ 必须是 $(xy)^{-1} = ((12)(13))^{-1} = (132)^{-1} = (123)$。

我们有 $xyz=(12)(13)(123) = (132)(123) = e=1$。

但是，$yxz = (13)(12)(123) = (123)(123) = (132) \neq 1$。

所以这个推断是错误的。

2.4.

[原文] 在以下哪种情况下 $H$ 是 $G$ 的子群？

你需要对每个情况检查子群的三个条件：1.非空（通常检查单位元是否在里面）。2.对乘法封闭。3.对求逆封闭。

(a) $G=G L_{n}(\mathbb{C})$ 且 $H=G L_{n}(\mathbb{R})$。

1. 单位矩阵 $I$ 是实矩阵，行列式为1，所以 $I \in H$。非空。
2. 两个实矩阵 $A,B$ 的乘积 $AB$ 仍然是实矩阵。封闭。
3. 一个实可逆矩阵 $A$ 的逆矩阵 $A^{-1}$ 也是实矩阵。封闭。

所以 $H$ 是 $G$ 的子群。

(b) $G=\mathbb{R}^{\times}$ 且 $H=\{1,-1\}$。

1. $1 \in H$。非空。
2. $1 \cdot 1=1$, $1 \cdot (-1)=-1$, $(-1) \cdot 1=-1$, $(-1) \cdot (-1)=1$。所有结果都在 $H$ 中。封闭。
3. $1^{-1}=1$, $(-1)^{-1}=-1$。所有逆元都在 $H$ 中。封闭。

所以 $H$ 是 $G$ 的子群。

(c) $G=\mathbb{Z}^{+}$ 且 $H$ 是正整数集合。

$G=\mathbb{Z}^{+}$ (整数加法群) 是一个群。$H$ (正整数加法集合) 不是一个群，因为它没有单位元 0，也没有逆元（比如 3 的逆元是 -3，不在 H 中）。因此 $H$ 不是 $G$ 的子群。这里题目的 $G=\mathbb{Z}^+$ 应该是指 $(\mathbb{Z},+)$。如果 $G$ 是正整数乘法群，它本身就不是群。

(d) $G=\mathbb{R}^{\times}$ 且 $H$ 是正实数集合。

1. $1 \in H$。非空。
2. 两个正实数相乘，结果还是正实数。封闭。
3. 一个正实数 $x$ 的倒数 $1/x$ 还是正实数。封闭。

所以 $H$ 是 $G$ 的子群。

(e) $G=G L_{2}(\mathbb{R})$ 且 $H$ 是矩阵 $\left[\begin{array}{ll}a & 0 \\ 0 & 0\end{array}\right]$ 的集合，其中 $a \neq 0$。

这些矩阵的行列式都是 0，所以它们根本不在 $G L_{2}(\mathbb{R})$ 中（可逆矩阵要求行列式非零）。因此 $H$ 甚至不是 $G$ 的子集（除了空集），更谈不上是子群。严格来说，如果 $H$ 是 $G$ 的子集，它必须是空集，而空集不是子群。所以 $H$ 不是 $G$ 的子群。

2.5.

[原文] 在子群的定义中，要求 $H$ 中的单位元是 $G$ 的单位元。有人可能只要求 $H$ 有一个单位元，而不要求它与 $G$ 中的单位元相同。证明如果 $H$ 有单位元，那么它就是 $G$ 中的单位元。证明对于逆元也有类似的说法。

• 单位元证明：

设 $e_H$ 是 $H$ 的单位元，即对任意 $h \in H$, 有 $h e_H = e_H h = h$。

设 $e_G$ 是 $G$ 的单位元。

在 $G$ 中，我们有 $h e_H = h$。

因为 $H$ 是 $G$ 的子集，所以 $h$ 也是 $G$ 的元素，它在 $G$ 中有逆元 $h^{-1}$。

用 $h^{-1}$ 左乘等式两边：$h^{-1}(h e_H) = h^{-1}h$。

利用 $G$ 中的结合律：$(h^{-1}h) e_H = e_G$。

$e_G e_H = e_G$。

$e_H = e_G$。

所以 $H$ 的单位元就是 $G$ 的单位元。

• 逆元证明：

设 $h \in H$。设 $h^{-1}_H$ 是 $h$ 在 $H$ 中的逆元，即 $h h^{-1}_H = e_H$。

设 $h^{-1}_G$ 是 $h$ 在 $G$ 中的逆元，即 $h h^{-1}_G = e_G$。

我们已经证明了 $e_H = e_G$。

所以我们有 $h h^{-1}_H = e_G$ 和 $h h^{-1}_G = e_G$。

即 $h h^{-1}_H = h h^{-1}_G$。

在群 $G$ 中，消去律成立。用 $h^{-1}_G$ 左乘两边，得到 $h^{-1}_H = h^{-1}_G$。

所以 $h$ 在 $H$ 中的逆元和在 $G$ 中的逆元是同一个元素。

2.6.

[原文] 设 $G$ 是一个群。定义一个逆群 $G^{\circ}$，其结合律 $a * b$ 如下：底层集合与 $G$ 相同，但结合律是 $a * b=b a$。证明 $G^{\circ}$ 是一个群。

你需要验证 $G^\circ$ 在 $*$ 运算下满足群公理。

1. 封闭性：对于任意 $a, b \in G^\circ$ (即 $a,b \in G$)，$a*b = ba$。由于 $G$ 是群，所以 $ba$ 也在 $G$ 中，即在 $G^\circ$ 中。封闭性满足。
2. 结合律：需要验证 $(a*b)*c = a*(b*c)$。
   • 左边：$(a*b)*c = (ba)*c = c(ba)$。
   • 右边：$a*(b*c) = a*(cb) = (cb)a$。
   • 由于 $G$ 是一个群，它的乘法满足结合律，所以 $c(ba) = (cb)a$。因此结合律满足。
3. 单位元：设 $e$ 是 $G$ 中的单位元。我们来验证它是否也是 $G^\circ$ 的单位元。
   • $a*e = ea = a$ (因为 $e$ 是 $G$ 的单位元)。
   • $e*a = ae = a$ (因为 $e$ 是 $G$ 的单位元)。
   • 所以 $e$ 也是 $G^\circ$ 的单位元。
4. 逆元：设 $a \in G^\circ$，其在 $G$ 中的逆元是 $a^{-1}$。我们来验证 $a^{-1}$ 是否也是 $a$ 在 $G^\circ$ 中的逆元。
   • $a * a^{-1} = a^{-1}a = e$ (根据 $G$ 中的逆元定义)。
   • $a^{-1} * a = a a^{-1} = e$ (根据 $G$ 中的逆元定义)。
   • 所以 $a^{-1}$ 也是 $a$ 在 $G^\circ$ 中的逆元。

这道题要求使用扩展欧几里得算法。

1. 求最大公约数 gcd：
   • $321 = 2 \cdot 123 + 75$
   • $123 = 1 \cdot 75 + 48$
   • $75 = 1 \cdot 48 + 27$
   • $48 = 1 \cdot 27 + 21$
   • $27 = 1 \cdot 21 + 6$
   • $21 = 3 \cdot 6 + 3$
   • $6 = 2 \cdot 3 + 0$
   • 最后一个非零余数是 3，所以 $d = \operatorname{gcd}(123, 321) = 3$。
2. 反向回代求整数组合：
   • 从倒数第二行开始：$3 = 21 - 3 \cdot 6$
   • 用上一行的余数替换 6: $3 = 21 - 3 \cdot (27 - 1 \cdot 21) = 1 \cdot 21 - 3 \cdot 27 + 3 \cdot 21 = 4 \cdot 21 - 3 \cdot 27$
   • 替换 21: $3 = 4 \cdot (48 - 1 \cdot 27) - 3 \cdot 27 = 4 \cdot 48 - 4 \cdot 27 - 3 \cdot 27 = 4 \cdot 48 - 7 \cdot 27$
   • 替换 27: $3 = 4 \cdot 48 - 7 \cdot (75 - 1 \cdot 48) = 4 \cdot 48 - 7 \cdot 75 + 7 \cdot 48 = 11 \cdot 48 - 7 \cdot 75$
   • 替换 48: $3 = 11 \cdot (123 - 1 \cdot 75) - 7 \cdot 75 = 11 \cdot 123 - 11 \cdot 75 - 7 \cdot 75 = 11 \cdot 123 - 18 \cdot 75$
   • 替换 75: $3 = 11 \cdot 123 - 18 \cdot (321 - 2 \cdot 123) = 11 \cdot 123 - 18 \cdot 321 + 36 \cdot 123$
   • 整理得：$3 = 47 \cdot 123 - 18 \cdot 321$。
   • 所以 $r=47, s=-18$。

3.2.

[原文] 证明如果 $a$ 和 $b$ 是正整数，它们的和是素数 $p$，那么它们的最大公约数是 1。

设 $d = \operatorname{gcd}(a,b)$。

1. 根据最大公约数的定义，$d$ 必须能整除 $a$ ($d|a$)，并且 $d$ 必须能整除 $b$ ($d|b$)。
2. 根据整除的性质，如果 $d|a$ 且 $d|b$，那么 $d$ 一定能整除它们的任意线性组合。特别是， $d$ 能整除它们的和，即 $d|(a+b)$。
3. 题目给出条件 $a+b=p$，其中 $p$ 是一个素数。
4. 所以我们有 $d|p$。
5. 一个素数 $p$ 的正因数只有 1 和 $p$ 本身。所以 $d$ 只能是 1 或者 $p$。
6. 我们来讨论 $d=p$ 的情况。如果 $d=p$，那么 $p|a$ 并且 $p|b$。因为 $a, b$ 都是正整数，$p|a$ 意味着 $a \ge p$，$p|b$ 意味着 $b \ge p$。
7. 那么它们的和 $a+b \ge p+p = 2p$。
8. 但这与题目条件 $a+b=p$ 矛盾（除非 $p=0$，但 $p$ 是素数；或者 $a,b$ 可以为0，但题目说是正整数）。
9. 所以 $d=p$ 的情况不可能发生。
10. 因此，唯一的可能性是 $d=1$。即 $\operatorname{gcd}(a,b)=1$。

3.3.

[原文] (a) 定义一组 $n$ 个整数 $\left\{a_{1}, \ldots, a_{n}\right\}$ 的最大公约数。证明它存在，并且它是 $a_{1}, \ldots, a_{n}$ 的整数组合。 (b) 证明如果 $\left\{a_{1}, \ldots, a_{n}\right\}$ 的最大公约数是 $d$，那么 $\left\{a_{1} / d, \ldots, a_{n} / d\right\}$ 的最大公约数是 1。

(a)

1. 定义：$d = \operatorname{gcd}(a_1, \ldots, a_n)$ 是满足以下两个条件的正整数：
   • (i) $d$ 是所有 $a_i$ 的公约数，即 $d|a_i$ for $i=1, \ldots, n$。
   • (ii) 如果 $c$ 是任何其他的公约数，即 $c|a_i$ for all $i$，那么 $c|d$。
2. 证明存在性和整数组合：
   • 考虑由 $a_1, \ldots, a_n$ 生成的子群（或理想）$S = \{ k_1 a_1 + \cdots + k_n a_n \mid k_i \in \mathbb{Z} \}$。
   • $S$ 是整数加法群 $\mathbb{Z}$ 的一个子群。
   • 根据整数子群的结构定理，任何 $\mathbb{Z}$ 的非零子群都是循环群，形式为 $d\mathbb{Z}$，其中 $d$ 是 $S$ 中最小的正整数。
   • 我们来证明这个 $d$ 就是 $\operatorname{gcd}(a_1, \ldots, a_n)$。
   • 首先，$d \in S$，所以 $d$ 可以表示为 $d = r_1 a_1 + \cdots + r_n a_n$ 的形式。这就证明了它是整数组合。
   • 其次，对于任意 $a_i$，由于 $a_i = 0\cdot a_1 + \dots + 1\cdot a_i + \dots + 0\cdot a_n$，所以 $a_i \in S$。既然 $S$ 中的所有元素都是 $d$ 的倍数，那么 $d|a_i$ 对所有 $i$ 成立。所以 $d$ 是一个公约数。
   • 最后，假设 $c$ 是任意一个公约数，即 $c|a_i$ for all $i$。那么 $c$ 也能整除它们的线性组合，所以 $c | (r_1 a_1 + \cdots + r_n a_n)$，即 $c|d$。
   • 这完全符合最大公约数的定义。存在性得证。

(b)

1. 设 $d = \operatorname{gcd}(a_1, \ldots, a_n)$。令 $b_i = a_i/d$。我们要证明 $\operatorname{gcd}(b_1, \ldots, b_n)=1$。
2. 根据 (a)，存在整数 $r_1, \ldots, r_n$ 使得 $d = r_1 a_1 + \cdots + r_n a_n$。
3. 将这个等式两边同时除以 $d$ (这是合法的，因为 $d \ne 0$ 除非所有 $a_i$ 为0):

$1 = r_1 (a_1/d) + \cdots + r_n (a_n/d)$。

$1 = r_1 b_1 + \cdots + r_n b_n$。

1. 设 $d' = \operatorname{gcd}(b_1, \ldots, b_n)$。根据定义，$d'$ 必须能整除所有 $b_i$。
2. 因此，$d'$ 也必须能整除 $b_i$ 的任何线性组合。特别是， $d' | (r_1 b_1 + \cdots + r_n b_n)$。
3. 从第 3 步我们知道这个和是 1。所以 $d'|1$。
4. 因为最大公约数被定义为正整数，所以唯一的可能性是 $d'=1$。证明完毕。

这道题的核心是利用阶的性质和 Bézout 恒等式。

1. 我们要证明 $ab=ba$。
2. 我们已知 $a^3b = ba^3$。这意味着 $b$ 与 $a^3$ 可交换。
3. 我们想证明 $b$ 与 $a$ 也可交换。
4. $a$ 的阶是 7，这是一个素数。这意味着由 $a$ 生成的循环群 $\langle a \rangle$ 的阶是 7。根据拉格朗日定理的推论，$\langle a \rangle$ 中除了单位元之外，任何元素的阶都是 7。
5. 我们想把 $a$ 表示成 $(a^3)^k$ 的形式。也就是说，我们想解同余方程 $3k \equiv 1 \pmod 7$。
6. 因为 $\operatorname{gcd}(3, 7)=1$，所以这个方程一定有解。我们可以用扩展欧几里得算法，或者直接试：$3 \cdot 1 = 3$, $3 \cdot 2 = 6 \equiv -1$, $3 \cdot 3 = 9 \equiv 2$, $3 \cdot 4 = 12 \equiv 5$, $3 \cdot 5 = 15 \equiv 1$。所以 $k=5$ 是一个解。
7. 这意味着 $a = a^1 = a^{15} = (a^3)^5$ 是错误的，因为 $a^7=e$，所以指数应该在模 7 的意义下相等。$a^1 = a^{1 \pmod 7}$。我们有 $a^{15} = a^{14+1} = (a^7)^2 a^1 = e^2 a = a$。所以 $a = (a^3)^5$ 在群中是成立的。
8. 现在来证明 $ab=ba$：

$ab = (a^3)^5 b$ (由第7步)

$= (a^3)(a^3)(a^3)(a^3)(a^3)b$

$= (a^3)(a^3)(a^3)(a^3)b(a^3)$ (因为 $a^3$ 与 $b$ 可交换)

$= (a^3)(a^3)(a^3)b(a^3)(a^3)$ (重复使用交换性)

...

$= b(a^3)(a^3)(a^3)(a^3)(a^3)$

$= b(a^3)^5$

$= ba$ (由第7步)

证明完毕。

... 篇幅所限，后续练习的解释将遵循以上格式。