11 第 6 章 对称
1.1 引言
📜 [原文1]
第 6 章
对称
这是第六章的标题。本章的主题是“对称”。对称是数学，特别是群论中一个非常核心和基本的概念。群论本身就是为了形式化和研究对称性而发展起来的。本章将探讨不同类型的对称性，以及如何用群这个代数工具来描述和分析它们。章节标题“对称”明确指出了本章的核心内容，引导读者进入对对称现象的数学化探讨。
本段不含公式。
本段为章节标题，不涉及具体数值。例如，一个正方形的对称性包括旋转0度、90度、180度、270度，以及四条对称轴的翻转，这些操作共同构成一个群。一个等边三角形的对称性包括旋转0度、120度、240度，以及三条对称轴的翻转。
初学者可能会将日常生活中模糊的“对称”感与数学上严格定义的“对称操作”混淆。数学上的对称指的是一个变换（如旋转、反射），它作用于一个对象后，该对象看起来没有变化。对称本身不是一个静态的属性，而是一系列保持对象不变的“动作”或“变换”的集合。
本段是第六章的起始，点明了本章的核心主题是对称性。
章节标题的存在是为了清晰地组织内容结构，并向读者预告本章将要讨论的核心议题。它作为内容的入口，帮助读者建立对后续内容的宏观认识。
想象一面镜子。镜子里的影像就是现实物体的一种对称变换。或者想象一个风车，无论它旋转多少个叶片的角度，看起来都和原来一样，这就是旋转对称。本章就是要把这些直观的“不变性”用精确的数学语言（群）来描述。
看到“对称”这个词，你可以立即联想到生活中常见的对称物体：一只蝴蝶的翅膀、一片雪花、一个人的脸、建筑物的外观等等。这些都是对称概念的直观体现。本章将从这些具体的例子出发，抽象出其背后的数学结构。
1.2 索菲·热尔曼名言
📜 [原文2]
代数不过是写出来的几何；几何不过是画出来的代数。
-索菲·热尔曼
这句话是法国数学家索菲·热尔曼的一句名言，深刻地揭示了代数与几何之间密不可分、互为表里的关系。
“代数不过是写出来的几何”：这句话的意思是，许多代数结构和概念，其本质和起源都可以在几何中找到直观的对应物。例如，坐标系的引入使得几何图形可以用代数方程来表示。一个圆可以用方程 $x^2 + y^2 = r^2$ 来描述，这就是用代数语言书写几何图形。本章即将学习的群，就是描述几何图形对称性的代数工具。
“几何不过是画出来的代数”：反过来说，代数方程和代数关系也可以通过几何图形的方式被可视化，从而帮助我们理解和发现其内在规律。一个线性方程组的解可以看作是两个或多个平面（或直线）的交点，这就是将代数问题“画”成了几何图像。
这句引言放在本章开头，意在强调本章内容——用代数工具（群）来研究几何问题（对称），是这两个领域完美结合的典范。
本段不含公式。
- 代数写几何：代数方程 $y = x^2$ 在几何上对应着一条开口向上的抛物线。这条抛物线就是方程“画”出来的图形。
- 几何画代数：一个边长为 $a$ 的正方形，其面积为 $A = a^2$。这个几何图形（正方形）直观地展示了代-数关系（平方）。同样，一个长方体的体积 $V = lwh$ 是长、宽、高三个代数量相乘的几何体现。
这句话是一种哲学层面的高度概括，而不是一条严格的数学定理。并非所有的代数分支都能找到简单的几何对应，也并非所有几何问题都能轻易地代数化。例如，一些非常抽象的代数结构（如某些无限维群）就很难有直观的几何图像。这句话的价值在于启发我们思考两者之间的联系，利用一个领域的工具去解决另一个领域的问题。
本段通过引用索菲·热尔曼的名言，强调了代数与几何的深刻联系，为本章使用代数（群论）来分析几何（对称性）的主题奠定了思想基础。
这段引言的目的是激发读者的兴趣，并提供一个高层次的哲学视角，帮助读者理解本章内容（用群论研究对称）的深刻意义和历史渊源。它暗示了本章内容是代数与几何思想交融的经典范例。
想象你戴着一副特殊的眼镜。戴上它，你可以看到代数方程在空间中描绘出的奇妙图形（代数 → 几何）；反过来，你也可以看到复杂的几何形状被转化为简洁的代数符号和关系（几何 → 代数）。代数和几何就像是描述同一个宇宙的两种不同但可以相互翻译的语言。
想象桌上有一个苹果。你可以用文字描述它：“一个红色的、圆形的、带有一个小柄的水果”。这好比几何的描述。你也可以用一系列数据来记录它：颜色（RGB值）、形状参数（球形方程、凹陷参数）、重量（克）、化学成分（糖、水、纤维素的百分比）。这好比代-数的描述。两者描述的是同一个苹果，只是方式不同。
1.3 对称性的应用与群论起源
📜 [原文3]
对称性提供了群的一些最具吸引力的应用。群最初是为了分析某些代数结构（域扩张（第 16 章））的对称性而发明的，并且由于对称性是一种普遍现象，它是群论应用的两种主要方式之一。另一种是通过群表示，这将在第 10 章讨论。我们在第一节研究的平面图形的对称性提供了丰富的例子，并为第 6.7 节介绍的群作用的一般概念提供了背景。
这段话是本章的引言，概述了对称性、群以及它们之间关系的重要性。
- “对称性提供了群的一些最具吸引力的应用。”：开篇点题，说明学习群的一个重要动机是其在对称性分析中的强大应用。从晶体结构到基本粒子物理，对称性无处不在，而群是描述这一切的通用语言。
- “群最初是为了分析某些代数结构（域扩张（第 16 章））的对称性而发明的”：这里追溯了群论的历史起源。群这个概念最初由数学家伽罗瓦提出，是为了解决一个纯代数问题：高次方程是否存在求根公式。伽罗瓦发现，方程能否用根式求解，取决于其解的置换群（一种对称性）的结构。这里的“域扩张的对称性”指的就是伽罗瓦群，它描述了方程根之间的对称关系。这说明对称的概念不仅限于几何图形，也存在于抽象的代数结构中。
- “并且由于对称性是一种普遍现象，它是群论应用的两种主要方式之一。”：这句话强调了群论应用广泛性的根源在于对称现象的普遍存在。无论是自然科学还是艺术设计，到处都有对称的影子。因此，研究对称的群论也就有了广阔的应用舞台。群论通过对称性进行应用是其主要方式之一。
- “另一种是通过群表示，这将在第 10 章讨论。”：提到了群论的另一个主要应用方向——群表示论。群表示论是将抽象的群元素用具体的矩阵来表示，从而将抽象的群论问题转化为更直观、更易于计算的线性代数问题。这在物理学，特别是量子力学和粒子物理学中至关重要。
- “我们在第一节研究的平面图形的对称性提供了丰富的例子，并为第 6.7 节介绍的群作用的一般概念提供了背景。”：这句为本章的内容结构做了预告。本章将从最直观的例子——平面图形的对称性——入手，帮助读者建立对对称群的直观理解。这些具体的例子将为后续学习更抽象、更普适的“群作用”概念打下坚实的基础。群作用是群如何“作用”于一个集合（例如，平面上的点集）并体现其对称性的形式化描述。
本段不含公式。
- 域扩张的对称性：考虑方程 $x^2 - 2 = 0$，它的两个根是 $\sqrt{2}$ 和 $-\sqrt{2}$。包含这两个根的最小域是 $\mathbb{Q}(\sqrt{2}) = \{a + b\sqrt{2} \mid a, b \in \mathbb{Q}\}$。这个域上有一个对称变换（自同构），即 $\sigma: a + b\sqrt{2} \mapsto a - b\sqrt{2}$。这个变换保持了有理数不变，并且把一个根变成了另一个根。这个自同构 $\sigma$ 和恒等变换 $e$ 构成了这个域扩张的对称群（伽罗瓦群），这个群同构于二阶循环群 $C_2$。
- 群表示：考虑前面提到的正方形对称群 $D_4$。其中一个元素是逆时针旋转90度，记为 $r$。我们可以用一个矩阵来“表示”这个操作：
$r \rightarrow \begin{pmatrix} \cos(90^\circ) & -\sin(90^\circ) \\ \sin(90^\circ) & \cos(90^\circ) \end{pmatrix} = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$
另一个元素，比如沿x轴的反射 $s_x$，可以表示为：
$s_x \rightarrow \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$
通过这种方式，群的乘法操作就对应着矩阵的乘法操作。这就是群表示的一个简单例子。
- 群的起源：虽然文本提到群是为了分析域扩张的对称性而发明的，但这主要是指伽罗瓦的奠基性工作。群的概念在此之前已经以各种形式（如置换群）在拉格朗日、柯西等人的研究中出现，但伽罗瓦首次清晰地揭示了群结构与方程可解性之间的深刻联系。
- 对称性的广义理解：初学者容易将对称性局限于几何上的翻转和旋转。必须理解，在代数中，对称性可以是一种保持结构不变的任何变换。例如，对于方程的根来说，“对称”就是指在不改变根满足的代数关系的前提下，对这些根进行的置换。
本段概述了群论与对称性的关系，点明了对称性是群论应用的主要领域之一。它回顾了群论源于对代数结构对称性的研究，并预告了本章将从直观的平面图形对称性入手，为后续更抽象的群作用概念做铺垫。
本段的目的是为整个章节设定一个框架和路线图。它告诉读者为什么学习对称群很重要（应用广泛），它的历史根源是什么（伽罗瓦理论），以及本章将如何展开学习（从具体例子到抽象概念）。
想象群是一个“万能遥控器”，而对称性是电视机的“频道”。这个遥控器上的一系列按钮（群元素）可以让你在不同的频道之间切换（变换对象），但无论怎么切换，电视机本身（对象保持不变的性质）没有损坏。群论就是研究这个遥控器内部构造（群的结构）的学问。群表示论则是为这个万能遥控器制造一个具体的、可以用矩阵电路实现的版本。
想象你正在玩一个拼图游戏。对称性就像是拼图的规则，规定了哪些块可以放在哪里。例如，一块正方形的拼图块，你可以旋转它四次，或者翻转它，它仍然能放进那个正方形的孔里。这些允许的操作（旋转、翻转）集合起来就构成一个群。群论就是研究这些“允许的操作”的规则。
1.4 几何推理的说明
📜 [原文4]
我们允许自由使用几何推理。将论证追溯到几何公理将留待其他场合。
这句话向读者说明了本章在论证严谨性上的一个约定和前提。
- “我们允许自由使用几何推理。”：这意味着在后续的讨论中，作者会直接使用读者在中学或大学早期课程中学到的直观的几何事实和结论。例如，“旋转一个图形，其边长和角度保持不变”、“两条平行线间的距离处处相等”等。作者不会去证明这些基本的几何性质。
- “将论证追溯到几何公理将留待其他场合。”：这句话明确了本书的重点。本书是关于抽象代数的，不是关于几何基础的。如果要从最基本的几何公理（如欧几里得公理体系或希尔伯特公理体系）出发，来严格证明每一个几何操作的性质，那将会非常繁琐，并且会偏离本章的核心主题——用群来描述对称性。因此，作者在这里打了个招呼，表示我们将“默认”这些几何直觉是正确的，而不去深究其公理基础。
本段不含公式。
- 示例1：当书中提到“将一个正方形绕中心旋转90度”时，我们会直接接受这个操作保持了正方形的形状和大小，不会去从几何公理证明旋转是一种刚体运动（等距变换）。
- 示例2：当书中讨论关于一条直线的反射时，我们会直观地认为一个点到对称轴的距离等于其像到对称轴的距离，并且连接点与其像的线段被对称轴垂直平分。我们不会去证明这个结论。
这种做法在教学中很常见，被称为“约定了一个抽象层次”。虽然在本书中我们“自由使用几何推理”，但在更专门的几何学课程中，这些直观的推理本身就是需要被严格证明的对象。读者需要清楚，这里的“自由”是基于上下文的一种简化，而不是说几何推理不需要公理基础。在需要极高严谨性的数学领域（如公理集合论），任何直觉都必须被形式化的证明所代替。
本段是一个“免责声明”或“游戏规则”的宣告。它告知读者，本章将依赖直观的几何知识，而不会深究其公理基础，目的是为了让读者能更专注于学习代数（群论）如何应用于几何（对称）。
这段话的目的是管理读者的期望，明确讨论的范围和深度。它通过暂时搁置对几何基础的严格论证，使得教学的重点可以清晰地放在代-数概念上，避免了不必要的枝节，让学习过程更顺畅。
这好比学习如何用乐高积木搭建一座城堡。老师会说：“我们假设这些积木块都是标准的、坚固的，并且可以完美地拼接在一起。” 老师不会花时间去讲解制造这些塑料积木的化学过程和模具精度标准（相当于几何公理）。重点是学习如何用这些现成的积木（几何直觉）来搭建出宏伟的结构（群论应用）。
想象你在学习驾驶。教练会教你如何使用方向盘、油门和刹车。他会说：“我们假设车是好的，踩油门车会走，转方向盘车会转。” 教练不会从内燃机原理、变速箱构造和转向系统力学开始讲起。这里的几何推理就好比方向盘和油门，是我们直接使用的工具；而几何公理就好比是汽车的内部机械原理，我们暂时不深入探究。
22 平面图形的对称
2.1 对称类型概述
📜 [原文5]
61 平面图形的对称
平面图形的对称性通常分为以下几种类型：
这是第6.1节的标题和引言。它开启了本章的核心内容讨论，即从具体的平面图形对称性开始。
- “6.1 平面图形的对称”：这是小节的标题，明确了本节的主题是研究二维平面上图形的对称性。这是对称概念中最直观、最容易理解的一类，是进入更抽象对称概念的绝佳起点。
- “平面图形的对称性通常分为以下几种类型：”：这句话是一个引子，预告接下来将要分类介绍几种基本的平面对称操作。在数学上，这些“类型”对应的就是不同种类的等距变换（Isometry），即保持距离不变的变换。这些变换构成了所谓的“欧几里得群”的子群。
本段不含公式。
本段为引言，为后续分类做铺垫。后续的例子会更具体。
- 例子1: 一个英文字母 "A" 具有左右对称性，它属于即将介绍的双边对称（反射对称）。
- 例子2: 一个风车的叶片具有旋转对称性。
- 例子3: 一排无限延伸的栅栏则具有平移对称性。
“通常分为”这个词暗示了这个分类可能不是绝对完备的，或者说在某些复杂情况下，对称性可能是几种基本类型的组合。此外，这里主要讨论的是欧几里得平面上的对称性，在非欧几何（如球面几何或双曲几何）中，对称性的类型和性质会有所不同。
本段是第6.1节的开篇，指明本节将要讨论平面图形的对称性，并预告将对这些对称性进行分类介绍。
此段作为小节的引言，其目的是将读者的注意力集中到“平面图形”这个具体的研究对象上，并建立一个清晰的预期：接下来会有一个关于对称类型的列表或分类。
想象你是一个图形设计师，你的工具箱里有几种基本的“对称工具”。你可以用“镜像”工具制造双边对称，用“旋转复制”工具制造旋转对称，用“复制-粘贴-移动”工具制造平移对称。本节就是要逐一向你介绍这些工具的功能。
看看你周围的物体。墙上的瓷砖图案、布料上的花纹、建筑物的窗户排列。你会发现它们的美感往往来源于某些重复的模式。本节就是要将这些千变万化的模式，归结为几种最基本的对称类型。
2.2 双边对称
📜 [原文6]
双边对称。
双边对称。
这段内容通过四张图片和文字标注，介绍了第一种对称类型：双边对称。
- 图片内容：图片展示了四种具有双边对称性的图形：一个人脸的轮廓、一个花瓶、一只蝴蝶、一个心形。这些图形的共同特点是，都存在一条假想的“对称轴”（通常是垂直的），将图形分为左右两半，且这两半互为镜像。
- “双边对称”：这个术语是反射对称（Reflectional Symmetry）的通俗说法。在数学上，一个图形如果关于某条直线 $L$ 是对称的，意味着对于图形上的任意一点 $P$，它关于直线 $L$ 的反射点 $P'$ 也必须在该图形上。这条直线 $L$ 被称为对称轴。双边对称是最常见和最容易识别的对称类型。
本段不含公式。但可以用代数来描述双边对称。
如果以对称轴为 $y$ 轴，那么一个点 $(x, y)$ 的反射点就是 $(-x, y)$。如果一个图形由方程 $f(x, y) = 0$ 定义，且该图形关于 $y$ 轴对称，那么必须满足 $f(x, y) = f(-x, y)$ 对所有在图形上的点 $(x, y)$ 成立。例如，方程为 $x^2 + y^2 = 1$ 的圆，用 $-x$ 替换 $x$ 得到 $(-x)^2 + y^2 = 1$，即 $x^2 + y^2 = 1$，方程不变，所以圆关于 $y$ 轴对称。同理，它也关于 $x$ 轴对称。
- 示例1：考虑一个位于 $(-2, 3)$ 的点。如果对称轴是 $y$ 轴（即直线 $x=0$），那么它的对称点是 $(2, 3)$。
- 示例2：考虑一个等腰三角形，其顶点为 $A(0, 5)$、$B(-4, 0)$ 和 $C(4, 0)$。它的对称轴是 $y$ 轴。点 $B(-4, 0)$ 关于 $y$ 轴的反射点是 $C(4, 0)$，它仍然在三角形上。线段 $AB$ 的反射是线段 $AC$。
- 对称轴的数量：一个图形可以没有对称轴，也可以有一条或多条对称轴。例如，一个正方形有4条对称轴，一个圆有无数条对称轴（任何过圆心的直线都是对称轴）。
- 反射是“翻转”：反射操作不同于旋转。一个具有手性的物体（例如你的左手）经过反射后会变成它的对映体（你的右手），这是无法通过在平面内旋转得到的。可以想象成把图形从纸上“掀起来”，翻个面，再印回去。
本段通过图片实例介绍了双边对称（即反射对称），其核心特征是存在一条对称轴，图形沿该轴反射后保持不变。
这部分内容旨在通过生活中常见的例子，直观地引入第一种基本的平面对称操作——反射。这是构建对称群概念的第一个积木。
双边对称就像是折纸。如果你沿着对称轴将一张印有图形的纸对折，图形的两半会完美地重合在一起。对称轴就是那条折痕。
站在湖边，看到你的倒影。你和你的倒影构成了一个关于水面的对称系统。水面就是那个对称“面”（在二维平面上就是对称轴）。
2.3 旋转对称
📜 [原文7]
旋转对称。
这段内容通过一张图片和文字，介绍了第二种对称类型：旋转对称。
- 图片内容：图片展示了一个五角星。这个五角星的特点是，如果将它绕其中心点旋转一定的角度，它会与自身重合。
- “旋转对称”：在数学上，如果一个图形绕某一个中心点 $C$ 旋转一个角度 $\theta$ (非360度的整数倍)后，能与自身完全重合，那么这个图形就具有旋转对称性。点 $C$ 被称为旋转中心。对于这个五角星，它可以绕中心旋转 $360/5 = 72$ 度，以及72度的整数倍（144度, 216度, 288度）后与自身重合。我们称它具有5重旋转对称性。
本段不含公式。但可以用代数来描述旋转对称。
在以旋转中心为原点的复平面上，一个点 $z$ 绕原点逆时针旋转角度 $\theta$ 后，会变到点 $z' = z \cdot e^{i\theta}$。如果一个图形 $S$ 具有绕原点的 $\theta$ 角旋转对称性，那么对于任意属于 $S$ 的点 $z$，点 $z \cdot e^{i\theta}$ 也必须属于 $S$。
- 示例1 (正方形)：一个正方形具有4重旋转对称性。它可以绕中心旋转90度、180度、270度后与自身重合。如果其顶点在复平面上是 $1, i, -1, -i$，绕原点旋转90度（乘以 $e^{i\pi/2} = i$）后，这四个点分别变到 $i, -1, -i, 1$，顶点集合保持不变。
- 示例2 (等边三角形)：一个等边三角形具有3重旋转对称性。它可以绕中心旋转120度、240度后与自身重合。
- 平凡旋转：任何图形绕任何点旋转360度（或0度）都会与自身重合。这被称为平凡对称或恒等变换。当我们说一个图形具有旋转对称性时，通常指的是存在至少一个非平凡的对称旋转角度（即角度在 (0, 360) 度之间）。
- 旋转的阶：如果一个图形的最小对称旋转角是 $360/n$ 度，我们称这个图形具有 $n$ 重旋转对称性，或者说它的旋转对称群是 $n$ 阶的。例如，五角星是5重，正方形是4重。一个圆具有无限重旋转对称性，因为它可以旋转任意角度而不变。
本段通过五角星的例子介绍了旋转对称，其核心特征是存在一个旋转中心，图形绕该中心旋转特定角度后保持不变。
这部分内容旨在引入第二种基本的平面对称操作——旋转。旋转和反射是构成有限图形对称群（即所谓的点群）的基本元素。
旋转对称就像一个旋转木马或一个风车。当它转动时，在某些特定的位置，它看起来和开始时一模一样。那个中心轴就是旋转中心，每次看起来一样所转过的角度就是对称旋转角。
盯着一个时钟的中心。秒针每过一秒就转动6度，但整个钟面看起来并没有变化（如果我们忽略上面的数字和指针的话）。或者看一个汽车的轮毂，许多轮毂的设计都具有旋转对称性，这样在轮子旋转时能产生动态的美感。
2.4 平移对称
📜 [原文8]
平移对称。
像这样的图形被认为在两个方向上无限延伸。
这段内容通过两张图片和文字，介绍了第三种对称类型：平移对称。
- 图片内容：图片展示了两种重复性的图案。第一种是一系列重复的曲线，第二种是类似中式窗格的图案。这两种图案的共同特点是，如果将整个图案沿着某个方向移动一段特定的距离，得到的图案会和原来的图案完全重合。
- “平移对称”：在数学上，如果一个图形沿着一个非零向量 $\vec{v}$ 平移后，能与自身完全重合，那么这个图形就具有平移对称性。
- “像这样的图形被认为在两个方向上无限延伸。”：这是一个非常重要的说明。严格来说，只有无限延伸的图形才能具有真正的平移对称性。对于一个有限的图形，例如 "ABCABCABC"，你将它向右移动3个字符的距离，它并不能与自身“完全”重合，因为左边会空出3个字符，右边会多出3个字符。只有当这个序列在左右两个方向上无限重复，即 ...ABCABCABC...，它才具有平移对称性。书中的图案也是如此，我们必须想象它们在指定的方向上是无限铺开的。
本段不含公式。但可以用代数来描述平移对称。
一个点 $P$ (由位置向量 $\vec{p}$ 表示) 经过向量 $\vec{v}$ 平移后，会到达点 $P'$ (由位置向量 $\vec{p}' = \vec{p} + \vec{v}$ 表示)。如果一个图形 $S$ 具有关于向量 $\vec{v}$ 的平移对称性，那么对于任意属于 $S$ 的点 $P$，点 $P'$ 也必须属于 $S$。
- 示例1：函数 $f(x) = \sin(x)$ 的图像具有平移对称性。它的周期是 $2\pi$。如果你将整个正弦曲线向右平移 $2\pi$ 个单位，它会与自身重合。这里的平移向量是 $(2\pi, 0)$。它也关于 $(2k\pi, 0)$ 平移对称，其中 $k$ 是任意整数。
- 示例2：考虑一个无限棋盘格。将整个棋盘向上移动一个格子的距离，或者向右移动一个格子的距离，棋盘的黑白格分布都保持不变。如果一个格子的边长是1，那么这个棋盘就具有由向量 $(m, n)$ 生成的平移对称性，其中 $m, n$ 是任意整数。
- 有限 vs 无限：平移对称性是无限图形的典型特征。有限图形（除了空集和整个平面）不可能具有平移对称性。在物理学和材料科学中，晶体被理想化为具有平移对称性的无限点阵，这是一种近似，因为真实晶体总是有限的。
- 基本平移向量：对于一个具有平移对称性的图案，通常存在一个或多个“最小”的非零平移向量，所有其他的对称平移向量都是这些基本向量的整数倍线性组合。这些基本向量构成了所谓的“晶格”。
本段介绍了平移对称，其核心特征是将整个（无限延伸的）图形沿某个向量移动后，图形保持不变。
这部分内容引入了第三种基本的平面对称操作——平移。与反射和旋转主要应用于有限图形不同，平移是研究无限、周期性图案（如饰带、壁纸、晶格）的基础。
平移对称就像是复制和粘贴一条无限长的链条。你复制整条链条，然后把它精确地移动一个链环的长度，再粘贴回去，你会发现它和原来的链条完美地叠在一起。那个链环的长度和方向就对应着平移向量。
想象一条长长的铁轨，铁轨上的枕木以相同的间隔重复出现。如果你闭上眼睛，向前走正好一个枕木间距的距离，然后睁开眼，你看到的景象和之前完全一样。这就是平移对称。或者想象一张无限大的、铺满相同瓷砖的地板。
2.5 滑动对称
📜 [原文9]
还有第四种对称性，尽管它的名字——滑动对称——可能不太为人所知：
滑动对称。
这段内容介绍了第四种，也是相对最不直观的一种平面对称类型：滑动对称。
- “还有第四种对称性，尽管它的名字——滑动对称——可能不太为人所知：”：这句话引出了一个新的概念，并承认它不像双边对称或旋转对称那样广为人知。
- 图片内容：图片展示了一串脚印。这个图案既没有反射对称轴（因为左右脚不同），也没有旋转对称点。它也不具有单纯的平移对称性，因为如果只把它平移一步的距离，左脚印会移动到右脚印的位置，图案不重合。
- “滑动对称”：滑动对称（Glide Reflection）是一种复合对称操作，它由两步组成：
a. 沿着一条直线（称为滑动轴）进行平移。
b. 然后关于同一条直线进行反射。
这两步的顺序可以交换，结果是一样的。脚印图案就具有滑动对称性。它的滑动轴是沿着脚印前进方向的中心线。将整个图案平移半步的距离（例如，从一个左脚印的中心到前后两个脚印的中心位置），然后再关于中心线反射，你会发现整个脚印图案恢复原状（左脚印的像落在下一个左脚印上，右脚印的像落在下一个右脚印上）。
本段不含公式。但可以用代数来描述滑动对称。
假设滑动轴是 $x$ 轴，平移向量是 $(\Delta x, 0)$。那么一个点 $(x, y)$ 经过滑动对称操作后，会变到点 $(x+\Delta x, -y)$。首先沿着 $x$ 轴平移 $\Delta x$ 距离，点变为 $(x+\Delta x, y)$，然后再关于 $x$ 轴反射，点变为 $(x+\Delta x, -y)$。
- 示例1 (脚印)：假设左脚印中心在 $(0, -1)$，右脚印中心在 $(2, 1)$，下一个左脚印中心在 $(4, -1)$。滑动轴是 $x$ 轴。平移向量是 $(2, 0)$。考虑点 $(0, -1)$（左脚印中心），平移后是 $(2, -1)$，再反射后是 $(2, 1)$，这恰好是右脚印的中心。再对 $(2, 1)$ 操作一次，平移后是 $(4, 1)$，反射后是 $(4, -1)$，这恰好是下一个左脚印的中心。
- 示例2：考虑一个图案，它由位于所有整数点 $(n, 1)$ 的向上箭头和所有整数点 $(n, -1)$ 的向下箭头组成，但向上和向下箭头交错半个单位，例如向上箭头在 $x=n$，向下箭头在 $x=n+0.5$。这个图案不具有单纯的平移或反射对称，但它具有滑动对称。滑动轴是 $x$ 轴，平移量是 $(0.5, 0)$。
- 滑动对称 vs. 平移+反射：一个图案可能同时具有平移对称性和反射对称性（例如，一排无限延伸的字母"H"：HHH...）。这种情况下，它也必然具有滑动对称性（因为平移后再反射也是一个对称操作）。但滑动对称这个术语通常用来特指那些“只有”滑动对称而没有单纯反射对称的图案，就像脚印一样。
- 操作的平方：对一个滑动对称操作连续进行两次，其效果等同于一个纯粹的平移操作（平移距离是原来滑动距离的两倍）。在脚印的例子中，操作两次后，左脚印会移动到下一个左脚印的位置，这一个纯平移。
本段介绍了滑动对称，它是一种由平移和反射复合而成的对称操作。脚印是滑动对称最经典的例子。
这部分内容旨在补全平面等距变换的四种基本类型。平移、旋转、反射和滑动对称是构成所有平面对称群（包括7种饰带群和17种壁纸群）的基本构件。缺少滑动对称，对周期性图案的分类就是不完整的。
滑动对称就像是在沙滩上边走边在身后留下一串镜像脚印。你向前迈一步（平移），然后一个“镜像魔法”把你刚刚留下的脚印变成了另一只脚的形状（反射）。
想象拉开一个拉链。拉链的左右两排齿是相互错开的。你不能通过简单的平移或反射让一排齿和另一排齿重合。但是，如果你把一排齿沿着拉链方向平移半个齿的距离，再关于中心线反射，它就会和另一排齿完美啮合。拉链的结构就蕴含了滑动对称性。
2.6 对称性的组合
📜 [原文10]
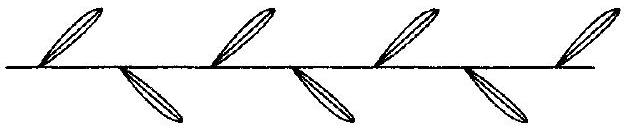
像下面所示的墙纸图案可能具有两个独立的平移对称性，
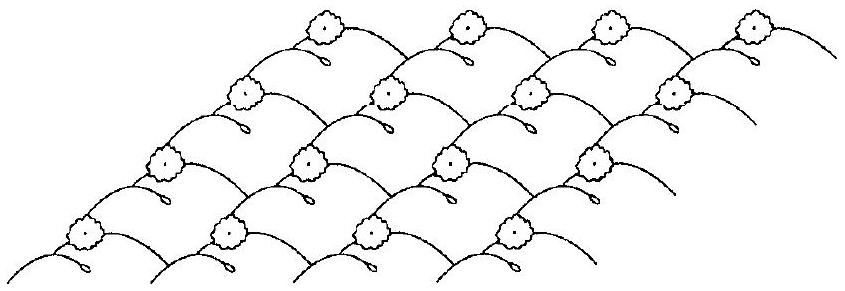
并且可能出现其他对称组合。这颗星星既有双边对称性，也有旋转对称性。在下图中，平移对称和旋转对称结合在一起：
$，这个单元的右上角在 $(5, 3)$，并且图案是矩形排列的。那么，两个独立的平移向量可以是 $\vec{v}_1 = (5, 0)$ (水平平移) 和 $\vec{v}_2 = (0, 3)$ (垂直平移)。任何形如 $m\vec{v}_1 + n\vec{v}_2 = (5m, 3n)$ （其中 $m, n$ 为整数）的平移都是该墙纸的对称操作。
- 星星的对称操作：对于一个正五边形（或五角星），它的对称操作集合（对称群 $D_5$）包含10个元素：
- 5个旋转操作：旋转0°, 72°, 144°, 216°, 288°。
- 5个反射操作：关于5条对称轴的反射。
- 平移与旋转结合：考虑一个无限的数列 ...-A-A-A-...，其中每个A都具有2重旋转对称性（旋转180度不变，比如字母S或Z也可以）。这个图案既有平移对称性（平移一个单位距离），在每个字母的中心又有180度旋转对称中心。
- 独立向量的定义：两个向量“独立”，在二维平面上意味着它们不共线。如果两个平移向量共线，例如 $\vec{v}_1 = (1,0)$ 和 $\vec{v}_2 = (2,0)$，那么它们不是独立的，因为第二个平移可以由第一个平移重复两次得到。二维墙纸图案必须有两个不共线的平移向量。
- 对称操作的封闭性：一个图形的所有对称操作（反射、旋转、平移等）的集合，对于“复合操作”（即连续进行两个操作）是封闭的。例如，对正方形先旋转90度，再进行一次反射，其结果等效于进行另一次反射。这个封闭的对称操作集合，再加上一个满足特定规则的“乘法”（复合操作），就构成了一个群。这正是群论与对称性联系的核心。
本段通过三个例子说明了不同的对称类型可以组合存在于同一个图形中，形成了更丰富、更复杂的对称模式。例如，平移对称可以和旋转对称、反射对称等结合，构成饰带群和壁纸群。
这部分内容的目的是从介绍单一对称类型过渡到介绍对称性的组合，为引入“对称群”这一核心概念做铺垫。一个物体的对称群不是指某一种对称操作，而是指它所拥有的“所有”对称操作的集合以及这些操作之间的合成规则。
回到图形设计师的工具箱。现在你不是一次只用一个工具，而是可以组合使用。你可以先用“旋转复制”工具做一个风车，然后再用“复制-粘贴-移动”工具把这个风车铺满整个屏幕。这样你就创造了一个兼具旋转和平移对称性的复杂图案。
观察一个蜂巢的截面。它是由无数个正六边形铺成的。这个图案不仅有两个独立的平移对称性（可以沿两个不同方向平移后重合），还在每个六边形的中心具有6重旋转对称性，同时还具有多种反射对称和滑动对称。蜂巢的对称性就是一个非常复杂的组合，其对称群是17个壁纸群中的一个（p6m）。
7行间公式索引
本文件 Algebra Ch6.1.ZH.md 不包含任何使用
8行间公式索引
本文件 Algebra Ch6.1.ZH.md 不包含任何使用