11. 平面等距变换的代数与几何描述
1.1. 引言:研究目标与方法
📜 [原文1]
在本节中,我们将从代数和几何两方面描述平面的等距变换。
我们将平面的等距变换群记为 $M$。为了在该群中进行计算,我们选择一些特殊的等距变换作为生成元,并获得它们之间的关系。这些关系在某种程度上类似于定义对称群 $S_{3}$ 的关系,但由于 $M$ 是无限的,因此关系更多。
本段是这一节的开篇,阐述了本节的核心目标和研究方法。
- 研究对象: 平面的等距变换(isometries of the plane)。等距变换指的是平面上的一种变换(可以想象成移动或翻转),它保持任意两点之间的距离不变。就像你移动一张刚性纸片,纸片上任意两个点之间的距离在移动前后都是一样的。这种变换不会拉伸、压缩或撕裂平面。常见的等距变换包括平移、旋转和反射。
- 研究角度: 作者提出了两个角度来描述这些变换:
- 代数角度:将这些变换看作是一个代数结构——群 (Group) 的元素。群是一个集合,配上一种二元运算(在这里是变换的复合,即先做一个变换再做另一个),满足一些特定的公理(封闭性、结合律、存在单位元、存在逆元)。我们会用符号、公式和方程来描述这些变换以及它们之间的相互作用。
- 几何角度:关注这些变换在视觉上是如何改变平面的。例如,一个变换是把整个平面向右移动了3个单位,还是绕着某个点旋转了90度。
- 研究方法:
- 将所有平面的等距变换的集合记为 $M$。这个 $M$ 和变换的复合运算一起构成了一个群,称为平面的等距变换群。
- 为了研究这个群 $M$,我们不需要列出其中所有的变换(因为有无穷多个)。相反,我们采用一种更高效的方法:找到一小组最基本的变换,称为生成元 (generators)。通过反复组合这些生成元,我们可以得到 $M$ 中的任何一个等距变换。这就像用红、黄、蓝三种基本颜色可以混合出各种颜色一样。
- 定义了生成元之后,我们需要了解它们之间是如何相互作用的。这些相互作用的规则被称为关系 (relations)。例如,一个旋转和一个平移组合起来,会得到一个新的变换,这个新变换是什么?这就是关系要回答的问题。
- 类比: 作者用对称群 $S_3$ 来类比。$S_3$ 是一个包含6个元素的有限群,它可以被一个旋转和一个反射这两个生成元所生成,并且它们之间满足一些简单的关系。而我们现在研究的等距变换群 $M$ 是一个无限群,因为它包含无数个平移(可以向任何方向移动任何距离)和旋转(可以绕任何点旋转任何角度)。因此,$M$ 的生成元之间的关系会比 $S_3$ 更复杂、更多样。
- 等距变换: 想象平面上的两个点 $A=(0,0)$ 和 $B=(3,4)$。它们之间的距离是 $\sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9+16} = \sqrt{25} = 5$。现在我们对整个平面进行一个平移,把每个点 $(x,y)$ 都移动到 $(x+2, y+1)$。那么点 $A$ 移动到 $A'=(2,1)$,点 $B$ 移动到 $B'=(5,5)$。新点 $A'$ 和 $B'$ 之间的距离是 $\sqrt{(5-2)^2 + (5-1)^2} = \sqrt{3^2 + 4^2} = \sqrt{9+16} = 5$。距离没有改变,所以这个平移是一个等距变换。
- 生成元与关系 (类比): 想象你在一个一维的无限数轴上,你只能做两种操作:向右走一步 (记为 $R$) 和向左走一步 (记为 $L$)。$R$ 和 $L$ 就是这个运动群的生成元。它们之间的关系是什么?很明显,先向右走一步再向左走一步,等于没动。这个关系可以写成 $R \circ L = \text{Identity}$ (恒等操作)。通过组合 $R$ 和 $L$,你可以到达数轴上的任何整数点。平面的等距变换也是类似的道理,只是更复杂。
- 变换的顺序: 变换的复合(运算)通常不满足交换律。例如,先平移再旋转,和先旋转再平移,得到的结果一般是不同的。这在后面的关系部分会详细体现。
- 群和集合的区别: $M$ 不仅仅是一个集合,它是一个群。这意味着我们关心元素(等距变换)之间的运算(复合)。只罗列元素而不谈运算规则是没有意义的。
- 无限群的复杂性: 不要低估从有限群(如 $S_3$)到无限群(如 $M$)的跨越。无限群的结构要复杂得多,关系的数量和形式也会更丰富。
本段设定了本节的舞台:我们将使用代数工具(群、生成元、关系)来系统地、精确地描述和分类平面上所有保持距离不变的几何变换。
本段的目的是为读者建立一个清晰的路线图。它告知读者,我们将要从两个不同但互补的视角(代数与几何)来探索同一个核心概念(平面等距变换)。通过引入群、生成元和关系这些代数概念,它预示了我们将采用一种结构化、公理化的方法来处理一个看似直观的几何问题,从而实现更深刻的理解和更强的计算能力。
想象你有一块无限大的、画着方格的硬纸板(平面)。你可以对这块纸板做的所有操作,只要保证纸板本身不被弯曲或拉伸(保持距离不变),都属于平面等geom变换**。这些操作包括:
- 把整块纸板沿着某个方向滑动(平移)。
- 找一个点,用钉子钉住,然后转动纸板(旋转)。
- 沿着一条线,把纸板翻个面(反射)。
本节的目标就是把所有这些可能的操作(无穷多种)进行分类,并找出它们背后的“语法规则”(代数关系)。
想象你站在一个无边无际的冰面上。你可以在冰面上滑行到任何位置(平移),可以原地打转(绕你所在点的旋转),甚至可以想象有一个镜子立在冰面上,你看到了一个镜像的你(反射)。本节就是要研究所有这些运动方式的数学本质。
1.2. 等距变换的生成元
📜 [原文2]
我们选择一个坐标系并用它来将平面 $P$ 识别为空间 $\mathbb{R}^{2}$。然后我们选择平移、关于原点的旋转以及关于 $e_{1}$-轴的反射作为生成元。我们将通过角度 $\theta$ 的旋转记为 $\rho_{\theta}$,将关于 $e_{1}$-轴的反射记为 $r$。这些是线性算子,它们的矩阵 $R$ 和 $S_{0}$ 之前已经展示过(参见 (5.1.17) 和 (5.1.16))。
这段话定义了研究平面等距变换群 $M$ 所需的“基本积木”——生成元。
- 建立坐标系: 为了用代数(数字和矩阵)来描述几何(点和变换),我们首先要在平面 $P$ 上建立一个笛卡尔坐标系。这样,平面上的每一个点都可以用一个坐标对 $(x_1, x_2)$ 来表示。这个坐标对可以看作是二维实数空间 $\mathbb{R}^2$ 中的一个向量 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$。这么做的本质是“数字化”几何空间。
- 选择生成元: 作者没有选择所有类型的等距变换,而是只选了三种最基本的、特殊的变换作为生成元:
- 平移 (translation): 记为 $t_a$,表示将平面上的每个点都移动一个向量 $a$ 的距离和方向。
- 关于原点的旋转 (rotation about the origin): 记为 $\rho_{\theta}$,表示将平面上的每个点都绕着坐标系的原点 $(0,0)$ 逆时针旋转一个角度 $\theta$。
- 关于 $e_1$-轴的反射 (reflection about the $e_1$-axis): 记为 $r$。这里的 $e_1$-轴就是我们通常说的 $x$-轴。这个变换就像沿着 $x$-轴放了一面镜子,把每个点都翻到它的镜像位置。
- 生成元的特殊性: 注意,这里选择的旋转和反射都是非常特殊的。旋转必须是绕着原点的,反射必须是关于 $x$-轴的。为什么可以做这样的简化?因为后面会证明,任何等距变换(比如绕任意点 $p$ 的旋转,或关于任意直线 $\ell$ 的反射)都可以通过这三种基本生成元的组合来得到。
- 符号约定:
- $\rho_{\theta}$: 表示绕原点逆时针旋转角度 $\theta$。$\rho$ 是 rotation 的希腊字母写法。
- $r$: 表示关于 $x$-轴($e_1$-轴)的反射。$r$ 是 reflection 的首字母。
- 与线性代数关联: 作者提到,旋转 $\rho_{\theta}$ 和反射 $r$ 都是线性算子。这意味着它们可以用矩阵来表示。一个变换 $f$ 是线性的,如果它满足 $f(x+y)=f(x)+f(y)$ 和 $f(cx)=cf(x)$。绕原点的旋转和关于过原点的直线的反射都满足这个性质。而平移(只要平移向量非零)不是线性算子,因为它不满足 $f(0)=0$(它会把原点移动到其他地方)。
- 平移不是线性变换: 这是一个非常关键的区别。旋转 $\rho_{\theta}$ 和反射 $r$ 可以用一个 $2 \times 2$ 矩阵与坐标向量相乘来表示,但平移 $t_a$ 只能表示为向量加法。这个区别是理解后续复合规则的关键。
- 生成元的选择不是唯一的: 我们可以选择其他三、四种基本变换作为生成元。例如,我们可以选择两个不同直线(比如 $x$ 轴和 $y$ 轴)的反射作为生成元。但当前的选择(平移、绕原点旋转、关于 $x$ 轴反射)在代数计算上特别方便。
本段将研究等距变换的策略具体化:通过建立坐标系,将问题转化为 $\mathbb{R}^2$ 上的向量和矩阵运算,并选定了一组最基本的变换——任意平移、绕原点旋转、沿 $x$ 轴反射——作为构建所有等距变换的生成元。
本段的目的是奠定整个代数分析的基础。通过将几何问题坐标化,并将无穷的等距变换归结为三种基本生成元,它为后续的公式化和计算铺平了道路。这是一种化繁为简的经典数学策略。
这就像玩乐高积木。你有一堆各种各样(无穷无尽)的复杂积木块(所有的等距变换)。为了更好地理解它们,你发现其实只需要三种最基本的积木块:一种是“移动块”(平移),一种是“绕中心旋转块”(绕原点旋转),一种是“翻转块”(沿x轴反射)。通过组合这三种基本块,你可以拼出任何一个复杂的积木块。本段就是在定义这三种“基本乐高块”。
想象一张透明的坐标纸盖在另一张固定的地图上。
- 平移 $t_a$:你把整张透明纸平着滑动,不旋转。
- 旋转 $\rho_{\theta}$:你用一根针把透明纸的原点钉在地图的原点上,然后转动透明纸。
- 反射 $r$:你捏住透明纸的 $x$ 轴,然后把它像书页一样翻过来。
这三种基本动作就是我们的生成元。
1.3. 生成元的具体公式
📜 [原文3]
- 向量 $a$ 的平移 $t_{a}$: $t_{a}(x)=x+a=\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]+\left[\begin{array}{l}a_{1} \\ a_{2}\end{array}\right]$。
- 关于原点以角度 $\theta$ 的旋转 $\rho_{\theta}$: $\rho_{\theta}(x)=\left[\begin{array}{rr}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]$。
- 关于 $e_{1}$-轴的反射 $r$: $r(x)=\left[\begin{array}{rr}1 & 0 \\ 0 & -1\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]$。
这一部分给出了上一段提到的三种生成元的具体数学公式。
- 平移 (Translation):
- $t_a(x) = x + a$:这是平移的向量表示。$t_a$ 是作用在点 $x$ 上的变换,其结果是点 $x$ 的位置向量与平移向量 $a$ 相加。
- $\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]+\left[\begin{array}{l}a_{1} \\ a_{2}\end{array}\right]$:这是分量表示。点 $(x_1, x_2)$ 被移动到点 $(x_1+a_1, x_2+a_2)$。$x$ 坐标移动 $a_1$, $y$ 坐标移动 $a_2$。
- 旋转 (Rotation):
- $\rho_{\theta}(x) = R_{\theta}x$:这是旋转的矩阵表示。绕原点旋转一个角度 $\theta$ 的变换 $\rho_{\theta}$ 可以通过将点的坐标向量 $x$ 左乘一个 $2 \times 2$ 的旋转矩阵来实现。
- $\left[\begin{array}{rr}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]$:这是著名的二维旋转矩阵。当它乘以一个向量 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ 时,得到的新向量就是原向量绕原点逆时针旋转 $\theta$ 角后的位置。
- 反射 (Reflection):
- $r(x) = S_0 x$: 这是关于 $x$ 轴($e_1$ 轴)反射的矩阵表示。这个变换 $r$ 也是一个线性变换,可以通过左乘一个反射矩阵 $S_0$ 来实现。
- $\left[\begin{array}{rr}1 & 0 \\ 0 & -1\end{array}\right]$: 这是关于 $x$ 轴的反射矩阵。当它乘以一个向量 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ 时,结果是 $\begin{pmatrix} 1 \cdot x_1 + 0 \cdot x_2 \\ 0 \cdot x_1 + (-1) \cdot x_2 \end{pmatrix} = \begin{pmatrix} x_1 \\ -x_2 \end{pmatrix}$。这正是点 $(x_1, x_2)$ 关于 $x$ 轴的镜像点。
- 公式1: 平移 $t_{a}(x)=x+a$
- $t_a$: 一个函数/算子,表示“由向量 $a$ 定义的平移”。下标 $a$ 指明了平移的方向和大小。
- $x$: 输入,一个平面上的点,用其位置向量 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ 表示。
- $a$: 平移向量 $\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$。
- $x+a$: 向量加法,输出是平移后的新点的位置向量。
- 公式2: 旋转 $\rho_{\theta}(x)=\left[\begin{array}{rr}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]$
- $\rho_\theta$: 表示“绕原点逆时针旋转角度 $\theta$”的算子。
- $\left[\begin{array}{rr}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta\end{array}\right]$: 旋转矩阵 $R_\theta$。我们可以推导它:假设点 $P(x,y)$ 极坐标为 $(l, \alpha)$,则 $x = l \cos \alpha, y = l \sin \alpha$。旋转 $\theta$ 角后到点 $P'(x', y')$,其极坐标为 $(l, \alpha+\theta)$。所以 $x' = l \cos(\alpha+\theta) = l(\cos\alpha\cos\theta - \sin\alpha\sin\theta) = x\cos\theta - y\sin\theta$。同理 $y' = l \sin(\alpha+\theta) = l(\sin\alpha\cos\theta + \cos\alpha\sin\theta) = y\cos\theta + x\sin\theta$。写成矩阵形式就是:$\begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$。
- 公式3: 反射 $r(x)=\left[\begin{array}{rr}1 & 0 \\ 0 & -1\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]$
- $r$: 表示“关于 $x$ 轴的反射”的算子。
- $\left[\begin{array}{rr}1 & 0 \\ 0 & -1\end{array}\right]$: 反射矩阵。这个矩阵的作用是保持 $x_1$ 分量不变 ($1 \cdot x_1$),并将 $x_2$ 分量取反 ($-1 \cdot x_2$)。这正是关于 $x$ 轴做镜像的几何意义。
- 示例1: 平移
- 令平移向量 $a = \begin{pmatrix} 3 \\ -2 \end{pmatrix}$,作用于点 $x = \begin{pmatrix} 1 \\ 4 \end{pmatrix}$。
- $t_a(x) = x + a = \begin{pmatrix} 1 \\ 4 \end{pmatrix} + \begin{pmatrix} 3 \\ -2 \end{pmatrix} = \begin{pmatrix} 1+3 \\ 4-2 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix}$。
- 点 $(1,4)$ 被平移到了点 $(4,2)$。
- 示例2: 旋转
- 令旋转角度 $\theta = 90^\circ$ (或 $\pi/2$ 弧度)。$\cos(90^\circ)=0, \sin(90^\circ)=1$。
- 旋转矩阵为 $\left[\begin{array}{rr}0 & -1 \\ 1 & 0\end{array}\right]$。
- 作用于点 $x = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$。
- $\rho_{90^\circ}(x) = \left[\begin{array}{rr}0 & -1 \\ 1 & 0\end{array}\right] \begin{pmatrix} 2 \\ 3 \end{pmatrix} = \begin{pmatrix} 0 \cdot 2 + (-1) \cdot 3 \\ 1 \cdot 2 + 0 \cdot 3 \end{pmatrix} = \begin{pmatrix} -3 \\ 2 \end{pmatrix}$。
- 点 $(2,3)$ 被逆时针旋转 $90^\circ$ 后到达点 $(-3,2)$。
- 示例3: 反射
- 作用于点 $x = \begin{pmatrix} 5 \\ -6 \end{pmatrix}$。
- $r(x) = \left[\begin{array}{rr}1 & 0 \\ 0 & -1\end{array}\right] \begin{pmatrix} 5 \\ -6 \end{pmatrix} = \begin{pmatrix} 1 \cdot 5 + 0 \cdot (-6) \\ 0 \cdot 5 + (-1) \cdot (-6) \end{pmatrix} = \begin{pmatrix} 5 \\ 6 \end{pmatrix}$。
- 点 $(5, -6)$ 关于 $x$ 轴的镜像点是 $(5, 6)$。
- 角度单位: 在旋转矩阵的公式中,$\theta$ 通常使用弧度制。如果题目给的是角度制,需要先转换。例如 $90^\circ = \pi/2$ 弧度。
- 旋转方向: 这里的旋转矩阵是逆时针旋转。顺时针旋转 $\theta$ 等价于逆时针旋转 $-\theta$。由于 $\cos(-\theta)=\cos\theta, \sin(-\theta)=-\sin\theta$,顺时针旋转的矩阵为 $\left[\begin{array}{rr}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta\end{array}\right]$。
- 矩阵乘法顺序: 矩阵必须在向量的左边,即 $Rx$ 而不是 $xR$。矩阵乘法不满足交换律。
本段将三种生成元(平移、绕原点旋转、沿 $x$ 轴反射)从抽象概念转化为具体的、可计算的代数表达式:平移是向量加法,旋转和反射是矩阵乘法。
本段的目的是为“计算”做准备。通过提供这些明确的公式,我们就拥有了分析和组合这些变换的工具。任何复杂的等距变换,原则上都可以通过反复应用这些公式来计算其最终效果。这是连接几何直观与代数严谨性的桥梁。
这就像是给你的三种乐高基本块(移动、旋转、翻转)写下了详细的“使用说明书”。说明书用数学语言精确地告诉你,当你使用这些积木块时,平面上每个点的坐标会发生怎样的确切变化。
- 平移:在坐标网格上,所有点都像一个整体,沿着向量 $a$ 的箭头方向滑动。
- 旋转:想象坐标网格的原点有一个图钉。整个网格绕着图钉旋转,而网格线本身的角度也跟着改变。
- 反射:想象 $x$ 轴是一面镜子。每个点都跳到镜子另一侧同样距离的位置,它的 $y$ 坐标数值不变,但符号变了。
1.4. 生成元的完备性
📜 [原文4]
我们还没有列出所有的等距变换。不包括不通过原点的旋转,也不包括关于其他直线的反射,或滑移反射。然而,$M$ 的每个元素都是这些等距变换的乘积,因此它们生成了群。
这段话处理了一个潜在的疑问,并做出了一个核心论断。
- 提出疑问/承认不足: 作者坦诚,我们刚刚定义的三种基本操作(平移、$t_a$;绕原点旋转、$\rho_\theta$;关于 $x$ 轴反射,$r$)显然不是全部的等距变换。例如:
- 不通过原点的旋转: 比如,绕点 $(1,1)$ 旋转 $45^\circ$。这是一个合法的等距变换,但它不是我们定义的 $\rho_{45^\circ}$。
- 关于其他直线的反射: 比如,关于直线 $y=x$ 的反射。
- 滑移反射 (glide reflection): 这是一种更复杂的变换,它由一个反射和一个平行于反射轴的平移组合而成。想象在雪地上走路的脚印,左脚印和右脚印大致是镜像对称的,但又向前错开了一段距离。
- 核心论断: 尽管我们只列出了三种“特殊”的变换,但这个集合已经足够了。这个论断是:“$M$ 的每个元素都是这些等距变换的乘积”。
- “乘积”在这里指的是变换的复合(composition)。例如,$\rho_\theta \circ t_a$ 表示先进行平移 $t_a$,再进行旋转 $\rho_\theta$。(注意:函数复合的顺序是从右到左)。
- 这个论断意味着,任何你能想到的平面等距变换,无论它看起来多么复杂(如绕任意点的旋转或滑移反射),都可以被拆解成一系列我们定义的三种基本变换的组合。
- 生成群 (generate the group): 这个核心论断直接引出了结论——我们选出的这三种变换(平移、绕原点旋转、关于 $x$ 轴反射)是等距变换群 $M$ 的一个生成集 (generating set)。它们是构建整个群 $M$ 的基本材料。
- 如何生成一个“不通过原点的旋转”?
- 目标:将平面绕点 $p=(1,1)$ 旋转 $90^\circ$。我们称这个变换为 $R_{90, p}$。
- 分解步骤:我们可以利用我们已有的工具(绕原点的旋转 $\rho_{90}$ 和平移 $t_a$)来“拼凑”出这个变换。
- 第一步:将旋转中心平移到原点。使用平移 $t_{-p}$,即 $t_{(-1,-1)}$,将点 $p=(1,1)$ 移动到原点 $(0,0)$。
- 第二步:执行我们熟悉的绕原点旋转。现在旋转中心已经在原点了,我们可以使用 $\rho_{90}$ 进行旋转。
- 第三步:将原点平移回原来的旋转中心。使用平移 $t_p$,即 $t_{(1,1)}$,将原点移回到点 $p=(1,1)$。
- 代数表示: 整个变换的复合为 $R_{90, p} = t_p \circ \rho_{90} \circ t_{-p}$。
- 我们成功地用生成元(一个旋转和两个平移)的复合表示了一个更复杂的变换。
- 复合顺序至关重要: $t_p \circ \rho_{90} \circ t_{-p}$ 的顺序不能错。它是把一个点 $x$ 先做 $t_{-p}$,再做 $\rho_{90}$,最后做 $t_p$。写出来就是 $t_p(\rho_{90}(t_{-p}(x)))$。如果顺序颠倒,例如变成 $t_{-p} \circ \rho_{90} \circ t_p$,那将是绕 $(-1,-1)$ 点的旋转,完全不同。
本段的核心思想是“完备性”。它申明我们选出的三种基本变换(生成元)虽然看起来很特殊、很简单,但它们的组合能力是完备的,足以构建出整个平面等距变换群 $M$ 中的任何一个元素。
本段的目的是打消读者的疑虑,建立信心。在只介绍了三种特殊变换后,读者很自然会问“这够用吗?”。本段直接回答了这个问题:“够用”,并解释了“够用”的含义,即任何变换都可以由它们“生成”。这为后续只研究这三种生成元及其关系的合理性提供了辩护。
回到乐高积木的比喻。你可能觉得只有三种基本块,怎么可能拼出宇宙飞船模型呢?本段告诉你,这三种基本块设计得非常好,通过不同的方式组合、堆叠它们(对应变换的复合),你确实可以拼出任何你想要的复杂模型(任何等距变换)。
想象你的工具箱里只有三种工具:一把能让你在平面上滑动的“滑动器”(平移),一个只能在原点打桩旋转的“圆规”(绕原点旋转),和一把只能沿着 $x$ 轴翻折的“折尺”(关于 $x$ 轴反射)。本段告诉你,即使工具这么有限,只要你足够聪明地组合使用它们,你就能实现任何对平面的刚性操作。例如,想绕任意点 $P$ 旋转,你可以先用“滑动器”把 $P$ 点滑到原点,再用“圆规”旋转,最后再用“滑动器”把原点滑回 $P$ 点。
22. 等距变换的代数结构
2.1. 等距变换的唯一分解定理
📜 [原文5]
定理 6.3.2 令 $m$ 为平面的等距变换。那么 $m=t_{v} \rho_{\theta}$,或者 $m=t_{v} \rho_{\theta} r$,其中 $v$ 是一个唯一确定的向量,$\theta$ 是一个唯一确定的角度,可能为零。
这个定理是本节第一个重要的结构性结论。它为平面上的任何一个等距变换 $m$ 提供了一个“标准范式”或“标准分解式”。
- 定理内容: 它说,任何一个等距变换 $m$ 都可以被写成以下两种形式之一:
- 形式一: $m = t_v \rho_\theta$。这是一个绕原点的旋转 $\rho_\theta$,后面跟着一个平移 $t_v$。
- 形式二: $m = t_v \rho_\theta r$。这是一个关于 $x$ 轴的反射 $r$,然后是一个绕原点的旋转 $\rho_\theta$,最后是一个平移 $t_v$。(注意复合顺序从右到左)。
- 唯一性: 这种表示法是唯一的。对于一个给定的等距变换 $m$,能把它写成上述形式的平移向量 $v$ 和旋转角度 $\theta$ 是独一无二的。
- 分类: 这个定理实际上将所有等距变换分成了两大类:
- 保持定向 (orientation-preserving) 的变换,它们可以被写成 $t_v \rho_\theta$ 的形式。直观上,这些变换像是把平面作为一个刚性物体来移动和旋转,但不会“翻面”。比如,如果你在平面上画了一个顺时针的圆,经过这类变换后,它依然是顺时针的。平移和旋转都属于这一类。
- 改变定向 (orientation-reversing) 的变换,它们可以被写成 $t_v \rho_\theta r$ 的形式。这些变换中包含了一次反射(翻面操作)。经过这类变换后,原来顺时针的圆会变成逆时针的。反射和滑移反射属于这一类。
- $\theta$ 可能为零: 定理中提到 $\theta$ 可能为零。如果 $\theta=0$,那么 $\rho_0$ 就是恒等变换(不做任何旋转),因为旋转矩阵变成单位矩阵 $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$。
- 当 $\theta=0$ 时,形式一 $m=t_v \rho_0 = t_v$,就是一个纯粹的平移。
- 当 $\theta=0$ 时,形式二 $m=t_v \rho_0 r = t_v r$,就是一个反射再加一个平移。这就是滑移反射的一般形式。
[证明思路解析]
📜 [原文6]
证明。推论 6.2.7 断言任何等距变换 $m$ 都可以唯一地写成 $m=t_{v} \varphi$ 的形式,其中 $\varphi$ 是一个正交算子。空间 $\mathbb{R}^{2}$ 上的正交线性算子是关于原点的旋转 $\rho_{\theta}$ 和关于通过原点的直线的反射。这些反射具有 $\rho_{\theta} r$ 的形式(参见 (5.1.17))。
- 引用先前的结论 (推论 6.2.7): 证明的第一步是引用一个更早的结论:任何等距变换 $m$ 都可以被唯一地分解为一个平移 $t_v$ 和一个正交算子 $\varphi$ 的复合,即 $m = t_v \varphi$。
- 正交算子 $\varphi$ 是一个保持原点不变的等距变换。在几何上,它保持向量的长度和向量之间的夹角不变。在线性代数中,它的矩阵 $Q$ 满足 $Q^T Q = I$(正交矩阵)。
- 分类二维正交算子: 证明的第二步是具体化在二维平面 $\mathbb{R}^2$ 上,正交算子 $\varphi$ 到底有哪些。结论是,它们只有两种:
- 旋转: 绕原点的旋转 $\rho_\theta$。这些变换的矩阵是 $\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}$,其行列式为 $\cos^2\theta - (-\sin^2\theta) = 1$。这些是保持定向的正交算子。
- 反射: 关于一条穿过原点的直线的反射。之前的章节 (5.1.17) 已经证明,任何这样的一条反射都可以表示为“先做一个标准的关于 $x$ 轴的反射 $r$,然后再做一个合适的绕原点的旋转 $\rho_\theta$”。也就是说,任何关于过原点直线的反射都可以写成 $\rho_\theta r$ 的形式。这些变换的矩阵行列式为 $-1$,是改变定向的正交算子。
- 组合结论: 将步骤1和2结合起来:
- 既然任何等距变换是 $m = t_v \varphi$,而 $\varphi$ 要么是 $\rho_\theta$,要么是 $\rho_\theta r$。
- 那么 $m$ 就必然是 $m = t_v \rho_\theta$ 或者 $m = t_v \rho_\theta r$。
- 由于 $m=t_v\varphi$ 的分解是唯一的,而 $\varphi$ 到 $\rho_\theta$ 或 $\rho_\theta r$ 的表示也是唯一的,因此整个分解 $m=t_v\rho_\theta$ 或 $m=t_v\rho_\theta r$ 中的 $v$ 和 $\theta$ 也是唯一的。
这个定理极其强大,它为所有看起来杂乱无章的平面等距变换提供了一个统一的、唯一的“身份证”。每个变换都可以被两个参数(平移向量 $v$)和(旋转角度 $\theta$)以及一个“翻转”标志(是否包含 $r$)来唯一标识。
这个定理的目的是为了“标准化”。有了这个标准形式,我们在处理一个任意的等距变换时,就有了一个固定的入手点。我们可以先确定它是保持定向还是改变定向,然后找出它的平移部分和旋转/反射部分。这为后续的分类和计算提供了极大的便利。
想象你在整理一个大仓库,里面堆满了各式各样的椅子(等距变换)。你发现所有椅子都可以被归为两类:“正着放的椅子”(保持定向)和“倒着放的椅子”(改变定向)。然后你进一步发现,任何一把“正着放的椅子”,它的位置和朝向都可以通过“先在仓库中心转一个角度,再把它搬到某个地方”来描述。任何一把“倒着放的椅子”,其位置和姿态都可以通过“先在仓库中心把它上下翻转并转一个角度,再把它搬到某个地方”来描述。这个定理就是这个整理仓库的“万能描述法则”。
2.2. 定向的保持与改变
📜 [原文7]
$t_{v} \rho_{\theta}$ 形式的等距变换保持定向,而 $t_{v} \rho_{\theta} r$ 改变定向。
这段话是对定理 6.3.2 分类的几何意义的阐述。
- 定向 (Orientation): 平面的定向可以直观地理解为“顺时针”和“逆时针”方向的区分。你可以在平面上画一个带箭头的圆弧,或者画一个带顶点顺序的三角形(如 $ABC$)。
- 保持定向 (Orientation-Preserving): 一个变换如果保持定向,意味着它不会改变这种“顺时针/逆时针”的性质。
- 如果你有一个按 $A \rightarrow B \rightarrow C$ 顺序为逆时针的三角形,经过变换后得到新三角形 $A'B'C'$,那么 $A' \rightarrow B' \rightarrow C'$ 的顺序也必须是逆时针的。
- 平移 $t_v$ 只是把图形平移,显然不改变定向。
- 旋转 $\rho_\theta$ 只是把图形转动,也不改变定向。
- 它们的复合 $t_v \rho_\theta$ 自然也保持定向。
- 从线性代数角度看,这种变换的线性部分(即 $\rho_\theta$)的矩阵行列式为 $+1$。
- 改变定向 (Orientation-Reversing): 一个变换如果改变定向,意味着它会颠倒“顺时针/逆时针”的性质。
- 如果原来的三角形 $ABC$ 是逆时针的,变换后的 $A'B'C'$ 会变成顺时针的。
- 这本质上是一个“翻面”操作,就像你看镜子里的自己,你的左手在镜像里变成了“右手”(相对于镜像身体的左右)。
- 反射 $r$ 是最基本的改变定向的变换。
- 任何包含奇数次反射的复合变换都会改变定向。形式 $t_v \rho_\theta r$ 中包含了一次反射 $r$,所以它改变定向。
- 从线性代数角度看,这种变换的线性部分(即 $\rho_\theta r$)的矩阵行列式为 $-1$。
- 保持定向示例:
- 考虑三个点 $O(0,0), A(1,0), B(0,1)$。从 $O \rightarrow A \rightarrow B$ 是逆时针顺序。
- 应用变换 $m = t_{(2,1)}\rho_{90}$。
- 先旋转 $\rho_{90}$: $O \rightarrow O'(0,0)$, $A \rightarrow A'(0,1)$, $B \rightarrow B'(-1,0)$。顺序 $O' \rightarrow A' \rightarrow B'$ 仍然是逆时针。
- 再平移 $t_{(2,1)}$: $O' \rightarrow O''(2,1)$, $A' \rightarrow A''(2,2)$, $B' \rightarrow B''(1,1)$。顺序 $O'' \rightarrow A'' \rightarrow B''$ 依然是逆时针。
- 改变定向示例:
- 还是用 $O(0,0), A(1,0), B(0,1)$,逆时针。
- 应用变换 $m=r$ (关于 $x$ 轴反射)。
- $O \rightarrow O'(0,0)$, $A \rightarrow A'(1,0)$, $B \rightarrow B'(0,-1)$。
- 现在我们看新的顺序 $O' \rightarrow A' \rightarrow B'$。从 $(0,0)$ 到 $(1,0)$ 再到 $(0,-1)$,这是一个顺时针的顺序。定向被改变了。
本段用定向这个几何概念,给定理 6.3.2 的两种标准形式赋予了直观的物理意义:一种是刚体在平面内的移动和旋转,另一种是刚体移动旋转后再翻个面。
这不仅是一个解释,更是一个重要的分类标准。在群论中,所有保持定向的等距变换构成一个子群,称为特殊欧几里得群 $SE(2)$。这个子群在整个等距变换群 $M$ 中是一个指数为2的正规子群,这是群论中一个非常重要的结构。
2.3. 生成元的复合规则(关系)
📜 [原文8]
在 $M$ 中的计算可以使用符号 $t_{v}, \rho_{\theta}$ 和 $r$ 进行,并使用以下组合规则。这些规则可以通过公式 6.3.1 进行验证(另请参见 (6.2.8))。
这段给出了我们选定的生成元之间进行复合运算的“语法规则”,即关系。这些关系是进行代数计算的基础。我们逐条分析:
- $\rho_{\theta} t_{v} =t_{v^{\prime}} \rho_{\theta}, \text{ 其中 } v^{\prime}=\rho_{\theta}(v)$
- 含义: “先平移 $v$ 再绕原点旋转 $\theta$”,这个组合变换等价于“先绕原点旋转 $\theta$,再平移另一个向量 $v'$”。而这个新的平移向量 $v'$ 正是原来的平移向量 $v$ 被旋转 $\theta$ 角后得到的向量。
- 直观理解: 想象一个点 $P$。先把它平移 $v$ 到 $P+v$,再把结果绕原点旋转 $\theta$ 得到 $\rho_\theta(P+v)$。由于旋转是线性的,所以 $\rho_\theta(P+v) = \rho_\theta(P) + \rho_\theta(v)$。这个结果可以看作是:先把 $P$ 点旋转 $\theta$ 得到 $\rho_\theta(P)$,然后再把它平移一个向量 $\rho_\theta(v)$。这正是 $t_{\rho_\theta(v)} \rho_\theta$ 作用在 $P$ 上的结果。
- 核心: 旋转和平移的顺序可以交换,但代价是必须把平移向量也旋转一下。
- $r t_{v} =t_{v^{\prime}} r, \text{ 其中 } v^{\prime}=r(v)$
- 含义: “先平移 $v$ 再关于 $x$ 轴反射”,等价于“先关于 $x$ 轴反射,再平移一个新的向量 $v'$”。这个新向量 $v'$ 是原平移向量 $v$ 被 $x$ 轴反射后的向量。
- 证明类似于上一条,利用了反射 $r$ 也是线性的性质:$r(P+v) = r(P) + r(v)$。
- $r \rho_{\theta} =\rho_{-\theta} r$
- 含义: “先绕原点旋转 $\theta$ 再关于 $x$ 轴反射”,等价于“先关于 $x$ 轴反射,再绕原点旋转 $-\theta$(即顺时针旋转 $\theta$)”。
- 直观理解: 想象你面前有一本书,你先把它逆时针转了30度,然后上下翻个面。这和你先把它上下翻个面,再顺时针转30度,最后得到书的姿态是一样的。反射会把旋转的方向颠倒。
- $t_{v} t_{w} =t_{v+w}, \quad \rho_{\theta} \rho_{\eta}=\rho_{\theta+\eta}, \quad \text{且} \quad r r=1$
- 这三条是同类变换复合的规则。
- $t_{v} t_{w} =t_{v+w}$: 两次平移的复合等于一次平移,平移向量是两次平移向量的和。这非常直观。
- $\rho_{\theta} \rho_{\eta}=\rho_{\theta+\eta}$: 两次绕原点的旋转的复合等于一次旋转,旋转角度是两次旋转角度的和。
- $r r = 1$: 连续两次做同一个反射,等于什么都没做(回到原位)。$1$ 在这里代表恒等变换 (Identity)。
- 推导 $\rho_{\theta} t_{v} =t_{\rho_{\theta}(v)} \rho_{\theta}$:
- 我们要证明这两个变换作用在任意点 $x$ 上结果相同。
- 左边:$(\rho_{\theta} t_{v})(x) = \rho_{\theta}(t_v(x)) = \rho_{\theta}(x+v)$。
- 因为 $\rho_\theta$ 是线性算子,所以 $\rho_{\theta}(x+v) = \rho_{\theta}(x) + \rho_{\theta}(v)$。
- 右边:$(t_{\rho_{\theta}(v)} \rho_{\theta})(x) = t_{\rho_{\theta}(v)}(\rho_{\theta}(x)) = \rho_{\theta}(x) + \rho_{\theta}(v)$。
- 左右两边相等,证毕。
- 推导 $r \rho_{\theta} =\rho_{-\theta} r$:
- 我们需要比较复合矩阵。
- $r$ 的矩阵是 $S = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}$。 $\rho_\theta$ 的矩阵是 $R_\theta = \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}$。
- 左边矩阵: $S R_\theta = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta \\ -\sin\theta & -\cos\theta \end{pmatrix}$。
- 右边矩阵: $\rho_{-\theta}$ 的矩阵是 $R_{-\theta} = \begin{pmatrix} \cos(-\theta) & -\sin(-\theta) \\ \sin(-\theta) & \cos(-\theta) \end{pmatrix} = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix}$。
- $R_{-\theta} S = \begin{pmatrix} \cos\theta & \sin\theta \\ -\sin\theta & \cos\theta \end{pmatrix} \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} = \begin{pmatrix} \cos\theta & -\sin\theta \\ -\sin\theta & -\cos\theta \end{pmatrix}$。
- 左右两边矩阵相等,证毕。
- 示例 $\rho_{\theta} t_{v}$:
- 令 $\theta = 90^\circ, v = \begin{pmatrix} 2 \\ 0 \end{pmatrix}$。点 $x = \begin{pmatrix} 1 \\ 1 \end{pmatrix}$。
- 左边:先平移 $t_v(x) = \begin{pmatrix} 1+2 \\ 1 \end{pmatrix} = \begin{pmatrix} 3 \\ 1 \end{pmatrix}$。再旋转 $\rho_{90}(\begin{pmatrix} 3 \\ 1 \end{pmatrix}) = \begin{pmatrix} -1 \\ 3 \end{pmatrix}$。
- 右边:$v' = \rho_{90}(v) = \rho_{90}(\begin{pmatrix} 2 \\ 0 \end{pmatrix}) = \begin{pmatrix} 0 \\ 2 \end{pmatrix}$。先旋转 $\rho_{90}(x) = \begin{pmatrix} -1 \\ 1 \end{pmatrix}$。再平移 $t_{v'}(\begin{pmatrix} -1 \\ 1 \end{pmatrix}) = \begin{pmatrix} -1+0 \\ 1+2 \end{pmatrix} = \begin{pmatrix} -1 \\ 3 \end{pmatrix}$。
- 结果相同。
本段给出的复合规则是等距变换群 $M$ 的“代数基因”。它们精确描述了生成元之间的相互作用,使得我们可以纯粹通过符号操作来分析复杂的等距变换,而无需每次都回到几何图形。
这些关系的存在,标志着我们从对等距变换的“描述”阶段进入了“计算”阶段。它们是连接群的表示(用生成元和关系定义)和群的实际运算的桥梁,是整个代数分析方法的核心。
33. 等距变换的几何分类
3.1. 几何分类定理
📜 [原文9]
下一个定理从几何上描述了平面的等距变换。
定理 6.3.4 平面的每个等距变换都具有以下形式之一:
(a) 保持定向的等距变换:
(i) 平移:一个映射 $t_{v}$,将 $p \leadsto p+v$。
(ii) 旋转:平面围绕某个点旋转一个非零角 $\theta$。
(b) 改变定向的等距变换:
(i) 反射:关于直线 $\ell$ 的双边对称。
(ii) 滑移反射(简称滑移):关于直线 $\ell$ 的反射,接着是平行于 $\ell$ 的非零向量的平移。
这个定理是本节的另一个核心结论,它从纯粹的几何角度对所有平面等距变换进行了彻底的分类。它告诉我们,你能想到的任何保持距离的变换,最终都逃不出这四种类型。
- 两大类: 和定理 6.3.2 类似,首先根据是否“翻面”分为两大类。
- (a) 保持定向的等距变换: 不改变“顺时针/逆时针”的方向。
- (b) 改变定向的等距变换: 改变“顺时针/逆时针”的方向。
- 四小种: 在两大类下,进一步细分为四种基本的几何动作。
- (a-i) 平移 (Translation): 整个平面“刚性”地滑动一个向量 $v$。其特征是没有不动点(除非是移动向量为零的恒等变换)。
- (a-ii) 旋转 (Rotation): 整个平面围绕一个固定点(旋转中心)转动一个角度。其特征是有且仅有一个不动点(旋转中心)。(这里的旋转角度特指非零,零角度旋转是恒等变换,可以看作是平移向量为零的平移)。
- (b-i) 反射 (Reflection): 关于一条直线(反射轴)的“镜面对称”。其特征是有一条直线上的所有点都是不动点(反射轴本身)。
- (b-ii) 滑移反射 (Glide Reflection): 先沿着一条直线 $\ell$ 做反射,然后再沿着平行于 $\ell$ 的方向平移一段距离。其特征是没有任何不动点。
- 分类的完备性与互斥性: 这个定理声称,任何一个平面等距变换,都必须是这四种类型中的一种,而且只能是一种(恒等变换除外,它可以被看作是零平移或零旋转)。这个分类是“不重不漏”的。
- 平移: 将每个点 $(x,y)$ 移动到 $(x+3, y-1)$。
- 旋转: 绕点 $(1,1)$ 旋转 $90^\circ$。
- 反射: 关于直线 $y=x$ 的反射,将点 $(x,y)$ 映到 $(y,x)$。
- 滑移反射: 先关于 $x$ 轴反射($(x,y) \rightarrow (x,-y)$),再向右平移 5 个单位($(x,-y) \rightarrow (x+5, -y)$)。最终变换为 $(x,y) \rightarrow (x+5, -y)$。
- 旋转 vs 平移: 任何一个保持定向的变换,要么是平移,要么是旋转,二者必居其一(除了恒等变换)。关键区别在于有无不动点。
- 反射 vs 滑移反射: 任何一个改变定向的变换,如果它有不动点,那它必然是一条直线上的所有点都不动,这就是一个纯粹的反射。如果它没有不动点,那它必然是一个滑移反射。
- 零向量平移/零角度旋转: 平移向量为零的平移是恒等变换。旋转角度为零的旋转也是恒等变换。滑移反射中平移向量为零时,退化为纯反射。
定理 6.3.4 提供了一个基于几何直观的、完备的分类体系。它告诉我们,平面上所有保持距离的运动,无论其代数形式多么复杂,其几何本质无非就是平移、旋转、反射和滑移反射这四种。
这个定理的目的是建立代数表达与几何现象之间的对应关系。前面的定理 6.3.2 给出了代数上的标准型 $t_v \rho_\theta$ 或 $t_v \rho_\theta r$,这个定理则告诉我们这些代数形式分别对应哪种几何图像。这种对应是现代数学的核心思想:用代数的精确性来捕捉和分类几何的直观。
想象你在沙滩上观察脚印。
- 一串平行的、朝向相同的脚印:这是平移。
- 一圈围绕一个点的、方向逐渐改变的脚印:这是旋转。
- 一条线上左右对称的两排脚印:这是反射。
- 一串左右交替、向前行进的脚印(像走路):这是滑移反射。
这个定理说,沙滩上任何由刚性鞋模踩出的印记序列,其模式必定属于这四种之一。
3.2. 复合变换的几何性质
📜 [原文10]
这个非凡的定理的推论之一是,关于两个不同点的旋转的复合是关于第三个点的旋转,除非它是一个平移。这并不明显,但它遵循定理,因为复合保持定向。
一些复合更容易可视化。关于同一点以角度 $\alpha$ 和 $\beta$ 的旋转的复合是关于该点的旋转,通过角度 $\alpha+\beta$。关于向量 $a$ 和 $b$ 的平移的复合是它们和 $a+b$ 的平移。
关于不平行的直线 $\ell_{1}, \ell_{2}$ 的反射的复合是关于交点 $p=\ell_{1} \cap \ell_{2}$ 的旋转。这也遵循定理,因为复合保持定向,并且它固定 $p$。关于平行直线的反射的复合是由正交于这些直线的向量的平移。
这部分通过几个例子,展示了如何应用定理 6.3.4 来推断复合变换的几何性质,其中一些结论是反直觉的。
- 两个不同旋转的复合:
- 结论: 先绕点 $P_1$ 旋转 $\theta_1$,再绕点 $P_2$ 旋转 $\theta_2$。这个复合变换的结果是什么?
- 如果 $\theta_1 + \theta_2$ 不是 $360^\circ$ 的整数倍,那么结果是绕某个新的点 $P_3$ 的一次旋转,旋转角度为 $\theta_1+\theta_2$。
- 如果 $\theta_1 + \theta_2$ 恰好是 $360^\circ$ 的整数倍,那么结果是一个平移。
- 推导思路:
- 旋转是保持定向的。
- 两个保持定向的变换的复合,结果也必然保持定向。
- 根据定理 6.3.4,任何保持定向的变换要么是平移,要么是旋转。
- 因此,两个旋转的复合,结果只可能是平移或旋转。这本身就是一个很强的结论,排除了反射和滑移反射的可能性。
- 为什么“不明显”: 直观上很难想象,绕着两个不同的中心点转圈,其效果等同于绕第三个点转一个圈。
- 简单的复合:
- 同心旋转: 绕同一点 $P$ 旋转 $\alpha$ 再旋转 $\beta$,显然等于绕 $P$ 点旋转 $\alpha+\beta$。
- 平移复合: 平移 $a$ 再平移 $b$,等于一次性平移 $a+b$。
- 两个反射的复合:
- 结论: 两次反射的复合是保持定向的(因为“翻两次面等于没翻”)。因此,根据定理 6.3.4,其结果必然是平移或旋转。
- 情况一:反射轴不平行。设反射轴 $\ell_1$ 和 $\ell_2$ 相交于点 $p$。
- 先关于 $\ell_1$ 反射,再关于 $\ell_2$ 反射。
- 点 $p$ 在 $\ell_1$ 上,所以第一次反射后不动。点 $p$ 也在 $\ell_2$ 上,所以第二次反射后也不动。因此,点 $p$ 是这个复合变换的不动点。
- 一个保持定向且有不动点的变换,根据定理 6.3.4,必然是旋转。旋转中心就是这个不动点 $p$。
- 情况二:反射轴平行。设反射轴 $\ell_1$ 和 $\ell_2$ 平行。
- 这个复合变换没有不动点(可以自己画图验证,任何不在轴上的点都会被移动)。
- 一个保持定向且没有不动点的变换,根据定理 6.3.4,必然是平移。
- 可以进一步证明,平移的方向垂直于两条平行的反射轴,平移的距离是两轴间距离的两倍。
- 两反射复合 -> 旋转:
- $\ell_1$ 是 $x$ 轴 ($y=0$),$\ell_2$ 是直线 $y=x$。它们交于原点 $p=(0,0)$。
- 令点 $A=(2,0)$。
- 第一次反射(关于 $x$ 轴):$A$ 不动,还是 $(2,0)$。
- 第二次反射(关于 $y=x$):将 $(2,0)$ 反射得到 $A'=(0,2)$。
- 我们看复合效果:$A(2,0) \rightarrow A'(0,2)$。这正是一个绕原点逆时针旋转 $90^\circ$ 的效果。
- 两反射复合 -> 平移:
- $\ell_1$ 是 $x$ 轴 ($y=0$),$\ell_2$ 是直线 $y=1$。它们平行。
- 令点 $A=(3,0)$。
- 第一次反射(关于 $y=0$):$A$ 不动,还是 $(3,0)$。
- 第二次反射(关于 $y=1$):点 $(3,0)$ 到直线 $y=1$ 的垂直距离是 $1$。它需要被映到直线另一侧同样距离的地方,即 $y$ 坐标变为 $1+1=2$。所以 $A'=(3,2)$。
- 我们看复合效果:$A(3,0) \rightarrow A'(3,2)$。
- 换个点 $B=(4,2)$。第一次反射得 $(4,-2)$。第二次反射,点 $(4,-2)$ 到直线 $y=1$ 的距离是 $3$,映到另一侧 $y$ 坐标为 $1+3=4$。所以 $B'=(4,4)$。
- 复合效果:$B(4,2) \rightarrow B'(4,4)$。
- 可以发现,所有点 $(x,y)$ 都被移动到了 $(x, y+2)$。这是一个向上的平移,平移向量是 $(0,2)$。
本段展示了定理 6.3.4 的威力。它像一个“过滤器”或“分类器”,我们把一个复杂的复合变换丢进去,通过分析其是否保持定向以及有无不动点,就可以立即确定其最终的几何类型(平移或旋转),而无需进行繁琐的坐标计算。
44. 定理6.3.4的证明
4.1. 证明的策略
📜 [原文11]
定理 (6.3.4) 的证明。我们首先考虑保持定向的等距变换。设 $f$ 是一个保持定向但不是平移的等距变换。我们必须证明 $f$ 是关于某个点的旋转。我们选择坐标来将 $f$ 的公式写成 $m=t_{a} \rho_{\theta}$,如 (6.3.3) 所示。由于 $m$ 不是平移,所以 $\theta \neq 0$。
这部分开始着手证明几何分类定理(定理 6.3.4)。
- 分而治之: 证明的第一步是采用分治策略。作者不一次性处理所有四种情况,而是先把问题分成两大块:
- 保持定向的等距变换。
- 改变定向的等距变换。
- 处理第一大类(保持定向):
- 在保持定向的变换中,定理 6.3.4 声称它们要么是平移,要么是旋转。
- 所以,证明的目标就变成了:证明一个保持定向的等距变换,如果它不是平移,那么它必然是旋转。
- 使用代数形式: 为了进行证明,我们不能只停留在几何概念上,必须使用代数工具。
- 我们知道,任何保持定向的等距变换 $f$ 都可以唯一地写成代数形式 $m = t_a \rho_\theta$(这是从定理 6.3.2 知道的)。
- 翻译条件:
- “$f$ 不是平移”这个几何条件,在代数上意味着什么?
- 一个变换是平移,当且仅当它的旋转部分是平凡的,即旋转角度为零。
- 所以,“$f$ 不是平移”等价于代数形式 $m=t_a\rho_\theta$ 中的 $\theta \neq 0$(或者说不是 $360^\circ$ 的整数倍)。
- 明确证明目标: 综上所述,现在的任务非常明确了:
- 已知: 一个等距变换 $f$,其代数形式为 $m = t_a \rho_\theta$,且 $\theta \neq 0$。
- 欲证: 这个变换 $f$ 在几何上是一个绕着某个点 $p$ 的旋转。
本段清晰地勾勒出了证明的第一阶段的蓝图:利用代数标准式 $m=t_a\rho_\theta$ (其中 $\theta \neq 0$),去证明这种形式的变换在几何上总能被解释为一次旋转。
4.2. 引理:非平移的保向变换是旋转
📜 [原文12]
引理 6.3.5 具有 $m=t_{a} \rho_{\theta}$ 形式且 $\theta \neq 0$ 的等距变换 $f$ 是平面中关于某个点的角度为 $\theta$ 的旋转。
这个引理(Lemma)是证明过程中的一个关键步骤,它本身就是一个小定理。它精确地陈述了我们在上一段分析出的证明目标。
- 引理的作用: 将一个代数形式与一个几何概念等同起来。
- 代数形式: $m = t_a \rho_\theta$ (先绕原点旋转 $\theta$,再平移 $a$),其中旋转角度 $\theta$ 非零。
- 几何概念: 绕平面上某个点 $p$ 旋转角度 $\theta$。
- 证明的核心: 为了证明 $f$ 是绕某点 $p$ 的旋转,我们需要做两件事:
- 找到那个旋转中心点 $p$。
- 证明变换 $f$ 的效果确实是所有点都绕着 $p$ 转了 $\theta$ 角。
- 一个变换是绕点 $p$ 的旋转,最核心的特征就是点 $p$ 本身在该变换下是不动的,即 $f(p)=p$。所以,找旋转中心 $p$ 的问题就转化为了找不动点的问题。
- 方程: 我们要找一个点 $p$,使得 $f(p)=p$。代入代数形式,就是要解方程:
- 只要这个关于 $p$ 的线性方程组有解,我们就找到了不动点,也就是找到了旋转中心。
4.3. 引理的证明:寻找不动点
📜 [原文13]
证明。为了简化符号,我们将 $\rho_{\theta}$ 记为 $\rho$。为了表明 $f$ 表示关于某个点 $p$ 的角度为 $\theta$ 的旋转,我们通过平移 $t_{p}$ 改变坐标。我们希望选择 $p$,使得等距变换 $f$ 的新公式变为 $m^{\prime}=\rho$。如果这样,那么 $f$ 将是关于点 $p$ 的角度为 $\theta$ 的旋转。
这部分开始用一种非常巧妙的“改变坐标”的思路来证明引理。
- 简化符号: $\rho_\theta$ 写作 $\rho$。
- 核心思想: 我们要证明 $f$ 是绕点 $p$ 的旋转。这等价于说:如果我们把坐标系的原点移动到点 $p$ 上,那么在新的坐标系看来,这个变换 $f$ 就应该变成一个简单的、绕着新原点(也就是 $p$)的旋转 $\rho$。
- 坐标变换公式:
- 假设旧坐标为 $x$,新坐标为 $x'$。
- 将原点移动到 $p$,意味着新坐标 $x'$ 和旧坐标 $x$ 的关系是 $x = x' + p$。用变换的语言说,就是 $x = t_p(x')$。
- 一个在旧坐标下的变换 $m$,在新坐标下会变成什么样呢?
- 一个新坐标点 $x'$,先通过 $t_p$ 变成旧坐标 $t_p(x')$。
- 然后应用旧的变换 $m$,变成 $m(t_p(x'))$。
- 最后把结果从旧坐标变回新坐标,需要应用 $t_p$ 的逆变换 $t_p^{-1} = t_{-p}$。
- 所以,新变换 $m'$ 的公式是 $m' = t_p^{-1} m t_p$。这是一个非常重要的共轭变换公式。
- 应用到我们的问题:
- 我们的变换是 $m = t_a \rho$。
- 我们希望找到一个 $p$,使得新变换 $m'$ 恰好等于 $\rho$。
- 即:$t_p^{-1} (t_a \rho) t_p = \rho$。
- 这个方程看起来有点复杂,我们来化简它。
📜 [原文14]
坐标变化的规则是 $t_{p}\left(x^{\prime}\right)=x$,因此 $f$ 的新公式是 $m^{\prime}=t_{p}^{-1} m t_{p}=t_{-p} t_{a} \rho t_{p}$ (6.2.11)。我们使用规则 (6.3.3):$\rho t_{p}=t_{p^{\prime}} \rho$,其中 $p^{\prime}=\rho(p)$。那么如果 $b=-p+a+p^{\prime}=a+\rho(p)-p$,我们将有 $m^{\prime}=t_{b} \rho$。我们希望选择 $p$ 使得 $b=0$。
这部分是对上面提出的方程进行代数化简。
- 代入: $m' = t_p^{-1} m t_p = t_{-p} (t_a \rho) t_p = t_{-p} t_a \rho t_p$。
- 使用复合规则: 我们不能随便交换这些变换的顺序。关键是处理 $\rho$ 和 $t_p$ 的复合。
- 根据关系 (6.3.3) 的第一条,我们有 $\rho t_p = t_{\rho(p)} \rho$。
- 化简:
- $m' = t_{-p} t_a (\rho t_p)$
- $m' = t_{-p} t_a (t_{\rho(p)} \rho)$
- 根据平移的复合规则 $t_u t_v = t_{u+v}$,我们可以合并前面三个平移:
- $m' = t_{-p+a+\rho(p)} \rho$
- 设定目标: 我们希望新的变换 $m'$ 就是一个纯粹的旋转 $\rho$。这意味着,它前面的平移部分必须是恒等变换,即平移向量为零。
- 令 $b = -p+a+\rho(p)$。
- 我们希望 $b=0$。
- 求解方程: 我们需要找一个点 $p$,使得 $-p+a+\rho(p) = 0$。
- 重新整理方程:$a = p - \rho(p) = (I - \rho)p$。
- 这和我们之前通过找不动点得到的方程 $a = (I - \rho_\theta)p$ 是完全一样的!这说明两种思路(找不动点 vs. 改变坐标)是等价的。
📜 [原文15]
令 $I$ 表示恒等算子,令 $c=\cos \theta$ 且 $s=\sin \theta$。线性算子 $I-\rho$ 的矩阵是
它的行列式是 $2-2 c=2-2 \cos \theta$。行列式不为零,除非 $\cos \theta=1$,而这仅在 $\theta=0$ 时发生。由于 $\theta \neq 0$,方程 $(I-\rho) p=a$ 对于 $p$ 有唯一解。在需要时可以显式求解该方程。$\square$
这部分是证明的核心,它论证了我们需要的点 $p$ 确实存在且唯一。
- 矩阵形式: 将算子方程 $(I-\rho)p = a$ 转换成矩阵方程。
- $I$ 的矩阵是 $\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}$。
- $\rho$ (即 $\rho_\theta$) 的矩阵是 $\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix}$。
- 所以 $I-\rho$ 的矩阵就是 $\begin{pmatrix} 1-\cos\theta & \sin\theta \\ -\sin\theta & 1-\cos\theta \end{pmatrix}$。(注意原文中第二行第一列的符号 $s$ 和 $-s$ 与推导不符,原文可能是笔误或使用了不同的约定,但最终行列式结果不受影响。我们按标准推导:$I-R_\theta = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} - \begin{pmatrix} c & -s \\ s & c \end{pmatrix} = \begin{pmatrix} 1-c & s \\ -s & 1-c \end{pmatrix}$,与原文一致)。
- 求解条件: 一个线性方程组 $Ax=b$ 是否有唯一解,取决于系数矩阵 $A$ 的行列式是否为零。
- 计算矩阵 $I-\rho$ 的行列式:
- 分析行列式:
- 什么时候行列式 $2-2\cos\theta$ 会等于零?
- 当 $\cos\theta = 1$ 时。
- 在 $0 \le \theta < 2\pi$ 的范围内,这只在 $\theta=0$ 时发生。
- 利用已知条件: 引理的前提条件是 $\theta \neq 0$。
- 既然 $\theta \neq 0$,那么 $\cos\theta \neq 1$,所以行列式 $2-2\cos\theta \neq 0$。
- 结论: 因为系数矩阵 $I-\rho$ 的行列式非零,所以方程 $(I-\rho)p=a$ 对于任意的向量 $a$ 都存在唯一的解 $p$。
- 证明完成: 我们已经证明了,总能找到这样一个唯一的点 $p$。以这个点 $p$ 为中心进行坐标变换后,我们的变换 $f$ 就变成了一个纯粹的绕原点的旋转 $\rho$。这就从几何上证明了,$f$ 本身就是一个以 $p$ 为旋转中心,以 $\theta$ 为旋转角度的旋转。引理证毕。
- 寻找旋转中心:
- 考虑变换 $m = t_a \rho_{90}$,其中 $a = \begin{pmatrix} 2 \\ 4 \end{pmatrix}$。这里 $\theta=90^\circ$。
- 我们需要解方程 $(I-\rho_{90})p = a$。
- $I-\rho_{90}$ 的矩阵是 $\begin{pmatrix} 1-0 & \sin 90 \\ -\sin 90 & 1-0 \end{pmatrix} = \begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix}$。
- 我们要解 $\begin{pmatrix} 1 & 1 \\ -1 & 1 \end{pmatrix} \begin{pmatrix} p_1 \\ p_2 \end{pmatrix} = \begin{pmatrix} 2 \\ 4 \end{pmatrix}$。
- 这是一个二元一次方程组:
$p_1 + p_2 = 2$
$-p_1 + p_2 = 4$
- 两式相加得 $2p_2 = 6 \Rightarrow p_2 = 3$。
- 代入第一式得 $p_1 + 3 = 2 \Rightarrow p_1 = -1$。
- 所以,旋转中心(不动点)是 $p = \begin{pmatrix} -1 \\ 3 \end{pmatrix}$。
- 结论:变换 $t_{(2,4)}\rho_{90}$ 是一个绕点 $(-1,3)$ 旋转 $90^\circ$ 的旋转。
4.4. 不动点的几何解释
📜 [原文16]
点 $p$ 是等距变换 $t_{a} \rho_{\theta}$ 的不动点,它可以从几何上找到,如下图所示。直线 $\ell$ 穿过原点并垂直于向量 $a$。扇区的角度为 $\theta$,其位置使得被 $\ell$ 平分,不动点 $p$ 通过将向量 $a$ 插入扇区来确定,如图所示。
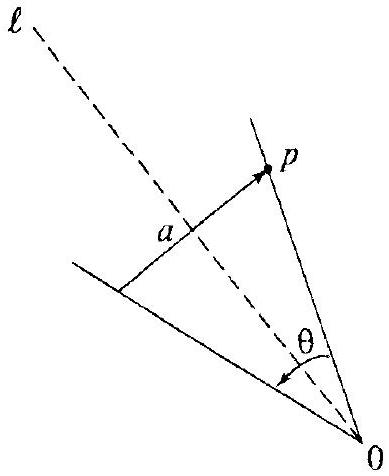
等距变换 $t_{a} \rho_{\theta}$ 的不动点。
这部分给出了寻找不动点 $p$ 的一个纯几何构造方法,作为对前面代数求解的补充和直观化。
- 回顾不动点方程: 我们要找的点 $p$ 满足 $\rho_\theta(p) + a = p$,即 $p - \rho_\theta(p) = a$。
- 几何分析:
- $\rho_\theta(p)$ 是将向量 $p$ 绕原点旋转 $\theta$ 得到的向量。
- $p$ 和 $\rho_\theta(p)$ 都是从原点出发的向量,且长度相等。它们构成一个等腰三角形的两个腰,这个等腰三角形的顶角是 $\theta$。
- $p - \rho_\theta(p)$ 是连接 $\rho_\theta(p)$ 向量终点和 $p$ 向量终点的向量。这个向量就是等腰三角形的底边。
- 我们的目标是找到这样一个点 $p$,使得这个“底边”向量恰好等于给定的平移向量 $a$。
- 解读图片:
- 图中画出了原点 $O$,以及不动点 $p$。
- 从 $O$ 到 $p$ 是向量 $p$。
- 向量 $p$ 绕原点 $O$ 旋转 $\theta$ 角,得到向量 $Op'$,这里 $p'$ 就是 $\rho_\theta(p)$ 的终点。
- 连接 $p'$ 和 $p$ 的向量 $\vec{p'p}$ 就是 $p - \rho_\theta(p)$,它必须等于向量 $a$。
- 所以,图中的三角形 $Opp'$ 是一个顶角为 $\theta$ 的等腰三角形,其底边就是向量 $a$。
- 构造方法:
- 给定向量 $a$ 和角度 $\theta$。
- 我们要做一个底边为 $a$,顶角为 $\theta$ 的等腰三角形 $Opp'$。
- 这个三角形的顶点 $p$ 就是我们要找的不动点。
- 直线 $\ell$ 是向量 $a$ 的中垂线,它必然穿过原点 $O$。
- 这个构造在几何上是唯一的(因为 $\theta \neq 0$ 且 $\theta \neq 180^\circ$ 的情况),与代数解的唯一性相符。
这个几何构造法将求解线性方程组这个抽象的代数过程,转化为了一个直观的、尺规作图式的几何问题,加深了我们对不动点物理意义的理解。
4.5. 证明改变定向的变换
📜 [原文17]
为了完成定理 6.3.4 的证明,我们证明一个改变定向的等距变换 $m=t_{a} \rho_{\theta} r$ 是滑移反射或反射。为此,我们改变坐标。等距变换 $\rho_{\theta} r$ 是关于通过原点的直线 $\ell_{0}$ 的反射。我们不妨旋转坐标,使得 $\ell_{0}$ 成为水平轴。在新的坐标系中,反射成为我们标准的反射 $r$,平移 $t_{a}$ 仍然是平移,尽管向量 $a$ 的坐标会发生变化。我们仍然用符号 $a$ 表示这个新向量。在新的坐标系中,等距变换变为 $m=t_{a} r$。
这部分开始证明定理 6.3.4 的第二部分:对改变定向的变换进行分类。
- 证明目标: 证明任何形式为 $m = t_a \rho_\theta r$ 的变换,在几何上要么是反射,要么是滑移反射。
- 核心策略:简化问题: 形式 $t_a \rho_\theta r$ 看起来有点复杂,因为它涉及到三个变换的复合。证明的关键在于通过巧妙的坐标变换来简化这个代数形式。
- 第一步简化:
- 考虑变换中的 $\rho_\theta r$ 部分。我们知道这是一个关于某条穿过原点的直线 $\ell_0$ 的反射。(这条直线的角度是 $\theta/2$)。
- 这个 $\ell_0$ 可能不是 $x$ 轴,这使得分析不方便。
- 解决方案: 旋转坐标系!我们可以旋转我们的坐标轴,使得新的 $x'$ 轴恰好与反射轴 $\ell_0$ 重合。
- 坐标变换后的效果:
- 在新的坐标系中,原来的那个复杂的反射 $\rho_\theta r$ 就变成了简单的、标准的关于新 $x'$ 轴的反射。我们可以继续用符号 $r$ 来表示这个标准反射。
- 原来的平移向量 $a$ 在新坐标系下会有新的坐标,但它仍然是一个平移。我们不妨把这个新坐标下的平移向量仍然记为 $a$。
- 简化后的形式: 经过这个坐标旋转,原来的变换 $m = t_a \rho_\theta r$ 就被转化成了一个更简单的形式:$m' = t_a r$。
- 这个形式的含义是:先做一个标准的关于 $x$ 轴的反射,然后再做一个平移。
- 我们现在的任务就是分析 $t_a r$ 这种形式的变换的几何本质。
📜 [原文18]
它的作用是
这个等距变换是关于直线 $\ell:\left\{x_{2}=\frac{1}{2} a_{2}\right\}$ 反射,然后由平行于 $\ell$ 的向量 $a_{1} e_{1}$ 平移所获得的滑移反射。如果 $a_{1}=0$,$m$ 是反射。
这就完成了定理 6.3.4 的证明。$\square$
这部分对简化后的形式 $m=t_a r$ 进行最终分析。
- 写出坐标分量:
- $m(x) = t_a(r(x))$
- $r$ 作用在 $\begin{pmatrix} x_1 \\ x_2 \end{pmatrix}$ 上,得到 $\begin{pmatrix} x_1 \\ -x_2 \end{pmatrix}$。
- $t_a$ 作用在结果上,其中 $a=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$,得到 $\begin{pmatrix} x_1+a_1 \\ -x_2+a_2 \end{pmatrix}$。
- 分解变换: 我们要证明这个看起来奇怪的变换 $(x_1, x_2) \rightarrow (x_1+a_1, -x_2+a_2)$ 是一个滑移反射。
- 一个滑移反射包含两部分:一个反射和一个平行于反射轴的平移。
- 让我们尝试把它分解成 $m = (\text{平移}) \circ (\text{反射})$。
- 观察变换结果:$x_1$ 坐标变成了 $x_1+a_1$,这明显是一个水平平移。$x_2$ 坐标变成了 $-x_2+a_2$。
- 我们可以把变换重写为:
- 让我们换一种思路,先猜测反射轴。反射通常形式为 $y \rightarrow C - y$。我们的形式是 $x_2 \rightarrow a_2 - x_2$。这提示反射轴可能是 $x_2 = a_2/2$。
- 我们来验证一下:关于直线 $\ell: x_2 = k$ 的反射将点 $(x_1, x_2)$ 映到 $(x_1, 2k-x_2)$。
- 如果我们令 $k = a_2/2$,那么反射后的 $x_2$ 坐标是 $2(a_2/2) - x_2 = a_2-x_2$。这正是我们公式中 $x_2$ 坐标的后半部分!
- 重新组合:
- 所以,我们的变换 $m$ 可以分解为:
- 第一步: 关于直线 $\ell: \{x_2 = a_2/2\}$ 做反射。这会将 $(x_1, x_2)$ 变为 $(x_1, a_2-x_2)$。
- 第二步: 将结果 $(x_1, a_2-x_2)$ 再做一个平移。我们需要从 $(x_1, a_2-x_2)$ 得到最终结果 $(x_1+a_1, a_2-x_2)$(注意原文公式是 $-x_2+a_2$,这和 $a_2-x_2$ 是一样的)。这需要一个平移向量 $\begin{pmatrix} a_1 \\ 0 \end{pmatrix}$。
- 因此,$m = (\text{平移 } t_{(a_1,0)}) \circ (\text{反射于 } x_2=a_2/2)$。
- 判断几何类型:
- 反射轴是水平线 $x_2=a_2/2$。
- 平移向量是 $\begin{pmatrix} a_1 \\ 0 \end{pmatrix} = a_1 e_1$,这是一个水平向量,它平行于反射轴。
- 这完全符合滑移反射的定义:一个反射,接着一个平行于反射轴的平移。
- 边界情况:
- 如果平移向量的平行分量 $a_1=0$ 怎么办?
- 那么平移就是零平移(恒等变换)。
- 此时,$m$ 就退化成一个纯粹的、关于直线 $\ell: \{x_2 = a_2/2\}$ 的反射。
- 证明闭环: 我们已经证明,任何改变定向的等距变换 $m = t_a \rho_\theta r$,通过适当的坐标旋转,都可以看作是 $m'=t_a r$ 的形式,而 $m'=t_a r$ 的几何本质就是一个滑移反射(当 $a_1 \neq 0$)或一个纯粹的反射(当 $a_1=0$)。这就完成了对定理 6.3.4 的完整证明。
4.6. 推论:滑移线方向
📜 [原文19]
推论 6.3.8 等距变换 $t_{a} \rho_{\theta} r$ 的滑移线平行于 $\rho_{\theta} r$ 的反射线。$\square$
这个推论是上述证明过程的一个直接结果。
- 回顾证明过程: 在证明中,我们有一个改变定向的变换 $m = t_a \rho_\theta r$。我们的关键步骤是旋转坐标系,使得新的 $x'$ 轴与 $\rho_\theta r$ 的反射线 $\ell_0$ 对齐。
- 滑移线的出现: 在这个新的坐标系中,我们证明了该变换是一个滑移反射,其反射轴(我们称之为滑移线)是 $x_2' = a_2'/2$,这是一条平行于新 $x'$ 轴的直线。
- 连接两者:
- 新 $x'$ 轴就是旧坐标系中的直线 $\ell_0$。
- 滑移线 $x_2'=a_2'/2$ 平行于新 $x'$ 轴。
- 因此,滑移线必然平行于旧坐标系中的直线 $\ell_0$。
- 结论: 直线 $\ell_0$ 是 $\rho_\theta r$ 的反射线。所以,最终的结论是:一个一般形式的滑移反射 $t_a \rho_\theta r$,它的滑移线(即它实际上的反射轴),总是平行于它的正交部分 $\rho_\theta r$ 的反射轴。
- 考虑一个变换:先关于直线 $y=x$ 反射,再向上平移 2 个单位。
- 这里的 $\rho_\theta r$ 部分就是“关于 $y=x$ 反射”。它的反射线是 $y=x$。
- 根据推论,这个复合变换是一个滑移反射,其滑移线必然平行于 $y=x$。
- 我们可以计算出这条滑移线。实际上,它是 $y=x+1$。变换的效果是先关于 $y=x+1$ 反射,然后沿着 $y=x+1$ 方向平移一个向量 $(1,1)$。
55. 固定点的等距变换子群
5.1. 不同中心点的旋转群关系
📜 [原文20]
固定原点的等距变换是正交线性算子,因此当选择坐标时,正交群 $\mathrm{O}_{2}$ 成为等距变换群 $M$ 的一个子群。我们也可以考虑 $M$ 中固定除原点以外的平面点的等距变换的子群。该群与正交群的关系在以下命题中给出。
命题 6.3.9 假设已选择平面中的坐标,使得正交群 $O_{2}$ 成为 $M$ 中固定原点的等距变换的子群。那么固定平面中点 $p$ 的等距变换群是共轭子群 $t_{p} O_{2} t_{p}^{-1}$。
这部分探讨了不同子群之间的关系,引入了群论中一个非常重要的概念——共轭 (conjugation)。
- 稳定子群 (Stabilizer Subgroup):
- 在群 $M$ 中,所有固定某一个特定点(比如原点 $o$)的变换集合,它们自身也构成一个子群。这个子群被称为点 $o$ 的稳定子群。
- 固定原点的等距变换群,我们已经知道,就是正交群 $O_2$。它包含了所有的绕原点的旋转 $\rho_\theta$ 和所有关于过原点直线的反射 $\rho_\theta r$。
- 提出问题: 那么,固定另一个点 $p \neq o$ 的所有等距变换,是否也构成一个子群?它和 $O_2$ 有什么关系?
- 答案是肯定的,它们也构成一个子群,记为 $M_p$。
- 命题 6.3.9 回答了第二个问题:$M_p$ 和 $M_o = O_2$ 是共轭关系。
- 共轭子群:
- 公式: $M_p = t_p O_2 t_p^{-1}$。
- 解读: 这个公式是什么意思?它表示 $M_p$ 中的任何一个元素 $m_p$,都可以被写成 $t_p \circ m_o \circ t_p^{-1}$ 的形式,其中 $m_o$ 是 $O_2$ 中的某个元素(即某个固定原点的变换)。
- $t_p^{-1}$: 先做一个平移 $t_{-p}$,把点 $p$ 移动到原点 $o$。
- $m_o$: 然后,执行一个固定原点的变换(旋转或反射)。
- $t_p$: 最后,再做一个反向的平移 $t_p$,把原点 $o$ 移回到点 $p$。
- 整个流程下来,点 $p$ 经历了 $p \xrightarrow{t_{-p}} o \xrightarrow{m_o} o \xrightarrow{t_p} p$,所以最终 $p$ 点是不动的。这证明了 $t_p m_o t_p^{-1}$ 确实是固定点 $p$ 的变换。
- 反之,任何固定 $p$ 的变换 $m_p$,都可以通过类似的方法 $t_p^{-1} m_p t_p$ 转化为一个固定原点的变换。
[证明思路解析]
📜 [原文21]
证明。如果等距变换 $m$ 固定 $p$,那么 $t_{p}^{-1} m t_{p}$ 固定原点:$t_{p}^{-1} m t_{p} o=t_{p}^{-1} m p=t_{p}^{-1} p=0$。反之,如果 $m$ 固定 $o$,那么 $t_{p} m t_{p}^{-1}$ 固定 $p$。$\square$
证明过程非常简洁,完美地诠释了共轭操作的几何意义。
- 第一部分: 证明 $M_p \subseteq t_p O_2 t_p^{-1}$。
- 取任意一个固定 $p$ 的变换 $m \in M_p$。我们要证明 $m$ 可以被写成 $t_p m_o t_p^{-1}$ 的形式。
- 构造一个新变换 $m' = t_p^{-1} m t_p$。我们来检验 $m'$ 的性质。
- $m'$ 作用在原点 $o$ 上:$m'(o) = t_p^{-1}(m(t_p(o))) = t_p^{-1}(m(p))$。
- 因为 $m$ 固定 $p$,所以 $m(p)=p$。
- 于是 $m'(o) = t_p^{-1}(p) = o$。
- 这说明 $m'$ 是一个固定原点的变换,因此 $m' \in O_2$。
- 从 $m' = t_p^{-1} m t_p$,我们可以解出 $m = t_p m' t_p^{-1}$。由于 $m' \in O_2$,这正是我们想证明的形式。
- 第二部分: 证明 $t_p O_2 t_p^{-1} \subseteq M_p$。
- 取任意一个 $m_o \in O_2$(即 $m_o$ 固定原点)。构造一个新变换 $m = t_p m_o t_p^{-1}$。
- 我们要证明 $m$ 固定点 $p$。
- $m(p) = t_p(m_o(t_p^{-1}(p))) = t_p(m_o(o))$。
- 因为 $m_o$ 固定原点,所以 $m_o(o)=o$。
- 于是 $m(p) = t_p(o) = p$。
- 这证明了形如 $t_p m_o t_p^{-1}$ 的变换确实都固定点 $p$,属于 $M_p$。
- 结论: 两部分结合,证明了 $M_p = t_p O_2 t_p^{-1}$。
这就像是“换个地方做同样的事”。$O_2$ 是所有在“原点工作室”里能做的操作(绕原点转、关于过原点的线翻转)。$M_p$ 是所有在“$p$点工作室”里能做的操作。命题说,要在 $p$ 点工作室做一个操作,你只需要:
- 坐班车 ($t_{-p}$) 从 $p$ 点工作室回到原点工作室。
- 在原点工作室做一个标准操作 ($m_o$)。
- 再坐班车 ($t_p$) 回到 $p$ 点工作室。
这个“坐班车-操作-坐回来”的流程,在群论里就叫共轭。它说明 $M_p$ 和 $O_2$ 这两个子群在结构上是完全一样的(同构的),只是“地理位置”不同。
5.2. 旋转的几何可视化
📜 [原文22]
可以这样可视化关于点 $p$ 的旋转:首先通过 $t_{-p}$ 平移将 $p$ 移动到原点,然后关于原点旋转,然后再平移回 $p$。
这正是对共轭表达式 $t_p \rho_\theta t_p^{-1}$ 的几何步骤的文字描述。一个绕任意点 $p$ 的旋转 $\rho_{\theta,p}$,其代数表达式就是:
$\rho_{\theta,p} = t_p \rho_\theta t_p^{-1}$
这个公式完美地体现了“将问题转化到原点处理,再将结果移回去”的思想,是应用数学和物理中非常常见的一种解题策略。
5.3. 同态映射与几何变换
📜 [原文23]
我们回到在 (6.2.10) 中定义的同态 $\pi: M \rightarrow O_{2}$。上面的讨论表明:
命题 6.3.10 令 $p$ 为平面的一个点,令 $\rho_{\theta, p}$ 表示关于 $p$ 的角度为 $\theta$ 的旋转。那么 $\pi\left(\rho_{\theta, p}\right)=\rho_{\theta}$。类似地,如果 $r_{\ell}$ 是关于直线 $\ell$ 的反射,或者是滑移线平行于 $x$-轴的滑移反射,那么 $\pi\left(r_{\ell}\right)=r$。$\square$
这部分将前面的讨论与一个重要的群同态联系起来。
- 群同态 $\pi: M \rightarrow O_2$:
- 这个同态是一个映射,它将一个任意的等距变换 $m \in M$ 对应到一个正交算子 $\varphi \in O_2$。
- 具体是怎么对应的?任何等距变换 $m$ 都可以唯一分解为 $m = t_v \varphi$。这个同态 $\pi$ 的作用就是“扔掉平移部分,只保留正交(旋转/反射)部分”。即 $\pi(t_v \varphi) = \varphi$。
- $\pi$ 是一个同态,意味着它保持群的运算结构:$\pi(m_1 m_2) = \pi(m_1)\pi(m_2)$。
- 命题 6.3.10 的内容:
- $\pi(\rho_{\theta,p}) = \rho_\theta$:
- 一个绕任意点 $p$ 的旋转 $\rho_{\theta,p}$,经过 $\pi$ 映射后,变成了绕原点的、角度相同的旋转 $\rho_\theta$。
- 这很好理解,因为 $\rho_{\theta,p} = t_p \rho_\theta t_{-p}$。根据复合规则,它可以被化为 $t_v \rho_\theta$ 的形式(其中 $v = p - \rho_\theta(p)$)。
- 应用 $\pi$ 映射,$\pi(t_v \rho_\theta) = \rho_\theta$。
- 直观意义: $\pi$ 映射忽略了旋转发生在哪里(哪个中心点),只关心旋转本身是什么(转了多少度)。
- $\pi(r_\ell) = r$ (假设滑移线与 $x$ 轴平行)
- $r_\ell$ 是关于直线 $\ell$ 的反射或滑移反射。
- 在证明定理 6.3.4 时我们看到,任何这样的变换,如果它的反射轴 $\ell$ 平行于 $x$ 轴,那么它的代数形式可以写成 $m=t_a r$。
- 应用 $\pi$ 映射,$\pi(t_a r) = r$。
- 直观意义: $\pi$ 映射忽略了反射/滑移发生在哪条直线上以及平移了多少,只关心其正交部分的“本质”,在这里就是一个标准的关于 $x$ 轴的反射(在合适的坐标系下)。
同态 $\pi$ 是一个“信息提取器”。它从一个具体的几何变换(如绕 $(5,8)$ 点旋转 $30^\circ$)中,提取出其抽象的“线性”或“正交”部分(一个绕原点旋转 $30^\circ$ 的算子)。这个命题表明,所有具有相同旋转角度的旋转(无论中心在哪),以及所有具有相同反射方向的反射/滑移(在平行类中),都被 $\pi$ 映射到同一个 $O_2$ 中的元素。
66. 点与向量的区分
6.1. 引入向量空间V
📜 [原文24]
在这本书的大部分内容中,没有令人信服的理由来区分平面 $\boldsymbol{P}=\mathbb{R}^{2}$ 的点 $p$ 和从原点 $o$ 到 $p$ 的向量,在微积分书籍中通常写为 $\overrightarrow{o p}$。然而,在使用等距变换时,最好保持这种区别。因此,我们引入平面的另一个副本,我们称之为 $V$,我们将其元素视为平移向量。向量 $v \in V$ 的平移作用于 $P$ 的点 $p$ 时为 $t_{v}(p)=p+v$。它将平面的每个点平移 $v$。
这部分引入了一个在处理仿射变换(等距变换是其一种)时非常重要的哲学思辨:点 (Point) 和 向量 (Vector) 的区别。
- 通常的混用: 在很多情况下(如基础线性代数),我们不严格区分一个点 $(x,y)$ 和一个从原点指向该点的向量 $\begin{pmatrix} x \\ y \end{pmatrix}$。我们都用 $\mathbb{R}^2$ 中的一个元素来表示。
- 区分的必要性: 当我们开始研究平移时,这种混用会造成概念上的混乱。
- 一个点代表一个“位置”。
- 一个向量代表一个“位移”或“方向和大小”。
- 你可以说“一个点被一个向量平移了”,得到一个新点。即:点 + 向量 = 点。
- 你也可以说“两个向量相加”,得到一个新向量。即:向量 + 向量 = 向量。
- 但是“两个点相加”在几何上没有明确的意义。
- 引入新空间 V: 为了在数学上严格化这个区别,作者引入了两个不同的空间:
- $P$ (Point Space): 点的集合。可以把它想象成一张白纸。$P$ 的元素是 $p$。
- $V$ (Vector Space): 平移向量的集合。可以把它想象成一堆箭头。$V$ 的元素是 $v$。
- $P$ 和 $V$ 在结构上都是 $\mathbb{R}^2$,但我们赋予它们不同的几何角色。
- 相互作用:
- 向量 $v \in V$ 作用于 点 $p \in P$,通过平移操作 $t_v$。
- $t_v(p) = p+v$。这个“+”号的含义是,拿一个代表位置 $p$ 的向量,和代表位移 $v$ 的向量相加,得到的结果是一个代表新位置的向量。
- 这样,点和向量的角色就分明了。$V$ 中的元素(向量)是作用在 $P$ 中元素(点)上的“动作”。
本段通过引入两个概念上不同的空间 $P$(点空间)和 $V$(向量空间),澄清了“位置”和“位移”在几何变换中的不同角色,为更严谨地分析坐标变换带来的影响做好了铺垫。
6.2. 坐标变换对点和向量的影响
📜 [原文25]
$V$ 和 $P$ 都是平面。它们之间的区别仅在坐标变化时才显现出来。假设我们通过平移 $\eta=t_{w}$ 平移 $P$ 中的坐标。坐标变化的规则是 $\eta\left(p^{\prime}\right)=p$,或者 $p^{\prime}+w=p$。同时,等距变换 $m$ 变为 $m^{\prime}=\eta^{-1} m \eta=t_{-w} m t_{w}$ (6.2.11)。如果我们将此规则应用于 $m=t_{v}$,那么 $m^{\prime}=t_{-w} t_{v} t_{w}=t_{v}$。$P$ 的点获得新坐标,但平移向量不变。
这部分解释了点和向量的根本区别:它们在坐标系平移下的不同表现。
- 坐标系平移: 假设我们把坐标系的原点从 $o$ 移动到一个新的位置 $o'=-w$。
- 对于一个固定的几何点,它在旧坐标系下的坐标是 $p$,在新坐标系下的坐标是 $p'$。
- 它们的关系是 $p = p' + w$ 或 $p' = p - w$。比如,原点本身,旧坐标是 $(0,0)$,新坐标是 $(0-w_1, 0-w_2) = -w$。
- 平移变换自身的变化:
- 考虑一个由向量 $v$ 定义的平移变换 $m=t_v$。
- 在新的坐标系下,这个变换会变成什么样?我们使用共轭公式 $m' = \eta^{-1} m \eta$,其中 $\eta = t_w$ 是坐标变换。
- $m' = t_w^{-1} t_v t_w = t_{-w} t_v t_w$。
- 根据平移的复合规则,这等于 $t_{-w+v+w} = t_v$。
- 惊人的结论:
- 平移变换 $t_v$ 在坐标系平移后,其形式完全不变!它仍然是 $t_v$。
- 几何意义:平移这个“动作”(比如“向右移动5米”)的描述,与你把坐标系的原点放在哪里无关。
- 对比: 点的坐标会改变 ($p' = p-w$),但定义平移的向量 $v$ 不会变。
- 这就是点和向量的本质区别。点的坐标是相对的,依赖于原点选择。向量(作为位移)是绝对的,不依赖于原点。
📜 [原文26]
另一方面,如果我们通过正交算子 $\varphi$ 改变坐标,那么 $\varphi\left(p^{\prime}\right)=p$,并且如果 $m=t_{v}$,那么 $m^{\prime}=\varphi^{-1} t_{v} \varphi=t_{v^{\prime}}$,其中 $v^{\prime}=\varphi^{-1} v$。所以 $\varphi v^{\prime}=v$。正交算子改变坐标的效果在 $P$ 和 $V$ 上是相同的。
这里讨论另一种坐标变换——旋转或反射坐标系。
- 坐标系旋转/反射: 我们保持原点不动,但旋转/反射坐标轴。这由一个正交算子 $\varphi$ 描述。
- 一个固定的几何点,旧坐标为 $p$,新坐标为 $p'$。关系是 $p = \varphi(p')$ 或 $p'=\varphi^{-1}(p)$。
- 平移变换的变化:
- 还是考虑平移变换 $m=t_v$。
- 在新坐标系下,它变成 $m' = \varphi^{-1} m \varphi = \varphi^{-1} t_v \varphi$。
- 使用复合规则: $t_v \varphi = \varphi t_{\varphi^{-1}(v)}$(这是 $\rho_\theta t_v=t_{\rho_\theta(v)}\rho_\theta$ 规则的变体)。所以 $t_v = \varphi t_{\varphi^{-1}(v)} \varphi^{-1}$。
- 因此 $\varphi^{-1} t_v \varphi = \varphi^{-1} (\varphi t_{\varphi^{-1}(v)} \varphi^{-1}) \varphi = t_{\varphi^{-1}(v)}$。
- 结论:
- 在旋转/反射的坐标变换下,平移变换 $t_v$ 变成了 $t_{v'}$,其中新的平移向量 $v'$ 是旧的平移向量 $v$ 被坐标变换的逆变换 $\varphi^{-1}$ 作用后的结果。
- 几何意义:如果你把坐标轴转了 $30^\circ$,那么原来一个“向东”的平移向量,在新坐标系下看起来就是“向南偏东 $30^\circ$”了。它的分量会改变。
- 在这种坐标变换下,点的坐标和向量的坐标(分量)以同样的方式变化,即 $p'=\varphi^{-1}(p)$ 且 $v' = \varphi^{-1}(v)$。
📜 [原文27]
$P$ 和 $V$ 之间唯一的区别是 $P$ 中的原点不必是固定的,而零向量在 $V$ 中被选为原点。
正交算子作用于 $V$,但它们不作用于 $P$,除非选择了原点。
这几句是画龙点睛的总结。
- P与V的唯一区别:
- 在点空间 $P$ 中,没有哪个点是天生特殊的。“原点”只是我们为了方便计算而人为选择的一个参考点,它可以被随意平移。
- 在向量空间 $V$ 中,零向量 $\begin{pmatrix} 0 \\ 0 \end{pmatrix}$ 是一个绝对的、特殊的元素。它是加法的单位元,代表“没有位移”。你不能随意改变零向量的定义。
- 算子的作用对象:
- 正交算子(如 $\rho_\theta, r$)天生是作用在向量上的(它们是线性算子,保持零向量不变),所以它们作用于 $V$。
- 正交算子不能直接“作用于点空间 $P$”,因为 $P$ 没有一个固定的中心。只有当你为 $P$ 人为地指定了一个原点 $o$ 时,你才能把点和从 $o$ 出发的向量等同起来,从而让正交算子作用在这些向量上,实现对点的变换。这就是为什么我们总是说“绕原点的旋转”。如果你不指定“原点”,那么“旋转”这个词本身是无意义的。
通过区分点空间 $P$ 和向量空间 $V$,并考察它们在不同坐标变换下的行为,我们深化了对仿射几何基本概念的理解。点是位置,其坐标依赖于原点选择。向量是位移,其本身不依赖于原点,但其坐标分量依赖于坐标轴的方向。这个区别是理解平移在等距变换群中扮演的特殊角色的关键。
7行间公式索引
1. 平移变换公式
该公式定义了平移变换 $t_a$,它将点 $x$ 的位置向量加上一个平移向量 $a$。
2. 旋转变换公式
该公式定义了绕原点逆时针旋转角度 $\theta$ 的变换 $\rho_\theta$,通过左乘一个 $2 \times 2$ 的旋转矩阵来实现。
3. 反射变换公式
该公式定义了关于 $e_1$ 轴($x$ 轴)的反射变换 $r$,通过左乘一个反射矩阵实现,该矩阵将 $x_2$ 坐标取反。
4. 等距变换群的复合规则(关系)
这组公式描述了等距变换群 $M$ 的生成元(平移 $t_v$、旋转 $\rho_\theta$、反射 $r$)之间的代数复合规则。
5. 求解不动点的线性算子矩阵
该矩阵是线性算子 $I-\rho_\theta$ 的矩阵表示,用于求解变换 $t_a\rho_\theta$ 的不动点 $p$ 的方程 $(I-\rho_\theta)p = a$。
6. 改变定向变换的坐标表示
该公式给出了一个简化后的改变定向的等距变换 $m = t_a r$ 作用在任意点 $(x_1, x_2)$ 上的具体坐标变化结果。