11. 6.6 平面晶体学群
11. 引言与背景回顾
1.1.1. 原文
我们回到等距变换的离散群 $G \subset M$。我们已经看到,当 $L$ 是平凡群时,$G$ 是循环群或二面体群。离散群 $G$ 使得 $L$ 是无限循环群 (6.5.5)(b) 是带状图案的对称群,如 (6.1.3), (6.1.4) 所示。我们把这些群的分类留作练习。
1.1.2. 逐步解释
这段话是本节的引言,它首先将我们的注意力带回到之前讨论过的一个核心概念上:等距变换的离散群。让我们一步步拆解这句话。
1. “我们回到等距变换的离散群 $G \subset M$”:
* M (Motion Group):首先,$M$ 代表了平面上所有等距变换(Isometry)组成的群。等距变换是指保持距离不变的变换,具体包括平移 (translation)、旋转 (rotation)、反射 (reflection) 和滑移反射 (glide reflection)。这些变换可以组合(复合),并且都有逆变换,因此构成一个群。
* G (Group):$G$ 是 $M$ 的一个子群。这意味着 $G$ 是一些等距变换的集合,这个集合也满足群的四个基本公理(封闭性、结合律、存在单位元、存在逆元)。
* 离散群 (Discrete Group):这是 $G$ 的一个关键性质。“离散”意味着群里的变换不是“连续”的。直观地讲,如果你对一个点反复应用群中的任何一个变换(除了单位变换),这个点不会无限逼近它的初始位置,而是会“跳”到一系列孤立的位置。一个更精确的定义是,对于平面上的任意一个点 $p$,它在群 $G$ 作用下的轨道 $G p = \{g(p) | g \in G\}$ 是一个离散点集。这意味着每个点的周围都有一个小的邻域,这个邻域内不再有轨道中的其他点。想象一下,一个图案上的对称操作,比如一个正方形绕中心旋转90度,你只能得到4个不同的朝向,这些朝向是离散的,你不可能旋转一个任意小的角度还保持对称。
2. “我们已经看到,当 $L$ 是平凡群时,$G$ 是循环群或二面体群”:
* L (Translation Subgroup):这里的 $L$ 是指群 $G$ 中所有纯平移变换组成的子群,称为平移子群。对于任意一个等距变换群 $G$,它的平移子群 $L$ 要么是平凡群(只包含一个单位变换,即不动),要么是无限循环群(所有平移都在一条直线上),要么是一个格(平移分布在两个不同方向上)。
* 平凡群 (Trivial Group):$L$ 是平凡群意味着对称群 $G$ 中没有任何非平凡的平移对称性。也就是说,你无法将图案平移一段距离后还能与自身重合。
* 结论:如果一个离散等距变换群没有平移对称性,那么它必然是关于某一个点对称的。这样的群只有两种:
* 循环群 $C_n$:只包含绕一个中心点的旋转(包括0度旋转)。例如,一个风车图案的对称群。
* 二面体群 $D_n$:除了包含循环群 $C_n$ 的所有旋转外,还包含反射。例如,一个正 $n$ 边形的对称群。
3. “离散群 $G$ 使得 $L$ 是无限循环群 (6.5.5)(b) 是带状图案的对称群...”:
* 无限循环群 (Infinite Cyclic Group):$L$ 是无限循环群意味着图案的平移对称性只存在于一个方向上。你可以沿着某个向量 $v$ 和它的整数倍 $-v, 2v, -2v, ...$ 方向平移,图案会与自身重合。
* 带状图案 (Frieze Pattern):这种只有单一方向平移对称性的图案就是所谓的带状图案或饰带图案。想象一下墙壁上的腰线、花边或者古代建筑的饰带,它们在水平方向上不断重复。
* 分类:作者提到,这些带状图案的对称群(共有7种,称为饰带群)的分类问题,作为一个练习留给读者。这暗示了本节将要处理的是比带状图案更复杂的情况。
1.1.3. 具体数值示例
* 示例 1:平凡群 $L$ -> 二面体群 $D_4$
* 图案:一个静止的正方形。
* 平移子群 $L$:你无法将这个正方形平移任何非零的距离后使其与自身完全重合。所以它的平移子群 $L$ 只包含“平移0距离”这个单位变换,即 $L = \{t_0\}$,这是平凡群。
* 对称群 $G$:这个正方形的对称群是 $D_4$。它包含:
* 绕中心旋转 $0^\circ, 90^\circ, 180^\circ, 270^\circ$ (构成子群 $C_4$)。
* 4条反射轴(穿过对边中点的2条,穿过对角的2条)。
* 这个例子验证了“当 $L$ 是平凡群时,$G$ 是二面体群”的说法。
* 示例 2:无限循环群 $L$ -> 带状图案
* 图案:想象一排无限延伸的字母 ... H H H H ...。
* 平移子群 $L$:设一个 'H' 的宽度是 $w$。你可以将整个图案向右平移 $w, 2w, 3w, ...$ 的距离,或者向左平移 $-w, -2w, ...$ 的距离,图案都保持不变。所有的这些平移构成了一个无限循环群,由基本平移 $t_w$ (向右平移 $w$) 生成。即 $L = \{ t_{kw} \mid k \in \mathbb{Z} \}$。
* 对称群 $G$:除了平移,这个图案还有其他的对称性,比如绕每个 'H' 中心的 $180^\circ$ 旋转,以及穿过 'H' 中间横杠的水平反射轴,还有穿过两个 'H' 之间空隙的竖直反射轴。所有这些变换构成了这个带状图案的对称群。
1.1.4. 易错点与边界情况
* 离散 vs. 连续:很容易混淆离散群和连续群。一个圆形的对称群是连续的,因为你可以绕圆心旋转任意角度,它都保持不变。而一个正六边形的对称群是离散的,你只能旋转 $60^\circ$ 的整数倍。本节讨论的晶体学群都是离散的。
* $L$ 的维度:要清楚平移子群 $L$ 的“维度”。
* 0维:$L$ 是平凡群(对应点群)。
* 1维:$L$ 是无限循环群(对应饰带群)。
* 2维:$L$ 是一个格(对应平面晶体学群),这是本节的重点。
* 群 vs. 图案:要区分对称群 $G$(一个抽象的代数结构)和它所作用的图案(一个具体的几何对象)。同一个对称群可以对应无数个看起来不一样的图案。
1.1.5. 总结
本段的核心作用是承上启下。它回顾了两种已经(或将被作为练习)分析过的离散等距变换群:没有平移对称性的(点群 $C_n, D_n$)和只有一维平移对称性的(饰带群)。通过这种回顾,作者将讨论的焦点自然地引向了下一个、也是更复杂的情况:具有二维平移对称性的群。
1.1.6. 存在目的
这一段的目的是为即将展开的对平面晶体学群的讨论设置舞台。它通过回顾已知知识,明确了研究对象在整个等距变换群分类体系中的位置。这有助于读者理解,我们正在从最简单的情况(0维平移)逐步过渡到更复杂的情况(1维平移),最终进入本节的主题(2维平移)。这是一种系统性的、由简入繁的数学研究方法。
1.1.7. 直觉心智模型
想象你是一个设计师,手上有几种基本的几何操作工具:平移、旋转和反射。
1. 情况1(点群):你只能站在一个点上进行操作,不能移动。你所有的设计都围绕这个点展开。你能创造出的对称图案就是风车(只有旋转)或者雪花(有旋转和反射)。
2. 情况2(饰带群):你现在可以沿着一条直线来回移动你的操作中心。你创造的图案会在这个方向上无限重复,就像一条花边。
3. 情况3(晶体学群):现在你获得更大的自由,可以在整个平面上任意移动,但你的移动必须遵循一个网格的结构,比如只能在棋盘的格点上落脚。你创造出的图案会在两个不同的方向上无限重复,就像一块铺满整个房间的瓷砖。本节就是要研究这种“棋盘式”对称性的所有可能性。
1.1.8. 直观想象
想象一下站在一个无边无际的、用完全相同的地砖铺成的广场上。
* 如果你低头只看一块地砖的中心,并考虑这块地砖自身的对称性(比如它是正方形的),这对应于点群的概念。
* 如果你沿着一排地砖往前看,你会发现地砖在你的前进方向上不断重复,这体现了一维平移对称性,就像带状图案。
* 现在,你意识到不仅你前进的方向有重复,你左边和右边也都是完全相同的地砖,整个广场在两个方向上都无限重复。这种遍布整个平面的、具有二维重复性的对称结构,就是平面晶体学群所要描述的对象。
12. 晶体学群的定义与晶体学限制
1.2.1. 原文
当 $L$ 是格时,$G$ 称为二维晶体学群。这些晶体学群是二维晶体的对称群,如石墨。我们设想晶体是无限大的。那么,分子排列规则的事实意味着它们形成了一个具有两个独立平移对称的阵列。墙纸图案也在两个不同的方向上重复——一次是沿着纸条,因为图案是用滚筒印刷的,另一次是因为纸条并排粘在墙上。晶体学限制限制了可能性,并
允许将晶体学群分类为 17 种类型。具有各种对称类型的代表性图案如图 (6.6.2) 所示。
1.2.2. 逐步解释
1. “当 $L$ 是格时,$G$ 称为二维晶体学群”:这是平面晶体学群(Plane Crystallographic Group)或墙纸群(Wallpaper Group)的核心定义。
* L 是格 (Lattice):回顾一下,$L$ 是对称群 $G$ 中的平移子群。说 $L$ 是一个格,意味着存在两个线性无关的向量 $v_1$ 和 $v_2$(即它们不在同一条直线上),使得 $L$ 中所有的平移都可以表示为 $t_{av_1 + bv_2}$ 的形式,其中 $a$ 和 $b$ 是任意整数。换句话说,这个图案的平移对称性是在两个独立方向上重复出现的。这就像一个无限大的棋盘,你可以沿着行平移任意格,也可以沿着列平移任意格,图案都会保持不变。
2. “这些晶体学群是二维晶体的对称群,如石墨”:这里给出了物理世界中的一个例子。
* 二维晶体:像石墨(graphene,单层石墨)或云母的原子排列,可以在一个平面上形成高度规则的、重复的结构。
* 对称群:描述这些原子排列方式的所有对称操作(平移、旋转、反射等)的集合,就构成了一个晶体学群。
* 无限大设想:在数学上,我们处理的是理想化的无限大晶体或图案。这样做是为了避免边界效应,从而能纯粹地研究其内在的、重复的对称结构。
3. “墙纸图案也在两个不同的方向上重复...”:这里用一个更生活化的例子——墙纸——来解释二维重复性。
* 滚筒印刷产生了第一个方向的重复(沿墙纸条的长度方向)。
* 将墙纸条并排粘贴在墙上,产生了第二个方向的重复(垂直于墙纸条长度的方向)。
* 这两个方向上的重复,共同构成了一个二维的格。
4. “晶体学限制限制了可能性,并允许将晶体学群分类为 17 种类型”:这是一个非常重要且深刻的结论。
* 晶体学限制 (Crystallographic Restriction):这是一个定理,它指出:如果一个离散等距变换群的平移子群是一个格,那么该群中任何旋转的阶(即旋转多少次能回到原始位置)只能是 1, 2, 3, 4 或 6。也就是说,你只能找到能够旋转 $360^\circ$ (阶1), $180^\circ$ (阶2), $120^\circ$ (阶3), $90^\circ$ (阶4) 或 $60^\circ$ (阶6) 而保持图案不变的中心点。你永远找不到一个无限重复的墙纸图案,它具有 $72^\circ$ 旋转对称性(五重对称)。
* 为什么会有这个限制? 直观地想,五边形或七边形无法像三角形、正方形、六边形那样无缝地铺满整个平面。如果你试图用正五边形地砖铺地,它们之间必然会留下空隙。这个几何上的限制反映到代数上,就是对旋转阶的限制。
* 17 种类型:基于晶体学限制以及对平移、旋转、反射和滑移反射组合方式的详尽分析,数学家们证明了,平面上总共只有 17 种本质上不同的晶体学群。图 (6.6.2) 展示了这 17 种对称类型的示例图案。
1.2.3. 具体数值示例
* 示例 1:一个简单的晶体学群 (p1)
* 图案:想象一个无限平面上,每个整数坐标点 $(m, n)$(其中 $m, n$ 是整数)上都画了一个没有对称性的小逗号 ","。
* 平移子群 $L$:这个图案的平移对称由两个基向量 $v_1 = (1, 0)$ 和 $v_2 = (0, 1)$ 生成。你可以将图案平移向量 $m v_1 + n v_2 = (m, n)$,图案会完全重合。这个 $L$ 就是一个正方格。
* 对称群 $G$:除了平移,这个图案没有任何旋转或反射对称性。所以 $G$ 就是平移子群 $L$ 本身。这是最简单的一种晶体学群,记作 p1。
* 示例 2:具有旋转对称的晶体学群 (p4)
* 图案:在无限棋盘的每个格子的中心,都画一个风车图案。
* 平移子群 $L$:同样,由 $v_1 = (1, 0)$ 和 $v_2 = (0, 1)$(假设格子边长为1)生成的正方格。
* 对称群 $G$:这个图案不仅有平移对称,还有旋转对称。
* 在每个格子中心,都有一个 $90^\circ, 180^\circ, 270^\circ$ 旋转对称中心。
* 在每个格子的顶点,也有一个 $90^\circ$ 旋转对称中心。
* 在每条边的中点,有一个 $180^\circ$ 旋转对称中心。
* 所有这些平移和旋转操作共同构成了晶体学群 p4。
1.2.4. 易错点与边界情况
* 晶体学限制的误用:晶体学限制(只能有1,2,3,4,6重旋转)仅适用于具有格状平移对称性的离散群。对于只有一个不动点的点群,不存在这个限制。例如,一个孤立的正五边形具有5重旋转对称,它的对称群是 $D_5$,但它不能铺满平面。
* 17这个数字的含义:这不是指有17种图案,而是指有17种不同的对称群结构。无数种外形的图案可能共享同一种对称结构。例如,一个铺满棋盘的万字饰图案和一个铺满棋ard的风车图案,可能都属于 p4 群。
* 群和格的关系:$L$ (格) 是 $G$ (晶体学群) 的一个子群,而且是一个非常重要的正规子群。研究 $G$ 的结构,很大程度上依赖于分析 $L$ 以及商群 $G/L$(即点群 $\bar{G}$)。
1.2.5. 总结
本段正式定义了平面晶体学群,即其平移子群 $L$ 是一个二维格的离散等距变换群。通过晶体和墙纸的例子,它直观地解释了这种二维重复性的含义。最关键的信息是晶体学限制的存在,它极大地缩减了旋转对称的可能性,并最终导致平面上只有 17 种这样的对称群。
1.2.6. 存在目的
本段的目的是从上一段的铺垫过渡到本节的核心主题。它通过一个明确的定义($L$ 是一个格),将我们的研究范围锁定在平面晶体学群上。同时,它通过引出“17”这个最终的分类数字,为整个章节设定了一个明确的目标:理解这些群是如何被分类的,并最终能够识别和区分它们。这激发了读者的好奇心,并提供了一个清晰的学习路径图。
1.2.7. 直觉心智模型
想象你在玩一个特殊的乐高游戏。你有无限量的相同积木块(比如一个不对称的小人仔)。
1. 定义:晶体学群就是你摆放这些积木块所遵循的“对称规则手册”。这个手册必须包含一个“网格移动”规则:你可以把整个积木阵列沿着两个不同方向的网格线移动,整体看起来和移动前一样。
2. 例子:石墨就是大自然用碳原子当积木,按照六边形网格规则手册拼出来的作品。墙纸是人类用图案当积木,按照长方形或正方形网格规则手册印出来的作品。
3. 晶体学限制:你的规则手册里关于“旋转一块区域”的规则是受限的。你不能制定一个“将这 $2 \times 2$ 区域的积木旋转 $72^\circ$”的规则,因为这样旋转后,它们就没法跟周围的积木对齐了。你只能制定旋转 $180^\circ, 120^\circ, 90^\circ, 60^\circ$ 的规则。
4. 17种类型:这本“对称规则手册”总共只有 17 个版本。无论你看到的墙纸、地砖、布料图案多么千变万化,它们内在的对称性都逃不出这 17 种。
1.2.8. 直观想象
站在一个巨大的、铺满图案的房间里,这个图案无限延伸。
* 格:你可以找到两个不同的方向,比如“向前3步”和“向右2步”,只要你按照这个步法移动,你脚下看到的图案和你出发时完全一样。所有这些可能的“对称步法”构成了一个网格,这就是格 $L$。
* 晶体学限制:你在房间里寻找一个可以作为“旋转中心”的点。你发现,如果你站在某个点上旋转身体,只有当你转了 $180^\circ$(比如一个砖块图案的中心)、$120^\circ$(比如一个蜂巢图案的中心)、$90^\circ$ 或 $60^\circ$ 时,你看到的整个房间的景象才和旋转前一样。你永远找不到一个能让你转 $72^\circ$(五分之一圈)后景象不变的点。
* 17种:这个无限房间的整体对称性,总共只有 17 种可能的设计蓝图。
13. 点群与滑移反射
1.3.1. 原文
点群 $\bar{G}$ 和平移群 $L$ 并不能完全确定群 $G$。事情变得复杂,因为 $\bar{G}$ 中的反射不一定是 $G$ 中反射的像。在 $G$ 中,它可能仅由滑移表示,如砖块图案所示。这种图案(我最喜欢的)相对微妙,因为它的对称群不包含反射。它在每块砖块中心处具有角度为 $\pi$ 的旋转对称。所有这些旋转都代表点群 $\bar{G}$ 的相同元素 $\bar{\rho}_{\pi}$。除了 0 和 $\pi$ 之外,没有非平凡的旋转对称。该图案还在图中虚线所示方向上具有滑移对称,因此 $\bar{G}=D_{2}=\left\{1, \overline{\rho_{\pi}}, \bar{r}, \overline{\rho_{\pi} r}\right\}$。
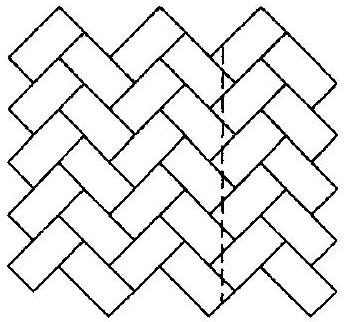
1.3.2. 逐步解释
1. “点群 $\bar{G}$ 和平移群 $L$ 并不能完全确定群 $G$”:这是本段的核心论点。
* 点群 $\bar{G}$ (Point Group):对于一个等距变换 $g = t_v \rho$(先旋转/反射 $\rho$,再平移 $t_v$),它的“线性部分” $\rho$ 就是它在点群 $\bar{G}$ 中对应的元素 $\bar{g}$。点群 $\bar{G}$ 描述的是对称群 $G$ 中所有变换的“旋转和反射”部分,它忽略了平移分量。可以证明 $\bar{G}$ 本身也是一个群,并且根据晶体学限制,它必然是 $C_n$ 或 $D_n$ 中的一种(其中 $n \in \{1,2,3,4,6\}$)。
* $L$ (平移群/格):描述了群 $G$ 的纯平移对称性。
* 为什么不能完全确定? 作者指出,即使我们知道了 $L$(图案的重复网格)和 $\bar{G}$(图案包含哪些类型的旋转和反射),我们还是无法唯一地确定整个对称群 $G$ 的结构。这就像知道了一支军队有多少个师($L$),以及每个师里士兵的兵种构成($\bar{G}$),但你不知道这些兵种是如何部署和协同作战的($G$ 的具体结构)。
2. “事情变得复杂,因为 $\bar{G}$ 中的反射不一定是 $G$ 中反射的像”:这里解释了复杂性的来源。
* $\bar{G}$ 中有一个反射元素 $\bar{r}$,意味着图案“在某种意义上”是左右对称的。
* 但是,这种“左右对称”在实际的对称群 $G$ 中,可以有两种实现方式:
* 纯反射 (Reflection):$G$ 中确实包含一个关于某条直线 $l$ 的反射变换 $r_l$。这个 $r_l$ 的线性部分就是 $\bar{r}$。
* 滑移反射 (Glide Reflection):$G$ 中可能不包含任何纯反射,但它包含一个滑移反射 $g$。滑移反射是指先沿着一条直线 $l$ 做反射,然后再沿着 $l$ 的方向平移一段距离。这个变换 $g$ 的线性部分同样是 $\bar{r}$。
* 因此,当我们在点群 $\bar{G}$ 中看到一个反射元素时,我们必须回到原来的对称群 $G$ 中去检查,实现这个反射元素的,到底是一个纯反射还是一个滑移反射。这两种不同的实现方式会导致两个本质上不同的晶体学群。
3. “如砖块图案所示...”:作者用一个具体的例子来说明这种复杂性。
* 图案:一个经典的砖墙图案,上下两排砖块交错排列。
* 旋转对称:在每块砖的中心,你都可以将图案旋转 $180^\circ$ ($\pi$ 弧度),图案会与自身重合。所以 $G$ 包含 $180^\circ$ 旋转。因此,点群 $\bar{G}$ 至少包含一个 $180^\circ$ 旋转元素 $\bar{\rho}_\pi$。
* 反射对称?:你试试在砖墙图案上画一条水平或垂直的直线,然后沿这条线做反射。你会发现图案无法与自身重合。例如,沿一条水平灰缝反射,上排的砖块会跑到下排,但它们的位置是错开的,无法重合。所以,这个图案的对称群 $G$ 不包含任何纯反射。
* 滑移对称 (Glide Symmetry):观察图中虚线。如果你先把整个图案沿着这条虚线做反射,然后再把图案沿着虚线的方向平移半块砖的宽度,你会发现图案与自身完美重合。这个“反射+平移”的复合操作就是一个滑移反射。
* 结论:这个滑移反射操作在点群 $\bar{G}$ 中的像就是一个反射 $\bar{r}$。因此,这个砖墙图案的点群 $\bar{G}$ 同时包含了 $180^\circ$ 旋转 $\bar{\rho}_\pi$ 和反射 $\bar{r}$。由这两个元素生成的群是 $D_2 = \{1, \bar{\rho}_\pi, \bar{r}, \bar{\rho}_\pi \bar{r}\}$。然而,实际的对称群 $G$ 却不包含纯反射,只包含滑移反射。这就证明了,$L$ 和 $\bar{G}$ 不足以确定 $G$。
1.3.3. 具体数值示例
* 示例 1:群 pm (有反射)
* 图案:想象一排无限重复的字母 B B B B。并且在它下面是它的镜像 p p p p(这里p是B的镜像)。
* L:沿水平方向的平移构成一维格(技术上这是个饰带群,但原理相通)。
* $\bar{G}$:这个图案显然有水平反射对称轴(穿过B和p的中间)。所以 $\bar{G}$ 包含反射元素 $\bar{r}$。
* G:对称群 $G$ 中真实地包含一个纯反射操作。
* 这个群的点群和砖墙图案的点群(如果只看一维)类似,但群 $G$ 的结构不同。
* 示例 2:群 pg (只有滑移反射,砖墙图案的抽象)
* 图案:想象一排脚印 ... 🐾 🐾 🐾 🐾 ...,但每个脚印都指向前方。
* L:从一只左脚印到下一只左脚印的平移是对称操作。
* $\bar{G}$:这个图案的点群包含一个反射元素。为什么?因为滑移反射(从左脚印到右脚印)的线性部分是一个反射。
* G:群 $G$ 中不包含纯反射。你找不到一条线,能把左脚印变成右脚印而不移动它。但是它包含一个滑移反射:沿着脚印中间的路径反射,同时向前平移一步。
* 这就是 pm 和 pg 这两个不同晶体学群的区别。它们有相同的平移格 $L$ 和相同的点群 $\bar{G}$,但一个是纯反射实现,另一个是滑移反射实现。
1.3.4. 易错点与边界情况
* 混淆 G 和 $\bar{G}$:这是最核心的易错点。$\bar{G}$ 是一个“简化版”的群,它只告诉你“有什么样的转动和镜面对称”,但没告诉你这些对称是“纯粹的”还是“带滑动的”。$G$ 才是包含所有完整信息的“完全版”对称群。
* 寻找滑移反射:滑移反射比纯反射更难被直观地发现。检查一个图案是否有纯反射比较容易,如果没有,不要立刻断定它没有反射类对称,而要去寻找是否存在滑移反射。
* 点群的确定:如原文所述,$\bar{G}$ 中存在反射元素 $\bar{r}$,可能是因为 $G$ 中有纯反射,也可能是因为 $G$ 中有滑移反射。只要两者有其一,$\bar{G}$ 就会包含反射元素。
1.3.5. 总结
本段通过“砖墙图案”这个经典例子,生动地揭示了晶体学群分类中的一个关键复杂点:点群 $\bar{G}$ 和平移格 $L$ 不足以唯一确定群 $G$。根本原因在于,点群中的一个反射元素,在实际的群 $G$ 中可以由一个纯反射来实现,也可以由一个滑移反射来实现,而这两种实现方式会产生结构不同的群。
1.3.6. 存在目的
这一段的目的是为了深化读者对晶体学群结构的理解,指出分类工作不能仅仅停留在分析点群和格上。它引入了滑移反射这个重要的概念,并阐明了它在群分类中的核心作用。这为后面更形式化、更代数的分类方法铺平了道路,解释了为什么需要进行更细致的分析,而不仅仅是看 $L$ 和 $\bar{G}$ 就够了。
1.3.7. 直觉心智模型
回到乐高游戏。你现在知道你的规则手册由“网格移动规则 ($L$)”和“旋转/反射规则 ($\bar{G}$)”组成。
* 假设 $\bar{G}$ 规则说:“允许镜像操作”。
* 情况A (纯反射):你的手册里有一条具体指令:“拿起一块积木,沿着一条红线翻转到对面。” 这是一个纯反射。
* 情况B (滑移反射):你的手册里可能有另一条指令:“拿起一块积木,沿着一条蓝线翻转到对面,然后顺着蓝线向前推半格。” 这是一个滑移反射。
* 问题:当你只看“允许镜像操作”这条高层规则 ($\bar{G}$)时,你不知道手册里写的到底是情况A还是情况B。但A和B是两种完全不同的拼搭方式,会产生两种不同的整体图案。砖墙图案就是用情况B的规则拼出来的。因此,为了完全理解手册 ($G$),你必须打开看里面的具体指令,而不能只看封面上的规则摘要 ($\bar{G}$)。
1.3.8. 直观想象
想象你站在一条河边,河对岸有棵树。
* 纯反射:你在水中的倒影,就是你关于河岸线的一个纯反射。你和你的倒影在垂直于河岸的方向上是“面对面”的。
* 滑移反射:现在想象河水在流动。你在水中的倒影不仅是上下颠倒的,而且还被水流向下游冲走了一段距离。这个被冲走的倒影,就是你关于河岸线的一个滑移反射。
* 砖墙图案里的对称性,就像这条流动的河。上半部分的砖块在“对称之河”中的像,不是正好在它“对面”,而是被“冲走”了半块砖的距离。
14. 如何确定图案的点群
1.4.1. 原文
可以相当容易地通过两个步骤确定图案的点群:首先寻找旋转对称。它们通常相对容易找到。点群 $\bar{G}$ 中的旋转 $\bar{\rho}_{\theta}$ 在图案对称群 $G$ 中由具有相同角度的旋转表示。当找到旋转对称后,将知道整数 $n$,使得点群是 $C_{n}$ 或 $D_{n}$。然后,为了区分 $D_{n}$ 和 $C_{n}$,查看图案是否具有反射或滑移对称。如果具有,则 $\bar{G}=D_{n}$;如果没有,则 $\bar{G}=C_{n}$。
1.4.2. 逐步解释
这段话提供了一个实用的、两步走的策略,来确定任何一个给定墙纸图案的点群 $\bar{G}$。
第一步:寻找旋转对称
1. “首先寻找旋转对称。它们通常相对容易找到。”
* 这是确定点群的起点。你需要审视图案,找到所有能让图案旋转后保持不变的“中心点”和“角度”。
* 根据晶体学限制,这些角度只能是 $180^\circ$ (2重), $120^\circ$ (3重), $90^\circ$ (4重), 或 $60^\circ$ (6重)。
* 在图案中寻找旋转对称中心通常比寻找反射轴或滑移轴更直观。
2. “点群 $\bar{G}$ 中的旋转 $\bar{\rho}_{\theta}$ 在图案对称群 $G$ 中由具有相同角度的旋转表示。”
* 这是一个关键的简化!与反射可能由滑移反射实现不同,旋转总是“货真价实”的。如果点群 $\bar{G}$ 中有一个 $90^\circ$ 旋转元素,那么在实际的对称群 $G$ 中,必然存在一个或多个真实的、$90^\circ$ 旋转中心。旋转不存在“滑移旋转”这种对应物。
* 因此,通过观察图案中有哪些旋转,我们就能直接知道点群 $\bar{G}$ 中有哪些旋转元素。
3. “当找到旋转对称后,将知道整数 $n$,使得点群是 $C_n$ 或 $D_n$。”
* 一个有限点群中的旋转元素总是形成一个循环子群 $C_n$。$n$ 是图案中具有最高阶的旋转对称的阶数。
* 例如,如果你在图案中找到的最高阶旋转是 $90^\circ$(4重),那么 $n=4$。这意味着点群 $\bar{G}$ 的所有旋转操作构成了 $C_4 = \{0^\circ, 90^\circ, 180^\circ, 270^\circ\}$。
* 此时,整个点群 $\bar{G}$ 就只有两种可能:
* $C_n$:如果群里除了旋转,没有其他类型的操作(即没有反射类操作)。
* $D_n$:如果群里除了旋转,还包含了反射类操作。
第二步:区分 $C_n$ 和 $D_n$
1. “然后,为了区分 $D_n$ 和 $C_n$,查看图案是否具有反射或滑移对称。”
* 在确定了最高旋转阶数 $n$ 之后,任务就变成了判断点群是单纯的循环群 $C_n$ 还是更复杂的二面体群 $D_n$。
* 这个判断的依据就是检查图案中是否存在任何“反转方向”的对称操作。
2. “如果具有,则 $\bar{G}=D_{n}$;如果没有,则 $\bar{G}=C_{n}$。”
* “具有”:指的是图案的对称群 $G$ 中,存在纯反射或滑移反射。只要两者有其一,就意味着点群 $\bar{G}$ 中包含了反射元素。在这种情况下,$\bar{G}$ 就是二面体群 $D_n$。$D_n$ 由 $n$ 个旋转和 $n$ 个反射类元素构成。
* “没有”:指的是图案的对称群 $G$ 中,既没有纯反射,也没有滑移反射。这意味着 $G$ 中所有的变换都是保持方向的(平移和旋转)。在这种情况下,点群 $\bar{G}$ 只包含旋转元素,因此 $\bar{G}$ 就是循环群 $C_n$。
1.4.3. 具体数值示例
假设我们正在分析一个未知的墙纸图案:
* 示例 1:确定点群为 $C_4$
1. 第一步 (找旋转):我们仔细观察图案,发现了很多旋转中心。经过检查,我们找到的最高阶旋转是 $90^\circ$(4重)。比如,某个位置旋转 $90^\circ, 180^\circ, 270^\circ$ 图案都重合。我们没有发现任何 $60^\circ$ 或 $120^\circ$ 的旋转中心。因此,我们确定 $n=4$。点群要么是 $C_4$,要么是 $D_4$。
2. 第二步 (区分 $C_4/D_4$):我们开始寻找反射轴和滑移反射轴。我们尝试了所有可能的直线,发现无论如何做纯反射或滑移反射,图案都无法与自身重合。
3. 结论:因为没有反射或滑移对称,所以点群 $\bar{G} = C_4$。这个图案对应的晶体学群是 p4。
* 示例 2:确定点群为 $D_2$
1. 第一步 (找旋转):我们观察另一个图案(比如之前的砖墙图案)。我们找不到 $90^\circ, 60^\circ$ 的旋转。但是,我们发现在每块砖的中心,都可以旋转 $180^\circ$(2重)。这是最高阶的旋转。所以 $n=2$。点群要么是 $C_2$,要么是 $D_2$。
2. 第二步 (区分 $C_2/D_2$):我们检查反射和滑移。我们发现虽然没有纯反射轴,但存在一条滑移反射轴(砖缝之间的虚线)。
3. 结论:因为存在滑移对称,所以点群 $\bar{G} = D_2$。这个图案对应的晶体学群是 pgg。
1.4.4. 易错点与边界情况
* 找全旋转中心:要确定最高的旋转阶数 $n$,理论上需要检查所有不同类型的旋转中心。一个图案里可能同时存在2重、3重、6重的旋转中心(例如 p6m 群),此时 $n=6$。
* 滑移反射的隐藏性:再次强调,滑移反射是最容易被忽略的对称操作。如果一个图案看起来“有点像”对称但又不是纯反射对称,那很可能就是滑移反射。
* $n=1$ 的情况:如果一个图案没有任何旋转对称性(除了 $360^\circ$),那么 $n=1$。
* 如果它还没有任何反射或滑移,那么点群是 $C_1$ (平凡群)。
* 如果它有反射或滑移,那么点群是 $D_1$ (等价于 $C_2$,包含单位元和一次反射)。
1.4.5. 总结
本段给出了一个鉴定墙纸图案点群的实用算法:
1. 找到图案中最高阶的旋转对称,阶数为 $n$。这确定了点群的基本框架是 $C_n$ 或 $D_n$。
2. 检查图案中是否存在任何纯反射或滑移反射。
3. 如果存在,则点群为 $D_n$。如果不存在,则点群为 $C_n$。
这个流程极大地简化了点群的识别过程。
1.4.6. 存在目的
本段的目的是从理论转向实践。在上一段指出了滑移反射带来的复杂性之后,这一段立即提供了一个清晰、可操作的方法来应对这种复杂性,至少在确定点群这个层面上是如此。它告诉读者,尽管 $G$ 的结构复杂,但确定其点群 $\bar{G}$ 是一个有章可循的过程。这给予了读者分析具体图案的工具和信心。
1.4.7. 直觉心智模型
你是一名侦探,面对一个复杂的犯罪现场(墙纸图案),你的任务是确定幕后黑手团伙的“高层领导结构”(点群 $\bar{G}$)。
1. 第一步:寻找“头目”。你先不在意小喽啰(平移),而是寻找现场的“指挥中心”,即旋转中心。你发现现场有好几个指挥中心,其中最高级别的能下达“全体旋转90度”的命令。你断定这个团伙的“核心领导层”是一个四人旋转小组 ($C_4$)。那么这个团伙的完整高层结构,要么就是这个纯粹的四人旋转小组 ($C_4$),要么是一个更复杂的、包含“卧底”(反射)的八人小组 ($D_4$)。
2. 第二步:寻找“卧底”。你开始排查现场是否留下了“卧底”的痕迹。“卧底”有两种:一种是直接露脸的(纯反射),另一种是伪装后行动的(滑移反射)。你在现场的蛛丝马迹中发现了一些需要“先镜像,再平移”才能解释的痕迹。你找到了“卧底”存在的证据。
3. 结论:因此,你断定这个团伙的高层结构是包含“卧底”的八人小组 $D_4$,而不是纯粹的四人旋转小组 $C_4$。
1.4.8. 直观想象
你手里拿着一张透明的塑料片,上面画着一个基本的图案单元。你的目标是移动这张塑料片,使其与墙纸上的另一个图案单元重合。
1. 旋转:你把塑料片钉在墙纸的某个点上,然后旋转它。如果转了 $90^\circ$ 后,你的塑料片和下面的墙纸图案完美重合,你就找到了一个4重旋转中心。记下这个最高的旋转角度。
2. 反射:你把塑料片从墙上拿下来,翻个面(像翻书一样),再试着对齐墙纸。如果能找到一条线,使得翻面后的塑料片能与墙纸重合,你就找到了纯反射。
3. 滑移反射:你把塑料片翻个面,发现对不齐。但你没有放弃,你把翻过面的塑料片沿着某个方向滑动了一段距离,发现它与墙纸重合了。你就找到了滑移反射。
4. 判断:
* 如果你在第1步找到了最高 $n$ 重旋转,但在第2、3步一无所获,那么点群就是 $C_n$。
* 如果你在第1步找到了最高 $n$ 重旋转,并且在第2步或第3步中至少有一样成功了,那么点群就是 $D_n$。
22. 具有四重旋转的平面晶体学群
21. 引言与分析目标
2.1.1. 原文
作为用于分类等距变换的离散群的方法的一个例子,我们分析点群为 $C_{4}$ 或 $D_{4}$ 的群。
2.1.2. 逐步解释
这句话设定了本节后续内容的具体目标。作者不打算对全部17种晶体学群进行完整和冗长的分类推导,而是选择其中一个子集作为案例研究,来展示分类所使用的典型方法和逻辑。
1. “作为...的一个例子”: 这明确告诉读者,接下来的内容是一个示范,而不是一个全面的推导。其目的是教学,让读者“管中窥豹”,理解整个分类过程的精神和技巧。
2. “分析点群为 $C_4$ 或 $D_4$ 的群”: 这里选定了要分析的对象。
* 我们从上一节的“两步法”知道,当一个图案的最高阶旋转对称是4重($90^\circ$)时,它的点群 $\bar{G}$ 不是 $C_4$ 就是 $D_4$。
* $C_4$:点群只包含 $0^\circ, 90^\circ, 180^\circ, 270^\circ$ 旋转。对应的图案有4重旋转对称,但没有任何反射或滑移对称。
* $D_4$:点群除了包含 $C_4$ 的四个旋转外,还包含4个反射类元素。对应的图案既有4重旋转对称,又有反射或滑移对称。
* 选择这个例子是因为4重对称在几何上和代数上都具有足够丰富的结构,能够很好地展示分类中的关键思想,但又不像6重对称那样复杂。
2.1.3. 具体数值示例
* 图案示例 (点群 $C_4$): 想象一个无限棋盘,在每个格子的中心画一个万字饰“卍”。这个图案有 $90^\circ$ 旋转对称,但没有反射或滑移对称。它的对称群的点群就是 $C_4$。
* 图案示例 (点群 $D_4$): 想象一个无限棋盘,每个格子就是简单的白色或黑色交替(标准的棋盘格)。这个图案在每个格子中心、每个顶点都有 $90^\circ$ 旋转对称。同时,它还有穿过格子边缘和对角线的反射轴。它的对称群的点群就是 $D_4$。
2.1.4. 易错点与边界情况
* 不要误以为本节会讨论所有17种群。焦点被严格限定在那些具有4重对称的群上。
* 要时刻记住 $C_4$ 和 $D_4$ 是点群 $\bar{G}$,而不是晶体学群 $G$ 本身。本节的目标是找出所有以 $C_4$ 或 $D_4$ 为点群的晶体学群 $G$。
2.1.5. 总结
本段是一个引子,它清晰地陈述了接下来要执行的任务:以点群为 $C_4$ 或 $D_4$ 的晶体学群为例,演示对这类群进行分类的方法。
2.1.6. 存在目的
这段话的目的是为后续的详细数学推导提供一个清晰的导向和范围限定。它让读者知道,我们将要深入研究一个具体的、重要的案例,而不是泛泛而谈。这有助于集中注意力,并为读者提供一个可消化、可理解的知识块。
2.1.7. 直觉心智模型
想象我们是生物学家,目标是对世界上所有的动物进行分类。这是一个浩大的工程。为了向学生展示分类学的方法,我们不说“今天我们来分类所有动物”,而是说“今天我们以‘有四条腿的哺乳动物’为例,来演示如何进行科学分类”。这里的“四条腿的哺乳动物”就对应“点群为 $C_4$ 或 $D_4$ 的群”。我们通过解剖这一个具体的类别,来学习通用的方法论。
2.1.8. 直观想象
想象我们面前有所有17种墙纸图案。我们从中挑出所有那些“看起来有正方形感觉的”(即具有 $90^\circ$ 旋转对称)图案。然后,我们的任务就是对这一小堆图案进行再细分,看看它们内部还有哪些不同的对称结构。
22. 格的形状
2.2.1. 原文
设 $G$ 是这样一个群,设 $\bar{\rho}$ 表示 $\bar{G}$ 中角度为 $\pi / 2$ 的旋转,设 $L$ 是 $G$ 的格,即向量 $v$ 的集合,使得 $t_{v}$ 在 $G$ 中。
引理 6.6.2 格 $L$ 是正方形的。
证明。我们选择 $L$ 中长度最小的非零向量 $a$。点群作用于 $L$,因此 $\bar{\rho}(a)=b$ 在 $L$ 中并与 $a$ 正交。我们声称 $(a, b)$ 是 $L$ 的格基。
假设不是。那么根据引理 6.5.8,在区域 $\Pi^{\prime}$ 中将有一个 $L$ 的点,该区域由 $0 \leq r_{i}<1$ 的点 $r_{1} a+r_{2} b$ 组成。这样一个点 $w$ 将距离正方形的四个顶点 $0, a, b, a+b$ 中的一个小于 $|a|$。称该顶点为 $v$。那么 $v-w$ 也在 $L$ 中,且 $|v-w|<|a|$。这与 $a$ 的选择相矛盾。$\square$
2.2.2. 逐步解释
这一部分是整个分析的第一步,也是至关重要的一步:确定平移格 $L$ 的几何形状。结论是,只要一个晶体学群含有四重旋转对称,它的平移格必然是正方形的。
引理的陈述与前提
* 前提:我们有一个晶体学群 $G$,其点群 $\bar{G}$ 包含一个 $90^\circ$(即 $\pi/2$ 弧度)的旋转元素 $\bar{\rho}$。$L$ 是 $G$ 的平移格。
* 结论:$L$ 必须是一个正方格。这意味着 $L$ 可以由两个长度相等且相互垂直的向量生成。
证明的步骤详解
1. “我们选择 $L$ 中长度最小的非零向量 $a$”:
* 因为 $L$ 是一个格,它包含了除原点 $(0,0)$ 之外的无数个点。这些点到原点的距离各不相同。因为 $L$ 是离散的,所以一定存在一个或多个点,它们到原点的距离是所有非零距离中最小的。我们从中随便选一个,代表的向量记为 $a$。$|a|$ 就是这个最小距离。
2. “点群作用于 $L$,因此 $\bar{\rho}(a)=b$ 在 $L$ 中并与 $a$ 正交”:
* 点群作用于格 (Point group acts on the lattice): 这是一个基本性质。$L$ 是 $G$ 的一个正规子群,商群 $G/L$ 同构于点群 $\bar{G}$。$\bar{G}$ 的作用可以这样理解:对 $L$ 中的任意向量 $v$,以及 $\bar{G}$ 中的任意元素 $\bar{g}$,向量 $\bar{g}(v)$ 必然也在 $L$ 中。直观地说,如果你对整个对称图案做一个旋转或反射,原来的平移对称向量会变成新的平移对称向量。
* 应用 $\bar{\rho}$: $\bar{\rho}$ 是一个 $90^\circ$ 的旋转。我们将它作用在向量 $a$ 上,得到一个新的向量 $b = \bar{\rho}(a)$。
* $b$ 在 $L$ 中: 根据上述性质,因为 $a \in L$ 且 $\bar{\rho} \in \bar{G}$,所以 $b$ 也必须在 $L$ 中。
* $b$ 与 $a$ 的关系: 旋转 $90^\circ$ 保持向量的长度,所以 $|b| = |a|$。同时,旋转 $90^\circ$ 使得新向量与原向量垂直,所以 $b \perp a$。
* 至此,我们已经在格 $L$ 中找到了两个长度相等且互相垂直的向量 $a$ 和 $b$。这已经有了正方形的雏形。
3. “我们声称 $(a, b)$ 是 $L$ 的格基”:
* 一个格基是指能通过整数组合 $m a + n b$ ($m, n \in \mathbb{Z}$) 生成格 $L$ 中所有向量的一组基向量。
* 我们现在需要证明,仅仅用 $a$ 和 $b$ 就足以构建出整个格 $L$,没有任何“漏网之鱼”。
4. “假设不是。那么根据引理 6.5.8,在区域 $\Pi'$ 中将有一个 $L$ 的点...”:
* 这里使用反证法。我们假设 $(a, b)$ 不是一个格基。
* 引理 6.5.8 (或类似结论) 的内容是:如果两个向量 $(a,b)$ 不是格 $L$ 的基,那么在它们张成的基本平行四边形(这里是正方形)的内部或边界(不包括原点外的三个顶点)上,必然还存在其他的格点。
* 这里的区域 $\Pi'$ 是由 $a,b$ 张成的基本区域:$\Pi' = \{r_1 a + r_2 b \mid 0 \leq r_1 < 1, 0 \leq r_2 < 1\}$。这个区域是一个左闭右开的正方形。
* 所以,假设 $(a,b)$ 不是基,就意味着存在一个格点 $w = r_1 a + r_2 b$ 在这个 $\Pi'$ 区域内,且 $w$ 不为零向量。
5. “这样一个点 $w$ 将距离正方形的四个顶点 $0, a, b, a+b$ 中的一个小于 $|a|$”:
* 这是一个纯粹的几何论证。想象一个边长为 $s$ 的正方形,四个顶点是 $(0,0), (s,0), (0,s), (s,s)$。在这个正方形(包括边界)内的任何一个点,它到四个顶点中最近的一个顶点的距离,最大可能是在正方形的中心点 $(\frac{s}{2}, \frac{s}{2})$。这个中心点到四个顶点的距离都是 $\sqrt{(\frac{s}{2})^2 + (\frac{s}{2})^2} = \frac{s}{\sqrt{2}} < s$。对于其他任何点,它到最近顶点的距离会更小。
* 在我们的情况中,$s = |a|$。所以,这个在 $\Pi'$ 中的格点 $w$,它到 $0, a, b, a+b$ 这四个格点中最近的一个(我们称之为 $v$)的距离,必然小于 $|a|$。
6. “称该顶点为 $v$。那么 $v-w$ 也在 $L$ 中,且 $|v-w|<|a|$”:
* 因为 $v$(是 $0, a, b, a+b$ 之一)和 $w$ 都是格 $L$ 中的向量,而格对于减法是封闭的(因为它是群),所以它们的差 $v-w$ 也必须是 $L$ 中的一个向量。
* 我们刚刚从几何上论证了,向量 $w-v$(或 $v-w$)的长度是 $|v-w| < |a|$。
* 这个向量 $v-w$ 不可能是零向量,因为 $w$ 在 $\Pi'$ 区域内,而 $v$ 是顶点。
7. “这与 $a$ 的选择相矛盾。$\square$”:
* 我们得到了一个惊人的结论:我们找到了一个新的格向量 $v-w$,它的长度小于 $|a|$。
* 但这与我们证明的第一步——“选择 $L$ 中长度最小的非零向量 $a$”——直接矛盾。
* 既然出现了矛盾,说明我们最初的假设——“$(a, b)$ 不是一个格基”——是错误的。
* 因此,$(a, b)$ 必须是 $L$ 的一个格基。
* 因为 $(a, b)$ 是一个格基,且 $|a|=|b|, a \perp b$,所以这个格 $L$ 就是一个正方格。证明完毕。
2.2.3. 具体数值示例
* 示例:假设一个晶体学群 $G$ 有 $90^\circ$ 旋转对称。
1. 我们通过某种方式(比如X射线衍射)探测到它的平移格 $L$ 中有一个点 $(3, 0)$。我们不知道它是不是最短的,先假设它是。令 $a = (3, 0)$。它的长度是 $|a| = 3$。
2. 因为群有 $90^\circ$ 旋转,所以向量 $\bar{\rho}(a)$ 也必须在格 $L$ 中。$\bar{\rho}$ 将 $(3,0)$ 旋转 $90^\circ$ 得到 $b = (0, 3)$。所以 $(0, 3)$ 也一定是格点。
3. 现在我们声称 $(a,b)$,即 $((3,0), (0,3))$,是这个格的基。
4. 反证:假设它们不是基。那么在由 $r_1(3,0) + r_2(0,3)$ 构成的 $3 \times 3$ 的正方形区域($0 \le r_1 < 1, 0 \le r_2 < 1$)内,还存在另一个格点 $w$。
5. 比如,假设我们发现 $w = (1, 2)$ 竟然也是一个格点。
6. 现在我们计算 $w$ 到四个顶点 $0=(0,0), a=(3,0), b=(0,3), a+b=(3,3)$ 的距离。
* $|w-0| = |(1,2)| = \sqrt{1^2+2^2} = \sqrt{5} \approx 2.236$。
* $|w-a| = |(1-3, 2-0)| = |(-2,2)| = \sqrt{(-2)^2+2^2} = \sqrt{8} \approx 2.828$。
* $|w-b| = |(1-0, 2-3)| = |(1,-1)| = \sqrt{1^2+(-1)^2} = \sqrt{2} \approx 1.414$。
* $|w-(a+b)| = |(1-3, 2-3)| = |(-2,-1)| = \sqrt{(-2)^2+(-1)^2} = \sqrt{5} \approx 2.236$。
7. 最近的顶点是 $b=(0,3)$。新构造的格向量是 $w-b = (1, -1)$ 或 $b-w = (-1, 1)$。它的长度是 $\sqrt{2} \approx 1.414$。
8. 我们发现了一个新的格向量 $b-w$,其长度 $\sqrt{2}$ 小于我们最初假设的最小长度 $|a|=3$。
9. 这就产生了矛盾。这个矛盾说明我们最初的假设“$a=(3,0)$ 是最短向量”是错的。真正的最短向量长度必然小于等于 $\sqrt{2}$。
10. 这个逻辑可以一直迭代下去,直到我们找到真正的最短向量 $a'$。一旦我们以真正的最短向量 $a'$ 开始论证,那么就不可能再找到一个更短的向量,反证法的矛盾就会迫使我们接受 $(a', \bar{\rho}(a'))$ 是格基的结论。最终证明格一定是正方形的。
2.2.4. 易错点与边界情况
* 最短向量不唯一:在一个正方格中,最短的非零向量至少有4个(例如 $a, -a, b, -b$)。我们只需任选其一即可。
* 引理 6.5.8 的理解:这个引理是证明的关键,它保证了如果选的不是基,就一定能在基本平行四边形里找到“更基本”的格点。
* 几何论证的严谨性: "距离四个顶点之一小于 $|a|$" 这一步需要严格的几何证明,虽然直观上很明显。任何在边长为 $s$ 的正方形内的点,到最近顶点的距离不会超过中心点到顶点的距离 $s/\sqrt{2}$,而这个距离是小于 $s$ 的。
2.2.5. 总结
本段通过一个优雅的反证法证明了一个重要的基础性结论:任何具有四重旋转对称的二维周期性图案,其重复的网格(平移格)必须是正方形。这个证明的核心思想是:如果格不是由最短向量及其旋转90度后的向量生成的,那么我们总能利用这个“多余”的格点,构造出一个比“最短向量”更短的格向量,从而导出矛盾。
2.2.6. 存在目的
这个引理的目的是为后续的分类工作奠定一个坚实的基础。通过将平移格 $L$ 的形状唯一地确定为正方形,它极大地简化了后续的分析。我们可以方便地建立一个直角坐标系,将格点与整数坐标点 $(m,n)$ 对应起来,从而将复杂的几何问题代数化、坐标化。没有这个引理,我们就需要处理倾斜的、任意形状的平行四边形格,分析过程将变得异常繁琐。
2.2.7. 直觉心智模型
你想用一种形状的地砖铺满一个巨大的广场,并要求铺好后的图案具有 $90^\circ$ 旋转对称性(即你闭上眼转 $90^\circ$ 再睁开,看到的景象和原来一样)。
这个引理告诉你:你唯一能选择的地砖形状就是正方形。
为什么?假设你试图用长方形地砖(非正方形)来铺。比如 $1 \times 2$ 的地砖。你可以把它们铺成一个有平移对称的图案。但是,你在这个图案上找不到任何一个点,能让你旋转 $90^\circ$ 后图案还保持原样。如果你绕着某块地砖的中心旋转 $90^\circ$,这块地砖会从“竖着”变成“横着”,跟周围的地砖就对不上了。
为了让 $90^\circ$ 旋转成为一个合法的对称操作,这个操作作用在任何一块地砖上,都必须把它变成另一块地砖。唯一能做到这一点的地砖形状就是正方形。
2.2.8. 直观想象
想象一张无限大的、由许多看不见的钉子构成的钉板,这些钉子就是格点 $L$。我们知道,如果我们站在任何一个钉子上,把整个钉板旋转 $90^\circ$,每个钉子都会正好落在另一个钉子的位置上。
现在,从原点(一个钉子)出发,拉一根橡皮筋到离它最近的另一个钉子 $A$。这根橡皮筋的长度就是最短的格距。
现在,把整个钉板绕原点旋转 $90^\circ$。钉子 $A$ 会跑到新的位置 $B$,$B$ 也必然是一个钉子。连接原点和 $B$ 的橡皮筋长度和原来一样,并且与原来的橡皮筋垂直。
这个引理的证明告诉我们,整个钉板上所有的钉子,都可以通过从原点出发,沿着第一根橡皮筋的方向走整数步,再沿着第二根橡皮筋的方向走整数步来到达。不会有任何钉子遗漏在这张正方形网格之外。
23. 坐标系的选择
2.3.1. 原文
我们选择坐标并重新缩放,使得 $a$ 和 $b$ 成为标准基向量 $e_{1}$ 和 $e_{2}$。然后 $L$ 成为具有整数坐标的向量的格,而 $\Gamma^{\prime}$ 成为具有 $0 \leq s<1$ 和 $0 \leq t<1$ 的向量 $(s, t)^{\mathrm{t}}$ 的集合。这确定了平面 $P$ 中的坐标,直到平移。
2.3.2. 逐步解释
这一小段是承接上文引理的技术性步骤,目的是简化后续的计算和讨论。
1. “我们选择坐标并重新缩放...”:这是数学证明中常用的一种技巧,叫做“不失一般性”(Without Loss of Generality, WLOG)。既然我们已经证明了格 $L$ 是由两个等长且正交的向量 $a$ 和 $b$ 生成的,那么我们可以通过旋转整个坐标系并调整单位长度,来让后续的计算变得最简单。
* 选择坐标(旋转): 我们旋转我们的坐标轴,使得x轴与向量 $a$ 的方向重合,y轴与向量 $b$ 的方向重合。
* 重新缩放(伸缩): 我们调整坐标系中的“单位长度”,使得向量 $a$ 的长度正好是1。由于 $|b|=|a|$,向量 $b$ 的长度也自动变成了1。
2. “...使得 $a$ 和 $b$ 成为标准基向量 $e_1$ 和 $e_2$”:
* 经过上述操作,$a$ 就变成了代表x方向单位长度的向量,即 $e_1 = (1, 0)$。
* $b$ 就变成了代表y方向单位长度的向量,即 $e_2 = (0, 1)$。
3. “然后 $L$ 成为具有整数坐标的向量的格...”:
* 因为 $L$ 是由 $a$ 和 $b$ 生成的,即 $L = \{m a + n b \mid m, n \in \mathbb{Z}\}$。
* 在新的坐标系下,这就变成了 $L = \{m e_1 + n e_2 \mid m, n \in \mathbb{Z}\} = \{m(1,0) + n(0,1) \mid m, n \in \mathbb{Z}\} = \{(m, n) \mid m, n \in \mathbb{Z}\}$。
* 这正是整数格 $\mathbb{Z}^2$。也就是说,经过坐标变换,我们的平移格变成了平面上所有整数坐标点构成的集合。这是一个巨大的简化。
4. “而 $\Gamma^{\prime}$ 成为具有 $0 \leq s<1$ 和 $0 \leq t<1$ 的向量 $(s, t)^{\mathrm{t}}$ 的集合”:
* $\Gamma'$(原文是 $\Pi'$)是之前证明中使用过的基本区域。它是由基向量 $a$ 和 $b$ 张成的“左闭右开”平行四边形。
* 在新的坐标系下,这个区域就变成了一个单位正方形,包含x坐标从0到(但不包括)1,y坐标从0到(但不包括)1的所有点。这个区域通常被称为基本单元或基本域。
5. “这确定了平面 $P$ 中的坐标,直到平移”:
* 我们固定了坐标轴的方向和单位长度,但没有固定坐标原点的位置。我们可以把这个整数格点构成的坐标系在平面上任意平移,它仍然描述的是同一个格。在后续的步骤中,我们将会通过选择一个合适的旋转中心作为原点,来彻底固定坐标系。
2.3.3. 具体数值示例
* 假设我们通过实验发现一个晶体的平移格是由两个向量 $a = (5, 5)$ 和 $b = (-5, 5)$ 生成的。
* 首先检查:$|a| = \sqrt{5^2+5^2} = \sqrt{50}$,$|b| = \sqrt{(-5)^2+5^2} = \sqrt{50}$。它们的长度相等。它们的点积 $a \cdot b = 5(-5) + 5(5) = -25+25=0$。它们相互垂直。所以这是一个正方格。
* 选择坐标并重新缩放:
1. 旋转: 当前的基向量 $a, b$ 与标准坐标轴 $x, y$ 呈 $45^\circ$ 角。我们把整个坐标系逆时针旋转 $45^\circ$。新的 $x'$ 轴将指向原 $a$ 的方向,新的 $y'$ 轴将指向原 $b$ 的方向。
2. 缩放: 在这个新的坐标系中,基向量的长度是 $\sqrt{50}$。我们把单位长度定义为 $\sqrt{50}$。也就是说,我们把整个平面缩小 $\sqrt{50}$ 倍。
* 结果:
* 原来的向量 $a=(5,5)$ 在新坐标系下变成了 $e_1 = (1, 0)$。
* 原来的向量 $b=(-5,5)$ 在新坐标系下变成了 $e_2 = (0, 1)$。
* 原来的一个普通格点,例如 $2a+3b = 2(5,5)+3(-5,5) = (10,10)+(-15,15) = (-5, 25)$,在新坐标系下就对应着整数点 $(2, 3)$。
* 通过这种方式,我们把一个看起来很复杂的格 $L$ 简化成了最标准、最容易处理的整数格 $\mathbb{Z}^2$。
2.3.4. 易错点与边界情况
* 这只是一个坐标选择,并没有改变群 $G$ 的内在几何结构。就像我们给一个几何图形拍照,可以用不同的角度和焦距,但图形本身不变。我们选择了一个最“正”的角度和最方便的焦距。
* “直到平移”这个限定很重要。我们还没有确定原点。原点的位置选择会影响旋转和反射的代数表示,这是下一步要处理的关键。
2.3.5. 总结
本段描述了一个关键的数学技巧:通过合理的选择坐标系(旋转和缩放),将前面证明得到的正方格 $L$ 标准化为整数格 $\mathbb{Z}^2$。这使得后续的代数运算变得异常简洁,所有平移都可以用整数向量 $(m,n)$ 来表示。
2.3.6. 存在目的
此步骤的目的是为了“清理战场”,为接下来的核心战斗(分析旋转和反射的组合)做好准备。通过坐标标准化,我们可以从繁琐的具体数值(如 $\sqrt{50}$)中解脱出来,专注于研究对称操作之间的组合关系,这些关系现在可以用简单的整数和矩阵来表达。
2.3.7. 直觉心智模型
你是一个棋盘设计师。你已经知道你的棋盘必须是正方形格子的。现在你要在电脑上画设计图。你不会把棋盘斜着画,也不会把每个格子画成 $3.14$ 像素宽。最聪明的做法是:
1. 把棋盘摆正,让格线与屏幕的水平和垂直方向对齐。
2. 把一个格子的边长定义为“1个单位”。
这样,棋盘上任何一个格点的位置都可以用一对整数 $(m, n)$ 来表示。你所做的,就是建立了一个最方便的“数字地址系统”来描述你的棋盘。
2.3.8. 直观想象
想象你手上有一张透明的方格纸。这就是你的新坐标系。你可以把这张纸盖在任何一个具有四重对称的墙纸图案上。通过旋转和缩放这张纸,你总能让纸上的网格线与墙纸图案的重复网格(平移格 $L$)完美对齐。一旦对齐,墙纸上所有的重复单元的左下角,就都对应了你方格纸上的整数坐标点。
24. 点群 $C_4$ 的情况
2.4.1. 原文
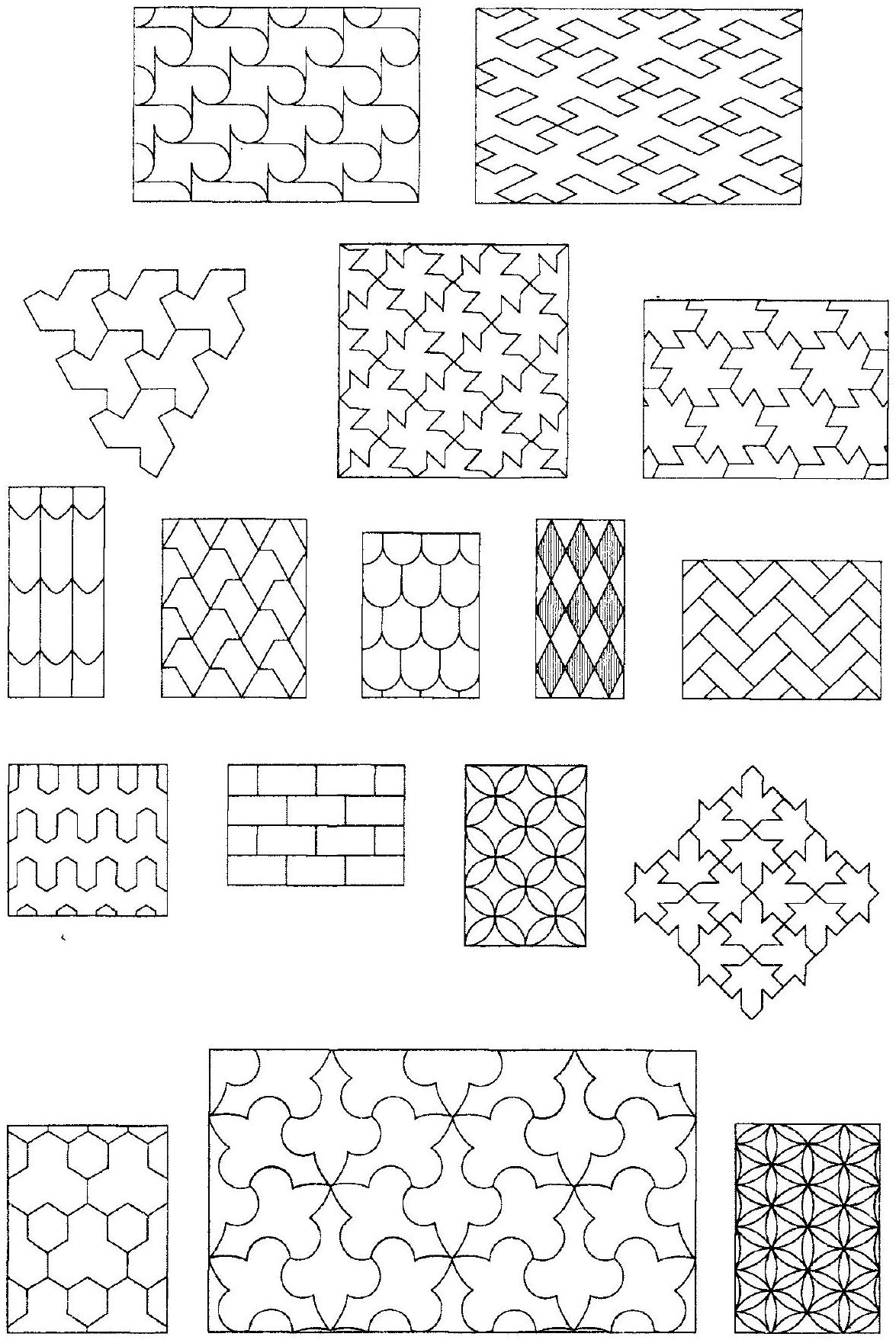
(6.6.2)
17 种平面晶体学群的样本图案。
作用于 $V$ 并将 $L$ 映射到自身的正交算子形成由通过 $\pi / 2$ 角度的旋转 $\bar{\rho}$ 和标准反射 $\bar{r}$ 生成的二面体群 $D_{4}$。我们的假设是 $\bar{\rho}$ 在 $\bar{G}$ 中。如果 $\bar{r}$ 也在 $\bar{G}$ 中,那么 $\bar{G}$ 是二面体群 $D_{4}$。如果不是,则 $\bar{G}$ 是循环群 $C_{4}$。我们首先描述当 $G$ 是 $C_{4}$ 时的群 $G$。设 $g$ 是 $G$ 中的一个元素,其在 $\bar{G}$ 中的像是一个角度为 $\pi / 2$ 的旋转。那么 $g$ 是绕平面中某个点 $p$ 的角度为 $\pi / 2$ 的旋转。我们平移平面 $P$ 中的坐标,使得点 $p$ 成为原点。在这个坐标系中,$G$ 包含绕原点的旋转 $\rho=\rho_{\pi / 2}$。
命题 6.6.3 设 $G$ 是一个平面晶体学群,其点群 $\bar{G}$ 是循环群 $C_{4}$。在选择坐标使得 $L$ 是具有整数坐标的点的格,并且 $\rho=\rho_{\pi / 2}$ 是 $G$ 的一个元素的情况下,群 $G$ 由 $t_{v} \rho^{i}$ 的乘积组成,其中 $v$ 在 $L$ 中且 $0 \leq i<4$:
证明。设 $G^{\prime}$ 表示形如 $t_{v} \rho^{i}$ 的元素集合,其中 $v$ 在 $L$ 中。我们必须证明 $G^{\prime}=G$。根据 $L$ 的定义,$t_{v}$ 在 $G$ 中,并且 $\rho$ 也在 $G$ 中。因此 $t_{v} \rho^{i}$ 在 $G$ 中,所以 $G^{\prime}$ 是 $G$ 的一个子集。
为了证明相反的包含关系,设 $g$ 是 $G$ 的任意元素。由于点群 $\bar{G}$ 是 $C_{4}$,所以 $G$ 的每个元素都保持方向。因此 $g$ 具有 $g=t_{u} \rho_{\alpha}$ 的形式,其中 $u$ 是某个平移向量,$\alpha$ 是某个角度。此元素在点群中的像是 $\bar{\rho}_{\alpha}$,所以 $\alpha$ 是 $\pi / 2$ 的倍数,并且 $\rho_{\alpha}=\rho^{i}$ 对于某个 $i$。由于 $\rho$ 在 $G$ 中,$g \rho^{-i}=t_{u}$ 在 $G$ 中且 $u$ 在 $L$ 中。因此 $g$ 在 $G^{\prime}$ 中。$\square$
2.4.2. 逐步解释
这部分开始对第一种情况进行分类:点群为 $C_4$ 的晶体学群。结论是,这种情况只对应唯一一种晶体学群结构(在17种群里记为 p4)。
前提分析
1. “作用于 $V$ 并将 $L$ 映射到自身的正交算子形成...$D_4$”:
* $L$ 是我们已经标准化的整数格 $\mathbb{Z}^2$。
* 一个正交算子(旋转或反射)如果能将整数格映射到自身,就被称为格的对称操作。
* 对于一个正方格,它的对称操作包括:旋转 $0, 90, 180, 270$ 度,以及关于水平、垂直、两条对角线的4条反射。这些操作恰好构成了二面体群 $D_4$。
* 这说明,对于一个正方格,与它兼容的点群 $\bar{G}$ 必须是 $D_4$ 的一个子群。
2. “我们的假设是 $\bar{\rho}$ 在 $\bar{G}$ 中”:
* 这是本节分析的大前提,即我们只考虑具有四重对称的群。$\bar{\rho}$ 是 $90^\circ$ 旋转。
3. “如果 $\bar{r}$ 也在 $\bar{G}$ 中,那么 $\bar{G}=D_4$。如果不是,则 $\bar{G}=C_4$”:
* 根据群论,一个包含 $\bar{\rho}$($D_4$ 的生成元之一)的 $D_4$ 的子群,如果它还包含任何一个反射,它就必须是整个 $D_4$。如果它不包含任何反射,那它就只能是 $C_4$。所以只有这两种可能。
4. “我们首先描述当 $\bar{G}$ 是 $C_4$ 时的群 $G$”:
* 我们先分析简单的情况:点群 $\bar{G}$ 是 $C_4 = \{1, \bar{\rho}, \bar{\rho}^2, \bar{\rho}^3\}$。这意味着我们的图案有 $90^\circ$ 旋转对称,但没有任何反射或滑移对称。
5. “设 $g \in G$ ... 其像为 $\bar{\rho}$ ... $g$ 是绕某个点 $p$ 的 $90^\circ$ 旋转”:
* 因为点群中有 $\bar{\rho}$,所以在群 $G$ 中一定存在一个或多个元素 $g$,它们的线性部分是 $90^\circ$ 旋转。任何这样的 $g$ 本身是一个等距变换,它要么是一个纯旋转,要么是“滑移旋转”(但这种变换不存在)。所以 $g$ 一定是一个绕着某个点 $p$ 的 $90^\circ$ 纯旋转。
6. “我们平移平面 $P$ 中的坐标,使得点 $p$ 成为原点”:
* 还记得我们之前说的坐标系只确定到平移吗?现在我们终于可以把原点定下来了。我们就把其中一个 $90^\circ$ 旋转中心选作我们的坐标原点 $(0,0)$。
* 这是一个非常关键的步骤。通过这个选择,我们使得“绕原点旋转 $90^\circ$”这个操作(记为 $\rho$)本身就是我们对称群 $G$ 的一个元素。
命题 6.6.3 的陈述
* 前提:
1. $G$ 是一个晶体学群。
2. 它的点群 $\bar{G}=C_4$。
3. 我们已经做好了坐标选择:$L$ 是整数格 $\mathbb{Z}^2$,并且绕原点的 $90^\circ$ 旋转 $\rho$ 是 $G$ 的一个元素。
* 结论: $G$ 中的每一个元素,都可以表示成“先绕原点旋转 $0, 90, 180, 270$ 度中的一个角度($\rho^i$),然后再进行一次格点平移($t_v, v \in L$)”的形式。
* 公式: $G = \{t_v \rho^i \mid v \in L, i=0,1,2,3\}$。这完全确定了群 $G$ 的结构。
证明的详解
1. 证明 $G' \subseteq G$ (直接包含):
* $G'$ 是我们构造出来的集合 $G' = \{t_v \rho^i\}$。
* 根据平移格 $L$ 的定义,所有平移 $t_v$ ($v \in L$) 都在 $G$ 中。
* 根据我们对坐标原点的选择,$\rho$ 也在 $G$ 中。
* 因为 $G$ 是一个群,所以对其中的元素进行任意次的乘法(复合)操作,结果仍然在 $G$ 中。所以 $\rho^i$ 在 $G$ 中,进而 $t_v \rho^i$ 也在 $G$ 中。
* 因此,我们构造的集合 $G'$ 是真实对称群 $G$ 的一个子集。
2. 证明 $G \subseteq G'$ (反向包含):
* 我们需要证明,真实的对称群 $G$ 里没有“多余的”元素。
* 从 $G$ 中任意取一个元素 $g$。
* “由于点群 $\bar{G}$ 是 $C_4$,所以 $G$ 的每个元素都保持方向”: $C_4$ 只包含旋转,不包含反射。旋转和平移都是保向变换(不会把左手变成右手),而反射和滑移反射是反向变换。因为 $\bar{G}$ 没有反射类元素,所以 $G$ 中也不可能有任何反向变换。
* 一个保向的平面等距变换只有两种可能:纯平移或纯旋转。两者都可以统一写成 $g = t_u \rho_\alpha$ 的形式(先绕原点旋转 $\alpha$,再平移 $u$)。
* “此元素在点群中的像是 $\bar{\rho}_\alpha$”: $g$ 的线性部分就是 $\rho_\alpha$。根据点群的定义,这个线性部分必须是 $\bar{G}$ 的一个元素。
* “所以 $\alpha$ 是 $\pi/2$ 的倍数,并且 $\rho_\alpha = \rho^i$”: 因为 $\bar{G} = C_4 = \{1, \bar{\rho}, \bar{\rho}^2, \bar{\rho}^3\}$,所以 $\bar{\rho}_\alpha$ 只能是这四个元素之一。这意味着旋转角度 $\alpha$ 只能是 $0, 90, 180, 270$ 度之一。因此,旋转部分 $\rho_\alpha$ 就可以写成我们那个绕原点的标准旋转 $\rho$ 的幂次 $\rho^i$。
* 所以,任意一个元素 $g$ 都可以写成 $g = t_u \rho^i$ 的形式,其中 $i \in \{0,1,2,3\}$。
* “由于 $\rho$ 在 $G$ 中,$g \rho^{-i} = t_u$ 在 $G$ 中”: 我们知道 $g \in G$,也知道 $\rho \in G$,所以 $\rho^{-i}$ 也一定在 $G$ 中。两个 $G$ 中元素的乘积 $g \rho^{-i}$ 也必然在 $G$ 中。而 $g \rho^{-i} = (t_u \rho^i) \rho^{-i} = t_u$。
* “且 $u$ 在 $L$ 中”: 我们刚刚证明了 $t_u$ 是一个在 $G$ 中的纯平移。根据平移格 $L$ 的定义,它包含了 $G$ 中所有的纯平移。所以,向量 $u$ 必须属于格 $L$。
* “因此 $g$ 在 $G'$ 中”: 我们已经证明了任意一个 $g \in G$ 都可以写成 $g = t_u \rho^i$ 的形式,并且 $u \in L, i \in \{0,1,2,3\}$。这完全符合我们构造的集合 $G'$ 的定义。所以 $g \in G'$。
3. 结论: 因为我们证明了 $G' \subseteq G$ 并且 $G \subseteq G'$,所以 $G = G'$。证明完毕。
2.4.3. 具体数值示例
* 群: p4 (对应 $\bar{G}=C_4$ 的情况)
* 坐标: $L=\mathbb{Z}^2$,原点是一个4重旋转中心。
* 元素示例1: 绕点 $(1,0)$ 旋转 $90^\circ$。这个点不是原点,但它也是一个对称中心。这个操作是群 $G$ 的一个元素 $g$。我们来验证它是否可以写成 $t_v \rho^i$ 的形式。
* 一个绕点 $p$ 旋转 $\theta$ 的变换,可以分解为:先平移 $-p$,再绕原点旋转 $\theta$,最后平移 $p$。在这里是 $p=(1,0), \theta=90^\circ$。
* 这个操作 $g$ 作用于一个点 $x$ 的效果是 $g(x) = \rho(x-p)+p = \rho x - \rho p + p$。
* 这可以写成 $t_{p-\rho p} \rho (x)$。
* 我们计算平移向量 $u = p - \rho p = (1,0) - \rho(1,0) = (1,0) - (0,1) = (1, -1)$。
* 向量 $(1,-1)$ 的坐标是整数,所以它在格 $L$ 中。
* 因此,这个绕 $(1,0)$ 旋转 $90^\circ$ 的变换 $g$,可以表示为 $t_{(1,-1)} \rho^1$。这符合 $G = \{t_v \rho^i\}$ 的形式。
* 元素示例2: 绕点 $(0.5, 0.5)$ 旋转 $180^\circ$。在 p4 图案中,单位正方形的中心是一个2重旋转中心。
* 这个变换 $g$ 是 $g(x) = \rho^2(x-p)+p$,其中 $p=(0.5, 0.5)$。
* 分解为 $g(x) = \rho^2 x - \rho^2 p + p$。
* 平移向量是 $u = p - \rho^2 p = (0.5, 0.5) - (-0.5, -0.5) = (1, 1)$。
* 向量 $(1,1)$ 在格 $L$ 中。
* 因此,这个变换可以表示为 $t_{(1,1)} \rho^2$。这也符合 $G = \{t_v \rho^i\}$ 的形式。
2.4.4. 易错点与边界情况
* 原点的选择是关键:如果当初我们没有选择一个 $90^\circ$ 旋转中心作为原点,那么 $\rho$ 本身就不在 $G$ 中,命题的表述和证明会复杂得多。例如,如果我们选择 $(0.5, 0.5)$ 作为原点,那么 $G$ 中没有任何一个元素是绕新原点的旋转。
* $G$ 不是直积:虽然 $G$ 的元素可以写成 $t_v \rho^i$ 的形式,但这并不意味着 $G$ 是平移群 $L$ 和旋转群 $C_4$ 的直积(Direct Product)。它是半直积(Semidirect Product),记作 $L \rtimes C_4$。因为旋转操作会影响平移向量,$\rho t_v \rho^{-1} = t_{\rho(v)}$,两类操作的次序不满足交换律。
2.4.5. 总结
本段完整地分析了点群为 $C_4$ 的晶体学群。通过巧妙地选择坐标系(以一个四重旋转中心为原点,以格向量为坐标轴),证明了这类群具有唯一的、非常简洁的结构:它由整数格平移和绕原点的四重旋转通过复合生成。所有其他的对称操作(如在其他位置的旋转)都可以由这两个基本操作组合而成。
2.4.6. 存在目的
本段的目的是完成分类任务的第一部分。它展示了,对于给定的点群 $C_4$ 和与之兼容的正方格 $L$,只存在一种可能的晶体学群 $G$。这个推导过程本身就是一个典范,展示了如何利用坐标系选择、群的封闭性以及点群的性质来精确刻画一个无限离散群的结构。
2.4.7. 直觉心智模型
你是一个程序员,在编写一个绘图程序,这个程序需要能生成具有 p4 对称性的图案。
* 数据结构:你的平移格 $L$ 就是 (int m, int n) 整数对。你的旋转操作就是一个函数 rotate90(point)。
* 命题 6.6.3 告诉你:你的程序中所有可能的对称画笔操作,都可以通过一个函数库 Library G 实现。这个库只需要两个基础功能:
1. translate(m, n): 将画笔移动到任意一个整数格点。
2. rotate_at_origin(i): 将画笔的朝向(以及它画出的图案)绕原点旋转 $i \times 90$ 度。
* 结论:任何复杂的对称操作,比如“在点(10, 8)的位置旋转180度”,你的程序都可以通过调用 translate(m, n) 和 rotate_at_origin(i) 的组合来实现。你不需要为每一个对称中心都编写一个独立的旋转函数。整个对称性被两个最基本的模块完全掌控了。
2.4.8. 直观想象
想象你站在一个 p4 图案的墙纸前,比如前面提到的“卍”字图案。
* 你找到了一个“卍”的中心,并把它定为原点 $(0,0)$。
* 这个图案的对称群 $G$ 就是你能对这个墙纸做的所有“看不出变化”的操作的集合。
* 命题 6.6.3 的意思是:你任何一个复杂的操作,比如跑到右边第10个、上面第8个“卍”字那里,然后把整个墙纸绕那个中心转 $180^\circ$,这个操作的效果,等同于一个更简单的操作序列:
1. 首先,你站在原点,原地转一个角度($0, 90, 180, 270$ 度之一)。
2. 然后,你再沿着网格线把自己平移一段整数距离。
* 通过这一套“先转后移”的简单动作,你可以复现出所有可能的神奇对称操作。
25. 点群 $D_4$ 的情况
2.5.1. 原文
我们现在考虑点群 $\bar{G}$ 是 $D_{4}$ 的情况。
命题 6.6.4 设 $G$ 是一个平面晶体学群,其点群 $\bar{G}$ 是二面体群 $D_{4}$。设坐标被选择,使得 $L$ 是具有整数坐标的点的格,并且 $\rho=\rho_{\pi / 2}$ 是 $G$ 的一个元素。此外,设 $c$ 表示向量 $\left(\frac{1}{2}, \frac{1}{2}\right)^{\mathrm{t}}$。有两种可能性:
(a) $G$ 的元素是 $t_{v} \varphi$ 的乘积,其中 $v$ 在 $L$ 中,$\varphi$ 在 $D_{4}$ 中,
(b) $G$ 的元素是 $t_{x} \varphi$ 的乘积,其中 $\varphi$ 在 $D_{4}$ 中。如果 $\varphi$ 是旋转,那么 $x$ 在 $L$ 中,如果 $\varphi$ 是反射,那么 $x$ 在陪集 $c+L$ 中:
证明。设 $H$ 是 $G$ 中保持方向的等距变换的子集。这是 $G$ 的一个子群,其平移格是 $L$,并且它包含 $\rho$。因此其点群是 $C_{4}$。命题 6.6.3 告诉我们 $H$ 由元素 $t_{v} \rho^{i}$ 组成,其中 $v$ 在 $L$ 中。
点群还包含反射 $\bar{r}$。我们选择 $G$ 中一个元素 $g$,使得 $\bar{g}=\bar{r}$。它将具有 $g=t_{u} r$ 的形式,其中 $u$ 是某个向量,但我们不知道 $u$ 是否在 $L$ 中。分析这种情况将需要一些调整。假设 $u=(p, q)^{t}$。
我们可以将 $g$ 左乘 $G$ 中的平移 $t_{v}$ (即 $v$ 在 $L$ 中),以将 $u$ 移动到点 $0 \leq p, q<1$ 的区域 $\Pi^{\prime}$。假设这已经完成。
我们用 $g=t_{u} r$ 进行计算,使用公式 (6.3.3):
这些都是 $G$ 的元素,所以 $u+r u=(2 p, 0)^{\mathrm{t}}$ 和 $u+r \rho u=(p-q, q-p)^{\mathrm{t}}$ 都在格 $L$ 中。它们是具有整数坐标的向量。由于 $0 \leq p, q<1$ 且 $2 p$ 是一个整数,所以 $p$ 要么是 0,要么是 $\frac{1}{2}$。由于 $p-q$ 也是一个整数,所以如果 $p=0$,则 $q=0$;如果 $p=\frac{1}{2}$,则 $q=\frac{1}{2}$。因此 $u$ 只有两种可能性:要么 $u=(0,0)^{\mathrm{t}}$,要么 $u=c=\left(\frac{1}{2}, \frac{1}{2}\right)^{\mathrmt}$。在第一种情况下,$g=r$,所以 $G$ 包含一个反射。这是命题的 (a) 种情况。第二种可能性是 (b) 种情况。$\square$
2.5.2. 逐步解释
这部分是本节的分析核心,处理更复杂的情况:点群为 $D_4$ 的晶体学群。结论是,这种情况会分化出两种不同的群结构(在17种群里分别记为 p4m 和 p4g)。
命题 6.6.4 的陈述
* 前提:
1. $G$ 是一个晶体学群。
2. 它的点群 $\bar{G}=D_4$。
3. 坐标系已选择好:$L=\mathbb{Z}^2$,并且绕原点的 $90^\circ$ 旋转 $\rho$ 在 $G$ 中。
* 结论: 存在两种可能。为了理解这两种可能,我们先要定义 $r$ 和 $c$。
* $r$:代表绕x轴的标准反射,即 $r(x,y) = (x,-y)$。
* $c$: 一个特殊的向量 $c = (\frac{1}{2}, \frac{1}{2})$,代表单位正方形的中心。
* 可能性 (a) - (p4m 群):
* 群 $G$ 由两部分组成:
* 保向部分:$t_v \rho^i$ (与 $C_4$ 情况完全一样)。
* 反向部分:$t_v \rho^i r$。这里的平移向量 $v$ 依然来自整数格 $L$。
* 这个公式意味着,反射类操作可以由绕原点的标准反射 $r$、绕原点的旋转 $\rho^i$ 和格点平移 $t_v$ 组合而成。特别是,当 $v=0, i=0$ 时,$t_0 \rho^0 r = r$ 本身就在群里。这意味着群 $G$ 包含一个纯反射(绕x轴的反射)。
* 可能性 (b) - (p4g 群):
* 群 $G$ 也由两部分组成:
* 保向部分:$t_v \rho^i$ (依然和之前一样)。
* 反向部分:$t_u \rho^i r$。这里的关键区别在于,平移向量 $u$ 来自一个陪集 $c+L$。
* 陪集 $c+L$: 这是将整数格 $L$ 的每一个点都平移向量 $c$ 后得到的点的集合。即 $\{ (m+\frac{1}{2}, n+\frac{1}{2}) \mid m,n \in \mathbb{Z} \}$。这是所有“半整数”坐标点的集合。
* 这个公式意味着,任何一个反射类的操作 $g$,它都自带一个“非整数”的平移分量。例如,最简单的反射类操作是 $t_c r$ (令 $u=c, i=0$)。这是一个滑移反射!它先绕x轴反射,再平移 $(\frac{1}{2}, \frac{1}{2})$。这个群 $G$ 不包含纯反射 $r$。
证明的详解
1. “设 $H$ 是 $G$ 中保持方向的等距变换的子集”:
* $G$ 中的元素分为两类:保向的(旋转、平移)和反向的(反射、滑移反射)。
* 所有保向的元素构成 $G$ 的一个正规子群 $H$,其指数为2($H$ 的元素数量是 $G$ 的一半)。
* 这个子群 $H$ 本身也是一个晶体学群。它的平移格仍然是 $L$。它的点群 $\bar{H}$ 是 $\bar{G}=D_4$ 中所有保向元素组成的群,即 $C_4$。
* “命题 6.6.3 告诉我们 $H$ 由元素 $t_v \rho^i$ 组成”: 我们直接应用上一节的结论,确定了 $G$ 中所有保向元素的结构。这就是两种可能性中共同的那一部分。
2. “点群还包含反射 $\bar{r}$。我们选择 $G$ 中一个元素 $g$,使得 $\bar{g}=\bar{r}$”:
* 现在我们要分析反向的部分。因为 $\bar{G}=D_4$,所以 $\bar{G}$ 中一定有反射元素 $\bar{r}$。
* 这意味着,在群 $G$ 中,必然存在一个元素 $g$,它的线性部分是反射 $r$。
* 这个 $g$ 的一般形式是 $g = t_u r$ (先反射,再平移 $u$)。这就是滑移反射的一般形式(如果 $u$ 平行于反射轴)或“反射+不平行平移”的组合。纯反射是 $u=0$ 的特殊情况。
* “但我们不知道 $u$ 是否在 $L$ 中”: 这是问题的核心。如果 $u \in L$,我们就可以把 $t_u$ 看作一个独立的格点平移,从而把 $g$ 分解。但如果 $u \notin L$,这个平移就是“内嵌”在 $g$ 这个操作里的。
3. “我们可以将 $g$ 左乘 $G$ 中的平移 $t_v$... 以将 $u$ 移动到点 $0 \leq p, q<1$ 的区域 $\Pi'$”:
* 我们有一个 $g=t_u r$。我们可以用 $G$ 中的另一个元素来“简化”它。选择一个合适的格点平移 $t_v$ ($v \in L$),我们考察一个新的元素 $g' = t_{-v} g = t_{-v} t_u r = t_{u-v} r$。
* $g'$ 也是 $G$ 中的一个元素,它的线性部分也是 $r$。我们可以选择合适的整数向量 $v$,使得新的平移向量 $u' = u-v$ 落在基本单元 $\Pi'$(即 $x,y$ 坐标在 $[0,1)$ 内)里。
* 这步操作不失一般性,因为我们只是在分析 $G$ 中具有反射部分的所有元素中的一个代表。我们可以分析这个“简化版”的 $g'$,得出的结论将适用于所有同类元素。为方便起见,我们仍然把这个简化后的元素记为 $g=t_u r$,但现在我们有了约束条件 $u=(p,q)^t$ 且 $0 \le p, q < 1$。
4. “我们用 $g=t_u r$ 进行计算... $g^2 = t_{u+ru}$ 和 $(g\rho)^2 = t_{u+r\rho u}$”:
* 因为 $g$ 在群 $G$ 中,所以 $g^2=g \circ g$ 也必须在 $G$ 中。
* $g^2 = (t_u r)(t_u r) = t_u (r t_u r^{-1}) r^2 = t_u t_{ru} (I) = t_{u+ru}$。(这里用到了变换规则 $r t_u r^{-1} = t_{ru}$ 和 $r^2=I$)。
* $g^2$ 是一个纯平移。所以它必须是 $L$ 中的一个格点平移。这意味着向量 $u+ru$ 必须是一个整数坐标向量。
* 同样,$g \in G, \rho \in G$,所以 $g\rho \in G$,进而 $(g\rho)^2 \in G$。
* $(g\rho)^2 = (t_u r \rho)(t_u r \rho) = t_u (r\rho t_u (r\rho)^{-1}) (r\rho)^2 = t_u t_{r\rho(u)} (I) = t_{u+r\rho u}$。
* 这个结果也是一个纯平移,所以向量 $u+r\rho u$ 也必须是整数坐标向量。
5. “$u+r u=(2 p, 0)^{\mathrm{t}}$ 和 $u+r \rho u=(p-q, q-p)^{\mathrm{t}}$ 都在格 $L$ 中”:
* 计算 $u+ru$: $u=(p,q)$, $r$ 是关于x轴反射, $r(u) = (p, -q)$。所以 $u+ru = (p,q) + (p,-q) = (2p, 0)$。
* 计算 $u+r\rho u$: $\rho$ 是 $90^\circ$ 旋转,$\rho(u) = (-q, p)$。$r\rho(u) = r(-q,p) = (-q, -p)$。所以 $u+r\rho u = (p,q) + (-q, -p) = (p-q, q-p)$。
* 这两个向量都必须在整数格 $L=\mathbb{Z}^2$ 中。
6. “由于 $0 \leq p, q<1$ ... $u$ 只有两种可能性...”:
* 从 $(2p, 0) \in \mathbb{Z}^2$ 可知,$2p$ 必须是整数。因为 $0 \le p < 1$,所以 $0 \le 2p < 2$。那么 $2p$ 只能是 0 或 1。这意味着 $p=0$ 或 $p=1/2$。
* 从 $(p-q, q-p) \in \mathbb{Z}^2$ 可知,$p-q$ 必须是整数。
* Case 1: $p=0$。那么 $0-q = -q$ 必须是整数。因为 $0 \le q < 1$,唯一的可能是 $q=0$。所以 $u=(0,0)$。
* Case 2: $p=1/2$。那么 $1/2 - q$ 必须是整数。因为 $0 \le q < 1$,所以 $-1 < -q \le 0$,进而 $-1/2 < 1/2-q \le 1/2$。这个范围内唯一的整数是 0。所以 $1/2-q=0$,即 $q=1/2$。所以 $u=(1/2, 1/2)$。
7. 结论:
* 可能性 (a): 如果 $u=(0,0)$,那么我们找到的那个代表性元素就是 $g = t_0 r = r$。这意味着纯反射 $r$ 本身就在群 $G$ 中。这对应于命题的 (a) 部分,即 p4m 群。
* 可能性 (b): 如果 $u=(1/2, 1/2)=c$,那么我们找到的代表性元素是 $g=t_c r$。这是一个滑移反射。我们无法通过乘以格点平移来消掉这个 $t_c$ 部分,因为 $c \notin L$。这意味着群 $G$ 中没有纯反射,但有滑移反射。这对应于命题的 (b) 部分,即 p4g 群。
2.5.3. 具体数值示例
* 群 (a): p4m
* 图案: 一个标准的无限棋盘格。
* 坐标: $L=\mathbb{Z}^2$ (格点在顶点),原点在某个顶点。$\rho$ 是绕原点的 $90^\circ$ 旋转。
* 保向部分 $H$: $t_{(m,n)} \rho^i$。例如 $t_{(1,0)}\rho^0$ (向右平移一格),$\rho$ (绕原点旋转90度)。
* 反向部分: $t_{(m,n)} \rho^i r$。例如 $r$ (关于x轴的反射,这是一条格线)。$t_{(1,0)}r$ (先关于x轴反射,再向右平移一格)。
* 这个群包含纯反射,例如 $r$ (沿格线反射) 和 $t_{(1,0)} \rho r \rho^{-1}$ (可以算出是沿 $x=1/2$ 线反射)。
* 群 (b): p4g
* 图案: 想象一个棋盘,但在每个白色格子的中心画一个逆时针的“卍”,在每个黑色格子的中心画一个顺时针的“卐”。
* 坐标: $L=\mathbb{Z}^2$ (格点在同色格子的中心),原点在一个“卍”的中心。$\rho$ 是绕原点的 $90^\circ$ 旋转。
* 保向部分 $H$: $t_{(m,n)} \rho^i$。这部分操作只会把“卍”变到“卍”,把“卐”变到“卐”。
* 反向部分: $t_{u} \rho^i r$ 其中 $u \in (\frac{1}{2}, \frac{1}{2}) + L$。
* 考虑一个最简单的反向操作 $g$。它应该把“卍”变成“卐”。你无法通过纯反射做到。
* 但你可以先沿着对角线方向(例如 $y=x$)做反射,这会把“卍”变成一个镜像,然后再沿着该对角线平移一段距离,就可以和另一个“卐”重合。
* 这个操作经过坐标变换后,就对应着 $t_c r$ 这样的滑移反射。你找不到任何一个纯反射是这个图案的对称操作。
2.5.4. 易错点与边界情况
* $g^2$ 和 $(g\rho)^2$ 的作用: 这两个计算是整个证明的“引擎”。它们的作用是把一个一般性的等距变换 $g$(可能很复杂)的平方,转化成一个纯平移。这就建立了一座桥梁,使得我们可以用平移格 $L$ 的离散性质(必须是整数坐标)来约束 $g$ 的平移分量 $u$。
* $u$ 的归一化: 将 $u$ 移动到基本单元 $\Pi'$ 内的操作是合法的,因为我们是在 $G$ 的一个陪集 $H g$ 中选取代表元。$H t_u r$ 和 $H t_{u-v} r$ 是同一个陪集。选择哪个代表元进行分析,不影响最终结论。
* 两种可能性的互斥性: 一个群不可能既是(a)又是(b)。因为它要么包含纯反射 $r$,要么不包含。这是个非此即彼的判断。
2.5.5. 总结
本段通过精妙的代数推导,完成了对点群为 $D_4$ 的晶体学群的分类。证明的核心在于,通过分析反射类元素 $g=t_u r$ 的平方以及与旋转复合后的平方,迫使 $g$ 的平移分量 $u$ 只能取两个值:$(0,0)$ 或 $(\frac{1}{2}, \frac{1}{2})$。这两种可能分别对应于群 $G$ 中包含纯反射 (p4m) 和只包含滑移反射 (p4g) 两种本质不同的结构。
2.5.6. 存在目的
本段的目的是完成四重对称群的分类,并展示处理滑移反射这类“隐藏对称性”的代数方法。它完美地回应了之前提出的问题:“点群和格不足以确定群”。通过这里的分析,我们看到了为什么不足够,以及如何通过更深入的计算来区分这些“同点群、同格”但结构不同的群。这为理解全部17个群的分类提供了最关键的范例。
2.5.7. 直觉心智模型
你是一名化学家,你通过实验知道一种晶体的原子排列具有正方格结构 ($L$),并且整体上看具有正方形的对称性 ($\bar{G}=D_4$)。现在你想确定原子的精确排布方式 ($G$)。
这个命题告诉你,只有两种可能的“分子内部结构”:
* 模型A (p4m): 原子就直接摆在格点上,并且关于格线是镜面对称的。这是一种高度对称、很“坦率”的结构。它有纯反射对称。
* 模型B (p4g): 原子不是直接在格点上,而是稍微偏离一点。并且,对称性是以一种更“扭曲”的方式实现的。你看似镜面对称的两个原子,其实一个是另一个的“镜像”再“平移”一点点的结果。它没有纯反射,只有滑移反射。
你的任务就是通过更精密的实验(比如分析特定的衍射斑点),来判断你手头的晶体属于模型A还是模型B。
2.5.8. 直观想象
回到墙纸图案。所有看起来有“正方形感”的墙纸,可以分为两大类。
1. 第一类 (p4m):你可以找到一条真正的“镜子线”。你把一张半透明的纸盖在图案上,沿着这条线描出图案,然后把纸翻过来,描出的图案会和线另一边的墙纸完全重合。标准的棋盘格就属于这一类。
2. 第二类 (p4g):你找不到任何一条这样的“镜子线”。但是,你能找到一条“滑移镜子线”。当你沿着这条线描好图案,翻过纸来,发现对不上。但是,你把翻过来的纸沿着这条线滑动半个基本单位的距离,就完美重合了。前面说的“卍卐交错”的图案就属于这一类。
这两种墙纸在“宏观”上都是 $D_4$ 对称的,但“微观”的实现方式有本质区别。
3行间公式索引
1.
解释: 这个公式描述了点群为 $C_4$ 的晶体学群 p4 的结构,其所有元素都由一个格点平移 $t_v$ 和一个绕原点的旋转 $\rho^i$ 复合而成。
2.
解释: 这个公式描述了点群为 $D_4$ 的第一种可能情况 p4m,其反射类操作由标准的反射、旋转和格点平移复合而成,这意味着群中包含纯反射。
3.
解释: 这个公式描述了点群为 $D_4$ 的第二种可能情况 p4g,其反射类操作的平移分量 $u$ 来自陪集 $c+L$,这意味着群中不包含纯反射,而是包含滑移反射。
4.
解释: 这组公式是证明命题6.6.4的关键计算,它将一个反射类元素 $g=t_ur$ 的平方及其与旋转复合后的平方,都转化为了纯平移变换,从而可以用平移格的性质来约束其平移分量 $u$。