1. 计数公式

这部分内容是在回顾一个群论中的基础且重要的定理——拉格朗日定理。它描述了一个有限群的阶（元素个数）与其任意子群的阶之间的关系。

1. 起点：我们从一个有限群 $G$ 开始。“有限”意味着群 $G$ 中的元素数量是有限的。“群”是一个代数结构，包含一个集合和在这个集合上的一个二元运算，满足封闭性、结合律、有单位元和每个元素都有逆元。
2. 子群：我们考虑 $G$ 的一个子群 $H$。子群是 $G$ 的一个子集，它本身也满足群的四个条件（使用与 $G$ 相同的运算）。
3. 陪集：对于 $H$ 和 $G$ 中的任意一个元素 $g$，我们可以构造一个叫做“陪集”的集合。左陪集 $gH$ 的定义是 $\{gh \mid h \in H\}$，即用 $g$ 去乘 $H$ 中的每一个元素。类似的，右陪集 $Hg$ 是 $\{hg \mid h \in H\}$。
4. 陪集的性质：一个关键的事实是，$G$ 中由 $H$ 形成的所有不同的左陪集（或右陪集）构成 $G$ 的一个划分（Partition）。这意味着：
   • $G$ 中的每一个元素都恰好属于一个左陪集。
   • 任意两个左陪集要么完全相同，要么完全不相交。
   • 所有左陪集的大小都和子群 $H$ 本身的大小一样，即 $|gH| = |H|$。
5. 指数：所有不同左陪集的集合，我们记为 $G/H$。这个集合的大小，也就是不同左陪集的个数，被称为 $H$ 在 $G$ 中的指数，记为 $[G:H]$。所以， $|G/H| = [G:H]$。
6. 核心关系：既然 $G$ 被划分成了 $[G:H]$ 个互不相交的部分，每个部分的大小都是 $|H|$，那么把这些部分加起来就等于 $G$ 的总大小。这就好像把一个大饼切成若干个同样大小的小块，大饼的总重量等于一小块的重量乘以小块的数量。这就得到了拉格朗日定理的公式。

这部分引入了群作用背景下的核心计数公式，通常被称为“轨道-稳定化子定理”。它将群的阶与它作用在一个集合上时产生的轨道和稳定化子的阶联系起来。

1. 群作用：首先，我们需要一个群 $G$ 和一个集合 $S$。“$G$ 在 $S$ 上作用”是一个形式化的概念，意味着 $G$ 中的每个元素 $g$ 都能以一种与群运算兼容的方式“移动”$S$ 中的元素。具体来说，这个作用是一个映射 $G \times S \to S$，记作 $(g, s) \mapsto g \cdot s$，满足：
   • $e \cdot s = s$ (单位元不做任何移动)
   • $(g_1g_2) \cdot s = g_1 \cdot (g_2 \cdot s)$ (连续两次移动等价于两次移动的复合)
2. 轨道 (Orbit)：给定 $S$ 中的一个元素 $s$，它的轨道 $O_s$ 是 $s$ 在 $G$ 中所有元素作用下可能被移动到的所有位置的集合。即 $O_s = \{ g \cdot s \mid g \in G \}$。直观上，就是从 $s$ 出发，群 $G$ 能把它带到的所有地方。
3. 稳定化子 (Stabilizer)：给定 $S$ 中的一个元素 $s$，它的稳定化子 $G_s$ 是 $G$ 中所有那些“固定”$s$ 不动的元素构成的集合。即 $G_s = \{ g \in G \mid g \cdot s = s \}$。一个重要的事实是，$G_s$ 始终是 $G$ 的一个子群。
4. 核心思想：轨道-稳定化子定理揭示了一个深刻的平衡关系。群 $G$ 的“力量”（由其阶 $|G|$ 体现）被分成了两部分：一部分力量用来“移动”元素 $s$ 到轨道上的不同位置（体现在轨道的阶 $|O_s|$ 上），另一部分力量则“浪费”在了保持 $s$ 不动上（体现在稳定化子的阶 $|G_s|$ 上）。公式 $|G| = |G_s| |O_s|$ 精确地量化了这种平衡。
5. 与拉格朗日定理的联系：原文提到“这由 (6.9.1) 和命题 (6.8.4) 得出”。命题 (6.8.4)（此处未给出，但标准教材中会证明）指出，元素 $s$ 的轨道 $O_s$ 的元素个数，与稳定化子 $G_s$ 在 $G$ 中的陪集个数是一一对应的。也就是说，$|O_s| = [G:G_s] = |G/G_s|$。
   • 把这个结论代入我们刚刚回顾的拉格朗日定理 $|G| = |H| |G/H|$ 中。
   • 将子群 $H$ 替换为稳定化子 $G_s$（因为 $G_s$ 是一个子群），我们得到 $|G| = |G_s| |G/G_s|$。
   • 再将 $|G/G_s|$ 替换为 $|O_s|$，就得到了计数公式：$|G| = |G_s| |O_s|$。

这一小段是对上一段计数公式的直接推论和解读。

1. 轨道的阶等于稳定化子的指数：这是轨道-稳定化子定理证明过程中的核心关系，这里把它明确地写成一个独立的公式。
   • 我们有拉格朗日定理：$|G| = |G_s| \cdot [G:G_s]$，其中 $[G:G_s]$ 是子群 $G_s$ 的指数。
   • 我们也有轨道-稳定化子定理：$|G| = |G_s| \cdot |O_s|$。
   • 比较这两个公式，两边同时除以 $|G_s|$（因为 $|G_s| \ge 1$），我们立刻得到 $|O_s| = [G:G_s]$。
   • 这个等式意味着，轨道里有多少个元素，就对应着稳定化子有多少个不同的陪集。
2. 它整除群的阶：“它”指的是轨道的阶 $|O_s|$。
   • 从公式 $|G| = |G_s| \cdot |O_s|$ 可以看出，$|G|$ 是 $|O_s|$ 和 $|G_s|$ 的乘积。
   • 在整数算术中，如果 $A = B \cdot C$，那么 $B$ 和 $C$ 都是 $A$ 的因子（divisor）。
   • 因此，$|O_s|$ 必然整除 $|G|$。同样，$|G_s|$ 也必然整除 $|G|$（这从拉格朗日定理也能直接看出，因为 $G_s$ 是子群）。
   • 这是一个非常重要的结论，它限制了在一个群作用中可能出现的轨道大小。轨道的大小不可能是任意的，它必须是群阶的一个约数。
3. 对于S的每个元素s都有这样一个公式：这句话强调了这个定理的普适性。无论你从集合 $S$ 中挑选哪个元素 $s$ 开始分析，轨道-稳定化子定理都成立。当然，对于不同的 $s$，其轨道 $O_s$ 和稳定化子 $G_s$ 可能是不同的。但是，如果你选的另一个元素 $s'$ 恰好在 $s$ 的轨道里（即 $s' \in O_s$），那么它们的轨道是完全相同的（$O_s = O_{s'}$），并且它们的稳定化子是共轭的（$G_{s'} = g G_s g^{-1}$，其中 $s' = g \cdot s$），因此稳定化子的阶也是相同的（$|G_s| = |G_{s'}|$）。

这部分介绍了另一个基于群作用的计数公式，它关注的是如何计算被作用的集合 $S$ 的总大小。这个公式通常被称为类方程（Class Equation）的基础，或者直接叫轨道划分公式。

1. 轨道是一种等价关系：在群作用的背景下，我们可以定义一个等价关系 $\sim$ 。对于 $S$ 中的两个元素 $s_1, s_2$，我们说 $s_1 \sim s_2$ 当且仅当存在一个群元 $g \in G$ 使得 $g \cdot s_1 = s_2$。换句话说，两个元素等价，如果它们在同一个轨道里。
   • 自反性：$s \sim s$ 因为 $e \cdot s = s$。
   • 对称性：如果 $s_1 \sim s_2$，则存在 $g$ 使 $g \cdot s_1 = s_2$。那么 $g^{-1} \cdot s_2 = g^{-1} \cdot (g \cdot s_1) = (g^{-1}g) \cdot s_1 = e \cdot s_1 = s_1$，所以 $s_2 \sim s_1$。
   • 传递性：如果 $s_1 \sim s_2$ 且 $s_2 \sim s_3$，则存在 $g_1, g_2$ 使 $g_1 \cdot s_1 = s_2$ 和 $g_2 \cdot s_2 = s_3$。那么 $(g_2g_1) \cdot s_1 = g_2 \cdot (g_1 \cdot s_1) = g_2 \cdot s_2 = s_3$，所以 $s_1 \sim s_3$。
2. 等价类就是轨道：既然 $\sim$ 是一个等价关系，它就会把集合 $S$ 划分成一系列互不相交的等价类。而根据定义，一个元素 $s$ 的等价类，就是所有能从 $s$ 到达的元素的集合——这正是轨道 $O_s$ 的定义。
3. 集合的划分：因此，群作用产生的轨道，天然地把整个集合 $S$ 分割成了若干个互不相干的小块。每个小块就是一个轨道。
4. 加总：既然 $S$ 被划分成了 $k$ 个互不相交的轨道 $O_1, O_2, \dots, O_k$，那么 $S$ 的总元素个数 $|S|$ 就等于所有这些轨道的元素个数之和。这就得到了公式 $|S| = |O_1| + |O_2| + \dots + |O_k|$。

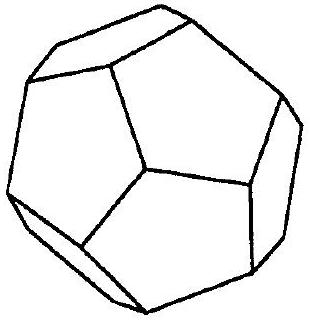
这个例子绝佳地展示了如何应用轨道-稳定化子定理（公式 6.9.2）来计算一个复杂对象的对称群的阶。这里的对象是正十二面体，一个由12个正五边形面构成的正多面体。

思路一：作用于“面”

1. 群和集合：
   • $G$：正十二面体的所有旋转对称操作构成的群。我们的目标是求 $|G|$。
   • $S=F$：正十二面体的12个面的集合。$|F|=12$。
2. 作用是传递的：“传递作用”意味着只存在一个轨道，这个轨道就是整个集合 $F$。直观上，对于任意两个面 $f_1, f_2$，我们总能找到一个旋转操作，把十二面体从 $f_1$ 正对着你的位置，转到 $f_2$ 正对着你的位置。所以，$|O_f| = |F| = 12$。
3. 计算稳定化子：我们选择一个特定的面 $f$（比如正对着我们的那个）。它的稳定化子 $G_f$ 是什么？就是那些能让这个面 $f$ 保持在原位的旋转操作。
   • 想象一下，你盯着一个正五边形的面。能让这个五边形回到原位的旋转，只有绕着穿过它中心的轴进行的旋转。
   • 旋转 $360/5 = 72$ 度（即 $2\pi/5$ 弧度），五边形回到原位。
   • 旋转 $2 \times 72, 3 \times 72, 4 \times 72, 5 \times 72 = 360$ 度，五边形都回到原位。
   • 这5个旋转操作（旋转0, 72, 144, 216, 288度）构成了 $f$ 的稳定化子 $G_f$。它是一个5阶的循环群。所以 $|G_f| = 5$。
4. 应用公式：根据轨道-稳定化子定理 $|G| = |G_f| \cdot |O_f|$。
   • 代入数值：$|G| = 5 \cdot 12 = 60$。
   • 结论：正十二面体的旋转对称群的阶是60。

思路二：作用于“顶点”

1. 群和集合：
   • $G$：同上。
   • $S=V$：正十二面体的20个顶点的集合。$|V|=20$。
2. 作用是传递的：同样，你可以通过旋转，把任意一个顶点转到任意另一个顶点的位置。所以作用是传递的，$|O_v| = |V| = 20$。
3. 计算稳定化子：选择一个顶点 $v$。它的稳定化子 $G_v$ 是什么？这个顶点是3个正五边形面的交点。
   • 能让这个顶点 $v$ 保持在原位的旋转，是绕着穿过这个顶点和其对跖点的轴进行的旋转。
   • 从这个顶点看去，你会看到3个面和3条边汇集于此。旋转 $360/3=120$ 度（$2\pi/3$ 弧度）后，整个图形看起来和原来一样。
   • 这3个旋转操作（旋转0, 120, 240度）构成了 $v$ 的稳定化子 $G_v$。它是一个3阶的循环群。所以 $|G_v| = 3$。
4. 应用公式：$|G| = |G_v| \cdot |O_v|$。
   • 代入数值：$|G| = 3 \cdot 20 = 60$。
   • 这个结果与从面计算得到的结果一致，验证了我们的计算。

思路三：作用于“边”

1. 群和集合：
   • $G$：同上。
   • $S=E$：正十二面体的边的集合。我们暂时不知道 $|E|$ 是多少。
2. 作用是传递的：所有边都是等价的，可以通过旋转相互转换。所以 $|O_e| = |E|$。
3. 计算稳定化子：选择一条边 $e$。它的稳定化子 $G_e$ 是什么？
   • 能让这条边 $e$ 保持在原位的旋转，是绕着穿过这条边中点并且垂直于它的轴进行的。
   • 这种旋转只有两种可能：旋转0度（恒等元）和旋转180度（$\pi$ 弧度）。旋转180度会把边的两端点互换，但边本身占据的空间位置不变。
   • 所以 $G_e = \{e, R_{\pi}\}$，$|G_e| = 2$。
4. 应用公式：$|G| = |G_e| \cdot |O_e|$。
   • 我们已经知道 $|G|=60$，$|G_e|=2$。所以 $60 = 2 \cdot |O_e|$。
   • 解得 $|O_e|=30$。因为作用是传递的，所以 $|E|=|O_e|=30$。
   • 结论：正十二面体有30条边。这个方法不仅验证了群的阶，还帮我们计算出了边的数量。

这部分探讨了一个更精细的技巧：考察一个子群的作用。大群 $G$ 的作用可能比较粗糙（比如是传递的，只有一个大轨道），但当我们只用 $G$ 的一部分力量——一个子群 $H$——去作用时，原来那个大轨道可能会碎裂成几个更小的 $H$-轨道，从而揭示出更精细的结构。

1. 限制作用：如果群 $G$ 能作用于集合 $S$，那么它的任何一个子群 $H$ 自然也能作用于 $S$。因为 $H$ 的元素本来就是 $G$ 的元素，它们对 $S$ 元素的“移动”规则是完全一样的。这称为作用的限制。
2. 轨道碎裂：
   • 一个 $G$-轨道 $O_s^G = \{g \cdot s \mid g \in G\}$ 是用 $G$ 的所有力量能到达的地方。
   • 一个 $H$-轨道 $O_s^H = \{h \cdot s \mid h \in H\}$ 是只用 $H$ 的力量能到达的地方。
   • 因为 $H \subseteq G$，所以 $O_s^H \subseteq O_s^G$。$H$-轨道总是包含在相应的 $G$-轨道之内。
   • 因此，一个大的 $G$-轨道，在子群 $H$ 的作用下，会被划分成一个或多个互不相交的 $H$-轨道。

第一个例子：面的稳定化子 H 的作用

1. 群和集合：
   • 集合 $S=F$ 是十二面体的12个面。$|F|=12$。
   • 子群 $H$ 是我们之前找到的、固定某个面 $f$ 的稳定化子 $G_f$。它是一个5阶循环群，由绕 $f$ 中心的旋转（0, 72, 144, 216, 288度）构成。$|H|=5$。
2. H作用于F：我们现在用这个5阶的子群 $H$ 去作用于全部12个面。
   • 根据轨道-稳定化子定理（这次是对于 $H$ 的作用），任何 $H$-轨道的大小必须整除 $|H|=5$。所以轨道大小只能是1或5。
   • 我们使用轨道划分公式（6.9.4）：$|F| = 12 = \sum |O_i|$，其中每个 $|O_i|$ 只能是1或5。
3. 寻找轨道：我们需要将数字12用数字1和5来凑。
   • 阶为1的轨道：哪些面在 $H$ 的所有5个旋转操作下都保持不动？
   • 首先，面 $f$ 本身。$H$ 的定义就是固定 $f$ 的，所以 $f$ 自己构成一个1阶轨道：$\{f\}$。
   • 再想想几何结构，当绕穿过 $f$ 中心的轴旋转时，这个轴的另一端会穿过正十二面体正对面的那个面 $f_{opp}$。因此，对面的那个面 $f_{opp}$ 也会被这5个旋转操作固定。所以 $\{f_{opp}\}$ 也构成一个1阶轨道。
   • 我们找到了两个1阶轨道。总数12个面，还剩下 $12 - 1 - 1 = 10$ 个面。
   • 阶为5的轨道：剩下的10个面，必须被划分成若干个5阶轨道。$10 = 5+5$ 是唯一的可能。
   • 几何上，这10个面可以分成两圈，一圈是与 $f$ 相邻的5个面，另一圈是与 $f_{opp}$ 相邻的5个面。$H$ 的旋转会使每一圈内的5个面轮换，从而形成两个5阶轨道。
4. 最终划分：$H$ 作用于 $F$ 产生的轨道划分是：$12 = 1 + 1 + 5 + 5$。这完美地解释了12个面在这个5阶子群作用下的结构。

第二个例子：顶点的稳定化子 K 的作用

1. 群和集合：
   • 集合 $S=F$ 还是12个面。$|F|=12$。
   • 子群 $K$ 是我们之前找到的、固定某个顶点 $v$ 的稳定化子 $G_v$。它是一个3阶循环群，由绕 $v$ 的旋转（0, 120, 240度）构成。$|K|=3$。
2. K作用于F：我们用这个3阶的子群 $K$ 去作用于全部12个面。
   • 任何 $K$-轨道的大小必须整除 $|K|=3$。所以轨道大小只能是1或3。
   • 轨道划分公式：$|F| = 12 = \sum |O_i|$，其中每个 $|O_i|$ 只能是1或3。
3. 寻找轨道：我们需要将数字12用数字1和3来凑。
   • 阶为1的轨道：有面被 $K$ 固定吗？$K$ 是绕一个顶点 $v$ 旋转。这个顶点是3个面的交点。当绕 $v$ 旋转120度时，这3个面会相互轮换位置，没有一个面被固定不动。所以不存在1阶轨道。
   • 阶为3的轨道：既然没有1阶轨道，那么所有轨道都必须是3阶的。$12 = 3+3+3+3$。
   • 这意味着12个面被划分成了4个轨道，每个轨道里有3个面。
   • 几何上，绕顶点 $v$ 旋转时，与 $v$ 相邻的那3个面构成一个3阶轨道。另外9个面则会根据它们离旋转轴的距离和方位，被分成另外3组，每组3个面，在旋转下相互轮换，构成另外3个3阶轨道。
4. 最终划分：$K$ 作用于 $F$ 产生的轨道划分是：$12 = 3+3+3+3$。