13 构造自由群的前奏:自由半群
📜 [原文3]
为了描述自由群,我们从一个任意集合开始,例如 $S=\{a, b, c, \ldots\}$。我们称其元素为“符号”,并定义一个字是符号的有限字符串,其中允许重复。例如,$a, a a, b a$ 和 $a a b a$ 都是字。两个字可以通过并置来组合,即把它们并排放置:
这是字集合 $W$ 上的结合律。我们将“空字”包含在 $W$ 中作为单位元,并用符号 $1$ 表示它。那么集合 $W$ 就变成了所谓的集合 $S$ 上的自由半群。它不是一个群,因为它缺少逆元,而添加逆元会使事情变得稍微复杂。
这一段开始着手,一步步地、形式化地构造自由群。作者采取的策略是“循序渐进”,先从一个更简单的结构——自由半群 (Free Semigroup) ——开始。
- 第一步:定义原材料
- 我们从一个集合 $S$ 开始,这个集合可以是任何东西,比如 $S=\{a, b, c\}$ 或者 $S=\{\text{猫}, \text{狗}\}$。
- $S$ 中的元素被称为符号 (symbols) 或字母 (letters)。它们是构建一切的基础,就像字母表里的字母。
- 第二步:定义“字”
- 一个字 (word) 就是由这些符号组成的一个有限长度的序列(字符串)。
- 允许重复: 就像在英文单词 "book" 中 'o' 可以重复一样,我们也可以有字 "aa"。
- 例子: 如果 $S=\{a, b\}$,那么
- $a$ 是一个字(长度为1)。
- $aa$ 是一个字(长度为2)。
- $ba$ 是一个字(长度为2)。
- $aaba$ 是一个字(长度为4)。
- 顺序很重要:$ba$ 和 $ab$ 是两个不同的字。
- 第三步:定义运算
- 我们定义一个操作,叫做并置 (concatenation),就是简单地把两个字首尾相连。
- 比如,字 $w_1 = aa$ 和字 $w_2 = ba$,它们的并置 $w_1w_2$ 就是 $aaba$。
- 这个操作是天生就满足结合律 (associative law) 的。比如,$(w_1 w_2) w_3$ (先把 $w_1, w_2$ 连接,再连上 $w_3$) 和 $w_1 (w_2 w_3)$ (先把 $w_2, w_3$ 连接,再把 $w_1$ 连在前面) 得到的结果显然是一样的。例如,$("ab")"c"$ 和 $"a"("bc")$ 都得到 $"abc"$。
- 第四步:引入单位元
- 为了让这个结构更接近群,我们引入一个特殊的字,叫做空字 (empty word)。它不包含任何符号,长度为0。
- 我们用符号 $1$ 来表示空字。
- 空字的作用是单位元 (identity element)。任何字 $w$ 与空字 $1$ 进行并置,都等于 $w$ 本身。$w \cdot 1 = 1 \cdot w = w$。例如,$aba \cdot 1 = aba$。
- 第五步:命名这个结构
- 到目前为止,我们有了一个集合 $W$(所有字的集合,包括空字),以及一个满足结合律的运算(并置),并且还有一个单位元(空字)。
- 这种代数结构(有结合律和单位元的集合)被称为幺半群 (Monoid)。文中称之为 $S$ 上的自由半群,更准确的说是自由幺半群 (Free Monoid)。
- 半群 (Semigroup) 仅要求运算满足结合律。幺半群在半群的基础上还要求有单位元。
- 最后一步:指出缺陷
- 作者明确指出,这个自由半群 $W$ 还不是一个群。
- 为什么?因为它缺少逆元 (inverses)。对于一个非空的字,比如 $a$,你在 $W$ 中找不到另一个字 $w'$,使得 $a \cdot w' = 1$(空字)。把任何非空字符串接在 $a$ 后面,只会让它变得更长,永远变不回空字。
- 添加逆元是构造自由群的下一步,也是更复杂的一步。
- $aa$: 一个由符号 'a' 重复两次构成的字。
- $ba$: 一个由符号 'b' 后跟符号 'a' 构成的字。
- ,: 分隔符,表示这是两个独立的字。
- $\rightsquigarrow$: 一个表示“产生”或“组合成”的箭头符号。在这里,它就代表并置操作。
- $aaba$: 并置操作的结果,一个新的、更长的字。
这个“公式”其实是一个操作示例,展示了并置是如何工作的。
- 示例1: 字母表 $S = \{x, y, z\}$
- 符号: $x, y, z$
- 字 (Words): $x, y, z, xx, xy, yx, zzz, xyzy, \ldots$
- 空字: $1$
- 并置操作:
- 令 $w_1 = xy$,$w_2 = zx$。
- $w_1 w_2 = (xy)(zx) = xyZX$。
- 令 $w_3 = 1$ (空字)。
- $w_1 w_3 = (xy)(1) = xy$。
- 这个结构不是群: 找不到一个字 $w'$ 使得 $(xy)w' = 1$。
- 示例2: 二进制字母表 $S = \{0, 1\}$
- 这在计算机科学中非常常见。
- 符号: $0, 1$
- 字 (Words): $0, 1, 00, 01, 10, 11, 10101, \ldots$ (所有二进制字符串)
- 空字: $1$ (或者用 $\epsilon$ 表示)
- 并置操作: 把两个二进制字符串连起来。
- 101 和 011 并置得到 101011。
- 这个结构是自由半群/幺半群: 它在形式语言理论和计算理论中是基础。同样,它也不是群。
- 半群 vs. 幺半群 vs. 群:
- 半群: 只要求结合律。
- 幺半群 (Monoid): 结合律 + 单位元。本段描述的 $W$ 实际上是幺半群。
- 群: 结合律 + 单位元 + 逆元。
- 作者使用“自由半群”可能是一个稍微不那么精确但可接受的说法,因为重点在于它“不是群”。
- 空字的角色: 空字 $1$ 是一个真实存在的元素,是单位元,不是“无”。集合 $W$ 包含了这个元素。
- 字与元素的区别: 在这个阶段,每一个不同的字符串就是一个不同的元素。ab 和 ba 是两个不同的元素。之后为了构造群,我们会引入“等价”的概念,情况会改变。
本段通过定义符号、字、并置和空字,构造了一个名为自由半群(或更精确地说是自由幺半群)的代数结构。这个结构具有结合律和单位元,但因缺少逆元而不能成为一个群。这是向着构造完整自由群迈出的第一步。
这一部分的目的是“打地基”。直接定义自由群比较抽象,所以作者选择了一个“建设性”的路线。从最简单的元素(符号)开始,用最简单的操作(并置)构建出一个初步的结构(自由半群)。这使得整个构造过程更加清晰、有条理。同时,通过明确指出这个初步结构“缺少逆元”,自然地引出了下一步需要解决的核心问题,使得叙述逻辑流畅。
- 自由半群就像一个只有“录音”功能的磁带播放器。
- 符号 $S=\{a, b, c\}$ 就是你可以念的几个音节。
- 一个字就是你录下的一段声音,比如“a-b-a”。
- 并置操作就是“追加录音”。你在“a-b-a”后面接着录“c-a”,磁带上的内容就变成了“a-b-a-c-a”。
- 空字 $1$ 就是一盘空白磁带。在任何录音前后追加一段“无声的录音”,原录音不变。
- 缺少逆元的问题是:这个播放器没有“撤销”或“倒带”按钮。你一旦录了“a”,就无法通过再录一段什么东西让磁带重新变回完全空白。你只能让录音越来越长。
想象你在用字母积木块 $S=\{A, B, C\}$ 玩游戏。
- 一个字就是你把一些积木块排成一排,例如 A-B-B-A。
- 并置就是把两排积木首尾相连。你有一排 A-B,我有一排 C-A,我们把它俩接起来,就成了一长排 A-B-C-A。
- 空字就是你的桌子上空空如也,什么积木都没放。你在空桌子上放一排 A-B,那桌子上就是 A-B。
- 这个游戏为什么不是群?因为你一旦把积木 A 放上去了,你就不能通过再放一个什么积木块,让 A 消失掉。你只能越放越多。要让它变成群,我们就需要引入一种能让积木“湮灭”的新规则,这就是下一步要做的。
14 构造自由群的核心:引入逆元和约化
📜 [原文4]
令 $S^{\prime}$ 是由 $S$ 中每个 $a$ 的符号 $a$ 和 $a^{-1}$ 组成的集合:
并令 $W^{\prime}$ 是使用 $S^{\prime}$ 中符号构成的字的半群。如果一个字看起来像
对于 $S$ 中的某个 $x$,我们可以同意抵消这两个符号 $x$ 和 $x^{-1}$ 以减少字的长度。如果不能进行这样的抵消,则称一个字是约化的。从 $W^{\prime}$ 中的任何字 $w$ 开始,我们可以执行有限次抵消序列,并且最终必须得到一个约化字 $w_{0}$,可能是空字 $1$。我们称 $w_{0}$ 为 $w$ 的约化形式。
这一段是构造自由群的关键一步。我们解决了上一段提出的“缺少逆元”的问题,方法是:
- 显式地为每个符号添加一个对应的逆符号。
- 定义一个“抵消”规则,让符号和其逆符号可以互相消除。
让我们分解这个过程:
- 扩大字母表:
- 之前我们的字母表是 $S = \{a, b, c, \ldots\}$。
- 现在我们创建一个新的、更大的字母表,叫做 $S'$。
- 对于 $S$ 中的每一个符号 $a$,我们在 $S'$ 中放入两样东西:符号 $a$ 本身,以及一个全新的符号,我们记作 $a^{-1}$。
- $a^{-1}$ 被称为 $a$ 的逆符号 (inverse symbol)。它目前只是一个形式上的记号,看起来像幂,但其实只是一个新字母。
- 所以,如果 $S=\{a, b\}$,那么新的字母表就是 $S'=\{a, a^{-1}, b, b^{-1}\}$。
- 创建新的字集:
- 和之前一样,我们用新字母表 $S'$ 中的符号来构成字。所有这些新字的集合,我们称之为 $W'$。
- $W'$ 本身也是一个自由半群(或幺半群),运算同样是并置。
- 现在的字可以包含逆符号了,例如:$ab^{-1}$, $a^{-1}a$, $bba^{-1}b$ 都是 $W'$ 中的字。
- 定义核心规则:抵消 (Cancellation)
- 这是最关键的创新。我们规定:在一个字中,如果一个符号和它的逆符号紧挨在一起,它们就可以被“抵消”或“删除”。
- 这个规则有两种形式:
- 一个符号后面跟着它的逆符号,如 $aa^{-1}$。
- 一个逆符号后面跟着它对应的原符号,如 $a^{-1}a$。
- 抵消会使字的长度变短。例如,在字 $ba a^{-1} c$ 中,中间的 $aa^{-1}$ 可以被抵消,得到更短的字 $bc$。
- 定义“约化”:
- 约化字 (Reduced Word): 如果一个字里面已经没有任何可以抵消的部分了(即找不到任何相邻的 $xx^{-1}$ 或 $x^{-1}x$),那么这个字就被称为约化的。
- 例如:$ab^{-1}c$ 是约化的,因为 $a$ 和 $b^{-1}$ 不能抵消,$b^{-1}$ 和 $c$ 也不能。$aab$ 也是约化的。
- 而 $abb^{-1}a$ 不是约化的,因为中间有 $bb^{-1}$。
- 约化形式 (Reduced Form): 从任何一个字 $w$ 开始,我们可以不断地进行抵消操作。因为每次抵消都会使字的长度减少,这个过程必然会在有限步内结束。当不能再进行任何抵消时,我们得到的那个约化字,就称为 $w$ 的约化形式。
- 例如,字 $w = c a^{-1} a b b^{-1}$。
- 抵消 $a^{-1}a$ 得到 $c b b^{-1}$。
- 再抵消 $b b^{-1}$ 得到 $c$。
- $c$ 本身是约化的,所以 $c$ 就是 $w$ 的约化形式。
- 另一个例子:$w = a b^{-1} b a^{-1}$。抵消 $b^{-1}b$ 得到 $aa^{-1}$。再抵消 $aa^{-1}$ 得到空字 $1$。所以 $w$ 的约化形式是 $1$。
- $S'$: 一个新的集合,是构造自由群所用的扩展字母表。
- $\{ \ldots \}$: 集合的表示法。
- $a, b, c, \ldots$: 这些是来自原始集合 $S$ 的符号。
- $a^{-1}, b^{-1}, c^{-1}, \ldots$: 这些是新引入的逆符号。每个逆符号 $x^{-1}$ 都与一个原始符号 $x \in S$ 相关联。
- $(7.9.1)$: 公式的标签或编号,方便在文本中引用。
* $\cdots$: 省略号,表示字中可能存在的其他符号。
* $x$: 一个占位符,它可以代表任何来自原始集合 $S$ 的符号(如 $a, b, \ldots$)。
* $x^{-1}$: $x$ 对应的逆符号。
* $x x^{-1}$: 表示符号 $x$ 和其逆符号 $x^{-1}$ 相邻出现,这是一个可以被抵消的组合。
* $x^{-1} x$: 表示逆符号 $x^{-1}$ 和其对应的符号 $x$ 相邻出现,这也是一个可以被抵消的组合。
* 或: 表示这两种情况都适用。
- 示例1:求 $w = a b b^{-1} c^{-1} c a$ 的约化形式
- 原始字: $w = a b b^{-1} c^{-1} c a$
- 观察: 我们发现中间有两对可以抵消的:$b b^{-1}$ 和 $c^{-1} c$。
- 抵消 $b b^{-1}$: 字变为 $a (b b^{-1}) c^{-1} c a \to a c^{-1} c a$。
- 抵消 $c^{-1} c$: 字变为 $a (c^{-1} c) a \to a a$。
- 最终结果: $aa$。这个字中没有相邻的逆符号对,所以它是约化的。因此,$aa$ 是 $w$ 的约化形式。
- 示例2:求 $w = x y^{-1} z z^{-1} y x^{-1} x$ 的约化形式
- 原始字: $w = x y^{-1} z z^{-1} y x^{-1} x$
- 抵消 $z z^{-1}$: 得到 $x y^{-1} y x^{-1} x$。
- 抵消 $y^{-1} y$: 得到 $x x^{-1} x$。
- 抵消 $x x^{-1}$: 得到 $x$。
- 最终结果: $x$ 是约化的,所以它是 $w$ 的约化形式。
- 示例3:约化为空字
- 原始字: $w = a^{-1} b^{-1} b a$
- 抵消 $b^{-1} b$: 得到 $a^{-1} a$。
- 抵消 $a^{-1} a$: 得到空字 $1$。
- 最终结果: $1$ 是 $w$ 的约化形式。
- $a^{-1}$ 只是一个符号: 再次强调,$a^{-1}$ 不是“$a$的倒数”,它是一个独立的、与 $a$ 配对的符号。我们只是借用了幂的写法,因为它在后续的群运算中行为类似逆元。
- 抵消必须是相邻的: 只能抵消紧挨在一起的 $xx^{-1}$ 或 $x^{-1}x$。在字 $a b a^{-1}$ 中,$a$ 和 $a^{-1}$ 不相邻,它们之间隔了一个 $b$,所以不能抵消。$a b a^{-1}$ 本身就是一个约化字。
- 什么是 $(a^{-1})^{-1}$?: 为了让系统完整,我们通常定义 $a$ 的逆符号是 $a^{-1}$,而 $a^{-1}$ 的逆符号就是 $a$。即 $(a^{-1})^{-1} = a$。这样, $x$ 可以代表 $S'$ 中的任何元素(包括 $a^{-1}$),而 $x^{-1}$ 就代表它的配对符号。
- 约化过程的顺序: 从一个字出发,可能有多种抵消顺序(如下一段所述)。一个重要的问题是:不同的抵消顺序是否会得到不同的最终约化字?下一段的命题将回答这个问题。
本段在构造自由群的道路上迈出了关键一步。通过引入逆符号来扩展字母表,并定义了抵消规则,我们获得了一种“缩短”字的机制。这引出了约化字(无法再缩短的字)和约化形式(任何字最终缩短成的形态)的核心概念,为定义群的元素和运算铺平了道路。
本段的目的是解决自由半群中“缺少逆元”的根本问题。通过形式上地引入逆符号和抵消规则,我们正在模拟群中逆元的核心性质:$g \cdot g^{-1} = 1$。这里的抵消就相当于“乘以逆元得到单位元”,而约化形式就将是未来自由群中真正的元素。这一步是连接字的组合世界和抽象群论世界的桥梁。
- 回到我们的“路径”模型:$S=\{a, b\}$ 分别代表“向东”和“向北”。
- 引入 $S' = \{a, a^{-1}, b, b^{-1}\}$ 就意味着我们现在有了四种指令:“东”($a$),“西”($a^{-1}$), “北”($b$),“南”($b^{-1}$)。
- 字就是一连串的移动指令,比如 $w = a b b^{-1} a$ 代表 “东-北-南-东”。
- 抵消规则 $bb^{-1} \to 1$ 的含义是:“向北走一步,然后立刻向南走一步”这个组合动作,净效果是“原地不动”。
- 约化一个字,就是把路径中所有这种“原地打转”的无效操作全部去掉,找到从起点到终点的最直接路径。
- 对于 $w = a b b^{-1} a$,你先向东,再向北,再向南(回到只向东一步的位置),最后再向东。整个路径的净效果,等同于一开始就“向东走两步”,即 $aa$。所以 $aa$ 是 $w$ 的约化形式。
- 继续用“珠子”模型:我们现在有红珠子($a$)、反红珠子($a^{-1}$)、蓝珠子($b$)、反蓝珠子($b^{-1}$)。
- 抵消规则:任何时候,一个普通珠子和它的反物质珠子挨在一起(比如 红-反红 或 反红-红),它们就会一起“湮灭”消失。
- 一个字是一长串各种珠子,例如:红-蓝-反蓝-红 ($a b b^{-1} a$)。
- 约化就是让 این串珠子内部所有能湮灭的对都湮灭掉,看看最后剩下什么。
- 在 $a b b^{-1} a$ 这串珠子中,中间的 蓝-反蓝 ($b b^{-1}$) 会湮灭消失。
- 最后剩下两颗红珠子:红-红 ($aa$)。这就是约化形式。
1.5 约化的唯一性
📜 [原文5]
抵消过程可能有不止一种方式。例如,从 $w=a b b^{-1} c^{-1} c b$ 开始,我们可以通过两种方式进行:
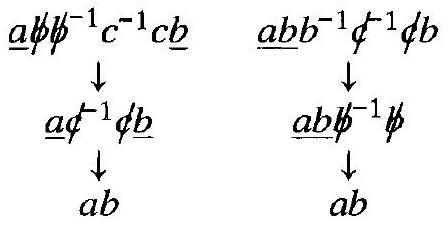
最终得到的是同一个约化字,尽管这些符号在原始字中的位置不同。(最后保留的符号已被下划线标出。)这种情况总是成立的。
命题 7.9.2 给定字 $w$ 只有一个约化形式。
这一部分解决了一个至关重要的问题:约化过程的最终结果是否依赖于我们选择的抵消顺序?如果不同的顺序导致不同的约化字,那么我们的整个构造就会陷入混乱。本段通过一个例子和一则命题,给出了一个明确的答案:最终结果是唯一的。
- 问题的提出:
- 在一个字中,可能同时存在多个可以抵消的相邻对。
- 例如,在字 $w = a b b^{-1} c^{-1} c b$ 中,我们既可以先抵消中间的 $b b^{-1}$,也可以先抵消它旁边的 $c^{-1} c$。
- 这就引出了一个问题:我选择先抵消哪个,会影响最终的结果吗?
- 通过例子建立直觉:
- 作者给出了 $w = a \underline{b} \underline{b}^{-1} \underline{c}^{-1} \underline{c} \underline{b}$ 的例子。(原文中下划线的符号是最终保留的,这里我用下划线标出可操作的对来解释)
- 方式一 (先抵消 $bb^{-1}$):
- $a (b b^{-1}) c^{-1} c b \to a c^{-1} c b$
- $a (c^{-1} c) b \to a b$
- 最终得到 $ab$。
- 方式二 (先抵消 $c^{-1}c$):
- $a b b^{-1} (c^{-1} c) b \to a b b^{-1} b$
- $a (b b^{-1}) b \to a b$
- 最终也得到 $ab$。
- 例子的结论: 在这个例子中,无论我们先处理哪一对,最终得到的约化字都是 $ab$。这暗示我们,最终结果可能是唯一的。
- 正式的结论:命题 7.9.2
- 作者将这个观察提升为一个普适的数学命题。
- 命题 7.9.2: 对于任何一个给定的字 $w$,无论你采用什么样的抵消顺序,最终得到的那个无法再抵消的约化字(即约化形式)是独一无二的。
- 这个命题是整个自由群理论的基石。它保证了“约化形式”这个概念是良好定义的 (well-defined)。因为每个字都对应着一个唯一的约化形式,我们才能放心地把这个约化形式当作是群里的一个规范的元素代表。
本段的“公式”是那个图片,它用图形化的方式展示了两种抵消路径。我们可以用文本形式复现它。
原始字: $w = a b b^{-1} c^{-1} c b$
- 路径1:
- 路径2:
- 两种路径都汇集到同一个终点 $ab$。
- 示例1: $w = x y^{-1} y x^{-1} x y$
- 可抵消对: $y^{-1}y$ 和 $x^{-1}x$
- 路径A (先抵消 $y^{-1}y$):
- $x (y^{-1} y) x^{-1} x y \to x x^{-1} x y$
- $ (x x^{-1}) x y \to x y$
- 结果: $xy$
- 路径B (先抵消 $x^{-1}x$):
- $x y^{-1} y (x^{-1} x) y \to x y^{-1} y y$
- $x (y^{-1} y) y \to x y$
- 结果: $xy$
- 两种顺序得到相同的结果。
- 示例2: $w = a b c c^{-1} b^{-1} a^{-1} a b$
- 可抵消对: $cc^{-1}$ 和 $a^{-1}a$
- 路径A (先抵消 $cc^{-1}$):
- $a b (c c^{-1}) b^{-1} a^{-1} a b \to a b b^{-1} a^{-1} a b$
- $a (b b^{-1}) a^{-1} a b \to a a^{-1} a b$
- $(a a^{-1}) a b \to a b$
- $ab$
- 路径B (先抵消 $a^{-1}a$):
- $a b c c^{-1} b^{-1} (a^{-1} a) b \to a b c c^{-1} b^{-1} b$
- $a b c c^{-1} (b^{-1} b) \to a b c c^{-1}$
- $a b (c c^{-1}) \to a b$
- $ab$
- 再次验证,结果唯一。
- 不要被“重叠”迷惑: 在 $w = a b^{-1} b a^{-1}$ 中, $b^{-1}b$ 是唯一的可抵消对。在 $w = a b b^{-1} a$ 中也是如此。但在 $w = a b b^{-1} b a$ 中,$b b^{-1}$ 和 $b^{-1} b$ 看起来“重叠”了,但它们是两个不同的潜在抵消操作。你选择了其中一个,另一个就不存在了。
- $a (b b^{-1}) b a \to a b a$
- $a b (b^{-1} b) a \to a b a$
- 结果仍然是唯一的。
- 该命题的重要性: 如果没有这个命题,我们就无法定义一个字的“身份”。如果 $w$ 可以被约化成 $w_1$ 和 $w_2$ 两个不同的约化字,那么 $w$ 到底代表哪个元素呢?这个命题保证了每个字都有一个唯一的“身份证”,即它的约化形式。
本段提出了一个关键问题:不同的抵消顺序是否会导致不同的结果?通过一个直观的例子和一则核心的命题 7.9.2,本段确认了答案是否定的。任何一个字,无论经过何种顺序的抵消,最终都会达到同一个、唯一的约化形式。这个唯一性是后续所有理论的基石。
本段的目的是为了确保我们即将建立的数学结构是“稳固”和“一致”的。在数学中,一个操作的结果必须是明确无歧义的,这个性质称为“良定义 (well-defined)”。本段的核心任务就是证明“取一个字的约化形式”这个操作是良定义的。没有这个保证,我们就无法将字的等价类(所有具有相同约化形式的字)定义为群的元素,整个自由群的构造就会失败。
- 回到“在平原上行走”的模型。一个字是一串行走指令,约化是去掉所有“来回走”的无效步骤。
- 字: "东-北-南-西-东-东" ($a b b^{-1} a^{-1} a a$)
- 你可以在地图上模拟这个路径。
- 路径1 (先去掉 北-南): 你的指令单变成 "东-西-东-东"。你先走一步东,再走一步西(回到起点),再走两步东。净效果是“向东两步”。
- 路径2 (先去掉 西-东): 你的指令单变成 "东-北-南-东"。你先走一步东,再向北,再向南(回到只走了一步东的位置),再向东。净效果也是“向东两步”。
- 命题的含义: 不管你先擦掉哪段“回头路”,你最终都会发现,这趟复杂的行程,其净效果等同于一个唯一的、最简单的行程(约化形式)。起点和终点之间的最短有效路径是唯一的。
- 想象你在整理一串打结的绳子,绳子上有各种活结。
- 一个字就是这串绳子。
- 一个“可抵消对” $xx^{-1}$ 就像一个简单的、可以被轻易拉开的活结。
- 约化就是把所有这些活结都拉开,让绳子变直。
- 命题的含义: 绳子上可能有很多处活结。不管你先拉开哪一个,只要你把所有能拉开的结都拉开,最终得到的“拉直了的绳子”(约化形式)总会是同一根。
1.6 约化形式唯一性的证明
📜 [原文6]
证明。我们对 $w$ 的长度使用归纳法。如果 $w$ 是约化的,则无需证明。如果不是,则必定存在可以抵消的符号对,例如下划线标注的对
(我们允许 $x$ 表示 $S^{\prime}$ 的任何元素,条件是如果 $x=a^{-1}$ 则 $x^{-1}=a$。)如果我们证明通过首先抵消 $x x^{-1}$ 可以得到 $w$ 的每个约化形式,则根据归纳法,该命题将成立,因为字 $\cdots x x^{-1} \cdots$ 更短。
令 $w_{0}$ 是 $w$ 的约化形式。它通过某个抵消序列从 $w$ 得到。第一种情况是我们的对 $\underline{x x^{-1}}$ 在该序列的某个步骤中被抵消。如果是这样,我们不妨先抵消 $x x^{-1}$。因此这种情况已解决。另一方面,由于 $w_{0}$ 是约化的,所以对 $x x^{-1}$ 不能保留在 $w_{0}$ 中。这两个符号中至少有一个必须在某个时候被抵消。如果该对本身没有被抵消,则涉及该对的第一次抵消必须看起来像
请注意,通过这种抵消获得的字与通过抵消对 $x x^{-1}$ 获得的字相同。因此,在此阶段,我们可以抵消原始对。然后我们回到第一种情况,因此该命题得证。$\square$
这是对命题 7.9.2(约化形式唯一性)的证明。证明的核心思想是数学归纳法,并结合对抵消过程的精细分析。
- 证明策略:数学归纳法
- 证明是基于字的长度 $n$ 来进行的。
- 基本情况 (Base Case): 如果字 $w$ 的长度很短(比如0或1),它本身就是约化的,只有一个约化形式(它自己)。或者,如果一个字 $w$ 本身就是约化的,那么它的约化形式就是它自己,显然是唯一的。这部分是平凡的,所以证明中直接说“无需证明”。
- 归纳假设 (Inductive Hypothesis): 假设对于所有长度小于 $n$ 的字,它们的约化形式都是唯一的。
- 归纳步骤 (Inductive Step): 我们需要证明,对于一个长度为 $n$ 的字 $w$,它的约化形式也是唯一的。
- 证明的逻辑流程
- 取一个长度为 $n$ 的、非约化的字 $w$。因为它非约化,所以它内部至少包含一个可抵消的对,我们不妨把它记作 $\underline{xx^{-1}}$。
- 我们的目标是证明:$w$ 的任何一个约化形式,都可以通过先抵消 $\underline{xx^{-1}}$ 这一步,然后对得到的更短的字 $w'$ 进行约化来得到。
- 令 $w'$ 是抵消 $\underline{xx^{-1}}$ 后得到的字。即 $w' = \text{(一些符号)(另一些符号)}$。
- $w'$ 的长度是 $n-2$,比 $w$ 的长度 $n$ 要短。
- 根据归纳假设,$w'$ 有一个唯一的约化形式,我们称之为 $w'_{red}$。
- 如果我们可以证明 $w$ 的所有可能的约化形式都等于这个 $w'_{red}$,那么就证明了 $w$ 的约化形式也是唯一的。
- 核心论证:分析任意一个约化过程
- 假设我们有一个任意的抵消序列,它把 $w$ 变成了某个约化形式 $w_0$。我们来分析这个序列中,最初的那对 $\underline{xx^{-1}}$ 发生了什么。
- 可能性1:$\underline{xx^{-1}}$ 这对符号在某个步骤中被直接抵消了。
- 比如,序列是 $w \to w_1 \to \dots \to w_k \to \dots \to w_0$,在第 $k$ 步,我们把最初的那个 $xx^{-1}$ 对给抵消了。
- 证明指出,我们可以调整抵消顺序,把“抵消 $\underline{xx^{-1}}$”这一步提到最前面来做,这不会影响后续的抵消。这在直觉上是显然的,因为抵消这对符号只影响它们自身,不影响远处的其他符号对。
- 所以,这种情况下的约化形式 $w_0$,确实可以通过先抵消 $\underline{xx^{-1}}$ 得到。这符合我们的目标。
- 可能性2:$\underline{xx^{-1}}$ 这对符号从来没有被“直接”抵消过,但它们最终还是消失了。
- 它们为什么会消失?因为 $w_0$ 是约化的,所以 $x$ 和 $x^{-1}$ 不可能还挨在一起。这意味着,它们中的至少一个,比如 $x$,肯定在某个步骤中跟它旁边的另一个符号抵消了。
- 那么,这个与 $x$ 抵消的符号必须是 $x^{-1}$。这个 $x^{-1}$ 从哪里来?它只能是原先紧挨着 $x$ 的那个 $x^{-1}$ 的邻居。
- 所以,这种情况必然是形如 $\dots y \underline{x^{-1} x} x^{-1} y^{-1} \dots$ 的结构,我们抵消了中间的 $x^{-1}x$。但更具体地,我们看 $w = \dots \underline{x x^{-1}} \dots$。如果 $x$ 或 $x^{-1}$ 要和别的符号抵消,那一定是下面这两种情况之一的第一次发生:
证明中给出的形式是更微妙的一层:
或者
我们来分析第一种:$\cdots x^{-1} \underline{x x^{-1}} \cdots$。
- 在这个字里,如果某个抵消步骤是抵消了 $x^{-1}x$ (下划线左边的 $x^{-1}$ 和 $x$),那么字会变成 $\cdots x^{-1} \cdots$。
- 但是,如果我们不这么做,而是先抵消我们最开始选定的 $\underline{xx^{-1}}$,那么字会变成 $\cdots x^{-1} \cdots$。
- 关键观察: 两种不同的抵消步骤,得到的结果是完全一样的!
- 这意味着,即使抵消序列看起来没有“直接”处理我们选定的 $\underline{xx^{-1}}$,它在某个中间步骤产生的效果,也和我们先处理 $\underline{xx^{-1}}$ 是等价的。
- 因此,我们可以“劫持”这个过程,把它看作是先抵消了 $\underline{xx^{-1}}$,然后再继续。这样一来,这种情况也被转化为了可能性1。
- 结论
- 我们证明了,对于 $w$ 的任何一个约化形式 $w_0$,它所对应的抵消过程,都可以被看作是“先抵消我们选定的 $\underline{xx^{-1}}$,然后约化更短的 $w'$” 这一过程。
- 由于 $w'$ 的约化形式根据归纳假设是唯一的,那么 $w$ 的约化形式也就是唯一的。
- 归纳步骤完成,命题得证。
- 这代表一个非约化字 $w$,其中有一个明确标记的可抵消对 $\underline{xx^{-1}}$。
- 这展示了证明中关键的第二种情况。
- $\cdots x^{-1} x x^{-1} \cdots$: 考虑子串 $x^{-1} x x^{-1}$。
- 如果抵消左边的 $x^{-1}x$,结果是 $x^{-1}$。
- 如果抵消右边的 $xx^{-1}$,结果也是 $x^{-1}$。
- 这说明抵消顺序不影响局部结果。
- $\cdots x x^{-1} x \cdots$: 考虑子串 $x x^{-1} x$。
- 如果抵消左边的 $xx^{-1}$,结果是 $x$。
- 如果抵消右边的 $x^{-1}x$,结果也是 $x$。
- 这也说明抵消顺序不影响局部结果。
- 这个观察是证明的核心,它允许我们将看似不同的抵消路径统一起来,从而完成归纳。
这个证明是高度抽象的,很难用具体数值示例来“验证”证明本身,但我们可以用示例来理解证明中的情况。
- 示例: 理解证明中的“第二种情况”
- 令 $w = a b b^{-1} b$。这个字的长度为4。
- 归纳假设: 所有长度小于4的字,其约化形式唯一。
- 我们选定 $w$ 中的第一个可抵消对:$b b^{-1}$。
- $w = a \, \underline{b b^{-1}} \, b$
- 约化路径A (先抵消选定对):
- $a \, (\underline{b b^{-1}}) \, b \to a b$
- $ab$ 是约化的,结果是 $ab$。
- 约化路径B (抵消另一对):
- $w$ 中还有另一对可抵消的:$b^{-1} b$。
- $a b \, (\underline{b^{-1} b}) \to ab$
- $ab$ 是约化的,结果是 $ab$。
- 证明如何看待路径B?
- 证明的逻辑是:路径B的第一步是处理了 $b^{-1}b$。这个抵消发生在子串 $b b^{-1} b$ 内部。
- 这完全符合证明中描述的 $\cdots x x^{-1} x \cdots$ 的情况(这里 $x=b$)。
- 证明指出,抵消 $b^{-1}b$ 得到 $b$,与先抵消 $bb^{-1}$ 再留下 $b$ 得到的结果 $b$ 是相同的。
- 因此,即使你走了路径B,也可以把它理解为在效果上等同于走了路径A。因为两种路径都将 $w$ 变成了 $ab$,而 $ab$ 是长度为2的字,根据归纳假设,它只有一个约化形式(就是它自己)。
- 所以 $w$ 的约化形式唯一,就是 $ab$。
- 证明的精髓: 这个证明的巧妙之处在于它并没有去追踪所有可能的、极其复杂的抵消路径。它只抓住一点:任意一个非约化字 $w$,随便选一个可抵消对 $\underline{xx^{-1}}$。然后证明所有的约化路径,无论多么曲折,其最终结果都必然和“先抵消 $\underline{xx^{-1}}$,再处理剩下的”这个标准路径的结果相同。这就把一个未知的问题($w$ 的约化形式是否唯一)转化为了一个已知的问题(更短的字 $w'$ 的约化形式是否唯一)。
- 归纳法不是循环论证: 有时学生会觉得归纳法像循环论证(用结论证明结论)。但它不是。它是多米诺骨牌:我们证明了(1)第一张牌会倒(基本情况),以及(2)如果第 $k$ 张牌倒了,那么第 $k+1$ 张也一定会倒(归纳步骤)。这样我们就能断定所有牌都会倒。在这里,我们证明了短字的唯一性可以“传递”给长字。
本段给出了命题 7.9.2 的一个严谨证明。该证明使用数学归纳法,通过分析任意抵消序列中特定符号对的“命运”,论证了任何抵消路径的最终结果都等同于先进行某一次特定抵消、再处理更短字符串的结果。由于更短字符串的约化形式在归纳假设下是唯一的,因此原字符串的约化形式也是唯一的。
在数学中,仅仅通过例子观察到一种模式是不够的,必须给出严格的证明,才能将其作为后续理论的可靠基石。本段的目的就是提供这个证明,为“约化形式”这一核心概念的“良定义性”提供无可辩驳的逻辑支持。没有这个证明,自由群的整个理论大厦将建立在流沙之上。
- 钻石切割定理 (Diamond Lemma): 这个证明的思想与组合数学中的“钻石引理”或“汇合性质 (Confluence)”非常相似。
- 想象一个状态图,每个节点是一个字,每条有向边是一次抵消操作。
- $w$ 是一个起始节点。从 $w$ 出发,可以有多条路径(不同的抵消选择)。
- 约化形式是图中的“终点站”,即没有出边的节点。
- 命题说的是:从任何一个节点 $w$ 出发,所有可能的路径最终都会汇入同一個终点站。
- 证明中的 $\cdots x x^{-1} x \cdots$ 的情况,就像图中一个“钻石”形状:
- $w_1$ 可以通过两条不同的路(比如 $w_1 \to w_2$ 和 $w_1 \to w_3$)走。
- 但证明说明了,$w_2$ 和 $w_3$ 最终都能走到同一个节点 $w_4$。
- $w_1 \to w_2 \to w_4$ 和 $w_1 \to w_3 \to w_4$ 形成了一个菱形(钻石)。只要每个小分岔都能重新汇合,那么整个系统最终就会汇合到唯一的终点。
- 想象你在一座山的山顶(非约化字 $w$),山脚下有一个湖(唯一的约化形式)。
- 从山顶到湖边有很多条下山的小路(不同的抵消序列)。
- 命题说的是:无论你选择哪条小路往下走,只要你一直往下走(一直在做抵消),你最终必然会到达同一个湖,而不是跑到其他地方去。
- 证明的逻辑是:在任何一个岔路口,你选了左边的路或者右边的路。证明告诉你,这两条路在不远处就会重新汇合。既然所有的小岔路都能汇合,那么所有的大路最终也必然通向同一个终点。
17 定义等价关系与群的元素
📜 [原文7]
我们称 $W^{\prime}$ 中两个字 $w$ 和 $w^{\prime}$ 等价,记作 $w \sim w^{\prime}$,如果它们具有相同的约化形式。这是一种等价关系。
命题 7.9.3 等价字的乘积是等价的:如果 $w \sim w^{\prime}$ 且 $v \sim v^{\prime}$,则 $w v \sim w^{\prime} v^{\prime}$。
在证明了约化形式的唯一性之后,我们现在可以利用这个强大的工具来定义自由群的元素了。思路是:不把每个字都看作一个独立的元素,而是把所有能被约化成同一个约化字的字“捆绑”在一起,看作一个整体。
- 定义等价关系 ~:
- 我们定义一种新的关系,称为“等价”,用符号 ~ 表示。
- 定义: 两个字 $w$ 和 $w'$ 是等价的 (写成 $w \sim w'$),当且仅当它们的约化形式完全相同。
- 例子:
- 令 $w = a b b^{-1} c$,它的约化形式是 $ac$。
- 令 $w' = a c c^{-1} c$,它的约化形式也是 $ac$。
- 因为它们的约化形式相同,所以我们说 $w$ 和 $w'$ 是等价的,即 $a b b^{-1} c \sim a c c^{-1} c$。
- 而字 $ab$ 的约化形式是 $ab$,与 $ac$ 不同,所以 $ab \nsim w$。
- 验证这是一个等价关系:
- 一个关系要成为等价关系 (Equivalence Relation),必须满足三个性质:
- 自反性 (Reflexivity): 对任何字 $w$,都有 $w \sim w$。
- 这是显然的,因为 $w$ 的约化形式和它自己的约化形式当然是同一个。
- 对称性 (Symmetry): 如果 $w \sim w'$,那么 $w' \sim w$。
- 这也很好理解。如果 $w$ 和 $w'$ 的约化形式相同,那么 $w'$ 和 $w$ 的约化形式自然也相同。
- 传递性 (Transitivity): 如果 $w \sim w'$ 并且 $w' \sim w''$,那么 $w \sim w''$。
- 如果 $w$ 和 $w'$ 有相同的约化形式(比如 $w_{red}$),$w'$ 和 $w''$ 也有相同的约化形式(也必须是 $w_{red}$),那么 $w$ 和 $w''$ 就必然拥有共同的约化形式 $w_{red}$。因此 $w \sim w''$。
- 既然三个性质都满足,那么 ~ 确实是一种等价关系。
- 等价关系的作用:
- 等价关系会把整个集合 $W'$(所有字的集合)分割成一个个互不相交的子集,这些子集被称为等价类 (Equivalence Classes)。
- 每个等价类由所有具有相同约化形式的字组成。
- 例如,等价类 $[ac]$ (用约化形式 $ac$ 来命名这个类) 包含了字 $ac$, $abb^{-1}c$, $acc^{-1}c$, $ad^{-1}dac$ 等等所有能约化成 $ac$ 的字。
- 这些等价类,未来就会成为我们自由群中的元素!
- 为群运算铺路:命题 7.9.3
- 我们想在这些等价类上定义一个运算(乘法)。自然的想法是:[w] * [v] = [wv]。也就是说,两个等gao类相乘,就是从每个类里随便挑一个代表字 $w$ 和 $v$,把它们并置成 $wv$,然后看看 $wv$ 属于哪个等价类。
- 但这里有一个严重的问题:这个运算的结果是否依赖于我们挑选的代表?
- 例子: 假设 $[w] = [w']$ 且 $[v] = [v']$。我们定义的运算必须保证 $[wv] = [w'v']$。否则,这个运算就是不“良定义”的。
- 命题 7.9.3 正是来解决这个问题的。它保证了:如果你从两个等价的字 $w, w'$ 和另外两个等价的字 $v, v'$ 开始,把它们分别并置起来得到 $wv$ 和 $w'v'$,那么这两个新的、更长的字也一定是等价的。
- 这个命题确保了我们可以在等价类上定义一个一致的、无歧义的乘法运算。
[原文](逐字逐句) (命题7.9.3的证明)
证明。为了获得与乘积 $w v$ 等价的约化字,我们首先可以在 $w$ 和 $v$ 中尽可能多地抵消,将 $w$ 约化为 $w_{0}$,将 $v$ 约化为 $v_{0}$。然后 $w v$ 被约化为 $w_{0} v_{0}$。现在我们继续在 $w_{0} v_{0}$ 中抵消,直到该字被约化。如果 $w \sim w^{\prime}$ 且 $v \sim v^{\prime}$,则将相同的过程应用于 $\boldsymbol{w}^{\prime} \boldsymbol{v}^{\prime}$,它也会通过 $w_{0} v_{0}$,因此它会得到相同的约化字。$\square$
这个证明非常直观。它解释了为什么在等价类上定义的乘法是合理的。
- 证明的目标: 证明如果 $w \sim w'$ 且 $v \sim v'$,那么 $wv \sim w'v'$。根据定义,这等价于证明 $wv$ 和 $w'v'$ 有相同的约化形式。
- 分析 $wv$ 的约化过程:
- 如何求 $wv$ 的约化形式?一个自然的方法是分步进行:
- 应用到 $w'v'$:
- 现在我们对 $w'v'$ 做同样的事情。
- 因为我们已知 $w \sim w'$,根据定义,这意味着 $w$ 和 $w'$ 有相同的约化形式。所以 $w'$ 的约化形式也必须是 $w_0$。
- 同理,因为 $v \sim v'$,所以 $v'$ 的约化形式也必须是 $v_0$。
- 因此,当我们约化 $w'v'$ 时,我们同样会先得到中间步骤 $w_0v_0$。
- 从 $w_0v_0$ 开始,后续的抵消过程对于 $wv$ 和 $w'v'$ 来说是完全一样的。
- 既然它们经过了完全相同的后续处理步骤,它们最终得到的约化形式也必然是完全相同的。
- 结论:
- 我们证明了 $wv$ 和 $w'v'$ 具有相同的约化形式。
- 因此,$wv \sim w'v'$ 成立。
- 命题得证。
- 示例1:
- 令 $w = a b b^{-1}$,$v = c^{-1} c d$。
- 令 $w' = a x x^{-1}$,$v' = y^{-1} y d$。
- 步骤1:检查等价性
- $w = a b b^{-1}$ 的约化形式是 $a$。
- $w' = a x x^{-1}$ 的约化形式是 $a$。
- 所以 $w \sim w'$ 成立。它们的共同约化形式 $w_0 = a$。
- $v = c^{-1} c d$ 的约化形式是 $d$。
- $v' = y^{-1} y d$ 的约化形式是 $d$。
- 所以 $v \sim v'$ 成立。它们的共同约化形式 $v_0 = d$。
- 步骤2:计算 $wv$ 的约化形式
- $wv = (a b b^{-1})(c^{-1} c d)$。
- 直接在 $wv$ 上约化:$a b b^{-1} c^{-1} c d \to a c^{-1} c d \to a d$。
- 或者按照证明的思路:先约化 $w,v$ 得到 $w_0v_0 = ad$。$ad$ 本身就是约化的。
- 所以 $wv$ 的约化形式是 $ad$。
- 步骤3:计算 $w'v'$ 的约化形式
- $w'v' = (a x x^{-1})(y^{-1} y d)$。
- 直接在 $w'v'$ 上约化:$a x x^{-1} y^{-1} y d \to a y^{-1} y d \to a d$。
- 或者按照证明的思路:先约化 $w',v'$ 得到 $w_0v_0 = ad$。$ad$ 本身就是约化的。
- 所以 $w'v'$ 的约化形式也是 $ad$。
- 结论: 因为 $wv$ 和 $w'v'$ 有相同的约化形式 ($ad$),所以 $wv \sim w'v'$。这验证了命题 7.9.3。
- 区分“字”和“等价类”: $w$ 是一个具体的字符串,而 $[w]$ 是一个集合,包含了 $w$ 和所有与它等价的字符串。自由群的元素是后者。
- 命题的重要性: 如果没有这个命题,群的运算就无法定义。想象一下,如果 $(2+3)$ 和 $(1+4)$ 都等于5,但我们有一个操作 f,使得 f(2,3) 不等于 f(1,4),那么我们就不能在“结果为5”的这些数对上定义操作 f。这里的并置操作通过了这个考验。
- 证明的简洁性: 证明过程非常简洁,它依赖于前面已证的“约化形式唯一性”。它没有陷入繁琐的细节,而是抓住了核心:所有等价的字都共享同一个“标准型”(约化形式),因此它们的行为在组合时必然是一致的。
本段定义了字之间的等价关系:如果两个字可以被约化成同一个约化字,它们就是等价的。这个关系将所有字的集合 $W'$ 划分成多个等价类,每个等价类将成为自由群的一个元素。接着,命题 7.9.3 及其证明确保了在这些等价类上可以定义一个良好、一致的乘法(即并置),为最终定义群结构扫清了最后的障碍。
本段的目的是从“字”的世界过渡到“群元素”的世界。单个的、未约化的字太多太乱,比如 $a$, $abb^{-1}$, $acc^{-1}$ 都应该代表同一个“东西”。通过引入等价关系和等价类,我们实现了“多对一”的映射,把无限多的冗余字符串,归纳到有限个(对于给定的等价类)或可数无限个(对于整个群)规范的元素(约化字所代表的等gao类)上。命题 7.9.3 则是确保这个新世界里的运算规则(乘法)是自洽的、有意义的。
- 等价类就像是“同义词”。字 $w_1 = $ "big", $w_2 = $ "large"。它们是不同的字符串,但在语义上等价。它们的“约化形式”就是它们共同的“意思”。
- 命题 7.9.3 的意思是,同义词替换不影响句子的最终意思。
- $w \sim w'$ (e.g., "big" $\sim$ "large")
- $v \sim v'$ (e.g., "house" $\sim$ "home")
- 那么 "big house" ($wv$) 和 "large home" ($w'v'$) 的意思也是等价的 ($wv \sim w'v'$)。
- 自由群的元素不是具体的单词,而是那个抽象的“意思”。
- 想象一堆分数。字就像是分数 $\frac{1}{2}, \frac{2}{4}, \frac{3}{6}, \frac{100}{200}$。它们是不同的写法。
- 约化形式就像是最简分数 $\frac{1}{2}$。
- 等价关系就是数值上的相等。$\frac{1}{2} = \frac{2}{4}$。
- 等价类就是所有数值等于0.5的分数的集合。这个等价类就可以被看作是有理数 $0.5$ 这个元素。
- 命题 7.9.3 在这里是什么意思?
- $\frac{1}{2} \sim \frac{2}{4}$ 并且 $\frac{1}{3} \sim \frac{2}{6}$。
- 那么,它们的乘积 $\frac{1}{2} \times \frac{1}{3} = \frac{1}{6}$ 和 $\frac{2}{4} \times \frac{2}{6} = \frac{4}{24}$ 也必须是等价的。
- 我们检查一下:$\frac{4}{24}$ 的约化形式是 $\frac{1}{6}$。确实等价。
- 这保证了我们可以在“有理数”这个抽象的等价类上定义乘法,而不用担心我们用的是 $\frac{1}{2}$ 还是 $\frac{2}{4}$ 来计算。自由群的构造与此非常相似。
18 自由群的诞生
📜 [原文8]
根据这个命题,字的等价类可以相乘:
命题 7.9.4 字的等价类的集合 $\mathcal{F}$ 是一个群,其复合律由 $W^{\prime}$ 中的乘法(并置)诱导。
证明。乘法具有结合律以及空字 $1$ 的等价类是单位元的事实,是根据 $W^{\prime}$ 中相应的事实得出的(参见引理 2.12.8)。我们必须检查 $\mathcal{F}$ 的所有元素是否都可逆。但显然,如果 $w$ 是 $S^{\prime}$ 元素的乘积 $x y \cdots z$,那么 $z^{-1} \cdots y^{-1} x^{-1}$ 的等价类是 $w$ 的等价类的逆。$\square$
这是构造过程的高潮。我们终于将前面所有的铺垫组合起来,正式声明我们已经成功构建了一个群——自由群。
- 集合 $\mathcal{F}$ 的定义:
- $\mathcal{F}$ 是由所有字的等价类构成的集合。
- 回顾一下,一个等价类 $[w]$ 是所有与字 $w$ 具有相同约化形式的字的集合。
- 因此,$\mathcal{F}$ 中的每一个元素,都是 $W'$ 中的一个子集。例如,$[a], [b], [ab], [a^{-1}b]$ 都是 $\mathcal{F}$ 中不同的元素。
- 运算的定义:
- 我们在 $\mathcal{F}$ 上定义一个二元运算(我们称之为乘法),这个运算是由字的并置操作“诱导”出来的。
- 定义: 两个等价类 $[w]$ 和 $[v]$ 的乘积,被定义为 $[w][v] = [wv]$。
- 诱导 (induced) 这个词的意思是,我们在新集合(等价类的集合)上的运算,是借助旧集合(字的集合)上的运算来定义的。
- 上一个命题 7.9.3 已经保证了这个运算是“良定义的”,即结果不依赖于你从等价类中选择哪个字作为代表。
- 命题 7.9.4 的声明:
- 这个命题的核心声明是:集合 $\mathcal{F}$ 和我们定义的乘法运算一起,构成了一个群。
- 证明 (验证群公理):
- 要证明 $(\mathcal{F}, \cdot)$ 是一个群,我们需要验证它满足群的四个基本公理(闭包性已由运算定义保证)。
- a. 结合律 (Associativity):
- 我们需要证明对任意三个元素 $[w], [v], [u] \in \mathcal{F}$,都有 $([w][v])[u] = [w]([v][u])$。
- 左边: $([w][v])[u] = [wv][u] = [(wv)u]$。
- 右边: $[w]([v][u]) = [w][vu] = [w(vu)]$。
- 在字的层面,我们知道并置操作是满足结合律的,即 $(wv)u = w(vu)$。这两个是完全相同的字符串。
- 既然 $(wv)u$ 和 $w(vu)$ 是同一个字,它们当然属于同一个等gao类。所以 $[(wv)u] = [w(vu)]$。
- 结论: 结合律成立。它直接继承自字的并置操作的结合律。
- b. 单位元 (Identity Element):
- 我们需要在 $\mathcal{F}$ 中找到一个元素 $[e]$,使得对任何 $[w] \in \mathcal{F}$,都有 $[w][e] = [e][w] = [w]$。
- 考虑空字 $1$。它自己就是约化的。我们来看看它所在的等价类 $[1]$。
- $[w][1] = [w \cdot 1] = [w]$。
- $[1][w] = [1 \cdot w] = [w]$。
- 这完全符合单位元的定义。
- 结论: 空字的等价类 $[1]$ 就是 $\mathcal{F}$ 中的单位元。
- c. 逆元 (Inverse Element):
- 这是最关键的一步。对于 $\mathcal{F}$ 中的任意一个元素 $[w]$,我们能否找到另一个元素 $[w'] \in \mathcal{F}$,使得 $[w][w'] = [w'][w] = [1]$?
- 设 $w$ 是一个字,比如 $w = x y \cdots z$,其中 $x, y, z$ 是来自扩展字母表 $S'$ 的符号。
- 我们构造一个新的字 $w_{inv} = z^{-1} \cdots y^{-1} x^{-1}$。这个构造方法是“把原来的字倒过来,再把每个符号换成它的逆符号”。
- 现在我们来计算 $[w][w_{inv}]$:
- $[w][w_{inv}] = [w \cdot w_{inv}] = [(x y \cdots z)(z^{-1} \cdots y^{-1} x^{-1})]$。
- 我们来约化这个长字 $w \cdot w_{inv}$:
- $(x y \cdots z)(z^{-1} \cdots y^{-1} x^{-1})$
- 中间的 $z$ 和 $z^{-1}$ 相邻,可以抵消。
- $(x y \cdots)(y^{-1} x^{-1})$
- 中间的 $y$ 和 $y^{-1}$ 现在相邻了,也可以抵消。
- 这个过程一直持续下去,直到最后只剩下 $x x^{-1}$,它们也抵消。
- 最终结果是空字 $1$。
- 所以,$w \cdot w_{inv}$ 的约化形式是 $1$。这意味着 $[w \cdot w_{inv}] = [1]$。
- 同理,我们计算 $[w_{inv}][w]$:
- $[w_{inv}][w] = [(z^{-1} \cdots y^{-1} x^{-1})(x y \cdots z)]$
- 中间的 $x^{-1}$ 和 $x$ 相邻,抵消。然后是 $y^{-1}$ 和 $y$,等等。
- 最终结果也是空字 $1$。所以 $[w_{inv} \cdot w] = [1]$。
- 结论: 对于任意等价类 $[w]$,它的逆元就是 $[w_{inv}]$,其中 $w_{inv}$ 是通过“反转并取逆”得到的字。所有元素都可逆。
- 最终结论:
- 既然结合律、单位元、逆元都已满足,我们证明了 $(\mathcal{F}, \cdot)$ 确实是一个群。
本段没有新的行间公式,但证明中用到了符号化的逆元构造。
- 如果 $w = x y \cdots z$:
- $w$: 代表一个任意的字。
- $x, y, \ldots, z$: 构成字 $w$ 的一连串符号,它们来自 $S'=\{a, a^{-1}, b, b^{-1}, \ldots\}$。
- 那么逆是 $z^{-1} \cdots y^{-1} x^{-1}$:
- $z^{-1}, \ldots, y^{-1}, x^{-1}$: 分别是 $z, \ldots, y, x$ 的逆符号。注意,如果 $x$ 本身是 $a^{-1}$,那么 $x^{-1}$ 就是 $(a^{-1})^{-1} = a$。
- 顺序颠倒: 这个构造方法和矩阵的逆 $(AB)^{-1} = B^{-1}A^{-1}$ 或者置换的逆非常相似,这被称为“袜子-鞋子原理”:你穿的时候是先穿袜子再穿鞋,脱的时候必须先脱鞋再脱袜子。
- 示例1:验证结合律
- 令 $[w]=[a], [v]=[b^{-1}c], [u]=[c^{-1}]$。
- 左边: $([a][b^{-1}c])[c^{-1}] = [ab^{-1}c][c^{-1}] = [(ab^{-1}c)c^{-1}] = [ab^{-1}cc^{-1}]$。
- 约化 $cc^{-1}$,得到 $[ab^{-1}]$。
- 右边: $[a]([b^{-1}c][c^{-1}]) = [a][(b^{-1}c)c^{-1}] = [a][b^{-1}cc^{-1}]$。
- 先约化等价类内部:$[b^{-1}cc^{-1}]$ 的约化形式是 $b^{-1}$,所以它就是 $[b^{-1}]$。
- $[a][b^{-1}] = [ab^{-1}]$。
- 左右相等,结合律成立。
- 示例2:寻找逆元
- 令一个元素为 $[ab^{-1}c]$。它的代表字是 $w = ab^{-1}c$。
- 构造逆字:
- 将 $w$ 颠倒: $c b^{-1} a$。
- 将每个符号取逆: $c^{-1}, (b^{-1})^{-1}, a^{-1}$,即 $c^{-1}, b, a^{-1}$。
- 组合起来: $w_{inv} = c^{-1} b a^{-1}$。
- 验证: 它的逆元应该是 $[c^{-1} b a^{-1}]$。我们来计算乘积:
- $[ab^{-1}c][c^{-1} b a^{-1}] = [(ab^{-1}c)(c^{-1} b a^{-1})]$
- $= [ab^{-1} (c c^{-1}) b a^{-1}]$
- $= [ab^{-1} b a^{-1}]$
- $= [a (b^{-1} b) a^{-1}]$
- $= [a a^{-1}]$
- $= [1]$
- 验证成功,$[c^{-1} b a^{-1}]$ 确实是 $[ab^{-1}c]$ 的逆元。
- 群的元素是等价类: 一定要牢记,我们谈论的群 $\mathcal{F}$,它的成员不是字,而是字的等价类。尽管在实际计算时,我们总是通过操作它们的代表字(通常是唯一的约化字)来完成。
- 单位元 [1]: 单位元是包含空字 $1$ 的那个等价类。这个等价类还包含许多其他非空字,例如 $aa^{-1}, b^{-1}b, cdd^{-1}c^{-1}$ 等等,所有能被完全抵消的字都在这里。
- 引理 2.12.8: 作者在这里引用了一个外部的引理,这个引理的大意是:如果在一个代数结构(如幺半群 $W'$)上有一个等价关系 ~,并且这个关系与运算(如并置)兼容(即命题 7.9.3 的内容),那么我们可以在等价类的集合上定义一个诱导运算,并且这个新运算会自动继承原运算的结合律和单位元性质。这是一个标准的代数构造手法,称为商构造 (Quotient Construction)。
本段完成了自由群的构造。它明确了自由群 $\mathcal{F}$ 是由所有字的等价类组成的集合。乘法由字的并置诱导。证明部分依次检验了结合律、单位元和逆元三条群公理,确认了 $\mathcal{F}$ 确实构成一个群。其中,逆元的存在性通过一个“反转并取逆”的显式构造得到了保证。
这是整个构造过程的终点和成果展示。前面的所有定义(逆符号、约化、唯一性、等价关系)都是为了在这一刻服务。本段的目的是将这些零件组装起来,并严格地依据群的定义进行最终的“质量检验”,从而庄严地宣布一个全新的、重要的数学对象——自由群——已经成功诞生。
- 我们成功地为“语义”(等价类)定义了运算。
- 结合律: ("big" "house") "is" $\Leftrightarrow$ "big" ("house" "is") (句子的结合方式不影响最终意思的组合)
- 单位元: "big house" + (一个代表“无”的词) $\Leftrightarrow$ "big house"。
- 逆元: 如果一个操作是“向东走,再向北走”($ab$),它的逆操作就是“先向南走,再向西走”($b^{-1}a^{-1}$)。执行完第一套操作,再执行第二套,最终会回到起点。
- 想象我们现在拥有了所有从一个起点出发的、不走回头路的最短路径的集合。每条这样的路径(一个约化字)代表一个群的元素。
- 群的乘法 $(ab) \cdot (b^{-1}c)$ 是什么?
- 取第一条路径 $ab$ (东,然后北)。
- 在它的终点,接上第二条路径 $b^{-1}c$ (南,然后(假设c是)上)。
- 整个行程是“东-北-南-上”。
- 去掉回头路“北-南”,最终的净路径是“东-上”,即 $ac$。
- 所以 $[ab][b^{-1}c] = [ac]$。
- 这个路径的集合,以及“路径相连并化简”这个操作,就构成了一个自由群。
19 自由群的最终描述和性质
📜 [原文9]
集合 $S^{\prime}$ 中字的等价类的群 $\mathcal{F}$ 被称为集合 $S$ 上的自由群。$\mathcal{F}$ 的一个元素恰好对应于 $W^{\prime}$ 中的一个约化字。要乘约化字,进行组合和抵消:$\left(a b c^{-1}\right)(c b) \rightsquigarrow a b c^{-1} c b=a b b$。
可以使用幂符号:$a a a b^{-1} b^{-1}=a^{3} b^{-2}$。
注:单元素集合 $S=\{a\}$ 上的自由群就是一个无限循环群。相比之下,两个或更多元素的集合上的自由群则相当复杂。
这一段是对刚刚构造出的自由群进行总结,并给出了更实用、更直观的计算方式和一些基本性质。
- 正式命名:
- 我们把历经千辛万苦构造出来的那个群 $\mathcal{F}$(由 $S'$ 中字的等价类构成),正式命名为“集合 $S$ 上的自由群 (Free group on the set S)”。
- 这里的 $S$ 是我们最开始选定的生成元集合 $\{a, b, c, \ldots\}$。
- 如果 $S$ 有 $n$ 个元素,对应的自由群通常记作 $F_n$。
- 元素的一一对应:
- 虽然我们把群的元素定义为等价类(一个集合),但在实际操作中,这样做太繁琐了。
- 我们知道,每一个等价类中,都包含一个且仅一个约化字。
- 因此,我们可以把群的元素与约化字建立一个一一对应的关系。
- 这极大地简化了我们对自由群的看法:可以不严谨但很有效地认为,“自由群的元素就是所有的约化字”。
- 例如,当我们说自由群的元素 $[ab^{-1}c]$ 时,我们脑子里想的就是那个唯一的约化字 $ab^{-1}c$。
- 实用的乘法规则:
- 基于“元素就是约化字”这个看法,两个元素的乘法就变得非常具体:
- 要计算两个约化字 $w_1$ 和 $w_2$ 的乘积:
- 组合 (Concatenate): 把它们并置起来,形成一个新的、更长的字 $w_1w_2$。
- 抵消 (Cancel/Reduce): 对这个新字 $w_1w_2$ 进行约化,即在 $w_1$ 的尾部和 $w_2$ 的头部之间寻找并消除所有可抵消的对,直到得到最终的约化字。
- 例子: 计算 $(abc^{-1})$ 和 $(cb)$ 的乘积。
- 组合: $(abc^{-1})(cb) \to abc^{-1}cb$。
- 抵消: 中间的 $c^{-1}c$ 可以抵消,得到 $ab b$。
- $abb$ 是约化字,这就是乘积的结果。
- 引入幂符号:
- 为了书写方便,我们可以使用幂 (power) 的简写形式。
- $aaa$ 可以写成 $a^3$。
- $b^{-1}b^{-1}$ 可以写成 $b^{-2}$。
- 于是,像 $aaab^{-1}b^{-1}$ 这样的约化字就可以简洁地写成 $a^3b^{-2}$。
- 注意: 只有相同的符号(或逆符号)连续出现时才能合并。$a^2b^3$ 不能再化简了。
- 基本例子和性质:
- 一个生成元的自由群 ($F_1$):
- 如果 $S=\{a\}$,那么 $S'=\{a, a^{-1}\}$。
- 所有的约化字是什么?是形如 $a^k$ 的字,其中 $k$ 是任意整数(正数表示 $a$ 的重复,负数表示 $a^{-1}$ 的重复,0表示空字 $1$)。例如 $a^3=aaa$, $a^{-2}=a^{-1}a^{-1}$, $a^0=1$。
- 乘法就是指数相加:$a^k \cdot a^m = a^{k+m}$。
- 这和整数加法群 $(\mathbb{Z}, +)$ 的结构是完全一样的(数学上称为同构)。
- 它是一个无限循环群,由 $a$ (或 $a^{-1}$) 生成。
- 两个或更多生成元的自由群 ($F_n, n \ge 2$):
- 如果 $S=\{a, b\}$,约化字就五花八门了,比如 $a, b, ab, ba, a^2b, ab^{-1}a^2, \ldots$。
- 由于 $ab \neq ba$,这个群是非交换的。
- 可以证明,这种群的结构“相当复杂”,具有许多深刻和有趣的数学性质。它们是组合群论和几何群论的核心研究对象。
- $\left(a b c^{-1}\right)(c b) \rightsquigarrow a b c^{-1} c b=a b b$
- $(abc^{-1})$: 第一个约化字(第一个群元素)。
- $(cb)$: 第二个约化字(第二个群元素)。
- $\rightsquigarrow$: 箭头表示“进行运算”。
- $abc^{-1}cb$: 并置的结果。
- $=$: 等号表示“约化为”。
- $abb$: 最终的乘积结果,一个约化字。
- $a a a b^{-1} b^{-1}=a^{3} b^{-2}$
- 这是一个符号简写规则的展示。
- $aaa$ 被简写为 $a^3$。
- $b^{-1}b^{-1}$ 被简写为 $b^{-2}$。
- 这只是记法上的方便,不改变其作为约化字的本质。
- 示例1: 在 $F_2$ (由 $a,b$ 生成) 中计算
- 计算 $(a^2b^{-1}) \cdot (ba^{-1})$。
- 展开幂: $(aab^{-1}) \cdot (ba^{-1})$。
- 组合: $aab^{-1}ba^{-1}$。
- 抵消: 中间的 $b^{-1}$ 和 $b$ 不相邻,不能抵消。$a$ 和 $a^{-1}$ 也不相邻。
- 结果: $aab^{-1}ba^{-1}$ 本身就是一个约化字。所以 $(a^2b^{-1})(ba^{-1}) = a^2b^{-1}ba^{-1}$。
- 示例2: 在 $F_2$ 中计算,有抵消发生
- 计算 $(ab^2) \cdot (b^{-2}a^{-1})$。
- 展开幂: $(abb) \cdot (b^{-1}b^{-1}a^{-1})$。
- 组合: $abbb^{-1}b^{-1}a^{-1}$。
- 抵消:
- $ab(bb^{-1})b^{-1}a^{-1} \to abb^{-1}a^{-1}$
- $a(bb^{-1})a^{-1} \to aa^{-1}$
- $aa^{-1} \to 1$ (空字)
- 结果: 乘积是单位元 $1$。这说明 $(ab^2)$ 和 $(b^{-2}a^{-1})$ 在自由群中互为逆元,这也符合我们之前推导的逆元构造法则。
- $a^3b^{-2}$ 不是 $a^3/b^2$: 幂符号只是一个计数器,不是算术运算。$a$ 和 $b$ 之间没有任何交换或除法关系。
- $F_2$ 是非交换的: $ab \neq ba$。这是自由群最关键的性质之一。不要习惯性地交换它们的顺序。$(ab)^2 = abab$,它不等于 $a^2b^2 = aabb$。
- 复杂性: 不要低估 $F_2$ 的复杂性。它包含无限多个元素,并且其内部结构非常丰富。例如,它包含一个同构于 $F_3, F_4, \dots$ 甚至 $F_\infty$(无限生成元)的子群。
本段为自由群提供了一个实用、具体的工作模型。我们可以将自由群的元素就看作是所有可能的约化字。两个元素的乘法就是将两个约化字连接起来,然后进行化简。本段还介绍了方便的幂次记法,并指出了最简单的自由群 $F_1$ 与整数加法群 $\mathbb{Z}$ 的关系,同时强调了具有更多生成元的自由群的非交换性和复杂性。
经过前面漫长而抽象的理论构造,本段的目的是“落地”。它告诉读者在实践中如何看待和使用自由群。通过将抽象的“等价类”与具体的“约化字”等同起来,使得自由群的计算变得直观可行。这为读者使用自由群作为工具来研究其他数学问题(如在代数拓扑中计算基本群)提供了具体的操作指南。
- 自由群就是一个“最纯粹”的符号操作系统。
- 元素: 所有不能再简化的符号串(约化字)。
- 乘法: “拼接并化简”。
- 这个系统里没有任何“意外”的等式。除非一个等式是由“拼接并化简”这个基本规则直接导致的(例如 $(ab)(b^{-1}a^{-1})=1$),否则它就不成立(例如 $ab=ba$ 不成立)。这就是“自由”的最终体现。
- 想象一个理想的、无限大的乐高仓库。你有红、蓝、绿……等各种颜色的积木块(生成元 $a, b, c, \dots$),以及它们对应的“反物质”积木块(逆元 $a^{-1}, b^{-1}, c^{-1}, \dots$)。
- 自由群的元素就是你用这些积木块拼成的、任何一个无法再“湮灭”(即积木和反物质积木相邻)的拼接成品。
- 群运算就是把你的作品A和我的作品B首尾相连,形成一个更大的作品A+B。然后,我们检查连接处,如果A的尾巴和B的头是互为反物质的一对积木,它们就“湮灭”消失,让作品缩短。我们重复这个湮灭过程,直到连接处稳定为止。最终得到的那个稳定的新作品,就是A和B的乘积。
- $F_1$ 就像你只有一种颜色的积木(和它的反物质),所有的作品都是一长条同色的积木,可以用长度(正或负)来描述。
- $F_2$ 就像你有红蓝两种积木,你可以拼出千变万化的、五彩斑斓的作品,其结构远比单色的长条要丰富多彩。
[[END_OF_EXPLANATION]]所有正文部分解释已全部输出完毕
2行间公式索引
1. 字与字的并置操作示例
一句话解释:这个例子展示了两个字“aa”和“ba”通过并置(首尾相连)组合成一个新字“aaba”的过程。
2. 扩展字母表的定义 (7.9.1)
一句话解释:这个公式定义了一个新的字母表 $S'$,它在原有符号(如a, b, c)的基础上,为每个符号增加了一个形式上的逆符号(如$a^{-1}, b^{-1}, c^{-1}$)。
3. 可抵消的符号对
一句话解释:这指出了在一个字中,任何符号与其逆符号(或逆符号与其符号)紧密相邻的组合,都是可以被“抵消”或删除的基本模式。
4. 证明中标记的待抵消的字
一句话解释:在证明约化形式唯一性时,用此公式代表一个非约化字 $w$,并明确标出其中一个可以被抵消的符号对 $\underline{x x^{-1}}$。
5. 证明中的关键局部结构
一句话解释:这个公式展示了证明中讨论的一种情况,即一个符号对的抵消可能与相邻的符号有关,但无论先抵消哪一对,局部结果都相同。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。