1现代代数1
第三周笔记
Aise Johan de Jong 教授
11 等价关系
1. 1 第 4 讲:等价关系
定义 1.1. 给定 $\mathcal{R} \subseteq X \times X$,我们记作
如果它满足以下条件,则这是一个等价关系:
(i) $x \sim x$ 对于所有 $x \in X$ (自反性)
(ii) $x \sim y \Rightarrow y \sim x$ (对称性)
(iii) $x \sim y, y \sim z \Rightarrow x \sim z$ (传递性)
定义 1.2. $x$ 的等价类是:
命题 1.3. 令 $\sim$ 是 $X$ 上的一个等价关系。那么对于 $x, y \in X$,我们有:
证明. 令 $z \in[x] \cap[y]$。那么 $z \sim x$ 且 $z \sim y$。
要证明 $[x] \subseteq[y]$:选取 $w \in[x]$,那么 $w \sim x$。通过传递性,$w \sim z$ 且 $z \sim y$ 意味着 $w \sim y$,所以 $w \in[y]$。
$x$ 和 $y$ 的角色可以互换以证明 $[y] \subseteq[x]$。因此 $[x]=[y]$。
反向是平凡的。
注 1.4. 其他刻画:
- 每个 $x \in X$ 都包含在恰好一个等价类中。
- $X$ 是等价类的不相交并集。
定义 1.5. 对于 $X$ 上的等价关系 $\sim$,我们用 $X / \sim$ 表示所有等价类的集合:
这称为等价关系的商集。
有一个自然映射 $\pi: X \rightarrow X / \sim$,定义为 $\pi(x)=[x]$,它将每个元素映射到其等价类。
注 1.6. $\pi$ 的纤维(元素的逆像)恰好是等价类。
1. 2 $X / \sim$ 的例子
例子 1.7 (1). 如果 $\sim$ 等于 $=$,那么 $X / \sim=\{\{x\} \mid x \in X\}$。
$\pi: X \rightarrow X / \sim$ 是一个双射。
虽然(严格来说)$X$ 和 $X / \sim$ 是不同的集合,但我们经常将它们识别。
例子 1.8 (2). 如果 $\sim$ 对应于 $\emptyset, \mathcal{R}=X \times X$,即对于所有 $x, y \in X$,有 $x \sim y$,那么
例子 1.9 (3). 对于自然数 $n \in \mathbb{N}$,对于 $\mathbb{Z}$ 上的等价关系 $\equiv(\bmod n)$,我们记作 $\mathbb{Z} / n \mathbb{Z}=\mathbb{Z} / \sim$。
上次我们看到:
例子 1.10 (4). 如果 $X=\mathbb{Z} \times(\mathbb{Z} \backslash\{0\})$ 且 $C_{a, b} \sim C_{c, d}$,如果 $ad=bc$,那么我们记作
记法 1.11. 对于 $(a, b) \in X$,我们记作
$\mathbb{Q}$ 的一个元素称为有理数。
我们现在知道有理数是什么,但我们可能希望通过定义运算来施加一些额外的结构。
1. 3 商集上的运算定义
假设 $X, Y$ 是集合。$\sim$ 是 $X$ 上的等价关系。
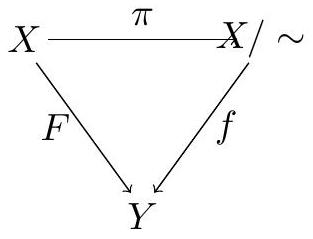
目标:某个函数 $f: X / \sim \rightarrow Y$
步骤:从一个函数 $F: X \rightarrow Y$ 开始,并尝试定义 $f([x])=F(x)$。
这可能不起作用,因为如果 $x \sim y$,那么需要检查 $F(x)=F(y)$。
如果是这样,对于所有 $x \sim y$,那么这个规则有效。
在这种情况下:$F:$ 域
例子 1.12. 假设我们要定义一个函数 $\mathbb{Z} / 2 \mathbb{Z} \rightarrow\{ \pm 1\}$。那么我们可以取 $F: \mathbb{Z} \rightarrow\{ \pm 1\}, F(n)=(-1)^{n}$。
为了得到 $f$,我需要检查:
$\star \quad n \equiv m(\bmod 2)$
因此,$f$ 是良定义的。
$f$ 是什么?
例子 1.13 (弧度制角)。让我们在 $\mathbb{R}$ 上定义一个等价关系,通过说明 $x \equiv y (\bmod 2 \pi)$ 当且仅当 $x-y$ 是 $2 \pi$ 的整数倍。
这是一个等价关系。
记法 1.14. 商集 $\mathbb{R} / 2 \pi \mathbb{Z}$ 记作 $\mathbb{R} / 2 \pi \mathbb{Z}$。
1. 4 周期函数
假设我要定义一个映射
什么样的 $F: \mathbb{R} \rightarrow \mathbb{R}$ 会给出这样的 $f$ 呢?这恰好在 $F$ 是周期为 $2 \pi$ 的周期函数时成立。
例子:正弦,余弦。
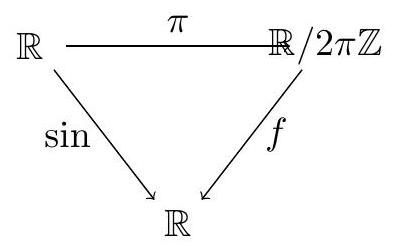
$F$ 是周期函数意味着对于所有 $x \in \mathbb{R}$,有 $F(x)=F(x+2 \pi)$
命题 1.15. 函数 $F: \mathbb{R} \rightarrow \mathbb{R}^{2}$ 定义为 $F(x)=(\cos x, \sin x)$,它诱导一个从 $\mathbb{R} / 2 \pi \mathbb{Z}$ 到 $\mathbb{R}^{2}$ 中单位圆的双射。
2探讨:
如何从 $X / \sim$ 生成一个到 $Y=X^{\prime} / \sim^{\prime}$ 的映射?
从 $F \circ \phi: X \rightarrow X^{\prime}$ 开始并检查:
⇒ 如何定义一个映射 $X / \sim \rightarrow X^{\prime} / \sim^{\prime}$?
这里会再次尝试 $F: X \times X \rightarrow X$,其性质是对于所有 $x_{1}, x_{2} \in X$,有 $y_{1} \sim y_{2} \Rightarrow F\left(x_{1}, y_{1}\right) \sim^{\prime} F\left(x_{2}, y_{2}\right)$。
1. 5 商集上的映射定义
定义 1.16. 令 $X=\mathbb{Z} \times(\mathbb{Z} \backslash\{0\})$ 且 $\sim$ 如前所述以构造 $\mathbb{Q}$。那么:
具有所需的性质并诱导映射 $\mathbb{Q} \times \mathbb{Q} \rightarrow \mathbb{Q}$,通常表示为 + 和 $\cdot$
证明. 将会是检查 $(a, b) \sim\left(a^{\prime}, b^{\prime}\right)$ 和 $(c, d) \sim\left(c^{\prime}, d^{\prime}\right) \Rightarrow(a d+b c, b d) \sim\left(a^{\prime} d^{\prime}+b^{\prime} c^{\prime}, b^{\prime} d^{\prime}\right)$,对于另一个也类似。
阅读 2.33 和 2.34。
注 1.17. 对于 $\mathbb{R} / 2 \pi \mathbb{Z}$ 我们仍然有加法:
但没有乘法!!!
32 $\S 3: \mathbb{N}, \mathbb{Q}, \mathbb{R}, \mathbb{C}$
2. 1 自然数
$\mathbb{N}$:概念:
(i) 从 $1 \in \mathbb{N}$ 开始。
(ii) 每个 $n \in \mathbb{N}$ 都有一个后继。
(iii) 概念:有一个后继函数 $S: \mathbb{N} \rightarrow \mathbb{N}$。
皮亚诺公理:
(1) $S$ 是内射的:$S(n)=S(m) \Rightarrow n=m$
(2) 存在唯一的 $1 \in \mathbb{N}$,它不是任何其他 $n \in \mathbb{N}$ 的后继。
(3) 归纳原理:如果 $X \subseteq \mathbb{N}$ 使得 $1 \in X$ 且如果 $S(n) \in X$,那么 $X=\mathbb{N}$。
加法:你定义 $n+1=S(n)$。
通过归纳定义 $n+m$:如果 $m=S\left(m^{\prime}\right)$ 那么
乘法:类似地。
幂运算、阶乘、序也来自公理。
2. 2 良序原理
良序原理:令 $A$ 是 $\mathbb{N}$ 的一个非空子集。那么 $A$ 有一个最小元素,即一个元素 $a \in A$ 使得对于所有其他元素 $a'$,有 $a \leq a'$。
2. 3 复数
复数可以由实数构造。我们有数系的演进:
其中第一个箭头使用等价关系和戴德金切割(或柯西序列)。
定义 2.1 (复数)。一个复数的形式为
其中 $a=\operatorname{Re}(z)$ 是实部,$b=\operatorname{Im}(z)$ 是虚部。我们可以将 $\mathbb{C} \cong \mathbb{R}^{2}$ 识别。
复数上有加法和乘法,这使得 $\mathbb{C}$ 成为一个域:
那么 $\mathbb{C}$ 有 0 和 1,加法和乘法是交换的和结合的,分配律成立,并且每个非零复数都有乘法逆元。
2. 4 复共轭
定义 2.2. 如果 $z=a+b i$,那么复共轭是 $\bar{z}=a-b i$。
性质:
- $\overline{z_{1}+z_{2}}=\bar{z}_{1}+\bar{z}_{2}$
- $\overline{z_{1} \cdot z_{2}}=\bar{z}_{1} \cdot \bar{z}_{2}$
- $z \bar{z}=0 \Leftrightarrow z=0$
注意 $z \bar{z}=(a+b i)(a-b i)=a^{2}+b^{2}$ 总是非负实数。
定义 2.3. $|z|=\sqrt{z \bar{z}}$ 称为 $z$ 的绝对值、长度或模。
命题 2.4. $\left|z_{1} \cdot z_{2}\right|=\sqrt{z_{1} z_{2} \bar{z}_{1} \bar{z}_{2}}=\sqrt{z_{1} \bar{z}_{1}} \sqrt{z_{2} \bar{z}_{2}}=\left|z_{1}\right| \cdot\left|z_{2}\right|$
命题 2.5 (三角不等式)。 $\left|z_{1}+z_{2}\right| \leq\left|z_{1}\right|+\left|z_{2}\right|$
2. 5 乘法逆元
如果 $z \neq 0$,那么我们可以找到乘法逆元:
我们可以验证:$z \cdot z^{-1}=z \cdot \frac{\bar{z}}{z \bar{z}}=1$。
例子 2.6.
注 2.7. 非零复数的集合 $\mathbb{C}^{*}$ 在乘法下构成一个群。
2. 6 单位圆
定义 2.8. $U_{1}=\{z \in \mathbb{C}| | z \mid=1\}$ 是 $\mathbb{C} \cong \mathbb{R}^{2}$ 中的单位圆。
注 2.9. 由于 $U_{1}$ 中两个元素的乘积仍在 $U_{1}$ 中,并且 $z \in U_{1}$ 的逆元(即当 $|z|=1$ 时的 $z^{-1}=\bar{z}$)的长度也为 1,我们看到 $U_{1} \subseteq \mathbb{C}^{*}$ 是一个子群。
2. 7 极坐标
极坐标:
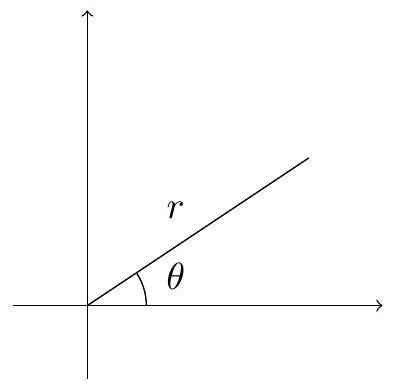
我们将把角 $\theta$ 视为 $\mathbb{R} / 2 \pi \mathbb{Z}$ 的一个元素(我们称之为 $z$ 的辐角)。
乘法:
$z_{1} z_{2}$ 的极坐标是 $\left(r_{1} r_{2}, \theta_{1}+\theta_{2}\right)$。
2. 8 欧拉恒等式
例子 2.10. 考虑 $(1+i)^{2}$。使用标准乘法:$(1+i)^{2}=1+2 i+i^{2}= 1+2 i-1=2 i$。
使用极坐标:$1+i=\sqrt{2}\left(\cos \frac{\pi}{4}+\sin \frac{\pi}{4} i\right)$,所以
定义 2.11. 对于任何实数 $\lambda$,我们定义
更一般地,对于 $z=a+b i \in \mathbb{C}$,我们定义
2. 9 指数的事实
- 每个非零 $y \in \mathbb{C}$ 都可以写成 $e^{z}$ 对于某个 $z \in \mathbb{C}$。
- $e^{z_{1}} \cdot e^{z_{2}}=e^{z_{1}+z_{2}}$ (指数序列对于任何 $z$ 都是绝对收敛的)
欧拉恒等式:$e^{\pi i}+1=0$
命题 2.12. 令 $z$ 是一个非零复数。方程 $x^{n}=z$ 恰好有 $n$ 个解。
即,如果 $z=r e^{i \theta}$,那么解是
证明梗概。我们需要 $x^{n}=z$。如果 $x=s e^{i \phi}$,那么 $x^{n}=s^{n} e^{i n \phi}$。为了使其等于 $r e^{i \theta}$,我们需要 $s^{n}=r$(因此 $s=r^{1 / n}$)并且 $n \phi=\theta+2 \pi k$ 对于某个整数 $k$。
因此 $\phi=\frac{\theta+2 \pi k}{n}$。两个值 $k$ 和 $\ell$ 模 $2 \pi$ 给出相同的 $\phi$ 当且仅当 $k \equiv \ell(\bmod n)$,这给了我们恰好 $n$ 个不同的解。
例子 2.13. 找到 $z=1+\sqrt{3} i$ 的 5 次根。
首先,转换为极坐标形式:$z=2\left(\cos \frac{\pi}{3}+\sin \frac{\pi}{3} i\right)=2 e^{i \pi / 3}$。
5 次根是:
即:
定义 2.14. 对于 $n \geq 1$,我们定义
即 $n$ 次单位根的群。
根据我们之前的命题:
或等价地
注 2.15. $U_{n}$ 是 $U_{1}$ 的一个子群。确实,如果 $\xi, \eta \in U_{n}$,那么 $(\xi \eta)^{n}=\xi^{n} \eta^{n}=1 \cdot 1=1$,所以 $\xi \eta \in U_{n}$。此外,如果 $\xi^{n}=1$,那么 $\left(\xi^{-1}\right)^{n}=\left(\xi^{n}\right)^{-1}=1$,所以 $\xi^{-1} \in U_{n}$。
2. 10 根的计算
将 $\sin (5 \theta)$ 表示为 $\sin \theta$ 和 $\cos \theta$ 的多项式?