1内容
好的,我将根据您提供的ZH.md文件内容,并严格遵循解释工作流WorkFlow.md中的工作流程,为您生成一份详尽的、逐步的解释。解释将涵盖源文件的所有内容和细节,并包含您要求的所有结构化部分。
21. 商群性质与正规子群
11.1 商群的性质示例
1. 1.1 例子 (ii)
📜 [原文1]
(ii) 商群 $G/H$ 是阿贝尔群并不意味着 $G$ 是阿贝尔群。例如,在 $H$ 在 $G$ 中的指数为二的情况下,例如在 $G=S_{n}$ 和 $H=A_{n}$ 的情况下,那么 $G / H$ 的阶为二,因此同构于 $\mathbb{Z} / 2 \mathbb{Z}$。但如果 $n \geq 3$,$S_{n}$ 就不是阿贝尔群。
这段话的核心思想是揭示一个关于群论中商群的重要性质:商群的性质不能完全反推回原群的性质。具体来说,即使我们发现一个商群 $G/H$ 是阿贝尔群(即群内任意两个元素的运算都满足交换律),我们也不能草率地断定原来的群 $G$ 也是阿贝尔群。
- 提出论点: 商群 $G/H$ 是阿贝尔群,推不出 $G$ 是阿贝尔群。这是一个“反例”性质的论述,旨在打破一种可能的直觉误解。很多人可能会想,既然商群是从原群“构造”出来的,那么商群的美好性质(如交换律)应该也源于原群。但事实并非如此。
- 寻找特例: 为了证明这个论点,作者需要一个具体的例子。这个例子需要满足:
- 存在一个群 $G$ 和它的一个正规子群 $H$。
- $G$ 本身不是阿贝尔群。
- 构造出的商群 $G/H$ 恰好是阿贝尔群。
- 给出普遍情况: 作者首先给出了一个普遍成立的特例类别:“$H$ 在 $G$ 中的指数为二”。
- 指数的定义:一个子群 $H$ 在群 $G$ 中的指数,记作 $[G:H]$,是指 $H$ 在 $G$ 中的左陪集(或右陪集)的个数。
- 当指数为 2 时,意味着 $G$ 可以被划分为两个不相交的部分:$H$ 本身,以及另一个陪集 $gH$(其中 $g$ 是任意一个不在 $H$ 中的元素)。所以 $G = H \cup gH$。
- 一个重要的定理是:任何指数为 2 的子群都是正规子群。所以这里的前提是天然满足构造商群的条件的。
- 商群 $G/H$ 的元素就是这些陪集。当指数为 2 时,商群 $G/H$ 只有两个元素:$\{H, gH\}$。
- 任何只有两个元素的群,它的阶为 2。根据群论的基本知识,阶为素数的群一定是循环群,而所有循环群都是阿贝尔群。特别地,阶为 2 的群必然同构于 $\mathbb{Z}/2\mathbb{Z}$,它是一个非常简单的阿贝尔群。
- 给出具体例子: 作者从上述普遍情况中,挑选了一个最经典、最重要的例子:对称群 $S_n$ 和交错群 $A_n$。
- $G = S_n$:$n$ 个元素的所有置换构成的群。其阶为 $n!$。
- $H = A_n$:$n$ 个元素的所有偶置换构成的群。它是 $S_n$ 的一个子群,其阶为 $n!/2$。
- 计算指数: $[S_n : A_n] = |S_n| / |A_n| = (n!) / (n!/2) = 2$。这完美地符合了“指数为二”的普遍情况。
- 因此,$A_n$ 是 $S_n$ 的一个指数为 2 的正规子群。
- 构造商群 $S_n/A_n$。根据上面的分析,这个商群的阶为 2,因此它同构于 $\mathbb{Z}/2\mathbb{Z}$,是一个阿贝尔群。
- 验证结论: 现在需要检查原群 $G=S_n$ 是否是非阿贝尔群。
- 当 $n \geq 3$ 时,对称群 $S_n$ 不是阿贝尔群。例如,在 $S_3$ 中,我们有置换 $(1,2)$ 和 $(1,3)$。它们的复合运算不满足交换律:
- $(1,2)(1,3) = (1,3,2)$
- $(1,3)(1,2) = (1,2,3)$
- 显然 $(1,3,2) \neq (1,2,3)$。
- 所以,$S_n$ (当 $n \geq 3$ 时) 不是阿贝尔群。
- 得出最终结论: 我们找到了一个群 $G=S_n$ ($n \geq 3$),它不是阿贝尔群,但它的商群 $S_n/A_n$ 是阿贝尔群。这雄辩地证明了最初的论点:“商群是阿贝尔群”并不能保证“原群是阿贝尔群”。
- 示例 1: 使用 $G=S_3$
- 原群: $G = S_3 = \{e, (1,2), (1,3), (2,3), (1,2,3), (1,3,2)\}$。这是一个非阿贝尔群,因为 $(1,2)(1,3) = (1,3,2)$,而 $(1,3)(1,2) = (1,2,3)$。
- 正规子群: $H = A_3 = \{e, (1,2,3), (1,3,2)\}$。这是所有偶置换构成的子群。$|S_3|=6$, $|A_3|=3$。
- 指数: $[S_3:A_3] = |S_3|/|A_3| = 6/3 = 2$。
- 陪集: $A_3$ 在 $S_3$ 中有两个陪集:
- $eA_3 = A_3 = \{e, (1,2,3), (1,3,2)\}$
- $(1,2)A_3 = \{(1,2)e, (1,2)(1,2,3), (1,2)(1,3,2)\} = \{(1,2), (2,3), (1,3)\}$
- 商群: $G/H = S_3/A_3 = \{A_3, (1,2)A_3\}$。这个商群只有两个元素。
- 商群的运算: 它的运算表如下(其中 $I=A_3$,$O=(1,2)A_3$):
| * | I | O |
|---|---|---|
| I | I | O |
| O | O | I |
这个运算表与 $\mathbb{Z}/2\mathbb{Z}$ 的加法表同构(将 $I$ 对应于 0,将 $O$ 对应于 1)。
- 结论: 商群 $S_3/A_3$ 是阿贝尔群(同构于 $\mathbb{Z}/2\mathbb{Z}$),但原群 $S_3$ 不是阿贝尔群。这验证了原文的论点。
- 示例 2: 使用二面体群 $G=D_4$
- 原群: $G = D_4$ 是正方形的对称群,阶为 8。它包含4个旋转和4个翻转。这是一个非阿贝尔群。例如,旋转90度后再水平翻转,与先水平翻转再旋转90度的结果不同。
- 正规子群: 考虑由旋转构成的子群 $H = \{R_0, R_{90}, R_{180}, R_{270}\}$,其中 $R_i$ 表示旋转 $i$ 度。$H$ 是一个循环群,阶为 4。可以验证 $H$ 是 $D_4$ 的正规子群,且指数为 $[D_4:H] = 8/4 = 2$。
- 商群: 商群 $D_4/H$ 的阶为 2。
- 结论: 根据上面的分析,任何阶为 2 的群都是阿贝尔群。因此商群 $D_4/H$ 是阿贝尔群,但原群 $D_4$ 不是阿贝尔群。
- 易错点1: 将商群的性质等同于原群的性质。这是最核心的易错点。必须记住商群丢失了原群的很多信息。它只反映了原群“模掉”正规子群 $H$ 之后的结构。
- 易错点2: 混淆指数与阶。子群的阶是子群中元素的个数,而指数是陪集的个数。两者通过拉格朗日定理关联:$|G| = |H| \cdot [G:H]$。
- 易错点3: 认为任何子群都可以用来构造商群。只有正规子群才能保证陪集的乘法是良定义的,从而构成一个群。对于指数为 2 的子群,它恰好总是正规子群,这是一个非常方便的性质。
- 边界情况:
- 当 $n=1$ 或 $n=2$ 时,$S_n$ 是阿贝尔群。$S_1$ 是平凡群,只有一个元素。$S_2$ 有两个元素,同构于 $\mathbb{Z}/2\mathbb{Z}$。所以“$S_n$ 是非阿贝尔群”的条件是 $n \geq 3$。
- 如果 $G$ 本身就是阿贝尔群,那么它的任何子群都是正规子群,且其任何商群 $G/H$ 也必然是阿贝尔群。这个方向的推论是成立的。
本段通过一个经典且重要的反例——对称群 $S_n$ 与其正规子群 交错群 $A_n$——清晰地阐明了群论中的一个关键概念:商群 $G/H$ 的交换性(是阿贝尔群)并不蕴含原群 $G$ 的交换性。这个例子基于一个更普遍的原理:任何指数为 2 的子群都是正规的,并且其对应的商群阶为 2,因此必然是阿贝尔群。
本段的目的是为了加深学生对商群概念的理解,防止他们形成错误的直觉。在数学学习中,通过反例来精确界定一个概念的适用范围是至关重要的方法。它告诉我们,从 $G$ 到 $G/H$ 的商映射是一个“信息压缩”或“信息丢失”的过程,商群只保留了原群的一部分结构信息,因此商群的性质不能随意地“逆推”回原群。
想象一下“取模”运算。例如,整数环 $\mathbb{Z}$ 是一个阿贝尔群。商群 $\mathbb{Z}/12\mathbb{Z}$ 就是我们熟悉的钟表算术。13点就是1点,14点就是2点。这个商群也是阿贝尔群。
现在,把这个想法推广到非阿贝尔群。想象一个复杂的三维物体(代表非阿贝尔群 $G$),它有旋转、翻转等多种对称操作。现在,我们戴上一副特殊的“模糊眼镜”(代表正规子群 $H$)。戴上这副眼镜后,我们不再能区分某些操作。例如,眼镜可能让我们无法区分“旋转180度”和“不作任何操作”。所有这些被我们视为“一样”的操作集合,就构成了 $H$。而我们能区分开的几大类操作,就构成了商群 $G/H$ 的元素(即陪集)。
在 $S_n$ 与 $A_n$ 的例子中,我们的“模糊眼镜” $A_n$ 让我们无法区分任何偶置换,把它们都看作是“平凡操作”。我们唯一能区分的是“这个操作是偶置换”还是“这个操作是奇置换”。于是,在我们的模糊视野里,世界只剩下了两种状态:“偶”和“奇”。这两种状态的运算规则很简单:“偶+偶=偶”,“偶+奇=奇”,“奇+奇=偶”。这显然是一个满足交换律的简单系统(阿贝尔群),但它完全掩盖了背后那个复杂、非阿贝尔的置换世界 $S_n$。
想象一条由许多彩色珠子串成的复杂项链,珠子的排列顺序很重要,交换任意两个珠子的位置会得到一条完全不同的项链(这代表非阿贝尔群 $G=S_n$)。现在,我们不再关心每个珠子的具体颜色,只关心它是“深色”还是“浅色”。我们将所有只改变“深色”珠子之间顺序或“浅色”珠子之间顺序的操作,都看作是等价的(这代表子群 $H=A_n$,即那些不改变“奇偶性”的置换)。这样一来,我们能观察到的宏观变化就只剩下两种:“保持深浅模式不变”和“交换所有深浅珠子的位置”。这两种宏观变化构成的简单系统,就是商群 $G/H$。这个宏观系统非常简单且满足交换律(阿贝尔群),但它隐藏了项链内部复杂的珠子排列规则(非阿贝尔性质)。
1. 1.2 例子 (iii)
📜 [原文2]
(iii) It is easy to see that, if $G$ is 循环的,那么$G / H$是循环的。例如,设 $G=\mathbb{Z} / n \mathbb{Z}$。那么对于每个 $d \mid n$,我们有子群 $H=\langle d\rangle$,阶为 $n / d$。由于 $G$是阿贝尔群,$H$自动成为 $G$的正规子群。因此 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle$是一个循环群,其阶等于 $\langle d\rangle$在 $\mathbb{Z} / n \mathbb{Z}$中的指数,即 $n /(n / d)=d$。因此 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$。(我们稍后将为此提供另一个证明。)
这段话阐述了与上一段相反方向的一个性质:如果原群 $G$ 是循环群,那么它的任何商群 $G/H$ 也必然是循环群。这说明“循环性”这个性质是可以被商群继承的。
- 提出论点: 如果 $G$ 是循环的,则 $G/H$ 也是循环的。
- 循环群的定义:一个群 $G$ 被称为循环群,如果存在一个元素 $g \in G$,使得 $G$ 中的每一个元素都可以表示为 $g$ 的幂次(或在加法群中是 $g$ 的倍数)。这个元素 $g$ 被称为群 $G$ 的生成元。
- 证明这个论点:设 $G = \langle g \rangle$。商群 $G/H$ 的元素是形如 $aH$ 的陪集,其中 $a \in G$。因为 $a$ 是 $G$ 的元素,所以 $a$ 可以被写成 $g^k$ 的形式(对于某个整数 $k$)。因此,任何一个陪集都可以写成 $(g^k)H$。根据陪集乘法的定义,$(g^k)H = (gH)^k$。这意味着商群 $G/H$ 中的每一个元素都是陪集 $gH$ 的幂次。所以,$gH$ 是商群 $G/H$ 的一个生成元。因此,$G/H$ 是一个循环群。
- 给出具体例子: 作者选择了有限循环群 $G = \mathbb{Z}/n\mathbb{Z}$ 作为例子来具体说明这个原理。$\mathbb{Z}/n\mathbb{Z}$ 是所有模 $n$ 的同余类的集合,在模 $n$ 加法下构成一个循环群,其生成元是 $[1]$。
- 寻找子群: 在循环群 $\mathbb{Z}/n\mathbb{Z}$ 中,对于任何一个整除 $n$ 的正整数 $d$,都存在一个唯一的阶为 $n/d$ 的子群。这个子群就是由元素 $d$(或说同余类 $[d]$)生成的循环子群,记作 $H = \langle d \rangle$。它的元素是 $\{[0], [d], [2d], \dots, [(\frac{n}{d}-1)d]\}$。
- 验证正规性: 因为 $G = \mathbb{Z}/n\mathbb{Z}$ 是一个阿贝尔群(加法满足交换律),所以它的任何子群都是正规子群。因此,我们总可以用 $H = \langle d \rangle$ 来构造商群。
- 构造商群: 我们可以构造商群 $(\mathbb{Z}/n\mathbb{Z})/\langle d \rangle$。
- 分析商群:
- 根据第一步的普适性结论,因为原群 $\mathbb{Z}/n\mathbb{Z}$ 是循环的,所以这个商群也一定是循环的。
- 商群的阶: 商群的阶等于子群的指数。即 $|G/H| = [G:H] = |G|/|H|$。
- $|G| = |\mathbb{Z}/n\mathbb{Z}| = n$。
- $|H| = |\langle d \rangle| = n/d$。
- 所以,商群的阶为 $n / (n/d) = d$。
- 得出结论: 我们得到了一个阶为 $d$ 的循环群。在同构的意义下,阶为 $d$ 的循环群是唯一的,就是 $\mathbb{Z}/d\mathbb{Z}$。因此,我们得出结论:$(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$。
- 预告: 作者提到,这个结论后面还会用另一种方法(通常是第一同构定理)来再次证明,这暗示了这个结论的重要性。
- $d \mid n$: 读作 "$d$ 整除 $n$",意味着 $n$ 是 $d$ 的整数倍,即存在整数 $k$ 使得 $n = dk$。
- $G = \mathbb{Z}/n\mathbb{Z}$: 这是模 $n$ 的整数加法群。它的元素是 $\{[0], [1], \dots, [n-1]\}$,运算是模 $n$ 加法。它是一个阶为 $n$ 的循环群。
- $H = \langle d \rangle$: 这是由元素 $d$(在 $\mathbb{Z}/n\mathbb{Z}$ 的上下文中指同余类 $[d]$)生成的循环子群。它的元素是 $d$ 的所有倍数模 $n$ 的集合。由于 $d$ 是 $n$ 的因子,这个子群的阶是 $n/d$。
- $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$:
- 左边: 是一个商群。原群是 $\mathbb{Z}/n\mathbb{Z}$,我们“除以”或“模掉”了它的正规子群 $\langle d \rangle$。
- 右边: 是一个阶为 $d$ 的循环群。
- $\cong$: 表示“群同构”,意味着左右两边的群在结构上是完全一样的,只是元素的叫法可能不同。
- 推导过程:
- 商群的阶: $|(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle| = [\mathbb{Z}/n\mathbb{Z} : \langle d \rangle] = |\mathbb{Z}/n\mathbb{Z}| / |\langle d \rangle| = n / (n/d) = d$。
- 商群的循环性: 因为原群 $\mathbb{Z}/n\mathbb{Z}$ 是循环的,所以商群也必定是循环的。
- 结论: 一个阶为 $d$ 的循环群必然同构于 $\mathbb{Z}/d\mathbb{Z}$。因此结论成立。
- 示例 1: $n=12, d=4$
- 原群: $G = \mathbb{Z}/12\mathbb{Z} = \{0,1,2,3,4,5,6,7,8,9,10,11\}$。这是一个阶为 12 的循环群。
- 因子: $d=4$ 整除 $n=12$。
- 子群: $H = \langle 4 \rangle = \{0, 4, 8\}$。这是一个阶为 $12/4 = 3$ 的子群。
- 商群: 我们要考察商群 $G/H = (\mathbb{Z}/12\mathbb{Z})/\langle 4 \rangle$。
- 商群的阶: 应该是 $d=4$。我们来验证一下。$|G/H| = |G|/|H| = 12/3 = 4$。正确。
- 商群的元素 (陪集):
- $H = 0+H = \{0, 4, 8\}$
- $1+H = \{1, 5, 9\}$
- $2+H = \{2, 6, 10\}$
- $3+H = \{3, 7, 11\}$
- 商群的运算: 以 $1+H$ 为生成元:
- $(1+H)^1 = 1+H$
- $(1+H)^2 = (1+H)+(1+H) = 2+H$
- $(1+H)^3 = 3+H$
- $(1+H)^4 = 4+H = H$ (因为 $4 \in H$,所以 $4+H=H$,这是商群的单位元)。
- 结论: $(\mathbb{Z}/12\mathbb{Z})/\langle 4 \rangle$ 是一个阶为 4 的循环群,因此它同构于 $\mathbb{Z}/4\mathbb{Z}$。这验证了公式 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$ 对于 $n=12, d=4$ 成立。
- 示例 2: $n=6, d=3$
- $G = \mathbb{Z}/6\mathbb{Z} = \{0,1,2,3,4,5\}$。
- $d=3$ 整除 $n=6$。
- $H = \langle 3 \rangle = \{0, 3\}$。这是一个阶为 $6/3=2$ 的子群。
- 商群 $G/H$ 的阶应为 $d=3$。验证:$|G/H| = |G|/|H| = 6/2 = 3$。正确。
- 商群是一个阶为 3 的循环群,因此同构于 $\mathbb{Z}/3\mathbb{Z}$。
- 结论: $(\mathbb{Z}/6\mathbb{Z})/\langle 3 \rangle \cong \mathbb{Z}/3\mathbb{Z}$。
- 易错点: 混淆 $d$ 和 $n/d$ 的角色。子群 $\langle d \rangle$ 的阶是 $n/d$,而商群的阶是 $d$。这是一个非常容易出错的地方。可以这样记忆:我们“模掉”了与 $d$ 的倍数相关的结构,最终得到的群的规模与 $d$ 相关。
- 边界情况:
- 如果 $d=n$,则 $H = \langle n \rangle = \langle 0 \rangle = \{0\}$。这是平凡子群。商群为 $(\mathbb{Z}/n\mathbb{Z})/\{0\} \cong \mathbb{Z}/n\mathbb{Z}$。公式成立。
- 如果 $d=1$,则 $H = \langle 1 \rangle = \mathbb{Z}/n\mathbb{Z}$。这是整个群。商群为 $(\mathbb{Z}/n\mathbb{Z})/(\mathbb{Z}/n\mathbb{Z}) \cong \{e\}$ (平凡群)。而 $\mathbb{Z}/1\mathbb{Z}$ 也是平凡群。公式成立。
本段的核心论点是“循环群的商群也是循环群”。它通过分析循环群的生成元在商群中的对应元素(一个陪集)也必然是商群的生成元来证明这一点。然后,文章使用标准的有限循环群 $\mathbb{Z}/n\mathbb{Z}$ 作为具体示例,详细推导了其对于任意因子 $d$ 的子群 $\langle d \rangle$ 所构成的商群 $(\mathbb{Z}/n\mathbb{Z})/\langle d \rangle$ 的结构。最终结论是这个商群是一个阶为 $d$ 的循环群,因此同构于 $\mathbb{Z}/d\mathbb{Z}$。
这一段的目的是展示与前一段相反的情况:有些重要的群性质是可以被商群完美继承的,“循环性”就是其中之一。这有助于学生建立一个更平衡的观点,理解商群既会丢失信息,也会保留信息。同时,这个例子 $(\mathbb{Z} / n \mathbb{Z}) /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$ 本身是群论中一个非常基础和有用的结论,它在后续学习(如环论中的商环)中会反复出现。
继续使用钟表模型。
- 原群 $G=\mathbb{Z}/12\mathbb{Z}$ 是一个有12个刻度的普通时钟。它的“循环性”体现在我们可以通过“前进1小时”这个操作(即元素1),重复12次,走遍所有的12个点。
- 子群 $H=\langle 4 \rangle = \{0, 4, 8\}$ 可以想象成时钟上的三个特殊标记点(12点、4点、8点)。我们现在要“模掉”这个子群,意思是说,我们不再关心精确的时间,只关心时间除以4的余数。
- 商群的元素(陪集)就是这种“模糊时间”:
- $1+H = \{1, 5, 9\}$ 构成了“余数为1”的集合。
- $2+H = \{2, 6, 10\}$ 构成了“余数为2”的集合。
- $3+H = \{3, 7, 11\}$ 构成了“余数为3”的集合。
- $0+H = \{0, 4, 8\}$ 构成了“余数为0”的集合。
- 这个商群就是一个只有4个状态的“季节时钟”(春、夏、秋、冬)。这个新的、更粗糙的时钟本身也是循环的:从春天开始,不断“前进一个季节”,可以遍历春夏秋冬。这就是商群的循环性。这个阶为4的“季节时钟”同构于 $\mathbb{Z}/4\mathbb{Z}$。
想象一个沿着圆形跑道跑步的运动员。跑道的总长度是 $n$ 米。运动员每跑1米,就相当于循环群 $\mathbb{Z}/n\mathbb{Z}$ 中的元素 1。这是一个循环群。
现在,我们在跑道上每隔 $d$ 米设置一个检查点。总共有 $n/d$ 个检查点。这个检查点集合就类似于子群 $\langle d \rangle$。
我们构造商群,相当于我们不再关心运动员在跑道上的精确位置,只关心他“位于第几个 $d$ 米的区间内”。
例如,当 $n=1200$米,$d=400$米时,跑道上有3个检查点(0米,400米,800米)。
- 陪集 $0+H$: 运动员位于 $[0, 399]$ 米区间的某个位置。
- 陪集 $1+H$: 这不标准,应该是用生成元。
- 陪集 $H$: 位置在0, 400, 800米。
- 陪集 $100+H$: 位置在100, 500, 900米。
- 商群 $(\mathbb{Z}/1200\mathbb{Z})/\langle 400 \rangle$ 就相当于只观察运动员在哪一圈(这里圈的概念不对)。
让我们换个想象。原群 $\mathbb{Z}/n\mathbb{Z}$ 是一个有 $n$ 个珠子的项链。我们现在用一种颜色把第 $d, 2d, 3d, \dots$ 个珠子染上色。然后我们把项链盘起来,让所有染色的珠子对齐。这样项链就变成了一个有 $d$ 股的绳圈。这个新的绳圈,它的“周长”是 $d$,它本身也是一个循环的结构,这就是商群 $\mathbb{Z}/d\mathbb{Z}$。
21.2 正规子群的一些性质
📜 [原文3]
For future reference, we collect some facts about 正规子群. The 证明s are straightforward.
命题 2.3.14. Let $G$ be a 群 and let $H$ and $K$ be 子群 of $G$. Then:
(i) If $H \triangleleft G$ and $K \triangleleft G$,那么$H \cap K \triangleleft G$。
(ii) If $H \triangleleft G$ and $K \leq G$,那么$H \cap K \triangleleft K$。
(iii) If $H \leq K \leq G$ and $H \triangleleft G$,那么$H \triangleleft K$。
(iv) If $H \triangleleft G$ and $K \leq G$,那么子集
is a 子群 of $G$.
这部分内容是为后续的讨论和证明做铺垫,集中列出了几个关于正规子群的基本但非常重要的性质。这些性质在处理复杂的群结构时会经常用到。
- 引言: 作者明确指出,这些事实是为“未来参考”而收集的,并提到它们的证明都很“直接”(straightforward),鼓励读者自行思考或验证。
- 命题 2.3.14 (i): 两个正规子群的交集仍然是正规子群。
- 前提: $H$ 是 $G$ 的正规子群 ($H \triangleleft G$),并且 $K$ 也是 $G$ 的正规子群 ($K \triangleleft G$)。
- 结论: 它们的交集 $H \cap K$ 也是 $G$ 的正规子群 ($H \cap K \triangleleft G$)。
- 证明思路:
- 首先,两个子群的交集必然还是一个子群(这是子群的基本性质)。
- 然后需要证明其正规性。要证明 $H \cap K \triangleleft G$,我们需要对任意 $x \in H \cap K$ 和任意 $g \in G$,证明 $gxg^{-1} \in H \cap K$。
- 因为 $x \in H$ 且 $H \triangleleft G$,所以 $gxg^{-1} \in H$。
- 因为 $x \in K$ 且 $K \triangleleft G$,所以 $gxg^{-1} \in K$。
- 既然 $gxg^{-1}$ 同时属于 $H$ 和 $K$,那么它必然属于它们的交集 $H \cap K$。
- 证明完毕。
- 命题 2.3.14 (ii): 一个正规子群与任何一个子群的交集,是那个子群的正规子群。
- 前提: $H$ 是 $G$ 的正规子群 ($H \triangleleft G$),$K$ 是 $G$ 的一个(不一定是正规的)子群 ($K \leq G$)。
- 结论: 它们的交集 $H \cap K$ 是 $K$ 的一个正规子群 ($H \cap K \triangleleft K$)。
- 证明思路:
- $H \cap K$ 是 $K$ 的一个子群,这是显然的。
- 要证明 $H \cap K \triangleleft K$,我们需要对任意 $x \in H \cap K$ 和任意 $k \in K$,证明 $kxk^{-1} \in H \cap K$。
- 因为 $x \in H \cap K$,所以 $x \in H$ 并且 $x \in K$。
- 因为 $k \in K$ 且 $x \in K$,并且 $K$ 是一个子群,所以 $kxk^{-1}$ 必然也在 $K$ 中(子群对共轭运算是封闭在其自身内部的)。
- 因为 $x \in H$ 且 $H \triangleleft G$,并且 $k$ 也是 $G$ 中的一个元素,所以根据 $H$ 的正规性,我们有 $kxk^{-1} \in H$。
- 既然 $kxk^{-1}$ 同时属于 $H$ 和 $K$,那么它必然属于它们的交集 $H \cap K$。
- 证明完毕。这个性质也被称为Dedekind's modular law的特例。
- 命题 2.3.14 (iii): 如果一个子群在整个大群中是正规的,那么它在任何包含它的中间子群中也必然是正规的。
- 前提: $H \leq K \leq G$(形成一个子群链),并且 $H$ 在大群 $G$ 中是正规的 ($H \triangleleft G$)。
- 结论: $H$ 在中间那个群 $K$ 中也是正规的 ($H \triangleleft K$)。
- 证明思路:
- 要证明 $H \triangleleft K$,我们需要对任意 $h \in H$ 和任意 $k \in K$,证明 $khk^{-1} \in H$。
- 因为 $k \in K$ 且 $K \leq G$,所以 $k$ 也是 $G$ 的一个元素。
- 我们已知 $H \triangleleft G$,这意味着对于任意 $g \in G$,都有 $ghg^{-1} \in H$。
- 既然这个性质对所有 $G$ 中的元素都成立,那么它自然也对 $G$ 的子集 $K$ 中的所有元素 $k$ 成立。
- 因此,$khk^{-1} \in H$。证明完毕。
- 命题 2.3.14 (iv): 如果两个子群中至少有一个是正规的,那么它们的积集 HK 构成一个子群。
- 前提: $H$ 是 $G$ 的正规子群 ($H \triangleleft G$),$K$ 是 $G$ 的一个子群 ($K \leq G$)。
- 结论: 集合 $HK = \{hk : h \in H, k \in K\}$ 是 $G$ 的一个子群。
- 证明思路 (使用子群判别法):
- 非空: 因为 $H$ 和 $K$ 都是子群,它们都包含单位元 $e$。所以 $e = e \cdot e \in HK$。$HK$ 非空。
- 封闭性: 取任意两个元素 $x_1, x_2 \in HK$。则 $x_1 = h_1k_1$, $x_2 = h_2k_2$。我们需要证明 $x_1x_2 \in HK$。
$x_1x_2 = (h_1k_1)(h_2k_2) = h_1(k_1h_2)k_2$。
这里的关键是处理 $k_1h_2$。因为 $H \triangleleft G$,所以对于任意 $h_2 \in H$ 和 $k_1 \in G$ (这里 $k_1 \in K \leq G$),我们有 $k_1H = Hk_1$。这意味着 $k_1h_2 \in k_1H = Hk_1$,所以存在一个 $h_3 \in H$ 使得 $k_1h_2 = h_3k_1$。
代入上式:$x_1x_2 = h_1(h_3k_1)k_2 = (h_1h_3)(k_1k_2)$。
因为 $h_1, h_3 \in H$,所以 $h_1h_3 \in H$。因为 $k_1, k_2 \in K$,所以 $k_1k_2 \in K$。
因此 $x_1x_2$ 的形式是一个 $H$ 中的元素乘以一个 $K$ 中的元素,所以 $x_1x_2 \in HK$。
- 逆元: 取任意 $x = hk \in HK$。我们需要证明 $x^{-1} \in HK$。
$x^{-1} = (hk)^{-1} = k^{-1}h^{-1}$。
同样地,因为 $H \triangleleft G$,我们有 $k^{-1}H = Hk^{-1}$。这意味着 $k^{-1}h^{-1} \in k^{-1}H = Hk^{-1}$,所以存在 $h' \in H$ 使得 $k^{-1}h^{-1} = h'k^{-1}$。
因为 $h' \in H$ 且 $k^{-1} \in K$ (因为 $K$ 是子群),所以 $x^{-1} = h'k^{-1} \in HK$。
- 根据子群判别法,HK 是 $G$ 的子群。
- $H \triangleleft G$: 读作 "$H$ 是 $G$ 的正规子群" (H is a normal subgroup of G)。定义是:对于所有 $g \in G$ 和所有 $h \in H$,都有 $ghg^{-1} \in H$。等价地,对于所有 $g \in G$,都有 $gH = Hg$。
- $K \leq G$: 读作 "$K$ 是 $G$ 的子群" (K is a subgroup of G)。
- $H \cap K$: 集合的交集,即所有同时属于 $H$ 和 $K$ 的元素的集合。
- $H K=\{h k: h \in H \text { and } k \in K\}$: 子集的积。这是一个集合,由一个来自 $H$ 的元素和一个来自 $K$ 的元素的所有可能的乘积构成。注意,一般情况下 $hk$ 不等于 $kh$,所以 $HK$ 不一定等于 $KH$。但是如果 $H$ 或 $K$ 中有一个是正规的,可以证明 $HK=KH$。
- 示例 for (i) 和 (iv):
- 令 $G = \mathbb{Z}/12\mathbb{Z}$。这是一个阿贝尔群,所以它的所有子群都是正规子群。
- 取 $H = \langle 2 \rangle = \{0, 2, 4, 6, 8, 10\}$。$H \triangleleft G$。
- 取 $K = \langle 3 \rangle = \{0, 3, 6, 9\}$。$K \triangleleft G$。
- (i) 验证 $H \cap K \triangleleft G$:
- $H \cap K = \{0, 6\} = \langle 6 \rangle$。
- $\langle 6 \rangle$ 是 $\mathbb{Z}/12\mathbb{Z}$ 的一个子群,并且因为 $\mathbb{Z}/12\mathbb{Z}$ 是阿贝尔群,所以 $\langle 6 \rangle$ 自动是正规子群。性质(i)成立。
- (iv) 验证 $HK$ 是子群:
- $HK = H+K = \{h+k \pmod{12} \mid h \in H, k \in K\}$。
- $H+K = \langle \text{gcd}(2,3) \rangle = \langle 1 \rangle = \mathbb{Z}/12\mathbb{Z} = G$。
- 因为 $\text{gcd}(2,3)=1$,所以通过 $h=2a, k=3b$ 的线性组合可以凑出 1,例如 $3(-1)+2(2)=1$。所以 $H+K$ 包含了生成元 1,因此 $H+K=G$。而 $G$ 本身当然是一个子群。性质(iv)成立。
- 示例 for (ii) 和 (iii):
- 令 $G = S_4$。
- 取正规子群 $H = V_4 = \{e, (12)(34), (13)(24), (14)(23)\}$。$H \triangleleft S_4$。
- 取一个非正规子群 $K = S_3$ (嵌入到 $S_4$ 中,作为固定元素4的置换群)。$K = \{e, (12), (13), (23), (123), (132)\}$。$K \leq S_4$。
- (ii) 验证 $H \cap K \triangleleft K$:
- $H \cap K = \{e\}$。平凡子群总是任何群的正规子群。所以 $\{e\} \triangleleft K$。性质(ii)成立。
- 取另一个子群链:$H=V_4$, $K=A_4$。我们有 $H \leq A_4 \leq S_4$。
- 已知 $H=V_4$ 是 $S_4$ 的正规子群 ($H \triangleleft S_4$)。
- (iii) 验证 $H \triangleleft A_4$:
- 我们需要证明对于任意 $\pi \in A_4$ 和任意 $h \in H$,都有 $\pi h \pi^{-1} \in H$。
- 因为 $\pi \in A_4 \subset S_4$,而我们已经知道 $H$ 在整个 $S_4$ 中都是正规的,所以对于任何 $S_4$ 中的元素(自然包括 $A_4$ 中的元素)的共轭操作,都会把 $H$ 的元素变回 $H$ 里。因此 $H \triangleleft A_4$ 必然成立。
- 易错点1: 对于性质(iv),必须有一个子群是正规的。如果 $H$ 和 $K$ 都不是正规子群,那么 $HK$ 很可能不是一个子群。下面的Remark中就给出了这个反例。
- 易错点2: 混淆 $HK$ 和 $\langle H, K \rangle$。$HK$ 只是 $h$ 和 $k$ 的乘积的集合,而 $\langle H, K \rangle$ 是由 $H$ 和 $K$ 的所有元素生成的子群,它包含所有形如 $h_1k_1h_2k_2\dots$ 的有限乘积。当 $H$ 或 $K$ 正规时,恰好有 $HK = KH = \langle H, K \rangle$。
- 边界情况:
- 如果 $H$ 或 $K$ 是平凡子群 $\{e\}$,所有命题都平凡地成立。例如,若 $H=\{e\}$,$H \triangleleft G$。则 (i) $\{e\} \cap K = \{e\} \triangleleft G$ 不一定,应该是 $\{e\} \cap K = \{e\} \triangleleft K$。这里原文(i)的前提是H, K都是G的正规子群。 (ii) $\{e\} \cap K = \{e\} \triangleleft K$ 成立。(iii) $\{e\} \leq K \leq G, \{e\} \triangleleft G \Rightarrow \{e\} \triangleleft K$ 成立。(iv) $\{e\}K = K$ 是子群,成立。
- 如果 $H \leq K$,则 $H \cap K = H$。那么命题 (i) 变为 “若 $H, K \triangleleft G$ 且 $H \leq K$,则 $H \triangleleft G$”,这是同义反复。命题 (ii) 变为“若 $H \triangleleft G$ 且 $H \leq K \leq G$,则 $H \triangleleft K$”,这与命题 (iii) 完全相同。
该命题总结了正规子群在交集、子群链和与其它子群乘积运算下的四个关键性质:
- 正规性对交集运算封闭:两个正规子群之交仍为正规子群。
- 正规性的遗传性 (对子群):正规子群与任一子群的交,在该子群中是正规的。
- 正规性的向下传递性: 在大群中正规的子群,在任何包含它的中间子群中也正规。
- 乘积构成子群的条件: 一正规子群与一任意子群的积集,本身构成一个子群。
这些性质是后续证明(特别是同构定理)的重要工具。
本段的目的是提供一个“工具箱”,将这些证明中反复使用的引理集中起来,方便随时调用。通过将它们作为命题先行陈述,可以使后续的定理证明更加流畅,逻辑更加清晰,而不必在每个定理中都重复证明这些基础事实。这也体现了数学论述的模块化思想。
想象正规子群 $H$ 是一种非常“稳定”和“对称”的结构。
- (i) 两个“稳定”结构的共同部分 $H \cap K$,自然也应该是“稳定”的。
- (ii) 一个“稳定”结构 $H$ 在一个普通结构 $K$ 内部的投影 $H \cap K$,在 $K$ 的视角看来,也是“稳定”的。就像一个在三维空间中绝对圆的球体,它与任何一个平面的交集(一个圆盘),在这个平面上看来也是一个完美的圆形。
- (iii) 一个在整个大环境 $G$ 中都表现出“稳定性”的结构 $H$,那么把它放到一个更小的环境 $K$ 中($H \subset K$),它当然也表现出“稳定性”。
- (iv) 一个“稳定”结构 $H$ 和一个任意结构 $K$ 相结合,由于 $H$ 的“稳定性”($kH=Hk$),它能“吸收”和“整理”任意来自 $K$ 的元素 $k$ 的扰动,使得它们的组合 $HK$ 能够形成一个封闭、完整的结构(子群),而不会因为运算顺序的混乱而“散架”。
- 把群 $G$ 想象成一个大广场。子群是广场上的人群。
- 正规子群 $H$ 是一群穿着统一制服、行动一致的仪仗队员。无论广场上其他人(元素 $g$)怎么跑动,仪仗队的整体队形和结构 $H$ 看起来都是不变的($gH=Hg$)。
- (i) 有两队仪仗队 $H$ 和 $K$,它们的制服和动作都与广场整体协调。那么,同时属于这两队的人(交集 $H \cap K$)组成的那个小编队,显然也和广场整体是协调的。
- (ii) 有一队仪仗队 $H$ 和一队普通的游客群 $K$。那么,仪仗队中恰好也是游客的那些人(交集 $H \cap K$),在游客群 $K$ 的内部看来,他们的行为模式(正规性)是相对于游客群 $K$ 而言的,也是非常规律的。
- (iv) 仪仗队 $H$ 和游客群 $K$ 混合在一起。因为仪仗队有严格的规则,可以和游客进行有序的互动($kh = h'k$),所以他们混合后形成的整个大群体 $HK$ 依然是一个有组织的、封闭的团体(子群),而不是一盘散沙。
31.3 关于性质(iv)的补充说明与反例
📜 [原文4]
Remark 2.3.15. (i) Warning: It is possible that, in the above notation, we could have $H \triangleleft K$ and $K \triangleleft G$ but that $H$ is not a 正规子群 of $G$. In other words, the 性质 of being a 正规子群通常不具有传递性。习题 4.20中给出了示例。
(ii) If $H$ and $K$ are two arbitrary 子群 of $G$,neither one of which is 正规的,那么上述(4)中定义的$H K$不一定是子群。例如,取 $G=S_{3}, H=\langle(1,2)\rangle=\{1,(1,2)\}$ and $K=\langle(2,3)\rangle=\{1,(2,3)\}$,很容易看出
In particular, $\#(H K)=4$ and so $H K$ cannot be a 子群,since otherwise we would get a contradiction to 拉格朗日定理。
这部分是对上一个命题的补充说明,通过两个重要的“警告”(Warning)来指出一些容易误解的边界情况。
- Remark (i): 正规性不具有传递性
- 论点: “$H$ 是 $K$ 的正规子群” ($H \triangleleft K$) 并且 “$K$ 是 $G$ 的正规子群” ($K \triangleleft G$),这两个条件放在一起,并不能保证 “$H$ 是 $G$ 的正规子群” ($H \triangleleft G$)。
- 对比命题2.3.14(iii): 命题(iii)说的是 $H \triangleleft G \implies H \triangleleft K$ (当 $H \leq K$),这是“向下传递”。而这里讨论的是 $H \triangleleft K$ 和 $K \triangleleft G$ 是否能“向上传递”到 $H \triangleleft G$,结论是不能。
- 直觉理解: $H$ 在 $K$ 中正规,意味着用 $K$ 内部的元素去做共轭运算,不会把 $H$ 的元素变出 $H$。$K$ 在 $G$ 中正规,意味着用 $G$ 内部的元素去做共轭运算,不会把 $K$ 的元素变出 $K$。但是,当我们用一个不在 $K$ 中的 $G$ 的元素 $g$ 去对 $H$ 的元素 $h$ 做共轭运算 $ghg^{-1}$ 时,我们只知道 $gKg^{-1}=K$,但 $g$ 对 $K$ 内部的 $h$ 会产生什么影响,是未知的。$g$ 可能会把 $h$ 变成一个不在 $H$ 中,但仍在 $K$ 中的元素。
- 例子预告: 作者没有在这里给出具体的例子,而是说在习题4.20中会给出一个。一个经典的例子是:
- $G = D_4$ (8阶二面体群)。
- $K = \{e, r^2, h, v\}$ (其中 $h, v$ 是水平和垂直翻转),$K$ 是一个 V4 型子群,可以验证 $K \triangleleft D_4$。
- $H = \{e, h\}$,是一个2阶子群。因为 $K$ 是阿贝尔群,所以 $H \triangleleft K$。
- 但是,$H$ 在 $D_4$ 中不是正规的。例如,用旋转 $r$ 来做共轭运算:$rhr^{-1} = v \notin H$。所以 $H$ 不满足 $H \triangleleft G$。
- Remark (ii): 两个非正规子群的积集不一定是子群
- 论点: 这是对命题 2.3.14(iv) 的反向说明。如果前提“$H$ 或 $K$ 中至少有一个是正规的”不满足,那么结论“$HK$ 是一个子群”就可能不成立。
- 提供反例:
- 选择群和子群:
- $G = S_3$ (6阶对称群)。
- $H = \langle(1,2)\rangle = \{e, (1,2)\}$。这是一个2阶子群。它在 $S_3$ 中不是正规的(例如 $(1,3)(1,2)(1,3)^{-1}=(2,3) \notin H$)。
- $K = \langle(2,3)\rangle = \{e, (2,3)\}$。这也是一个2阶子群,同样不是正规的。
- 计算积集 $HK$:
- $HK = \{hk \mid h \in H, k \in K\}$。
- $e \cdot e = e = 1$ (为了和原文符号统一,用1表示单位元)。
- $e \cdot (2,3) = (2,3)$。
- $(1,2) \cdot e = (1,2)$。
- $(1,2) \cdot (2,3) = (1,2,3)$。
- 所以,$HK = \{1, (1,2), (2,3), (1,2,3)\}$。
- 验证 $HK$ 是否是子群:
- 方法一:检查元素个数。
- $HK$ 这个集合里有4个元素,所以 $\#(HK) = 4$。
- 拉格朗日定理指出,子群的阶(元素的个数)必须能整除整个群的阶。
- 这里,群 $G=S_3$ 的阶是 $3! = 6$。
- 数字 4 不能整除数字 6。
- 因此,$HK$ 不可能是一个子群。这是最快捷的判断方法。
- 方法二:检查封闭性 (虽然已经有结论了,但可以验证一下)。
- 取 $HK$ 中的元素 $(1,2)$ 和 $(2,3)$。它们的乘积是 $(1,2)(2,3)=(1,2,3)$,这个元素在 $HK$ 中。
- 取 $HK$ 中的元素 $(1,2,3)$ 和 $(1,2,3)$。它们的乘积是 $(1,2,3)(1,2,3)=(1,3,2)$。但是 $(1,3,2)$ 并不在集合 $HK=\{1, (1,2), (2,3), (1,2,3)\}$ 中。
- 所以 $HK$ 对乘法不封闭,故不是一个子群。
- $H K=\{1,(1,2),(2,3),(1,2)(2,3)=(1,2,3)\}$:
- 这是一个集合的构建过程。
- $H = \{1, (1,2)\}$
- $K = \{1, (2,3)\}$
- $1 \cdot 1 = 1$
- $1 \cdot (2,3) = (2,3)$
- $(1,2) \cdot 1 = (1,2)$
- $(1,2) \cdot (2,3) = (1,2,3)$
- 将所有结果收集起来,并去除重复项(本例无重复),得到 $HK = \{1, (1,2), (2,3), (1,2,3)\}$。
- $\#(H K)=4$: 符号 $\#(S)$ 或 $|S|$ 表示集合 $S$ 的基数(元素的个数)。这里是说 $HK$ 这个集合里有4个元素。
本段本身就是一个完整的具体数值示例,因此无需再提供新的示例。它已经用 $G=S_3$ 完美地展示了当两个子群都不是正规时,它们的积集 $HK$ 如何“失败”成为一个子群。
- 易错点: 误以为正规性是可以传递的。这是群论初学者一个非常常见的错误。必须牢记 $H \triangleleft K \triangleleft G \not\Rightarrow H \triangleleft G$。
- 易错点: 在计算 $HK$ 时,忘记了群乘法不满足交换律,并且漏掉了某些组合或计算错误。
- 易错点: 看到 $HK$ 就想当然地认为它是一个子群。必须先验证前提条件($H$ 或 $K$ 正规)或者直接用子群的定义去检验。
- 边界情况: 正如命题2.3.14(iv)所示,只要 $H$ 和 $K$ 中有一个是正规的,$HK$ 就是子群。这个Remark展示的是两者都非正规的情况。如果其中一个正规,例如在 $S_3$ 中取正规子群 $A_3 = \{1, (1,2,3), (1,3,2)\}$ 和非正规子群 $H=\langle(1,2)\rangle = \{1, (1,2)\}$。那么它们的积集 $A_3H$ 是一个子群吗?
- $A_3H = \{1, (1,2,3), (1,3,2), (1,2), (1,2,3)(1,2)=(2,3), (1,3,2)(1,2)=(1,3)\}$
- $A_3H = \{1, (1,2), (1,3), (2,3), (1,2,3), (1,3,2)\} = S_3$。
- $S_3$ 当然是 $S_3$ 的子群。这验证了命题2.3.14(iv)。
这段附注(Remark)通过两个方面对正规子群的理解进行了深化和澄清:
- 正规性不传递: 指出了 $H \triangleleft K \triangleleft G$ 的链式结构不能保证 $H \triangleleft G$,打破了对正规性具有传递性的错误直觉。
- 积集构成子群的必要条件: 通过在 $S_3$ 中构造一个具体的反例,清晰地表明如果两个子群都不是正规的,它们的积集 $HK$ 不一定是一个子群,从而反向强调了命题2.3.14(iv)中正规性前提的重要性。
本段的目的是通过“反例”和“警告”来帮助读者精确地掌握概念的边界。数学不仅要知道“是什么”,还要知道“不是什么”。通过指出常见的误区(如正规性的传递性)和使结论失效的条件($HK$何时不是子群),可以极大地加深对正规子群和相关命题的理解,避免在未来的应用和证明中犯错。
- 正规性不传递: 想象公司里的部门。研发部(H)的管理规则在整个技术中心(K)内是统一协调的($H \triangleleft K$)。技术中心(K)的政策在整个公司(G)内是统一协调的($K \triangleleft G$)。但是,一个销售部的人(g)直接去干涉研发部的一个项目(h),即 $ghg^{-1}$,他可能并不懂研发部的内部规则,导致项目被搅乱,变成了一个不属于原来研发部的东西 (但可能还在技术中心的范畴内)。也就是说,销售部的协调能力只到技术中心这一层,穿不透到研发部内部。
- HK非子群: 想象两组人,A组只说英语($H$),B组只说德语($K$),而且他们都很固执,不学对方的语言,也没有统一的交流规则(非正规)。他们聚在一起($HK$),一个A组人对一个B组人说话,完全无法沟通。这个混合群体($HK$)无法形成一个有凝聚力的、能有效协作的团队(子群),因为缺乏基本的交流规则(封闭性等)。而如果其中A组是正规的,就好像他们是双语接待员,总能把德语转换成英语再传递信息,使得整个团队可以运作起来。
- 正规性不传递: 想象一套俄罗斯套娃。最里面的小娃(H)相对于中间的娃(K)是居中的($H \triangleleft K$)。中间的娃(K)相对于最外面的大娃(G)也是居中的($K \triangleleft G$)。但是,如果你直接摇晃最外面的大娃(G),最里面的小娃(H)可能会在中间娃(K)的内部晃来晃去,不再相对于大娃(G)保持居中($H \not\triangleleft G$)。
- HK非子群: 想象两种乐高积木,一种是方形的($H$),一种是圆形的($K$),并且它们没有设计成可以互相拼接的样子(非正规)。你把它们倒在一起($HK$),可以得到一堆积木。但是你没法用这堆积木搭出一个稳固的结构(不是子群),因为它们之间无法“封闭”地连接起来。如果你拿起一个方块和一个圆块,拼在一起,再想跟另一个方块拼,可能就失败了。
32. 正规子群与同态
12.1. 同态基本定理
2. 1.1. 同态与商群的关系
📜 [原文5]
3.1. 同态基本定理. We begin with a discussion of the relationship between 商群与同态。If $G$ is a 群 and $H \triangleleft G$,then we have the 商群 $G / H$ and the 商同态 $\pi: G \rightarrow G / H$,with 核 $\operatorname{Ker} \pi=H$。Conversely, suppose that $f: G_{1} \rightarrow G_{2}$ is a 同态 from a 群 $G_{1}$ to another 群 $G_{2}$。We want to analyze $f$ in terms of 商群。A first step is the following:
这段话是第一同构定理章节的引言,旨在建立同态与商群这两个核心概念之间的双向联系。
- 章节标题: “同态基本定理”,这预示着接下来的内容是群论中一个极其核心和基础的定理。这个定理在很多文献中也被称为“第一同构定理”。
- 建立联系: 作者开宗明义,指出本节的目的是讨论“商群与同态”之间的关系。这种关系是双向的。
- 方向一:从商群到同态 (已知)
- 起点: 我们有一个群 $G$ 和它的一个正规子群 $H \triangleleft G$。
- 构造: 基于这个前提,我们可以定义商群 $G/H$。
- 自然的映射: 伴随着商群的定义,天然存在一个从原群 $G$ 到商群 $G/H$ 的映射,称为“商同态”或“自然同态”,通常用 $\pi$ 表示。
- 商同态的定义: $\pi: G \rightarrow G/H$ 的定义是 $\pi(g) = gH$。它将 $G$ 中的每个元素 $g$ 映射到它所在的 $H$ 的陪集。
- 商同态的性质: 这个映射 $\pi$ 是一个满同态(因为 $G/H$ 中的每个陪集 $gH$ 都至少有一个元素 $g$ 从 $G$ 中映射过来)。
- 商同态的核: 同态的核(Kernel)被定义为所有被映射到目标群单位元的元素的集合。在商群 $G/H$ 中,单位元是陪集 $H$ (也就是 $eH$)。因此,$\text{Ker } \pi = \{g \in G \mid \pi(g) = H\} = \{g \in G \mid gH = H\}$。根据陪集的性质, $gH=H$ 当且仅当 $g \in H$。所以,我们得到一个至关重要的结论:商同态 $\pi$ 的核正好就是我们用来构造商群的那个正规子群 $H$。即 $\text{Ker } \pi = H$。
- 小结: 这个方向告诉我们,任何一个商群的构造过程,都内在地定义了一个以该正规子群为核的满同态。
- 方向二:从同态到商群 (待分析)
- 起点: 现在反过来,我们有一个任意的群同态 $f: G_1 \rightarrow G_2$。我们对这个同态一无所知,只知道它保持群的运算结构。
- 目标: 作者提出,我们的目标是“in terms of 商群”来分析这个同态 $f$。也就是说,我们希望把这个抽象的同态 $f$ 与我们刚刚讨论过的、更具体的商群结构联系起来。
- 第一步: 为了用商群来理解 $f$,我们首先需要一个正规子群。那么,从同态 $f$ 本身,我们能自然地找到一个正规子群吗?答案是肯定的,那就是 $f$ 的核。接下来的引理将证明这一点。
这段引言精炼地勾勒出了同态与商群之间深刻的对偶关系。一方面,由正规子群 $H$ 构造的商群 $G/H$ 自然地引出以 $H$ 为核的商同态 $\pi$。另一方面,任意一个同态 $f$ 也内涵了一个正规子群——它的核,这暗示了我们可以利用这个核来构造一个商群,从而反过来理解 $f$ 本身。这为第一同构定理的提出和证明铺平了道路,该定理将精确地阐明这种对偶关系:任何同态的像都同构于其定义域群对核的商群。
本段的目的是设置舞台,引入第一同构定理的核心思想。通过建立商群与同态之间的双向联系,激发读者思考:既然从 $H \triangleleft G$ 能得到核为 $H$ 的同态 $\pi$,那么从一个核为 $K$ 的同态 $f$ 是否也能得到一个与 $K$ 相关的商群,并且这个商群与 $f$ 有什么关系?这种设问式的引导是启发式教学的典型方法,让读者带着问题进入下一部分的学习。
想象一个投影仪和屏幕。
- 方向一 (从商群到同态): 你有一张三维的复杂物体(群 $G$),你决定忽略它的厚度信息(模掉正规子群 $H$),只看它在墙上的二维投影(商群 $G/H$)。这个“投影”的动作本身,就是一个映射(商同态 $\pi$)。所有在投影方向上重叠在一起的点(厚度方向上的点)都被映射到了投影图像上的同一个点。那些被映射到投影原点的点,就是那些在“零厚度”平面上的点,这个平面就是核 $H$。
- 方向二 (从同态到商群): 现在你只知道有一个投影过程 $f$ (一个同态),它把一个物体 $G_1$ 变成了某个图像 $G_2$。你想理解这个投影过程。一个自然的想法是,研究哪些点被这个投影过程“压扁”了,也就是哪些点被映射到了图像的原点。这些被“压扁”的点的集合,就是核 $\text{Ker } f$。这个核本身构成了一个特殊的子结构(正规子群)。接下来的定理会告诉你,原来这个投影图像 $G_2$ (的像 $\text{Im} f$) 的结构,和你直接把原物体 $G_1$ 按照这个“压扁”的方式(即模掉核)所得到的结构 $G_1/\text{Ker } f$ 是一模一样的(同构)。
- 方向一: 你有一堆彩色积木(群 $G$),你决定把所有“蓝色”的积木都看成是“一样的”(正规子群 $H$)。然后你把积木按颜色分类,得到“红色类”、“黄色类”、“蓝色类”等几个大盒子(商群 $G/H$)。从“任意一块积木”映射到“它所属的颜色盒子”,这个过程就是商同态 $\pi$。“蓝色”积木构成的集合 $H$ 就是这个映射的核。
- 方向二: 你有一个函数 $f$,它能告诉你每块积木的“重量”(映射到群 $G_2$)。你想搞清楚这个函数。你发现,所有“蓝色”的积木,它们的“重量”都是0(被映射到单位元)。这个“蓝色积木”的集合就是核 $\text{Ker } f$。同构定理将告诉你,你最终得到的“重量”的种类和结构(像 $\text{Im} f$),和你直接按颜色分类得到的“颜色盒子”的结构(商群 $G/\text{Ker } f$)是完全一样的。
2. 1.2. 引理 3.1.1:同态的核是正规子群
📜 [原文6]
引理 3.1.1. If $f: G_{1} \rightarrow G_{2}$ is a 同态,那么核 $\operatorname{Ker} f$是$G_{1}$的正规子群。
证明. We must show that, for all $h \in \operatorname{Ker} f$ and for all $g \in G, g h g^{-1} \in \operatorname{Ker} f$,or equivalently that $f\left(g h g^{-1}\right)=1$。But, since $h \in \operatorname{Ker} f$,根据定义,$f(h)=1$,hence
Thus $\operatorname{Ker} f \triangleleft G_{1}$。
这个引理是连接同态和商群的桥梁,它确立了从任意一个同态出发,我们总能获得一个正规子群,即该同态的核。
- 引理陈述: 任何一个群同态 $f: G_1 \rightarrow G_2$,它的核 $\text{Ker } f$ 不仅仅是 $G_1$ 的一个子群(这在更早的章节通常已经证明),而且还是一个正规子群。
- 证明目标:
- 首先回顾核的定义: $\text{Ker } f = \{x \in G_1 \mid f(x) = e_2\}$,其中 $e_2$ 是目标群 $G_2$ 的单位元。为了简洁,通常也写成 $f(x)=1$。
- 回顾正规子群的定义: 一个子群 $N \leq G_1$ 是正规的,如果对于任意 $g \in G_1$ 和任意 $n \in N$,都有 $gng^{-1} \in N$。
- 所以,我们的目标是证明:对于任意 $g \in G_1$ 和任意 $h \in \text{Ker } f$,我们必须证明 $ghg^{-1}$ 这个元素也属于 $\text{Ker } f$。
- 应用核的定义来转化证明目标:
- 要证明 $ghg^{-1} \in \text{Ker } f$,根据核的定义,我们只需要证明 $f(ghg^{-1}) = 1$ 即可。这就是原文中 "or equivalently that $f\left(g h g^{-1}\right)=1$" 这句话的来源。
- 开始证明:
- 利用同态性质: 因为 $f$ 是一个同态,所以它可以把乘积的像拆成像的乘积:$f(ghg^{-1}) = f(g)f(h)f(g^{-1})$。
- 利用 $h$ 在核中: 我们知道 $h \in \text{Ker } f$,所以根据定义,$f(h) = 1$。代入上式,得到 $f(g) \cdot 1 \cdot f(g^{-1})$。
- 利用同态对逆元的性质: 同态还保持逆元运算,即 $f(g^{-1}) = (f(g))^{-1}$。代入上式,得到 $f(g) \cdot 1 \cdot (f(g))^{-1}$。
- 化简: 在目标群 $G_2$ 中,任何元素乘以单位元 1 等于其自身,所以表达式变为 $f(g) \cdot (f(g))^{-1}$。
- 得到最终结果: 在任何群中,一个元素乘以它自己的逆元,结果都是单位元 1。所以 $f(g) \cdot (f(g))^{-1} = 1$。
- 完成证明: 我们已经成功证明了 $f(ghg^{-1}) = 1$,这意味着 $ghg^{-1} \in \text{Ker } f$。由于这个结论对于任意的 $g \in G_1$ 和 $h \in \text{Ker } f$ 都成立,所以根据定义,$\text{Ker } f$ 是 $G_1$ 的一个正规子群。
- $\operatorname{Ker} f$: 同态 $f$ 的核 (Kernel)。
- $f\left(g h g^{-1}\right)=f(g) f(h) f\left(g^{-1}\right)=f(g) \cdot 1 \cdot f(g)^{-1}=1$: 这是整个证明的核心推导链。
- 第一步 $f(ghg^{-1}) = f(g)f(h)f(g^{-1})$: 这是因为 $f$ 是同态,它保持群的运算结构。$f(ab)=f(a)f(b)$ 对所有 $a,b$ 成立。这里我们把 $ghg^{-1}$ 看作 $g \cdot h \cdot g^{-1}$ 的乘积。
- 第二步 $\dots = f(g) \cdot 1 \cdot f(g)^{-1}$: 这是因为 $h$ 是从核 $\text{Ker } f$ 中取出的,所以 $f(h)=1$ (目标群的单位元)。
- 第三步 $\dots = 1$: 这是因为 $f(g^{-1}) = f(g)^{-1}$ (同态保持逆元),所以整个表达式是 $f(g) \cdot f(g)^{-1}$,这在目标群中等于单位元 1。
- 示例: 考虑行列式映射 $\det: GL_n(\mathbb{R}) \rightarrow \mathbb{R}^*$。
- 同态: $f = \det$。这是一个从一般线性群 $GL_n(\mathbb{R})$ (所有 $n \times n$ 的可逆实数矩阵在矩阵乘法下构成的群) 到非零实数乘法群 $\mathbb{R}^* = (\mathbb{R} \setminus \{0\}, \times)$ 的群同态。这是因为矩阵乘积的行列式等于行列式的乘积: $\det(AB) = \det(A)\det(B)$。
- 核: $\text{Ker}(\det) = \{A \in GL_n(\mathbb{R}) \mid \det(A) = 1\}$。目标群 $\mathbb{R}^*$ 的单位元是 1。这个核有一个专门的名字,叫做特殊线性群,记作 $SL_n(\mathbb{R})$。
- 引理的应用: 根据本引理,我们不需要任何额外的计算,就可以直接得出结论:$SL_n(\mathbb{R})$ 是 $GL_n(\mathbb{R})$ 的一个正规子群。即 $SL_n(\mathbb{R}) \triangleleft GL_n(\mathbb{R})$。
- 验证 (可选): 我们可以手动验证一下。取任意矩阵 $A \in SL_n(\mathbb{R})$ (即 $\det(A)=1$) 和任意可逆矩阵 $B \in GL_n(\mathbb{R})$。我们需要证明共轭矩阵 $BAB^{-1}$ 也在 $SL_n(\mathbb{R})$ 中。
计算其行列式:
$\det(BAB^{-1}) = \det(B) \det(A) \det(B^{-1})$
$= \det(B) \cdot 1 \cdot (\det(B))^{-1}$
$= 1$。
因为 $BAB^{-1}$ 的行列式也是 1,所以 $BAB^{-1} \in SL_n(\mathbb{R})$。因此 $SL_n(\mathbb{R})$ 确实是正规子群。这个例子完美地印证了引理的结论。
- 易错点: 忘记同态的性质。整个证明完全依赖于 $f(ab)=f(a)f(b)$ 和 $f(a^{-1})=f(a)^{-1}$ 这两个基本性质。如果对同态定义不熟,就无法进行证明。
- 易错点: 混淆 $G_1$ 和 $G_2$ 中的运算。例如,在 $f(g) \cdot 1 \cdot f(g)^{-1}$ 这一步,所有的运算都是在目标群 $G_2$ 中进行的。
- 边界情况:
- 如果 $f$ 是一个单射(一对一)同态,那么它的核只包含单位元 $\text{Ker } f = \{e_1\}$。平凡子群 $\{e_1\}$ 总是任何群的正规子群,所以引理依然成立。
- 如果 $f$ 是将所有元素都映射到单位元的平凡同态,$f(g) = e_2$ for all $g \in G_1$。那么 $\text{Ker } f = G_1$。一个群总是其自身的正规子群,所以引理也成立。
该引理揭示了同态与正规子群之间的一个基本联系:任何群同态的核都天然地是一个正规子群。证明过程非常直接,仅仅利用了同态保持乘法和逆元运算的定义,以及正规子群的共轭封闭性定义。这个引理是第一同构定理的基石,因为它保证了我们总能从一个同态 $f$ 出发,找到一个正规子群 $\text{Ker } f$,从而可以构造商群 $G_1/\text{Ker } f$,为后续的同构关系讨论提供了对象。
本引理的存在目的就是为了给第一同构定理的证明提供一个关键的、必不可少的步骤。它解决了“给定一个同态 $f$,我们如何构造一个与之相关的商群?”这个问题的第一部分,即“如何找到用于构造商群的正规子群?”。答案就是:直接取 $f$ 的核。
再次使用投影仪模型。一个同态 $f$ 是一个投影过程。核 $\text{Ker } f$ 是所有被投影到原点的点构成的集合。为什么这个集合是正规子群?
想象你在原物体空间 $G_1$ 中进行一个“共轭操作” $g(\cdot)g^{-1}$。这可以理解为:
- 做一个操作 $g^{-1}$ (比如向右移动)。
- 放置一个在核中的物体 $h$。
- 再做一个反向操作 $g$ (比如向左移动)。
整个过程是 $ghg^{-1}$。引理说的是,如果 $h$ 本来是被投影到原点的,那么经过这一番“先移走,再放,再移回来”的折腾之后,新的物体 $ghg^{-1}$ 依然会被投影到原点。
这是因为同态(投影)的性质。$f(ghg^{-1}) = f(g)f(h)f(g)^{-1}$。这可以理解为,物体在移动前后的投影效果,等于先对投影图像进行移动,再投影物体,再把投影图像移回去。因为 $f(h)=1$ (h被投影到原点),所以整个过程变成了 $f(g) \cdot 1 \cdot f(g)^{-1} = 1$。这意味着,对原像做共轭操作,等价于对像做共轭操作。既然 $h$ 的像是单位元 1,对单位元做任何共轭操作 $f(g) \cdot 1 \cdot f(g)^{-1}$ 结果还是单位元 1。所以 $ghg^{-1}$ 的像也必然是单位元 1,即 $ghg^{-1}$ 仍然在核中。
想象一个滤镜(同态 $f$),它可以滤掉(映射到单位元“无色”)所有“蓝色”的物体(核 $\text{Ker } f$)。现在,你有一个“蓝色”的球 $h$。你把它用一个夹子 $g$ 夹起来,在空中旋转了半圈(这个动作是 $g(\cdot)g^{-1}$)。那个被旋转后的球 $ghg^{-1}$ 还是不是蓝色的?当然是。因为夹取和旋转这个动作 $g$ 不会改变球本身的颜色。所以,经过这番操作后,它通过滤镜时,依然会被滤掉(映射到“无色”)。因此,旋转后的球 $ghg^{-1}$ 仍然在“蓝色物体”这个集合(核)中。这个“颜色不会因旋转而改变”的性质,就直观地对应了核的正规性。
2. 1.3. 第一同构定理
📜 [原文7]
第一同构定理,also called the 同态基本定理,states among other things that every 同态 between two 群s is built up out of three basic types of 同态s: 商同态、同构和包含映射。
定理 3.1.2. Let $G_{1}$ and $G_{2}$ be 群s, let $f: G_{1} \rightarrow G_{2}$ be a 同态,and set $K=\operatorname{Ker} f \triangleleft G_{1}$ and $H=\operatorname{Im} f \leq G_{2}$。Then $G_{1} / K \cong H$。More precisely, if $\pi: G_{1} \rightarrow G_{1} / K$ is the 商同态 and if $i: H \rightarrow G_{2}$ is the 包含同态,then there is a unique 同构 $\tilde{f}: G_{1} / K \rightarrow H$ such that $f=i \circ \tilde{f} \circ \pi$。The situation is summarized by the following 图示:
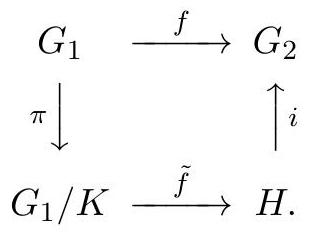
这部分正式陈述了第一同构定理(或称同态基本定理)。这个定理是群论乃至整个抽象代数的基石之一。
- 定理的非正式描述:
- 定理首先给出了一个高度概括但非常深刻的描述:任何一个群同态,无论它看起来多么复杂,本质上都可以被“分解”成三个标准、简单的步骤(三种基本的同态):
- 商同态 ($\pi$): 这是从一个群 $G_1$ 到其商群 $G_1/K$ 的映射,可以理解为一种“压缩”或“打包”的过程,把核 $K$ 里的所有元素都压缩成一个点(单位元)。
- 同构 ($\tilde{f}$): 这是一个结构完全相同的双射。它表明“压缩”后的群 $G_1/K$ 和原同态的目标像 $H$ 在结构上是一模一样的。这是定理的核心。
- 包含映射 ($i$): 这是从子群 $H$ 到包含它的大群 $G_2$ 的映射,简单地把 $H$ 的元素看作是 $G_2$ 的元素。这可以理解为一种“放置”或“嵌入”的过程。
- 这个描述的意义在于,它将任意同态 $f$ 的行为模式标准化了:$f$ 的作用,无非就是先把定义域 $G_1$ 按照其核 $K$ “捏合”一下得到商群 $G_1/K$,然后发现这个“捏合”后的东西恰好就是同态的像 $H$,最后再把这个像 $H$ 放到目标空间 $G_2$ 中去。
- 定理的正式陈述 (定理 3.1.2):
- 前提:
- 有两个群 $G_1, G_2$。
- 有一个从 $G_1$ 到 $G_2$ 的同态 $f: G_1 \rightarrow G_2$。
- 定义符号:
- $K = \text{Ker } f$: $f$ 的核。根据引理3.1.1,我们知道 $K$ 是 $G_1$ 的一个正规子群 ($K \triangleleft G_1$)。
- $H = \text{Im } f$: $f$ 的像,即 $f(G_1) = \{f(g) \mid g \in G_1\}$。根据同态的性质,我们知道 $H$ 是 $G_2$ 的一个子群 ($H \leq G_2$)。
- 核心结论: $G_1/K \cong H$。
- 左边: $G_1/K$ 是源群 $G_1$ 关于其核 $K$ 的商群。
- 右边: $H$ 是同态 $f$ 的像群。
- $\cong$: 表示这两个群是同构的。这意味着存在一个从 $G_1/K$ 到 $H$ 的双射,并且这个双射保持群的运算结构。
- 这个结论的威力在于,它把对抽象同态 $f$ 的研究,转化为了对更具体的商群 $G_1/K$ 的研究。
- 定理的更精确陈述 (交换图):
- 这部分用范畴论的语言(交换图)来更精确地描述这个同构关系。
- 涉及的映射:
- $f: G_1 \rightarrow G_2$: 我们开始时拥有的任意同态。
- $\pi: G_1 \rightarrow G_1/K$: 商同态,定义为 $\pi(g) = gK$。
- $i: H \rightarrow G_2$: 包含同态,定义为 $i(h) = h$ (只是把 $h$ 看作 $G_2$ 的元素)。
- 核心断言: 存在一个唯一的同构 $\tilde{f}: G_1/K \rightarrow H$,使得 $f = i \circ \tilde{f} \circ \pi$。
- $f = i \circ \tilde{f} \circ \pi$ 的含义: 这意味着从 $G_1$ 到 $G_2$ 有两条路径:
- 直接走 $f$。
- 绕道走 $\pi$,然后走 $\tilde{f}$,最后走 $i$。
定理说这两条路的结果是完全一样的。用一个元素 $g \in G_1$ 来说明:$f(g) = i(\tilde{f}(\pi(g)))$。
- 图示的意义:
- 图中的箭头代表同态。
- $G_1$ 在左上角, $G_2$ 在右下角。
- 从 $G_1$ 到 $G_2$ 的直接箭头是 $f$。
- $G_1 \xrightarrow{\pi} G_1/K \xrightarrow{\tilde{f}} H \xrightarrow{i} G_2$ 是一条迂回的路径。
- 图是“交换的”(commutative),意味着从任意一个起点到任意一个终点,所有路径的结果都相同。在这里就是 $f = i \circ \tilde{f} \circ \pi$。
- $\tilde{f}$ 上的波浪线和同构符号 ($\cong$) 强调了它是整个构造的核心,是一个同构。
第一同构定理是群论的中心定理之一。它揭示了任何群同态 $f: G_1 \rightarrow G_2$ 的内在结构。定理的核心思想是,同态的像($\text{Im } f$)与定义域群对核($\text{Ker } f$)的商群($G_1/\text{Ker } f$)在结构上是完全一样的(同构)。更精确地,原同态 $f$ 可以被唯一地分解为一个商同态、一个同构和一个包含映射的复合。这个定理为我们提供了一个强大的工具,可以通过构造一个合适的同态来识别未知的商群,或者通过分析商群来理解同态的性质。
这个定理的存在目的,是为整个抽象代数提供一个基本的结构性定理。它统一了同态、正规子群、商群和同构这四个核心概念,揭示了它们之间密不可分的联系。它使得我们可以:
- 识别商群: 想要知道 $G/N$ 是个什么群?只需构造一个从 $G$ 出发,且核正好是 $N$ 的同态 $f$,那么 $G/N$ 就同构于 $f$ 的像 $\text{Im } f$。很多时候,$\text{Im } f$ 是一个我们非常熟悉的群。
- 理解同态: 想要理解一个复杂的同态 $f$?通过研究它的核与像,我们可以把它分解成标准、简单的步骤,从而看清其本质。
- 构造群: 它可以作为从已知群构造新群的理论依据。
想象一个黏土工匠(同态 $f$)要把一大块黏土(群 $G_1$)塑造成一个雕塑(群 $G_2$ 的一个子群 $H$)。
- 核 $K = \text{Ker } f$: 在塑造过程中,有一些黏土被挤压掉了,或者说被揉捏到了一起,无法分辨了。这些“被浪费掉”或“被整合掉”的黏土就是核。引理 3.1.1 告诉我们,这些“废料”本身具有很好的对称性(正规子群)。
- 商群 $G_1/K$: 工匠在塑造前,先把所有注定要被“浪费”的黏土 $K$ 全部移除,把剩下的黏土重新组织起来。这个“预处理”过的黏土块就是商群 $G_1/K$。
- 像 $H = \text{Im } f$: 工匠最终完成的雕塑成品就是像 $H$。
- 第一同构定理 $G_1/K \cong H$: 定理告诉我们一个惊人的事实:工匠经过“预处理”后得到的黏土块 $G_1/K$,其形状、大小、结构已经和最终的雕塑成品 $H$ 一模一样了!从 $G_1/K$ 到 $H$ 的过程($\tilde{f}$)只是一个“上釉”或者“抛光”的过程,没有改变任何结构,是一个同构。
- 交换图 $f = i \circ \tilde{f} \circ \pi$: 这描述了工匠的整个工作流程。把黏土 $G_1$ 变成雕塑 $H$ (并放入展厅 $G_2$),这个过程 $f$ 可以分解为:
- 先把“废料” $K$ 去掉,得到“预处理”黏土块 $G_1/K$ (过程 $\pi$)。
- 对“预处理”黏土块进行“抛光”,得到成品 $H$ (过程 $\tilde{f}$)。
- 把成品 $H$ 放到展厅 $G_2$ 中 (过程 $i$)。
想象用一台榨汁机(同态 $f$)处理一堆水果(群 $G_1$),得到果汁(群 $G_2$ 的子群 $H$)。
- 核 $K = \text{Ker } f$: 榨汁过程中产生的果渣,就是核。
- 商群 $G_1/K$: 如果我们有一种魔法,能预先从水果中分离出所有会变成“果渣”的部分,剩下的“纯果肉”部分就是商群 $G_1/K$。
- 像 $H = \text{Im } f$: 最终得到的纯果汁就是像。
- 第一同构定理 $G_1/K \cong H$: 定理告诉你,我们用魔法分离出的“纯果肉”($G_1/K$) 和最终榨出的“纯果汁”($H$),在营养成分和结构上是完全等价的(同构)。从“纯果肉”到“纯果汁”的过程 $\tilde{f}$ 只是一个形态的转换。
- 交换图 $f = i \circ \tilde{f} \circ \pi$: 整个榨汁过程 $f$ (从水果到放在杯子里的果汁) 可以分解为:
- 分离果渣,得到纯果肉 ($\pi$)。
- 将纯果肉榨成纯果汁 ($\tilde{f}$)。
- 将纯果汁倒入杯子 ($G_2$) 中 ($i$)。
这三个步骤合起来,就等价于直接榨汁。
2. 1.4. 第一同构定理的证明
📜 [原文8]
证明. We begin by trying to define the 函数 $\tilde{f}: G_{1} / K \rightarrow H$。Clearly, the only natural way to define $\tilde{f}$ on a 陪集 $g K$ is to set $\tilde{f}(g K)=f(g)$。In fact, this is also forced on us if we want $f=i \circ \tilde{f} \circ \pi$,because we must have $f(g)=i(\tilde{f}(\pi(g)))=i(\tilde{f}(g K))$,so $\tilde{f}(g K)=f(g)$。We must check that this is 良定义的,i.e. independent of the choice of 代表元 $g \in g K$。If instead we choose a different 代表元 of $g K$,necessarily of the form $g k$,then $f(g k)=f(g) f(k)=f(g) \cdot 1=f(g)$,hence $\tilde{f}$ is 良定义的,and its values $\tilde{f}(g K)=f(g)$ lie in $H=\operatorname{Im} f$。So we can view $\tilde{f}$ as a 函数 $G_{1} / K \rightarrow H$,and it is clearly 满射。Moreover, $\tilde{f}$ is a 同态 since
To see that it is an 同构,since we know that it is 满射,it suffices to show that it is 单射。Equivalently we must show that 核 $\operatorname{Ker} \tilde{f}=\{K\}$,the single element set consisting of the identity in $G_{1} / K$,namely the 单位陪集。Suppose that $\tilde{f}(g K)=1$。By definition $f(g)=\tilde{f}(g K)=1$,hence $g \in K$ and therefore $g K=K$。Thus 核 $\operatorname{Ker} \tilde{f}=\{K\}$ and hence $\tilde{f}$ is 单射,thus an 同构。(Compare also Remark 1.2.5.)
Finally we establish that $f=i \circ \tilde{f} \circ \pi$。To see that these two 函数 are equal, it is enough to check that they take the same value for every $g \in G$。But
where when we write $i(f(g))$ we view the term $f(g)$ as an element of $H=\operatorname{Im} f$ and in the final step of the equality we view $f(g)$ as an element of $G_{2}$。Thus $i \circ \tilde{f} \circ \pi(g)=f(g)$ for all $g \in G_{1}$,so that $f=i \circ \tilde{f} \circ \pi$。
这部分是第一同构定理的详细证明。证明的逻辑非常清晰,分为四个主要步骤:
- 定义映射 $\tilde{f}$ 并证明其良定义性。
- 证明 $\tilde{f}$ 是一个满同态。
- 证明 $\tilde{f}$ 是一个单射,从而证明它是同构。
- 证明交换图成立,即 $f=i \circ \tilde{f} \circ \pi$。
第一步:定义映射 $\tilde{f}$ 并证明其良定义性 (Well-defined)
- 定义 $\tilde{f}$: 我们的目标是建立从商群 $G_1/K$到像群 $H$ 的一个映射 $\tilde{f}$。商群的元素是陪集,形如 $gK$。最自然、也是唯一合理的定义方式就是:将陪集 $gK$ 映射到原先 $g$ 被 $f$ 映射到的地方。即定义 $\tilde{f}(gK) = f(g)$。
- 作者还补充说,如果我们想要满足交换图 $f = i \circ \tilde{f} \circ \pi$,这个定义是“被逼无奈”的唯一选择。因为 $f(g) = i(\tilde{f}(\pi(g))) = i(\tilde{f}(gK)) = \tilde{f}(gK)$ (因为 $i$ 是包含映射,不起实际作用),所以必须这么定义。
- 证明良定义性: 这是定义在商集上的映射最关键的一步。一个陪集 $gK$ 可以由不同的代表元来表示。例如,$g$ 和 $gk$ (其中 $k \in K$) 都代表同一个陪集。我们必须证明,无论我们选择哪个代表元,$\tilde{f}$ 的映射结果都是一样的。否则,这个映射就是模糊不清、没有意义的。
- 设 $g'$ 是 $gK$ 的另一个代表元。那么 $g'$ 必然可以写成 $g' = gk$ 的形式,其中 $k$ 是核 $K$ 中的某个元素。
- 我们来计算 $\tilde{f}(g'K)$,根据定义,它等于 $f(g')$。
- $f(g') = f(gk)$。
- 因为 $f$ 是同态,所以 $f(gk) = f(g)f(k)$。
- 因为 $k \in K = \text{Ker } f$,所以根据核的定义,$f(k) = 1$ (目标群的单位元)。
- 所以 $f(gk) = f(g) \cdot 1 = f(g)$。
- 我们发现,用新的代表元 $g'$ 计算出的结果 $f(g')$ 和用旧的代表元 $g$ 计算出的结果 $f(g)$ 是完全一样的!
- 这就证明了 $\tilde{f}(gK) = f(g)$ 这个定义是良定义的,它不依赖于陪集代表元的选择。
第二步:证明 $\tilde{f}$ 是满同态
- 证明 $\tilde{f}$ 是同态: 我们需要证明 $\tilde{f}$ 保持群运算。即 $\tilde{f}((g_1K)(g_2K)) = \tilde{f}(g_1K)\tilde{f}(g_2K)$。
- 从左边开始:$\tilde{f}((g_1K)(g_2K))$
- 根据商群的乘法定义:$(g_1K)(g_2K) = (g_1g_2)K$。所以左边等于 $\tilde{f}((g_1g_2)K)$。
- 根据我们对 $\tilde{f}$ 的定义:$\tilde{f}((g_1g_2)K) = f(g_1g_2)$。
- 因为 $f$ 本身是同态:$f(g_1g_2) = f(g_1)f(g_2)$。
- 再次使用 $\tilde{f}$ 的定义,把 $f(g_1)$ 和 $f(g_2)$ 换回去:$f(g_1) = \tilde{f}(g_1K)$,$f(g_2) = \tilde{f}(g_2K)$。
- 所以,我们得到 $\tilde{f}((g_1K)(g_2K)) = \tilde{f}(g_1K)\tilde{f}(g_2K)$。
- 证明完毕,$\tilde{f}$ 是一个同态。
- 证明 $\tilde{f}$ 是满射 (Surjective): 我们需要证明,对于像群 $H$ 中的任意一个元素 $h$,都存在商群 $G_1/K$ 中的一个元素(一个陪集)被 $\tilde{f}$ 映射到 $h$。
- 取任意 $h \in H = \text{Im } f$。
- 根据像的定义,必然存在一个 $g \in G_1$,使得 $f(g) = h$。
- 现在我们考虑商群中的元素 $gK$。
- 根据 $\tilde{f}$ 的定义,$\tilde{f}(gK) = f(g)$。
- 而我们知道 $f(g) = h$,所以 $\tilde{f}(gK) = h$。
- 我们成功地为任意的 $h$ 找到了一个原像 $gK$。
- 因此,$\tilde{f}$ 是满射。这一步在原文中被描述为“clearly 满射”。
第三步:证明 $\tilde{f}$ 是单射,从而证明是同构
- 证明 $\tilde{f}$ 是单射 (Injective): 对于一个同态而言,证明它是单射等价于证明它的核只包含单位元。
- 商群 $G_1/K$ 的单位元是陪集 $K$ 本身 (即 $eK$)。
- 我们的目标是证明 $\text{Ker } \tilde{f} = \{K\}$。
- 设 $gK$ 是 $\text{Ker } \tilde{f}$ 中的任意一个元素。根据核的定义,这意味着 $\tilde{f}(gK) = 1$ (这里的 1 是 $H$ 的单位元,也就是 $G_2$ 的单位元)。
- 根据 $\tilde{f}$ 的定义,$\tilde{f}(gK) = f(g)$。所以我们有 $f(g) = 1$。
- 根据 $f$ 的核的定义,如果 $f(g)=1$,那么 $g \in \text{Ker } f$,即 $g \in K$。
- 根据陪集的性质,如果一个陪集的代表元 $g$ 属于子群 $K$,那么这个陪集 $gK$ 就等于子群 $K$ 本身。所以 $gK = K$。
- 这说明,$\text{Ker } \tilde{f}$ 中唯一的元素就是陪集 $K$。
- 因此 $\tilde{f}$ 的核是平凡的,所以 $\tilde{f}$ 是单射。
- 结论: 我们已经证明了 $\tilde{f}$ 是一个同态,并且它既是满射又是单射。因此,根据定义,$\tilde{f}$ 是一个同构。这就证明了定理的核心部分:$G_1/K \cong H$。
第四步:证明交换图成立
- 目标: 证明 $f = i \circ \tilde{f} \circ \pi$。
- 证明方法: 要证明两个函数相等,我们只需证明它们对定义域中的每一个元素所作用的结果都相等。
- 开始证明: 取任意一个元素 $g \in G_1$。
- 计算迂回路径的结果:$(i \circ \tilde{f} \circ \pi)(g)$。
- 根据函数复合的定义,这等于 $i(\tilde{f}(\pi(g)))$。
- 根据商同态 $\pi$ 的定义,$\pi(g) = gK$。所以表达式变为 $i(\tilde{f}(gK))$。
- 根据我们对 $\tilde{f}$ 的定义,$\tilde{f}(gK) = f(g)$。所以表达式变为 $i(f(g))$。
- 根据包含映射 $i$ 的定义,它只是把一个元素“看作”是更大集合里的元素,不做任何改变。所以 $i(f(g)) = f(g)$。
- 我们得到 $(i \circ \tilde{f} \circ \pi)(g) = f(g)$。
- 这个等式对所有 $g \in G_1$ 都成立,因此两个函数是相等的:$f = i \circ \tilde{f} \circ \pi$。
至此,第一同构定理的所有部分都得到了完整的证明。
- $\tilde{f}\left(g_{1} K g_{2} K\right)=\tilde{f}\left(g_{1} g_{2} K\right)=f\left(g_{1} g_{2}\right)=f\left(g_{1}\right) f\left(g_{2}\right)=\tilde{f}\left(g_{1} K\right) \tilde{f}\left(g_{2} K\right) .$: 这是证明 $\tilde{f}$ 是同态的完整链条,详细解释见上文第二步。
- $i \circ \tilde{f} \circ \pi(g)=i \circ \tilde{f}(g K)=i(f(g))=f(g),$: 这是证明交换图成立的完整链条,详细解释见上文第四步。
- 最核心的易错点: 忘记证明良定义性 (well-definedness)。任何时候当你在一个商集(元素是等价类,如陪集)上定义一个函数,并且定义的方式依赖于等价类中代表元的选择时,你都必须首先证明这个定义是良定义的。这是一个极其重要的习惯和步骤。
- 易错点: 混淆 $f$ 和 $\tilde{f}$。$f$ 的定义域是 $G_1$,而 $\tilde{f}$ 的定义域是 $G_1/K$。它们是完全不同的函数。
- 易错点: 对同态、核、像、商群、陪集、单射、满射、同构等基本概念的定义不熟悉,导致无法跟上证明的每一步。这个定理的证明是这些基本概念的一次综合演练。
- 易错点: 在证明 $\tilde{f}$ 是单射时,不清楚其核的单位元是什么。要记住,商群 $G_1/K$ 的单位元是陪集 $K$。
第一同构定理的证明过程是严谨而优美的,它完美地展示了抽象代数中定义和逻辑的力量。证明的核心在于巧妙地定义了一个新的映射 $\tilde{f}(gK)=f(g)$,然后按部就班地验证这个映射具备我们所期望的所有性质:
- 良定义性:保证了映射的合法性,这是建立在核 $K$ 的性质之上的。
- 同态性:保证了映射保持了群的结构,这是建立在 $f$ 的同态性质和商群运算定义之上的。
- 满射性:保证了映射覆盖了整个像群 $H$,这是由 $H$ 本身的定义决定的。
- 单射性:保证了映射是一对一的,这是通过分析 $\tilde{f}$ 的核,并将其与 $f$ 的核 $K$ 关联起来实现的。
最后,通过简单的函数复合演算,证明了整个映射关系可以用一个交换图来完美地概括。
4行间公式索引
- 积集 HK 的定义:
这个公式定义了两个子群 H 和 K 的积集 HK,它包含了所有形如一个 H 中的元素乘以一个 K 中的元素的乘积。
- 积集 HK 的一个具体计算:
这个公式展示了在群 S3 中,两个非正规子群 H=< (1,2)> 和 K=< (2,3)> 的积集 HK 的具体元素。
- 第一同构定理的交换图:
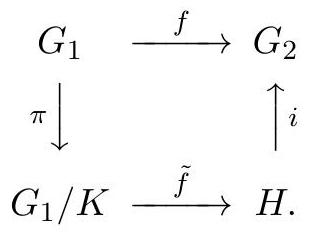
这个图示化了第一同构定理,表明从 G1 到 G2 的同态 f 可以分解为商同态 π、同构 f̃ 和包含映射 i 的复合。
- 证明 f̃ 是同态:
这个公式链证明了通过 f 定义的映射 f̃ 保持了商群的乘法运算,因此是一个群同态。
- 证明交换图成立:
这个公式链通过对任意元素 g 进行计算,验证了直接映射 f 与绕道 π、f̃、i 的复合映射结果相同。
- 推论中的同态核:
这个公式定义了一个从 ZxZ 到 Z 的满同态,其核是由 <(a,b)> 生成的子群,其中 gcd(a,b)=1。
- 商群的直积分解:
这个同构关系表明,直积群的商群同构于商群的直积。
- 直积群商去一个因子的特例:
这是上一个公式的特例,说明将直积群 G1xG2 模掉第二个因子 G2 后,得到的商群同构于第一个因子 G1。
- 第三同构定理 (消去定理):
这个公式被称为第三同构定理或“消去定理”,它表明对商群再做商运算,可以简化为对原群做更大的商运算,形式上如同分数的约分。
- 第二同构定理:
这个公式是第二同构定理,它揭示了由正规子群 H 和任意子群 K 构成的两个不同商群之间的同构关系。
- 有限群阶数的乘积公式:
这个公式是第二同构定理在有限群情况下的一个重要推论,它给出了积子群 HK 的阶数计算方法。
2. 1.5. 推论 3.1.3
📜 [原文9]
推论 3.1.3. Let $G$ be a 群 and $H$ a 子群 of $G$。If there exists a 群 $G^{\prime}$ and a 满同态 $f: G \rightarrow G^{\prime}$ such that 核 $\operatorname{Ker} f=H$,then $H$ is a 正规子群 of $G$ and $G / H \cong G^{\prime}$。
这个推论是第一同构定理最直接、最常用的一个应用形式。它告诉我们如何通过构造一个同态来快速识别一个商群的结构。
- 推论的条件:
- 有一个群 $G$ 和它的一个子群 $H$。注意,这里一开始并没有假设 $H$ 是正规子群。
- 关键条件是:我们能够找到某个目标群 $G'$ 以及一个从 $G$ 到 $G'$ 的同态 $f$。
- 这个同态 $f$ 必须满足两个条件:
- 它是一个满射(surjective),意味着 $f$ 的像 $\text{Im } f$ 恰好就是整个目标群 $G'$。
- 它的核 $\text{Ker } f$ 恰好就是我们开始时关注的那个子群 $H$。
- 推论的结论:
- 如果上述条件全部满足,那么我们可以立即得出两个重要结论:
- $H$ 必然是 $G$ 的一个正规子群。
- 由 $H$ 构造的商群 $G/H$ 同构于我们找到的那个目标群 $G'$。
- 证明思路: 这个推论的证明完全依赖于第一同构定理。
- 证明 H 是正规子群:
- 我们知道有一个同态 $f$ 的核是 $H$。
- 根据引理 3.1.1,任何同态的核都必然是一个正规子群。
- 因此,$H = \text{Ker } f$ 是 $G$ 的一个正规子群。这个结论是直接的。
- 证明 G/H 同构于 G':
- 第一同构定理告诉我们:对于任何同态 $f: G \rightarrow G'$,我们有 $G/\text{Ker } f \cong \text{Im } f$。
- 根据本推论的条件,我们有 $\text{Ker } f = H$。
- 根据本推论的条件,我们还知道 $f$ 是一个满同态,这意味着 $\text{Im } f = G'$。
- 将这两个条件代入第一同构定理的核心结论,我们得到:$G/H \cong G'$。
- 证明完毕。
这个推论为我们提供了一个强大的“配对”策略,用于识别商群。当我们面对一个陌生的商群 $G/H$ 时,如果我们能够机智地构造一个从 $G$ 出发的满同态 $f$,并且让这个 $f$ 的“失效”部分(即核)正好是 $H$,那么 $f$ 的“产出”部分(即像,也就是目标群 $G'$)就和我们想要研究的商群 $G/H$ 在结构上是完全一样的。
本推论的目的是将第一同构定理这个比较抽象的理论,转化为一个具有高度可操作性的实用工具。它为后续的大量例子提供了一个统一的解题模板。相比于直接用陪集的定义去分析商群的结构(这通常很繁琐),构造一个合适的同态往往要简洁和深刻得多。
这就像是做一道“看图识物”的题。
- 商群 $G/H$: 你手上有一张经过特殊处理的、模糊的图片(商群)。你想知道这张图片到底是什么。
- 同态 $f$ 和群 $G'$: 这时,你找到了一个魔法相机(同态 $f$)和一个清晰的原版照片(群 $G'$)。
- 核 Ker f = H: 你发现这个魔法相机有一个特点,它会自动把背景里所有“蓝色”的东西(子群 $H$)全部变成透明(映射到单位元)。
- 满射 Im f = G': 你还发现,这个相机拍出的照片,除了背景变透明外,照片的主体内容正好填满了你手上的那张原版照片 $G'$。
- 结论 G/H ≅ G': 于是你恍然大悟,你手上那张模糊的图片 $G/H$(把原图 $G$ 按“蓝色”与否 $H$ 进行模糊化处理),其内容和结构,其实和那张清晰的原版照片 $G'$ 是一回事。
你有一个复杂的机械装置 $G$,你移除了它的一些内部零件 $H$。你想知道剩下的框架结构 $G/H$ 是什么样子的。
现在,你找到了另一个完整的、现成的机器 $G'$。你发现有一个操作流程 $f$,可以将你的复杂装置 $G$ 变成机器 $G'$。而且你注意到,在操作过程中,所有被你移除的零件 $H$ 都在流程中被“丢弃”了(核是 $H$),并且你的装置 $G$ 刚好不多不少,正好能完整地变成一台机器 $G'$(满射)。
那么你就可以得出结论:你拆掉零件后剩下的那个框架 $G/H$,其结构和功能,与那台现成的机器 $G'$ 是完全一样的(同构)。
2. 1.6. 使用推论识别商群的示例
📜 [原文10]
We can sometimes use the 推论 to identify 商群 $G / H$ as more familiar 群s. The idea is to find a 同态 $f$ such that $H=\operatorname{Ker} f$。Here are some 示例:
例 3.1.4. (1) Let $G$ be a 群 and let $g \in G$。We have seen that there is a unique 同态 $f: \mathbb{Z} \rightarrow G$ such that $f(a)=g^{a}$ for all $a \in \mathbb{Z}$。Hence 像 $\operatorname{Im} f=\langle g\rangle$。If $g$ has 无限阶,then $f$ is 单射。If $g$ has 有限阶 $n$,then 核 $\operatorname{Ker} f=\langle n\rangle=n \mathbb{Z}$。Hence there is a unique 诱导同构 $\tilde{f}: \mathbb{Z} / n \mathbb{Z} \rightarrow G$ such that $\tilde{f}\left([a]_{n}\right)=g^{a}$ for all $a \in \mathbb{Z}$。
(2) The 同态 $f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(n, m)=n-m$ is 满射,and 核 $\operatorname{Ker} f= \{(n, n): n \in \mathbb{Z}\}=\langle(1,1)\rangle$。Hence $(\mathbb{Z} \times \mathbb{Z}) /\langle(1,1)\rangle \cong \mathbb{Z}$。More generally, if $\operatorname{gcd}(a, b)=1$,there is a 满同态 $\mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ with 核 $\langle(a, b)\rangle$,namely
Thus $(\mathbb{Z} \mathbb{Z}) /\langle(a, b)\rangle \cong \mathbb{Z}$ provided that $\operatorname{gcd}(a, b)=1$。
(3) We have seen that $f(t)=e^{i t}$ defines a 满同态 from $\mathbb{R}$(在加法下)到 $U(1)$ whose 核是 $\langle 2 \pi\rangle=2 \pi \mathbb{Z}$。Hence $\mathbb{R} / 2 \pi \mathbb{Z} \cong U(1)$ (a fact which also has 拓扑学意义)。Since multiplication by $2 \pi$ defines an 同构 from $\mathbb{R}$ to $\mathbb{R}$ such that the 像 of $\mathbb{Z}$ is $2 \pi \mathbb{Z}$,it follows easily that $\mathbb{R} / \mathbb{Z}$ is also 同构 to $U(1)$。In fact, the 同态 $g(t)=e^{2 \pi i t}$ has 核 $\mathbb{Z}$ and 像 $U(1)$,and thus $\mathbb{R} / \mathbb{Z} \cong U(1)$ as well。Using this 同构,we see that the 挠子群 of $U(1)$,which by definition is $\mu_{\infty}$,is 同构 to $\mathbb{Q} / \mathbb{Z}$。
(4) Let $G_{1}$ and $G_{2}$ be two 群s, with 正规子群 $H_{1} \triangleleft G_{1}$ and $H_{2} \triangleleft G_{2}$,and let $\pi_{1}: G_{1} \rightarrow G_{1} / H_{1}$ and $\pi_{2}: G_{2} \rightarrow G_{2} / H_{2}$ be the 商同态。Then there is a 同态
defined by $\pi\left(g_{1}, g_{2}\right)=\left(\pi_{1}\left(g_{1}\right), \pi_{2}\left(g_{2}\right)\right)=\left(g_{1} H_{1}, g_{2} H_{2}\right)$。Clearly $\pi$ is 满射 and 核 $\operatorname{Ker} \pi= H_{1} \times H_{2}$。Thus
In particular, taking $H_{1}=\{1\}$ and $H_{2}=G_{2}$ shows that
For example, taking $G_{1}=G_{2}=\mathbb{Z}$,we see that $(\mathbb{Z} \times \mathbb{Z}) /(\{0\} \times \mathbb{Z}) \cong \mathbb{Z}$,where $\{0\} \times \mathbb{Z}= \langle(0,1)\rangle$。Similarly, if $W$ is a 向量子空间 of the 有限维向量空间 $V$,say $\operatorname{dim} V=n$ and $\operatorname{dim} W=d$,then there is a 基 $e_{1}, \ldots, e_{n}$ of $V$ such that $W= \operatorname{span}\left\{e_{1}, \ldots, e_{d}\right\}$。This identifies $V$ with $\mathbb{R}^{n}$ and $W$ with the 向量子空间 $\mathbb{R}^{d}$ consisting of all vectors whose last $n-d$ coordinates are zero。Hence $V \cong \mathbb{R}^{n} \cong \mathbb{R}^{d} \times \mathbb{R}^{n-d}$,in such a way that the 子空间 $W$ is identified with the first factor $\mathbb{R}^{d}$,so that the 商空间 $V / W \cong \mathbb{R}^{n-d}$。Here, $V / W$ is more than just a 群,since $W$ is more than just a 子群 of $V$ (it is in addition closed under 标量乘法),and in fact $V / W$ is a 向量空间 in its own right。
12.1.6.1. 示例 (1): 循环群的起源
📜 [原文11]
(1) Let $G$ be a 群 and let $g \in G$。We have seen that there is a unique 同态 $f: \mathbb{Z} \rightarrow G$ such that $f(a)=g^{a}$ for all $a \in \mathbb{Z}$。Hence 像 $\operatorname{Im} f=\langle g\rangle$。If $g$ has 无限阶,then $f$ is 单射。If $g$ has 有限阶 $n$,then 核 $\operatorname{Ker} f=\langle n\rangle=n \mathbb{Z}$。Hence there is a unique 诱导同构 $\tilde{f}: \mathbb{Z} / n \mathbb{Z} \rightarrow G$ such that $\tilde{f}\left([a]_{n}\right)=g^{a}$ for all $a \in \mathbb{Z}$。
这个例子实际上是在重新阐述循环群的定义和基本结构,但这一次是从第一同构定理的视角来看。
- 构造同态:
- 对于任何一个群 $G$ 中的任意一个元素 $g$,我们总可以定义一个从整数加法群 $(\mathbb{Z}, +)$ 到 $G$ 的同态 $f$。
- 定义方式为 $f(a) = g^a$。
- 验证它是同态: $f(a+b) = g^{a+b} = g^a g^b = f(a)f(b)$。性质成立。这个同态是研究循环群的基础。
- 分析同态的像 (Image):
- $f$ 的像 $\text{Im } f$ 是 $G$ 中所有形如 $g^a$($a$ 为任意整数)的元素的集合。
- 根据定义,这个集合就是由 $g$ 生成的循环子群 $\langle g \rangle$。
- 所以 $\text{Im } f = \langle g \rangle$。
- 分析同态的核 (Kernel):
- $\text{Ker } f = \{a \in \mathbb{Z} \mid f(a) = e_G\} = \{a \in \mathbb{Z} \mid g^a = e_G\}$。即所有能将 $g$ 变回单位元的整数指数的集合。
- 这里需要分两种情况讨论:
- 情况一: $g$ 的阶是无限的。这意味着除了 $a=0$ 之外,没有任何整数 $a$ 能让 $g^a=e_G$。此时,$\text{Ker } f = \{0\}$。当一个同态的核是平凡的,这个同态就是单射。
- 情况二: $g$ 的阶是有限的,为 $n$。这意味着 $n$ 是最小的使得 $g^n=e_G$ 的正整数。那么,所有能使 $g^a=e_G$ 的整数 $a$ 恰好是 $n$ 的所有倍数。因此,$\text{Ker } f = \{k \cdot n \mid k \in \mathbb{Z}\}$。这个集合就是由 $n$ 生成的 $\mathbb{Z}$ 的子群,记作 $\langle n \rangle$ 或 $n\mathbb{Z}$。
- 应用第一同构定理 (有限阶情况):
- 我们现在有一个同态 $f: \mathbb{Z} \rightarrow G$。
- 它的定义域是 $\mathbb{Z}$。
- 它的核是 $K = n\mathbb{Z}$。
- 它的像是 $H = \langle g \rangle$。
- 根据第一同构定理,$G_1/K \cong H$,即 $\mathbb{Z}/n\mathbb{Z} \cong \langle g \rangle$。
- 定理的更精确版本告诉我们,存在一个唯一的诱导同构 $\tilde{f}: \mathbb{Z}/n\mathbb{Z} \rightarrow \langle g \rangle$。
- 这个同构 $\tilde{f}$ 的具体形式是什么?根据证明过程,我们知道 $\tilde{f}$ 作用在陪集(这里是模 $n$ 的同余类 $[a]_n$)上,结果就是 $f$ 作用在代表元 $a$ 上的结果。
- 所以,$\tilde{f}([a]_n) = f(a) = g^a$。
- 最终结论: 这段话从同构定理的角度,严谨地证明了:任何一个阶为 $n$ 的循环群 $\langle g \rangle$ 都与 $\mathbb{Z}/n\mathbb{Z}$ 同构。这是群论中最基本的结论之一。
这个例子展示了第一同构定理如何为循环群的结构提供了一个深刻而严谨的解释。它表明,任何循环群都可以看作是整数加法群 $\mathbb{Z}$ 的一个“同态像”。如果这个循环群是无限的,它就和 $\mathbb{Z}$ 本身同构;如果它是有限的(阶为 $n$),它就和 $\mathbb{Z}$ 的一个商群 $\mathbb{Z}/n\mathbb{Z}$ 同构。这完美地统一了所有循环群的来源。
本例的目的是用全新的、更抽象的视角来审视一个我们已经熟悉的概念——循环群。通过展示即便是像“所有阶为n的循环群都同构于$\mathbb{Z}/n\mathbb{Z}$”这样基础的结论也可以被优雅地置于同构定理的框架下,作者旨在强调同构定理的普适性和基础性。
22.1.6.2. 示例 (2): $\mathbb{Z} \times \mathbb{Z}$ 的商群
📜 [原文12]
(2) The 同态 $f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ defined by $f(n, m)=n-m$ is 满射,and 核 $\operatorname{Ker} f= \{(n, n): n \in \mathbb{Z}\}=\langle(1,1)\rangle$。Hence $(\mathbb{Z} \times \mathbb{Z}) /\langle(1,1)\rangle \cong \mathbb{Z}$。More generally, if $\operatorname{gcd}(a, b)=1$,there is a 满同态 $\mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$ with 核 $\langle(a, b)\rangle$,namely
Thus $(\mathbb{Z} \mathbb{Z}) /\langle(a, b)\rangle \cong \mathbb{Z}$ provided that $\operatorname{gcd}(a, b)=1$。
这个例子展示了如何使用第一同构定理来识别一个看起来更复杂的商群 $(\mathbb{Z} \times \mathbb{Z}) / H$ 的结构。
第一部分:简单情况
- 构造同态:
- 定义一个从二维整数格点群 $(\mathbb{Z} \times \mathbb{Z}, +)$ 到整数加法群 $(\mathbb{Z}, +)$ 的映射 $f$。
- 定义为 $f(n, m) = n - m$。
- 验证它是同态:
- 分析同态的像 (Image):
- 我们需要确定这个 $f$ 是不是满射。即,对于目标群 $\mathbb{Z}$ 中的任意一个整数 $k$,我们能找到一个 $(n, m) \in \mathbb{Z} \times \mathbb{Z}$ 使得 $f(n, m) = n-m = k$ 吗?
- 答案是肯定的。我们可以很简单地取 $n=k, m=0$,那么 $f(k, 0) = k-0=k$。或者取 $n=0, m=-k$,那么 $f(0, -k) = 0 - (-k) = k$。
- 既然对于任何整数 $k$ 都能找到原像,所以 $f$ 是满射,$\text{Im } f = \mathbb{Z}$。
- 分析同态的核 (Kernel):
- $\text{Ker } f = \{(n, m) \in \mathbb{Z} \times \mathbb{Z} \mid f(n, m) = 0\}$。
- $f(n,m)=n-m=0$ 意味着 $n=m$。
- 所以,核是所有两个分量都相等的整数对的集合:$\text{Ker } f = \{(n, n) \mid n \in \mathbb{Z}\}$。
- 这个集合可以被看作是由单个元素 $(1,1)$ 生成的循环子群。因为任何一个形如 $(n,n)$ 的元素都可以写成 $n \cdot (1,1)$。
- 所以 $\text{Ker } f = \langle(1,1)\rangle$。
- 应用第一同构定理:
- 我们有一个满同态 $f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$。
- 它的核是 $\langle(1,1)\rangle$。
- 根据推论 3.1.3,我们直接得到:$(\mathbb{Z} \times \mathbb{Z}) / \langle(1,1)\rangle \cong \mathbb{Z}$。
- 结论: 这个看起来复杂的商群——二维整数格点群模掉其对角线子群——其结构竟然和一维的整数加法群是完全一样的。
第二部分:推广情况
- 推广条件: 将核从 $\langle(1,1)\rangle$ 推广到 $\langle(a,b)\rangle$,其中 $a,b$ 是任意两个互质的整数 ($\text{gcd}(a,b)=1$)。
- 构造同态: 我们需要找到一个新的满同态 $f: \mathbb{Z} \times \mathbb{Z} \rightarrow \mathbb{Z}$,使得它的核恰好是 $\langle(a,b)\rangle$。
- 作者给出了这个同态: $f(n,m) = -bn + am$。
- 验证它是同态: 这和前面的验证类似,是线性的,所以是同态。
- 分析同态的像 (满射):
- $f$ 是满射吗?即对于任意整数 $k \in \mathbb{Z}$,方程 $-bn+am=k$ 是否总有整数解 $(n,m)$?
- 这正是数论中的裴蜀定理(Bézout's identity)的应用。裴蜀定理说,对于不全为零的整数 $a, b$,方程 $ax+by=d$ 有整数解 $(x,y)$ 的充要条件是 $d$ 是 $\text{gcd}(a,b)$ 的倍数。
- 在本例中,方程是 $am - bn = k$。因为前提是 $\text{gcd}(a,b)=1$,所以 1 整除任何整数 $k$。因此,对于任意的 $k$,这个方程总是有整数解 $(m, n)$ 的。
- 所以 $f$ 是满射。
- 分析同态的核:
- $\text{Ker } f = \{(n, m) \in \mathbb{Z} \times \mathbb{Z} \mid -bn + am = 0\}$。
- $-bn + am = 0 \implies am = bn$。
- 因为 $\text{gcd}(a,b)=1$ (a和b互质),所以要使等式成立,必然有 $m$ 是 $b$ 的倍数,$n$ 是 $a$ 的倍数,并且它们是同一个倍数。即存在整数 $t$ 使得 $n = ta$ 且 $m = tb$。
- 所以,核中的元素都是形如 $(ta, tb) = t(a,b)$ 的向量。
- 这正是由向量 $(a,b)$ 生成的循环子群 $\langle(a,b)\rangle$。
- 所以 $\text{Ker } f = \langle(a,b)\rangle$。
- 应用第一同构定理:
- 我们找到了一个满同态 $f(n,m)=-bn+am$,它的核是 $\langle(a,b)\rangle$。
- 根据推论 3.1.3,我们得到:$(\mathbb{Z} \times \mathbb{Z}) / \langle(a,b)\rangle \cong \mathbb{Z}$,只要 $\text{gcd}(a,b)=1$。
- 推广情况的例子: 设 $a=2, b=3$。$\text{gcd}(2,3)=1$。
- 我们要研究的商群是 $(\mathbb{Z} \times \mathbb{Z})/\langle(2,3)\rangle$。
- 构造同态 $f(n,m) = -3n + 2m$。
- 满射性: 方程 $-3n+2m=k$ 对任意整数 $k$ 都有解。例如,如果 $k=1$,解可以是 $n=1, m=2$ ($-3+4=1$)。如果 $k=5$,解可以是 $n=1, m=4$ ($-3+8=5$)。
- 核: $\text{Ker } f = \{(n,m) \mid -3n+2m=0\}$。$2m=3n$。因为 2 和 3 互质,所以 $n$ 必须是 2 的倍数,$m$ 必须是 3 的倍数。设 $n=2t$,则 $m=3t$。所以核是所有形如 $(2t, 3t) = t(2,3)$ 的元素,即 $\langle(2,3)\rangle$。
- 结论: 应用定理,我们得到 $(\mathbb{Z} \times \mathbb{Z})/\langle(2,3)\rangle \cong \mathbb{Z}$。
- 易错点: 对裴蜀定理不熟悉,导致无法理解为何 $f(n,m)=-bn+am$ 在 $\text{gcd}(a,b)=1$ 时是满射。
- 易错点: 在求解核 $am=bn$ 时,忘记了使用 $a,b$ 互质的条件,从而无法得出解的形式是 $t(a,b)$。
- 边界情况: 如果 $\text{gcd}(a,b)=d > 1$ 会怎么样?
- 例如,取 $(a,b)=(2,4)$。这时 $\text{gcd}(2,4)=2$。我们仍然可以定义 $f(n,m) = -4n+2m$。
- 像: 它的像是所有形如 $-4n+2m = 2(-2n+m)$ 的整数。这显然是所有偶数的集合 $2\mathbb{Z}$。它不再是满射到 $\mathbb{Z}$ 了。
- 核: $\text{Ker } f = \{(n,m) \mid -4n+2m=0\} \implies m=2n$。所以核是 $\langle(1,2)\rangle$。
- 应用第一同构定理: $G_1/K \cong H \implies (\mathbb{Z} \times \mathbb{Z})/\langle(1,2)\rangle \cong 2\mathbb{Z}$。而我们知道 $2\mathbb{Z}$ 是和 $\mathbb{Z}$ 同构的(通过映射 $x \mapsto x/2$)。所以结论 $(\mathbb{Z} \times \mathbb{Z})/\langle(1,2)\rangle \cong \mathbb{Z}$ 仍然成立。
- 这个例子说明,即使 $\text{gcd}(a,b) \neq 1$,只要构造得当,结论也可能成立。但原文中的构造方法 $f(n,m)=-bn+am$ 依赖于 $\text{gcd}(a,b)=1$ 来保证满射到 $\mathbb{Z}$。
这个例子极好地展示了第一同构定理的威力。通过巧妙地构造一个线性映射作为同态,我们发现二维整数格点群在模掉任何一个由互质坐标分量构成的向量生成的循环子群后,都会“坍缩”成一个一维的整数群 $\mathbb{Z}$。这在几何上可以理解为,将整个平面格点沿着向量 $(a,b)$ 的方向进行“投影”,得到的投影图像在结构上是等距分布的,与一维的整数点集同构。
32.1.6.3. 示例 (3): 实数轴与单位圆
📜 [原文13]
(3) We have seen that $f(t)=e^{i t}$ defines a 满同态 from $\mathbb{R}$(在加法下)到 $U(1)$ whose 核是 $\langle 2 \pi\rangle=2 \pi \mathbb{Z}$。Hence $\mathbb{R} / 2 \pi \mathbb{Z} \cong U(1)$ (a fact which also has 拓扑学意义)。Since multiplication by $2 \pi$ defines an 同构 from $\mathbb{R}$ to $\mathbb{R}$ such that the 像 of $\mathbb{Z}$ is $2 \pi \mathbb{Z}$,it follows easily that $\mathbb{R} / \mathbb{Z}$ is also 同构 to $U(1)$。In fact, the 同态 $g(t)=e^{2 \pi i t}$ has 核 $\mathbb{Z}$ and 像 $U(1)$,and thus $\mathbb{R} / \mathbb{Z} \cong U(1)$ as well。Using this 同构,we see that the 挠子群 of $U(1)$,which by definition is $\mu_{\infty}$,is 同构 to $\mathbb{Q} / \mathbb{Z}$。
这个例子将第一同构定理应用到连续群上,揭示了实数加法群 $\mathbb{R}$、整数加法群 $\mathbb{Z}$ 与复平面单位圆上的乘法群 $U(1)$ 之间的深刻联系。
第一部分: $\mathbb{R} / 2 \pi \mathbb{Z} \cong U(1)$
- 构造同态:
- 定义一个从实数加法群 $(\mathbb{R}, +)$ 到复平面单位圆乘法群 $U(1) = \{z \in \mathbb{C} \mid |z|=1\}$ 的映射 $f$。
- 定义为 $f(t) = e^{it}$ (欧拉公式 $e^{it} = \cos(t) + i\sin(t)$)。
- 验证它是同态: $f(t_1+t_2) = e^{i(t_1+t_2)} = e^{it_1}e^{it_2} = f(t_1)f(t_2)$。性质成立。
- 分析同态的像 (Image):
- 当实数 $t$ 从 0 变到 $2\pi$ 时,$e^{it}$ 会在复平面的单位圆上走完一整圈。当 $t$ 取遍所有实数时,$e^{it}$ 会在单位圆上转无数圈,覆盖单位圆上的每一个点。
- 所以,这个同态是满射,$\text{Im } f = U(1)$。
- 分析同态的核 (Kernel):
- $\text{Ker } f = \{t \in \mathbb{R} \mid f(t) = 1\}$。目标群 $U(1)$ 的单位元是复数 1。
- 我们需要解方程 $e^{it} = 1$。根据欧拉公式,$e^{it} = \cos(t)+i\sin(t)$。要使其等于 1,必须有 $\cos(t)=1$ 且 $\sin(t)=0$。
- 这当且仅当 $t$ 是 $2\pi$ 的整数倍时成立。
- 所以,$\text{Ker } f = \{2\pi k \mid k \in \mathbb{Z}\}$。这个集合是在 $\mathbb{R}$ 中由 $2\pi$ 生成的循环子群,记作 $\langle 2\pi \rangle$ 或 $2\pi\mathbb{Z}$。
- 应用第一同构定理:
- 我们有一个满同态 $f: \mathbb{R} \rightarrow U(1)$,其核为 $2\pi\mathbb{Z}$。
- 根据推论 3.1.3,我们直接得到:$\mathbb{R} / 2\pi\mathbb{Z} \cong U(1)$。
- 几何意义: 这个同构关系有非常直观的几何和拓扑学意义。它意味着,如果你拿一根无限长的实数轴 $\mathbb{R}$,然后把它“模掉” $2\pi\mathbb{Z}$,相当于每隔 $2\pi$ 的长度就剪断,然后把所有的这些长度为 $2\pi$ 的线段叠在一起,首尾相接。最终得到的东西就是一个周长为 $2\pi$ 的圆圈,这正是 $U(1)$。
第二部分: $\mathbb{R} / \mathbb{Z} \cong U(1)$
- 方法一 (通过同构变换):
- 作者提出了一个巧妙的论证。考虑映射 $\phi: \mathbb{R} \rightarrow \mathbb{R}$,定义为 $\phi(t) = 2\pi t$。这是一个从 $\mathbb{R}$ 到自身的群同构(线性映射)。
- 在这个同构下,整数子群 $\mathbb{Z} \subset \mathbb{R}$ 被映射到了子群 $2\pi\mathbb{Z} \subset \mathbb{R}$。
- 因为 $\phi$ 是同构,它保持所有结构。所以“$\mathbb{R}$ 模掉 $\mathbb{Z}$”得到的结构,应该和“$\phi(\mathbb{R})$ 模掉 $\phi(\mathbb{Z})$”得到的结构是一样的。
- 即 $\mathbb{R} / \mathbb{Z} \cong \phi(\mathbb{R}) / \phi(\mathbb{Z}) = \mathbb{R} / 2\pi\mathbb{Z}$。
- 结合第一部分的结论 $\mathbb{R} / 2\pi\mathbb{Z} \cong U(1)$,我们通过传递性得到 $\mathbb{R} / \mathbb{Z} \cong U(1)$。
- 方法二 (构造新的同态):
- 这是更直接的方法。定义一个新的同态 $g: \mathbb{R} \rightarrow U(1)$,为 $g(t) = e^{2\pi i t}$。
- 这个 $g$ 仍然是一个从 $(\mathbb{R},+)$ 到 $(U(1), \times)$ 的满同态。
- 分析其核: 我们需要解方程 $e^{2\pi i t} = 1$。这当且仅当指数 $2\pi t$ 是 $2\pi$ 的整数倍时成立。
- $2\pi t = 2\pi k$ (for $k \in \mathbb{Z}$) $\implies t=k$。
- 所以,$\text{Ker } g = \mathbb{Z}$。
- 应用第一同构定理: 我们有一个满同态 $g: \mathbb{R} \rightarrow U(1)$,其核为 $\mathbb{Z}$。因此,$\mathbb{R} / \mathbb{Z} \cong U(1)$。
- 几何意义: 这意味着把实数轴按整数长度剪断,然后把所有 $[k, k+1]$ 的线段叠在一起,得到的就是一个单位圆。这通常被称为“实数的小数部分”构成的群。任何实数 $t$ 都可以写成 $t = \lfloor t \rfloor + \{t\}$ (整数部分 + 小数部分)。在商群 $\mathbb{R}/\mathbb{Z}$ 中,我们忽略了整数部分,只看小数部分。小数部分 $[0,1)$ 通过映射 $x \mapsto e^{2\pi ix}$ 就卷成了一个圆。
第三部分: 挠子群 $\mu_\infty$ 与 $\mathbb{Q}/\mathbb{Z}$
- 挠子群 (Torsion subgroup): 一个群的挠子群是其所有有限阶元素的集合。
- $U(1)$ 的挠子群 $\mu_\infty$: $U(1)$ 中的元素是 $e^{i\theta}$。一个元素要有有限阶 $n$,意味着 $(e^{i\theta})^n = e^{in\theta} = 1$。这要求 $n\theta$ 是 $2\pi$ 的整数倍,即 $\theta = k \frac{2\pi}{n}$。这些点正是复平面上的 $n$ 次单位根。当 $n$ 取遍所有正整数时,所有的单位根构成了 $U(1)$ 的挠子群 $\mu_\infty$。这些元素的幅角都是 $2\pi$ 的有理数倍。
- 同构到 $\mathbb{Q}/\mathbb{Z}$:
- 我们已经建立了同构 $g^{-1}: U(1) \rightarrow \mathbb{R}/\mathbb{Z}$ (这里 $g$ 是 $g(t)=e^{2\pi it}$)。
- 同构会把挠子群映射到挠子群。所以 $g^{-1}(\mu_\infty)$ 是 $\mathbb{R}/\mathbb{Z}$ 的挠子群。
- $\mathbb{R}/\mathbb{Z}$ 中的一个元素是形如 $t+\mathbb{Z}$ 的陪集。它有有限阶 $n$ 意味着 $n(t+\mathbb{Z}) = nt+\mathbb{Z} = \mathbb{Z}$ (商群的单位元)。
- $nt+\mathbb{Z} = \mathbb{Z}$ 当且仅当 $nt$ 是一个整数。即 $t = k/n$ 必须是一个有理数。
- 所以,$\mathbb{R}/\mathbb{Z}$ 的挠子群是所有 $q+\mathbb{Z}$ ($q \in \mathbb{Q}$) 构成的集合。这个子群就是 $\mathbb{Q}/\mathbb{Z}$。
- 因此,我们得出结论:$\mu_\infty \cong \mathbb{Q}/\mathbb{Z}$。这是一个非常深刻和重要的结论,连接了数论中的单位根和有理数。
本例通过欧拉公式 $e^{it}$ 构造了连接实数加法群和单位圆乘法群的桥梁。利用第一同构定理,它得出了两个核心结论:
- $\mathbb{R}/2\pi\mathbb{Z} \cong U(1)$
- $\mathbb{R}/\mathbb{Z} \cong U(1)$
这两个结论在群论、拓扑学和分析学中都至关重要。最后,通过分析这个同构如何作用在有限阶元素上,进一步推导出了一个更精细的结论:单位圆上的所有单位根构成的群 $\mu_\infty$ 与有理数模整数群 $\mathbb{Q}/\mathbb{Z}$ 是同构的。
42.1.6.4. 示例 (4): 直积群的商群
📜 [原文14]
(4) Let $G_{1}$ and $G_{2}$ be two 群s, with 正规子群 $H_{1} \triangleleft G_{1}$ and $H_{2} \triangleleft G_{2}$,and let $\pi_{1}: G_{1} \rightarrow G_{1} / H_{1}$ and $\pi_{2}: G_{2} \rightarrow G_{2} / H_{2}$ be the 商同态。Then there is a 同态
defined by $\pi\left(g_{1}, g_{2}\right)=\left(\pi_{1}\left(g_{1}\right), \pi_{2}\left(g_{2}\right)\right)=\left(g_{1} H_{1}, g_{2} H_{2}\right)$。Clearly $\pi$ is 满射 and 核 $\operatorname{Ker} \pi= H_{1} \times H_{2}$。Thus
In particular, taking $H_{1}=\{1\}$ and $H_{2}=G_{2}$ shows that
For example, taking $G_{1}=G_{2}=\mathbb{Z}$,we see that $(\mathbb{Z} \times \mathbb{Z}) /(\{0\} \times \mathbb{Z}) \cong \mathbb{Z}$,where $\{0\} \times \mathbb{Z}= \langle(0,1)\rangle$。Similarly, if $W$ is a 向量子空间 of the 有限维向量空间 $V$,say $\operatorname{dim} V=n$ and $\operatorname{dim} W=d$,then there is a 基 $e_{1}, \ldots, e_{n}$ of $V$ such that $W= \operatorname{span}\left\{e_{1}, \ldots, e_{d}\right\}$。This identifies $V$ with $\mathbb{R}^{n}$ and $W$ with the 向量子空间 $\mathbb{R}^{d}$ consisting of all vectors whose last $n-d$ coordinates are zero。Hence $V \cong \mathbb{R}^{n} \cong \mathbb{R}^{d} \times \mathbb{R}^{n-d}$,in such a way that the 子空间 $W$ is identified with the first factor $\mathbb{R}^{d}$,so that the 商空间 $V / W \cong \mathbb{R}^{n-d}$。Here, $V / W$ is more than just a 群,since $W$ is more than just a 子群 of $V$ (it is in addition closed under 标量乘法),and in fact $V / W$ is a 向量空间 in its own right。
这个例子探讨了群的直积与商群运算如何相互作用,并得出了一个非常符合直觉的“分配律”。
第一部分: 一般结论
- 构造同态:
- 起点: 有两个群 $G_1, G_2$ 和它们各自的正规子群 $H_1, H_2$。我们可以构造商群 $G_1/H_1$ 和 $G_2/H_2$。
- 定义域: $\mathbb{G}_1 \times G_2$,即 $G_1$ 和 $G_2$ 的直积群。其元素是序对 $(g_1, g_2)$。
- 目标域: $(G_1/H_1) \times (G_2/H_2)$,即两个商群的直积群。其元素是序对 $(g_1H_1, g_2H_2)$。
- 定义映射 $\pi$: 很自然地,我们将一个序对映射到对应分量的陪集构成的序对。
- 这个映射 $\pi$ 是一个同态,因为它在每个分量上都是同态。
- 分析同态的像 (Image):
- $\pi$ 是满射吗?是的。对于目标群中的任意元素 $(g_1H_1, g_2H_2)$,我们总能找到原像 $(g_1, g_2)$,因为 $\pi(g_1, g_2)$ 正好就是它。原文中用 "Clearly $\pi$ is 满射" 来描述。
- 分析同态的核 (Kernel):
- $\text{Ker } \pi = \{(g_1, g_2) \in G_1 \times G_2 \mid \pi(g_1, g_2) = \text{单位元}\}$。
- 目标群的单位元是 $(H_1, H_2)$ (两个商群各自的单位元构成的序对)。
- 所以 $\pi(g_1, g_2) = (g_1H_1, g_2H_2) = (H_1, H_2)$。
- 这当且仅当 $g_1H_1 = H_1$ 并且 $g_2H_2 = H_2$。
- $g_1H_1 = H_1 \iff g_1 \in H_1$。
- $g_2H_2 = H_2 \iff g_2 \in H_2$。
- 所以,核是所有形如 $(h_1, h_2)$ (其中 $h_1 \in H_1, h_2 \in H_2$) 的元素的集合。这正是子群 $H_1$ 和 $H_2$ 的直积群 $H_1 \times H_2$。
- 所以 $\text{Ker } \pi = H_1 \times H_2$。
- 应用第一同构定理:
- 我们有一个满同态 $\pi: G_1 \times G_2 \rightarrow (G_1/H_1) \times (G_2/H_2)$。
- 它的核是 $H_1 \times H_2$。
- 根据推论 3.1.3,我们得到:$(G_1 \times G_2) / (H_1 \times H_2) \cong (G_1/H_1) \times (G_2/H_2)$。
- 结论: 直积的商群等于商群的直积。这个性质非常有用,它允许我们将对高维结构的商运算分解为对低维结构的商运算。
第二部分: 特例与应用
- 特例: 商掉一个因子
- 在上述通用公式中,取 $H_1 = \{1\}$ ( $G_1$ 的平凡子群) 和 $H_2 = G_2$ ( $G_2$ 本身)。
- 代入公式:$(G_1 \times G_2) / (\{1\} \times G_2) \cong (G_1/\{1\}) \times (G_2/G_2)$。
- 我们知道 $G_1/\{1\} \cong G_1$ (模掉平凡子群等于自身)。
- 我们知道 $G_2/G_2 \cong \{1\}$ (模掉自身等于平凡群)。
- 所以右边是 $G_1 \times \{1\}$,这个群显然同构于 $G_1$。
- 最终结论: $(G_1 \times G_2) / (\{1\} \times G_2) \cong G_1$。
- 直觉理解: 在直积 $G_1 \times G_2$ 中,我们把所有第二个分量的信息都“忽略”掉了(模掉了 $G_2$),那么剩下的自然就只有第一个分量的结构 $G_1$ 了。
- 具体例子:
- 取 $G_1 = \mathbb{Z}, G_2 = \mathbb{Z}$。子群 $\{0\} \times \mathbb{Z}$ 就是 y-轴上的所有整点,这个子群是由 $(0,1)$ 生成的,即 $\langle(0,1)\rangle$。
- 应用上面的特例结论:$(\mathbb{Z} \times \mathbb{Z}) / (\{0\} \times \mathbb{Z}) \cong \mathbb{Z}$。
- 几何意义: 将二维平面上的所有格点,沿着 y-轴方向进行“压缩”,投射到 x-轴上,得到的投影就是 x-轴上的所有整数点,其结构是 $\mathbb{Z}$。这与示例(2)的结论互为补充。
- 向量空间的应用:
- 将群的概念推广到向量空间。(向量空间首先是一个在向量加法下的阿贝尔群)。
- $V$ 是一个 $n$ 维向量空间,$W$ 是它的一个 $d$ 维子空间。
- 我们可以选择一组基,使得 $V$ 同构于 $\mathbb{R}^n$,而 $W$ 同构于 $\mathbb{R}^d \times \{0\}^{n-d}$ (即前 $d$ 个坐标任意,后 $n-d$ 个坐标为0的空间)。
- 此时,整个空间 $V$ 可以看作是两个子空间的直和(类似于群的直积):$V \cong W \oplus U$,其中 $U \cong \mathbb{R}^{n-d}$ 是与 $W$ 互补的子空间。
- $V \cong \mathbb{R}^d \times \mathbb{R}^{n-d}$,而 $W$ 对应于第一个因子 $\mathbb{R}^d$。
- 那么商空间 $V/W$ 就相当于 $(\mathbb{R}^d \times \mathbb{R}^{n-d}) / (\mathbb{R}^d \times \{0\})$。
- 根据我们上面证明的特例,$V/W \cong \mathbb{R}^{n-d}$。
- 结论: $n$ 维空间模掉一个 $d$ 维子空间,得到的商空间是一个 $(n-d)$ 维的空间。这个结论是线性代数中的基本事实,这里展示了它可以被看作是群论同构定理的一个自然推论。
- 补充: 作者还指出,$V/W$ 不仅仅是一个商群,它本身还继承了标量乘法的运算,构成一个向量空间。
本例通过构造一个分量式的同态,证明了商群运算与群的直积运算可以“交换”,即 $(G_1 \times G_2) / (H_1 \times H_2) \cong (G_1/H_1) \times (G_2/H_2)$。这个一般性的结论有许多重要的应用,例如,它直观地解释了为什么一个直积空间模掉其中一个因子空间后,会得到另一个因子空间。这个思想也无缝推广到线性代数中的商向量空间,并给出了其维度的合理解释。
12.2. 第二同构定理与第三同构定理
2. 2.1. 引言
📜 [原文15]
3.2. 第二同构定理与第三同构定理. One reason to call $G / H$ a 商群 is that the notation $G / H$ has many properties that look like the analogous ones for 分数。For example, $G / G \cong\{1\}$ and $G /\{1\} \cong G$。We have also seen that, for $H_{1} \triangleleft G_{1}$ and $H_{2} \triangleleft G_{2},\left(G_{1} \times\right. \left.G_{2}\right) /\left(H_{1} \times H_{2}\right) \cong\left(G_{1} / H_{1}\right) \times\left(G_{2} / H_{2}\right)$。Another property is the following: We called 定理 3.1.2 the 第一同构定理,so we naturally expect there to be other 同构定理s as well。We shall first state and 证明 the 第三同构定理:
这部分是第二和第三同构定理章节的引言,旨在通过类比分数运算来引入这两个定理,并解释了为什么先讲第三同构定理。
- 类比分数: 作者提出了一个帮助理解商群记号 $G/H$ 的启发性想法:可以把它类比成分数。这种类比并不严谨,但有助于直观记忆和预测某些定理的形式。
- 类比1: $G/G \cong \{1\}$ 对应于 $a/a = 1$。一个群模掉它自身,只剩下单位元构成的平凡群。
- 类比2: $G/\{1\} \cong G$ 对应于 $a/1 = a$。一个群模掉平凡子群,结构没有任何改变,仍然是它自身。
- 类比3: $(G_1 \times G_2) / (H_1 \times H_2) \cong (G_1/H_1) \times (G_2/H_2)$。这有点像分数的乘法 $(\frac{a}{b} \times \frac{c}{d})$,虽然形式上不完全一样,但体现了运算的可分配性或可分解性。
- 引出新定理: 基于这种分数类比,作者引出了即将要讲的定理。这种类比会使得第三同构定理的形式看起来非常自然,就像分数的约分一样。
- 预告顺序: 作者明确表示,虽然标题是“第二和第三同构定理”,但他将首先陈述和证明第三同构定理。这通常是因为第三同构定理的形式与分数类比的联系更强,更容易记忆,并且其证明也直接依赖于第一同构定理,逻辑上更连贯。
本段引言的核心作用是“启发”和“引导”。它通过建立商群记号与我们熟悉的分数运算之间的直观类比,降低了后续定理的认知门槛,使得定理的形式不再显得那么抽象和突兀。同时,它也解释了接下来的论述顺序,让读者有所准备。
本段的目的是为了教学上的便利。直接抛出第二和第三同构定理的抽象陈述可能会让学生感到困惑和难以记忆。通过一个简单的“分数类比”作为“脚手架”,可以帮助学生建立直观的印象,并利用这种印象来“猜测”或“记忆”定理的公式。这是一种有效的教学策略。
2. 2.2. 定理 3.2.1 (第三同构定理)
📜 [原文16]
定理 3.2.1. Let $G$ be a 群 and let $H$ and $K$ be 正规子群 of $G$ with $H \leq K$。Let $\pi: G \rightarrow G / H$ be the 商同态。Then $K / H=\pi(K)$ is a 正规子群 of $G / H$,and
(The way to remember this is that, if we think the expressions $G / H, K / H$ as 分数,then the denominators above cancel each other.)
这部分正式陈述了第三同构定理,有时也称为“消去律”或“对应定理”的一部分。
- 定理的条件:
- 有一个群 $G$。
- 有两个正规子群 $H$ 和 $K$。
- 这两个正规子群形成一个包含关系链:$H \leq K \leq G$。(由于两者都是 $G$ 的正规子群,所以 $H$ 在 $K$ 中也必然是正规的,见命题2.3.14(iii))。
- 定理的结论:
- 结论一: $K/H$ 是 $G/H$ 的一个正规子群。
- 这里 $K/H$ 是什么?作者给出了一个解释:$K/H = \pi(K)$。
- $\pi: G \rightarrow G/H$ 是标准的商同态,$\pi(g)=gH$。
- $\pi(K)$ 就是 $K$ 中所有元素在商同态下的像的集合,即 $\{kH \mid k \in K\}$。
- 这正是商群 $K/H$ 的标准定义(因为 $H \triangleleft K$,所以可以构造 $K/H$)。
- 所以,结论一是说,大正规子群 $K$ 在模掉小正规子群 $H$ 之后,得到的陪集集合,构成了大商群 $G/H$ 中的一个正规子群。
- 结论二: $(G / H) /(K / H) \cong G / K$。
- 左边: 是一个“商群的商群”。我们先用 $H$ 对 $G$ 做商,得到 $G/H$。然后,再用刚刚证明的正规子群 $K/H$ 对 $G/H$ 做商。
- 右边: 是一个更直接的商群,直接用大的正规子群 $K$ 对 $G$ 做商。
- $\cong$: 表示左右两边这两个看起来很不一样的东西,在结构上是完全同构的。
- 记忆技巧:
- 作者再次强调了分数类比法。将表达式 $(G/H)/(K/H)$ 想象成分数 $\frac{G/H}{K/H}$。形式上,“分子分母”中的 $H$ 可以“约掉”,剩下 $G/K$。这提供了一个非常强大且不容易忘记的记忆方式。
第三同构定理处理的是一种“子群塔” $H \leq K \leq G$ 的情况。它揭示了对一个群进行两次连续的“求商”操作(先模 $H$,再模 $K/H$),其结果等价于一次性进行一个更大的“求商”操作(直接模 $K$)。这个定理在简化涉及多层商群的复杂结构时非常有用。
本定理的目的是建立不同层次商群之间的联系。它构成了所谓的“对应定理”的核心部分,该定理建立了 $G$ 中包含 $H$ 的子群与 $G/H$ 中的子群之间的一一对应关系。这个定理使得我们可以通过研究结构可能更简单的商群 $G/H$ 的子群结构,来反推原群 $G$ 中更复杂的子群结构。
想象一个三层楼的建筑 ($G$)。
- $K$ 是指“一楼和二楼”这个整体。$H$ 是指“一楼”。$H \leq K \leq G$。两者都是“特殊区域”(正规子群)。
- $G/K$:你站在三楼,把一楼和二楼看成一个整体“地基”,你只关心三楼相对于这个“地基”是什么样的。
- $G/H$:你站在二楼或三楼,把一楼看成“地基”,你关心的是二楼和三楼相对于一楼是什么样的。这个新的“建筑”就是 $G/H$。
- $K/H$:在 $G/H$ 这个新视角下,“原来的二楼”相对于“原来的地基一楼”是什么样的。
- $(G/H)/(K/H)$:在你已经忽略了一楼的视角下($G/H$),你再把“新视角下的二楼”($K/H$) 也忽略掉。
- 定理: 这样做之后,你剩下的东西(三楼),和你一开始就直接忽略一楼和二楼($G/K$)所剩下的东西(三楼)是一样的。
你有一张分辨率非常高的地图 $G$。
- $H$:你决定忽略所有“街道”级别的信息。
- $K$:你决定忽略所有“城市”级别的信息(自然也包括了街道)。
- $G/K$:你直接看一张只显示“国家”轮廓的地图。
- $G/H$:你看一张显示“城市”和“国家”轮廓的地图(街道被抹去)。
- $K/H$:在这张没有街道的地图上,“城市”本身这个概念。
- $(G/H)/(K/H)$:你在这张没有街道的地图上,再把“城市”的轮廓也抹去。
- 定理: 这样操作后得到的地图,和你一开始就直接看那张只显示“国家”轮廓的地图,是一样的。两次连续的“模糊化”操作,等价于一次性进行最大程度的“模糊化”。
2. 2.3. 第三同构定理的证明
📜 [原文17]
证明. We will 证明 the 定理 by applying the 第一同构定理。Begin by defining $f: G / H \rightarrow G / K$ by: $f(g H)=g K$。Here $f$ is a 函数 defined on the set of 陪集 $G / H$ by choosing a 代表元,so we must check that $f$ is 良定义的。If $g^{\prime} \in g H$ is another 代表元,then $g^{\prime}=g h$ for some $h \in H$ and so $g^{\prime} K=g h K=g K$,since $g h$ and $g$ differ by an element of $H$ and hence of $K$ since $H \subseteq K$。Clearly $f$ is 满射。Also,
Hence $f$ is a 同态。Finally,
Hence $K / H \triangleleft G / H$ and $(G / H) /(K / H) \cong G / K$ by the 第一同构定理。
这个证明再次展示了第一同构定理作为“万能工具”的威力。思路是巧妙地构造一个同态,其定义域是 $(G/H)$,目标域是 $G/K$,然后通过分析这个同态的核与像来得出结论。
- 构造同态:
- 定义域: $G/H$
- 目标域: $G/K$
- 定义映射 $f$: 将陪集 $gH$ 映射到陪集 $gK$。即 $f(gH) = gK$。
- 证明良定义性:
- 定义依赖于代表元 $g$,必须检查。
- 设 $g'$ 是 $gH$ 的另一个代表元,则 $g' = gh$ (对于某个 $h \in H$)。
- 我们需要证明 $f(g'H) = f(gH)$。
- $f(g'H) = g'K = (gh)K$。
- 因为 $H \leq K$ (前提条件),所以 $h \in H$ 蕴含了 $h \in K$。
- 根据陪集的性质,$xK=K$ 当且仅当 $x \in K$。所以 $(gh)K = g(hK) = gK$。
- 因此 $f(g'H) = gK = f(gH)$。良定义性得证。
- 分析同态的像 (Image):
- $f$ 是满射吗?对于目标群 $G/K$ 中的任意元素 $gK$,我们能找到原像吗?
- 是的,源群 $G/H$ 中的元素 $gH$ 就是一个原像,因为 $f(gH)=gK$。
- 所以 $f$ 是满射。$\text{Im } f = G/K$。
- 证明是同态:
- 我们需要证明 $f((g_1H)(g_2H)) = f(g_1H)f(g_2H)$。
- $f((g_1H)(g_2H)) = f((g_1g_2)H)$ (根据 $G/H$ 的运算)
- $= (g_1g_2)K$ (根据 $f$ 的定义)
- $= (g_1K)(g_2K)$ (根据 $G/K$ 的运算)
- $= f(g_1H)f(g_2H)$ (根据 $f$ 的定义)
- 所以 $f$ 是一个同态。
- 分析同态的核 (Kernel):
- $\text{Ker } f = \{gH \in G/H \mid f(gH) = \text{单位元}\}$。
- 目标群 $G/K$ 的单位元是陪集 $K$。
- 所以 $\text{Ker } f = \{gH \mid gK=K\}$。
- 条件 $gK=K$ 等价于 $g \in K$。
- 所以 $\text{Ker } f = \{gH \mid g \in K\}$。
- 这个集合正是我们之前定义的 $K/H$。所以 $\text{Ker } f = K/H$。
- 应用第一同构定理:
- 我们现在有一个满同态 $f: G/H \rightarrow G/K$。
- 它的核是 $K/H$。
- 根据推论 3.1.3,我们可以直接得出两个结论:
- 核 $K/H$ 是定义域群 $G/H$ 的正规子群。这证明了定理的第一个结论。
- (定义域群)/(核) $\cong$ (目标群),即 $(G/H)/(K/H) \cong G/K$。这证明了定理的第二个结论。
- 整个证明一气呵成。
第三同构定理的证明是应用第一同构定理的一个典范。通过在两个不同的商群之间建立一个自然的同态 $f(gH)=gK$,然后系统地分析这个新构造的同态 $f$ 的良定义性、满射性、同态性以及它的核,最后将这些要素代入第一同构定理的框架,就直接得到了所要证明的全部结论。这个证明过程本身也加深了我们对商群之间关系的理解。
2. 2.4. 评述 3.2.2 (Remark 3.2.2)
📜 [原文18]
Remark 3.2.2. An equivalent formulation is the following: Suppose that $f: G \rightarrow G^{\prime}$ is a 满同态 and that $N^{\prime}$ is a 正规子群 of $G^{\prime}$。Then $f^{-1}\left(N^{\prime}\right)=N$ is a 正规子群 of $G$ and the 复合同态 $G \rightarrow G^{\prime} / N^{\prime}$ is a 满射 with 核 $N$。Hence, by the 第一同构定理,$G / N \cong G^{\prime} / N^{\prime}$。
这个评述提供了第三同构定理的另一种等价的表述方式。这种表述不直接涉及三层的群塔,而是用同态和原像的语言来描述,有时在应用中更为方便。
- 等价表述的条件:
- 有一个满同态 $f: G \rightarrow G'$。
- 在目标群 $G'$ 中有一个正规子群 $N'$。
- 等价表述的结论:
- 结论一: $N = f^{-1}(N')$ 是 $G$ 中的一个正规子群。
- $f^{-1}(N')$ 是 $N'$ 在 $f$ 下的原像,即 $\{g \in G \mid f(g) \in N'\}$。
- 为什么 $N$ 是正规子群?可以证明。取任意 $n \in N$ 和 $g \in G$。我们需要证明 $gng^{-1} \in N$。这等价于证明 $f(gng^{-1}) \in N'$。
- $f(gng^{-1}) = f(g)f(n)f(g^{-1}) = f(g)f(n)(f(g))^{-1}$。
- 因为 $n \in N = f^{-1}(N')$,所以 $f(n) \in N'$。
- 因为 $N' \triangleleft G'$,所以对于任意 $y \in G'$ 和 $n' \in N'$,都有 $yn'y^{-1} \in N'$。
- 这里取 $y = f(g) \in G'$ 和 $n' = f(n) \in N'$,所以 $f(g)f(n)(f(g))^{-1} \in N'$。
- 因此 $f(gng^{-1}) \in N'$,这证明了 $gng^{-1} \in N$。所以 $N$ 是 $G$ 的正规子群。
- 结论二: 考虑一个复合同态: $\phi: G \rightarrow G'/N'$。
- 这个同态 $\phi$ 是先走 $f$ 到 $G'$,再走商同态 $\pi: G' \rightarrow G'/N'$。即 $\phi = \pi \circ f$。
- 这个复合同态是满射吗?是的。因为 $f$ 是满射到 $G'$,$\pi$ 是满射到 $G'/N'$,两个满射的复合依然是满射。
- 这个复合同态的核是什么?$\text{Ker } \phi = \{g \in G \mid \phi(g) = \text{单位元}\}$。$G'/N'$ 的单位元是 $N'$。
- $\phi(g) = \pi(f(g)) = N'$。这当且仅当 $f(g) \in N'$。
- 根据 $N$ 的定义,$f(g) \in N' \iff g \in f^{-1}(N') = N$。
- 所以 $\text{Ker } \phi = N$。
- 结论三: 应用第一同构定理。
- 我们有了一个满同态 $\phi: G \rightarrow G'/N'$,它的核是 $N$。
- 根据推论 3.1.3,我们得到 $G/N \cong G'/N'$。
- 与原定理的联系:
- 如何看出这和 $(G/H)/(K/H) \cong G/K$ 是等价的?
- 我们可以做一个对应:
- 取 $f$ 为商同态 $\pi_H: G \rightarrow G/H$。这是一个满同态。所以 $G' = G/H$。
- 在 $G'$ 中取一个正规子群 $N'$。根据对应定理,$G/H$ 中的任何正规子群都唯一对应于 $G$ 中一个包含 $H$ 的正规子群 $K$,并且 $N' = K/H$。
- 计算 $N = f^{-1}(N') = (\pi_H)^{-1}(K/H)$。根据定义,$(\pi_H)^{-1}(K/H) = \{g \in G \mid \pi_H(g) \in K/H\} = \{g \in G \mid gH \in K/H\}$。
- $gH \in K/H$ 的意思是 $gH = kH$ 对于某个 $k \in K$,这等价于 $g \in K$。所以 $N=K$。
- 现在把这些代入等价表述的结论 $G/N \cong G'/N'$:
- $G/K \cong (G/H)/(K/H)$。
- 这正是第三同构定理的原始形式。因此两种表述是等价的。
这个评述提供了一种看待第三同构定理的替代视角。它将定理的适用场景从“群塔” $H \leq K \leq G$ 推广到任何存在满同态 $f: G \rightarrow G'$ 的情况。它揭示了满同态 $f$ 在正规子群和商群结构上的“保持”性质:$G'$ 的正规子群 $N'$ 向上“拉回”到 $G$ 中得到正规子群 $f^{-1}(N')$,并且 $G$ 对这个“拉回”的子群求商,其结果与 $G'$ 对原子群 $N'$ 求商的结果是同构的。
2. 2.5. 示例 3.2.3
📜 [原文19]
例 3.2.3. Suppose that $n, d \in \mathbb{N}$ and that $d \mid n$。Then $\langle n\rangle \leq\langle d\rangle \leq \mathbb{Z}$,and all 子群 of $\mathbb{Z}$ are 正规的 since $\mathbb{Z}$是阿贝尔群。The 像 of $\langle d\rangle$ in $\mathbb{Z} /\langle n\rangle=\mathbb{Z} / n \mathbb{Z}$ is the 循环子群 generated by $d$ viewed as an element of $\mathbb{Z} / n \mathbb{Z}$。Applying the 第三同构定理,we see that $\mathbb{Z} / n \mathbb{Z} /\langle d\rangle \cong \mathbb{Z} / d \mathbb{Z}$,which we have also argued by a direct inspection of the 陪集 and the 群运算。
这个例子将第三同构定理应用到我们熟悉的整数循环群上,为之前在示例(iii)中得到的一个结论提供了另一种证明方法。
- 建立群塔:
- 设 $G = \mathbb{Z}$ (整数加法群)。
- 因为 $d$ 整除 $n$ ($d \mid n$),所以任何 $n$ 的倍数也必然是 $d$ 的倍数。这意味着 $n\mathbb{Z} \subseteq d\mathbb{Z}$。
- 在群论的记号中,这写作 $\langle n \rangle \leq \langle d \rangle$。
- 所以我们有了一个子群塔:$\langle n \rangle \leq \langle d \rangle \leq \mathbb{Z}$。
- 因为 $\mathbb{Z}$ 是阿贝尔群,所以它的所有子群都是正规子群。这样,第三同构定理的条件就满足了。
- 对应关系:$G = \mathbb{Z}$, $K = \langle d \rangle = d\mathbb{Z}$, $H = \langle n \rangle = n\mathbb{Z}$。
- 应用第三同构定理:
- 定理公式为 $(G/H)/(K/H) \cong G/K$。
- 代入我们的具体群和子群:
- $G/H = \mathbb{Z}/\langle n \rangle = \mathbb{Z}/n\mathbb{Z}$。
- $G/K = \mathbb{Z}/\langle d \rangle = \mathbb{Z}/d\mathbb{Z}$。
- $K/H = \langle d \rangle / \langle n \rangle$。这是 $G/H = \mathbb{Z}/n\mathbb{Z}$ 中的一个子群。这个子群是什么呢?它是由 $d$ 在 $\mathbb{Z}/n\mathbb{Z}$ 中生成的循环子群,也就是 $\langle [d] \rangle$。
- 将这些代入公式,得到:$(\mathbb{Z}/n\mathbb{Z}) / \langle [d] \rangle \cong \mathbb{Z}/d\mathbb{Z}$。
- 与之前的结论对比:
- 这个结论正是我们在分析商群性质的示例(iii)中得到的结论。
- 在示例(iii)中,我们的论证是:原群是循环的,所以商群也是循环的,然后通过计算商群的阶为 $d$ 来确定它同构于 $\mathbb{Z}/d\mathbb{Z}$。
- 在这里,我们使用了更强大的第三同构定理,通过形式化的符号“约分”,直接得出了这个同构关系,而无需关心商群的生成元或具体运算。
- 设 $n=12, d=4$。我们有 $\langle 12 \rangle \leq \langle 4 \rangle \leq \mathbb{Z}$。
- $G = \mathbb{Z}, H=\langle 12 \rangle, K=\langle 4 \rangle$。
- $G/H = \mathbb{Z}/12\mathbb{Z}$。
- $G/K = \mathbb{Z}/4\mathbb{Z}$。
- $K/H = \langle 4 \rangle / \langle 12 \rangle$。这是 $\mathbb{Z}/12\mathbb{Z}$ 中由 4 生成的子群,即 $\langle 4 \rangle_{12} = \{0, 4, 8\}$。
- 根据第三同构定理:$(\mathbb{Z}/12\mathbb{Z}) / \{0,4,8\} \cong \mathbb{Z}/4\mathbb{Z}$。
- 这与我们之前手动计算的结果完全一致:一个阶为 12 的群模掉一个阶为 3 的子群,得到一个阶为 4 的商群,并且由于结构上的“约分”,它恰好同构于 $\mathbb{Z}/4\mathbb{Z}$。
本例为同一个结论 $(\mathbb{Z}/n\mathbb{Z})/\langle d \rangle \cong \mathbb{Z}/d\mathbb{Z}$ 提供了第二次证明。第一次证明是基于商群的循环性和阶的计算,更为具体。第二次证明是基于第三同构定理,更为抽象和普适。通过同一个例子,展示了不同定理的应用方式,有助于学生对比和理解这些定理的威力所在。
2. 2.6. 第二同构定理的引言
📜 [原文20]
To describe the 第二同构定理,we recall from 习题 4.25 that, if $H$ and $K$ are two 子群 of $G$,with $H \triangleleft G$,then $H K$ is a 子群 of $G, H \triangleleft H K$ and $H \cap K \triangleleft K$。Thus, we can consider the 商群 $H K / H$。The 第二同构定理 gives another description of this 商:
这部分是第二同构定理的引言,旨在设置定理的舞台,明确定理要研究的对象和前提条件。
- 前提条件:
- 有一个群 $G$。
- 有两个子群 $H$ 和 $K$。
- 这两个子群的地位不是对等的:其中一个 $H$ 必须是 $G$ 的正规子群 ($H \triangleleft G$),而另一个 $K$ 只是一个普通的子群 ($K \leq G$)。
- 由前提条件引出的性质:
- 作者引用了一个习题的结论(这在之前命题2.3.14中也已证明),在上述前提下,我们可以得到几个重要的结构性事实:
- 积集 $HK$ 是一个子群: 因为 $H$ 是正规的,所以 $HK$ 是 $G$ 的一个子群。
- $H$ 在 $HK$ 中是正规的 ($H \triangleleft HK$): 因为 $H \triangleleft G$,根据命题2.3.14(iii),$H$ 在任何包含它的中间子群中都是正规的。既然 $H \leq HK \leq G$,那么 $H \triangleleft HK$ 自然成立。
- $H \cap K$ 在 $K$ 中是正规的 ($H \cap K \triangleleft K$): 这是命题2.3.14(ii) 的直接结论。
- 引出研究对象:
- 基于上述性质,我们知道构造以下两个商群是合法的、有意义的:
- 商群1: $HK/H$ (因为 $H \triangleleft HK$)
- 商群2: $K/(H \cap K)$ (因为 $H \cap K \triangleleft K$)
- 这两个商群看起来毫无关系。它们是由不同的群和不同的正规子群构造出来的。
- 定理的预告:
- 第二同构定理的核心任务,就是揭示这两个表面上无关的商群 $HK/H$ 和 $K/(H \cap K)$ 之间令人惊讶的联系:它们实际上是同构的。
- 定理为商群 $HK/H$ 提供了“另一种描述”。
本段引言清晰地陈述了第二同构定理的背景设定。它从一个正规子群 $H$ 和一个任意子群 $K$ 出发,利用已知的命题确认了可以合法地构造出两个商群 $HK/H$ 和 $K/(H \cap K)$。然后,它明确指出,第二同构定理就是要证明这两个看似不同的商群在结构上是完全一样的。
2. 2.7. 定理 3.2.4 (第二同构定理)
📜 [原文21]
定理 3.2.4. Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Then
In particular, if $H$ and $K$ are both 有限的,then
这部分正式陈述了第二同构定理及其在有限群中的重要推论。
- 定理的条件:
- $G$ 是一个群。
- $H$ 是 $G$ 的一个正规子群 ($H \triangleleft G$)。
- $K$ 是 $G$ 的一个子群 ($K \leq G$)。
- 定理的结论 (同构关系):
- $HK/H \cong K/(H \cap K)$
- 左边: 是由积子群 $HK$ 模掉其正规子群 $H$ 得到的商群。
- 右边: 是由子群 $K$ 模掉其正规子群 $H \cap K$ 得到的商群。
- $\cong$: 表明这两个群同构。
- 直观理解 (分数类比): 这个定理有时被称为“平行四边形法则”。想象一个由向量 $H$ 和 $K$ 张成的平行四边形 $HK$。$HK/H$ 像是把平行四边形沿着 $H$ 的方向“压扁”,得到一条长度为 $K$ 的线段。$K/(H \cap K)$ 像是从线段 $K$ 中“减去”了它与 $H$ 重叠的部分 $H \cap K$。定理说这两种操作得到的结果在结构上是等价的。
- 定理的推论 (有限群阶数公式):
- 前提: 在原定理的基础上,增加条件 $H$ 和 $K$ 都是有限群。
- 推论: $\#(HK) = \frac{\#(H)\#(K)}{\#(H \cap K)}$。
- 证明思路:
- 因为 $HK/H \cong K/(H \cap K)$,所以这两个有限群的阶必然相等。
- $|HK/H| = |HK| / |H|$ (根据拉格朗日定理)。
- $|K/(H \cap K)| = |K| / |H \cap K|$ (根据拉格朗日定理)。
- 所以 $|HK| / |H| = |K| / |H \cap K|$。
- 将分母 $|H|$ 乘到右边,就得到 $\#(HK) = \frac{\#(H)\#(K)}{\#(H \cap K)}$。
- 这个公式非常有用,它给出了计算两个子群(其中一个正规)的积子群大小的方法。它在形式上和集合论中的容斥原理 $|A \cup B| = |A| + |B| - |A \cap B|$ 有类似之处,但这里是乘除关系。
第二同构定理,又称“钻石同构定理”(因其相关的子群格图形状像钻石),揭示了一个正规子群和一个普通子群之间相互作用的深刻结构。它表明,从积子群 $HK$ 中“除掉”$H$ 的部分,其结果与从 $K$ 中“除掉”它们公共的部分 $H \cap K$ 是一样的。其在有限群中的推论——积子群阶数公式——是一个在组合计数和结构分析中极其常用的工具。
2. 2.8. 第二同构定理的证明
📜 [原文22]
证明. By 习题 4.25,$H \cap K \triangleleft K$ (although we will see this directly as well),$H K \leq G$ and $H \triangleleft H K$。
To prove the 定理,we shall find a 满同态 $f$ from $K$ to $H K / H$ whose 核是 $H \cap K$。The 第一同构定理 then says that $K /(H \cap K) \cong H K / H$。Define $f(k)=k H$,包含$k$的$H$-陪集。Thus $f$ is the 复合映射 $\pi \circ i$,where $i: K \rightarrow H K$ is the 包含映射 and $\pi: H K \rightarrow H K / H$ is the 商同态。Hence $f$ is a 同态 since it is a 复合映射 of two 同态s, and clearly 核 $\operatorname{Ker} f=\operatorname{Ker} \pi \cap K=H \cap K$。
We will be done if we show that $f$ is 满射,in other words that every 陪集 $x H$,with $x \in H K$,is equal to some 陪集 of the form $k H$ with $k \in K$。But since $x \in H K, x=h k$ for some $h \in H$ and $k \in K$。Since $H$ is 正规的,$h k=k h^{\prime}$ for some $h^{\prime} \in H$,and clearly $k h^{\prime} H=k H$。Thus $x H=h k H=k h^{\prime} H=k H=f(k)$,so that $f$ is 满射。The final equality holds since then
这个证明再次娴熟地运用了第一同构定理。策略是构造一个从 $K$ 到 $HK/H$ 的同态。
- 证明策略:
- 我们的目标是证明 $K/(H \cap K) \cong HK/H$。
- 根据第一同构定理的“配对”策略(推论 3.1.3),如果我们能构造一个满同态 $f: K \rightarrow HK/H$,并且证明它的核恰好是 $H \cap K$,那么定理就得证了。
- 构造同态:
- 定义域: $K$
- 目标域: $HK/H$
- 定义映射 $f$: 对于 $K$ 中的任意元素 $k$,定义 $f(k) = kH$。这个 $kH$ 是 $HK/H$ 中的一个元素(一个 $H$ 的陪集)。
- 验证是同态: 作者给出了一个优雅的看法。这个映射 $f$ 可以看作是两个已知同态的复合:
- $i: K \rightarrow HK$: 这是一个包含映射,将 $K$ 中的元素 $k$ 看作是 $HK$ 中的元素 $k$。这显然是同态。
- $\pi: HK \rightarrow HK/H$: 这是标准的商同态,$\pi(x) = xH$。这也是同态。
- $f(k) = kH = \pi(k) = \pi(i(k)) = (\pi \circ i)(k)$。
- 因为 $f$ 是两个同态的复合,所以 $f$ 本身也必然是一个同态。
- 分析同态的核 (Kernel):
- $\text{Ker } f = \{k \in K \mid f(k) = \text{单位元}\}$。
- 目标群 $HK/H$ 的单位元是陪集 $H$。
- 所以 $\text{Ker } f = \{k \in K \mid kH = H\}$。
- 条件 $kH = H$ 等价于 $k \in H$。
- 所以,核是那些既属于 $K$ 又属于 $H$ 的元素的集合。这正是交集 $H \cap K$。
- 所以 $\text{Ker } f = H \cap K$。
- (这里也顺便直接证明了 $H \cap K \triangleleft K$,因为它是同态 $f: K \rightarrow HK/H$ 的核。)
- 分析同态的像 (Image - 证明满射):
- 我们需要证明 $f$ 是满射,即对于目标群 $HK/H$ 中的任意元素,都能在定义域 $K$ 中找到原像。
- 取 $HK/H$ 中的任意一个元素,它必然形如 $xH$,其中 $x \in HK$。
- 根据 $HK$ 的定义,$x$ 可以写成 $x=hk$ 的形式,其中 $h \in H, k \in K$。
- 所以这个任意元素是 $(hk)H$。
- 根据陪集的性质,$(hk)H = h(kH)$。因为 $h \in H$,所以 $h$ 乘以一个陪集等于该陪集本身,即 $h(kH)=kH$。
- 所以,任意一个元素 $xH = (hk)H$ 实际上就等于 $kH$。
- 而 $kH$ 正是定义域 $K$ 中元素 $k$ 的像 $f(k)$。
- 这就证明了,对于任意的目标元素 $xH$,我们总能找到一个原像 $k \in K$ (就是 $x$ 的 $K$ 部分)。
- 因此,$f$ 是满射。
- (原文中用到了 $H$ 的正规性 $hk=kh'$,然后 $hkH=kh'H=kH$,结论是一样的,但直接用陪集性质 $h(kH)=kH$ 更简洁。)
- 应用第一同构定理:
- 我们成功构造了一个满同态 $f: K \rightarrow HK/H$,其核为 $H \cap K$。
- 根据推论 3.1.3,我们得到 $(K)/(H \cap K) \cong HK/H$。
- 定理证明完毕。
- 最后阶数公式的说明:
- 原文最后一句 "The final equality holds since then..." 是在解释那个有限群阶数公式的由来。
- 它来自于对同构关系 $HK/H \cong K/(H \cap K)$ 两边取阶。
- $\#(HK/H) = \#(K/(H \cap K))$。
- 根据拉格朗日定理,$\#(HK)/\#(H) = \#(K)/\#(H \cap K)$。
- 这就是原文中给出的等式。
第二同构定理的证明再次完美地演绎了如何利用第一同构定理。其核心在于识别出正确的定义域 ($K$) 和目标域 ($HK/H$),并定义一个最自然的映射 $f(k)=kH$。剩下的工作就是按部就班地验证这个映射是满同态,并找出其核。一旦完成这些,结论便水到渠成。这个证明过程不仅给出了定理的逻辑依据,也深化了我们对陪集 $kH$ 和 $hkH$ 之间关系的理解。
2. 2.9. 推论 3.2.5
📜 [原文23]
推论 3.2.5. Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $H K=G$ and that $H \cap K=\{1\}$。Then $G / H \cong K$。
这个推论是第二同构定理在一种特殊且重要情况下的直接应用。这种情况在讨论半直积时非常关键。
- 推论的条件:
- $H \triangleleft G$ (H是正规子群)。
- $K \leq G$ (K是子群)。
- $HK = G$: 它们的积子群恰好是整个群 $G$。
- $H \cap K = \{1\}$: 它们的交集是平凡的,只包含单位元。
- 推论的结论:
- $G/H \cong K$。
- 直观理解: 如果群 $G$ 可以被一个正规子群 $H$ 和一个子群 $K$ “无重叠地完全覆盖”($H \cap K=\{1\}, HK=G$),那么从 $G$ 中“模掉”$H$ 的部分,剩下的结构就和 $K$ 的结构一模一样。
- 证明思路:
- 直接应用第二同构定理的公式:$HK/H \cong K/(H \cap K)$。
- 将本推论的特殊条件代入公式:
- 将左边的 $HK$ 替换为 $G$,得到 $G/H$。
- 将右边的 $H \cap K$ 替换为 $\{1\}$,得到 $K/\{1\}$。
- 所以公式变为 $G/H \cong K/\{1\}$。
- 我们知道任何群模掉平凡子群 $\{1\}$ 都同构于其自身,即 $K/\{1\} \cong K$。
- 通过传递性,我们得到 $G/H \cong K$。
- 证明完毕。
这个推论描述了一种将群 $G$ 分解为 $H$ 和 $K$ 两部分的情况。当正规子群 $H$ 和子群 $K$ 的交集平凡且它们的乘积等于全群时,商群 $G/H$ 就同构于子群 $K$。这为识别形如 $G/H$ 的商群提供了一个非常有力的工具:只需在 $G$ 中找到一个与 $H$ “互补”的子群 $K$ 即可。
2. 2.10. 推论 3.2.6
📜 [原文24]
推论 3.2.6. Let $G$ be a 有限群 and $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $H \cap K=\{1\}$ and that $\#(G)=\#(H) \#(K)$。Then $G / H \cong K$。
这个推论是上一个推论在有限群背景下的一个变种。它将上一个推论中难以验证的条件 $HK=G$ 替换为了一个更容易计算的阶数条件。
- 推论的条件:
- $G$ 是一个有限群。
- $H \triangleleft G$。
- $K \leq G$。
- $H \cap K = \{1\}$ (交集平凡)。
- $\#(G) = \#(H)\#(K)$ (群的阶数等于两个子群阶数的乘积)。
- 推论的结论:
- $G/H \cong K$。
- 证明思路:
- 我们的目标是应用上一个推论 (3.2.5)。上一个推论的条件是 $HK=G$ 和 $H \cap K=\{1\}$。
- 本推论已经给出了 $H \cap K=\{1\}$。所以我们唯一需要证明的就是 $HK=G$。
- 证明 HK=G:
- 因为 $H \triangleleft G$,我们知道 $HK$ 是 $G$ 的一个子群。
- 我们来计算这个子群 $HK$ 的阶数。根据第二同构定理的阶数公式:$\#(HK) = \frac{\#(H)\#(K)}{\#(H \cap K)}$。
- 将条件 $H \cap K = \{1\}$ 代入,得到分母 $\#(H \cap K)=1$。
- 所以 $\#(HK) = \#(H)\#(K)$。
- 根据本推论的另一个条件,我们知道 $\#(G) = \#(H)\#(K)$。
- 因此,我们得到 $\#(HK) = \#(G)$。
- 我们现在有一个子群 $HK$,它的阶数和整个群 $G$ 的阶数相等。对于有限群来说,这意味着这个子群只能是全群本身。
- 所以 $HK=G$。
- 应用推论3.2.5:
- 我们已经证明了 $HK=G$ 并且已知 $H \cap K=\{1\}$。这完全满足了推论3.2.5的条件。
- 因此,我们可以直接得出结论 $G/H \cong K$。
- 证明完毕。
这个推论在处理有限群时非常实用。它告诉我们,要证明 $G/H \cong K$,我们不必去费力地计算积集 $HK$ 来验证它是否等于 $G$,只需要简单地比较阶数即可。如果 $H$ 和 $K$ 的阶数之积恰好等于 $G$ 的阶数,并且它们的交集只有单位元,那么这个同构关系就成立。
2. 2.11. 示例 3.2.7
📜 [原文25]
例 3.2.7. Consider the 群 $S_{4}$。We have seen that the 子群
is a 正规子群 of $S_{4}$,with $\#(H)=4$。There is also the (非正规) 子群 $H_{4}$ of $S_{4}$:$H_{4}=\left\{\sigma \in S_{4}: \sigma(4)=4\right\}$。Then $H_{4} \cong S_{3}$ and $\#\left(H_{4}\right)=6$,so that $\#(H) \#\left(H_{4}\right)=24=\#\left(S_{4}\right)$。Finally, by inspection $H \cap H_{4}=\{1\}$。Thus $S_{4} / H \cong S_{3}$。
这个例子是推论 3.2.6 的一个具体应用,用它来识别一个重要的商群 $S_4/V_4$ 的结构。
- 设定群和子群:
- $G = S_4$,阶为 $4! = 24$ 的4次对称群。
- $H = \{1, (12)(34), (13)(24), (14)(23)\}$。这个群通常被称为克莱因四元群 $V_4$。它是一个阶为 4 的阿贝尔群。之前已经指出(或可以验证)$H$ 是 $S_4$ 的一个正规子群 ($H \triangleleft S_4$)。
- $K = H_4 = \{\sigma \in S_4 \mid \sigma(4)=4\}$。这是 $S_4$ 中所有固定元素 '4' 的置换构成的子群。
- 这些置换只作用于集合 $\{1,2,3\}$,因此这个子群在结构上与 $S_3$ 是完全一样的,即 $K \cong S_3$。
- 因此它的阶是 $|S_3| = 3! = 6$。
- $K$ 在 $S_4$ 中不是正规子群。
- 验证推论 3.2.6 的条件:
- G是有限群: $S_4$ 的阶是 24,是有限群。
- H triangleleft G: 已知 $H=V_4$ 是 $S_4$ 的正规子群。
- K ≤ G: $H_4$ 是 $S_4$ 的子群。
- 阶数条件: $\#(G) = 24$。$\#(H) = 4$。$\#(K) = 6$。计算乘积 $\#(H)\#(K) = 4 \times 6 = 24$。我们发现 $\#(G) = \#(H)\#(K)$。条件满足。
- 交集条件: 我们需要检查 $H \cap K$。
- $H = \{1, (12)(34), (13)(24), (14)(23)\}$。
- $K = H_4$ 是所有固定 '4' 的置换。
- 我们逐个检查 $H$ 中的非单位元元素是否固定 '4':
- $(12)(34)$: 它把 3 映到 4,4 映到 3。它不固定 '4'。
- $(13)(24)$: 它把 2 映到 4,4 映到 2。它不固定 '4'。
- $(14)(23)$: 它把 1 映到 4,4 映到 1。它不固定 '4'。
- 所以 $H$ 中唯一固定 '4' 的元素只有单位元 1。
- 因此 $H \cap K = \{1\}$。条件满足。
- 应用推论得出结论:
- 所有条件都满足了。根据推论 3.2.6,我们可以直接得出结论:$G/H \cong K$。
- 代入具体的群:$S_4/V_4 \cong S_3$。
这个例子完美地展示了推论 3.2.6 的应用流程。通过识别 $S_4$ 中的正规子群 $V_4$ 和一个“互补”的子群 $S_3$,并通过简单的阶数计算和交集检查,我们成功地识别出商群 $S_4/V_4$ 的结构就是我们非常熟悉的 $S_3$。这比直接去分析 $S_4/V_4$ 的6个陪集以及它们之间的乘法运算要简单得多。
2. 2.12. 推论 3.2.8
📜 [原文26]
Here is another 推论 that will come up later:
推论 3.2.8. Let $G$ be a 有限群 with $\#(G)=n m$ and $\operatorname{gcd}(n, m)=1$。Let $H$ and $K$ be two 子群 of $G$,with $H \triangleleft G$。Suppose that $\#(H)=n$ and that $\#(K)=m$。Then $G / H \cong K$。
这个推论是推论 3.2.6 的进一步特殊化,将阶数条件与数论中的互质条件联系起来。
- 推论的条件:
- $G$ 是一个有限群,其阶 $\#(G)=nm$。
- $n$ 和 $m$ 是两个互质的正整数,即 $\text{gcd}(n,m)=1$。
- $H \triangleleft G$,并且 $H$ 的阶是 $\#(H)=n$。
- $K \leq G$,并且 $K$ 的阶是 $\#(K)=m$。
- 推论的结论:
- $G/H \cong K$。
- 证明思路:
- 我们的目标是应用推论 3.2.6。该推论的条件是: $H \cap K=\{1\}$ 和 $\#(G)=\#(H)\#(K)$。
- 验证阶数条件:
- 我们已知 $\#(H)=n$ 和 $\#(K)=m$。
- 所以 $\#(H)\#(K) = nm$。
- 我们又已知 $\#(G)=nm$。
- 所以 $\#(G)=\#(H)\#(K)$。阶数条件自动满足。
- 验证交集条件 ($H \cap K = \{1\}$):
- 考虑交集子群 $H \cap K$。
- 因为 $H \cap K$ 是 $H$ 的一个子群,根据拉格朗日定理,它的阶 $\#(H \cap K)$ 必须整除 $H$ 的阶 $\#(H)=n$。
- 因为 $H \cap K$ 也是 $K$ 的一个子群,根据拉格朗日定理,它的阶 $\#(H \cap K)$ 必须整除 $K$ 的阶 $\#(K)=m$。
- 所以,$\#(H \cap K)$ 是 $n$ 和 $m$ 的一个公因数。
- 根据前提条件,$\text{gcd}(n,m)=1$。$n$ 和 $m$ 唯一的正公因数就是 1。
- 因此,$\#(H \cap K)$ 只能是 1。
- 一个阶为 1 的群只包含单位元。所以 $H \cap K = \{1\}$。交集条件得证。
- 应用推论 3.2.6:
- 我们已经证明了 $H \cap K=\{1\}$ 和 $\#(G)=\#(H)\#(K)$。
- 因此,根据推论 3.2.6,结论 $G/H \cong K$ 成立。
- 证明完毕。
这个推论在处理有限群的阶数满足特定数论属性(可以分解为互质的两个因子)时非常有用。它告诉我们,如果群 $G$ 恰好有一个正规子群和一个子群,它们的阶分别对应于这两个互质的因子,那么我们就可以立即得到一个商群的同构关系。这个推论在西罗定理等更深入的有限群结构理论中会扮演重要角色。
22.3. 单群与有限群的分类
2. 3.1. 小阶有限群
📜 [原文27]
4.1. 小阶有限群. How can we describe all 有限群?Before we address this question, let's write down a list of all the 有限群 of small 阶 $\leq 15$,up to 同构。We have seen almost all of these already。If $G$ is 阿贝尔群,it is easy to write down all possible $G$ of a given 阶,using the 有限阿贝尔群基本定理:$G$ must be 同构 to a 循环群的直积,and any 同构 between two such 直积s is a consequence of the 中国剩余定理。For example, if $\#(G)=n$ and $n$ is a product of 不同素数 then $G$ is 循环的,and hence 同构于 $\mathbb{Z} / n \mathbb{Z}$。The only cases where this doesn't happen for $n \leq 15$ are:
- $n=4$ and $G \cong \mathbb{Z} / 4 \mathbb{Z}$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$。
- $n=8$ and $G \cong \mathbb{Z} / 8 \mathbb{Z}, G \cong(\mathbb{Z} / 4 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z})$。
- $n=9$ and $G \cong \mathbb{Z} / 9 \mathbb{Z}$ or $G \cong(\mathbb{Z} / 3 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$。
- $n=12$ and $G \cong(\mathbb{Z} / 4 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$ or $G \cong(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 2 \mathbb{Z}) \times(\mathbb{Z} / 3 \mathbb{Z})$。
Note that, for $n=16$,there are already 5 possibilities for $G$。
In case $G$ is not 阿贝尔群,there are many 阶 which can't arise。For example, if $\#(G)=p$,where $p$是素数,then we have seen that $G$是阿贝尔群。We will show soon that, if $\#(G)=p^{2}$,where $p$是素数,then $G$是阿贝尔群。Also, if $\#(G)=p q$,where $p$ and $q$ are distinct 素数,say $p<q$,then $G$是阿贝尔群 unless $q \equiv 1 \bmod p$,and in this case all of the 非阿贝尔群 $G$ of 阶 $p q$ are 同构 and can be described quite explicitly。Thus for example every 阶为15的群都是阿贝尔群,因此是循环群。The only possibilities then for 阶至多为15的非阿贝尔群,up to 同构,are given by:
- $n=6$ and $G \cong S_{3} \cong D_{3}$。
- $n=8; G \cong D_{4}$ or 四元数群 $Q$。
- $n=10$ and $G \cong D_{5}$。
- $n=12; G \cong D_{6}, G \cong A_{4}$, or $G \cong(\mathbb{Z} / 3 \mathbb{Z}) \rtimes(\mathbb{Z} / 4 \mathbb{Z})$,a certain 群 which we shall describe later, time permitting。(Note: $S_{3} \times(\mathbb{Z} / 2 \mathbb{Z})$也是阶为12的非阿贝尔群,but in fact $S_{3} \times(\mathbb{Z} / 2 \mathbb{Z}) \cong D_{6}$。)
- $n=14$ and $G \cong D_{7}$。
Lest one conclude that the list seems manageable, we mention that for $n=16$,there are already 5 非同构阿贝尔群 of 阶 16 as well as 9 非同构非阿贝尔群 of 阶 16,and it is rather complicated to describe them all。Of course, if $\#(G)$ has 阶 17,$G$同构于 $\mathbb{Z} / 17 \mathbb{Z}$且是循环的(particularly 阿贝尔的)。In general, though, if $n$可被素数 $p$的高次幂整除,then it becomes very difficult to list all 群 $G$ with $\#(G)=n$ up to 同构。
这部分内容是对有限群分类问题的一个概述和初步探索,特别是针对阶数比较小(不大于15)的群。它将问题分为阿贝尔群和非阿贝尔群两部分来讨论。
引言
- 提出问题: 我们如何描述所有的有限群?这是一个宏大而困难的问题,是有限群理论的核心。
- 简化问题: 作者并不直接解决这个问题,而是先从一个更小、更具体的目标入手:列出所有阶数 $\leq 15$ 的有限群(在同构意义下)。
第一部分:小阶阿贝尔群
- 分类工具: 对于有限阿贝尔群,我们有一个非常强大的分类工具——有限阿贝尔群基本定理。
- 定理内容: 该定理指出,任何一个有限阿贝尔群都同构于一个或多个循环群的直积。具体形式是 $G \cong \mathbb{Z}_{p_1^{k_1}} \times \mathbb{Z}_{p_2^{k_2}} \times \dots$,其中 $p_i$ 是素数。
- 同构的判断: 不同的直积形式何时表示同一个群?这可以用中国剩余定理来判断。例如,$\mathbb{Z}/6\mathbb{Z} \cong \mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}$,因为 2 和 3 互质。但 $\mathbb{Z}/4\mathbb{Z}$ 和 $\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$ 是两个不同的4阶群。
- 特殊情况: 如果群的阶 $n$ 是无平方因子的(即 $n$ 是不同素数的乘积),那么任何阶为 $n$ 的阿贝尔群都必然是循环群,且同构于 $\mathbb{Z}/n\mathbb{Z}$。
- 例如,阶为 $15=3 \times 5$ 的阿贝尔群,只能是 $\mathbb{Z}/15\mathbb{Z}$ (或同构于它的 $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z}$)。
- 列出例外情况 ($n \leq 15$): 作者列出了在阶数15以内,存在多个不同构的阿贝尔群的阶数:
- $n=4=2^2$: $\mathbb{Z}/4\mathbb{Z}$ 和 $\mathbb{Z}/2\mathbb{Z} \times \mathbb{Z}/2\mathbb{Z}$ (V4群)。
- $n=8=2^3$: 有三种,$\mathbb{Z}/8\mathbb{Z}$,$(\mathbb{Z}/4\mathbb{Z}) \times (\mathbb{Z}/2\mathbb{Z})$,以及 $(\mathbb{Z}/2\mathbb{Z})^3$。
- $n=9=3^2$: $\mathbb{Z}/9\mathbb{Z}$ 和 $\mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/3\mathbb{Z}$。
- $n=12=2^2 \times 3$: $(\mathbb{Z}/4\mathbb{Z}) \times (\mathbb{Z}/3\mathbb{Z}) \cong \mathbb{Z}/12\mathbb{Z}$ 和 $(\mathbb{Z}/2\mathbb{Z})^2 \times \mathbb{Z}/3\mathbb{Z}$。
- 复杂性的增长: 作者指出,当阶数增加时,可能性会迅速增多。例如 $n=16$ 时,已经有5种不同的阿贝尔群。
第二部分:小阶非阿贝尔群
- 不存在非阿贝尔群的阶: 很多阶数是排除了非阿贝尔群的。
- 阶为素数 $p$: 任何阶为素数的群都是循环群,因此是阿贝尔群。
- 阶为 $p^2$: 作者预告将证明,任何阶为素数平方的群也是阿贝尔群。所以阶为 4, 9 的群都是阿贝尔群。
- 阶为 $pq$ ($p<q$ 为素数): 这类群是阿贝尔群,除非满足一个特殊的数论条件 $q \equiv 1 \pmod p$。如果不满足这个条件(例如 $15 = 3 \times 5$,而 $5 \not\equiv 1 \pmod 3$),则所有阶为15的群都是阿贝尔群(并且是循环群)。如果满足条件,那么所有非阿贝尔的群都同构于一个特定的半直积结构。
- 列出存在的非阿贝尔群 ($n \leq 15$):
- $n=6=2 \times 3$: $3 \equiv 1 \pmod 2$。存在一个非阿贝尔群 $S_3$(也同构于 $D_3$)。
- $n=8=2^3$: 这是素数的幂,情况复杂。有两个著名的非阿贝尔群:二面体群 $D_4$ 和四元数群 $Q_8$。
- $n=10=2 \times 5$: $5 \equiv 1 \pmod 2$。存在一个非阿贝尔群 $D_5$。
- $n=12=2^2 \times 3$: 阶数因子复杂,导致可能性增多。有三种:$D_6$, $A_4$ (12阶交错群),以及一个用半直积表示的群 $(\mathbb{Z}/3\mathbb{Z}) \rtimes (\mathbb{Z}/4\mathbb{Z})$。作者还特意注释了 $S_3 \times (\mathbb{Z}/2\mathbb{Z})$ 也是12阶非阿贝尔群,但它恰好和 $D_6$ 同构。
- $n=14=2 \times 7$: $7 \equiv 1 \pmod 2$。存在一个非阿贝尔群 $D_7$。
- 阶数1, 2, 3, 4, 5, 7, 9, 11, 13, 15 都不存在非阿贝尔群。
结论
- 复杂性的警告: 作者最后警告读者,不要因为这个列表看起来还算“可管理”就掉以轻心。他再次以 $n=16$ 为例,指出该阶存在9个不同的非阿贝尔群,分类已经相当复杂。
- 素数阶的简单性: 阶为17(素数)的群很简单,只有循环群 $\mathbb{Z}/17\mathbb{Z}$。
- 困难的根源: 作者总结道,当群的阶 $n$ 包含素数的高次幂时(如 $2^3=8, 3^2=9, 2^4=16$),分类问题会变得异常困难。这部分理论被称为 $p$-群理论,是有限群论中最复杂的分支之一。
本段通过对阶数不超过15的有限群进行分类的尝试,为读者描绘了一幅有限群世界复杂性的全景图。它表明:
- 有限阿贝尔群的分类问题已经完全解决,其结构由有限阿贝尔群基本定理给出。
- 非阿贝尔群的分类则要困难得多。其存在性与群的阶的数论性质(如是否为素数、素数平方、$pq$ 型等)密切相关。
- 当群的阶包含素数的高次幂时,群的种类会爆炸式增长,分类变得非常困难。
这段文字通过具体的列表和前瞻性的论述,既展示了已知理论的威力,也指出了未知或困难领域的所在,为后续更深入地学习有限群结构理论(如西罗定理和半直积)提供了动机。
5行间公式索引
- 积集 HK 的定义:
这个公式定义了两个子群 H 和 K 的积集 HK,它包含了所有形如一个 H 中的元素乘以一个 K 中的元素的乘积。
- 积集 HK 的一个具体计算:
这个公式展示了在群 S3 中,两个非正规子群 H=< (1,2)> 和 K=< (2,3)> 的积集 HK 的具体元素。
- 第一同构定理的交换图:
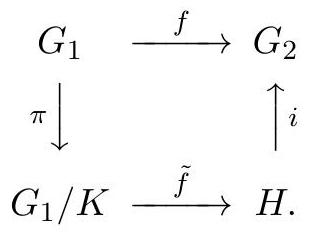
这个图示化了第一同构定理,表明从 G1 到 G2 的同态 f 可以分解为商同态 π、同构 f̃ 和包含映射 i 的复合。
- 证明 f̃ 是同态:
这个公式链证明了通过 f 定义的映射 f̃ 保持了商群的乘法运算,因此是一个群同态。
- 证明交换图成立:
这个公式链通过对任意元素 g 进行计算,验证了直接映射 f 与绕道 π、f̃、i 的复合映射结果相同。
- 推广的同态定义:
这个公式定义了一个从 ZxZ 到 Z 的满同态,当 gcd(a,b)=1 时,其核是由 <(a,b)> 生成的子群。
- 直积群商群的同态:
这个公式定义了一个从直积群到商群的直积的自然同态,用于证明直积与求商运算的“分配律”。
- 直积的商群同构于商群的直积:
这个同构关系表明,对直积群求商,其结果同构于先对各个分量求商再做直积。
- 直积群商去一个因子的特例:
这是上一个公式的特例,说明将直积群 G1xG2 模掉第二个因子 G2 后,得到的商群同构于第一个因子 G1。
- 第三同构定理 (消去定理):
这个公式被称为第三同构定理或“消去定理”,它表明对商群再做商运算,可以简化为对原群做更大的商运算,形式上如同分数的约分。
- 第二同构定理:
这个公式是第二同构定理,它揭示了由正规子群 H 和任意子群 K 构成的两个不同商群之间的同构关系。
- 有限群阶数的乘积公式:
这个公式是第二同构定理在有限群情况下的一个重要推论,它给出了积子群 HK 的阶数计算方法。
- 第二同构定理证明中的阶数关系:
这个等式是阶数乘积公式的直接来源,通过对第二同构定理两边取阶数并应用拉格朗日定理得到。
- S4中V4子群的定义:
这个公式定义了S4中的克莱因四元群子群H(也记作V4),它是一个4阶正规子群。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。