11. COMS 3261 讲义 2B:确定性有限自动机练习解答
📜 [原文1]
COMS 3261 讲义 2B:确定性有限自动机练习解答
Angel Cui 和 Owen Keith
2024 秋季
这部分是文档的标题和作者信息。
- COMS 3261:这是课程代码,代表哥伦比亚大学的一门课程,通常与“计算机科学理论”或“计算理论导论”相关。
- 讲义 2B:这表明该文档是系列讲义中的一部分,具体是第二单元B部分的内容,专注于练习题的解答。
- 确定性有限自动机 (DFA):这是本次讲义的核心主题。DFA 是一种计算模型,用于识别正则语言。它由有限数量的状态、一个字母表(允许的输入符号集合)、一个转移函数(根据当前状态和输入符号决定下一个状态)、一个起始状态和一个接受状态集合组成。
- Angel Cui 和 Owen Keith:文档的作者。
- 2024 秋季:文档所属的学期。
这部分为文档提供了上下文,明确了其主题(DFA练习解答)、来源(COMS 3261课程)和归属信息,帮助读者定位和理解文档的用途。
可以把这份文档想象成一本练习册的答案解析。标题和作者信息就是这本解析的封面,告诉你这是哪门课、哪个章节的答案,由谁编写。
22. 问题一:判断字符串接受情况
2.1 原文叙述
📜 [原文2]
确定 $\varepsilon, 11,010,10,0101$ 中哪些被该 DFA 接受。
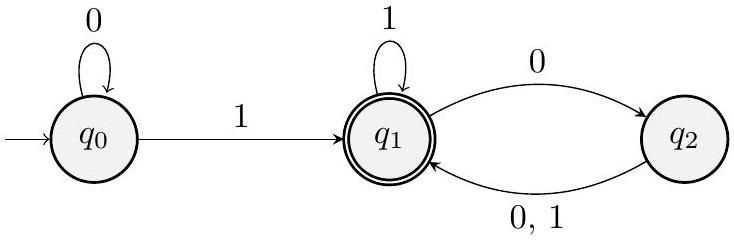
这部分提出了第一个问题:给定一个确定性有限自动机 (DFA) 的状态图,要求我们判断一系列给定的字符串是否被这个 DFA 接受。
- DFA 状态图:这是 DFA 的一种可视化表示。
- 圆圈:代表状态。图中有三个状态:$q_0, q_1, q_2$。
- 指向 $q_0$ 的无源箭头:表示 $q_0$ 是起始状态。DFA 的计算总是从这里开始。
- 双层圆圈:代表接受状态。图中 $q_1$ 是一个接受状态。如果一个字符串处理完毕后,DFA 恰好停在接受状态,那么该字符串就被接受。
- 带标签的箭头:代表转移函数 $\delta$。例如,从 $q_0$ 出发,有一个标着 "0" 的箭头指回 $q_0$,这表示当 DFA 处于 $q_0$ 状态时,如果读入符号 "0",它将转移到 $q_0$ 状态。$\delta(q_0, 0) = q_0$。同样,$\delta(q_0, 1) = q_1$。
- 接受 (Acceptance):一个字符串被 DFA 接受,当且仅当 DFA 从起始状态开始,按顺序读完字符串中的每一个符号并进行相应的状态转移后,最终停留的状态是一个接受状态。
- 待检测字符串:
- $\varepsilon$:空字符串,不包含任何符号。
- $11$
- $010$
- $10$
- $0101$
2.2 解答与分析
📜 [原文3]
我们从 起始状态 开始,逐步“遵循”给定的 字符串 通过 DFA,并检查它是否在 接受状态 结束。具体而言,
- $\varepsilon$ 不被 接受,因为其 计算 中的 状态序列 为 $\left(q_{0}\right)$,而 $q_{0}$ 不是一个 接受状态。
- 11 被 接受,因为其 计算 中的 状态序列 为 $\left(q_{0}, q_{1}, q_{1}\right)$,而 $q_{1}$ 是一个 接受状态。
- 010 不被 接受,因为其 计算 中的 状态序列 为 ( $q_{0}, q_{0}, q_{1}, q_{2}$ ),而 $q_{2}$ 不是一个 接受状态。
- 10 不被 接受,因为其 计算 中的 状态序列 为 ( $q_{0}, q_{1}, q_{2}$ ),而 $q_{2}$ 不是一个 接受状态。
- 0101 被 接受,因为其 计算 中的 状态序列 为 $\left(q_{0}, q_{0}, q_{1}, q_{2}, q_{1}\right)$,而 $q_{1}$ 是一个 接受状态。
这里详细解释了每个字符串的“计算过程”,即状态的演变序列。
- 处理字符串 $\varepsilon$:
- 计算开始:DFA 处于起始状态 $q_0$。
- 读取字符串:$\varepsilon$ 是空字符串,没有符号可读。
- 计算结束:DFA 停留在 $q_0$。
- 判断:$q_0$ 不是接受状态(不是双圈)。
- 结论:$\varepsilon$ 不被接受。
- 状态序列: $(q_0)$
- 处理字符串 $11$:
- 计算开始:DFA 处于起始状态 $q_0$。
- 读取第一个 '1':根据转移 $\delta(q_0, 1) = q_1$,DFA 从 $q_0$ 转移到 $q_1$。
- 读取第二个 '1':根据转移 $\delta(q_1, 1) = q_1$,DFA 从 $q_1$ 转移到 $q_1$。
- 计算结束:字符串读取完毕,DFA 停留在 $q_1$。
- 判断:$q_1$ 是接受状态(是双圈)。
- 结论:$11$ 被接受。
- 状态序列: $(q_0, q_1, q_1)$
- 处理字符串 $010$:
- 计算开始:DFA 处于起始状态 $q_0$。
- 读取第一个 '0':根据转移 $\delta(q_0, 0) = q_0$,DFA 停留在 $q_0$。
- 读取第二个 '1':根据转移 $\delta(q_0, 1) = q_1$,DFA 转移到 $q_1$。
- 读取第三个 '0':根据转移 $\delta(q_1, 0) = q_2$,DFA 转移到 $q_2$。
- 计算结束:字符串读取完毕,DFA 停留在 $q_2$。
- 判断:$q_2$ 不是接受状态。
- 结论:$010$ 不被接受。
- 状态序列: $(q_0, q_0, q_1, q_2)$
- 处理字符串 $10$:
- 计算开始:DFA 处于起始状态 $q_0$。
- 读取第一个 '1':根据转移 $\delta(q_0, 1) = q_1$,DFA 转移到 $q_1$。
- 读取第二个 '0':根据转移 $\delta(q_1, 0) = q_2$,DFA 转移到 $q_2$。
- 计算结束:字符串读取完毕,DFA 停留在 $q_2$。
- 判断:$q_2$ 不是接受状态。
- 结论:$10$ 不被接受。
- 状态序列: $(q_0, q_1, q_2)$
- 处理字符串 $0101$:
- 计算开始:DFA 处于起始状态 $q_0$。
- 读取第一个 '0':$\delta(q_0, 0) = q_0$。当前状态 $q_0$。
- 读取第二个 '1':$\delta(q_0, 1) = q_1$。当前状态 $q_1$。
- 读取第三个 '0':$\delta(q_1, 0) = q_2$。当前状态 $q_2$。
- 读取第四个 '1':$\delta(q_2, 1) = q_1$。当前状态 $q_1$。
- 计算结束:字符串读取完毕,DFA 停留在 $q_1$。
- 判断:$q_1$ 是接受状态。
- 结论:$0101$ 被接受。
- 状态序列: $(q_0, q_0, q_1, q_2, q_1)$
- 示例1:字符串 "101"
- 从 $q_0$ 开始。
- 读 '1',转移到 $q_1$。
- 读 '0',转移到 $q_2$。
- 读 '1',转移到 $q_1$。
- 结束在 $q_1$。$q_1$ 是接受状态,所以 "101" 被接受。
- 示例2:字符串 "000"
- 从 $q_0$ 开始。
- 读 '0',转移到 $q_0$。
- 读 '0',转移到 $q_0$。
- 读 '0',转移到 $q_0$。
- 结束在 $q_0$。$q_0$ 不是接受状态,所以 "000" 不被接受。
- 空字符串 $\varepsilon$:初学者容易忽略空字符串。对空字符串的判断非常简单:只需看起始状态本身是否是接受状态。
- 混淆状态和转移:必须严格按照箭头和标签来转移。例如在 $q_1$ 读到 '1',箭头指回 $q_1$ 自身,而不是去别的状态。
- 只看最后一个符号:DFA 的最终状态取决于整个字符串的计算路径,而不仅仅是最后一个符号。例如,对于 "010" 和 "10",它们都以 '0' 结尾,但前者不被接受,后者也不被接受,但它们的路径是不同的。
该问题考察了 DFA 的基本工作原理。核心思想是模拟字符串在 DFA 上的执行过程:从起始状态出发,根据输入符号,沿着转移函数定义的路径一步步改变状态,最终检查停留的状态是否属于接受状态集合。
这个练习的目的是为了巩固学生对 DFA 计算过程的理解,即将一个抽象的计算模型应用到具体的输入上,并得出确定的输出(接受或拒绝)。
可以把 DFA 想象成一个简单的棋盘游戏。
- 棋盘:就是状态图。
- 棋子:代表当前的计算位置。
- 起点:起始状态 $q_0$。
- 骰子:就是输入的字符串。你按顺序掷出字符串的每个符号。
- 移动规则:转移箭头。每次掷出一个符号,你就根据当前棋子位置(状态)和掷出的符号,把棋子移动到下一个位置。
- 胜利条件:当所有符号都掷完后,如果棋子停在了一个“胜利格子”(接受状态)上,你就赢了(字符串被接受)。
33. 问题二:DFA 的形式化定义
3.1 原文叙述
📜 [原文4]
下方的 DFA 状态图 定义在 字母表 $\Sigma=\{a, b, c\}$ 上。写出其 形式化定义(作为一个 五元组)。在指定 转移函数 $\delta$ 时,画出一个 表格。
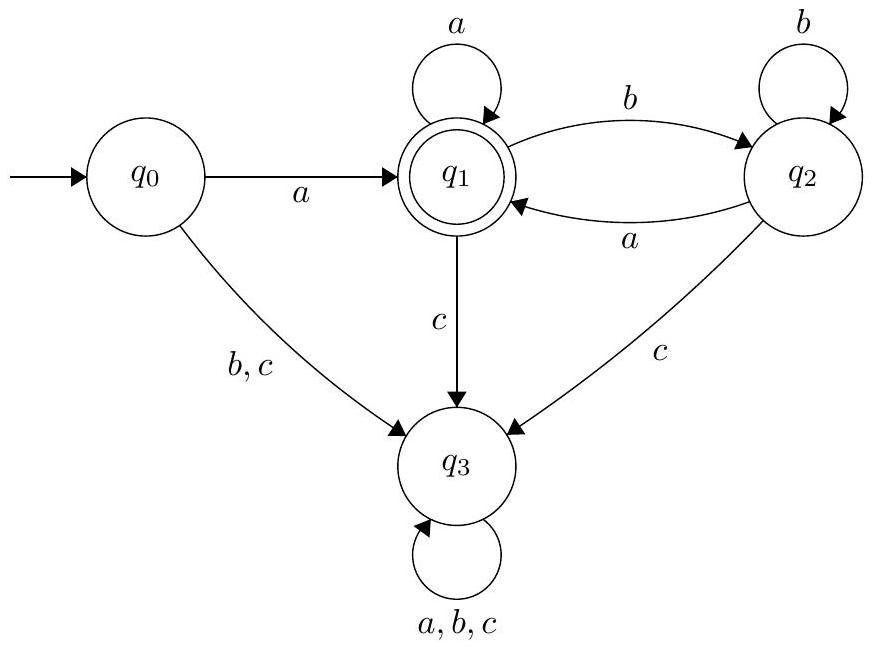
这个问题要求我们将一个给定的 DFA 状态图 翻译成其形式化定义。形式化定义是描述 DFA 的一种精确、无歧义的数学语言。
- 形式化定义 (五元组):一个 DFA $D$ 被定义为一个五元组 $D = (Q, \Sigma, \delta, q_0, F)$,其中:
- $Q$:一个有限的状态集合 (a finite set of states)。
- $\Sigma$:一个有限的字母表 (a finite alphabet),即输入符号的集合。
- $\delta: Q \times \Sigma \to Q$:转移函数 (the transition function)。它接受当前状态和当前输入符号,输出下一个状态。
- $q_0 \in Q$:起始状态 (the start state)。
- $F \subseteq Q$:接受状态的集合 (the set of accept states)。
- 分析状态图:
- 状态 $Q$:图中有四个圆圈,分别标记为 $q_0, q_1, q_2, q_3$。所以 $Q = \{q_0, q_1, q_2, q_3\}$。
- 字母表 $\Sigma$:题目已给出 $\Sigma = \{a, b, c\}$。
- 起始状态 $q_0$:$q_0$ 有一个无源的指向它的箭头,所以 $q_0$ 是起始状态。
- 接受状态 $F$:$q_1$ 是双层圆圈,所以 $F = \{q_1\}$。注意,只有一个接受状态,所以它被放在一个集合中。
- 转移函数 $\delta$:我们需要根据图中的箭头来构建一个表格。表格的行是当前状态,列是输入符号,表格单元格是下一个状态。
3.2 解答与分析
📜 [原文5]
因此我们有 $D=\left\{Q, \Sigma, \delta, q_{0}, F\right\}$,其中:
- $Q=\left\{q_{0}, q_{1}, q_{2}, q_{3}\right\}$
- $\Sigma=\{a, b, c\}$
- $\delta$ 描述如下:
| a | b | c | |
|---|---|---|---|
| $q_{0}$ | $q_{1}$ | $q_{3}$ | $q_{3}$ |
| $q_{1}$ | $q_{1}$ | $q_{2}$ | $q_{3}$ |
| $q_{2}$ | $q_{1}$ | $q_{2}$ | $q_{3}$ |
| $q_{3}$ | $q_{3}$ | $q_{3}$ | $q_{3}$ |
- $q_{0}$ 是 起始状态
- $F=\left\{q_{1}\right\}$ 是 接受状态 集合
这部分给出了完整的五元组定义。
- $Q = \{q_0, q_1, q_2, q_3\}$:正确地列出了图中所有的状态。
- $\Sigma = \{a, b, c\}$:正确地使用了题目给出的字母表。
- $\delta$ 的表格:这个表格是对转移函数的完整描述。让我们逐行核对:
- 行 $q_0$:
- 读 'a':$\delta(q_0, a)$,从 $q_0$ 有个标 'a' 的箭头指向 $q_1$。所以是 $q_1$。正确。
- 读 'b':$\delta(q_0, b)$,从 $q_0$ 有个标 'b' 的箭头指向 $q_3$。所以是 $q_3$。正确。
- 读 'c':$\delta(q_0, c)$,从 $q_0$ 有个标 'c' 的箭头指向 $q_3$。所以是 $q_3$。正确。
- 行 $q_1$:
- 读 'a':$\delta(q_1, a)$,从 $q_1$ 有个标 'a' 的箭头指回 $q_1$。所以是 $q_1$。正确。
- 读 'b':$\delta(q_1, b)$,从 $q_1$ 有个标 'b' 的箭头指向 $q_2$。所以是 $q_2$。正确。
- 读 'c':$\delta(q_1, c)$,从 $q_1$ 有个标 'c' 的箭头指向 $q_3$。所以是 $q_3$。正确。
- 行 $q_2$:
- 读 'a':$\delta(q_2, a)$,从 $q_2$ 有个标 'a' 的箭头指向 $q_1$。所以是 $q_1$。正确。
- 读 'b':$\delta(q_2, b)$,从 $q_2$ 有个标 'b' 的箭头指回 $q_2$。所以是 $q_2$。正确。
- 读 'c':$\delta(q_2, c)$,从 $q_2$ 有个标 'c' 的箭头指向 $q_3$。所以是 $q_3$。正确。
- 行 $q_3$:
- 读 'a', 'b', 'c':从 $q_3$ 有一个标有 "a, b, c" 的箭头指回 $q_3$ 自身。这意味着对于任何输入符号,状态都保持不变。所以 $\delta(q_3, a)=q_3$, $\delta(q_3, b)=q_3$, $\delta(q_3, c)=q_3$。全部正确。
- $q_0$ 是起始状态:正确识别。
- $F = \{q_1\}$:正确识别接受状态并将其放入集合中。
- $D=\left\{Q, \Sigma, \delta, q_{0}, F\right\}$:
- $D$: 代表这个DFA本身。
- $Q$: 状态集合,在此例中为 $\{q_0, q_1, q_2, q_3\}$。
- $\Sigma$: 字母表,在此例中为 $\{a, b, c\}$。
- $\delta$: 转移函数,以表格形式给出。例如,$\delta(q_1, b) = q_2$。
- $q_0$: 起始状态,就是 $q_0$。
- $F$: 接受状态集合,在此例中为 $\{q_1\}$。
- 示例1: 形式化表示的用途
- 假设我们要追踪字符串 "ab"。
- 开始于 $q_0$。
- 读取 'a'。我们查找 $\delta(q_0, a)$。根据表格,$\delta(q_0, a) = q_1$。转移到 $q_1$。
- 读取 'b'。我们查找 $\delta(q_1, b)$。根据表格,$\delta(q_1, b) = q_2$。转移到 $q_2$。
- 字符串结束,停在 $q_2$。因为 $q_2 \notin F$,所以 "ab" 不被接受。
- 示例2: 字符串 "ac"
- 开始于 $q_0$。
- 读取 'a'。$\delta(q_0, a) = q_1$。转移到 $q_1$。
- 读取 'c'。$\delta(q_1, c) = q_3$。转移到 $q_3$。
- 字符串结束,停在 $q_3$。因为 $q_3 \notin F$,所以 "ac" 不被接受。
- $F$ 不是集合:一个常见的错误是写 $F = q_1$。接受状态的定义是一个集合,所以即使只有一个接受状态,也必须写成 $F = \{q_1\}$。
- $\delta$ 不是函数:DFA 的转移函数 $\delta$ 必须是完全的 (total),即对于每个状态和每个字母表中的符号,都必须有且只有一个转移。表格的形式强制了这一点,每一格都必须被填满。
- 忘记起始/接受状态:五元组的每个部分都至关重要,缺一不可。
3.3 关于死状态的说明
📜 [原文6]
注意 $q_{3}$ 是一个 死状态 $/$ 拒绝状态 $/$ 坏状态。${ }^{1}$ 我们也可以不画出这个 $q_{3}$ 状态,因为对于 DFA,我们有一个 约定,即当存在缺失的 转移 时,意味着它们将进入一个 死状态 $/$ 拒绝状态 $/$ 坏状态。然而,在 DFA 的 正式规范 中,我们必须包含所有 状态。
[^0]: ${ }^{1}$ 一个“死”状态是指一个不是 接受状态 的 状态 $q$,且对于每个 符号 $\sigma$,我们都有 $\delta(q, \sigma)=q$
- 死状态 (Dead State):也称为陷阱状态 (Trap State) 或垃圾状态 (Garbage State)。它是一个特殊的非接受状态,一旦进入,就再也无法离开。从图中可以看到,$q_3$ 就是一个死状态,因为所有从 $q_3$ 出发的转移都指回它自己,而且 $q_3$ 不是接受状态。一旦计算路径到达 $q_3$,无论后面还有什么输入符号,DFA 都会一直停留在 $q_3$,因此该字符串最终一定会被拒绝。
- 省略死状态的约定:在绘制 DFA 状态图时,为了简化图形,人们常常会省略死状态以及所有指向它的转移。如果从某个状态出发,对于某个输入符号,图中没有画出对应的转移箭头,那么就默认这个转移是指向一个不可见的死状态。
- 形式化定义的要求:尽管在画图时可以省略死状态,但在编写形式化定义时,DFA 的转移函数 $\delta$ 必须是完全的。这意味着定义域 $Q \times \Sigma$ 中的每一个元素都必须有对应的输出。因此,死状态必须被明确地包含在状态集 $Q$ 中,并且所有指向它的转移也必须在转移函数 $\delta$ 中明确定义。
这个问题考察了从 DFA 的状态图(可视化表示)转换到其形式化五元组定义(数学表示)的能力。这需要准确识别状态集 $Q$、字母表 $\Sigma$、起始状态 $q_0$、接受状态集 $F$,并以表格或函数列表的形式完整描述转移函数 $\delta$。同时,该问题也引入了“死状态”的概念及其在形式化定义和状态图约定中的不同处理方式。
这个练习的目的是让学生熟练掌握 DFA 的两种核心表示方法(状态图和形式化定义)之间的转换。形式化定义是理论分析和证明的基础,而状态图则提供了直观的理解。
- 状态图就像一张手绘的城市地图,标出了地点(状态)和路线(转移)。
- 形式化定义就像一份用GPS坐标和精确街道名称写成的导航指令文档。
- 死状态就像地图上的一个“黑洞”区域或一个“有进无出”的迷宫。一旦开车进去,就只能在里面兜圈子,永远到不了任何目的地(接受状态)。在手绘地图上,为了简洁,你可能干脆不画这个“黑洞”,只告诉别人“没有路就是死路”。但在精确的导航指令中,你必须明确指出这条路通向“黑洞”。
44. 问题三:构造 DFA
4.1 构造 DFA (a): 语言补集法
41.1 原文叙述
📜 [原文7]
画出 识别 以下 语言 的 DFA:
(a) $L=\left\{w \in\{a, b\}^{*} \mid w \text{ 不包含恰好两个 } a \right\}$
这个问题要求我们为一个特定的语言 $L$ 设计一个 DFA。
- 语言 $L$ 的描述:
- 字母表是 $\{a, b\}$。
- 语言中的字符串 $w$ 满足一个条件:$w$ 中 'a' 的数量不等于 2。
- 这意味着 'a' 的数量可以是 0, 1, 3, 4, 5, ... 等等,但唯独不能是 2。
📜 [原文8]
我们在课上看到 正则语言 的 补集 也是 正则 的,即如果 $L$ 是 正则 的,那么 $\bar{L}$ 也是 正则 的。有时,为 $\bar{L}$ 构造一个 DFA 会更容易,然后通过我们在课上看到的构造方法,翻转所有 接受状态 和 拒绝状态,从而得到 $L$ 的 DFA。
我们有 $\bar{L}=\left\{w \in\{a, b\}^{*} \mid w \text{ 包含恰好两个 } a \right\}$,因此 $\bar{L}$ 的 DFA 如下所示。不难看出以下是一个 $\bar{L}$ 的 DFA。

这里提出了一种非常重要的解题策略:通过构造补集语言的 DFA 来解决。
- 补集语言 (Complement Language) $\bar{L}$:
- 对于一个定义在字母表 $\Sigma$ 上的语言 $L$,它的补集 $\bar{L}$ 包含了所有不在 $L$ 中,但由 $\Sigma$ 中的符号构成的字符串。
- 在本例中,$\Sigma^* = \{a,b\}^*$ 是所有可能的 'a' 和 'b' 构成的字符串集合。
- $L$ 是 “'a' 的数量不是 2” 的字符串集合。
- 那么 $\bar{L}$ 就是 “‘a’ 的数量是 2” 的字符串集合。
- 为什么先构造 $\bar{L}$ 的 DFA:
- 描述“恰好有两个 'a'”比描述“'a' 的数量不是 2”要直接得多。我们可以用状态来计数 'a' 的出现次数。
- 状态 $q_0$:表示到目前为止看到了 0 个 'a'。
- 状态 $q_1$:表示到目前为止看到了 1 个 'a'。
- 状态 $q_2$:表示到目前为止看到了 2 个 'a'。
- 状态 $q_3$:表示到目前为止看到了 超过 2 个 'a'。
- 分析 $\bar{L}$ 的 DFA:
- 起始状态 $q_0$(0 个 'a')。
- 从 $q_0$ 读到 'b','a' 的数量不变,留在 $q_0$。读到 'a','a' 的数量变为 1,转移到 $q_1$。
- 从 $q_1$ 读到 'b','a' 的数量不变,留在 $q_1$。读到 'a','a' 的数量变为 2,转移到 $q_2$。
- 从 $q_2$ 读到 'b','a' 的数量不变,留在 $q_2$。读到 'a','a' 的数量变为 3,超过了 2,转移到 $q_3$ (一个死状态,因为一旦超过 2 个 'a',就不可能再满足“恰好 2 个”的条件)。
- 从 $q_3$ 读到任何符号,'a' 的数量仍然大于 2,留在 $q_3$。
- 接受状态:语言 $\bar{L}$ 要求字符串结束时有“恰好两个 'a'”。这正好对应状态 $q_2$。所以 $q_2$ 是唯一的接受状态。
- 图中所示的 DFA 完全符合这个逻辑。
📜 [原文9]
因此,$L$ 的 DFA 将会是:
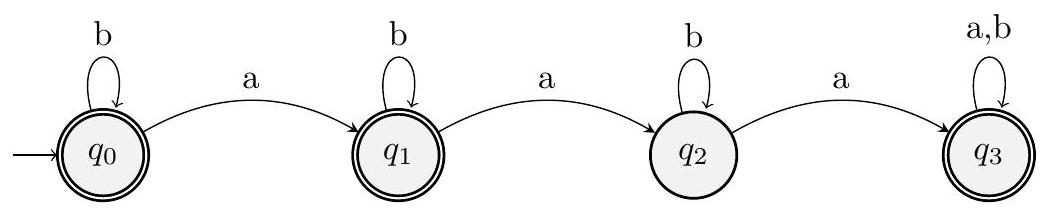
- 从 $\bar{L}$ 的 DFA 构造 $L$ 的 DFA:
- 理论基础:如果一个 DFA $M = (Q, \Sigma, \delta, q_0, F)$ 识别 语言 $\bar{L}$,那么 DFA $M' = (Q, \Sigma, \delta, q_0, Q \setminus F)$ 将识别 语言 $L$。
- $Q \setminus F$ 表示从状态全集 $Q$ 中去掉原接受状态集 $F$ 后剩下的状态。
- 直观操作:将原来所有的接受状态变成非接受状态,同时将原来所有的非接受状态变成接受状态。
- 应用到本题:
- 原 DFA (for $\bar{L}$) 中:
- $Q = \{q_0, q_1, q_2, q_3\}$
- $F = \{q_2\}$ (唯一的接受状态)
- 非接受状态是 $\{q_0, q_1, q_3\}$。
- 新 DFA (for $L$) 中:
- 状态、字母表、转移函数、起始状态都保持不变。
- 新的接受状态集 $F'$ 就是原来的非接受状态集。所以 $F' = \{q_0, q_1, q_3\}$。
- 检查新的DFA:
- 起始状态 $q_0$ 变为接受状态。这接受了 'a' 数量为 0 的字符串 (例如 $\varepsilon$, "b", "bb")。正确。
- $q_1$ 变为接受状态。这接受了 'a' 数量为 1 的字符串 (例如 "a", "bab")。正确。
- $q_2$ 变为非接受状态。这拒绝了 'a' 数量恰好为 2 的字符串 (例如 "aa", "aba")。正确。
- $q_3$ 变为接受状态。这接受了 'a' 数量大于 2 的字符串 (例如 "aaa", "ababa")。正确。
- 这个新的 DFA 正确地识别了语言 $L$。
- 对 $\bar{L}$ 的 DFA (恰好两个 'a'):
- 字符串 "aba": $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_1 \xrightarrow{a} q_2$。停在 $q_2$ (接受)。
- 字符串 "bb": $q_0 \xrightarrow{b} q_0 \xrightarrow{b} q_0$。停在 $q_0$ (拒绝)。
- 字符串 "aaab": $q_0 \xrightarrow{a} q_1 \xrightarrow{a} q_2 \xrightarrow{a} q_3 \xrightarrow{b} q_3$。停在 $q_3$ (拒绝)。
- 对 $L$ 的 DFA (不恰好两个 'a'):
- 字符串 "aba": $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_1 \xrightarrow{a} q_2$。停在 $q_2$ (拒绝)。
- 字符串 "bb": $q_0 \xrightarrow{b} q_0 \xrightarrow{b} q_0$。停在 $q_0$ (接受)。
- 字符串 "aaab": $q_0 \xrightarrow{a} q_1 \xrightarrow{a} q_2 \xrightarrow{a} q_3 \xrightarrow{b} q_3$。停在 $q_3$ (接受)。
- 忘记翻转所有状态:在从 $\bar{L}$ 的 DFA 构造 $L$ 的 DFA 时,必须翻转每一个状态的接受属性,不能遗漏。
- 补集思想的误用:补集法只适用于DFA。对于非确定性有限自动机 (NFA),简单地翻转接受/非接受状态并不总是能得到其补集语言的 NFA。
- 死状态的处理:在翻转时,原来的死状态(如 $q_3$)会变成一个新的接受状态。这是正确的,因为一旦进入 $q_3$,意味着 'a' 的数量已经大于2,这符合“不等于2”的条件。
本题展示了一个强大的 DFA 设计技巧:当直接设计目标语言 $L$ 的 DFA 比较复杂时,可以尝试设计其补集语言 $\bar{L}$ 的 DFA,然后通过“翻转”所有状态的接受/非接受属性来获得 $L$ 的 DFA。
这个练习旨在教授和巩固正则语言的闭包性质之一——对补集运算封闭。它提供了一个具体的构造性证明,并展示了如何利用这一性质简化 DFA 的设计过程。
想象你要雇一个保安,他的任务是“不允许恰好两个人进入大楼”。
- 直接方法(设计 $L$ 的 DFA):你告诉保安:“如果进来的人数是0, 1, 3, 4, 5, ...,就亮绿灯。如果是2个人,就亮红灯。” 这个指令有点绕。
- 补集方法(设计 $\bar{L}$ 的 DFA,然后翻转):你换一种方式告诉保安:“你的任务是只在恰好有两个人进来的时候亮红灯,其他任何时候都亮绿灯。” 这个指令更清晰。
- 你先训练一个“实习保安”($\bar{L}$ 的 DFA),告诉他:“当且仅当有两个人进来时,你就按下警报。” 他只需要计数到2,然后一直盯着就行了。
- 然后你告诉“正式保安”($L$ 的 DFA):“你就看着实习保安。只要他不按警报,你就一直让大门敞开(接受)。他一按警报,你就关门(拒绝)。”
4.2 构造 DFA (b): 语言交集法
42.1 原文叙述
📜 [原文10]
(b) $L=\left\{w \in\{a, b\}^{*} \mid w \text{ 具有偶数长度且包含奇数个 } a \right\}$
这里,$L$ 是两个更简单 语言 的 交集。即 $L=L_{1} \cap L_{2}$,其中
$$
\begin{gathered}
L_{1}=\left\{w \in\{a, b\}^{*} \mid w \text{ 具有偶数长度} \right\} \\
L_{2}=\left\{w \in\{a, b\}^{*} \mid w \text{ 具有奇数个 } a \right\}
\end{gathered}
$$
这个问题要求为语言 $L$ 设计一个 DFA,该语言的字符串需要同时满足两个条件:
- 字符串的总长度是偶数。
- 字符串中 'a' 的个数是奇数。
解题思路是将这个复杂的语言分解为两个更简单的语言的交集:
- $L_1$:所有偶数长度的字符串的语言。
- $L_2$:所有包含奇数个 'a' 的字符串的语言。
- $L = L_1 \cap L_2$。
这个思路是基于正则语言的另一个闭包性质:正则语言对交集运算是封闭的。这意味着如果 $L_1$ 和 $L_2$ 都是正则语言(即它们各自都有对应的 DFA),那么它们的交集 $L$ 也一定是正则语言,并且我们可以通过一个标准的构造方法(笛卡尔积构造)从 $L_1$ 和 $L_2$ 的 DFA 得到 $L$ 的 DFA。
42.2 构造 L1 和 L2 的 DFA
📜 [原文11]
让我们为 $L_{1}$ 和 $L_{2}$ 构造 DFA,然后应用我们在课上看到的构造方法来得到 $L$ 的 DFA。
$L_{1}$ 的 DFA 为:
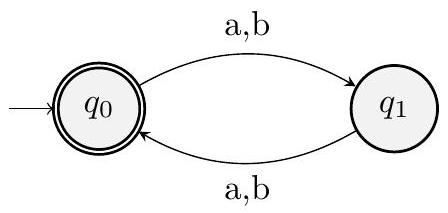
$L_{2}$ 的 DFA 为:
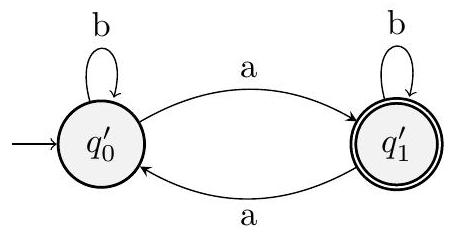
- 构造 $L_1$ (偶数长度) 的 DFA ($M_1$):
- 我们需要记录字符串长度的奇偶性。
- 状态 $q_e$ (even):表示到目前为止读过的字符串长度为偶数。
- 状态 $q_o$ (odd):表示到目前为止读过的字符串长度为奇数。
- 起始状态:空字符串 $\varepsilon$ 的长度是 0(偶数),所以起始状态是 $q_e$。
- 转移:无论读到 'a' 还是 'b',字符串长度都加 1。这会使长度的奇偶性翻转。所以,从 $q_e$ 读任何符号都到 $q_o$;从 $q_o$ 读任何符号都到 $q_e$。
- 接受状态:语言 $L_1$ 要求偶数长度,所以 $q_e$ 是接受状态。
- 图中 $p_0$ 对应这里的 $q_e$ (even),$p_1$ 对应 $q_o$ (odd)。该 DFA 正确。
- 构造 $L_2$ (奇数个 'a') 的 DFA ($M_2$):
- 我们需要记录字符串中 'a' 个数的奇偶性。
- 状态 $r_e$ (even):表示到目前为止读过的 'a' 的个数为偶数。
- 状态 $r_o$ (odd):表示到目前为止读过的 'a' 的个数为奇数。
- 起始状态:空字符串 $\varepsilon$ 中 'a' 的个数是 0(偶数),所以起始状态是 $r_e$。
- 转移:
- 如果读到 'b','a' 的个数不变,所以奇偶性不变。状态保持不变 ($r_e \xrightarrow{b} r_e$, $r_o \xrightarrow{b} r_o$)。
- 如果读到 'a','a' 的个数加 1,奇偶性翻转。状态发生切换 ($r_e \xrightarrow{a} r_o$, $r_o \xrightarrow{a} r_e$)。
- 接受状态:语言 $L_2$ 要求奇数个 'a',所以 $r_o$ 是接受状态。
- 图中 $s_0$ 对应这里的 $r_e$ (even),$s_1$ 对应 $r_o$ (odd)。该 DFA 正确。
42.3 笛卡尔积构造
📜 [原文12]
现在通过课上的 笛卡尔积构造, $L$ 的 DFA 将会是:
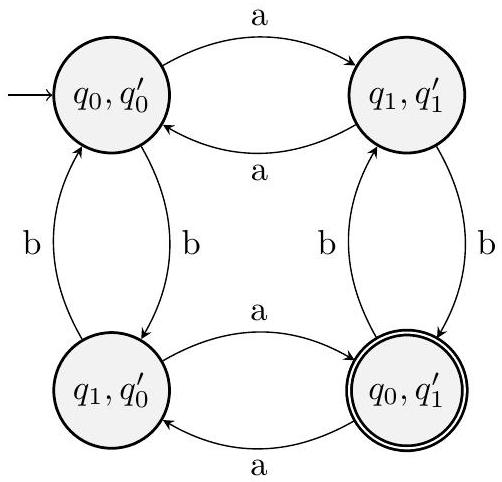
笛卡尔积构造 (Cartesian Product Construction) 是一种标准算法,用于从两个 DFA $M_1 = (Q_1, \Sigma, \delta_1, q_{0,1}, F_1)$ 和 $M_2 = (Q_2, \Sigma, \delta_2, q_{0,2}, F_2)$ 构造一个识别它们交集语言 $L(M_1) \cap L(M_2)$ 的新 DFA $M = (Q, \Sigma, \delta, q_0, F)$。
- 新状态集 $Q$:是 $Q_1$ 和 $Q_2$ 的笛卡尔积,$Q = Q_1 \times Q_2$。新状态是一个有序对 $(p, r)$,其中 $p \in Q_1, r \in Q_2$。这个状态对同时追踪 $M_1$ 和 $M_2$ 的状态。
- $Q_1 = \{p_0, p_1\}$, $Q_2 = \{s_0, s_1\}$。
- $Q = \{(p_0, s_0), (p_0, s_1), (p_1, s_0), (p_1, s_1)\}$。图中这四个状态分别被命名为 $q_0, q_1, q_2, q_3$。
- $q_0 = (p_0, s_0)$: (偶数长, 偶数个a)
- $q_1 = (p_0, s_1)$: (偶数长, 奇数个a)
- $q_2 = (p_1, s_0)$: (奇数长, 偶数个a)
- $q_3 = (p_1, s_1)$: (奇数长, 奇数个a)
- 新起始状态 $q_0$:是原起始状态的有序对。
- $q_0 = (q_{0,1}, q_{0,2}) = (p_0, s_0)$。图中 $q_0$ 被正确设为起始状态。
- 新转移函数 $\delta$:对于任何新状态 $(p, r)$ 和输入符号 $\sigma$,新转移定义为 $\delta((p, r), \sigma) = (\delta_1(p, \sigma), \delta_2(r, \sigma))$。即两个 DFA 并行运行,各自独立进行转移。
- 以 $(p_0, s_0)$ 为例:
- 读 'a': $\delta((p_0, s_0), a) = (\delta_1(p_0, a), \delta_2(s_0, a)) = (p_1, s_1)$。所以从 $(p_0, s_0)$ 有一条标 'a' 的箭头指向 $(p_1, s_1)$。图中即 $q_0 \xrightarrow{a} q_3$。正确。
- 读 'b': $\delta((p_0, s_0), b) = (\delta_1(p_0, b), \delta_2(s_0, b)) = (p_1, s_0)$。所以从 $(p_0, s_0)$ 有一条标 'b' 的箭头指向 $(p_1, s_0)$。图中即 $q_0 \xrightarrow{b} q_2$。正确。
- 以 $(p_1, s_1)$ 为例:
- 读 'a': $\delta((p_1, s_1), a) = (\delta_1(p_1, a), \delta_2(s_1, a)) = (p_0, s_0)$。所以从 $(p_1, s_1)$ 有一条标 'a' 的箭头指向 $(p_0, s_0)$。图中即 $q_3 \xrightarrow{a} q_0$。正确。
- 读 'b': $\delta((p_1, s_1), b) = (\delta_1(p_1, b), \delta_2(s_1, b)) = (p_0, s_1)$。所以从 $(p_1, s_1)$ 有一条标 'b' 的箭头指向 $(p_0, s_1)$。图中即 $q_3 \xrightarrow{b} q_1$。正确。
- (其余转移可同理验证,图中均正确)
- 新接受状态集 $F$:一个字符串要被交集语言接受,必须同时被 $M_1$ 和 $M_2$ 接受。这意味着最终状态必须在 $F_1$ 和 $F_2$ 中。所以,新接受状态是那些两个分量都分别是原接受状态的状态对。
- $F = F_1 \times F_2 = \{p \in F_1 \text{ and } r \in F_2 \mid (p,r) \in Q\}$
- 在本题中,$F_1 = \{p_0\}$, $F_2 = \{s_1\}$。
- $F = \{(p_0, s_1)\}$。
- 对应的状态是 $q_1$。图中 $q_1$ 是唯一的接受状态。正确。
- 字符串 "ab":
- $M_1$ 路径: $p_0 \xrightarrow{a} p_1 \xrightarrow{b} p_0$。停在 $p_0$ (接受)。
- $M_2$ 路径: $s_0 \xrightarrow{a} s_1 \xrightarrow{b} s_1$。停在 $s_1$ (接受)。
- $M$ (乘积机) 路径: $(p_0, s_0) \xrightarrow{a} (p_1, s_1) \xrightarrow{b} (p_0, s_1)$。停在 $(p_0, s_1)$。
- 结果: "ab" 长度为2(偶数),'a' 个数为1(奇数)。符合条件。最终状态 $(p_0, s_1)$ 也是接受状态。
- 字符串 "aab":
- $M_1$ 路径: $p_0 \xrightarrow{a} p_1 \xrightarrow{a} p_0 \xrightarrow{b} p_1$。停在 $p_1$ (拒绝)。
- $M_2$ 路径: $s_0 \xrightarrow{a} s_1 \xrightarrow{a} s_0 \xrightarrow{b} s_0$。停在 $s_0$ (拒绝)。
- $M$ (乘积机) 路径: $(p_0, s_0) \xrightarrow{a} (p_1, s_1) \xrightarrow{a} (p_0, s_0) \xrightarrow{b} (p_1, s_0)$。停在 $(p_1, s_0)$。
- 结果: "aab" 长度为3(奇数),'a' 个数为2(偶数)。不符合条件。最终状态 $(p_1, s_0)$ 也不是接受状态。
- 混淆交集和并集的接受状态:对于交集 ($L_1 \cap L_2$),新的接受状态集是 $F_1 \times F_2$(两个都要接受)。对于并集 ($L_1 \cup L_2$),新的接受状态集是 $(F_1 \times Q_2) \cup (Q_1 \times F_2)$(至少一个接受就行)。
- 转移函数计算错误:必须保证新DFA的每个转移都分别对应两个旧DFA的转移。
- 状态命名与实际对应的混淆:最终图中的 $q_0, ..., q_3$ 只是个名字,关键是理解它们背后代表的状态对,如 $q_1$ 代表 (偶数长度, 奇数个a)。
本题展示了如何使用笛卡尔积构造来设计一个识别两个正则语言交集的 DFA。该方法的核心思想是创建一个新的“并行”自动机,其状态是原自动机状态的组合,从而可以同时跟踪多个属性(本例中为长度奇偶性和'a'个数奇偶性)。
该练习旨在教授和巩固正则语言对交集运算的闭包性质,并让学生掌握笛卡尔积构造这一具体的、算法化的构造过程。这是计算理论中一个非常基础且重要的构造方法。
想象你有两个独立的监视器。
- 监视器1 ($M_1$):只关心进来的人数是奇数还是偶数。它有两个灯:”偶数“灯和”奇数“灯。
- 监视器2 ($M_2$):只关心进来的人里穿红衣服的是奇数个还是偶数个。它也有两个灯:”偶数红衣“和”奇数红衣“。
- 你想知道什么时候“总人数是偶数 且 穿红衣的人是奇数”。
- 笛卡尔积构造就是把这两个监视器组合成一个超级监视器。这个超级监视器有四个状态灯,每个灯都显示了两个基础信息:
- (偶数总人数, 偶数红衣)
- (偶数总人数, 奇数红衣) $\leftarrow$ 这是你想要的,把它设为“警报”灯(接受状态)
- (奇数总人数, 偶数红衣)
- (奇数总人数, 奇数红衣)
每进来一个人,这个超级监视器的状态就会根据两个基础监视器的变化而更新。
4.3 构造 DFA (c): 有限语言
43.1 原文叙述
📜 [原文13]
(c) $L=\{11,101,010,0110\}$
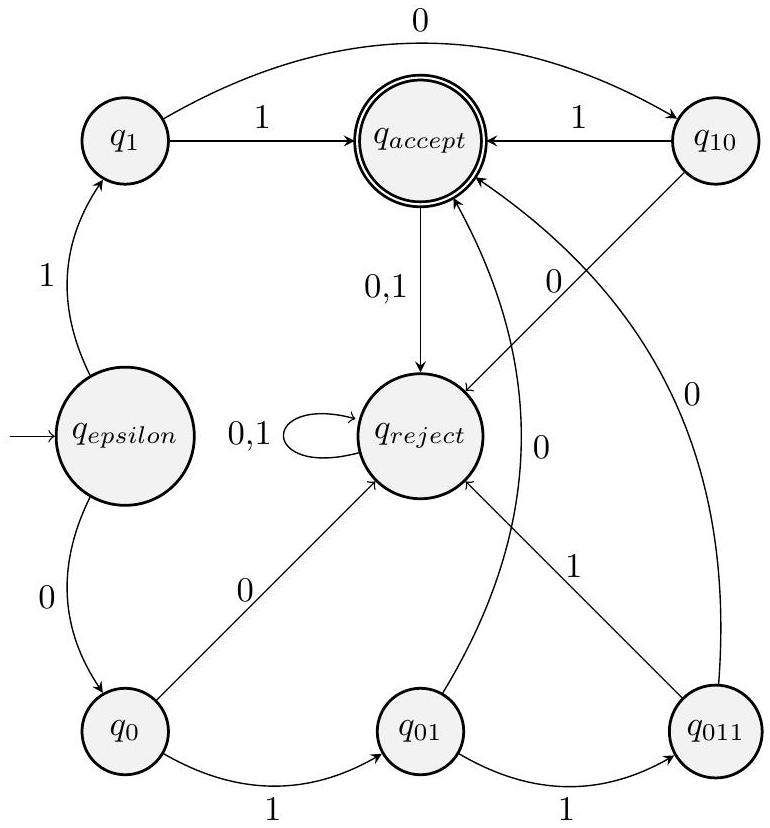
这个问题要求为一个有限语言 $L$ 设计一个 DFA。有限语言是指其包含的字符串数量是有限的。所有有限语言都是正则语言。
- 语言 $L$:只包含 "11", "101", "010", "0110" 这四个字符串。
构造有限语言的 DFA 的一种直接方法是:
- 为语言中所有字符串的所有前缀(包括空字符串 $\varepsilon$ 和字符串本身)创建一个状态。
- 起始状态是代表空字符串 $\varepsilon$ 的状态。
- 转移函数:如果当前在代表前缀 $p$ 的状态,读入符号 $\sigma$,则转移到代表前缀 $p\sigma$ 的状态。
- 接受状态:所有代表语言 $L$ 中字符串的状态都是接受状态。
- 死状态:如果一个转移会产生一个不属于任何语言内字符串的前缀的字符串,那么该转移指向一个死状态。
让我们来分析图中的 DFA 是否符合这个思想:
- 状态的命名:
- $q_{\text{start}}$: 代表前缀 $\varepsilon$。
- $q_1$: 代表前缀 "1"。
- $q_0$: 代表前缀 "0"。
- $q_{11}$: 代表前缀 "11"。它是语言中的一个词,所以可以是接受状态。
- $q_{10}$: 代表前缀 "10"。
- $q_{01}$: 代表前缀 "01"。
- $q_{101}$: 代表前缀 "101"。
- $q_{010}$: 代表前缀 "010"。
- $q_{011}$: 代表前缀 "011"。
- $q_{0110}$: 代表前缀 "0110"。
- 图中设计思路的微小区别:
- 图中的设计者并没有严格为每个前缀都创建一个状态(例如 "01" 的前缀 "0" 和 "1" 的前缀 "1" 最终都可能导向别的路径)。但大体思路是为语言中的每个字符串构建一条“成功路径”。
- 它引入了一个通用的接受状态 $q_{\text{accept}}$ 和一个通用的拒绝状态 $q_{\text{reject}}$。
43.2 解答分析
📜 [原文14]
该 DFA 对 语言 中任何 字符串 的每个 真前缀 都有一个不同的 状态(注意我们可以这样做是因为该 语言 是 有限的,所以这类 前缀 也是 有限的),以及一个额外的 接受状态 和一个 拒绝状态。当输入是 L 中的 字符串 时,DFA 将在 $q_{\text {accept }}$ 中结束 计算,而当 字符串 不在 L 中时,它将最终处于 $q_{\text {reject }} \cdot$
这里,$q_{\text {reject }}$ 是一个 死状态/拒绝状态/坏状态,为了简单起见,也可以从图中省略。我们可以根据上面提到的 约定 移除 $q_{\text {reject }}$ 及其所有指向它的 转移。
此外,你始终可以以有助于使事情更清晰的方式为 状态 命名。
- DFA 的工作方式:
- 路径 "11": $q_{\text{start}} \xrightarrow{1} q_1 \xrightarrow{1} q_{11}$。在 $q_{11}$ 之后,原文图中没有画出从 $q_{11}$ 出发的箭头,这通常意味着转移到死状态。但如果我们将 $q_{11}$ 本身就视为一个临时的接受状态,或者像图中一样,在识别出"11"后需要一个明确的结束信号,这里的设计有些不标准。更规范的画法是从 $q_{11}$ 出发,如果后面还有字符,则转移到$q_{reject}$。但这里的图似乎把 $q_{11}, q_{101}, q_{010}, q_{0110}$ 直接画成了最终的接受状态(虽然它们不是双圈,但没有后续路径)。然而,解答的文字描述是有一个统一的 $q_{accept}$,这与图不符。我们以图的结构为准进行分析。
- 让我们重新解读这个图:$q_{11}, q_{101}, q_{010}, q_{0110}$ 就是接受状态。
- 路径 "11": $q_{\text{start}} \xrightarrow{1} q_1 \xrightarrow{1} q_{11}$。结束在 $q_{11}$ (接受)。
- 路径 "101": $q_{\text{start}} \xrightarrow{1} q_1 \xrightarrow{0} q_{10} \xrightarrow{1} q_{101}$。结束在 $q_{101}$ (接受)。
- 路径 "010": $q_{\text{start}} \xrightarrow{0} q_0 \xrightarrow{1} q_{01} \xrightarrow{0} q_{010}$。结束在 $q_{010}$ (接受)。
- 路径 "0110": $q_{\text{start}} \xrightarrow{0} q_0 \xrightarrow{1} q_{01} \xrightarrow{1} q_{011} \xrightarrow{0} q_{0110}$。结束在 $q_{0110}$ (接受)。
- $q_{reject}$ (死状态): 任何不属于上述四个字符串及其前缀的路径都会导向 $q_{reject}$。
- 例如,字符串 "00": $q_{\text{start}} \xrightarrow{0} q_0 \xrightarrow{0} q_{reject}$。
- 例如,字符串 "110": $q_{\text{start}} \xrightarrow{1} q_1 \xrightarrow{1} q_{11} \xrightarrow{0} q_{reject}$。
- 例如,字符串 "10": $q_{\text{start}} \xrightarrow{1} q_1 \xrightarrow{0} q_{10}$。停在 $q_{10}$,它不是接受状态,并且任何后续输入都会进入 $q_{reject}$。所以 "10" 不被接受。
- 关于 $q_{reject}$ 的省略: 如前所述,为了简化 DFA 图,可以省略死状态 $q_{reject}$ 和所有指向它的箭头。这样,任何在图中“无路可走”的转移都默认进入一个不可见的死状态。
- 字符串 "0110" (在语言 L 中)
- 开始于 $q_{start}$。
- 读 '0' $\to q_0$。
- 读 '1' $\to q_{01}$。
- 读 '1' $\to q_{011}$。
- 读 '0' $\to q_{0110}$。
- 结束。$q_{0110}$ 是接受状态 (根据我们的解读)。所以 "0110" 被接受。
- 字符串 "1011" (不在语言 L 中)
- 开始于 $q_{start}$。
- 读 '1' $\to q_1$。
- 读 '0' $\to q_{10}$。
- 读 '1' $\to q_{101}$。
- 读 '1' $\to q_{reject}$ (因为从 $q_{101}$ 读 '1' 没有定义路径)。
- 结束。$q_{reject}$ 是非接受状态。所以 "1011" 不被接受。
- 前缀与完整字符串的混淆:一个字符串是另一个字符串的前缀时要特别小心。例如 "11" 和 "110"。DFA 必须确保在读完 "11" 时停在接受状态,但如果后面还有 "0",则必须离开该接受状态进入一个非接受状态。图中从 $q_{11}$ 到 $q_{reject}$ 的转移就处理了这种情况。
- 状态复用:如果不同字符串有相同的前缀,它们的路径可以共享状态。例如 "010" 和 "0110" 共享了从 $q_{start}$ 到 $q_{01}$ 的路径。
- 不完整的转移:在设计时,必须为每个状态(非死状态)和每个字母表中的符号都定义一个转移。如果某个转移在图中缺失,要明确这是指向一个省略的死状态。
本题展示了如何为有限语言构造一个 DFA。基本策略是构建一个“前缀树”(Trie)结构,其中每个节点是一个状态,代表一个前缀。凡是代表语言中完整字符串的节点都设为接受状态。所有不匹配的路径都导向一个统一的死状态(拒绝状态)。
这个练习的目的是让学生理解任何有限语言都是正则的,并掌握一种为有限语言系统地构造 DFA 的方法。这强化了 DFA 识别字符串前缀的概念。
想象一个自动售货机,它只接受几种特定的硬币序列 (例如 "1角-1角", "1角-5角-1角" 等)。
- 状态:售货机内部记录当前已投币序列的记忆。
- 起始状态:未投币。
- 转移:每投一个硬币,售货机就更新它的记忆,进入下一个状态。
- 接受状态:当投入的硬币序列恰好是它接受的某一种时,它就进入一个“出货”状态。
- 拒绝/死状态:如果投币序列错误(例如 "5角-5角"),机器就进入“吞币”状态,之后再投什么也没用了。
这个 DFA 就是这个售货机的逻辑电路图。
55. 问题四:描述 DFA 识别的语言
5.1 描述 DFA (a)
51.1 原文叙述
📜 [原文15]
给定 DFA,指定它所 识别 的 语言:
(a) DFA $M$ :
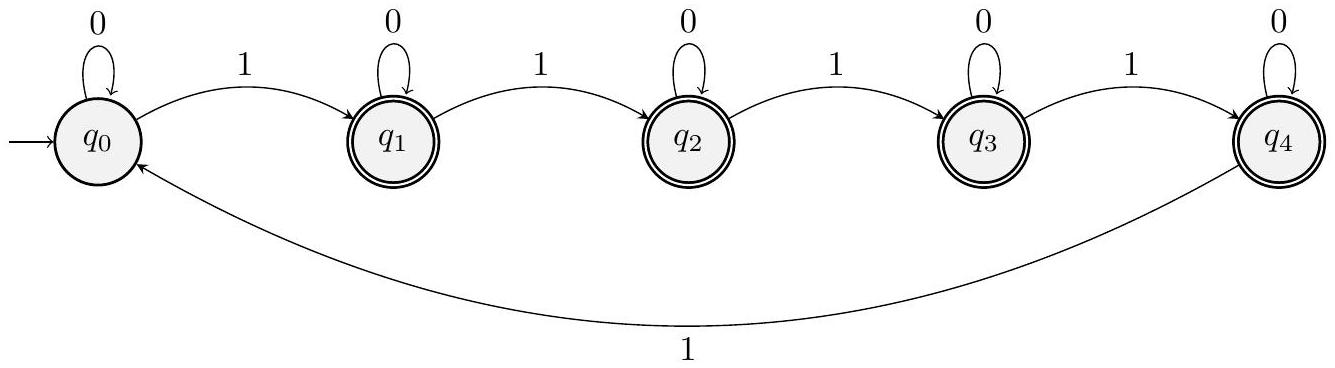
📜 [原文16]
如何处理此问题:
首先,我们可以检查哪些 状态 是 接受状态。
这里,$\left\{q_{1}, q_{2}, q_{3}, q_{4}\right\}$ 是 接受状态。
然后我们可以检查一些被该 DFA 接受 的 字符串 和一些被该 DFA 拒绝 的 字符串。例如,0, 11111, 011111, 0101010101, 1111111111 是该 DFA 拒绝 的一些 字符串。01, 010, 011, 0101, 1, 10, 11, 111111111 是该 DFA 接受 的一些 字符串。
我们可以发现,被该 DFA 拒绝 的 字符串 始终具有 $\{0, 5, 10, 15, 20, \ldots\}$ 个 1。
这个问题是之前问题的“逆问题”:给定一个 DFA,要求我们用自然语言或集合符号来描述它所识别的语言。
分析步骤:
- 识别 DFA 的基本组件:
- 状态 $Q = \{q_0, q_1, q_2, q_3, q_4\}$。
- 字母表 $\Sigma = \{0, 1\}$。
- 起始状态是 $q_0$。
- 接受状态 $F = \{q_1, q_2, q_3, q_4\}$。唯一的非接受状态是 $q_0$。
- 理解状态的含义: 这是关键一步。我们需要弄清楚每个状态代表了字符串的什么属性。
- 读 '0':在任何状态下读 '0',状态都保持不变。这意味着 '0' 不影响我们正在追踪的属性。
- 读 '1':
- $q_0 \xrightarrow{1} q_1$
- $q_1 \xrightarrow{1} q_2$
- $q_2 \xrightarrow{1} q_3$
- $q_3 \xrightarrow{1} q_4$
- $q_4 \xrightarrow{1} q_0$
- 这个结构是一个环!每次读到一个 '1',状态就在这个环上前进一格。这表明 DFA 正在对 '1' 的数量进行模运算(modulo)。环的大小是 5,所以是模 5。
- 让我们验证一下:
- 状态 $q_0$: 表示到目前为止 '1' 的数量是 $0 \pmod 5$。
- 状态 $q_1$: 表示到目前为止 '1' 的数量是 $1 \pmod 5$。
- 状态 $q_2$: 表示到目前为止 '1' 的数量是 $2 \pmod 5$。
- 状态 $q_3$: 表示到目前为止 '1' 的数量是 $3 \pmod 5$。
- 状态 $q_4$: 表示到目前为止 '1' 的数量是 $4 \pmod 5$。
- 结合接受状态得出结论:
- 接受状态是 $\{q_1, q_2, q_3, q_4\}$。
- 这意味着,只要字符串处理完毕后,'1' 的数量模 5 的结果是 1, 2, 3, 或 4,该字符串就被接受。
- 换句话说,只要 '1' 的数量不是 0 (模 5),字符串就被接受。
- “'1' 的数量是 $0 \pmod 5$” 等价于 “'1' 的数量是 5 的整数倍”。
- 因此,被接受的字符串是那些 '1' 的数量不是 5 的整数倍的字符串。
51.2 解答分析
📜 [原文17]
解答:
该 DFA 识别 以下 语言:
$L=\left\{w \in\{0,1\}^{*} \mid w \text{ 中 1 的数量不是 5 的整数倍}\right\}$
我们可以看到,对于任何 字符串,如果 M 的 计算 到达 $q_{i}$,这意味着到目前为止我们已经看到了 $\mathrm{i} \bmod 5$ 个 1。唯一不被 接受 的 字符串 是那些 1 的数量为 5 的 整数倍 的 字符串(注意 0 也是 5 的 整数倍)。
解答完全正确,并清晰地指出了每个状态 $q_i$ 的含义是代表已经看到了 $i$ 个 '1' (模 5)。
- 语言 $L$ 的形式化描述: $L = \{ w \in \{0,1\}^* \mid (\text{count}_1(w) \pmod 5) \neq 0 \}$,其中 $\text{count}_1(w)$ 是 $w$ 中 '1' 的数量。
- 关于 0: 空字符串 $\varepsilon$ 中有 0 个 '1'。$0 \pmod 5 = 0$。计算路径是停在 $q_0$,而 $q_0$ 是非接受状态。所以 $\varepsilon$ 不被接受。这符合“0 是 5 的倍数”的逻辑。
- 字符串 "1011":
- '1' 的数量是 3。$3 \pmod 5 = 3$。应该被接受。
- 路径: $q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_1 \xrightarrow{1} q_2 \xrightarrow{1} q_3$。结束在 $q_3$。$q_3$ 是接受状态。正确。
- 字符串 "110111":
- '1' 的数量是 5。$5 \pmod 5 = 0$。应该被拒绝。
- 路径: $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2 \xrightarrow{0} q_2 \xrightarrow{1} q_3 \xrightarrow{1} q_4 \xrightarrow{1} q_0$。结束在 $q_0$。$q_0$ 是非接受状态。正确。
- 混淆状态索引和计数值: 在这个例子中,状态 $q_i$ 恰好对应计数值 $i \pmod 5$,但并非总是如此。需要仔细分析才能确定每个状态的真正含义。
- 忽略不改变状态的转移: '0' 在这个 DFA 中是“中性”的,它不改变状态。在分析时,这些转移和改变状态的转移同样重要。
- 对“0是...的倍数”的理解: 0 是任何非零整数的倍数。这是一个数学上的约定,也符合模运算的定义。
本题的核心是“破解” DFA 的设计意图。通过观察状态转移的模式(特别是循环结构),可以推断出状态所代表的抽象属性(例如计数、奇偶性、模运算结果)。再结合接受状态,就可以完整地描述出语言的特征。
该练习旨在培养学生逆向工程 DFA 的能力,从一个具体的自动机抽象出它所定义的语言的通用规则。这是理解计算模型和其所能表达的语言之间关系的关键一步。
这个 DFA 就像一个有5个槽位的旋转拨盘(槽位 0 到 4)。
- 拨盘初始在 0 号槽位。
- 每当来一个 '1',拨盘就顺时针转一格。
- 每当来一个 '0',拨盘不动。
- 只要最后拨盘停在 1、2、3、4 号槽位中的任何一个,就亮绿灯(接受)。
- 只有当拨盘恰好停在 0 号槽位时,才亮红灯(拒绝)。
- 这个机器实际上是在检查 '1' 的个数是不是 5 的倍数。
5.2 描述 DFA (b)
52.1 原文叙述
📜 [原文18]
(b) DFA N:
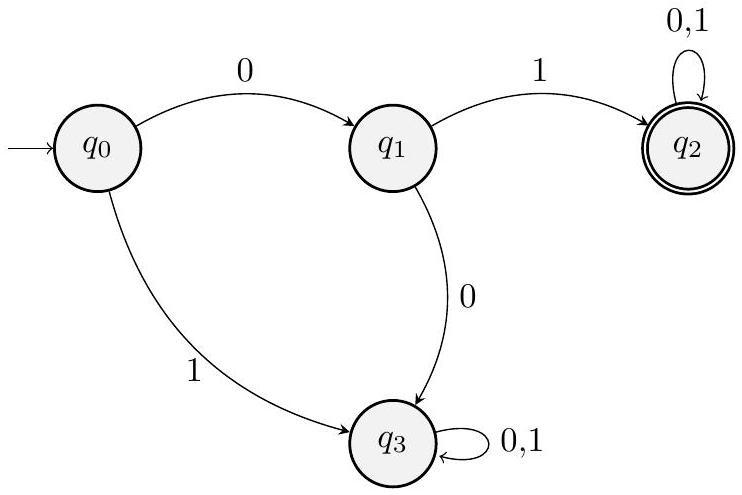
如何处理此问题:
类似地,我们可以先检查哪些 状态 是 接受状态。
这里,$\left\{q_{2}\right\}$ 是 接受状态。我们可以很容易地看出 $q_{3}$ 是一个 死状态/拒绝状态/坏状态。
然后我们可以检查一些被该 DFA 接受 的 字符串 和一些被该 DFA 拒绝 的 字符串。例如,0, 00, 1, 11, 000, 001, 100, 101 是该 DFA 拒绝 的一些 字符串。01, 010, 011, 0101 是该 DFA 接受 的一些 字符串。
我们可以看出该 DFA 仅 接受 以 前缀 01 开头的 字符串。
同样,我们来分析这个 DFA。
- 识别 DFA 的基本组件:
- 状态 $Q = \{q_0, q_1, q_2, q_3\}$。
- 字母表 $\Sigma = \{0, 1\}$。
- 起始状态是 $q_0$。
- 接受状态 $F = \{q_2\}$。
- 分析状态转移路径:
- 从起始状态 $q_0$ 出发:
- 如果第一个符号是 '1',路径是 $q_0 \xrightarrow{1} q_3$。$q_3$ 是一个死状态(所有出边都指向自身,且非接受)。所以任何以 '1' 开头的字符串都会被拒绝。
- 如果第一个符号是 '0',路径是 $q_0 \xrightarrow{0} q_1$。这开启了一条通往接受状态的可能路径。
- 从状态 $q_1$ 出发 (已经读了 '0'):
- 如果第二个符号是 '0',路径是 $q_1 \xrightarrow{0} q_3$。进入死状态。所以任何以 "00" 开头的字符串都会被拒绝。
- 如果第二个符号是 '1',路径是 $q_1 \xrightarrow{1} q_2$。进入了接受状态 $q_2$!
- 从状态 $q_2$ 出发 (已经读了 "01"):
- 无论读到 '0' 还是 '1',状态都保持在 $q_2$ ($q_2 \xrightarrow{0,1} q_2$)。
- 这意味着,一旦字符串的前缀是 "01",DFA 就会进入并永远停留在接受状态 $q_2$。
- 总结:
- 只有以 "01" 开头的字符串才能到达接受状态 $q_2$。
- 一旦到达 $q_2$,就再也不会离开。
- 因此,这个 DFA 接受所有以 "01" 为前缀的字符串。
52.2 解答分析
📜 [原文19]
解答:
该 DFA 识别 以下 语言:
$L=\left\{w \in\{0,1\}^{*} \mid w \text{ 以前缀 01 开头}\right\}$
任何以 01 开头的 字符串,其 计算 都会以 状态 ( $q 0, q 1, q 2$ ) 开始,然后在 字符串 的剩余部分保持在 $q 2$,因此它被 接受。任何不以 01 开头的 字符串,要么以 1 开始,然后其 计算 从 $q 0$ 转到 $q 3$ 并停留在 $q 3$;要么以 00 开始,然后 计算 以 ( $q 0, q 1, q 3$ ) 开始,并停留在 $q 3$。
注意:
注意这里 $q_{3}$ 是一个 死状态/拒绝状态/坏状态,可以像下面这样省略:
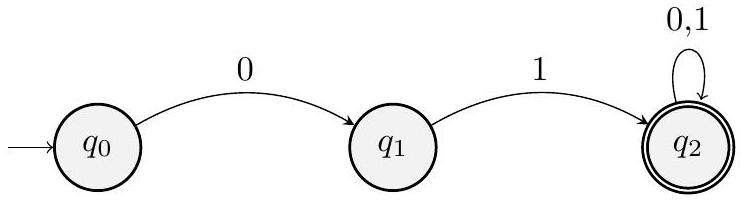
- 解答是完全正确的。它准确地描述了语言为“所有以'01'为前缀的字符串的集合”。
- 解答还清晰地分析了两种被拒绝的情况:以 '1' 开头和以 "00" 开头,这两种情况都会导致计算陷入死状态 $q_3$。
- 关于省略死状态的图示:最后的图示展示了省略死状态 $q_3$ 后的简化版 DFA。
- 从 $q_0$ 出发,标 '1' 的箭头被移除了。
- 从 $q_1$ 出发,标 '0' 的箭头被移除了。
- 按照约定,这些缺失的转移都默认指向一个不可见的死状态。这个简化图与原图在功能上是完全等价的,但视觉上更简洁。
- 字符串 "01001" (以 "01" 开头):
- 路径: $q_0 \xrightarrow{0} q_1 \xrightarrow{1} q_2 \xrightarrow{0} q_2 \xrightarrow{0} q_2 \xrightarrow{1} q_2$。结束于 $q_2$ (接受)。
- 字符串 "0" (不以 "01" 开头):
- 路径: $q_0 \xrightarrow{0} q_1$。结束于 $q_1$ (非接受)。
- 字符串 "101" (不以 "01" 开头):
- 路径: $q_0 \xrightarrow{1} q_3 \xrightarrow{0} q_3 \xrightarrow{1} q_3$。结束于 $q_3$ (非接受)。
- 只检查前两个字符: 不能简单地认为这是一个只检查前两个字符的机器。它必须能处理任意长度的字符串。$q_2$ 上的自循环是确保在 "01" 之后无论跟什么,字符串仍然被接受的关键。
- 状态的含义:
- $q_0$: 初始状态,什么都没看到。
- $q_1$: 看到了前缀 "0"。
- $q_2$: 看到了前缀 "01"。
- $q_3$: 已经确定字符串不可能是以 "01" 开头,进入“失败”状态。
这个 DFA 的设计模式是“前缀检测器”。它通过一系列状态来匹配一个特定的前缀。一旦前缀匹配成功,就进入一个“永久接受”的状态。如果匹配中途失败,就进入一个“永久拒绝”(死)状态。
这个练习让学生熟悉一种常见的 DFA 应用场景:识别具有特定前缀的语言。它也再次强调了“死状态”的作用以及在绘图时为了简化而省略它的约定。
这台 DFA 就像一个保险箱的密码锁,但它只检查密码的开头两位。
- 密码必须是 "01..."。
- $q_0$: 等待输入第一位。
- 你输入 '0' ($q_0 \to q_1$):锁芯转动了一下,似乎对了。
- 你输入 '1' ($q_0 \to q_3$):错了,锁卡死了,再转什么都没用。
- 在 $q_1$ 状态,你输入 '1' ($q_1 \to q_2$):对了!锁“咔嗒”一声打开了(进入接受状态)。一旦打开,它就保持打开状态,你再随便按什么数字都无所谓了。
- 在 $q_1$ 状态,你输入 '0' ($q_1 \to q_3$):错了,锁卡死了。
6行间公式索引
1. 语言L1和L2的定义:将一个复杂语言分解为两个简单语言L1(偶数长度)和L2(奇数个'a')的交集。
76. 附录:脚注解释
6.1 “死状态”的定义
📜 [原文20]
[^0]: ${ }^{1}$ 一个“死”状态是指一个不是 接受状态 的 状态 $q$,且对于每个 符号 $\sigma$,我们都有 $\delta(q, \sigma)=q$
这部分是文档末尾的一个脚注,它为在正文中多次提到的“死状态”提供了一个精确的、形式化的定义。理解这个定义对于掌握 DFA 的完整概念至关重要。让我们将这个定义分解成它的两个核心组成部分来详细解释。
- 一个不是 接受状态 的 状态 q: 这是成为一个死状态的首要条件。死状态本质上是一个拒绝状态;它永远不能是接受状态(即在状态图中,它永远不会是双圈)。这意味着,只要一个字符串的计算过程最终停留在死状态,该字符串就一定被拒绝。这个特性是死状态“失败”属性的根本来源。
- 对于每个 符号 σ,我们都有 δ(q, σ)=q: 这是第二个关键条件,它描述了死状态的行为模式。
- 这里的 q 指的就是我们正在定义的这个死状态。
- σ (sigma) 是一个变量,代表字母表 Σ 中的任意一个符号。
- δ(q, σ) = q 是转移函数的表达。它说明:“如果你当前处于状态 q,并且你读入了任何一个符号 σ,那么你接下来要转移到的状态仍然是 q。”
- 综合起来,这句话的含义是:一旦自动机的计算路径进入了死状态,它就再也无法离开。无论后续输入什么字符串,它都会永远被“困”在这个状态里。这就像一个计算的“黑洞”。
将这两个条件合在一起,我们得到一个完整的画像:死状态是一个非接受状态,并且它会将计算永久地困在自身内部。
- δ(q, σ)=q:
- δ (delta): 这是 DFA 的转移函数的通用符号。它是一个数学函数,其输入是“当前状态”和“当前输入符号”,其输出是“下一个状态”。
- q: 在这个公式中,q 代表一个特定的状态,也就是我们正在定义的死状态。
- σ (sigma): 代表一个来自字母表 Σ 的通用符号。例如,如果 Σ = {a, b, c},那么 σ 可以是 a、b 或 c 中的任何一个。
- =: 等号表示函数调用的结果。整个表达式的含义是,对于状态 q 和任何可能的输入符号 σ,转移函数 δ 的计算结果总是返回状态 q 本身。
让我们以讲义问题2中的 DFA 为例来具体说明。
- 问题2的DFA信息:
- 状态集: $Q = \{q_0, q_1, q_2, q_3\}$
- 字母表: $\Sigma = \{a, b, c\}$
- 接受状态集: $F = \{q_1\}$
- 在该 DFA 中,状态 $q_3$ 就是死状态。
- 验证 $q_3$ 是否符合定义:
- 它是非接受状态吗? 是的。接受状态只有 $q_1$,$q_3$ 不在接受状态集 $F$ 中。满足条件一。
- 它会困住计算吗? 我们需要检查对于字母表中的所有符号 {a, b, c},从 $q_3$ 的转移是否都回到 $q_3$。
- 输入 'a': 从状态图中看到,$\delta(q_3, a) = q_3$。是的。
- 输入 'b': 从状态图中看到,$\delta(q_3, b) = q_3$。是的。
- 输入 'c': 从状态图中看到,$\delta(q_3, c) = q_3$。是的。
- 满足条件二。
- 因为 $q_3$ 同时满足两个条件,所以它被严格地定义为一个死状态。
- 计算示例: 让我们追踪字符串 "acb" 的计算过程。
- 从起始状态 $q_0$ 开始。
- 读入 'a',根据 $\delta(q_0, a) = q_1$,转移到 $q_1$。
- 读入 'c',根据 $\delta(q_1, c) = q_3$,转移到 $q_3$。此时,自动机已经进入了死状态。
- 读入 'b',根据 $\delta(q_3, b) = q_3$,停留在 $q_3$。
- 字符串处理完毕,最终状态是 $q_3$。因为 $q_3$ 是非接受状态,所以字符串 "acb" 被拒绝。一旦进入 $q_3$,就注定了被拒绝的命运。
- 并非所有非接受状态都是死状态: 这是一个非常关键的区别。一个状态可以是非接受的,但它不是一个“终点”。例如,在问题2中,$q_0$ 是非接受状态,但它不是死状态,因为从 $q_0$ 出发,可以通过读入 'a' 到达接受状态 $q_1$。死状态是一个不可逆转的失败点。
- 图的简化与形式化定义: 在绘制状态图时,为了让图形更简洁,通常会省略死状态以及所有指向它的转移。当你在图中发现某个状态在面对某个输入符号时“无路可走”,你应该默认那条缺失的路是指向一个未画出的死状态。然而,在编写形式化定义(即五元组)时,转移函数 δ 必须是完备的(Total Function),即必须为每一个“状态-符号”对都明确指定一个转移。因此,死状态必须被包含在状态集 $Q$ 中,并且所有相关的转移都必须在函数 δ 中被明确写出。
该脚注为“死状态”这一概念提供了严谨的数学定义。它必须同时满足两个条件:(1)它本身不是一个接受状态;(2)对于任何可能的输入符号,它都只会转移回自身。它在 DFA 中的功能是充当一个统一的、永久性的“失败”收集器,将所有不符合语言规则的计算路径都导向这个不可逃脱的陷阱,从而使自动机的逻辑变得清晰。
设立此脚注的目的是为了给出一个在正文中被非正式使用的术语的严格定义。在计算理论中,精确性是至关重要的。该脚注确保了读者能够从数学上准确地理解“死状态”的含义,而不仅仅停留在“坏状态”或“陷阱”的直观感觉上。
把 DFA 的计算过程想象成在一个有许多房间(状态)的建筑里寻宝。
- 接受状态:是藏有宝藏的房间。你的目标是停在其中一个房间。
- 其他状态:是普通的、空无一物的房间。
- 死状态:是一间“储藏室”,它的门是单向的,只能进不能出,而且里面没有宝藏。
- 你一旦走进这间储藏室(进入死状态),门就在你身后锁上了。
- 房间里没有任何通往其他房间的门,你无论做什么(读入任何符号),你都只能留在储藏室里(转移到自身)。
- 因为储藏室里没有宝藏(它是非接受状态),所以你的寻宝之旅就此失败了。
8行间公式索引
1. 语言L1和L2的定义:将一个复杂语言分解为两个简单语言L1(偶数长度)和L2(奇数个'a')的交集。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。