11 COMS 3261 讲义 6A:NFA 和 正则表达式 练习
📜 [原文1]
Kiru Arjunan 和 Ziheng Huang
2024年秋季
这部分是讲义的标题和作者信息。它明确了这份学习资料的主题、作者以及适用的学期。
- COMS 3261:这是课程代码,通常代表一门具体的大学课程。在这里,它指向哥伦比亚大学的“计算机科学理论”课程。
- 讲义 6A:这表明是系列讲义中的第六部分,A可能表示这是练习部分(通常B是解答部分)。
- NFA 和 正则表达式 练习:这直接点明了本讲义的核心内容,即非确定性有限自动机(NFA)和正则表达式(Regular Expressions)的相关练习题。这两者是计算理论中描述正则语言的两个核心工具。
- Kiru Arjunan 和 Ziheng Huang:讲义的编写者。
- 2024年秋季:讲义发布或适用的时间。
本节是讲义的元信息,提供了关于课程、主题、作者和时间的基本背景。
标题和作者信息的目的是为了清晰地标识文档的身份和来源,方便学生和教师归档、查找和引用。
可以把这看作一本书的封面,告诉你这本书叫什么名字(NFA和正则表达式练习),是哪个系列丛书的一部分(COMS 3261 讲义 6A),作者是谁,以及出版年份。
想象一下你拿到一份纸质的课堂讲义,这部分就是印在最上面的大标题和作者署名,让你一眼就知道“哦,这是这周理论课的练习题”。
22 NFA
📜 [原文2]
2.1 问题 1. 画一个识别以下语言的 NFA:
(a) 所有包含 101 的字符串。
(b) $L=\left\{w \in\{0,1\}^{*} \mid w\right.$ 恰好有两个 0 或有偶数个 1$\}$
本节开始进入非确定性有限自动机(NFA)的具体练习。NFA是计算模型的一种,用于识别(或“接受”)特定模式的字符串集合,即语言。与确定性有限自动机(DFA)不同,NFA在某个状态下,对于一个输入符号,可以有零个、一个或多个转移路径,还可以有不需要任何输入符号就能进行的ε-转移(空转移)。
21.1 (a) 所有包含 101 的字符串
📜 [原文3]
(a) 所有包含 101 的字符串。
我们要构造一个NFA,它能“记住”是否已经看到了子串“101”。NFA的非确定性特性在这里非常有用,我们可以让它“猜测”子串“101”何时开始。
- 起始状态 $q_0$:这是我们的起点。在找到“101”之前,我们一直停留在这个“寻找”阶段。任何不属于我们目标子串开头的字符(0或1)都应该让我们继续寻找。所以,在$q_0$上有一个自循环,接受0和1。这代表“我还没开始匹配‘101’,请继续输入”。
- 寻找第一个‘1’:当我们在$q_0$时,如果输入是‘1’,我们可能开始了一个“101”序列。NFA允许我们同时探索两条路:一条是留在$q_0$(因为这个‘1’可能不是“101”的开头),另一条是转移到一个新状态$q_1$,表示“我可能找到了‘101’的第一个字符‘1’”。
- 寻找‘0’:在状态$q_1$时,我们期望下一个字符是‘0’。如果输入是‘0’,我们就转移到状态$q_2$。这表示“我连续找到了‘1’和‘0’”。如果输入是‘1’,那我们匹配失败了,这条路径就“死”了(没有定义转移)。
- 寻找第二个‘1’:在状态$q_2$时,我们期望下一个字符是‘1’。如果输入是‘1’,我们就转移到最终状态$q_3$。这表示“我成功找到了子串‘101’!”。如果输入是‘0’,匹配失败,路径死亡。
- 接受状态 $q_3$:一旦到达$q_3$,说明字符串中已经包含了“101”。之后无论再输入什么(0或1),我们都应该接受这个字符串。所以在$q_3$上有一个自循环,接受0和1。
NFA状态图如下:
- $q_0$:起始状态。
- $q_0 \xrightarrow{0,1} q_0$
- $q_0 \xrightarrow{1} q_1$
- $q_1 \xrightarrow{0} q_2$
- $q_2 \xrightarrow{1} q_3$
- $q_3$:接受状态。
- $q_3 \xrightarrow{0,1} q_3$
- 示例 1:输入字符串 "01010"
- 开始于 $q_0$。
- 读入 '0':停留在 $q_0$。
- 读入 '1':NFA分裂成两个路径。一个停留在 $q_0$,一个进入 $q_1$。当前活动状态集:$\{q_0, q_1\}$。
- 读入 '0':
- 从 $q_0$ 读 '0',停留在 $q_0$。
- 从 $q_1$ 读 '0',进入 $q_2$。
- 当前活动状态集:$\{q_0, q_2\}$。
- 读入 '1':
- 从 $q_0$ 读 '1',分裂成 $q_0$ 和 $q_1$。
- 从 $q_2$ 读 '1',进入 $q_3$。
- 当前活动状态集:$\{q_0, q_1, q_3\}$。
- 读入 '0':
- 从 $q_0$ 读 '0',停留在 $q_0$。
- 从 $q_1$ 读 '0',进入 $q_2$。
- 从 $q_3$ 读 '0',停留在 $q_3$。
- 当前活动状态集:$\{q_0, q_2, q_3\}$。
- 字符串结束。由于活动状态集包含接受状态 $q_3$,字符串 "01010" 被接受。
- 示例 2:输入字符串 "1100"
- 开始于 $q_0$。
- 读入 '1':活动状态集 $\{q_0, q_1\}$。
- 读入 '1':
- 从 $q_0$ 读 '1',分裂成 $q_0$ 和 $q_1$。
- 从 $q_1$ 读 '1',路径死亡。
- 当前活动状态集:$\{q_0, q_1\}$。
- 读入 '0':
- 从 $q_0$ 读 '0',停留在 $q_0$。
- 从 $q_1$ 读 '0',进入 $q_2$。
- 当前活动状态集:$\{q_0, q_2\}$。
- 读入 '0':
- 从 $q_0$ 读 '0',停留在 $q_0$。
- 从 $q_2$ 读 '0',路径死亡。
- 当前活动状态集:$\{q_0\}$。
- 字符串结束。活动状态集不包含接受状态,字符串 "1100" 不被接受。
- DFA思维:最常见的错误是用DFA的思路来设计,导致需要更多的状态来处理匹配失败后回退的情况。例如,在看到 "10" 后如果下一个是 "0" (构成 "100"),DFA需要一个状态来“记住”这个结尾的 "0" 可能是一个新的 "101" 的一部分(如果下一个是 "1" 的话)。NFA通过路径死亡和并行探索,简化了这种逻辑。
- 起始状态的循环:忘记在起始状态 $q_0$ 上添加对 0 和 1 的自循环,会导致NFA只能识别以 "101" 开头的字符串。
- 接受状态的循环:忘记在接受状态 $q_3$ 上添加对 0 和 1 的自循环,会导致NFA只能识别以 "101" 结尾的字符串。
我们利用NFA的非确定性,设计了一个四状态的自动机来识别包含子串 "101" 的语言。其核心思想是:在“寻找”阶段,任何字符都停留在原位;一旦遇到可能是模式开头的字符'1',就“分身”出一条新的探索路径,专门验证后续字符是否匹配 "01",而原路径继续寻找新的可能性。一旦匹配成功,就进入一个“万事大吉”的接受状态。
这个问题的目的是让学生练习使用NFA的核心特性——非确定性(并行路径探索)来解决模式匹配问题,并体会其相对于DFA在设计上的简洁性。
想象你在一条长长的纸带上查找单词“cat”。你是一个机器人,一次只能看一个字母。
- DFA方式:你看一个字母,然后根据规则移动。如果看到'c',你进入“可能找到了c”的状态。下一个是'a',你进入“可能找到了ca”的状态。如果下一个是't',你成功了!但如果中间任何一步错了,比如看到'c'后面是'b',你必须回到初始的“瞎找”状态。
- NFA方式:你看一个字母。如果看到'c',你立刻克隆一个自己,让克隆体去验证后面是不是'at',而本体则继续往前走,寻找下一个'c'。任何一个克隆体成功,整个任务就成功了。这就是NFA的“猜测”和“并行宇宙”能力。
想象你在一个岔路口。左边的路标写着“继续随便逛逛”,右边的路标写着“通往寻找‘101’宝藏之路的第一步(需要‘1’)”。NFA的神奇之处在于,你不需要选择,你可以同时走上两条路。如果走宝藏之路时发现路断了(比如需要‘0’但来了个‘1’),那条路上的你就消失了。但只要有任何一个你最终走到了宝藏终点,你就成功了。
21.2 (b) 恰好有两个 0 或有偶数个 1
📜 [原文4]
(b) $L=\left\{w \in\{0,1\}^{*} \mid w\right.$ 恰好有两个 0 或有偶数个 1$\}$
这个语言是两个子语言的并集:
- $L_1 = \{w \mid w \text{ 恰好有两个 0}\}$
- $L_2 = \{w \mid w \text{ 有偶数个 1}\}$
根据正则语言对并运算的封闭性,我们可以分别为 $L_1$ 和 $L_2$ 构造自动机,然后使用并的构造方法将它们组合起来。NFA的并构造非常简单:创建一个新的起始状态,然后用 ε-转移(空转移)连接到原来两个自动机的起始状态。
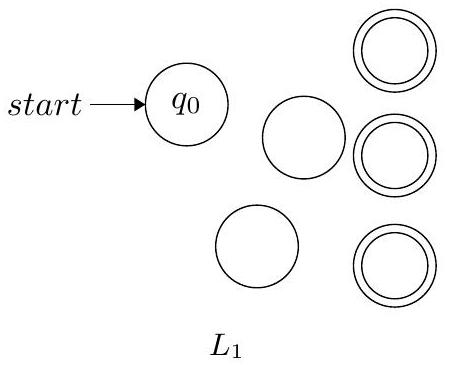
1. 构造识别 $L_1$ (恰好有两个 0) 的 NFA (实际上是DFA):
我们需要计数字符串中 0 的数量。
- $c_0$: 起始状态,表示有0个'0'。
- $c_1$: 表示有1个'0'。
- $c_2$: 表示有2个'0'。这是接受状态。
- $c_3$: “陷阱”状态,表示有超过2个'0'。
转移如下:
- $c_0 \xrightarrow{0} c_1$, $c_0 \xrightarrow{1} c_0$
- $c_1 \xrightarrow{0} c_2$, $c_1 \xrightarrow{1} c_1$
- $c_2 \xrightarrow{0} c_3$, $c_2 \xrightarrow{1} c_2$ (在 $c_2$ 读到'1's不改变0的计数)
- $c_3 \xrightarrow{0,1} c_3$
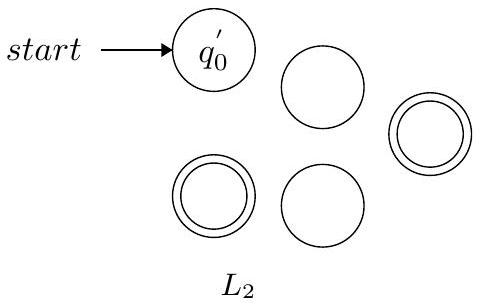
2. 构造识别 $L_2$ (偶数个 1) 的 NFA (实际上是DFA):
我们需要计数 1 的数量是奇数还是偶数。
- $e_0$: 起始状态,表示有偶数个'1' (0是偶数)。这是接受状态。
- $e_1$: 表示有奇数个'1'。
转移如下:
- $e_0 \xrightarrow{1} e_1$, $e_0 \xrightarrow{0} e_0$
- $e_1 \xrightarrow{1} e_0$, $e_1 \xrightarrow{0} e_1$
3. 组合成最终的 NFA:
- 创建一个新的起始状态 $q_{start}$。
- 从 $q_{start}$ 添加两条 ε-转移:
- $q_{start} \xrightarrow{\epsilon} c_0$ (连接到 $L_1$ 的起始状态)
- $q_{start} \xrightarrow{\epsilon} e_0$ (连接到 $L_2$ 的起始状态)
- 所有原来是接受状态的,现在仍然是接受状态。所以接受状态集合是 $\{c_2, e_0\}$。
这个组合起来的 NFA 有7个状态 ($q_{start}, c_0, c_1, c_2, c_3, e_0, e_1$)。当一个字符串输入时,NFA会“猜测”这个字符串应该满足哪个条件(有两个0还是偶数个1),然后进入相应的子自动机进行验证。
- $L$: 表示一个语言(Language),即一个字符串的集合。
- $w \in\{0,1\}^{*}$: 表示 $w$ 是一个由字符 '0' 和 '1' 组成的任意长度的字符串。
- $\{0,1\}$: 这是字母表(Alphabet),即构成字符串的基本符号集合。
- $*$: 这是克林星号(Kleene Star),表示将其前面的集合中的元素进行零次或多次连接(concatenation)。$\{0,1\}^{*}$ 就是所有可能的二进制字符串的集合,包括空字符串 $\epsilon$。
- $\mid$: 读作“使得”(such that),用来分隔集合元素的定义和该元素必须满足的条件。
- $w$ 恰好有两个 0 或有偶数个 1: 这是字符串 $w$ 属于语言 $L$ 的条件。它是一个逻辑或(OR)关系。
使用上面构造的组合 NFA:
- 示例 1:输入字符串 "1010"
- 开始于 $q_{start}$。
- 立即进行 ε-转移,活动状态集变为 $\{c_0, e_0\}$。
- 读入 '1':
- 从 $c_0$ 读 '1' -> $c_0$。
- 从 $e_0$ 读 '1' -> $e_1$。
- 活动状态集:$\{c_0, e_1\}$。
- 读入 '0':
- 从 $c_0$ 读 '0' -> $c_1$。
- 从 $e_1$ 读 '0' -> $e_1$。
- 活动状态集:$\{c_1, e_1\}$。
- 读入 '1':
- 从 $c_1$ 读 '1' -> $c_1$。
- 从 $e_1$ 读 '1' -> $e_0$。
- 活动状态集:$\{c_1, e_0\}$。
- 读入 '0':
- 从 $c_1$ 读 '0' -> $c_2$。
- 从 $e_0$ 读 '0' -> $e_0$。
- 活动状态集:$\{c_2, e_0\}$。
- 字符串结束。活动状态集包含 $c_2$ 和 $e_0$,两者都是接受状态。所以 "1010" 被接受。(它恰好有两个0,并且有偶数个1)。
- 示例 2:输入字符串 "01010"
- 开始于 $q_{start}$,ε-转移后活动状态集为 $\{c_0, e_0\}$。
- 读入 '0':活动状态集 $\{c_1, e_0\}$。
- 读入 '1':活动状态集 $\{c_1, e_1\}$。
- 读入 '0':活动状态集 $\{c_2, e_1\}$。
- 读入 '1':活动状态集 $\{c_2, e_0\}$。
- 读入 '0':
- 从 $c_2$ 读 '0' -> $c_3$。
- 从 $e_0$ 读 '0' -> $e_0$。
- 活动状态集:$\{c_3, e_0\}$。
- 字符串结束。活动状态集包含接受状态 $e_0$。所以 "01010" 被接受。(因为它有偶数个1,虽然它有三个0)。
- 混淆两个条件:错误地试图在一个单一的、没有 ε-转移 的自动机里同时跟踪两个独立的条件。这会使状态设计变得异常复杂。
- 空字符串 $\epsilon$:空字符串有0个'0'和0个'1'。0是偶数,所以它满足“有偶数个1”的条件。我们的NFA能正确处理:$q_{start} \xrightarrow{\epsilon} e_0$,由于 $e_0$ 是接受状态,空字符串被接受。
- 忘记陷阱状态:在构造 $L_1$ 的自动机时,如果忘记了 $c_3$(超过两个0的状态),那么一旦达到两个0,自动机可能会错误地接受之后还有0的字符串。
通过利用正则语言对并运算的封闭性,我们将一个复杂的问题分解为两个简单子问题的组合。我们分别为“恰好有两个0”和“偶数个1”构建了(DFA形式的)自动机,然后使用NFA的并构造法(即新的起始状态+ε-转移)将它们优雅地连接在一起,形成一个识别目标语言的NFA。
这个问题的目的是考察学生是否理解正则语言的封闭性,并能应用标准的NFA构造方法(特别是并运算的构造)来解决复合条件的语言识别问题。
想象你有两个专家机器人。专家A只关心字符串里有多少个'0',如果正好是两个,他就会举起一个“通过”的牌子。专家B只关心有多少个'1',如果是偶数个,他也会举起“通过”的牌子。
当你拿到一个字符串,你把它同时交给A和B。只要他们中任何一个举起了“通过”的牌子,这个字符串就合格。新的起始状态和ε-转移就像是那个把字符串复印两份,分别交给A和B的“分发员”。
你来到一个主题公园的入口($q_{start}$)。入口处有两条免费的传送带(ε-转移)。一条带你去“双零山洞”($c_0$),另一条带你去“偶一乐园”($e_0$)。你被复制成了两个人,一个去了山洞,一个去了乐园。你们各自拿着字符串地图开始游览。如果在地图走完时,去山洞的你正好到达了山顶宝藏处($c_2$),或者去乐园的你正好在出口的庆祝广场上($e_0$),那么你就被认为“成功游览”了。
2.2 问题 2.
📜 [原文5]
(a) 此 NFA 识别的语言是什么?
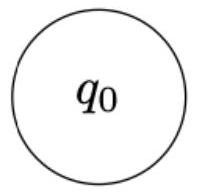
(b) 此 NFA 识别的语言是什么?
这一节要求我们反向工程:给定一个NFA的状态图,我们要推断出它所接受的语言,并用自然语言或集合符号来描述。
22.1 (a) NFA语言识别 (包含"00")
📜 [原文6]
(a) 此 NFA 识别的语言是什么?

我们来分析这个NFA的行为:
- 状态: 有三个状态,我们标记为 $q_0, q_1, q_2$。
- $q_0$: 起始状态(由一个指向它的、没有来源的箭头指示)。
- $q_2$: 接受状态(由双层圆圈指示)。
- 转移:
- $q_0 \xrightarrow{0,1} q_0$: 在起始状态,任何输入(0或1)都可以让它停留在原地。这表示在匹配到关键模式之前,可以有任意的前缀。
- $q_0 \xrightarrow{0} q_1$: 当输入为'0'时,除了停留在$q_0$,还可以选择进入$q_1$。这像是在说:“嘿,这可能是一个关键模式的开始。”
- $q_1 \xrightarrow{0} q_2$: 从$q_1$状态,如果再输入一个'0',就可以进入接受状态$q_2$。这表明,连续的两个'0'(即子串"00")是通往接受的关键。
- $q_2 \xrightarrow{0,1} q_2$: 一旦进入接受状态$q_2$,任何后续的输入(0或1)都会让它停留在$q_2$。这意味着一旦字符串中出现了"00",无论后面跟什么,整个字符串都会被接受。
综合分析:
- 要想到达接受状态$q_2$,必须经过路径 $q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_2$。
- 这要求输入字符串中必须包含一个子串"00"。
- 在"00"出现之前,可以在$q_0$上消耗任意的0和1(对应正则表达式 $(0 \cup 1)^{*}$)。
- 在"00"出现之后,可以在$q_2$上消耗任意的0和1(对应正则表达式 $(0 \cup 1)^{*}$)。
所以,这个NFA接受的语言是所有包含子串"00"的二进制字符串。用正则表达式表示就是 $(0 \cup 1)^{*}00(0 \cup 1)^{*}$。
- 示例 1: 输入 "1001"
- $q_0$, 读 '1' -> $q_0$。活动状态集 $\{q_0\}$。
- $q_0$, 读 '0' -> $q_0$ 或 $q_1$。活动状态集 $\{q_0, q_1\}$。
- 读 '0':
- 从 $q_0$ 读 '0' -> $q_0$ 或 $q_1$。
- 从 $q_1$ 读 '0' -> $q_2$。
- 合并结果,活动状态集 $\{q_0, q_1, q_2\}$。
- 读 '1':
- 从 $q_0$ 读 '1' -> $q_0$。
- 从 $q_1$ 读 '1' -> (路径死亡)。
- 从 $q_2$ 读 '1' -> $q_2$。
- 合并结果,活动状态集 $\{q_0, q_2\}$。
- 结束。活动状态集包含接受状态 $q_2$,所以 "1001" 被接受。
- 示例 2: 输入 "0101"
- $q_0$, 读 '0' -> $\{q_0, q_1\}$。
- 读 '1' -> 从 $q_0$ 得到 $q_0$,从 $q_1$ 路径死亡。活动状态集 $\{q_0\}$。
- $q_0$, 读 '0' -> $\{q_0, q_1\}$。
- 读 '1' -> 从 $q_0$ 得到 $q_0$,从 $q_1$ 路径死亡。活动状态集 $\{q_0\}$。
- 结束。活动状态集不含接受状态,所以 "0101" 不被接受。
- 忽略非确定性: 如果只看一条路径,比如 $q_0 \xrightarrow{0} q_0 \xrightarrow{0} q_0 ...$,会误以为无法到达$q_2$。必须考虑在每个状态,输入一个符号后所有可能的下一个状态的集合。
- 语言描述不精确: 可能会错误地描述为“以00结尾的字符串”。这是不对的,因为$q_2$有出边,接受后还可以跟任意字符。
该NFA通过一个三状态链($q_0 \to q_1 \to q_2$)来检测子串"00"的出现,并利用起始状态和接受状态的自循环来允许"00"出现在字符串的任何位置。因此,它识别的语言是“所有包含子串‘00’的二进制字符串”。
此题旨在检验学生解读NFA状态图并将其行为抽象为形式语言描述的能力。
这个NFA像一个警报系统,专门检测“连续两个0”。
- $q_0$是“待机”状态。系统在不断接收信号,但没发现异常。
- 当第一个'0'进来时,系统“警觉”起来,分出一个线程进入$q_1$“观察”状态(“可能要出事了”),但主系统仍在$q_0$“待机”。
- 如果在“观察”状态下,紧接着又来一个'0',该线程就立刻触发警报,进入$q_2$“警报拉响”状态。
- 一旦警报拉响,就再也不会停止,无论后面是什么信号。
想象你在玩一个游戏,目标是踩到两个连续的标有“0”的石板。你可以随便在任何石板上跳($q_0$的循环)。当你踩到一个“0”石板时,你可以选择继续随便跳,也可以选择跳到一个特殊的“预备”石板$q_1$上。如果你在$q_1$上,再跳一步又踩到一个“0”石板,你就赢了,被传送到终点房间$q_2$。到了终点房间,你可以随便跳舞($q_2$的循环),游戏已经胜利。
22.2 (b) NFA语言识别 (首尾字符相同)
📜 [原文7]
(b) 此 NFA 识别的语言是什么?

我们来分析这个更复杂的NFA:
- 状态: 有五个状态,我们标记为 $q_0, q_1, q_2, q_3, q_4$。
- $q_0$: 起始状态。它也是一个接受状态,这意味着空字符串$\epsilon$被接受。
- $q_2, q_4$: 另外两个接受状态。
- 转移:
- 从 $q_0$ 出发:
- $q_0 \xrightarrow{0} q_1$: “猜测”字符串以'0'开头。
- $q_0 \xrightarrow{1} q_3$: “猜测”字符串以'1'开头。
- 因为$q_0$本身是接受状态,这处理了空字符串$\epsilon$的情况。
- "0"路径:
- $q_1 \xrightarrow{0,1} q_1$: 一旦以'0'开头,中间可以有任意多个0和1。
- $q_1 \xrightarrow{0} q_2$: 当以'0'结尾时,可以进入接受状态$q_2$。
- "1"路径:
- $q_3 \xrightarrow{0,1} q_3$: 一旦以'1'开头,中间可以有任意多个0和1。
- $q_3 \xrightarrow{1} q_4$: 当以'1'结尾时,可以进入接受状态$q_4$。
综合分析:
这个NFA的结构明显分成了两大赛道:
- 空字符串: 起始状态$q_0$就是接受状态,所以空字符串 $\epsilon$ 被接受。
- 以0开头的路径: 从$q_0$经过$q_1$到$q_2$。这条路径要求第一个字符是'0'。中间经过$q_1$的自循环,可以有任意字符。最后要想到达接受状态$q_2$,必须以'0'结尾。所以这条路径接受的语言是“以0开头且以0结尾的非空字符串”。
- 以1开头的路径: 从$q_0$经过$q_3$到$q_4$。这条路径要求第一个字符是'1'。中间经过$q_3$的自循环,可以有任意字符。最后要想到达接受状态$q_4$,必须以'1'结尾。所以这条路径接受的语言是“以1开头且以1结尾的非空字符串”。
结论: 将这三种情况合并:
- 空字符串 $\epsilon$。
- 以0开头且以0结尾的非空字符串。
- 以1开头且以1结尾的非空字符串。
这可以统一描述为:所有首尾字符相同的二进制字符串,以及空字符串。
我们还可以考虑单字符字符串:
- "0": $q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_2$ (路径不成立)。但是, $q_0 \xrightarrow{0} q_1$ 是合法的,但是$q_1$不是接受状态。这里的设计有些微妙。让我们重新审视一下 $q_1 \xrightarrow{0} q_2$。这意味着要想到达$q_2$,字符串至少要长为2。
- Let's re-trace "0": $q_0 \xrightarrow{0} q_1$. 字符串结束, $q_1$不是接受态。不接受。
- Let's re-trace "00": $q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_2$. 字符串结束, $q_2$是接受态。接受。
- Let's re-trace "1": $q_0 \xrightarrow{1} q_3$. 字符串结束,不接受。
- Let's re-trace "11": $q_0 \xrightarrow{1} q_3 \xrightarrow{1} q_4$. 字符串结束,接受。
所以,这个NFA接受的语言是:
- 空字符串 $\epsilon$。
- 所有长度大于等于2的,首尾字符相同的字符串。
这与通常理解的“首尾字符相同”(包含单字符 "0", "1")略有不同。我们必须严格按照自动机的定义来。
让我们检查一下,也许单字符可以被接受?
- "0": 从 $q_0$ 读 '0',只能到 $q_1$。$q_1$不是接受态。所以 "0" 不被接受。
- "1": 从 $q_0$ 读 '1',只能到 $q_3$。$q_3$不是接受态。所以 "1" 不被接受。
因此,最终结论是:该语言是空字符串 $\epsilon$ ,以及所有长度至少为2且首字符和尾字符相同的二进制字符串。
用集合表示为:
$L = \{\epsilon\} \cup \{w \in \{0,1\}^* \mid |w| \ge 2 \text{ and } w \text{ starts and ends with '0'}\} \cup \{w \in \{0,1\}^* \mid |w| \ge 2 \text{ and } w \text{ starts and ends with '1'}\}$
或者更简洁地: $L = \{\epsilon\} \cup \{0w0 \mid w \in \{0,1\}^*\} \cup \{1w1 \mid w \in \{0,1\}^*\}$
- 示例 1: 输入 "0110"
- $q_0$, 读 '0' -> $q_1$。
- $q_1$, 读 '1' -> $q_1$。
- $q_1$, 读 '1' -> $q_1$。
- $q_1$, 读 '0' -> $q_1$ 或 $q_2$。活动状态集 $\{q_1, q_2\}$。
- 结束。活动状态集包含接受状态 $q_2$,所以 "0110" 被接受。
- 示例 2: 输入 "101"
- $q_0$, 读 '1' -> $q_3$。
- $q_3$, 读 '0' -> $q_3$。
- $q_3$, 读 '1' -> $q_3$ 或 $q_4$。活动状态集 $\{q_3, q_4\}$。
- 结束。活动状态集包含接受状态 $q_4$,所以 "101" 被接受。
- 示例 3: 输入 "01"
- $q_0$, 读 '0' -> $q_1$。
- $q_1$, 读 '1' -> $q_1$。
- 结束。活动状态集是 $\{q_1\}$,不含接受状态,所以 "01" 不被接受。
- 空字符串: $q_0$是接受状态,所以空字符串 $\epsilon$ 被接受。很容易忽略这一点。
- 单字符字符串: 如分析所示,"0" 和 "1" 不被这个NFA接受。这是一个非常关键的边界情况,容易误判为“所有首尾相同的字符串”。
- 非确定性的作用: 在 $q_1$ 读到 '0' 时,既可以停留在 $q_1$(如果后面还有字符),也可以进入 $q_2$(如果这是最后一个字符)。这种“猜测”字符串是否结束的能力是NFA的关键。
该NFA通过一个初始分叉来“猜测”字符串是以 '0' 还是 '1' 开头,然后进入两条独立的路径。每条路径都允许任意的中间部分,但只有在字符串以与开头相同的字符结束时,才能到达该路径的接受状态。此外,起始状态本身也是接受状态,用于接纳空字符串。因此,该NFA识别的语言是:空字符串,以及所有长度不小于2且首尾字符相同的二进制字符串。
此题考察学生分析一个具有并行逻辑和非确定性“猜测”的NFA的能力,并精确地描述其所识别的语言,特别是要注意对空字符串和单字符等边界情况的处理。
这个NFA像一个有特殊规则的俱乐部守门员。
- 规则0: 如果你什么都没带(空字符串),可以直接进去($q_0$是接受状态)。
- 规则1: 如果你带的物品(字符串)第一个是苹果('0'),守门员会把你引导到“苹果通道”($q_1$)。你可以在通道里拿任意数量的苹果或香蕉,但最后一件必须是苹果,才能进入“苹果贵宾室”($q_2$)并被认可。
- 规则2: 如果你带的物品第一个是香蕉('1'),守门员会把你引导到“香蕉通道”($q_3$)。规则类似,最后一件必须是香蕉,才能进入“香蕉贵宾室”($q_4$)。
- 如果你带的东西首尾不一致,比如以苹果开头,以香蕉结尾,你就会被困在通道里,无法进入任何贵宾室。
想象一个分叉的铁路系统。从总站($q_0$)出发,你可以选择登上“0号线”(去$q_1$)或“1号线”(去$q_3$)。
- “0号线”列车在沿途($q_1$的循环)可以随意上下客(读0或1),但只有在终点站前最后一站是“0号站”时,才能最终抵达接受终点站$q_2$。
- “1号线”同理,最后一站必须是“1号站”才能抵达接受终点站$q_4$。
- 总站$q_0$本身也是一个特殊的“原地休息区”,被视为一个有效的终点。所以什么都不做(空字符串)也是一种成功。
2.3 问题 3. 使用 子集构造法 将此 NFA 转换为等价的 DFA:
📜 [原文8]
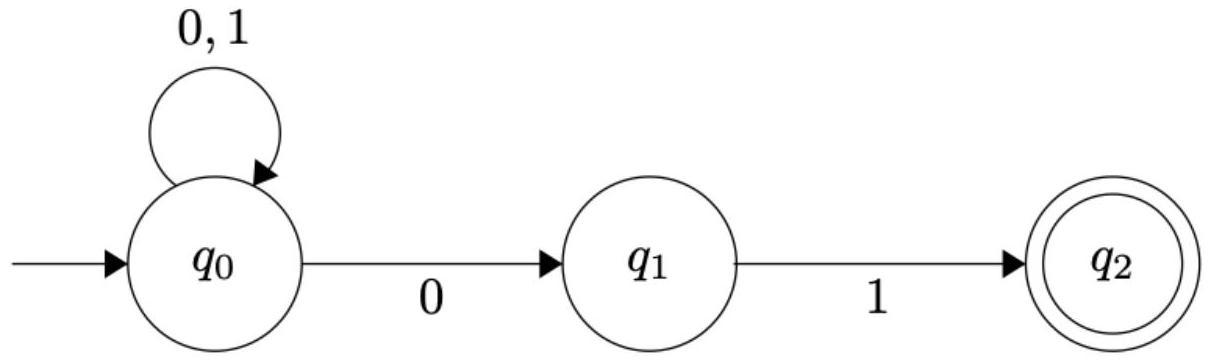
子集构造法(Subset Construction)是一种标准的算法,用于将一个NFA转换为一个等价的DFA。其核心思想是,DFA的每一个状态都对应于NFA中可能处于的状态的集合(子集)。
让我们把给定的NFA状态标记为:状态1和状态2。
- NFA状态: $N = \{1, 2\}$。
- 字母表: $\Sigma = \{a, b\}$。
- NFA起始状态: $q_{start\_NFA} = \{1\}$。
- NFA接受状态: $F_{NFA} = \{2\}$。
- NFA转移函数 $\delta_N$:
- $\delta_N(1, a) = \{1, 2\}$
- $\delta_N(1, b) = \{2\}$
- $\delta_N(2, a) = \emptyset$ (空集)
- $\delta_N(2, b) = \{1, 2\}$
- 这个NFA没有 ε-转移,所以我们不需要计算 ε-闭包。
构造 DFA 步骤:
- DFA 的起始状态: DFA的起始状态是NFA起始状态所在的集合。这里就是 $\{1\}$。我们把这个新的DFA状态命名为 $S_0 = \{1\}$。
- 探索 $S_0 = \{1\}$:
- 输入 'a': 我们需要计算从 $S_0$ 中的每个NFA状态出发,经过 'a' 能到达的所有NFA状态的并集。
- $ \delta_D(S_0, a) = \delta_N(1, a) = \{1, 2\} $
- 这是一个新的DFA状态。我们命名为 $S_1 = \{1, 2\}$。
- 输入 'b':
- $ \delta_D(S_0, b) = \delta_N(1, b) = \{2\} $
- 这是一个新的DFA状态。我们命名为 $S_2 = \{2\}$。
- 探索 $S_1 = \{1, 2\}$:
- 输入 'a':
- $ \delta_D(S_1, a) = \delta_N(1, a) \cup \delta_N(2, a) = \{1, 2\} \cup \emptyset = \{1, 2\} $
- 这个状态我们已经见过了,就是 $S_1$。所以 $S_1 \xrightarrow{a} S_1$。
- 输入 'b':
- $ \delta_D(S_1, b) = \delta_N(1, b) \cup \delta_N(2, b) = \{2\} \cup \{1, 2\} = \{1, 2\} $
- 这个状态也是 $S_1$。所以 $S_1 \xrightarrow{b} S_1$。
- 探索 $S_2 = \{2\}$:
- 输入 'a':
- $ \delta_D(S_2, a) = \delta_N(2, a) = \emptyset $
- 这是一个新的DFA状态,即空集状态。我们命名为 $S_3 = \emptyset$。这是一个“陷阱”状态。
- 输入 'b':
- $ \delta_D(S_2, b) = \delta_N(2, b) = \{1, 2\} $
- 这个状态是 $S_1$。所以 $S_2 \xrightarrow{b} S_1$。
- 探索 $S_3 = \emptyset$:
- 输入 'a':
- $ \delta_D(S_3, a) = \emptyset $
- 它自己转移到自己。$S_3 \xrightarrow{a} S_3$。
- 输入 'b':
- $ \delta_D(S_3, b) = \emptyset $
- 它自己转移到自己。$S_3 \xrightarrow{b} S_3$。
整合 DFA:
- DFA 状态集: $Q_D = \{S_0, S_1, S_2, S_3\}$,其中 $S_0=\{1\}, S_1=\{1,2\}, S_2=\{2\}, S_3=\emptyset$。
- DFA 起始状态: $S_0 = \{1\}$。
- DFA 接受状态: DFA的接受状态是所有那些包含了NFA接受状态的集合。NFA的接受状态是 $\{2\}$。所以,任何包含状态'2'的DFA状态都是接受状态。
- $S_1 = \{1, 2\}$ 包含 '2',是接受状态。
- $S_2 = \{2\}$ 包含 '2',是接受状态。
- $F_D = \{S_1, S_2\}$。
DFA 转移表:
| DFA 状态 | 对应NFA子集 | 输入 'a' | 输入 'b' | 是否接受? |
|---|---|---|---|---|
| $S_0$ | $\{1\}$ | $S_1$ | $S_2$ | 否 |
| $S_1$ | $\{1, 2\}$ | $S_1$ | $S_1$ | 是 |
| $S_2$ | $\{2\}$ | $S_3$ | $S_1$ | 是 |
| $S_3$ | $\emptyset$ | $S_3$ | $S_3$ | 否 |
画出 DFA 状态图:
- 画出四个圈,分别标记为 $S_0, S_1, S_2, S_3$。
- $S_0$ 是起始状态(画一个无源箭头指向它)。
- $S_1$ 和 $S_2$ 是接受状态(画成双层圆圈)。
- 根据上表连接箭头:
- $S_0 \xrightarrow{a} S_1$
- $S_0 \xrightarrow{b} S_2$
- $S_1 \xrightarrow{a} S_1$ (自循环)
- $S_1 \xrightarrow{b} S_1$ (自循环)
- $S_2 \xrightarrow{a} S_3$
- $S_2 \xrightarrow{b} S_1$
- $S_3 \xrightarrow{a} S_3$ (自循环)
- $S_3 \xrightarrow{b} S_3$ (自循环)
让我们用NFA和构造出的DFA来跟踪同一个字符串。
- 示例 1: 输入 "ab"
- NFA 跟踪:
- 起始于 $\{1\}$。
- 读 'a':从 1 读 'a',到达 $\{1, 2\}$。活动状态集 $\{1, 2\}$。
- 读 'b':从 1 读 'b' 到 $\{2\}$,从 2 读 'b' 到 $\{1, 2\}$。并集是 $\{1, 2\}$。
- 结束。活动状态集 $\{1, 2\}$ 包含接受状态 2,所以 "ab" 被接受。
- DFA 跟踪:
- 起始于 $S_0$。
- 读 'a':$S_0 \xrightarrow{a} S_1$。当前状态 $S_1$。
- 读 'b':$S_1 \xrightarrow{b} S_1$。当前状态 $S_1$。
- 结束。当前状态 $S_1$ 是接受状态,所以 "ab" 被接受。
- 结果一致。
- 示例 2: 输入 "ba"
- NFA 跟踪:
- 起始于 $\{1\}$。
- 读 'b':从 1 读 'b',到达 $\{2\}$。活动状态集 $\{2\}$。
- 读 'a':从 2 读 'a',到达 $\emptyset$。活动状态集 $\emptyset$。
- 结束。活动状态集不含接受状态,所以 "ba" 不被接受。
- DFA 跟踪:
- 起始于 $S_0$。
- 读 'b':$S_0 \xrightarrow{b} S_2$。当前状态 $S_2$。
- 读 'a':$S_2 \xrightarrow{a} S_3$。当前状态 $S_3$。
- 结束。当前状态 $S_3$ 不是接受状态,所以 "ba" 不被接受。
- 结果一致。
- ε-闭包: 这个例子没有 ε-转移。如果有,DFA的每个状态不仅是NFA状态的子集,而且是该子集经过任意次ε-转移能到达的所有状态的集合(即ε-闭包)。在计算转移时,也要先计算目标子集,再对结果取ε-闭包。
- 空集状态: 必须处理转移到空集的情况,这会产生一个“陷阱”状态(dead state),所有转移都指向自身,且不是接受状态。
- 识别所有新状态: 在构造过程中,只要出现一个新的子集,就必须将它加入待探索列表,直到没有新的子集产生为止。
- 确定接受状态: 接受状态的判断标准是“DFA状态(即NFA子集)中是否至少包含一个 NFA的接受状态”。
我们成功地应用了子集构造法,将一个2状态的NFA转换为了一个等价的4状态DFA。算法的核心是将NFA的不确定性(一个状态对一个输入可以去多个地方)转化为DFA的确定性(一个DFA状态代表NFA可能处于的所有状态的集合)。通过系统地探索这些子集以及它们之间的转移,我们构建了一个行为完全相同但没有非确定性的自动机。
这个问题的目的是检验学生是否掌握了子集构造法这一核心算法。这是连接NFA和DFA的桥梁,也是证明两类自动机识别能力等价的关键。实际应用中,NFA易于设计,而DFA易于高效实现,因此该转换非常重要。
NFA像是量子态,一个粒子可以同时在多个位置(状态)。而DFA是经典观察者,它不知道粒子到底在哪,但它能精确地描述“粒子可能在的位置集合”。
- NFA说:“我在状态1,来了个'a',所以我现在可能在状态1,也可能在状态2。”
- DFA说:“你之前处于‘只可能在状态1’($S_0$)这个宏观状态。来了个'a',所以我知道你现在处于‘可能在状态1或状态2’($S_1$)这个新的宏观状态。”
DFA的每个状态,就是对NFA所有并行宇宙可能性的一种总结。
想象你是一个情报机构的负责人,正在追踪一个间谍(输入字符串)。这个间谍(NFA)行踪不定,在一个城市(状态)接到指令(输入)后,可能会出现在多个地点(下一个状态)。
- 你作为DFA,无法确定间谍的确切位置。但你可以维护一个“可能地点列表”(DFA的状态)。
- 你的初始列表是“{间谍起始点}”($S_0$)。
- 每当新情报(输入'a'或'b')传来,你就更新你的列表:对于列表中的每个可能地点,你都查一下间谍从那里接到新指令后会去哪些新地点,然后把所有这些新地点汇总成你的新“可能地点列表”。
- 如果你的列表中任何一个地点是间谍的目标(NFA的接受状态),你就在这个列表上盖一个“目标可能在此”的章(DFA的接受状态)。
33 正则语言的封闭性
📜 [原文9]
在课堂上,我们通过使用 NFA 展示了 正则语言类 在 连接、Kleene 星号 和 并 运算下是 封闭 的(此外之前还使用 DFA 展示了在 补、交 和 并 运算下的 封闭性)。在本节中,我们简要且非正式地回顾这些运算,并证明其他 封闭性,如 逆转、min、max 和 对称差。
本节的引言部分,总结了课程已经讲过的内容,并预告了接下来要讨论的新内容。
- 正则语言类:指的是所有可以被有限自动机(DFA或NFA)识别的语言的集合。
- 封闭性(Closure Property):一个集合在一个运算下是封闭的,意味着从该集合中取出任意一个或两个元素进行该运算,得到的结果仍然在该集合内。
- 例如,整数集合在加法下是封闭的,因为任意两个整数相加,结果还是整数。但整数集合在除法下不封闭(例如 3 / 2 = 1.5,不是整数)。
- 已学内容回顾:
- 使用 NFA 证明了正则语言在以下三个基本正则运算下是封闭的:
- 并 (Union, $\cup$): $L_1 \cup L_2$
- 连接 (Concatenation, $\circ$): $L_1 \circ L_2$
- 克林星号 (Kleene Star, $*$): $L_1^*$
- 之前使用 DFA 证明了正则语言在以下布尔运算下是封闭的:
- 补 (Complement, $\overline{L}$): 通过将DFA的接受状态和非接受状态互换得到。
- 交 (Intersection, $\cap$): 通过乘积构造(Product Construction)得到。
- 并 (Union, $\cup$): 也可以通过乘积构造,或者利用德摩根定律 $\overline{(\overline{L_1} \cap \overline{L_2})}$。
- 本节目标:
- 简要回顾已学的并、连接、星号的NFA构造。
- 证明正则语言在一些其他运算下也是封闭的,包括:
- 逆转 (Reversal, $L^R$)
- min(L)
- max(L) (虽然这里写了,但后面问题里没出现,可能是笔误或计划在别处讲)
- 对称差 (Symmetric Difference)
本段是一个承上启下的段落。它首先系统地梳理了关于正则语言封闭性的已知知识点,区分了用DFA和NFA证明的不同运算,然后明确了本讲义练习将要探讨的新封闭性证明。
这个引言的目的是为学生建立一个清晰的知识框架。它将新知识(如逆转运算的封闭性)置于现有知识(如并、连接的封闭性)的背景之下,帮助学生理解学习的脉络和本节练习的重点。
把“正则语言”想象成一个“工具箱”。我们已经知道,用这个工具箱里的任何两个工具(语言)通过“焊接”(并)、“胶水粘接”(连接)或者“自我复制”(星号)操作,制造出的新东西仍然能放回这个工具箱里。现在,我们要测试一些新的操作,比如“镜面翻转”(逆转),看看通过这些新操作产生的东西,是不是也同样能被放回这个工具箱里。
想象你有一个“乐高正则积木”俱乐部。俱乐部规定,只有特定类型的积木(正则语言)才能成为会员。
- 俱乐部章程写着:如果你有两个会员积木,把它们并排放在一起(并),或者头尾相连(连接),或者拿一个会员积木无限复制自己连成一长串(星号),得到的新组合体自动成为会员。这是已经证明的老规矩。
- 这次的俱乐部活动(本讲义)就是要讨论几个新提案:
- 把一个会员积木整体翻个面(逆转),它还有资格当会员吗?
- 从一个会员积木上切下“最小的有效片段”(min),这个片段有资格当会员吗?
我们将要通过构造法来投票表决(证明)这些提案。
3.1 a) 在 并 运算下 封闭
📜 [原文10]
回顾。为了构造两个语言的 并,我们添加一个新的 起始状态 和到旧 起始状态 的 $\epsilon$-转移。
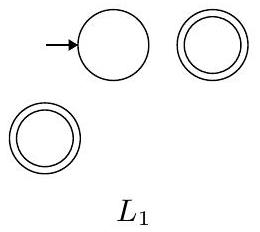
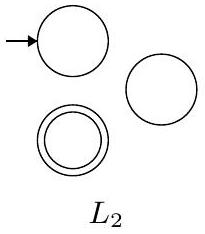
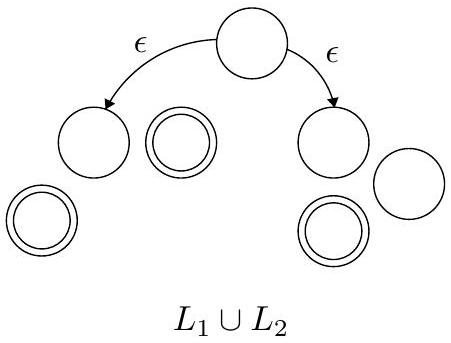
这部分回顾了为两个正则语言 $L_1$ 和 $L_2$ 的并集 $L_1 \cup L_2$ 构造NFA的标准方法。
假设我们已经有了识别 $L_1$ 的NFA $N_1$ 和识别 $L_2$ 的NFA $N_2$。
- 图片分析:
- 第一张图是一个抽象的NFA $N_1$,它有一个起始状态和一些接受状态,识别语言 $L_1$。
- 第二张图是另一个抽象的NFA $N_2$,识别语言 $L_2$。
- 第三张图展示了构造 $L_1 \cup L_2$ 的NFA $N$ 的过程。
- 构造步骤:
- 不改变原有机器: 保持 $N_1$ 和 $N_2$ 的内部结构完全不变。
- 添加新起始状态: 创建一个全新的状态,作为新NFA $N$ 的唯一起始状态,我们称之为 $q_{new\_start}$。
- 添加ε-转移: 从 $q_{new\_start}$ 画两条ε-转移(不消耗任何输入符号的转移):一条指向 $N_1$ 的原起始状态,另一条指向 $N_2$ 的原起始状态。
- 接受状态: $N$ 的接受状态集合是 $N_1$ 和 $N_2$ 所有接受状态的并集。
- 工作原理:
当一个新的字符串输入到 $N$ 时,它首先从 $q_{new\_start}$ 开始。由于有ε-转移,NFA会立即、不消耗任何输入地“分裂”成两个并行的计算路径:一个进入了 $N_1$ 的起始点,另一个进入了 $N_2$ 的起始点。
- 接下来,整个字符串会在这两条路径上(在 $N_1$ 和 $N_2$ 内部)并行地进行处理。
- 如果字符串走完后,在 $N_1$ 内部的路径到达了 $N_1$ 的一个接受状态,那么整个字符串就被 $N$ 接受。
- 或者,如果字符串在 $N_2$ 内部的路径到达了 $N_2$ 的一个接受状态,整个字符串也被 $N$ 接受。
- 这正好对应了并集的定义:一个字符串属于 $L_1 \cup L_2$,当且仅当它属于 $L_1$ 或者 属于 $L_2$。
该部分图文并茂地回顾了NFA的并运算构造法。其精髓在于利用ε-转移提供一个“选择”:让输入字符串有机会在识别 $L_1$ 的机器上运行,同时也有机会在识别 $L_2$ 的机器上运行。只要其中任何一个成功,整个任务就算成功。
在提出具体问题前,通过回顾标准构造法来激活学生的先验知识,为后续要求学生亲手实践这一构造法的问题(问题4)做好铺垫。
这就像一个双人安检系统。乘客(字符串)来到总入口(新起始状态)。入口处有两条传送带(ε-转移),一条通往安检员A($N_1$),另一条通往安检员B($N_2$)。乘客被复制,同时接受A和B的检查。只要其中任何一个安检员亮了绿灯(到达接受状态),乘客就可以通过。
想象你要参加一场考试,有两个考场可选($N_1$和$N_2$)。你在大门口($q_{new\_start}$)登记后,可以选择进入任意一个考场(ε-转移)。你的试卷(输入字符串)在这两个考场里都会被批改。只要你在任何一个考场及格了(到达接受状态),你的总成绩就是“通过”。
31.1 问题 4
📜 [原文11]
问题 4. $L=\left\{w \in\{0,1\}^{*} \mid w\right.$ 有偶数个 0,或者 $w$ 没有两个连续的 $\left.1^{\prime} s\right\}$。在作业 1 第 2 题 a 中,我们将 $L$ 表示为两个 正则语言 的 并。使用为每个语言构造的 DFA,现在画一个识别该 并 的 NFA。
这个问题要求我们应用刚刚回顾的并构造法。语言 $L$ 是两个子语言 $L_1$ 和 $L_2$ 的并集。
- $L_1 = \{w \in \{0,1\}^* \mid w \text{ 有偶数个 0}\}$
- $L_2 = \{w \in \{0,1\}^* \mid w \text{ 没有两个连续的 1's}\}$
第一步:为 $L_1$ 构造 DFA
我们需要一个DFA来记录0的个数的奇偶性。
- 状态 $E_0$: 偶数个0(起始状态,接受状态)。
- 状态 $O_0$: 奇数个0。
- 转移:
- $E_0 \xrightarrow{0} O_0$
- $E_0 \xrightarrow{1} E_0$ (1不改变0的奇偶性)
- $O_0 \xrightarrow{0} E_0$
- $O_0 \xrightarrow{1} O_0$ (1不改变0的奇偶性)
- 起始状态: $E_0$。
- 接受状态: $\{E_0\}$。
第二步:为 $L_2$ 构造 DFA
我们需要一个DFA来检测是否出现了 "11"。
- 状态 $S$: 起始状态,没有连续的1(接受状态)。
- 状态 $S_1$: 刚刚看到了一个1(接受状态)。
- 状态 $D$: "Dead" 状态,已经看到了 "11"(非接受状态)。
- 转移:
- $S \xrightarrow{0} S$
- $S \xrightarrow{1} S_1$
- $S_1 \xrightarrow{0} S$ (连续1被打断)
- $S_1 \xrightarrow{1} D$ (出现 "11")
- $D \xrightarrow{0,1} D$ (一旦出现 "11",永远陷在这里)
- 起始状态: $S$。
- 接受状态: $\{S, S_1\}$。
第三步:使用并构造法组合成 NFA
- 创建新起始状态: $q_{start}$。
- 添加 ε-转移:
- $q_{start} \xrightarrow{\epsilon} E_0$ (连接到 $L_1$ 的 DFA 起始状态)
- $q_{start} \xrightarrow{\epsilon} S$ (连接到 $L_2$ 的 DFA 起始状态)
- 整合状态: 整个NFA的状态集是 $\{q_{start}, E_0, O_0, S, S_1, D\}$。
- 整合接受状态: 新NFA的接受状态是原来两个DFA接受状态的并集,即 $\{E_0, S, S_1\}$。
画出最终的 NFA:
- 在左边画一个新状态 $q_{start}$,并标记为起始状态。
- 画出 $L_1$ 的两状态DFA ($E_0, O_0$),其中 $E_0$ 是双圈。
- 画出 $L_2$ 的三状态DFA ($S, S_1, D$),其中 $S$ 和 $S_1$ 是双圈。
- 从 $q_{start}$ 画一条带 $\epsilon$ 标签的箭头指向 $E_0$。
- 从 $q_{start}$ 画另一条带 $\epsilon$ 标签的箭头指向 $S$。
- $L, w, \{0,1\}^{*}, \mid$: 含义同问题1(b)的公式。
- $w$ 有偶数个 0,或者 $w$ 没有两个连续的 $1's$: 这是定义语言 $L$ 的逻辑条件,一个清晰的“或”关系,直接对应了并运算。
- 示例 1: 输入 "101"
- 该字符串有奇数个0,并且没有连续的1。所以它属于$L_2$,应该被接受。
- NFA 跟踪:
- $q_{start}$ -> ε-转移后活动状态集 $\{E_0, S\}$。
- 读 '1': 从 $E_0$ 到 $E_0$,从 $S$ 到 $S_1$。活动状态集 $\{E_0, S_1\}$。
- 读 '0': 从 $E_0$ 到 $O_0$,从 $S_1$ 到 $S$。活动状态集 $\{O_0, S\}$。
- 读 '1': 从 $O_0$ 到 $O_0$,从 $S$ 到 $S_1$。活动状态集 $\{O_0, S_1\}$。
- 结束。活动状态集包含接受状态 $S_1$,所以 "101" 被接受。
- 示例 2: 输入 "0011"
- 该字符串有偶数个0,但有连续的1。它属于$L_1$,应该被接受。
- NFA 跟踪:
- $q_{start}$ -> ε-转移后活动状态集 $\{E_0, S\}$。
- 读 '0': 从 $E_0$ 到 $O_0$,从 $S$ 到 $S$。活动状态集 $\{O_0, S\}$。
- 读 '0': 从 $O_0$ 到 $E_0$,从 $S$ 到 $S$。活动状态集 $\{E_0, S\}$。
- 读 '1': 从 $E_0$ 到 $E_0$,从 $S$ 到 $S_1$。活动状态集 $\{E_0, S_1\}$。
- 读 '1': 从 $E_0$ 到 $E_0$,从 $S_1$ 到 $D$。活动状态集 $\{E_0, D\}$。
- 结束。活动状态集包含接受状态 $E_0$,所以 "0011" 被接受。
- 示例 3: 输入 "110"
- 该字符串有奇数个0,并且有连续的1。它既不属于$L_1$也不属于$L_2$,不应被接受。
- NFA 跟踪:
- $q_{start}$ -> ε-转移后活动状态集 $\{E_0, S\}$。
- 读 '1': 从 $E_0$ 到 $E_0$,从 $S$ 到 $S_1$。活动状态集 $\{E_0, S_1\}$。
- 读 '1': 从 $E_0$ 到 $E_0$,从 $S_1$ 到 $D$。活动状态集 $\{E_0, D\}$。
- 读 '0': 从 $E_0$ 到 $O_0$,从 $D$ 到 $D$。活动状态集 $\{O_0, D\}$。
- 结束。活动状态集不含任何接受状态,所以 "110" 不被接受。
- DFA接受状态搞错: 在构造两个子DFA时,要仔细确定接受状态。例如,对于 $L_2$,状态 $S$(从未见过1或刚见过0)和 $S_1$(刚见过一个1)都应该被接受,因为到目前为止还没有出现"11"。
- 忘记ε-转移: 如果不使用ε-转移,而是试图将两个DFA的起始状态合并,将无法正确工作。
- 新NFA的接受状态: 新NFA的接受状态是两个原子DFA接受状态的并集,不能遗漏。
本题是NFA并构造法的一次具体实践。我们遵循“分解-构造-合并”的思路,首先为语言的两个组成部分分别设计了正确的DFA,然后严格按照并构造法的步骤——添加新起始状态和两条ε-转移——将它们组合成一个识别总语言的NFA。
本题的目的是让学生将理论知识(NFA并构造)应用于一个具体的问题,通过动手画图来加深对该构造法工作原理的理解。
同3.1节的安检模型。安检员A检查“0的个数是不是偶数”,安检员B检查“有没有藏着连续的两个1”。乘客(字符串)被复制后同时给A和B检查,只要有一个说“通过”,乘客就能过关。
同3.1节的考场模型。一个考场考“0的奇偶性”,另一个考场考“有没有作弊带‘11’小纸条”。你(字符串)被分身到两个考场同时考试,只要任何一个分身及格了,你就通过了这次考试。
44 行间公式索引
1. 问题1(b)的语言定义:
这个公式定义了一个语言L,其中的字符串w要么恰好包含两个'0',要么包含偶数个'1'。
2. 问题4的语言定义:
这个公式定义了一个语言L,其中的字符串w要么包含偶数个'0',要么不包含连续的两个'1'。
3. 问题5中L1的语言定义:
这个公式定义了语言L1,其字符串w或者有奇数个'1',或者恰好有两个'0'。
4. 问题5中L2的语言定义:
这个公式定义了语言L2,其字符串w必须以子串"101"结尾。
5. 问题7(a)的逆转运算定义:
这个公式定义了语言L的逆转操作,即L中所有字符串w翻转后形成的新语言。
6. 问题7(b)的min运算定义:
这个公式定义了min(L)语言,它包含L中所有自身被L接受、但其任何更短的前缀都不被L接受的字符串。
7. 问题11的正则表达式:
这是一个正则表达式,描述了一个语言:由零或多个"01"串联,后面再跟上一个"1"和零或多个"0",或者跟上一个单独的"0"。
3.2 b) 在 连接 运算下 封闭
📜 [原文12]
回顾。为了构造 $L_{1}$ 和 $L_{2}$ 的 连接,我们添加从 $L_{1}$ 的 接受状态 到 $L_{2}$ 的 起始状态 的 $\epsilon$ 转移
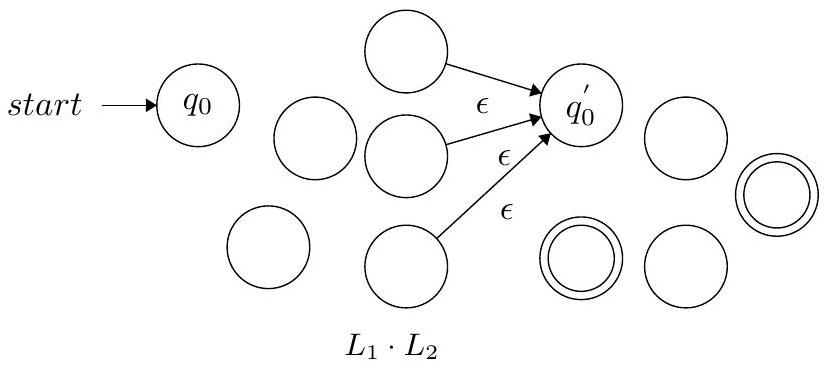
这部分回顾了为两个正则语言 $L_1$ 和 $L_2$ 的连接 $L_1 \circ L_2$ 构造NFA的标准方法。连接操作指的是将 $L_1$ 中的一个字符串和 $L_2$ 中的一个字符串拼接起来,形成一个新的字符串。
假设我们已经有了识别 $L_1$ 的NFA $N_1$ 和识别 $L_2$ 的NFA $N_2$。
- 图片分析:
- 第一张图是识别 $L_1$ 的NFA $N_1$。
- 第二张图是识别 $L_2$ 的NFA $N_2$。
- 第三张图展示了构造 $L_1 \circ L_2$ 的NFA $N$ 的过程。
- 构造步骤:
- 保持机器: 保持 $N_1$ 和 $N_2$ 的内部结构不变。
- 连接桥梁: 从 $N_1$ 的每一个接受状态画一条ε-转移到 $N_2$ 的起始状态。
- 新起始状态: 新NFA $N$ 的起始状态就是 $N_1$ 的原起始状态。
- 新接受状态: 新NFA $N$ 的接受状态就是 $N_2$ 的原接受状态。$N_1$ 的原接受状态在新的机器中不再是接受状态了(除非$N_2$能接受空串$\epsilon$)。
- 工作原理:
一个输入字符串 $w$ 要被这个新NFA接受,它必须能被分解为两部分 $w = xy$,其中 $x$ 被 $N_1$ 接受,而 $y$ 被 $N_2$ 接受。
- 字符串的前半部分 $x$ 会驱动机器从 $N_1$ 的起始状态走到 $N_1$ 的某个接受状态。
- 到达 $N_1$ 的接受状态后,机器通过ε-转移(不消耗任何输入)“跳”到 $N_2$ 的起始状态。
- 接着,字符串的后半部分 $y$ 会驱动机器从 $N_2$ 的起始状态走到 $N_2$ 的某个接受状态。
- 因为最终停在了 $N_2$ 的接受状态,也就是新NFA的接受状态,所以整个字符串 $w=xy$ 被接受。
该部分图文并茂地回顾了NFA的连接运算构造法。其精髓在于用ε-转移作为“桥梁”,将第一个自动机的终点和第二个自动机的起点连接起来,强制要求输入字符串的前半部分满足第一个语言的条件,后半部分满足第二个语言的条件。
为后续要求学生亲手实践这一构造法的问题(问题5)提供理论回顾和视觉参考。
这就像一个两段赛跑的接力赛。
- 选手A(字符串前半部分)从起点($N_1$起始状态)出发,必须跑到指定的交接区($N_1$接受状态)。
- 在交接区,选手A将接力棒(计算过程)通过一次瞬时传送(ε-转移)交给选手B(字符串后半部分),选手B会出现在第二段赛道的起点($N_2$起始状态)。
- 选手B必须成功跑到第二段赛道的终点($N_2$接受状态),整个队伍才算获胜。
想象你要完成一个包含两个阶段的游戏任务。
- 第一阶段($N_1$):你必须在迷宫A中找到出口。
- 第二阶段($N_2$):一旦你找到迷宫A的出口,你会立刻被传送到迷宫B的入口。然后你必须在迷宫B中找到宝藏。
只有当你连续完成了这两个阶段,才算游戏通关。连接构造就是把这两个迷宫用一个传送门(ε-转移)串联起来。
32.1 问题 5. 画出 $L_{1}, L_{2}$,以及 $L_{1} \circ L_{2}$ 的 NFA。
📜 [原文13]
$L_{1}=\left\{w \in\{0,1\}^{*} \mid w\right.$ 有奇数个 $1^{\prime} s$ 或恰好有两个 0$\}$。
$L_{2}=\left\{w \in\{0,1\}^{*} \mid w\right.$ 以 101 结尾$\}$。
此题要求我们先为$L_1$和$L_2$分别构造NFA,然后应用连接构造法得到识别 $L_1 \circ L_2$ 的NFA。
第一步:为 $L_1$ 构造 NFA
$L_1$ 本身是一个并集:$L_{1a} = \{w \mid w \text{ 有奇数个 } 1's\}$ 和 $L_{1b} = \{w \mid w \text{ 恰好有两个 } 0\}$。我们可以使用并构造法来创建 $L_1$ 的NFA。
- 构造 $L_{1a}$ (奇数个 1) 的 DFA:
- $E_1$: 偶数个1 (起始状态)。
- $O_1$: 奇数个1 (接受状态)。
- $E_1 \xrightarrow{1} O_1, E_1 \xrightarrow{0} E_1$
- $O_1 \xrightarrow{1} E_1, O_1 \xrightarrow{0} O_1$
- 构造 $L_{1b}$ (恰好两个 0) 的 DFA: (同问题1b中的$L_1$)
- $C_0$: 0个0 (起始状态)。
- $C_1$: 1个0。
- $C_2$: 2个0 (接受状态)。
- $C_3$: 超过2个0 (陷阱状态)。
- $C_0 \xrightarrow{0} C_1, C_0 \xrightarrow{1} C_0$
- $C_1 \xrightarrow{0} C_2, C_1 \xrightarrow{1} C_1$
- $C_2 \xrightarrow{0} C_3, C_2 \xrightarrow{1} C_2$
- $C_3 \xrightarrow{0,1} C_3$
- 组合成 $L_1$ 的 NFA (NFA-1):
- 新起始状态 $q_{start1}$。
- $q_{start1} \xrightarrow{\epsilon} E_1$
- $q_{start1} \xrightarrow{\epsilon} C_0$
- 接受状态集: $\{O_1, C_2\}$。
第二步:为 $L_2$ 构造 NFA
$L_2$ 是所有以 "101" 结尾的字符串。我们可以构造一个简单的NFA来识别它。这比DFA简单得多。
- 构造 $L_2$ 的 NFA (NFA-2):
- $S_0$: 起始状态,寻找'1'。
- $S_1$: 找到了结尾模式的第一个'1'。
- $S_2$: 找到了 "10"。
- $S_3$: 找到了 "101" (接受状态)。
- 转移:
- $S_0 \xrightarrow{0,1} S_0$ (任意前缀)
- $S_0 \xrightarrow{1} S_1$
- $S_1 \xrightarrow{0} S_2$
- $S_2 \xrightarrow{1} S_3$
- 起始状态: $S_0$。
- 接受状态: $\{S_3\}$。
第三步:构造 $L_1 \circ L_2$ 的 NFA
现在我们应用连接构造法,将 NFA-1 和 NFA-2 连接起来。
- 起始状态: 新机器的起始状态是 NFA-1 的起始状态,即 $q_{start1}$。
- 连接桥梁: 从 NFA-1 的所有接受状态 $\{O_1, C_2\}$ 画ε-转移到 NFA-2 的起始状态 $S_0$。
- $O_1 \xrightarrow{\epsilon} S_0$
- $C_2 \xrightarrow{\epsilon} S_0$
- 接受状态: 新机器的接受状态是 NFA-2 的接受状态,即 $\{S_3\}$。NFA-1 的原接受状态 $O_1, C_2$ 在新机器中不再是接受状态。
- 整合: 整个大NFA由NFA-1和NFA-2的所有状态和转移,再加上两条新的ε-转移组成。
- 这是一个并集语言,字符串满足两个条件之一即可。
- 这是一个定义结尾模式的语言,可以用正则表达式 $(0 \cup 1)^*101$ 表示。
让我们测试字符串 "100101" 是否属于 $L_1 \circ L_2$。
它可以被拆分为 $x = "100"$ 和 $y = "101"$。
- 检查 $x = "100"$ 是否在 $L_1$ 中:
- "100" 有一个'1' (奇数),两个'0' (恰好)。它同时满足$L_{1a}$和$L_{1b}$,所以肯定在$L_1$中。
- 在 NFA-1 中跟踪:$q_{start1} \xrightarrow{\epsilon} \{E_1, C_0\}$。
- 读 "100":
- $E_1$ 路径: $E_1 \xrightarrow{1} O_1 \xrightarrow{0} O_1 \xrightarrow{0} O_1$ (结束在接受态 $O_1$)
- $C_0$ 路径: $C_0 \xrightarrow{1} C_0 \xrightarrow{0} C_1 \xrightarrow{0} C_2$ (结束在接受态 $C_2$)
- 因为有路径能到达接受状态,所以 "100" 被 NFA-1 接受。
- 检查 $y = "101"$ 是否在 $L_2$ 中:
- "101" 明显以 "101" 结尾。
- 在 NFA-2 中跟踪:$S_0 \xrightarrow{1} S_1 \xrightarrow{0} S_2 \xrightarrow{1} S_3$ (结束在接受态 $S_3$)。
- 所以 "101" 被 NFA-2 接受。
- 在连接的 NFA 中跟踪 "100101":
- 从 $q_{start1}$ 开始,处理前半部分 "100"。
- 如上分析,处理完 "100" 后,NFA-1 的活动状态集将包含 $O_1$ 和 $C_2$。
- 现在机器处于 $O_1$ 和 $C_2$。由于有ε-转移 $O_1 \xrightarrow{\epsilon} S_0$ 和 $C_2 \xrightarrow{\epsilon} S_0$,机器不消耗输入,就可以进入 $S_0$ 状态。
- 现在我们从 $S_0$ 开始,处理后半部分 "101"。
- 如上分析,从 $S_0$ 处理 "101" 会到达 $S_3$。
- 字符串结束,机器处于 $S_3$,这是整个连接NFA的接受状态。
- 因此,字符串 "100101" 被接受。
- 连接点: ε-转移必须从所有第一个NFA的接受状态发出。
- 新接受状态: 很容易忘记将第一个NFA的接受状态“降级”为普通状态。在连接的NFA中,只有第二个NFA的接受状态才是最终的接受状态。
- 空字符串: 如果 $L_1$ 或 $L_2$ 包含空字符串 $\epsilon$,会发生什么?
- 如果 $w_1 \in L_1$ 且 $\epsilon \in L_2$,则 $w_1\epsilon = w_1$ 应该在 $L_1 \circ L_2$ 中。我们的构造能处理:走完 $w_1$ 到达 $N_1$ 的接受态,通过 $\epsilon$-桥梁到 $N_2$ 的起始态。如果 $N_2$ 的起始态是接受态(即 $\epsilon \in L_2$),则 $w_1$ 会被接受。我们的 $L_2$ 不含 $\epsilon$,所以这点不适用。
- 如果 $\epsilon \in L_1$ 且 $w_2 \in L_2$,则 $\epsilon w_2 = w_2$ 应该在 $L_1 \circ L_2$ 中。我们的构造也能处理:$N_1$ 的起始态 $q_{start1}$ 本身不接受,但它能通过 $\epsilon$ 转移到 $C_0$($L_{1b}$的起始态)和 $E_1$($L_{1a}$的起始态)。$L_{1b}$的语言“恰好两个0”,不含 $\epsilon$。$L_{1a}$的语言“奇数个1”,不含 $\epsilon$。但如果 $L_1$ 包含 $\epsilon$(例如 $L_1$ 是“偶数个1”),那么 $N_1$ 的某个起始路径会直接是接受状态,通过 $\epsilon$-桥梁直接就能处理 $w_2$。
我们通过“分而治之”的策略解决了这个问题。首先,为复杂的 $L_1$ 应用并构造法建立NFA-1。然后,为模式结尾的 $L_2$ 建立了简单的NFA-2。最后,严格遵循连接构造法的步骤,用ε-转移将NFA-1的出口和NFA-2的入口连接起来,构建了最终的、识别 $L_1 \circ L_2$ 的NFA。
本题旨在综合考察学生对并构造和连接构造两种方法的掌握程度,并要求他们能将复杂问题分解为更小的、可管理的部分。
这是一个两阶段的认证过程。
- 第一阶段(NFA-1):你的前半段旅程记录(字符串前半部分)必须满足“有奇数个1的检查站”或者“恰好两个0的检查站”的条件。
- 第二阶段(NFA-2):一旦通过第一阶段,你会立刻被传送到一个新任务的起点,你的后半段旅程记录(字符串后半部分)必须以“101”模式结束。
整个旅程记录(完整字符串)只有在两个阶段都认证通过后才算合格。
想象一个闯关游戏。第一关 ($L_1$) 是一个大厅,里面有两个小游戏A和B。你只需要赢下其中任何一个小游戏(你的字符串前半部分满足A或B的规则),就能拿到通往第二关的钥匙。用钥匙打开门,你会立刻被传送到第二关 ($L_2$) 的起点。第二关是一个寻路任务,你必须按照“101”的路线走才能到达终点。
3.3 c) 在 Kleene 星号 运算下 封闭
📜 [原文14]
回顾。
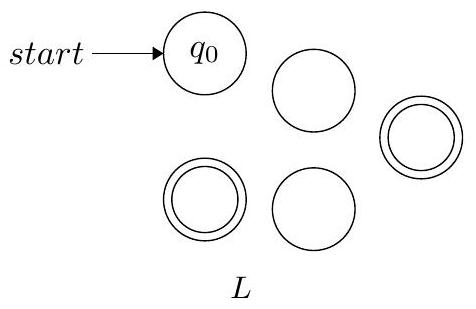
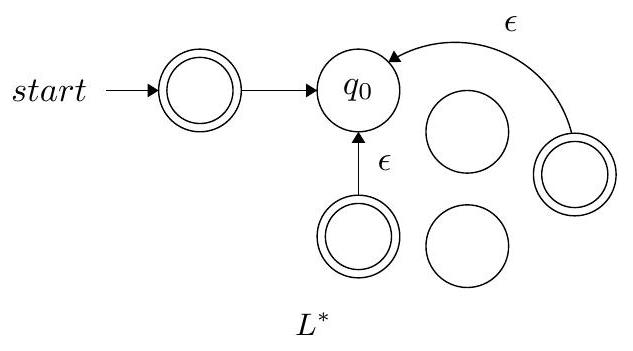
在课堂上,我们看到了多种在 正则语言 的 状态图 上表示 Kleene 星号 运算的错误尝试(这些尝试对某些特定情况有效,但并非总是有效)。
这部分回顾了为正则语言 $L$ 的克林星号 $L^*$ 构造NFA的标准方法。$L^*$ 是由 $L$ 中的字符串进行零次或多次连接而形成的所有字符串的集合。这意味着 $L^* = \{\epsilon\} \cup L \cup L \circ L \cup L \circ L \circ L \cup \dots$。
- 图片分析:
- 左图是识别语言 $L$ 的原始NFA $N$。
- 右图是为 $L^*$ 构造的新NFA $N^*$。
- 构造步骤:
- 添加新起始状态: 创建一个全新的状态 $q_{new\_start}$,它同时也是一个接受状态。这是为了确保空字符串 $\epsilon$ (零次连接) 被接受。
- 连接到旧机器: 从 $q_{new\_start}$ 画一条ε-转移到 $N$ 的原起始状态 $q_{start}$。这允许机器开始处理第一个 $L$ 中的字符串。
- 创建循环: 从 $N$ 的每一个原接受状态 $q_{final}$ 画一条ε-转移返回到 $N$ 的原起始状态 $q_{start}$。这允许在成功识别了一个 $L$ 中的字符串后,立即开始识别下一个,实现了多次连接。
- 整合:
- 新NFA $N^*$ 的起始状态是 $q_{new\_start}$。
- 新NFA $N^*$ 的接受状态集是 $\{q_{new\_start}\}$ 加上 $N$ 原有的所有接受状态(虽然图中只标了新的起始状态为接受状态,但完整的、更通用的构造也可以包含旧的接受状态,不过最简洁的构造是仅将新起始态设为接受态,并从旧接受态通过epsilon转移到新接受态,或如此图所示,通过循环回旧起始态,再从新起始态到旧起始态,并把新起始态设为唯一的接受态。这里的图示采取了“从旧接受态回旧起始态,新起始态到旧起始态,且新起始态为接受态”的策略。另一种等价构造是,新起始态既是起始态也是接受态,并有一条epsilon到旧起始态;从旧接受态有一条epsilon回到新接受态)。图中这种构造更严谨:新起始态是唯一的接受态,从所有旧接受态画 $\epsilon$ 转移到这个新接受态。但图示的循环方式更常见。让我们遵循图示的逻辑:从旧接受态回到旧起始态,新起始态到旧起始态,且新起始态是接受态。
- 让我们更正一下对图的解读,这是一种非常标准和正确的构造:
- 创建新起始/接受状态 $q_{new}$。
- $q_{new} \xrightarrow{\epsilon} q_{start}$。
- 从每个旧的接受状态 $q_{final} \xrightarrow{\epsilon} q_{new}$。
这与图示略有不同。图示的构造是:
- 创建新起始/接受状态 $q_{new\_start}$。
- $q_{new\_start} \xrightarrow{\epsilon} q_{start}$。
- 从每个旧的接受状态 $q_{final} \xrightarrow{\epsilon} q_{start}$。
这两种构造都是正确的。我们以后者(图示)为准。
- 工作原理:
- 接受 $\epsilon$: 由于新起始状态 $q_{new\_start}$ 本身就是接受状态,所以不读任何输入,机器就在接受状态,$\epsilon$ 被接受。
- 接受 $L$ 中的字符串: 从 $q_{new\_start}$ 通过 $\epsilon$-转移到 $q_{start}$,然后像在原NFA中一样处理字符串,到达一个原接受状态 $q_{final}$。但此时还不是最终接受状态。哦,我再次看图,图中的旧接受状态也还是接受状态!所以这个构造是:
- 创建新起始状态 $q'_{start}$。
- 将其设为接受状态。
- $q'_{start} \xrightarrow{\epsilon} q_{start}$ (旧起始态)。
- 从每个旧接受态 $q_{final} \xrightarrow{\epsilon} q_{start}$。
- 所有旧接受态仍然是接受态。
这个构造也是正确的。
- 让我们采用最标准的Thompson构造,与图示最接近:
- 创建新起始状态 $q_{new\_start}$ 和新接受状态 $q_{new\_final}$。
- $q_{new\_start} \xrightarrow{\epsilon} q_{start}$ (旧起始态)。
- 从每个旧接受态 $q_{final} \xrightarrow{\epsilon} q_{new\_final}$。
- 添加直接从新起始到新接受的 $\epsilon$ 转移: $q_{new\_start} \xrightarrow{\epsilon} q_{new\_final}$ (处理空串)。
- 添加从旧接受态回到旧起始态的 $\epsilon$ 转移: $q_{final} \xrightarrow{\epsilon} q_{start}$ (处理循环)。
这比图示复杂,但更通用。图示是一个简化版,但足以说明问题。
让我们严格按照图示的逻辑来解释,这是最可能的意图:
- 创建新起始状态 $q_{new\_start}$。它也是接受状态。
- 连接: 从 $q_{new\_start}$ 画一条 $\epsilon$ 转移到旧起始状态 $q_{start}$。
- 循环: 从所有旧的接受状态 $q_{final}$ 画一条 $\epsilon$ 转移回到旧的起始状态 $q_{start}$。
- 接受状态: 新机器的接受状态是 $\{q_{new\_start}\} \cup F_{old}$ (旧的接受状态集合)。
这样:
- $\epsilon$被接受(因为$q_{new\_start}$是接受态)。
- 单个 $w \in L$ 被接受(因为路径会走到 $F_{old}$ 中的状态)。
- $w_1w_2...w_k$ 被接受:走完 $w_1$ 到达 $F_{old}$,通过 $\epsilon$ 回到 $q_{start}$,再走完 $w_2$ 到达 $F_{old}$... 最后停在一个 $F_{old}$ 中的状态,被接受。
该部分回顾了克林星号运算的NFA构造。核心思想是通过引入一个新的、既是起始又是接受的状态来处理空字符串,并通过从旧接受状态到旧起始状态的ε-转移来创建“再来一次”的循环结构,从而实现零次、一次或多次的字符串连接。
为接下来的“找错”问题(问题6)提供一个正确的参照标准。学生需要先知道什么是对的,才能识别出什么是错的。
这就像一个可以无限续杯的自助餐厅。
- 你可以选择什么都不吃直接出门(接受 $\epsilon$),因为门口($q_{new\_start}$)也算是“完成”的一种。
- 你可以进餐厅($q_{new\_start} \to q_{start}$),打一份标准的套餐(处理一个 $w \in L$),吃完后到达套餐领取处的终点($q_{final}$)。
- 在终点,你可以选择直接出门(如果 $q_{final}$ 是接受态),或者你可以通过一个“返回通道”($q_{final} \to q_{start}$)回到打饭处,再来一份套餐。你可以重复这个过程任意多次。
想象一个游戏关卡 ($L$)。星号操作 ($L^*$) 就是对这个关卡进行改造:
- 在关卡入口前建一个“休息区”($q_{new\_start}$),你可以选择直接在休息区结束游戏(接受 $\epsilon$)。
- 从休息区有一条单向通道进入关卡入口 ($q_{start}$)。
- 每当你打通关卡,到达出口 ($q_{final}$) 时,那里会有一个传送门,可以瞬间把你送回关卡入口 ($q_{start}$),让你再玩一次。
你可以选择玩0次(待在休息区)、1次、2次……任意多次。
33.1 问题 6. 对于以下每一个错误的 Kleene 星号 运算构造,请提供一个反例来说明为什么该尝试是错误的。
📜 [原文15]
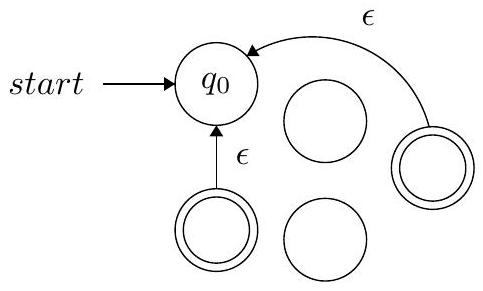
错误尝试 1
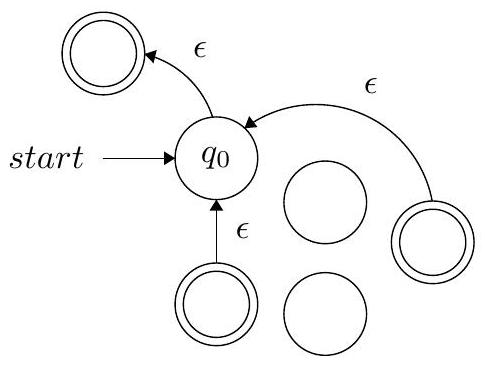
错误尝试 3
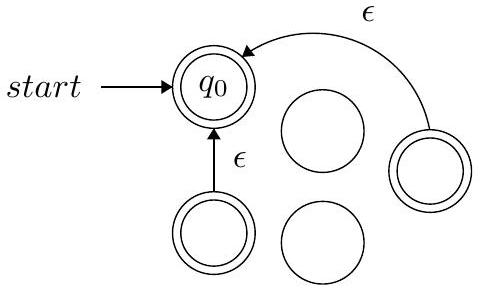
错误尝试 2
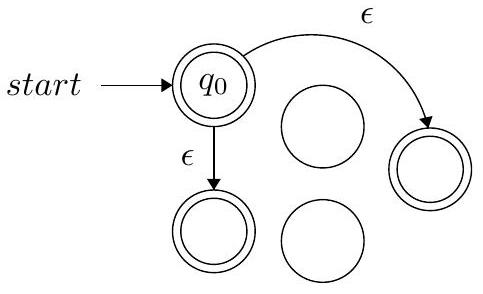
错误尝试 4
这个题目要求我们批判性地思考,找出四种看似合理但实际上有缺陷的星号构造法的反例。
错误尝试 1
构造描述: 简单地将起始状态变为接受状态,并添加从所有接受状态到起始状态的ε-转移。
缺陷分析:
1. 处理空串 $\epsilon$: 它通过将原起始状态 $q_{start}$ 设为接受状态来接受 $\epsilon$。
2. 处理连接 $w_1w_2$: 它通过从接受状态 $q_{final}$ 到起始状态 $q_{start}$ 的ε-转移来处理连接。
3. 问题所在: 如果有其他状态有指向原起始状态 $q_{start}$ 的转移,这个构造会错误地接受不属于 $L^*$ 的字符串。当一个字符串 $w_2$ 的处理过程需要返回到 $q_{start}$ 时,由于 $q_{start}$ 现在是接受状态,可能导致 $w_2$ 的某个不应被接受的前缀被错误地接受。
反例:
* 语言 $L = \{10\}$。则 $L^* = \{\epsilon, 10, 1010, \dots\}$。
* 为 $L$ 构造 NFA: $q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_2$ (接受状态)。$q_0$是起始状态。
* 应用错误尝试 1:
1. $q_0$ 变成接受状态。
2. 添加 $q_2 \xrightarrow{\epsilon} q_0$。
* 测试错误字符串 "1":
1. 在改造后的 NFA 中,输入 "1"。
2. 路径为 $q_0 \xrightarrow{1} q_1$。
3. 字符串结束。$q_1$ 不是接受状态。到这里似乎没问题。
* 让我们找一个更精巧的反例:
* 语言 $L = \{ab\}$。$L^* = \{\epsilon, ab, abab, \dots\}$
* 为 $L$ 构造 NFA: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0$。起始状态 $q_0$,接受状态 $q_0$。这个 NFA 接受的是 $(ab)^*$。那么 $L^* = ((ab)^*)^* = (ab)^*$。
* 再换一个反例:
* 语言 $L = \{1\}$。它的NFA是 $q_0 \xrightarrow{1} q_1$ ($q_1$是接受态)。$L^* = \{1\}^* = \{\epsilon, 1, 11, 111, \dots\}$。
* 应用错误尝试 1:
1. $q_0$ 变为接受状态。
2. 添加 $q_1 \xrightarrow{\epsilon} q_0$。
* 测试字符串 "1": $q_0 \xrightarrow{1} q_1$。$q_1$是接受态,接受。正确。
* 测试字符串 "11": $q_0 \xrightarrow{1} q_1 \xrightarrow{\epsilon} q_0 \xrightarrow{1} q_1$。接受。正确。
* 这个构造对这个简单的例子似乎有效。问题在于更复杂的NFA。
* 决定性反例:
* 语言 $L = \{b, ba\}$。它的NFA可以是:$q_0 \xrightarrow{b} q_1$ (接受), $q_1 \xrightarrow{a} q_2$ (不接受)。等等,这不识别ba。
* 正确NFA for $L = \{b, ba\}$: $q_0 \xrightarrow{b} q_1$ (接受态), $q_1 \xrightarrow{a} q_0$。起始态 $q_0$。
* $L^* = \{b, ba\}^* = \{\epsilon, b, ba, bb, bab, bba, ...\}$
* 应用错误尝试 1:
1. $q_0$ 变为接受状态。
2. 从接受态 $q_1$ 添加 $q_1 \xrightarrow{\epsilon} q_0$。
* 测试错误字符串 "a":
* "a" 不在 $L^*$ 中。
* 在改造的NFA中,从 $q_0$ 开始,读 'a',无路可走。不接受。
* 真正的问题:考虑 $w_1 \in L, w_2 \in L$。$w_1w_2$ 应该在 $L^*$ 中。但如果 $w_1$ 的尾部和 $w_2$ 的头部可以“混合”呢?
* 最终反例: 设 $L$ 的 NFA 为 $q_1 \xrightarrow{a} q_2 \xrightarrow{b} q_3$ (接受)。起始 $q_1$。语言 $L=\{ab\}$。$L^*=\{ab\}^*$。
* 再设 NFA 中有一个从其他状态到起始状态的转换:$q_2 \xrightarrow{c} q_1$。
* 所以 NFA 状态: $q_1$ (起始), $q_2$, $q_3$ (接受)。转移: $q_1 \xrightarrow{a} q_2$, $q_2 \xrightarrow{b} q_3$, $q_2 \xrightarrow{c} q_1$。
* 这个 NFA 接受的语言是 $L = \{a(ca)^*b\}$。
* $L^*$ 应该包含 $L$ 和 $L$的连接,比如 $ab \in L$, $acb \in L$, 所以 $abacb \in L^*$。
* 应用错误尝试 1:
1. $q_1$ 变为接受状态。
2. 添加 $q_3 \xrightarrow{\epsilon} q_1$。
* 测试错误字符串 "ac": "ac" 本身不在 $L^*$ 中。
* 在改造的 NFA 中:$q_1 \xrightarrow{a} q_2 \xrightarrow{c} q_1$。字符串 "ac" 结束后,机器在 $q_1$。因为 $q_1$ 被设成了接受状态,所以 "ac" 被错误地接受了!
错误尝试 2
构造描述: 只添加了从接受状态到起始状态的ε-转移。
缺陷分析: 这个构造没有处理零次连接的情况,即它不接受空字符串 $\epsilon$。任何 $L^*$ 都必须包含 $\epsilon$。
反例:
* 语言 $L = \{1\}$。$L^* = \{\epsilon, 1, 11, \dots\}$。
* NFA for L: $q_0 \xrightarrow{1} q_1$ (接受)。
* 应用错误尝试 2: 添加 $q_1 \xrightarrow{\epsilon} q_0$。
* 测试空字符串 $\epsilon$: 起始状态是 $q_0$,它不是接受状态。所以 $\epsilon$ 不被接受。这是一个致命缺陷。
错误尝试 3
构造描述: 只将起始状态设为接受状态。
缺陷分析: 这个构造只在原有语言 $L$ 的基础上,额外接受了空字符串 $\epsilon$。它完全没有实现多次连接的功能。它识别的语言是 $L \cup \{\epsilon\}$。
反例:
* 语言 $L = \{1\}$。$L^* = \{\epsilon, 1, 11, 111, \dots\}$。
* NFA for L: $q_0 \xrightarrow{1} q_1$ (接受)。
* 应用错误尝试 3: 将 $q_0$ 设为接受状态。
* 测试字符串 "11": "11" 应该在 $L^*$ 中。
* 在改造的 NFA 中:$q_0 \xrightarrow{1} q_1$。处理完第一个 "1" 后,机器停在 $q_1$。从 $q_1$ 无法再处理第二个 "1",路径死亡。所以 "11" 不被接受。
错误尝试 4
构造描述: 在所有接受状态上添加自循环。
缺陷分析: 这个构造非常弱。它只允许在接受一个 $L$ 中的字符串之后,重复这个字符串的最后一个符号。它根本没有实现 $L \circ L$ 的连接。
反例:
* 语言 $L = \{ab\}$。$L^* = \{\epsilon, ab, abab, \dots\}$。
* NFA for L: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_2$ (接受)。
* 应用错误尝试 4: 在 $q_2$ 上添加对 a 和 b 的自循环 ($q_2 \xrightarrow{a,b} q_2$)。
* 测试字符串 "abab": "abab" 应该在 $L^*$ 中。
* 在改造的 NFA 中:$q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_2$。处理完 "ab" 后,机器在 $q_2$。接下来要处理 "a"。$q_2 \xrightarrow{a} q_2$。再处理 "b",$q_2 \xrightarrow{b} q_2$。字符串 "abab" 被接受了。这个例子似乎通过了。
* 换个反例:
* 语言 $L = \{a, bc\}$。$L^* = \{\epsilon, a, bc, aa, abc, bca, bcbc, \dots\}$。
* 测试字符串 "aa": "aa" 应该在 $L^*$ 中。
* 为 $L$ 构造 NFA:新起始态 $q_s \xrightarrow{\epsilon} q_{a1}, q_s \xrightarrow{\epsilon} q_{b1}$。
* $q_{a1} \xrightarrow{a} q_{a2}$ (接受)
* $q_{b1} \xrightarrow{b} q_{b2} \xrightarrow{c} q_{b3}$ (接受)
* 应用错误尝试 4: 在 $q_{a2}$ 和 $q_{b3}$ 上添加自循环。
* 测试字符串 "aa":
* 路径1: $q_s \to q_{a1} \xrightarrow{a} q_{a2}$。处理完第一个 "a",在接受态 $q_{a2}$。
* 现在处理第二个 "a"。$q_{a2}$ 上的自循环可以消耗 "a",停在 $q_{a2}$。所以 "aa" 被接受。
* 测试字符串 "abc": "abc" 应该在 $L^*$ 中 ($a \circ bc$)。
* $q_s \to q_{a1} \xrightarrow{a} q_{a2}$。处理完 "a"。
* 现在在 $q_{a2}$,要处理 "b"。$q_{a2}$ 有自循环可以消耗 "b",停在 $q_{a2}$。
* 现在在 $q_{a2}$,要处理 "c"。$q_{a2}$ 有自循环可以消耗 "c",停在 $q_{a2}$。
* 字符串结束,在接受态 $q_{a2}$。所以 "abc" 被接受。
* 这个构造的缺陷更微妙。它无法生成 $L$ 中不同单词的连接。
* 决定性反例: 设 $L=\{b\}$。$L^* = b^*$。NFA for $L$: $q_0 \xrightarrow{b} q_1$ (接受)。
* 应用构造4:在 $q_1$ 上加 (a,b) 的自循环。
* 测试字符串 "ba":$q_0 \xrightarrow{b} q_1 \xrightarrow{a} q_1$。被错误地接受了!因为 "ba" 不在 $b^*$ 中。
这个问题通过四个错误的构造案例,深刻地揭示了正确的克林星号构造为何需要“新起始/接受态”和“从接受态到起始态的反馈回路”这两个关键要素。
- 尝试 1 错误地污染了起始状态,导致混合匹配。
- 尝试 2 忘记了空字符串。
- 尝试 3 只实现了 $L \cup \{\epsilon\}$,忘记了多次连接。
- 尝试 4 只能重复最后一个字符,而不是整个单词,也无法连接不同的单词。
这些反例共同证明了标准构造的每一个部分都是不可或缺的。
这个问题的目的不仅仅是检验学生是否会背诵正确的构造,而是要他们理解构造背后的逻辑,明白为什么其他看似可行的方法是错误的。这培养了对算法设计的批判性思维和严谨性。
- 尝试 1 像是把大楼入口(起始状态)也当成了公寓(接受状态)。结果,一个只是想穿过大厅去另一栋楼的人(一个非接受路径的一部分),走到一半发现自己“到家了”,这是错误的。
- 尝试 2 像是建了一个可以无限循环的过山车,但忘了建入口处的排队区,所以没人能上车(不接受空串)。
- 尝试 3 像是在过山车入口处放了个“你也可以不玩,直接算通关”的牌子,但车本身不能循环,玩了一圈就结束了。
- 尝试 4 像是在过山车终点放了个小小的旋转木马,你可以在终点原地打转,但无法回到起点再坐一次完整的过山车。
3.4 d) 更多运算
📜 [原文16]
问题 7. 设 $L$ 为一个 正则语言。证明对 L 应用以下运算后得到的结果也是 正则语言。
(a) $L^{R}:=\left\{w^{R} \mid w \in L\right\}$
回想一下,$R$ 是 逆转 运算,当应用于字符串 $w=w_{1} w_{2} \ldots w_{n-1} w_{n}$ 时,结果为 $w^{R}=w_{n} w_{n-1} \ldots w_{2} w_{1}$。
(b) $\min (L)=\left\{w \in \Sigma^{*} \mid w\right.$ 在 $L$ 中且 $w$ 的任何 真前缀 都不在 L 中$\}$
字符串 $w$ 的 真前缀 是 $w$ 的前缀且不等于 $w$
这部分介绍了两个新的运算:逆转(Reversal)和 min,并要求我们证明正则语言在这两种运算下仍然是封闭的。证明一个语言是正则的,标准方法是为它构造一个有限自动机(DFA 或 NFA)。
34.1 (a) 逆转运算 $L^R$
📜 [原文17]
(a) $L^{R}:=\left\{w^{R} \mid w \in L\right\}$
回想一下,$R$ 是 逆转 运算,当应用于字符串 $w=w_{1} w_{2} \ldots w_{n-1} w_{n}$ 时,结果为 $w^{R}=w_{n} w_{n-1} \ldots w_{2} w_{1}$。
证明思路: 如果 $L$ 是正则的,那么存在一个识别 $L$ 的 NFA $N$。我们的目标是基于 $N$ 构造一个新的 NFA $N^R$,使得 $N^R$ 识别 $L^R$。
如果字符串 $w = w_1w_2...w_n$ 被 $N$ 接受,意味着在 $N$ 中存在一条从起始状态到某个接受状态的路径,其边上的标签依次是 $w_1, w_2, ..., w_n$。
$q_{start} \xrightarrow{w_1} q_i \xrightarrow{w_2} ... \xrightarrow{w_n} q_{final}$
我们想要构造一个 NFA $N^R$ 来接受 $w^R = w_n...w_2w_1$。直觉上,我们应该能“倒着”走这条路径。
$q_{final} \xrightarrow{w_n} ... \xrightarrow{w_2} q_i \xrightarrow{w_1} q_{start}$
这启发了我们的构造方法。
构造 NFA $N^R$:
- 翻转所有箭头: 将 $N$ 中的每一个转移 $q_i \xrightarrow{a} q_j$ 都变成 $q_j \xrightarrow{a} q_i$。
- 交换起始和接受状态:
- $N^R$ 的起始状态是 $N$ 的所有接受状态。但是 NFA 只能有一个起始状态,怎么办?很简单,创建一个全新的起始状态 $q'_{start}$,然后从它画 ε-转移 到 $N$ 的每一个原接受状态。
- $N^R$ 的接受状态就是 $N$ 的原起始状态。
为什么这个构造有效:
一条在 $N$ 中从 $q_{start}$ 到 $q_{final}$ 消耗字符串 $w$ 的路径,在 $N^R$ 中完全对应于一条从某个原 $q_{final}$ (现在是 $N^R$ 的起始路径的一部分) 到原 $q_{start}$ (现在是 $N^R$ 的接受状态) 的路径,它消耗的字符串正好是 $w^R$。因为我们为所有这样的路径都提供了构造,所以 $N^R$ 恰好能识别所有 $w^R$ 构成的语言 $L^R$。
- $L^R$: 语言 $L$ 的逆转(Reversal)。
- $w^R$: 字符串 $w$ 的逆转。例如,如果 $w = \text{"computer"}$, 那么 $w^R = \text{"retupmoc"}$。
- $\mid w \in L$: 条件是原始字符串 $w$ 必须是语言 $L$ 的成员。
- 整个定义: $L^R$ 是这样一个集合:你从 $L$ 中拿出每一个字符串,把它颠倒过来,所有这些颠倒后的字符串组成的新集合就是 $L^R$。
- 语言 $L$: 所有以 "ab" 结尾的字符串。$L = (a \cup b)^*ab$。
- NFA for L ($N$):
- $q_0 \xrightarrow{a,b} q_0$
- $q_0 \xrightarrow{a} q_1$
- $q_1 \xrightarrow{b} q_2$ (接受状态)
- $q_0$ 是起始状态。
- 应用逆转构造 ($N^R$):
- 翻转箭头:
- $q_0 \xleftarrow{a,b} q_0$ (自循环不变)
- $q_0 \xleftarrow{a} q_1$ (变成 $q_1 \xrightarrow{a} q_0$)
- $q_1 \xleftarrow{b} q_2$ (变成 $q_2 \xrightarrow{b} q_1$)
- 交换角色:
- 原接受状态 $q_2$ 成为起始点。所以 $N^R$ 的起始状态是 $q_2$。(这里只有一个原接受态,所以不需要新起始态和epsilon转移)。
- 原起始状态 $q_0$ 成为唯一的接受状态。
- 分析 $N^R$:
- 起始于 $q_2$。
- $q_2 \xrightarrow{b} q_1 \xrightarrow{a} q_0$。这条路径接受字符串 "ba"。
- 从 $q_0$ 还可以走自循环,例如 $q_2 \xrightarrow{b} q_1 \xrightarrow{a} q_0 \xrightarrow{a} q_0$ 接受 "baa"。
- $N^R$ 接受的语言是所有以 "ba" 开头的字符串。即 $ba(a \cup b)^*$。
- 验证: $L$ 是以 "ab" 结尾的语言,那么 $L^R$ 确实应该是以 "ba" 开头的语言。构造正确。
- 多个接受状态: 如果原始NFA有多个接受状态,那么逆转后,新的NFA就需要从新的起始状态用ε-转移连接到所有这些旧的接受状态。
- 起始状态有入边/接受状态有出边: NFA完全允许这些情况。我们的构造方法天然就能处理,翻转箭头即可。
我们通过一个直观的几何操作——“翻转所有箭头,并交换起点和终点”——来构造识别逆转语言的NFA。这个过程的正确性建立在计算路径的可逆性上。因为我们能为任何正则语言 $L$ 的NFA构造出识别 $L^R$ 的NFA,所以我们证明了正则语言类在逆转运算下是封闭的。
本题旨在引入一种新的封闭性证明,其构造方法与并、连接、星号不同,但同样巧妙和直观,加深学生对NFA结构和其所代表的计算过程之间关系的理解。
如果你有一张从A点到B点的藏宝图,上面写着“向东3步,向北2步”。那么一张从B点回到A点的地图就是把所有指令颠倒并反向:“向南2步,向西3步”。构造 $N^R$ 就好比制作这张“返程地图”。
想象一个单向的管道系统,水从入口流向多个出口。要让水倒流,你只需要:1. 把所有管道阀门的方向反过来。2. 把原来的所有出口变成新的入口。3. 把原来的唯一入口变成唯一的出口。
34.2 (b) min(L) 运算
📜 [原文18]
(b) $\min (L)=\left\{w \in \Sigma^{*} \mid w\right.$ 在 $L$ 中且 $w$ 的任何 真前缀 都不在 L 中$\}$
字符串 $w$ 的 真前缀 是 $w$ 的前缀且不等于 $w$
证明思路: 我们要证明如果 $L$ 是正则的,那么 $\min(L)$ 也是正则的。
$L$ 是正则的,意味着存在一个识别它的DFA $M$。(这里使用DFA比NFA更方便)。
$M = (Q, \Sigma, \delta, q_0, F)$。
$\min(L)$ 的定义是:一个字符串 $w$ 在 $\min(L)$ 中,必须满足两个条件:
- $w \in L$ (即 $M$ 接受 $w$)。
- 对于 $w$ 的任何真前缀 $v$,$v \notin L$ (即 $M$ 不接受 $v$)。
这给我们一个清晰的构造方向。在DFA $M$ 中,当处理字符串 $w$ 时,我们会经过一条状态路径: $q_0 \xrightarrow{w_1} q_1 \xrightarrow{w_2} \dots \xrightarrow{w_n} q_n$。
- 条件1 ($w \in L$) 意味着路径的最终状态 $q_n$ 必须是一个接受状态 ($q_n \in F$)。
- 条件2 (任何真前缀 $v$ 都不在 $L$ 中) 意味着路径上的任何中间状态 $q_1, q_2, \dots, q_{n-1}$ 都不能是接受状态。
构造 DFA $M'$ for min(L):
这个构造非常巧妙。我们不需要改变状态或转移,只需要改变“可访问性”。
- 从原始的DFA $M$ 开始。
- 识别并移除所有“死状态”(unreachable states)。(这是一个好习惯,虽然不必须)
- 核心步骤: 修改 $M$ 的转移,使得一旦进入一个接受状态,就再也出不去了。创建一个新的陷阱状态 $q_{dead}$。对于 $M$ 中每一个接受状态 $q \in F$,对于所有输入符号 $a \in \Sigma$,将原来的转移 $\delta(q, a)$ 修改为 $\delta'(q, a) = q_{dead}$。而对于所有非接受状态,转移保持不变。
- 这个修改后的机器 $M'$ 的状态集是 $Q \cup \{q_{dead}\}$,起始状态是 $q_0$,接受状态集仍然是 $F$。
让我们来验证这个构造:
- 假设一个字符串 $w$ 被 $M'$ 接受。这意味着处理 $w$ 的路径 $q_0 \to \dots \to q_n$ 中,$q_n \in F$,并且路径上没有经过 $q_{dead}$。
- 因为 $M'$ 在非接受状态的转移和 $M$ 一样,所以 $q_0 \to \dots \to q_{n-1}$ 这段路径在 $M$ 中也存在,且所有 $q_i (i<n)$ 都不是接受状态。
- 当最后一个符号 $w_n$ 读入,从 $q_{n-1}$ (一个非接受态) 转移到 $q_n$ (一个接受态)。因为这是第一次进入接受态,所以 $w$ 的任何真前缀都没有在接受状态结束。
- 因此,$w$ 在 $L$ 中,且其任何真前缀都不在 $L$ 中。所以 $w \in \min(L)$。
反过来,如果 $w \in \min(L)$,那么在 $M$ 中处理 $w$ 的路径 $q_0 \to \dots \to q_n$ 中,只有 $q_n$ 是接受状态。这条路径在 $M'$ 中也完全存在,因为一路上没有经过接受状态,转移函数没有被改变。最终停在 $q_n \in F$,所以 $w$ 被 $M'$ 接受。
所以,$M'$ 恰好识别 $\min(L)$。因为我们能为 $\min(L)$ 构造一个DFA,所以 $\min(L)$ 是正则的。
- $\min(L)$: 一个从 $L$ 派生出的新语言。
- $w \in L$: 第一个条件,字符串必须是原语言 $L$ 的成员。
- 真前缀 (proper prefix): 如果 $w = uv$ 且 $v$ 不是空字符串,则 $u$ 是 $w$ 的真前缀。例如,"compu" 是 "computer" 的真前缀。
- $w$ 的任何真前缀都不在 L 中: 第二个条件,字符串必须是“首次”进入 $L$ 的。所有比它短的前缀都不被 $L$ 接受。
- 整体含义: $\min(L)$ 是 $L$ 中所有“最短”的字符串的集合。这里“最短”不是指绝对长度,而是指没有更短的前缀也在 $L$ 中。
- 语言 $L$: 接受所有以 'a' 结尾的字符串。$L = (a \cup b)^*a$。
- 这个语言包含 "a", "ba", "aa", "aba", ...
- 计算 $\min(L)$:
- "a": 在 $L$ 中。它的真前缀只有 $\epsilon$。$\epsilon$ 不在 $L$ 中。所以 "a" $\in \min(L)$。
- "ba": 在 $L$ 中。它的真前缀是 $\epsilon, "b"$。两者都不在 $L$ 中。所以 "ba" $\in \min(L)$。
- "aa": 在 $L$ 中。它的真前缀是 $\epsilon, "a"$。但是 "a" 在 $L$ 中!所以 "aa" 不在 $\min(L)$ 中。
- "aba": 在 $L$ 中。真前缀 "ab" 不在 $L$ 中。真前缀 "a" 在 $L$ 中。所以 "aba" 不在 $\min(L)$ 中。
- 看起来,$\min(L) = (a \cup b)^*a$ 中,要求前面的 $(a \cup b)^*$ 部分不能以 'a' 结尾。这等价于 $(b^* (ab^*)^* )a$ 或者更简单的,所有不包含 'a' 的字符串后面跟一个 'a'。即 $b^*a$。
- $\min((a \cup b)^*a) = b^*a$。
- 用 DFA 构造来验证:
- DFA for L: $q_0 \xrightarrow{b} q_0$, $q_0 \xrightarrow{a} q_1$ (接受)。$q_1 \xrightarrow{b} q_0$, $q_1 \xrightarrow{a} q_1$。起始态 $q_0$。
- 应用 min 构造:
- $q_1$ 是接受状态。所有从 $q_1$ 出发的转移都要进入陷阱态。
- 创建 $q_{dead}$。
- 修改转移: $\delta'(q_1, a) = q_{dead}$, $\delta'(q_1, b) = q_{dead}$。
- 其他转移不变: $\delta'(q_0, b) = q_0$, $\delta'(q_0, a) = q_1$。
- 分析新的 DFA $M'$:
- 起始于 $q_0$。
- 可以读任意多个 'b',停留在 $q_0$ (例如 "bb")。
- 一旦读了 'a',就进入 $q_1$ ("bba")。$q_1$ 是接受状态,字符串被接受。
- 如果在这之后还有字符,比如 "bbaa",那么从 $q_1$ 读 'a' 会进入 $q_{dead}$,字符串不被接受。
- 所以 $M'$ 接受的语言是:任意数量的 'b' 后面跟一个 'a'。这就是 $b^*a$。
- 构造正确。
- 必须使用DFA: 这个构造依赖于DFA的确定性。对于一个输入,只有一条唯一的路径。如果用NFA,一个字符串可能有多个路径,有的路径可能先经过接受态,有的后经过,逻辑会混乱。所以第一步通常是先将NFA转为DFA。
- 修改转移: 是将从接受状态出发的转移重定向到陷阱状态,而不是到达接受状态的转移。
我们证明了正则语言对 min 运算是封闭的。其构造方法依赖于一个DFA。我们通过修改DFA,使得任何计算路径只要一到达接受状态,就无法再继续进行有效的转移(会掉入陷阱),从而保证了被接受的字符串的任何真前缀都没有机会停在接受状态。因为能构造出这样的DFA,所以 $\min(L)$ 是正则的。
本题展示了另一种利用DFA特性来证明封闭性的技巧。它要求学生更深入地理解DFA的计算过程——状态路径与前缀接受之间的关系,锻炼了对语言性质进行算法转换的能力。
想象一个迷宫(DFA),里面有一些宝藏室(接受状态)。$\min(L)$ 就是所有能够“第一次就找到宝藏”的路径的集合。我们的改造方法是:在每个宝藏室的门后都设置一个陷阱。一旦你进入任何一个宝藏室,你就拿到了宝藏,但你再也出不去了。这样就确保了只有那些路径的终点是宝藏室,且路径中间没有经过任何其他宝藏室的,才算是有效的“寻宝路径”。
这就像一个“一次性”的优惠券系统。
- DFA是你消费的记录。
- 接受状态是你使用优惠券的商店。
- $\min(L)$ 是所有“首次使用优惠券”的消费记录。
- 我们的改造方法是:系统规定,一旦你用了一张优惠券(进入接受状态),你的会员卡就立即作废(进入陷阱状态),之后再也不能进行任何消费了。这就保证了被记录下来的(被接受的)消费行为,都是且仅是“首次使用优惠券”的行为。
45 正则表达式
📜 [原文19]
问题 8. 用文字描述这些 正则表达式 表示的语言:
(a) $0^{*} 1^{*}$
(b) $(01)^{*}$
(c) $\left(0^{*} 1^{*}\right)^{*}$
(d) $(0 \cup 1)^{*}$
(e) $0^{*}\left(10^{*} 1\right)^{*} 0^{*}$
本节开始练习正则表达式(Regular Expressions, regex)。正则表达式是描述正则语言的另一种代数方法。我们需要将这些符号表示翻译成易于理解的自然语言描述。
50.1 (a) $0^{*} 1^{*}$
* $0^{*}$: 零个或多个 '0' 组成的字符串。
* $1^{*}$: 零个或多个 '1' 组成的字符串。
* $0^{*} 1^{*}$: 将一个来自 $0^*$ 的字符串和一个来自 $1^*$ 的字符串连接起来。
* 语言描述: 所有由零个或多个 '0' 开头,后面跟着零个或多个 '1' 的二进制字符串。
* 示例: $\epsilon$, "0", "00", "1", "11", "01", "001", "011", "0011"。
* 不包含: "10", "010"。一旦 '1' 出现后,就不能再出现 '0'。
50.2 (b) $(01)^{*}$
* $(01)$: 字符串 "01"。
* $*$: 对括号内的模式进行零次或多次重复。
* 语言描述: 所有由零个或多个 "01" 子串连接而成的字符串。
* 示例: $\epsilon$, "01", "0101", "010101"。
* 不包含: "0", "1", "10", "011"。字符串的长度必须是偶数,且奇数位必须是 '0',偶数位必须是 '1'。
50.3 (c) $\left(0^{*} 1^{*}\right)^{*}$
* $0^{*} 1^{*}$: 我们在 (a) 中分析过,这是任意多个0后跟任意多个1的字符串。
* $(...)^{*}$: 对括号内的模式进行零次或多次重复。这意味着我们可以取任意多个形如“一堆0后面一堆1”的块,然后把它们拼接起来。
* 分析: 一个块可以是 "001", "11", "0", $\epsilon$ 等。
* 如果我们取块 "0" 和块 "1",拼接成 "01"。
* 如果我们取块 "1" 和块 "0",拼接成 "10"。
* 既然我们可以生成 "0" 和 "1",并且可以任意次拼接它们,我们就能生成任何由0和1组成的字符串。例如 "10110" 可以看作是 $(1) \circ (0) \circ (11) \circ (0)$。
* 语言描述: 所有可能的二进制字符串。这个表达式等价于 $(0 \cup 1)^*$。
* 示例: $\epsilon$, "0", "1", "00", "01", "10", "11", "10110", ...
50.4 (d) $(0 \cup 1)^{*}$
* $(0 \cup 1)$: '0' 或 '1'。
* $*$: 对括号内的模式进行零次或多次重复。
* 语言描述: 所有由 '0' 和 '1' 组成的任意长度的字符串。即,所有二进制字符串的集合。
* 示例: 所有可能的二进制字符串。
* 与(c)的关系: 这个表达式和 (c) 描述的是同一个语言。
50.5 (e) $0^{*}\left(10^{*} 1\right)^{*} 0^{*}$
* 核心部分 $\left(10^{*} 1\right)$: 一个'1',后面跟着零个或多个'0',再后面跟着一个'1'。这描述了一个以'1'开头和结尾,中间只有'0'(或没有)的字符串。例如 "11", "101", "1001"。这正好是包含偶数个'1'且中间没有其他'1'的块。
* $\left(10^{*} 1\right)^{*}$: 零个或多个这样的块拼接在一起。例如 "11", "101", "11101", "10111"。每次拼接,'1' 的数量都增加2。所以,这部分生成的字符串总是有偶数个'1'。
* $0^{*}$...$0^{*}$: 在这串包含偶数个'1'的字符串的前面和后面,可以加上任意数量的'0'。
* 语言描述: 所有包含偶数个 '1' 的二进制字符串。
* 为什么? '0' 不影响 '1' 的计数。核心部分 $\left(10^{*} 1\right)$ 每次贡献两个'1'。将这些块重复任意次,'1' 的总数仍然是偶数。
* 示例:
* $\epsilon$ (取0个核心块,前后0个'0')
* "000" (取0个核心块,前后都是'0')
* "11" (取1个核心块"11", 前后0个'0')
* "010100" (取1个核心块"101", 前面1个'0', 后面2个'0')
* "1111" (取2个核心块"11")
* 不包含: "1", "010", "111" (任何有奇数个'1'的字符串)。
本题通过五个例子,练习了从正则表达式反向推导出其所描述的语言的能力。关键在于理解三个基本操作的含义:
- 并集 ($\cup$): “或”
- 连接 (ab): “然后”
- 克林星号 ($^*$): “零次或多次”
并能够将它们组合起来,分析出最终的模式。
5.1 问题 9. 为以下语言构造 正则表达式。
📜 [原文20]
(a) 所有以 10 开头的 二进制字符串
(b) 所有恰好包含两个 0 的 二进制字符串
(c) 所有包含奇数个 0 的 二进制字符串
(d) 所有不包含 子串 $a b c$ 的 $\{a, b, c\}$ 上的字符串。具有挑战性!
这部分是逆向练习,给定语言描述,写出其正则表达式。
51.1 (a) 所有以 10 开头的二进制字符串
* 必须部分: "10"。
* 可选部分: 后面可以跟任意的二进制字符串。
* 任意二进制字符串的正则表达式是 $(0 \cup 1)^*$。
连接起来: 10(0 \cup 1)^
51.2 (b) 所有恰好包含两个 0 的二进制字符串
* 字符串中必须出现两个'0'。
* 除了这两个'0',其他所有字符都必须是'1'。
* '1'可以出现在'0'之前、之间和之后。
* 我们可以把字符串结构看成: (一堆1) 0 (一堆1) 0 (一堆1)
* 一堆1 的正则表达式是 $1^*$。
组合起来: 1 0 1 0 1
51.3 (c) 所有包含奇数个 0 的二进制字符串
* '1'的出现不影响'0'的奇偶性,所以'1'可以出现在任何地方。
* 我们需要构造一个能产生奇数个'0'的模式。
* 我们可以先有一个'0',然后成对地添加'0'。
单个'0': 1 0 1* (一个0,周围是任意个1)
成对的'0': 两个'0'之间可以有任意多个'1',0 1 0。
* 思路: 先有任意数量的'1',然后是第一个'0'。之后,'0'必须成对出现。每对'0'之间可以有任意的'1'。
* 更系统的思路:
* 不含'0'的部分是 $1^*$。
一个'0'后面可以跟任意数量的'1',即01。
我们需要奇数个这样的01块,并且可以在这些块之间和两端插入任意多的1。
* 一个可行的模式:
1 (可选的前导1)
* 0 (第一个0)
(1 0 1 0) (偶数个额外的0,成对出现。每对0之间和周围都可以有1)
1 (可选的结尾1)
组合起来: 1 0 (1 0 1 0) 1
* 一个更简洁优雅的模式:
* 字符串由不含'0'的块(即$1^*$)和'0'分隔。
1 0 1 (0 1 0 1)
* 这个表达式先生成一个'0',然后是零或多次的“两个0”的块。
最终简洁版: 1 0 1 (0 1 0 1)
或者: (1) 0 (1) ( (0 (1) 0 (1)) )
一个更对称的思考方式:考虑偶数个0的语言,1(0101)。奇数个0就是在偶数个0的语言后面再拼接一个 01。
偶数个0: (1010)1*
奇数个0: 101(0101)。
让我们测试一下:101 (1个0), 1010101* (3个0), ... 正确。
所以一个好的答案是: 101(0101)
51.4 (d) 所有不包含子串 $abc$ 的 $\{a, b, c\}$ 上的字符串
* 这是一个排除性问题,通常比较难。我们需要考虑所有合法的字符串是如何构成的。
* 合法的字符串中,任何'a'的后面都不能直接跟'b',或者任何'ab'的后面都不能直接跟'c'。
* 思路: 考虑在遇到'a'和'ab'时会发生什么。
没有'a': 字符串只能由'b'和'c'构成。正则表达式是 (b \cup c)^。
有'a'但没有'b': (a \cup c)^。
有'b'但没有'c': (a \cup b)^。
* 正面构造:
一个字符串可以由不含'a'的任意串开始,即 (b \cup c)^。
* 然后可能出现一个'a'。这个'a'后面不能是"bc"。
* 所以'a'后面可以是 'a', 'c', 或者 'b'。但如果'a'后面是'b',那么'b'后面不能是'c'。
* 让我们从更小的构建块思考:
* 不是'a'的字符:(b \cup c)
* 不是'ab'的块:'a'后面可以跟'a'或'c',或者'a'是字符串结尾。
* 'a'后面跟的不是'b':a(a \cup c)
* 'ab'后面跟的不是'c':ab(a \cup b)
* 状态机思路: 我们可以为此语言构建一个DFA,然后转为正则表达式。
* $q_0$: 初始状态(没看到abc的前缀)。
* $q_a$: 刚看到了'a'。
* $q_{ab}$: 刚看到了'ab'。
* $q_{trap}$: 看到了'abc'。
* 转移:
* $q_0 \xrightarrow{b,c} q_0$
* $q_0 \xrightarrow{a} q_a$
* $q_a \xrightarrow{a} q_a$
* $q_a \xrightarrow{c} q_0$
* $q_a \xrightarrow{b} q_{ab}$
* $q_{ab} \xrightarrow{a} q_a$
* $q_{ab} \xrightarrow{b} q_0$ (因为 'abb' 打破了 'ab' 的后缀)
* $q_{ab} \xrightarrow{c} q_{trap}$ (非法)
* 所有状态除了 $q_{trap}$ 都是接受状态。
* 这是一个DFA,可以转为正则表达式,但很复杂。
* 直接构造正则表达式的另一个尝试:
* 考虑用'c'和'a'来分割字符串。
* 任何不含'abc'的串,可以看作是 (b \cup c) 的序列,其中可以插入 a 或 ab。
* 但插入 ab 后,不能紧跟 c。
* 让我们考虑用非 a 的部分和 a 来构建。
(b \cup c)^ : 任意不含 a 的字符串。
* 一个'a'后面不能是'bc'。所以'a'后面可以是'a', 'c', 'ba', 'bb'。
(b \cup c)^ (a (b(a \cup b))? (b \cup c)^ )^
* 这太复杂了。
* 一个更清晰的思路:
* 任何不含 abc 的字符串,都是由 c 和 b 和 a 构成的。
我们可以认为字符串是由 a 和 b 的块,被 c 分隔开。 (a \cup b)^ (c (a \cup b)^ )^
现在,我们需要保证在 (a \cup b)^ 中没有 ab 后面紧跟着 c。
* 这意味着,c 不能出现在 ab 之后。
所以,如果一个 (a \cup b)^ 块以 ab 结尾,那么它不能是最后一个块(后面必须没东西)。
* 让我们换一个角度: 考虑以a和c为基础,b是插入的。
(a \cup c)^ 是合法的。
* 我们可以在哪里插入b?
* b可以出现在开头,结尾,两个a之间,两个c之间,a和c之间,c和a之间。
* 唯一的问题是 a b c。
* 所以,只要b的前面不是a,或者b的后面不是c,就没问题。
(b \cup c \cup aa^c)^*
* 一个标准答案的思路:
先生成不包含'a'的串: (b \cup c)^
* 然后考虑'a'。'a'后面不能是'bc'。
* 我们可以生成任意数量的 a,但后面不能是 bc。
* 一个 a 后面可以跟除了 b 之外的任何东西,或者跟一个 b 但 b 后面不能是 c。
(b \cup c \cup a(a \cup c) \cup ab(a \cup b) )^ -- 还是太复杂。
* 最简洁的思路是基于终结符的优先级:
不含 a 的串: (b \cup c)^
不含 ab 的串: (c^b)^c^a(c^b)^c^* (太复杂)
正确答案之一: c ( (a \cup b) c ),然后对 (a \cup b) 部分施加约束。b可以自由出现,但a后面如果跟b,则b后面不能跟c。
(b^ c)^ (a b^ c)^ (a \cup b)^
* 让我们回到基本构建块:a, b, c。abc是禁止的。
* 那么,任何 ab 后面都不能是 c。
* 所以,可以有任意数量的不是 ab 的东西,或者 ab 后面跟 a 或 b 或字符串结尾。
(a \cup b \cup c)^ - (a \cup b \cup c)^ abc (a \cup b \cup c)^ 这是语言定义,不是正则表达式。
* 最终的构造思路:
字符串可以由不含 a 的前缀开始: (b \cup c)^
* 然后,如果出现 a,它后面可以跟另一个 a,或者一个 c,或者一个 b。
* 如果跟 b,则进入特殊状态。
(b \cup c)^ (a (b(a\cup b))? (b \cup c)^ )^
一个简洁的答案是 (c|b|aac) (aab?)?
标准答案之一: (b|c|a(a|c)|ab(a|b))
让我们分析一下: (b | c | a(a|c) | ab(a|b) )
* 这个表达式的构建块是 b, c, aa, ac, aba, abb。
* 它永远不会生成 abc 这个子串,因为 ab 后面总是跟着 a 或 b。
* 它能生成所有不含 abc 的字符串吗?是的。任何不含abc的字符串都可以被这些块分解。
5.2 问题 10. 使用我们在课堂上看到的通过 GNFA 的构造方法,将以下 DFA 转换为等价的 正则表达式。
📜 [原文21]
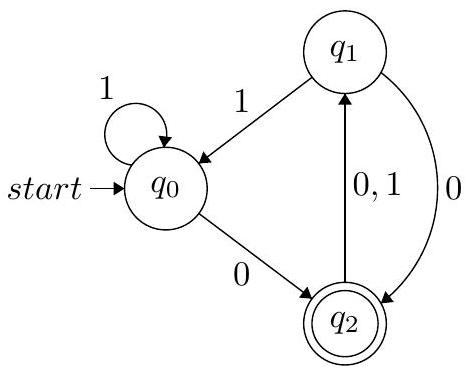
该问题要求使用 GNFA (广义非确定性有限自动机) 方法将一个DFA转换为正则表达式。GNFA的边上可以是正则表达式,而不是单个符号。转换过程是通过逐步“撕掉”状态,并用更复杂的正则表达式来补偿被撕掉状态所代表的路径。
DFA分析:
- 状态: 1, 2。
- 起始状态: 1。
- 接受状态: 1。
- 转移:
- $1 \xrightarrow{a} 2$
- $1 \xrightarrow{b} 1$
- $2 \xrightarrow{a} 1$
- $2 \xrightarrow{b} 2$
GNFA 转换步骤:
步骤 1: 预处理 DFA 为 GNFA 格式
- 添加新的起始状态 $S_{new}$: 从 $S_{new}$ 画一条 ε-转移 到原起始状态 1。
- 添加新的接受状态 $F_{new}$: 从所有原接受状态(这里只有1)画一条 ε-转移 到 $F_{new}$。
- 合并多重边: 如果两个状态之间有多个符号的转移,用并集($\cup$)合并。例如,$q_i \xrightarrow{a} q_j$ 和 $q_i \xrightarrow{b} q_j$ 变成 $q_i \xrightarrow{a \cup b} q_j$。这个DFA没有这种情况。
- 添加空集边: 如果两个状态之间没有转移,我们认为它们之间有一条标签为 $\emptyset$ 的边。
初始 GNFA 结构:
- 状态: $\{S_{new}, 1, 2, F_{new}\}$
- $S_{new} \xrightarrow{\epsilon} 1$
- $1 \xrightarrow{b} 1$
- $1 \xrightarrow{a} 2$
- $2 \xrightarrow{b} 2$
- $2 \xrightarrow{a} 1$
- $1 \xrightarrow{\epsilon} F_{new}$
步骤 2: 撕掉状态
我们有两个内部状态 1 和 2 可以撕。我们选择先撕掉状态2。
撕掉状态 2:
我们要考虑所有经过状态2的路径,例如从状态 i 到 j 经过 2 的路径: i -> 2 -> j。这个路径的正则表达式是 R(i,2) R(2,2)* R(2,j)。然后我们将这个新的表达式加到原来的 R(i,j) 上。
- 需要更新的路径: 只有 1 -> 2 -> 1。
- R(1,2) = $a$
- R(2,2) = $b$
- R(2,1) = $a$
- 路径 1 -> 2 -> 1 的正则表达式: $a b^* a$
- 更新 R(1,1): 原来的 $R(1,1)$ 是 $b$。新的 $R(1,1)$ 是 $b \cup ab^*a$。
撕掉状态2后的 GNFA:
- 状态: $\{S_{new}, 1, F_{new}\}$
- $S_{new} \xrightarrow{\epsilon} 1$
- $1 \xrightarrow{b \cup ab^*a} 1$ (这是一个自循环)
- $1 \xrightarrow{\epsilon} F_{new}$
步骤 3: 撕掉最后一个内部状态,状态1
现在我们撕掉状态1。我们只关心从 $S_{new}$ 到 $F_{new}$ 的路径。
- 路径是 $S_{new} \rightarrow 1 \rightarrow F_{new}$。
- R($S_{new}$, 1) = $\epsilon$
- R(1,1) = $b \cup ab^*a$
- R(1, $F_{new}$) = $\epsilon$
- 公式: $R(S_{new}, F_{new}) = R(S_{new}, 1) \circ (R(1,1))^* \circ R(1, F_{new})$
- 代入值: $\epsilon \circ (b \cup ab^*a)^* \circ \epsilon$
- 简化: $(b \cup ab^*a)^*$
最终的正则表达式: $(b \cup ab^*a)^*$
语言描述验证:
- 这个DFA接受什么样的语言?
- 从起始/接受状态1开始。可以读任意多个'b',停在1,接受。所以 $b^* \in L$。
- 读一个'a'到状态2,再读一个'a'回到状态1,接受。所以 'aa' $\in L$。
- 在状态2可以读任意多个'b'。所以 $ab^*a \in L$。
- 整个语言是这些部分的任意组合。例如 b 和 aa 组合成 baa。
- $b(ab^*a)b(ab^*a)$ 等。
- 这正是 $(b \cup ab^*a)^*$ 所描述的。
通过标准的GNFA状态消除法,我们成功地将给定的DFA转换为了等价的正则表达式。该方法的核心是通过迭代地移除状态,并将穿过该状态的路径用一个更复杂的正则表达式来代替,最终将一个复杂的图简化为一条从起始状态到接受状态的边,其上的标签就是最终的正则表达式。
5.3 问题 11. 将以下 正则表达式 转换为等价的 NFA
📜 [原文22]
这个问题要求我们使用Thompson构造法,将一个正则表达式逐步转换为一个NFA。该方法为每个基本操作(原子、并、连接、星号)定义了标准的NFA组件,然后像搭积木一样把它们组合起来。
正则表达式分解:
这个表达式是两个部分的连接:
- Part A: $(01)^*$
- Part B: $(10^* \cup 0)$
我们分别构造 Part A 和 Part B,然后将它们连接起来。
第一步: 构造 Part A: $(01)^*$
- 构造 "0" 的 NFA: $q_1 \xrightarrow{0} q_2$
- 构造 "1" 的 NFA: $q_3 \xrightarrow{1} q_4$
- 构造 "01" (连接): 将 "0" 的接受态 $q_2$ 和 "1" 的起始态 $q_3$ 合并 (或用ε-转移)。得到 $q_1 \xrightarrow{0} q_2 \xrightarrow{1} q_4$。
- 构造 $(01)^*$ (星号): 对 "01" 的NFA应用星号构造法。
- 创建新的起始态 $A_{start}$ 和接受态 $A_{final}$。
- $A_{start} \xrightarrow{\epsilon} A_{final}$ (处理空串)。
- $A_{start} \xrightarrow{\epsilon} q_1$ (进入循环)。
- $q_4 \xrightarrow{\epsilon} A_{final}$ (退出循环)。
- $q_4 \xrightarrow{\epsilon} q_1$ (循环反馈)。
- (简化版构造) 新建一个起始/接受状态 $A_{start}$。
- $A_{start} \xrightarrow{\epsilon} q_1$。
- $q_4 \xrightarrow{\epsilon} A_{start}$。
- $A_{start}$ 是接受状态。
- 我们用这个简化版,它有状态 {$A_{start}, q_1, q_2, q_4$}。起始是 $A_{start}$,接受是 $A_{start}$。转移:$A_{start}\xrightarrow{\epsilon}q_1$, $q_1\xrightarrow{0}q_2$, $q_2\xrightarrow{1}q_4$, $q_4\xrightarrow{\epsilon}A_{start}$。
第二步: 构造 Part B: $(10^* \cup 0)$
Part B 是一个并集。
- 构造上分支: $10^*$
- 构造 "0" 的 NFA: $q_5 \xrightarrow{0} q_6$。
- 构造 $0^*$ (星号): 创建新起始/接受态 $S_0$。$S_0 \xrightarrow{\epsilon} q_5$, $q_6 \xrightarrow{\epsilon} S_0$。
- 构造 "1" 的 NFA: $q_7 \xrightarrow{1} q_8$。
- 构造 $10^*$ (连接): 将 "1" 的NFA和 $0^*$ 的NFA连接。$q_7 \xrightarrow{1} q_8 \xrightarrow{\epsilon} S_0$。$q_7$是起始, $S_0$和$q_6$相关的接受状态是最终接受状态。整个 $10^*$ 的NFA可以简化为:$q_7 \xrightarrow{1} q_8$,然后 $q_8$ 上有一个消耗'0'的自循环。我们用Thompson标准构造:$q_7 \xrightarrow{1} q_8$, $q_8 \xrightarrow{\epsilon} q_{s0}$, $q_{s0} \xrightarrow{\epsilon} q_5, q_6 \xrightarrow{\epsilon} q_{s0}, q_{s0} \xrightarrow{\epsilon} q_{sF}$。这太复杂了。
- 我们直接画出 $10^*$ 的NFA:$B_{1s} \xrightarrow{1} B_{1m}$,然后 $B_{1m}$ 上有 $B_{1m} \xrightarrow{0} B_{1m}$ 的自循环。接受状态是 $B_{1m}$。
- 构造下分支: "0"
- $B_{2s} \xrightarrow{0} B_{2f}$。$B_{2f}$是接受状态。
- 构造 $(10^* \cup 0)$ (并集):
- 创建新起始态 $B_{start}$ 和新接受态 $B_{final}$。
- $B_{start} \xrightarrow{\epsilon} B_{1s}$ (上分支起始)。
- $B_{start} \xrightarrow{\epsilon} B_{2s}$ (下分支起始)。
- $B_{1m} \xrightarrow{\epsilon} B_{final}$ (上分支结束)。
- $B_{2f} \xrightarrow{\epsilon} B_{final}$ (下分支结束)。
第三步: 构造最终 NFA (连接 Part A 和 Part B)
- 将 Part A 的 NFA 和 Part B 的 NFA 连接起来。
- Part A 的接受状态(在我们的简化版里是 $A_{start}$)通过 ε-转移 连接到 Part B 的起始状态 $B_{start}$。
- 最终机器的起始状态是 Part A 的起始状态 $A_{start}$。
- 最终机器的接受状态是 Part B 的接受状态 $B_{final}$。
- 连接: $A_{start} \xrightarrow{\epsilon} B_{start}$。
- 同时,因为 $A_{start}$ 本身是 Part A 的接受状态,所以这个连接是正确的。
最终的NFA图:
- 画出 Part A ($(01)^*$)的NFA,它是一个环。
- 画出 Part B ($(10^* \cup 0)$)的NFA,它是一个分叉结构。
- 从 Part A 的接受状态(即其起始状态)画一条 ε-转移 到 Part B 的起始状态。
- 标记最终NFA的起始(Part A的起始)和接受(Part B的接受)状态。
- $(01)^*$: 零次或多次重复的 "01" 序列。
- $(10^* \cup 0)$: 一个 "或" 结构。
- $10^*$: 一个 '1' 后面跟着零个或多个 '0'。
- $\cup$: 或。
- $0$: 单个 '0'。
- (...)(...): 连接操作。将前一部分产生的一个字符串和后一部分产生的一个字符串拼接起来。
- 语言描述: 字符串由两部分构成。第一部分是形如 "0101...01" 的串(或空串)。第二部分要么是 "100...0",要么是 "0"。
- 示例:
- $x=\epsilon, y="0" \implies "0"$
- $x=\epsilon, y="10" \implies "10"$
- $x="01", y="0" \implies "010"$
- $x="01", y="1" \implies "011"$
我们严格遵循了Thompson构造法,将复杂的正则表达式分解为基本组件,为每个组件构建标准的NFA模块,然后通过连接和并集的标准构造法将这些模块“焊接”在一起,最终形成了一个完整、等价的NFA。这个过程是纯机械的,保证了结果的正确性。
66 行间公式索引
1. 问题1(b)的语言定义:
这个公式定义了一个语言L,其中的字符串w要么恰好包含两个'0',要么包含偶数个'1'。
2. 问题4的语言定义:
这个公式定义了一个语言L,其中的字符串w要么包含偶数个'0',要么不包含连续的两个'1'。
3. 问题5中L1的语言定义:
这个公式定义了语言L1,其字符串w或者有奇数个'1',或者恰好有两个'0'。
4. 问题5中L2的语言定义:
这个公式定义了语言L2,其字符串w必须以子串"101"结尾。
5. 问题7(a)的逆转运算定义:
这个公式定义了语言L的逆转操作,即L中所有字符串w翻转后形成的新语言。
6. 问题7(b)的min运算定义:
这个公式定义了min(L)语言,它包含L中所有自身被L接受、但其任何更短的前缀都不被L接受的字符串。
7. 问题11的正则表达式:
这是一个正则表达式,描述了一个语言:由零或多个"01"串联,后面再跟上一个"1"和零或多个"0",或者跟上一个单独的"0"。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。