1COMS W3261: 计算机科学理论
作者:William Pires 和 Zachary Thayer
并基于 Rahul Gosain、Benjamin Kuykendall 先前的材料
期末复习
21. 关键术语
📜 [原文1]
集合:一组对象,我们称之为它的元素。这些“对象”可以是任何东西:符号、数字、字符串,或者集合本身。我们有多种方式定义集合:
这部分内容介绍了计算理论中最基础、最核心的概念之一:集合 (Set)。集合是构建后续所有复杂概念(如字母表、字符串、语言、自动机等)的基石。
- 什么是集合?
- 集合就是一个“容器”或“袋子”,里面装着一些东西。
- 这些“东西”被称为集合的元素 (elements)。
- 一个集合的关键特征是它的确定性(一个对象要么在集合里,要么不在,没有模棱两可的情况)和无序性(元素之间没有先后顺序,{1, 2} 和 {2, 1} 是同一个集合)以及互异性(一个元素在集合中只出现一次,{1, 1, 2} 会被自动看作 {1, 2})。
- 元素可以是任何东西:
- 符号 (symbols):比如 {a, b, c},这是字母表的基础。
- 数字 (numbers):比如 {0, 1, 2, 3},这是自然数集的一部分。
- 字符串 (strings):比如 {"apple", "banana", "cherry"}。
- 集合本身 (sets):一个集合的元素也可以是另一个集合,比如 {{1, 2}, {3, 4}}。这个集合有两个元素,每个元素都是一个集合。这在定义幂集时非常重要。
- 定义集合的方式:
- 计算机科学中,我们需要用精确的、无歧义的方式来描述一个集合,所以这里介绍了三种主要方法。
- 示例 1 (数字集合):集合 $S_1 = \{2, 4, 6, 8\}$。这里的对象是数字。元素 4 在集合 $S_1$ 中,而元素 5 不在。
- 示例 2 (符号集合):一个字母表 $\Sigma = \{'0', '1'\}$。这里的对象是符号。这个集合是构建二进制字符串的基础。
- 示例 3 (字符串集合):一个语言 $L = \{"cat", "dog", "bird"\}$。这里的对象是字符串。
- 示例 4 (集合的集合):集合 $S_2 = \{\emptyset, \{a\}, \{b\}\}$。这个集合有三个元素:空集 $\emptyset$、只包含元素 a 的集合 {a}、只包含元素 b 的集合 {b}。
- 混淆元素和集合:对于集合 $A = \{\{1, 2\}, 3\}$,元素 1 和 2 并不直接属于 $A$。$A$ 只有两个元素:集合 $\{1, 2\}$ 和数字 3。即 $\{1, 2\} \in A$ 且 $3 \in A$,但 $1 \notin A$。
- 忽略无序性:集合 $\{a, b, c\}$ 和 $\{c, b, a\}$ 是完全相同的集合,因为元素的顺序不重要。
- 忽略互异性:在定义集合时,如果写下 $\{1, 2, 2, 3\}$,它实际上就是集合 $\{1, 2, 3\}$。重复的元素会被自动忽略。
本段定义了集合及其元素的基本概念。集合是容纳对象(元素)的容器。元素可以是数字、符号、字符串,甚至是其他集合。
集合是数学和计算机科学的通用语言。在计算理论中,几乎所有概念都建立在集合之上。没有对集合的清晰理解,就无法学习后续的语言、自动机和可计算性等概念。这是搭建整个理论体系的第一块砖。
你可以把集合想象成一个透明的塑料袋。袋子里的每个物品就是一个元素。
- 你可以清楚地看到袋子里有什么(确定性)。
- 物品在袋子里的位置可以随意晃动,不影响袋子的内容(无序性)。
- 如果你想放一个和袋子里已有的完全一样的物品进去,它实际上还是只有一个(互异性)。
- 袋子里还可以装其他更小的袋子(元素可以是集合)。
想象一个玩具箱,里面有各种积木块。
- 这个玩具箱就是一个集合。
- 每一块积木就是一个元素。
- 积木可以是不同形状(方块、圆柱)、不同颜色(红色、蓝色),这代表元素可以是不同类型的对象。
- 玩具箱里还可以放一个小的收纳盒,收纳盒里又装着更小的积木,这就像一个集合里包含另一个集合。
1.1. 定义集合的方式
📜 [原文2]
列举有限集合的项目:例如 $\{1\},\{1,2,3\},\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$。
使用省略号表示模式无限延续:例如 $\{1,2,3, \ldots\},\{1,11,111, \ldots\}$。
给出成员资格条件:例如 $\left\{n \mid n=m^{2}\right.$ for some $\left.m \in \mathbb{N}\right\}$。
这部分详细说明了三种定义或描述集合内容的常用方法。
- 列举法 (Roster Notation):
- 这是最直接的方法,尤其适用于元素数量不多的有限集合。
- 你把集合中所有的元素一个一个地写出来,用逗号隔开,然后用大括号 {} 包围起来。
- 例如:
- $\{1\}$:表示只包含数字 1 的集合。
- $\{1, 2, 3\}$:表示包含数字 1、2、3 的集合。
- $\{\mathrm{a}, \mathrm{b}, \mathrm{c}\}$:表示包含符号 'a', 'b', 'c' 的集合。
- 模式法 (Pattern Notation) / 省略号法:
- 当集合是无限的,或者有限但元素太多不方便一一列举时,如果元素之间存在明显的规律,就可以使用这种方法。
- 你写出开头的几个元素以展示规律,然后使用省略号 ... 来表示“照此规律继续下去”。
- 例如:
- $\{1, 2, 3, \ldots\}$:这通常表示所有正整数的集合(即 $\mathbb{Z}^+$)。规律是逐个加 1。
- $\{1, 11, 111, \ldots\}$:这个集合的元素是由数字 1 组成的字符串,长度依次增加。
- 描述法 / 构造法 (Set-Builder Notation):
- 这是最强大、最精确的方法,尤其适用于描述无限集合或具有复杂成员资格规则的集合。
- 格式通常是 {变量 | 对变量的描述或条件}。竖线 | 读作“使得 (such that)”。
- 例如: $\left\{n \mid n=m^{2} \text{ for some } m \in \mathbb{N}\right\}$
- {n | ...}: 这个集合由满足特定条件的元素 n 组成。
- n = m^2: 条件是 n 必须是某个数的平方。
- for some m ∈ ℕ: 那个“某个数” m 必须是自然数 (Natural Number, $\mathbb{N}=\{0, 1, 2, 3, ...\}$)。
- 所以,这个集合是所有自然数的平方组成的集合,即 $\{0, 1, 4, 9, 16, \ldots\}$。
- 示例 1 (列举法):
- 一个字母表可以定义为 $\Sigma = \{\text{'A'}, \text{'B'}, \dots, \text{'Z'}\}$。
- 一个包含哥大课程的集合 $C = \{\text{"COMS W3261"}, \text{"COMS W4118"}, \text{"COMS W4701"}\}$。
- 示例 2 (模式法):
- 所有偶数的集合:$E = \{0, 2, 4, 6, \ldots\}$。
- 所有 10 的次方的集合:$P_{10} = \{1, 10, 100, 1000, \ldots\}$。
- 示例 3 (描述法):
- 描述所有偶数集合 $E$: $E = \{x \mid x = 2k \text{ for some } k \in \mathbb{Z}\}$ (其中 $\mathbb{Z}$ 是整数集)。
- 描述所有长度为 3 的二进制字符串的集合 $L$: $L = \{w \mid w \in \{0,1\}^* \text{ and } |w|=3\}$。这个集合用列举法就是 $\{000, 001, 010, 011, 100, 101, 110, 111\}$。
- 模式法的模糊性: 省略号 ... 依赖于读者能正确理解其模式。例如,$\{1, 2, 4, \ldots\}$ 可能表示“2的幂次” $\{1, 2, 4, 8, 16, \ldots\}$,也可能表示“下一个数是前几个数的和” $\{1, 2, 4, 7, 13, \ldots\}$。因此,在需要严格精确的场合,描述法是更好的选择。
- 描述法的域 (Domain): 在描述法中,需要明确变量的取值范围。例如,$\{x \mid x > 2\}$ 是不明确的,x 是整数、有理数还是实数?应该写成 $\{x \in \mathbb{R} \mid x > 2\}$ (大于2的实数集合) 或 $\{x \in \mathbb{Z} \mid x > 2\}$ (大于2的整数集合 $\{3, 4, 5, \ldots\}$),这两者是截然不同的。
本段介绍了定义集合的三种方法:列举法用于有限小集合,模式法用于有明显规律的无限或大集合,描述法则提供了最通用和最精确的定义方式。
为了在计算理论中进行严谨的讨论和证明,我们必须能够清晰、无歧义地定义我们正在研究的对象(集合)。这三种方法为我们提供了不同场景下的工具,使我们能够精确地沟通。
- 列举法: 像是一张购物清单,上面明确列出了你要买的所有东西。
- 模式法: 像是告诉朋友:“帮我买序列号从 1 开始的所有苹果手机,iPhone 1, iPhone 2, iPhone 3,以此类推...” 你不用说完,朋友也知道你的意思。
- 描述法: 像是在法律条款中定义一个群体:“本法案适用于所有持有纽约州驾照且年龄在 21 岁及以上的个人。” 这是一个非常精确的筛选标准。
想象你在图书馆找书:
- 列举法: 你的书单上直接写着《百年孤独》、《追风筝的人》和《三体》。你直接按书名找。
- 模式法: 你想找《哈利波特》全集,你跟图书管理员说:“就是从第一部到第七部的那一套”。
- 描述法: 你想找所有“由 19 世纪法国作家撰写的,并且页数超过 500 页的小说”。这是一个明确的规则,图书管理员可以根据这个规则去筛选。
1.2. 集合的符号与操作
📜 [原文3]
我们有成员和子集的符号:
成员资格:如果 $x$ 是 $S$ 的元素,则说 $x \in S$(或“ $x$ 在 $S$ 中”)。
子集:如果 $T$ 中的每个元素也在 $S$ 中,则说 $T \subseteq S$(或“ $T$ 是 $S$ 的子集”)。
幂集:令 $\mathcal{P}(X)$(或“ $X$ 的所有子集的集合”)为 $\mathcal{P}(X)=\{S \mid S \subseteq X\}$。
注意 $\varnothing \in \mathcal{P}(X)$ 且 $X \in \mathcal{P}(X)$。
我们对集合有一些基本操作。例如
并集: $A \cup B=\{x \mid x \in A$ or $x \in B\}$。
交集: $A \cap B=\{x \mid x \in A$ and $x \in B\}$。
差集: $A \backslash B=\{x \mid x \in A$ and $x \notin B\}$。
这部分引入了用于描述集合之间关系和进行集合运算的基本符号和操作。
- 成员资格 (Membership):
- 符号: $\in$
- 含义: $x \in S$ 表示对象 x 是集合 S 的一个元素。
- 这是判断一个对象和一个集合之间最基本的关系。
- 子集 (Subset):
- 符号: $\subseteq$
- 含义: $T \subseteq S$ 表示集合 T 是集合 S 的一个子集。这意味着,T 里面的所有元素,都可以在 S 里面找到。
- 这是一个集合与另一个集合之间的关系。
- 注意区分 $\in$ 和 $\subseteq$。前者是元素与集合的关系,后者是集合与集合的关系。
- 幂集 (Power Set):
- 符号: $\mathcal{P}(X)$
- 含义: $\mathcal{P}(X)$ 是一个特殊的集合,它的元素是原集合 X 的所有可能的子集。
- 这是一个“集合的集合”。
- 关键点:
- 空集 $\varnothing$ (不含任何元素的集合) 永远是任何集合的子集,所以 $\varnothing \in \mathcal{P}(X)$。
- 任何集合都是其自身的子集,所以 $X \in \mathcal{P}(X)$。
- 如果集合 $X$ 有 n 个元素,那么它的幂集 $\mathcal{P}(X)$ 就有 $2^n$ 个元素。
- 基本集合操作:
- 并集 (Union): $A \cup B$
- 含义: 把集合 A 和 B 的所有元素合并在一起,形成一个新的集合。重复的元素只保留一个。
- 条件: 一个元素只要在 A 中 或者 (or) 在 B 中,它就在并集中。
- 交集 (Intersection): $A \cap B$
- 含义: 找出集合 A 和 B 共同拥有的元素,形成一个新的集合。
- 条件: 一个元素必须同时在 A 中 并且 (and) 在 B 中,它才在交集中。
- 差集 (Difference): $A \backslash B$
- 含义: 从集合 A 中,移除所有也存在于集合 B 中的元素,剩下的元素形成一个新的集合。
- 条件: 一个元素必须在 A 中 并且 (and) 不在 B 中。
- 成员与子集示例:
- 令 $S = \{1, 2, 3\}$。
- $1 \in S$ (1 是 S 的一个元素)。
- $\{1\} \subseteq S$ (只包含1的集合是 S 的子集)。
- 但是 $1 \not\subseteq S$ (1 不是一个集合),且 $\{1\} \notin S$ (S 的元素是数字1, 2, 3,而不是集合{1})。
- 幂集示例:
- 令 $X = \{a, b\}$。X 有 2 个元素。
- X 的子集有:
- 不含任何元素的子集:$\varnothing$
- 含一个元素的子集:$\{a\}$, $\{b\}$
- 含两个元素的子集:$\{a, b\}$
- 因此,X 的幂集是 $\mathcal{P}(X) = \{\varnothing, \{a\}, \{b\}, \{a, b\}\}$。$\mathcal{P}(X)$ 有 $2^2 = 4$ 个元素。
- 集合操作示例:
- 令 $A = \{1, 2, 3\}$, $B = \{3, 4, 5\}$。
- 并集: $A \cup B = \{1, 2, 3, 4, 5\}$。
- 交集: $A \cap B = \{3\}$。
- 差集:
- $A \backslash B = \{1, 2\}$ (从 A 中去掉 B 里也有的元素 3)。
- $B \backslash A = \{4, 5\}$ (从 B 中去掉 A 里也有的元素 3)。
- 成员 ($\in$) vs. 子集 ($\subseteq$): 这是初学者最常见的错误。$a \in \{a, b\}$ 是正确的,但 $\{a\} \in \{a, b\}$ 是错误的。$\{a\} \subseteq \{a, b\}$ 是正确的。
- 空集作为元素: 考虑 $S = \{\varnothing, 1\}$。这里,空集 $\varnothing$ 是 $S$ 的一个元素,所以 $\varnothing \in S$。同时,空集也是 $S$ 的一个子集,所以 $\varnothing \subseteq S$。这是少数情况 $\in$ 和 $\subseteq$ 同时成立。
- 幂集的大小: 如果一个集合有 n 个元素,它的幂集有 $2^n$ 个元素。这个数字增长非常快。一个有 10 个元素的集合,其幂集就有 $2^{10} = 1024$ 个元素。
- 差集不对称: $A \backslash B$ 和 $B \backslash A$ 通常是不同的。
本段定义了集合的成员关系 ($\in$)、子集关系 ($\subseteq$),以及如何由一个集合生成其所有子集的集合——幂集 ($\mathcal{P}(X)$)。同时介绍了三种基本的集合运算:并集 ($\cup$)、交集 ($\cap$) 和差集 ($\backslash$)。
这些符号和操作构成了集合论的基本语法。它们是精确描述和推理计算理论中各种概念(如语言的补集、正则语言的闭包性质等)所必需的工具。没有它们,我们的讨论将变得冗长和模糊。
- 成员与子集: 你的一个朋友是你朋友圈(集合)里的一个成员 ($\in$)。你朋友中的一小撮人(比如你们的篮球队友)是你朋友圈的一个子集 ($\subseteq$)。
- 幂集: 想象你有一盒披萨,上面有三种配料:蘑菇、香肠、青椒。幂集就是你能做出的所有可能的披萨组合:什么都不加的(空集)、只加蘑菇的、只加香肠的、只加青椒的、加蘑菇和香肠的……一直到把三种配料都加上。总共有 $2^3=8$ 种组合。
- 操作:
- 并集: 你和你朋友的书单合并在一起,得到一个更大的书单。
- 交集: 找出你和你朋友书单上共同有的书。
- 差集: 在你的书单上,划掉你朋友也有的那些书。
用文氏图 (Venn Diagram) 来想象:
- 并集: 两个圆圈覆盖的总面积。
- 交集: 两个圆圈重叠部分的面积。
- 差集 $A \backslash B$: A 圆圈中不与 B 重叠的那部分面积。
1.3. 字母表、字符串和编码
📜 [原文4]
字母表:一个非空有限符号集合,通常表示为 $\Sigma$。例如
$\{0,1\},\{0,1, \ldots, 9\},\{\mathrm{a}, \mathrm{b}, \mathrm{c}\},\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \ldots, \mathrm{z}\}$。
字符串:由字母表中符号组成的有限序列。例如
$\varepsilon$(空字符串,没有符号)
1, 11, 111, 1996, benjamin
编码:有限数学对象可以用任何语言的字符串进行编码。例如
整数(使用它们的 $n$ 进制表示)
列表和集合(通过逗号分隔对象)
图(通过列出顶点和边)
有限集合之间的函数(通过列出对 $(x, f(x))$)
此外,由于我们所有的计算模型都是集合和函数的元组,我们可以编码 DFA、NFA、PDA和TM。如果 $x$ 是一个对象,其编码表示为 $\langle x\rangle$。
一般来说,并非所有字符串都是有效的编码。例如,如果我们将整数对编码为 $x \# y$ 格式,则 $123\#321$ 是一个有效编码,但 $\#\#$ 不是。
这部分将集合的概念具体化,引入了计算理论的核心处理对象:字符串,以及如何将其他数学对象表示为字符串(即编码)。
- 字母表 (Alphabet):
- 定义: 字母表是一个特殊的集合,用符号 $\Sigma$ (Sigma) 表示。
- 特征:
- 非空: 字母表里至少要有一个符号。
- 有限: 字母表里的符号数量是有限的。
- 作用: 字母表规定了我们可以用来构建字符串的所有“合法字符”。
- 字符串 (String):
- 定义: 字符串是从字母表 $\Sigma$ 中选取符号并按一定顺序排列形成的有限序列。
- 关键特征:
- 有限性: 字符串的长度必须是有限的。
- 有序性: 符号的顺序很重要。ab 和 ba 是两个不同的字符串。
- 特殊字符串:
- 空字符串 (empty string) $\varepsilon$ (Epsilon):它是一个长度为 0 的特殊字符串,不包含任何符号。
- 编码 (Encoding):
- 核心思想: 图灵机等计算模型的输入本质上是字符串。为了让图灵机能处理各种数学对象(如数字、图、甚至其他图灵机),我们必须找到一种方法,将这些对象转换成字符串表示。这个转换过程就是编码。
- 表示法: 如果 x 是一个数学对象(比如一个图 G),它的编码(一个字符串)通常被写作 $\langle x \rangle$(比如 $\langle G \rangle$)。
- 编码的应用:
- 整数: 可以用二进制 (如101) 或十进制 (5) 字符串表示。
- 图: 可以编码为一个顶点列表和边列表的字符串,例如 ({v1,v2,v3},{(v1,v2),(v2,v3)})。
- 计算模型: DFA、NFA、TM 本身就是由状态集、字母表、转移函数等组成的元组,这些组成部分都可以被系统地描述成一个长字符串。这就意味着一台图灵机可以把另一台图灵机的描述(编码)作为自己的输入来分析。这是可计算性理论(如停机问题)的核心。
- 有效编码:
- 概念: 对于一种编码方案,不是所有字符串都有意义。
- 例子: 我们约定用 数字#数字 的格式来编码一对整数。
- 字母表是 $\{0, 1, \dots, 9, \#\}$。
- 123#321 是一个有效编码,它表示数对 (123, 321)。
- ##,12#,#321 等都是无效编码,因为它们不符合我们约定的格式,没有对应的数学对象。
- 字母表与字符串示例:
- 字母表: $\Sigma = \{a, b\}$。
- 该字母表上的字符串: $\varepsilon$, a, b, aa, ab, ba, bb, aaa, ...
- 编码示例:
- 对象: 一个简单的无向图 $G$,有两个顶点 1 和 2,之间有一条边。
- 编码方案: $\langle G \rangle = "(V, E)"$,其中 $V$ 是顶点集,E是边集。
- 编码结果: $\langle G \rangle$ 可以是字符串 ({1,2},{{1,2}})。这个字符串就在某个字母表(包含 {, }, (, ), 1, 2 等符号)上。
- DFA 编码示例:
- 对象: 一个接受以 '1' 结尾的二进制字符串的 DFA $M$。
- $Q = \{q_0, q_1\}$ (状态集)
- $\Sigma = \{0, 1\}$ (字母表)
- $\delta$ (转移函数): $\delta(q_0, 0) = q_0$, $\delta(q_0, 1) = q_1$, $\delta(q_1, 0) = q_0$, $\delta(q_1, 1) = q_1$
- $q_0$ (开始状态)
- $F = \{q_1\}$ (接受状态集)
- 编码结果 $\langle M \rangle$: 我们可以将这些信息串联成一个字符串,例如:({q0,q1},{0,1},{(q0,0,q0),(q0,1,q1),(q1,0,q0),(q1,1,q1)},q0,{q1})。
- 字符串 vs. 集合: {a, b} 是一个包含两个元素 a 和 b 的集合,是无序的。ab 是一个长度为 2 的字符串,a 在 b 之前,是有序的。
- 空字符串 $\varepsilon$: $\varepsilon$ 是一个真实存在的字符串,只是它的长度是 0。它和空集 $\varnothing$ (不包含任何元素的集合) 是完全不同的概念。
- 编码的唯一性: 对于同一个对象,可以有多种不同的编码方案。我们通常假设在讨论某个问题时,已经预先固定了一种“合理”的编码方案。
- 对象 vs. 它的编码: 一定要区分数学对象本身(如图 G)和代表它的字符串 $\langle G \rangle$。图灵机处理的是后者。
本段定义了计算理论的基本数据单位:字母表是字符的集合,字符串是这些字符的有限序列。编码是将任何数学对象(如图、数字、甚至图灵机本身)转换为字符串的过程,从而使计算模型能够对其进行处理。
编码是连接抽象数学世界和具体计算世界的桥梁。通过编码,我们可以将关于图、数论或逻辑的问题,转化为对字符串的判定问题,然后用图灵机这样的形式化模型来研究这些问题的可计算性和复杂性。这是整个理论能够应用于广泛领域的前提。
[直觉心- 1.4. 语言及其补集
📜 [原文5]
语言:来自相同字母表的字符串集合。例如
$\varnothing$ (空字符串集合)
$\Sigma^{*}$ (所有 $\Sigma$ 上的字符串集合)
$A=\left\{w \in\{0,1\}^{*} \mid w\right.$ contains a 1$\}$
$G_{C}=\{\langle G\rangle \mid G$ is a cyclic graph $\}$
$M_{0110}=\{\langle M\rangle \mid M$ is a TM that accepts 0110\}
语言的补集:补集 $\bar{L}$ 是 $\Sigma^{*}$ 中但不在 $L$ 中的字符串集合。或者用集合论符号表示 $\bar{L}:=\Sigma^{*} \backslash L$。例如
这部分定义了计算理论的核心研究对象——语言,以及它的基本集合运算——补集。
- 语言 (Language):
- 定义: 一个语言就是一个字符串的集合。
- 前提: 一个语言中的所有字符串都必须构建于同一个字母表 $\Sigma$ 之上。
- 本质: 语言就是从所有可能的字符串(这个全集通常记作 $\Sigma^*$)中,根据某个规则挑选出来的一个子集。
- 计算理论的核心问题: 给定一个语言 L 和一个字符串 w,判断 w 是否属于 L(即 $w \in L$ ?)。这就是所谓的成员资格问题 (Membership Problem)。
- 例子分析:
- $\varnothing$: 空语言,它是一个集合,但是里面没有任何字符串。
- $\Sigma^{*}$: 全语言,包含由字母表 $\Sigma$ 能构成的所有有限长度的字符串(包括空字符串 $\varepsilon$)。星号 * 在这里是克莱尼星号 (Kleene Star),表示“零个或多个”的串联。
- $A=\left\{w \in\{0,1\}^{*} \mid w\right.$ contains a 1$\}$: 这是一个在二进制字母表 $\{0,1\}$ 上的语言。规则是“字符串中至少包含一个 '1'”。例如, 1, 010, 111 属于 A, 但 0, 000, $\varepsilon$ 不属于 A。
- $G_{C}=\{\langle G\rangle \mid G$ is a cyclic graph $\}$: 这是一个更抽象的语言。它的字母表是用来编码图的符号集合。它的字符串不是普通的文本,而是图的编码。如果一个字符串是一个有环图的有效编码,那么这个字符串就在这个语言里。
- $M_{0110}=\{\langle M\rangle \mid M$ is a TM that accepts 0110\}: 这是一个关于图灵机的语言。它的字符串是图灵机的编码。如果一个字符串 $\langle M \rangle$ 所代表的图灵机 M 能够接受特定的字符串 "0110",那么 $\langle M \rangle$ 就属于这个语言。
- 语言的补集 (Complement of a Language):
- 定义: 给定一个语言 $L$(它是 $\Sigma^*$ 的一个子集),它的补集 $\bar{L}$ 是所有“不在” $L$ 里的字符串组成的集合。
- 前提: 补集是相对于全集 $\Sigma^*$ 而言的。
- 集合论表示: $\bar{L} = \Sigma^* \backslash L$。
- 例子分析:
- $\bar{\varnothing}=\Sigma^{*}$: 空语言的补集是全语言。因为没有任何字符串在空语言里,所以所有字符串都在它的补集里。
- $\overline{\Sigma^{*}}=\varnothing$: 全语言的补集是空语言。
- 对于 $A = \{w \in \{0,1\}^* \mid w \text{ contains a 1}\}$,它的补集 $\bar{A}$ 是所有“不包含任何 '1'”的二进制字符串。这些字符串只能由 '0' 组成,包括空字符串 $\varepsilon$。所以 $\bar{A} = \{0^n \mid n \ge 0\} = \{\varepsilon, 0, 00, 000, \ldots\}$。
- 对于 $G_C$ (有环图的编码),它的补集 $\overline{G_C}$ 包含两种字符串:一种是无效的图编码(比如格式错误的字符串),另一种是无环图的有效编码。
- 对于 $M_{0110}$ (接受 "0110" 的图灵机编码),它的补集 $\overline{M_{0110}}$ 包含两种字符串:一种是无效的TM编码,另一种是那些“不接受” "0110" 的图灵机的有效编码。(“不接受”包括拒绝和循环)。
- 语言示例:
- 字母表: $\Sigma = \{a, b\}$。
- 语言 $L_1$: 所有以 'a' 开头的字符串。$L_1 = \{a, aa, ab, aaa, aab, aba, abb, \ldots\}$。
- 语言 $L_2$: 所有长度为偶数的字符串。$L_2 = \{\varepsilon, aa, ab, ba, bb, aaaa, \ldots\}$。
- 补集示例:
- 全集: $\Sigma^* = \{\varepsilon, a, b, aa, ab, ba, bb, \ldots\}$。
- $\overline{L_1}$: 所有不以 'a' 开头的字符串。这包括空字符串 $\varepsilon$ 和以 'b' 开头的字符串。$\overline{L_1} = \{\varepsilon, b, ba, bb, baa, \ldots\}$。
- $\overline{L_2}$: 所有长度为奇数的字符串。$\overline{L_2} = \{a, b, aaa, aab, \ldots\}$。
- 空字符串 $\varepsilon$ 的归属: 在求补集时,很容易忘记考虑空字符串。例如,对于语言“所有非空字符串”的补集是 $\{\varepsilon\}$,而不是 $\varnothing$。
- 补集与无效编码: 对于像 $\langle G \rangle$ 或 $\langle M \rangle$ 这样的编码语言,其补集总是包含了所有“格式错误”的字符串。这是一个非常重要且容易忽略的细节,尤其是在构造性证明中。
- 语言 vs. 字符串: 语言是集合,字符串是元素。可以说 "$w \in L$",但不能说 "$w = L$" (除非 L 只包含 w 这一个字符串,且 w 本身不是一个集合)。
本段将计算理论的焦点从单个字符串转移到了字符串的集合——语言。语言是判定问题的形式化表达。补集运算是研究语言性质(如可判定性下的闭包)的一个基本工具。
整个计算理论,从有限自动机到图灵机,其最终目的都是为了回答关于语言的问题:一个给定的语言能否被某种计算模型所“识别”或“判定”?它属于哪个复杂性类?定义语言和补集,为提出和研究这些核心问题搭建了舞台。
- 字母表: 英文字母表 (A-Z)。
- $\Sigma^*$: 所有可能的英文单词、胡言乱语、甚至包括空的纸条 ($\varepsilon$) 的集合。这是一个无限大的字典。
- 语言: 从这个无限大的字典里,挑出一部分有意义的词。例如,所有合法的英语单词组成的集合就是一个语言。
- 补集: 在这个无限大的字典里,所有不是合法英语单词的字符串(比如 "xyzzy", "applepie" 如果它不是一个词的话)组成的集合。
想象一条数轴代表所有实数(类似 $\Sigma^*$)。
- 一个语言就像数轴上的一个区间,比如 [0, 1]。
- 它的补集就是数轴上除了这个区间之外的所有部分,即 $(-\infty, 0) \cup (1, \infty)$。
1.5. 图灵机、识别器和判定器
📜 [原文6]
图灵机:我们稍后将正式定义图灵机;目前,考虑在字符串 $w$ 上运行图灵机 $M$ 时可能出现的三种结果:
经过一些步骤后,机器进入接受状态:说“ $M$ 接受 $w$ ”。
经过一些步骤后,机器进入拒绝状态:说“ $M$ 拒绝 $w$ ”。
机器既未达到接受状态也未达到拒绝状态:说“ $M$ 在 $w$ 上循环”。
如果 $M$ 接受或拒绝 $w$,我们说“ $M$ 在 $w$ 上停机”。
识别器:当
时,“ $M$ 识别 $L$ ”。
由 $M$ 识别的语言是唯一的,即 $L(M)=\left\{w \in \Sigma^{*} \mid M\right.$ accepts $\left.w\right\}$。
判定器:当
时,“ $M$ 判定 $L$ ”。
或者等价地说:
如果 $M$ 识别 $L$ 并且 $M$ 在所有输入上停机。
同样,如果 $M$ 判定任何语言,该语言就是 $L(M)$。
这部分介绍了计算理论中最终极的计算模型——图灵机 (Turing Machine, TM),并定义了它与语言之间的两种核心关系:识别 (Recognize) 和 判定 (Decide)。
- 图灵机的三种结果:
- 接受 (Accept): 图灵机在有限步骤内完成计算,并进入一个特殊的“接受”状态。这通常表示输入字符串“是”我们想要的。
- 拒绝 (Reject): 图灵机在有限步骤内完成计算,并进入一个特殊的“拒绝”状态。这通常表示输入字符串“不是”我们想要的。
- 循环 (Loop): 图灵机永不停止,一直在无限地计算下去。它既不接受也不拒绝。
- 停机 (Halt): 如果一个图灵机对于某个输入,最终结果是接受或拒绝,而不是循环,我们就说它停机了。
- 识别器 (Recognizer):
- 定义: 一个图灵机 M 如果能识别一个语言 L,意味着:
- 对于任何在语言 L 中的字符串 w ($w \in L$),M 最终一定会接受 w。
- 对于任何不在语言 L 中的字符串 w ($w \notin L$),M 永不接受 w。这里“永不接受”包含了两种可能:M 拒绝 w,或者 M 在 w 上循环。
- 非对称性: 识别器对“是”的回答是明确的(一定会接受并停机),但对“否”的回答可能是不确定的(可能拒绝,也可能永远没有回音)。
- 识别的语言: 对于一个图灵机 M,它所识别的语言被记为 $L(M)$,这个集合包含了所有能被 M 接受的字符串。
- 判定器 (Decider):
- 定义: 一个图灵机 M 如果能判定一个语言 L,意味着:
- 对于任何在语言 L 中的字符串 w ($w \in L$),M 最终一定会接受 w。
- 对于任何不在语言 L 中的字符串 w ($w \notin L$),M 最终一定会拒绝 w。
- 对称性/确定性: 判定器对于任何输入,无论是“是”还是“否”,都必须在有限时间内给出明确的答复(接受或拒绝)。它从不循环。
- 与识别器的关系:
- 所有的判定器都是识别器。
- 一个判定器就是一个“保证停机”的识别器。
- 识别器: $w \in L \Longleftrightarrow M \text { accepts } w$
- $\Longleftrightarrow$ 是逻辑符号“当且仅当”,表示双向蕴涵。
- 正向 ($w \in L \Longrightarrow M \text{ accepts } w$): 如果字符串在语言里,机器必须接受它。
- 反向 ($M \text{ accepts } w \Longrightarrow w \in L$): 如果机器 接受了某个字符串,那么这个字符串必须是在语言里。这隐含了如果 $w \notin L$,M 绝不能接受它。
- 判定器: $w \in L \Longrightarrow M \text { accepts } w \text{ and } w \notin L \Longrightarrow M \text { rejects } w$
- 这是一个更强的条件。它由两个独立的蕴涵句构成。
- 第一部分 ($w \in L \Longrightarrow M \text{ accepts } w$) 和识别器一样。
- 第二部分 ($w \notin L \Longrightarrow M \text{ rejects } w$) 明确要求对于不在语言中的字符串,机器必须拒绝,排除了循环的可能性。
- 语言: $L = \{010\}$,只包含一个字符串 "010"。字母表 $\Sigma = \{0, 1\}$。
- 一个 L 的判定器 M1:
- 读入输入字符串 w。
- 如果 w 等于 "010",则接受。
- 否则,拒绝。
- 这个图灵机对于任何输入都会在有限步骤内给出接受或拒绝的答案,所以它是判定器。
- 一个 L 的识别器 M2 (不是判定器):
- 读入输入字符串 w。
- 如果 w 等于 "010",则接受。
- 如果 w 不等于 "010",则进入一个无限循环(例如,不停地将磁带头左右移动)。
- 这个图灵机满足识别器的定义:对于属于 L 的 "010",它接受;对于不属于 L 的任何其他字符串,它不接受(而是循环)。但因为它会循环,所以它不是判定器。
- 不可识别语言的例子: 停机问题的补集 $\overline{A_{TM}}$ 是一个著名的不可识别语言的例子。没有任何图灵机能识别它。
- 识别器对“否”的处理: 学生常常忘记识别器在处理不属于语言的字符串时,除了拒绝之外,还可以循环。这是识别器和判定器最关键的区别。
- 可识别 (Recognizable) vs. 可判定 (Decidable):
- 一个语言是可识别的,意味着存在一个识别器来识别它。这类语言也叫图灵可识别语言或递归可枚举语言。
- 一个语言是可判定的,意味着存在一个判定器来判定它。这类语言也叫图灵可判定语言或递归语言。
- 可判定语言的集合是可识别语言集合的一个真子集。即,所有可判定语言都是可识别的,但存在一些可识别的语言是不可判定的(如停机问题 $A_{TM}$)。
本段定义了图灵机的三种输出行为(接受、拒绝、循环)。基于这些行为,定义了两种语言类别:可识别语言(其成员可被图灵机验证,非成员则可能导致拒绝或循环)和可判定语言(其成员资格可被图灵机在有限时间内给出明确的“是”或“否”的回答)。
识别器和判定器的概念是计算理论的中心。它们对语言(即问题)进行了第一次,也是最重要的一次难度划分。
- 可判定语言代表了我们理想中的“可解决”问题,算法可以对任何实例给出答案。
- 可识别但不可判定的语言代表了一类“半可解决”的问题,我们只能验证“是”的答案,但无法确切地判定所有的“否”。
- 不可识别的语言则代表了彻底无法用算法解决的问题。
这个分类体系是理解计算极限的基础。
假设你在向一位非常严谨但可能有点问题的专家提问。
- 判定器专家: 对于你提的任何问题,他总能在有限时间内给你一个明确的“是”或“否”。他非常可靠。
- 识别器专家: 对于你提的问题,如果答案是“是”,他一定会在有限时间内告诉你“是”。但如果答案是“否”,他可能会告诉你“否”,也可能会陷入沉思,永远不给你答复(循环)。你只能确信他的“是”答案,但如果他长时间不回答,你无法知道答案是“否”还是他只是在思考。
- 判定器: 像一个完美的自动化测试程序。对于任何提交的代码,它总能运行完毕并报告“测试通过”或“测试失败”。
- 识别器: 像一个可能会有死循环的程序。如果代码正确,它可能会打印“成功”并退出。但如果代码有错误,它可能会打印“失败”并退出,也可能直接卡死,程序无响应。
1.6. 可计算函数
📜 [原文7]
可计算函数:一个函数 $f: \Sigma^{*} \rightarrow \Sigma^{*}$ 是可计算的,当存在某个图灵机(技术上是输入-输出图灵机),在输入字符串 $x$ 上,当它停机时,磁带上将包含 $f(x)$。
这部分将图灵机的能力从“判断(是/否)”扩展到了“计算/转换”。
- 什么是函数?
- 在数学上,函数 $f: A \rightarrow B$ 是一个规则,它为定义域 A 中的每一个输入 x,都指定了值域 B 中唯一的一个输出 y,记为 $f(x)=y$。
- 在这里,我们关注的函数是字符串到字符串的函数,即 $f: \Sigma^* \rightarrow \Sigma^*$。输入是一个字符串,输出也是一个字符串。
- 什么是可计算函数 (Computable Function)?
- 一个函数 f 是可计算的,如果我们可以设计一台图灵机 M 来“实现”这个函数。
- “实现”的含义是:
- 将输入字符串 x 写在图灵机的初始磁带上。
- 启动图灵机 M。
- M 最终必须停机。
- 当 M 停机时,磁带上留下的内容不多不少,正好是字符串 $f(x)$。
- 输入-输出图灵机:
- 这是一个技术细节。标准的图灵机有接受/拒绝状态,用于判定语言。
- 用于计算函数的图灵机通常没有接受/拒绝状态,只有一个停机状态 (Halt state)。它的目的不是说是或否,而是产出结果。
- 在实践中,我们可以用标准图灵机来模拟它:比如约定,图灵机进入接受状态就意味着计算完成,此时磁带上的内容就是结果。
- 与判定器的关系:
- 判定一个语言 L,可以看作是计算一个特殊的特征函数 (characteristic function) $\chi_L$:
- $\chi_L(w) = \text{"1"}$ 如果 $w \in L$
- $\chi_L(w) = \text{"0"}$ 如果 $w \notin L$
- 如果一个语言 L 是可判定的,那么它的特征函数 $\chi_L$ 就是一个可计算函数。我们可以构造一个图灵机,输入 w,如果判定结果是接受,就在磁带上擦掉所有内容写入 "1" 并停机;如果是拒绝,就写入 "0" 并停机。
- 函数 1: $f(w) = w_1w_2...w_n \rightarrow w_nw_{n-1}...w_1$ (字符串反转)。
- 例如, $f(\text{"abc"}) = \text{"cba"}$。
- 这个函数是可计算的,因为我们可以设计一个图灵机来完成这个任务:
- 从左到右扫描到字符串末尾。
- 记住最后一个字符,把它写到一个新的空白区域。
- 回去把原字符串的最后一个字符擦除。
- 重复以上步骤,直到原字符串为空。
- 函数 2: $f(\langle n \rangle) = \langle n+1 \rangle$ (二进制加一)。
- 例如, $f(\text{"101"}) = \text{"110"}$ (5 -> 6)。
- 这个函数是可计算的。图灵机可以实现二进制加法的算法:从右到左,遇到 '0' 变成 '1' 并停机;遇到 '1' 变成 '0' 并继续向左进位。
- 不可计算函数的例子: 海狸函数 (Beaver Function) $BB(n)$,它的值是所有 n-状态图灵机中,在空输入上停机时,在磁带上留下最多 '1' 的数量。这个函数被证明是不可计算的,它增长得比任何可计算函数都快。
- 必须停机: 可计算函数的定义要求图灵机对所有定义域内的输入都必须停机。如果对于某个输入 x,图灵机 M 循环了,那么 M 就不算计算了一个在 x 处有定义的函数。
- 部分可计算函数 (Partial Computable Function): 如果我们放宽要求,允许图灵机在某些输入上循环,那么它计算的就是一个部分函数(即定义域不是全部 $\Sigma^*$)。在停机问题的语境下,这个概念很重要。
可计算函数将图灵机的角色从一个决策者 (Decision Maker) 扩展为一个转换器 (Transducer)。如果一个从字符串到字符串的函数可以通过一个保证停机的图灵机来实现,那么这个函数就是可计算的。
这个概念是归约 (Reduction) 的基础。映射归约 $A \le_m B$ 的核心就是要求存在一个可计算函数 f,能将语言 A 的成员资格问题转换为语言 B 的成员资格问题。没有可计算函数的定义,归约就无从谈起。它也形式化了我们通常理解的“算法”——一个接收输入并产生输出的过程。
- 判定器像一个法官,对案件(输入字符串)只给出“有罪”或“无罪”的判决。
- 计算函数的图灵机像一个翻译官,他接收一句话(输入字符串),然后把它翻译成另一种语言(输出字符串)。他必须完成翻译工作并给出结果,不能中途放弃或卡住。
想象一个函数是数学公式 $y = x^2$。
- 一个可计算函数的图灵机就像一个计算器程序。
- 你输入 x=5。
- 程序运行乘法算法。
- 最终,程序输出 25 并停止。
- 这个过程就是“计算”函数 $x^2$。
1.7. 语言集合
📜 [原文8]
语言集合:像任何数学对象一样,我们可以拥有语言集合。例如
$\{A\}$(只包含语言 $A$ 的集合)
$\{L \mid L \subseteq\{0,1\}\}$(四个语言 $\varnothing,\{0\},\{1\}$, 和 $\{0,1\}$)
$\left\{L \mid L \subseteq \Sigma^{*}\right.$ and $L$ is recognizable (or regular, decidable, unrecognizable ...)
$\left\{L \mid L \subseteq \Sigma^{*}\right.$ and $L$ can be decided in polynomial time $\}$(P 类)
$\left\{L \mid L \subseteq \Sigma^{*}\right.$ and $L$ can be verified in polynomial time $\}$(NP 类)
能够区分不同类型的集合很重要:字符串集合(语言)与语言集合。这里有一些你应理解的棘手的语言集合示例。例如
$\{\varnothing\}$(只包含语言 $\varnothing$ 的集合)
$\varnothing$(不包含任何语言的集合)
$\left\{L \mid L \subseteq \Sigma^{*}\right\}$(所有 $\Sigma^{*}$ 上语言的集合)
$\left\{\Sigma^{*}\right\}$(只包含语言 $\Sigma^{*}$ 的集合)
这部分引入了一个更高层次的抽象概念:语言的集合 (Set of Languages)。这在讨论语言的性质和对语言进行分类时非常关键。
- 从“字符串的集合”到“语言的集合”:
- 我们已经知道,一个语言是字符串的集合。
- 现在,我们可以把语言本身看作一个对象,然后把多个这样的对象(语言)放在一个更大的集合里,这个更大的集合就是“语言的集合”。
- 例子分析:
- $\{A\}$: 这是一个最简单的语言集合,它里面只有一个元素,这个元素就是语言 A。
- $\{L \mid L \subseteq\{0,1\}\}$:
- 这里的字母表是 $\Sigma=\{0,1\}$ 的一个子集,我们假设是 $\{0,1\}$ 本身。不,原文是 $L \subseteq \{0,1\}$。这意味着语言 L 中的字符串只能是 "0" 或 "1"。哦,我理解错了。$\{0,1\}$ 不是字母表,而是一个包含两个字符串 "0" 和 "1" 的语言。
- 让我们重新分析:L 是 { "0", "1" } 这个语言的子集。
- 一个集合的子集有哪些?这就要用到幂集的概念。
- { "0", "1" } 的幂集是:
- $\mathcal{P}(\{ \text{"0"}, \text{"1"} \}) = \{\varnothing, \{\text{"0"}\}, \{\text{"1"}\}, \{\text{"0"}, \text{"1"}\}\}$
- 这四个集合本身都是语言。所以,这个语言集合就是 {\varnothing, {"0"}, {"1"}, {"0", "1"}}。它是一个包含四个语言的集合。
- $\{L \mid L \subseteq \Sigma^* \text{ and } L \text{ is recognizable}\}$:
- 这是一个非常重要的语言集合,它代表了所有图灵可识别语言的集合,通常记作 RE。
- 它的元素是语言,筛选条件是“这个语言必须是可识别的”。
- 类似的,我们有所有正则语言的集合,所有可判定语言的集合(记作 R)。
- P 类 (Class P): $\{L \mid L \text{ can be decided in polynomial time}\}$
- 这是复杂性理论中的一个核心概念。它是一个语言集合。
- 它的元素是语言,筛选条件是“这个语言不仅是可判定的,而且存在一个判定器(图灵机),它能在多项式时间内完成判定”。
- NP 类 (Class NP): $\{L \mid L \text{ can be verified in polynomial time}\}$
- 这是另一个核心的复杂性类。它也是一个语言集合。
- 筛选条件是“对于这个语言中的任何字符串,我们都可以在多项式时间内验证它的一个‘证据’(证书)”。
- 棘手的例子分析:
- 区分类型: 关键在于搞清楚集合里的元素是什么。
- 字符串集合 (语言): 元素是字符串。例如 $L = \{\text{"a"}, \text{"b"}\}$。
- 语言集合: 元素是语言。例如 $C = \{L_1, L_2\}$,其中 $L_1=\{\text{"a"}\}, L_2=\{\text{"b"}\}$。
- $\{\varnothing\}$: 这是一个语言集合。它里面有一个元素,这个元素是空语言 $\varnothing$。它不是空的!
- $\varnothing$: 这是空集。如果把它看作语言集合,它是一个不包含任何语言的集合。如果把它看作语言,它是一个不包含任何字符串的集合。上下文很重要。
- $\{L \mid L \subseteq \Sigma^*\}$: 这是“所有语言的集合”,也就是全语言 $\Sigma^*$ 的幂集 $\mathcal{P}(\Sigma^*)$。这是一个极其巨大的集合。
- $\{\Sigma^*\}$: 这是一个语言集合。它里面只有一个元素,这个元素是全语言 $\Sigma^*$。
- 令字母表为 $\Sigma=\{a\}$。
- $\Sigma^*$ (全语言) = $\{\varepsilon, a, aa, aaa, \ldots\}$。
- $L_{even} = \{\varepsilon, aa, aaaa, \ldots\}$ (偶数长度的字符串语言)。
- $L_{odd} = \{a, aaa, aaaaa, \ldots\}$ (奇数长度的字符串语言)。
- $L_{finite} = \{a, aa\}$ (一个有限语言)。
- $C_1 = \{L_{even}, L_{odd}\}$。这是一个语言集合,它有两个元素。
- $C_2 = \{L_{finite}\}$。这是一个语言集合,它有一个元素。
- $L_{even} \cup L_{odd} = \Sigma^*$ (两个语言的并集是一个语言)。
- $\{L_{even}\} \cup \{L_{odd}\} = \{L_{even}, L_{odd}\} = C_1$ (两个语言集合的并集是一个语言集合)。
- 类型的混淆: 最根本的易错点是混淆元素的类型。问自己:“这个集合里的东西是什么?” 是字符串?还是语言(字符串的集合)?
- $\varnothing$ vs. $\{\varnothing\}$:
- $\varnothing$ 是一个空集,它的基数(大小)是 0。
- $\{\varnothing\}$ 是一个非空集合,它的基数是 1。它唯一的元素就是空集 $\varnothing$。
- $L$ vs. $\{L\}$:
- $L$ 是一个语言(一个字符串的集合)。
- $\{L\}$ 是一个语言集合,它只包含 $L$ 这一个语言。
本段通过引入“语言集合”的概念,将我们的视角提升了一个层次。我们不再仅仅研究单个语言,而是开始研究具有共同性质的语言所构成的集合,这些集合通常被称为语言类或复杂性类(如正则语言类、P、NP)。
语言集合是进行分类和抽象的必要工具。计算理论的一个主要目标就是根据“解决难度”来对所有可能的问题(语言)进行分类。P 类、NP 类、可判定语言类等都是语言集合,它们构成了计算复杂性的版图。没有这个概念,我们就无法讨论“所有正则语言都具有XX性质”或“P 是否等于 NP”这类高层问题。
[直觉心- 2. 集合基数
📜 [原文9]
集合的基数是它的大小,表示为 $|S|$。对于有限集合, $|S|$ 就是元素的数量。无限集合也有基数。为了证明两个集合具有相同的基数,即 $|S|=|T|$,我们需要从 $S$ 到 $T$ 的双射 $f$(回想一下,当且仅当对于每个 $y \in T$,存在唯一的 $x \in S$ 使得 $f(x)=y$ 时, $f$ 是双射)。
这部分引入了衡量集合大小的概念——基数 (Cardinality),并给出了比较两个集合大小的严格数学方法,特别是对于无限集合。
- 基数是什么?
- 基数就是集合中元素的数量。
- 符号: 一个集合 S 的基数记作 $|S|$。
- 对于有限集合: 这很简单,就是数一下有多少个元素。例如,如果 $S = \{a, b, c\}$,那么 $|S| = 3$。
- 无限集合的基数:
- 我们不能像数数一样去数无限集合的元素。那么,如何比较两个无限集合的大小呢?比如,整数多还是自然数多?
- 核心思想: 德国数学家康托 (Cantor) 提出了一个天才的想法:如果两个集合的元素可以建立一个“一一对应”的关系,那么我们就说它们一样大。
- 这个“一一对应”关系,在数学上就叫做双射 (Bijection)。
- 双射 (Bijection):
- 一个从集合 S 到集合 T 的函数 $f: S \rightarrow T$ 是一个双射,如果它同时满足两个条件:
- 单射 (Injection): 不会“多对一”。即如果 $x_1 \neq x_2$,那么一定有 $f(x_1) \neq f(x_2)$。每个输入都对应一个独一无二的输出。
- 满射 (Surjection): 不会“漏掉”。即对于集合 T 中的任何一个元素 y,我们总能在 S 中找到至少一个元素 x,使得 $f(x) = y$。
- 双射的直观理解: 就像在舞会上,如果男士(集合 S)和女士(集合 T)能够正好配成一对对,不多不少,那么男士和女士的数量就是一样多的。函数 f 就是这个配对的规则。
- 定义总结: 如果能在集合 S 和 T 之间找到一个双射函数,我们就定义它们具有相同的基数,记为 $|S| = |T|$。
- 有限集合示例:
- $S = \{a, b, c\}$, $T = \{1, 2, 3\}$。
- 我们可以定义一个双射函数 $f: S \rightarrow T$ 如下:
- $f(a) = 1$
- $f(b) = 2$
- $f(c) = 3$
- 这个函数是单射的(不同的字母对应不同的数字),也是满射的(T中的每个数字都被对应了)。
- 因此,我们得出 $|S| = |T| = 3$。
- 无限集合示例 (将在后续部分展示):
- 我们可以证明,所有自然数的集合 $\mathbb{N} = \{0, 1, 2, ...\}$ 和所有偶数的集合 $E = \{0, 2, 4, ...\}$ 的基数是相等的。
- 双射函数是 $f(n) = 2n$。对于每个自然数 n,都有一个唯一的偶数 $2n$ 与之对应,反之亦然。
- 这说明,尽管偶数集合看起来只是自然数集合的一部分,但从基数的角度看,它们“一样大”。这是无限集合反直觉的特性之一。
- 有限直觉的误用: 不能用处理有限集合的直觉来处理无限集合。对于有限集合,一个真子集的大小总是小于原集合。但对于无限集合,如上面的偶数例子,一个真子集的大小可以等于原集合。
- 双射是证明工具: 要证明 $|S|=|T|$,你需要实际地构造出一个双射函数 $f: S \rightarrow T$,并证明它的单射性和满射性。仅仅感觉它们一样大是不够的。
本段定义了基数作为衡量集合大小的尺度。对于有限集合,基数就是元素个数。对于无限集合,我们通过是否存在双射来判断两个集合的基数是否相等。
基数理论,特别是可数与不可数的区分,是计算理论中一个至关重要的证明工具。它被用来证明某些对象的数量远远多于另一些对象的数量。例如,通过证明“所有语言的集合是不可数的”而“所有图灵机的集合是可数的”,我们可以直接得出结论:必然存在一些语言是任何图灵机都无法识别的。这是证明不可识别语言存在性的最高层、最优雅的方法。
- 基数: 就像给每个集合(一个装满东西的袋子)贴上一个标签,上面写着这个袋子有多“满”。
- 双射: 想象有两个这样的袋子,你想知道里面的东西是不是一样多。你从第一个袋子里拿一个东西,再从第二个袋子里拿一个东西,把它们配成一对放在旁边。如果你能不断地这样做,直到两个袋子同时变空,那么它们里面的东西就是一样多的。这个配对过程就是双射。
想象你有两排椅子,一排红色,一排蓝色。你想知道两排椅子的数量是否相等。
- 你不需要去数每一排有多少把椅子。
- 你只需要尝试用绳子把红椅子和蓝椅子一一对应地绑起来。
- 如果每把红椅子都正好绑到了一把蓝椅子上,而且没有蓝椅子剩下,也没有红椅子剩下,那么两排椅子的数量就是相等的。这个“绑绳子”的规则就是双射函数。
2.1. 比较集合基数
📜 [原文10]
- 对于两个集合 $S, T$,如果存在一个双射 $f: S \rightarrow T$,我们说 $|S|=|T|$。
- 如果存在一个单射 $f: S \rightarrow T$,我们说 $|S| \leq|T|$。
我们还考虑以下重要事实。如果 $S \subseteq T$,则 $|S| \leq|T|$。
定义 2。如果集合 $S$ 是有限的或 $|S|=|\mathbb{N}|$ ,则 $S$ 是可数的。如果一个集合不是可数的,它就是不可数的。
或者,一个集合是可数的当且仅当每个元素都有一个有限字符串的描述,或者我们可以列举集合中的每个元素。注意 $\Sigma^{*}$ 总是可数的,所以我们可以将 $\Sigma^{*}$ 中的每个字符串列举为 $w_{1}, w_{2}, \ldots$。
这部分在上一节的基础上,给出了比较基数大小(≤)的定义,并引入了计算理论中最重要的基数分类:可数 (Countable) 与 不可数 (Uncountable)。
- 比较基数:
- 相等 ($|S|=|T|$): 存在从 S 到 T 的双射 (bijection)。
- 小于等于 ($|S| \le |T|$): 存在从 S 到 T 的单射 (injection)。
- 单射意味着“不重复”,即 S 中的每个元素都对应 T 中一个独一无二的元素。这就像把 S 中的所有元素都“塞进” T 中,并且没有两个 S 的元素被塞到同一个 T 的位置。这直观地说明了 T 的“容量”至少和 S 一样大。
- 重要事实 ($S \subseteq T \implies |S| \le |T|$): 如果 S 是 T 的子集,那么 S 的大小自然不会超过 T 的大小。我们可以构造一个最简单的单射函数 $f(x) = x$。对于 S 中的每个 x,它本身也在 T 中,所以这个函数是合法的单射。
- 可数集 (Countable Set):
- 定义: 一个集合 S 是可数的,如果满足以下两个条件之一:
- S 是有限集。
- S 的基数与自然数集 $\mathbb{N} = \{0, 1, 2, 3, \ldots\}$ 的基数相等,即 $|S| = |\mathbb{N}|$。这种情况也称为可数无限 (countably infinite)。
- 直观理解: 一个集合是可数的,意味着我们可以给它的所有元素“编号”,或者说,可以把它们排成一个(可能是无限的)列表,像 $e_0, e_1, e_2, \ldots$ 这样,不重不漏。这个列表的下标 (0, 1, 2, ...) 就来自自然数集 $\mathbb{N}$。这个列表过程本身就构造了一个从 $\mathbb{N}$ 到该集合的双射。
- 不可数集 (Uncountable Set):
- 定义: 如果一个集合不是可数的,那它就是不可数的。
- 直观理解: 不可数集是如此“巨大”,以至于我们无法用自然数去给它的所有元素编号。你永远无法列出一个完整的列表来包含它的所有元素,无论你的列表有多长,总会有元素被遗漏。
- 可数性的另一个视角:
- 有限描述: 一个集合是可数的,等价于它的每个元素都可以用一个有限长度的字符串来描述。既然每个元素都能表示成一个字符串,而所有字符串的集合 $\Sigma^*$ 本身是可数的(见下文),那么这个集合自然也是可数的。
- $\Sigma^*$ 是可数的: 我们可以按长度,再按字典序,将 $\Sigma^*$ 中的所有字符串排列成一个列表。例如,对于 $\Sigma=\{0, 1\}$:
- 长度 0: $\varepsilon$
- 长度 1: 0, 1
- 长度 2: 00, 01, 10, 11
- 长度 3: ...
- 这个列表 $w_0=\varepsilon, w_1=0, w_2=1, w_3=00, \ldots$ 不重不漏地包含了所有二进制字符串,所以 $\Sigma^*$ 是可数的。
- $|S| \le |T|$ 的示例:
- $S = \{a, b\}$, $T = \{1, 2, 3\}$。
- 我们可以构造一个单射函数 $f: S \rightarrow T$:$f(a)=1, f(b)=2$。
- 这个函数不是满射(3没有被用到),但它是单射。因此 $|S| \le |T|$。这符合我们的直觉 $2 \le 3$。
- 可数集示例:
- 有限集: $\{a, b, c\}$ 是可数的。
- 自然数集 $\mathbb{N}=\{0, 1, 2, \ldots\}$ 是可数无限的(这是定义)。
- 整数集 $\mathbb{Z}=\{\ldots, -2, -1, 0, 1, 2, \ldots\}$ 是可数无限的。我们可以这样列举它:$0, 1, -1, 2, -2, 3, -3, \ldots$。
- 有理数集 $\mathbb{Q}$ (所有可以表示为 p/q 的分数) 也是可数无限的(证明略复杂,通常用康托的对角线方法的变体)。
- 不可数集示例:
- 实数集 $\mathbb{R}$ 是不可数的。我们无法将所有实数(包括 $\pi, \sqrt{2}$ 等无理数)排成一个列表。
- 任何一个区间,如 [0, 1] 里的所有实数,也是不可数的。
- 一个集合的幂集 $\mathcal{P}(\mathbb{N})$ 是不可数的。
- 可数 vs. 可数无限: “可数”包含了“有限”和“可数无限”两种情况。在讨论无限集合时,通常说“可数无限”更精确。
- Cantor-Bernstein-Schroeder 定理: 这是一个更强的结论:如果 $|S| \le |T|$ 并且 $|T| \le |S|$,那么 $|S| = |T|$。也就是说,如果你能构造两个方向的单射,就不必非得构造一个双射来证明大小相等。这在证明中非常有用。
- 所有语言的集合是不可数的: 因为所有语言的集合就是 $\mathcal{P}(\Sigma^*)$,而 $\Sigma^*$ 是可数无限的,根据康托定理,一个无限集合的幂集是不可数的。
本段定义了比较集合大小的方法,并以此为基础将集合划分为可数和不可数两类。可数集可以被一一列举,而不可数集则大到无法被列举。所有字符串的集合 $\Sigma^*$ 是可数的。
这个划分是计算理论中一个至关重要的分水岭。因为图灵机(及其编码)是“有限字符串描述”的,所以所有图灵机的集合是可数的。然而,所有问题(语言)的集合却是不可数的。这个简单的基数对比,直接证明了“问题”的数量远远多于“解决方案”(图灵机)的数量,因此必然存在无法解决的问题。
- 可数集: 就像一个书架上的书,即使书有无限多本,你也可以给它们编号:第1本,第2本,...。
- 不可数集: 就像海滩上所有的沙子。你无法给每一粒沙子一个唯一的编号,因为它们太多了,而且是连续存在的。
- 列举整数集 $\mathbb{Z}$: 想象一条无限长的拉链。拉链的起点是 0。你往一个方向拉,拉出 1, 2, 3, ...;再往另一个方向拉,拉出 -1, -2, -3, ...。通过来回拉动,你可以遍历到每一个整数。
- 无法列举实数集 $\mathbb{R}$: 想象一条直线。你可以在上面标出 0, 1, 2, ...。但 0 和 1 之间还有无限多的点 (0.5, 0.333..., $\sqrt{0.5}$ 等)。无论你把这个列表做得多么密集,两个点之间永远有新的点,你永远也列不完。
2.2. 基数示例证明
📜 [原文11]
示例 1:
令 $\mathbb{Z}=\{\ldots,-2,-1,0,1,2, \ldots\}$(整数)和 $\mathbb{Z}_{\geq 0}=\{0,1,2,3, \ldots\}$(非负整数)。我们声称 $|\mathbb{Z}|=\left|\mathbb{Z}_{\geq 0}\right|$。遵循上述证明模板:构造一个函数 $f: \mathbb{Z} \rightarrow \mathbb{Z}_{\geq 0}$:
考虑 $\mathbb{Z}$ 中的两个元素 $x, y$。如果 $f(x)=f(y)$ 且值是偶数,那么我们知道 $x=f(x) / 2=f(y) / 2=y$。否则,如果是奇数,我们知道 $x=-(f(x)-1) / 2= -(f(y)-1) / 2=y$。所以得出 $f(x)=f(y)$ 当且仅当 $x=y$。因此,$f$ 是单射的,给出 $|\mathbb{Z}| \leq\left|\mathbb{Z}_{\geq 0}\right|$。
此外,由于 $\mathbb{Z}_{\geq 0} \subseteq \mathbb{Z}$,我们知道 $|\mathbb{Z}| \geq\left|\mathbb{Z}_{\geq 0}\right|$。得出 $|\mathbb{Z}|=\left|\mathbb{Z}_{\geq 0}\right|$。
这个例子通过一个具体的构造性证明,展示了如何应用基数理论来证明两个无限集合的大小相等。这里要证明的是整数集 $\mathbb{Z}$ 和非负整数集 $\mathbb{Z}_{\ge 0}$(也就是自然数集 $\mathbb{N}$)是“一样大”的。
- 证明目标: 证明 $|\mathbb{Z}| = |\mathbb{Z}_{\ge 0}|$。
- 证明策略: 根据上一节的定义,我们可以选择两种主要策略:
- 策略 A (双射): 构造一个从 $\mathbb{Z}$ 到 $\mathbb{Z}_{\ge 0}$ 的双射函数 f,并证明其单射性和满射性。
- 策略 B (双向单射): 分别构造两个方向的单射函数:一个 $f_1: \mathbb{Z} \to \mathbb{Z}_{\ge 0}$ 和另一个 $f_2: \mathbb{Z}_{\ge 0} \to \mathbb{Z}$。根据 Cantor-Bernstein-Schroeder 定理,这同样能证明它们基数相等。
- 这里的文本采用的是策略 B,虽然它构造的那个函数 f 实际上就是一个双射。
- 构造函数:
- 思路: 如何把所有整数(有正有负)不重不漏地映射到所有非负整数上?一个常见的想法是“交错”映射:把非负整数 (0, 1, 2, ...) 映射到偶数 (0, 2, 4, ...),把负整数 (-1, -2, -3, ...) 映射到奇数 (1, 3, 5, ...)。
- 函数定义:
- 当输入 x 是非负整数时(0, 1, 2, ...),输出是 $2x$(0, 2, 4, ...),即所有的偶数。
- 当输入 x 是负整数时(-1, -2, -3, ...),输出是 $1-2x$(3, 5, 7, ...)。咦,这里好像和我的想法有点出入,让我们代入算一下:
- $f(-1) = 1 - 2(-1) = 3$
- $f(-2) = 1 - 2(-2) = 5$
- $f(-3) = 1 - 2(-3) = 7$
- 它把负整数映射到了从3开始的奇数。那么数字1去哪了?让我们检查一下原文,原文是 $1-2x$。啊,如果 x < 0,-2x 是正偶数,1-2x 才是奇数。
- 让我们换个更常见的函数来理解这个思路:
- $g(0)=0, g(1)=2, g(2)=4, \ldots$ (映射到偶数)
- $g(-1)=1, g(-2)=3, g(-3)=5, \ldots$ (映射到奇数)
- 这个 g(x) 是一个完美的双射。原文中的 f(x) 似乎有点问题,因为它没有映射到1。让我们假设原文的 $1-2x$ 应该是 $-2x-1$ 或者类似能覆盖所有奇数的函数。不过,我们还是按照原文的逻辑来分析它的证明过程。
- 证明过程 (按原文):
- 第一步:证明 $|\mathbb{Z}| \le |\mathbb{Z}_{\ge 0}|$
- 这需要证明存在一个单射 $f: \mathbb{Z} \to \mathbb{Z}_{\ge 0}$。
- 原文声称它构造的 $f(x)$ 是单射的。
- 证明单射性: 需要证明如果 $f(x) = f(y)$,那么必然 $x=y$。
- 情况1: 如果 $f(x) = f(y)$ 是一个偶数,那么 x 和 y 必定都是 $\ge 0$ 的(因为只有上半部分规则产生偶数)。所以 $2x = 2y$,推出 $x=y$。
- 情况2: 如果 $f(x) = f(y)$ 是一个奇数,那么 x 和 y 必定都是 $<0$ 的。所以 $1-2x = 1-2y$,推出 $-2x = -2y$,再次推出 $x=y$。
- 情况3: 不可能一个偶数等于一个奇数。
- 综上所述,只要 $f(x)=f(y)$,就一定有 $x=y$。所以 f 是单射的。
- 根据定义,这证明了 $|\mathbb{Z}| \le |\mathbb{Z}_{\ge 0}|$。
- 第二步:证明 $|\mathbb{Z}| \ge |\mathbb{Z}_{\ge 0}|$
- 这需要证明存在一个单射 $g: \mathbb{Z}_{\ge 0} \to \mathbb{Z}$。
- 原文用了一个更简单的事实:$\mathbb{Z}_{\ge 0}$ 是 $\mathbb{Z}$ 的一个子集。
- 根据上一节的结论 "$S \subseteq T \implies |S| \le |T|$",我们直接可以得到 $|\mathbb{Z}_{\ge 0}| \le |\mathbb{Z}|$,这等价于 $|\mathbb{Z}| \ge |\mathbb{Z}_{\ge 0}|$。
- 第三步:结论
- 既然我们证明了 $|\mathbb{Z}| \le |\mathbb{Z}_{\ge 0}|$ 和 $|\mathbb{Z}| \ge |\mathbb{Z}_{\ge 0}|$,根据 Cantor-Bernstein-Schroeder 定理,我们可以得出结论:$|\mathbb{Z}| = |\mathbb{Z}_{\ge 0}|$。
- 这是一个分段函数 (piecewise function)。它的行为取决于输入 x 的范围。
- 上半部分 ($x \ge 0$): $f(x) = 2x$。
- $f(0) = 0$
- $f(1) = 2$
- $f(2) = 4$
- ... (将非负整数映射到非负偶数)
- 下半部分 ($x < 0$): $f(x) = 1 - 2x$。
- $f(-1) = 1 - 2(-1) = 3$
- $f(-2) = 1 - 2(-2) = 5$
- $f(-3) = 1 - 2(-3) = 7$
- ... (将负整数映射到从3开始的奇数)
- 这个函数的像集 (Image/Range) 是 $\{0, 2, 3, 4, 5, 6, 7, \ldots\}$。它不包含 1。因此,这个函数不是满射,也就不是双射。但是,它确实是单射的,所以原文用它来证明 $|\mathbb{Z}| \le |\mathbb{Z}_{\ge 0}|$ 的逻辑是成立的。
- 使用原文的 f(x):
- 输入 5 (>= 0),输出 $2*5 = 10$。
- 输入 -3 (< 0),输出 $1 - 2*(-3) = 7$。
- 不同的输入确实映射到了不同的输出。
- 使用我们改进的 g(x) (这是一个双射):
- $g(x)= \begin{cases}2 x & \text { if } x \geq 0 \\ -2x - 1 & \text { if } x<0\end{cases}$
- $g(0) \to 0$
- $g(1) \to 2$
- $g(-1) \to 1$
- $g(2) \to 4$
- $g(-2) \to 3$
- 这个映射关系是 0 -> 0, 1 -> 2, 2 -> 4, ... 和 -1 -> 1, -2 -> 3, ...。
- 它完美地将 $\mathbb{Z}$ 中的元素与 $\mathbb{Z}_{\ge 0}$ 中的元素一一对应起来,不重不漏。这直接证明了 $|\mathbb{Z}| = |\mathbb{Z}_{\ge 0}|$。
- 构造函数的正确性: 在构造函数时,要仔细检查它是否真的满足单射或双射的性质。如我们分析的,原文的 f(x) 并不是一个双射,但它足以完成证明的第一部分。
- 证明的完备性: 要证明基数相等,严格来说需要双向的小于等于关系,或者一个完整的双射证明。原文的证明是有效的,因为它使用了双向小于等于的策略。
本段通过一个具体的例子,展示了如何使用构造单射函数的方法来证明整数集和非负整数集的基数相等。这个结论本身说明了整数集是可数无限的。
这个例子是基数理论应用的入门。它训练学生如何思考无限集合的对应关系,并使用数学工具(构造函数并证明其性质)来严格地论证反直觉的结论。这是后续理解更复杂的基数论证(如康托的对角线法)的必要练习。
证明 $|\mathbb{Z}| = |\mathbb{Z}_{\ge 0}|$ 就像整理一排无限长的队伍。队伍里有正数、负数和零,乱糟糟的。你想证明这群人和另一排只有 0, 1, 2, 3... 的队伍人数一样多。
你的策略是:
- 让 0 号(来自 $\mathbb{Z}$)站到新队伍的 0 号位置。
- 让 1 号(来自 $\mathbb{Z}$)站到新队伍的 2 号位置。
- 让 -1 号(来自 $\mathbb{Z}$)站到新队伍的 1 号位置。
- 让 2 号(来自 $\mathbb{Z}$)站到新队伍的 4 号位置。
- 让 -2 号(来自 $\mathbb{Z}$)站到新队伍的 3 号位置。
...
通过这种方式,你把原来乱糟糟的队伍里的每一个人,都安排到了新队伍的一个唯一的位置上,并且新队伍的所有位置也都被占满了。这就证明了两边人一样多。
想象一根无限长的绳子,上面每隔一米有一个标记,标记着整数 ..., -2, -1, 0, 1, 2, ...。
现在你把这根绳子在 0 点处对折,但是不完全重合,而是把负数部分拉到正数部分的空隙里。
- 0 还在原地。
- 1 的位置是 1。
- -1 被你拉到了 2 的位置。
- 2 的位置是 3。
- -2 被你拉到了 4 的位置。
...
通过这种操作,你把原来双向无限的绳子变成了一条单向无限的、更“紧凑”的绳子,但上面的标记一个都不少。这直观地展示了它们可以一一对应。
2.3. 基数的分类与关系
📜 [原文12]
我们有一些形容词来描述具有某些基数的集合:“无限”集合要么是可数无限的,要么是不可数无限的,“可数”集合要么是有限的,要么是可数无限的,而“不可数”集合是不可数无限的。
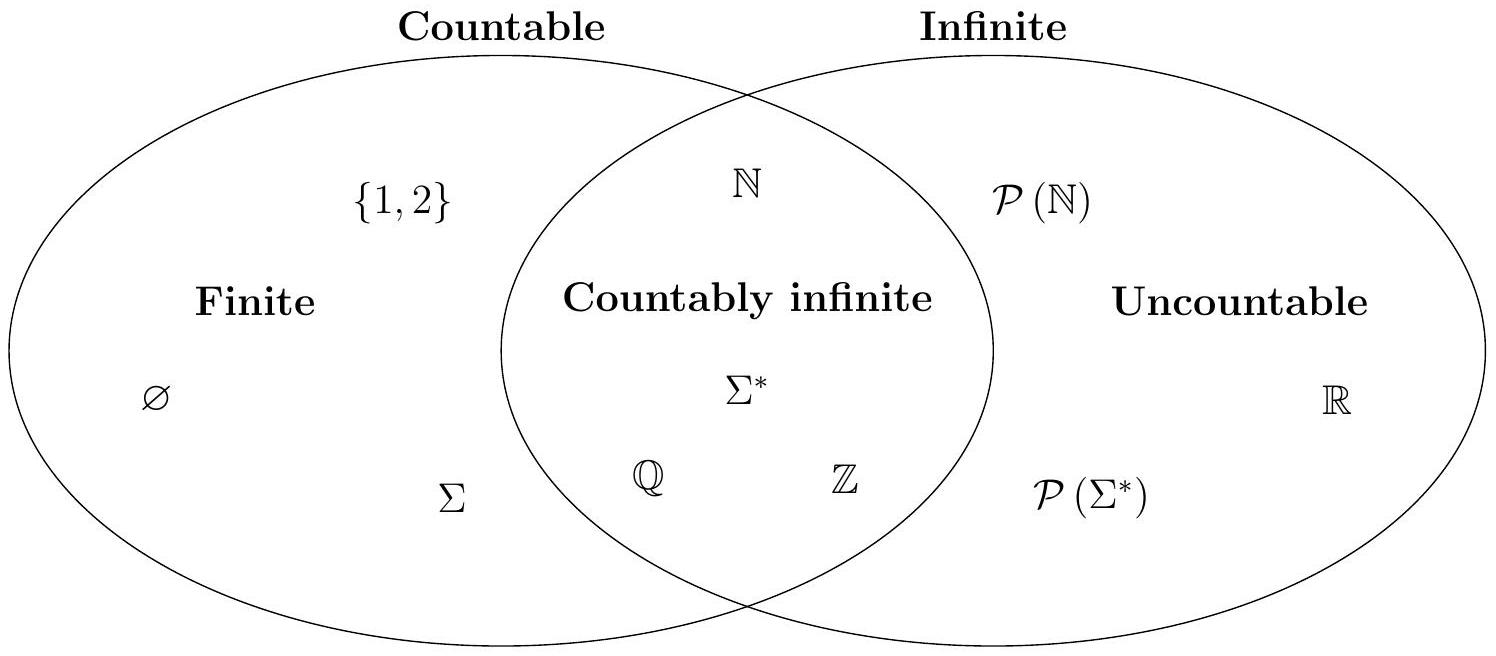
图 1:不同类型基数之间的关系。
这部分内容和配图是为了梳理和澄清之前引入的各种关于集合大小的术语之间的逻辑关系。
- 术语梳理:
- 有限 (Finite): 元素个数是有限的。例如 $|\{a,b\}|=2$。
- 无限 (Infinite): 不是有限的。
- 可数无限 (Countably Infinite): 与自然数集 $\mathbb{N}$ 等大的无限集合。例如 $|\mathbb{Z}|=|\mathbb{N}|$。
- 不可数无限 (Uncountably Infinite): 比自然数集 $\mathbb{N}$ 更大的无限集合。例如 $|\mathbb{R}| > |\mathbb{N}|$。也简称为不可数 (Uncountable)。
- 可数 (Countable): 这是一个更宽泛的概念,它包括了所有有限集和所有可数无限集。
- 图 1 解读:
- 最外层的椭圆代表“所有集合”。
- “所有集合”被一条竖线分成了两部分:左边的“有限集”和右边的“无限集”。这两部分互不相交,且并集是所有集合。
- 在右边的“无限集”内部,又被分成了两部分:左边的“可数无限集”和右边的“不可数无限集”。
- 图中用一个更大的椭圆框住了“有限集”和“可数无限集”,并标记为“可数集”。这清晰地表明了“可数 = 有限 或 可数无限”。
- 图中“不可数无限集”也被标记为“不可数集”,说明“不可数”和“不可数无限”是同义词,因为不存在“有限的不可数集”。
- 逻辑关系总结:
- 集合 = 可数集 $\cup$ 不可数集
- 可数集 = 有限集 $\cup$ 可数无限集
- 无限集 = 可数无限集 $\cup$ 不可数集
- 不可数集 = 不可数无限集
- 有限集:
- $A = \{1, 2, 3\}$, $|A|=3$。A 是有限的,因此也是可数的。
- 可数无限集:
- $\mathbb{N} = \{0, 1, 2, \ldots\}$。$\mathbb{N}$ 是可数无限的,因此是可数的,也是无限的。
- $\Sigma^*$, $\mathbb{Z}$, $\mathbb{Q}$ 也都属于这一类。
- 不可数集 (即不可数无限集):
- $\mathbb{R}$ (实数集)。$\mathbb{R}$ 是不可数的,也是无限的。
- $\mathcal{P}(\mathbb{N})$ (自然数集的幂集)。这也是不可数的。
- $\mathcal{P}(\Sigma^*)$ (所有语言的集合)。这也是不可数的。
- “可数” vs. “可数无限”: 在口语或非严格讨论中,人们有时会用“可数”来指代“可数无限”。但在严格的数学语境下,要记住“可数”也包含有限的情况。例如,提问“正则语言的集合是可数的吗?” 和 “正则语言的集合是可数无限的吗?” 是有细微差别的(尽管在这个特定例子中答案都是“是”)。
- “无限” vs. “不可数”: 无限是一个更大的概念,它包含了可数无限和不可数两种。不要把两者混淆。整数集 $\mathbb{Z}$ 是无限的,但它是可数的,不是不可数的。
本段通过文字和图表,系统地梳理了有限、无限、可数、可数无限、不可数这五个核心术语的定义和它们之间的层级与包含关系。
在进行计算理论的证明时,精确地使用这些术语至关重要。例如,当我们说“图灵机的集合是可数的”,我们实际上指的是它是可数无限的。当我们说“语言的集合是不可数的”,我们指的是它是不可数无限的。清晰的术语是进行清晰推理的前提,这张图帮助学习者建立一个清晰的心理框架,避免混淆。
想象一个图书馆的分类系统:
- 所有集合: 整个图书馆的所有书籍。
- 有限集: 单卷本的书。
- 无限集: 多卷册的系列丛书,而且这个系列永远出不完。
- 可数无限集: 像《读者文摘》合订本,你可以清楚地标号:1980年卷,1981年卷...
- 不可数无限集: 一本“魔法书”,每一页之间都还能翻出新的一页,你永远无法给所有页码编号。
- 可数集: 图书馆里所有单卷本的书 + 所有可以按卷编号的系列丛书。
把集合想象成不同类型的珠子。
- 有限集: 一小把珠子,你能数得清。
- 可数无限集: 一条无限长的项链,珠子一颗接一颗,你可以沿着项链数下去:第1颗,第2颗...
- 不可数集: 一大桶黏土。你无法从中“分离”出独立的“珠子”来数,因为它们是连续混合在一起的。
2.4. 康托对角线法及其应用
📜 [原文13]
康托对角线法证明了 $|\mathbb{N}|<|\mathcal{P}(\mathbb{N})|$。(事实上,对于任何无限集合 $X$,我们知道 $\mathcal{P}(X)$ 是不可数的)。换句话说,可数集合比不可数集合小。由此我们知道不存在从 $\mathbb{N}$ 到 $\mathcal{P}(\mathbb{N})$ 的满射。
21 应用于可识别性
令 $\mathbb{M}$ 为所有图灵机的集合。考虑编码映射 $f(M)=\langle M\rangle$。由于编码是从 $\mathbb{M}$ 到 $\Sigma^{*}$ 的单射,并且 $\Sigma^{*}$ 是可数的,这表明 $\mathbb{M}$ 是可数的。让我们继续用基数来描述我们从图灵机研究中知道的集合:
```
\Sigma: 有限的。
\Sigma*: 可数的。
L\in \Sigma* (任何语言): 可数的。
M (图灵机集合): 可数无限的。
P(5*)(所有语言的集合): 不可数的。
```
现在考虑从图灵机到它识别的语言的函数 $L: \mathbb{M} \rightarrow \mathcal{P}\left(\Sigma^{*}\right)$。由于 $\mathcal{P}\left(\Sigma^{*}\right)$ 是不可数的,我们知道映射不能是满射。换句话说,存在某个语言 $S \in \mathcal{P}\left(\Sigma^{*}\right)$ 使得没有图灵机识别 $S$。同样的证明技术可以用来表明任何不可数语言集合都包含一些不可识别语言。
这部分是基数理论在计算理论中的第一个高潮应用。它使用康托对角线法 (Cantor's Diagonalization Argument) 的结论,通过简单的集合大小比较,直接证明了不可解问题的存在性。
- 康托对角线法:
- 这是一个著名的数学证明方法,由康托提出。
- 其核心结论是:对于任何集合 X,其幂集 $\mathcal{P}(X)$ 的基数严格大于 X 本身的基数。即 $|X| < |\mathcal{P}(X)|$。
- 应用到自然数集 $\mathbb{N}$ 上,我们得到 $|\mathbb{N}| < |\mathcal{P}(\mathbb{N})|$。
- 因为 $|\mathbb{N}|$ 是可数无限的“标杆”,所以这个不等式意味着 $\mathcal{P}(\mathbb{N})$ 是不可数的。
- $|S| < |T|$ 意味着不存在从 S 到 T 的满射 (surjection)。也就是说,你无法用 S 中的元素去“覆盖” T 中的所有元素,T 总是会有剩下的。
- 应用于可识别性:
- 核心论证步骤:
- 确定“解决方案”的集合有多大。
- 确定“问题”的集合有多大。
- 比较两者的大小。
- 步骤 1:解决方案有多大?
- “解决方案”就是图灵机。我们要确定所有图灵机的集合 $\mathbb{M}$ 的基数。
- 每个图灵机 M 都可以被编码为一个有限字符串 $\langle M \rangle$。
- 这个编码过程 $f(M) = \langle M \rangle$ 是一个单射(不同的图灵机有不同的编码)。
- 所以, $|\mathbb{M}| \le |\Sigma^*|$ (所有字符串的集合)。
- 我们已经知道 $\Sigma^*$ 是可数的。
- 因此,图灵机的集合 $\mathbb{M}$ 也是可数的。
- 步骤 2:问题有多大?
- “问题”就是语言。我们要确定所有语言的集合的基数。
- 所有语言的集合,根据定义,就是 $\mathcal{P}(\Sigma^*)$ (所有字符串集合的子集的集合)。
- 因为 $\Sigma^*$ 是可数无限的(等价于 $\mathbb{N}$),根据康托定理,它的幂集 $\mathcal{P}(\Sigma^*)$ 是不可数的。
- 步骤 3:比较大小
- 解决方案的集合 $\mathbb{M}$ 是可数的。
- 问题的集合 $\mathcal{P}(\Sigma^*)$ 是不可数的。
- 可数集严格小于不可数集。
- 最终结论:
- 我们有一个从图灵机集合 $\mathbb{M}$ 到语言集合 $\mathcal{P}(\Sigma^*)$ 的映射 $L$,它为每个图灵机 M 指定它所识别的语言 $L(M)$。
- 由于定义域 $\mathbb{M}$ 是可数的,而值域 $\mathcal{P}(\Sigma^*)$ 是不可数的,这个映射不可能是满射。
- “不可能是满射”意味着,在值域(所有语言的集合)中,必然存在一些语言,是没有任何图灵机(来自定义域)能够映射到它的。
- 换句话说:存在一些语言,是任何图灵机都无法识别的。这些就是不可识别语言。
- 基数总结表:
- $\Sigma$ (字母表): 有限。
- $\Sigma^*$ (所有字符串): 可数无限。
- $L \subseteq \Sigma^*$ (任何一个语言): 最多是可数无限的(因为它是可数集 $\Sigma^*$ 的子集),也可能是有限的。所以是可数的。
- $\mathbb{M}$ (所有图灵机): 可数无限。
- $\mathcal{P}(\Sigma^*)$ (所有语言): 不可数。 (原文 P(5*) 疑似笔误,应为 $\mathcal{P}(\Sigma^*)$)
这个证明是高度抽象的,很难用简单的数值示例来展示。但我们可以做一个类比:
- 假设你的“解决方案”是整数 $\mathbb{Z} = \{\ldots, -1, 0, 1, \ldots\}$。
- 假设你的“问题”是实数 $\mathbb{R}$。
- 我们知道整数集是可数的,实数集是不可数的。
- 现在你想用每个整数去“代表”一个实数。
- 你的映射 $f: \mathbb{Z} \to \mathbb{R}$ 可以是 $f(i) = i$。这会代表所有的整数实数。
- 但无论你怎么设计这个映射,你都无法用可数的整数去覆盖掉所有不可数的实数。像 $\pi, \sqrt{2}, 0.5$ 这样的实数很可能就没被你代表到。
- 结论:实数比整数“多得多”,因此必然存在无法被整数代表的实数。
- 把“整数”换成“图灵机”,把“实数”换成“语言”,就是这个证明的逻辑。
- 误认为所有无限集都一样大: 这是康托理论打破的主要错误直觉。无限是有“大小”等级的,可数无限是最低的等级。
- 语言 vs. 语言的集合: 任何单个语言 L,因为它只是字符串的集合,所以它必然是可数的。而所有这些可数的语言汇集在一起形成的集合 $\mathcal{P}(\Sigma^*)$ 却是不可数的。这个层次的跳跃是关键。
本段展示了计算理论中一个最深刻、最优雅的证明。通过比较“图灵机”集合(可数)和“语言”集合(不可数)的基数,我们无需构造任何具体的语言,就能直接证明不可识别语言(即算法无法解决的问题)必然存在。
这个非构造性的存在性证明,为我们探索计算的边界提供了理论基础。它告诉我们,寻找所有问题的通用算法是注定要失败的,我们的任务变成了去划分哪些问题是可解的,哪些是不可解的。它为停机问题等具体不可判定问题的发现铺平了道路。
想象一个酒店,它有无限但可数的房间(房间号是 1, 2, 3, ...)。
现在来了一群客人,这群客人的数量是不可数的(比如,每个客人的名字是 [0,1] 区间的一个实数)。
酒店经理(映射函数)尝试给每个客人安排一个房间。
因为房间是可数的,而客人是不可数的,客人比房间“多得多”。
所以无论经理怎么安排,必然会有客人没地方住。
- 酒店房间 -> 图灵机 (解决方案)
- 客人 -> 语言 (问题)
- 没地方住的客人 -> 不可识别语言 (无法解决的问题)
想象一条无限长的单行道,上面每隔一米停着一辆车(图灵机,可数)。
现在天上要降下无数的雨滴(语言,不可数)。
每一滴雨都要落在路面上。
由于路面上的车的数量(可数)远远少于雨滴的数量(不可数),必然有无数的雨滴会落到没有车的地方。
那些落在空地上的雨滴,就代表着没有图灵机能“接住”(识别)的语言。
3. 图灵机
3.1. 形式定义
📜 [原文14]
图灵机是一个 7-元组 ( $Q, \Sigma, \Gamma, \delta, q_{0}, q_{\text {accept }}, q_{\text {reject }}$ ),其中
- $Q$ 是一个有限状态集合,
- $\Sigma$ 是输入字母表, $\sqcup \notin \Sigma$,
- $\Gamma$ 是磁带字母表, $\sqcup \in \Gamma$ 且 $\Sigma \subset \Gamma$,
- $\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}$ 是转移函数,
- $q_{0} \in Q$ 是开始状态,
- $q_{\text {accept }} \in Q$ 是接受状态,
- $q_{\text {reject }} \in Q$ 是拒绝状态, $q_{\text {accept }} \neq q_{\text {reject }}$。
这可能看起来很难处理。然而,一旦你理解了转移函数的工作原理,这个定义的每一行都应该变得有意义。机器通过读取磁头处的字符 $\gamma$,计算 $\delta(q, \gamma)=\left(q^{\prime}, \gamma^{\prime}, D\right)$,在当前位置的磁带上写入 $\gamma^{\prime}$,根据 $D$ 向左或向右移动磁头,并进入状态 $q^{\prime}$ 来操作。它重复此过程,只有当达到 $q_{\text {accept }}$ 或 $q_{\text {reject }}$ 时才停止。
这部分给出了图灵机 (Turing Machine, TM) 的严格数学定义。图灵机是一个抽象的计算模型,旨在模拟任何计算机算法能做的事情。这个 7-元组定义了图灵机的所有组成部分及其规则。
- $Q$ (状态集):
- 定义: 一个有限的状态集合。
- 作用: 状态代表了图灵机的“内存”。在任何时刻,图灵机都处于这些状态之一。例如,一个状态可能表示“正在寻找一个1”,另一个状态可能表示“已经找到了一个1,正在返回磁带开头”。因为集合是有限的,所以图灵机的“内部程序”是有限的。
- $\Sigma$ (输入字母表):
- 定义: 用于书写初始输入字符串的符号集合。
- 约束: 它不能包含空白符 $\sqcup$。
- 作用: 定义了图灵机要解决的问题所使用的字符集。例如,对于二进制字符串问题,$\Sigma=\{0,1\}$。
- $\Gamma$ (磁带字母表):
- 定义: 图灵机可以在其磁带上读写的符号集合。
- 约束:
- 它必须包含空白符 $\sqcup$。空白符代表磁带上未使用的格子。
- 它必须包含整个输入字母表 ($\Sigma \subset \Gamma$)。这意味着图灵机至少能读懂输入,并且它还可以在磁带上写入一些额外的“草稿”符号。
- 作用: 提供了图灵机的工作空间和工作符号。例如,为了标记某个位置,图灵机可以在磁带上写一个不在 $\Sigma$ 中的特殊符号,如 'X'。
- $\delta$ (转移函数):
- 定义: 这是图灵机的“程序”或“大脑”。它是一个函数,告诉图灵机在特定情况下该做什么。
- 输入: $\delta$ 的输入是一个二元组 (当前状态, 当前磁带头下的符号)。
- 输出: $\delta$ 的输出是一个三元组 (下一个状态, 要写入磁带的符号, 磁带头移动方向)。
- 格式: $\delta: Q \times \Gamma \rightarrow Q \times \Gamma \times \{\mathrm{L}, \mathrm{R}\}$
- $Q \times \Gamma$: 当前状态和当前磁带符号。
- $\rightarrow$: "映射到"。
- $Q \times \Gamma \times \{\mathrm{L}, \mathrm{R}\}$: 新状态,要写入的新符号,以及移动方向(L代表向左,R代表向右)。
- 例子: $\delta(q_1, 'a') = (q_2, 'b', R)$ 的意思是:“如果机器当前在状态 $q_1$,并且磁带头下方的符号是 'a',那么:1. 将状态切换到 $q_2$;2. 在当前位置的磁带上写入 'b';3. 将磁带头向右移动一格。”
- $q_0$ (开始状态):
- 定义: $Q$ 中的一个特殊状态。
- 作用: 图灵机的计算总是从这个状态开始。
- $q_{\text{accept}}$ (接受状态):
- 定义: $Q$ 中的一个特殊状态。
- 作用: 一旦图灵机进入这个状态,计算立即停止,并宣布接受输入。
- $q_{\text{reject}}$ (拒绝状态):
- 定义: $Q$ 中的一个特殊状态。
- 约束: 它必须与接受状态不同 ($q_{\text{accept}} \ne q_{\text{reject}}$)。
- 作用: 一旦图灵机进入这个状态,计算立即停止,并宣布拒绝输入。
让我们设计一个简单的图灵机,它判定语言 $L = \{w \in \{0\}^* \mid |w| \text{ is even}\}$ (由偶数个 '0' 组成的字符串)。
- $Q$: $\{q_0, q_1, q_{\text{accept}}, q_{\text{reject}}\}$
- $q_0$: 开始状态,也代表“目前已读过偶数个0”。
- $q_1$: 代表“目前已读过奇数个0”。
- $\Sigma$: $\{0\}$ (输入字母表)
- $\Gamma$: $\{0, \sqcup\}$ (磁带字母表,这里不需要额外符号)
- $q_0$: $q_0$
- $q_{\text{accept}}$: $q_{\text{accept}}$
- $q_{\text{reject}}$: $q_{\text{reject}}$
- $\delta$ (转移函数):
- $\delta(q_0, 0) = (q_1, 0, R)$: 在 $q_0$ (偶数) 状态读到 0,变成奇数状态 $q_1$,向右移动。
- $\delta(q_1, 0) = (q_0, 0, R)$: 在 $q_1$ (奇数) 状态读到 0,变回偶数状态 $q_0$,向右移动。
- $\delta(q_0, \sqcup) = (q_{\text{accept}}, \sqcup, R)$: 在 $q_0$ (偶数) 状态读到结尾的空白,说明总共有偶数个0,接受。
- $\delta(q_1, \sqcup) = (q_{\text{reject}}, \sqcup, R)$: 在 $q_1$ (奇数) 状态读到结尾的空白,说明总共有奇数个0,拒绝。
- (为完备性,还需定义在 $q_0, q_1$ 读到非0符号的情况,都转到 $q_{reject}$,这里省略)。
- 运行示例: 输入 00
- 开始: 状态 $q_0$, 磁带 _0_0_sqcup_..., 读头在第一个 0。
- $\delta(q_0, 0) \to (q_1, 0, R)$: 状态变 $q_1$, 磁带不变, 读头移到第二个 0。
- $\delta(q_1, 0) \to (q_0, 0, R)$: 状态变 $q_0$, 磁带不变, 读头移到 $\sqcup$。
- $\delta(q_0, \sqcup) \to (q_{\text{accept}}, \sqcup, R)$: 状态变 $q_{\text{accept}}$,停机并接受。
- 确定性: 这个定义的图灵机是确定性图灵机 (Deterministic Turing Machine, DTM),因为转移函数 $\delta$ 的输出是唯一的。对于任何 (状态, 符号) 组合,只有一种行动方案。
- 无限磁带: 图灵机的关键在于其拥有一个双向无限长的磁带,这给了它无限的存储空间。
- 元组的严谨性: 形式化定义要求写全所有7个部分。在考试或作业中,如果要求形式化定义,就必须把所有这些集合和函数都清晰地列出来。
本段给出了确定性图灵机的7元组形式化定义。这个定义精确地描述了图灵机的静态构成(状态、字母表)和动态行为(转移函数),是所有后续图灵机理论的基石。
形式化定义是进行严格数学证明的基础。虽然我们之后更多地使用“高级描述”,但所有这些高级描述最终都必须能够被翻译成符合这个7元组定义的、具体的图灵机。这个定义确保了我们讨论的“算法”是一个有坚实数学基础的、无歧义的对象。
想象一个在一条无限长的铁轨上工作的小机器人。
- 磁带: 铁轨,被划分成一格一格的。
- 符号: 每一格上可以画上不同的标记 (0, 1, X, ...)。
- 磁带头: 机器人本身,它一次只能站在一格铁轨上,并能看到这一格的标记。
- 状态 ($Q$): 机器人内部有一个显示屏,显示它当前的“工作模式”(例如,“模式A:寻找0”,“模式B:返回起点”)。
- 转移函数 ($\delta$): 机器人有一本操作手册。它根据自己当前的“工作模式”(状态)和脚下铁轨的标记(符号),去查手册。手册会告诉它三件事:1. 下一个工作模式是什么;2. 在脚下的格子里画上什么新标记;3. 向左走一格还是向右走一格。
- $q_0, q_{accept}, q_{reject}$: 手册里规定了“开机模式”,以及两种“关机模式”(一种是“任务成功”,一种是“任务失败”)。
你正在用纸带和铅笔做长除法。
- 磁带: 无限长的方格纸。
- 符号: 数字0-9,小数点等。
- 磁带头: 你的眼睛和铅笔尖,一次只能聚焦在一个位置。
- 状态: 你心里的计算步骤(“现在在做减法”,“现在要把下一位数字拿下来”)。
- 转移函数: 你学过的长除法规则。根据你当前在做的步骤和看到的数字,你决定下一步写什么、以及看哪个位置的数字。
这个过程可以被一个图灵机精确地模拟。
3.2. 高级描述
📜 [原文15]
我们图灵机和算法互换使用。在课堂上,我们展示了图灵机能够执行许多涉及字符串和数字的操作;事实上,它们更强大。任何你可以在编程语言中编写的算法都可以通过图灵机来模拟:丘奇-图灵论题假定图灵机可以模拟任何合理的计算模型。因此,在给出图灵机规范时,我们经常使用高级描述(即伪代码)来描述一台机器。
允许的语法和操作示例包括以下内容:
- 变量:赋值变量并使用它们的值,添加或删除有限列表和集合中的元素,检查有限列表或集合中的成员资格。
- 控制流:使用循环,条件跳转,或if-then-else语句。
- 字符串操作:移动字符串,追加字符串,反转字符串,查找字符串的第 $n$ 个字符,查找和替换子字符串。
- 算术运算:整数或有理数的加、减、乘、除或幂运算,检查一个数字是否能被另一个数字整除,比较或检查相等性。
- 图:检查图编码是否有效,检查顶点是否有邻居,添加或删除边和顶点,在边和顶点上放置标记。
- 图灵机:检查编码是否有效,在输入上运行图灵机,在输入上运行图灵机若干步骤,并编写一台新的图灵机。
图灵机上的操作可能很微妙。因为图灵机可以永远运行(并且无法检查图灵机是否会永远运行,因为我们证明了 $\mathrm{HALT}_{\mathrm{TM}}$ 是不可判定的),我们必须在我们的构造中考虑这一点。
这部分解释了为什么我们在描述图灵机时,可以并且应该从繁琐的形式化定义转向更易于理解的高级描述,并列举了哪些操作被认为是“合法的”高级操作。
- 图灵机 = 算法:
- 丘奇-图灵论题 (Church-Turing Thesis): 这是一个非常重要的哲学论点,而不是一个可以被证明的数学定理。它声称,任何我们直觉上认为的“可计算的”、“机械的”过程或“算法”,都可以被一台图灵机所模拟。
- 实践意义: 这意味着,如果我们能用任何一种编程语言(如 Python, C++, Java)写出一个算法,或者用伪代码清晰地描述一个算法步骤,那么我们就有信心相信,存在一台等价的图灵机。这给了我们一个巨大的解放:我们不需要再纠结于具体的状态和转移函数,而是可以直接用类似编程的语言来描述图灵机的行为。
- 高级描述 (High-Level Description):
- 定义: 使用接近自然语言或伪代码的方式来描述图灵机的算法。
- 目标: 关注算法的逻辑,而不是底层的实现细节。
- 分层:
- 形式化描述: 完整的 7-元组。
- 实现级别描述: 描述磁带头如何移动、如何读写磁带,但不具体到状态。
- 高级描述: 完全忽略磁带操作,直接描述算法逻辑,如同编写程序注释。
- 允许的高级操作:
- 这里的列表给出了一些可以被认为是“基本构建块”的操作,我们相信这些操作都可以被一个(可能很复杂的)图灵机子程序实现。
- 变量和数据结构: 图灵机可以通过在磁带的特定区域存储和更新信息来模拟变量。列表和集合可以通过在磁带上用特殊符号分隔元素来表示。
- 控制流: if-then-else 可以通过不同的状态路径来实现。循环可以通过跳转回之前的状态来实现。
- 字符串和算术: 我们已经知道可以构造图灵机来做字符串复制、反转,以及整数的加减乘除。
- 图操作: 给定一个图的编码(例如,邻接矩阵或邻接表的字符串形式),图灵机可以扫描这个字符串来模拟图算法,比如查找邻居或标记顶点(通过在编码字符串上做标记)。
- 图灵机操作 (元操作): 这是最高级的操作。一台图灵机 U(通用图灵机)可以接收另一台图灵机 M 的编码 $\langle M \rangle$ 和一个输入 w,然后模拟 M 在 w 上的运行。这使得“调用”一个图灵机作为子程序成为可能。
- 需要注意的微妙之处:
- 停机问题: 当你的高级描述中包含“运行图灵机 M 在输入 w 上”这样的步骤时,你必须意识到这个步骤可能永远不会结束(如果 M 在 w 上循环)。
- 构造中的处理: 如果你的算法依赖于一个子程序的返回结果,而这个子程序(一个被模拟的图灵机)可能会循环,那么你的整个算法也可能会卡住。因此,在设计归约或其他涉及模拟的算法时,必须明确如何处理这种潜在的无限循环。
- 问题: 判定语言 $L = \{a^n b^n c^n \mid n \ge 0\}$。
- 形式化描述: 会非常巨大和复杂,几乎无法手写。
- 实现级别描述:
- 从左到右扫描,寻找一个 'a' 并用 'X' 标记它。
- 继续向右扫描,跳过所有 'a' 和 'Y',寻找一个 'b' 并用 'Y' 标记它。
- 继续向右扫描,跳过所有 'b' 和 'Z',寻找一个 'c' 并用 'Z' 标记它。
- 将磁带头移回最左端。
- 重复步骤 1-4。
- 如果在任何一步找不到对应的 'a', 'b', 或 'c',则拒绝。
- 当再也找不到未标记的 'a' 时,向右扫描检查是否还有未标记的 'b' 或 'c'。如果没有,则接受;如果有,则拒绝。
- 高级描述:
- 扫描磁带,检查 w 是否是 $a...ab...bc...c$ 的形式。如果不是,拒绝。
- 重复以下操作,直到磁带上没有 'a':
a. 在磁带上划掉最左边的 'a'。
b. 划掉最左边的 'b'。如果找不到 'b',拒绝。
c. 划掉最左边的 'c'。如果找不到 'c',拒绝。
- 如果磁带上还剩下 'b' 或 'c',拒绝。否则,接受。"
- 滥用高级描述: 不能想当然地写下无法实现的操作。例如,不能写“1. 检查图灵机 M 是否在输入 w 上停机。2. 如果是,则...”。因为停机问题本身是不可判定的,所以第一步这个操作就不存在一个对应的图灵机能实现。
- 忽略资源: 高级描述虽然方便,但它隐藏了时间和空间复杂性。一个简单的“排序列表”操作,在图灵机上实现起来可能需要非常多的步骤。在复杂性理论中,我们需要回头关注这些细节。
本段的核心是丘奇-图灵论题,它允许我们用更直观、更易于理解的高级描述(伪代码)来代替复杂的形式化定义来描述图灵机的算法。这大大简化了计算理论中的算法设计和论证过程,但使用者必须清楚哪些操作是合法的,并警惕停机问题等陷阱。
如果计算理论的所有论证都必须在 7-元组的层面进行,那整个领域将变得寸步难行。高级描述是一种必要的抽象,它让我们能够站在更高的视角思考算法的本质,从而设计出更复杂的构造(如归约)来证明深刻的结论。
这就像现代程序员写代码一样。
- 形式化描述: 相当于用机器码或汇编语言编程,需要手动管理内存地址和寄存器。
- 高级描述: 相当于用 Python 或 Java 编程。你可以直接写 list.sort(),而不需要自己去实现快速排序算法的每一个细节。你相信编程语言的解释器或编译器能够把你的高级指令翻译成底层的机器操作。
- 丘奇-图灵论题: 就是那个信念——“只要我能用 Python 写出来,就一定能用汇编实现”。
你在教一个机器人做饭。
- 形式化描述: 你要告诉它:“左臂马达旋转30度,夹爪压力增加到5牛顿,伸展20厘米,拿起那个鸡蛋...”。这非常繁琐。
- 高级描述: 你直接告诉它:“1. 拿一个鸡蛋。2. 打在碗里。3. 搅拌均匀。” 你相信机器人内部的程序能将这些高级指令分解成底层的动作。
- 微妙之处: 如果你给它一个指令“想出一个宇宙的终极真理”,机器人可能会卡在那里永远不动(循环)。
3.3. 图灵机构造的微妙之处
📜 [原文16]
示例 2:
设 $M$ 是一台图灵机。我们将构造另一台图灵机如下。
$N=$“在输入 $w$ 上,
1. 模拟 $M$ 在 $w$ 上的运行。
2. 如果 $M$ 接受,则拒绝。
3. 如果 $M$ 拒绝,则接受。”
如果 $M$ 判定 $L$,那么我们知道 $N$ 判定 $\bar{L}$。为了证明正确性,请观察:
然而,如果 $M$ 只识别 $L$,则 $N$ 可能在步骤 1 中永远循环。例如,考虑 $M$ 从不拒绝的情况:相反,每当它遇到输入 $w \notin L$ 时,它就永远循环。在这种情况下:
因此,在这种情况下,$N$ 不接受任何字符串;换句话说,它识别 $\varnothing$。
为了处理循环,我们可以使用一种称为交错运行的技术,使用并行性,或者利用非确定性图灵机。
这个例子通过一个非常经典的构造,深刻地揭示了识别器和判定器之间的关键区别,以及在构造图灵机时必须如何小心处理停机问题。
- 构造的目标:
- 给定一个图灵机 M,我们想构造一个新的图灵机 N,它的行为与 M “相反”。
- “相反”的直接想法是:M 接受的,N 就拒绝;M 拒绝的,N 就接受。
- 构造的算法 (高级描述):
- N 的算法很简单:
- 在输入 w 上,先完整地模拟 M 在 w 上的运行。
- 等待 M 给出结果。
- 如果 M 的结果是“接受”,N 就输出“拒绝”。
- 如果 M 的结果是“拒绝”,N 就输出“接受”。
- 分析构造 (分两种情况):
- 情况 1: M 是一个判定器 (Decider)
- 前提: 判定器对任何输入都保证停机(接受或拒绝)。
- 分析:
- 当 N 模拟 M 时,步骤 1 必然会在有限时间内结束。
- 如果 $w \in L(M)$,M 接受 w,于是 N 进入步骤 2,拒绝 w。
- 如果 $w \notin L(M)$,M 拒绝 w,于是 N 进入步骤 3,接受 w。
- 结论: N 接受所有不在 $L(M)$ 中的字符串,并拒绝所有在 $L(M)$ 中的字符串。N 也对所有输入都停机。因此,N 判定了 $L(M)$ 的补集 $\overline{L(M)}$。
- 重要推论: 如果一个语言 L 是可判定的,那么它的补集 $\bar{L}$ 也一定是可判定的。(可判定语言类对补集运算是封闭的)。
- 情况 2: M 只是一个识别器 (Recognizer)
- 前提: 识别器对于不属于其语言的输入,可能会拒绝,也可能会循环。
- 分析:
- 如果 $w \in L(M)$,M 接受 w,N 的步骤 1 会结束,然后 N 拒绝 w。这部分没问题。
- 如果 $w \notin L(M)$,现在有两种可能:
- (a) M 拒绝 w。那么 N 的步骤 1 结束,N 接受 w。
- (b) M 在 w 上循环。那么 N 在模拟 M 的步骤 1 中,也会跟着永远循环下去,永远到不了步骤 2 或 3。
- 最坏情况: 假设 M 是一个只识别 L 的图灵机,它对于所有 $w \notin L$ 的情况都循环。
- 在这种情况下,N 的行为变成:
- 对于 $w \in L$, N 拒绝 w。
- 对于 $w \notin L$, N 在 w 上循环。
- 结论: 这个 N 接受了哪些字符串?答案是:一个都没有。所以 $L(N) = \varnothing$。它识别了空语言。它并没有像我们期望的那样识别 $\bar{L}$。
- 如何处理循环:
- 这个例子说明,简单的“模拟然后翻转结果”的策略在面对可能循环的图灵机时会失效。
- 文中提到了更高级的技术来处理这种情况,例如:
- 交错运行 (Dovetailing): 如果要同时模拟两个可能循环的计算(比如 M 在 w 上和 M' 在 w' 上),你可以模拟 M 的第1步,然后模拟 M' 的第1步,然后 M 的第2步,M' 的第2步... 这样交替进行,确保如果其中任何一个能停机,你最终都能发现。
- 这在证明“可识别语言对并集和交集封闭”时很有用。
- 情况 1 (M 是判定器):
- 这两行完美地符合了 N 判定 $\bar{L}$ 的定义。
- 情况 2 (M 是识别器且对非成员循环):
- 分析 N 的行为:
- $L(N) = \{w \mid N \text{ accepts } w\}$。根据上面的分析,没有 w 能让 N 接受,所以 $L(N) = \varnothing$。
- $\overline{L(N)} = \Sigma^*$。
- 混淆识别和判定: 这个例子是检验是否真正理解识别和判定区别的试金石。关键就在于对“循环”这个第三种可能性的处理。
- 对角线证明的影子: 这个“翻转结果”的构造,是康托对角线证明和停机问题不可判定性证明的核心思想的简化版。在证明停机问题时,我们会构造一个“刁民”程序 D,它接收另一个程序 M 的编码 $\langle M \rangle$,然后模拟 M 在自己的编码 $\langle M \rangle$ 上的运行,并做出相反的动作。这个例子的逻辑与之一脉相承。
本例通过构造一个“反向器”图灵机 N,清晰地展示了:
- 如果一个语言 L 是可判定的,那么它的补集 $\bar{L}$ 也是可判定的。
- 如果仅知道一个语言 L 是可识别的,我们不能通过简单地翻转识别器 M 的接受/拒绝结果来构造出 $\bar{L}$ 的识别器,因为 M 可能在某些输入上循环,导致我们的构造失效。
这个例子至关重要,因为它直接导向了计算理论中一个非常深刻的定理:一个语言 L 是可判定的,当且仅当 L 和它的补集 $\bar{L}$ 都- 3.4. 图灵机示例
📜 [原文17]
33 示例
考虑语言
我们将给出三种图灵机,以不同的格式,它们都识别 $L$. $\unlhd^{1}$
这部分将通过一个非常简单的语言作为例子,来具体展示前面提到的三种不同层次的图灵机描述方法:形式化描述、实现级别描述和高级描述。
- 目标语言:
- $L = \{w \in \{0,1\}^* \mid w \text{ contains no 1's}\}$
- 字母表: $\Sigma = \{0, 1\}$
- 语言描述: 这个语言包含所有仅由 '0' 组成的二进制字符串,以及空字符串 $\varepsilon$。
- 等价描述: $L = \{0^n \mid n \ge 0\}$。
- 示例:
- 属于 L 的字符串: $\varepsilon$, 0, 00, 0000
- 不属于 L 的字符串: 1, 010, 11
- 目标任务:
- 为这个语言 L 设计一个图灵机。因为这个语言非常简单,我们可以轻易地设计出一个判定器(即一个对所有输入都停机的图灵机),这个判定器自然也是一个识别器。
- 下面的内容将用三种不同的“画风”来描述同一个判定器。
本节的引言部分,提出了一个具体的、简单的目标语言——“所有不含 '1' 的二进制字符串”,并预告将用三种不同抽象层次的方法来为它设计图灵机。
通过这个简单的例子,让学生直观地感受到三种描述方式的差异:形式化描述的繁琐和精确,实现级别描述的折衷,以及高级描述的简洁和直观。这有助于学生理解为什么高级描述在后续的学习中是必要且方便的。
📜 [原文18]
[^0]
33.1 形式描述
其中 $\delta$ 定义为
或者,同一图灵机表示为状态图:
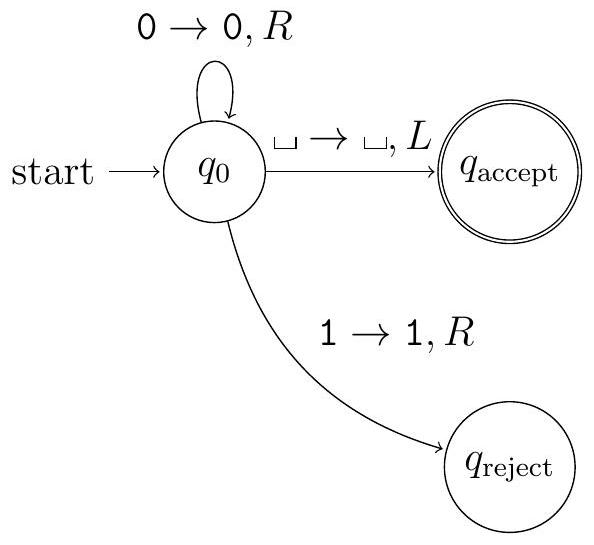
这是描述图灵机最底层、最精确的方式。
- 7-元组定义:
- $Q = \{q_0, q_{\text{accept}}, q_{\text{reject}}\}$: 状态集。这里只需要一个工作状态 $q_0$ 加上两个终止状态。
- $\Sigma = \{0, 1\}$: 输入字母表。
- $\Gamma = \{0, 1, \sqcup\}$: 磁带字母表。这里我们不需要额外的草稿符号。
- $\delta$: 转移函数,是核心。下面详细解释。
- $q_0$: 开始状态。
- $q_{\text{accept}}$: 接受状态。
- $q_{\text{reject}}$: 拒绝状态。
- 转移函数 $\delta$ 详解:
- 算法思路: 从左到右扫描输入字符串。只要没遇到 '1',就继续前进。如果遇到了 '1',立刻拒绝。如果一路平安走到了字符串的末尾(即读到了空白符 $\sqcup$),就说明没有 '1',于是接受。
- $\delta(q_0, 0) = (q_0, 0, R)$:
- 情况: 在开始状态 $q_0$ 读到了一个 '0'。
- 动作: '0' 是允许的。保持在 $q_0$ 状态,把 '0' 写回磁带(实际上没变),然后磁带头向右 (R) 移动,继续检查下一个符号。
- $\delta(q_0, 1) = (q_{\text{reject}}, 1, R)$:
- 情况: 在开始状态 $q_0$ 读到了一个 '1'。
- 动作: '1' 是不允许的。立刻跳转到拒绝状态 $q_{\text{reject}}$,计算停止。写入什么和向哪移动已经不重要了,因为机器已经停机。
- $\delta(q_0, \sqcup) = (q_{\text{accept}}, \sqcup, L)$:
- 情况: 在开始状态 $q_0$ 读到了空白符 $\sqcup$。
- 动作: 这意味着我们已经成功扫描完了整个字符串而没有遇到任何 '1'。立刻跳转到接受状态 $q_{\text{accept}}$,计算停止。向左 (L) 移动是可选的,没有实际影响。
- 状态图 (State Diagram) 解读:
- 节点: 图中的圆圈代表状态 ($q_0, q_{\text{accept}}, q_{\text{reject}}$)。
- 箭头: 代表状态之间的转移。
- 箭头上的标签: 格式是 读入符号 -> 写入符号, 移动方向。
- 从 $q_0$ 指向自己的箭头,标签是 $0 \to 0, R$。这对应了 $\delta(q_0, 0) = (q_0, 0, R)$。
- 从 $q_0$ 指向 $q_{\text{reject}}$ 的箭头,标签是 $1 \to 1, R$。这对应了 $\delta(q_0, 1) = (q_{\text{reject}}, 1, R)$。
- 从 $q_0$ 指向 $q_{\text{accept}}$ 的箭头,标签是 $\sqcup \to \sqcup, L$。这对应了 $\delta(q_0, \sqcup) = (q_{\text{accept}}, \sqcup, L)$。
- 状态图是形式化描述的一种图形化表示,对于简单的图灵机来说更直观。
- 输入: 00
- 初始: 状态 $q_0$, 读头在第一个 0。
- 根据 $\delta(q_0, 0)$, 状态仍为 $q_0$, 读头右移,指向第二个 0。
- 根据 $\delta(q_0, 0)$, 状态仍为 $q_0$, 读头右移,指向 sqcup。
- 根据 $\delta(q_0, \sqcup)$, 状态变为 $q_{\text{accept}}$。接受。
- 输入: 010
- 初始: 状态 $q_0$, 读头在第一个 0。
- 根据 $\delta(q_0, 0)$, 状态仍为 $q_0$, 读头右移,指向 1。
- 根据 $\delta(q_0, 1)$, 状态变为 $q_{\text{reject}}$。拒绝。
- 输入: $\varepsilon$ (空字符串)
- 初始: 状态 $q_0$, 读头直接就在第一个 sqcup 上。
- 根据 $\delta(q_0, \sqcup)$, 状态变为 $q_{\text{accept}}$。接受。
本段给出了判定语言 $\{0^n \mid n \ge 0\}$ 的图灵机的完整形式化描述,包括 7-元组和状态图两种形式。
📜 [原文19]
33.2 实现级别描述
检查磁带是否为空,如果是则接受。
重复以下操作:
检查当前字符是否为 1,如果是则拒绝。
检查当前字符是否为空格,如果是则接受。
否则将磁头向右移动。
这是描述图灵机的中间层次,它关注磁带和磁带头的操作,但不涉及具体的状态名。
- “检查磁带是否为空,如果是则接受。”:
- 这对应了形式化描述中,机器一启动,如果读头下是空白符 $\sqcup$(意味着输入是空字符串 $\varepsilon$),就直接进入接受状态的情况。即 $\delta(q_0, \sqcup) = (q_{\text{accept}}, \dots)$。
- “重复以下操作:”:
- 这描述了一个循环,对应形式化描述中从 $q_0$ 状态到 $q_0$ 状态的自循环。
- “检查当前字符是否为 1,如果是则拒绝。”:
- 这对应了转移 $\delta(q_0, 1) = (q_{\text{reject}}, \dots)$。在循环的任何一步,只要碰到 '1',就跳出循环并拒绝。
- “检查当前字符是否为空格,如果是则接受。”:
- 这对应了当字符串不为空时,在扫描完所有非空白字符后遇到空白符的情况。这也是循环的终止条件,并导向接受。
- “否则将磁头向右移动。”:
- “否则”在这里意味着当前字符既不是 '1' 也不是空白符。在我们的字母表 $\{0,1\}$ 中,那就只剩下 '0' 了。
- 这对应了转移 $\delta(q_0, 0) = (q_0, \dots, R)$。遇到 '0',就继续循环(保持在 $q_0$),并将读头右移以检查下一个字符。
本段用更接近自然语言的伪代码,描述了图灵机的磁带操作逻辑,它比形式化描述更易读,但仍然保留了对机器底层操作(移动磁带头、检查字符)的关注。
📜 [原文20]
33.3 高级描述
$M=$“在输入 $x \in\{0,1\}^{*}$ 上,检查 $x$ 是否包含任何 1。如果是,则拒绝,否则接受”
这是描述图灵机最高、最抽象的层次。它完全不关心图灵机的内部工作细节(状态、磁带),只陈述它要解决的算法问题和最终结果。
- “在输入 $x \in \{0,1\}^*$ 上”:
- 声明了图灵机 M 的输入类型。
- “检查 $x$ 是否包含任何 1”:
- 这是一个高度抽象的指令。我们相信(基于丘奇-图灵论题)这个检查过程可以被一台图灵机实现,但我们在这里不关心具体如何实现。它可能涉及一个从左到右的扫描循环,就像我们在前面两个描述中看到的那样。
- “如果是,则拒绝,否则接受”:
- 这直接说明了算法的判断逻辑和最终输出。
- “是”(包含 '1')对应 $x \notin L$,结果是拒绝。
- “否则”(不包含 '1')对应 $x \in L$,结果是接受。
本段用一句话描述了算法的核心逻辑,完全抽象掉了图灵机的物理操作。这是我们在进行复杂构造和证明(如归约)时最常用、最方便的描述方式。
- 三种描述的等价性: 对于同一个问题,这三种描述本质上是在描述同一个算法,只是抽象层次不同。高级描述必须是“可编译”的,即原则上可以被翻译成实现级别乃至形式化的描述。
- 选择合适的描述层次:
- 当需要严谨证明图灵机具体构造时,形式化描述是不可避免的。
- 当需要解释一个相对简单的算法的工作原理时,实现级别描述很有用。
- 当构建复杂算法或进行高层理论证明时,高级描述是首选。
这三个示例放在一起,旨在清晰地展示从具体到抽象的三个层次,并合理化我们为什么在计算理论的后续学习中,绝大多数时候都停留在高级描述的层面。它解放了我们的思维,让我们能专注于问题本身的逻辑,而不是陷入底层实现的泥潭。
3.5. 非确定性图灵机
📜 [原文21]
非确定性图灵机可以从给定的配置中进行多种可能的移动(类似于 NFA)。像 NFA 一样,当且仅当存在导致接受状态的序列时,它们才接受输入。非确定性可以被认为是让算法“猜测”,然后我们需要验证当且仅当某些幸运猜测能够使**非- 4. 可判定性、可识别性、归约和莱斯定理
4.1. 可识别性
📜 [原文22]
回顾以下定义:
定义 3。如果存在一个(确定性)图灵机 $M$ 使得:
则语言 $L$ 是可识别的。
也就是说,$M$ 接受 $L$ 中的每个字符串,并拒绝或无限循环不在 $L$ 中的字符串。如果一个语言不可识别,它就是不可识别的。
可识别语言在补集下不封闭。例如,我们知道 $\mathrm{A}_{\text {TM }}:= \{\langle M, x\rangle \mid M$ 是一个接受 $x$ 的 TM $\}$ 是可识别的,但 $\overline{\mathrm{A}_{\text {TM }}}$ 不是。
然而,请注意,对于可识别语言,可以等价地使用非确定性图灵机。
定义 4。如果存在一个非确定性图灵机 $M$ 使得:
- 如果 $x \in L$,则存在某个非确定性分支, $M$ 在该分支上接受 $x$。
- 如果 $x \notin L$,则对于所有非确定性分支,$M$ 不接受 $x$。
特别是,图灵机允许在某些非确定性分支上循环。
这部分重新审视并深化了可识别性 (Recognizability) 的概念,强调了其核心特征和一些重要性质。
- 可识别性的核心定义 (使用 DTM):
- 一个语言 L 是可识别的 (Recognizable),如果存在一个确定性图灵机 (DTM) M,它能做到:
- 对于“是”的实例: 如果一个字符串 w 在 L 里 ($w \in L$),M 必须在有限时间内停机并接受 w。
- 对于“否”的实例: 如果一个字符串 w 不在 L 里 ($w \notin L$),M 绝对不能接受 w。这意味着 M 要么停机并拒绝 w,要么永不停机(循环)。
- 这个定义的关键在于其不对称性。它对“是”的回答给出了强有力的承诺(一定有答案),但对“否”的回答则没有(可能没答案)。
- 可识别语言也被称为图灵可识别语言或递归可枚举语言 (Recursively Enumerable Language, RE)。
- 在补集运算下不封闭:
- 这是一个非常重要的性质。“不封闭”意味着,如果一个语言 L 是可识别的,我们不能保证它的补集 $\bar{L}$ 也一定是可识别的。
- 经典例子: 停机问题 $A_{TM} = \{\langle M, x \rangle \mid M \text{ accepts } x\}$。
- $A_{TM}$ 是可识别的。我们可以构造一个识别器 U(通用图灵机),它模拟 M 在 x 上的运行。如果 M 接受 x,U 就接受 $\langle M, x \rangle$。如果 M 拒绝或循环,U 也会跟着拒绝或循环。这符合识别器的定义。
- $\overline{A_{TM}}$ (它的补集) 被证明是不可识别的。这意味着不存在任何图灵机能够识别 $\overline{A_{TM}}$。
- 可识别性的等价定义 (使用 NTM):
- 一个重要的定理是:一个语言能被确定性图灵机 (DTM) 识别,当且仅当它能被非确定性图灵机 (NTM) 识别。换句话说,在可识别性的层面上,非确定性没有增加额外的计算能力。
- 用 NTM 定义可识别性: 一个语言 L 是可识别的,如果存在一个 NTM N,它能做到:
- 对于“是”的实例: 如果 $w \in L$,那么在 N 的所有计算分支中,至少存在一个分支能够停机并接受 w。
- 对于“否”的实例: 如果 $w \notin L$,那么 N 的所有计算分支都不能接受 w。(它们可以拒绝,也可以循环)。
- 这个定义与 NTM 的接受机制完全一致,因此 NTM 接受的语言就是可识别语言。
- $x \in L \Longleftrightarrow M \text { accepts } x$
- 这个双向蕴涵关系是识别器定义的核心。
- $x \in L \Longrightarrow M \text{ accepts } x$: “是”的必须接受。
- $M \text{ accepts } x \Longrightarrow x \in L$: 接受的必须是“是”。这反过来意味着,如果 $x \notin L$,那么 $M$ 不能接受 x,即 $M$ 只能拒绝或循环。
- 语言: 停机问题 $A_{TM}$。
- 识别器 U:
- 输入: $\langle M, w \rangle$ (一个图灵机 M 的编码和输入 w)。
- 算法:
- 检查输入格式是否正确。如果不是 $\langle M, w \rangle$ 的有效编码,拒绝。
- 模拟 M 在输入 w 上的运行。
- 如果模拟中的 M 接受了 w,那么 U 就接受 $\langle M, w \rangle$。
- 如果模拟中的 M 拒绝了 w,那么 U 就拒绝 $\langle M, w \rangle$。
- (隐含) 如果模拟中的 M 循环了,那么 U 也会在模拟过程中循环。
- 分析:
- 如果 $\langle M, w \rangle \in A_{TM}$ (即 M 接受 w),U 最终会接受。
- 如果 $\langle M, w \rangle \notin A_{TM}$ (即 M 拒绝或循环),U 最终会拒绝或循环,但绝不会接受。
- 这完全符合识别器的定义。因此 $A_{TM}$ 是可识别的。
- DTM 与 NTM 的能力: 在可识别性层面,DTM 和 NTM 等价。但在复杂性理论(如 P 与 NP)中,非确定性是否比确定性更强大(在多项式时间内)是核心问题。不要将不同层次的结论混淆。
- 不封闭的含义: “在补集下不封闭”不代表所有可识别语言的补集都不可识别。例如,所有可判定语言都是可识别的,而它们的补集也都是可判定的(因此也是可识别的)。“不封闭”仅仅意味着“不保证总是封闭”,存在至少一个反例(如 $A_{TM}$)。
本段再次强调了可识别语言 (RE) 的核心定义:存在一个图灵机,对语言内的字符串保证接受,对语言外的字符串则拒绝或循环。同时指出了该语言类的一个重要性质(对补集不封闭),并给出了其与非确定性图灵机的等价关系。
精确理解可识别性是掌握计算理论后半部分的关键。它是区分“半可解”问题(可识别但不可判定)和“完全不可解”问题(不可识别)的界线。了解其性质(如对补集不封闭)和等价定义(NTM)为后续的证明和理论(如莱斯定理)打下基础。
- 可识别问题: 就像一个数学猜想(如哥德巴赫猜想)。如果你能找到一个反例(“是”的答案),你就能停机并发表论文(接受)。但如果你一直找不到反例,你无法确定是因为它不存在(答案是“否”),还是因为你找得还不够久(循环)。你永远无法确定地发表一篇论文说“这个猜想绝对成立”,因为可能明天就有人找到反例。
[直- 4.2. 可判定性
📜 [原文23]
可判定性很像可识别性,只是我们对图灵机施加了一个额外的条件:它必须拒绝所有不在 $L$ 中的字符串。
定义 5。如果存在一个(确定性)图灵机 $M$ 使得:
也就是说,一个判定器总是能在有限时间内为所有可能的输入给出答案。
我们还有以下定理:
定理 1。一个语言 $L$ 是可判定的当且仅当 $L$ 和 $\bar{L}$ 都是可识别的。
可判定语言在补集下封闭。也就是说,如果 $A$ 是可判定的,那么 $\bar{A}$ 也是可判定的。我们也可以使用 NTM
定义 6。如果存在一个非确定性图灵机 $M$ 使得:
- 如果 $x \in L$,则存在某个非确定性分支, $M$ 在该分支上接受 $x$。
- 如果 $x \notin L$,则对于所有非确定性分支,$M$ 拒绝 $x$。
你需要小心并确保没有非确定性分支会永远运行。这里有一个示例。考虑以下 NTM:
```
算法 1 $\mathrm{A}_{\mathrm{TM}}$ 的判定器?
输入:$\langle M, x\rangle$,其中 $M$ 是一台 TM
非确定性地选择 $k \geq 0$
运行 $M$ 在 $x$ 上 $k$ 步。
如果 $M$ 接受 $x$ 则
接受 $\langle M, x\rangle$。
否则
拒绝 $\langle M, x\rangle$。
结束 如果
```
这里,显然如果 $M$ 不接受 $x$,无论我们选择什么 $k$,NTM 都会拒绝。另一方面,如果 $M$ 接受 $x$,选择足够大的 $k$ 意味着 $M$ 将在第 3 行接受,所以我们接受。但是 $\mathrm{A}_{\mathrm{TM}}$ 是不可判定的,所以一定有什么问题。特别是考虑行“非确定性地选择 $k \geq 0$”,这只是一个简写,它应该读作:
```
$k=0$
while True do
选择一个:“退出 while 循环”或“将 $k$ 增加 1”。
end while
```
并且观察到,在这里,我们可以清楚地看到 NTM 可能永远不会在某个分支上停机,它会不断增加 $k$。
经验法则:在要求给出识别器时使用 NTM 是很好的,但在要求给出判定器时可能不是最好的。如果你想使用 NTM 来给出判定器,请确保你“非确定性地猜测”的内容来自一个有限集合(这样“猜测永远不会持续下去”)。
这部分详细阐述了比可识别性更强的概念——可判定性 (Decidability),并探讨了它与补集、非确定性的关系,以及使用 NTM 来构造判定器时的一个典型陷阱。
- 可判定性的核心定义 (使用 DTM):
- 一个语言 L 是可判定的 (Decidable),如果存在一个确定性图灵机 (DTM) M,它对任何输入字符串 w 都保证在有限时间内停机,并给出明确的“是”或“否”的答案。
- 如果 $w \in L$, M 接受 w。
- 如果 $w \notin L$, M 拒绝 w。
- 关键区别: 判定器从不循环。它总是能给出答案。
- 可判定语言也被称为图灵可判定语言或递归语言 (Recursive Language, R)。
- 重要的定理和性质:
- 定理 1: $L \text{ is decidable} \iff L \text{ is recognizable and } \bar{L} \text{ is recognizable.}$
- 直观解释 (=>): 如果 L 是可判定的,那么存在一个判定器 $M_L$。$M_L$ 本身就是一个识别器。同时,我们可以构造 $\bar{L}$ 的判定器 $M_{\bar{L}}$ (通过翻转 $M_L$ 的接受/拒绝状态),所以 $\bar{L}$ 也是可判定的,因此也是可识别的。
- 直观解释 (<=): 如果我们有 L 的识别器 $M_1$ 和 $\bar{L}$ 的识别器 $M_2$。为了判定一个输入 w,我们可以并行地(或交错地)同时运行 $M_1(w)$ 和 $M_2(w)$。因为 w 要么在 L 中,要么在 $\bar{L}$ 中,所以这两个识别器中必然有一个会在有限时间内停机并接受。
- 如果 $M_1$ 先接受,我们就知道 $w \in L$,于是我们的判定器就接受 w。
- 如果 $M_2$ 先接受,我们就知道 $w \in \bar{L}$ (即 $w \notin L$),于是我们的判定器就拒绝 w。
- 这个过程保证了总能停机并给出答案。
- 在补集运算下封闭: 如果 L 是可判定的,那么 $\bar{L}$ 也是可判定的。这从上面的定理可以轻松推导出。
- 可判定性的 NTM 定义与陷阱:
- NTM 判定器定义: 一个 NTM N 是判定器,如果它对任何输入 w,所有计算分支都在有限时间内停机(接受或拒绝),并且:
- 如果 $w \in L$,至少有一个分支接受。
- 如果 $w \notin L$,所有分支都拒绝。
- 陷阱示例: 尝试为 $A_{TM}$ 构造一个 NTM 判定器。
- 算法思想: 非确定性地“猜”一个运行步数 k,然后模拟 M 在 x 上运行 k 步。如果 M 在这 k 步内接受了,那么 NTM 就接受。否则,这个分支就拒绝。
- 表面上的正确性:
- 如果 $M(x)$ 确实接受(比如在 $k_0$ 步),那么 NTM 只要“猜”对了 $k=k_0$ (或任何 $k \ge k_0$),这个分支就会接受。
- 如果 $M(x)$ 不接受(拒绝或循环),那么对于任何有限的 k,模拟 k 步后都不会发现它接受,所以所有这些分支都会拒绝。
- 问题所在: “非确定性地选择 $k \ge 0$” 这一步本身就包含了无限的可能性。NTM 的一个计算分支可以是“猜 k=0”,另一个是“猜 k=1”,...,但它还有一个分支是“永远在猜测 k 的过程中”。如文中所述,这个非确定性选择可以被实现为一个循环,而这个循环本身可以永不退出。因此,这个 NTM 存在无限循环的分支,它不满足 NTM 判定器要求所有分支都停机的条件。所以这个构造失败了。
- 经验法则: 使用 NTM 来做非确定性“猜测”时,如果猜测的对象来自一个无限集合(如此处的步数 k),要特别小心,这通常是引入无限循环的根源,因此不适用于构造判定器。如果猜测的对象来自一个有限集合(比如“非确定性地选择图中的一个顶点”),那么所有分支都必然是有限的,这种用法是安全的。
- $L \text{ is decidable} \iff (L \in \text{RE} \text{ and } \bar{L} \in \text{RE})$
- RE 是递归可枚举语言(可识别语言)的集合。
- 这个公式是定理 1 的符号化表示,是连接可判定性和可识别性的桥梁。
- 可判定语言: $E_{DFA} = \{\langle A \rangle \mid A \text{ is a DFA and } L(A) = \varnothing\}$ (DFA的空语言问题)。
- 这是一个可判定的语言。我们可以构造一个判定器:
- 输入 $\langle A \rangle$。
- 检查编码是否是一个合法的 DFA。如果不是,拒绝。
- 在 DFA 的状态图上,从开始状态出发,执行一个图遍历算法(如 BFS 或 DFS),看是否能到达任何一个接受状态。
- 如果能到达任何一个接受状态,说明这个 DFA 至少能接受一个字符串,因此 $L(A) \neq \varnothing$。于是拒绝 $\langle A \rangle$。
- 如果遍历结束都无法到达任何接受状态,说明 $L(A) = \varnothing$。于是接受 $\langle A \rangle$。
- 这个算法对于任何 DFA 编码都会在有限时间内结束(因为 DFA 的状态是有限的),所以它是一个判定器。
- 认为 NTM 判定器允许部分分支循环: 这是一个常见误解。NTM 识别器允许循环,但 NTM 判定器要求所有分支都必须停机。
- 忽略对无限猜测的严格定义: “非确定性地选择一个自然数”听起来像一个单一的操作,但它的图灵机实现涉及到可能无限的循环,这正是陷阱所在。
本段定义了可判定语言 (R),其判定器保证对所有输入在有限时间内停机并给出接受或拒绝的答案。它揭示了可判定性与可识别性的重要关系($R = RE \cap co-RE$),并指出了使用非确定性构造判定器时的一个关键陷阱:不能从无限集合中进行“猜测”。
可判定性是算法理论的“黄金标准”。可判定的问题是我们认为的“理想的可计算问题”。将问题分为可判定、可识别但不可判定、不可识别这三个层次,是计算理论的核心任务。理解可判定性的严格要求,对于理解为什么像停机问题这样的语言不属于这个“理想”类别至关重要。
- 可判定问题: 就像一个有明确答案并且总能被找到答案的是非题。例如,“13579是否是一个质数?”。你可以通过一个有限的算法(试除法)来得到确切的“否”的答案。
- 可识别但不可判定的问题 ($A_{TM}$): 就像问“这个程序(可能很复杂)在输入X时,最终会打印出'Hello World'吗?”。如果它真的打印了,你就得到了“是”的答案。但如果它一直没打印,你不知道是它永远不会打印,还是只是运行得慢。你无法为所有程序都给出一个确定的答案。
- 判定器: 一个完美的法官,对于任何案卷,他总能在规定时间内审理完毕,并给出“有罪”或“无罪”的判决。
- 识别器: 一个可能会拖延的侦探。对于有确凿证据的案子,他能很快结案(接受)。对于没有证据的案子,他可能会说证据不足(拒绝),也可能会说“我再查查”,然后就没了下文(循环)。
- 定理1的想象: 如果你有两个侦探,一个专门找“有罪”的证据(识别 L),另一个专门找“无罪”的证据(识别 $\bar{L}$)。把同一个案卷给他们俩,因为案子最终要么有罪要么无罪,所以其中一个侦探必然能在有限时间内找到证据并报告。这样,这个“侦探组合”就成了一个完美的法官(判定器)。
4.3. 归约
📜 [原文24]
一般来说,归约是一种根据问题的难度对其进行排序的方式。形式上,我们说 $A \leq B$ 或“ $A$ 可归约到 $B$ ”。以下是该陈述的三种英语解释,它们很好地说明了归约的直觉:
归约有多种形式:我们研究了 $\leq_{\mathrm{T}}, \leq_{\mathrm{m}}, \text{ 和 } \leq_{\mathrm{p}}$。
定义 7。设 $A, B$ 是两个语言:
图灵归约。如果给定一个判定 $B$ 的 TM $M$,存在一个判定 $A$ 的判定器 $N$,我们说 $A$ 图灵可归约到 $B$,记作 $A \leq_{\mathrm{T}} B$。
映射归约 如果存在一个可计算函数 $f$ 使得
我们说 $A$ 映射可归约到 $B$,记作 $A \leq_{\mathrm{m}} B$。
我们知道如果 $A \leq_{\mathrm{m}} B$,那么 $A \leq_{\mathrm{T}} B$。因此,无论何时需要图灵归约,你都可以使用映射归约。然而,反之不成立:在某些情况下,存在从 $A$ 到 $B$ 的图灵归约,但没有从 $A$ 到 $B$ 的映射归约。在下一节中,我们将介绍如何使用这两种归约来解决问题。但是在此之前,我们先回顾以下定理:
定理 2。
- $A \leq_{T} B \Longleftrightarrow \bar{A} \leq_{T} B \Longleftrightarrow A \leq_{T} \bar{B} \Longleftrightarrow \bar{A} \leq_{T} \bar{B}$
- $A \leq_{M} B \Longleftrightarrow \bar{A} \leq_{M} \bar{B}$
我们还有以下重要定理:
定理 3。
- 如果 $A \leq_{T} B$ 且 $B$ 是可判定的,那么 $A$ 是可判定的。
- 如果 $A \leq_{M} B$ 且 $B$ 是可识别的,那么 $A$ 是可识别的。
推论 4。
- 如果 $A \leq_{T} B$ 且 $A$ 是不可判定的,那么 $B$ 是不可判定的。
- 如果 $A \leq_{M} B$ 且 $A$ 是不可识别的,那么 $B$ 是不可识别的。
提示:在进行映射归约 $A \leq_{\mathrm{m}} B$ 时,你可以忽略错误编码的输入(即不是 TM、DNA、CNF 等...),方法是首先说“如果 $x$ 是错误编码,我们只需将其映射到某个 $y \notin B$”。然后,在证明 $x \in A \Longleftrightarrow f(x) \in B$ 时,可以忽略错误编码。
这部分是计算理论的核心技术——归约 (Reduction)。归约是用来证明新问题的不可判定性或不可识别性的主要工具。
- 归约的直觉:
- 归约是一种比较两个问题 A 和 B 难度关系的方法。
- $A \le B$ 的核心意思是,我们可以利用一个解决 B 问题的“黑盒子”(子程序),来帮助我们解决 A 问题。
- 这就好比说,“如果你能帮我把这堆苹果去核(问题B),那么我就能做出苹果派(问题A)”。这说明做苹果派的难度“小于等于”苹果去核的难度(假设其他步骤都很简单)。
- 因此,$A \le B$ 意味着 B 至少和 A 一样难。如果 A 是一个已知的难题,那么 B 也不可能简单。
- 两种归约的定义:
- 图灵归约 ($A \le_T B$):
- 这是一种非常通用的归约。它说,如果我们有一个能判定 B 的图灵机 $M_B$ (我们称之为一个神谕 (Oracle)),我们就可以构造一个能判定 A 的图灵机 $N^B$。
- 这个 $N^B$ 在计算过程中,可以随时“调用” $M_B$ 这个黑盒子。它可以向 $M_B$ 提问:“某个字符串 y 在不在 B 里?”,并立即得到“是”或“否”的答案。$N^B$ 可以调用这个黑盒子任意多次。
- 例子: $A_{TM} \le_T \overline{A_{TM}}$。假设有判定 $\overline{A_{TM}}$ 的神谕。要判定 $A_{TM}$ 的输入 $\langle M, w \rangle$,我们直接问神谕“$\langle M, w \rangle$ 是否在 $\overline{A_{TM}}$ 中?”。如果神谕回答“是”,我们就拒绝;如果回答“否”,我们就接受。我们只调用了一次神谕。
- 映射归约 ($A \le_m B$):
- 这是一种更严格、更受限的归约。
- 它要求存在一个可计算函数 f,这个函数能把 A 问题的任何一个实例 x,转换成 B 问题的一个实例 $f(x)$。
- 并且这个转换必须保持“是/否”答案的一致性:x 是 A 的“是”实例,当且仅当 $f(x)$ 是 B 的“是”实例。
- 映射归约中,解决 A 的过程分为两步:
- 用图灵机计算 $f(x)$。
- 把 $f(x)$ 扔给解决 B 的黑盒子,B 的答案就是 A 的答案。
- 与图灵归约的区别: 映射归约只能调用一次黑盒子,并且必须在所有计算的最后一步调用,且黑盒子的答案就是最终答案,不能再做任何后处理。而图灵归约可以在计算过程中多次调用黑盒子,并根据返回结果进行后续计算。
- 重要的定理和推论:
- 定理 2 (与补集的关系):
- 图灵归约: $A \le_T B$ 和 $A \le_T \bar{B}$ 是等价的。因为如果有一个 B 的神谕,你总能通过反转其输出来得到一个 $\bar{B}$ 的神谕,反之亦然。
- 映射归约: $A \le_m B \iff \bar{A} \le_m \bar{B}$。这是因为 $x \in A \iff f(x) \in B$ 等价于 $x \notin A \iff f(x) \notin B$。这个可计算函数 f 同时建立了 $\bar{A}$ 和 $\bar{B}$ 之间的归约。注意,$A \le_m B$ 通常并不意味着 $A \le_m \bar{B}$。
- 定理 3 (传播“简单性”):
- 如果 B 是可判定的,并且 A 能图灵归约到 B,那么 A 也是可判定的。(用一个简单的东西解决了一个更简单的东西)。
- 如果 B 是可识别的,并且 A 能映射归约到 B,那么 A 也是可识别的。
- 推论 4 (传播“困难性”): 这是我们使用归约最主要的方式!
- 证明不可判定性: 要证明 B 是不可判定的,我们只需找到一个已知不可判定的问题 A (通常是 $A_{TM}$),然后构造一个从 A 到 B 的归约 ($A \le_T B$ 或 $A \le_m B$)。如果 B 是可判定的,那么根据定理 3,A 也将是可判定的,这与 A 不可判定的前提矛盾。所以 B 必须是不可判定的。
- 证明不可识别性: 要证明 B 是不可识别的,我们只需找到一个已知不可识别的问题 A (通常是 $\overline{A_{TM}}$),然后构造一个从 A 到 B 的映射归约 ($A \le_m B$)。
- 处理错误编码的提示:
- 在构造映射归约 $f: A \to B$ 时,输入 x 可能是格式错误的(比如,A 是关于图灵机的问题,但 x 根本不是一个合法的图灵机编码)。
- 对于这些格式错误的输入,它们肯定不属于 A。所以,我们只需要把它们映射到一个确定不属于 B 的实例 $y_{no} \notin B$。这样就满足了 $x \notin A \implies f(x) \notin B$ 的条件。
- 这使得我们在证明的核心部分,可以只关注那些格式正确的输入。
- $A \leq_{\mathrm{m}} B$ via computable function $f$:
- $x \in A \Longleftrightarrow f(x) \in B$
- 证明模板:
- 构造函数 f: 描述一个算法,它接收问题 A 的一个实例 x,并输出一个问题 B 的实例 y。这个算法必须是可计算的(即能被一个图灵机实现且总能停机)。
- 证明正向 ($x \in A \Longrightarrow f(x) \in B$): 假设 x 是 A 的一个“是”实例,然后根据 f 的构造,论证 f(x) 必须是 B 的一个“是”实例。
- 证明反向 ($f(x) \in B \Longrightarrow x \in A$): 假设 f(x) 是 B 的一个“是”实例,然后根据 f 的构造,论证 x 必须是 A 的一个“是”实例。有时证明其逆否命题 ($x \notin A \Longrightarrow f(x) \notin B$) 会更容易。
- 问题: 证明语言 $HALT_{TM} = \{\langle M, w \rangle \mid M \text{ halts on input } w\}$ 是不可判定的。
- 策略: 我们使用推论 4,通过归约 $A_{TM} \le_T HALT_{TM}$ 来证明。
- 已知: $A_{TM}$ 是不可判定的。
- 归约构造:
- 我们的目标是构造一个判定 $A_{TM}$ 的图灵机 $N$,它可以使用一个能判定 $HALT_{TM}$ 的神谕 $H$。
- $N$ 的算法如下,输入为 $\langle M, w \rangle$:
- 调用神谕 $H$,问它:“$\langle M, w \rangle$ 是否在 $HALT_{TM}$ 中?” (即 M 在 w 上是否停机?)
- 如果 $H$ 回答“否”(M 不停机,即循环),那么 M 肯定不会接受 w。所以 N 直接拒绝 $\langle M, w \rangle$。
- 如果 $H$ 回答“是”(M 停机),现在我们知道 M 不会循环了,它只可能接受或拒绝。于是,我们就可以安全地模拟 M 在 w 上的运行,直到它停机。
- 如果 M 的模拟结果是接受,N 就接受 $\langle M, w \rangle$。
- 如果 M 的模拟结果是拒绝,N 就拒绝 $\langle M, w \rangle$。
- 结论: 这个图灵机 N 确实能判定 $A_{TM}$。既然我们从“$HALT_{TM}$ 是可判定的”这个假设,推导出了“$A_{TM}$ 是可判定的”这个结论,而我们已知 $A_{TM}$ 是不可判定的,那么最初的假设一定是错误的。因此,$HALT_{TM}$ 必须是不可判定的。
- 归约方向: $A \le B$ 意味着 A 不比 B 难。要证明 B 难,就要从一个已知的难题 A 出发,归约到 B。方向搞反是初学者最常见的错误。
- 区分图灵归约和映射归约: 映射归约是图灵归约的特例。在证明不可识别性时,必须使用映射归约,因为图灵归约不保持可识别性。
- 可计算函数 f 必须停机: 在构造映射归约时,用于转换实例的函数 f 自身必须是一个算法,即它必须对所有输入都在有限时间内完成转换。
本段定义了归约作为比较问题难度的方法,并介绍了两种主要形式:通用的图灵归约和受限但更强的映射归约。归约的核心应用是,通过将一个已知的困难问题(如 $A_{TM}$)归约到一个新问题 B,来证明 B 至少和 A 一样困难(即不可判定或不可识别)。
在证明了第一个不可判定问题 $A_{TM}$ 之后,归约就成了我们扩展不可判定性“版图”的主要武器。我们不再需要每次都从头使用对角线方法,而是可以建立一个“归约链”:$A_{TM} \le B \le C \le \dots$,从而证明 B, C, ... 都是不可判定的。这是计算理论和复杂性理论中最重要的证明技术。
- 归约: 你想解决一个新任务“把大象放进冰箱里”(问题 A)。你发现,如果你能解决“打开冰箱门”(问题 B)这个子任务,那么剩下的步骤(把大象推进去,关上门)都很简单。所以,你把解决 A 的问题归约到了解决 B。这说明“打开冰箱门”是整个任务的关键难度所在。$A \le B$。
- 证明 B 难: 假设你知道“造一台冰箱” (问题 A) 是非常难的。你又发现,如果你能“打开任何东西的门”(问题 B),你就能轻易地造出一台冰箱(比如,打开通往材料仓库的门,打开工具箱的门等)。这说明 $A \le B$。因为 A 已知很难,所以 B 也一定很难。
- 映射归约: 你要翻译一篇中文文章到英文(问题 A)。你找到一个可计算函数 f,它能把这篇中文文章转换成一篇法文文章($f(x)$),并且原文是通顺的当且仅当转换后的法文文章是通顺的。然后,你有一个只会判断法文文章是否通顺的专家(黑盒 B)。你把转换后的法文文章给专家看,他的判断就是你对中文文章的最终判断。
- 图灵归约: 还是翻译中文文章。这次你有一个更厉害的法语专家(神谕 B),你可以在翻译的任何时候向他提问,比如“这个法语句子‘Je ne sais quoi’通顺吗?”,他会立刻告诉你。你可以一边翻译,一边向他咨询无数次,最后完成你的翻译工作。这个过程比映射归约更灵活。
4.4. 莱斯定理
📜 [原文25]
注意,我们学到的许多不可判定语言都符合一个共同的模式。也就是说,它们是形式为 $\{\langle M\rangle \mid M$ 是一台 TM 且 $L(M)$ 满足... $\}$ 的语言。我们将此类语言称为“可识别语言的性质”。形式上,
定义 8。如果 $P \subseteq\{\langle M\rangle \mid M$ 是一台 TM $\}$ 并且如果 $L\left(M_{1}\right)=L\left(M_{2}\right)$ 则 $\left\langle M_{1}\right\rangle \in P \Longleftrightarrow\left\langle M_{2}\right\rangle \in P$,则 $P$ 是可识别语言的性质。
定义 9。可识别语言的性质 $P$ 是非平凡的,如果 $P \neq \emptyset$ 且 $P \neq\{\langle M\rangle \mid M$ 是一台 TM $\}$。
特别是,我们有以下非常方便的定理来判断这种形式的语言是否可判定 / 可识别。
定理 5(莱斯定理)。设 $P$ 是可识别语言的非平凡性质。那么 $P$ 是不可判定的。
以下更强的版本(非必需)告诉我们性质的可识别性。
定理 6(精炼莱斯定理)。设 $P$ 是可识别语言的非平凡性质。设 $M_{\emptyset}$ 是一台 TM 使得 $L\left(M_{\emptyset}\right)=\emptyset$。那么:
- 如果 $\left\langle M_{\emptyset}\right\rangle \in P$,则 $P$ 是不可识别的。
- 如果 $\left\langle M_{\emptyset}\right\rangle \in P$,则 $\bar{P}$ 是不可识别的。
这部分介绍了一个极其强大的“批量处理”工具——莱斯定理 (Rice's Theorem),它可以一次性证明一大类关于图灵机的问题都是不可判定的。
- 问题的模式:
- 我们之前遇到的很多问题(语言)都是在问图灵机本身的一些特性。比如:
- $A_{TM} = \{\langle M, w \rangle \mid \dots \}$: 这是问一个图灵机和一个输入。
- $E_{TM} = \{\langle M \rangle \mid L(M) = \varnothing\}$: 这是问图灵机 M 所识别的语言是不是空语言。
- $REGULAR_{TM} = \{\langle M \rangle \mid L(M) \text{ is regular}\}$: 这是问图灵机 M 所识别的语言是不是正则语言。
- 莱斯定理关注的是后一类问题:只给一个图灵机的编码 $\langle M \rangle$,然后问它所识别的语言 $L(M)$ 是否具有某种“性质”。
- 性质 (Property) 的形式化定义:
- 一个关于图灵机的语言 P 被称为是一个“性质”,如果它只关心图灵机的行为(即它识别的语言),而不关心其实现(即具体的状态和转移函数)。
- 形式化定义: 如果两个图灵机 $M_1$ 和 $M_2$ 识别同一个语言 ($L(M_1) = L(M_2)$),那么它们的编码 $\langle M_1 \rangle$ 和 $\langle M_2 \rangle$ 必须要么都属于 P,要么都不属于 P。
- 例子:
- $P_1 = \{\langle M \rangle \mid L(M) \text{ contains '01'}\}$ 是一个性质。因为判断 $\langle M \rangle$ 是否在 $P_1$ 中,只取决于 $L(M)$,和 M 的内部构造无关。
- $P_2 = \{\langle M \rangle \mid M \text{ has exactly 10 states}\}$ 不是一个性质。因为我们可以轻易构造两个图灵机 $M_1$ (有10个状态) 和 $M_2$ (有20个状态),但它们都识别同一个语言(比如空语言)。那么 $\langle M_1 \rangle \in P_2$ 但 $\langle M_2 \rangle \notin P_2$,违反了定义。
- 非平凡性质 (Non-trivial Property):
- 一个性质 P 是非平凡的,如果它不是“空性质”也不是“全性质”。
- $P \ne \varnothing$: 至少存在一台图灵机,它所识别的语言具有该性质。
- $P \ne \{\text{all TM encodings}\}$: 至少存在一台图灵机,它所识别的语言不具有该性质。
- 直观理解: “非平凡”意味着这个性质是有区分度的,不是所有语言都有或者所有语言都没有。例如,“识别的语言是否是可识别的”是一个平凡性质,因为所有图灵机识别的语言定义上就是可识别的。
- 莱斯定理 (Theorem 5):
- 内容: 任何关于图灵机所识别语言的非平凡性质都是不可判定的。
- 威力: 这个定理是一个“超级武器”。只要我们能确定一个问题是在问图灵机语言的某个非平凡性质,我们就可以立刻宣称它是不可判定的,无需再做任何从 $A_{TM}$ 出发的归约。
- 证明思路: 其标准证明就是从 $A_{TM}$ 归约到任意一个非平凡性质 P。
- 精炼莱斯定理 (Rice's Theorem, Refined):
- 这个更强的版本不仅告诉我们可判定性,还告诉我们可识别性。
- 判断标准: 看一下“最简单”的图灵机 $M_\varnothing$(它识别空语言 $\varnothing$,比如一台启动后立刻拒绝所有输入的图灵机)是否满足这个性质。
- Case 1: 如果 $M_\varnothing$ 满足性质 P (即 $\langle M_\varnothing \rangle \in P$)
- 那么 P 是不可识别的。
- 直觉: 这类性质通常是“负面”或“受限”的,比如“语言为空”、“语言不包含'01'”、“语言是有限的”。判断一个图灵机的语言是否有限是不可识别的,因为它需要你确保图灵机不会在无穷多个输入上接受。
- Case 2: 如果 $M_\varnothing$ 不满足性质 P (即 $\langle M_\varnothing \rangle \notin P$)
- 那么 P 的补集 $\bar{P}$ 是不可识别的。(注意,这并不直接告诉我们 P 的可识别性,但如果 P 本身是可识别的,那么根据 $co-RE$ 的性质,它就不是不可识别的)。
- 直觉: 这类性质通常是“正面”或“存在性”的,比如“语言非空”、“语言包含'01'”、“语言是无限的”。例如,“语言非空”这个性质是可识别的(非确定性地猜一个 w 和步数 k,看 M 能否接受 w),但它的补集(“语言为空”)是不可识别的。
让我们用莱斯定理来判断以下语言的可判定性:
- 问题 1: $L_1 = \{\langle M \rangle \mid L(M) \text{ is finite}\}$ (M 的语言是有限的)
- 是性质吗?: 是。只关心 $L(M)$,不关心 M 的实现。
- 是平凡的吗?: 否。存在图灵机识别有限语言(如接受 {01} 的),也存在图灵机识别无限语言(如接受 $\{0\}^*$ 的)。所以是非平凡的。
- 结论 (莱斯定理): $L_1$ 是不可判定的。
- 进一步分析 (精炼莱斯定理): $M_\varnothing$ 识别空语言 $\varnothing$,空语言是有限的。所以 $\langle M_\varnothing \rangle \in L_1$。根据第一条规则,$L_1$ 是不可识别的。
- 问题 2: $L_2 = \{\langle M \rangle \mid M \text{ accepts the string '101'}\}$
- 是性质吗?: 是。因为 "$L(M)$ 包含 '101'" 是一个关于 $L(M)$ 的性质。
- 是平凡的吗?: 否。有的图灵机接受 '101',有的不接受。
- 结论 (莱斯定理): $L_2$ 是不可判定的。
- 进一步分析 (精炼莱斯定理): $M_\varnothing$ 识别空语言,不包含 '101'。所以 $\langle M_\varnothing \rangle \notin L_2$。根据第二条规则,$\overline{L_2}$ 是不可识别的。($L_2$ 本身是可识别的:只需模拟 M 在 '101' 上的运行即可)。
- 问题 3: $L_3 = \{\langle M \rangle \mid M \text{ halts on all inputs}\}$
- 是性质吗?: 是。"$L(M)$ 是可判定的" 是一个关于 $L(M)$ 的性质。
- 是平凡的吗?: 否。有的图灵机在所有输入上停机,有的则不。
- 结论 (莱斯定理): $L_3$ 是不可判定的。
- 应用范围: 莱斯定理只适用于判断关于图灵机所识别语言 (L(M)) 的性质。对于那些涉及图灵机实现细节(如状态数、运行时间)或涉及具体输入(如 $A_{TM} = \{\langle M, w \rangle \dots\}$)的问题,莱斯定理不适用,必须使用归约。
- 精炼莱斯定理的第二条: $\langle M_\varnothing \rangle \notin P \implies \bar{P}$ 是不可识别的。这没有直接说 P 的可识别性。通常,这类 P 是可识别的,因此形成了 $RE \setminus R$ 的经典例子(可识别但不可判定)。
莱斯定理提供了一个强大的“快捷方式”,用于证明所有关于图灵机语言行为的非平凡问题都是不可判定的。精炼版的莱斯定理进一步根据“空语言”是否满足该性质,来判断该问题(或其补集)的可识别性。
在发现了一系列不可判定问题($A_{TM}, HALT_{TM}, E_{TM}$ 等)后,数学家们发现它们的证明(都从 $A_{TM}$ 归约)具有高度的相似性。莱斯定理就是对这种相似性的终极抽象。它将所有这些单独的证明统一成了一个单一的、更具普遍性的定理。学习它使得我们能够快速分类一大批新遇到的问题,而无需重复繁琐的归约构造。
- 莱斯定理: 就像一个“万能检测器”,但它只能检测“黑盒程序”的输入输出行为,无法窥探其内部代码。
- 定理内容: 这个检测器想检测一个非平凡的行为性质 P(比如,“这个程序是否会输出质数?”)。莱斯定理说,这样一个通用的、仅凭行为来判断的检测器是不可能存在的(不可判定)。
- 原因: 如果存在这样的检测器,我们就可以用它来解决停机问题。我们可以构造一个特殊的程序,它只有在某个图灵机 M 停机时,才表现出性质 P。通过检测这个特殊程序是否具有性质 P,我们就能知道 M 是否停机,但这与停机问题不可判定相矛盾。
想象你想开发一个“代码质量分析”软件。
- 性质 P: “这段代码实现的算法,在功能上是否等价于快速排序?”
- 莱斯定理说: 你不可能做出一个完美的软件,能对任何给定的代码,都准确判断出它是不是一个“快速排序”。
- 为什么: 因为代码的写法千奇百怪(两个图灵机可以有不同实现但语言相同),有的代码可能包含恶意的无限循环。要完全确定一个程序的外部行为,在所有情况下都与“快速排序”一致,本质上需要解决停机问题,这是不可能的。你也许能检查一些简单情况,但无法做到100%精确。
4行间公式索引
1. 识别器定义: $w \in L \Longleftrightarrow M \text { accepts } w .$
* 该公式定义了图灵机 M 识别语言 L 的条件:M 接受一个字符串当且仅当该字符串在 L 中。
2. 判定器定义: $w \in L \Longrightarrow M \text { accepts } w \text { and } w \notin L \Longrightarrow M \text { rejects } w .$
* 该公式定义了图灵机 M 判定语言 L 的条件:对于语言内的字符串,M 接受;对于语言外的字符串,M 拒绝,从不循环。
3. 语言补集的例子:
* 该公式组列举了几个典型语言的补集,展示了补集是相对于全集 $\Sigma^*$ 而言的。
4. 整数集映射到非负整数集的函数:
* 该公式定义了一个从整数集到非负整数集的单射函数,用于证明整数集是可数的。
5. 判定器工作流的逻辑蕴涵:
* 该公式组展示了当 M 是一个判定器时,通过翻转其结果构造的图灵机 N 如何成功地判定了 M 所识别语言的补集。
6. 识别器工作流的逻辑蕴涵:
* 该公式组展示了当 M 只是一个识别器且在某些输入上循环时,简单翻转其结果的构造会失败,无法正确识别其补集。
7. 示例语言的定义:
* 该公式定义了一个简单的正则语言,用于后续展示图灵机的不同描述方式。
8. 图灵机形式化描述 (7-元组):
* 该公式给出了一个具体图灵机的完整形式化定义,包含其状态集、字母表等所有七个组成部分。
9. 图灵机转移函数定义:
* 该公式组具体定义了示例图灵机的转移函数,即其核心“程序逻辑”。
10. 归约的直觉解释:
* 该公式组用三种不同的自然语言方式解释了归约 $A \le B$ 的核心思想:问题 A 的解决可以依赖于问题 B 的解决,因此 A 的难度不高于 B。
11. 图灵归约的蕴涵:
* 该公式简明地表达了图灵归约的含义:一个判定 B 的图灵机的存在,可以用来构造一个判定 A 的图灵机。
12. 映射归约的等价条件:
* 该公式定义了映射归约的核心条件:一个可计算函数 f 必须保持实例从问题 A 到问题 B 的“是/否”性质不变。
- 问题: 合数问题 (COMPOSITES) = $\{x \in \mathbb{N} \mid x \text{ is a composite number}\}$。
- 用 NTM 解决:
- 输入: 一个整数 x 的编码 $\langle x \rangle$。
- 猜测: 非确定性地选择两个整数 p 和 q,使得 $1 < p, q < x$。
- 这会产生很多计算分支,每个分支对应一对 (p, q) 的猜测。
- 验证: 在每个分支中,计算 p 和 q 的乘积。
- 如果 $p \times q = x$,则该分支接受。
- 如果 $p \times q \ne x$,则该分支拒绝。
- 分析:
- 如果 x 是合数(例如 12),那么它必然可以写成两个更小的数的乘积(例如 $3 \times 4$)。因此,必然存在一个“幸运的猜测”分支(猜 p=3, q=4),在这个分支上,验证会成功,NTM 就会接受 12。
- 如果 x 是质数(例如 13),那么不存在这样的 p 和 q。因此,所有的猜测分支最终都会验证失败,NTM 就不会接受 13。
- NTM 不是并行计算机: NTM 是一个数学模型,不是物理上并行处理的机器。它的“并行分支”是一种逻辑上的抽象。
- DTM vs. NTM: 一个重要的定理是,任何 NTM 都可以被一个 DTM 模拟。这意味着 NTM 并不比 DTM 更强大(在可计算性的层面上,它们识别相同的语言类,即图灵可识别语言)。但是,模拟过程可能会消耗指数级增长的时间。P vs NP 问题本质上就是在问,这种指数级的时间爆炸是否是不可避免的。
本段介绍了非确定性图灵机 (NTM),它的转移函数可以有多个选择,其接受标准是只要存在一个计算分支接受即可。理解 NTM 的最佳方式是“猜测并验证”模型,它极大地简化了某些算法的设计,并且是计算复杂性理论中 NP 类的基础。
非确定性是计算理论,特别是复杂性理论中的一个核心概念。它让我们能够定义 NP 这样的重要复杂性类。虽然在可计算性层面它不比确定性更强大,但在多项式时间的限制下,非确定性是否比确定性更强大(即 P 是否等于 NP)是计算机科学中最重大的未解之谜。
- DTM: 一个按部就班、循规蹈矩的侦探。他会一个一个地排查所有线索。
- NTM: 一个拥有“直觉”的侦探。他能“猜到”谁是凶手(猜测),然后他只需要去验证这个嫌疑人是不是真的凶手(验证)。如果他的直觉是对的,他就能很快破案。如果所有直觉都是错的,他就破不了案。
你身处一个巨大的迷宫的入口,要去寻找出口。
- DTM 的方法: 使用“右手扶墙”法则。你始终沿着一条路走,遇到分岔路就按固定规则选一条,走到死胡同再退回来尝试另一条。你最终能走遍整个迷宫,但可能会花很长时间。
- NTM 的方法: 在每个分岔路口,你都“分裂”成多个你,每个你都去探索一条路。只要其中任何一个你找到了出口,整个“你”就成功了。
34.1. NTM 示例:可达性问题
📜 [原文26]
示例 我们给出一个 NTM 来判定以下语言(与讲义 8 相同):
可达性 = $\{\langle G, s, t\rangle \mid G$ 是一个图,$s, t$ 是顶点,在 $G$ 中存在从 $s$ 到 $t$ 的路径 $\}$
我们的 NTM $N$ 操作如下:
在输入 $w=\langle G, s, t\rangle$ 上,其中 $G$ 是一个图,$s, t$ 是 $G$ 中的顶点,执行以下操作:
- 将当前顶点设置为 $s$。
- 将当前顶点标记为已访问。
- 如果所有通过边连接到当前顶点的顶点集合都被标记:
- 拒绝。
- 否则:
- 非确定性地将当前顶点设置为该集合中未被标记的顶点。
- 如果当前顶点是 $t$,则接受 $w$。否则返回步骤 2。
为什么这有效:假设 $w \in$ 可达性:那么根据可达性的定义,存在一条路径,即由边连接的从 $s$ 到 $t$ 的顶点序列。因此,存在一系列 $N$ 可以做出的幸运选择以从 $s$ 到 $t$,所以 $N$ 接受 $w$。
假设 $w \notin$ 可达性:那么不存在从 $s$ 到 $t$ 的这种可猜测的路径,所以所有可能的猜测都使 $N$ 拒绝 $w$。
最后,图灵机最多只能返回第 2 行一次,每个 $G$ 中的顶点。所以图灵机必须总是停机,不能永远运行。
这个例子展示了如何使用 NTM 的“猜测”能力来优雅地解决图的可达性问题。
- 问题定义:
- 语言: 可达性 (REACHABILITY)
- 输入: 一个图 G 的编码,以及两个顶点 s (起点) 和 t (终点)。
- 问题: 图 G 中是否存在一条从 s 到 t 的路径?
- NTM 算法 (高级描述):
- 核心思想: 从起点 s 开始,非确定性地在图中“漫游”,看看能否“撞到”终点 t。
- 步骤 1 & 2: 初始化。把当前位置设为 s,并标记 s 已经访问过(防止在两个顶点间来回走死循环)。
- 步骤 3 & 4: 死胡同判断。如果当前顶点的所有邻居都已经被访问过了,说明从这条路走不通了,此计算分支拒绝。
- 步骤 5 & 6: 非确定性的移动。这是算法的核心。从当前顶点的所有未被访问过的邻居中,“猜测”一个作为下一个要移动到的顶点。NTM 会分裂出多个分支,每个分支探索一个邻居。
- 步骤 7: 终止条件。在移动到新的当前顶点后,检查它是不是终点 t。如果是,那么这个分支就成功了,接受输入。如果不是,就回到步骤 2,标记新顶点,继续探索。
- 正确性分析 (Why this works):
- 如果存在路径 ($w \in$ 可达性): 假设存在一条路径 $s \to v_1 \to v_2 \to \dots \to t$。那么,NTM 就存在一个“幸运的猜测”序列:在 s 时猜到 $v_1$,在 $v_1$ 时猜到 $v_2$,... 一路下去,最终猜到 t。在这个计算分支上,NTM 会在步骤 7 接受。根据 NTM 的接受定义,只要有一个分支接受,整个机器就接受。
- 如果不存在路径 ($w \notin$ 可达性): 那么从 s 出发,无论怎么走都到不了 t。在 NTM 的所有计算分支中,每一次移动都是沿着图中实际存在的边进行的。因为没有路径到 t,所以没有任何一个分支能最终将当前顶点设置为 t。所有分支最终都会因为走到“死胡同”(步骤 4)而拒绝。因此,没有分支会接受,整个机器不接受。
- 停机分析:
- 这个 NTM 是一个判定器,因为它总是会停机。
- 原因在于步骤 2 “将当前顶点标记为已访问”,以及步骤 6 只选择“未被标记的顶点”。
- 一个计算分支的路径长度,最多只能经过图中的每个顶点一次。
- 因为图 G 的顶点数量是有限的,所以任何一个计算分支的长度都是有限的。
- 因此,机器不可能无限循环,它总是会在有限步内接受或拒绝。
- 图 G: $V=\{s, a, b, t\}$, $E=\{(s,a), (s,b), (a,t), (b,b)\}$
- 输入: $\langle G, s, t \rangle$
- 运行:
- 当前顶点 s。标记 s。
- s 的邻居是 a 和 b,都未标记。
- NTM 分裂成两个分支:
- 分支 1: 非确定性地选择 a。
- 当前顶点 a。标记 a。
- 检查 a 是否是 t。不是。返回步骤 2。
- a 的邻居是 s 和 t。s 已被标记。
- 非确定性地选择 t。
- 当前顶点 t。标记 t。
- 检查 t 是否是 t。是。此分支接受。
- 因为有一个分支接受了,整个 NTM 接受 $\langle G, s, t \rangle$。
- 分支 2: 非确定性地选择 b。
- 当前顶点 b。标记 b。
- 检查 b 是否是 t。不是。返回步骤 2。
- b 的邻居是 s 和 b。s 和 b 都已被标记。
- 所有邻居都被标记了。此分支拒绝。
- 与 DTM 的区别: 一个确定性图灵机 (DTM) 要解决这个问题,通常需要使用系统的图搜索算法,如广度优先搜索 (BFS) 或深度优先搜索 (DFS)。这需要一个队列或栈的数据结构,在磁带上实现起来更复杂。NTM 则通过“猜测”巧妙地避免了显式管理这些数据结构。
- 判定器 vs 识别器: 这个 NTM 是一个判定器,因为它的所有分支都会在有限步内停机。如果图中有环,标记已访问顶点的策略保证了不会在环里无限转圈。
本例展示了 NTM 如何利用其“猜测”能力,将一个搜索问题(寻找一条路径)转化为一个简单的“漫游”过程。非确定性使得算法的描述变得非常简洁和直观。通过保证所有分支都会停机,这个 NTM 实际上成为了该语言的一个判定器。
这个例子是为了具体地展示“猜测并验证”模型的威力,并说明 NTM 在算法设计上的便利性。可达性问题本身是可判定的(甚至在P类中),这个例子并非要证明什么不可判定性,而是要让学生熟悉 NTM 的思维方式,为后续理解 NP 类问题(如哈密顿路径、SAT等)的 NTM 解法打下基础。
你站在迷宫起点s,想到达终点t。你有很多“克隆体”(非确定性)。在每个路口,你都派出一个克隆体去走一条路,同时自己也走另一条。只要有一个克隆体最终到达了终点t,他就立刻通过心灵感应告诉所有人“找到了!”,任务成功(接受)。如果所有的克隆体都走到了死胡同,任务失败(拒绝)。为了防止在迷宫里绕圈,每个走过的地方都会被画上标记,不再走第二遍。
想象洪水从 s 点注入一个管网 G。非确定性就像是水流会同时涌入所有相连的管道。如果 t 点最终湿了,说明存在一条从 s 到 t 的路径(接受)。如果水流遍了所有能到达的地方,t 点还是干的,说明路径不存在(拒绝)。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。