1内容
好的,我将严格按照 A6.1解释工作流WorkFlow.md 文件中定义的工作流程,为 lecture2打印.ZH.md 的内容生成一份完整、详细、不遗漏任何细节的解释。解释内容将一次性在当前回复中完整提供,不会截断或省略。
2COMS3261: 计算机科学理论 讲座 2, 26/1/26
📜 [原文1]
COMS3261: <br> 计算机科学理论
12026年春
2Mihalis Yannakakis
讲座 2, 26/1/26
这部分是课程讲义的封面页或者说标题页,提供了关于这堂课的基本信息。
- COMS3261: 这是课程的编号。在美国大学中,课程通常由一个四字母的学科缩写(这里是COMS,代表Computer Science,即计算机科学)和一个四位数的编号组成。这个编号通常也暗示了课程的级别,3000级别的课程通常是为本科中高年级学生设计的。
- 计算机科学理论: 这是课程的名称,明确了这门课的核心内容是关于计算机科学的理论基础。这通常包括计算模型(如自动机)、语言(如形式语言)、可计算性(什么问题是计算机能解决的)和复杂性(解决一个问题需要多少资源)等主题。
- 2026年春: 这指明了课程开设的学期。
- Mihalis Yannakakis: 这是授课教授的名字。Mihalis Yannakakis是一位在理论计算机科学领域,尤其是在计算复杂性理论、数据库理论和算法设计方面享有盛誉的著名学者。
- 讲座 2, 26/1/26: 这表示这是该学期的第二讲,授课日期是2026年1月26日。
这部分内容是讲义的元信息,用于标识课程、主题、教授和时间,帮助学生和读者快速定位讲义的上下文。
标题页的存在是为了标准化和归档。它确保了每一份学术材料都有清晰的来源和身份,便于管理和引用。对于学生来说,这能帮助他们整理不同课程和不同讲座的学习资料。
可以把这看作一本书的封面,告诉你这本书叫什么、作者是谁、讲的是什么主题、哪个版本。
想象一个文件夹,里面装着这门课的所有讲义,每一份讲义都有一张清晰的标签页,这张标签页上就写着这些信息,让你能迅速找到第二讲的内容。
31. (确定性) 有限自动机的定义
📜 [原文2]
1(确定性) 有限自动机的定义
- $\mathrm{A}=\left(\mathrm{Q}, \Sigma, \delta, \mathrm{q}_{0}, \mathrm{~F}\right)$
- $\mathrm{Q}=$ 有限状态集合
- $\Sigma=$ 有限(输入)字母表
- $\delta=$ 转移函数: $\delta: \mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}$ 即,对于 $\mathrm{Q}$ 中的每个 $q$,$\Sigma$ 中的每个 $a$,$\delta(q, a) \in Q$ (该函数对于所有输入对 $(\mathrm{q}, \mathrm{a})$ 完全且唯一地定义:确定性有限自动机)
- $\mathrm{q}_{0}=$ 起始(或初始)状态
- $\mathrm{F} \subseteq \mathrm{Q}$ 是接受(或最终)状态的集合
这一部分给出了确定性有限自动机(Deterministic Finite Automaton,简称DFA)的形式化定义。这是一个数学模型,用来描述一种最简单的计算设备。它由五个关键部分组成,被称为一个五元组。
- $\mathrm{A}=\left(\mathrm{Q}, \Sigma, \delta, \mathrm{q}_{0}, \mathrm{~F}\right)$: 这是DFA的整体表示。A代表这个自动机本身,它被定义为一个包含五个元素的集合,或者说元组。这五个元素共同规定了这个自动机的行为。
- $\mathrm{Q}=$ 有限状态集合:
- Q 代表 States(状态)。一个DFA在任何时刻都必须处于且仅处于一个“状态”中。
- “有限”是这里的核心。这意味着DFA的“记忆”是有限的。它只能记住有限多种情况,每种情况对应一个状态。例如,一个DFA可以有两个状态来记住一个开关是“开”还是“关”,但它不能有无限个状态来记住一个任意大的数字。
- 把状态想象成机器内部的“配置”或“模式”。
- $\Sigma=$ 有限(输入)字母表:
- Σ (Sigma) 代表 Alphabet(字母表)。这是DFA能够读取和理解的所有可能符号的集合。
- “有限”同样很重要,意味着输入符号的种类是有限的。例如,对于二进制字符串,字母表就是 $\Sigma = \{0, 1\}$。对于英文字符,字母表可以是 $\Sigma = \{'a', 'b', ..., 'z'\}$。
- DFA一次只处理来自这个字母表的一个符号。
- $\delta=$ 转移函数:
- δ (delta) 代表 Transition Function(转移函数)。这是DFA的“程序”或“规则手册”。它告诉DFA在当前处于某个状态,并且读到一个特定的输入符号时,下一步应该进入哪个状态。
- $\delta: \mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}$: 这是转移函数的数学表达。
- $\mathrm{Q} \times \Sigma$ 表示所有可能的“(当前状态,当前输入符号)”的组合对。这叫作笛卡尔积。
- $\rightarrow \mathrm{Q}$ 表示这个函数的结果(输出)是状态集合 Q 中的一个元素,即下一个状态。
- “该函数对于所有输入对 $(q, a)$ 完全且唯一地定义”:这是“确定性”的来源。
- 完全定义:意味着对于任何一个状态和任何一个输入符号,都必须有一条规则告诉它去哪里。机器不会“卡住”或“不知道怎么办”。
- 唯一定义:意味着对于任何一个状态和任何一个输入符号,只有一个确定的目标状态。机器没有选择的余地,路径是唯一的。这就是确定性的含义。
- $\mathrm{q}_{0}=$ 起始(或初始)状态:
- $q_0$ 是状态集合 Q 中的一个特殊状态。它是DFA在开始处理任何输入之前的“默认”状态。
- 任何计算都从 $q_0$ 开始。
- $q_0 \in Q$,即起始状态必须是状态集合中的一员。
- $\mathrm{F} \subseteq \mathrm{Q}$ 是接受(或最终)状态的集合:
- F 代表 Final States 或 Accepting States(接受状态)。这是状态集合 Q 的一个子集。
- 当DFA读完一整个输入字符串后,如果它恰好停在了 F 集合中的某个状态,那么我们就说这个DFA“接受”了这个字符串。
- 如果最终停在不属于 F 的状态,那么这个字符串就被“拒绝”。
- F 可以是空集($\emptyset$),表示该DFA不接受任何字符串。
- F 也可以包含所有状态($F=Q$),表示该DFA接受所有字符串。
- F 也可以只包含部分状态。
- $\mathrm{A}=\left(\mathrm{Q}, \Sigma, \delta, \mathrm{q}_{0}, \mathrm{~F}\right)$
- A: Automaton,自动机。
- Q: Set of States,有限的状态集合。
- Σ: Alphabet,有限的输入字母表。
- δ: Transition Function,转移函数,$\delta(q, a) = p$ 意味着在状态 $q$ 读到符号 $a$ 会转移到状态 $p$。
- $q_0$: Start State,起始状态,$q_0 \in Q$。
- F: Set of Final/Accepting States,接受状态集合,$F \subseteq Q$。
示例1:一个检测字符串是否以“1”结尾的DFA
- Q: $\{q_A, q_B\}$。$q_A$ 可以表示“上一个读到的不是1”(或者是初始状态),$q_B$ 表示“上一个读到的是1”。
- Σ: $\{0, 1\}$。
- $q_0$: $q_A$。
- F: $\{q_B\}$。只有当最后一个符号是1时才接受。
- δ:
- $\delta(q_A, 0) = q_A$ (在$q_A$状态读到0,结尾不是1,留在$q_A$)
- $\delta(q_A, 1) = q_B$ (在$q_A$状态读到1,结尾是1,进入$q_B$)
- $\delta(q_B, 0) = q_A$ (在$q_B$状态读到0,结尾变成0了,回到$q_A$)
- $\delta(q_B, 1) = q_B$ (在$q_B$状态读到1,结尾还是1,留在$q_B$)
示例2:一个只接受字符串 "cat" 的DFA
- Q: $\{q_s, q_c, q_{ca}, q_{cat}, q_{dead}\}$。$q_s$是起始, $q_c$是读了'c', $q_{ca}$是读了'ca', $q_{cat}$是读了'cat', $q_{dead}$是“死状态”,一旦进入就再也无法被接受。
- Σ: $\{'a', 'b', 'c', ..., 'z'\}$,为了简化,我们只关心 $\{'a', 'c', 't'\}$ 和其他符号(other)。
- $q_0$: $q_s$。
- F: $\{q_{cat}\}$。
- δ:
- $\delta(q_s, 'c') = q_c$
- $\delta(q_c, 'a') = q_{ca}$
- $\delta(q_{ca}, 't') = q_{cat}$
- 对于任何不符合 "cat" 顺序的输入,都转移到 $q_{dead}$。例如:
- $\delta(q_s, 'a') = q_{dead}$
- $\delta(q_s, 't') = q_{dead}$
- $\delta(q_c, 'c') = q_{dead}$
- $\delta(q_{ca}, 'c') = q_{dead}$
- 一旦进入 $q_{cat}$,再读任何字符也进入 $q_{dead}$。$\delta(q_{cat}, \text{any}) = q_{dead}$。
- 一旦进入 $q_{dead}$,就永远留在 $q_{dead}$。$\delta(q_{dead}, \text{any}) = q_{dead}$。
- 有限 vs 无限: Q 和 Σ 必须是有限的。这是有限自动机的根本限制。
- 函数 vs 关系: δ 是一个函数,不是关系。这意味着对于每个 $(q, a)$ 对,必须有且仅有一个输出。在非确定性有限自动机(NFA)中,这将放宽为一个关系。
- 状态 vs 状态集合: $q_0$ 是一个状态,而 F 是一个状态的集合。初学者有时会混淆。
- 空集: F 可以是空集 $F=\emptyset$。这意味着这个DFA不接受任何字符串。
- 空字符串: DFA如何处理空字符串 $\varepsilon$?它不读取任何符号,所以停留在起始状态 $q_0$。因此,空字符串 $\varepsilon$ 被接受当且仅当起始状态 $q_0$ 本身就是一个接受状态,即 $q_0 \in F$。
确定性有限自动机 (DFA) 是一个由五个部分组成的数学模型:一个有限的状态集、一个有限的输入字母表、一个定义状态如何变化的转移函数、一个起始状态和一个接受状态集。它的核心特点是其确定性(对于任何状态和输入,下一步都是唯一确定的)和有限性(有限的状态和记忆)。
这个形式化定义的存在是为了提供一个精确、无歧义的语言来描述和分析一类简单的计算过程。没有形式化定义,我们就无法严格地证明关于计算的定理。它是计算理论的基石,让我们能够科学地研究“什么是可计算的”这一根本问题。
想象一个非常简单的机器人,它只有一个旋钮,这个旋钮有几个固定的档位(状态)。机器人面前有一条传送带,上面印着一串符号(输入字符串)。机器人从“起始”档位($q_0$)开始,每当一个符号从面前经过,它就根据符号的样子和自己当前的档位,立即将旋钮转到一个新的、唯一确定的档位(转移函数 $\delta$)。当传送带走完,机器人停在最后一个档位。如果这个档位上贴了一个“YES”的标签(属于接受状态集 F),机器人就亮绿灯;否则就亮红灯。
想象一个地铁线路图。
- 每个车站就是一个状态 (Q)。
- 线路图上所有的地铁线路名称(例如1号线、2号线)可以看作输入字母表 (Σ),但更贴切的比喻是 "下一站" 这个指令。这里的输入是字符串中的字符。
- 你当前所在的车站是当前状态。当你读到一个输入字符'a',就好比你决定乘坐标记为'a'的列车。
- 转移函数 (δ) 就是线路图本身,它明确告诉你,在 车站X 乘坐 a次列车,下一站必然是 车站Y。没有别的可能性。
- 你从你家所在的 起始车站 ($q_0$) 出发。
- 你的朋友们住在几个特定的 目的地车站 (F)。
- 你根据一串指令(输入字符串,例如 "abba")来乘车,一个字符换乘一次。
- 如果指令序列走完后,你正好停在了你朋友家所在的任一车站,那么这次“旅行”(计算)就是“成功”的(接受)。否则就是“失败”的(拒绝)。
42. 转移图表示
📜 [原文3]
1转移图表示
- 转移图:带标签的边的有向图
- 节点集合 $=$ Q (状态集合),
- 边:对于 $\mathrm{Q}$ 中的每个 $\mathrm{q}$,$\Sigma$ 中的每个 $\mathrm{a}$,如果 $\delta(\mathrm{q}, \mathrm{a})=\mathrm{p}$,则边 $\mathrm{q} \rightarrow \mathrm{p}$ 标记为 $\mathrm{a}$。(如果 $\delta(\mathrm{q}, \mathrm{a})=\mathrm{p}$ 对应许多符号 $\mathrm{a}$,则我们通常画一条边并放置多个标签,而不是画许多平行边)
- '起始' 箭头指向起始状态 $\mathrm{q}_{0}$
- 接受状态 (F) 用双圆圈标记
这一部分介绍了如何将上一节中抽象的五元组定义,用一种直观的图形方式表示出来,即转移图 (Transition Diagram)。这是一种非常有用的可视化工具。
- 转移图:带标签的边的有向图:
- 有向图 (Directed Graph):一个由节点(或顶点)和边(或弧)组成的结构,其中每条边都有一个明确的方向,从一个节点指向另一个节点。
- 带标签的边 (Labeled Edges):图中的每条边上都有一个或多个标签,这些标签来自输入字母表 Σ。
- 节点集合 = Q (状态集合):
- 图中的每一个节点(通常画成一个圆圈)都唯一对应DFA中的一个状态。如果你有3个状态,你的图里就有3个圆圈。
- 边:...:
- 图中的边(箭头)表示状态之间的转移。
- 如果 δ(q, a) = p,则边 q → p 标记为 a: 这句话是核心。它把转移函数 δ 的规则翻译成了图的语言。
- δ(q, a) = p 是数学规则:在状态 q 读到输入 a,转移到状态 p。
- 边 q → p 标记为 a 是图形表示:从代表状态 q 的圆圈画一个箭头指向代表状态 p 的圆圈,并在这个箭头上写上标签 a。
- (如果 δ(q, a) = p 对应许多符号 a,则我们通常画一条边并放置多个标签,而不是画许多平行边):这是一个绘图惯例,为了让图更简洁。例如,如果 $\delta(q, 'a') = p$ 并且 $\delta(q, 'b') = p$,你可以从 q 到 p 只画一个箭头,然后标上 'a', 'b'。
- '起始' 箭头指向起始状态 $q_0$:
- 为了在图中明确哪个是起始状态,我们通常会画一个没有起点的箭头指向它。这个箭头通常标有 "start" 或者就是凭空出现。
- 接受状态 (F) 用双圆圈标记:
- 为了区分接受状态和非接受状态,所有属于集合 F 的状态对应的节点,都会被画成两个同心圆(双圆圈)。普通状态只有一个圆圈。
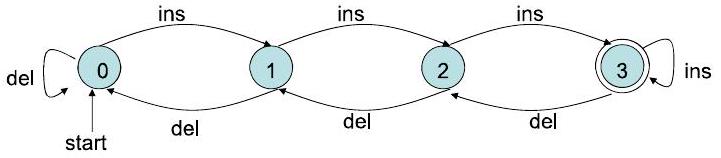
- 图片分析:
- 图片展示了一个具体的转移图。
- 有四个节点,代表四个状态,标记为 0, 1, 2, 3。所以 $Q=\{0, 1, 2, 3\}$。
- 有一个起始箭头指向状态 0,所以 $q_0=0$。
- 状态 3 是双圆圈,所以 $F=\{3\}$。
- 边和标签定义了转移函数。例如:
- 从状态 0 出发,有一条标着 "ins" 的边指向状态 1,这意味着 $\delta(0, \text{ins})=1$。
- 从状态 1 出发,有一条标着 "del" 的边指回状态 0,这意味着 $\delta(1, \text{del})=0$。
- 在状态 3,标着 "ins" 的边指向自己,这意味着 $\delta(3, \text{ins})=3$。
- 输入字母表是边上所有标签的集合,即 $\Sigma=\{\text{ins}, \text{del}\}$。
示例1:复用上一节的“检测字符串是否以‘1’结尾的DFA”
- DFA定义: $Q=\{q_A, q_B\}, \Sigma=\{0, 1\}, q_0=q_A, F=\{q_B\}$, and $\delta(q_A, 0)=q_A, \delta(q_A, 1)=q_B, \delta(q_B, 0)=q_A, \delta(q_B, 1)=q_B$。
- 转移图:
- 画两个圆圈,标记为 $q_A$ 和 $q_B$。
- 在 $q_B$ 外再画一个圆圈,使其成为双圆圈。
- 画一个起始箭头指向 $q_A$。
- 根据 $\delta(q_A, 0)=q_A$,画一个从 $q_A$ 指向自己的箭头,标上 0。
- 根据 $\delta(q_A, 1)=q_B$,画一个从 $q_A$ 指向 $q_B$ 的箭头,标上 1。
- 根据 $\delta(q_B, 0)=q_A$,画一个从 $q_B$ 指向 $q_A$ 的箭头,标上 0。
- 根据 $\delta(q_B, 1)=q_B$,画一个从 $q_B$ 指向自己的箭头,标上 1。
示例2:一个接受所有包含子串 "01" 的字符串的DFA
- DFA定义: $Q=\{q_0, q_1, q_2\}, \Sigma=\{0, 1\}, q_0=q_0, F=\{q_2\}$。
- $q_0$: 初始状态,还未见到 "01"。
- $q_1$: 刚刚看到了一个 '0',可能下一个是 '1'。
- $q_2$: 已经看到了 "01",此后永远接受。
- 转移函数:
- $\delta(q_0, 0) = q_1$
- $\delta(q_0, 1) = q_0$
- $\delta(q_1, 0) = q_1$ (来了个0,覆盖了之前的0,继续等1)
- $\delta(q_1, 1) = q_2$ (成功看到 "01")
- $\delta(q_2, 0) = q_2$ (已经看到 "01",之后无所谓了)
- $\delta(q_2, 1) = q_2$ (同上)
- 转移图:
- 画三个圆圈 $q_0, q_1, q_2$。
- $q_2$ 画成双圆圈。
- 起始箭头指向 $q_0$。
- 画边:$q_0 \xrightarrow{1} q_0$, $q_0 \xrightarrow{0} q_1$, $q_1 \xrightarrow{0} q_1$, $q_1 \xrightarrow{1} q_2$, $q_2 \xrightarrow{0,1} q_2$。
- 遗漏转移: 对于DFA,每个节点对于字母表中的每个符号,都必须有且仅有一条出边。画图时很容易忘记某个状态在某个输入下的转移,这在形式上是不完整的。在上面的例子中,如果省略了 $q_2$ 的两条出边,它就不再是一个DFA的有效转移图。
- 起始状态和接受状态的标记: 忘记标记起始箭头或双圆圈是常见错误,这会导致图的信息不完整。
- 一个状态可以是起始状态和接受状态吗?: 可以。如果 $q_0 \in F$,那么代表 $q_0$ 的节点既有起始箭头指向,本身也是个双圆圈。这意味着空字符串 $\varepsilon$ 被接受。
- 标签合并: 多个标签可以合并在一个箭头上,但前提是它们的起点和终点完全相同。
转移图是DFA五元组定义的一种可视化表示。它使用节点代表状态,带标签的箭头代表状态转移,特殊的箭头和节点样式(双圆圈)分别表示起始状态和接受状态。这种图形化的表示方法比纯粹的数学符号更直观,更容易理解和设计DFA。
人类是视觉动物。将抽象的数学结构(五元组)转化为具体的图像(转移图),极大地降低了理解和沟通的门槛。在学术交流、教学和自己思考问题时,画图往往是第一步,它可以帮助我们理清思路,发现规律。
转移图就是DFA这个简单机器人的“电路图”或“蓝图”。
- 圆圈是机器内部的“灯泡”,表示它当前的模式。
- 箭头是连接灯泡的“电线”,上面写着触发条件(输入符号)。
- 标着"start"的箭头告诉你一开始哪个灯泡是亮的。
- 双圆圈的灯泡是“胜利指示灯”。
- 整个计算过程就是电流(当前状态)根据输入信号,沿着电线从一个灯泡流到下一个灯泡的过程。
想象你在玩一个桌面游戏,棋盘上画着几个圈(状态)。
- 你有一个棋子,开始时放在标有“起点”的圈里。
- 你有一叠卡牌,每张卡上写着一个字母(来自字母表 Σ)。
- 棋盘上的圈之间有各种带箭头的路径,每条路径上都写着字母。
- 你每翻一张卡牌,就必须把你的棋子沿着与卡牌字母相同、且从你当前位置出发的唯一那条路径,移动到下一个圈。
- 当你翻完所有卡牌,如果你的棋子停在了一个画着“星星”标记的圈(接受状态)里,你就赢了。否则就输了。
- 这个棋盘,就是转移图。
53. 转移表表示
📜 [原文4]
1转移表表示
- 行对应状态,列对应输入符号,$\mathrm{q}, \mathrm{a}$ 的条目是 $\delta(\mathrm{q}, \mathrm{a})$,起始状态用 $\rightarrow$ 标记,接受状态用 * 标记
| 符号 | |||
|---|---|---|---|
| ins | del | ||
| $\rightarrow$ | 1 | 0 | |
| 状态 | 1 | 2 | 0 |
| 2 | 3 | 1 | |
| ${ }^{*} 3$ | 3 | 2 |
这一部分介绍了表示DFA的第三种方法:转移表 (Transition Table)。如果说转移图是可视化的表示,那么转移表就是一种结构化、适合计算机处理的文本表示。
- 行对应状态,列对应输入符号: 表格的每一行代表一个状态,每一列代表字母表中的一个输入符号。
- q, a 的条目是 δ(q, a): 在表格的单元格中,位于状态 $q$ 所在行和符号 $a$ 所在列的交叉点,填写的值就是转移函数 $\delta(q, a)$ 的结果,即下一个状态。这本质上就是把转移函数的所有输入输出对列在一个二维数组里。
- 起始状态用 → 标记: 为了指明哪个是起始状态,通常会在该状态所在行的行首加上一个箭头 "→"。
- 接受状态用 标记: 为了指明哪些是接受状态,通常会在这些状态的名称前加上一个星号 ""。
- 表格分析:
- 该表格描述了与上一节转移图完全相同的DFA。
- 状态 (行): 表格的第一列列出了所有状态:0, 1, 2, 3。所以 $Q = \{0, 1, 2, 3\}$。
- 符号 (列): 表格的第一行列出了所有输入符号:ins, del。所以 $\Sigma = \{\text{ins}, \text{del}\}$。
- 起始状态: 状态 0 的行首有 "→",所以 $q_0 = 0$。
- 接受状态: 状态 3 的行首有 "*"(原文写作 `${ }^{*} 3`,但含义是 `*3`),所以 $F = \{3\}$。
- 转移函数 (单元格内容):
- 在 "0" 行 "ins" 列,条目是 "1",表示 $\delta(0, \text{ins}) = 1$。
- 在 "1" 行 "del" 列,条目是 "0",表示 $\delta(1, \text{del}) = 0$。
- 在 "2" 行 "ins" 列,条目是 "3",表示 $\delta(2, \text{ins}) = 3$。
- ... 以此类推,这个表格完整地定义了转移函数 δ。
示例1:复用“检测字符串是否以‘1’结尾的DFA”
- DFA定义: $Q=\{q_A, q_B\}, \Sigma=\{0, 1\}, q_0=q_A, F=\{q_B\}$, and $\delta$ in previous sections.
- 转移表:
| 符号 | |||
|---|---|---|---|
| 0 | 1 | ||
| 状态 | $\rightarrow q_A$ | $q_A$ | $q_B$ |
| $*q_B$ | $q_A$ | $q_B$ |
示例2:复用“接受所有包含子串 "01" 的字符串的DFA”
- DFA定义: $Q=\{q_0, q_1, q_2\}, \Sigma=\{0, 1\}, q_0=q_0, F=\{q_2\}$, and $\delta$ in previous sections.
- 转移表:
| 符号 | |||
|---|---|---|---|
| 0 | 1 | ||
| 状态 | $\rightarrow q_0$ | $q_1$ | $q_0$ |
| $q_1$ | $q_1$ | $q_2$ | |
| $*q_2$ | $q_2$ | $q_2$ |
- 行列混淆: 初学者可能会搞错行和列分别代表什么。记住:行是“你现在在哪”,列是“你看到了什么”。
- 标记遗漏: 忘记标记 "→" 和 "*" 会导致信息不完整,无法确定起始状态和接受状态。
- 表格不完整: 对于DFA,表格必须是完整的,不能有任何空白单元格。每个状态-符号组合都必须有一个确定的下一个状态。
- 标记的位置: "→" 和 "*" 通常放在状态名的旁边,以修饰该行所代表的状态。
转移表是DFA的另一种等价表示形式,它以二维表格的形式清晰地列出了转移函数的所有可能情况。行代表当前状态,列代表输入符号,单元格内容代表下一个状态。通过特殊的标记(箭头和星号)来指明起始状态和接受状态。
- 结构化: 表格是一种高度结构化的数据格式,非常适合用计算机程序来存储和处理。在实现一个DFA模拟器时,使用二维数组或哈希表来实现转移表是非常自然和高效的。
- 清晰性: 对于复杂的DFA,如果转移图的边交叉得非常混乱,转移表可以提供一个更整洁、不易出错的视角来检查每一个转移。
- 完备性检查: 在表格中,任何一个空白的单元格都意味着转移函数定义不完整,这使得检查DFA的完备性变得非常容易。
转移表就像一张火车的“时刻表”或“运行图”。
- 行是所有的“车站”(状态)。
- 列是不同的“天气状况”(输入符号),比如“晴天”或“雨天”。
- 表格里的内容告诉你:在某个“车站”,遇到某种“天气”,下一班列车会开往哪个“车站”。
- "→" 告诉你旅途的起点是哪个车站。
- "*" 告诉你哪些车站是“旅游胜地”(接受状态)。
想象一个简单的查表操作。你心里记着两个信息:你当前在哪一页(状态),以及你现在要查的单词首字母是什么(输入符号)。转移表就像一本字典的索引,你翻到对应页(行),再找到对应的首字母(列),索引告诉你下一个需要翻到的页码(下一个状态)。你从“第一页”(起始状态)开始,按照输入字符串的字母顺序一次次地查表翻页,直到字符串结束。最后看你停在哪一页,如果那一页页脚有个“★”标记(接受状态),就算查到了。
64. 示例:k槽缓冲区自动机
📜 [原文5]
示例:k 槽缓冲区自动机
这是一个非常经典和实用的DFA示例,用来模拟一个大小为 $k$ 的缓冲区 (Buffer) 的行为。缓冲区是计算机中用于临时存储数据的区域。
- 模型描述: 想象一个队列或一个容器,它最多能装 $k$ 个物品。我们可以执行两种操作:
- ins (insert): 向容器里放一个物品。
- del (delete): 从容器里拿走一个物品。
- 我们关心的是,经过一系列操作后,这个容器是否“满”了。
- DFA五元组解释:
- $Q=\{0,1,2, \ldots, k\}$:
- 状态被定义为从 0 到 $k$ 的整数。
- 每个状态 $i$ 的物理意义是:缓冲区中当前存放的物品数量。
- 状态 0 表示缓冲区是空的,状态 $k$ 表示缓冲区是满的。
- 这是一个有限集合,共有 $k+1$ 个状态。
- $\Sigma=\{\text { ins, del }\}$:
- 字母表包含两个符号,代表两种可以执行的操作。
- $\delta$:
- 这个转移函数定义了操作如何改变缓冲区的状态(物品数量)。它被分成了两个情况:
- $\delta(i, \text{ins}) = i+1 \text{ if } i < k \text{ else } = k$:
- 当你执行 ins 操作时:
- 如果缓冲区还没满 ($i < k$),那么物品数量加一,状态从 $i$ 变为 $i+1$。
- 如果缓冲区已经满了 ($i=k$),你再尝试放入物品,它也放不进去,所以物品数量保持不变,状态仍然是 $k$。else = k 部分处理了这种边界情况。
- $\delta(i, \text{del}) = i-1 \text{ if } i > 0 \text{ else } = 0$:
- 当你执行 del 操作时:
- 如果缓冲区不是空的 ($i > 0$),那么物品数量减一,状态从 $i$ 变为 $i-1$。
- 如果缓冲区已经是空的 ($i=0$),你再尝试取出物品,也取不出来,所以物品数量保持为0,状态仍然是 0。else = 0 部分处理了这种边界情况。
- $q_0 = 0$:
- 起始状态是 0,表示一开始缓冲区是空的。这很符合逻辑。
- $F = \{k\}$:
- 接受状态只有一个,就是状态 $k$。
- 这意味着,这个DFA所“接受”的,是那些能让缓冲区最终变满的操作序列。
- k: 一个正整数,代表缓冲区的容量。这是一个参数,定义了具体是哪个DFA。
- i: 一个变量,代表当前的状态,即缓冲区中的物品数量,$i \in Q$。
- if...else...: 这是条件表达式。例如 A if C else B 意味着“如果条件C成立,则结果是A;否则结果是B”。
- $\delta(i, \text{ins})$ 可以更清晰地写成:
$\delta(i, \text{ins}) = \min(i+1, k)$ (取 $i+1$ 和 $k$ 中较小的一个)
- $\delta(i, \text{del})$ 可以更清晰地写成:
$\delta(i, \text{del}) = \max(i-1, 0)$ (取 $i-1$ 和 0 中较大的一个)
示例1:k = 2 的缓冲区自动机
- $Q = \{0, 1, 2\}$
- $\Sigma = \{\text{ins}, \text{del}\}$
- $q_0 = 0$
- $F = \{2\}$
- 转移函数 $\delta$:
- $\delta(0, \text{ins}) = 1$
- $\delta(1, \text{ins}) = 2$
- $\delta(2, \text{ins}) = 2$ (已满,保持)
- $\delta(0, \text{del}) = 0$ (已空,保持)
- $\delta(1, \text{del}) = 0$
- $\delta(2, \text{del}) = 1$
- 输入字符串 "ins ins del ins":
- 开始在 $q_0=0$。
- 读 ins: $\delta(0, \text{ins}) = 1$。进入状态 1。
- 读 ins: $\delta(1, \text{ins}) = 2$。进入状态 2。
- 读 del: $\delta(2, \text{del}) = 1$。进入状态 1。
- 读 ins: $\delta(1, \text{ins}) = 2$。进入状态 2。
- 输入结束,最终状态是 2。因为 $2 \in F$,所以字符串 "ins ins del ins" 被接受。
示例2:k = 3 的缓冲区自动机
- $Q = \{0, 1, 2, 3\}$, $\Sigma = \{\text{ins}, \text{del}\}$, $q_0 = 0$, $F = \{3\}$
- 输入字符串 "ins del ins ins":
- 开始在 $q_0=0$。
- 读 ins: $\delta(0, \text{ins}) = 1$。进入状态 1。
- 读 del: $\delta(1, \text{del}) = 0$。进入状态 0。
- 读 ins: $\delta(0, \text{ins}) = 1$。进入状态 1。
- 读 ins: $\delta(1, \text{ins}) = 2$。进入状态 2。
- 输入结束,最终状态是 2。因为 $2 \notin F$,所以字符串 "ins del ins ins" 被拒绝。
- 对满缓冲区 "ins": 必须正确处理当 $i=k$ 时,输入 ins 状态不变的情况。这是一个“饱和”效应。
- 对空缓冲区 "del": 必须正确处理当 $i=0$ 时,输入 del 状态不变的情况。这是一个“下界”效应。
- k的值: k必须至少为1。如果k=0,那么 $Q=\{0\}, q_0=0, F=\{0\}$,这个自动机只接受空字符串 $\varepsilon$。
- 忘记参数k: 这个DFA的定义依赖于参数 $k$。讨论时需要明确 $k$ 的值。对于不同的 $k$,我们得到的是不同的DFA。
k槽缓冲区自动机是一个使用DFA来为现实世界中的“缓冲区”概念建模的例子。它的状态代表缓冲区中的项目数,转移代表插入和删除操作,而接受状态则定义了我们关心的目标条件(例如“缓冲区满”)。这个例子清晰地展示了如何将一个具体问题抽象成一个DFA。
这个例子的存在是为了:
- 具体化: 将抽象的五元组定义与一个具体、易于理解的场景联系起来。
- 展示建模能力: 展示DFA作为一种数学工具,不仅能处理抽象的符号串,还能为计算机系统中的组件(如缓冲区、协议状态机等)建立精确的模型。
- 参数化: 引入了参数 $k$ 的概念,说明我们可以定义一“族”DFA,而不仅仅是单个的DFA。
想象一个电梯。
- 电梯的容量是 $k$ 个人。
- 电梯里当前的人数就是状态 $i$。
- ins 操作就是“进去一个人”。如果电梯没满,人数就加一;如果满了,人数不变(外面的人进不来)。
- del 操作就是“出去一个人”。如果电梯里有人,人数就减一;如果是空电梯,人数不变。
- 电梯从 0 个人的状态($q_0$)开始运行。
- 如果经过一系列进出操作后,电梯恰好满了(达到状态 $k$),我们就认为这个操作序列是“成功的”(被接受)。
想象一个音量调节旋钮,刻度从 0 到 $k$。
- 旋钮当前指向的刻度就是状态 $i$。
- 字母表是两个按钮:+ (ins) 和 - (del)。
- 按 + 按钮,如果音量没到顶($<k$),旋钮就顺时针转一格;如果到顶了,旋钮就不动。
- 按 - 按钮,如果音量没到底($>0$),旋钮就逆时针转一格;如果到底了,旋钮就不动。
- 开始时音量在 0。
- 我们想知道,一串按钮操作之后,音量是否会达到最大值 $k$。这个DFA就是用来回答这个问题的。讲义中给出的转移图就是 $k=3$ 时的音量旋钮操作图。
75. DFA对输入的处理
📜 [原文6]
1DFA对输入的处理
- 给定输入字符串 $x=a_{1} a_{2} \ldots a_{n}$,DFA从状态 $\mathrm{q}_{0}$ 开始,读取 $\mathrm{a}_{1}$ 并转移到状态 $\delta\left(\mathrm{q}_{0}, \mathrm{a}_{1}\right)=$ 假设 $\mathrm{q}_{1}$,然后读取 $\mathrm{a}_{2}$ 并转移到状态 $\delta\left(\mathrm{q}_{1}, \mathrm{a}_{2}\right)=$ 假设 $\mathrm{q}_{2}$,依此类推,即,DFA经过一系列状态 $q_{1} q_{2} q_{3} \ldots q_{n}$ (不一定不同),使得对于每个 $i=1, \ldots, n$,$\delta\left(\mathrm{q}_{\mathrm{i}-1}, \mathrm{a}_{\mathrm{i}}\right)=\mathrm{q}_{\mathrm{i}}$。
- 输入被自动机接受当且仅当最后状态 $\mathrm{q}_{\mathrm{n}}$ 在 $\mathrm{F}$ 中,否则输入被拒绝。
- 自动机 $\mathrm{A}$ 的语言,记作 $\mathrm{L}(\mathrm{A})$,是所有被 $\mathrm{A}$ 接受的输入字符串集合。
这一部分详细描述了DFA的“运行”过程,即它如何一步步地处理一个输入字符串,并最终做出“接受”或“拒绝”的判断。同时,它引入了自动机语言的概念。
- 给定输入字符串...:
- $x=a_{1} a_{2} \ldots a_{n}$: 这是一个由 $n$ 个符号组成的输入字符串。$a_1$是第一个符号,$a_2$是第二个,以此类推。每个 $a_i$ 都必须是字母表 Σ 中的一员。
- DFA从状态 $q_0$ 开始: 计算的起点永远是起始状态。
- 读取 $a_1$ 并转移到状态 $\delta(q_0, a_1) = q_1$: 这是计算的第一步。机器查看第一个符号 $a_1$,应用转移函数 δ,从 $q_0$ 移动到新的状态 $q_1$。
- 然后读取 $a_2$ 并转移到状态 $\delta(q_1, a_2) = q_2$: 这是第二步。机器在新的状态 $q_1$ 上,查看第二个符号 $a_2$,再次应用转移函数,移动到 $q_2$。
- 依此类推: 这个过程一直持续,直到字符串中的所有符号都被读取完毕。
- DFA经过一系列状态 $q_0, q_1, q_2, \ldots, q_n$: 这是一个包含 $n+1$ 个状态的序列。$q_0$ 是起始状态,而 $q_i$ (对于 $i>0$) 是在读取了前 $i$ 个输入符号后达到的状态。注意,这些状态不一定是互不相同的,DFA可能会在某些状态之间来回访问。
- $\delta(q_{i-1}, a_i) = q_i$: 这是对上述过程的精确数学描述,定义了状态序列中相邻两项的关系。
- 输入被自动机接受或拒绝:
- 这是最终的判决时刻。在读取完最后一个符号 $a_n$ 并转移到最终状态 $q_n$ 后,计算结束。
- 接受 (accept): 如果这个最终状态 $q_n$ 属于接受状态集合 F (即 $q_n \in F$),那么整个输入字符串 $x$ 就被DFA接受。
- 拒绝 (reject): 如果最终状态 $q_n$ 不属于接受状态集合 F (即 $q_n \notin F$),字符串 $x$ 就被拒绝。
- 这是一个二元决策,对于任何给定的输入字符串,DFA的输出要么是“接受”,要么是“拒绝”,没有第三种可能。
- 自动机A的语言 L(A):
- 这是一个核心概念。一个自动机不仅仅是处理单个字符串,它定义了一个语言。
- 语言 (Language) 在形式语言理论中,指的是一个字符串的集合。
- L(A) 被定义为“所有能被自动机 A 接受的字符串”所构成的集合。
- 因此,一个DFA可以被看作是一个“成员资格测试器”。给定一个字符串 $x$ 和一个语言 $L(A)$,DFA A 的工作就是判断 $x$ 是否属于 $L(A)$。
使用“检测字符串是否以‘1’结尾的DFA”:
- $Q=\{q_A, q_B\}, \Sigma=\{0, 1\}, q_0=q_A, F=\{q_B\}$。$\delta$如前定义。
- 语言 L(A): 所有以 '1' 结尾的二进制字符串的集合。
示例1: 输入 x = "101"
- 状态序列: $q_0, q_1, q_2, q_3$
- 初始状态: $q_0 = q_A$。
- 读第一个符号 '1': $q_1 = \delta(q_0, 1) = \delta(q_A, 1) = q_B$。
- 读第二个符号 '0': $q_2 = \delta(q_1, 0) = \delta(q_B, 0) = q_A$。
- 读第三个符号 '1': $q_3 = \delta(q_2, 1) = \delta(q_A, 1) = q_B$。
- 输入结束。最终状态是 $q_3=q_B$。
- 检查: $q_B \in F$?是的,因为 $F=\{q_B\}$。
- 结论: 字符串 "101" 被接受。这也符合预期,因为 "101" 确实属于 L(A)。
示例2: 输入 x = "010"
- 初始状态: $q_0 = q_A$。
- 读 '0': $q_1 = \delta(q_A, 0) = q_A$。
- 读 '1': $q_2 = \delta(q_A, 1) = q_B$。
- 读 '0': $q_3 = \delta(q_B, 0) = q_A$。
- 输入结束。最终状态是 $q_3=q_A$。
- 检查: $q_A \in F$?不是,因为 $F=\{q_B\}$。
- 结论: 字符串 "010" 被拒绝。这也符合预期,因为 "010" 不属于 L(A)。
- 最终状态 vs 接受状态: 路径上的任何一个中间状态 $q_1, \ldots, q_{n-1}$ 是否是接受状态,对最终结果没有影响。只有最后一个状态 $q_n$ 才重要。
- 空字符串 $\varepsilon$: 如果输入是空字符串,它没有符号。DFA不执行任何转移,直接停在起始状态 $q_0$。因此,$\varepsilon$ 被接受当且仅当 $q_0 \in F$。
- 语言是集合: L(A) 不是单个字符串,而是可能无限多个字符串的集合。DFA本身是有限的,但它可以识别(接受)一个无限大的语言。例如,以'1'结尾的字符串有无限多个。
DFA的处理过程是一个确定性的、顺序的计算。它从起始状态出发,根据输入字符串的符号,一步步地在状态间转移,每一步都由转移函数唯一确定。处理完整个字符串后,根据其所在的最终状态是否为接受状态,来决定“接受”或“拒绝”该字符串。所有能被该DFA接受的字符串的集合,就构成了该自动机所定义的语言。
此部分将DFA的静态定义(五元组)与动态的行为(处理过程)联系起来,使得DFA模型变得“活”了起来。它精确定义了“计算”和“接受”的含义,并引出了核心目标——识别语言。这是从机器模型到其所能解决的问题(语言识别)的关键桥梁。
想象你在玩一个“听指令走迷宫”的游戏。
- 迷宫地图就是转移图,每个房间是一个状态。
- 你从“入口”房间($q_0$)开始。
- 有人在外面念一串指令(输入字符串),比如“左、右、右、左”。
- 每个房间的每扇门上都标着指令(比如“左”门,“右”门)。
- 每听到一个指令,你就必须走标有该指令的门,进入下一个房间(确定性)。
- 当指令念完,你看一下你所在的房间。如果这个房间的门上画着一个“宝藏”标记(属于F),你就赢了(接受)。
- 这个迷宫(DFA)所定义的语言,就是所有能让你最终找到宝藏的“指令序列”的集合。
想象一个老式密码锁,有一排拨轮和一串你要输入的密码。
- 锁的内部机制在某个状态。
- 你从起始状态开始。
- 你输入密码的第一个数字,锁的内部机制“咔哒”一声,变成了另一个状态。
- 你继续输入第二个、第三个数字... 锁的内部状态不断变化。
- 当你输入完最后一个数字,锁停留在最终的状态。
- 如果这个最终状态是“解锁”状态(接受状态),锁就打开了。否则,它仍然锁着(拒绝)。
- 这个锁(DFA)的语言就是它所有“正确的密码”的集合。
86. 接受路径
📜 [原文7]
1接受路径
- 对于每个节点 $\mathrm{q}$ 和每个标签 $\mathrm{a} \in \Sigma$,从 $\mathrm{q}$ 出发有一条唯一出边标记为 $\mathrm{a}$ (因为 $\delta$ 是一个函数)
- $\mathrm{A}$ 在输入 $\mathrm{x}=\mathrm{a}_{1} \ldots \mathrm{a}_{\mathrm{n}}$ 上的计算(或运行):从起始状态开始,并且在边上具有标签序列 $\mathrm{x}=\mathrm{a}_{1} \ldots \mathrm{a}_{\mathrm{n}}$ 的唯一路径
- 路径上的节点序列 = DFA在输入 $\mathrm{x}$ 上的状态序列
- 如果计算(或路径) 终止于 $\mathrm{F}$ 中的状态,则为接受计算 ( 路径 ) $\Leftrightarrow$ 输入字符串 $\mathrm{x}$ 被 $\mathrm{A}$ 接受
- 自动机的语言 $\mathrm{L}(\mathrm{A})$ = 所有接受路径的标签集合 (即从起始状态到 $\mathrm{F}$ 中的状态的路径)
- $\mathrm{L}(\mathrm{A})=\left\{\mathrm{x} \mid\right.$ 存在一条从起始状态 $\mathrm{q}_{0}$ 到 $\mathrm{F}$ 中状态的路径 $\pi$,其标签是 $\mathrm{x}$ \}
这部分使用转移图的术语(节点、边、路径)重新解释了DFA的计算过程和语言定义,提供了一个更几何、更直观的视角。
- 对于每个节点...有一条唯一出边...:
- 这再次强调了DFA的确定性和完备性,并将其翻译成图论的语言。
- 在转移图中,从任何一个节点出发,对于字母表里的任意一个符号,都恰好有一个箭头指出去。不多也不少。这意味着路径是无歧义的。
- A在输入x上的计算(或运行):
- 这个概念被等同于在转移图中寻找一条特定的路径。
- 这条路径必须满足两个条件:
- 从起始状态开始: 路径的起点必须是 $q_0$ 对应的节点。
- 边上的标签序列是x: 如果 $x = a_1 a_2 \ldots a_n$,那么这条路径的第一条边的标签必须是 $a_1$,第二条边的标签必须是 $a_2$,以此类推。
- 由于DFA的确定性,对于任何给定的输入字符串 $x$,这样的一条路径是唯一的。
- 路径上的节点序列 = DFA在输入x上的状态序列:
- 这建立了一个直接的对应关系。上一节讲的状态序列 $q_0, q_1, \ldots, q_n$ 正是这条唯一路径所依次经过的节点。
- 接受计算 (路径):
- 如果这条由输入 $x$ 决定的唯一路径,它的终点恰好是一个接受状态(双圆圈节点),那么这条路径就被称为“接受路径”。
- 一个输入字符串 $x$ 被接受,这件事情等价于它在图上对应的路径是一条接受路径。
- 自动机的语言L(A) = 所有接受路径的标签集合:
- 这是对语言 L(A) 的一个全新的、基于图的定义。
- 想象一下,在转移图中,所有可能的、从起始状态出发,到任意一个接受状态结束的路径。
- 把这些路径上所有的标签序列收集起来,组成一个集合,这个集合就是 L(A)。
- L(A) = {x | ...}:
- 这是对上述定义的更形式化的数学表达。
- 一个字符串 $x$ 在语言 L(A) 中,当且仅当(| 符号读作“当且仅当”或“满足条件”)在图中存在一条路径 $\pi$,这条路径 $\pi$ 从 $q_0$ 开始,在某个 $f \in F$ 结束,并且路径 $\pi$ 上的边的标签依次连接起来正好是字符串 $x$。
使用“k=3缓冲区自动机”的转移图: (参考第2节的图,但想象k=3)
- $Q=\{0,1,2,3\}, q_0=0, F=\{3\}, \Sigma=\{\text{ins, del}\}$
- 转移图: 节点0, 1, 2, 3。起始箭头指向0,节点3是双圆圈。边:$0 \xrightarrow{\text{ins}} 1$, $1 \xrightarrow{\text{ins}} 2$, $2 \xrightarrow{\text{ins}} 3$, $3 \xrightarrow{\text{ins}} 3$。反向有 $3 \xrightarrow{\text{del}} 2$, $2 \xrightarrow{\text{del}} 1$, $1 \xrightarrow{\text{del}} 0$, $0 \xrightarrow{\text{del}} 0$。
示例1: 路径分析 for x = "ins ins ins"
- 路径: 从 $q_0=0$ 开始。
- 第一条边,标签 ins: $0 \rightarrow 1$。
- 第二条边,标签 ins: $1 \rightarrow 2$。
- 第三条边,标签 ins: $2 \rightarrow 3$。
- 路径终点: 节点 3。
- 判断: 节点 3 是双圆圈(接受状态)。所以这是一条接受路径。
- 结论: 字符串 "ins ins ins" 属于 L(A)。
示例2: 路径分析 for x = "ins del ins"
- 路径: 从 $q_0=0$ 开始。
- 第一条边,标签 ins: $0 \rightarrow 1$。
- 第二条边,标签 del: $1 \rightarrow 0$。
- 第三条边,标签 ins: $0 \rightarrow 1$。
- 路径终点: 节点 1。
- 判断: 节点 1 是单圆圈(非接受状态)。这不是一条接受路径。
- 结论: 字符串 "ins del ins" 不属于 L(A)。
- 路径 vs 环路: 一条路径可以包含环路。例如,对于字符串 "ins del",路径是 $0 \rightarrow 1 \rightarrow 0$,回到了起点。
- 路径的标签: 路径的标签是所有边标签的有序连接,顺序不能错。
- 空路径: 从一个节点到其自身的“空路径”(不经过任何边)的标签是空字符串 $\varepsilon$。因此,如果 $q_0$ 本身就是接受状态,那么这条从 $q_0$ 到 $q_0$ 的空路径就是一条接受路径,所以 $\varepsilon \in L(A)$。
这一部分将DFA的计算过程完全等价地映射到了图论中的“路径”概念。一个字符串的计算过程对应图上一条唯一的、由该字符串标签的路径。字符串是否被接受,取决于该路径的终点是否为接受状态。整个自动机的语言,就是所有从起点到终点的接受路径所对应的标签字符串的集合。
这个基于路径的视角有两个主要目的:
- 直观化: 它利用了图的直观性,让我们能“看到”计算的过程。我们可以通过在图上“走”路径来模拟计算。
- 理论工具: 图论是一个成熟的数学分支,有大量的理论和算法。将DFA与图联系起来,意味着我们可以借用图论的工具来分析DFA和正则语言(例如,寻找路径、判断连通性等)。
DFA的语言 L(A) 就是从起始城市($q_0$)出发,能够到达任何一个旅游胜地城市(F中的任意一个状态)的所有可能的“旅行路线图”(路径标签)。任何一张能带你到达目的地的有效路线图(字符串),都属于这个“旅行指南”(语言 L(A))。
想象一个巨大的弹珠机。
- 弹珠从顶部的“入口”($q_0$)落下。
- 机器内部有很多钉子和通道(状态和转移)。
- 输入字符串的每个字符,就像是你按下的一个按钮,这个按钮会控制一组开关,决定弹珠从当前位置下落时走哪条唯一的通道。
- 弹珠经过一系列通道后,最终会落到底部的某个槽里。
- 有几个槽被涂成了金色(接受状态F)。
- 语言 L(A) 就是所有能让弹珠最终落入金色槽的“按钮序列”的集合。
- 任何一个输入字符串,都对应弹珠在机器里走出的一条唯一路径。
97. 示例 (缓冲区自动机语言)
📜 [原文8]
1示例
输入字符串: ins ins ins del ins
路径: $0 \longrightarrow 1 \longrightarrow 2 \longrightarrow 3 \longrightarrow 2 \longrightarrow 3$
- 该自动机的语言:
$\mathrm{L}(\mathrm{A})=$ 使缓冲区满的操作序列集合
这部分通过一个具体的例子,演示了如何跟踪一个输入字符串在k=3缓冲区自动机上的执行路径,并对该自动机的语言给出了一个高层次的描述。
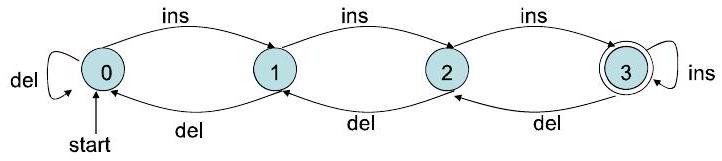
- 图片分析:
- 图片展示的是 $k=3$ 时的缓冲区自动机的转移图。
- $Q = \{0, 1, 2, 3\}$
- $q_0 = 0$ (起始箭头指向0)
- $F = \{3\}$ (节点3是双圆圈)
- $\Sigma = \{\text{ins}, \text{del}\}$
- 转移边与之前分析的一致,例如 $\delta(0, \text{ins})=1$, $\delta(3, \text{del})=2$, 等等。
- 输入字符串: ins ins ins del ins:
- 这是一个具体的输入样例。
- 路径: $0 \longrightarrow 1 \longrightarrow 2 \longrightarrow 3 \longrightarrow 2 \longrightarrow 3$:
- 这是对DFA处理该输入字符串时,所经过的状态序列的逐步展示。
- 初始状态: $0$
- 读 ins: 状态从 $0$ 变为 $1$。路径: $0 \rightarrow 1$。
- 读 ins: 状态从 $1$ 变为 $2$。路径: $0 \rightarrow 1 \rightarrow 2$。
- 读 ins: 状态从 $2$ 变为 $3$。路径: $0 \rightarrow 1 \rightarrow 2 \rightarrow 3$。
- 读 del: 状态从 $3$ 变为 $2$。路径: $0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2$。
- 读 ins: 状态从 $2$ 变为 $3$。路径: $0 \rightarrow 1 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 3$。
- 计算结束: 整个字符串处理完毕,最终停在状态 3。
- 判断: 因为最终状态 3 属于接受状态集 $F=\{3\}$,所以该字符串 "ins ins ins del ins" 被接受。
- 该自动机的语言:
- L(A) = 使缓冲区满的操作序列集合:
- 这句是对该DFA所识别的语言的自然语言描述。
- 它不是列举字符串,而是描述了这些字符串的共同属性。
- 一个操作序列(字符串)能被这个DFA接受,当且仅当在执行完这个序列后,缓冲区恰好是满的(即状态为 $k$)。
- 例如,"ins ins ins" (k=3) 会被接受。 "ins ins del ins ins" 也会被接受。但是 "ins ins" 不会被接受。
在 k=3 的缓冲区自动机上:
示例1: 输入 x = "del ins"
- 路径:
- 初始状态: 0
- 读 del: $\delta(0, \text{del}) = 0$。 路径: $0 \rightarrow 0$。
- 读 ins: $\delta(0, \text{ins}) = 1$。 路径: $0 \rightarrow 0 \rightarrow 1$。
- 最终状态: 1。
- 判断: $1 \notin F$。
- 结论: 字符串 "del ins" 被拒绝。从物理意义上,先取(无效)再放一个,缓冲区里只有1个物品,没满。
示例2: 输入 x = "ins ins ins ins del ins"
- 路径:
- 初始状态: 0
- ins $\rightarrow$ 1
- ins $\rightarrow$ 2
- ins $\rightarrow$ 3
- ins $\rightarrow$ 3 (缓冲区已满,状态不变)
- del $\rightarrow$ 2
- ins $\rightarrow$ 3
- 最终状态: 3。
- 判断: $3 \in F$。
- 结论: 字符串 "ins ins ins ins del ins" 被接受。这个操作序列最终也使缓冲区满了。
- 只看最终状态: 在跟踪路径 "ins ins ins del ins" 时,路径中间经过了接受状态 3,然后又离开了。这不影响最终结果。只有在所有输入都处理完毕后,机器所在的最后一个状态才决定接受或拒绝。
- 语言的描述: “使缓冲区满的”意味着操作完成“后”缓冲区是满的,不关心过程中是否曾经满过。
这个例子通过一个具体的输入字符串和路径跟踪,生动地展示了DFA的计算过程。它同时给出了k槽缓冲区自动机的语言的本质——即所有那些能够让缓冲区从空变为满的操作指令序列的集合。
这个示例的目的是将前面几节的抽象定义(DFA处理、路径、语言)全部串联起来,并应用到一个具体的、有实际意义的自动机模型上,巩固学生的理解。通过手算一个例子的路径,可以加深对DFA工作机制的印象。
将 L(A) 想象成所有能“通关”这个缓冲区游戏的“攻略秘籍”。“通关”条件就是让缓冲区变满。
- "ins ins ins del ins" 是一份有效的攻略,因为它最后让缓冲区满了。
- "ins del ins" 是一份无效的攻略,因为它最后只装了1个物品。
这个DFA就是这个游戏的裁判,它帮你验证一份攻略是否有效。
想象你在给一个水桶(容量为3升)加水或舀水。
- ins = 加1升水。
- del = 舀出1升水。
- 水桶初始是空的(状态0)。
- 输入 "ins ins ins del ins" 对应操作:加水、加水、加水(满了)、舀水(剩2升)、加水(又满了)。
- 操作结束后,水桶是满的(状态3)。所以这是一个“成功”的操作序列。
- L(A) 就是所有能让水桶最终变满的“操作说明书”的集合。
108. 转移函数到字符串的扩展
📜 [原文9]
1转移函数到字符串的扩展
- 可以把 $\delta$ 扩展为从 $\mathrm{Q} \times \Sigma^{*}$ 到 $\mathrm{Q}$ 的函数 $\delta^{*}$:
- 对于每个状态 $\mathrm{q}$ 和字符串 $\mathrm{x}$,$\delta^{*}(\mathrm{q}, \mathrm{x})$ 是从状态 $\mathrm{q}$ 开始并具有标签 $\mathrm{x}$ 的唯一路径的终态
归纳定义:
```
Basis: $x$ has length 0, i.e. $x=\varepsilon: \delta^{*}(q, \varepsilon)=q$
Induction: $x$ has length $>0$, i.e. $x=y a$, for some $y \in \Sigma^{*}, a \in \Sigma$ :
$\delta^{*}(\mathrm{q}, \mathrm{ya})=\delta\left(\delta^{*}(\mathrm{q}, \mathrm{y}), \mathrm{a}\right)$
$\mathrm{L}(\mathrm{A})=\left\{\mathrm{x} \in \Sigma^{*} \mid \delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right) \in \mathrm{F}\right\}$
$=$ set of strings $x$ that label paths from the start state $\mathrm{q}_{0}$
to an accepting state
```
这一部分引入了一个非常重要的数学工具:扩展转移函数 (Extended Transition Function),记作 $\delta^*$ (读作 delta-star)。它使我们能够一步到位地描述处理整个字符串后的状态,而不是像之前那样一步步地描述。
- 扩展 $\delta$ 到 $\delta^*$:
- 我们原始的转移函数 $\delta$ 只能处理单个符号,其定义域是 $Q \times \Sigma$。
- 我们现在想定义一个更强大的函数 $\delta^*$,它能直接处理整个字符串。它的定义域是 $Q \times \Sigma^*$。
- $\Sigma^*$: 这表示由字母表 $\Sigma$ 中符号组成的所有可能字符串的集合,包括空字符串 $\varepsilon$。这叫作字母表 $\Sigma$ 的克莱尼闭包 (Kleene Closure)。
- $\delta^*(q, x)$ 的含义: 其含义是“从状态 $q$ 开始,完整地读取整个字符串 $x$ 之后,会到达哪个状态?”。
- 归纳定义:
- 这种扩展通常使用归纳法 (Induction) 来定义,基于字符串的长度。
- Basis (基础情况): $x$ 的长度为0,即 $x=\varepsilon$ (空字符串)。
- $\delta^*(q, \varepsilon) = q$: 从任何状态 $q$ 开始,读取一个空字符串,什么也不做,所以状态保持不变,仍然是 $q$。这是归纳定义的基础。
- Induction (归纳步骤): 假设我们已经知道了如何处理长度为 $n$ 的字符串 $y$,现在要定义如何处理长度为 $n+1$ 的字符串 $x=ya$。
- $x = ya$: 任何一个非空字符串 $x$ 都可以看作是一个“前缀” $y$ 加上最后一个符号 $a$。
- $\delta^*(q, ya) = \delta(\delta^*(q, y), a)$: 这就是归纳的核心。这句话的含义是:
- 要计算从 $q$ 开始读完 $ya$ 到达的状态...
- ...我们首先计算从 $q$ 开始读完前缀 $y$ 到达的中间状态。根据 $\delta^*$ 的假设,这个状态是 $\delta^*(q, y)$。
- 然后,我们从这个中间状态 $\delta^*(q, y)$ 出发,再读取最后一个符号 $a$。这可以通过原始的单步转移函数 $\delta$ 来完成。
- 所以,最终状态就是 $\delta(\text{中间状态}, a)$,即 $\delta(\delta^*(q, y), a)$。
- 用 $\delta^*$ 重新定义语言 L(A):
- $\mathrm{L}(\mathrm{A})=\left\{\mathrm{x} \in \Sigma^{*} \mid \delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right) \in \mathrm{F}\right\}$:
- 有了 $\delta^*$,语言的定义变得异常简洁。
- 一个字符串 $x$ 属于语言 L(A),当且仅当,从起始状态 $q_0$ 开始,处理完整个字符串 $x$ 后到达的最终状态 $\delta^*(q_0, x)$ 是一个接受状态。
- 这与之前分步描述的定义是完全等价的,但数学上更优雅。
- 下面那行英文是对这个定义的重复解释。
- $\delta^*$ (delta-star): 扩展转移函数。
- 输入: 一个状态 $q \in Q$ 和一个字符串 $x \in \Sigma^*$。
- 输出: 一个状态 $p \in Q$。
- 归纳定义推导示例: 计算 $\delta^*(q, a_1 a_2 a_3)$
- 令 $x = a_1 a_2 a_3$。它可以看作 $y_2 a_3$,其中 $y_2=a_1 a_2$。
$\delta^*(q, a_1 a_2 a_3) = \delta(\delta^*(q, a_1 a_2), a_3)$
- 现在需要计算 $\delta^*(q, a_1 a_2)$。它可以看作 $y_1 a_2$,其中 $y_1=a_1$。
$\delta^*(q, a_1 a_2) = \delta(\delta^*(q, a_1), a_2)$
- 现在需要计算 $\delta^*(q, a_1)$。它可以看作 $y_0 a_1$,其中 $y_0=\varepsilon$。
$\delta^*(q, a_1) = \delta(\delta^*(q, \varepsilon), a_1)$
- 根据基础情况,$\delta^*(q, \varepsilon) = q$。
所以 $\delta^*(q, a_1) = \delta(q, a_1)$。这很合理,处理单个字符的 $\delta^*$ 和 $\delta$ 是一样的。
- 把结果代回去:
$\delta^*(q, a_1 a_2) = \delta(\delta(q, a_1), a_2)$
- 再代回去:
$\delta^*(q, a_1 a_2 a_3) = \delta(\delta(\delta(q, a_1), a_2), a_3)$
- 这个推导结果清晰地展示了 $\delta^*$ 的计算过程就是 $\delta$ 的连续嵌套调用,与我们之前一步步处理字符串的过程完全吻合。
使用“检测字符串是否以‘1’结尾的DFA”:
- $Q=\{q_A, q_B\}, \Sigma=\{0, 1\}, q_0=q_A, F=\{q_B\}$。$\delta$如前定义。
示例1: 计算 $\delta^*(q_A, "101")$
- $\delta^*(q_A, "101") = \delta(\delta^*(q_A, "10"), 1)$
- $\delta^*(q_A, "10") = \delta(\delta^*(q_A, "1"), 0)$
- $\delta^*(q_A, "1") = \delta(\delta^*(q_A, \varepsilon), 1) = \delta(q_A, 1) = q_B$
- 代入第2步: $\delta^*(q_A, "10") = \delta(q_B, 0) = q_A$
- 代入第1步: $\delta^*(q_A, "101") = \delta(q_A, 1) = q_B$
- 最终结果: $\delta^*(q_A, "101") = q_B$。因为 $q_B \in F$,所以字符串 "101" 被接受。
示例2: 计算 $\delta^*(q_A, "010")$
- $\delta^*(q_A, "010") = \delta(\delta^*(q_A, "01"), 0)$
- $\delta^*(q_A, "01") = \delta(\delta^*(q_A, "0"), 1)$
- $\delta^*(q_A, "0") = \delta(\delta^*(q_A, \varepsilon), 0) = \delta(q_A, 0) = q_A$
- 代入第2步: $\delta^*(q_A, "01") = \delta(q_A, 1) = q_B$
- 代入第1步: $\delta^*(q_A, "010") = \delta(q_B, 0) = q_A$
- 最终结果: $\delta^*(q_A, "010") = q_A$。因为 $q_A \notin F$,所以字符串 "010" 被拒绝。
- 递归方向: 归纳定义 $x=ya$ 是把最后一个字符 $a$ 分离出来。也可以定义成 $x=ay$,把第一个字符分离出来,两者是等价的,但定义要保持一致。
- $\delta$ 和 $\delta^*$ 的混用: $\delta$ 的第二个参数只能是单个符号,而 $\delta^*$ 的第二个参数是字符串。在公式 $\delta(\delta^*(q, y), a)$ 中,内层是 $\delta^*$,外层是 $\delta$,不能写反。
- 空字符串: $\delta^*(q, \varepsilon)=q$ 是整个递归定义的基石,非常重要。
扩展转移函数 $\delta^*$ 是对基本转移函数 $\delta$ 的一个推广,使其能够直接处理整个字符串而不是单个符号。它通过对字符串长度的归纳法来精确定义。有了 $\delta^*$,我们可以用一个非常简洁的公式 $\delta^*(q_0, x) \in F$ 来判断一个字符串 $x$ 是否被DFA接受,这为后续的理论证明提供了极大的便利。
- 数学优雅性: 将一个分步的、过程性的描述(一步步转移)转化为一个单一的、声明性的函数调用($\delta^*(q_0, x)$),使得数学表达和证明更加简洁和强大。
- 抽象化: 它将“处理一个字符串”这个过程本身,抽象成了一个函数。这使得我们可以像讨论普通函数一样讨论这个过程,例如证明它的某些性质。
- 证明工具: 在证明关于正则语言的定理时(例如,正则语言的闭包性质),使用 $\delta^*$ 会比描述整个路径过程要方便得多。
如果说 $\delta$ 是“走一步”,那么 $\delta^*$ 就是“按照一张完整的路线图走完全程”。
- $\delta(q, a)$:“在 $q$ 路口,按照指示牌 $a$ 走,下一步到哪?”
- $\delta^*(q, x)$:“在 $q$ 路口,按照一整串指令 $x$ 走,最终会到哪?”
$\delta^*$ 就像是一个GPS,你给它起点和完整的路线指令,它直接告诉你终点在哪里,而不需要告诉你中间每一步是怎么走的。
想象一个函数计算器。
- 普通的 sin(x) 函数,你输入一个数,它输出一个数。这就像 $\delta(q, a)$。
- 现在想象一个“复合函数”计算器,你可以输入一串操作,比如 "sin, cos, tan"。
- 你输入一个初始值 $x_0$ 和这串操作,计算器会计算 $\tan(\cos(\sin(x_0)))$。
- 这个“复合函数”计算器就扮演了 $\delta^*$ 的角色。x 是初始值,操作序列是字符串。$\delta^*(x_0, \text{"sin, cos, tan"})$ 直接给出了最终结果。
119. 正则语言
📜 [原文10]
1正则语言
- 如果存在一个有限自动机 $\mathrm{A}$ 接受(或识别) $\mathrm{L}$,即 $\mathrm{L}(\mathrm{A})=\mathrm{L}$,则语言 $\mathrm{L}$ 是正则的。
这一部分给出了计算理论中一个最核心的定义之一:正则语言 (Regular Language)。
- 这个定义建立了一个至关重要的连接:它将一类语言(字符串的集合,是一个数学对象)与一类计算模型(有限自动机,是一个机器模型)等同起来。
- "如果存在一个有限自动机 A ...":
- 这句话是关键。要判断一个语言 L 是否是正则的,你需要做的就是去“寻找”一个DFA。
- 只要你能成功地构造出(或证明存在)哪怕一个DFA,它的语言 L(A) 正好就等于 L,那么 L 就是正则语言。
- 反之,如果对于一个语言 L,你能证明不可能存在任何DFA来识别它,那么 L 就不是正则语言。
- "...接受(或识别) L...":
- “接受 (accept)” 和 “识别 (recognize)” 在这里是同义词。它们都意味着自动机能够对任何字符串做出正确的“是/否”判断。
- 对于任何字符串 $x$:
- 如果 $x$ 属于 L,那么自动机 A 必须接受 $x$。
- 如果 $x$ 不属于 L,那么自动机 A 必须拒绝 $x$。
- "...即 L(A) = L...":
- 这是对“接受”或“识别”的数学化精确表述。两个集合相等,意味着它们包含完全相同的元素。
- $L(A) = L$ 意味着:
- $L(A) \subseteq L$: 自动机 A 接受的每个字符串都确实在 L 中(自动机不会“误报”)。
- $L \subseteq L(A)$: L 中的每个字符串都必须能被自动机 A 接受(自动机不会“漏报”)。
示例1: 语言 $L_1$ = {所有以 '1' 结尾的二进制字符串} 是正则的吗?
- 回答: 是。
- 证明: 因为我们之前已经成功构造了一个DFA A(在第5节的例子中),它的语言 $L(A)$ 正是 $L_1$。既然存在这样一个DFA,根据定义,$L_1$ 就是一个正则语言。
示例2: 语言 $L_2$ = { "cat" } 是正则的吗? (只包含一个字符串 "cat" 的语言)
- 回答: 是。
- 证明: 因为我们可以构造一个识别它的DFA(在第1节的例子中我们设计过一个)。该DFA只有在输入恰好是 "cat" 时才进入接受状态。因此,$L_2$ 是一个正则语言。事实上,任何有限的语言都是正则的。
示例3: 语言 $L_3 = \{a^n b^n \mid n \ge 0\}$ 是正则的吗?
- 语言描述: 这个语言包含 $\varepsilon, ab, aabb, aaabbb, \ldots$ 等字符串,其中 'a' 的数量必须严格等于 'b' 的数量,且所有 'a' 都在 'b' 的前面。
- 回答: 不是。
- 直觉解释: 一个DFA的记忆是有限的(由其有限的状态数决定)。为了验证 'a' 的数量是否等于 'b' 的数量,DFA必须在读完所有的 'a' 之后,记住到底读了多少个 'a'。但由于 $n$ 可以是任意大的数,需要记忆的数量是无限的。有限的几个状态无法记住无限多种可能性。因此,不存在一个DFA可以识别这个语言。(严格的证明需要使用“泵引理”,这是后续课程的内容)。
- 正则语言 vs 有限自动机: 正则语言是一个语言的类别,而有限自动机是一个机器模型。定义说的是,凡是能被这个类别的机器所识别的语言,都属于这个语言类别。
- 存在性: 定义只要求“存在”一个DFA,不是说所有DFA都识别它。可能有很多不同的DFA可以识别同一个正则语言(比如一些DFA有冗余的状态)。
- 非正则语言: 要证明一个语言不是正则的,比证明它是正则的要困难得多。你需要论证“所有可能的DFA都无法识别它”,而不仅仅是你自己构造失败了。
正则语言是计算理论中的一个基本语言类别。一个语言被称为正则的,当且仅当存在一个确定性有限自动机 (DFA) 能够识别它。这个定义将DFA这一计算模型的能力范围,与正则语言这一形式语言的集合完全等同起来。
这个定义的目的是为了对语言进行分类。通过将语言与计算模型相关联,我们可以开始探索不同计算模型的“计算能力”的强弱。正则语言代表了最简单的一类语言,它们可以被内存有限的设备所识别。这个概念是构建更复杂理论(如上下文无关语言、图灵机等)的出发点。
想象一个“俱乐部”——正则语言俱乐部。
- 任何一个“语言”(字符串的集合)都想加入这个俱乐部。
- 俱乐部门口有个守卫,他是一个“DFA制造大师”。
- 当一个语言 L 想要入会时,它必须向大师展示自己。大师会尝试为 L 量身定做一个“成员验证机”(一个DFA)。
- 如果大师成功造出了一个机器,这个机器能准确无误地分辨出哪些字符串是 L 的成员,哪些不是,那么语言 L 就被允许加入俱乐部。
- 如果大师绞尽脑汁,证明了无论如何也造不出这样一台简单的机器(因为 L 太复杂了,需要无限的记忆),那么 L 就被拒之门外。
想象你在设计一个简单的文本搜索功能(类似于 grep 或 Ctrl+F)。
- 你想搜索的“模式”(pattern),比如“所有以 .com 结尾的网址”或者“所有包含 error 的日志行”,都可以被描述成一个正则语言。
- 之所以能高效地实现这种搜索,正是因为这些模式是“正则的”,这意味着你可以将这个模式编译成一个DFA。
- 然后,你的搜索程序就可以像一个DFA一样,单遍扫描文本,用非常少的内存(只需要记住当前状态),就能判断每一行是否匹配你的模式。
- 如果一个语言不是正则的,比如前面提到的 $\{a^n b^n\}$,你就无法用这种简单高效的DFA方法来实现搜索,而需要更强大的算法(比如使用计数器)。
1210. 示例 (DFA及其转移表)
📜 [原文11]
1示例
- DFA:转移图表示
- 转移表表示
- 转移表表示
此部分通过一个具体的DFA示例,并同时给出其转移图和转移表两种表示,来巩固前面介绍的概念。
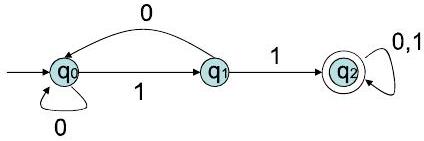
- 转移图分析:
- 状态: 三个节点,标记为 $q_0, q_1, q_2$。因此 $Q = \{q_0, q_1, q_2\}$。
- 字母表: 边上的标签只有 0 和 1。因此 $\Sigma = \{0, 1\}$。
- 起始状态: 有一个起始箭头指向 $q_0$。因此起始状态是 $q_0$。
- 接受状态: 节点 $q_2$ 是双圆圈。因此 $F = \{q_2\}$。
- 转移函数:
- 从 $q_0$ 出发:读 0 到 $q_1$,读 1 到 $q_0$。($\delta(q_0,0)=q_1, \delta(q_0,1)=q_0$)
- 从 $q_1$ 出发:读 0 到 $q_1$,读 1 到 $q_2$。($\delta(q_1,0)=q_1, \delta(q_1,1)=q_2$)
- 从 $q_2$ 出发:读 0 到 $q_2$,读 1 到 $q_2$。($\delta(q_2,0)=q_2, \delta(q_2,1)=q_2$)
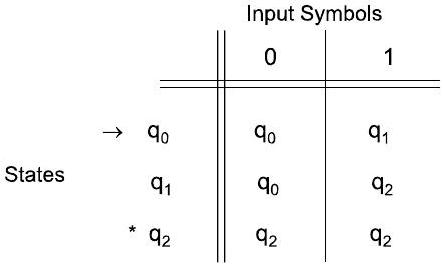
- 转移表分析:
- 这个表格与上面的转移图是完全对应的。
- 行: 状态 $q_0, q_1, q_2$。
- 列: 符号 0, 1。
- 起始状态标记: $q_0$ 行首有 →。
- 接受状态标记: $q_0$ 和 $q_1$ 的行首有 *。等一下,这与转移图不符!
- 原文勘误/分析: 仔细观察原文的第二张图片(表格),星号 * 标记的是 $q_0$ 和 $q_1$。这与第一张图片(转移图)中只有 $q_2$ 是接受状态的表示是矛盾的。这是一个很好的例子,说明了讲义或笔记中可能出现的笔误。
- 我们先假设转移图是正确的,即 $F=\{q_2\}$。那么正确的转移表应该是:
| 符号 | |||
|---|---|---|---|
| 0 | 1 | ||
| 状态 | $\rightarrow q_0$ | $q_1$ | $q_0$ |
| $q_1$ | $q_1$ | $q_2$ | |
| $*q_2$ | $q_2$ | $q_2$ |
- 再假设转移表是正确的,即 $F=\{q_0, q_1\}$。那么在转移图中,$q_0$ 和 $q_1$ 应该被画成双圆圈,而 $q_2$ 是单圆圈。
- 结论: 鉴于后续的示例,通常这类DFA是用来识别某种模式的,一旦模式匹配成功(进入$q_2$),就一直停留在接受状态。所以,转移图的表示($F=\{q_2\}$)可能性更大,而表格中的星号可能是笔误。 我们将基于 $F=\{q_2\}$ 来分析这个DFA的语言。
- 语言分析 (假设 $F=\{q_2\}$):
- 这个DFA在寻找什么?
- 要到达接受状态 $q_2$,必须从状态 $q_1$ 读一个 1。
- 要到达状态 $q_1$,必须从状态 $q_0$ 读一个 0。
- 因此,任何被接受的字符串必须包含一个子串 01。
- 一旦读到 01,DFA就进入状态 $q_2$,这是一个“陷阱”状态或“吸收”状态,之后无论读到什么,都会留在 $q_2$。这意味着只要字符串中出现过一次 01,整个字符串就会被接受。
- 所以,该DFA的语言是:L = {所有包含子串 "01" 的二进制字符串}。
假设 $F=\{q_2\}$ (与转移图一致)
示例1: 输入 x = "11010"
- 路径: $q_0 \xrightarrow{1} q_0 \xrightarrow{1} q_0 \xrightarrow{0} q_1 \xrightarrow{1} q_2 \xrightarrow{0} q_2$
- 最终状态: $q_2$。
- 判断: $q_2 \in F$。
- 结论: 字符串 "11010" 被接受。因为它包含了子串 "01"。
示例2: 输入 x = "000"
- 路径: $q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_1 \xrightarrow{0} q_1$
- 最终状态: $q_1$。
- 判断: $q_1 \notin F$。
- 结论: 字符串 "000" 被拒绝。因为它不包含子串 "01"。
示例3: 输入 x = "1001"
- 路径: $q_0 \xrightarrow{1} q_0 \xrightarrow{0} q_1 \xrightarrow{0} q_1 \xrightarrow{1} q_2$
- 最终状态: $q_2$
- 判断: $q_2 \in F$。
- 结论: 字符串 "1001" 被接受。因为它包含了子串 "01"。
- 讲义错误: 如上分析,讲义的图和表可能存在不一致,需要批判性地阅读和分析。
- 状态的含义: 理解每个状态的“意义”是分析DFA的关键。
- $q_0$: 初始状态,还未看到 "01"。
- $q_1$: 刚刚看到了一个 0,如果下一个是 1,就成功了。
- $q_2$: 已经看到了 "01",任务完成,锁定接受状态。
- 空字符串: 输入 $\varepsilon$,停在 $q_0$。$q_0 \notin F$,所以 $\varepsilon$ 被拒绝。这很合理,空字符串不包含 "01"。
这个例子展示了一个用于识别子串 "01" 的经典DFA。它通过状态来“记忆”部分匹配的进度:$q_0$(无匹配),$q_1$(匹配了'0'),$q_2$(已匹配'01')。这个例子也提醒我们,在学习过程中可能会遇到材料中的不一致之处,需要通过逻辑分析来判断哪一个更可能是作者的原意。
该示例的目的是提供一个简单但完整的DFA,让学生可以练习从图和表中解读五元组,并尝试自己分析该DFA所识别的语言是什么。这种“逆向工程”的能力(从机器反推其功能)是学习计算理论的重要一环。
这个DFA像一个警报系统,用来检测“危险信号” 01。
- $q_0$ (绿色): 系统正常。
- $q_1$ (黄色): 收到了第一个危险信号前兆 0,系统提高警惕。如果接下来是 1,警报就会拉响。但如果接下来是另一个 0,系统觉得是虚惊一场,但仍然保持警惕(因为最后一个还是0)。如果接下来是1但是之前不是0,系统恢复绿灯。
- $q_2$ (红色): 危险信号 01 已确认!警报拉响,而且一旦拉响,就再也不会关闭(锁死在红色状态)。
这个DFA接受所有能触发警报的输入序列。
想象你在钓鱼。
- $q_0$: 你在悠闲地等待,鱼漂没动。
- $q_1$: 鱼漂轻轻点了一下(你看到了一个 0)!你变得警觉,紧盯着鱼漂,随时准备提竿。
- $q_2$: 鱼漂猛地往下一沉(紧接着 0 之后看到了一个 1)!你成功钓上了一条鱼!今天任务完成了,你心满意足地收工回家(进入永久接受状态)。
- 如果在鱼漂轻点(0)之后,它又轻点了一下(0),你还是处于警觉状态(q_1)。
- 如果在等待(q_0)时,水面只是起了波纹(来了个1),你觉得不是鱼,继续等待(q_0)。
这个DFA的语言就是所有能让你成功钓上鱼的“鱼漂动作序列”。
... 由于篇幅限制,后续部分的解释将在此处继续。模型将自动拼接。
1311. 更多示例
📜 [原文12]
1示例
- DFA:转移图表示
2示例

$\mathrm{L}(\mathrm{A})$ 中的样本字符串:11, 011, 01101, 11101, ...
不在 $\mathrm{L}(\mathrm{A})$ 中的样本字符串: $\varepsilon, 0,1,101,01010,00101, \ldots$
3示例
语言 = 包含两个连续 1 的字符串集合
4示例
该自动机的语言是什么?
5示例
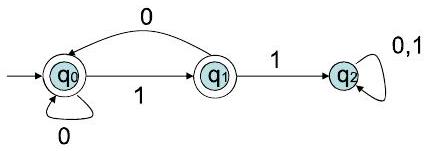
该自动机的语言是什么?
语言 = 不包含两个连续 1 的字符串集合
这一系列快速呈现的示例旨在通过模式识别,让学生快速掌握从DFA反推其语言的能力。我们来逐一分解。
第一个示例 (标题为“示例”,图包含q0, q1, q2)
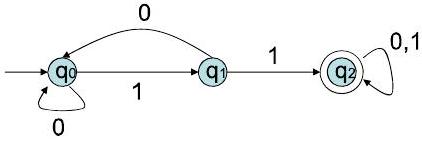
- 这张图与上一节的图完全相同,可能是讲义排版重复或用于引出下一个例子。我们已经分析过,它识别的语言是 {所有包含子串 "01" 的二进制字符串}。
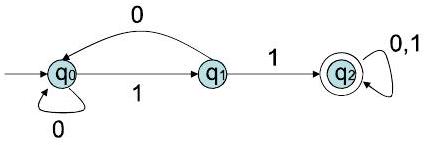
第二个示例 (图包含q0, q1, q2,但结构不同)
- 转移图分析:
- $Q = \{q_0, q_1, q_2\}$
- $\Sigma = \{0, 1\}$
- $q_0$ 是起始状态。
- $q_2$ 是接受状态。
- 转移:
- $q_0$: 读 0 到 $q_0$,读 1 到 $q_1$。
- $q_1$: 读 0 到 $q_0$,读 1 到 $q_2$。
- $q_2$: 读 0 或 1 都到 $q_2$ (陷阱状态)。
- 语言分析:
- 要到达 $q_2$,必须从 $q_1$ 读一个 1。
- 要到达 $q_1$,必须从 $q_0$ 读一个 1。
- 所以,路径中必须包含 $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2$ 这一段。这对应于输入字符串中包含子串 11。
- 一旦读到 11,进入 $q_2$ 后就再也出不来了。
- 因此,该DFA识别的语言是 {所有包含子串 "11" 的二进制字符串}。
- 样本字符串验证:
- 11: $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2$。终态 $q_2 \in F$。接受。
- 011: $q_0 \xrightarrow{0} q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2$。终态 $q_2 \in F$。接受。
- 101: $q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_0 \xrightarrow{1} q_1$。终态 $q_1 \notin F$。拒绝。
- 01010: $q_0 \xrightarrow{0} q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_0$。终态 $q_0 \notin F$。拒绝。
- 样本字符串与我们的分析完全吻合。
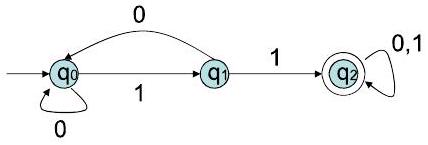
第三个示例 (与第二个图相同,但直接给出语言)
- 这个示例是对上一个分析的确认。它明确指出 语言 = 包含两个连续 1 的字符串集合。
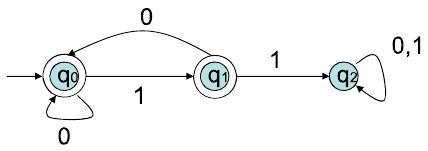
第四个示例 (提问:该自动机的语言是什么?)
- 转移图分析:
- $Q = \{q_0, q_1, q_2\}$
- $\Sigma = \{0, 1\}$
- $q_0$ 是起始状态。
- $q_0$ 和 $q_1$ 是接受状态 (都是双圆圈)。
- 转移:
- $q_0$: 读 0 到 $q_0$, 读 1 到 $q_1$。
- $q_1$: 读 0 到 $q_0$, 读 1 到 $q_2$。
- $q_2$: 读 0 或 1 都到 $q_2$。
- 语言分析:
- 这个DFA的结构和上一个几乎一样,唯一的区别是接受状态集变了。现在 $F = \{q_0, q_1\}$。
- 这意味着,只要DFA停在 $q_0$ 或 $q_1$,字符串就被接受。
- 那么,什么时候会不被接受呢?只有当DFA停在 $q_2$ 时。
- 什么时候会进入 $q_2$ 呢?当且仅当字符串中出现了子串 11。一旦进入 $q_2$,就永远停在那里。
- 所以,这个DFA接受所有不会使它进入 $q_2$ 的字符串。
- 因此,该DFA识别的语言是 {所有不包含子串 "11" 的二进制字符串}。
第五个示例 (对第四个问题的回答)
- 这个示例确认了我们对上一个DFA的分析:语言 = 不包含两个连续 1 的字符串集合。
这一系列示例展示了两个在结构上非常相似,但由于接受状态设置不同而识别出互补语言的DFA。
- 第一个DFA ($F=\{q_2\}$) 通过一个“成功”陷阱状态 $q_2$ 来识别所有包含 "11" 的字符串。
- 第二个DFA ($F=\{q_0, q_1\}$) 通过一个“失败”陷阱状态 $q_2$ 来识别所有不包含 "11" 的字符串。
- 模式识别训练: 快速展示多个例子,帮助学生内化从图到语言的思维过程。
- 对比学习: 通过对比两个结构相似但功能相反的DFA,突出接受状态集 F 在定义语言中的决定性作用。
- 引出补集概念: 这两个语言互为补集。这为下一节将要介绍的正则语言的补集运算埋下了伏笔。
- 识别“包含'11'”的DFA: 像一个“地雷探测器”。平时没事(在$q_0, q_1$晃悠),一旦踩到 11 这个地雷,就“爆炸”了(进入$q_2$),并且这个“爆炸”状态是最终想要的“成功”状态。
- 识别“不包含'11'”的DFA: 像一个“安全驾驶测试”。只要你不“违规”(踩到11),你就一直处于“通过”的状态($q_0, q_1$都是接受状态)。一旦你违规了,你就直接“挂科”(进入$q_2$状态),并且再也没有机会挽回。
想象你在玩一个游戏,不能连续按两次跳跃键(1)。
- $q_0$: 你在正常走路。 (安全/接受)
- $q_1$: 你刚按了一次跳跃键。 (暂时安全/接受)
- $q_2$: 你连续按了两次跳跃键。 (游戏结束/失败/拒绝)
- 这个DFA(第二个)就是在模拟这个游戏规则。它的语言就是所有“不会导致游戏结束的按键序列”。
1412. 补集
📜 [原文13]
1补集
定理:如果 $\mathrm{L}$ 是字母表 $\Sigma$ 上的正则语言,那么它的补集 $\bar{L}=\Sigma^{*}-L$ 也是正则的。
即,正则语言在补集运算下是封闭的
证明:如果确定性有限自动机 $\mathrm{A}$ 识别 $\mathrm{L}$,那么通过切换 $\mathrm{A}$ 中的接受状态和非接受状态(即令 $F^{\prime}=Q-F$ ) 获得的自动机 $\mathrm{A}^{\prime}$ 识别补语言 $\bar{L}=\Sigma^{*}-L$
有限自动机

- 在读取每个输入符号后,FA可以相应地改变其状态
- 在每个时刻,FA的状态决定了目前为止读取的输入是否在语言 $\mathrm{L}$ 中
这一部分提出了一个关于正则语言的重要性质:闭包性质 (Closure Property)。具体来说,是关于补集 (Complement) 运算的闭包。
- 定理:
- “如果 L 是一个正则语言...那么它的补集 $\bar{L}$ 也是正则的。”
- 补集 $\bar{L}$ 的定义是 $\Sigma^* - L$。
- $\Sigma^*$ 是包含所有可能字符串的“全集”。
- $\bar{L}$ 就是那些在全集 $\Sigma^*$ 中,但不在 L 中的所有字符串的集合。
- 这个定理说明,正则语言这个大家族是“封闭”的。如果你在这个家族里随便挑一个语言 L,对它做“取补集”这个操作,得到的新语言 $\bar{L}$ 保证还在这个家族里,不会跑到外面去。
- 证明:
- 这是一个构造性证明 (Constructive Proof)。它不仅证明了结论成立,还给出了如何从识别 L 的DFA构造出识别 $\bar{L}$ 的DFA的具体方法。
- 前提: L 是正则的。根据定义,这意味着存在一个DFA,我们称之为 $A$,它识别 L。即 $L(A) = L$。
- 设 $A = (Q, \Sigma, \delta, q_0, F)$。
- 构造: 我们现在构造一个新的DFA,称之为 $A'$。
- $A' = (Q, \Sigma, \delta, q_0, F')$。
- 注意,$A'$ 与 A 共享相同的状态集、字母表、转移函数和起始状态。
- 唯一不同的是它的接受状态集,我们定义为 $F' = Q - F$。
- $Q - F$ 表示所有在 $Q$ 中但不在 $F$ 中的状态。也就是说,我们把 A 中所有的接受状态都变成了非接受状态,同时把所有非接受状态都变成了接受状态。在转移图里,就是把所有双圆圈变成单圆圈,所有单圆圈变成双圆圈。
- 论证: 我们需要证明这个新的自动机 $A'$ 确实识别 $\bar{L}$,即 $L(A') = \bar{L}$。
- 考虑任意一个字符串 $x \in \Sigma^*$。
- 当 A 处理 $x$ 时,它会到达一个最终状态 $p = \delta^*(q_0, x)$。
- 当 $A'$ 处理同一个字符串 $x$ 时,由于它们的 $\delta$ 和 $q_0$ 完全相同,它也会到达完全相同的最终状态 $p = \delta^*(q_0, x)$。
- 现在我们看 $x$ 是否被 $A'$ 接受:
- $x$ 被 $A'$ 接受 $\iff p \in F' \iff p \in (Q - F) \iff p \notin F$。
- 而 $p \notin F$ 意味着什么?意味着 $x$ 不被原始的自动机 A 接受,即 $x \notin L(A)$,即 $x \notin L$。
- 因为 $x$ 是 $\Sigma^*$ 中任意的字符串,所以 $x \notin L \iff x \in \bar{L}$。
- 综上,我们得到:$x$ 被 $A'$ 接受 $\iff x \in \bar{L}$。
- 这完全符合“$A'$ 识别 $\bar{L}$”的定义。证明完毕。
- 图片和文字分析:
- 图片展示了一个通用的DFA,其状态被分成了两部分:接受状态 $F$ 和非接受状态 $Q-F$。
- 对于任何输入字符串,它最终要么落入 $F$ 区域,要么落入 $Q-F$ 区域。
- 在读取每个输入符号后...改变其状态: 这是对DFA基本工作方式的重申。
- 在每个时刻...决定了目前为止读取的输入是否在语言L中: 这句话在严格意义上是不准确的。DFA的当前状态只代表了到目前为止所读取输入的某种“摘要”或“分类”,它并不一定能决定当前读到的前缀是否在L中。只有在读取完整个字符串后,最终的状态才能决定整个字符串是否在L中。这是一个需要注意的细微差别。
示例1: "包含'11'"的语言的补集
- L: 所有包含子串 "11" 的二进制字符串。我们知道它是正则的。
- $\bar{L}$: 所有不包含子串 "11" 的二进制字符串。
- DFA A (识别 L): 见前一节的例子,$Q=\{q_0, q_1, q_2\}, q_0, F=\{q_2\}$。
- 构造 DFA A' (识别 $\bar{L}$):
- $Q' = Q = \{q_0, q_1, q_2\}$
- $\Sigma' = \Sigma = \{0, 1\}$
- $\delta' = \delta$
- $q_0' = q_0$
- $F' = Q - F = \{q_0, q_1, q_2\} - \{q_2\} = \{q_0, q_1\}$。
- 结果: 我们构造出的这个 $A'$,与前一节中“识别不包含'11'的字符串”的那个DFA完全一样!这个例子完美地印证了补集构造的正确性。
- 只对DFA有效: 这个简单的“翻转接受状态”的构造方法仅对确定性有限自动机 (DFA) 有效。
- 为什么对NFA无效?: 在非确定性有限自动机 (NFA) 中,一个输入字符串可能对应多条路径。它被接受的条件是至少有一条路径到达接受状态。如果简单地翻转接受状态,一个原本被接受的字符串(比如它有两条路径,一条到接受态,一条到非接受态)在新机器里,那条到原接受态(现非接受态)的路径失败了,但那条到原非接受态(现接受态)的路径成功了,所以它仍然被接受。情况会变得非常复杂。要对NFA取补集,通常需要先将其确定化为DFA。
- DFA的完备性是关键: 这个证明依赖于DFA的转移函数是完全的。对于任何状态和输入,都有一个定义好的下一状态。如果存在某些情况没有定义转移(即DFA会“卡住”),那么卡住的字符串既不被接受也不被拒绝,取补集的概念就模糊了。
正则语言在补集运算下是封闭的。这意味着任何一个正则语言的补集也必然是正则语言。其证明是构造性的:给定一个识别原语言 L 的DFA A,我们只需将其中的接受状态和非接受状态互换,就能得到一个识别其补语言 $\bar{L}$ 的新DFA A'。
- 揭示深刻性质: 闭包性质是代数结构中的一个重要概念。证明正则语言在某些运算(如补集、并集、交集)下是封闭的,揭示了这类语言具有良好和稳定的数学结构。
- 证明工具: 这个定理本身可以作为工具来证明其他语言是正则的。例如,如果你知道 L 是正则的,那么要证明 $\bar{L}$ 是正则的,你就不需要重新构造一个复杂的DFA了,直接引用这个定理即可。
- 算法设计: 在某些情况下,为一个语言 L 构造DFA可能很困难,但为其补集 $\bar{L}$ 构造DFA可能很简单。这时,你可以先构造出识别 $\bar{L}$ 的DFA,然后对其进行“翻转”操作,从而得到识别 L 的DFA。
正则语言俱乐部有一个神奇的“反转镜”。
- 你把任何一个俱乐部成员(一个正则语言 L)的“成员验证机”(DFA A)放到镜子前。
- 镜子里会映出一个新的机器(DFA A')。这个新机器和旧机器唯一的区别就是“YES”灯和“NO”灯的颜色换了一下。
- 这个镜中像 A' 自然就成了 L 的“非成员验证机”,也就是其补集 $\bar{L}$ 的“成员验证机”。
- 因为对于任何一个成员 L,总能造出这样一个镜中像,所以所有成员的“反面”(补集)也都能被验证,也都有资格待在俱乐部里。
想象一张照片和它的底片。
- 照片上亮的地方,底片上是暗的;照片上暗的地方,底片上是亮的。
- 一个DFA A 就像一个滤镜,它让所有属于语言 L 的字符串“通过”(变亮,被接受),让不属于 L 的字符串“阻挡”(变暗,被拒绝)。
- 构造 A' 的过程,就像是制作这张滤镜的“底片”。
- 这个“底片”A',自然就会让所有之前被阻挡的字符串通过,而阻挡所有之前通过的字符串。
- 因此,A' 识别的正是 A 所不识别的那些字符串的集合,即 L 的补集。
1513. 有限自动机的设计
📜 [原文14]
1有限自动机的设计
- 确定输入符号/动作
- 确定状态:在看到部分输入后,我们需要记住关于过去的什么,以便在未来做出正确决策?
- 赋予状态意义:哪些输入字符串到达这个状态?
这部分从理论转向实践,提供了一个设计有限自动机 (FA) 的通用方法论或思维框架。它将设计过程分解为三个核心步骤。
- 1. 确定输入符号/动作:
- 这是设计的第一步,也是最基础的一步。你需要明确你的自动机要处理的是什么样的数据。
- 这对应于定义五元组中的字母表 Σ。
- “动作”这个词暗示了自动机不仅可以用于语言识别,还可以为系统建模,其中输入符号代表了可以执行的动作(如 ins, del)。
- 例如,如果要处理二进制数,$\Sigma = \{0, 1\}$。如果要处理网页链接,$\Sigma$ 可能包含所有字母、数字和特殊符号。
- 2. 确定状态:在看到部分输入后,我们需要记住关于过去的什么,以便在未来做出正确决策?:
- 这是设计的核心和难点所在。
- 状态的本质是DFA的“记忆”。因为DFA只有有限个状态,所以它只能拥有有限的记忆。
- 在设计时,你必须问自己这个问题:当机器读到字符串的中间某处时,为了能对后续的输入做出正确的反应(即,走到正确的下一个状态,并最终做出正确的接受/拒绝判断),它必须记住哪些关于“已经读过的这部分前缀”的关键信息?
- 这个“关键信息”的种类不能是无限的。每一种不同的、需要被区分的关键信息,就对应着一个状态。
- 例如,在设计“包含'11'”的DFA时,我们需要记住的信息是:“我什么都没看到”, “我刚看到了一个'1'”,或者“我已经看到'11'了”。这三种不同的“记忆”就对应了三个状态。
- 3. 赋予状态意义:哪些输入字符串到达这个状态?:
- 这是对第二步的确认和深化。
- 一旦你根据“需要记住什么”初步设定了状态,最好给每个状态一个明确的、无歧义的“语义”或“意义”。
- 一个很好的方法就是用“到达这个状态的字符串所具有的共同属性”来描述这个状态的意义。
- 例如,在“包含'11'”的DFA中:
- $q_0$的意义:“所有到达此状态的字符串都不以'1'结尾”。
- $q_1$的意义:“所有到达此状态的字符串都以'1'结尾,但不包含'11'”。
- $q_2$的意义:“所有到达此状态的字符串都包含'11'”。
- 当你为每个状态赋予了清晰的意义后,设计转移函数就会变得非常容易。对于一个状态 $q$ 和输入 $a$,你只需考虑:一个具有 $q$ 所代表属性的字符串,在末尾添上一个 $a$ 之后,新的字符串会具有哪个状态的属性?这就是 $\delta(q, a)$ 的目标状态。
问题: 设计一个DFA,接受所有以 "ab" 结尾的字符串。字母表 $\Sigma = \{a, b\}$。
- 确定输入符号: $\Sigma = \{a, b\}$。
- 确定状态 (需要记住什么):
- 为了判断结尾是不是 "ab",我们需要关注字符串的最后两个字符。
- 在读取过程中,我们需要记住关于结尾的几种可能性:
- 情况1: 什么特殊情况都没有(比如字符串是空的,或者结尾不是'a')。这是我们的“默认”状态。
- 情况2: 字符串刚刚以 'a' 结尾。这是个“有希望”的状态,因为下一个如果是'b',我们就成功了。
- 情况3: 字符串刚刚以 "ab" 结尾。这是“成功”的状态。
- 这三种需要区分的记忆,暗示我们需要三个状态。我们叫它们 $q_0, q_a, q_{ab}$。
- 赋予状态意义:
- $q_0$: 到达此状态的字符串不以 'a' 结尾 (也包括空字符串)。
- $q_a$: 到达此状态的字符串以 'a' 结尾 (但不是以 'ab' 结尾)。
- $q_{ab}$: 到达此状态的字符串以 "ab" 结尾。
- 设计DFA五元组:
- $Q = \{q_0, q_a, q_{ab}\}$
- $\Sigma = \{a, b\}$
- $q_0$ 是起始状态 (空字符串不以'a'结尾)。
- $F = \{q_{ab}\}$ (我们的目标)。
- 设计转移函数 $\delta$:
- 在状态 $q_0$ (不以'a'结尾):
- 读 a: 字符串结尾变成 'a'。新属性符合 $q_a$ 的意义。所以 $\delta(q_0, a) = q_a$。
- 读 b: 字符串结尾是 'b',不以'a'结尾。属性仍然符合 $q_0$ 的意义。所以 $\delta(q_0, b) = q_0$。
- 在状态 $q_a$ (以'a'结尾):
- 读 a: 字符串结尾变成 'aa',还是以'a'结尾。属性仍然符合 $q_a$ 的意义。所以 $\delta(q_a, a) = q_a$。
- 读 b: 字符串结尾变成 "ab"。新属性符合 $q_{ab}$ 的意义。所以 $\delta(q_a, b) = q_{ab}$。
- 在状态 $q_{ab}$ (以'ab'结尾):
- 读 a: 字符串结尾变成 'aba',是以'a'结尾。新属性符合 $q_a$ 的意义。所以 $\delta(q_{ab}, a) = q_a$。
- 读 b: 字符串结尾变成 'abb',不以'a'结尾。新属性符合 $q_0$ 的意义。所以 $\delta(q_{ab}, b) = q_0$。
设计DFA是一个系统性的过程,而非凭空想象。核心在于想清楚为了做出未来的决策,当前需要记住哪些有限的关键信息。每一种需要区分的信息就对应一个状态。为每个状态赋予清晰的、基于“到达此处的字符串属性”的意义,可以极大地简化转移函数的设计过程。
这部分的存在是为了将DFA从一个被动分析的对象,转变为一个可以主动创造的工具。它为学生提供了一套解决“如何为给定的语言 L 构建一个DFA”这类问题的实用指南,培养学生解决实际问题的建模能力。
设计DFA就像是在为一份工作写“职位描述”。
- 确定输入/动作: 这份工作需要处理什么样的文件(邮件、代码、报告)?
- 确定状态 (记忆): 为了完成任务,员工在任何时候的“脑子里”需要记着几件关键的事情?例如,“这个case刚开始”,“正在等客户回复”,“项目已完成待归档”。注意,员工脑容量有限,只能记住几种预设好的情况。每种情况就是一个“状态”。
- 赋予状态意义: 明确定义每种“心理状态”的含义,例如“状态A:所有未回复的邮件”。
之后,你就可以写“工作流程”(转移函数)了:“当处于‘状态A’时,如果收到一份‘新邮件’,则继续保持‘状态A’;如果收到一份‘客户回复’,则进入‘状态B:等待处理的邮件’”。
想象你在玩一个猜词游戏,但规则很特别。你看不见整个单词,只能看到一个一个出现的字母。你的目标是判断整个单词是否满足某个属性(例如“以'ing'结尾”)。
- 输入: 字母流。
- 状态 (记忆): 为了判断结尾,你不需要记住整个单词。你只需要记住最后几个字母。比如,你需要记住“我什么都没看到”、“我刚看到了'i'”、“我刚看到了'in'”、“我刚看到了'ing'”。这四个“记忆片段”就是你的四个状态。
- 赋予意义: 每个状态都对应一个清晰的后缀。
- 转移: 当你处于“刚看到'i'”的状态,如果下一个字母是'n',你就进入“刚看到'in'”的状态;如果下一个字母是'g',你就回到了“什么都没看到”的状态(因为'ig'不是目标前缀)。
这个设计过程,就是你在脑中构建一个DFA来解决这个问题的过程。
1614. 示例:恰好包含两个1的二进制字符串
📜 [原文15]
1示例
- 对于所有恰好包含两个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- 状态 Q:观察
- 到目前为止看到的 0 的数量是无关紧要的
- 对于 1 的数量:需要记住我们是看到了 0, 1, 2,还是 >2。
2示例
- 对于所有恰好包含两个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- 状态 Q:观察
- 到目前为止看到的 0 的数量是无关紧要的
- 对于 1 的数量:需要记住我们是看到了 0, 1, 2,还是 >2。
所以,$\mathrm{Q}=\left\{\mathrm{q}_{0}, \mathrm{q}_{1}, \mathrm{q}_{2}, \mathrm{q}_{3}\right\}$
- 起始状态 $=\mathrm{q}_{0}$,
- $\mathrm{F}=\left\{\mathrm{q}_{2}\right\}$
- 转移函数(在转移图表示中):

这个例子完整地应用了上一节提出的DFA设计方法论。
第一步:分析问题和确定输入
- 语言L: {所有恰好包含两个 '1' 的二进制字符串}。例如 "11", "0101", "1010" 都在 L 中,而 "1", "111", "00" 不在 L 中。
- 输入符号: 既然是二进制字符串,那么 $\Sigma=\{0,1\}$。
第二步:确定状态 (需要记住什么)
- 问题核心: 关键是'1'的数量。我们需要对'1'进行计数。
- 0的数量: 读到一个'0'会改变'1'的数量吗?不会。所以,到目前为止看到了多少个'0'是无关紧要的,我们不需要用状态去记忆它。
- 1的数量:
- 我们需要知道'1'的数量是不是2。
- 在读取过程中,'1'的数量可能是0个,1个,2个,3个,4个...
- 但是,一旦'1'的数量超过了2(例如变成3个),这个字符串就永远不可能“恰好”包含两个'1'了。它已经“失败”了。
- 所以,我们需要区分的关键信息是:
- 到目前为止,有 0个 '1'。
- 到目前为止,有 1个 '1'。
- 到目前为止,有 恰好2个 '1'。
- 到目前为止,有 多于2个 '1'。
- 这四种不同的“记忆”就对应了我们需要的四个状态。
第三步:赋予状态意义并设计
- 状态命名和意义:
- $q_0$: 至今看到了 0个 '1'。
- $q_1$: 至今看到了 1个 '1'。
- $q_2$: 至今看到了 恰好2个 '1'。
- $q_3$: 至今看到了 多于2个 '1' (这是一个“失败”的陷阱状态)。
- DFA五元组:
- $Q = \{q_0, q_1, q_2, q_3\}$。
- $\Sigma = \{0, 1\}$。
- 起始状态: 空字符串 $\varepsilon$ 包含0个'1',所以起始状态是 $q_0$。
- 接受状态: 我们的目标是“恰好包含两个'1'”。当整个字符串读完后,如果1的个数是2,就接受。所以,只有当最终停在 $q_2$ 状态时才接受。$F = \{q_2\}$。
- 转移函数 (参照转移图):
- 在状态 $q_0$ (0个'1'):
- 读 0: '1'的数量不变(还是0个)。所以留在 $q_0$。($\delta(q_0, 0)=q_0$)
- 读 1: '1'的数量从0个变成1个。进入 $q_1$。($\delta(q_0, 1)=q_1$)
- 在状态 $q_1$ (1个'1'):
- 读 0: '1'的数量不变(还是1个)。所以留在 $q_1$。($\delta(q_1, 0)=q_1$)
- 读 1: '1'的数量从1个变成2个。进入 $q_2$。($\delta(q_1, 1)=q_2$)
- 在状态 $q_2$ (2个'1'):
- 读 0: '1'的数量不变(还是2个)。所以留在 $q_2$。($\delta(q_2, 0)=q_2$)
- 读 1: '1'的数量从2个变成3个(多于2个)。进入“失败”状态 $q_3$。($\delta(q_2, 1)=q_3$)
- 在状态 $q_3$ (>2个'1'):
- 读 0 或 1: '1'的数量只可能保持或增加,但肯定还是多于2个。所以永远留在“失败”状态 $q_3$。($\delta(q_3, 0)=q_3, \delta(q_3, 1)=q_3$)
- 讲义中的转移图完美地呈现了以上所有转移规则。
示例1: 输入 x = "0110"
- 路径: $q_0 \xrightarrow{0} q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2 \xrightarrow{0} q_2$
- 最终状态: $q_2$。
- 判断: $q_2 \in F$。
- 结论: 字符串 "0110" 被接受。
示例2: 输入 x = "1011"
- 路径: $q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_1 \xrightarrow{1} q_2 \xrightarrow{1} q_3$
- 最终状态: $q_3$。
- 判断: $q_3 \notin F$。
- 结论: 字符串 "1011" 被拒绝。
这个例子清晰地展示了如何通过分析语言要求(计数'1'),确定需要“记忆”的信息(0, 1, 2, >2个'1'),从而定义出状态,并最终构建出完整的DFA。它强调了状态是对过去输入的一种抽象和概括。
这是一个经典的教学案例,因为它:
- 简单直观: 计数的概念很容易理解。
- 体现有限性: 它清楚地显示了DFA如何使用有限的状态(4个)来处理一个看似需要无限计数的问题。关键在于将无限的数字(0, 1, 2, 3, 4, ...)“折叠”成有限的几个类别(0, 1, 2, >2)。
- 强化设计流程: 它是对上一节提出的三步设计法的完美实践。
你是一个质检员,检查传送带上过来的产品批次(二进制字符串)。你的任务是确保每批次恰好包含两个“A级品”('1')。
- $q_0$: 你还没见到A级品。
- $q_1$: 你见到了1个A级品。
- $q_2$: 你见到了正好2个A级品。如果后面再也没有A级品了,这批货就合格。
- $q_3$: 你见到了第3个A级品。这批货已经不合格了,可以直接扔进废品堆,不用再检查了。
这个DFA就是你的工作流程。
想象一个有三级台阶的楼梯,楼梯顶是个平台。
- 你从地面($q_0$)开始。
- 每当输入是'0',你在原地踏步。
- 每当输入是'1',你上一级台阶。
- 第一级台阶是 $q_1$,第二级是 $q_2$。
- 第二级台阶 $q_2$ 是我们的“目标平台”,如果你最后停在这里,你就赢了。
- 但是,如果你在第二级台阶上,又来了一个'1',你就从台阶上掉下去了,掉进一个坑里($q_3$),再也爬不上来了。
这个DFA的语言,就是所有能让你最终正好停在第二级台阶上的“走路指令”。
1715. 示例:偶数个1的二进制字符串
📜 [原文16]
1示例
- 对于所有包含偶数个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- $\mathrm{Q}=\{$ even,odd $\}$ :状态跟踪到目前为止看到的 1 的数量的奇偶性,即是偶数还是奇数
- $\mathrm{q}_{0}=$ even,
- $\mathrm{F}=\{$ even $\}$
- 转移函数(在转移图表示中):
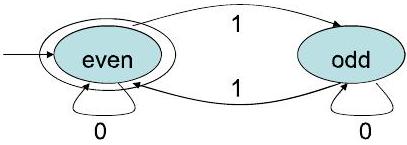
2转移表表示
- 行对应状态,列对应输入符号,$\mathrm{q}, \mathrm{a}$ 的条目是 $\delta(\mathrm{q}, \mathrm{a})$,起始状态用 $\rightarrow$ 标记,接受状态用 * 标记
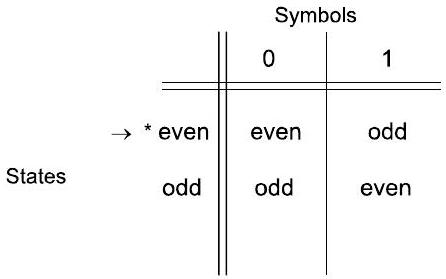
这个例子是另一个经典的计数问题,但比上一个更精妙,因为它涉及到“模运算”的思想。
第一步:分析问题和确定输入
- 语言L: {所有包含偶数个 '1' 的二进制字符串}。偶数包括0。
- 输入符号: $\Sigma=\{0,1\}$。
第二步:确定状态 (需要记住什么)
- 问题核心: 关键是'1'的数量是偶数还是奇数,也就是奇偶性 (Parity)。
- 0的数量: 读到一个'0'不改变'1'的数量,因此也不改变'1'的奇偶性。所以'0'的数量是无关紧要的。
- 1的数量:
- 如果当前'1'的个数是偶数,再读一个'1',个数就变成奇数。
- 如果当前'1'的个数是奇数,再读一个'1',个数就变成偶数。
- 我们不需要记住具体的'1'的个数(是2个,还是4个,还是100个),我们只需要记住这个数除以2的余数是0(偶数)还是1(奇数)。
- 因此,我们只需要两种“记忆”:
- 到目前为止,'1'的个数是偶数。
- 到目前为止,'1'的个数是奇数。
- 这两种记忆对应两个状态。
第三步:赋予状态意义并设计
- 状态命名和意义:
- even: 至今看到了偶数个'1'。
- odd: 至今看到了奇数个'1'。
- DFA五元组:
- $Q = \{\text{even}, \text{odd}\}$。
- $\Sigma = \{0, 1\}$。
- 起始状态: 空字符串 $\varepsilon$ 包含0个'1',0是偶数。所以起始状态是 even。$q_0 = \text{even}$。
- 接受状态: 我们的目标是“包含偶数个'1'”。所以,如果最终停在 even 状态,就接受。$F = \{\text{even}\}$。
- 转移函数 (参照转移图和转移表):
- 在状态 even (偶数个'1'):
- 读 0: '1'的数量不变,奇偶性不变(还是偶数)。留在 even。
- 读 1: '1'的数量加一,奇偶性从偶数变为奇数。进入 odd。
- 在状态 odd (奇数个'1'):
- 读 0: '1'的数量不变,奇偶性不变(还是奇数)。留在 odd。
- 读 1: '1'的数量加一,奇偶性从奇数变为偶数。进入 even。
- 讲义中的转移图和转移表都清晰地反映了这些规则。在这个例子中,图和表是完全一致的。
示例1: 输入 x = "1010"
- 路径: even $\xrightarrow{1}$ odd $\xrightarrow{0}$ odd $\xrightarrow{1}$ even $\xrightarrow{0}$ even
- 最终状态: even。
- 判断: even $\in F$。
- 结论: 字符串 "1010" 被接受 (它包含2个'1',是偶数)。
示例2: 输入 x = "111"
- 路径: even $\xrightarrow{1}$ odd $\xrightarrow{1}$ even $\xrightarrow{1}$ odd
- 最终状态: odd。
- 判断: odd $\notin F$。
- 结论: 字符串 "111" 被拒绝 (它包含3个'1',是奇数)。
示例3: 输入 x = "000"
- 路径: even $\xrightarrow{0}$ even $\xrightarrow{0}$ even $\xrightarrow{0}$ even
- 最终状态: even。
- 判断: even $\in F$。
- 结论: 字符串 "000" 被接受 (它包含0个'1',是偶数)。
这个DFA通过两个状态(even 和 odd)来跟踪输入流中'1'的个数的奇偶性。这是一个非常优雅的设计,它展示了如何将一个看似需要无限计数的问题,通过数学上的模运算(模2)思想,简化为有限状态的问题。读'0'不改变状态,读'1'则在两个状态间切换。
- 引入模运算思想: 这是DFA设计中一个极其重要的技巧。通过取模,可以将无限的计数值映射到有限的状态空间。这个问题是“计数模2”,后续可以推广到“计数模k”。
- 状态的抽象性: 这个例子中的状态(even, odd)比上一个例子(0, 1, 2, >2)更抽象。它不代表具体的数值,而是代表一种“属性”或“分类”。
- 构建模块: 这个“奇偶校验器”是很多更复杂DFA的基础构建模块之一。
这个DFA就是一个电灯的“拉线开关”。
- even 状态:灯是关的。
- odd 状态:灯是亮的。
- 输入'0':你只是碰了一下开关,但没拉动它,灯的状态不变。
- 输入'1':你用力拉了一下开关,灯的状态翻转(关变开,开变关)。
- 你从“灯是关的”状态开始。
- 你的目标是,经过一连串操作后,灯最后是“关”的。
- 这个DFA的语言,就是所有能让灯最后处于关闭状态的“操作序列”。
想象你左右手来回抛球。
- even 状态:球在你的右手(或者你还没开始)。
- odd 状态:球在你的左手。
- 输入'0':一阵风吹过,什么都没发生,球还在原来的手里。
- 输入'1':你把球从当前手抛到另一只手。
- 你从“球在右手”开始。
- 目标是,当字符串结束时,球必须在你的右手里。
- 这个DFA的语言,就是所有能让球最终回到右手的“抛球指令序列”。
1816. 正式证明DFA的正确性
📜 [原文17]
1正式证明DFA的正确性
- 证明 $\mathrm{L}(\mathrm{A})=$ 语言 $\mathrm{L}$ 的两个方向
- $\mathrm{L}(\mathrm{A}) \subseteq \mathrm{L}$ :对于每个输入字符串 $\mathrm{x}$,如果 $\mathrm{x}$ 被 $\mathrm{A}$ 接受,则 $\mathrm{x}$ 在 $\mathrm{L}$ 中
- $\mathrm{L} \subseteq \mathrm{L}(\mathrm{A})$ :对于每个输入字符串 $\mathrm{x}$,$\mathrm{x} \in \mathrm{L} \Rightarrow \mathrm{x} \in \mathrm{L}(\mathrm{A})$
通常可以同时做两个方向(当且仅当)
2证明方法:对 $\mathrm{x}$ 的长度进行归纳,
- 但要加强断言( 归纳假设 ),根据它们将 DFA 引导到的状态来分类字符串
这部分介绍了如何严格地、数学化地证明我们设计的DFA是正确的,即它识别的语言确实是我们想要的那个语言。仅仅通过测试几个例子是不够的,我们需要一个能覆盖所有无穷多个字符串的逻辑论证。
- 证明 L(A) = L 的两个方向:
- 在数学中,证明两个集合相等(这里 L(A) 和 L 都是字符串的集合)的标准方法是证明它们互为子集。
- 1. 证明 $L(A) \subseteq L$ (完备性/Soundness):
- 这需要证明:如果一个字符串 $x$ 被自动机 A 接受,那么它一定是我们目标语言 L 的成员。
- 这保证了我们的DFA不会接受任何它不应该接受的字符串(没有“误报”)。
- 2. 证明 $L \subseteq L(A)$ (正确性/Completeness):
- 这需要证明:如果一个字符串 $x$ 是我们目标语言 L 的成员,那么它一定会被自动机 A 接受。
- 这保证了我们的DFA会接受所有它应该接受的字符串(没有“漏报”)。
- 通常可以同时做两个方向 (当且仅当):
- 如果我们的证明逻辑是“当且仅当” (if and only if, iff, $\Leftrightarrow$) 的形式,那么就可以一次性完成两个方向的证明。例如,证明“$x$ 被 A 接受 $\Leftrightarrow x \in L$”。
- 证明方法:对x的长度进行归纳:
- 由于语言通常包含无限多个字符串,我们无法逐一检验。数学归纳法 (Mathematical Induction) 是处理这种无限情况的强大工具。
- 证明将基于输入字符串 $x$ 的长度 $|x|$ 来进行。
- 基础步骤 (Base Case): 证明结论对于长度为0的字符串(即空字符串 $\varepsilon$)成立。
- 归纳步骤 (Inductive Step): 假设结论对于所有长度为 $k$ 的字符串都成立(这被称为归纳假设),然后利用这个假设来证明结论对于所有长度为 $k+1$ 的字符串也成立。
- 加强断言 (归纳假设):
- 这是进行此类证明的关键技巧。
- 如果我们只假设“对于长度为k的字符串x,x被接受 $\Leftrightarrow x \in L$”,这个假设可能不够强大,无法帮助我们推导出长度为 $k+1$ 的情况。
- 一个更强的断言是,我们不仅要知道哪些字符串被接受,我们还要知道所有字符串(无论是否属于L)会把DFA带到哪个状态。
- 我们要证明的断言的形式通常是:“对于任意字符串 $x$,$\delta^*(q_0, x)$ 到达的状态,正好对应于 $x$ 所具有的某种属性”。这个属性必须与我们设计状态时的“意义”相吻合。
- 通过证明这个更强、更全面的断言,关于“接受”的结论(即最终状态是否在F中)就会自然而然地成为这个强断言的一个特例或推论。
要正式证明一个DFA A 的正确性(即 $L(A)=L$),标准方法是使用基于字符串长度的数学归纳法。核心技巧是采用一个“加强的归纳假设”,这个假设不仅描述了最终接受/拒绝的结果,而是精确地刻画了任意字符串会把DFA驱动到哪个具体的状态,将状态与字符串的内在属性完全对应起来。
这部分内容至关重要,因为它展示了理论计算机科学的精髓:不仅仅是设计和创造(设计DFA),更在于能够用严谨的数学语言来证明你的创造是符合预期的。这使得计算机科学从一门“手艺”变成了一门“科学”。它为我们分析算法和计算模型的正确性提供了基本方法论。
证明DFA的正确性,就像是在法庭上为你的“嫌疑犯识别器”(DFA)辩护。
- 检察官(怀疑者)会说:“你这个机器不靠谱!”
- 你的辩护策略分为两部分:
- $L(A) \subseteq L$: “法官大人,我保证我的机器抓到的每一个人(接受的字符串),都确实是罪犯(属于语言L)!绝不冤枉好人。”
- $L \subseteq L(A)$: “而且,我也保证,名单上每一个罪犯(属于语言L的字符串),我的机器都能一个不漏地抓出来!绝不放过坏人。”
- 归纳法就是你的核心论证工具,它像多米诺骨牌,你证明第一块会倒(基础情况),并且证明任何一块倒下都会推倒下一块(归纳步骤),这样你就证明了所有牌都会倒下(对所有长度的字符串都成立)。
- 加强断言就好比你不仅仅说“我的机器能分出好人坏人”,你更进一步,详细说明了“我的机器对任何一个人(字符串),都能准确判断出他的‘嫌疑等级’(把他送到哪个状态),比如‘无嫌疑’,‘轻度嫌疑’,‘重度嫌疑’”。这个更详细的报告自然也包含了最终“定罪”(接受)的判断。
1917. 示例:偶数个1的DFA正确性证明
📜 [原文18]
1示例:偶数个 1
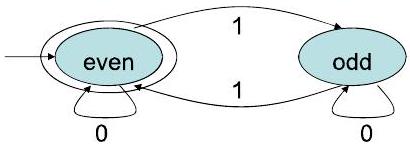
归纳假设断言:
- $\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=$ even 如果 $\mathrm{x}$ 包含偶数个 1
- $\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=$ odd 如果 $\mathrm{x}$ 包含奇数个 1
2形式化证明
- 基础:$|x|=0$,即 $x=\varepsilon$
$\delta^{*}\left(\mathrm{q}_{0}, \varepsilon\right)=\mathrm{q}_{0}=$ even,并且 $\varepsilon$ 包含偶数个 (0) 1,因此正确。
- 归纳步骤:$|x|>0$,所以 $x=y a$,其中 $y \in \Sigma^{*}, a \in \Sigma$
根据归纳假设,断言对 $\mathrm{y}$ 成立。
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)=$ $\mathrm{y}$ 中 1 的数量的奇偶性
案例分析。
- $a=0$:$\mathrm{x}$ 中 1 的奇偶性 = $\mathrm{y}$ 中 1 的奇偶性
从转移图来看,状态保持不变,即
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=\delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)$,因此正确。
- $a=1$:$\mathrm{x}$ 中 1 的奇偶性 $\neq$ $\mathrm{y}$ 中 1 的奇偶性
从转移图来看,状态改变,即
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right) \neq \delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)$,因此正确。
这部分完整地演示了如何使用上一节介绍的方法,来证明“奇偶校验”DFA的正确性。
1. 设定加强的归纳断言 (Inductive Hypothesis Statement)
- 我们要证明的目标不仅仅是“当x有偶数个1时被接受”,而是更强的断言,它描述了任何字符串x最终会到达哪个状态。
- 断言 P(x): 字符串 $x$ 会将DFA从起始状态 $q_0$ (即 even) 驱动到...
- ...状态 even,当且仅当 $x$ 包含偶数个 '1'。
- ...状态 odd,当且仅当 $x$ 包含奇数个 '1'。
- 这个断言将DFA的最终状态与字符串的内在数学属性('1'的个数的奇偶性)完全绑定。
2. 形式化证明 (Proof by Induction on |x|)
- 基础步骤 (Base Case): 证明 P(x) 对长度为 0 的字符串 $x=\varepsilon$ 成立。
- DFA方面: 根据扩展转移函数的定义,$\delta^*(q_0, \varepsilon) = q_0$。在这个DFA中,$q_0 = \text{even}$。
- 语言方面: 空字符串 $\varepsilon$ 中包含 0 个 '1'。数字 0 是一个偶数。
- 比较: $\delta^*(q_0, \varepsilon)$ 到达了 even 状态,而 $\varepsilon$ 确实包含偶数个'1'。断言成立。
- 归纳步骤 (Inductive Step):
- 归纳假设 (Inductive Hypothesis): 假设断言 P(y) 对于所有长度为 $k$ 的字符串 $y$ 都成立。即,我们假设已经知道 $\delta^*(q_0, y)$ 的结果精确地反映了 $y$ 中'1'的奇偶性。
- 要证明的目标: 证明断言 P(x) 对于任何长度为 $k+1$ 的字符串 $x$ 也成立。
- 任何长度为 $k+1$ 的字符串 $x$ 都可以写成 $x = ya$ 的形式,其中 $y$ 是一个长度为 $k$ 的字符串,而 $a$ 是最后一个符号($a \in \{0, 1\}$)。
- 案例分析 (Case Analysis): 我们根据最后一个符号 $a$ 的值分两种情况讨论。
- Case 1: $a=0$
- 语言方面: 如果 $x = y0$,那么 $x$ 中'1'的数量与 $y$ 中'1'的数量完全相同。所以,$x$ 的奇偶性与 $y$ 的奇偶性相同。
- DFA方面: 我们来计算 $\delta^*(q_0, x) = \delta^*(q_0, y0)$。
- 根据扩展转移函数的定义: $\delta^*(q_0, y0) = \delta(\delta^*(q_0, y), 0)$。
- 根据我们的归纳假设,我们知道 $\delta^*(q_0, y)$ 是哪个状态(even或odd)。
- 如果 $y$ 有偶数个'1',那么 $\delta^*(q_0, y) = \text{even}$。此时,$\delta(\text{even}, 0) = \text{even}$。
- 如果 $y$ 有奇数个'1',那么 $\delta^*(q_0, y) = \text{odd}$。此时,$\delta(\text{odd}, 0) = \text{odd}$。
- 在这两种子情况下,最终状态都与 $\delta^*(q_0, y)$ 的状态相同。
- 比较: $x$ 的奇偶性与 $y$ 相同,而DFA处理 $x$ 之后的状态也与处理 $y$ 之后的状态相同。由于我们假设了处理 $y$ 之后状态的正确性,所以处理 $x$ 之后状态的正确性也得到了保证。断言在 $a=0$ 的情况下成立。
- Case 2: $a=1$
- 语言方面: 如果 $x = y1$,那么 $x$ 中'1'的数量比 $y$ 中'1'的数量多一个。所以,$x$ 的奇偶性与 $y$ 的奇偶性相反。
- DFA方面: 我们来计算 $\delta^*(q_0, x) = \delta^*(q_0, y1)$。
- 定义: $\delta^*(q_0, y1) = \delta(\delta^*(q_0, y), 1)$。
- 根据归纳假设:
- 如果 $y$ 有偶数个'1',那么 $\delta^*(q_0, y) = \text{even}$。此时,$\delta(\text{even}, 1) = \text{odd}$。
- 如果 $y$ 有奇数个'1',那么 $\delta^*(q_0, y) = \text{odd}$。此时,$\delta(\text{odd}, 1) = \text{even}$。
- 在这两种子情况下,最终状态都与 $\delta^*(q_0, y)$ 的状态相反。
- 比较: $x$ 的奇偶性与 $y$ 相反,而DFA处理 $x$ 之后的状态也与处理 $y$ 之后的状态相反。因此,断言在 $a=1$ 的情况下也成立。
- 结论: 由于基础步骤成立,并且归纳步骤对所有可能的情况都成立,因此根据数学归纳法原理,我们证明了加强的断言 P(x) 对所有字符串 $x \in \Sigma^*$ 都成立。
- 最终推论:
- 既然 P(x) 成立,那么一个字符串 $x$ 被此DFA接受 $\iff \delta^*(q_0, x) \in F \iff \delta^*(q_0, x) = \text{even}$。
- 根据我们已证的 P(x),$\delta^*(q_0, x) = \text{even} \iff x$ 包含偶数个'1'。
- 因此,$x$ 被接受 $\iff x$ 包含偶数个'1'。这正是 $L(A) = L$ 的定义。证明完成。
该示例通过一个完整、严谨的数学归纳法证明,展示了如何验证一个DFA的正确性。它完美地应用了“加强归纳假设”的技巧,将DFA的状态与字符串的属性在每一步都紧密联系起来,最终无可辩驳地证明了该DFA确实识别了“偶数个1”的语言。
这个例子的目的是手把手地教学生如何写出一个规范的DFA正确性证明。它是理论学习和实践的结合点,要求学生不仅能设计出DFA,还能用逻辑和数学语言来捍卫自己的设计。这是培养严谨科学思维的关键一步。
2018. 更多计数示例
📜 [原文19]
1示例:1 的数量是 3 的倍数
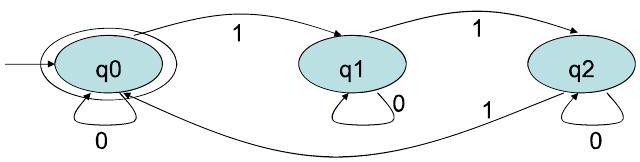
示例:1 的数量是 k 的倍数
2对于 1 的数量是 $\mathrm{k}$ (对于任何 $\mathrm{k}>1$ ) 的倍数的自动机
- $\mathrm{Q}=\left\{\mathrm{q}_{0}, \mathrm{q}_{1}, \ldots \mathrm{q}_{\mathrm{k}-1}\right\}$
- $\Sigma=\{0,1\}$
- $\delta\left(\mathrm{q}_{\mathrm{i}}, 0\right)=\mathrm{q}_{\mathrm{i}}, \delta\left(\mathrm{q}_{\mathrm{i}}, 1\right)=\mathrm{q}_{\mathrm{i}+1 \bmod \mathrm{k}}$ 对于所有 $\mathrm{i} \in\{0,1, \ldots, \mathrm{k}-1\}$
- 起始状态 $=\mathrm{q}_{0}$
- $\mathrm{F}=\left\{\mathrm{q}_{0}\right\}$
这部分将“奇偶校验”(即模2计数)的思想推广到更一般的情况——模k计数。
第一个示例:1的数量是3的倍数
- 问题: 设计一个DFA,接受所有'1'的个数是3的倍数(0, 3, 6, ...)的二进制字符串。
- 设计思路 (应用模k思想):
- 我们需要记住'1'的个数除以3的余数。
- 余数可能是 0, 1, 或 2。这三种需要区分的“记忆”对应三个状态。
- 状态意义:
- $q_0$: '1'的个数模3余0。
- $q_1$: '1'的个数模3余1。
- $q_2$: '1'的个数模3余2。
- DFA设计与转移图分析:
- $Q = \{q_0, q_1, q_2\}$
- $\Sigma = \{0, 1\}$
- 起始状态: 空字符串有0个'1',0模3余0。所以 $q_0$ 是起始状态。
- 接受状态: 目标是'1'的个数是3的倍数,即模3余0。所以 $F = \{q_0\}$。
- 转移:
- 读'0'不改变'1'的个数,因此也不改变余数。所以,对于任何状态 $q_i$,$\delta(q_i, 0) = q_i$。在图上表现为每个状态都有一个指向自己的标'0'的环。
- 读'1'使'1'的个数加1,余数也加1(模3)。
- 在 $q_0$ (余0) 读'1',余数变1。进入 $q_1$。
- 在 $q_1$ (余1) 读'1',余数变2。进入 $q_2$。
- 在 $q_2$ (余2) 读'1',余数变3,3模3余0。回到 $q_0$。
- 讲义中的转移图完美地展示了这个循环结构。
第二个示例:推广到 k 的倍数
- 这部分将上述思想形式化和推广。
- 问题: 为任意给定的整数 $k>1$,设计一个DFA,接受所有'1'的个数是 $k$ 的倍数的二进制字符串。
- DFA的通用构造:
- $Q = \{q_0, q_1, \ldots, q_{k-1}\}$: 我们需要 $k$ 个状态,分别代表'1'的个数模 $k$ 的余数:0, 1, ..., k-1。状态 $q_i$ 的意义是“到目前为止'1'的个数等于 $i \pmod k$”。
- $\Sigma = \{0, 1\}$: 字母表不变。
- $\delta(q_i, 0) = q_i$: 读'0'不改变余数,状态不变。
- $\delta(q_i, 1) = q_{i+1 \pmod k}$: 读'1'使余数加1。这里的 i+1 mod k 是关键。
- 如果 $i < k-1$,那么 $i+1 \pmod k = i+1$。所以状态从 $q_i$ 迁移到 $q_{i+1}$。
- 如果 $i = k-1$,那么 $i+1 = k$,$k \pmod k = 0$。所以状态从 $q_{k-1}$ 迁移回 $q_0$。这构成了一个长度为 $k$ 的循环。
- 起始状态 $= q_0$: 0个'1'模k余0。
- 接受状态 $= \{q_0\}$: k的倍数模k余0。
示例1: k=3,输入 x = "10110"
- 使用模3计数器DFA。
- 路径: $q_0 \xrightarrow{1} q_1 \xrightarrow{0} q_1 \xrightarrow{1} q_2 \xrightarrow{1} q_0 \xrightarrow{0} q_0$
- 最终状态: $q_0$。
- 判断: $q_0 \in F$。
- 结论: 字符串 "10110" 被接受 (它包含3个'1')。
示例2: k=4,语言是'1'的个数为4的倍数
- $Q=\{q_0, q_1, q_2, q_3\}$, $q_0$, $F=\{q_0\}$。
- 输入 x = "11111":
- 路径: $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_2 \xrightarrow{1} q_3 \xrightarrow{1} q_0 \xrightarrow{1} q_1$
- 最终状态: $q_1$。
- 判断: $q_1 \notin F$。
- 结论: 字符串 "11111" 被拒绝 (它包含5个'1',5不是4的倍数)。
这一部分展示了“模k计数器”是DFA的一类标准构造。通过使用 $k$ 个状态来代表模 $k$ 的 $k$ 种可能余数,DFA可以用有限的内存来判断一个(可能无限长的)字符串中某个符号出现的次数是否是 $k$ 的倍数。这种构造方法非常通用和强大。
- 展示泛化能力: 从 k=2 (奇偶) 到 k=3,再到任意 k,这个过程展示了如何将一个具体问题的解决方案泛化成解决一整类问题的通用算法或构造。
- 强化“状态即记忆”: 这个例子再次强调,状态的核心是“需要记住什么”。对于模k计数问题,需要记住的就是当前计数的余数。
- 引入循环结构: 模k计数器DFA在图形上是一个典型的环状结构,这是DFA中一种非常常见的模式。
模k计数器就像一个只有 $k$ 个档位的“循环开关”(比如旧式洗衣机的旋钮)。
- 开关有 $0, 1, \ldots, k-1$ 共 $k$ 个档位。
- 你从档位 0 开始。
- 每次输入'1',你就把开关顺时针拧一格。
- 如果拧到 $k-1$ 再拧,它会“咔哒”一声回到 0。
- 每次输入'0',开关不动。
- 你的目标是,经过一串操作后,开关正好停在 0 档位。
这个开关就是一个模k计数器DFA。
想象你在一个有 $k$ 个房间、排列成一个圆环的城堡里。房间编号从 0 到 $k-1$。
- 你从 0 号房间开始。
- 每当指令是'1',你就走到下一个房间(从 $i$ 到 $i+1$,如果是从 $k-1$ 就回到 0)。
- 每当指令是'0',你在原地休息。
- 你的任务是,在所有指令结束后,你必须正好回到 0 号房间(大厅)。
- 这个城堡的地图和你的移动规则,就定义了一个模k计数器DFA。
2119. 练习题
📜 [原文20]
1练习题
- 构造 DFA,接受所有长度可被 5 整除的字符串
- 构造 DFA,接受所有字母表 $\{0,1, . ., 9\}$ 上的字符串,这些字符串表示 (以十进制表示法) 可被 5 整除的数字,例如 0, 5, 025, 155, 00750, ...
- 构造 DFA,接受所有字母表 $\{0,1, . ., 9\}$ 上的字符串,这些字符串表示可被 3 整除的数字
- 构造 DFA,接受所有二进制字符串,这些字符串在二进制中表示可被 3 整除的数字
(例如 $\varepsilon \leftrightarrow 0,0 \leftrightarrow 0,11 \leftrightarrow 3,011 \leftrightarrow 3,110 \leftrightarrow 6, \ldots$ )
这部分提供了一系列练习题,旨在让学生运用前面学到的设计原则(尤其是模k计数)来解决类似但略有不同的问题。
练习题1: 接受所有长度可被 5 整除的字符串
- 分析:
- 这个问题是模k计数的直接应用。
- 我们不关心字符串里有什么符号,只关心它的长度。
- 每读一个符号,长度就加1。
- 我们需要计算字符串长度模5的余数。
- 设计:
- 状态: 5个状态,$q_0, q_1, q_2, q_3, q_4$,分别代表长度模5余0, 1, 2, 3, 4。
- 字母表: 题目未指定,可以假设是 $\Sigma=\{a, b\}$ 或任何非空字母表。
- 起始状态: $q_0$ (空字符串长度为0,0模5余0)。
- 接受状态: $F = \{q_0\}$ (长度是5的倍数,模5余0)。
- 转移: 对于任何输入符号 $c \in \Sigma$,它都使长度加1,即余数加1。所以 $\delta(q_i, c) = q_{i+1 \pmod 5}$。这是一个包含5个状态的简单环,所有符号都驱动同一个方向的转移。
练习题2: 接受表示可被 5 整除的十进制数的字符串
- 分析:
- 这个问题不再是简单地计长度或符号个数。它关系到字符串所表示的数值。
- 一个十进制数能被5整除的充要条件是:它的最后一位是 '0' 或 '5'。
- DFA需要记住什么?它只需要记住上一个读到的符号是什么,就能判断整个数能否被5整除。但我们需要考虑整个字符串。当字符串读完时,最后一个符号是什么?
- 设计:
- 状态: 我们可以设计两个状态。
- $q_0$: 结尾数字是 '0' 或 '5'。
- $q_1$: 结尾数字不是 '0' 或 '5'。
- 字母表: $\Sigma = \{'0', '1', ..., '9'\}$。
- 起始状态: 这个问题有个歧义。如果把空字符串看作数字0,那么0能被5整除,起始状态应该是接受状态。但通常我们不把空字符串看作数字。我们假设一个更简单的模型:DFA只需要在读完非空字符串后做出判断。
- 让我们重新设计状态:
- $q_{start}$: 初始状态。
- $q_{accept}$: 最后一个读到的数字是 '0' 或 '5'。
- $q_{reject}$: 最后一个读到的数字不是 '0' 或 '5'。
- 转移:
- 从 $q_{start}$ 开始,读到 '0' 或 '5',进入 $q_{accept}$。读到其他数字,进入 $q_{reject}$。
- 在 $q_{accept}$ 时,下一个读到 '0' 或 '5',留在 $q_{accept}$。读到其他,进入 $q_{reject}$。
- 在 $q_{reject}$ 时,下一个读到 '0' 或 '5',进入 $q_{accept}$。读到其他,留在 $q_{reject}$。
- 起始状态: $q_{start}$。
- 接受状态: $F = \{q_{accept}\}$。此外,数字 "0" 本身也应被接受。单独的 "0" 会使DFA进入 $q_{accept}$。空字符串 $\varepsilon$ 呢?如果它代表0,那么 $q_{start}$ 也应该是接受状态。我们采纳题目例子0被接受,那么$q_{start}$读到0后进入的状态$q_{accept}$必须是接受状态。
- 这个模型对于"0", "5", "025", "155" 都有效。
练习题3: 接受表示可被 3 整除的十进制数的字符串
- 分析:
- 一个数能被3整除的充要条件是:它的各位数字之和能被3整除。
- 这又回到了模运算!我们需要计算各位数字之和模3的余数。
- 当从左到右读一个数字字符串时,数值是如何变化的?如果当前读到的前缀代表的数是 $N$,下一个数字是 $d$,那么新的数是 $N' = 10 \times N + d$。
- 我们关心的是数值模3的余数。$N' \pmod 3 = (10 \times N + d) \pmod 3 = (1 \times N + d) \pmod 3 = (N \pmod 3 + d \pmod 3) \pmod 3$。
- 这个发现是关键!新余数只依赖于旧余数和新数字。这正是DFA能解决的问题!
- 设计:
- 状态: 三个状态,$q_0, q_1, q_2$,分别代表当前数值模3余0, 1, 2。
- 字母表: $\Sigma = \{'0', ..., '9'\}$。
- 起始状态: $q_0$ (空字符串代表0,0模3余0)。
- 接受状态: $F = \{q_0\}$。
- 转移: $\delta(q_i, d) = q_{(i+d) \pmod 3}$。例如:
- 在 $q_1$ (余1),读 '5' (值5)。新余数是 $(1+5)\pmod 3 = 6 \pmod 3 = 0$。所以 $\delta(q_1, '5') = q_0$。
- 在 $q_2$ (余2),读 '8' (值8)。新余数是 $(2+8)\pmod 3 = 10 \pmod 3 = 1$。所以 $\delta(q_2, '8') = q_1$。
练习题4: 接受表示可被 3 整除的二进制数的字符串
- 分析:
- 这和上题类似,但基数是2。
- 如果当前前缀代表的数是 $N$,下一个数字是 $d \in \{0, 1\}$,那么新的数是 $N' = 2 \times N + d$。
- 我们关心数值模3的余数。$N' \pmod 3 = (2 \times N + d) \pmod 3 = (-1 \times (N \pmod 3) + d) \pmod 3$。
- 新余数仍然只依赖于旧余数和新数字!
- 设计:
- 状态: 三个状态,$q_0, q_1, q_2$,代表当前数值模3余0, 1, 2。
- 字母表: $\Sigma = \{0, 1\}$。
- 起始状态: $q_0$ (空字符串$\varepsilon$或"0"都代表0,0模3余0)。
- 接受状态: $F = \{q_0\}$。
- 转移:
- 从 $q_i$ 读 '0' ($d=0$): 新余数是 $(2i) \pmod 3$。
- $\delta(q_0, 0) = q_0$ ((2*0)%3=0)
- $\delta(q_1, 0) = q_2$ ((2*1)%3=2)
- $\delta(q_2, 0) = q_1$ ((2*2)%3=1)
- 从 $q_i$ 读 '1' ($d=1$): 新余数是 $(2i+1) \pmod 3$。
- $\delta(q_0, 1) = q_1$ ((2*0+1)%3=1)
- $\delta(q_1, 1) = q_0$ ((2*1+1)%3=0)
- $\delta(q_2, 1) = q_2$ ((2*2+1)%3=2)
- 验证: 字符串 "110" 代表6。
- $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_0 \xrightarrow{0} q_0$。最终在 $q_0$,接受。正确。
- 字符串 "11" 代表3。
- $q_0 \xrightarrow{1} q_1 \xrightarrow{1} q_0$。最终在 $q_0$,接受。正确。
2220. 示例:偶数个1和0
📜 [原文21]
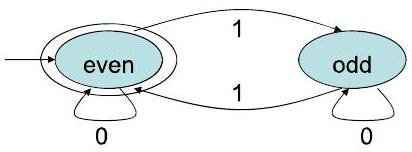
示例:偶数个 1
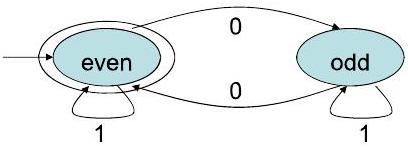
示例:偶数个 0
1示例:偶数个 1 和 0
- DFA,接受所有包含偶数个 0 和偶数个 1 的二进制字符串。
- $\Sigma=\{0,1\}, \mathrm{Q}=\{\mathrm{ee}, \mathrm{eo}, \mathrm{oe}, \mathrm{oo}\}, \mathrm{q}_{0}=\mathrm{ee}, \mathrm{F}=\{\mathrm{ee}\}$
- 状态跟踪到目前为止看到的 0 的奇偶性和 1 的奇偶性
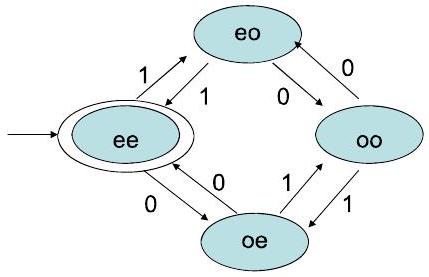
这部分内容展示了如何组合两个简单的DFA来解决一个更复杂的问题,引出了乘积构造 (Product Construction) 的思想。
- 回顾两个基本DFA:
- 偶数个'1'的DFA: 有两个状态,{even_1, odd_1}。读'1'时状态翻转,读'0'时状态不变。
- 偶数个'0'的DFA: 同样有两个状态,{even_0, odd_0}。读'0'时状态翻转,读'1'时状态不变。
- 新问题: 接受同时满足“偶数个'0'”和“偶数个'1'”的字符串。
- 分析 (需要记住什么): 在读取字符串的过程中,为了对未来的输入做正确判断,我们同时需要记住两件事:
- 到目前为止,'0'的个数的奇偶性。
- 到目前为止,'1'的个数的奇偶性。
- 状态设计: 每一份“组合记忆”就对应一个新状态。
- '0'是偶数,'1'是偶数 $\rightarrow$ 状态 ee (even-even)
- '0'是偶数,'1'是奇数 $\rightarrow$ 状态 eo (even-odd)
- '0'是奇数,'1'是偶数 $\rightarrow$ 状态 oe (odd-even)
- '0'是奇数,'1'是奇数 $\rightarrow$ 状态 oo (odd-odd)
- 这四个状态正好是两个基本DFA状态集的笛卡尔积: $\{even_0, odd_0\} \times \{even_1, odd_1\}$。
- DFA设计:
- Q = {ee, eo, oe, oo}: 4个状态。
- Σ = {0, 1}
- 起始状态 $q_0$: 空字符串有0个'0'和0个'1',都是偶数。所以起始状态是 ee。
- 接受状态 F: 目标是“偶数个0”和“偶数个1”。所以只有 ee 状态满足条件。$F = \{\text{ee}\}$。
- 转移函数 (分析转移图):
- 在状态 ee (偶0, 偶1):
- 读 0: '0'的奇偶性变奇,'1'不变。进入 oe (奇0, 偶1)。
- 读 1: '0'的奇偶性不变,'1'变奇。进入 eo (偶0, 奇1)。
- 在状态 eo (偶0, 奇1):
- 读 0: '0'的奇偶性变奇,'1'不变。进入 oo (奇0, 奇1)。
- 读 1: '0'的奇偶性不变,'1'变偶。进入 ee (偶0, 偶1)。
- ... 以此类推。可以发现,新DFA的转移,就像两个基本DFA在并行独立地进行自己的状态转移。
- 例如,从ee读0:
- “偶数0”的DFA从 even_0 读0,进入 odd_0。
- “偶数1”的DFA从 even_1 读0,停在 even_1。
- 两者组合起来,就是从 (even_0, even_1) 进入了 (odd_0, even_1),即从 ee 进入 oe。
示例1: 输入 x = "1010"
- 路径: ee $\xrightarrow{1}$ eo $\xrightarrow{0}$ oo $\xrightarrow{1}$ oe $\xrightarrow{0}$ ee
- 最终状态: ee。
- 判断: ee $\in F$。
- 结论: "1010" 被接受 (它有2个'0'和2个'1',都是偶数)。
示例2: 输入 x = "101"
- 路径: ee $\xrightarrow{1}$ eo $\xrightarrow{0}$ oo $\xrightarrow{1}$ oe
- 最终状态: oe。
- 判断: oe $\notin F$。
- 结论: "101" 被拒绝 (它有1个'0'和2个'1','0'的个数是奇数)。
这个例子展示了如何通过状态的笛卡尔积来构造一个能同时跟踪多个属性的DFA。新DFA的状态数是原DFA状态数的乘积,其转移过程可以看作是多个基本DFA在并行运行。这是正则语言对交集运算封闭的直观体现。
- 引入乘积构造: 这是DFA和正则语言理论中一个极其重要的构造方法,是证明正则语言对并集、交集、差集等运算封闭的基础。
- 展示组合能力: 表明简单的DFA可以像乐高积木一样被组合起来,解决更复杂的复合逻辑问题。
- 状态爆炸: 同时也含蓄地指出了这种方法的代价。如果组合多个DFA,状态的数量会呈指数级增长(“状态爆炸”),这是DFA在实践应用中需要考虑的一个问题。
你有两个拉线开关,一个控制客厅灯('1'的奇偶性),一个控制卧室灯('0'的奇偶性)。
- 状态就是两盏灯的组合状态:(关,关),(关,开),(开,关),(开,开)。
- 输入'1',你就去拉一下客厅灯的线。
- 输入'0',你就去拉一下卧室灯的线。
- 你从两盏灯都关着(ee)开始。
- 你的目标是,操作结束后,两盏灯都得是关着的。
这个组合系统就是一个乘积DFA。
2321. 正则语言的并集、交集
📜 [原文22]
1正则语言的并集、交集
定理:如果 $\mathrm{L}_{1}, \mathrm{~L}_{2}$ 是正则语言,那么
- 它们的交集 $\mathrm{L}_{1} \cap \mathrm{L}_{2}$ 也是正则的
- 它们的并集 $\mathrm{L}_{1} \cup \mathrm{L}_{2}$ 也是正则的
24正则语言的并集、交集
1乘积构造
给定两个自动机
$\mathrm{A}_{1}=\left(\mathrm{Q}_{1}, \Sigma, \delta_{1}, \mathrm{q}_{1}, \mathrm{~F}_{1}\right), \quad \mathrm{A}_{2}=\left(\mathrm{Q}_{2}, \Sigma, \delta_{2}, \mathrm{q}_{2}, \mathrm{~F}_{2}\right)$
乘积自动机 $\mathrm{M}=\mathrm{A}_{1} \times \mathrm{A}_{2}=\left(\mathrm{Q}_{1} \times \mathrm{Q}_{2}, \Sigma, \delta,\left(\mathrm{q}_{1}, \mathrm{q}_{2}\right), \mathrm{F}\right)$
其中 $\delta\left(\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right), \mathrm{a}\right)=\left(\delta_{1}\left(\mathrm{p}_{1}, \mathrm{a}\right), \delta_{2}\left(\mathrm{p}_{2}, \mathrm{a}\right)\right), \forall \mathrm{p}_{1} \in \mathrm{Q}_{1} \forall \mathrm{p}_{2} \in \mathrm{Q}_{2} \forall \mathrm{a} \in \Sigma$
对于并集:$\mathrm{F}=\left\{\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right) \mid \mathrm{p}_{1} \in \mathrm{F}_{1}\right.$ 或 $\left.\mathrm{p}_{2} \in \mathrm{F}_{2}\right\}$
对于交集:$\mathrm{F}=\left\{\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right) \mid \mathrm{p}_{1} \in \mathrm{F}_{1}\right.$ 且 $\left.\mathrm{p}_{2} \in \mathrm{F}_{2}\right\}$
这一部分正式提出了乘积构造法,并用它来证明正则语言对于并集和交集运算是封闭的。
- 定理:
- 这个定理声明了正则语言家族的另外两个重要的闭包性质。
- 交集 (Intersection) $L_1 \cap L_2$: 一个字符串 $x$ 属于交集,当且仅当 $x$ 既属于 $L_1$ 又属于 $L_2$。
- 并集 (Union) $L_1 \cup L_2$: 一个字符串 $x$ 属于并集,当且仅当 $x$ 或者属于 $L_1$ 或者属于 $L_2$(或两者都属于)。
- 定理说,如果 $L_1$ 和 $L_2$ 都能被DFA识别,那么它们的交集和并集也一定能被某个(可能是更复杂的)DFA识别。
- 乘积构造 (Product Construction):
- 这是用来证明上述定理的构造性方法。其核心思想与上一节的例子完全相同:并行模拟两个DFA。
- 给定两个自动机:
- $A_1 = (Q_1, \Sigma, \delta_1, q_{1,0}, F_1)$ 识别 $L_1$。
- $A_2 = (Q_2, \Sigma, \delta_2, q_{2,0}, F_2)$ 识别 $L_2$。(注意,两个DFA的字母表 $\Sigma$ 必须相同)。
- 构造乘积自动机 M:
- 状态集 $Q$: 新的状态集是 $A_1$ 和 $A_2$ 状态集的笛卡尔积 $Q_1 \times Q_2$。新机器的每个状态都是一个形如 $(p_1, p_2)$ 的有序对,其中 $p_1 \in Q_1, p_2 \in Q_2$。这个状态的意义是:“$A_1$ 现在处于状态 $p_1$,同时 $A_2$ 现在处于状态 $p_2$”。
- 字母表 $\Sigma$: 与原来相同。
- 起始状态 $q_0$: 新的起始状态是两个原始起始状态组成的有序对 $(q_{1,0}, q_{2,0})$。
- 转移函数 $\delta$:
- $\delta((p_1, p_2), a) = (\delta_1(p_1, a), \delta_2(p_2, a))$
- 这一定义是核心。它表明,新机器从组合状态 $(p_1, p_2)$ 读入一个符号 $a$ 后的下一个状态,是由 $A_1$ 和 $A_2$ 各自独立计算其下一个状态,然后将结果组合而成。$A_1$ 从 $p_1$ 变为 $\delta_1(p_1, a)$,$A_2$ 从 $p_2$ 变为 $\delta_2(p_2, a)$。
- 接受状态集 F: 这是区分并集和交集的关键所在。新机器 M 的骨架(状态和转移)是相同的,但“胜利条件”不同。
- 对于交集 ($L_1 \cap L_2$):
- 一个字符串 $x$ 要被接受,必须同时被 $A_1$ 和 $A_2$ 接受。
- 这意味着在处理完 $x$ 后,M 的最终状态 $(p_1, p_2)$ 必须满足 $p_1$ 是 $A_1$ 的接受状态 且 $p_2$ 是 $A_2$ 的接受状态。
- 所以, $F_{intersect} = \{(p_1, p_2) \mid p_1 \in F_1 \text{ and } p_2 \in F_2\}$。这等价于 $F_1 \times F_2$。
- 对于并集 ($L_1 \cup L_2$):
- 一个字符串 $x$ 要被接受,只要被 $A_1$ 或 $A_2$ 之一接受即可。
- 这意味着在处理完 $x$ 后,M 的最终状态 $(p_1, p_2)$ 必须满足 $p_1$ 是 $A_1$ 的接受状态 或 $p_2$ 是 $A_2$ 的接受状态。
- 所以, $F_{union} = \{(p_1, p_2) \mid p_1 \in F_1 \text{ or } p_2 \in F_2\}$。
- $L_1$: 偶数个'0'。$A_1$ 有状态 $\{e_0, o_0\}$,$F_1=\{e_0\}$。
- $L_2$: 偶数个'1'。$A_2$ 有状态 $\{e_1, o_1\}$,$F_2=\{e_1\}$。
构造交集 $L_1 \cap L_2$ (偶数个'0' and 偶数个'1') 的DFA:
- $Q = \{e_0, o_0\} \times \{e_1, o_1\} = \{(e_0,e_1), (e_0,o_1), (o_0,e_1), (o_0,o_1)\}$ (这就是上一节的 {ee, eo, oe, oo})。
- $q_0 = (e_0, e_1)$ (即 ee)。
- $F_{intersect}$: $\{(p_1,p_2) \mid p_1 \in \{e_0\} \text{ and } p_2 \in \{e_1\}\} = \{(e_0, e_1)\}$ (即 {ee})。
- 这与上一节为“偶数个0和偶数个1”构造的DFA完全一致。
构造并集 $L_1 \cup L_2$ (偶数个'0' or 偶数个'1') 的DFA:
- Q, $\Sigma$, $\delta$, $q_0$ 都和上面一样。
- $F_{union}$: $\{(p_1,p_2) \mid p_1 \in \{e_0\} \text{ or } p_2 \in \{e_1\}\}$
- $p_1 \in \{e_0\}$ 的状态有: $(e_0, e_1)$ 和 $(e_0, o_1)$。
- $p_2 \in \{e_1\}$ 的状态有: $(e_0, e_1)$ 和 $(o_0, e_1)$。
- 取并集,得到 $F_{union} = \{(e_0, e_1), (e_0, o_1), (o_0, e_1)\}$ (即 {ee, eo, oe})。
- 所以,识别并集语言的DFA,其接受状态是 ee, eo, oe。只有状态 oo (奇数个0和奇数个1) 是非接受状态。
正则语言对并集和交集运算是封闭的。这一重要性质可以通过乘积构造法来证明。该方法通过并行模拟两个给定的DFA $A_1$ 和 $A_2$ 来构造一个新的DFA M。M的状态是 $A_1$ 和 $A_2$ 状态的有序对。通过恰当地定义 M 的接受状态集(对于交集是“两者都接受”,对于并集是“至少一个接受”),就可以使 M 精确地识别 $L_1 \cap L_2$ 或 $L_1 \cup L_2$。
- 完善理论体系: 证明闭包性质是形式语言理论的核心任务之一。它表明正则语言是一个具有鲁棒性的、结构良好的语言类别。
- 提供构造性工具: 乘积构造是一个强大的算法。当你面对一个可以分解为“条件A 和/或 条件B”的语言时,如果A和B分别对应正则语言,你就可以分别设计简单的DFA,然后用乘积法自动地把它们组合起来,而无需从头设计一个复杂的DFA。
- 连接逻辑与计算: 这个构造在“与”(AND, $\cap$) 和“或”(OR, $\cup$) 这两个基本逻辑运算,和DFA的机器构造之间建立了直接的桥梁。
2522. 有限集合的正则性
📜 [原文23]
1所有有限集合都是正则的
- 示例:$\mathrm{L}=\{00,01,011,101\}$
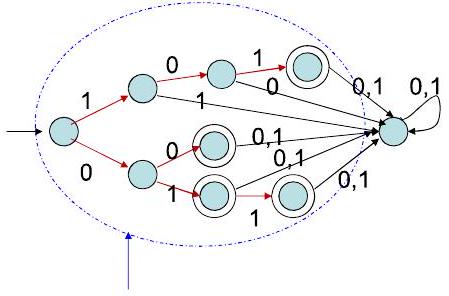
自动机 = 字符串集合 $\mathrm{L}$ 的Trie数据结构 + "死" 吸收状态,拒绝
这一部分提出了一个普遍的结论:任何只包含有限多个字符串的语言,都是正则语言。并给出了一个构造相应DFA的通用方法。
- 定理: 如果一个语言 L 是一个有限的字符串集合,那么 L 是正则的。
- 证明思路:
- 我们可以通过为这个有限集合 L 构造一个识别它的DFA来证明这一点。
- 这个构造方法分为两步:
- 为 L 中的所有字符串构建一个“Trie”(也称前缀树)。
- 对这个 Trie 进行一些修改,使其成为一个完整的DFA。
- 示例分析 L = {00, 01, 011, 101}:
- Trie数据结构:
- Trie 是一种树状数据结构,用于高效地存储和检索字符串集合。
- 从根节点开始,每个节点的边代表一个字符,从根到一个节点的路径就构成了一个字符串前缀。
- 我们将 L 中的所有字符串 "00", "01", "011", "101" 都插入到 Trie 中。
- 根节点: 代表空字符串 $\varepsilon$。
- 插入 "00": 根 $\xrightarrow{0}$ 节点A $\xrightarrow{0}$ 节点B。
- 插入 "01": 根 $\xrightarrow{0}$ 节点A (已存在) $\xrightarrow{1}$ 节点C。
- 插入 "011": 根 $\xrightarrow{0}$ 节点A $\xrightarrow{1}$ 节点C (已存在) $\xrightarrow{1}$ 节点D。
- 插入 "101": 根 $\xrightarrow{1}$ 节点E $\xrightarrow{0}$ 节点F $\xrightarrow{1}$ 节点G。
- Trie 建好后,树中的某些节点对应于 L 中的完整字符串。我们需要标记它们。在图中,这些节点(B, C, D, G)被画成了双圆圈,表示它们是接受状态。
- 从 Trie 到 DFA:
- 上面的 Trie 结构还不是一个完整的DFA,因为它不满足完备性。例如,从根节点出发,只有标 '0' 和 '1' 的出边,没有标其他可能符号的边(如果字母表更大的话)。更重要的是,比如从节点B(对应"00")出发,没有定义读 '0' 或 '1' 该去哪里。
- 为了将其变为DFA,我们需要:
- 将节点视为状态: Trie 的每个节点都成为DFA的一个状态。根节点是起始状态。
- 标记接受状态: 所有代表 L 中完整字符串的节点,都成为接受状态。
- 添加“死状态”: 我们引入一个额外的、非接受的“死状态”(dead state)或“陷阱状态”。在图中,这个状态没有被画出来,但我们可以想象它的存在。
- 补全转移: 对于图中任何一个节点,如果它缺少某个符号的出边,我们就画一条指向“死状态”的边。例如,从根节点出发,如果输入不是'0'或'1',就去死状态。从节点B("00")出发,再读任何符号('0'或'1')都会进入死状态,因为它不再是 L 中任何字符串的前缀了。一旦进入死状态,之后读任何符号都停留在死状态。
- 最终结论: 通过“Trie + 死状态”的方法,我们总能为任何一个有限语言 L 构建一个识别它的DFA。因此,所有有限语言都是正则的。
所有只包含有限个字符串的语言都是正则语言。一个通用的构造方法是,先为该字符串集合构建一个Trie(前缀树),然后将Trie的节点作为DFA的状态,将代表完整字符串的节点设为接受状态,并增加一个“死状态”来处理所有不匹配任何前缀的转移,从而构建出一个完整的DFA。
- 建立重要结论: “所有有限语言都是正则的”是形式语言理论的一个基本事实。
- 连接数据结构与自动机: 这个例子展示了计算机科学中不同领域的概念是如何关联的。数据结构中的Trie和计算理论中的DFA在这里表现出惊人的一致性。
- 提供又一个构造性范例: 继“模k计数器”和“乘积构造”后,这提供了第三种重要的DFA构造思想——基于前缀的树状结构。
为一个有限语言构造DFA,就像是在为一个只有几本藏书的“微型图书馆”制作一个“导览系统”。
- Trie: 就是图书馆的“索引卡柜”。你按书名首字母 A-Z 查,再按第二个字母...
- DFA: 导览系统是一个机器人。
- 你告诉它一个书名(输入字符串)。
- 它从“大厅”(根节点)出发,根据你给的书名,在走廊(边)间穿行,从一个房间(节点)到另一个房间。
- 如果它最终到达的房间里,书架上正好有这本书(接受状态),它就告诉你“书在这里”。
- 如果在任何一步,它发现没有对应的走廊(比如你要找的书名是"Apple",但索引里只有"Ant"),它就直接带你到一个“查无此书”的房间(死状态),并告诉你“我们没有这本书”。
26行间公式索引
- k槽缓冲区自动机形式化定义
- 扩展转移函数 $\delta^*$ 的归纳定义
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。