10.2
数学概念和术语
正如任何数学学科一样,我们从讨论我们期望使用的基本数学对象、工具和符号开始。
集合
集合是一组作为整体表示的对象。集合可以包含任何类型的对象,包括数字、符号,甚至其他集合。集合中的对象称为其元素或成员。集合可以通过几种方式正式描述。
一种方式是列出集合的元素并用花括号括起来。因此,集合
包含元素 7、21 和 57。符号 $\in$ 和 $\notin$ 表示集合成员身份和非成员身份。我们写 $7 \in\{7,21,57\}$ 和 $8 \notin\{7,21,57\}$。对于两个集合 $A$ 和 $B$,如果 $A$ 的每个成员也是 $B$ 的成员,我们说 $A$ 是 $B$ 的子集,写作 $A \subseteq B$。如果 $A$ 是 $B$ 的子集且不等于 $B$,我们说 $A$ 是 $B$ 的真子集,写作 $A \subsetneq B$。
描述集合的顺序无关紧要,成员的重复也无关紧要。通过写作 $\{57,7,7,7,21\}$ 得到相同的集合 $S$。如果我们要考虑成员出现的次数,我们将该组称为多重集而不是集合。因此 $\{7\}$ 和 $\{7,7\}$ 作为多重集是不同的,但作为集合是相同的。一个无限集包含无限多个元素。我们无法列出无限集的所有元素,所以我们有时使用“...”符号表示“永远继续序列”。因此,我们将自然数集 $\mathcal{N}$ 写为
整数集 $\mathcal{Z}$ 写为
没有成员的集合称为空集,写作 $\emptyset$。具有一个成员的集合有时称为单例集,具有两个成员的集合称为无序对。
当我们想描述一个根据某种规则包含元素的集合时,我们写 $\{n \mid \text{关于 } n \text{ 的规则}\}$。因此,$\left\{n \mid n=m^{2} \text{ 且 } m \in \mathcal{N}\right\}$ 表示完全平方数集。
如果我们有两个集合 $A$ 和 $B$, $A$ 和 $B$ 的并集,写作 $A \cup B$,是我们通过将 $A$ 和 $B$ 中的所有元素组合成一个集合而得到的集合。 $A$ 和 $B$ 的交集,写作 $A \cap B$,是同时在 $A$ 和 $B$ 中的元素集。 $A$ 的补集,写作 $\bar{A}$,是所考虑的所有元素中不在 $A$ 中的元素集。
在数学中,通常情况下,一张图片有助于澄清概念。对于集合,我们使用一种称为文氏图的图片。它将集合表示为由圆形线条包围的区域。设集合 START-t 是所有以字母“t”开头的英文单词的集合。例如,图中,圆圈代表集合 START-t。该集合的几个成员以圆圈内的点的形式表示。
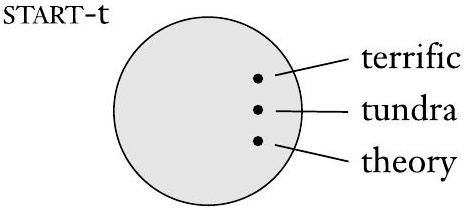
图 0.1
以“t”开头的英文单词集合的文氏图
类似地,我们在下图中表示以“z”结尾的英文单词的集合 END-z。
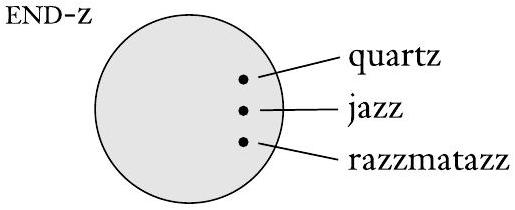
图 0.2
以“z”结尾的英文单词集合的文氏图
要在同一个文氏图中表示这两个集合,我们必须将它们绘制成重叠的,表示它们共享一些元素,如下图所示。例如,单词 topaz 在这两个集合中。该图还包含一个表示集合 START-j 的圆圈。它与 START-t 的圆圈不重叠,因为没有单词同时属于这两个集合。
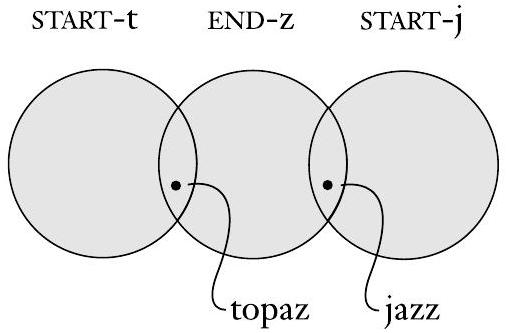
图 0.3
重叠的圆圈表示共同的元素
接下来的两个文氏图描绘了集合 $A$ 和 $B$ 的并集和交集。
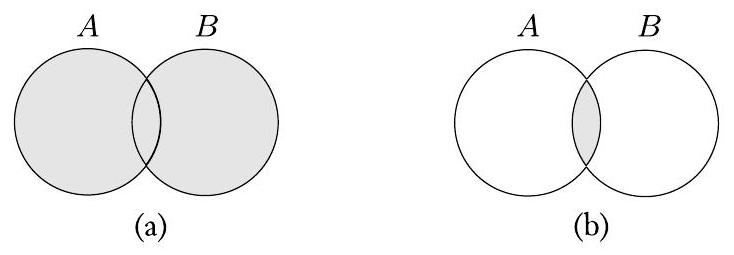
图 0.4
(a) $A \cup B$ 和 (b) $A \cap B$ 的图示
序列和元组
对象的序列是这些对象按一定顺序排列的列表。我们通常通过将列表写在括号内来表示序列。例如,序列 7, 21, 57 将写为
在集合中,顺序无关紧要,但在序列中则不然。因此 $(7,21,57)$ 与 $(57,7,21)$ 不同。类似地,重复在序列中很重要,但在集合中则无关紧要。因此 $(7,7,21,57)$ 与其他两个序列都不同,而集合 $\{7,21,57\}$ 与集合 $\{7,7,21,57\}$ 完全相同。
与集合一样,序列可以是有限的也可以是无限的。有限序列通常称为元组。一个包含 $k$ 个元素的序列是一个 $k$-元组。因此 $(7,21,57)$ 是一个 3-元组。一个 2-元组也称为有序对。
集合和序列可以作为其他集合和序列的元素出现。例如,$A$ 的幂集是 $A$ 的所有子集的集合。如果 $A$ 是集合 $\{0,1\}$,则 $A$ 的幂集是集合 $\{\emptyset,\{0\},\{1\},\{0,1\}\}$。所有元素为 0 和 1 的有序对的集合是 $\{(0,0),(0,1),(1,0),(1,1)\}$。
如果 $A$ 和 $B$ 是两个集合,$A$ 和 $B$ 的笛卡尔积或叉积,写作 $A \times B$,是所有有序对的集合,其中第一个元素是 $A$ 的成员,第二个元素是 $B$ 的成员。
示例 0.5
如果 $A=\{1,2\}$ 且 $B=\{x, y, z\}$,
$\square$
我们也可以取 $k$ 个集合 $A_{1}, A_{2}, \ldots, A_{k}$ 的笛卡尔积,写作 $A_{1} \times A_{2} \times \cdots \times A_{k}$。它是由所有 $k$-元组 $(a_{1}, a_{2}, \ldots, a_{k})$ 组成的集合,其中 $a_{i} \in A_{i}$。
示例 0.6
如果 $A$ 和 $B$ 与示例 0.5 中相同,
如果我们有一个集合与自身的笛卡尔积,我们使用简写
示例 0.7
集合 $\mathcal{N}^{2}$ 等于 $\mathcal{N} \times \mathcal{N}$。它由所有自然数的有序对组成。我们也可以将其写为 $\{(i, j) \mid i, j \geq 1\}$。
函数和关系
函数是数学的核心。函数是一种建立输入-输出关系的对象。函数接受输入并产生输出。在每个函数中,相同的输入总是产生相同的输出。如果 $f$ 是一个函数,当输入值为 $a$ 时,输出值为 $b$,我们写
函数也称为映射,如果 $f(a)=b$,我们说 $f$ 将 $a$ 映射到 $b$。
例如,绝对值函数 $abs$ 接受一个数字 $x$ 作为输入,如果 $x$ 为正则返回 $x$,如果 $x$ 为负则返回 $-x$。因此 $abs(2)=abs(-2)=2$。加法是函数的另一个例子,写作 $add$。加法函数的输入是有序对的数字,输出是这些数字的和。
函数的可能输入集称为其域。函数的输出来自一个称为其值域的集合。表示 $f$ 是一个函数,其域为 $D$,值域为 $R$ 的符号表示是
在函数 $abs$ 的情况下,如果我们处理的是整数,则域和值域都是 $\mathcal{Z}$,所以我们写 $abs: \mathcal{Z} \longrightarrow \mathcal{Z}$。在整数的加法函数的情况下,域是整数对的集合 $\mathcal{Z} \times \mathcal{Z}$,值域是 $\mathcal{Z}$,所以我们写 $add: \mathcal{Z} \times \mathcal{Z} \longrightarrow \mathcal{Z}$。请注意,函数不一定使用指定值域的所有元素。函数 $abs$ 永远不会取值 -1,即使 $-1 \in \mathcal{Z}$。使用值域所有元素的函数被称为满射。
我们可以通过几种方式描述一个特定的函数。一种方式是使用一个从指定输入计算输出的过程。另一种方式是使用一个列出所有可能输入并给出每个输入的输出的表格。
示例 0.8
考虑函数 $f:\{0,1,2,3,4\} \longrightarrow\{0,1,2,3,4\}$。
| $n$ | $f(n)$ |
| :---: | :------: |
| 0 | 1 |
| 1 | 2 |
| 2 | 3 |
| 3 | 4 |
| 4 | 0 |
这个函数将其输入加 1,然后输出结果模 5。一个数模 $m$ 是除以 $m$ 后的余数。例如,钟面上的分针是模 60 计数。当我们进行模运算时,我们定义 $\mathcal{Z}_{m}=\{0,1,2, \ldots, m-1\}$。使用这个符号,上述函数 $f$ 的形式是 $f: \mathcal{Z}_{5} \longrightarrow \mathcal{Z}_{5}$。
示例 0.9
如果函数的域是两个集合的笛卡尔积,有时会使用二维表格。这是另一个函数 $g: \mathcal{Z}_{4} \times \mathcal{Z}_{4} \longrightarrow \mathcal{Z}_{4}$。表格中标记为 $i$ 的行和标记为 $j$ 的列中的条目是 $g(i, j)$ 的值。
| $g$ | 0 | 1 | 2 | 3 |
| :---- | :- | :- | :- | :- |
| 0 | 0 | 1 | 2 | 3 |
| 1 | 1 | 2 | 3 | 0 |
| 2 | 2 | 3 | 0 | 1 |
| 3 | 3 | 0 | 1 | 2 |
函数 $g$ 是模 4 的加法函数。
当函数 $f$ 的域是某个集合 $A_{1}, \ldots, A_{k}$ 的笛卡尔积 $A_{1} \times \cdots \times A_{k}$ 时,$f$ 的输入是一个 $k$-元组 $(a_{1}, a_{2}, \ldots, a_{k})$,我们称 $a_{i}$ 为 $f$ 的参数。一个带有 $k$ 个参数的函数称为 $k$-元函数, $k$ 称为函数的元数。如果 $k$ 为 1,$f$ 有一个参数, $f$ 称为一元函数。如果 $k$ 为 2,$f$ 是二元函数。某些熟悉的二元函数以特殊的中缀表示法书写,函数的符号放在其两个参数之间,而不是以前缀表示法书写,符号放在前面。例如,加法函数 $add$ 通常以中缀表示法书写,用 + 符号放在其两个参数之间,如 $a+b$,而不是前缀表示法 $add(a, b)$。
谓词或属性是值域为 {TRUE, FALSE} 的函数。例如,设 $even$ 是一个属性,如果其输入是偶数则为 TRUE,如果其输入是奇数则为 FALSE。因此 $even(4)=$ true 且 $even(5)=$ FALSE。
域是 $k$-元组集合 $A \times \cdots \times A$ 的属性称为关系, $k$-元关系,或A上的$k$-元关系。一个常见的情况是二元关系。在涉及二元关系的表达式中,我们习惯使用中缀表示法。例如,“小于”是一种关系,通常用中缀运算符 < 来书写。“等于”,用 = 符号书写,是另一个熟悉的关系。如果 $R$ 是一个二元关系,语句 $a R b$ 意味着 $a R b=$ TRUE。类似地,如果 $R$ 是一个 $k$-元关系,语句 $R\left(a_{1}, \ldots, a_{k}\right)$ 意味着 $R\left(a_{1}, \ldots, a_{k}\right)=$ TRUE。
示例 0.10
在儿童游戏“剪刀-石头-布”中,两名玩家同时从集合 {SCISSORS, PAPER, STONE} 中选择一个成员,并用手势表示他们的选择。如果两个选择相同,游戏重新开始。如果选择不同,则一名玩家获胜,根据关系 $beats$。
| beats | SCISSORS | PAPER | STONE |
| :------: | :------: | :---: | :---: |
| SCISSORS | FALSE | TRUE | FALSE |
| PAPER | FALSE | FALSE | TRUE |
| STONE | TRUE | FALSE | FALSE |
从这个表格中我们确定 SCISSORS beats PAPER 是 TRUE,PAPER beats SCISSORS 是 FALSE。
有时用集合而不是函数描述谓词更方便。谓词 $P: D \longrightarrow\{\text{TRUE, FALSE}\}$ 可以写成 $(D, S)$,其中 $S=\{a \in D \mid P(a)=\text{TRUE}\}$,如果域 $D$ 很明显,则简写为 $S$。因此,关系 $beats$ 可以写成
一种特殊类型的二元关系,称为等价关系,捕捉了两个对象在某些特征上相等这一概念。二元关系 $R$ 是等价关系,如果 $R$ 满足三个条件:
- $R$ 具有自反性:对于每个 $x$,$x R x$;
- $R$ 具有对称性:对于每个 $x$ 和 $y$,如果 $x R y$ 则 $y R x$;
- $R$ 具有传递性:对于每个 $x, y$ 和 $z$,如果 $x R y$ 且 $y R z$ 则 $x R z$。
示例 0.11
在自然数上定义一个等价关系,写作 $\equiv_{7}$。对于 $i, j \in \mathcal{N}$,如果 $i-j$ 是 7 的倍数,则称 $i \equiv_{7} j$。这是一个等价关系,因为它满足三个条件。首先,它具有自反性,因为 $i-i=0$,是 7 的倍数。其次,它具有对称性,因为如果 $i-j$ 是 7 的倍数,则 $j-i$ 也是 7 的倍数。第三,它具有传递性,因为每当 $i-j$ 是 7 的倍数且 $j-k$ 是 7 的倍数时,那么 $i-k=(i-j)+(j-k)$ 是两个 7 的倍数的和,因此也是 7 的倍数。
图
无向图,或简称图,是一组点和连接其中一些点的线。这些点称为节点或顶点,这些线称为边,如下图所示。
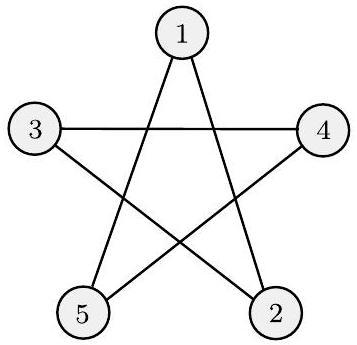
(a)
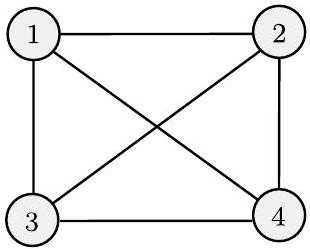
(b)
图 0.12
图的示例
特定节点上的边的数量称为该节点的度。在图 0.12(a) 中,所有节点的度都为 2。在图 0.12(b) 中,所有节点的度都为 3。任意两个节点之间最多只允许有一条边。我们可能允许从一个节点到自身的边,称为自环,具体取决于情况。
在包含节点 $i$ 和 $j$ 的图 $G$ 中,对 $(i, j)$ 表示连接 $i$ 和 $j$ 的边。在无向图中,$i$ 和 $j$ 的顺序无关紧要,因此对 $(i, j)$ 和 $(j, i)$ 表示同一条边。有时我们用集合表示法 $\{\{i, j\}\}$ 来描述无向边。如果 $V$ 是 $G$ 的节点集, $E$ 是边集,我们说 $G=(V, E)$。我们可以用图示或更正式地通过指定 $V$ 和 $E$ 来描述一个图。例如,图 0.12(a) 中图的正式描述是
图 0.12(b) 中图的正式描述是
图经常用于表示数据。节点可以是城市,边可以是连接它们的公路,或者节点可以是人,边可以是他们之间的友谊。有时,为了方便,我们给图的节点和/或边添加标签,这称为带标签的图。图 0.13 描绘了一个图,其节点是城市,其边用如果可能在这些城市之间进行直飞旅行,则最便宜的直飞机票的美元成本标记。
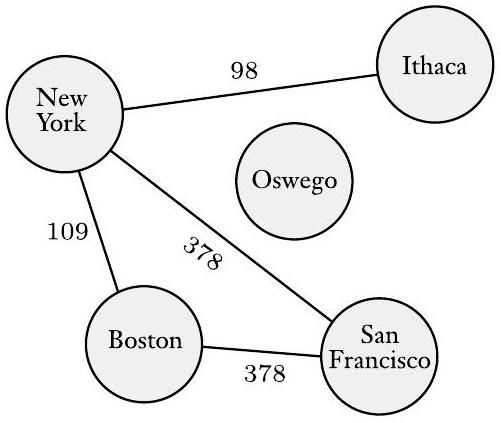
图 0.13
各城市之间最便宜的直飞航班票价
我们说图 $G$ 是图 $H$ 的子图,如果 $G$ 的节点是 $H$ 的节点的子集,并且 $G$ 的边是 $H$ 在相应节点上的边。下图显示了一个图 $H$ 和一个子图 $G$。
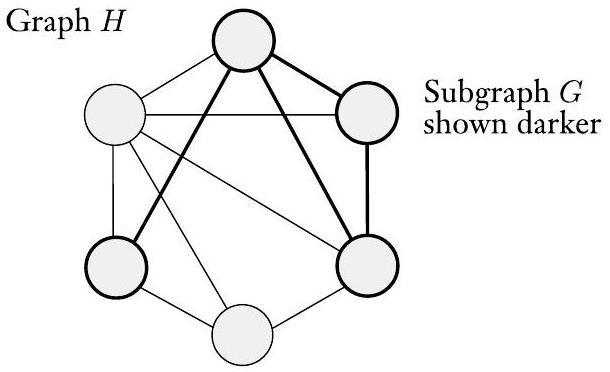
图 0.14
图 $G$ (显示为深色) 是 $H$ 的子图
图中的路径是按边连接的节点序列。简单路径是不重复任何节点的路径。如果任意两个节点之间都有一条路径,则该图是连通图。路径是一个环,如果它始于并终于同一节点。简单环是包含至少三个节点并且只重复第一个和最后一个节点的环。如果一个图是连通图且没有简单环,则它是一个树,如图 0.15 所示。树可能包含一个特殊指定的节点,称为根。树中度为 1 的节点,除了根之外,称为树的叶子。
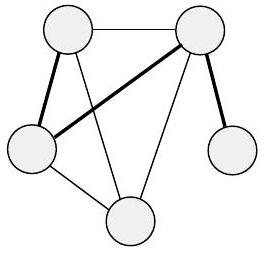
(a)
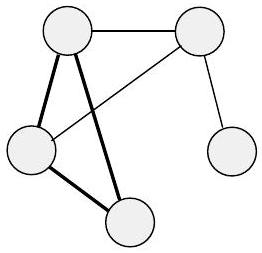
(b)
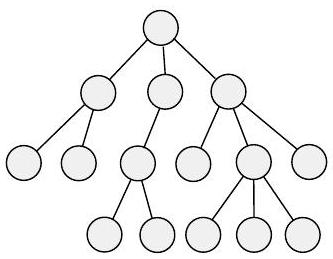
(c)
图 0.15
(a) 图中的路径,(b) 图中的环,和 (c) 树
有向图有箭头而不是线,如下图所示。从特定节点指向的箭头数量是该节点的出度,指向特定节点的箭头数量是入度。
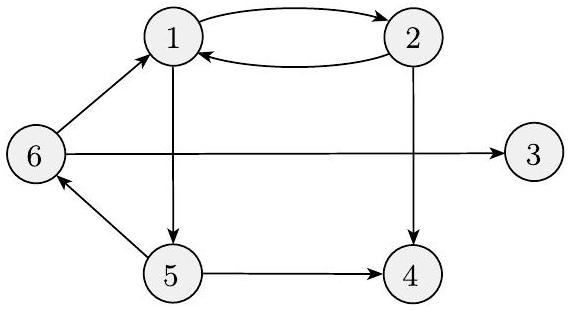
图 0.16
有向图
在有向图中,我们将从 $i$ 到 $j$ 的边表示为对 $(i, j)$。有向图 $G$ 的正式描述是 $(V, E)$,其中 $V$ 是节点集, $E$ 是边集。图 0.16 中图的正式描述是
其中所有箭头方向与其步骤方向相同的路径称为有向路径。如果任意两个节点之间都有有向路径连接,则该有向图是强连通的。有向图是描绘二元关系的便捷方式。如果 $R$ 是一个二元关系,其域是 $D \times D$,则带标签的图 $G=(D, E)$ 表示 $R$,其中 $E=\{(x, y) \mid x R y\}$。
示例 0.17
这里所示的有向图表示示例 0.10 中给出的关系。
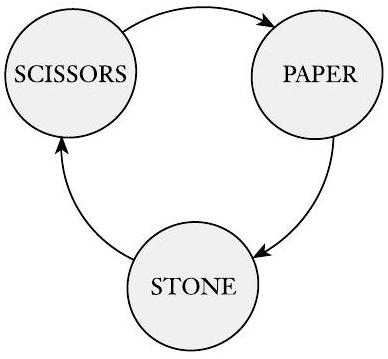
图 0.18
关系 $beats$ 的图
字符串和语言
字符字符串是计算机科学中的基本构建块。定义字符串的字母表可能因应用程序而异。为了我们的目的,我们将字母表定义为任何非空有限集合。字母表的成员是字母表的符号。我们通常使用大写希腊字母 $\Sigma$ 和 $\Gamma$ 来表示字母表,并使用打字机字体表示字母表中的符号。以下是几个字母表的示例。
一个字符串是字母表中符号的有限序列,通常并排书写,不被逗号分隔。如果 $\Sigma_{1}=\{0,1\}$,那么 01001 是 $\Sigma_{1}$ 上的一个字符串。如果 $\Sigma_{2}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \ldots, \mathrm{z}\}$,那么 abracadabra 是 $\Sigma_{2}$ 上的一个字符串。如果 $w$ 是 $\Sigma$ 上的字符串,$w$ 的长度,写作 $|w|$,是它包含的符号的数量。长度为零的字符串称为空字符串,写作 $\varepsilon$。空字符串在数字系统中扮演 0 的角色。如果 $w$ 的长度为 $n$,我们可以写 $w=w_{1} w_{2} \cdots w_{n}$,其中每个 $w_{i} \in \Sigma$。$w$ 的逆序,写作 $w^{\mathcal{R}}$,是通过将 $w$ 以相反顺序(即 $w_{n} w_{n-1} \cdots w_{1}$)书写而得到的字符串。字符串 $z$ 是 $w$ 的子串,如果 $z$ 在 $w$ 中连续出现。例如,cad 是 abracadabra 的子串。
如果我们有长度为 $m$ 的字符串 $x$ 和长度为 $n$ 的字符串 $y$, $x$ 和 $y$ 的拼接,写作 $xy$,是通过将 $y$ 追加到 $x$ 的末尾而得到的字符串,如 $x_{1} \cdots x_{m} y_{1} \cdots y_{n}$。要将一个字符串自身拼接多次,我们使用上标表示法 $x^{k}$ 表示
字符串的字典序与熟悉的字典顺序相同。我们偶尔会使用一种修改过的字典序,称为短前缀序或简称字符串顺序,它与字典序相同,只是较短的字符串排在较长的字符串之前。因此,字母表 $\{0,1\}$ 上所有字符串的字符串顺序是
如果存在一个字符串 $z$ 使得 $xz=y$,则称字符串 $x$ 是字符串 $y$ 的前缀;如果除了 $x \neq y$ 之外,则称 $x$ 是 $y$ 的真前缀。语言是字符串集。如果语言中没有一个成员是另一个成员的真前缀,则该语言是无前缀的。
布尔逻辑
布尔逻辑是一个围绕 TRUE 和 FALSE 两个值构建的数学系统。尽管最初被认为是纯数学,但该系统现在被认为是数字电子和计算机设计的基础。值 TRUE 和 FALSE 称为布尔值,通常用值 1 和 0 表示。我们在有两种可能性的情况下使用布尔值,例如可能具有高电压或低电压的电线,可能为真或假的命题,或可能回答是或否的问题。
我们可以使用布尔运算来操纵布尔值。最简单的布尔运算是否定或非运算,用符号 $\neg$ 表示。布尔值的否定是相反的值。因此 $\neg 0=1$ 和 $\neg 1=0$。我们用符号 $\wedge$ 表示合取或与运算。两个布尔值的合取在两个值都为 1 时为 1。析取或或运算用符号 $\vee$ 表示。两个布尔值的析取在其中任一个值为 1 时为 1。我们总结如下。
我们使用布尔运算将简单语句组合成更复杂的布尔表达式,就像我们使用算术运算 + 和 $\times$ 来构建复杂的算术表达式一样。例如,如果 $P$ 是表示语句“太阳正在发光”为真的布尔值, $Q$ 表示语句“今天是星期一”为真的布尔值,我们可以写 $P \wedge Q$ 来表示语句“太阳正在发光且今天是星期一”的真值,同样,用或代替且的 $P \vee Q$ 也是如此。值 $P$ 和 $Q$ 称为运算的操作数。
其他几个布尔运算偶尔也会出现。异或(或 XOR)运算用 $\oplus$ 符号表示,当其两个操作数中只有一个为 1 而非两个都为 1 时为 1。相等运算,用符号 $\leftrightarrow$ 表示,当其两个操作数具有相同值时为 1。最后,蕴含运算用符号 $\rightarrow$ 表示,当其第一个操作数为 1 且第二个操作数为 0 时为 0;否则,$\rightarrow$ 为 1。我们总结如下。
我们可以建立这些运算之间的各种关系。事实上,我们可以用与运算和非运算表示所有布尔运算,如下面的恒等式所示。每行中的两个表达式是等价的。每行都用左侧列中的运算及其上方的运算、以及与运算和非运算来表示。
与和或的分配律在布尔表达式操作时非常有用。它类似于加法和乘法的分配律,即 $a \times(b+c)=(a \times b)+(a \times c)$。布尔版本有两种形式:
- $P \wedge(Q \vee R)$ 等于 $(P \wedge Q) \vee(P \wedge R)$,及其对偶
- $P \vee(Q \wedge R)$ 等于 $(P \vee Q) \wedge(P \vee R)$。
数学术语总结
| 术语 | 定义 |
| :----------------- | :--------------------------------------------------------------------------------------------------------------------- |
| 字母表 | 由符号组成的有限非空集合 |
| 参数 | 函数的输入 |
| 二元关系 | 域为对集合的关系 |
| 布尔运算 | 对布尔值进行的运算 |
| 布尔值 | 值 TRUE 或 FALSE,通常用 1 或 0 表示 |
| 笛卡尔积 | 对集合进行的运算,形成由各个集合中元素组成的所有元组的集合 |
| 补集 | 对集合进行的运算,形成所有不在该集合中的元素集 |
| 拼接 | 将字符串连接在一起的运算 |
| 合取 | 布尔与运算 |
| 连通图 | 任意两个节点之间都有路径的图 |
| 环 | 始于并终于同一节点的路径 |
| 有向图 | 点和连接某些点对的箭头的集合 |
| 析取 | 布尔或运算 |
| 域 | 函数的可能输入集 |
| 边 | 图中的线 |
| 元素 | 集合中的对象 |
| 空集 | 没有成员的集合 |
| 空字符串 | 长度为零的字符串 |
| 等价关系 | 具有自反性、对称性和传递性的二元关系 |
| 函数 | 将输入转换为输出的运算 |
| 图 | 点和连接某些点对的线的集合 |
| 交集 | 对集合进行的运算,形成共同元素的集合 |
| k-元组 | 包含$k$ 个对象的列表 |
| 语言 | 字符串集 |
| 成员 | 集合中的对象 |
| 节点 | 图中的点 |
| 有序对 | 包含两个元素的列表 |
| 路径 | 图中按边连接的节点序列 |
| 谓词 | 值域为 {TRUE, FALSE} 的函数 |
| 属性 | 谓词 |
| 值域 | 函数输出所来自的集合 |
| 关系 | 谓词,最典型的是当域是k-元组集合时 |
| 序列 | 对象的列表 |
| 集合 | 对象的集合 |
| 简单路径 | 不重复的路径 |
| 单例集 | 包含一个成员的集合 |
| 字符串 | 字母表中符号的有限列表 |
| 符号 | 字母表的成员 |
| 树 | 没有简单环的连通图 |
| 并集 | 对集合进行的运算,将所有元素组合成一个集合 |
| 无序对 | 包含两个成员的集合 |
| 顶点 | 图中的点 |
```
```