10.3
定义、定理和证明
定理和证明是数学的心脏和灵魂,定义则是它的精神。这三个实体是包括我们这门学科在内的所有数学主题的核心。
定义描述了我们使用的对象和概念。一个定义可能很简单,就像本章前面给出的集合的定义,也可能很复杂,就像密码系统中安全性的定义。精度对于任何数学定义都是必不可少的。在定义某个对象时,我们必须清楚什么构成了这个对象,什么不构成。
在定义了各种对象和概念之后,我们通常会对其作出数学陈述。通常,陈述表达了某个对象具有某种属性。这个陈述可能为真,也可能为假;但像定义一样,它必须是精确的。不允许对其含义有任何模糊之处。
证明是一种令人信服的逻辑论证,表明一个陈述是真的。在数学中,一个论证必须是无懈可击的;也就是说,在绝对意义上是令人信服的。在日常生活中或法律中,证明的标准较低。谋杀案的审判要求“排除一切合理怀疑”的证明。证据的分量可能会迫使陪审团接受嫌疑人的清白或有罪。然而,证据在数学证明中不起作用。数学家要求毫无疑问的证明。
定理是经证明为真的数学陈述。通常我们将这个词保留给具有特殊兴趣的陈述。偶尔我们证明的陈述仅因为它们有助于证明另一个更重要的陈述而有趣。这样的陈述称为引理。偶尔,一个定理或其证明可能使我们很容易得出其他相关陈述为真。这些陈述称为该定理的推论。
寻找证明
确定一个数学陈述真假唯一的方法是数学证明。不幸的是,寻找证明并不总是容易的。它不能简化为一套简单的规则或过程。在本课程中,你将被要求证明各种陈述。不要对这种前景感到绝望!尽管没有人有产生证明的秘诀,但有一些有用的通用策略可用。
首先,仔细阅读你想证明的陈述。你理解所有符号吗?用你自己的话改写陈述。将其分解并分别考虑每个部分。
有时,多部分陈述的部分并不立竿见影。一种经常出现的多部分陈述的形式是“ $P$ 当且仅当 $Q$ ”,通常写作“ $P$ iff $Q$ ”,其中 $P$ 和 $Q$ 都是数学陈述。这个符号是两部分陈述的简写。第一部分是“ $P$ 仅当 $Q$ ”,意思是:如果 $P$ 为真,则 $Q$ 为真,写作 $P \Rightarrow Q$。第二部分是“ $P$ 如果 $Q$ ”,意思是:如果 $Q$ 为真,则 $P$ 为真,写作 $P \Leftarrow Q$。这些部分中的第一个是原始陈述的正向,第二个是反向。我们把“ $P$ 当且仅当 $Q$ ”写作 $P \Longleftrightarrow Q$。要证明这种形式的陈述,你必须证明这两个方向。通常,其中一个方向比另一个更容易证明。
另一种多部分陈述的形式是陈述两个集合 $A$ 和 $B$ 相等。第一部分陈述 $A$ 是 $B$ 的子集,第二部分陈述 $B$ 是 $A$ 的子集。因此,证明 $A=B$ 的一种常见方法是证明 $A$ 的每个成员也是 $B$ 的成员,并且 $B$ 的每个成员也是 $A$ 的成员。
接下来,当你想证明一个陈述或其部分时,试着对它为什么应该是真的有一个直观的、“直觉的”感觉。实验例子特别有帮助。因此,如果陈述说某种类型的所有对象都具有特定的属性,请选择该类型的几个对象,并观察它们确实具有该属性。之后,尝试找到一个不具有该属性的对象,称为反例。如果陈述确实为真,你将无法找到反例。当你试图找到反例时,看到你在哪里遇到困难,可以帮助你理解为什么陈述为真。
示例 0.19
假设你想证明“对于每个图 $G$,图 $G$ 中所有节点的度数之和是一个偶数。”这个陈述。
首先,选择几个图并观察这个陈述的实际作用。这里有两个例子。
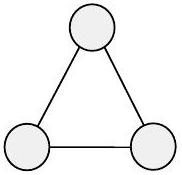
和 $=2+2+2 =6$
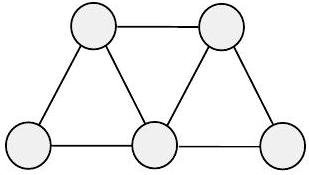
和 $=2+3+4+3+2 =14$
接下来,尝试找到一个反例;也就是说,一个图中度数之和是奇数。
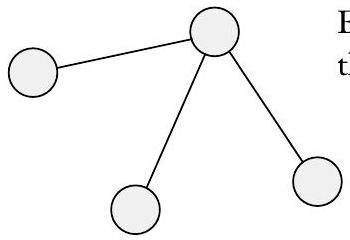
每次添加边时,和都会增加 2。
你现在能开始明白为什么陈述为真以及如何证明它了吗?
如果你在证明一个陈述时仍然感到困难,请尝试一些更容易的方法。尝试证明该陈述的一个特例。例如,如果你试图证明某个属性对于每个 $k>0$ 都为真,首先尝试证明 $k=1$。如果你成功了,就尝试 $k=2$,依此类推,直到你能理解更普遍的情况。如果一个特例很难证明,请尝试一个不同的特例,或者可能是特例的特例。
最后,当你认为你找到了证明时,你必须正确地写出来。一份编写良好的证明是陈述的序列,其中每个陈述都通过简单推理从序列中先前的陈述得出。仔细编写证明很重要,这既是为了让读者理解它,也是为了确保它没有错误。
以下是生成证明的一些技巧。
- 耐心。寻找证明需要时间。如果你没有立即知道如何去做,不要担心。研究人员有时需要工作数周甚至数年才能找到一个证明。
- 回头再看。查看你想证明的陈述,思考一下,离开,然后几分钟或几小时后再回来。让你的潜意识、直觉部分有机会发挥作用。
- 整洁。当你在为你想证明的陈述建立直觉时,使用简单、清晰的图片和/或文本。你正在努力培养对陈述的洞察力,而粗心会阻碍洞察力。此外,当你为别人阅读而编写解决方案时,整洁将帮助那个人理解它。
- 简洁。简洁有助于你在不迷失于细节的情况下表达高层次的思想。良好的数学符号有助于简洁地表达思想。但请务必在编写证明时包含足够的推理,以便读者可以轻松理解你想要表达的内容。
为了练习,让我们证明德摩根定律之一。
定理 0.20
对于任何两个集合 $A$ 和 $B, \overline{A \cup B}=\bar{A} \cap \bar{B}$。
首先,这个定理的含义清楚吗?如果你不理解符号 $\cup$ 或 $\cap$ 或上划线的含义,请回顾第 4 页的讨论。
为了证明这个定理,我们必须表明两个集合 $\overline{A \cup B}$ 和 $\bar{A} \cap \bar{B}$ 是相等的。回想一下,我们可以通过显示一个集合的每个元素也是另一个集合的元素,反之亦然来证明两个集合相等。在查看以下证明之前,请考虑几个例子,然后尝试自己证明它。
证明 这个定理指出两个集合 $\overline{A \cup B}$ 和 $\bar{A} \cap \bar{B}$ 是相等的。我们通过显示一个集合的每个元素也是另一个集合的元素,反之亦然来证明这个断言。
假设 $x$ 是 $\overline{A \cup B}$ 的一个元素。那么根据集合补集的定义,$x$ 不在 $A \cup B$ 中。因此,根据两个集合的并集的定义,$x$ 不在 $A$ 中,也不在 $B$ 中。换句话说,$x$ 在 $\bar{A}$ 中,并且 $x$ 在 $\bar{B}$ 中。因此,两个集合交集的定义表明 $x$ 在 $\bar{A} \cap \bar{B}$ 中。
对于另一个方向,假设 $x$ 在 $\bar{A} \cap \bar{B}$ 中。那么 $x$ 既在 $\bar{A}$ 中,也在 $\bar{B}$ 中。因此,$x$ 既不在 $A$ 中,也不在 $B$ 中,因此不在这些两个集合的并集中。因此 $x$ 在这些集合的并集的补集中;换句话说,$x$ 在 $\overline{A \cup B}$ 中,这完成了定理的证明。
现在让我们证明示例 0.19 中的陈述。
定理 0.21
对于每个图 $G$,图 $G$ 中所有节点的度数之和是一个偶数。
证明 图 $G$ 中的每条边都连接到两个节点。每条边对它所连接的每个节点的度数贡献 1。因此,每条边对所有节点的度数之和贡献 2。因此,如果 $G$ 包含 $e$ 条边,那么图 $G$ 中所有节点的度数之和是 $2e$,这是一个偶数。
O. 4 "-"-"-"-"-"-"-"-"-"-"-"-"-"
证明类型
在数学证明中,有几种论证类型经常出现。在这里,我们描述一些在计算理论中经常出现的类型。请注意,一个证明可能包含不止一种论证类型,因为证明本身可能包含几个不同的子证明。
构造性证明
许多定理陈述特定类型的对象存在。证明这种定理的一种方法是演示如何构造该对象。这种技术是构造性证明。
让我们使用构造性证明来证明以下定理。我们将图定义为k-正则,如果图中的每个节点的度数都是 $k$。
定理 0.22
对于每个大于 2 的偶数 $n$,存在一个具有 $n$ 个节点的 3-正则图。
证明 令 $n$ 为大于 2 的偶数。构造图 $G=(V, E)$,其中有 $n$ 个节点,如下所示。 $G$ 的节点集是 $V=\{0,1, \ldots, n-1\}$, $G$ 的边集是集合
想象一下,这个图的节点按顺序排列在一个圆周上。在这种情况下, $E$ 的第一行描述的边连接圆上相邻的对。 $E$ 的第二行描述的边连接圆上相对两侧的节点。这种心理图像清楚地表明 $G$ 中的每个节点的度数都是 3。
反证法
在证明定理的一种常见论证形式中,我们假设定理是假的,然后证明这个假设导致一个显然是假的结果,称为矛盾。我们在日常生活中经常使用这种推理类型,如下例所示。
示例 0.23
杰克看到刚从外面进来的吉尔。看到她完全是干的,他知道外面没有下雨。他证明外面没有下雨的“证据”是:如果外面正在下雨(假设陈述是假的),吉尔就会是湿的(显然是假的结果)。因此,外面一定没有下雨。
接下来,让我们用反证法证明 2 的平方根是一个无理数。一个数是有理数,如果它是一个分数 $\frac{m}{n}$,其中 $m$ 和 $n$ 是整数;换句话说,一个有理数是整数 $m$ 和 $n$ 的比值。例如, $\frac{2}{3}$ 显然是一个有理数。一个数是无理数,如果它不是有理数。
定理 0.24
$\sqrt{2}$ 是无理数。
证明 首先,为了以后得到矛盾,我们假设 $\sqrt{2}$ 是有理数。因此
其中 $m$ 和 $n$ 是整数。如果 $m$ 和 $n$ 都可以被大于 1 的同一个整数整除,则将它们都除以这个最大的整数。这样做不会改变分数的值。现在,$m$ 和 $n$ 中至少有一个必须是奇数。
我们将方程两边乘以 $n$,得到
我们将方程两边平方,得到
因为 $m^{2}$ 是整数 $n^{2}$ 的 2 倍,我们知道 $m^{2}$ 是偶数。因此,$m$ 也是偶数,因为奇数的平方总是奇数。所以我们可以写 $m=2 k$,其中 $k$ 是某个整数。然后,用 $2k$ 代替 $m$,我们得到
将方程两边除以 2,我们得到
但这个结果表明 $n^{2}$ 是偶数,因此 $n$ 是偶数。因此我们已经确定 $m$ 和 $n$ 都是偶数。但我们之前已经将 $m$ 和 $n$ 约分,使得它们不同时是偶数——这是一个矛盾。
归纳法证明
归纳法证明是一种高级方法,用于表明一个无限集的所有元素都具有特定的属性。例如,我们可以使用归纳法证明来表明一个算术表达式对于其变量的每个赋值都计算出所需数量,或者一个程序在所有步骤或所有输入下都能正确工作。
为了说明归纳法证明的工作原理,让我们把无限集设为自然数 $\mathcal{N}=\{1,2,3, \ldots\}$,并说这个属性称为 $\mathcal{P}$。我们的目标是证明对于每个自然数 $k$, $\mathcal{P}(k)$ 为真。换句话说,我们想证明 $\mathcal{P}(1)$ 为真,以及 $\mathcal{P}(2)$、 $\mathcal{P}(3)$、 $\mathcal{P}(4)$ 等等。
每个归纳法证明由两部分组成:基础和归纳步骤。每部分都是一个独立的证明。基础证明 $\mathcal{P}(1)$ 为真。归纳步骤证明对于每个 $i \geq 1$,如果 $\mathcal{P}(i)$ 为真,则 $\mathcal{P}(i+1)$ 也为真。
当我们证明了这两部分时,所需结果就随之而来——即 $\mathcal{P}(i)$ 对于每个 $i$ 都为真。为什么?首先,我们知道 $\mathcal{P}(1)$ 为真,因为基础单独就证明了它。其次,我们知道 $\mathcal{P}(2)$ 为真,因为归纳步骤证明了如果 $\mathcal{P}(1)$ 为真,那么 $\mathcal{P}(2)$ 也为真,而我们已经知道 $\mathcal{P}(1)$ 为真。第三,我们知道 $\mathcal{P}(3)$ 为真,因为归纳步骤证明了如果 $\mathcal{P}(2)$ 为真,那么 $\mathcal{P}(3)$ 也为真,而我们已经知道 $\mathcal{P}(2)$ 为真。这个过程对所有自然数都持续下去,表明 $\mathcal{P}(4)$ 为真, $\mathcal{P}(5)$ 为真,依此类推。
一旦你理解了前一段,你就可以轻松理解相同思想的变体和概括。例如,基础不一定需要从 1 开始;它可以从任何值 $b$ 开始。在这种情况下,归纳证明表明 $\mathcal{P}(k)$ 对于每个至少为 $b$ 的 $k$ 都为真。
在归纳步骤中,假设 $\mathcal{P}(i)$ 为真称为归纳假设。有时,拥有更强的归纳假设,即对于每个 $j \leq i$, $\mathcal{P}(j)$ 都为真,是很有用的。归纳证明仍然有效,因为当我们想证明 $\mathcal{P}(i+1)$ 为真时,我们已经证明了 $\mathcal{P}(j)$ 对于每个 $j \leq i$ 都为真。
归纳法证明的写作格式如下。
基础:证明 $\mathcal{P}(1)$ 为真。
$\vdots$
归纳步骤:对于每个 $i \geq 1$,假设 $\mathcal{P}(i)$ 为真,并使用此假设来表明 $\mathcal{P}(i+1)$ 为真。
$\vdots$
现在,让我们用归纳法证明用于计算房屋抵押贷款月付款大小的公式的正确性。在购买房屋时,许多人会借入购买所需的部分资金,并在一定年限内偿还这笔贷款。通常,这种偿还的条款规定每月支付固定金额,以支付利息以及部分原始金额,以便在 30 年内全额偿还。计算月付款大小的公式笼罩在神秘之中,但实际上非常简单。它触及了许多人的生活,所以你应该会觉得它很有趣。我们使用归纳法来证明它有效,这很好地说明了这种技术。
首先,我们设定几个变量的名称和含义。设 $P$ 为本金,即原始贷款的金额。设 $I>0$ 为贷款的年利率,其中 $I=0.06$ 表示 6% 的利率。设 $Y$ 为月付款。为方便起见,我们使用 $I$ 来定义另一个变量 $M$,即月乘数。它是贷款每月因利息而变化的比率。按照标准银行惯例,月利率是年利率的十二分之一,因此 $M=1+I / 12$,并且利息按月支付(按月复利)。
每个月会发生两件事。首先,贷款金额因月乘数而趋于增加。其次,贷款金额因月付款而趋于减少。设 $P_{t}$ 为第 $t$ 个月后未偿还的贷款金额。那么 $P_{0}=P$ 是原始贷款的金额,$P_{1}=M P_{0}-Y$ 是一个月后的贷款金额,$P_{2}=M P_{1}-Y$ 是两个月后的贷款金额,依此类推。现在我们准备用对 $t$ 的归纳法来陈述和证明一个给出 $P_{t}$ 值的公式的定理。
定理 0.25
对于每个 $t \geq 0$,
证明
基础:证明该公式对于 $t=0$ 成立。如果 $t=0$,则公式陈述
我们可以通过观察 $M^{0}=1$ 来简化右侧。因此我们得到
这成立,因为我们已将 $P_{0}$ 定义为 $P$。因此,我们已证明归纳的基础成立。
归纳步骤:对于每个 $k \geq 0$,假设公式对于 $t=k$ 成立,并表明它对于 $t=k+1$ 成立。归纳假设陈述
我们的目标是证明
我们通过以下步骤来做到这一点。首先,根据 $P_{k+1}$ 从 $P_{k}$ 的定义,我们知道
因此,使用归纳假设来计算 $P_{k}$,
乘以 $M$ 并重写 $Y$ 得到
因此,公式对于 $t=k+1$ 是正确的,这证明了定理。
问题 0.14 要求你使用上述公式计算实际的抵押贷款付款。
习题
0.1 检查以下集合的形式描述,以便你理解它们包含的成员。为每个集合写一个简短的非正式英语描述。
a. $\{1,3,5,7, \ldots\}$
b. $\{\ldots,-4,-2,0,2,4, \ldots\}$
c. $\{n \mid n=2 m$ 对于某个自然数 $m\}$
d. $\{n \mid n=2 m$ 对于某个自然数 $m$,并且 $n=3 k$ 对于某个自然数 $k\}$
e. $\{w \mid w$ 是一个由 0 和 1 组成的字符串,并且 $w$ 等于 $w$ 的反向 $\}$
f. $\{n \mid n$ 是一个整数,并且 $n=n+1\}$
0.2 写出以下集合的形式描述。
a. 包含数字 1、10 和 100 的集合
b. 包含所有大于 5 的整数的集合
c. 包含所有小于 5 的自然数的集合
d. 包含字符串 aba 的集合
e. 包含空字符串的集合
f. 完全不包含任何内容的集合
0.3 设 $A$ 为集合 $\{\mathrm{x}, \mathrm{y}, \mathrm{z}\}$, $B$ 为集合 $\{\mathrm{x}, \mathrm{y}\}$。
a. $A$ 是 $B$ 的子集吗?
b. $B$ 是 $A$ 的子集吗?
c. $A \cup B$ 是什么?
d. $A \cap B$ 是什么?
e. $A \times B$ 是什么?
f. $B$ 的幂集是什么?
0.4 如果 $A$ 有 $a$ 个元素,$B$ 有 $b$ 个元素,那么 $A \times B$ 中有多少个元素?解释你的答案。
0.5 如果 $C$ 是一个有 $c$ 个元素的集合,那么 $C$ 的幂集中有多少个元素?解释你的答案。
0.6 设 $X$ 是集合 $\{1,2,3,4,5\}$,$Y$ 是集合 $\{6,7,8,9,10\}$。一元函数 $f: X \longrightarrow Y$ 和二元函数 $g: X \times Y \longrightarrow Y$ 在下表中描述。
| $n$ | $f(n)$ |
| :---: | :---: |
| 1 | 6 |
| 2 | 7 |
| 3 | 6 |
| 4 | 7 |
| 5 | 6 |
| $g$ | 6 | 7 | 8 | 9 | 10 |
| :---: | :---: | :---: | :---: | :---: | :---: |
| 1 | 10 | 10 | 10 | 10 | 10 |
| 2 | 7 | 8 | 9 | 10 | 6 |
| 3 | 7 | 7 | 8 | 8 | 9 |
| 4 | 9 | 8 | 7 | 6 | 10 |
| 5 | 6 | 6 | 6 | 6 | 6 |
a. $f(2)$ 的值是多少?
b. $f$ 的值域和定义域是什么?
c. $g(2,10)$ 的值是多少?
d. $g$ 的值域和定义域是什么?
e. $g(4, f(4))$ 的值是多少?
0.7 对于每个部分,给出一个满足条件的关系。
a. 自反和对称但不传递
b. 自反和传递但不对称
c. 对称和传递但不自反
0.8 考虑无向图 $G=(V, E)$,其中节点集 $V$ 是 $\{1,2,3,4\}$,边集 $E$ 是 $\{\{1,2\},\{2,3\},\{1,3\},\{2,4\},\{1,4\}\}$。绘制图 $G$。每个节点的度数是多少?在你的图 $G$ 上标示一条从节点 3 到节点 4 的路径。
0.9 写出以下图的形式描述。