11. 正则表达式
1.1 表达式的构建
📜 [原文1]
在算术中,我们可以使用 + 和 × 运算来构建表达式,例如
类似地,我们可以使用正则运算来构建描述语言的表达式,这些表达式被称为正则表达式。一个例子是:
算术表达式的值是数字 32。正则表达式的值是语言。在这种情况下,其值是包含所有以 0 或 1 开头,后跟任意数量 0 的字符串的语言。我们通过将表达式分解为各个部分来获得此结果。首先,符号 0 和 1 是集合 $\{0\}$ 和 $\{1\}$ 的简写。因此 $(0 \cup 1)$ 表示 $(\{0\} \cup\{1\})$。这部分的值是语言 $\{0,1\}$。部分 $0^{*}$ 表示 $\{0\}^{*}$,其值是包含任意数量 0 的字符串的语言。其次,就像代数中的 × 符号一样,连接符号 ∘ 在正则表达式中通常是隐式的。因此 $(0 \cup 1) 0^{*}$ 实际上是 $(0 \cup 1) \circ 0^{*}$ 的简写。连接将来自两个部分的字符串连接起来,以获得整个表达式的值。
这段引言的核心思想是通过类比来帮助我们理解一个全新的概念:正则表达式。它将我们熟悉的算术表达式与即将学习的正则表达式进行对比,揭示它们在结构和求值上的相似与不同之处。
- 类比的起点:算术表达式
- 我们从小就学习算术,知道如何使用数字(如 5, 3, 4)和运算符(如 + 和 ×)组合成一个表达式,例如 $(5+3) \times 4$。
- 这个表达式有一个明确的“值”。通过计算,我们知道 $(5+3) \times 4 = 8 \times 4 = 32$。这个值是一个数字。
- 引入新概念:正则表达式
- 现在,我们将这种“构建表达式”的思想迁移到一个新的领域:形式语言理论。
- 在这个新领域里,我们操作的对象不再是数字,而是“语言”(语言是字符串的集合)。
- 构建表达式所用的运算符也不同,不再是加号和乘号,而是三种正则运算:并 (Union, 符号是 $\cup$)、连接 (Concatenation, 符号是 $\circ$) 和 星号 (Star, 符号是 $^{*}$)。
- 使用这些正则运算构建出的表达式,就叫做正则表达式 (Regular Expression)。
- 一个正则表达式的实例剖析
- 书中给出了一个例子:$(0 \cup 1) 0^{*}$。
- 这个表达式看起来有些陌生,但我们可以像分析算术表达式一样拆解它。
- 核心区别:算术表达式的值是一个数字,而正则表达式的值是一个语言(即一个字符串的集合)。
- 分步拆解 $(0 \cup 1) 0^{*}$
- 第一部分:$(0 \cup 1)$
- 在正则表达式中,单个字符(如 '0' 或 '1')本身就是一种最简单的正则表达式。
- 正则表达式 '0' 代表的语言是只包含一个字符串 "0" 的集合,即 $\{0\}$。
- 同理,正则表达式 '1' 代表的语言是 $\{1\}$。
- 符号 $\cup$ 是并运算,它对语言(集合)进行操作。所以,$(0 \cup 1)$ 的含义是 $L(0) \cup L(1)$,也就是 $\{0\} \cup \{1\}$。
- 这个并集的结果是一个新的语言:$\{0, 1\}$。这个语言包含两个字符串:"0" 和 "1"。
- 第二部分:$0^{*}$
- 符号 $^{*}$ 是星号运算,也叫克林闭包 (Kleene Star)。它作用于一个语言。
- $0^{*}$ 表示对语言 $\{0\}$ 进行星号运算,即 $\{0\}^{*}$。
- 一个语言的星号运算结果是:从该语言中任意选取 0 个、1 个、2 个、...、n 个字符串,并按任意顺序连接起来形成的所有可能的新字符串的集合。
- 对于 $\{0\}^{*}$:
- 选 0 个字符串:得到空字符串 $\varepsilon$。
- 选 1 个字符串:得到 "0"。
- 选 2 个字符串:得到 "0" 连接 "0",即 "00"。
- 选 3 个字符串:得到 "000"。
- ... 以此类推。
- 所以,$0^{*}$ 所代表的语言是 $\{\varepsilon, 0, 00, 000, \dots\}$,即包含任意数量(包括零个)0 的字符串的集合。
- 第三部分:连接运算
- 在算术中,乘法符号 $\times$ 有时可以省略,比如 $4a$ 表示 $4 \times a$。
- 在正则表达式中,连接 (concatenation) 运算符 $\circ$ 也通常被省略。
- 因此,表达式 $(0 \cup 1) 0^{*}$ 的完整写法是 $(0 \cup 1) \circ 0^{*}$。
- 连接运算的作用是:从第一个语言中取出一个字符串,从第二个语言中取出一个字符串,然后将它们拼接在一起。结果是所有这种拼接可能性的集合。
- 在这里,就是从语言 $\{0, 1\}$ 中取一个字符串,再从语言 $\{\varepsilon, 0, 00, \dots\}$ 中取一个字符串,进行拼接。
- 让我们看看拼接结果:
- 取 "0" 和 $\varepsilon$ $\rightarrow$ "0"。
- 取 "0" 和 "0" $\rightarrow$ "00"。
- 取 "0" 和 "00" $\rightarrow$ "000"。
- ...
- 取 "1" 和 $\varepsilon$ $\rightarrow$ "1"。
- 取 "1" 和 "0" $\rightarrow$ "10"。
- 取 "1" 和 "00" $\rightarrow$ "100"。
- ...
- 将所有这些结果汇集起来,得到的语言是 $\{0, 00, 000, \dots, 1, 10, 100, \dots\}$。
- 这个语言可以用一句话描述:所有以一个 '0' 或一个 '1' 开头,后面跟着任意数量(包括零个)的 '0' 的字符串的集合。
- 算术表达式: $(5+3) \times 4$
- $5, 3, 4$: 操作数,它们是数字。
- $+, \times$: 运算符,分别代表加法和乘法。
- $()$: 括号,用于改变运算的优先级。
- 推导:
- 首先计算括号内的部分: $5 + 3 = 8$。
- 然后执行乘法: $8 \times 4 = 32$。
- 值: 最终结果是一个数字 32。
- 正则表达式: $(0 \cup 1) 0^{*}$
- $0, 1$: 基本正则表达式,它们代表最简单的语言。
- $L(0) = \{0\}$ (一个只包含字符串 "0" 的语言)
- $L(1) = \{1\}$ (一个只包含字符串 "1" 的语言)
- $\cup$: 并运算符 (Union)。它将两个语言合并成一个语言。
- $L(R_1 \cup R_2) = L(R_1) \cup L(R_2)$
- $^{*}$: 星号或克林闭包运算符 (Star / Kleene Star)。它作用于一个语言,表示该语言中字符串的零次或多次连接。
- $L(R^{*}) = (L(R))^{*}$
- $\circ$ (通常省略): 连接运算符 (Concatenation)。它将第一个语言中的每个字符串与第二个语言中的每个字符串进行拼接。
- $L(R_1 \circ R_2) = \{xy \mid x \in L(R_1) \text{ and } y \in L(R_2)\}$
- 推导:
- 步骤 1: 计算 $L(0 \cup 1)$。
- $L(0 \cup 1) = L(0) \cup L(1) = \{0\} \cup \{1\} = \{0, 1\}$。
- 步骤 2: 计算 $L(0^{*})$。
- $L(0^{*}) = (L(0))^{*} = \{0\}^{*}$。
- 这意味着从集合 $\{0\}$ 中取字符串进行 0 次或多次连接。
- 0 次连接: 产生空字符串 $\varepsilon$。
- 1 次连接: 产生 "0"。
- 2 次连接: 产生 "00"。
- ...
- 所以 $L(0^{*}) = \{\varepsilon, 0, 00, 000, \dots\}$。
- 步骤 3: 计算 $L((0 \cup 1) \circ 0^{*})$。
- $L((0 \cup 1) \circ 0^{*}) = L(0 \cup 1) \circ L(0^{*}) = \{0, 1\} \circ \{\varepsilon, 0, 00, \dots\}$。
- 我们需要将第一个集合中的每个元素与第二个集合中的每个元素拼接。
- 以 "0" 开头的: $0\varepsilon=0, 00, 000, \dots$
- 以 "1" 开头的: $1\varepsilon=1, 10, 100, \dots$
- 值: 最终结果是一个语言(字符串的集合),即 $\{w \mid w \text{ 以 0 或 1 开头,后跟任意数量的 0}\}$。
- 示例 1: 检验字符串 "100" 是否属于语言 $L((0 \cup 1) 0^{*})$
- 目标: 我们要判断 "100" 能否由正则表达式 $(0 \cup 1) 0^{*}$ 生成。
- 分解: 我们需要将 "100" 分成两部分,第一部分 $x$ 必须属于 $L(0 \cup 1) = \{0, 1\}$,第二部分 $y$ 必须属于 $L(0^{*}) = \{\varepsilon, 0, 00, \dots\}$。
- 尝试:
- 令 $x = 1$。这部分是合法的,因为 $1 \in \{0, 1\}$。
- 剩下的部分是 $y = 00$。这部分也是合法的,因为 $00 \in \{\varepsilon, 0, 00, \dots\}$。
- 结论: 因为我们可以将 "100" 分解为 $x="1"$ 和 $y="00"$,并且 $x \in L(0 \cup 1)$,$y \in L(0^{*})$,所以字符串 "100" 属于该正则表达式描述的语言。
- 示例 2: 检验字符串 "010" 是否属于语言 $L((0 \cup 1) 0^{*})$
- 目标: 判断 "010" 能否由正则表达式 $(0 \cup 1) 0^{*}$ 生成。
- 分解: 同样,需要将 "010" 分解为 $x \in \{0, 1\}$ 和 $y \in \{\varepsilon, 0, 00, \dots\}$。
- 尝试:
- 可能 1: 令 $x=0$。那么 $y$ 必须是 "10"。但是 "10" 并不属于 $L(0^{*})$,因为 $L(0^{*})$ 只包含由 '0' 组成的字符串和空字符串。所以此路不通。
- 可能 2: 令 $x=1$。这是不可能的,因为字符串以 '0' 开头。
- 可能 3: 尝试其他分解方式?根据连接的定义,我们必须从开头取一个前缀作为 $x$。唯一的可能是 $x=0$。
- 结论: 由于我们无法找到一个合法的分解方式,所以字符串 "010" 不属于该正则表达式描述的语言。
- 隐式的连接: 初学者最容易忘记正则表达式中并列的项之间存在一个看不见的连接运算。$(0 \cup 1) 0^{*}$ 不是指一个集合里的元素,而是指两个语言的连接。
- 星号运算包含空字符串: $R^{*}$ 永远包含空字符串 $\varepsilon$。这是一个非常重要的边界情况。例如,在 $(0 \cup 1) 0^{*}$ 中,如果从 $0^{*}$ 中选取 $\varepsilon$,那么字符串 "0" (来自 $0 \circ \varepsilon$) 和 "1" (来自 $1 \circ \varepsilon$) 都是合法的。
- 运算优先级: 如果没有括号,运算的优先级是:星号 > 连接 > 并。例如,$0 \cup 10^{*}$ 等价于 $0 \cup (1(0^{*}))$,而不是 $(0 \cup 1)0^{*}$。括号在这里是至关重要的。
- 语言 vs. 字符串: 正则表达式的值是一个语言(集合),而不是单个字符串。说 $(0 \cup 1) 0^{*}$ 的值是 "100" 是错误的;正确的说法是 "100" 是属于语言 $L((0 \cup 1) 0^{*})$ 的一个成员。
本段通过与算术表达式的类比,引入了正则表达式的概念。它阐明了核心区别:算术表达式的值是数字,而正则表达式的值是语言(字符串的集合)。通过拆解一个实例 $(0 \cup 1) 0^{*}$,本段逐一介绍了三个基本的正则运算——并($\cup$)、星号($^{*}$)和连接($\circ$)——以及它们如何作用于语言来构建更复杂的语言。同时,它也指出了连接符号通常是隐式省略的。
本段的目的是为读者建立一个关于正则表达式的基本框架。它利用读者已有的知识(算术)作为桥梁,来理解一个抽象的新概念。通过一个具体的例子,它将抽象的正则运算具象化,让读者初步掌握如何“阅读”和“计算”一个简单的正则表达式,为后续更形式化的定义和更复杂的应用打下基础。
你可以把正则表达式想象成一个“字符串模式的配方”。
- 基本成分: 单个字符,如 '0', '1', 'a' 等。
- 混合指令:
- 并 $\cup$: "或者"。$(0 \cup 1)$ 意味着“一个 '0' 或者一个 '1'”。
- 连接 $\circ$: "然后"。$ab$ 意味着“一个 'a' 然后一个 'b'”。
- 星号 $^{*}$: "任意数量的...(包括没有)"。$0^{*}$ 意味着“任意数量的 '0'”。
- 制作过程: 按照这个“配方”,你就可以“生产”出所有符合该模式的字符串。$(0 \cup 1) 0^{*}$ 的配方就是:“先来一个 '0' 或者一个 '1',然后跟上任意数量的 '0'”。
想象一条字符串生产流水线:
- 第一个工位: 这个工位上有一个岔路。一条路生产 '0',另一条路生产 '1'。出来的半成品要么是 "0",要么是 "1"。这就是 $(0 \cup 1)$ 的作用。
- 第二个工位: 这个工位有一个特殊的机器,它可以生产出任意长度的 '0' 字符串,包括什么都不生产(即生产出一个看不见的空字符串 $\varepsilon$)。这就是 $0^{*}$ 的作用。
- 最终组装: 流水线将第一个工位出来的半成品和第二个工位出来的产品拼接在一起。
- 如果第一个工位出了 "1",第二个工位生产了 "00",最终产品就是 "100"。
- 如果第一个工位出了 "0",第二个工位什么都没生产 (出了 $\varepsilon$),最终产品就是 "0"。
1.2 正则表达式的应用与优先级
📜 [原文2]
正则表达式在计算机科学应用中扮演着重要角色。在涉及文本的应用中,用户可能希望搜索符合特定模式的字符串。正则表达式提供了一种描述此类模式的强大方法。UNIX 中的 awk 和 grep 等实用程序、Perl 等现代编程语言以及文本编辑器都提供了使用正则表达式描述模式的机制。
这一段从理论转向了实践,阐述了正则表达式的现实意义和广泛应用。它告诉我们,正则表达式不仅仅是理论家们在象牙塔里研究的抽象概念,更是程序员和计算机用户日常工作中不可或缺的强大工具。
- 核心应用领域:文本处理和模式匹配
- 我们每天都在和文本打交道:代码、日志文件、网页、文档等等。
- 很多时候,我们需要的不是一个特定的、一成不变的字符串,而是一类符合某种“模式”的字符串。
- 例如,我想在一个文件中找到所有的电子邮件地址。电子邮件地址的模式是什么?通常是“一串字符 @ 另一串字符 . 顶级域名”。这个模式用普通文本搜索是无法完成的。
- 正则表达式正是为了解决这类问题而生。它提供了一种精确、灵活的语言来定义这些模式。
- 具体的工具和编程语言
- UNIX/Linux 工具:
- grep: 这是 Global Regular Expression Print 的缩写,是UNIX系统中最经典的文件搜索工具。它的核心功能就是使用正则表达式在文件中查找匹配的行。例如,grep "error" log.txt 会找出 log.txt 中所有包含 "error" 的行。而 grep "^[0-9]" data.txt 则会使用更复杂的正则表达式找出所有以数字开头的行。
- awk: 这是一个更强大的文本处理工具,它能将文件逐行读入,并使用正则表达式对行中的字段进行匹配和处理。
- 编程语言:
- Perl: 这门语言因其强大的内置正则表达式功能而闻名,被誉为文本处理的“瑞士军刀”。在Perl中,正则表达式是一等公民,使用起来非常自然和高效。
- 几乎所有现代编程语言,如 Python, Java, JavaScript, C#, Ruby, Go 等,都内置了对正则表达式的支持(通常通过标准库提供)。这使得开发者可以在自己的程序中轻松实现复杂的文本匹配、验证、替换和提取功能。
- 文本编辑器:
- 像 VS Code, Sublime Text, Vim, Emacs 等专业的文本编辑器,它们的查找和替换功能都支持正则表达式模式。这对于批量修改代码或文本格式非常有用。例如,你可以用一个正则表达式一次性将所有 var name = "value"; 格式的变量声明替换为 const name = "value";。
- 示例 1: 使用 grep 查找有效的电话号码
- 场景: 你有一个包含大量文本的文件 contacts.txt,里面混杂着各种信息,你想把所有北美格式的电话号码(如 123-456-7890 或 (123) 456-7890)找出来。
- 普通搜索: 你无法用一个固定的词来搜索。
- 正则表达式搜索: 你可以在 grep 中使用一个正则表达式。一个(简化的)正则表达式可能是 \b[0-9]{3}-[0-9]{3}-[0-9]{4}\b。
- \b: 表示单词边界,确保我们匹配的是完整的号码,而不是某个更长数字的一部分。
- [0-9]{3}: 表示连续三个 0到9 的数字。
- -: 匹配连字符。
- 命令: grep -E "\b[0-9]{3}-[0-9]{3}-[0-9]{4}\b" contacts.txt (-E 表示启用扩展正则表达式)
- 结果: 这条命令会只打印出文件中所有符合 xxx-xxx-xxxx 格式的行。
- 示例 2: 在 Python 中验证用户输入的邮箱格式
- 场景: 你正在写一个网站的注册页面,需要确保用户输入的电子邮件地址格式基本正确。
- 正则表达式: 一个常用的(但非完美的)邮箱正则表达式是 ^[a-zA-Z0-9._%+-]+@[a-zA-Z0-9.-]+\.[a-zA-Z]{2,}$
- ^: 匹配字符串的开始。
- [a-zA-Z0-9._%+-]+: 匹配一个或多个字母、数字或特定符号(用户名部分)。
- @: 匹配 "@" 符号。
- [a-zA-Z0-9.-]+: 匹配一个或多个字母、数字、点或连字符(域名部分)。
- \.: 匹配点 . (需要转义,因为 . 在正则中有特殊含义)。
- [a-zA-Z]{2,}: 匹配两个或更多字母(顶级域名,如 com, net)。
- $: 匹配字符串的结束。
- Python 代码:
```python
import re
email = "test.user@example.com"
pattern = r"^[a-zA-Z0-9._%+-]+@[a-zA-Z0-9.-]+\.[a-zA-Z]{2,}$"
if re.match(pattern, email):
print("有效的邮箱格式")
else:
print("无效的邮箱格式")
```
- 结果: 程序会输出“有效的邮箱格式”。如果 email 是 "hello-world",则会输出“无效的邮箱格式”。
- 方言 (Flavors): 不同的工具和编程语言实现的正则表达式语法会有细微的差别,被称为“方言”。例如,Perl 兼容正则表达式(PCRE)非常流行,但与其他版本(如 POSIX ERE)在某些高级功能上可能不完全兼容。在使用时需要注意你所用环境的具体语法。
- 过度匹配 (Greedy Matching): 正则表达式中的量词(如 和 +)默认是“贪婪的”,它们会尽可能多地匹配字符。例如,对于字符串 <b>bold</b> and <i>italic</i>,正则表达式 <.> 会从第一个 < 一直匹配到最后一个 >,结果是 <b>bold</b> and <i>italic</i>,而不是我们期望的 <b> 和 <i>。需要使用非贪婪匹配 *? 来解决。
- 性能问题: 写得不好的正则表达式可能会导致灾难性的性能问题,称为“灾难性回溯”(Catastrophic Backtracking)。这通常发生在复杂的嵌套量词中,匹配时间会随输入长度呈指数级增长。
本段强调了正则表达式的实用价值,指出它是在计算机科学,特别是文本处理领域,用于描述和匹配字符串模式的一种强大工具。它通过列举 grep、Perl 和各种文本编辑器等具体实例,证明了正则表达式已被广泛集成到我们日常使用的软件和开发语言中,是解决现实世界中复杂文本搜索、验证和替换问题的关键技术。
这一段的目的是为了激发读者的学习兴趣和动机。在介绍了抽象的定义之后,它立即将正则表达式与实际应用联系起来,告诉读者“你学习这个东西是有用的”。通过展示其在流行工具和语言中的核心地位,本段为读者建立了一个清晰的认知:掌握正则表达式是一项具有高度回报的实践技能。
把正则表达式想象成一把“瑞士军刀”上的一个特殊工具——“模式匹配锯”。
- 普通锯子: 只能锯直的、固定的形状。这就像普通的文本搜索,只能找固定的单词。
- 模式匹配锯: 你可以给这个锯子安装一个“模板”(即正则表达式),然后它就能自动找出所有符合这个模板形状的木块。模板可以是“所有圆形木块”、“所有长方形且边长在5到10厘米之间的木块”等等。
- 在计算机世界里,这把“锯子”就是 grep、Python 的 re 模块等工具,而“木块”就是文本数据。
想象你在一个巨大的图书馆里找书,但你忘记了书名。
- 普通搜索: 你只能问图书管理员:“有叫《编译原理》的书吗?”
- 正则表达式搜索: 你可以给图书管理员一个更灵活的指令:“请帮我找所有书名里包含‘龙’或‘魔法’,并且是2000年以后出版,作者名是‘J.’开头的所有书。”
这个复杂的指令就是正则表达式。它让你能够根据模式,而不是固定的值,来筛选海量信息。
📜 [原文3]
示例 1.51
正则表达式的另一个例子是
它以语言 $(0 \cup 1)$ 开始,并应用 星号运算。这个表达式的值是包含所有可能的 0 和 1 字符串的语言。如果 $\Sigma=\{0,1\}$,我们可以将 $\Sigma$ 写成正则表达式 $(0 \cup 1)$ 的简写。更一般地,如果 $\Sigma$ 是任何字母表,正则表达式 $\Sigma$ 描述的是该字母表上所有长度为 1 的字符串组成的语言,而 $\Sigma^{*}$ 描述的是该字母表上所有字符串组成的语言。类似地,$\Sigma^{*} 1$ 是包含所有以 1 结尾的字符串的语言。语言 $\left(0 \Sigma^{*}\right) \cup\left(\Sigma^{*} 1\right)$ 包含所有以 0 开头或以 1 结尾的字符串。
在算术中,我们说 × 具有比 + 更高的优先级,意思是当有选择时,我们先执行 × 运算。因此在 $2+3 \times 4$ 中,$3 \times 4$ 在加法之前完成。为了让加法先完成,我们必须添加括号以获得 $(2+3) \times 4$。在正则表达式中,星号运算先完成,其次是连接,最后是并,除非括号改变了通常的顺序。
这个示例和后续的段落通过一系列具体的正则表达式,进一步深化我们对正则运算的理解,并引入了运算符优先级的重要概念。
- 核心示例:$(0 \cup 1)^{*}$
- 这是一个非常基础且重要的正则表达式。让我们再次分解它。
- 内部: $(0 \cup 1)$。我们已经知道,它描述的语言是 $\{0, 1\}$。这个语言包含了所有长度为 1 的、由 0 和 1 组成的字符串。
- 外部: $^{*}$(星号运算)。这个运算作用于语言 $\{0, 1\}$。
- 星号运算的含义是:从基础语言(这里是 $\{0, 1\}$)中,任意挑选 0 次、1 次、2 次、...、n 次字符串,然后把它们拼接起来。
- 推演过程:
- 挑选 0 次: 得到空字符串 $\varepsilon$。
- 挑选 1 次: 可以选 "0",也可以选 "1"。得到 $\{0, 1\}$。
- 挑选 2 次: 可能的组合有 "0"后面跟"0" (00), "0"后面跟"1" (01), "1"后面跟"0" (10), "1"后面跟"1" (11)。得到 $\{00, 01, 10, 11\}$。
- 挑选 3 次: 得到所有长度为 3 的二进制字符串,如 "000", "001", ..., "111"。
- ... 以此类推。
- 结论: 将所有这些可能的结果集合在一起,我们就得到了由 '0' 和 '1' 构成的所有可能的字符串,包括空字符串。这正是字母表 $\Sigma=\{0,1\}$ 上所有字符串的集合,通常记作 $\Sigma^{*}$。
- 引入简写符号 $\Sigma$
- 字母表 (Alphabet) $\Sigma$ 是一个字符的有限集合。在我们的例子中,$\Sigma = \{0, 1\}$。
- 书中提出了一个方便的简写:当我们在正则表达式中写 $\Sigma$ 时,它就等同于 $(0 \cup 1 \cup \dots)$,即字母表中所有单个字符的并集。
- 所以,如果 $\Sigma = \{0, 1\}$,那么正则表达式 $\Sigma$ 就等同于 $(0 \cup 1)$。它描述的语言是 $\{0, 1\}$,即所有长度为 1 的字符串。
- 相应地,正则表达式 $\Sigma^{*}$ 就等同于 $(0 \cup 1)^{*}$,它描述的语言是 $\Sigma^{*}$,即该字母表上的所有字符串。
- 利用简写构建更复杂的表达式
- $\Sigma^{*} 1$:
- 这是两个正则表达式 $\Sigma^{*}$ 和 $1$ 的连接。
- $L(\Sigma^{*})$ 是所有由 '0' 和 '1' 组成的字符串的语言。
- $L(1)$ 是语言 $\{1\}$。
- 连接它们:从 $L(\Sigma^{*})$ 中取一个字符串 $w$,然后在其末尾拼接上一个 '1'。
- 例如:取 $\varepsilon$ 拼接 '1' $\rightarrow$ "1";取 "0" 拼接 '1' $\rightarrow$ "01";取 "101" 拼接 '1' $\rightarrow$ "1011"。
- 这个表达式描述的语言是:所有以 '1' 结尾的字符串。
- $(0 \Sigma^{*}) \cup (\Sigma^{*} 1)$:
- 这是一个并集,由两部分组成。
- 第一部分 $0 \Sigma^{*}$: 描述所有以 '0' 开头的字符串。 (例如: "0", "01", "0011"...)
- 第二部分 $\Sigma^{*} 1$: 描述所有以 '1' 结尾的字符串。 (例如: "1", "01", "1101"...)
- 并集 $\cup$: 将这两个语言(集合)合并。一个字符串只要满足其中至少一个条件,就属于这个语言。
- 例如: "0110" 属于该语言(因为它以 '0' 开头)。"1101" 属于该语言(因为它以 '1' 结尾)。"01" 属于该语言(因为它既以 '0' 开头,又以 '1' 结尾)。"10" 则不属于该语言(因为它以 '1' 开头,以 '0' 结尾,两个条件都不满足)。
- 所以,这个表达式描述的语言是:所有以 '0' 开头或以 '1' 结尾的字符串。
- 引入运算符优先级
- 这个概念和算术完全一样,是为了在没有括号时消除歧义。
- 算术优先级: 乘法($\times$) > 加法($+$)。$2+3 \times 4$ 被解释为 $2+(3 \times 4)$。
- 正则表达式优先级:
- 最高: 星号 ($^{*}$)
- 次高: 连接 ($\circ$)
- 最低: 并 ($\cup$)
- 这意味着,当你看到一个没有括号的正则表达式时,要先处理所有的星号,然后处理所有的连接,最后处理所有的并。
- 例如:$a \cup b c^{*}$
- 首先计算 $c^{*}$,得到语言 $L(c^{*})$。
- 然后计算 $b \circ (c^{*})$,得到语言 $L(bc^{*})$。
- 最后计算 $a \cup (bc^{*})$,得到最终的语言 $L(a) \cup L(bc^{*})$。
- 括号的作用: 括号可以覆盖默认的优先级。$(a \cup b)c^{*}$ 则会先计算 $a \cup b$,得到语言 $L(a \cup b)$,然后再对此语言进行星号运算。这和 $a \cup bc^{*}$ 是完全不同的。
- 表达式: $(0 \cup 1)^{*}$
- $0 \cup 1$: 正则表达式,代表语言 $L_1 = \{0, 1\}$。
- $^{*}$: 星号运算。
- 推导: $L((0 \cup 1)^{*}) = (L(0 \cup 1))^{*} = \{0, 1\}^{*}$。这个集合包含由字母表 $\{0,1\}$ 中字符组成的所有有限长度的字符串,包括空字符串 $\varepsilon$。例如 $\varepsilon, 0, 1, 00, 01, 10, 11, 000, \dots$。
- 表达式: $\Sigma^{*}$
- $\Sigma$: 字母表的简写形式。如果 $\Sigma = \{a, b, c\}$,则在正则表达式中,$\Sigma$ 代表 $(a \cup b \cup c)$。
- $\Sigma^{*}$: 描述了由字母表 $\Sigma$ 中字符组成的所有可能字符串的语言。
- 表达式: $\Sigma^{*} 1$ (假设 $\Sigma=\{0,1\}$)
- $\Sigma^{*}$: 正则表达式,代表语言 $L_1 = \{0, 1\}^{*}$。
- $1$: 正则表达式,代表语言 $L_2 = \{1\}$。
- (隐式连接): $L(\Sigma^{*} 1) = L_1 \circ L_2 = \{w \circ '1' \mid w \in L_1\}$。
- 值: 所有以 '1' 结尾的字符串集合。
- 表达式: $\left(0 \Sigma^{*}\right) \cup\left(\Sigma^{*} 1\right)$ (假设 $\Sigma=\{0,1\}$)
- $0\Sigma^{*}$: 正则表达式,代表所有以 '0' 开头的字符串的语言 $L_A$。
- $\Sigma^{*}1$: 正则表达式,代表所有以 '1' 结尾的字符串的语言 $L_B$。
- $\cup$: 并运算。
- 推导: $L(\left(0 \Sigma^{*}\right) \cup\left(\Sigma^{*} 1\right)) = L(0\Sigma^{*}) \cup L(\Sigma^{*}1) = L_A \cup L_B$。
- 值: 所有以 '0' 开头或以 '1' 结尾的字符串的集合。
- 示例 1: 优先级应用,解释 $01^{*} \cup 1$
- 分析: 根据优先级规则:星号 > 连接 > 并。
- 步骤 1 (星号): 先看 $1^{*}$。它代表的语言是 $\{\varepsilon, 1, 11, 111, \dots\}$。
- 步骤 2 (连接): 再看 $01^{*}$。这是 '0' 与 $1^{*}$ 的连接。
- $L(01^{*}) = L(0) \circ L(1^{*}) = \{0\} \circ \{\varepsilon, 1, 11, \dots\} = \{0, 01, 011, 0111, \dots\}$。
- 步骤 3 (并): 最后处理 $\cup$。
- $L(01^{*} \cup 1) = L(01^{*}) \cup L(1) = \{0, 01, 011, \dots\} \cup \{1\}$。
- 最终语言: $\{1, 0, 01, 011, 0111, \dots\}$。
- 对比: 如果是 $(01)^{*} \cup 1$,那么会先连接0和1得到语言 $\{01\}$,然后做星号得到 $\{\varepsilon, 01, 0101, \dots\}$,最后与 $\{1\}$ 取并集,结果完全不同。
- 示例 2: 判断字符串 "010" 是否属于语言 $L(\left(0 \Sigma^{*}\right) \cup\left(\Sigma^{*} 1\right))$
- 目标: 检验 "010"。
- 条件: 字符串必须满足 (以 '0' 开头) 或 (以 '1' 结尾) 中的至少一个。
- 检查条件1: "010" 是否以 '0' 开头?是的。
- 结论: 因为满足了第一个条件,所以 "010" 属于这个语言。我们无需再检查第二个条件。
- 示例 3: 判断字符串 "100" 是否属于语言 $L(\left(0 \Sigma^{*}\right) \cup\left(\Sigma^{*} 1\right))$
- 目标: 检验 "100"。
- 条件: (以 '0' 开头) 或 (以 '1' 结尾)。
- 检查条件1: "100" 是否以 '0' 开头?不是。
- 检查条件2: "100" 是否以 '1' 结尾?不是。
- 结论: 两个条件都不满足,所以 "100" 不属于这个语言。
- $\Sigma$ 的含义: $\Sigma$ 本身是字母表(一个集合),但在正则表达式的上下文中,它是一个代表语言的简写,即 $L(\Sigma)$ 是字母表中所有单个字符组成的字符串的集合。不要将其与语言 $\Sigma^{*}$(所有字符串的集合)混淆。
- 优先级的混淆: $a \cup bc^{*}$ 极易被误解为 $(a \cup b)c^{*}$ 或 $a \cup (bc)^{*}$。必须牢记优先级顺序是 星号 > 连接 > 并,并养成在不确定时主动添加括号的习惯。
- 空字符串 $\varepsilon$ 的角色: 在 $\Sigma^{*}1$ 中,$\Sigma^{*}$ 部分可以匹配空字符串 $\varepsilon$,此时整个表达式匹配 "1"。所以 "1" 是属于 $L(\Sigma^{*}1)$ 的。这是一个常见的边界情况。
本节通过分析核心的正则表达式 $(0 \cup 1)^{*}$,引出了使用字母表符号 $\Sigma$ 作为正则表达式简写的便利方法,其中 $\Sigma$ 代表语言中所有长度为1的字符串,$\Sigma^{*}$ 代表所有可能的字符串。随后,本节借助 $\Sigma$ 构建了更复杂的表达式来描述如“以...结尾”或“以...开头或以...结尾”的语言。最重要的是,本节明确定义了正则表达式的运算符优先级规则:星号具有最高优先级,其次是连接,并的优先级最低。这个规则与算术中的优先级类似,是正确解析无括号正则表达式的关键。
此段的目的是多重的:1) 通过一个非常通用的例子 $(0 \cup 1)^{*}$ 来巩固对星号运算的理解。2) 引入 $\Sigma$ 这一方便的记号,简化未来对语言的描述。3) 建立运算符优先级的规则,这是形式化定义和无歧义解析正则表达式的基石。这为下一节的形式化定义做好了铺垫,使得读者能够处理更复杂的、不带括号的表达式。
将正则表达式的优先级想象成英语语法中的词性变化:
- 星号 $^{*}$ 就像名词的复数 -s 或者动词的过去式 -ed。它作用于紧邻它前面的那个“单词”(正则表达式),改变其形态。例如 dog 中的 只作用于 g。
- 连接就像形容词修饰名词,或者副词修饰动词。big dog 是一个词组,big 和 dog 紧密结合在一起。在 $a \cup bc$ 中,bc 就是一个紧密结合的词组。
- 并 $\cup$ 就像连词 or。它连接两个独立的“概念”(词组或单词)。在 I like cats or big dogs 中,or 连接的是 cats 和 big dogs 这两个概念。同理,$a \cup bc$ 就是连接 a 和 bc 这两个“词组”。
想象你在按一个菜谱做菜:
- 星号: "把盐撒上,撒任意多"。这个指令只针对盐,不针对旁边的糖。
- 连接: "面粉和鸡蛋混合"。这是一个固定的组合步骤,它们要先在一起变成面糊。
- 并: "(面粉鸡蛋混合物) 或者 (现成的披萨饼底)"。这是两种选择,是最高层级的决策。
当你看到一个菜谱“盐,面粉和鸡蛋混合,或者现成的披萨饼底”,你会自然地按照(混合面粉鸡蛋)>(加盐)>(与披萨饼底二选一)的逻辑去理解。正则表达式的优先级就是这种内在逻辑的形式化规定。
1.3 正则表达式的形式化定义
📜 [原文4]
定义 1.52
如果 $R$ 是正则表达式,则 $R$ 是以下之一:
- 字母表 $\Sigma$ 中某个 $a$。
- $\varepsilon$。
- $\emptyset$。
- ( $R_{1} \cup R_{2}$ ),其中 $R_{1}$ 和 $R_{2}$ 是正则表达式。
- $\left(R_{1} \circ R_{2}\right)$,其中 $R_{1}$ 和 $R_{2}$ 是正则表达式。
- $\left(R_{1}^{*}\right)$,其中 $R_{1}$ 是正则表达式。
这是对正则表达式的一个形式化、递归的定义。这种定义方式在数学和计算机科学中非常常见,它通过两种方式来确定一个对象是否属于某个集合:
- 基础情况 (Base Cases): 定义最简单、最基本的成员。
- 归纳/递归步骤 (Inductive/Recursive Steps): 定义如何从已有的成员通过某些规则组合出新的、更复杂的成员。
让我们逐条拆解这个定义:
基础情况 (原子正则表达式)
这三条定义了构成所有正则表达式的最基本“积木”,它们自身就是正则表达式,不能再被分解。
- 1. 字母表中的符号 $a$:
- 含义: 字母表 $\Sigma$ 中的任何一个单独的符号(比如 'a', 'b', '0', '1')都是一个合法的正则表达式。
- 它描述的语言: 这个正则表达式 $a$ 所描述的语言是 $L(a) = \{a\}$,一个只包含单个字符串 $a$ 的集合。
- 例子: 如果 $\Sigma = \{0, 1\}$,那么 0 是一个正则表达式,1 也是一个正则表达式。
- 2. 空字符串符号 $\varepsilon$:
- 含义: 符号 $\varepsilon$ 本身就是一个合法的正则表达式。
- 它描述的语言: 它描述的语言是 $L(\varepsilon) = \{\varepsilon\}$,一个只包含空字符串的集合。
- 注意: 空字符串不是“没有东西”,它是一个实际存在的、长度为零的字符串。
- 3. 空集符号 $\emptyset$:
- 含义: 符号 $\emptyset$ 本身就是一个合法的正则表达式。
- 它描述的语言: 它描述的语言是 $L(\emptyset) = \{\}$,即空语言,一个不包含任何字符串的集合。
- 与 $\varepsilon$ 的区别: 这是初学者极易混淆的地方。$L(\varepsilon)$ 是一个包含 一个 元素的集合(这个元素是空字符串),而 $L(\emptyset)$ 是一个包含 零个 元素的集合。想象一个钱包,$L(\varepsilon)$ 是钱包里有一张 0 元的钞票,而 $L(\emptyset)$ 是钱包里什么都没有,是空的。
归纳/递归步骤 (复合正则表达式)
这三条定义了如何使用正则运算,将已经存在的正则表达式组合成新的、更复杂的正则表达式。
- 4. 并 (Union): $(R_1 \cup R_2)$
- 含义: 如果你已经有了两个合法的正则表达式 $R_1$ 和 $R_2$,那么用括号把它们的并运算括起来,即 $(R_1 \cup R_2)$,得到的结果也是一个合法的正则表达式。
- 它描述的语言: 新表达式描述的语言是两个子表达式所描述语言的并集,即 $L(R_1 \cup R_2) = L(R_1) \cup L(R_2)$。
- 例子: 因为 0 和 1 都是正则表达式,所以 (0 U 1) 也是一个正则表达式。
- 5. 连接 (Concatenation): $(R_1 \circ R_2)$
- 含义: 如果 $R_1$ 和 $R_2$ 是正则表达式,那么将它们用连接符号 $\circ$ 连接并用括号括起来,即 $(R_1 \circ R_2)$,也是一个合法的正则表达式。在实践中,$\circ$ 和外层括号常常省略。
- 它描述的语言: 新表达式描述的语言是两个子语言的连接,即从 $L(R_1)$ 中取一个字符串,后面拼接上一个从 $L(R_2)$ 中取的字符串。
- 例子: 因为 (0 U 1) 和 0 都是正则表达式,所以 ((0 U 1) o 0) 也是一个正则表达式。
- 6. 星号 (Star): $(R_1^*)$
- 含义: 如果 $R_1$ 是一个正则表达式,那么在它后面加上星号并用括号括起来,即 $(R_1^*)$,也是一个合法的正则表达式。
- 它描述的语言: 新表达式描述的语言是子语言 $L(R_1)$ 的克林闭包(Kleene Star),即从 $L(R_1)$ 中取任意 0 个或多个字符串进行拼接得到的所有字符串的集合。
- 例子: 因为 0 是正则表达式,所以 (0*) 也是一个正则表达式。
递归的本质
这个定义是递归的,因为规则 4, 5, 6 在定义“什么是正则表达式”时,引用了“正则表达式”自身。但这不是一个无效的循环定义,因为用于构建新表达式的 $R_1$ 和 $R_2$ 总是比生成的表达式 $(R_1 \cup R_2)$ 要“更小”或“更简单”。我们可以从最基础的原子表达式(a, $\varepsilon$, $\emptyset$)出发,像搭乐高积木一样,一层一层地构建出任意复杂的正则表达式。
- 示例 1: 验证 $(a \cup b)^{*}$ 是一个合法的正则表达式
- 步骤 1: 根据规则 1,a 是一个正则表达式。
- 步骤 2: 根据规则 1,b 是一个正则表达式。
- 步骤 3: 根据规则 4,因为 a 和 b 都是正则表达式,所以 (a U b) 也是一个合法的正则表达式。
- 步骤 4: 根据规则 6,因为 (a U b) 是一个正则表达式,所以 ((a U b)*) 是一个合法的正则表达式。(在实践中,外层括号通常省略,写成 $(a \cup b)^{*}$)。
- 结论: 验证通过。我们从最基础的规则出发,通过递归步骤构建出了目标表达式。
- 示例 2: 验证 $a\cup$ 不是一个合法的正则表达式
- 分析: 我们尝试用定义的六条规则来构建 $a\cup$。
- a 是合法的(规则 1)。
- U 运算符需要两个正则表达式参数,$R_1$ 和 $R_2$,形成 $(R_1 \cup R_2)$。
- 在 $a\cup$ 中,$R_1$ 是 a,但是 $R_2$ 缺失了。它不符合规则 4 的 (R1 U R2) 结构。
- 它也不符合任何其他规则。
- 结论: $a\cup$ 不是一个合法的正则表达式。这个形式化定义非常严格,保证了表达式的结构是完整和无歧义的。
- 括号的重要性: 在形式化定义中,规则 4, 5, 6 都带了括号。这强调了运算的范围。虽然我们后面会根据优先级省略一些括号,但在最严格的定义层面,括号是结构的一部分。
- 递归定义的理解:不要把递归定义看成是“用自己定义自己”的悖论。应该将其理解为“如何从小零件组装成大机器”的说明书。基础情况是“零件”,归纳步骤是“组装规则”。
- $\varepsilon$ 和 $\emptyset$ 的再次强调:
- $L(a \cup \varepsilon) = \{a, \varepsilon\}$ (语言里多了个空字符串)
- $L(a \cup \emptyset) = \{a\} \cup \{\} = \{a\} = L(a)$ (语言没变)
- $L(a \circ \varepsilon) = \{a\varepsilon\} = \{a\} = L(a)$ (语言没变)
- $L(a \circ \emptyset) = \{a\} \circ \{\} = \{\}$ (语言变成了空集!)
定义 1.52 为正则表达式提供了一个严格的、数学上无歧义的归纳定义。它首先通过三条 基础规则 定义了最简单的“原子”正则表达式:单个字母表符号 a、空字符串 ε 和 空集 ∅。然后,它通过三条 归纳规则 定义了如何使用并、连接和星号这三种正则运算,将已有的正则表达式组合成更复杂的正则表达式。这个定义是所有正则表达式理论的基石,确保了任何一个合法的正则表达式都可以被分解为更简单的部分,直至最基本的原子表达式。
这个形式化定义的目的是消除任何关于“什么才是正则表达式”的歧义。在非正式讨论中,我们可以凭感觉写出一些模式,但为了进行严格的数学证明和构建算法(比如将正则表达式转换为自动机),我们必须有一个精确的、所有人都认可的定义。这个归纳定义完美地实现了这一点,它像语言的语法规则一样,精确规定了所有合法表达式的结构。
将正则表达式的形式化定义想象成“合法算术表达式”的规则:
- 基础: 任何一个数字(如 7, 12.5)都是一个合法的算术表达式。
- 归纳:
- 如果 A 和 B 都是合法的算术表达式,那么 (A + B) 也是。
- 如果 A 和 B 都是合法的算术表达式,那么 (A * B) 也是。
- 如果 A 是合法的算术表达式,那么 (-A) 也是。
想象一个乐高积木工厂:
- 规则 1, 2, 3 (基础): 工厂生产三种最基本的积木块:红色的方块 (代表 a),透明的、几乎看不见的薄片 (代表 ε),以及一个代表“虚无”的空盒子 (代表 ∅)。
- 规则 4 (并): 你可以拿两个已有的积木(或组合体)$R_1$ 和 $R_2$,用一个“或”连接器把它们并排放在一个大盒子里,这个新盒子就是 $(R_1 \cup R_2)$。
- 规则 5 (连接): 你可以拿两个已有的积木 $R_1$ 和 $R_2$,把 $R_2$ 粘在 $R_1$ 的后面,形成一个新的、更长的组合体 $(R_1 \circ R_2)$。
- 规则 6 (星号): 你可以拿一个已有的积木 $R_1$,然后工厂给你一个魔法袋子,里面装着无限多个 $R_1$ 的复制品,你可以从里面拿出任意多个(包括不拿)粘在一起,这个可能性集合就是 $(R_1^*)$。
任何你能通过以上规则从最基础的三种积木块搭建出来的结构,都是一个合法的正则表达式。
📜 [原文5]
在项目 1 和 2 中,正则表达式 $a$ 和 $\varepsilon$ 分别表示语言 $\{a\}$ 和 $\{\varepsilon\}$。在项目 3 中,正则表达式 $\emptyset$ 表示空语言。在项目 4、5 和 6 中,表达式表示通过对语言 $R_{1}$ 和 $R_{2}$ 执行并或连接,或对语言 $R_{1}$ 执行星号运算所获得的语言。
不要混淆正则表达式 $\varepsilon$ 和 $\emptyset$。表达式 $\varepsilon$ 表示包含一个单一字符串(即空字符串)的语言,而 $\emptyset$ 表示不包含任何字符串的语言。
表面上,我们似乎有陷入用自身来定义正则表达式概念的危险。如果属实,我们将有一个循环定义,这是无效的。然而,$R_{1}$ 和 $R_{2}$ 总是小于 $R$。因此,我们实际上是根据较小的正则表达式来定义正则表达式,从而避免了循环性。这种类型的定义被称为归纳定义。
这段内容是对定义 1.52 的进一步阐释和说明,主要解决了两个问题:一是明确正则表达式与其所代表语言之间的关系;二是解释为什么这个定义是有效的,而不是一个无效的循环定义。
- 正则表达式与语言的映射关系
- 核心思想: 正则表达式本身是一个“符号序列”或“句法结构”,而它的“意义”或“值”是一个语言(即一个字符串的集合)。这就像算术表达式 (5+3)*4 是一个符号序列,而它的值是数字 32。
- 基础情况的映射:
- 正则表达式 a $\rightarrow$ 语言 $\{a\}$
- 正则表达式 ε $\rightarrow$ 语言 $\{\varepsilon\}$
- 正则表达式 ∅ $\rightarrow$ 语言 ∅ 或 {} (空集)
- 归纳步骤的映射:
- 正则表达式 $(R_1 \cup R_2)$ $\rightarrow$ 语言 $L(R_1) \cup L(R_2)$
- 正则表达式 $(R_1 \circ R_2)$ $\rightarrow$ 语言 $L(R_1) \circ L(R_2)$
- 正则表达式 $(R_1^*)$ $\rightarrow$ 语言 $(L(R_1))^*$
- 这里的关键是,正则运算符($\cup, \circ, ^{*}$)既可以看作是组合正则表达式的语法符号,也可以看作是作用于语言(集合)的实际运算。形式化定义是在语法层面定义的,而这里是在语义(意义)层面进行解释。
- 辨析 $\varepsilon$ 和 $\emptyset$
- 这部分内容是对前面易错点的再次强调,因为它非常重要且容易混淆。
- 正则表达式 $\varepsilon$:
- 它描述的语言是 $L(\varepsilon) = \{\varepsilon\}$。
- 这是一个非空的语言。它包含一个成员,这个成员就是空字符串 ε。
- 类比: 一个钱包里有一张“零元”的纸币。钱包不是空的,它里面有东西。
- 正则表达式 $\emptyset$:
- 它描述的语言是 $L(\emptyset) = \{\}$。
- 这是一个空语言(空集)。它里面没有任何成员,一个字符串也没有。
- 类比: 一个空钱包。里面什么都没有。
- 归纳定义的有效性
- 潜在的问题(循环定义): 有人可能会质疑,规则 4 说“如果 $R_1, R_2$ 是正则表达式,那么 $(R_1 \cup R_2)$ 也是正则表达式”,这听起来像是在用“正则表达式”这个词来定义它自己,陷入了“鸡生蛋还是蛋生鸡”的困境。
- 解答(归纳的本质): 这不是一个无效的循环,因为用于构建的组件 ($R_1, R_2$) 总是比最终的产物 ($R$) “更小”或“更简单”。
- “更小”可以从结构上理解。比如,表达式 (a U b) 的长度是 5 (包括括号),而它的组件 a 和 b 的长度都是 1。
- “更简单”可以从构建的层级来理解。我们总是从第 0 层的原子表达式(a, ε, ∅)开始,然后用它们构建第 1 层的表达式(如 (a U b)),再用第 0 层和第 1 层的表达式构建第 2 层的表达式(如 ((a U b)*)),以此类推。
- 避免了循环: 因为我们永远是用已经定义好或构建好的、更简单的东西去定义更复杂的新东西,所以这个过程是有方向、有终点的,它会终止于最基础的原子表达式,从而避免了无限循环。
- 名称: 这种依赖于更小自身实例来定义新实例的方法,在逻辑和数学中被称为归纳定义 (Inductive Definition)。
- 示例 1: 比较 $L(0^*)$ 和 $L(\emptyset^*)$
- $L(0^*)$:
- 根据规则 6,这是对正则表达式 0 进行星号运算。
- 0 描述的语言是 $L(0) = \{0\}$。
- 对语言 $\{0\}$ 进行星号运算,得到 $\{\varepsilon, 0, 00, 000, \dots\}$。这是一个无限集。
- $L(\emptyset^*)$:
- 根据规则 6,这是对正则表达式 ∅ 进行星号运算。
- ∅ 描述的语言是 $L(\emptyset) = \{\}$ (空集)。
- 对语言 {} 进行星号运算,意味着从空集中挑选 0 个或多个字符串进行拼接。
- 你唯一能做的操作就是“挑选 0 个字符串”。这个操作的结果是空字符串 ε。
- 你无法挑选 1 个或更多字符串,因为集合里根本没有东西给你挑。
- 所以,$L(\emptyset^*) = \{\varepsilon\}$。这是一个只包含一个元素的集合。
- 对比: $L(0^*)$ 是一个无限语言,而 $L(\emptyset^*)$ 是一个只包含空字符串的有限语言。
- 示例 2: 归纳定义的构建过程,以 $((a \circ b) \cup c)$ 为例
- 第 0 层 (基础): 我们有正则表达式 a, b, c (根据规则 1)。
- 第 1 层 (第一次归纳): 使用 a 和 b,根据规则 5,我们可以构建出新的正则表达式 $R_1 = (a \circ b)$。$R_1$ 比 a 和 b 都更“大”。
- 第 2 层 (第二次归纳): 使用第 1 层的结果 $R_1$ 和第 0 层的 c,根据规则 4,我们可以构建出最终的正则表达式 $R = (R_1 \cup c) = ((a \circ b) \cup c)$。$R$ 比 $R_1$ 和 c 都更“大”。
- 这个过程清晰地展示了从小到大、从简单到复杂的构建过程,不存在循环定义。
- 循环定义的误解: 务必理解归纳定义和无效循环定义的区别。关键在于是否存在一个“良序”(well-ordered) 的基础,使得定义过程可以终止。在这里,表达式的结构复杂度(或长度)就是这个良序的基础。
- 混淆语法和语义: 正则表达式 (a U b) 是一个语法结构,而语言 $\{a, b\}$ 是它的语义(含义)。在思考时要能在这两者之间灵活切换,但要清楚地区分它们。
- $R \circ \emptyset = \emptyset$: 任何语言与空语言进行连接,结果都是空语言。因为你无法从空语言中取出任何字符串来完成拼接操作。
- $R \cup \emptyset = R$: 任何语言与空语言取并集,结果还是其自身。因为你只是合并了一个不包含任何新元素的集合。
本段对形式化定义进行了补充说明。首先,它明确了正则表达式(语法)和它所描述的语言(语义)之间的对应关系。其次,它再次强调了 $\varepsilon$(代表含空字符串的语言)和 $\emptyset$(代表空语言)这两个关键概念的根本区别。最后,它解释了为何定义 1.52 是一个有效的归纳定义,而非无效的循环定义,因为它总是用更小的、已知的正则表达式来构建更大的、新的正则表达式,保证了定义过程的有效性和层次性。
此段旨在扫清读者在理解形式化定义时可能产生的两个主要障碍。第一个障碍是对符号意义的困惑(特别是 $\varepsilon$ 和 $\emptyset$),第二个障碍是对定义本身逻辑有效性的怀疑。通过清晰的阐释和类比,本段巩固了形式化定义的根基,让读者可以更有信心地接受和使用它。
将归纳定义想象成一份家族族谱的生成规则:
- 基础: 亚当和夏娃是人类(最基础的成员)。
- 归纳: 如果 A 和 B 是人类,他们的后代也是人类。
这个定义不是循环的,因为“后代”总是比“祖先”在辈分上更“晚”(更“大”)。你永远可以用祖先去定义后代,一直追溯到最初的亚当和夏娃。正则表达式的归纳定义同理,最简单的 a, ε, ∅ 就是“亚当和夏娃”。
想象一个化学反应的规则:
- 循环定义会是:“水是由水组成的。” 这毫无用处。
- 归纳定义则是:
- 基础: 氢原子(H)和氧原子(O)是基本元素。
- 归纳: 两个氢原子和一个氧原子可以化合成一个水分子(H₂O)。
- 归纳: ...
我们用更基本的元素(原子)来定义了更复杂的物质(分子)。这正是归纳定义的精髓,它为复杂事物的构建提供了清晰、有效、无循环的路径。
📜 [原文6]
为方便起见,我们将 $R^{+}$简写为 $R R^{*}$。换句话说,尽管 $R^{*}$ 包含来自 $R$ 的 0 次或更多次连接字符串的所有字符串,但语言 $R^{+}$包含来自 $R$ 的 1 次或更多次连接字符串的所有字符串。因此 $R^{+} \cup \varepsilon=R^{*}$。此外,我们将 $R^{k}$ 简写为 $k$ 个 $R$ 相互连接。
当我们想区分正则表达式 $R$ 和它所描述的语言时,我们用 $L(R)$ 来表示 $R$ 的语言。
这一部分引入了几个非常有用的简写符号(语法糖, Syntactic Sugar),并正式提出了一个表示法来区分正则表达式本身和它所描述的语言。
- 正闭包 (Positive Closure) $R^{+}$
- 定义: $R^{+}$ 是 $R R^{*}$ 的简写。
- 拆解:
- $R$ 代表从语言 $L(R)$ 中取一个字符串。
- $R^{*}$ 代表从语言 $L(R)$ 中取 0 个或多个字符串进行拼接。
- $R R^{*}$ (即 $R \circ R^{*}$) 表示,先从 $L(R)$ 中取一个字符串(这是 $R$ 的部分),然后从 $L(R^{*})$ 中再取一个字符串(这是 $R^{*}$ 的部分),把它们拼接起来。
- 实际效果:
- $L(R^{*}) = \{\text{0次拼接}\}\ \cup\ \{\text{1次或多次拼接}\}$
- $L(R) \circ L(R^{*}) = L(R) \circ (\{\varepsilon\} \cup L(R^{+})) = (L(R) \circ \{\varepsilon\}) \cup (L(R) \circ L(R^{+})) = L(R) \cup \dots$
- 一个更直观的理解是:$R R^{*}$ 的结果,必然至少包含一个来自 $R$ 的连接。这恰好就是 “1 次或更多次连接” 的含义。
- 与 $R^{*}$ 的关系:
- $R^{*}$:代表 “0 次或多次” 的连接。
- $R^{+}$:代表 “1 次或多次” 的连接。
- 它们唯一的区别就在于是否包含 “0 次连接” 的情况,即空字符串 $\varepsilon$。
- 因此,我们有这个非常重要的关系:$L(R^{*}) = L(R^{+}) \cup \{\varepsilon\}$。反过来写就是 $R^{+} \cup \varepsilon=R^{*}$。
- 幂次运算 $R^{k}$
- 定义: $R^{k}$ 是 $k$ 个 $R$ 连接在一起的简写。
- 展开形式: $R^{k} = \underbrace{R \circ R \circ \dots \circ R}_{k \text{ 个}}$
- 它描述的语言: 从语言 $L(R)$ 中取 $k$ 个字符串,依次拼接起来。
- 例子:
- $R^2 = R \circ R$。$L(R^2)$ 就是从 $L(R)$ 中取两个字符串 $w_1, w_2$ 拼接成 $w_1w_2$ 的所有可能。
- $R^3 = R \circ R \circ R$。
- $R^1 = R$。
- $R^0 = \varepsilon$。这是约定俗成的定义,代表 0 次连接,其结果是空字符串。
- 语言表示法 $L(R)$
- 动机: 到目前为止,我们一直在正则表达式(比如 0*)和它所描述的语言(比如 {ε, 0, 00, ...} )之间切换。有时这种混用会产生歧义。
- 定义: 为了严格区分,我们引入记号 $L(R)$。
- $R$:指正则表达式这个句法结构本身,它是一串符号。
- $L(R)$:指正则表达式 $R$ 所描述的那个语言,它是一个字符串的集合。
- 作用: 这个记号在进行理论推导和证明时非常有用,可以使论述更加严谨。例如,我们可以清晰地写出并运算的语义:$L(R_1 \cup R_2) = L(R_1) \cup L(R_2)$。左边的 $\cup$ 是正则表达式语法的一部分,而右边的 $\cup$ 是集合论中的并集运算。
- 示例 1: $R = (a \cup b)$,分析 $R^{+}, R^{*}, R^2$
- $L(R) = \{a, b\}$
- $R^{+}$: 表示 1 次或多次连接。
- 1 次: $\{a, b\}$
- 2 次: $\{aa, ab, ba, bb\}$
- ...
- $L(R^{+})$ 就是所有由 a 和 b 组成的非空字符串的集合。
- $R^{*}$: 表示 0 次或多次连接。
- $L(R^{*})$ 就是 $L(R^{+}) \cup \{\varepsilon\}$,即所有由 a 和 b 组成的字符串的集合(包括空字符串)。
- $R^2$: 表示 2 次连接。
- $L(R^2) = L(R) \circ L(R) = \{a, b\} \circ \{a, b\} = \{aa, ab, ba, bb\}$。
- 示例 2: $R = a b^{*}$,分析 $R^{+}$ 和 $R^2$
- 首先分析 $L(R)$: $L(ab^{*}) = L(a) \circ L(b^{*}) = \{a\} \circ \{\varepsilon, b, bb, \dots\} = \{a, ab, abb, abbb, \dots\}$。即一个 'a' 后面跟任意数量 'b' 的字符串。
- $R^{+}$: 1 次或多次连接 $L(R)$ 中的字符串。
- 1 次: $\{a, ab, abb, \dots\}$
- 2 次: 比如取 $a \in L(R)$ 和 $ab \in L(R)$,拼接得到 aab。取 $ab \in L(R)$ 和 $abb \in L(R)$,拼接得到 ababb。$L(R^{+})$ 包含了所有这些可能,非常复杂。
- $R^2$: 2 次连接 $L(R)$ 中的字符串。
- $L(R^2) = L(R) \circ L(R) = \{a, ab, abb, \dots\} \circ \{a, ab, abb, \dots\}$。
- 这个集合里包含了像 aa (来自 $a \circ a$), aab (来自 $a \circ ab$), aba (来自 $ab \circ a$) 等等字符串。
- $R^{+}$ 不包含空字符串: 除非 $L(R)$ 本身包含 $\varepsilon$ (例如 $R = (a \cup \varepsilon)$),否则 $L(R^{+})$ 通常不包含 $\varepsilon$。这是它与 $R^{*}$ 的核心区别。
- $R^0 = \varepsilon$: k=0 是一个特殊的边界情况,需要记住 $R^0$ 按照惯例定义为 $\varepsilon$。
- $L(R)$ 符号的理解: 不要把 $L(R)$ 当成一个函数调用那么复杂。它仅仅是一个标记,提醒我们“现在我们讨论的是这个表达式所代表的那个集合,而不是表达式的写法本身”。
本段引入了三个重要的辅助记号。$R^{+}$(正闭包)是 $R^{*}$ 的一个变体,表示“一次或多次”连接,与 $R^{*}$ 的“零次或多次”仅差一个空字符串。$R^{k}$ 表示对正则表达式 $R$ 进行 $k$ 次自我连接。最后,$L(R)$ 是一个形式化的表示法,用于清晰地区分正则表达式 $R$ 这个“语法对象”和它所描述的语言(字符串集合)这个“语义对象”,这对于进行严谨的理论分析至关重要。
引入这些简写符号和表示法的主要目的是为了让后续的讨论和定义更加简洁和精确。
- $R^{+}$ 和 $R^k$ 是非常常见的模式,给它们一个简写的名字可以大大简化正则表达式的书写。
- $L(R)$ 的引入则是为了学术上的严谨性,避免在证明和复杂讨论中产生混淆。它是一种“元语言”工具,帮助我们更清晰地谈论形式语言。
- $R^{+}$ vs $R^{*}$:
- $R^{*}$ 像一个自助餐厅的饮料机,你可以选择“不喝”(0次),或者喝1杯,2杯,...
- $R^{+}$ 就像是“购买了套餐必须选一杯饮料”,你至少要选1杯,不能不选。
- $R^k$: 就像菜谱里的“重复此步骤k次”。比如 $R=$"打一个鸡蛋",那么 $R^3$ 就是“打一个鸡蛋,再打一个鸡蛋,再打一个鸡蛋”。
- $L(R)$: 就像区分“菜谱本身”(一张写着字的纸,即 $R$)和“按照菜谱做出来的菜”(一盘可以吃的食物,即 $L(R)$)。菜谱不是菜,但它描述了如何做出菜。
想象你在用代码写一个循环:
- for (int i = 0; i < n; i++) { ... } 这个循环会执行 n 次。这就像是 $R^n$ 的概念。
- 一个 while 循环 while (condition) { ... } 可能会执行 0 次或多次。这就像是 $R^{*}$。
- 一个 do-while 循环 do { ... } while (condition) 保证了循环体至少执行 1 次。这就像是 $R^{+}$。
- $L(R)$ 就像是代码 R 和它在运行时产生的输出 L(R) 之间的区别。一个是静态的文本,一个是动态的结果。
1.4 更多正则表达式示例
📜 [原文7]
[^3]如果我们让 $R$ 是任意正则表达式,我们有以下恒等式。它们是检验你是否理解定义的好方法。
$R \cup \emptyset=R$。
将空语言添加到任何其他语言都不会改变它。
$R \circ \varepsilon=R$。
将空字符串连接到任何字符串都不会改变它。
然而,在前面的恒等式中交换 $\emptyset$ 和 $\varepsilon$ 可能会导致等式失效。
$R \cup \varepsilon$ 可能不等于 $R$。
例如,如果 $R=0$,则 $L(R)=\{0\}$ 但 $L(R \cup \varepsilon)=\{0, \varepsilon\}$。
$R \circ \emptyset$ 可能不等于 $R$。
例如,如果 $R=0$,则 $L(R)=\{0\}$ 但 $L(R \circ \emptyset)=\emptyset$。
正则表达式是编程语言编译器设计中的有用工具。编程语言中的基本对象,称为词法单元 (tokens),例如变量名和常量,可以用正则表达式描述。例如,一个可能包含小数部分和/或符号的数值常量可以用语言
的成员来描述,其中 $D=\{0,1,2,3,4,5,6,7,8,9\}$ 是十进制数字的字母表。生成的字符串示例有:$72,3.14159,+7$. 和 $-.01$。
一旦用正则表达式根据其词法单元描述了编程语言的语法,自动化系统就可以生成词法分析器 (lexical analyzer),它是编译器中初步处理输入程序的组成部分。
这一部分混合了几个要点:首先通过一组恒等式来深化对 $\varepsilon$ 和 $\emptyset$ 的理解,然后给出一个复杂的、实际应用中的正则表达式例子(数值常量),并最终点出正则表达式在编译器设计中的核心角色——定义词法单元并生成词法分析器。
- 重要的恒等式
- 这些恒等式揭示了 $\varepsilon$ 和 $\emptyset$ 在正则运算中扮演着类似于算术中 1 和 0 的角色,但又不完全相同。
- $R \cup \emptyset = R$:
- 语义: $L(R \cup \emptyset) = L(R) \cup L(\emptyset) = L(R) \cup \{\}$。一个集合与一个空集取并集,结果还是原来的集合。
- 类比: 这就像算术中的 x + 0 = x。$\emptyset$ 在并运算中是“单位元”。
- $R \circ \varepsilon = R$:
- 语义: $L(R \circ \varepsilon) = L(R) \circ L(\varepsilon) = L(R) \circ \{\varepsilon\}$。将一个语言中的每个字符串 $w$ 与空字符串 $\varepsilon$ 连接,结果仍然是 $w$ ($w\varepsilon = w$)。所以语言不变。
- 类比: 这就像算术中的 x * 1 = x。$\varepsilon$ 在连接运算中是“单位元”。
- 打破对称性:交换 $\varepsilon$ 和 $\emptyset$
- 这里展示了为什么不能简单地将 $\varepsilon$ 和 $\emptyset$ 互换。
- $R \cup \varepsilon$ 可能不等于 $R$:
- 语义: $L(R \cup \varepsilon) = L(R) \cup \{\varepsilon\}$。这个操作向语言 $L(R)$ 中添加了空字符串 $\varepsilon$。
- 例子: 如果 $R=0$,$L(R)=\{0\}$。那么 $L(R \cup \varepsilon) = \{0\} \cup \{\varepsilon\} = \{0, \varepsilon\}$。显然 $\{0\} \neq \{0, \varepsilon\}$。
- 什么时候相等?: 只有当 $L(R)$ 本身已经包含了 $\varepsilon$ 时,等式才成立。
- $R \circ \emptyset$ 可能不等于 $R$:
- 语义: $L(R \circ \emptyset) = L(R) \circ L(\emptyset) = L(R) \circ \{\}$。将一个语言与空语言进行连接。因为无法从空语言中取出任何字符串进行拼接,所以结果是空语言 $\emptyset$。
- 例子: 如果 $R=0$,$L(R)=\{0\}$。那么 $L(R \circ \emptyset) = \{0\} \circ \{\} = \{\}$。显然 $\{0\} \neq \{\}$。
- 类比: 这就像算术中的 x * 0 = 0。$\emptyset$ 在连接运算中是“零元”,它具有“吞噬”一切的特性。
- 实际应用:定义数值常量
- 这里给出了一个非常实用的正则表达式,用于描述编程语言中常见的数字格式。
- 表达式: $(+\cup-\cup \varepsilon)\left(D^{+} \cup D^{+} . D^{*} \cup D^{*} . D^{+}\right)$
- 字母表: $D = \{0,1,2,3,4,5,6,7,8,9\}$。
- 分解:
- 第一部分: $(+\cup-\cup \varepsilon)$
- 这部分描述数字的符号。
- 它可以是 +,或者是 -,或者什么都没有 (ε)。
- 匹配 +, - 或空。
- 第二部分: $\left(D^{+} \cup D^{+} . D^{*} \cup D^{*} . D^{+}\right)$
- 这部分描述数字本身,由三个用并运算连接的子模式组成。
- 子模式1: $D^{+}$
- $D$ 代表任一数字 (0 | 1 | ... | 9)。
- $D^{+}$ 表示“一个或多个数字”。
- 这匹配的是整数,如 72。
- 子模式2: $D^{+} . D^{*}$
- $D^{+}$: 小数点前至少有一个数字。
- .: 小数点本身 (注意,在很多正则引擎里 . 是特殊字符,需要转义成 \.,但这里是理论描述,就直接写了)。
- $D^{*}$: 小数点后有零个或多个数字。
- 这匹配的是 72. 或 3.14159 这样的数。
- 子模式3: $D^{*} . D^{+}$
- $D^{*}$: 小数点前有零个或多个数字。
- .: 小数点。
- $D^{+}$: 小数点后至少有一个数字。
- 这匹配的是 .01 或 0.01 这样的数。
- 组合: 整个表达式的含义是:一个可选的符号,后面跟着一个数字部分,这个数字部分可以是整数、或者带有小数点的浮点数。
- 示例匹配:
- 72: 符号部分匹配 $\varepsilon$,数字部分匹配 $D^{+}$。
- 3.14159: 符号部分匹配 $\varepsilon$,数字部分匹配 $D^{+} . D^{*}$。
- +7.: 符号部分匹配 +,数字部分匹配 $D^{+} . D^{*}$。
- -.01: 符号部分匹配 -,数字部分匹配 $D^{*} . D^{+}$。
- 在编译器中的角色:词法分析
- 编译器 (Compiler): 将人类编写的高级语言代码(如 C++, Java)翻译成计算机可以执行的机器代码的程序。
- 词法单元 (Token): 编程语言中最小的有意义的语法单位。就像英语中的单词。例如,在代码 int x = 10; 中,int, x, =, 10, ; 都是词法单元。
- 词法分析器 (Lexical Analyzer / Lexer / Scanner): 编译器的第一个部分。它的工作就是读取原始的源代码文本(一长串字符),然后将其切分成一个个的词法单元。
- 正则表达式的作用: 正则表达式正是用来定义每一种词法单元的模式的。
- 变量名 (Identifier): (a-zA-Z_)(a-zA-Z0-9_)* (以字母或下划线开头,后跟任意数量的字母、数字或下划线)
- 整数: [0-9]+
- 关键字: if, else, while (可以直接匹配)
- 操作符: +, -, *, /, =
- 自动化: 一旦我们为一门编程语言的所有词法单元都写好了正则表达式,就可以使用像 Lex 或 Flex 这样的自动化工具,它们会读取这些正则表达式,并自动生成一个高效的词法分析器程序。
- 表达式: $(+\cup-\cup \varepsilon)\left(D^{+} \cup D^{+} . D^{*} \cup D^{*} . D^{+}\right)$
- $+\cup-\cup \varepsilon$:
- $L(+\cup-\cup \varepsilon) = L(+) \cup L(-) \cup L(\varepsilon) = \{+\} \cup \{-\} \cup \{\varepsilon\} = \{+, -, \varepsilon\}$。
- 这是一个描述可选符号的语言。
- $D$:
- 这是一个字母表的简写, $D=\{0,1, \dots, 9\}$。在正则表达式中,它代表 $(0 \cup 1 \cup \dots \cup 9)$。
- $D^{+}$:
- $L(D^{+})$ 是由数字组成的非空字符串集合。例如 {"0", "1", ..., "9", "10", ...}。
- $D^{+} . D^{*}$:
- $L(D^{+} . D^{*}) = L(D^{+}) \circ L(.) \circ L(D^{*})$
- 这是小数点前至少一位数字,小数点后任意位数字的字符串集合。例如 {"1.", "1.2", "12.34", ...}。
- $D^{*} . D^{+}$:
- $L(D^{*} . D^{+}) = L(D^{*}) \circ L(.) \circ L(D^{+})$
- 这是小数点前任意位数字,小数点后至少一位数字的字符串集合。例如 "{.1", ".12", "0.1", ...}。
- 整个数字部分:
- $L(\text{数字部分}) = L(D^{+}) \cup L(D^{+} . D^{*}) \cup L(D^{*} . D^{+})$。
- 它合并了三种情况:纯整数,小数点后可以为空的数,小数点前可以为空的数。
- 最终推导:
- $L(\text{总表达式}) = L(\text{符号部分}) \circ L(\text{数字部分})$。
- 将符号集合中的每个元素与数字集合中的每个元素进行连接。
- 示例 1: 检验恒等式 $R \circ \emptyset = \emptyset$
- 令 $R = a \cup b$。则 $L(R) = \{a, b\}$。
- $L(R \circ \emptyset) = L(R) \circ L(\emptyset) = \{a, b\} \circ \{\}$。
- 根据连接的定义,我们需要从第一个集合取一个元素,从第二个集合取一个元素,然后拼接。
- 我们可以从 $\{a, b\}$ 中取出 'a' 或 'b'。
- 但是,我们无法从空集 {} 中取出任何元素。
- 因为无法完成拼接操作,所以最终结果的集合是空的。即 {} ,也就是 $L(\emptyset)$。
- 所以 $L((a \cup b) \circ \emptyset) = L(\emptyset)$,验证了恒等式。
- 示例 2: 使用数值常量表达式匹配 "-3.14"
- 目标: 匹配字符串 "-3.14"。
- 第一部分 (符号): 字符串以 - 开头,这匹配了 $(+\cup-\cup \varepsilon)$ 中的 -。
- 第二部分 (数字): 剩下的部分是 "3.14"。我们需要看它是否匹配 $\left(D^{+} \cup D^{+} . D^{*} \cup D^{*} . D^{+}\right)$。
- 它不匹配 $D^{+}$ (因为有小数点)。
- 它匹配 $D^{+} . D^{*}$ 吗?
- "3" 匹配 $D^{+}$ (一个或多个数字)。
- "." 匹配 .。
- "14" 匹配 $D^{*}$ (零个或多个数字)。
- 是的,它匹配 $D^{+} . D^{*}$。
- 结论: 因为符号部分和数字部分都找到了匹配,所以 "-3.14" 是由该正则表达式描述的语言的一个成员。
- $R \cup \varepsilon$ 不改变语言的特殊情况: 只有当 $\varepsilon \in L(R)$ 时,$L(R \cup \varepsilon) = L(R)$。例如,如果 $R = a^{*}$,那么 $L(R)$ 已经包含了 $\varepsilon$,此时再与 $\varepsilon$ 取并集就不会改变语言。
- 理论 vs 实践中的 .: 在形式化的正则表达式理论中,. 只是一个普通字符。但在 grep, Python 等实际应用中,. 是一个元字符,代表“任意单个字符”。要匹配小数点本身,需要写成 \.。这是一个重要的理论与实践的差异。
- $D^{+}$ 与 $D^{*}$ 的区别: $D^{+}$ 要求至少一个数字,而 $D^{*}$ 允许零个数字。这个区别在定义如 $D^{+} . D^{*}$ 和 $D^{*} . D^{+}$ 中至关重要,它决定了小数点哪边必须有数字。
本段首先通过一组关于 $\varepsilon$ 和 $\emptyset$ 的恒等式及其反例,深刻揭示了这两个特殊正则表达式在并和连接运算中的不同代数属性,巩固了基础概念。接着,它展示了一个复杂的、用于描述数值常量的真实世界正则表达式,并详细拆解了其结构。最后,本段将正则表达式与编译器理论联系起来,阐明了其在词法分析阶段作为定义词法单元(如变量名、数字等)模式的核心工具,并引出了词法分析器可以被自动化系统根据正则表达式生成的重要思想。
这一段的目的是将前面建立的抽象理论与实际应用连接起来,展示正则表达式的强大威力。通过恒等式的辨析,它加强了读者的理论深度。通过数值常量的例子,它展示了组合复杂模式的能力。通过介绍词法分析,它揭示了正则表达式在计算机科学核心领域——编译器构造中的根本性作用,极大地提升了学习该理论的价值感和实用性。
- 恒等式: 把 $\varepsilon$ 和 $\emptyset$ 想象成特殊的人。
- $\emptyset$ (空): 一个“隐形人”。你把他加入任何一个团队($\cup$),团队成员不变($R \cup \emptyset = R$)。但如果你要求任何人和他合作完成一个任务($\circ$),这个任务就无法完成,结果是“空”($R \circ \emptyset = \emptyset$)。
- $\varepsilon$ (空串): 一个“万能助手”。你让他加入一个团队($\cup$),团队就多了一个人,除非他已在队里($R \cup \varepsilon \neq R$)。如果你让他和任何人合作($\circ$),他对任务没有影响,结果就是那个人自己完成的样貌($R \circ \varepsilon = R$)。
- 词法分析器: 把它想象成一个厨房里的自动切菜机。
- 源代码: 一整颗大白菜。
- 正则表达式: 你给切菜机设置的“刀模”,比如“切成丝”、“切成块”、“把根去掉”。
- 词法分析器 (切菜机): 读取你设置的刀模(正则表达式),然后自动把大白菜(源代码)处理成一盘盘切好的菜丝、菜块(词法单元),方便下一步炒菜(语法分析)。
想象你在整理一大堆杂乱的邮件。
- 正则表达式: 你写下了一些规则,比如:
- 规则1(发票):“主题包含‘发票’或‘invoice’,并且附件是.pdf文件”
- 规则2(垃圾邮件):“发件人是‘@spam.com’结尾,或者内容包含‘赢大奖’”
- 规则3(会议邀请):“主题以‘邀请:’开头”
- 词法分析器: 一个智能助手,它读取你的这些规则(正则表达式),然后遍历你的收件箱,给每一封邮件贴上标签:“发票”、“垃圾邮件”、“会议邀请”或“其他”。
这个贴标签的过程,就是词法分析。它将一长串无结构的邮件流,转换成了一个个带有明确类别(词法单元类型)的、结构化的邮件对象。
1.5 与有限自动机的等价性
📜 [原文8]
正则表达式和有限自动机在描述能力上是等价的。这一事实令人惊讶,因为有限自动机和正则表达式表面上看起来截然不同。然而,任何正则表达式都可以转换为识别其所描述语言的有限自动机,反之亦然。回想一下,正则语言是指被某个有限自动机识别的语言。
定理 1.54
一个语言是正则语言当且仅当某个正则表达式描述它。
这个定理有两个方向。我们分别将每个方向陈述并证明为一个独立的引理。
这是本章乃至整个计算理论的一个核心结论。它在两个看似完全不同的世界——正则表达式的世界和有限自动机的世界——之间建立了一座坚固的桥梁。
- 两个世界的对比
- 有限自动机 (Finite Automata - FA):
- 本质: 一种计算模型,可以想象成一个带有状态和转换规则的机器。
- 工作方式: 它一次读取输入字符串的一个字符,并根据当前状态和读到的字符,“跳转”到下一个状态。当字符串读完后,如果机器停在接受状态,则该字符串被“接受”。
- 描述方式: 声明式 (Declarative) 或 操作式 (Operational)。它通过一系列操作步骤来定义一个语言。我们用状态转换图来可视化它。
- 正则表达式 (Regular Expressions - RE):
- 本质: 一种描述字符串模式的代数表达式。
- 工作方式: 它通过并、连接、星号等运算来组合字符,从而定义一个语言。
- 描述方式: 代数式 (Algebraic) 或 描述式 (Descriptive)。它直接描述了一个语言的结构。
- 令人惊讶的等价性
- 从表面上看,一个像流程图一样的有限自动机和一个像数学公式一样的正则表达式,两者毫无共同之处。
- “等价”这个词在这里有非常精确的含义:对于任何一个能被有限自动机识别的语言,我们都能找到一个正则表达式来描述它;反之,对于任何一个能被正则表达式描述的语言,我们也都能构造出一个有限自动机来识别它。
- 这意味着,有限自动机和正则表达式只是描述同一类语言——即正则语言 (Regular Languages)——的两种不同方式。它们是同一枚硬币的两面。
- 定理 1.54 的陈述
- 定理: 一个语言是正则语言当且仅当某个正则表达式描述它。
- 这是一个“当且仅当”(if and only if, iff) 的陈述,意味着它包含两个方向的证明:
- 方向一 (充分性): 如果一个语言可以被正则表达式描述,那么它是一个正则语言。
- 要证明这一点,我们需要展示如何将任意一个正则表达式 $R$ 转换成一个能识别语言 $L(R)$ 的有限自动机 (特别是 NFA,因为 NFA 更容易构造)。
- 方向二 (必要性): 如果一个语言是正则语言,那么它一定能被某个正则表达式描述。
- 正则语言的定义是“能被有限自动机(DFA)识别的语言”。
- 所以,要证明这一点,我们需要展示如何将任意一个 DFA 转换成一个等价的正则表达式。
- 这两个方向的证明将作为两个独立的引理在后面给出。
- 示例 1: 一个简单的等价对
- 语言: 所有由偶数个 'a' 组成的字符串的语言(包括空字符串)。
- 有限自动机描述:
- 一个有两个状态的 DFA。状态 $q_0$ 是起始状态和接受状态,代表目前为止读了偶数个 'a'。状态 $q_1$ 是非接受状态,代表读了奇数个 'a'。
- 从 $q_0$ 读到 'a' -> 跳转到 $q_1$。
- 从 $q_1$ 读到 'a' -> 跳转到 $q_0$。
- 这个机器精确地识别了上述语言。
- 正则表达式描述:
- 表达式: (aa)*
- aa 表示语言 {aa}。
- (aa)* 表示对语言 {aa} 进行零次或多次连接。
- 0 次: $\varepsilon$
- 1 次: aa
- 2 次: aaaa
- ...
- 这个表达式也精确地描述了同一个语言。
- 这直观地展示了,对于同一个语言,存在两种截然不同的描述方式。
- 示例 2: 另一个等价对
- 语言: 所有以 'b' 结尾的字符串的语言。
- 有限自动机描述:
- 一个有两个状态的 DFA。状态 $q_0$ 是起始状态。状态 $q_1$ 是接受状态。
- 从 $q_0$ 读到 'a' -> 停留在 $q_0$。
- 从 $q_0$ 读到 'b' -> 跳转到 $q_1$。
- 从 $q_1$ 读到 'a' -> 跳转到 $q_0$。
- 从 $q_1$ 读到 'b' -> 停留在 $q_1$。
- 这个机器只有在最后一个字符是 'b' 时才会停在 $q_1$。
- 正则表达式描述:
- 表达式: (a | b)* b (在我们的记号中是 $(a \cup b)^{*}b$)
- (a | b)*: 匹配任意由 'a' 和 'b' 组成的字符串(包括空串)。
- b: 匹配一个 'b'。
- 连接起来,就是任意字符串后面跟着一个 'b'。这正是“以 'b' 结尾的字符串”。
- 再次说明了等价性。
- 等价性是“描述能力”的等价: 这不意味着任何一个正则表达式都“长得像”一个自动机。它们在形式上完全不同。等价性是指它们能描述的语言的集合是完全相同的,这个集合就是正则语言。
- 证明的复杂性: 虽然直观上可以通过例子感受等价性,但严格的数学证明(即将要展开的两个引理)是相当构造性和技术性的,需要耐心理解其算法过程。
- NFA 的角色: 在“正则表达式 -> 自动机”的证明中,我们通常构造的是 NFA(非确定型有限自动机),而不是 DFA。这是因为 NFA 的构造方式与正则表达式的递归结构能够完美契合,构造起来简单得多。我们已经知道任何 NFA 都可以转换成等价的 DFA,所以这并不影响结论。
本段提出了计算理论中的一个里程碑式的结论:正则表达式和有限自动机在描述语言的能力上是等价的。尽管它们在形式上——一个是代数表达式,一个是状态机模型——看起来完全不同,但它们所能描述的语言集合是完全重合的,这个集合就是正则语言的集合。为了证明这个重要的定理 1.54,作者指出需要从两个方向分别进行证明:1) 证明任何正则表达式都可以转换成一个等价的有限自动机;2) 证明任何有限自动机都可以转换成一个等价的正则表达式。这两个证明将作为后续的两个引理展开。
本段的目的是作为一个“路标”,宣告一个极其重要的理论结果,并为接下来的两个核心证明(引理 1.55 和 引理 1.60)设定好舞台。它连接了本章前面的有限自动机内容和当前的正则表达式内容,将它们统一在“正则语言”这个大旗之下。这个等价性定理是后续所有关于正则语言性质讨论的基础。
想象你要描述“如何从家走到公司”。
- 方法一 (正则表达式): 你写下一段文字描述:“出门右转,直走(任意多个路口),直到看到星巴克,然后左转,再走两个路口”。这是一段描述性的、基于规则的指令。
- 方法二 (有限自动机): 你画了一张地图,上面标注了你家、公司、以及沿途的每个路口(状态)。每个路口都画了箭头,指示“在这里如果直走会到哪个路口”、“在这里如果左转会到哪个路口”。这是一个基于状态和转换的模型。
这两种方法看起来完全不同,但它们描述的是同一件事:从家到公司的路径集合。定理 1.54 说的就是,这两种方法在“描述路径”的能力上是等价的。任何你能用文字描述的路径,都能在地图上画出来;任何你能在地图上画出的路径,也都能用文字描述出来。
想象两种不同的乐谱。
- 一种是五线谱 (有限自动机)。音符在谱上的位置(状态)和时间的推进,精确地告诉你每一步要弹什么音,持续多久,非常操作化。
- 另一种是吉他六线谱 (正则表达式)。它可能用更简洁的符号告诉你“在这里弹一个C和弦(一个组合模式),然后重复4遍(星号),接一个G和弦...”。它更偏向于描述模式和结构。
定理 1.54 就像在说:任何能用五线谱写出的(某种类型的)音乐,也都能用六线谱写出来,反之亦然。它们只是记录音乐的两种不同但表达能力相同的语言。
1.6 引理 1.55:从正则表达式到 NFA
📜 [原文9]
引理 1.55
如果一个语言被正则表达式描述,那么它是正则语言。
证明思路 假设我们有一个描述某个语言 $A$ 的正则表达式 $R$。我们展示如何将 $R$ 转换为一个识别 $A$ 的 NFA (非确定型有限自动机)。根据推论 1.40,如果一个 NFA 识别 $A$,那么 $A$ 是正则语言。
证明 让我们将 $R$ 转换为一个 NFA $N$。我们考虑正则表达式形式化定义中的六种情况。
- $R=a$,对于字母表 $\Sigma$ 中的某个 $a$。那么 $L(R)=\{a\}$,以下 NFA 识别 $L(R)$。
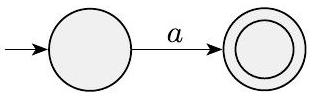
请注意,这台机器符合 NFA 的定义,但不符合 DFA (确定型有限自动机) 的定义,因为它对于每个可能的输入符号,有些状态没有离开的箭头。当然,我们可以在这里展示一个等价的 DFA;但我们现在只需要 NFA,而且它更容易描述。
形式上,$N=\left(\left\{q_{1}, q_{2}\right\}, \Sigma, \delta, q_{1},\left\{q_{2}\right\}\right)$,其中我们通过说明 $\delta\left(q_{1}, a\right)=\left\{q_{2}\right\}$ 以及对于 $r \neq q_{1}$ 或 $b \neq a$ 时 $\delta(r, b)=\emptyset$ 来描述 $\delta$。
- $R=\varepsilon$。那么 $L(R)=\{\varepsilon\}$,以下 NFA 识别 $L(R)$。
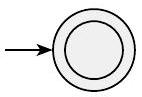
形式上,$N=\left(\left\{q_{1}\right\}, \Sigma, \delta, q_{1},\left\{q_{1}\right\}\right)$,其中对于任何 $r$ 和 $b$,$\delta(r, b)=\emptyset$。
- $R=\emptyset$。那么 $L(R)=\emptyset$,以下 NFA 识别 $L(R)$。
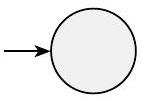
形式上,$N=(\{q\}, \Sigma, \delta, q, \emptyset)$,其中对于任何 $r$ 和 $b$,$\delta(r, b)=\emptyset$。
这是定理 1.54 第一个方向的证明。它旨在说明,任何正则表达式所描述的语言都是正则语言。证明的核心策略是一个构造性证明:它提供了一个具体的算法,能够将任意给定的正则表达式 $R$ 转换成一个识别相同语言 $L(R)$ 的 NFA。
- 证明的逻辑链
- 前提: 我们有一个正则表达式 $R$,它描述了语言 $A$ (即 $L(R) = A$)。
- 目标: 证明 $A$ 是一个正则语言。
- 回顾正则语言的定义: 一个语言是正则语言,如果存在一个 DFA 识别它。
- 回顾 NFA 与 DFA 的关系 (推论 1.40): 任何能被 NFA 识别的语言都是正则语言(因为任何 NFA 都能被转换成一个等价的 DFA)。
- 证明策略: 我们只需要展示如何为任意正则表达式 $R$ 构造一个等价的 NFA。只要能做到这一点,根据推论 1.40,语言 $L(R)$ 就是正则语言,引理得证。
- 构造方法:模仿正则表达式的归纳定义
- 正则表达式是通过归纳定义的,它有 3 个基础情况和 3 个归纳步骤。我们的构造算法将完美地模仿这个结构。我们将为每一种情况给出一个构造 NFA 的方法。
- 这种方法保证了我们可以处理任意复杂的正则表达式,因为任何正则表达式都可以被分解成这六种基本情况之一。
- 处理基础情况 (原子正则表达式)
- 情况 1: $R = a$
- 语言: $L(R) = \{a\}$,只包含单个字符串 a。
- NFA 构造: 我们需要一个 NFA,它只接受字符串 a。
- 创建一个起始状态 $q_1$。
- 创建一个接受状态 $q_2$。
- 从 $q_1$ 到 $q_2$ 画一个箭头,并用符号 a 标记它。
- 工作原理:
- 输入 a: 从 $q_1$ 开始,读到 a,沿着箭头到达 $q_2$。字符串结束,机器在接受状态,所以 a 被接受。
- 输入任何其他字符串 (如 b, aa, $\varepsilon$): 机器无法从 $q_1$ 离开(或无法匹配完整),最终无法停在接受状态 $q_2$。所以其他字符串都被拒绝。
- 与 DFA 的区别: 这个构造出的机器是一个 NFA,因为它不是对所有状态和所有输入符号都有定义转换。例如,在 $q_1$,如果输入是 b (假设 $b \neq a$),没有对应的转换箭头。这在 DFA 中是不允许的(DFA 需要一个完整的转换函数),但在 NFA 中是合法的(缺失的转换被认为是指向一个“死亡状态”)。选择构造 NFA 是因为它更简单、更灵活。
- 情况 2: $R = \varepsilon$
- 语言: $L(R) = \{\varepsilon\}$,只包含空字符串。
- NFA 构造: 我们需要一个 NFA,它只接受空字符串。
- 创建一个起始状态 $q_1$。
- 让这个起始状态 $q_1$ 同时也是一个接受状态。
- 工作原理:
- 输入 $\varepsilon$: 机器从 $q_1$ 开始,字符串立即结束。此时机器在接受状态 $q_1$ 上,所以 $\varepsilon$ 被接受。
- 输入任何非空字符串 (如 a): 机器从 $q_1$ 开始,读到 a,但没有任何地方可以去。字符串未读完机器就卡住了,所以 a 被拒绝。
- 情况 3: $R = \emptyset$
- 语言: $L(R) = \{\}$,即空语言,不接受任何字符串。
- NFA 构造: 我们需要一个不接受任何东西的 NFA。
- 创建一个起始状态 $q$。
- 不要设置任何接受状态。
- 工作原理: 无论输入什么字符串,机器运行结束后,它所在的最终状态都不可能是接受状态(因为根本就没有接受状态),所以任何字符串都会被拒绝。
- 示例 1: 构造 R = 'b' 的 NFA
- 适用规则: 情况 1,$a = 'b'$。
- 语言: $L(b) = \{b\}$。
- 构造:
- 创建起始状态 $q_{start}$。
- 创建接受状态 $q_{accept}$。
- 从 $q_{start}$ 到 $q_{accept}$ 画一个箭头,标记为 'b'。
- 结果: 一个简单的两状态 NFA,它只在输入为 'b' 时从起始状态走到接受状态。
- 示例 2: 理解 R = ε 的 NFA
- 适用规则: 情况 2。
- 语言: $L(\varepsilon) = \{\varepsilon\}$。
- 构造:
- 创建起始状态 $q_0$。
- 将 $q_0$ 圈上双圈,表示它也是接受状态。
- 测试:
- 输入 $\varepsilon$: 从 $q_0$ 开始,输入结束。当前状态 $q_0$ 是接受状态。接受。
- 输入 "a": 从 $q_0$ 开始,读入 'a'。没有从 $q_0$ 出发的 'a' 转换。机器卡住。拒绝。
- NFA vs. DFA: 必须清楚地认识到,这些简单的构造步骤之所以简单,是因为我们构建的是 NFA。如果试图直接为这些基础情况构造 DFA,会需要额外的“陷阱状态”(trap state) 来处理所有未明确定义的转换,从而使图形变得更复杂。
- $R = \varepsilon$ 的 NFA: 其特点是起始状态就是接受状态。这是一种特殊但非常重要的模式。
- $R = \emptyset$ 的 NFA: 其特点是没有接受状态。这是最简单的“什么都不接受”的机器。
- 状态命名: 书中使用的 $q_1, q_2$ 只是代号,你可以使用任何你喜欢的名字,如 $q_{start}, q_{accept}$,关键是它们的角色(起始/接受)和它们之间的转换关系。
本段启动了定理 1.54 的第一个关键证明(引理 1.55),即从正则表达式到正则语言的转换。证明的策略是为任意正则表达式 $R$ 构造一个等价的 NFA。本段处理了构造性证明的第一部分:基础情况。它展示了如何为三种最原子的正则表达式——a (单个符号),ε (空串),和 ∅ (空集)——分别构造出简单、正确的 NFA。这些基础的 NFA 将作为后续构造更复杂正则表达式对应 NFA 的“积木块”。
这部分内容是整个构造性证明的基石。没有这些基础“积木”,就无法通过递归步骤构建更复杂的机器。它为后续的并、连接和星号运算的NFA构造提供了起点,并再次强调了 NFA 在这种构造中的便利性。
把“将正则表达式转为 NFA”的过程想象成“用电路元件搭建一个逻辑门”:
- 正则表达式: 逻辑表达式,例如 A AND B。
- NFA: 实际的电路图。
- 本段内容 (基础情况): 对应着最基本的元件:
- R = a: 像一个“信号检测器”,只有当输入信号是 a 时,它才会亮灯(到达接受状态)。
- R = ε: 像一个“默认开启”的开关。你什么都不用做(输入空字符串),它就已经是通路状态(在接受状态)。
- R = ∅: 像一个“永久断路”的开关。无论你做什么,它永远不会导通(到达接受状态)。
接下来的步骤将展示如何用“与门”、“或门”等组合这些基本元件。
想象你在为一个极其简单的游戏设计关卡:
- R = a: 这一关只有一个平台,上面写着 'a'。玩家必须踩到这个 'a' 平台才能过关。任何其他的操作(比如跳到旁边)都算失败。
- R = ε: 玩家一进关卡就发现自己站在终点线上。什么都不用做就通关了。
- R = ∅: 这个关卡里根本没有终点线。无论玩家怎么走,都不可能通关。
这些是最简单的“关卡”。下一部分将展示如何把这些小关卡“并联”、“串联”或“循环”起来,形成更复杂的关卡。
📜 [原文10]
- $R=R_{1} \cup R_{2}$。
- $R=R_{1} \circ R_{2}$。
- $R=R_{1}^{*}$。
对于最后三种情况,我们使用正则语言类在正则运算下封闭的证明中给出的构造。换句话说,我们从 $R_{1}$ 和 $R_{2}$(或在情况 6 中仅 $R_{1}$)的 NFA 以及适当的封闭构造来构建 $R$ 的 NFA。
这结束了定理 1.54 证明的第一部分,给出了“当且仅当”条件的较容易方向。在继续讨论另一个方向之前,我们先通过一些示例来了解如何使用此过程将正则表达式转换为 NFA。
这部分内容处理了引理 1.55 证明的归纳步骤。它解释了如何为由并、连接和星号三种正则运算构成的复合正则表达式来构造 NFA。
- 归纳假设 (Inductive Hypothesis)
- 这个证明方法的核心是归纳。当我们处理 $R = R_1 \cup R_2$ 时,我们假设我们已经知道如何为它的子表达式 $R_1$ 和 $R_2$ 构造出对应的 NFA。
- 设 NFA $N_1$ 识别 $L(R_1)$,NFA $N_2$ 识别 $L(R_2)$。我们的任务是,利用 $N_1$ 和 $N_2$ 这两个已有的“积木”,来搭建一个新的、更大的 NFA $N$,使得 $N$ 能够识别语言 $L(R_1 \cup R_2)$。
- 引用已有的结论
- 作者在这里指出,我们其实已经做过这项工作了。在之前学习“正则语言的封闭性”时,我们已经证明了:
- 如果 $L_1$ 和 $L_2$ 是正则语言,那么它们的并集 $L_1 \cup L_2$ 也是正则语言。
- 如果 $L_1$ 和 $L_2$ 是正则语言,那么它们的连接 $L_1 \circ L_2$ 也是正则语言。
- 如果 $L_1$ 是正则语言,那么它的星号 $L_1^*$ 也是正则语言。
- 当时的证明就是构造性的:我们给出了具体的算法,展示了如何从识别 $L_1$ 和 $L_2$ 的自动机出发,构造出识别新语言的自动机。
- 现在,我们直接“重用”那些构造方法。
- 三种归纳情况的构造方法回顾
- 情况 4: $R = R_1 \cup R_2$ (并)
- 目标: 构造一个 NFA $N$ 来识别 $L(N_1) \cup L(N_2)$。
- 构造 (Thompson's Construction 算法):
- 创建一个新的起始状态 $q_{new\_start}$。
- 从 $q_{new\_start}$ 画两条 $\varepsilon$-转移箭头,分别指向 $N_1$ 的起始状态和 $N_2$ 的起始状态。
- 创建一个新的接受状态 $q_{new\_accept}$。
- 从 $N_1$ 的所有接受状态画 $\varepsilon$-转移箭头到 $q_{new\_accept}$。
- 从 $N_2$ 的所有接受状态画 $\varepsilon$-转移箭头到 $q_{new\_accept}$。
- 将 $N_1$ 和 $N_2$ 原本的接受状态都变成普通状态。
- 直觉: 新机器开始时,通过 $\varepsilon$-转移“猜测”要去匹配 $L(N_1)$ 还是 $L(N_2)$。如果任意一条路径成功,整个字符串就被接受。
- 情况 5: $R = R_1 \circ R_2$ (连接)
- 目标: 构造一个 NFA $N$ 来识别 $L(N_1) \circ L(N_2)$。
- 构造:
- 将 $N_1$ 的起始状态作为新机器 $N$ 的起始状态。
- 将 $N_2$ 的接受状态作为新机器 $N$ 的接受状态。
- 从 $N_1$ 的所有接受状态画 $\varepsilon$-转移箭头,指向 $N_2$ 的起始状态。
- 将 $N_1$ 原本的接受状态都变成普通状态。
- 直觉: 机器首先必须完整地匹配一个 $L(N_1)$ 中的字符串,走到 $N_1$ 的终点,然后通过 $\varepsilon$-转移“无缝衔接”到 $N_2$ 的起点,接着必须完整地匹配一个 $L(N_2)$ 中的字符串。
- 情况 6: $R = R_1^*$ (星号)
- 目标: 构造一个 NFA $N$ 来识别 $(L(N_1))^*$。
- 构造:
- 创建一个新的起始状态 $q_{new\_start}$,它同时也是接受状态(为了处理 0 次重复,即接受 $\varepsilon$)。
- 创建一个新的接受状态 $q_{new\_accept}$。
- 从 $q_{new\_start}$ 画一条 $\varepsilon$-转移到 $N_1$ 的起始状态,和一条 $\varepsilon$-转移直接到 $q_{new\_accept}$。
- 从 $N_1$ 的所有接受状态画 $\varepsilon$-转移,一条指回 $N_1$ 的起始状态(实现循环),另一条指向 $q_{new\_accept}$(结束循环)。
- $N_1$ 原本的起始和接受状态都变成普通状态。
- 简化版构造:
- 创建一个新的起始状态 $q_{new\_start}$,同时也是接受状态。
- 从 $q_{new\_start}$ 画一条 $\varepsilon$ 边到 $N_1$ 的起始状态。
- 从 $N_1$ 的所有接受状态画 $\varepsilon$ 边到 $q_{new\_start}$。
- 直觉: 机器可以从头($q_{new\_start}$)直接到尾,接受 $\varepsilon$。或者,它可以进入 $N_1$ 子模块,匹配一个 $L(N_1)$ 中的字符串,然后通过 $\varepsilon$-转移回到起点,准备再次进入 $N_1$ 匹配下一个,或者选择结束。这个循环结构允许匹配任意多次。
- 证明完成
- 通过为 3 种基础情况和 3 种归纳情况都提供了具体的 NFA 构造方法,我们完整地展示了如何将任何一个正则表达式转换为等价的 NFA。
- 这个算法(通常称为 Thompson's Construction)是递归的、确定性的,保证能为任何合法的正则表达式生成一个 NFA。
- 因此,引理 1.55 成立:任何被正则表达式描述的语言,都能被一个 NFA 识别,故它是一个正则语言。这完成了定理 1.54 "if" 部分的证明。
- 示例 1: 构造 $R = a \cup b$ 的 NFA
- 分解: $R_1 = a$, $R_2 = b$。
- 子模块: 我们已经知道如何构造 $N_a$ 和 $N_b$ (都是两状态的简单 NFA)。
- 并运算构造:
- 创建新起始状态 $q_{start}$。
- 从 $q_{start}$ 画 $\varepsilon$-转移分别到 $N_a$ 的起点和 $N_b$ 的起点。
- 创建新接受状态 $q_{accept}$。
- 从 $N_a$ 的终点和 $N_b$ 的终点画 $\varepsilon$-转移到 $q_{accept}$。
- 结果: 得到一个有 6 个状态的 NFA,它在开始时“选择”走上面匹配 'a' 的路径或下面匹配 'b' 的路径。
- 示例 2: 构造 $R = a^*$ 的 NFA
- 分解: $R_1 = a$。
- 子模块: 我们有 NFA $N_a$。
- 星号运算构造:
- 创建新起始状态 $q_{start}$,它也是接受状态。
- 从 $q_{start}$ 画 $\varepsilon$-转移到 $N_a$ 的起点。
- 从 $N_a$ 的终点画 $\varepsilon$-转移回到 $q_{start}$。
- 结果: 得到一个 NFA。它可以直接接受 $\varepsilon$(因为 $q_{start}$ 是接受的)。或者,它可以通过 $\varepsilon$ 边进入 $N_a$ 子模块,匹配一个 'a',然后通过另一条 $\varepsilon$ 边回到起点,准备匹配下一个 'a',或者就此停留在起点并接受。
- $\varepsilon$-转移的滥用: Thompson's Construction 大量使用 $\varepsilon$-转移。在分析这些构造出的 NFA 如何工作时,必须时刻记住机器可以在不消耗任何输入字符的情况下沿着 $\varepsilon$ 箭头移动。
- 状态的复用: 在构造过程中,子模块 $N_1$ 和 $N_2$ 的状态集必须是不相交的,否则会产生混乱。在实践中,每次递归调用构造时,都应该使用全新的状态名称。
- 旧的接受/起始状态: 在组合时,子模块原本的“接受”或“起始”角色通常会被新的状态取代,它们自身变回了普通状态。这是一个很关键的细节。
本段完成了引理 1.55 的归纳步骤证明。它指出,对于复合正则表达式 $R_1 \cup R_2$, $R_1 \circ R_2$, 和 $R_1^*$,我们可以通过重用之前在证明正则语言封闭性时所使用的NFA构造算法,来从其子表达式的 NFA ($N_1, N_2$) 构建出整个表达式的 NFA。由于我们已经为所有基础情况和所有归纳情况都提供了构造方法,这个递归的算法(Thompson's Construction)能够将任何正则表达式转换为等价的 NFA。这证明了任何被正则表达式描述的语言都是正则语言。
这部分的目的是完成整个构造性证明的核心逻辑。通过将问题递归地分解,并重用已知的封闭性构造结论,它优雅地、系统地解决了“如何将任意正则表达式转换为自动机”的难题。这不仅是一个理论证明,其本身(Thompson's Construction)就是一个可以在编译器和文本处理工具中实现的具体算法。
这个过程就像用函数式编程来处理一个表达式树。
- 正则表达式: 一个树形数据结构。叶子节点是 a, ε, ∅。内部节点是 U, o, *。
- NFA 构造器: 一个递归函数 build_nfa(regex)。
- 如果 regex 是叶子节点 a,返回基础的“a-检测器”NFA。
- 如果 regex 是叶子节点 ε,返回基础的“默认接受”NFA。
- 如果 regex 是叶子节点 ∅,返回基础的“永不接受”NFA。
- 如果 regex 是 R1 U R2,那么递归调用 nfa1 = build_nfa(R1) 和 nfa2 = build_nfa(R2),然后用“并联”的方式将 nfa1 和 nfa2 组合起来。
- 如果 regex 是 R1 o R2,则递归调用后用“串联”的方式组合。
- 如果 regex 是 R1*,则递归调用后用“加循环”的方式改造。
这个递归过程保证了树上的每个节点都会被正确地“翻译”成 NFA 的一部分。
想象你在用乐高积木搭建一个复杂的模型,说明书是正则表达式。
- 说明书的基础部分告诉你:“这是一个红色2x1的块 (a)”,“这是一个透明的1x1的块 (ε)”。
- 说明书的组合部分告诉你:
- 并: “把红色块和蓝色块并排摆放,它们俩构成一个组件 (a U b)”。
- 连接: “把绿色块插在黄色块后面 (g o y)”。
- 星号: “拿一个橙色块,你可以在它上面再叠任意多个橙色块 (o*)”。
引理 1.55 的证明过程,就是这本“乐高说明书”本身,它告诉你无论多么复杂的模型,都可以通过这几种基本操作搭建出来。
1.7 示例:将 (ab U a)* 转换为 NFA
📜 [原文11]
示例 1.56
我们分阶段将正则表达式 $(\mathrm{ab} \cup \mathrm{a})^{*}$ 转换为 NFA。我们从最小的子表达式开始构建,逐步到较大的子表达式,直到我们拥有原始表达式的 NFA,如下图所示。请注意,此过程通常不会给出状态最少的 NFA。在此示例中,该过程给出了一个有八个状态的 NFA,但最小的等价 NFA 只有两个状态。你能找到它吗?
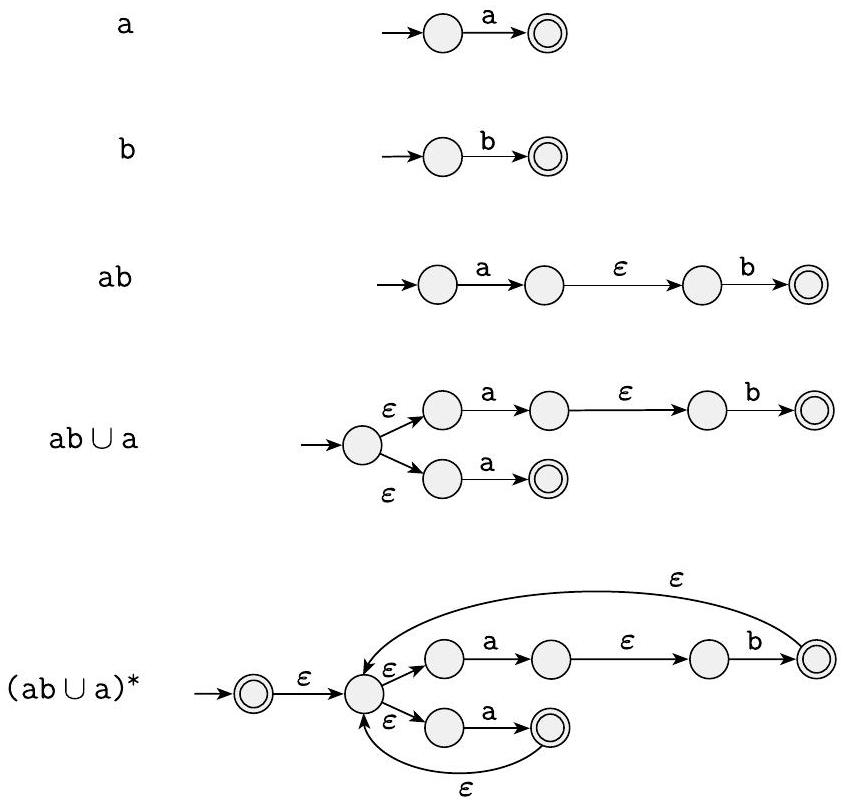
图 1.57
从正则表达式 $(\mathrm{ab} \cup \mathrm{a})^{*}$ 构建 NFA
这个例子完整地演示了前面描述的 Thompson's Construction 算法。它严格遵循从内到外、从简单到复杂的构建顺序,将一个具体的正则表达式 $(\mathrm{ab} \cup \mathrm{a})^{*}$ 一步步地转换成一个 NFA。
分析表达式的结构树
首先,我们需要像解析一个数学公式一样,分析 $(\mathrm{ab} \cup \mathrm{a})^{*}$ 的结构:
- 最外层是星号运算 *。
- 星号内部是并运算 U。
- 并运算的左边是连接运算 ab。
- 并运算的右边是 a。
- 最底层的原子表达式是 a 和 b。
所以,构建的顺序应该是:
- 构造 a 和 b 的 NFA。
- 使用 a 和 b 的 NFA 构造 ab 的 NFA。
- 我们已经有 a 的 NFA。
- 使用 ab 和 a 的 NFA 构造 ab U a 的 NFA。
- 最后,使用 ab U a 的 NFA 构造 (ab U a)* 的 NFA。
图 1.57 的分步详解
- 第一行: a 和 b (基础情况)
- 左图 (a): 对应正则表达式 a。根据基础规则 1,构造一个两状态 NFA,中间由 a 箭头连接。
- 右图 (b): 对应正则表达式 b。同样,构造一个两状态 NFA,中间由 b 箭头连接。
- 这是我们最小的“积木块”。
- 第二行: ab (连接运算)
- 目标: 构造正则表达式 ab 的 NFA。这是 a 和 b 的连接。
- 方法: 使用连接的构造规则。
- 取 a 的 NFA ($N_a$) 和 b 的 NFA ($N_b$)。
- 将 $N_a$ 的接受状态通过一条 $\varepsilon$-转移箭头连接到 $N_b$ 的起始状态。
- $N_a$ 的起始状态成为新机器的起始状态。
- $N_b$ 的接受状态成为新机器的接受状态。
- 图中结果: 将第一行的 a 的 NFA 的终点,通过 $\varepsilon$ 连接到 b 的 NFA 的起点,形成了一个三状态的链。这个链只接受字符串 ab。
- 第三行: ab U a (并运算)
- 目标: 构造 ab U a 的 NFA。
- 子模块: 我们需要 ab 的 NFA (来自第二行) 和 a 的 NFA (来自第一行)。
- 方法: 使用并的构造规则。
- 创建一个新的起始状态。
- 从新起点画两条 $\varepsilon$-转移,分别指向 ab 的 NFA 的起点和 a 的 NFA 的起点。
- 创建一个新的接受状态。
- 从 ab 的 NFA 的终点和 a 的 NFA 的终点画 $\varepsilon$-转移到新终点。
- 图中结果: 一个菱形的结构。机器开始时,可以选择走上面的路径(匹配 ab)或者走下面的路径(匹配 a)。
- 第四行: (ab U a)* (星号运算)
- 目标: 构造 (ab U a)* 的 NFA。
- 子模块: 我们需要 ab U a 的 NFA (来自第三行)。
- 方法: 使用星号的构造规则。
- 创建一个新的起始状态,它同时也是接受状态(为了匹配空字符串 $\varepsilon$)。
- 从新起点画一条 $\varepsilon$-转移到 ab U a 的 NFA (即第三行的菱形结构) 的起点。
- 从 ab U a 的 NFA 的终点画一条 $\varepsilon$-转移回到新起点(形成循环)。
- (在书中的画法中,还额外有一个新的接受状态,并且从旧的接受状态和新的起始状态都有 $\varepsilon$ 边连过去,这是一种等价但更严格的画法,保证单一出口)。
- 图中结果: 整个菱形结构被一个大的循环和出入口包裹起来。机器可以:
- 直接从新起点到新终点(通过最外围的 $\varepsilon$ 边),接受 $\varepsilon$。
- 进入菱形,匹配一个 ab 或 a,然后回到起点,准备下一次匹配。
- 在任意次匹配后,从菱形的终点退出到最终的接受状态。
关于状态最少的 NFA
- 算法的产物: Thompson's Construction 生成的 NFA 有 8 个状态,并且有大量的 $\varepsilon$-转移。它虽然保证正确,但通常是冗余的。
- 语言的本质: 让我们分析一下语言 $L((ab \cup a)^*)$。它是由 ab 和 a 进行任意次数的拼接。
- 这个语言里包含了 a, aa, ab, aab, aba 等等。
- 实际上,这个语言就是所有由 a 和 b 组成,且不以 b 开头,并且没有任何两个连续的 b 的字符串的集合。或者更简单地想:它等价于所有以 a 开头的字符串,只要其中不出现 bb 子串。
- 一个更简单的等价正则表达式是 a(aba)a*。
- 更直接地看,任何由 a 和 b 组成的字符串,只要它以 a 开头,并且 b 后面必须跟着 a,似乎都可以。不,aa可以,ab可以, aba可以。其实就是所有不含 bb 子串且不以 b 开头的字符串。
- 让我们再思考一下,这个语言其实就是所有以 'a' 开头,并且任意一个 'b' 后面必须紧跟着一个 'a' 的字符串。
- 不,(ab U a)* 可以生成 a,也可以生成 ab,也可以生成 aab,aba。
- 其实 $L((ab \cup a)^*)$ 就是 $L((a(b \cup \varepsilon))^*)$。 这代表了所有由 a 和 ab 组成的字符串。这意味着所有字符串都以 a 开头,并且b前面必须有a。
- 一个更简单的想法:这个语言包含空字符串。所有非空字符串都必须以 a 开头。在 a 之后,可以有另一个 a,也可以有一个 b,但 b 之后不能再跟 b。
- 最小的等价 NFA:
- 状态0 (起始, 接受): 代表空字符串或一个合法的字符串结尾。
- 状态1 (接受): 代表刚读完一个a,也是合法的结尾。
- 从状态0读 a -> 状态1. (可以开始一个新的 a... 或者 ab... 序列)
- 从状态1读 a -> 状态1. (...aa...)
- 从状态1读 b -> 状态0. (...ab...,此时必须重新以a开头)
- 这个 NFA 似乎可行。让我们检查一下:
- 输入 a: 0 -> 1 (接受)
- 输入 ab: 0 -> 1 -> 0 (接受)
- 输入 aba: 0 -> 1 -> 0 -> 1 (接受)
- 输入 aa: 0 -> 1 -> 1 (接受)
- 输入 b: (从0无法读b) 拒绝。正确。
- 输入 bb: (无路径) 拒绝。正确。
- 所以,一个两状态的 NFA 确实可以实现。状态0(起始,接受)和状态1(接受)。从0读a到1。从1读a到1。从1读b到0。所有其他转换都到“死亡状态”。这个机器接受所有由 a 和 ab 组成的字符串,这正是 (a U ab),也就等价于 (ab U a)。
- 机械化 vs. 优化: Thompson's Construction 是一个完全机械化的过程。它的优点是保证正确,无需思考。缺点是结果冗余。在实际应用中,可能会有后续的NFA最小化步骤来优化它。
- 不要跳步: 在手动执行这个算法时,严格按照表达式的结构树从叶子到根的顺序进行,不要试图“智能地”跳过某些步骤,否则很容易出错。
- ε-转移的处理: 最终得到的 NFA 包含大量 $\varepsilon$-转移。要正确理解它的行为,必须考虑所有可能的 $\varepsilon$-闭包。
示例 1.56 通过一个具体的正则表达式 $(\mathrm{ab} \cup \mathrm{a})^{*}$,完整地、分步地展示了 Thompson's Construction 算法 的应用。它从最基本的原子表达式 a 和 b 的 NFA 开始,然后依次应用连接、并和星号的构造规则,像搭积木一样,最终构建出一个完整但冗余的 NFA。这个例子直观地证明了引理 1.55 的构造性证明是可行的。同时,它也提醒读者,这个算法的产物在状态数量上通常不是最优的,存在很大的简化空间。
这个例子的主要目的是将前面抽象的构造规则具象化。通过一个完整的、手把手的演练,读者可以更深刻地理解 Thompson's Construction 算法 的递归本质和操作流程。它弥合了抽象理论描述与实际动手操作之间的差距,为读者独立完成类似转换或理解相关自动化工具的内部工作原理打下了基础。
这个过程就像用基本逻辑门(AND, OR, NOT)搭建一个复杂的数字电路。
- a, b 的 NFA 是最基础的电线和传感器。
- ab (连接) 的构造,就像把两个元件串联起来。
- ab U a (并) 的构造,就像把两个元件并联起来。
- (ab U a)* (星号) 的构造,就像给一个电路模块加上了反馈循环和旁路开关。
整个过程就是一份详细的电路组装蓝图,告诉你如何用标准件拼装出任何你想要的逻辑功能。
想象你在画一幅流程图来描述一个任务。
- a: 一个简单的步骤,“执行任务A”。
- b: “执行任务B”。
- ab: 一个顺序流程,“先执行A,然后立刻执行B”。
- ab U a: 一个分支,“你可以选择‘先A后B’这条路,也可以选择只‘执行A’这条路”。
- (ab U a)*: 一个循环结构,“你可以重复任意次‘分支选择’这个过程,也可以一次都不做直接退出”。
图 1.57 就是将这个任务描述,一步步地画成了一张完整、精确但可能有些绕的流程图。
1.8 示例:将 (a U b)*aba 转换为 NFA
📜 [原文12]
示例 1.58
在图 1.59 中,我们将正则表达式 $(\mathrm{a} \cup \mathrm{b})^{*} \mathrm{aba}$ 转换为 NFA。其中一些次要步骤未显示。
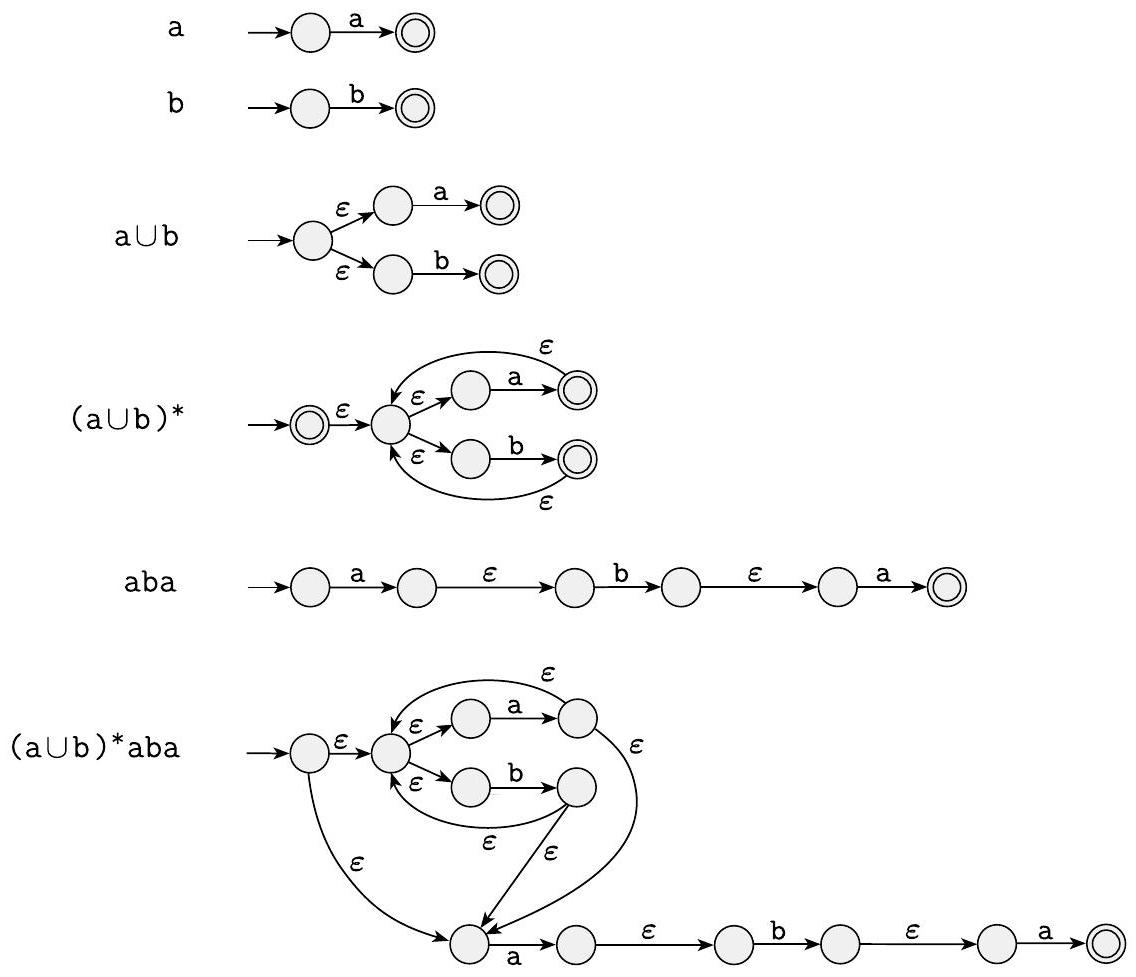
图 1.59
从正则表达式 $(\mathrm{a} \cup \mathrm{b})^{*} \mathrm{aba}$ 构建 NFA $\square$
这个例子比上一个更复杂,它组合了并、星号和多次连接。它旨在展示 Thompson's Construction 算法处理更长序列的能力,并省略了一些中间步骤以突出关键的组合过程。
分析表达式的结构树
正则表达式是 $(\mathrm{a} \cup \mathrm{b})^{*} \mathrm{aba}$。根据优先级(星号 > 连接 > 并),它的结构是:
$(((\mathrm{a} \cup \mathrm{b})^{*}) \circ \mathrm{a}) \circ \mathrm{b}) \circ \mathrm{a}$
这是一个由四个主要部分连接而成的长链:
- 部分1: $(\mathrm{a} \cup \mathrm{b})^{*}$
- 部分2: $\mathrm{a}$
- 部分3: $\mathrm{b}$
- 部分4: $\mathrm{a}$
所以,构建的顺序是:
- 构造 a 和 b 的 NFA (基础)。
- 使用它们构造 a U b 的 NFA (并)。
- 使用 a U b 的 NFA 构造 (a U b)* 的 NFA (星号)。这是第一大块。
- 构造 a, b, a 各自的 NFA (基础)。
- 使用连接规则,将 (a U b)* 的 NFA、a 的 NFA、b 的 NFA、a 的 NFA 像串珠子一样串联起来。
图 1.59 的分步详解
- a, b (未显示,但为基础)
- 与上例相同,我们脑中已有 a 和 b 的两状态 NFA 作为零件。
- a U b (第一行)
- 目标: 构造 a U b 的 NFA。
- 方法: 应用并的构造规则。创建一个新起点,用 $\varepsilon$-转移连接到 a 和 b 的 NFA 的起点。创建一个新终点,a 和 b 的 NFA 的终点都用 $\varepsilon$-转移连接到它。
- 图中结果: 一个包含 6 个状态的菱形结构,与上一个例子的第三步类似。
- (a U b)* (第二行)
- 目标: 构造 (a U b)* 的 NFA。
- 子模块: 使用第一行得到的 a U b 的 NFA。
- 方法: 应用星号的构造规则。
- 创建一个新的起始/接受状态。
- 从新起点画 $\varepsilon$-转移到 a U b NFA 的起点。
- 从 a U b NFA 的终点画 $\varepsilon$-转移回到新起点。
- 图中结果: 一个大的循环结构,包裹着 a U b 的菱形。这个模块可以匹配任意由 a 和 b 组成的字符串。
- aba (第三行)
- 目标: 构造 aba 的 NFA。这是 a $\circ$ b $\circ$ a 的连接。
- 方法: 应用两次连接的构造规则。
- 取一个 a 的 NFA ($N_a$)。
- 将其终点用 $\varepsilon$-转移连接到 b 的 NFA ($N_b$) 的起点。
- 将 $N_b$ 的终点用 $\varepsilon$-转移连接到另一个 a 的 NFA ($N_{a'}$)。
- 图中结果: 一个由 a 弧、$\varepsilon$ 弧、b 弧、$\varepsilon$ 弧、a 弧串起来的链条。这个模块只接受字符串 aba。
- (a U b)*aba (第四行)
- 目标: 构造最终的正则表达式。
- 子模块: 第二行的 (a U b)* NFA 和第三行的 aba NFA。
- 方法: 应用连接的构造规则。
- 取 (a U b)* 的 NFA (我们称之为 $N_{star}$)。
- 取 aba 的 NFA (我们称之为 $N_{aba}$)。
- 将 $N_{star}$ 的接受状态通过一条 $\varepsilon$-转移连接到 $N_{aba}$ 的起始状态。
- $N_{star}$ 的起始状态是新机器的起点。
- $N_{aba}$ 的接受状态是新机器的终点。
- 图中结果: 将第二行的整个循环结构和第三行的整个链条结构,通过一个 $\varepsilon$ 箭头“焊接”在一起。
最终 NFA 的工作流程
这个最终构造出的复杂 NFA 如何识别一个字符串,比如 aababa?
- 字符串 aab 会在第一部分 (a U b)* 的循环中被匹配。机器可能会在循环体里走三次,分别匹配 a, a, b。
- 匹配完 aab 后,机器到达了原 $N_{star}$ 的接受状态。
- 通过关键的 $\varepsilon$-转移,机器“跳”到了 $N_{aba}$ 的起始状态。这个过程不消耗任何输入字符。
- 此时,输入字符串还剩下 aba。
- 机器在 $N_{aba}$ 子模块中,依次匹配 a, b, a。
- 最终,机器恰好在消耗完所有输入的同时,到达了整个 NFA 的最终接受状态。
- 因此,字符串 aababa 被接受。
- 省略的步骤: 图中为了简洁,没有画出最基础的 a 和 b 的 NFA,而是直接从 a U b 开始。在实际操作时,第一步总是从最原子的元素开始。
- 状态的唯一性: 在画图时,虽然我们复用了 a 和 b 的 NFA 概念,但在一个最终的 NFA 中,每个状态都应该是唯一的。例如,aba 中的两个 a 弧,它们连接的是完全不同的状态。
- 理解连接点: 理解 $\varepsilon$-转移在“连接处”的作用是关键。它像一个胶水,把两个独立的 NFA 模块粘合在一起,允许计算流从一个模块无缝地传递到下一个模块。
示例 1.58 进一步强化了 Thompson's Construction 算法 的应用。它通过构造一个更复杂的正则表达式 $(\mathrm{a} \cup \mathrm{b})^{*} \mathrm{aba}$ 的 NFA,展示了如何处理一个由星号、并和多次连接组合而成的序列。该示例清晰地表现了如何将正则表达式分解成主要部分(这里是 (a U b)* 和 aba),分别构造它们的 NFA,然后使用连接规则将这些大的子模块“焊接”在一起,形成最终的 NFA。
这个例子的目的是展示 Thompson's Construction 的通用性和模块化特性。它告诉我们,无论正则表达式看起来多长多复杂,我们总能将其分解为几个主要部分的连接,或者一个部分的并,或者一个部分的星号。通过为每个部分(递归地)构建 NFA,然后像组装零件一样将它们组合起来,我们总能得到最终的结果。这为算法的正确性和普适性提供了强有力的直观证据。
这个过程就像写一个复杂的程序函数。
- 正则表达式: process_data(data)
- 分解: result1 = step1_loop(data),然后 final_result = step2_process_fixed_pattern(result1)。
- (a U b)* 的 NFA: 就像一个 while 循环或者 for 循环模块 step1_loop,它可以处理任意长度的输入。
- aba 的 NFA: 就像一个 if-else 链或者 switch 语句 step2_process_fixed_pattern,它严格匹配一个固定的模式。
- 最终的 NFA: 就是将这两个函数调用顺序地连接起来。step1_loop 的输出作为 step2 的输入。在 NFA 中,这种“连接”是通过 $\varepsilon$-转移实现的。
想象一个闯关游戏的两段连续关卡。
- 第一段关卡 (对应 (a U b)*): 一个广阔的迷宫。里面有无数的 'a' 房间和 'b' 房间,你可以随意穿行,任意走动(匹配任意 a 和 b 的组合),甚至可以直接找到一个传送门跳过整个迷宫(匹配 $\varepsilon$)。迷宫的出口就是通往第二段关卡的门。
- 第二段关卡 (对应 aba): 一条笔直的走廊。上面依次有三道门,分别需要 'a' 钥匙,'b' 钥匙,和 'a' 钥匙才能打开。必须严格按顺序通过。
- 整个游戏: 玩家必须先成功走出迷宫(匹配 (a U b)* 部分),然后立刻进入走廊,并按顺序用 aba 三把钥匙通过。最终能到达终点的玩家,其行走路径(输入的字符串)就属于语言 $L((\mathrm{a} \cup \mathrm{b})^{*} \mathrm{aba})$。
1.9 引理 1.60:从 NFA 到正则表达式
📜 [原文13]
现在让我们转向定理 1.54 证明的另一个方向。
引理 1.60
如果一个语言是正则语言,那么它被正则表达式描述。
证明思路 我们需要证明如果一个语言 $A$ 是正则语言,那么一个正则表达式描述它。因为 $A$ 是正则语言,它被一个 DFA 接受。我们描述一个将 DFA 转换为等价正则表达式的过程。
我们将此过程分为两部分,使用一种新型的有限自动机,称为广义非确定型有限自动机 (GNFA)。首先,我们展示如何将 DFA 转换为 GNFA,然后将 GNFA 转换为正则表达式。
这是定理 1.54 第二个方向的证明,也是更难、更具技巧性的一个。它旨在说明,任何正则语言(即任何能被 DFA 识别的语言)都可以用一个正则表达式来描述。
- 证明的逻辑链
- 前提: 我们有一个正则语言 $A$。
- 根据正则语言的定义: 存在一个 DFA (确定型有限自动机) $M$,它能识别语言 $A$ (即 $L(M) = A$)。
- 目标: 找到一个正则表达式 $R$,使得 $L(R) = A$。
- 证明策略: 我们需要一个算法,这个算法的输入是一个 DFA,输出是一个等价的正则表达式。
- 引入一个中间工具:GNFA
- 直接从 DFA 转换到正则表达式在思路上比较困难。作者在这里引入了一个非常聪明的中间步骤——广义非确定型有限自动机 (Generalized Nondeterministic Finite Automaton, GNFA)。
- 这个转换过程被分成了两步,使得每一步都更容易处理:
- 第一步: 将输入的 DFA 转换成一个特定形式的 GNFA。这一步相对直接,主要是格式上的调整。
- 第二步: 通过一个递归的状态消除过程,将这个 GNFA 逐步简化,直到它变成一个非常简单的 GNFA,其等价的正则表达式可以被直接读出。这是整个证明的核心和难点。
- 什么是 GNFA?
- 广义 (Generalized) 这个词是关键。它“广义”在什么地方?
- 转移箭头的标签:
- 在普通的 NFA 或 DFA 中,状态之间的转移箭头上的标签只能是一个单一的字符 (来自字母表 $\Sigma$),或者是 $\varepsilon$。
- 在 GNFA 中,转移箭头上的标签可以是任何一个正则表达式!
- 工作方式:
- 普通的 NFA 一次只“消耗”一个字符(或不消耗,对于 $\varepsilon$)。
- GNFA 在从状态 A 移动到状态 B 时,可以一次性“消耗”掉输入字符串中的一个子串。这个子串必须是箭头标签上的正则表达式所描述的语言中的一员。
- 例子: 如果从状态 $q_1$ 到 $q_2$ 的箭头上标签是正则表达式 (ab)*c,那么 GNFA 可以从 $q_1$ 开始,在读完输入字符串中的 ababc 这个子串后,直接到达状态 $q_2$。
- 两步走战略的优势
- DFA -> GNFA: 这一步是“升维”。我们把简单的、只带字符标签的 DFA,变成一个复杂的、带正则表达式标签的 GNFA。这看起来似乎把问题搞复杂了,但实际上是为了第二步做准备。在这一步,原 DFA 的字符标签 a 会被看作是正则表达式 a。
- GNFA -> 正则表达式: 这一步是“降维”。我们通过不断地“消除状态”,把一个有 N 个状态的 GNFA 变成一个等价的、只有 N-1 个状态的 GNFA。每消除一个状态,我们就把经过它的路径信息,通过正则运算(并、连接、星号)“合并”到保留下来的状态之间的箭头的正则表达式标签上。这个过程一直持续,直到 GNFA 只剩下起始状态和接受状态。此时,从起始状态到接受状态的唯一箭头上的那个(可能非常复杂的)正则表达式,就是我们最终要找的答案。
- 示例: 从 DFA 到 GNFA 的初步转换 (概念)
- DFA 中: 从 $q_1$到 $q_2$ 有一条标记为 a 的边,还有一条标记为 b 的边。
- 转换到 GNFA: 为了让 GNFA 结构更统一(任意两个状态间只有一个方向的一条边),我们会把这两条边合并成一条。新的边从 $q_1$ 指向 $q_2$,它的标签是正则表达式 a U b。这个新的正则表达式标签包含了原来两条边的所有路径信息。
- DFA 中: 从 $q_3$ 到 $q_4$ 没有边。
- 转换到 GNFA: 我们会在 $q_3$ 和 $q_4$ 之间添加一条边,其标签是正则表达式 ∅。因为没有任何字符串属于语言 $L(\emptyset)$,所以这条边实际上是无法通行的,这等价于原来没有边。
- GNFA 是一个工具,不是一个新的计算模型类别: GNFA 只是为了这个证明而引入的辅助工具。它和 NFA、DFA 的计算能力是等价的(都是正则语言)。不要把它看成是比 NFA 更强大的模型。
- 状态消除的顺序: 在将 GNFA 转换为正则表达式的过程中,消除状态的顺序可以是任意的(只要不是起始和最终接受状态)。不同的消除顺序可能会得到不同形式、但语言等价的正则表达式。
- 证明的构造性: 这个证明也是构造性的。它提供了一个明确的算法。这意味着,只要你给我任何一个 DFA,我都可以按照这个菜谱,一步步地计算出对应的正则表达式。
本段介绍了定理 1.54 的第二个证明方向(引理 1.60)的总体策略。该策略旨在证明任何正则语言(由一个 DFA 接受)都可以被一个正则表达式描述。为了实现从 DFA 到正则表达式的转换,作者引入了一个中间工具——广义非确定型有限自动机 (GNFA),其转移箭头上可以标记任意正则表达式。整个证明过程被分解为两个主要步骤:首先,将给定的 DFA 规范化成一个特定形式的 GNFA;其次,通过一个递归的状态消除算法,逐步将 GNFA 简化,直至可以直接读出等价的正则表达式。
本段的目的是为整个证明过程中最复杂的部分搭建一个清晰的脚手架。通过明确“两步走”的策略并引入 GNFA 这个关键概念,它让读者对即将到来的复杂算法有了一个宏观的认识。它回答了“我们该如何从一个图(DFA)得到一个代数式(正则表达式)”这个核心问题,其答案是“通过一个中间的、允许图和代数式混合的表示(GNFA),并逐步将图的部分消除,最终只剩下代数式”。
这个过程就像解一个复杂的多元一次方程组。
- DFA: 原始的方程组,每个状态是一个变量,每个转换是一条方程。
- GNFA: 仍然是方程组,但我们允许系数是更复杂的表达式(正则表达式)。
- 状态消除过程: 这就像代数中的“消元法”。我们选择一个变量(状态),通过代入和化简,将这个变量从所有方程中消除。这个过程会导致其他方程的系数(其他边的正则表达式)变得更加复杂。
- 重复消元: 我们不断地重复这个过程,每次减少一个变量(状态)。
- 最终结果: 当方程组只剩下一个变量(比如从起点到终点)时,它的系数就是我们要求的解(最终的正则表达式)。
想象你在解决一个城市交通问题。
- DFA: 一张详细的城市地图,上面有成百上千个路口(状态),和单行道(转换)。
- 目标: 你想用一句话(一个正则表达式)来描述从你家(起始状态)到公司(接受状态)的所有可能路线。
- 状态消除: 这个过程就像“城市规划改造”。
- 你选择一个路口(比如市中心广场)进行改造,将它“铲平”(消除状态)。
- 为了不影响交通,你必须修建新的“立交桥”(更新正则表达式)。比如,原来从A点必须经过广场才能到B点,现在你修了一座从A直达B的立交桥。这座“立交桥”的通行规则(新的正则表达式)会比原来走地面道路更复杂,因为它必须包含所有原来可以经过广场的走法。
- 你不断地“铲平”路口并修建更复杂的“立交桥”。
- 最终,整个城市只剩下你家和公司两个点,以及一座巨大、复杂的“超级立交桥系统”(最终的正则表达式),这座系统包含了原来城市中所有从你家到公司的可能路径。
1.10 GNFA 的定义与转换过程
📜 [原文14]
广义非确定型有限自动机只是非确定型有限自动机,其中转移箭头可以有任何正则表达式作为标签,而不是仅仅是字母表的成员或 $\varepsilon$。GNFA 从输入中读取符号块,不一定像普通 NFA 那样一次只读取一个符号。GNFA 通过读取输入中的符号块,沿着连接两个状态的转移箭头移动,这些符号块本身构成了一个由该箭头上的正则表达式描述的字符串。GNFA 是非确定型的,因此可能有几种不同的方法来处理相同的输入字符串。如果其处理能够使 GNFA 在输入结束时处于接受状态,则它接受其输入。下图展示了一个 GNFA 的示例。
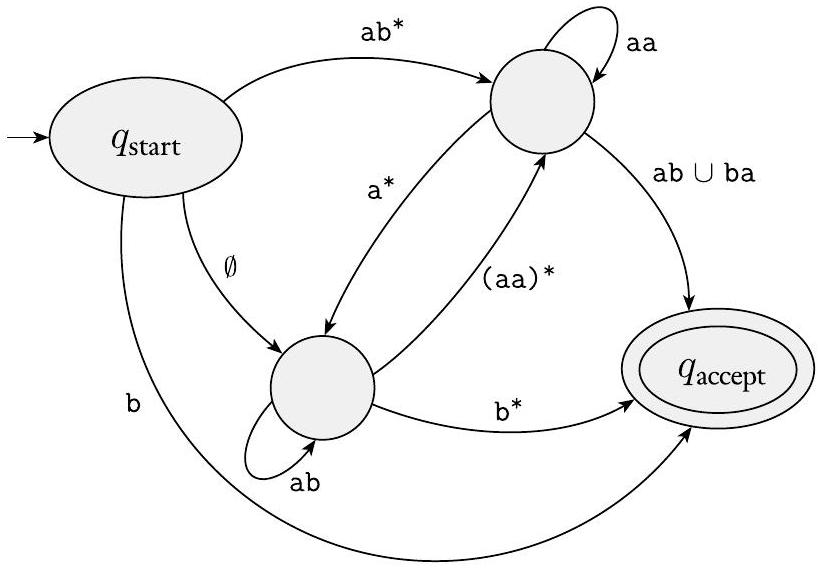
图 1.61
一个广义非确定型有限自动机
为方便起见,我们要求 GNFA 始终具有满足以下条件的特殊形式。
- 起始状态有指向所有其他状态的转移箭头,但没有从任何其他状态进入的箭头。
- 只有一个接受状态,它有从所有其他状态进入的箭头,但没有指向任何其他状态的箭头。此外,接受状态与起始状态不同。
- 除了起始状态和接受状态外,每个状态到每个其他状态以及每个状态到自身都有一条箭头。
我们可以很容易地将 DFA 转换为特殊形式的 GNFA。我们只需添加一个带 $\varepsilon$ 箭头的新起始状态到旧的起始状态,以及一个带 $\varepsilon$ 箭头的新接受状态从旧的接受状态。如果任何箭头有多个标签(或者在两个状态之间有多个指向同一方向的箭头),我们用一个标签是先前标签的并的单一箭头替换每个箭头。最后,我们在没有箭头的状态之间添加标记为 $\emptyset$ 的箭头。这最后一步不会改变所识别的语言,因为标记为 $\emptyset$ 的转移永远不会被使用。从现在开始,我们假设所有 GNFA 都处于特殊形式。
本段详细定义了 GNFA 及其为了方便转换而规定的“特殊形式”,并说明了如何将一个普通的 DFA 转换成这种特殊形式的 GNFA。这是 DFA -> 正则表达式 转换算法的第一步。
- GNFA 的核心特征
- 标签是正则表达式: 这是它与 NFA 最根本的区别。NFA 的边上是单个字符或 $\varepsilon$,而 GNFA 的边上可以是任意复杂的正则表达式,如 (a|b)* 或 a(b|c)d。
- 消耗符号块: 当 GNFA 沿着一条边从 $q_i$ 移动到 $q_j$ 时,它不是消耗一个字符,而是消耗一个“符号块”,即一个字符串。这个被消耗的字符串 $w$ 必须是边上正则表达式 $R$ 所描述的语言 $L(R)$ 的一员。
- 非确定性: 与 NFA 类似,GNFA 也是非确定型的。这意味着对于一个输入字符串,可能有多条计算路径。例如,如果输入是 ab,一条边是 a,另一条是 ab,机器可以“猜测”走哪条路。只要存在至少一条合法的路径能让机器在消耗完整个输入后到达接受状态,该输入就被接受。
- 图 1.61 示例解读
- 这个 GNFA 有三个状态:$q_{start}$, $q_1$, $q_{accept}$。
- 从 $q_{start}$ 到 $q_1$ 的边标签是 (a U b)*。这意味着机器可以消耗任意 a,b 串,从 $q_{start}$ 到达 $q_1$。
- $q_1$ 有一个自循环,标签是 a。这意味着在 $q_1$ 时,可以消耗一个 a 然后回到 $q_1$。
- 从 $q_1$ 到 $q_{accept}$ 的边标签是 b。这意味着必须消耗一个 b 才能从 $q_1$ 到达接受状态。
- 这个 GNFA 接受什么语言?
- 一个字符串要被接受,必须能从 $q_{start}$ 走到 $q_{accept}$。
- 路径是 $q_{start} \rightarrow q_1 \rightarrow \dots \rightarrow q_1 \rightarrow q_{accept}$。
- $q_{start} \rightarrow q_1$:消耗一个字符串 $w_1 \in L((a \cup b)^*)$。
- $q_1 \rightarrow \dots \rightarrow q_1$:在 $q_1$ 循环 $k$ 次,消耗 $k$ 个 a,即字符串 $a^k$。
- $q_1 \rightarrow q_{accept}$:消耗一个 b。
- 所以,被接受的字符串的结构是 $w_1 \circ a^k \circ b$。其中 $w_1$ 是任意 a,b 串,$k \geq 0$。
- $w_1 \circ a^k$ 的组合实际上还是一个任意的 a,b 串。
- 所以这个 GNFA 接受的语言是所有以 b 结尾的字符串,即 $L((a \cup b)^*b)$。
- GNFA 的“特殊形式” (Canonical Form)
- 为了让后续的“状态消除”算法能够统一、方便地进行,我们对 GNFA 的结构做了一些严格的规定。这就像在解方程前,我们先把所有方程都整理成“标准形式”。
- 规则 1 (起始状态): 有一个唯一的起始状态,它只出不进。即,有从它出发到所有其他状态的边,但没有任何边指向它。这确保了计算总有一个干净的起点。
- 规则 2 (接受状态): 只有一个唯一的接受状态,它只进不出。即,有从所有其他状态指向它的边,但没有从它出发的边。这确保了计算总有一个明确的终点。并且,起始状态和接受状态不能是同一个状态。
- 规则 3 (全连接): 除了起始和接受状态,任何两个状态 $q_i, q_j$ 之间都有一条从 $q_i$到 $q_j$ 的边(包括 $q_i$ 到自身的自循环边)。这保证了我们在进行状态消除时,总能找到需要更新的边,算法逻辑可以统一。
- 将 DFA 转换为特殊形式的 GNFA
- 这是转换算法的第一步,非常程序化。
- 步骤 1 (添加新起点/终点):
- 在原 DFA 的基础上,创建一个全新的起始状态 $q_{start\_new}$。从 $q_{start\_new}$ 画一条 $\varepsilon$-转移边到原 DFA 的起始状态。
- 创建一个全新的接受状态 $q_{accept\_new}$。从原 DFA 的所有接受状态画 $\varepsilon$-转移边到 $q_{accept\_new}$。
- 这样就满足了“只出不进”的起点和“只进不出”的终点规则。
- 步骤 2 (合并多重边):
- 在原 DFA 中,如果从状态 A 到状态 B 有多条边(例如,NFA 中可能出现),比如一条标 a,一条标 b。在 GNFA 中,我们将它们合并成一条边,其标签是原标签的并,即 a U b。
- 步骤 3 (添加缺失边):
- 为了满足“全连接”规则,检查任意两个状态之间是否缺少边。如果从 $q_i$ 到 $q_j$ 没有边,就添加一条,并标记为 ∅。
- 为什么标记 ∅?因为 $L(\emptyset) = \{\}$,没有任何字符串属于这个语言,所以这条边在计算中永远不会被走到。这在逻辑上等价于“没有边”。
- 经过这三步,任何 DFA(或 NFA)都可以被转换成一个行为完全等价的、满足特殊形式的 GNFA。
- 示例: 将一个简单的 DFA 转换为特殊形式的 GNFA
- DFA:
- 状态: $q_0$ (起始), $q_1$ (接受)
- 转换: $\delta(q_0, a) = q_0$, $\delta(q_0, b) = q_1$, $\delta(q_1, a) = q_1$, $\delta(q_1, b) = q_0$
- 这个 DFA 接受所有包含奇数个 b 的字符串。
- 转换为 GNFA:
- 添加新起点/终点:
- 创建新起点 $S$,新终点 $A$。
- 添加边: $S \xrightarrow{\varepsilon} q_0$, $q_1 \xrightarrow{\varepsilon} A$。
- 合并/转换标签:
- 原 $q_0 \xrightarrow{a} q_0$ 变为 $q_0 \xrightarrow{a} q_0$ (标签 a 视为正则表达式 a)。
- 原 $q_0 \xrightarrow{b} q_1$ 变为 $q_0 \xrightarrow{b} q_1$。
- 原 $q_1 \xrightarrow{a} q_1$ 变为 $q_1 \xrightarrow{a} q_1$。
- 原 $q_1 \xrightarrow{b} q_0$ 变为 $q_1 \xrightarrow{b} q_0$。
- 添加缺失边 (标记为 ∅):
- $S$ 到 $q_1, A$ 的边: $S \xrightarrow{\emptyset} q_1, S \xrightarrow{\emptyset} A$。
- $q_0$到 $A$ 的边: $q_0 \xrightarrow{\emptyset} A$。
- $q_1$到 $S$ 的边: (没有到起点的边)。
- ... 等等,所有原来没有连接的地方都用 ∅ 补上。
- 最终我们得到一个 4 状态的 GNFA ($S, q_0, q_1, A$),它满足所有特殊形式的规定,并且接受的语言与原 DFA 相同。
- 为什么要特殊形式: 如果没有特殊形式,状态消除算法会变得非常复杂,需要处理各种边界情况(比如消除的是起始状态怎么办?消除的状态和其他状态没有完全连接怎么办?)。特殊形式将所有这些情况都统一了。
- $\varepsilon$ 和 $\emptyset$ 的使用: 在 DFA -> GNFA 的转换中,$\varepsilon$ 和 $\emptyset$ 这两个特殊的正则表达式扮演了关键角色。$\varepsilon$ 用于“无损”地连接新旧起点/终点,而 $\emptyset$ 用于“无害”地补全图的结构。
- 接受状态与起始状态不能相同: 这个规定是为了简化算法的终止条件。如果它们是同一个,算法在只剩一个状态时会很尴尬。通过一开始就添加新起点和新终点,保证了它们在整个过程中都是分离的。
本段首先详细定义了广义非确定型有限自动机 (GNFA),阐明其核心特征是转移箭头的标签可以是任意正则表达式。接着,为了简化后续的转换算法,它提出了一种GNFA的“特殊形式”,要求机器有唯一的、只出不进的起始状态,唯一的、只进不出的接受状态,并且内部状态之间是全连接的。最后,本段给出了一个清晰的、程序化的三步方法,用于将任何一个 DFA 转换为一个等价的、满足这种特殊形式的 GNFA。这个转换是整个 DFA -> 正则表达式 证明的第一步。
本段的目的是为后续核心的“状态消除”算法准备好一个标准化的、易于处理的输入。通过将各种不规则的 DFA 都统一转换成同一种“特殊形式”的 GNFA,后续的算法就可以不必再考虑各种烦人的边界情况,只需专注于核心的状态消除和正则表达式更新逻辑。这是一种典型的“预处理”思想,在算法设计中非常常见。
这个过程就像做一道菜前的“备料”阶段。
- DFA: 各种形状不一的蔬菜(胡萝卜、土豆、青椒)。
- 特殊形式的 GNFA: 所有蔬菜都被切成了统一大小的方块。
- 转换过程: 就是“切菜”的过程。
- 添加新起点/终点: 就像在切菜板两边放上“生料碗”和“熟料碗”。
- 合并多重边: 如果胡萝卜和土豆都要下锅,就把它们放在同一个盘子里,标记为“混合蔬菜”。
- 添加 ∅ 边: 为了让工作台看起来整齐,任何两个没有菜的盘子之间,你都放一个空的“占位盘”。
- 目的: 把原料都处理成标准化的样子,下一步的“炒菜”(状态消除)步骤就可以用同一个动作来处理所有食材,而不用考虑它是胡萝卜还是土豆。
想象你在组织一次会议的座位安排。
- DFA: 一个随意的座位图,人们可以随便坐。
- 特殊形式的 GNFA: 一个非常正式的、有严格规定的座位图。
- 转换过程:
- 添加新起点/终点: 在门口安排一个“迎宾员”(新起点),在主席台安排一个“主持人”(新终点)。迎宾员负责引导“主讲人”(原起点)入场,所有发言完毕的人都要到主持人那里报道。
- 合并多重边: 如果 A 和 B 之间可以谈论“话题1”也可以谈论“话题2”,现在规定他们之间只有一个交流通道,通道上标记着“可以谈论话题1或话题2”。
- 添加 ∅ 边: 为了保证结构完整,规定任何两个人之间都必须有一个“名义上的”交流通道。如果他们实际上没什么好谈的,就在通道上标记“禁止交流”(∅)。
经过这番改造,座位图变得非常规整,便于下一步进行更复杂的操作。
1.11 状态消除算法
📜 [原文15]
现在我们展示如何将 GNFA 转换为正则表达式。假设 GNFA 有 $k$ 个状态。那么,因为 GNFA 必须有一个起始状态和一个接受状态,并且它们必须彼此不同,我们知道 $k \geq 2$。如果 $k>2$,我们构造一个具有 $k-1$ 个状态的等价 GNFA。此步骤可以在新的 GNFA 上重复,直到它减少到两个状态。如果 $k=2$,GNFA 有一个从起始状态到接受状态的单一箭头。此箭头的标签就是等价的正则表达式。例如,将一个三状态 DFA 转换为等价正则表达式的阶段如下图所示。
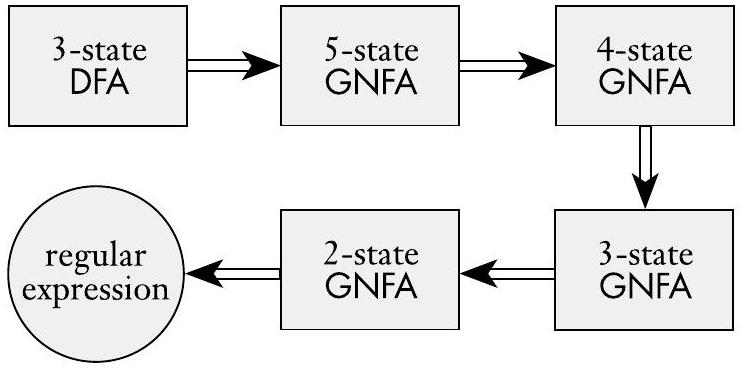
图 1.62
将 DFA 转换为正则表达式的典型阶段
关键步骤是当 $k>2$ 时,构造一个状态更少一个的等价 GNFA。我们通过选择一个状态,将其从机器中移除,并修复其余部分,以便仍然识别相同的语言来实现。任何状态都可以,只要它不是起始状态或接受状态。我们保证这样的状态将存在,因为 $k>2$。我们称被移除的状态为 $q_{\text {rip}}$。
移除 $q_{\text {rip}}$ 后,我们通过修改标记每个剩余箭头的正则表达式来修复机器。新的标签弥补了 $q_{\text {rip}}$ 的缺失,通过添加回丢失的计算。从状态 $q_{i}$ 到状态 $q_{j}$ 的新标签是一个正则表达式,它描述了所有可以直接或通过 $q_{\text {rip}}$ 将机器从 $q_{i}$ 带到 $q_{j}$ 的字符串。我们将在图 1.63 中说明这种方法。
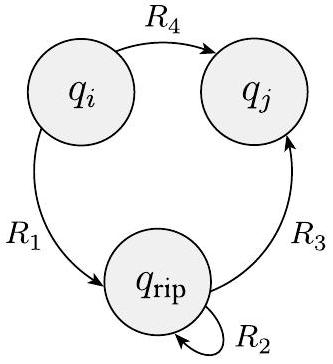
之前
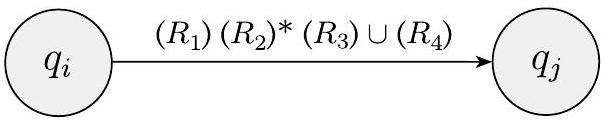
之后
图 1.63
构造一个状态更少一个的等价 GNFA
在旧机器中,如果
- $q_{i}$ 通过标记为 $R_{1}$ 的箭头到 $q_{\mathrm{rip}}$,
- $q_{\text {rip }}$ 通过标记为 $R_{2}$ 的箭头到自身,
- $q_{\text {rip }}$ 通过标记为 $R_{3}$ 的箭头到 $q_{j}$,并且
- $q_{i}$ 通过标记为 $R_{4}$ 的箭头到 $q_{j}$,
那么在新机器中,从 $q_{i}$ 到 $q_{j}$ 的箭头将获得标签
我们为从任何状态 $q_{i}$ 到任何状态 $q_{j}$ 的每个箭头进行此更改,包括 $q_{i}=q_{j}$ 的情况。新机器识别原始语言。
这是整个 DFA -> 正则表达式 证明的核心算法:状态消除法。它描述了一个递归过程,通过不断减少 GNFA 的状态数量,最终得到一个只含起始和接受状态的二状态 GNFA,从而直接读出等价的正则表达式。
- 算法的总体流程 (递归)
- 输入: 一个有 $k$ 个状态的、处于“特殊形式”的 GNFA。
- 终止条件 (Base Case): 如果 $k=2$,那么这个 GNFA 只剩下起始状态 $q_{start}$ 和接受状态 $q_{accept}$。由于是特殊形式,它们之间只有一条从 $q_{start}$ 到 $q_{accept}$ 的边。这条边上的正则表达式 $R$ 就描述了从起点到终点的所有路径。因此,这个 $R$ 就是我们要求的最终结果。算法结束。
- 递归步骤 (Recursive Step): 如果 $k > 2$,执行以下操作:
- 选择: 从 GNFA 中选择一个“待消除”的状态 $q_{rip}$。这个状态不能是起始状态或接受状态。因为 $k>2$,所以这样的状态一定存在。
- 转换: 创建一个新的、$k-1$ 个状态的 GNFA。这个新 GNFA 中不包含 $q_{rip}$。
- 修复: 为了补偿 $q_{rip}$ 的消失,需要更新新 GNFA 中所有剩余的边的标签。
- 递归: 对这个新的、$k-1$ 状态的 GNFA,重新调用本算法。
- 核心操作:修复边的标签 (状态消除公式)
- 这是整个算法最关键的部分。当我们把状态 $q_{rip}$ 从图中“撕掉”后,原来所有经过 $q_{rip}$ 的路径都断了。我们需要通过修改其他边的标签,把这些断掉的路径信息“嫁接”回去。
- 考虑任意一对剩下的状态 $q_i$ 和 $q_j$($q_i$ 不能是接受状态,$q_j$ 不能是起始状态)。我们要计算从 $q_i$ 到 $q_j$ 的新标签。
- 原来的路径: 从 $q_i$ 到 $q_j$ 的路径有两种:
- 直接路径: 不经过 $q_{rip}$,直接从 $q_i$ 到 $q_j$。这条路径由原来的边 $q_i \xrightarrow{R_4} q_j$ 上的正则表达式 $R_4$ 描述。
- 间接路径: 必须经过 $q_{rip}$。这条路径可以分解为三步:
- 第一步: 从 $q_i$ 到 $q_{rip}$。由边 $q_i \xrightarrow{R_1} q_{rip}$ 描述。
- 第二步: 在 $q_{rip}$ 上“兜圈子”。$q_{rip}$ 可能有一个自循环边 $q_{rip} \xrightarrow{R_2} q_{rip}$。计算流可以在这里循环 0 次或任意多次。这个循环过程由正则表达式 $(R_2)^*$ 描述。
- 第三步: 从 $q_{rip}$ 到 $q_j$。由边 $q_{rip} \xrightarrow{R_3} q_j$ 描述。
- 将这三步连接起来,就构成了所有经过 $q_{rip}$ 一次(或一连串循环)的路径,由正则表达式 $(R_1)(R_2)^*(R_3)$ 描述。
- 新标签的组合: 新的从 $q_i$到 $q_j$ 的路径,可以是原来的直接路径,或者是新的间接路径。在正则表达式中,“或者”就是并运算 $\cup$。
- 最终公式:
- $R_1$: 从 $q_i$ 到 $q_{rip}$ 的旧标签。
- $R_2$: 从 $q_{rip}$ 到 $q_{rip}$ 的旧标签(自循环)。
- $R_3$: 从 $q_{rip}$ 到 $q_j$ 的旧标签。
- $R_4$: 从 $q_i$ 到 $q_j$ 的旧标签。
- 重要: 这个更新公式需要对所有可能的 $q_i, q_j$ 组合($q_i \neq q_{accept}, q_j \neq q_{start}$)都执行一遍,包括 $q_i = q_j$ 的情况(即更新自循环边的标签)。
- 图 1.62 和 1.63 的解读
- 图 1.62: 宏观地展示了整个流程。从一个多状态的 DFA 开始,首先转换为一个 $k$ 状态的 GNFA (这里 $k=3+2=5$,但图中简化了,假设为4),然后消除一个状态变成 $k-1=3$ 状态的 GNFA,最后再消除一个状态,变成 $k-2=2$ 状态的 GNFA。在这个最终的 2 状态 GNFA 中,从起点到终点的边上就是最终的正则表达式。
- 图 1.63: 微观地展示了单次状态消除的核心操作。它直观地画出了公式的来源:从 $q_i$ 到 $q_j$ 的新路径,等于老路径 $R_4$ 加上那条绕道 $q_{rip}$ 的新路径。
- 状态消除公式:
- $R_4$: 这部分代表了“保守”的选择,即不使用被移除的 $q_{rip}$,直接走原来的老路。
- $(R_1)(R_2)^*(R_3)$: 这部分代表了所有“必须利用”被移除的 $q_{rip}$ 的新路径。
- $R_1$: "进入" $q_{rip}$ 的路径。
- $(R_2)^*$: "在" $q_{rip}$ 内部循环任意次的路径。这至关重要,因为计算流可能在 $q_{rip}$ 处多次往返才离开。星号完美地捕捉了“0次或多次循环”这个行为。
- $R_3$: "离开" $q_{rip}$ 的路径。
- $\cup$: 最后的并运算将“走老路”和“走新路”这两种可能性合并起来,确保了新 GNFA 的行为等价于旧 GNFA。
- 示例: 假设我们要消除 $q_{rip}$,并计算从 $q_1$ 到 $q_2$ 的新标签。
- 旧的标签:
- $q_1 \xrightarrow{a} q_{rip}$ (所以 $R_1 = a$)
- $q_{rip} \xrightarrow{b} q_{rip}$ (所以 $R_2 = b$)
- $q_{rip} \xrightarrow{c} q_2$ (所以 $R_3 = c$)
- $q_1 \xrightarrow{d} q_2$ (所以 $R_4 = d$)
- 应用公式:
$R_{new} = (R_1)(R_2)^*(R_3) \cup (R_4) = (a)(b)^*(c) \cup (d) = ab^*c \cup d$
- 解释: 新的从 $q_1$ 到 $q_2$ 的边,可以匹配字符串 d(走老路),也可以匹配任何形如 ac, abc, abbc, ... 的字符串(走绕道 $q_{rip}$ 的新路)。
- 示例 2 (如果 R4 不存在):
- 旧的标签: 假设从 $q_1$ 到 $q_2$ 原来没有直接的边。根据特殊形式的规定,这条边应该标记为 ∅。所以 $R_4 = \emptyset$。
- 应用公式:
$R_{new} = (a)(b)^*(c) \cup (\emptyset) = ab^*c \cup \emptyset$
- 根据恒等式 $R \cup \emptyset = R$,上式可以简化为 $R_{new} = ab^*c$。
- 解释: 这很符合直觉。如果原来没有直达的路,那么消除 $q_{rip}$ 后,所有从 $q_1$ 到 $q_2$ 的路就必须经过 $q_{rip}$。
- $R_2 = \emptyset$: 如果 $q_{rip}$ 没有自循环,那么 $R_2 = \emptyset$。此时 $(R_2)^* = (\emptyset)^* = \varepsilon$。公式简化为 $R_{new} = (R_1)(\varepsilon)(R_3) \cup (R_4) = R_1R_3 \cup R_4$。
- $R_1, R_3$ 或 $R_4$ 为 $\emptyset$: 如果任意一条进入、离开或直达的路径不存在,对应的 $R$ 就是 $\emptyset$。在代入公式时要特别注意,因为 $\emptyset$ 在连接中有“吞噬”作用 ($R \circ \emptyset = \emptyset$)。
- 更新所有边: 在消除一个状态后,必须计算所有剩下节点对 $(q_i, q_j)$ 之间的新标签,不能遗漏。
- 选择哪个 $q_{rip}$: 理论上,选择任何一个非起始/接受状态都可以。但在手动计算时,选择一个连接较少的“简单”状态来消除,可以使计算过程中的正则表达式不至于过早地变得异常复杂。
本段详细阐述了 GNFA -> 正则表达式 转换的核心算法:递归状态消除法。算法的流程是,如果 GNFA 状态多于2个,就选择一个中间状态 $q_{rip}$ 将其移除,并通过一个关键的更新公式 $R_{new} = (R_1)(R_2)^*(R_3) \cup (R_4)$ 来修复图中其余边的标签,以补偿被移除状态所承载的路径信息。这个过程不断递归进行,每次减少一个状态,直到 GNFA 只剩下起始和接受两个状态为止。此时,连接这两个状态的唯一箭头上的标签,就是与原始 DFA 等价的正则表达式。
本段的目的是提供一个从图模型(DFA/GNFA)到代数模型(正则表达式)的桥梁。这个状态消除算法是构造性的,它不仅证明了转换的可能性,还给出了一个具体的操作“配方”。它是计算理论中一个非常经典和巧妙的算法,完美地利用了正则表达式的三种运算(连接、星号、并)来概括和吸收被消除的状态的路径信息。
这个过程就像是在简化一个复杂的通信网络图。
- 状态: 城市。
- 边上的正则表达式: 两个城市间所有直达交通方式的描述(比如“可以坐火车,也可以坐飞机”)。
- 消除一个状态 $q_{rip}$: 假设我们要关闭城市 $q_{rip}$ 的中转功能。
- 更新标签: 对于原来从城市 $q_i$ 经过 $q_{rip}$ 到达 $q_j$ 的旅客,我们现在需要为他们提供新的“联程票”信息。
- $R_1$: 从 $q_i$ 到 $q_{rip}$ 的所有交通方式。
- $R_2$: 在 $q_{rip}$ 市内观光/换乘的所有方式。$(R_2)^*$ 表示可以观光任意久。
- $R_3$: 从 $q_{rip}$ 到 $q_j$ 的所有交通方式。
- $R_4$: 原来从 $q_i$ 直达 $q_j$ 的所有交通方式。
- 新标签: 新的从 $q_i$ 到 $q_j$ 的“交通总览”就是:“你可以继续走原来的直达方式($R_4$),或者($\cup$),你也可以选择我们新推出的、经由旧 $q_{rip}$ 地区的联运套餐($(R_1)(R_2)^*(R_3)$)”。
通过不断地关闭中转站并更新“联运套餐”,最终从起点到终点的唯一“总套餐”描述,就是最终的正则表达式。
想象你在手动解一个迷宫。你有一支红色的笔。
- 你找到迷宫中的一个岔路口(状态 $q_{rip}$),决定“消除”它。
- 你用红色笔,画出所有必须经过这个岔路口的新路径。比如,从路口A进入该岔路,然后从该岔路的路口B出去,你就在A和B之间直接画一条新的红线。
- 如果这个岔路口本身是个环岛($R_2$),那么你画的红线旁边就要标注“这里可以绕任意圈”。
- 画完所有经过该岔路口的新红线后,你就可以把这个岔路口从地图上涂掉了。
- 你不断重复这个过程,消除一个个岔路口,地图上的红线(正则表达式)会变得越来越复杂。
- 最终,地图上只剩下起点和终点,以及连接它们的一条极其复杂的红线。这条红线上所有的标注,就是最终的答案。
1.12 GNFA 的形式化定义与转换算法
📜 [原文16]
证明 现在我们正式执行这个想法。首先,为了方便证明,我们正式定义引入的新型自动机。GNFA 类似于非确定型有限自动机,除了转移函数,其形式为
符号 $\mathcal{R}$ 是字母表 $\Sigma$ 上所有正则表达式的集合,$q_{\text {start }}$ 和 $q_{\text {accept }}$ 是起始状态和接受状态。如果 $\delta\left(q_{i}, q_{j}\right)=R$,则从状态 $q_{i}$ 到状态 $q_{j}$ 的箭头以正则表达式 $R$ 作为标签。转移函数的域是 $\left(Q-\left\{q_{\text {accept }}\right\}\right) \times\left(Q-\left\{q_{\text {start }}\right\}\right)$,因为除了没有从 $q_{\text {accept }}$ 出发或指向 $q_{\text {start }}$ 的箭头外,每个状态都连接到每个其他状态。
定义 1.64
广义非确定型有限自动机是一个 5 元组 $\left(Q, \Sigma, \delta, q_{\text {start }}, q_{\text {accept }}\right)$,其中
- $Q$ 是有限状态集,
- $\Sigma$ 是输入字母表,
- $\delta:\left(Q-\left\{q_{\text {accept }}\right\}\right) \times\left(Q-\left\{q_{\text {start }}\right\}\right) \longrightarrow \mathcal{R}$ 是转移函数,
- $q_{\text {start }}$ 是起始状态,
- $q_{\text {accept }}$ 是接受状态。
如果 $w=w_{1} w_{2} \cdots w_{k}$,其中每个 $w_{i}$ 都在 $\Sigma^{*}$ 中,并且存在状态序列 $q_{0}, q_{1}, \ldots, q_{k}$ 使得
- $q_{0}=q_{\text {start }}$ 是起始状态,
- $q_{k}=q_{\text {accept }}$ 是接受状态,并且
- 对于每个 $i$,我们有 $w_{i} \in L\left(R_{i}\right)$,其中 $R_{i}=\delta\left(q_{i-1}, q_{i}\right)$;换句话说,$R_{i}$ 是从 $q_{i-1}$ 到 $q_{i}$ 的箭头上的表达式,则 GNFA 接受 $\Sigma^{*}$ 中的字符串 $w$。
这一部分提供了 GNFA 的严格数学定义,并形式化地描述了 GNFA 是如何“接受”一个字符串的。这是将前面直观的描述转化为严谨的数学语言的关键步骤。
- GNFA 的形式化五元组定义
- 与 DFA 和 NFA 类似,GNFA 也被定义为一个五元组 $\left(Q, \Sigma, \delta, q_{\text {start }}, q_{\text {accept }}\right)$。我们来逐项分析:
- 1. $Q$ (有限状态集): 与 NFA/DFA 相同,是一组有限的状态。
- 2. $\Sigma$ (输入字母表): 与 NFA/DFA 相同,是构成字符串的基本字符集。
- 3. $\delta$ (转移函数): 这是与 NFA/DFA 核心区别所在。
- 函数签名: $\delta:\left(Q-\left\{q_{\text {accept }}\right\}\right) \times\left(Q-\left\{q_{\text {start }}\right\}\right) \longrightarrow \mathcal{R}$
- 输入 (Domain): $\left(Q-\left\{q_{\text {accept }}\right\}\right) \times\left(Q-\left\{q_{\text {start }}\right\}\right)$
- 这是一个笛卡尔积,代表一个“状态对” $(q_{from}, q_{to})$。
- $q_{from}$ 可以是任何状态,但不能是接受状态 ($q_{\text {accept }}$)。这对应了“接受状态只进不出”的规则。
- $q_{to}$ 可以是任何状态,但不能是起始状态 ($q_{\text {start }}$)。这对应了“起始状态只出不进”的规则。
- 这个定义域精确地编码了我们对“特殊形式” GNFA 的结构要求。
- 输出 (Range): $\mathcal{R}$
- $\mathcal{R}$ 代表了在字母表 $\Sigma$ 上所有可能的正则表达式的集合。
- 这意味着,$\delta$ 函数的返回值不是一个状态或一个状态集,而是一个正则表达式。
- 含义: $\delta(q_i, q_j) = R$ 表示从状态 $q_i$ 到 $q_j$ 的边的标签是正则表达式 $R$。
- 4. $q_{start}$ (起始状态): 一个特殊指定的起始状态。
- 5. $q_{accept}$ (接受状态): 一个特殊指定的、唯一的接受状态。
- GNFA 的接受条件 (形式化定义)
- 这段定义了 GNFA 如何工作。一个字符串 $w$ 被 GNFA 接受,需要满足以下所有条件:
- 1. 字符串的分解: 字符串 $w$ 必须能够被分解成一连串的子字符串 $w_1, w_2, \dots, w_k$,即 $w = w_1w_2\dots w_k$。注意这里的 $w_i$ 不是单个字符,而是字符串。
- 2. 状态路径的存在性: 必须存在一个状态序列 $q_0, q_1, \dots, q_k$:
- 这个路径的起点必须是起始状态 ($q_0 = q_{start}$)。
- 这个路径的终点必须是接受状态 ($q_k = q_{accept}$)。
- 3. 每一步的合法性: 对于路径中的每一步(从 $q_{i-1}$ 到 $q_i$),对应的字符串块 $w_i$ 必须属于连接这两个状态的边上的正则表达式 $R_i = \delta(q_{i-1}, q_i)$ 所描述的语言。即,$w_i \in L(R_i)$。
- 总结: 如果我们能找到一种方法,把输入字符串 $w$ 切割成几段,并且能找到一条从起始状态到接受状态的状态路径,使得切割的每一段字符串都能被路径上对应步骤的边的正则表达式所匹配,那么字符串 $w$ 就被接受。
- 转移函数 $\delta$:
- $Q-\left\{q_{\text {accept }}\right\}$: 状态集 $Q$ 中除去接受状态 $q_{accept}$ 后的集合。这是所有可能的“出发”状态。
- $Q-\left\{q_{\text {start }}\right\}$: 状态集 $Q$ 中除去起始状态 $q_{start}$ 后的集合。这是所有可能的“到达”状态。
- $\times$: 笛卡尔积。表示从第一个集合取一个元素,从第二个集合取一个元素,组成一个有序对。
- $\longrightarrow$: 表示这是一个函数映射关系。
- $\mathcal{R}$: 所有正则表达式的集合。
- 示例: 使用定义 1.64 判断字符串 "aba" 是否被图 1.61 接受
- GNFA (图 1.61):
- $\delta(q_{start}, q_1) = (a \cup b)^*$
- $\delta(q_1, q_1) = a$
- $\delta(q_1, q_{accept}) = b$
- 目标: 判断 w = "aba" 是否被接受。
- 尝试寻找切割和路径:
- 尝试 1:
- 切割: $w_1 = "ab"$, $w_2 = "a"$. $w \neq w_1w_2$。失败。
- 尝试 2:
- 切割: $w_1 = "a"$, $w_2 = "b"$, $w_3 = "a"$. $w = w_1w_2w_3$。
- 寻找路径: $q_0, q_1, q_2, q_3$
- $q_0 = q_{start}$。
- 检查 $w_1 = "a"$: 是否 $a \in L(\delta(q_0, q_1))$?
- $R_1 = \delta(q_{start}, q_1) = (a \cup b)^*$。
- $a \in L((a \cup b)^*)$。是的。所以第一步合法,可以从 $q_{start}$ 到 $q_1$。
- 检查 $w_2 = "b"$: 是否 $b \in L(\delta(q_1, q_2))$?
- 这里 $q_2$ 是路径的下一个状态。我们可以让 $q_2 = q_{accept}$。
- $R_2 = \delta(q_1, q_{accept}) = b$。
- $b \in L(b)$。是的。所以第二步合法,可以从 $q_1$ 到 $q_{accept}$。
- 此时,路径是 $q_{start}, q_1, q_{accept}$,消耗了字符串 "ab"。但我们的输入是 "aba",字符串还没消耗完,但我们已经到了接受状态。根据定义,路径的终点必须是消耗完整个字符串后到达的。所以这个路径不匹配。
- 尝试 3:
- 切割: $w_1 = "a"$, $w_2 = "b"$, $w_3 = "a"$. 我们需要一条 4 状态的路径。
- 路径: $q_{start}, q_1, q_1, q_{accept}$ (在 $q_1$ 停留一次)。
- $q_0 = q_{start}$。
- 第一步: $w_1 = "a"$. $q_0 \rightarrow q_1$. $a \in L(\delta(q_{start}, q_1)) = L((a \cup b)^*)$。合法。
- 第二步: $w_2 = "b"$. $q_1 \rightarrow q_1$. $b \in L(\delta(q_1, q_1)) = L(a)$? 不,$b \notin \{a\}$。此路不通。
- 正确的路径和切割:
- 切割: $w_1 = "ab"$, $w_2 = "a"$.
- 路径: $q_{start}, q_1, q_{accept}$。
- 第一步: $w_1 = "ab"$. $q_{start} \rightarrow q_1$. $ab \in L((a \cup b)^*)$。合法。
- 第二步: $w_2 = "a"$. $q_1 \rightarrow q_{accept}$. $a \in L(\delta(q_1, q_{accept})) = L(b)$? 不。
- 结论: 看起来 "aba" 不被接受。让我们回顾一下图1.61的语言:以b结尾的串。 "aba" 不以b结尾。所以它确实不该被接受。
- 示例 2: 使用定义 1.64 判断字符串 "ab" 是否被图 1.61 接受
- 目标: 判断 w = "ab" 是否被接受。
- 切割: $w_1 = "a"$, $w_2 = "b"$.
- 路径: $q_0 = q_{start}, q_1, q_2 = q_{accept}$。
- 第一步: $w_1 = "a"$. $q_0 \rightarrow q_1$. $a \in L(\delta(q_{start}, q_1)) = L((a \cup b)^*)$。合法。
- 第二步: $w_2 = "b"$. $q_1 \rightarrow q_2$. $b \in L(\delta(q_1, q_{accept})) = L(b)$。合法。
- 检查: 字符串消耗完毕,且机器到达了接受状态 $q_{accept}$。
- 结论: 字符串 ab 被接受。
- w_i 可以是空字符串: 如果某条边上的正则表达式 $R$ 包含 $\varepsilon$ (例如 $R=a^*$),那么对应的 $w_i$ 可以是 $\varepsilon$。这意味着 GNFA 可以在不消耗任何输入的情况下,沿着这条边转移状态。
- 与 NFA 计算的区别: NFA 的计算是基于单个字符的,而 GNFA 的计算是基于字符串块的。要验证一个 GNFA 的计算,关键在于如何对输入字符串 w 进行“切分”,这是一个非确定性的选择。
- 定义域的严格性: $\delta$ 的定义域严格排除了到起始状态的转换和从接受状态出发的转换。这使得形式化的算法描述变得非常干净。
本段为广义非确定型有限自动机 (GNFA) 提供了严格的数学基础。它通过一个形式化的五元组定义,精确描述了 GNFA 的组成部分,特别是其独特的转移函数 $\delta$,该函数将一对状态映射到一个正则表达式。此外,它还形式化地定义了 GNFA 的“接受”条件:当且仅当一个输入字符串可以被分割成多个子串,并且存在一条从起始状态到接受状态的状态路径,使得每个子串都被路径上对应边的正则表达式所匹配时,该字符串被接受。这个形式化的框架是执行和证明后续状态消除算法正确性的必要前提。
在计算机科学理论中,从直观想法到形式化定义是至关重要的一步。本段的目的就是完成这个步骤。没有这个严谨的定义,后续的证明就会是空中楼阁,缺乏数学上的说服力。通过精确定义 GNFA 是什么以及它如何工作,我们为状态消除算法的每一步都提供了可以严格引用的依据,从而确保整个证明的逻辑链是完整和可靠的。
GNFA 的接受定义就像一个“多段接力旅行”的签证检查。
- 输入字符串 w: 你的整个旅行计划,比如从北京到纽约。
- 状态: 途中的各个机场(状态)。北京是起始状态,纽约是接受状态。
- w 的切割: 你将整个旅行分成几段:北京->东京, 东京->洛杉矶, 洛杉矶->纽约。这对应 $w = w_1w_2w_3$。
- 边的正则表达式: 每一段航程的“签证要求”。比如北京->东京的边上写着“需要日本签证”($R_1$),东京->洛杉矶的边上写着“需要美国签证”($R_2$)。
- $w_i \in L(R_i)$: 你的护照(子串 $w_i$)必须符合该段航程的签证要求(正则表达式 $R_i$)。
- 接受: 只有当你能规划出一条航线(状态序列),并且你的护照能满足每一段航程的签证要求,最终成功抵达纽约,你的整个旅行计划(字符串 w)才被认为是“合法的”(被接受)。
想象一个电脑游戏里的“组合技能”系统。
- 输入字符串: 你在键盘上按下的按键序列,比如 A-A-B-C。
- GNFA 状态: 你的人物当前所处的“架势”(stance)。比如“防御姿态”、“攻击姿态”。
- 边上的正则表达式: 释放一个“组合技”的按键要求。比如从“防御姿态”到“攻击姿态”的边上,正则表达式是 A(A|B)*,意思是“按一个A,后面再跟任意数量的A或B”。
- 接受: 如果你按下的 A-A-B-C 序列,可以被解释为一连串合法的“组合技”释放,并且最终让你的人物进入了“胜利姿态”(接受状态),那么你这个按键序列就被游戏“接受”了。比如,A-A-B 触发了组合技让你进入了“攻击姿态”,然后 C 又触发了另一个技能让你进入了“胜利姿态”。
📜 [原文17]
回到引理 1.60 的证明,我们设 $M$ 是语言 $A$ 的 DFA。然后我们通过添加新起始状态和新接受状态以及必要的额外转移箭头将 $M$ 转换为 GNFA $G$。我们使用过程 CONVERT( $G$ ),它接受一个 GNFA 并返回一个等价的正则表达式。此过程使用递归,这意味着它会调用自身。通过该过程仅在处理状态少一个的 GNFA 时调用自身来避免无限循环。GNFA 具有两个状态的情况无需递归处理。
Convert $(G)$:
- 设 $k$ 为 $G$ 的状态数。
- 如果 $k=2$,则 $G$ 必须由一个起始状态、一个接受状态和一个连接它们的单个箭头组成,该箭头标记为正则表达式 $R$。
返回表达式 $R$。
- 如果 $k>2$,我们选择任何一个不同于 $q_{\text {start }}$ 和 $q_{\text {accept }}$ 的状态 $q_{\text {rip }} \in Q$,并设 $G^{\prime}$ 为 GNFA ( $\left.Q^{\prime}, \Sigma, \delta^{\prime}, q_{\text {start }}, q_{\text {accept }}\right)$,其中
并且对于任何 $q_{i} \in Q^{\prime}-\left\{q_{\text {accept }}\right\}$ 和任何 $q_{j} \in Q^{\prime}-\left\{q_{\text {start }}\right\}$,设
其中 $R_{1}=\delta\left(q_{i}, q_{\text {rip }}\right)$,$R_{2}=\delta\left(q_{\text {rip }}, q_{\text {rip }}\right)$,$R_{3}=\delta\left(q_{\text {rip }}, q_{j}\right)$,和 $R_{4}=\delta\left(q_{i}, q_{j}\right)$。
- 计算 Convert $\left(G^{\prime}\right)$ 并返回此值。
这一部分形式化地定义了前面讨论的状态消除算法,并将其包装成一个名为 CONVERT 的递归过程。
- 算法的起点
- 证明的第一步(在调用 CONVERT 之前)是将给定的 DFA $M$ 转换成一个满足“特殊形式”的 GNFA $G$。这个预处理步骤我们已经讨论过,它确保了我们交给 CONVERT 的输入是标准化的。
- CONVERT(G) 过程详解
- 这是一个递归算法,其设计思想是“分而治之”(Divide and Conquer)。
- 输入: 一个 GNFA $G$。
- 输出: 一个与 $G$ 等价的正则表达式。
- 步骤 1: 获取状态数
- 设 k 为 G 的状态数。
- $k$ 的大小是驱动递归的关键变量。
- 步骤 2: 终止条件 (Base Case)
- 如果 k=2,... 返回表达式 R。
- 这是递归的出口。当 GNFA 被简化到只剩下起始状态和接受状态时,我们不再需要递归。
- 由于 GNFA 是特殊形式,这两个状态之间只有一条从起点到终点的边。
- 这条边上的正则表达式 $R$ 自然地描述了从头到尾所有可能的路径(因为已经没有中间状态可以绕路了)。所以这个 $R$ 就是答案。
- 步骤 3: 递归步骤 (Recursive Step)
- 如果 k > 2,...
- 这是算法的核心,对应“分治”中的“治”。
- a. 选择一个状态 $q_{rip}$:
- 从除了起始和接受状态之外的中间状态中,随便选一个出来,作为本次要“撕掉”的目标。
- b. 构建简化的 $G'$:
- 定义一个新的 GNFA $G'$,它的状态集 $Q'$ 就是原来的状态集 $Q$ 减去 $q_{rip}$。所以 $G'$ 的状态数是 $k-1$。
- $G'$ 的起点、终点、字母表都和 $G$ 一样。
- c. 计算新的转移函数 $\delta'$ (核心公式):
- 这是最关键的一步:为 $G'$ 中的每一条边计算新的正则表达式标签。
- 对于任何一对状态 $(q_i, q_j)$ (其中 $q_i$ 不是终点, $q_j$ 不是起点),新的标签 $\delta'(q_i, q_j)$ 由以下公式给出:
- 这里的 $R_1, R_2, R_3, R_4$ 都是从旧的 GNFA $G$ 的转移函数 $\delta$ 中取出的值:
- $R_1 = \delta(q_i, q_{rip})$ (从 $q_i$ 到 $q_{rip}$ 的路径)
- $R_2 = \delta(q_{rip}, q_{rip})$ (在 $q_{rip}$ 的自循环路径)
- $R_3 = \delta(q_{rip}, q_j)$ (从 $q_{rip}$到 $q_j$ 的路径)
- $R_4 = \delta(q_i, q_j)$ (从 $q_i$ 到 $q_j$ 的不经过 $q_{rip}$ 的直接路径)
- 这个公式的含义我们前面已经深入讨论过:它将所有经过 $q_{rip}$ 的路径信息,通过正则运算,编码并合并到了不经过 $q_{rip}$ 的路径上。
- 步骤 4: 递归调用
- 计算 Convert(G') 并返回此值。
- 现在我们有了一个新的、状态数减一的 GNFA $G'$。我们把这个更小的问题,扔回给 CONVERT 函数自己去解决。
- 因为每次递归调用,问题的规模(状态数 $k$)都在减小,所以这个递归过程最终必然会达到 $k=2$ 的终止条件,从而保证算法会结束。
- $Q^{\prime}=Q-\left\{q_{\mathrm{rip}}\right\}$:
- $Q'$: 新 GNFA 的状态集。
- $Q$: 原 GNFA 的状态集。
- $-$ : 集合减法。
- $\left\{q_{\mathrm{rip}}\right\}$: 只包含被移除状态的集合。
- 含义: 新的状态集就是旧的集合里去掉了 $q_{rip}$ 这个元素。
- $\delta^{\prime}\left(q_{i}, q_{j}\right)=\left(R_{1}\right)\left(R_{2}\right)^{*}\left(R_{3}\right) \cup\left(R_{4}\right)$:
- $\delta'$: 新 GNFA $G'$ 的转移函数。
- $\delta$: 旧 GNFA $G$ 的转移函数。
- 这整个公式是 CONVERT 算法的核心,是算法正确性的关键。它保证了 $G'$ 和 $G$ 是等价的。
- 示例: CONVERT 算法的一次递归调用
- 输入: 一个 3 状态的 GNFA $G$ (状态为 $q_{start}, q_{mid}, q_{accept}$)。
- k=3, 大于 2,进入递归步骤。
- 1. 选择: 我们只能选择 $q_{mid}$ 作为 $q_{rip}$。
- 2. 构建 G': 新的 $G'$ 只有两个状态:$q_{start}, q_{accept}$。
- 3. 计算新标签: $G'$ 只有一个需要计算的边,就是从 $q_{start}$ 到 $q_{accept}$。我们设这对状态为 $(q_i, q_j)$。
- $q_i = q_{start}$
- $q_j = q_{accept}$
- $q_{rip} = q_{mid}$
- 4. 从 G 中查找旧标签:
- $R_1 = \delta(q_{start}, q_{mid})$
- $R_2 = \delta(q_{mid}, q_{mid})$
- $R_3 = \delta(q_{mid}, q_{accept})$
- $R_4 = \delta(q_{start}, q_{accept})$
- 5. 应用公式:
- $\delta'(q_{start}, q_{accept}) = (R_1)(R_2)^*(R_3) \cup (R_4)$
- 6. 递归调用: CONVERT(G')
- 此时 $G'$ 的状态数 $k=2$。满足终止条件。
- CONVERT 直接返回 $G'$ 中从起点到终点的边的标签,也就是我们刚算出来的 $(R_1)(R_2)^*(R_3) \cup (R_4)$。
- 最终结果: 对于一个 3 状态的 GNFA,经过一次递归,就得到了最终的正则表达式。
- 递归的信任: 理解递归算法的关键在于“信任”。你不需要知道 CONVERT(G') 内部是如何解决那个更小的问题的,你只需要相信它能正确地返回一个与 $G'$ 等价的正则表达式。你的任务只是确保你这一层(从 $k$ 到 $k-1$)的转换是正确的。
- 公式的普适性: 这个公式对所有合法的 $(q_i, q_j)$ 对都适用,包括 $q_i=q_j$ 的情况(更新自循环)。
- 初始转换: 整个过程的正确性依赖于第一步:将 DFA 正确地转换为“特殊形式”的 GNFA。如果初始的 GNFA 格式不对,算法的前提就不成立。
本段以伪代码的形式,给出了从 GNFA 到正则表达式的转换算法 CONVERT(G) 的形式化描述。该算法是一个递归过程。其终止条件是当输入的 GNFA 只有2个状态(起始和接受)时,直接返回它们之间边的正则表达式。其递归步骤是:当状态多于2个时,选择并移除一个中间状态 $q_{rip}$,然后使用一个核心的更新公式 $\left(R_{1}\right)\left(R_{2}\right)^{*}\left(R_{3}\right) \cup\left(R_{4}\right)$ 来计算新的、状态数减一的 GNFA $G'$ 的边标签,最后递归调用 CONVERT 来处理这个更小的 $G'$。这个算法系统地、确定地将一个图结构逐步转化为一个纯粹的代数表达式。
本段的目的是将前面直观的“状态消除”思想,固化成一个可以被严格分析和执行的算法。伪代码的引入使得整个过程无歧义,为后续的正确性证明(断言 1.65)提供了坚实的基础。它展示了如何将一个复杂的图论问题通过递归和代数替换,转化为一个更小、更简单的同类问题,是算法设计中一个经典的范例。
CONVERT 函数就像一个“俄罗斯套娃”拆解师。
- GNFA: 一个大的、复杂的俄罗斯套娃。
- k=2: 拆到最后只剩一个最小的、实心的娃娃,上面刻着一行字(最终的正则表达式)。拆解师直接读出这行字。
- k>2: 拆解师打开当前这层套娃,拿出里面那个小一号的套娃 ($G'$)。但在拿出之前,他需要把当前这层外壳上雕刻的复杂花纹(经过 $q_{rip}$ 的路径信息)用一种特殊的墨水(更新公式)重新绘制到里面那个小套娃的表面。这样,信息就不会丢失。
- 递归: 拆解师把这个“重绘”过的小套娃,交给另一个“自己”(递归调用),让他去继续拆解。
这个过程保证了,无论拆了多少层,所有的花纹信息最终都会被累加到最小那个娃娃的表面上。
想象你在做一道非常复杂的代数化简题,比如 f(x) = ...。
- CONVERT(G): 就像是函数 simplify(expression)。
- k=2: expression 已经是最简形式(比如 x+1),直接返回。
- k>2: expression 里含有一个复杂的项,比如 sin(y)。
- 消除状态 $q_{rip}$: 就像是你决定用一个代换,比如令 z = cos(y),来消除 sin(y) 项(依据 $\sin^2y + \cos^2y = 1$)。
- 更新标签: 做出这个代换后,表达式中其他部分都会变得更复杂。tan(y) 会变成 sqrt(1-z^2)/z 等等。这对应着更新正则表达式标签。
- 递归调用: 现在你有了一个不含 sin(y) 但可能更复杂的关于 z 的表达式。你调用 simplify 去处理这个新问题。
这个过程通过不断地代换和化简,最终得到一个最简结果。
1.13 算法正确性证明
📜 [原文18]
接下来我们证明 CONVERT 返回一个正确的值。
断言 1.65
对于任何 GNFA $G$,Convert $(G)$ 等价于 $G$。
我们通过对 $k$(GNFA 的状态数)进行归纳来证明此断言。
基础情况:证明断言对于 $k=2$ 个状态成立。如果 $G$ 只有两个状态,它只能有一个从起始状态到接受状态的单个箭头。此箭头上的正则表达式标签描述了所有允许 $G$ 到达接受状态的字符串。因此,此表达式等价于 $G$。
归纳步骤:假设断言对于 $k-1$ 个状态成立,并使用此假设来证明断言对于 $k$ 个状态成立。首先我们证明 $G$ 和 $G^{\prime}$ 识别相同的语言。假设 $G$ 接受输入 $w$。那么在计算的接受分支中,$G$ 进入一个状态序列:
如果其中没有一个是移除的状态 $q_{\text {rip }}$,则显然 $G^{\prime}$ 也接受 $w$。原因是标记 $G^{\prime}$ 箭头的每个新正则表达式都包含旧正则表达式作为并的一部分。
如果 $q_{\text {rip }}$ 确实出现,则移除每个连续的 $q_{\text {rip }}$ 状态的运行会形成 $G^{\prime}$ 的接受计算。限定运行的状态 $q_{i}$ 和 $q_{j}$ 在它们之间的箭头上有一个新的正则表达式,它描述了所有通过 $G$ 上的 $q_{\text {rip }}$ 将 $q_{i}$ 带到 $q_{j}$ 的字符串。因此 $G^{\prime}$ 接受 $w$。
反之,假设 $G^{\prime}$ 接受输入 $w$。由于 $G^{\prime}$ 中任何两个状态 $q_{i}$ 和 $q_{j}$ 之间的每个箭头都描述了在 $G$ 中直接或通过 $q_{\text {rip }}$ 将 $q_{i}$ 带到 $q_{j}$ 的字符串集合,因此 $G$ 也必须接受 $w$。因此 $G$ 和 $G^{\prime}$ 是等价的。
归纳假设表明,当算法递归调用自身处理输入 $G^{\prime}$ 时,结果是一个等价于 $G^{\prime}$ 的正则表达式,因为 $G^{\prime}$ 具有 $k-1$ 个状态。因此,此正则表达式也等价于 $G$,并且算法被证明是正确的。
这结束了断言 1.65、引理 1.60 和定理 1.54 的证明。
这是对 CONVERT 算法正确性的形式化证明,它使用了数学归纳法。证明的核心是论证,每一步状态消除操作所产生的新的、更小的 GNFA $G'$,与原来的 GNFA $G$ 在语言识别能力上是完全等价的。
证明结构:对状态数 k 进行归纳
- 断言 (Claim): 我们要证明的命题是 “对于任何有 $k$ 个状态的 GNFA $G$,CONVERT(G) 返回的正则表达式 $R$ 满足 $L(R) = L(G)$”。
- 基础情况 (Base Case): k = 2
- 论述: 当一个 GNFA 只有 2 个状态时,它必然只包含起始状态 $q_{start}$ 和接受状态 $q_{accept}$。根据其“特殊形式”,从 $q_{start}$ 到 $q_{accept}$ 有且只有一条边,设其标签为正则表达式 $R$。
- 根据 GNFA 的接受定义,一个字符串 $w$ 被这个二状态 GNFA 接受,当且仅当 $w$ 可以被分解成一段 $w_1$,使得 $w_1 \in L(R)$,并且路径是 $q_{start} \rightarrow q_{accept}$。由于 $w$ 只能被分解成它自身,所以这意味着 $w \in L(R)$。
- 因此,这个 GNFA 接受的语言就是 $L(R)$。
- CONVERT 算法在 $k=2$ 时,正是返回了这个正则表达式 $R$。
- 结论: 在 $k=2$ 的情况下,断言成立。
- 归纳步骤 (Inductive Step)
- 归纳假设 (Inductive Hypothesis): 假设断言对于所有状态数为 $k-1$ 的 GNFA 都成立。也就是说,我们相信 CONVERT 算法对于 $k-1$ 个状态的 GNFA 能够给出正确的结果。
- 目标: 在这个假设下,证明断言对于状态数为 $k$ 的 GNFA 也成立。
- 核心论点: 我们需要证明,CONVERT 算法中从 $k$ 状态的 $G$ 构造出的 $k-1$ 状态的 $G'$,与 $G$ 是等价的,即 $L(G) = L(G')$。
- 如果能证明这一点,那么逻辑链就是:
- $L(G) = L(G')$ (我们将要证明的)。
- CONVERT(G) 的执行过程是返回 CONVERT(G') 的结果。
- 根据归纳假设,CONVERT(G') 返回的正则表达式 $R$ 与 $G'$ 等价,即 $L(R) = L(G')$。
- 综合 1 和 3,我们得到 $L(R) = L(G)$。
- 这就证明了 CONVERT(G) 返回了与 $G$ 等价的正则表达式。断言对于 $k$ 成立。
- 证明 $L(G) = L(G')$
- 这是一个集合相等的证明,需要证明两个方向:$L(G) \subseteq L(G')$ 和 $L(G') \subseteq L(G)$。
- 方向一: 证明如果 $w \in L(G)$,那么 $w \in L(G')$
- 假设 $w$ 被 $G$ 接受。这意味着在 $G$ 中存在一条接受路径 $q_{start}, q_1, \dots, q_{accept}$,以及对 $w$ 的一个切分 $w_1, \dots, w_m$。
- 情况 A: 接受路径中不包含被移除的状态 $q_{rip}$
- 那么这条路径在 $G'$ 中也完全存在。
- 路径中每一步 $q_i \rightarrow q_j$ 对应的边,在 $G$ 中的标签是 $R_4 = \delta(q_i, q_j)$。在 $G'$ 中,新标签是 $R_{new} = \dots \cup R_4$。
- 因为 $L(R_4) \subseteq L(R_{new})$,所以原来合法的每一步在 $G'$ 中也仍然合法。
- 因此,$G'$ 也接受 $w$。
- 情况 B: 接受路径中包含了 $q_{rip}$
- 路径看起来像 $\dots, q_i, q_{rip}, \dots, q_{rip}, q_j, \dots$。
- 考虑任何一段从 $q_i$ 进入 $q_{rip}$,在 $q_{rip}$ 可能自循环若干次,然后从 $q_{rip}$ 离开到 $q_j$ 的子路径。
- 这段子路径消耗的输入子串,正好是由正则表达式 $(R_1)(R_2)^*(R_3)$ 描述的。
- 在 $G'$ 中,我们用一条从 $q_i$ 到 $q_j$ 的新边取代了这段子路径。这条新边的标签 $R_{new}$ 通过 $\cup$ 运算包含了 $(R_1)(R_2)^*(R_3)$。
- 因此,原来在 $G$ 中需要经过 $q_{rip}$ 的多步跳转,在 $G'$ 中可以被一步等价地完成。
- 通过将 $G$ 中所有经过 $q_{rip}$ 的子路径都替换成 $G'$ 中的单步跳转,我们可以为 $w$ 构造出一条在 $G'$ 中的接受路径。
- 因此,$G'$ 也接受 $w$。
- 方向二: 证明如果 $w \in L(G')$,那么 $w \in L(G)$
- 这个方向更直接。假设 $w$ 被 $G'$ 接受。这意味着在 $G'$ 中存在一条接受路径。
- 考虑这条路径中的任意一步,从 $q_i$ 到 $q_j$,消耗了子串 $w_{sub}$。
- $w_{sub}$ 必须属于新标签 $R_{new} = (R_1)(R_2)^*(R_3) \cup (R_4)$。
- 如果 $w_{sub} \in L(R_4)$: 那么在 $G$ 中,我们可以直接通过 $q_i \xrightarrow{R_4} q_j$ 这条旧的边来完成这一步。
- 如果 $w_{sub} \in L((R_1)(R_2)^*(R_3))$: 那么在 $G$ 中,我们可以通过 $q_i \xrightarrow{R_1} q_{rip} \xrightarrow{(R_2)^*} \dots \xrightarrow{R_3} q_j$ 这一系列的跳转来消耗掉 $w_{sub}$。
- 这意味着,$G'$ 中的每一步跳转,都可以在 $G$ 中被模拟出来(或者直接走,或者绕道 $q_{rip}$)。
- 因此,我们可以在 $G$ 中为 $w$ 构造出一条接受路径。$w$ 也被 $G$ 接受。
- 结论: 既然两个方向都成立,那么 $L(G) = L(G')$。
- 最终结论
- 通过数学归纳法,我们证明了 CONVERT(G) 对于任何状态数的 GNFA $G$ 都是正确的。
- 这完成了对断言 1.65 的证明。
- 断言 1.65 的成立直接保证了引理 1.60 的正确性(因为我们可以将任何 DFA 转换成 GNFA,然后调用 CONVERT)。
- 引理 1.60(DFA -> RE)和之前的引理 1.55(RE -> NFA)共同完成了对定理 1.54 的双向证明。
- 归纳证明的逻辑: 理解归纳证明的关键是分离“归纳假设”和“需要证明的步骤”。不要在证明 $k$ 的情况时,对 $k-1$ 的情况的正确性有任何怀疑,因为那是你的前提。
- $G$ 和 $G'$ 等价的精髓: 其核心在于更新公式 $(R_1)(R_2)^*(R_3) \cup (R_4)$ 完美地、不多不少地捕捉了所有路径。$\cup R_4$ 保证了不经过 $q_{rip}$ 的旧路径得以保留。$(R_1)(R_2)^*(R_3)$ 保证了所有必须经过 $q_{rip}$ 的路径都被等价地转换。
- 证明的严谨性: 这段证明虽然是文字描述,但其每一步都依赖于形式化的定义(如 GNFA 的接受条件),因此是严谨的。
本段使用数学归纳法对 CONVERT 算法的正确性(即断言 1.65)进行了严谨的证明。
- 基础情况 ($k=2$) 被证明是平凡成立的。
- 归纳步骤的核心是证明算法中用于从 $k$ 状态的 GNFA $G$ 构造 $k-1$ 状态的 GNFA $G'$ 的那一步是“保义”的,即 $L(G) = L(G')$。这个等价性通过双向包含($L(G) \subseteq L(G')$ 和 $L(G') \subseteq L(G)$)得以证明,其关键在于状态消除公式 $\left(R_{1}\right)\left(R_{2}\right)^{*}\left(R_{3}\right) \cup\left(R_{4}\right)$ 精确地补偿了被移除状态 $q_{rip}$ 的路径功能。
- 基于归纳假设(即相信算法对 $k-1$ 状态是正确的),$G$ 和 $G'$ 的等价性保证了算法对 $k$ 状态也是正确的。
- 该断言的成立,最终完成了引理 1.60 和整个定理 1.54 的证明,牢固地建立了有限自动机和正则表达式之间的等价关系。
一个算法被提出后,其正确性必须得到证明,否则它就只是一个未经证实的猜想。本段的目的就是为 CONVERT 算法提供这个至关重要的正确性保证。通过使用标准的数学归纳法,它将算法的正确性建立在坚实的逻辑基础之上。这是计算理论中典型的“提出算法 -> 证明正确性”的思维模式。
这就像证明一个递归的阶乘函数 factorial(n) 是正确的。
- factorial(n) = n * factorial(n-1)
- 基础情况 (n=0): factorial(0) 返回 1。正确。
- 归纳步骤:
- 归纳假设: 相信 factorial(n-1) 能正确计算出 (n-1)!。
- 证明: 我们的算法返回 n factorial(n-1),根据假设,这等于 n (n-1)!,这正是 n! 的定义。
- 结论: 我们的算法在第 n 步也是正确的。
本段的证明结构与此完全相同,只是处理的对象从数字和乘法,换成了 GNFA 和正则运算。证明 $L(G)=L(G')$ 就好比证明 n! = n * (n-1)! 这个递归关系是正确的。
想象你在做一笔复杂的财务审计。
- G: 完整的、包含所有明细账目的总账本。
- $q_{rip}$: 一个中间账户,比如“待处理费用”。
- 消除 $q_{rip}$: 你决定结清并注销“待处理费用”这个账户。
- 更新标签: 为了让账目平掉,所有原来流入和流出“待处理费用”账户的钱,现在必须重新分配到其他账户的往来中。比如,原来“销售部”给“待处理费用”100元,然后“待处理费用”给“采购部”100元。现在注销了中间账户,你就在“销售部”和“采购部”之间直接记一笔100元的往来。
- 证明 $L(G)=L(G')$: 就是在证明,经过这番操作后,整个公司的总资产(语言)没有发生任何变化。每一分钱的来龙去脉(每条计算路径)都仍然被完整地记录着,只是记录的方式变了。
1.14 示例:将 DFA 转换为正则表达式 (1)
📜 [原文19]
示例 1.66
在此示例中,我们使用上述算法将 DFA 转换为正则表达式。我们从图 1.67(a) 中的两状态 DFA 开始。
在图 1.67(b) 中,我们通过添加一个新起始状态和一个新接受状态(为了方便绘制,分别称为 $s$ 和 $a$,而不是 $q_{\text {start }}$ 和 $q_{\text {accept }}$)来制作一个四状态 GNFA。为了避免图形混乱,我们不绘制标记为 $\emptyset$ 的箭头,即使它们存在。请注意,我们将 DFA 上状态 2 的自循环上的标签 $\mathrm{a}, \mathrm{b}$ 替换为 GNFA 上相应位置的标签 $\mathrm{a} \cup \mathrm{b}$。我们这样做是因为 DFA 的标签表示两个转移,一个用于 a,另一个用于 b,而 GNFA 可能只有一个从 2 到自身的转移。
在图 1.67(c) 中,我们移除状态 2 并更新剩余的箭头标签。在这种情况下,唯一改变的标签是从 1 到 $a$ 的标签。在 (b) 部分中它是 $\emptyset$,但在 (c) 部分中它是 $\mathrm{b}(\mathrm{a} \cup \mathrm{b})^{*}$。我们通过遵循 CONVERT 过程的步骤 3 获得此结果。状态 $q_{i}$ 是状态 1,状态 $q_{j}$ 是 $a$,并且 $q_{\text {rip }}$ 是 2,因此 $R_{1}=\mathrm{b}$,$R_{2}=\mathrm{a} \cup \mathrm{b}$,$R_{3}=\varepsilon$,和 $R_{4}=\emptyset$。因此,从 1 到 $a$ 的箭头上的新标签是 $(\mathrm{b})(\mathrm{a} \cup \mathrm{b})^{*}(\varepsilon) \cup \emptyset$。我们将此正则表达式简化为 $\mathrm{b}(\mathrm{a} \cup \mathrm{b})^{*}$。
在图 1.67(d) 中,我们从 (c) 部分移除状态 1 并遵循相同的过程。由于只剩下起始状态和接受状态,连接它们的箭头上的标签就是等价于原始 DFA 的正则表达式。
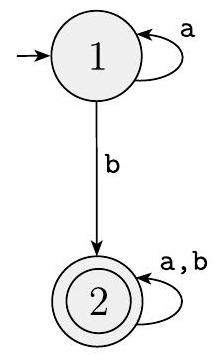
(a)
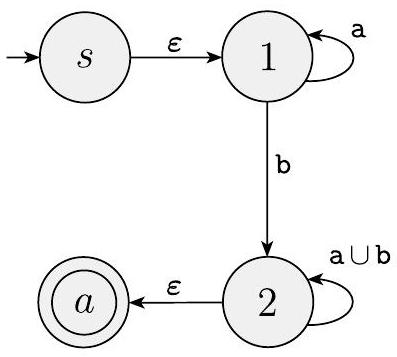
(b)
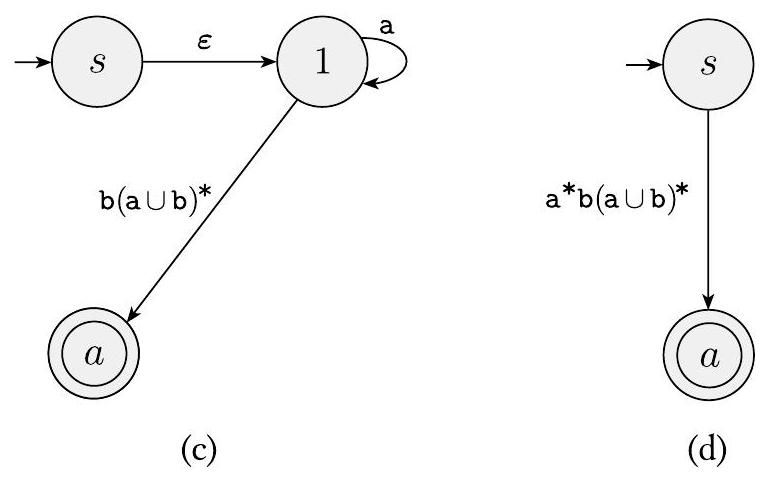
图 1.67
将两状态 DFA 转换为等价正则表达式 $\square$
这个例子完整地演示了从 DFA 到正则表达式的转换算法。
第一步:分析原始 DFA (图 1.67(a))
- 状态: 状态1 (起始), 状态2 (接受)。
- 转换:
- 在状态1,读 a -> 状态1 (自循环)。
- 在状态1,读 b -> 状态2。
- 在状态2,读 a 或 b -> 状态2 (自循环)。
- 语言: 这个 DFA 接受什么语言?
- 必须读到一个 b 才能从状态1到达状态2。
- 一旦到达状态2,就永远不会离开,所以之后可以跟任意 a 或 b 的序列。
- 在读到第一个 b 之前,可以在状态1上读任意数量的 a。
- 所以,语言是:以任意数量的 a 开头,然后跟一个 b,然后跟任意由 a,b 组成的字符串。
- 用正则表达式直观地描述就是:ab(a U b)。
- 我们的目标是通过算法推导出这个或一个等价的正则表达式。
第二步:转换为特殊形式的 GNFA (图 1.67(b))
- 添加新起点和终点:
- 创建一个新起始状态 s。
- 创建一个新接受状态 a (这里用 a 表示 accept,不是字母 a)。
- 添加 $\varepsilon$ 边: $s \xrightarrow{\varepsilon} 1$ 和 $2 \xrightarrow{\varepsilon} a$。
- 合并/转换标签:
- 原 DFA 的边被转换成 GNFA 的边。
- $1 \xrightarrow{a} 1$ 变为 $1 \xrightarrow{a} 1$。
- $1 \xrightarrow{b} 2$ 变为 $1 \xrightarrow{b} 2$。
- $2$ 上的自循环,原来是两条边(一条 a,一条 b),被合并成一条边,标签为正则表达式 a U b。即 $2 \xrightarrow{a \cup b} 2$。
- 添加缺失边:
- 图中为了简洁,省略了所有标签为 ∅ 的边。例如,从 s 到 2,从 1 到 a 等,都应该有一条 ∅ 边。我们心里知道它们存在就行。
第三步:第一次状态消除,移除状态 2 (图 1.67(c))
- 目标: 移除状态 2。
- 需要更新的边: 状态 2 被移除后,剩下 s, 1, a。我们需要检查所有状态对之间的边并更新。
- s 到 1? 不经过 2,不变。
- 1 到 1? 不经过 2,不变。
- s 到 a?
- 1 到 a?
- ... 实际上,因为 2 是一个“汇点”(只进不出,除了到新终点 a),它只影响指向它的状态到它指向的状态的路径。即,从 1 到 a 的路径。
- 计算从 1 到 a 的新标签:
- 我们使用状态消除公式: $R_{new} = (R_1)(R_2)^*(R_3) \cup (R_4)$。
- $q_i = 1$, $q_j = a$, $q_{rip} = 2$。
- 在图(b)中查找旧标签:
- $R_1 = \delta(1, 2) = b$。
- $R_2 = \delta(2, 2) = a \cup b$。
- $R_3 = \delta(2, a) = \varepsilon$。
- $R_4 = \delta(1, a) = \emptyset$ (因为原来没有直达的边)。
- 代入公式:
$R_{new} = (b)(a \cup b)^*(\varepsilon) \cup (\emptyset)$
- 简化:
- $(a \cup b)^*(\varepsilon) = (a \cup b)^*$ (任何东西连接 $\varepsilon$ 都不变)。
- $(b)(a \cup b)^*$。
- $\cup (\emptyset)$ (与空集取并集不变)。
- 最终结果是: $b(a \cup b)^*$。
- 更新图: 在 (c) 中,我们看到从 1到 a 的边标签被更新为 $b(a \cup b)^*$。其他相关边不变。
第四步:第二次状态消除,移除状态 1 (图 1.67(d))
- 目标: 移除状态 1。
- 剩下状态: s, a。
- 需要更新的边: 只有从 s 到 a 这一条。
- 计算从 s 到 a 的新标签:
- $q_i = s$, $q_j = a$, $q_{rip} = 1$。
- 在图(c)中查找旧标签:
- $R_1 = \delta(s, 1) = \varepsilon$。
- $R_2 = \delta(1, 1) = a$。
- $R_3 = \delta(1, a) = b(a \cup b)^*$。
- $R_4 = \delta(s, a) = \emptyset$ (原来没有直达的边)。
- 代入公式:
$R_{new} = (\varepsilon)(a)^*(b(a \cup b)^*) \cup (\emptyset)$
- 简化:
- $(\varepsilon)(a)^* = a^*$。
- $a^*(b(a \cup b)^*)$。
- $\cup (\emptyset)$ 不变。
- 最终结果是: $a^*b(a \cup b)^*$。
- 更新图: 在 (d) 中,我们看到 s 和 a 之间只剩下一条边,其标签就是我们计算出的结果。
第五步:算法终止
- 现在 GNFA 只有 2 个状态 ($k=2$)。算法终止。
- 返回从起始状态到接受状态的边的标签。
- 最终正则表达式: $a^*b(a \cup b)^*$。
- 这与我们最初凭直觉分析 DFA 得出的语言描述完全一致!
- 标签的查找: 在应用公式时,务必在上一步的图中查找 $R_1, R_2, R_3, R_4$ 的值,而不是更早的图。
- 对 $\varepsilon$ 和 $\emptyset$ 的简化: 正确运用恒等式 $R\varepsilon=R$, $\varepsilon R=R$, $R \cup \emptyset=R$, $R \circ \emptyset = \emptyset$ 是简化计算的关键。
- 选择消除顺序: 在这个例子中,我们先消除了 2,再消除 1。如果先消除 1,计算过程会不同,但最终的正则表达式在语言上是等价的(尽管写法可能不同)。
示例 1.66 提供了一个将一个具体的两状态 DFA 转换为正则表达式的完整、分步的演练。该过程严格遵循了前面定义的状态消除算法:
- 将 DFA 转换为一个4状态的“特殊形式” GNFA。
- 通过应用核心更新公式,消除了一个中间状态 2,得到一个3状态的 GNFA。
- 再次应用公式,消除了另一个中间状态 1,得到一个2状态的 GNFA。
- 算法终止,并从最终的2状态 GNFA 中直接读出了等价的正则表达式 $a^*b(a \cup b)^*$。
这个例子雄辩地证明了状态消除算法的有效性和可操作性。
这个例子的目的是为了让读者不再停留在对状态消除算法抽象的理解上,而是能亲手(或亲眼)看到算法的每一个步骤是如何在一个具体的图上执行的。它展示了代数公式如何与图的操作精确对应,以及复杂的正则表达式是如何从简单的标签通过递归的“累加”而生成的。这对于建立对该算法的信心和深入理解至关重要。
这个过程就像在解一个“路径谜题”。
- 原始DFA: 谜题的初始版图。
- 添加s和a: 在起点放一个“入口”标志,在终点放一个“出口”标志。
- 消除状态2: 你发现所有通往“出口”的路都必须先经过一个叫“检查点2”的地方。你决定撤掉“检查点2”,然后印发一份新的“过路指南”。
- 更新边 (1,a): 新指南上写着:“所有原来要去‘出口’的人,现在在‘检查点1’这里,可以直接走一条新的秘密通道。走法是:先按‘b’钮,然后可以任意按‘a’或‘b’钮,最后按‘ε’钮。” 这就是 $b(a \cup b)^*\varepsilon$。
- 消除状态1: 你又决定撤掉“检查点1”。
- 更新边 (s,a): 你再次更新“过路指南”:“所有从‘入口’来的人,你们现在有一条直达‘出口’的超级高速路。走法是:可以任意按‘a’钮,然后走那条通往旧‘检查点2’的秘密通道($b(a \cup b)^*$)。” 这就是 $a^*b(a \cup b)^*$。
最终,这份指南本身(正则表达式)就描述了所有能从入口到出口的走法。
想象你是一名程序员,在重构一段包含很多 goto 语句的意大利面式代码。
- DFA: 原始的、混乱的 goto 代码。状态是代码行号。
- 消除状态: 你决定消除某一个代码标签 LABEL_2:。
- 更新边: 所有 goto LABEL_2; 的地方,你都需要分析 LABEL_2 后面代码的逻辑,然后将那段逻辑直接“内联”到 goto 的地方。如果 LABEL_2 后面是一个循环,内联后的代码就会包含一个循环。这就像正则表达式中出现 *。如果 LABEL_2 后面是一个 if-else,内联后就会出现 U。
- 最终结果: 通过不断地消除 goto 标签并内联代码,你最终得到了一段没有 goto 的、结构化的代码。这段代码可能看起来更长、更复杂(就像最终的正则表达式),但它在功能上与原始代码是等价的。
1.15 示例:将 DFA 转换为正则表达式 (2)
📜 [原文20]
示例 1.68
在此示例中,我们从一个三状态 DFA 开始。转换步骤如下图所示。
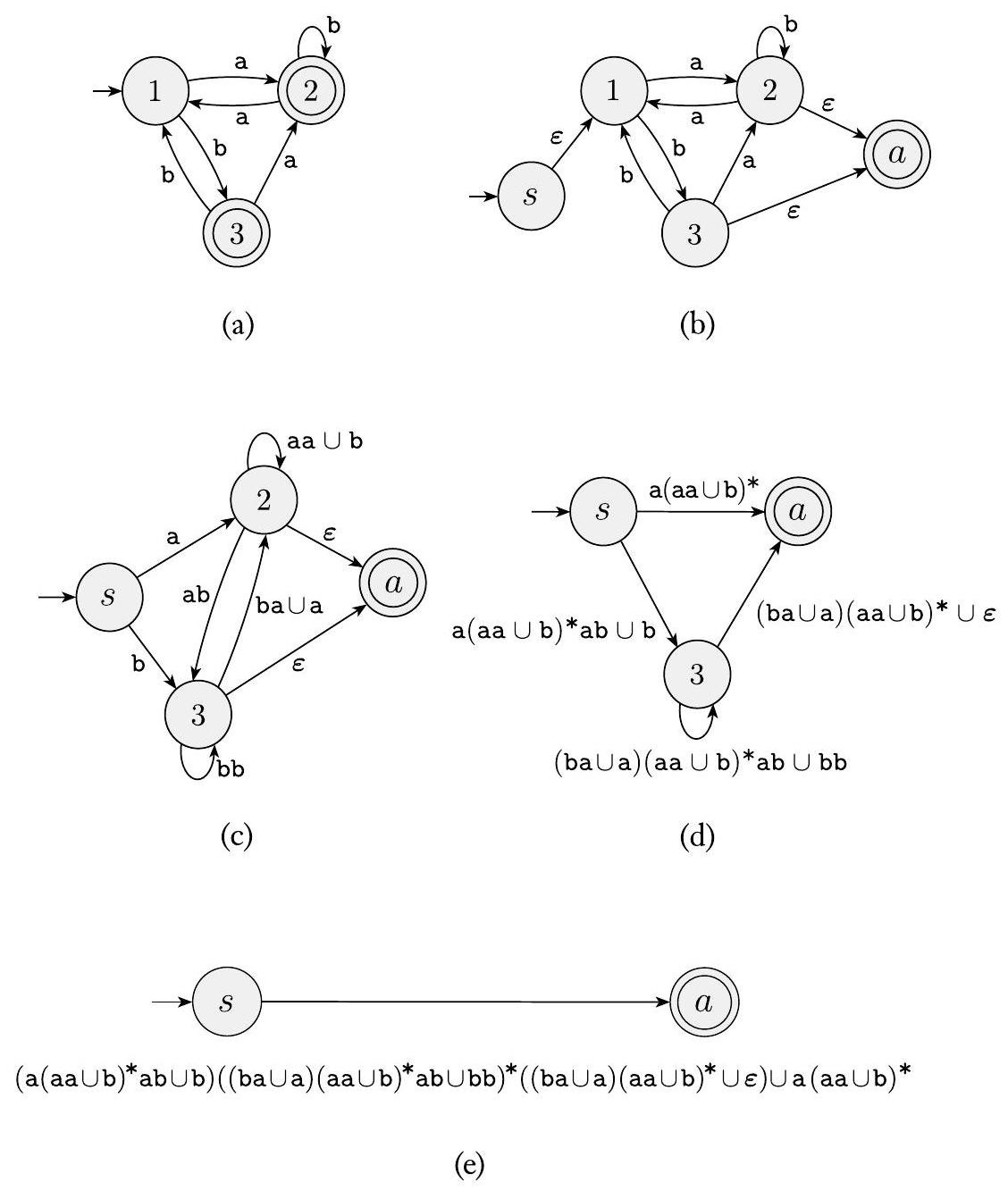
图 1.69
将三状态 DFA 转换为等价正则表达式 $\square$
这个例子比上一个更进了一步,从一个三状态的 DFA 开始,需要消除更多的中间状态,从而导致更复杂的正则表达式运算。
第一步:分析原始 DFA (图 1.69(a))
- 状态: 状态1 (起始), 状态2, 状态3 (接受)。
- 语言: 这个 DFA 接受什么语言?
- 它接受空字符串 $\varepsilon$ 吗?不,因为起始状态1不是接受状态。
- 要到达接受状态3,必须经过状态2。
- 路径 $1 \xrightarrow{a} 2 \xrightarrow{a} 3$ 接受 aa。
- 路径 $1 \xrightarrow{a} 2 \xrightarrow{b} 2 \xrightarrow{a} 3$ 接受 aba。
- 路径 $1 \xrightarrow{b} 1 \xrightarrow{a} 2 \xrightarrow{a} 3$ 接受 baa。
- 核心特征: 必须以一个 a 结尾才能从状态2跳到状态3。在状态2可以有任意 b 的循环。在状态1可以有任意 b 的循环。
- 直观描述: 任意数量的b(可能没有)和a交错,但a不能连续出现,后面可以跟任意数量的b,最后必须以a结尾。不对,再分析。
- 任何被接受的串,必须以 a 结尾。在 a 之前,是从状态1出发,经过一系列转换到达状态2。
- 从状态1到状态2,路径可以是:$1 \xrightarrow{a} 2$ (消耗a),或者 $1 \xrightarrow{b} 1 \xrightarrow{a} 2$ (消耗ba),或者 $1 \xrightarrow{a} 2 \xrightarrow{b} 2$ (消耗ab后在状态2)。
- 让我们用更简单的方式思考:所有被接受的字符串都必须以 a 结尾。最后一个 a 之前的字符串必须能把机器带到状态2。什么样的字符串能把机器带到状态2?
- 任意数量 b 后跟一个 a (b*a)。
- 或者,到了状态2后,可以跟任意数量的 b,然后再跟一个 a 到状态1,再想办法回来... 这个思路太复杂了。
- 让我们相信算法,看它能推导出什么。
第二步:转换为 GNFA (图 1.69(b))
- 这是一个 5 状态的 GNFA。
- 添加新起点 s 和新终点 a。
- 添加 $\varepsilon$ 边: $s \xrightarrow{\varepsilon} 1$, $3 \xrightarrow{\varepsilon} a$。
- 原 DFA 的边被照搬过来,标签视为正则表达式。
- 所有缺失的边都被隐式地认为是 ∅。
第三步:消除状态 3 (图 1.69(c))
- 选择: 消除状态 3。
- 分析: 状态 3 是一个“终极汇点”,没有出边。因此,消除它只会影响从其他状态到新终点 a 的路径。
- 计算从 2 到 a 的新标签:
- $q_i=2, q_j=a, q_{rip}=3$。
- $R_1 = \delta(2,3) = a$。
- $R_2 = \delta(3,3) = \emptyset$ (状态3没有自循环)。
- $R_3 = \delta(3,a) = \varepsilon$。
- $R_4 = \delta(2,a) = \emptyset$。
- $R_{new} = (a)(\emptyset)^*(\varepsilon) \cup \emptyset = a\varepsilon\varepsilon \cup \emptyset = a$。
- 结果: 从 2 到 a 的新边标签是 a。其他边不受影响。
第四步:消除状态 2 (图 1.69(d))
- 选择: 消除状态 2。
- 分析: 状态 2 是一个核心中转站。它的消除会影响 1->1, 1->a 的边。
- 计算从 1 到 1 的新标签 (更新自循环):
- $q_i=1, q_j=1, q_{rip}=2$。
- $R_1 = \delta(1,2) = a$ (在图c中查找)。
- $R_2 = \delta(2,2) = b$。
- $R_3 = \delta(2,1) = a$。
- $R_4 = \delta(1,1) = b$。
- $R_{new} = (a)(b)^*(a) \cup (b) = ab^*a \cup b$。
- 结果: 1 的自循环标签变为 $b \cup ab^*a$。
- 计算从 1 到 a 的新标签:
- $q_i=1, q_j=a, q_{rip}=2$。
- $R_1 = \delta(1,2) = a$。
- $R_2 = \delta(2,2) = b$。
- $R_3 = \delta(2,a) = a$。
- $R_4 = \delta(1,a) = \emptyset$。
- $R_{new} = (a)(b)^*(a) \cup \emptyset = ab^*a$。
- 结果: 从 1 到 a 的边标签变为 $ab^*a$。
第五步:消除状态 1 (图 1.69(e))
- 选择: 消除状态 1。
- 剩下: s, a。
- 计算从 s 到 a 的新标签:
- $q_i=s, q_j=a, q_{rip}=1$。
- $R_1 = \delta(s,1) = \varepsilon$ (在图d中查找)。
- $R_2 = \delta(1,1) = b \cup ab^*a$。
- $R_3 = \delta(1,a) = ab^*a$。
- $R_4 = \delta(s,a) = \emptyset$。
- $R_{new} = (\varepsilon)(b \cup ab^*a)^*(ab^*a) \cup \emptyset$。
- 简化: 最终结果是 $(b \cup ab^*a)^*(ab^*a)$。
最终结果分析
- 最终正则表达式: $(b \cup ab^*a)^*(ab^*a)$。
- 它描述的语言:
- 后缀: 字符串必须以 ab^*a 结尾。
- ab^a 能产生什么? aa (当 b 是 $\varepsilon$), aba, abba, abbba, ...
- 前缀: 在这个后缀之前,可以有 0 个或多个由 b 或者 ab^*a 组成的块。
- 让我们验证几个字符串:
- aa: 前缀为空,后缀为 aa。匹配。
- aba: 前缀为空,后缀为 aba。匹配。
- baa: 前缀为 b,后缀为 aa。匹配。
- babaa: 前缀 b,后缀 aba。
- 这个表达式完美地描述了原始 DFA 的行为,尽管它的形式非常复杂,凭直觉很难直接写出来。
- 括号的重要性: 在最终表达式中,括号是至关重要的。$(b \cup ab^*a)^*$ 和 $b \cup (ab^*a)^*$ 是完全不同的。
- 逐步计算: 随着状态的消除,正则表达式会迅速变得复杂。在手动计算时,必须非常小心,不要在代数化简时出错。
- 选择消除顺序的影响: 如果我们先消除状态1,再消除2,再消除3,得到的正则表达式可能会是不同的写法,但它们描述的语言一定是相同的。例如,另一个等价的正则表达式可能是 (b | a(b|aa)a) a(b|aa)*。证明两个复杂的正则表达式等价本身就是一个难题。
- 代数运算的复杂性: 这个例子表明,随着状态的增多,手动进行状态消除会变得非常容易出错。每一步的正则表达式都在膨胀,任何一个小小的代数化简错误都会导致最终结果的谬误。这凸显了算法的机械性对于保证正确性的重要。
- 选择消除顺序: 本例选择先消除3再消除2。如果选择先消除2,那么第一次更新就会涉及到 1->1, 1->3, 3->1, 3->3 等多条边的更新,计算会变得非常繁琐。选择一个“出口”或“入口”附近、连接简单的状态先消除,通常是手动计算时的明智策略。
- 最终表达式的等价性: 最终得到的 (b U aba)(ab*a) 只是众多可能等价正则表达式中的一个。它在功能上是正确的,但在形式上可能不是最简洁的。例如,它是否等价于另一个可能的结果?验证两个复杂的正则表达式是否等价本身就是一个困难的问题。我们在这里信任算法的正确性。
示例 1.68 演示了将一个更复杂的三状态 DFA 转换为正则表达式的全过程。通过严格遵循状态消除算法,该示例展示了如何处理具有多个中间状态和更复杂循环结构的自动机。
- 首先,三状态 DFA 被转换为一个五状态的“特殊形式” GNFA。
- 然后,通过一系列递归步骤,依次消除了中间状态 3 和 2。
- 每一步消除都涉及到应用核心的更新公式 $R_{new} = (R_1)(R_2)^*(R_3) \cup R_4$,这使得边的正则表达式标签变得越来越复杂。
- 最终,算法终止于一个二状态的 GNFA,其唯一转换边上的标签 $(b \cup ab^*a)^*(ab^*a)$ 就是与原始 DFA 等价的正则表达式。
这个例子生动地说明了算法的机械性和威力,即便是对于一个直观上难以立即写出正则表达式的 DFA,该算法也能系统地、确定地推导出正确的结果。
这个例子的存在是为了证明状态消除算法的通用性,不仅仅适用于最简单的两状态 DFA。通过展示如何处理一个包含多个循环和路径选择的三状态 DFA,它增强了读者对算法处理更一般情况的能力的信心。它也暴露了该算法在手动执行时的一个现实问题:正则表达式的复杂性会迅速增长。这反过来暗示了为什么我们需要一个自动化的、机械的算法,而不是依赖于人类的直觉来完成这种转换。
这个过程就像在进行高级的“代码重构”,目标是把一个包含多个函数和跳转的程序,重构成一个单一的、巨大的 main 函数,而且不能使用任何函数调用。
- DFA: 原始程序,有 main (状态1), func2 (状态2), func3 (状态3) 等。
- 消除状态3: 决定内联 func3。找到所有调用 func3 的地方,把 func3 的代码(可能很简单,比如 return a;)直接替换掉调用。
- 消除状态2: 决定内联 func2。func2 可能很复杂,它内部有循环(b自循环),还可能调用 func1 (a边回到状态1)。当你内联 func2 时,所有这些循环和调用逻辑都必须以某种代数形式(正则表达式)被嵌入到调用者 func1 的代码中。这就导致了 func1 的自调用逻辑(自循环标签)变得极其复杂:b U ab*a。
- 消除状态1: 最后,把重构后的 func1 的所有逻辑都内联到 main 函数的入口点。
- 最终结果: main 函数现在变成了一个巨大的、嵌套的、包含所有逻辑的正则表达式。它功能正确,但可读性极差。
想象你在绘制一张从你家(状态1)到三个不同商店(状态2, 3等)再回家的所有可能购物路线的总图。
- 消除状态3 (杂货店): 你决定以后不去杂货店了。那么,所有原来“去完A店,再去杂货店,再去B店”的路线,现在都要变成一张新的“A店到B店的联运票”,票上说明了原来经过杂货店的走法。
- 消除状态2 (书店): 你又决定不去书店了。书店是你购物路线的核心中转站,你可能在书店里逛很久(自循环),也可能从书店去杂货店,也可能从书店回家。现在你必须把所有这些经过书店的复杂路线,全部重新规划成不经过书店的“超级联运票”。
- 结果: 原来“从家到书店”的票,“书店内部闲逛”的票,“书店到杂货店”的票……所有这些简单的票,现在都合并成了几张极其复杂的“全程通票”,比如“从家直接到家”的票(自循环),和“从家直接到出口”的票。这张“从家到出口”的最终通票上所写的路线规则,就是那个复杂的正则表达式。
2行间公式索引
- 一个算术表达式的例子:
- 一个描述以0或1开头,后跟任意数量0的语言的正则表达式:
- 一个描述所有0和1组成的字符串的语言的正则表达式:
- 一个描述数值常量的正则表达式:
- GNFA状态消除算法中更新边的核心公式:
- GNFA转移函数的形式化定义:
- GNFA中一条接受计算的通用状态序列:
- GNFA状态消除中新状态集的定义:
- GNFA状态消除算法中新转移函数的形式化定义:
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。