12 上下文无关语言
📜 [原文1]
在第 1 章中,我们介绍了两种不同但等效的语言描述方法:有限自动机和正则表达式。我们展示了许多语言可以用这种方式描述,但某些简单的语言,例如 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$,则不能。
这段话是本章的引言,旨在承上启下。它首先回顾了前一章(第 1 章)的核心内容,即有限自动机(Finite Automata, FA)和正则表达式(Regular Expressions, RE)。这两个工具是计算理论中用于描述和识别一类被称为正则语言(Regular Languages)的强大工具。
“不同但等效”是一个关键点。有限自动机是一种计算模型,像一台简单的机器,通过状态转移来“读取”并判断一个字符串是否属于某个语言。而正则表达式是一种代数表达式,是一种描述性的文本模式,用来定义一个字符串集合。尽管它们的形式完全不同(一个是机器模型,一个是代数表达式),但它们所能描述的语言集合是完全相同的,这个集合就是正则语言。这就是“等效”的含义。这个等价性是计算理论中的一个基本且重要的结论。
接着,段落指出了有限自动机和正则表达式的局限性。虽然它们可以描述很多有用的语言(例如,电子邮件地址的格式、特定格式的日期等),但它们的能力是有限的。存在一些结构上看起来很简单,但有限自动机无法处理的语言。
这里给出的经典例子是语言 $L = \left\{0^{n} 1^{n} \mid n \geq 0\right\}$。这个语言包含的字符串是由任意数量(包括零)的 '0' 后面跟着相同数量的 '1' 组成的。例如,空字符串 $\varepsilon$ (当 $n=0$ 时)、"01" (当 $n=1$ 时)、"0011" (当 $n=2$ 时)、"000111" (当 $n=3$ 时) 等都属于这个语言。而 "011"、"001"、"10" 等则不属于。
为什么有限自动机无法识别这个语言呢?直观地理解,有限自动机的“记忆力”是有限的。它的记忆力体现在它的状态数量上。要判断一个字符串是否属于 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$,机器在读完所有的 '0' 之后,必须准确地记住 '0' 的数量 $n$,以便在接下来读取 '1' 时进行匹配。但是,$n$ 可以是任意大的非负整数。一个只有有限个状态的机器,无法存储一个可能无限增长的计数值。这就是有限自动机的根本局限性,这个局限性通常用泵引理(Pumping Lemma for Regular Languages)来形式化地证明。
因此,这段引言的目的是告诉我们,现有的工具(有限自动机和正则表达式)已经不够用了,我们需要一种更强大的方法来描述像 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 这样更复杂的语言。这为引入本章的主角——上下文无关文法——埋下了伏笔。
- 语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$
- {... | ...}: 这是集合的标准表示法,称为集合构建符号(Set-builder notation)。竖线 | 左边是集合中元素的形式,右边是这些元素必须满足的条件。
- $0^{n} 1^{n}$: 这描述了集合中字符串的结构。它表示一个由 $n$ 个符号 '0' 组成的字符串,紧跟着一个由 $n$ 个符号 '1' 组成的字符串。这里的上标 $n$ 表示符号重复的次数。例如,$0^3$ 就是 "000"。
- $n \geq 0$: 这是变量 $n$ 必须满足的条件。$n$ 是一个大于或等于 0 的整数。这意味着 $n$ 可以是 0, 1, 2, 3, ...。
- 综合解释: 这个语言集合包含了所有由若干个 '0' 后面跟着相同数量的 '1' 构成的字符串。
- 示例 1: $n=3$
- 根据条件 $n=3$,我们构建字符串 $0^{3}1^{3}$。
- $0^3$ 表示 "000"。
- $1^3$ 表示 "111"。
- 所以,字符串是 "000111"。这个字符串属于语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$。
- 示例 2: $n=0$
- 根据条件 $n=0$,我们构建字符串 $0^{0}1^{0}$。
- 在形式语言理论中,任何符号的 0 次方都表示空串 $\varepsilon$。
- 所以,$0^0 = \varepsilon$ 且 $1^0 = \varepsilon$。
- 拼接起来就是 $\varepsilon\varepsilon = \varepsilon$。
- 因此,空串 $\varepsilon$ 也属于这个语言。
- 反例: 字符串 "001"
- 这个字符串中 '0' 的数量是 2 ($n=2$),而 '1' 的数量是 1。
- 数量不相等,不满足 $0^{n}1^{n}$ 的形式。
- 因此,"001" 不属于这个语言。
- 忘记 $n=0$ 的情况: 一个常见的遗漏是忘记考虑 $n=0$ 的情况。这导致认为该语言不包含空串 $\varepsilon$。但根据定义 $n \geq 0$,当 $n=0$ 时,我们得到空串,所以 $\varepsilon$ 是该语言的成员。
- 误认为顺序可以颠倒: 语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 对符号的顺序有严格要求,必须是所有的 '0' 在前,所有的 '1' 在后。像 "0101" 这样的字符串,虽然 '0' 和 '1' 的数量相等(都是2),但顺序是交错的,所以它不属于这个语言。
- 与 $\left\{w \mid w \text{ 中 0 和 1 的数量相等}\right\}$ 混淆: 后者是一个更宽泛的语言,它包含了 "0101", "1100" 等字符串,而前者只是它的一个子集。识别后者也需要超越正则语言的能力。
- 认为 $n$ 有上限: 语言的定义中 $n$ 是任意非负整数,没有上限。正是这种无限的可能性,使得有限自动机的有限记忆无法应对。
本段是第 2 章的开篇,通过回顾第 1 章的有限自动机和正则表达式,引出了它们的局限性。它以经典的非正则语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 为例,说明了需要更强大的描述工具来处理具有递归或依赖计数特性的语言,从而为本章引入上下文无关文法做了铺垫。
本段的目的是在知识体系上建立一座桥梁,连接已学的正则语言和将要学习的上下文无关语言。它通过指出旧工具的“能力天花板”,来论证学习新工具的必要性和动机,使得内容的展开显得自然且有逻辑。
你可以把有限自动机想象成一个只有短期记忆的人。他可以记住几个(有限个)关键信息,比如“我刚刚看到了一个'a'”或“我已经看到了奇数个'b'”。但如果你让他数一数一本书里总共有多少个'a',然后再告诉你这个数字,他就做不到了,因为书里的'a'可能非常多,超出了他的记忆极限。语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 就需要这种无限的计数能力,而有限自动机不具备。
想象一条单行道的隧道,汽车只能从一端进,另一端出。有限自动机就像一个站在隧道口的收费员,他只有一个小本子,上面只能记有限页的东西(状态)。如果规则是“进来多少辆红车,就必须紧跟着出去多少辆蓝车”,当红车源源不断地进来时($n$ 可以非常大),收费员的小本子很快就记满了,他无法确切知道到底进来了多少辆红车,也就无法在蓝车出去时进行核对。这就是有限自动机的困境。
📜 [原文2]
在本章中,我们将介绍上下文无关文法,这是一种更强大的语言描述方法。这类文法可以描述具有递归结构的某些特征,这使其在各种应用中都很有用。
这段话正式引入了本章的核心概念——上下文无关文法(Context-Free Grammar, CFG)。在上一段指出有限自动机的局限性之后,这里直接给出了解决方案。
“更强大的语言描述方法”是对上下文无关文法的一个定位。这里的“强大”是形式化的,意味着由上下文无关文法所能描述的语言集合(即上下文无关语言)是正则语言集合的一个超集。也就是说,所有正则语言都可以用上下文无关文法来描述,但上下文无关文法还能描述一些非正则语言,比如上一段提到的 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$。
接下来解释了上下文无关文法之所以“强大”的关键在于它能够描述“递归结构”。递归(Recursion)是指一个结构或规则的定义中包含了它自身的引用。在语言中,递归结构表现为“一个短语类型可以包含同类型的更小的短语”。例如,一个算术表达式可以由两个更小的算术表达式通过加号连接而成。 ( (3 + 4) * 5 ) 就是一个例子,外层的表达式包含了内层的 (3 + 4)。这种能够自我嵌套的特性,正是上下文无关文法所擅长描述的,也是有限自动机无法处理的。
最后,段落提到了上下文无关文法的实用性——“在各种应用中都很有用”。这表明上下文无关文法不仅仅是一个理论工具,它在实际中有着广泛的应用。这为后面详细介绍其应用场景(如人类语言学和编程语言编译)做了引子。
- 示例 1: 递归结构在语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 中的体现
- 考虑字符串 "0011"。它可以被看作是在字符串 "01" 的外部包裹了一对 "0" 和 "1"。
- 即: "0011" = "0" + "01" + "1"。
- 这里的 "01" 本身也是该语言的一个成员。
- 这种“一个合法的字符串可以通过在另一个合法的字符串外面包裹一层符号来生成”的模式,就是一种递归的体现。一个上下文无关文法规则可以写成 S -> 0S1 来捕捉这种递归结构。
- 示例 2: 英语中的递归结构
- 考虑名词短语 "the cat on the mat"。
- 这个短语中包含了一个介词短语 "on the mat"。
- 而介词短语 "on the mat" 自身又包含了一个名词短语 "the mat"。
- 所以我们看到一个名词短语的定义里可以包含另一个名词短语。这就是递归结构。例如,一个规则可以写成 <名词短语> -> <名词短语> <介词短语>。
- 误认为“更强大”意味着能描述所有语言**:上下文无关文法虽然比有限自动机强大,但它也不是万能的。同样存在它无法描述的语言,例如 $\left\{a^{n} b^{n} c^{n} \mid n \geq 0\right\}$。这类语言需要更强大的工具,如上下文相关文法或图灵机**来描述。
- 对“递归”的理解过于狭隘: 递归不仅仅是 A -> ...A... 这种直接递归,也包括间接递归,如 A -> B,B -> A。只要在推导过程中,一个变量能够推导出包含自身的字符串,就体现了递归性。
本段明确提出了本章要介绍的核心工具——上下文无关文法 (CFG)。它将 CFG 定位为一种比有限自动机更强大的语言描述方法,其强大之处在于能够捕捉语言中的递归结构。同时,它也强调了 CFG 的实用价值,预示了其在多个领域的广泛应用。
本段的核心目的是为读者建立对上下文无关文法的初步认知。它回答了三个基本问题:1. 我们要学什么?(上下文无关文法) 2. 它有什么特点?(更强大,能描述递归结构) 3. 学它有什么用?(应用广泛)。这为后续深入学习打下了概念基础。
如果说有限自动机是只有短期记忆的人,那么上下文无关文法就像一套俄罗斯套娃的制作说明书。说明书告诉你:“一个套娃可以由一个更小的套娃涂上油漆再装进一个外壳里组成”。通过反复应用这条规则,你可以制作出任意多层的套娃。这个“自我引用”的制作规则就是递归。上下文无关文法就是这样一套规则,它能生成具有嵌套或递归特性的语言。
想象一下你在用乐高积木搭建。有限自动机的规则集就像是“红砖旁边只能放蓝砖,蓝砖旁边只能放绿砖”这类简单的“邻接规则”。你只能搭出一条彩色的线。而上下文无关文法的规则集则像是“一个‘房子’可以由四面‘墙’和一个‘屋顶’组成”,而一面‘墙’又可以由很多‘砖块’组成,甚至一个‘大房子’的院子里可以建一个‘小房子’。这种分层、嵌套的组合能力,就是上下文无关文法描述递归结构能力的直观体现。
📜 [原文3]
上下文无关文法最初用于研究人类语言。理解名词、动词、介词等术语及其各自短语之间关系的一种方法,自然会导致一种递归,因为名词短语可能出现在动词短语中,反之亦然。上下文无关文法帮助我们组织和理解这些关系。
这段话介绍了上下文无关文法的第一个重要应用领域:自然语言处理(Natural Language Processing, NLP),特别是其在语言学中的起源。
“最初用于研究人类语言”点明了其历史背景。在计算机科学领域之外,语言学家(如诺姆·乔姆斯基)为了形式化地描述人类语言的语法结构,发展了这套理论。
接下来,段落解释了为什么上下文无关文法适合描述人类语言。人类语言的句子不是单词的随意堆砌,而是具有层次化的语法结构。句子由短语构成,短语又由更小的短语或单词构成。这里提到了几个基本的语法单位:“名词”、“动词”、“介词”以及它们构成的“短语”(如名词短语、动词短语)。
核心思想在于这些短语之间的“递归”关系。“名词短语可能出现在动词短语中”,例如,在动词短语“sees the boy”(看见那个男孩)中,“the boy”是一个名词短语。“反之亦然”指的是动词短语也可能出现在名词短语中,虽然这种情况在英语中不那么直接,但可以通过从句等形式实现,例如名词短语“the man who runs fast”(跑得快的男人)中,"who runs fast"起到了修饰作用,其核心是动词"runs"。更典型的例子是,一个名词短语可以包含另一个名词短语,如“the corner of the room”(房间的角落),其中“the room”是内嵌在更大的名词短语里的。
“上下文无关文法帮助我们组织和理解这些关系”是对其作用的总结。通过一套形式化的规则,语言学家可以精确地描述哪些句子是合法的,哪些是不合法的,并且能够揭示句子的内部结构。这种结构化的分析对于理解语言、机器翻译和人机对话等任务至关重要。
- 示例 1: 名词短语出现在动词短语中
- 句子: "The dog chases the cat." (狗追猫。)
- 动词短语 (Verb Phrase): "chases the cat"
- 在这个动词短语中,"the cat" 是一个名词短语 (Noun Phrase)。
- 我们可以用一条文法规则来表示这种关系: <Verb-Phrase> -> <Verb> <Noun-Phrase> (动词短语由一个动词和一个名词短语构成)。
- 示例 2: 递归的名词短语
- 名词短语: "the key to the door of the house" (房门的钥匙)
- 整个字符串是一个大的名词短语。
- 它包含一个介词短语 "to the door of the house"。
- 这个介词短语中又包含一个名词短语 "the door of the house"。
- 这个名词短语又包含一个介词短语 "of the house"。
- 这个介词短语又包含一个名词短语 "the house"。
- 我们看到名词短语一层套一层,这就是典型的递归。可以用规则如 <Noun-Phrase> -> <Noun-Phrase> <Prepositional-Phrase> 来描述。
- 高估了上下文无关文法的能力: 虽然上下文无关文法在描述句子结构方面很强大,但它无法捕捉人类语言中的所有现象。例如,英语中的主谓一致("The boy runs" vs "The boys run"),动词 "run" 的形式取决于主语 "boy" 是单数还是复数。这种依赖于“上下文”(主语的数)的特性,上下文无关文法很难处理。这类问题通常需要上下文相关文法或更复杂的模型。
- “上下文无关”的误解: 这个术语指的是替换规则的应用是“无关上下文”的。比如有一条规则 A -> X,那么在任何包含 A 的字符串中,这个 A 都可以被替换为 X,而不需要考虑 A 前后是什么符号。这与前面提到的主谓一致问题形成了对比,在那个场景下,动词的选择是“有关上下文”(即主语)的。
本段阐述了上下文无关文法在语言学中的起源和核心应用。它通过分析人类语言中短语之间普遍存在的递归和嵌套关系,说明了上下文无关文法是组织和理解这些复杂语法结构的有力工具。
本段的目的是展示上下文无关文法的第一个,也是最原始的应用场景——人类语言研究。这不仅丰富了我们对该工具的认识,也通过一个我们熟悉的领域(自己的母语或外语)帮助我们直观地理解抽象的“递归结构”概念。
想象一下你在分析一个复杂的句子,就像在画一棵语法树。你会先把句子分成主语(一个名词短语)和谓语(一个动词短语)。然后你再分别去看主语和谓语的构成,可能会发现它们里面又包含了更小的短语。这个过程不断地分解下去,直到你分析到单个的单词为止。上下文无关文法就是这套分解规则的集合。它告诉你什么样的组合是合法的,以及如何进行这种层次化的分解。
把一个句子想象成一个公司组织架构图。CEO是整个句子(SENTENCE)。他下面有几个副总裁,比如“名词短语部”和“动词短语部”。每个副总裁下面又有经理(比如“介词短语”、“形容词”),经理下面是普通员工(具体的单词 "the", "boy", "sees")。有时候,“名词短语部”的一个项目需要从“介词短语部”借调一个团队,而那个团队里可能又有一个来自“名词短语部”的顾问。这种部门间的嵌套和调用关系,就是上下文无关文法所描述的递归关系。
📜 [原文4]
上下文无关文法的一个重要应用是编程语言的规范和编译。编程语言的文法通常作为人们学习语言语法时的参考。编程语言的编译器和解释器设计者通常从获取语言的文法开始。大多数编译器和解释器都包含一个称为解析器的组件,它在生成编译代码或执行解释之前提取程序的意义。一旦有了上下文无关文法,许多方法都能促进解析器的构建。有些工具甚至可以根据文法自动生成解析器。
这段话介绍了上下文无关文法在计算机科学领域最核心的应用:编程语言。
“编程语言的规范和编译”点出了两个关键环节。
- 规范 (Specification): 上下文无关文法为编程语言提供了一个精确、无歧义的语法定义。这就像一部语言的“法典”。当我们学习一门新的编程语言(如 Python, Java)时,官方文档中描述的语法规则(比如 if 语句的格式,函数定义的格式)就是基于其上下文无关文法的。这为所有使用者和开发者提供了统一的标准。
- 编译 (Compilation): 编译是将人类可读的源代码(高级语言)转换成机器可执行的代码(低级语言)的过程。上下文无关文法在编译过程中扮演着至关重要的角色。
段落接着详细阐述了文法在编译过程中的作用。编译器或解释器的设计者首先需要得到该语言的上下文无关文法。这是设计的第一步。
编译器和解释器中有一个核心组件叫解析器(Parser)。解析器的任务是读取源代码字符串,并根据文法规则来分析其语法结构,判断代码是否符合语法。这个过程称为解析(Parsing)或语法分析。如果语法正确,解析器会生成一个数据结构来表示代码的层次化意义,这个结构通常是抽象语法树(Abstract Syntax Tree, AST),它捕捉了代码的运算顺序、依赖关系等。这个“提取程序的意义”的过程是后续生成可执行代码或进行解释执行的基础。
例如,对于代码 a = b + c d,解析器会根据文法中定义的运算符优先级,生成一棵树,表明应该先计算 c d,然后将其结果与 b 相加,最后再将总结果赋值给 a。没有文法和解析器,编译器就无法理解这段代码的真正意图。
最后一段强调了文法的工具价值。“一旦有了上下文无关文法”,构建解析器就变得有章可循。存在许多成熟的理论和算法(如 LL 解析、LR 解析)来指导如何手动编写一个解析器。更方便的是,存在一些“解析器生成器”(Parser Generator)工具,例如 YACC (Yet Another Compiler-Compiler) 或 Bison。你只需要把语言的上下文无关文法作为输入提供给这些工具,它们就能自动生成对应的解析器代码。这极大地简化了编译器和解释器的开发工作。
- 示例 1: C 语言的 if 语句
- 一个简化的 if 语句文法规则可能是:<if-statement> -> if ( <expression> ) <statement>
- 规范: 这条规则清晰地定义了 if 语句的结构:必须以关键字 if 开头,后跟一个括号括起来的表达式,最后是一个语句。任何不符合这个模式的代码(如 if x > 0 { ... },括号缺失)都会被解析器认为是语法错误。
- 解析: 当解析器读到源代码 if (a == 10) x = 1; 时,它会匹配这条规则,并识别出 <expression> 是 a == 10,<statement> 是 x = 1;。然后它会递归地去解析表达式和语句,最终构建出一棵完整的语法树。
- 示例 2: 解析器生成器 YACC/Bison
- 假设我们要为一个简单的计算器定义文法,我们可以在一个 .y 文件中这样写 (Bison 格式):
```yacc
%token NUMBER
%%
expr: expr '+' term { $$ = $1 + $3; }
| term { $$ = $1; }
;
term: term '*' factor { $$ = $1 * $3; }
| factor { $$ = $1; }
;
factor: '(' expr ')' { $$ = $2; }
| NUMBER { $$ = $1; }
;
%%
```
- 这个文件定义了表达式 (expr)、项 (term) 和因子 (factor) 的文法规则,以及相应的计算动作。
- 把这个文件输入到 Bison 工具中,它会自动生成一个 C 语言的解析器文件。我们只需要再提供一个词法分析器(用于识别出 NUMBER, +, * 等符号)并编译它们,就能得到一个可以工作的计算器程序。这展示了文法如何驱动自动化工具的开发。
- 混淆解析与词法分析: 解析(语法分析)是编译的第二阶段。在它之前还有一个词法分析(Lexical Analysis)阶段。词法分析器(Scanner)负责将源代码的字符流切分成一个个有意义的单元,称为词法单元或记号(Token),例如关键字 if、标识符 my_variable、数字 123、运算符 +。解析器处理的是这些词法单元流,而不是原始的字符流。
- 文法的歧义性问题: 在设计编程语言的文法时,必须非常小心地避免歧义。一个有歧义的文法可能对同一段代码产生两种或多种不同的解析树,这意味着代码的意义不唯一,这是不可接受的。例如,a + b c 如果文法有歧义,可能被解析为 (a + b) c 或 a + (b * c)。因此,编程语言的文法必须是无歧义的。
本段详细阐述了上下文无关文法在计算机科学中的核心应用:作为编程语言的规范和编译/ 解释过程的基础。它解释了文法如何被解析器用来分析代码结构、提取意义,并强调了文法对于自动化构建编译器工具(如解析器生成器)的重要性。
本段的目的是将上下文无关文法这个理论工具与一个非常具体、重要的实践领域——编程语言开发——联系起来。这不仅展示了其巨大的实用价值,也为学习计算机科学的学生提供了强烈的学习动机,因为这直接关系到他们日常使用的工具(编译器、解释器)是如何工作的。
上下文无关文法就像一本编程语言的“官方食谱”。解析器就是一位严格按照食谱做菜的厨师。源代码是顾客的订单。厨师(解析器)拿到订单(源代码),会逐行对照食谱(文法),检查订单写得是否规范。如果规范,他就知道这道菜(程序)的烹饪步骤(运算顺序和结构),然后开始备料、烹饪(生成机器代码)。如果订单不符合食谱(语法错误),厨师就会拒绝服务并指出哪里写错了。像 YACC 这样的工具,则是一个“食谱机器人”,你给它食谱,它就能变出一个严格的厨师来。
想象一下你正在组装一件宜家家具。那本只有图画和零件编号的说明书,就是这件家具的“文法”。它规定了A零件必须和B零件用C号螺丝连接,然后整体再插入D零件的孔中。你(解析器)看着一堆零件(源代码),严格按照说明书(文法)的步骤进行组装(解析)。如果你发现少了个零件,或者想把A零件强行接到Z零件上(说明书里没这么画),你就知道出错了(语法错误)。当你严格按照说明书组装完成后,你就得到了一个具有特定结构和功能的椅子(程序的语法树),而不是一堆无意义的木板和螺丝。
📜 [原文5]
与上下文无关文法相关的语言集合称为上下文无关语言。它们包括所有正则语言以及许多额外的语言。在本章中,我们给出上下文无关文法的形式化定义,并研究上下文无关语言的性质。我们还将介绍下推自动机,这是一类识别上下文无关语言的机器。下推自动机很有用,因为它们使我们能够更深入地了解上下文无关文法的力量。
这段话是整个引言的总结,并预告了本章即将展开的主要内容。
“与上下文无关文法相关的语言集合称为上下文无关语言 (Context-Free Languages, CFLs)。” 这句话给出了一个核心定义。就像由正则表达式描述的语言集合被称为正则语言一样,所有能够被某一个上下文无关文法生成的语言,其集合被称为上下文无关语言。这是一个新的、更庞大的语言类别。
“它们包括所有正则语言以及许多额外的语言。” 这句话阐明了上下文无关语言和正则语言之间的关系。正则语言是上下文无关语言的真子集(Proper Subset)。这意味着:
- 任何一个正则语言,都必定是一个上下文无关语言。(我们总能为它找到一个上下文无关文法来描述)。
- 存在一些上下文无关语言,它们不是正则语言(比如 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$)。
这在形式上确认了上下文无关文法是比有限自动机或正则表达式“更强大”的描述工具。
接下来是本章的内容路线图:
- “给出上下文无关文法的形式化定义”:前面都是直观描述,接下来要用数学的语言精确定义什么是文法、什么是推导等。
- “研究上下文无关语言的性质”:这包括探讨这类语言在并、交、补等运算下的封闭性,以及它们的其他特性(例如,是否存在泵引理)。
- “介绍下推自动机 (Pushdown Automata, PDA)”:这是本章的另一个核心内容。回顾第 1 章,我们有正则表达式(描述工具)和有限自动机(识别机器),它们是等价的。类似地,本章也将为上下文无关文法(描述工具)引入一个与之等价的计算模型——下推自动机。
- “下推自动机是一类识别上下文无关语言的机器。” 这明确了 PDA 的角色,它是一个识别器,用于判断一个给定的字符串是否属于某个上下文无关语言。
- “下推自动机很有用,因为它们使我们能够更深入地了解上下文无关文法的力量。” 这说明了引入 PDA 的意义。通过研究一个具体的机器模型,我们可以从另一个角度理解上下文无关语言的内在特性。下推自动机比有限自动机多了一个栈(stack)作为无限的记忆体,正是这个栈结构,使得它能够处理像 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 这样需要计数的语言。研究 PDA 的工作原理,能让我们更深刻地理解为什么上下文无关语言能处理递归和匹配,以及它们的计算能力的边界在哪里。
- 示例 1: 正则语言也是上下文无关语言****
- 正则语言 $L = \{ (01)^* \}$ (由任意数量的 "01" 串联而成,如 $\varepsilon$, "01", "0101", ...)。
- 它可以被正则表达式 (01)* 描述。
- 它也可以被上下文无关文法 $G$ 描述:S -> 01S | ε。
- 例如,生成 "0101" 的过程是: S => 01S => 0101S => 0101ε => 0101。
- 这说明了正则语言确实可以被 CFG 描述。
- 示例 2: 下推自动机识别 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 的直观工作方式
- 机器: 一个带栈的有限自动机 (PDA)。
- 输入: "0011"
- 过程:
- PDA 开始读第一个 '0',它将一个特殊符号(比如 '$')推入栈中。
- 读到第二个 '0',它再推入一个 '$' 到**栈**中。现在**栈**里有两个 '$'。
- 接着读到第一个 '1',它从栈顶弹出一个 '$'。
- 读到第二个 '1',它再从栈顶弹出一个 '$'。
- 字符串读完,同时栈也空了。
- PDA 进入接受状态,宣布 "0011" 是合法的。
- 失败情况 (输入 "001"):
- 读完两个 '0',栈里有两个 '$'。
- 读到一个 '1',弹出一个 '$'。
- 字符串读完,但栈里还剩一个 '$'。
- PDA 进入拒绝状态。
- 这个栈就像一个计数器,完美解决了有限自动机记忆力不足的问题。
- 对“识别”和“生成”的混淆: 上下文无关文法是“生成”语言的工具,它提供一套规则来构建语言中的所有字符串。下推自动机是“识别”语言的工具,它判断一个给定的字符串是否符合语言的规则。这两个概念一个主动一个被动,但描述的是同一类语言。
- 认为所有 PDA 都是确定的: 有限自动机有确定性(DFA)和非确定性(NFA)之分,但它们的计算能力是等价的。对于下推自动机,确定性下推自动机(DPDA)的能力弱于非确定性下推自动机(NPDA)。NPDA 才与上下文无关文法等价。存在一些上下文无关语言,它们可以被 NPDA 识别,但不能被任何 DPDA 识别。
本段作为引言的结尾,明确定义了上下文无关语言 (CFL) 这一核心概念,并阐述了它与正则语言的层级关系(CFL 包含所有正则语言)。同时,它清晰地勾勒出本章的学习路线:学习上下文无关文法的形式化定义、研究 CFL 的性质,并引入与之等价的计算模型——下推自动机,以从机器识别的角度加深理解。
本段的目的是为读者提供一个清晰的“学习地图”。在进入具体的、可能充满细节和数学符号的内容之前,让读者对本章的整体结构、核心概念及其相互关系有一个宏观的把握。这有助于读者在学习过程中保持方向感,更好地组织和吸收新知识。
把学习计算理论的过程想象成升级你的工具箱。第 1 章你得到了锤子(正则表达式)和螺丝刀(有限自动机),它们很好用,但只能处理一些简单的钉子和螺丝(正则语言)。本章告诉你,有一个更复杂的任务(比如处理 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$),你需要新工具。于是,你将得到一本“蓝图”(上下文无关文法)和一台“3D 打印机”(下推自动机)。蓝图告诉你如何设计和生成复杂的零件(上下文无关语言),而 3D 打印机可以根据设计来实际制造或验证这些零件。它们的能力比锤子和螺丝刀更强。
想象一场法庭辩论。上下文无关文法就像是检察官,他要“构建”一个完整的犯罪故事(生成一个字符串),从动机到行为,一步步推导出结论。下推自动机则像是辩护律师,他面对一个给定的“指控”(输入字符串),需要用证据(栈操作)来一步步“验证”这个指控是否成立。虽然角色不同,但他们都围绕着同一套法律(语言规则)工作。本章就是要学习这套更高级的法律以及检察官和律师的工作方法。
22.1 上下文无关文法
📜 [原文6]
以下是上下文无关文法的一个示例,我们称之为 $G_{1}$。
文法由一系列替换规则组成,也称为产生式。每条规则都以文法中的一行出现,包含一个符号和一个由箭头分隔的字符串。该符号称为变量。该字符串由变量和称为终结符的其他符号组成。变量符号通常用大写字母表示。终结符类似于输入字母表,通常用小写字母、数字或特殊符号组成。其中一个变量被指定为开始变量。它通常出现在最顶层规则的左侧。例如,文法 $G_{1}$ 包含三条规则。$G_{1}$ 的变量是 $A$ 和 $B$,其中 $A$ 是开始变量。它的终结符是 0, 1 和 \#。
这一部分开始正式介绍上下文无关文法(CFG)的具体构成。它通过一个非常经典的例子 $G_1$ 来展开说明。
首先,给出了一个名为 $G_1$ 的文法,它包含三条规则:
- $A \rightarrow 0A1$
- $A \rightarrow B$
- $B \rightarrow \#$
然后,对文法的组成要素进行了详细拆解:
- 规则 (Rules) / 产生式 (Productions): 文法的核心是一系列规则。每一条规则定义了一种“替换”或“生成”的可能性。例如,规则 $A \rightarrow 0A1$ 意味着,当你在构建字符串的过程中遇到符号 $A$ 时,你可以将它替换成字符串 "0A1"。这个过程就像一个转换指令。
- 箭头 →: 这个符号读作“导出”或“生成”。它分隔了规则的左右两部分。左边是被替换的对象,右边是替换后的结果。
- 变量 (Variables): 出现在规则左侧的符号被称为变量。它们是文法的“非终结符”(Non-terminals)。你可以把它们看作是构造过程中的“中间产品”或“占位符”。它们不是最终语言字符串的一部分,必须在生成过程中被完全替换掉。按照惯例,变量通常用大写字母表示。在 $G_1$ 中,$A$ 和 $B$ 就是变量。
- 终结符 (Terminals): 在规则右侧出现的,且不是变量的符号,被称为终结符。它们是构成最终语言字符串的“基本材料”或“字母”。一旦生成,它们就不能再被替换。它们类似于有限自动机的输入字母表。在 $G_1$ 中,0,1 和 # 就是终结符。它们通常用小写字母、数字或特殊符号表示。
- 开始变量 (Start Variable): 在所有变量中,有一个是特殊的,被称为开始变量。它是一切生成过程的起点。按照惯例,如果没有特别说明,出现在第一条规则左侧的变量就是开始变量。在 $G_1$ 中,$A$ 就是开始变量。
最后,对 $G_1$ 进行了总结:
- 规则: 共 3 条。
- 变量: $A$ 和 $B$。
- 开始变量: $A$。
- 终结符: 0, 1, #。
这一段通过一个实例,清晰地定义了上下文无关文法的四个基本组成部分:变量、终结符、规则和开始变量。这是理解后续所有内容的基础。
- $A \rightarrow 0 A 1$
- A (左侧): 这是一个变量。
- →: “导出”符号。
- 0 (右侧): 这是一个终结符。
- A (右侧): 这是同一个变量 $A$ 的递归引用。
- 1 (右侧): 这是一个终结符。
- 规则含义: 这是一条递归规则。它表示一个变量 $A$ 可以被替换为在它自身两侧各加上一个 '0' 和一个 '1'。这个规则是用来生成对称的 '0' 和 '1' 串的。
- $A \rightarrow B$
- A (左侧): 变量。
- →: “导出”符号。
- B (右侧): 另一个变量。
- 规则含义: 这是一条单元规则 (Unit Rule)。它表示变量 $A$ 的生成过程可以转交给变量 $B$ 来继续。这通常用于在不同的生成阶段之间进行切换。
- $B \rightarrow \#$
- B (左侧): 变量。
- →: “导出”符号。
- # (右侧): 终结符。
- 规则含义: 这是一条终结规则。它表示变量 $B$ 可以被替换为一个终结符 #,从而结束这一分支的生成过程。
- 示例 1: 分析文法** $G_{\text{example}}$
- 文法:
```
S -> aSb
S -> ε
```
- 规则: 有 2 条规则, S -> aSb 和 S -> ε。
- 变量: 只有 1 个变量 S。
- 开始变量: S。
- 终结符: a 和 b。(ε 是空串,是一个特殊的符号,不计入终结符字母表)。
- 示例 2: 分析文法** $G_{\text{expr}}$
- 文法:
```
E -> E + T
E -> T
T -> T * F
T -> F
F -> (E)
F -> id
```
- 规则: 有 6 条规则。
- 变量: E, T, F (通常代表 Expression, Term, Factor)。
- 开始变量: E。
- 终结符: +, *, (, ), id (代表标识符,如变量名)。
- 变量与终结符混淆: 初学者可能分不清哪些是变量,哪些是终结符。关键判断依据是:出现在规则左侧的必定是变量;没有出现在任何规则左侧的符号就是终结符。大写/小写的惯例有助于区分,但最终定义要看规则本身。
- 开始变量的确定: 如果没有明确指定,默认第一条规则的左侧变量是开始变量。但在一些复杂的文法定义中,可能会显式地指出开始变量是哪一个。
- 规则右侧可以为空: 一条规则的右侧可以是空串 $\varepsilon$,例如 A -> ε。这种规则被称为 $\varepsilon$-规则,它表示一个变量可以直接“消失”,结束生成。
本段通过一个具体的例子 $G_1$,详细介绍了构成上下文无关文法 (CFG) 的四个基本组件:规则(或产生式)、变量(非终结符)、终结符和开始变量。它建立了后续讨论 CFG 工作方式所必需的基础词汇和概念。
此段的目的是从一个具体的、简单的实例入手,避免一开始就进行抽象的形式化定义,从而降低读者的认知门槛。通过“解剖麻雀”的方式,让读者对文法的组成部分有一个直观且准确的认识,为理解文法如何“工作”做好准备。
一个上下文无关文法就像一套菜谱。
- 终结符 (0, 1, #) 是厨房里最基本的食材,比如盐、糖、面粉。
- 变量 (A, B) 是菜谱里的半成品菜名,比如“红烧肉酱汁”、“面团”。它们本身不能直接吃,需要进一步加工。
- 规则 (A -> 0A1) 是具体的烹饪步骤,比如“(步骤5)制作‘豪华版红烧肉酱汁’:取一份‘普通版红烧肉酱汁’,加入一勺糖和一勺酱油”。
- 开始变量 (A) 是你最终想要做的那道主菜的名字,比如“红烧肉”。整个做菜过程就从这道主菜开始。
想象你是一个玩具工厂的生产线控制器。
- 终结符是构成玩具的最小零件:螺丝、塑料片、轮子。
- 变量是各种组件的代号:WHEEL_ASSEMBLY (车轮组件), MAIN_BODY (主体框架)。
- 规则是装配指令:WHEEL_ASSEMBLY -> AXLE + WHEEL + WHEEL (一个车轮组件由一根轴和两个轮子构成)。
- 开始变量是最终产品的型号:TOY_CAR_MODEL_S。
你的任务就是从最终产品的型号开始,按照装配指令不断地把组件代号替换成更小的组件或基本零件,直到最后只剩下基本零件的组合,一个完整的玩具车就生产出来了。
📜 [原文7]
你通过以下方式生成该语言的每个字符串来使用文法描述语言。
- 写下开始变量。它是顶层规则左侧的变量,除非另有说明。
- 找到一个已写下的变量以及一个以该变量开头的规则。用该规则的右侧替换已写下的变量。
- 重复步骤 2,直到没有变量为止。
例如,文法 $G_{1}$ 生成字符串 000\#111。获取字符串的替换序列称为推导。文法 $G_{1}$ 中字符串 000\#111 的推导是
你也可以用分析树以图形方式表示相同的信息。分析树的一个示例如图 2.1 所示。
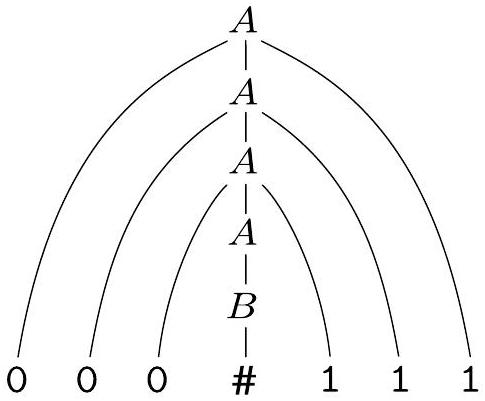
图 2.1
文法 $G_{1}$ 中 000\#111 的分析树
这一部分详细描述了如何使用一个文法来生成语言中的字符串,并引入了两个关键概念:推导和分析树。
首先,给出了一个三步走的算法流程,解释了“生成”一个字符串的过程:
- 初始化: 从开始变量出发。这是所有生成的起点。对于 $G_1$,我们从 $A$ 开始。
- 迭代替换: 在当前生成的字符串(初始为开始变量)中,选择一个变量。然后,在文法的规则集中,找到一条以这个变量为左侧的规则。将所选变量替换为该规则的右侧内容。这个步骤可以重复进行。选择哪一个变量(如果当前字符串中有多个),以及选择哪一条规则(如果一个变量对应多条规则),都会影响生成的路径和最终结果。
- 终止: 当生成的字符串中不再含有任何变量,只剩下终结符时,生成过程结束。这个最终的终结符串就是文法所生成的语言中的一个成员。
接着,通过一个具体的例子来演示这个过程。目标是使用文法 $G_1$ 生成字符串 000#111。这个一步步替换的过程被称为推导 (Derivation)。
推导过程的符号是 $\Rightarrow$,读作“一步推导出”。
$A \Rightarrow 0A1$:
- 开始于开始变量 $A$。
- 应用规则 $A \rightarrow 0A1$。将 $A$ 替换为 0A1。
$0A1 \Rightarrow 00A11$:
- 当前字符串是 0A1。其中唯一的变量是 $A$。
- 再次应用规则 $A \rightarrow 0A1$。将中间的 $A$ 替换为 0A1。
- 得到 0 + 0A1 + 1,即 00A11。
$00A11 \Rightarrow 000A111$:
- 当前字符串是 00A11。
- 第三次应用规则 $A \rightarrow 0A1$。
- 得到 00 + 0A1 + 11,即 000A111。
$000A111 \Rightarrow 000B111$:
- 当前字符串是 000A111。
- 现在我们选择应用另一条规则 $A \rightarrow B$。
- 将 $A$ 替换为 $B$,得到 000B111。
- 这一步是递归的终止,转向下一个阶段。
$000B111 \Rightarrow 000\#111$:
- 当前字符串是 000B111。唯一的变量是 $B$。
- 应用规则 $B \rightarrow \#$。
- 将 $B$ 替换为 #,得到 000#111。
- 此时,字符串 000#111 中已没有任何变量。推导结束。
这个序列完整地展示了从开始变量 $A$ 如何一步步生成最终字符串 000#111 的过程。
最后,引入了分析树(Parse Tree)或推导树(Derivation Tree)的概念。它是推导过程的图形化表示,能更直观地展示字符串的语法结构。
- 树根 (Root): 是开始变量($A$)。
- 内部节点 (Internal Nodes): 是变量($A, B$)。
- 叶子节点 (Leaves): 是终结符(0, 1, #)或空串 $\varepsilon$。
- 父子关系: 如果有一个规则 $X \rightarrow Y_1 Y_2 \dots Y_k$,那么在树中,节点 $X$ 会有 $k$ 个子节点,从左到右依次是 $Y_1, Y_2, \dots, Y_k$。
- 分析树的产出: 将分析树的所有叶子节点从左到右串联起来,得到的就是被生成的字符串。在图 2.1 中,从左到右读取叶子节点,得到 0 0 0 # 1 1 1。
分析树清晰地展示了字符串的层次结构,例如,000#111 是由一个顶层的 $A$ 结构生成,这个 $A$ 分解为 0、一个子 $A$ 和 1,这个子 $A$ 又同样分解...直到最后通过 $B$ 产生 #。
- $A \Rightarrow 0 A 1 \Rightarrow 00 A 11 \Rightarrow 000 A 111 \Rightarrow 000 B 111 \Rightarrow 000 \# 111$
- $X \Rightarrow Y$: 这个符号表示字符串 $X$ 可以通过一次规则应用,推导出字符串 $Y$。
- 第一步 $A \Rightarrow 0A1$: 应用规则 $A \rightarrow 0A1$。
- 第二步 $0A1 \Rightarrow 00A11$: 在 0A1 中,对变量 $A$ 应用规则 $A \rightarrow 0A1$。
- 第三步 $00A11 \Rightarrow 000A111$: 在 00A11 中,对变量 $A$ 应用规则 $A \rightarrow 0A1$。
- 第四步 $000A111 \Rightarrow 000B111$: 在 000A111 中,对变量 $A$ 应用规则 $A \rightarrow B$。
- 第五步 $000B111 \Rightarrow 000\#111$: 在 000B111 中,对变量 $B$ 应用规则 $B \rightarrow \#$。
- 整个序列构成了一个完整的推导过程。
- 示例 1: 使用 $G_1$ 推导字符串 "0#1"
- 推导:
$A \Rightarrow 0A1$ (应用 $A \rightarrow 0A1$ 一次)
$\Rightarrow 0B1$ (应用 $A \rightarrow B$)
$\Rightarrow 0\#1$ (应用 $B \rightarrow \#$)
- 分析树:
- 根是 $A$。
- $A$ 有三个孩子: 0, $A$, 1。
- 中间的 $A$ 有一个孩子: $B$。
- $B$ 有一个孩子: #。
- 叶子节点从左到右是 0, #, 1。
- 示例 2: 使用 $G_1$ 推导字符串 "#"
- 推导:
$A \Rightarrow B$ (应用 $A \rightarrow B$)
$\Rightarrow \#$ (应用 $B \rightarrow \#$)
- 分析树:
- 根是 $A$。
- $A$ 有一个孩子: $B$。
- $B$ 有一个孩子: #。
- 叶子节点就是 #。
- 混淆推导和语言: 推导是生成一个字符串的过程。语言是所有可能被推导出来的终结符串的集合。一个推导只产生语言里的一个成员。
- 分析树的唯一性: 对于同一个字符串,可能存在多种不同的推导顺序(例如,如果一个中间字符串有多个变量,先替换哪个?)。但如果文法是无歧义的,那么这个字符串只会对应唯一的一棵分析树。分析树关注的是结构,而不是推导的步骤顺序。
- 叶子节点必须是终结符: 在一个完整的分析树中,所有的叶子节点都必须是终结符或 $\varepsilon$。如果叶子节点还有变量,说明推导还未完成。
本段解释了如何使用上下文无关文法通过一个称为推导的逐步替换过程来生成语言中的字符串。它还引入了分析树作为推导过程的图形化表示,它能更清晰地揭示生成字符串的层次化语法结构。
本段的目的是将静态的文法规则和动态的字符串生成过程联系起来,让读者明白文法是如何“运作”的。通过推导和分析树这两个核心概念,为后续讨论语言的定义、文法的歧义性等问题奠定了操作基础。
推导就像是在执行一份菜谱的步骤。你从主菜名(开始变量)开始,然后一步步地执行指令(应用规则),把半成品(变量)替换成更小的半成品或者基本食材(终结符),直到最后得到一道完整的菜(最终字符串)。
分析树就像是这道菜的“解构图”。它展示了这道菜最终是由哪些基本食材,通过哪些半成品步骤组合而成的。比如,最终的“红烧肉”是由“炒好的糖色”和“焯过水的五花肉”组成,而“炒好的糖色”又是由“冰糖”和“油”加热而来。这个层次关系就是分析树。
想象一下你正在用 Photoshop 进行图像合成。
- 推导是你操作的序列:
- 新建一个图层,命名为“最终图像”(开始变量)。
- 在“最终图像”图层上,你决定它由“背景”和“前景人物”两个子部分组成(应用规则 最终图像 -> 背景 + 前景人物)。
- 选择“前景人物”这个占位符,你决定用“人物剪影”来替换它(应用规则 前景人物 -> 人物剪影)。
- 选择“背景”,用一张“星空图片”替换它(应用规则 背景 -> 星空图片.jpg)。
- ...直到所有占位符都被具体的图片(终结符)替换掉。
- 分析树就是你最终看到的 Photoshop 图层面板。它显示了“最终图像”是由“背景”和“前景人物”两个图层组构成的,而每个图层组又包含具体的图片图层。这个图层结构就是分析树。
📜 [原文8]
以这种方式生成的所有字符串构成文法的语言。我们将文法 $G_{1}$ 的语言表示为 $L\left(G_{1}\right)$。对文法 $G_{1}$ 进行一些实验,我们发现 $L\left(G_{1}\right)$ 是 $\left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$。任何可以通过某些上下文无关文法生成的语言都称为上下文无关语言 (CFL)。为方便起见,在呈现上下文无关文法时,我们将几个具有相同左侧变量的规则(例如 $A \rightarrow 0 A 1$ 和 $A \rightarrow B$)缩写为一行 $A \rightarrow 0 A 1 \mid B$,其中符号 " $\mid$ " 表示 "或"。
这段话正式定义了由文法生成的语言,并介绍了一些约定俗成的表示法。
- 文法生成的语言: 一个文法 $G$ 所生成的语言,记作 $L(G)$,是所有可以从该文法的开始变量出发,经过一系列推导步骤,最终得到的终结符串的集合。换句话说,它是该文法所有可能产出的集合。
- $L(G_1)$ 的分析: 通过对文法 $G_1$ 进行“实验”(即尝试进行各种可能的推导),我们可以归纳出它生成的语言的模式。
- 规则 $A \rightarrow 0A1$ 是一个递归规则。每应用一次,就在中间的 $A$ 两侧分别增加一个 '0' 和一个 '1'。如果这个规则被应用 $n$ 次,我们就会得到一个形如 $0^n A 1^n$ 的字符串。
- 规则 $A \rightarrow B$ 和 $B \rightarrow \#$ 提供了一个终止递归并产生中心符号 # 的方式。
- 组合起来看:我们首先可以应用 $A \rightarrow 0A1$ 共 $n$ 次($n \ge 0$),得到 $0^n A 1^n$。然后,应用 $A \rightarrow B$,得到 $0^n B 1^n$。最后应用 $B \rightarrow \#$,得到最终字符串 $0^n \# 1^n$。
- 由于 $n$ 可以是 0, 1, 2, ...,所以这个文法能够生成 $\left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$ 集合中的所有字符串。例如:
- $n=0$: $A \Rightarrow B \Rightarrow \#$
- $n=1$: $A \Rightarrow 0A1 \Rightarrow 0B1 \Rightarrow 0\#1$
- $n=2$: $A \Rightarrow 0A1 \Rightarrow 00A11 \Rightarrow 00B11 \Rightarrow 00\#11$
- 因此,我们得出结论:$L(G_1) = \left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$。
- 上下文无关语言 (CFL) 的定义: 这里给出了上下文无关语言的正式定义。如果一个语言 $L$ 存在一个上下文无关文法 $G$ 能够生成它(即 $L=L(G)$),那么 $L$ 就被称为一个上下文无关语言。这个定义将文法(一种描述工具)和语言(一个字符串集合)联系了起来。
- 文法缩写: 最后介绍了一个书写惯例,以简化文法的表示。当有多条规则具有相同的左侧变量时,可以将它们合并成一行,用竖线 | 分隔右侧部分。竖线 | 读作“或”。
- 例如,规则 $A \rightarrow 0A1$ 和 $A \rightarrow B$ 可以合并写成 $A \rightarrow 0A1 \mid B$。
- 这仅仅是一种语法糖(syntactic sugar),一种简便的写法,它不改变文法的任何数学性质,但使得文法看起来更紧凑、更易读。
- $L(G_1)$:
- $L$: 代表语言 (Language)。
- $(G_1)$: 括号中的 $G_1$ 指明是文法 $G_1$ 生成的语言。
- 含义: 符号 $L(G_1)$ 表示由文法 $G_1$ 生成的所有终结符串的集合。
- $\left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$:
- 含义: 这个集合包含了所有由 $n$ 个 '0' 开头,中间是一个 '#',然后由 $n$ 个 '1' 结尾的字符串,其中 $n$ 是任意非负整数。
- $A \rightarrow 0 A 1 \mid B$:
- $A \rightarrow 0A1$: 一条规则。
- $A \rightarrow B$: 另一条规则。
- |: “或”符号,用于连接具有相同左侧变量的多条规则的右侧。
- 含义: 这行缩写等价于两条独立的规则:$A \rightarrow 0A1$ 和 $A \rightarrow B$。它表示变量 $A$ 可以被替换为 0A1 或者被替换为 B。
- 示例 1: 缩写文法**
- 原始规则:
```
E -> E + T
E -> T
```
- 缩写形式:
```
E -> E + T | T
```
- 示例 2: 另一个文法的语言****
- 文法 $G_x$: S -> aS | ε
- 推导:
- $n=0$: S -> ε
- $n=1$: S -> aS -> aε -> a
- $n=2$: S -> aS -> aaS -> aaε -> aa
- $n=3$: S -> aS -> aaS -> aaaS -> aaaε -> aaa
- 语言: 我们可以看出 $L(G_x)$ 生成的是由任意数量 'a' 组成的字符串,包括空串。用集合表示就是 $L(G_x) = \{ a^n \mid n \ge 0 \}$。这是一个正则语言,也符合上下文无关语言的定义。
- 并非所有语言都是上下文无关的: 必须明确,CFL 只是所有可能语言中的一个子集。存在一些语言,比如 $\{a^n b^n c^n \mid n \ge 0\}$,是找不到任何 CFG 来生成它的。
- 一个语言可以有多个文法: 同一个上下文无关语言可能可以被多个不同的上下文无关文法生成。这些文法在结构上可能完全不同,但它们的生成能力是等价的。例如,$\left\{a^{n} \mid n \ge 1 \right\}$ 可以由 S -> aS | a 生成,也可以由 S -> Sa | a 生成。
本段将文法的生成能力与语言的概念正式挂钩,定义了文法的语言 $L(G)$。通过分析 $G_1$ 的生成过程,得出其语言为 $\left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$。在此基础上,给出了上下文无关语言 (CFL) 的一般定义。最后,介绍了一种常用的文法书写简化规则 |。
此段的目的是完成从“文法如何工作”到“文法定义了什么”的关键一步。它正式定义了上下文无关语言这一核心研究对象,并将前面所有的技术细节(推导、变量、终结符)汇集到一个有意义的集合——语言——上,为后续的理论分析(如语言的性质、分类)建立了基础。
文法 $G$ 是一台“字符串制造机”的设计蓝图。$L(G)$ 就是这台机器所有可能生产出来的、并且通过了质检(即不含任何半成品零件/变量)的“最终产品”的完整目录。上下文无关语言就是所有可以用这种“蓝图+机器”模式制造出来的产品的总类别。| 规则就像蓝图上的一个注释:“在第5步,你可以使用A号螺丝,也可以使用B号螺丝”。
想象一个分形图案的生成规则(例如科赫雪花)。
- 文法就是那套递归的生成指令:“将一条直线替换为一条带有凸起的折线”。
- 推导就是你一步步应用这套指令的过程。
- $L(G)$ 就是所有可能生成的、包含了无限细节的最终分形图案的集合。
- 上下文无关语言就是所有能用这类递归绘图指令画出来的图案的总称。
- | 规则就是指令里说:“你可以向上凸起,也可以向下凸起”。
📜 [原文9]
以下是上下文无关文法的第二个示例,称为 $G_{2}$,它描述了英语的一个片段。
```
$\langle$ SENTENCE $\rangle \rightarrow\langle$ NOUN-PHRASE $\rangle\langle$ VERB-PHRASE $\rangle$
$\langle$ NOUN-PHRASE $\rangle \rightarrow\langle$ CMPLX-NOUN $\rangle \mid\langle$ CMPLX-NOUN $\rangle\langle$ PREP-PHRASE $\rangle$
$\langle$ VERB-PHRASE $\rangle \rightarrow\langle$ CMPLX-VERB $\rangle \mid\langle$ CMPLX-VERB $\rangle\langle$ PREP-PHRASE $\rangle$
$\langle$ PREP-PHRASE $\rangle \rightarrow\langle$ PREP $\rangle\langle$ CMPLX-NOUN $\rangle$
$\langle$ CMPLX-NOUN $\rangle \rightarrow\langle$ ARTICLE $\rangle\langle$ NOUN $\rangle$
$\langle$ CMPLX-VERB $\rangle \rightarrow\langle$ VERB $\rangle \mid\langle$ VERB $\rangle\langle$ NOUN-PHRASE $\rangle$
$\langle$ ARTICLE $\rangle \rightarrow \mathrm{a} \mid$ the
〈NOUN〉 → boy | girl | flower
|VERB → touches | likes | sees
$\langle$ PREP $\rangle \rightarrow$ with
```
文法 $G_{2}$ 有 10 个变量(括号内大写的语法术语);27 个终结符(标准英文字母加上一个空格字符);以及 18 条规则。$L\left(G_{2}\right)$ 中的字符串包括:
```
a boy sees
the boy sees a flower
a girl with a flower likes the boy
```
这些字符串中的每一个在文法 $G_{2}$ 中都有推导。以下是此列表中第一个字符串的推导。
这一部分通过一个更复杂、更实际的例子 $G_2$ 来进一步展示上下文无关文法的应用,这次是模拟自然语言——英语的语法。
首先,给出了文法 $G_2$ 的所有规则。
- 变量: 使用尖括号 <...> 括起来的术语,如 <SENTENCE> (句子), <NOUN-PHRASE> (名词短语), <VERB> (动词) 等。这些都是语言学中的语法成分。
- 终结符: 具体的英文单词,如 a, the, boy, touches 等,以及用于分隔单词的空格。
- 规则: 定义了语法成分之间的组合关系。例如:
- <SENTENCE> -> <NOUN-PHRASE><VERB-PHRASE>: 一个句子由一个名词短语(主语)后跟一个动词短语(谓语)构成。
- <NOUN-PHRASE> -> <CMPLX-NOUN> | <CMPLX-NOUN><PREP-PHRASE>: 一个名词短语可以是一个简单的复合名词,也可以是一个复合名词后面跟着一个介词短语(起修饰作用)。这条规则体现了递归潜力,因为介词短语里可能又包含名词短语。
- <CMPLX-VERB> -> <VERB> | <VERB><NOUN-PHRASE>: 一个复合动词可以只是一个动词,也可以是一个动词后面跟着一个名词短语(作宾语)。
- <ARTICLE> -> a | the: 冠词可以是 'a' 或 'the'。这展示了如何定义一个词类。
接下来,对 $G_2$ 的规模进行了统计:10 个变量,27 个终结符(26个字母+空格),18 条规则(通过计算 | 的数量可以得出)。
然后,列举了三个可以通过这个文法生成的句子,展示了该文法的生成能力:
- a boy sees (一个男孩看见)
- the boy sees a flower (那个男孩看见一朵花)
- a girl with a flower likes the boy (一个带着花的女孩喜欢那个男孩)
最后,为了证明这些句子确实是语言 $L(G_2)$ 的成员,详细演示了第一个句子 a boy sees 的推导过程。这个推导从开始变量 <SENTENCE> 出发,一步步应用规则,将变量替换为更小的变量或终结符,最终得到了完全由终结符构成的目标句子。
这个推导过程清晰地展示了句子的语法结构是如何被文法规则逐步构建出来的:
- 一个句子分解为主语(名词短语)和谓语(动词短语)。
- 名词短语被具体化为一个复合名词。
- 复合名词由冠词和名词组成。
- 冠词和名词被替换为具体的单词 'a' 和 'boy'。
- 动词短语被具体化为一个复合动词。
- 复合动词被简化为一个动词。
- 动词被替换为具体的单词 'sees'。
整个过程就像一个语法分析的逆过程,从最高层的句子结构逐步填充细节,直至生成最终的单词序列。
- <SENTENCE> -> <NOUN-PHRASE><VERB-PHRASE>
- <...>: 尖括号用于表示这是一个变量(非终结符),以区别于终结符单词。
- 规则含义: 定义了一个 <SENTENCE>(句子)的结构。它由一个 <NOUN-PHRASE>(名词短语)紧跟着一个 <VERB-PHRASE>(动词短语)组成。这是英语简单句最基本的主谓结构。
- 推导过程:
- X ⇒ Y: 表示 $X$ 在一步之内推导出 $Y$。
- <s> ⇒ <np><vp>: <SENTENCE> 缩写为 <s>, <NOUN-PHRASE> 缩写为 <np>, <VERB-PHRASE> 缩写为 <vp>。应用第一条规则。
- ⇒ <cn><vp>: 应用规则 <np> -> <cn>(<CMPLX-NOUN> 缩写为 <cn>)。将 <np> 替换为 <cn>。
- ⇒ <art><n><vp>: 应用规则 <cn> -> <art><n>(<ARTICLE> 缩写为 <art>, <NOUN> 缩写为 <n>)。
- ⇒ a <n><vp>: 应用规则 <art> -> a。将 <art> 替换为终结符 'a'。
- ⇒ a boy <vp>: 应用规则 <n> -> boy。
- ⇒ a boy <cv>: 应用规则 <vp> -> <cv>(<CMPLX-VERB> 缩写为 <cv>)。
- ⇒ a boy <v>: 应用规则 <cv> -> <v>(<VERB> 缩写为 <v>)。
- ⇒ a boy sees: 应用规则 <v> -> sees。推导完成。
- 示例 1: 推导 "the girl likes a flower"
- 推导:
<SENTENCE>
⇒ <NOUN-PHRASE><VERB-PHRASE>
⇒ <CMPLX-NOUN><VERB-PHRASE>
⇒ <ARTICLE><NOUN><VERB-PHRASE>
⇒ the <NOUN><VERB-PHRASE>
⇒ the girl <VERB-PHRASE>
⇒ the girl <CMPLX-VERB>
⇒ the girl <VERB><NOUN-PHRASE> (这次动词带宾语)
⇒ the girl likes <NOUN-PHRASE>
⇒ the girl likes <CMPLX-NOUN>
⇒ the girl likes <ARTICLE><NOUN>
⇒ the girl likes a <NOUN>
⇒ the girl likes a flower
- 示例 2: 展示递归的推导 "a boy with a flower sees"
- 推导 (部分):
<SENTENCE>
⇒ <NOUN-PHRASE><VERB-PHRASE>
⇒ <CMPLX-NOUN><PREP-PHRASE><VERB-PHRASE> (应用了 <NP> -> <CN><PP> 规则)
⇒ <ARTICLE><NOUN><PREP-PHRASE><VERB-PHRASE>
⇒ a boy <PREP-PHRASE><VERB-PHRASE>
⇒ a boy <PREP><CMPLX-NOUN><VERB-PHRASE> (应用了 <PP> -> <P><CN>)
⇒ a boy with <CMPLX-NOUN><VERB-PHRASE>
⇒ a boy with <ARTICLE><NOUN><VERB-PHRASE>
⇒ a boy with a flower <VERB-PHRASE>
... (后续过程类似)
- 这个例子展示了文法如何通过递归的规则(名词短语包含介词短语,介词短语又包含名词短语)来生成更复杂的句子结构。
- 过度泛化: 这个文法 $G_2$ 只是英语语法的一个极度简化的“片段”。它生成的句子非常有限,而且存在很多不符合自然语言习惯的组合(例如,它无法区分及物动词和不及物动词,可能生成 "a boy sees a girl" 也可能生成 "a boy touches",后者在没有宾语时通常不完整)。
- 忽略空格: 在书写终结符时,a, boy 等单词后面都隐含了一个空格,这在文法的终结符集合中已说明。如果忽略空格,生成的字符串将是 aboysees,这与目标不符。在实际的解析器中,词法分析器会处理空格和单词的切分。
- 文法的歧义性: 正如引言中所述,自然语言的文法常常是有歧义的。例如,句子 "the girl touches the boy with the flower" 可以有两种解析方式:(the girl touches) (the boy with the flower) [女孩触摸了那个带着花的男孩],或者 (the girl touches the boy) (with the flower) [女孩用花触摸了那个男孩]。这个文法 $G_2$ 同样允许这两种推导,因此它是一个有歧义的文法。
本段通过一个描述部分英语语法的上下文无关文法 $G_2$ 作为实例,具体展示了 CFG 如何用于建模自然语言。它详细列出了文法的规则、组成成分,并给出了几个生成句子的例子,最后还完整演示了其中一个句子的推导过程,从而将抽象的文法规则与具体的句子生成实践联系起来。
本段的目的是提供一个比 $G_1$ 更大规模、更贴近实际应用的例子,以巩固读者对 CFG 的理解。通过使用读者熟悉的自然语言作为模型,可以更直观地理解文法规则如何捕捉层次化结构(句子-短语-单词),以及推导过程如何模拟句子的构建。
这个文法就像一个“句子自动生成器”的程序。程序从 "生成一个句子" 的指令开始,然后根据内部的语法规则库,随机(或按一定策略)选择规则来逐步构建。比如,它先决定句子是“主语+谓语”结构,然后决定主语是“冠词+名词”,再决定冠词是'a',名词是'boy',一步步往下走,最终拼凑出一个完整的、语法正确的句子。
想象你在玩一个语法版的“疯狂填词”游戏。你有一张卡片,上面写着 ______ (一个 <SENTENCE>)。游戏规则书(文法)说,你可以把它换成两张更小的卡片:______(一个 <NOUN-PHRASE>) 和 ______(一个 <VERB-PHRASE>)。你继续查规则书,发现 <NOUN-PHRASE> 卡片可以换成 <ARTICLE> 和 <NOUN> 两张卡片。最后,规则书告诉你 <ARTICLE> 可以直接填入单词 'a' 或 'the'。你不断地将这些代表“语法槽位”的卡片替换成更小的槽位,或者直接填入单词,直到所有卡片上都填满了单词,一个完整的句子就诞生了。这个填词的过程就是推导。
32.2 上下文无关文法的形式化定义
📜 [原文10]
让我们将上下文无关文法 (CFG) 的概念形式化。
定义 2.2
上下文无关文法是一个四元组 ( $V, \Sigma, R, S$ ),其中
- $V$ 是一个有限集合,称为变量,
- $\Sigma$ 是一个有限集合,与 $V$ 不相交,称为终结符,
- $R$ 是一个有限的规则集合,每条规则都是一个变量和一个变量与终结符的字符串,并且
- $S \in V$ 是开始变量。
如果 $u, v$ 和 $w$ 是变量和终结符的字符串,并且 $A \rightarrow w$ 是文法的一条规则,我们说 $u A v$ 导出 $u w v$,记作 $u A v \Rightarrow u w v$。如果 $u=v$ 或存在一个序列 $u_{1}, u_{2}, \ldots, u_{k}$,其中 $k \geq 0$ 且
我们说 $u$ 推导 $v$,记作 $u \stackrel{*}{\Rightarrow} v$。
文法的语言是 $\left\{w \in \Sigma^{*} \mid S \stackrel{*}{\Rightarrow} w\right\}$。
这一部分从直观描述转向了严格的数学定义,将上下文无关文法及其相关概念形式化。
首先,定义 2.2 将上下文无关文法 (CFG) 定义为一个四元组 $(V, \Sigma, R, S)$。这是一种在数学和计算机科学中常见的定义方式,通过一个元组来精确地规定一个对象的构成要素。
- $V$ (Variables): 这是一个有限集合,包含了文法中所有的变量(非终结符)。例如,在 $G_1$ 中,$V = \{A, B\}$。有限性是重要的,意味着文法规则是有限的。
- $\Sigma$ (Terminals): 这是另一个有限集合,包含了所有的终结符(字母表)。关键约束是 $V$ 和 $\Sigma$ 不相交 ($V \cap \Sigma = \emptyset$),这意味着一个符号不能既是变量又是终结符,二者身份必须明确。在 $G_1$ 中,$\Sigma = \{0, 1, \#\}$。
- $R$ (Rules): 这是一个有限的规则集合。定义中描述了每条规则的形式:它由一个变量(来自 $V$)和箭头 → 以及一个由变量和终结符混合组成的字符串构成。形式上,$R$ 是 $V \times (V \cup \Sigma)^*$ 的一个有限子集。其中 $(V \cup \Sigma)^*$ 表示由 $V$ 和 $\Sigma$ 中所有符号组成的任意有限长度的字符串集合(包括空串)。在 $G_1$ 中,$R = \{ (A, 0A1), (A, B), (B, \#) \}$。
- $S$ (Start Variable): 这是开始变量,它必须是 $V$ 集合中的一个成员 ($S \in V$)。它是所有推导的起点。在 $G_1$ 中,$S=A$。
接下来,形式化定义了推导过程:
- 一步推导 (yields): 符号为 $\Rightarrow$。如果有一个字符串 uAv(其中 u 和 v 可以是任何由变量和终结符构成的串,甚至是空串),并且文法中有一条规则 $A \rightarrow w$,那么我们可以应用这条规则将 uAv 转换为 uwv。这个过程被称为 uAv 一步推导出 uwv,记作 $uAv \Rightarrow uwv$。这个定义强调了“上下文无关”的特性:只要有变量 $A$,就可以替换它,而无需关心它的上下文 u 和 v 是什么。
- 多步推导 (derives): 符号为 $\stackrel{*}{\Rightarrow}$。这表示零步或多步推导。我们说 u 推导 v(记作 $u \stackrel{*}{\Rightarrow} v$)有两种情况:
- $u = v$ (零步推导,任何字符串都可以推导出它自身)。
- 存在一个推导序列 $u \Rightarrow u_1 \Rightarrow u_2 \Rightarrow \dots \Rightarrow v$。
这个 * 符号是克莱尼星号(Kleene Star)的推广,表示“零次或多次应用”。
最后,基于多步推导,给出了由文法 $G$ 生成的语言 $L(G)$ 的形式化定义:
- $L(G) = \left\{w \in \Sigma^{*} \mid S \stackrel{*}{\Rightarrow} w\right\}$
- 这个语言是一个集合。
- 集合中的成员 $w$ 必须满足两个条件:
- $w \in \Sigma^{*}$: $w$ 必须是一个完全由终结符组成的字符串(* 表示包括空串)。这意味着推导必须终止,不能留下任何变量。
- $S \stackrel{*}{\Rightarrow} w$: 必须存在一个从开始变量 $S$ 出发,经过零步或多步推导,能够得到字符串 $w$ 的过程。
这个定义精确、无歧义地界定了上下文无关文法是什么,以及它是如何工作的。
- $(V, \Sigma, R, S)$:
- 这是一个四元组,用于形式化定义一个数学对象。
- $V$: 变量集合 (a finite set of variables)。
- $\Sigma$: 终结符字母表 (a finite set of terminals)。
- $R$: 规则集合 (a finite set of rules)。
- $S$: 开始变量 (the start variable)。
- $u A v \Rightarrow u w v$:
- $u, v, w$: 是 $(V \cup \Sigma)^*$ 中的字符串,即由变量和终结符构成的任意串。
- $A$: 是 $V$ 中的一个变量。
- 含义: 这是“一步推导”的定义。它形式化地表达了在一个更长的字符串中应用一条规则 $A \rightarrow w$ 的过程。
- $u \stackrel{*}{\Rightarrow} v$:
- $\stackrel{*}{\Rightarrow}$: 表示“零步或多步推导”。
- 含义: u 可以通过应用零次或多次规则,最终变成 v。这是对一步推导 $\Rightarrow$ 的自反传递闭包(Reflexive Transitive Closure)。
- $\left\{w \in \Sigma^{*} \mid S \stackrel{*}{\Rightarrow} w\right\}$:
- 含义: 这是文法 $G$ 的语言 $L(G)$ 的定义。它是一个集合,包含了所有满足以下两个条件的字符串 $w$:1) $w$ 只包含终结符;2) $w$ 可以从开始变量 $S$ 推导出来。
- 示例 1: 形式化描述文法 $G_1$
- $V = \{A, B\}$
- $\Sigma = \{0, 1, \#\}$
- $R = \{ A \rightarrow 0A1, A \rightarrow B, B \rightarrow \# \}$
- $S = A$
- 推导示例:
- 一步推导: 因为有规则 $A \rightarrow 0A1$,所以 $A \Rightarrow 0A1$。
- 多步推导: 因为 $A \Rightarrow 0A1$ 且 $0A1 \Rightarrow 0B1$,所以我们可以说 $A \stackrel{*}{\Rightarrow} 0B1$。
- 语言成员: 字符串 0#1 是 $L(G_1)$ 的成员,因为 0#1 完全由终结符构成,并且 $S = A \stackrel{*}{\Rightarrow} 0\#1$ (推导过程: $A \Rightarrow 0A1 \Rightarrow 0B1 \Rightarrow 0\#1$)。
- 示例 2: 形式化描述文法 $G_x$: S -> aS | ε
- $V = \{S\}$
- $\Sigma = \{a\}$
- $R = \{ S \rightarrow aS, S \rightarrow \varepsilon \}$
- $S = S$
- 语言成员:
- aa $\in L(G_x)$ 吗?
- 1. aa $\in \Sigma^*$ ? 是的,a 是终结符。
- 2. $S \stackrel{*}{\Rightarrow}$ aa ?
- $S \Rightarrow aS$ (应用 $S \rightarrow aS$)
- $aS \Rightarrow aaS$ (应用 $S \rightarrow aS$)
- $aaS \Rightarrow aa\varepsilon$ (应用 $S \rightarrow \varepsilon$)
- $aa\varepsilon$ 就是 aa。
- 所以 $S \stackrel{*}{\Rightarrow} aa$ 成立。
- 结论: aa 是 $L(G_x)$ 的成员。
- $V$ 和 $\Sigma$ 的不相交性: 这是一个严格的要求。在设计文法时,不能让一个符号既当变量又当终结符。例如,不能有 a -> aA 这样的规则,如果 a 被定义为终结符的话。
- $k=0$ 的情况: 在多步推导的定义中,$k=0$ 的情况意味着 $u \Rightarrow v$ 这个序列不存在,此时 $u=v$。这保证了自反性,即任何字符串都能推导出自身。这在一些形式化证明中很重要。
- 语言只包含终结符串: 最终语言 $L(G)$ 的成员必须是纯终结符串。像 0A1 这样的中间产物不属于语言,它们只是推导过程的一部分。
本节为上下文无关文法 (CFG) 提供了一个严格的、基于集合论的形式化定义。它将 CFG 定义为一个四元组 $(V, \Sigma, R, S)$,并精确定义了“一步推导” ($\Rightarrow$)、“多步推导” ($\stackrel{*}{\Rightarrow}$) 和文法生成的语言 $L(G)$。这套形式化体系是后续所有理论分析和证明的基石。
本段的目的是将之前通过例子建立的直观理解,提升到数学上严谨的层面。在科学和工程中,形式化是必不可少的一步,它消除了模糊性,使得概念可以被精确地操作和推理。这为后续证明文法的等价性、研究语言的性质、设计算法等工作铺平了道路。
形式化定义就像是为之前直观的“菜谱”模型编写了一份“ISO 国际标准”。
- 四元组 $(V, \Sigma, R, S)$ 就是标准的第一章,它规定了菜谱必须包含四个部分:半成品列表 ($V$),基础食材列表 ($\Sigma$),烹饪步骤说明书 ($R$),以及最终主菜名 ($S$)。
- 一步推导的定义,是在标准中精确说明了“执行一个烹饪步骤”意味着什么。
- 多步推导的定义,则说明了“完成一道菜”意味着从主菜名开始,执行零或多个烹饪步骤。
- 语言的定义,就是这份标准认证的所有“合格成品”的名录。
想象一下你在为乐高积木编写官方的设计规范。
- 四元组就是规范的封面页,声明了本文档包含:1. 所有非基础的“组合模块”清单 ($V$);2. 所有最基础的“原子砖块”清单 ($\Sigma$);3. 所有的“组装规则” ($R$);4. 本套玩具的最终“成品型号” ($S$)。
- 推导的定义是规范中的核心条款,它精确描述了“根据一条组装规则,将一个组合模块替换为其 constituent parts”这个动作。
- 语言的定义则是这份规范所能涵盖的、所有能从“成品型号”开始、完全由“原子砖块”搭建起来的、所有可能的最终成品的集合。
📜 [原文11]
在文法 $G_{1}$ 中,$V=\{A, B\}$,$\Sigma=\{0,1, \#\}$,$S=A$,且 $R$ 是第 102 页上出现的三条规则的集合。在文法 $G_{2}$ 中,
$\Sigma=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \ldots, \mathrm{z}$, " " $\}$。符号 " " 是空格符号,不可见地放在每个单词(a, boy 等)之后,这样单词就不会连在一起。
我们通常只通过写下文法的规则来指定文法。我们可以将变量识别为出现在规则左侧的符号,并将终结符识别为其余的符号。按照惯例,开始变量是第一条规则左侧的变量。
这段话将前面给出的形式化定义应用到之前的两个例子 $G_1$ 和 $G_2$ 上,并阐述了在实际操作中描述一个文法的常用惯例。
首先,它精确地用四元组的形式“翻译”了文法 $G_1$:
- 变量集合 $V$ 是 $\{A, B\}$。
- 终结符集合 $\Sigma$ 是 $\{0, 1, \#\}$。
- 开始变量 $S$ 是 $A$。
- 规则集合 $R$ 就是之前列出的那三条规则 $\{A \rightarrow 0A1, A \rightarrow B, B \rightarrow \#\}$。
这展示了如何将一个写出的文法映射到其形式化定义的四元组上。
接着,它对更复杂的文法 $G_2$ 也做了同样的分析:
- 变量集合 $V$ 被明确列出,包含了所有用尖括号括起来的 10 个语法术语。
- 终结符集合 $\Sigma$ 被描述为所有小写英文字母加上一个空格符号。这里特别解释了空格符号的作用:它是语言的一部分,用来分隔单词,否则生成的句子会是 aboysees 这样的连体词。这强调了终结符可以是任何符号,包括那些不可见的。
然后,引出了一套非常重要的书写惯例。在实践中,每次都写出完整的四元组 $(V, \Sigma, R, S)$ 会非常繁琐。因此,大家约定俗成了一套简化表示法:
- 只写规则: 我们通常只把规则集合 $R$ 写出来。
- 推断变量: 凡是出现在任何规则左侧的符号,都被自动识别为变量。
- 推断终结符: 那些只出现在规则右侧,且不是变量的符号,就被自动识别为终结符。
- 推断开始变量: 除非特别声明,第一条写出的规则的左侧变量,就被默认为是开始变量。
这套惯例大大简化了文法的书写,使得我们可以仅通过规则列表就能完整地、无歧义地定义一个文法。前面的 $G_1$ 和 $G_2$ 就是按照这个惯例给出的。
- $V=\{ \langle\text { SENTENCE }\rangle, \dots, \langle\text { PREP }\rangle\}$:
- 这是一个集合的显式列举。
- $V$: 代表文法 $G_2$ 的变量集合。
- <...>: 尖括号在这里是符号名称的一部分,用于清晰地标识这些是语法概念的变量。
- $\Sigma=\{\mathrm{a}, \mathrm{b}, \ldots, \mathrm{z}, \text{ " " }\}$:
- $\Sigma$: 代表文法 $G_2$ 的终结符集合。
- a, b, ..., z: 代表 26 个小写英文字母。
- " ": 代表空格符号,它也是字母表中的一个合法终结符。
- 示例 1: 根据惯例解释文法****
- 给出的文法:
```
E -> E + T | T
T -> T * F | F
F -> (E) | id
```
- 根据惯例推断:
- 规则: 就是写出的这 3 行(展开是 6 条)。
- 变量: 在左侧出现过的有 E, T, F。所以 $V = \{E, T, F\}$。
- 终结符: +, *, (, ), id。它们都只出现在右侧,且不是变量。所以 $\Sigma = \{+, *, (, ), id\}$。
- 开始变量: 第一条规则的左侧是 E。所以 $S = E$。
- 这样,我们就从简化的写法中还原出了完整的四元组定义。
- 示例 2: 显式指定开始变量
- 在某些教科书或工具中,可能会这样写:
```
// Grammar for simple assignments
// Start symbol is <assign>
<assign> -> <id> = <expr>
<expr> -> <id> + <id> | <id>
<id> -> a | b | c
```
- 在这种情况下,尽管 <assign> 是第一条规则的左侧变量,但注释明确地再次强调了它是开始变量。如果注释说开始变量是 <expr>,那么就应该以 <expr> 为准。惯例是默认选项,但可以被显式声明覆盖。
- 空格的地位: 在处理编程语言或自然语言时,空格、换行符等“空白字符”的角色需要明确。在 $G_2$ 中,空格是语言的一部分,是终结符。但在很多编程语言的文法中,空白字符通常在词法分析阶段就被忽略了,它们不作为终结符出现在文法规则中,其作用仅仅是分隔词法单元。
- 惯例的适用范围: 这套惯例在学术界和大多数工具中是通用的,但并非绝对。在阅读新的资料或使用新的工具时,最好先确认其是否遵循这套标准惯例,或者有无自己的特殊规定。
本段将形式化定义与具体例子相结合,演示了如何将一个实际的文法表示为四元组。更重要的是,它阐明了一套广泛使用的书写惯例:仅通过书写规则,就可以隐式地、无歧义地定义整个上下文无关文法的四个组成部分 ($V, \Sigma, R, S$)。这为后续所有文法的呈现方式提供了背景说明。
本段的目的是在严谨的形式化定义和便捷的日常实践之间架起一座桥梁。它告诉读者,虽然我们有了精确的数学基础,但在交流和工作中,我们会使用一套更简洁的“速记法”。理解这套速记法是如何工作的,对于能够读懂和写出文法至关重要。
这就像在化学中,一个水分子的形式化定义是“由两个氢原子和一个氧原子通过共价键连接而成的化合物”。但在实践中,我们几乎总是直接写它的化学式 $H_2O$。这个化学式就是一种“惯例”,我们看到它就能自动推断出所有的组成信息(有哪些原子,分别有几个,是什么连接方式)。本段解释的就是上下文无关文法的“化学式”写法。
想象你在网上分享一个菜谱。
- 形式化定义:你需要写一个 JSON 文件,严格规定:
```json
{
"start_dish": "红烧肉",
"semi_finished_products": ["面团", "酱汁"],
"basic_ingredients": ["猪肉", "酱油", "糖"],
"steps": [
{"from": "红烧肉", "to": "焯水的猪肉 + 酱汁"},
...
]
}
```
- 惯例写法:你只需要在美食博客上写下:
红烧肉 -> 焯水的猪肉 + 酱汁
酱汁 -> 酱油 + 糖
...
- 读者(以及专门的菜谱解析软件)看到这个博客,就能自动明白:“红烧肉”是主菜(开始变量),“酱汁”是半成品(变量),而“酱油”、“糖”是基本食材(终行符)。本段就是在解释为什么我们可以这样“偷懒”地写。
42.3 上下文无关文法的例子
📜 [原文12]
例子 2.3
考虑文法 $G_{3}=(\{S\},\{\mathrm{a}, \mathrm{b}\}, R, S)$。规则集 $R$ 是
这个文法生成像 abab、aaabbb 和 aababb 这样的字符串。如果你将 a 视为左括号 "(",b 视为右括号 ")",你就能更容易地看出这种语言是什么。从这个角度看,$L\left(G_{3}\right)$ 是所有正确嵌套括号的字符串的语言。请注意,规则的右侧可以是空串 $\varepsilon$。
这个例子介绍了一个非常经典的上下文无关文法 $G_3$,它用来生成所有正确嵌套括号的字符串。
首先,明确了文法 $G_3$ 的形式化定义:
- 变量 $V = \{S\}$。只有一个变量 $S$。
- 终结符 $\Sigma = \{a, b\}$。
- 开始变量就是 $S$。
- 规则集 $R$ 包含三条规则,通过 | 缩写在一行:$S \rightarrow \mathrm{a} S \mathrm{~b}$, $S \rightarrow S S$, 和 $S \rightarrow \varepsilon$。
接下来分析这三条规则的作用:
- $S \rightarrow \mathrm{a} S \mathrm{~b}$: 这是一条递归规则,用于嵌套。它表示一个合法的括号串 ($S$),可以在其外部包裹一层括号 (a 和 b),形成一个新的、更长的合法括号串。例如,如果 ab 是合法的,那么 a(ab)b 即 aabb 也是合法的。
- $S \rightarrow S S$: 这也是一条递归规则,用于并列或连接。它表示两个合法的括号串 ($S$) 相邻放置,形成的新字符串也是一个合法的括号串。例如,如果 ab 和 ab 都是合法的,那么它们的连接 (ab)(ab) 即 abab 也是合法的。
- $S \rightarrow \varepsilon$: 这是基本情况(base case)或终止规则。它表示空串 $\varepsilon$ 本身就是一个合法的括号串。这是所有推导的终点,也是生成最短合法串的方式。
通过这三条规则的组合,可以生成所有形式的合法括号串。
- 嵌套: 通过反复应用 $S \rightarrow \mathrm{a}S\mathrm{b}$ 实现。
- 并列: 通过应用 $S \rightarrow SS$ 实现。
- 结束: 通过应用 $S \rightarrow \varepsilon$ 终止递归。
段落给出了几个 $G_3$ 生成的字符串例子:abab, aaabbb, aababb。
为了帮助理解,段落提出了一个绝佳的类比:将 'a' 想象成左括号 (, 将 'b' 想象成右括号 )。
- $S \rightarrow (S)$: 在一个合法括号串外面加一对括号。
- $S \rightarrow SS$: 将两个合法括号串并列。
- $S \rightarrow \varepsilon$: 空串是合法的。
在这个类比下,$L(G_3)$ 就是所有正确嵌套括号的语言。例如:
- () 对应 ab。
- ()() 对应 abab。
- ((())) 对应 aaabbb。
- (())() 对应 aababb。
最后,再次强调了 ε 规则的重要性,它是递归能够终止的基础。没有它,推导将无限进行下去,无法生成任何有限长度的字符串。
- $S \rightarrow \mathrm{a} S \mathrm{~b}|S S| \varepsilon$:
- $S \rightarrow \mathrm{a}S\mathrm{b}$ (嵌套规则): 生成一个被 a 和 b 包围的、更小的合法串。
- 推导示例: $S \Rightarrow aSb \Rightarrow a(a S b)b \Rightarrow a(a(\varepsilon)b)b \Rightarrow aabb$
- $S \rightarrow SS$ (并列规则): 生成两个并列的合法串。
- 推导示例: $S \Rightarrow SS \Rightarrow (aSb)S \Rightarrow (a\varepsilon b)S \Rightarrow abS \Rightarrow ab(aSb) \Rightarrow ab(a\varepsilon b) \Rightarrow abab$
- $S \rightarrow \varepsilon$ (基本规则): 生成空串,终止推导。
- 推导示例: $S \Rightarrow \varepsilon$
- 示例 1: 推导字符串 aababb (对应 (())())
- $S \Rightarrow SS$ (选择并列规则开始)
- $\Rightarrow (aSb)S$ (对第一个 $S$ 应用嵌套规则)
- $\Rightarrow (a(aSb)b)S$ (对内部的 $S$ 再次应用嵌套规则)
- $\Rightarrow (a(a\varepsilon b)b)S$ (对最内部的 $S$ 应用终止规则)
- $\Rightarrow (aabb)S$ (化简)
- $\Rightarrow aabb(aSb)$ (对第二个 $S$ 应用嵌套规则)
- $\Rightarrow aabb(a\varepsilon b)$ (对最后的 $S$ 应用终止规则)
- $\Rightarrow aabbab$ (化简,完成推导)
- 示例 2: 推导字符串 aaabbb (对应 ((())))
- $S \Rightarrow aSb$
- $\Rightarrow a(aSb)b$
- $\Rightarrow a(a(aSb)b)b$
- $\Rightarrow a(a(a\varepsilon b)b)b$
- $\Rightarrow aaabbb$
- 反例: 为什么无法生成 abb?
- 要生成 abb,你必须以 a 开头,所以第一步必须是 $S \Rightarrow aSb$。
- 现在我们得到了 aSb,需要从中间的 $S$ 生成 b。
- 但是文法规则中没有任何一条能让 $S$ 直接或间接生成单独一个 b。$S$ 只能生成成对的 ab、并列的 $S$ 或者空串。
- 因此,abb 不属于 $L(G_3)$。这与我们的直觉(()) 不是合法括号串)相符。
- 歧义性: 这个文法 $G_3$ 是有歧义的。例如,字符串 ababab (对应 ()()()) 可以有多种推导方式。
- 推导 1: $S \Rightarrow SS \Rightarrow (SS)S \Rightarrow (aSb)SS \Rightarrow \dots \Rightarrow ababab$
- 推导 2: $S \Rightarrow SS \Rightarrow S(SS) \Rightarrow S(aSb)S \Rightarrow \dots \Rightarrow ababab$
这两种推导对应不同的分析树,一种是 (S S) S 结构,另一种是 S (S S) 结构。对于编程语言来说,这种歧义通常是需要避免的。
- 空串是语言的一部分: 由于有 $S \rightarrow \varepsilon$ 规则,空串 $\varepsilon$ 是 $L(G_3)$ 的一个合法成员。
- 规则的组合: 理解这个文法的关键是认识到三条规则的协同作用。只有嵌套规则,你只能生成 aa...bb 这样的串;只有并列规则,你什么也生成不了(因为无法终止);终止规则是递归的出口。
本例介绍了一个重要且经典的上下文无关文法 $G_3$,它精确地生成了所有正确嵌套括号的语言。通过类比括号,该例子清晰地解释了文法中递归的两种主要形式:嵌套 ($S \rightarrow \mathrm{a}S\mathrm{b}$) 和并列 ($S \rightarrow SS$),以及基本情况 ($S \rightarrow \varepsilon$) 如何共同作用来定义一个复杂的、具有递归结构的语言。
本段的目的是通过一个与 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 类似但结构更丰富的例子,来深化读者对 CFG 递归能力的理解。它展示了 CFG 不仅能处理简单的“匹配计数”(如 $G_1$),还能处理更复杂的结构,即嵌套和并列的任意组合,这在描述程序结构、数学表达式等方面非常常见。
想象你在写一个数学证明。
- $S \rightarrow (S)$: 这条规则说:“如果你有一个已证明的引理,你可以把它放在一个‘假设...则...’的框架里,得到一个新的有效论证。”
- $S \rightarrow SS$: 这条规则说:“如果你有两个独立证明的引理,你可以把它们并列在一起,它们共同构成一个有效的论证。”
- $S \rightarrow \varepsilon$: 这条规则代表“公理”或“无需证明的事实”,是所有论证的起点。
通过这些规则,你可以从公理出发,构建出任意复杂的证明体系。
想象你在吹泡泡。
- $S \rightarrow \varepsilon$: 代表你还没有开始吹,只有一个空的泡泡棒。
- $S \rightarrow aSb$: 你吹出了一个泡泡 ($S$),然后又在它外面吹了一个更大的泡泡,把它包裹了起来。a 和 b 就是这个外层泡泡的“膜”。
- $S \rightarrow SS$: 你连续吹了两个独立的泡泡,它们挨在一起。
$L(G_3)$ 就是你用这两种方式(包裹、并列)能吹出的所有泡泡组合的形态。
📜 [原文13]
例子 2.4
考虑文法 $G_{4}=(V, \Sigma, R,\langle\mathrm{EXPR}\rangle)$。
$V$ 是 $\{\langle \text{EXPR} \rangle,\langle \text{TERM} \rangle,\langle \text{FACTOR} \rangle\}$,$\Sigma$ 是 $\{\mathrm{a},+, \times,(), \ \}$。规则是
字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 和 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 可以用文法 $G_{4}$ 生成。分析树如下图所示。
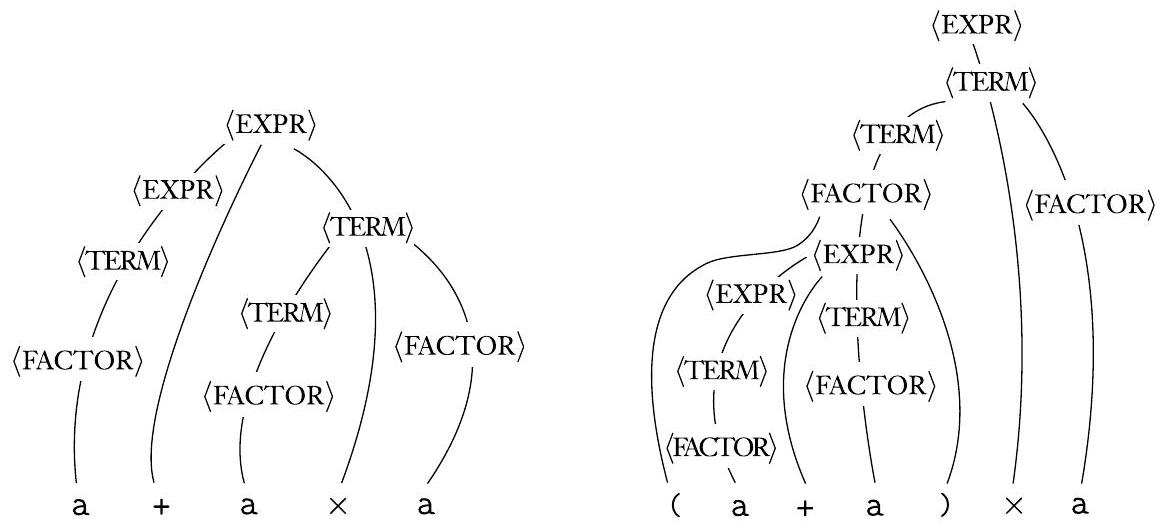
图 2.5
字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 和 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 的分析树
这个例子展示了上下文无关文法在描述编程语言中算术表达式的强大能力,特别是如何利用文法结构来强制实现运算符的优先级和结合性。
首先,给出了文法 $G_4$ 的形式化定义:
- 变量 $V = \{\langle \text{EXPR} \rangle, \langle \text{TERM} \rangle, \langle \text{FACTOR} \rangle\}$。这三个变量分别代表表达式 (Expression)、项 (Term) 和因子 (Factor)。
- 终结符 $\Sigma = \{\mathrm{a}, +, \times, (, )\}$。a 代表一个操作数(比如一个数字或变量),+ 和 × 是运算符,( 和 ) 是括号。
- 开始变量是 $\langle \text{EXPR} \rangle$。
- 规则集分为三组,分别定义了表达式、项和因子:
- $\langle\mathrm{EXPR}\rangle \rightarrow \langle\mathrm{EXPR}\rangle+\langle\mathrm{TERM}\rangle \mid \langle\mathrm{TERM}\rangle$
- 一个表达式可以是一个表达式加上一个项,或者直接就是一个项。
- 这组规则处理加法 +。+ 是左结合的(因为递归的
出现在 + 的左边),并且优先级最低。
- $\langle\mathrm{TERM}\rangle \rightarrow \langle\mathrm{TERM}\rangle \times\langle\mathrm{FACTOR}\rangle \mid \langle\mathrm{FACTOR}\rangle$
- 一个项可以是一个项乘以一个因子,或者直接就是一个因子。
- 这组规则处理乘法 ×。× 是左结合的,它的优先级高于加法,因为一个表达式是由项组成的,而乘法是在项的层次上定义的。要看到加号,你必须先处理完所有的乘法。
- $\langle\mathrm{FACTOR}\rangle \rightarrow (\langle\mathrm{EXPR}\rangle) \mid \mathrm{a}$
- 一个因子可以是一个被括号括起来的表达式,或者直接就是一个操作数 a。
- 这组规则是递归的终点。括号 () 提供了改变默认优先级的机制,因为它允许一个完整的表达式(可以包含加法)出现在一个需要因子的地方。a 是最基本的操作数。
这个三层结构(表达式-项-因子)是编译器设计中用于处理带优先级的表达式的经典文法设计模式。
接着,展示了用这个文法生成的两个字符串 a+a×a 和 (a+a)×a 的分析树。
- 对于 a+a×a:
- 分析树的结构显示,顶层是 + 运算。+ 的左边是一个表达式,最终归结为第一个 a。+ 的右边是一个项,这个项内部是 × 运算 a×a。
- 这棵树的结构强制了 a×a 先被计算(因为它在一个较低的子树 <TERM> 中),其结果再和第一个 a 相加。这正确地反映了乘法优先级高于加法的规则。
- 对于 (a+a)×a:
- 分析树的结构显示,顶层是 × 运算。× 的左边是一个项,这个项最终来自一个因子 (<EXPR>),即 (a+a)。× 的右边是第二个 a。
- 这棵树的结构强制了括号内的 a+a 先被计算,其结果再和后面的 a 相乘。这正确地反映了括号覆盖默认优先级的规则。
这个例子有力地证明了,一个精心设计的上下文无关文法不仅能定义哪些字符串是合法的,还能通过其推导结构(即分析树的形状)来赋予字符串唯一的、正确的语义解释。
- $\langle\mathrm{EXPR}\rangle \rightarrow\langle\mathrm{EXPR}\rangle+\langle\mathrm{TERM}\rangle \mid\langle\mathrm{TERM}\rangle$:
- EXPR: Expression,表达式。
- TERM: Term,项。
- 左递归: <EXPR> 出现在规则的左侧,这被称为左递归。E -> E + T 形式的左递归规则通常用于定义左结合的运算符。这意味着 a+b+c 会被解析为 (a+b)+c。
- 优先级: 因为一个 EXPR 是由 TERM 组成的,这意味着要形成一个 EXPR,你必须先形成 TERM。加法在 EXPR 层面,乘法在 TERM 层面,所以乘法比加法“更深层”,优先级更高。
- $\langle\mathrm{TERM}\rangle \rightarrow\langle\mathrm{TERM}\rangle \times\langle\mathrm{FACTOR}\rangle \mid\langle\mathrm{FACTOR}\rangle$:
- FACTOR: Factor,因子。
- 左递归: T -> T F 也是左递归,定义了 × 的左结合性 (abc 被解析为 (ab)*c)。
- 优先级: TERM 由 FACTOR 构成,所以 FACTOR 层面定义的运算(括号)比 TERM 层面的乘法优先级更高。
- $\langle\mathrm{FACTOR}\rangle \rightarrow(\langle\mathrm{EXPR}\rangle) \mid \mathrm{a}$:
- 递归入口: ( <EXPR> ) 规则允许整个文法重新从顶层的 EXPR 开始,这使得括号内可以有任意复杂的表达式。
- 基本情况: a 是最底层的操作数,是递归的终点。
- 示例 1: 推导 a+a×a (展示乘法优先)
- <EXPR>
⇒ <EXPR> + <TERM> (顶层是加法)
⇒ <TERM> + <TERM> (左边的 <EXPR> 简化为 <TERM>)
⇒ <FACTOR> + <TERM> (再简化)
⇒ a + <TERM> (最终简化为 a)
⇒ a + <TERM> × <FACTOR> (右边的 <TERM> 展开为乘法)
⇒ a + <FACTOR> × <FACTOR> (左边的 <TERM> 简化)
⇒ a + a × <FACTOR> (简化为 a)
⇒ a + a × a (简化为 a)
- 这个推导过程(这是一个最左推导)生成的分析树与图 2.5 左侧一致。
- 示例 2: 推导 (a+a)×a (展示括号优先)
- <EXPR>
⇒ <TERM> (顶层结构是一个 TERM,因为最终是乘法)
⇒ <TERM> × <FACTOR>
⇒ <FACTOR> × <FACTOR>
⇒ ( <EXPR> ) × <FACTOR> (左边的 <FACTOR> 展开为括号表达式)
⇒ ( <EXPR> + <TERM> ) × <FACTOR> (括号内的 <EXPR> 展开为加法)
... (继续在括号内进行推导,最终得到 (a+a))
⇒ (a+a) × a (右边的 <FACTOR> 简化为 a)
- 这个推导生成的分析树与图 2.5 右侧一致。
- 左递归与解析器: 像 E -> E + T 这样的左递归规则,对于某些类型的解析器(如递归下降解析器或 LL 解析器)来说是致命的,会导致无限递归。因此,在为这些解析器编写文法时,需要将左递归消除,改写成等价的右递归形式,例如 E -> T E' 和 E' -> + T E' | ε。但对于 LR 类的解析器(如 YACC/Bison 使用的),左递归是高效且推荐的写法。
- 文法的无歧义性: 这个文法 $G_4$ 是无歧义的。对于任何一个合法的表达式字符串,它只能生成唯一的一棵分析树。这是通过精巧的表达式-项-因子分层结构实现的,这种设计是文法工程中的一个重要技巧。
本例通过文法 $G_4$ 展示了如何使用上下文无关文法来描述算术表达式,并巧妙地利用文法的层次结构(表达式-项-因子)来编码运算符的优先级(乘法高于加法)和结合性(左结合)。通过对比 a+a×a 和 (a+a)×a 的分析树,清晰地说明了该文法如何确保表达式被正确地、无歧义地解析,这在编译器设计中至关重要。
本段的目的是展示 CFG 在解决实际编程问题中的一个核心应用和高级技巧。它超越了简单的语言成员识别,进入到如何利用文法来表达“语义”的层面。通过这个例子,读者可以理解文法设计不仅仅是“能生成就行”,更是“要生成得有意义、无歧义”,这为理解编译器前端的工作原理提供了深刻的洞见。
这个文法就像一个严格的数学老师在教你运算顺序。
- 老师说:“一个因子是最基本的东西,比如一个数字 a,或者一个被括号括起来的整体 (<EXPR>)。括号里的东西要先算,把它看成一个整体。”
- 然后老师说:“一个项是由一个或多个因子通过乘法连起来的。所以你要先把所有乘法都算完。”
- 最后老师说:“一个表达式是由一个或多个项通过加法连起来的。所以加法是最后算的。”
这个从因子到项再到表达式的逐级定义,就自然而然地规定了“先括号,再乘法,最后加法”的运算顺序。
想象一条装配线,有三个工位:因子工位、项工位、表达式工位。
- 因子工位: 负责处理最基本的零件 a,或者把一个完整的、从表达式工位运回来的“成品”(括号里的内容)打包成一个“标准模块”。
- 项工位: 从因子工位接收“标准模块”,然后用 × 号螺丝把它们组装起来。
- 表达式工位: 从项工位接收“乘法组件”,然后用 + 号螺丝把它们组装起来,形成最终产品。
这个流水线的顺序(因子 -> 项 -> 表达式)决定了组装的顺序,× 号螺丝总是在 + 号螺丝之前被使用。
📜 [原文14]
编译器将用编程语言编写的代码转换为另一种形式,通常是更适合执行的形式。为此,编译器在称为解析的过程中提取待编译代码的含义。这种含义的一种表示是代码的分析树,它位于编程语言的上下文无关文法中。我们将在定理 7.16 和问题 7.22 中讨论一种解析上下文无关语言的算法。
文法 $G_{4}$ 描述了与算术表达式相关的编程语言片段。请注意图 2.5 中的分析树如何“分组”操作。字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的树将 $\times$ 运算符及其操作数(后两个 a)分组为 + 运算符的一个操作数。在字符串 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 的树中,分组顺序颠倒。这些分组符合乘法先于加法的标准优先级,以及使用括号覆盖标准优先级。文法 $G_{4}$ 旨在捕获这些优先级关系。
这段话是对例子 2.4 的进一步阐述和总结,旨在强调文法、分析树与编译器工作原理之间的深刻联系。
第一段首先概括了编译器的核心功能:代码转换。然后聚焦于编译过程中的一个关键步骤——解析(Parsing)。
- 解析的目的: “提取待编译代码的含义”。源代码本身只是一串文本字符,编译器需要通过解析来理解这串文本的结构和意图。
- 含义的表示: 分析树(Parse Tree)或其变体抽象语法树(AST)是承载代码含义的关键数据结构。它不是线性的文本,而是层次化的树状结构,能清晰地表示运算的顺序、代码块的嵌套关系等。
- 分析树的来源: 分析树是在特定编程语言的上下文无关文法的框架下构建的。没有文法,就没有构建分析树的依据。
- 预告: 这里提到了后续章节(定理 7.16 和问题 7.22)会讨论具体的解析算法,暗示了这是一个重要且有具体实现方法的主题(例如 CYK 算法或 Earley 算法)。
第二段则将这些通用概念应用回例子 $G_4$。
- $G_4$ 的作用: 明确指出 $G_4$ 就是用来描述编程语言中算术表达式这部分的文法。
- 分析树的“分组”功能: 这是对分析树作用的非常直观的描述。“分组”就是指分析树的子树结构。一个子树将一个运算符和它的操作数“圈”在一起,形成一个独立的计算单元。
- 对 a+a×a 的分析: 分析树将 a×a 圈成一个子树(一个 <TERM>),这个子树整体作为 + 的右操作数。这体现了分组,也即是实现了“先算乘法”。
- 对 (a+a)×a 的分析: 分析树将 a+a 圈在另一个子树里(一个由括号产生的 <FACTOR>),这个子树作为 × 的左操作数。分组顺序发生了颠倒。
- 与编程规则的对应: 这种由文法和分析树强制实现的“分组”,完美地对应了我们在编程时所熟知的两条规则:
- 标准优先级: 乘法先于加法。
- 括号覆盖: 括号内的运算最先执行。
- $G_4$ 的设计意图: 最后总结,$G_4$ 的设计目的就是为了通过其结构来精确地“捕获”这些优先级关系,确保代码被无歧义地理解。
- 示例 1: C++ 代码 cout << 1+2*3;
- 代码含义: 我们期望的计算顺序是 2*3 先算得 6,然后 1+6 得 7,最后输出 7。
- 编译器工作: C++ 的编译器(如 g++)内置了一个遵循 C++ 上下文无关文法的解析器。这个文法的设计与 $G_4$ 类似,规定了 * 的优先级高于 +。
- 解析过程会为 1+23 生成一棵分析树,其结构类似于 a+a×a 的分析树,强制 23 先“分组”计算。
- 如果文法设计不当,可能会错误地解析为 (1+2)*3,导致结果为 9,这是灾难性的。
- 示例 2: Python 代码 x = (a if b else c) + d
- 代码含义: 这是一个条件表达式。它的优先级通常较低。我们期望先计算 (a if b else c) 的结果,再与 d 相加。
- 解析: Python 的解释器在解析这段代码时,其文法定义了条件表达式的优先级和结构。() 使得条件表达式被“分组”为一个独立的单元(一个 <FACTOR>),其结果再参与 + 运算。分析树会清晰地体现出 + 是顶层操作,它的左操作数是整个条件表达式的结果。
- 分析树 vs. 抽象语法树 (AST): 在实际的编译器中,解析器通常生成的是抽象语法树 (AST),而不是严格的分析树。分析树包含了所有的语法细节,包括推导过程中的所有变量节点(如 <EXPR>, <TERM>),比较冗余。AST 是分析树的简化版,它只保留了代码的核心结构和语义信息,去掉了那些用于解析过程的中间变量节点,使得后续处理更方便。例如,对于 a+b,分析树可能有 E -> E+T -> T+T -> F+T -> a+T -> ... 很多层,而 AST 可能就是一个 + 节点,左右孩子分别是 a 和 b。
- “含义”的层次: 解析提取的是“语法含义”。编译器的后续阶段,如语义分析 (Semantic Analysis),会提取更高层次的“语义含义”,例如检查变量是否已声明、类型是否匹配等。上下文无关文法主要负责语法层面。
本段是对例子 2.4 的升华。它将文法 $G_4$ 的具体设计与编译器的通用工作原理联系起来,强调了上下文无关文法和其产生的分析树在“提取代码含义”这一核心任务中的关键作用。通过“分组”这一直观概念,它解释了文法结构如何被用来精确地编码和实现如运算符优先级等重要的编程语言规则。
本段的目的是为了让读者不仅仅停留在“这个文法能生成这些字符串”的表面理解上,而是深入到“为什么文法要这样设计”的层面。它揭示了文法设计背后的“语义动机”,即通过语法结构来约束和定义程序的意义。这对于理解语言设计和编译器原理至关重要。
分析树就像是句子的“骨架”。对于 a+a×a,文法 $G_4$ 给出的“骨架”是,+ 是主心骨(脊椎),一个 a 是一条胳膊,而 a×a 整体是另一条胳膊。a×a 这条胳膊本身又有自己的骨架,× 是其骨干。你要想理解整个骨架,必须先理解每条胳膊的构造。这种骨架的层次结构就决定了你“理解”这个句子的顺序。
想象一下你在阅读一份复杂的法律合同。
- 源代码: 合同的原始文本。
- 文法: 起草合同所遵循的法律格式和术语规定。
- 解析: 律师(解析器)阅读合同的过程。
- 分析树: 律师在头脑中或草稿纸上画出的合同结构图,标明了哪个条款是哪个条款的附加条件,哪个定义适用于哪个章节。
- 分组: 律师会把“除外责任”这一整块内容“圈起来”看作一个整体,再去看它如何影响主要的保险条款。这个“圈起来”的动作就是“分组”。文法 $G_4$ 的设计,就相当于法律格式规定了“附件中的条款(乘法)必须先于正文章节(加法)进行解释”。
52.4 设计上下文无关文法
📜 [原文15]
正如 1.1 节(第 41 页)讨论的有限自动机设计一样,上下文无关文法的设计也需要创造力。事实上,上下文无关文法比有限自动机更难构建,因为我们更习惯于为特定任务编写机器程序,而不是用文法描述语言。当面临构建 CFG 的问题时,以下技术(单独或组合使用)会很有帮助。
这段话是设计上下文无关文法 (CFG) 这一主题的引言。它首先定性地描述了这项任务的特点和难点,并预告了接下来将要介绍一些有用的设计技巧。
- 类比与难度:
- 它将设计 CFG 与之前学习过的设计有限自动机 (FA) 进行了类比,指出两者都需要“创造力”,都不是简单的机械性工作。
- 紧接着,它做了一个重要的难度对比:“上下文无关文法比有限自动机更难构建”。这为读者设定了合理的预期,承认了这项任务的挑战性。
- 难度原因分析:
- 段落给出了一个深刻的解释,说明了为什么设计 CFG 更难。这源于我们人类,特别是受过编程训练的人的思维习惯。
- “我们更习惯于为特定任务编写机器程序”:设计有限自动机或编写程序,是一种“过程式”或“指令式”的思维。我们思考的是“第一步做什么,第二步做什么,遇到什么情况就转移到哪个状态”。这是一种动态的、描述“如何做”的思维方式。
- “而不是用文法描述语言”:设计文法,则是一种“声明式”或“描述式”的思维。我们思考的是“一个合法的对象是由哪些部分组成的”,或者“什么样的结构是合法的”。这是一种静态的、描述“是什么”的思维方式。
- 由于我们的教育和实践更多地倾向于前者,所以转换到后一种思维方式会感觉不自然,从而增加了难度。
- 提供解决方案:
- 在指出了困难之后,该段落立即给出了积极的引导:“以下技术……会很有帮助”。这表明,虽然设计 CFG 有挑战,但并非无章可循。存在一些通用的策略和模式可以学习和应用。
- 这些技术可以“单独或组合使用”,暗示了设计的灵活性,可能需要根据具体问题综合运用多种方法。
- 示例 1: 思维方式对比 - 识别语言 $\{a^n b^n | n \ge 1\}$
- 机器程序思维 (类似 PDA):
- 创建一个计数器,初始化为 0。
- 开始读取输入字符串。
- 只要读到 'a',计数器就加 1。
- 一旦读到第一个 'b',就改变策略。
- 接下来,每读到一个 'b',计数器就减 1。
- 在读取 'b' 的过程中如果又读到 'a',则失败。
- 字符串读完后,如果计数器正好为 0,则成功;否则失败。
这是在描述一个“过程”。
- 文法描述思维 (CFG):
- 思考这个语言的结构是什么?它的核心是“一个 'a' 和一个 'b' 的匹配对”。
- 这种匹配结构有递归性:一个大的匹配对 a...b 内部可以包含一个小的匹配对。
- 如何表达这种递归?S -> aSb。
- 递归的终点是什么?最小的合法串是 ab。所以我们需要一个规则来终止递归并产生 ab。我们可以让 S -> aSb 中的 $S$ 最终变成 $\varepsilon$,但题目要求 $n \ge 1$,所以最小单位是 ab。因此,终止规则是 S -> ab。
- 组合起来,文法是 S -> aSb | ab。
这是在描述一个“结构”。
- 将过程式思维带入文法设计: 初学者在设计文法时,常常不自觉地试图用文法规则来模拟机器的“状态转移”。例如,试图用不同的变量代表“我已经读了3个a”的状态。这种方法通常会变得非常复杂且不可行,因为文法的变量是有限的,无法表示无限的状态。正确的方法是思考语言的递归结构。
- 完美主义: 不必追求一次就设计出最完美、最简洁的文法。通常可以先从一个能生成正确语言但可能比较复杂或有冗余的文法开始,然后再逐步优化和简化它。
本段作为“设计 CFG”部分的开场白,首先承认了设计上下文无关文法是一项富有挑战性的创造性活动,并从人类思维习惯的角度解释了其难度所在(过程式思维 vs. 描述式思维)。最后,它积极地预告了接下来将要介绍一系列实用的设计技巧,以帮助读者应对这一挑战。
本段的目的是进行心理建设和方法论引导。它通过“丑话说在前面”的方式,让读者对任务难度有合理的预期,避免因挫败感而气馁。同时,通过点明思维方式的差异,引导读者有意识地从“如何做”转换到“是什么”的视角来思考问题,为学习后续的具体技巧做好思维准备。
设计有限自动机就像是导演一场戏,你要安排每个演员(状态)在特定时间(接到输入)做什么动作(状态转移)。而设计上下文无关文法就像是编剧写剧本,你要定义角色的构成(“一个英雄角色由一个悲惨的过去和一个坚定的目标组成”),而不是指挥演员的每一个动作。我们通常更习惯当导演,而不是当编剧。
想象两种描述“楼梯”的方式。
- 机器程序思维: “向上走一步,再向上走一步,再向上走一步...”。这是在描述一个动作序列。
- 文法描述思维: “一个楼梯,由一个台阶,和另一个位于其上方的楼梯组成。最简单的楼梯就是一个台阶。” 这是一个递归的结构定义。
设计文法要求我们用后一种思维方式来描述语言。
📜 [原文16]
首先,许多 CFL 是更简单 CFL 的并集。如果你必须为可以分解为更简单部分的 CFL 构建 CFG,那么这样做,然后为每个部分构建单独的文法。这些单独的文法可以很容易地合并为原始语言的文法,方法是组合它们的规则,然后添加新规则 $S \rightarrow S_{1}\left|S_{2}\right| \cdots \mid S_{k}$,其中变量 $S_{i}$ 是各个文法的开始变量。解决几个更简单的问题通常比解决一个复杂的问题更容易。
例如,为了获得语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\} \cup\left\{1^{n} 0^{n} \mid n \geq 0\right\}$ 的文法,首先构建语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 的文法
以及语言 $\left\{1^{n} 0^{n} \mid n \geq 0\right\}$ 的文法
然后添加规则 $S \rightarrow S_{1} \mid S_{2}$,得到文法
这里介绍了设计上下文无关文法 (CFG) 的第一个核心技术:分解与合并,专门用于处理由并集 (Union) 构成的语言。
核心思想: “分而治之” (Divide and Conquer)。
- 分解 (Divide): 当你面对一个复杂的语言 $L$ 时,首先观察它是否能被看作是几个更简单的语言 $L_1, L_2, \dots, L_k$ 的并集。即 $L = L_1 \cup L_2 \cup \dots \cup L_k$。
- 解决子问题 (Conquer): 如果可以分解,那么就暂时忽略整个复杂问题,转而为每一个简单的子语言 $L_i$ 单独设计一个 CFG,我们称之为 $G_i$。设 $G_i$ 的开始变量是 $S_i$。
- 合并 (Combine): 将所有子文法的规则全部放在一起。然后,引入一个新的、全局的开始变量 $S$,并为它添加一条新的规则 $S \rightarrow S_1 | S_2 | \dots | S_k$。这条规则的意思是:“要生成语言 $L$ 的一个字符串,你可以选择去生成 $L_1$ 的一个字符串(从 $S_1$ 开始),或者选择去生成 $L_2$ 的一个字符串(从 $S_2$ 开始),以此类推。”
这个技巧的有效性基于上下文无关语言对于并集运算是封闭的这一性质。也就是说,如果 $L_1$ 和 $L_2$ 都是 CFL,那么它们的并集 $L_1 \cup L_2$ 也必然是 CFL。这个构造性证明本身就提供了设计文法的方法。
例子分析:
- 目标语言: $L = \left\{0^{n} 1^{n} \mid n \geq 0\right\} \cup\left\{1^{n} 0^{n} \mid n \geq 0\right\}$。这个语言包含两种类型的字符串:要么是若干个 '0' 后面跟相同数量的 '1',要么是若干个 '1' 后面跟相同数量的 '0'。
- 分解:
- $L_1 = \left\{0^{n} 1^{n} \mid n \geq 0\right\}$。
- $L_2 = \left\{1^{n} 0^{n} \mid n \geq 0\right\}$。
- 显然 $L = L_1 \cup L_2$。
- 解决子问题:
- 为 $L_1$ 设计文法 $G_1$。我们已经知道它的递归结构是外部包裹 0 和 1,中心是空串。所以文法是 $S_1 \rightarrow 0S_1 1 \mid \varepsilon$。
- 为 $L_2$ 设计文法 $G_2$。结构完全类似,只是包裹的终结符变成了 1 和 0。所以文法是 $S_2 \rightarrow 1S_2 0 \mid \varepsilon$。
- 合并:
- 将 $G_1$ 和 $G_2$ 的规则放在一起。
- 引入新的开始变量 $S$。
- 添加规则 $S \rightarrow S_1 \mid S_2$。
- 最终文法:
```
S -> S1 | S2
S1 -> 0S1 1 | ε
S2 -> 1S2 0 | ε
```
这个文法的工作方式是:从 $S$ 开始,你第一步必须选择走 $S_1$ 的路径还是 $S_2$ 的路径。一旦选定,比如选了 $S_1$,你就进入了 $L_1$ 的生成模式,之后的所有推导都遵循 $G_1$ 的规则,不可能再跳到 $S_2$ 的规则里去。这样就保证了生成的字符串要么完全符合 $L_1$ 的格式,要么完全符合 $L_2$ 的格式。
- $\left\{0^{n} 1^{n} \mid n \geq 0\right\} \cup\left\{1^{n} 0^{n} \mid n \geq 0\right\}$:
- $\cup$: 并集运算符。$A \cup B$ 表示包含所有属于 $A$ 或属于 $B$ 的元素的集合。
- 含义: 这个语言集合包含了所有形如 $0^n 1^n$ 的字符串,以及所有形如 $1^n 0^n$ 的字符串。
- $S \rightarrow S_{1}\left|S_{2}\right| \cdots \mid S_{k}$:
- $S$: 新的、总的开始变量。
- $S_i$: 第 $i$ 个子语言 $L_i$ 的开始变量。
- |: “或”选择。
- 含义: 这是合并步骤的核心规则,它提供了一个顶层的选择,让推导可以进入任何一个子文法的生成过程中。
- 示例 1: 设计语言 $L = \{a^n \mid n \text{ is even}\} \cup \{b^m \mid m \text{ is odd}\}$ 的文法****
- 分解:
- $L_1 = \{a^n \mid n \text{ is even}\}$: 由偶数个 'a' 组成的字符串。
- $L_2 = \{b^m \mid m \text{ is odd}\}$: 由奇数个 'b' 组成的字符串。
- 解决子问题:
- 文法 $G_1$ for $L_1$: 每次添加两个 'a'。$S_1 \rightarrow aaS_1 \mid \varepsilon$。
- 文法 $G_2$ for $L_2$: 每次添加两个 'b',但基础是单个 'b'。$S_2 \rightarrow bbS_2 \mid b$。
- 合并:
```
S -> S1 | S2
S1 -> aaS1 | ε
S2 -> bbS2 | b
```
- 示例 2: 为 a 或 b 设计文法****
- 语言 $L = \{a^n \mid n \ge 0\} \cup \{b^m \mid m \ge 0\}$。
- 分解: $L_1 = \{a^n \mid n \ge 0\}$, $L_2 = \{b^m \mid m \ge 0\}$。
- 子文法: $S_1 \rightarrow aS_1 \mid \varepsilon$ 和 $S_2 \rightarrow bS_2 \mid \varepsilon$。
- 合并后文法:
```
S -> S1 | S2
S1 -> aS1 | ε
S2 -> bS2 | ε
```
- 忘记引入新的开始变量: 一个常见的错误是直接把两个文法的规则合并,然后试图让原来的某个开始变量(比如 $S_1$)担当总的开始变量。这是不行的,因为从 $S_1$ 开始你永远无法生成 $L_2$ 的字符串。必须引入一个更高层级的、全新的开始变量 $S$ 来提供选择。
- 变量名冲突: 在合并多个文法时,要确保它们的变量集合是不相交的(除了开始变量,可以重命名)。如果 $G_1$ 和 $G_2$ 都用了一个叫 $X$ 的变量,在合并前最好将其中一个重命名为 $X'$,以避免规则混淆。在这个例题中,$S_1$ 和 $S_2$ 的变量集合本身就是不相交的(分别是 $\{S_1\}$ 和 $\{S_2\}$),所以没有这个问题。
- 此方法不适用于交集: 上下文无关语言对交集运算不封闭。也就是说,$L_1$ 和 $L_2$ 都是 CFL,但 $L_1 \cap L_2$ 不一定是 CFL。因此,没有一个通用的方法可以通过组合两个文法来获得其语言交集的文法。
本段介绍了一种强大而系统的 CFG 设计技术:对于由并集构成的语言,采用“分而治之”的策略。通过为每个子语言单独设计文法,然后用一个新的开始变量和选择规则将它们“粘合”在一起,可以将一个复杂问题简化为几个简单问题的组合。这个方法既直观又可靠。
本段的目的是为 CFG 设计提供第一个具体的、可操作的“设计模式”。这让读者从完全依赖“创造力”的困境中解脱出来,开始掌握一些结构化的设计方法。通过展示如何处理并集,它也从侧面引入了上下文无关语言的封闭性质这一重要理论概念。
这就像是做一个“套餐选择”菜单。
- $L_1$ 是“中餐菜单”,$L_2$ 是“西餐菜单”。为它们分别设计菜品(子文法)是相对独立的任务。
- 你的总餐厅菜单 $L$ 提供“中餐或西餐”。
- 合并的过程就是,在菜单的首页写上(新的开始变量 $S$):
今日特选 (S):
- 请翻到中餐部(选择 $S_1$)
- 请翻到西餐部(选择 $S_2$)
- 顾客一旦选择了去哪个“部”,就只能点那个部的菜了。
想象你在为一个大型活动规划不同的入口。
- $L_1$ 是 VIP 通道,有一套自己的安检和验证流程(文法 $G_1$)。
- $L_2$ 是普通观众通道,有另一套流程(文法 $G_2$)。
- 整个活动的入口系统(文法 $G$)是在最外面设置一个大的分流点(开始变量 $S$)。工作人员在这里指示你:“VIP 请走左边($S \rightarrow S_1$),普通观众请走右边($S \rightarrow S_2$)”。一旦你进入了某条通道,就必须按该通道的规则走到底,不能中途换道。
📜 [原文17]
其次,如果一种语言恰好是正则的,那么构建它的 CFG 就很容易,如果你能先为该语言构建一个 DFA。你可以将任何 DFA 转换为等效的 CFG,如下所示。为 DFA 的每个状态 $q_{i}$ 创建一个变量 $R_{i}$。如果 $\delta\left(q_{i}, a\right)=q_{j}$ 是 DFA 中的一个转移,则将规则 $R_{i} \rightarrow a R_{j}$ 添加到 CFG 中。如果 $q_{i}$ 是 DFA 的接受状态,则添加规则 $R_{i} \rightarrow \varepsilon$。将 $R_{0}$ 作为文法的开始变量,其中 $q_{0}$ 是机器的开始状态。请自行验证,由此产生的 CFG 生成的语言与 DFA 识别的语言相同。
这里介绍了设计上下文无关文法 (CFG) 的第二个技术:从确定性有限自动机 (DFA) 进行转换。这个技术专门用于为正则语言构建 CFG。
背景知识: 我们已经知道,所有正则语言都是上下文无关语言。这意味着任何一个可以用 DFA(或 NFA,或正则表达式)描述的语言,都必然存在一个 CFG 可以生成它。本段就提供了一个将 DFA 自动转换为等效 CFG 的算法。
转换算法:
- 变量映射: 文法的变量和 DFA 的状态一一对应。为 DFA 的每一个状态 $q_i$,创建一个名为 $R_i$ 的变量。这个变量 $R_i$ 的直观含义是:“从状态 $q_i$ 开始,能够识别的字符串的集合”。
- 转移转换: DFA 的转移函数 $\delta(q_i, a) = q_j$ 表示在状态 $q_i$ 读到输入符号 $a$ 会转移到状态 $q_j$。这个过程被转换成一条 CFG 规则:$R_i \rightarrow a R_j$。这条规则的直观含义是:“要生成一个能从 $q_i$ 开始被识别的字符串,你可以先生成一个 a,然后生成一个能从 $q_j$ 开始被识别的字符串。” 这完美地模拟了 DFA 的一步转移。
- 接受状态转换: 如果 $q_i$ 是一个接受状态,这意味着机器到达这个状态时,已经读取的字符串是合法的。在 DFA 中,从接受状态开始,如果不再读入任何字符(即读入空串 $\varepsilon$),当前路径是接受的。因此,为每个接受状态 $q_i$ 添加一条规则 $R_i \rightarrow \varepsilon$。这条规则表示“从接受状态 $q_i$ 出发,可以生成空串”,它为推导提供了一个终止点。
- 开始状态映射: DFA 的开始状态 $q_0$ 对应的变量 $R_0$ 被指定为 CFG 的开始变量。这保证了文法的生成过程是从模拟 DFA 的初始状态开始的。
正确性验证 (直观):
- 考虑 DFA 识别一个字符串 $w = a_1 a_2 \dots a_k$ 的过程。这个过程是一个状态序列:$q_0 \xrightarrow{a_1} q_{i_1} \xrightarrow{a_2} q_{i_2} \dots \xrightarrow{a_k} q_{i_k}$,并且 $q_{i_k}$ 是一个接受状态。
- 在构造出的 CFG 中,这个过程对应一个推导:
$R_0 \Rightarrow a_1 R_{i_1} \Rightarrow a_1 a_2 R_{i_2} \Rightarrow \dots \Rightarrow a_1 a_2 \dots a_k R_{i_k}$。
- 因为 $q_{i_k}$ 是接受状态,所以我们有一条规则 $R_{i_k} \rightarrow \varepsilon$。
- 继续推导:$a_1 a_2 \dots a_k R_{i_k} \Rightarrow a_1 a_2 \dots a_k \varepsilon = w$。
- 这就证明了,任何被 DFA 接受的字符串都可以被这个 CFG 生成。反之亦然。
这个技巧非常强大,因为它将一个可能需要创造力的设计问题,转换为了一个完全机械化的、算法性的转换过程。只要你能为正则语言画出 DFA,就能自动得到它的 CFG。
- 示例 1: DFA 识别以 1 结尾的二进制串
- DFA:
- 状态: $q_0$ (开始), $q_1$ (接受)
- 转移:
- $\delta(q_0, 0) = q_0$
- $\delta(q_0, 1) = q_1$
- $\delta(q_1, 0) = q_0$
- $\delta(q_1, 1) = q_1$
- CFG 转换:
- 变量: $R_0$ (对应 $q_0$), $R_1$ (对应 $q_1$)。
- 开始变量: $R_0$。
- 转移规则:
- $\delta(q_0, 0) = q_0 \rightarrow R_0 \rightarrow 0 R_0$
- $\delta(q_0, 1) = q_1 \rightarrow R_0 \rightarrow 1 R_1$
- $\delta(q_1, 0) = q_0 \rightarrow R_1 \rightarrow 0 R_0$
- $\delta(q_1, 1) = q_1 \rightarrow R_1 \rightarrow 1 R_1$
- 接受状态规则: $q_1$ 是接受状态 $\rightarrow R_1 \rightarrow \varepsilon$。
- 最终 CFG:
- 推导验证 (生成 01): $R_0 \Rightarrow 0R_0 \Rightarrow 01R_1 \Rightarrow 01\varepsilon = 01$。 (这里推导 01 应该是 $R_0 \Rightarrow 1R_1 \Rightarrow 1\varepsilon = 1$。推导 01 应该是 $R_0 \Rightarrow 0 R_0 \Rightarrow 01 R_1 \Rightarrow 01\varepsilon=01$)
- 示例 2: DFA 识别包含子串 ab 的语言
- DFA:
- 状态: $q_0$ (开始), $q_1$, $q_2$ (接受)
- 转移:
- $\delta(q_0, b) = q_0$, $\delta(q_0, a) = q_1$
- $\delta(q_1, a) = q_1$, $\delta(q_1, b) = q_2$
- $\delta(q_2, a) = q_2$, $\delta(q_2, b) = q_2$
- CFG 转换:
- 变量: $R_0, R_1, R_2$
- 开始变量: $R_0$
- 规则:
```
R0 -> bR0 | aR1
R1 -> aR1 | bR2
R2 -> aR2 | bR2 | ε // R2是接受状态
```
- 这个文法就能生成所有包含 ab 的字符串。
- NFA 到 CFG: 这个算法是针对 DFA 的。如果你有一个 NFA,你需要先将它转换为等效的 DFA,然后再应用这个算法。直接从 NFA 转换会更复杂,因为一个状态对一个输入可能转移到多个状态。
- 接受状态是开始状态: 如果 DFA 的开始状态 $q_0$ 本身就是接受状态,那么语言包含空串 $\varepsilon$。我们的算法能正确处理这种情况:因为 $q_0$ 是接受状态,我们会添加规则 $R_0 \rightarrow \varepsilon$。那么从开始变量 $R_0$ 出发,一步就可以推导出 $\varepsilon$。
- 文法的形式: 这种方法生成的 CFG 是一种特殊的正则文法(Right-Regular Grammar),其所有规则都形如 $A \rightarrow aB$ 或 $A \rightarrow \varepsilon$。所有正则文法生成的都是正则语言。
本段提出了一个将任何 DFA 转换为等效 CFG 的确定性算法。这个方法为所有正则语言提供了一个标准化的 CFG 构建流程,将设计问题转化为了一个机械的转换过程。其核心思想是让文法的变量模拟 DFA 的状态,让文法的规则模拟 DFA 的转移。
本段的目的是提供一个处理正则语言这一大类 CFL 的“银弹”。它不仅再次强调了“所有正则语言都是上下文无关的”,并且给出了一个构造性的证明。这使得设计师在面对一个已知是正则的语言时,有了一个非常可靠和简单的工具,而不必去重新进行创造性思考。
[直觉心-智模型]
这个转换过程就像是为自动售货机 (DFA) 编写一份“用户可读的说明书” (CFG)。
- DFA 状态: 售货机的内部状态(“待机”、“已投币5角”、“已投币1元”)。
- CFG 变量: 说明书中的章节名($R_0$: “第一章:从待机状态开始的操作”)。
- DFA 转移: 售货机的物理反应(在“已投币5角”状态下,再投5角,变为“已投币1元”状态)。
- CFG 规则: 说明书中的一句话($R_{5角} \rightarrow \text{投5角币 } R_{1元}$:“在‘已投币5角’时,你可以‘投一个5角币’,然后参考‘第二章:已投币1元的操作’。”)。
- DFA 接受状态: 售货机可以出货的状态。
- CFG $\varepsilon$-规则: 说明书里说:“在‘已足额’状态下,你可以选择‘什么都不做’(按出货按钮),交易完成。”
想象一个迷宫游戏 (DFA)。
- 每个房间是一个状态。
- 每条带颜色的门是一个转移(在A房间,走红门,到B房间)。
- 出口房间是接受状态。
- 将这个迷宫翻译成一本“路书” (CFG) 的过程:
- 为每个房间(如 Room_A)创建一个章节(变量 $R_A$)。
- 对于“在A房间,走红门,到B房间”这条路,你在A章节里写一条规则:“$R_A \rightarrow \text{走红门 } R_B$”(要从A房间走出迷宫,你可以先走红门,然后按B章节的指示走)。
- 对于出口房间 Exit_Room,你在 Exit_Room 章节里加一条规则:“$R_{Exit} \rightarrow \text{停步走出}$ ($\varepsilon$)”(到了出口,你就成功了,路程结束)。
- 路书的开始章节自然是迷宫的入口房间。
📜 [原文18]
第三,某些上下文无关语言包含带有两个子串的字符串,这两个子串是“关联”的,这意味着针对此类语言的机器需要记住有关其中一个子串的无限量信息,以验证它是否与另一个子串正确对应。这种情况发生在语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 中,因为机器需要记住 0 的数量,以验证它是否等于 1 的数量。你可以通过使用 $R \rightarrow u R v$ 形式的规则来构建 CFG 以处理这种情况,该规则生成字符串,其中包含 $u$ 的部分对应于包含 $v$ 的部分。
这里介绍了设计上下文无关文法的第三个,也是最核心的一个技巧:使用递归规则处理关联子串。这个技巧是用来处理那些超越了正则语言能力的、需要“计数”或“匹配”的语言。
- 问题识别:
- 首先,要识别出语言的特性。这类语言的字符串通常可以被分成几个部分,其中两个(或多个)部分存在某种“关联”。
- 最常见的关联是“数量相等”,例如 $\left\{0^{n} 1^{n}\right\}$ 中 '0' 和 '1' 的数量相等。
- 另一种关联是“逆序匹配”,例如回文语言 $\left\{w w^{R} \mid w \in \{0,1\}^{*}\right\}$,其中后半部分是前半部分的反转。
- “机器需要记住...无限量信息”是对这种关联的计算挑战的描述。正如之前讨论的,有限自动机的有限状态无法存储一个可能无限增长的计数值 $n$。
- 解决方案:
- CFG 通过递归来解决这个问题,而不需要显式的“计数器”。
- 核心技巧: 使用形如 $R \rightarrow u R v$ 的规则。
- $R$ 是一个递归调用的变量。
- u 和 v 是终结符(或终结符串)。
- 工作原理: 这条规则有一种“同时生长”或“对称生成”的效应。每应用一次,就在递归的变量 $R$ 的两侧同时“种下”u 和 v。
- $R \Rightarrow uRv$
- $\Rightarrow u(uRv)v = u^2 R v^2$
- $\Rightarrow u^2(uRv)v^2 = u^3 R v^3$
- ... 经过 $n$ 次递归,我们会得到 $u^n R v^n$。
- 通过这种方式,u 和 v 的数量被文法的递归结构本身隐式地、完美地绑定在了一起,始终保持一致。
- 最后,只需要一个终止规则(例如 $R \rightarrow \varepsilon$ 或 $R \rightarrow w_0$)来替换掉最后的 $R$,就完成了字符串的生成。
- 例子回顾:
- 对于语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$:
- 关联的子串是 0...0 和 1...1。
- u 就是 0,v 就是 1。
- 所以核心规则是 $S \rightarrow 0S1$。
- 递归的终点是当 $n=0$ 时,此时字符串是空串 $\varepsilon$。所以终止规则是 $S \rightarrow \varepsilon$。
- 最终文法: $S \rightarrow 0S1 \mid \varepsilon$。
这个技巧是设计非正则 CFL 文法的基石,它直接利用了 CFG 最强大的武器——递归。
- 示例 1: 语言 $L = \{a^n b^{2n} \mid n \ge 0\}$
- 分析: b 的数量总是 a 的两倍。两个子串 a...a 和 b...b 是关联的。
- 设计: 我们需要每次递归生成一个 a 和两个 b。
- u = a
- v = bb
- 核心规则: $S \rightarrow aSbb$。
- 终止条件: 当 $n=0$ 时,字符串是 $\varepsilon$。
- 最终文法: $S \rightarrow aSbb \mid \varepsilon$。
- 推导验证 (n=2, aabbbb): $S \Rightarrow aSbb \Rightarrow a(aSbb)bb = aaSbbbb \Rightarrow aa\varepsilon bbbb = aabbbb$。
- 示例 2: 语言 $L$ = 所有偶数长度的回文串 (palindromes) over $\{0, 1\}$
- 分析: 回文串的特点是左右对称。例如 0110,1001。第一个字符和最后一个字符匹配,第二个字符和倒数第二个字符匹配,以此类推。这是一个典型的“关联子串”问题。
- 设计: 我们需要一个规则,在两侧同时添加相同的符号。
- $S \rightarrow 0S0$: 在一个更小的回文串两侧添加 0。
- $S \rightarrow 1S1$: 在一个更小的回文串两侧添加 1。
- 终止条件: 最短的偶数长度回文串是空串 $\varepsilon$。
- 最终文法: $S \rightarrow 0S0 \mid 1S1 \mid \varepsilon$。
- 推导验证 (0110): $S \Rightarrow 0S0 \Rightarrow 0(1S1)0 = 01S10 \Rightarrow 01\varepsilon10 = 0110$。
- 中心点或分隔符: 某些语言在关联的子串之间可能有一个中心标记。例如 $\left\{0^{n} \# 1^{n}\right\}$。在这种情况下,终止规则应该生成那个中心标记,而不是空串。例如,$S \rightarrow 0S1 \mid \#$。
- 奇数长度回文串: 如果要生成奇数长度的回文串(如 010, 111),它们的中心是一个单独的字符。这意味着递归的终点不再是空串,而是单个的终结符 0 或 1。所以可以添加规则 $S \rightarrow 0$ 和 $S \rightarrow 1$。生成所有回文串的文法就是 $S \rightarrow 0S0 \mid 1S1 \mid 0 \mid 1 \mid \varepsilon$。
- 关联不止一对: 某些语言可能有多于一对的关联,例如 $\left\{a^n b^m c^m d^n \mid n,m \ge 0\right\}$。这种语言可以通过组合递归规则来解决。例如:$S \rightarrow aSd \mid A$, $A \rightarrow bAc \mid \varepsilon$。这里,$S$ 负责外层的 a-d 匹配,$A$ 负责内层的 b-c 匹配。
本段介绍了设计 CFG 的一个关键策略:使用形如 $R \rightarrow uRv$ 的递归规则来处理语言中“关联子串”的匹配问题。这种方法通过文法结构本身实现了隐式的计数或对称性检查,是生成非正则的上下文无关语言的核心技巧。
本段的目的是揭示上下文无关文法超越有限自动机的根本原因和实现方式。它为读者提供了一把“钥匙”,以解决所有需要无限“记忆”来匹配或计数的语言的设计问题。这是从正则语言思维迈向上下文无关语言思维的最重要一步。
这种递归规则就像一个“对称的生长指令”。想象你有一棵神奇的树 ($R$)。
- 指令 $R \rightarrow uRv$ 说:“每一次生长,树的左边会长出一根 u 枝,右边同时长出一根 v 枝。”
- 无论生长多少次,两边的枝条数量(或结构)都保持着完美的对应关系。
- 最后,用一个终止规则把树心 ($R$) 换成一颗种子或一朵花,生长就结束了。
想象你在用双手同时串珠子。
- 规则 $S \rightarrow \text{左手穿红珠 } S \text{ 右手穿蓝珠}$。
- 你每次都严格执行这个指令,左手穿一颗红珠子的同时,右手必须穿一颗蓝珠子。
- 当你决定结束时(应用 $S \rightarrow \varepsilon$),你停下来。
- 结果是,你得到一串珠子,左半部分全是红珠子,右半部分全是蓝珠子,并且两边的数量绝对相等。你不需要脑子去数数,这个“同步动作”的规则本身就保证了结果的正确性。
📜 [原文19]
最后,在更复杂的语言中,字符串可能包含递归地作为其他(或相同)结构的一部分出现的某些结构。这种情况发生在例子 2.4 中生成算术表达式的文法中。每当出现符号 a 时,一个完整的括号表达式可能会递归地出现。为了实现这种效果,将生成结构的变量符号放置在规则中对应于该结构可能递归出现的位置。
这里介绍了设计上下文无关文法的第四个技巧:结构替换式递归。这个技巧用于处理那些一个语法结构可以出现在另一个(或自身)语法结构内部的语言,这是构建复杂层次结构的关键。
- 问题识别:
- 这类语言的特点是“一个东西里面可以有另一个东西”。这与第三个技巧的“两端匹配”不同,这里的递归是“整体替换”。
- 最典型的例子就是算术表达式,如例子 2.4 所示。一个最基本的元素(操作数,如 a)出现的位置,往往可以被一个更复杂的、同类型的结构(一个完整的、带括号的表达式,如 (a+a*b))所替换。
- 另一个例子是编程语言中的语句块。一个 if 语句的 then 分支里可以只是一条简单的赋值语句,也可以是另一个完整的 if-else 语句,或者一个 while 循环。
- 解决方案:
- 核心技巧: 在文法规则中,将代表“小结构”的符号和代表“大结构”的变量并列作为可选项。
- 回顾文法 $G_4$ 中的规则 $\langle\mathrm{FACTOR}\rangle \rightarrow (\langle\mathrm{EXPR}\rangle) \mid \mathrm{a}$。
- a 在这里代表最简单的、原子的结构(一个操作数)。
- (
) 代表复杂的、递归的结构。是整个文法的开始变量,代表了一个可以任意复杂的完整表达式。 - | “或”符号将这两者并列,意味着:任何需要一个 FACTOR 的地方,你既可以提供一个简单的 a,也可以提供一个用括号括起来的、任意复杂的完整表达式。
- 通用模式: A -> B | C,其中 B 派生出原子结构,C 派生出包含顶层结构(比如开始变量)的递归结构。
- 实现效果: "将生成结构的变量符号放置在规则中对应于该结构可能递归出现的位置"。在 $G_4$ 中,
这个代表完整结构的变量,被放置在了 FACTOR 的规则中,也就是一个 a 原本可以出现的位置。
这个技巧是构建具有任意深度嵌套能力的文法的关键,广泛应用于编程语言、数据格式(如 JSON)等领域。
- 示例 1: JSON 对象的简化文法
- 分析: JSON 的 value 可以是一个简单的字符串、数字等,也可以是一个完整的 object 或 array,这就是结构替换式递归。
- 文法 (简化版):
```
<value> -> <object> | <string> | <number>
<object> -> { <members> }
<members> -> <pair> | <pair>, <members>
<pair> -> <string> : <value> // <-- 关键递归点
```
- 解释: pair 的定义是 <string> : <value>。这里的 <value> 可以是简单的 <string> 或 <number>,也可以是一个完整的 <object>。这就允许了对象的嵌套,例如 { "name": "John", "address": { "city": "New York" } }。代表整体结构的 <value> 被放置在了代表局部结构的 <pair> 的规则中。
- 示例 2: 简化的 if-else 语句
- 分析: if 语句的执行体可以是一条简单语句,也可以是另一条复合语句(如 if 或 while)。
- 文法:
```
<stmt> -> <if-stmt> | <assign-stmt> | ...
<if-stmt> -> if (<expr>) <stmt> else <stmt> // <-- 关键递归点
<assign-stmt> -> <id> = <expr>
```
- 解释: <if-stmt> 的规则中,then 和 else 部分需要的是一个 <stmt>。这个 <stmt> 可以是一个简单的赋值语句 <assign-stmt>,也可以是另一个 <if-stmt>,从而实现了 if 语句的任意嵌套。if (x>0) if (y>0) z=1; else z=0;
- 无限循环: 如果设计不当,可能会导致无意义的无限递归。例如,规则 A -> A 或 A -> B, B -> A 如果没有其他出口,将导致推导永远无法终止。结构替换式递归必须有一个非递归的出口(如 $G_4$ 中的 a)。
- 与第三个技巧的区别:
- 第三个技巧 ($R \rightarrow uRv$) 是线性递归或尾递归的变体,通常用于字符串两端的“匹配”,构建的是一维的对称性。
- 第四个技巧是树状递归,一个节点可以被一整棵子树替换,构建的是层次化的、嵌套的结构。
本段介绍了 CFG 设计的第四个技巧:通过在规则中将代表原子结构的选项和代表完整递归结构的选项并列,来实现复杂的、任意深度的结构嵌套。这个技巧的核心是“把代表整体的变量,放到一个代表局部成分的规则里”,如 $G_4$ 中 FACTOR -> (EXPR) | a 所做的那样。这是构建如编程语言等复杂层次结构语言文法的基石。
本段的目的是介绍一种比“对称匹配”更强大的递归模式,即“结构替换”。这使得读者能够理解和设计那些具有复杂嵌套特性的语言的文法,比如编程语言中的表达式、语句块,或数据格式中的嵌套对象。这进一步拓宽了读者可以解决的问题范围。
这就像是“梦想成真”的规则。
- 规则说:“你可以选择拥有一块金子 (a),或者选择拥有一个‘愿望宝盒’ (<EXPR>)”。
- 而“愿望宝盒”的规则是,打开它可以实现任何愿望,包括获得更多的金子,或者获得另一个“愿望宝盒”。
- 通过这个机制,你可以构建出任意复杂的财富结构,比如“一个愿望宝盒,里面装着金子和另一个愿望宝盒”。
想象一下你的电脑文件系统。
- 一个“文件夹”(<FACTOR>)里面可以放什么?
- 可以放一个“文件”(a)。
- 也可以放另一个“文件夹”((<EXPR>),这里的括号代表进入下一层目录)。
- FACTOR -> (EXPR) | a 这条规则就完美地描述了文件系统的这种递归嵌套能力。一个文件夹里可以有文件,也可以有子文件夹,而子文件夹里又可以有文件和子子文件夹,以此类推,形成一个树状结构。
62.5 二义性
📜 [原文20]
有时,一个文法可以用几种不同的方式生成同一个字符串。这样的字符串将有几个不同的分析树,因此有几个不同的含义。这对于某些应用(例如编程语言)可能是不希望的,因为程序应该具有唯一的解释。
如果一个文法以几种不同的方式生成同一个字符串,我们说该字符串在该文法中是二义性地推导的。如果一个文法二义性地生成了某个字符串,我们说该文法是二义性的。
例如,考虑文法 $G_{5}$:
这个文法二义性地生成了字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$。下图显示了两个不同的分析树。
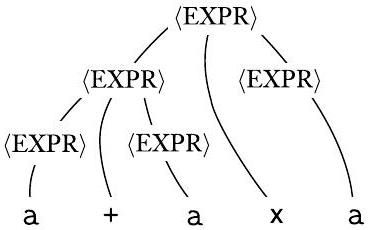
图 2.6
文法 $G_{5}$ 中字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的两个分析树
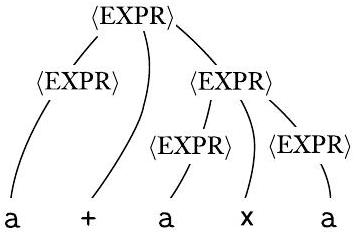
图 2.6
文法 $G_{5}$ 中字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的两个分析树
这一部分引入了上下文无关文法中的一个核心问题——二义性 (Ambiguity)。
首先,对二义性进行了直观的定义和解释:
- 现象: 一个文法可以用多种不同的方式生成同一个字符串。
- 后果: 这个字符串会对应多个不同的分析树。因为分析树代表了字符串的结构和含义,所以多个分析树就意味着“多种含义”。
- 危害: 在某些应用中,多种含义是不可接受的。最典型的例子就是编程语言。一个程序 a+bc 必须有唯一确定的计算方式,不能有时解释为 (a+b)c,有时又解释为 a+(b*c)。程序的行为必须是确定的。因此,用于编程语言的文法必须是无二义性的。
接着,给出了两个形式化的术语:
- 二义性推导 (ambiguously derived): 当一个字符串可以被一个文法以多种方式生成(即对应多棵分析树)时,我们说这个字符串是被二义性推导的。
- 二义性文法 (ambiguous grammar): 如果一个文法中至少存在一个字符串可以被二义性推导,那么这个文法本身就被称为二义性文法。
然后,通过一个具体的文法 $G_5$ 来演示二义性。
- 文法 $G_5$: <EXPR> -> <EXPR>+<EXPR> | <EXPR>×<EXPR> | (<EXPR>) | a
- 这个文法看起来很直观,它说一个表达式可以是两个表达式相加,或两个表达式相乘,或括号括起来,或一个 a。
- 问题所在: 这个文法没有规定 + 和 × 的优先级。规则 <EXPR> -> <EXPR>+<EXPR> 和 <EXPR> -> <EXPR>×<EXPR> 处于同一“层级”,推导时可以随意选择先应用哪个。
- 二义性字符串: a+a×a。
- 两个分析树:
- 第一棵树 (左图): 顶层是 + 节点。这棵树的结构对应于 (a) + (a×a)。它先将 a×a 解析为一个子
,然后将这个结果与第一个 a 相加。这符合我们期望的乘法优先。 - 第二棵树 (右图): 顶层是 × 节点。这棵树的结构对应于 (a+a) × (a)。它先将 a+a 解析为一个子
,然后将结果与第三个 a 相乘。这违反了标准的运算符优先级。
因为文法 $G_5$ 允许为同一个字符串 a+a×a 生成这两棵结构完全不同(即含义完全不同)的分析树,所以 $G_5$ 是一个二义性文法。
- $\langle\mathrm{EXPR}\rangle \rightarrow\langle\mathrm{EXPR}\rangle+\langle\mathrm{EXPR}\rangle|\langle\mathrm{EXPR}\rangle \times\langle\mathrm{EXPR}\rangle|(\langle\mathrm{EXPR}\rangle) \mid \mathrm{a}$:
- <EXPR> -> <EXPR>+<EXPR>: 这条规则本身就带来了两种二义性:
- 优先级二义性: 与
-> 规则没有层次区分。× - 结合性二义性: 对于 a+a+a,这条规则既可以解析为 (a+a)+a (左结合),也可以解析为 a+(a+a) (右结合)。因为它在 + 的两边都用了相同的变量
。 - 与 $G_4$ 的对比:
- $G_5$: E -> E+E | E*E | ... (对称的,无层次)
- $G_4$: E -> E+T, T -> T*F, F -> ... (非对称,有层次)
- $G_4$ 通过引入不同的变量 E, T, F 并建立它们的推导层次关系,从而消除了 $G_5$ 中存在的二义性。
- 示例 1: $G_5$ 中 a+a+a 的二义性
- 字符串: a+a+a
- 分析树 1 (左结合):
- 顶层是第二个 +。
- 左子树是 a+a。
- 右子树是 a。
- 含义: (a+a)+a。
- 分析树 2 (右结合):
- 顶层是第一个 +。
- 左子树是 a。
- 右子树是 a+a。
- 含义: a+(a+a)。
- 由于加法满足结合律,这在数学上结果相同,但在编译器生成代码时,计算顺序不同,可能会影响性能或浮点数计算的精度。
- 示例 2: "dangling else" 问题
- 语言片段: if (c1) if (c2) s1 else s2
- 简化文法: <stmt> -> if (<cond>) <stmt> | if (<cond>) <stmt> else <stmt> | ...
- 二义性: else s2 到底跟哪个 if 匹配?
- 匹配内层 if: if (c1) { if (c2) s1 else s2 }
- 匹配外层 if: if (c1) { if (c2) s1 } else s2
- 大多数编程语言(如C, Java)规定 else 与最近的未匹配的 if 结合,即第一种解释。它们的文法经过了精巧的设计以消除这种二义性。
- 二义性 vs. 多种推导: 一个字符串可能有很多不同的推导序列,但如果这些推导序列最终对应的是同一棵分析树,那么它不是二义性的。二义性的本质是有多棵结构不同的分析树。后面会引入“最左推导”的概念来标准化推导过程,如果一个字符串有两个不同的最左推导,那它就是二义性的。
- 二义性是文法的属性,不是语言的: 一个语言可能是可以用无二义性文法描述的,但我们恰好为它写了一个有二义性的文法(如 $G_5$)。我们可以通过修改文法(如改成 $G_4$)来消除二义性。这种情况下,语言本身不是“固有二义性的”。
本段引入了上下文无关文法的一个关键问题——二义性。它定义了当一个文法可以为同一个字符串生成多棵不同的分析树(从而产生多种含义)时,该文法就是二义性的。通过文法 $G_5$ 和字符串 a+a×a 的例子,直观地展示了二义性是如何产生的(缺乏优先级和结合性规定),以及它为什么在编程语言等需要确定性解释的应用中是不可接受的。
本段的目的是让读者认识到文法设计中的一个重要陷阱和挑战。它说明了设计一个能生成目标语言的 CFG 只是第一步,保证这个 CFG 是无二义性的(如果可能的话)同样重要,尤其是在编译器设计等实际应用中。这为后续讨论如何消除二义性(如 $G_4$ 的设计)和固有二义性语言等更深层次的话题埋下伏笔。
一个二义性文法就像是一份有歧义的法律条文。
- 条文: “所有未戴帽子的男性和女性都必须罚款。”
- 解释1 (分析树1): (未戴帽子的男性) 和 (女性) -> 只有未戴帽子的男性以及所有女性(无论戴帽与否)被罚款。
- 解释2 (分析树2): 未戴帽子的 (男性和女性) -> 未戴帽子的男性和未戴帽子的女性被罚款。
- 因为条文有歧义,导致对同一个人(一个戴了帽子的女性)是否罚款,可以有两种不同的解释。在法律和编程中,这种不确定性都是要极力避免的。
想象一句有歧义的英文句子:“I saw a man on a hill with a telescope.”
- 分析树 1: (I saw) (a man on a hill) (with a telescope) -> 我用望远镜看到了山上的一个人。(with a telescope 修饰 saw)
- 分析树 2: (I saw) (a man on a hill with a telescope) -> 我看到了山上的一个人,那个人带着望远镜。(with a telescope 修饰 man)
- 分析树 3: (I saw) (a man) (on a hill with a telescope) -> 我看到了一个人,他在一个有望远镜的山上。(with a telescope 修饰 hill)
一个二义性文法就如同英语语法本身,允许对同一句话产生多种不同的结构理解。
📜 [原文21]
这个文法没有捕捉到通常的优先级关系,因此它可能先分组 + 运算符,后分组 × 运算符,反之亦然。相比之下,文法 $G_{4}$ 生成完全相同的语言,但每个生成的字符串都有唯一的分析树。因此 $G_{4}$ 是无二义性的,而 $G_{5}$ 是二义性的。
文法 $G_{2}$(第 103 页)是二义性文法的另一个例子。句子 the girl touches the boy with the flower 有两种不同的推导。在练习 2.8 中,你将被要求给出两个分析树,并观察它们与阅读该句子的两种不同方式的对应关系。
这段话是对二义性例子的补充说明和总结,并引出了另一个关于自然语言文法的二义性例子。
第一段,对文法 $G_4$ 和 $G_5$ 进行了直接的对比和定性。
- $G_5$ 的问题: 明确指出 $G_5$ 的根本缺陷在于“没有捕捉到通常的优先级关系”。它把 + 和 × 放在了同等地位,导致解析器在“分组”(构建子树)时可以随意选择,从而产生了二义性。
- $G_4$ 的优点:
- 它生成“完全相同的语言”,即所有合法的算术表达式串。在生成能力上,它和 $G_5$ 是等价的。
- 但是,它对每个合法的字符串,都能生成“唯一的分析树”。
- 结论: 基于以上对比,给出了明确的判定:$G_4$ 是无二义性的 (unambiguous),而 $G_5$ 是二义性的 (ambiguous)。这强调了对于同一个语言,可能存在好的(无二义性)和坏的(二义性)文法。
第二段,将二义性的概念扩展回自然语言的例子。
- 另一个例子: 指出之前介绍的用于描述英语片段的文法 $G_2$ 也是一个二义性文法。这说明二义性不仅是设计数学表达式文法时的问题,在自然语言处理中也普遍存在。
- 二义性句子: "the girl touches the boy with the flower"。
- 歧义来源: 介词短语 with the flower 到底修饰谁?
- 修饰 the boy: (the boy with the flower),男孩带着花。整个句意是:女孩触摸了那个带着花的男孩。
- 修饰 touches: (touches ... with the flower),用花来触摸。整个句意是:女孩用花去触摸那个男孩。
- 两种推导/分析树: 文法 $G_2$ 的规则设计使得这两种解析结构都是合法的,因此可以为这个句子生成两棵不同的分析树,分别对应这两种不同的含义。
- 留作练习: 文本没有在此处画出这两棵树,而是将其作为一个练习(练习 2.8),让读者亲自去推导和构建分析树,从而更深刻地体会文法规则是如何导致语义二义性的。
- 示例 1: 消除 $G_5$ 结合性二义性的方法
- 问题: $G_5$ 的规则 E -> E+E 导致 a+a+a 有两种分析树(左结合/右结合)。
- 解决方案 (如 $G_4$ 所示): 使用左递归来强制左结合。将规则改为 E -> E+T。
- 分析: 要推导 a+a+a,使用新规则,你只能这样推导(最左推导):
E ⇒ E+T ⇒ E+T+T ⇒ T+T+T ⇒ a+T+T ⇒ a+a+T ⇒ a+a+a
这唯一对应于 (a+a)+a 的分析树结构。通过非对称的规则 E -> E+T,我们消除了结合性的二义性。
- 示例 2: $G_2$ 中 "the girl touches the boy with the flower" 的两种推导概要
- 推导 1 (with the flower 修饰 the boy):
<SENTENCE> ⇒ <NP> <VP>
... ⇒ the girl <VP>
⇒ the girl <CMPLX-VERB>
⇒ the girl <VERB> <NP> (动词带宾语)
⇒ the girl touches <NP>
⇒ the girl touches <CMPLX-NOUN> <PREP-PHRASE> (宾语名词短语自身带修饰)
... ⇒ the girl touches the boy with the flower
这棵树中,<PREP-PHRASE> 是 <NP> (the boy) 的子节点。
- 推导 2 (with the flower 修饰 touches):
<SENTENCE> ⇒ <NP> <VP>
... ⇒ the girl <VP>
⇒ the girl <VERB-PHRASE> <PREP-PHRASE> (整个动词短语被修饰)
⇒ the girl <CMPLX-VERB> <PREP-PHRASE>
... ⇒ the girl touches the boy with the flower
这棵树中,<PREP-PHRASE> 和 <CMPLX-VERB> 是兄弟节点,都属于顶层的 <VERB-PHRASE>。
- 所有权与二义性: 自然语言中很多二义性都源于修饰语的归属不明确。上下文无关文法天然地难以处理这些需要深层语义信息的归属问题。
- 二义性不总是坏事: 在编程语言中,二义性几乎总是不好的。但在自然语言理解或文学分析中,识别并理解所有可能的二义性解释本身就是任务的一部分。一个二义性文法可能恰恰因为它能反映出这些多种可能性而“有用”。
- 消除二义性的代价: 有时为了消除二义性,需要引入更多的变量和规则,可能会使文法变得更复杂、不那么直观(对比 $G_4$ 和 $G_5$)。这是一个在简洁性和精确性之间的权衡。
本段通过对比文法 $G_4$ 和 $G_5$,强调了一个语言可以有二义性和无二义性两种不同的文法,并指出无二义性对于编程语言等应用的重要性。同时,它以自然语言中介词短语修饰不明确的经典例子,进一步说明了二义性是一个普遍存在的问题,并将其与不同的分析树结构和语义解释直接关联起来。
本段的目的是巩固读者对二义性概念的理解,并将其从数学表达式的领域扩展到更熟悉的自然语言领域。通过对比“好文法”($G_4$)和“坏文法”($G_5$),它强化了“设计一个无二义性的文法”是文法工程中的一个核心目标。通过自然语言的例子,它让抽象的“多棵分析树”概念与我们日常生活中就能体验到的“一句话有多种理解”现象联系起来,使得概念更易于吸收。
[直觉心-智模型]
这就像是比较两份建筑蓝图(文法)。
- 蓝图 $G_5$ (二义性): 一份潦草的草图,上面画着“客厅旁边是厨房”,也画着“客厅旁边是餐厅”,但没说清楚厨房和餐厅的相对位置。工人拿去看,可能会把厨房建在客厅左边,也可能建在右边,导致建出两种不同的房子。
- 蓝图 $G_4$ (无二义性): 一份精密的施工图,明确标注了客厅、厨房、餐厅的精确位置和连接方式。所有工人拿去看,只能建出唯一一种布局的房子。
两份蓝图描述的都是“一个有客厅、厨房、餐厅的房子”(同一个语言),但 $G_4$ 是更好的设计,因为它不会产生误解。
想象一下你在给一个机器人下达指令。
- 指令: “去拿桌子上的杯子和瓶子”。
- 二义性文法: 机器人无法确定是“桌子上的(杯子和瓶子)”还是“(桌子上的杯子)和(任何地方的瓶子)”。
- 无二义性文法: 对应的指令可能是“去拿(位于桌子上的(杯子和瓶子))”或“去拿(位于桌子上的杯子)和(位于冰箱里的瓶子)”,通过明确的“分组”来消除歧义。
$G_2$ 这样的文法就类似于第一种有歧义的自然语言指令。
📜 [原文22]
现在我们形式化二义性的概念。当我们说一个文法二义性地生成一个字符串时,我们指的是该字符串有两个或多个不同的分析树,而不是两个不同的推导。两个推导可能仅仅因为替换变量的顺序不同而不同,但它们的整体结构是相同的。为了专注于结构,我们定义一种以固定顺序替换变量的推导类型。如果每一步都替换最左边的剩余变量,那么文法 $G$ 中字符串 $w$ 的推导就是最左推导。定义 2.2(第 104 页)之前的推导就是最左推导。
定义 2.7
如果字符串 $w$ 具有两个或多个不同的最左推导,则称其在上下文无关文法 $G$ 中二义性地推导。如果文法 $G$ 二义性地生成了某个字符串,则称该文法是二义性的。
这一部分为二义性提供了一个更严格、更便于操作的形式化定义。
首先,它澄清了一个关键点:二义性的本质在于分析树的不同,而不是推导序列的不同。
- 一个字符串可以有很多个推导序列。例如,对于中间字符串 A + B,你可以选择先替换 A,也可以选择先替换 B。这会产生两个不同的推导步骤序列。
- 但是,如果这两种替换顺序最终产生的分析树是完全一样的(即 + 的左右子树分别是 A 和 B 的推导结果),那么这种推导顺序的不同是无关紧要的,不构成二义性。它只是到达同一个“结构”的不同路径而已。
- 二义性的真正问题是,同一个字符串存在结构上不同的分析树。
为了消除这种因推导顺序不同而产生的“假性”多样性,从而能专注于真正的结构性二义性,这里引入了一个标准化的推导方法:最左推导 (Leftmost Derivation)。
- 定义: 在最左推导中,每一步推导都必须替换当前字符串中最左边的那个变量。这是一个严格的规定,使得在每一步,选择哪个变量进行替换是唯一确定的。
- 作用: 通过固定替换顺序,最左推导与分析树之间建立了一一对应的关系。每一棵特定的分析树都唯一对应一个最左推导,反之亦然。
- 因此,判断“一个字符串是否有两棵不同的分析树”这个比较抽象的问题,被转换为了一个更具体、更容易操作的问题:“一个字符串是否有两个不同的最左推导”。
基于最左推导,定义 2.7 给出了二义性的形式化定义:
- 二义性推导: 如果一个字符串 $w$ 在文法 $G$ 中存在两个或更多的、不同的最左推导序列,那么它就是被二义性推导的。
- 二义性文法: 如果一个文法 $G$ 中至少存在一个这样的字符串,那么文法 $G$ 就是二义性的。
这个定义比“多棵分析树”的定义更便于在数学证明或算法中进行判断。
最后,文本回顾了一下,指出在前面(定义 2.2 之前)为 a boy sees 做的推导,实际上就是一个最左推导的例子。
- 示例 1: a+a 的最左推导 (使用 $G_5$)
- 文法: E -> E+E | a
- 字符串: a+a
- 推导过程:
- E ⇒ E+E (替换最左的 E)
- ⇒ a+E (替换最左的 E)
- ⇒ a+a (替换最左的 E)
- 这是唯一的最左推导,所以 a+a 在这个片段文法中是无二义性的。
- 示例 2: a+a*a 的两个最左推导 (使用 $G_5$)
- 文法: E -> E+E | E*E | a
- 字符串: a+a*a
- 最左推导 1 (对应加法优先):
- E ⇒ E * E (选择乘法规则)
- ⇒ (E+E) * E (替换最左的 E,选择加法规则)
- ⇒ (a+E) * E (替换最左的 E)
- ⇒ (a+a) * E (替换最左的 E)
- ⇒ (a+a) * a (替换最左的 E)
- 最左推导 2 (对应乘法优先):
- E ⇒ E + E (选择加法规则)
- ⇒ a + E (替换最左的 E)
- ⇒ a + (E*E) (替换最左的 E,选择乘法规则)
- ⇒ a + (a*E) (替换最左的 E)
- ⇒ a + (a*a) (替换最左的 E)
- 由于字符串 a+a*a 存在两个不同的最左推导,因此根据定义 2.7,该字符串是二义性推导的,文法 $G_5$ 是二义性的。
- 最右推导: 类似地,也可以定义最右推导(Rightmost Derivation),即每一步都替换最右边的变量。一个字符串有两棵不同的分析树,当且仅当它有两个不同的最左推导,当且仅当它有两个不同的最右推导。三者是等价的判断标准。
- 检查所有可能的推导: 如果不使用最左推导或最右推导的约束,要证明二义性会很困难,因为你需要证明在所有可能(成千上万种)的推导序列中,存在两个对应不同的分析树。而使用最左推导,你只需要找到两个不同的序列即可。
本段为二义性提供了更严格的形式化定义。它首先澄清二义性的本质在于分析树的结构差异,而非推导步骤的顺序差异。为了标准化比较,引入了最左推导的概念,即每一步都替换最左边的变量。最终,将二义性定义为:一个文法是二义性的,如果它能为某个字符串提供两个或以上不同的最左推导。这个定义将抽象的分析树比较问题转化为了具体的推导序列比较问题。
本段的目的是将对二义性的直观理解转化为一个在数学上和算法上都易于处理的精确工具。在计算机科学中,能够形式化地、无歧义地定义一个概念是进行自动分析、证明和算法设计的前提。通过最左推导,为判断二义性提供了一个坚实可靠的操作性标准。
这就像在规范如何阅读一本书。
- 不同的推导: 读者 A 从第一章读到第五章,然后跳回去读第二章的注释。读者 B 先读第一章,然后直接读第二章的注释,再继续读第二章正文。他们的“阅读序列”不同。
- 相同的分析树: 但如果他们最终对这本书的章节结构、论点脉络的理解(分析树)是完全一样的,那么这种阅读顺序的差异是无关紧要的。
- 最左推导: 这相当于规定了所有人都必须严格地从前到后、一字不漏地阅读。
- 二义性: 如果在严格遵守这个“从前到后”的阅读规则下,两个读者对某句话的语法结构还是得出了两种不同的理解(比如断句方式不同),那么这句话本身就是有歧-义的。
想象你在做一道多步骤的数学题。
- 非标准推导: 你可以先算第二步,再回头算第一步,只要逻辑上允许。
- 最左推导: 相当于老师规定,你必须严格按照从左到右,从上到下的顺序书写每一步。
- 二义性: 如果即使你严格遵守了这个书写顺序,你仍然发现有两种不同的方法可以进行下一步计算(例如,2+34,你可以先算 2+3,也可以先算 34,因为规则不明确),并且这两种方法导致了不同的“计算路径”(不同的最左推导序列),那么这个问题(文法)就是有歧义的。
📜 [原文23]
有时,当我们有一个二义性文法时,我们可以找到一个生成相同语言的无二义性文法。然而,有些上下文无关语言只能由二义性文法生成。这类语言被称为固有二义性语言。问题 2.41 要求你证明语言 $\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i=j \text{ 或 } j=k\right\}$ 是固有二义性的。
这段话讨论了二义性问题的两种可能结果,并引入了一个新的重要概念:固有二义性语言。
- 可消除的二义性:
- “有时,当我们有一个二义性文法时,我们可以找到一个生成相同语言的无二义性文法。”
- 这是一种“好”情况。它说明二义性是出在我们的文法设计上,而不是语言本身的问题。
- 例子: 文法 $G_5$ (E -> E+E | EE | ...) 是二义性的,但它生成的算术表达式语言可以通过文法 $G_4$ (E -> E+T, T -> TF, ...) 来无二义性地生成。
- 这意味着,我们可以通过“重写文法”或“文法转换”的技术来消除二义性。这在编译器设计中是常规操作。
- 不可消除的二义性:
- “然而,有些上下文无关语言只能由二义性文法生成。”
- 这是一种“坏”情况,它揭示了二义性问题的深层本质。这里的二义性根植于语言的内在结构,是其固有属性,无论我们如何巧妙地设计文法,都无法消除。
- 固有二义性语言 (Inherently Ambiguous Language): 这就是对这类语言的正式命名。一个语言 $L$ 如果是固有二义性的,意味着所有能够生成 $L$ 的上下文无关文法都必然是二义性的。
- 这个概念非常重要,因为它设定了无二义性解析的边界。对于固有二义性语言,我们无法构建出一个能为其所有字符串提供唯一分析树的 CFG 解析器。
- 固有二义性语言的例子:
- 文本给出了一个经典的固有二义性语言的例子:$L = \left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i=j \text{ 或 } j=k\right\}$。
- 这个语言由两部分并集而成:
- $L_1 = \{a^i b^i c^k \mid i,k \ge 0\}$ (a 和 b 数量相等)
- $L_2 = \{a^i b^j c^j \mid i,j \ge 0\}$ (b 和 c 数量相等)
- 二义性的来源: 考虑字符串的形式为 $a^n b^n c^n$。这种字符串既满足 $i=j$ 的条件(属于 $L_1$),也满足 $j=k$ 的条件(属于 $L_2$)。
- 直观上,一个文法为了生成这个语言,很可能需要一个部分来处理 a-b 的匹配,另一个部分来处理 b-c 的匹配。对于 $a^n b^n c^n$ 这样的字符串,它既可以被“a-b匹配”的逻辑生成(把它看作 $a^n b^n$ 后面跟了 $c^n$),也可以被“b-c匹配”的逻辑生成(把它看作 $a^n$ 后面跟了 $b^n c^n$)。这两种不同的生成逻辑会对应两种不同的分析树,从而导致二义性。
- 证明一个语言是固有二义性的通常很困难,需要用到上下文无关语言的泵引理的变体或其他高级技术。文本在此处只是提出问题,将证明留作练习。
- 示例 1: $L = \left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i=j \text{ 或 } j=k\right\}$ 中字符串 abc 的潜在二义性
- 字符串: abc (即 $i=1, j=1, k=1$)
- 视角 1 (来自 $L_1$): 它可以被看作是 ab ($i=j=1$) 后面跟了一个 c ($k=1$)。分析树的结构会体现出 a 和 b 的紧密匹配关系。
- 视角 2 (来自 $L_2$): 它可以被看作是 a ($i=1$) 后面跟了一个 bc ($j=k=1$)。分析树的结构会体现出 b 和 c 的紧密匹配关系。
- 由于一个字符串可以有两种不同的结构来源,任何试图同时捕捉这两种来源的文法都很可能在这个交集点上产生二义性。
- 示例 2: 一个非固有二义性语言的二义性文法
- 语言: $L = \{a, b\}$ 的所有非空字符串,即 (a|b)+。这是一个正则语言,因此肯定不是固有二义性的。
- 一个二义性文法 $G_{amb}$: S -> S S | a | b
- 字符串 aba 的二义性:
- 推导 1: S ⇒ SS ⇒ aS ⇒ a(SS) ⇒ a(bS) ⇒ a(ba) -> 结构是 a 和 ba 的并列。
- 推导 2: S ⇒ SS ⇒ (SS)S ⇒ (aS)S ⇒ (ab)S ⇒ aba -> 结构是 ab 和 a 的并列。
- 一个无二义性文法 $G_{unamb}$: S -> aS | bS | a | b
- 这个文法是右递归的,对任何字符串只会产生唯一的分析树。例如,aba 的唯一推导是 S ⇒ aS ⇒ a(bS) ⇒ a(ba)。
- 这说明了二义性是 $G_{amb}$ 的问题,而不是语言 $L$ 的问题。
- 并集不一定导致固有二义性: 在前面的技巧中,我们看到 $\left\{0^{n} 1^{n}\right\} \cup\left\{1^{n} 0^{n}\right\}$ 的文法是通过一个顶层选择 $S \rightarrow S_1 | S_2$ 来构建的。这个文法是无二义性的,因为两个子语言的交集是空集(除了可能的空串)。没有任何一个非空字符串同时属于两个子语言。
- 固有二义性的关键在于两个子语言的交集部分是“复杂的”或“无限的”,并且这两部分语言的内在结构不同,导致在交集处的字符串无法避免地拥有两种结构来源。
本段区分了两种二义性:可消除的二义性和不可消除的二义性。前者是文法设计不佳的结果,可以通过重写文法来解决;后者则源于语言本身的内在结构性冲突,这类语言被称为固有二义性语言。并给出了一个经典的固有二义性语言例子,$\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i=j \text{ 或 } j=k\right\}$,其二义性源于满足两种匹配条件的字符串(如 $a^n b^n c^n$)的存在。
本段的目的是为了揭示二义性问题的全部图景,告诉读者并非所有的二义性问题都有解决方案。这引入了计算理论中一个深刻的限制性结论,即存在一些上下文无关语言,它们在本质上就是“模糊”的,无法用任何一个 CFG 进行唯一解析。这对于理解 CFL 的能力边界和解析理论的局限性至关重要。
这就像是给照片分类。
- 可消除的二义性: 你有一套分类规则:“是猫的照片放A堆,是动物的照片放B堆”。一张猫的照片既可以放A堆也可以放B堆,规则有歧义。你可以修改规则为:“是猫的照片放A堆,是不是猫的其他动物放B堆”,这样就无二义性了。
- 固有二义性语言: 想象一张“鸭兔图”(一张可以看作鸭子也可以看作兔子的图片)。这个图片本身就是固有二义性的。你无法设计一个“无二义性”的分类规则来处理它。任何规则,只要它能识别鸭子也能识别兔子,当遇到这张图时,都会面临两种可能的分类结果。这个图片就类似于固有二义性语言中的字符串。
想象一个人的身份。
- 可消除的二义性: 一个人既是“公司的员工”,又是“项目的负责人”。这两个身份描述不冲突,我们可以设计一个清晰的组织架构图(无二义性文法)来同时体现这两个角色。
- 固有二义性语言: 某个间谍,他同时拥有两个完全合法、但互不兼容的国民身份,一个是A国公民,一个是B国公民。对于需要明确国籍的场合(例如国际法庭),他这个“字符串”就产生了固有二义性。任何试图描述他身份的系统(文法),只要承认这两个身份都是合法的,就无法避免在他身上产生身份的二义性。
72.6 乔姆斯基范式
📜 [原文24]
在使用上下文无关文法时,通常将它们简化形式会很方便。最简单且最有用的形式之一被称为乔姆斯基范式。乔姆斯基范式在给出处理上下文无关文法的算法时很有用,正如我们在第 4 章和第 7 章中所做的那样。
定义 2.8
上下文无关文法是乔姆斯基范式,如果每条规则都采用以下形式
其中 $a$ 是任何终结符,$A, B$ 和 $C$ 是任何变量——但 $B$ 和 $C$ 不能是开始变量。此外,我们允许规则 $S \rightarrow \varepsilon$,其中 $S$ 是开始变量。
这一部分引入了一个重要的文法“标准化”形式——乔姆斯基范式 (Chomsky Normal Form, CNF)。
首先,引言部分解释了为什么需要这种范式:
- 目的: “简化形式会很方便”。原始的 CFG 规则形式多样,可以很长,可以混合变量和终结符,这使得设计和分析处理 CFG 的算法变得复杂。
- CNF 的地位: 它是“最简单且最有用的形式之一”。这意味着它在理论和实践中都有很高的价值。
- 用途: “在给出处理上下文无关语言的算法时很有用”。后面章节(第 4 章和第 7 章)将会介绍一些算法,例如,判断一个字符串是否属于某个 CFL 的成员资格算法(如 CYK 算法),或者关于 CFL 的其他性质证明。这些算法的设计通常都假设输入的文法已经是 CNF 形式,因为这种简单的规则形式极大地简化了算法的逻辑。
接着,定义 2.8 给出了乔姆斯基范式的严格定义。一个 CFG 要成为 CNF,它的所有规则(除了一个特殊情况)必须满足以下两种形式之一:
- $A \rightarrow BC$:
- 规则的右侧必须是两个变量。不能是一个,不能是三个或更多,也不能是变量和终结符的混合。
- $A, B, C$ 都是变量。
- 一个额外的约束是 $B$ 和 $C$ 都不能是开始变量 $S$。这个约束在某些严格的定义中出现,旨在简化某些证明,但并非所有教科书都包含此条。
- $A \rightarrow a$:
- 规则的右侧必须是一个终结符。不能是多个终结符,也不能是空串 $\varepsilon$。
- $A$ 是一个变量,$a$ 是一个终结符。
特殊情况:
- $S \rightarrow \varepsilon$: 如果语言包含空串 $\varepsilon$,那么允许有一条从开始变量 $S$ 直接生成空串的规则。
- 约束: 如果存在 $S \rightarrow \varepsilon$ 这条规则,那么开始变量 $S$ 就不能出现在任何其他规则的右侧。这也是为了简化算法和证明。后面的转换过程会展示如何实现这一点。
总结 CNF 的特点:
- 规则右侧长度: 所有规则(除 $S \rightarrow \varepsilon$)的右侧长度要么是 1(一个终结符),要么是 2(两个变量)。
- 符号类型分离: 变量和终结符不会出现在同一条规则的右侧。要么全是变量,要么全是终结符。
- 无 $\varepsilon$-规则 (基本): 除了可能的 $S \rightarrow \varepsilon$,没有其他规则可以生成空串。
- 无单元规则: 没有形如 $A \rightarrow B$ 的规则。
这种高度规范化的形式,使得分析树的结构也变得非常规整:每个变量节点要么有两个变量子节点,要么有一个终结符子节点。这对于动态规划类的解析算法(如 CYK)来说是完美的基础。
- $A \rightarrow B C$:
- $A, B, C \in V$ ($A, B, C$ 都是变量)。
- 这条规则的作用是将一个变量的推导分解为两个子问题,每个子问题由一个子变量负责。这是构建二叉分析树的基础。
- $A \rightarrow a$:
- $A \in V$, $a \in \Sigma$ ($A$ 是变量,$a$ 是终结符)。
- 这是推导的终点,将一个变量最终转换为一个语言的基本符号。
- $S \rightarrow \varepsilon$:
- $S$ 是开始变量,$\varepsilon$ 是空串。
- 这是处理语言包含空串这一特殊情况的唯一合法途径。
- 示例 1: 一个已经是 CNF 的文法
- 文法:
```
S -> AB
A -> CD | a
B -> b
C -> c
D -> d
```
- 检查:
- S -> AB: 符合 $A \rightarrow BC$ 形式。
- A -> CD: 符合 $A \rightarrow BC$ 形式。
- A -> a: 符合 $A \rightarrow a$ 形式。
- B -> b, C -> c, D -> d: 都符合 $A \rightarrow a$ 形式。
- 结论: 这个文法是 CNF。
- 示例 2: 一个不是 CNF 的文法
- 文法: $S \rightarrow 0S1 \mid \varepsilon$
- 检查:
- S -> 0S1: 规则右侧长度为 3,且混合了终结符和变量。不符合。
- S -> ε: $S$ 是开始变量,这条规则是允许的。但是,S 出现在了 0S1 规则的右侧,这违反了当 $S \rightarrow \varepsilon$ 存在时,$S$ 不能出现在任何右侧的约束。
- 结论: 这个文法不是 CNF。后续的定理将说明如何将其转换为 CNF。
- $S \rightarrow \varepsilon$ 的约束: 对于允许空串的语言,CNF 文法必须满足两个条件:1) 存在 $S \rightarrow \varepsilon$ 规则;2) $S$ 不能出现在任何规则的右侧。后面将会看到,这是通过引入一个新的开始变量 $S_0$ 和规则 $S_0 \rightarrow S \mid \varepsilon$ 来实现的。
- 变量数量: $A \rightarrow BC$ 规则右侧必须是恰好两个变量。
- 终结符数量: $A \rightarrow a$ 规则右侧必须是恰好一个终结符。像 A -> ab 这样的规则是不允许的。
本段引入了乔姆斯基范式 (CNF),一种对上下文无关文法进行标准化的重要形式。它定义了 CNF 文法的规则必须满足的两种严格形式($A \rightarrow BC$ 或 $A \rightarrow a$),以及处理空串的特殊规则 ($S \rightarrow \varepsilon$)。并阐明了使用 CNF 的主要动机:它极大地简化了处理 CFG 的算法的设计和分析。
本段的目的是介绍一种“规范化”工具。在数学和计算机科学中,将研究对象转换到一个统一的、简单的“标准型”或“范式”是一种常用且强大的技术。这可以去除无关的复杂性,使我们能集中于核心问题。CNF 就是 CFG 的一个标准型,它的引入是为了后续的算法和理论推导服务的。
乔姆斯基范式就像是把所有食谱都统一成一种极简风格。
- 原始食谱: “将牛肉、土豆、胡萝卜一起炖煮2小时。”(规则右侧很长,混合多种成分)。
- CNF 食谱:
- 一道主菜 -> 一份肉类 + 一份蔬菜 (规则 $A \rightarrow BC$)
- 一份肉类 -> 牛肉 (规则 $A \rightarrow a$)
- 一份蔬菜 -> 一份根茎蔬菜 + 一份调味蔬菜
- ...
- 所有步骤都被分解为“一个东西由两个半成品组成”或“一个半成品就是一种基础食材”。这种二叉分解的结构非常规整,便于计算机程序(算法)去分析和处理。
想象一下你在用最基础的 1x1 和 1x2 的乐高积木来复制一个复杂的模型。
- 原始模型: 可能包含各种奇形怪状的大块积木。
- 转换为 CNF: 就是一个将所有大块积木分解,最终只用两种标准操作来重构整个模型的过程:
- A -> BC: “一个较大的组件 A,总是由两个较小的组件 B 和 C 拼成。”(所有连接都是二合一)
- A -> a: “一个最基础的组件 A,就是一块颜色为 a 的 1x1 积木。”
- 通过这种方式,任何复杂的结构都被分解为一系列简单的二叉组合,其结构一目了然。
📜 [原文25]
定理 2.9
任何上下文无关语言都由乔姆斯基范式中的上下文无关文法生成。
证明思路 我们可以将任何文法 $G$ 转换为乔姆斯基范式。这种转换有几个阶段,其中违反条件的规则被替换为等效的令人满意的规则。首先,我们添加一个新的开始变量。然后,我们消除所有 $A \rightarrow \varepsilon$ 形式的$\varepsilon$ 规则。我们还消除所有 $A \rightarrow B$ 形式的单元规则。在这两种情况下,我们都会修补文法,以确保它仍然生成相同的语言。最后,我们将剩余的规则转换为正确的形式。
这一部分提出了一个核心定理并概述了其证明思路。
定理 2.9:
- 陈述: “任何上下文无关语言都由乔姆斯基范式中的上下文无关文法生成。”
- 含义: 这个定理的意义非常重大。它说明乔姆斯基范式这种“受限的”文法形式,其生成能力并没有减弱。对于任何一个可以用任意复杂 CFG 描述的语言,我们总能找到一个等价的、但形式上非常简单的 CNF 文法来生成它。
- 推论: 这意味着,当我们要设计一个处理所有 CFL 的通用算法时,我们可以放心地假设输入的文法已经是 CNF 形式。因为如果不是,我们总可以通过一个预处理步骤将它转换成 CNF,而不会改变它所代表的语言。这极大地扩展了 CNF 的实用性。
证明思路 (Proof Idea):
定理的证明是构造性的。它不只是说“存在”一个 CNF 文法,而是给出了一个具体的算法,可以将任何给定的 CFG 转换为等效的 CNF。这个算法分为几个清晰的阶段,每个阶段旨在消除一种不符合 CNF 要求的规则。
- 阶段 1: 添加新开始变量 (START)
- 目的: 为了处理语言包含空串 $\varepsilon$ 的情况,并确保开始变量不会出现在任何规则的右侧。这是 CNF 的一个严格要求。
- 操作: 创建一个全新的开始变量 $S_0$,并添加一条规则 $S_0 \rightarrow S$,其中 $S$ 是原始的开始变量。$S_0$ 成为文法的新起点。如果原始语言包含 $\varepsilon$,通常会在这里处理,比如添加 $S_0 \rightarrow \varepsilon$。
- 阶段 2: 消除 $\varepsilon$-规则 (TERM)
- 目的: CNF 中除了 $S_0 \rightarrow \varepsilon$(如果需要),不允许有其他形如 $A \rightarrow \varepsilon$ 的规则。
- 操作: 找到一条规则 $A \rightarrow \varepsilon$ 并删除它。然后,必须“补偿”因 A 可以消失而带来的影响。具体做法是:在整个文法中,找到所有在右侧包含 $A$ 的规则,对于每一条这样的规则,都添加一个“A消失了”的版本。例如,如果存在规则 $R \rightarrow uAv$,就要添加一条新规则 $R \rightarrow uv$。如果规则是 $R \rightarrow uAvAw$,则需要添加 $R \rightarrow uvAw$, $R \rightarrow uAvw$, 和 $R \rightarrow uvw$ 三个新版本。这个过程需要迭代,直到所有非开始变量的 $\varepsilon$-规则都被消除。
- 阶段 3: 消除单元规则 (UNIT)
- 目的: CNF 不允许有形如 $A \rightarrow B$ 的规则,其中右侧只有一个变量。
- 操作: 找到一条单元规则 $A \rightarrow B$ 并删除它。然后进行“补偿”:找到所有以 $B$ 为左侧的规则,比如 $B \rightarrow w$。为 $A$ 添加一条新规则 $A \rightarrow w$。这样做相当于把 $B$ 的能力“复制”给了 $A$。这个过程也需要迭代,例如,如果 $A \rightarrow B$ 且 $B \rightarrow C$,最终需要把 $C$ 的所有规则都复制给 $A$。
- 阶段 4: 转换剩余规则 (CLEANUP)
- 目的: 经过前几个阶段,剩下的规则可能仍然不符合 CNF 的两种形式。例如,可能存在 A -> aBC (混合终结符和变量) 或 A -> BCD (右侧多于两个变量)。
- 操作:
- 对于混合终结符和变量的规则,将终结符“外包”出去。例如,对于 A -> aBC,引入一个新变量 $U_a$ 和新规则 $U_a \rightarrow a$,然后将原规则替换为 A -> U_a BC。
- 对于右侧变量多于两个的规则,进行“二叉化分解”。例如,对于 A -> BCD,引入一个新变量 $A_1$,将原规则分解为两条新规则:A -> B A_1 和 A_1 -> CD。这样,每条规则的右侧都只有两个变量了。
通过这四个阶段的处理,任何一个 CFG 都可以被系统地、算法化地转换为一个生成相同语言的 CNF 文法。
- 示例 1: 阶段 1 - 添加新开始变量
- 原始文法: S -> SS | ε
- 问题: S 既是开始变量,又生成 $\varepsilon$,还出现在了 SS 规则的右侧。
- 转换: 引入新开始变量 $S_0$。
```
S0 -> S
S -> SS | ε
```
(后续步骤会进一步处理 $S \rightarrow \varepsilon$)
- 示例 2: 阶段 2 - 消除 $\varepsilon$-规则
- 文法: S -> aAb, A -> ε
- 转换:
- 删除 A -> ε。
- 找到使用 A 的规则 S -> aAb。
- 添加一个 A“消失”的版本:S -> ab。
- 最终文法:
- 示例 3: 阶段 3 - 消除单元规则
- 文法: A -> B, B -> c | d
- 转换:
- 删除 A -> B。
- 找到 B 的规则 B -> c 和 B -> d。
- 为 A 添加这些规则的副本:A -> c 和 A -> d。
- 最终文法:
- 示例 4: 阶段 4 - 清理
- 文法: A -> bCD
- 转换:
- 处理终结符 b。引入新变量 $U_b$ 和规则 Ub -> b。原规则变为 A -> Ub CD。
- 处理三个变量。引入新变量 $A_1$。原规则分解为 A -> Ub A1 和 A1 -> CD。
- 最终规则集:
- 步骤顺序: 这几个阶段的执行顺序很重要。通常,START -> TERM -> UNIT -> CLEANUP 是一个可靠的顺序。如果先清理再消除单元规则,可能会引入新的不合规的规则。
- 迭代的重要性: 消除 $\varepsilon$-规则和单元规则的过程必须是迭代的,直到没有这类规则可以被消除为止。例如,A -> B, B -> C, C -> ε,需要多次迭代才能将 C -> ε 的影响传递到 A。
- 语言不变性: 每一步转换都必须保证生成的语言不变。这是整个证明的核心。例如,在消除 $\varepsilon$-规则时,添加新规则就是为了“补偿”被删除规则的生成能力,确保没有丢失任何字符串。
本段提出了一个根本性的定理(任何 CFL 都有一个 CNF 文法),并给出了其构造性证明的详细步骤概览。这个证明本身就是一个强大的算法,可以将任意 CFG 转换为等价的乔姆斯基范式。转换过程分为四个主要阶段:添加新开始变量、消除 $\varepsilon$-规则、消除单元规则,以及将剩余规则分解为 CNF 形式。
本段的目的是证明乔姆斯基范式的普适性和强大性。通过提供一个具体的转换算法,它不仅在理论上确立了 CNF 文法的表达能力没有损失,也在实践上为后续所有依赖 CNF 的算法提供了一个必要的前置工具。它告诉我们,我们可以“随心所欲”地设计一个方便的文法,然后总有办法把它“打磨”成标准、规整的 CNF 形式。
这个转换过程就像是“代码重构”。
- 原始文法: 一段功能正确但结构混乱、风格不一的代码。
- 转换为 CNF: 一个遵循严格编码规范(例如,每个函数不超过10行,每个函数只有一个出口,变量命名有规则等)的重构过程。
- 阶段 1 (START): 创建一个新的 main() 函数,所有旧的逻辑都从这里调用,保持 main 函数的简洁。
- 阶段 2 (TERM): 消除所有返回 null 或空对象的函数,将它们的逻辑直接内联到调用处。
- 阶段 3 (UNIT): 消除所有简单的包装函数(即 function A() { return B(); }),直接让调用者调用 B()。
- 阶段 4 (CLEANUP): 将所有长函数分解成一系列小的、只做一件事的二元调用函数。
- 最终结果: 功能完全一样,但结构清晰、标准,便于自动化工具(如静态分析器)进行分析。
这就像是把一篇长篇散文(任意 CFG)改编成一部格律严格的五言绝句诗集 (CNF)。
- 原始散文: 句子长短不一,结构复杂。
- 转换过程:
- START: 给诗集起一个新的总标题。
- TERM: 删除所有无意义的空行($\varepsilon$-规则),并调整上下文以保持意思连贯。
- UNIT: 删除所有同义词替换的句子(单元规则),直接使用最根本的词。
- CLEANUP:
- 把所有长句子(超过两个词组)断成几个短句,用新的主语连接。(A->BCD 变成 A->BA1, A1->CD)
- 把所有带状语、定语的词组(混合终结符和变量)拆分,变成纯粹的名词-动词结构。
- 最终结果: 意思(语言)保持不变,但所有句子都变成了“五言”($A \rightarrow BC$)或单个的意象词($A \rightarrow a$)。
📜 [原文26]
证明 首先,我们添加一个新的开始变量 $S_{0}$ 和规则 $S_{0} \rightarrow S$,其中 $S$ 是原始的开始变量。此更改保证开始变量不会出现在规则的右侧。
其次,我们处理所有$\varepsilon$ 规则。我们删除$\varepsilon$ 规则 $A \rightarrow \varepsilon$,其中 $A$ 不是开始变量。然后对于规则右侧出现的每个 $A$,我们添加一条删除该出现的新规则。换句话说,如果 $R \rightarrow u A v$ 是一条规则,其中 $u$ 和 $v$ 是变量和终结符的字符串,我们添加规则 $R \rightarrow u v$。我们对每个 $A$ 的出现都这样做,因此规则 $R \rightarrow u A v A w$ 会导致我们添加 $R \rightarrow u v A w, R \rightarrow u A v w$ 和 $R \rightarrow u v w$。如果存在规则 $R \rightarrow A$,我们添加 $R \rightarrow \varepsilon$,除非我们之前已经删除了规则 $R \rightarrow \varepsilon$。我们重复这些步骤,直到消除所有不涉及开始变量的$\varepsilon$ 规则。
第三,我们处理所有单元规则。我们删除单元规则 $A \rightarrow B$。然后,每当出现规则 $B \rightarrow u$ 时,我们添加规则 $A \rightarrow u$,除非这是之前删除的单元规则。与之前一样,$u$ 是变量和终结符的字符串。我们重复这些步骤,直到消除所有单元规则。
最后,我们将所有剩余的规则转换为正确的形式。我们将每条规则 $A \rightarrow u_{1} u_{2} \cdots u_{k}$(其中 $k \geq 3$ 且每个 $u_{i}$ 是变量或终结符符号)替换为规则 $A \rightarrow u_{1} A_{1}, A_{1} \rightarrow u_{2} A_{2}, A_{2} \rightarrow u_{3} A_{3} \ldots$ 和 $A_{k-2} \rightarrow u_{k-1} u_{k}$。$A_{i}$ 是新变量。我们将上述规则中的任何终结符 $u_{i}$ 替换为新变量 $U_{i}$,并添加规则 $U_{i} \rightarrow u_{i}$。
这一部分是定理 2.9 的正式证明,它详细描述了将任意 CFG 转换为 CNF 的四步算法。
第一步:处理开始变量 (START)
- 操作:
- 引入一个全新的变量 $S_0$。
- 添加一条新规则 $S_0 \rightarrow S$,其中 $S$ 是原来的开始变量。
- 将 $S_0$ 设为文法的新开始变量。
- 目的: 这一步的目的是为了“隔离”开始变量。通过这个操作,新的开始变量 $S_0$ 就绝对不会出现在任何规则的右侧了。这为后续处理(尤其是处理 $S \rightarrow \varepsilon$)铺平了道路,满足了 CNF 关于开始变量的严格要求。语言显然没有改变,因为任何从 $S$ 能推导出的东西,现在都可以从 $S_0$ 经过一步额外推导得到。
第二步:消除 $\varepsilon$-规则 (TERM)
- 目标: 消除所有形如 $A \rightarrow \varepsilon$ 的规则 (除非是 $S_0 \rightarrow \varepsilon$,并且 $S_0$ 不在右侧出现)。
- 算法:
- 首先,确定所有“可为空的”变量 (nullable variables)。一个变量 $A$ 是可为空的,如果 $A \stackrel{*}{\Rightarrow} \varepsilon$。这可以通过一个迭代算法来找到:初始时,所有有 $A \rightarrow \varepsilon$ 规则的 $A$ 是可为空的;然后,如果存在规则 $B \rightarrow C_1 C_2 \dots C_k$ 并且所有的 $C_i$ 都已经是可为空的,那么 $B$ 也变成可为空的,如此迭代直到没有变化。
- 对于每一条规则 $R \rightarrow w$,如果 $w$ 中包含一个或多个可为空的变量,那么就要为这条规则创建所有可能的“消失”版本。
- 详细操作: 遍历所有规则 $R \rightarrow u_1 u_2 \dots u_k$。对于右侧的每个符号 $u_i$,如果它是一个可为空的变量,那么我们就有两种选择:保留它或删除它。我们必须生成包含所有这些选择组合的新规则。例如,规则 $R \rightarrow uAvAw$ 中,如果 $A$ 是可为空的,则需要添加三条新规则:
- $R \rightarrow uvAw$ (第一个 $A$ 消失)
- $R \rightarrow uAvw$ (第二个 $A$ 消失)
- $R \rightarrow uvw$ (两个 $A$ 都消失)
- 最后,删除所有原始的 $A \rightarrow \varepsilon$ 形式的规则 (除了可能的 $S_0 \rightarrow \varepsilon$)。
- 特殊情况: 如果在上述过程中,一条规则 $R \rightarrow A$ 因为 $A$ 可为空而需要添加 $R \rightarrow \varepsilon$,那么就添加它。但后续如果 $R$ 的 $\varepsilon$-规则也要被消除,这个过程会继续。这个过程保证了任何可以生成 $\varepsilon$ 的路径都被保留了下来。
第三步:消除单元规则 (UNIT)
- 目标: 消除所有形如 $A \rightarrow B$ 的规则,其中 $A$ 和 $B$ 都是变量。
- 算法:
- 同样,这是一个迭代过程。对于每个变量 $A$,计算它可以推导出的所有变量的集合(即所有满足 $A \stackrel{*}{\Rightarrow} B$ 的 $B$)。
- 然后,对于每一对满足 $A \stackrel{*}{\Rightarrow} B$ 的 $(A, B)$,将所有 $B$ 的非单元规则(形如 $B \rightarrow w$,$w$ 不是单个变量)都“复制”给 $A$,即添加规则 $A \rightarrow w$。
- 简化操作描述: 对于一条单元规则 $A \rightarrow B$,删除它。然后,对于所有以 $B$ 开头的规则 $B \rightarrow u$,添加新规则 $A \rightarrow u$。如果新添加的规则 $A \rightarrow u$ 又是单元规则(比如 $u$ 是一个变量 $C$),则重复此过程,直到没有新的单元规则产生。
- 最后,删除所有原始的单元规则。
- 目的: 这保证了任何通过一系列变量传递的推导能力,都被一个直接的规则所取代。
第四步:清理剩余规则 (CLEANUP)
- 目标: 将所有现有规则转换为 $A \rightarrow BC$ 或 $A \rightarrow a$ 的形式。此时,所有规则的右侧长度至少为1(除了 $S_0 \rightarrow \varepsilon$),且不含单元规则。
- 算法分为两部分:
- 处理混合终端符和变量/长终端符串:
- 遍历所有规则。如果一条规则 $A \rightarrow w$ 的右侧 $w$ 长度大于1,并且包含任何终结符,那么就为每个这样的终结符 a 创建一个全新的变量 $U_a$ 和一条新规则 $U_a \rightarrow a$。然后,在原规则 $w$ 中,用变量 $U_a$ 替换掉终结符 a。
- 例如,A -> aB 变为 A -> U_a B 和 U_a -> a。A -> ab 变为 A -> U_a U_b,U_a -> a, U_b -> b。
- 经过这一步,所有长度大于1的规则右侧都只包含变量。
- 处理长变量串:
- 遍历所有规则。如果一条规则形如 $A \rightarrow A_1 A_2 \dots A_k$ 且 $k \ge 3$,则将其分解。
- 引入一系列新的变量 $N_1, N_2, \dots, N_{k-2}$。
- 将原规则替换为一组新规则:
- $A \rightarrow A_1 N_1$
- $N_1 \rightarrow A_2 N_2$
- ...
- $N_{k-2} \rightarrow A_{k-1} A_k$
- 这就像将一个长链条从左到右断开,每次只保留两个环节。
- 最终结果: 经过这两部分处理,所有规则都变成了 CNF 的两种标准形式之一。
这个四步过程保证了任何 CFG 都可以被机械地转换为等效的 CNF 文法。
- 新变量的唯一性: 在第四步中,每次引入新变量时,必须确保它们是全新的,不会与文法中
已有的任何变量(包括之前步骤中新引入的)相冲突。
本段详细描述了将任何一个上下文无关文法 (CFG) 转换为等效的乔姆斯基范式 (CNF) 的四步构造性证明算法。
- 第一步 (START): 引入新开始变量 $S_0$ 并添加规则 $S_0 \rightarrow S$,以隔离开始变量,确保其不出现在任何规则的右侧。
- 第二步 (TERM): 通过寻找“可为空变量”并添加规则的“消失”版本,来系统地消除所有非平凡的 $\varepsilon$-规则 ($A \rightarrow \varepsilon$)。
- 第三步 (UNIT): 通过将推导链“短路”,即把下层变量的规则复制给上层变量,来消除所有单元规则 ($A \rightarrow B$)。
- 第四步 (CLEANUP): 通过引入新变量,将所有剩余的长规则或混合规则分解,最终使所有规则都符合 $A \rightarrow BC$(两个变量)或 $A \rightarrow a$(一个终结符)的形式。
这个算法是证明定理 2.9 的核心,展示了 CNF 的普适性。
本段的目的是提供定理 2.9 的一个严谨、详细的构造性证明。它不仅仅是理论阐述,更是一个可以被计算机程序实现的具体算法。这为计算机科学家和编译器设计者提供了一个强大的工具,使他们可以将任何复杂的 CFG “预处理”成一种简单、标准的形式,从而极大地简化后续解析算法(如 CYK 算法)的设计与实现。
这套算法就像一个“文法精炼厂”。
- 输入: 任意开采出来的“原油” (任意 CFG)。
- 第一步 (START): 在精炼厂入口设立一个新的总控制室 ($S_0$),原有的入口 ($S$) 降级为一级车间。
- 第二步 (TERM): 移除所有会产生“空产品”($\varepsilon$)的生产线,但为了不影响产量,在所有使用该“空产品”作为原料的地方,都增加一条“无此原料”的备用生产方案。
- 第三步 (UNIT): 取消所有“外包”工序($A \rightarrow B$),直接让 A 车间学会 B 车间的所有生产技能。
- 第四步 (CLEANUP): 对所有生产线进行标准化改造。任何需要超过两种原料的工序,都拆分成多个“两两混合”的子工序;任何直接使用“基础原料”(终结符)和“半成品”(变量)混合的工序,都改成先将“基础原料”包装成标准的“半成品”,再进行混合。
- 输出: 高度标准化的“汽油” (CNF),其本质用途(语言)与“原油”完全相同。
想象一下你在整理一堆乱七八糟的电线。
- 原始状态 (CFG): 一大团电线,长的短的,各种颜色缠绕在一起。
- 第一步 (START): 你拿出一个新的总插排 ($S_0$),把原来这团线的总电源线 ($S$) 插在上面。
- 第二步 (TERM): 你找到所有没接任何东西的“空接头”($\varepsilon$-规则),把它们剪掉。但如果某个设备原来可以接这个空接头,你现在就得给它一个“跳线”,让它在没有这个接头的情况下也能工作。
- 第三步 (UNIT): 你找到所有“延长线”($A \rightarrow B$),即一根线只是简单地连接到另一根线。你把延长线拔掉,把需要用电的设备直接插到被延长的那根线上。
- 第四步 (CLEANUP):
- 你看到一个一拖三的插头,你把它换成一个一拖二的插头,第二个口再接一个一拖二的插头,实现“二叉化”。
- 你看到一个设备直接连在火线和另一捆电线上,你把火线先接在一个标准插座上,再用标准插头从插座取电去连接那捆线。
- 最终状态 (CNF): 所有连接都变成了“一个插座带两个插头” ($A \rightarrow BC$),或者“一个插座直接给一个设备供电” ($A \rightarrow a$)。整个电路(文法)的功能没变,但布线变得极度规整、清晰。
82.7 例子 2.10
📜 [原文27]
令 $G_{6}$ 为以下 CFG,并使用刚刚给出的转换过程将其转换为乔姆斯基范式。所呈现的文法系列说明了转换中的步骤。粗体显示的规则是刚添加的。灰色显示的规则是刚删除的。
- 原始 CFG $G_{6}$ 显示在左侧。应用第一步创建新开始变量的结果显示在右侧。
- 删除$\varepsilon$ 规则 $B \rightarrow \varepsilon$(左侧显示)和 $A \rightarrow \varepsilon$(右侧显示)。
3a. 删除单元规则 $S \rightarrow S$(左侧显示)和 $S_{0} \rightarrow S$(右侧显示)。
3b. 删除单元规则 $A \rightarrow B$ 和 $A \rightarrow S$。
- 通过添加额外的变量和规则将剩余的规则转换为正确的形式。最终的乔姆斯基范式文法等效于 $G_{6}$。(实际上,定理 2.9 中给出的过程会生成多个变量 $U_{i}$ 和多个规则 $U_{i} \rightarrow \text{a}$。我们通过使用单个变量 $U$ 和规则 $U \rightarrow \text{a}$ 来简化结果文法。)
这个例子通过一个完整的、循序渐进的过程,演示了如何将一个给定的文法 $G_6$ 转换为乔姆斯基范式 (CNF)。每一步都严格遵循了前面证明中描述的算法。
初始文法 $G_6$:
```
S -> ASA | aB
A -> B | S
B -> b | ε
```
第 1 步: 添加新开始变量 (START)
- 操作: 引入新变量 $S_0$,添加规则 $S_0 \rightarrow S$。$S_0$ 成为新的开始变量。
- 结果:
```
S0 -> S
S -> ASA | aB
A -> B | S
B -> b | ε
```
- 目的: 隔离开始变量。现在 $S_0$ 不在任何规则的右侧,为后续步骤做好了准备。
第 2 步: 消除 $\varepsilon$-规则 (TERM)
这是一个迭代的过程。
- 第一次迭代 (消除 $B \rightarrow \varepsilon$):
- 可为空变量: $B$ 是可为空的 ($B \rightarrow \varepsilon$)。
- 操作:
- 找到使用 $B$ 的规则: $A \rightarrow B$ 和 $S \rightarrow aB$。
- 对于 $S \rightarrow aB$,添加 $B$ 消失的版本: $S \rightarrow a$。
- 对于 $A \rightarrow B$,添加 $B$ 消失的版本: $A \rightarrow \varepsilon$。
- 删除 $B \rightarrow \varepsilon$。
- 结果 (左栏):
- 第二次迭代 (消除 $A \rightarrow \varepsilon$):
- 可为空变量: 现在 $A$ 变成可为空的了 ($A \rightarrow \varepsilon$)。
- 操作:
- 找到使用 $A$ 的规则: $S \rightarrow ASA$。
- $S \rightarrow ASA$ 有两个 $A$,所以要添加三个新版本:
- 第一个 $A$ 消失: $S \rightarrow SA$
- 第二个 $A$ 消失: $S \rightarrow AS$
- 两个 $A$ 都消失: $S \rightarrow S$ (这是一个新的单元规则)
- 删除 $A \rightarrow \varepsilon$。
- 结果 (右栏):
第 3 步: 消除单元规则 (UNIT)
这也是一个迭代过程。
- 3a. 第一次迭代 (消除 $S \rightarrow S$ 和 $S_0 \rightarrow S$):
- 消除 $S \rightarrow S$: 这是一条无用的规则,直接删除即可。
- 结果 (左栏): S -> ASA | aB | a | SA | AS
- 消除 $S_0 \rightarrow S$:
- 删除 $S_0 \rightarrow S$。
- 将所有 $S$ 的规则右侧复制给 $S_0$:
$S_0 \rightarrow ASA | aB | a | SA | AS$
- 结果 (右栏):
```
S0 -> ASA | aB | a | SA | AS
S -> ASA | aB | a | SA | AS
A -> B | S
B -> b
```
- 3b. 第二次迭代 (消除 $A \rightarrow B$ 和 $A \rightarrow S$):
- 消除 $A \rightarrow B$:
- 删除 $A \rightarrow B$。
- B 的规则是 B -> b。
- 添加新规则 $A \rightarrow b$。
- 中间结果: A -> S | b
- 消除 $A \rightarrow S$:
- 删除 $A \rightarrow S$。
- 将所有 S 的规则右侧 ASA | aB | a | SA | AS 复制给 A。
- 添加新规则 $A \rightarrow ASA | aB | a | SA | AS$。
- 最终结果:
第 4 步: 清理剩余规则 (CLEANUP)
- 目标: 将所有规则转换为 $X \rightarrow YZ$ 或 $X \rightarrow x$ 的形式。
- 操作:
- 处理终结符:
- 规则 ... -> aB 和 ... -> a 中的 a 需要处理。
- 引入新变量 U 和规则 $U \rightarrow a$。
- 将所有 aB 替换为 UB。
- 将所有单独的 a 保留(因为它已经是 A->a 形式)。
- B -> b 和 A -> b 中的 b 也已经是 A->a 形式,无需处理。
- 处理长规则:
- 规则 ... -> ASA 右侧长度为 3。
- 引入新变量 A1。
- 将 ASA 分解为两条规则:... -> A A1 和 $A1 \rightarrow SA$。
- 组合和整理:
- 将上述变换应用到 S0, S, A 的所有规则上。
- S0 的规则 ASA | aB | a | SA | AS 变为:
- ASA -> A A1
- aB -> U B
- a -> a (保留)
- SA -> S A (已经是 CNF)
- AS -> A S (已经是 CNF)
- 对 S 和 A 的规则做同样处理。
- 最终结果 (如文中所列):
- 关于简化的说明: 文本中提到,严格按照算法,每个终结符都会有一个自己的变量(如 $U_a, U_b$ 等)。但如果多个地方都需要同一个终结符 a,可以复用同一个新变量 U (代表 a),以使最终文法更简洁。这是一种无伤大雅的优化。
本例是一个将 CFG 转换为 CNF 的完整、手把手的教程。它严格遵循了定理 2.9 证明中提出的四步算法(START, TERM, UNIT, CLEANUP),并通过粗体和灰色标记清晰地展示了每一步中规则的增加和删除。通过这个具体的例子,读者可以直观地看到一个复杂的文法是如何被一步步地分解、替换、重组,最终“精炼”成一个结构高度统一的乔姆斯基范式文法的。
本段的目的是为了具象化抽象的转换算法。理论证明给出了“怎么做”,而这个例子展示了“这样做出来的结果是什么样”。通过一个足够复杂(但又可以手动追踪)的文法 $G_6$,它让读者能够亲手或在头脑中演练整个转换过程,从而深刻理解每个步骤的具体操作和目的,巩固对 CNF 转换过程的掌握。
这就像是在解一个复杂的代数方程。
- 原始文法: 一个包含分数、括号、多层嵌套的复杂方程。
- 步骤1 (START): 令整个方程等于一个新的变量 x,x = ...。
- 步骤2 (TERM): “去分母”,将所有分数形式都通过乘以公分母来消除。
- 步骤3 (UNIT): “合并同类项”,将所有 (3y) 这种简单的包裹形式展开。
- 步骤4 (CLEANUP): “因式分解”和“展开”,将所有多项式都分解成二次或一次项的组合。
- 最终结果 (CNF): 整个方程组被转换为一系列形如 x = y*z 或 x = 5 的、最简单的二次或线性方程,虽然方程数量变多了,但每个方程的形式都极为简单。
这就像是为一篇长文章(原始文法)生成一份“核心要点摘要” (CNF),但要求摘要遵循非常严格的格式。
- 原始文章: 自由发挥,长句短句,各种修辞。
- 第1步: 给文章加一个总标题 "$S_0$"。
- 第2步: 删除所有“嗯、啊”之类的语气词 ($\varepsilon$-规则),但把它们的情感色彩融入到相邻的句子中。
- 第3步: 找到所有“如前所述”、“换句话说”之类的引用(单元规则),把它们替换成被引用的实际内容。
- 第4步:
- 把所有长句(主谓宾定状补齐全)都拆成一系列“主-谓-宾”的简单句。
- 把所有带修饰词的短语(如“漂亮的女孩”)拆成两个独立的句子:“她是一个女孩”和“她是漂亮的”。
- 最终摘要 (CNF): 文章内容(语言)不变,但所有句子都被重写成了“A是B和C”($X \rightarrow YZ$)或“A是a”($X \rightarrow x$)这种极度简化的逻辑命题形式。
9行间公式索引
- 文法 G1 的三条替换规则或产生式:
- 文法 G1 中字符串 000#111 的推导过程:
- 文法 G2 中字符串 "a boy sees" 的推导过程:
- 多步推导的形式化定义序列:
- 文法 G3 的规则集,用于生成正确嵌套的括号字符串:
- 文法 G4 的规则集,用于无歧义地生成算术表达式:
- 有歧义的文法 G5 的规则集:
- 用于并集语言的子文法 G1 的规则:
- 用于并集语言的子文法 G2 的规则:
- 通过合并子文法 G1 和 G2 得到的最终文法:
- 乔姆斯基范式 (CNF) 允许的两种主要规则形式:
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。