12.3
非上下文无关语言
在本节中,我们将介绍一种证明某些语言不是上下文无关的技术。回想一下,在第 1.4 节中,我们引入了泵引理来证明某些语言不是正则的。在这里,我们为上下文无关语言介绍了一个类似的泵引理。它指出,每个上下文无关语言都具有一个称为泵长度的特殊值,使得语言中所有较长的字符串都可以被“泵送”。这一次,“泵送”的含义要复杂一些。它意味着字符串可以被分成五部分,以便第二部分和第四部分可以一起重复任意次数,并且生成的字符串仍然保留在该语言中。
上下文无关语言的泵引理
定理 2.34
上下文无关语言的泵引理 如果 $A$ 是一个上下文无关语言,那么存在一个数 $p$(泵长度),使得对于 $A$ 中任何长度至少为 $p$ 的字符串 $s$,可以将 $s$ 分为五个部分 $s=u v x y z$,满足以下条件:
- 对于每个 $i \geq 0, u v^{i} x y^{i} z \in A$,
- $|v y|>0$,并且
- $|v x y| \leq p$。
当 $s$ 被分为 $uvxyz$ 时,条件 2 表示 $v$ 或 $y$ 都不是空字符串。否则,该定理将是显然成立的。条件 3 声明 $v、x$ 和 $y$ 这些部分的长度总和至多为 $p$。这个技术条件有时在证明某些语言不是上下文无关时很有用。
证明思想 设 $A$ 是一个 CFL,并设 $G$ 是生成它的 CFG。我们必须证明 $A$ 中任何足够长的字符串 $s$ 都可以被泵送并保留在 $A$ 中。这种方法背后的思想很简单。
设 $s$ 是 $A$ 中一个非常长的字符串。(我们稍后会明确“非常长”的含义。)因为 $s$ 在 $A$ 中,所以它可以由 $G$ 派生,因此有一个分析树。$s$ 的分析树必须非常高,因为 $s$ 非常长。也就是说,分析树中必须包含从树根处的起始变量到叶子处终结符号之一的某条长路径。在这条长路径上,某些变量符号 $R$ 必定会重复出现,因为鸽巢原理。如下图所示,这种重复允许我们用第一个 $R$ 出现处的子树替换第二个 $R$ 出现处的子树,并且仍然得到一个合法的分析树。因此,我们可以将 $s$ 分为五个部分 $u v x y z$,如图所示,并且我们可以重复第二部分和第四部分,从而得到一个仍在语言中的字符串。换句话说,$u v^{i} x y^{i} z$ 对于任何 $i \geq 0$ 都在 $A$ 中。
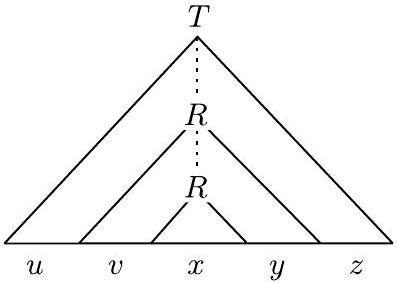
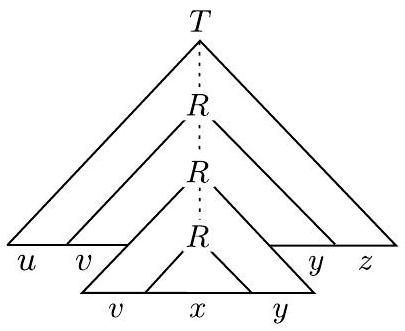
图 2.35
分析树上的手术
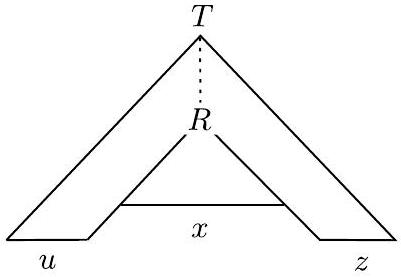
图 2.35
分析树上的手术
现在我们转向细节,以获得泵引理的所有三个条件。我们还将展示如何计算泵长度 $p$。
证明 设 $G$ 是 CFL $A$ 的一个 CFG。设 $b$ 是规则右侧符号的最大数量(假设至少为 2)。在任何使用该文法的分析树中,我们知道一个节点最多可以有 $b$ 个子节点。换句话说,最多有 $b$ 个叶子距离起始变量 1 步;最多有 $b^{2}$ 个叶子距离起始变量 2 步;最多有 $b^{h}$ 个叶子距离起始变量 $h$ 步。因此,如果分析树的高度至多为 $h$,则生成的字符串的长度至多为 $b^{h}$。反之,如果生成的字符串至少长 $b^{h}+1$,则其每个分析树的高度必须至少为 $h+1$。
设 $|V|$ 是 $G$ 中变量的数量。我们将泵长度 $p$ 设置为 $b^{|V|+1}$。现在,如果 $s$ 是 $A$ 中的一个字符串,且其长度为 $p$ 或更多,则其分析树的高度必须至少为 $|V|+1$,因为 $b^{|V|+1} \geq b^{|V|}+1$。
要了解如何泵送任何此类字符串 $s$,设 $\tau$ 是其分析树之一。如果 $s$ 有多个分析树,则选择 $\tau$ 作为节点数量最少的分析树。我们知道 $\tau$ 的高度必须至少为 $|V|+1$,因此从根到叶子的最长路径的长度至少为 $|V|+1$。该路径至少有 $|V|+2$ 个节点;一个在终结符处,其余在变量处。因此,该路径至少有 $|V|+1$ 个变量。由于 $G$ 只有 $|V|$ 个变量,因此某些变量 $R$ 在该路径上出现不止一次。为了以后的方便,我们选择 $R$ 作为在该路径上最低的 $|V|+1$ 个变量中重复出现的变量。
我们根据图 2.35 将 $s$ 分为 $uvxyz$。$R$ 的每次出现都有一个子树,生成字符串 $s$ 的一部分。$R$ 的上部出现有一个较大的子树并生成 $vxy$,而下部出现只生成 $x$ 和一个较小的子树。这两个子树都由相同的变量生成,因此我们可以用一个子树替换另一个子树,并且仍然获得有效的分析树。重复用较大的子树替换较小的子树会为每个 $i>1$ 的字符串 $u v^{i} x y^{i} z$ 生成分析树。用较小的子树替换较大的子树会生成字符串 $uxz$。这确立了引理的条件 1。现在我们转向条件 2 和条件 3。
为了获得条件 2,我们必须确保 $v$ 和 $y$ 不都是 $\varepsilon$。如果它们都是,那么用较小的子树替换较大的子树所获得的分析树的节点数量将少于 $\tau$,并且仍会生成 $s$。这个结果是不可能的,因为我们已经选择 $\tau$ 作为节点数量最少的 $s$ 的分析树。这就是这样选择 $\tau$ 的原因。
为了获得条件 3,我们需要确保 $vxy$ 的长度至多为 $p$。在 $s$ 的分析树中,$R$ 的上部出现生成 $vxy$。我们选择 $R$ 使得两次出现都落在路径上最低的 $|V|+1$ 个变量中,并且我们选择了分析树中最长的路径,因此 $R$ 生成 $vxy$ 的子树的高度至多为 $|V|+1$。这个高度的树可以生成长度至多为 $b^{|V|+1}=p$ 的字符串。
有关使用泵引理证明语言不是上下文无关的一些技巧,请回顾示例 1.73(第 80 页)之前的文本,其中我们讨论了使用正则语言的泵引理证明非正则性的相关问题。
示例 2.36
使用泵引理证明语言 $B=\left\{\mathrm{a}^{n} \mathrm{~b}^{n} \mathrm{c}^{n} \mid n \geq 0\right\}$ 不是上下文无关的。
我们假设 $B$ 是一个 CFL 并得到矛盾。设 $p$ 是泵引理保证存在的 $B$ 的泵长度。选择字符串 $s=\mathrm{a}^{p} \mathrm{~b}^{p} \mathrm{c}^{p}$。显然 $s$ 是 $B$ 的成员,且长度至少为 $p$。泵引理指出 $s$ 可以被泵送,但我们证明它不能。换句话说,我们证明无论我们将 $s$ 分为 $uvxyz$ 多少种方式,引理的三个条件之一都会被违反。
首先,条件 2 规定 $v$ 或 $y$ 都不是空的。然后我们考虑两种情况之一,这取决于子字符串 $v$ 和 $y$ 是否包含多于一种字母符号类型。
- 当 $v$ 和 $y$ 都只包含一种字母符号类型时,$v$ 不包含 'a' 和 'b' 或 'b' 和 'c',$y$ 也是如此。在这种情况下,字符串 $u v^{2} x y^{2} z$ 不能包含相同数量的 'a'、'b' 和 'c'。因此,它不能是 $B$ 的成员。这违反了引理的条件 1,因此是矛盾。
- 当 $v$ 或 $y$ 包含多于一种符号类型时,$u v^{2} x y^{2} z$ 可能包含相同数量的三个字母符号,但顺序不正确。因此它不能是 $B$ 的成员,并且发生矛盾。
这两种情况之一必须发生。因为两种情况都导致矛盾,所以矛盾是不可避免的。因此,假设 $B$ 是 CFL 必须是错误的。因此我们证明了 $B$ 不是一个 CFL。
示例 2.37
设 $C=\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid 0 \leq i \leq j \leq k\right\}$。我们使用泵引理证明 $C$ 不是一个 CFL。该语言类似于示例 2.36 中的语言 $B$,但证明它不是上下文无关要复杂一些。
假设 $C$ 是一个 CFL 并得到矛盾。设 $p$ 是泵引理给出的泵长度。我们使用我们之前用过的字符串 $s=\mathrm{a}^{p} \mathrm{~b}^{p} \mathrm{c}^{p}$,但这次我们必须“向下泵”以及“向上泵”。设 $s=u v x y z$,并再次考虑示例 2.36 中出现的两种情况。
- 当 $v$ 和 $y$ 都只包含一种字母符号类型时,$v$ 不包含 'a' 和 'b' 或 'b' 和 'c',$y$ 也是如此。请注意,之前在情况 1 中使用的推理不再适用。原因是 $C$ 包含 'a'、'b' 和 'c' 数量不等的字符串,只要数量不递减。我们必须更仔细地分析情况,以证明 $s$ 不能被泵送。观察到因为 $v$ 和 $y$ 只包含一种字母符号类型,所以 'a'、'b' 或 'c' 中的一个符号没有出现在 $v$ 或 $y$ 中。我们根据哪个符号没有出现将这种情况进一步细分为三个子情况。
a. 'a' 没有出现。那么我们尝试向下泵送以获得字符串 $u v^{0} x y^{0} z=u x z$。它包含与 $s$ 相同数量的 'a',但包含更少的 'b' 或更少的 'c'。因此,它不是 $C$ 的成员,并且发生矛盾。
b. 'b' 没有出现。那么 'a' 或 'c' 必须出现在 $v$ 或 $y$ 中,因为它们不能都是空字符串。如果 'a' 出现,字符串 $u v^{2} x y^{2} z$ 包含的 'a' 比 'b' 多,所以它不在 $C$ 中。如果 'c' 出现,字符串 $u v^{0} x y^{0} z$ 包含的 'b' 比 'c' 多,所以它不在 $C$ 中。无论哪种情况,都会发生矛盾。
c. 'c' 没有出现。那么字符串 $u v^{2} x y^{2} z$ 包含的 'a' 或 'b' 比 'c' 多,所以它不在 $C$ 中,并且发生矛盾。
- 当 $v$ 或 $y$ 包含多于一种符号类型时,$u v^{2} x y^{2} z$ 将不会以正确的顺序包含符号。因此它不能是 $C$ 的成员,并且发生矛盾。
因此我们已经证明 $s$ 不能被泵送,这违反了泵引理,并且 $C$ 不是上下文无关的。
示例 2.38
设 $D=\left\{w w \mid w \in\{0,1\}^{*}\right\}$。使用泵引理证明 $D$ 不是一个 CFL。假设 $D$ 是一个 CFL 并得到矛盾。设 $p$ 是泵引理给出的泵长度。
这次选择字符串 $s$ 不那么明显。一种可能性是字符串 $0^{p} 10^{p} 1$。它是 $D$ 的成员,并且长度大于 $p$,所以它看起来是一个不错的候选。但是这个字符串可以通过以下方式划分来泵送,因此它不适合我们的目的。
让我们尝试另一个 $s$ 的候选。直观上,字符串 $0^{p} 1^{p} 0^{p} 1^{p}$ 似乎比之前的候选更捕捉到语言 $D$ 的“本质”。事实上,我们可以证明这个字符串确实有效,如下所示。
我们证明字符串 $s=0^{p} 1^{p} 0^{p} 1^{p}$ 不能被泵送。这次我们使用泵引理的条件 3 来限制 $s$ 的划分方式。它说我们可以通过将 $s=u v x y z$ 划分为 $|v x y| \leq p$ 来泵送 $s$。
首先,我们证明子字符串 $vxy$ 必须跨越 $s$ 的中点。否则,如果子字符串只出现在 $s$ 的前半部分,将 $s$ 向上泵送至 $u v^{2} x y^{2} z$ 会将一个 '1' 移动到后半部分的第一个位置,因此它不能是 $ww$ 的形式。类似地,如果 $vxy$ 出现在 $s$ 的后半部分,将 $s$ 向上泵送至 $u v^{2} x y^{2} z$ 会将一个 '0' 移动到前半部分的最后一个位置,因此它不能是 $ww$ 的形式。
但是如果子字符串 $vxy$ 跨越 $s$ 的中点,当我们尝试将 $s$ 向下泵送至 $uxz$ 时,它具有 $0^{p} 1^{i} 0^{j} 1^{p}$ 的形式,其中 $i$ 和 $j$ 不能都为 $p$。这个字符串不是 $ww$ 的形式。因此 $s$ 不能被泵送,并且 $D$ 不是一个 CFL。