1DPDAs 和 DCFGs 的关系
在本节中,我们将证明 DPDA 和 DCFG 描述同一类带结束标记的语言。首先,我们将展示如何将 DCFG 转换为等价的 DPDA。这种转换在所有情况下都有效。其次,我们将展示如何进行反向转换,即将 DPDA 转换为等价的 DCFG。后一种转换仅适用于带结束标记的语言。我们将等价性限制在带结束标记的语言,因为如果没有此限制,这些模型是不等价的。我们之前已经证明结束标记不影响 DPDA 识别的语言类别,但它们确实影响 DCFG 生成的语言类别。没有结束标记,DCFG 只生成 DCFL 的子类——那些无前缀的语言(参见问题 2.22)。请注意,每个带结束标记的语言都是无前缀的。
定理 2.57
一个带结束标记的语言可由确定性上下文无关文法生成当且仅当它是确定性上下文无关的。
我们有两个方向需要证明。首先,我们将证明每个 DCFG 都有一个等价的 DPDA。然后,我们将证明每个识别带结束标记的语言的 DPDA 都有一个等价的 DCFG。我们将在单独的引理中处理这两个方向。
引理 2.58
每个 DCFG 都有一个等价的 DPDA。
证明思路 我们展示如何将 DCFG $G$ 转换为等价的 DPDA $P$。$P$ 使用 DFA $DK$ 进行操作,如下所示。它模拟 $DK$ 对从输入中读取的符号,直到 $DK$ 接受。如定理 2.52 的证明所示,$DK$ 的接受状态指示一个特定的带点规则,因为 $G$ 是确定性的,并且该规则识别出扩展到目前为止它已看到的输入的某个有效字符串的句柄。此外,由于 $G$ 是确定性的,这个句柄适用于每个有效扩展,特别是如果输入在 $L(G)$ 中,它将适用于 $P$ 的完整输入。因此 $P$ 可以使用这个句柄来识别其输入字符串的第一个规约步骤,即使此时它只读取了部分输入。
$P$ 如何识别第二个和后续的规约步骤?一个想法是直接在输入字符串上执行规约步骤,然后像我们上面那样通过 $DK$ 运行修改后的输入。但是输入既不能被修改也不能被重新读取,所以这个想法行不通。另一种方法是将输入复制到栈上并在那里执行规约步骤,但那样的话 $P$ 需要弹出整个栈才能通过 $DK$ 运行修改后的输入,因此修改后的输入将无法用于后续步骤。
这里的技巧是在栈上存储 $DK$ 的状态,而不是在栈上存储输入字符串。每次 $P$ 读取一个输入符号并模拟 $DK$ 中的一个移动时,它会通过将 $DK$ 的状态压入栈中来记录。当它使用规约规则 $T \rightarrow u$ 执行规约步骤时,它会从栈中弹出 $|u|$ 个状态,显示 $DK$ 在读取 $u$ 之前所处的状态。它将 $DK$ 重置为该状态,然后模拟它在输入 $T$ 上,并将结果状态压入栈中。然后 $P$ 继续读取和处理输入符号,就像以前一样。
当 $P$ 将开始变量压入栈中时,它已经找到了其输入到开始变量的归约,因此它进入接受状态。
接下来我们证明定理 2.57 的另一个方向。
引理 2.59
每个识别带结束标记语言的 DPDA 都有一个等价的 DCFG。
证明思路 该证明是引理 2.27 第 121 页构造的修改,该引理描述了 PDA $P$ 到等价 CFG $G$ 的转换。
这里 $P$ 和 $G$ 是确定性的。在引理 2.27 的证明思路中,我们修改了 $P$,使其在接受时清空栈并进入一个特定的接受状态 $q_{\text{accept}}$。PDA 无法直接确定它是否在输入的末尾,因此 $P$ 利用其非确定性来猜测它处于这种情况。我们不想在构造 DPDA $P$ 时引入非确定性。相反,我们使用 $L(P)$ 是带结束标记的假设。我们修改 $P$,使其在读取结束标记 $\dashv$ 后进入其原始接受状态之一时,清空栈并进入 $q_{\text{accept}}$。
接下来,我们应用文法构造来获得 $G$。简单地将原始构造应用于 DPDA 会产生一个几乎确定性的文法,因为 CFG 的推导与 DPDA 的计算密切对应。该文法在一个微小但可修复的方面未能实现确定性。
原始构造引入了形式为 $A_{pq} \rightarrow A_{pr} A_{rq}$ 的规则,这些规则可能导致歧义。这些规则涵盖了 $A_{pq}$ 生成一个字符串的情况,该字符串将 $P$ 从状态 $p$ 带到状态 $q$,其栈在两端都为空,并且栈中途清空。替换对应于在该点划分计算。但是,如果栈多次清空,则可能进行多次划分。每个划分都会产生不同的分析树,因此所得文法是有歧义的。我们通过修改文法来解决这个问题,使其仅在栈中途清空的最后一点划分计算,从而消除这种歧义。例如,在有歧义的文法中也出现了类似但更简单的情况:
这等价于无歧义且确定性的文法:
接下来我们使用 DK 检验来证明 $G$ 是确定性的。为此,我们将分析 $P$ 如何在有效字符串上操作,通过扩展其输入字母表和转移函数来处理变量符号和终结符号。我们将所有符号 $A_{pq}$ 添加到 $P$ 的输入字母表,并通过定义 $\delta\left(p, A_{p q}, \boldsymbol{\varepsilon}\right)=(q, \boldsymbol{\varepsilon})$ 来扩展其转移函数 $\delta$。将所有其他涉及 $A_{pq}$ 的转移设置为 $\emptyset$。为了保持 $P$ 的确定性行为,如果 $P$ 从输入中读取 $A_{pq}$,则不允许 $\varepsilon$ 输入移动。
以下断言适用于 $L(G)$ 中任何字符串 $w$ 的推导,例如
断言 2.60
如果 $P$ 读取包含变量 $A_{pq}$ 的 $v_i$,它会在读取 $A_{pq}$ 之前进入状态 $p$。
证明采用关于 $i$(从 $A_{q_0, q_{\text{accept}}}$ 推导 $v_i$ 的步骤数)的归纳法。
基础情况:$i=0$。
在这种情况下,$v_i=A_{q_0, q_{\text{accept}}}$ 并且 $P$ 从状态 $q_0$ 开始,因此基础情况成立。
归纳步骤:假设对 $i$ 断言成立,并证明对 $i+1$ 成立。
首先考虑情况 $v_i=x A_{pq} y$ 并且 $A_{pq}$ 是在步骤 $v_i \Rightarrow v_{i+1}$ 中被替换的变量。归纳假设意味着 $P$ 在读取 $x$ 之后,读取符号 $A_{pq}$ 之前进入状态 $p$。根据 $G$ 的构造,替换规则可以是两种类型:
- $A_{pq} \rightarrow A_{pr} a A_{st} b$ 或
- $A_{pp} \rightarrow \varepsilon$。
因此,根据使用哪种类型的规则,$v_{i+1}=x A_{pr} a A_{st} b y$ 或 $v_{i+1}=xy$。在第一种情况下,当 $P$ 读取 $v_{i+1}$ 中的 $A_{pr} a A_{st} b$ 时,我们知道它从状态 $p$ 开始,因为它刚刚完成读取 $x$。当 $P$ 读取 $v_{i+1}$ 中的 $A_{pr} a A_{st} b$ 时,由于替换规则的构造,它将按顺序进入状态 $r, s, t$ 和 $q$。因此,它在读取 $A_{pr}$ 之前进入状态 $p$,并在读取 $A_{st}$ 之前进入状态 $s$,从而确立了对这两个变量出现的断言。断言在 $y$ 部分的变量出现上成立,因为在 $P$ 读取 $b$ 之后,它进入状态 $q$,然后它读取字符串 $y$。在输入 $v_i$ 上,它也在读取 $y$ 之前进入 $q$,因此计算在 $v_i$ 和 $v_{i+1}$ 的 $y$ 部分上一致。显然,计算在 $x$ 部分上一致。因此,断言对 $v_{i+1}$ 成立。在第二种情况下,没有引入新变量,所以我们只需观察计算在 $v_i$ 和 $v_{i+1}$ 的 $x$ 和 $y$ 部分上一致。这证明了断言。
断言 2.61
$G$ 通过 DK 检验。
我们证明 $DK$ 的每个接受状态都满足 DK 检验要求。选择这些接受状态之一。它包含一个已完成规则 $R$。这个已完成规则可能有两种形式:
- $A_{pq} \rightarrow A_{pr} a A_{st} b.$
- $A_{pp} \rightarrow .$
在这两种情况下,我们都需要证明接受状态不能包含
a. 另一个已完成规则,并且
b. 一个点后立即跟着终结符号的带点规则。
我们分别考虑这四种情况。在每种情况下,我们首先考虑一个字符串 $z$, $DK$ 在其上进入我们上面选择的接受状态。
情况 1a。这里 $R$ 是一个已完成的类型 1-2 规则。对于此接受状态中的任何规则,$z$ 必须以该规则中点之前的符号结尾,因为 $DK$ 在 $z$ 上进入该状态。因此,点之前的符号在所有此类规则中必须一致。这些符号在 $R$ 中是 $A_{pr} a A_{st} b$,因此任何其他类型 1-2 的已完成规则都必须在右侧具有完全相同的符号。由此可知,左侧的变量也必须一致,因此规则必须相同。
假设接受状态包含 $R$ 和某个类型 3 已完成 $\varepsilon$ 规则 $T$。从 $R$ 我们知道 $z$ 以 $A_{pr} a A_{st} b$ 结尾。此外,我们知道 $P$ 在 $z$ 的末尾弹出其栈,因为在 $R$ 中在该点发生了弹出,这是由于 $G$ 的构造。根据我们构建 $DK$ 的方式,状态中已完成的 $\varepsilon$ 规则必须派生自位于同一状态的带点规则,其中点不在开头,并且点紧接在某个变量之前。(在 $DK$ 的开始状态中可能出现异常,其中点可能出现在规则的开头,但此接受状态不能是开始状态,因为它包含一个已完成的类型 1-2 规则。)在 $G$ 中,这意味着 $T$ 派生自一个类型 1-2 的带点规则,其中点位于第二个变量之前。从 $G$ 的构造来看,在点之前发生了一个压入操作。这意味着 $P$ 在 $z$ 的末尾进行了一次压入移动,这与我们之前的陈述相矛盾。因此,已完成的 $\varepsilon$ 规则 $T$ 不可能存在。无论哪种情况,此接受状态中不能出现第二个已完成规则。
情况 2a。这里 $R$ 是一个已完成的 $\varepsilon$ 规则 $A_{pp} \rightarrow .$。我们证明没有其他已完成的 $\varepsilon$ 规则 $A_{qq} \rightarrow .$ 可以与 $R$ 共存。如果共存,前面的断言表明 $P$ 在读取 $z$ 后必须处于 $p$ 状态,并且在读取 $z$ 后也必须处于 $q$ 状态。因此 $p=q$,并且这两个已完成的 $\boldsymbol{\varepsilon}$ 规则是相同的。
情况 1b。这里 $R$ 是一个已完成的类型 1-2 规则。从情况 1a 我们知道 $P$ 在 $z$ 的末尾弹出其栈。假设接受状态也包含一个带点规则 $T$,其点后立即跟着终结符号。从 $T$ 我们知道 $P$ 在 $z$ 的末尾不弹出其栈。这个矛盾表明这种情况不可能发生。
情况 2b。这里 $R$ 是一个已完成的 $\varepsilon$ 规则。假设接受状态还包含一个带点规则 $T$,其点后立即跟着终结符号。因为 $T$ 是类型 1-2,变量符号紧接在点之前,因此 $z$ 以该变量符号结尾。此外,在 $P$ 读取 $z$ 后,它已准备好读取一个非 $\varepsilon$ 输入符号,因为终结符号紧接在点之后。如情况 1a 所示,已完成的 $\varepsilon$ 规则 $R$ 派生自类型 1-2 的带点规则 $S$,其中点紧接在第二个变量之前。(同样,此接受状态不能是 $DK$ 的开始状态,因为点不出现在 $T$ 的开头。)因此,某个符号 $\hat{a} \in \Sigma_{\varepsilon}$ 紧接在 $S$ 中的点之前,因此 $z$ 以 $\hat{a}$ 结尾。$\hat{a} \in \Sigma$ 或 $\hat{a}=\varepsilon$,但由于 $z$ 以变量符号结尾,$\hat{a} \notin \Sigma$,因此 $\hat{a}=\varepsilon$。因此,在 $P$ 读取 $z$ 但在它进行 $\varepsilon$ 输入移动以处理 $\hat{a}$ 之前,它已准备好读取一个 $\varepsilon$ 输入。我们上面还证明了 $P$ 在这一点已准备好读取一个非 $\varepsilon$ 输入符号。但是,DPDA 不允许在给定状态和栈的情况下同时进行 $\varepsilon$ 输入移动和读取非 $\varepsilon$ 输入符号的移动,因此上述情况是不可能的。因此,这种情况不可能发生。
解析和 LR(K) 文法
确定性上下文无关语言具有重要的实际意义。它们的成员资格和解析算法基于 DPDA,因此效率高,并且它们包含丰富的 CFL 类别,其中包括大多数编程语言。然而,DCFG 有时不便于表达特定的 DCFL。所有句柄都必须是强制的要求通常是设计直观 DCFG 的障碍。
幸运的是,一个更广泛的文法类别,称为 LR(k) 文法,为我们提供了两全其美的优点。它们与 DCFG 足够接近,可以直接转换为 DPDA。然而,它们对于许多应用来说表达能力足够强。
LR(k) 文法的算法引入了前瞻 (lookahead)。在 DCFG 中,所有句柄都是强制的。句柄仅取决于有效字符串中(包括句柄本身)的符号,而不取决于句柄后面的终结符号。在 LR(k) 文法中,句柄也可能取决于句柄后面的符号,但仅限于这些符号的前 $k$ 个。缩写 LR(k) 代表:从左到右的输入处理 (Left to right input processing)、最右推导(或等价地,最左归约)(Rightmost derivations),以及 $k$ 个前瞻符号 (k symbols of lookahead)。
为了使其精确,设 $h$ 是有效字符串 $v=xhy$ 的句柄。我们说 $h$ 由前瞻 $k$ 强制,如果 $h$ 是每个有效字符串 $x h \hat{y}$ 的唯一句柄,其中 $\hat{y} \in \Sigma^{*}$,并且 $y$ 和 $\hat{y}$ 在它们的前 $k$ 个符号上一致。(如果任一字符串的长度小于 $k$,则这些字符串必须一致到较短字符串的长度。)
定义 2.62
LR(k) 文法是一种上下文无关文法,其中每个有效字符串的句柄都由前瞻 $k$ 强制。
因此,DCFG 与 LR(0) 文法相同。我们可以证明对于每个 $k$,我们可以将 LR(k) 文法转换为 DPDA。我们已经证明 DPDA 等价于 LR(0) 文法。因此 LR(k) 文法对于所有 $k$ 在能力上是等价的,并且都准确描述了 DCFL。以下示例表明 LR(1) 文法比 DCFG 更方便指定某些语言。
为避免繁琐的符号和技术细节,我们仅在 $k=1$ 的特殊情况下展示如何将 LR(k) 文法转换为 DPDA。一般情况下的转换方式基本相同。
首先,我们将介绍 DK 检验的变体,为 LR(1) 文法进行了修改。我们称之为带前瞻 1 的 DK 检验,或简称为 $DK_1$ 检验。和以前一样,我们将构造一个 NFA,这里称为 $K_1$,并将其转换为 DFA $DK_1$。 $K_1$ 的每个状态都有一个带点规则 $T \rightarrow u . v$ 和一个终结符号 $a$,称为前瞻符号,表示为 $T \rightarrow u . v \quad a$。此状态表示 $K_1$ 最近读取了字符串 $u$,如果 $v$ 在 $u$ 之后,$a$ 在 $v$ 之后,那么 $u v$ 将是句柄的一部分。
形式构造与之前大致相同。开始状态对每个涉及开始变量 $S_1$ 的规则和每个 $a \in \Sigma$ 都有一个到 $S_{1 \rightarrow .ua}$ 的 $\varepsilon$ 移动。移进转移将 $T \rightarrow u . x v a$ 转换为 $T \rightarrow ux . va$,输入为 $x$,其中 $x$ 是变量符号或终结符号。$\varepsilon$ 转移将 $T \rightarrow u . Cva \quad a$ 转换为 $C \rightarrow . r \quad b$,对于每个规则 $C \rightarrow r$,其中 $b$ 是可以从 $v$ 派生的任何终结符串的第一个符号。如果 $v$ 派生 $\varepsilon$,则添加 $b=a$。接受状态是所有 $B \rightarrow u \cdot a$,用于已完成规则 $B \rightarrow u.$ 和 $a \in \Sigma$。
设 $R_1$ 是一个已完成规则,前瞻符号为 $a_1$,设 $R_2$ 是一个带点规则,前瞻符号为 $a_2$。如果满足以下条件,则称 $R_1$ 和 $R_2$ 是一致的:
- $R_2$ 已完成且 $a_1=a_2$,或
- $R_2$ 未完成且 $a_1$ 紧接在其点之后。
现在我们准备描述 $DK_1$ 检验。构造 DFA $DK_1$。检验规定每个接受状态不得包含任何两个一致的带点规则。
定理 2.63
$G$ 通过 $DK_1$ 检验当且仅当 $G$ 是 LR(1) 文法。
证明思路 推论 2.51 仍然适用于 $DK_1$,因为我们可以忽略前瞻符号。
示例 2.64
这个示例表明以下文法通过了 $DK_1$ 检验。回想一下,在示例 2.53 中,这个文法未能通过 DK 检验。因此,它是一个 LR(1) 文法但不是 DCFG 的例子。
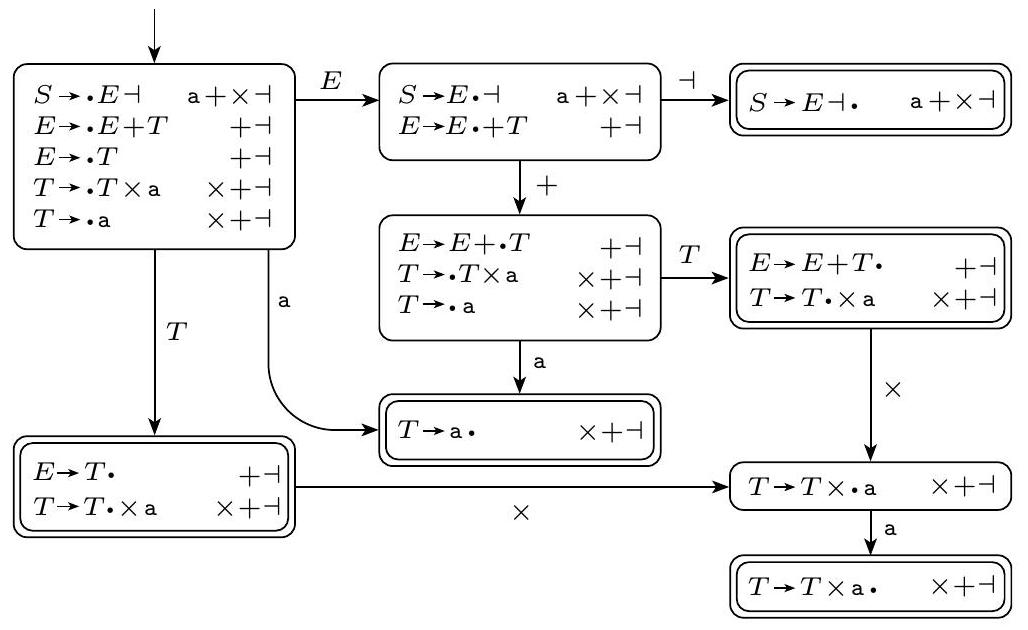
图 2.65
通过 $DK_1$ 检验
定理 2.66
一个带结束标记的语言可由 LR(1) 文法生成当且仅当它是一个 DCFL。
我们已经证明每个 DCFL 都有一个 LR(0) 文法,因为 LR(0) 文法与 DCFG 相同。这证明了定理的反向。剩下的是以下引理,它展示了如何将 LR(1) 文法转换为 DPDA。
引理 2.67
每个 LR(1) 文法都有一个等价的 DPDA。
证明思路 我们构造 $P_1$,它是我们在引理 2.67 中介绍的 DPDA $P$ 的修改版本。 $P_1$ 读取其输入并模拟 $DK_1$,同时使用栈来跟踪 $DK_1$ 如果所有规约步骤都应用到目前为止的输入,它将处于什么状态。此外,$P_1$ 超前读取 1 个符号,并将此前瞻信息存储在其有限状态存储器中。每当 $DK_1$ 达到接受状态时,$P_1$ 都会查阅其前瞻以查看是否执行规约步骤,以及如果在此状态中出现多种可能性,执行哪个步骤。只能应用一个选项,因为文法是 LR(1)。
练习
2.1 回想一下我们在示例 2.4 中给出的 CFG $G_4$。为方便起见,我们将其变量重命名为单个字母,如下所示。
给出每个字符串的分析树和推导。
a. a
b. a+a
c. a+a+a
d. ((a))
2.2 a. 使用语言 $A=\left\{\mathrm{a}^{m} \mathrm{~b}^{n} \mathrm{c}^{n} \mid m, n \geq 0\right\}$ 和 $B=\left\{\mathrm{a}^{n} \mathrm{~b}^{n} \mathrm{c}^{m} \mid m, n \geq 0\right\}$ 以及示例 2.36 来证明上下文无关语言类在交集下不封闭。
b. 使用 (a) 部分和德摩根定律 (定理 0.20) 来证明上下文无关语言类在补运算下不封闭。
${ }^{\text{A}}$ 2.3 对以下上下文无关文法 $G$ 的每个部分回答。
a. $G$ 的变量是什么?
i. 对或错:$T \stackrel{*}{\Rightarrow} T$。
b. $G$ 的终结符是什么?
j. 对或错:$XXX \xrightarrow{*}$ aba。
c. $G$ 的开始变量是哪个?
k. 对或错:$X \stackrel{*}{\Rightarrow}$ aba。
d. 给出 $L(G)$ 中的三个字符串。
l. 对或错:$T \stackrel{*}{\Rightarrow} XX$。
e. 给出不在 $L(G)$ 中的三个字符串。
m. 对或错:$T \stackrel{*}{\Rightarrow} XXX$。
f. 对或错:$T \Rightarrow$ aba。
n. 对或错:$S \stackrel{*}{\Rightarrow} \varepsilon$。
g. 对或错:$T \stackrel{*}{\Rightarrow}$ aba。
o. 用英语描述 $L(G)$。
h. 对或错:$T \Rightarrow T$。
2.4 给出生成以下语言的上下文无关文法。在所有部分中,字母表 $\Sigma$ 是 $\{0,1\}$。
${ }^{\text{A}}$ a. $\{w \mid w \text{ 包含至少三个 } 1 \text{s}\}$
b. $\{w \mid w \text{ 以相同符号开始和结束}\}$
c. $\{w \mid w \text{ 的长度为奇数}\}$
${ }^{\text{A}}$ d. $\{w \mid w \text{ 的长度为奇数且其中间符号为 } 0\}$
e. $\{w \mid w=w^{\mathcal{R}} \text{,即 } w \text{ 是回文}\}$
f. 空集
2.5 给出练习 2.4 中语言的下推自动机的非形式化描述和状态图。
2.6 给出生成以下语言的上下文无关文法。
${ }^{\text{A}}$ a. 字母表 $\{\mathrm{a}, \mathrm{b}\}$ 上 a 比 b 多的字符串集
b. 语言 $\left\{\mathrm{a}^{n} \mathrm{~b}^{n} \mid n \geq 0\right\}$ 的补集
${ }^{\text{A}}$ c. $\left\{w \# x \mid w^{\mathcal{R}} \text{ 是 } x \text{ 的子字符串,其中 } w, x \in\{0,1\}^{*}\right\}$
d. $\left\{x_{1} \# x_{2} \# \cdots \# x_{k} \mid k \geq 1\text{,每个 } x_{i} \in\{\mathrm{a}, \mathrm{b}\}^{*}\text{,并且对于某个 } i \text{ 和 } j\text{,} x_{i}=x_{j}^{\mathcal{R}}\right\}$
${ }^{\text{A}}$ 2.7 给出练习 2.6 中语言的 PDA 的非形式化英语描述。
${ }^{\text{A}}$ 2.8 证明字符串 the girl touches the boy with the flower 在第 103 页的文法 $G_2$ 中有两个不同的最左推导。用英语描述这个句子的两种不同含义。
2.9 给出生成语言
的上下文无关文法。您的文法是否有歧义?为什么或为什么不?
2.10 给出识别练习 2.9 中语言 $A$ 的下推自动机的非形式化描述。
2.11 使用定理 2.20 中给出的过程,将练习 2.1 中给出的 CFG $G_4$ 转换为等价的 PDA。
2.12 使用定理 2.20 中给出的过程,将练习 2.3 中给出的 CFG $G$ 转换为等价的 PDA。
2.13 令 $G=(V, \Sigma, R, S)$ 为以下文法。$V=\{S, T, U\};\Sigma=\{0, \#\}$;$R$ 是规则集:
a. 用英语描述 $L(G)$。
b. 证明 $L(G)$ 不是正则的。
2.14 使用定理 2.9 中给出的过程,将以下 CFG 转换为乔姆斯基范式中的等价 CFG。
2.15 给出反例,以证明以下构造未能证明上下文无关语言类在星运算下是闭合的。设 $A$ 是由 CFG $G=(V, \Sigma, R, S)$ 生成的 CFL。添加新规则 $S \rightarrow SS$,并将所得文法命名为 $G'$。这个文法应该生成 $A^*$。
2.16 证明上下文无关语言类在正则运算、并集、连接和星运算下是闭合的。
2.17 使用练习 2.16 的结果,给出另一个证明,证明每个正则语言都是上下文无关的,通过展示如何将正则表达式直接转换为等价的上下文无关文法。