13.2 "8"8"8"8"-8"-8"-"-"-"-"-"-"
图灵机的变体
图灵机的替代定义比比皆是,包括带有多条磁带或带有非确定性的版本。它们被称为图灵机模型的变体。原始模型及其合理的变体都具有相同的能力——它们识别相同类的语言。在本节中,我们将描述其中一些变体以及它们在能力上等价的证明。我们将这种对定义中某些改变的不变性称为鲁棒性。有限自动机和下推自动机都是具有一定鲁棒性的模型,但图灵机具有惊人的鲁棒性。
为了说明图灵机模型的鲁棒性,我们来改变允许的转移函数类型。在我们的定义中,转移函数强制磁头在每一步之后向左或向右移动;磁头不能仅仅停留在原地。假设我们允许图灵机具有停留在原地的能力。那么转移函数的形式将是 $\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$。这个特性是否会使图灵机能够识别额外的语言,从而增加模型的威力呢?当然不会,因为我们可以将任何具有“停留在原地”功能的图灵机转换为没有该功能的图灵机。我们通过将每个“停留在原地”的转移替换为两个转移来实现:一个向右移动,第二个再向左移动。
这个小例子包含了证明图灵机变体等价性的关键。要证明两个模型是等价的,我们只需要证明一个可以模拟另一个。
多带图灵机
一个多带图灵机就像一个普通的图灵机,但有几条磁带。每条磁带都有自己的磁头用于读写。最初,输入出现在磁带 1 上,其他磁带则为空白。转移函数被修改以允许同时在部分或所有磁带上进行读、写和磁头移动。形式上,它是
其中 $k$ 是磁带的数量。表达式
表示如果机器处于状态 $q_{i}$ 并且磁头 1 到 $k$ 正在读取符号 $a_{1}$ 到 $a_{k}$,则机器进入状态 $q_{j}$,写入符号 $b_{1}$ 到 $b_{k}$,并根据规定指示每个磁头向左或向右移动,或停留在原地。
多带图灵机似乎比普通图灵机更强大,但我们可以证明它们在能力上是等价的。回想一下,如果两台机器识别相同的语言,则它们是等价的。
定理 3.13
每个多带图灵机都具有一个等价的单带图灵机。
证明 我们展示如何将多带图灵机 $M$ 转换为等价的单带图灵机 $S$。关键思想是展示如何用 $S$ 模拟 $M$。
假设 $M$ 有 $k$ 条磁带。那么 $S$ 通过将其信息存储在其单条磁带上来模拟 $k$ 条磁带的效果。它使用新符号 \# 作为分隔符来分隔不同磁带的内容。除了这些磁带的内容之外,$S$ 还必须跟踪磁头的位置。它通过写入一个带有圆点的磁带符号来标记该磁带上的磁头所在的位置。将这些视为“虚拟”磁带和磁头。像以前一样,“带点”的磁带符号只是添加到磁带字母表中的新符号。下图说明了如何使用一条磁带表示三条磁带。
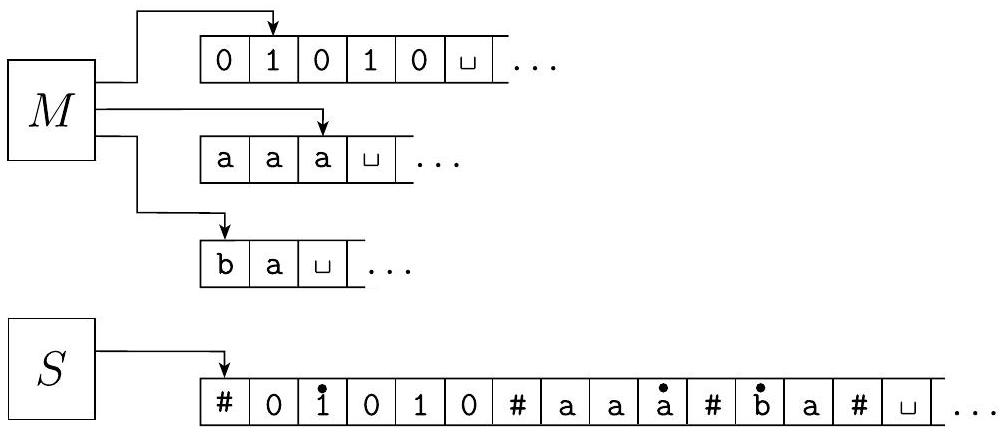
图 3.14
用一条磁带表示三条磁带
$S=$ “在输入 $w=w_{1} \cdots w_{n}$ 上:
- 首先,$S$ 将其磁带格式化,以表示 $M$ 的所有 $k$ 条磁带。格式化后的磁带包含
- 为了模拟单个移动,$S$ 扫描其磁带,从第一个 \#(标记左端)到第 $(k+1)$ 个 \#(标记右端),以确定虚拟磁头下的符号。然后 $S$ 进行第二次扫描,根据 $M$ 的转移函数的规定更新磁带。
- 如果在任何时候 $S$ 将其中一个虚拟磁头向右移动到 \# 上,这个动作表示 $M$ 已将相应的磁头移动到该磁带先前未读取的空白部分。因此,$S$ 在该磁带单元格上写入一个空白符号,并将磁带内容从该单元格向右移动一位,直到最右边的 \#。然后它像以前一样继续模拟。”
推论 3.15
当且仅当某些多带图灵机识别该语言时,该语言才是图灵可识别的。
证明 图灵可识别语言由普通(单带)图灵机识别,而普通(单带)图灵机是多带图灵机的一种特殊情况。这证明了这个推论的一个方向。另一个方向则由定理 3.13 得出。
非确定性图灵机
非确定性图灵机以预期的方式定义。在计算中的任何一点,机器都可以根据几种可能性进行。非确定性图灵机的转移函数形式为
非确定性图灵机的计算是一棵树,其分支对应于机器的不同可能性。如果计算的某个分支导致接受状态,则机器接受其输入。如果您觉得需要复习非确定性,请参阅第 1.2 节(第 47 页)。现在我们证明非确定性不影响图灵机模型的能力。
定理 3.16
每个非确定性图灵机都具有一个等价的确定性图灵机。
证明思想 我们可以用确定性图灵机 $D$ 模拟任何非确定性图灵机 $N$。模拟背后的思想是让 $D$ 尝试 $N$ 的非确定性计算的所有可能分支。如果 $D$ 在这些分支中的一个上找到了接受状态,则 $D$ 接受。否则,$D$ 的模拟将不会终止。
我们将 $N$ 在输入 $w$ 上的计算视为一棵树。树的每个分支代表非确定性的一个分支。树的每个节点是 $N$ 的一个配置。树的根是开始配置。图灵机 $D$ 在这棵树中搜索一个接受配置。仔细进行此搜索至关重要,以免 $D$ 未能访问整个树。一个诱人的,但糟糕的想法是让 $D$ 使用深度优先搜索来探索树。深度优先搜索策略会一直向下遍历一个分支,然后再回溯探索其他分支。如果 $D$ 以这种方式探索树,则 $D$ 可能会永远沿着一个无限分支向下,并错过其他分支上的接受配置。因此,我们设计 $D$ 改用广度优先搜索来探索树。该策略会探索所有深度相同的分支,然后再继续探索下一个深度的任何分支。这种方法保证 $D$ 将访问树中的每个节点,直到遇到接受配置。
证明 模拟确定性图灵机 $D$ 有三条磁带。根据定理 3.13,这种安排等同于拥有一条单条磁带。机器 $D$ 以特殊方式使用其三条磁带,如下图所示。磁带 1 始终包含输入字符串,并且从不改变。磁带 2 维护 $N$ 在其非确定性计算的某个分支上的磁带副本。磁带 3 跟踪 $D$ 在 $N$ 的非确定性计算树中的位置。
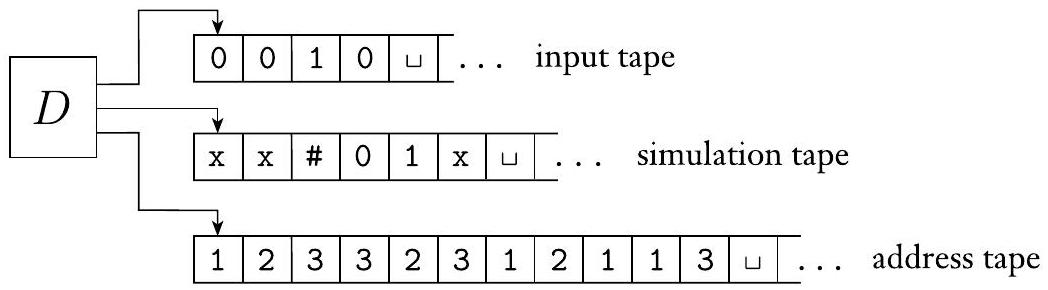
图 3.17
确定性图灵机 $D$ 模拟非确定性图灵机 $N$
首先,我们考虑磁带 3 上的数据表示。树中的每个节点最多可以有 $b$ 个子节点,其中 $b$ 是由 $N$ 的转移函数给出的可能选择的最大集合的大小。我们给树中的每个节点分配一个地址,该地址是字母表 $\Gamma_{b}=\{1,2, \ldots, b\}$ 上的字符串。我们将地址 231 分配给通过从根开始,转到其第 2 个子节点,再转到该节点的第 3 个子节点,最后转到该节点的第 1 个子节点而到达的节点。字符串中的每个符号告诉我们在模拟 $N$ 的非确定性计算中一个分支的一个步骤时接下来要做出的选择。有时,如果一个配置的选择太少,一个符号可能不对应任何选择。在这种情况下,地址无效,并且不对应任何节点。磁带 3 包含一个 $\Gamma_{b}$ 上的字符串。它表示 $N$ 的计算从根到由该字符串寻址的节点的分支,除非地址无效。空字符串是树根的地址。现在我们准备描述 $D$。
- 最初,磁带 1 包含输入 $w$,磁带 2 和 3 为空。
- 将磁带 1 复制到磁带 2,并将磁带 3 上的字符串初始化为 $\varepsilon$。
- 使用磁带 2 模拟 $N$ 在其非确定性计算的一个分支上输入 $w$。在 $N$ 的每一步之前,查阅磁带 3 上的下一个符号,以确定在 $N$ 的转移函数所允许的选择中做出哪个选择。如果磁带 3 上没有更多符号,或者此非确定性选择无效,则通过转到第 4 阶段来中止此分支。如果遇到拒绝配置,也转到第 4 阶段。如果遇到接受配置,则接受输入。
- 将磁带 3 上的字符串替换为字符串排序中的下一个字符串。通过转到第 2 阶段来模拟 $N$ 计算的下一个分支。
推论 3.18
当且仅当某些非确定性图灵机识别该语言时,该语言才是图灵可识别的。
证明 任何确定性图灵机自动也是非确定性图灵机,因此这个推论的一个方向立即得出。另一个方向则由定理 3.16 得出。
我们可以修改定理 3.16 的证明,以便如果 $N$ 总是终止其计算的所有分支,则 $D$ 也将总是终止。如果非确定性图灵机的所有分支在所有输入上都终止,我们称之为判定器。练习 3.3 要求您以这种方式修改证明,以获得定理 3.16 的以下推论。
推论 3.19
当且仅当某些非确定性图灵机判定该语言时,该语言才是可判定的。
枚举器
正如我们之前提到的,有些人用递归可枚举语言来指代图灵可识别语言。这个术语起源于一种称为枚举器的图灵机变体。广义地讲,枚举器是一种带有打印机的图灵机。图灵机可以使用该打印机作为输出设备来打印字符串。每当图灵机想要将一个字符串添加到列表中时,它就会将该字符串发送到打印机。练习 3.4 要求您给出枚举器的正式定义。下图描绘了此模型的示意图。
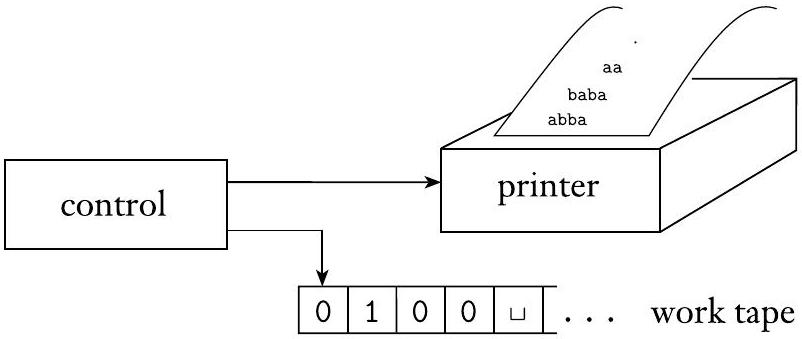
图 3.20
枚举器示意图
一个枚举器 $E$ 在其工作磁带上以空白输入开始。如果枚举器不停止,它可能会打印一个无限的字符串列表。由 $E$ 枚举的语言是它最终打印出的所有字符串的集合。此外,$E$ 可以按任何顺序生成语言的字符串,可能带有重复。现在我们准备阐述枚举器和图灵可识别语言之间的联系。
定理 3.21
当且仅当某个枚举器枚举该语言时,该语言才是图灵可识别的。
证明 首先我们证明,如果我们有一个枚举器 $E$ 枚举语言 $A$,则图灵机 $M$ 识别 $A$。图灵机 $M$ 按以下方式工作。
$M=$ “在输入 $w$ 上:
- 运行 $E$。每次 $E$ 输出一个字符串时,将其与 $w$ 进行比较。
- 如果 $w$ 曾出现在 $E$ 的输出中,则接受。”
显然,$M$ 接受出现在 $E$ 列表中的那些字符串。
现在我们做另一个方向的证明。如果图灵机 $M$ 识别语言 $A$,我们可以为 $A$ 构建以下枚举器 $E$。假设 $s_{1}, s_{2}, s_{3}, \ldots$ 是 $\Sigma^{*}$ 中所有可能字符串的列表。
$E=$ “忽略输入。
- 对 $i=1,2,3, \ldots$ 重复以下操作。
- 对每个输入 $s_{1}, s_{2}, \ldots, s_{i}$,运行 $M$ $i$ 步。
- 如果任何计算接受,则打印出相应的 $s_{j}$。”
如果 $M$ 接受一个特定的字符串 $s$,它最终会出现在 $E$ 生成的列表中。事实上,它会无限次地出现在列表中,因为 $M$ 在步骤 1 的每次重复中都会从头开始在每个字符串上运行。这个过程产生了在所有可能的输入字符串上并行运行 $M$ 的效果。
与其他模型的等价性
到目前为止,我们已经介绍了图灵机模型的几种变体,并证明它们在能力上是等价的。许多其他通用计算模型也已被提出。其中一些模型非常像图灵机,但另一些则大相径庭。它们都共享图灵机的基本特征——即不受限制地访问无限内存——这使它们区别于有限自动机和下推自动机等较弱的模型。值得注意的是,所有具有该特征的模型,只要满足合理的要求,最终都被证明在能力上是等价的。 ${ }^{3}$
[^1]为了理解这种现象,请考虑编程语言的类似情况。许多编程语言,例如 Pascal 和 LISP,在风格和结构上彼此看起来非常不同。是否可以在其中一种编程语言中编程某个算法而不能在其他编程语言中编程呢?当然不是——我们可以将 LISP 编译成 Pascal,将 Pascal 编译成 LISP,这意味着这两种语言描述了完全相同一类的算法。所有其他合理的编程语言也是如此。计算模型的普遍等价性正是出于相同的原因。任何满足某些合理要求的两个计算模型都可以相互模拟,因此在能力上是等价的。
这种等价现象具有重要的哲学推论。尽管我们可以想象许多不同的计算模型,但它们所描述的算法类别保持不变。虽然每个单独的计算模型在其定义上都具有一定的任意性,但它所描述的算法的底层类别是自然的,因为其他模型也达到了相同且独特的类别。这种现象对数学产生了深远的影响,我们将在下一节中展示。