📝 我的笔记

还没有笔记

选中页面文字后点击「高亮」按钮添加

4_可判定性4.1.ZH

📜 原文
📖 逐步解释
∑ 公式拆解
💡 数值示例
⚠️ 易错点
📝 总结
🎯 存在目的
🧠 直觉心智模型
💭 直观想象

14

可判定性

在第3章中，我们介绍了图灵机作为通用计算机模型，并通过丘奇-图灵论题定义了算法的概念。

在本章中，我们开始研究算法解决问题的能力。我们将展示某些可以通过算法解决的问题，以及其他无法解决的问题。我们的目标是探索算法可解性的极限。您可能对算法的可解性很熟悉，因为许多计算机科学都致力于解决问题。某些问题的不可解性可能会让您感到惊讶。

为什么要研究不可解性？毕竟，如果您必须解决一个问题，那么证明一个问题是不可解的似乎没有任何用处。您需要研究这种现象有两个原因。首先，了解一个问题何时在算法上不可解是有用的，因为这样您就会意识到在找到算法解决方案之前，必须简化或改变该问题。像任何工具一样，计算机也有其能力和局限性，如果想很好地使用它们，就必须认识到这些。第二个原因是文化上的。即使您处理的问题显然是可解的，对不可解问题的一瞥也能激发您的想象力，并帮助您对计算获得重要的视角。

4.1 "8"8"8"8"8"8"8"8"-8"-8"-8"-8"

可判定语言

在本节中，我们将给出一些算法可判定语言的示例。我们重点关注与自动机和文法相关的语言。例如，我们提出了一个算法，用于测试一个字符串是否是上下文无关语言 (CFL)的成员。这些语言之所以有趣，有几个原因。首先，这类问题的某些与应用相关。测试CFG是否生成字符串的问题与编程语言中程序识别和编译的问题相关。其次，其他一些与自动机和文法相关的问题是算法不可判定的。从可判定性可能的示例开始，有助于您理解不可判定的示例。

关于正则语言的可判定问题

我们从一些关于有限自动机的计算问题开始。我们给出算法，用于测试有限自动机是否接受字符串，有限自动机的语言是否为空，以及两个有限自动机是否等价。

请注意，我们选择用语言来表示各种计算问题。这样做很方便，因为我们已经建立了处理语言的术语。例如，测试特定确定性有限自动机是否接受给定字符串的DFA的接受问题可以表示为一种语言，$A_{\text {DFA }}$。这种语言包含所有DFA的编码以及DFA所接受的字符串。设

$$ A_{\mathrm{DFA}}=\{\langle B, w\rangle \mid B \text { is a DFA that accepts input string } w\} . $$

测试DFA $B$ 是否接受输入 $w$ 的问题与测试 $\langle B, w\rangle$ 是否是语言 $A_{\text {dfa }}$ 的成员的问题相同。同样，我们可以将其他计算问题表述为测试语言的成员资格。证明语言是可判定的与证明计算问题是可判定的相同。

在下面的定理中，我们证明 $A_{\text {DFA }}$ 是可判定语言。因此，该定理表明，测试给定有限自动机是否接受给定字符串的问题是可判定的。

定理 4.1

$A_{\text {DFA }}$ 是可判定语言。

证明思路 我们只需要提出一个图灵机 $M$ 来判定 $A_{\text {DFA }}$。

$M=$ "在输入 $\langle B, w\rangle$ 上，其中 $B$ 是一个DFA，$w$ 是一个字符串：

  1. 模拟 $B$ 在输入 $w$ 上的运行。
  2. 如果模拟在接受状态结束，则接受。如果模拟在非接受状态结束，则拒绝。"

证明 我们只提及本证明的一些实现细节。对于熟悉使用任何标准编程语言编写程序的读者，请想象您会如何编写一个程序来执行此模拟。

首先，让我们检查输入 $\langle B, w\rangle$。它是DFA $B$ 和字符串 $w$ 的表示。 $B$ 的一个合理表示就是其五个组成部分的列表：$Q, \Sigma, \delta, q_{0}$ 和 $F$。当 $M$ 接收其输入时，$M$ 首先确定它是否正确表示了DFA $B$ 和字符串 $w$。如果不是，$M$ 拒绝。

然后 $M$ 直接执行模拟。它通过在其磁带上写下此信息来跟踪 $B$ 的当前状态和 $B$ 在输入 $w$ 中的当前位置。最初，$B$ 的当前状态是 $q_{0}$， $B$ 的当前输入位置是 $w$ 的最左边的符号。状态和位置根据指定的转移函数 $\delta$ 进行更新。当 $M$ 完成处理 $w$ 的最后一个符号时，如果 $B$ 处于接受状态，则 $M$ 接受输入；如果 $B$ 处于非接受状态，则 $M$ 拒绝输入。

我们可以为非确定性有限自动机证明类似的定理。设

$$ A_{\mathrm{NFA}}=\{\langle B, w\rangle \mid B \text { is an NFA that accepts input string } w\} . $$

定理 4.2

$A_{\text {NFA }}$ 是可判定语言。

证明 我们提出了一个图灵机 $N$ 来判定 $A_{\text {NFA }}$。我们可以将 $N$ 设计成像 $M$ 一样运行，模拟NFA而不是DFA。相反，我们将以不同的方式进行，以说明一个新想法：让 $N$ 使用 $M$ 作为子程序。由于 $M$ 旨在与DFA一起工作，$N$ 首先将它作为输入接收的NFA转换为等价的 DFA，然后将其传递给 $M$。

$N=$ "在输入 $\langle B, w\rangle$ 上，其中 $B$ 是一个NFA，$w$ 是一个字符串：

  1. 使用定理1.39中给出的转换过程，将NFA $B$ 转换为等价的 DFA $C$。
  2. 在输入 $\langle C, w\rangle$ 上运行定理4.1中的图灵机 $M$。
  3. 如果 $M$ 接受，则接受；否则，拒绝。"

在第二阶段运行图灵机 $M$ 意味着将 $M$ 作为子程序纳入 $N$ 的设计中。

同样，我们可以确定正则表达式是否生成给定的字符串。设 $A_{\text {REX }}=\{\langle R, w\rangle \mid R$ is a regular expression that generates string $w\}$。

定理 4.3

$A_{\text {REX }}$ 是可判定语言。

证明 以下图灵机 $P$ 判定 $A_{\text {REX }}$。

$P=$ "在输入 $\langle R, w\rangle$ 上，其中 $R$ 是一个正则表达式，$w$ 是一个字符串：

  1. 使用定理1.54中给出的转换过程，将正则表达式 $R$ 转换为等价的 NFA $A$。
  2. 在输入 $\langle A, w\rangle$ 上运行图灵机 $N$。
  3. 如果 $N$ 接受，则接受；如果 $N$ 拒绝，则拒绝。"

定理4.1、4.2和4.3说明，出于可判定性的目的，向图灵机提供DFA、NFA或正则表达式是等价的，因为机器可以将一种编码形式转换为另一种。

现在我们转向另一种关于有限自动机的问题：有限自动机的语言的空性测试。在前面的三个定理中，我们必须确定有限自动机是否接受一个特定的字符串。在下一个证明中，我们必须确定有限自动机是否接受任何字符串。设

$$ E_{\mathrm{DFA}}=\{\langle A\rangle \mid A \text { is a DFA and } L(A)=\emptyset\} . $$

定理 4.4

$E_{\text {DFA }}$ 是可判定语言。

证明 DFA 接受某些字符串当且仅当从起始状态沿着DFA的箭头到达接受状态是可能的。为了测试这个条件，我们可以设计一个图灵机 $T$，它使用类似于例3.23中使用的标记算法。

$T=$ "在输入 $\langle A\rangle$ 上，其中 $A$ 是一个DFA：

  1. 标记 $A$ 的起始状态。
  2. 重复直到没有新的状态被标记：
  3. 标记所有从已被标记的任何状态传入转换的状态。
  4. 如果没有接受状态被标记，则接受；否则，拒绝。"

下一个定理指出，确定两个DFA是否识别相同的语言是可判定的。设

$$ E Q_{\mathrm{DFA}}=\{\langle A, B\rangle \mid A \text { and } B \text { are DFAs and } L(A)=L(B)\} . $$

定理 4.5

$E Q_{\text {DFA }}$ 是可判定语言。

证明 为了证明这个定理，我们使用定理4.4。我们从 $A$ 和 $B$ 构造一个新的DFA $C$，其中 $C$ 只接受那些由 $A$ 或 $B$ 接受但不能同时由两者接受的字符串。因此，如果 $A$ 和 $B$ 识别相同的语言， $C$ 将不接受任何东西。 $C$ 的语言是

$$ L(C)=(L(A) \cap \overline{L(B)}) \cup(\overline{L(A)} \cap L(B)) . $$

这个表达式有时被称为 $L(A)$ 和 $L(B)$ 的对称差，如下图所示。这里，$\overline{L(A)}$ 是 $L(A)$ 的补集。对称差在这里很有用，因为 $L(C)=\emptyset$ 当且仅当 $L(A)=L(B)$。我们可以通过证明正则语言类在补集、并集和交集运算下封闭的构造从 $A$ 和 $B$ 构造 $C$。这些构造是图灵机可以执行的算法。一旦我们构造了 $C$，我们就可以使用定理4.4来测试 $L(C)$ 是否为空。如果为空，则 $L(A)$ 和 $L(B)$ 必须相等。

$F=$ "在输入 $\langle A, B\rangle$ 上，其中 $A$ 和 $B$ 是DFA：

  1. 按照描述构造DFA $C$。
  2. 在输入 $\langle C\rangle$ 上运行定理4.4中的图灵机 $T$。
  3. 如果 $T$ 接受，则接受。如果 $T$ 拒绝，则拒绝。"

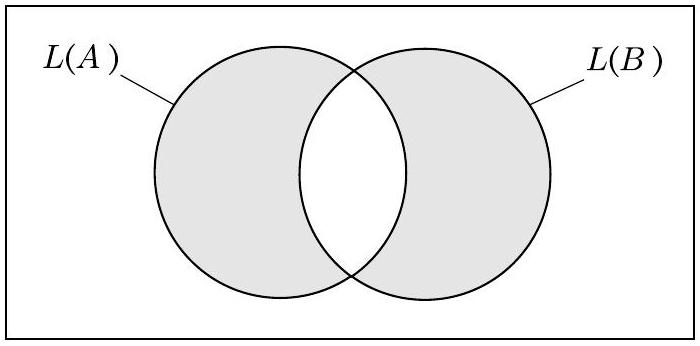
图 4.6

$L(A)$ 和 $L(B)$ 的对称差

关于上下文无关语言的可判定问题

在这里，我们描述算法，用于确定CFG是否生成特定字符串，以及确定CFG的语言是否为空。设

$$ A_{\mathrm{CFG}}=\{\langle G, w\rangle \mid G \text { is a CFG that generates string } w\} . $$

定理 4.7

$A_{\text {CFG }}$ 是可判定语言。

证明思路 对于CFG $G$ 和字符串 $w$，我们想确定 $G$ 是否生成 $w$。一个想法是使用 $G$ 遍历所有推导，以确定是否有任何推导是 $w$ 的推导。这个想法行不通，因为可能需要尝试无限多的推导。如果 $G$ 不生成 $w$，这个算法将永远不会停止。这个想法给出了一个图灵机，它是一个识别器，但不是 $A_{\text {CFG }}$ 的判定器。

为了将这个图灵机变成一个判定器，我们需要确保算法只尝试有限数量的推导。在问题2.38（第158页）中，我们表明如果 $G$ 是乔姆斯基范式，则 $w$ 的任何推导都有 $2n-1$ 步，其中 $n$ 是 $w$ 的长度。在这种情况下，只需检查具有 $2n-1$ 步的推导即可确定 $G$ 是否生成 $w$。只有有限数量的这种推导存在。我们可以通过使用第2.1节中给出的过程将 $G$ 转换为乔姆斯基范式。

证明 $A_{\text {CFG }}$ 的图灵机 $S$ 如下。

$S=$ "在输入 $\langle G, w\rangle$ 上，其中 $G$ 是一个CFG，$w$ 是一个字符串：

  1. 将 $G$ 转换为乔姆斯基范式中的等价文法。
  2. 列出所有具有 $2n-1$ 步的推导，其中 $n$ 是 $w$ 的长度；除非 $n=0$，否则列出所有具有一步的推导。
  3. 如果这些推导中的任何一个生成 $w$，则接受；否则，拒绝。"

确定CFG是否生成特定字符串的问题与编程语言的编译问题相关。图灵机 $S$ 中的算法效率非常低，在实践中永远不会使用，但它很容易描述，我们在此不关心效率。在本书的第三部分，我们将讨论算法的运行时间和内存使用问题。在定理7.16的证明中，我们描述了一种更有效的识别通用上下文无关语言的算法。对于识别确定性上下文无关语言，甚至可以实现更高的效率。

回想一下，我们已经在定理2.20中给出了CFG和PDA之间相互转换的过程。因此，我们关于CFG相关问题的可判定性所说的一切都同样适用于PDA。

现在我们转向CFG的语言的空性测试问题。正如我们对DFA所做的那样，我们可以证明确定CFG是否生成任何字符串的问题是可判定的。设

$$ E_{\mathrm{CFG}}=\{\langle G\rangle \mid G \text { is a CFG and } L(G)=\emptyset\} . $$

定理 4.8

$E_{\text {CFG }}$ 是可判定语言。

证明思路 为了找到这个问题的算法，我们可能会尝试使用定理4.7中的图灵机 $S$。它指出我们可以测试CFG是否生成某个特定字符串 $w$。为了确定 $L(G)=\emptyset$，算法可能会尝试逐个遍历所有可能的 $w$。但是有无限多的 $w$ 可以尝试，所以这种方法可能会永远运行下去。我们需要采取不同的方法。

为了确定文法的语言是否为空，我们需要测试起始变量是否可以生成终结符号串。算法通过解决一个更一般的问题来做到这一点。它为每个变量确定该变量是否能够生成终结符号串。当算法确定一个变量可以生成某些终结符号串时，算法通过在该变量上放置一个标记来跟踪此信息。

首先，算法标记文法中的所有终结符号。然后，它扫描文法的所有规则。如果它发现一个规则允许某个变量被替换为一些符号串，并且所有这些符号都已被标记，那么算法就知道这个变量也可以被标记。算法以这种方式继续，直到不能标记任何额外的变量。图灵机 $R$ 实现了这个算法。

证明

$R=$ "在输入 $\langle G\rangle$ 上，其中 $G$ 是一个CFG：

  1. 标记 $G$ 中的所有终结符号。
  2. 重复直到没有新的变量被标记：
  3. 标记任何变量 $A$，其中 $G$ 有一个规则 $A \rightarrow U_{1} U_{2} \cdots U_{k}$ 并且每个符号 $U_{1}, \ldots, U_{k}$ 都已被标记。
  4. 如果起始变量未被标记，则接受；否则，拒绝。"

接下来，我们考虑确定两个上下文无关文法是否生成相同语言的问题。设

$$ E Q_{\mathrm{CFG}}=\{\langle G, H\rangle \mid G \text { and } H \text { are CFGs and } L(G)=L(H)\} . $$

定理4.5给出了一个算法，它判定了有限自动机的类似语言 $E Q_{\mathrm{DFA}}$。我们使用 $E_{\text {DFA }}$ 的判定过程来证明 $E Q_{\text {DFA }}$ 是可判定的。由于 $E_{\text {CFG }}$ 也是可判定的，您可能认为我们可以使用类似的策略来证明 $E Q_{\mathrm{CFG}}$ 是可判定的。但是这个想法有问题！上下文无关语言类在补集或交集运算下不封闭，正如您在练习2.2中证明的那样。实际上，$E Q_{\mathrm{CFG}}$ 是不可判定的。证明方法将在第5章中介绍。

现在我们证明上下文无关语言是图灵机可判定的。

定理 4.9

每个上下文无关语言都是可判定的。

证明思路 设 $A$ 是一个CFL。我们的目标是证明 $A$ 是可判定的。一个（糟糕的）想法是将 $A$ 的PDA直接转换为图灵机。这并不难做到，因为用图灵机更通用的磁带模拟栈很容易。$A$ 的PDA可能是非确定性的，但这似乎没问题，因为我们可以将其转换为非确定性图灵机，并且我们知道任何非确定性图灵机都可以转换为等价的确定性图灵机。然而，存在一个困难。PDA的某些计算分支可能会永远运行下去，读取和写入栈而永不停止。那么，模拟图灵机的计算中也会有一些非停止分支，因此该图灵机将不是一个判定器。需要一个不同的想法。相反，我们用我们在定理4.7中设计的图灵机 $S$ 来证明这个定理，以判定 $A_{\text {CFG }}$。

证明 设 $G$ 是 $A$ 的一个CFG，并设计一个图灵机 $M_{G}$ 来判定 $A$。我们将 $G$ 的一个副本构建到 $M_{G}$ 中。它的工作原理如下。

$M_{G}=$ "在输入 $w$ 上：

  1. 在输入 $\langle G, w\rangle$ 上运行图灵机 $S$。
  2. 如果该机器接受，则接受；如果它拒绝，则拒绝。"

定理4.9提供了我们迄今为止描述的四种主要语言类之间关系的最终环节：正则语言、上下文无关语言、可判定语言和图灵可识别语言。图4.10描绘了这种关系。

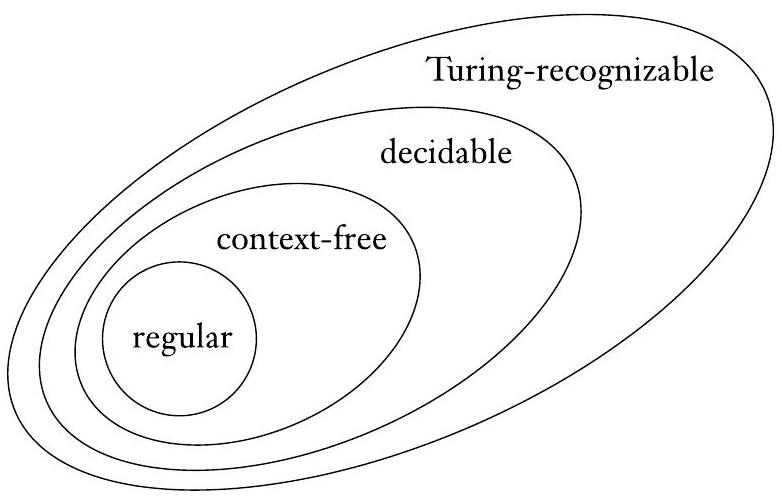
图 4.10

语言类之间的关系