14.2 不可判定性 (UNDECIDABILITY)
在本节中,我们将证明计算理论中一个哲学上最重要的定理:存在一个特定的问题是算法不可解的。计算机看起来如此强大,你可能会认为所有问题最终都将迎刃而解。这里提出的定理表明计算机在根本上是受限制的。
什么样的问题是计算机不可解的?它们是深奥的,只存在于理论家的思想中吗?不是!即使是一些人们想要解决的普通问题,也被证明是计算上不可解的。
在一种不可解的问题中,你得到一个计算机程序和一个关于该程序应该做什么的精确规范(例如,对数字列表进行排序)。你需要验证程序是否按规范执行(即,它是正确的)。由于程序和规范都是数学上精确的对象,你希望通过将这些对象输入到一台经过适当编程的计算机中来自动化验证过程。然而,你会感到失望。软件验证的通用问题是计算机不可解的。
在本节和第5章中,你将遇到几个计算上不可解的问题。我们的目标是帮助你对不可解的问题类型形成一种感觉,并学习证明不可解性的技术。
现在我们转向第一个确立特定语言不可判定性的定理:判定图灵机是否接受给定输入字符串的问题。我们将其称为 $A_{\text {TM }}$,类似于 $A_{\text {DFA }}$ 和 $A_{\text {CFG }}$。但是,虽然 $A_{\text {DFA }}$ 和 $A_{\text {CFG }}$ 是可判定的, $A_{\text {TM }}$ 却不是。设
定理 (THEOREM) 4.11
$A_{\text {TM }}$ 是不可判定的。
在进行证明之前,我们首先观察到 $A_{\text {TM }}$ 是图灵可识别的。因此,这个定理表明识别器比判定器更强大。要求图灵机在所有输入上都停机限制了它能识别的语言种类。以下图灵机 $U$ 识别 $A_{\text {TM }}$。
$U=$ “在输入 $\langle M, w\rangle$ 上,其中 $M$ 是一个图灵机,$w$ 是一个字符串:
- 模拟 $M$ 在输入 $w$ 上的运行。
- 如果 $M$ 进入其接受状态,则接受;如果 $M$ 进入其拒绝状态,则拒绝。”
请注意,如果 $M$ 在 $w$ 上循环,这台机器在输入 $\langle M, w\rangle$ 上也会循环,这就是为什么这台机器不判定 $A_{\mathrm{TM}}$ 的原因。如果算法有某种方法来判定 $M$ 在 $w$ 上没有停机,它就可以在这种情况下拒绝。然而,算法没有办法做出这个判定,正如我们将看到的。
图灵机 $U$ 本身也很有趣。它是艾伦·图灵在1936年首次提出的通用图灵机的一个例子。这台机器被称为通用的,因为它能够根据对机器的描述来模拟任何其他图灵机。通用图灵机在存储程序计算机的发展早期发挥了重要的作用。
对角化方法 (THE DIAGONALIZATION METHOD)
$A_{\text {TM }}$ 不可判定性的证明使用了一种称为对角化的技术,该技术由数学家格奥尔格·康托尔于1873年发现。康托尔关注的是测量无限集大小的问题。如果我们有两个无限集,我们如何判断一个是否比另一个大,或者它们是否大小相同?对于有限集,当然,回答这些问题很容易。我们只需数数有限集中的元素,结果的数字就是它的大小。但是如果我们尝试数数无限集中的元素,我们将永远数不完!所以我们不能使用数数方法来判定无限集的相对大小。
例如,取偶数集和所有二进制字符串集。这两个集都是无限的,因此都比任何有限集大,但其中一个是否比另一个大?我们如何比较它们的相对大小?
康托尔提出了一个相当巧妙的解决方案来解决这个问题。他观察到,如果一个集的元素可以与另一个集的元素配对,那么这两个有限集的大小相同。这种方法在不数数的情况下比较大小。我们可以将这个想法扩展到无限集。更精确地说是这样的。
定义 (DEFINITION) 4.12
假设我们有集合 $A$ 和 $B$ 以及一个从 $A$ 到 $B$ 的函数 $f$。如果 $f$ 从不将两个不同的元素映射到同一个位置——也就是说,如果当 $a \neq b$ 时 $f(a) \neq f(b)$,则称 $f$ 是一对一的。如果 $f$ 击中 $B$ 中的每个元素——也就是说,对于每个 $b \in B$,都存在一个 $a \in A$ 使得 $f(a)=b$,则称 $f$ 是满射的。如果存在一个一对一的、满射的函数 $f: A \longrightarrow B$,则称 $A$ 和 $B$ 大小相同。既是一对一又是满射的函数称为一一对应。在一一对应中, $A$ 的每个元素都映射到 $B$ 的一个唯一元素,并且 $B$ 的每个元素都有一个 $A$ 的唯一元素映射到它。一一对应仅仅是将 $A$ 的元素与 $B$ 的元素配对的一种方式。
这些函数类型的另一种常用术语是单射 (injective) 代表一对一,满射 (surjective) 代表满射,以及双射 (bijective) 代表一对一和满射。
示例 (EXAMPLE) 4.13
设 $\mathcal{N}$ 是自然数集 $\{1,2,3, \ldots\}$,设 $\mathcal{E}$ 是偶自然数集 $\{2,4,6, \ldots\}$。使用康托尔对大小的定义,我们可以看到 $\mathcal{N}$ 和 $\mathcal{E}$ 具有相同的大小。将 $\mathcal{N}$ 映射到 $\mathcal{E}$ 的一一对应 $f$ 简单地是 $f(n)=2 n$。我们可以借助表格更容易地可视化 $f$。
| $n$ | $f(n)$ |
| :--------: | :--------: |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| $\vdots$ | $\vdots$ |
当然,这个例子看起来很奇怪。直观上, $\mathcal{E}$ 似乎比 $\mathcal{N}$ 小,因为 $\mathcal{E}$ 是 $\mathcal{N}$ 的一个真子集。但是,可以将 $\mathcal{N}$ 的每个成员与 $\mathcal{E}$ 的一个成员配对,所以我们声明这两个集的大小相同。
定义 (DEFINITION) 4.14
如果集合 $A$ 是有限的,或者它与 $\mathcal{N}$ 的大小相同,则称 $A$ 是可数的。
示例 (EXAMPLE) 4.15
现在我们来看一个更奇怪的例子。如果我们设 $\mathcal{Q}=\left\{\left.\frac{m}{n} \right\rvert\, m, n \in \mathcal{N}\right\}$ 为正有理数集, $\mathcal{Q}$ 看起来比 $\mathcal{N}$ 大得多。然而,根据我们的定义,这两个集的大小相同。我们给出一个与 $\mathcal{N}$ 的一一对应,以表明 $\mathcal{Q}$ 是可数的。一个简单的方法是列出 $\mathcal{Q}$ 的所有元素。然后我们将列表中的第一个元素与 $\mathcal{N}$ 中的数字1配对,将列表中的第二个元素与 $\mathcal{N}$ 中的数字2配对,依此类推。我们必须确保 $\mathcal{Q}$ 的每个成员在列表中只出现一次。
为了得到这个列表,我们制作一个包含所有正有理数的无限矩阵,如图4.16所示。第 $i$ 行包含所有分子为 $i$ 的数字,第 $j$ 列包含所有分母为 $j$ 的数字。因此,数字 $\frac{i}{j}$ 出现在第 $i$ 行和第 $j$ 列中。
现在我们将这个矩阵变成一个列表。一个(不好的)尝试方法是,用第一行中的所有元素开始列表。这不是一个好方法,因为第一行是无限的,所以列表永远不会到达第二行。相反,我们列出对角线上的元素,这些元素叠加在图中,从角落开始。第一条对角线包含单个元素 $\frac{1}{1}$,第二条对角线包含两个元素 $\frac{2}{1}$ 和 $\frac{1}{2}$。因此,列表中的前三个元素是 $\frac{1}{1}, \frac{2}{1}$ 和 $\frac{1}{2}$。在第三条对角线中,出现了一个复杂情况。它包含 $\frac{3}{1}, \frac{2}{2}$ 和 $\frac{1}{3}$。如果我们简单地将这些添加到列表中,我们将重复 $\frac{1}{1}=\frac{2}{2}$。我们通过在出现重复时跳过一个元素来避免这种情况。所以我们只添加两个新元素 $\frac{3}{1}$ 和 $\frac{1}{3}$。以这种方式继续,我们得到 $\mathcal{Q}$ 的所有元素的列表。
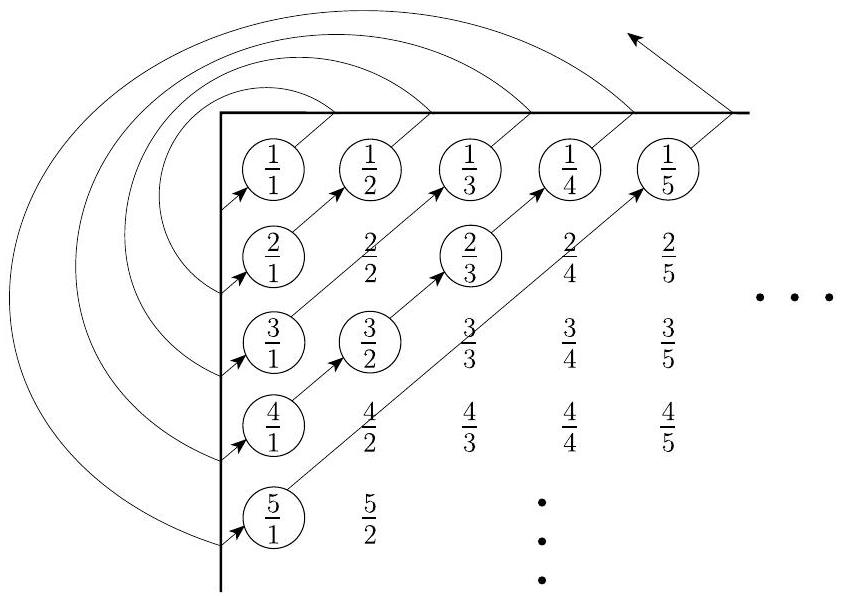
图 4.16
$\mathcal{N}$ 和 $\mathcal{Q}$ 的一一对应
在看到 $\mathcal{N}$ 和 $\mathcal{Q}$ 的一一对应之后,你可能会认为任何两个无限集都可以被证明具有相同的大小。毕竟,你只需要证明一个一一对应,这个例子表明确实存在令人惊讶的一一对应。然而,对于某些无限集,不存在与 $\mathcal{N}$ 的一一对应。这些集太大了。这样的集称为不可数。
实数集就是一个不可数集的例子。实数是具有小数表示的数字。数字 $\pi=3.1415926 \ldots$ 和
$\sqrt{2}=1.4142135 \ldots$ 是实数的例子。设 $\mathcal{R}$ 是实数集。康托尔证明了 $\mathcal{R}$ 是不可数的。在证明过程中,他引入了对角化方法。
定理 (THEOREM) 4.17
$\mathcal{R}$ 是不可数的。
证明:为了表明 $\mathcal{R}$ 是不可数的,我们表明 $\mathcal{N}$ 和 $\mathcal{R}$ 之间不存在一一对应。该证明采用反证法。假设 $\mathcal{N}$ 和 $\mathcal{R}$ 之间存在一个一一对应 $f$。我们的任务是表明 $f$ 未能按其应有的方式工作。为了使其成为一一对应, $f$ 必须将 $\mathcal{N}$ 的所有成员与 $\mathcal{R}$ 的所有成员配对。但我们将发现 $\mathcal{R}$ 中存在一个 $x$,它未与 $\mathcal{N}$ 中的任何事物配对,这将是我们的矛盾。
我们通过实际构造 $x$ 来找到这个 $x$。我们选择 $x$ 的每个数字,以使 $x$ 与与 $\mathcal{N}$ 中的元素配对的实数中的一个不同。最后,我们确信 $x$ 不同于任何已配对的实数。
我们可以通过举例来说明这个想法。假设存在一一对应 $f$。设 $f(1)=3.14159 \ldots, f(2)=55.55555 \ldots, f(3)=\ldots$,依此类推,只是为了编造一些 $f$ 的值。然后 $f$ 将数字1与 $3.14159 \ldots$ 配对,将数字2与 $55.55555 \ldots$ 配对,依此类推。下表显示了 $\mathcal{N}$ 和 $\mathcal{R}$ 之间假设的一一对应 $f$ 的一些值。
| $n$ | $f(n)$ |
| :--------: | ------------------: |
| 1 | $3.14159 \ldots$ |
| 2 | $55.55555 \ldots$ |
| 3 | $0.12345 \ldots$ |
| 4 | $0.50000 \ldots$ |
| $\vdots$ | $\vdots$ |
我们通过给出其小数表示来构造所需的 $x$。它是一个介于0和1之间的数字,因此其所有有效数字都是小数点后的小数位。我们的目标是确保对于任何 $n$, $x \neq f(n)$。为了确保 $x \neq f(1)$,我们让 $x$ 的第一位数字与 $f(1)=3.14159 \ldots$ 的第一个小数位1不同。我们任意地将其设为4。为了确保 $x \neq f(2)$,我们让 $x$ 的第二位数字与 $f(2)=55.555555 \ldots$ 的第二个小数位5不同。我们任意地将其设为6。 $f(3)=0.12 \underline{3} 45 \ldots$ 的第三个小数位是3,所以我们让 $x$ 是任何不同的数字——例如4。以这种方式沿着 $f$ 表的对角线继续,我们得到 $x$ 的所有数字,如下表所示。我们知道 $x$ 不是任何 $f(n)$,因为它与 $f(n)$ 在第 $n$ 个小数位上不同。(一个小问题出现了,因为某些数字,例如 $0.1999 \ldots$ 和 $0.2000 \ldots$,即使它们的小数表示不同,也相等。我们在构造 $x$ 时从不选择数字0或9来避免这个问题。)
| $n$ | $f(n)$ | |
| :--------- | -------------------------------: | :------------------ |
| 1 | $3.14159 \ldots$ | |
| 2 | $55.55555 \ldots$ | |
| 3 | $0.12 \underline{3} 45 \ldots$ | $x=0.4641 \ldots$ |
| 4 | $0.500 \underline{0} 0 \ldots$ | |
| $\vdots$ | $\vdots$ | |
前面的定理对计算理论有着重要的应用。它表明有些语言是不可判定的,甚至不是图灵可识别的,原因在于语言是不可数的,而图灵机只有可数个。因为每台图灵机只能识别一种语言,并且语言的数量多于图灵机的数量,所以有些语言不被任何图灵机识别。这样的语言是图灵不可识别的,正如我们在以下推论中所述。
推论 (corollary) 4.18
有些语言是图灵不可识别的。
证明:为了表明所有图灵机的集是可数的,我们首先观察到任何字母表 $\Sigma$ 的所有字符串 $\Sigma^{*}$ 的集是可数的。对于每个长度的有限数量的字符串,我们可以通过写下所有长度为0、长度为1、长度为2等字符串来形成 $\Sigma^{*}$ 的列表。
所有图灵机的集是可数的,因为每个图灵机 $M$ 都有一个编码成字符串 $\langle M\rangle$。如果我们简单地省略那些不是合法图灵机编码的字符串,我们就可以得到所有图灵机的列表。
为了表明所有语言的集是不可数的,我们首先观察到所有无限二进制序列的集是不可数的。无限二进制序列是0和1的无限序列。设 $\mathcal{B}$ 是所有无限二进制序列的集。我们可以通过使用类似于定理4.17中用于表明 $\mathcal{R}$ 是不可数的对角化证明来表明 $\mathcal{B}$ 是不可数的。
设 $\mathcal{L}$ 是字母表 $\Sigma$ 上的所有语言的集。我们通过给出与 $\mathcal{B}$ 的一一对应来表明 $\mathcal{L}$ 是不可数的,从而表明这两个集的大小相同。设 $\Sigma^{*}=\left\{s_{1}, s_{2}, s_{3}, \ldots\right\}$。 $\mathcal{L}$ 中的每种语言 $A$ 在 $\mathcal{B}$ 中都有一个唯一的序列。该序列的第 $i$ 位是1,如果 $s_{i} \in A$,如果 $s_{i} \notin A$,则为0,这被称为 $A$ 的特征序列。例如,如果 $A$ 是字母表 $\{0,1\}$ 上所有以0开头的字符串的语言,其特征序列 $\chi_{A}$ 将是
函数 $f: \mathcal{L} \longrightarrow \mathcal{B}$,其中 $f(A)$ 等于 $A$ 的特征序列,是一对一的且是满射的,因此是一一对应。因此,由于 $\mathcal{B}$ 是不可数的, $\mathcal{L}$ 也是不可数的。
因此,我们已经表明所有语言的集不能与所有图灵机的集建立一一对应。我们得出结论,有些语言不被任何图灵机识别。
一个不可判定的语言 (AN UNDECIDABLE LANGUAGE)
现在我们准备证明定理4.11,$A_{\mathrm{TM}}$ 语言的不可判定性:
证明:我们假设 $A_{\mathrm{TM}}$ 是可判定的并得到矛盾。假设 $H$ 是 $A_{\mathrm{TM}}$ 的一个判定器。在输入 $\langle M, w\rangle$ 上,其中 $M$ 是一个图灵机,$w$ 是一个字符串,如果 $M$ 接受 $w$,则 $H$ 停机并接受。此外,如果 $M$ 不接受 $w$,则 $H$ 停机并拒绝。换句话说,我们假设 $H$ 是一个图灵机,其中
现在我们构造一个以 $H$ 为子程序的新图灵机 $D$。这个新图灵机调用 $H$ 来判定当 $M$ 的输入是它自己的描述 $\langle M\rangle$ 时 $M$ 会做什么。一旦 $D$ 获得此信息,它就会做相反的事情。也就是说,如果 $M$ 接受,它就拒绝;如果 $M$ 不接受,它就接受。以下是 $D$ 的描述。
$D=$ “在输入 $\langle M\rangle$ 上,其中 $M$ 是一个图灵机:
- 在输入 $\langle M,\langle M\rangle\rangle$ 上运行 $H$。
- 输出与 $H$ 输出相反的结果。也就是说,如果 $H$ 接受,则拒绝;如果 $H$ 拒绝,则接受。”
不要被在一个机器上运行它自己的描述这种概念所困扰!这类似于运行一个程序并以它自己作为输入,这在实践中偶尔会发生。例如,编译器是一个翻译其他程序的程序。一个用 Python 编写的 Python 编译器,用它自己作为输入来运行也是有意义的。总而言之,
当我们用它自己的描述 $\langle D\rangle$ 作为输入来运行 $D$ 时会发生什么?在这种情况下,我们得到
无论 $D$ 做什么,它都被迫做相反的事情,这显然是一个矛盾。因此,图灵机 $D$ 和图灵机 $H$ 都不可能存在。
让我们回顾一下这个证明的步骤。假设图灵机 $H$ 判定 $A_{\mathrm{TM}}$。使用 $H$ 构建一个图灵机 $D$,它接受输入 $\langle M\rangle$,其中 $D$ 接受其输入 $\langle M\rangle$ 当且仅当 $M$ 不接受其输入 $\langle M\rangle$。最后,在 $D$ 上运行 $D$ 本身。因此,这些机器采取以下行动,最后一行是矛盾。
- $H$ 接受 $\langle M, w\rangle$ 当且仅当 $M$ 接受 $w$。
- $D$ 拒绝 $\langle M\rangle$ 当且仅当 $M$ 接受 $\langle M\rangle$。
- $D$ 拒绝 $\langle D\rangle$ 当且仅当 $D$ 接受 $\langle D\rangle$。
定理4.11的证明中的对角化在哪里?当你检查图灵机 $H$ 和 $D$ 的行为表时,它就会变得显而易见。在这些表中,我们列出了所有图灵机( $M_{1}, M_{2}, \ldots$)在行中,以及它们的所有描述( $\left\langle M_{1}\right\rangle,\left\langle M_{2}\right\rangle, \ldots$)在列中。条目说明给定行中的机器是否接受给定列中的输入。如果机器接受输入,则条目为“接受”,如果它拒绝或循环,则为空白。我们编造了下图中的条目来说明这个想法。
| | $\left\langle M_{1}\right\rangle$ | $\left\langle M_{2}\right\rangle$ | $\left\langle M_{3}\right\rangle$ | $\left\langle M_{4}\right\rangle$ | $\ldots$ |
| :--------: | :---------------------------------: | :---------------------------------: | :---------------------------------: | :---------------------------------: | :--------: |
| $M_{1}$ | accept | | accept | | |
| $M_{2}$ | accept | accept | accept | accept | |
| $M_{3}$ | | | | | $\ldots$ |
| $M_{4}$ | accept | accept | | | |
| $\vdots$ | | | $\vdots$ | | |
图 4.19
条目 $i, j$ 为接受,如果 $M_{i}$ 接受 $\left\langle M_{j}\right\rangle$
在下图中,条目是在与图4.19对应的输入上运行 $H$ 的结果。因此,如果 $M_{3}$ 不接受输入 $\left\langle M_{2}\right\rangle$,则 $M_{3}$ 行和 $\left\langle M_{2}\right\rangle$ 列的条目为拒绝,因为 $H$ 拒绝输入 $\left\langle M_{3},\left\langle M_{2}\right\rangle\right\rangle$。
| | $\left\langle M_{1}\right\rangle$ | $\left\langle M_{2}\right\rangle$ | $\left\langle M_{3}\right\rangle$ | $\left\langle M_{4}\right\rangle$ | $\cdots$ |
| :--------: | :---------------------------------: | :---------------------------------: | :---------------------------------: | :---------------------------------: | :--------: |
| $M_{1}$ | accept | reject | accept | reject | |
| $M_{2}$ | accept | accept | accept | accept | $\ldots$ |
| $M_{3}$ | reject | reject | reject | reject | |
| $M_{4}$ | accept | accept | reject | reject | |
| $\vdots$ | | | $\vdots$ | | |
图 4.20
条目 $i, j$ 是 $H$ 在输入 $\left\langle M_{i},\left\langle M_{j}\right\rangle\right\rangle$ 上的值
在下图中,我们将 $D$ 添加到图4.20中。根据我们的假设,$H$ 是一个图灵机,$D$ 也是。因此,它必须出现在所有图灵机的列表 $M_{1}, M_{2}, \ldots$ 中。请注意, $D$ 计算的是对角线条目的相反。矛盾发生在问号处,该处的条目必须与自身相反。
| | $\left\langle M_{1}\right\rangle$ | $\left\langle M_{2}\right\rangle$ | $\left\langle M_{3}\right\rangle$ | $\left\langle M_{4}\right\rangle$ | ⋯ | $\langle D\rangle$ | ⋯ |
| :-------- | :---------------------------------- | :---------------------------------- | :---------------------------------- | :---------------------------------- | :- | :------------------- | :- |
| $M_{1}$ | accept | reject | accept | reject | | accept | |
| $M_{2}$ | accept | accept | accept | accept | … | accept | |
| $M_{3}$ | reject | reject | reject | reject | | reject | |
| $M_{4}$ | accept | accept | reject | $\underline{\text { reject }}$ | | accept | |
| ⋮ | | | ⋮ | | ⋱ | | |
| D | reject | reject | accept | accept | | ? | |
| : | | | ⋮ | | | | ⋱ |
图 4.21
如果 $D$ 在图中,问号处就会发生矛盾
一个图灵不可识别的语言 (A TURING-UNRECOGNIZABLE LANGUAGE)
在上一节中,我们展示了一种不可判定的语言——即 $A_{\text {TM }}$。现在我们展示一种甚至不是图灵可识别的语言。请注意, $A_{\text {TM }}$ 不能用于此目的,因为我们已经证明 $A_{\text {TM }}$ 是图灵可识别的(第202页)。以下定理表明,如果一种语言及其补集都是图灵可识别的,那么该语言就是可判定的。因此,对于任何不可判定的语言,它或它的补集都不是图灵可识别的。回想一下,一种语言的补集是由所有不属于该语言的字符串组成的语言。如果一种语言是图灵可识别语言的补集,我们称之为协同图灵可识别的。
定理 (THEOREM) 4.22
一种语言是可判定的当且仅当它是图灵可识别的且是协同图灵可识别的。
换句话说,一种语言是可判定的,当且仅当它和它的补集都是图灵可识别的。
证明:我们需要证明两个方向。首先,如果 $A$ 是可判定的,我们可以很容易地看到 $A$ 和它的补集 $\bar{A}$ 都是图灵可识别的。任何可判定的语言都是图灵可识别的,可判定的语言的补集也是可判定的。
另一方面,如果 $A$ 和 $\bar{A}$ 都是图灵可识别的,我们设 $M_{1}$ 为 $A$ 的识别器, $M_{2}$ 为 $\bar{A}$ 的识别器。以下图灵机 $M$ 是 $A$ 的判定器。
$M=$ “在输入 $w$ 上:
- 在输入 $w$ 上并行运行 $M_{1}$ 和 $M_{2}$。
- 如果 $M_{1}$ 接受,则接受;如果 $M_{2}$ 接受,则拒绝。”
并行运行这两台机器意味着 $M$ 有两条磁带,一条用于模拟 $M_{1}$,另一条用于模拟 $M_{2}$。在这种情况下,$M$ 轮流模拟每台机器的一个步骤,直到其中一台接受。
现在我们表明 $M$ 判定 $A$。每个字符串 $w$ 要么在 $A$ 中,要么在 $\bar{A}$ 中。因此, $M_{1}$ 或 $M_{2}$ 必须接受 $w$。因为当 $M_{1}$ 或 $M_{2}$ 接受时 $M$ 就会停机,所以 $M$ 总是停机,因此它是一个判定器。此外,它接受 $A$ 中的所有字符串,并拒绝不在 $A$ 中的所有字符串。所以 $M$ 是 $A$ 的一个判定器,因此 $A$ 是可判定的。
推论 (corollary) 4.23
$\overline{A_{\text {TM }}}$ 是图灵不可识别的。
证明:我们知道 $A_{\text {TM }}$ 是图灵可识别的。如果 $\overline{A_{\text {TM }}}$ 也是图灵可识别的,那么 $A_{\text {TM }}$ 将是可判定的。定理4.11告诉我们 $A_{\text {TM }}$ 是不可判定的,所以 $\overline{A_{\mathrm{TM}}}$ 必然不是图灵可识别的。
练习 (EXERCISES)
${ }^{\text {A }}$ 4.1 对于以下 DFA $M$,回答所有部分并给出理由。
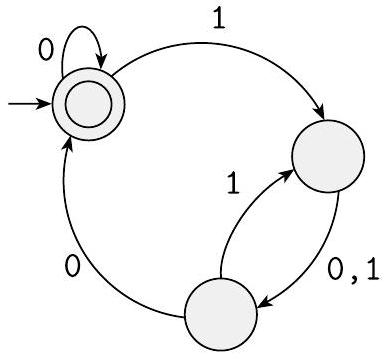
a. $\langle M, 0100\rangle \in A_{\mathrm{DFA}}$ 吗?
b. $\langle M, 011\rangle \in A_{\mathrm{DFA}}$ 吗?
c. $\langle M\rangle \in A_{\text {DFA }}$ 吗?
d. $\langle M, 0100\rangle \in A_{\text {REX }}$ 吗?
e. $\langle M\rangle \in E_{\text {DFA }}$ 吗?
f. $\langle M, M\rangle \in E Q_{\text {DFA }}$ 吗?
4.2 考虑判定一个 DFA 和一个正则表达式是否等价的问题。将这个问题表示为一种语言并表明它是可判定的。
4.3 设 $A L L_{\mathrm{DFA}}=\left\{\langle A\rangle \mid A\right.$ 是一个 DFA 且 $\left.L(A)=\Sigma^{*}\right\}$。表明 $A L L_{\mathrm{DFA}}$ 是可判定的。
4.4 设 $A \varepsilon_{\mathrm{CFG}}=\{\langle G\rangle \mid G$ 是一个生成 $\varepsilon$ 的 CFG $\}$。表明 $A \varepsilon_{\mathrm{CFG}}$ 是可判定的。
${ }^{\text {A }}$ 4.5 设 $E_{\mathrm{TM}}=\{\langle M\rangle \mid M$ 是一个 TM 且 $L(M)=\emptyset\}$。表明 $\overline{E_{\mathrm{TM}}}$,即 $E_{\text {TM }}$ 的补集,是图灵可识别的。
4.6 设 $X$ 是集合 $\{1,2,3,4,5\}$, $Y$ 是集合 $\{6,7,8,9,10\}$。我们在下表中描述函数 $f: X \longrightarrow Y$ 和 $g: X \longrightarrow Y$。回答每个部分并给出每个否定答案的理由。
| $n$ | $f(n)$ |
| :---: | :------: |
| 1 | 6 |
| 2 | 7 |
| 3 | 6 |
| 4 | 7 |
| 5 | 6 |
| $n$ | $g(n)$ |
| :---: | :------: |
| 1 | 10 |
| 2 | 9 |
| 3 | 8 |
| 4 | 7 |
| 5 | 6 |
${ }^{\text {A }}$ a. $f$ 是一对一的吗?
${ }^{\text {A }}$ d. $g$ 是一对一的吗?
b. $f$ 是满射的吗?
e. $g$ 是满射的吗?
c. $f$ 是一一对应吗?
f. $g$ 是一一对应吗?
4.7 设 $\mathcal{B}$ 是所有二进制序列的集。使用对角化证明表明 $\mathcal{B}$ 是不可数的。
4.8 设 $T=\{(i, j, k) \mid i, j, k \in \mathcal{N}\}$。表明 $T$ 是可数的。
4.9 回顾我们在定义4.12(第203页)中定义集合大小相同的方式。表明“大小相同”是一种等价关系。