5_可归约性5.2.ZH

15.2

一个简单的不可判定问题

在本节中，我们将展示不可判定性现象不仅限于与自动机相关的问题。我们将举一个关于字符串简单操作的不可判定问题的例子。它被称为邮政对应问题（PCP）。

我们可以很容易地将这个问题描述为一种谜题。我们从一堆多米诺骨牌开始，每张多米诺骨牌两面各有一个字符串。一张多米诺骨牌看起来像

一堆多米诺骨牌看起来像

任务是列出这些多米诺骨牌（允许重复），使得从上方读出的字符串与从下方读出的字符串相同。这个列表称为一个匹配。例如，以下列表是这个谜题的一个匹配。

从上方读出字符串得到abcaaabc，这与从下方读出的相同。我们也可以通过将多米诺骨牌变形，使上方和下方对应的符号对齐来描绘这个匹配。

对于某些多米诺骨牌集合，可能无法找到匹配。例如，集合

不可能包含匹配，因为每个上方字符串都比对应的下方字符串长。

邮政对应问题是确定一组多米诺骨牌是否具有匹配。这个问题是算法无法解决的。

在正式阐述这个定理及其证明之前，让我们精确地说明这个问题，然后将其表示为一种语言。PCP 的实例是一组多米诺骨牌 $P$

而匹配是序列 $i_{1}, i_{2}, \ldots, i_{l}$，其中 $t_{i_{1}} t_{i_{2}} \cdots t_{i_{l}}=b_{i_{1}} b_{i_{2}} \cdots b_{i_{l}}$。问题是确定 $P$ 是否具有匹配。令

定理 5.15

PCP 是不可判定的。

证明思路 从概念上讲，这个证明很简单，尽管它涉及许多细节。主要技术是利用接受计算历史从 $A_{\text {TM }}$ 进行归约。我们展示，对于任何图灵机 $M$ 和输入 $w$，我们可以构造一个实例 $P$，其中一个匹配就是 $M$ 在 $w$ 上的接受计算历史。如果我们可以确定该实例是否具有匹配，我们就能确定 $M$ 是否接受 $w$。

我们如何构造 $P$，使得匹配是 $M$ 在 $w$ 上的接受计算历史？我们选择 $P$ 中的多米诺骨牌，使得形成匹配强制模拟 $M$ 的发生。在匹配中，每张多米诺骨牌将一个格局中的一个或多个位置与下一个格局中对应的一个或多个位置连接起来。

在进行构造之前，我们处理三个小的技术点。（在您初次阅读此构造时，不必过于担心它们。）首先，为了方便构造 $P$，我们假设 $M$ 在 $w$ 上从不试图将其磁头移出纸带的左端。这需要首先修改 $M$ 以防止这种行为。其次，如果 $w=\varepsilon$，我们在构造中使用符号 $\sqcup$ 代替 $w$。第三，我们修改 PCP 以要求匹配从第一张多米诺骨牌开始，

稍后我们将展示如何消除此要求。我们将此问题称为修改的邮政对应问题（MPCP）。令

现在让我们深入到证明的细节，并设计 $P$ 来模拟 $M$ 在 $w$ 上的行为。

证明 我们让图灵机 $R$ 判定 PCP，并构造图灵机 $S$ 来判定 $A_{\text {TM }}$。令

其中 $Q, \Sigma, \Gamma$ 和 $\delta$ 分别是 $M$ 的状态集、输入字母表、纸带字母表和转移函数。

在这种情况下，$S$ 构造 PCP 的一个实例 $P$，当且仅当 $M$ 接受 $w$ 时，该实例才具有匹配。为此，$S$ 首先构造 MPCP 的一个实例 $P^{\prime}$。我们将构造过程分为七个部分，每个部分都完成模拟 $M$ 在 $w$ 上的一个特定方面。为了解释我们正在做的事情，我们穿插了构造过程和一个构造实例。

第 1 部分。构造以以下方式开始。

因为 $P^{\prime}$ 是 MPCP 的一个实例，匹配必须以这张多米诺骨牌开始。因此，底部字符串正确地以 $C_{1}=q_{0} w_{1} w_{2} \cdots w_{n}$ 开始，这是 $M$ 在 $w$ 上的接受计算历史中的第一个格局，如下图所示。

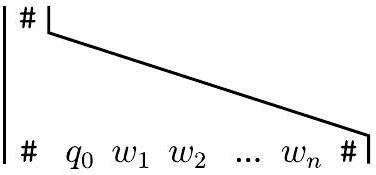
图 5.16

MPCP 匹配的开始

在此部分匹配的描绘中，底部字符串由 $\# q_{0} w_{1} w_{2} \cdots w_{n} \#$ 组成，而顶部字符串仅由 $\#$ 组成。为了获得匹配，我们需要扩展顶部字符串以匹配底部字符串。我们提供额外的多米诺骨牌以允许这种扩展。这些额外的多米诺骨牌通过强制 $M$ 的单步模拟，使得 $M$ 的下一个格局出现在底部字符串的扩展中。

在第 2、3 和 4 部分中，我们向 $P^{\prime}$ 添加执行模拟主要部分的多米诺骨牌。第 2 部分处理磁头向右移动，第 3 部分处理磁头向左移动，第 4 部分处理不与磁头相邻的纸带单元格。

第 2 部分。对于每个 $a, b \in \Gamma$ 和每个 $q, r \in Q$ 且 $q \neq q_{\text {reject}}$，

第 3 部分。对于每个 $a, b, c \in \Gamma$ 和每个 $q, r \in Q$ 且 $q \neq q_{\text {reject}}$，

第 4 部分。对于每个 $a \in \Gamma$，

现在我们举一个假设的例子来说明我们目前所构建的内容。令 $\Gamma=\{0,1,2, \sqcup\}$。假设 $w$ 是字符串 $0100$，并且 $M$ 的起始状态是 $q_{0}$。在状态 $q_{0}$ 中，读取一个 $0$ 后，假设转移函数规定 $M$ 进入状态 $q_{7}$，在纸带上写入一个 $2$，并将磁头向右移动。换句话说，$\delta\left(q_{0}, 0\right)=\left(q_{7}, 2, \mathrm{R}\right)$。

第 1 部分将多米诺骨牌

放入 $P^{\prime}$ 中，匹配开始

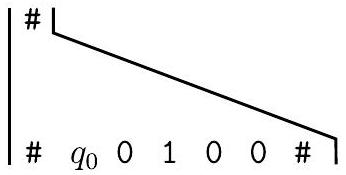
此外，第 2 部分将多米诺骨牌

放入 $P^{\prime}$，因为 $\delta\left(q_{0}, 0\right)=\left(q_{7}, 2, \mathrm{R}\right)$，第 4 部分将多米诺骨牌

放入 $P^{\prime}$，因为 $0,1,2$ 和 $\sqcup$ 是 $\Gamma$ 的成员。结合第 5 部分，这使我们能够将匹配扩展到

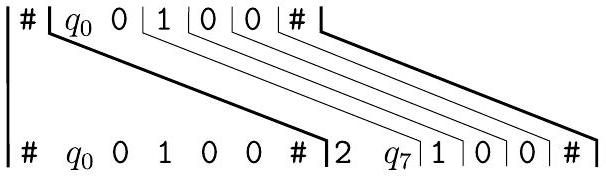
因此，第 2、3 和 4 部分的多米诺骨牌允许我们通过在第一个格局之后添加第二个格局来扩展匹配。我们希望这个过程继续下去，添加第三个格局，然后是第四个，依此类推。为此，我们需要再添加一张多米诺骨牌来复制符号 $\#$。

第 5 部分。

第一张多米诺骨牌允许我们复制标记格局之间分隔的符号 $\#$。此外，第二张多米诺骨牌允许我们在格局末尾添加一个空白符号 $\sqcup$，以模拟当我们写入格局时被抑制的无限多个右侧空白。

继续举例，假设在状态 $q_{7}$ 中，读取一个 $1$ 后，$M$ 进入状态 $q_{5}$，写入一个 $0$，并将磁头向右移动。也就是说，$\delta\left(q_{7}, 1\right)= \left(q_{5}, 0, \mathrm{R}\right)$。那么我们有多米诺骨牌

所以最新的部分匹配扩展到

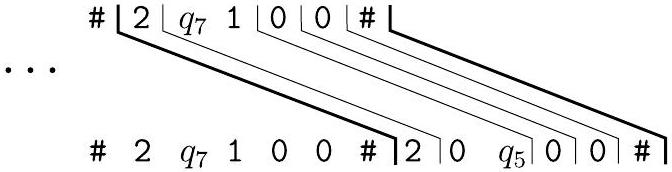
然后，假设在状态 $q_{5}$ 中，读取一个 $0$ 后，$M$ 进入状态 $q_{9}$，写入一个 $2$，并将磁头向左移动。所以 $\delta\left(q_{5}, 0\right)=\left(q_{9}, 2, \mathrm{~L}\right)$。那么我们有多米诺骨牌

第一个是相关的，因为磁头左侧的符号是 $0$。前面的部分匹配扩展到

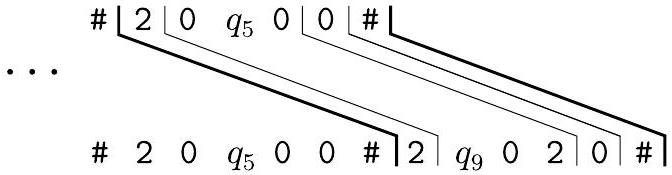
请注意，当我们构造一个匹配时，我们被迫模拟 $M$ 在输入 $w$ 上的行为。这个过程一直持续到 $M$ 达到停机状态。如果出现接受状态，我们希望部分匹配的顶部与底部“赶上”，以便匹配完成。我们可以通过添加额外的多米诺骨牌来安排这种情况。

第 6 部分。对于每个 $a \in \Gamma$，

此步骤的效果是在图灵机停机状态后添加“伪步骤”，其中磁头“吃掉”相邻符号直到没有剩余。继续举例，如果机器在接受状态停机状态时的部分匹配是

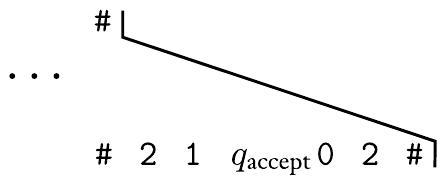
我们刚刚添加的多米诺骨牌允许匹配继续：

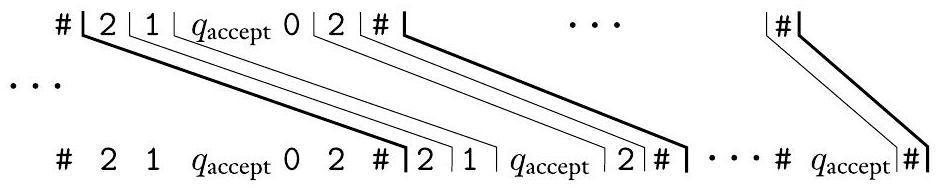
第 7 部分。最后，我们添加多米诺骨牌

并完成匹配：

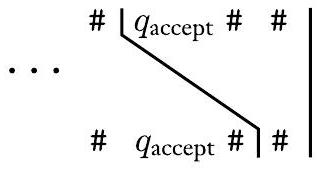
这样就完成了 $P^{\prime}$ 的构造。回想一下， $P^{\prime}$ 是 MPCP 的一个实例，其中匹配模拟 $M$ 在 $w$ 上的计算。为了完成证明，我们回想一下 MPCP 与 PCP 的不同之处在于，匹配必须从列表中的第一张多米诺骨牌开始。如果我们将 $P^{\prime}$ 视为 PCP 的实例而不是 MPCP 的实例，那么无论 $M$ 是否接受 $w$，它显然都具有匹配。你能找到它吗？（提示：它非常短。）

我们现在展示如何将 $P^{\prime}$ 转换为 $P$，一个 PCP 的实例，它仍然模拟 $M$ 在 $w$ 上的行为。我们通过一个有点技术性的技巧来做到这一点。这个想法是，将匹配必须从第一张多米诺骨牌开始的要求直接构建到问题实例本身中，使其自动强制执行。之后，就不再需要这个要求了。我们引入一些符号来实现这个想法。

令 $u=u_{1} u_{2} \cdots u_{n}$ 为任意长度为 $n$ 的字符串。将 $\star u, u \star$ 和 $\star u \star$ 定义为三个字符串

这里，$\star u$ 在 $u$ 中的每个字符前添加符号 ，$u \star$ 在 $u$ 中的每个字符后添加一个 ，而 $\star u \star$ 则在 $u$ 中的每个字符前和后都添加一个 *。

要将 $P^{\prime}$ 转换为 PCP 的实例 $P$，我们执行以下操作。如果 $P^{\prime}$ 是集合

我们令 $P$ 为集合

将 $P$ 视为 PCP 的实例，我们看到唯一可能开始匹配的多米诺骨牌是第一张，

因为它是在上方和下方都以相同符号（即 ）开始的唯一一张。除了强制匹配从第一张多米诺骨牌开始之外， 的存在不会影响可能的匹配，因为它们只是与原始符号交错。原始符号现在出现在匹配的偶数位置。多米诺骨牌

的存在是为了让上方在匹配的末尾添加额外的 *。