17.3 NP类
正如我们在7.2节中观察到的,我们可以在许多问题中避免暴力搜索并获得多项式时间解。然而,在某些其他问题(包括许多有趣和有用的问题)中,避免暴力搜索的尝试并未成功,并且尚未知道存在解决这些问题的多项式时间算法。
为什么我们未能为这些问题找到多项式时间算法?我们不知道这个重要问题的答案。也许这些问题具有尚未被发现的、基于未知原理的多项式时间算法。或者可能其中一些问题根本无法在多项式时间内解决。它们可能本质上是困难的。
关于这个问题的一个显著发现表明,许多问题的复杂性是相互关联的。一个此类问题的多项式时间算法可以用来解决一整类问题。为了理解这种现象,让我们从一个例子开始。
在有向图 $G$ 中的哈密顿路径是一条有向路径,它恰好经过每个节点一次。我们考虑测试有向图是否包含连接两个指定节点的哈密顿路径的问题,如下图所示。令
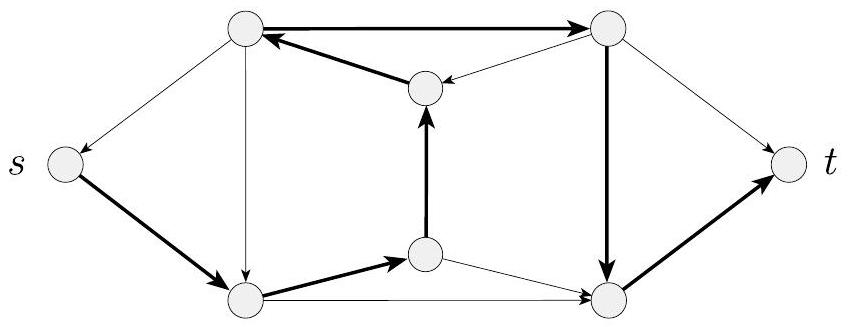
图 7.17
哈密顿路径恰好经过每个节点一次
我们可以通过修改定理7.14中给出的PATH的暴力算法,轻松地获得HAMPATH问题的指数时间算法。我们只需要添加一个检查,以验证潜在路径是哈密顿的。没有人知道HAMPATH是否可以在多项式时间内解决。
HAMPATH问题具有一种称为多项式可验证性的特性,这对于理解其复杂性很重要。尽管我们不知道一种快速(即多项式时间)方法来确定一个图是否包含哈密顿路径,但如果通过某种方式(可能使用指数时间算法)发现了这样一条路径,我们可以通过简单地呈现它来轻松说服其他人它的存在。换句话说,验证哈密顿路径的存在可能比确定它的存在要容易得多。
另一个多项式可验证的问题是合数。回想一下,一个自然数是合数,如果它是两个大于1的整数的乘积(即,合数不是素数)。令
我们可以很容易地验证一个数字是否是合数——所需要的只是该数字的一个约数。最近,发现了一种测试一个数字是素数还是合数的多项式时间算法,但它比前面验证合数的方法复杂得多。
有些问题可能不是多项式可验证的。例如,考虑HAMPATH的补集 $\overline{H A M P A T H}$。即使我们能够(以某种方式)确定一个图不包含哈密顿路径,我们也不知道别人验证其不存在的方法,除非使用相同的指数时间算法进行最初的确定。下面是正式定义。
定义 7.18
语言 $A$ 的验证器是一个算法 $V$,其中
我们只根据 $w$ 的长度来衡量验证器的时间,因此多项式时间验证器在 $w$ 的长度上以多项式时间运行。如果语言 $A$ 具有多项式时间验证器,则称其为多项式可验证的。
验证器使用附加信息(在定义7.18中用符号 $c$ 表示)来验证字符串 $w$ 是 $A$ 的成员。此信息称为 $A$ 中成员资格的证书或证明。请注意,对于多项式验证器,证书具有多项式长度(相对于 $w$ 的长度),因为这是验证器在其时间限制内可以访问的全部内容。让我们将此定义应用于HAMPATH和COMPOSITES语言。
对于HAMPATH问题,字符串 $\langle G, s, t\rangle \in H A M P A T H$ 的证书就是一条从 $s$ 到 $t$ 的哈密顿路径。对于COMPOSITES问题,合数 $x$ 的证书就是它的一个约数。在这两种情况下,当给定证书时,验证器可以在多项式时间内检查输入是否在语言中。
定义 7.19
NP是具有多项式时间验证器的语言类。
NP类很重要,因为它包含许多具有实际意义的问题。从前面的讨论中,HAMPATH和COMPOSITES都是NP的成员。正如我们所提到的,COMPOSITES也是P的成员,P是NP的子集;但证明这个更强的结果要困难得多。术语NP来自非确定性多项式时间,并且源自使用非确定性多项式时间图灵机的另一种表征。NP中的问题有时称为NP问题。
以下是一个非确定性图灵机(NTM),它在非确定性多项式时间内判定HAMPATH问题。回想一下,在定义7.9中,我们将非确定性机器的时间定义为最长计算分支所使用的时间。
$N_{1}=$ "在输入 $\langle G, s, t\rangle$ 上,其中 $G$ 是一个具有节点 $s$ 和 $t$ 的有向图:
- 写下 $m$ 个数字的列表,$p_{1}, \ldots, p_{m}$,其中 $m$ 是 $G$ 中的节点数。列表中的每个数字都是非确定性地选择的,介于 1 和 $m$ 之间。
- 检查列表中是否有重复。如果发现任何重复,则拒绝。
- 检查 $s=p_{1}$ 和 $t=p_{m}$。如果任何一个失败,则拒绝。
- 对于 1 到 $m-1$ 之间的每个 $i$,检查 $(p_{i}, p_{i+1})$ 是否是 $G$ 的一条边。如果任何一个不是,则拒绝。否则,所有测试都已通过,因此接受。"
为了分析这个算法并验证它在非确定性多项式时间内运行,我们检查它的每个阶段。在阶段1中,非确定性选择显然在多项式时间内运行。在阶段2和3中,每个部分都是一个简单的检查,因此它们总共在多项式时间内运行。最后,阶段4也显然在多项式时间内运行。因此,该算法在非确定性多项式时间内运行。
定理 7.20
一个语言在NP中当且仅当它被某个非确定性多项式时间图灵机判定。
证明思路 我们展示如何将多项式时间验证器转换为等效的多项式时间NTM,反之亦然。NTM通过猜测证书来模拟验证器。验证器通过使用接受分支作为证书来模拟NTM。
证明 对于本定理的正向,设 $A \in \mathrm{NP}$ 并证明 $A$ 被一个多项式时间NTM $N$ 判定。设 $V$ 是 $A$ 的多项式时间验证器,根据NP的定义存在。假设 $V$ 是一个在时间 $n^{k}$ 内运行的图灵机,并构造 $N$ 如下。
$N=$ "在长度为 $n$ 的输入 $w$ 上:
- 非确定性地选择长度至多为 $n^{k}$ 的字符串 $c$。
- 在输入 $\langle w, c\rangle$ 上运行 $V$。
- 如果 $V$ 接受,则接受;否则,拒绝。"
为了证明定理的另一个方向,假设 $A$ 被一个多项式时间NTM $N$ 判定,并构造一个多项式时间验证器 $V$ 如下。
$V=$ "在输入 $\langle w, c\rangle$ 上,其中 $w$ 和 $c$ 是字符串:
- 在输入 $w$ 上模拟 $N$,将 $c$ 的每个符号视为在每一步进行非确定性选择的描述(如定理3.16的证明中所示)。
- 如果 $N$ 的这个计算分支接受,则接受;否则,拒绝。"
我们将非确定性时间复杂度类 NTIME$(t(n))$ 定义为类似于确定性时间复杂度类 TIME$(t(n))$。
定义
7.21
$\mathbf{N T I M E}(\boldsymbol{t}(\boldsymbol{n}))=\{L \mid L$ 是由一个 $O(t(n))$ 时间非确定性图灵机判定的语言\}。
推论 7.22
$\mathrm{NP}=\bigcup_{k} \operatorname{NTIME}\left(n^{k}\right)$。
NP类对合理非确定性计算模型的选择不敏感,因为所有这些模型都是多项式等价的。在描述和分析非确定性多项式时间算法时,我们遵循前面关于确定性多项式时间算法的约定。非确定性多项式时间算法的每个阶段必须在合理非确定性计算模型上具有显而易见的非确定性多项式时间实现。我们分析算法以表明每个分支最多使用多项式个阶段。
NP中的问题示例
无向图中的团是一个子图,其中任意两个节点都由一条边连接。一个 $k$-团是一个包含 $k$ 个节点的团。图7.23展示了一个包含一个5-团的图。
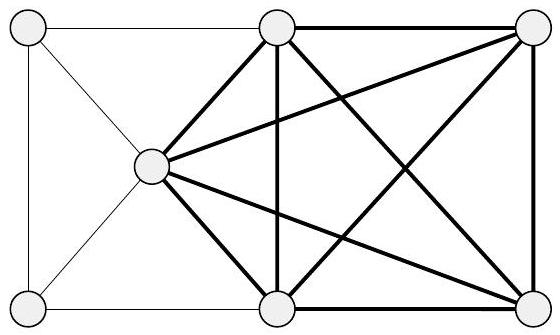
图 7.23
一个包含5-团的图
团问题是确定一个图是否包含指定大小的团。令
CLIQUE $=\{\langle G, k\rangle \mid G$ 是一个包含 $k$-团的无向图\}。
定理 7.24
CLIQUE在NP中。
证明思路 团就是证书。
证明 以下是CLIQUE的验证器 $V$。
$V=$ "在输入 $\langle\langle G, k\rangle, c\rangle$ 上:
- 测试 $c$ 是否是 $G$ 中具有 $k$ 个节点的子图。
- 测试 $G$ 是否包含连接 $c$ 中所有节点的边。
- 如果两者都通过,则接受;否则,拒绝。"
替代证明 如果您倾向于从非确定性多项式时间图灵机的角度思考NP,您可以通过给出一个判定CLIQUE的非确定性多项式时间图灵机来证明这个定理。观察这两个证明之间的相似性。
$N=$ "在输入 $\langle G, k\rangle$ 上,其中 $G$ 是一个图:
- 非确定性地选择 $G$ 中 $k$ 个节点的子集 $c$。
- 测试 $G$ 是否包含连接 $c$ 中所有节点的边。
- 如果是,则接受;否则,拒绝。"
接下来,我们考虑关于整数算术的子集和问题(SUBSET-SUM)。我们给定一个数字集合 $x_{1}, \ldots, x_{k}$ 和一个目标数字 $t$。我们想确定该集合是否包含一个加起来等于 $t$ 的子集合。
因此,
例如,$\langle\{4,11,16,21,27\}, 25\rangle \in$ SUBSET-SUM 因为 $4+21=25$。注意,$\left\{x_{1}, \ldots, x_{k}\right\}$ 和 $\left\{y_{1}, \ldots, y_{l}\right\}$ 被认为是多重集,因此允许元素重复。
定理 7.25
SUBSET-SUM在NP中。
证明思路 子集就是证书。
证明 以下是SUBSET-SUM的验证器 $V$。
$V=$ "在输入 $\langle\langle S, t\rangle, c\rangle$ 上:
- 测试 $c$ 是否是加起来等于 $t$ 的数字集合。
- 测试 $S$ 是否包含 $c$ 中的所有数字。
- 如果两者都通过,则接受;否则,拒绝。"
替代证明 我们也可以通过为SUBSET-SUM给出一个非确定性多项式时间图灵机来证明这个定理,如下所示。
$N=$ "在输入 $\langle S, t\rangle$ 上:
- 非确定性地选择 $S$ 中数字的一个子集 $c$。
- 测试 $c$ 是否是加起来等于 $t$ 的数字集合。
- 如果测试通过,则接受;否则,拒绝。"
请注意,这些集合的补集,$\overline{\text { CLIQUE }}$ 和 $\overline{\text { SUBSET-SUM }}$,并非明显是NP的成员。验证某个东西不存在似乎比验证它存在更困难。我们创建一个单独的复杂度类,称为coNP,它包含NP中语言的补集。我们不知道coNP是否与NP不同。
P 对 NP 问题
正如我们一直所说,NP是可以在非确定性图灵机上以多项式时间解决的语言类;或者,等效地,它是在多项式时间内可以验证成员资格的语言类。P是可以在多项式时间内测试成员资格的语言类。我们总结这些信息如下,其中我们粗略地将多项式时间可解决称为“快速”可解决。
$\mathrm{P}=$ 成员资格可以快速判定的语言类。
$\mathrm{NP}=$ 成员资格可以快速验证的语言类。
我们已经提出了NP成员但尚未知道是否在P中的语言示例,例如HAMPATH和CLIQUE。多项式可验证性的力量似乎比多项式可判定性的力量大得多。但是,尽管难以想象,P和NP可能相等。我们无法证明NP中存在任何不在P中的语言。
P等于NP的问题是理论计算机科学和当代数学中最大的未解决问题之一。如果这些类相等,那么任何多项式可验证的问题都将是多项式可判定的。大多数研究人员认为这两个类不相等,因为人们已经投入了巨大的努力来寻找NP中某些问题的多项式时间算法,但没有成功。研究人员也曾尝试证明这些类不相等,但这将需要证明不存在替代暴力搜索的快速算法。这样做目前超出了科学范围。下图显示了两种可能性。
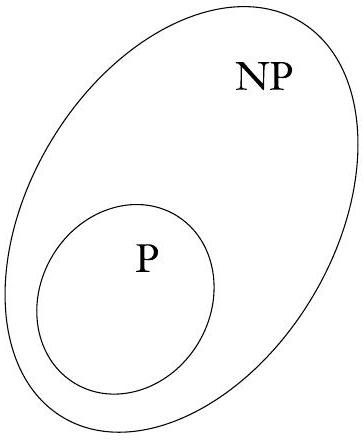
图 7.26
这两种可能性之一是正确的
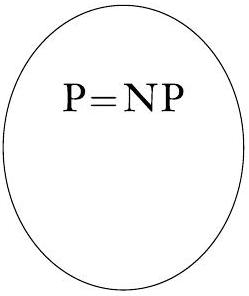
图 7.26
这两种可能性之一是正确的
目前已知用于判定NP中语言的最佳确定性方法使用指数时间。换句话说,我们可以证明
但我们不知道NP是否包含在较小的确定性时间复杂度类中。