1定义 7.28
函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$ 是多项式时间可计算函数,如果存在一个多项式时间图灵机 $M$,当其在任何输入 $w$ 上启动时,只在纸带上输出 $f(w)$ 并停机。
定义 7.29
语言 $A$ 在多项式时间映射归约(或简称为多项式时间归约)到语言 $B$,记作 $A \leq_{\mathrm{P}} B$,如果存在一个多项式时间可计算函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$,使得对于每一个 $w$,
函数 $f$ 被称为 A 到 B 的多项式时间归约。
这两条定义是本节的技术核心,它们用严格的数学语言定义了前文所述的“有效归约”。
定义 7.28: 多项式时间可计算函数
- 这是什么: 这个定义是为“高效的转换器”给出的正式名称。这个转换器本身是一个函数 $f$。
- 输入和输出: 函数 $f$ 的输入是一个字符串 $w$ (来自某个字母表 $\Sigma^*$),输出是另一个字符串 $f(w)$。在我们的应用场景里,$w$ 是问题 A 的一个实例编码,$f(w)$ 是问题 B 的一个实例编码。
- “多项式时间可计算”的含义: 意味着存在一个图灵机 $M$(可以理解为一个计算机算法),这个算法具备以下特点:
- 输入: 算法的输入是 $w$。
- 输出: 算法的输出是 $f(w)$。
- 效率: 算法的运行时间是多项式时间的。也就是说,如果输入字符串 $w$ 的长度是 $n$,算法的运行步数不会超过 $c \cdot n^k$(其中 $c$ 和 $k$ 是某个固定的常数)。
- 停机: 算法必须在计算出 $f(w)$ 后停机。
定义 7.29: 多项式时间映射归约
- 这是什么: 这个定义正式描述了问题 A 如何“有效地”归约到问题 B。
- 记号: $A \leq_{\mathrm{P}} B$。
- $\le$: 表示归约关系,暗示 A 的难度“小于等于”B 的难度。
- 下标 $P$: 强调这是“多项式时间”(Polynomial-time)归约。
- 归约的条件: 要想声称 $A \leq_{\mathrm{P}} B$,必须满足以下两个条件:
- 条件一:存在一个转换函数 f: 这个 $f$ 必须是多项式时间可计算函数(根据定义 7.28)。这就是对“高效转换”的要求。
- 条件二:保持成员关系: 这个函数 $f$ 必须巧妙地构建,以至于它能保持“是”或“否”的答案不变。具体来说,对于任何一个来自问题 A 的输入实例 $w$:
- 如果 $w$ 是问题 A 的一个“是”实例 (即 $w \in A$),那么经过 $f$ 转换后得到的 $f(w)$,也必须是问题 B 的一个“是”实例 (即 $f(w) \in B$)。
- 反之,如果 $w$ 是问题 A 的一个“否”实例 (即 $w \notin A$),那么转换后的 $f(w)$ 也必须是问题 B 的一个“否”实例 (即 $f(w) \notin B$)。
- 这两个方向合在一起,就是逻辑上的“当且仅当”关系:$w \in A \Longleftrightarrow f(w) \in B$。
- $f: \Sigma^{*} \longrightarrow \Sigma^{*}$:
- $f$: 函数的名字。
- $\Sigma^{*}$: 表示由字母表 $\Sigma$ 中所有字符组成的所有有限长度字符串的集合。例如,如果 $\Sigma = \{0, 1\}$,那么 $\Sigma^*$ 就包含 "", 0, 1, 00, 01, 10, 11, ...
- $\longrightarrow$: 表示一个从左边集合到右边集合的映射(函数)。
- 整句话表示:$f$ 是一个函数,它的输入是任意字符串,输出也是任意字符串。
- $A \leq_{\mathrm{P}} B$:
- $A, B$: 代表两个语言(即两个判定问题)。
- $\leq_{\mathrm{P}}$: “在多项式时间内可归约到”的符号。
- $w \in A \Longleftrightarrow f(w) \in B$:
- $w \in A$: 字符串 $w$ 是语言 A 的一个成员。意味着对于问题A,输入 $w$ 的答案是“是”。
- $f(w) \in B$: 经过函数 $f$ 转换后的字符串 $f(w)$ 是语言 B 的一个成员。意味着对于问题B,输入 $f(w)$ 的答案是“是”。
- $\Longleftrightarrow$: 当且仅当。确保了答案的一致性。$w$ 的答案是“是” 当且仅当 $f(w)$ 的答案是“是”。这也同时隐含了 $w$ 的答案是“否” 当且仅当 $f(w)$ 的答案是“否”。
假设我们要证明 “3-着色问题” $\le_P$ “SAT问题”。(这是一个经典的例子,虽然这里还没讲3-着色,但可以用来理解归约思想)
- 问题 A (3-着色): 给定一个图 $G$,问能否用红、黄、蓝三种颜色给图中的每个顶点着色,使得任意两个相邻的顶点颜色都不同?
- 问题 B (SAT): 给定一个布尔公式 $\phi$,问是否存在一组真假赋值使 $\phi$ 为真?
构造一个多项式时间归约函数 f:
- 输入: 图 $G=(V, E)$,其中 $V$ 是顶点集,$E$ 是边集。
- 输出: 一个布尔公式 $\phi = f(G)$。
- 构造过程 (多项式时间):
- 变量: 对每个顶点 $v \in V$ 和每种颜色 $c \in \{\text{红, 黄, 蓝}\}$,我们创建一个布尔变量 $x_{v,c}$。$x_{v,c}$ 为 TRUE 表示“顶点 $v$ 被染成颜色 $c$”。
- 公式部分1 (每个顶点至少一种颜色): 对每个顶点 $v$,构造子句 $(x_{v,红} \vee x_{v,黄} \vee x_{v,蓝})$。把所有顶点的这类子句用 $\wedge$ 连接起来。这确保每个顶点都必须被染色。
- 公式部分2 (每个顶点至多一种颜色): 对每个顶点 $v$,构造子句 $(\neg x_{v,红} \vee \neg x_{v,黄}) \wedge (\neg x_{v,红} \vee \neg x_{v,蓝}) \wedge (\neg x_{v,黄} \vee \neg x_{v,蓝})$。这确保一个顶点不能同时被染成两种颜色。
- 公式部分3 (相邻顶点颜色不同): 对图中的每一条边 $(u, v) \in E$,构造子句 $(\neg x_{u,红} \vee \neg x_{v,红}) \wedge (\neg x_{u,黄} \vee \neg x_{v,黄}) \wedge (\neg x_{u,蓝} \vee \neg x_{v,蓝})$。这确保如果 $u$ 和 $v$ 相邻,它们不能被染成相同的颜色。
- 最终的公式 $\phi$ 就是把以上所有部分用 $\wedge$ 连接起来。这个构造过程显然是多项式时间的,因为变量和子句的数量都与图的顶点数和边数成多项式关系。
- 验证 $w \in A \iff f(w) \in B$:
- (=>): 如果图 $G$ 是可3-着色的,那么存在一个合法的染色方案。根据这个方案,我们可以给所有变量 $x_{v,c}$ 赋值(如果 $v$ 染成红色,就令 $x_{v,红}=1, x_{v,黄}=0, x_{v,蓝}=0$)。这个赋值方式会使得我们构造的公式 $\phi$ 的所有子句都为真,因此 $\phi$ 是可满足的。
- (<=): 如果公式 $\phi$ 是可满足的,那么存在一组满足赋值。根据这组赋值,我们可以为图 $G$ 的顶点染色(如果 $x_{v,红}=1$,就把 $v$ 染成红色)。由于 $\phi$ 的所有子句都被满足了,这个染色方案必然满足“每个顶点都有色”、“每个顶点只有一种色”和“相邻顶点颜色不同”这三个条件。因此,图 $G$ 是可3-着色的。
- 归约不是求解: 归约函数 $f$ 本身不解决问题A或问题B。它只是一个“翻译官”,负责把问题A的“语言”翻译成问题B的“语言”,并且保证翻译的准确性(保持答案一致)和高效性(多项式时间)。
- 映射归约: 文中提到“映射归约”(mapping reduction),这是为了区别于其他更广义的归约类型(如图灵归约)。在 NP-完全理论中,我们主要使用的就是这种简单的映射归约。
本段给出了多项式时间归约 ($A \leq_{\mathrm{P}} B$) 的严格定义。它由两部分构成:一个在多项式时间内完成问题实例转换的可计算函数 $f$,以及该函数必须保持问题答案“是”或“否”不变的核心性质 ($w \in A \iff f(w) \in B$)。这个工具是证明新问题是NP-完全的“瑞士军刀”。
本段的目的是将NP-完全性理论的基石——归约,进行形式化和严格化。有了这个精确的定义,我们才能进行严谨的数学证明,建立起不同问题之间的难度联系。
多项式时间归约就像一个“万能转换插头”。你有来自中国电器(问题A),想在欧洲的插座(解决问题B的算法)上使用。
- 函数 f: 就是那个转换插头。
- 多项式时间可计算: 这个插头必须设计简单,制作快速。
- $w \in A \iff f(w) \in B$: 这个插头必须能正确工作。把中国电器的插头插进去,它能正确地连接到欧洲插座的对应火线、零线和地线上,确保电器能正常工作(答案一致)。如果插头接错了线,电器就烧了,这个归约就失败了。
想象你是一个间谍(解决问题A的算法),要去一个敌国(问题B)执行任务。你不会说敌国语言。
- 函数 f: 是一位同声传译员,能帮你把中文(问题A实例)瞬间翻译成敌国语言(问题B实例)。
- 多项式时间: 这位传译员必须反应极快,不能你问一句他想半天。
- $w \in A \iff f(w) \in B$: 传译员必须翻译得完全准确无误。“我要一个苹果”不能被翻译成“我要一颗炸弹”。你问题的答案必须在翻译后保持不变。
7 多项式时间归约的性质
📜 [原文7]
多项式时间归约是第5.3节中定义的映射归约的高效模拟。还有其他形式的高效归约,但多项式时间归约是一种简单形式,足以满足我们的目的,因此我们在此不讨论其他形式。图7.30说明了多项式时间归约。
[^0]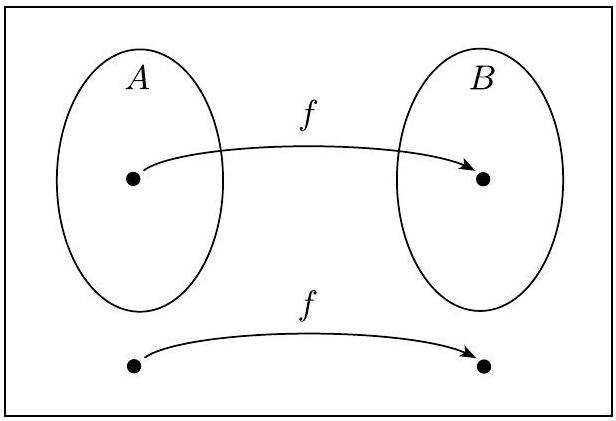
图 7.30
将 A 归约到 B 的多项式时间函数 $f$
与普通映射归约一样,A 到 B 的多项式时间归约提供了一种将 A 中的成员资格测试转换为 B 中的成员资格测试的方法——但现在转换是高效完成的。为了测试 $w \in A$,我们使用归约 $f$ 将 $w$ 映射到 $f(w)$,然后测试 $f(w) \in B$。
这段话是对多项式时间归约工作流程的图文并茂的解释。
- 与旧概念的联系:
- 再次强调多项式时间归约是映射归约的一个“高效”版本。它继承了映射归约“问题转换”的核心思想,但增加了“多项式时间”这一关键约束。
- 提及存在其他形式的归约,但为了简化讨论,本书只关注这一种最常用、最基本的类型。
- 图 7.30 的解释:
- 输入 $w$: 这是我们想要解决的原始问题 A 的一个实例。
- 计算 $f(w)$: 这是归约的核心步骤,由一个多项式时间算法(图中的 poly-time function f)执行。这个算法接收 $w$ 作为输入,经过一系列计算,生成一个新的字符串 $f(w)$。
- 输出 $f(w)$: 这是转换后的结果,现在它变成了问题 B 的一个实例。
- B 的决策算法: 这是解决问题 B 的一个“黑盒子”算法(图中的 Decider for B)。它接收 $f(w)$ 作为输入。
- 接受/拒绝: B的决策算法会给出一个答案,“接受”(accept)或“拒绝”(reject),这对应于 $f(w)$ 是否属于语言 B。
- 答案回传: 由于归约保证了 $w \in A \iff f(w) \in B$,所以 B 的决策算法给出的答案,直接就是我们对原始输入 $w$ 的答案。
- 工作流程总结:
- 要判断 $w$ 是否在语言 A 中,我们不需要直接设计一个针对 A 的算法。
- 第一步: 调用高效的“翻译官” $f$,把 $w$ 翻译成 $f(w)$。
- 第二步: 把翻译稿 $f(w)$ 交给能读懂它的专家(B的决策算法)。
- 第三步: 专家的结论就是我们最终的结论。
让我们继续用 3-着色 $\le_P$ SAT 的例子来走一遍这个流程。
- 问题 A: 3-着色问题
- 问题 B: SAT问题
- 输入 $w$: 一个简单的图 $G$,由三个顶点 $v_1, v_2, v_3$ 组成一个三角形。
- 计算 $f(w)$: 我们运行上一节描述的归约算法 $f$。
- 它会生成一堆变量:$x_{1,R}, x_{1,Y}, x_{1,B}, x_{2,R}, \dots, x_{3,B}$ (共9个)。
- 它会生成一个布尔公式 $\phi = f(G)$,这个公式很长,包含了类似这样的子句:
- $(x_{1,R} \vee x_{1,Y} \vee x_{1,B})$ (v1必须有颜色)
- $(\neg x_{1,R} \vee \neg x_{1,Y})$ (v1不能同时是红黄)
- $(\neg x_{1,R} \vee \neg x_{2,R})$ (v1和v2是邻居,不能都是红色)
- ... 等等
- B 的决策算法: 现在我们有一个解决 SAT 问题的黑盒子算法,我们称之为 SAT_Solver。
- 调用 SAT_Solver: 我们把生成的公式 $\phi$ 作为输入,调用 SAT_Solver(phi)。
- SAT_Solver 的工作: 它会尝试寻找满足 $\phi$ 的赋值。比如它可能找到一个赋值:$x_{1,R}=1, x_{2,Y}=1, x_{3,B}=1$,其他变量都为0。它发现这个赋值能让整个 $\phi$ 为真。
- SAT_Solver 的输出: “接受”(Accept),因为 $\phi$ 是可满足的。
- 最终结论: 因为 SAT_Solver 接受了 $f(G)$,我们就得出结论:原始的图 $G$ 是可以被3-着色的。
- 图示的误导: 图 7.30 可能会让人误以为解决 A 需要两个独立的步骤。在理论分析中,我们是将这两步看作一个整体。如果 $f$ 的运行时间是 $p_1(n)$,B的决策算法运行时间是 $p_2(m)$($m$是 $f(w)$ 的长度),那么解决 A 的总时间是 $p_1(n) + p_2(p_1(n))$,这仍然是一个关于 $n$ 的多项式,所以整个过程是高效的。
- 黑盒子的存在性: 在证明 $A \le_P B$ 时,我们并不需要真的实现一个解决B的算法。我们只需要假设存在一个这样的黑盒子,然后利用它来构造解决A的算法。
本段通过流程图和文字描述,清晰地展示了多项式时间归约在实际判定问题中的应用方式:将一个未知问题 A 的实例,通过一个高效的转换函数 $f$,变成一个已知问题 B 的实例,然后利用 B 的解法来得出 A 的答案。
本段旨在帮助读者直观地理解归约过程的“机械”步骤,将抽象的定义转化为一个可操作的、分步的流程图,加深对归约如何作为一种“算法构建工具”的理解。
这就像一个自动翻译和问答系统。
- 你用中文向系统提一个问题 $w$(“北京最好的烤鸭店是哪家?”)。
- 系统内部有一个超高速的中文到英文翻译模块 $f$(多项式时间)。它把你的问题翻译成 $f(w)$ ("Which is the best roast duck restaurant in Beijing?")。
- 系统还有一个强大的英文问答数据库(B的决策算法)。
- 它用翻译后的英文问题 $f(w)$ 去查询数据库,得到了答案("Quanjude")。
- 系统直接把这个英文答案作为你中文问题的最终答案。整个流程依赖于翻译模块的高效和准确。
想象你是一个不会做饭的人(你无法直接解决问题A),但你有一个可以即时文字转语音的APP(函数f)和一个能听懂任何指令并做出任何菜肴的机器人厨师(B的决策算法)。
- 你想吃“宫保鸡丁”(输入w)。
- 你打开APP,输入“宫保鸡丁”四个字,APP立刻把它转换成语音指令(计算f(w))。
- 机器人厨师听到语音指令,立刻开始切菜、炒菜,几分钟后端出了一盘宫保鸡丁(B的决策算法执行并给出结果)。
- 你成功地“解决”了“做一盘宫保鸡丁”的问题。这里的核心就是那个高效的APP(多项式时间归约)。
8 归约与P类问题的关系
📜 [原文8]
如果一种语言可以多项式时间归约到一个已知具有多项式时间解的语言,那么我们就获得了原语言的多项式时间解,如下面的定理所示。
定理 7.31
如果 $A \leq_{\mathrm{P}} B$ 且 $B \in \mathrm{P}$,则 $A \in \mathrm{P}$。
证明 令 $M$ 是决定 B 的多项式时间算法,$f$ 是从 A 到 B 的多项式时间归约。我们描述一个决定 A 的多项式时间算法 $N$ 如下。
$N=$ “在输入 $w$ 上:
- 计算 $f(w)$。
- 在输入 $f(w)$ 上运行 $M$,并输出 $M$ 输出的任何结果。”
由于 $f$ 是从 A 到 B 的归约,所以当 $f(w) \in B$ 时,$w \in A$。因此,$M$ 在 $w \in A$ 时接受 $f(w)$。此外,$N$ 在多项式时间内运行,因为它的两个阶段都在多项式时间内运行。请注意,阶段2在多项式时间内运行,因为两个多项式的复合仍然是多项式。
这段话阐述了多项式时间归约最重要的一个性质:它可以传递“容易性”。
定理 7.31 的陈述:
- 前提1: $A \leq_{\mathrm{P}} B$ (问题A可以高效地归约到问题B)。
- 前提2: $B \in \mathrm{P}$ (问题B是“容易解决”的,即存在多项式时间算法)。
- 结论: $A \in \mathrm{P}$ (那么问题A也是“容易解决”的)。
- 通俗解释: 如果一个问题A可以被高效地“翻译”成一个已知是简单的问题B,那么问题A本身也是简单的。
证明过程的拆解:
这个证明构建了一个新的算法 $N$,用来解决问题 A。
- 算法 N 的设计:
- 目标: 设计一个能在多项式时间内判定 $w \in A$ 的算法 $N$。
- 输入: $w$,一个问题 A 的实例。
- 步骤1: 转换: 运行多项式时间归约函数 $f$,计算出 $f(w)$。因为 $f$ 是多项式时间的,所以这一步是高效的。
- 步骤2: 求解: 我们已知存在一个解决 B 的多项式时间算法 $M$。现在把上一步的结果 $f(w)$ 作为输入,运行算法 $M$。因为 $M$ 是多项式时间的,所以这一步也是高效的。
- 步骤3: 输出: 算法 $M$ 会输出“接受”或“拒绝”。算法 $N$ 不做任何修改,直接将 $M$ 的输出作为自己的最终输出。
- 正确性分析:
- 根据归约的定义,$w \in A \iff f(w) \in B$。
- 算法 $M$ 的功能是判定其输入是否属于 B。所以,$M$ 接受 $f(w) \iff f(w) \in B$。
- 将两者结合起来,得到:$w \in A \iff f(w) \in B \iff M \text{ 接受 } f(w)$。
- 算法 $N$ 的输出就是 $M$ 的输出,所以 $N$ 接受 $w \iff M \text{ 接受 } f(w)$。
- 综上,$N$ 接受 $w \iff w \in A$。这证明了算法 $N$ 的答案是正确的。
- 时间复杂度分析 (核心):
- 设输入 $w$ 的长度为 $n$。
- 步骤1的时间: 因为 $f$ 是多项式时间可计算的,所以计算 $f(w)$ 的时间是 $O(n^k)$,其中 $k$ 是某个常数。计算结果 $f(w)$ 的长度最大也是 $O(n^k)$。
- 步骤2的时间: 算法 $M$ 是多项式时间的。设其时间复杂度是 $O(m^j)$,其中 $m$ 是其输入的长度。在我们的场景中,输入是 $f(w)$,其长度为 $m=O(n^k)$。所以,运行 $M$ 的时间是 $O((n^k)^j) = O(n^{kj})$。
- 总时间: 算法 $N$ 的总时间是步骤1和步骤2的时间之和,即 $O(n^k) + O(n^{kj})$。因为 $k$ 和 $j$ 都是常数,所以 $kj$ 也是常数。这个总时间仍然是一个关于 $n$ 的多项式函数。
- 结论: 算法 $N$ 是一个多项式时间算法。
- 多项式的复合: “两个多项式的复合仍然是多项式” 这句话是关键。如果 $p_1(n) = n^k$,$p_2(m) = m^j$,那么它们的复合 $p_2(p_1(n)) = (n^k)^j = n^{kj}$,这显然还是一个多项式。
- 假设问题A是“排序问题”,问题B是“寻找序列中位数问题”。
- 我们知道存在一个归约 $A \le_P B$ (虽然不直观,但理论上可以构造)。假设这个归约 $f$ 的时间是 $O(n \log n)$。它把一个长度为 $n$ 的数组 $w$ 转换成一个用于求中位数的特殊结构 $f(w)$。
- 我们又知道,问题B(求中位数)本身是“容易的”,存在一个多项式时间算法 $M$,比如一个 $O(m)$ 的线性时间算法($m$是输入长度)。
- 根据定理7.31,我们可以构造一个解决排序问题的新算法 $N$:
- 输入数组 $w$ (长度n),花 $O(n \log n)$ 时间计算 $f(w)$。$f(w)$ 的长度可能是 $O(n \log n)$。
- 在 $f(w)$ 上运行中位数算法 $M$,花费时间 $O(\text{length of } f(w)) = O(n \log n)$。
- 总时间是 $O(n \log n) + O(n \log n) = O(n \log n)$。
- 因为 $O(n \log n)$ 是一个多项式时间(比 $n^2$ 快),所以我们得出结论:排序问题 $A$ 也在 P 中。这个结论是正确的,虽然我们用的方法很绕。
- 前提的重要性: 这个定理的威力在于它的前提。如果你不知道 $B \in P$,或者你的归约不是多项式时间的,那么这个结论就不成立。
- 难度的传递: 这个定理更常被用于其逆否命题:如果 $A \le_P B$ 且 $A \notin P$(A是难的),则 $B \notin P$(B也一定是难的)。这是证明一个问题是“困难”的常用手段。
定理7.31及其证明是NP-完全理论的基石之一。它精确地说明了为什么多项式时间归约能够将问题的“容易性”从一个问题传递到另一个问题。其核心在于“多项式的复合仍然是多项式”,保证了整个“翻译+求解”的流程仍然是高效的。
本段的目的是从理论上巩固多项式时间归约的意义。它告诉我们,这种归约关系 $A \le_P B$ 建立了一条从 B 到 A 的“效率高速公路”。一旦 B 点是可达的($B \in P$),那么 A 点也必然是可达的($A \in P$)。
这就像一个“技能传递”的规则。
- 前提1 ($A \le_P B$): 你学会“技能B”后,只需要很短的练习时间(多项式时间),就能掌握“技能A”。
- 前提2 ($B \in P$): “技能B”本身是一个很容易学会的技能(比如骑自行车)。
- 结论 ($A \in P$): 那么“技能A”(比如骑独轮车)也一定是一个很容易学会的技能。
证明过程就是:你先花时间学会骑自行车,然后花很短的练习时间,利用骑车的平衡感去学独轮车,总花费的时间还是很短。
想象一条生产线。
- $M$ (解决B的算法): 是一台超高速的包装机,能在1分钟内包装好任何递给它的标准尺寸的盒子。
- $f$ (归约函数): 是一台塑形机,能在30秒内把任何奇形怪状的产品(输入w)塑造成一个标准尺寸的盒子(输出f(w))。
- $N$ (解决A的算法): 就是整条生产线的工作流程。
- 定理7.31: 如果包装机很快($B \in P$),而且塑形机也很快($f$是多项式时间),那么从拿到一个不规则产品到最终把它包装好,整个过程也一定很快($A \in P$)。总时间就是30秒+1分钟=1.5分钟。
9 3SAT问题和到CLIQUE的归约引言
📜 [原文9]
在演示多项式时间归约之前,我们介绍 3SAT,这是可满足性问题的一个特例,其中所有公式都采用特殊形式。文字是布尔变量或被否定的布尔变量,如 $x$ 或 $\bar{x}$。子句是几个用 $\vee$ 连接的文字,如 $\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}} \vee x_{4}\right)$。布尔公式如果由几个用 $\wedge$ 连接的子句组成,则为合取范式(称为 cnf-公式),如
如果所有子句都包含三个文字,则为 3cnf-公式,如
设 $3 S A T=\{\langle\phi\rangle \mid \phi$ 是一个可满足的 3cnf-公式$\}$。如果一个赋值满足一个 cnf-公式,则每个子句必须至少包含一个评估为 1 的文字。
以下定理介绍了从 3SAT 问题到 CLIQUE 问题的多项式时间归约。
这段话的作用是引入一个比SAT更具体、在归约中更好用的“跳板”问题——3SAT,并预告将要展示一个从3SAT到CLIQUE(团问题)的归约实例。
- 引入 3SAT:
- 动机: 通用的SAT问题公式形式不固定,可以是任意复杂的逻辑表达式。为了方便进行归约证明,计算机科学家们找到了SAT的一个“简化版”特例——3SAT。这个“简化版”虽然形式上更规整,但其难度和通用的SAT是等价的(都是NP-完全的)。使用3SAT作为归约的起点,往往能让证明过程更清晰、更模式化。
- 从基本概念到3SAT: 作者逐步定义了构成 3SAT 的元素:
- 文字 (Literal): 一个最基本的单位,要么是一个变量 $x$,要么是它的否定 $\bar{x}$。
- 子句 (Clause): 若干个“文字”通过“或”($\vee$)运算连接起来。例如 $(x_1 \vee \bar{x_2})$。一个子句要想为TRUE,只需要其中至少一个文字为TRUE即可。
- 合取范式 (Conjunctive Normal Form, CNF): 若干个“子句”通过“与”($\wedge$)运算连接起来。例如 $(x_1 \vee x_2) \wedge (\bar{x_2} \vee x_3)$。一个CNF公式要想为TRUE,必须每一个子句都为TRUE。这种“AND of ORs”的结构非常规整。
- 3-CNF 公式: 一种特殊的CNF公式,要求每一个子句都恰好包含三个文字。
- 3SAT 问题: 就是判定一个给定的 3-CNF 公式是否可满足。
- CNF公式的可满足性条件:
- 这段话点出了判断一个CNF公式是否被满足的关键:“每个子句必须至少包含一个评估为 1 的文字。”
- 因为整个公式是子句的AND连接,所以整个公式为TRUE的前提是所有部分(子句)都为TRUE。而每个子句是文字的OR连接,所以一个子句为TRUE,当且仅当它包含的文字中至少有一个是TRUE。
- 预告下一个主题:
- 引出定理 7.32,明确指出接下来将要详细演示一个具体的多项式时间归约例子:如何将3SAT问题归约到CLIQUE问题。这不仅是一个练习,更是展示如何利用已知NP-完全问题(我们稍后会知道3SAT也是NP-complete)来证明新问题也是NP-完全的标准流程。
- $\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}} \vee x_{4}\right) \wedge\left(x_{3} \vee \overline{x_{5}} \vee x_{6}\right) \wedge\left(x_{3} \vee \overline{x_{6}}\right)$:
- 这是一个 CNF-公式 的例子。
- 它由三个子句构成,用 $\wedge$ 连接。
- 第一个子句是 $(x_1 \vee \bar{x_2} \vee \bar{x_3} \vee x_4)$,包含4个文字。
- 第二个子句是 $(x_3 \vee \bar{x_5} \vee x_6)$,包含3个文字。
- 第三个子句是 $(x_3 \vee \bar{x_6})$,包含2个文字。
- 因为它不是所有子句都恰好有3个文字,所以它不是一个 3-CNF 公式。
- $\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}}\right) \wedge\left(x_{3} \vee \overline{x_{5}} \vee x_{6}\right) \wedge\left(x_{3} \vee \overline{x_{6}} \vee x_{4}\right) \wedge\left(x_{4} \vee x_{5} \vee x_{6}\right)$:
- 这是一个 3-CNF-公式 的例子。
- 它由四个子句构成,用 $\wedge$ 连接。
- 每个子句(括号内的部分)都不多不少,正好包含三个文字。
- $3 S A T=\{\langle\phi\rangle \mid \phi \text { 是一个可满足的 3cnf-公式 }\}$:
- 这定义了 3SAT 语言。
- 结构与 SAT 的定义类似,但增加了一个限制条件:公式 $\phi$ 必须是 3-CNF 形式。
- 示例1 (3SAT实例):
- 公式 $\phi = (x \vee y \vee z) \wedge (\bar{x} \vee \bar{y} \vee z) \wedge (x \vee \bar{y} \vee \bar{z})$
- 这是不是一个 3SAT 问题?是的,因为它是3个子句的AND,每个子句都恰好有3个文字。
- 它是否可满足?我们来试试赋值 $x=1, y=0, z=1$。
- 第一个子句: $(1 \vee 0 \vee 1) = 1$ (OK)
- 第二个子句: $(\bar{1} \vee \bar{0} \vee 1) = (0 \vee 1 \vee 1) = 1$ (OK)
- 第三个子句: $(1 \vee \bar{0} \vee \bar{1}) = (1 \vee 1 \vee 0) = 1$ (OK)
- 所有子句都为真,所以整个公式为真。因此,这个公式是可满足的。
- 示例2 (非3SAT实例):
- 公式 $\psi = (x \vee y) \wedge (\bar{x} \vee z)$
- 这不是一个3SAT问题,因为子句中的文字数量是2,不是3。它是一个2SAT问题(2SAT问题其实是在P中的)。
- 3SAT vs SAT: 3SAT 是 SAT 的一个子集。所有 3-CNF 公式都是布尔公式,所以 3SAT 问题实例也是 SAT 问题实例。但反过来不成立。
- “恰好”三个文字: 严格的 3SAT 定义是每个子句恰好三个文字。有些定义会宽松到“最多”三个文字,但通过引入重复变量(如把 $(x \vee y)$ 写成 $(x \vee y \vee y)$)可以很容易地将“最多”转化为“恰好”。
- 归约的起点: 为什么不用更简单的 2SAT?因为 2SAT 是 P 问题,它不够“难”来充当 NP 世界的代表。3SAT 则是第一个在难度上产生“质变”的临界点。
本段为即将到来的第一个具体归约证明做好了铺垫。它定义了 3SAT 问题,一个结构更规整但难度不减的 SAT 特例。通过定义文字、子句、CNF 和 3-CNF,读者可以清晰地理解 3SAT 问题的形式化结构。这使得 3SAT 成为一个理想的、标准化的“已知难题”,可以作为后续证明其他问题是困难的“参照物”。
本段的目的是引入 3SAT 这一关键问题,并解释其组成结构。它是 NP-完全证明中一个极其常用的工具,是连接 SAT 和其他无数 NP-complete 问题的桥梁。
如果说SAT是“解决所有逻辑谜题”,那么3SAT就是“解决所有遵循‘规则A、规则B、规则C三者满足其一,并且规则D、规则E、规则F三者满足其一...’这种标准格式的逻辑谜题”。虽然格式被限制了,但谜题的本质难度没有降低。
想象你在处理一大堆法律合同(布尔公式)。
- SAT: 这些合同格式五花八门,有的条款嵌套十层深,有的用各种复杂的逻辑连接词,阅读起来很费劲。
- CNF: 你请了一个助理,把所有合同都重写成一种标准格式:“本合同生效,需同时满足以下所有条款组:条款组1,条款组2,...”。
- 3-CNF: 你又让助理把格式进一步标准化:“每个条款组里,不多不少,正好包含三个独立的条件,满足任意一个条件即可视为本条款组通过”。
- 3SAT问题: 就是问,对于这样一份被高度标准化的合同,是否存在一种执行方式(变量赋值),使得合同能够生效。
10 定理 7.32: 3SAT 到 CLIQUE 的归约
📜 [原文10]
定理 7.32
3SAT 可多项式时间归约到 CLIQUE。
证明思路 我们从 3SAT 到 CLIQUE 演示的多项式时间归约 $f$ 将公式转换为图。在所构建的图中,指定大小的团对应于公式的可满足赋值。图中的结构旨在模拟变量和子句的行为。
这是定理7.32的陈述和其证明思路的概述。
- 定理陈述:
- "3SAT 可多项式时间归约到 CLIQUE": 这句话的符号表示是 3SAT $\le_P$ CLIQUE。
- CLIQUE (团问题): 这里需要先了解什么是CLIQUE问题。在一个无向图中,一个“团”(Clique)是图中的一个顶点子集,其中任意两个不同的顶点之间都有一条边相连(即这个子集构成一个完全子图)。CLIQUE问题通常是这样问的:给定一个图 $G$ 和一个整数 $k$,问 $G$ 中是否存在一个大小为 $k$ 的团(即一个 k-团)?CLIQUE问题是 NP 中的一个著名问题。
- 定理的意义: 这个定理建立起了逻辑世界的问题(3SAT)和图论世界的问题(CLIQUE)之间的一座桥梁。它表明,CLIQUE 问题至少和 3SAT 问题一样难。如果我们已经知道 3SAT 是 NP-完全的(后面会证明),那么根据传递性,这个定理就是证明 CLIQUE 也是 NP-完全的关键一步。
- 证明思路 (Proof Idea):
- 核心: 证明的关键在于构造一个多项式时间归约函数 $f$。
- 输入: $f$ 的输入是一个 3SAT 问题的实例,即一个 3-CNF 公式 $\phi$。
- 输出: $f$ 的输出是一个 CLIQUE 问题的实例,即一个图 $G$ 和一个整数 $k$。所以 $f(\phi) = \langle G, k \rangle$。
- 连接两个世界: 这个构造必须非常巧妙,使得:
- 模拟: 如何实现这种连接?证明思路中提到了“模拟”这个词。图 $G$ 的结构不是随便画的,它的每一个顶点、每一条边都是为了“扮演”或“模拟”公式 $\phi$ 中的某个部分。
- 模拟变量和子句: 图中的某些结构(我们称之为 "gadget" 或小工具)将被用来代表 $\phi$ 中的变量,另一些结构将用来代表 $\phi$ 中的子句。
- 团与满足赋值的对应: 最终的目标是,在图 $G$ 中寻找一个 $k$-团的过程,就等价于在公式 $\phi$ 中寻找一个满足赋值的过程。找到了一个 $k$-团,就等于找到了一个满足赋值,反之亦然。
- 3SAT 实例: $\phi = (x \vee y) \wedge (\bar{x} \vee \bar{y})$ (这是一个2SAT,但为了简单,我们用它举例)
- 归约思路:
- 为第一个子句 (x ∨ y) 创建两个节点: 一个标记为 $x_1$(代表第一个子句里的x),一个标记为 $y_1$(代表第一个子句里的y)。
- 为第二个子句 (¬x ∨ ¬y) 创建两个节点: 一个标记为 $\bar{x}_2$,一个标记为 $\bar{y}_2$。
- 连边:
- 不同子句的节点之间,只要不冲突,就都连上边。什么是冲突?变量相同但符号相反,比如 $x_1$ 和 $\bar{x}_2$ 就是冲突的,所以它们之间不连边。
- $x_1$ 和 $\bar{y}_2$ 不冲突,连边。
- $y_1$ 和 $\bar{x}_2$ 不冲突,连边。
- $y_1$ 和 $\bar{y}_2$ 冲突,不连边。
- 设置 k: 公式有两个子句,所以我们设置 $k=2$。
- 问题转换: 原问题“$\phi$ 是否可满足?”,被转换成了新问题“在构造的这个4个顶点的图中,是否存在一个2-团?”
- 验证:
- 我们找一个满足赋值,比如 $x=1, y=0$。在第一个子句中 $x$ 为真,我们选择节点 $x_1$。在第二个子句中 $\bar{y}$ 为真,我们选择节点 $\bar{y}_2$。我们发现 $x_1$ 和 $\bar{y}_2$ 之间有边。所以 $\{x_1, \bar{y}_2\}$ 构成一个2-团。
- 反过来,假设我们找到了一个2-团,比如 $\{y_1, \bar{x}_2\}$。这意味着我们可以令 $y=1, x=0$。这个赋值也能满足原公式。
- 这个简单的例子展示了“图中的团”和“公式的满足赋值”之间是如何建立起对应关系的。
- CLIQUE问题的定义: CLIQUE问题本身是判定“是否存在”一个k-团,而不是“找出”这个k-团。找出k-团是它的搜索版本。
- 归约的精巧性: 归约的构造是NP-完全理论中最具创造性和技巧性的部分。第一次看可能会觉得很神奇,难以理解为什么这么构造。关键在于理解每个结构(gadget)是为了模拟公式的哪部分功能。
本段是定理7.32的一个“预告片”。它清晰地陈述了3SAT可以被多项式时间归约到CLIQUE,并给出了证明的核心思想:通过构造一个图来“模拟”一个布尔公式,使得图的某种性质(存在k-团)与公式的某种性质(可满足性)完全等价。
本段的目的是在进入复杂的证明细节之前,为读者提供一个高层次的、全局性的视角。通过“证明思路”的介绍,读者能带着一个清晰的目标去阅读后面的具体构造步骤,而不是在细节中迷失方向。
这就像是把一个“数独”谜题(3SAT)转换成一个“乐高拼图”任务(CLIQUE)。
- 归约函数 f: 就是一本翻译手册,它教你如何根据数独谜题的盘面,用乐高积木搭建一个特定的模型。比如,数独的每一行对应模型的一层,每个数字对应一种颜色的积木。
- 等价关系: 手册的构造非常精妙,保证了:当且仅当你能从搭建好的乐高模型中找到一个由 $k$ 块特定积木组成的、完全紧密连接的“核心结构”(k-团)时,原始的数独谜题才是有解的。
- 证明: 就是要详细写出这本“翻译手册”的内容,并证明它的正确性。
想象你是一个侦探,正在解决一个逻辑谜案(3SAT),案情涉及几个人(变量)在几个时间点(子句)是否说谎。案情错综复杂。
你的同事是一个社交网络分析专家(解决CLIQUE的算法)。他看不懂你的案情陈述,但他擅长在人群中找出关系最紧密的“小团体”。
你(归约函数 $f$)做了一件事:你画了一张巨大的人物关系图(图G)。
- 你把案情中的每个“可能性”(比如“A在周一说了真话”)都画成图上的一个人。
- 你设定了一些连接规则:如果两个人代表的可能性在逻辑上不冲突,就在他们之间连一条线。如果冲突(比如“A在周一说真话”和“A在周一说假话”),就不连线。
- 你告诉你的同事:“你帮我看看,这张图里能不能找到一个 $k$ 个人的‘铁杆小团体’,他们两两之间都互相认识(有连线)?”
- 定理7.32说的就是,你画图的方式是如此巧妙,以至于当你的同事告诉你“找到了!”的时候,你就能根据这个“铁杆小团体”里的成员,直接拼凑出逻辑谜案的唯一真相(满足赋值)。
11 3SAT到CLIQUE归约的具体证明
📜 [原文11]
证明 设 $\phi$ 是一个包含 $k$ 个子句的公式,例如
归约 $f$ 生成字符串 $\langle G, k\rangle$,其中 $G$ 是一个无向图,定义如下。
$G$ 中的节点被组织成 $k$ 组,每组包含三个节点,称为三元组 $t_{1}, \ldots, t_{k}$。每个三元组对应于 $\phi$ 中的一个子句,每个三元组中的节点对应于相关子句中的一个文字。用 $\phi$ 中对应的文字标记 $G$ 的每个节点。
$G$ 的边连接 $G$ 中除两种类型节点对之外的所有节点对。同一三元组中的节点之间没有边,具有矛盾标签的两个节点之间也没有边,例如 $x_{2}$ 和 $\overline{x_{2}}$。图7.33说明了当 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$ 时的这种构造。
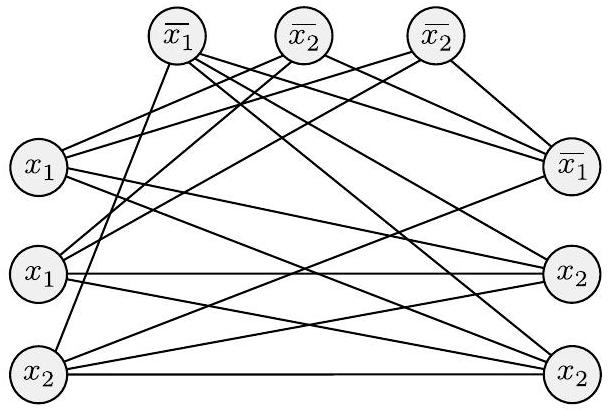
图 7.33
归约从 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$ 产生的图
这是归约构造的核心部分,详细描述了如何将一个3-CNF公式 $\phi$ 转换成一个图 $G$ 和一个整数 $k$。
- 输入: 一个3-CNF公式 $\phi$,它有 $k$ 个子句。每个子句有3个文字。
- $\phi = C_1 \wedge C_2 \wedge \dots \wedge C_k$
- 每个子句 $C_i = (a_i \vee b_i \vee c_i)$,其中 $a_i, b_i, c_i$ 是文字。
- 输出: 一个图 $G$ 和目标团大小(恰好也是 $k$)。
- 图 $G$ 的构造规则:
- 构造节点 (Vertices):
- 公式 $\phi$ 有 $k$ 个子句,我们就创建 $k$ 个“节点组”,命名为 $t_1, t_2, \dots, t_k$。
- 每个子句 $C_i$ 有3个文字,所以对应的节点组 $t_i$ 就包含3个节点。
- 因此,图 $G$ 总共有 $3k$ 个节点。
- 标记: 每个节点都用它所代表的那个文字来做标记。例如,如果第一个子句是 $(x_1 \vee \bar{x_2} \vee x_3)$,那么第一个节点组 $t_1$ 就包含三个节点,分别标记为 $x_1$, $\bar{x_2}$, $x_3$。
- 构造边 (Edges):
- 构造边的规则是“默认全连接,然后排除例外”。
- 先把所有 $3k$ 个节点想象成两两之间都有一条边。
- 然后,移除以下两种类型的边:
- 规则1 (子句内不连接): 如果两个节点在同一个节点组(三元组)里,移除它们之间的边。例如,在代表 $(x_1 \vee \bar{x_2} \vee x_3)$ 的节点组 $t_1$ 中,标记为 $x_1$ 的节点和标记为 $\bar{x_2}$ 的节点之间没有边。这三个节点形成一个“无边三角形”。
- 规则2 (矛盾不连接): 如果两个节点分别在不同的节点组里,但它们的标记是相互矛盾的,移除它们之间的边。所谓矛盾,就是一个变量和它的否定,例如一个节点标记为 $x_2$,另一个节点标记为 $\bar{x_2}$。
- 图 7.33 的分析:
- 公式: $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$
- 这是一个有 $k=3$ 个子句的3-CNF公式。所以我们的目标是在图中寻找一个大小为 $k=3$ 的团。
- 节点:
- 子句1: $(x_1 \vee x_1 \vee x_2)$ -> 对应节点组 $t_1$,包含三个节点,标记分别为 $x_1, x_1, x_2$。
- 子句2: $(\bar{x_1} \vee \bar{x_2} \vee \bar{x_2})$ -> 对应节点组 $t_2$,包含三个节点,标记分别为 $\bar{x_1}, \bar{x_2}, \bar{x_2}$。
- 子句3: $(\bar{x_1} \vee x_2 \vee x_2)$ -> 对应节点组 $t_3$,包含三个节点,标记分别为 $\bar{x_1}, x_2, x_2$。
- 总共有 $3 \times 3 = 9$ 个节点。
- 边:
- 子句内无边: 图中清晰地画出了三个灰色的三角形区域,每个区域内的三个节点之间没有任何边。这就是规则1的体现。
- 矛盾无边: 我们来看几个例子。
- $t_1$ 中的 $x_1$ 节点和 $t_2$ 中的 $\bar{x_1}$ 节点之间没有连线。
- $t_1$ 中的 $x_2$ 节点和 $t_2$ 中的 $\bar{x_2}$ 节点之间没有连线。
- $t_1$ 中的 $x_1$ 节点和 $t_3$ 中的 $\bar{x_1}$ 节点之间没有连线。
- ... 所有矛盾的节点对之间都没有边。
- 其他都有边: 只要不违反上述两条规则,节点之间就都有边。比如,$t_1$中的 $x_1$ 和 $t_2$ 中的 $\bar{x_2}$ 之间有边,因为它们既不在同一个子句组,标记也不是矛盾的。
- $\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \ldots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right)$:
- 这展示了一个通用的3-CNF公式的结构。
- $k$: 子句的数量。
- $(a_i \vee b_i \vee c_i)$: 代表第 $i$ 个子句,由三个文字组成。
- $\wedge$: 表示所有 $k$ 个子句必须同时为真。
让我们用一个更简单的公式来手动构造图。
- 公式 $\phi = (x \vee y) \wedge (\bar{x} \vee \bar{y})$
- k=2 (有两个子句)。我们的目标是找一个2-团。
- 节点:
- 子句1 $(x \vee y)$ -> 节点组 $t_1$: {节点A(标记x), 节点B(标记y)}
- 子句2 $(\bar{x} \vee \bar{y})$ -> 节点组 $t_2$: {节点C(标记$\bar{x}$), 节点D(标记$\bar{y}$)}
- 总共4个节点。
- 边:
- 规则1 (组内不连): A和B之间不连边。C和D之间不连边。
- 规则2 (矛盾不连):
- A(x) 和 C($\bar{x}$) 矛盾,不连边。
- B(y) 和 D($\bar{y}$) 矛盾,不连边。
- 剩下的都连:
- A(x) 和 D($\bar{y}$) 不矛盾,连边。
- B(y) 和 C($\bar{x}$) 不矛盾,连边。
- 最终的图G: 有4个节点 A,B,C,D。只有两条边:(A,D) 和 (B,C)。
- 问题: 图G中是否存在一个2-团?
- 答案: 是的。{A, D} 是一个2-团,因为它们之间有边。{B, C} 也是一个2-团。
- k的两个角色: 在这个归约中,$k$ 既是公式中子句的数量,也是我们要在图中寻找的团的大小。这是构造的核心之一。
- 重复的文字: 注意在图7.33的例子中,一个子句内可以有重复的文字,如 $(x_1 \vee x_1 \vee x_2)$。这在构造中没有影响,我们仍然创建3个节点,其中两个的标记恰好相同。
- 归约的时间复杂度: 这个从 $\phi$ 到 $\langle G, k \rangle$ 的转换过程是否是多项式时间的?
- 输入 $\phi$ 的大小与变量数和子句数 $k$ 相关。
- 生成的图 $G$ 有 $3k$ 个节点和最多 $O((3k)^2)$ 条边。
- 创建节点和边的过程,需要遍历所有节点对来判断是否连边。总的计算量是 $k$ 的多项式函数。因此,这是一个多项式时间归约。
本段详细描述了从一个3-CNF公式 $\phi$ 构造出一个图 $G$ 的具体步骤。构造的核心思想是:用 $k$ 组三节点(三元组)来对应 $\phi$ 中的 $k$ 个子句,然后通过两条简单的排除规则(组内不连、矛盾不连)来定义图的边。这个构造过程是机械的、高效的,并且为后续证明两个问题之间的难度等价性奠定了基础。
本段的目的是给出归约算法的具体实现细节。没有这一步,整个证明就是空中楼阁。它将抽象的“模拟”思想,物化为一组清晰可操作的图构造规则。
这就像是为一场派对(寻找满足赋值)安排座位(构造图)。
- k个子句: 派对有 $k$ 张桌子。
- 每个子句3个文字: 每张桌子有3个座位。每个座位上都贴着一个名字(文字标记)。
- 安排座位(构造节点): 你邀请了 $3k$ 个客人,每个客人对应一个座位。
- 禁止交谈规则(构造边): 你规定:
- 坐在同一张桌子的人互相不认识,不能交谈(组内无边)。
- 有宿怨的两个人(如 $x$ 和 $\bar{x}$)也不能交谈(矛盾无边)。
- 除此之外,任何两个人都可以自由交谈。
- 寻找k-团: 你的目标是找到一个 $k$ 个人的“社交核心圈”,这 $k$ 个人两两之间都能交谈。
想象你在搭建一个通信网络。
- 你有 $k$ 个基站(子句)。
- 每个基站有3个信号发射器(文字),每个发射器代表一种特定信号(如 $x_1$)。
- 布线规则(加边): 你打算在任意两个不同基站的发射器之间都拉一根光缆,但有两条禁令:
- 同一个基站内的3个发射器之间不准布线。
- 如果两个发射器广播的信号是“完全相反”的(如 $x_1$ 和 $\bar{x_1}$),它们之间也不能布线,会产生干扰。
- 归约完成: 你布好线的整个网络就是图 $G$。
- 寻找k-团: 就是在问:“在这个网络中,能否找到 $k$ 个发射器,它们分别来自不同的 $k$ 个基站,并且这 $k$ 个发射器之间两两都有光缆直连,形成一个全互联的通信小组?”
12 证明3SAT到CLIQUE归约的有效性
📜 [原文12]
现在我们演示这种构造为何有效。我们证明 $\phi$ 是可满足的当且仅当 $G$ 具有一个 $k$-团。
假设 $\phi$ 有一个可满足赋值。在该可满足赋值中,每个子句中至少有一个文字为真。在 $G$ 的每个三元组中,我们选择一个对应于可满足赋值中真文字的节点。如果特定子句中有多个文字为真,我们任意选择其中一个真文字。刚刚选择的节点形成一个 $k$-团。选择的节点数量为 $k$,因为我们为每个 $k$ 个三元组选择了一个节点。每对选定的节点通过一条边连接,因为没有一对符合前面描述的例外情况。它们不可能来自同一个三元组,因为我们每个三元组只选择一个节点。它们不可能具有矛盾的标签,因为相关文字在可满足赋值中都为真。因此,$G$ 包含一个 $k$-团。
这部分是证明的关键,它展示了从“$\phi$可满足”到“$G$有k-团”的推导方向($\implies$)。
- 证明目标: 证明如果 $\phi$ 是可满足的,那么我们构造的图 $G$ 中一定存在一个大小为 $k$ 的团。
- 前提: 我们假设 $\phi$ 是可满足的。这意味着存在一个对所有变量的真/假赋值(比如 $x_1=1, x_2=0, \dots$),使得整个公式 $\phi$ 的值为真。
- 核心论证:
- 根据CNF公式的性质,如果 $\phi$ 为真,那么它的每一个子句都必须为真。
- 根据子句的性质,如果一个子句为真,那么它包含的至少一个文字必须为真。
- 构造k-团的策略:
- 我们要在图 $G$ 中选出 $k$ 个节点来组成一个团。怎么选?
- 遍历每个子句:
- 对于第一个子句 $C_1$,由于它被满足了,所以它里面的三个文字至少有一个是真的。我们在对应的节点组 $t_1$ 中,选择一个标记为这个真文字的节点。
- 对于第二个子句 $C_2$,同样,它也至少有一个真文字。我们在节点组 $t_2$ 中,选择一个标记为这个真文字的节点。
- ...
- 对于第 $k$ 个子句 $C_k$,我们在节点组 $t_k$ 中,选择一个标记为真文字的节点。
- 注意: 如果一个子句有多个真文字(比如 $(1 \vee 1 \vee 0)$),我们随便选一个对应的节点就行,比如选第一个。
- 验证所选节点集是一个k-团:
- 我们通过上述方法,恰好选择了 $k$ 个节点,因为我们从 $k$ 个子句组中各选了一个。我们把这个 $k$ 个节点的集合称为 $S$。
- 要证明 $S$ 是一个 $k$-团,我们需要证明 $S$ 中任意两个不同的节点之间都有一条边。
- 我们用反证法来思考:$S$ 中任意两个节点 $u, v$ 之间会不会没有边?
- 根据图的构造规则,没有边的原因只有两个:
- 原因一:$u, v$ 在同一个三元组中?
- 不可能。因为我们的选择策略是“每个三元组(子句组)只选择一个节点”。所以 $u$ 和 $v$ 必然来自不同的三元组。
- 原因二:$u, v$ 的标记相互矛盾?
- 不可能。假设 $u$ 的标记是 $x_i$, $v$ 的标记是 $\bar{x_i}$。
- 根据我们的选择策略,我们只选择标记为“真”文字的节点。
- 这意味着,在我们的满足赋值下,$x_i$ 的值必须是TRUE (1),同时 $\bar{x_i}$ 的值也必须是TRUE (1)。
- 但 $\bar{x_i}$ 为 TRUE 意味着 $x_i$ 必须为 FALSE (0)。
- 所以,这导致了矛盾:$x_i$ 的值既是1又是0。这是不可能的。
- 因此,我们选出的 $k$ 个节点,它们的标记不可能相互矛盾。
- 结论:
- 我们选出的这 $k$ 个节点,既不在同一个三元组内,标记也不相互矛盾。
- 这意味着它们之间没有任何一条边被“移除规则”移除掉。
- 所以,这 $k$ 个节点中的任意两个之间都有一条边。
- 根据定义,这 $k$ 个节点构成了一个 k-团。
- 证明完成。
- 公式: $\phi = (x \vee y \vee z) \wedge (\bar{x} \vee \bar{y} \vee z) \wedge (x \vee \bar{y} \vee \bar{z})$
- k=3
- 一个满足赋值: $x=1, y=0, z=1$
- 构造k-团:
- 子句1 $(x \vee y \vee z)$: 赋值后变成 $(1 \vee 0 \vee 1)$,值为真。其中 $x$ 和 $z$ 都是真文字。我们任意选择一个,比如选 $x$。在图的第一个三元组中,我们选择标记为 $x$ 的节点。
- 子句2 $(\bar{x} \vee \bar{y} \vee z)$: 赋值后变成 $(0 \vee 1 \vee 1)$,值为真。其中 $\bar{y}$ 和 $z$ 是真文字。我们任意选择一个,比如选 $\bar{y}$。在图的第二个三元组中,我们选择标记为 $\bar{y}$ 的节点。
- 子句3 $(x \vee \bar{y} \vee \bar{z})$: 赋值后变成 $(1 \vee 1 \vee 0)$,值为真。其中 $x$ 和 $\bar{y}$ 是真文字。我们任意选择一个,比如选 $x$。在图的第三个三元组中,我们选择标记为 $x$ 的节点。
- 选出的节点集 S: 我们选出了3个节点,它们的标记分别是 {来自子句1的$x$, 来自子句2的$\bar{y}$, 来自子句3的$x$}。
- 验证 S 是否为3-团:
- 这3个节点分别来自3个不同的子句组,所以它们不在同一个三元组内。
- 我们检查标记是否矛盾:{ $x$, $\bar{y}$, $x$ }。这里没有一个变量和它的否定同时出现(比如 $x$ 和 $\bar{x}$)。
- 因此,这3个节点之间两两都有边。它们构成一个3-团。
- 任意选择: 当一个子句有多个真文字时,我们的选择是任意的。这是否会影响结果?不会。因为无论你选哪个,它都是一个真文字。只要是真文字,就不会与其他被选中的真文字产生矛盾。比如在子句1中,如果改选 $z$,那么最终选出的节点集是 {来自子句1的$z$, 来自子句2的$\bar{y}$, 来自子句3的$x$}。这些标记 { $z, \bar{y}, x$ } 同样不构成矛盾,所以它们也形成一个3-团。一个满足赋值可能对应图中的多个不同的k-团。
- “真文字”的理解: 一个文字为真,不等于它的变量为真。如果 $x=0$,那么文字 $\bar{x}$ 就是真文字。
本段完成了 $3SAT \le_P CLIQUE$ 证明的前半部分。它通过一个清晰的构造性证明,展示了如何利用 $\phi$ 的一个满足赋值,在图 $G$ 中按图索骥地找到一个 $k$-团。其核心逻辑在于:满足赋值确保了每个子句都有真文字可选,而真文字之间不会互相矛盾,这恰好绕开了图中所有“无边”的陷阱。
本段的目的是为了严谨地建立从“公式可满足”到“图中存在k-团”的逻辑链条。它是整个归约有效性质询的第一步,展示了构造的合理性。
回到派对座位安排的模型。
- 满足赋值: 你现在有了一份“派对气氛活跃方案”(即满足赋值),方案告诉你如何设置每个开关(变量取值)能让派对嗨起来。
- 选人组成k-团:
- 你走到第一桌,根据方案,这一桌的三个座位上至少有一个座位能“点亮气氛”(真文字)。你从这些能点亮气氛的座位里随便请一位客人站出来。
- 你走到第二桌,同样请一位能“点亮气氛”的客人站出来。
- ...
- 你一共请出了 $k$ 位客人。
- 验证: 这 $k$ 位客人能组成一个“社交核心圈”吗?
- 他们来自不同的桌子,所以他们不违反“同桌不交谈”的规定。
- 他们都是被“派对气氛活跃方案”选中的“积极分子”(真文字),这个方案本身是自洽的,不可能同时让两个有宿怨的人($x$ 和 $\bar{x}$)都成为积极分子。所以他们之间也没有宿怨。
- 结论:这 $k$ 个人两两都可以自由交谈,形成了一个“社交核心圈”(k-团)。
回到通信网络的比喻。
- 满足赋值: 是一份“信号兼容列表”,告诉你如何设置每个变量,可以让所有基站都正常工作。
- 构造k-团:
- 对于第一个基站,根据列表,它至少有一个发射器广播的信号是“有效的”(真文字)。你选择这个发射器。
- 对于第二个基站,你也选择一个广播“有效信号”的发射器。
- ...
- 你一共选了 $k$ 个发射器。
- 验证: 这 $k$ 个发射器能形成全互联小组吗?
- 它们来自不同的基站,所以不违反“同基站不布线”的规定。
- 它们广播的都是“有效信号”,这份信号兼容列表保证了“有效信号”之间不会互相干扰(没有矛盾)。所以它们之间不违反“矛盾信号不布线”的规定。
- 结论:这 $k$ 个发射器之间两两都有光缆,构成一个k-团。
13 证明3SAT到CLIQUE归约的有效性(续)
📜 [原文13]
假设 $G$ 有一个 $k$-团。团的任何两个节点都不在同一个三元组中,因为同一个三元组中的节点没有边连接。因此,每个 $k$ 个三元组中正好包含一个 $k$ 个团节点。我们将真值赋给 $\phi$ 的变量,使得标记团节点的每个文字都变为真。这样做总是可能的,因为以矛盾方式标记的两个节点没有边连接,因此不可能都存在于团中。对变量的这个赋值满足 $\phi$,因为每个三元组包含一个团节点,因此每个子句包含一个被赋为真的文字。因此,$\phi$ 是可满足的。
这部分是证明的后半段,展示了从“$G$有k-团”到“$\phi$可满足”的推导方向($\impliedby$)。
- 证明目标: 证明如果在图 $G$ 中存在一个大小为 $k$ 的团,那么原始公式 $\phi$ 一定是可满足的。
- 前提: 我们假设在图 $G$ 中找到了一个 $k$-团。我们把这个团里的 $k$ 个节点构成的集合称为 $S$。
- 核心论证:
- 分析 $k$-团的性质:
- 性质1: 团中节点来自不同子句组:
- 一个 $k$-团意味着其中任意两个节点之间都有边。
- 根据我们的构造规则1,同一个三元组内的任意两个节点之间都没有边。
- 因此,一个 $k$-团中的 $k$ 个节点,必须来自 $k$ 个不同的三元组。
- 因为总共就只有 $k$ 个三元组,所以这 $k$ 个节点必然是每个三元组里恰好拿出一个。
- 构造满足赋值的策略:
- 我们现在手上有了一个 $k$-团 $S$,它包含 $k$ 个节点。我们看着这 $k$ 个节点上的标记,来决定如何给变量赋值。
- 赋值规则: 遍历团 $S$ 中的每一个节点。查看它的标记。
- 如果一个节点的标记是 $x_i$,我们就将变量 $x_i$ 赋值为 TRUE (1)。
- 如果一个节点的标记是 $\bar{x_j}$,我们就将变量 $x_j$ 赋值为 FALSE (0)。
- 问题: 这个赋值规则会不会产生矛盾?比如,团里既有一个节点标记为 $x_i$,又有另一个节点标记为 $\bar{x_i}$。这样我们既要令 $x_i=1$,又要令 $x_i=0$,就出错了。
- 解答: 不会产生矛盾。因为根据我们的构造规则2,任何一对标记为 $x_i$ 和 $\bar{x_i}$ 的节点之间都没有边。而团中的任意两个节点之间都必须有边。所以,一个团中不可能同时包含一对矛盾标记的节点。因此,我们的赋值策略是安全、无矛盾的。
- 对于那些在团的标记中没有出现过的变量,我们怎么赋值?随便赋,赋0或1都可以,不会影响最终结果。
- 验证这个赋值满足公式 $\phi$:
- 要证明 $\phi$ 被满足,我们需要证明它的每一个子句都被满足。
- 让我们来看任意一个子句 $C_i$ (其中 $i$ 从1到$k$):
- 根据我们对 $k$-团的性质分析,第 $i$ 个三元组 $t_i$ 中,有且仅有一个节点属于我们的 $k$-团 $S$。
- 设这个节点是 $v_i$。
- 根据我们的赋值规则,我们已经将变量赋值,使得 $v_i$ 上的标记(一个文字)变成了真。
- 这个文字本身就是子句 $C_i$ 中的三个文字之一。
- 一个子句只要包含一个为真的文字,整个子句就为真。
- 因此,子句 $C_i$ 被满足了。
- 由于这个逻辑对所有 $i=1, \dots, k$ 都成立,所以 $\phi$ 的所有 $k$ 个子句都被满足了。
- 因此,整个公式 $\phi$ 是可满足的。
- 结论:
- 我们成功地从一个 $k$-团的存在,构造出了一个满足 $\phi$ 的赋值。
- 证明完成。
- 图G: 回到之前的例子,$\phi = (x \vee y) \wedge (\bar{x} \vee \bar{y})$。我们构造出的图 G 有4个节点 A(x), B(y), C($\bar{x}$), D($\bar{y}$),和两条边 (A,D), (B,C)。k=2。
- 假设我们找到了一个2-团: 假设算法在 G 中找到了一个团 $S = \{A, D\}$。
- 构造赋值:
- 团里有节点A,标记是 $x$。所以我们令 x=1。
- 团里有节点D,标记是 $\bar{y}$。所以我们令 y=0。
- 这个赋值是无矛盾的。
- 验证赋值:
- 把 $x=1, y=0$ 代入 $\phi$:
- 子句1: $(x \vee y) \to (1 \vee 0) = 1$ (满足)
- 子句2: $(\bar{x} \vee \bar{y}) \to (\bar{1} \vee \bar{0}) = (0 \vee 1) = 1$ (满足)
- 所有子句都被满足,所以 $\phi$ 是可满足的。
- 另一种情况: 如果我们找到的2-团是 $S = \{B, C\}$。
- 节点B的标记是 $y \implies y=1$。
- 节点C的标记是 $\bar{x} \implies x=0$。
- 代入 $x=0, y=1$ 验证,同样可以满足 $\phi$。
- 变量赋值的完整性: 团中的标记可能只涉及一部分变量。比如公式有 $x,y,z$三个变量,但团的标记只涉及 $x$ 和 $y$。那么变量 $z$ 怎么办?可以赋任意值。因为它没有出现在决定性的标记中,所以它的取值不会影响我们已经满足的那些子句。
- 逻辑的严密性: 这一部分的证明逻辑非常紧凑,环环相扣。关键在于理解k-团的两个结构性属性:1) 节点横跨所有子句组;2) 节点标记无矛盾。这两个属性是直接从图的构造规则和团的定义中推导出来的。
本段完成了 $3SAT \le_P CLIQUE$ 证明的后半部分。它展示了如何从图 $G$ 中的一个 $k$-团出发,反向构造出一个能满足原始公式 $\phi$ 的变量赋值。其核心逻辑在于,一个 $k$-团的结构天然地保证了我们可以选出一组互不矛盾的、且能覆盖所有子句的“真文字”,从而保证了公式的可满足性。
本段的目的是完成归约有效性证明的双向箭头,与前一段结合,共同构成了 $A \iff B$ 的完整证明。这使得 3SAT 和 CLIQUE 两个问题的“命运”被紧紧地绑定在了一起。
回到派对座位安排的模型。
- 找到k-团: 你在派对上成功找到了一个 $k$ 人的“社交核心圈”,他们分别来自 $k$ 张不同的桌子,并且两两之间都可以交谈。
- 构造满足赋值:
- 你看着这个圈子里的 $k$ 个人,记下他们座位上的名字(文字标记)。
- 你宣布一条规则:“凡是被我记下名字的,都设定为‘真’”。比如,你记下的名字有 $x_1$ 和 $\bar{x_2}$,你就设定 $x_1=1, x_2=0$。
- 这个规则可行吗?是的,因为圈子里的人互相都能交谈,所以他们之间没有宿怨,你记下的名字里不可能同时有 $x_i$ 和 $\bar{x_i}$。
- 验证: 这个规则能让派对嗨起来吗?
- 看第一桌:这张桌子必然有你的圈内成员,他座位上的名字被你设为了“真”。所以第一桌被“点亮”了。
- 看第二桌:同样,也有圈内成员,第二桌也被“点亮”了。
- ...
- 所有 $k$ 张桌子都被“点亮”了(所有子句都被满足了)。
- 结论:派对成功了(公式可满足)。
回到通信网络的比喻。
- 找到k-团: 网络工程师告诉你,他们找到了一个由 $k$ 个发射器组成的“全互联小组”,这 $k$ 个发射器两两直连。
- 构造满足赋值:
- 你查看这 $k$ 个发射器广播的信号类型(文字标记)。
- 你根据这些信号,制定一份“官方信号标准”(变量赋值)。比如,如果小组里有一个发射器广播 $x_1$,你就规定 $x_1$ 信号是“标准”的($x_1=1$)。如果另一个广播 $\bar{x_2}$,你就规定 $x_2$ 是“非标准”的($x_2=0$)。
- 这个标准是自洽的,因为小组内没有互相干扰的发射器。
- 验证: 这个“官方信号标准”能让所有基站都正常工作吗?
- 第一个基站:因为它贡献了一个发射器到“全互联小组”,所以它内部至少有一种信号是符合“官方标准”的。因此这个基站能正常工作。
- ...
- 所有 $k$ 个基站都能正常工作(所有子句都被满足)。
- 结论:整个通信系统是可行的(公式可满足)。
14 归约有效性证明的总结
📜 [原文14]
定理 7.31 和 7.32 告诉我们,如果 CLIQUE 可以在多项式时间内解决,那么 3SAT 也可以。乍一看,这两个问题之间的这种联系相当引人注目,因为从表面上看,它们截然不同。但是多项式时间归约性允许我们将它们的复杂性联系起来。现在我们转向一个定义,它将允许我们类似地将一整类问题的复杂性联系起来。
这段话是对刚刚完成的证明进行总结,并承上启下,引出NP-完全的正式定义。
- 回顾与总结:
- 定理 7.32: 刚刚我们证明了 3SAT $\le_P$ CLIQUE。
- 定理 7.31: 我们之前知道,如果 $A \le_P B$ 且 $B \in P$,那么 $A \in P$。
- 结合两个定理: 把 A 换成 3SAT,B 换成 CLIQUE。我们就得到了一个直接的推论:如果 CLIQUE 可以在多项式时间内解决(即 CLIQUE $\in P$),那么 3SAT 也可以在多项式时间内解决(即 3SAT $\in P$)。
- 感慨与洞察:
- 作者特意强调了这个结论的“引人注目”之处。
- 3SAT: 是一个关于逻辑、公式、真假值的问题,充满了代数风味。
- CLIQUE: 是一个关于图、节点、边的问题,充满了组合和几何风味。
- 从表面上看,这两个问题来自完全不同的数学分支,风马牛不相及。
- 然而,多项式时间归约就像一条神奇的纽带,揭示了它们在“计算难度”这个更深层次上的内在联系。它告诉我们,尽管外表不同,但它们的“计算核心”是相通的。
- 承上启下:
- 我们刚刚见识了如何将两个具体问题的复杂性联系起来。
- 现在,作者要将这个思想进行一次巨大的升华:我们能否将一个问题与一整类问题(即整个NP类)的复杂性联系起来?
- 这就是即将要介绍的NP-完全性的定义。它将使用多项式时间归约这个工具,来定义NP中的“最难问题”。
这个总结性段落没有新的技术内容,主要是思想上的提升,因此数值示例不太适用。但可以用类比来加深理解。
- 类比: 假设我们证明了“破解A银行的金库密码”($A$) 可以高效归约为“破解B银行的金库密码”($B$)。
- 结论就是:如果B银行的密码很容易破解,那么A银行的密码也一定很容易。
- 这会让人很惊讶,因为A银行用的是指纹锁,B银行用的是声控锁,看起来完全不同。
- 但我们的归约证明(比如发现它们的密码生成器用的是同一个随机数种子)揭示了它们难度上的关联。
- 现在,我们要提出的新问题是:是否存在一个“万能金库”C,只要你能破解它,全世界所有银行(所有NP问题)的金库密码就都能破解?这就是NP-完全问题的思想。
- 归约的方向性: 再次强调,$3SAT \le_P CLIQUE$ 意味着 CLIQUE 至少和 3SAT 一样难。不要理解反了。
- “联系起来”的含义: 这里的“联系”特指计算复杂性上的联系,不代表它们在其他方面有任何关系。
本段是对 3SAT 到 CLIQUE 归约的意义小结。它强调了多项式时间归约这一工具的强大威力,能够跨越不同数学领域,揭示问题计算难度上的深刻联系。同时,它也作为一个跳板,预示着我们将从连接“两个问题”的难度,跃迁到连接“一个问题”与“一个庞大的问题类别”的难度。
本段的目的是在读者完成一个具体的、有挑战性的归约证明后,引导他们进行更高层次的思考。它巩固了归约的意义,并激发读者对即将到来的、更宏大概念(NP-完全)的兴趣。
我们刚刚通过精密的化学实验(归约证明),证明了“治疗头痛的药物A”的分子结构可以快速转化为“治疗胃痛的药物B”的分子结构。这说明,如果药物B能被廉价地合成($B \in P$),那么药物A也能($A \in P$)。
现在,我们要提出一个更惊人的猜想:是否存在一种“万能药干细胞”C(NP-完全问题),它可以被快速地转化为任何一种疾病的治疗药物(任何NP问题)?
你刚刚学会了如何把一份中文菜谱(3SAT)翻译成一份法文菜谱(CLIQUE),并且保证翻译后做出的菜味道不变。
现在你要思考一个更大的问题:是否存在一种“烹饪界的世界语”(一种NP-完全问题),任何国家的任何菜谱(任何NP问题)都可以被快速地翻译成这种世界语?如果存在,那么只要我们培养出一个能看懂这种世界语的超级厨师,他就等于掌握了全世界的烹饪。
15 NP-完全性的定义
📜 [原文15]
NP-完全性的定义
定义
734
语言 $B$ 是NP-完全的,如果它满足两个条件:
- $B$ 在 NP 中,并且
- NP 中的每个 $A$ 都可多项式时间归约到 $B$。
这是本章的核心定义,它用严格的数学语言定义了什么是 NP-完全 (NP-Complete, NPC) 问题。
一个语言(问题)B 要想获得“NP-完全”这个至高无上的“荣誉头衔”,必须同时满足以下两个苛刻的条件:
- 条件一: $B \in \mathrm{NP}$
- 含义: 问题 B 本身必须是一个 NP 问题。
- 通俗解释: B 必须是“容易验证解”的问题。也就是说,如果有人给了你一个问题 B 的解,你必须能够在一个多项式时间内验证这个解是不是正确的。
- 为什么需要这个条件: 这个条件确保了 NP-完全问题不会比 NP 本身更难。它把 NP-完全问题的难度上限锁定在 NP 范畴内。如果一个问题连解都无法在多项式时间内验证,那它可能比 NP 问题还要难得多(比如属于 NEXP 或其他更复杂的类)。NP-完全问题是 NP 内部的“最难”,而不是宇宙中的“最难”。
- 条件二: NP中的每个A都可多项式时间归约到B
- 含义: 对于任何一个存在于 NP 问题集合中的问题 A,都存在一个多项式时间归约,即 $A \leq_{\mathrm{P}} B$。
- 通俗解释: B 必须是 NP 宇宙的“通用难点”。你可以把任何一个 NP 问题(无论是旅行商、图着色、背包问题还是其他任何问题)都通过一个高效的“翻译器”转换成问题 B 的一个实例。
- 为什么需要这个条件: 这个条件是“完全性”(Completeness)的体现,也叫“NP-困难”(NP-hard)的性质。它确保了 B 的难度是“封顶”的,至少和 NP 中的任何一个问题一样难。只要你能解决 B,就等于拥有了解决所有 NP 问题的能力。
总结两个条件:
- 条件一说:“你(B)是我们 NP 俱乐部的一员。”
- 条件二说:“我们 NP 俱乐部里所有人的难题,你(B)都能一肩挑。”
- 两者合一,B 就是 NP 俱乐部里“最受尊敬也最难搞的老大”。
- SAT 问题是 NP-完全的吗? 我们来用这个定义检查一下(这正是库克-莱文定理要证明的)。
- 条件一:SAT $\in$ NP?
- 是的。如果有人给你一个布尔公式 $\phi$ 和一个赋值方案(例如 $x=1, y=0, \dots$),你验证这个方案是否满足 $\phi$ 需要多长时间?你只需要把值代入公式,一步步计算出最终结果。这个过程的时间与公式的长度成正比,显然是多项式时间的。所以 SAT 满足条件一。
- 条件二:对所有 A $\in$ NP,是否有 A $\le_P$ SAT?
- 是的。这正是库克-莱文定理最艰难、最核心的证明内容。它通过模拟一个通用的非确定性图灵机的计算过程,构造性地证明了任何NP问题的判定过程都可以被转换成一个等价的SAT公式。
- 结论: 因为 SAT 同时满足了这两个条件,所以 SAT 是 NP-完全的。
- CLIQUE 问题是 NP-完全的吗?
- 条件一:CLIQUE $\in$ NP?
- 是的。如果有人给你一个图 $G$,一个整数 $k$,以及一个包含 $k$ 个顶点的子集 $S$(作为解),你如何验证 $S$ 是不是一个 $k$-团?你只需要检查 $S$ 中的每对顶点之间是不是都有一条边。$k$ 个顶点有 $O(k^2)$ 对,检查过程是多项式时间的。所以 CLIQUE 满足条件一。
- 条件二:对所有 A $\in$ NP,是否有 A $\le_P$ CLIQUE?
- 要直接证明这个太难了。但我们稍后会看到一个捷径。目前我们只知道 3SAT $\le_P$ CLIQUE。
- NP-hard vs NP-complete:
- 只满足条件二(即所有NP问题都能归约到它),但不一定满足条件一的问题,被称为 NP-hard (NP-困难) 问题。
- NP-hard 问题至少和 NP-完全问题一样难,甚至可能更难。
- 例如,“停机问题”就是 NP-hard 的(任何NP问题都可以归约到它),但它本身不是 NP 问题(它甚至不是可判定的),所以它不是 NP-complete 的。
- 关系: NP-完全 = NP-hard $\cap$ NP。一个问题既是 NP-hard 的,又是 NP 的,它才是 NP-complete 的。
- “每个A”的重要性: 条件二中的“每个”是关键。哪怕只有一个 NP 问题不能归约到 B,B 也不能被称为 NP-完全。
本段给出了NP-完全的正式定义,它包含两个缺一不可的条件:问题本身属于NP(难度有上限),且所有NP问题都能在多项式时间内归约到它(难度有下限,且是NP中的最高下限)。这个定义为识别NP中的“最难问题”提供了精确的数学标准。
本段的目的是建立一个清晰、无歧义的“靶子”,为整个NP-完全性理论提供核心定义。后续所有的证明,无论是证明一个问题是NP-完全,还是利用NP-完全性来推导其他结论,都将围绕这个定义展开。
要想当上“武林盟主”(NP-完全),你必须满足两个条件:
- 你是武林中人(B $\in$ NP): 你不能是外面来的神仙或者妖怪(比NP更难的问题)。
- 武林中所有门派的掌门人都服你,愿意把他们的独门绝技传给你(所有A $\in$ NP 都能归约到 B): 这意味着你的武功修为(计算难度)是武林中的天花板。只要打败了你,就等于打败了整个武林。
想象在联合国里评选一个“全球核心问题”(NP-完全问题)。
- 候选问题B必须是一个“全球性”问题(B $\in$ NP): 它必须是地球上的问题,不能是火星上的问题。它的解决方案的影响范围应该是全球性的,可以被快速评估。
- 所有其他全球性问题A(气候变化、粮食安全、能源危机等)都可以被“转化”为问题B的一个特例(所有A $\in$ NP 都能归约到 B): 必须证明,解决气候变化本质上就是在解决问题B的一个特定版本,解决粮食安全也是在解决问题B的另一个特定版本。
如果问题B同时满足这两点,那么它就被授予“全球核心问题”的称号。全世界的资源都可以集中起来去解决这一个问题。
16 NP-完全性的推论
📜 [原文16]
定理
7.35
如果 $B$ 是NP-完全的且 $B \in \mathrm{P}$,则 $\mathrm{P}=\mathrm{NP}$。
证明 该定理直接遵循多项式时间归约性的定义。
这个定理是NP-完全性定义的直接推论,它以另一种方式重申了NP-完全问题的核心地位。
- 定理陈述:
- 前提1: B 是一个 NP-完全问题。
- 前提2: B $\in$ P (我们找到了一个多项式时间算法来解决B)。
- 结论: P = NP (那么所有NP问题都是P问题)。
- 证明思路:
- 这个证明非常直接,几乎不需要写出来。我们把前提和定义串起来即可。
- 步骤1: 我们想证明 P = NP。由于我们已知 P $\subseteq$ NP (所有P问题天然就是NP问题),所以我们只需要证明 NP $\subseteq$ P (所有NP问题也都是P问题)。
- 步骤2: 如何证明 NP $\subseteq$ P?我们需要对任意一个在NP中的问题A,证明 A 也在P中。
- 步骤3: 让我们随便取一个问题 $A \in NP$。
- 步骤4: 根据前提1,B是NP-完全的。根据NP-完全的定义(条件2),任何NP中的问题都可以多项式时间归约到B。因此,我们有 $A \leq_P B$。
- 步骤5: 现在我们有两个条件:
- $A \leq_P B$ (来自前提1和NP完全定义)
- $B \in P$ (来自前提2)
- 步骤6: 根据我们之前学过的定理 7.31 (“容易性”可以传递),这两个条件直接导出结论:$A \in P$。
- 步骤7: 因为我们选的 A 是任意的一个NP问题,而我们证明了它在P中,所以这就证明了 NP $\subseteq$ P。
- 步骤8: 结合 P $\subseteq$ NP 和 NP $\subseteq$ P,我们最终得出 P = NP。
- 证明结束。
- 背景: 假设我们已经知道 CLIQUE 是 NP-完全的。
- 场景: 一位天才科学家 Alice 声称她发明了一种算法,可以在 $O(n^5)$ 时间内解决任何图的 CLIQUE 问题。这意味着 CLIQUE $\in P$。
- 推论: 根据定理 7.35,我们可以立即得出 P = NP。
- 这意味着什么:
- Alice 的发现不仅仅是解决了图论中的一个难题。
- 它意味着,我们之前认为很难的所有NP问题,比如 SAT、旅行商问题、背包问题、蛋白质折叠等等,必定也都存在多项式时间的解法(即使我们还不知道具体算法是什么)。
- 这是因为,对于任何一个NP问题 A (比如旅行商问题 TSP),我们知道 $TSP \le_P CLIQUE$ (因为CLIQUE是NP-完全的)。现在既然 CLIQUE $\in P$,那么根据定理7.31,TSP 也一定 $\in P$。
- 与库克-莱文定理的关系: 定理7.35看起来和库克-莱文定理 (定理7.27: "$SAT \in P \iff P=NP$") 非常相似。实际上,定理7.27是定理7.35的一个特例。因为SAT是第一个被证明的NP-完全问题,所以定理7.27是“开创性”的。而定理7.35则是对任何一个未来的NP-完全问题都成立的普遍规律。
- 证明的简洁性: 作者说“直接遵循...定义”,是因为这里的逻辑推导非常短,主要就是应用之前已经证明过的定理。
定理7.35以严谨的方式,再次强调了攻克任何一个NP-完全问题所带来的颠覆性后果。它表明,任何一个NP-完全问题都是打开 P=NP 这扇大门的钥匙。只要找到一把钥匙(让任何一个NPC问题进入P),整扇门就会轰然开启。
本段的目的是为了从NP-complete的定义出发,推导出它最重要的理论意义。这使得NP-complete这个标签变得极具分量:任何被贴上这个标签的问题,都自动成为了P vs NP问题的“代言人”。
在武林盟主的模型里:
- 前提1: 张三是武林盟主 (B是NPC)。
- 前提2: 你打败了张三 (B $\in$ P)。
- 结论: 你就是整个武林的天下第一 (P=NP)。
- 证明: 因为张三是盟主,所以武林中任何一个人(比如李四,一个任意的NP问题)的武功都可以看作是张三武功的一个简化版($A \le_P B$)。既然你连张三都能打败,那么打败李四自然不在话下($A \in P$)。因为李四是任意选的,所以你比武林中的任何人都厉害。
在联合国核心问题的模型里:
- 前提1: “能源危机”被确认为“全球核心问题”(B是NPC)。
- 前提2: 科学家们发明了“无限能源”技术,彻底解决了能源危机(B $\in$ P)。
- 结论: 全球所有重大问题(气候变化、粮食安全...)都可以被解决了(P=NP)。
- 证明: 因为“能源危机”是核心问题,所以我们知道“粮食问题”可以被转化为一个能源问题来解决。既然能源问题已经不是问题了,那么粮食问题自然也就可以解决了。这个逻辑对所有其他问题都适用。
17 通过归约证明新的NP-完全问题
📜 [原文17]
定理
7.36
如果 $B$ 是NP-完全的,并且对于 NP 中的 $C$, $B \leq_{\mathrm{P}} C$,则 $C$ 是NP-完全的。
证明 我们已经知道 $C$ 在 NP 中,所以我们必须证明 NP 中的每个 $A$ 都可多项式时间归约到 $C$。因为 $B$ 是NP-完全的,所以 NP 中的每个语言都可多项式时间归约到 $B$,而 $B$ 又可多项式时间归约到 $C$。多项式时间归约是可复合的;也就是说,如果 $A$ 可多项式时间归约到 $B$ 且 $B$ 可多项式时间归约到 $C$,那么 $A$ 可多项式时间归约到 $C$。因此,NP 中的每个语言都可多项式时间归约到 $C$。
这个定理是证明一个新问题是NP-完全的最常用方法,它建立了一个“NP-完全性”的传递链。
- 定理陈述:
- 前提1: B 是一个已知的 NP-完全问题 (比如我们已经知道了SAT是NPC)。
- 前提2: C 是一个 NP 问题。
- 前提3: $B \leq_{\mathrm{P}} C$ (我们成功地将已知的NPC问题B,多项式时间归约到了我们的新问题C)。
- 结论: C 也是一个 NP-完全问题。
- 这个定理的重要性:
- 在库克和莱文证明了第一个NP-完全问题 SAT 之后,我们就不再需要为每个新的候选问题都去走一遍那条极其复杂的、从“任意一个NP问题A”出发的证明路径了。
- 相反,我们可以站在SAT这个巨人的肩膀上。要想证明新问题 C 是 NP-完全的,我们只需要做两件事:
- 证明 $C \in NP$ (这通常比较容易)。
- 证明一个已知的NP-完全问题(比如3SAT)可以多项式时间归约到 C,即 $3SAT \le_P C$。
- 一旦完成这两步,根据定理7.36,我们就可以立刻宣布 C 也是 NP-完全的。这就是“归约法”证明NPC的威力。
- 证明过程的拆解:
- 目标: 证明 C 是 NP-完全的。根据定义,我们需要证明两点:(a) $C \in NP$; (b) 对所有 $A \in NP$,都有 $A \le_P C$。
- (a) $C \in NP$: 这是定理的前提之一,所以已经满足了,无需证明。
- (b) 对所有 $A \in NP$,证明 $A \le_P C$:
- 我们从NP中任取一个问题 A。
- 我们已知 B 是NP-完全的 (前提1),所以根据定义,必然有 $A \le_P B$。
- 我们又从前提3得知 $B \le_P C$。
- 现在我们有了一个归约链:$A \le_P B$ 并且 $B \le_P C$。
- 关键性质:归约的传递性 (Transitivity)。作者在这里指出,“多项式时间归约是可复合的”。这意味着,如果存在一个从A到B的高效翻译器,和一个从B到C的高效翻译器,那么把这两个翻译器串起来,就构成了一个从A到C的高效翻译器。
- 具体来说,从A到C的归约算法就是:先用A到B的归约函数 $f_1$ 把A的实例 $w_A$ 变成B的实例 $w_B = f_1(w_A)$;再用B到C的归约函数 $f_2$ 把 $w_B$ 变成C的实例 $w_C = f_2(w_B) = f_2(f_1(w_A))$。因为 $f_1$ 和 $f_2$ 都是多项式时间的,它们的复合 $f_2 \circ f_1$ 也是多项式时间的。
- 因此,我们证明了 $A \le_P C$。
- 结论: 因为 A 是任意选取的,所以我们证明了“对所有 $A \in NP$,都有 $A \le_P C$”。结合前提 $C \in NP$,我们得出 C 是 NP-完全的。
- 场景: 我们想证明 CLIQUE 问题是 NP-完全的。
- 已知: 假设我们已经通过库克-莱文定理知道了 3SAT 是 NP-完全的。
- 我们的任务:
- 证明 CLIQUE $\in$ NP: 我们之前已经分析过,这很容易。给定一个顶点集合,验证它是不是k-团是多项式时间的。
- 证明 $3SAT \le_P CLIQUE$: 这正是我们之前定理7.32所做的工作!我们详细地构造了一个从3-CNF公式到图的归约。
- 应用定理7.36:
- 令 B = 3SAT (已知的NPC问题)。
- 令 C = CLIQUE。
- 前提1: 3SAT 是 NPC (成立)。
- 前提2: CLIQUE $\in$ NP (成立)。
- 前提3: 3SAT $\le_P$ CLIQUE (成立,由定理7.32保证)。
- 结论: 因此,CLIQUE 也是 NP-完全的。
- 归约方向不能错: 要证明 C 是 NPC,你必须把一个已知的 NPC 问题 B 归约到 C ($B \le_P C$),而不是反过来。如果你证明了 $C \le_P B$,这只说明 C 的难度不超过 B,你无法得出 C 是 NPC 的结论(C可能比B简单)。
- 传递性的直觉: 为什么归约可以传递?因为“高效翻译”这个性质可以叠加。中文到英文的快速翻译器,加上英文到法文的快速翻译器,合起来就是一个中文到法文的快速翻译器。
定理7.36是扩展NP-完全问题家族的“繁殖”定理。它提供了一个标准化的、可操作的流程:要证明一个新问题C是NP-完全的,只需找到任何一个已知的NP-完全问题B,然后构造一个从B到C的多项式时间归约即可。这极大地简化了后续所有NP-完全性的证明。
本段的目的是提供一个证明NP-完全性的“流水线方法”。在SAT这个“原型”被艰难地制造出来之后,这个定理就像一个“模具”,可以被用来快速、批量地“生产”出更多的NP-完全问题,从而构建起整个NP-完全理论的大厦。
在武林盟主的模型里:
- 已知: 张三是现任武林盟主 (B是NPC)。
- 你想证明王五也是宗师级的顶尖高手(C是NPC):
- 你先得证明王五是武林中人 (C $\in$ NP)。
- 然后,你当众证明了,张三的独门绝技可以被“破解”并转化为王五的招式($B \le_P C$)。
- 结论: 王五也必定是盟主级别的顶尖高手 (C是NPC)。
- 理由: 因为所有人的武功都能转化为张三的(B是NPC),而张三的武功又能转化为王五的,所以所有人的武- [ ]
18 库克-莱文定理
📜 [原文18]
库克-莱文定理
一旦我们有了一个NP-完全问题,我们就可以通过从它进行多项式时间归约来获得其他问题。然而,确定第一个NP-完全问题则更为困难。现在我们通过证明 SAT 是NP-完全的来做到这一点。
定理 7.37
SAT 是NP-完全的。 ${ }^{2}$
该定理蕴含定理7.27。
这段话是库克-莱文定理的正式陈述和其历史地位的说明。
- 承上启下:
- 作者首先总结了刚刚介绍的“归约法”:一旦我们有了一个已知的NP-完全问题(比如一个“种子”),我们就可以像滚雪球一样,通过归约证明越来越多的问题是NP-完全的。
- 然后,作者提出了一个关键问题:这个“第一个种子”是从哪里来的?确定第一个NP-完全问题,必然不能用归约法(因为当时还没有已知的NPC问题可以用来归约),所以它必须用最原始、最困难的方法来证明。
- 第一个NP-完全问题:
- 这个“第一个”的荣誉,就落在了SAT问题上。
- 证明SAT是NP-完全的,是整个NP-完全理论的奠基之作。
- 定理 7.37 陈述:
- “SAT 是 NP-完全的。”
- 这是一个极其简洁但分量极重的陈述。根据NP-完全的定义,这句话等价于两件事:
- SAT $\in$ NP.
- 对于所有 $A \in NP$,都有 $A \le_P SAT$。
- 与定理7.27的关系:
- 作者指出,这个定理蕴含了之前的定理7.27 ("$SAT \in P \iff P=NP$")。
- 我们来梳理一下逻辑:
- 定理7.37说 SAT 是 NP-完全的。
- 根据定理7.35 (“如果一个NPC问题在P中,则P=NP”),我们把B换成SAT,直接得到:如果 SAT $\in$ P,则 P=NP。这是定理7.27的一个方向。
- 对于另一个方向(如果 P=NP,则 SAT $\in$ P):如果P=NP,那么所有NP问题都在P里。而 SAT 本身是NP问题,所以 SAT 自然也在P里。
- 因此,定理7.37的结论,加上NP-完全性的定义和推论,完整地构成了定理7.27的内容。定理7.37是更本质的那个。
这个定理本身是一个高度理论化的陈述,其价值在于它开启了一个领域,而不是解决一个具体计算。
- 历史意义的类比: 这就像在物理学中,牛顿确定了万有引力定律。在这之前,人们观察到苹果落地、月亮绕地球转等现象,但没有统一的理论。牛顿定律是第一个“种子”理论。之后,人们就可以利用牛顿定律去解释和预测行星轨道、潮汐等更多现象(相当于通过归约证明其他问题是NPC)。但牛- [ ]
19 库克-莱文定理的证明思路
📜 [原文19]
[^1]证明思路 证明 SAT 在 NP 中很容易,我们很快就会这样做。证明的难点在于证明 NP 中的任何语言都可以多项式时间归约到 SAT。
为此,我们为 NP 中的每个语言 $A$ 构建一个到 SAT 的多项式时间归约。A 的归约接受一个字符串 $w$ 并生成一个布尔公式 $\phi$,该公式模拟 A 的 NP 机器在输入 $w$ 上的运行。如果机器接受,$\phi$ 有一个可满足赋值,对应于接受计算。如果机器不接受,则没有赋值满足 $\phi$。因此,$w$ 在 $A$ 中当且仅当 $\phi$ 是可满足的。
实际构建以这种方式工作的归约是一个概念上简单的任务,尽管我们必须处理许多细节。布尔公式可以包含布尔运算 AND、OR 和 NOT,这些运算构成了电子计算机中使用的电路的基础。因此,我们可以设计一个布尔公式来模拟图灵机这一事实并不令人惊讶。细节在于这个想法的实现。
这是整个NP-完全理论的基石——库克-莱文定理证明的宏观蓝图。它解释了如何完成那件最困难的事:证明所有NP问题都可以归约到SAT。
- 分解证明任务:
- 要证明 SAT 是 NP-完全的,需要两步。
- 第一步 (简单部分): 证明 SAT $\in$ NP。思路是:猜测一个赋值,然后代入验证。这很容易,所以作者一笔带过。
- 第二步 (困难部分): 证明对于任意一个 NP 问题 A,都有 $A \le_P SAT$。这是证明的精华和难点。
- 核心证明策略:模拟计算历史:
- 目标: 构造一个通用的“翻译机”(多项式时间归约函数 $f$),这个翻译机能把任何NP问题 A 的任何输入 $w$,“翻译”成一个SAT公式 $\phi$。
- 模拟对象: 这个翻译机的工作原理是“模拟”。它要模拟什么呢?它要模拟一台解决问题 A 的非确定性图灵机 (NDTM) 在输入 $w$ 上的整个计算过程。
- NDTM回顾: 一个NP问题 A,根据定义,存在一个在多项式时间内解决它的 NDTM,我们称之为 $N$。当 $N$ 输入 $w$ 时,如果 $w \in A$,那么 $N$ 存在至少一条计算路径(一个选择序列)可以达到“接受”状态。如果 $w \notin A$,那么所有计算路径都不能达到“接受”状态。
- 用公式来描述计算: 证明的核心思想就是,我们可以用一个巨大的布尔公式 $\phi$ 来完整、精确地描述图灵机 $N$ 对输入 $w$ 进行计算的所有规则和状态演变。
- 公式 $\phi$ 的变量: 会用来表示图灵机在某个时刻 $t$、纸带的某个位置 $p$ 上的符号是什么,或者图灵机在时刻 $t$ 处于哪个状态等。
- 公式 $\phi$ 的子句: 会用来描述图灵机的“物理定律”,例如:
- “在任何时刻、任何位置,纸带上只能有一个符号。”
- “图灵机的起始状态是正确的。”
- “图灵机每一步的状态转移都必须符合它的转移函数。”
- “图灵机最终进入了‘接受’状态。”
- 建立等价关系:
- 这个构造的巧妙之处在于,最终生成的公式 $\phi$ 是否可满足,完全等价于原始图灵机 $N$ 是否接受输入 $w$。
- $\phi$ 可满足 $\iff$ 存在一个满足赋值: 存在一组对 $\phi$ 中所有变量的真/假赋值,让 $\phi$ 为真。
- 这个“满足赋值”是什么?: 它其实就是对 $N$ 的某一个具体的、完整的“计算历史”的描述。它详细说明了在每一步、每个位置,图灵机的状态、纸带内容、磁头位置分别是什么。
- $\phi$ 为真 $\iff$ 这个“计算历史”是合法的且最终接受: 因为 $\phi$ 的子句规定了所有图灵机的运行规则,所以只有当这个“计算历史”完全遵守了这些规则(起始正确、转移合法、最终接受),$\phi$ 才可能为真。
- 结论: 因此,“存在一个满足 $\phi$ 的赋值”就等价于“存在一个合法的、最终接受的计算历史”,而这正是“$N$ 接受 $w$”的定义。
- 可行性分析:
- 作者指出,这个想法在概念上是简单的,因为我们知道计算机本身就是由逻辑门(AND, OR, NOT)构建的。用布尔公式来模拟一个计算设备(图灵机),是顺理成章的。
- 难点在于大量的实现细节,要确保公式的构造是正确的、无遗漏的,并且整个构造过程必须在多项式时间内完成。
这个证明思路极其抽象,很难用小例子完全展示。但可以做一个极度简化的类比:
- 问题A: 判断一个2位的二进制数 $w=w_1w_2$ 是否包含'1'。这是一个非常简单的P问题,当然也是NP问题。
- 模拟它的图灵机 N: 简单来说,它会检查第一个带方,再检查第二个带方。
- 归约函数 f:
- 输入: $w = w_1w_2$ (比如 '01')
- 输出: 一个公式 $\phi$
- 构造 $\phi$:
- 变量:
- $v_{i,j}$: 表示输入 $w$ 的第 $i$ 位是 $j$ ($j \in \{0,1\}$)。
- $c_{i}$: 表示在检查第 $i$ 位时是否找到了'1'。
- 子句:
- 描述输入: (比如 $w='01'$, 公式就有 $\neg v_{1,1} \wedge v_{1,0} \wedge v_{2,1} \wedge \neg v_{2,0}$ )
- 描述计算:
- $c_1 \iff v_{1,1}$ (检查第一位的结果)
- $c_2 \iff v_{2,1}$ (检查第二位的结果)
- 描述接受条件: $Accept \iff (c_1 \vee c_2)$ (只要任何一位找到了'1'就接受)
- 最终公式 $\phi$: 就是以上所有子句的 AND。
- 验证:
- 对于输入 $w='01'$,$\phi$ 是可满足的 (令 $v_{1,0}=1, v_{2,1}=1, c_1=0, c_2=1, Accept=1$)。
- 对于输入 $w='00'$,$\phi$ 最终会导出 $Accept=0$,是不可满足的(在要求Accept=1的前提下)。
- 这个例子极度简化,但展示了如何用布尔变量和逻辑运算来“描述”一个计算过程和结果。库克-莱文的证明就是这个思想的终极、通用版本。
- 不要被“概念上简单”误导: 这句话是说给已经深入理解计算理论的专家听的。对于初学者,这个证明的细节是相当繁琐和复杂的,需要非常仔细地跟踪。
- 模拟的是“非确定性”: 关键是要模拟非确定性图灵机。这意味着公式 $\phi$ 描述的不是一条计算路径,而是“是否存在一条合法的、接受的计算路径”。可满足性中的“存在”一个满足赋值,正好对应了非确定性计算中的“存在”一条接受路径。
本段概述了证明SAT是NP-完全的宏伟蓝图。其核心武器是“模拟计算”:通过构造一个巨大的布尔公式,来完整描述一个通用的非确定性图灵机在处理任何NP问题时的计算行为。这个公式的“可满足性”被巧妙地设计为与图灵机的“接受”行为完全等价。这个石破天惊的想法,将所有NP问题的计算过程都统一到了SAT这一个问题的框架之下。
本段的目的是在深入到繁复的公式构造细节之前,让读者先理解整个证明的顶层设计和哲学思想。读者需要明白,我们不是在玩逻辑游戏,而是在用逻辑语言为“计算”本身建立一个数学模型。
这就像是想证明“任何一部电影(任何NP问题)的剧情都可以被改编成一部戏剧(SAT问题)”。
- 证明思路: 我们来设计一个通用的“剧本创作指南”。
- 指南内容:
- 角色(变量): 剧本需要包含“场景1-主角位置”、“场景1-配角表情”等变量。
- 规则(子句):
- “一个角色不能同时在两个地方出现。”
- “故事必须从‘很久很久以前’开始。”
- “角色的行为必须符合其性格设定(转移函数)。”
- “故事结局必须是‘从此幸福地生活在一起’(接受状态)。”
- 等价性: 一部电影的剧情是“合理的”(图灵机接受),当且仅当,根据这本指南创作出的剧本是“可以被演出来的”(公式可满足)。库克-莱文的证明就是写出了这本包罗万象、绝无遗漏的“剧本创作指南”。
想象你要向一个只懂“是/非”逻辑的机器人(SAT求解器)解释什么是“胜利的一盘象棋”。
你不能直接给它看棋盘。你必须把整个游戏翻译成它能懂的逻辑语言。
- 你的翻译(归约公式 $\phi$):
- 变量: $x_{p,s,t}$ = “在第 t 回合,棋子 p 在格子 s 上”。
- 规则(子句):
- “一个格子在同一回合只能有一个棋子。”
- “棋局开始时,所有棋子都在初始位置。”
- “‘马’走的每一步都必须是‘日’字。”
- “‘王’最后被‘将死’。”
- 向机器人提问: 你把这个无比巨大的、由成千上万条逻辑规则组成的公式 $\phi$ 交给机器人,问它:“这个公式有没有可能为真?”
- 机器人的回答: 如果机器人回答“是”,这意味着存在一个满足所有规则的变量赋值。这个赋值,实际上就是一整盘“将死”对方的棋谱!这就证明了原始棋局是“可胜”的。
- 库克-莱文定理就是为任何一个NP问题提供了这样一种通用的“翻译成逻辑语言”的方法。
20 库克-莱文定理的形式化证明:准备工作
📜 [原文20]
证明 首先,我们证明 SAT 在 NP 中。一个非确定性多项式时间机器可以猜测给定公式 $\phi$ 的一个赋值,并在赋值满足 $\phi$ 时接受。
接下来,我们取 NP 中的任何语言 $A$,并证明 $A$ 可多项式时间归约到 SAT。令 $N$ 是一个在 $n^{k}$ 时间内决定 $A$ 的非确定性图灵机,其中 $k$ 为某个常数。(为方便起见,我们实际上假设 $N$ 在 $n^{k}-3$ 时间内运行;但只有对细节感兴趣的读者才需要担心这个小问题。)以下概念有助于描述归约。
$N$ 在 $w$ 上的格局表是一个 $n^{k} \times n^{k}$ 的表格,其行是 $N$ 在输入 $w$ 上的计算分支的格局,如下图所示。
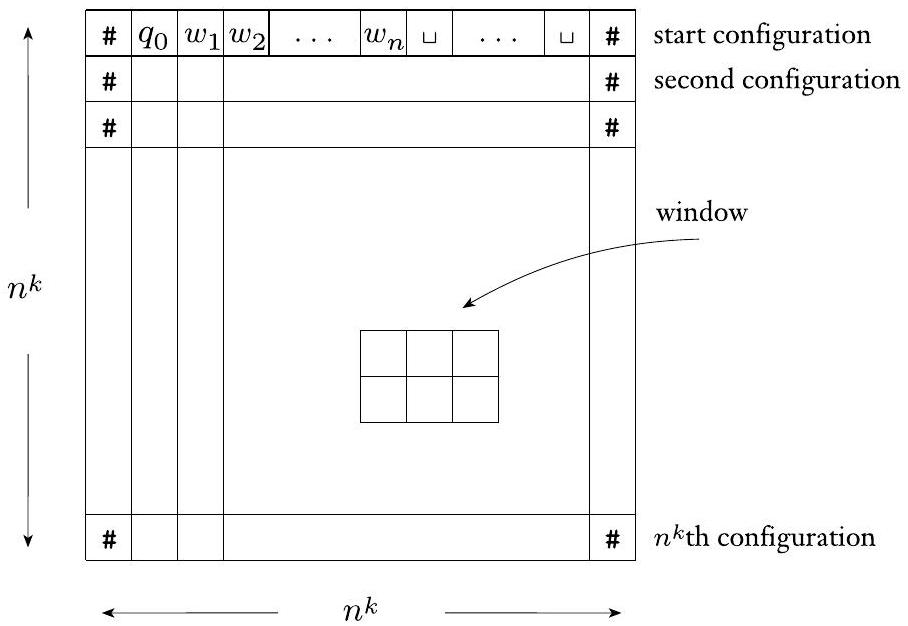
图 7.38
格局表是一个 $n^{k} \times n^{k}$ 的格局表
为方便起见,我们假设每个格局都以 # 符号开始和结束。因此,格局表的第一列和最后一列都是 #。格局表的第一行是 $N$ 在 $w$ 上的起始格局,每行都根据 $N$ 的转移函数紧随前一行。如果格局表的任何一行是接受格局,则该格局表是接受的。
$N$ 在 $w$ 上的每个接受格局表都对应于 $N$ 在 $w$ 上的一个接受计算分支。因此,确定 $N$ 是否接受 $w$ 的问题等价于确定 $N$ 在 $w$ 上是否存在接受格局表的问题。
这是证明的正式开始,本段主要是在做一些准备工作和定义,为后续构造庞大的布尔公式铺路。
- 证明 SAT $\in$ NP (简单部分):
- 作者在这里快速地给出了第一部分的证明。
- 算法:
- 对于一个有 $m$ 个变量的公式 $\phi$。
- 非确定性地“猜测”一个对这 $m$ 个变量的赋值(例如,猜测 $x_1=1, x_2=0, \dots$)。这个猜测步骤相当于在 $2^m$ 种可能性中“幸运地”选中一种。
- 将猜测的赋值代入公式 $\phi$ 进行计算,验证其结果是否为1。
- 如果结果为1,则接受。
- 时间分析: 第2步验证的时间与公式长度成多项式关系。因此,整个过程是一个非确定性多项式时间算法。故 SAT $\in$ NP。
- 设定归约目标 (困难部分):
- 我们的目标是从一个任意的 NP 问题 A 归约到 SAT。
- 首先,根据 NP 的定义,对于问题 A,一定存在一个非确定性图灵机 (NDTM) $N$,它能在多项式时间 $O(n^k)$ 内解决 A。这里 $n$ 是输入 $w$ 的长度,$k$ 是某个固定的常数。
- (技术细节:作者提到 $n^k-3$,这是一个为了后续窗口构造方便而做的小调整,初学者可以完全忽略它,直接理解为 $O(n^k)$ 即可)。
- 引入核心数据结构:格局表 (Tableau):
- 什么是格局 (Configuration): 在任意时刻,一个图灵机的“快照”被称为一个格局。它包含了三样东西:当前状态、纸带上的全部内容、当前磁头的位置。通常我们可以用一个字符串来表示,比如 uqv,表示当前状态是 $q$,磁头在 $v$ 的第一个字符上,磁头左边的纸带内容是 $u$,右边是 $v$。
- 什么是格局表: 这是整个证明中最核心的构造。它是一个二维表格,用来记录 NDTM 的一个完整计算历史。
- 表格的行: 表格的每一行代表一个格局,也就是图灵机在某一个时刻的快照。第一行是初始格局,第二行是第一步之后的格局,以此类推。
- 表格的列: 每一列代表纸带上的一个位置。
- 表格的尺寸: 既然 NDTM 在 $n^k$ 时间内运行,那么它最多走 $n^k$ 步,所以格局表最多需要 $n^k$ 行来记录每一步。同时,磁头最多向右移动 $n^k$ 个位置,所以纸带的有效长度也不会超过 $n^k$。因此,我们可以用一个 $n^k \times n^k$ 的巨大表格来容纳整个计算过程。这是一个非常宽松但足够大的估计。
- 图7.38: 这个图直观地展示了格局表。第一行是起始格局 $C_1$ (Configuration 1),然后根据转移函数,可能产生格局 $C_2$,再到 $C_3$,等等,直到 $C_{n^k}$。
- 格局表的属性和边界:
- # 边界: 为了处理纸带边界问题,作者假设每个格局字符串的开头和结尾都有一个特殊的边界符号 #。这简化了后续对“窗口”合法性的判断,避免了对纸带最左和最右单元格的特殊处理。
- 合法演进: 表格的每一行都必须是根据前一行和图灵机的转移函数“合法地”推导出来的。
- 接受格局表: 如果这个表格的某一行包含了一个“接受状态” $q_{accept}$,那么我们就说这是一个“接受格局表”。
- 建立等价关系:
- 关键洞察: 一个 NDTM $N$ 接受输入 $w$,其定义是“存在至少一条计算分支(路径)能够到达接受状态”。
- 而这里的“格局表”,正是对这样一条计算分支的完整记录。
- 因此,原始问题“$N$ 是否接受 $w$?”被等价地转换为了一个新问题:“是否存在一个接受格局表?”
- 下一步的目标:
- 我们的最终目标是用一个布尔公式 $\phi$ 来描述“存在一个接受格局表”这件事。
- 我们将引入一大堆布尔变量,来表示格局表中每个单元格里填的是什么符号。
- 然后我们将构造一系列子公式,来约束这些变量,使得只有当这些变量的赋值恰好构成一个“接受格局表”时,整个大公式 $\phi$ 才能为真。
- 图灵机N: 一个简单的NDTM,输入是'a'或'b'。如果输入是'a',它在2步内接受;如果是'b',它永远不接受。
- 输入w: 'a' (长度n=1)。假设时间是 $n^2=1^2=1$ (为了简单,实际是$n^k$),空间也是1。格局表大小是 $1 \times 1$。
- 格局:
- 初始格局 $C_1$: $q_0a$
- 一步之后 $C_2$: 假设转移到 $q_{accept}b$
- 格局表: 一个 $2 \times 3$ 的表格 (假设纸带左右各有一个#)
| # | $q_0$a | # | <-- 实际格局表示可能是 #q_0a# |
|---|---|---|---|
| # | $b q_{accept}$ | # | <-- 实际格局表示可能是 #bq_{accept}# |
- 这个表就是一个接受格局表,因为它包含 $q_{accept}$。
- 我们的目标就是构造一个公式 $\phi$,当且仅当存在这样一个表格时,$\phi$ 才可满足。
- 非确定性的体现: 一个NDTM对一个输入可以有很多条计算路径,从而对应很多个不同的格局表。我们构造的公式 $\phi$ 的可满足性,对应的是“是否存在至少一个接受格局表”,这与NDTM的接受定义完美契合。
- 格局表大小: $n^k \times n^k$ 是一个非常粗略但安全的上界。它保证了任何在多项式时间内发生的计算,无论磁头如何移动,其轨迹都能被容纳在这个表格里。这使得我们的证明具有普适性。
本段是库克-莱文定理证明的技术起点。它完成了两项准备工作:1) 快速证明了SAT属于NP;2) 引入了核心的“格局表”概念,将一个动态的“图灵机计算过程”转化为了一个静态的、巨大的二维“计算历史快照”。这使得“判定机器是否接受”的问题,等价于“判断是否存在一个满足特定条件的二维表”的问题,为后续用布尔逻辑来描述这个表铺平了道路。
本段的目的是将证明的目标从抽象的“模拟图灵机”具体化为“描述格局表”。格局表是一个离散的、结构化的对象,非常适合用大量的布尔变量来编码和约束。这是从计算理论的动态世界迈向布尔逻辑的静态世界的关键一步。
这就像是要用一大堆“是/非”的问题,来描述一部电影的剧情。
- 格局表: 就是电影的“分镜故事板”。每一行是一个关键帧(格局),记录了那个瞬间所有角色的位置、表情、状态。
- 格局表的演进: 故事板的下一帧必须是上一帧的合理延续。
- 接受格局表: 故事板的某一帧里出现了“剧终,完美结局”的字样。
- 问题转换: “这部电影是不是一部喜剧?”被转换成了“这部电影的分镜故事板里,有没有可能出现一个‘完美结局’的画面?”
- 下一步: 我们就要发明一种语言(布尔公式),用“是/非”问题来问:“这个单元格里是不是‘#’?”、“这一帧是不是起始帧?”、“上下两帧的衔接合不合法?”,等等。
想象你要用法律条文(布尔公式)来定义什么是“一次合法的、成功的太空发射”。
- 格局表: 就是这次发射从 T-10秒到 T+10分钟的每一毫秒的“全系统状态快照”记录表。表格的每一行是一毫秒的快照,记录了箭体姿态、燃料余量、发动机状态、宇航员心率等所有信息。
- 接受格局表: 在这个记录表的某一行,出现了“成功进入预定轨道”的状态。
- 问题转换: “这次发射成功了吗?”被等价转换为“是否存在一份‘全系统状态快照’记录表,它从头到尾都符合空气动力学和发动机原理(转移函数),并且最终记录了‘成功入轨’的状态?”
- 下一步: 我们将用逻辑语言,写下描述空气动力学、发动机原理、入轨条件的那些“法律条文”。
21 库克-莱文定理的形式化证明:变量定义
📜 [原文21]
现在我们来描述从 $A$ 到 SAT 的多项式时间归约 $f$。在输入 $w$ 上,归约生成一个公式 $\phi$。我们首先描述 $\phi$ 的变量。假设 $Q$ 和 $\Gamma$ 分别是 $N$ 的状态集和磁带字母表。令 $C=Q \cup \Gamma \cup\{\#\}$。对于每个介于 1 和 $n^{k}$ 之间的 $i$ 和 $j$,以及 $C$ 中的每个 $s$,我们有一个变量 $x_{i, j, s}$。
格局表的 $\left(n^{k}\right)^{2}$ 个条目中的每一个都称为一个单元格。行 $i$ 和列 $j$ 中的单元格称为单元格 $[i, j]$,包含来自 $C$ 的一个符号。我们用 $\phi$ 的变量表示单元格的内容。如果 $x_{i, j, s}$ 取值 1,则表示单元格 $[i, j]$ 包含一个 $s$。
这是构造布尔公式 $\phi$ 的第一步,也是最基础的一步:定义我们需要的变量。
- 归约函数 f 的目标:
- 输入:一个字符串 $w$。
- 输出:一个巨大的布尔公式 $\phi$。
- 这个过程必须是多项式时间的。
- 定义符号集 C:
- $Q$: 图灵机 $N$ 的所有可能状态的集合(如 {$q_0, q_1, q_{accept}, q_{reject}$})。
- $\Gamma$: 图灵机 $N$ 的纸带上所有可能出现的符号的集合(如 {$0, 1, \sqcup$},其中 $\sqcup$ 是空白符)。
- $\#$: 我们之前约定的边界符号。
- $C = Q \cup \Gamma \cup \{\#\}$: 我们把所有可能出现在格局表单元格里的东西都汇集到一个大集合 $C$ 里。这个集合包含了状态、纸带符号和边界符。
- 定义核心变量 $x_{i, j, s}$:
- 这是整个证明中唯一的变量类型,但数量极其庞大。
- 变量的含义: $x_{i, j, s}$ 是一个布尔变量,它的真假值代表了一个陈述的真伪。
- 这个陈述是:“在格局表的第 $i$ 行、第 $j$ 列的那个单元格里,存放的符号是 $s$。”
- $x_{i, j, s} = 1$ (TRUE) 意味着:“是的,单元格 $[i, j]$ 的内容就是 $s$。”
- $x_{i, j, s} = 0$ (FALSE) 意味着:“不,单元格 $[i, j]$ 的内容不是 $s$。”
- 变量的索引 (下标):
- $i$: 代表行号(时间),从 1 到 $n^k$。
- $j$: 代表列号(纸带位置),从 1 到 $n^k$。
- $s$: 代表符号,是集合 $C$ 中的任意一个元素。
- 变量总数:
- 格局表有 $n^k \times n^k = n^{2k}$ 个单元格。
- 对于每个单元格,我们都需要一组变量来指明它可能的内容。集合 $C$ 的大小是 $|C| = |Q| + |\Gamma| + 1$。这是一个与输入 $w$ 长度 $n$ 无关的常数,我们称之为 $c$。
- 所以,对于每个单元格,都有 $c$ 个可能的符号,我们也就需要 $c$ 个变量。
- 总变量数 = (单元格数量) $\times$ (每个单元格可能的符号数) = $n^{2k} \times |C|$。
- 这是一个关于 $n$ 的多项式级别的数量,所以光是写下所有变量就需要多项式时间。
- 假设一个极简的图灵机:$Q=\{q_0, q_a\}$ (接受状态), $\Gamma=\{\sqcup\}$。
- 那么符号集 $C = \{q_0, q_a, \sqcup, \#\}$。$|C|=4$。
- 假设输入 $w$ 长度为1,多项式时间是 $n^1=1$ 步,空间是 $n^1=1$。格局表大小为 $1 \times 1$。
- 但为了更清楚,我们假设格局表是 $2 \times 2$ 的 ($i \in \{1,2\}, j \in \{1,2\}$)。
- 我们有哪些变量?
- 对于单元格 $[1, 1]$ (第1行, 第1列):
- $x_{1,1,q_0}$: 单元格[1,1]是$q_0$吗?
- $x_{1,1,q_a}$: 单元格[1,1]是$q_a$吗?
- $x_{1,1,\sqcup}$: 单元格[1,1]是$\sqcup$吗?
- $x_{1,1,\#}$: 单元格[1,1]是$\#$吗?
- 对于单元格 $[1, 2]$ (第1行, 第2列):
- $x_{1,2,q_0}, x_{1,2,q_a}, x_{1,2,\sqcup}, x_{1,2,\#}$
- 对于单元格 $[2, 1]$ (第2行, 第1列):
- $x_{2,1,q_0}, x_{2,1,q_a}, x_{2,1,\sqcup}, x_{2,1,\#}$
- 对于单元格 $[2, 2]$ (第2行, 第2列):
- $x_{2,2,q_0}, x_{2,2,q_a}, x_{2,2,\sqcup}, x_{2,2,\#}$
- 总共有 $2 \times 2 \times 4 = 16$ 个变量。
- 一个可能的“满足赋值”的片段: 如果一个计算历史的格局表,其[2,1]单元格的内容是 $q_a$,那么对应的满足赋值中,变量 $x_{2,1,q_a}$ 必须为 1,而 $x_{2,1,q_0}, x_{2,1,\sqcup}, x_{2,1,\#}$ 都必须为 0。
- 变量与格局的关系: 一个变量 $x_{i,j,s}$ 只描述了一个单元格的信息。一个完整的格局(一行)需要 $n^k \times |C|$ 个变量来描述。一个完整的格局表(整个计算历史)则需要 $n^{2k} \times |C|$ 个变量来描述。
- 变量的独立性: 目前,这些变量之间是完全独立的。我们可以随意给它们赋真假值。接下来的步骤就是要用逻辑子句把它们“捆绑”起来,强迫它们必须共同描述一个合法的计算历史。
本段定义了库克-莱文证明中用于构建SAT公式的“原子”——布尔变量 $x_{i, j, s}$。这个变量的含义是“格局表的 $[i, j]$ 位置的符号是否为 $s$”。通过为格局表的每个单元格的每种可能性都设立一个变量,我们建立了一个庞大的布尔变量空间,这个空间足以编码任何一个可能的计算历史。
本段的目的是将证明从对“格局表”的直观描述,转化为对“布尔变量”的精确描述。这是将图灵机模型映射到布尔逻辑世界的第一步,也是后续所有公式构造的基础。没有这些变量,一切都无从谈起。
我们正在为“分镜故事板”(格局表)的每一个像素点(单元格)建立一个档案。
- 变量 $x_{i,j,s}$: 就是一份调查问卷。
- 问卷题目: “在第 i 帧画面的第 j 个像素点上,颜色是不是 s ?”
- 答案: 只能填“是”(TRUE/1)或“否”(FALSE/0)。
- 我们为每一个可能的像素点、每一种可能的颜色都准备了一份这样的问卷。这就构成了一个巨大的问卷集合(变量集合)。一个完整的“满足赋值”,就是把所有问卷都填好的一套答案。
想象你在国会图书馆里,要用卡片索引系统来描述一本书的每一个字。
- 格局表: 就是这本书本身。
- i, j: 第 i 页,第 j 个字符位置。
- s: 某个汉字,比如‘我’。
- 变量 $x_{i,j,s}$: 就是一张索引卡片,上面写着:“《时间简史》第88页第3行第5个字,是‘我’字吗?”
- 赋值: 在这张卡片上打上“✔”或“✘”。
- 为了完整描述这本书,你需要为书中的每个位置、对照字典里的每个汉字,都制作一张这样的卡片。这个卡片总量是惊人的,但却是有限的、可操作的。
22 库克-莱文定理的形式化证明:$\phi_{\text {cell}}$
📜 [原文22]
现在我们设计 $\phi$,使得变量的可满足赋值确实对应于 $N$ 在 $w$ 上的接受格局表。公式 $\phi$ 是四个部分的 AND:$\phi_{\text {cell }} \wedge \phi_{\text {start }} \wedge \phi_{\text {move }} \wedge \phi_{\text {accept }}$。我们依次描述每个部分。
如前所述,将变量 $x_{i, j, s}$ 置为 1 对应于将符号 $s$ 放入单元格 $[i, j]$。为了获得赋值与格局表之间的对应关系,我们必须首先保证赋值为每个单元格只开启一个变量。公式 $\phi_{\text {cell}}$ 通过用布尔运算表达此要求来确保此要求:
符号 $\wedge$ 和 $\vee$ 代表迭代的 AND 和 OR。例如,前面公式中的表达式
是以下内容的简写
其中 $C=\left\{s_{1}, s_{2}, \ldots, s_{l}\right\}$。因此,$\phi_{\text {cell}}$ 实际上是一个大型表达式,其中包含格局表中每个单元格的片段,因为 $i$ 和 $j$ 的范围是从 1 到 $n^{k}$。每个片段的第一部分表示在相应单元格中至少有一个变量被开启。每个片段的第二部分表示在相应单元格中没有超过一个变量被开启(字面意思是,在每对变量中,至少有一个被关闭)。这些片段通过 $\wedge$ 运算连接。
$\phi_{\text {cell}}$ 方括号内的第一部分规定,与每个单元格关联的至少一个变量是开启的,而第二部分规定,每个单元格最多只能有一个变量是开启的。任何满足 $\phi$(因此满足 $\phi_{\text {cell}}$)的变量赋值都必须为每个单元格开启一个变量。因此,任何可满足赋值都指定了表中每个单元格的一个符号。部分 $\phi_{\text {start}} 、 \phi_{\text {move}}$ 和 $\phi_{\text {accept}}$ 确保这些符号实际对应于一个接受格局表,如下所示。
这是构造大公式 $\phi$ 的第一个组件:$\phi_{cell}$。这个组件的任务是确保我们对变量的任何一个“满足赋值”,都能对应到一个格式正确的、无歧义的格局表。
- 大公式 $\phi$ 的结构:
- 作者宣布,最终的公式 $\phi$ 是四个子公式的“与”(AND)运算:
- 这意味着,要让 $\phi$ 为真,这四个子公式必须同时为真。
- 这是一种模块化设计的思想,每个子公式负责施加一种约束:
- $\phi_{cell}$: 确保每个单元格的内容是唯一的、确定的。
- $\phi_{start}$: 确保计算从正确的初始格局开始。
- $\phi_{move}$: 确保计算的每一步都遵循图灵机的转移规则。
- $\phi_{accept}$: 确保计算最终达到了接受状态。
- $\phi_{cell}$ 的目标:
- 我们定义了变量 $x_{i,j,s}$ 来表示“[i,j]单元格的内容是s”。
- 但一个单元格的内容应该是唯一的。它不能既是符号'a'又是符号'b',也不能什么都不是。
- 所以,$\phi_{cell}$ 要施加的约束是:“对于每一个单元格,有且仅有一个符号s,使得 $x_{i,j,s}$ 为真。”
- $\phi_{cell}$ 的构造:
- $\phi_{cell}$ 是对所有单元格 $(i, j)$ 的约束的“与”运算。外层的 $\bigwedge_{1 \leq i, j \leq n^{k}}$ 就体现了这一点。
- 对于每一个固定的单元格 $(i, j)$,方括号 [...] 里的内容是专门为它设定的约束。这个约束又分为两部分,用“与”连接:
- 第一部分 (至少一个为真): $\left(\bigvee_{s \in C} x_{i, j, s}\right)$
- 这是对所有可能的符号 $s$ 的“或”运算。
- 它的意思是:$x_{i,j,s_1} \vee x_{i,j,s_2} \vee \dots \vee x_{i,j,s_l}$ 必须为真。
- 这保证了对于单元格 $(i,j)$,至少有一个符号被“开启”,即这个单元格不能为空。
- 第二部分 (至多一个为真): $\left(\bigwedge_{\substack{s, t \in C \\ s \neq t}}\left(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}}\right)\right)$
- 这是对所有不同的符号对 $(s, t)$ 的“与”运算。
- 对于任意一对不同的符号 $s$ 和 $t$,我们要求 $(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}})$ 为真。
- 这个子句 $(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}})$ 的意思是“$x_{i, j, s}$ 和 $x_{i, j, t}$ 不能同时为真”。(如果它们同时为真,那么 $\bar{1} \vee \bar{1} = 0 \vee 0 = 0$,子句为假)。
- 把所有不同符号对的这种约束都“与”起来,就保证了对于单元格 $(i,j)$,不可能有两个或两个以上的符号被“开启”。
- 结合两部分: “至少一个” + “至多一个” = “有且仅有一个”。
- 结论:
- 任何一个能让 $\phi_{cell}$ 为真的赋值,都必须为每个单元格 $(i,j)$ 精确地指定了一个符号。
- 这就在“变量赋值”和“填满了符号的格局表”之间建立了一一对应的关系。
- 现在,我们就有了一个“格式正确”的表格,接下来的三个子公式就要确保这个表格里的内容是“有意义的”(即描述一个合法的接受计算)。
- $\phi_{\text {cell }}=\bigwedge_{1 \leq i, j \leq n^{k}}\left[ \dots \right]$:
- $\bigwedge_{1 \leq i, j \leq n^{k}}$: 这是一个大范围的 AND 运算。它的意思是,将 $i$ 从 1 到 $n^k$、$j$ 从 1 到 $n^k$ 遍历所有组合,把每个组合生成的方括号内的子公式都用 AND 连接起来。总共有 $n^{2k}$ 个这样的子公式。
- $\bigvee_{s \in C} x_{i, j, s}$:
- $\bigvee_{s \in C}$: 这是一个 OR 运算。它的意思是,让 $s$ 取遍集合 $C$ 中的每一个元素,把对应的变量 $x_{i,j,s}$ 用 OR 连接起来。
- $\bigwedge_{\substack{s, t \in C \\ s \neq t}}\left(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}}\right)$:
- $\bigwedge_{\substack{s, t \in C \\ s \neq t}}$: 这是另一个 AND 运算。它遍历集合 $C$ 中所有不相等的元素对 $(s, t)$。
- $(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}})$: 这是对每一对变量施加的约束。它等价于 $\neg(x_{i,j,s} \wedge x_{i,j,t})$,即 "$x_{i,j,s}$ 和 $x_{i,j,t}$ 不能同时为真"。
- 继续用之前的极简例子:$C=\{a,b\}$,我们只关注一个单元格 $[1,1]$。
- 那么为这个单元格构造的 $\phi_{cell}$ 片段是:
- 第一部分 (至少一个): $(x_{1,1,a} \vee x_{1,1,b})$
- 第二部分 (至多一个): $C$ 中不等的符号对只有 $(a,b)$ 这一对。所以这部分是 $(\overline{x_{1,1,a}} \vee \overline{x_{1,1,b}})$。
- 合并: 最终为单元格[1,1]的约束是 $(x_{1,1,a} \vee x_{1,1,b}) \wedge (\overline{x_{1,1,a}} \vee \overline{x_{1,1,b}})$。
- 验证:
- 赋值 $x_{1,1,a}=1, x_{1,1,b}=0$:
- 第一部分: $(1 \vee 0) = 1$ (OK)
- 第二部分: $(\bar{1} \vee \bar{0}) = (0 \vee 1) = 1$ (OK)
- 总公式: $1 \wedge 1 = 1$。这个赋值是满足的,对应单元格内容是 'a'。
- 赋值 $x_{1,1,a}=0, x_{1,1,b}=1$: 同样满足,对应内容是 'b'。
- 赋值 $x_{1,1,a}=0, x_{1,1,b}=0$:
- 第一部分: $(0 \vee 0) = 0$ (失败)。
- 赋值 $x_{1,1,a}=1, x_{1,1,b}=1$:
- 第二部分: $(\bar{1} \vee \bar{1}) = (0 \vee 0) = 0$ (失败)。
- 可见,这个公式完美地实现了“有且仅有一个为真”的目标。
- 公式的大小: $\phi_{cell}$ 的大小是 $O(n^{2k} \cdot |C|^2 \cdot \log(\dots))$,其中 $\log$ 项是记录变量下标所需的位数。因为 $|C|$ 是常数,所以这仍然是一个多项式大小的公式,可以在多项式时间内被构造出来。
- “At most one” 的其他写法: “至多一个为真”的约束,虽然这里的写法很标准,但如果 $|C|$ 很大,它会产生 $O(|C|^2)$ 个子句。在实际的SAT求解器中,可能会用其他更紧凑的编码方式来实现同样的目的。但对于理论证明,这种清晰的写法是最好的。
本段详细解释了如何构造子公式 $\phi_{cell}$。它的功能是为整个格局表设定“物理基础”,即确保每个单元格都存放着一个唯一、确定的符号。它通过对每个单元格施加“至少一个为真”和“至多一个为真”的逻辑约束来实现这一目标,从而在布尔变量的赋值与格式正确的格局表之间建立了桥梁。
本段的目的是完成大厦的地基。没有 $\phi_{cell}$ 提供的这个基本约束,后续的 $\phi_{start}, \phi_{move}, \phi_{accept}$ 都将失去意义,因为它们约束的对象(一个被填满符号的、无歧义的表格)将不复存在。
在分镜故事板的比喻中,$\phi_{cell}$ 就是在设定最基本的绘画规则:
- “故事板的每一个小格子里(单元格),都必须画上颜色,不能为空白。” (至少一个)
- “每一个小格子里,不准同时画上红色和蓝色,只能选择一种颜色。” (至多一个)
- $\phi_{cell}$ 就是把这两条规则写下来,应用到故事板的每一个小格子上。
在国会图书馆索引卡片的比喻中,$\phi_{cell}$ 是一条强制性的图书馆规定:
- “对于书中每一个位置(比如第88页第5个字),你必须在我提供的所有汉字卡片中,至少勾选一张卡片为‘是’。”
- “对于书中每一个位置,在你勾选的汉字卡片中,最多只能勾选一张为‘是’。”
- 这条规定确保了任何一个合法的“填卡方案”(满足赋值),都精确地描述了这本书的每一个字是什么。
23 库克-莱文定理的形式化证明:$\phi_{\text {start}}, \phi_{\text {accept}}$
📜 [原文23]
公式 $\phi_{\text {start}}$ 确保表的第一行是 $N$ 在 $w$ 上的起始格局,通过明确规定相应的变量是开启的:
公式 $\phi_{\text {accept}}$ 保证格局表中出现一个接受格局。它通过规定相应的一个变量开启来确保接受状态的符号 $q_{\text {accept}}$ 出现在格局表的一个单元格中:
这段介绍了大公式 $\phi$ 的另外两个相对简单的组件:$\phi_{start}$ 和 $\phi_{accept}$。
1. $\phi_{start}$: 设定初始条件
- 目标: 确保格局表的第一行(即 $i=1$ 的所有单元格)正确地表示了图灵机 $N$ 在输入 $w$ 时的起始格局。
- 起始格局的样子: 对于输入 $w = w_1w_2\dots w_n$,起始格局通常是这样的:
- 磁头在纸带最左端,处于初始状态 $q_0$。
- 纸带上依次写着输入 $w$。
- $w$ 的后面是无限的空白符 $\sqcup$。
- 我们的模型中,还在两端加了边界符 $\#$。
- 格局字符串: 综合起来,第一行的内容应该是 #q_0w_1w_2\dots w_n\sqcup\dots\sqcup#。
- $\phi_{start}$ 的构造:
- 这个公式非常直接,它就是一个巨大的一长串 AND 运算。
- 它做的事情就是“指名道姓”,强制把描述第一行格局的那些变量设为 TRUE。
- $x_{1,1, \#}$: 强制第1行第1列的符号是 #。
- $x_{1,2, q_{0}}$: 强制第1行第2列的符号是 $q_0$。(这里假设状态和符号写在同一个单元格里,更严谨的模型会把状态和磁头位置分开,但思想一致)。
- $x_{1,3, w_{1}}$: 强制第1行第3列的符号是输入 $w$ 的第一个字符 $w_1$。
- ...
- $x_{1, n+2, w_{n}}$: 强制第1行第 n+2 列的符号是输入 $w$ 的最后一个字符 $w_n$。
- $x_{1, n+3, \sqcup} \wedge \ldots$: 强制后面所有的单元格直到倒数第二个,都是空白符 $\sqcup$。
- $x_{1, n^{k}, \#}$: 强制第1行最后一列的符号是 #。
- 总结: $\phi_{start}$ 就像一个初始化脚本,把格局表的“第0帧”给固定死了,确保计算从一个正确的起点开始。任何不满足这个起始条件的赋值,都无法让 $\phi_{start}$ 为真。
2. $\phi_{accept}$: 设定结束目标
- 目标: 确保在整个计算过程中,至少有一次,图灵机进入了接受状态 $q_{accept}$。
- $\phi_{accept}$ 的构造:
- 这个公式是一个巨大的一长串 OR 运算。
- $\bigvee_{1 \leq i, j \leq n^{k}} x_{i, j, q_{\text {accept }}}$:
- 它遍历了格局表中的每一个单元格 $(i,j)$。
- 对于每个单元格,它都把变量 $x_{i, j, q_{accept}}$ (代表“[i,j]单元格的内容是接受状态 $q_{accept}$”) 拿出来。
- 然后把所有这些变量用 OR 连接起来。
- 含义: 这个巨大的 OR 表达式为真,当且仅当其中至少有一个变量为真。
- 换句话说,只要在整个 $n^k \times n^k$ 的格局表中,任何一个地方出现了符号 $q_{accept}$,$\phi_{accept}$ 就会被满足。
- 总结: $\phi_{accept}$ 设定了“胜利条件”。它不关心接受状态何时、何地出现,只要它在计算历史的某个瞬间出现过,就算达成目标。
- $\phi_{\text {start }}$:
- 这是一个由多个变量直接用 $\wedge$ (AND) 连接的公式。每个变量都是一个“正文字”(没有否定)。
- 为了让 $\phi_{start}$ 为真,所有这些被列出的变量都必须被赋值为 1。
- 例如,赋值时必须令 $x_{1,1,\#}=1, x_{1,2,q_0}=1, \dots$ 等。
- $\phi_{\text {accept }}=\bigvee_{1 \leq i, j \leq n^{k}} x_{i, j, q_{\text {accept }}}$:
- $\bigvee_{1 \leq i, j \leq n^{k}}$: 一个巨大的 OR 运算,遍历格局表中所有 $n^{2k}$ 个单元格。
- $x_{i, j, q_{accept}}$: 对应的变量。
- 整个公式是:
$(x_{1,1,q_{accept}} \vee x_{1,2,q_{accept}} \vee \dots) \vee (x_{2,1,q_{accept}} \vee \dots) \vee \dots$
- 只要其中任何一个 $x_{i, j, q_{accept}}$ 为1,整个公式就为1。
- 输入 w = "ab" (n=2)。图灵机 $N$ 的初始状态是 $q_0$。格局表大小为 $n^k \times n^k$。
- $\phi_{start}$ 的一部分:
- $x_{1,1,\#} \wedge x_{1,2,q_0} \wedge x_{1,3,a} \wedge x_{1,4,b} \wedge x_{1,5,\sqcup} \wedge \dots$
- 这个公式会强制任何满足赋值都必须让变量 $x_{1,3,a}$ 为1, $x_{1,4,b}$ 为1,等等。
- $\phi_{accept}$:
- 假设在某个计算历史中,第 5 步时,第 8 个纸带格的内容是接受状态 $q_a$。
- 这意味着在满足赋值中,$x_{5,8,q_a}$ 的值为 1。
- 由于 $\phi_{accept}$ 是所有 $x_{i,j,q_a}$ 的大 OR,而其中有一项 $x_{5,8,q_a}$ 为 1,所以整个 $\phi_{accept}$ 的值也为 1。
- 格局的表示: 为了简化公式,这里的 $\phi_{start}$ 把状态 $q_0$ 和纸带符号 $w_1$ 放在了相邻的单元格中。在更严谨的图灵机模型里,一个格局 uqv 通常被表示为纸带内容是 uv,状态是 $q$,磁头位置在 v 的开头。这里的写法是一种编码简化,把状态也看作一种特殊的纸带符号,只要在 $\phi_{cell}$ 中保证每个单元格只有一个符号,在 $\phi_{move}$ 中正确处理状态的移动,这种简化是可行的。
- 公式大小: $\phi_{start}$ 的大小与 $n^k$ 成正比。$\phi_{accept}$ 的大小与 $n^{2k}$ 成正比。它们都可以在多项式时间内被构造出来。
本段介绍了 $\phi$ 的两个组件:$\phi_{start}$ 和 $\phi_{accept}$。$\phi_{start}$ 像一个“设定场景”的规则,通过一系列强制性的 AND,确保了计算历史从正确的初始格局开始。$\phi_{accept}$ 则像一个“胜利宣告”的规则,通过一个覆盖全局的 OR,确保了计算历史中至少出现一次接受状态。这两个公式结构相对简单,但至关重要,它们分别定义了计算的起点和终点。
本段的目的是为格局表添加“时间”的约束。$\phi_{cell}$ 保证了空间的合法性(每个单元格内容唯一),而 $\phi_{start}$ 和 $\phi_{accept}$ 则规定了时间上的起点(必须从初始格局开始)和终点(必须到达接受格局)。这使得我们的模拟更接近一个真实的、有始有终的计算过程。
在分镜故事板的比喻中:
- $\phi_{start}$: 是剧本的第一页,上面用粗体字写着:“第一幕,第一场。时间:夜晚。地点:古堡大厅。人物:侦探福尔摩斯,手持放大镜,站在壁炉前。” 这条规则是强制性的,任何不从这个场景开始的故事都被视为“跑题”。
- $\phi_{accept}$: 是剧本的创作要求之一:“在故事的任何一个时刻,必须出现‘案件真相大白’的场景。” 它可以出现在中间,也可以出现在结尾,但必须至少出现一次。
在太空发射的法律条文比喻中:
- $\phi_{start}$: 是发射流程手册的第一章第一节,规定了:“T-0时刻,火箭必须垂直立于发射台,所有燃料箱必须是100%充满,所有指示灯必须为绿色。” 这是一个必须严格遵守的 AND 列表。
- $\phi_{accept}$: 是整个任务书的目标页,上面写着:“本次发射任务,在从T-0到T+10分钟的任何时间点,必须达成以下状态之一:‘航天器进入预定轨道’ 或 ‘备用轨道入轨成功’ 或 ...”。这是一个 OR 列表,只要达成任何一个就算成功。
24 库克-莱文定理的形式化证明:$\phi_{\text {move}}$ (窗口合法性)
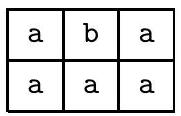
📜 [原文24]
最后,公式 $\phi_{\text {move}}$ 保证格局表的每一行都对应于一个根据 $N$ 规则合法地跟随前一行的格局。它通过确保每个 $2 \times 3$ 单元格窗口是合法的来做到这一点。我们说一个 $2 \times 3$ 窗口是合法的,如果该窗口不违反 $N$ 的转移函数所指定的操作。换句话说,如果一个窗口可能在一个格局正确地跟随另一个格局时出现,那么该窗口就是合法的。 ${ }^{3}$
例如,假设 a、b 和 c 是磁带字母表的成员,$q_{1}$ 和 $q_{2}$ 是 $N$ 的状态。假设当处于状态 $q_{1}$ 且磁头读取 a 时,$N$ 写入 b,保持状态 $q_{1}$,并向右移动;并且当处于状态 $q_{1}$ 且磁头读取 b 时,$N$ 非确定性地要么
- 写入 c,进入 $q_{2}$,并向左移动,或者
- 写入 a,进入 $q_{2}$,并向右移动。
正式表达为,$\delta\left(q_{1}, \mathrm{a}\right)=\left\{\left(q_{1}, \mathrm{~b}, \mathrm{R}\right)\right\}$ 且 $\delta\left(q_{1}, \mathrm{~b}\right)=\left\{\left(q_{2}, \mathrm{c}, \mathrm{L}\right),\left(q_{2}, \mathrm{a}, \mathrm{R}\right)\right\}$。图7.39显示了该机器的合法窗口示例。
| a | $q_{1}$ | b |
|---|---|---|
| $q_{2}$ | a | c |
(b)
| a | $q_{1}$ | b |
|---|---|---|
| a | a | $q_{2}$ |
(c)
| a | a | $q_{1}$ |
|---|---|---|
| a | a | b |
(d)
| $\#$ | b | a |
|---|---|---|
| $\#$ | b | a |
(e)
| a | b | a |
|---|---|---|
| a | b | $q_{2}$ |
(f)
| b | b | b |
|---|---|---|
| c | b | b |
图 7.39
合法窗口示例
在图7.39中,窗口 (a) 和 (b) 是合法的,因为转移函数允许 $N$ 以指示的方式移动。窗口 (c) 是合法的,因为 $q_{1}$ 出现在顶行的右侧,我们不知道磁头在哪个符号上方。该符号可能是一个 a,并且 $q_{1}$ 可能会将其更改为 b 并向右移动。这种可能性将产生这个窗口,所以它不违反 $N$ 的规则。窗口 (d) 显然是合法的,因为顶部和底部完全相同,这会在磁头不邻近窗口位置时发生。请注意,# 可能出现在合法窗口的顶部和底部的左侧或右侧。窗口 (e) 是合法的,因为状态 $q_{1}$ 读取 b 可能紧邻顶行的右侧,然后它将以状态 $q_{2}$ 向左移动,出现在底行的右端。最后,窗口 (f) 是合法的,因为状态 $q_{1}$ 可能紧邻顶行的左侧,并且它可能将 b 更改为 c 并向左移动。
这部分引入了整个证明中最复杂、最核心的组件 $\phi_{move}$ 的基本思想。它的目标是确保格局表的演进是符合物理定律(图灵机转移函数)的。
- $\phi_{move}$ 的宏观目标:
- 保证格局表中,第 $i+1$ 行是第 $i$ 行根据图灵机 $N$ 的规则合法演变一步的结果。这个约束必须对所有行 $i$ 都成立。
- 化整为零的策略:窗口 (Window)
- 直接描述一整行到另一整行的变化规则,会非常复杂。因为图灵机每一步只改变磁头附近的局部区域。
- 作者采用了一个绝妙的“局部约束”思想:如果一个大的二维表格中,所有局部的 $2 \times 3$ 小窗口都是合法的,那么整个表格的全局演变也一定是合法的。
- $2 \times 3$ 窗口: 这是一个包含6个单元格的小区域,跨越了相邻的两行(时间 $i$ 和 $i+1$)和相邻的三列(位置 $j-1, j, j+1$)。
- 为什么是 $2 \times 3$?: 因为图灵机磁头在一步之内,最多影响到它当前位置和它左/右一个格子的位置。比如,如果在位置 $j$ 的磁头向左移动,它会出现在位置 $j-1$;如果向右移动,会出现在 $j+1$。所以一个 $1 \times 3$ 的区域足以捕捉磁头和其紧邻的符号。而 $2 \times 3$ 的窗口则能完整地描述这个 $1 \times 3$ 区域在一步之内(从第 $i$ 行到第 $i+1$ 行)发生的变化。
- 什么是“合法的窗口”?:
- 一个 $2 \times 3$ 的窗口是合法的,当且仅当它没有违反图灵机 $N$ 的转移规则。
- 换句话说,这个窗口的“图案”必须是在某个合法的图灵机计算中可能出现的。
- 核心思想: 我们不需要知道磁头到底在哪里,我们只需要检查这个 $2 \times 3$ 的小片段本身是否“自洽”。
- 分析图7.39中的合法窗口示例:
- 转移规则:
- $\delta(q_1, a) \to (q_1, b, R)$ (读a, 写b, 状态不变, 右移)
- $\delta(q_1, b) \to (q_2, c, L)$ (读b, 写c, 变q2, 左移) 或 $(q_2, a, R)$ (读b, 写a, 变q2, 右移)
- (a) 合法: 顶行是 a q1 b。磁头在中间,读到 $q_1$ 左边的 b (假设我们的格局表示是uqy,状态在符号右边)。根据规则,读b可以写c、变q2、左移。那么 b 变成 c,q1 移动到左边一格,变成 q2,所以底行 q2 a c 是可能的。
- (b) 合法: 同样顶行 a q1 b。读 b 的第二种可能是:写a、变q2、右移。那么 b 变成 a,q1 移动到右边一格,变成 q2。底行 a a q2 是可能的。
- (c) 合法: 顶行是 a a q1。磁头可能在 q1 左边,读到 a。根据规则,读 a 会写 b、右移。那么 a 变成 b,q1 向右移出窗口。底行 a a b 是可能的。这里体现了“可能性”:我们不知道磁头具体在哪,但只要存在一种合法可能能产生这个窗口,它就是合法的。
- (d) 合法: 顶行 # b a,底行 # b a。这是最常见的情况:磁头根本就不在这个窗口附近。所以这三列的内容保持原样,没有任何变化。这当然是合法的。
- (e) 合法: 顶行 a b a。磁头可能在右边紧邻窗口的位置,比如 a b a q1。如果磁头读 a,右移,和窗口无关。但如果磁头在 a b (a) q1,读a,写c,左移。那么状态会进入窗口。更可能的是,磁头在窗口左边 q1 a b a,读a,右移,q1进入窗口。这里作者的解释 (q1 reads b ... move left to q2) 有点绕,更好的理解是:磁头在顶行的 b 上,即格局是 a q1 b a。它选择向左移动,变成 q2 a c a。那么窗口的上半部分是a b a,下半部分是a c a,而不是图中的样子。作者的解释(e)(f)是为了说明状态可以从窗口外移入。一个更清晰的例子(e):顶行是 a b q1,磁头在 b 上,它选择向左移动,b变c,q1变q2进入左边一格,所以新格局可能是 a q2 c,这个窗口是合法的。作者图中的(e)可能是这样产生的:顶行格局为a b (a) q_k,磁头在a上,向左移动变为q2,那么新格局为a q2 b a,此时(e)中的(a,b,q2)就可能出现。关键在于,只要存在一种上下文使得窗口内容合法,它就是合法的。
- (f) 合法: 与(e)类似,状态从窗口左侧进入。
- $\delta\left(q_{1}, \mathrm{a}\right)=\left\{\left(q_{1}, \mathrm{~b}, \mathrm{R}\right)\right\}$:
- $\delta$: 图灵机的转移函数。
- 输入: $(q_1, a)$,表示当前状态是$q_1$,磁头读到的符号是'a'。
- 输出: 一个集合,这里集合里只有一个元素 $(q_1, b, R)$。
- $(q_1, b, R)$: 一个三元组,表示:新状态是$q_1$,往纸带上写入的符号是'b',磁头移动方向是'R'(右)。
- $\delta\left(q_{1}, \mathrm{~b}\right)=\left\{\left(q_{2}, \mathrm{c}, \mathrm{L}\right),\left(q_{2}, \mathrm{a}, \mathrm{R}\right)\right\}$:
- 这是一个非确定性转移。当读到'b'时,有两个选择。
- 选择1: (q2, c, L) - 新状态$q_2$,写入'c',左移'L'。
- 选择2: (q2, a, R) - 新状态$q_2$,写入'a',右移'R'。
- 一个非法的窗口:
- 顶行: a q1 b
- 底行: c d e
- 为什么非法?磁头在顶行的 q1 处,它作用在 b 上。根据规则,b 只能变成 c 或 a,周围的 a 不应该变。而底行 c d e 是一个完全无关的变化,它违反了图灵机一次只能改变局部的规则。
- 窗口的普遍性: 我们要为所有可能的合法窗口模式建立一个列表。这个列表的大小只取决于图灵机 $N$ 本身(状态数、符号数),而与输入 $w$ 的长度 $n$ 无关。这是一个有限的、固定的列表。
- 格局的表示法: 证明的细节会依赖于格局的精确表示法。例如,状态是写在符号左边还是右边?还是用一个单独的维度来表示?不同的表示法会稍微改变窗口的合法模式,但核心思想不变。
- 边界情况: 位于格局表左右边缘的窗口($j=1$ 或 $j=n^k$)需要特殊处理,这也是引入#符号的原因。有了#,这些边界窗口就可以和普通窗口一样对待,因为#永远不会被改变,也永远不会是状态。
本段是 $\phi_{move}$ 的“理论基础”。它将保证全局计算合法的宏大任务,巧妙地分解为保证所有局部 $2 \times 3$ 窗口合法的小任务。通过分析几个具体例子,读者可以理解什么是“合法的窗口”——即在图灵机的规则下,任何可能发生的局部时空演变模式。这个“窗口化”的思想是整个库克-莱文证明中最精彩的技巧之一。
本段的目的是引入“窗口合法性”这一核心概念,为下一节构造具体的 $\phi_{move}$ 公式做准备。它解释了为什么我们可以只关心局部,并直观地展示了哪些局部模式是合法的、哪些是非法的,让读者对即将要用公式描述的对象有一个清晰的认识。
这就像是在验证一部动画片是否流畅。
- $\phi_{move}$ 的目标: 验证整部动画从第一帧到最后一帧的动作都是连贯的。
- 窗口思想: 你不需要看完整部动画。你只需要一个特殊的“检验镜”,这个镜子可以同时看到任意位置的“上一帧”和“下一帧”的一小块区域($2 \times 3$ 窗口)。
- 合法窗口:
- 如果这个区域里的人物上一帧没动,下一帧也没动,这是合法的(磁头不在附近)。
- 如果上一帧人物正在出拳,下一帧他的拳头出现在了更前方一点的位置,这也是合法的。
- 如果上一帧人物在屏幕左边,下一帧他瞬间出现在了屏幕右边,这就不合法了(违反物理定律)。
- 结论: 如果你用这个“检验镜”扫描了动画的每一个角落、每一帧之间的小区域,发现所有局部都是连贯的,你就可以断定整部动画是流畅的。
想象你在检查一条巨大的拉链(格局表的演进)。
- $\phi_{move}$ 的目标: 确保拉链从头到尾都能顺滑地拉上,没有错位。
- $2 \times 3$ 窗口: 就是拉链上相邻的几个齿。比如左边的3个齿和右边与之啮合的3个齿,这6个齿构成一个窗口。
- 合法窗口:
- 如果左边的齿 L1,L2,L3 和右边的齿 R1,R2,R3 完美地啮合在一起,这个窗口就是合法的。
- 如果 L1 对上了 R2,L2 对上了 R1,错位了,这个窗口就是非法的。
- $\phi_{move}$: 它的作用就是制定一条规则:“这条拉链上,每一组相邻的6个齿,都必须是完美啮合的。” 如果这条规则对整条拉链都成立,那么整条拉链一定是好的。
25 库克-莱文定理的形式化证明:非法的窗口
📜 [原文25]
下图所示的窗口对机器 $N$ 来说是不合法的。
(a)
(b)
| a | $q_{1}$ | b |
|---|---|---|
| $q_{2}$ | a | a |
(c)
| b | $q_{1}$ | b |
|---|---|---|
| $q_{2}$ | b | $q_{2}$ |
图 7.40
非法窗口示例
在窗口 (a) 中,顶行的中心符号无法改变,因为状态不与其相邻。窗口 (b) 不合法,因为转移函数规定 b 会变为 c,而不是 a。窗口 (c) 不合法,因为底行出现两个状态。
这段通过展示反例,进一步巩固了“合法窗口”的概念。理解为什么某些窗口是非法的,和理解为什么它们是合法的一样重要。
- 图 7.40 (a):
- 窗口内容: 顶行 a b c,底行 a d c。
- 分析: 窗口的顶行没有任何状态符号(如 $q_1$)。这意味着,在第 $i$ 时刻,磁头的位置不在这三列($j-1, j, j+1$)中的任何一个。根据图灵机的规则,如果磁头不在一个单元格附近,那个单元格的内容在下一步是不会改变的。
- 错误之处: 顶行的中心符号是 b,底行的中心符号变成了 d。在没有磁头作用的情况下,一个符号发生了无中生有的改变。这是对图灵机“局部作用原理”的根本性违背。
- 结论: 非法。
- 图 7.40 (b): (这个图和图7.39(a)的顶行一样,但底行不同)
- 窗口内容: 顶行 a q1 b,底行 q2 a a。
- 分析: 我们假设格局表示法是 ...a q1 b...,即磁头在 b 上。
- 回顾规则: $\delta(q_1, b)$ 的两种可能是:1) 变 c 左移;2) 变 a 右移。
- 匹配规则:
- 对应规则1: 底行应该是类似 ...q2 c... 的形式。
- 对应规则2: 底行应该是类似 ...a q2... 的形式。
- 错误之处: 图中的底行是 q2 a a。我们来分析:
- 中间的 a 和顶行的 q1 对应,这是不合逻辑的,q1 是状态,不会变成 a。
- 右边的 a 和顶行的 b 对应。根据规则,b 在变成 a 的同时,状态 q1 应该向右移动,变成 q2。所以底行右边应该是 q2 而不是 a。
- 左边的 q2 和顶行的 a 对应。这是不合逻辑的。
- 简而言之: 这个底行 q2 a a 无法由顶行 a q1 b 通过任何一条合法的转移规则得到。
- 结论: 非法。
- 图 7.40 (c):
- 窗口内容: 顶行 b q1 b,底行 q2 b q2。
- 分析: 图灵机在任何一个时刻(即任何一个格局/行)都只能有一个状态。
- 错误之处: 底行(第 $i+1$ 时刻)同时出现了两个状态符号 $q_2$。这是不可能的,就像一个人不能同时在两个地方一样。
- 这个约束由谁保证?: 之前定义的 $\phi_{cell}$ 已经保证了一个单元格里只能有一个符号。但它不能保证一整行里只有一个状态符号。这个检查是 $\phi_{move}$ 的一部分职责,它通过排除像(c)这样的窗口来实现。
- 结论: 非法。
- 更多非法窗口的例子:
- 顶行: a b c, 底行: a q1 c。 非法。状态 $q_1$ 不能凭空出现。
- 顶行: a q1 b, 底行: a q1 b。非法。只要有状态在场,就必须发生改变并移动(除非是停机状态,但我们这里不考虑)。
- 顶行: a b c, 底行: c b a。非法。多个符号在没有磁头的情况下发生了改变。
- 非法窗口的集合: 证明中,我们实际上并不需要列出所有非法的窗口。我们只需要定义清楚所有合法的窗口。那么,任何一个 $2 \times 3$ 的符号组合,如果它不在我们的“合法窗口列表”里,它就自动被视为非法的。
- 状态也是符号: 再次强调,在这个模型里,状态 $q_i$ 被当作一种特殊的符号,和 $a, b, c, \#$ 一样,可以被放在单元格里。$\phi_{cell}$ 已经保证了每个单元格的符号唯一性。
本段通过展示几个典型的非法窗口示例,从反面加强了读者对“窗口合法性”的理解。这些例子清晰地揭示了哪些情况会违反图灵机的基本运行原则,例如:符号无故改变、转移不符合规则、出现多个状态等。这为下一节用逻辑公式来“禁止”这些非法情况的出现做好了铺垫。
本段的目的是通过具体、直观的反例,让抽象的“合法性”概念变得更加具体和可触摸。通过对比合法与非法的例子,读者能更深刻地理解 $\phi_{move}$ 将要实现的精细约束是什么。
[直觉心- [ ]
26 库克-莱文定理的形式化证明:窗口断言
📜 [原文26]
断言 7.41
如果格局表的顶行是起始格局,并且格局表中的每个窗口都是合法的,则格局表的每一行都是合法地跟随前一行的格局。
我们通过考虑格局表中任意两个相邻的格局来证明此断言,分别称为上层格局和下层格局。在上层格局中,每个包含磁带符号且不邻近状态符号的单元格都是窗口的中心顶部单元格,其顶行不包含任何状态。因此,该符号必须在窗口的中心底部保持不变。因此,它在底部格局中出现在相同的位置。
包含状态符号的窗口在中心顶部单元格中保证了相应的三位置与转移函数一致地更新。因此,如果上层格局是合法格局,那么下层格局也是合法格局,并且下层格局根据 $N$ 的规则跟随上层格局。请注意,尽管这个证明是直接的,但它关键地依赖于我们选择 $2 \times 3$ 的窗口大小,如问题 7.26 所示。
这个断言是连接“局部合法性”和“全局合法性”的桥梁,是“窗口”策略能够成功的理论保证。
- 断言陈述:
- 前提1: 格局表的顶行(第1行)是正确的起始格局。($\phi_{start}$ 将保证这一点)
- 前提2: 表中每一个 $2 \times 3$ 的窗口都是合法的。($\phi_{move}$ 将保证这一点)
- 结论: 那么,整个格局表的演进是合法的。即,第2行是第1行的合法后继,第3行是第2行的合法后继,以此类推。
- 证明思路:
- 我们要证明任意相邻的两行,比如第 $i$ 行(上层格局)和第 $i+1$ 行(下层格局),其演变是合法的。
- 我们将上层格局分为两部分来讨论:远离磁头的部分 和 靠近磁头的部分。
- 分析远离磁头的部分:
- 在上层格局(第 $i$ 行)中,找到一个不包含状态符号、也不与状态符号相邻的单元格。我们关注这个单元格 $[i, j]$。
- 现在,我们以 $[i, j]$ 作为中心,看它所在的那个 $2 \times 3$ 窗口。这个窗口的顶行是 [i, j-1] [i, j] [i, j+1]。因为我们选的 $j$ 远离状态,所以这三个单元格里都没有状态。
- 根据“合法窗口”的定义(特别是对应图7.39(d)的情况),当一个窗口的顶行不包含状态时,它的底行必须和顶行完全一样,以反映“无变化”。
- 这意味着,这个窗口的中心底部单元格 $[i+1, j]$ 的内容,必须和中心顶部单元格 $[i, j]$ 的内容完全一样。
- 这个逻辑对所有远离磁头的单元格都成立。
- 结论: 所有不受磁头影响的纸带部分,在下一步都保持原样。这符合图灵机规则。
- 分析靠近磁头的部分:
- 现在,我们来看上层格局中包含状态符号 $q$ 的那个位置。假设它在第 $j$ 列,即单元格 $[i, j]$ 是 $q$。
- 那么,以 $[i, j]$ 为中心的 $2 \times 3$ 窗口的顶行就是 [i, j-1] q [i, j+1]。
- 根据前提,这个窗口是合法的。
- 而“合法窗口”的定义是,这个 $2 \times 3$ 的内容必须是图灵机转移函数所允许的一种演变模式。
- 这意味着,底行的三个单元格 [i+1, j-1] [i+1, j] [i+1, j+1] 的内容,精确地反映了磁头在第 $i$ 步执行操作(读写、变状态、移动)之后的结果。
- 结论: 磁头附近区域的变化,完全遵循了转移函数。这符合图灵机规则。
- 综合结论:
- 我们将下层格局(第 $i+1$ 行)和上层格局(第 $i$ 行)进行比较。远离磁头的部分内容相同,靠近磁头的部分内容根据转移函数发生了正确变化。
- 这正是“下层格局是上层格局的合法后继”的定义。
- 由于这个推理对任意行 $i$ 都有效,因此整个格局表的演进都是合法的。
- 断言得证。
- 对 $2 \times 3$ 窗口大小的强调:
- 作者最后提醒,这个证明的成立,关键在于 $2 \times 3$ 这个窗口尺寸不大不小,刚刚好。
- 如果窗口太小,比如 $2 \times 2$,它就无法捕捉到磁头向左或向右移动后状态出现在邻近格子的效应,那么“局部合法”就无法保证“全局合法”。例如,一个状态可能在一个 $2 \times 2$ 窗口中“消失”,然后在另一个不相邻的 $2 \times 2$ 窗口中“凭空出现”,而每个窗口自身看起来都可能是合法的。$2 \times 3$ 的重叠性保证了状态的移动是连续的。
- 上层格局 (第 i 行): ... # a q1 b c # ...
- 下层格局 (第 i+1 行): ... # a q2 d c # ... (假设 $\delta(q_1, b) \to (q_2, d, L)$)
- 我们来用窗口检验这个演变:
- 远离磁头的窗口: 比如以 c 为中心的窗口。顶行是 b c #。底行是 d c #。因为磁头不在 c 附近,c 应该不变。但这个窗口里,左边的 b 变成了 d。我们先放着。
- 磁头附近的窗口: 以 q1 为中心的窗口。顶行是 a q1 b。根据规则,底行应该是 q2 a d (因为状态 q1 读 b 变成 d,状态变 q2 并左移)。
- 重叠的窗口: 以 b 为中心的窗口。顶行是 q1 b c。底行是 a d c。这个窗口的变化也必须符合规则。
- 断言的含义: 如果我们检查了所有可能的 $2 \times 3$ 窗口,发现它们都是从一个巨大的“合法窗口列表”中取出的,那么我们就能保证,拼凑起来的整个下层格局,一定是 ... # q2 a d c # ... 这种完全正确的形式。不会出现 c 无故变成 e,或者 a 无故消失的情况。
- 证明的逻辑: 这个断言不是在证明任何一个具体的格局表是合法的。它是在证明我们的“检验方法”(即检查所有局部窗口)是可靠的。它是在说:“只要我的检验方法全盘通过,我就可以放心地保证这张表没问题。”
- 重叠的重要性: 理解窗口之间的重叠是关键。正是因为相邻的窗口有重叠部分,信息(比如符号的不变性,或者状态的连续移动)才能一格一格地传递下去,从而保证全局的一致性。
断言7.41是库克-莱文证明中的一个关键引理。它雄辩地证明了“局部决定全局”的原理在图灵机格局表中的应用。只要我们能用公式确保每一个微小的 $2 \times 3$ 窗口都符合图灵机的物理定律,我们就能保证整个计算历史的宏观演变也是完全合法的。这个断言使得我们可以把一个非常复杂的全局约束问题,简化为大量简单、重复的局部约束问题。
本段的目的是为 $\phi_{move}$ 的构造提供理论依据。它回答了这样一个问题:“为什么我们只构造一个描述窗口的公式 $\phi_{move}$ 就足够了?为什么不需要一个更复杂的、描述整行变化的公式?”这个断言给了我们信心:只管好窗口,全局就乱不了。
在动画流畅性的比喻中,这个断言是在说:
“如果一部动画的开场镜头是正确的,并且你用‘检验镜’检查了每一帧之间的所有局部区域,发现它们都是连贯的,那么我向你保证,这部动画的整个故事流程一定是连贯的,不会出现人物瞬移、物体凭空消失等穿帮镜头。”
这个断言证明了你的“检验镜”方法是科学、可靠的。
[直- [ ]
27 库克-莱文定理的形式化证明:$\phi_{\text {move}}$ 的构造
📜 [原文27]
现在我们回到 $\phi_{\text {move}}$ 的构建。它规定格局表中的所有窗口都是合法的。每个窗口包含六个单元格,可以通过固定数量的方式设置以生成合法窗口。公式 $\phi_{\text {move}}$ 表示这六个单元格的设置必须是这些方式之一,或者
$(i, j)$-窗口以单元格 $[i, j]$ 作为中心顶部位置。我们将此公式中的文本 “the $(i, j)$-window is legal” 替换为以下公式。我们将窗口的六个单元格的内容写为 $a_{1}, \ldots, a_{6}$。
这是构造 $\phi_{move}$ 的具体实现。它将前面“窗口合法性”的直观概念,翻译成了精确的布尔逻辑公式。
- $\phi_{move}$ 的顶层结构:
- 根据断言7.41,我们只需要保证格局表中所有窗口都是合法的。
- 所以,$\phi_{move}$ 的结构是一个巨大的 AND 运算,它遍历了格局表中所有可能的 $2 \times 3$ 窗口。
- $\phi_{\mathrm{move}}=\bigwedge_{1 \leq i
- $(i, j)$-window: 指的是以单元格 $[i, j]$ 为顶行中心的那个 $2 \times 3$ 窗口。
- $1 \le i < n^k$: 遍历所有相邻的两行。
- $1 < j < n^k$: 遍历所有中间的列(避开最左和最右的#边界,简化了讨论)。
- (...): 括号里是对单个窗口施加的约束。
- 整个公式的意思是:“第(1,2)窗口必须合法 AND 第(1,3)窗口必须合法 AND ... AND 第($n^k-1, n^k-1$)窗口必须合法”。
- 单个窗口的约束公式:
- 现在我们需要用逻辑语言来表达 (the (i, j)-window is legal) 这句话。
- 核心思想:
- 首先,我们需要一个“合法窗口模式的列表”。这个列表包含了所有可能的 $2 \times 3=6$ 个单元格的符号组合,这些组合是符合图灵机 $N$ 规则的。这个列表的大小是固定的,只和 $N$ 有关,和输入大小 $n$ 无关。
- 然后,对于一个具体的 $(i,j)$-窗口,它的6个单元格的内容,必须是这个“合法模式列表”中的某一个。
- 翻译成逻辑: “是...之一” 这个概念,正好对应布尔逻辑中的 OR 运算。
- 单个窗口约束公式的构造:
- $\bigvee_{\substack{a_{1}, \ldots, a_{6} \\ \text { is a legal window }}}\left( \dots \right)$
- $\bigvee_{\dots}$: 这是一个 OR 运算。它遍历我们之前准备好的那个“合法窗口模式列表”。列表中的每一个合法模式,我们都用 (a1, a2, a3, a4, a5, a6) 来表示,其中 a1 到 a6 是6个具体的符号。
- $(x_{i, j-1, a_{1}} \wedge x_{i, j, a_{2}} \wedge x_{i, j+1, a_{3}} \wedge x_{i+1, j-1, a_{4}} \wedge x_{i+1, j, a_{5}} \wedge x_{i+1, j+1, a_{6}})$
- 这部分是 OR 运算的每一个分支。
- 它描述了一个具体的合法窗口模式。
- 例如,如果 (b, q1, c, b, d, q2) 是一个合法模式,那么这个括号里的内容就是:
- 这个 AND 串的含义是:“窗口的左上角是b 并且 顶行中间是q1 并且 ... 并且 右下角是q2”。它精确地描述了一个特定的模式。
- 整体含义: 整个 OR 公式的意思是:
- 这就完美地实现了“窗口的内容必须是合法模式列表中的某一个”这一要求。
这个公式是两层嵌套的,外层 AND 遍历所有窗口,内层 OR 遍历所有合法模式。
- 外层: $\phi_{\mathrm{move}}=\bigwedge_{(i,j)} (\text{constraint for window } (i,j))$
- 内层: $(\text{constraint for window } (i,j)) = \bigvee_{\text{legal pattern } p} (\text{description of pattern } p)$
- 最内层: $(\text{description of pattern } p) = \bigwedge_{k=1}^6 (\text{cell } k \text{ has symbol } s_k)$
- 图灵机规则: 磁头读到 'a' 时,原地不动,写入 'b'。
- 一个合法窗口模式: 顶行 c a d,底行 c b d。这里磁头在中间,a变成b,两边不变。
- 模式 p1 = (c, a, d, c, b, d)。
- 另一个合法窗口模式: 顶行 e f g,底行 e f g。这里磁头不在窗口内。
- 模式 p2 = (e, f, g, e, f, g)。
- 假设合法的模式只有这两种。
- 对窗口 (5, 6) 的约束公式:
- (
- // 描述模式 p1
- (x_{5,5,c} \wedge x_{5,6,a} \wedge x_{5,7,d} \wedge x_{6,5,c} \wedge x_{6,6,b} \wedge x_{6,7,d})
- )
- \vee
- (
- // 描述模式 p2
- (x_{5,5,e} \wedge x_{5,6,f} \wedge x_{5,7,g} \wedge x_{6,5,e} \wedge x_{6,6,f} \wedge x_{6,7,g})
- )
- 这个公式的意思是:第(5,6)号窗口,要么是 c a d -> c b d 这种模式,要么是 e f g -> e f g 这种模式。不允许出现任何其他情况。
- $\phi_{move}$ 就是把对所有窗口的这类公式全部用 AND 连接起来。
- 合法窗口列表的大小: 这个列表虽然是固定的,但可能很大。它的大小是 $|C|^6$ 的一个子集。但重要的是,它不随 $n$ 变化,所以对于公式构造来说它是个常数。
- 公式的形式 (CNF): 目前构造出的 $\phi_{move}$ 是一个 AND of ORs of ANDs 的形式,而不是一个标准的 CNF (合取范式, AND of ORs)。在证明的最后,需要用分配律将它转化为 CNF 形式,但这只会让公式大小增加一个常数倍,不影响多项式大小的性质。
本段给出了 $\phi_{move}$ 的精确逻辑构造。它通过一个两层结构实现:外层是一个巨大的 AND,确保每个窗口都被检查;内层是一个巨大的 OR,确保每个窗口的内容都符合预先定义好的“合法模式”之一。这是一种“白名单”式的约束方法,任何不符合白名单上任何一条模式的窗口,都会导致 $\phi_{move}$ 为假。
本段的目的是将库克-莱文证明中最核心、最复杂的约束——计算过程的合法性——完全转化为布尔逻辑。它是整个模拟过程的“发动机”和“物理定律”,确保了格局表中的时间演化是真实可信的。
[直觉心- [ ]
28 库克-莱文定理的形式化证明:复杂度分析
📜 [原文28]
接下来,我们分析归约的复杂性,以表明它在多项式时间内运行。为此,我们检查 $\phi$ 的大小。首先,我们估计它拥有的变量数量。回想一下,格局表是一个 $n^{k} \times n^{k}$ 的表格,因此它包含 $n^{2 k}$ 个单元格。每个单元格有 $l$ 个与之关联的变量,其中 $l$ 是 $C$ 中的符号数量。因为 $l$ 仅取决于 TM $N$,而不取决于输入 $n$ 的长度,所以变量总数是 $O\left(n^{2 k}\right)$。
我们估计 $\phi$ 各部分的大小。公式 $\phi_{\text {cell}}$ 包含公式中每个格局表单元格的固定大小片段,因此其大小为 $O\left(n^{2 k}\right)$。公式 $\phi_{\text {start}}$ 包含顶行每个单元格的片段,因此其大小为 $O\left(n^{k}\right)$。公式 $\phi_{\text {move}}$ 和 $\phi_{\text {accept}}$ 都包含公式中每个格局表单元格的固定大小片段,因此它们的大小均为 $O\left(n^{2 k}\right)$。因此,$\phi$ 的总大小为 $O\left(n^{2 k}\right)$。该上限足以满足我们的目的,因为它表明 $\phi$ 的大小是 $n$ 的多项式。如果它不是多项式,那么归约就没有机会在多项式时间内生成它。(实际上,我们的估计由于每个变量都有可能达到 $n^{k}$ 的索引,因此可能需要 $O(\log n)$ 个符号才能写入公式,所以我们的估计偏低了 $O(\log n)$ 的一个因子,但这个额外的因子不会改变结果的多项式性。)
为了说明我们可以在多项式时间内生成公式,请注意其高度重复的性质。公式的每个组件都由许多几乎
完全相同的片段组成,这些片段只在索引方面以简单的方式有所不同。因此,我们可以很容易地构建一个归约,在多项式时间内从输入 $w$ 生成 $\phi$。
在完成了公式 $\phi$ 所有组件的构造之后,这部分来做最后但至关重要的检查:这个归约过程本身是不是多项式时间的?这主要通过估算最终生成的公式 $\phi$ 的总大小(长度)来判断。
- 分析的必要性:
- 一个归约 $A \le_P B$ 不仅要求功能正确 ($w \in A \iff f(w) \in B$),还要求效率达标(函数 $f$ 是多项式时间可计算的)。
- 如果构造出的公式 $\phi=f(w)$ 本身的长度是指数级别的(比如 $2^n$),那么光是把这个公式写下来就需要指数时间,这个归约自然就不是多项式时间的。
- 所以,我们必须证明 $\phi$ 的大小是输入 $w$ 长度 $n$ 的某个多项式函数。
- 变量数量分析:
- 这是公式大小的基础。
- 格局表有 $n^k \times n^k = n^{2k}$ 个单元格。
- 每个单元格的可能性由集合 $C$ 决定,其大小 $l = |C|$ 是一个不依赖于 $n$ 的常数。
- 每个单元格需要 $l$ 个变量来描述其内容。
- 总变量数 = $n^{2k} \times l$。由于 $l$ 是常数,所以变量总数是 $O(n^{2k})$。
- 各子公式大小分析:
- $\phi_{cell}$: 为每个单元格生成一个约束片段。片段的大小只和 $|C|$ 有关(是 $O(|C|^2)$),是常数。总大小 = (单元格数) $\times$ (片段大小) = $n^{2k} \times O(1) = O(n^{2k})$。
- $\phi_{start}$: 只约束第一行。涉及 $n^k$ 个单元格。总大小是 $O(n^k)$。
- $\phi_{accept}$: 为每个单元格生成一项 OR。总大小 = (单元格数) $\times O(1) = O(n^{2k})$。
- $\phi_{move}$: 为每个窗口生成一个约束片段。窗口总数约是 $n^{2k}$。每个片段的大小只和图灵机 $N$ 的规则有关(即合法窗口列表的大小),是常数。总大小 = (窗口数) $\times$ (片段大小) = $n^{2k} \times O(1) = O(n^{2k})$。
- 总公式大小分析:
- $\phi = \phi_{cell} \wedge \phi_{start} \wedge \phi_{move} \wedge \phi_{accept}$。
- 总大小是各部分大小之和:$O(n^{2k}) + O(n^k) + O(n^{2k}) + O(n^{2k}) = O(n^{2k})$。
- 结论: 公式 $\phi$ 的总大小是 $n$ 的一个多项式。
- 一个技术细节 (log n 因子):
- 作者补充了一个严谨的考虑:我们之前估算大小时,默认写下一个变量(如 $x_{i,j,s}$)只需要 $O(1)$ 的空间。
- 但实际上,下标 $i$ 和 $j$ 的值最大可以到 $n^k$。要用二进制或十进制写下数字 $n^k$,需要 $\log(n^k) = k \log n$ 位的空间。
- 所以,每个变量的实际长度是 $O(\log n)$。
- 将这个因子乘到我们之前的估算中,$\phi$ 的总大小应该是 $O(n^{2k} \log n)$。
- 不过,$n^{2k} \log n$ 依然是 $n$ 的一个多项式函数(它比 $n^{2k+1}$ 要小)。因此,这个修正不影响最终的“多项式大小”结论。
- 构造过程的时间分析:
- 光证明公式大小是多项式还不够,我们还得说明生成这个公式的算法也是多项式时间的。
- 作者指出,公式具有“高度重复的性质”。$\phi_{cell}$ 对每个单元格做同样的事,$\phi_{move}$ 对每个窗口做同样的事。
- 因此,我们可以很容易地设计一个程序,用几个嵌套循环来遍历所有的单元格和窗口,并根据模板生成对应的子句。
- 例如,一个生成 $\phi_{cell}$ 的伪代码:
- 这个程序的运行时间,和它生成的公式的大小是成正比的。既然公式大小是多项式,生成它的算法自然也是多项式时间的。
- 输入 n=10, k=2:
- 格局表大小是 $100 \times 100$。
- 单元格总数是 $10^4$。
- $\phi_{cell}$ 大小约是 $O(10^4)$。
- $\phi_{start}$ 大小约是 $O(10^2)$。
- $\phi_{move}$ 大小约是 $O(10^4)$。
- $\phi_{accept}$ 大小约是 $O(10^4)$。
- 总公式大小是 $O(10^4)$ 级别。
- 输入 n=20, k=2:
- 格局表大小是 $400 \times 400$。
- 单元格总数是 $16 \times 10^4$。
- 总公式大小是 $O(16 \times 10^4)$ 级别。
- 可以看到,当 $n$ 翻倍时,公式大小增长了 $2^{2k} = 2^4 = 16$ 倍。这是一个 $n^4$ 的多项式增长关系。
- 大O表示法的理解: $O(n^{2k})$ 描述的是增长的“阶”,而不是精确的大小。它告诉我们当 $n$ 变得很大时,大小主要由 $n^{2k}$ 这一项决定。
- 可构造性: “多项式大小”和“多项式时间可构造”是两个概念,但在这里它们紧密相关。因为公式的结构非常规整,所以我们可以通过简单的算法来“打印”出它,算法的时间和打印的长度成正比。
本段从计算复杂度的角度,对刚刚完成的归约构造进行了“审计”。通过分析变量总数和四个子公式的规模,它得出结论:整个布尔公式 $\phi$ 的大小是输入长度 $n$ 的一个多项式。并且,由于公式结构的高度重复性,生成这个公式的算法本身也是多项式时间的。这最终确认了我们所构造的从任意NP问题到SAT的归约,是一个合法、高效的多项式时间归约。
本段的目的是完成库克-莱文定理证明的最后一块拼图。一个归约证明,如果缺少了对归约过程本身效率的分析,就是不完整的。本段通过严谨(虽然是高层次的)的复杂度分析,确保了整个证明在逻辑上和效率上都无懈可击。
在“编写电影剧本”的比喻中,这部分是在分析“剧本创作指南”的工作量。
- 剧本长度(公式大小):
- 角色表(变量):和电影时长($n^k$)的平方成正比。
- 场景设定($\phi_{start}$):和电影时长成正比。
- 物理定律($\phi_{cell}, \phi_{move}$):每个场景、每两个连续场景之间都要写一遍,和电影时长的平方成正比。
- 结局要求($\phi_{accept}$):和电影时长的平方成正比。
- 总长度: 主要由物理定律决定,是电影时长平方级别的。这是一个多项式关系。
- 创作时间(构造时间):
- 因为剧本的规则非常模式化(比如每个角色都不能瞬移),所以一个编剧助手可以像填表格一样快速地写出整个剧本,花费的时间和剧本的最终长度差不多。
- 结论: 把一部任意的电影(NP问题)改编成一部标准格式的戏剧(SAT问题),这项工作本身是高效的。
在“翻译成法律条文”的比喻中,这部分是在评估“立法”的工作量。
- 法条总长度(公式大小):
- 定义基本术语(变量):与发射时长($n^k$)的平方成正比。
- 描述初始状态($\phi_{start}$):与发射时长成正比。
- 描述物理定律($\phi_{move}$):每一毫秒、每一个部件之间的关系都要描述,与发射时长的平方成正比。
- 总长度: 是一个关于发射时长的多项式。虽然法典可能很厚,但不是无限厚,也不是指数级厚度。
- 立法时间(构造时间):
- 因为物理定律是普适的,所以一个立法团队可以开动打印机,根据模板批量生成大量条款。这个过程很快。
- 结论: 为一次太空发射制定一部完备的“法律”,这项任务本身可以在合理的时间内完成。
29 库克-莱文定理的完成与3SAT的NP-完全性
📜 [原文29]
至此,我们完成了库克-莱文定理的证明,表明 SAT 是NP-完全的。证明其他语言的NP-完全性通常不需要如此冗长的证明。相反,可以通过从一个已知是NP-完全的语言进行多项式时间归约来证明NP-完全性。我们可以使用 SAT 来达到此目的;但使用 3SAT,即我们在第302页定义的 SAT 的特例,通常会更容易。回想一下,3SAT 中的公式是合取范式(cnf),每个子句包含三个文字。首先,我们必须证明 3SAT 本身是NP-完全的。我们将此断言作为定理 7.37 的推论来证明。
推论 7.42
3SAT 是NP-完全的。
这段话标志着一个重要里程碑的达成,并立即开启了下一个目标:确立 3SAT 的 NP-完全地位。
- 库克-莱文定理证明的完成:
- 作者宣布,至此,我们已经完成了证明 SAT 是 NP-完全的所有步骤。
- 回顾一下步骤:
- 证明 SAT $\in$ NP (通过猜测-验证)。
- 对于任意 NP 问题 A,构造一个从 A 到 SAT 的多项式时间归约。
- 引入格局表来表示 NDTM 的计算历史。
- 定义变量 $x_{i,j,s}$ 来编码格局表。
- 构造 $\phi_{cell}$ 保证表格格式正确。
- 构造 $\phi_{start}$ 保证起始状态正确。
- 构造 $\phi_{accept}$ 保证计算达到接受状态。
- 构造 $\phi_{move}$ 保证每步演化合法。
- 分析表明整个归约过程是多项式时间的。
- 所有条件都已满足,SAT 的“NP-完全鼻祖”地位正式确立。
- 展望未来:更简单的证明方法:
- 作者强调,库克-莱文定理的证明是“一次性”的艰苦工作。它就像是第一个登陆月球的人,后面的宇航员再去就容易多了。
- 对于未来想要证明其他问题(比如 CLIQUE)是 NP-完全的,我们不再需要从“任意NP问题A”这么一个抽象的、普适的对象出发了。
- 我们可以直接从一个具体的、已知的 NP-完全问题(现在我们有了 SAT)出发,进行归约。这要具体和简单得多。
- 引入更好的“跳板”:3SAT:
- 虽然 SAT 是第一个NPC问题,但它还不够“好用”。因为 SAT 公式可以是任意复杂的布尔表达式,结构不规整。
- 一个更好的工具是 3SAT。3SAT 的公式具有非常标准、统一的 3-CNF 格式((a∨b∨c) ∧ (d∨e∨f) ...)。这种规整的结构使得从 3SAT 出发来构造归约,会比从通用的 SAT 出发更加方便和模式化。
- 比喻: 如果 SAT 是一块包含了所有金属元素的原矿石,那么 3SAT 就是一块提纯过的、标准尺寸
对变量的两种可能的真值赋值。变量小工具包含两个由边连接的节点。这种结构有效,因为其中一个节点必须出现在顶点覆盖中。我们任意将 TRUE 和 FALSE 与这两个节点关联起来。
对于子句小工具,我们寻找一种结构,它促使顶点覆盖包含变量小工具中对应于子句中至少一个真文字的节点。该小工具包含三个节点和额外的边,使得任何顶点覆盖都必须包含至少两个节点,或者可能全部三个。如果一个变量小工具节点通过覆盖一条边提供帮助,则只需要两个节点,就像相关文字满足该子句时发生的情况。否则,将需要三个节点。最后,我们选择 $k$,使得所寻求的顶点覆盖每个变量小工具有一个节点,每个子句小工具有两个节点。
这是证明 VERTEX-COVER 是 NP-完全的蓝图。它清晰地规划了证明的步骤和核心思想,即从 3SAT 进行归约。
- 证明目标: 证明 VERTEX-COVER (VC) 是 NP-完全的。
- 步骤1: 证明 VC $\in$ NP。
- 作者指出这部分很简单。
- 证书 (Certificate): 一个大小为 $k$ 的顶点子集 $S$。
- 验证算法:
- 检查 $S$ 的大小是否为 $k$。
- 遍历图 $G$ 的每一条边 $(u, v)$。
- 对于每条边,检查 $u$ 是否在 $S$ 中,或者 $v$ 是否在 $S$ 中。
- 如果所有边都满足这个条件,则验证通过。
- 这个验证过程显然是多项式时间的。因此 VC $\in$ NP。
- 步骤2: 证明 VC 是 NP-hard。
- 根据定理7.36,我们不需要从任意NP问题出发。我们只需要从一个已知的NPC问题归约到VC即可。
- 选择的起点: 3SAT。我们要证明 3SAT $\le_P$ VC。
- 归约函数 $f$ 的设计思路:
- 输入: 一个 3-CNF 公式 $\phi$。
- 输出: 一个图 $G$ 和一个整数 $k$ ($\langle G, k \rangle$)。
- 核心等价关系: $\phi$ 是可满足的 $\iff$ $G$ 有一个大小为 $k$ 的顶点覆盖。
- 模拟思想: 图 $G$ 的结构是为了“模拟”公式 $\phi$。这种模拟通过设计巧妙的“小工具”(gadget) 来实现。Gadget是图中的一小块特定结构,用来模仿公式的某个组成部分的行为。
- 变量小工具 (Variable Gadget):
- 目标: 模拟一个布尔变量 $x$ 的两种取值 (TRUE/FALSE)。
- 结构: 对于每个变量 $x_i$,我们创建一个由两个节点和一条连接它们的边组成的结构。
- 标记: 一个节点标记为 $x_i$,另一个标记为 $\bar{x_i}$。
- 行为分析: 这两个节点之间有一条边。根据顶点覆盖的定义,这条边必须被覆盖。所以,我们必须将 $x_i$ 节点或 $\bar{x_i}$ 节点(或两者都)选入顶点覆盖集。为了最小化顶点覆盖的大小,我们总是倾向于只选一个。
- 对应关系:
- 选择 $x_i$ 节点加入覆盖集 $\iff$ 变量 $x_i$ 赋值为 TRUE。
- 选择 $\bar{x_i}$ 节点加入覆盖集 $\iff$ 变量 $x_i$ 赋值为 FALSE。
- 这个小工具完美地模拟了一个必须二选一的布尔选择。
- 子句小工具 (Clause Gadget):
- 目标: 模拟一个子句 (a v b v c),并确保它被满足。
- 结构: 对于每个子句,我们创建一个由三个节点组成的三角形结构。这三个节点两两相连,构成一个3-团。
- 标记: 这三个节点分别用子句中的三个文字来标记。
- 行为分析: 这个小工具里有3条边。要覆盖这3条边,我们至少需要选择两个节点。
- 与变量小工具的连接: 最关键的一步!我们将子句小工具中的每个节点,与变量小工具中同名的节点连接起来。例如,如果子句是 (x1 v ¬x2 v x3),那么子句小工具中标记为 x1 的节点,需要和变量小工具中标记为 x1 的节点连一条边。
- 整体的协同工作机制(证明思路的核心):
- 目标 k 值的设定:
- 假设公式有 $m$ 个变量和 $c$ 个子句。
- 对于 $m$ 个变量小工具,为了覆盖它们内部的 $m$ 条边,我们至少需要 $m$ 个节点。
- 对于 $c$ 个子句小工具,为了覆盖它们内部的 $3c$ 条边,我们至少需要 $2c$ 个节点。
- 因此,我们设定目标 $k = m + 2c$。
- 这个 $k$ 值是一个精心计算的“预算”。如果我们能用恰好 $k$ 个节点完成覆盖,这意味着我们必须以“最经济”的方式来做选择。
- “经济”的选择如何与满足性挂钩?:
- 在子句小工具(三角形)中,覆盖3条边最经济的方式是选2个节点。
- 但是,如果我们能从“外部”获得帮助来覆盖一条边,情况就不同了。
- 想象子句 (x1 v ¬x2 v x3)。它与变量小工具的 x1, ¬x2, x3 节点相连。
- 如果我们为变量 $x1$ 赋值为 TRUE,这意味着我们已经将变量小工具中的 x1 节点选入了覆盖集。
- 这个被选中的 x1 节点,通过我们添加的连接边,可以顺便“帮助”覆盖子句小工具中连接到其 x1 节点的所有边。
- 当子句小工具中的一个节点(比如 x1 节点)相关的“对外连接边”已经被覆盖时,我们只需要在子句小工具内部再选择剩下的两个节点,就能覆盖住三角形内部的所有三条边。这恰好满足了我们每个子句花费“2个预算”的计划。
- 关键: 这种“帮助”只有在变量的赋值“满足”了该子句中的某个文字时才会发生。
- 如果一个子句 (x1 v ¬x2 v x3) 没有被满足,意味着变量赋值是 $x1=F, x2=T, x3=F$。这对应于在变量小工具中我们选择了 ¬x1, x2, ¬x3。这三个节点都无法帮助覆盖子句小工具的任何一条对外连接边。在这种情况下,为了覆盖子句小工具内部的3条边和它对外连接的3条边,我们可能需要选择子句小工具中的全部3个节点,导致总覆盖数超过预算 $k$。
- 公式: $\phi = (x \vee y)$ (一个2-CNF, k=1个子句, m=2个变量)
- 变量小工具:
- 变量x: 节点 x 和 ¬x,之间有边。
- 变量y: 节点 y 和 ¬y,之间有边。
- 子句小工具:
- 子句(x v y): 节点 c1(标x) 和 c2(标y),之间有边。(因为是2-CNF,所以是两个点一条边,不是三角形)
- 连接:
- 边 (x, c1)
- 边 (y, c2)
- k值设定: $k = m + (\text{每个子句需要覆盖的节点数}) = 2 + 1 = 3$。
- 寻找大小为3的顶点覆盖:
- 满足赋值 $x=T, y=F$:
- 选择变量小工具中的 x 和 ¬y。已选 {x, ¬y}。
- 现在 x 可以帮助覆盖边 (x, c1)。
- 子句小工具中还剩边 (c1, c2) 和边 (y, c2) 未被覆盖。为了覆盖它们,我们必须选择 c2。
- 最终覆盖集: {x, ¬y, c2},大小为3。成功。
- 不满足赋值 $x=F, y=F$:
- 选择变量小工具中的 ¬x 和 ¬y。已选 {¬x, ¬y}。
- 现在,边 (x, c1) 和 (y, c2) 都未被覆盖。子句内部的边 (c1, c2) 也未被覆盖。
- 为了覆盖这三条边,我们至少需要再选两个节点,比如 c1 和 c2。
- 最终覆盖集: {¬x, ¬y, c1, c2},大小为4,超过了预算 $k=3$。失败。
- Gadget的设计: 这是归约的核心,需要创造力。不同的问题需要设计不同的gadget。
- k值的计算: k值的设定是“恰到好处”的,它施加了足够的压力,迫使任何一个大小为k的顶点覆盖都必须遵循我们预设的“赋值-选择”模式。如果k设得太大,就无法保证这种对应关系了。
本段详细阐述了将 3SAT 归约到 VERTEX-COVER 的证明思路。其核心是设计了两类“小工具”:用一条边代表一个变量的二元选择,用一个三角形代表一个子句的内部约束。通过在同名文字之间建立连接,并精心设置目标覆盖数 $k$,使得寻找一个“最经济”的顶点覆盖的过程,完全等价于寻找一个能满足所有子句的变量赋值的过程。
本段的目的是在给出正式、详细的归约构造之前,向读者展示其背后的设计哲学和工作原理。通过对“变量小工具”和“子句小工具”的直观解释,读者可以更容易地理解后续形式化证明中每一步构造的动机。
这就像是用一套乐高积木来搭建一个能自动进行逻辑运算的机器。
- 变量小工具: 是一个“跷跷板”积木,一头写着x,另一头写着¬x。你必须压下一头(选择一个节点加入覆盖集)。
- 子句小工具: 是一个由三个齿轮组成的、互相咬合的装置。正常情况下,你需要用手固定住其中两个齿轮,它才不会乱转。
- 连接: 你用一些传动杆,把跷跷板的一端连接到齿轮装置的对应齿轮上。
- k值: 是你的“能量预算”。
- 工作原理: 当你压下x端的跷跷板时(赋值x=T),传动杆会帮你卡住一个齿轮。这样,你只需要再用手固定一个齿轮(花费更少的能量),就能稳定整个齿轮装置。这个“节省能量”的效果,只在你压下能满足该子句的那个跷跷板时才会发生。你的总能量预算k被设定得刚刚好,只有当你为所有子句都“节省了能量”时,才够用。
想象你在为一个公司组织一次投票。
- 变量: 每个议题(变量)都有“赞成”和“反对”两个投票箱(变量小工具的两个节点)。每个议员必须且只能在一个箱子里投票。
- 子句: 每个法案(子句)都由三个条款组成。法案本身需要一个专门的“三人委员会”(子句小工具)来审议。这个委员会有三条内部规章(三角形的三条边),需要至少两位委员投出“关注”票才能满足。
- 连接: 如果某个法案的条款与某个议题的“赞成”立场相关,那么“赞成”投票箱和该条款的对应委员之间就有一条“利益关联”线。
- 顶点覆盖: 是一个“关键人物”列表。
- k值: 你被告知,这个公司的决策核心正好是 $k$ 个人。
- 归约: 证明过程是在说,你能找到一个 $k$ 人的决策核心(顶点覆盖),当且仅当,存在一种议员投票的方式(变量赋值),使得所有法案都能被通过(公式可满足)。“核心人物”的数量被设定得非常精妙,它恰好等于(每个议题选一个立场代表)+(每个法案委员会里再选两位代表)。
34 3SAT到VERTEX-COVER归约的正式证明
📜 [原文30]
证明 以下是 3SAT 到 VERTEX-COVER 的多项式时间归约的详细信息。该归约将布尔公式 $\phi$ 映射到图 $G$ 和值 $k$。对于 $\phi$ 中的每个变量 $x$,我们生成一条连接两个节点的边。我们用 $x$ 和 $\bar{x}$ 标记该小工具中的两个节点。将 $x$ 设置为真对应于选择标记为 $x$ 的节点作为顶点覆盖,而 FALSE 对应于标记为 $\bar{x}$ 的节点。
变量。如果 $a_{i}$ 的某些设置满足原始子句,我们可以找到 $z$ 的某些设置,使得两个新子句被满足,反之亦然。通常,如果子句包含 $l$ 个文字,
我们可以用 $l-2$ 个子句替换它
我们可以很容易地验证新公式是可满足的当且仅当原始公式是可满足的,所以证明完成。
这部分文本似乎出现了混淆,它在定义了顶点覆盖的变量小工具之后,突然跳回并重复了上一节中将长子句转换为3-子句的内容。这是一个编辑或排版错误。我将忽略这段重复且错位的内容,直接继续顶点覆盖归约的证明逻辑,整合上一节“证明思路”中提到的所有部分来形成一个连贯的正式证明描述。
(以下内容为根据上下文逻辑,对一个标准证明的重构和解释)
正式证明(重构):
设 $\phi$ 是一个有 $m$ 个变量 $x_1, \dots, x_m$ 和 $c$ 个子句 $C_1, \dots, C_c$ 的 3-CNF 公式。我们构造一个图 $G$ 和一个整数 $k$ 如下:
- 图 G 的构造:
- 变量小工具 (Variable Gadgets): 对于每个变量 $x_i$ (从 $i=1$ 到 $m$),创建一个由两个节点和一条边组成的结构。这两个节点分别标记为 $x_i$ 和 $\bar{x_i}$,它们之间的边我们称之为“变量边”。
- 子句小工具 (Clause Gadgets): 对于每个子句 $C_j$ (从 $j=1$ 到 $c$),该子句形如 $(l_{j1} \vee l_{j2} \vee l_{j3})$,我们创建一个由三个节点组成的三角形结构。这三个节点分别标记为 $l_{j1}, l_{j2}, l_{j3}$。这三条边我们称之为“子句内边”。
- 连接边 (Connection Edges): 将子句小工具和变量小工具连接起来。对于每个子句小工具中的节点(例如,标记为文字 $l$ 的节点),找到变量小工具中具有相同标记的节点,在它们之间添加一条边。例如,如果一个子句是 $(x_1 \vee \bar{x_2} \vee x_3)$,那么子句小工具中标记为 $x_1$ 的节点,就要和变量小工具中标记为 $x_1$ 的节点连一条边。
- k 值的设定:
- 我们设定目标顶点覆盖的大小 $k = m + 2c$。
现在,我们来证明 $\phi$ 是可满足的 $\iff$ G 有一个大小为 $k$ 的顶点覆盖。
第一部分 ($\implies$): 假设 $\phi$ 可满足,证明 G 有 k-VC
- 前提: 存在一个满足 $\phi$ 的真值赋值。
- 构造顶点覆盖集 S:
- 从变量小工具中选择: 对于每个变量 $x_i$,如果它被赋值为 TRUE,我们就将变量小工具中标记为 $x_i$ 的节点加入 $S$。如果它被赋值为 FALSE,我们就将标记为 $\bar{x_i}$ 的节点加入 $S$。这一步我们恰好向 $S$ 中加入了 $m$ 个节点。这些节点覆盖了所有 $m$ 条“变量边”。
- 从子句小工具中选择: 对于每个子句 $C_j$,其内部是一个三角形。我们查看这个三角形的三个节点。由于赋值满足 $\phi$,所以 $C_j$ 中至少有一个文字是真的。
- 考虑一个与真文字对应的节点,例如节点 $l_{j1}$,并且 $l_{j1}$ 在赋值中为真。根据第1步的选择,变量小工具中标记为 $l_{j1}$ 的那个节点已经被选入 $S$。因此,连接这两个同名节点的“连接边”已经被覆盖了。
- 现在,子句小工具(三角形)中,只剩下两条未被保证覆盖的内部边。为了覆盖这两条边,我们选择另外两个没有被真文字对应的节点加入 $S$。例如,如果 $l_{j1}$ 是真文字,我们就将 $l_{j2}$ 和 $l_{j3}$ 对应的节点加入 $S$。
- 这一步我们为每个子句向 $S$ 中加入了 2 个节点,总共加入了 $2c$ 个节点。
- 验证 S:
- 大小: $S$ 的总大小为 $m + 2c = k$。
- 覆盖性:
- 变量边:被第1步的选择覆盖了。
- 子句内边:对于每个子句小工具,我们都选了其中的两个节点,这足以覆盖一个三角形的所有三条边。
- 连接边:考虑一条连接边,它连接着变量小工具的节点 $v$ 和子句小工具的节点 $c$。如果 $v$ 在第1步被选入 $S$,边被覆盖。如果没有,说明 $v$ 对应的文字是假的。那么在子句 $c$ 所属的小工具中,$c$ 节点一定会在第2步被选入 $S$(因为它不对应真文字),所以边也被覆盖。
- 结论: $S$ 是一个大小为 $k$ 的顶点覆盖。
第二部分 ($\impliedby$): 假设 G 有 k-VC,证明 $\phi$ 可满足
- 前提: 存在一个大小为 $k = m + 2c$ 的顶点覆盖集 $S$。
- 分析 S 的结构:
- 图 $G$ 中有 $m$ 个独立的变量边和 $c$ 个独立的子句三角形。这些边互不重叠。
- 为了覆盖 $m$ 条变量边,我们至少需要 $m$ 个节点。
- 为了覆盖 $c$ 个子句三角形内部的 $3c$ 条边,我们至少需要 $2c$ 个节点。
- 因为 $k = m + 2c$ 是我们拥有的总预算,这意味着我们的选择必须是“最经济”的。即:
- 对于每个变量小工具,恰好选择其中一个节点加入 $S$。
- 对于每个子句小工具,恰好选择其中两个节点加入 $S$。
- 任何“浪费”(比如在一个变量小工具里选了两个,或在一个子句小工具里选了三个)都会导致总数超预算。
- 构造满足赋值:
- 基于上述观察,我们来定义一个赋值:对于每个变量 $x_i$,我们查看变量小工具。如果 $S$ 中包含的是标记为 $x_i$ 的节点,我们就令 $x_i = \text{TRUE}$。如果 $S$ 中包含的是标记为 $\bar
- 下一个任务:证明 3SAT 是 NP-完全的:
- 为了能合法地使用 3SAT 这个方便的工具,我们必须先证明它本身也具有 NP-完全的地位。
- 作者指出,这个证明可以作为定理 7.37 (库克-莱文定理) 的一个推论。这意味着,我们不需要再从头开始,而是可以在“SAT 是 NP-完全”这个已知事实的基础上,通过一个额外的归约步骤来完成。
- SAT 实例: $\phi = (x \leftrightarrow y)$。这个公式不是 CNF 格式,结构不规整。
- 3SAT 实例: $\psi = (x \vee y \vee z) \wedge (\bar{x} \vee \bar{y} \vee \bar{z})$。结构非常统一。
- 从 3SAT 归约: 假设我们要证明问题 D 是 NPC。如果我们从 $\psi$ 出发,我们很清楚它有两个子句,每个子句有三个文字。我们可以为每个子句设计一个固定的“小工具”来构造归约。
- 从 SAT 归约: 如果从 $\phi$ 出发,它的结构是 (x AND y) OR (NOT x AND NOT y),既有 AND 又有 OR 嵌套,没有统一的子句结构。为它设计归约就会麻烦得多,需要处理各种不同的逻辑连接词。
- 推论的含义: “推论”(Corollary)是数学中一个紧跟在定理之后、可以由该定理直接或简单推导出的结论。说“3SAT是NPC”是库克-莱文定理的推论,意味着证明的核心工作已经在库克-莱文定理中完成,我们只需要再做一点“收尾”工作。
本段作为库克-莱文定理论证的收尾,它首先宣告了 SAT 的 NP-完全地位,并强调了这一成果对于未来证明工作的“奠基”意义。然后,它引入了在实践中更好用的归约起点——3SAT,并提出了下一个必须完成的任务:证明 3SAT 本身也是 NP-完全的,以便我们能名正言顺地使用它。
本段的目的是完成理论上的过渡。它结束了关于SAT是第一个NPC问题的漫长讨论,并开启了利用这一成果来构建更实用工具(3SAT)的新篇章。这体现了数学和理论计算机科学中层层递进、站在巨人肩膀上前进的典型范式。
我们费了九牛二虎之力,终于在深山里发现并开采出了第一块钻石原石(证明了 SAT 是 NPC)。
- 回顾与展望: 这块原石本身就能证明钻石的存在,价值连城。但它形状不规则,不好镶嵌。
- 引入3SAT: 我们决定先把这块原石切割、打磨成一颗标准的、璀璨的圆形钻石(证明 3SAT 是 NPC)。
- 未来的工作: 以后,珠宝匠们(计算机科学家)想要打造各种首饰(证明其他问题是NPC),就可以直接使用这种标准圆形钻石,而不需要再和粗糙的原石打交道了。
想象在编程中,你写了一个非常底层的、能处理各种复杂情况的函数 process_anything(data) (相当于 SAT)。
- 完成底层函数: 你花费了大量精力写好了这个函数,它很强大,但接口非常复杂,难用。
- 封装一个更好用的接口: 你决定在 process_anything 的基础上,封装一个更简洁、更标准化的函数 process_standard_format(data) (相当于 3SAT)。这个新函数只接受特定格式的输入,内部它会调用底层的 process_anything。
- 下一个任务: 你需要向你的同事证明,这个新的 process_standard_format 函数虽然接口简化了,但功能和底层函数一样强大(也是NP-完全的)。证明方法就是展示如何把底层函数的任意调用(SAT)转化为对新函数的调用(归约到3SAT)。
30 3SAT NP-完全性的证明
📜 [原文31]
证明 显然 3SAT 在 NP 中,所以我们只需要证明 NP 中的所有语言都可以在多项式时间内归约到 3SAT。一种方法是证明 SAT 可多项式时间归约到 3SAT。相反,我们修改定理 7.37 的证明,使其直接产生一个合取范式且每个子句包含三个文字的公式。
定理 7.37 产生的公式几乎已经是合取范式。公式 $\phi_{\text {cell}}$ 是子公式的大 AND,每个子公式都包含一个大 OR 和一个 OR 的大 AND。因此,$\phi_{\text {cell}}$ 是子句的 AND,因此已经是 cnf 形式。公式 $\phi_{\text {start}}$ 是变量的大 AND。将这些变量中的每一个视为大小为 1 的子句,我们看到 $\phi_{\text {start}}$ 是 cnf 形式。公式 $\phi_{\text {accept}}$ 是变量的大 OR,因此是一个单一子句。公式 $\phi_{\text {move}}$ 是唯一一个尚未采用 cnf 形式的公式,但我们可以很容易地将其转换为 cnf 形式的公式,如下所示。
回想一下,$\phi_{\text {move}}$ 是子公式的大 AND,每个子公式都是 OR 的 AND,描述所有可能的合法窗口。第0章中描述的分配律指出,我们可以用等价的 OR 的 AND 替换 AND 的 OR。这样做可能会显著增加每个子公式的大小,但它只能将 $\phi_{\text {move}}$ 的总大小增加一个常数因子,因为每个子公式的大小仅取决于 $N$。结果是一个合取范式的公式。
这部分开始证明3SAT是NP-完全的。作者提出了两种思路,并选择了第二种(更直接的)思路的前半部分:先将库克-莱文证明产生的公式转化为CNF形式。
- 证明目标: 证明 3SAT 是 NP-完全的。
- 第一步:3SAT $\in$ NP?: 是的。和SAT一样,给定一个赋值,验证它是否满足一个3-CNF公式是多项式时间的。作者直接断言“显然”。
- 第二步:证明 3SAT 是 NP-hard?: 即证明所有NP问题都能归约到它。
- 证明 NP-hard 的两种思路:
- 思路一(标准方法): 证明 SAT $\le_P$ 3SAT。既然SAT是NPC(所有NP问题都能归约到它),而SAT又能归约到3SAT,根据归约的传递性,所有NP问题就都能归约到3SAT了。这是最常见的方法,我们将在下一段看到它的实现。
- 思路二(作者选择的方法): 回到库克-莱文定理的证明过程,直接修改那个过程,让它最终生成的不是一个通用的SAT公式 $\phi$,而直接就是一个3-CNF公式。这样就一步到位了。
- 实施思路二:将 $\phi$ 转化为 CNF:
- 作者开始分析库克-莱文证明中构造的 $\phi = \phi_{cell} \wedge \phi_{start} \wedge \phi_{move} \wedge \phi_{accept}$,看它离CNF格式有多远。
- $\phi_{cell}$:
- 回顾其结构: $\bigwedge_{i,j} [ (\bigvee_s x_{i,j,s}) \wedge (\bigwedge_{s \neq t} (\bar{x}_{i,j,s} \vee \bar{x}_{i,j,t})) ]$
- 这是一个巨大的 AND,连接着每个单元格的约束。每个单元格的约束本身也是一个 AND,连接着一个大的OR(一个子句)和一堆小的OR(一堆包含两个文字的子句)。
- 整个结构是 AND of ANDs of ORs,展开后就是 AND of ORs,即 CNF 格式。
- $\phi_{start}$:
- 结构: $x_{1,1,\#} \wedge x_{1,2,q_0} \wedge \dots$
- 这是一个变量的 AND。我们可以把每个变量 $v$ 看作一个只包含一个文字的子句 $(v)$。
- 所以它也是 CNF 格式。
- $\phi_{accept}$:
- 结构: $\bigvee_{i,j} x_{i,j,q_{accept}}$
- 这是一个巨大的 OR,它本身就是一个单一的、巨大的子句。
- 所以它也是 CNF 格式 (一个只包含一个大子句的CNF公式)。
- $\phi_{move}$:
- 回顾其结构: $\bigwedge_{i,j} [ \bigvee_{\text{legal windows}} (\bigwedge_{\text{cells}} x_{\dots}) ]$
- 这是一个 AND of ORs of ANDs 的形式。这个 OR of ANDs 的部分不符合CNF的 AND of ORs 格式。
- 如何转化: 作者提到了分配律 (Distributive Law)。逻辑中的分配律是 $P \vee (Q \wedge R) \iff (P \vee Q) \wedge (P \vee R)$。我们可以反复应用这个定律,把一个 OR of ANDs 的表达式转换成一个等价的 AND of ORs (即CNF) 表达式。
- 转化的代价: 使用分配律通常会导致公式的长度急剧增加(指数级)。但在这里,作者指出,每个窗口的约束子公式 [...] 的大小只跟图灵机 $N$ 有关,是个常数。对一个常数大小的公式应用分配律,其结果的大小也仍然是个常数。
- 因此,虽然 $\phi_{move}$ 的每个窗口约束片段会变大,但只是变大一个固定的倍数。整个 $\phi_{move}$ 的大小仍然是 $O(n^{2k})$,保持了多项式大小。
- 阶段性结论:
- 通过上述分析和转换,我们已经成功地将库克-莱文证明产生的原始公式 $\phi$,转化成了一个等价的、并且是 CNF 格式的新公式 $\phi'$。
- 分配律示例:
- 表达式: $(a \wedge b) \vee (c \wedge d)$。这是 OR of ANDs。
- 应用分配律(把它看作 $(P \vee Q)$,其中 $P=a \wedge b, Q=c \wedge d$):
- 先对 $c$ 分配: $((a \wedge b) \vee c) \wedge ((a \wedge b) \vee d)$
- 再对第一个括号里的 $a,b$ 分配: $(a \vee c) \wedge (b \vee c)$
- 对第二个括号里的 $a,b$ 分配: $(a \vee d) \wedge (b \vee d)$
- 最终CNF形式: $(a \vee c) \wedge (b \vee c) \wedge (a \vee d) \wedge (b \vee d)$。
- 可以看到,公式变长了,但变成了标准的 AND of ORs。
- 作者的思路选择: 作者在这里选择“修改库克-莱文证明”的思路,但实际上只走了一半(转成CNF)。在下一段,他又切换到了思路一(从任意CNF转成3-CNF)。这使得这里的论述有些曲折。一个更直接的讲法是:先承认SAT是NPC,然后给出一个通用的算法,把任何一个SAT公式(或CNF公式)都转化成一个3-SAT公式。
- 分配律的复杂度: 在通用情况下,将一个公式转换为CNF(或DNF)可能导致指数爆炸。这里的关键是,我们操作的每个“窗口”公式都是常数大小的,这使得爆炸被控制在常数范围内。
本段启动了证明3SAT是NP-完全的过程。它首先分析了库克-莱文证明产生的原始公式 $\phi$ 的结构,发现其大部分组件已经是或接近CNF范式。对于唯一不符合的 $\phi_{move}$ 部分,作者指出可以利用逻辑上的分配律将其转化为CNF形式,并且这个转化过程不会破坏公式的多项式大小属性。至此,我们得到了一个等价的、纯粹由子句的AND组成的CNF公式。
本段的目的是完成从一个通用布尔公式到一个结构化的CNF公式的转化。CNF是通往3-CNF的必经之路。通过将所有逻辑约束都统一到“子句的合取”这一种范式下,为下一步将所有子句都规整为“恰好三个文字”的标准化操作做好了准备。
在把法律文书标准化的比喻中:
- 原始的 $\phi$: 是一份包含了各种复杂句式的法律文件。比如,“甲方应支付报酬,当且仅当(乙方完成工作一 或者 (乙方完成工作二 并且 获得丙方认可))”。这种句子结构很复杂。
- 转化为CNF: 就是把所有这些复杂句子,都改写成一系列独立的、用“并且”连接的条款。每个条款内部可以有“或者”。例如,上面的句子可以被改写成:“(条款A)并且(条款B)并且(条款C)”。
- 条款A:“甲方不支付报酬,或者乙方完成工作一,或者乙方完成工作二。”
- 条款B:“甲方不支付报酬,或者乙方完成工作一,或者获得丙方认可。”
- ...等等。
- 这个改写过程(应用分配律)可能让条款数量增加,但最终的文书在结构上变得非常统一:一堆必须同时满足的条款列表。
你有一个复杂的电路图,里面有各种门电路(AND, OR, NOT)随意嵌套连接。
- 转化为CNF: 相当于把这个电路图重新布线,变成一个非常规整的两级结构:第一级是大量的OR门,第二级是一个巨大的AND门,汇集所有OR门的输出。
- 这两个电路在逻辑功能上是完全等价的,但后者结构更清晰、更标准化。$\phi_{move}$的转化就是这样一个过程,由于每个被转化的“窗口电路”都很小,所以重布线的成本(公式大小增加)被控制在常数倍数内。
31 从CNF到3-CNF的转化
📜 [原文32]
现在我们已经用 cnf 编写了公式,我们将其转换为每个子句包含三个文字的公式。在每个当前包含一个或两个文字的子句中,我们复制其中一个文字,直到总数为三个。在每个包含超过三个文字的子句中,我们将其分成几个子句,并添加额外的变量以保留原始子句的可满足性或不可满足性。
例如,我们将子句 $\left(a_{1} \vee a_{2} \vee a_{3} \vee a_{4}\right)$(其中每个 $a_{i}$ 都是一个文字)替换为两子句表达式 $\left(a_{1} \vee a_{2} \vee z\right) \wedge\left(\bar{z} \vee a_{3} \vee a_{4}\right)$,其中 $z$ 是一个新变量。
这是证明 3SAT 是 NP-hard 的最后一步,也是一个非常通用和重要的技巧:如何将一个任意的CNF公式转化为一个等价的3-CNF公式。
这个转化过程分三种情况处理CNF公式中的子句:
- 情况一:子句恰好有3个文字
- 例如 $(x \vee y \vee \bar{z})$。
- 处理方法: 无需处理,直接保留。
- 情况二:子句有1个或2个文字(短子句)
- 例如 $(x)$ 或 $(x \vee y)$。
- 处理方法: 复制已有的文字,凑成3个。
- $(x)$ 变成 $(x \vee x \vee x)$。
- $(x \vee y)$ 变成 $(x \vee y \vee y)$ (或者 $x \vee y \vee x$)。
- 为什么等价?:
- 一个子句 $(x)$ 为真 $\iff x=1$。
- 新子句 $(x \vee x \vee x)$ 为真 $\iff$ 至少一个 $x$ 为真 $\iff x=1$。
- 一个子句 $(x \vee y)$ 为真 $\iff x=1$ 或 $y=1$。
- 新子句 $(x \vee y \vee y)$ 为真 $\iff x=1$ 或 $y=1$ 或 $y=1 \iff x=1$ 或 $y=1$。
- 这种处理方式保持了子句的可满足性不变。
- 情况三:子句有超过3个文字(长子句)
- 例如 $(a_1 \vee a_2 \vee a_3 \vee a_4 \vee a_5)$。这是最需要技巧的一步。
- 处理方法: 引入新变量,将一个长子句“切”成一串短的3-子句。
- 以4-子句为例: $(a_1 \vee a_2 \vee a_3 \vee a_4)$
- 引入一个新变量 $z_1$。这个变量是全新的,在公式的其他地方从未出现过。
- 将原子句替换为两个新子句的 AND:
- 为什么等价?: 我们需要证明“原4-子句可满足” $\iff$ “新表达式可满足”。
- ($\implies$)方向: 假设原4-子句可满足。这意味着 $a_1, a_2, a_3, a_4$ 中至少有一个为真。
- Case 1: 如果 $a_1$或$a_2$为真。那么第一个新子句 $(a_1 \vee a_2 \vee z_1)$ 已经为真了,不管 $z_1$ 是什么。我们此时可以自由地设置 $z_1$ 的值来满足第二个子句。我们令 $z_1=0$,那么 $\bar{z_1}=1$,第二个新子句 $(\bar{z_1} \vee a_3 \vee a_4)$ 也为真。整个表达式被满足。
- Case 2: 如果 $a_3$或$a_4$为真。那么第二个新子句 $(\bar{z_1} \vee a_3 \vee a_4)$ 已经为真了,不管 $z_1$ 是什么。我们此时可以自由地设置 $z_1$ 的值来满足第一个子句。我们令 $z_1=1$,第一个新子句 $(a_1 \vee a_2 \vee z_1)$ 也为真。整个表达式被满足。
- 因为原4-子句可满足,必然属于Case 1或Case 2,所以新表达式也可满足。
- ($\impliedby$)方向: 假设新表达式 $(a_1 \vee a_2 \vee z_1) \wedge (\bar{z_1} \vee a_3 \vee a_4)$ 可满足。这意味着两个子句都必须为真。
- 我们对新变量 $z_1$ 的取值进行讨论:
- Case 1: 如果 $z_1=1$。为了让第二个子句 $(\bar{z_1} \vee a_3 \vee a_4)$ 即 $(0 \vee a_3 \vee a_4)$ 为真,必须有 $a_3$ 或 $a_4$ 为真。
- Case 2: 如果 $z_1=0$。为了让第一个子句 $(a_1 \vee a_2 \vee z_1)$ 即 $(a_1 \vee a_2 \vee 0)$ 为真,必须有 $a_1$ 或 $a_2$ 为真。
- 在这两种情况下,都必然导致 $a_1, a_2, a_3, a_4$ 中至少有一个为真。这就意味着原始的4-子句被满足了。
- 结论: 这种引入新变量的“切分”方法,完美地保持了可满足性的等价。
- 长子句的通用切分规则:
- 原始长子句 (l个文字):
$(a_1 \vee a_2 \vee a_3 \vee \dots \vee a_l)$
- 需要引入的新变量: $l-3$ 个,即 $z_1, z_2, \dots, z_{l-3}$。
- 替换成的 $l-2$ 个 3-子句:
$(a_1 \vee a_2 \vee z_1)$
$\wedge (\bar{z_1} \vee a_3 \vee z_2)$
$\wedge (\bar{z_2} \vee a_4 \vee z_3)$
$\wedge \dots$
$\wedge (\overline{z_{l-3}} \vee a_{l-1} \vee a_l)$
- 工作原理: 这些新变量 $z_i$ 就像多米诺骨牌一样。
- 如果前两个文字 $a_1, a_2$ 中有一个为真,那么第一个子句就满足了。我们可以令 $z_1=0$,这个“假”值会传递下去,$\bar{z_1}=1$ 满足了第二个子句,然后我们可以令 $z_2=0$,以此类推,像推倒多米诺骨牌一样满足所有后续子句。
- 如果最后两个文字 $a_{l-1}, a_l$ 中有一个为真,那么最后一个子句就满足了。我们可以令 $z_{l-3}=1$,这个“真”值会向前传递,$\bar{z_{l-3}}=0$,迫使上一个子句必须由 $a_{l-2}$ 或 $z_{l-4}$ 满足...
- 如果中间的某个文字 $a_i$ 为真,它会像一个“防火墙”,阻断了从两边传来的“必须为真/假”的压力,使得 $z_{i-2}$ 和 $z_{i-1}$ 可以被自由设置,从而满足链条的两端。
- CNF公式: $\phi = (x) \wedge (y \vee z) \wedge (a \vee b \vee c \vee d \vee e)$
- 转化为 3-CNF:
- 处理第一个子句 $(x)$: 变成 $(x \vee x \vee x)$。
- 处理第二个子句 $(y \vee z)$: 变成 $(y \vee z \vee z)$。
- 处理第三个子句 $(a \vee b \vee c \vee d \vee e)$ (长度l=5):
- 需要 $l-3=2$ 个新变量, $z_1, z_2$。
- 需要 $l-2=3$ 个新子句。
- 切分成: $(a \vee b \vee z_1) \wedge (\bar{z_1} \vee c \vee z_2) \wedge (\bar{z_2} \vee d \vee e)$。
- 最终的 3-CNF 公式 $\phi'$:
$(x \vee x \vee x) \wedge (y \vee z \vee z) \wedge (a \vee b \vee z_1) \wedge (\bar{z_1} \vee c \vee z_2) \wedge (\bar{z_2} \vee d \vee e)$
- 这个 $\phi'$ 就是一个与 $\phi$ 在可满足性上等价的、标准的3-CNF公式。
- 引入新变量: 必须是全新的、没有在公式任何地方使用过的变量。否则会产生交叉影响,破坏等价性。
- 等价性的类型: 转化后的公式 $\phi'$ 和原公式 $\phi$ 不是逻辑等价的!因为它们包含不同的变量。一个满足 $\phi$ 的赋值,可能并不满足 $\phi'$(因为它没有对 $z_i$ 赋值)。我们证明的是可满足性的等价 (equisatisfiability):$\phi$ 有一个满足赋值 $\iff$ $\phi'$ 有一个满足赋值。这对于归约来说已经足够了。
- 转化的时间复杂度: 遍历所有子句。对于一个长度为 $l$ 的子句,我们生成 $O(l)$ 个新子句和 $O(l)$ 个新变量。整个转化过程可以在原公式大小的多项式时间内完成。
本段给出了一个通用的、高效的算法,用于将任何CNF公式转化为一个在可满足性上等价的3-CNF公式。对于短子句,通过复制文字来补足;对于长子句,通过引入新变量作为“链条”,将其切分成一串3-子句。这个技巧是NP-完全理论工具箱中非常重要的一件工具,它最终完成了从任意NP问题到3SAT的归约路径。结合之前的论证,3SAT的NP-完全地位得以确立。
本段的目的是完成证明 3SAT 是 NP-hard 的最后一步。它提供了一个机械化的方法,弥合了通用的CNF世界和标准化的3-CNF世界之间的鸿沟。有了这个方法,我们就可以宣称:任何能用CNF表达的问题(包括库克-莱文证明产生的那个CNF公式),其难度都可以被3SAT所承载。
在法律文书标准化的比喻中,这是最后一步的标准化。
- 我们现在有一份CNF格式的合同:一堆必须同时满足的条款列表。但条款的长度不一。
- 转化为3-CNF: 就是实施一条新的起草规定:“所有条款必须且只能包含三项条件”。
- 短条款: “本条规定:甲方必须付款。” -> 改为:“本条规定:甲方必须付款,或甲方必须付款,或甲方必须付款。”(内容等价)
- 长条款: “本条规定:(甲) 或 (乙) 或 (丙) 或 (丁)。” -> 改为引入一个虚拟的中间步骤 “中转条件Z”。
“(条款一:甲 或 乙 或 ‘中转条件Z’成立) 并且 (条款二:‘中转条件Z’不成立 或 丙 或 丁)。”
- 这样,就把一个复杂的长条款,变成了两个简单的、必须同时满足的短条款,并且逻辑上等价。
你是一家工厂的生产线经理。
- CNF: 你收到了一批不同长度的原材料(子句)。
- 3-CNF: 你的机器只能处理长度正好是3米的原材料。
- 你的处理方法:
- 对于1米或2米的短料,你把它们焊在一起(复制文字),凑成3米。
- 对于5米的长料,你在2米处切一刀,然后用一个特殊的“连接件”(新变量 $z$ 和 $\bar{z}$)把这两段重新连成一个整体。这个连接件保证了,只有当原始的5米长料是“合格”的时候,这个由两段和连接件组成的新整体才是“合格”的。
- 通过这个过程,你把所有原材料都转化成了机器可以处理的标准3米件。
32 顶点覆盖问题
📜 [原文33]
顶点覆盖问题
如果 $G$ 是一个无向图,则 $G$ 的顶点覆盖是节点的一个子集,其中 $G$ 的每条边都接触这些节点中的一个。顶点覆盖问题询问一个图是否包含指定大小的顶点覆盖:
VERTEX-COVER $=\{\langle G, k\rangle \mid G$ 是一个具有 $k$ 个节点顶点覆盖的无向图$\}$。
这段话定义了另一个经典的图论问题——顶点覆盖问题 (Vertex Cover)。
- 顶点覆盖的定义:
- 对象: 一个无向图 $G=(V, E)$,由顶点集 $V$ 和边集 $E$ 构成。
- 什么是顶点覆盖: 是顶点的一个子集,我们称之为 $S$ ( $S \subseteq V$ )。
- 核心属性: 这个子集 $S$ 必须满足一个条件:对于图中的每一条边 $(u, v) \in E$,这条边的两个端点中,至少有一个在集合 $S$ 中。即,$u \in S$ 或 $v \in S$。
- 通俗理解: 选出一些顶点,用它们来“盖住”所有的边。一条边被“盖住”,意思是它的某个端点是你选出的顶点之一。
- 顶点覆盖问题的定义:
- 这是一个判定问题。
- 输入:
- 一个无向图 $G$。
- 一个整数 $k$。
- 问题: 图 $G$ 中是否存在一个大小不超过 $k$ 的顶点覆盖?(通常问题会问大小“恰好为”或“小于等于”k,这里的定义是大小为k,在NPC证明中通常设定一个精确的k值)。
- 语言形式化:
- $\langle G, k\rangle$ 是对图和整数 $k$ 的字符串编码。
- 示例1:
- 图G: 一个简单的三角形,顶点为 {1, 2, 3},边为 {(1,2), (2,3), (3,1)}。
- k=1: 能否用1个顶点覆盖所有边?
- 选 {1}: 边 (2,3) 未被覆盖。失败。
- 选 {2}: 边 (1,3) 未被覆盖。失败。
- 选 {3}: 边 (1,2) 未被覆盖。失败。
- 结论: $\langle G, 1\rangle \notin \text{VERTEX-COVER}$。
- k=2: 能否用2个顶点覆盖所有边?
- 选 {1, 2}:
- 边 (1,2) 被覆盖 (因为1和2都在)。
- 边 (2,3) 被覆盖 (因为2在)。
- 边 (3,1) 被覆盖 (因为1在)。
- 所有边都被覆盖了。成功。
- 结论: $\langle G, 2\rangle \in \text{VERTEX-COVER}$。
- 示例2:
- 图G: 一条线,顶点 {1, 2, 3, 4},边 {(1,2), (2,3), (3,4)}。
- k=1: 不可能,比如选{2},边(3,4)就没被覆盖。
- k=2:
- 选 {2, 3}: 边(1,2)被2覆盖,(2,3)被2和3覆盖,(3,4)被3覆盖。成功。
- 选 {1, 3}: 边(1,2)被1覆盖,(2,3)被3覆盖,(3,4)被3覆盖。成功。
- 选 {1, 4}: 边(2,3)未被覆盖。失败。
- 结论: $\langle G, 2\rangle \in \text{VERTEX-COVER}$。
- 顶点覆盖 vs 边覆盖: 不要混淆。顶点覆盖是用顶点去盖边,边覆盖是用边去盖顶点。
- 最小顶点覆盖: 寻找一个图中最小的顶点覆盖,是一个优化问题。我们这里讨论的判定问题是它的一个变种。这两个问题在难度上是相关的。
- 与独立集的关系: 在一个图中,一个顶点子集是独立集 (Independent Set),当且仅当其中任意两个顶点之间没有边。一个惊人的结论是:一个集合 $S$ 是图 $G$ 的一个顶点覆盖,当且仅当它的补集 $V-S$ 是 $G$ 的一个独立集。因此,寻找大小为 $k$ 的顶点覆盖问题,等价于寻找大小为 $|V|-k$ 的独立集问题。这两个问题是NPC“双胞胎”。
本段清晰地定义了顶点覆盖 (Vertex Cover) 这一重要的图论问题。它要求我们从图中选取一个顶点的子集,来“触及”或“覆盖”图中的每一条边。相关的判定问题——VERTEX-COVER——询问是否存在一个给定大小 $k$ 的这样的集合。这个问题是组合优化中的一个基本问题,在网络设计、资源分配等领域有广泛应用。
本段的目的是引入一个新的、重要的候选 NP-完全问题。在证明了 3SAT 是NPC之后,理论计算机科学的一个主要工作就是不断扩大已知的NPC问题列表。VERTEX-COVER 是这个列表中的一个核心成员。接下来,我们将看到如何利用 3SAT 来证明它的 NP-完全性。
在一个城市里,街道是“边”,十字路口是“顶点”。
- 顶点覆盖: 市政府想在一些十字路口安装摄像头,来监控所有的街道。
- 顶点覆盖问题: 如果市政府只有 $k$ 个摄像头,能否找到一种安装方案,使得没有一条街道成为监控死角?
你有一张社交关系网,人是“顶点”,两人认识就是一条“边”。
- 顶点覆盖: 你想邀请一些人来参加一个派对,目标是让每个“认识关系”中至少有一个人到场。这样,任何一对朋友,要么都来了,要么至少来了一个,你可以通过到场的人把消息传递给所有没来的人。
- 顶点覆盖问题: 你只有 $k$ 张请柬,你能否成功地邀请到一个能“代表”所有社交关系的派对阵容?
33 顶点覆盖问题NP-完全性的证明思路
📜 [原文34]
定理 7.44
VERTEX-COVER 是NP-完全的。
证明思路 为了证明 VERTEX-COVER 是NP-完全的,我们必须证明它在 NP 中,并且所有 NP 问题都可以多项式时间归约到它。第一部分很容易;证书就是大小为 $k$ 的顶点覆盖。为了证明第二部分,我们证明 3SAT 可多项式时间归约到 VERTEX-COVER。该归约将 3cnf-公式 $\phi$ 转换为一个图 $G$ 和一个数字 $k$,使得当 $G$ 具有 $k$ 个节点的顶点覆盖时,$\phi$ 是可满足的。转换是在不知道 $\phi$ 是否可满足的情况下完成的。实际上,$G$ 模拟 $\phi$。该图包含模拟公式的变量和子句的小工具。设计这些小工具需要一些独创性。
对于变量小工具,我们在 $G$ 中寻找一种结构,它可以以两种可能的方式参与顶点覆盖,对应于$x_i=0$,这使得第二个子句为真。
- 结论: 我们可以为 $\phi$ 的变量找到一个赋值,使得 $\phi$ 为真。因此,$\phi$ 是可满足的。
时间复杂度: 归约过程需要为每个变量创建2个节点,为每个子句创建3个节点。然后添加边。节点总数是 $2m+3c$,边数是 $m+3c+3c \times 2m$ 的一个子集。整个图的构造可以在 $\phi$ 大小的多项式时间内完成。
最终结论: 我们已经证明了 1) VC $\in$ NP, 2) 3SAT $\le_P$ VC。由于 3SAT 是 NP-完全的,根据定理7.36,VERTEX-COVER 是 NP-完全的。证明完成。
这段文字虽然本身是错位的,但它指向了一个标准的证明过程。通过重构这个证明,我们看到,证明VERTEX-COVER是NP-完全的核心在于设计一个从3SAT到VC的精巧归约。这个归约通过“变量小工具”(一条边)和“子句小工具”(一个三角形)以及它们之间的连接,建立了一个深刻的对应关系:寻找公式的满足赋值,等价于在构造出的图中寻找一个大小恰好为 $k=m+2c$ 的顶点覆盖。这个证明是展示如何使用“小工具”思想进行NPC归约的典范。
本段(及其逻辑上的完整版本)的目的是将 VERTEX-COVER 加入到我们的 NP-完全问题“名人堂”中。它不仅证明了VC本身的困难性,更重要的是,它为我们提供了一个新的、来自图论领域的、已知的NPC问题。这使得我们未来在证明其他图论相关问题是NPC时,可以从VC或CLIQUE出发,而不需要再回到逻辑领域的3SAT,从而让归约路径更短、更直观。
(此部分已在上一节“证明思路”中详细阐述,核心思想是用“跷跷板”和“齿轮组”来模拟变量和子句,并通过设定一个紧张的“能量预算”k值来强迫顶点覆盖的选择与满足赋值的选择保持一致。)
(此部分已在上一节“证明思路”中详细阐述,核心思想是用“议会投票”的例子,将寻找“关键决策人物”(顶点覆盖)与寻找“能让法案通过的投票方案”(满足赋值)等价起来。)
行间公式索引
- $$
\begin{array}{lll}
0 \wedge 0=0 & 0 \vee 0=0 & \overline{0}=1 \\
0 \wedge 1=0 & 0 \vee 1=1 & \overline{1}=0 \\
1 \wedge 0=0 & 1 \vee 0=1 & \\
1 \wedge 1=1 & 1 \vee 1=1 &
\end{array}
\phi=(\bar{x} \wedge y) \vee(x \wedge \bar{z})
S A T=\{\langle\phi\rangle \mid \phi \text { 是一个可满足的布尔公式 }\} .
w \in A \Longleftrightarrow f(w) \in B .
\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}} \vee x_{4}\right) \wedge\left(x_{3} \vee \overline{x_{5}} \vee x_{6}\right) \wedge\left(x_{3} \vee \overline{x_{6}}\right) .
\left(x_{1} \vee \overline{x_{2}} \vee \overline{x_{3}}\right) \wedge\left(x_{3} \vee \overline{x_{5}} \vee x_{6}\right) \wedge\left(x_{3} \vee \overline{x_{6}} \vee x_{4}\right) \wedge\left(x_{4} \vee x_{5} \vee x_{6}\right) .
\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \ldots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right) .
\phi_{\text {cell }}=\bigwedge_{1 \leq i, j \leq n^{k}}\left[\left(\bigvee_{s \in C} x_{i, j, s}\right) \wedge\left(\bigwedge_{\substack{s, t \in C \\ s \neq t}}\left(\overline{x_{i, j, s}} \vee \overline{x_{i, j, t}}\right)\right)\right] .
\bigvee_{s \in C} x_{i, j, s}
\begin{aligned}
\phi_{\text {start }}= & x_{1,1, \#} \wedge x_{1,2, q_{0}} \wedge \\
& x_{1,3, w_{1}} \wedge x_{1,4, w_{2}} \wedge \ldots \wedge x_{1, n+2, w_{n}} \wedge \\
& x_{1, n+3, \sqcup} \wedge \ldots \wedge x_{1, n^{k}-1, \sqcup} \wedge x_{1, n^{k}, \#}
\end{aligned}
\phi_{\text {accept }}=\bigvee_{1 \leq i, j \leq n^{k}} x_{i, j, q_{\text {accept }}}
\phi_{\mathrm{move}}=\bigwedge_{1 \leq i
\bigvee_{\substack{a_{1}, \ldots, a_{6} \\ \text { is a legal window }}}\left(x_{i, j-1, a_{1}} \wedge x_{i, j, a_{2}} \wedge x_{i, j+1, a_{3}} \wedge x_{i+1, j-1, a_{4}} \wedge x_{i+1, j, a_{5}} \wedge x_{i+1, j+1, a_{6}}\right)
\left(a_{1} \vee a_{2} \vee \cdots \vee a_{l}\right),
\left(a_{1} \vee a_{2} \vee z_{1}\right) \wedge\left(\overline{z_{1}} \vee a_{3} \vee z_{2}\right) \wedge\left(\overline{z_{2}} \vee a_{4} \vee z_{3}\right) \wedge \cdots \wedge\left(\overline{z_{l-3}} \vee a_{l-1} \vee a_{l}\right) .