11. 额外的NP-完全问题
1.1. NP-完全现象的普遍性
📜 [原文1]
NP-完全现象普遍存在。NP-完全问题出现在许多领域。由于人们不完全了解的原因,大多数自然出现的 NP 问题要么已知属于 P 类,要么属于 NP-完全类。如果你正在为新的 NP 问题寻找多项式时间算法,那么投入部分精力尝试证明它属于 NP-完全是明智的,因为这样做可以防止你为寻找一个不存在的多项式时间算法而徒劳。
这段话是对 NP-完全 (NP-Complete) 这个概念在现实世界中的普遍性和重要性的一个宏观介绍。
- “NP-完全现象普遍存在。NP-完全问题出现在许多领域。”
- 这句话指出,NP-完全问题不是计算理论中一个罕见的、孤立的特例,而是一种广泛存在的现象。
- 在计算机科学的许多分支,如运筹学(例如旅行商问题)、人工智能(例如规划问题)、网络设计(例如顶点覆盖)、密码学、生物信息学等领域,都会遇到大量的 NP-完全问题。它们是“自然出现”的,而不是被人为构造出来的难题。
- “由于人们不完全了解的原因,大多数自然出现的 NP 问题要么已知属于 P 类,要么属于 NP-完全类。”
- 这里提到了一个有趣的观察,被称为“NP 问题的二分法”或“拉德纳定理 (Ladner's Theorem)”的某种体现。
- P 类问题 (Polynomial time) 是指那些存在多项式时间算法,能够在合理时间内解决的问题。例如,排序、查找最短路径。
- NP 类问题 (Nondeterministic Polynomial time) 是指那些解的正确性可以在多项式时间内验证的问题。
- NP-完全问题 是 NP 问题中最难的一类。
- 这句话的意思是,当我们发现一个新的 NP 问题时,它很大概率最终会被证明要么是“简单的”(属于 P 类),要么是“最难的”(属于 -完全)。介于两者之间的“NP-中间问题”(即,既不是 P 也不是 NP-完全)虽然理论上存在(由拉德纳定理证明),但在实践中非常罕见。整数分解问题和图同构问题曾被认为是 NP-中间问题的候选者,但它们的确切地位仍是未解之谜。
- 这个现象的原因尚不完全清楚,但它指导着我们研究问题的策略。
- “如果你正在为新的 NP 问题寻找多项式时间算法,那么投入部分精力尝试证明它属于 NP-完全是明智的...”
- 这提供了一个非常实用的研究建议。当你面对一个你不知道解法复杂度的 NP 问题时,你有两条路可以走:
- 尝试设计一个多项式时间算法来解决它。如果成功,你就证明了这个问题属于 P 类,这是一个重大的理论突破(如果该问题之前被认为是难的)。
- 尝试证明这个问题是 NP-完全的。
- 这个建议的核心在于,这两条路是互斥的(假设 P ≠ NP)。如果一个问题是 NP-完全的,那么它就不可能存在多项式时间算法。
- “...因为这样做可以防止你为寻找一个不存在的多项式时间算法而徒劳。”
- 这是上述建议的直接结果。如果你成功地证明了一个问题是 NP-完全的,你就得到了一个“坏消息”,但这个坏消息非常有价值。它告诉你,不要再浪费时间和资源去尝试寻找一个高效的、精确的、能在所有情况下都快速解决问题的算法了,因为这样的算法(在 P ≠ NP 的前提下)根本不存在。
- 知道一个问题是 NP-完全的,可以让你改变策略,转而寻求近似算法、启发式算法、或者只针对特定情况的特例算法,而不是一头扎进一个死胡同。
- 示例1:旅行商问题 (TSP)
- 问题描述:给定一系列城市和每对城市之间的距离,求一条访问每个城市恰好一次并返回起点的最短路径。
- 分类:这是一个经典的 NP-完全问题。
- 研究策略:一个刚接触此问题的研究者可能会尝试各种算法(如贪心法、动态规划)来寻找一个在任何城市规模下都很快的最优解法。然而,当他了解到 TSP 是 NP-完全的之后,他就会明白,对于大规模问题(例如几百个城市),寻找精确的最短路径是极其耗时的。他可能会转向设计近似算法,比如找到一条长度不超过最优路径长度 1.5 倍的路径,这样的算法是存在的且运行速度快得多。
- 示例2:2-SAT 问题 (2-Satisfiability)
- 问题描述:给定一个由若干子句组成的布尔公式,其中每个子句都是两个文字(变量或其否定)的析取(或运算),判断是否存在一组变量赋值使得整个公式为真。例如:$(x_1 \lor \overline{x_2}) \land (\overline{x_1} \lor x_3) \land (x_2 \lor \overline{x_3})$。
- 分类:这是一个 P 类问题。存在线性的时间复杂度的算法可以解决它。
- 研究策略:对于 2-SAT,研究者可以放心大胆地去设计高效算法,因为他们知道这样的算法是存在的。他们不必担心这个问题是“不可解”的(在多项式时间内)。这与 3-SAT(每个子句有三个文字)形成鲜明对比,3-SAT 是 NP-完全的。
- 误解1:NP 问题都是难解的。
- 辨析:这是最常见的误解。NP 只是一个分类,它包含了所有 P 类问题。P 类问题是“容易”的。所以,说一个问题是 NP 问题,只说明它的解容易验证,并没有说明它本身是否难解。只有 NP-完全或 NP-难问题才被认为是“难解”的。
- 误解2:如果我证明了一个问题是 NP-完全的,就意味着它永远无法解决。
- 辨析:并非如此。NP-完全的证明只是说,在 P ≠ NP 的假设下,不存在一个在最坏情况下运行时间是多项式级别的精确算法。对于实际应用中的许多 NP-完全问题实例,我们仍然可以:
- 用指数级算法解决小规模的实例。
- 找到近似解(例如,找到一个接近最优的解)。
- 使用启发式方法,在大多数“典型”实例上表现良好,尽管在某些最坏情况下可能很慢或找不到解。
- 解决问题的某个有特殊结构的子集。
- 边界情况:P vs NP 问题。
- 整个讨论都建立在 P ≠ NP 这个悬而未决的猜想之上。如果有一天有人证明了 P = NP,那么所有 NP-完全问题都将拥有多项式时间算法,这里的“明智建议”就会失效。但目前,学术界和工业界普遍基于 P ≠ NP 的假设进行工作。
本段是关于 NP-完全问题研究策略的指导性引言。它强调了 NP-完全问题的普遍性,并指出了一个重要的研究现象:大多数 NP 问题要么简单 (属于 P),要么极难 (属于 NP-完全)。基于此,它提出了一个实用的建议:在为一个新的 NP 问题寻找高效算法时,应同时尝试证明其为 NP-完全。成功证明其 NP-完全性虽然意味着找不到通用的高效解法,但能避免在错误的方向上浪费精力,从而引导研究转向更现实的解决方案,如近似算法。
本段的目的是为后续介绍具体的 NP-完全问题证明做铺垫。它首先建立起一个“为什么要证明一个问题是 NP-完全”的宏观认知。它告诉读者,进行这种证明不仅仅是一个理论练习,更是一种在算法研究和应用开发中至关重要的策略性步骤,可以帮助我们识别问题的内在难度,从而做出明智的决策。
你可以把所有 NP 问题想象成一个巨大的“问题大陆”。
- 大陆上有一片富饶的、容易开发的平原,叫做“P 域”,这里的问题都有现成的、快速的解决方法(多项式时间算法)。
- 大陆上还有一片极其险峻、无法逾越的山脉,叫做“NP-完全山脉”,这里的问题本质上都一样难,只要你能征服其中一座山峰,你就等于能征服所有山峰。
- 当你遇到一个新问题,它就像是降落在这片大陆的一个未知地点。你的任务是确定你的位置。
- 本段的建议是:你不要只朝着平原(P 域)的方向埋头猛冲。你应该同时观察一下周围的地形,看看有没有迹象表明你其实身处“NP-完全山脉”的脚下。如果你能证明自己就在山脉脚下,你就知道攀登是徒劳的(在现有技术下),应该考虑绕路(近似算法)或者造一架飞机(量子计算等未来技术)。
想象你是一个寻宝猎人,宝藏是一个能解决某个问题的“高效算法”。你面前有一张藏宝图,上面标记了“NP 问题”这个区域。
- 你知道这个区域里有些地方埋着“P 类”宝藏,很容易挖到。
- 但也有些地方被下了“NP-完全”魔咒,任何试图直接挖掘宝藏的人都会陷入无尽的循环,永远也挖不到。
- 本段文字就像一位老猎人给你的忠告:“孩子,在你开始疯狂挖掘之前,先花点时间研究一下你脚下的土地。学会识别‘NP-完全’魔咒的迹象。如果你发现这里被施了魔咒,就别挖了,赶紧换个地方,或者改变目标,挖点旁边的‘近似解’小宝石也好。否则,你只会在这里白白浪费一生。”
1.2. 归约策略概述
📜 [原文2]
在本节中,我们介绍额外的定理,表明各种语言是 NP-完全的。这些定理提供了这类证明中使用的技术的例子。我们的通用策略是展示从 3SAT 到相关语言的多项式时间归约,尽管为了方便,我们有时会从其他 NP-完全语言进行归约。
这段话简要说明了本节内容的核心——如何证明一个问题是 NP-完全的,并点明了所采用的主要技术手段。
- “在本节中,我们介绍额外的定理,表明各种语言是 NP-完全的。”
- 这明确了本节的目标:不是介绍一个,而是介绍一系列的 NP-完全问题。这里的“语言”是形式语言理论中的术语,可以理解为“问题”的严格数学定义。例如,CLIQUE 语言是所有编码了“包含特定大小团的图”的字符串集合。证明一个语言是 NP-完全的,等价于证明对应的问题是 NP-完全的。
- “这些定理提供了这类证明中使用的技术的例子。”
- 本节的目的不仅仅是罗列 NP-完全问题,更重要的是教学。通过展示几个具体的证明过程,让读者学习和掌握证明 NP-完全性的一般方法和技巧。这些技巧,特别是“归约”的构造,是计算复杂性理论的核心技能之一。
- “我们的通用策略是展示从 3SAT 到相关语言的多项式时间归约...”
- 这里揭示了核心战术:多项式时间归约 (Polynomial-time reduction)。
- 要证明一个新问题 B 是 NP-完全的,标准的两步流程是:
- 证明 B 属于 NP。(这通常比较简单,只需说明给定一个解,可以在多项式时间内验证其正确性)。
- 证明一个已知的 NP-完全问题 A 可以多项式时间归约到 B(记作 $A \le_P B$)。
- “从 3SAT” 指的是,我们将选择 3SAT 问题作为那个“已知的 NP-完全问题 A”。3SAT 是第一个被证明为 NP-完全的问题(根据库克-莱文定理),并且它的结构(与、或、非逻辑)非常基础,适合用来模拟和构造其他问题。它就像是 NP-完全世界里的“万恶之源”或“干细胞”,可以“分化”成各种各样其他的问题。
- “...尽管为了方便,我们有时会从其他 NP-完全语言进行归约。”
- 这补充说明了归约的灵活性。虽然从 3SAT 出发是最根本的方法,但有时并不方便。
- NP-完全性具有传递性:如果 $A \le_P B$ 且 $B \le_P C$,那么 $A \le_P C$。
- 这意味着一旦我们证明了某个新问题 B 是 NP-完全的,我们就可以把它加入我们的“已知 NP-完全问题工具箱”。在将来要证明另一个问题 C 是 NP-完全时,如果发现从 B 归约到 C 比从 3SAT 归约到 C 更简单、更直观,我们完全可以这么做。这形成了一个“归约链”。例如,在证明 哈密顿路径 (HAMPATH) 是 NP-完全之后,要证明它的无向版本 UHAMPATH 是 NP-完全的,从 HAMPATH 出发就比从 3SAT 出发简单得多。
- 示例:归约链 (Reduction Chain)
- 起点:SAT (布尔可满足性问题) 是 NP-完全的 (库克-莱文定理)。
- 第1步:我们可以证明 SAT $\le_P$ 3SAT。这样,3SAT 就成了我们工具箱里的第一个成员。
- 第2步:在本章中,我们将看到如何证明 3SAT $\le_P$ CLIQUE (团问题)。现在 CLIQUE 也被证明是 NP-完全的,可以加入工具箱。
- 第3步:假设我们现在想证明一个新的问题,叫做“独立集问题 (INDEPENDENT SET)”是 NP-完全的。独立集是指图中的一个点集,其中任意两点之间都没有边。我们可以发现,一个图 G 中大小为 k 的团 (CLIQUE),正好对应于它的补图 $\overline{G}$ (有边变没边,没边变有边) 中大小为 k 的独立集。这个转换非常简单,是多项式时间的。因此,我们可以方便地证明 CLIQUE $\le_P$ INDEPENDENT SET,而不需要再费力地从 3SAT 开始构造。
- 归约方向错误:初学者最常犯的错误是搞反归约方向。要证明 B 是 NP-完全的,必须是 $A \le_P B$,其中 A 是已知的 NP-完全问题。这意味着“用 B 的解法器来解决 A”。直观上,这意味着 B 至少和 A 一样难。如果搞成 $B \le_P A$,那只说明 B 不比 A 难,无法证明 B 是 NP-完全的。
- 忘记“多项式时间”:归约过程本身必须是高效的,即在多项式时间内完成。如果把问题 A 转换成问题 B 的过程需要指数时间,那么这个归约是无效的。例如,用暴力搜索解决 A,然后把答案编码到 B 的一个简单实例中,这不是一个有效的归约。
本段是全节内容的方法论纲领。它明确指出,本节将通过一系列实例来教授证明 NP-完全性的核心技术——多项式时间归约。通用的策略是从经典的 3SAT 问题出发进行归约,但为了证明的便利性,也会利用 NP-完全性的传递性,从其他已被证明的 NP-完全问题进行归约。
本段的目的是为读者设定清晰的预期。在深入到复杂的证明细节之前,它先给出了一个高层次的路线图,告诉读者接下来会看到什么(一系列 NP-完全性证明),以及这些证明背后的统一思想是什么(多项式时间归约)。这有助于读者带着一个清晰的框架去理解后续复杂的“小工具 (gadget)”构造和逻辑推导。
[直觉心-模型]
想象你要证明新来的一块石头 “B” 非常坚硬。
- 你手里已经有一块公认的、已知最坚硬的石头,叫做 “3SAT 石头”。
- 多项式时间归约就像是制造一台机器,这台机器可以在很短的时间内(多项式时间),把任何在 “3SAT 石头” 上刻字的任务,都转化成在 “B 石头” 上刻字的任务。
- 如果你能造出这台机器,就说明 “B 石头” 至少和 “3SAT 石头” 一样坚硬。因为如果 “B 石头” 很软(很容易刻字),你就可以通过你的机器,间接地在 “3SAT 石头” 上轻松刻字了,这与 “3SAT 石头” 是最坚硬的这一事实相矛盾。
- 因此,证明 $A \le_P B$ 就好比是建造了这样一台“任务转换机”。
- 本段还提到,有时我们会发现另一块已经被证明和 “3SAT 石头” 一样硬的石头 “C”,从 “C” 改造任务到 “B” 更方便,我们也可以这么做。
你是一名特工,你的任务是证明一个代号为“CLIQUE”的新锁和传说中最难破解的“3SAT 锁”一样复杂。
- 多项式时间归约就是你的行动计划:你设计一个方案,能把任何一个“3SAT 锁”的实例,在很短的时间内,重新组装成一个“CLIQUE 锁”的实例。
- 并且,这个组装方案必须保证:原来的“3SAT 锁”能被打开,当且仅当新组装的“CLIQUE 锁”能被打开。
- 如果你成功了,就意味着任何能开“CLIQUE 锁”的人,也一定能通过你的方案打开任何“3SAT 锁”。这说明“CLIQUE 锁”的破解难度至少和“3SAT 锁”一样高。
- 本段说,我们的主要策略就是学习如何设计这种“锁的重组方案”,并且主要从“3SAT 锁”开始学。但学会之后,我们也可以从其他同样复杂的锁(如“顶点覆盖”锁)开始重组,只要更方便就行。
1.3. 归约中的“小工具”
📜 [原文3]
在构建从 3SAT 到某种语言的多项式时间归约时,我们寻找该语言中可以模拟布尔公式中的变量和子句的结构。这些结构有时被称为小工具(gadgets)。例如,在从 3SAT 到 CLIQUE 的归约中(定理 7.32),单个节点模拟变量,三元组节点模拟子句。单个节点可以属于或不属于团,对应于变量可以为真或为假。每个子句必须包含一个被赋值为真的文字。相应地,每个三元组必须包含一个团中的节点(以便达到目标大小)。定理 7.32 的以下推论表明 CLIQUE 是 NP-完全的。
这段话介绍了 NP-完全性归约证明中的一个核心思想和术语:“小工具 (gadget)”。
- “在构建从 3SAT 到某种语言的多项式时间归约时,我们寻找该语言中可以模拟布尔公式中的变量和子句的结构。”
- 这是归约构造的核心思路。我们要从 3SAT 归约,就要在新问题中“复刻”出 3SAT 的核心元素。
- 3SAT 公式的核心元素是什么?就是变量 (variables) 和子句 (clauses)。
- 变量可以取值为“真”或“假”,这是一个二元选择。
- 子句是由三个文字(变量或其否定)通过“或”连接起来的,整个公式要求所有子句都必须为“真”。
- 因此,归约的关键就在于,在目标问题(例如 CLIQUE 问题)的实例(例如一个图)中,找到一些局部结构,用这些结构来一一对应地模仿 3SAT 的变量和子句,并确保它们之间的相互作用能准确反映原公式的逻辑约束。
- “这些结构有时被称为小工具(gadgets)。”
- 这里给出了一个非常形象的术语。Gadget,即“小装置”或“小工具”,就是指我们为了模拟 3SAT 的某个特定部分(如一个变量或一个子句)而在目标问题中精心设计的局部构造。
- 变量小工具 (Variable Gadget):它的作用是模拟一个布尔变量的“真/假”二选一。它必须具有某种“双稳态”特性。
- 子句小工具 (Clause Gadget):它的作用是确保对应的子句必须被满足。它通常与相关的变量小工具有联系,并施加一个约束,即这些变量小工具中至少有一个要处于“满足该子句”的状态。
- “例如,在从 3SAT 到 CLIQUE 的归约中(定理 7.32),单个节点模拟变量,三元组节点模拟子句。”
- 这里用一个(虽然在原文中未详细展开的)例子来具体说明 gadget 的概念。这个例子与后续的 VERTEX-COVER 归约中的 gadget 不同,是另一种思路。在 3SAT 到 CLIQUE 的归约中:
- 变量模拟:对于每个变量 $x_i$,我们不是用一个结构,而是为它的每个出现(在不同子句中)创建一个节点。
- 子句模拟:我们将属于同一个子句的文字对应的节点组织在一起,但不在它们之间连边。
- 约束:我们在两个节点之间连边,当且仅当它们分别代表的文字是相容的(即,它们可以同时为真)。这有两层意思:1) 它们属于不同的子句。2) 它们不是一对矛盾的文字(如 $x_i$ 和 $\overline{x_i}$)。
- 目标:如果公式有 $k$ 个子句,那么寻找一个大小为 $k$ 的团 (CLIQUE) 就等价于为每个子句挑选一个为真的文字,且这些选择互不矛盾。
- “单个节点可以属于或不属于团,对应于变量可以为真或为假。每个子句必须包含一个被赋值为真的文字。相应地,每个三元组必须包含一个团中的节点(以便达到目标大小)。”
- 这段话似乎将 CLIQUE 的归约和 VERTEX-COVER 的归约中的概念有所混淆,或者是在用一个更泛化的方式来描述。让我们聚焦于 gadget 的核心思想:
- 状态对应:“属于或不属于团” 对应 “真或假”。这是 gadget 的核心功能,即将目标问题的解的某种属性(一个节点是否在团里,一条边是否被覆盖)映射到源问题(3SAT)的解的属性(一个变量是真是假)。
- 约束对应:“每个子句必须满足” 对应 “每个子句小工具必须满足某个结构要求”。例如,在 VERTEX-COVER 归约中,是要求子句小工具的内部边必须被覆盖。在 CLIQUE 归约中,是要求最终选出的 $k$ 个节点中,必须每个子句都贡献一个。
- “定理 7.32 的以下推论表明 CLIQUE 是 NP-完全的。”
- 这句是承上启下,说明在证明 CLIQUE 是 NP 成员之后,只要完成了从 3SAT 到 CLIQUE 的多项式时间归约,就可以得出 CLIQUE 是 NP-完全的结论。
让我们以 3SAT 到 顶点覆盖 (VERTEX-COVER) 的归约为蓝本,来说明 gadget 的具体构造(这比原文模糊的例子更清晰,也与后面的内容更一致)。
假设我们有 3SAT 公式 $\phi = (x_1 \lor \overline{x_2} \lor x_3)$。
- 变量小工具 (Variable Gadgets):
- 为变量 $x_1$ 创建两个节点,分别标记为 $v_{1,T}$ 和 $v_{1,F}$,并在它们之间连接一条边。这个结构就是一个 变量小工具。要覆盖这条边,我们必须选择 $v_{1,T}$ 或 $v_{1,F}$ 加入顶点覆盖集。这完美地模拟了变量 $x_1$ 必须被赋值为“真”或“假”的二元选择。
- 同样为 $x_2$ 创建 $v_{2,T}, v_{2,F}$ 和边,为 $x_3$ 创建 $v_{3,T}, v_{3,F}$ 和边。
- 子句小工具 (Clause Gadget):
- 为子句 $c_1 = (x_1 \lor \overline{x_2} \lor x_3)$ 创建一个由三个节点 $u_{1,1}, u_{1,2}, u_{1,3}$ 组成的三角形(三条边)。这是一个 子句小工具。要覆盖这三条边,我们至少需要选择其中两个节点。
- 连接小工具:
- 现在连接变量和子句。因为子句 $c_1$ 包含 $x_1$,我们就连接 $v_{1,T}$ 和 $u_{1,1}$。
- 因为子句 $c_1$ 包含 $\overline{x_2}$,我们就连接 $v_{2,F}$ 和 $u_{1,2}$。(注意是 F,代表 $\overline{x_2}$ 为真)。
- 因为子句 $c_1$ 包含 $x_3$,我们就连接 $v_{3,T}$ 和 $u_{1,3}$。
这个由各种节点和边构成的复杂结构,就是 VERTEX-COVER 问题的实例。Gadget 就是指其中的“变量对”和“子句三角形”这些有特定功能的模块化组件。
- 小工具设计不当:Gadget 的设计是归约的艺术所在,也是最容易出错的地方。一个好的 gadget 必须忠实地、无歧义地模拟源问题的行为。
- 不完备:如果 gadget 的某种状态在源问题中没有对应,或者源问题的某种状态在 gadget 中无法体现,那么归约就是失败的。
- 有副作用:如果 gadget 之间的交互产生了意料之外的约束,破坏了模拟的纯粹性,归约也会失败。例如,两个不相关的变量的 gadget 在图中产生了不应有的联系。
- 混淆不同归约的 Gadget:不同的归约(如 3SAT 到 CLIQUE,3SAT 到 VERTEX-COVER)会使用完全不同的 gadget。学习时必须清楚地区分,不能张冠李戴。原文的例子本身就有点模糊,容易让人和后面 VERTEX-COVER 的 gadget 混淆。
本段引入了在 NP-完全归约证明中一个至关重要的概念——小工具 (gadget)。Gadget 是在目标问题实例中,为了模拟源问题(通常是 3SAT)的核心组成部分(变量和子句)而精心设计的局部结构。通过将变量的二元选择和子句的满足条件,转化为 gadget 必须满足的某种属性(如节点是否被选中,边是否被覆盖),从而建立起两个问题之间的等价性。这个思想是理解和构造归约的关键。
本段的目的是将抽象的“归约”思想具体化、工具化。它给出了一个可操作的思路:不要把归约看作一个整体的、天马行空的变换,而是看作一个模块化的“翻译”过程。你需要为源语言的每个“词汇”(变量、子句)找到目标语言中对应的“短语”(gadget),然后把它们组装起来。这使得复杂的归约构造过程变得更有条理、更易于理解和设计。
想象你在用乐高积木(目标问题,如图)来搭建一个能工作的布尔电路(源问题,3SAT)。
- 变量小工具:你设计了一种乐高组合(例如,一个跷跷板结构),它只有两种稳定的状态:左边翘起或右边翘起。这正好可以代表一个变量的“真”或“假”。
- 子句小工具:你又设计了另一种乐高组合(例如,一个由三个开关控制的灯),只有当三个开关中至少有一个被按下时,灯才会亮。这代表一个子句必须被满足。
- 连接:然后你用乐高杆件把代表变量的跷跷板和代表子句的开关灯连接起来。例如,如果子句里有 $x_i$,你就把 $x_i$ 跷跷板“真”的那一端连到子句灯的一个开关上。
- 整个归约过程,就是用这些设计好的“乐高小工具”把整个 3SAT 电路图复刻出来。问原来的电路能否被满足,就等价于问你搭建的这个复杂的乐高模型能否达到某个整体目标(例如,让所有的灯都亮起来)。
你是一个电影导演,要把一部小说(3SAT 公式)改编成电影(例如,一个关于寻找哈密顿路径的迷宫冒险故事)。
- 小说里有一个主角叫“变量 $x_1$”,他有两个选择:去“真理之城”或去“谎言之城”。
- 变量小工具:你在电影里设计了一个特殊的“菱形岔路口”,冒险者从一端进入,只能选择两条路中的一条(例如,靠上走或靠下走)穿过它,这分别对应主角选择去“真理之城”或“谎言之城”。
- 小说里有一个情节是“主角必须打开三个锁中的一个才能过关”(一个子句)。
- 子句小工具:你在电影里设计了一个“神庙”,冒险者必须拜访这个神庙才能继续前进。
- 连接:你设计了从“菱形岔路口”的不同路径到“神庙”的隐藏通道。例如,如果主角选择走“真理之城”那条路,就会有一条捷径可以让他顺路访问某个神庙。
- 整个归约过程,就是把小说中的所有人物选择和情节要求,都用电影场景中的“岔路口”、“神庙”和“隐藏通道”这些“小工具”来表现出来。小说是否有一个皆大-欢喜的结局(公式可满足),就等价于电影中的冒险者是否有一条能走遍所有必经之地(如所有神庙)的通关路线(哈密顿路径)。
1.4. CLIQUE 的 NP-完全性
📜 [原文4]
推论 7.43
CLIQUE 是 NP-完全的。
这部分内容非常简洁,它是一个推论的陈述。
- “推论 7.43”: 这是一个编号,表明这个结论是基于前面某个定理(这里是未详细展开的定理 7.32)直接得出的。在数学和理论著作中,“推论 (Corollary)” 是指一个可以从前面的定理或证明中轻易、直接地推导出来的结论,无需复杂的新证明。
- “CLIQUE 是 NP-完全的。”: 这是本节的核心结论。
- CLIQUE (团问题):输入是一个图 $G$ 和一个整数 $k$,问题是 $G$ 中是否存在一个大小为 $k$ 的团。团是图中的一个完全子图,即子图中的任意两个节点之间都有边相连。
- NP-完全 (NP-complete):意味着 CLIQUE 问题同时满足两个条件:
- CLIQUE $\in$ NP:这个问题属于 NP 类。这一点比较容易理解。如果你给我一个图 $G$ 和一个由 $k$ 个节点组成的集合,我可以在多项式时间内验证这个集合是否构成一个团。我只需要检查两件事:这个集合的大小是不是 $k$,以及集合中任意一对节点之间是否存在边。这个验证过程的复杂度大约是 $O(k^2 \cdot |E|)$ 或更优,是多项式级别的。
- CLIQUE 是 NP-难 (NP-hard):任何 NP 问题都可以多项式时间归约到 CLIQUE。正如前面几段所讨论的,我们通过证明一个已知的 NP-完全问题(如 3SAT)可以归约到 CLIQUE(即 3SAT $\le_P$ CLIQUE)来证明这一点。
- 这个推论的成立,是基于“定理 7.32”已经完成了 3SAT $\le_P$ CLIQUE 的证明。因此,结合 CLIQUE $\in$ NP,我们就能得出 CLIQUE 是 NP-完全的最终结论。
- 示例1:一个有团的图
- 输入:图 $G$ 有节点 {1, 2, 3, 4, 5},边为 {(1,2), (1,3), (1,4), (2,3), (2,4), (3,4), (4,5)}。$k=4$。
- 问题:$G$ 中是否存在大小为 4 的团?
- 解:是。节点集合 {1, 2, 3, 4} 就是一个大小为 4 的团,因为其中任意两个节点之间都有边。
- 验证:给我 {1, 2, 3, 4} 这个解,我检查:(1,2)有边,(1,3)有边,(1,4)有边,(2,3)有边,(2,4)有边,(3,4)有边。所有 6 对节点之间都有边。验证通过。这说明了 CLIQUE $\in$ NP。
- 示例2:一个没有团的图
- 输入:同样的图 $G$,$k=5$。
- 问题:$G$ 中是否存在大小为 5 的团?
- 解:否。因为节点 5 只和节点 4 相连,它不可能与 1, 2, 3 同时构成团。
- NP-完全的含义:对于这个小图,我们很容易看出答案。但当图有成千上万个节点时,要找出是否存在一个例如大小为 100 的团,就没有已知的快速通用方法了。暴力搜索需要检查所有大小为 100 的节点组合,这是一个天文数字。CLIQUE 是 NP-完全的,意味着(在 P ≠ NP 的假设下)这样的快速通用方法不存在。
- 推论的依赖性:必须理解这是一个“推论”,它的正确性完全依赖于前文(定理 7.32)已经成功证明了 3SAT $\le_P$ CLIQUE。如果那个证明有误,这个推论也就不成立。
- CLIQUE vs 最大 CLIQUE:CLIQUE 问题是一个判定问题(回答“是”或“否”)。它还有一个兄弟版本,叫做“最大团问题 (Maximum Clique Problem)”,这是一个优化问题,要求找到图中最大的那个团。这两个问题密切相关,最大团问题是 NP-难的。通常说的 CLIQUE 是指判定版本。
本段以推论的形式,明确宣告了 CLIQUE (团问题) 是一个 NP-完全问题。这是计算复杂性理论中的一个里程碑式的结论。它意味着寻找图中是否存在特定大小的完全子图,在本质上和解决 3SAT 问题一样困难,并且(在 P ≠ NP 假设下)不存在通用的高效算法。
本段的目的是将 CLIQUE 问题正式加入到我们的“已知 NP-完全问题工具箱”中。在证明了 3SAT 的 NP-完全性之后,CLIQUE 是我们通过归约方法拿下的第一个重要“战利品”。从现在开始,当我们需要证明其他图论相关问题是 NP-完全的时,我们就可以选择从 CLIQUE 出发进行归约,这往往比从 3SAT 出发更直观、更方便。
回到“NP-完全山脉”的比喻。
- 库克和莱文首先发现了这座险峻山脉,并确认了第一座无法攀登的山峰,叫做“SAT 峰”。
- 然后人们发现,从“SAT 峰”可以很容易地修一条路到旁边的“3SAT 峰”,说明它也一样高,无法攀登。
- 本段的“定理 7.32”就好比是探险家们又从“3SAT 峰”修建了一条栈道,通向了一座新的、看起来完全不同的山峰,叫做“CLIQUE 峰”。
- 这个“推论 7.43”就是探险队在“CLIQUE 峰”顶插上的一面旗帜,上面写着:“此峰已被证实为‘NP-完全山脉’的一部分,无法从底部攀登。”
- 从此以后,其他探险队想探索附近的山峰时,就可以直接从“CLIQUE 峰”出发,而不用再回到遥远的“3SAT 峰”了。
想象一个“已知犯罪团伙名单”,这个名单上的团伙都是最顶级的、最难抓捕的,代号为“NP-完全”。
- 一开始,名单上只有 FBI 认定的始祖级团伙 “3SAT”。
- 一个侦探(卡普)通过卧底调查,发现了一个新的街头帮派 “CLIQUE”。他写了一份详细的报告(定理 7.32),报告证明了任何 “3SAT” 团伙策划的犯罪活动,都可以通过一套固定的流程,转化成 “CLIQUE” 帮派的一次行动,并且前者的成败完全取决于后者的成败。
- “推论 7.43” 就是局长看完报告后下的最终定论:“把‘CLIQUE’也加入‘NP-完全’犯罪团伙名单!它的危险等级和‘3SAT’一样高。”
- 从此,其他侦探在调查新帮派时,如果发现新帮派和“CLIQUE”有直接联系,就可以直接引用这份报告,快速将其也列为“NP-完全”团伙,而无需再从最原始的“3SAT”开始调查了。
22. 从3SAT到顶点覆盖(Vertex Cover)的归约
注意:原文此处开始的文字描述的是从 3SAT 到 顶点覆盖 (VERTEX-COVER) 问题的归约,但标题和前面的例子却是指向 CLIQUE。这是一个常见的教材编写中的混淆或笔误。接下来的解释将严格按照原文的 文字内容 (即 VERTEX-COVER 的归约) 进行,尽管它被错误地放在了 CLIQUE 的标题之下。我们将把这个归约视为对 VERTEX-COVER 问题的 NP-完全性证明。顶点覆盖问题是:给定一个图 $G$ 和一个整数 $k$,是否存在一个大小为 $k$ 的节点集合,使得图中每条边都至少与该集合中的一个节点相连。
2.1. 子句的小工具
📜 [原文5]
子句的小工具(gadgets)稍微复杂一些。每个子句小工具是一个三元组节点,它们用子句的三个文字进行标记。这三个节点相互连接,并连接到变量小工具中具有相同标记的节点。因此,$G$ 中出现的节点总数为 $2m+3l$,其中 $\phi$ 有 $m$ 个变量和 $l$ 个子句。令 $k$ 为 $m+2l$。
这段话描述了用于 顶点覆盖 归约的 子句小工具 (Clause Gadget) 的构造,以及整个图的规模。
- “子句的小工具(gadgets)稍微复杂一些。”
- 这句话暗示之前已经讨论过一个相对简单的 gadget,即 变量小工具。一个典型的 变量小工具 是为每个变量 $x_i$ 创建两个节点(比如标记为 $x_i$ 和 $\overline{x_i}$)并在它们之间连一条边。要覆盖这条边,必须选两者之一,这模拟了变量的真假赋值。
- “每个子句小工具是一个三元组节点,它们用子句的三个文字进行标记。”
- 这里开始描述 子句小工具 的内部结构。对于 3SAT 公式中的每一个子句 $c_j$,我们都创建一个对应的 gadget。
- 这个 gadget 由三个节点组成。为了方便理解,我们可以将这三个节点与子句中的三个文字一一对应。例如,如果子句是 $(x_1 \lor \overline{x_2} \lor x_3)$,那么这三个节点就可以想象成代表 $x_1$ 在此子句中的出现、$\overline{x_2}$ 在此子句中的出现、以及 $x_3$ 在此子句中的出现。
- “这三个节点相互连接...”
- 这是 子句小工具 内部结构的关键。这三个节点构成一个三角形(一个大小为 3 的团)。这意味着它们之间有三条边。
- 这个结构的作用是什么?在一个顶点覆盖问题中,要覆盖一个三角形的三条边,我们至少需要选择其中的两个节点。选择一个节点只能覆盖与其相连的两条边,还剩下一条对边未被覆盖。因此,这个三角形结构强制要求我们必须从这三个节点中,至少选出两个放入顶点覆盖集中。
- “...并连接到变量小工具中具有相同标记的节点。”
- 这描述了 子句小工具 和 变量小工具 之间的连接方式,这是整个归约的核心所在,它建立了逻辑约束。
- 假设我们已经为每个变量 $x_i$ 创建了 变量小工具,即两个节点 $v_i$ (代表 $x_i$ 为真) 和 $\overline{v_i}$ (代表 $x_i$ 为假),以及它们之间的边。
- 现在,如果一个子句 $c_j$ 包含文字 $x_1$,我们就将 $c_j$ 的 子句小工具 中代表 $x_1$ 的那个节点,与 变量小工具 $x_1$ 中的 $v_1$ 节点连接起来。
- 如果子句 $c_j$ 包含文字 $\overline{x_2}$,我们就将 $c_j$ 的 子句小工具 中代表 $\overline{x_2}$ 的那个节点,与 变量小工具 $x_2$ 中的 $\overline{v_2}$ 节点连接起来。
- 这个连接的作用是传递“赋值”信息。如果一条边 $(u, v)$ 要被覆盖,我们可以选择 $u$,也可以选择 $v$。这个连接边建立了一个选择的关联:我们可以通过选择 变量小工具 中的节点来帮助覆盖这条连接边,从而影响我们在 子句小工具 中的选择。
- “因此,$G$ 中出现的节点总数为 $2m+3l$,其中 $\phi$ 有 $m$ 个变量和 $l$ 个子句。”
- 这里在计算整个构造出来的图 $G$ 的节点总数。
- 变量小工具:每个变量 $x_i$ (共 $m$ 个) 对应两个节点。所以总共有 $2m$ 个变量节点。
- 子句小工具:每个子句 $c_j$ (共 $l$ 个) 对应三个节点。所以总共有 $3l$ 个子句节点。
- 总节点数 = 变量节点数 + 子句节点数 = $2m + 3l$。
- “令 $k$ 为 $m+2l$。”
- 这里定义了顶点覆盖问题实例的目标大小 $k$。这个 $k$ 的取值是精心设计的,是整个归约能够成功的关键。
- $k = m + 2l$ 的含义是什么?
- $m$:来自 $m$ 个变量小工具。每个变量小工具是一条边,至少需要 1 个节点来覆盖。为了覆盖所有 $m$ 个变量小工具内部的边,我们总共至少需要 $m$ 个节点。我们计划恰好选择 $m$ 个节点,即每个变量二选一。
- $2l$:来自 $l$ 个子句小工具。每个子句小工具是一个三角形,至少需要 2 个节点来覆盖其内部的三条边。为了覆盖所有 $l$ 个子句小工具内部的边,我们总共至少需要 $2l$ 个节点。我们计划恰好选择 $2l$ 个节点。
- 这个目标值 $k$ 是一个“紧张”的预算。它恰好等于我们在每个小工具内部为了满足覆盖要求而必须选择的节点数量之和。这个“不多不少”的预算,正是强制逻辑关系成立的关键。
- 示例:
- 3SAT 公式 $\phi$:$(x_1 \lor \overline{x_2}) \land (x_2 \lor x_3)$。
- 参数:这里我们用一个包含两个文字的子句为例,虽然是 2-SAT,但足以说明构造。
- 变量数 $m = 3$ ($x_1, x_2, x_3$)。
- 子句数 $l = 2$ ($c_1, c_2$)。
- 节点总数:$2m + 2l = 2*3 + 2*2 = 10$。(注意这里每个子句是2个文字,所以是 $2m+2l$)。如果严格按原文的 3-SAT,假设 $c_1=(x_1 \lor \overline{x_2} \lor x_1)$,$c_2=(x_2 \lor x_3 \lor x_2)$,则 $m=3, l=2$。
- 变量节点 (6个): $v_1, \overline{v_1}, v_2, \overline{v_2}, v_3, \overline{v_3}$。
- 子句节点 (6个): 属于 $c_1$ 的 $u_{1,1}, u_{1,2}, u_{1,3}$;属于 $c_2$ 的 $u_{2,1}, u_{2,2}, u_{2,3}$。
- 总节点数:$2*3 + 3*2 = 12$。
- 顶点覆盖目标大小 k:
- $k = m + 2l = 3 + 2*2 = 7$。
- 构造出的图 G 的 k 值的意义:
- 我们需要在 $G$ 中找到一个大小为 7 的顶点覆盖集。
- 这个预算的分配是固定的:必须从 3 个变量小工具中各选 1 个节点(共 3 个),从 2 个子句小工具中各选 2 个节点(共 4 个)。总共 $3+4=7$ 个。
- 任何其他的选择方案(比如在某个变量小工具中选了 2 个节点,或者在某个子句小工具中只选了 1 个节点)都会导致预算超支,或者无法覆盖所有边。这个“紧张的预算”是证明的关键。
- k 值的计算:$k$ 的值是归约成功的核心,必须精确计算并理解其构成。$k=m+2l$ 这个公式是针对 3SAT 到 VERTEX-COVER 归约的特定设计,不能滥用到其他归约中。
- 小工具的命名:为了清晰,最好使用一致且有意义的命名法来标记小工具的节点,例如用 $v$ 表示变量节点,用 $u$ 表示子句节点,并用下标指明其所属的变量/子句和具体代表的文字。
- 原文的混淆:再次强调,这部分描述的是 VERTEX-COVER 的归约,而非 CLIQUE。如果强行理解为 CLIQUE,整个逻辑都是不通的。例如,在 CLIQUE 中,我们是寻找密集连接的子图,而 VERTEX-COVER 是寻找能“打散”所有边的节点集,两者目标相反。
本段详细阐述了 3SAT 到 VERTEX-COVER 归约中 子句小工具 的构造方法及其与 变量小工具 的连接方式。每个子句被转换为一个三角形节点组,这种结构强制要求至少选择两个节点才能覆盖其内部。整个图的节点数被确定为 $2m+3l$,而顶点覆盖的目标大小 $k$ 被精巧地设定为 $m+2l$。这个紧凑的预算 $k$ 强制要求任何有效的顶点覆盖解都必须在每个变量小工具中恰好选择一个节点,在每个子句小工具中恰好选择两个节点,从而为模拟布尔逻辑奠定了基础。
本段的目的是具体化归约的构造细节,特别是 子句小工具 的设计和图的整体参数设定。它展示了如何将 3SAT 的一个核心约束(子句必须被满足)转化为图论问题的一个结构性约束(三角形的边必须被覆盖)。通过设定精确的节点总数和目标覆盖数 $k$,它为后续的正确性证明(即证明公式可满足当且仅当图存在大小为 $k$ 的顶点覆盖)铺平了道路。
[直觉心-模型]
想象一个安保系统设计问题。
- 变量小工具:你有 $m$ 个房间,每个房间都有一个前门和一个后门(节点 $v_i, \overline{v_i}$)。前后门之间有一条红外线(边 $(v_i, \overline{v_i})$)。你必须在每个房间的前门或后门之一安装一个摄像头,才能监控到这条红外线。你的预算是 $m$ 个摄像头。
- 子句小工具:你有 $l$ 个保险柜。每个保险柜由一个三角形的玻璃柜保护(节点 $u_{j,1}, u_{j,2}, u_{j,3}$ 及它们之间的三条边)。要确保玻璃柜的所有三面都被监控到,你必须在三个角中的至少两个角上安装摄像头。你的预算是每个保险柜 2 个摄像头。
- 连接:每个保险柜都与某些房间的门有特定的关联。例如,保险柜 $j$ 的第一个角($u_{j,1}$)和房间 $i$ 的前门($v_i$)之间也有一条红外线。
- 总预算 k:你的总预算是 $k = m + 2l$ 个摄像头。
- 问题:能否用这 $k$ 个摄像头,监控到所有的红外线(图的所有边)?
- 本段的设计就表明,你必须严格按照“每个房间1个,每个保险柜2个”的方式来分配摄像头。你没有额外的摄像头去处理连接房间和保险柜的那些红外线。唯一的办法是,你在房间里选择的那个摄像头,正好也能顺便监控到连接保险柜的红外线。这就模拟了变量的赋值如何满足子句。
你是一个派对策划人,正在安排座位。
- 变量小工具:有 $m$ 对夫妇(变量 $x_i$)。每对夫妇(节点 $v_i, \overline{v_i}$)之间关系紧张,不能同时请来,必须二选一。这构成了一个约束(边)。
- 子句小工具:有 $l$ 张圆桌,每张桌子只有三个座位(子句 $c_j$)。这三个座位上的人互相认识,形成一个小圈子(三角形)。
- 连接:你有一些额外的安排规则,比如A桌的1号位客人,和B夫妇里的丈夫是好朋友(连接边)。
- 总人数 k:你的派对总共只能容纳 $k = m + 2l$ 人。
- 目标(顶点覆盖):你需要选出一个大小为 $k$ 的宾客名单,使得所有“关系”(边)都至少有一个人在场。
- 推导:
- 为了满足“夫妇二选一”的约束,你必须从 $m$ 对夫妇中各选一人,这就占了 $m$ 个名额。
- 为了让每张圆桌的“小圈子”关系被代表,你需要从每桌的三个座位中至少请来两人,这就占了 $2l$ 个名额。
- 你的名额 $k=m+2l$ 刚好用完。
- 现在要考虑连接夫妇和餐桌的那些“朋友关系”。由于你没有多余的名额,唯一的办法是,你从夫妇中选出的那个人,正好也是某个餐桌上被邀请的客人,这样他/她一个人就能同时满足两种“关系”。
- 一个可满足的赋值,就对应一个成功的派对安排方案。
2.2. 归约图示与示例
📜 [原文6]
例如,如果 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$,则归约从 $\phi$ 产生 $\langle G, k\rangle$,其中 $k=8$,且 $G$ 采用下图所示的形式。
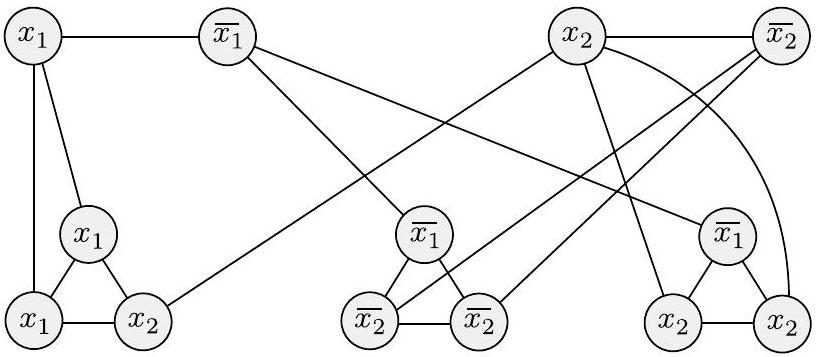
图 7.45
由 $\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$ 产生的图 $G$
这部分通过一个具体的 3SAT 公式实例,展示了归约过程生成的图 $G$ 和目标值 $k$。然而,这里的图示与前文描述的用于 VERTEX-COVER 的小工具构造完全不同。 这个图示实际上是 3SAT 到 CLIQUE (团) 或者 3SAT 到 INDEPENDENT SET (独立集) 归约中使用的构造。我们在此处对其进行忠实解释,并指出它与前后文的矛盾之处。
让我们先分析这个图示本身代表的归约方法(即 3SAT 到 CLIQUE):
- 公式 $\phi$:$\phi=\left(x_{1} \vee x_{1} \vee x_{2}\right) \wedge\left(\overline{x_{1}} \vee \overline{x_{2}} \vee \overline{x_{2}}\right) \wedge\left(\overline{x_{1}} \vee x_{2} \vee x_{2}\right)$。
- 这个公式有 2 个变量 ($x_1, x_2$) 和 3 个子句 ($c_1, c_2, c_3$)。
- 注意子句中可以有重复的文字,例如 $c_1$ 中的 $x_1$ 和 $c_2$ 中的 $\overline{x_2}$。
- 图 $G$ 的构造:
- 节点:图中的节点是根据子句来组织的。每个子句对应一组节点,节点数量等于子句中文字的数量。
- $c_1 = (x_1 \lor x_1 \lor x_2)$ 对应图顶部的三个节点,分别标记为 $x_1, x_1, x_2$。
- $c_2 = (\overline{x_1} \lor \overline{x_2} \lor \overline{x_2})$ 对应图中左下角的三个节点,标记为 $\overline{x_1}, \overline{x_2}, \overline{x_2}$。
- $c_3 = (\overline{x_1} \lor x_2 \lor x_2)$ 对应图中右下角的三个节点,标记为 $\overline{x_1}, x_2, x_2$。
- 总共有 $3+3+3=9$ 个节点。
- 边:图中边的连接规则是:
- 规则 A (不同子句):只有当两个节点属于不同的子句时,它们之间才可能有边。属于同一个子句的节点之间(如图中顶部的三个 $c_1$ 节点之间)绝对没有边。
- 规则 B (不矛盾):如果两个节点属于不同子句,我们检查它们标记的文字是否矛盾。如果不矛盾,则在它们之间连一条边。“不矛盾”意味着它们不是形如 $x_i$ 和 $\overline{x_i}$ 的一对。
- 例如:
- 顶部 $c_1$ 的第一个 $x_1$ 节点,与左下角 $c_2$ 的 $\overline{x_2}$ 节点之间有边,因为它们属于不同子句,且 $x_1$ 和 $\overline{x_2}$ 不矛盾。
- 顶部 $c_1$ 的第一个 $x_1$ 节点,与左下角 $c_2$ 的 $\overline{x_1}$ 节点之间没有边,因为 $x_1$ 和 $\overline{x_1}$ 是矛盾的。
- 顶部 $c_1$ 的第一个 $x_1$ 节点,与顶部 $c_1$ 的第二个 $x_1$ 节点之间没有边,因为它们属于同一个子句。
- 目标值 $k$:
- 原文给出的 $k=8$ 是错误的,并且与 CLIQUE 归约的目标不符。在 3SAT 到 CLIQUE 的归约中,目标 $k$ 值应该等于子句的数量。
- 在这个例子中,有 3 个子句,所以正确的 $k$ 值应该是 $k=3$。
- 归约的目标:证明 $\phi$ 可满足 $\iff$ 图 $G$ 中存在大小为 $k=3$ 的团 (CLIQUE)。
解释这个 CLIQUE 归约为什们有效:
- 从可满足赋值到团:
- 假设 $\phi$ 有一个满足赋值,例如 $x_1=$ 真, $x_2=$ 假。
- 我们为每个子句挑选一个在此赋值下为真的文字。
- $c_1=(x_1 \lor x_1 \lor x_2)$: $x_1$ 为真,我们选择顶部的一个 $x_1$ 节点。
- $c_2=(\overline{x_1} \lor \overline{x_2} \lor \overline{x_2})$: $\overline{x_2}$ 为真 (因为 $x_2$ 为假),我们选择左下角的一个 $\overline{x_2}$ 节点。
- $c_3=(\overline{x_1} \lor x_2 \lor x_2)$: $\overline{x_1}$ 为假,两个 $x_2$ 都为假,这个例子中的赋值无法满足 $c_3$。让我们换一个赋值。
- 换个赋值:$x_1=$ 假, $x_2=$ 真。
- $c_1=(x_1 \lor x_1 \lor x_2)$: $x_2$ 为真。我们选择顶部的 $x_2$ 节点。
- $c_2=(\overline{x_1} \lor \overline{x_2} \lor \overline{x_2})$: $\overline{x_1}$ 为真。我们选择左下角的 $\overline{x_1}$ 节点。
- $c_3=(\overline{x_1} \lor x_2 \lor x_2)$: $\overline{x_1}$ 和 $x_2$ 都为真。我们选择右下角的一个 $x_2$ 节点。
- 我们选出的三个节点是:来自 $c_1$ 的 $x_2$,来自 $c_2$ 的 $\overline{x_1}$,来自 $c_3$ 的 $x_2$。
- 这三个节点来自不同的子句,并且它们代表的文字 ($x_2$, $\overline{x_1}$) 是相容的。根据我们的构造规则,这三个节点两两之间都有边,因此它们构成一个大小为 3 的团。
- 从团到可满足赋值:
- 假设我们在 $G$ 中找到了一个大小为 3 的团。
- 由于团中任意两点都有边,根据构造规则 A,这 3 个节点必须来自 3 个不同的子句,即每个子句恰好贡献一个节点。
- 根据构造规则 B,这 3 个节点代表的文字不能相互矛盾。
- 我们就可以构造一个赋值:对于团中选中的节点所代表的文字,将其赋值为真。例如,如果团中的节点是 $x_1, \overline{x_2}, x_3$,我们就令 $x_1=$真, $x_2=$假, $x_3=$真。这个赋值是无矛盾的。
- 由于每个子句都贡献了一个节点到团中,这意味着每个子句都至少有一个文字在这个赋值下为真。因此,整个公式 $\phi$ 是可满足的。
关于原文中 $k=8$ 的错误分析:
这个 $k=8$ 完全不符合 CLIQUE 归约的逻辑。它看起来更像是前文 VERTEX-COVER 归约中 $k=m+2l$ 公式的误用。对于这个公式 $\phi$,$m=2, l=3$。如果套用那个公式,$k=m+2l = 2+2*3 = 8$。这表明作者在写这段时,脑子里想的还是 VERTEX-COVER 的归约,但配的图却是 CLIQUE 归约的图,并且把前者的 $k$ 值错误地安在了后者上,造成了严重的混淆。
本段提供了一个将具体 3SAT 公式转化为图 $G$ 的实例。然而,该实例存在严重的不一致性:它展示的图构造方法是用于“3SAT 到 CLIQUE”归约的,但给出的目标值 $k=8$ 却是错误地套用了“3SAT 到 VERTEX-COVER”归约的公式。正确的 CLIQUE 归约目标值应为子句数,即 $k=3$。这个例子如果按照 CLIQUE 归约的正确逻辑来理解(即寻找大小为 3 的团),可以很好地展示归约如何建立公式可满足性与图中是否存在特定大小团之间的等价关系。
本段的意图是通过一个具体的、可视化的例子来帮助读者理解归约的构造过程。尽管例子本身存在错误和不一致,但其初衷是好的:将抽象的构造规则应用于一个实际的公式,并画出结果图,让读者能更直观地看到变量和子句是如何“变形”成图中的节点和边的。
想象你在组织一个国际会议,有 $l$ 个国家代表团(子句),每个代表团有 3 名代表(节点)。
- 规则1:同一个代表团的成员互相看不顺眼,不能同时被选入核心委员会。
- 规则2:如果两个不同代表团的代表所持的政治立场(文字,如 $x_i$ 和 $\overline{x_i}$)有冲突,他们也不能同时被选入核心委员会。
- 建图:你画了一张关系图,只有互相没有矛盾的代表之间才连线。
- 目标:你要组建一个大小为 $l$ 的核心委员会(大小为 $k=l$ 的团),要求委员会里人人关系和谐(两两之间都有连线)。
- 等价性:
- 能成功组建这样的委员会 $\iff$ 你可以从每个国家的代表团里各挑一个人,并且这些人的政治立场互不冲突。
- 这就等价于,你可以找到一种满足所有政治约束(公式可满足)的方案,让每个国家都有代表“满意”(子句被满足)。
你正在玩一个拼图游戏。
- 原料:给你 3 堆积木(子句),每堆有 3 块,积木上写着 $x_1, \overline{x_2}$ 等标签(文字)。
- 连接规则:如果两块积木来自不同堆,并且标签不冲突(不是 $x_i$ 和 $\overline{x_i}$),你就可以用一根“磁力棒”(边)把它们连起来。
- 目标:你需要在图中找到 3 块积木,它们两两之间都由磁力棒连接(构成一个三角形的团)。
- 结论:你能找到这样的一个“磁力三角形”,当且仅当你可以从每堆积木中各拿一块,而这三块积木的标签所代表的逻辑赋值不互相矛盾。这正对应于原布尔公式是可满足的。
2.3. 归约的正确性证明(顶点覆盖版本)
📜 [原文7]
为了证明这个归约是有效的,我们需要证明 $\phi$ 是可满足的当且仅当 $G$ 具有 $k$ 个节点的顶点覆盖。我们从一个满足赋值开始。我们首先将变量小工具中与赋值中真文字对应的节点放入顶点覆盖中。然后,我们选择每个子句中的一个真文字,并将每个子句小工具中剩余的两个节点放入顶点覆盖中。现在我们总共有 $k$ 个节点。它们覆盖了所有边,因为每个变量小工具的边都已明确覆盖,每个子句小工具内部的所有三条边都已覆盖,并且变量小工具和子句小工具之间的所有边也都已覆盖。因此 $G$ 具有 $k$ 个节点的顶点覆盖。
其次,如果 $G$ 具有 $k$ 个节点的顶点覆盖,我们通过构造满足赋值来证明 $\phi$ 是可满足的。顶点覆盖必须包含每个变量小工具中的一个节点和每个子句小工具中的两个节点,以覆盖变量小工具的边和子句小工具内部的三条边。这占据了所有节点,因此没有节点剩余。我们取顶点覆盖中变量小工具的节点,并将相应的文字赋值为 TRUE。这个赋值满足 $\phi$,因为连接变量小工具和每个子句小工具的三条边中的每一条都已覆盖,并且子句小工具中只有两个节点在顶点覆盖中。因此,其中一条边必须由来自变量小工具的节点覆盖,因此该赋值满足相应的子句。
这部分是 3SAT 到 VERTEX-COVER 归约的正确性证明的核心。它分为两个方向:($\Rightarrow$) 可满足性推导出顶点覆盖,和 ($\Leftarrow$) 顶点覆盖推导出可满足性。这部分内容完全是基于 VERTEX-COVER 的归约,与上一节的图示无关。
第一部分:证明 $\phi$ 可满足 $\Rightarrow G$ 存在大小为 $k$ 的顶点覆盖
- “我们从一个满足赋值开始。”
- 这是证明的起点。我们假设我们已经有了一个能让公式 $\phi$ 为真的变量赋值方案,例如 $x_1=$真, $x_2=$假, ...
- “我们首先将变量小工具中与赋值中真文字对应的节点放入顶点覆盖中。”
- 这是构建顶点覆盖集 $C$ 的第一步。我们根据已知的满足赋值来选择变量节点。
- 对于每个变量 $x_i$(共 $m$ 个):
- 如果 $x_i$ 赋值为真,我们就把代表“真”的节点(我们称之为 $v_i$)放入集合 $C$ 中。
- 如果 $x_i$ 赋值为假,我们就把代表“假”的节点(我们称之为 $\overline{v_i}$)放入集合 $C$ 中。
- 经过这一步,我们恰好选择了 $m$ 个节点。这些选择直接覆盖了所有 $m$ 个变量小工具的内部边(即 $(v_i, \overline{v_i})$)。
- “然后,我们选择每个子句中的一个真文字,并将每个子句小工具中剩余的两个节点放入顶点覆盖中。”
- 这是构建顶点覆盖集 $C$ 的第二步,处理子句小工具。
- 因为我们假设 $\phi$ 是可满足的,所以每个子句 $c_j$ 都至少包含一个为真的文字。
- 我们为每个子句 $c_j$(共 $l$ 个)任意选择一个在当前赋值下为真的文字。假设这个文字是 $L$。
- 在 $c_j$ 的子句小工具(一个由三个节点组成的三角形)中,有一个节点是与代表 $L$ 的变量节点相连的。我们不选这个节点。
- 我们选择这个三角形中剩下的两个节点,将它们放入集合 $C$。
- 对所有 $l$ 个子句都执行这个操作,我们就向 $C$ 中加入了 $2l$ 个节点。
- “现在我们总共有 $k$ 个节点。”
- 我们从变量小工具中选了 $m$ 个节点,从子句小工具中选了 $2l$ 个节点。
- 集合 $C$ 的总大小为 $m + 2l$,这正好是我们预设的目标值 $k$。
- “它们覆盖了所有边...”
- 现在需要验证我们选出的这 $k$ 个节点是否构成了 $G$ 的一个顶点覆盖,即是否图中的每一条边都至少有一个端点在 $C$ 中。图中的边有三类:
- 变量小工具内部的边:形如 $(v_i, \overline{v_i})$。我们对每个变量都选择了 $v_i$ 或 $\overline{v_i}$ 中的一个,所以这些边肯定被覆盖了。
- 子句小工具内部的边:每个子句小工具是三角形,有三条边。我们选择了其中的两个节点,这两个节点必然覆盖了这三条边。
- 连接变量和子句的边:这是最关键的部分。考虑连接变量小工具和子句小工具 $c_j$ 的一条边 $(v, u)$,其中 $v$ 在变量小工具中, $u$ 在子句小工具中。
- 根据我们的选择规则(第3步),我们特意在每个子句 $c_j$ 中找到了一个真文字 $L$,并且没有选择与 $L$ 对应的那个子句节点 $u_L$。
- 那么连接到 $u_L$ 的那条边 $(v_L, u_L)$ 是如何被覆盖的呢?
- 因为 $L$ 是真文字,所以根据我们的规则(第2步),它对应的变量节点 $v_L$ 一定被选入了集合 $C$!
- 因此,这条连接边被来自变量小工具的节点 $v_L$ 覆盖了。
- 对于子句小工具中其他的连接边,它们的子句端节点已经被我们选入 $C$ 了,所以它们也被覆盖了。
- “因此 $G$ 具有 $k$ 个节点的顶点覆盖。”
- 我们成功地用一个满足赋值构造出了一个大小为 $k=m+2l$ 的顶点覆盖。证明了这一半。
第二部分:证明 $G$ 存在大小为 $k$ 的顶点覆盖 $\Rightarrow \phi$ 可满足
- “如果 $G$ 具有 $k$ 个节点的顶点覆盖,我们通过构造满足赋值来证明 $\phi$ 是可满足的。”
- 这是反方向的证明。我们假设已经找到了一个大小为 $k=m+2l$ 的顶点覆盖集 $C$。我们要利用这个 $C$ 来找出一个能满足 $\phi$ 的变量赋值。
- “顶点覆盖必须包含每个变量小工具中的一个节点和每个子句小工具中的两个节点...”
- 这是一个关键的结构性断言。为什么必须这样?
- 变量小工具是 $m$ 条独立的边(它们之间不共享节点),要覆盖这 $m$ 条边,你至少需要 $m$ 个节点。
- 子句小工具是 $l$ 个独立的三角形,要覆盖这 $l$ 个三角形内部的所有 $3l$ 条边,你至少需要 $2l$ 个节点(每个三角形至少2个)。
- 覆盖这两部分内部的边总共就需要至少 $m+2l = k$ 个节点。
- 而我们的总预算恰好就是 $k$。这意味着我们没有丝毫浪费的余地。为了用恰好 $k$ 个节点覆盖所有边,我们必须:
- 在每个变量小工具中恰好选择 1 个节点。
- 在每个子句小工具中恰好选择 2 个节点。
- 任何其他选择方案(比如在某个变量小工具选2个,或某个子句小工具选3个)都会导致节点总数超过 $k$ 才能覆盖所有内部边。
- “这占据了所有节点,因此没有节点剩余。”
- 顶点覆盖集 $C$ 中的所有 $k$ 个节点,都被完美地分配给了 $m$ 个变量小工具和 $l$ 个子句小工具。
- “我们取顶点覆盖中变量小工具的节点,并将相应的文字赋值为 TRUE。”
- 这是构造赋值的方法。我们遍历顶点覆盖集 $C$ 中来自变量小工具的那 $m$ 个节点。
- 对于每个变量 $x_i$:
- 如果 $C$ 中包含的是 $v_i$(代表“真”的节点),我们就将 $x_i$ 赋值为真。
- 如果 $C$ 中包含的是 $\overline{v_i}$(代表“假”的节点),我们就将 $x_i$ 赋值为假。
- 因为每个变量小工具恰好有一个节点在 $C$ 中,所以这个赋值是明确且无矛盾的。
- “这个赋值满足 $\phi$...”
- 现在需要证明这个构造出来的赋值方案确实能让 $\phi$ 为真,即让每个子句 $c_j$ 都为真。
- 考虑任意一个子句 $c_j$。我们知道它的子句小工具(三角形)中有两个节点在 $C$ 中。这意味着有一个节点 $u$ 不在 $C$ 中。
- 考虑连接到这个节点 $u$ 的边,它形如 $(v, u)$,其中 $v$ 是某个变量小工具中的节点。
- 因为 $C$ 是一个顶点覆盖,所以边 $(v, u)$ 必须被覆盖。
- 我们已经知道 $u$ 不在 $C$ 中,那么覆盖这条边的责任就落在了 $v$ 身上。因此,节点 $v$ 必须在 $C$ 中。
- 节点 $v$ 在 $C$ 中,意味着什么?根据我们构造赋值的规则,它所代表的那个文字被赋值为真了!
- 而这个文字,正是子句 $c_j$ 中的一个文字。
- 所以,我们证明了,对于任意子句 $c_j$,它都至少包含一个被赋值为真的文字。
- “因此,$\phi$ 得到满足。”
- 所有子句都被满足,所以整个公式 $\phi$ 是可满足的。证明了另一半。
本段是 3SAT 到 VERTEX-COVER 归约的核心逻辑证明。它完美地展示了两个问题之间的等价性是如何通过精心设计的 gadget 和目标值 $k$ 建立起来的。
- 正向证明展示了如何将一个逻辑上的“满足”状态,转化为一个物理结构上的“覆盖”状态。通过在变量和子句 gadget 中做出特定选择,可以构造一个大小恰好为 $k$ 的顶点覆盖。关键在于,变量赋值为真可以“帮助”覆盖与之相连的子句边。
- 反向证明则展示了结构上的“最优性”(用最少的节点覆盖)如何强制产生逻辑上的“满足”。大小为 $k$ 的顶点覆盖是一个“紧绷”的解,它没有冗余。这种紧绷性迫使变量节点的选择必须能够满足所有子句,因为子句小工具自身留出了一个“缺口”,这个缺口必须由一个值为“真”的变量节点来填补。
这段证明的存在目的,是为“VERTEX-COVER 是 NP-完全的”这个结论提供严格的数学依据。它不是在描述构造,而是在验证这个构造的正确性。这是所有 NP-完全性证明中最关键、最需要严谨逻辑的部分。它展示了归约不仅仅是形式上的转换,更是逻辑等价性的深刻映射。
再次回到安保系统模型:$k = m+2l$ 个摄像头。
- 正向:假设你知道一个安全的密码组合(满足赋值)。你按照这个密码组合,在对应的门上(变量)安装摄像头。由于密码是正确的,每个保险柜(子句)至少有一个关联的门是“安全”的。你就在这个保险柜的另外两个“不安全”的角上装摄像头。这样一来,你恰好用了 $k$ 个摄像头,并且可以证明所有红外线都被监控到了。因为那些连接“安全”门和保险柜的红外线,被你装在门上的摄像头搞定了。
- 反向:假设你找到了一个只用 $k$ 个摄像头的完美布防方案。由于预算太紧张,你分析后发现,这个方案必须是“每个房间门口装1个,每个保险柜角落装2个”。然后你去看每个保险柜,都发现有一个角没装摄像头。连接这个角的红外线怎么办呢?它必须被另一头的——也就是某个房间门口的摄像头——监控到。于是,你记下所有这些“起到了关键作用”的房门,把它们的状态(前门还是后门)组合起来,就得到了那个唯一的、能使整个安保系统成立的密码组合。
再次回到派对策划模型:$k=m+2l$ 个宾客名额。
- 正向:假设你有一份“和谐人际关系”名单(满足赋值),告诉你每对夫妻请谁来能让大家都开心。你按照名单邀请,这就占了 $m$ 个名额。因为关系是和谐的,所以每张桌子(子句)上都至少有一个“关键人物”其伴侣没来。然后你在这张桌子剩下的两个座位上随便邀请两个人填满。这样你恰好用了 $2l$ 个名额来处理桌子。总共 $k$ 个名额,并且你会发现所有“关系”(边)都被满足了。
- 反向:假设你有一份大小为 $k$ 的完美宾客名单,它满足了所有的关系。你发现,由于名额太紧张,名单必然是“每对夫妻来一人,每张桌子来两人”的结构。你检查每张桌子,都发现有一个空位。连接这个空位的“朋友关系”怎么办?必然是被另一端——也就是某个夫妻中的来宾——所满足了。你把所有这些“起到了关键作用”的夫妻来宾记录下来,他们的组合(丈夫来还是妻子来)就构成了一份“和谐人际关系”名单,证明这样的和谐关系是可能存在的。
33. 哈密顿路径问题
3.1. 问题定义
📜 [原文8]
哈密顿路径问题
回想一下 哈密顿路径问题 询问输入图是否包含一条从 $s$ 到 $t$ 且经过每个节点恰好一次的路径。
这部分简单地重申了 哈密顿路径问题 (Hamiltonian Path Problem, HAMPATH) 的定义。
- “哈密顿路径问题”: 这是问题的名称。它以爱尔兰数学家威廉·罗恩·哈密顿命名,他研究了相关的问题。
- “询问输入图是否包含一条...”: 这说明 HAMPATH 是一个判定问题 (Decision Problem),它的答案是“是”或“否”。它不要求你找出那条路径,只问你是否存在。
- “从 $s$ 到 $t$”: 这是指路径有指定的起点 $s$ 和终点 $t$。这是 HAMPATH 问题的特定版本,有时也称为“$s-t$ 哈密顿路径问题”。有些版本的定义不指定起点和终点,只问图中是否存在任何一条哈密顿路径。指定起点和终点使得问题更具体,也更容易用于归约。
- “经过每个节点恰好一次”: 这是哈密顿路径的核心定义。一条路径如果访问了图中的所有节点,并且每个节点都只访问了一次,那么它就是一条哈密顿路径。
- “所有节点”: 不能有遗漏。如果图有 $V$ 个节点,路径必须包含所有 $V$ 个节点。
- “恰好一次”: 不能重复访问。路径是一个简单的路径 (simple path),没有环。
- 示例1:存在哈密顿路径
- 输入:一个图 $G$,节点集 $V=\{s, a, b, t\}$,边集 $E=\{(s,a), (a,b), (b,t)\}$。起点为 $s$,终点为 $t$。
- 问题:是否存在从 $s$ 到 $t$ 的哈密顿路径?
- 解:是。路径 $s \rightarrow a \rightarrow b \rightarrow t$ 经过了所有四个节点,且每个节点恰好一次。
- 示例2:不存在哈密顿路径
- 输入:一个图 $G$,节点集 $V=\{s, a, b, t\}$,边集 $E=\{(s,a), (s,b), (a,t), (b,t)\}$(一个菱形)。起点为 $s$,终点为 $t$。
- 问题:是否存在从 $s$ 到 $t$ 的哈密顿路径?
- 解:否。任何从 $s$ 到 $t$ 的路径,例如 $s \rightarrow a \rightarrow t$,都遗漏了节点 $b$。另一条路径 $s \rightarrow b \rightarrow t$ 则遗漏了节点 $a$。你无法在一条路径中同时访问 $a$ 和 $b$ 并满足起点终点要求。
- 示例3:有向图中的哈密顿路径
- 输入:一个有向图 $G$,节点 $V=\{s, a, b, t\}$,有向边 $E=\{s \to a, a \to b, b \to t, t \to s, a \to t\}$。起点 $s$,终点 $t$。
- 解:是。路径 $s \to a \to b \to t$ 是一条哈密顿路径。注意,即使图中存在其他边如 $a \to t$,我们也不使用它。
- 哈密顿路径 vs 欧拉路径:这是一个经典的易混淆概念。
- 哈密顿路径:访问每个节点恰好一次。
- 欧拉路径:走过每条边恰好一次。
- 一个图可能存在其中一种路径,而没有另一种。判断是否存在欧拉路径有简单的充要条件(关于节点度数的奇偶性),属于 P 类问题。而 HAMPATH 是 NP-完全的。
- 路径 vs 环:
- 哈密顿路径:从一个节点开始,到另一个节点结束。
- 哈密顿环 (Hamiltonian Cycle):一条哈密顿路径,并且其起点和终点之间也有一条边,从而形成一个闭环。哈密顿环问题 (HAMCYCLE) 也是一个著名的 NP-完全问题,它和 HAMPATH 密切相关,可以相互归约。
本段对 哈密顿路径问题 (HAMPATH) 进行了清晰的定义。该问题要求判断一个给定的图中,是否存在一条从指定起点 $s$ 到指定终点 $t$ 的路径,这条路径必须不重不漏地访问图中的每一个节点。这是一个经典的 NP-完全图论问题。
本段的目的是为接下来的 NP-完全性证明设定目标。在引入了一个新的复杂证明之前,首先要确保读者对这个问题的定义有清晰、准确的理解。这是任何严格证明的必要前提。接下来的内容将围绕这个定义展开,展示如何将 3SAT 的逻辑结构“编码”到一个图的结构中,使得图是否存在哈密顿路径等价于公式是否可满足。
想象一个“一笔画”游戏,但规则不同。
- 棋盘:一个图,节点是棋盘上的点,边是连接点的线。
- 规则:你需要从起点 $s$ 出发,用一笔画出一条线,这条线必须经过棋盘上所有的点,每个点只能经过一次,最后停在终点 $t$。你不能抬笔,也不能走重复的点。
- 问题:这样的画法是否存在?
- HAMPATH 问题就是问,对于给定的棋盘和起终点,这个游戏有没有解。
你是一个游客,想要规划一次城市观光。
- 城市地图:一个图,节点是景点,边是连接景点的公交线路。
- 你的计划:你计划从酒店(起点 $s$)出发,必须游览完地图上标记的所有景点,每个景点只去一次,最后到达机场(终点 $t$)。
- HAMPATH 问题:是否存在这样一条完美的、不走回头路的观光路线?
- 对于小城市,你可能一眼就看出来了。但如果是一个有几百个景点的大都市,规划这样一条路线将变得异常困难,这就是 HAMPATH 问题的难点所在。
3.2. HAMPATH 的 NP-完全性
📜 [原文9]
定理 7.46
HAMPATH 是 NP-完全的。
这是一个定理的陈述,是本节的一个核心结论。
- “定理 7.46”: 这是该定理的编号。
- “HAMPATH 是 NP-完全的。”:
- HAMPATH: 正如刚刚定义的,是在一个图中寻找一条经过所有节点恰好一次的 $s-t$ 路径的判定问题。
- NP-完全: 这个断言意味着 HAMPATH 问题同时具备两个属性:
- HAMPATH $\in$ NP: 这个问题属于 NP 类。这一点很容易证明。如果有人给了你一条声称是哈密顿路径的节点序列(例如 $s, v_1, v_2, ..., t$),你可以在多项式时间内验证它。你需要检查:(a) 路径的起点是 $s$,终点是 $t$;(b) 序列中包含了图的所有节点;(c) 序列中没有重复节点;(d) 序列中相邻的每一对节点之间在图中确实存在一条边。这些检查都可以在多项式时间内完成。
- HAMPATH 是 NP-难 (NP-hard): 任何 NP 问题都可以多项式时间归约到 HAMPATH。接下来的“证明思路”和“证明”部分,就是要通过证明 3SAT $\le_P$ HAMPATH 来证实这一点。
- NP-完全的实际意义:
- 假设你为一个物流公司工作,需要为一架无人机规划一条投送路线,它需要从仓库($s$)出发,访问 $N$ 个客户投送点,然后飞到充电站($t$)。为了节省能源,你希望无人机每个点只访问一次。
- 这个问题就是一个 HAMPATH 问题的实例。
- 由于 HAMPATH 是 NP-完全的,当客户数量 $N$ 很大时(比如 50 个),你的公司不应该期望能找到一个软件,在任何情况下都能在几秒钟内计算出是否存在这样一条完美路线。
- 知道这一点后,公司可能会改变策略,比如:
- 开发一个近似算法,寻找一条尽可能短的、访问所有客户的路线(这变成了旅行商问题,也是 NP-难的)。
- 开发一个启发式算法,在大多数实际的城市布局中能快速找到一个不错的解,但不保证在所有奇怪的布局中都有效。
- 对问题进行限制,例如,如果所有客户都在一条直线上,问题就变得很简单。
- 有向图 vs 无向图: 这里的 HAMPATH 通常指的是有向图版本(directed HAMPATH),因为归约中构造的图是带方向的。无向图版本 UHAMPATH 也是 NP-完全的,并且可以由有向版本归约而来,后面会讲到。必须分清正在讨论的是哪个版本。
- 证明的完备性: 这个定理的陈述只是一个结论。它的成立,完全依赖于后续的、非常复杂的归约证明。在没有看到那个证明之前,我们只是“接受”这个结论。
本段以定理的形式,庄重地宣告了 哈密顿路径问题 (HAMPATH) 是 NP-完全的。这意味着它在计算复杂性上属于最难的一类 NP 问题,与 3SAT、CLIQUE、VERTEX-COVER 等问题等价。这个结论对于算法设计和实际应用具有重要的指导意义,它告诉我们不要期望为大规模的 HAMPATH 问题找到通用的高效解法。
本段的目的是清晰地提出本节证明的目标。它像一个章节的标题,预告了接下来的长篇证明将要达成的最终结论。通过先给出结论,再展开证明,可以让读者带着明确的目标去阅读和理解复杂的归约构造过程。
回到“NP-完全山脉”的比喻。
- 前面我们已经通过修建栈道,在“3SAT 峰”和“CLIQUE 峰”上插上了旗帜。
- 现在,探险队看上了另一座风格迥异的山峰,叫做“HAMPATH 峰”,这座山峰的挑战是“一笔画问题”。
- 这个定理就是探险队立下的军令状:“我们的目标是证明 HAMPATH 峰也和 3SAT 峰一样高,无法攀登。”
- 接下来的所有关于菱形、子句节点的复杂构造,都是在修建一条从“3SAT 峰”通往“HAMPATH 峰”的、极其精巧的、带有方向性的空中索道。
你是一名法官,正在审理一个案子。
- 被告:HAMPATH 问题。
- 指控:它和臭名昭著的黑帮头目“3SAT”是一伙的,属于“NP-完全”犯罪集团。
- 证据(属于 NP):检察官首先证明,验证 HAMPATH 的不在场证明(给出一个路径)很容易(多项式时间),所以它符合“NP 成员”的基本特征。
- 核心指证(NP-难):检察官(在本案中是卡普或库克/莱文)将要向法庭展示一个复杂的证据链(归约),证明任何“3SAT”策划的犯罪,都可以转化为一个“HAMPATH”的行动。
- 定理 7.46 就是最终的判决书:“经审理,HAMPATH 问题 NP-完全罪名成立,即刻生效。”
3.3. 证明思路
📜 [原文10]
证明思路 我们在 7.3 节中证明了 HAMPATH 属于 NP。为了证明每个 NP 问题都可以多项式时间归约到 HAMPATH,我们证明 3SAT 可以多项式时间归约到 HAMPATH。我们给出一种将 3 cnf-公式转换为图的方法,其中哈密顿路径对应于公式的满足赋值。图包含模拟变量和子句的小工具(gadgets)。变量小工具是一个菱形结构,可以通过两种方式遍历,对应于两种真值设置。子句小工具是一个节点。确保路径经过每个子句小工具对应于确保满足赋值中每个子句都得到满足。
这部分概述了证明 HAMPATH 是 NP-完全的整体策略和核心创意。
- “我们在 7.3 节中证明了 HAMPATH 属于 NP。”
- 这重申了证明 NP-完全性的两步中的第一步已经完成。验证一个给定的路径是否是哈密顿路径是容易的。
- “为了证明每个 NP 问题都可以多项式时间归约到 HAMPATH,我们证明 3SAT 可以多项式时间归约到 HAMPATH。”
- 这再次明确了证明 NP-难的标准策略:我们不需要把所有的 NP 问题都归约到 HAMPATH,只需要把一个已知的“代表”(NP-完全问题,这里选 3SAT)归约到 HAMPATH 即可。利用 NP-完全的传递性,就足以证明 HAMPATH 的 NP-难度。
- “我们给出一种将 3 cnf-公式转换为图的方法,其中哈密顿路径对应于公式的满足赋值。”
- 这是归约的核心目标:建立“哈密顿路径的存在性”与“公式的可满足性”之间的当且仅当关系。我们要设计的这个转换(从公式到图的算法)必须保证:
- 如果公式可满足,那么转换出的图中必定存在一条哈密顿路径。
- 如果图中存在一条哈密顿路径,那么原公式必定是可满足的。
- “图包含模拟变量和子句的小工具(gadgets)。”
- 这里点出了实现上述目标的技术手段,即再次使用“小工具”的思想。我们需要在图中设计出两种不同功能的结构模块。
- “变量小工具是一个菱形结构,可以通过两种方式遍历,对应于两种真值设置。”
- 这是对变量小工具设计的核心创意的首次揭示。
- 为每个变量 $x_i$ 设计一个“菱形”的子图结构。
- 这个菱形结构的关键特性是,任何一条想要“穿过”它的哈密顿路径,都只有两种走法。例如,“从左到右”走或者“从右到左”走(原文用“之字形”和“反之字形”更准确地描述了内部走法)。
- 我们将这两种走法强制与变量的赋值对应起来:走法 A 代表 $x_i$ 为真,走法 B 代表 $x_i$ 为假。这是一个非常漂亮的“二元选择”的物理模拟。
- “子句小工具是一个节点。”
- 子句小工具的设计在这里看起来非常简单:每个子句 $c_j$ 就只对应图中的一个孤零零的节点。
- “确保路径经过每个子句小工具对应于确保满足赋值中每个子句都得到满足。”
- 这是整个归约的“画龙点睛”之笔。
- 哈密顿路径要求必须经过图中每一个节点。这意味着,路径必须想办法“拜访”到每一个代表子句的节点。
- 如何拜访?这些子句节点会通过特定的连接边,与变量小工具联系起来。
- 连接方式的设计将非常精巧,它要保证:只有当某个变量的赋值(即其变量小工具的遍历方式)满足了某个子句时,哈密顿路径才有机会“顺路”去拜访那个子句对应的节点。
- 因此,“路径必须访问所有子句节点”这个图论上的要求,就被转化为了“赋值必须满足所有子句”这个逻辑上的要求。
- 变量小工具的直观想象:
- 想象一条长长的走廊代表变量 $x_i$。走廊里有一排房间。
- 你可以选择“从上向下”访问这些房间,这代表 $x_i=$ 真。
- 你也可以选择“从下向上”访问这些房间,这代表 $x_i=$ 假。
- 但你必须访问完所有房间,并且只能选择一种顺序。
- 子句小工具和连接的直观想象:
- 假设子句 $c_j = (x_i \lor ...)$。这意味着如果 $x_i$ 为真,则 $c_j$ 被满足。
- 在我们的图中,有一个代表 $c_j$ 的“宝藏”节点。
- 我们在代表 $x_i$ 的那条走廊里,如果你选择了“从上向下”($x_i=$ 真)的路线,那么在某个特定的房间,会出现一条岔路,让你能够“顺便”去访问一下“宝藏”节点 $c_j$ 再回来,而不影响你继续走完走廊。
- 但如果你选择了“从下向上”($x_i=$ 假)的路线,那么在那同一个房间,通往宝藏节点的岔路是“逆行”的,你无法使用它。
- 因此,变量的赋值(走廊的遍历方向)决定了你是否能“解锁”通往特定宝藏节点的路径。
- 由于哈密顿路径要求你必须拿到所有宝藏,你就必须为每个宝藏(子句)至少解锁一条通往它的路径,这等价于每个子句至少要被一个文字满足。
- 小工具的隔离性:变量小工具的设计必须保证路径只能“进入再出来”,不能从中间“跳”到别的变量小工具里去。菱形结构两端的“瓶颈”设计就是为了保证这一点。
- 绕行的代价:去访问子句节点的“绕行”必须是无缝的,即路径访问完子句节点后,必须能完美地回到它出发的地方,继续走完变量小工具,并且不能因此跳过变量小工具里的任何一个节点。
- 证明的复杂性:这个“证明思路”只是一个高度概括的蓝图。实际的证明需要非常精细地设计菱形内部的节点数量和连接方式,以防止出现意料之外的“捷径”或“死路”,破坏归约的逻辑。
本段清晰地勾勒出了 3SAT 到 HAMPATH 归约的证明蓝图。其核心思想是使用巧妙设计的“小工具”将逻辑世界中的概念映射到图论世界中:用具有两种遍历方式的“菱形结构”来模拟变量的真/假赋值,用单个“节点”来代表子句。通过精心设计的连接,使得哈密顿路径“必须访问所有子句节点”的图论约束,等价于“赋值必须满足所有子句”的逻辑约束。这个思路将一个静态的逻辑满足问题,转化为了一个动态的路径寻找问题。
本段的目的是在读者陷入繁复的图构造细节之前,提供一个高层次的、直观的理解框架。它回答了最重要的问题:“这个复杂的图到底想干什么?”通过提前揭示菱形结构代表变量、单个节点代表子句以及“必须访问”等价于“必须满足”的核心思想,它让读者在后续阅读中能够有的放矢,理解每个构造细节背后的意图。
[直觉心-模型]
想象一个由多个“开关组”和多个“指示灯”组成的电路。
- 变量小工具:每个“开关组”(变量)是一个菱形的轨道,上面有一个小球。小球可以从左到右滚过,也可以从右到左滚过(二元选择),这代表了变量的赋值。
- 子句小工具:每个“指示灯”(子句)是一个需要被小球触碰一下才能点亮的装置。
- 连接:轨道上布满了精巧的触发器。例如,如果小球在“变量$x_i$”的轨道上“从左到右”滚动($x_i$=真),它就会在某个位置触发一个弹射杆,把另一个小球弹出去,正好能碰到“子句$c_j$”的指示灯。
- HAMPATH:一条哈密顿路径,就是小球的一条总运动轨迹,它必须穿过所有开关组,并且点亮所有指示灯。
- 等价性:是否存在这样一条轨迹,等价于是否存在一种设置所有开关的方式(赋值),使得所有指示灯都被点亮(所有子句都被满足)。
你是一个特技飞行员,要完成一项挑战。
- 场地:由 $l$ 个“菱形峡谷”(变量)和 $k$ 个“目标气球”(子句)组成。
- 规则:
- 你必须从起点 $s$ 起飞,飞越每一个菱形峡谷,最后降落在终点 $t$。
- 对于每个菱形峡谷,你只能选择两种固定航线中的一种飞过它(例如,“Z”字形或反“Z”字形)。
- 你必须在飞行过程中,撞破所有的目标气球。
- 连接:不同的航线会让你在峡谷的不同位置,有机会做出一个短暂的“侧飞”,去撞破特定的气球,然后马上飞回主航线。选择“Z”字航线($x_i$=真)可能会让你有机会撞破A气球,而选择反“Z”字航线($x_i$=假)则没有这个机会。
- HAMPATH 问题:是否存在一套航线选择方案(为每个峡谷选择一种飞法),使得你能够规划出一条连续的、不重复的飞行路径,飞越所有峡谷,并撞破所有气球?
- 这个问题的答案,直接对应了原 3SAT 公式是否存在一个满足赋值。
由于篇幅限制,后续的详细解释将在下一个回复中继续。
4行间公式索引
- $$
\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \cdots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right),
\begin{aligned}
& S \rightarrow R T \\
& R \rightarrow T R \mid \mathrm{a} \\
& T \rightarrow T R \mid \mathrm{b}
\end{aligned}
(x \vee y) \wedge(x \vee \bar{y}) \wedge(\bar{x} \vee y) \wedge(\bar{x} \vee \bar{y})
y_{1}, z_{1}, y_{2}, z_{2}, \ldots, y_{l}, z_{l} \quad \text { 和 } \quad g_{1}, h_{1}, g_{2}, h_{2}, \ldots, g_{k}, h_{k}
\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \cdots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right),
\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \cdots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right),
s, u_{1}, u_{2}, \ldots, u_{k}, t,
s^{\text {out }}, u_{1}^{\text {in }}, u_{1}^{\text {mid }}, u_{1}^{\text {out }}, u_{2}^{\text {in }}, u_{2}^{\text {mid }}, u_{2}^{\text {out }}, \ldots, t^{\text {in }} .
y_{1}, z_{1}, y_{2}, z_{2}, \ldots, y_{l}, z_{l} \quad \text { 和 } \quad g_{1}, h_{1}, g_{2}, h_{2}, \ldots, g_{k}, h_{k}
\left(x_{1} \vee \overline{x_{2}} \vee x_{3}\right) \wedge\left(x_{2} \vee x_{3} \vee \cdots\right) \wedge \cdots \wedge\left(\overline{x_{3}} \vee \cdots \vee \cdots\right) .
\phi=\left(a_{1} \vee b_{1} \vee c_{1}\right) \wedge\left(a_{2} \vee b_{2} \vee c_{2}\right) \wedge \cdots \wedge\left(a_{k} \vee b_{k} \vee c_{k}\right),
s, u_{1}, u_{2}, \ldots, u_{k}, t,
s^{\text {out }}, u_{1}^{\text {in }}, u_{1}^{\text {mid }}, u_{1}^{\text {out }}, u_{2}^{\text {in }}, u_{2}^{\text {mid }}, u_{2}^{\text {out }}, \ldots, t^{\text {in }} .
y_{1}, z_{1}, y_{2}, z_{2}, \ldots, y_{l}, z_{l} \quad \text { 和 } \quad g_{1}, h_{1}, g_{2}, h_{2}, \ldots, g_{k}, h_{k}
\left(x_{1} \vee \overline{x_{2}} \vee x_{3}\right) \wedge\left(x_{2} \vee x_{3} \vee \cdots\right) \wedge \cdots \wedge\left(\overline{x_{3}} \vee \cdots \vee \cdots\right) .
\begin{aligned}
& S \rightarrow R T \\
& R \rightarrow T R \mid \mathrm{a} \\
& T \rightarrow T R \mid \mathrm{b}
\end{aligned}
(x \vee y) \wedge(x \vee \bar{y}) \wedge(\bar{x} \vee y) \wedge(\bar{x} \vee \bar{y})