1CSEE 3827:计算机系统基础(2026 年春季学期)
1. 第 1 讲
授课教师:Dan Rubenstein 教授
电子邮箱:danr@cs.columbia.edu
1Ch1. 快速公告 Quick Announcements P1
- 请填写办公时间可用性,链接如下:
- http://uribe.cs.columbia.edu/sched/table.php(截止日期:1 月 24 日,**星期六)
- 作业 #0:可以先尝试!不要提交!解答将很快提供(可能在星期五)
2Ch2. 关于讲义的说明 A note on lecture slides P2
- 本学期共有 13 份讲义
- 它们按主题分组
- 显然,我们不可能总是在一堂课中完成一套讲义。有些可能需要 2、3 或 4 次课堂讲座
3Ch3. 议程 (M&K 章节 1, 3.11, 9.7) Agenda P3
- 从(非常高层次)数字视角看计算机
- 数字/二进制
- 与十进制、十六进制
- 术语:
- 位/字节/字 & 字长
- 最高有效位 (most significant) 位,最低有效位 (least significant) 位
- 负数格式:
- 符号/幅度
- 1 的补码
- 2 的补码
- 通过二进制的浮点 (P&H 3.5 - 跳过 MIPS 子节中的 FP)
- 加法
- 乘法
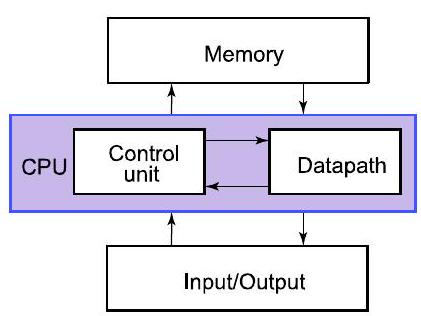
4Ch4. 课程概述:构建计算机(数字视角) Course Overview: Building a computer (digital perspective) P4
- CPU:计算机的“大脑”
- 控制单元对数据通路中的数据进行计算
- 内存:存储数据(供以后使用)
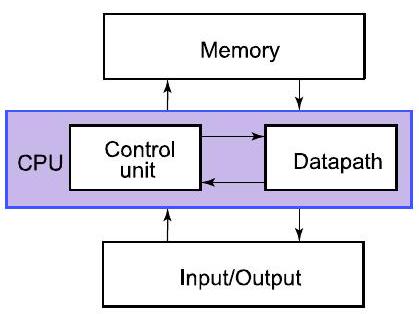
- 输入/输出:与外部的接口(磁盘、网络、显示器、键盘、鼠标等)
- 课程:从这种更简单的视图(下一幻灯片)开始
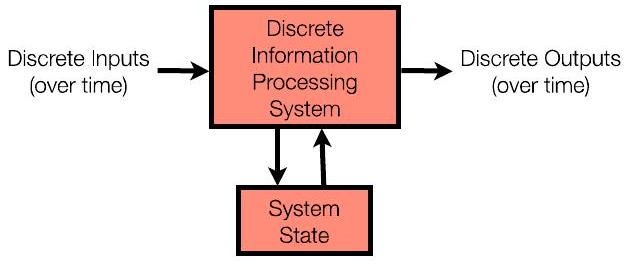
1Ch4.1. 课程概述:第一季度 Course Overview: 1st quarter P5
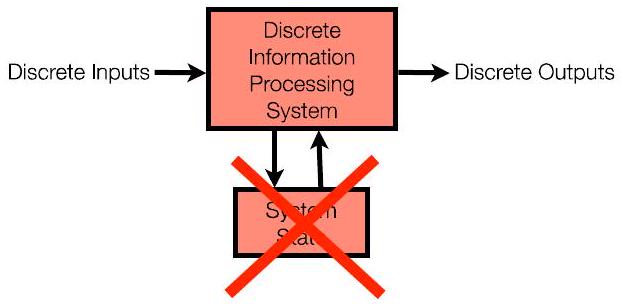
- 课程第一季度:非常简单的视图:“计算机”不维护状态
- 输入 → 计算 → 输出(仅仅是数学函数)
- 输入相同,输出相同
2Ch4.2. 课程概述:第二季度 Course Overview: 2nd quarter P6
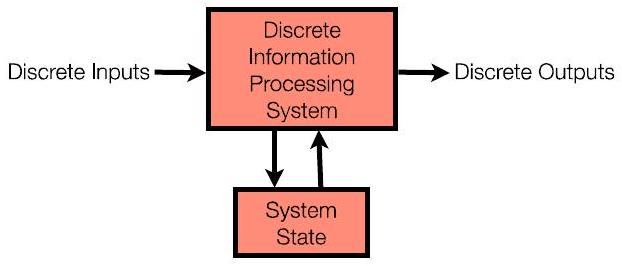
- 第二季度:“计算机”有内存(系统状态)
- 可以使用输入和内存中存储的内容来确定输出
3Ch4.3. 课程概述:后半部分 Course Overview: 2nd Half P7
计算机处理程序(存储在内存中)
- 程序由指令序列组成
- 程序修改也存储在内存中的数据
本学期稍后会详细介绍...
- 丹尼尔必须“打蜡,擦拭”才能掌握空手道..


- 你也必须“打蜡,擦拭”,然后我们才能进入更有趣的内容
到五月...

到五月...

到五月...


5Ch5. 不同进制的加法 Addition in different bases P8
1Ch5.1. 数制回顾:10 进制 (十进制) Number systems review: Base 10 (Decimal) P9
- 人类(通常)处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例:4537.8 基数 10 又名 $(4537.8)_{10}$
1. 数制回顾:10 进制 (十进制) Number systems review: Base 10 (Decimal) P10
- 人类(通常)处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例:4537.8 基数 10 又名 $(4537.8)_{10}$
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$
- 示例:$(1011.1)_{2}$
2Ch5.2. 数制:2 进制 (二进制) Number systems: Base 2 (Binary) P11
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$:我们将二进制数字称为位
- 示例:$(1011.1)_{2}$
将一列向左移会使数字的值乘以 2
3Ch5.3. 数制:16 进制 (十六进制) Number systems: Base 16 (Hexadecimal) P12
- (书呆子)人类与计算机交互的方式
- 16 个数字 = \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}
| 基数 16 (十六进制) 值 | 基数 2 (二进制) 值 | 基数 10 值 |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
1. 数制:16 进制 (十六进制) Number systems: Base 16 (Hexadecimal) P13
- (书呆子)人类与计算机交互的方式
- 16 个数字 = \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}
- 示例:$(26 \mathrm{BA})$ [十六进制的替代表示法:0x26BA]
- (书呆子)人类与计算机交互的方式
- 16 个数字 $=\{0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F\}$
- 示例:$(26 \mathrm{BA})$ [十六进制的替代表示法:0x26BA]
| 2 | 6 | B | A |
|---|---|---|---|
| $\times 16^{3}$ | $\times 16^{2}$ | $\times 16^{1}$ | $\times 16^{0}$ |
- 将一列向左移会使数字的值乘以 $(16)_{10}$
- 为何重要:比二进制更简洁,但相关(2 的幂)
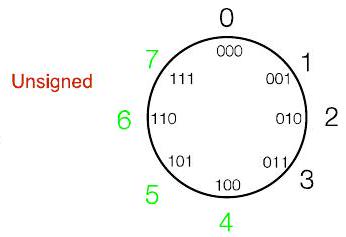
6Ch6. 数字范围 Number ranges P14
- 无法在有限内存中映射无限的数字:限制在某个有限的范围内:必须为计算机选择表示形式
- 我可以用...来表示多少个数字
...5 个十进制数字? $10^{5}$ 可能值 $(100,000)_{10}$
...8 个二进制数字? $2^{8}$ 可能值 $(256)_{10}$
...4 个十六进制数字? $16^{4}$ 可能值 $(65,536)_{10}$
7Ch7. 为什么基数 16 (十六进制) 有用 Why Base 16 (Hexadecimal) is useful P15
- 计算机以基数 2 (二进制) 工作
- 书写基数 2 数字令人困惑/费力
- 例如,$74,638_{(10)}=10110110001111000110_{(2)}$
- 基数 2 与基数 16 之间转换容易,原因如下:
- 取任何基数-2 值:
- 例如,1010111111010110101101
- 从右开始,将位分组成 4 个一组:
- 1010111111010110101101
- 从左边用 0 位填充,直到每组有 4 位:
- 001010111111010110101101
- 填充没有改变基数-2 值(接下一页)
1Ch7.1. 为什么基数 16 (十六进制) 有用(续) Why Base 16 (Hexadecimal) is useful (cont'd) P16
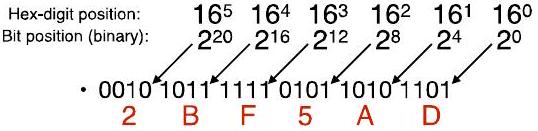
- 请注意,每组基数-4 位将表示 0 到 15 之间的值:用十六进制值表示
- 第 i 个数字(从右边开始)在十六进制中应该在的位置!
- 例如,看“1010” $=1 \cdot 2^{7}+0 \cdot 2^{6}+1 \cdot 2^{5}+0 \cdot 2^{4}$
- 26BA
- $=2000+600+\mathrm{BO}+\mathrm{A}$
- = 2(左移 3)+ 6(左移 2)+ B(左移 1)+ A [这些是十六进制数字]
- = 0010(左移 12)+ 0110(左移 8)+1011(左移 4)+ 1010 [这些是二进制数字]
- $=0010000000000000+011000000000+10110000+1010$
- = 0010011010111010
26 B A
2Ch7.2. 使用基数 16 Using Base 16 P17
- 对长序列的二进制\\表示很有用,例如,32-位量:
- 01101010111110100000110000111111
- 6 A F A 0 C 3 F
- 即,32-位量可以写作 6AFA0C3F,它是
- 01101010111110100000110000111111
8Ch8. 定义 & 术语 Defs & Terminology P18
1Ch8.1. 从数字视角看计算机 Computer from Digital Perspective P19
- (数字)信息:仅仅是二进制(0 和 1)的序列
- 真 = 1,假 = 0
- 数字:当计算机“看到”时转换为二进制形式
- 例如,19(10 进制)= 10011(2 进制)
. 即,$(16(1)+8(0)+4(0)+2(1)+1(1))$ 在二进制中
- 字符:分配一个特定的数值(ASCII 标准)
- 例如,' A ' $=65$ [10 进制] = 1000001 [2 进制],' a ' $= 97 = 1100001$
- 文本是字符序列:
- “你好” = 72, 105, 32, 116, 104, 101, 114, 101
[10 进制]
- $=1001000,1101001, \ldots$
[二进制]
- 位:一个单一的二进制数字(一个‘0’或一个‘1’)
- 字节:8 位的分组,例如,10110010。问:存在多少个不同的字节?
- 字:依赖于计算机架构的位分组
- 计算机架构可以一次处理的位数
- 例如,64-位字架构期望数据以 64-位分组\\传入(并返回输出)
- 架构使用的位数称为其字长
- 观察:计算机对一次能处理的输入量有限制
- 字长限制同时的位数,限制了它们能处理的数字大小(在单个计算周期内)
2Ch8.2. 术语 2:最高/最低位/有效位 Terminology 2: Highest / Lowest Order / significant bits P20
- 左边的位是最高位(又名最重要位)
- 右边的位是最低位(又名最不重要位)

- 较高的位在作为数字读取时代表“更大”的值
- 例如,上面是 $64+16+4+2+1=87$ 如果作为无符号二进制读取
- $k$-位值的常用参考表示法:$b_{k-1} b_{k-2} b_{k-3} \ldots b_{1} b_{0}$
- 或者替代地:$\mathrm{b}_{\mathrm{k}} \mathrm{b}_{\mathrm{k}-1} \mathrm{~b}_{\mathrm{k}-2} \ldots \mathrm{~b}_{2} \mathrm{~b}_{1}$
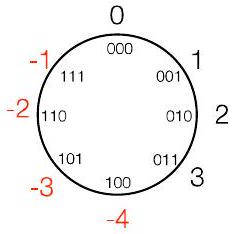
9Ch9. 模运算 Modular Arithmetic P21
1Ch9.1. 定义与基本示例 Definition & Basic Examples P22
- 定义:$X \bmod Y = \text{余数}(X / Y)$(即 0 到 $Y-1$ 之间的值)
- 例如,
- $10 \bmod 8$ 是多少?
- 定义:$\mathrm{X} \bmod \mathrm{Y} = \text{余数}(\mathrm{X} / \mathrm{Y})$(即 0 到 $\mathrm{Y}-1$ 之间的值)
- 例如,
- $10 \bmod 8$ 是多少?
- 是 2!
- 那么 $-10 \bmod 8$ 呢?
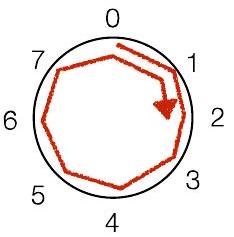
“风车”表示法:对正数顺时针移动,
对负数逆时针移动
这个风车是用于 $\bmod 8$
2Ch9.2. 负数模运算与风车表示法 Negative Modular Arithmetic & Pinwheel P23
- 定义:$X \bmod Y = \text{余数}(X / Y)$(即 0 到 $Y-1$ 之间的值)
- 例如,
- $10 \bmod 8$ 是多少?
- 是 2!
- 那么 $-10 \bmod 8$ 呢?
- 是 6!
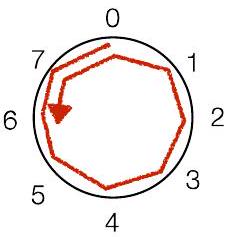
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$
3Ch9.3. 模运算性质与更多示例 Properties & More Examples P24
- 定义:$X \bmod Y = \text{余数}(X / Y)$(即 0 到 $Y-1$ 之间的值)
- 例如,
$22 \bmod 5=2$
$22=5 * 4+2)$
- $100 \bmod 9=1$,
- $-10 \bmod 3=-1 \bmod 3=2 \bmod 3\left(-4^{*} 3+2\right)$
- 观察:当 $X=Z+K Y$ 对于某个整数 $K$ 时, $X \bmod Y=Z \bmod Y$
- 例如,$1 \bmod 9=100 \bmod 9: X=1, Z=100, Y=9, K=-11$
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$
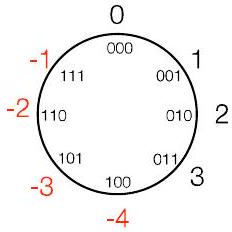
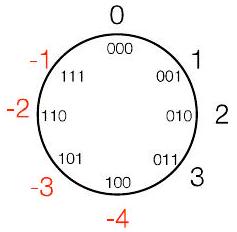
10Ch10. 带负数表示的模运算 Modular Arithmetic with negative representations P25
- 对于 $\mathrm{X} \bmod \mathrm{Y}$,我们通常将余数定义为 0 到 $\mathrm{Y}-1$ 之间的值
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 例如,$\bmod 8$ 将使用 -4 到 3 的余数值:
- 注意:
- 7 变为 -1(它们在 $\bmod 8$ 下是相同的)
- 6 变为 -2(在 $\bmod 8$ 下也相同)
- 一直到 4 变为 -4(在 $\bmod 8$ 下相同)
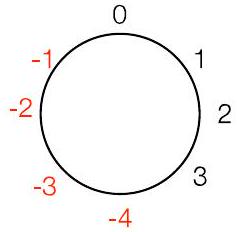
“风车”表示法:对正数顺时针移动,
对负数逆时针移动
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中, $10 \bmod 8$ 是多少?
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$ (范围 $\mathbf{- 4}$ 到 $\mathbf{3}$ )
对 2 的补码很重要(稍后讨论)
1Ch10.1. 替代余数定义(负范围) Alternative Remainder Definition (Negative Range) P26
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中, $10 \bmod 8$ 是多少?
- 仍然是 2!
- 那么 $-10 \bmod 8$ 呢?
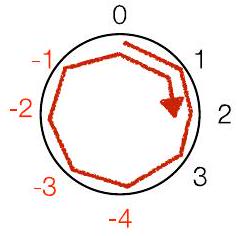
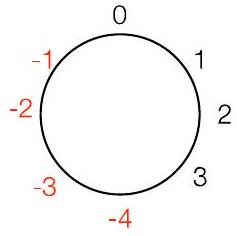
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$ (范围 -4 到 3 )
对 2 的补码很重要(稍后讨论)
2Ch10.2. 负范围模运算示例 Negative Range Modular Arithmetic Examples P27
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中, $10 \bmod 8$ 是多少?
- 仍然是 2!
- 那么 $-10 \bmod 8$ 呢?
- 现在是 -2!
- 那么 4 呢?
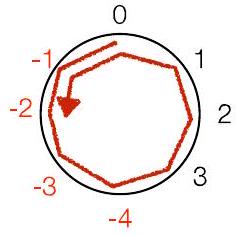
“风车”表示法:对正数顺时针移动,对负数逆时针移动
这个风车是用于 $\bmod 8$ (范围 -4 到 3 )
对 2 的补码很重要(稍后讨论)
3Ch10.3. 更多负范围示例与补码关联 More Examples & Complement Connection P28
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中, $10 \bmod 8$ 是多少?
- 仍然是 2!
- 那么 $-10 \bmod 8$ 呢?
- 现在是 -2!
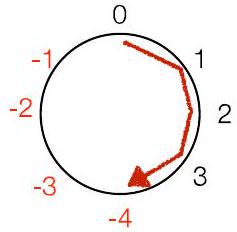
- 那么 4 呢?
- 现在是 -4(没有 4 的表示)
- 对于 $X \bmod Y$,我们通常将余数定义为 0 到 $Y-1$ 之间的值
- 有用的替代方法:将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 例如,$\bmod 8$ 将使用 -4 到 3 的余数值:
- $4 \bmod 8=-4 \quad\left(4=8^{*} 1+(-4)\right)$
- $7 \bmod 8=-1 \quad\left(7=8^{*} 1+(-1)\right.$
- $-5 \bmod 8=3\left(-5=8^{*}-1+3\right)$
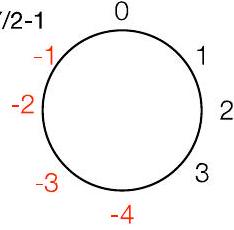
“风车”表示法:对正数顺时针移动,
对负数逆时针移动
- $30 \bmod 8=-2\left(30=8^{*} 4+(-2)\right)$
这个风车是用于 $\bmod 8$ (范围 $\mathbf{- 4}$ 到 $\mathbf{3}$ )
- $30 \bmod 10=0\left(30=10^{\star} 3+0\right)$
对 2 的补码很重要(稍后讨论)
11Ch11. 整数 # 格式(带字长限制) Integer # Formats (with word size restriction) P29
假设 字长 $=k$(例如, $k=3$)
- 有多少不同的位序列
具有 字长 $k$?
- $2^{k}$(例如,对于 $k=3, 2^{3}=8$)
假设 字长 $=k$(例如, $k=3$)
- 有多少不同的位序列
具有 字长 $k$?
- $2^{k}$(例如,对于 $k=3, 2^{3}=8$)
- 可以将每个数值分配给一个不同的位序列:最多可以有 $2^{k}$ 个不同的数值
| 字 | 值 |
|---|---|
| 000 | 15 |
| 001 | -7 |
| 010 | 42 |
| 011 | 42 |
| 100 | 7 |
| 101 | 9 |
| 110 | $\mathrm{e}^{7}$ |
| 111 | 0.004 |
- 二进制序列仅表示非负值(正数或 0)
- 例如,字长 $=4$(计算机“思考”时一次使用 4 位)
- $0000=0$
- $0011=3$
- $1011=11$
- $1111=15$
- 不能用字长为 4 的无符号二进制表示 16 或更大的数字!!
- 不能用无符号二进制表示负数
12Ch12. 二进制加法算法(无符号数) Binary Addition Algorithm (of unsigned numbers) P30
- 类似于常规(基数 10)加法算法,除了:
- $1+1=0$ 带进位 1,$1+1+1=1$ 带进位 1
- 例如,字长 $=5$(所有数值表示限制为 5 位)
- 加 11110 和 $10101 (30+21)$
1Ch12.1. 二进制加法算法(无符号数) Binary Addition Algorithm (of unsigned numbers) P31
- 类似于常规(基数 10)加法,除了:
- $1+1=0$ 带进位 1,$1+1+1=1$ 带进位 1
- 例如,字长 = 5,加 11110 和 $10101 (30+21)$
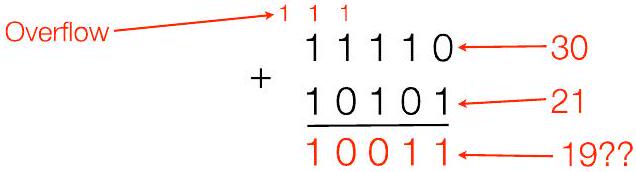
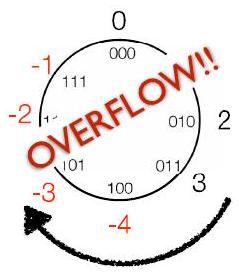
- 溢出:当结果不能\\适合字长\\约束时
- 例如,上面,“正确”的答案 $110011(=51)$ 需要 6 位:不能仅用 5 位在无符号表示中表示
2Ch12.2. 模运算和溢出 Modular Arithmetic and Overflow P32
- 假设我们没有限制字长,允许\\解决方案使用\\额外的位
- 解决方案将是 $110011=51$
- 字长限制阻止了我们包含\\位 = 32
- 结果 $(19)$ 差 32,但模 $32 = \bmod 2$ 字长是正确的
- 即,$19=51 \bmod 2^{5}$
- 换句话说,固定字长内的算术计算\\余数,即正确的结果 $\bmod 2$ 字长
- 给定:计算机有固定字长(例如,4)
- 问:当受到固定字长\\约束时,如何表示正数和负数?
- 注意:我们需要位序列到值的替代映射(与无符号二进制使用的不同),以便某些位序列\\表示负数
- 答:有几种方法可以做到,有些对人类更容易,有些对计算机...
负数 \# 表示:符号位 1 的补码 2 的补码
13Ch13. 负数:符号幅度表示 Negative Numbers: Signed Magnitude representation P33
- 最高位 ($b_{k-1}$) 表示符号:$0$=正,$1$=负
- 剩余位表示幅度
- 例如,$0011=3$
- 例如,$1011=-3$
- 例如,$1000=0000=0$
- 符号幅度中的正数与无符号表示中的位数相同
- 对人类来说\\易于解释,但对计算机来说\\进行加法/减法操作\\不是最简单的形式(我们很快会看到...)
- 再次,最高位 ($b_{k-1}$) 表示符号:$0$=正,$1$=负
- 非负数与无符号数(和带符号位)表示方式相同
- 要取反一个 \#,翻转所有位(不只是\\像带符号位一样的最高位)
- 请注意,翻转所有位也会翻转最高位(符号位)
- 例如,字长 $=4$
- $0010=2$
- $1101=-2$
- 非负数与无符号数(和带符号位)表示方式相同
- 要取反一个 \#,翻转所有位(不只是\\像带符号位一样的最高位)
- 例如,字长 $=4$
- $0010=2$
- $1101=-2$
- 问:假设字长是 8,当 11101011 以 1 的补码表示一个 \# 时,它的值是多少?
- 答:设 $X=11101011$(这是一个负数)
- 通过翻转所有位来取反 X:$-\mathrm{X}=00010100$
- $-X=20$,所以 $X=-20$
14Ch14. 负数:1 的补码表示 Negative Numbers: 1's Complement representation P34
- 非负数与无符号数(和带符号位)表示方式相同
- 要取反一个 \#,翻转所有位(不只是\\像带符号位一样的最高位)
- 例如,字长 $=4$
- $0010=2$
- $1101=-2$
- 问:假设字长是 8,当 11101011 以 1 的补码表示一个 \# 时,它的值是多少?
- 答:设 $X=11101011$(这是一个负数)
- 通过翻转所有位来取反 X:$-\mathrm{X}=00010100$
- $-\mathrm{X}=20$,所以 $X=-20$
- 注意:1 的补码中表示 0 的两种方式:全 0 和全 1
- 例如,对于字长 8,00000000 和 11111111 在 1 的补码中都是 0
15Ch15. 有符号幅度 & 1 的 补码的问题 Problems with signed mag & 1's C P35
- 假设我们想要一种包含负数的表示方法,其中我们可以应用\\二进制加法算法 (BAA) 执行加法:
- 1 的补码和有符号幅度并非总是\\有效
- 例如,4-位字示例:
使用二进制加法算法
1Ch15.1. 二进制加法算法在有符号幅度下的局限性 BAA Limitations in Signed Magnitude P36
- 假设我们想要一种包含负数的表示方法,其中我们可以应用\\二进制加法算法 (BAA) 执行加法:
- 1 的补码和有符号幅度并非总是\\有效
- 例如,4-位字示例:
2Ch15.2. 符号幅度加法错误示例 Signed Magnitude Addition Error Example P37
- 假设我们想要一种包含负数的表示方法,其中我们可以应用\\二进制加法算法 (BAA) 执行加法:
- 1 的补码和有符号幅度并非总是\\有效
- 例如,4-位字示例:
使用二进制加法算法 (BAA)
3Ch15.3. 1的补码加法的问题 Problems with 1's Complement Addition P38
- 假设我们想要一种包含负数的表示方法,其中我们可以应用\\二进制加法算法执行加法:
- 1 的补码和有符号幅度并非总是\\有效
- 例如,4 位示例:

使用二进制加法算法 (BAA)
16Ch16. 负数:2 的补码表示 Negative Numbers: 2's complement representation P39
- 非负数的形式与无符号数(和有符号位)相同
- 要取反一个 \#,翻转所有位,然后(使用二进制加法算法)加 1
- 忽略溢出(只在取反 0 时发生)
- 例如,字长 = 4
- $0010=2$,所以 $1101+0001=1110=-2$
- $0011=3$,所以 $1100+0001=1101=-3$
- $1101=-3$,所以 $0010+0001=0011=3$(也可以取反\\负数!)
- $0000=0$,所以 $1111+0001=0000=0$(0 在 2 的补码中是唯一的)
- 注意:取反两种方式都适用(从正到负或从负到正)
- 例外:一个 1 后跟所有 0,例如 1000
- 对于字长 $k$,值为 $-2^{k-1}$,例如 $k=4$,值为 -8
- 注意:在 2 的补码形式中,不能用 $k$ 位表示 $2^{k-1}$ 的正值
17Ch17. 数字编码 Number encodings P40
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
有符号幅度和 1 的补码浪费了一个位模式:2 个表示 0
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
|---|---|---|---|---|
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | -0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | -0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
1Ch17.1. 数字编码 Number encodings P41
| 2 的补码:最小的负数在表示中没有正数对应 翻转位并加 1 的过程不能\\成功地取反该数字 | ||||
|---|---|---|---|---|
| 无符号 | 符号 & 幅度 | 1 的补码 | 2 的补码 | |
| 000 | 0 | +0 | +0 | +0 |
| 001 | 1 | +1 | +1 | +1 |
| 010 | 2 | +2 | +2 | +2 |
| 011 | 3 | +3 | +3 | +3 |
| 100 | 4 | 0 | -3 | -4 |
| 101 | 5 | -1 | -2 | -3 |
| 110 | 6 | -2 | -1 | -2 |
| 111 | 7 | -3 | 0 | -1 |
| 8个值 | 7个值,2 个零 | 7个值,2 个零 | 8个值,1 个零 |
在 2 的补码中,二进制加法算法总是有效的(除非发生溢出)!
2Ch17.2. 使用二进制加法算法 Using binary addition algorithm P42
当发生溢出时,结果将差 $2^{\text{字长}}$
18Ch18. 2 的补码的特殊之处 What's special about 2's complement P43
- 与无符号数类似,当使用 BAA 进行加法时,结果在 $\bmod 2^{\mathrm{k}}$ 下是正确的( $k$ 是字长)
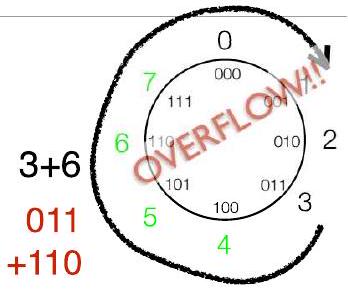
- 无论是无符号还是 2 的 补码形式,都将落在模 $2^{k}$ 正确的值上,但如果不在\\风车上则实际值不正确
- 思考模运算(例如,$\bmod 8$)
- 如果我们选择“无符号” $\bmod 8 = (0,1,2,3,4,5,6,7)$
- $3+6 \bmod 8=1$(即 $\text{余数}(9/8)$)
- $3-6 \bmod 8=5$
1Ch18.1. 模运算与溢出的关联 Modular Arithmetic & Overflow P44
- 思考模运算(例如,$\bmod 8$)
- 如果我们选择“无符号” $\bmod 8 = (0,1,2,3,4,5,6,7)$
- $3+6 \bmod 8=1$(即 $\text{余数}(9/8)$)
- $3-6 \bmod 8=5$(也溢出)
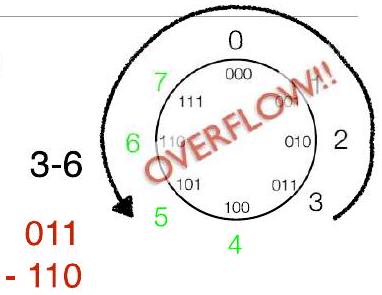
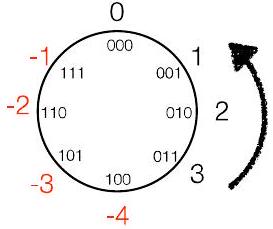
2Ch18.2. 补码环形表示(风车) Pinwheel Representation P45
- 但也可以选择“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$
- 6(即 110)将变为 -2
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
011
+110
3Ch18.3. C语言中的补码示例 C Example P46
- 但也可以选择“2 的 补码” $\bmod 8 = (-4,-3,-2,-1,0,1,2,3)$
011
- 6(即 110)将变为 -2
- $3+(-2) \bmod 8 = 3-2 \bmod 8 = 1$
- $3-(-2) \bmod 8 = 3+2 \bmod 8 = -3$
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
```
你(无意中)在哪里使用过 2 的补码?
```
int main() {
int x = 47;
int y=-50;
unsigned int z = 50;
printf("%d %d %uln", x, y, z);
}
- The computer represents
- x and y as signed 2 's complement
- $z$ as an unsigned
- C Demo: https://onlinegdb.com/49zlpDA9P8
- Note:
- $0 \times F$ (in Hex) is $15=1111$ in (unsigned) binary
- $0 \times 8$ (in Hex) is $8=1000$ in (unsigned) binary
- $2^{32}=4,294,967,296$ and $2^{31}=2,147,483,648$
```
4Ch18.4. “翻转位+1”的直观解释 Flip bits + 1 Intuitive Proof P47
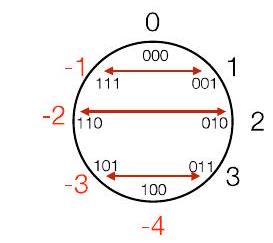
负值正好在对面
2 的补码

所有位翻转的值比\\正好在对面的值顺时针少 1 刻度
5Ch18.5. “翻转位+1”的正式证明 Flip bits + 1 Formal Proof P48
- 从任何 $k$-位字 $X$(除了 $100 \ldots 000$)开始,并以 2 的补码表示它
- 设 $Y = X$ 并翻转所有位
- $X+Y=11 \ldots 1111$(使用二进制加法算法)
- 因此,$X+Y=-1$ 在 2 的补码表示中(在“风车”上从 $00 \ldots 0000$ 逆时针旋转 1 位)
- 然后 $X+Y+1=00 \ldots 0000$(使用二进制加法算法)
- 所以 $Y+1=-X$(并且回想 $Y$ 是 $X$ 翻转所有位)
19Ch19. 表示 vs. 操作 Representation vs. Operation P49
1Ch19.1. k-位字 & 各种表示的范围 k-bit Words & Ranges P50
- 给定一个 $k$-位字,可以表示的数字范围是:
- 无符号:0 到 $2^{k}-1$(例如,$k=8$,0 到 255)
- 有符号幅度:$-2^{k-1}+1$ 到 $2^{k-1}-1$(例如,$k=8$,-127 到 127 [2 种表示 0 的方式])
- 1 的补码:与有符号幅度相同(但负数表示方式不同)
- 2 的补码:$-2^{k-1}$ 到 $2^{k-1}-1$(例如,$k=8$,-128 到 127 [1 种表示 0 的方式])
20Ch20. 获取表示 Getting representation P51
- 问:给定 8-位字长,10001011 的值是多少?
1Ch20.1. 获取表示 Getting representation P52
- 问:给定 8-位字长,10001011 的值是多少?
- 答:它是以无符号、有符号幅度、1 的补码还是 2 的补码表示?
- 无符号:$128+8+2+1=139$
- 有符号幅度:$-1 * (8+2+1)=-11$
- 1 的补码:01110100 的取反 $=-116$
- 2 的补码:01110101 的取反 $=-117$
- 注意:对于给定的一组位,当 \# 为负数时,2 的补码比 1 的补码小 1
21Ch21. 表示 vs. 操作 (总结) Representation vs. Operation (Summary) P53
- 我们已经讨论了表示整数的各种方法
- 无符号、有符号幅度、1 的补码、2 的补码
- 还有以位为单位的操作,名称相同
- 1 的补码操作:翻转所有位
- 2 的补码操作:翻转所有位并(BAA)加 1
- 操作可以在数字上执行,无论\\表示形式如何
- 例如,设 10111 是一个有符号幅度形式的数字(值为 -7)
- 在 10111 上执行 2 的补码(操作) $=01001$(在有符号幅度形式中值为 9)
- 观察:
- 当数字\\使用 2 的补码表示时,2 的补码操作会取反该数字
- 当数字\\使用 1 的补码表示时,1 的补码操作会取反该数字
22Ch22. 自动化减法 Automating Subtraction P54
- 问:为什么我们对 2 的补码感兴趣,尽管它\\看起来如此不直观?
- 答:自动化减法(即加符号相反的 \#)要容易得多
- 例如,字长 6,使用有符号幅度表示执行 14-21
1Ch22.1. 自动化减法示例 Automating Subtraction Example P55
- 问:为什么我们对 2 的补码感兴趣,尽管它\\看起来如此不直观?
- 答:自动化减法(即加符号相反的 \#)要容易得多
- 例如,字长 6,使用有符号幅度表示执行 14-21
- 有符号幅度有很多潜在的“繁重工作”
- 例如,翻转顶部 & 底部,“从较高位借位”等。
23Ch23. 2 的补码减法:利用 BAA 2's-complement subtraction: make use of BAA P56
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21
1Ch23.1. 补码减法示例 Complement Subtraction Example P57
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21
2 的补码减法:利用 BAA
- 只需取反减数(减法中的底数)并加
- 例如,字长 6,使用 2 的补码表示执行 14-21

$X=111001, -X=000111=7, X=-7$
24Ch24. 检测溢出 Detecting Overflow P58
- 问:如何判断计算结果是否溢出(即结果无法在字长约束内表示)
- 例如,4-位字,无符号:1110 + $1010 (14 + 10)$
- 结果是 24,无法在 4-位无符号中表示(只有 0-15 的值)
- 因此,溢出
- 无符号检测\\容易:
- 加法溢出
| 对于无符号 | 111 |
|---|---|
| 1110 | |
| $\underline{1010}$ | |
| 1000 |
- 减法:减数大于 \#(结果为负),则溢出
25Ch25. 2 的补码中的溢出检测很简单 Overflow detection in 2's-complement is easy P59
| -如果最终\\两个进位匹配,则没有溢出 - 如果\\不同,则溢出 - 例如,字长 $=4$ |
|||
|---|---|---|---|
| $5+1=6$ | $-5+-3=-8$ | $-2+7=5$ | $-2+-7=-9$ |
| 00 | 11 | 11 | 10 |
| + | + | + | + |
| $\underline{0001}$ | $\underline{1101}$ | 0111 | $\underline{1001}$ |
| 0110 | 1000 | 0101 | 0111 |
- 需要考虑 3 种情况:
- 两个 \# 都是正数(即最高位都是 0)
- 两个 \# 都是负数(即最高位都是 1)
- 一个是正数(最高位 0),另一个\\是负数(最高位 1)
26Ch26. 为什么 2 的补码溢出检测有效的证明 Proof of why 2's complement overflow detection works P60
- 情况 1:两者皆正:
- 写下两个最高位\\进位为 A 和 B
- 写下两个最高位\\进位为 $A$ 和 $B \quad A B$
- $A=$ 进位 B $+0+0 O X_{k-2} X_{k-3} \ldots X_{0}$
$O Y_{k-2} Y_{k-3} \ldots Y_{0}$
- A 始终为 0!
- 最高位 $= B+0+0$
- $B=1$:将结果解释为负数?
错误
- $B=0$:正常(刚刚执行了无符号 $K-1$ 位
加法)
1Ch26.1. 情况2:两者皆负 Case 2: both negative P61
- 情况 2:两者皆负:
- 写下两个最高位\\进位为 A 和 B
- $A=$ 进位 B $+1+1$
- A 始终为 1!
- 最高位 = B + 1 + 1
- $B=0$:最高位 = 0:正数 \#?错误
- $B=1$:负数:正常(并且 $\bmod 2^{\mathrm{k}}$ 正确)
2Ch26.2. 情况3:一正一负 Case 3: one positive, other negative P62
- 情况 3:一个正数,另一个负数:
- 写下两个最高位\\进位为 $A$ 和 $B+X_{k-2} X_{k-3} \ldots X_{0}$
- $A=$ 进位 $(B+1): B=0 \rightarrow A=0, B=1 \rightarrow A=1 \quad 1 Y_{k-2} Y_{k-3} \ldots Y_{0}$
- 所以永远不会溢出?
- 没错!
- 注意 $X+(-Y)$ 将小于 $X$ 且大于 $-Y$
- 如果 $X$ 可以用 2 的补码表示,并且 $-Y$ 可以\\用 2 的补码表示,那么任何 $Z$ 在 $-Y \leq Z \leq X$ 之间也都可以表示。
- 不能过分强调\\溢出意味着结果无法在字长内表示(不一定\\是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字\\映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
27Ch27. 关于溢出的最后思考 Final thoughts on Overflow P63
- 不能过分强调\\溢出意味着结果无法在字长内表示(不一定\\是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字\\映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
1Ch27.1. 溢出示例分析 Overflow Example Analysis P64
- 不能过分强调\\溢出意味着结果无法在字长内表示(不一定\\是结果太大)!
- 示例:假设我选择一个(奇怪的)方式将 2-位字\\映射到值,如下所示:
| 两位字 word |
关联值 Value |
|---|---|
| 00 | 1 |
| 01 | 3 |
| 10 | 6 |
| 11 | 2 |
$1+3$ 应该等于 4,但没有 2-位组合表示 4
因此,对于此表示,00+01 导致溢出
28Ch28. 浮点 Floating Point P65
29Ch29. 需要更大的范围?浮点表示 Need a bigger range? Floating Point Representation P66
- 改变编码。
- 浮点(用于以紧凑方式表示\\非常大的数字)
- 很像科学记数法:
尾数
注意:尾数总是采用 X.XX... 形式**
(又名小数部分)
(**小数点前一位)
1Ch29.1. 浮点表示示例 Floating Point Representation Example P67
- 改变编码。
- 浮点(用于以紧凑方式表示\\非常大的数字)
- 很像科学记数法:
尾数
注意:尾数总是采用 X.XX... 形式**
(又名小数部分)
(**小数点前一位)
- 但对于本课程,请考虑二进制:
注意:在正确形式中,对于二进制,尾数总是 1.XX... (小数点前一位,且该位\\总是 1)
唯一例外:$0=0.0 \times 2^{0}$
30Ch30. 浮点数的标准形式 Standard Forms for Floating Point Numbers P68
- 如何在 32-位字的限制内表示浮点数
- 字的位分成不同的\\字段
3130292827262524232221201918171615141312111009080706050403020100
符号 小数部分 (尾数)
- IEEE 754 标准规定
- 哪些位表示哪些\\字段(位 31 是符号位,位 30-23 是 8-位指数,位 22-00 是 23-位小数部分)
- 如何解释每个字段
31Ch31. IEEE 754 浮点描述 IEEE 754 Floating Point description P69
3130292827262524232221201918171615141312111009080706050403020100
| 符号 | 指数 | 小数部分 (尾数) |
|---|
- 符号:0 = 正数 \#,1 = 负数 \#(像有符号幅度)
- 指数:无符号,偏移量为 127
- 指数值 = 8 位无符号二进制表示 -127
- 小数部分:回想小数部分总是1.XXXXXX形式
- 省略‘1’,只表示“XXXXXXX”部分
3130292827262524232221201918171615141312111009080706050403020100
1000011011010000000000000000000
- $=(-1) \times 1.101_{(2)} \times 2^{13-127}=-1.625_{(10)} \times 2^{-114}=-7.82409 \times 10^{-35}$
- 因为表示总是 $\pm 1.\mathrm{XXXX} \times 2^{\text{yyy}}$ 形式,不能表示真正的 0
- 注意:所有位都设为 0 等于 $1.0 \times 2^{-127}$,一个非常非常小的数字,实际上是 0
32Ch32. 偏移量和浮点数比较 Bias and Comparing floats P70
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
1Ch32.1. 步骤2:检查指数 Step 2: Check exponents P71
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
2Ch32.2. 步骤3:检查小数部分 Step 3: Check fraction P72
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
- 步骤 3 (A 和 B 符号相同,指数相同): 检查小数部分
- (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B
- (A 为负且 A.小数部分 > B.小数部分) 或 (A 为正且 A.小数部分 < B.小数部分),返回 A < B
3Ch32.3. 步骤4:完全相等与有符号比较的相似性 Step 4: Full Equality & Signed Comparison P73
- 偏移量允许指数在 -127(非常小)和 128(非常大)之间
- 问:为什么使用偏移量而不是 2 的补码或无符号幅度?
- 答:比较两个浮点数 A & B 哪个更大很容易
- 步骤 1:检查符号。A 为正,B 为负,返回 A > B。A 为负,B 为正,返回 A < B
- 步骤 2 (A 和 B 符号相同): 检查指数
- (A 为正且 A.指数 > B.指数) 或 (A 为负且 A.指数 < B.指数),返回 A > B
- (A 为负且 A.指数 > B.指数) 或 (A 为正且 A.指数 < B.指数),返回 A < B
- 步骤 3 (A 和 B 符号相同,指数相同): 检查小数部分
- (A 为正且 A.小数部分 > B.小数部分) 或 (A 为负且 A.小数部分 < B.小数部分),返回 A > B
- (A 为负且 A.小数部分 > B.小数部分) 或 (A 为正且 A.小数部分 < B.小数部分),返回 A < B
- 步骤 4 (A 和 B 符号相同,指数相同,小数部分相同): 返回 A = B
- 观察:当位按照符号、指数、幅度排序时,过程\\与比较 2 个有符号幅度数相同
哪个 IEEE 754 FP \# 最大?

- 所有 + \#s,$B > A$(指数更大),$B > C$(指数相同,小数部分更大)
- 如果 \#s 简单地视为有符号幅度,会怎样?
- 结果相同:$B > C > A$
33Ch33. IEEE 754 64-位 (双精度) IEEE 754 64-bit (double) precision P74
- 在 32-位架构中描述为两个 32-位字
| 字 1 | 31/30292827262524232221201918171615141312111009080706050403020100 | |
|---|---|---|
| 指数 | 小数部分 (高位) |
3130292827262524232221201918171615141312111009080706050403020100
字 2 小数部分 (低位)
- 11-位指数,偏移量为 1023
- 小数部分长 52 位(字 1 中 20 个高位,字 2 中剩余 32 个低位)
34Ch34. 下溢 Underflow P75
- 当值的幅度\\太小而无法用表示形式描述时
- 例如,在 IEEE 754 浮点中:
- $X = 1 \times 2^{-100}$ 可以通过标准表示(指数字段中的位集是什么?)
- 但是,$X^2$ 等于 $2^{-200}$ 太小,无法表示
- 最小可能指数是 -127
- 因此,尝试计算 $X*X$ 会导致下溢
35Ch35. 讲座结束 Lecture End P76
- 课程其余部分的重要要点:
- 计算机的高层视角(数字化视角):字长这一概念
- 二进制数:负数表示法(二进制补码)
- 加法、减法、溢出、溢出检测
```
```