📜 原文
📖 逐步解释
∑ 公式拆解
💡 数值示例
⚠️ 易错点
📝 总结
🎯 存在目的
🧠 直觉心智模型
💭 直观想象
1CSEE 3827：计算机系统基础（2026 年春季学期）
1. 第 1 讲
授课教师：Dan Rubenstein 教授
电子邮箱：danr@cs.columbia.edu
11. 快速公告
- 请填写办公时间可用性，链接如下：
- http://uribe.cs.columbia.edu/sched/table.php（截止日期：1 月 24 日，星期六）
- 作业 #0：可以先尝试！不要提交！解答将很快提供（可能在星期五）
22. 关于讲义的说明
- 本学期共有 13 份讲义
- 它们按主题分组
- 显然，我们不可能总是在一堂课中完成一套讲义。有些可能需要 2、3 或 4 次课堂讲座
33. 议程 (M&K 章节 1, 3.11, 9.7)
- 从（非常高层次）数字视角看计算机
- 数字/二进制
- 与十进制、十六进制
- 术语：
- 位/字节/字 & 字长
- 最高有效位 (most significant) 位，最低有效位 (least significant) 位
- 负数格式：
- 符号/幅度
- 1 的补码
- 2 的补码
- 通过二进制的浮点 (P&H 3.5 - 跳过 MIPS 子节中的 FP)
- 加法
- 乘法
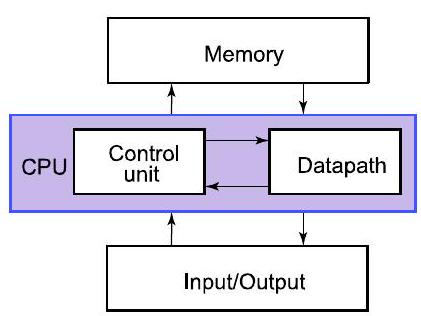
44. 课程概述：构建计算机（数字视角）
- CPU：计算机的“大脑”
- 控制单元对数据通路中的数据进行计算
- 内存：存储数据（供以后使用）
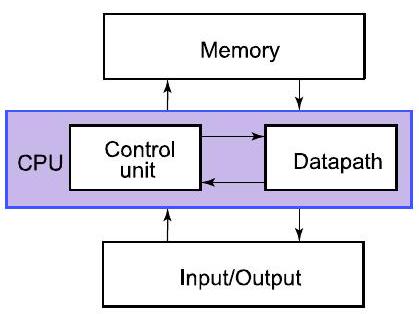
- 输入/输出：与外部的接口（磁盘、网络、显示器、键盘、鼠标等）
- 课程：从这种更简单的视图（下一幻灯片）开始
14.1 课程概述：第一季度
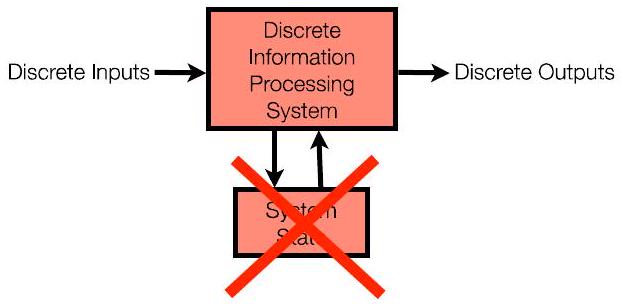
- 课程第一季度：非常简单的视图：“计算机”不维护状态
- 输入 → 计算 → 输出（仅仅是数学函数）
- 输入相同，输出相同
24.2 课程概述：第二季度
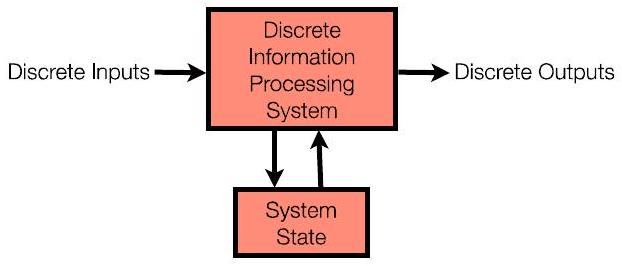
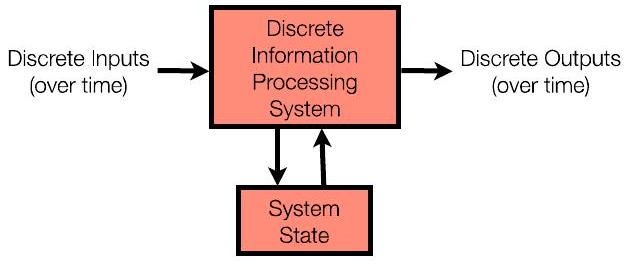
- 第二季度：“计算机”有内存（系统状态）
- 可以使用输入和内存中存储的内容来确定输出
34.3 课程概述：后半部分
计算机处理程序（存储在内存中）
- 程序由指令序列组成
- 程序修改也存储在内存中的数据
本学期稍后会详细介绍...
- 丹尼尔必须“打蜡，擦拭”才能掌握空手道..
- 你也必须“打蜡，擦拭”，然后我们才能进入更有趣的内容
到五月...
到五月...
到五月...
55. 不同进制的加法
15.1 数制回顾：10 进制 (十进制)
- 人类（通常）处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例：4537.8 基数 10 又名 $(4537.8)_{10}$
$$
\begin{array}{cccc}
4 & 5 & 3 & 7 \\
\times 10^{3} & \times 10^{2} \\
\hline 4000 & \times 10^{1} & \times 10^{0} & \times 10^{-1} \\
500 & \times 30 & +7 & +8=4537.8
\end{array}
$$
25.1.1 数制回顾：10 进制 (十进制)
- 人类（通常）处理数字的方式
- 10 个数字 $=\{0,1,2,3,4,5,6,7,8,9\}$
- 示例：4537.8 基数 10 又名 $(4537.8)_{10}$
$$
\begin{array}{cccc}
4 & 5 & 3 & 7 \\
\times 10^{3} & \times 10^{2} \\
\hline 4000 & \times 10^{1} & \times 10^{0} & \times 10^{-1} \\
500 & +30 & +7 & +8=4537.8
\end{array}
$$
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$
- 示例：$(1011.1)_{2}$
$$
\begin{gathered}
1 \\
\times 2^{3} \times 2^{2} \times \frac{1}{1} \times 2^{1} \times 2^{0} \times \frac{\times 2^{-1}}{8}+\frac{1}{2}=(11.5)_{10}
\end{gathered}
$$
35.2 数制：2 进制 (二进制)
- 计算机如何“思考”数字
- 2 个数字 $=\{0,1\}$：我们将二进制数字称为位
- 示例：$(1011.1)_{2}$
$$
\begin{gathered}
1 \\
\times 2^{3} \times 2^{2} \times \frac{1}{1} \times 2^{1} \times 2^{0} \times \frac{\times 2^{-1}}{8}+\frac{1}{2}=(11.5)_{10}
\end{gathered}
$$
将一列向左移会使数字的值乘以 2
45.3 数制：16 进制 (十六进制)
- （书呆子）人类与计算机交互的方式
- 16 个数字 = \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}
| 基数 16 (十六进制) 值 | 基数 2 (二进制) 值 | 基数 10 值 |
|---|---|---|
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
55.3.1 数制：16 进制 (十六进制)
- （书呆子）人类与计算机交互的方式
- 16 个数字 = \{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F\}
- 示例：$(26 \mathrm{BA})$ [十六进制的替代表示法：0x26BA]
$$
\begin{array}{cccc}
2 & 6 & \text { B } & \text { A } \\
\times 16^{3} & \times 16^{2} \\
\hline 8192 & \times 16^{1} & \times 16^{0} \\
& =(9914)_{10}
\end{array}
$$
- （书呆子）人类与计算机交互的方式
- 16 个数字 $=\{0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F\}$
- 示例：$(26 \mathrm{BA})$ [十六进制的替代表示法：0x26BA]
| 2 | 6 | B | A |
|---|---|---|---|
| $\times 16^{3}$ | $\times 16^{2}$ | $\times 16^{1}$ | $\times 16^{0}$ |
$$
8192+1536+176+10=(9914)_{10}
$$
- 将一列向左移会使数字的值乘以 $(16)_{10}$
- 为何重要：比二进制更简洁，但相关（2 的幂）
66. 数字范围
- 无法在有限内存中映射无限的数字：限制在某个有限的范围内：必须为计算机选择表示形式
- 我可以用...来表示多少个数字
...5 个十进制数字？ $10^{5}$ 可能值 $(100,000)_{10}$
...8 个二进制数字？ $2^{8}$ 可能值 $(256)_{10}$
...4 个十六进制数字？ $16^{4}$ 可能值 $(65,536)_{10}$
77. 为什么基数 16 (十六进制) 有用
- 计算机以基数 2 (二进制) 工作
- 书写基数 2 数字令人困惑/费力
- 例如，$74,638_{(10)}=10110110001111000110_{(2)}$
- 基数 2 与基数 16 之间转换容易，原因如下：
- 取任何基数-2 值：
- 例如，1010111111010110101101
- 从右开始，将位分组成 4 个一组：
- 1010111111010110101101
- 从左边用 0 位填充，直到每组有 4 位：
- 001010111111010110101101
- 填充没有改变基数-2 值（接下一页）
17.1 为什么基数 16 (十六进制) 有用（续）
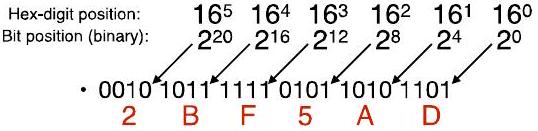
- 请注意，每组基数-4 位将表示 0 到 15 之间的值：用十六进制值表示
- 第 i 个数字（从右边开始）在十六进制中应该在的位置！
- 例如，看“1010” $=1 \cdot 2^{7}+0 \cdot 2^{6}+1 \cdot 2^{5}+0 \cdot 2^{4}$
$$
\begin{aligned}
& =2^{4} \cdot\left(1 \cdot 2^{3}+0 \cdot 2^{2}+1 \cdot 2^{1}+0 \cdot 2^{0}\right) \\
& =16^{1}{ }_{(10)} \cdot 10_{(10)} \\
& =10_{(\mathrm{Hex})} \cdot A_{(\mathrm{Hex})}(A \text { in 2nd column })
\end{aligned}
$$
- 26BA
- $=2000+600+\mathrm{BO}+\mathrm{A}$
- = 2（左移 3）+ 6（左移 2）+ B（左移 1）+ A [这些是十六进制数字]
- = 0010（左移 12）+ 0110（左移 8）+1011（左移 4）+ 1010 [这些是二进制数字]
- $=0010000000000000+011000000000+10110000+1010$
- = 0010011010111010
26 B A
27.2 使用基数 16
- 对长序列的二进制表示很有用，例如，32-位量：
- 01101010111110100000110000111111
- 6 A F A 0 C 3 F
- 即，32-位量可以写作 6AFA0C3F，它是
- 01101010111110100000110000111111
88. 定义 & 术语
18.1 从数字视角看计算机
- （数字）信息：仅仅是二进制（0 和 1）的序列
- 真 = 1，假 = 0
- 数字：当计算机“看到”时转换为二进制形式
- 例如，19（10 进制）= 10011（2 进制）
. 即，$(16(1)+8(0)+4(0)+2(1)+1(1))$ 在二进制中
- 字符：分配一个特定的数值（ASCII 标准）
- 例如，' A ' $=65$ [10 进制] = 1000001 [2 进制]，' a ' $= 97 = 1100001$
- 文本是字符序列：
- “你好” = 72, 105, 32, 116, 104, 101, 114, 101
[10 进制]
- $=1001000,1101001, \ldots$
[二进制]
- 位：一个单一的二进制数字（一个‘0’或一个‘1’）
- 字节：8 位的分组，例如，10110010。问：存在多少个不同的字节？
- 字：依赖于计算机架构的位分组
- 计算机架构可以一次处理的位数
- 例如，64-位字架构期望数据以 64-位分组传入（并返回输出）
- 架构使用的位数称为其字长
- 观察：计算机对一次能处理的输入量有限制
- 字长限制同时的位数，限制了它们能处理的数字大小（在单个计算周期内）
28.2 术语 2：最高/最低位/有效位
- 左边的位是最高位（又名最重要位）
- 右边的位是最低位（又名最不重要位）
- 较高的位在作为数字读取时代表“更大”的值
- 例如，上面是 $64+16+4+2+1=87$ 如果作为无符号二进制读取
- $k$-位值的常用参考表示法：$b_{k-1} b_{k-2} b_{k-3} \ldots b_{1} b_{0}$
- 或者替代地：$\mathrm{b}_{\mathrm{k}} \mathrm{b}_{\mathrm{k}-1} \mathrm{~b}_{\mathrm{k}-2} \ldots \mathrm{~b}_{2} \mathrm{~b}_{1}$
99. 模运算
19.1 定义与基本示例
- 定义：$X \bmod Y = \text{余数}(X / Y)$（即 0 到 $Y-1$ 之间的值）
- 例如，
- $10 \bmod 8$ 是多少？
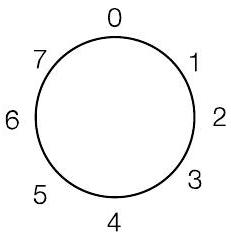
- 定义：$\mathrm{X} \bmod \mathrm{Y} = \text{余数}(\mathrm{X} / \mathrm{Y})$（即 0 到 $\mathrm{Y}-1$ 之间的值）
- 例如，
- $10 \bmod 8$ 是多少？
- 是 2！
- 那么 $-10 \bmod 8$ 呢？
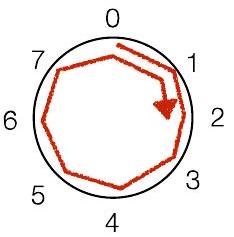
“风车”表示法：对正数顺时针移动，
对负数逆时针移动
这个风车是用于 $\bmod 8$
29.2 负数模运算与风车表示法
- 定义：$X \bmod Y = \text{余数}(X / Y)$（即 0 到 $Y-1$ 之间的值）
- 例如，
- $10 \bmod 8$ 是多少？
- 是 2！
- 那么 $-10 \bmod 8$ 呢？
- 是 6！
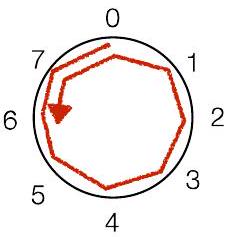
“风车”表示法：对正数顺时针移动，对负数逆时针移动
这个风车是用于 $\bmod 8$
39.3 模运算性质与更多示例
- 定义：$X \bmod Y = \text{余数}(X / Y)$（即 0 到 $Y-1$ 之间的值）
- 例如，
$22 \bmod 5=2$
$22=5 * 4+2)$
- $100 \bmod 9=1$,
- $-10 \bmod 3=-1 \bmod 3=2 \bmod 3\left(-4^{*} 3+2\right)$
- 观察：当 $X=Z+K Y$ 对于某个整数 $K$ 时， $X \bmod Y=Z \bmod Y$
- 例如，$1 \bmod 9=100 \bmod 9: X=1, Z=100, Y=9, K=-11$
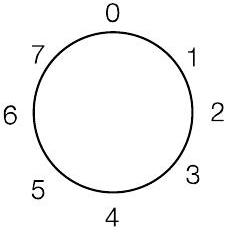
“风车”表示法：对正数顺时针移动，对负数逆时针移动
这个风车是用于 $\bmod 8$
1010. 带负数表示的模运算
- 对于 $\mathrm{X} \bmod \mathrm{Y}$，我们通常将余数定义为 0 到 $\mathrm{Y}-1$ 之间的值
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 例如，$\bmod 8$ 将使用 -4 到 3 的余数值：
- 注意：
- 7 变为 -1（它们在 $\bmod 8$ 下是相同的）
- 6 变为 -2（在 $\bmod 8$ 下也相同）
- 一直到 4 变为 -4（在 $\bmod 8$ 下相同）
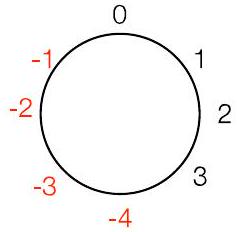
“风车”表示法：对正数顺时针移动，
对负数逆时针移动
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中， $10 \bmod 8$ 是多少？
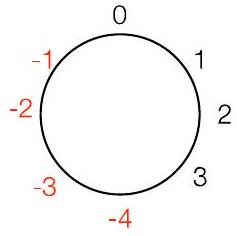
“风车”表示法：对正数顺时针移动，对负数逆时针移动
这个风车是用于 $\bmod 8$ （范围 $\mathbf{- 4}$ 到 $\mathbf{3}$ ）
对 2 的补码很重要（稍后讨论）
110.1 替代余数定义（负范围）
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中， $10 \bmod 8$ 是多少？
- 仍然是 2！
- 那么 $-10 \bmod 8$ 呢？
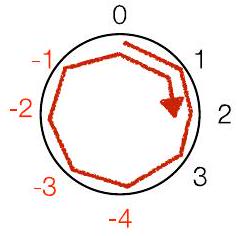
“风车”表示法：对正数顺时针移动，对负数逆时针移动
这个风车是用于 $\bmod 8$ （范围 -4 到 3 ）
对 2 的补码很重要（稍后讨论）
210.2 负范围模运算示例
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中， $10 \bmod 8$ 是多少？
- 仍然是 2！
- 那么 $-10 \bmod 8$ 呢？
- 现在是 -2！
- 那么 4 呢？
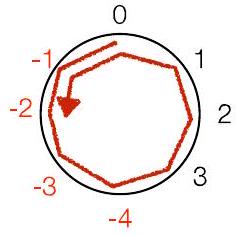
“风车”表示法：对正数顺时针移动，对负数逆时针移动
这个风车是用于 $\bmod 8$ （范围 -4 到 3 ）
对 2 的补码很重要（稍后讨论）
310.3 更多负范围示例与补码关联
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 在此替代表示法中， $10 \bmod 8$ 是多少？
- 仍然是 2！
- 那么 $-10 \bmod 8$ 呢？
- 现在是 -2！
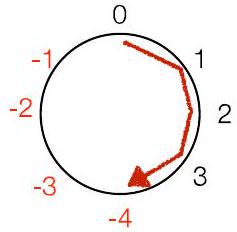
- 那么 4 呢？
- 现在是 -4（没有 4 的表示）
- 对于 $X \bmod Y$，我们通常将余数定义为 0 到 $Y-1$ 之间的值
- 有用的替代方法：将余数定义在 $-\mathrm{Y} / 2$ 和 $\mathrm{Y}/2-1$ 之间
- 例如，$\bmod 8$ 将使用 -4 到 3 的余数值：
- $4 \bmod 8=-4 \quad\left(4=8^{*} 1+(-4)\right)$
- $7 \bmod 8=-1 \quad\left(7=8^{*} 1+(-1)\right.$
- $-5 \bmod 8=3\left(-5=8^{*}-1+3\right)$
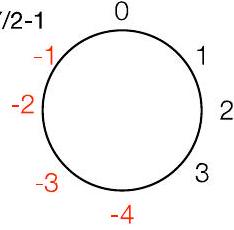
“风车”表示法：对正数顺时针移动，
对负数逆时针移动
- $30 \bmod 8=-2\left(30=8^{*} 4+(-2)\right)$
这个风车是用于 $\bmod 8$ （范围 $\mathbf{- 4}$ 到 $\mathbf{3}$ ）
- $30 \bmod 10=0\left(30=10^{\star} 3+0\right)$
对 2 的补码很重要（稍后讨论）
1111. 整数 # 格式（带字长限制）
假设 字长 $=k$（例如， $k=3$）
- 有多少不同的位序列
具有 字长 $k$？
- $2^{k}$（例如，对于 $k=3, 2^{3}=8$）
假设 字长 $=k$（例如， $k=3$）
- 有多少不同的位序列
具有 字长 $k$？
- $2^{k}$（例如，对于 $k=3, 2^{3}=8$）
- 可以将每个数值分配给一个不同的位序列：最多可以有 $2^{k}$ 个不同的数值
| 字 | 值 |
|---|---|
| 000 | 15 |
| 001 | -7 |
| 010 | 42 |
| 011 | 42 |
| 100 | 7 |
| 101 | 9 |
| 110 | $\mathrm{e}^{7}$ |
| 111 | 0.004 |
- 二进制序列仅表示非负值（正数或 0）
- 例如，字长 $=4$（计算机“思考”时一次使用 4 位）
- $0000=0$
- $0011=3$
- $1011=11$
- $1111=15$
- 不能用字长为 4 的无符号二进制表示 16 或更大的数字！！
- 不能用无符号二进制表示负数
1212. 二进制加法算法（无符号数）
- 类似于常规（基数 10）加法算法，除了：
- $1+1=0$ 带进位 1，$1+1+1=1$ 带进位 1
- 例如，字长 $=5$（所有数值表示限制为 5 位）
- 加 11110 和 $10101 (30+21)$
$$
\begin{array}{r}
11110 \\
+\quad 10101 \\
\hline
\end{array}
$$
112.1 二进制加法算法（无符号数）
- 类似于常规（基数 10）加法，除了：
- $1+1=0$ 带进位 1，$1+1+1=1$ 带进位 1
- 例如，字长 = 5，加 11110 和 $10101 (30+21)$
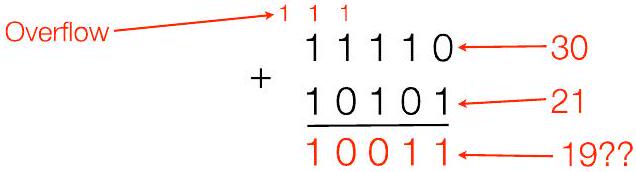
- 溢出：当结果不能适合字长约束时
- 例如，上面，“正确”的答案 $110011(=51)$ 需要 6 位：不能仅用 5 位在无符号表示中表示
212.2 模运算和溢出
$$
\begin{array}{r}
11110 \\
+\quad 30 \\
\hline 10101 \\
\hline 10011
\end{array}
$$
- 假设我们没有限制字长，允许解决方案使用额外的位
- 解决方案将是 $110011=51$
- 字长限制阻止了我们包含位 = 32
- 结果 $(19)$ 差 32，但模 $32 = \bmod 2$ 字长是正确的
- 即，$19=51 \bmod 2^{5}$
- 换句话说，固定字长内的算术计算余数，即正确的结果 $\bmod 2$ 字长
- 给定：计算机有固定字长（例如，4）
- 问：当受到固定字长约束时，如何表示正数和负数？
- 注意：我们需要位序列到值的替代映射（与无符号二进制使用的不同），以便某些位序列表示负数
- 答：有几种方法可以做到，有些对人类更容易，有些对计算机...
负数 \# 表示：符号位 1 的补码 2 的补码
1313. 负数：符号幅度表示
- 最高位 ($b_{k-1}$) 表示符号：$0$=正，$1$=负
- 剩余位表示幅度
- 例如，$0011=3$
- 例如，$1011=-3$
- 例如，$1000=0000=0$
- 符号幅度中的正数与无符号表示中的位数相同
- 对人类来说易于解释，但对计算机来说进行加法/减法操作不是最简单的形式（我们很快会看到...）
- 再次，最高位 ($b_{k-1}$) 表示符号：$0$=正，$1$=负
- 非负数与无符号数（和带符号位）表示方式相同
- 要取反一个 \#，翻转所有位（不只是像带符号位一样的最高位）
- 请注意，翻转所有位也会翻转最高位（符号位）
- 例如，字长 $=4$
- $0010=2$
- $1101=-2$
- 非负数与无符号数（和带符号位）表示方式相同
- 要取反一个 \#，翻转所有位（不只是像带符号位一样的最高位）
- 例如，字长 $=4$
- $0010=2$
- $1101=-2$
- 问：假设字长是 8，当 11101011 以 1 的补码表示一个 \# 时，它的值是多少？
- 答：设 $X=11101011$（这是一个负数）
- 通过翻转所有位来取反 X：$-\mathrm{X}=00010100$
- $-X=20$，所以 $X=-20$
1414. 负数：1 的补码表示
- 非负数与无符号数（和带符号位）表示方式相同
- 要取反一个 \#，翻转所有位（不只是像带符号位一样的最高位）
- 例如，字长 $=4$
- $0010=2$
- $1101=-2$
- 问：假设字长是 8，当 11101011 以 1 的补码表示一个 \# 时，它的值是多少？
- 答：设 $X=11101011$（这是一个负数）
- 通过翻转所有位来取反 X：$-\mathrm{X}=00010100$
- $-\mathrm{X}=20$，所以 $X=-20$
- 注意：1 的补码中表示 0 的两种方式：全 0 和全 1
- 例如，对于字长 8，00000000 和 11111111 在 1 的补码中都是 0
1515. 有符号幅度 & 1 的 补码的问题
- 假设我们想要一种包含负数的表示方法，其中我们可以应用二进制加法算法 (BAA) 执行加法：
- 1 的补码和有符号幅度并非总是有效
- 例如，4-位字示例：
$$
\begin{array}{r}
0101 \\
+1101 \\
\hline
\end{array}
$$
使用二进制加法算法
115.1 二进制加法算法在有符号幅度下的局限性
- 假设我们想要一种包含负数的表示方法，其中我们可以应用二进制加法算法 (BAA) 执行加法：
- 1 的补码和有符号幅度并非总是有效
- 例如，4-位字示例：
$$
\begin{array}{r}
111 \\
+0101 \\
1101 \\
\hline 0010
\end{array}
$$
215.2 符号幅度加法错误示例
- 假设我们想要一种包含负数的表示方法，其中我们可以应用二进制加法算法 (BAA) 执行加法：
- 1 的补码和有符号幅度并非总是有效
- 例如，4-位字示例：
$$
\begin{array}{cc}
1 \quad 1 \quad 1 & \text { Signed magnitude } \\
+0101 & +5 \\
+1101 & +-5 \\
\hline 0010 & \text { Result should be } 0, \text { not } 2
\end{array}
$$
使用二进制加法算法 (BAA)
315.3 1的补码加法的问题
- 假设我们想要一种包含负数的表示方法，其中我们可以应用二进制加法算法执行加法：
- 1 的补码和有符号幅度并非总是有效
- 例如，4 位示例：
使用二进制加法算法 (BAA)
1616. 负数：2 的补码表示
- 非负数的形式与无符号数（和有符号位）相同
- 要取反一个 \#，翻转所有位，然后（使用二进制加法算法）加 1
- 忽略溢出（只在取反 0 时发生）
- 例如，字长 = 4
- $0010=2$，所以 $1101+0001=1110=-2$
- $0011=3$，所以 $1100+0001=1101=-3$
- $1101=-3$，所以 $0010+0001=0011=3$（也可以取反负数！）
- $0000=0$，所以 $1111+0001=0000=0$（0 在 2 的补码中是唯一的）
- 注意：取反两种方式都适用（从正到负或从负到正）
- 例外：一个 1 后跟所有 0，例如 1000
- 对于字长 $k$，值为 $-2^{k-1}$，例如 $k=4$，值为 -8
- 注意：在 2 的补码形式中，不能用 $k$ 位表示 $2^{k-1}$ 的正值