
< br > [美]Michael A.Nielsen < br > Isaac L.Chuang < br > 孙晓明 尚云 李绿周 等译Quantum Computation and Quantum Information
MICHAEL A.NIELSEN and ISAAC L.CHUANG
Quantum Computation and Quantum Information
10th Anniversary Edition
量子计算 ${ }^{\text {a }}$量子信息 (10周年版)
Quantum Computation and Quantum Information: 10th Anniversary Edition
[美]Michael A.Nielsen Isaac L.Chuang@著孙晓明 尚云 李绿周 尹璋琦 魏朝晖 田国敬〇译
本书介绍了量子计算和量子信息领域的主要思想和技术。该领域的快速发展及其跨学科的性质使得新来者很难全面地了解其中重要的技术和研究成果。本书共分为 3 部分:第 1 部分概述了量子计算和量子信息领域的主要思想和研究成果,并介绍了计算机科学,数学和物理学领域的相关背景材料,这些材料是深人理解量子计算和量子信息所必需的;第 2 部分详细描述了量子计算;第 3 部分是关于量子信息的,内容涉及什么是量子信息,如何使用量子态表示和交流信息,以及如何描述和处理量子信息和经典信息的破坏。
本书适合对量子计算和量子信息感兴趣的学习者阅读。 This is a Simplified Chinese translation edition of the following title published by Cambridge University Press: Quantum Computation and Quantum Information:10th Anniversary Edition 9781107002173.This publication is in copyright.Subject to statutory exception and to the provisions of relevant collective licensing agreements,no reproduction of any part may take place without the written permission of Cambridge University Press.
This Simplified Chinese translation edition for the mainland of China(excluding Hong Kong,Macau SAR and Taiwan)is published by arrangement with the Press Syndicate of the University of Cambridge,Cambridge,United Kingdom.© Cambridge University Press and Publishing House of Electronics Industry Co.,Ltd 2021.This Simpli- fied Chinese translation edition is authorized for sale in the mainland of China(excluding Hong Kong,Macau SAR and Taiwan)only.Unauthorised export of this Simplified Chinese translation edition is a violation of the Copyright Act.No part of this publication may be reproduced or distributed by any means,or stored in a database or retrieval system,without the prior written permission of Cambridge University Press and Publishing House of Electronics Industry Co.,Ltd.
Copies of this book sold without a Cambridge University Press sticker on the cover are unauthorized and illegal.本书封面贴有 Cambridge University Press 防伪标签,无标签者不得销售。 本书中文简体版专有版权由 Cambridge University Press 授予电子工业出版社。专有出版权受法律保护。版权贸易合同登记号 图字:01-2020-4039
图书在版编目(CIP)数据
量子计算与量子信息: 10 周年版/(美)迈克尔 A.尼尔森(Michael A.Nielsen),(美)艾萨克 L.庄(Isaac L.Chuang)著;孙晓明等译.一北京:电子工业出版社, 2022.2 书名原文:Quantum Computation and Quantum Information:10th Anniversary Edition ISBN 978-7-121-42687-2 I.(1)量 $\cdots$ II.(1)迈 $\cdots$(2)艾 $\cdots$(3)子小 $\cdots$ III.(1)量子计算机(2)量子力学-信息技术 IV.(1)TP385(2)O413.1 中国版本图书馆 CIP 数据核字(2022)第 014538 号 责任编辑:官 杨 印 刷:北京天宇星印刷厂 装 订:北京天宇星印刷厂 出版发行:电子工业出版社 北京市海淀区万寿路 173 信箱 邮编: 100036 开 本: $787 \times 1092$ 1/16 印张: 38.75 字数:973千字 版 次:2022年2月第1版 印 次:2022年2月第1次印刷 定 价: 168.00 元 凡所购买电子工业出版社图书有缺损问题,请向购买书店调换。若书店售缺,请与本社发行部联系,联系及邮购电话:(010)88254888,88258888。
质量投诉请发邮件至 zlts@phei.com.cn,盗版侵权举报请发邮件至 dbqq@phei.com.cn。 本书咨询联系方式:(010)51260888-819 faq@phei.com.cn。
近年来量子计算发展非常迅速,国内外在实验方面不断有突破性的进展涌现。但是国内计算机领域从事量子计算研究的学者,特别是从事量子算法与理论研究的科研人员非常少。导致这一现象的原因是多方面的,其中之一是缺乏好的量子计算中文教材。
由 Michael A.Nielsen 和 Isaac L.Chuang 合著的《Quantum Computation and Quantum Informa- tion》毫无疑问是量子计算和量子信息领域最优秀的教材之一,全书近 700 页,覆盖了量子计算和量子信息的基础知识。自 2000 年由英国剑桥大学出版社出版以后,全球许多高校都使用该书作为量子计算课程的教材。据统计,该书是量子信息领域,乃至物理领域被引用次数最高的图书之一。2004 年清华大学赵千川老师等曾翻译过该书的早期版本,三年前电子工业出版社购买了该书最新版的版权,组织团队翻译该版图书。中国科学院计算所孙晓明研究员领衔,邀请了数学所尚云教授,中山大学李绿周教授,北理工尹璋琦教授,清华大学魏朝晖助理教授和中科院计算所田国敬副研究员等五位活跃在量子计算一线的研究人员,从2018年9月开始翻译,直到 2020年夏天完成翻译初稿,之后又花了一年的时间打磨校对,真可谓呕心沥血,为关心量子计算的读者提供了一本高质量的译作。
孙晓明研究员发邮件邀请我为此书写一篇序,我感到十分为难。因为我未在量子计算的第一线做过科研和教学工作,只是在自学量子计算这门课的一名"老学生"。上世纪 80 年代我留学回国,就已经开始阅读早期关于量子计算的文献,如 David Deutsch 1985 年发表的经典论文 "Quantum theory,the Church-Turing principle and the universal quantum computer"和有关可逆计算的论文,但一直是"观潮者"。由我为《量子计算和量子信息》这本经典教材写序言,就如同叫一个拉拉队员为精彩的球赛写述评,肯定写不到点子上。但另一方面,我也观察到,多数计算机界的学者是通过报刊或者自媒体上的报道来了解量子计算,有时会受非科班的媒体记者的误导。他们急于跨进量子计算的大门又苦于找不到人口。由我这个与他们经历类似的研究传统计算机的人做"导游",也许会打消一点他们心中的困惑,于是我硬着头皮答应写这篇序。
最近几年各种媒体频繁报道量子计算机的新闻,似乎实用化的量子计算机已呼之欲出。Google, IBM 等几家大公司正在努力研制 50 位量子比特以上的量子计算机,试图做到解决某个特殊问题的速度超过世界上任何传统计算机,领先宣布取得所谓"量子霸权(quantum supremacy )"。量子计算机的计算能力是否超过以图灵计算机为模型的传统计算机,这是一个重大的科学问题。严谨
的教科书与大众媒体文章的差别在于,对科技术语都有严格的定义,对科学与技术的判断都有明确的前提条件和结论成立的边界,《量子计算与量子信息》这本教材在这方面不愧为经典。
本书的许多章节都讨论了量子计算机的能力极限,书中明确指出,量子计算机也遵循丘奇-图灵论题,即任何算法过程都可以使用图灵机有效地模拟,也就是说,量子计算机与图灵机可计算的函数类相同。学过一点计算机科学理论的大学生都知道 P 和 NP 问题类,还有一类范围可能更大的问题类叫 PSPACE,是指所有可以通过合理内存(多项式空间)来解决的问题(可以任意时间)。所有能用量子计算机解决的问题叫 BQP 问题类,即可以用多项式大小的量子线路在有界错误概率内解决的判定问题。目前还不知道 BQP 与 P,NP,PSPACE 的准确关系,只知道量子计算机能有效地求解 P 类问题,但是 PSPACE 以外的问题不能有效求解。量子计算复杂性最著名的结果之一是 $B Q P \subseteq P S P A C E$ ,即 $B Q P$ 处在 $P$ 和 PSPACE 中间的某个位置,量子计算机能不能有效解决 NP 问题现在还没有结论。学习这些理论知识有什么用?进人量子计算这个新领域,首先要知道,什么类型的问题可以在量子计算机上有效地解决,与传统计算机上可有效解决的问题相比有什么优势。量子计算最激动人心的事就是对这些问题的答案知之甚少,为后进人者提供了巨大的研究空间。
研究量子计算机最初的出发点是试图突破图灵计算机的极限,主要是讨论可计算性这类理论问题,只有少数学者关心。1994 年量子计算掀开新的一页,进人蓬勃发展阶段。这是因为 Peter Shor 教授展示了与密码学有关的两个重要问题——寻找整数的素因子问题和离散对数问题在量子计算机上可以在多项式时间内解决(在经典计算中这两个问题具有指数级的时间复杂性),预示量子计算在计算效率上对于传统计算有本质性的提高。这一颠覆性的量子算法研究成果引发了量子计算机的研制热潮。从量子计算机的发展历史可以看出,量子算法的研究对量子计算机的发展起到了关键的推动作用。这也表明,量子计算技术的发展不仅仅是物理学界的事,计算机界也必须积极参与,争取做出更大的贡献。量子算法是本书的重点内容之一,不但阐述了量子算法的入门知识,详细介绍了 Shor 算法,Grover 算法等经典量子算法,而且尖锐地指出:量子算法研究"过去十年的进展喜忧参半。尽管独具匠心并付出了巨大的努力,但主要的算法见解仍停留在 10 年前。虽然已经取得了相当大的技术进步,但我们仍不了解究竞是什么使量子计算机变得强大,或者它们在哪些类别的问题上可以胜过传统计算机。"本书英文版出版后又过了十年,至今可提供指数级加速的量子算法仍然只有 Shor 算法,可见量子算法的研究任重道远。
为什么量子算法的突破如此艰难?媒体上普遍解释量子计算的加速是由于指数级的并行处理,这种理解没有触及量子计算的本质,因为量子计算完全不同于计算机界耳熟能详的"并行处理"。在一个量子比特的状态里,大自然隐藏了大量的"隐含信息",量子算法必须利用量子世界独特的干涉和纠缠特性。经典的并行性是用多个电路同时计算 $f(x)$ ,而量子并行性是利用不同量子状态的叠加,用单个 $f(x)$ 电路同时计算多个 $x$ 的函数值。"纠缠"不是简单的并行,而是我们在宏观世界从未接触过的新的"自然资源"。人类的直觉植根于经典世界,如果只是借助于我们已有的知识和直觉来设计算法,就跳不出经典思维的局限。为设计好的量子算法,需要部分地"关闭"经典直觉,巧妙地利用量子效应去达到期望的算法目的。Shor 教授曾出版过诗集,是一个具有诗人一样浪漫思维的标新立异的学者。他采用不同寻常的思路,将整数质因数分解重构为一个新问题:确定一个序列的重复周期。这本质上是一种傅里叶变换,可以通过在量子比特的
全集上使用全局运算找到这个序列。上世纪 80 年代人们就知道量子计算机可以实现傅里叶变换,但由于在量子计算机上,振幅不能通过测量直接访问,也没有有效的方法来制备傅里叶变换的初始态,因此寻找量子傅里叶变换的应用希望渺茫。Shor 教授找到了在不测量计算的情况下测量误差的巧妙办法,用量子傅里叶变换解决了整数因子分解和离散对数问题。量子计算将计算机科学推向物理学的最前沿,如果没有对量子纠缠的深刻理解,只在传统的并行处理上动脑筋,就难以找到比传统算法更有效的量子算法。
学习与研究量子算法的另一个难点是,传统算法已经研究了几十年,各个领域都有大量成熟的算法,如果我们设计的量子算法与已有的算法相比,没有明显的优势,就没有必要"杀鸡用牛刀"了。尽管量子计算机的物理实现有较大进展,但运行 Shor 算法破解 1024 位 RSA 的加密信息仍需要比当前量子计算机的规模扩大五个数量级,错误率则要再降低两个数量级,估计近十年内难以实现。在有噪声的中尺度量子计算机上能有效运行哪些有重大科学和经济价值的量子算法,是当前应优先考虑的研究方向。在量子搜索,量子组合优化,量子机器学习,量子游走,变分量子算法等方向都有可能做出实用化的量子算法。在未来的 10 到 15 年内,量子计算机可能是与传统计算机互补的协处理器或加速器,量子算法与传统算法的协同值得高度重视。
一谈到量子计算,人们首先想到的是超低温的精密物理设备,似乎与计算机科学技术无关,所以许多计算机学者在等待量子计算机商品化以后才开始考虑进入这个新的领域,其实了解量子计算并不需要对复杂的物理设备有很深人的理解。本书有一章从基本原理的角度介绍量子计算机的物理实现,包含 5 种物理模型系统:简谐振子,光子与非线性光学介质,腔量子电动力学器件,离子阱和分子核磁共振。目前在研制的量子计算机大致可分成三类:模拟量子计算机(如 D-Wave 公司做的量子退火器等),数字 NISQ 计算机(有噪声的中尺度量子计算机)和 QEC 量子计算机(完全误差校正量子计算机)。目前较普遍采用的物理实现方法是超导系统,离子阱和量子点技术,但现在就下注哪一种技术会胜出还为时过早,因而有必要学习多种技术实现原理。在这本教材中,"量子计算机"与"计算的量子电路模型"同义,因此花了较多篇幅详细讲解量子电路及其基本元件,通用门族,这是理解量子计算的基础。理解量子电路的前提是掌握线性代数知识,从课程学习的角度而言,学好量子计算这门课必须先打好线性代数的底子。物理学家描述量子力学用的 Dirac 记号不同于大学生们熟悉的线性代数表示方法,初学者可能一开始感到不习惯,但这不应当成为学习量子计算的拦路虎。
本书的内容不限于量子计算,而是采取从具体开始逐步抽象的原则,在介绍量子信息处理的一般原理之前先介绍较为具体的量子计算实例,在介绍量子信息理论更一般的结果之前,先给出特定的量子纠错码。由于量子比特和量子门本质上不能拒绝物理电路中出现的噪声,量子计算机最重要的设计参数之一是错误率。噪声对量子计算机的影响可以有效地数字化,即使存在有限量的噪声,量子计算的优势仍然存在。本书第 8 章介绍了量子噪声的属性,第 10 章介绍了量子纠错码。学过计算机课程的学生都知道奇偶纠错码和常用的纠错检验技术,但量子计算中出现错误的概率比传统计算机大得多,在量子计算机中运行量子误差校正算法来模拟无噪声或者完全校正噪声引起的错误,可能需要比传统计算机多几十倍的纠错码。纠错技术是量子计算能否实用的关键,学习量子计算要特别关注这一技术。本书的最后两章介绍了量子信息的更抽象的理论,包括量子通信和量子密码理论等,进一步扩大了读者的视野。
人类花费了很长时间才认识到使用量子力学系统可以进行信息处理,为量子计算和量子信息提供基本概念的领域很多,包括量子力学,计算机科学,线性代数,信息论和密码体系等,要透彻地理解量子计算,需要数学思维,物理思维和计算思维。本书在第一部分"基础概念"中,分别从物理学家,计算机科学家,信息论学家和密码学家的视角,多角度地概述了量子计算和量子信息学,对形成正确"量子信息观"颇有帮助。计算机专业的读者了解一点量子力学的基础知识,物理专业的读者了解一点计算机科学的基本理论,十分必要。建议初学量子计算和量子信息的读者认真学习第一部分,首先对一些最基本的概念形成正确的认识。
一本好的教科书必须有加深对教材理解的习题。本书的特点是这些习题直接出现在正文中,成为教材不可分割的一部分。除了习题,每章的末尾还提出一些深层次的问题,目的是介绍那些在正文中没有足够的空间来阐述的新的有趣的材料,包括一些仍未解决的科学技术问题。每章的结束语是"背景资料与延伸阅读",描述了本章主要思想的发展,给出了整章的引用和参考。这些内容的选取作者是费了心思的,将有关技术的来龙去脉交代得清清楚楚。这本书不仅是一本高质量的教科书,也是一本合适的自学参考书和该领域研究人员有价值的参考资料。由于量子计算和量子信息本质上的跨学科性,不管是上这门大学或研究生课程,还是自学,都要沉下心来,对跨进一个新的前沿领域的难度应有足够的思想准备。
这本书最新的一版出版于 2010 年,最近十来年量子计算和量子信息技术又有许多新的发展。量子计算机不仅需要新的硬件,更需要新的软件栈。近年来量子软件的研究已经提上日程,调试量子计算的专用软件工具和连接量子算法与底层量子芯片的操控平台也已开始研制。这方面的内容本书没有涉及,关心量子软件技术的学者需要阅读其他的相关文献资料。

中科院计算所研究员 2021年9月25日
近年来,以量子计算,量子通信和量子精密测量为代表的量子信息技术迅猛发展,引发了国内外广泛关注。2020年10月16日,中共中央政治局就量子科技研究和应用前景举行了第二十四次集体学习,习近平总书记发表重要讲话,强调量子科技发展具有重大科学意义和战略价值,是一项对传统技术体系产生冲击,进行重构的重大颠覆性技术创新,将引领新一轮科技革命和产业变革方向。总书记特别指出,要围绕量子科技前沿方向,加强相关学科和课程体系建设。我对总书记加强量子科技相关学科和课程体系建设的要求,有切身的体会。
国际上量子计算的实用化方案,目前有七八种,需要进一步深人研究和探索。只有加强后备人才培养,才能满足量子计算发展走向实用化,工程化的需要。而要培养后备人才,则离不开优秀的教材。
由 Nielsen 和 Chuang 合著的《Quantum Computation and Quantum Information》,是量子信息与量子计算领域的经典教材。全书近七百页,涵盖了量子信息与量子计算的基本知识,且自成体系,方便读者自学。自从 2000 年出版以来,本书已经被全世界许多大学选为量子信息和量子计算课程的标准教科书。多年的教学实践表明,这是一本优秀的教材。由于撰写时精心组织和设计, 2010 年本书再版时,只是更正了部分错漏,全书的内容并没有做大的修改。作为一个正在迅速发展的新领域的教科书,这是极为难得的。
3 年前电子工业出版社购买了本书最新版的版权,并委托中科院计算所孙晓明研究员领衔组织团队翻译本书,团队成员包括中科院数学所尚云教授,中山大学李绿周教授,北京理工大学尹璋琦教授,清华大学魏朝晖助理教授和中科院计算所田国敬副研究员等人,他们都是国内活跃在量子信息与量子计算领域的青年研究人员。经过两年的翻译校对打磨,他们高质量地完成了这本译作。
译作出版前,孙晓明研究员请我撰写一篇序言。读完译稿后,我觉得这本教材的出版适逢其时,很好地回应了总书记对量子科技发展的要求,并将对支撑我国量子信息相关学科课程体系建设起到重要作用,因此我欣然应允作序。
本书包含基本概念,量子计算以及量子信息三部分。量子信息与量子计算是量子物理的交叉学科,不论是物理学背景还是计算机背景的科研人员,在进人这个领域开展研究时,都会遇到不少基本概念上的理解难题。为了解决此难题,在本书第一部分"基本概念"中,先用一章描绘了
量子信息与量子计算的整体图像,然后简明扼要介绍了量子物理,计算机科学方面的基本概念,帮助不同背景的研究者扫清概念上的障碍,树立基本图像,为后继的学习和研究打下基础。在第二部分,本书介绍了量子计算的量子电路模型,以及量子傅里叶算法,量子搜索算法及其应用,最后还介绍了几种典型的量子计算机的物理实现路径。第三部分涉及量子计算中的量子噪声和量子纠畆的度量,量子信息的基本理论,以及量子纠错和容错量子计算。在本书 2000 年出版乃至 2010 年再版时,容错量子计算都似乎可望而不可即。随着 2019 年量子计算相对经典计算机的优越性得到实验证明,量子纠错和容错量子计算已成为量子计算研究领域正在集中攻关的关键课题。对这些基本理论的学习,能让读者迅速进人量子计算研究的前沿,为量子计算的实用化贡献力量。
需要指出,本书已经出版二十余年,最近这些年量子计算又有一些重要的进展,本书并末涉及。比如可自动纠错的拓扑量子计算,本书就没有介绍。量子计算重要的实现路径,超导量子计算的基本物理原理,本书也只是一笔带过。建议读者可参阅相关文献和综述来学习。

2021年12月20日
1981年理论物理学家理查德•费曼提出了"大自然不是经典的,所以如果你想模拟它的话,那你最好用量子力学"(原文:Nature isn't classical,and if you want to make a simulation of nature, you'd better make it quantum mechanical.)的观点,这催生了量子计算领域的兴起与发展。在过去的四十年里,学者们已经在理论上成功基于量子力学原理设计算法来求解某些经典难于计算的问题,提出量子密码协议来进行信息的安全高效传输;同时在实验上也已经可以实现数十个量子比特的精准操控,以及卫星与地面之间的量子密钥分发。这些或许是费曼等量子计算先驱们始料未及的——"这盛世,如你所愿"!
但"革命尚未成功,前路依旧崎岖",目前高效求解困难问题的量子算法还太少,现有的量子算法还不能很好地在当前量子硬件设备上运行,而实验方面量子比特数还很少且噪声影响严重。解决这些问题最需要的是集中不同领域的科研人员协同攻关,但从长远看量子计算与量子信息领域专业人才的培养也至关重要。据 2018 年《纽约时报》的报道,在全球范围能够从事量子计算创新性研究的人才不足千人。而人才培养离不开一本好的教材,这是本书所有译者的动力来源,也是本书所有译者的共同心愿。
《Quantum Computation and Quantum Information》一书是国内外几乎所有量子计算与量子信息科研人员的必读书籍,尤其对于本科专业是数学,计算机或其他学科学习量子计算的学生和老师更加友好,只需要线性代数的基础即可开始学习。而对于刚刚开始学习量子计算的同学来说,中文版显然比英文原版更容易接受和人门。于是在2018年冬天中科院计算所孙晓明研究员便联合了来自中科院,中山大学,北京理工大学,清华大学等高校或科研院所的其他 5 位从事量子计算与量子信息研究的同仁,开始了本书的翻译工作。我们都深知,翻译书是一件费力不讨好的工作,但大家还是本着推动和普及我国量子计算发展的初心承担了这一任务,历时近三年终于完工了。
孙晓明研究员的主要研究领域为算法与计算复杂性,量子计算,组合数学等。作为发起人负责整体翻译工作的推进与协调,并负责完成了第 1 章"简介与概述"和第 3 章"计算机科学简介",以及附录的翻译。中科院数学所尚云研究员,主要从事量子计算与量子逻辑,量子点元胞电路的自动设计,以及量子程序语言等方向的研究,负责完成了本书第 2 章"量子力学基础"和第4章"量子电路"的翻译。中山大学李绿周教授的主要研究兴趣为量子计算模型,算法与复杂
性,量子机器学习等,负责完成了本书第 5 章"量子傅里叶变换及其应用"和第 6 章"量子搜索算法"的翻译。北京理工大学尹璋琦教授的科研方向为光力学与微腔光子学,量子信息处理的物理实现,量子物理的基本问题等,负责完成了本书第 7 章"量子计算机:物理实现"和第 8 章 "量子噪声与量子操作"的翻译。清华大学魏朝晖副教授长期从事量子信息与量子计算,计算复杂度,量子机器学习,量子程序方面的研究,负责完成了本书第 9 章"量子信息的距离度量"和第 10 章"量子纠错"的翻译。中科院计算所田国敬副研究员的主要研究方向是量子算法设计,量子电路优化,量子非局域性等,负责完成了本书第 11 章"熵与信息"和第 12 章"量子信息论"的翻译。
因为是多人合作翻译,一件非常重要的事情是术语和表达的统一,所以在翻译工作开始之前我们就先确定专有名词,统一语言习惯。虽然所有译者都是量子计算与量子信息领域的一线科研人员,但是对于诸多术语的中文翻译仍不尽相同,譬如"eigenstate",数学或计算机学科的老师会翻译为"特征态",而物理学的同事会翻译为"本征态"。这当然没有本质上的区别,也不会影响读者对内容的理解,但是作为一本书我们必须要保持一致性。另外一点是语言习惯的统一,不同人的写作表达方式不同,这也是我们前期必须解决的问题。所以在2019年1月份,我们先统一专有名词的写法,再分别对几个比较难的段落进行了试译,讨论确定翻译的句式并在以后的翻译过程中逐步完善。正式的集中翻译是从2019年寒假阶段开展的,由于各位译者都承担着多项重要的科研和教学的任务,翻译工作虽几易寒暑,但时间仍不免有些捉襟见肘。在我们完成翻译的初稿后,又烦劳出版社的编辑和工作人员协助进行排版,画图等,之后我们便开始一遍又一遍地校对和勘误。即使到了在撰写这一序言时,我们仍在努力进行检查,尽量避免错误的出现。尽管我们已经校对多遍,但是由于能力所限,翻译版中仍然不免有一些错误或者翻译不够准确的地方,敬请读者批评指正。
最后,衷心感谢本书的两位原作者 Michael Nielsen 和 Isaac Chuang 教授,感谢李国杰院士与薛其坤院士为本书作序,感谢电子工业出版社的编辑团队,感谢中科院计算所算法理论与量子计算实验室的各位同事和同学。
全体译者 2021年12月于计算所
孙晓明,中国科学院计算技术研究所研究员。主要研究领域为算法与计算复杂性,量子计算等。曾获首批国家自然科学基金优秀青年基金资助,入选中组部首批万人计划青年拔尖人才,获得中国密码学会优秀青年奖,密码创新二等奖。目前担任中国计算机学会理论计算机科学专委会主任,全国量子计算与测量标准化技术委员会委员,还担任《软件学报》《计算机研究与发展》《中国科学:信息科学》《Information and Computation》《JCST》《FCS》等杂志编委或青年编委。
尚云,中国科学院数学与系统科学研究院研究员,CCF 量子计算专委会常务委员,CCF 杰出会员。主要研究兴趣是量子计算基础理论,量子游走,量子机器学习,量子点元胞自动机电路的自动设计与优化等,发表论文 50 多篇。获 CCF 科学技术奖自然科学二等奖( $1 / 5,2021$ ),英国皇家物理学会 IOP 高引用作者奖(2021),王宽诚优秀女科学家专项奖(2012)等。
李绿周,中山大学计算机学院量子计算与计算机理论研究所教授,中国计算机学会(CCF)量子计算专业组副主任,CCF 理论计算机科学专委会常务委员,CCF 杰出会员。2009年6月毕业于中山大学计算机科学系,获博士学位。长期从事量子计算方面的研究,目前研究兴趣具体包括量子算法与复杂性,量子机器学习,量子线路优化等,在国内外知名学术期刊发表论文 60 余篇,出版学术专著 1 部,"量子计算模型与算法的研究"获得广东省杰出青年基金项目资助。
尹璋琦,北京理工大学物理学院量子技术研究中心教授,CCF 量子计算专委委员。1999年到2009年,在西安交通大学先后获物理学学士,硕士和博士学位。2007年至2009年在美国密歇根大学公派联合培养。2010 年到 2019 年先后在中科院武汉物理与数学研究所,中国科学技术大学和清华大学工作。2019年调人北京理工大学,研究兴趣为量子信息与量子精密测量,宏观系统量子效应等,发表论文 70 余篇。人选教育部青年长江学者(2020),任《中国科学:物理学力学天文学(英文版)》青年编委。
魏朝晖,清华大学丘成桐数学科学中心助理教授,CCF 量子计算专委委员。2009 年于清华大学计算机系获得博士学位后前往新加坡量子研究中心任 Research Fellow,于 2018 年返回清华任教。长期从事量子计算方面的理论研究,主要研究兴趣包括量子计算复杂性,量子信息论,量子算法,量子纠错,量子人工智能等,学术成果发表在包括《IEEE Transactions on Information Theory》《Mathematical Programming》《Physical Review Letters》等在内的知名学术期刊上。2020
年获得北京市优秀本科毕业论文指导教师奖。 田国敬,中科院计算所副研究员,CCF 量子计算专业组委员,CCF 理论计算机专委委员。主要研究方向是量子算法设计,量子电路优化,量子非局域性,量子模拟等,目前共发表论文 17篇,博士毕业论文被评为中国通信学会优秀博士学位论文(全国共 10 篇)。作为项目负责人,先后获得了北京市自然科学基金和国家自然科学基金青年项目的资助,并于 2019 年人选了博士后创新人才支持计划(全国计算机专业共 16 人)。
量子力学的奇妙之处在于,它是我们的科学理论中最成功的理论,同时也是最神秘的理论。它的发展是量身定制的,始于1900年到1920年的非凡时代,并在1920年代后期逐渐成熟并发展成现在的形态。在 1920 年后的几十年中,物理学家在运用量子力学了解自然界的基本粒子和自然力方面取得了巨大的成功,最终发展出了粒子物理学的标准模型。在同一时期,物理学家在运用量子力学来理解我们的世界中从聚合物到半导体,从超流体到超导体的各种现象方面也取得了巨大的成功。但是,尽管这些发展深刻地增进了我们对自然界的理解,但它们对增进我们对量子力学的理解作用有限。
这种情况在 20 世纪七八十年代开始发生改变,当时一些先驱者受到启发,开始考虑计算机科学和信息论的一些基本问题是否可以应用于量子系统的研究。相比将量子系统纯粹视为自然界中可以解释的现象,他们将量子系统视为可以设计的系统。这似乎是观念上的微小变化,但意义是深远的。量子世界不再仅仅是呈现出来的,而是可以创造出来的。其结果是一幅全新的景象,不仅激发了人们对量子力学基本原理的兴趣,还有融合了物理学,计算机科学和信息论的许多新问题。这些问题包括:构建量子态所需的空间和时间的基本物理限制是什么?实现给定的动态操作需要多少时间和空间?是什么使量子系统难以通过传统的经典方法来理解和模拟?
在 20 世纪 90 年代后期写作这本书时,我们很幸运,这些还有其他一些基本问题才刚刚浮现出来。十年后再来回顾,很明显这些问题为物理学和计算机科学的基础研究提供了持续的动力。量子信息科学已广为接受。尽管该领域的理论基础与我们十年前所讨论的相似,但在许多领域的详细知识却取得了长足的进步。这本书最初是对该领域的全面概述,为的是将读者引人研究的前沿。如今,这本书为理解这一领域提供了基础,它既适合那些渴望对量子信息科学有广阔视野的人,也适合想进一步研究最新文献的入门者。当然,这个领域仍然存在着许多基本挑战,而应对这些挑战有望激发物理学,计算机科学和信息论的许多不同部分之间令人兴奋且出乎意料的联系。我们对未来的几十年充满期待!
自本书第 1 版上市以来的十年中,量子信息科学发生了巨大的变化,在本文中,我们甚至无法总结其中的一小部分。这里将提一些特别引人注目的发展,也许会激发你的兴趣。
也许最令人印象深刻的进展是在实验实现领域。尽管我们距离构建大型量子计算机还很遥远,但截至本文撰写时已经取得了很大的进步。超导电路已被用于实现简单的两比特量子算法,而三量子比特系统也几乎可以实现。使用基于核自旋和单光子的量子比特已经分别用来进行量子误差校正和量子模拟的简单形式的原理验证。但是,最令人印象深刻的进步是离子阱系统所取得的成就,该系统已被用于实现许多两量子比特和三量子比特算法及算法构造模块,包括量子搜索算法和量子傅里叶变换。囚禁离子也已被用来展示基本的量子通信原语,包括量子纠错和量子隐形传态。
第二个方面的进展是了解量子计算需要哪些物理资源。也许最有趣的突破是发现量子计算可以仅通过测量来完成。多年以来,传统观念认为,保持相干叠加的酉动力学是量子计算机功能的重要组成部分。认识到量子计算可以完全不需要任何酉动力学来完成,这震撼了传统的认识。取而代之的是,在某些新的量子计算模型中,可以单独使用量子测量进行任意量子计算。在该模型中,唯一相互耦合的资源是量子存储器,即存储量子信息的能力。这些模型的一个特别有趣的例子是单向量子计算机或簇状态计算机。要在簇状态模型中进行量子计算,只需要实验者拥有一个固定的通用状态即簇量子态即可。有了簇量子态,可以简单地通过执行一系列单比特量子测量来实现量子计算,具体的计算取决于测量哪些量子比特,何时测量,以及如何测量。这非常了不起:给你固定的量子态,然后通过适当的方式"观察"各个量子比特来进行量子计算。
第三个方面的进展是量子系统的经典模拟。费曼于1982年发表的有关量子计算的开创性论文的一部分动机是,他观察到,通常很难在传统的经典计算机上模拟量子系统。当然,当时对在普通经典计算机上模拟不同量子系统的难易程度只有很少的了解。但是在 1990 年代,尤其是到了 2000 年,我们已经了解到哪些量子系统很容易模拟,哪些很困难。许多巧妙的算法被开发出来,以模拟许多以前被认为难以模拟的量子系统,特别是在一维空间中的许多量子系统,以及某些二维量子系统。借助发展具有洞察力的量子系统的某些经典描述,这些经典算法得以实现,这些描述以紧凑的方式捕获了所讨论系统的大部分或全部基本物理特性。与此同时,我们了解到某些以前看起来很简单的系统其实非常复杂。例如,人们早就知道基于某种类型的光学组件的量子
系统——所谓的线性光学系统——很容易经典地模拟。因此,当发现添加两个看似"无害"的组件(单光子源和光电探测器)就能使线性光学器件具有量子计算的全部功能时,十分令人惊讶。这些和类似的研究加深了我们对哪些量子系统易于模拟,哪些量子系统难以模拟,以及相关原因的理解。
第四个方面的进展是对量子通信信道的理解大大加深。关于纠缠的量子态如何协助量子信道上的经典通信的一套优美而完整的理论已经发展起来。大量不同的通信量子协议已被组织成一个完整的家族(以"母亲"和"父亲"协议为首),统一了我们对量子信息可能的不同通信类型的绝大部分理解。取得进展的迹象之一是本书中记述的一个关键的未解决猜想被证明是不成立的,即拥有乘积态的量子信道的通信能力等于不受约束情形下的通信能力(即允许任何纠缠态作为输人)。但是,尽管取得了进展,仍然有很多我们尚未理解的问题。例如,令人惊讶的是直到最近才发现,两个零容量的量子信道在一起使用时,其量子容量可以为正。众所周知,在经典信道上具有经典容量的类似结果是不可能发生的。
量子信息科学工作的主要动力之一是快速量子算法有望解决重要的计算问题。在这里,过去十年的进展喜忧参半。尽管研究人员独具匠心并付出了巨大的努力,但主要的算法见解仍停留在十年前。虽然已经取得了相当大的技术进步,但我们仍不了解究竟是什么使量子计算机变得强大,或者它们在哪些类别的问题上可以胜过传统计算机。
但是,令人兴奋的是,量子计算的思想已被用来证明有关经典计算的各种定理,例如关于在离散格点中找到某些隐藏向量的困难性的结果。在这些证明中引人注目的特征是,利用量子计算的思想,这些证明有时比以前的经典证明更为简洁和优雅。因此,人们已经意识到,量子计算可能是比经典模型更自然的计算模型,也许通过量子计算的思想可以更容易地揭示根本性的结果。
本书介绍量子计算和量子信息领域的主要思想和技术。该领域的快速发展及其跨学科的性质使得新来者很难全面地了解其中重要的技术和研究成果。
因此,写作本书的目的是双重的。第一个目的是介绍理解量子计算和量子信息所必需的计算机科学,数学和物理学的背景材料,具有这三个学科中至少一科或多个学科背景知识的新研究生都能够理解这些内容;最重要的要求是具备一定程度的数学基础,以及对学习量子计算和量子信息的兴趣。第二个目的是详细介绍量子计算和量子信息的主要结果。通过全面的学习,读者应该对这一令人兴奋的领域的基本工具和结果有实际的了解,这既可以作为其通识教育的一部分,也可以作为开展量子计算和量子信息独立研究的序幕。
本书的基本结构如图 1 所示。本书共分 3 部分。一般的策略是在可能的情况下从具体开始,逐步抽象。因此,我们在研究量子信息之前先研究量子计算;在介绍量子信息理论更一般的结果之前,先给出特定的量子纠错码。全书始终尝试在讨论一般理论之前先介绍实例。
第 1 部分概述量子计算和量子信息领域的主要思想和结果,并介绍计算机科学,数学和物理学的背景材料,这些材料是深人理解量子计算和量子信息所必需的。第1章是导论性章节,概述该领域的历史发展和基本概念,突出沿途的一些重要开放问题。相关材料的结构使得即使没有计算机科学或物理学背景也可以理解。第2章和第3章拓展用于更详细理解的背景材料,分别深人论述量子力学和计算机科学的基本概念。读者可以根据自己的背景,或多或少地阅读这一部分的不同章节,并在必要时返回查阅,以弥补对量子力学和计算机科学基础知识的缺失。
第2部分详细描述量子计算。第4章介绍执行量子计算所需要的基本要素,并介绍许多可用于开发更复杂的量子计算应用的基本运算。第 5 章和第 6 章分别介绍量子傅里叶变换和量子搜索算法,这是目前已知的两种基本量子算法。第 5 章还解释如何使用量子傅里叶变换来解决大整数素数分解和离散对数问题,以及这些结果对密码学的重要性。第7章以在实验室中成功演示的几种实现为例,介绍量子计算机好的物理实现的一般设计原则和标准。
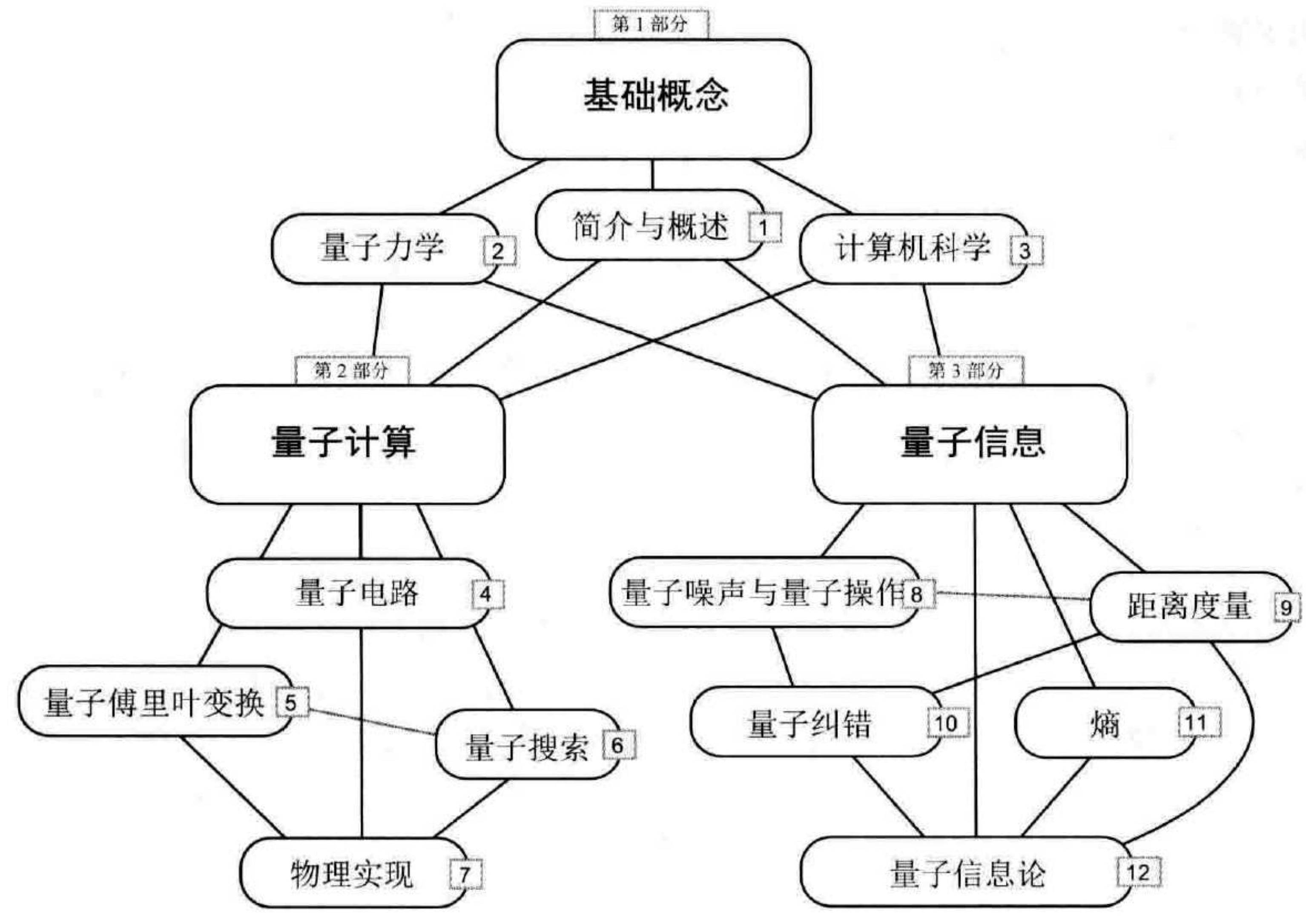
图1 本书结构
第3部分是关于量子信息的:什么是量子信息,如何使用量子态表示和交流信息,以及如何描述和处理量子信息和经典信息的破坏。第8章介绍了解现实世界中的量子信息处理所需的量子噪声的属性,以及量子运算形式主义,这是一种了解量子噪声的强大数学工具。第 9 章描述量子信息的距离度量,它使我们能够在数量上精确地说出两个量子信息相似的含义。第 10 章介绍量子纠错码,可用于保护量子计算不受噪声影响。本章的一个重要结果是阈值定理,它表明对于现实的噪声模型,噪声在原则上不会严重阻碍量子计算。第 11 章介绍熵的基本信息论概念,解释经典信息论和量子信息论中摘的许多性质。最后,第 12 章讨论量子态和量子通信通道的信息携带特性,详细介绍这种系统对于经典信息和量子信息的传输,以及秘密信息的传输可能具有的许多奇怪和有趣的特性。
大量的习题和问题贯穿整本书。习题旨在巩固对基本材料的理解,并出现在正文中。除少数例外,只需要几分钟即可轻松解决这些习题。问题出现在每章的末尾,目的是介绍那些在正文中没有足够的空间来介绍的新的有趣的材料。这些问题通常是多方面的,目的是在某种程度上深人拓展特定的思路。在本书付印之时,一些问题仍未解决。在这种情况下,将在问题说明中予以注明。每章都以本章主要结果的摘要作为结尾,并以"背景资料与延伸阅读"部分作为结束语,该部分描述本章主要思想的发展,给出整章的引用和参考文献,并提供建议供进一步阅读。
本书的文前包含详细的目录,建议浏览。还有一个术语和符号指南,可以帮助你阅读本书。本书的文后包含 6 个附录和一个参考文献列表。
附录 A 回顾基础概率论中的一些基本定义,符号和结果。我们假定读者熟悉这些材料的内
容,为了便于参考而将它们包括在此。同样,附录 B 回顾群论中的一些基本概念,收录这些材料的主要目的是方便参考。附录 C 包含 Solovay-Kitaev 定理的证明,这是量子计算中的一个重要结果,它表明可以使用一组有限的量子门来快速近似任意量子门。附录 D 回顾理解大整数素因数分解和离散对数问题的量子算法所需的数论基础知识,以及 RSA 密码系统。RSA 密码系统本身在附录 E 中进行回顾。附录 F 包含 Lieb 定理的证明,这是量子计算和量子信息中最重要的结果之一,也是重要的熵不等式的先驱,例如著名的强次可加性不等式。Solovay-Kitaev 定理和 Lieb定理的证明十分冗长,我们认为把它们放到正文之外是恰当的。
参考文献包含书中引用的所有参考资料的清单。对于所有出于无意而被遗漏引用的研究人员,我们深表歉意。
近年来,量子计算和量子信息领域的发展如此之快,以至于我们无法涵盖所有主题。有 3 个主题值得特别提及。首先是纠缠度量的主题。正如我们在书中解释的那样,纠缠是影响诸如量子隐形传态,快速量子算法和量子纠错等效应的关键因素。简而言之,它是在量子计算和量子信息中非常有用的资源。目前,蓬勃发展的研究团体正在不断充实纠缠的概念,将其作为一种新型的物理资源,并找到支配其操纵和利用的原理。我们认为,这些研究虽然前景广阔,但还不够完善,不足以保证像我们在本书中对其他主题进行的广泛介绍,因此,我们仅在第 12 章中进行简要介绍。类似地,分布式量子计算(有时称为量子通信复杂性)这一主题是一个非常有前途的主题,且在不断积极发展,但由于担心在本书出版之前我们所写的内容就会过时,因而没有在书中对它进行任何讲解。量子信息处理机器的实现也已经发展成为一个迷人且丰富的领域,但我们只花一个章节在这一主题上。显然,关于物理实现可以说的话题非常之多,但这将涉及物理,化学和工程的更多领域,这里我们没有更多的空间留给它们。
本书可以多种方式使用。它可以用作各种课程的基础,不管是有关量子计算和量子信息的特定主题的短期讲座课程,还是涵盖整个领域的全年课程。对想要了解一点量子计算和量子信息的读者,或者想要了解研究前沿的学者,它可以用来自学。它也可以用作该领域当前研究人员的参考书。我们希望新进人这个领域的研究者会发现它作为一份介绍材料是十分有价值的。
本书被设计为对自学者也是易于理解的。全书拥有大量的习题,可以作为理解正文内容的自我测验。目录和章末的总结可用以快速确定要深人学习的章节。依赖图(图1)有助于确定书中内容的阅读顺序。
本书涵盖了广泛的主题,因此可以用作各种课程的基础。
对于一学期的量子计算课程,可以根据班级的背景从第 1 章到第 3 章中选择部分内容,接着是关于量子电路的第 4 章,关于量子算法的第 5 章和第 6 章,以及从关于物理实现的第 7 章中选择的内容和理解量子纠错的第 8 章到第 10 章,其中第 10 章应特别关注。
对于一学期的量子信息课程,可以根据班级的背景从第 1 章到第 3 章中选择部分内容,接着是关于量子纠错的第 8 章到第 10 章,以及分别关于量子嫡和量子信息论的第 11 章和第 12 章。
对于一整年的课程,可以覆盖书中的所有内容,且有时间可从若干章节的"背景资料与延伸阅读"部分选择额外的内容阅读。量子计算和量子信息也非常适合于学生的独立研究项目。
除了用于量子计算和量子信息的课程,我们还希望有另外一种使用本书的方式,即作为物理系学生量子力学人门课的课本。传统的量子力学的介绍严重依赖于偏微分方程的数学框架,我们认为这常常掩盖了其中的基本思想。量子计算与量子信息为理解量子力学的基本概念和独特之处提供了一个出色的概念上的试验场,而无须基于繁重的数学机制。此类课程的重点是第 2 章中的量子力学人门,第4章中关于量子电路的基础内容,第 5 章和第 6 章中关于量子算法的部分内容,第 7 章中量子计算的物理实现,以及根据个人品味从本书第 3 部分中任意选取的内容。
我们编写这本书时尽可能使其自洽。主要的例外是,有时我们省略了那些需要读者自行验证才能相信的论证,这些通常作为习题给出。建议读者在阅读本书时至少应该尝试所有的习题。除少数例外,这些习题均可以在几分钟内完成。如果在大量习题中遇到很多困难,这可能表明需要回顾一个或多个关键的概念。
如前所述,每一章都以"背景资料与延伸阅读"部分结尾,还有一些读者可能会感兴趣的范围广泛的参考资料。Preskill 精湛的讲义[Pre98b]从与本书略有不同的角度介绍了量子计算和量子信息。关于特定主题的出色的综述性文章包括(按在本书中的出现顺序):Aharonov 对量子计算的综述[Aha99b],Kitaev 对算法和纠错的综述[Kit97b],Mosca 关于量子算法的博士论文 [Mos99],Fuchs 关于量子信息中的可区分性和远距离测量的博士论文[Fuc96],Gottesman 关于量子纠错的博士论文[Got97],Preskill 对量子纠错的综述[Pre97],Nielsen 关于量子信息论的博士论文[Nie98],以及 Bennett 和 Shor ${ }^{[B S 98]}$ 与 Bennett 和 DiVincenzo ${ }^{[B D 00]}$ 关于量子信息论的综述。其他有用的参考资料还包括 Gruska 的专著[Gru99],以及由 Lo,Spiller 和 Popescu 编辑的综述文章合辑[LSP98]。
任何冗长的文字都难免会包含错误和遗漏,本书当然也不例外。如果发现与本书有关的任何错误或有其他意见,请通过电子邮件将其发送至 qci@squint.org。需要勘误时,我们会将相关内容添加到本书网站上维护的列表中。
一些人对我们如何看待量子计算和量子信息产生了决定性的影响。许多有趣的讨论有助于塑造和完善我们的观点,为此 Michael A.Nielsen 要感谢 Carl Caves,Chris Fuchs,Gerard Milburn,John Preskill 和 Ben Schumacher,Isaac L.Chuang 要感谢 Tom Cover,Umesh Vazirani,Yoshi Yamamoto和 Bernie Yurke。
许多人直接或间接地为本书的编写提供了帮助。部分名单包括:Dorit Aharonov,Andris Am- bainis,Nabil Amer,Howard Barnum,Dave Beckman,Harry Buhrman,Caltech Quantum Optics Foosballers,Andrew Childs,Fred Chong,Richard Cleve,John Conway,John Cortese,Michael DeS- hazo,Ronald de Wolf,David DiVincenzo,Steven van Enk,Henry Everitt,Ron Fagin,Mike Freedman, Michael Gagen ,Neil Gershenfeld,Daniel Gottesman,Jim Harris,Alexander Holevo,Andrew Huibers, Julia Kempe,Alesha Kitaev,Manny Knill,Shing Kong,Raymond Laflamme,Andrew Landahl,Ron Legere,Debbie Leung,Daniel Lidar,Elliott Lieb,Theresa Lynn,Hideo Mabuchi,Yu Manin,Mike Mosca,Alex Pines,Sridhar Rajagopalan,Bill Risk,Beth Ruskai,Sara Schneider,Robert Schrader, Peter Shor,Sheri Stoll,Volker Strassen,Armin Uhlmann,Lieven Vandersypen,Anne Verhulst,Debby Wallach,Mike Westmoreland,Dave Wineland,Howard Wiseman,John Yard,Xinlan Zhou 和 Wojtek Zurek。
感谢剑桥大学出版社的帮助,使得本书从构想变成了现实。特别感谢周到而热情的编辑 Simon Capelin,她主持这个项目 3 年多,还要感谢 Margaret Patterson 及时而彻底地审阅手稿。
在本书的各个部分完成时,Michael A.Nielsen 是加州理工学院的托尔曼奖研究员,Los Alamos国家实验室的 T-6 理论天体物理学小组的成员,以及新墨西哥大学高等研究中心的成员,而 Isaac L.Chuang 是 IBM Almaden 研究中心的研究人员,斯坦福大学电气工程系顾问助理教授,加利福尼亚大学伯克利分校计算机科学系客座研究员,Los Alamos 国家实验室 T-6 理论天体物理学小组成员,以及加利福尼亚大学圣塔芭芭拉分校理论物理研究所的客座研究员。我们也感谢 Aspen 物理中心的热情款待,本书末尾的证明都在此完成。
Michael A.Nielsen 和 Isaac L.Chuang 非常感谢 NMRQC 研究计划的 DARPA 和陆军研究办公室管理的 QUIC 研究所的支持,也感谢美国国家科学基金会,国家安全局,海军研究办公室和 IBM 的慷慨支持。
在量子计算和量子信息领域中,有个别术语和符号具有两种或以上的常用含义。为了避免引起混淆,这里汇集了这些术语和符号中更常用的那些意义,以及本书遵循的惯例『。
除非另有说明,否则所有向量空间均假定是有限维的。在很多情况下,此限制是不必要的,或者可以通过一些额外的技术手段予以消除,但是统一加以限制可以使得整个陈述更易于理解,并且不会对这些结果预期中的应用产生太大的影响。
正算子 $A$ 是使得对所有的 $|\psi\rangle,\langle\psi| A|\psi\rangle \geqslant 0$ 的算子。正定算子 $A$ 是使得对所有 $|\psi\rangle \neq 0$ , $\langle\psi| A|\psi\rangle > 0$ 的算子。一个算子的支集定义为正交于其核空间的向量空间。对于厄米算子,这意味着由算子的特征值非零的特征向量所张成的向量空间。
符号 $U$( $V$ 通常也是如此,但并非总是)一般用于表示西算子或矩阵。 $H$ 通常用于表示量子逻辑门——阿达玛门(Hadamard gate),有时也用于表示量子系统的哈密顿量,其具体含义从上下文中可以明显看出。
向量有时也写作列向量的形式,例如,
$$ \left[\begin{array}{l} 1 \tag{0.1}\\ 2 \end{array}\right] $$
有时为了提高可读性,也写作 $(1,2)$ 。后者应理解为列向量的简写。对于作为量子比特的两能级量子系统,我们通常使用向量 $(1,0)$ 标识状态 $|0\rangle$ ,类似地,用 $(0,1)$ 标识状态 $|1\rangle$ 。我们还按照惯例定义泡利(Pauli)西格玛矩阵——参见下面的"常用量子门和电路符号"。最重要的是,我们约定泡利西格玛 $z$ 矩阵是 $\sigma_{z}|0\rangle=|0\rangle$ 和 $\sigma_{z}|1\rangle=-|1\rangle$ ,这与某些物理学家(但通常不是计算机科学家或数学家)直观上的期望相反。这种不和谐的根源是,物理学家通常把 $\sigma_{z}$ 的本征态 +1作为所谓的"激发态",对于许多人来说,把它等同于 $|1\rangle$ 似乎是自然的,而不是像本书一样等同于 $|0\rangle$ 。我们的选择是为了与线性代数中矩阵元素常用的下标保持一致,因此把 $\sigma_{z}$ 的第 1 列与 $\sigma_{z}$ 在 $|0\rangle$ 上的操作等同,把第 2 列与在 $|1\rangle$ 上的操作等同是自然的。这一选择也被整个量子计算和量子信息学界所使用。除了泡利西格玛矩阵的常规符号 $\sigma_{x}, \sigma_{y}, \sigma_{z}$ ,对于这 3 个矩阵使用符号 $\sigma_{1}, \sigma_{2}, \sigma_{3}$ ,并将 $\sigma_{0}$ 定义为 $2 \times 2$ 的单位矩阵也会带来很多方便。但最常见的情况是,我们分别使用符号 $I, X, Y, Z$ 来代替 $\sigma_{0}, \sigma_{1}, \sigma_{2}, \sigma_{3}$ 。
与优秀的信息论专家一致,对数始终以 2 为底,除非另有说明。我们使用 $\log (x)$ 表示以 2为底的对数;而在我们希望采用自然对数的极少数情况下,使用 $\ln (x)$ 表示。术语概率分布用于表示满足 $p_{x} \geqslant 0$ 且 $\sum_{x} p_{x}=1$ 的有限个实数 $p_{x}$ 。正算子 $A$ 相对正算子 $B$ 的相对摘定义为 $S(A | B) \equiv \operatorname{tr}(A \log A)-\operatorname{tr}(A \log B)$ 。
$\oplus$ 表示模二加法。
某些示意图符号常常用于表示西变换,这在量子电路的设计中十分有用。为了方便读者,我们把很多这样的符号汇总在下面。西变换的行和列从左到右,从上到下分别被标记为从 $00 \cdots 0$ , $00 \cdots 1$ 到 $11 \cdots 1$ ,底端的导线表示最低位。注意 $\mathrm{e}^{\mathrm{i} \pi / 4}$ 是 i 的平方根,因此 $\pi / 8$ 门=e^pi/4是相位门e^pi/2的平方根,而相位门本身是泡利 $Z$ 门=e^pi/2的平方根。
| 阿达玛门 | $-H-$ | $\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1 & 1 \\ 1 & -1\end{array}\right]$ |
|---|---|---|
| 泡利$X$ 门 | $-X$ | $\left[\begin{array}{cc}0 & 1 \\ 1 & 0\end{array}\right]$ |
| 泡利$Y$ 门 | $-Y$ | $\left[\begin{array}{cc}0 & -\mathrm{i} \\ \mathrm{i} & 0\end{array}\right]$ |
| 泡利$Z 门$ | $-Z$ | $\left[\begin{array}{cc}1 & 0 \\ 0 & -1\end{array}\right]$ |
| 相位门 | $-\sqrt{S}-$ | $\left[\begin{array}{cc}1 & 0 \\ 0 & \mathrm{i}\end{array}\right]$ |
| $\pi / 8 门$ | $-T$ | $\left[\begin{array}{cc}1 & 0 \\ 0 & \mathrm{e}^{\mathrm{i} \pi / 4}\end{array}\right]$ |
| 受控非门 |  |
$\left[\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0\end{array}\right]$ |
|---|---|---|
| 交换门 | $\underset{*}{*}$ | $\left[\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1\end{array}\right]$ |
| 受控$Z$ 门 |  |
$\left[\begin{array}{cccc}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1\end{array}\right]$ |
| 受控相位门 |  |
$\left[\begin{array}{llll}1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & \mathrm{i}\end{array}\right]$ |
| Toffoli 门 |  |
$\left[\begin{array}{llllllll}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0\end{array}\right]$ |
| Fredkin门(受控交换门) |  |
$\left[\begin{array}{llllllll}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1\end{array}\right]$ |
| 测量 | $\square$ | 投影到$|0\rangle$ 和 $|1\rangle$ |
| 量子比特 | - | 单量子比特的连线 (时间从左向右流逝) |
| 经典比特 | $\underline{\square}$ | 单经典比特的连线 |
| $n$ 量子比特 | $1^{n}$ | $n$ 量子比特的连线 |
第1部分 基础概念 ..... 1
第1章 简介与概述 ..... 2
1.1 全貌 ..... 3
1.1.1 量子计算和量子信息的历史 ..... 3
1.1.2 未来发展方向 ..... 10
1.2 量子比特 ..... 11
1.3 量子计算 ..... 14
1.3.1 单量子比特门 ..... 14
1.3.2 多量子比特门 ..... 17
1.3.3 除计算基外的测量 ..... 18
1.3.4 量子电路 ..... 19
1.3.5 量子比特复制电路? ..... 20
1.3.6 示例:贝尔态 ..... 21
1.3.7 示例:量子隐形传态 ..... 22
1.4 量子算法 ..... 24
1.4.1 量子计算机的经典计算 ..... 24
1.4.2 量子并行性 ..... 25
1.4.3 Deutsch 算法 ..... 27
1.4.4 Deutsch-Jozsa 算法 ..... 28
1.4.5 量子算法总结 ..... 30
1.5 实验量子信息处理 ..... 35
1.5.1 Stern-Gerlach 实验 ..... 35
1.5.2 实用量子信息处理的前景 ..... 38
1.6 量子信息 ..... 41
1.6.1 量子信息理论:一些问题 ..... 42
1.6.2 更广泛背景下的量子信息 ..... 47
第2章 量子力学基础 ..... 49
2.1 线性代数 ..... 50
2.1.1 基和线性无关性 ..... 51
2.1.2 线性算子和矩阵 ..... 52
2.1.3 泡利矩阵 ..... 53
2.1.4 内积 ..... 54
2.1.5 特征向量和特征值 ..... 57
2.1.6 伴随和厄米算子 ..... 58
2.1.7 张量积 ..... 60
2.1.8 算子函数 ..... 63
2.1.9 对易式和反对易式 ..... 65
2.1.10 极式分解和奇异值分解 ..... 67
2.2 量子力学的假设 ..... 68
2.2.1 状态空间 ..... 68
2.2.2 演化 ..... 69
2.2.3 量子测量 ..... 72
2.2.4 区分量子状态 ..... 73
2.2.5 投影测量 ..... 74
2.2.6 POVM 测量 ..... 77
2.2.7 相位 ..... 79
2.2.8 复合系统 ..... 80
2.2.9 量子力学:总览 ..... 82
2.3 应用:超密编码 ..... 83
2.4 密度算子 ..... 84
2.4.1 量子状态的系综 ..... 84
2.4.2 密度算子的一般性质 ..... 87
2.4.3 约化密度算子 ..... 91
2.5 施密特分解与纯化 ..... 94
2.6 EPR 和贝尔不等式 ..... 97
第3章 计算机科学简介 ..... 104
3.1 计算模型 ..... 105
3.1.1 图灵机 ..... 106
3.1.2 电路 ..... 112
3.2 计算问题的分析 ..... 115
3.2.1 如何量化计算资源 ..... 116
3.2.2 计算复杂性 ..... 118
3.2.3 判定性问题与复杂性类 P 与 NP ..... 120
3.2.4 更多的复杂性类 ..... 128
3.2.5 能量与计算 ..... 131
3.3 关于计算科学的观点 ..... 137
第2部分 量子计算 ..... 144
第4章 量子电路 ..... 145
4.1 量子算法 ..... 146
4.2 单量子比特操作 ..... 147
4.3 受控操作 ..... 151
4.4 测量 ..... 158
4.5 通用量子门 ..... 160
4.5.1 两级酉门是通用的 ..... 160
4.5.2 单量子比特门和受控非门是通用的 ..... 163
4.5.3 通用运算的一个离散集合 ..... 165
4.5.4 逼近任意西门一般是难的 ..... 169
4.5.5 量子计算复杂度 ..... 171
4.6 量子电路模型计算总结 ..... 172
4.7 量子系统的模拟 ..... 173
4.7.1 行为模拟 ..... 174
4.7.2 量子模拟算法 ..... 176
4.7.3 说明性示例 ..... 179
4.7.4 量子模拟展望 ..... 180
第5章 量子傅里叶变换及其应用 ..... 184
5.1 量子傅里叶变换 ..... 185
5.2 相位估计 ..... 189
5.3 应用:求阶与因子分解问题 ..... 193
5.3.1 应用:求阶 ..... 193
5.3.2 应用:因子分解 ..... 199
5.4 量子傅里叶变换的一般应用 ..... 202
5.4.1 周期查找 ..... 202
5.4.2 离散对数问题 ..... 204
5.4.3 隐含子群问题 ..... 206
5.4.4 其他的量子算法? ..... 208
第6章 量子搜索算法 ..... 212
6.1 量子搜索算法 ..... 212
6.1.1 Oracle ..... 212
6.1.2 过程 ..... 214
6.1.3 几何可视化 ..... 215
6.1.4 性能 ..... 217
6.2 作为量子模拟的量子搜索 ..... 219
6.3 量子计数 ..... 223
6.4 NP 完全问题解的加速 ..... 225
6.5 无结构数据库的量子搜索 ..... 226
6.6 捜索算法的最优性 ..... 229
6.7 黑盒算法的极限 ..... 232
第7章 量子计算机:物理实现 ..... 237
7.1 指导性原则 ..... 238
7.2 量子计算的条件 ..... 239
7.2.1 量子信息的表示 ..... 239
7.2.2 执行酉变换 ..... 240
7.2.3 制备基准初态 ..... 241
7.2.4 测量输出结果 ..... 241
7.3 谐振子量子计算机 ..... 242
7.3.1 物理装置 ..... 242
7.3.2 哈密顿量 ..... 243
7.3.3 量子计算 ..... 245
7.3.4 缺陷 ..... 246
7.4 光学光量子计算机 ..... 246
7.4.1 物理装置 ..... 247
7.4.2 量子计算 ..... 249
7.4.3 缺陷 ..... 254
7.5 光学腔量子电动力学 ..... 255
7.5.1 物理装置 ..... 256
7.5.2 哈密顿量 ..... 259
7.5.3 单光子单原子吸收与折射 ..... 260
7.5.4 量子计算 ..... 263
7.6 离子阱 ..... 266
7.6.1 物理装置 ..... 267
7.6.2 哈密顿量 ..... 273
7.6.3 量子计算 ..... 274
7.6.4 实验 ..... 276
7.7 核磁共振 ..... 279
7.7.1 物理装置 ..... 279
7.7.2 哈密顿量 ..... 281
7.7.3 量子计算 ..... 285
7.7.4 实验 ..... 290
7.8 其他实现方案 ..... 296
第3部分 量子信息 ..... 304
第8 章 量子噪声与量子操作 ..... 305
8.1 经典噪声与马尔可夫过程 ..... 306
8.2 量子操作 ..... 307
8.2.1 概述 ..... 307
8.2.2 环境与量子操作 ..... 309
8.2.3 算子和表示 ..... 310
8.2.4 量子操作的公理化方法 ..... 316
8.3 量子噪声与量子操作的例子 ..... 323
8.3.1 迹与偏迹 ..... 323
8.3.2 单量子比特操作的几何图像 ..... 324
8.3.3 比特翻转与相位翻转信道 ..... 325
8.3.4 退极化信道 ..... 327
8.3.5 振幅阻尼 ..... 328
8.3.6 相位阻尼 ..... 332
8.4 量子操作的应用 ..... 335
8.4.1 主方程 ..... 335
8.4.2 量子过程层析 ..... 337
8.5 量子操作形式体系的局限 ..... 343
第9章 量子信息的距离度量 ..... 346
9.1 经典信息的距离度量 ..... 346
9.2 两个量子态有多接近 ..... 349
9.2.1 迹距离 ..... 350
9.2.2 保真度 ..... 355
9.2.3 距离度量之间的关系 ..... 361
9.3 量子信道保护信息的效果怎么样 ..... 363
第 10 章 量子纠错 ..... 371
10.1 背景介绍 ..... 372
10.1.1 三量子比特的比特翻转编码 ..... 373
10.1.2 三量子比特的相位翻转编码 ..... 376
10.2 Shor 编码 ..... 377
10.3 量子纠错理论 ..... 379
10.3.1 错误的离散化 ..... 384
10.3.2 独立错误模型 ..... 385
10.3.3 简并编码 ..... 388
10.3.4 量子汉明界 ..... 388
10.4 构造量子编码 ..... 389
10.4.1 经典线性编码 ..... 389
10.4.2 Calderbank-Shor-Steane 编码 ..... 393
10.5 稳定子编码 ..... 396
10.5.1 稳定子形式 ..... 397
10.5.2 西逻辑门和稳定子形式 ..... 402
10.5.3 稳定子形式中的测量 ..... 405
10.5.4 Gottesman-Knill 定理 ..... 406
10.5.5 稳定子编码的构造 ..... 407
10.5.6 例子 ..... 409
10.5.7 稳定子编码的标准形式 ..... 412
10.5.8 编码,解码和纠错的量子电路 ..... 414
10.6 容错量子计算 ..... 416
10.6.1 容错:全局视角 ..... 416
10.6.2 容错量子逻辑 ..... 422
10.6.3 容错测量 ..... 427
10.6.4 自恢复量子计算的元素 ..... 431
第 11 章 熵与信息 ..... 436
11.1 香农熵 ..... 436
11.2 熵的基本性质 ..... 439
11.2.1 二元熵 ..... 439
11.2.2 相对熵 ..... 440
11.2.3 条件熵与互信息 ..... 441
11.2.4 数据处理不等式 ..... 445
11.3 冯-诺伊曼嫡 ..... 446
11.3.1 量子相对熵 ..... 447
11.3.2 摘的基本性质 ..... 449
11.3.3 测量和熵 ..... 450
11.3.4 次可加性 ..... 451
11.3.5 熵的凹性 ..... 452
11.3.6 量子态混合的熵 ..... 453
11.4 强次可加性 ..... 455
11.4.1 强次可加性的证明 ..... 455
11.4.2 强次可加性:基本应用 ..... 457
第12章 量子信息论 ..... 463
12.1 量子态的区分与可达信息 ..... 464
12.1.1 霍列沃界 ..... 466
12.1.2 霍列沃界的应用实例 ..... 468
12.2 数据压缩 ..... 471
12.2.1 香农无噪声信道编码定理 ..... 471
12.2.2 Schumacher 量子无噪声信道编码定理 ..... 476
12.3 噪声信道上的经典信息 ..... 481
12.3.1 经典噪声信道中的通信 ..... 481
12.3.2 噪声量子信道中的通信 ..... 486
12.4 有噪声量子信道的量子信息 ..... 493
12.4.1 嫡交换和量子费诺不等式 ..... 493
12.4.2 量子数据处理不等式 ..... 495
12.4.3 量子辛格顿界限 ..... 499
12.4.4 量子纠错码,制冷和麦克斯韦妖 ..... 500
12.5 作为一种物理资源的纠缠 ..... 502
12.5.1 两体纯态纠缠变换 ..... 503
12.5.2 纠缠蒸馏与稀释 ..... 508
12.5.3 纠畆蒸馏与量子纠错 ..... 510
12.6 量子密码学 ..... 512
12.6.1 私钥密码学 ..... 512
12.6.2 隐私放大和信息协调 ..... 513
12.6.3 量子密钥分发 ..... 515
12.6.4 隐私和相干信息 ..... 520
12.6 .5 量子密钥分发的安全性 ..... 521
附录 $\mathbf{A}$ 概率论基础 ..... 535
附录 B 群论 ..... 537
附录 C Solovay-Kitaev 定理 ..... 543
附录 D 数论 ..... 550
附录 E 公钥密码和 RSA 密码系统 ..... 565
附录 F Lieb 定理的证明 ..... 569
参考文献 ..... 574