第4章

波斯数学家、诗人欧玛尔 • 海亚姆（1048 -1131）的塑像，他写于1070年的代数著作首次详细研究了三次多项式。

多项式

这简短的一章包含关于多项式的内容，我们在讨论算子时要用到这些材料。本章的很多结果你可能已经从其他课程熟悉了，把它们写在这里只是为了完整性。
因为这一章不是关于线性代数的，所以老师可能会讲得很快。你无需把所有的证明都仔细看一遍，但至少要把本章中所有结论的陈述看一遍，并且理解它们——本书的后续章节要用到这些结论。
在本章中我们总做如下假定：

4.1 记号 F

F F F\mathbf{F}F 表示 R R R\mathbf{R}R 或 C C C\mathbf{C}C 。

本章的学习目标

  • 多项式的带余除法
  • C 上多项式的分解
■ R 上多项式的分解

复共轭与绝对值

在讨论复系数或实系数多项式之前, 我们需要多学一点复数知识.
4.2 定义 实部（real part）， Re z Re z Re z\operatorname{Re} zRez 、虚部（imaginary part）， Im z Im z Im z\operatorname{Im} zImz
设 z = a + b i z = a + b i z=a+biz=a+b \mathrm{i}z=a+bi, 其中 a a aaa 和 b b bbb 均为实数.
  • z z zzz 的实部（记作 Re z Re z Re z\operatorname{Re} zRez ）定义为 Re z = a Re z = a Re z=a\operatorname{Re} z=aRez=a.
  • z z zzz 的虚部（记作 Im z Im z Im z\operatorname{Im} zImz ）定义为 Im z = b Im z = b Im z=b\operatorname{Im} z=bImz=b 。
于是对每个复数 z z zzz 都有 z = Re z + ( Im z ) i z = Re z + ( Im z ) i z=Re z+(Im z)iz=\operatorname{Re} z+(\operatorname{Im} z) \mathrm{i}z=Rez+(Imz)i.
4.3 定义 复共轮 (complex conjugate), z ¯ z ¯ bar(z)\bar{z}z¯ 、绝对值（absolute value）, | z | | z | |z||z||z|
设 z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C.
  • z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C 的复共轭（记作 z ¯ z ¯ bar(z)\bar{z}z¯ ）定义为 z ¯ = Re z − ( Im z ) i z ¯ = Re z − ( Im z ) i bar(z)=Re z-(Im z)i\bar{z}=\operatorname{Re} z-(\operatorname{Im} z) \mathrm{i}z¯=Rez−(Imz)i.
  • 复数 z z zzz 的绝对值（记作 | z | | z | |z||z||z| ）定义为 | z | = ( Re z ) 2 + ( Im z ) 2 | z | = ( Re z ) 2 + ( Im z ) 2 |z|=sqrt((Re z)^(2)+(Im z)^(2))|z|=\sqrt{(\operatorname{Re} z)^{2}+(\operatorname{Im} z)^{2}}|z|=(Rez)2+(Imz)2.
    4.4 例 设 z = 3 + 2 i z = 3 + 2 i z=3+2iz=3+2 \mathrm{i}z=3+2i. 则
  • Re z = 3 Re z = 3 Re z=3\operatorname{Re} z=3Rez=3 且 Im z = 2 Im z = 2 Im z=2\operatorname{Im} z=2Imz=2;
  • z ¯ = 3 − 2 i ; z ¯ = 3 − 2 i ; bar(z)=3-2i;\bar{z}=3-2 \mathrm{i} ;z¯=3−2i;
  • | z | = 3 2 + 2 2 = 13 | z | = 3 2 + 2 2 = 13 |z|=sqrt(3^(2)+2^(2))=sqrt13|z|=\sqrt{3^{2}+2^{2}}=\sqrt{13}|z|=32+22=13.
请验证 z = z ¯ z = z ¯ z= bar(z)z=\bar{z}z=z¯ 当且仅当 z z zzz 是实数。注意：对于每个 z ∈ C , | z | z ∈ C , | z | z inC,|z|z \in \mathbf{C},|z|z∈C,|z| 都是非负实数。实部、虚部、复共轭和绝对值具有以下性质。

4.5 复数的性质

设 w , z ∈ C w , z ∈ C w,z inCw, z \in \mathbf{C}w,z∈C. 则
z z zzz 与 z ¯ z ¯ bar(z)\bar{z}z¯ 的和: z + z ¯ = 2 Re z z + z ¯ = 2 Re z z+ bar(z)=2Re zz+\bar{z}=2 \operatorname{Re} zz+z¯=2Rez;
z z zzz 与 z ¯ z ¯ bar(z)\bar{z}z¯ 的差: z − z ¯ = 2 ( Im z ) i z − z ¯ = 2 ( Im z ) i z- bar(z)=2(Im z)iz-\bar{z}=2(\operatorname{Im} z) \mathrm{i}z−z¯=2(Imz)i;
z z zzz 与 z ¯ z ¯ bar(z)\bar{z}z¯ 的积: z z ¯ = | z | 2 z z ¯ = | z | 2 z bar(z)=|z|^(2)z \bar{z}=|z|^{2}zz¯=|z|2;
复共轭的可加性与可乘性： w + z ― = w ¯ + z ¯ w + z ¯ = w ¯ + z ¯ bar(w+z)= bar(w)+ bar(z)\overline{w+z}=\bar{w}+\bar{z}w+z―=w¯+z¯ 且 w z ― = w ¯ z ¯ w z ¯ = w ¯ z ¯ bar(wz)= bar(w) bar(z)\overline{w z}=\bar{w} \bar{z}wz―=w¯z¯;
共轭的共轴： z ¯ ― = z z ¯ ¯ = z bar(bar(z))=z\overline{\bar{z}}=zz¯―=z ；
实部与虚部有界于 | z | : | Re z | ≤ | z | | z | : | Re z | ≤ | z | |z|:quad|Re z| <= |z||z|: \quad|\operatorname{Re} z| \leq|z||z|:|Rez|≤|z| 且 | Im z | ≤ | z | | Im z | ≤ | z | |Im z| <= |z||\operatorname{Im} z| \leq|z||Imz|≤|z|;
复共轭的绝对值: | z ¯ | = | z | | z ¯ | = | z | | bar(z)|=|z||\bar{z}|=|z||z¯|=|z|;
绝对值的可乘性： | w z | = | w | | z | | w z | = | w | | z | |wz|=|w||z||w z|=|w||z||wz|=|w||z|;
三角不等式: | w + z | ≤ | w | + | z | | w + z | ≤ | w | + | z | |w+z| <= |w|+|z||w+z| \leq|w|+|z||w+z|≤|w|+|z|.
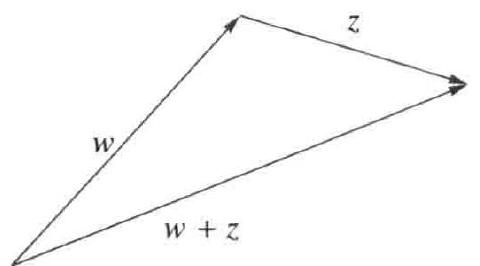
证明 除了最后一条, 其余性质的验证留给读者. 为了验证最后一条, 我们有
| w + z | 2 = ( w + z ) ( w ¯ + z ¯ ) = w w ¯ + z z ¯ + w z ¯ + z w ¯ = | w | 2 + | z | 2 + w z ¯ + w z ¯ ― = | w | 2 + | z | 2 + 2 Re ( w z ¯ ) ≤ | w | 2 + | z | 2 + 2 | w z ¯ | = | w | 2 + | z | 2 + 2 | w | | z | = ( | w | + | z | ) 2 . | w + z | 2 = ( w + z ) ( w ¯ + z ¯ ) = w w ¯ + z z ¯ + w z ¯ + z w ¯ = | w | 2 + | z | 2 + w z ¯ + w z ¯ ¯ = | w | 2 + | z | 2 + 2 Re ( w z ¯ ) ≤ | w | 2 + | z | 2 + 2 | w z ¯ | = | w | 2 + | z | 2 + 2 | w | | z | = ( | w | + | z | ) 2 . {:[|w+z|^(2)=(w+z)( bar(w)+ bar(z))],[=w bar(w)+z bar(z)+w bar(z)+z bar(w)],[=|w|^(2)+|z|^(2)+w bar(z)+ bar(w( bar(z)))],[=|w|^(2)+|z|^(2)+2Re(w bar(z))],[ <= |w|^(2)+|z|^(2)+2|w bar(z)|],[=|w|^(2)+|z|^(2)+2|w||z|],[=(|w|+|z|)^(2).]:}\begin{aligned} |w+z|^{2} & =(w+z)(\bar{w}+\bar{z}) \\ & =w \bar{w}+z \bar{z}+w \bar{z}+z \bar{w} \\ & =|w|^{2}+|z|^{2}+w \bar{z}+\overline{w \bar{z}} \\ & =|w|^{2}+|z|^{2}+2 \operatorname{Re}(w \bar{z}) \\ & \leq|w|^{2}+|z|^{2}+2|w \bar{z}| \\ & =|w|^{2}+|z|^{2}+2|w||z| \\ & =(|w|+|z|)^{2} . \end{aligned}|w+z|2=(w+z)(w¯+z¯)=ww¯+zz¯+wz¯+zw¯=|w|2+|z|2+wz¯+wz¯―=|w|2+|z|2+2Re(wz¯)≤|w|2+|z|2+2|wz¯|=|w|2+|z|2+2|w||z|=(|w|+|z|)2.
在不等式 | w + z | 2 ≤ ( | w | + | z | ) 2 | w + z | 2 ≤ ( | w | + | z | ) 2 |w+z|^(2) <= (|w|+|z|)^(2)|w+z|^{2} \leq(|w|+|z|)^{2}|w+z|2≤(|w|+|z|)2 两端取平方根, 即得到所要证明的不等式.

多项式系数的唯一性

回忆一下, 对于函数 p : F → F p : F → F p:FrarrFp: \mathbf{F} \rightarrow \mathbf{F}p:F→F, 若存在 a 0 , … , a m ∈ F a 0 , … , a m ∈ F a_(0),dots,a_(m)inFa_{0}, \ldots, a_{m} \in \mathbf{F}a0,…,am∈F 使得对所有 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 都有
4.6
p ( z ) = a 0 + a 1 z + a 2 z 2 + ⋯ + a m z m p ( z ) = a 0 + a 1 z + a 2 z 2 + ⋯ + a m z m p(z)=a_(0)+a_(1)z+a_(2)z^(2)+cdots+a_(m)z^(m)p(z)=a_{0}+a_{1} z+a_{2} z^{2}+\cdots+a_{m} z^{m}p(z)=a0+a1z+a2z2+⋯+amzm
则称函数 p p ppp 为系数在 F F F\mathbf{F}F 中的多项式.

4.7 若一个多项式是零函数，则其所有系数均为 0

设 a 0 , … , a m ∈ F a 0 , … , a m ∈ F a_(0),dots,a_(m)inFa_{0}, \ldots, a_{m} \in \mathbf{F}a0,…,am∈F. 若对任意 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有
a 0 + a 1 z + ⋯ + a m z m = 0 a 0 + a 1 z + ⋯ + a m z m = 0 a_(0)+a_(1)z+cdots+a_(m)z^(m)=0a_{0}+a_{1} z+\cdots+a_{m} z^{m}=0a0+a1z+⋯+amzm=0
则 a 0 = ⋯ = a m = 0 a 0 = ⋯ = a m = 0 a_(0)=cdots=a_(m)=0a_{0}=\cdots=a_{m}=0a0=⋯=am=0.
证明 我们将证明逆否命题. 如果并非所有系数均为 0 , 则通过改变 m m mmm 我们可以假定 a m ≠ 0 a m ≠ 0 a_(m)!=0a_{m} \neq 0am≠0. 设
z = | a 0 | + | a 1 | + ⋯ + | a m − 1 | | a m | + 1 . z = a 0 + a 1 + ⋯ + a m − 1 a m + 1 . z=(|a_(0)|+|a_(1)|+cdots+|a_(m-1)|)/(|a_(m)|)+1.z=\frac{\left|a_{0}\right|+\left|a_{1}\right|+\cdots+\left|a_{m-1}\right|}{\left|a_{m}\right|}+1 .z=|a0|+|a1|+⋯+|am−1||am|+1.
注意 z ≥ 1 z ≥ 1 z >= 1z \geq 1z≥1, 于是对 j = 0 , 1 , … , m − 1 j = 0 , 1 , … , m − 1 j=0,1,dots,m-1j=0,1, \ldots, m-1j=0,1,…,m−1 有 z j ≤ z m − 1 z j ≤ z m − 1 z^(j) <= z^(m-1)z^{j} \leq z^{m-1}zj≤zm−1 。使用三角不等式, 我们有
| a 0 + a 1 z + ⋯ + a m − 1 z m − 1 | ≤ ( | a 0 | + | a 1 | + ⋯ + | a m − 1 | ) z m − 1 < | a m z m | a 0 + a 1 z + ⋯ + a m − 1 z m − 1 ≤ a 0 + a 1 + ⋯ + a m − 1 z m − 1 < a m z m |a_(0)+a_(1)z+cdots+a_(m-1)z^(m-1)| <= (|a_(0)|+|a_(1)|+cdots+|a_(m-1)|)z^(m-1) < |a_(m)z^(m)|\left|a_{0}+a_{1} z+\cdots+a_{m-1} z^{m-1}\right| \leq\left(\left|a_{0}\right|+\left|a_{1}\right|+\cdots+\left|a_{m-1}\right|\right) z^{m-1}<\left|a_{m} z^{m}\right||a0+a1z+⋯+am−1zm−1|≤(|a0|+|a1|+⋯+|am−1|)zm−1<|amzm|
于是 a 0 + a 1 z + ⋯ + a m − 1 z m − 1 ≠ − a m z m a 0 + a 1 z + ⋯ + a m − 1 z m − 1 ≠ − a m z m a_(0)+a_(1)z+cdots+a_(m-1)z^(m-1)!=-a_(m)z^(m)a_{0}+a_{1} z+\cdots+a_{m-1} z^{m-1} \neq-a_{m} z^{m}a0+a1z+⋯+am−1zm−1≠−amzm. 所以 a 0 + a 1 z + ⋯ + a m − 1 z m − 1 + a m z m a 0 + a 1 z + ⋯ + a m − 1 z m − 1 + a m z m a_(0)+a_(1)z+cdots+a_(m-1)z^(m-1)+a_(m)z^(m)a_{0}+a_{1} z+\cdots+a_{m-1} z^{m-1}+a_{m} z^{m}a0+a1z+⋯+am−1zm−1+amzm ≠ 0 ≠ 0 !=0\neq 0≠0.
上述结果表明多项式的系数是唯一确定的（因为若一个多项式有两组不同的系数，则该多项式的这两个表达式相减即与上述结果矛盾）。
回忆一下, 若多项式 p p ppp 可以写成 4.6 的形式, 其中 a m ≠ 0 a m ≠ 0 a_(m)!=0a_{m} \neq 0am≠0, 则说 p p ppp 是 m m mmm 次的,记为 deg p = m deg p = m deg p=m\operatorname{deg} p=mdegp=m 。
规定多项式 0 的次数为 − ∞ − ∞ -oo-\infty−∞ ，很多结果就不再有例外。例如，即使 p = 0 p = 0 p=0p=0p=0 也有 deg ( p q ) = deg p + deg ( p q ) = deg p + deg(pq)=deg p+\operatorname{deg}(p q)=\operatorname{deg} p+deg(pq)=degp+ deg q deg q deg q\operatorname{deg} qdegq.
多项式 0 的次数规定为 − ∞ − ∞ -oo-\infty−∞. 必要时可以使用关于 − ∞ − ∞ -oo-\infty−∞ 的显然算术。例如，对任意整数 m m mmm 有 − ∞ < m − ∞ < m -oo < m-\infty<m−∞<m 和 − ∞ + m = − ∞ − ∞ + m = − ∞ -oo+m=-oo-\infty+m=-\infty−∞+m=−∞ 。

多项式的带余除法

若 p p ppp 和 s s sss 是非负整数且 s ≠ 0 s ≠ 0 s!=0s \neq 0s≠0, 则存在非负整数 q q qqq 和 r r rrr 使得
p = s q + r p = s q + r p=sq+rp=s q+rp=sq+r
且 r < s r < s r < sr<sr<s. 上式可解释为 p p ppp 除以 s s sss, 得到了商 q q qqq 及余数 r r rrr. 下面的任务是对多项式证明类似结果.
可将多项式的带余除法理解为多项式 p p ppp 除以 s s sss 得到了余式 r r rrr 。
下面的结果通常称为带余除法，尽管这里的表述并不是一个真正的算法，而只是一个有用的命题。
回忆一下, P ( F ) P ( F ) P(F)\mathcal{P}(\mathbf{F})P(F) 表示系数在 F F F\mathbf{F}F 中的所有多项式构成的向量空间, P m ( F ) P m ( F ) P_(m)(F)\mathcal{P}_{m}(\mathbf{F})Pm(F) 表示系数在 F F F\mathbf{F}F 中的次数不超过 m m mmm 的所有多项式构成的 P ( F ) P ( F ) P(F)\mathcal{P}(\mathbf{F})P(F) 的子空间。
下面的结果可以不使用线性代数的知识来证明, 但这里给出的使用线性代数的证明对于一本线性代数教材是合适的。

4.8 多项式的带余除法

设 p , s ∈ P ( F ) p , s ∈ P ( F ) p,s inP(F)p, s \in \mathcal{P}(\mathbf{F})p,s∈P(F) 且 s ≠ 0 s ≠ 0 s!=0s \neq 0s≠0. 则存在唯一的多项式 q , r ∈ P ( F ) q , r ∈ P ( F ) q,r inP(F)q, r \in \mathcal{P}(\mathbf{F})q,r∈P(F) 使得
p = s q + r p = s q + r p=sq+rp=s q+rp=sq+r
且 deg r < deg s deg r < deg s deg r < deg s\operatorname{deg} r<\operatorname{deg} sdegr<degs.
证明 设 n = deg p , m = deg s n = deg p , m = deg s n=deg p,m=deg sn=\operatorname{deg} p, m=\operatorname{deg} sn=degp,m=degs. 若 n < m n < m n < mn<mn<m, 取 q = 0 , r = p q = 0 , r = p q=0,r=pq=0, r=pq=0,r=p 即可. 于是我们可以假定 n ≥ m n ≥ m n >= mn \geq mn≥m 。
定义 T : P n − m ( F ) × P m − 1 ( F ) → P n ( F ) T : P n − m ( F ) × P m − 1 ( F ) → P n ( F ) T:P_(n-m)(F)xxP_(m-1)(F)rarrP_(n)(F)T: \mathcal{P}_{n-m}(\mathbf{F}) \times \mathcal{P}_{m-1}(\mathbf{F}) \rightarrow \mathcal{P}_{n}(\mathbf{F})T:Pn−m(F)×Pm−1(F)→Pn(F) 为
T ( q , r ) = s q + r T ( q , r ) = s q + r T(q,r)=sq+rT(q, r)=s q+rT(q,r)=sq+r
容易验证 T T TTT 是线性映射. 若 ( q , r ) ∈ ( q , r ) ∈ (q,r)in(q, r) \in(q,r)∈ null T T TTT, 则 s q + r = 0 s q + r = 0 sq+r=0s q+r=0sq+r=0, 这表明 q = 0 q = 0 q=0q=0q=0 且 r = 0 r = 0 r=0r=0r=0 (因为, 否则 deg s q ≥ m , s q deg s q ≥ m , s q deg sq >= m,sq\operatorname{deg} s q \geq m, s qdegsq≥m,sq 也就不可能等于 − r − r -r-r−r ). 于是 dim null T = 0 dim null T = 0 dim null T=0\operatorname{dim} \operatorname{null} T=0dimnullT=0 (这就证明了命题中的 "唯一" 性)。
由 3.76 我们有
dim ( P n − m ( F ) × P m − 1 ( F ) ) = ( n − m + 1 ) + ( m − 1 + 1 ) = n + 1 dim P n − m ( F ) × P m − 1 ( F ) = ( n − m + 1 ) + ( m − 1 + 1 ) = n + 1 dim(P_(n-m)(F)xxP_(m-1)(F))=(n-m+1)+(m-1+1)=n+1\operatorname{dim}\left(P_{n-m}(\mathbf{F}) \times \mathcal{P}_{m-1}(\mathbf{F})\right)=(n-m+1)+(m-1+1)=n+1dim(Pn−m(F)×Pm−1(F))=(n−m+1)+(m−1+1)=n+1
线性映射基本定理 3.22 和上面的等式表明 dim range T = n + 1 dim range T = n + 1 dim range T=n+1\operatorname{dim} \operatorname{range} T=n+1dimrangeT=n+1 ，从而等于 dim P n ( F ) dim P n ( F ) dimP_(n)(F)\operatorname{dim} \mathcal{P}_{n}(\mathbf{F})dimPn(F) 。于是 range T = P n ( F ) T = P n ( F ) T=P_(n)(F)T=\mathcal{P}_{n}(\mathbf{F})T=Pn(F), 因此存在 q ∈ P n − m ( F ) q ∈ P n − m ( F ) q inP_(n-m)(F)q \in \mathcal{P}_{n-m}(\mathbf{F})q∈Pn−m(F) 和 r ∈ P m − 1 ( F ) r ∈ P m − 1 ( F ) r inP_(m-1)(F)r \in \mathcal{P}_{m-1}(\mathbf{F})r∈Pm−1(F) 使得 p = T ( q , r ) = p = T ( q , r ) = p=T(q,r)=p=T(q, r)=p=T(q,r)= s q + r s q + r sq+rs q+rsq+r.

多项式的零点

求解方程 p ( z ) = 0 p ( z ) = 0 p(z)=0p(z)=0p(z)=0 在多项式 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F) 的研究中起着至关重要的作用. 因此这些解有一个特别的名字.
4.9 定义 多项式的零点（zero of a polynomial）
称数 λ ∈ F λ ∈ F lambda inF\lambda \in \mathbf{F}λ∈F 为多项式 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F) 的零点（或根），如果 p ( λ ) = 0 p ( λ ) = 0 p(lambda)=0p(\lambda)=0p(λ)=0 。

4.10 定义 因式（factor）

称多项式 s ∈ P ( F ) s ∈ P ( F ) s inP(F)s \in \mathcal{P}(\mathbf{F})s∈P(F) 为多项式 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F) 的因式，如果存在多项式 q ∈ P ( F ) q ∈ P ( F ) q inP(F)q \in \mathcal{P}(\mathbf{F})q∈P(F) 使得 p = s q p = s q p=sqp=s qp=sq.
我们首先证明 λ λ lambda\lambdaλ 是多项式 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F) 的零点当且仅当 ( z − λ ) ( z − λ ) (z-lambda)(z-\lambda)(z−λ) 是 p p ppp 的因式.

4.11 多项式的每个零点对应一个一次因式

设 p ∈ P ( F ) , λ ∈ F p ∈ P ( F ) , λ ∈ F p inP(F),lambda inFp \in \mathcal{P}(\mathbf{F}), \lambda \in \mathbf{F}p∈P(F),λ∈F. 则 p ( λ ) = 0 p ( λ ) = 0 p(lambda)=0p(\lambda)=0p(λ)=0 当且仅当存在多项式 q ∈ P ( F ) q ∈ P ( F ) q inP(F)q \in \mathcal{P}(\mathbf{F})q∈P(F) 使得对每个 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有 p ( z ) = ( z − λ ) q ( z ) p ( z ) = ( z − λ ) q ( z ) p(z)=(z-lambda)q(z)p(z)=(z-\lambda) q(z)p(z)=(z−λ)q(z) 。
证明 证明的一个方面是显然的。即，假设存在多项式 q ∈ P ( F ) q ∈ P ( F ) q inP(F)q \in \mathcal{P}(\mathbf{F})q∈P(F) 使得对所有 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有 p ( z ) = ( z − λ ) q ( z ) p ( z ) = ( z − λ ) q ( z ) p(z)=(z-lambda)q(z)p(z)=(z-\lambda) q(z)p(z)=(z−λ)q(z) 。则 p ( λ ) = ( λ − λ ) q ( λ ) = 0 p ( λ ) = ( λ − λ ) q ( λ ) = 0 p(lambda)=(lambda-lambda)q(lambda)=0p(\lambda)=(\lambda-\lambda) q(\lambda)=0p(λ)=(λ−λ)q(λ)=0 。
要证明另一个方面，设 p ( λ ) = 0 p ( λ ) = 0 p(lambda)=0p(\lambda)=0p(λ)=0 。则多项式 z − λ z − λ z-lambdaz-\lambdaz−λ 的次数为 1 . 由于次数小于 1的多项式是常函数，所以多项式的带余除法 4.8 表明存在多项式 q ∈ P ( F ) q ∈ P ( F ) q inP(F)q \in \mathcal{P}(\mathbf{F})q∈P(F) 和数 r ∈ F r ∈ F r inFr \in \mathbf{F}r∈F使得对每个 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有
p ( z ) = ( z − λ ) q ( z ) + r . p ( z ) = ( z − λ ) q ( z ) + r . p(z)=(z-lambda)q(z)+r.p(z)=(z-\lambda) q(z)+r .p(z)=(z−λ)q(z)+r.
上述等式以及 p ( λ ) = 0 p ( λ ) = 0 p(lambda)=0p(\lambda)=0p(λ)=0 表明 r = 0 r = 0 r=0r=0r=0. 于是对每个 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有 p ( z ) = ( z − λ ) q ( z ) p ( z ) = ( z − λ ) q ( z ) p(z)=(z-lambda)q(z)p(z)=(z-\lambda) q(z)p(z)=(z−λ)q(z).
现在我们可以证明多项式不会有太多的零点.

4.12 多项式零点的个数不超过它的次数

设 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F) 是 m m mmm 次多项式， m ⩾ 0 m ⩾ 0 m >= 0m \geqslant 0m⩾0. 则 p p ppp 在 F F F\mathbf{F}F 中最多有 m m mmm 个互不相同的零点.
证明 若 m = 0 m = 0 m=0m=0m=0, 则 p ( z ) = a 0 ≠ 0 p ( z ) = a 0 ≠ 0 p(z)=a_(0)!=0p(z)=a_{0} \neq 0p(z)=a0≠0, 因此 p p ppp 没有零点.
若 m = 1 m = 1 m=1m=1m=1, 则 p ( z ) = a 0 + a 1 z p ( z ) = a 0 + a 1 z p(z)=a_(0)+a_(1)zp(z)=a_{0}+a_{1} zp(z)=a0+a1z, 其中 a 1 ≠ 0 a 1 ≠ 0 a_(1)!=0a_{1} \neq 0a1≠0, 因此 p p ppp 恰有一个零点, 即 − a 0 / a 1 − a 0 / a 1 -a_(0)//a_(1)-a_{0} / a_{1}−a0/a1.
现在设 m > 1 m > 1 m > 1m>1m>1 。对 m m mmm 用归纳法，假设每个 m − 1 m − 1 m-1m-1m−1 次多项式最多有 m − 1 m − 1 m-1m-1m−1 个不同的零点. 如果 p p ppp 在 F F F\mathbf{F}F 中没有零点, 则结论成立. 如果 p p ppp 有一个零点 λ ∈ F λ ∈ F lambda inF\lambda \in \mathbf{F}λ∈F, 则由 4.11可知，存在一个多项式 q q qqq 使得对所有 z ∈ F z ∈ F z inFz \in \mathbf{F}z∈F 均有
p ( z ) = ( z − λ ) q ( z ) p ( z ) = ( z − λ ) q ( z ) p(z)=(z-lambda)q(z)p(z)=(z-\lambda) q(z)p(z)=(z−λ)q(z)
显然 deg q = m − 1 deg q = m − 1 deg q=m-1\operatorname{deg} q=m-1degq=m−1. 上面的等式表明：若 p ( z ) = 0 p ( z ) = 0 p(z)=0p(z)=0p(z)=0 ，则 z = λ z = λ z=lambdaz=\lambdaz=λ 或者 q ( z ) = 0 q ( z ) = 0 q(z)=0q(z)=0q(z)=0 。 也就是说， p p ppp 的零点是由 λ λ lambda\lambdaλ 和 q q qqq 的零点组成的。由归纳法假设， q q qqq 在 F F F\mathbf{F}F 中至多有 m − 1 m − 1 m-1m-1m−1 个不同的零点。因此 p p ppp 在 F F F\mathbf{F}F 中至多有 m m mmm 个不同的零点。

C 上多项式的分解

到目前为止，通过约定 F F F\mathbf{F}F 代表 R R R\mathbf{R}R 或 C C C\mathbf{C}C ，我们已经同时处理了复系数多项式和实系数多项式。现在我们将会看到这两种情形之间的区别。我们先处理复系数多项式。然后利用这些关于复系数多项式的结果来证明实系数多项式的相应结果。
代数学基本定理是一个存在性定理。其证明并没有给出求多项式零点的方法。二次求根公式明确地给出了二次多项式的零点。三次或四次多项式也有类似的但要复杂得多的求根公式。五次或五次以上的多项式就没有这样的求根公式了。
下面的命题，虽然称为代数学基本定理，但是它的证明却需要分析学的知识，这里给出的简短证明用到了复分析的工具。如果你还没有学过复分析方面的课程，那么这个证明对你而言就不太有意义。要是这样的话，只要将代数学基本定理当作一种事实来接受就可以了，其证明所用到的高级工具在后续的课程中才能学到。

4.13 代数学基本定理

每个非常数的复系数多项式都有零点.
证明 设 p p ppp 为非常数的复系数多项式。假设 p p ppp 没有零点，则 1 / p 1 / p 1//p1 / p1/p 是 C C C\mathbf{C}C 上的解析函数。进一步，当 | z | → ∞ | z | → ∞ |z|rarr oo|z| \rightarrow \infty|z|→∞ 时 | p ( z ) | → ∞ | p ( z ) | → ∞ |p(z)|rarr oo|p(z)| \rightarrow \infty|p(z)|→∞ ，这说明当 | z | → ∞ | z | → ∞ |z|rarr oo|z| \rightarrow \infty|z|→∞ 时 1 / p → 0 1 / p → 0 1//p rarr01 / p \rightarrow 01/p→0 。因此 1 / p 1 / p 1//p1 / p1/p 是 C C C\mathbf{C}C上的有界解析函数。根据刘维尔定理，任何这样的函数都一定是常数。但若 1 / p 1 / p 1//p1 / p1/p 是常数, 则 p p ppp 是常数, 这与 p p ppp 不是常数的假设矛盾.
三次求根公式发现于十六世纪，下面把它写出来只是为了满足你的好奇心，不要去背这个公式。
设多项式 p ( x ) = a x 3 + b x 2 + c x + d p ( x ) = a x 3 + b x 2 + c x + d p(x)=ax^(3)+bx^(2)+cx+dp(x)=a x^{3}+b x^{2}+c x+dp(x)=ax3+bx2+cx+d,其中 a ≠ 0 a ≠ 0 a!=0a \neq 0a≠0 。 令
u = 9 a b c − 2 b 3 − 27 a 2 d 54 a 3 v = u 2 + ( 3 a c − b 2 9 a 2 ) 3 u = 9 a b c − 2 b 3 − 27 a 2 d 54 a 3 v = u 2 + 3 a c − b 2 9 a 2 3 {:[u=(9abc-2b^(3)-27a^(2)d)/(54a^(3))],[v=u^(2)+((3ac-b^(2))/(9a^(2)))^(3)]:}\begin{aligned} & u=\frac{9 a b c-2 b^{3}-27 a^{2} d}{54 a^{3}} \\ & v=u^{2}+\left(\frac{3 a c-b^{2}}{9 a^{2}}\right)^{3} \end{aligned}u=9abc−2b3−27a2d54a3v=u2+(3ac−b29a2)3
假设 v ≥ 0 v ≥ 0 v >= 0v \geq 0v≥0. 则
− b 3 a + u + v 3 + u − v 3 − b 3 a + u + v 3 + u − v 3 -(b)/(3a)+root(3)(u+sqrtv)+root(3)(u-sqrtv)-\frac{b}{3 a}+\sqrt[3]{u+\sqrt{v}}+\sqrt[3]{u-\sqrt{v}}−b3a+u+v3+u−v3
是 p p ppp 的零点。
虽然上面的证明可能是代数学基本定理的最短的证明，但是通过网页搜索你会找到一些使用其他方法的证明，所有这些证明都需要使用一些分析学的知识，这是因为，例如，如果将 C C C\mathbf{C}C 换成所有 c + d i c + d i c+dic+d \mathrm{i}c+di 构成的数集（其中 c c ccc 和 d d ddd是有理数），则该定理不再成立。
值得注意的是，数学家们已经证明了五次及五次以上的多项式不存在这样的求根公式。但是计算机或计算器可以使用巧妙的数值方法寻找任意多项式的近似零点，即使无法找到确切的零点。
例如，人们无法找到多项式
p ( x ) = x 5 − 5 x 4 − 6 x 3 + 17 x 2 + 4 x − 7 p ( x ) = x 5 − 5 x 4 − 6 x 3 + 17 x 2 + 4 x − 7 p(x)=x^(5)-5x^(4)-6x^(3)+17x^(2)+4x-7p(x)=x^{5}-5 x^{4}-6 x^{3}+17 x^{2}+4 x-7p(x)=x5−5x4−6x3+17x2+4x−7
的零点的确切公式. 但是, 计算机或符号计算器可以找到这个多项式的近似零点.
代数学基本定理给出了复系数多项式的如下分解定理。在下面的分解中数 λ 1 , … , λ m λ 1 , … , λ m lambda_(1),dots,lambda_(m)\lambda_{1}, \ldots, \lambda_{m}λ1,…,λm 恰为 p p ppp 的零点, 因为只有 z z zzz 的这些取值才能使得下面等式的右端等于 0.

4.14 C 上多项式的分解

若 p ∈ P ( C ) p ∈ P ( C ) p inP(C)p \in \mathcal{P}(\mathbf{C})p∈P(C) 是非常数多项式，则 p p ppp 可以唯一分解（不计因式的次序）为
p ( z ) = c ( z − λ 1 ) ⋯ ( z − λ m ) , p ( z ) = c z − λ 1 ⋯ z − λ m , p(z)=c(z-lambda_(1))cdots(z-lambda_(m)),p(z)=c\left(z-\lambda_{1}\right) \cdots\left(z-\lambda_{m}\right),p(z)=c(z−λ1)⋯(z−λm),
其中 c , λ 1 , … , λ m ∈ C c , λ 1 , … , λ m ∈ C c,lambda_(1),dots,lambda_(m)inCc, \lambda_{1}, \ldots, \lambda_{m} \in \mathbf{C}c,λ1,…,λm∈C.
证明 设 p ∈ P ( C ) , m = deg p p ∈ P ( C ) , m = deg p p inP(C),m=deg pp \in \mathcal{P}(\mathbf{C}), m=\operatorname{deg} pp∈P(C),m=degp. 对 m m mmm 用归纳法. 若 m = 1 m = 1 m=1m=1m=1, 则分解显然存在且唯一.假设 m > 1 m > 1 m > 1m>1m>1 ，并设对于 m − 1 m − 1 m-1m-1m−1 次多项式分解存在且唯一。
我们首先证明 p p ppp 的分解存在。由代数学基本定理4.13, p p ppp 有一个根 λ λ lambda\lambdaλ. 由 4.11,存在多项式 q q qqq 使得对所有 z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C 均有
p ( z ) = ( z − λ ) q ( z ) p ( z ) = ( z − λ ) q ( z ) p(z)=(z-lambda)q(z)p(z)=(z-\lambda) q(z)p(z)=(z−λ)q(z)
由于 deg q = m − 1 deg q = m − 1 deg q=m-1\operatorname{deg} q=m-1degq=m−1, 归纳法假设表明 q q qqq 的分解存在, 将这一分解代入上面的等式即可得 p p ppp 的分解。
现在考虑唯一性问题。显然 c c ccc 由 z m z m z^(m)z^{m}zm 的系数唯一确定。因此我们只需证明不计次序的话， λ 1 , … , λ m λ 1 , … , λ m lambda_(1),dots,lambda_(m)\lambda_{1}, \ldots, \lambda_{m}λ1,…,λm 是唯一确定的. 如果对所有 z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C 均有
( z − λ 1 ) ⋯ ( z − λ m ) = ( z − τ 1 ) ⋯ ( z − τ m ) z − λ 1 ⋯ z − λ m = z − τ 1 ⋯ z − τ m (z-lambda_(1))cdots(z-lambda_(m))=(z-tau_(1))cdots(z-tau_(m))\left(z-\lambda_{1}\right) \cdots\left(z-\lambda_{m}\right)=\left(z-\tau_{1}\right) \cdots\left(z-\tau_{m}\right)(z−λ1)⋯(z−λm)=(z−τ1)⋯(z−τm)
那么, 因为当 z = λ 1 z = λ 1 z=lambda_(1)z=\lambda_{1}z=λ1 时上面等式的左端等于 0 , 所以右端一定有某个 τ τ tau\tauτ 等于 λ 1 λ 1 lambda_(1)\lambda_{1}λ1. 重置下标, 可设 τ 1 = λ 1 τ 1 = λ 1 tau_(1)=lambda_(1)\tau_{1}=\lambda_{1}τ1=λ1. 现在对于 z ≠ λ 1 z ≠ λ 1 z!=lambda_(1)z \neq \lambda_{1}z≠λ1, 上式两端都除以 z − λ 1 z − λ 1 z-lambda_(1)z-\lambda_{1}z−λ1, 则
( z − λ 2 ) ⋯ ( z − λ m ) = ( z − τ 2 ) ⋯ ( z − τ m ) z − λ 2 ⋯ z − λ m = z − τ 2 ⋯ z − τ m (z-lambda_(2))cdots(z-lambda_(m))=(z-tau_(2))cdots(z-tau_(m))\left(z-\lambda_{2}\right) \cdots\left(z-\lambda_{m}\right)=\left(z-\tau_{2}\right) \cdots\left(z-\tau_{m}\right)(z−λ2)⋯(z−λm)=(z−τ2)⋯(z−τm)
对除 z = λ 1 z = λ 1 z=lambda_(1)z=\lambda_{1}z=λ1 之外的所有 z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C 都成立。 事实上, 上面的等式一定对所有的 z ∈ C z ∈ C z inCz \in \mathbf{C}z∈C 都成立。否则，从等式的左端减去右端将得到一个具有无限多个零点的非零多项式。由上面的等式及我们的归纳法假设可知，不计次序的话，诸 λ λ lambda\lambdaλ 与诸 τ τ tau\tauτ 是相同的，这就完成唯一性的证明。

R 上多项式的分解

实系数多项式有可能没有实的零点，例如多项式 1 + x 2 1 + x 2 1+x^(2)1+x^{2}1+x2 就没有实的零点。
为了得到 R 上的分解定理，我们将利用 C上的分解定理。首先证明以下命题。
代数学基本定理对 R R R\mathbf{R}R 不成立，这反映了实向量空间和复向量空间上算子的区别，在后面的章节中我们将会看到这一点.

4.15 实系数多项式的非实零点是成对出现的

设 p ∈ P ( C ) p ∈ P ( C ) p inP(C)p \in \mathcal{P}(\mathbf{C})p∈P(C) 是实系数多项式. 若 λ ∈ C λ ∈ C lambda inC\lambda \in \mathbf{C}λ∈C 是 p p ppp 的零点，则 λ ¯ λ ¯ bar(lambda)\bar{\lambda}λ¯ 也是 p p ppp 的零点.
证明 设
p ( z ) = a 0 + a 1 z + ⋯ + a m z m p ( z ) = a 0 + a 1 z + ⋯ + a m z m p(z)=a_(0)+a_(1)z+cdots+a_(m)z^(m)p(z)=a_{0}+a_{1} z+\cdots+a_{m} z^{m}p(z)=a0+a1z+⋯+amzm
其中 a 0 , … , a m a 0 , … , a m a_(0),dots,a_(m)a_{0}, \ldots, a_{m}a0,…,am 均为实数. 设 λ ∈ C λ ∈ C lambda inC\lambda \in \mathbf{C}λ∈C 是 p p ppp 的零点. 则
a 0 + a 1 λ + ⋯ + a m λ m = 0 a 0 + a 1 λ + ⋯ + a m λ m = 0 a_(0)+a_(1)lambda+cdots+a_(m)lambda^(m)=0a_{0}+a_{1} \lambda+\cdots+a_{m} \lambda^{m}=0a0+a1λ+⋯+amλm=0
等式两端取复共轭得
a 0 + a 1 λ ¯ + ⋯ + a m λ ¯ m = 0 a 0 + a 1 λ ¯ + ⋯ + a m λ ¯ m = 0 a_(0)+a_(1) bar(lambda)+cdots+a_(m) bar(lambda)^(m)=0a_{0}+a_{1} \bar{\lambda}+\cdots+a_{m} \bar{\lambda}^{m}=0a0+a1λ¯+⋯+amλ¯m=0
此处我们使用了复共轭的一些基本性质（见 4.5）。上式表明 λ ¯ λ ¯ bar(lambda)\bar{\lambda}λ¯ 是 p p ppp 的零点。
考虑一下二次求根公式与 4.16 之间的联系。
我们想要得到实系数多项式的分解定理。为此，需要先来描述可以写成两个一次实系数多项式之积的二次实系数多项式。

4.16 二次多项式的分解

设 b , c ∈ R b , c ∈ R b,c inRb, c \in \mathbf{R}b,c∈R. 则存在 λ 1 , λ 2 ∈ R λ 1 , λ 2 ∈ R lambda_(1),lambda_(2)inR\lambda_{1}, \lambda_{2} \in \mathbf{R}λ1,λ2∈R 使得分解式
x 2 + b x + c = ( x − λ 1 ) ( x − λ 2 ) x 2 + b x + c = x − λ 1 x − λ 2 x^(2)+bx+c=(x-lambda_(1))(x-lambda_(2))x^{2}+b x+c=\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)x2+bx+c=(x−λ1)(x−λ2)
成立当且仅当 b 2 ≥ 4 c b 2 ≥ 4 c b^(2) >= 4cb^{2} \geq 4 cb2≥4c.
证明 注意到
x 2 + b x + c = ( x + b 2 ) 2 + ( c − b 2 4 ) . x 2 + b x + c = x + b 2 2 + c − b 2 4 . x^(2)+bx+c=(x+(b)/(2))^(2)+(c-(b^(2))/(4)).x^{2}+b x+c=\left(x+\frac{b}{2}\right)^{2}+\left(c-\frac{b^{2}}{4}\right) .x2+bx+c=(x+b2)2+(c−b24).
上述等式是一个基本技坅，即所谓配方法。
首先假设 b 2 < 4 c b 2 < 4 c b^(2) < 4cb^{2}<4 cb2<4c. 则对每个 x ∈ R x ∈ R x inRx \in \mathbf{R}x∈R 上式右端显然都是正的，因此多项式 x 2 + b x + c x 2 + b x + c x^(2)+bx+cx^{2}+b x+cx2+bx+c 没有实根。于是不能分解为 ( x − λ 1 ) ( x − λ 2 ) x − λ 1 x − λ 2 (x-lambda_(1))(x-lambda_(2))\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)(x−λ1)(x−λ2) 的形式，其中 λ 1 , λ 2 ∈ R λ 1 , λ 2 ∈ R lambda_(1),lambda_(2)inR\lambda_{1}, \lambda_{2} \in \mathbf{R}λ1,λ2∈R 。
反之，设 b 2 ≥ 4 c b 2 ≥ 4 c b^(2) >= 4cb^{2} \geq 4 cb2≥4c 。则存在实数 d d ddd 使得 d 2 = b 2 4 − c d 2 = b 2 4 − c d^(2)=(b^(2))/(4)-cd^{2}=\frac{b^{2}}{4}-cd2=b24−c 。由本证明第二行的等式得
x 2 + b x + c = ( x + b 2 ) 2 − d 2 = ( x + b 2 + d ) ( x + b 2 − d ) x 2 + b x + c = x + b 2 2 − d 2 = x + b 2 + d x + b 2 − d x^(2)+bx+c=(x+(b)/(2))^(2)-d^(2)=(x+(b)/(2)+d)(x+(b)/(2)-d)x^{2}+b x+c=\left(x+\frac{b}{2}\right)^{2}-d^{2}=\left(x+\frac{b}{2}+d\right)\left(x+\frac{b}{2}-d\right)x2+bx+c=(x+b2)2−d2=(x+b2+d)(x+b2−d)
这就是我们要的分解.
下面的定理给出了 R R R\mathbf{R}R 上多项式的分解。证明的思路是把 p p ppp 看作复系数多项式来使用分解 4.14. p p ppp 的非实数的复根是成对出现的，见 4.15. 于是，如果 p p ppp 作为 P ( C ) P ( C ) P(C)\mathcal{P}(\mathbf{C})P(C)中的元素，其分解包含形如 ( x − λ ) ( x − λ ) (x-lambda)(x-\lambda)(x−λ) 的项，其中 λ λ lambda\lambdaλ 是非实数的复数，那么 ( x − λ ¯ ) ( x − λ ¯ ) (x- bar(lambda))(x-\bar{\lambda})(x−λ¯) 也是该分解中的一项。将这两项相乘就得到
( x 2 − 2 ( Re λ ) x + | λ | 2 ) x 2 − 2 ( Re λ ) x + | λ | 2 (x^(2)-2(Re lambda)x+|lambda|^(2))\left(x^{2}-2(\operatorname{Re} \lambda) x+|\lambda|^{2}\right)(x2−2(Reλ)x+|λ|2)
即所需的二次项。
上一段简要描述的思路基本上给出了分解存在性的证明。但是，有一点需要注意，假设 λ λ lambda\lambdaλ 是一个非实数的复根，并且 ( x − λ ) ( x − λ ) (x-lambda)(x-\lambda)(x−λ) 是 p p ppp 作为 P ( C ) P ( C ) P(C)\mathcal{P}(\mathbf{C})P(C) 中元素的分解中的一
项。根据 4.15， ( x − λ ¯ ) ( x − λ ¯ ) (x- bar(lambda))(x-\bar{\lambda})(x−λ¯) 也是这个分解中的一项，但是 4.15 并没说这两个因子出现的次数相同，而这正是使上面的思路可行所必需的。不过，我们将证明这一点的确是成立的。
在下面的定理中， m m mmm 或 M M MMM 都可能等于 0 。数 λ 1 , … , λ m λ 1 , … , λ m lambda_(1),dots,lambda_(m)\lambda_{1}, \ldots, \lambda_{m}λ1,…,λm 恰为 p p ppp 的实零点，因为它们是使得下面的等式右端等于 0 的唯一一组实数。

4.17 R 上多项式的分解

设 p ∈ P ( R ) p ∈ P ( R ) p inP(R)p \in \mathcal{P}(\mathbf{R})p∈P(R) 是非常数多项式. 则 p p ppp 可以唯一分解（不计因子的次序）为
p ( x ) = c ( x − λ 1 ) ⋯ ( x − λ m ) ( x 2 + b 1 x + c 1 ) ⋯ ( x 2 + b M x + c M ) p ( x ) = c x − λ 1 ⋯ x − λ m x 2 + b 1 x + c 1 ⋯ x 2 + b M x + c M p(x)=c(x-lambda_(1))cdots(x-lambda_(m))(x^(2)+b_(1)x+c_(1))cdots(x^(2)+b_(M)x+c_(M))p(x)=c\left(x-\lambda_{1}\right) \cdots\left(x-\lambda_{m}\right)\left(x^{2}+b_{1} x+c_{1}\right) \cdots\left(x^{2}+b_{M} x+c_{M}\right)p(x)=c(x−λ1)⋯(x−λm)(x2+b1x+c1)⋯(x2+bMx+cM)
其中 c , λ 1 , … , λ m , b 1 , … , b M , c 1 , … , c M ∈ R c , λ 1 , … , λ m , b 1 , … , b M , c 1 , … , c M ∈ R c,lambda_(1),dots,lambda_(m),b_(1),dots,b_(M),c_(1),dots,c_(M)inRc, \lambda_{1}, \ldots, \lambda_{m}, b_{1}, \ldots, b_{M}, c_{1}, \ldots, c_{M} \in \mathbf{R}c,λ1,…,λm,b1,…,bM,c1,…,cM∈R, 并且对每个 j j jjj 均有 b j 2 < 4 c j b j 2 < 4 c j b_(j)^(2) < 4c_(j)b_{j}{ }^{2}<4 c_{j}bj2<4cj.
证明 将 p p ppp 视为 P ( C ) P ( C ) P(C)\mathcal{P}(\mathbf{C})P(C) 中的元素。如果 p p ppp 的所有（复）零点均为实数，则由 4.14 知结论成立。故设 p p ppp 有一个零点 λ ∈ C λ ∈ C lambda inC\lambda \in \mathbf{C}λ∈C 使得 λ ∉ R λ ∉ R lambda!inR\lambda \notin \mathbf{R}λ∉R 。由4.15, λ ¯ λ ¯ bar(lambda)\bar{\lambda}λ¯ 也是 p p ppp 的零点. 则有某个次数比 p p ppp 低 2 次的多项式 q ∈ P ( C ) q ∈ P ( C ) q inP(C)q \in \mathcal{P}(\mathbf{C})q∈P(C) 使得
p ( x ) = ( x − λ ) ( x − λ ¯ ) q ( x ) = ( x 2 − 2 ( Re λ ) x + | λ | 2 ) q ( x ) p ( x ) = ( x − λ ) ( x − λ ¯ ) q ( x ) = x 2 − 2 ( Re λ ) x + | λ | 2 q ( x ) p(x)=(x-lambda)(x- bar(lambda))q(x)=(x^(2)-2(Re lambda)x+|lambda|^(2))q(x)p(x)=(x-\lambda)(x-\bar{\lambda}) q(x)=\left(x^{2}-2(\operatorname{Re} \lambda) x+|\lambda|^{2}\right) q(x)p(x)=(x−λ)(x−λ¯)q(x)=(x2−2(Reλ)x+|λ|2)q(x)
如果我们能证明 q q qqq 是实系数的，那么通过对 p p ppp 的次数用归纳法就可以断定： ( x − λ ) ( x − λ ) (x-lambda)(x-\lambda)(x−λ)与 ( x − λ ¯ ) ( x − λ ¯ ) (x- bar(lambda))(x-\bar{\lambda})(x−λ¯) 在 p p ppp 的分解中出现的次数一样多。
要证明 q q qqq 是实系数的, 从上面的方程解出 q q qqq 可得, 对所有 x ∈ R x ∈ R x inRx \in \mathbf{R}x∈R 有
q ( x ) = p ( x ) x 2 − 2 ( Re λ ) x + | λ | 2 q ( x ) = p ( x ) x 2 − 2 ( Re λ ) x + | λ | 2 q(x)=(p(x))/(x^(2)-2(Re lambda)x+|lambda|^(2))q(x)=\frac{p(x)}{x^{2}-2(\operatorname{Re} \lambda) x+|\lambda|^{2}}q(x)=p(x)x2−2(Reλ)x+|λ|2
这表明对所有 x ∈ R x ∈ R x inRx \in \mathbf{R}x∈R 均有 q ( x ) ∈ R q ( x ) ∈ R q(x)inRq(x) \in \mathbf{R}q(x)∈R. 把 q q qqq 写成
q ( x ) = a 0 + a 1 x + ⋯ + a n − 2 x n − 2 q ( x ) = a 0 + a 1 x + ⋯ + a n − 2 x n − 2 q(x)=a_(0)+a_(1)x+cdots+a_(n-2)x^(n-2)q(x)=a_{0}+a_{1} x+\cdots+a_{n-2} x^{n-2}q(x)=a0+a1x+⋯+an−2xn−2
其中 n = deg p n = deg p n=deg pn=\operatorname{deg} pn=degp 且 a 0 , … , a n − 2 ∈ C a 0 , … , a n − 2 ∈ C a_(0),dots,a_(n-2)inCa_{0}, \ldots, a_{n-2} \in \mathbf{C}a0,…,an−2∈C ，则对所有 x ∈ R x ∈ R x inRx \in \mathbf{R}x∈R 有
0 = Im q ( x ) = ( Im a 0 ) + ( Im a 1 ) x + ⋯ + ( Im a n − 2 ) x n − 2 0 = Im q ( x ) = Im a 0 + Im a 1 x + ⋯ + Im a n − 2 x n − 2 0=Im q(x)=(Ima_(0))+(Ima_(1))x+cdots+(Ima_(n-2))x^(n-2)0=\operatorname{Im} q(x)=\left(\operatorname{Im} a_{0}\right)+\left(\operatorname{Im} a_{1}\right) x+\cdots+\left(\operatorname{Im} a_{n-2}\right) x^{n-2}0=Imq(x)=(Ima0)+(Ima1)x+⋯+(Iman−2)xn−2
由此可得 Im a 0 , … , Im a n − 2 Im a 0 , … , Im a n − 2 Ima_(0),dots,Ima_(n-2)\operatorname{Im} a_{0}, \ldots, \operatorname{Im} a_{n-2}Ima0,…,Iman−2 均等于 0 （由于 4.7）. 因此 q q qqq 的所有系数都是实数, 这就证明了分解的存在性。
现在考虑分解的唯一性问题。当 b j 2 < 4 c j b j 2 < 4 c j b_(j)^(2) < 4c_(j)b_{j}{ }^{2}<4 c_{j}bj2<4cj 时， p p ppp 的形如 x 2 + b j x + c j x 2 + b j x + c j x^(2)+b_(j)x+c_(j)x^{2}+b_{j} x+c_{j}x2+bjx+cj 的因式可以唯一地写成 ( x − λ j ) ( x − λ j ― ) x − λ j x − λ j ¯ (x-lambda_(j))(x- bar(lambda_(j)))\left(x-\lambda_{j}\right)\left(x-\overline{\lambda_{j}}\right)(x−λj)(x−λj―) ，其中 λ j ∈ C λ j ∈ C lambda_(j)inC\lambda_{j} \in \mathbf{C}λj∈C 。稍加思索便知，如果 p p ppp 作为 P ( R ) P ( R ) P(R)\mathcal{P}(\mathbf{R})P(R) 中元素有两个不同的分解，那么 p p ppp 作为 P ( C ) P ( C ) P(C)\mathcal{P}(\mathbf{C})P(C) 中元素也有两个不同的分解，与 4.14 矛盾。

习题 4

1 证明 4.5 中除最后一条之外的所有结论.
2 设 m m mmm 是正整数. 集合 { 0 } ∪ { p ∈ P ( F ) : deg p = m } { 0 } ∪ { p ∈ P ( F ) : deg p = m } {0}uu{p inP(F):deg p=m}\{0\} \cup\{p \in \mathcal{P}(\mathbf{F}): \operatorname{deg} p=m\}{0}∪{p∈P(F):degp=m} 是 P ( F ) P ( F ) P(F)\mathcal{P}(\mathbf{F})P(F) 的子空间吗？
3 集合 { 0 } ∪ { p ∈ P ( F ) : deg p { 0 } ∪ { p ∈ P ( F ) : deg p {0}uu{p inP(F):deg p\{0\} \cup\{p \in \mathcal{P}(\mathbf{F}): \operatorname{deg} p{0}∪{p∈P(F):degp 是偶数 } } }\}} 是 P ( F ) P ( F ) P(F)\mathcal{P}(\mathbf{F})P(F) 的子空间吗？
4 设 m m mmm 和 n n nnn 均为正整数， m ≤ n m ≤ n m <= nm \leq nm≤n ，并设 λ 1 , … , λ m ∈ F λ 1 , … , λ m ∈ F lambda_(1),dots,lambda_(m)inF\lambda_{1}, \ldots, \lambda_{m} \in \mathbf{F}λ1,…,λm∈F 。证明存在多项式 p ∈ P ( F ) p ∈ P ( F ) p inP(F)p \in \mathcal{P}(\mathbf{F})p∈P(F)满足 deg p = n deg p = n deg p=n\operatorname{deg} p=ndegp=n 和 0 = p ( λ 1 ) = ⋯ = p ( λ m ) 0 = p λ 1 = ⋯ = p λ m 0=p(lambda_(1))=cdots=p(lambda_(m))0=p\left(\lambda_{1}\right)=\cdots=p\left(\lambda_{m}\right)0=p(λ1)=⋯=p(λm) ，且 p p ppp 没有其他的零点。
5 设 m m mmm 是非负整数， z 1 , … , z m + 1 z 1 , … , z m + 1 z_(1),dots,z_(m+1)z_{1}, \ldots, z_{m+1}z1,…,zm+1 是 F F F\mathbf{F}F 中的一些不同的元素，且 w 1 , … , w m + 1 ∈ F w 1 , … , w m + 1 ∈ F w_(1),dots,w_(m+1)inFw_{1}, \ldots, w_{m+1} \in \mathbf{F}w1,…,wm+1∈F 。证明存在唯一一个多项式 p ∈ P m ( F ) p ∈ P m ( F ) p inP_(m)(F)p \in \mathcal{P}_{m}(\mathbf{F})p∈Pm(F) 使得 p ( z j ) = w j p z j = w j p(z_(j))=w_(j)p\left(z_{j}\right)=w_{j}p(zj)=wj ，其中 j = 1 , … , m + 1 j = 1 , … , m + 1 j=1,dots,m+1j=1, \ldots, m+1j=1,…,m+1 。这个结果可以不用线性代数来证明. 试用线性代数的知识给出一个简短的证明.
6 设 p ∈ P ( C ) p ∈ P ( C ) p inP(C)p \in \mathcal{P}(\mathbf{C})p∈P(C) 的次数为 m m mmm 。证明 p p ppp 有 m m mmm 个不同的零点当且仅当 p p ppp 与其导式 p ′ p ′ p^(')p^{\prime}p′ 没有公共零点。
7 证明每个奇数次的实系数多项式都有实的零点.
8 8 8\mathbf{8}8 定义 T : P ( R ) → R R T : P ( R ) → R R T:P(R)rarrR^(R)T: \mathcal{P}(\mathbf{R}) \rightarrow \mathbf{R}^{\mathbf{R}}T:P(R)→RR 为
T p = { p − p ( 3 ) x − 3 , 若 x ≠ 3 , p ′ ( 3 ) , 若 x = 3 . T p = p − p ( 3 ) x − 3 ,       若  x ≠ 3 , p ′ ( 3 ) ,       若  x = 3 . Tp={[(p-p(3))/(x-3)","," 若 "x!=3","],[p^(')(3)","," 若 "x=3.]:}T p= \begin{cases}\frac{p-p(3)}{x-3}, & \text { 若 } x \neq 3, \\ p^{\prime}(3), & \text { 若 } x=3 .\end{cases}Tp={p−p(3)x−3, 若 x≠3,p′(3), 若 x=3.
证明对每个多项式 p ∈ P ( R ) p ∈ P ( R ) p inP(R)p \in \mathcal{P}(\mathbf{R})p∈P(R) 均有 T p ∈ P ( R ) T p ∈ P ( R ) Tp inP(R)T p \in \mathcal{P}(\mathbf{R})Tp∈P(R) ，且 T T TTT 是线性映射。
9 设 p ∈ P ( C ) p ∈ P ( C ) p inP(C)p \in \mathcal{P}(\mathbf{C})p∈P(C) 。定义 q : C → C q : C → C q:CrarrCq: \mathbf{C} \rightarrow \mathbf{C}q:C→C 为 q ( z ) = p ( z ) p ( z ¯ ) ― q ( z ) = p ( z ) p ( z ¯ ) ¯ q(z)=p(z) bar(p(( bar(z))))q(z)=p(z) \overline{p(\bar{z})}q(z)=p(z)p(z¯)― 。证明 q q qqq 是实系数多项式.
10 设 m m mmm 是非负整数， p ∈ P m ( C ) p ∈ P m ( C ) p inP_(m)(C)p \in \mathcal{P}_{m}(\mathbf{C})p∈Pm(C) ，且存在不同的实数 x 0 , x 1 , … , x m x 0 , x 1 , … , x m x_(0),x_(1),dots,x_(m)x_{0}, x_{1}, \ldots, x_{m}x0,x1,…,xm 使得 p ( x j ) ∈ R p x j ∈ R p(x_(j))inRp\left(x_{j}\right) \in \mathbf{R}p(xj)∈R ，其中 j = 0 , 1 , … , m j = 0 , 1 , … , m j=0,1,dots,mj=0,1, \ldots, mj=0,1,…,m 。证明 p p ppp 的系数均为实数。
11 设 p ∈ P ( F ) , p ≠ 0 p ∈ P ( F ) , p ≠ 0 p inP(F),p!=0p \in \mathcal{P}(\mathbf{F}), p \neq 0p∈P(F),p≠0. 令 U = { p q : q ∈ P ( F ) } U = { p q : q ∈ P ( F ) } U={pq:q inP(F)}U=\{p q: q \in \mathcal{P}(\mathbf{F})\}U={pq:q∈P(F)}.
(a) 证明 dim P ( F ) / U = deg p dim P ( F ) / U = deg p dimP(F)//U=deg p\operatorname{dim} \mathcal{P}(\mathbf{F}) / U=\operatorname{deg} pdimP(F)/U=degp.
(b) 求 P ( F ) / U P ( F ) / U P(F)//U\mathcal{P}(\mathbf{F}) / UP(F)/U 的一个基.