11. 讲义标题与元信息
📜 [原文1]
COMS W3261: 计算机理论。
讲师:Tal Malkin
日期:2024 年 9 月
讲义 3:Myhill-Nerode 定理及其影响
这部分内容是讲义的元信息,用于标识课程、讲师、发布日期以及本讲义的主题。
- COMS W3261: 这是课程代码,代表哥伦比亚大学计算机科学系的 W3261 课程,课程名称是“计算机理论”。
- 讲师:Tal Malkin: 指明了授课教授的名字。
- 日期:2024 年 9 月: 表明了这份讲义发布或适用的时间。
- 讲义 3:Myhill-Nerode 定理及其影响: 这是讲义的标题,明确指出了本讲义的核心内容是 Myhill-Nerode 定理 以及由该定理引申出的相关概念和应用(即“其影响”)。
这部分是标准的讲义开头,提供了基本的上下文信息,让学生了解这份材料所属的课程、作者、时间及主题。
这部分的存在是为了标准化文档格式,方便学生归档和快速识别讲义内容。它起到了一个“封面”的作用。
可以把它想象成一本书的封面和扉页,上面写着书名、作者和出版社信息。它告诉你这本书是关于什么的,是谁写的,属于哪个系列。
就像你在图书馆里拿到一本书,首先看到封面上的标题“Myhill-Nerode 定理及其影响”,然后翻开第一页,看到作者是“Tal Malkin”,属于“COMS W3261 计算机理论”这门课的系列讲义。这让你对这份资料有了一个初步的定位。
22. 概述
2.1. Myhill-Nerode 定理的定位与作用
📜 [原文2]
Myhill-Nerode 定理是正则语言理论中的一个基本结果。它提供了正则语言的一个特征刻画,因此可以用来证明一个语言 $L$ 是否是正则的。如果 $L$ 是正则的,它还可以用来寻找识别 $L$ 的 DFA 中的最小状态数。事实上,这个定理是高效 DFA 最小化算法的核心。在这里,我们介绍 Myhill-Nerode 定理,并给出一些将其应用于正则和非正则语言的例子。
这段话是整篇讲义的引言,旨在告诉我们 Myhill-Nerode 定理是什么,以及它为什么重要。
- “Myhill-Nerode 定理是正则语言理论中的一个基本结果。”
- 这句话给定了定理的领域和地位。它不属于某个偏僻的角落,而是计算理论中关于正则语言这一核心分支的基础性、关键性成果。
- “它提供了正则语言的一个特征刻画”
- “特征刻画”(Characterization)是一个很强的数学术语。它的意思是,这个定理提供了一个与“正则语言”完全等价的条件。也就是说,“一个语言是正则的” 当且仅当 “它满足 Myhill-Nerode 定理描述的某个性质”。这就像说“一个整数是偶数”的特征刻画是“它能被2整除”。这两件事是完全等价的。
- “因此可以用来证明一个语言 $L$ 是否是正则的。”
- 这是特征刻画带来的第一个直接应用。因为有了一个等价条件,我们就有了一个新的工具(除了 DFA、NFA、正则表达式、泵引理之外)来判断一个语言的正则性。
- 证明一个语言是正则的:证明它满足 Myhill-Nerode 定理的条件。
- 证明一个语言不是正则的:证明它不满足 Myhill-Nerode 定理的条件。
- “如果 $L$ 是正则的,它还可以用来寻找识别 $L$ 的 DFA 中的最小状态数。”
- 这是定理的第二个重要应用。它不仅能判断“是或不是”,还能给出“是多少”的答案。对于一个正则语言,总存在一个识别它的、拥有最少状态的 DFA,我们称之为最小 DFA。Myhill-Nerode 定理能精确地告诉我们这个最小状态数是多少。这对于设计最高效的机器非常重要。
- “事实上,这个定理是高效 DFA 最小化算法的核心。”
- 这揭示了该定理在实践中的价值。存在一些算法,可以将一个任意的、可能有很多冗余状态的 DFA,转化为一个状态最少的等价 DFA。这些算法的理论基础正是 Myhill-Nerode 定理。
- “在这里,我们介绍 Myhill-Nerode 定理,并给出一些将其应用于正则和非正则语言的例子。”
- 这句话预告了本讲义的结构:首先会介绍定理本身,然后通过具体的例子来展示如何使用它。
- $L$: 在计算理论中,通常用大写字母 $L$ (Language) 来表示一个语言。语言是一个字符串的集合。例如,$L = \{ "a", "ab", "aba" \}$ 就是一个包含三个字符串的语言。
- DFA: Deterministic Finite Automaton,确定性有限自动机。是一种计算模型,用于识别正则语言。
- 最小状态数: 对于一个正则语言 $L$,可能存在多个不同的 DFA 都能识别它。这些 DFA 的状态数量可能不同。其中,状态数量最少的那个 DFA 的状态个数,就是最小状态数。这个最小 DFA 在结构上是唯一的(同构意义下)。
- 判断正则性: 假设我们要判断语言 $L = \{0^n1^n \mid n \ge 0\}$ (等数量的0后面跟着等数量的1) 是否正则。我们已经知道用泵引理可以证明它不是。Myhill-Nerode 定理提供了另一种方法:我们将证明这个语言会导致无限个“区分”情况,因此它不是正则的。
- 寻找最小状态数: 考虑语言 $L' = \{w \mid w \text{ 以1结尾}\}$。这是一个正则语言。我们可以构造一个识别它的 DFA。Myhill-Nerode 定理可以帮助我们确定,识别这个语言最少需要多少个状态。答案是2个状态:(1)一个表示“最近没有看到1”的状态(初始状态);(2)一个表示“刚刚看到了1”的状态(接受状态)。定理会从理论上确认,2就是最小状态数。
- 特征刻画 vs. 单向含意: 泵引理只是一个单向条件:如果一个语言是正则的,那么它必须满足泵引理的性质。但满足泵引理性质的语言不一定是正则的(虽然很少见)。而 Myhill-Nerode 定理是“当且仅当”的双向关系,是充要条件,因此更加强大。
- 最小状态数: 定理给出的是最小 DFA 的状态数。非确定性有限自动机 (NFA) 的最小状态数可能比 DFA 少。例如,识别“倒数第 $n$ 个字符是1”的语言,DFA 需要 $2^n$ 个状态,而 NFA 只需要 $n+1$ 个状态。
本段介绍了 Myhill-Nerode 定理的“江湖地位”和三大核心功能:
- 身份鉴定: 提供了一个判断语言是否正则的充要条件。
- 效率评估: 能够确定识别一个正则语言的最小 DFA 需要多少个状态。
- 优化指导: 是 DFA 最小化算法的理论基石。
本段的目的是在深入技术细节之前,先给出一个高度概括的“执行摘要”(Executive Summary)。它告诉读者为什么要学习这个定理,它的价值在哪里,激发读者的学习兴趣和动机。
Myhill-Nerode 定理就像一把“瑞士军刀”。对于一个语言,这把刀不仅能测出它是不是“正则”这块料(像一个试纸),还能精确测量出如果要为它打造一个最高效的 DFA 机器,这台机器最少需要几个齿轮(状态)。
想象一下,你是一个汽车工程师,面前有一堆设计图(语言)。你想知道某张设计图(某个语言 $L$)能不能用一套标准的、有限的零件(DFA)造出来。
- 泵引理就像一个“不合格”检测器:你找个地方(字符串)一“泵”(重复),如果车子散架了(产生矛盾),那这图纸肯定造不出来。但就算没散架,也不保证它一定合格。
- Myhill-Nerode 定理则是一位经验丰富的老师傅。他看一眼图纸,就能通过分析图纸的内在“区分需求”,告诉你两件事:
- “这张图纸啊,内在需求是有限的,能用标准零件造出来(是正则的)。” 或者 “这张图纸内在需求是无限的,标准零件不够用,造不出来(不是正则的)。”
- 如果能造,他还会告诉你:“要造这辆车,最少需要 $k$ 个核心部件(状态),一个都不能少。”
2.2. 讲义来源与定位
📜 [原文3]
这份讲义由 Tal Malkin 编写,部分基于 2017 年助教 Michael Tong、2024 年助教 Hans Shen 和 Hellen Zhao 编写的材料,以及 Luca Trevisan 的讲课笔记。Sipser 的教科书将 Myhill-Nerode 定理作为其已解答习题 1.52 的一部分(等价关系在问题 1.51 中定义)。Hopcroft, Motwani, Ullman 的教科书在第 4.4 节中有更详尽的论述。
这份讲义被推荐给感兴趣的学生阅读,如果你愿意,你可以使用 Myhill-Nerode 定理来解决作业和考试中的问题。然而,它不属于本学期课程的必修内容,也不会假定你已知晓该定理。
这部分内容提供了学术诚信信息和课程定位。
- 致谢与来源: 第一段话说明了这份讲义的知识来源,是对前人工作的致谢,体现了学术严谨性。同时,它也为感兴趣的学生提供了进一步的参考资料:
- Sipser 的教科书: 经典教材《计算理论导引》,定理在习题中出现,说明它在某些教学体系中被视为进阶或拓展内容。
- Hopcroft, Motwani, Ullman 的教科书: 另一本经典教材《自动机理论、语言和计算导论》(俗称“龙书”),其中有更详细的章节,说明这是深入学习的好去处。
- 课程要求: 第二段明确了该定理在 COMS W3261 这门课中的地位。
- 推荐阅读: 这不是强制要求掌握的内容,而是作为补充材料。
- 可以使用: 虽然不强制,但学了就可以在作业和考试中用。这给了学生一个选择,可以用更强大的工具解决问题。
- 不属于必修内容: 考试不会专门出一道题考“请陈述 Myhill-Nerode 定理”,课程的后续内容也不会基于你已经学会这个定理的前提来展开。这为不想深入这部分的同学减轻了负担。
本段澄清了讲义的学术背景和在课程中的定位:它是一份受多方资料启发的、推荐给学有余力的学生的选修内容,学会了可以在解题时使用,但不是强制要求。
这部分的存在是为了管理学生的期望和学习负担。它清楚地界定了哪些是核心要求,哪些是拓展知识,避免学生在非核心内容上花费过多精力而影响对必修内容的掌握。同时,提供参考文献也方便了希望深入研究的学生。
这就像游戏中的一个“支线任务”或“隐藏秘籍”。主线剧情(必修内容)不要求你完成它,但如果你完成了这个支线任务(学习了 Myhill-Nerode 定理),你可能会获得一把强大的武器,让后续的战斗(解决问题)变得更容易。
你正在参加一个烹饪课程。老师发了一份“分子料理技术简介”的讲义。他说:“这份资料大家有兴趣可以看看。我们这门课不强制要求,考试也不会直接考。但如果你们学会了,做菜时可以用这些技术,可能会做出更棒的菜肴。想深入了解的,可以去看《现代主义烹饪》这本书。” 这份讲义就扮演着同样的角色。
33. Myhill-Nerode 定理
3.1. 关键概念:区别扩展
📜 [原文4]
Myhill-Nerode 定理背后的一个关键概念是区别扩展。
定义 2.1。令 $L \subseteq \Sigma^{*}$ 为字母表 $\Sigma$ 上的任意语言。对于 $x, y \in \Sigma^{*}$,如果 $x z$ 和 $y z$ 中恰好有一个在 $L$ 中(其中 $x z$ 是 $x$ 和 $z$ 的连接),我们称 $z \in \Sigma^{*}$ 为 $x$ 和 $y$ 的区别扩展。如果存在这样的 $z$,我们说 $x$ 和 $y$ 对于 $L$ 是可区分的;否则,我们说 $x$ 和 $y$ 对于 $L$ 是不可区分的。
这是 Myhill-Nerode 定理的基石。整个定理都建立在这个定义之上。让我们一步步拆解它。
- “令 $L \subseteq \Sigma^{*}$ 为字母表 $\Sigma$ 上的任意语言。”
- 这设定了舞台。我们讨论的是一个语言 $L$。这个语言是基于某个字母表 $\Sigma$ 的。例如,$\Sigma = \{0, 1\}$,那么 $L$ 就是一个由0和1组成的字符串的集合。
- “对于 $x, y \in \Sigma^{*}$”
- 我们从这个字母表能构成的所有字符串($\Sigma^{*}$)中,任意挑选两个字符串,称它们为 $x$ 和 $y$。
- “如果 $x z$ 和 $y z$ 中恰好有一个在 $L$ 中”
- 这是核心判断标准。我们现在要找第三个字符串 $z$($z$ 也可以是空字符串 $\epsilon$)。
- 我们把 $z$ 分别拼接到 $x$ 和 $y$ 的后面,形成两个新字符串 $xz$ 和 $yz$。
- 然后我们检查这两个新字符串的“命运”:
- $xz \in L$ 并且 $yz \notin L$ ($xz$ 在语言里,$yz$ 不在)
- 或者 $xz \notin L$ 并且 $yz \in L$ ($xz$ 不在语言里,$yz$ 在)
- 只要满足上述两种情况之一(即它们的成员身份不一致),我们就找到了一个特殊的 $z$。
- “我们称 $z \in \Sigma^{*}$ 为 $x$ 和 $y$ 的区别扩展。”
- 那个能让 $x$ 和 $y$ “命运”分离的字符串 $z$,就被赋予了一个名字,叫做“区别扩展”(Distinguishing Extension)。
- “如果存在这样的 $z$,我们说 $x$ 和 $y$ 对于 $L$ 是可区分的”
- 我们不需要检查所有的 $z$。只要能找到至少一个这样的 $z$,我们就可以立刻下结论:$x$ 和 $y$ 是可区分的(Distinguishable)。
- “否则,我们说 $x$ 和 $y$ 对于 $L$ 是不可区分的。”
- “否则”指的是什么情况?指的是我们找不到任何一个这样的 $z$。
- 也就是说,对于任意的字符串 $z \in \Sigma^{*}$,$xz$ 和 $yz$ 的命运总是相同的:要么它们都在 $L$ 中,要么它们都不在 $L$ 中。
- 只有在这种情况下,我们才能说 $x$ 和 $y$ 是不可区分的(Indistinguishable)。
- $L \subseteq \Sigma^{*}$:
- $\Sigma$: 一个有限的符号集合,称为字母表。例如 $\Sigma = \{a, b\}$。
- $\Sigma^{*}$: 由 $\Sigma$ 中符号组成的所有有限长度字符串的集合,包括空字符串 $\epsilon$。这被称为 $\Sigma$ 的克莱尼闭包 (Kleene Star)。
- $L$: 语言,是 $\Sigma^{*}$ 的一个子集。
- $x, y \in \Sigma^{*}$:
- $x$ 和 $y$ 是从所有可能的字符串中取出的两个实例。
- $z \in \Sigma^{*}$:
- $z$ 也是一个字符串,我们用它来“测试” $x$ 和 $y$。
- $xz$:
- 字符串的连接 (Concatenation)。如果 $x = "ab"$, $z = "cde"$, 那么 $xz = "abcde"$.
- $x$ 和 $y$ 可区分 (Distinguishable):
- 形式化定义: $\exists z \in \Sigma^{*} \text{ s.t. } (xz \in L \land yz \notin L) \lor (xz \notin L \land yz \in L)$.
- 符号 $\exists$ 读作 "存在"。$\land$ 读作 "与"。$\lor$ 读作 "或"。
- $x$ 和 $y$ 不可区分 (Indistinguishable):
- 形式化定义: $\forall z \in \Sigma^{*}, (xz \in L \iff yz \in L)$.
- 符号 $\forall$ 读作 "对于所有"。$\iff$ 读作 "当且仅当"。
示例 1:
- 字母表: $\Sigma = \{a, b\}$
- 语言: $L = \{w \mid w \text{ 以 } a \text{ 结尾}\}$ (所有以 'a' 结尾的字符串)
- 我们来比较: $x = "b"$ 和 $y = "ba"$
- 寻找区别扩展 $z$:
- 尝试 $z = \epsilon$ (空字符串):
- $xz = x\epsilon = "b"$. "b" 不在 $L$ 中。
- $yz = y\epsilon = "ba"$. "ba" 在 $L$ 中。
- 它们的“命运”不同!一个在 $L$ 中,一个不在。
- 结论: 我们找到了一个区别扩展 $z = \epsilon$。因此,$x="b"$ 和 $y="ba"$ 对于语言 $L$ 是可区分的。
示例 2:
- 语言: 还是 $L = \{w \mid w \text{ 以 } a \text{ 结尾}\}$
- 我们来比较: $x = "ab"$ 和 $y = "bb"$
- 寻找区别扩展 $z$:
- 让我们尝试任意的 $z$:
- 如果 $z$ 以 $a$ 结尾 (例如 $z="a"$, $z="bba"$), 那么 $xz$ 和 $yz$ 也都以 $a$ 结尾,所以 $xz \in L$ 且 $yz \in L$。命运相同。
- 如果 $z$ 不以 $a$ 结尾 (例如 $z=\epsilon$, $z="b"$, $z="bbb"$), 那么 $xz$ 和 $yz$ 也都不以 $a$ 结尾,所以 $xz \notin L$ 且 $yz \notin L$。命运仍然相同。
- 结论: 我们找不到任何一个 $z$ 能让 $xz$ 和 $yz$ 的命运不同。对于任何后缀 $z$,它们的结局(是否在 $L$ 中)都完全取决于 $z$ 自己是否以 $a$ 结尾,而与前缀是 $x$ 还是 $y$ 无关。因此,$x="ab"$ 和 $y="bb"$ 对于语言 $L$ 是不可区分的。
- 证明可区分 vs. 证明不可区分: 证明两个字符串可区分很简单,只需要找到一个区别扩展 $z$ 即可。但证明它们不可区分则困难得多,需要论证对于所有可能的 $z$ 都无法区分它们。
- 空字符串 $z=\epsilon$: 不要忘记 $z$ 可以是空字符串 $\epsilon$。这通常是最简单的测试。如果 $x$ 和 $y$ 本身一个在 $L$ 中一个不在,那么 $z=\epsilon$ 就是一个区别扩展。
- 语言是关键: 两个字符串是否可区分,完全取决于所讨论的语言 $L$。对于语言 $L_1$,$x$ 和 $y$ 可能
是可区分的;但对于语言 $L_2$,$同样的 $x$ 和 $y$ 可能就是不可区分的。
“可区分性”是衡量两个前缀字符串 $x$ 和 $y$ 是否有本质区别的一个标准。这个标准是:我们是否能找到一个“未来”的后缀 $z$,这个后缀能揭示出 $x$ 和 $y$ 的区别,导致一个通往“接受”的结局,另一个通往“拒绝”的结局。如果找不到任何这样的“未来”,那么这两个前缀就被认为是“没有本质区别的”,即不可区分。
这个定义的目的是将字符串的属性与 DFA 的状态联系起来。正如马上会看到的,如果两个字符串是可区分的,那么任何识别该语言的 DFA 在处理完这两个字符串后,必须处于不同的状态。这个定义是在为建立语言和机器之间的桥梁铺设第一块砖。
把 DFA 想象成一个只有短期记忆的机器人。它沿着字符串路径行走。
- 不可区分的字符串: $x$ 和 $y$ 是两条不同的路径,但它们都把机器人带到了同一个“决策点”(同一个状态)。从这个点出发,无论接下来走哪条小路 $z$,最终的结果(是到达宝藏点还是陷阱点)都是一样的。对于机器人来说,它是通过走 $x$ 还是 $y$ 到达这个决策点的,已经不重要了,因为历史不影响未来。
- 可区分的字符串: $x$ 和 $y$ 是两条路径,把机器人带到了不同的“决策点”(不同的状态)。存在至少一条后续的小路 $z$,从一个决策点走会找到宝藏,而从另一个决策点走会掉进陷阱。因此,机器人必须记住它是从 $x$ 来的还是从 $y$ 来的,因为它处在不同的状态,面临着不同的未来可能性。
想象你在一个分叉路口,路口前有两条路 $x$ 和 $y$。走完 $x$ 后,你站在 A 点。走完 $y$ 后,你站在 B 点。
- 可区分: 如果从 A 点和 B 点出发,有一条后续的路 $z$(比如“向前走10米然后左转”),导致一个在终点,一个不在。那么 A 点和 B 点就是有本质区别的。你必须知道自己身在 A 还是 B。因此,路径 $x$ 和 $y$ 就是可区分的。
- 不可区分: 如果无论你接下来怎么走(尝试所有可能的路径 $z$),从 A 点出发和从 B 点出发的最终结果总是一样的(要么都到终点,要么都到不了),那么 A 点和 B 点就没有本质区别。你可以认为它们是同一个“等效位置”。因此,路径 $x$ 和 $y$ 就是不可区分的。
3.2. 可区分性与 DFA 状态
📜 [原文5]
这个定义背后的直觉是,如果两个字符串 $x, y$ 对于 $L$ 是可区分的,那么在 $L$ 的任何可能 DFA 中(如果存在),DFA 在 $x$ 和 $y$ 上的计算必须结束于两个不同的状态。这是因为如果 $x$ 和 $y$ 到达 DFA 中的同一个状态,那么对于任何扩展 $z$,$x z$ 和 $y z$ 将到达同一个状态。这是允许证明以下引理的关键思想。
这段话解释了上一节定义的“直觉”目的,也就是它和 DFA 的关系。
- “如果两个字符串 $x, y$ 对于 $L$ 是可区分的,那么...DFA...必须结束于两个不同的状态。”
- 这是核心论点。可区分性(语言的属性)直接映射到 DFA 的物理结构(状态的分离)。
- 为什么?让我们用反证法来理解。
- “这是因为如果 $x$ 和 $y$ 到达 DFA 中的同一个状态...”
- 假设,为了找到矛盾,我们假设 $x$ 和 $y$ 是可区分的,但一个 DFA $M$ 在读取完 $x$ 和 $y$ 之后,都到达了同一个状态,我们叫它 $q$。
- 形式化地说,$\delta^*(q_0, x) = q$ 并且 $\delta^*(q_0, y) = q$。
- “...那么对于任何扩展 $z$,$x z$ 和 $y z$ 将到达同一个状态。”
- 这是 DFA 的本性决定的。DFA 是“确定性的”,它的后续行为只取决于当前状态和后续输入,与如何到达当前状态的历史无关。
- 既然从 $q$ 开始,输入相同的字符串 $z$,那么无论当初是通过 $x$ 还是 $y$ 到达的 $q$,最终到达的状态必然是相同的。
- 形式化地说,$\delta^*(q, z)$ 的结果是唯一的。因此 $\delta^*(q_0, xz) = \delta^*(\delta^*(q_0, x), z) = \delta^*(q, z)$ 和 $\delta^*(q_0, yz) = \delta^*(\delta^*(q_0, y), z) = \delta^*(q, z)$ 会是同一个结束状态。
- 矛盾的产生:
- 如果 $xz$ 和 $yz$ 总是结束在同一个状态,那么这个状态要么是接受状态,要么不是。
- 这意味着 DFA $M$ 要么同时接受 $xz$ 和 $yz$,要么同时拒绝它们。
- 但这与我们最初的假设“$x$ 和 $y$ 是可区分的”相矛盾!因为“可区分”意味着存在一个 $z$,使得 $xz$ 和 $yz$ 一个被接受,一个被拒绝。
- 既然假设“$x$ 和 $y$ 到达同一个状态”会导致矛盾,那么这个假设一定是错误的。
- 结论:
- 因此,如果 $x$ 和 $y$ 是可区分的,任何能正确识别该语言的 DFA 都必须将它们映射到不同的状态。
本段建立了“可区分性”和“DFA 状态”之间的关键桥梁:可区分的字符串必须被 DFA 映射到不同的状态。这是因为 DFA 的无记忆性(只看当前状态)决定了,如果两个字符串被映射到同一状态,它们后续的“命运”将永远被绑定在一起,从而使它们变得不可区分。
此段的目的是为了给下面的引理 2.2 提供逻辑基础。它将一个抽象的、基于语言的定义(可区分性)转化为了一个关于计算机器的、具体的、物理的约束(状态分离)。这是从语言理论迈向自动机理论的关键一步。
再次使用机器人模型。如果机器人需要区分路径 $x$ 和 $y$(因为它们有不同的潜在未来),它就不能在走完 $x$ 和 $y$ 之后,在自己的脑图(状态图)上把它们的目的地标记为同一个点。它必须用两个不同的标记,比如“A点”和“B点”,来记住这种区别,否则它就会“忘记”这个至关重要的信息,并在后续决策中犯错。
想象一个自动售货机(一个 DFA)。
- 语言 $L$ 是“所有能成功买到可乐的操作序列”。
- 假设投入“1元硬币”(字符串 $x$)和投入“5角硬币两次”(字符串 $y$)是可区分的。为什么?因为如果接下来你按“退币按钮”(区别扩展 $z$),前者会退还1元,后者会退还2个5角,结果不同。假设机器无法识别退币,我们简化一下。
- 设语言 $L$ 是“总投币金额达到或超过2元”。
- $x = $ "投入1元"。$y = $ "投入5角"。
- 它们是可区分的吗?找一个 $z$。设 $z = $ "投入1元"。
- $xz = $ "投入1元" + "投入1元",总额2元,$xz \in L$。
- $yz = $ "投入5角" + "投入1元",总额1.5元,$yz \notin L$。
- 是的,$x$ 和 $y$ 是可区分的。
- 这段话的直觉就是:售货机在处理完“投入1元”和“投入5角”之后,其内部记录的“当前金额”这个状态必须是不同的(比如一个是“已收1元”,一个是“已收5角”)。如果机器稀里糊涂地把这两种情况都记作同一个状态,比如“已收钱”,那它就无法正确判断接下来再投入1元时,总金额是否足够。
3.3. 引理 2.2:可区分集与状态数下界
📜 [原文6]
引理 2.2。令 $L \subseteq \Sigma^{*}$ 为字母表 $\Sigma$ 上的任意语言。假设存在一个包含 $k$ 个不同字符串的集合 $\left\{x_{1}, \ldots, x_{k}\right\}$,使得对于任何 $i \neq j$,$x_{i}$ 和 $x_{j}$ 对于 $L$ 是可区分的。那么不存在状态数少于 $k$ 且识别 $L$ 的 DFA。
这个引理是上一段逻辑的直接推论和量化。
- “假设存在一个包含 $k$ 个不同字符串的集合 $\left\{x_{1}, \ldots, x_{k}\right\}$”
- 我们找到了一个特殊的小团体,里面有 $k$ 个字符串。
- “使得对于任何 $i \neq j$,$x_{i}$ 和 $x_{j}$ 对于 $L$ 是可区分的。”
- 这个小团体的特殊之处在于,里面任意挑出两个不同的成员,它俩都是相互可区分的。我们称这样的集合为一个“两两可区分集”(pairwise distinguishable set)。
- “那么不存在状态数少于 $k$ 且识别 $L$ 的 DFA。”
- 这是结论。这个结论给出了识别 $L$ 的 DFA 的状态数量的一个下界。
- 换句话说,任何能够识别 $L$ 的 DFA,其状态数量至少为 $k$。
- 为什么?这可以用鸽巢原理 (Pigeonhole Principle) 来简单说明。
证明思路:
- 我们有 $k$ 个字符串 $x_1, \ldots, x_k$。把它们看作 $k$ 个“鸽子”。
- 假设我们有一个识别 $L$ 的 DFA,它有 $m$ 个状态。把这些状态看作 $m$ 个“鸽巢”。
- DFA 在处理完每个字符串 $x_i$ 后,会到达一个状态 $\delta^*(q_0, x_i)$。
- 根据上一节的结论,因为 $x_i$ 和 $x_j$ (对于 $i \neq j$) 是可区分的,所以它们必须到达不同的状态。即 $\delta^*(q_0, x_i) \neq \delta^*(q_0, x_j)$。
- 这意味着,我们的 $k$ 个“鸽子” ($x_1, \ldots, x_k$) 必须飞进 $k$ 个不同的“鸽巢”(状态)。
- 因此,鸽巢的数量(状态数 $m$)必须至少等于鸽子的数量(字符串数 $k$)。
- 所以,$m \ge k$。
- 这就证明了,状态数不可能少于 $k$。
- 语言: $L = \{w \in \{0,1\}^* \mid |w| \text{ is odd}\}$ (奇数长度的字符串)
- 字母表: $\Sigma = \{0, 1\}$
- 找一个两两可区分集:
- 考虑集合 $S = \{ \epsilon, 0 \}$。这里 $k=2$。
- 成员是 $x_1 = \epsilon$ (空字符串) 和 $x_2 = 0$。
- 它们可区分吗?找一个 $z$。
- 尝试 $z = \epsilon$。
- $x_1 z = \epsilon\epsilon = \epsilon$。长度为0 (偶数),不在 $L$ 中。
- $x_2 z = 0\epsilon = 0$。长度为1 (奇数),在 $L$ 中。
- 命运不同!所以 $\epsilon$ 和 $0$ 是可区分的。
- 应用引理:
- 我们找到了一个大小为 $k=2$ 的两两可区分集 $S = \{\epsilon, 0\}$。
- 根据引理 2.2,任何识别 $L$ 的 DFA 的状态数必须至少为 2。
- 事实上,识别这个语言的最小 DFA 正好有两个状态:一个代表“已读偶数个字符”,一个代表“已读奇数个字符”。
- 下界而非精确值: 这个引理只提供了一个下界。你找到一个大小为 $k$ 的可区分集,只能保证最小状态数 $\ge k$。可能存在一个更大的可区分集,从而得到一个更好的下界。Myhill-Nerode 定理的强大之处在于它能找到最大的那个可区分集的大小。
- 集合必须是“两两”可区分的: 仅仅找到 $k$ 个字符串还不够,必须保证它们中的每一对都是可区分的。
引理 2.2 将“可区分性”这个概念量化了。它说:如果能找到一个由 $k$ 个“互相看不顺眼”(两两可区分)的字符串组成的团伙,那么任何想要“管理”好它们(正确识别语言)的 DFA 老大,手下至少要有 $k$ 个小弟(状态),每个“刺头”都得有一个专门的状态去“看管”,否则就会乱套。
这个引理是 Myhill-Nerode 定理证明中的一个关键组成部分,特别是用来证明最小状态数的部分。它建立了一个从语言属性(可区分集的规模)到机器复杂度(状态数下界)的直接数学联系。它是我们用来证明一个语言非正则的有力工具的雏形:只要能找到一个无限大的两两可区分集,就意味着任何 DFA 都需要无限个状态,而这是不可能的,所以语言非正则。
想象一个酒店前台,他需要根据客人的预定信息(字符串 $x_i$)给他们不同的房间钥匙(状态)。如果有一群客人 $x_1, \ldots, x_k$,他们每个人的后续行程安排(区别扩展 $z$)都两两不兼容(比如 $x_1$ 和 $x_2$ 的客人,如果后续都参加“潜水”活动 $z$,一个能去一个去不了),那么前台必须给这 $k$ 个客人 $k$ 把完全不同的钥匙,让他们进入不同的房间。如果前台只有少于 $k$ 种钥匙(比如让 $x_i$ 和 $x_j$ 拿了同一把钥匙),那这两个客人就会被绑定在一起,导致后续行程安排出错。因此,房间(状态)的数量至少要等于这群特殊客人的数量。
你是一名老师,班里有 $k$ 个学生 $x_1, \ldots, x_k$。你知道他们中的任何两个,比如小明 ($x_i$) 和小红 ($x_j$),在未来的某次考试(区别扩展 $z$)中,成绩必然会一个及格一个不及格。为了准确预测他们未来的表现,你需要在你的脑子里(DFA)为这 $k$ 个学生建立 $k$ 个独立的档案(状态)。如果你试图把小明和小红放到同一个档案里(同一个状态),你就无法区分他们了,你的预测系统就会崩溃。因此,你脑中的档案数量(状态数)至少得有 $k$ 个。
3.4. 命题 2.3:不可区分性是一种等价关系
📜 [原文7]
不难检查,对于任何语言 $L$,对于 $L$ 的不可区分性是一个等价关系:
命题 2.3。令 $L \subseteq \Sigma^{*}$ 为一种语言。定义 $\sim_{L}$ 为 $\Sigma^{*}$ 上的关系,其中 $x \sim_{L} y$ 当且仅当 $x$ 和 $y$ 对于 $L$ 是不可区分的。那么 $\sim_{L}$ 是自反的、对称的、和传递的,因此 $\sim_{L}$ 是 $\Sigma^{*}$ 上的一个等价关系。
这部分引入了一个新的符号 $\sim_L$,并指出了它所代表的“不可区分性”关系具有一个非常重要的数学性质——它是一个等价关系。
- 定义 $\sim_L$:
- 我们用一个简洁的符号 $x \sim_L y$ 来表示“$x$ 和 $y$ 对于语言 $L$ 是不可区分的”。
- 回忆一下不可区分的定义:对于所有的字符串 $z \in \Sigma^*$,都有 $xz \in L \iff yz \in L$。
- 什么是等价关系?
- 在数学上,一个关系(比如“=”, “<”, “是...的朋友”)如果同时满足以下三个性质,就被称为等价关系:
- 自反性 (Reflexivity): 任何元素都与它自身有关系。 $a \sim a$.
- 对称性 (Symmetry): 如果 $a$ 与 $b$ 有关系,那么 $b$ 也与 $a$ 有关系。 $a \sim b \implies b \sim a$.
- 传递性 (Transitivity): 如果 $a$ 与 $b$ 有关系,且 $b$ 与 $c$ 有关系,那么 $a$ 也与 $c$ 有关系。 $a \sim b \land b \sim c \implies a \sim c$.
- 最经典的等价关系是“等于号 =”。
- 证明 $\sim_L$ 是等价关系:
- 自反性 ($x \sim_L x$):
- 我们需要证明 $x$ 和 $x$ 是不可区分的。
- 根据定义,我们要检查对于所有 $z$,$xz \in L \iff xz \in L$ 是否成立。
- 这是一个逻辑上的重言式(A if and only if A),它永远为真。
- 所以,$\sim_L$ 满足自反性。
- 对称性 ($x \sim_L y \implies y \sim_L x$):
- 假设 $x \sim_L y$。这意味着对于所有 $z$,$xz \in L \iff yz \in L$。
- 逻辑上的“当且仅当”($\iff$)关系本身就是对称的。如果 (A $\iff$ B) 成立,那么 (B $\iff$ A) 也成立。
- 所以,对于所有 $z$,$yz \in L \iff xz \in L$ 也成立。
- 这正是 $y \sim_L x$ 的定义。
- 所以,$\sim_L$ 满足对称性。
- 传递性 ($x \sim_L y \land y \sim_L w \implies x \sim_L w$):
- 假设 $x \sim_L y$ 并且 $y \sim_L w$。
- $x \sim_L y$ 意味着:对所有 $z$, ($xz \in L \iff yz \in L$)。 (关系1)
- $y \sim_L w$ 意味着:对所有 $z$, ($yz \in L \iff wz \in L$)。 (关系2)
- 我们要证明 $x \sim_L w$,即对于所有 $z$,$xz \in L \iff wz \in L$。
- 从关系1和关系2,我们可以看到 $xz \in L$ 的“命运”和 $yz \in L$ 的“命运”是绑定的,而 $yz \in L$ 的“命运”又和 $wz \in L$ 的“命运”是绑定的。
- 由于逻辑上的“当且仅当”关系具有传递性(如果 A $\iff$ B 且 B $\iff$ C,则 A $\iff$ C),我们可以得出结论:对于所有 $z$,$xz \in L \iff wz \in L$。
- 这正是 $x \sim_L w$ 的定义。
- 所以,$\sim_L$ 满足传递性。
- 结论:
- 因为 $\sim_L$ 同时满足自反、对称和传递三个性质,所以它是一个等价关系。
- $\sim_L$:
- 这是一个二元关系符号,定义在 $\Sigma^* \times \Sigma^*$ 上。
- $x \sim_L y$ 是 “$x$ and $y$ are indistinguishable with respect to language $L$” 的简写。
- 语言: $L = \{w \mid w \text{ 的长度是偶数}\}$
- 自反性: $x = "ab"$。显然,对于任何 $z$,"ab"z 和 "ab"z 的长度总是相同,所以它们要么同在 $L$ 中,要么同不在 $L$ 中。所以 "ab" $\sim_L$ "ab"。
- 对称性: 我们已知 "a" $\sim_L$ "c"。因为对于任何 $z$,"a"z 和 "c"z 的长度总是 $|z|+1$,所以它们总是同在或同不在 $L$ 中。那么 "c" $\sim_L$ "a" 吗?当然,判断条件完全一样。
- 传递性:
- 令 $x = "a"$, $y = "b"$, $w = "c"$.
- $x \sim_L y$? 对于任何 $z$,$|az| = |bz| = |z|+1$。所以它们同在或同不在 $L$ 中。是的,$x \sim_L y$。
- $y \sim_L w$? 对于任何 $z$,$|bz| = |cz| = |z|+1$。所以它们同在或同不在 $L$ 中。是的,$y \sim_L w$。
- 那么 $x \sim_L w$ 吗? 对于任何 $z$,$|az| = |cz| = |z|+1$。所以它们同在或同不在 $L$ 中。是的,$x \sim_L w$。
- 这个例子展示了传递性。
- 关系 vs. 等价关系: 并非所有关系都是等价关系。例如,小于关系 "<" 满足传递性($a<b, b<c \implies a<c$),但不满足自反性($a \not< a$)和对称性($a<b \not\implies b<a$)。“是...的朋友”关系满足对称性,但不一定满足传递性。
- 深刻理解“等价”: 等价关系的重要性在于它能对一个集合进行划分,下一节会讲到。所有相互等价的元素可以被归为一类,形成一个“等价类”。
本段的核心是为“不可区分性”这个概念赋予一个坚实的数学结构。通过证明它是自反、对称、传递的,我们确认了它是一种等价关系。这个结论意义重大,因为它允许我们利用等价关系的所有强大理论,特别是“划分”和“等价类”。
本段的目的是为引出“等价类”这一核心概念做铺垫。一旦我们确立了等价关系,我们就可以自然地将所有字符串根据这个关系进行分组,每一组就是一个等价类。而 Myhill-Nerode 定理的精髓,正是将这些等价类与 DFA 的状态一一对应起来。
等价关系就像给集合里的所有元素贴标签。
- 自反性: 每个人都有一个和自己一样的标签。
- 对称性: 如果你和我的标签一样,那么我和你的标签也一样。
- 传递性: 如果你的标签和我的标签一样,我的标签和他的标签一样,那么你的标签也和他的标签一样。
这个 $\sim_L$ 关系就是一种贴标签的规则:如果两个字符串从“语言 $L$ 的视角”来看,其未来发展(加任何后缀 $z$)没有任何区别,那么它俩就贴上相同的标签。
想象一下,所有字符串 $\Sigma^*$ 是一群人。语言 $L$ 是一个俱乐部。
- $x \sim_L y$ 的意思是:无论未来发生什么事(追加任何字符串 $z$),$x$ 和 $y$ 这两个人要么都能凭着追加的事件进入俱乐部,要么都不能。
- 自反性: 张三和张三自己,未来的结局当然总是一样的。
- 对称性: 如果张三和李四的未来结局总是一样,那么李四和张三的未来结局也总是一样。
- 传递性: 如果张三和李四的未来结局总是一样,李四和王五的未来结局也总是一样,那么张三和王五的未来结局必然也总是一样。
因此,“未来结局总是一样”这个关系,是一个等价关系。它可以把所有的人分成不同的小团体,每个团体里的人,他们的“命运”是紧紧绑定在一起的。这个小团体,就是“等价类”。
3.5. 等价类与划分
📜 [原文8]
现在回想一下,集合 $S$ 上的一个等价关系 $\sim$ 会导出等价类,这些等价类将 $S$ 划分为通过 $\sim$ 相互关联的元素的子集。例如,令 $\sim$ 为整数集(记作 $\mathbb{Z}$)上的关系,定义为 $a \sim b$ 当且仅当 $a \equiv b(\bmod 3)$。那么 $\sim$ 是一个等价关系,它将 $\mathbb{Z}$ 划分为三个等价类 [0], [1], [2],定义为 $[i]=\{n \in \mathbb{Z} \mid n \equiv i(\bmod 3)\}$。
这段话的作用是复习一个数学概念:等价关系如何引出等价类和划分。
- “等价关系 $\sim$ 会导出等价类”
- 一旦我们有了一个等价关系 $\sim$(比如上一节的 $\sim_L$),我们就可以定义等价类。
- 对于任何一个元素 $x$,它的等价类(通常记作 $[x]$)是集合中所有与 $x$ 等价的元素的集合。
- 形式化地:$[x] = \{ y \in S \mid x \sim y \}$。
- “这些等价类将 $S$ 划分为...”
- 划分 (Partition) 是一个非常重要的概念。一个集合 $S$ 的划分是指把 $S$ 分成若干个非空子集 $S_1, S_2, \ldots$,这些子集满足两个条件:
- 并集为全集: $S_1 \cup S_2 \cup \ldots = S$ (所有子集合并起来等于原集合,没有遗漏任何元素)。
- 两两不相交: 对于任何 $i \neq j$,$S_i \cap S_j = \emptyset$ (任意两个不同的子集都没有共同元素)。
- 等价类正好构成了对原集合的一个划分。每个元素都属于且仅属于一个等价类。
- 例子:模3同余
- 集合: $S = \mathbb{Z}$ (所有整数)。
- 等价关系: $a \sim b$ 当且仅当 $a$ 和 $b$ 除以 3 的余数相同。这记作 $a \equiv b \pmod 3$。这是一个标准的等价关系。
- 划分/等价类:
- [0]: 所有除以3余0的整数。$[0] = \{\ldots, -6, -3, 0, 3, 6, \ldots\}$。
- [1]: 所有除以3余1的整数。$[1] = \{\ldots, -5, -2, 1, 4, 7, \ldots\}$。
- [2]: 所有除以3余2的整数。$[2] = \{\ldots, -4, -1, 2, 5, 8, \ldots\}$。
- 这三个等价类 $[0], [1], [2]$ 就构成了对整数集 $\mathbb{Z}$ 的一个划分。
- 任何一个整数都必然属于这三类中的一类。
- 不可能有一个整数同时属于两类。
- 在这个例子中,等价类的数量是 3,是有限的。
- $\mathbb{Z}$: 代表整数集 (来自德语 Zahlen)。
- $a \equiv b \pmod 3$:
- 读作 "$a$ is congruent to $b$ modulo 3"。
- 意思是 $a$ 和 $b$ 除以 3 的余数相等。
- 等价地,意思是 $(a-b)$ 是 3 的倍数。
- $[i]$:
- 表示等价类。在这个上下文中,是所有与 $i$ 模3同余的整数的集合。
- 例如,$[1]$ 和 $[4]$ 表示的是同一个集合,因为 $1 \equiv 4 \pmod 3$。所以 $[1] = [4] = [-2] = \ldots$。
本段通过一个具体的“模3同余”的例子,形象地回顾了等价关系的核心作用:它能像切蛋糕一样,将一个大集合(如所有字符串 $\Sigma^*$)整齐地切分成若干个互不重叠的小块(等价类),每一块里的所有元素都具有某种共同的“本质”。对于 $\sim_L$ 关系,这个共同的“本质”就是拥有相同的“未来可能性”。
本段的目的是为了让读者对“等价类”和“划分”有一个具体、直观的理解。这是理解 Myhill-Nerode 定理陈述的关键一步,因为定理的核心就是关于 $\sim_L$ 关系所产生的等价类的数量。这个例子告诉我们,等价类的数量可以是有限的(比如3个),也可以是无限的。
等价关系就像一个分拣系统。
- 所有字符串 $\Sigma^*$ 是传送到分拣系统的包裹。
- 等价关系 $\sim_L$ 是分拣规则:“有相同未来命运的包裹去同一个篮子”。
- 等价类就是那些篮子。
- 划分就是指,每个包裹最终都会掉进且仅掉进一个篮子,整个场地被这些篮子占满了。
这个例子告诉你,对于“按除3余数”这个分拣规则,你只需要3个篮子就够了。
想象一个大地图,上面有无数个村庄(字符串)。你现在要给这些村庄分组(划分)。分组的规则(等价关系)是:“从两个村庄出发,无论你接下来按什么路线走,最终的旅行体验(比如是否能到达一个叫 $L$ 的旅游胜地)总是一样的,那么这两个村庄就分到一组。”
- 这样分出来的每一个组,就是一个等价类。
- 比如,所有“位于山谷里”的村庄可能是一组,所有“位于山顶上”的村庄是另一组。
- 这个模3的例子就像是按海拔把所有地点分为三类:“低海拔”、“中海拔”、“高海拔”。
3.6. 备注 2.4:等价类与语言成员身份
📜 [原文9]
备注 2.4。如果 $x \in L$ 且 $y \notin L$,那么 $x$ 和 $y$ 对于 $L$ 是可区分的:我们可以取区别扩展为空字符串 $\epsilon$。因此,每个等价类包含的字符串要么全部在 $L$ 中,要么全部不在 $L$ 中。
这是一个非常重要但又很简单的观察。
- “如果 $x \in L$ 且 $y \notin L$”
- 我们取了两个字符串 $x$ 和 $y$。它们自身的“命运”就已经不同了:一个本身就在语言 $L$ 中,另一个不在。
- “那么 $x$ 和 $y$ 对于 $L$ 是可区分的”
- 为什么?因为我们可以找到一个区别扩展。
- “我们可以取区别扩展为空字符串 $\epsilon$。”
- 让我们来验证一下 $z = \epsilon$ 是否是区别扩展。
- 考虑 $xz = x\epsilon = x$。我们已知 $x \in L$。
- 考虑 $yz = y\epsilon = y$。我们已知 $y \notin L$。
- 一个在 $L$ 中,一个不在 $L$ 中。这完全符合区别扩展的定义。
- 所以,$x$ 和 $y$ 确实是可区分的。
- “因此,每个等价类包含的字符串要么全部在 $L$ 中,要么全部不在 $L$ 中。”
- 这是上面结论的直接推论。
- 回想一下,一个等价类是由相互不可区分的字符串组成的。
- 如果一个等价类里,既有在 $L$ 中的字符串 $x$,又有不在 $L$ 中的字符串 $y$,那么根据我们刚刚的证明,$x$ 和 $y$ 将是可区分的。
- 这与“它们在同一个等价类中”这个前提相矛盾。
- 因此,这种情况不可能发生。
- 唯一可能的情况是:一个等价类里的所有字符串,要么都在 $L$ 里,要么都不在 $L$ 里。我们称这样的等价类是“纯洁的”。
- 语言: $L = \{w \mid w \text{ 以 } a \text{ 结尾}\}$
- 等价类 1: 我们在示例 2 中看到 $x="ab"$ 和 $y="bb"$ 是不可区分的。它们构成了某个等价类的一部分。
- $x="ab" \notin L$
- $y="bb" \notin L$
- 这个等价类中的所有字符串(所有不以 $a$ 结尾但前面有字符的字符串)都不在 $L$ 中。
- 等价类 2: 我们可以证明所有以 $a$ 结尾的字符串都是相互不可区分的。
- $x = "a"$, $y = "ba"$.
- $x \in L, y \in L$.
- 让我们看它们是否不可区分。对于任何 $z$:
- $az \in L \iff z$ 以 $a$ 结尾 (错!如果 $z$ 是b呢?az="ab"不在L)
- 让我重新思考一下。所有以a结尾的字符串真的不可区分吗?
- 设 $L = \{ w | |w| \text{为偶数} \}$。
- $x = "aa" \in L$, $y = "bb" \in L$。
- 它们不可区分吗?对任意 $z$,$|az|=|bz|=|z|+2$,$|xz|=|yz|=|z|+2$。$|aaz| = |z|+2$, $|bbz| = |z|+2$. 它们有相同的长度。所以$aaz \in L \iff bbz \in L$。
- $x="aa"$ 和 $y="bb"$ 是不可区分的。它们同属于一个等价类,且都在$L$中。
- 这个备注的重点是:一个等价类不能“跨界”。它不能既有 $L$ 的成员,又有非 $L$ 的成员。
本备注揭示了等价类的一个关键特性:等价类在语言 $L$ 的边界上是“泾渭分明”的。一个等价类要么完全在 $L$ 的“领土”内,要么完全在 $L$ 的“领土”外,绝不会横跨边界。
这个备注是为了后面构造 DFA 时定义“接受状态”做铺垫。既然等价类是“纯洁”的,那么我们可以将那些“完全在 $L$ 内”的等价类所对应的状态,直接标记为接受状态。这个属性保证了这种标记的合理性和一致性。
回到分拣包裹的例子。语言 $L$ 是“贵重品”。这个备注说,同一个篮子(等价类)里,不可能既有贵重品,又有普通品。如果发生了这种情况,说明你的分拣规则(等价关系)出错了,因为贵重品和普通品本身就是“可区分的”(一个贵重一个不贵重),它们就不应该被分到同一个篮子里。
在村庄分组的比喻中,旅游胜地 $L$ 是一个国家。这个备注的意思是,你划分出的每一个“组”(等价类),里面的村庄要么就全部属于这个国家,要么就全部不属于这个国家。不可能有一个组,其中一部分村庄在国境内,另一部分在国境外。
3.7. 定理 2.5:Myhill-Nerode 定理的完整陈述
📜 [原文10]
我们现在准备陈述 Myhill-Nerode 定理。
定理 2.5。令 $L \subseteq \Sigma^{*}$ 为一种语言。那么 $L$ 是正则的当且仅当 $\sim_{L}$ 的等价类数量是有限的。此外,如果 $L$ 是正则的,那么 $\sim_{L}$ 的等价类数量也是识别 $L$ 的最小 DFA 的状态数。
这是整篇讲义的核心,是前述所有铺垫的最终集结。我们将它分解成三个部分来理解。
第一部分:正则性的特征刻画
- “$L$ 是正则的当且仅当 $\sim_{L}$ 的等价类数量是有限的。”
- “当且仅当” (if and only if, iff): 这是一个双向箭头,意味着两边的陈述是完全等价的。
- 方向一 (=>): 如果 $L$ 是正则的,那么 $\sim_L$ 的等价类数量一定是有限的。
- 直觉:既然 $L$ 可以被一个状态有限的 DFA 识别,而 DFA 的状态本质上就是对字符串进行分类,那么这种分类的数量(即等价类的数量)也必然是有限的。
- 方向二 (<=): 如果 $\sim_L$ 的等价类数量是有限的,那么 $L$ 一定是正则的。
- 直觉:如果所有字符串可以被归结为有限多种“本质不同的类别”(等价类),我们就可以构造一个 DFA,让它的每一个状态正好对应一个等价类。因为等价类数量有限,所以这个 DFA 的状态数也是有限的,因此 $L$ 是正则的。
第二部分:最小状态数的确定
- “此外,如果 $L$ 是正则的,那么 $\sim_{L}$ 的等价类数量也是识别 $L$ 的最小 DFA 的状态数。”
- 这部分给出了一个惊人的精确结论。它不仅说等价类数量是有限的,还说这个数量不多不少,正好等于识别 $L$ 所需的最小状态数。
- 令 $k$ 为 $\sim_L$ 的等价类数量。
- 定理说:识别 $L$ 的最小 DFA 的状态数 = $k$。
- 这意味着什么?
- 下界: 我们不能用少于 $k$ 个状态来识别 $L$。为什么?因为 $k$ 个等价类中的每一个都与其他等价类中的字符串可区分。我们可以从每个等价类中取出一个代表字符串,形成一个大小为 $k$ 的两两可区分集。根据引理 2.2,DFA 至少需要 $k$ 个状态。
- 上界: 我们可以构造出一个正好有 $k$ 个状态的 DFA 来识别 $L$。证明部分将会展示这个构造过程。
整合理解:
Myhill-Nerode 定理完美地连接了三个概念:
- 语言的正则性 (一个抽象属性)
- 不可区分关系 $\sim_L$ 的等价类数量 (一个组合数学属性)
- 最小 DFA 的状态数 (一个计算模型复杂度属性)
定理说,这三者是紧密锁定的。语言是正则的 $\iff$ 等价类数量有限 $\iff$ 存在一个最小 DFA。并且,等价类的数量 == 最小 DFA 的状态数。
- 语言: $L = \{w \mid w \text{ 以 } a \text{ 结尾}\}$
- 等价类: 我们可以找到两个等价类。
- $[ \epsilon ]$: 所有不以 $a$ 结尾的字符串。例如 "b", "bb", "aba" (错了,"aba"以a结尾)。应该是:
- $[\epsilon]$: 所有不以 $a$ 结尾的字符串 (例如 $\epsilon$, "b", "ab", "bb", ...)。这些字符串后面如果跟一个 $z="a"$, 就会进入 $L$。
- $[a]$: 所有以 $a$ 结尾的字符串 (例如 "a", "aa", "ba", ...)。这些字符串无论后面跟什么,其是否属于$L$的命运和从[a]出发是一样的。
让我们更精确地思考:
- 类1: 所有以 $a$ 结尾的字符串。我们称之为 $[a]$。
- 类2: 所有不以 $a$ 结尾的字符串。我们称之为 $[b]$。(用 $b$ 作为代表)
- 它们是仅有的两个等价类吗?是的。任何两个以 $a$ 结尾的字符串 $x, y$,对于任何 $z$,$xz, yz$ 是否以 $a$ 结尾完全取决于 $z$ 是否以 $a$ 结尾。所以它们不可区分。任何两个不以 $a$ 结尾的字符串也是如此。但一个以 $a$ 结尾的 $x$ 和一个不以 $a$ 结尾的 $y$ 是可区分的 (用 $z=\epsilon$)。
- 等价类数量: 2。
- 定理应用:
- 因为等价类数量 (2) 是有限的,所以 $L$ 是正则的。
- 识别 $L$ 的最小 DFA 的状态数正好是 2。
- 事实上,这个最小 DFA 有两个状态:一个非接受状态(代表“当前已读字符串不以a结尾”),一个接受状态(代表“当前已读字符串以a结尾”)。
- 语言: $L' = \{0^n 1^n \mid n \ge 0\}$
- 等价类: 考虑字符串集合 $\{0, 00, 000, \ldots, 0^k, \ldots\}$。
- 对于任意两个不同的成员 $x=0^i$ 和 $y=0^j$ ($i \neq j$)。
- 令 $z = 1^i$。那么 $xz = 0^i 1^i \in L'$。但 $yz = 0^j 1^i \notin L'$。
- 所以 $0^i$ 和 $0^j$ 是可区分的。
- 这意味着,每一个 $0^k$ 都属于一个不同的等价类。
- 等价类数量: 无限多。
- 定理应用:
- 因为等价类数量是无限的,所以 $L'$ 不是正则的。
Myhill-Nerode 定理是一个“三位一体”的定理。它指出,一个语言的正则性、它的不可区分等价类的有限性、以及它的最小 DFA 状态数,这三者被一个精确的数学关系锁定在一起。这个关系就是:语言是正则的,当且仅当等价类数量是有限的,并且这个数量就等于最小 DFA 的状态数。
这是本讲义的高潮和核心。前面所有的定义、引理和备注都是为了能够清晰地陈述和理解这个定理。这个定理为我们提供了一个全新的、强大的视角来分析语言的正则性,并将抽象的语言属性与具体的机器复杂度直接挂钩。
Myhill-Nerode 定理是“语言需求”和“机器成本”之间的最终审计报告。
- 语言的需求: 一个语言 $L$ 内在地需要我们区分多少种不同的“前缀历史”?这个数量就是等价类的数量。
- 机器的成本: 我们为了满足这些需求,需要建造一个DFA,最少需要多少个“记忆单元”(状态)?
- 审计报告(定理): 报告说,成本不多不少,正好等于需求。如果需求是无限的,那么任何有限成本的机器都无法满足,任务失败(语言非正则)。如果需求是有限的 $k$,那么成本就是 $k$(最小状态数为 $k$)。
想象你要为全世界所有字符串(人)签发护照(状态)。
- 签发规则是:如果两个人(字符串 $x, y$)的“未来潜力”完全一样(对于任何后缀 $z$ 命运相同),他们就拿同一种护照(属于同一个等价类)。
- 定理说:
- 如果只需要有限种护照就能覆盖所有人,那么你的国家(语言 $L$)就是一个“正则国家”。否则就是“非正则国家”。
- 对于一个“正则国家”,你所需要的护照种类数量,不多不少,正好等于管理这个国家所需的最简化政府部门(最小 DFA)的数量(状态数)。
44. 证明梗概
📜 [原文11]
证明。我们在这里提供证明的梗概。我们需要证明以下三个陈述:
- 如果 $L$ 是正则的,那么 $\sim_{L}$ 有有限个等价类。
- 如果 $\sim_{L}$ 有有限个等价类,那么 $L$ 是正则的。
- 如果 $\sim_{L}$ 有有限个等价类,那么等价类的数量就是识别 $L$ 的最小 DFA 中的状态数。
这部分将定理的证明分解为三个逻辑步骤。前两步证明了定理的“当且仅当”部分,第三步证明了“最小状态数”部分。
- 陈述 1 (正则 $\implies$ 有限等价类): 这是证明定理的 "=>" 方向。假设我们已经有了一个能识别 $L$ 的 DFA(因为 $L$ 是正则的),我们要说明等价类的数量不可能是无限的。
- 陈述 2 (有限等价类 $\implies$ 正则): 这是证明定理的 "<=" 方向。假设我们知道等价类数量是有限的,我们要说明 $L$ 必须是正则的。证明的方法是构造性的:我们直接用这些等价类作为蓝图,来建造一个能识别 $L$ 的 DFA。
- 陈述 3 (等价类数量 = 最小状态数): 这部分是锦上添花,但也是定理的精髓。它利用了前两步的结论。
- 证明分为两半:
- (下界) 最小状态数 $\ge$ 等价类数量: 这在引理 2.2 已经暗示了。从每个等价类挑一个代表,它们两两可区分,所以DFA 至少需要那么多状态。
- (上界) 最小状态数 $\le$ 等价类数量: 陈述 2 的构造过程给出了一个状态数恰好等于等价类数量的 DFA。既然存在这样一个 DFA,那么最小的那个 DFA 的状态数肯定不会超过这个数量。
- 结合上下界,就证明了两者相等。
这部分是证明的路线图。它将一个复杂的双向证明拆解成三个更易于管理的部分:证明必要性、证明充分性、以及确定精确数量。
在给出详细的证明步骤之前,先列出大纲有助于读者跟上逻辑的脉络。这是一种清晰的学术写作风格,让读者知道接下来要“去哪里”以及“为什么要去那里”。
这就像一个律师要证明“被告有罪当且仅当他有作案动机,且动机的数量等于犯罪团伙的最少人数”。
- 第一步 (有罪 $\implies$ 有动机): 检察官说,既然他被定罪了(正则),我们肯定能从他的行为中找到有限的作案动机(有限等价类)。
- 第二步 (有动机 $\implies$ 有罪): 辩护律师反驳,如果他只有有限的几种动机(有限等价类),我就可以构建一个模型(DFA)来解释他的所有行为,这说明他的行为模式是可预测的(正则的)。
- 第三步 (动机数量 = 团伙人数): 法官总结,我们发现,他的动机种类(等价类数量)正好和他犯罪所需的最少同伙人数(最小状态数)一样多。
4.1. 证明 1:正则 $\implies$ 有限等价类
📜 [原文12]
证明 1:我们将证明其逆否命题。假设 $\sim_{L}$ 有无限个等价类。这意味着存在一个包含无限个字符串的集合(每个等价类取一个),使得其中每两个字符串对于 $L$ 都是可区分的。现在根据引理 2.2,对于我们选取的任何数量 $k$,都不可能存在具有 $k$ 个状态且识别 $L$ 的 DFA。因此,不存在识别 $L$ 的 DFA(具有任何有限数量的状态),这意味着 $L$ 不是正则的。
这部分的证明非常巧妙,它没有直接证明“$L$ 是正则的 $\implies$ 等价类有限”,而是证明了其逆否命题 (Contrapositive)。
- 原命题: $P \implies Q$ (如果P成立,那么Q成立)
- 逆否命题: $\neg Q \implies \neg P$ (如果Q不成立,那么P不成立)
- 在逻辑上,原命题和其逆否命题是完全等价的。证明了逆否命题,就等于证明了原命题。
在这里:
- $P$: $L$ 是正则的。
- $Q$: $\sim_L$ 的等价类数量是有限的。
- $\neg P$: $L$ 不是正则的。
- $\neg Q$: $\sim_L$ 的等价类数量是无限的。
- 要证明的逆否命题是: 如果 $\sim_L$ 的等价类数量是无限的,那么 $L$ 不是正则的。
证明步骤:
- “假设 $\sim_{L}$ 有无限个等价类。”
- 这是逆否命题的起点。
- “这意味着存在一个包含无限个字符串的集合...使得其中每两个字符串...是可区分的。”
- 如果有无限个等价类,我们可以从每个等价类中挑选一个代表字符串。由于不同等价类中的字符串必然是可区分的,这样我们就得到了一个无限的、两两可区分的字符串集合。
- “现在根据引理 2.2...”
- 引理 2.2 说,如果有一个大小为 $k$ 的两两可区分集,那么 DFA 至少需要 $k$ 个状态。
- 现在我们有一个无限的两两可区分集。
- “对于我们选取的任何数量 $k$,都不可能存在具有 $k$ 个状态且识别 $L$ 的 DFA。”
- 我们可以从这个无限集合中,轻松取出 $k+1$ 个字符串。这 $k+1$ 个字符串构成了一个大小为 $k+1$ 的两两可区分集。
- 根据引理 2.2,任何识别 $L$ 的 DFA 都至少需要 $k+1$ 个状态。
- 所以,一个只有 $k$ 个状态的 DFA 绝对不可能识别 $L$。
- 这里的 $k$ 是任意一个正整数。
- “因此,不存在识别 $L$ 的 DFA(具有任何有限数量的状态)”
- 既然对于任何有限数 $k$,一个 $k$ 状态的 DFA 都不够用,那就意味着没有任何一个具有有限状态的 DFA 能够识别 $L$。
- “这意味着 $L$ 不是正则的。”
- 根据正则语言的定义(一个语言是正则的,当且仅当存在一个有限自动机识别它),如果不存在任何有限状态的 DFA,那么 $L$ 就不是正则的。
- 证明完成。我们成功证明了逆否命题,因此原命题也成立。
证明1的逻辑链是:无限等价类 $\implies$ 无限大的两两可区分集 $\implies$ DFA 需要无限个状态(根据引理2.2) $\implies$ 不存在这样的 DFA $\implies$ 语言非正则。这是一个非常简洁且有力的论证。
这部分完成了定理证明的第一步,即从“正则”推导出“有限等价类”。它本质上是引理 2.2 的一个直接应用和推广。
这好比说:“如果一个公司是正规的(正则),那么它的部门数量必须是有限的(有限等价类)。”
证明方法是反过来:“假设一个公司需要设立无限个部门(无限等价类)。每个部门都处理完全不同的业务(两两可区分)。那么,无论你给这个公司多大的办公楼(任意有限的 $k$ 个房间/状态),都永远不够用。因此,这样的公司根本无法建成(非正则)。”
4.2. 证明 2:有限等价类 $\implies$ 正则
📜 [原文13]
证明 2:如果 $\sim_{L}$ 有有限个等价类,我们将通过构造一个 DFA 来证明 $L$ 是正则的(这个 DFA 也将被用来证明第 3 部分)。
提醒一下,对于字符串 $x$,符号 $[x]$ 指的是包含 $x$ 的等价类,即 $[x]$ 是所有满足 $x \sim_{L} y$ 的字符串 $y$ 的集合。所以如果 $x \sim_{L} y$,那么 $[x]$ 和 $[y]$ 相等并表示同一个等价类。
一个重要的观察是,当 $x \sim_{L} y$ 时,对于任何字符串 $w$,我们有 $[x w]=[y w]$。这是因为如果 $x$ 和 $y$ 是不可区分的,那么对于所有字符串 $z \in \Sigma^{*}$,$x z \in L$ 当且仅当 $y z \in L$。这包括形式为 $z=w u$ 的字符串,其中 $u$ 是任何字符串。由于对于任何字符串 $u$,$x w u \in L$ 当且仅当 $y w u \in L$,我们知道 $x w \sim_{L} y w$, 所以 $[x w]=[y w]$。
考虑到这一点,我们为 $L$ 构造一个 DFA ( $Q, \Sigma, \delta, q_{0}, F$ ) 如下。
$Q$ 对于 $\sim_{L}$ 的每个等价类 $[x]$,我们将有一个对应的状态。
$q_{0}$ 起始状态是 $[\epsilon]$,即包含空字符串的等价类。
F 正如备注 2.4 中提到的,每个等价类包含的字符串要么全部在 $L$ 中,要么全部不在 $L$ 中。我们将 $F$ 定义为对应于 $x \in L$ 的等价类 $[x]$ 的状态集。
$\delta$ 对于一个状态/等价类 $[x]$ 和字符 $a \in \Sigma$,让 DFA 从 $[x]$ 转移到 $[x a]$,即 $\delta([x], a)=[x a]$。我们需要检查这个函数是否是良定义的(如果 $[x]=\left[x^{\prime}\right]$,我们不希望 $\delta([x], a)=[x a]$ 和 $\delta\left(\left[x^{\prime}\right], a\right)=\left[x^{\prime} a\right]$ 是两个不同的输出)。但确实,如前所述,如果 $[x]=\left[x^{\prime}\right]$,那么对于包括字符 $a$ 在内的所有字符串 $z$,都有 $[x z]=\left[x^{\prime} z\right]$。
现在我们已经给出了 DFA 的有效定义,我们的最后一步是证明这个 DFA 确实识别 $L$。令 $x=x_{1} x_{2} \ldots x_{n}$ 为任意字符串。将其输入 DFA,我们的 DFA 将从 $[\epsilon]$ 开始,然后移动到状态 $\left[x_{1}\right]$,然后移动到 $\left[x_{1} x_{2}\right]$,依此类推,直到结束于状态 $\left[x_{1} \ldots x_{n}\right]$。根据构造,$\left[x_{1} \ldots x_{n}\right]=[x]$ 是一个接受状态当且仅当 $x \in L$。我们的 DFA 确实识别 $L$,所以 $L$ 是正则的。
这是一个构造性证明 (Constructive Proof)。它通过直接搭建一个满足条件的 DFA 来证明 $L$ 的正则性。
构造蓝图:
- 核心思想: 让 DFA 的状态直接与 $\sim_L$ 的等价类一一对应。
- 前提: 我们假设等价类的数量是有限的,比如有 $k$ 个。
第一步:重要的观察 (为转移函数的良定义性铺路)
- 观察: 如果 $x$ 和 $y$ 在同一个等价类中 (即 $x \sim_L y$),那么把它们分别加上同一个后缀 $w$ 之后,得到的新字符串 $xw$ 和 $yw$ 也必然在同一个等价类中 (即 $xw \sim_L yw$)。
- 证明: $x \sim_L y$ 意味着对任意的 $z'$, $xz' \in L \iff yz' \in L$。
- 我们想证明 $xw \sim_L yw$。这需要证明对任意的 $u$, $xwu \in L \iff ywu \in L$。
- 我们可以令 $z' = wu$。由于 $z'$ 也是一个合法的字符串,根据 $x \sim_L y$ 的前提,我们有 $x(wu) \in L \iff y(wu) \in L$。
- 这正是我们要证明的。所以这个观察成立。
- 意义: 这个观察保证了等价类的演化是“一致的”。从一个等价类中的任何字符串出发,经过相同的输入,都会到达同一个目标等价类。这对于定义一个“确定性”的转移至关重要。
第二步:构造 DFA M = ($Q, \Sigma, \delta, q_0, F$)
这是 DFA 的五元组定义。
- $Q$ (状态集):
- 集合 $Q$ 就是所有 $\sim_L$ 等价类的集合。
- 因为我们假设等价类数量有限,所以 $Q$ 是一个有限集,满足 DFA 的要求。
- $\Sigma$ (字母表):
- 就是语言 $L$ 的字母表。
- $q_0$ (起始状态):
- 我们需要一个状态作为起点。最自然的选择是代表“什么都还没读”的那个等价类。
- “什么都还没读”就是空字符串 $\epsilon$。
- 所以,起始状态就是等价类 $[\epsilon]$。
- $F$ (接受状态集):
- 哪些状态(等价类)应该是接受状态?
- 根据备注 2.4,一个等价类要么全在 $L$ 中,要么全不在 $L$ 中。
- 所以,我们把那些“全在 $L$ 中”的等价类定义为接受状态。
- 形式化地,$F = \{ [x] \in Q \mid x \in L \}$。这个定义是有效的,因为如果 $[x]$ 在 $F$ 中,对于 $[x]$ 中的任何其他成员 $y$,由于 $x \sim_L y$,且 $x\in L$,我们不能有 $y \notin L$ (否则 $z=\epsilon$ 会区分它们)。所以 $y$ 也必须在 $L$ 中。
- $\delta$ (转移函数):
- 这是最关键的部分。$\delta$ 的功能是:给定一个当前状态(一个等价类 $[x]$)和一个输入字符 $a$,它应该转移到哪个新状态?
- 定义: $\delta([x], a) = [xa]$。
- 解释: 如果机器当前在代表了所有与 $x$ 不可区分的字符串的状态 $[x]$,在读入一个字符 $a$ 之后,它会进入一个新的状态,这个状态代表了所有与 $xa$ 不可区分的字符串。
- 良定义性 (Well-definedness): 这个定义有没有问题?状态是等价类,但我们是用等价类中的一个代表元素 $x$ 来定义转移的。如果我用同一个等价类的另一个代表 $x'$ 来定义,结果会一样吗?
- 假设 $[x] = [x']$,即 $x \sim_L x'$。
- 我们需要验证 $\delta([x], a)$ 是否等于 $\delta([x'], a)$。
- $\delta([x], a) = [xa]$
- $\delta([x'], a) = [x'a]$
- 我们需要验证 $[xa]$ 是否等于 $[x'a]$,即 $xa \sim_L x'a$。
- 这正是我们在“第一步:重要的观察”中证明的结论(令 $w=a$)。
- 因此,转移函数的定义是“良定义的”,它不依赖于我们选择哪个代表元素,结果都是唯一的。
第三步:证明构造的 DFA 识别 L
- 我们需要证明,对于任何字符串 $w$,将 $w$ 输入我们构造的 DFA $M$,当且仅当 $w \in L$ 时,$M$ 停在接受状态。
- 令 $w = a_1 a_2 \ldots a_n$。
- DFA 的计算过程:
- 从 $q_0 = [\epsilon]$ 开始。
- 读 $a_1$: 转移到 $\delta([\epsilon], a_1) = [\epsilon a_1] = [a_1]$。
- 读 $a_2$: 转移到 $\delta([a_1], a_2) = [a_1 a_2]$。
- ...
- 读 $a_n$: 转移到 $\delta([a_1\ldots a_{n-1}], a_n) = [a_1\ldots a_n]$。
- 最终状态: 读完整个字符串 $w$ 后,DFA 停在状态 $[w]$。
- 接受条件: 根据我们对 $F$ 的定义,状态 $[w]$ 是接受状态当且仅当 $w \in L$。
- 结论: 这个 DFA $M$ 准确地识别了语言 $L$。因为我们成功构造了一个有限状态的 DFA,$L$ 根据定义是正则的。
证明2的核心是构造。它将抽象的等价类实体化为 DFA 的状态,将等价类的演化规则(追加字符)实体化为 DFA 的转移函数。通过证明这个构造是有效且正确的,它雄辩地证明了只要等价类有限,语言就必然正则。
这部分是 Myhill-Nerode 定理证明的核心和最精彩的部分。它不仅完成了逻辑推导,还给出了一个从语言的等价关系直接生成 DFA 的具体方法。这个构造方法本身就极具价值,是 DFA 最小化算法的理论基础。
这就像用乐高积木搭建一个模型。
- 有限等价类: 你手头有有限种类的乐高积木块。
- 构造 DFA:
- 状态: 每一种积木块,就是一种状态。
- 起始状态: “空”积木块(代表还没开始拼)就是起始状态 $[\epsilon]$。
- 接受状态: 那些本身就能构成一个完整小作品(字符串在 $L$ 中)的积木块,被涂上金色,成为接受状态。
- 转移函数: 你制定了一个拼接规则,“A类型积木”旁边接一个“红色小方块”,总会变成“B类型积木”。这个规则之所以有效,是因为无论你拿哪一个具体的“A类型积木”来拼,结果都是一样的(良定义性)。
- 证明: 通过这个拼接规则,你拼出来的任何一个作品(处理完一个字符串),最终的形态(最终状态)正好就决定了它是不是一个合格的作品(是否在 $L$ 中)。
4.3. 证明 3:等价类数量 = 最小 DFA 状态数
📜 [原文14]
证明 3:上面我们为 $L$ 构造了一个 DFA,其状态数与 $\sim_{L}$ 的等价类数量相同。此外,根据引理 2.2,不可能存在任何识别 $L$ 且状态数少于等价类数量的 DFA。因此,上面构造的 DFA 是 $L$ 的最小 DFA。
这部分证明非常简洁,因为它综合了前面的所有成果。它通过“夹逼”的方式证明等式。
- 证明:最小状态数 $\le$ 等价类数量
- 在“证明 2”中,我们构造了一个 DFA,我们称之为 $M_{MN}$ (Myhill-Nerode automaton)。
- 这个 $M_{MN}$ 的状态数恰好等于 $\sim_L$ 的等价类数量。
- 既然存在一个能够识别 $L$ 的 DFA,它的状态数是 $|Q_{M_{MN}}| = (\text{等价类数量})$,那么,所有能识别 $L$ 的 DFA 中,那个状态最少的(即最小 DFA),其状态数肯定不会超过这个值。
- 所以,$(\text{最小状态数}) \le (\text{等价类数量})$。
- 证明:最小状态数 $\ge$ 等价类数量
- 令 $k$ 为 $\sim_L$ 的等价类数量。
- 我们可以从这 $k$ 个不同的等价类中,每个取出一个代表字符串,形成一个集合 $S = \{x_1, x_2, \ldots, x_k\}$。
- 因为这些字符串来自不同的等价类,所以它们两两可区分。
- 我们得到了一个大小为 $k$ 的两两可区分集。
- 根据引理 2.2,任何识别 $L$ 的 DFA 的状态数必须至少为 $k$。
- 这当然也包括最小 DFA。
- 所以,$(\text{最小状态数}) \ge k = (\text{等价类数量})$。
- 结论
- 我们已经证明了:
- $(\text{最小状态数}) \le (\text{等价类数量})$
- $(\text{最小状态数}) \ge (\text{等价类数量})$
- 唯一能同时满足这两个不等式的情况就是相等。
- 因此,$(\text{最小状态数}) = (\text{等价类数量})$。
- 补充结论
- “因此,上面构造的 DFA 是 L 的最小 DFA。”
- 我们构造的 $M_{MN}$ 的状态数等于等价类数量。
- 我们又证明了最小 DFA 的状态数也等于等价类数量。
- 所以,我们构造的 $M_{MN}$ 的状态数就是最小状态数。
- 在自动机理论中,可以进一步证明,任何具有最小状态数的 DFA 在结构上都是唯一的(同构的)。这意味着我们构造的 $M_{MN}$ 不仅状态数最小,它本质上就是那个唯一的最小 DFA。
证明3利用“证明2”构造的 DFA 建立了一个上界,利用“引理2.2”建立了一个下界。通过上下夹逼,精确地证明了等价类的数量就等于最小 DFA 的状态数,并且“证明2”中构造的那个 DFA 正是最小 DFA 的一个实例。
这部分完成了整个定理的证明,将定理的所有部分都严密地串联了起来。它不仅确认了数量上的相等,还赋予了在“证明2”中构造的DFA一个特殊的地位——它就是我们能为这个语言找到的最高效的 DFA。
你想知道建造一座桥梁(识别语言 $L$)最少需要多少个桥墩(最小状态数)。
- 工程师A(构造法,证明2):他用一种叫“等价类”的特殊材料造了一座桥,用了 $k$ 个桥墩。他说:“你看,我用 $k$ 个桥墩就把桥造好了。所以,最少需要的桥墩数肯定不会超过 $k$。” (提供了上界)
- 地质学家B(引理2.2):他勘测了河床,发现河里有 $k$ 个必须支撑的特殊地质点(两两可区分集)。他说:“无论你怎么设计,这 $k$ 个点每个点上都必须放一个桥墩,否则桥会塌。所以,你最少也得用 $k$ 个桥墩。” (提供了下界)
- 结论(证明3):既然最少不少于 $k$,最多不过 $k$,那最少就正好是 $k$。而且工程师 A 造的那座桥,不多不少正好用了 $k$ 个桥墩,说明他的设计就是最省料的(最小 DFA)。
4.4. Myhill-Nerode 定理的使用
📜 [原文15]
使用 Myhill-Nerode 定理。Myhill-Nerode 定理对于正则语言非常有用,它允许我们将语言分解为最基本的片段,即等价类,这些等价类对应于该语言的最小 DFA。上面讨论的思想也是高效 DFA 最小化算法的核心(我们在这里不作介绍)。关键思想是,如上所述,在语言的任何 DFA 中,所有最终处于同一状态的字符串必须属于同一个等价类。另一方面,最终处于两个不同状态的字符串可能仍然属于同一个等价类。在这种情况下,这两个状态被称为是等价的,并且可以在不改变 DFA 行为的情况下合并为一个状态。
Myhill-Nerode 定理在证明语言 $L$ 不是正则的方面也非常有用。为此,我们需要证明等价类的数量是无限的。这可以通过找出无限多个字符串,使得其中没有两个是等价的(即,每对字符串对于 $L$ 都是可区分的)来实现。
这部分总结了 Myhill-Nerode 定理的两个主要应用方向。
应用一:分析和优化正则语言
- “将语言分解为最基本的片段,即等价类”:
- Myhill-Nerode 定理提供了一个独特的视角,让我们不从字符串本身,而是从“等价类”这个更高层次的抽象来理解语言。等价类是语言的“基因”或“原子成分”。
- “这些等价类对应于该语言的最小 DFA”:
- 等价类和最小 DFA 的状态之间存在一一对应的关系。这意味着,通过分析等价类,我们就能洞察最小 DFA 的结构和复杂性。
- DFA 最小化算法的核心:
- 虽然讲义不详细介绍,但它指明了方向。一个普通的、可能有冗余的 DFA 是怎么最小化的?
- “所有最终处于同一状态的字符串必须属于同一个等价类”: 这是证明1的推论。一个状态内的字符串,它们的未来命运被绑定了,所以它们必须不可区分。
- “最终处于两个不同状态的字符串可能仍然属于同一个等价类”: 这是DFA 存在冗余的关键!一个非最小的 DFA 可能用了两个或多个状态去做了本该一个状态就能做的事情。比如,状态 $q_1$ 和 $q_2$ 是不同的,但所有能到达 $q_1$ 的字符串,和所有能到达 $q_2$ 的字符串,它们其实都属于同一个大的等价类。
- “这两个状态被称为是等价的,并且可以...合并为一个状态”: 这就是最小化算法的核心操作。算法会去寻找并合并这些“等价的状态”,直到每个状态都恰好对应一个 Myhill-Nerode 等价类,此时 DFA 就最小化了。
应用二:证明语言非正则
- “证明等价类的数量是无限的”:
- 根据定理的“当且仅当”部分,语言非正则 $\iff$ 等价类数量无限。
- 所以,证明非正则性的任务,就转化为了证明等价类数量是无限的。
- “这可以通过找出无限多个字符串,使得其中没有两个是等价的...来实现”:
- 这是证明等价类数量无限的具体操作方法。
- 我们只需要构造一个无限的字符串集合 $S = \{s_1, s_2, s_3, \ldots\}$。
- 并且证明,对于这个集合里任意两个不同的成员 $s_i$ 和 $s_j$,它们都是可区分的 ($s_i \not\sim_L s_j$)。
- 如果能做到这一点,就说明每个 $s_i$ 都必须属于一个独一无二的等价类。
- 既然有无限个这样的 $s_i$,那就必须有无限个等价类。
- 任务完成,语言被证明为非正则。这比泵引理更直接,有时也更简单。
本段指出了 Myhill-Nerode 定理的两大用武之地:
- 对内 (分析正则语言): 理解语言的原子结构(等价类),并指导如何将一个臃肿的 DFA “瘦身”成最高效的最小 DFA。
- 对外 (判断非正则语言): 提供一个强大的“无限性”论证工具,通过构造一个无限的可区分集来证明一个语言不是正则的。
在理论证明之后,这部分将理论与实践联系起来,告诉学生“我们学这个到底能干嘛?”。它为接下来的具体例子部分设定了议程,让学生带着明确的目标去阅读示例。
Myhill-Nerode 定理就像一个细胞生物学家研究生物体。
- 应用一 (分析): 对于一个已知的生物(正则语言),他可以用定理来识别出构成这个生物的所有最基本的细胞种类(等价类),并理解这些细胞如何构成最高效的器官(最小 DFA)。他还可以指导外科医生(最小化算法)如何切除多余的组织(冗余状态)。
- 应用二 (鉴定): 面对一个未知的生物(语言),他通过寻找是否该生物含有无限多种类的细胞(无限等价类)。如果找到了,他就可以断定:“这不是一个我们已知的、结构有限的简单生物(非正则)。”
55. 例子
这部分将通过具体的例子来演示如何应用 Myhill-Nerode 定理。
5.1. 正则语言的例子
51.1. 例 3.1: 语言 $L=\left\{01^{n} \mid n \geq 0\right\}$
📜 [原文16]
例 3.1。令 $L=\left\{01^{n} \mid n \geq 0\right\}$。等价类是什么?首先注意 $\varepsilon$ 与 $\{0,1\}^{*}$ 中的所有其他字符串都是可区分的,因此它属于它自己的等价类。事实上,如果 $w$ 是一个非空二进制字符串,那么 $w 0$ 不在 $L$ 中,但 $\epsilon 0=0$ 在 $L$ 中。另一个等价类由不在正确“格式”中的字符串组成,因为那样无论添加什么扩展 $z$,字符串仍然不在语言中。这将包括以 1 开头的字符串和包含多个 0 的字符串。第三个等价类由 $L$ 中的字符串组成(你明白为什么对于这个语言,$L$ 中的所有字符串都在同一个等价类中吗?)。这些是仅有的 3 个等价类,因为根据 $L$ 的定义,每个字符串要么在 $L$ 中,要么是空的,要么以 1 开头,或者有多个 0。由于有 3 个等价类,我们知道 $L$ 是正则的,并且有一个具有 3 个状态的最小 DFA。
这个例子分析一个简单的正则语言 $L = \{0, 01, 011, 0111, \ldots\}$,并找出它的等价类。
第一步:识别不同的“命运”类别
我们要思考,一个字符串在被处理的过程中,有哪些“本质不同”的状态?
- 刚开始,什么都没读: 这是字符串 $\epsilon$。它的未来是充满希望的,如果接下来读到一个 '0',就走上了通往成功的正确道路。
- 走在正确的路上: 已经读了一个 '0',或者 '0' 后面跟了一些 '1'。比如 "0", "01", "011"。这些字符串本身就在语言 $L$ 中。它们接下来的命运是什么?如果再读一个 '1',它们依然在正确的路上。如果读一个 '0',就失败了。
- 已经走错了路,万劫不复: 字符串的格式已经错了,比如以 '1' 开头 ("1", "10"),或者包含了多个 '0' ("00", "010")。一旦到了这个地步,无论后面再追加什么字符串 $z$,最终结果都不可能再属于 $L$ 了。这是一个“死亡”状态。
第二步:将这些类别形式化为等价类
- 等价类 1: $[\epsilon]$ (初始状态)
- 这个类只包含空字符串 $\epsilon$。
- 为什么它自成一类?因为它和任何非空字符串 $w$ 都是可区分的。
- 证明: 取 $z=0$。$ \epsilon z = 0 \in L$。但对于任何非空 $w$,如果 $w$ 以0开头,则 $w0$ 含有两个0,不在L中;如果$w$以1开头,则$w0$以1开头,不在L中。所以 $w0 \notin L$。因此 $\epsilon$ 和任何非空 $w$ 可区分。
- 等价类 2: $[1]$ (死亡状态/垃圾桶状态)
- 这个类包含所有“格式错误”的字符串。
- 比如:以 '1' 开头的字符串 ("1", "10", "11", ...),包含多于一个 '0' 的字符串 ("00", "010", "001", ...),在 '0' 之前有 '1' 的字符串(这是以1开头的情况)。
- 为什么它们都属于一个等价类?因为它们都不可区分。
- 证明: 设 $x, y$ 都是格式错误的字符串。对于任何后缀 $z$,$xz$ 和 $yz$ 的格式也一定是错误的(比如 $x$ 有两个0,那么 $xz$ 至少有两个0),所以 $xz \notin L$ 且 $yz \notin L$。它们的命运完全相同(永远被拒绝)。因此它们不可区分。我们用 "1" 作为这个等价类的代表,记作 $[1]$(也可以用 "00" 等)。
- 等价类 3: $[0]$ (接受状态)
- 这个类包含所有在语言 $L$ 中的字符串。即 $L$ 本身: $\{0, 01, 011, \ldots\}$。
- 为什么它们都属于同一个等价类?
- 证明: 设 $x, y$ 都是 $L$ 中的字符串(比如 $x=01^i, y=01^j$)。对于任何后缀 $z$:
- 如果 $z$ 的形式是 $1^k$ (任意数量的1),那么 $xz = 01^{i+k}$ 也在 $L$ 中,$yz = 01^{j+k}$ 也在 $L$ 中。命运相同。
- 如果 $z$ 包含 '0' 或者不是全由 '1' 组成,那么 $xz$ 和 $yz$ 都会包含第二个 '0' 或其他非法字符,导致它们都不在 $L$ 中。命运也相同。
- 因此,任何两个 $L$ 中的字符串都是不可区分的。它们构成一个等价类。我们用 "0" 作为代表,记作 $[0]$。
第三步:应用 Myhill-Nerode 定理
- 我们找到了 3 个等价类: $[\epsilon]$, $[1]$, $[0]$。
- 等价类的数量是 3,是有限的。
- 结论:
- 语言 $L$ 是正则的。
- 识别 $L$ 的最小 DFA 恰好有 3 个状态。这三个状态就分别对应这三个等价类。
📜 [原文17]
另一方面,考虑以下最小 DFA:
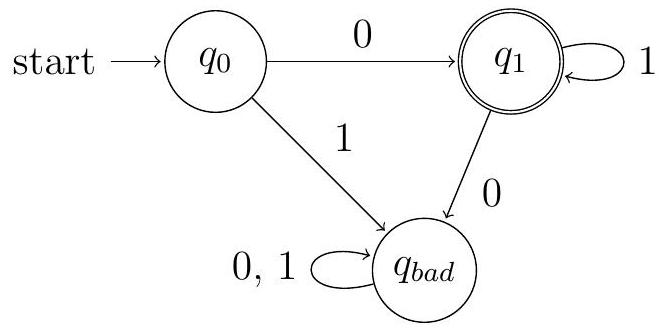
现在更清楚等价类如何与状态相关联:每个等价类仅由导致 DFA 处于同一状态的字符串组成。事实上,初始状态没有指向它的箭头,因此仅对应于字符串 $\epsilon$。状态 $q_{\text {bad }}$ 指的是具有“不正确格式”的字符串,DFA 认同这些字符串是以 1 开头或具有多个 0 的字符串。最后,状态 $q_{1}$ 指的是语言中的字符串。事实上,$L$ 本身完全包含在一个等价类中,这一事实对应于最小 DFA 只有一个接受状态这一事实。
这部分通过展示一个具体的 DFA 来验证我们之前的等价类分析。
- DFA 状态与等价类的对应:
- 初始状态 (unnamed): 这个状态只在开始时处于,没有任何箭头指向它。这完美对应了等价类 $[\epsilon]$,它只包含空字符串。当读入 '0',离开此状态;读入 '1',也离开此状态。之后再也回不来。
- 状态 $q_1$ (接受状态):
- 如何到达?从初始状态读 '0'。所以字符串 "0" 到达 $q_1$。
- 在 $q_1$ 时读 '1',会回到 $q_1$。所以 "01", "011", ... 都停在 $q_1$。
- 所有停在 $q_1$ 的字符串,恰好就是语言 $L$ 中的所有字符串。
- 这完美对应了等价类 $[0]$。
- 状态 $q_{bad}$ (垃圾桶状态):
- 如何到达?从初始状态读 '1';或从 $q_1$ 读 '0';或在 $q_{bad}$ 时读任何字符。
- 这包括了所有以 '1' 开头的字符串,以及所有包含多个 '0' 的字符串。
- 一旦进入 $q_{bad}$,就永远出不去了。
- 这完美对应了“格式错误”的等价类 $[1]$。
- “$L$ 本身完全包含在一个等价类中,这一事实对应于最小 DFA 只有一个接受状态这一事实”:
- 这是一个有趣的观察。因为所有 $L$ 中的字符串都是不可区分的,它们形成了一个大的等价类。所以在最小 DFA 中,它们都必须被映射到同一个状态。由于它们是接受字符串,这个状态必须是接受状态。如果最小 DFA 有两个或多个接受状态 $q_A, q_B$,那么到达 $q_A$ 的字符串和到达 $q_B$ 的字符串就必然是可区分的,从而它们属于不同的等价类。反之,如果所有 $L$ 里的字符串都属于同一个等价类,那么在最小 DFA 里它们只能对应一个状态,因此只有一个接受状态。
这个例子完美地展示了理论和实践的统一。我们通过抽象推理找出的3个等价类,与一个具体、直观的最小 DFA 的3个状态精确地一一对应。这让我们对等价类是什么有了更具体的感受:它就是最小 DFA 的状态在语言层面的“投影”。
51.2. 例 3.2: 语言 $L_{n}=\left\{w \in\{0,1\}^{*} \mid w \text{ 中的倒数第 } n \text{ 个符号是 } 1\right\}$
📜 [原文18]
例 3.2。对于任何 $n \in \mathbb{N}$,定义语言
我们证明对于任何 $n$,语言 $L_{n}$ 是正则的,并且识别它的最小 DFA 有 $2^{n}$ 个状态。
长度为 $n$ 的字符串有 $2^{n}$ 个。我们将证明它们中的每一对都有一个区别扩展,因此每一个相对于 $\sim_{L_{n}}$ 都属于不同的等价类。考虑任意两个字符串 $w=w_{1} \ldots w_{n} \in\{0,1\}^{n}$ 和 $w^{\prime}=w_{1}^{\prime} \ldots w_{n}^{\prime} \in\{0,1\}^{n}$,其中 $w \neq w^{\prime}$。由于 $w \neq w^{\prime}$,它们必须在至少一个位置上不同。取某个 $i \in\{1, \ldots, n\}$ 使得 $w_{i} \neq w_{i}^{\prime}$,这意味着 $w_{i}, w_{i}^{\prime}$ 中一个是 0,另一个是 1。选择长度为 $i-1$ 的扩展 $z$,例如,取 $z=0^{i-1}$。$w z$ 中的倒数第 $n$ 位是 $w_{i}$,$w^{\prime} z$ 中的倒数第 $n$ 位是 $w_{i}^{\prime}$,其中一个是 0,一个是 1。因此,$w z, w^{\prime} z$ 中有一个在 $L_{n}$ 中,另一个不在,所以 $w, w^{\prime}$ 是可区分的。
我们已经证明 $L_{n}$ 至少有 $2^{n}$ 个等价类(长度为 $n$ 的每个字符串对应一个)。我们现在声称 $L_{n}$ 恰好有 $2^{n}$ 个等价类。事实上,不难看出,每个长度为 $|w|>n$ 的字符串 $w$ 都等价于它的 $n$ 位后缀,而每个长度为 $|w|<n$ 的字符串 $w$ 都等价于 $n$ 位字符串 $0^{n-|w|} w$。因此,$L_{n}$ 的最小 DFA 恰好有 $2^{n}$ 个状态。
我们注意到,相比之下,对于任何 $n$,都存在一个具有 $n+1$ 个状态的 NFA 用于识别 $L_{n}$。
这个例子非常经典,它展示了 DFA 和 NFA 之间著名的指数级差距,并用 Myhill-Nerode 定理给出了 DFA 状态数的精确证明。
语言 $L_n$ 的直觉:
- 这个语言关心的是“倒数第 $n$ 位”。为了判断一个字符串 $w$ 是否在 $L_n$ 中,你至少需要看到 $n$ 个字符。当你读完整个字符串后,你需要“记住”最后 $n$ 个字符是什么,才能做出判断。
- 这暗示了 DFA 的状态必须编码关于“最近 $n$ 个字符”的信息。
证明部分一:证明至少有 $2^n$ 个等价类
- 目标: 找到一个大小为 $2^n$ 的两两可区分集。
- 候选集合: 最自然的候选者是所有长度为 $n$ 的二进制字符串。这个集合正好有 $2^n$ 个成员。例如,当 $n=3$ 时,集合是 $\{000, 001, 010, 011, 100, 101, 110, 111\}$。
- 证明两两可区分:
- 任取其中两个不同的字符串,记作 $w=w_1 w_2 \ldots w_n$ 和 $w'=w'_1 w'_2 \ldots w'_n$。
- 因为 $w \neq w'$,它们至少在某一位 $i$ 上不同。即 $w_i \neq w'_i$。
- 如何构造区别扩展 $z$?: 我们的目标是把这个不同的第 $i$ 位“推到”倒数第 $n$ 位去。
- 当前 $w_i$ 是 $w$ 的第 $i$ 位。在它后面追加一个长度为 $i-1$ 的字符串 $z$,那么 $w_i$ 就变成了新字符串 $wz$ 的第 $i$ 位,同时也是倒数第 $(n-i)+(i-1)+1 = n$ 位!
- 选择 $z$: 我们选择 $z = 0^{i-1}$ ( $i-1$ 个0)。
- 验证:
- 考虑 $wz = w_1 \ldots w_i \ldots w_n 0^{i-1}$。它的总长度是 $n + (i-1)$。它的倒数第 $n$ 位是哪个字符?从后往前数,先跳过 $i-1$ 个0,再跳过 $w_n, w_{n-1}, \ldots, w_{i+1}$ (共 $n-i$ 个字符),下一个就是 $w_i$。所以 $wz$ 的倒数第 $n$ 位是 $w_i$。
- 同理,$w'z$ 的倒数第 $n$ 位是 $w'_i$。
- 结论: 因为 $w_i \neq w'_i$,所以一个为 '1',一个为 '0'。这意味着 $wz$ 和 $w'z$ 中,一个在 $L_n$ 中,另一个不在。
- 因此,$w$ 和 $w'$ 是可区分的。
- 小结: 由于所有 $2^n$ 个长度为 $n$ 的字符串两两可区分,它们必须分属于 $2^n$ 个不同的等价类。所以,等价类的数量至少是 $2^n$。根据 Myhill-Nerode 定理,最小 DFA 的状态数至少是 $2^n$。
证明部分二:证明恰好有 $2^n$ 个等价类
- 目标: 证明任何字符串都与某个长度为 $n$ 的字符串不可区分。如果能证明这一点,就说明所有的字符串都可以被归入由长度为 $n$ 的字符串所代表的这 $2^n$ 个等价类中,不存在更多的等价类了。
- 直觉: 要判断一个长字符串 $wz$ 是否在 $L_n$ 中,重要的是 $wz$ 的最后 $n$ 个字符。而 $wz$ 的最后 $n$ 个字符,只取决于 $z$ 以及 $w$ 的最后若干个字符。更准确地说,对于任何字符串 $x$,它的“未来命运”完全由它的长度为n的后缀所决定。
- 形式化论证:
- 情况 1: $|w| > n$:
- 设 $w$ 的长度为 $n$ 的后缀是 $s$。即 $w=us$ 且 $|s|=n$。我们声称 $w \sim_{L_n} s$。
- 为什么?对于任何后缀 $z$,我们要比较 $wz$ 和 $sz$。
- $wz$ 是否在 $L_n$ 中,取决于 $wz$ 的最后 $n$ 个字符。这 $n$ 个字符完全由 $s$ 和 $z$ 决定。
- $sz$ 是否在 $L_n$ 中,也取决于 $sz$ 的最后 $n$ 个字符。
- $wz$ 和 $sz$ 的最后 $n$ 个字符是完全一样的!(因为 $w$ 中 $s$ 前面的 $u$ 部分已经被“挤掉”了,不影响最后 $n$ 位)。
- 所以,$wz \in L_n \iff sz \in L_n$。它们不可区分。
- 情况 2: $|w| < n$:
- 设 $w'$ 是在 $w$ 前面补上 $n-|w|$ 个 '0' 得到的字符串,即 $w' = 0^{n-|w|}w$。$|w'|=n$。我们声称 $w \sim_{L_n} w'$。
- 为什么?对于任何后缀 $z$,$wz$ 和 $w'z$ 的命运取决于它们各自的倒数第 $n$ 位。而这两个位置的字符是相同的(都来自于 $w$ 或者补上的 '0')。
- 结论: 任何字符串都与一个长度为 $n$ 的字符串等价。这意味着所有的等价类都可以由长度为 $n$ 的 $2^n$ 个字符串来代表。因此,等价类的数量恰好是 $2^n$。
最终结论:
- $L_n$ 的等价类数量是 $2^n$。
- 因为这个数是有限的,所以 $L_n$ 是正则的。
- 识别 $L_n$ 的最小 DFA 恰好有 $2^n$ 个状态。每个状态对应一个可能的长度为 $n$ 的后缀。
与 NFA 的对比:
- 识别 $L_n$ 的 NFA 可以非常简单。它“猜测”哪一位是倒数第 $n$ 位。
- NFA 构造:
- 一个初始状态 $q_0$。
- 在 $q_0$ 看到 '1' 时,可以非确定性地跳转到一个特殊的状态 $q_1$(这代表“我猜这个1是倒数第n位”),也可以留在 $q_0$。看到 '0' 只能留在 $q_0$。
- 从 $q_1$ 开始,需要再读 $n-1$ 个字符。我们用 $n-1$ 个状态 $q_2, \ldots, q_n$ 来“数”这 $n-1$ 步。
- $q_n$ 是唯一的接受状态。
- 总状态数是 $q_0, q_1, \ldots, q_n$,共 $n+1$ 个。
- 对比: DFA 需要 $2^n$ 个状态,而 NFA 只需要 $n+1$ 个。当 $n$ 很大时,这个差距是巨大的。这说明了 NFA 在某些问题上的简洁表达能力。
- $$ L_{n}=\left\{w \in\{0,1\}^{*} \mid w \text{ 中的倒数第 } n \text{ 个符号是 } 1\right\} $$
- $L_n$: 一个依赖于参数 $n$ 的语言。
- $w \in \{0,1\}^*$: $w$ 是一个由0和1组成的任意字符串。
- |: 读作“使得”(such that),后面是字符串 $w$ 必须满足的条件。
- “$w$ 中的倒数第 $n$ 个符号是 1”: 如果 $w=a_1 a_2 \ldots a_k$,这个条件是 $k \ge n$ 并且 $a_{k-n+1}=1$。
[具体数值示例 ($n=2$)]
- 语言: $L_2 = \{w \mid \text{倒数第2位是1}\}$。例如, "10", "11", "010", "111" 都在 $L_2$ 中。
- 最小 DFA 状态数预测: $2^2 = 4$。
- 找两两可区分集: 集合是所有长度为2的字符串 $\{00, 01, 10, 11\}$。
- 比较 $w=00$ 和 $w'=01$:
- $i=2$ 时不同 ($w_2=0, w'_2=1$)
- 选 $z=0^{2-1}=0$。
- $wz=000$。倒数第2位是0,不在 $L_2$ 中。
- $w'z=010$。倒数第2位是1,在 $L_2$ 中。
- 可区分。
- 比较 $w=01$ 和 $w'=11$:
- $i=1$ 时不同 ($w_1=0, w'_1=1$)
- 选 $z=0^{1-1}=\epsilon$。
- $wz=01$。倒数第2位是0,不在 $L_2$ 中。(注意:长度为2,倒数第2位就是第1位)
- $w'z=11$。倒数第2位是1,在 $L_2$ 中。
- 可区分。
- 等价类代表: $\{00, 01, 10, 11\}$。
- $[00]$: 所有以 "00" 结尾的字符串 (e.g., "00", "100", ...)。
- $[01]$: 所有以 "01" 结尾的字符串 (e.g., "01", "101", ...)。
- $[10]$: 所有以 "10" 结尾的字符串 (e.g., "10", "010", ...)。
- $[11]$: 所有以 "11" 结尾的字符串 (e.g., "11", "011", ...)。
- 最小 DFA 状态: 确实需要4个状态,每个状态记住最后两位是什么。
- 状态 $q_{00}$ (代表后缀是00)
- 状态 $q_{01}$ (代表后缀是01)
- 状态 $q_{10}$ (代表后缀是10) - 接受状态
- 状态 $q_{11}$ (代表后缀是11) - 接受状态
- (还需要处理长度小于2的初始状态,完整的DFA会更复杂一些,但核心是这4个状态)
5.2. 非正则语言的例子
📜 [原文19]
下面是两个我们在课堂上已经使用泵引理证明过不是正则的例子。在这里,我们使用 Myhill-Nerode 定理重新证明它们。在下一份讲义中,我们将看到一些非正则语言的例子,在这些例子中,使用泵引理来证明是很困难或不可能的,但使用 Myhill-Nerode 定理却有效。
这部分引出了 Myhill-Nerode 定理的第二个主要用途:证明语言的非正则性。它预告了将要用新方法解决老问题,并暗示了这个新方法的威力可能比泵引理更强。
证明非正则的策略回顾:
- 根据 Myhill-Nerode 定理,语言非正则 $\iff$ 等价类数量无限。
- 我们的任务就是去证明等价类数量是无限的。
- 具体方法: 构造一个无限的字符串集合 $S = \{s_1, s_2, s_3, \ldots\}$,并证明集合中任意两个不同的元素 $s_i, s_j$ 都是可区分的。
52.1. 例 3.3: 语言 $L=\{w \in\{0,1\}^{*} \mid w \text{ 中 0 的数量与 } 1 \text{ 的数量相同}\}$
📜 [原文20]
例 3.3。令 $L=\{w \in\{0,1\}^{*} \mid w \text{ 中 0 的数量与 } 1 \text{ 的数量相同}\}$。我们将证明 $L$ 有无限多个等价类,因此不是正则的。考虑所有形式为 $0^{k}$ 的字符串,对于任何 $k \geq 0$。这些是无限多个字符串,我们声称其中没有两个是等价的。事实上,对于任何 $k \neq j$,考虑字符串 $x=0^{k}$ 和 $y=0^{j}$。选择扩展 $z=1^{k}$ 得到 $x z=0^{k} 1^{k}$,它在 $L$ 中,而 $y z=0^{j} 1^{k}$ 不在 $L$ 中。因此,$L$ 的每个等价类最多只能包含一个形式为 $0^{k}$ 的字符串,所以必须有无限多个等价类。所以 $L$ 不是正则的。
- 语言: $L$ 是所有 0 和 1 数量相等的字符串的集合。例如, $\epsilon, 01, 10, 0011, 0101$ 都在 $L$ 中。
- 目标: 证明 $L$ 非正则。
- 策略: 找一个无限的、两两可区分的集合。
- 候选集合: 一个简单的无限集合是 $S = \{ \epsilon, 0, 00, 000, \ldots, 0^k, \ldots \}$。
- 证明两两可区分:
- 从 $S$ 中任取两个不同的字符串,令它们为 $x=0^k$ 和 $y=0^j$,其中 $k \neq j$ (假设 $k,j \ge 0$)。
- 我们需要找一个区别扩展 $z$。
- 直觉: $x$ "欠"了 $k$ 个 '1' 才能达到平衡。$y$ "欠"了 $j$ 个 '1'。我们可以通过添加适量的 '1' 来“帮助”其中一个达到平衡,而另一个则不能。
- 选择 $z$: 我们选择 $z=1^k$。这个 $z$ 是为 $x$ "量身定做"的。
- 验证:
- 考虑 $xz = 0^k 1^k$。这里 '0' 的数量是 $k$,'1' 的数量也是 $k$。它们相等。所以 $xz \in L$。
- 考虑 $yz = 0^j 1^k$。这里 '0' 的数量是 $j$,'1' 的数量是 $k$。因为 $j \neq k$,所以 '0' 和 '1' 的数量不相等。所以 $yz \notin L$。
- 结论: $xz$ 和 $yz$ 的命运不同。因此,$x=0^k$ 和 $y=0^j$ 是可区分的。
- 最终论证:
- 我们已经证明,对于集合 $S=\{0^k \mid k \ge 0\}$ 中的任意两个不同元素,它们都是可区分的。
- 这意味着它们必须属于不同的等价类。
- 由于集合 $S$ 是无限的,所以必然存在无限多个等价类。
- 根据 Myhill-Nerode 定理,如果等价类数量是无限的,那么语言 $L$ 就不是正则的。
- 区别扩展的选择: 选择 $z=1^k$ 是关键。如果错误地选择了 $z=1^j$,那么 $y$ 会被平衡,而 $x$ 不会,同样可以证明。关键是要根据其中一个字符串来定制区别扩展。
- 与泵引理的比较: 用泵引理证明此问题,需要选择一个足够长的字符串 $s \in L$ (如 $s=0^p 1^p$),然后对 $s$ 的一部分(只能是 $0^i$)进行“泵”,导致 0 和 1 的数量失衡。Myhill-Nerode 的方法感觉更直接,它直接指出了为什么 DFA 无法识别这个语言:DFA 必须能够区分无限多种“欠债”状态(欠1个1,欠2个1,欠3个1 ...),这需要无限个状态。
52.2. 例 3.4: 语言 $L=\left\{w \in\{a, b\}^{n} \mid w \text{ 是回文串}\right\}$
📜 [原文21]
例 3.4。令 $L=\left\{w \in\{a, b\}^{*} \mid w \text{ 是回文串}\right\}$。我们将通过证明该语言具有无限多个等价类来证明它不是正则的。同样,我们可以通过找出一个无限字符串集合的例子来实现这一点,使得其中没有两个字符串是等价的。我们考虑所有形式为 $a^{k}$($k \geq 0$)的字符串,并证明其中没有两个是等价的。对于任何 $k \neq j$,取 $x=a^{k}, y=a^{j}$。选择扩展 $z=b a^{k}$ 得到 $x z=a^{k} b a^{k} \in L$,而 $y z=a^{j} b a^{k} \notin L$。因此,所有这些对 $a^{k}, a^{j}$ 都是可区分的,我们有无限多个等价类,所以 $L$ 不是正则的。
- 语言: $L$ 是所有回文串的集合。回文串是指正读和反读都一样的字符串,例如 $\epsilon, a, b, aa, bb, aba, bab, abba$。
- 目标: 证明 $L$ 非正则。
- 策略: 找一个无限的、两两可区分的集合。
- 候选集合: 同样,一个简单的无限集合是 $S = \{ \epsilon, a, aa, aaa, \ldots, a^k, \ldots \}$。
- 证明两两可区分:
- 从 $S$ 中任取两个不同的字符串,令它们为 $x=a^k$ 和 $y=a^j$,其中 $k \neq j$ (假设 $k,j \ge 0$)。
- 我们需要找一个区别扩展 $z$。
- 直觉: $x=a^k$ 是一个前缀。要使整个字符串成为回文,后缀必须是 $x$ 的“镜像”。我们可以构造一个后缀,它正好是 $x$ 的镜像,但不是 $y$ 的镜像。
- 选择 $z$: 我们选择 $z = b a^k$。这里 'b' 是一个“分隔符”,后面跟着 $x$ 本身。
- 验证:
- 考虑 $xz = a^k b a^k$。这个字符串以 $b$ 为中心,左右两边都是 $a^k$,它是对称的,所以是一个回文串。因此 $xz \in L$。
- 考虑 $yz = a^j b a^k$。这个字符串的左边是 $a^j$,右边是 $a^k$。因为 $j \neq k$,所以它不是对称的,不是回文串。因此 $yz \notin L$。
- 结论: $xz$ 和 $yz$ 的命运不同。因此,$x=a^k$ 和 $y=a^j$ 是可区分的。
- 最终论证:
- 我们已经证明,对于集合 $S=\{a^k \mid k \ge 0\}$ 中的任意两个不同元素,它们都是可区分的。
- 这意味着它们必须属于不同的等价类。
- 由于集合 $S$ 是无限的,所以必然存在无限多个等价类。
- 根据 Myhill-Nerode 定理,语言 $L$ 不是正则的。
📜 [原文22]
注意:还有许多其他可能的无限字符串集合可供我们使用,其中每一对都是可区分的。事实上,在这个例子中,人们可以证明每个字符串都在它自己的等价类中,即没有两个字符串是等价的。但我们上面给出的证明更简单,足以说明 $L$ 不是正则的。
- 其他候选集: 我们可以选择 $S' = \{a, ab, abb, abbb, \ldots, ab^k, \ldots\}$。对于 $x=ab^k, y=ab^j$ ($k \neq j$),选择 $z = (ab^k)^R = b^k a$ 作为区别扩展。$xz$ 是回文,$yz$ 不是。
- “每个字符串都在它自己的等价类中”: 这个论断更强。它意味着对于任意两个不同的字符串 $x, y$,它们都是可区分的。证明起来可能更复杂,但直觉上是对的,因为要形成回文,需要的“镜像”后缀是完全由前缀决定的,不同的前缀需要不同的镜像。
- “但我们上面的证明更简单”: 这是一个重要的解题策略思想。我们不需要把所有等价类都找出来。为了证明非正则,我们只需要找到一个无限的、两两可区分的子集就足够了。选择最简单的那个子集(比如 $a^k$)来论证,可以大大简化证明过程。
这两个例子展示了使用 Myhill-Nerode 定理证明非正则性的标准流程:
- 确定要证明的语言 $L$。
- 提出一个无限的、简单的字符串集合 $S$ 作为候选(常见的有 $a^k$, $a^k b^k$ 等形式)。
- 从 $S$ 中任取两个不同元素 $x, y$。
- 根据 $x$ (或 $y$) 的结构,巧妙地构造一个区别扩展 $z$,使得 $xz \in L$ 而 $yz \notin L$ (或反之)。
- 得出结论:$S$ 中所有元素两两可区分,因此等价类无限,因此语言非正则。
66. 行间公式索引
1. 公式 1: $L_{n}=\left\{w \in\{0,1\}^{*} \mid w \text{ 中的倒数第 } n \text{ 个符号是 } 1\right\}$
- 解释: 定义了语言 $L_n$,它包含所有倒数第 $n$ 个字符是 '1' 的二进制字符串。
76. 行间公式索引
1. 公式 1:
- 解释: 定义了语言 $L_n$,它包含所有倒数第 $n$ 个字符是 '1' 的二进制字符串。
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。