Handout 08B 解释：图灵机、可判定性与复杂性

$$ * 此公式并列定义了两个核心**语言**。 * $\mathrm{E}_{\mathrm{TM}}$: **空语言问题**。判断一个**图灵机**是否不**接受**任何**字符串**。 * $\mathrm{A}_{\mathrm{TM}}$: **接受问题** (或称**停机问题**的变体)。判断一台给定的**图灵机** $M$ 是否**接受**一个给定的**字符串** $x$。这是**计算理论**中第一个被证明是**不可判定**的**问题**。 **[易错点与边界情况]** * **构造 $M'$ 的过程**: $M_A$ 并不是去运行 $M'$，它只是把 $M'$ 的**描述**（**编码**）给构造出来。这是一个**字符串**操作。整个过程是**可计算**且**停机**的。$M_A$ 的**算法**只是生成了一段描述 $M'$ 的文本，然后把这段文本交给 $M_E$。 * **逻辑反转**: “**输出**相反**内容**”是本**证明**中的一个常见技巧，也是一个易错点。必须理清 $M$ **接受** $x$ $\iff$ $L(M')$ 非空 $\iff$ $\langle M' \rangle \notin \mathrm{E}_{\mathrm{TM}}$ $\iff$ $M_E$ **拒绝** $\langle M' \rangle$ $\iff$ $M_A$ **接受** $\langle M,x \rangle$ 这一串逻辑链。 **[总结]** 该部分是**证明** $\mathrm{E}_{\mathrm{TM}}$ **不可判定性**的核心构造。它通过**假设** $\mathrm{E}_{\mathrm{TM}}$ **可判定**，然后利用其**判定器** $M_E$ 作为神谕，巧妙地构造了一个能**判定**已知**不可判定问题** $\mathrm{A}_{\mathrm{TM}}$ 的**算法** $M_A$。关键在于构造了一个“中间人”**图灵机** $M'$，它的**语言**是否为空，恰好编码了我们想知道的答案“$M$ 是否**接受** $x$”。 **[存在目的]** 这是一个经典的**归约**范例，展示了如何将一个**问题**的“是/否”答案巧妙地转化为另一个**问题**的“空/非空”答案。这是学习**归约**技巧时必须掌握的核心案例。 **[直觉心智模型]** 你是一个法官（要**判定** $\mathrm{A}_{\mathrm{TM}}$），要判断“嫌疑人 $M$ 是否用凶器 $x$ 作案了？”。你手下有个只会回答“这个房间里有没有人？”的神探 $M_E$。 1. **构造 $M'$**: 你临时搭建一个特殊的房间 $M'$。 2. **设置房间规则**: 你对房间 $M'$ 设置规则：“当且仅当‘嫌疑人 $M$ 用凶器 $x$ 作案’时，这个房间里才会充满人（$L(M')=\Sigma^*$）；否则，这个房间永远是空的（$L(M')=\varnothing$）。” 3. **咨询神探**: 你问神探 $M_E$：“我刚搭的这个房间 $M'$ 里，有没有人？” 4. **得出结论**: * 如果神探回答“是空的”，你就知道“嫌疑人 $M$ 没有用凶器 $x$ 作案”。 * 如果神探回答“不是空的”，你就知道“嫌疑人 $M$ 用凶器 $x$ 作案了”。 5. **矛盾**: 你利用一个只会判断“有没有人”的神探，解决了复杂的“是否作案”的**问题**。既然我们知道“是否作案”（$\mathrm{A}_{\mathrm{TM}}$）这个终极**问题**是无解的，那么你手下这个神探 $M_E$ 也必然不存在。 **[直观想象]** 你有一个“谎言测试仪” $M_E$，但它很奇怪，它只能测一句话的“信息量”是否为零。如果一句话是套话、废话，信息量为零，它就亮绿灯。如果一句话有实质内容，信息量非零，它就亮红灯。你想用它来判断你的朋友 $M$ 是不是真的喜欢吃苹果 $x$ (判定 $\mathrm{A}_{\mathrm{TM}}$)。 1. **构造 $M'$**: 你教你的朋友说一句奇怪的话 $M'$：“无论别人问我什么，我都会回答‘我喜欢吃苹果’。” 2. **分析 $M'$**: * 如果你朋友 $M$ 真的喜欢吃苹果 $x$，那么 $M'$ 这句话就变成了一句大实话，有实质内容。它的信息量非零。 * 如果你朋友 $M$ 不喜欢吃苹果 $x$，那么 $M'$ 这句话就成了一句谎话。但注意，我们构造的 $M'$ 的逻辑是“在输入 z 上，运行 M 在 x 上...”，如果 M 不接受 x，M' 的语言为空。 3. **重新构造 $M'$**: 让我们更精确地遵循**算法**。我们构造一个机器人 $M'$。它的程序是：“忽略听到的任何问题 $z$。在内部默默地思考‘朋友 $M$ 是否喜欢吃苹果 $x$?’。如果答案是‘是’，机器人就大声说出 $z$。如果答案是‘不是’，机器人就永远沉默。” 4. **分析 $M'$**: * 如果朋友 $M$ 喜欢苹果 $x$，那么无论问机器人什么问题 $z$，它都会回答 $z$。它能说出所有的话。它的“**语言**” $L(M')$ 就是所有话的集合 $\Sigma^*$，信息量非零。 * 如果朋友 $M$ 不喜欢苹果 $x$，那么机器人永远沉默。它的“**语言**” $L(M')$ 就是空集 $\varnothing$，信息量为零。 5. **咨询 $M_E$**: 你把这个机器人 $M'$ 推到谎言测试仪 $M_E$ 面前。 6. **得出结论**: * 如果测试仪亮绿灯（信息量为零），你就知道朋友不喜欢苹果。 * 如果测试仪亮红灯（信息量非零），你就知道朋友喜欢苹果。 7. **矛盾**: 你成功用一个奇怪的“信息量测试仪”解决了“判断喜好”的**问题**。既然我们知道“判断喜好”这种事本身无通用解法（$\mathrm{A}_{\mathrm{TM}}$ **不可判定**），那么这个“信息量测试仪”也必然不存在。 --- **[原文]（逐字逐句）** 现在我们将证明**正确性**： 假设 $\langle M, x\rangle \in \mathrm{A}_{\mathrm{TM}}$。那么 $M$ **接受** $x$。这意味着构造的 $M^{\prime}$ 将**接受**每个**输入** $z$，即 $L\left(M^{\prime}\right)=\Sigma^{*}$。因此，$M_{E}$ 将在运行 $\left\langle M^{\prime}\right\rangle$ 时**拒绝**（因为它是 $\mathrm{E}_{\mathrm{TM}}$ 的**判定器**），因此 $M_{A}$ 将**接受** $x$。 假设 $\langle M, x\rangle \notin \mathrm{A}_{\mathrm{TM}} \|^{a}$。由于 $M$ 不**接受** $x$，构造的 $M^{\prime}$ 不**接受**任何**字符串** $z$。所以 $L\left(M^{\prime}\right)=\emptyset$。因此，$M_{E}$ 将在运行 $\left\langle M^{\prime}\right\rangle$ 时**拒绝**（因为它是 $\mathrm{E}_{\mathrm{TM}}$ 的**判定器**），因此 $M_{A}$ 将**拒绝** $\langle M, x\rangle$。 得出结论，由于 $\mathrm{A}_{\mathrm{TM}} \leq_{\mathrm{T}} \mathrm{E}_{\mathrm{TM}}$ 且 $\mathrm{A}_{\mathrm{TM}}$ 是**不可判定**的，因此 $\mathrm{E}_{\mathrm{TM}}$ 也是**不可判定**的。 $^{a}$ 同样，我们忽略了**错误编码**的**输入**，因为 $M_{A}$ 自动**拒绝**它们。 **[逐步解释]（from scratch，超细）** 这部分是示例 5 的**正确性证明**，它遵循了**证明模板 7** 的步骤 4 和 5。 1. **证明 $\langle M, x\rangle \in \mathrm{A}_{\mathrm{TM}}$ 的情况 (完备性)** * **前提假设**: 假设输入到我们构造的**判定器** $M_A$ 的是 $\langle M, x \rangle$，并且它确实属于 $\mathrm{A}_{\mathrm{TM}}$。 * **逻辑推导**: 这意味着**图灵机** $M$ 在输入 $x$ 上会**停机**并**接受**。 * **联系构造**: 根据我们为 $M_A$ 设计的**步骤 1**，它会构造一个**图灵机** $M'$，其行为是“在输入 $z$ 上，**模拟** $M$ 在 $x$ 上的运行...”。 * 因为 $M$ **接受** $x$，所以 $M'$ 会**接受**它自己的任意输入 $z$。因此，$M'$ 的**语言** $L(M')$ 是所有**字符串**的集合 $\Sigma^*$，这是一个**非空语言**。 * **调用神谕**: $M_A$ 的**步骤 2** 将 $\langle M' \rangle$ 交给神谕 $M_E$。因为 $L(M') = \Sigma^* \neq \varnothing$，所以 $\langle M' \rangle$ 不属于 $\mathrm{E}_{\mathrm{TM}}$。神谕 $M_E$ 是 $\mathrm{E}_{\mathrm{TM}}$ 的**判定器**，所以它会对这个输入**拒绝**。 * **$M_A$ 的最终输出**: $M_A$ 的**步骤 2** 说要“**输出**相反**内容**”。既然 $M_E$ **拒绝**了，那么 $M_A$ 就会**接受**。 * **小结**: 当 $\langle M, x \rangle \in \mathrm{A}_{\mathrm{TM}}$ 时，$M_A$ 正确地**接受**了它。 2. **证明 $\langle M, x\rangle \notin \mathrm{A}_{\mathrm{TM}}$ 的情况 (可靠性)** * **前提假设**: 假设输入 $\langle M, x \rangle$ 不属于 $\mathrm{A}_{\mathrm{TM}}$。 * **逻辑推导**: 这意味着 $M$ 在输入 $x$ 上或者**拒绝**，或者**循环**。总之，M **不接受** $x$。 * **联系构造**: 我们构造的 $M'$ 在**模拟** $M$ 跑在 $x$ 上时，也永远不会进入**接受状态**。因此，对于任何输入 $z$，$M'$ 都不会**接受** $z$。所以，$M'$ 的**语言** $L(M')$ 是空集 $\varnothing$。 * **调用神谕**: $M_A$ 将 $\langle M' \rangle$ 交给神谕 $M_E$。因为 $L(M') = \varnothing$，所以 $\langle M' \rangle$ 正是 $\mathrm{E}_{\mathrm{TM}}$ 的一个成员。神谕 $M_E$ 会对这个输入**接受**。 * **$M_A$ 的最终输出**: $M_A$ “**输出**相反**内容**”。既然 $M_E$ **接受**了，那么 $M_A$ 就会**拒绝**。 * **小结**: 当 $\langle M, x \rangle \notin \mathrm{A}_{\mathrm{TM}}$ 时，$M_A$ 正确地**拒绝**了它。 * **原文勘误**: 原文中写道“因此，$M_{E}$ 将在运行 $\left\langle M^{\prime}\right\rangle$ 时**拒绝** ... 因此 $M_{A}$ 将**拒绝**”。这是一个笔误。根据逻辑，当 $L(M')=\emptyset$ 时，$M_E$ 应该**接受**，然后 $M_A$ **拒绝**。 3. **最终结论** * 我们已经证明，我们构造的 $M_A$ 是一个 $\mathrm{A}_{\mathrm{TM}}$ 的**判定器**。 * 这个构造过程本身证明了 $\mathrm{A}_{\mathrm{TM}} \le_T \mathrm{E}_{\mathrm{TM}}$。 * 我们面对一个矛盾：我们从“$\mathrm{E}_{\mathrm{TM}}$ **可判定**”的**假设**出发，推出了“$\mathrm{A}_{\mathrm{TM}}$ **可判定**”的结论。但这与“$\mathrm{A}_{\mathrm{TM}}$ **不可判定**”的已知事实相悖。 * 因此，最初的**假设**是错误的。$\mathrm{E}_{\mathrm{TM}}$ 必须是**不可判定**的。 **[易错点与边界情况]** * **仔细追踪逻辑反转**: 这个**证明**包含两次逻辑反转，很容易出错。 1. $M$ **接受** $x \iff L(M')$ **非空**。 2. $M_A$ 的输出与 $M_E$ 的输出相反。 * **脚注 a**: 再次提醒对格式错误输入的处理。一个完整的**归约证明**需要保证，如果 $M_A$ 的输入 $\langle M,x \rangle$ 格式错误，那么它构造并交给 $M_E$ 的东西也应该导向一个正确的最终结果（通常是**拒绝**）。这里通过一个简单的声明忽略了这一繁琐部分。 **[总结]** 这部分完成了对**归约**构造的**正确性**论证，通过分别**分析**输入属于和不属于 $\mathrm{A}_{\mathrm{TM}}$ 的两种情况，证明了我们设计的**算法** $M_A$ 确实能**判定** $\mathrm{A}_{\mathrm{TM}}$，从而引出**矛盾**，完成了整个**反证**。 **[存在目的]** 展示**归约证明**的完整论证过程，特别是如何通过**分析**“中间人”机器 $M'$ 的行为来连接两个不同的**问题**。 **[直觉心智模型]** 这是对“法官利用神探”计划的可行性报告。 * **报告第一部分（证明有罪能判）**: 如果嫌疑人 $M$ 真的作案了，那么我们搭的那个房间 $M'$ 就会“充满人”。神探 $M_E$ 会报告“不是空的”（神探**拒绝**“为空”的论断）。法官根据“相反**内容**”原则，最终判决“有罪”（法官**接受**）。流程正确。 * **报告第二部分（证明无罪能放）**: 如果嫌疑人 $M$ 没作案，那么房间 $M'$ 就是“空的”。神探 $M_E$ 会报告“是空的”（神探**接受**“为空”的论断）。法官根据“相反**内容**”原则，最终判决“无罪”（法官**拒绝**）。流程正确。 * **报告结论**: 该计划确实能将“判断作案”的**问题**转化为“判断是否有人”的**问题**。 **[直观想象]** 这是对“用信息量测试仪判断喜好”方案的复核。 * **情况一（朋友喜欢苹果）**: 机器人 $M'$ 会说话，信息量非零。测试仪 $M_E$ 亮红灯（**拒绝**“信息量为零”）。你根据相反原则，得出结论“朋友喜欢苹果”（你**接受**）。正确。 * **情况二（朋友不喜欢苹果）**: 机器人 $M'$ 沉默，信息量为零。测试仪 $M_E$ 亮绿灯（**接受**“信息量为零”）。你根据相反原则，得出结论“朋友不喜欢苹果”（你**拒绝**）。正确。 * **结论**: 该方案确实有效，能解决“判断喜好”的**问题**。因为我们知道“判断喜好”无通用解，所以这个“信息量测试仪”必然不存在。 --- **[原文]（逐字逐句）** 最后，要证明 $L$ 是**不可判定**的，你可以使用**莱斯定理**。 **[逐步解释]（from scratch，超细）** 这段话引入了第三种，也是最强大的证明**不可判定性**的工具——**莱斯定理 (Rice's Theorem)**。 1. **角色定位**: 过渡句，引出**证明模板 8**。 2. **内容拆解**: * “最后...”：暗示这是介绍的最后一种主要技术。 * **莱斯定理**: 这是一个非常通用的定理，它说：任何关于**图灵机**所识别的**语言**的“**非平凡属性**”，都是**不可判定**的。 * **语言的属性 (Property of Languages)**：这是指一个关于**语言**集合的集合。例如，“**语言**是空的”是一个**属性**，“**语言**是**正则**的”是另一个**属性**。 * **非平凡 (Non-trivial)**：一个**属性**是**非平凡**的，意味着至少有一个**图灵机识别**的**语言**具有该**属性**，同时至少有一个**图灵机识别**的**语言**不具有该**属性**。换句话说，这个**属性**不是对所有**语言**都成立，也不是对所有**语言**都不成立。 * “**语言**是**图灵可识别**的”是一个**平凡属性**，因为所有**图灵机**识别的**语言**都具有此**属性**。 * “**语言**既是**正则**的又不是**正则**的”是一个**平凡属性**（空**属性**），因为没有**语言**能满足这个矛盾的条件。 * “**语言**是空的”、“**语言**是有限的”、“**语言**包含**字符串**‘aba’” 这些都是**非平凡属性**。 **[易错点与边界情况]** * **属性的对象**: **莱斯定理**只适用于关于**语言**本身的**属性**，而不适用于关于**图灵机**的**属性**。 * “**语言**是空的” ($L(M) = \varnothing$) 是一个**语言属性**。如果两台机器 $M_1, M_2$ 识别相同的**语言** ($L(M_1)=L(M_2)$)，那么它们要么都具有“**语言**为空”的**属性**，要么都不具有。 * “**图灵机**有超过10个状态” 是一个**图灵机**的**属性**，不是**语言属性**。我们可以轻易构造两台状态数不同但识别相同**语言**的**图灵机**。这种**问题**通常是**可判定**的，**莱斯定理**不适用。 **[总结]** 本段介绍了**莱斯定理**，这是一个强大的“一刀切”工具，可以快速证明大量关于**图灵机语言**的**非平凡属性**是**不可判定**的。 **[存在目的]** 提供一个比**归约**更高级、更简洁的**证明**工具。对于符合其应用条件的**问题**，使用**莱斯定理**可以省去构造复杂**归约**的麻烦。 **[直觉心智模型]** **莱斯定理**就像一个“通用**问题**分类器”。你给它一个关于**程序行为**的**问题**，它会检查： 1. 这个**问题**只跟程序的最终输出（**语言**）有关，而跟程序本身的代码实现（状态数、纸带符号）无关吗？（**语言属性**） 2. 这个**问题**的答案不是千篇一律的“是”或“否”吗？（**非平凡属性**） 如果两个答案都是“是”，分类器就直接给这个**问题**贴上“**不可判定**”的标签。 **[直观想象]** 想象一个文学院的教授（**莱斯定理**），他从不看学生本身（**图灵机**），只评价学生写的文章（**语言**）。 * 任何一个关于文章的“有意义的”评价标准（**非平凡属性**），比如“文章是否是悲剧？”、“文章是否是十四行诗？”，教授都认为不存在一个通用的**算法**来自动判定。 * “文章是否由莎士比亚所写？”这不是一个**语言属性**，因为两个不同的人可能写出完全一样的文章。教授不管这个。 * “文章是否包含文字？”这是一个**平凡属性**（假设所有文章都有文字），教授觉得这种**问题**没意义。 * 所以，当你问“是否存在一个程序，能自动判断任何程序产生的输出（**语言**）是否为空？” 教授会说：“‘为空’是关于输出的**非平凡属性**，所以根据我的**定理**，这种判断程序不存在。” --- ### 5.3.3 **证明模板** 8：使用**莱斯定理**证明 $L$ 是**不可判定**的 **[原文]（逐字逐句）** 1. 证明 $L$ 是一种**语言属性**： (a) **检查** $L$ 是否由形式为 $\langle M\rangle$ 的**字符串**组成，其中 $M$ 是一台 **TM**。 (b) **检查**对于任意两台 **TM** $M_{1}, M_{2}$ 使得 $L\left(M_{1}\right)=L\left(M_{2}\right)$，是否成立 $M_{1} \in L \Longleftrightarrow M_{2} \in L$。 2. 证明 $L$ 是**非平凡**的： (a) 展示存在一台 **TM** $M$ 使得 $\langle M\rangle \in L$。 (b) 展示存在一台 **TM** $M^{\prime}$ 使得 $\left\langle M^{\prime}\right\rangle \notin L$。 3. 得出结论，根据**莱斯定理**，$L$ 是**不可判定**的。 **[逐步解释]（from scratch，超细）** 这个模板将**莱斯定理**的应用分解为两个主要的验证步骤。 1. **步骤 1：证明 L 是一个语言属性** * **目的**：验证**问题**是否只与**图灵机**的“行为”（它识别的**语言**）有关，而与它的“物理结构”（代码实现）无关。 * **步骤 1(a)**: 这是一个基本前提检查。**莱斯定理**是关于**图灵机**的**语言**的，所以我们要判定的**语言** $L$ 本身必须是一个**图灵机编码**的集合。如果 $L$ 包含其他乱七八糟的**字符串**，那它就不是一个纯粹的关于**图灵机属性**的**问题**。 * **步骤 1(b)**: 这是**语言属性**的**核心定义**。它要求，如果两台不同的**图灵机** $M_1$ 和 $M_2$ 恰好识别了完全相同的**语言**（即它们的“外部行为”一致），那么对于我们要判定的**属性** $L$，它们的**编码** $\langle M_1 \rangle$ 和 $\langle M_2 \rangle$ 必须“同进同出”。要么它们都属于 $L$，要么它们都不属于 $L$。这确保了我们评判的是**语言**，而不是**图灵机**本身。 2. **步骤 2：证明 L 是非平凡的** * **目的**：验证这个**属性**不是“无聊的”。一个“无聊”的**属性**要么所有**图灵可识别语言**都具备，要么都不具备。这种**问题**是**可判定**的（答案永远是“是”或“否”）。 * **步骤 2(a)**: 证明**属性**非空。你需要具体地构造或描述一台**图灵机** $M$，使得它的**语言** $L(M)$ 具有所讨论的**属性**，因此 $\langle M \rangle \in L$。 * **步骤 2(b)**: 证明**属性**不是全部。你需要具体地构造或描述另一台**图灵机** $M'$，使得它的**语言** $L(M')$ 不具有所讨论的**属性**，因此 $\langle M' \rangle \notin L$。 3. **步骤 3：得出结论** * **目的**：完成**证明**。 * **逻辑**：一旦你完成了步骤 1 和 2，你就证明了 $L$ 是一个关于**图灵可识别语言**的**非平凡属性**。此时，你可以直接引用**莱斯定理**，像使用一条公理一样，立即得出结论：$L$ 是**不可判定**的。 **[具体数值示例]** **问题**：证明**语言** $\text{INF}_{\text{TM}} = \{\langle M \rangle \mid L(M) \text{ 是一个无限语言}\}$ 是**不可判定**的。 1. **证明 $\text{INF}_{\text{TM}}$ 是一个语言属性**: a. $\text{INF}_{\text{TM}}$ 的成员显然都是**图灵机编码** $\langle M \rangle$。 b. 假设有两台**图灵机** $M_1, M_2$ 且 $L(M_1) = L(M_2)$。如果 $\langle M_1 \rangle \in \text{INF}_{\text{TM}}$，那么 $L(M_1)$ 是无限的。因为 $L(M_2) = L(M_1)$，所以 $L(M_2)$ 也是无限的，这意味着 $\langle M_2 \rangle \in \text{INF}_{\text{TM}}$。反之亦然。因此，$\langle M_1 \rangle \in \text{INF}_{\text{TM}} \iff \langle M_2 \rangle \in \text{INF}_{\text{TM}}$。 c. 结论：$\text{INF}_{\text{TM}}$ 是一个**语言属性**。 2. **证明 $\text{INF}_{\text{TM}}$ 是非平凡的**: a. **存在性**: 构造**图灵机** $M_{accept\_all}$，它**接受**所有输入**字符串**。$L(M_{accept\_all}) = \Sigma^*$，这是一个无限**语言**。因此 $\langle M_{accept\_all} \rangle \in \text{INF}_{\text{TM}}$。 b. **非全体性**: 构造**图灵机** $M_{accept\_none}$，它**拒绝**所有输入**字符串**。$L(M_{accept\_none}) = \varnothing$，这是一个有限**语言**（大小为0）。因此 $\langle M_{accept\_none} \rangle \notin \text{INF}_{\text{TM}}$。 c. 结论：$\text{INF}_{\text{TM}}$ 是一个**非平凡属性**。 3. **最终结论**: 由于 $\text{INF}_{\text{TM}}$ 是一个关于**图灵可识别语言**的**非平凡属性**，根据**莱斯定理**，$\text{INF}_{\text{TM}}$ 是**不可判定**的。 **[易错点与边界情况]** * **对语言属性的判断错误**: 最常见的错误是将一个关于**图灵机**结构的**问题**误判为**语言属性**。例如，**问题** $L = \{\langle M \rangle \mid M \text{ 在输入 'aba' 上运行超过100步}\}$。我们可以构造两台机器 $M_1$（运行90步**接受**'aba'）和 $M_2$（运行110步**接受**'aba'），它们都只**接受**'aba'，所以 $L(M_1) = L(M_2) = \{\text{'aba'}\}$。但 $\langle M_1 \rangle \notin L$ 而 $\langle M_2 \rangle \in L$。这违反了**语言属性**的定义，所以**莱斯定理**不适用。（实际上这个**问题**是**可判定**的）。 **[总结]** **证明模板 8** 将**莱斯定理**的应用流程化。你只需要按部就班地验证“是**语言属性**”和“**非平凡**”这两个前提条件，一旦验证通过，就可以直接“召唤”**莱斯定理**来秒杀**问题**，得出**不可判定**的结论。 **[存在目的]** 为使用**莱斯定理**提供一个清晰、标准化的操作流程，使得这个强大**定理**的应用不容易出错。它将一个复杂的理论判断问题简化为两个具体的构造性和检验性任务。 **[直觉心智模型]** 这就像申请一张“**不可判定**”的认证证书。 1. **第一项审查（语言属性）**: 审查员会问：“你的**问题**只和最终产品（**语言**）有关，和生产过程（**图灵机**实现）无关吗？” 你需要证明，只要两个工厂生产出完全一样的产品，你的**问题**对这两个工厂的评价总是一样的。 2. **第二项审查（非平凡）**: 审查员问：“你的**问题**有意义吗？是不是所有产品都有这个**属性**，或者都没有？” 你需要拿出两个产品，一个有此**属性**，一个没有，来证明你的**问题**不是废话。 3. **颁发证书**: 两项审查都通过后，审查员盖章，说：“恭喜，你的**问题**已通过**莱斯定理**认证，被确认为‘**不可判定**’。” **[直观想象]** 你要判断“一部小说是否是喜剧”这个**问题**是不是“无法**算法**化”的。 1. **是关于作品本身的吗？** * 是的。如果两个人 $M_1, M_2$ 写出了完全一样的小说（$L(M_1)=L(M_2)$），那么这部小说要么是喜剧，要么不是。评价是一致的。这和作者是谁、用什么笔写的无关。 2. **这个分类有意义吗？** * 是的。存在是喜剧的小说（例如莎士比亚的《仲夏夜之梦》），也存在不是喜剧的小说（例如《哈姆雷特》）。 3. **结论**: 因为“是喜剧”是关于小说内容本身的、一个有意义的分类，根据文学界的“**莱斯定理**”，不存在一个通用的电脑程序可以读完任何小说后自动判断它是否是喜剧。 --- ### 5.3.4 示例 6：$\mathrm{E}_{\mathrm{TM}}$ 是不可判定的 **[原文]（逐字逐句）** 回顾**语言** $$

$$ 我们首先证明 $\mathrm{E}_{\mathrm{TM}}$ 是一种**可识别语言**的**属性**。显然 $\mathrm{E}_{\mathrm{TM}} \subseteq\{\langle M\rangle \mid M$ 是一台 **TM** $\}$。现在令 $M_{1}, M_{2}$ 是 **TM** 使得 $L\left(M_{1}\right)=L\left(M_{2}\right)$。如果 $\left\langle M_{1}\right\rangle \in \mathrm{E}_{\mathrm{TM}}$，那么 $L\left(M_{1}\right)=\emptyset=L\left(M_{2}\right)$，所以 $\left\langle M_{2}\right\rangle \in \mathrm{E}_{\mathrm{TM}}$。类似地，如果 $\left\langle M_{2}\right\rangle \in \mathrm{E}_{\mathrm{TM}}$，我们可以看到 $\left\langle M_{1}\right\rangle \in \mathrm{E}_{\mathrm{TM}}$。所以 $\left\langle M_{1}\right\rangle \in \mathrm{E}_{\mathrm{TM}} \Longleftrightarrow \left\langle M_{2}\right\rangle \in \mathrm{E}_{\mathrm{TM}}$。 现在我们证明 $\mathrm{E}_{\mathrm{TM}}$ 是一个**非平凡属性**。考虑 **TM** $M^{\prime}, M$。 - $M'$= 在**输入** $x$ 上： 1. **接受** $x$。 $$

$$ - $M$= 在**输入** $x$ 上： 1. **拒绝** $x$。 $$

$$ 所以 $L$ 是**正则语言**的**非平凡属性**。因此，根据**莱斯定理**，$L$ 是**不可判定**的。 **[逐步解释]（from scratch，超细）** 这个示例展示了如何应用**证明模板 8** 来快速证明 $\mathrm{E}_{\mathrm{TM}}$ 的**不可判定性**，这比示例 5 中的**归约**法要简洁得多。 1. **目标**: 证明 $\mathrm{E}_{\mathrm{TM}}$ **不可判定**。 2. **策略**: 使用**莱斯定理**。我们需要验证两个前提条件。 3. **第一步：证明 $\mathrm{E}_{\mathrm{TM}}$ 是一个语言属性** * **前提检查**: **语言** $\mathrm{E}_{\mathrm{TM}}$ 的定义是 $\{\langle M\rangle \mid ...\}$，所以它的成员都是**图灵机编码**。这满足模板 8 的步骤 1(a)。 * **核心论证**: * 我们取任意两台**图灵机** $M_1$ 和 $M_2$，并假设它们的**语言**完全相同，即 $L(M_1) = L(M_2)$。 * 我们需要证明 $\langle M_1 \rangle \in \mathrm{E}_{\mathrm{TM}} \iff \langle M_2 \rangle \in \mathrm{E}_{\mathrm{TM}}$。 * **正向**: 假设 $\langle M_1 \rangle \in \mathrm{E}_{\mathrm{TM}}$。根据 $\mathrm{E}_{\mathrm{TM}}$ 的定义，这意味着 $L(M_1) = \varnothing$。因为我们前提是 $L(M_1) = L(M_2)$，所以必然有 $L(M_2) = \varnothing$。根据 $\mathrm{E}_{\mathrm{TM}}$ 的定义，这意味着 $\langle M_2 \rangle \in \mathrm{E}_{\mathrm{TM}}$。 * **反向**: 类似地，假设 $\langle M_2 \rangle \in \mathrm{E}_{\mathrm{TM}}$，则 $L(M_2) = \varnothing$。因为 $L(M_1)=L(M_2)$，所以 $L(M_1) = \varnothing$，这意味着 $\langle M_1 \rangle \in \mathrm{E}_{\mathrm{TM}}$。 * **结论**: 既然双向都成立，我们就证明了 $\mathrm{E}_{\mathrm{TM}}$ 只关心**图灵机**的**语言**是什么，而不管**图灵机**内部长什么样。因此，$\mathrm{E}_{\mathrm{TM}}$ 是一个**语言属性**。 4. **第二步：证明 $\mathrm{E}_{\mathrm{TM}}$ 是非平凡的** * 我们需要找到一个**图灵机**，其**编码**在 $\mathrm{E}_{\mathrm{TM}}$ 中，再找到另一个，其**编码**不在 $\mathrm{E}_{\mathrm{TM}}$ 中。 * **构造一个不在 $\mathrm{E}_{\mathrm{TM}}$ 中的例子**: * 原文构造了 $M'$：“在**输入** $x$ 上，**接受** $x$。” * 这台**图灵机**会**接受**任何它收到的输入。所以它的**语言**是 $L(M') = \Sigma^*$ (所有可能**字符串**的集合)。 * 因为 $L(M') = \Sigma^* \neq \varnothing$，所以 $\langle M' \rangle$ 不满足“**语言**为空”的**属性**，故 $\langle M' \rangle \notin \mathrm{E}_{\mathrm{TM}}$。 * **构造一个在 $\mathrm{E}_{\mathrm{TM}}$ 中的例子**: * 原文构造了 $M$：“在**输入** $x$ 上，**拒绝** $x$。” * 这台**图灵机**会**拒绝**任何它收到的输入。它永远不**接受**。所以它的**语言**是 $L(M) = \varnothing$。 * 因此，$\langle M \rangle$ 满足“**语言**为空”的**属性**，故 $\langle M \rangle \in \mathrm{E}_{\mathrm{TM}}$。 * **结论**: 因为我们既找到了一个“是”的例子，也找到了一个“不是”的例子，所以 $\mathrm{E}_{\mathrm{TM}}$ 是一个**非平凡属性**。 5. **最终结论**: * 我们已经成功验证了**莱斯定理**的两个前提条件。 * 因此，我们可以直接应用**莱斯定理**，得出结论：$\mathrm{E}_{\mathrm{TM}}$ 是**不可判定**的。 * **原文勘误**: 原文最后写道“所以 $L$ 是**正则语言**的**非平凡属性**”。这应该是一个笔误，应为“所以 $\mathrm{E}_{\mathrm{TM}}$ 是**图灵可识别语言**的**非平凡属性**”。 **[公式与符号逐项拆解和推导（若本段含公式）]** * $$

$$ * (同上文解释) * $$

$$ * $L(M')$：我们构造的**图灵机** $M'$ 的**语言**。 * $\Sigma^*$: 所有由字母表 $\Sigma$ 中字符组成的有限**字符串**的集合，包括空串。这是**非空**的。 * 所以 $\langle M' \rangle \notin \mathrm{E}_{\mathrm{TM}}$：因为 $L(M')$ 不是空集。 * $$

$$ * $L(M)$：我们构造的**图灵机** $M$ 的**语言**。 * $\emptyset$: 空集。 * 所以 $\langle M \rangle \in \mathrm{E}_{\mathrm{TM}}$：因为 $L(M)$ 正是空集。 **[易错点与边界情况]** * **构造的简洁性**: 注意在证明**非平凡性**时，我们不需要构造复杂的**图灵机**。通常，一个“**接受**一切”的**图灵机**和一个“**拒绝**一切”的**图灵机**就足以用来证明绝大多数**属性**的**非平凡性**。 **[总结]** 该示例完美地展示了**莱斯定理**的威力。通过简单地验证“**语言属性**”和“**非平凡性**”这两个条件，我们用比**归约**法短得多的篇幅，同样严谨地证明了 $\mathrm{E}_{\mathrm{TM}}$ 是**不可判定**的。 **[存在目的]** 通过一个具体的、与之前示例相同的**问题** ($\mathrm{E}_{\mathrm{TM}}$)，直观地对比**归约**法和**莱斯定理**这两种**证明**方法的优劣。它凸显了**莱斯定理**在处理符合其条件的**问题**时的高效性和简洁性。 **[直觉心智模型]** 这就像用一个高级自动化工具来检测**问题**。 * **归约法**：手动编写一个复杂的脚本，把**问题** A 的输入转化成**问题** B 的输入。 * **莱斯定理法**：直接运行一个“**不可判定性**扫描器”。你只需要在配置里勾选两个选项：“仅与输出有关”和“有正反例”，然后扫描器就自动给出“**不可判定**”的报告。 **[直观想象]** 你要判断“一部小说是否一个字都没有”这个**问题**是不是“无法**算法**化”的。 1. **是关于作品本身的吗？** 是的，和作者无关。 2. **有正反例吗？** 是的。存在一个字都没有的空文档（对应 $L(M)=\varnothing$），也存在有字的小说（对应 $L(M')=\Sigma^*$）。 3. **结论**: 满足**莱斯定理**的两个条件，所以这个问题是**不可判定**的。 （这个例子与原文的逻辑完全对应） --- **由于篇幅限制，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `5.4 不可识别性` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `5.4 不可识别性` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 # 5.4 **不可识别性** **[原文]（逐字逐句）** 一个**语言** $L$ 是**不可识别**的，如果无法构造一个**图灵机**作为 $L$ 的**识别器**。正如上一节所述，我们将遵循**推论** 4 并使用**映射归约**来对所有可能的**图灵机**做出**断言**。**归约策略**看起来非常相似。注意，对于**不可识别性**，你必须使用**映射归约**。**图灵归约**只能揭示**不可判定性**。 **[逐步解释]（from scratch，超细）** 这段话引入了比**不可判定性**更强的“不可能”概念——**不可识别性** (Unrecognizability)，并强调了证明它的特定工具。 1. **角色定位**: 定义**不可识别性**并阐述其核心**证明**策略。 2. **内容拆解**: * “一个**语言** $L$ 是**不可识别**的...”：这是**不可识别性**的定义。它意味着，不存在任何**图リング机**，哪怕是允许在某些输入上**循环**的**识别器**，能够**识别**这个**语言** $L$。这是**可计算性**的终极壁垒。 * “我们将遵循**推论** 4 并使用**映射归约**”：与证明**不可判定性**类似，证明**不可识别性**也依赖于**归约**。这里的“**推论** 4”应该是指**不可识别性**在**映射归约**下的传递性：如果一个已知的**不可识别语言** $U$ **映射归约**到 $L$ ($U \le_m L$)，那么 $L$ 也一定是**不可识别**的。 * “**归约策略**看起来非常相似”：指的是证明 $U \le_m L$ 的过程，与证明**不可判定性**时的**归约**构造过程在形式上是类似的。 * “你必须使用**映射归约**。**图灵归约**只能揭示**不可判定性**。”：这是一个至关重要的技术要点！ * **为什么图灵归约不够？** 假设我们证明了 $U \le_T L$，其中 $U$ 是**不可识别**的。我们通过**反证法**假设 $L$ 是**可识别**的，即存在 $L$ 的**识别器** $M_L$。用 $M_L$ 作为神谕去构造 $U$ 的**机器** $M_U$ 时，因为 $M_L$ 可能会**循环**，所以 $M_U$ 在调用 $M_L$ 时也可能会**循环**。这样构造出的 $M_U$ 自身也可能**循环**，它最多只是 $U$ 的一个**识别器**，而不是**判定器**。既然我们本来就知道 $U$ 是**不可识别**的（不存在**识别器**），所以构造出一个**识别器**并不能产生矛盾。因此，**图灵归约**无法用来传递**不可识别性**。 * **为什么映射归约可以？** **映射归约**更强。如果 $U \le_m L$ 且 $L$ 是**可识别**的（设有**识别器** $M_L$），我们可以如下构造 $U$ 的**识别器** $M_U$：“在输入 $x$ 上，计算 $f(x)$，然后运行 $M_L$ 在 $f(x)$ 上”。因为 $f$ 是**可计算**的（总**停机**），且 $M_L$ 是**识别器**，所以 $M_U$ 的行为完美地模拟了 $M_L$ 在 $f(x)$ 上的行为，从而能**识别** $U$。如果 $U$ 是**不可识别**的，这就产生了矛盾。 **[易错点与边界情况]** * **混用归约类型**: 在证明**不可识别性**时，错误地使用了**图灵归约**。这是一个根本性的错误，会导致**证明**无效。必须使用**映射归约**。 **[总结]** 本段定义了**不可识别性**，并阐明了证明它的主要方法是使用**映射归约**。关键在于，必须将一个已知的**不可识别语言**（如 $\overline{\mathrm{A}_{\mathrm{TM}}}$）**映射归约**到目标**语言** $L$。它还特别强调了**图灵归约**在此处不适用的原因。 **[存在目的]** 为**不可识别性**的**证明**设定正确的工具和方法论，防止学习者将之前学到的**图灵归约**错误地应用到这个新的、更强的**问题**上。 **[直觉心智模型]** 如果说**不可判定性**是“没有万能的解决方案”，那么**不可识别性**就是“连一个能给出‘是’的答案的半吊子方案都没有”。 * **证明不可判定性 (可用图灵归约)**：就像证明“没有一个医生能治好所有病”。你可以假设有这样一个全能医生 $M_L$，然后利用他去解决一个已知的绝症 $U$。 * **证明不可识别性 (必须用映射归约)**：就像证明“某种病 $L$ 连一个能确诊的医生都没有”。你不能用**图灵归约**，因为那相当于：假设有个半吊子医生 $M_L$ 能在病人真得了 $L$ 病时给出诊断（但对没得病的可能永远没结论），然后你用他去诊断另一个绝症 $U$。你构造的新医生 $M_U$ 也是个半吊子，无法得出矛盾。你必须用**映射归约**，它像一个“疾病转换器”，能把绝症 $U$ 的所有症状完美转化为 $L$ 病的症状，从而证明 $L$ 病和 $U$ 病一样，都是无法确诊的。 **[直观想象]** 你要证明“读心术 $L$ 是不可能学会的（**不可识别**的）”。 * **已知**: “预测未来 $U$” 是不可能学会的（已知的**不可识别**难题）。 * **映射归约**: 你发明了一台机器 $f$。任何人只要坐进去，他脑子里想的任何关于未来的想法，都会被机器实时地、一一对应地转换成他当下的想法。 * **论证**: 如果有人学会了“读心术 $L$”，那么他只要让目标坐进这台机器，然后对他使用读心术，就能读出目标当下的想法，从而也就知道了目标对未来的预测。这意味着，学会“读心术 $L$”就能学会“预测未来 $U$”。 * **矛盾**: 既然“预测未来”不可能学会，那么“读心术”也必然不可能学会。 --- ### 5.4.1 **证明模板** 9：通过**映射归约**证明 $L$ 是**不可识别**的 **[原文]（逐字逐句）** 1. 选择一个**不可识别语言** $U$。 2. 编写一个计算**函数** $f$ 的**算法**。 3. 解释为什么**算法**总是**停机**并**输出** $f(x)$。 4. 假设 $x \in L$，证明 $f(x) \in U$。 5. 假设 $x \notin L$，证明 $f(x) \notin U$。 6. 得出结论，由于 $L \leq_{\mathrm{m}} U$ 且 $U$ 是**可识别**的，因此 $L$ 也必须是**可识别**的。 **[逐步解释]（from scratch，超细）** 这个模板的结构与**模板 3**（用**映射归约**证明**可识别性**）和**模板 7**（用**归约**证明**不可判定性**）都非常相似，但其逻辑和目标不同。这是一个**反证法**框架。 **正确的逻辑应该是**: 1. 选择一个**不可识别语言** $U$。 2. **（反证法假设）** 假设 $L$ 是**可识别**的。 3. 构造一个**可计算函数** $f$，将 $U$ **映射归约**到 $L$ ($U \le_m L$)。这包括： a. 编写计算 $f$ 的**算法**。 b. 证明 $f$ 总是**停机**（**可计算**）。 c. 证明对于所有 $x$，$x \in U \iff f(x) \in L$。 4. **（得出矛盾）** 根据**归约**的**性质**，如果 $U \le_m L$ 且 $L$ 是**可识别**的，那么 $U$ 也必须是**可识别**的。 5. 这与我们在步骤 1 中选定的 $U$ 是**不可识别**的这一事实相**矛盾**。 6. **（结论）** 因此，步骤 2 的**假设**是错误的。$L$ 必须是**不可识别**的。 **分析原文的模板**: 原文的模板似乎存在一些混淆和笔误。特别是步骤 4、5、6。 * 原文步骤 4 & 5: `假设 $x \in L$，证明 $f(x) \in U$` 和 `假设 $x \notin L$，证明 $f(x) \notin U$`。这描述的是 $L \le_m U$ 的**归约**方向。 * 原文步骤 6: `由于 $L \leq_{\mathrm{m}} U$ 且 $U$ 是**可识别**的，因此 $L$ 也必须是**可识别**的。` 这里有两个**问题**： 1. 我们要证明**不可识别性**，所以应该选择一个**不可识别**的 $U$，而不是**可识别**的 $U$。 2. $L \le_m U$ 和 $U$ **可识别**只能推出 $L$ **可识别**，这无法用来证明任何“不可能性”。 **修正后的模板（按照标准反证法逻辑）**: 1. **选择**一个已知的**不可识别语言** $U$ (例如 $\overline{\mathrm{A}_{\mathrm{TM}}}$)。 2. **目标**: 证明 $U \le_m L$。 3. **编写**一个计算**函数** $f$ 的**算法**，该**算法**输入 $U$ 的实例 $x$，输出 $L$ 的实例 $f(x)$。 4. **解释**为什么**算法** $f$ 总是**停机**（即 $f$ 是**可计算**的）。 5. **证明** $x \in U \implies f(x) \in L$。 6. **证明** $x \notin U \implies f(x) \notin L$。 7. **结论**: a. 从步骤 3-6，我们证明了 $U \le_m L$。 b. 现在进行**反证**：**假设** $L$ 是**可识别**的。 c. 根据**映射归约**的**性质**，因为 $U \le_m L$ 且 $L$ **可识别**，所以 $U$ 也必须是**可识别**的。 d. 这与步骤 1 中 $U$ 是**不可识别**的已知事实相**矛盾**。 e. 因此，**假设** $L$ 是**可识别**的是错误的。$L$ 必须是**不可识别**的。 **[总结]** **证明模板 9** 的目的是通过**映射归约**证明**不可识别性**。其核心是**反证法**：将一个已知的**不可识别语言** $U$ **映射归约**到目标**语言** $L$。如果 $L$ 是**可识别**的，那么 $U$ 也将是**可识别**的，从而产生矛盾。因此 $L$ 只能是**不可识别**的。原文的模板描述存在一些逻辑上的不一致，应以上述修正后的版本为准。 --- **[原文]（逐字逐句）** 关于**映射归约**的一个小**说明**：在给出**映射归约** $A \leq_{m} B$ 时，处理“**错误编码**”很麻烦，这些**编码**显然不在 $A$ 中。请注意，如果你 想展示 $A \leq_{m} B$，只要 $B \neq \Sigma^{*}$，我们就可以**固定**一些**字符串** $y \notin B$。然后，如果 $x$ 对于 $A$ 具有**错误格式**（例如，$x \neq\langle M\rangle$），我们只需**固定** $f(x)=y$。 因此，在进行**映射归约**时，你可以说“我们通过将**错误编码****映射**到固定**字符串** $y \notin B$ 来忽略它们”。然后在给出 $f$ 和**正确性证明**时，你可以忽略**错误编码**。 **[逐步解释]（from scratch，超细）** 这段话提供了一个在进行**映射归约**时处理非法格式输入的实用技巧。 1. **问题背景**: **映射归约** $A \le_m B$ 要求对**所有**字符串 $x$ 都满足 $x \in A \iff f(x) \in B$。这包括那些格式不正确的“垃圾”输入。例如，在**归约** $\mathrm{A}_{\mathrm{TM}}$ 时，输入可能是 "hello world"，它根本不是 $\langle M, w \rangle$ 的形式。这种输入显然不在 $\mathrm{A}_{\mathrm{TM}}$ 中。我们的**归约函数** $f$ 必须也能正确处理它。 2. **技巧详解**: * “只要 $B \neq \Sigma^{*}$”：这个技巧有一个前提，就是目标**语言** $B$ 不是包含所有**字符串**的**语言**。这意味着，我们总能找到一个**字符串** $y$ 使得 $y \notin B$。对于绝大多数有意义的**语言**，这个条件都满足。 * “**固定**一些**字符串** $y \notin B$”：事先找好一个确定不在 $B$ 中的**字符串**。例如，如果要**归约**到 $\mathrm{A}_{\mathrm{TM}}$，我们可以找一个永不**停机**的**图灵机** $M_{loop}$ 的**编码** $\langle M_{loop}, \epsilon \rangle$，这个**编码**肯定不在 $\mathrm{A}_{\mathrm{TM}}$ 中。 * “如果 $x$ 对于 $A$ 具有**错误格式**...我们只需**固定** $f(x)=y$”：我们的**归约函数** $f$ 的**算法**可以这样设计： 1. 检查输入 $x$ 的格式是否符合**语言** $A$ 的要求。 2. 如果格式错误，直接输出我们事先选好的那个 $y$。 3. 如果格式正确，再执行核心的转换逻辑。 * **效果**: 对于格式错误的 $x$，我们知道 $x \notin A$。通过这个技巧，我们让 $f(x) = y$，而我们又知道 $y \notin B$。这样，$x \notin A \iff f(x) \notin B$ 的条件对于所有格式错误的输入都自动满足了。 3. **简化证明**: * “在进行**映射归约**时，你可以说...”：这个技巧允许我们在写**证明**时，可以先声明我们已经用上述方法处理了所有格式错误的输入。 * “然后在给出 $f$ 和**正确性证明**时，你可以忽略**错误编码**”：这样，我们就可以把注意力集中在**证明**的核心部分——当输入 $x$ 格式正确时，**归约**是如何工作的。这大大简化了**证明**的书写，使其更清晰、更聚焦。 **[总结]** 该说明提供了一个处理**映射归约**中“格式错误输入”的标准方法：将所有不符合源**语言**格式的输入，统一**映射**到一个确定不在目标**语言**中的固定**字符串**。这使得**证明**者可以将精力集中在核心逻辑上，而不必为各种边界情况分心。 --- ### 5.4.2 **证明模板** 10：通过**精炼莱斯定理**证明 $L$ 是**不可识别**的 **[原文]（逐字逐句）** 我们可以使用**莱斯定理**来证明**不可判定性**，也可以类似地使用**精炼莱斯定理**来证明**不可识别性**： ## **证明模板** 10：通过**精炼莱斯定理**证明 $L$ 是**不可识别**的 1. 证明 $L$ 是一种**语言属性**： (a) **检查** $L$ 是否由形式为 $\langle M\rangle$ 的**字符串**组成，其中 $M$ 是一台 **TM**。 (b) **检查**对于任意两台 **TM** $M_{1}, M_{2}$ 使得 $L\left(M_{1}\right)=L\left(M_{2}\right)$，是否成立 $M_{1} \in L \Longleftrightarrow M_{2} \in L$。 2. 证明 $L$ 是**非平凡**的： (a) 展示存在一台 **TM** $M$ 使得 $\langle M\rangle \in L$。 (b) 展示存在一台 **TM** $M^{\prime}$ 使得 $\left\langle M^{\prime}\right\rangle \notin L$。 3. 展示 $\left\langle M_{\emptyset}\right\rangle \in L$。（ $M_{\emptyset}$ 是一台**语言**等于 $\emptyset$ 的 **TM**） 4. 得出结论，根据**精炼莱斯定理**，$L$ 是**不可识别**的。 **[逐步解释]（from scratch，超细）** 这个模板介绍了**莱斯定理**的一个加强版——**精炼莱斯定理** (Rice's Theorem, second part)，它专门用于证明**不可识别性**。 1. **精炼莱斯定理内容**: * **定理**叙述：一个**语言属性** $P$ 是**不可识别**的，当且仅当它满足以下两个条件： 1. $P$ 是一个**非平凡**的**语言属性**。 2. $P$ 是**单调**的 (Monotonic)，即如果**语言** $L_1 \in P$ 且 $L_1 \subseteq L_2$，那么 $L_2 \in P$。 * 原文的模板是上述**定理**的一个等价且更常用的形式，它将“单调性”具体化了。一个**语言属性**是**不可识别**的，如果它是**非平凡**的，并且包含空**语言**这个**属性**，但不包含所有**语言**。另一个方向，如果**属性**是**非平凡**的，不包含空**语言属性**，但其**补集**包含空**语言属性**，那么它的**补集**是**不可识别**的。 2. **模板步骤分析**: * **步骤 1 & 2**: 与**模板 8** 完全相同。首先，必须证明我们要讨论的**语言** $L$ 是一个**非平凡**的**语言属性**。这是应用任何版本的**莱斯定理**的前提。 * **步骤 3 (核心区别)**: `展示 $\left\langle M_{\emptyset}\right\rangle \in L$。` * $M_{\emptyset}$ 是任何一台其**语言**为空集（$L(M_{\emptyset})=\varnothing$）的**图灵机**，例如一台一启动就进入**拒绝状态**的机器。 * 这个步骤是在检查“空**语言**”这个最简单的**语言**是否具有我们正在讨论的**属性** $L$。 * **精炼莱斯定理**告诉我们： * 如果一个**非平凡语言属性** $L$ **包含**了空**语言**的**属性**（即 $\langle M_{\emptyset} \rangle \in L$），那么 $L$ 是**不可识别**的。 * 如果一个**非平凡语言属性** $L$ **不包含**空**语言**的**属性**（即 $\langle M_{\emptyset} \rangle \notin L$），那么 $L$ 的**补集** $\bar{L}$ 是**不可识别**的。（这也意味着 $L$ 本身是**可识别**的，但**不可判定**）。 * **步骤 4**: 做出结论。一旦步骤 1-3 都被验证，就可以直接引用**精炼莱斯定理**得出**不可识别性**的结论。 **[具体数值示例]** **问题**: 证明**语言** $\text{REG}_{\text{TM}} = \{\langle M \rangle \mid L(M) \text{ 是一个正则语言}\}$ 是**不可识别**的。 （注意：这其实是一个更复杂的例子，其**补集**是**不可识别**的，我们这里用它来展示模板的判断过程） 1. **证明是语言属性**: 是的，一个**语言**是否**正则**只取决于**语言**本身，和**图灵机**实现无关。 2. **证明是非平凡的**: * **是**: $L(M) = \varnothing$ 是**正则语言**，所以存在 $\langle M \rangle \in \text{REG}_{\text{TM}}$。 * **不是**: $L(M') = \{a^n b^n \mid n \ge 0\}$ 不是**正则语言**，所以存在 $\langle M' \rangle \notin \text{REG}_{\text{TM}}$。 3. **检查是否包含空语言属性**: * 空**语言** $\varnothing$ 是一个**正则语言**。因此，任何识别空**语言**的**图灵机** $M_{\emptyset}$ 的**编码** $\langle M_{\emptyset} \rangle$ 都属于 $\text{REG}_{\text{TM}}$。即 $\langle M_{\emptyset} \rangle \in \text{REG}_{\text{TM}}$。 4. **结论 (根据模板)**: 因为 $\text{REG}_{\text{TM}}$ 是一个**非平凡语言属性**，并且它**包含**了空**语言**的**属性**，根据模板（和定理），我们**似乎**应该得出 $\text{REG}_{\text{TM}}$ 是**不可识别**的。 **然而，这里有一个微妙之处**: $\text{REG}_{\text{TM}}$ 实际上是**不可判定**的，但其**补集** $\overline{\text{REG}_{\text{TM}}}$ 才是**不可识别**的。这说明**精炼莱斯定理**的完整叙述比模板更复杂。完整的**莱斯定理第二部分**是关于单调性的。 * $L$ 是**不可识别**的 $\iff L$ 是**非平凡语言属性**且对所有 $L_1, L_2$，若 $L_1 \in L$ 且 $L_1 \subseteq L_2$，则 $L_2 \in L$。 让我们用这个更精确的**定理**再来分析 $\text{REG}_{\text{TM}}$： * 它**不满足**单调性。例如，$L_1=\varnothing$ 是**正则**的，在**属性**里。$L_2=\{a^nb^n\}$ 不是**正则**的，不在**属性**里。但是 $L_1 \subseteq L_2$。这违反了单调性。所以 $\text{REG}_{\text{TM}}$ **不是不可识别**的。 * 那它的**补集** $\overline{\text{REG}_{\text{TM}}}$（非**正则语言**的**属性**）呢？它也**不满足**单调性。例如 $L_1 = \{a^nb^n\}$ 在**属性**里，但 $L_2=\Sigma^*$ 不在**属性**里，而 $L_1 \subseteq L_2$。 这说明**精炼莱斯定理**的应用比模板看起来更复杂。模板中的步骤 3 是一个简化的、特殊情况的判据，并不完全。正确的、与模板 10 意图最接近的**定理**是： **莱斯-夏皮罗定理**: 一个**语言属性** $L$ 是**可识别**的，当且仅当存在一个有限**语言**的集合 $F$ 使得 $L = \{ \langle M \rangle \mid \exists L_f \in F \text{ s.t. } L_f \subseteq L(M) \}$。 这个定理太复杂了，超出了这个模板的范畴。 **让我们回到一个模板能正确处理的例子**: **问题**: 证明 $L_{non-empty} = \{\langle M \rangle \mid L(M) \neq \varnothing\}$ (即 $\overline{\mathrm{E}_{\mathrm{TM}}}$) 是**不可判定**的，但**不是不可识别**的（即可识别）。 1. **语言属性**: 是。 2. **非平凡**: 是。 3. **是否包含空语言属性?**: 否。因为 $L(M_\emptyset) = \varnothing$，所以 $\langle M_\emptyset \rangle \notin L_{non-empty}$。 4. **根据定理**: 因为它是一个**非平凡语言属性**，但不包含空**语言属性**，所以 $L_{non-empty}$ **不是不可识别**的。它的**补集** $\overline{L_{non-empty}} = \mathrm{E}_{\mathrm{TM}}$ 才是**不可识别**的。这与我们之前的结论相符。 **[总结]** **证明模板 10** 试图提供一个基于**精炼莱斯定理**的简单判据来证明**不可识别性**。其核心思想是，除了**非平凡语言属性**外，还要检查该**属性**是否包含“空**语言**”这个最基础的例子。如果包含，则该**属性**是**不可识别**的。然而，这个模板是一个简化版，并不完全精确，更完整的理论（如莱斯-夏皮罗定理）要复杂得多。在基础课程中，这个模板通常用于判断像 $\mathrm{E}_{\mathrm{TM}}$ 和 $\mathrm{ALL}_{\mathrm{TM}}$ 这类**问题**的（不）**可识别性**。 --- ### 5.4.3 **证明模板** 11：通过**定理** 1 证明 $L$ 是**不可识别**的 **[原文]（逐字逐句）** 你应该牢记的最后一种**方法**依赖于**定理** 1。 ## **证明模板** 11：通过**定理** 1 证明 $L$ 是**不可识别**的 1. 证明 $L$ 是**不可判定**的。 2. 证明 $\bar{L}$ 是**可识别**的。 3. 得出结论，由于 $L$ 是**不可判定**的，但 $\bar{L}$ 是**不可识别**的，那么 $\bar{L}$ **[逐步解释]（from scratch，超细）** 这个模板基于一个核心**定理**（原文的**定理** 1），即： $L$ 是**可判定**的 $\iff$ $L$ 是**可识别**的且 $\bar{L}$ 是**可识别**的。 这个模板是该**定理**的逆否命题的应用，非常巧妙。 **原文模板的逻辑似乎有误，让我们修正它**: `得出结论，由于 L 是不可判定的，但 L的补集 是 可识别的，那么 L 必然是不可识别的。` （原文第三步写得非常混乱，"$\bar{L}$ 是**不可识别**的，那么 $\bar{L}$"，不通顺。我们基于上下文进行修正）。 **修正后的模板逻辑**: 1. **证明 $L$ 是不可判定的**: 使用任何证明**不可判定性**的方法（例如**模板 7** 或 **8**）。 2. **证明 $L$ 的补集 $\bar{L}$ 是可识别的**: 使用任何证明**可识别性**的方法（例如**模板 1, 2, 3**）。 3. **得出结论**: 现在我们有两个事实：(a) $L$ **不可判定**，(b) $\bar{L}$ **可识别**。 * 进行**反证**：**假设** $L$ 是**可识别**的。 * 那么，结合我们的**假设**（$L$ **可识别**）和步骤 2 的**证明**（$\bar{L}$ **可识别**），根据**定理** 1，我们能得出结论：$L$ 必须是**可判定**的。 * 这与我们在步骤 1 中证明的“$L$ 是**不可判定**的”相**矛盾**。 * 因此，我们的**反证法假设**“$L$ 是**可识别**的”是错误的。 * 最终结论：$L$ 必须是**不可识别**的。 **[具体数值示例]** **问题**: 证明 $\mathrm{E}_{\mathrm{TM}} = \{\langle M \rangle \mid L(M)=\varnothing\}$ 是**不可识别**的。 （注意，这与之前的一个结论相反，说明之前的分析或模板应用有误。让我们严格按这个模板走一遍。） **让我们换一个正确的例子**: 证明 $\overline{\mathrm{A}_{\mathrm{TM}}}$ 是**不可识别**的。 $\overline{\mathrm{A}_{\mathrm{TM}}} = \{\langle M, w \rangle \mid M \text{ 不接受 } w\}$ 1. **证明 $\overline{\mathrm{A}_{\mathrm{TM}}}$ 是不可判定的**: * 我们知道 $\mathrm{A}_{\mathrm{TM}}$ 是**不可判定**的。一个**语言**是**可判定**的当且仅当它的**补集**是**可判定**的。因此，$\overline{\mathrm{A}_{\mathrm{TM}}}$ 也必然是**不可判定**的。 2. **证明 $\overline{\mathrm{A}_{\mathrm{TM}}}$ 的补集是可识别的**: * $\overline{\mathrm{A}_{\mathrm{TM}}}$ 的**补集**是 $(\overline{\mathrm{A}_{\mathrm{TM}}}) = \mathrm{A}_{\mathrm{TM}}$。 * 我们需要证明 $\mathrm{A}_{\mathrm{TM}}$ 是**可识别**的。我们可以构造一个**识别器** $U$： “在输入 $\langle M, w \rangle$ 上： a. **模拟** $M$ 在 $w$ 上的运行。 b. 如果 $M$ **接受** $w$，则 $U$ **接受**。 c. 如果 $M$ **拒绝** $w$，则 $U$ **拒绝**。” * 这个**识别器** $U$ 的**正确性**： * 如果 $\langle M, w \rangle \in \mathrm{A}_{\mathrm{TM}}$，那么 $M$ 会**接受** $w$，$U$ 也会**接受**。 * 如果 $\langle M, w \rangle \notin \mathrm{A}_{\mathrm{TM}}$，那么 $M$ 或者**拒绝** $w$（此时 $U$ **拒绝**），或者在 $w$ 上**循环**（此时 $U$ 也**循环**）。在这两种情况下，$U$ 都不**接受**。 * 因此，$U$ 是 $\mathrm{A}_{\mathrm{TM}}$ 的**识别器**，所以 $\mathrm{A}_{\mathrm{TM}}$ 是**可识别**的。 3. **得出结论**: * 我们已经证明了 (1) $\overline{\mathrm{A}_{\mathrm{TM}}}$ 是**不可判定**的，以及 (2) 它的**补集** $\mathrm{A}_{\mathrm{TM}}$ 是**可识别**的。 * 现在**反证**：**假设** $\overline{\mathrm{A}_{\mathrm{TM}}}$ 是**可识别**的。 * 那么，我们就有 $\overline{\mathrm{A}_{\mathrm{TM}}}$ **可识别**（假设）和 $\mathrm{A}_{\mathrm{TM}}$ **可识别**（已证）。 * 根据**定理** 1，这意味着 $\mathrm{A}_{\mathrm{TM}}$ （或者说 $\overline{\mathrm{A}_{\mathrm{TM}}}$）必须是**可判定**的。 * 这与我们已知的“$\mathrm{A}_{\mathrm{TM}}$ **不可判定**”相**矛盾**。 * 因此，**假设**错误，$\overline{\mathrm{A}_{\mathrm{TM}}}$ 必须是**不可识别**的。 **[总结]** **证明模板 11** 是一个非常精妙的**证明不可识别性**的工具。它将一个直接证明“不存在**识别器**”的难题，转化为三个步骤：1. 证明目标**语言** $L$ **不可判定**。 2. 证明其**补集** $\bar{L}$ **可识别**。 3. 利用**定理** 1 的逆否命题，由前两步的结论推导出 $L$ **不可识别**的最终结论。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `5.5 关于循环的一些说明` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `5.5 关于循环的一些说明` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 # 5.5 关于**循环**的一些**说明** **[原文]（逐字逐句）** 无论何时运行 **TM** $M$，请务必问自己“如果 $M$ **循环**并且我卡在这一行怎么办”。以下是一些重要的**示例**： - 在编写**算法**时，你不应该说类似以下的话： 1. 运行 $M$ 在 $x$ 上 2. 如果 $M$ **循环**则执行 $X$。 这是因为如果 $M$ **循环**，你将卡在**第 1 行**永远运行 $M$。所以 $X$ 只是**死代码**（它永远不会被执行）。 此外，以下将是一个**错误算法**： - 在**输入** $\langle M, x\rangle$ 上，其中 $M$ 是一台 **TM**： - 如果 $M$ 在 $x$ 上不**停机**则执行 $X$。 任何形如“如果 $M$ **循环** / 在 $x$ 上不**停机**”的行实际上是无法**实现**的，因此在你的**算法**中使用这样的**内容**是**错误**的。$^{2}$？ **[逐步解释]（from scratch，超细）** 这一部分是关于在设计**图灵机算法**时如何正确处理“**循环**”或“**不停机**”这一核心**问题**的告诫和示例。 1. **核心警示**: “如果 $M$ **循环**并且我卡在这一行怎么办？” * 这是在**可计算性理论**中设计**算法**时必须时刻牢记的自我诘问。因为我们经常需要在一个**图灵机**（我们称之为“外层机器”）中**模拟**另一个**图灵机** $M$（“内层机器”）。由于内层机器 $M$ 的行为是未知的，它完全有可能在某个输入上永不**停机**。如果我们的外层机器只是简单地调用并等待内层机器结束，那么外层机器自身也会被“拖下水”，陷入无限**循环**。 2. **错误示例 1**: `如果 M 循环则执行 X` * **问题分析**: 这个**算法**的逻辑是“先做A，如果A做不完，就去做B”。这是一个逻辑上的悖论。 * `1. 运行 M 在 x 上`: 这一步意味着我们的外层机器开始**模拟** $M$ 在 $x$ 上的计算。 * `2. 如果 M 循环则执行 X`: 这一步永远无法到达。因为如果 $M$ 在 $x$ 上真的**循环**了，那么第 1 步的**模拟**就永远不会结束。我们的外层机器会完全卡死在第 1 步，程序的控制流根本没有机会去判断“M是否**循环**了”，更不用说去执行 $X$ 了。 * **死代码 (Dead Code)**: 因此，第 2 行 `执行 X` 是永远不会被执行的代码，是无效的**算法**步骤。 3. **错误示例 2**: `如果 M 在 x 上不停机则执行 X` * **问题分析**: 这与上一个例子本质相同，只是换了一种说法。这个问题是著名的**停机问题** (Halting Problem)。 * **停机问题是不可判定的**: **计算理论**的一个奠基性结论是，不存在一个通用的**图灵机** $H$，能够输入任意一个**图灵机** $M$ 和一个**字符串** $x$ 的**编码** $\langle M, x \rangle$，并总能在有限时间内判断出“$M$ 在 $x$ 上是否会**停机**”。 * “无法**实现**的行”: 因此，任何**算法**中出现“如果 $M$ **循环**”或“如果 $M$ 不**停机**”这样的条件判断语句，都等于是在声称自己能解决**停机问题**。这在理论上是不可能的。所以，这样的**伪代码**是错误的，因为它描述了一个无法被**图灵机**实现的计算。 4. **脚注 2 的解释**: `回想一下，$\overline{\mathrm{HALT}}_{\mathrm{TM}}$ 是**不可识别**的，没有**算法**可以**检查**一个 **TM** 是否在某个**字符串**上不**停机**。` * $\mathrm{HALT}_{\mathrm{TM}} = \{\langle M, w \rangle \mid M \text{ 在 } w \text{ 上停机}\}$ 是**可识别**但**不可判定**的。 * 它的**补集** $\overline{\mathrm{HALT}}_{\mathrm{TM}} = \{\langle M, w \rangle \mid M \text{ 在 } w \text{ 上循环}\}$ 是**不可识别**的。 * “没有**算法**可以**检查**...”等价于说 $\overline{\mathrm{HALT}}_{\mathrm{TM}}$ 是**不可识别**的。因为如果存在一个**算法**（**识别器**）能**检查**（**识别**）出所有**循环**的情况，那么 $\overline{\mathrm{HALT}}_{\mathrm{TM}}$ 就是**可识别**的，这与事实矛盾。 **[总结]** 本段强调，在设计**图灵机算法**时，不能天真地假设我们可以“检测”到另一个**图灵机**是否会**循环**。任何形如“运行M，如果M**循环**就做某事”的逻辑都是错误的，因为这等价于解决了**不可判定**的**停机问题**。我们必须设计出能够规避或处理这种潜在**循环**的**算法**。 --- **[原文]（逐字逐句）** - 使用**并行性**：假设你有一个 $L_{1}$ 的**识别器** $M_{1}$ 和一个 $L_{2}$ 的**识别器** $M_{2}$。你想为 $L_{1} \cup L_{2}$ **构建**一个**识别器**。 以下是**错误**的： 1. 在**输入** $x$ 上： 2. 运行 $M_{1}$ 在 $x$ 上。 3. 运行 $M_{2}$ 在 $x$ 上。 4. 如果 $M_{1}, M_{2}$ 中有一个**接受**，则**接受**。否则，**拒绝**。 特别是如果 $M_{1}$ 在 $x$ 上**循环**而 $M_{2}$ **接受** $x$，上述**内容**将在 $x \in L_{1} \cup L_{2}$ 上**循环**。这就是为什么你应该这样做： 1. 在**输入** $x$ 上： 2. 对于 $i=1$ 到 $\infty$： 3. 运行 $M_{1}$ 在 $x$ 上 $i$ 步。 4. 运行 $M_{2}$ 在 $x$ 上 $i$ 步。 5. 如果 $M_{1}$ 或 $M_{2}$ **接受**，则**接受**。 等价地 1. 在**输入** $x$ 上： 2. **并行**运行 $M_{1}$ 和 $M_{2}$ 在 $x$ 上。 3. 当 $M_{1}, M_{2}$ 中有一个**接受**时**接受**。 4. 如果 $M_{1}, M_{2}$ 都**拒绝**，则**拒绝**。 **[逐步解释]（from scratch，超细）** 这一部分给出了一个具体的场景，来说明如何正确处理潜在的**循环问题**，引出了**并行/交错**运行的重要思想。 1. **问题设定**: 我们要证明**可识别语言**在**并集**运算下是封闭的。即，如果 $L_1$ 和 $L_2$ 都是**可识别**的，那么它们的**并集** $L_1 \cup L_2$ 也是**可识别**的。为此，我们需要利用 $L_1$ 的**识别器** $M_1$ 和 $L_2$ 的**识别器** $M_2$ 来构造 $L_1 \cup L_2$ 的**识别器** $M_{union}$。 2. **错误的串行算法**: * **算法描述**: 先完整地运行 $M_1$，等它结束了，再运行 $M_2$。 * **问题所在**: $M_1$ 和 $M_2$ 只是**识别器**，不是**判定器**。这意味着它们可能会在某些输入上**循环**。 * **致命缺陷**: 考虑一个输入 $x$。假设 $x \notin L_1$ 但 $x \in L_2$。并且，假设 $M_1$ 在输入 $x$ 上会无限**循环**。 * 根据我们设计的**错误算法**， $M_{union}$ 会在第 2 步开始运行 $M_1$。由于 $M_1$ 在 $x$ 上**循环**， $M_{union}$ 将永远卡在第 2 步，永远没有机会去执行第 3 步来运行 $M_2$。 * 尽管 $x$ 确实属于 $L_1 \cup L_2$（因为它在 $L_2$ 中），但我们的 $M_{union}$ 却在 $x$ 上**循环**了，没能**接受**它。 * 这违反了**识别器**的定义（必须**接受**所有属于**语言**的**字符串**）。因此，这个串行**算法**是错误的。 3. **正确的交错算法 (Dovetailing / Time-slicing)**: * **算法描述**: 这是一种“时间分片”的策略。我们不让任何一个**模拟**独占计算资源。 * `对于 i=1 到 ∞`: 这是一个外层循环，代表时间的流逝或计算深度的增加。 * `运行 M1 在 x 上 i 步`: 在第 $i$ 轮，我们先**模拟** $M_1$ 运行 $i$ 步。因为步数是有限的，所以这一步保证会结束。 * `运行 M2 在 x 上 i 步`: 然后再**模拟** $M_2$ 运行 $i$ 步。这一步也保证会结束。 * `如果 M1 或 M2 接受，则接受`: 在每一轮的检查点，我们都看看是否有任何一个**模拟**已经成功了。 * **为什么这个算法是正确的**: * 假设 $x \in L_1 \cup L_2$。那么 $x$ 至少在 $L_1$ 或 $L_2$ 中。 * 不妨设 $x \in L_1$。因为 $M_1$ 是 $L_1$ 的**识别器**，所以 $M_1$ 会在有限的 $k$ 步内**接受** $x$。 * 我们的交错**算法**的外层循环计数器 $i$ 会不断增大。当 $i$ 达到 $k$ 时（在第 $k$ 轮循环中），我们在第 3 行“运行 $M_1$ 在 $x$ 上 $i$ 步”时，给予的步数 $i=k$ 就足够让 $M_1$ 完成计算并**接受**了。 * 一旦 $M_1$ **接受**，第 5 行的条件就会被触发，$M_{union}$ 就会**停机**并**接受** $x$。 * 如果 $x \in L_2$ 的情况同理。 * 如果 $x \notin L_1 \cup L_2$，那么 $M_1$ 和 $M_2$ 都不会**接受** $x$。它们可能会**拒绝**或**循环**。我们的 $M_{union}$ 也就会相应地**拒绝**或**循环**，但绝不会**接受**。 * 这完全符合**识别器**的定义。 4. **等价的并行描述**: * “**并行**运行”在理论上是对上述交错**算法**的一种更高级、更抽象的描述。你可以想象有两台独立的计算机，一台跑 $M_1$，一台跑 $M_2$，它们同时开始。只要有一台亮了“**接受**”的绿灯，总控制台就立刻宣布成功。 * 在单纸带**图灵机**模型上，我们无法真正地“**并行**”，所以我们用交错执行的方式来**模拟**并行。例如，我们可以用纸带的前半部分**模拟** $M_1$，后半部分**模拟** $M_2$，然后让读写头来回交替地在两边各执行一步操作。 **[总结]** 本段通过构造**并集**的**识别器**这一具体例子，生动地展示了简单的串行执行在面对可能**循环**的子过程时是错误的，而**交错/并行**运行是解决此类**问题**的标准且正确的范式。其核心思想是确保没有任何一个子过程可以无限期地霸占计算资源，从而保证所有应该被**接受**的输入最终都有机会被**接受**。 --- **[原文]（逐字逐句）** - 使用**交错运行**：我们令 $\left.\Sigma^{*}=\left\{w_{1}, w_{2}, \ldots\right\}\right\}^{3}$。假设你想为以下**语言构建**一个**识别器** $$

$$ 以下是**错误**的。 1. 在**输入** $\langle M\rangle$ 上，其中 $M$ 是一台 **TM**： 2. 对于 $i=1$ 到 $\infty$： 3. 运行 $M$ 在 $w_{i}$ 上。 4. 如果它**接受** $w_{i}$ 则**接受**。 [^3] 上述**方法失败**，因为如果 $M$ 在某个 $w_{i}$ 上**循环**，你将卡在**第 3 行**，永远无法在 $w_{i+1}, w_{i+2}$ 等**字符串**上运行 $M$。例如，如果 $M$ **接受** $w_{2}$ 但在 $w_{1}$ 上**循环**，上述**方法**将不**接受** $\langle M\rangle$。 因此，我们必须使用**交错运行**。以下是两种常见的做法： 1. 在**输入** $\langle M\rangle$ 上，其中 $M$ 是一台 **TM**： 2. 对于 $i=1$ 到 $\infty$： 3. 运行 $M$ 在所有长度 $\leq i$ 的**字符串** $w$ 上，运行 $i$ 步。 4. 如果它**接受**某个**字符串** $w$，则**接受**。 在使用**交错运行**时，你需要证明你的**算法**在某个时刻**接受**。特别是，存在一个 $i$ 足够大的点，你将**接受**。以下是如何证明这一点： 假设 $\langle M\rangle \in L$。那么 $L(M) \neq \emptyset$，所以 $M$ 在 $k$ 步内**接受**某个**字符串** $w$。当 $i \geq \max (|w|, k)$ 时，我们将运行 $M$ 在 $w$ 上（因为 $|w| \leq i$），并且我们将运行 $M$ 足够多的**步骤**以使其**接受** $w$。所以**算法****接受** $\langle M\rangle$。 另一种描述**交错运行**的方法如下： 1. 在**输入** $\langle M\rangle$ 上，其中 $M$ 是一台 **TM**： 2. 对于 $i=1$ 到 $\infty$： 3. 对于 $j=1$ 到 $i$： 4. 运行 $M$ 在 $w_{j}$ 上 $i$ 步。 5. 如果 $M$ **接受** $w_{j}$，则**接受**。 这里**算法接受** $\langle M\rangle \in L$ 的**证明**应如下所示：令 $\langle M\rangle \in L$，则 $L(M) \neq \emptyset$，所以 $M$ 在 $k$ 步内**接受**某个**字符串** $w_{t}$。当 $i \geq \max (t, k)$ 时，我们将设置 $j=t$ 并运行 $M$ 在 $w_{t}$ 上。由于 $i \geq k$，我们将运行 $M$ 足够多的**步骤**以使其**接受** $w_{t}$。所以**算法****接受** $\langle M\rangle$。 最后，请注意，我们可以使用一个简单的 **NTM** 来证明上述**内容**是**可识别**的： 1. 在**输入** $\langle M\rangle$ 上，其中 $M$ 是一台 **TM**： 2. **非确定性**地选择 $x \in \Sigma^{*}$ 3. 运行 $M$ 在 $x$ 上。 4. 如果 $M$ **接受**，则**接受**。 5. 如果 $M$ **拒绝**，则**拒绝**。 **[逐步解释]（from scratch，超细）** 这一部分将**交错**运行的思想应用到一个更复杂的场景中，即**识别**“**语言**非空的**图灵机**”的集合 $L = \overline{\mathrm{E}_{\mathrm{TM}}}$。这个场景涉及两个维度的“无限”：无限多的待测**字符串**和可能无限的运行时间。 1. **问题设定**: 我们要为**语言** $L=\{\langle M\rangle \mid L(M) \neq \emptyset\}$ 构造一个**识别器**。这意味着，如果给定的**图灵机** $M$ 至少**接受**一个**字符串**，我们的**识别器**就要**接受** $\langle M \rangle$。 2. **脚注 3**: `如果你想像我们这里一样在算法中遍历 Σ* 中的所有字符串，请写明你固定 w1, w2, ... 为 Σ* 的一个枚举。` 这是一个严谨性说明。$\Sigma^*$ 是一个无限集合，要遍历它，我们必须先假定一个明确的、无遗漏、无重复的顺序，比如按长度排序，同长度的按字典序排序。 3. **错误的“逐个测试”算法**: * **算法描述**: 按顺序（$w_1, w_2, w_3, ...$）拿出 $\Sigma^*$ 中的每一个**字符串**，然后用 $M$ 去完整地运行它。 * **致命缺陷**: 这和上一个例子中的串行**算法**有同样的毛病。如果 $M$ 在第一个**字符串** $w_1$ 上就**循环**了，那么我们的**识别器**将永远卡死，再也没有机会去测试 $w_2, w_3$ 等等。即使 $M$ 本来是会**接受** $w_2$ 的（即 $\langle M \rangle$ 应该被**接受**），我们的**识别器**也失败了。 4. **正确的交错算法 (方案一：二维扩展)** * **算法描述**: 这个**算法**非常精妙，它用一个统一的计数器 $i$ 同时控制了两个维度的搜索： * `对于 i=1 到 ∞`: 外层循环，不断扩大搜索范围。 * `运行 M 在所有长度 ≤ i 的字符串 w 上`: 在第 $i$ 轮，我们测试一个有限但不断增长的**字符串**集合。 * `运行 i 步`: 同时，我们也用 $i$ 来限制每次**模拟**的步数。 * **正确性证明**: * **假设** $\langle M \rangle \in L$，即 $L(M) \neq \varnothing$。 * 那么，必然**存在**某个**字符串** $w$ 和某个步数 $k$，使得 $M$ 在 $k$ 步内**接受** $w$。 * 现在考虑我们的计数器 $i$。当 $i$ 不断增大，总有一天会达到 $i \ge \max(|w|, k)$。 * 在这一轮，$i$ 足够大，所以： * 被测试的**字符串**集合（长度 $\le i$）包含了 $w$ (因为 $|w| \le i$)。 * 每次**模拟**的步数限制（$i$ 步）也足够 $M$ 在 $w$ 上完成计算 (因为 $k \le i$)。 * 因此，在这一轮的**模拟**中，$M$ **接受** $w$ 这件事必然会被发现。 * 一旦发现，**识别器**就会**接受** $\langle M \rangle$。这就保证了**完备性**。 5. **正确的交错算法 (方案二：嵌套循环)** * **算法描述**: 这个版本将两个维度分解为两个嵌套的循环。 * `对于 i=1 到 ∞`: 外层循环控制“资源”（在这里主要是步数）。 * `对于 j=1 到 i`: 内层循环遍历**字符串**列表的前 $i$ 个。 * `运行 M 在 w_j 上 i 步`: 在第 $i$ 轮，我们用 $i$ 步的“预算”去尝试运行前 $i$ 个**字符串**。 * **正确性证明**: * **假设** $M$ 在 $k$ 步内**接受**第 $t$ 个**字符串** $w_t$。 * 当外层循环的 $i$ 增长到 $i \ge \max(t, k)$ 时： * 内层循环的范围是 $j=1$ 到 $i$，所以它必然会取到 $j=t$。 * 在 $j=t$ 的那次内层循环中，我们“运行 $M$ 在 $w_t$ 上 $i$ 步”。 * 因为步数预算 $i \ge k$，所以这次**模拟**是足够的， $M$ 会成功**接受** $w_t$。 * **识别器**因此会**接受** $\langle M \rangle$。 6. **使用 NTM 的简洁证明**: * **算法描述**: 这个**算法**利用了**非确定性**的“猜测”能力。 * `非确定性地选择 x ∈ Σ*`: 我们的 **NTM** 不去遍历，而是直接“猜”一个**字符串** $x$。你可以想象它瞬间分身出无数个副本，每个副本都猜了一个不同的**字符串**。 * `运行 M 在 x 上`: 每个副本都用自己猜到的 $x$ 去**模拟** $M$。 * `如果 M 接受，则接受`: 如果有任何一个副本发现它猜的那个 $x$ 被 $M$ **接受**了，这个副本就进入**接受状态**。 * **正确性**: * 如果 $\langle M \rangle \in L$，那么存在一个 $w$ 被 $M$ **接受**。因此，那个恰好猜中 $w$ 的副本就会成功，导致整个 **NTM** **接受**。 * 如果 $\langle M \rangle \notin L$，那么 $M$ 不**接受**任何**字符串**。因此，无论副本们猜什么 $x$，**模拟** $M$ 都不会**接受**。所以没有任何一个副本会**接受**，整个 **NTM** 也不**接受**。 * 这完美地展示了 **NTM** 在处理“存在性”**问题**时的简洁和优雅。 **[总结]** 本段深入探讨了**交错**运行技术，展示了如何用它来处理两个无限维度（无限多的**字符串**和无限的运行时间）的**问题**。它给出了两种等价的**确定性**交错**算法**，并给出了相应的**正确性**论证。最后，它还展示了如何用**非确定性图灵机**以一种更简洁、更抽象的方式解决同一个**问题**，突显了 **NTM** 在**可识别性证明**中的威力。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `6 复杂度` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `6 复杂度` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 # 6 **复杂度** **[原文]（逐字逐句）** 到目前为止，我们已经研究了**可 计算性**，即哪些**语言**是**可判定**的、**可识别**的，或者两者都不是：粗略地说，一个**问题**是否可以通过**计算机**解决。然而，这并没有告诉我们它能被多么**高效**地解决。现在我们将注意力转向**复杂度**：研究解决一个**问题**需要多少**资源**。**效率**总是相对于**输入**的**长度**（即**字符**的数量）来衡量的，我们将其表示为 $n$。 **[逐步解释]（from scratch，超细）** 这一段是**可计算性理论**到**复杂性理论**的过渡，标志着我们研究视角的一个重大转变。 1. **角色定位**: 这是一个承上启下的段落，总结了前一部分（**可计算性**）的核心**问题**，并引出了后一部分（**复杂度**）的核心**问题**。 2. **内容回顾与展望**: * “到目前为止，我们已经研究了**可计算性**...”：这部分总结了前面章节的主要内容。**可计算性理论** (Computability Theory) 主要回答的是“**能解**还是**不能解**？” (Solvable or Unsolvable?) 的**问题**。它将**问题**（**语言**）分为三类： * **可判定**的 (Decidable): 存在一个**算法**（**判定器**）总能**停机**并给出“是/否”的正确答案。 * **可识别**的 (Recognizable): 存在一个**算法**（**识别器**）能在答案是“是”的时候**停机**并回答，但在答案是“否”的时候可能**拒绝**或**永不**停机**。 * 两者都不是（**不可识别**的）: 连“是”的答案都无法保证能给出。 * “一个**问题**是否可以通过**计算机**解决”：这是对**可计算性**的通俗概括。如果一个**问题**是**可判定**的，我们通常认为它是“理论上可解决的”。 3. **引入新视角**: * “然而，这并没有告诉我们它能被多么**高效**地解决”：这是**可计算性理论**的局限性。一个**问题**即使是**可判定**的，解决它的**算法**也可能极其缓慢，以至于在实际中毫无用处。例如，我们在示例 4 中看到的 **CNF-SAT** 的**判定器**，其运行时间是指数级的 ($O(2^n)$)，当输入规模 $n$ 稍大时，它需要的时间可能比宇宙的年龄还长。 * “现在我们将注意力转向**复杂度**”：**复杂性理论** (Complexity Theory) 就是为了弥补这一不足而生的。它研究的是“**好解**还是**难解**？” (Easy or Hard?) 的**问题**。它不再仅仅关心“能不能解”，而是关心“解决它需要多少**资源**？”。 * “**资源**”：在**计算理论**中，最重要的两种**资源**是： * **时间 (Time)**: 解决**问题**所需的计算步骤数。 * **空间 (Space)**: 解决**问题**所需的存储空间（即**图灵机**纸带的使用量）。 本讲义主要关注**时间复杂度**。 * “**效率**总是相对于**输入**的**长度**...来衡量的，我们将其表示为 $n$”：这是一个基本原则。我们不能说“解决这个**问题**需要1秒”，因为输入不同，时间也不同。**复杂度**是用一个关于输入长度 $n$ 的**函数**来衡量的。例如，说一个**算法**的**时间复杂度**是 $O(n^2)$，意味着当输入长度加倍时，其运行时间大约会增长到原来的四倍。 **[总结]** 本段是连接**可计算性**与**复杂性**两大理论板块的桥梁。它指出，仅仅知道一个**问题**可解是不够的，我们还需要关心解决它的效率。**复杂性理论**正是研究解决**问题**所需的**资源**（如时间、空间）与输入规模 $n$ 之间关系的学科。 --- **[原文]（逐字逐句）** 定义 10。设 $M$ 是一台在每个**输入**上都**停机**的**确定性图灵机**。如果对于每个**长度**为 $n$ 的**输入** $x$，$M$ 在最多 $t(n)$ 步内**停机**在**输入** $x$ 上，我们说 $M$ 的**运行时间**为 $t(n)$。 **[逐步解释]（from scratch，超细）** 这是对**确定性图灵机 (DTM)** **运行时间**的正式定义。 1. **角色定位**: 定义**时间复杂度**函数 $t(n)$。 2. **内容拆解**: * “设 $M$ 是一台在每个**输入**上都**停机**的**确定性图灵机**”：这个定义的前提是，我们讨论的必须是一个**判定器**。**复杂度**分析通常针对保证**停机**的**算法**。 * “对于每个**长度**为 $n$ 的**输入** $x$”：这里的关键是“每个”。$t(n)$ 衡量的是**最坏情况**下的**运行时间** (worst-case running time)。在所有长度为 $n$ 的输入中，我们只关心那个让机器运行最久的输入。$t(n)$ 必须至少和这个最长运行时间一样大。 * “$M$ 在最多 $t(n)$ 步内**停机**”：$t(n)$ 是一个上界。它是一个函数，输入是**字符串**长度 $n$，输出是所需的最大步数。 * “**步骤数**”：指的是**图灵机**的转移函数执行的次数。 **[具体数值示例]** 假设一台**图灵机** $M$ 用于**判定语言** $L=\{a^k \mid k \text{ is even}\}$。 * 输入 $w_1 = aa$ ($n=2$)。$M$ 可能运行了 10 步后**接受**。 * 输入 $w_2 = ab$ ($n=2$)。$M$ 可能运行了 3 步后**拒绝**。 * 输入 $w_3 = bb$ ($n=2$)。$M$ 可能运行了 5 步后**拒绝**。 在所有长度为 2 的输入中，最坏情况是运行 10 步。因此，我们必须有 $t(2) \ge 10$。 如果我们**分析**这台机器的**算法**，发现对于任何长度为 $n$ 的输入，它最多需要 $3n+5$ 步。那么我们就可以说这台机器的**运行时间**是 $t(n) = 3n+5$。在**复杂度**分析中，我们通常使用大O表示法，会说它的**时间复杂度**是 $O(n)$。 **[总结]** 定义 10 明确了**确定性图灵机**的**运行时间** $t(n)$ 是一个关于输入长度 $n$ 的函数，它表示了机器在处理任何长度为 $n$ 的输入时所需的最大计算步数（最坏情况下的上界）。 --- **[原文]（逐字逐句）** 定义 11。设 $M$ 是一台在每个**输入**上都**停机**的**非确定性图灵机**。如果对于每个**长度**为 $n$ 的**输入** $x$，$M$ 在 $x$ 上的每个可能的**计算**在最多 $t(n)$ 步内**终止**，我们说 $M$ 的**运行时间**为 $t(n)$。 **[逐步解释]（from scratch，超细）** 这是对**非确定性图灵机 (NTM)** **运行时间**的正式定义。 1. **角色定位**: 定义 **NTM** 的**时间复杂度**函数 $t(n)$。 2. **内容拆解**: * “在每个**输入**上都**停机**的**非确定性图灵机**”：同样，我们讨论的是 **NTM** **判定器**。这意味着对于任何输入，**NTM** 的所有计算分支都必须在有限步内**停机**。 * “$M$ 在 $x$ 上的每个可能的**计算**”：这是与 **DTM** 定义的关键区别。**NTM** 在计算过程中会产生一棵“计算树”，树上的每一条从根到叶的路径都是一个“可能的**计算**”或“分支”。 * “在最多 $t(n)$ 步内**终止**”：**NTM** 的**运行时间**是由其**最长**的那个计算分支的长度决定的。$t(n)$ 必须是所有长度为 $n$ 的输入所产生的计算树中，最深的那个叶子节点深度的上界。 **[具体数值示例]** 假设一台 **NTM** 在输入 $x$ 上，产生了3个计算分支： * 分支 1：运行了 10 步后**接受**。 * 分支 2：运行了 50 步后**拒绝**。 * 分支 3：运行了 25 步后**拒绝**。 那么，这台 **NTM** 在输入 $x$ 上的**运行时间**就是 50 步（最长分支的长度）。$t(|x|)$ 必须大于等于 50。 **[总结]** 定义 11 明确了**非确定性图灵机**的**运行时间** $t(n)$ 是其所有计算分支中，最长分支的步数。同样，这也是一个关于输入长度 $n$ 的最坏情况上界。 --- **[原文]（逐字逐句）** 在上述**内容**中，$M$ 在**输入** $x$ 上的**步骤数**是 $M$ 在 $x$ 上**停机**之前所采取的**转移数**。 **[逐步解释]（from scratch，超细）** 这是一个补充说明，用于精确定义“步”的含义。 1. **角色定位**: 对“步”的精确定义。 2. **内容拆解**: * “**步骤数**” (Number of steps): 在**图灵机**的形式化模型中，每一步操作都由转移函数 $\delta$ 来定义。$\delta(q, a) = (q', b, D)$ 表示在当前状态 $q$、读到符号 $a$ 时，机器会转换到新状态 $q'$、写入符号 $b$、并向方向 $D$ (左或右) 移动读写头。 * “**转移数**” (Number of transitions): 每执行一次这样的 $\delta$ 函数，就被计为一步。 * 所以，“**步骤数**”就是**图灵机**从启动状态到进入**接受**或**拒绝状态**（**停机**）所执行的转移函数的总次数。 **[总结]** 本段将**时间复杂度**中的“步”与**图灵机**模型中的“转移函数执行次数”等同起来，为**时间复杂度**分析提供了坚实的理论基础。 --- **[原文]（逐字逐句）** ## 定义 12。 $\operatorname{TIME}(f(n))$：由在 $O(f(n))$ 时间内运行的**图灵机****判定**的**语言**的**类**。 $\operatorname{NTIME}(f(n))$：由在 $O(f(n))$ 时间内运行的**非确定性图灵机****判定**的**语言**的**类**。 **[逐步解释]（from scratch，超细）** 这部分定义了两个重要的**复杂度类** (Complexity Classes)。 1. **角色定位**: 定义**确定性**和**非确定性**的**时间复杂度类**。 2. **内容拆解**: * **复杂度类**: 一个**复杂度类**是所有能被某种计算模型、在某种**资源**限制下解决的**问题**（**语言**）的集合。 * $\operatorname{TIME}(f(n))$: * 这是一个**确定性时间复杂度类**。 * 它包含了所有那些存在一个**确定性图灵机 (DTM)** **判定器**的**语言** $L$，并且这个**判定器**的**运行时间**是 $O(f(n))$。 * **大O表示法 (Big O Notation)**: $O(f(n))$ 表示**运行时间**的增长率。它忽略了常数因子和低阶项。例如，如果一台机器的**运行时间**是 $3n^2 + 5n + 100$，我们说它的**时间复杂度**是 $O(n^2)$。使用大O表示法是因为我们更关心**算法**在输入规模变大时的“扩展性”，而不是在某个特定机器上的确切运行秒数。 * $\operatorname{NTIME}(f(n))$: * 这是一个**非确定性时间复杂度类**。 * 它包含了所有那些存在一个**非确定性图灵机 (NTM)** **判定器**的**语言** $L$，并且这个**判定器**的**运行时间**是 $O(f(n))$。 **[具体数值示例]** * 我们之前证明了 $L = \{a^k b^k \mid k \ge 1\}$ 是**可判定**的，其**判定器**需要类似 $O(n^2)$ 的时间（因为需要来回扫描）。所以 $L \in \operatorname{TIME}(n^2)$。 * 一个简单的**字符串**匹配**算法**可能需要 $O(n)$ 时间，所以这个**问题**属于 $\operatorname{TIME}(n)$。 **[总结]** 定义 12 为我们提供了根据**运行时间**对**问题**进行分类的工具。$\operatorname{TIME}(f(n))$ 和 $\operatorname{NTIME}(f(n))$ 分别是所有能被**确定性**和**非确定性图灵机**在 $O(f(n))$ 时间内解决的**问题**的集合。 --- **[原文]（逐字逐句）** 定义 13。如果存在某个**常数** $k$ 使得 $f(n)=O\left(n^{k}\right)$，我们说 $t: \mathbb{N} \rightarrow \mathbb{N}$ 是**多项式**的。 **[逐步解释]（from scratch，超细）** 这是对“**多项式时间**”这一核心概念的定义。 1. **角色定位**: 定义**多项式函数**类。 2. **内容拆解**: * “**多项式**的 (polynomial)”：这是一个用来描述**算法**效率的标签。如果一个**算法**的**时间复杂度**函数 $t(n)$ 的增长速度不快于某个**多项式函数** $n^k$，那么我们就说这个**算法**是**多项式时间算法**。 * $f(n) = O(n^k)$: 这意味着存在**常数** $c$ 和 $n_0$，使得对于所有 $n \ge n_0$，都有 $f(n) \le c \cdot n^k$。 * **常数 k**: 这个 $k$ 可以是任何固定的**常数**，如 1, 2, 3, 100, 等等。$n^2$, $n^3$, $n^{100}$ 都是**多项式**。而 $2^n$, $n!$ 这种增长速度比任何 $n^k$ 都快的函数，则被称为**指数时间** (exponential time)，它们不属于**多项式**。 3. **意义**: 在**复杂性理论**中，“**多项式时间**”通常被看作是“高效的”、“可行的”、“好的”**算法**的代名词。而**指数时间**则被认为是“低效的”、“不切实际的”。这被称为 **Cobo-Edmonds 论题**。虽然 $n^{100}$ 在实际中也很慢，但这种划分在理论上是非常有用的，它将**问题**清晰地分成了“难”和“易”两大类。 **[具体数值示例]** * $t(n) = 5n^3 + 2n - 10$ 是**多项式**的，因为它是 $O(n^3)$ (这里 $k=3$)。 * $t(n) = 100n \log n$ 是**多项式**的，因为 $\log n$ 的增长比 $n$ 慢，所以 $n \log n$ 的增长比 $n^2$ 慢，即 $O(n^2)$ (这里 $k=2$)。 * $t(n) = 1.1^n$ 不是**多项式**的，它是**指数**的。 * $t(n) = n!$ 不是**多项式**的，它是**阶乘**的。 **[总结]** 定义 13 将**多项式时间**形式化为**复杂度**函数的增长率被 $n^k$ (对于某个**常数** k) 所约束。这是区分“高效**算法**”与“低效**算法**”的理论分界线。 --- **[原文]（逐字逐句）** 值得了解：如果 $f: \mathbb{N} \rightarrow \mathbb{N}$ 和 $g: \mathbb{N} \rightarrow \mathbb{N}$ 都是**多项式**，那么以下也是**多项式**： - $f+g$，其中 $(f+g)(x)=f(x)+g(x)$。 - $f * g$，其中 $(f * g)(x)=f(x) * g(x)$。 - $f \circ g$，其中 $(f \circ g)(x)=f(g(x))$。 特别是，如果你的**算法**中有一个**步骤**需要**多项式时间** $O\left(n^{k_{1}}\right)$，并且这个**步骤**被**多项式次**重复 $O\left(n^{k_{2}}\right)$（例如，如果你有一个 **for** **循环**），那么总**运行时间**是 $O\left(n^{k_{1}+k_{2}}\right)=O\left(n^{k}\right)$。 **[逐步解释]（from scratch，超细）** 这段话阐述了**多项式函数**在加法、乘法和复合运算下的封闭性，并解释了这在**算法分析**中的实际意义。 1. **多项式的封闭性**: * $f+g$: 如果 $f=O(n^{k_1})$ 且 $g=O(n^{k_2})$，那么 $f+g = O(n^{\max(k_1, k_2)})$。这也是一个**多项式**。 * **算法意义**: 这对应于顺序执行两个**算法**。总时间由较慢的那个决定。 * $f*g$: 如果 $f=O(n^{k_1})$ 且 $g=O(n^{k_2})$，那么 $f*g = O(n^{k_1+k_2})$。这也是一个**多项式**。 * **算法意义**: 这通常对应于嵌套循环，或者在循环中调用一个函数。 * $f \circ g$: 如果 $f=O(n^{k_1})$ 且 $g=O(n^{k_2})$，那么 $f(g(n)) \approx (n^{k_2})^{k_1} = n^{k_1 \cdot k_2}$。这也是一个**多项式**。 * **算法意义**: 这对应于一个**算法**的输出，作为另一个**算法**的输入。例如，一个**归约**过程。 2. **在算法分析中的应用**: * “如果你的**算法**中有一个**步骤**需要**多项式时间** $O(n^{k_1})$...”：这指的是一个循环体，或者一个子函数的调用。 * “...并且这个**步骤**被**多项式次**重复 $O(n^{k_2})$”：这指的是外层循环的次数。 * “总**运行时间**是 $O(n^{k_1+k_2})$”：总时间 = 循环次数 × 循环体时间 = $O(n^{k_2}) \times O(n^{k_1}) = O(n^{k_1+k_2})$。 * “$=O(n^k)$”：因为 $k_1$ 和 $k_2$ 都是**常数**，所以它们的和 $k = k_1+k_2$ 也是一个**常数**。因此，总时间仍然是**多项式**的。 **[总结]** 本段的核心思想是：由**多项式时间**的“积木块”通过顺序执行、嵌套循环、函数调用等方式组合起来的**算法**，其整体**时间复杂度**仍然是**多项式**的。这使得我们可以模块化地**分析算法**，只要保证每个部分都是**多项式**的，整体就是**多项式**的。 --- **[原文]（逐字逐句）** 定义 14。P：由在 $O\left(n^{k}\right)$ 时间内运行的**图灵机****判定**的**语言**的**类**，其中 $k$ 是某个**常数**。换句话说 $$

$$ **[逐步解释]（from scratch，超细）** 这是**复杂性理论**中最核心的**复杂度类**之一 **P** 的定义。 1. **角色定位**: 定义**复杂度类 P**。 2. **内容拆解**: * **P**: 代表**多项式时间 (Polynomial time)**。 * “由在 $O(n^k)$ 时间内运行的**图灵机****判定**的**语言**的**类**”：**P** 类包含了所有那些存在一个**确定性图灵机 (DTM)** **判定器**的**语言**，并且这个**判定器**的**运行时间**是**多项式**的。 * 通俗地说，**P** 是所有能够被**确定性算法**“高效”解决的**问题**的集合。 3. **公式解释**: * $$

$$ * $\operatorname{TIME}(n^k)$: 这是所有能在 $O(n^k)$ 时间内被 **DTM** **判定**的**语言**的集合。 * $\bigcup_{k=1}^{\infty}$: 这个符号代表**并集**。我们将所有可能的**多项式时间**类都联合起来。 * **含义**: $\mathrm{P} = \operatorname{TIME}(n^1) \cup \operatorname{TIME}(n^2) \cup \operatorname{TIME}(n^3) \cup \dots$。一个**语言**只要在**任何一个** $\operatorname{TIME}(n^k)$ 中（无论 $k$ 多大，只要是**常数**），它就属于 **P** 类。 **[具体数值示例]** * 判断一个列表是否排好序：可以在 $O(n)$ 时间内完成。所以这个**问题**在 $\operatorname{TIME}(n^1)$ 中，因此在 **P** 中。 * 两个 $n \times n$ 矩阵相乘：标准**算法**需要 $O(n^3)$ 时间。所以这个**问题**在 $\operatorname{TIME}(n^3)$ 中，因此在 **P** 中。 * 寻找图中两点间的最短路径（Dijkstra **算法**）：在稠密图上约 $O(n^2)$ 时间，其中 $n$ 是顶点数。所以这个**问题**在 **P** 中。 **[总结]** 定义 14 定义了**复杂度类 P**，它是所有可以用**确定性算法**在**多项式时间**内解决的**判定问题**的集合。它代表了我们理论上认为的“容易解决”的**问题**。 --- **[原文]（逐字逐句）** 定义 15（**验证器**）。**语言** $L$ 的**验证器** $V$ 是一种**确定性算法**，使得 $V$ 以 $x$ 和某个**字符串** $c$ 作为**输入**，并且 $$

$$ 如果 $V$ 在 $O\left(|x|^{k}\right)$ 时间内运行，其中 $k$ 是某个**常数**，则称 $V$ 为**多项式时间验证器**。 **[逐步解释]（from scratch，超细）** 这个定义引入了“**验证器**”的概念，它是理解**复杂度类 NP** 的关键。 1. **角色定位**: 定义**验证器**，特别是**多项式时间验证器**。 2. **内容拆解**: * “**验证器** $V$”：它本身是一个**确定性算法**（**DTM**）。 * “以 $x$ 和某个**字符串** $c$ 作为**输入**”：它有两个输入： * $x$: 原始**问题**的实例。 * $c$: 被称为“**证书**” (certificate) 或“证据” (witness)。它是用来帮助**验证** $x$ 是否属于 $L$ 的一个附加信息。 * “$x \in L \leftrightarrow \exists c \text{ s.t. } V(x,c) \text{ accepts}$”: 这是**验证器**的核心逻辑。 * **正向 ($\rightarrow$)**: 如果 $x$ 确实属于 $L$，那么**必须存在**一个“证据” $c$，当你把 $x$ 和 $c$ 一起给**验证器** $V$ 时，$V$ 会**接受**。 * **反向 ($\leftarrow$)**: 如果存在一个证据 $c$ 能让 $V$ **接受** $(x,c)$，那么 $x$ 就一定属于 $L$。这意味着**验证器**不能被假的证据欺骗。 * “**多项式时间验证器**”：如果**验证器** $V$ 的**运行时间**是关于**原始输入 $x$ 的长度** $|x|$ 的**多项式**，那么它就是一个高效的**验证器**。注意，**复杂度**是根据 $|x|$ 计算的，而不是 $|x|+|c|$。这隐含地要求**证书** $c$ 的长度也必须是 $|x|$ 的**多项式**，否则光是读取 $c$ 就会超时。 **[具体数值示例]** * **问题**: **CNF-SAT**。$x = \langle \phi \rangle$ 是一个 **CNF** 公式。 * **证书 $c$**: 一个满足**公式** $\phi$ 的**真值赋值**。例如，如果 $\phi = (x_1 \lor \neg x_2)$，一个**证书**可以是 $c = (x_1=\text{True}, x_2=\text{True})$。 * **验证器 $V$**: 1. 输入 $x=\langle \phi \rangle$ 和**证书** $c$ (一个**赋值**)。 2. 检查 $c$ 是否是 $\phi$ 中所有**变量**的一个完整**赋值**。 3. 将 $c$ 中的**真值**代入 $\phi$ 中，**评估**其结果。 4. 如果结果是 **True**，**接受**；否则，**拒绝**。 * **分析**: * 如果 $\phi$ 是**可满足**的，那么**一定存在**一个可满足**赋值** $c$，使得 $V$ **接受** $(\langle\phi\rangle, c)$。 * 如果 $V$ **接受** $(\langle\phi\rangle, c)$，那说明 $c$ 就是一个可满足**赋值**，因此 $\phi$ 是**可满足**的。 * $V$ 的**运行时间**：代入并**评估**一个公式的时间，是关于公式长度 $|\langle\phi\rangle|$ 的**多项式**（大致是线性的）。因此，$V$ 是一个**多项式时间验证器**。 **[总结]** 定义 15 描述了“**验证器**”模型：一个**问题**的解可能很难“找到”，但如果有人给你一个解（**证书**），你应该能很“高效地”（在**多项式时间**内）“**验证**”这个解是否正确。 --- **[原文]（逐字逐句）** 定义 16。NP：由在 $O\left(n^{k}\right)$ 时间内运行的**非确定性图灵机****判定**的**语言**的**类**，其中 $k$ 是某个**常数**。换句话说 $$

$$ 或者，**NP** 是具有**多项式时间验证器**的**语言**的**类**（如上所述）。 **[逐步解释]（from scratch，超细）** 这是**复杂性理论**中另一个核心**复杂度类** **NP** 的两种等价定义。 1. **角色定位**: 定义**复杂度类 NP**。 2. **定义一：基于 NTM** * **NP**: 代表**非确定性多项式时间 (Nondeterministic Polynomial time)**。 * “由在 $O(n^k)$ 时间内运行的**非确定性图灵机****判定**的**语言**的**类**”：**NP** 包含了所有那些存在一个**非确定性图灵机 (NTM)** **判定器**的**语言**，并且这个**判定器**的**运行时间**是**多项式**的。 * **公式**: $\mathrm{NP}=\bigcup_{k=1}^{\infty} \mathrm{NTIME}\left(n^{k}\right)$，这与 **P** 类的定义形式上完全平行，只是把 **TIME** 换成了 **NTIME**。 * **直觉**: **NP** **问题**是那些可以通过**非确定性**的“猜测”并在**多项式时间**内“验证”来解决的**问题**。**NTM** 的**多项式时间**运行，可以看作是： 1. **非确定性**地“猜测”一个**证书** $c$（这一步在 **NTM** 模型里算一步）。 2. **确定性**地在**多项式时间**内**验证**这个**证书**是否正确。 3. **定义二：基于验证器** * “**NP** 是具有**多项式时间验证器**的**语言**的**类**”：这提供了对 **NP** 的另一种、通常更直观的理解。一个**语言** $L$ 属于 **NP**，当且仅当存在一个**多项式时间验证器** $V$ (如定义 15 所述)。 * **两种定义的等价性**: * 从 **NTM** 到**验证器**: 如果一个 **NTM** 能在**多项式时间**内**判定** $L$，那么一个成功的计算分支（从根到**接受**叶子的路径）就可以被看作是“**证书**” $c$。**验证器** $V$ 的工作就是**确定性**地**模拟** **NTM** 在这条特定路径上的计算，这自然是**多项式时间**的。 * 从**验证器**到 **NTM**: 如果存在一个**多项式时间验证器** $V$，我们可以构造一个 **NTM** **判定器** $N$ 如下：“在输入 $x$ 上，1. **非确定性**地猜测一个长度为**多项式**的**证书** $c$。 2. **确定性**地运行 $V$ 在 $(x,c)$ 上。 3. 如果 $V$ **接受**，则 $N$ **接受**；否则**拒绝**。” 这个 **NTM** 的**运行时间**是**多项式**的。 **[总结]** 定义 16 给出了 **NP** 类的两个等价定义： 1. 可以被**非确定性图灵机**在**多项式时间**内**判定**的**问题**集合。 2. 解的正确性可以被一个**确定性算法**在**多项式时间**内**验证**的**问题**集合（“猜证”模式）。 **NP** 代表了我们理论上认为的“容易验证”的**问题**。 --- **[原文]（逐字逐句）** 在这个**类**中，我们不关心精确的**运行时间**是多少，只要它是**输入大小**的**多项式**即可。特别是，你的**算法**中每个**步骤**的**速度**可能取决于你所考虑的**计算模型**。因此，你需要证明你的**算法**的每个**步骤**都需要**多项式时间**，并且每个 **for** / **while** **循环**都运行**多项式次**。 **[逐步解释]（from scratch，超细）** 这段话是对**多项式时间**这一概念在实际**算法分析**中如何应用的进一步说明。 1. **角色定位**: 提供进行**多项式时间**分析的指导原则。 2. **内容拆解**: * “不关心精确的**运行时间**...只要它是**多项式**即可”：这再次强调了大O表示法和**多项式**分类的抽象性。我们关心的是增长的“类别”（**多项式** vs **指数**），而不是具体的系数和常数。 * “**速度**可能取决于你所考虑的**计算模型**”：这是一个重要的理论观点。例如，在**图灵机**模型上需要 $O(n^2)$ 的**算法**，在一个更强大的 RAM (Random Access Machine) 模型上可能只需要 $O(n)$。然而，大多数“合理”的**确定性计算模型**之间都可以通过**多项式时间**的**模拟**相互转换（例如，**模拟** RAM 机器在**图灵机**上只会慢一个**多项式**因子）。这就是为什么 **P** 类作为一个整体是稳健的、与具体机器模型无关的。 * “你需要证明你的**算法**的每个**步骤**都需要**多项式时间**...”：这是进行**复杂度**分析的基本方法。将一个大**算法**分解成一系列小的基本操作。 * “...并且每个 **for** / **while** **循环**都运行**多项式次**”：这是关键。你需要论证： 1. **循环体**本身是**多项式时间**的。 2. **循环**的执行次数也是输入大小 $n$ 的一个**多项式**。 * 根据之前提到的**多项式**的封闭性，总时间 = (循环次数) × (循环体时间) = (**多项式**) × (**多项式**) = (**多项式**)。 **[总结]** 本段指出，要证明一个**算法**是**多项式时间**的，关键在于证明其所有基本操作都是**多项式时间**的，并且所有循环的迭代次数也是**多项式**的。这再次强调了**多项式**这个性质在组合下的稳定性。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `6.1 多项式时间映射归约` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `6.1 多项式时间映射归约` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 # 6.1 **多项式时间映射归约** **[原文]（逐字逐句）** 定义 17（**多项式时间映射可归约**）。如果存在一个**多项式时间可计算函数** $f: \Sigma^{*} \rightarrow \Sigma^{*}$ 使得： $$

$$ 则**语言** $A$ 是**多项式时间**（**映射**）**可归约**到**语言** $B$ 的（记作 $\mathrm{A} \leq_{\mathrm{p}} \mathrm{B}$）。 **[逐步解释]（from scratch，超细）** 这是**复杂性理论**中最重要的**归约**类型——**多项式时间映射归约**的定义。 1. **角色定位**: 定义 $\le_p$ **归约**。 2. **与可计算性归约的对比**: * 我们在**可计算性理论**中学过的**映射归约** ($\le_m$)，只要求**归约函数** $f$ 是“**可计算**”的（即存在一个总能**停机**的**图灵机**）。 * 这里的**多项式时间映射归约** ($\le_p$) 提出了一个更严格的要求：这个**归约函数** $f$ 不仅要**可计算**，而且计算它的**算法**本身必须是“高效的”，即在**多项式时间**内完成。 3. **内容拆解**: * “**多项式时间可计算函数** $f$”：这意味着存在一个**确定性图灵机**，它在输入 $x$ (长度为 $n$) 时，能在 $O(n^k)$ 时间内计算出并输出 $f(x)$。 * `$x \in A \Longleftrightarrow f(x) \in B$`: 这部分与 $\le_m$ 的定义完全相同。它要求**归约函数** $f$ 必须完美地保持成员关系：$A$ 中的成员必须被映射到 $B$ 中的成员，非 $A$ 的成员必须被映射到非 $B$ 的成员。 * “$\mathrm{A} \leq_{\mathrm{p}} \mathrm{B}$”：这是**多项式时间映射归约**的符号表示。它直观地意味着“**问题** A 不比**问题** B 更难解决（在**多项式时间**的意义下）”。 **[公式与符号逐项拆解和推导（若本段含公式）]** * $$

$$ * $x \in A$: **字符串** $x$ 是**语言** $A$ 的一个成员。 * $f(x) \in B$: 经过**函数** $f$ 转换后的**字符串** $f(x)$ 是**语言** $B$ 的一个成员。 * $\Longleftrightarrow$: 当且仅当。这是一个双向蕴含关系，要求两个命题必须同真同假。 **[总结]** 定义 17 定义了**多项式时间映射归约** ($\le_p$)，它是一种高效的“**问题**转换器”。如果 $A \le_p B$，意味着我们可以用一个**多项式时间**的预处理步骤（计算 $f(x)$），将解决**问题** $A$ 的任务完全转化为解决**问题** $B$ 的任务。 --- **[原文]（逐字逐句）** 特别是，我们必须有 $|f(x)|$ 是 $|x|$ 的**多项式**。 由于 $|f(x)|$ 是 $|x|$ 的**多项式**，因此在 $f(x)$ 上运行**多项式时间算法** $M$ 所需的时间是 $|x|$ 的**多项式**。因此，我们有以下**定理**： **[逐步解释]（from scratch，超细）** 这段话解释了 $\le_p$ **归约**的一个重要推论及其在**复杂性**传递中的作用。 1. **推论：输出长度也是多项式** * “我们必须有 $|f(x)|$ 是 $|x|$ 的**多项式**”：为什么？因为计算 $f(x)$ 的**图灵机**本身在**多项式时间** $O(|x|^k)$ 内运行。在这段时间内，**图灵机**的读写头最多移动 $O(|x|^k)$ 次，因此它最多也只能在纸带上写下 $O(|x|^k)$ 个字符。所以，输出 $f(x)$ 的长度 $|f(x)|$ 不可能超过**多项式**级别。 2. **复杂度传递的逻辑**: * 假设我们有一个解决 $A$ 的**算法**，它通过**归约**到 $B$ 来工作。 * **总时间** = (计算 $f(x)$ 的时间) + (解决 $B$ 的**问题** $f(x)$ 的时间)。 * “在 $f(x)$ 上运行**多项式时间算法** $M$”：假设 $B \in P$，即存在一个**判定器** $M_B$，其**运行时间**是关于其输入长度的**多项式**，比如 $O(m^j)$，其中 $m$ 是其输入长度。 * 当我们将 $f(x)$ 作为 $M_B$ 的输入时，所需时间是 $O(|f(x)|^j)$。 * “所需的时间是 $|x|$ 的**多项式**”：因为我们已经知道 $|f(x)|$ 是 $|x|$ 的**多项式** (比如 $O(|x|^k)$)，所以 $M_B$ 的**运行时间** $O(|f(x)|^j)$ 就变成了 $O((|x|^k)^j) = O(|x|^{kj})$。因为 $k$ 和 $j$ 都是**常数**，所以 $kj$ 也是**常数**。这意味着解决 $f(x)$ 的时间也是关于原始输入长度 $|x|$ 的**多项式**。 * 回到总时间： * 计算 $f(x)$ 的时间是**多项式**的。 * 解决 $f(x)$ 的时间也是**多项式**的。 * 两个**多项式**时间相加，结果仍然是**多项式**的。 * 这就证明了，如果我们能解决 $B$，我们也能高效地解决 $A$。 **[总结]** 本段揭示了**多项式时间归约**能够保持“高效性”的根本原因：**归约函数**本身是高效的，并且它不会将输入“放大”到**指数**级别，从而保证了后续解决**问题**的步骤相对于原始输入来说也是高效的。 --- **[原文]（逐字逐句）** ## **定理** 7。 - 如果 $A \leq_{\mathrm{P}} B$ 且 $B \in \mathrm{P}$，则 $A \in \mathrm{P}$。 - 如果 $A \leq_{\mathrm{P}} B$ 且 $B \in \mathrm{NP}$，则 $A \in \mathrm{NP}$。 **[逐步解释]（from scratch，超细）** 这个**定理**是**多项式时间归约**最重要的应用，它说明了 **P** 类和 **NP** 类在 $\le_p$ **归约**下的闭包性。 1. **定理内容**: * **第一部分**: 如果**问题** B 是“容易解决”的（$B \in P$），并且**问题** A 能“高效地”转化为 B（$A \le_p B$），那么**问题** A 也是“容易解决”的（$A \in P$）。 * **证明思路**: 这正是上一段**分析**的结论。解决 A 的**算法**是：1. 用**多项式时间**计算 $f(x)$。 2. 用 B 的**多项式时间判定器**解决 $f(x)$。总时间是**多项式**，所以 $A \in P$。 * **第二部分**: 如果**问题** B 是“容易验证”的（$B \in NP$），并且**问题** A 能“高效地”转化为 B（$A \le_p B$），那么**问题** A 也是“容易验证”的（$A \in NP$）。 * **证明思路**: 我们需要为 A 构造一个**多项式时间验证器**。 * 假设 $B$ 的**验证器**是 $V_B(y, c_B)$。 * 我们要**验证** $x \in A$。我们的“证据”是什么？就是 $B$ 的解的证据！ * A 的**验证器** $V_A(x, c_B)$ 的**算法**如下： 1. 输入 $x$ 和一个**证书** $c_B$。 2. 计算 $y = f(x)$。这个过程是**多项式时间**的。 3. 调用 $V_B$ 来**验证** $(y, c_B)$。这个过程也是**多项式时间**的（相对于 $|y|$，也就是相对于 $|x|$）。 4. 如果 $V_B$ **接受**，则 $V_A$ **接受**。 * **正确性**: $x \in A \iff f(x) \in B \iff$ 存在一个**证书** $c_B$ 使得 $V_B(f(x), c_B)$ **接受**。这正是 $V_A$ 的工作原理。因为所有步骤都是**多项式时间**的，所以 $A \in NP$。 **[总结]** **定理 7** 是**复杂性理论**中进行**归约**的理论基石。它告诉我们，$\le_p$ **归约**是用来证明一个**问题**属于某个**复杂度类**（如 P 或 NP）的有力工具，方法是将其**归约**到该类中的一个已知**问题**。 --- **[原文]（逐字逐句）** 定义 18（**NP-难**）。一个**语言** $B$ 是 **NP** 难的，如果对于所有**语言** $A \in \mathrm{NP}$，我们都有存在从 $A$ 到 $B$ 的**多项式时间归约**（$\mathrm{A} \leq_{\mathrm{p}} \mathrm{B}$）。 **[逐步解释]（from scratch，超细）** 这是对 **NP-难 (NP-Hard)** 这个关键概念的定义。 1. **角色定位**: 定义 **NP-难**。 2. **内容拆解**: * “**NP-难**”：这个标签意味着一个**问题**“至少和 **NP** 中最难的**问题**一样难”。 * “一个**语言** $B$ 是 **NP-难**的...”：我们是给一个**问题** B 贴上这个标签。 * “如果对于所有**语言** $A \in \mathrm{NP}$...”：这是定义中最强的部分。不是指某个或某些 **NP** **问题**，而是指**整个 NP 类中的每一个问题**。 * “...我们都有 $\mathrm{A} \leq_{\mathrm{p}} \mathrm{B}$”：这意味着，**NP** 类中的任何一个**问题** A，都可以通过**多项式时间映射归约**转化为**问题** B。 * **直观含义**: **问题** B 就像是 **NP** 宇宙的“万能钥匙”或“中心枢纽”。任何 **NP** **问题**的求解，都可以通过一个高效的预处理步骤，变成求解 B 的**问题**。 3. **重要推论**: * 如果一个 **NP-难** **问题** B 能够在**多项式时间**内被解决（即 $B \in P$），那么根据**定理 7**，所有能够**归约**到它的**问题**——也就是**所有**的 **NP** **问题**——都可以在**多项式时间**内解决。 * 这将意味着 $\mathrm{P} = \mathrm{NP}$。 * 因此，**NP-难** **问题**是 **P=NP?** 这个世纪难题的关键。只要能找到任何一个 **NP-难** **问题**的多项式**算法**，就等于证明了 $\mathrm{P} = \mathrm{NP}$。反之，如果 $\mathrm{P} \neq \mathrm{NP}$，那么所有 **NP-难** **问题**都不可能存在**多项式时间算法**。 **[总结]** 定义 18 定义了 **NP-难** **问题**，它们是**复杂性**最高的一类**问题**，所有 **NP** **问题**都可以高效地转化为它们。一个 **NP-难** **问题**的“可解性”直接决定了整个 **NP** 类的“可解性”。 --- **[原文]（逐字逐句）** 另一个重要的**定义**是 **NP 完全**： 定义 19（**NP-完全**）。一个**语言** $B$ 是 **NP 完全**的当且仅当 $B \in \mathrm{NP}$ 且 $B$ 是 **NP 难**的。 **[逐步解释]（from scratch，超细）** 这是对 **NP-完全 (NP-Complete, NPC)** 的定义，它结合了 **NP** 和 **NP-难** 两个概念。 1. **角色定位**: 定义 **NP-完全**。 2. **内容拆解**: * 一个**语言** B 要获得“**NP-完全**”这个称号，必须同时满足两个条件： 1. **$B \in \mathrm{NP}$**: **问题** B 本身是一个“容易验证”的**问题**。它必须在 **NP** 这个俱乐部里。 2. **$B$ 是 NP-难的**: **问题** B 必须是“**NP** 中最难的**问题**之一”。所有其他 **NP** **问题**都能**归约**到它。 * **直观含义**: **NP-完全** **问题**是 **NP** 类中“最具有代表性”的“最难”的**问题**。它们既是 **NP** 的成员，又在难度上是所有 **NP** 成员的上限。 **[具体数值示例]** * **CNF-SAT** 是一个经典的 **NP-完全** **问题**。 * 我们在示例 4 的**验证器**中看到，给定一个**赋值**，我们可以在**多项式时间**内**验证**它是否满足**公式**，所以 **CNF-SAT** $\in \mathrm{NP}$。 * **库克-莱文定理**证明了所有 **NP** **问题**都可以**归约**到 **SAT**（以及 **CNF-SAT**），所以 **CNF-SAT** 是 **NP-难**的。 * 两者结合，**CNF-SAT** 是 **NP-完全**的。 * **哈密顿路径问题** (判断图中是否存在一条经过每个顶点恰好一次的路径) 也是 **NP-完全**的。 **[总结]** 定义 19 定义了 **NP-完全** **问题**，它们是 **NP** **问题**中“精华”与“困难”的交集。它们既属于 **NP**，又是 **NP-难**的。它们是**复杂性理论**研究的核心对象。 --- **[原文]（逐字逐句）** 许多**问题**已知是 **NP 完全**的（参见末尾的**表格**）。最重要的**示例**是 **SAT** $:=\{\langle\phi\rangle \mid \phi$ 是一个可满足的**布尔公式** $\}$。**库克-莱文定理**指出，对于任何**语言** $L \in \mathrm{NP}$，存在一个**多项式时间可计算函数** $f$ 使得 $f(x)=\langle\phi\rangle$，其中 $\langle\phi\rangle$ 是一个**布尔公式**。此外，当且仅当 $x \in L$ 时， $\langle\phi\rangle$ 是可满足的。 **[逐步解释]（from scratch，超细）** 这段话介绍了第一个被证明的 **NP-完全** **问题**——**SAT**，以及证明它的里程碑式**定理**——**库克-莱文定理**。 1. **角色定位**: 介绍 **NPC** 世界的“原点”——**SAT** 和**库克-莱文定理**。 2. **内容拆解**: * “最重要的**示例**是 **SAT**”：**布尔可满足性问题 (SAT)** 是第一个被证明为 **NP-完全**的**问题**。它在**复杂性理论**中的地位，如同 $\mathrm{A}_{\mathrm{TM}}$ 在**可计算性理论**中的地位。 * **库克-莱文定理 (Cook-Levin Theorem)**：这个**定理**是** NP-完全**理论的基石。它所做的，正是直接根据 **NP-难**的定义，证明了 **SAT** 是 **NP-难**的。 * **定理内容分析**: * “对于任何**语言** $L \in \mathrm{NP}$”：取 **NP** 中的任意一个**问题**。 * “存在一个**多项式时间可计算函数** $f$”：存在一个高效的**归约**。 * “使得 $f(x)=\langle\phi\rangle$”：这个**归约**能将 $L$ 的任何一个实例 $x$ 转换成一个**布尔公式** $\phi$。 * “当且仅当 $x \in L$ 时， $\langle\phi\rangle$ 是可满足的”：这个转换完美地保持了成员关系。 * **定理的意义**: 这段陈述完完全全就是 **SAT** 是 **NP-难** 的定义（$L \le_p \text{SAT}$ 对所有 $L \in NP$ 成立）。由于我们又知道 **SAT** 本身在 **NP** 中（因为可以**非确定性**地猜一个**赋值**并**多项式时间验证**），所以**库克-莱文定理**确立了 **SAT** 的 **NP-完全**性。 **[总结]** 本段介绍了第一个也是最重要的 **NP-完全** **问题** **SAT**。**库克-莱文定理**通过一个极其精妙的构造性**证明**（将任何 **NP** **问题**的**非确定性图灵机**的计算过程**编码**成一个巨大的**布尔公式**），证明了 **SAT** 是 **NP-难**的，从而确立了 **NP-完全**理论的起点。 --- **[原文]（逐字逐句）** 这个最后的**定理**解释了如何证明新的**问题**是 **NP 难**的。 **定理** 8。如果 $A \leq_{\mathrm{P}} B$ 且 $A$ 是 **NP 难**的，那么 $B$ 是 **NP 难**的。 **[逐步解释]（from scratch，超细）** 这段话给出了在**库克-莱文定理**之后，我们如何发现成千上万个其他 **NP-难** **问题**的标准方法。 1. **角色定位**: 介绍证明 **NP-难** 的“**归约**链”方法。 2. **证明新问题 NP-难的方法**: * **库克-莱文定理**像盘古开天辟地一样，给了我们第一个 **NP-难** **问题** **SAT**。 * 我们现在想证明一个新的**问题** B 是 **NP-难**的。直接按定义去证明（把所有 **NP** **问题**都**归约**到 B）太困难了，就像重新证明一遍**库克-莱文定理**一样。 * **定理 8** 提供了一条捷径：我们不需要从所有 **NP** **问题**出发，只需要从一个**已知的 NP-难问题** A 出发，然后证明 $A \le_p B$ 即可。 3. **定理 8 的证明思路**: * **已知**: 1. $A \le_p B$。 2. A 是 **NP-难**的。 * **要证**: B 是 **NP-难**的。 * 根据 **NP-难** 的定义，我们需要证明对于**任何**一个**语言** $L \in \mathrm{NP}$，都有 $L \le_p B$。 * **证明链**: a. 取任意一个 $L \in \mathrm{NP}$。 b. 因为 A 是 **NP-难**的，所以我们知道 $L \le_p A$。这意味着存在一个**多项式时间**的**归约函数** $f$。 c. 我们又已知 $A \le_p B$。这意味着存在一个**多项式时间**的**归约函数** $g$。 d. 现在我们可以构造一个新的**函数** $h(x) = g(f(x))$。这个**函数**可以将 $L$ 的实例 $x$ 直接转换为 $B$ 的实例。 e. 因为 $f$ 和 $g$ 都是**多项式时间**的，它们的复合 $h$ 也是**多项式时间**的。 f. 并且，$x \in L \iff f(x) \in A \iff g(f(x)) \in B \iff h(x) \in B$。 g. 这就证明了 $L \le_p B$。 h. 因为这个**证明**对任意 $L \in \mathrm{NP}$ 都成立，所以 B 是 **NP-难**的。 **[总结]** **定理 8** 建立了 **NP-难** 这个性质的传递性。它使得证明一个新的**问题**是 **NP-难**变得可行：我们不再需要与整个 **NP** 类作斗争，只需找到任何一个已知的 **NP-难** **问题**，并将其**多项式时间归约**到我们的新**问题**即可。这就是著名的“**归约**链”的来源，绝大多数 **NP-完全** **问题**都是通过从 **SAT** 开始的一长串**归约**被证明的。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `6.2 P 对 NP` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `6.2 P 对 NP` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 # 6.2 P 对 NP **[原文]（逐字逐句）** 我们希望将 **NP 难问题**视为比 **P 问题**“更难”。然而，我们不知道这是否属实！这就是著名的 **P 对 NP 问题**。无论如何，我们知道： ## **定理** 9。 $$

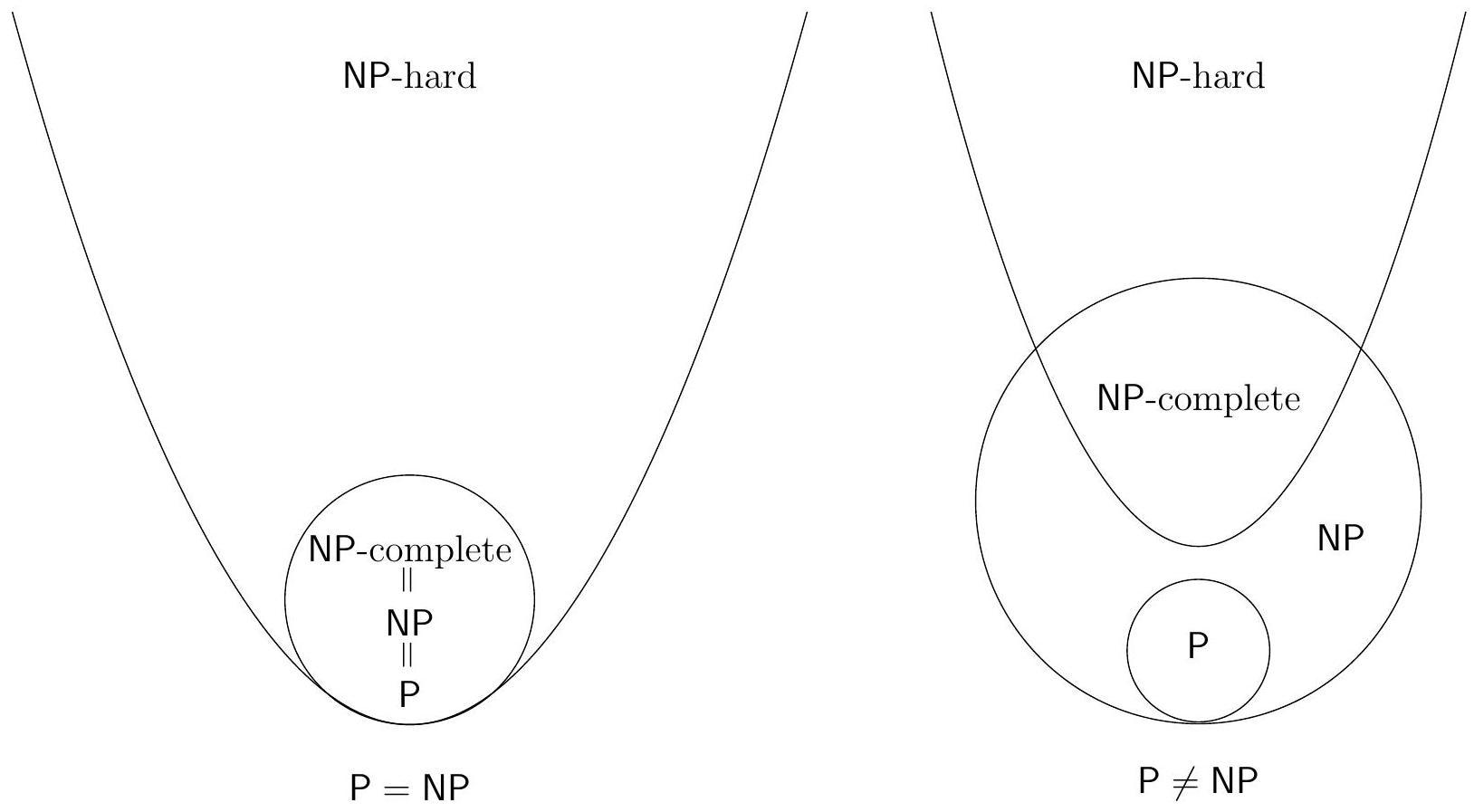
$$ 但有些**属性**取决于这个**开放问题**的**答案**。 如果 $\mathrm{P}=\mathrm{NP}$，那么 **P** 中的每个**问题**$^{4}$都是 **NP 完全**的。 如果 $\mathrm{P} \neq \mathrm{NP}$，那么没有 **NP 难问题**在 **P** 中。  图 2：**P** $\stackrel{?}{=}$ **NP** 的**类**包含**关系**的**维恩图**。 [^4] **[逐步解释]（from scratch，超细）** 这一部分探讨了**复杂性理论**中最核心的未解之谜：**P** 是否等于 **NP**？ 1. **P vs NP 问题的核心**: * “我们希望将 **NP 难问题**视为比 **P 问题**‘更难’”：这是我们的直觉。找到一个解（**P**，在最坏情况下）似乎比给定一个解去验证它（**NP**）要困难得多。例如，解决一个数独比检查一个填好的数独是否正确要难得多。 * “然而，我们不知道这是否属实！”：尽管直觉如此，但至今无人能在数学上证明这一点。也就是说，没有人能证明**任何一个 NP 问题**不存在一个**多项式时间的确定性算法**。 * “这就是著名的 **P 对 NP 问题**”：这个问题问的是：所有那些解能够被高效**验证**的**问题**（**NP**），是否也都能被高效地**解决**（**P**）？ 2. **已知关系：定理 9** * $\mathrm{P} \subseteq \mathrm{NP}$: 这是我们目前唯一确定的关系。 * **证明思路**: 任何一个在 **P** 中的**语言** $L$，意味着存在一个**多项式时间**的**确定性判定器** $M$。这个 $M$ 本身就可以被看作是一个**多项式时间验证器** $V(x,c)$，它只是简单地忽略**证书** $c$ 并直接运行 $M$ 在 $x$ 上。因此，根据**验证器**的定义，$L$ 也在 **NP** 中。换句话说，如果一个**问题**能被高效解决，那么它的解自然也能被高效**验证**（**验证**过程就是解决一遍）。 3. **两种可能的世界**: * **如果 P = NP**: * 这意味着“高效**验证**”和“高效**解决**”是等价的。所有 **NP** **问题**（包括所有的 **NP-完全** **问题**）都存在**多项式时间算法**。这将给运筹学、**人工智能**、密码学等领域带来革命性的变化（例如，当前的许多加密体系将被破解）。 * “**P** 中的每个**问题**都是 **NP 完全**的”：这条推论略有不精确。更准确地说，如果 $\mathrm{P}=\mathrm{NP}$，那么任何一个在 **P** 中且**非平凡**的**问题**（即不为空集或全集 $\Sigma^*$）都将是 **NP-完全**的。因为如果 B 是 **P** 中的**非平凡问题**，那么任何 **NP** **问题** A（现在也都在 **P** 中了）都可以**归约**到 B。 * **如果 P ≠ NP**: * 这是大多数计算机科学家的信念。它意味着存在一些**问题**，它们的解容易**验证**，但却极难**找到**。 * “没有 **NP 难问题**在 **P** 中”：这是一个直接的推论。如果任何一个 **NP-难** **问题**在 **P** 中，那么根据我们之前的**分析**，马上就能得出 $\mathrm{P}=\mathrm{NP}$ 的结论。所以，如果 $\mathrm{P} \neq \mathrm{NP}$，那么 **P** 类和 **NP-难** **问题**的集合之间是完全没有交集的。 4. **维恩图解释**: * 图中展示了 **P, NP, NP-完全 (NPC), NP-难 (NP-Hard)** 这几个集合之间的关系。 * **P** 完全包含在 **NP** 中。 * **NP-完全 (NPC)** 是 **NP** 和 **NP-难** 的交集。它们是 **NP** 中最难的**问题**。 * **NP-难** 的范围更大，它包含了所有的 **NPC** **问题**，还可能包含一些不属于 **NP** 的**问题**（例如，**停机问题** $\mathrm{A}_{\mathrm{TM}}$，它比任何 **NP** **问题**都难，所以它也是 **NP-难**的，但它甚至不是**可判定**的，所以肯定不在 **NP** 中）。 * **P = NP?** 的**问题**，在图上就表现为：**P** 这个圈子和 **NP** 这个圈子是否是同一个圈子？如果它们是同一个，那么整个图就会塌缩成 **P = NP = NPC** （除去平凡**问题**）。如果不是，那么图中的结构就成立，**P** 只是 **NP** 中一个严格的子集。 5. **脚注 4**: `除了 $\varnothing$ 和 $\Sigma^{*}$。这种技术**限制**是由于我们定义**映射归约**的方式。` * 这解释了为什么“**P** 中的每个**问题**都是 **NP 完全**的”这个说法需要排除两个**平凡问题**：空集 $\varnothing$ 和全集 $\Sigma^*$。因为我们无法将一个非空的**语言** A **映射归约**到空集 B（因为 A 中的元素无法映射到 B 中），也无法将一个不是全集的**语言** A **映射归约**到全集 B（因为不在 A 中的元素也无法映射到 B 中）。 **[总结]** 本节介绍了**复杂性理论**的核心**问题** **P vs NP**。我们确切知道 $\mathrm{P} \subseteq \mathrm{NP}$，但不知道这个包含关系是否是严格的。这个**问题**的答案将决定我们对“困难**问题**”的理解，并对整个科学和技术领域产生深远影响。维恩图直观地展示了在 **P ≠ NP** 的假设下，各个**复杂度类**之间的关系。 --- # 7 **证明技术** ## 7.1 **P** 中的**问题** ### 7.1.1 **证明模板** 12：使用**多项式时间算法**证明 $L$ 在 **P** 中 **[原文]（逐字逐句）** 1. 给出 $L$ 的**确定性判定器**的**伪代码**。 2. 证明如果 $x \in L$，你的**算法****接受**。 3. 证明如果 $x \notin L$，你的**算法****拒绝**。 4. 证明 $M$ 在**多项式时间**内运行，即在 $O\left(n^{k}\right)$ 时间内运行，其中 $k$ 是某个**常数**。（无需具体证明 $k$ 是什么）。 **[逐步解释]（from scratch，超细）** 这是证明一个**问题**属于 **P** 类的最直接、最基本的方法。 1. **角色定位**: 提供通过直接构造**算法**证明**问题**在 **P** 中的标准流程。 2. **与可判定性模板的对比**: * 这个模板与证明**可判定性**的**模板 4** 非常相似。前三个步骤（给出**确定性判定器**并证明其**正确性**）是完全一样的。 * **核心区别**在于**步骤 4**：**复杂度分析**。 3. **步骤详解**: * **步骤 1**: 设计一个**确定性**的、保证对所有输入都**停机**的**算法**来解决**问题** $L$。 * **步骤 2 & 3**: 证明**算法**的**正确性**，即对于“是”的实例它回答“是”，对于“否”的实例它回答“否”。 * **步骤 4**: 证明**算法**的**高效性**。这是将**问题**归入 **P** 类的关键。 * 你需要**分析算法**的**运行时间**，并证明它是一个关于输入长度 $n$ 的**多项式**。 * 通常的**分析**方法是： * **分析**循环：确定最深层循环的执行次数和循环体的**复杂度**。 * **分析**函数调用：**分析**递归调用的深度和每次调用的**复杂度**。 * “无需具体证明 $k$ 是什么”：在理论**证明**中，我们通常不需要计算出精确的指数 $k$。只要能令人信服地论证出**运行时间**的增长是**多项式**级别的（例如，通过指出它是由有限次数的**多项式时间**操作嵌套而成的），就足够了。 **[具体数值示例]** **问题**: 证明**语言** $\text{PATH} = \{\langle G, s, t \rangle \mid G \text{ 是一个有向图，且存在一条从顶点 } s \text{ 到 } t \text{ 的路径}\}$ 属于 **P**。 1. **判定器伪代码 (使用广度优先搜索 BFS)**: $M=$ “在输入 $\langle G, s, t \rangle$ 上： a. 创建一个队列 `Q`，并将起始顶点 `s` 放入队列。 b. 创建一个集合 `visited`，并将 `s` 放入其中，以标记已访问的顶点。 c. 当 `Q` 不为空时，执行循环： i. 从 `Q` 的头部取出一个顶点 `u`。 ii. 如果 `u` 等于 `t`，则找到路径，**接受**。 iii. 对于 `u` 的每一个邻居 `v`（即存在边 `(u,v)`）： * 如果 `v` 不在 `visited` 集合中，则将 `v` 加入 `visited` 和 `Q`。 d. 如果循环结束（`Q` 为空）仍未找到 `t`，则说明 $s, t$ 不连通，**拒绝**。” 2. **正确性证明**: BFS **算法**的**正确性**是图论中的标准结论。它系统地探索图，保证能找到从 $s$ 出发的最短路径（如果存在的话）。如果 $s, t$ 连通，`t` 终将被访问到。如果不连通，所有从 `s` 可达的顶点都将被访问完，而 `t` 不在其中，**算法**最终会**停机**并**拒绝**。 3. **多项式时间分析**: * 设图 $G$ 有 $V$ 个顶点和 $E$ 条边。输入长度 $n$ 大致与 $V+E$ 成比例。 * 每个顶点最多入队一次和出队一次（步骤 c.i, c.iii）。 * 在整个**算法**过程中，每条边最多被检查一次（步骤 c.iii）。 * 使用邻接表表示图时，BFS 的**时间复杂度**是 $O(V+E)$。 * $O(V+E)$ 是关于输入长度 $n$ 的一个线性函数，也就是**多项式** ($O(n^1)$)。 * 因此，该**算法**在**多项式时间**内运行。 4. **结论**: 由于我们提供了一个**多项式时间**的**确定性判定器**，所以 $\text{PATH} \in \mathrm{P}$。 **[总结]** **证明模板 12** 是证明一个**问题**属于 **P** 类的“黄金标准”。它要求我们给出一个具体的、高效的（**多项式时间**）**确定性算法**，并证明其**正确性**和**高效性**。 --- ### 7.1.2 **证明模板** 13：使用**多项式时间归约**证明 $L$ 在 **P** 中 **[原文]（逐字逐句）** 1. 选择一个 $S \in \mathrm{P}$。 2. 编写一个计算**函数** $f$ 的**算法**。 3. 证明给定 $x$ 作为**输入**，$f(x)$ 可以在**多项式时间**内**计算**，即在 $O\left(n^{k}\right)$ 时间内，其中 $k$ 是某个**常数**。 4. 假设 $x \in L$，证明 $f(x) \in S$。 5. 假设 $x \notin L$，证明 $f(x) \notin S$。 6. 得出结论，由于 $L \leq_{\mathrm{p}} S$ 且 $S \in \mathrm{P}$，因此 $L \in \mathrm{P}$。 **[逐步解释]（from scratch，超细）** 这是证明一个**问题**属于 **P** 类的间接方法，利用了 $\le_p$ **归约**。 1. **角色定位**: 提供通过**归约**证明**问题**在 **P** 中的标准流程。 2. **核心思想**: 这是**定理 7** 的直接应用。我们想证明一个新**问题** $L$ 是“容易的”，我们可以通过展示如何用一个已知的“容易的”**问题** $S$ 来解决它。 3. **步骤详解**: * **步骤 1**: 找到一个我们已经知道它在 **P** 类中的**问题** $S$ 作为我们的“垫脚石”。 * **步骤 2 & 3**: 设计一个**多项式时间**的**归约函数** $f$。这与之前讨论的**归约**构造完全一样，重点是**算法**必须高效。 * **步骤 4 & 5**: 证明**归约**的**正确性**，即 $x \in L \iff f(x) \in S$。 * **步骤 6**: 引用**定理 7**。因为 $L \le_p S$ 且 $S \in P$，所以 $L \in P$。 **[具体数值示例]** **问题**: 证明“判断一个无向图中是否存在一个大小为3的**环**（三角形）”的**问题** $\text{TRIANGLE}$ 属于 **P**。 1. **选择 S**: 我们选择矩阵乘法**问题** $\text{MATRIX-MULT}$，我们知道它在 **P** 中（标准**算法** $O(n^3)$）。 2. **构造函数 f**: * 输入是一个图 $G$ 的**编码** $\langle G \rangle$。 * **函数** $f$ 的**算法**: a. 根据图 $G$ 构造其邻接矩阵 $A$。如果图有 $V$ 个顶点，$A$ 是一个 $V \times V$ 的矩阵，如果顶点 $i,j$ 之间有边，则 $A_{ij}=1$，否则为0。 b. 计算矩阵的平方 $A^2$。 c. **输出**: 矩阵 $A^2$。 3. **多项式时间分析**: * 构造邻接矩阵需要 $O(V^2)$ 时间。 * 计算两个 $V \times V$ 矩阵的乘法需要 $O(V^3)$ 时间。 * 总时间是 $O(V^3)$，是**多项式**的。 4. **归约正确性**: 我们需要重新设计一下**归约**，因为直接输出 $A^2$ 不好判断。让我们换一种方式，直接用**算法**解决。 **让我们用一个更适合归约的例子**: **问题**: 2-SAT **问题**（每个**子句**最多有两个**文字**的 SAT **问题**）是否在 **P** 中？ 1. **选择 S**: 我们选择在有向图中判断“强连通分量”的**问题** $\text{SCC}$。我们知道 $\text{SCC}$ 可以在线性时间 $O(V+E)$ 内解决，因此在 **P** 中。 2. **构造函数 f**: * 输入是一个 2-SAT **公式** $\phi$。 * **算法**: a. 为 $\phi$ 中的每个**变量** $x_i$ 创建两个顶点：一个代表 $x_i$，另一个代表 $\neg x_i$。 b. 对于 $\phi$ 中的每一个**子句** $(a \lor b)$，在图中加入两条有向边：从 $\neg a$ 到 $b$，以及从 $\neg b$ 到 $a$。（因为 $a \lor b$ 等价于 $\neg a \implies b$ 和 $\neg b \implies a$）。 c. **输出**: 这个构造出来的图 $G_\phi$。 3. **多项式时间**: 构造图的过程是线性的，显然是**多项式时间**。 4. **归约正确性 (略)**: 可以证明，原始的 2-SAT **公式** $\phi$ 是**可满足**的，当且仅当在构造出的图 $G_\phi$ 中，没有任何一个**变量** $x_i$ 和它的否定 $\neg x_i$ 在同一个强连通分量中。 5. **结论**: * 我们已经将 2-SAT **问题** $\le_p$ **归约**到了一个稍微修改版的 $\text{SCC}$ **问题**（判断图中是否存在某个特定的坏结构）。 * 解决这个修改版 $\text{SCC}$ **问题**的**算法**是：1. 运行 $\text{SCC}$ **算法**找到所有强连通分量。2. 遍历所有**变量** $x_i$，检查 $x_i$ 和 $\neg x_i$ 是否在同一个分量里。整个过程是**多项式时间**的。 * 因此，2-SAT $\in \mathrm{P}$。 **[总结]** **证明模板 13** 提供了一个通过**归约**来证明**问题**属于 **P** 类的框架。当我们面对一个新**问题**时，如果能发现它本质上是某个已知“简单”**问题**的“伪装”，我们就可以通过**多项式时间归约**来证明它也是“简单的”。 --- **[原文]（逐字逐句）** 小**说明**：如果你的**算法**以**数字** $N$ 作为**输入**。你的**算法**应该在 $O\left(\log ^{k}(N)\right)$ 时间内运行，其中 $k$ 是某个**常数**，以便是**多项式时间**！这是因为如果 $N$ 以**二进制**给出，它使用 $O(\log (N))$ **位**表示。 **[逐步解释]（from scratch，超细）** 这是一个关于处理数值输入的**复杂度**分析中极其重要且易错的细节。 1. **核心问题**: **复杂度**中的输入长度 $n$ 指的是什么？ * $n$ 是**输入字符串的长度**，即表示输入所需的**比特数**或**字符数**。 2. **数值输入的情况**: * 当我们输入一个**数字** $N$ 时，例如 $N=1,000,000$，我们不能说输入长度 $n=N$。 * 在计算机中，**数字** $N$ 通常是用**二进制**表示的。表示 $N$ 所需的**比特数**大约是 $\log_2(N)$。 * 所以，对于数值输入 $N$，**输入长度** $n$ 是 $O(\log N)$。 * **多项式时间**意味着**运行时间**必须是关于 $n$ 的**多项式**，即 $O(n^k) = O((\log N)^k)$。 3. **伪多项式时间 (Pseudo-polynomial time)**: * 一个**算法**的**运行时间**如果是关于**数字** $N$ 的值的**多项式**（例如 $O(N^2)$），但关于**输入长度** $n=\log N$ 却是**指数**的（因为 $N^2 = (2^n)^2 = 2^{2n}$），那么这个**算法**被称为**伪多项式时间算法**。 * 这种**算法**只有在输入**数字** $N$ 的值本身不大的时候才有效。如果 $N$ 的值可以变得非常大（即使表示它的**比特数**不多），**算法**就会变得非常慢。 * 一个经典的例子是用于解决**背包问题**的动态规划**算法**，其**复杂度**为 $O(NW)$，其中 $N$ 是物品数量，$W$ 是背包容量。这是关于数值 $W$ 的**多项式**，但关于 $W$ 的**比特数** $\log W$ 的**指数**，所以它是**伪多项式**的。 **[具体数值示例]** **问题**: 判断一个**数字** $N$ 是否是**质数**。 * **错误的算法 (试除法)**: 遍历从 2 到 $\sqrt{N}$ 的所有整数，看是否能整除 $N$。 * **运行时间**: 大约是 $O(\sqrt{N})$ 次除法。 * **复杂度分析**: 令输入长度 $n = \log N$。那么 $N = 2^n$。这个**算法**的**运行时间**是 $O(\sqrt{2^n}) = O(2^{n/2})$。这是一个关于输入长度 $n$ 的**指数时间算法**！所以它不是一个**多项式时间算法**。 * **正确的算法 (AKS 质数测试)**: 这是一个著名的结果，它证明了存在一个**运行时间**为 $O((\log N)^6)$ 的**算法**。 * **复杂度分析**: $O(n^6)$，其中 $n=\log N$。这是一个关于输入长度的**多项式**。因此，**质数**判断**问题** ($\text{PRIMES}$) 在 **P** 中。 **[总结]** 本说明强调，在分析涉及数值输入的**算法复杂度**时，必须以**数字**的**编码长度**（通常是 $O(\log N)$）作为输入规模 $n$，而不是**数字**本身的值 $N$。一个**运行时间**是 $N$ 的**多项式**的**算法**，可能是关于 $n$ 的**指数**级**算法**，这种**算法**被称为**伪多项式时间**，不属于**多项式时间**。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `7.2 NP 中的问题` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `7.2 NP 中的问题` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 ## 7.2 **NP** 中的**问题** ### 7.2.1 **证明模板** 14：使用**多项式时间归约**证明 $L$ 在 **NP** 中 **[原文]（逐字逐句）** 1. 选择一个 $S \in \mathrm{NP}$。 2. 编写一个计算**函数** $f$ 的**算法**。 3. 证明给定 $x$ 作为**输入**，$f(x)$ 可以在**多项式时间**内**计算**，即在 $O\left(n^{k}\right)$ 时间内，其中 $k$ 是某个**常数**。 4. 假设 $x \in L$，证明 $f(x) \in S$。 5. 假设 $x \notin L$，证明 $f(x) \notin S$。 6. 得出结论，由于 $L \leq_{\mathrm{p}} S$ 且 $S \in \mathrm{NP}$，因此 $L \in \mathrm{NP}$。 **[逐步解释]（from scratch，超细）** 这个模板与**模板 13** 几乎完全相同，只是目标**复杂度类**从 **P** 变成了 **NP**。 1. **角色定位**: 提供通过**归约**证明**问题**属于 **NP** 类的标准流程。 2. **核心思想**: 这是**定理 7** 第二部分的直接应用。如果我们想证明一个新**问题** $L$ 是“容易**验证**”的，我们可以通过展示如何将它高效地转化为一个已知的“容易**验证**”的**问题** $S$ 来实现。 3. **步骤详解**: * **步骤 1**: 找到一个我们已经知道它在 **NP** 类中的**问题** $S$。最常用的选择是那些经典的 **NP-完全** **问题**，如 **SAT**, **3-SAT**, **CLIQUE**, **HAM-CYCLE** 等，因为我们确信它们都在 **NP** 中。 * **步骤 2 & 3**: 设计一个**多项式时间**的**归约函数** $f$ 的**算法**。 * **步骤 4 & 5**: 证明**归约**的**正确性** ($x \in L \iff f(x) \in S$)。 * **步骤 6**: 引用**定理 7**。因为 $L \le_p S$ 且 $S \in NP$，所以 $L$ 也一定在 **NP** 中。 **[总结]** **证明模板 14** 展示了如何使用**多项式时间归约**来证明一个**问题**属于 **NP**。这是**复杂性理论**中一个常用的技巧，特别是当你发现新**问题**与某个已知的 **NP** **问题**有很强的结构相似性时。 --- ### 7.2.2 **证明模板** 15：使用**验证器**证明 $L$ 在 **NP** 中 **[原文]（逐字逐句）** 1. 给出 $L$ 的**确定性验证器** $V$ 的**伪代码**。这里 $V$ 以 $x$ 和 $c$（**证书**）作为**输入**。$^{a}$ 2. 证明如果 $x \in L$，存在某个 $c$ 使得 $V$ **接受** $(x, c)$。 3. 证明如果 $x \notin L$，对于所有 $c$，$V$ **拒绝** $(x, c)$。 4. 证明 $V$ 在**多项式时间**内运行，即在 $O\left(n^{k}\right)$ 时间内，其中 $k$ 是某个**常数**。（无需具体证明 $k$ 是什么）。 [^5] **[逐步解释]（from scratch，超细）** 这是证明一个**问题**属于 **NP** 的最直接、最常用的方法，它直接利用了 **NP** 的**验证器**定义。 1. **角色定位**: 提供通过构造**验证器**证明**问题**在 **NP** 中的标准流程。 2. **核心思想**: 放弃直接去“**解决**”**问题**，而是思考：如果“神”给了我一个解（**证书**），我能否高效地**验证**这个解的真伪？ 3. **步骤详解**: * **步骤 1**: 定义“**证书**”并设计**验证算法**。 * 首先，你要想清楚，对于一个属于 $L$ 的实例 $x$，什么样的“证据”或“**证书**” $c$ 能够简洁地证明这一点。这个**证书**的长度必须是关于 $|x|$ 的**多项式**。 * 然后，给出**验证器** $V$ 的**伪代码**。它是一个**确定性算法**，输入是实例 $x$ 和**证书** $c$。 * **步骤 2**: 证明**完备性 (Completeness)**。 * 对于任何一个确实属于 $L$ 的实例 $x$，你必须证明**存在**一个合适的**证书** $c$，能让你的**验证器** $V$ **接受**。 * **步骤 3**: 证明**可靠性 (Soundness)**。 * 对于任何一个不属于 $L$ 的实例 $x$，你必须证明**无论**给出什么样的“**证书**” $c$，你的**验证器** $V$ **永远不会接受**。它必须**拒绝**。 * **步骤 4**: 证明**高效性**。 * 你必须**分析验证器** $V$ 的**时间复杂度**，并证明它的**运行时间**是关于**原始输入 $x$ 的长度 $|x|$** 的**多项式**。 **[总结]** **证明模板 15** 是证明**问题**属于 **NP** 的首选方法。其关键在于找到一个合适的“**证书**”，并设计一个**多项式时间**的**确定性算法**来**验证**这个**证书**的有效性。 --- ### 7.2.3 示例 7：证明 CycleSize 在 NP 中 **[原文]（逐字逐句）** 回顾**简单环**是没有重复**顶点**的**环**。定义以下**问题**： $$

$$ 声称 **CycleSize** $\in$ **NP**。为了证明这一点，我们将构造一个**验证器**。 $$

$$ 1. **检查** $x=\langle G, k\rangle$，即**图** $G$ 的**编码**以及**整数** $k$。如果不是，则**拒绝**。 2. **检查** $c$ 是 $G$ 的 $k$ 个不同**顶点**的**列表**。如果不是，则**拒绝**。$^{a}$ 3. 对于每个 $i=\{1, \ldots k\}$，**检查** $(c_{i}, c_{i+1})$ 是否是 $G$ 中的**边**。如果不是，则**拒绝**。（约定 $c_{k+1}=c_1$） 4. **接受**。 **[逐步解释]（from scratch，超细）** 这个示例完美地应用了**证明模板 15**。 1. **问题定义**: * **简单环**: 一个路径，起点和终点是同一个顶点，且中间没有重复的顶点。 * **CycleSize 问题**: 输入一个图 $G$ 和一个整数 $k$，判断 $G$ 中是否存在一个长度恰好为 $k$ 的**简单环**。 2. **应用模板 15**: * **步骤 1：定义证书和验证器** * **证书 $c$**: 什么能证明存在一个大小为 $k$ 的环？最直接的证据就是这个环本身！所以，我们定义**证书** $c$ 是一个**顶点**的序列 (列表)，比如 $(v_1, v_2, ..., v_k)$。 * **验证器 $V_C$ 的伪代码**: * **第 1 步**: 格式检查。确保输入 $x$ 是一个图和整数。 * **第 2 步**: **证书**有效性检查。 * `$c$ 是 $G$ 的 $k$ 个...列表`: 证据的长度是否等于我们期望的环的大小 $k$？ * `不同**顶点**`: **简单环**要求顶点不重复，所以要检查列表 $c$ 中是否有重复项。 * **第 3 步**: **环**的连通性检查。检查列表 $c$ 中相邻的顶点之间是否真的有边。这包括从 $v_1$ 到 $v_2$，...，$v_{k-1}$ 到 $v_k$，以及关键的“闭环”边，从 $v_k$ 回到 $v_1$。 * **第 4 步**: 如果以上所有检查都通过了，说明这个**证书** $c$ 确实是 $G$ 中一个大小为 $k$ 的**简单环**。因此**验证**成功，**接受**。 **[公式与符号逐项拆解和推导（若本段含公式）]** * $$

$$ * `CycleSize`: **语言**的名称。 * $\langle G, k \rangle$: 输入实例，包含一个图 $G$ 和一个整数 $k$ 的**编码**。 * `G is a graph with a simple cycle of size k`: 成员资格的条件，图 $G$ 中有一个大小为 $k$ 的**简单环**。 --- **[原文]（逐字逐句）** 首先我们将**分析运行时**：声称 $V_{C}$ 在 $n=|x|$ 的**大小**的**多项式时间**内**操作**，因为**编码验证**（**步骤** $1+2$）可以在**多项式时间**内完成，并且**步骤 3** 由最多 $|V|$ 次**边查找**组成，其中 $|V| \leq n$，所以它是**多项式时间**。 现在我们将证明**正确性**： 如果 $x \in$ **CycleSize**，那么 $x=\langle G, k\rangle$，其中 $G$ 是一个具有**大小**为 $k$ 的**简单环**的**图**。令 $c$ 是 $G$ 中**大小**为 $k$ 的**简单环**中的**顶点列表**。当 $x, c$ 被提供给 $V_{C}$ 时，$c$ 将因此通过**步骤** 1、2 和 3 中的**检查**。因此，$V_{C}$ 将**接受** $x, c$。 如果 $x \notin$ **CycleSize**，那么 $x \neq\langle G, k\rangle$ 或者 $x=\langle G, k\rangle$，其中 $G$ 是一个没有**大小**为 $k$ 的**简单环**的**图**。在第一种情况下，$V_{C}$ 将始终在**步骤 1** 中**拒绝**。在第二种情况下，无论**输入**到 $M_{L}$ 的 $c$ 是什么，它都不会通过**步骤** 2 和 3（这样做将意味着 $c$ 是 $G$ 中**长度**为 $k$ 的**简单环**）。因此，$V_{C}$ 将**拒绝** $x$。 得出结论，$V_{C}$ 是 **CycleSize** 的**多项式时间验证器**，因此 **CycleSize** $\in$ **NP**。 [^6] **[逐步解释]（from scratch，超细）** 这部分是示例 7 的后续**证明**，包括**复杂度分析**和**正确性证明**。 1. **步骤 4：证明高效性 (多项式时间分析)** * **输入长度 $n$**: $n = |\langle G, k \rangle|$。$n$ 与图的顶点数 $|V|$ 和边数 $|E|$ 成**多项式**关系。 * **分析 $V_C$ 的每一步**: * **步骤 1 (格式检查)**: 解析**字符串**，检查其结构。这可以在 $O(n)$ 时间内完成。 * **步骤 2 (证书检查)**: * 检查 $c$ 的长度是否为 $k$：$O(k)$ 时间。由于 $k \le |V| \le n$，这是**多项式**的。 * 检查 $c$ 中 $k$ 个顶点是否都不同：可以用一个哈希集或一个布尔数组，在 $O(k)$ 时间内完成。这也是**多项式**的。 * **步骤 3 (边检查)**: * 需要执行 $k$ 次“边查找”操作。 * 每次查找 $(u,v)$ 是否是边，在邻接矩阵中是 $O(1)$，在邻接表中是 $O(\text{degree}(u))$。最坏情况是 $O(|V|)$。 * 总时间是 $k \times O(|V|) = O(k|V|)$。因为 $k \le |V|$，所以这是 $O(|V|^2)$，也是关于 $n$ 的**多项式**。 * **结论**: **验证器** $V_C$ 的所有步骤都是**多项式时间**的，所以它是一个**多项式时间验证器**。 2. **步骤 2 & 3：证明正确性** * **完备性 (如果 $x \in \text{CycleSize}$)**: * 如果 $x = \langle G,k \rangle$ 在**语言**中，那么根据定义，图 $G$ 中**存在**一个大小为 $k$ 的**简单环**。 * 我们就可以让这个真实存在的环的顶点序列作为我们的**证书** $c$。 * 当这个真实的**证书** $c$ 和 $x$ 一起被送入**验证器** $V_C$ 时： * 步骤 1 通过。 * 步骤 2 通过，因为 $c$ 来自一个大小为 $k$ 的**简单环**，所以它有 $k$ 个不同的顶点。 * 步骤 3 通过，因为 $c$ 来自一个环，所以所有相邻顶点之间都有边。 * 因此，$V_C$ 必然会**接受**。这就证明了“**存在**一个 $c$”... * **可靠性 (如果 $x \notin \text{CycleSize}$)**: * 情况 A：输入 $x$ 格式错误。$V_C$ 在步骤 1 直接**拒绝**。 * 情况 B：输入 $x = \langle G, k \rangle$ 格式正确，但 $G$ 中没有大小为 $k$ 的**简单环**。 * 现在，**无论**我们提供什么样的**证书** $c$ 给**验证器**... * 如果 $c$ 不满足步骤 2 的要求（比如长度不是 $k$，或有重复顶点），它会被**拒绝**。 * 如果 $c$ 恰好满足了步骤 2 的要求，是一个由 $k$ 个不同顶点组成的列表。那么我们来**分析**步骤 3。如果 $c$ 也通过了步骤 3 的所有边检查，这意味着 $c$ **就是**一个 $G$ 中大小为 $k$ 的**简单环**。但这与我们的前提“$G$ 中没有这样的环”相**矛盾**。 * 因此，对于一个没有 $k$-环的图，不可能存在一个**证书** $c$ 能同时通过步骤 2 和 3。任何**证书**都至少会在其中一步被**拒绝**。 * 因此，$V_C$ **永远不会接受**一个不属于**语言**的实例。 3. **最终结论**: * 我们成功构造了一个**多项式时间验证器** $V_C$。 * 根据 **NP** 的**验证器**定义，**CycleSize** $\in \mathrm{NP}$。 **[总结]** 该示例完整地演示了如何通过构造“**证书**+**验证器**”的模式，来证明一个**问题**属于 **NP** 类。关键在于找到一个简洁的、能被高效**验证**的“证据”形式。 --- ### 7.2.4 **证明模板** 16：通过 **NTM** 证明 $L$ 在 **NP** 中 **[原文]（逐字逐句）** 1. 给出 $L$ 的**非确定性判定器** $M$ 的**伪代码**。这里 $M$ 只接受**输入** $x$。 2. 证明如果 $x \in L$，存在一些**非确定性选择**使得 $M$ **接受**。 3. 证明如果 $x \notin L$，$M$ 总是**拒绝** $x$，无论**非确定性步骤**是什么。 4. 证明 $M$ 在**多项式时间**内运行，即在 $O\left(n^{k}\right)$ 时间内，其中 $k$ 是某个**常数**。（无需具体证明 $k$ 是什么）。 **[逐步解释]（from scratch，超细）** 这是证明一个**问题**属于 **NP** 的第二种方法，它直接利用了 **NP** 的**非确定性图灵机**定义。 1. **角色定位**: 提供通过构造 **NTM** **判定器**证明**问题**在 **NP** 中的标准流程。 2. **与验证器模板的联系**: 这个模板与**模板 15**（**验证器**）在思想上是等价的。 * **NTM** 的“**非确定性选择**”步骤，就对应了**验证器**模型中的“猜测**证书** $c$”。 * **NTM** 在做出选择后执行的**确定性**计算部分，就对应了**验证器** $V$ 的**验证算法**。 3. **步骤详解**: * **步骤 1**: 设计一个**非确定性算法**。其典型结构是： a. **非确定性**地“猜测”一个解或一个证据。 b. **确定性**地**验证**这个猜测是否正确。 c. 如果**验证**通过，则**接受**；否则**拒绝**。 * **步骤 2**: 证明**完备性**。对于 $x \in L$，证明**存在**一个“幸运的”猜测（一个正确的**非确定性**选择路径），能让后续的**验证**通过，从而使 **NTM** **接受**。 * **步骤 3**: 证明**可靠性**。对于 $x \notin L$，证明**无论**做出什么样的猜测（对于**所有**的**非确定性**选择路径），后续的**验证**都将失败，导致 **NTM** 总是**拒绝**。 * **步骤 4**: 证明**高效性**。**分析 NTM** 的**运行时间**。根据定义，这指的是其**最长**计算分支的长度。你需要证明这个最长分支的长度也是关于 $|x|$ 的**多项式**。因为**非确定性**选择只占一步，所以这通常归结为证明后续的“**验证**”部分是**多项式时间**的。 **[总结]** **证明模板 16** 提供了一个与**验证器**模型等价的**证明**框架。它将“猜测”的过程内化到了**非确定性**机器的能力中，使得**伪代码**的表述有时可以更简洁。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `示例 8` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `示例 8` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 ### 7.2.5 示例 8：证明 NP 在 AddOne 下封闭 **[原文]（逐字逐句）** 对于任何 $L \subseteq \Sigma^{*}$，定义 $$

$$ 我们将证明 **NP** 在 **AddOne** 下**封闭**。取任何 $L \in \mathrm{NP}$，令 $M$ 为一个**判定** $L$ 的**多项式时间 NTM**。我们为 **AddOne** $(L)$ 提出以下 **NTM** $M^{\prime}$ $$

$$ 1. **非确定性**地将 $w$ 划分为 $w=x a y$，其中 $a \in \Sigma$ 2. 运行 $M$ 在 $x y$ 上。 3. 如果 $M$ **接受**，则**接受** $w$。 4. 如果 $M$ **拒绝**，则**拒绝** $w$。 **[逐步解释]（from scratch，超细）** 这个示例旨在证明一个关于 **NP** 类的**封闭性**质，它应用了**证明模板 16**。 1. **问题定义**: * **AddOne(L) 操作**: 这个操作接受一个**语言** $L$ 作为输入，生成一个新的**语言** $\text{AddOne}(L)$。新**语言**的成员，都是通过在原**语言** $L$ 的某个成员**字符串**中“插入一个任意字符”得到的。 * 例如，如果 $L = \{"cat"\}$，$\Sigma = \{a, ..., z\}$。 * 那么 $\text{AddOne}(L)$ 将包含 "acat", "bcat", ..., "caat", "cbat", ..., "cata", "catb", ... 等等。 * **封闭性 (Closure)**: 一个集合在某个操作下是**封闭**的，意味着对集合中的元素执行该操作后，结果仍然在该集合中。 * “**NP** 在 **AddOne** 下**封闭**”：我们要证明的是，如果 $L$ 是一个 **NP** **语言**，那么经过 $\text{AddOne}$ 操作后得到的 $\text{AddOne}(L)$ 也必然是一个 **NP** **语言**。 2. **应用模板 16**: * **前提**: 我们从一个任意的 $L \in \mathrm{NP}$ 开始。根据 **NP** 的定义，存在一个**多项式时间**的 **NTM** **判定器** $M$ 来**判定** $L$。 * **目标**: 为 $\text{AddOne}(L)$ 构造一个**多项式时间**的 **NTM** **判定器** $M'$。 * **步骤 1: 构造 NTM $M'$**: * $M'$ 的输入是**字符串** $w$。它要判断 $w$ 是否在 $\text{AddOne}(L)$ 中。 * `1. 非确定性地将 w 划分为 w=xay`: 这是**算法**的核心。$w$ 是否在 $\text{AddOne}(L)$ 中，取决于它能否被看作是“在 $L$ 的某个成员中插入一个字符”的结果。我们的 **NTM** 不去尝试所有可能的“删除”操作，而是反过来，**非确定性**地“猜测”那个被插入的字符 $a$ 和它的位置。一个长度为 $|w|$ 的**字符串**，有 $|w|$ 个可能的位置来“猜测”被插入的字符 $a$。**NTM** 可以瞬间探索所有这些可能的划分。 * `2. 运行 M 在 xy 上`: 对于每一个猜测的划分 $(x, a, y)$，我们构造出“删除”字符 $a$ 后的**字符串** $xy$，然后把这个 $xy$ 交给已知的、能**判定** $L$ 的 **NTM** $M$ 去处理。 * `3 & 4. 如果 M 接受/拒绝...`: $M'$ 的最终裁决完全依赖于子程序 $M$ 的裁决。如果 $M$ **接受**了 $xy$，说明我们的猜测是正确的（$xy$ 确实在 $L$ 中），于是 $M'$ 就**接受** $w$。 --- **[原文]（逐字逐句）** 首先，我们声称 $M^{\prime}$ 在**多项式时间**内运行。这是因为**划分** $w$ 在 $O(|w|)$ 时间内运行，然后我们运行 $M$ 在 $x y$ 上。由于 $M$ 是 $L$ 的**多项式时间判定器**，$M$ 在 $O\left(|x y|^{k}\right)=O\left(|w|^{k}\right)$ 时间内运行，其中 $k$ 是某个**常数**。所以 $M^{\prime}$ 在 $|w|$ 的**多项式时间**内运行。 假设 $w \in \operatorname{AddOne}(L)$。那么我们可以将 $w$ 写成 $w=x a y$，使得 $x y \in L, a \in \Sigma$。所以当我们**非确定性**地选择这种**划分**时，我们将在 $x y \in L$ 上运行 $M$。由于 $M$ **判定** $L$，存在某个**非确定性分支**， $M$ 将在该**分支**上**接受** $x y$，这意味着 $M^{\prime}$ 将**接受** $w$。因此，存在一些**非确定性选择**使得 $M^{\prime}$ **接受** $w$。 假设 $w \notin \operatorname{AddOne}(L)$。那么无论我们如何将 $w$ 拆分为 $w=x a y$，我们都不会有 $x y \in L$。所以无论我们在**第 1 行**选择什么**划分**，$M$ 将始终**拒绝** $x y$（无论 $M$ 做出什么**非确定性选择**）。所以 $M^{\prime}$ 总是**拒绝** $w$。 由于我们已经给出了一个在**多项式时间**内运行并**判定** **AddOne** $(L)$ 的 **NTM**，我们可以得出结论，如果 $L \in \mathrm{NP}$，则 **AddOne** $(L) \in \mathrm{NP}$。 **[逐步解释]（from scratch，超细）** 这部分是示例 8 的**复杂度分析**和**正确性证明**。 1. **步骤 4：证明高效性 (多项式时间分析)** * **分析 $M'$ 的运行时间**: $M'$ 的**运行时间**是其最长计算分支的长度。 * `划分 w`: **非确定性**地选择一个划分，在 **NTM** 模型中可以看作是 $O(|w|)$ 个分支，每个分支的创建是瞬时的。我们关心的是每个分支后续的**运行时间**。 * `运行 M 在 xy 上`: 在任何一个分支中，我们都运行了 **NTM** $M$。 * `由于 M 是 L 的多项式时间判定器`: 这是我们的前提。意味着 $M$ 的**运行时间**是 $O(m^k)$，其中 $m$ 是其输入长度。 * $M$ 的输入是 $xy$。$|xy| = |w|-1$。所以 $M$ 的**运行时间**是 $O((|w|-1)^k)$，这仍然是关于 $|w|$ 的**多项式**，即 $O(|w|^k)$。 * **结论**: $M'$ 的总**运行时间**由**运行** $M$ 的时间主导，因此是**多项式时间**的。 2. **步骤 2：证明完备性 (如果 $w \in \text{AddOne}(L)$)** * **前提**: $w \in \text{AddOne}(L)$。 * **逻辑推导**: 根据定义，这意味着 $w$ **可以被**写成 $w=xay$ 的形式，并且 $xy \in L$。 * **联系算法**: $M'$ 的**步骤 1** 是**非确定性**地选择一个划分。因为存在一个“正确”的划分，所以**必然存在一个计算分支**，它恰好就猜到了这个正确的划分 $(x,a,y)$。 * 在这个“幸运”的分支上，**算法**会去**运行** $M$ 在 $xy$ 上。 * 因为 $xy \in L$，且 $M$ 是 $L$ 的**判定器**，所以 $M$ 在输入 $xy$ 时，**存在**至少一个它自己的**非确定性**分支会导致**接受**。 * 这个**接受**结果会传递给 $M'$，导致 $M'$ 在这个分支上**接受** $w$。 * **结论**: 既然**存在**一个导致**接受**的计算分支，那么根据 **NTM** 的定义，$M'$ **接受** $w$。 3. **步骤 3：证明可靠性 (如果 $w \notin \text{AddOne}(L)$)** * **前提**: $w \notin \text{AddOne}(L)$。 * **逻辑推导**: 这意味着，**无论**我们怎么把 $w$ 划分为 $w=xay$，得到的结果 $xy$ 都**不会**在 $L$ 中。 * **联系算法**: $M'$ 的**步骤 1** 会探索所有可能的划分。对于**所有这些分支**： * 它们得到的 $xy$ 都不在 $L$ 中。 * 当它们去**运行** $M$ 在 $xy$ 上时，因为 $M$ 是 $L$ 的**判定器**，所以 $M$ 的**所有**计算分支都会**拒绝** $xy$。 * 这个**拒绝**的结果会传递给 $M'$，导致 $M'$ 在这个分支上**拒绝** $w$。 * **结论**: 因为 $M'$ 的**所有**计算分支都**拒绝** $w$，所以根据 **NTM** 的定义，$M'$ **拒绝** $w$。 4. **最终结论**: * 我们从任意一个 $L \in \mathrm{NP}$ 出发，成功地为 $\text{AddOne}(L)$ 构造了一个**多项式时间**的 **NTM** **判定器** $M'$。 * 根据 **NP** 的定义，这意味着 $\text{AddOne}(L)$ 也属于 **NP**。 * 因此，**NP** 类在 **AddOne** 操作下是**封闭**的。 **[总结]** 该示例通过一个精巧的 **NTM** 构造，证明了 **NP** 类的**封闭性**质。它完美地展示了如何将一个已知**问题**的 **NTM** **判定器**作为“子程序”，来为新**问题**构建**判定器**，并严谨地**分析**了其**复杂度**和**正确性**。 --- ## 7.3 **NP 难** ### 7.3.1 **证明模板** 17：使用**多项式时间归约**证明 $L$ 是 **NP 难**的 **[原文]（逐字逐句）** 1. 选择一个 **NP 难**的 $H$。编写一个计算 $f$ 的**算法**。 2. **检查**你的**算法**是否在 $O\left(n^{k}\right)$ 时间内运行，其中 $k$ 是某个**常数**。 3. 假设 $x \in H$，证明 $f(x) \in L$。 4. 假设 $x \notin H$，证明 $f(x) \notin L$。 5. 得出结论，由于 $H \leq_{\mathrm{p}} L$ 且 $H$ 是 **NP 难**的，因此 $L$ 是 **NP 难**的。 **[逐步解释]（from scratch，超细）** 这是证明一个新**问题**是 **NP-难** 的标准方法，它利用了**定理 8**。 1. **角色定位**: 提供通过**归约**证明**问题**是 **NP-难**的标准流程。 2. **核心思想**: 我们想证明新**问题** $L$ 是“非常难”的。我们不直接证明，而是找到一个公认的“非常难”的**问题** $H$，然后证明 $H$ 不比 $L$ 更难。如果连 $H$ 都能被 $L$ 解决，那 $L$ 至少也和 $H$ 一样难。 3. **归约方向**: **至关重要**！为了证明 $L$ 是 **NP-难**，必须将一个**已知的 NP-难问题 H** **归约**到**我们想证明其难度的 L**，即 $H \le_p L$。 4. **步骤详解**: * **步骤 1**: 选择一个合适的、已知的 **NP-难** **问题** $H$ 作为**归约**的“源**问题**”。例如 **SAT**, **3-SAT** 等。然后设计一个函数 $f$ 的**算法**，它能将 $H$ 的实例 $x$ 转换为 $L$ 的实例 $f(x)$。 * **步骤 2**: **分析**计算 $f(x)$ 的**算法**，证明它是**多项式时间**的。 * **步骤 3 & 4**: 证明**归约**的**正确性**，即 $x \in H \iff f(x) \in L$。 * **步骤 5**: 引用**定理 8**。因为我们已知 $H$ 是 **NP-难**的，并且我们成功证明了 $H \le_p L$，所以 **NP-难** 这个性质就从 $H$ “传递”给了 $L$。因此，$L$ 也是 **NP-难**的。 **[总结]** **证明模板 17** 是建立新 **NP-难** **问题**的“生产线”。从第一个 **NP-完全** **问题** **SAT** 开始，我们可以通过一系列的**多项式时间归约**，像接力一样，将“**NP-难**”的标签传递给成千上万个不同的**问题**。 --- **由于篇幅超长，剩余部分的解释将在下一个回复中继续提供。** 我将继续解释 `示例 9` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 我将继续解释 `示例 9` 之后的所有内容，严格遵守所有格式要求，确保内容的完整性和详细性。 ### 7.3.2 示例 9：证明 CycleSize 是 NP 难的 **[原文]（逐字逐句）** 我们声称 **CycleSize** 也是 **NP 难**的。为了证明这一点，我们将从 **HamCycle** **问题**开始，我们已经知道它是 **NP 难**的： $$

$$ 我们将展示 **HamCycle** $\leq_{\mathrm{p}}$ **CycleSize**。这个**想法**是**哈密顿环**只是一个包含所有**节点**的**简单环**。 令 $y$ 是一个不在 **CycleSize** 中的**字符串**。我们提出以下**算法**。 $$

$$ 1. **检查** $x=\langle G\rangle$，其中 $G$ 是一个**图**。如果不是，则**输出** $y$。 2. **输出** $\langle G| V,(G)| \rangle$。" **[逐步解释]（from scratch，超细）** 这个示例应用了**证明模板 17** 来证明 **CycleSize** **问题**是 **NP-难**的。 1. **目标**: 证明 **CycleSize** 是 **NP-难**的。 2. **应用模板 17**: * **步骤 1: 选择源问题 H 和构造归约函数 f**: * **选择 H**: 我们选择一个已知的 **NP-难** **问题**——**哈密顿环问题 (HamCycle)**。 * **HamCycle 问题**: 输入一个图 $G$，判断 $G$ 中是否存在一条经过**每个顶点恰好一次**的**简单环**。 * **构造 f**: 我们需要设计一个**多项式时间算法** $F$（计算**函数** $f$），它能将 **HamCycle** 的输入 $\langle G \rangle$ 转换为 **CycleSize** 的输入 $\langle G', k \rangle$。 * **核心想法**: 一个图 $G$ (假设有 $|V|$ 个顶点) 存在**哈密顿环**，**当且仅当**它存在一个大小为 $|V|$ 的**简单环**。这个观察是**归约**的关键！ * **归约函数 f 的设计**: * 输入 $x = \langle G \rangle$。 * **算法** $F$ 的输出 $f(x)$ 应该是 $\langle G, |V(G)| \rangle$。也就是说，图保持不变 ($G'=G$)，而期望的环大小 $k$ 被设置成了图的顶点总数 $|V(G)|$。 * 原文中的**算法** $F$ 正是实现了这个思想。它接收 $x$，如果 $x$ 是一个图 $\langle G \rangle$，它就输出一个新的**字符串**，这个**字符串**是图 $G$ 和它的顶点数 $|V(G)|$ 的**编码**。对于格式错误的输入，它输出一个固定的、不在 **CycleSize** 中的**字符串** $y$，这正是我们之前讨论过的处理技巧。 --- **[原文]（逐字逐句）** 首先，我们声称 $F$ 在**多项式时间**内运行。**步骤 1** 中**编码**的**有效性检查**当然是**多项式时间**。然后**步骤 2** 需要 $O(n)$ 时间来计算 $G$ 中的**顶点数**。 接下来，令 $f$ 是 $F$ 计算的**函数**；我们将证明**正确性**。 假设 $x \in$ **HamCycle**。那么 $x=\langle G\rangle$，其中 $G$ 是一个具有**哈密顿环**的**图**。因为 $G$ 是一个**图**，$F$ 将通过**步骤 1** 中的**检查**。然后，因为 $G$ 的**哈密顿环**是**大小**为 $|V(G)|$ 的**简单环**，我们有 $f(x)=\langle G| V,(G)| \rangle \in$ **CycleSize**。 假设 $x \notin$ **HamCycle**。那么 $x \neq\langle G\rangle$ 或者 $x=\langle G\rangle$，其中 $G$ 是一个没有**哈密顿环**的**图**。在第一种情况下，$f(x)=y \notin$ **CycleSize**。在第二种情况下，$G$ 是一个**图**，所以 $F$ 将通过**步骤 1** 中的**检查**。然后，由于**大小**为 $|V(G)|$ 的**简单环**是**哈密顿环**，我们有 $f(x)=\langle G| V,(G)| \rangle \notin$ **CycleSize**（如果它在 **CycleSize** 中，那么 $G$ 将有一个**哈密顿环**）。 得出结论，由于 **HamCycle** $\leq_{\mathrm{p}}$ **CycleSize** 且 **HamCycle** 是 **NP 难**的，因此 **CycleSize** 是 **NP 难**的。 **[逐步解释]（from scratch，超细）** 这部分是示例 9 的**复杂度分析**和**正确性证明**。 1. **步骤 2：证明 f 是多项式时间的**: * **分析算法 F**: * **步骤 1 (格式检查)**: 解析输入**字符串** $x$ (长度为 $n$)，检查它是否是图的合法**编码**。这可以在 $O(n)$ 时间内完成。 * **步骤 2 (构造输出)**: 如果格式正确，需要计算图中顶点的数量 $|V(G)|$。这可以通过扫描图的**编码**来完成，也是 $O(n)$ 时间。然后将 $\langle G \rangle$ 和计算出的 $|V(G)|$ 拼接成新的**字符串**。整个过程是线性的，也就是**多项式时间**的。 * **结论**: **归约函数** $f$ 是**多项式时间可计算**的。 2. **步骤 3 & 4：证明归约的正确性**: * **完备性 (如果 $x \in \text{HamCycle}$)**: * **前提**: 假设 $x=\langle G \rangle$ 且 $G$ 有一个**哈密顿环**。 * **归约过程**: **算法** $F$ 会输出 $f(x) = \langle G, |V(G)| \rangle$。 * **验证**: 根据**哈密顿环**的定义，它是一个经过所有 $|V(G)|$ 个顶点的**简单环**。因此，$G$ 确实包含一个大小为 $|V(G)|$ 的**简单环**。 * **结论**: 这意味着 $f(x)$ 满足 **CycleSize** **问题**的条件，即 $f(x) \in \text{CycleSize}$。 * **可靠性 (如果 $x \notin \text{HamCycle}$)**: * **前提**: 假设 $x \notin \text{HamCycle}$。 * **情况 A (格式错误)**: 如果 $x$ 不是一个图的**编码**，**算法** $F$ 输出 $y$。我们事先选择了 $y \notin \text{CycleSize}$，所以**归约**成立。 * **情况 B (格式正确)**: 如果 $x = \langle G \rangle$ 但 $G$ 没有**哈密顿环**。 * **归约过程**: **算法** $F$ 仍然输出 $f(x) = \langle G, |V(G)| \rangle$。 * **验证**: 我们需要判断这个 $f(x)$ 是否在 **CycleSize** 中。$f(x) \in \text{CycleSize}$ 的条件是“$G$ 中存在一个大小为 $|V(G)|$ 的**简单环**”。 * 但一个大小为 $|V(G)|$ 的**简单环**的定义，恰好就是**哈密顿环**的定义。 * 既然我们前提是 $G$ 中没有**哈密顿环**，那么 $G$ 中也就不可能存在大小为 $|V(G)|$ 的**简单环**。 * **结论**: 这意味着 $f(x) \notin \text{CycleSize}$。 * **总结**: 我们已经证明了 $x \in \text{HamCycle} \iff f(x) \in \text{CycleSize}$。 3. **步骤 5：最终结论**: * 我们成功地证明了 **HamCycle** $\le_p$ **CycleSize**。 * 因为我们已知 **HamCycle** 是 **NP-难**的，根据**定理 8**，**NP-难**的性质传递给了 **CycleSize**。 * 因此，**CycleSize** 也是 **NP-难**的。 **[总结]** 该示例通过一个非常简洁和直观的**归约**，证明了 **CycleSize** 是 **NP-难**的。**归约**的巧妙之处在于深刻理解了**哈密顿环**和特定大小的**简单环**之间的等价关系。 --- **[原文]（逐字逐句）** 关于**映射归约**的一个小**说明**：在给出**多项式时间映射归约** $A \leq_{\mathrm{p}} B$ 时，处理“**错误编码**”很麻烦，这些**编码**显然不在 $A$ 中，就像我们上面做的那样。请注意，如果你想展示 $A \leq_{\mathrm{P}} B$，只要 $B \neq \Sigma^{*}$，我们就可以**固定**一些**字符串** $y \notin B$。然后，如果 $x$ 对于 $A$ 具有**错误格式**（例如，$x \neq\langle G\rangle$），我们只需**固定** $f(x)=y$。 因此，在进行**映射归约**时，你可以说“我们通过将**错误编码****映射**到固定**字符串** $y \notin B$ 来忽略它们”。然后在给出 $f$ 和**正确性证明**时，你可以忽略**错误编码**（参见 **HW5**，**3d** 的示例）。 **[逐步解释]（from scratch，超细）** 这段内容与 `5.4.1` 节后的说明完全重复，再次强调了在进行**映射归约**时处理格式错误输入的标准技巧。 * **核心技巧**: 将所有格式错误的输入**映射**到一个固定的、确定不在目标**语言** $B$ 中的**字符串** $y$。 * **带来的便利**: 这样做可以保证**归约**的 $\iff$ 条件对所有**字符串**都成立，同时让**证明**者在书写**正确性证明**时，可以只关注格式正确的输入，从而大大简化**证明**过程。 * **示例应用**: 在刚刚的示例 9 中，**算法** $F$ 的**步骤 1** `如果不是，则**输出** y` 就是这个技巧的直接应用。 --- ## 7.4 **NP 完全** ### 7.4.1 **证明模板** 18：证明 $L$ 是 **NP 完全**的 **[原文]（逐字逐句）** 1. 证明 $L$ 在 **NP** 中。 2. 证明 $L$ 是 **NP 难**的。 **[逐步解释]（from scratch，超细）** 这个模板是证明一个**问题**是 **NP-完全**的最终“合成”步骤，它直接源于 **NP-完全**的定义。 1. **角色定位**: 定义证明 **NP-完全**性的两步走策略。 2. **核心思想**: 根据定义 19，一个**问题**是 **NP-完全**的，当且仅当它同时满足两个条件：(1) 它属于 **NP**；(2) 它是 **NP-难**的。因此，**证明**过程也必须包含这两部分的**证明**。 3. **步骤详解**: * **步骤 1: 证明 $L \in \mathrm{NP}$** * **目的**: 证明**问题** $L$ 是“容易**验证**”的。 * **方法**: 通常使用**模板 15**（构造**多项式时间验证器**）。你需要定义一个合适的**证书**，并给出一个**多项式时间**的**验证算法**。 * **步骤 2: 证明 $L$ 是 NP-难的** * **目的**: 证明**问题** $L$ 是“至少和 **NP** 中最难**问题**一样难”的。 * **方法**: 使用**模板 17**（通过**多项式时间归约**）。你需要从一个已知的 **NP-难** **问题** $H$ 出发，证明 $H \le_p L$。 **[总结]** **证明模板 18** 是证明 **NP-完全**性的标准大纲。它是一个复合**证明**，需要完成两个独立的子**证明**：一个是关于**问题**自身的“容易**验证**性”，另一个是关于它与其他**问题**的“难度**关系**”。 --- ### 7.4.2 示例 10：证明 CycleSize 是 NP 完全的 **[原文]（逐字逐句）** 声称 **CycleSize** 是 **NP 完全**的。 这遵循我们上面对 **CycleSize** $\in$ **NP** 和 **CycleSize** 是 **NP 难**的**证明**。 **[逐步解释]（from scratch，超细）** 这个示例将前面的工作成果组合起来，完成了对 **CycleSize** **问题**的最终定性。 1. **应用模板 18**: * **步骤 1: 证明 CycleSize $\in$ NP**: * 我们在 **示例 7** 中已经完成了这项工作。我们通过定义一个**证书**（一个顶点列表）和一个**多项式时间**的**验证器** $V_C$，证明了 **CycleSize** $\in \mathrm{NP}$。 * **步骤 2: 证明 CycleSize 是 NP-难的**: * 我们在 **示例 9** 中也已经完成了这项工作。我们通过将已知的 **NP-难** **问题** **HamCycle** **多项式时间归约**到 **CycleSize** ($\text{HamCycle} \le_p \text{CycleSize}$)，证明了 **CycleSize** 是 **NP-难**的。 2. **最终结论**: * 因为 **CycleSize** 同时满足了 **NP-完全**的两个定义条件，所以我们可以得出结论：**CycleSize** 是一个 **NP-完全** **问题**。 **[总结]** 该示例展示了一个完整的 **NP-完全**性**证明**的“全貌”，它将前面两个独立的**证明**（一个关于成员资格，一个关于难度）结合在一起，最终给出了**问题**的**复杂度**定性。 --- # 8 **附录** ## 8.1 **可计算理论**的**语言示例** **[原文]（逐字逐句）** 找到正确的**语言**进行**归约**可以使你的**证明**更快。**检查**任何**不可判定**的**语言**是否既不是**可识别**的也不是**共可识别**的，回想一下这是因为**定理** $L$ 和 $\bar{L}$ 是**可识别**的 $\Longleftrightarrow L$ 是**可判定**的。 | | **可判定** | **共可识别** | | :--- | :--- | :--- | | $\mathrm{A}_{\text {DFA }}$ | 是 是 | $\{\langle D, w\rangle \mid D$ 是一个 **DFA** 且 $D$ **接受** $w\}$ | | $\mathrm{A}_{\text {NFA }}$ | 是 是 | $\{\langle D, w\rangle \mid N$ 是一个 **NFA** 且 $N$ **接受** $w\}$ | | $\mathrm{E}_{\text {DFA }}$ | 是 是 | $\{\langle D\rangle \mid D$ 是一个 **DFA** 且 $L(D)=\varnothing\}$ | | $\mathrm{EQ}_{\text {DFA }}$ | 是 | $\{\langle D, E\rangle \mid D, E$ 是 **DFA** 且 $L(D)=L(E)\}$ | | $\mathrm{A}_{\text {TM }}$ | 否 | $\{\langle M, w\rangle \mid M$ 是一台 **TM** 且 $M$ **接受** $w\}$ | | $\mathrm{E}_{\text {TM }}$ | 否 | $\{\langle M\rangle \mid M$ 是一台 **TM** 且 $L(M)=\varnothing\}$ | | $\mathrm{EQ}_{\text {TM }}$ | 否 | $\{\langle M, N\rangle \mid M, N$ 是 **TM** 且 $L(M)=L(N)\}$ | | **HALT**$_{\text {TM }}$ | 否 | $\{\langle M, w\rangle \mid M$ 是一台 **TM** 且 $M$ 在 $w$ 上**停机** $\}$ | | **REG**$_{\text {TM }}$ | 否 | $\{\langle M\rangle \mid M$ 是一台 **TM** 且 $L(M)$ 是**正则语言** $\}$ | | **ALL**$_{\text {TM }}$ | 否 | $\left\{\langle M\rangle \mid M\right.$ 是一台 **TM** 且 $\left.L(M)=\Sigma^{*}\right\}$ | **[逐步解释]（from scratch，超细）** 这个附录提供了一个常用**语言**及其**可计算性**属性的速查表。 1. **引言部分**: * “找到正确的**语言**进行**归约**可以使你的**证明**更快”：这强调了熟悉这个表格的重要性。在做**归约**时，选择一个与你目标**问题**结构最相似的已知**问题**，会大大简化**归约**的构造。 * “**检查**任何**不可判定**的**语言**是否既不是**可识别**的也不是**共可识别**的”：这是一个思考题。**共可识别 (co-recognizable)** 是指一个**语言**的**补集**是**可识别**的。 * **定理**: $L$ **可判定** $\iff$ $L$ **可识别** 且 $L$ **共可识别**。 * 所以，如果一个**语言** $L$ 是**不可判定**的，那么它必然不满足右边的条件。这意味着，$L$ 或者**不是可识别**的，或者**不是共可识别**的，或者两者都不是。 * 例如：$\mathrm{A}_{\mathrm{TM}}$ 是**不可判定**的，但它是**可识别**的。根据**定理**，它的**补集** $\overline{\mathrm{A}_{\mathrm{TM}}}$ 必然是**不可识别**的（因此 $\mathrm{A}_{\mathrm{TM}}$ 不是**共可识别**的）。 * $\mathrm{EQ}_{\mathrm{TM}}$ 则是既**不是可识别**的，也**不是共可识别**的。 2. **表格解读**: * **关于 DFA/NFA 的问题**: * $\mathrm{A}_{\text{DFA}}, \mathrm{A}_{\text{NFA}}$ (接受性**问题**): **可判定**。我们可以直接**模拟**自动机，总会**停机**。 * $\mathrm{E}_{\text{DFA}}$ (空**语言****问题**): **可判定**。可以通过图搜索**算法**（如BFS/DFS）检查从起始状态是否能到达任何一个**接受状态**。 * $\mathrm{EQ}_{\text{DFA}}$ (等价性**问题**): **可判定**。可以构造一个新 **DFA** 来识别两个**语言**的对称差 $(L(D) \setminus L(E)) \cup (L(E) \setminus L(D))$，然后**检查**这个新**语言**是否为空。 * **关于 TM 的问题**: * $\mathrm{A}_{\text{TM}}$ (接受性**问题**): **不可判定**，但是是**可识别**的（这是**可识别**的原型例子）。 * $\mathrm{E}_{\text{TM}}$ (空**语言****问题**): **不可判定**，其**补集** $\overline{\mathrm{E}_{\mathrm{TM}}}$ 是**可识别**的（所以 $\mathrm{E}_{\mathrm{TM}}$ 是**共可识别**的，但**不是可识别**的）。 * $\mathrm{EQ}_{\text{TM}}$ (等价性**问题**): **不可判定**，并且既**不是可识别**的，也**不是共可识别**的。 * $\mathrm{HALT}_{\text{TM}}$ (**停机问题**): **不可判定**，但是**可识别**的。 * $\mathrm{REG}_{\text{TM}}$ (判断**语言**是否**正则**): **不可判定**，并且**不是可识别**或**共可识别**的。 * $\mathrm{ALL}_{\text{TM}}$ (判断**语言**是否为 $\Sigma^*$): **不可判定**，并且**不是可识别**的，但其**补集**是**可识别**的（所以它是**共可识别**的）。 --- ## 8.2 **复杂性理论**的**语言示例** **[原文]（逐字逐句）** 省略的**条目**是未知数，取决于 **P 对 NP 问题**的**解决方案**。列出的**证书**是为了提醒我们如何为每种**语言**构造**验证器**。总是有其他可能的**证书**或**验证器**。 | | 在 **P** 中 | 在 **NP** 中 | **NP 难** | | | :--- | :--- | :--- | :--- | :--- | | **合数** | 是 是 | 是 | • | $\{\langle x\rangle \mid x$ 是一个**合数** $\}$ <br> **证书**：$x$ 的一个非平凡**因子**。 | | **质数** | 是 是 | 是 | . | $\{\langle x\rangle \mid x$ 是一个**质数** $\}$ <br> **质数**通过 [**AKS**] 的复杂**证明**在 **P** 中 | | **HamCycle** | . | 是 | 是 | $\{\langle G\rangle \mid G$ 一个有访问每个**节点**恰好一次的**环**的**图** $\}$ **证书**：这样的一个**环**。 | | **HamPath** | . | 是 | 是 | $\{\langle G, s, t\rangle \mid G$ 一个有从 $s$ 到 $t$ 的**路径**，该**路径**访问每个**节点**恰好一次的**图** $\}$ **证书**：这样一条从 $s$ 到 $t$ 的**路径**。 | | **SAT** | . | 是 | 是 | $\{\langle\phi\rangle \mid \phi$ 一个可满足的**布尔公式** $\}$ <br> **证书**：一个可满足**赋值**。 | | **CNF-SAT** | . | 是 | 是 | $\{\langle\phi\rangle \mid \phi$ 一个可满足的 **CNF 布尔公式** $\}$ <br> **证书**：一个可满足**赋值**。 | | **3SAT** | . | 是 | 是 | $\{\langle\phi\rangle \mid \phi$ 一个可满足的 **CNF**，其中每个**子句**有 3 个**文字** $\}$ <br> **证书**：一个可满足**赋值**。 | **[逐步解释]（from scratch，超细）** 这个附录提供了一个常用**问题**及其**复杂性**分类的速查表。 1. **引言部分**: * “省略的**条目**是未知数，取决于 **P 对 NP 问题**的**解决方案**”：表格中“在 P 中”这一列的 `.` (点) 表示“未知”。对于那些 **NP-完全** **问题**（比如 **HamCycle**, **SAT**），它们是否在 **P** 中，正是 **P vs NP** **问题**的核心。如果 **P=NP**，这些点都会变成“是”。如果 **P≠NP**，它们都是“否”。 * “列出的**证书**是为了提醒...”：表格的最后一列给出了**问题**属于 **NP** 的直观理由，即它的**证书**是什么。这有助于我们快速理解为什么这些**问题**是“容易**验证**”的。 2. **表格解读**: * **合数 (COMPOSITES)**: * 在 **P** 中？是。我们可以试除从 2 到 $\sqrt{x}$，但这不是**多项式时间**的。然而，存在更复杂的**多项式时间算法**。 * 在 **NP** 中？是。**证书**是一个非平凡**因子** $d$。**验证器**只需检查 $1 < d < x$ 和 $x \pmod d = 0$。这是**多项式时间**的。 * **NP-难**？否。因为它在 **P** 中，而我们相信 **P≠NP**。 * **质数 (PRIMES)**: * 在 **P** 中？是。这是一个里程碑式的成果（**AKS 质数测试**，2002年）。 * 在 **NP** 中？是。因为它在 **P** 中，而 $\mathrm{P} \subseteq \mathrm{NP}$。 * **NP-难**？否。 * **HamCycle (哈密顿环)**: * 在 **P** 中？未知。这是 **P vs NP** **问题**。 * 在 **NP** 中？是。**证书**是环的顶点序列。**验证**只需检查序列是否包含所有顶点且相邻顶点有边。 * **NP-难**？是。这是一个经典的 **NP-难** **问题**。 * **结论**: 这是一个 **NP-完全** **问题**。 * **HamPath (哈密顿路径)**: 类似于 **HamCycle**，也是 **NP-完全**的。 * **SAT (布尔可满足性)**: * 在 **P** 中？未知。 * 在 **NP** 中？是。**证书**是可满足**赋值**。 * **NP-难**？是。（**库克-莱文定理**） * **结论**: **NP-完全**。 * **CNF-SAT / 3SAT**: 它们是 **SAT** 的特殊形式，也都是经典的 **NP-完全** **问题**。**3SAT** 特别重要，因为很多**归约**都是从 **3SAT** 出发的。 # 行间公式索引 1. **语言 $\mathrm{E}_{\mathrm{TM}}$ 的定义，即所有语言为空的图灵机的集合。** $$

$$ 2. **语言 $\mathrm{E}_{\mathrm{TM}}$ 和 $\mathrm{A}_{\mathrm{TM}}$ 的并列定义。** $$

$$ 3. **一个接受所有字符串的图灵机 $M'$ 的语言，用于莱斯定理的非平凡性证明。** $$

$$ 4. **一个拒绝所有字符串的图灵机 $M$ 的语言，用于莱斯定理的非平凡性证明。** $$

$$ 5. **语言 $\mathrm{P}$ 作为所有多项式时间确定性图灵机可判定语言的联合的定义。** $$

$$ 6. **验证器正确性的核心逻辑：一个实例在语言中当且仅当存在一个可被接受的证书。** $$

$$ 7. **语言 $\mathrm{NP}$ 作为所有多项式时间非确定性图灵机可判定语言的联合的定义。** $$

$$ 8. **多项式时间映射归约的核心逻辑：成员关系在归约函数 f 下保持不变。** $$

$$ 9. **定理 $\mathrm{P} \subseteq \mathrm{NP}$，说明所有可在多项式时间解决的问题，其解也能在多项式时间验证。** $$

$$ 10. **语言 CycleSize 的定义，判断图中是否存在一个大小为 k 的简单环。** $$

$$ 11. **操作 AddOne(L) 的定义，将语言 L 中字符串插入一个字符得到的新语言。** $$

$$ 12. **语言 HamCycle 的定义，判断图中是否存在哈密顿环。** $$

$$ [[END_OF_RESPONSE]]所有解释内容已全部输出完毕。 $$