📜 原文
📖 逐步解释
∑ 公式拆解
💡 数值示例
⚠️ 易错点
📝 总结
🎯 存在目的
🧠 直觉心智模型
💭 直观想象
1COMS3261:
Computer Science Theory
Spring 2026<br>Mihalis Yannakakis
Lecture 1, 1/21/26
2Ch1. 课程概况 (Course Introduction) P1
1Ch1.1. 课程信息 Course Information P1
- 网站: Courseworks
文件:
-课程信息: 一般信息，包括后勤、政策、评分方案、办公时间等。
-暂定时间表
- 作业 ...
2Ch1.2. 课程工作 Course Work P1
- 作业、期中考试、期末考试
- 政策
- 迟交作业（每迟交一天或不足一天扣10%）
- 舍弃最低分作业
- 合作政策
- 学术诚信
- 评分：作业20%，期中考试40%，期末考试40%
- 考试：期中考试（3/25），期末考试（5/4）课堂进行
3Ch1.3. 教科书 Textbook P2
- 必读:
1. Introduction to the Theory of Computation, by M. Sipser P2
- 其他:
2. Introduction to Automata Theory, Languages and Computation, by Hopcroft, Motwani, Ullman P2
3Ch2. 课程核心主题 (Core Topics) P2
1Ch2.1. 基本问题：可计算性 Basic Questions: Computability P2
- 可计算性：哪些计算问题可以由计算机解决？
- 并非所有！
- 示例：给定程序P（比如Java）和一个输入x，P会在输入x上终止还是会永远运行下去？
- 语法正确的程序（即合法的Java）与语义正确的程序（即做它应该做的事情）
- 给定一个数学陈述（例如所有整数都具有某种属性，如Fermat's last theorem），它是一个真定理吗？
2Ch2.2. 基本问题：复杂性 Basic Questions: Complexity P3
- 复杂性：哪些问题可以高效计算（在合理的时间内）？
- 并非所有！
- 示例：排序、加法、乘法数字的快速算法，但没有因式分解的。因式分解的难度是当前加密协议的基础。
- 许多优化问题——调度、网络设计、资源分配等。
3Ch2.3. 计算模型 Models of Computation P3
- 计算模型
- 形式化的数学基础
- 建模和抽象在科学和工程中的重要性
- 图灵机 [Turing 1936]
- 简单的“朴素”模型，但其能力 ⇔ 计算机
- 精确捕捉可计算性
- 捕捉复杂性的粗略差异
4Ch2.4. 模型和规范形式化 Models and Specification Formalisms P4
- 其他规范形式化
- 更受限制的模型
- 文法和形式语言 [Chomsky 1950年代]
- 最初是自然（人类）语言的模型
- 用于编程语言
- 允许在高级别（而非低级别机器语言）指定计算，自动编译方法，新语言等。
4Ch3. 自动机理论导论 (Introduction to Automata Theory) P4
1Ch3.1. 自动机（状态机）定义 Automata (State Machines) P4
- 描述系统（硬件和软件）的行为，建模设备、世界的一部分等。
- 系统状态通过动作/事件/输入以离散步骤改变
- 特别关注有限自动机（有限个状态）
- McCulloch, Pitts, 神经网络（大脑模型）1943
- Mealy, Moore, Huffman 1954-56: 顺序开关电路
- 随后，许多其他应用
2Ch3.2. 自动机应用 Automata Applications P4
- 编译器中的词法分析
- 模式匹配：搜索关键字或更复杂的模式（grep, awk等）
- 语音、语言处理
- 协议建模——例如通信协议、安全协议
- 软件和硬件系统的验证：自动机用于建模系统和/或正确性属性
- ...
3Ch3.3. 课程更一般的目标 More General Goals of the Course P5
- 发展有用的抽象和模型
- 严谨地推理论证它们的能力
无论你之后做什么，这都是重要的技能。
5Ch4. 预备知识与实例 (Prerequisites & Examples) P5
1Ch4.1. 数学基础（书中第0章） Review Chapter 0 in book P5
- 基本数学概念和定义
1. 基础概念 Basic Math Concepts and Definitions P5
集合
函数和关系
图
字符串和语言
布尔逻辑
2. 证明方法 Proofs P5
- 证明
通过构造
通过反证法
通过归纳法
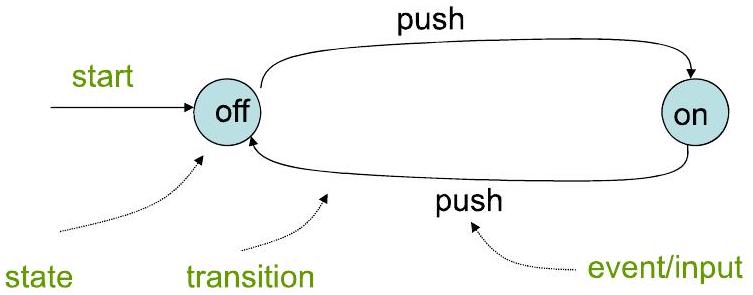
2Ch4.2. 有限自动机示例：开关 Finite Automata Examples P5
- 开关
操作：当你按下按钮时，如果灯亮着则关掉，如果灯灭着则打开
3Ch4.3. 有限自动机示例：3槽缓冲区 A 3-slot buffer P5
- 操作：可以插入一个项（如果缓冲区未满）或删除一个项（如果非空）
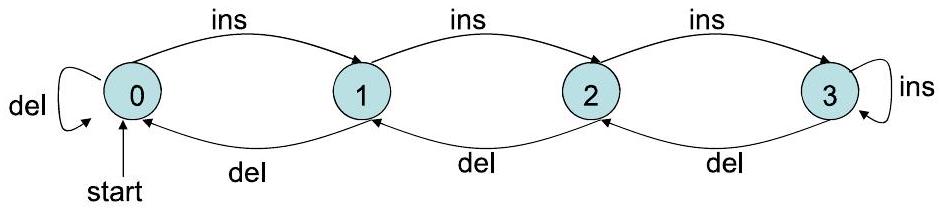
- 另外，对于满缓冲区中的插入或空缓冲区中的删除，可以转换为错误状态。
- 这个FA只跟踪缓冲区中项目的数量。如果我们还想跟踪项目本身的身份，我们需要一个更详细的自动机，并且还需要建模删除规则。
6Ch5. 形式化基础：字符串与语言 (Formal Strings & Languages) P6
1Ch5.1. 字符串、语言的基本概念 Basic Concepts on Strings, Languages P6
- 字母表 $\Sigma=$ 有限非空符号集
示例：$\{0,1\}$（二进制字符串，二进制数），$\{0,1, \ldots, 9\}$（十进制数），$\{a, b, \ldots, z\}$，ASCII characters，\{push\}，\{ins,del\}，\{up,down,left,right\}
- 字符串：由 $\Sigma$ 中的符号组成的有限序列
示例：010010, 2022, abba, then
- 空字符串 $\varepsilon=$ 不含符号的字符串
- 字符串的长度 = 符号的数量，表示法：$|\sigma|$
示例：$|\varepsilon|=0,|0100|=4$
2Ch5.2. 字符串操作 String Operations P6
- 字符串的前缀，字符串的后缀：字符串开头/结尾的子字符串
示例：abcd的前缀包括 $\varepsilon, a, ab, abc, abcd$，后缀包括 $\varepsilon, d, cd$等。
- 字符串 $x=a_{1} \ldots a_{i}$ 和 $y=b_{1} \ldots b_{j}$ 的连接是 $x \cdot y$ 或简写为 $xy=a_{1} \ldots a_{i} b_{1} \ldots b_{j}$
- 示例：$x=abra, y=cadabra \rightarrow xy=abracadabra$
对于每个字符串 $x, \varepsilon x=x \varepsilon=x$
- 字母表 $\Sigma$ 的幂
$\Sigma^{0}=\{\varepsilon\}, \Sigma^{1}=\Sigma, \Sigma^{k}=$ 长度为 $k$ 的 $\Sigma$ 上的字符串
$\Sigma^{*}=$ 任意长度的字符串 $=\Sigma^{0} \cup \Sigma^{1} \cup \Sigma^{2} \cup \cdots$
$\Sigma^{+}=$正长度的字符串 $=\Sigma^{1} \cup \Sigma^{2} \cup \cdots$
3Ch5.3. 语言 Languages P6
- 字母表 $\Sigma$ 上的语言 $L=$ $\Sigma^{*}$ 的任意子集，即 $\Sigma$ 上的任意字符串集
- 示例：$\varnothing, \Sigma, \Sigma^{*}$
- 英文字典中的所有单词（$\Sigma=\{\mathrm{a}, \ldots, \mathrm{z}\}$）
- 所有有效的C程序（$\Sigma=$ ASCII characters incl. newline CR）
- 十进制表示的所有偶数（$\Sigma=\{0, \ldots, 9\}$）
- 二进制表示的所有素数（$\Sigma=\{0,1\}$）
- 可以用二进制表示法（或ASCII）编码图、矩阵等 -> 所有平面图编码的集合
7Ch6. 确定性有限自动机 (DFA) (Deterministic Finite Automata) P7
1Ch6.1. 定义 Definition of DFA P7
- $A=(Q, \Sigma, \delta, q_{0}, F)$
- $Q=$ 有限状态集
- $\Sigma=$ 有限（输入）字母表
- $\delta=$ 转移函数：$\delta: Q \times \Sigma \rightarrow Q$
即，对于 $Q$ 中的每个 $q$ 和 $\Sigma$ 中的每个 $a, \delta(q, a) \in Q$
（该函数为所有输入对 $(q, a)$ 完全且唯一地定义：确定性FA）
- $q_{0}=$ 开始（或初始）状态
- $F \subseteq Q$ 是接受（或最终）状态集
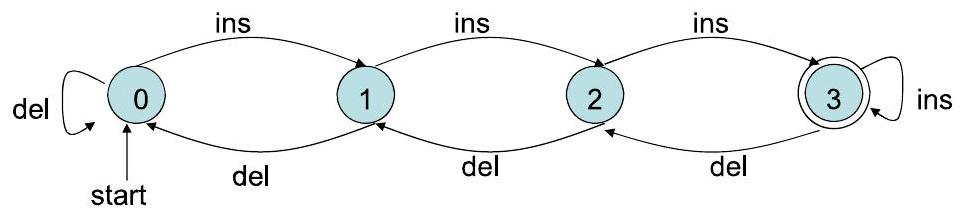
2Ch6.2. 转移图表示 Transition Diagram Representation P7
- 转移图：带有标记边的有向图
- 节点集 = $Q$（状态集），
- 边：对于每个 $q \in Q, a \in \Sigma$，如果 $\delta(q, a)=p$，则有边 $q \rightarrow p$ 标记为 $a$。（如果对于许多符号 $a, \delta(q, a)=p$，则我们通常画一条边并放置许多标记，而不是画许多平行边）
- “开始”箭头指向开始状态 $q_{0}$
- 接受状态 ($F$) 用双圈标记
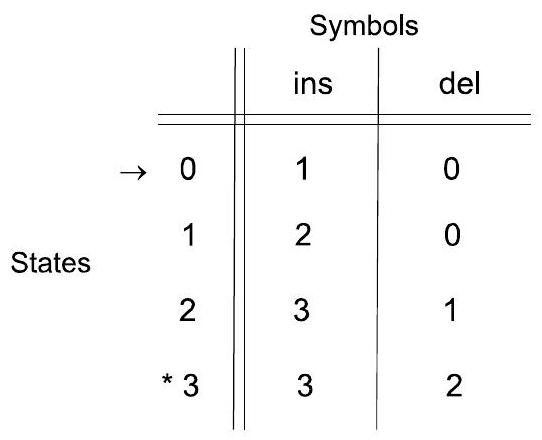
3Ch6.3. 转移表表示 Transition Table Representation P7
- 行对应状态，列对应输入符号，对于 $q, a$ 的条目是 $\delta(q, a)$，开始状态用 → 标记，接受状态用 * 标记
4Ch6.4. 符号表示 Symbolic Representation P8
示例：k-槽缓冲区自动机
$$
\begin{aligned}
& Q=\{0,1,2, \ldots, k\} \\
& \Sigma=\{\mathrm{ins}, \mathrm{del}\} \\
& \delta: \quad \delta(i, \mathrm{ins})=i+1 \text { if } i<k \text { else }=k \\
& \quad \delta(i, \mathrm{del})=i-1 \text { if } i>0 \text { else }=0 \\
& q_{0}=0 \\
& F=\{k\}
\end{aligned}
$$
5Ch6.5. DFA处理输入 Processing of Input by DFA P8
- 给定输入字符串 $x=a_{1} a_{2} \ldots a_{n}$，DFA从状态 $q_{0}$ 开始，读取 $a_{1}$ 并移动到状态 $\delta(q_{0}, a_{1})=$ 比如 $q_{1}$，然后读取 $a_{2}$ 并移动到状态 $\delta(q_{1}, a_{2})=$ 比如 $q_{2}$，依此类推，即 DFA 经历一个状态序列 $q_{1} q_{2} q_{3} \ldots q_{n}$（不一定不同），使得对于每个 $i=1, \ldots, n$，都有 $\delta(q_{i-1}, a_{i})=q_{i}$。
- 当且仅当最终状态 $q_{n}$ 在 $F$ 中时，自动机接受输入，否则拒绝。
- 自动机 $A$ 的语言，表示为 $L(A)$，是自动机 $A$ 接受的所有输入字符串的集合。
6Ch6.6. 综合示例 Example P8
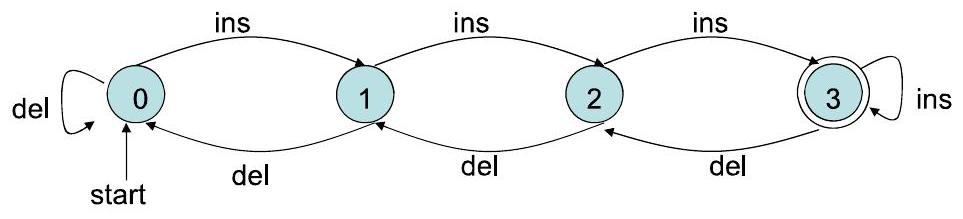
inputstring: ins ins ins del ins
path: $0 \longrightarrow 1 \longrightarrow 2 \longrightarrow 3 \longrightarrow 2 \longrightarrow 3$
- 这个自动机的语言：
$L(A)=$ 使缓冲区变满的操作序列集合