1内容
I will read the contents of lecture2打印.ZH.md and lecture2打印.md to align the Chinese and English titles and identify the page numbers for formatting.
2Ch2. COMS3261:
计算机科学理论 Computer Science Theory P1
11. 2026年春 Spring 2026 P1
22. Mihalis Yannakakis Mihalis Yannakakis P1
讲座 2, 26/1/26
33. (确定性) 有限自动机的定义 Definition of (Deterministic) Finite Automaton P1
- $\mathrm{A}=\left(\mathrm{Q}, \Sigma, \delta, \mathrm{q}_{0}, \mathrm{~F}\right)$
- $\mathrm{Q}=$ 有限状态集合
- $\Sigma=$ 有限(输入)字母表
- $\delta=$ 转移函数: $\delta: \mathrm{Q} \times \Sigma \rightarrow \mathrm{Q}$ 即,对于 $\mathrm{Q}$ 中的每个 $q$,$\Sigma$ 中的每个 $a$,$\delta(q, a) \in Q$ (该函数对于所有输入对 $(\mathrm{q}, \mathrm{a})$ 完全且唯一地定义:确定性有限自动机)
- $\mathrm{q}_{0}=$ 起始(或初始)状态
- $\mathrm{F} \subseteq \mathrm{Q}$ 是接受(或最终)状态的集合
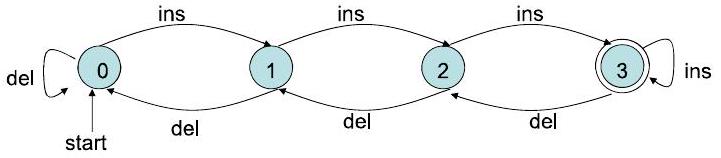
44. 转移图表示 Transition Diagram representation P1
- 转移图:带标签的边的有向图
- 节点集合 $=$ Q (状态集合),
- 边:对于 $\mathrm{Q}$ 中的每个 $\mathrm{q}$,$\Sigma$ 中的每个 $\mathrm{a}$,如果 $\delta(\mathrm{q}, \mathrm{a})=\mathrm{p}$,则边 $\mathrm{q} \rightarrow \mathrm{p}$ 标记为 $\mathrm{a}$。(如果 $\delta(\mathrm{q}, \mathrm{a})=\mathrm{p}$ 对应许多符号 $\mathrm{a}$,则我们通常画一条边并放置多个标签,而不是画许多平行边)
- '起始' 箭头指向起始状态 $\mathrm{q}_{0}$
- 接受状态 (F) 用双圆圈标记
55. 转移表表示 Transition table representation P2
- 行对应状态,列对应输入符号,$\mathrm{q}, \mathrm{a}$ 的条目是 $\delta(\mathrm{q}, \mathrm{a})$,起始状态用 $\rightarrow$ 标记,接受状态用 * 标记
| 符号 | |||
|---|---|---|---|
| ins | del | ||
| $\rightarrow$ | 1 | 0 | |
| 状态 | 1 | 2 | 0 |
| 2 | 3 | 1 | |
| ${ }^{*} 3$ | 3 | 2 |
示例:k 槽缓冲区自动机
66. DFA对输入的处理 Processing of input by DFA P2
- 给定输入字符串 $x=a_{1} a_{2} \ldots a_{n}$,DFA从状态 $\mathrm{q}_{0}$ 开始,读取 $\mathrm{a}_{1}$ 并转移到状态 $\delta\left(\mathrm{q}_{0}, \mathrm{a}_{1}\right)=$ 假设 $\mathrm{q}_{1}$,然后读取 $\mathrm{a}_{2}$ 并转移到状态 $\delta\left(\mathrm{q}_{1}, \mathrm{a}_{2}\right)=$ 假设 $\mathrm{q}_{2}$,依此类推,即,DFA经过一系列状态 $q_{1} q_{2} q_{3} \ldots q_{n}$ (不一定不同),使得对于每个 $i=1, \ldots, n$,$\delta\left(\mathrm{q}_{\mathrm{i}-1}, \mathrm{a}_{\mathrm{i}}\right)=\mathrm{q}_{\mathrm{i}}$。
- 输入被自动机接受当且仅当最后状态 $\mathrm{q}_{\mathrm{n}}$ 在 $\mathrm{F}$ 中,否则输入被拒绝。
- 自动机 $\mathrm{A}$ 的语言,记作 $\mathrm{L}(\mathrm{A})$,是所有被 $\mathrm{A}$ 接受的输入字符串集合。
77. 接受路径 Accepting paths P2
- 对于每个节点 $\mathrm{q}$ 和每个标签 $\mathrm{a} \in \Sigma$,从 $\mathrm{q}$ 出发有一条唯一出边标记为 $\mathrm{a}$ (因为 $\delta$ 是一个函数)
- $\mathrm{A}$ 在输入 $\mathrm{x}=\mathrm{a}_{1} \ldots \mathrm{a}_{\mathrm{n}}$ 上的计算(或运行):从起始状态开始,并且在边上具有标签序列 $\mathrm{x}=\mathrm{a}_{1} \ldots \mathrm{a}_{\mathrm{n}}$ 的唯一路径
- 路径上的节点序列 = DFA在输入 $\mathrm{x}$ 上的状态序列
- 如果计算(或路径) 终止于 $\mathrm{F}$ 中的状态,则为接受计算 ( 路径 ) $\Leftrightarrow$ 输入字符串 $\mathrm{x}$ 被 $\mathrm{A}$ 接受
- 自动机的语言 $\mathrm{L}(\mathrm{A})$ = 所有接受路径的标签集合 (即从起始状态到 $\mathrm{F}$ 中的状态的路径)
- $\mathrm{L}(\mathrm{A})=\left\{\mathrm{x} \mid\right.$ 存在一条从起始状态 $\mathrm{q}_{0}$ 到 $\mathrm{F}$ 中状态的路径 $\pi$,其标签是 $\mathrm{x}$ \}
88. 示例 Example P2
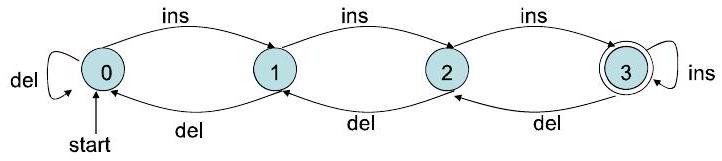
输入字符串: ins ins ins del ins
路径: $0 \longrightarrow 1 \longrightarrow 2 \longrightarrow 3 \longrightarrow 2 \longrightarrow 3$
- 该自动机的语言:
$\mathrm{L}(\mathrm{A})=$ 使缓冲区满的操作序列集合
99. 转移函数到字符串的扩展 Extension of transition function to strings P3
- 可以将 $\delta$ 扩展为从 $\mathrm{Q} \times \Sigma^{*}$ 到 $\mathrm{Q}$ 的函数 $\delta^{*}$:
- 对于每个状态 $\mathrm{q}$ 和字符串 $\mathrm{x}$,$\delta^{*}(\mathrm{q}, \mathrm{x})$ 是从状态 $\mathrm{q}$ 开始并具有标签 $\mathrm{x}$ 的唯一路径的终态
归纳定义:
```
Basis: $x$ has length 0, i.e. $x=\varepsilon: \delta^{*}(q, \varepsilon)=q$
Induction: $x$ has length $>0$, i.e. $x=y a$, for some $y \in \Sigma^{*}, a \in \Sigma$ :
$\delta^{*}(\mathrm{q}, \mathrm{ya})=\delta\left(\delta^{*}(\mathrm{q}, \mathrm{y}), \mathrm{a}\right)$
$\mathrm{L}(\mathrm{A})=\left\{\mathrm{x} \in \Sigma^{*} \mid \delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right) \in \mathrm{F}\right\}$
$=$ set of strings $x$ that label paths from the start state $\mathrm{q}_{0}$
to an accepting state
```
1010. 正则语言 Regular Languages P3
- 如果存在一个有限自动机 $\mathrm{A}$ 接受(或识别) $\mathrm{L}$,即 $\mathrm{L}(\mathrm{A})=\mathrm{L}$,则语言 $\mathrm{L}$ 是正则的。
1111. 示例 Example P3
- DFA:转移图表示
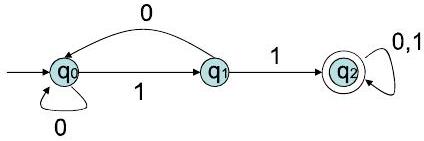
- 转移表表示
- 转移表表示
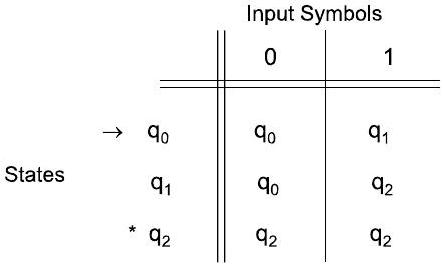
1212. 示例 Example P3
- DFA:转移图表示
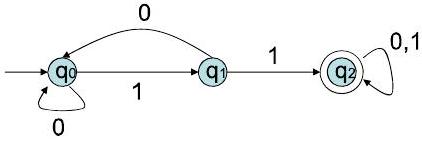
1313. 示例 Example P4
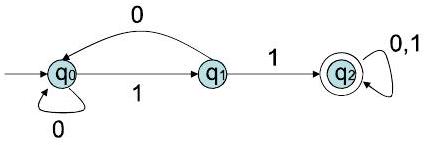

$\mathrm{L}(\mathrm{A})$ 中的样本字符串:11, 011, 01101, 11101, ...
不在 $\mathrm{L}(\mathrm{A})$ 中的样本字符串: $\varepsilon, 0,1,101,01010,00101, \ldots$
1414. 示例 Example P4
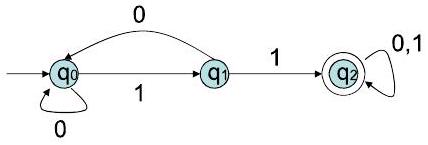
语言 = 包含两个连续 1 的字符串集合
1515. 示例 Example P4
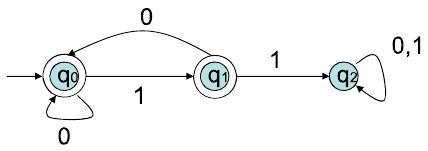
该自动机的语言是什么?
1616. 示例 Example P4
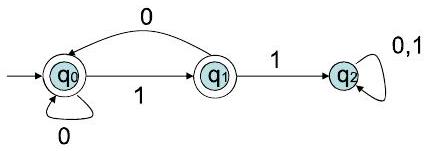
该自动机的语言是什么?
语言 = 不包含两个连续 1 的字符串集合
1717. 补集 Complement P5
定理:如果 $\mathrm{L}$ 是字母表 $\Sigma$ 上的正则语言,那么它的补集 $\bar{L}=\Sigma^{*}-L$ 也是正则的。
即,正则语言在补集运算下是封闭的
证明:如果确定性有限自动机 $\mathrm{A}$ 识别 $\mathrm{L}$,那么通过切换 $\mathrm{A}$ 中的接受状态和非接受状态(即令 $F^{\prime}=Q-F$ ) 获得的自动机 $\mathrm{A}^{\prime}$ 识别补语言 $\bar{L}=\Sigma^{*}-L$
有限自动机

- 在读取每个输入符号后,FA可以相应地改变其状态
- 在每个时刻,FA的状态决定了目前为止读取的输入是否在语言 $\mathrm{L}$ 中
1818. 有限自动机的设计 Design of Finite Automata P5
- 确定输入符号/动作
- 确定状态:在看到部分输入后,我们需要记住关于过去的什么,以便在未来做出正确决策?
- 赋予状态意义:哪些输入字符串到达这个状态?
1919. 示例 Example P6
- 对于所有恰好包含两个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- 状态 Q:观察
- 到目前为止看到的 0 的数量是无关紧要的
- 对于 1 的数量:需要记住我们是看到了 0, 1, 2,还是 >2。
2020. 示例 Example P6
- 对于所有恰好包含两个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- 状态 Q:观察
- 到目前为止看到的 0 的数量是无关紧要的
- 对于 1 的数量:需要记住我们是看到了 0, 1, 2,还是 >2。
所以,$\mathrm{Q}=\left\{\mathrm{q}_{0}, \mathrm{q}_{1}, \mathrm{q}_{2}, \mathrm{q}_{3}\right\}$
- 起始状态 $=\mathrm{q}_{0}$,
- $\mathrm{F}=\left\{\mathrm{q}_{2}\right\}$
- 转移函数(在转移图表示中):

2121. 示例 Example P6
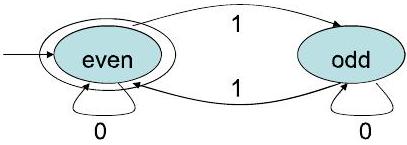
- 对于所有包含偶数个 1 的二进制字符串的语言 $\mathrm{L}$ 的FA。
- $\Sigma=\{0,1\}$
- $\mathrm{Q}=\{$ even,odd $\}$ :状态跟踪到目前为止看到的 1 的数量的奇偶性,即是偶数还是奇数
- $\mathrm{q}_{0}=$ even,
- $\mathrm{F}=\{$ even $\}$
- 转移函数(在转移图表示中):
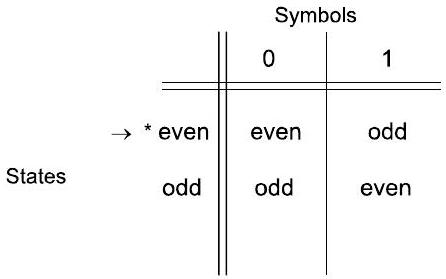
2222. 转移表表示 Transition table representation P6
- 行对应状态,列对应输入符号,$\mathrm{q}, \mathrm{a}$ 的条目是 $\delta(\mathrm{q}, \mathrm{a})$,起始状态用 $\rightarrow$ 标记,接受状态用 * 标记
2323. 正式证明DFA的正确性 Proving formally correctness of a DFA P7
- 证明 $\mathrm{L}(\mathrm{A})=$ 语言 $\mathrm{L}$ 的两个方向
- $\mathrm{L}(\mathrm{A}) \subseteq \mathrm{L}$ :对于每个输入字符串 $\mathrm{x}$,如果 $\mathrm{x}$ 被 $\mathrm{A}$ 接受,则 $\mathrm{x}$ 在 $\mathrm{L}$ 中
- $\mathrm{L} \subseteq \mathrm{L}(\mathrm{A})$ :对于每个输入字符串 $\mathrm{x}$,$\mathrm{x} \in \mathrm{L} \Rightarrow \mathrm{x} \in \mathrm{L}(\mathrm{A})$
通常可以同时做两个方向(当且仅当)
2424. 证明方法:对 $\mathrm{x}$ 的长度进行归纳, Proof Method: Induction on length of x , P7
- 但要加强断言( 归纳假设 ),根据它们将 DFA 引导到的状态来分类字符串
2525. 示例:偶数个 1 Example: even # of 1's P7
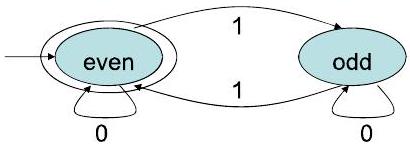
归纳假设断言:
- $\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=$ even 如果 $\mathrm{x}$ 包含偶数个 1
- $\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=$ odd 如果 $\mathrm{x}$ 包含奇数个 1
2626. 形式化证明 Formal Proof P7
- 基础:$|x|=0$,即 $x=\varepsilon$
$\delta^{*}\left(\mathrm{q}_{0}, \varepsilon\right)=\mathrm{q}_{0}=$ even,并且 $\varepsilon$ 包含偶数个 (0) 1,因此正确。
- 归纳步骤:$|x|>0$,所以 $x=y a$,其中 $y \in \Sigma^{*}, a \in \Sigma$
根据归纳假设,断言对 $\mathrm{y}$ 成立。
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)=$ $\mathrm{y}$ 中 1 的数量的奇偶性
案例分析。
- $a=0$:$\mathrm{x}$ 中 1 的奇偶性 = $\mathrm{y}$ 中 1 的奇偶性
从转移图来看,状态保持不变,即
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right)=\delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)$,因此正确。
- $a=1$:$\mathrm{x}$ 中 1 的奇偶性 $\neq$ $\mathrm{y}$ 中 1 的奇偶性
从转移图来看,状态改变,即
$\delta^{*}\left(\mathrm{q}_{0}, \mathrm{x}\right) \neq \delta^{*}\left(\mathrm{q}_{0}, \mathrm{y}\right)$,因此正确。
2727. 示例:1 的数量是 3 的倍数 Example: # of 1's multiple of 3 P7
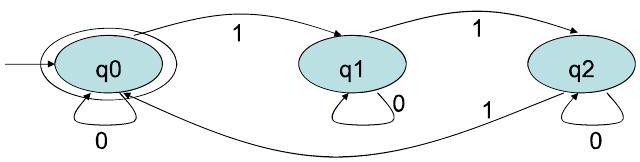
示例:1 的数量是 k 的倍数
2828. 对于 1 的数量是 $\mathrm{k}$ (对于任何 $\mathrm{k}>1$ ) 的倍数的自动机 Automaton for #1s multiple of $k$ (for any $k>1$ ) P8
- $\mathrm{Q}=\left\{\mathrm{q}_{0}, \mathrm{q}_{1}, \ldots \mathrm{q}_{\mathrm{k}-1}\right\}$
- $\Sigma=\{0,1\}$
- $\delta\left(\mathrm{q}_{\mathrm{i}}, 0\right)=\mathrm{q}_{\mathrm{i}}, \delta\left(\mathrm{q}_{\mathrm{i}}, 1\right)=\mathrm{q}_{\mathrm{i}+1 \bmod \mathrm{k}}$ 对于所有 $\mathrm{i} \in\{0,1, \ldots, \mathrm{k}-1\}$
- 起始状态 $=\mathrm{q}_{0}$
- $\mathrm{F}=\left\{\mathrm{q}_{0}\right\}$
2929. 练习题 Practice Problems P8
- 构造 DFA,接受所有长度可被 5 整除的字符串
- 构造 DFA,接受所有字母表 $\{0,1, . ., 9\}$ 上的字符串,这些字符串表示 (以十进制表示法) 可被 5 整除的数字,例如 0, 5, 025, 155, 00750, ...
- 构造 DFA,接受所有字母表 $\{0,1, . ., 9\}$ 上的字符串,这些字符串表示可被 3 整除的数字
- 构造 DFA,接受所有二进制字符串,这些字符串在二进制中表示可被 3 整除的数字
(例如 $\varepsilon \leftrightarrow 0,0 \leftrightarrow 0,11 \leftrightarrow 3,011 \leftrightarrow 3,110 \leftrightarrow 6, \ldots$ )
示例:偶数个 1
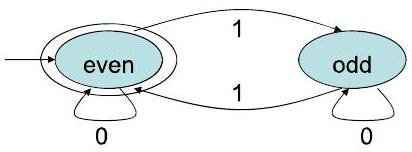
示例:偶数个 0
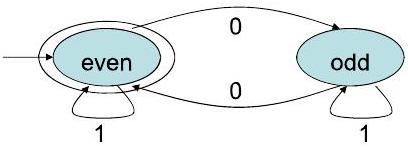
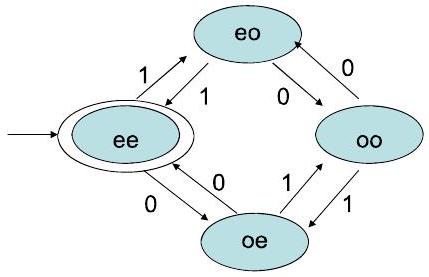
3030. 示例:偶数个 1 和 0 Example: Both even # 1's and 0's P8
- DFA,接受所有包含偶数个 0 和偶数个 1 的二进制字符串。
- $\Sigma=\{0,1\}, \mathrm{Q}=\{\mathrm{ee}, \mathrm{eo}, \mathrm{oe}, \mathrm{oo}\}, \mathrm{q}_{0}=\mathrm{ee}, \mathrm{F}=\{\mathrm{ee}\}$
- 状态跟踪到目前为止看到的 0 的奇偶性和 1 的奇偶性
3131. 正则语言的并集、交集 Union, Intersection of Regular Languages P8
定理:如果 $\mathrm{L}_{1}, \mathrm{~L}_{2}$ 是正则语言,那么
- 它们的交集 $\mathrm{L}_{1} \cap \mathrm{L}_{2}$ 也是正则的
- 它们的并集 $\mathrm{L}_{1} \cup \mathrm{L}_{2}$ 也是正则的
3Ch3. 正则语言的并集、交集 Union, Intersection of Regular Languages P9
1Ch3.1. 乘积构造 Product Construction P9
给定两个自动机
$\mathrm{A}_{1}=\left(\mathrm{Q}_{1}, \Sigma, \delta_{1}, \mathrm{q}_{1}, \mathrm{~F}_{1}\right), \quad \mathrm{A}_{2}=\left(\mathrm{Q}_{2}, \Sigma, \delta_{2}, \mathrm{q}_{2}, \mathrm{~F}_{2}\right)$
乘积自动机 $\mathrm{M}=\mathrm{A}_{1} \times \mathrm{A}_{2}=\left(\mathrm{Q}_{1} \times \mathrm{Q}_{2}, \Sigma, \delta,\left(\mathrm{q}_{1}, \mathrm{q}_{2}\right), \mathrm{F}\right)$
其中 $\delta\left(\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right), \mathrm{a}\right)=\left(\delta_{1}\left(\mathrm{p}_{1}, \mathrm{a}\right), \delta_{2}\left(\mathrm{p}_{2}, \mathrm{a}\right)\right), \forall \mathrm{p}_{1} \in \mathrm{Q}_{1} \forall \mathrm{p}_{2} \in \mathrm{Q}_{2} \forall \mathrm{a} \in \Sigma$
对于并集:$\mathrm{F}=\left\{\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right) \mid \mathrm{p}_{1} \in \mathrm{F}_{1}\right.$ 或 $\left.\mathrm{p}_{2} \in \mathrm{F}_{2}\right\}$
对于交集:$\mathrm{F}=\left\{\left(\mathrm{p}_{1}, \mathrm{p}_{2}\right) \mid \mathrm{p}_{1} \in \mathrm{F}_{1}\right.$ 且 $\left.\mathrm{p}_{2} \in \mathrm{F}_{2}\right\}$
2Ch3.2. 所有有限集合都是正则的 All finite sets are regular P9
- 示例:$\mathrm{L}=\{00,01,011,101\}$
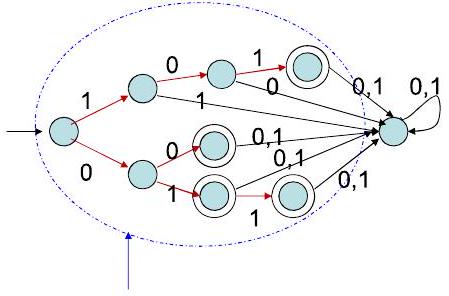
自动机 = 字符串集合 $\mathrm{L}$ 的Trie数据结构 + "死" 吸收状态,拒绝