0
引言
我们首先概述本课程中将要介绍的计算理论领域。之后,您将有机会学习和/或复习一些您稍后会需要的数学概念。
0.1
自动机、可计算性与复杂性
本书重点关注计算理论的三个传统核心领域:自动机、可计算性和复杂性。它们通过以下问题联系在一起:
计算机的基本能力和局限性是什么?
这个问题可以追溯到20世纪30年代,当时数理逻辑学家首次开始探索计算的含义。此后的技术进步大大增强了我们的计算能力,并将这个问题从理论领域带入了实际关注的世界。
在这三个领域——自动机、可计算性和复杂性——中,这个问题被赋予了不同的解释,答案也因解释而异。在本章引言之后,我们将在本书的
2 第0章 / 引言
不同部分中分别探讨每个领域。在这里,我们以倒序介绍这些部分,因为从结尾开始,您可以更好地理解开头的理由。
复杂性理论
计算机问题种类繁多;有些容易,有些困难。例如,排序问题就是一个容易的问题。假设您需要将一列数字按升序排列。即使是一台小型计算机也能相当快地排序一百万个数字。将其与调度问题进行比较。假设您必须为整所大学找到一个课程表,以满足一些合理的约束,例如没有两节课在同一时间占用同一教室。调度问题似乎比排序问题难得多。如果您只有一千门课,找到最佳调度可能需要几个世纪,即使使用超级计算机。
是什么使某些问题在计算上困难,而另一些则容易?
这是复杂性理论的核心问题。值得注意的是,我们不知道答案,尽管它已被深入研究了40多年。稍后,我们将探讨这个引人入胜的问题及其一些分支。
迄今为止,复杂性理论的一项重要成就,是研究人员发现了一种优雅的方案,可以根据计算难度对问题进行分类。它类似于根据化学性质对元素进行分类的元素周期表。使用这个方案,我们可以展示一种方法,为某些问题在计算上是困难的提供证据,即使我们无法证明它们是。
当您遇到一个看似计算困难的问题时,有几种选择。首先,通过理解问题的哪个方面是困难的根源,您也许能够改变它,从而使问题更容易解决。其次,您可能能够满足于次优解。在某些情况下,找到仅近似完美解的解决方案相对容易。第三,有些问题只在最坏情况下困难,但大多数时候都容易。根据应用,您可能对偶尔慢但通常运行快速的程序感到满意。最后,您可以考虑替代类型的计算,例如随机计算,这可以加快某些任务。
一个直接受复杂性理论影响的应用领域是古老的密码学领域。在大多数领域中,一个容易的计算问题比困难的更有利,因为容易的解决成本更低。密码学之所以不寻常,是因为它特别需要困难而非容易的计算问题。没有密钥或密码,秘密代码应该难以破解。复杂性理论为密码学家指明了计算困难问题的方向,他们围绕这些问题设计了革命性的新代码。
可计算性理论
在20世纪上半叶,库尔特·哥德尔、艾伦·图灵和阿隆佐·丘奇等数学家发现,某些基本问题无法由计算机解决。这种现象的一个例子是确定数学语句是真还是假的问题。这项任务是数学家的家常便饭。它似乎很适合计算机解决,因为它严格属于数学领域。但没有任何计算机算法可以执行这项任务。
这一深刻结果的后果之一是发展了关于计算机理论模型的思想,这些思想最终有助于实际计算机的建造。
可计算性和复杂性理论密切相关。在复杂性理论中,目标是将问题分类为容易的和困难的;而在可计算性理论中,问题的分类是可解决的和不可解决的。可计算性理论引入了复杂性理论中使用的几个概念。
自动机理论
自动机理论处理计算数学模型的定义和性质。这些模型在计算机科学的几个应用领域中发挥作用。一种模型,称为有限自动机,用于文本处理、编译器和硬件设计。另一种模型,称为上下文无关文法,用于编程语言和人工智能。
自动机理论是开始研究计算理论的绝佳起点。可计算性和复杂性理论需要对计算机进行精确定义。自动机理论允许在引入与计算机科学其他非理论领域相关的概念时,练习形式化的计算定义。
0.2
数学概念与术语
如同任何数学学科一样,我们首先讨论我们期望使用的基本数学对象、工具和符号。
集合
集合是一组作为整体表示的对象。集合可以包含任何类型的对象,包括数字、符号,甚至其他集合。集合中的对象称为其元素或成员。集合可以通过几种方式进行正式描述。
一种方法是将集合的元素列在大括号内。因此,集合
包含元素7、21和57。符号和表示集合成员关系和非成员关系。我们写和。对于两个集合和,如果的每个成员也是的成员,我们称是的子集,记作。如果是的子集且不等于,我们称是的真子集,记作。
描述集合的顺序无关紧要,其成员的重复也无关紧要。通过写,我们得到相同的集合。如果我们要考虑成员出现的次数,我们将该组称为多重集而不是集合。因此,和作为多重集是不同的,但作为集合是相同的。无限集包含无限多个元素。我们无法列出无限集的所有元素,所以我们有时使用“...”符号表示“永远继续序列”。因此,我们将自然数集写为
整数集写为
不含任何成员的集合称为空集,记作。包含一个成员的集合有时称为单元素集合,包含两个成员的集合称为无序对。
当我们要根据某种规则描述包含元素的集合时,我们写。因此,表示完全平方数集。
如果S我们有两个集合和,则和的并集,记作,是将和中的所有元素组合成一个集合而得到的集合。和的交集,记作,是同时属于和的元素集合。的补集,记作,是在考虑范围内的所有不属于的元素集合。
正如数学中常见的情况,图片有助于澄清概念。对于集合,我们使用一种称为维恩图的图片。它将集合表示为被圆形线包围的区域。设集合START-t是所有以字母“t”开头的英文单词的集合。例如,在图中,圆圈表示集合START-t。该集合的几个成员表示为圆圈内的点。
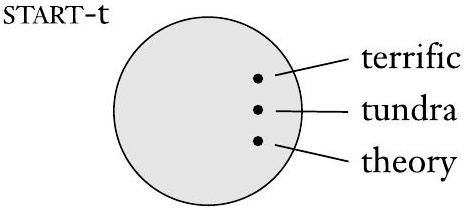 图 0.1
以“t”开头的英文单词集合的维恩图
图 0.1
以“t”开头的英文单词集合的维恩图
类似地,我们在下图中表示以“z”结尾的英文单词集END-z。
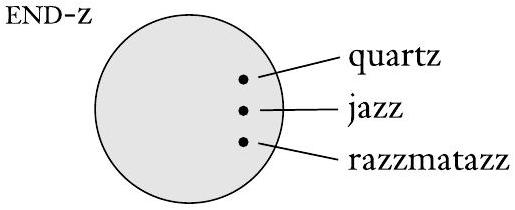 图 0.2
以“z”结尾的英文单词集合的维恩图
图 0.2
以“z”结尾的英文单词集合的维恩图
为了在同一维恩图中表示这两个集合,我们必须将它们绘制成重叠状态,表明它们共享一些元素,如下图所示。例如,单词topaz在这两个集合中。图中还包含一个表示START-j集合的圆圈。它不与START-t的圆圈重叠,因为没有单词同时属于这两个集合。
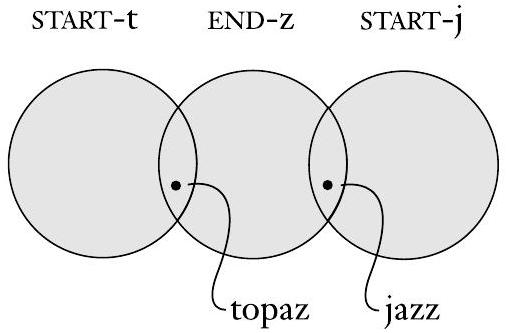 图 0.3
图 0.3
重叠的圆圈表示共同的元素
接下来的两个维恩图描绘了集合和的并集和交集。
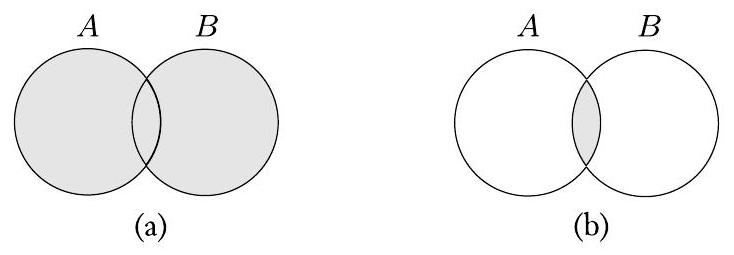 图 0.4
(a) 和(b) 的图示
图 0.4
(a) 和(b) 的图示
序列和元组
对象的序列是这些对象按一定顺序排列的列表。我们通常通过将列表写在括号内来指定一个序列。例如,序列7、21、57将写为
顺序在集合中不重要,但在序列中却很重要。因此与不同。类似地,重复在序列中很重要,但在集合中不重要。因此与另外两个序列都不同,而集合与集合相同。
与集合一样,序列可以是有限的或无限的。有限序列通常称为元组。一个包含个元素的序列是一个**-元组**。因此是一个3-元组。一个2-元组也称为有序对。
集合和序列可以作为其他集合和序列的元素出现。例如,的幂集是的所有子集的集合。如果是集合,则的幂集是集合。所有元素为0和1的有序对的集合是。
如果和是两个集合,和的笛卡尔积或叉积,记作,是所有有序对的集合,其中第一个元素是的成员,第二个元素是的成员。
示例 0.5
如果且,
A \times B=\{(1, x),(1, y),(1, z),(2, x),(2, y),(2, z)\} . $$ $\square$ 我们也可以取$k$个集合$A_{1}, A_{2}, \ldots, A_{k}$的笛卡尔积,记作$A_{1} \times A_{2} \times \cdots \times A_{k}$。它是所有$k$-元组$(a_{1}, a_{2}, \ldots, a_{k})$组成的集合,其中$a_{i} \in A_{i}$。 ## 示例 0.6 如果$A$和$B$如示例0.5所示,
\begin{aligned} A \times B \times A={ & (1, x, 1),(1, x, 2),(1, y, 1),(1, y, 2),(1, z, 1),(1, z, 2), \ & (2, x, 1),(2, x, 2),(2, y, 1),(2, y, 2),(2, z, 1),(2, z, 2)} . \end{aligned}
\overbrace{A \times A \times \cdots \times A}^{k}=A^{k} .
## 示例 0.7 集合$\mathcal{N}^{2}$等于$\mathcal{N} \times \mathcal{N}$。它由所有自然数有序对组成。我们也可以写成$\{(i, j) \mid i, j \geq 1\}$。 ## 函数与关系 **函数**是数学的核心。函数是建立输入-输出关系的对象。函数接受输入并产生输出。在每个函数中,相同的输入总是产生相同的输出。如果$f$是一个函数,当输入值为$a$时输出值为$b$,我们写
f(a)=b .
函数也称为**映射**,如果$f(a)=b$,我们说$f$将$a$映射到$b$。 例如,绝对值函数$abs$接受一个数$x$作为输入,如果$x$为正,则返回$x$;如果$x$为负,则返回$-x$。因此$abs(2)=abs(-2)=2$。加法是函数的另一个例子,写为$add$。加法函数的输入是一个有序的数对,输出是这些数的和。 函数的可能输入集合称为其**定义域**。函数的输出来自一个称为其**值域**的集合。表示$f$是一个定义域为$D$、值域为$R$的函数的符号是
f: D \longrightarrow R .
在函数$abs$的情况下,如果我们在整数范围内工作,定义域和值域都是$\mathcal{Z}$,所以我们写$abs: \mathcal{Z} \longrightarrow \mathcal{Z}$。在整数加法函数的情况下,定义域是整数对的集合$\mathcal{Z} \times \mathcal{Z}$,值域是$\mathcal{Z}$,所以我们写$add : \mathcal{Z} \times \mathcal{Z} \longrightarrow \mathcal{Z}$。请注意,函数不一定使用指定值域的所有元素。函数$abs$从不取值-1,即使$-1 \in \mathcal{Z}$。使用值域所有元素的函数被称为**满射**到值域上。 我们可以通过几种方式描述一个特定的函数。一种方式是使用计算从指定输入获得输出的过程。另一种方式是使用一个列出所有可能输入并给出每个输入输出的表格。 ## 示例 0.8 考虑函数$f:\{0,1,2,3,4\} \longrightarrow\{0,1,2,3,4\}$。 | $n$ | $f(n)$ | | :---: | :---: | | 0 | 1 | | 1 | 2 | | 2 | 3 | | 3 | 4 | | 4 | 0 | 这个函数将其输入加1,然后输出结果**模**5。一个数模$m$是除以$m$后的余数。例如,钟面上的分针计数是模60。当我们进行**模运算**时,我们定义$\mathcal{Z}_{m}=\{0,1,2, \ldots, m-1\}$。使用这个符号,上述函数$f$的形式是$f: \mathcal{Z}_{5} \longrightarrow \mathcal{Z}_{5}$。 ## 示例 0.9 如果函数的定义域是两个集合的笛卡尔积,有时会使用二维表格。这里是另一个函数$g: \mathcal{Z}_{4} \times \mathcal{Z}_{4} \longrightarrow \mathcal{Z}_{4}$。表格中标记为$i$的行和标记为$j$的列的条目是$g(i, j)$的值。 | $g$ | 0 | 1 | 2 | 3 | | :--- | :--- | :--- | :--- | :--- | | 0 | 0 | 1 | 2 | 3 | | 1 | 1 | 2 | 3 | 0 | | 2 | 2 | 3 | 0 | 1 | | 3 | 3 | 0 | 1 | 2 | 函数$g$是模4的加法函数。 当函数$f$的定义域是某些集合$A_{1}, \ldots, A_{k}$的$A_{1} \times \cdots \times A_{k}$时,$f$的输入是一个$k$-元组$(a_{1}, a_{2}, \ldots, a_{k})$,我们称$a_{i}$为$f$的**参数**。具有$k$个参数的函数称为**$k$-元函数**,$k$称为函数的**元数**。如果$k$为1,$f$有一个参数,称$f$为**一元函数**。如果$k$为2,$f$为**二元函数**。某些熟悉的二元函数以特殊的**中缀表示法**书写,其中函数符号放在其两个参数之间,而不是**前缀表示法**(符号放在前面)。例如,加法函数$add$通常以中缀表示法书写,其两个参数之间带有$+$符号,如$a+b$,而不是前缀表示法$add(a, b)$。 **谓词**或**性质**是一个值域为{TRUE, FALSE}的函数。例如,设$even$是一个性质,如果其输入是偶数则为TRUE,如果其输入是奇数则为FALSE。因此$even(4)=$ TRUE和$even(5)=$ FALSE。 定义域是$k$-元组集合$A \times \cdots \times A$的性质称为**关系**、**$k$-元关系**或**$A$上的$k$-元关系**。一个常见的情况是**2-元关系**,称为**二元关系**。在书写涉及二元关系的表达式时,我们通常使用中缀表示法。例如,“小于”是一种关系,通常用中缀运算符号$<$来书写。“相等”,用$=$符号书写,是另一种熟悉的关系。如果$R$是二元关系,语句$aRb$表示$aRb=$ TRUE。类似地,如果$R$是$k$-元关系,语句$R(a_{1}, \ldots, a_{k})$表示$R(a_{1}, \ldots, a_{k})=$ TRUE。 ## 示例 0.10 在一个名为“剪刀-石头-布”的儿童游戏中,两名玩家同时从集合{SCISSORS, PAPER, STONE}中选择一个,并用手势表示他们的选择。如果两个选择相同,游戏重新开始。如果选择不同,一名玩家获胜,根据“胜过”关系。 | 胜过 | SCISSORS | PAPER | STONE | | :---: | :---: | :---: | :---: | | SCISSORS | FALSE | TRUE | FALSE | | PAPER | FALSE | FALSE | TRUE | | STONE | TRUE | FALSE | FALSE | 从这个表格我们可以确定“SCISSORS胜过PAPER”为TRUE,“PAPER胜过SCISSORS”为FALSE。 有时用集合而不是函数描述谓词更方便。谓词$P: D \longrightarrow\{\text{TRUE, FALSE}\}$可以写成$(D, S)$,其中$S=\{a \in D \mid P(a)=\text{TRUE}\}$,或者如果定义域$D$在上下文中很明显,则简单写成$S$。因此,关系$beats$可以写成
{(\text{SCISSORS, PAPER), (PAPER, STONE), (STONE, SCISSORS)}. }
一种特殊的二元关系,称为**等价关系**,捕捉了两个对象在某些特征上相等 notion。二元关系$R$是等价关系,如果$R$满足三个条件: 1. $R$是**自反的**,如果对于每个$x$,有$xRx$; 2. $R$是**对称的**,如果对于每个$x$和$y$,有$xRy$蕴含$yRx$; 3. $R$是**传递的**,如果对于每个$x, y$和$z$,有$xRy$且$yRz$蕴含$xRz$。 ## 示例 0.11 在自然数上定义一个等价关系,记作$\equiv_{7}$。对于$i, j \in \mathcal{N}$,如果$i-j$是7的倍数,则称$i \equiv_{7} j$。这是一个等价关系,因为它满足三个条件。首先,它是自反的,因为$i-i=0$,它是7的倍数。其次,它是对称的,因为如果$i-j$是7的倍数,那么$j-i$也是7的倍数。第三,它是传递的,因为当$i-j$是7的倍数且$j-k$是7的倍数时,那么$i-k=(i-j)+(j-k)$是两个7的倍数的和,因此也是7的倍数。 ## 图 **无向图**,或简称**图**,是一组点,其中一些点之间有线连接。这些点称为**节点**或**顶点**,线称为**边**,如下图所示。 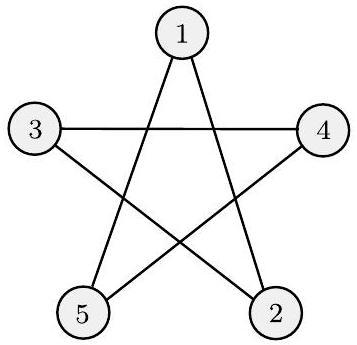 (a) 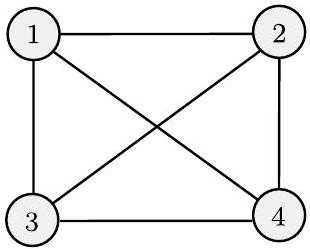 (b) ## 图 0.12 图的示例 特定节点上的边数称为该节点的**度**。在图0.12(a)中,所有节点的度都为2。在图0.12(b)中,所有节点的度都为3。任意两个节点之间最多允许一条边。根据情况,我们可能允许从一个节点到自身的边,称为**自环**。 在包含节点$i$和$j$的图$G$中,对$(i, j)$表示连接$i$和$j$的边。在无向图中,$i$和$j$的顺序无关紧要,因此对$(i, j)$和$(j, i)$表示同一条边。有时我们用集合符号$\{i, j\}$来描述无向边。如果$V$是$G$的节点集,$E$是边集,我们说$G=(V, E)$。我们可以用图表或更正式地通过指定$V$和$E$来描述一个图。例如,图0.12(a)的正式描述是
({1,2,3,4,5},{(1,2),(2,3),(3,4),(4,5),(5,1)}),
({1,2,3,4},{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}) .
图经常用于表示数据。节点可以是城市,边是连接的高速公路;或者节点可以是人,边是他们之间的友谊。有时,为了方便,我们给图的节点和/或边贴上标签,这称为**标记图**。图0.13描绘了一个图,其节点是城市,边标有这些城市之间最便宜的直飞航班票价(如果可以直飞)。 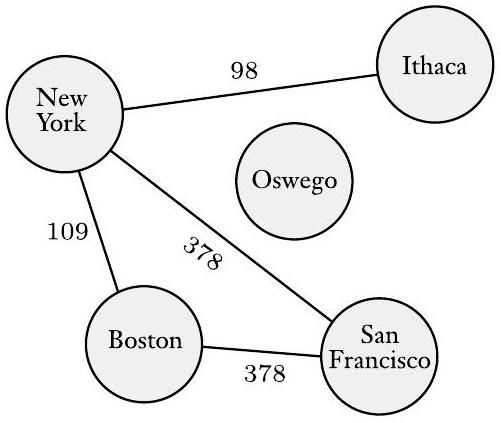 图 0.13 各城市之间最便宜的直飞航班票价 我们称图$G$是图$H$的**子图**,如果$G$的节点是$H$的节点的子集,并且$G$的边是$H$在相应节点上的边。下图显示了一个图$H$和一个子图$G$。 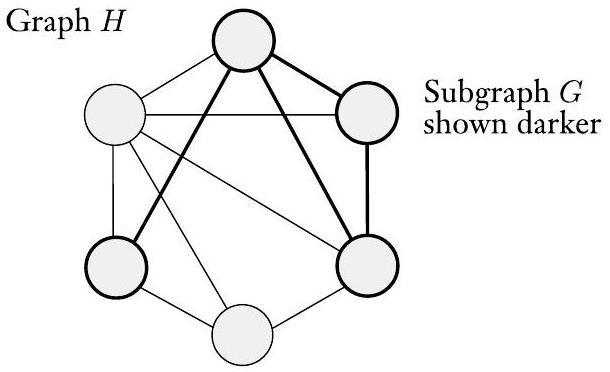 图 0.14 图G(颜色较深)是H的子图 图中的**路径**是边连接的节点序列。**简单路径**是不重复任何节点的路径。如果任意两个节点之间都有路径,则图是**连通的**。如果路径的起点和终点是同一个节点,则它是**环**。**简单环**是包含至少三个节点并且只重复第一个和最后一个节点的环。如果一个图是连通的且没有简单环,则它是一个**树**,如图0.15所示。树可以包含一个特殊指定的节点,称为**根**。树中度为1的节点(除了根)称为树的**叶子**。 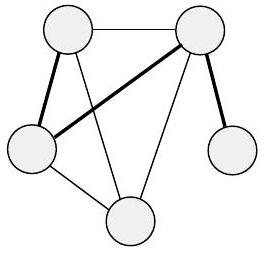 (a) 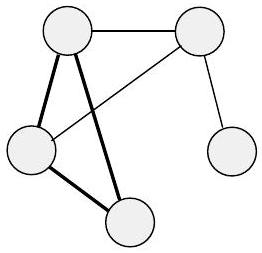 (b) 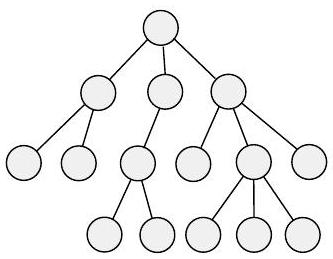 (c) 图 0.15 (a) 图中的一条路径,(b) 图中的一个环,和 (c) 一棵树 **有向图**有箭头而不是线,如下图所示。从特定节点指向的箭头数量是该节点的**出度**,指向特定节点的箭头数量是**入度**。 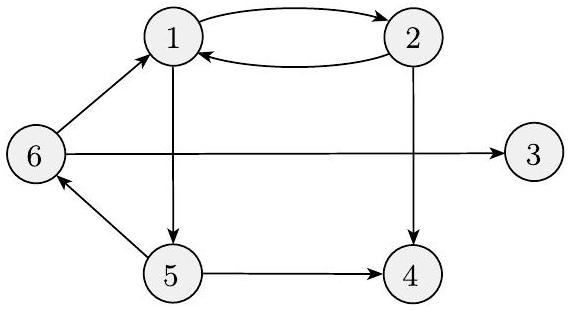 图 0.16 一个有向图 在有向图中,我们将从$i$到$j$的边表示为一对$(i, j)$。有向图$G$的正式描述是$(V, E)$,其中$V$是节点集,$E$是边集。图0.16的正式描述是
({1,2,3,4,5,6},{(1,2),(1,5),(2,1),(2,4),(5,4),(5,6),(6,1),(6,3)}) .
其中所有箭头指向与其步数相同方向的路径称为**有向路径**。如果任意两个节点之间都有有向路径连接,则有向图是**强连通的**。有向图是描绘二元关系的便捷方式。如果$R$是一个定义域为$D \times D$的二元关系,则标记图$G=(D, E)$表示$R$,其中$E=\{(x, y) \mid xRy\}$。 ## 示例 0.17 这里显示的有向图表示示例0.10中给出的关系。 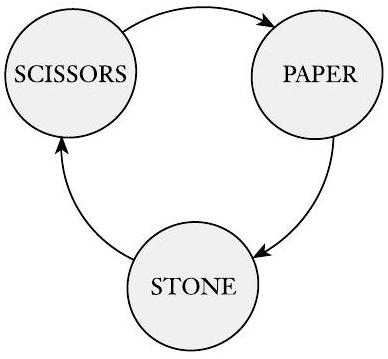 图 0.18 “胜过”关系的图 ## 字符串和语言 **字符**串是计算机科学中的基本构建块。定义字符串的**字母表**可能因应用而异。为了我们的目的,我们将字母表定义为任何非空的有限集。字母表的成员是字母表的**符号**。我们通常使用大写希腊字母$\Sigma$和$\Gamma$来表示字母表,并使用打字机字体来表示字母表中的符号。以下是几个字母表的示例。
\begin{aligned} \Sigma_{1} & ={0,1} \ \Sigma_{2} & ={\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}, \mathrm{e}, \mathrm{f}, \mathrm{g}, \mathrm{h}, \mathrm{i}, \mathrm{j}, \mathrm{k}, \mathrm{l}, \mathrm{m}, \mathrm{n}, \mathrm{o}, \mathrm{p}, \mathrm{q}, \mathrm{r}, \mathrm{s}, \mathrm{t}, \mathrm{u}, \mathrm{v}, \mathrm{w}, \mathrm{x}, \mathrm{y}, \mathrm{z}} \ \Gamma & ={0,1, \mathrm{x}, \mathrm{y}, \mathrm{z}} \end{aligned}
字母表上的**字符串**是该字母表中符号的有限序列,通常写在一起,不以逗号分隔。如果$\Sigma_{1}=\{0,1\}$,那么`01001`是$\Sigma_{1}$上的字符串。如果$\Sigma_{2}=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \ldots, \mathrm{z}\}$,那么`abracadabra`是$\Sigma_{2}$上的字符串。如果$w$是$\Sigma$上的字符串,$w$的**长度**,记作$|w|$,是它包含的符号数。长度为零的字符串称为**空字符串**,记作$\varepsilon$。空字符串在数字系统中扮演0的角色。如果$w$的长度为$n$,我们可以写$w=w_{1}w_{2}\cdots w_{n}$,其中每个$w_{i} \in \Sigma$。$w$的**逆序**,记作$w^{\mathcal{R}}$,是通过将$w$按相反顺序(即$w_{n}w_{n-1}\cdots w_{1}$)书写而得到的字符串。如果字符串$z$在$w$中连续出现,则$z$是$w$的**子串**。例如,`cad`是`abracadabra`的子串。 如果我们有一个长度为$m$的字符串$x$和一个长度为$n$的字符串$y$,$x$和$y$的**串联**,记作$xy$,是通过将$y$附加到$x$末尾而得到的字符串,如$x_{1}\cdots x_{m}y_{1}\cdots y_{n}$。要将一个字符串与自身串联多次,我们使用上标表示法$x^{k}$来表示
\overbrace{x x\cdots x}^{k} .
字符串的**字典序**与熟悉的字典顺序相同。我们偶尔会使用一种修改过的字典序,称为**短字符串优先字典序**或简称**字符串序**,它与字典序相同,但较短的字符串排在较长的字符串之前。因此,字母表$\{0,1\}$上所有字符串的字符串序是
(\varepsilon, 0,1,00,01,10,11,000, \ldots) .
如果存在字符串$z$使得$xz=y$,则称字符串$x$是字符串$y$的**前缀**,并且如果$x \neq y$,则$x$是$y$的**真前缀**。**语言**是一组字符串。如果没有任何成员是另一个成员的真前缀,则语言是**无前缀的**。 ## 布尔逻辑 **布尔逻辑**是一个围绕TRUE和FALSE这两个值建立的数学系统。尽管最初被认为是纯数学,但这个系统现在被认为是数字电子和计算机设计的基础。TRUE和FALSE值称为**布尔值**,通常用值1和0表示。我们在有两种可能性的情况下使用布尔值,例如可能具有高电压或低电压的导线、可能为真或为假的命题,或者可能回答是或否的问题。 我们可以使用**布尔运算**来操作布尔值。最简单的布尔运算是**否定**或**非运算**,用符号$\neg$表示。布尔值的否定是相反的值。因此$\neg 0=1$和$\neg 1=0$。我们用符号$\wedge$表示**合取**或**与运算**。两个布尔值的合取是1,如果这两个值都是1。**析取**或**或运算**用符号$\vee$表示。两个布尔值的析取是1,如果其中任一个值为1。我们总结这些信息如下。
\begin{array}{lll} 0 \wedge 0=0 & 0 \vee 0=0 & \neg 0=1 \ 0 \wedge 1=0 & 0 \vee 1=1 & \neg 1=0 \ 1 \wedge 0=0 & 1 \vee 0=1 & \ 1 \wedge 1=1 & 1 \vee 1=1 & \end{array}
我们使用布尔运算将简单语句组合成更复杂的布尔表达式,就像我们使用算术运算$+$和$\times$来构造复杂的算术表达式一样。例如,如果$P$是表示语句“太阳正在照耀”为真的布尔值,$Q$表示语句“今天是星期一”为真的布尔值,我们可以写$P \wedge Q$来表示语句“太阳正在照耀并且今天是星期一”的真值,类似地,对于$P \vee Q$则将`and`替换为`or`。值$P$和$Q$被称为运算的**操作数**。 其他一些布尔运算偶尔也会出现。**异或**(或XOR)运算用$\oplus$符号表示,如果其两个操作数中只有一个为1(而不是两个都为1),则结果为1。**等价运算**,用符号$\leftrightarrow$表示,如果其两个操作数具有相同的值,则结果为1。最后,**蕴含运算**用符号$\rightarrow$表示,如果其第一个操作数为1且第二个操作数为0,则结果为0;否则,$\rightarrow$为1。我们总结这些信息如下。
\begin{array}{lll} 0 \oplus 0=0 & 0 \leftrightarrow 0=1 & 0 \rightarrow 0=1 \ 0 \oplus 1=1 & 0 \leftrightarrow 1=0 & 0 \rightarrow 1=1 \ 1 \oplus 0=1 & 1 \leftrightarrow 0=0 & 1 \rightarrow 0=0 \ 1 \oplus 1=0 & 1 \leftrightarrow 1=1 & 1 \rightarrow 1=1 \end{array}
\begin{array}{ll} P \vee Q & \neg(\neg P \wedge \neg Q) \ P \rightarrow Q & \neg P \vee Q \ P \leftrightarrow Q & (P \rightarrow Q) \wedge(Q \rightarrow P) \ P \oplus Q & \neg(P \leftrightarrow Q) \end{array}
**与**和**或**的**分配律**在操作布尔表达式时非常有用。它类似于加法和乘法的分配律,即$a \times (b+c)=(a \times b)+(a \times c)$。布尔版本有两种形式: - $P \wedge (Q \vee R)$ 等于 $(P \wedge Q) \vee (P \wedge R)$,及其**对偶** - $P \vee (Q \wedge R)$ 等于 $(P \vee Q) \wedge (P \vee R)$。 ## 数学术语摘要 | 字母表 | 一个由称为符号的对象组成的有限非空集合 | | :--- | :--- | | 参数 | 函数的输入 | | 二元关系 | 定义域为对组集合的关系 | | 布尔运算 | 布尔值上的运算 | | 布尔值 | TRUE或FALSE的值,通常用1或0表示 | | 笛卡尔积 | 对集合的一种操作,形成由各集合元素的所有元组组成的集合 | | 补集 | 对集合的一种操作,形成所有不属于该集合的元素的集合 | | 串联 | 连接字符串的操作 | | 合取 | 布尔AND运算 | | 连通图 | 任意两节点之间都有路径连接的图 | | 环 | 起点和终点相同的路径 | | 有向图 | 点和连接某些点对的箭头的集合 | | 析取 | 布尔OR运算 | | 定义域 | 函数所有可能输入的集合 | | 边 | 图中的线 | | 元素 | 集合中的对象 | | 空集 | 不含任何成员的集合 | | 空字符串 | 长度为零的字符串 | | 等价关系 | 具有自反性、对称性和传递性的二元关系 | | 函数 | 将输入转换为输出的操作 | | 图 | 点和连接某些点对的线的集合 | | 交集 | 对集合的一种操作,形成共同元素的集合 | | $k$-元组 | 包含$k$个对象的列表 | | 语言 | 字符串的集合 | | 成员 | 集合中的对象 | | 节点 | 图中的点 | | 有序对 | 包含两个元素的列表 | | 路径 | 图中由边连接的节点序列 | | 谓词 | 值域为{TRUE, FALSE}的函数 | | 性质 | 谓词 | | 值域 | 函数输出的来源集合 | | 关系 | 谓词,最典型的是当定义域为$k$-元组集合时 | | 序列 | 对象的列表 | | 集合 | 对象的组 | | 简单路径 | 不重复任何节点的路径 | | 单元素集合 | 包含一个成员的集合 | | 字符串 | 字母表中符号的有限列表 | | 符号 | 字母表的成员 | | 树 | 没有简单环的连通图 | | 并集 | 对集合的一种操作,将所有元素组合成一个集合 | | 无序对 | 包含两个成员的集合 | | 顶点 | 图中的点 |