1正则语言
计算理论始于一个问题:什么是计算机?这或许是个愚蠢的问题,因为每个人都知道我正在敲字的这个东西就是计算机。但这些真实的计算机相当复杂——复杂到无法让我们直接建立一套可管理的数学理论。相反,我们使用一种理想化的计算机,称为计算模型。与任何科学模型一样,计算模型在某些方面可能准确,但在其他方面可能不准确。因此,我们将根据我们想要关注的特性,使用几种不同的计算模型。我们从最简单的模型开始,称为有限状态机或有限自动机。
1.1
有限自动机
有限自动机是计算机的良好模型,其内存量极其有限。具有如此小内存的计算机能做什么呢?许多有用的事情!事实上,我们一直都在与此类计算机交互,因为它们是各种机电设备的核心。
自动门的控制器就是此类设备的一个例子。自动门通常出现在超市入口和出口处,当控制器感应到有人靠近时,自动门就会自动打开。自动门前方有一个踏板,用于检测即将走过门口的人的存在。门后方还有一个踏板,以便控制器能让门开足够长的时间,让行人完全通过,同时也能防止门在开启时撞到站在后面的人。这种配置如下图所示。
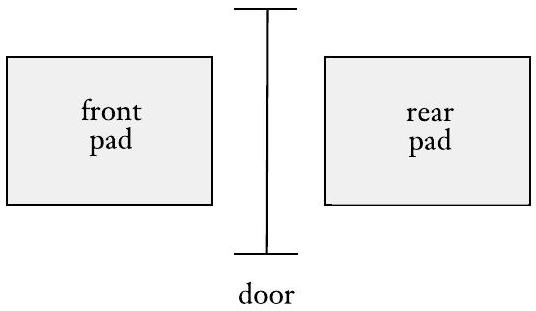
图 1.1
自动门顶视图
控制器处于两种状态之一:“OPEN”或“CLOSED”,分别表示门的相应状况。如下图所示,有四种可能的输入条件:“FRONT”(表示有人站在门前踏板上),“REAR”(表示有人站在门后踏板上),“BOTH”(表示有人站在两个踏板上),以及“neither”(表示两个踏板上都没人)。
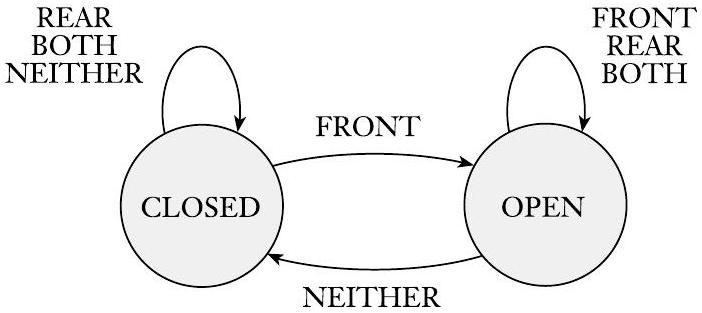
图 1.2
自动门控制器的状态图
输入信号
| | | NEITHER | FRONT | REAR | BOTH |
| :--- | :--- | :--- | :--- | :--- | :--- |
| 状态 | CLOSED | CLOSED | OPEN | CLOSED | CLOSED |
| | OPEN | CLOSED | OPEN | OPEN | OPEN |
图 1.3
自动门控制器的状态转移表
控制器根据其接收到的输入从一个状态转移到另一个状态。当处于 CLOSED 状态并接收到 NEITHER 或 REAR 输入时,它保持在 CLOSED 状态。此外,如果接收到 BOTH 输入,它仍然保持 CLOSED 状态,因为开门有撞倒后方踏板上的人的风险。但如果 FRONT 输入到达,它会转移到 OPEN 状态。在 OPEN 状态下,如果接收到 FRONT、REAR 或 BOTH 输入,它会保持在 OPEN 状态。如果 NEITHER 输入到达,它会返回到 CLOSED 状态。
例如,一个控制器可能从 CLOSED 状态开始,接收到一系列输入信号:front、rear、neither、front、both、neither、rear 和 NEITHER。然后它将经历一系列状态:CLOSED(起始)、OPEN、OPEN、CLOSED、OPEN、OPEN、CLOSED、CLOSED 和 CLOSED。
将自动门控制器视为有限自动机是有用的,因为它提示了如图 1.2 和 1.3 所示的标准表示方法。这个控制器是一个只有一位内存的计算机,能够记录控制器处于哪两种状态。其他常见设备拥有内存稍大的控制器。在电梯控制器中,一个状态可能代表电梯所在的楼层,输入可能是从按钮接收到的信号。这个计算机可能需要几位来跟踪这些信息。各种家用电器(如洗碗机和电子恒温器)以及数字手表和计算器的某些部件的控制器,是具有有限内存的计算机的其他例子。这些设备的设计需要牢记有限自动机的方法论和术语。
有限自动机及其概率对应物马尔可夫链是我们在尝试识别数据模式时的有用工具。这些设备用于语音处理和光学字符识别。马尔可夫链甚至被用于建模和预测金融市场中的价格变化。
我们现在将从数学角度更仔细地审视有限自动机。我们将发展有限自动机的精确定义、描述和操作有限自动机的术语,以及描述其能力和局限性的理论结果。除了让您更清楚地理解有限自动机是什么以及它们能做什么和不能做什么之外,这种理论发展还将使您能够在一个相对简单的环境中练习并更适应数学定义、定理和证明。
在开始描述有限自动机的数学理论时,我们抽象地进行,不涉及任何特定的应用。下图描绘了一个称为 $M_{1}$ 的有限自动机。
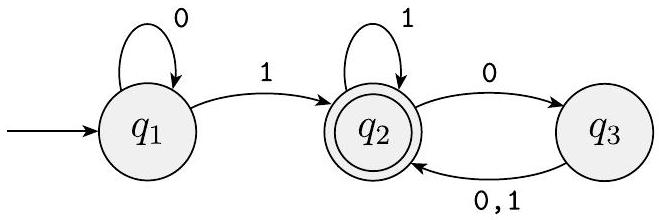
图 1.4
一个名为 $M_{1}$ 的有限自动机,它有三个状态
图 1.4 称为 $M_{1}$ 的状态图。它有三个状态,标记为 $q_{1}, q_{2}$ 和 $q_{3}$。起始状态 $q_{1}$ 由指向它的无源箭头表示。接受状态 $q_{2}$ 是双圆圈的那个。从一个状态到另一个状态的箭头称为转移。
当这个自动机接收到诸如 1101 的输入串时,它会处理该串并产生输出。输出要么是接受,要么是拒绝。为简单起见,我们现在只考虑这种是/否类型的输出。处理从 $M_{1}$ 的起始状态开始。自动机逐个从左到右读取输入串中的符号。读取每个符号后,$M_{1}$ 沿以该符号为标签的转移从一个状态转移到另一个状态。当它读取最后一个符号时,$M_{1}$ 产生其输出。如果 $M_{1}$ 现在处于接受状态,则输出为接受;如果不是,则为拒绝。
例如,当我们将输入串 1101 输入到图 1.4 中的机器 $M_{1}$ 时,处理过程如下:
- 从状态 $q_{1}$ 开始。
- 读取 1,沿转移从 $q_{1}$ 到 $q_{2}$。
- 读取 1,沿转移从 $q_{2}$ 到 $q_{2}$。
- 读取 0,沿转移从 $q_{2}$ 到 $q_{3}$。
- 读取 1,沿转移从 $q_{3}$ 到 $q_{2}$。
- 接受,因为 $M_{1}$ 在输入结束时处于接受状态 $q_{2}$。
对这台机器进行各种输入串的实验表明,它接受串 $1,01,11$ 和 $0101010101$。事实上,$M_{1}$ 接受任何以 1 结尾的串,因为它在读取符号 1 时都会进入其接受状态 $q_{2}$。此外,它接受串 $100,0100,110000$ 和 $0101000000$,以及任何以偶数个 0 跟随最后一个 1 结尾的串。它拒绝其他串,例如 $0,10,101000$。您能描述由 $M_{1}$ 接受的所有串组成的语言吗?我们很快就会这样做。
有限自动机的形式化定义
在上一节中,我们使用状态图介绍了有限自动机。现在我们形式化地定义有限自动机。虽然状态图在直观上更容易理解,但我们也需要形式化定义,原因有两个。
首先,形式化定义是精确的。它解决了关于有限自动机中允许什么操作的任何不确定性。如果您不确定有限自动机是否允许有 0 个接受状态,或者它们是否必须为每个可能的输入符号从每个状态恰好引出一条转移,您可以查阅形式化定义并验证答案在这两种情况下都是肯定的。其次,形式化定义提供了符号。良好的符号有助于您清晰地思考和表达您的想法。
形式化定义的语言有些深奥,与法律文件的语言有些相似。两者都需要精确,并且每个细节都必须详细说明。
一个有限自动机有几个部分。它有一组状态,以及根据输入符号从一个状态转移到另一个状态的规则。它有一个输入字母表,指示允许的输入符号。它有一个起始状态和一组接受状态。形式化定义指出,一个有限自动机是由这五个对象组成的列表:状态集、输入字母表、转移规则、起始状态和接受状态。在数学语言中,包含五个元素的列表通常称为五元组。因此,我们将有限自动机定义为由这五个部分组成的五元组。
我们使用一种称为转移函数(通常表示为 $\delta$)来定义转移规则。如果有限自动机有一个从状态 $x$ 到状态 $y$ 的箭头,并用输入符号 1 标记,这意味着如果自动机在状态 $x$ 时读取 1,它就会转移到状态 $y$。我们可以用转移函数表示同样的事情,即 $\delta(x, 1)=y$。这种表示法是一种数学速记。综合起来,我们就得到了有限自动机的形式化定义。
定义 1.5
有限自动机是一个五元组 $\left(Q, \Sigma, \delta, q_{0}, F\right)$,其中
- $Q$ 是一个有限集合,称为状态,
- $\Sigma$ 是一个有限集合,称为字母表,
- $\delta: Q \times \Sigma \longrightarrow Q$ 是转移函数, ${ }^{1}$
- $q_{0} \in Q$ 是起始状态,
- $F \subseteq Q$ 是接受状态集。 ${ }^{2}$
[^0]形式化定义精确地描述了我们所说的有限自动机的含义。例如,回到之前关于是否允许 0 个接受状态的问题,您可以看到将 $F$ 设置为空集 $\emptyset$ 会产生 0 个接受状态,这是允许的。此外,转移函数 $\delta$ 为状态和输入符号的每种可能组合精确地指定了一个下一个状态。这肯定地回答了我们的另一个问题,表明对于每个可能的输入符号,恰好有一个转移箭头从每个状态引出。
我们可以使用形式化定义的符号来描述单个有限自动机,通过指定定义 1.5中列出的五个部分。例如,让我们回到我们之前讨论的有限自动机 $M_{1}$,为方便起见在此重新绘制。
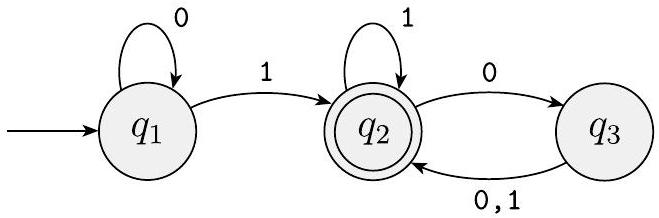
图 1.6
有限自动机 $M_{1}$
我们可以通过写 $M_{1}=\left(Q, \Sigma, \delta, q_{1}, F\right)$ 来形式化地描述 $M_{1}$,其中
- $Q=\left\{q_{1}, q_{2}, q_{3}\right\}$,
- $\Sigma=\{0,1\}$,
- $\delta$ 描述如下:
| | 0 | 1 |
| :---: | :---: | :---: |
| $q_{1}$ | $q_{1}$ | $q_{2}$ |
| $q_{2}$ | $q_{3}$ | $q_{2}$ |
| $q_{3}$ | $q_{2}$ | $q_{2}$, |
- $q_{1}$ 是起始状态,
- $F=\left\{q_{2}\right\}$。
如果 $A$ 是机器 $M$ 接受的所有串的集合,我们说 $A$ 是机器 $M$ 的语言,并写为 $L(M)=A$。我们说 $M$ 识别 $A$ 或 $M$ 接受 $A$。因为“接受”一词在指机器接受串和机器接受语言时有不同的含义,为了避免混淆,我们更倾向于对语言使用“识别”一词。
一台机器可以接受几个串,但它总是只识别一种语言。如果机器不接受任何串,它仍然识别一种语言——即空语言 $\emptyset$。
在我们的例子中,设
那么 $L\left(M_{1}\right)=A$,或者等价地说,$M_{1}$ 识别 $A$。
有限自动机的例子
例子 1.7
这是有限自动机 $M_{2}$ 的状态图。
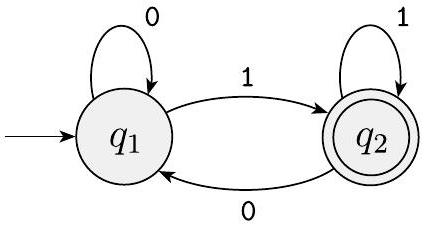
图 1.8
两状态有限自动机 $M_{2}$ 的状态图
在形式化描述中,$M_{2}$ 是 $\left(\left\{q_{1}, q_{2}\right\},\{0,1\}, \delta, q_{1},\left\{q_{2}\right\}\right)$。转移函数 $\delta$ 是
| | 0 | 1 |
| :---: | :---: | :---: |
| $q_{1}$ | $q_{1}$ | $q_{2}$ |
| $q_{2}$ | $q_{1}$ | $q_{2}$。 |
请记住,$M_{2}$ 的状态图和 $M_{2}$ 的形式化描述包含相同的信息,只是形式不同。您总能在必要时从一种形式转换到另一种形式。
理解任何机器的一个好方法是尝试一些示例输入串。当您进行这些“实验”以查看机器如何工作时,其工作方式通常会变得明显。在示例串 1101 上,机器 $M_{2}$ 从其起始状态 $q_{1}$ 开始,读取第一个 1 后首先进入状态 $q_{2}$,然后读取 1、0 和 1 后进入状态 $q_{2}、q_{1}$ 和 $q_{2}$。该串被接受,因为 $q_{2}$ 是一个接受状态。但串 110 使 $M_{2}$ 停留在状态 $q_{1}$,因此被拒绝。在尝试更多例子后,您会发现 $M_{2}$ 接受所有以 1 结尾的串。因此 $L\left(M_{2}\right)=\{w \mid w \text { 以 1 结尾}\}$。
例子 1.9
考虑有限自动机 $M_{3}$。
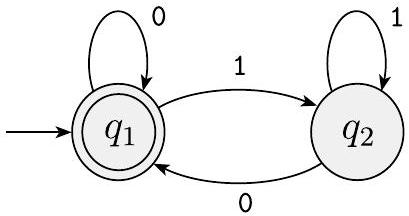
图 1.10
两状态有限自动机 $M_{3}$ 的状态图
机器 $M_{3}$ 与 $M_{2}$ 相似,只是接受状态的位置不同。像往常一样,机器接受所有在读完后使其停留在接受状态的串。请注意,由于起始状态也是一个接受状态,$M_{3}$ 接受空串 $\varepsilon$。一旦机器开始读取空串,它就到达了末尾;因此,如果起始状态是接受状态,则 $\varepsilon$ 被接受。除了空串之外,这台机器还接受任何以 0 结尾的串。这里,
例子 1.11
下图显示了一个五状态机器 $M_{4}$。
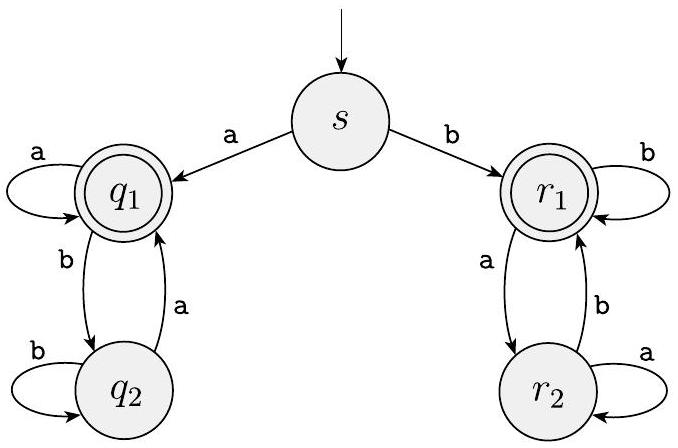
图 1.12
有限自动机 $M_{4}$
机器 $M_{4}$ 有两个接受状态 $q_{1}$ 和 $r_{1}$,并在字母表 $\Sigma=\{\mathrm{a}, \mathrm{b}\}$ 上操作。一些实验表明它接受串 a, b, aa, bb 和 bab,但不接受串 ab, ba 或 bbba。这台机器从状态 $s$ 开始,读取输入中的第一个符号后,它要么向左进入 $q$ 状态,要么向右进入 $r$ 状态。在这两种情况下,它都无法返回到起始状态(与前面的例子相反),因为它没有办法从任何其他状态回到 $s$。如果输入串中的第一个符号是 a,那么它向左移动并在串以 a 结尾时接受。类似地,如果第一个符号是 b,机器向右移动并在串以 b 结尾时接受。因此 $M_{4}$ 接受所有以相同符号开头和结尾的串。换句话说,$M_{4}$ 接受以相同符号开头和结尾的串。
例子 1.13
图 1.14 显示了三状态机器 $M_{5}$,它有一个四符号输入字母表,$\Sigma=\{\langle$ RESET $\rangle, 0,1,2\}$。我们将 $\langle$ RESET $\rangle$ 视为一个单一符号。
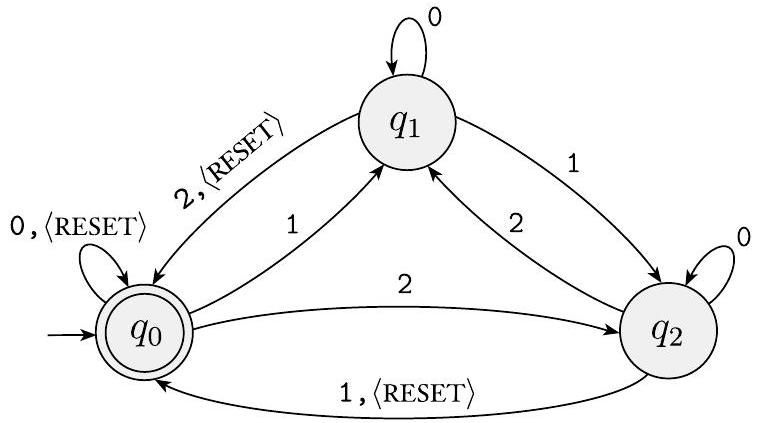
图 1.14
有限自动机 $M_{5}$
机器 $M_{5}$ 保持其读取的数值输入符号之和模 3 的运行计数。每当它接收到 $\langle$ RESET $\rangle$ 符号时,它将计数重置为 0。如果和是模 3 为 0,换句话说,如果和是 3 的倍数,它就接受。
在某些情况下,不可能通过状态图描述有限自动机。这可能发生在图太大而无法绘制时,或者像下一个例子一样,描述依赖于某些未指定的参数。在这些情况下,我们求助于形式化描述来指定机器。
例子 1.15
考虑例子 1.13的推广,使用相同的四符号字母表 $\Sigma$。对于每个 $i \geq 1$,设 $A_{i}$ 是所有串的语言,其中数字之和是 $i$ 的倍数,但每当出现符号 $\langle$ RESET $\rangle$ 时,和会重置为 0。对于每个 $A_{i}$,我们给出一个有限自动机 $B_{i}$,识别 $A_{i}$。我们形式化地描述机器 $B_{i}$ 如下:$B_{i}=\left(Q_{i}, \Sigma, \delta_{i}, q_{0},\left\{q_{0}\right\}\right)$,其中 $Q_{i}$ 是 $i$ 个状态的集合 $\left\{q_{0}, q_{1}, q_{2}, \ldots, q_{i-1}\right\}$,我们设计转移函数 $\delta_{i}$,使得对于每个 $j$,如果 $B_{i}$ 处于 $q_{j}$,则运行和是 $j$ 模 $i$。对于每个 $q_{j}$,设
计算的形式化定义
到目前为止,我们已经通过状态图和作为一个五元组的形式化定义非形式化地描述了有限自动机。非形式化描述起初更容易理解,但形式化定义对于使概念精确、解决非形式化描述中可能出现的任何歧义很有用。接下来,我们对有限自动机的计算也这样做。我们已经对它的计算方式有了非形式化的概念,现在我们将它数学形式化。
设 $M=\left(Q, \Sigma, \delta, q_{0}, F\right)$ 是一个有限自动机,设 $w=w_{1} w_{2} \cdots w_{n}$ 是一个串,其中每个 $w_{i}$ 是字母表 $\Sigma$ 的一个成员。那么 $M$ 接受 $w$ 如果存在一个状态序列 $r_{0}, r_{1}, \ldots, r_{n}$ 在 $Q$ 中,满足三个条件:
- $r_{0}=q_{0}$,
- $\delta\left(r_{i}, w_{i+1}\right)=r_{i+1}$,对于 $i=0, \ldots, n-1$,并且
- $r_{n} \in F$。
条件 1 表示机器从起始状态开始。条件 2 表示机器根据转移函数从一个状态转移到另一个状态。条件 3 表示如果机器最终停留在接受状态,则接受其输入。我们说 $M$ 识别语言 $A$ 如果 $A=\{w \mid M \text { 接受 } w\}$。
定义 1.16
如果某个有限自动机识别它,则称该语言为正则语言。
例子 1.17
以例子 1.13中的机器 $M_{5}$ 为例。设 $w$ 为串
10〈RESET〉22〈RESET〉012。
那么 $M_{5}$ 根据计算的形式化定义接受 $w$,因为它在计算 $w$ 时进入的状态序列是
满足这三个条件。$M_{5}$ 的语言是
由于 $M_{5}$ 识别这种语言,它是一种正则语言。
有限自动机的设计
无论是自动机还是艺术品,设计都是一个创造性过程。因此,它不能简化为简单的食谱或公式。然而,您可能会发现一种特定的方法在设计各种类型的自动机时很有帮助。也就是说,将自己置于您尝试设计的机器的位置,然后看看您将如何执行机器的任务。假装您是机器是一种心理技巧,有助于您的整个思维投入到设计过程中。
让我们使用刚刚描述的“读者即自动机”方法来设计有限自动机。假设给您一些语言,您想设计一个识别它的有限自动机。假装是自动机,您接收一个输入串,并且必须确定它是否是自动机应该识别的语言的成员。您将逐个看到串中的符号。在每个符号之后,您必须决定到目前为止所看到的串是否在语言中。原因是您,就像机器一样,不知道串何时结束,所以您必须始终准备好答案。
首先,为了做出这些决定,您必须弄清楚在读取串时需要记住哪些关于串的信息。为什么不简单地记住您看到的所有内容呢?请记住,您正在假装是有限自动机,而这种类型的机器只有有限数量的状态,这意味着有限的内存。想象一下输入非常长——比如说,从这里到月球——以至于您不可能记住整个内容。您有一个有限的内存——比如说,一张纸——它有有限的存储容量。幸运的是,对于许多语言,您不需要记住整个输入。您只需要记住某些关键信息。具体哪些信息是关键取决于所考虑的特定语言。
例如,假设字母表是 $\{0,1\}$,并且语言由所有包含奇数个 1 的串组成。您想构建一个有限自动机 $E_{1}$ 来识别这种语言。假装是自动机,您开始逐个符号接收由 0 和 1 组成的输入串。您需要记住到目前为止所看到的整个串,以便确定 1 的数量是奇数还是偶数吗?当然不需要。只需记住到目前为止所看到的 1 的数量是偶数还是奇数,并在读取新符号时跟踪这些信息。如果您读取 1,翻转答案;但如果您读取 0,保持答案不变。
但这如何帮助您设计 $E_{1}$ 呢?一旦您确定了在读取串时需要记住的关键信息,您就将这些信息表示为有限的可能性列表。在这种情况下,可能性将是
- 到目前为止是偶数,
- 到目前为止是奇数。
然后您为每种可能性分配一个状态。这些是 $E_{1}$ 的状态,如下图所示。
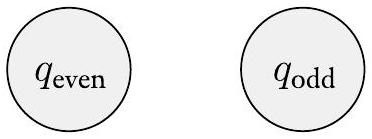
图 1.18
两个状态 $q_{\text {even }}$ 和 $q_{\text {odd }}$
接下来,您通过观察在读取符号后如何从一种可能性转移到另一种可能性来分配转移。因此,如果状态 $q_{\text {even }}$ 代表偶数可能性,状态 $q_{\text {odd }}$ 代表奇数可能性,您会将转移设置为在读取 1 时翻转状态,在读取 0 时保持不变,如下图所示。
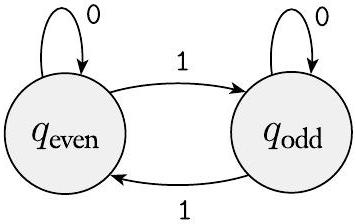
图 1.19
转移说明可能性如何重新安排
接下来,您将起始状态设置为对应于到目前为止已看到 0 个符号(空串 $\varepsilon$)的可能性的状态。在这种情况下,起始状态对应于状态 $q_{\text {even }}$,因为 0 是一个偶数。最后,将接受状态设置为对应于您想要接受输入串的可能性的状态。将 $q_{\text {odd }}$ 设置为接受状态,因为您希望在看到奇数个 1 时接受。这些添加如下图所示。
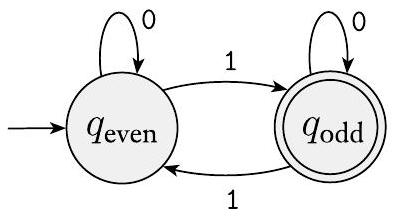
图 1.20
添加起始状态和接受状态
例子 1.21
这个例子展示了如何设计一个有限自动机 $E_{2}$ 来识别所有包含串 001 作为子串的正则语言。例如,0010、1001、001 和 11111110011111 都属于该语言,但 11 和 0000 不属于。如果您假装是 $E_{2}$,您将如何识别这种语言?当符号进来时,您最初会跳过所有的 1。如果您遇到一个 0,那么您可能会注意到您刚刚看到了您正在寻找的模式 001 中的三个符号中的第一个。如果此时您看到一个 1,则 0 的数量太少,所以您会回到跳过 1 的步骤。但是如果此时您看到一个 0,您应该记住您刚刚看到了模式中的两个符号。现在您只需要继续扫描直到看到一个 1。如果您找到了,请记住您成功找到了模式,并继续读取输入串直到结束。
所以有四种可能性:您
- 刚刚没有看到模式中的任何符号,
- 刚刚看到了一个 0,
- 刚刚看到了 00,或者
- 已经看到了整个模式 001。
将状态 $q, q_{0}, q_{00}$ 和 $q_{001}$ 分配给这些可能性。您可以通过观察从 $q$ 读取 1 时保持在 $q$,但读取 0 时转移到 $q_{0}$ 来分配转移。在 $q_{0}$ 中读取 1 时返回到 $q$,但读取 0 时转移到 $q_{00}$。在 $q_{00}$ 中读取 1 时转移到 $q_{001}$,但读取 0 时保持在 $q_{00}$。最后,在 $q_{001}$ 中读取 0 或 1 时保持在 $q_{001}$。起始状态是 $q$,唯一接受状态是 $q_{001}$,如图 1.22所示。
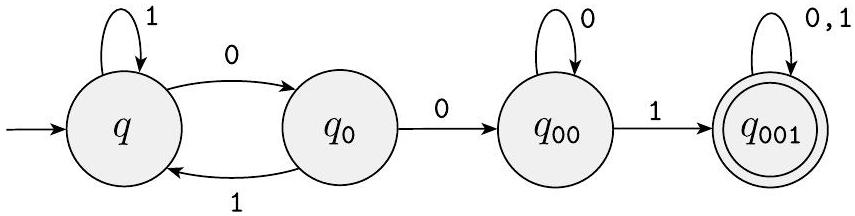
图 1.22
接受包含 001 的串
正则运算
在前两节中,我们介绍了有限自动机和正则语言并对其进行了定义。我们现在开始研究它们的性质。这样做将有助于开发一个用于设计自动机以识别特定语言的技术工具箱。该工具箱还将包括证明某些其他语言是非正则的(即,超出有限自动机的能力范围)的方法。
在算术中,基本对象是数字,而工具是用于操作它们的运算,例如 + 和 $\times$。在计算理论中,对象是语言,而工具包括专门用于操作它们的运算。我们定义语言上的三种运算,称为正则运算,并使用它们来研究正则语言的性质。
定义 1.23
设 $A$ 和 $B$ 是语言。我们定义正则运算并集、连接和星号如下:
- 并集:$A \cup B=\{x \mid x \in A \text { 或 } x \in B\}$。
- 连接:$A \circ B=\{x y \mid x \in A \text { 且 } y \in B\}$。
- 星号:$A^{*}=\left\{x_{1} x_{2} \ldots x_{k} \mid k \geq 0 \text { 且每个 } x_{i} \in A\right\}$。
您已经熟悉了并集运算。它只是将 $A$ 和 $B$ 中的所有串组合到一个语言中。
连接运算有点复杂。它以所有可能的方式将 $A$ 中的一个串附加在 $B$ 中的一个串前面,以获得新语言中的串。
星号运算与其他两个运算有点不同,因为它适用于单个语言而不是两个不同的语言。也就是说,星号运算是一元运算而不是二元运算。它通过将 $A$ 中的任意数量的串连接起来,以获得新语言中的串。因为“任意数量”包括 0 种可能性,所以空串 $\varepsilon$ 始终是 $A^{*}$ 的成员,无论 $A$ 是什么。
例子 1.24
设字母表 $\Sigma$ 是标准 26 个字母 $\{\mathrm{a}, \mathrm{b}, \ldots, \mathrm{z}\}$。如果 $A=\{\operatorname{good}, \mathrm{bad}\}$ 且 $B=\{$ boy, girl $\}$,那么
设 $\mathcal{N}=\{1,2,3, \ldots\}$ 为自然数集。当我们说 $\mathcal{N}$ 在乘法下是封闭的,我们的意思是对于 $\mathcal{N}$ 中的任意 $x$ 和 $y$,乘积 $x \times y$ 也在 $\mathcal{N}$ 中。相比之下,$\mathcal{N}$ 在除法下不是封闭的,因为 1 和 2 在 $\mathcal{N}$ 中,但 $1 / 2$ 不在。一般来说,如果对集合的成员应用某种运算后,结果仍然是该集合中的对象,则称该集合在该运算下封闭。我们证明正则语言集合在所有三种正则运算下都是封闭的。在第 1.3 节中,我们展示了这些是操作正则语言和理解有限自动机能力的有用工具。我们从并集运算开始。
定理 1.25
正则语言的类在并集运算下是封闭的。
换句话说,如果 $A_{1}$ 和 $A_{2}$ 是正则语言,那么 $A_{1} \cup A_{2}$ 也是正则语言。
证明思路 我们有正则语言 $A_{1}$ 和 $A_{2}$,并希望证明 $A_{1} \cup A_{2}$ 也是正则语言。因为 $A_{1}$ 和 $A_{2}$ 是正则语言,我们知道某个有限自动机 $M_{1}$ 识别 $A_{1}$,某个有限自动机 $M_{2}$ 识别 $A_{2}$。为了证明 $A_{1} \cup A_{2}$ 是正则语言,我们演示一个有限自动机,称之为 $M$,它识别 $A_{1} \cup A_{2}$。
这是一个构造性证明。我们从 $M_{1}$ 和 $M_{2}$ 构造 $M$。机器 $M$ 必须恰好在 $M_{1}$ 或 $M_{2}$ 接受其输入时接受其输入,以便识别并集语言。它通过模拟 $M_{1}$ 和 $M_{2}$ 并在其中任何一个模拟接受时接受来工作。
我们如何使机器 $M$ 模拟 $M_{1}$ 和 $M_{2}$ 呢?也许它首先在输入上模拟 $M_{1}$,然后模拟 $M_{2}$。但我们在这里必须小心!一旦输入符号被读取并用于模拟 $M_{1}$,我们就无法“回带输入磁带”来尝试在 $M_{2}$ 上进行模拟。我们需要另一种方法。
假装您是 $M$。当输入符号逐个到达时,您同时模拟 $M_{1}$ 和 $M_{2}$。这样,只需要对输入进行一次遍历。但是您能用有限的内存同时跟踪两个模拟吗?您只需要记住每台机器在读取到这一点时所处的状态。因此,您需要记住一个状态对。有多少种可能的状态对?如果 $M_{1}$ 有 $k_{1}$ 个状态,而 $M_{2}$ 有 $k_{2}$ 个状态,则状态对(一个来自 $M_{1}$,另一个来自 $M_{2}$)的数量是乘积 $k_{1} \times k_{2}$。这个乘积将是 $M$ 中的状态数量,每个状态对对应一个状态。$M$ 的转移从状态对到状态对,更新 $M_{1}$ 和 $M_{2}$ 的当前状态。$M$ 的接受状态是那些状态对,其中 $M_{1}$ 或 $M_{2}$ 处于接受状态。
证明
设 $M_{1}$ 识别 $A_{1}$,其中 $M_{1}=\left(Q_{1}, \Sigma, \delta_{1}, q_{1}, F_{1}\right)$,设 $M_{2}$ 识别 $A_{2}$,其中 $M_{2}=\left(Q_{2}, \Sigma, \delta_{2}, q_{2}, F_{2}\right)$。
构造 $M$ 以识别 $A_{1} \cup A_{2}$,其中 $M=\left(Q, \Sigma, \delta, q_{0}, F\right)$。
- $Q=\left\{\left(r_{1}, r_{2}\right) \mid r_{1} \in Q_{1} \text { 且 } r_{2} \in Q_{2}\right\}$。
这个集合是集合 $Q_{1}$ 和 $Q_{2}$ 的笛卡尔积,写为 $Q_{1} \times Q_{2}$。它是所有状态对的集合,第一个来自 $Q_{1}$,第二个来自 $Q_{2}$。
- $\Sigma$,字母表,与 $M_{1}$ 和 $M_{2}$ 中的相同。在这个定理和所有后续的类似定理中,为简单起见,我们假设 $M_{1}$ 和 $M_{2}$ 都具有相同的输入字母表 $\Sigma$。如果它们具有不同的字母表 $\Sigma_{1}$ 和 $\Sigma_{2}$,该定理仍然成立。那么我们将修改证明,使 $\Sigma=\Sigma_{1} \cup \Sigma_{2}$。
- $\delta$,转移函数,定义如下。对于每个 $\left(r_{1}, r_{2}\right) \in Q$ 和每个 $a \in \Sigma$,设
因此,$\delta$ 获取 $M$ 的一个状态(实际上是来自 $M_{1}$ 和 $M_{2}$ 的状态对),以及一个输入符号,并返回 $M$ 的下一个状态。
- $q_{0}$ 是状态对 $\left(q_{1}, q_{2}\right)$。
- $F$ 是状态对的集合,其中任何一个成员是 $M_{1}$ 或 $M_{2}$ 的接受状态。我们可以将其写为
这个表达式与 $F=\left(F_{1} \times Q_{2}\right) \cup\left(Q_{1} \times F_{2}\right)$ 相同。(请注意,它与 $F=F_{1} \times F_{2}$ 不同。那会给我们什么呢? ${ }^{3}$)
[^1]这结束了有限自动机 $M$ 的构造,它识别 $A_{1}$ 和 $A_{2}$ 的并集。这种构造相当简单,因此其正确性从证明思路中描述的策略显而易见。更复杂的构造需要额外的讨论来证明正确性。这种类型的构造的形式化正确性证明通常通过归纳法进行。有关证明正确的构造的例子,请参见定理 1.54的证明。您在本课程中遇到的大多数构造都相当简单,因此不需要形式化正确性证明。
我们刚刚展示了两个正则语言的并集是正则语言,从而证明了正则语言的类在并集运算下是封闭的。我们现在转向连接运算,并尝试证明正则语言的类在该运算下也是封闭的。
定理 1.26
正则语言的类在连接运算下是封闭的。
换句话说,如果 $A_{1}$ 和 $A_{2}$ 是正则语言,那么 $A_{1} \circ A_{2}$ 也是正则语言。
为了证明这个定理,让我们尝试一些类似于并集情况的证明。像以前一样,我们可以从识别正则语言 $A_{1}$ 和 $A_{2}$ 的有限自动机 $M_{1}$ 和 $M_{2}$ 开始。但是现在,构造自动机 $M$ 不再是如果 $M_{1}$ 或 $M_{2}$ 接受其输入就接受,而是如果其输入可以分成两部分,其中 $M_{1}$ 接受第一部分, $M_{2}$ 接受第二部分,它就必须接受。问题是 $M$ 不知道在哪里分割其输入(即,第一部分在哪里结束,第二部分在哪里开始)。为了解决这个问题,我们引入了一种新的技术,称为非确定性。