1_正则语言1.2.ZH

11.2

非确定性

非确定性是一个有用的概念，它对计算理论产生了巨大影响。到目前为止，在我们的讨论中，计算的每一步都以一种独特的方式从前一步推导出来。当机器处于给定状态并读取下一个输入符号时，我们知道下一个状态将是什么——它是确定的。我们称之为确定性计算。在非确定性机器中，在任何时候都可能存在多种选择以进入下一个状态。

非确定性是确定性的一种推广，因此每个确定性有限自动机自动也是非确定性有限自动机。正如图1.27所示，非确定性有限自动机可能具有额外的特性。

图 1.27

非确定性有限自动机 $N_{1}$

确定性有限自动机（缩写为DFA）与非确定性有限自动机（缩写为NFA）之间的区别显而易见。首先，DFA的每个状态对于字母表中的每个符号总是恰好有一条出转换箭头。图1.27所示的NFA违反了这一规则。状态$q_{1}$对0有一条出箭头，但对1有两条；$q_{2}$对0有一条箭头，但对1没有。在NFA中，一个状态对于每个字母表符号可以有零条、一条或多条出箭头。

其次，在DFA中，转换箭头上的标签是字母表中的符号。这个NFA有一条带标签$\varepsilon$的箭头。通常，NFA可能具有标有字母表成员或$\varepsilon$的箭头。从每个状态可以有零条、一条或多条带标签$\varepsilon$的箭头射出。

NFA如何计算？假设我们正在输入字符串上运行NFA，并到达一个有多种方式可以继续的状态。例如，假设我们在NFA $N_{1}$中的状态$q_{1}$，并且下一个输入符号是1。读取该符号后，机器会分裂成自身的多个副本并并行地遵循所有可能性。机器的每个副本都采取其中一种可能的方式继续，并像以前一样进行。如果存在后续选择，机器会再次分裂。如果下一个输入符号没有出现在机器副本所占据的状态的任何出箭头上，那么该机器副本以及与之相关的计算分支就会“死亡”。最后，如果这些机器副本中的任何一个在输入结束时处于接受状态，则NFA接受该输入字符串。

如果遇到带有$\varepsilon$符号的出箭头状态，也会发生类似的情况。不读取任何输入，机器会分裂成多个副本，一个副本遵循每个带有$\varepsilon$标签的出箭头，另一个副本停留在当前状态。然后机器像以前一样非确定性地进行。

非确定性可以看作是一种并行计算，其中多个独立的“进程”或“线程”可以并发运行。当NFA分裂以遵循多个选择时，这对应于一个进程“分叉”成多个子进程，每个子进程独立进行。如果至少有一个这样的进程接受，那么整个计算就接受。

考虑非确定性计算的另一种方式是将其视为一个可能性树。树的根对应于计算的开始。树中的每个分支点对应于机器有多种选择的计算点。如果至少一个计算分支以接受状态结束，则机器接受，如图1.28所示。

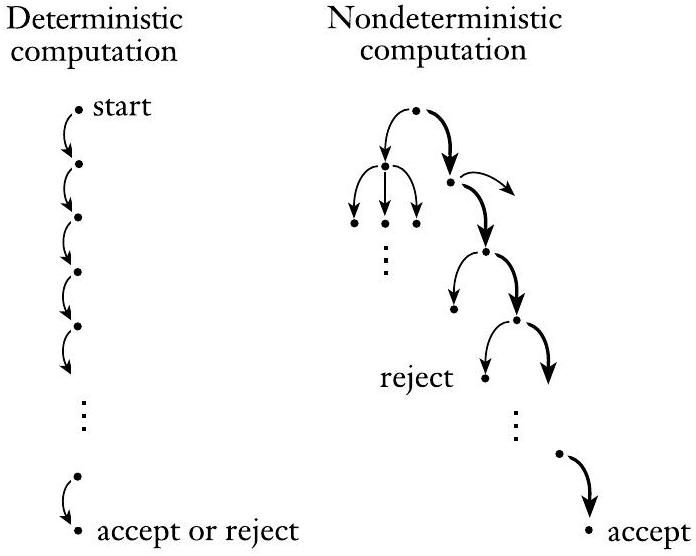
图 1.28

带有接受分支的确定性与非确定性计算

让我们考虑NFA $N_{1}$（如图1.27所示）的一些样本运行。$N_{1}$在输入010110上的计算如下图所示。

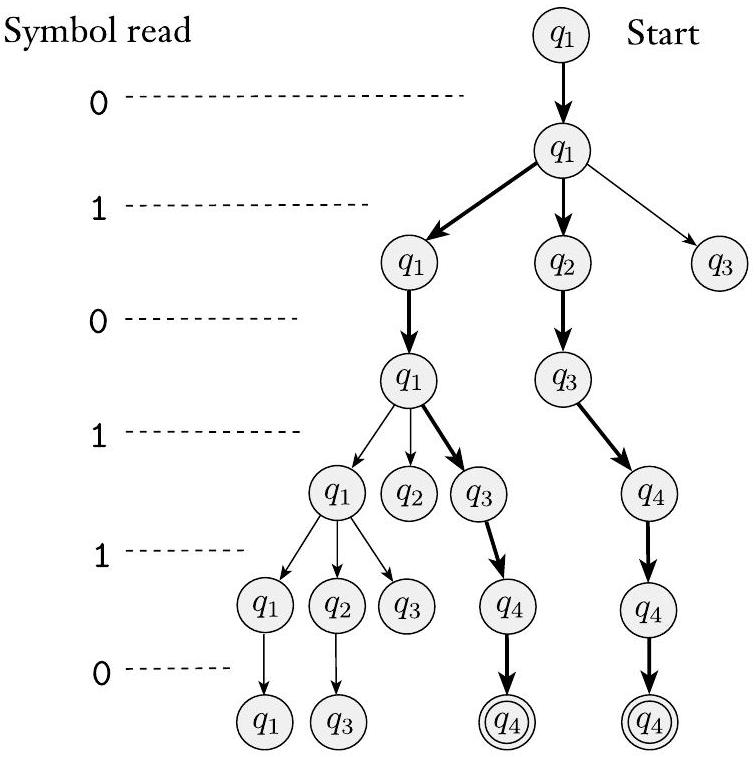
图 1.29

$N_{1}$在输入010110上的计算

在输入010110上，从起始状态$q_{1}$开始并读取第一个符号0。从$q_{1}$开始，对0只有一个去处——即回到$q_{1}$——所以停留在那里。接下来，读取第二个符号1。在$q_{1}$上读取1时，有两种选择：要么停留在$q_{1}$，要么移动到$q_{2}$。非确定性地，机器分裂成两个副本以遵循每个选择。通过在机器可能处于的每个状态上放置一个手指来跟踪这些可能性。所以你现在在状态$q_{1}$和$q_{2}$上都有手指。一个$\varepsilon$箭头从状态$q_{2}$射出，所以机器再次分裂；一个手指留在$q_{2}$上，另一个移动到$q_{3}$。你现在在$q_{1}$、$q_{2}$和$q_{3}$上都有手指。

读取第三个符号0时，依次取下每个手指。将$q_{1}$上的手指保持在原位，将$q_{2}$上的手指移动到$q_{3}$，并移除原本在$q_{3}$上的手指。最后一个手指没有0箭头可遵循，对应于一个简单地“死亡”的进程。此时，你的手指停留在状态$q_{1}$和$q_{3}$上。

读取第四个符号1时，将$q_{1}$上的手指分成$q_{1}$和$q_{2}$上的手指，然后将$q_{2}$上的手指进一步分裂以跟随$\varepsilon$箭头到$q_{3}$，并将原本在$q_{3}$上的手指移动到$q_{4}$。你现在在所有四个状态上都有手指。

读取第五个符号1时，正如你用第四个符号看到的那样，$q_{1}$和$q_{3}$上的手指会产生在状态$q_{1}$、$q_{2}$、$q_{3}$和$q_{4}$上的手指。$q_{2}$上的手指被移除。原本在$q_{4}$上的手指仍然停留在$q_{4}$上。现在你在$q_{4}$上有了两个手指，所以移除一个，因为你只需要记住$q_{4}$在此时是一个可能的州，而不是它可能因为多种原因。

读取第六个也是最后一个符号0时，将$q_{1}$上的手指保持在原位，将$q_{2}$上的手指移动到$q_{3}$，移除原本在$q_{3}$上的手指，并将$q_{4}$上的手指保持在原位。你现在处于字符串的末尾，如果某个手指处于接受状态，则你接受。你的手指停留在状态$q_{1}$、$q_{3}$和$q_{4}$上；由于$q_{4}$是一个接受状态，$N_{1}$接受这个字符串。

$N_{1}$在输入010上会做什么？从$q_{1}$开始放置一个手指。读取0后，你仍然只有一个手指在$q_{1}$上；但读取1后，手指会出现在$q_{1}$、$q_{2}$和$q_{3}$上（不要忘记$\varepsilon$箭头）。读取第三个符号0后，移除$q_{3}$上的手指，将$q_{2}$上的手指移动到$q_{3}$，并将$q_{1}$上的手指保持在原位。此时你已到达输入的末尾；由于没有手指处于接受状态，$N_{1}$拒绝此输入。

通过继续以这种方式进行实验，你将看到$N_{1}$接受所有包含子字符串101或11的字符串。

非确定性有限自动机在几个方面都很有用。正如我们将展示的，每个NFA都可以转换为等价的DFA，并且构建NFA有时比直接构建DFA更容易。NFA可能比其确定性对应物小得多，或者其功能可能更容易理解。有限自动机中的非确定性也是更强大的计算模型中非确定性的一个很好的介绍，因为有限自动机特别容易理解。现在我们来看几个NFA的例子。

例子 1.30

设$A$是所有包含一个1在倒数第三个位置的字符串组成的语言（例如，000100在$A$中，但0011不在）。下面的四状态NFA $N_{2}$识别$A$。

图 1.31

识别$A$的NFA $N_{2}$

看待这个NFA计算的一种好方法是说它停留在起始状态$q_{1}$，直到它“猜测”距离末尾还有三个位置。此时，如果输入符号是1，它分支到状态$q_{2}$并使用$q_{3}$和$q_{4}$来“检查”它的猜测是否正确。

如前所述，每个NFA都可以转换为等价的DFA；但有时DFA可能具有更多的状态。用于$A$的最小DFA包含八个状态。此外，理解NFA的功能要容易得多，你可以通过检查下面DFA的图来看到。

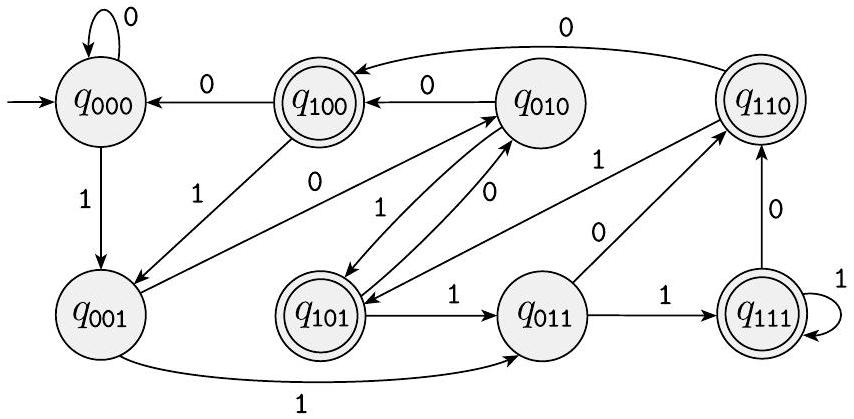
图 1.32

识别$A$的DFA

假设我们将$\boldsymbol{\varepsilon}$添加到机器$N_{2}$中从$q_{2}$到$q_{3}$以及从$q_{3}$到$q_{4}$的箭头上。这样，两条箭头都将带有标签$0,1, \varepsilon$，而不仅仅是$0,1$。$N_{2}$经过这种修改后会识别哪种语言？尝试修改图1.32中的DFA以识别该语言。

例子 1.33

下面的NFA $N_{3}$有一个只包含一个符号的输入字母表$\{0\}$。只包含一个符号的字母表称为一元字母表。

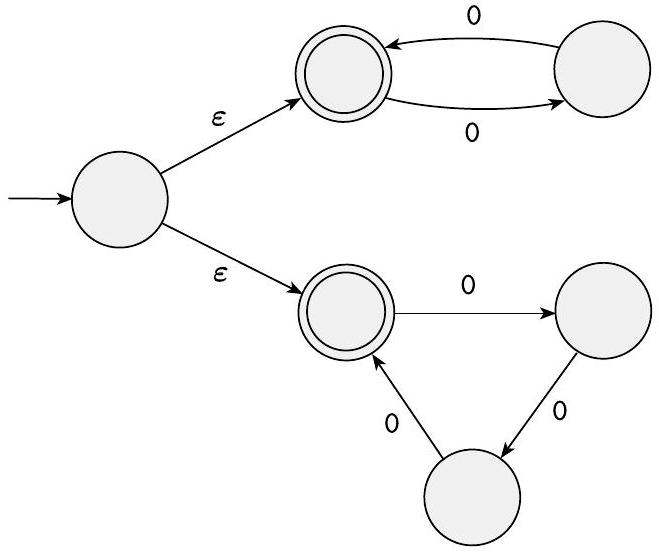
图 1.34

NFA $N_{3}$

这台机器展示了拥有$\varepsilon$箭头的便利性。它接受所有形式为$0^{k}$的字符串，其中$k$是2或3的倍数。（请记住，上标表示重复，而不是数字指数。）例如，$N_{3}$接受字符串$\varepsilon, 00,000,0000$和000000，但不接受0或00000。

设想机器通过最初猜测是测试2的倍数还是3的倍数来操作，通过分支到上面的循环或下面的循环，然后检查其猜测是否正确。当然，我们可以用一台没有$\varepsilon$箭头甚至没有任何非确定性的机器来代替这台机器，但所示的机器是针对这种语言最容易理解的机器。

例子 1.35

我们再举一个NFA的例子，见图1.36。练习一下，让自己确信它接受字符串$\varepsilon$、a、baba和baa，但不接受字符串b、bb和babba。稍后我们将使用这台机器来说明将NFA转换为DFA的过程。

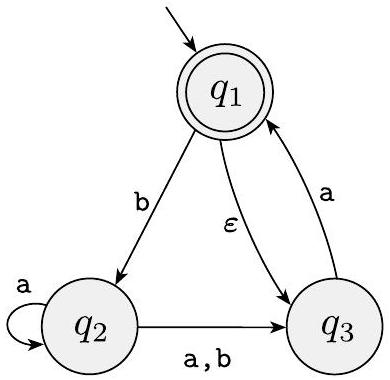
图 1.36

NFA $N_{4}$

非确定性有限自动机的形式定义

非确定性有限自动机的形式定义与确定性有限自动机的形式定义类似。两者都具有状态、输入字母表、转换函数、起始状态和接受状态集合。然而，它们在一个基本方面有所不同：转换函数的类型。在DFA中，转换函数接受一个状态和一个输入符号并产生下一个状态。在NFA中，转换函数接受一个状态和一个输入符号或空字符串并产生可能的下一个状态集合。为了编写形式定义，我们需要设置一些额外的符号。对于任何集合$Q$，我们用$\mathcal{P}(Q)$表示$Q$的所有子集集合。这里$\mathcal{P}(Q)$称为$Q$的幂集。对于任何字母表$\Sigma$，我们用$\Sigma_{\varepsilon}$表示$\Sigma \cup\{\varepsilon\}$。现在我们可以写出NFA中转换函数类型的形式描述为$\delta: Q \times \Sigma_{\varepsilon} \longrightarrow \mathcal{P}(Q)$。

定义 1.37

非确定性有限自动机是一个5元组$\left(Q, \Sigma, \delta, q_{0}, F\right)$，其中

1. $Q$是一个有限状态集，
2. $\Sigma$是一个有限字母表，
3. $\delta: Q \times \Sigma_{\varepsilon} \longrightarrow \mathcal{P}(Q)$是转换函数，
4. $q_{0} \in Q$是起始状态，并且
5. $F \subseteq Q$是接受状态集。

例子 1.38

回顾NFA $N_{1}$：

$N_{1}$的形式描述是$\left(Q, \Sigma, \delta, q_{1}, F\right)$，其中

1. $Q=\left\{q_{1}, q_{2}, q_{3}, q_{4}\right\}$，
2. $\Sigma=\{0,1\}$，
3. $\delta$如下所示

| | 0 | 1 | $\boldsymbol{\varepsilon}$ |

| :---: | :---: | :---: | :---: |

| $q_{1}$ | $\left\{q_{1}\right\}$ | $\left\{q_{1}, q_{2}\right\}$ | $\emptyset$ |

| $q_{2}$ | $\left\{q_{3}\right\}$ | $\emptyset$ | $\left\{q_{3}\right\}$ |

| $q_{3}$ | $\emptyset$ | $\left\{q_{4}\right\}$ | $\emptyset$ |

| $q_{4}$ | $\left\{q_{4}\right\}$ | $\left\{q_{4}\right\}$ | $\emptyset$， |

1. $q_{1}$是起始状态，并且
2. $F=\left\{q_{4}\right\}$。 $\square$

NFA的形式化计算定义与DFA类似。设$N=\left(Q, \Sigma, \delta, q_{0}, F\right)$是一个NFA，$w$是字母表$\Sigma$上的一个字符串。当我们可以将$w$写成$w=y_{1} y_{2} \cdots y_{m}$，其中每个$y_{i}$是$\Sigma_{\varepsilon}$的成员，并且在$Q$中存在一个状态序列$r_{0}, r_{1}, \ldots, r_{m}$，满足三个条件时，我们称$N$接受$w$：

1. $r_{0}=q_{0}$，
2. $r_{i+1} \in \delta\left(r_{i}, y_{i+1}\right)$，对于$i=0, \ldots, m-1$，并且
3. $r_{m} \in F$。

条件1表示机器从起始状态开始。条件2表示当$N$处于状态$r_{i}$并读取$y_{i+1}$时，状态$r_{i+1}$是允许的下一个状态之一。请注意，$\delta\left(r_{i}, y_{i+1}\right)$是允许的下一个状态集，因此我们说$r_{i+1}$是该集合的成员。最后，条件3表示如果最后一个状态是接受状态，则机器接受其输入。

NFA和DFA的等价性

确定性有限自动机和非确定性有限自动机识别相同类别的语言。这种等价性既令人惊讶又很有用。之所以令人惊讶，是因为NFA似乎比DFA拥有更强大的能力，所以我们可能预期NFA能识别更多的语言。之所以有用，是因为有时为给定语言描述NFA比直接描述DFA要容易得多。

如果两台机器识别相同的语言，我们称它们是等价的。

定理 1.39

每个非确定性有限自动机都具有一个等价的确定性有限自动机。

证明思想 如果一种语言被NFA识别，那么我们必须证明存在一个DFA也能识别它。其思想是将NFA转换为一个等价的DFA，该DFA模拟NFA。

回想一下设计有限自动机的“读者即自动机”策略。如果你假装是一个DFA，你将如何模拟NFA？在处理输入字符串时，你需要跟踪什么？在NFA的例子中，你通过在输入中给定点可能活跃的每个状态上放置一个手指来跟踪计算的各种分支。你根据NFA的操作方式通过移动、添加和移除手指来更新模拟。你只需要跟踪有手指的状态集。

如果$k$是NFA的状态数，那么它有$2^{k}$个状态子集。每个子集对应于DFA必须记住的一种可能性，因此模拟NFA的DFA将有$2^{k}$个状态。现在我们需要确定DFA的起始状态和接受状态，以及它的转换函数。在建立一些形式符号之后，我们可以更容易地讨论这个问题。

证明 设$N=\left(Q, \Sigma, \delta, q_{0}, F\right)$是识别语言$A$的NFA。我们构造一个识别$A$的DFA $M=\left(Q^{\prime}, \Sigma, \delta^{\prime}, q_{0}{ }^{\prime}, F^{\prime}\right)$。在进行完整构造之前，我们首先考虑$N$没有$\varepsilon$箭头的简单情况。稍后我们将考虑$\varepsilon$箭头。

1. $Q^{\prime}=\mathcal{P}(Q)$。

$M$的每个状态都是$N$的状态集。回想一下，$\mathcal{P}(Q)$是$Q$的子集集。

1. 对于$R \in Q^{\prime}$和$a \in \Sigma$，设$\delta^{\prime}(R, a)=\{q \in Q \mid q \in \delta(r, a) \text{ 对于某个 } r \in R\}$。如果$R$是$M$的一个状态，它也是$N$的一个状态集。当$M$在状态$R$中读取符号$a$时，它显示$a$将$R$中的每个状态带到何处。由于每个状态可以进入一个状态集，我们取所有这些集合的并集。另一种书写此表达式的方式是

1. $q_{0}{ }^{\prime}=\left\{q_{0}\right\}$。

$M$从仅包含$N$的起始状态的集合所对应的状态开始。

1. $F^{\prime}=\left\{R \in Q^{\prime} \mid R \text{ 包含 } N \text{ 的一个接受状态}\right\}$。

如果$N$在此时可能处于的状态中有一个是接受状态，则机器$M$接受。

[^2]现在我们需要考虑$\varepsilon$箭头。为此，我们设置一些额外的符号。对于$M$的任何状态$R$，我们定义$E(R)$为可以从$R$的成员仅沿着$\varepsilon$箭头到达的状态集合，包括$R$本身的成员。形式上，对于$R \subseteq Q$，$E(R)$定义为

然后我们修改$M$的转换函数，以便在每一步之后，将额外的“手指”放置在所有可以通过$\varepsilon$箭头到达的状态上。用$E(\delta(r, a))$替换$\delta(r, a)$即可实现此效果。因此

此外，我们需要修改$M$的起始状态，以将手指最初移动到所有可以通过$\varepsilon$箭头从$N$的起始状态到达的可能状态。将$q_{0}{ }^{\prime}$更改为$E\left(\left\{q_{0}\right\}\right)$即可实现此效果。我们现在已经完成了模拟NFA $N$的DFA $M$的构造。

$M$的构造显然工作正确。在$M$对输入进行计算的每一步中，它都清晰地进入一个状态，该状态对应于$N$在此时可能处于的状态子集。因此，我们的证明完成了。

定理1.39指出，每个NFA都可以转换为等价的DFA。因此，非确定性有限自动机提供了表征正则语言的另一种方式。我们将这一事实作为定理1.39的推论。

推论 1.40

一种语言是正则的当且仅当某个非确定性有限自动机识别它。

“当且仅当”条件的一个方向表明，如果某个NFA识别一种语言，则该语言是正则的。定理1.39表明，任何NFA都可以转换为等价的DFA。因此，如果NFA识别某种语言，那么某个DFA也识别它，因此该语言是正则的。 “当且仅当”条件的另一个方向表明，一种语言是正则的当且仅当某个NFA识别它。也就是说，如果一种语言是正则的，则某个NFA必须识别它。显然，这个条件是正确的，因为正则语言有一个DFA识别它，而任何DFA也是一个NFA。

例子 1.41

让我们用出现在例1.35中的机器$N_{4}$来说明定理1.39证明中给出的将NFA转换为DFA的过程。为了清晰起见，我们将$N_{4}$的状态重新标记为$\{1,2,3\}$。因此，在$N_{4}=(Q,\{\mathrm{a}, \mathrm{b}\}, \delta, 1,\{1\})$的形式描述中，状态集$Q$是$\{1,2,3\}$，如图1.42所示。

为了构造一个等价于$N_{4}$的DFA $D$，我们首先确定$D$的状态。$N_{4}$有三个状态$\{1,2,3\}$，所以我们构造一个有八个状态的$D$，每个状态对应于$N_{4}$状态集的一个子集。我们用相应的子集标记$D$的每个状态。因此$D$的状态集是

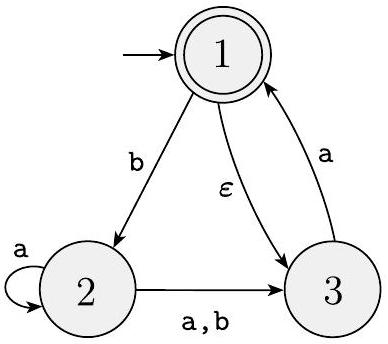
图 1.42

NFA $N_{4}$

接下来，我们确定$D$的起始状态和接受状态。起始状态是$E(\{1\})$，即可以通过沿着$\varepsilon$箭头从1到达的状态集合，包括1本身。一个$\varepsilon$箭头从1到3，所以$E(\{1\})=\{1,3\}$。新的接受状态是包含$N_{4}$接受状态的那些；因此是$\{\{1\},\{1,2\},\{1,3\},\{1,2,3\}\}$。

最后，我们确定$D$的转换函数。$D$的每个状态在输入a上都会到一个位置，在输入b上也会到一个位置。我们用几个例子来说明确定$D$的转换箭头放置的过程。

在$D$中，状态$\{2\}$在输入a时会变为$\{2,3\}$，因为在$N_{4}$中，状态2在输入a时会变为2和3，并且我们无法沿着$\varepsilon$箭头从2或3进一步移动。状态$\{2\}$在输入b时会变为状态$\{3\}$，因为在$N_{4}$中，状态2在输入b时只变为状态3，并且我们无法沿着$\varepsilon$箭头从3进一步移动。

状态$\{1\}$在a上变为$\emptyset$，因为没有a箭头从它射出。它在b上变为$\{2\}$。请注意，定理1.39中的过程规定，我们应该在读取每个输入符号后跟随$\varepsilon$箭头。另一种基于在读取每个输入符号前跟随$\varepsilon$箭头的方法同样有效，但该方法未在此示例中说明。

状态$\{3\}$在a上变为$\{1,3\}$，因为在$N_{4}$中，状态3在a上变为1，而1又通过$\varepsilon$箭头变为3。状态$\{3\}$在b上变为$\emptyset$。

状态$\{1,2\}$在a上变为$\{2,3\}$，因为1没有a箭头指向任何状态，2有a箭头指向2和3，并且两者都没有$\varepsilon$箭头指向任何地方。状态$\{1,2\}$在b上变为$\{2,3\}$。以这种方式继续，我们得到图1.43所示的$D$的图。

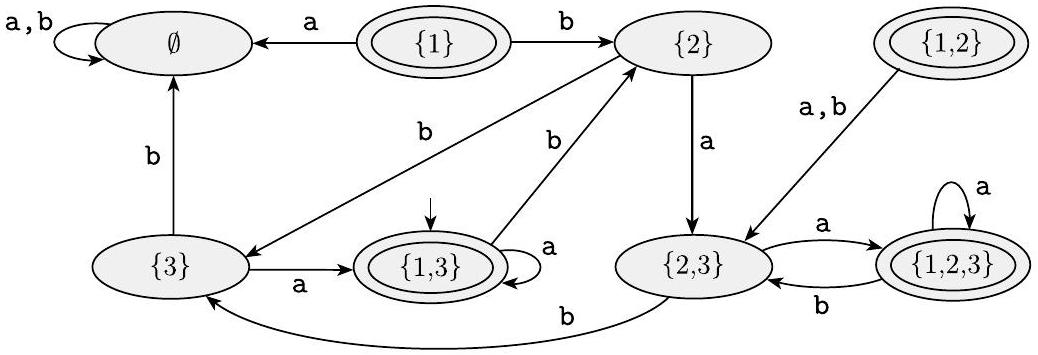
图 1.43

等价于NFA $N_{4}$的DFA $D$

我们可以通过观察状态$\{1\}$和$\{1,2\}$没有箭头指向它们来简化这台机器，这样就可以移除它们而不影响机器的性能。这样做会产生下图。

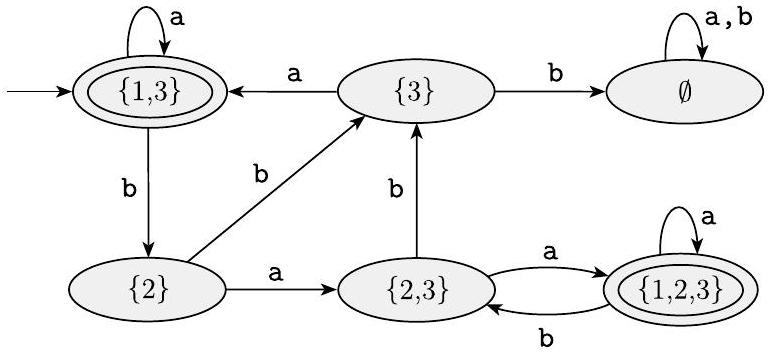
图 1.44

移除不必要状态后的DFA $D$

正则运算下的闭包

现在我们回到第1.1节开始讨论的正则语言类别在正则运算下的闭包。我们的目标是证明正则语言的并集、连接和星运算仍然是正则的。在处理连接运算过于复杂时，我们放弃了最初的尝试。非确定性的使用使证明变得容易得多。

首先，我们再次考虑在并集下的闭包。早些时候，我们通过笛卡尔积构造同时确定性地模拟两台机器来证明在并集下的闭包。我们现在给出一个新的证明来阐明

非确定性技术。回顾第45页的第一个证明，可能会发现新的证明更容易、更直观。

定理 1.45

正则语言类别在并集运算下是封闭的。

证明思想 我们有正则语言$A_{1}$和$A_{2}$，并希望证明$A_{1} \cup A_{2}$是正则的。其思想是取两个识别$A_{1}$和$A_{2}$的NFA $N_{1}$和$N_{2}$，并将它们组合成一个新的NFA $N$。

机器$N$必须在$N_{1}$或$N_{2}$接受其输入时接受其输入。新机器有一个新的起始状态，它通过$\varepsilon$箭头分支到旧机器的起始状态。通过这种方式，新机器非确定性地猜测哪台机器接受输入。如果其中一台接受输入，$N$也会接受它。

我们用下图表示这个构造。左侧，我们用大圆圈表示机器$N_{1}$和$N_{2}$的起始状态和接受状态，用小圆圈表示一些附加状态。右侧，我们展示了如何通过添加额外的转换箭头将$N_{1}$和$N_{2}$组合成$N$。

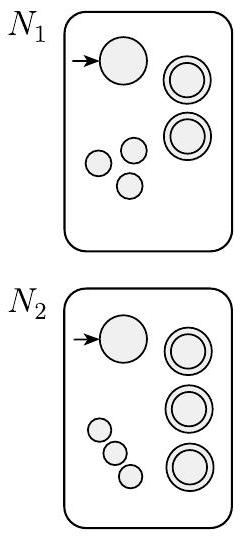
图 1.46

构造NFA $N$以识别$A_{1} \cup A_{2}$

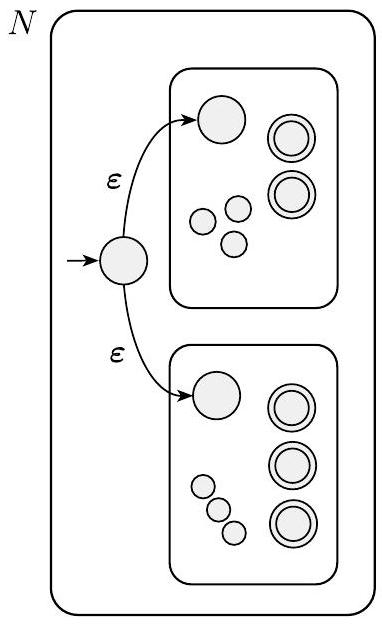
图 1.46

构造NFA $N$以识别$A_{1} \cup A_{2}$

证明

设$N_{1}=\left(Q_{1}, \Sigma, \delta_{1}, q_{1}, F_{1}\right)$识别$A_{1}$，且$N_{2}=\left(Q_{2}, \Sigma, \delta_{2}, q_{2}, F_{2}\right)$识别$A_{2}$。

构造$N=\left(Q, \Sigma, \delta, q_{0}, F\right)$来识别$A_{1} \cup A_{2}$。

1. $Q=\left\{q_{0}\right\} \cup Q_{1} \cup Q_{2}$。

$N$的状态是$N_{1}$和$N_{2}$的所有状态，加上一个新的起始状态$q_{0}$。

1. 状态$q_{0}$是$N$的起始状态。
2. 接受状态集$F=F_{1} \cup F_{2}$。

$N$的接受状态是$N_{1}$和$N_{2}$的所有接受状态。这样，$N$在$N_{1}$或$N_{2}$接受时接受。

1. 定义$\delta$，使得对于任何$q \in Q$和任何$a \in \Sigma_{\varepsilon}$，

现在我们可以证明在连接下的闭包。回想一下，早些时候，如果没有非确定性，完成证明将是困难的。

定理 1.47

正则语言类别在连接运算下是封闭的。

证明思想 我们有正则语言$A_{1}$和$A_{2}$，并希望证明$A_{1} \circ A_{2}$是正则的。其思想是取两个识别$A_{1}$和$A_{2}$的NFA $N_{1}$和$N_{2}$，并将它们组合成一个新的NFA $N$，就像我们在并集情况下所做的那样，但这次以不同的方式，如图1.48所示。

将$N$的起始状态指定为$N_{1}$的起始状态。$N_{1}$的接受状态具有额外的$\varepsilon$箭头，当$N_{1}$处于接受状态时，这些箭头非确定性地允许分支到$N_{2}$，这表示它已找到了构成$A_{1}$中字符串的输入初始部分。$N$的接受状态仅为$N_{2}$的接受状态。因此，当输入可以分成两部分，第一部分被$N_{1}$接受，第二部分被$N_{2}$接受时，它才接受。我们可以将$N$视为非确定性地猜测在哪里进行分割。

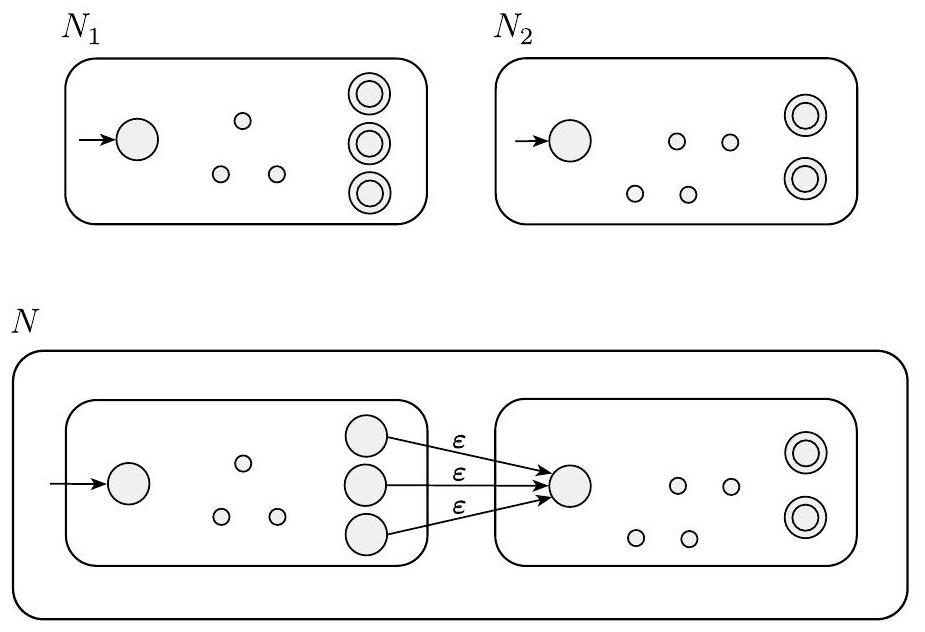
图 1.48

构造$N$以识别$A_{1} \circ A_{2}$

证明

设$N_{1}=\left(Q_{1}, \Sigma, \delta_{1}, q_{1}, F_{1}\right)$识别$A_{1}$，且

构造$N=\left(Q, \Sigma, \delta, q_{1}, F_{2}\right)$来识别$A_{1} \circ A_{2}$。

1. $Q=Q_{1} \cup Q_{2}$。

$N$的状态是$N_{1}$和$N_{2}$的所有状态。

1. 状态$q_{1}$与$N_{1}$的起始状态相同。
2. 接受状态$F_{2}$与$N_{2}$的接受状态相同。
3. 定义$\delta$，使得对于任何$q \in Q$和任何$a \in \Sigma_{\varepsilon}$，

定理 1.49

正则语言类别在星运算下是封闭的。

证明思想 我们有一个正则语言$A_{1}$，并希望证明$A_{1}^{*}$也是正则的。我们取一个识别$A_{1}$的NFA $N_{1}$，并修改它以识别$A_{1}^{*}$，如下图所示。生成的NFA $N$将在输入可以分成几部分且$N_{1}$接受每部分时接受其输入。

我们可以构造$N$像$N_{1}$一样，但在接受状态处增加额外的$\varepsilon$箭头返回到起始状态。这样，当处理到达$N_{1}$接受的一个片段的末尾时，机器$N$可以选择跳回到起始状态，尝试读取$N_{1}$接受的另一个片段。此外，我们必须修改$N$以使其接受$\varepsilon$，而$\varepsilon$始终是$A_{1}^{*}$的成员。一个（稍微不太好）的想法是简单地将起始状态添加到接受状态集。这种方法当然会将$\varepsilon$添加到识别的语言中，但它也可能添加其他不希望的字符串。练习1.15要求举例说明这种想法的失败。解决方法是添加一个新的起始状态，该状态也是接受状态，并且具有一个指向旧起始状态的$\varepsilon$箭头。这个解决方案具有在不添加任何其他内容的情况下将$\varepsilon$添加到语言中的期望效果。

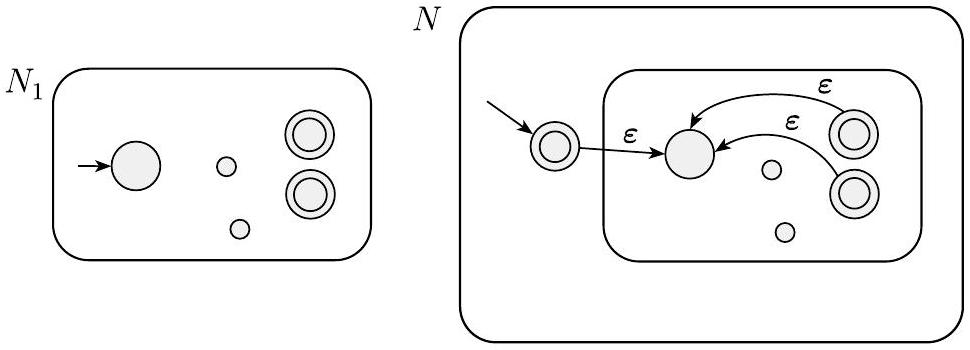
图 1.50

构造$N$以识别$A^{*}$

证明 设$N_{1}=\left(Q_{1}, \Sigma, \delta_{1}, q_{1}, F_{1}\right)$识别$A_{1}$。

构造$N=\left(Q, \Sigma, \delta, q_{0}, F\right)$来识别$A_{1}^{*}$。

1. $Q=\left\{q_{0}\right\} \cup Q_{1}$。

$N$的状态是$N_{1}$的状态加上一个新的起始状态。

1. 状态$q_{0}$是新的起始状态。
2. $F=\left\{q_{0}\right\} \cup F_{1}$。

接受状态是旧的接受状态加上新的起始状态。

1. 定义$\delta$，使得对于任何$q \in Q$和任何$a \in \Sigma_{\varepsilon}$，