1_正则语言1.4.ZH

11.4 非正则语言

为了理解有限自动机的能力，您还必须理解它们的局限性。在本节中，我们展示了如何证明某些语言无法被任何有限自动机识别。

让我们以语言 $B=\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 为例。如果我们试图找到一个识别 $B$ 的 DFA，我们会发现机器似乎需要在读取输入时记住已经看到了多少个 0。因为 0 的数量没有限制，机器将不得不跟踪无限数量的可能性。但是，它无法用任何有限数量的状态来做到这一点。

接下来，我们提出一种方法来证明像 $B$ 这样的语言是非正则的。难道前面已经给出的论证没有证明非正则性吗，因为 0 的数量是无限的？它没有。仅仅因为语言似乎需要无限的内存并不意味着它必然如此。对于语言 $B$ 来说确实是这样；但其他语言似乎需要无限数量的可能性，但实际上它们是正则的。例如，考虑字母表 $\Sigma=\{0,1\}$ 上的两种语言：

乍一看，在每种情况下，识别机器似乎都需要计数，因此这两种语言似乎都不是正则的。正如预期的那样，$C$ 是非正则的，但令人惊讶的是 $D$ 是正则的！$^{6}$ 因此，我们的直觉有时会误导我们，这就是为什么我们需要数学证明来确定。在本节中，我们展示了如何证明某些语言是非正则的。

正则语言的泵引理

我们证明非正则性的技术源于一个关于正则语言的定理，传统上称为泵引理。该定理指出，所有正则语言都具有一个特殊的性质。如果我们能证明一种语言不具备此性质，那么我们就可以确定它不是正则的。该性质表明，如果语言中的所有字符串的长度至少达到某个特殊值（称为泵浦长度），则它们可以被“泵浦”。这意味着每个这样的字符串都包含一个可以重复任意次数的部分，而生成的字符串仍然属于该语言。

[^4]定理 1.70

泵引理 如果 $A$ 是一个正则语言，那么存在一个数 $p$（泵浦长度），如果 $s$ 是 $A$ 中任何长度至少为 $p$ 的字符串，那么 $s$ 可以被分成三部分，$s=x y z$，满足以下条件：

1. 对于每个 $i \geq 0, x y^{i} z \in A$,
2. $|y|>0$, 并且
3. $|x y| \leq p$.

回想一下表示字符串 $s$ 长度的 $|s|$ 符号，$y^{i}$ 表示 $y$ 的 $i$ 个副本连接在一起，而 $y^{0}$ 等于 $\varepsilon$。

当 $s$ 被分成 $x y z$ 时，$x$ 或 $z$ 可以是 $\varepsilon$，但条件 2 说明 $y \neq \varepsilon$。请注意，如果没有条件 2，该定理将是显然成立的。条件 3 说明 $x$ 和 $y$ 两部分的长度最多为 $p$。这是一个额外的技术条件，我们在证明某些语言是非正则时偶尔会发现它很有用。有关条件 3 的应用，请参阅例 1.74。

证明思想 设 $M=\left(Q, \Sigma, \delta, q_{1}, F\right)$ 是一个识别 $A$ 的 DFA。我们将泵浦长度 $p$ 指定为 $M$ 的状态数。我们证明 $A$ 中任何长度至少为 $p$ 的字符串 $s$ 可以被分成三部分 $x y z$，满足我们的三个条件。如果 $A$ 中没有长度至少为 $p$ 的字符串怎么办？那么我们的任务甚至更容易，因为该定理就变成空洞地真：显然，如果不存在这样的字符串，则三个条件对所有长度至少为 $p$ 的字符串都成立。

如果 $A$ 中的 $s$ 的长度至少为 $p$，请考虑 $M$ 在使用输入 $s$ 进行计算时所经历的状态序列。它从起始状态 $q_{1}$ 开始，然后转到，比如说，$q_{3}$，然后，比如说，$q_{20}$，然后 $q_{9}$，依此类推，直到在状态 $q_{13}$ 处到达 $s$ 的末尾。由于 $s$ 在 $A$ 中，我们知道 $M$ 接受 $s$，所以 $q_{13}$ 是一个接受状态。

如果我们让 $n$ 为 $s$ 的长度，则状态序列 $q_{1}, q_{3}, q_{20}, q_{9}, \ldots, q_{13}$ 的长度为 $n+1$。因为 $n$ 至少为 $p$，所以我们知道 $n+1$ 大于 $M$ 的状态数 $p$。因此，该序列必须包含一个重复的状态。这个结果是鸽巢原理的一个例子，这是一个花哨的名称，用于说明一个相当明显的论点：如果将 $p$ 只鸽子放入少于 $p$ 个鸽巢中，那么某个鸽巢中必然不止一只鸽子。

下图显示了字符串 $s$ 和 $M$ 在处理 $s$ 时经过的状态序列。状态 $q_{9}$ 是重复的状态。

图 1.71

示例显示 $M$ 读取 $s$ 时状态 $q_{9}$ 重复

现在我们将 $s$ 分成 $x, y$ 和 $z$ 三部分。部分 $x$ 是 $s$ 中出现在 $q_{9}$ 之前的部分，部分 $y$ 是两个 $q_{9}$ 之间出现的部分，

部分 $z$ 是 $s$ 的剩余部分，出现在第二个 $q_{9}$ 之后。因此 $x$ 将 $M$ 从状态 $q_{1}$ 带到 $q_{9}$，$y$ 将 $M$ 从 $q_{9}$ 带回到 $q_{9}$，而 $z$ 将 $M$ 从 $q_{9}$ 带到接受状态 $q_{13}$，如下图所示。

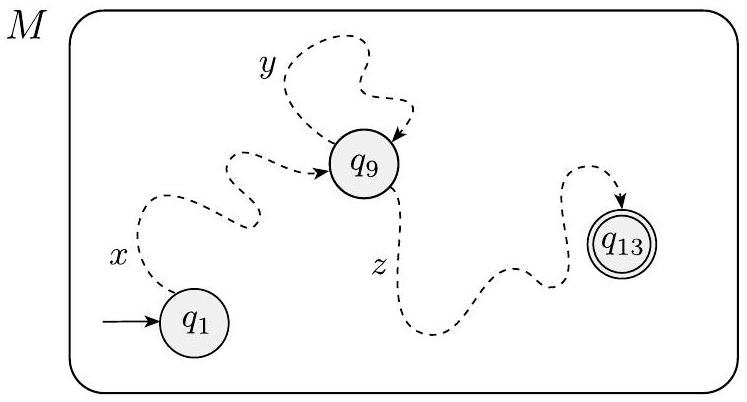
图 1.72

示例显示字符串 $x, y$ 和 $z$ 如何影响 $M$

让我们看看为什么这种对 $s$ 的划分满足这三个条件。假设我们运行 $M$ 在输入 $x y y z$ 上。我们知道 $x$ 将 $M$ 从 $q_{1}$ 带到 $q_{9}$，然后第一个 $y$ 将它从 $q_{9}$ 带回到 $q_{9}$，第二个 $y$ 也是如此，然后 $z$ 将它带到 $q_{13}$。由于 $q_{13}$ 是一个接受状态，$M$ 接受输入 $x y y z$。同样，它将接受任何 $i>0$ 的 $x y^{i} z$。对于 $i=0$ 的情况，$x y^{i} z=x z$，它也因类似原因被接受。这确立了条件 1。

检查条件 2，我们看到 $|y|>0$，因为它是 $s$ 中在状态 $q_{9}$ 的两次不同出现之间发生的部分。

为了得到条件 3，我们确保 $q_{9}$ 是序列中第一次重复。根据鸽巢原理，序列中前 $p+1$ 个状态必须包含一个重复。因此，$|x y| \leq p$。

证明 设 $M=\left(Q, \Sigma, \delta, q_{1}, F\right)$ 是一个识别 $A$ 的 DFA，且 $p$ 是 $M$ 的状态数。

设 $s=s_{1} s_{2} \cdots s_{n}$ 是 $A$ 中的一个长度为 $n$ 的字符串，其中 $n \geq p$。设 $r_{1}, \ldots, r_{n+1}$ 是 $M$ 在处理 $s$ 时进入的状态序列，因此对于 $1 \leq i \leq n$，有 $r_{i+1}=\delta\left(r_{i}, s_{i}\right)$。这个序列的长度为 $n+1$，至少为 $p+1$。根据鸽巢原理，序列中前 $p+1$ 个元素中必然有两个是相同的状态。我们称第一个为 $r_{j}$，第二个为 $r_{l}$。因为 $r_{l}$ 出现在从 $r_{1}$ 开始的序列中前 $p+1$ 个位置之内，所以 $l \leq p+1$。现在设 $x=s_{1} \cdots s_{j-1}, y=s_{j} \cdots s_{l-1}$, 且 $z=s_{l} \cdots s_{n}$。

由于 $x$ 将 $M$ 从 $r_{1}$ 带到 $r_{j}$，$y$ 将 $M$ 从 $r_{j}$ 带到 $r_{j}$，而 $z$ 将 $M$ 从 $r_{j}$ 带到接受状态 $r_{n+1}$，所以 $M$ 必须接受 $x y^{i} z$（对于 $i \geq 0$）。我们知道 $j \neq l$，所以 $|y|>0$；并且 $l \leq p+1$，所以 $|x y| \leq p$。因此我们满足了泵引理的所有条件。

要使用泵引理证明语言 $B$ 不是正则的，首先假设 $B$ 是正则的以得到矛盾。然后使用泵引理保证存在一个泵浦长度 $p$，使得 $B$ 中所有长度大于或等于 $p$ 的字符串都可以被泵浦。接下来，找到 $B$ 中一个长度大于或等于 $p$ 但不能被泵浦的字符串 $s$。最后，通过考虑将 $s$ 分成 $x, y, z$ 的所有方式（如果方便，考虑泵引理的条件 3），并对于每种这样的划分，找到一个 $i$ 值使得 $x y^{i} z \notin B$ 来证明 $s$ 不能被泵浦。这最后一步通常涉及将 $s$ 的各种划分方式分组为几种情况并单独分析它们。如果 $B$ 是正则的，那么 $s$ 的存在与泵引理相矛盾。因此 $B$ 不可能是正则的。

找到 $s$ 有时需要一些创造性的思考。您可能需要在几个 $s$ 的候选字符串中进行尝试，才能找到一个有效的。尝试 $B$ 中那些似乎展现了 $B$ 的非正则性“本质”的成员。在下面的一些例子中，我们将进一步讨论寻找 $s$ 的任务。

例 1.73

设 $B$ 为语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$。我们使用泵引理证明 $B$ 不是正则的。证明采用反证法。

假设 $B$ 是正则的，这与事实相反。设 $p$ 为泵引理给出的泵浦长度。选择 $s$ 为字符串 $0^{p} 1^{p}$。因为 $s$ 是 $B$ 的一个成员，并且 $s$ 的长度大于 $p$，所以泵引理保证 $s$ 可以被分成三部分，$s=x y z$，其中对于任何 $i \geq 0$，字符串 $x y^{i} z$ 都在 $B$ 中。我们考虑三种情况来证明这个结果是不可能的。

1. 字符串 $y$ 只由 0 组成。在这种情况下，字符串 $x y y z$ 的 0 的数量多于 1 的数量，因此不是 $B$ 的成员，违反了泵引理的条件 1。这种情况产生了矛盾。
2. 字符串 $y$ 只由 1 组成。这种情况也产生了矛盾。
3. 字符串 $y$ 由 0 和 1 组成。在这种情况下，字符串 $x y y z$ 可能有相同数量的 0 和 1，但是它们的顺序会错乱，一些 1 会在 0 之前。因此它不是 $B$ 的成员，这与事实矛盾。

因此，如果我们假设 $B$ 是正则的，那么矛盾是不可避免的，所以 $B$ 不是正则的。请注意，我们可以通过应用泵引理的条件 3 来简化此论证，以消除情况 2 和 3。

在此例中，寻找字符串 $s$ 很容易，因为 $B$ 中任何长度为 $p$ 或更长的字符串都可以。在接下来的两个例子中，某些 $s$ 的选择不起作用，因此需要额外小心。

例 1.74

设 $C=\{w \mid w \text { 包含相同数量的 } 0 \text { 和 } 1\}$。我们使用泵引理证明 $C$ 不是正则的。证明采用反证法。

假设相反，$C$ 是正则的。设 $p$ 为泵浦引理给出的泵浦长度。与例 1.73 中一样，设 $s$ 为字符串 $0^{p} 1^{p}$。由于 $s$ 是 $C$ 的成员，且其长度大于 $p$，泵浦引理保证 $s$ 可以被分成三部分，$s=x y z$，其中对于任何 $i \geq 0$，字符串 $x y^{i} z$ 都在 $C$ 中。我们希望证明这个结果是不可能的。但等等，它是可能的！如果我们将 $x$ 和 $z$ 设为空字符串，并将 $y$ 设为字符串 $0^{p} 1^{p}$，那么 $x y^{i} z$ 总是包含相同数量的 0 和 1，因此在 $C$ 中。所以看起来 $s$ 可以被泵浦。

这里，泵引理中的条件 3 是有用的。它规定当泵浦 $s$ 时，它必须被分割，使得 $|x y| \leq p$。对 $s$ 可以被分割方式的这种限制使得更容易证明我们选择的字符串 $s=0^{p} 1^{p}$ 不能被泵浦。如果 $|x y| \leq p$，那么 $y$ 必须只由 0 组成，所以 $x y y z \notin C$。因此，$s$ 不能被泵浦。这给了我们所需的矛盾。

在此例中选择字符串 $s$ 比在例 1.73 中需要更仔细。如果我们选择 $s=(01)^{p}$，我们就会遇到麻烦，因为我们需要一个不能被泵浦的字符串，而那个字符串可以被泵浦，即使考虑了条件 3。您能看出如何泵浦它吗？一种方法是设置 $x=\varepsilon, y=01$ 和 $z=(01)^{p-1}$。那么对于每个 $i$ 值，$x y^{i} z \in C$。如果您的第一次尝试未能找到不能被泵浦的字符串，请不要气馁。再试一个！

证明 $C$ 非正则的另一种方法来自于我们已知 $B$ 非正则的事实。如果 $C$ 是正则的，那么 $C \cap 0^{*} 1^{*}$ 也将是正则的。原因是语言 $0^{*} 1^{*}$ 是正则的，并且正则语言类在交集下是封闭的，这我们在脚注 3（第 46 页）中证明过。但是 $C \cap 0^{*} 1^{*}$ 等于 $B$，并且我们从例 1.73 中知道 $B$ 是非正则的。

例 1.75

设 $F=\left\{w w \mid w \in\{0,1\}^{*}\right\}$。我们使用泵引理证明 $F$ 是非正则的。

假设相反，$F$ 是正则的。设 $p$ 为泵引理给出的泵浦长度。设 $s$ 为字符串 $0^{p} 10^{p} 1$。因为 $s$ 是 $F$ 的成员，并且 $s$ 的长度大于 $p$，所以泵引理保证 $s$ 可以被分成三部分，$s=x y z$，满足引理的三个条件。我们证明这个结果是不可能的。

条件 3 再次至关重要，因为没有它，如果我们让 $x$ 和 $z$ 为空字符串，我们就可以泵浦 $s$。有了条件 3，证明成立，因为 $y$ 必须只由 0 组成，所以 $x y y z \notin F$。

请注意，我们选择 $s=0^{p} 10^{p} 1$ 是为了展示 $F$ 的非正则性“本质”的字符串，而不是例如字符串 $0^{p} 0^{p}$。尽管 $0^{p} 0^{p}$ 是 $F$ 的成员，但它未能证明矛盾，因为它能被泵浦。

例 1.76

这里我们演示一个非正则的一元语言。设 $D=\left\{1^{n^{2}} \mid n \geq 0\right\}$。换句话说，$D$ 包含所有长度为完全平方数的 1 字符串。我们使用泵引理证明 $D$ 不是正则的。证明采用反证法。

假设相反，$D$ 是正则的。设 $p$ 为泵引理给出的泵浦长度。设 $s$ 为字符串 $1^{p^{2}}$。因为 $s$ 是 $D$ 的成员，且其长度至少为 $p$，泵引理保证 $s$ 可以被分成三部分，$s=x y z$，其中对于任何 $i \geq 0$，字符串 $x y^{i} z$ 都在 $D$ 中。与前面例子一样，我们证明这个结果是不可能的。在这种情况下，这样做需要对完全平方数序列进行一些思考：

请注意此序列中连续成员之间不断增长的间隔。此序列中的大成员不能彼此靠近。

现在考虑字符串 $xyz$ 和 $xy^{2}z$。这些字符串仅通过一个 $y$ 的重复而不同，因此它们的长度差异为 $y$ 的长度。根据泵引理的条件 3，$|xy| \leq p$，因此 $|y| \leq p$。我们有 $|xyz|=p^{2}$，因此 $|xy^{2}z| \leq p^{2}+p$。但是 $p^{2}+p < p^{2}+2p+1=(p+1)^{2}$。此外，条件 2 意味着 $y$ 不是空字符串，因此 $|xy^{2}z|>p^{2}$。因此，$xy^{2}z$ 的长度严格介于连续的完全平方数 $p^{2}$ 和 $(p+1)^{2}$ 之间。因此，这个长度本身不可能是完全平方数。所以我们得到了矛盾 $xy^{2}z \notin D$，并得出结论 $D$ 不是正则的。

例 1.77

有时“向下泵浦”在应用泵引理时很有用。我们使用泵引理证明 $E=\left\{0^{i} 1^{j} \mid i>j\right\}$ 不是正则的。证明采用反证法。

假设 $E$ 是正则的。设 $p$ 为泵引理给出的 $E$ 的泵浦长度。设 $s=0^{p+1} 1^{p}$。那么 $s$ 可以分成 $x y z$，满足泵引理的条件。根据条件 3，$y$ 只包含 0。让我们检查字符串 $x y y z$ 以查看它是否可以在 $E$ 中。添加一个额外的 $y$ 副本会增加 0 的数量。但是，$E$ 包含所有 0 数量多于 1 数量的 $0^{*} 1^{*}$ 字符串，因此增加 0 的数量仍然会得到一个在 $E$ 中的字符串。没有发生矛盾。我们需要尝试其他方法。

泵引理指出，即使 $i=0$，也有 $x y^{i} z \in E$，所以我们考虑字符串 $x y^{0} z=x z$。删除字符串 $y$ 会减少 $s$ 中 0 的数量。回想一下 $s$ 中 0 的数量只比 1 的数量多一个。因此，$x z$ 不可能比 1 包含更多 0，所以它不能是 $E$ 的成员。因此我们得到一个矛盾。

习题

$^{\text {A }}$ 1.1 以下是两个 DFA $M_{1}$ 和 $M_{2}$ 的状态图。回答关于每个机器的以下问题。

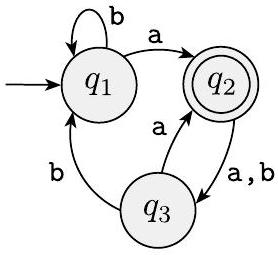
$M_{1}$

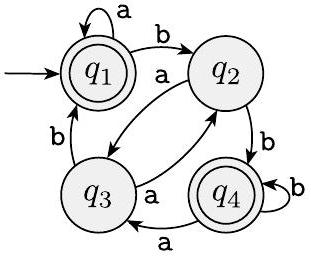
$M_{2}$

a. 起始状态是什么？

b. 接受状态集是什么？

c. 机器在输入 aabb 时经过的状态序列是什么？

d. 机器是否接受字符串 aabb？

e. 机器是否接受字符串 $\varepsilon$？

$^{\text {A }}$ 1.2 给出练习 1.1 中图示机器 $M_{1}$ 和 $M_{2}$ 的形式化描述。

1.3 DFA $M$ 的形式化描述是 $\left(\left\{q_{1}, q_{2}, q_{3}, q_{4}, q_{5}\right\},\{\mathrm{u}, \mathrm{d}\}, \delta, q_{3},\left\{q_{3}\right\}\right)$，其中 $\delta$ 由下表给出。给出该机器的状态图。

| | u | d |

| :---: | :---: | :---: |

| $q_{1}$ | $q_{1}$ | $q_{2}$ |

| $q_{2}$ | $q_{1}$ | $q_{3}$ |

| $q_{3}$ | $q_{2}$ | $q_{4}$ |

| $q_{4}$ | $q_{3}$ | $q_{5}$ |

| $q_{5}$ | $q_{4}$ | $q_{5}$ |

1.4 以下每种语言都是两种简单语言的交集。在每个部分中，为简单语言构造 DFA，然后使用脚注 3（第 46 页）中讨论的构造方法将它们组合起来，给出给定语言的 DFA 状态图。在所有部分中，$\Sigma=\{\mathrm{a}, \mathrm{b}\}$。

a. $\{w \mid w$ 至少有三个 a 和至少两个 b $\}$

$^{\text {A }}$ b. $\{w \mid w$ 恰好有两个 a 和至少两个 b $\}$

c. $\{w \mid w$ 有偶数个 a 和一个或两个 b $\}$

$^{\text {A }}$ d. $\{w \mid w$ 有偶数个 a，且每个 $\mathbf{a}$ 后面至少跟一个 $\mathbf{b}\}$

e. $\{w \mid w$ 以 $\mathbf{a}$ 开头且最多只有一个 $\mathbf{b}\}$

f. $\{w \mid w$ 有奇数个 a 且以 $\mathbf{b}$ 结尾 $\}$

g. $\{w \mid w$ 长度为偶数且有奇数个 a $\}$

1.5 以下每种语言都是一种更简单语言的补集。在每个部分中，为更简单语言构造一个 DFA，然后用它给出给定语言的 DFA 状态图。在所有部分中，$\Sigma=\{\mathrm{a}, \mathrm{b}\}$。

$^{\text {A }}$ a. $\{w \mid w$ 不包含子串 $\mathbf{ab}\}$

$^{\text {A }}$ b. $\{w \mid w$ 不包含子串 baba $\}$

c. $\{w \mid w$ 既不包含子串 ab 也不包含 ba $\}$

d. $\left\{w \mid w\right.$ 是任何不在 $\left.\mathbf{a}^{*} \mathbf{b}^{*} \text { 中的字符串 }\right\}$

e. $\left\{w \mid w\right.$ 是任何不在 $\left.\left(\mathbf{a b}^{+}\right)^{*} \text { 中的字符串 }\right\}$

f. $\left\{w \mid w\right.$ 是任何不在 $\mathrm{a}^{*} \cup \mathrm{b}^{*} \text { 中的字符串 }\right\}$

g. $\{w \mid w$ 是任何不包含恰好两个 a 的字符串 $\}$

h. $\{w \mid w$ 是除了 $\mathbf{a}$ 和 $\mathbf{b}$ 之外的任何字符串 $\}$

1.6 给出识别以下语言的 DFA 状态图。在所有部分中，字母表为 $\{0,1\}$。

a. $\{w \mid w$ 以 1 开头并以 0 结尾 $\}$

b. $\{w \mid w$ 包含至少三个 1$\}$

c. $\{w \mid w$ 包含子串 0101 (即，$w=x 0101 y$ 对于某些 $x$ 和 $y$ ) $\}$

d. $\{w \mid w$ 长度至少为 3 且其第三个符号为 0$\}$

e. $\{w \mid w$ 以 0 开头且长度为奇数，或以 1 开头且长度为偶数 $\}$

f. $\{w \mid w$ 不包含子串 110$\}$

g. $\{w \mid w$ 的长度最多为 5$\}$

h. $\{w \mid w$ 是除了 11 和 111 之外的任何字符串 $\}$

i. $\{w \mid w$ 的每个奇数位置都是 1$\}$

j. $\{w \mid w$ 包含至少两个 0 和最多一个 1$\}$

k. $\{\varepsilon, 0\}$

l. $\{w \mid w$ 包含偶数个 0，或包含恰好两个 1$\}$

m. 空集

n. 除了空字符串之外的所有字符串

1.7 给出具有指定状态数的 NFA 状态图，识别以下每种语言。在所有部分中，字母表为 $\{0,1\}$。

$^{\mathrm{A}}$ a. 语言 $\{w \mid w$ 以 00 结尾 $\}$ 具有三个状态

b. 练习 1.6c 的语言具有五个状态

c. 练习 1.6l 的语言具有六个状态

d. 语言 $\{0\}$ 具有两个状态

e. 语言 $0^{*} 1^{*} 0^{+}$具有三个状态

$^{\text {A }}$ f. 语言 $1^{*}\left(001^{+}\right)^{*}$ 具有三个状态

g. 语言 $\{\varepsilon\}$ 具有一个状态

h. 语言 $0^{*}$ 具有一个状态

1.8 使用定理 1.45 证明中的构造方法，给出识别下列语言并集的 NFA 状态图：

a. 练习 1.6a 和 1.6b。

b. 练习 1.6c 和 1.6f。

1.9 使用定理 1.47 证明中的构造方法，给出识别下列语言连接的 NFA 状态图：

a. 练习 1.6g 和 1.6i。

b. 练习 1.6b 和 1.6m。

1.10 使用定理 1.49 证明中的构造方法，给出识别下列语言星号操作的 NFA 状态图：

a. 练习 1.6b。

b. 练习 1.6j。

c. 练习 1.6m。

$^{\text {A }}$ 1.11 证明每个 NFA 都可以转换为一个具有单一接受状态的等价 NFA。

1.12 设 $D=\{w \mid w$ 包含偶数个 a 和奇数个 b，且不包含子串 ab$\}$。给出一个有五个状态的 DFA，它识别 $D$，并给出一个生成 $D$ 的正则表达式。（建议：更简单地描述 $D$。）

1.13 设 $F$ 是所有不包含被奇数个符号分隔的两个 1 的字符串的语言。给出一个有五个状态的 DFA 状态图，它识别 $F$。（您可能会发现，首先找到一个 4 状态的 $F$ 的补集的 NFA 会有所帮助。）

1.14 a. 证明如果 $M$ 是一个识别语言 $B$ 的 DFA，交换 $M$ 中的接受状态和非接受状态会产生一个识别 $B$ 的补集的新 DFA。得出正则语言类在补集操作下是封闭的结论。

b. 通过给出一个例子来证明，如果 $M$ 是一个识别语言 $C$ 的 NFA，交换 $M$ 中的接受状态和非接受状态不一定产生一个识别 $C$ 的补集的新 NFA。NFA 识别的语言类在补集操作下是封闭的吗？解释您的答案。

1.15 给出反例，说明以下构造未能证明定理 1.49，即正则语言类在星号操作下的封闭性。$^{7}$ 设 $N_{1}=\left(Q_{1}, \Sigma, \delta_{1}, q_{1}, F_{1}\right)$ 识别 $A_{1}$。构造 $N=\left(Q_{1}, \Sigma, \delta, q_{1}, F\right)$ 如下。$N$ 应该识别 $A_{1}^{*}$。

a. $N$ 的状态是 $N_{1}$ 的状态。

b. $N$ 的起始状态与 $N_{1}$ 的起始状态相同。

c. $F=\left\{q_{1}\right\} \cup F_{1}$。

接受状态 $F$ 是旧的接受状态加上其起始状态。

d. 定义 $\delta$ 使得对于任何 $q \in Q_{1}$ 和任何 $a \in \Sigma_{\varepsilon}$，

（建议：以图形方式展示此构造，如图 1.50 所示。）

[^5]1.16 使用定理 1.39 中给出的构造方法，将以下两个非确定性有限自动机转换为等价的确定性有限自动机。

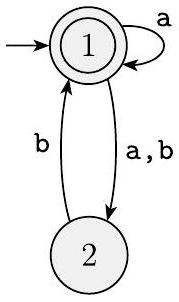
(a)

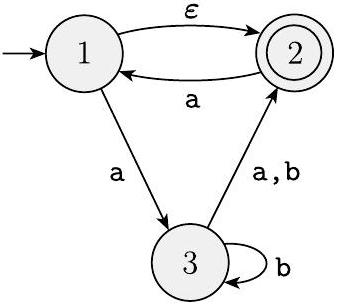
(b)

1.17 a. 给出一个 NFA，识别语言 $(01 \cup 001 \cup 010)^{*}$。

b. 将此 NFA 转换为等价的 DFA。只给出从起始状态可达的 DFA 部分。

1.18 给出生成练习 1.6 中语言的正则表达式。

1.19 使用引理 1.55 中描述的步骤将以下正则表达式转换为非确定性有限自动机。

a. $(0 \cup 1)^{*} 000(0 \cup 1)^{*}$

b. $\left(\left((00)^{*}(11)\right) \cup 01\right)^{*}$

c. $\emptyset^{*}$

1.20 对于以下每种语言，给出两个是成员的字符串和两个不是成员的字符串——每个部分总共四个字符串。在所有部分中，假设字母表 $\Sigma=\{\mathrm{a}, \mathrm{b}\}$。

a. $\mathrm{a}^{*} \mathrm{~b}^{*}$

b. $\mathrm{a}(\mathrm{ba})^{*} \mathrm{~b}$

c. $\mathrm{a}^{*} \cup \mathrm{b}^{*}$

d. $(\mathrm{aaa})^{*}$

e. $\Sigma^{*} \mathrm{a} \Sigma^{*} \mathrm{~b} \Sigma^{*} \mathrm{a} \Sigma^{*}$

f. $\mathrm{aba} \cup \mathrm{bab}$

g. $(\varepsilon \cup a) b$

h. $(\mathrm{a} \cup \mathrm{ba} \cup \mathrm{bb}) \Sigma^{*}$

1.21 使用引理 1.60 中描述的步骤将以下有限自动机转换为正则表达式。

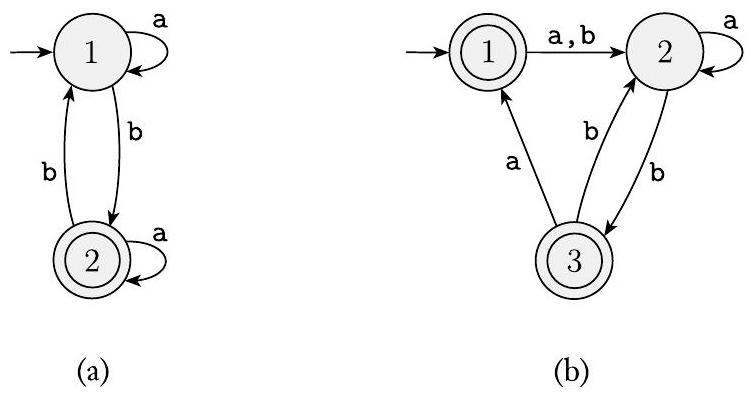
1.22 在某些编程语言中，注释出现在 /\# 和 \#/ 等分隔符之间。设 $C$ 为所有有效分隔注释字符串的语言。$C$ 的成员必须以 /\# 开头并以 \#/ 结尾，但不能有中间的 \#/。为简单起见，假设 $C$ 的字母表为 $\Sigma=\{\mathrm{a}, \mathrm{b}, /, \#\}$。

a. 给出识别 $C$ 的 DFA。

b. 给出生成 $C$ 的正则表达式。

$^{\text {A }}$ 1.23 设 $B$ 是字母表 $\Sigma$ 上的任何语言。证明 $B=B^{+}$当且仅当 $B B \subseteq B$。

1.24 有限状态传感器 (FST) 是一种确定性有限自动机，其输出是字符串，而不仅仅是接受或拒绝。以下是有限状态传感器 $T_{1}$ 和 $T_{2}$ 的状态图。

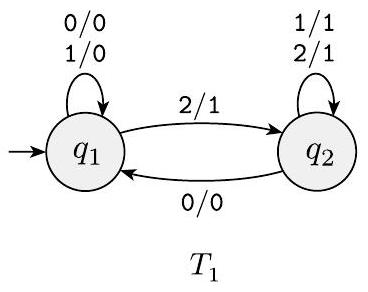
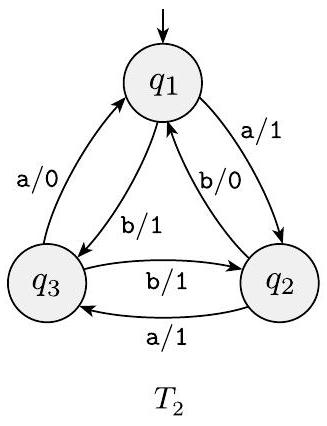
FST 的每个转换都标有两个符号，一个表示该转换的输入符号，另一个表示输出符号。这两个符号用斜杠 / 分隔。在 $T_{1}$ 中，从 $q_{1}$ 到 $q_{2}$ 的转换的输入符号是 2，输出符号是 1。某些转换可能具有多个输入-输出对，例如 $T_{1}$ 中从 $q_{1}$ 到自身的转换。当 FST 在输入字符串 $w$ 上进行计算时，它逐个读取输入符号 $w_{1} \cdots w_{n}$，并从起始状态开始，通过将输入标签与符号序列 $w_{1} \cdots w_{n}=w$ 匹配来遵循转换。每次它沿着一个转换移动时，它都会输出相应的输出符号。例如，在输入 2212011 上，机器 $T_{1}$ 进入状态序列 $q_{1}, q_{2}, q_{2}, q_{2}, q_{2}, q_{1}, q_{1}$ 并产生输出 1111000。在输入 abbb 上，$T_{2}$ 输出 1011。在以下每个部分中，给出进入的状态序列和产生的输出。

a. 输入 011 上的 $T_{1}$

b. 输入 211 上的 $T_{1}$

c. 输入 121 上的 $T_{1}$

d. 输入 0202 上的 $T_{1}$

e. 输入 b 上的 $T_{2}$

f. 输入 bbab 上的 $T_{2}$

g. 输入 bbbbbb 上的 $T_{2}$

h. 输入 $\varepsilon$ 上的 $T_{2}$

1.25 阅读练习 1.24 中给出的有限状态传感器非正式定义。根据定义 1.5（第 35 页）中的模式，给出该模型的形式化定义。假设 FST 有一个输入字母表 $\Sigma$ 和一个输出字母表 $\Gamma$，但没有一组接受状态。包括 FST 计算的形式化定义。（提示：FST 是一个 5 元组。其转换函数的形式为 $\delta: Q \times \Sigma \longrightarrow Q \times \Gamma$。）

1.26 使用您在练习 1.25 中给出的解决方案，给出练习 1.24 中描绘的机器 $T_{1}$ 和 $T_{2}$ 的形式化描述。

1.27 阅读练习 1.24 中给出的有限状态传感器非正式定义。给出一个具有以下行为的 FST 状态图。它的输入和输出字母表是 $\{0,1\}$。它的输出字符串在偶数位置与输入字符串相同，但在奇数位置反转。例如，在输入 0000111 上，它应该输出 1010010。

1.28 使用定理 1.54 中给出的步骤将以下正则表达式转换为 NFA。在所有部分中，$\Sigma=\{\mathrm{a}, \mathrm{b}\}$。

a. $\mathrm{a}(\mathrm{abb})^{*} \cup \mathrm{~b}$

b. $\mathrm{a}^{+} \cup(\mathrm{ab})^{+}$

c. $\left(a \cup b^{+}\right) a^{+} b^{+}$

1.29 使用泵引理证明以下语言不是正则的。

A. $A_{1}=\left\{0^{n} 1^{n} 2^{n} \mid n \geq 0\right\}$

b. $A_{2}=\left\{w w w \mid w \in\{\mathbf{a}, \mathbf{b}\}^{*}\right\}$

Ac. $A_{3}=\left\{\mathrm{a}^{2^{n}} \mid n \geq 0\right\}$ (此处，$\mathrm{a}^{2^{n}}$ 表示 $2^{n}$ 个 a 的字符串。)

1.30 描述以下“证明” $0^{*} 1^{*}$ 不是正则语言的错误。（错误必然存在，因为 $0^{*} 1^{*}$ 是正则的。）该证明采用反证法。假设 $0^{*} 1^{*}$ 是正则的。设 $p$ 为泵引理给出的 $0^{*} 1^{*}$ 的泵浦长度。选择 $s$ 为字符串 $0^{p} 1^{p}$。您知道 $s$ 是 $0^{*} 1^{*}$ 的成员，但例 1.73 表明 $s$ 不能被泵浦。因此您得到了一个矛盾。所以 $0^{*} 1^{*}$ 不是正则的。