11. 非正则语言导论
1.1 有限自动机的局限性
📜 [原文1]
为了理解有限自动机的能力,您还必须理解它们的局限性。在本节中,我们展示了如何证明某些语言无法被任何有限自动机识别。
这段话是本节内容的开篇,旨在设定学习目标。它强调了学习一个概念的两个方面:知道它能做什么(能力)和知道它不能做什么(局限性)。
- 有限自动机的能力:我们在前面的章节中已经学习到,有限自动机 (Finite Automata, FA),包括 DFA(确定性有限自动机) 和 NFA(非确定性有限自动机),它们的核心能力是识别正则语言。任何可以用正则表达式描述的语言,都可以构建一个对应的有限自动机来接受它。
- 有限自动机的局限性:然而,有限自动机并非万能。它的“有限”二字是其核心特征,也是其根本局限所在。这里的“有限”指的是状态的数量是有限的。这个限制意味着有限自动机的“记忆能力”是有限的。它无法处理那些需要无限记忆才能正确判断的语言。
- 本节目标:本节的核心任务就是从理论上严格地证明这种局限性的存在。我们将学习一种形式化的方法,用来论证某些特定的语言超出了有限自动机的识别能力范围,这些语言因此被称为“非正则语言”。
本段不包含数学公式或特殊符号。
- 能力示例:对于语言 $L = \{ w \mid w \text{以'ab'结尾} \}$,这是一个正则语言。我们可以轻松构建一个DFA来识别它。这个DFA只需要有限的几个状态(例如,一个初始状态,一个看到'a'的状态,一个看到'ab'的接受状态)就能完成任务,无论输入字符串有多长。它不需要“记住”整个字符串,只需要跟踪最后几个字符是否匹配'ab'。
- 局限性预告:对于语言 $B = \{ 0^n 1^n \mid n \ge 0 \}$,即等数量的0后面跟着等数量的1。如果一个字符串是 00000000001111111111(10个0,10个1),自动机在读完0之后,需要准确地知道它读了10个0,以便在后面匹配10个1。如果字符串是 0...0(一百万个0)1...1(一百万个1),自动机就需要记住“一百万”这个信息。由于n可以是任意大的数,需要记忆的可能性是无限的,而有限自动机的状态是有限的,因此直觉上它无法完成这个任务。
- 易错点:初学者可能会错误地认为,只要一个语言的描述看起来简单,它就是正则的。本节将通过例子证明,描述的简洁性与语言是否正则没有必然联系。
- 关键区别:能力与局限性的核心区别在于,问题是否可以用有限的记忆来解决。识别“以'ab'结尾”只需要记住最后两个字符,这是有限的记忆。而识别“等量的0和等量的1”则需要对任意数量的0进行计数,这需要无限的记忆。
1.2 直觉的挑战:需要计数的语言
📜 [原文2]
让我们以语言 $B=\left\\{0^{n} 1^{n} \mid n \geq 0\right\\}$ 为例。如果我们试图找到一个识别 $B$ 的 DFA,我们会发现机器似乎需要在读取输入时记住已经看到了多少个 0。因为 0 的数量没有限制,机器将不得不跟踪无限数量的可能性。但是,它无法用任何有限数量的状态来做到这一点。
这段话通过一个具体的例子 $B=\left\\{0^{n} 1^{n} \mid n \geq 0\right\\}$,来深化对有限自动机局限性的直观理解。
- 语言 B 的定义:语言 $B$ 由一串0后面跟着一串1组成,并且0的数量和1的数量必须完全相等。
- 构建 DFA 的思考过程:想象我们是一个 DFA,正在读取一个属于 $B$ 的字符串,比如 $000111$。
- 读到第一个 0,我们需要记住“看到了一个0”。
- 读到第二个 0,我们需要记住“看到了两个0”。
- 读到第三个 0,我们需要记住“看到了三个0”。
- 然后,开始读 1。读到第一个 1,我们需要将“三个0”的计数减一,变成“还需匹配两个1”。
- 读到第二个 1,计数减一,变成“还需匹配一个1”。
- 读到第三个 1,计数减为零。此时字符串结束,我们判断该字符串属于语言 $B$。
- 问题的核心:在这个过程中,“记住看到了多少个0”是关键。因为 $n$ (0的数量) 可以是任何非负整数(0, 1, 2, ..., 一百万, ...),所以理论上,DFA 需要有能力区分“看到1个0”、“看到2个0”、“看到3个0”... 直至无限多种情况。
- DFA的局限性:一个 DFA 的状态是有限的。我们可以用状态 $q_k$ 来代表“已经看到了 $k$ 个0”。但如果 DFA 只有 $m$ 个状态,它最多只能准确记录到 $m-1$ 个0。当输入的0的数量超过 $m-1$ 时,DFA必然会混淆,无法再精确记录0的数量。例如,一个有10个状态的DFA,无法区分输入是“10个0”还是“11个0”。
- 结论:因此,直观上判断,没有任何一个拥有有限状态的DFA能够完美识别语言 $B$。
- $B=\left\\{0^{n} 1^{n} \mid n \geq 0\right\\}$
- $B$:这是我们为这个特定语言起的名字。
- $\\{\dots\\}$:集合的表示法。语言在形式上被定义为字符串的集合。
- $0^{n} 1^{n}$:这描述了集合中每个字符串的形式。
- $0^{n}$:表示符号 '0' 连续出现 $n$ 次。
- $1^{n}$:表示符号 '1' 连续出现 $n$ 次。
- 整个表达式意味着字符串由 $n$ 个 '0' 紧接着 $n$ 个 '1' 构成。
- $\mid$:分隔符,读作“使得”(such that),用来分隔字符串的形式和其必须满足的条件。
- $n \geq 0$:这是变量 $n$ 必须满足的条件。它意味着 $n$ 可以是0, 1, 2, 3, ... 等任何非负整数。
- 示例 1 (属于 B):
- 取 $n=3$。字符串的形式是 $0^3 1^3$,即 000111。因为 000111 符合“$n$个0后面跟$n$个1”的形式,所以 000111 $\in B$。
- 示例 2 (属于 B, 边界情况):
- 取 $n=0$。字符串的形式是 $0^0 1^0$。任何符号的0次幂都是空字符串 $\varepsilon$。所以 $0^0 1^0 = \varepsilon \varepsilon = \varepsilon$。空字符串也属于语言 $B$。
- 示例 3 (不属于 B):
- 字符串 00111。这里有2个0和3个1。0和1的数量不相等($n$不统一),所以 00111 $\notin B$。
- 示例 4 (不属于 B):
- 字符串 0101。虽然0和1的数量相等(都是2个),但它的形式不是“所有0都在所有1之前”。它的形式是 0101 而不是 0011。所以 0101 $\notin B$。
- 易错点:混淆顺序。语言 $B$ 不仅仅是“包含相同数量的0和1”,它严格要求所有0必须出现在所有1之前。像 10 或 0101 这样的字符串就不属于 $B$。
- 边界情况:$n=0$。这个情况对应空字符串 $\varepsilon$。根据定义,$n=0$ 是允许的,所以 $\varepsilon$ 是语言 $B$ 的一员。任何试图识别 $B$ 的自动机都必须接受空字符串。
- 误解:无限语言 vs 非正则语言。语言 $B$ 是一个无限语言(包含无限多个字符串),但这并不直接意味着它是非正则的。例如,语言 $L = \{0^n \mid n \geq 0\}$ (所有由0组成的字符串,即 $0^*$) 也是无限语言,但它是正则的。关键区别在于是否需要无限记忆。
1.3 直觉不可靠的证明
📜 [原文3]
接下来,我们提出一种方法来证明像 $B$ 这样的语言是非正则的。难道前面已经给出的论证没有证明非正则性吗,因为 0 的数量是无限的?它没有。仅仅因为语言似乎需要无限的内存并不意味着它必然如此。对于语言 $B$ 来说确实是这样;但其他语言似乎需要无限数量的可能性,但实际上它们是正则的。例如,考虑字母表 $\\Sigma=\\{0,1\\}$ 上的两种语言:
这段话指出了一个关键问题:直觉虽然有启发性,但不能作为严格的数学证明。
- 对前面论证的质疑:我们刚刚在直觉上论证了,因为要计数的0的数量是无限的,所以语言 $B$ 看起来需要无限的内存,因此是非正则的。
- 直觉论证的缺陷:这段话明确指出,这种基于“似乎需要无限内存”的直觉论证是不充分的,它不是一个严格的数学证明。
- 为什么直觉不可靠:原因是,我们的直觉可能会被误导。有些语言,表面上看起来也需要无限计数,但通过巧妙的设计,实际上可以用有限状态的自动机来识别。这意味着它们是正则的。
- 引出反例:为了说明这一点,作者即将引入两个语言 $C$ 和 $D$。这两个语言从表面上看都需要对输入的符号进行计数,但结果一个是非正则的,另一个却是正则的。这恰恰证明了我们不能单凭直觉下判断。
- 预示后续内容:因此,我们需要一种比直觉更强大、更可靠的工具来进行判断。这个工具就是后面要介绍的泵引理 (Pumping Lemma)。
- $\Sigma=\\{0,1\\}$
- $\Sigma$ (Sigma):在形式语言理论中,$\Sigma$ 通常用来表示字母表 (alphabet),即构成语言中字符串的基本符号的集合。
- $\\{0,1\\}$:表示这个字母表由两个符号 '0' 和 '1' 组成。
- 直觉正确的例子(语言B):$B=\left\\{0^{n} 1^{n} \mid n \geq 0\right\\}$。我们的直觉是它需要无限记忆,而事实也的确如此,它是一个非正则语言。
- 直觉被误导的例子(语言D,将在下一段介绍):$D=\\{w \\mid w \text { 具有相同数量的子串 } 01 \text { 和 } 10 \text { 的出现 }\\}$。直觉上,要判断 01 和 10 的数量是否相等,似乎也需要两个计数器,这需要无限内存。但令人惊讶的是,这个语言是正则的。例如,字符串 010 中,01 出现一次,10 出现一次,数量相等。字符串 0110 中,01 出现一次,10 出现一次,数量也相等。事实证明,我们只需要检查字符串的起始符号和结束符号是否相同,就可以判断 01 和 10 的数量是否差1或相等,这可以用有限状态实现。
- 最大的易错点:将“看起来需要无限内存”等同于“非正则”。这是本段着力驳斥的观点。
- 学习重点:本段的目的是让读者建立一种意识——在形式科学中,必须使用严格的数学工具进行证明,而不能仅仅依赖主观直觉。直觉可以帮助我们形成猜想,但猜想需要被证明。
1.4 正则与非正则的惊人对比
📜 [原文4]
这里给出了两个语言 C 和 D 的形式化定义,用于展示直觉的不可靠性。
- 语言 C 的定义:
- $C$ 是一个集合,集合中的每个字符串 $w$ 都满足一个条件:$w$ 中符号 '0' 的总数等于符号 '1' 的总数。
- 这个定义不关心 '0' 和 '1' 的排列顺序。例如, 0011, 0101, 1010 都属于 $C$。
- 直觉上,为了验证一个长字符串是否属于 $C$,我们需要一个计数器。读到一个 '0' 就加一,读到一个 '1' 就减一(或反之)。因为字符串的长度没有上限,这个计数器的值也没有上限,所以看起来需要无限的内存。
- 语言 D 的定义:
- $D$ 也是一个字符串集合。它的成员 $w$ 满足的条件是:$w$ 中子串 "01" 出现的次数等于子串 "10" 出现的次数。
- 例如,在字符串 01010 中:
- 子串 "01" 出现了两次 (01010, 01010)。
- 子串 "10" 出现了两次 (01010, 01010)。
- 因为 2=2,所以 01010 $\in D$。
- 直觉上,这似乎比语言 $C$ 更复杂。我们好像需要两个独立的计数器,一个计 "01" 的数量,一个计 "10" 的数量,然后比较它们。这同样看起来需要无限的内存。
这段文字的核心就是呈现这两个在直觉上非常相似(都需要计数)的语言,为下一段揭示它们本质上的巨大差异埋下伏笔。
- $C=\\{w \\mid w \\text { 具有相同数量的 } 0 \\text { 和 } 1 \\mathrm{~s}\\}$
- $C$: 语言的名字。
- $\\{w \\mid \dots \\}$: 集合定义,表示 "$w$ 的集合,其中 $w$ 满足..."。
- $w$: 代表字母表 $\Sigma=\{0,1\}$ 上的任意一个字符串。
- "具有相同数量的 0 和 1s": 这是 $w$ 必须满足的属性。
- $D=\\{w \\mid w \\text { 具有相同数量的子串 } 01 \\text { 和 } 10 \\text { 的出现 }\\}$
- $D$: 语言的名字。
- "子串 01 和 10": 指的是字符串中连续出现的 "01" 或 "10" 片段。
- "出现的数量": 指在整个字符串 $w$ 中,"01" 作为子串总共出现了多少次,"10" 作为子串总共出现了多少次。
- 对于语言 C:
- 属于 C: 01, 10, 0011, 1100, 0101, 1010 (0和1的数量都是2)。空字符串 $\varepsilon$ 也属于 $C$ (0个0,0个1)。
- 不属于 C: 0, 1, 001, 110, 011 (0和1的数量不相等)。
- 对于语言 D:
- 属于 D:
- 010:num(01)=1, num(10)=1.
- 101:num(01)=1, num(10)=1.
- 00110:num(01)=1, num(10)=1.
- 0:num(01)=0, num(10)=0.
- 1:num(01)=0, num(10)=0.
- $\varepsilon$:num(01)=0, num(10)=0.
- 01:num(01)=1, num(10)=0. 等一下,这里我举例错了,需要重新分析。
- 让我们仔细分析一下 $D$。考虑一个字符串 $w$。扫描 $w$ 时,每次从0变到1,就产生一个 "01";每次从1变到0,就产生一个 "10"。
- 如果字符串以0开头,以0结尾 (e.g., 0...0),那么从0到1的切换次数必然等于从1到0的切换次数。例如 01110,一次0->1,一次1->0。
- 如果字符串以1开头,以1结尾 (e.g., 1...1),同理,切换次数也相等。例如 1001。
- 如果以0开头,以1结尾 (e.g., 0...1),那么0->1的切换会比1->0的切换多一次。例如 0101,两次0->1,一次1->0。
- 如果以1开头,以0结尾 (e.g., 1...0),那么1->0的切换会比0->1的切换多一次。例如 1010。
- 因此,语言 $D$ 实际上是 $\{w \mid (w \text{以0开头且以0结尾}) \lor (w \text{以1开头且以1结尾}) \lor w=\varepsilon \text{或单个字符} \}$。这是一个正则语言!可以用 0(0|1)0 | 1(0|1)1 | 0 | 1 | ε 这样的正则表达式描述。
- 所以,之前的数值示例需要修正:
- 属于 D: 010 (不属于), 101 (不属于)。01110 (属于), 1001 (属于), 0, 1, 00, 11, ε (都属于)。
- 不属于 D: 01, 10, 0101, 1010.
- 修正后的数值示例 (for D):
- 属于 D:
- $w = \varepsilon$: num(01)=0, num(10)=0.
- $w = 0$: num(01)=0, num(10)=0.
- $w = 1$: num(01)=0, num(10)=0.
- $w = 00110$: num(01)=1, num(10)=1.
- $w = 10101$: num(01)=2, num(10)=2.
- 不属于 D:
- $w = 01$: num(01)=1, num(10)=0.
- $w = 10$: num(01)=0, num(10)=1.
- $w = 0101$: num(01)=2, num(10)=1.
- 易错点 for C: 与语言 $B = \{0^n 1^n\}$ 混淆。$C$ 只要求数量相等,不要求顺序。$B$ 是 $C$ 的一个子集。
- 易错点 for D: 对子串计数的理解。子串可以重叠。例如,在 0101 中,10 和 01 是重叠的。最关键的易错点是凭直觉认为它需要无限计数,而实际上它只依赖于字符串的端点特性,这是一个非常令人惊讶和深刻的结论。
- 边界情况: 空字符串 $\varepsilon$ 和单个字符的字符串 '0', '1'。在两种语言中,num(0)=num(1)=0,num(01)=num(10)=0,所以它们都属于 $C$ 和 $D$。
1.5 直觉的证实与颠覆
📜 [原文5]
乍一看,在每种情况下,识别机器似乎都需要计数,因此这两种语言似乎都不是正则的。正如预期的那样,$C$ 是非正则的,但令人惊讶的是 $D$ 是正则的!$^{6}$ 因此,我们的直觉有时会误导我们,这就是为什么我们需要数学证明来确定。在本节中,我们展示了如何证明某些语言是非正则的。
这段话揭示了上一段设置的悬念,并最终点明了本节的核心目的。
- 重申直觉:作者首先再次强调了我们的第一印象:“乍一看...似乎都需要计数”。这指的是对于语言 $C$(等量0和1)和语言 $D$(等量子串"01"和"10"),我们的直觉都是它们需要无限的内存来进行计数。
- 揭晓答案:
- $C$ 是非正则的 (as expected):对于语言 $C$,我们的直觉是正确的。它的确需要无限的记忆来追踪0和1的数量差异,所以它不是正则语言。
- $D$ 是正则的 (surprisingly):对于语言 $D$,我们的直觉是错误的。尽管它表面上看起来需要计数,但实际上它有一个隐藏的、可以用有限状态表达的规律(即字符串的起始和结束符号是否相同)。因此,可以构建一个DFA来识别它,所以它是一个正则语言。
- 得出结论:这个惊人的对比有力地证明了“直觉会误导我们”。我们不能依赖主观感觉来判断一个语言是否正则。
- 引出解决方案:既然直觉不可靠,我们就需要一种客观、严格的数学工具。这个工具就是本节即将深入探讨的泵引理 (Pumping Lemma)。它的作用就是提供一个试金石,来形式化地、无可辩驳地证明一个语言是非正则的。
本段不包含新的数学公式或符号。
- 语言 C (非正则): 无法设计一个有固定状态数 $k$ 的DFA来区分 $0^k 1^k$ 和 $0^{k+1} 1^{k+1}$。它总会在某个点“耗尽内存”。
- 语言 D (正则): 我们可以构建一个简单的DFA来识别它。这个DFA只需要记住几件事:
- 起始状态 (尚未读取任何字符)。
- 读完第一个字符是 '0'。
- 读完第一个字符是 '1'。
- 当前在 '0' 后面。
- 当前在 '1' 后面。
- 根据当前状态和读入的下一个字符,可以判断是否产生了 '01' 或 '10' 的切换。更简单地说,一个DFA可以轻松检查一个字符串的第一个和最后一个字符。
- 一个识别 $D$ 的DFA可以设计如下:
- $q_0$ (初始状态, 接受状态, 因为 $\varepsilon, 0, 1$ 都属于 D)。
- 从 $q_0$ 读到 0 -> $q_s0$ (起始为0, 接受状态)。
- 从 $q_0$ 读到 1 -> $q_s1$ (起始为1, 接受状态)。
- 在 $q_s0$ 状态下,如果持续读 0,停留在 $q_s0$。如果读到 1,进入 $q_{mid}$ (非接受状态)。
- 在 $q_s1$ 状态下,如果持续读 1,停留在 $q_s1$。如果读到 0,进入 $q_{mid}$ (非接受状态)。
- 在 $q_{mid}$ 状态下,无论读 0 还是 1 都停留在 $q_{mid}$。
- 这是一个简化的思路,实际的DFA需要更严谨地跟踪最后一个字符。关键是,这是可以做到的,状态数量是有限的。
- 核心教训:不要相信你对“需要计数”的直觉。在没有严格证明之前,任何关于语言正则性的判断都只是一个猜想。
- 正则语言的隐藏属性:语言 $D$ 的例子揭示了,某些看似需要计数的属性,可能等价于某个可以用有限状态机跟踪的、更简单的属性。发现这种隐藏属性是理解正则语言的关键。
- 脚注6:原文中的上标 $^{6}$ 指向书末或页脚的注释,该注释通常会提供关于语言 $D$ 是正则的更详细解释或证明。
本章首先引入了有限自动机存在局限性的概念,即它们无法识别所有语言。通过核心示例语言 $B = \{0^n 1^n \mid n \ge 0\}$,直观地解释了这种局限性源于有限自动机只有有限的记忆能力(有限状态),无法处理需要无限计数的问题。然而,章节接着通过对比语言 $C$(相同数量的0和1)和语言 $D$(相同数量的子串01和10),有力地证明了直觉是不可靠的。$C$ 如预期一样是非正则的,而 $D$ 却惊人地是正则的。这个反差强调了建立一种严格的、非直觉的数学证明方法的必要性,从而为后续引入泵引理作为判断非正则语言的工具做好了铺垫。
这部分内容的存在,是为了在形式上定义和区分正则语言和非正则语言的边界。它扮演着一个承上启下的角色。
- 承上:在前文学习了有限自动机和正则表达式能“做什么”之后,本节开始探讨它们“不能做什么”,从而完整地描绘出这一计算模型的能力图谱。
- 启下:通过揭示直觉证明的不可靠性,强调了形式化证明工具的必要性,为即将登场的全章核心工具——泵引理——的引入,提供了充分的动机和背景。它告诉我们为什么需要学习泵引理。
- 有限状态机 = 一个记忆力有限的人。
- 想象一个人,他只能记住有限个数的东西,比如他只有 3 个口袋,每个口袋只能放一个写着数字的纸条。
- 识别正则语言:你让他判断一个句子是否以“你好”结尾。他不需要记住整个句子,只需要听最后两个字。当他听到“你”,就把“你”的纸条放进口袋1;接着听到“好”,就把“好”的纸条放进口袋2。任务完成。这是正则的,因为他需要的记忆(口袋数量)是固定的。
- 识别非正则语言 $B = \{0^n 1^n\}$:你让他判断一长串前半部分是“滴”,后半部分是“嗒”的声音,并且“滴”和“嗒”的次数要完全相等。他开始听“滴”,一个“滴”,他在口袋1放个“1”;两个“滴”,他在口袋2放个“2”;三个“滴”,他在口袋3放个“3”。当第四个“滴”传来时,他没有口袋放了!他的记忆耗尽了。他无法处理任意数量的“滴”。这就是非正则的本质。
- 识别语言D的陷阱:你让他判断“左右”和“右左”的切换次数是否相等。他一开始觉得需要两个计数器,感觉记忆又要耗尽。但后来他发现,只要记住第一个动作是“左”还是“右”,以及最后一个动作是“左”还是“右”,就能判断出来。例如,从左开始,到左结束,中间的“左右”和“右左”切换次数必然相等。他只需要记住开头和结尾,这是有限的记忆。这就是看似非正则,实则正则的语言。
- 有限自动机就像一个只有一个转盘密码锁的保险箱。这个密码锁只有固定的几位(有限的状态)。
- 识别正则语言,比如 (ab)*,就像这个锁的密码是 ab 或者 abab 或者 ababab... 但实际上,你只需要一个能识别 a 和 b 交替出现的状态机。这相当于密码锁的设计是:拨了a之后,下一个必须是b;拨了b之后,下一个必须是a。这个规则很简单,锁的内部结构是固定和有限的。
- 试图识别非正则语言 $B = \{0^n 1^n\}$,就像要求这个密码锁能识别 01, 0011, 000111, ... 一直到无限。这意味着密码锁需要能够“计数”你前面拨了多少个0,然后检查你后面是否拨了同样多的1。如果输入的0有一百万个,这个小小的密码锁就需要有一百万个齿轮来记录这个数字。这是不可能的,因为它的物理结构是有限的。它无法存储一个任意大的数字。
22. 证明非正则性的核心工具:泵引理
2.1 泵引理的陈述
📜 [原文6]
我们证明非正则性的技术源于一个关于正则语言的定理,传统上称为泵引理。该定理指出,所有正则语言都具有一个特殊的性质。如果我们能证明一种语言不具备此性质,那么我们就可以确定它不是正则的。该性质表明,如果语言中的所有字符串的长度至少达到某个特殊值(称为泵浦长度),则它们可以被“泵浦”。这意味着每个这样的字符串都包含一个可以重复任意次数的部分,而生成的字符串仍然属于该语言。
这段话是对泵引理 (Pumping Lemma) 的一个高度概括的介绍,阐述了它的核心思想和用途。
- 定位:泵引理是一个定理,它描述的是所有正则语言都必须遵守的一条普适性质。
- 核心用途:它是一种反证法的工具。它的逻辑是:
- 前提:所有正则语言都有属性 P。
- 待证:语言 L 是非正则的。
- 证明方法:我们来证明语言 L 没有属性 P。
- 结论:既然 L 没有属性 P,那它就不可能是正则语言。
- 性质 P 是什么? 这就是“**泵浦 (pumping)
**”性质。
- 这个性质是针对语言中足够长的字符串而言的。多长算“足够长”?这个长度由一个称为“泵浦长度 (pumping length)”的阈值决定。
- 对于任何一个长度超过这个阈值的字符串,它自身必然可以被拆分成三段。
- 中间那一段(非空)具有特殊的“可复制性”,就像一个泵一样。你可以把它“泵入”任意多次(包括0次,即删除),形成的新字符串必须仍然属于原来的语言。
- 直观理解“泵浦”:想象一根意大利面(足够长的字符串),你可以在靠近它的一头找到一小段(中间部分),你可以把这一小段复制粘贴任意多次,或者直接删掉,得到的新的意大利面(新字符串)仍然是“合格的”(属于该语言)。所有正则语言里的长字符串都必须有这样一小段可供“泵浦”的部分。
本段为引言,不包含具体的数学公式,但引入了核心概念:
- 泵引理 (Pumping Lemma):一个关于正则语言的定理。
- 泵浦长度 (pumping length):一个整数阈值,决定了字符串多长才适用泵引理。通常用符号 $p$ 表示。
- 泵浦 (pumping):指对字符串的某一部分进行复制或删除的操作。
- 语言: $L = \text{a(ba)}^*\text{b}$ (以a开头,以b结尾,中间是若干个ba)。这是一个正则语言。
- 泵浦长度: 假设这个语言对应的DFA有4个状态,那么泵浦长度 $p$ 可以是4。
- 足够长的字符串: 选一个长度大于4的字符串,例如 $s = \text{ababa}b \in L$ (长度为6)。
- 泵浦过程:
- 根据泵引理,我们可以把 $s$ 分成三部分。一种分法是:
- $x = \text{a}$
- $y = \text{ba}$
- $z = \text{bab}$
- 这里的中间部分 $y = \text{ba}$ 就是可以被“泵浦”的。
- 泵0次 (i=0): $xz = \text{a} + \text{bab} = \text{abab}$。这不属于$L$。这个分法不对。 泵引理要求分的 $x, y$ 长度和小于等于 $p$。
- 重新尝试泵浦过程 (遵循所有规则): $p=4$, $s = \text{ababa}b$
- $s$可以被拆分成 $xyz$。根据后面的条件3,$|xy| \le p=4$。这意味着 $x$ 和 $y$ 必须在字符串 "abab" 的内部。
- 一种拆分:$x = \text{a}$, $y = \text{ba}$, $z = \text{bab}$。这里 $|xy|=3 \le 4$。
- 泵0次 (i=0): $xz = \text{ab}ab$。这个分法还是不对,xz 必须属于 L。
让我们用一个更简单的正则语言来举例。
- 语言: $L = a^*b$ (任意多个a,后面跟一个b)。DFA有两个状态,泵浦长度 $p=2$。
- 足够长的字符串: $s = aaab$ (长度为4, 大于p)。
- 拆分: 根据 $|xy| \le p=2$,且 $|y|>0$,拆分必须在前两个字符 'aa' 中进行。
- 一种拆分方法:$x = a$, $y = a$, $z = ab$。
- 泵0次 (i=0): $xz = aab \in L$ (成立)。
- 泵1次 (i=1): $xyz = aaab \in L$ (原字符串, 成立)。
- 泵2次 (i=2): $xyyz = aaaab \in L$ (成立)。
- 泵k次 (i=k): $xy^kz = a^{k+1}ab = a^{k+2}b \in L$ (成立)。
- 这个例子成功展示了正则语言的“泵浦”性质。
- 易错点一: 泵引理不能用来证明一个语言是正则的。它是一个单向的结论:如果语言正则,那么它可被泵浦。反之不成立(一个非正则语言也可能有个别字符串能被泵浦)。
- 易错点二: 泵引理适用于语言中所有足够长的字符串。要证明一个语言非正则,你只需要找到一个足够长的字符串,证明它无论如何拆分都不能被泵浦。
- 易错点三: “泵浦”不是随便拆分的,它必须满足后面将要介绍的三个条件。
2.2 泵引理的形式化定义
📜 [原文7]
定理 1.70
泵引理 如果 $A$ 是一个正则语言,那么存在一个数 $p$(泵浦长度),如果 $s$ 是 $A$ 中任何长度至少为 $p$ 的字符串,那么 $s$ 可以被分成三部分,$s=x y z$,满足以下条件:
- 对于每个 $i \geq 0, x y^{i} z \in A$,
- $|y|>0$, 并且
- $|x y| \leq p$.
这是泵引理的形式化陈述,它精确地定义了上一段描述的“泵浦性质”。让我们逐条解析这个定理。
- "如果 A 是一个正则语言": 这是定理的大前提。下面说的一切都只对正则语言成立。
- "那么存在一个数 p (泵浦长度)": 对于任何一个正则语言 A,都必然存在一个与之对应的“魔数” $p$。这个 $p$ 只和语言 A (或识别它的DFA)有关,与具体要分析的字符串无关。
- "如果 s 是 A 中任何长度至少为 p 的字符串": 这个定理是针对 A 中所有足够长的字符串 $s$ 说的 (即 $|s| \ge p$)。对于那些短于 $p$ 的字符串,定理不做任何保证。
- "那么 s 可以被分成三部分, s = xyz": 对于任何一个满足上述条件的 $s$,都存在至少一种方法,能把它切成 $x$, $y$, $z$ 三段。$x$是前缀, $y$是中间部分, $z$是后缀。
- "满足以下条件": 这种切分不是任意的,必须同时满足以下三个约束条件:
- 条件1: $x y^{i} z \in A$ (对于每个 $i \ge 0$)
- 这是泵引理的核心,即“可泵浦性”。
- $y$ 部分可以像泵一样,被压入任意次。
- $i=1$: $xyz$ 就是原字符串 $s$,它本身当然在 $A$ 中。
- $i=2$: $xyyz$,即把 $y$ 复制一次,得到的新字符串也必须在 $A$ 中。
- $i=0$: $xz$,即把 $y$ 删除,得到的新字符串也必须在 $A$ 中。(这通常被称为“向下泵”)
- $i=k$: 把 $y$ 复制 $k-1$ 次,新字符串 $xy^kz$ 也必须在 $A$ 中。
- 条件2: $|y| > 0$
- 这保证了被泵浦的 $y$ 部分不是空字符串。
- 如果 $y$ 可以是空串,那条件1将变得毫无意义,因为复制任意多次空串都不会改变原字符串,定理就变成废话了。所以 $y$ 必须是“有料的”。
- 条件3: $|xy| \leq p$
- 这是一个非常关键的技术性约束。它规定了“可泵浦”的部分 $y$ 必须出现在字符串的早期。
- 具体来说,前缀 $x$ 和被泵浦的 $y$ 的总长度不能超过泵浦长度 $p$。
- 这意味着,对于一个很长的字符串,你不能跑到字符串的末尾去找一个 $y$ 来泵。你必须在字符串开头算起的前 $p$ 个字符内找到这个 $y$。这个条件极大地限制了 $y$ 的可能性,使得我们在使用泵引理进行反证时变得更加容易。
- $p$: 泵浦长度 (pumping length),一个正整数常量,其值取决于具体的正则语言 $A$。
- $s$: 语言 $A$ 中的一个字符串。
- $|s|$: 字符串 $s$ 的长度。
- $s=xyz$: 将字符串 $s$ 分解为三个连续的子串 $x, y, z$。
- $y^i$: 将子串 $y$ 重复 $i$ 次拼接起来。
- $y^0 = \varepsilon$ (空字符串)
- $y^1 = y$
- $y^2 = yy$
- $xy^iz$: 将字符串 $x$, $y^i$, 和 $z$ 依次拼接。
- $\in A$: “是语言 A 的一个成员”。
- $|y| > 0$: 字符串 $y$ 的长度大于0。等价于 $y \neq \varepsilon$。
- $|xy| \leq p$: 字符串 $x$ 和 $y$ 的长度之和小于或等于 $p$。
让我们再次使用语言 $L = a^*b$,其DFA有两个状态,所以泵浦长度 $p=2$。
- 选择 s: 选一个字符串 $s \in L$ 且 $|s| \ge p=2$。我们选 $s=ab$,长度为2。
- 寻找拆分 s=xyz: 我们需要寻找一种满足所有三个条件的拆分。
- 条件3 ($|xy| \le 2$) 意味着 $x$ 和 $y$ 必须来自 $s$ 的前两个字符 "ab"。
- 条件2 ($|y| > 0$) 意味着 $y$ 不能为空。
- 尝试拆分1: $x=\varepsilon, y=a, z=b$。
- $|y|=1>0$ (满足条件2)。
- $|xy|=1 \le 2$ (满足条件3)。
- 现在验证条件1:
- $i=0: xz = \varepsilon b = b \in L$ (成立)。
- $i=1: xyz = ab \in L$ (成立)。
- $i=2: xyyz = aab \in L$ (成立)。
- 通用情况: $xy^iz = a^ib$。所有这些字符串都属于 $L=a^*b$。
- 结论: 我们找到了一个满足所有条件的拆分。这符合泵引理的预期,因为 $L$ 是正则的。
- 逻辑顺序是关键:泵引理的逻辑是“对于所有足够长的字符串s,存在一种拆分xyz,满足...”。当我们用它来反证时,逻辑变成:“我们选择一个特定的足够长的s,然后证明对于所有可能的拆分xyz,它都无法满足...”。
- 条件3的重要性:这个条件是证明非正则性的利器。它将我们的注意力限制在字符串的开头部分,大大减少了需要考虑的拆分情况。例如,在证明 $B=\{0^n1^n\}$ 非正则时,如果我们选择 $s=0^p1^p$,条件3就保证了 $y$ 必须全部由0组成,从而使得证明变得简单。
2.3 泵引理中符号的含义
📜 [原文8]
回想一下表示字符串 $s$ 长度的 $|s|$ 符号,$y^{i}$ 表示 $y$ 的 $i$ 个副本连接在一起,而 $y^{0}$ 等于 $\\varepsilon$。
这一小段是对泵引理陈述中使用的一些基本符号的重申和解释,确保读者对这些记号有清晰的理解。
- $|s|$: 这个符号代表字符串 $s$ 的长度 (length)。长度就是字符串中包含的字符的数量。
- 例如,如果 $s = \text{automata}$,那么 $|s| = 8$。
- 如果 $s = \varepsilon$ (空字符串),那么 $|s| = 0$。
- $y^i$: 这个符号代表字符串 $y$ 的 $i$ 次幂 (power)。它表示将字符串 $y$ 自身连续拼接 $i$ 次。
- 例如,如果 $y = \text{ab}$:
- $y^1 = \text{ab}$
- $y^2 = \text{ab} \cdot \text{ab} = \text{abab}$ (其中 $\cdot$ 表示字符串拼接)
- $y^3 = \text{ab} \cdot \text{ab} \cdot \text{ab} = \text{ababab}$
- $y^0$: 这是幂运算的一个边界情况,即 $i=0$ 的情况。
- 任何字符串的 0 次幂被定义为空字符串 $\varepsilon$ (epsilon)。
- 所以,$y^0 = \varepsilon$。
- 这个定义在泵引理中非常重要,因为它对应着“向下泵”(pumping down)的情况,即从原字符串中移除 $y$ 部分。$xy^0z = x\varepsilon z = xz$。
这些都是形式语言理论中的标准记法,在此重申是为了确保后续的证明过程不会因为符号理解的偏差而出错。
- $|s|$: 字符串长度函数。输入一个字符串,输出一个非负整数。
- $y^i$: 字符串幂运算。
- 递归定义:
- $y^0 = \varepsilon$
- $y^i = y^{i-1} \cdot y$ (对于 $i \geq 1$)
- 操作性定义: 将 $y$ 连续写 $i$ 遍。
- 长度计算:
- $s_1 = 01101$, $|s_1|=5$。
- $s_2 = \varepsilon$, $|s_2|=0$。
- 幂运算:
- 设 $y = 01$。
- $y^0 = \varepsilon$
- $y^2 = 0101$
- $y^4 = 01010101$
- 结合泵引理的示例:
- 设 $s = abcde$, 并且通过某种方式拆分为 $x=a, y=bc, z=de$。
- 计算 $xy^2z$:
- $y^2 = (bc)^2 = bcbc$
- $xy^2z = a \cdot (bcbc) \cdot de = abcbcde$
- 计算 $xy^0z$:
- $y^0 = \varepsilon$
- $xy^0z = a \cdot \varepsilon \cdot de = ade$
- 混淆数字幂和字符串幂: 数字 $2^3 = 8$,而字符串 "2" 的三次方 "2"$^3$ = "222"。这是一个记法上的相似,但意义完全不同。
- 空字符串的角色: 务必记住 $| \varepsilon | = 0$ 和 $y^0 = \varepsilon$。空字符串是字符串拼接的单位元,即对于任何字符串 $w$,都有 $w \cdot \varepsilon = \varepsilon \cdot w = w$。这在处理 $i=0$ 的情况时至关重要。
2.4 对泵引理条件的进一步说明
📜 [原文9]
当 $s$ 被分成 $x y z$ 时,$x$ 或 $z$ 可以是 $\\varepsilon$,但条件 2 说明 $y \\neq \\varepsilon$。请注意,如果没有条件 2,该定理将是显然成立的。条件 3 说明 $x$ 和 $y$ 两部分的长度最多为 $p$。这是一个额外的技术条件,我们在证明某些语言是非正则时偶尔会发现它很有用。有关条件 3 的应用,请参阅例 1.74。
这段话对泵引理的三个条件进行了补充说明,特别是强调了条件2和条件3的重要性。
- 关于 x, y, z 的构成:
- $s = xyz$ 的拆分非常灵活。
- $x$ 可以是空字符串 $\varepsilon$。当可泵浦部分 $y$ 从字符串的开头开始时,就会出现这种情况。
- $z$ 也可以是空字符串 $\varepsilon$。当 $xy$ 恰好就是整个字符串 $s$ 时,就会出现这种情况。
- 但是,$y$ 绝对不能是空字符串 $\varepsilon$。这是由条件2 ($|y|>0$) 明确规定的。
- 条件2 ($|y|>0$) 的重要性:
- 作者指出,如果没有条件2,整个泵引理就变成了“显然成立 (trivially true)”的废话。
- 为什么?如果允许 $y=\varepsilon$,那么对于任何字符串 $s$,我们总可以这样拆分:$x=s, y=\varepsilon, z=\varepsilon$。
- 然后我们来验证条件1:$xy^iz = s \cdot \varepsilon^i \cdot \varepsilon = s \cdot \varepsilon = s$。因为 $s$ 本来就在语言 $A$ 中,所以 $xy^iz$ 也在 $A$ 中。这个结论对于任何 $i$ 都成立。
- 这样一来,任何字符串都能被“泵浦”了,定理就失去了区分正则和非正则语言的能力。所以,条件2是泵引理的灵魂,确保了“泵浦”操作必须对字符串产生实质性的改变(要么增加内容,要么删除内容)。
- 条件3 ($|xy| \le p$) 的重要性:
- 作者称之为“额外的技术条件 (extra technical condition)”,并强调它在证明中“偶尔会发现它很有用”。
- 这个条件将可泵浦的子串 $y$ 的位置限制在了字符串的开头部分(前 $p$ 个字符内)。
- 为什么有用?在进行反证时,我们的任务是证明“对于一个选定的字符串s,所有可能的拆分都不能满足泵引理”。条件3极大地缩小了“所有可能的拆分”的范围。我们不再需要考虑 $y$ 在字符串任意位置的情况,只需要考虑 $y$ 在开头的情况。
- 预告:作者明确指出,在后续的例 1.74 中,我们将看到一个绝佳的例子,展示了如果没有条件3,证明将无法进行;而有了条件3,证明则迎刃而解。
- $y \neq \varepsilon$: 这是对条件2 ($|y|>0$) 的另一种等价写法,表示 $y$ 不是空字符串。
- $|xy| \leq p$: 这是条件3的数学表达,前缀和泵浦部分的长度之和有上限。
- 演示条件2的重要性:
- 语言 $A = \{0^n 1^n \mid n \ge 0\}$ (我们想证明它非正则)。
- 选 $s = 0^p 1^p$。
- 如果泵引理没有条件2 (允许 $|y|=0$):
- 我们可以对 $s$ 做如下拆分:$x = 0^p 1^p$, $y = \varepsilon$, $z = \varepsilon$。
- 验证条件1: $xy^iz = (0^p 1^p)(\varepsilon)^i(\varepsilon) = 0^p 1^p = s$。
- 因为 $s \in A$,所以 $xy^iz \in A$ 永远成立。
- 这样一来,我们就无法通过泵浦 $s$ 来得到一个不在 $A$ 中的字符串,也就无法导出矛盾了。证明失败。
- 预演条件3的重要性 (来自例1.74):
- 语言 $C = \{w \mid w \text{ 中0和1数量相等}\}$ (我们想证明它非正则)。
- 选 $s = 0^p 1^p$。 $s \in C$ 且 $|s| = 2p \ge p$。
- 如果泵引理没有条件3 ($|xy| \le p$):
- 对手(试图证明C是正则的人)可以这样拆分 $s$: $x=\varepsilon$, $y=0^p1^p$, $z=\varepsilon$。
- 这个拆分满足 $|y|>0$。
- 验证条件1: $xy^iz = (0^p1^p)^i$。这个新字符串中,0的数量是 $p \times i$,1的数量也是 $p \times i$。数量始终相等!所以 $xy^iz \in C$ 永远成立。
- 我们又一次无法导出矛盾,证明失败。
- 现在加上条件3:
- 因为 $|xy| \le p$,并且 $s$ 的开头是 $p$ 个0,所以 $x$ 和 $y$ 都必须完全由0构成。
- 又因为 $|y|>0$,所以 $y$ 至少包含一个0。
- 现在我们泵浦:考虑 $xy^2z = xyyz$。这个新字符串比原来的 $s$ 多了至少一个0,而1的数量不变。因此0和1的数量不再相等。
- 所以 $xyyz \notin C$。这与泵引理的条件1相矛盾。
- 结论: 矛盾产生,$C$ 必须是非正则的。这个证明完全依赖于条件3。
- 不要忘记任何一个条件:在使用泵引理时,必须时刻牢记全部三个条件。它们共同构成了一个强大的逻辑约束。
- 条件3是你的朋友:在构造反证时,条件3是限制对手(即限制拆分方式)的最有力的工具,务必充分利用它来简化你的证明。
2.5 泵引理的证明思路
📜 [原文10]
证明思想 设 $M=\\left(Q, \\Sigma, \\delta, q_{1}, F\\right)$ 是一个识别 $A$ 的 DFA。我们将泵浦长度 $p$ 指定为 $M$ 的状态数。我们证明 $A$ 中任何长度至少为 $p$ 的字符串 $s$ 可以被分成三部分 $x y z$,满足我们的三个条件。如果 $A$ 中没有长度至少为 $p$ 的字符串怎么办?那么我们的任务甚至更容易,因为该定理就变成空洞地真:显然,如果不存在这样的字符串,则三个条件对所有长度至少为 $p$ 的字符串都成立。
这段话开始勾勒证明泵引理这个定理本身的思路。它告诉我们定理中的各个部分是如何与一个识别该语言的DFA联系起来的。
- 出发点: 既然 $A$ 是一个正则语言,那么根据定义,必然存在一个识别它的DFA,我们称之为 $M$。这个 $M$ 是我们证明的基石。
- 泵浦长度 $p$ 的来源: 定理中提到的那个神秘的“泵浦长度 $p$”是从哪里来的?证明思路直接给出了答案:$p$ 就是 DFA $M$ 的状态总数。即 $p = |Q|$。这是一个至关重要的联系,它将抽象的数字 $p$ 与具体的机器 $M$ 挂钩。
- 核心论证对象: 我们的目标是证明,对于 $A$ 中任意一个长字符串 $s$ (长度 $|s| \ge p$),都能找到满足那三个条件的 $xyz$ 拆分。
- 处理特殊情况 (vacuously true): 首先考虑一个简单的情况:如果语言 $A$ 中根本不存在长度大于或等于 $p$ 的字符串(例如,A是一个有限语言,且所有字符串都比 $p$ 短),会怎么样?
- 在这种情况下,泵引理的陈述 "如果 $s$ 是 $A$ 中任何长度至少为 $p$ 的字符串,那么..." 的前提永远是假的。
- 在逻辑学中,如果一个 "如果 P, 那么 Q" 的命题中,P 为假,那么整个命题被称为空洞地真 (vacuously true)。
- 所以,如果不存在这样的长字符串 $s$,泵引理自动成立,我们无需做任何事。这就像说“这个房间里所有会飞的大象都是粉色的”一样,因为房间里根本没有会飞的大象,所以这句话不会错。
这个“证明思想”的第一部分,为我们设置好了舞台:我们有了一个DFA $M$,并且把它的状态数定义为泵浦长度 $p$。现在,我们只需要处理主要情况:当语言 $A$ 中确实存在长度至少为 $p$ 的字符串 $s$ 时,如何证明它可以被泵浦。
- $M=\\left(Q, \\Sigma, \\delta, q_{1}, F\\right)$: DFA $M$ 的五元组形式化定义。
- $Q$: 有限的状态集合。
- $\Sigma$: 有限的输入字母表。
- $\delta$: 转移函数,$\delta: Q \times \Sigma \to Q$。
- $q_1$: 起始状态。
- $F$: 接受状态的集合,$F \subseteq Q$。
- $p = |Q|$: 证明的关键设定,将泵浦长度与DFA的状态数量等同起来。
- 语言: $A = a(a|b)^*$ (以a开头的任何字符串)。这是一个正则语言。
- DFA: 我们可以为它构建一个DFA $M$。
- $q_1$ (起始状态)。
- $q_2$ (接受状态)。
- $q_3$ (死亡状态)。
- 转移:$\delta(q_1, a) = q_2$, $\delta(q_1, b) = q_3$。$\delta(q_2, a) = q_2$, $\delta(q_2, b) = q_2$。$\delta(q_3, a) = q_3$, $\delta(q_3, b) = q_3$。
- 泵浦长度: 这个DFA有3个状态。所以,根据证明思路,我们设定泵浦长度 $p=3$。
- 检查空洞为真的情况: 语言 $A$ 中显然存在长度大于等于3的字符串,例如 aaa, abb 等。所以我们不能使用“空洞为真”的论证,必须进入下一步,对这些长字符串进行分析。
- 分析长字符串: 拿字符串 $s = \text{aabb}$ (长度为4,$|s| \ge p=3$) 来预演一下。
- $M$ 读取 $s$ 的状态序列将是: $q_1 \xrightarrow{a} q_2 \xrightarrow{a} q_2 \xrightarrow{b} q_2 \xrightarrow{b} q_2$。
- 这个状态序列是 $q_1, q_2, q_2, q_2, q_2$。
- 我们看到状态 $q_2$ 重复了。这正是下一段要利用的核心现象。
- 泵浦长度不是唯一的:虽然证明中将 $p$ 设为 $|Q|$,但泵引理只说“存在一个 $p$”。任何大于 $|Q|$ 的数也可以作为泵浦长度。证明中选择 $|Q|$ 是因为它恰好是能保证产生重复状态的最小长度阈值。
- 有限语言都是正则的:这段话中提到的“$A$中没有长度至少为$p$的字符串”这种情况,主要发生在 $A$ 是一个有限语言的时候。所有有限语言都是正则的,它们自然也满足泵引理(通常是以空洞为真的方式)。
2.6 鸽巢原理与状态重复
📜 [原文11]
如果 $A$ 中的 $s$ 的长度至少为 $p$,请考虑 $M$ 在使用输入 $s$ 进行计算时所经历的状态序列。它从起始状态 $q_{1}$ 开始,然后转到,比如说,$q_{3}$,然后,比如说,$q_{20}$,然后 $q_{9}$,依此类推,直到在状态 $q_{13}$ 处到达 $s$ 的末尾。由于 $s$ 在 $A$ 中,我们知道 $M$ 接受 $s$,所以 $q_{13}$ 是一个接受状态。
这部分继续深化证明思路,将焦点放在DFA处理一个长字符串时所经过的状态序列上。
- DFA 的计算过程: 当一个 DFA $M$ 读取一个输入字符串 $s = s_1s_2...s_n$ 时,它会经历一个状态序列。
- 从起始状态 $q_1$ 开始。
- 读取第一个字符 $s_1$,根据转移函数 $\delta(q_1, s_1)$,进入下一个状态。
- 读取第二个字符 $s_2$,再转移到下一个状态。
- ...这个过程一直持续,直到读完所有 $n$ 个字符。
- 状态序列的长度:
- 如果输入字符串 $s$ 的长度是 $n$ ($|s|=n$),那么DFA会进行 $n$ 次状态转移。
- 这个状态序列包含了起始状态,以及每读一个字符后的新状态。所以,总共会经过 $n+1$ 个状态。
- 例如,读取长度为3的字符串 abc,状态序列是 $q_{start}, q_{after\_a}, q_{after\_b}, q_{after\_c}$,共4个状态。
- 接受状态:
- 我们分析的字符串 $s$ 是从语言 $A$ 中选取的,而 $M$ 是识别 $A$ 的DFA。
- 因此,当 $M$ 读完整个字符串 $s$ 后,它必须停在一个接受状态 (accept state)。
- 在原文的例子中,这个最终状态是 $q_{13}$,所以 $q_{13} \in F$。
这一段的核心是建立一个清晰的图像:一个长度为 $n$ 的输入字符串,对应着一个长度为 $n+1$ 的状态访问历史记录。这个“历史记录”就是我们接下来要分析的关键对象。
- 状态序列 (Sequence of states): 设字符串 $s = s_1s_2\dots s_n$。设 $M$ 经过的状态序列为 $r_0, r_1, r_2, \dots, r_n$。
- $r_0 = q_1$ (起始状态)。
- $r_{i} = \delta(r_{i-1}, s_i)$ 对于 $1 \le i \le n$。
- 序列的长度是 $n+1$。
- 因为 $s \in A$,所以最终状态 $r_n$ 必须是接受状态,即 $r_n \in F$。
- DFA $M$: 假设一个DFA识别语言 $(a|b)^*b$ (以b结尾的字符串)。
- $Q=\{q_1, q_2\}$ ($q_1$是起始状态, $q_2$是接受状态)。
- $\delta(q_1, a) = q_1, \delta(q_1, b) = q_2, \delta(q_2, a) = q_1, \delta(q_2, b) = q_2$。
- 泵浦长度 $p$: $|Q| = 2$。
- 长字符串 $s$: 选取 $s = \text{aab}$ (长度为3, $|s| \ge p=2$)。$s$ 属于该语言。
- 状态序列:
- 初始在 $q_1$。
- 读第一个 a: $\delta(q_1, a) = q_1$。
- 读第二个 a: $\delta(q_1, a) = q_1$。
- 读第三个 b: $\delta(q_1, b) = q_2$。
- 整个状态序列是: $q_1, q_1, q_1, q_2$。
- 序列长度为 4 ($n+1=3+1$)。
- 最终状态 $q_2$ 是接受状态,符合预期。
- 状态 vs. 状态序列: 要分清DFA的状态集合 $Q$ (这是有限的) 和DFA在处理输入时经历的状态序列 (其长度随输入字符串长度而变)。
- 序列长度 $n+1$: 这是一个常见的细节,不要误认为是 $n$。因为包含了初始状态,所以长度是 $n+1$。这个“+1”正是触发鸽巢原理的关键。
2.7 鸽巢原理的应用
📜 [原文12]
如果我们让 $n$ 为 $s$ 的长度,则状态序列 $q_{1}, q_{3}, q_{20}, q_{9}, \\ldots, q_{13}$ 的长度为 $n+1$。因为 $n$ 至少为 $p$,所以我们知道 $n+1$ 大于 $M$ 的状态数 $p$。因此,该序列必须包含一个重复的状态。这个结果是鸽巢原理的一个例子,这是一个花fancy的名称,用于说明一个相当明显的论点:如果将 $p$ 只鸽子放入少于 $p$ 个鸽巢中,那么某个鸽巢中必然不止一只鸽子。
这是泵引理证明的核心步骤,它利用鸽巢原理指出了DFA在处理长字符串时必然会发生的事情——状态重复。
- 建立对应关系:
- 鸽子: DFA在处理输入时所经过的状态序列中的每一个状态。
- 鸽巢: DFA本身拥有的所有可用状态,即状态集 $Q$。
- 数量分析:
- 我们已经设定泵浦长度 $p$ 等于DFA的状态数,所以鸽巢的数量是 $p$ ($|Q|=p$)。
- 我们选取的字符串 $s$ 的长度为 $n$,并且 $n \ge p$。
- DFA处理 $s$ 所经过的状态序列长度是 $n+1$。
- 因为 $n \ge p$,所以 $n+1 \ge p+1$。
- 这意味着,鸽子的数量 ($n+1$) 至少是 $p+1$。
- 应用鸽巢原理:
- 我们有至少 $p+1$ 只鸽子 (状态序列中的位置)。
- 我们只有正好 $p$ 个鸽巢 (DFA的可用状态)。
- 把 $p+1$ 只鸽子放进 $p$ 个鸽巢里,必然导致至少有一个鸽巢里有两只或更多的鸽子。
- 翻译回DFA的场景:在DFA处理字符串 $s$ 的前 $p+1$ 个状态组成的序列中(即读取前 $p$ 个字符的过程中),必然至少有一个状态被访问了两次或以上。
- 结论: 只要输入字符串的长度大于等于DFA的状态数,DFA在处理这个字符串的过程中就不可避免地会重复进入某个状态。这个状态的重复,意味着在DFA的状态图中形成了一个环路 (loop)。这正是“泵浦”性质的根本来源。
- 鸽巢原理 (Pigeonhole Principle):
- 简单形式: 如果有 $k+1$ 个或更多的物体要放入 $k$ 个容器中,那么至少有一个容器会包含两个或更多的物体。
- 在本证明中:
- 物体 (鸽子): 状态序列中的前 $p+1$ 个状态 $r_0, r_1, \dots, r_p$。
- 容器 (鸽巢): DFA的状态集 $Q$。
- 物体数量是 $p+1$。
- 容器数量是 $|Q|=p$。
- 由于 $p+1 > p$,根据鸽巢原理,在序列 $r_0, \dots, r_p$ 中,必然存在两个不同的位置 $j$ 和 $l$ (其中 $0 \le j < l \le p$),使得 $r_j = r_l$。即状态发生了重复。
- DFA $M$: 假设一个DFA有 $p=10$ 个状态 ($q_1, \dots, q_{10}$)。
- 长字符串 $s$: 选取一个长度 $n=12$ 的字符串 $s$ ($n \ge p$)。
- 状态序列: $M$ 处理 $s$ 会生成一个长度为 $n+1=13$ 的状态序列: $r_0, r_1, r_2, \dots, r_{12}$。
- 应用鸽巢原理:
- 我们只看序列的前 $p+1=11$ 个状态:$r_0, r_1, \dots, r_{10}$。
- 我们有11个状态(鸽子),但DFA总共只有10个不同的状态(鸽巢)。
- 因此,在这11个状态中,必然有两个是相同的。
- 可能 $r_2 = q_5$ 并且 $r_9 = q_5$。这就是一个状态重复。
- 这意味着,DFA从处理完第2个字符后的状态,到处理完第9个字符后的状态,形成了一个环路,它从 $q_5$ 出发,经过一系列状态,最后又回到了 $q_5$。
- 重复发生的位置: 鸽巢原理保证了在前 $p+1$ 个状态(即读取前 $p$ 个字符的过程中)一定会出现重复。这直接导向了泵引理的条件3 ($|xy| \le p$)。因为 $y$ 就是这个环路对应的子串,而这个环路在读取前 $p$ 个字符内就形成了。
- “花哨的名称”: 作者说这是一个“花哨的名称”,是想强调其原理的朴素和显而易见性,让读者不要被术语吓到,而应专注于其简单的逻辑核心。
2.8 可视化状态重复
📜 [原文13]
下图显示了字符串 $s$ 和 $M$ 在处理 $s$ 时经过的状态序列。状态 $q_{9}$ 是重复的状态。

这段内容和图片一起,将前面抽象的“状态重复”概念进行了可视化,使其更加直观易懂。
- 上方的字符串 $s$:
- 图片顶部展示了输入字符串 $s$。它被隐式地分成了三段,对应下面的状态序列。
- 第一部分,从字符串开始到第一个 $q_9$ 对应的位置。
- 第二部分,在两个 $q_9$ 之间。
- 第三部分,从第二个 $q_9$ 之后到字符串结尾。
- 下方的状态序列:
- 图片底部是一个箭头,代表了DFA的状态转移路径。
- 它从起始状态 $q_1$ 开始。
- 依次经过 $q_3, q_{20}$ 等一系列状态。
- 关键点在于,序列中出现了两次状态 $q_9$。这是鸽巢原理所保证的状态重复。
- 序列最终结束于 $q_{13}$,这是一个接受状态。
- 图的意义:
- 这张图清晰地展示了,当一个DFA处理一个足够长的字符串时,它的轨迹必然会“打个结”或“绕个圈”。
- 第一次到达 $q_9$ 之前的部分,是DFA进入这个圈的路径。
- 两次 $q_9$ 之间的部分,是DFA在这个圈里绕行的路径。
- 第二次到达 $q_9$ 之后的部分,是DFA离开这个圈并走向最终接受状态的路径。
这张图是理解泵引理证明的关键。它将抽象的符号和序列转换成了具体的路径和环路,为接下来将字符串 $s$ 拆分为 $xyz$ 提供了直观的依据。
这张图是概念性的,没有引入新的公式。但它图示了以下关系:
- 设状态序列为 $r_0, r_1, \dots, r_n$。
- 图中 $q_1$ 对应 $r_0$。
- 图中第一个 $q_9$ 对应某个 $r_j$。
- 图中第二个 $q_9$ 对应某个 $r_l$,其中 $l>j$。
- 并且 $r_j = r_l = q_9$。
- 回到我们的例子:DFA识别 $(a|b)^*b$, $p=2$, 字符串 $s = \text{aab}$。
- 状态序列是 $r_0=q_1, r_1=q_1, r_2=q_1, r_3=q_2$。
- 重复的状态: $q_1$。它在 $r_0, r_1, r_2$ 处多次出现。
- 第一次重复: 我们可以在 $r_1$ 和 $r_2$ 处找到重复。
- 可视化:
- 字符串: a a b
- 状态: $q_1 \xrightarrow{a} q_1 \xrightarrow{a} q_1 \xrightarrow{b} q_2$
- 重复的状态是 $q_1$。
- 我们可以看到,DFA在状态 $q_1$ 上有一个由输入 a 形成的自环。这个自环就是泵引理中“环路”的来源。
- 哪个重复?: 状态序列中可能有很多重复。证明中通常选择第一个出现的重复状态,这有助于满足泵引理的条件3 ($|xy| \le p$)。图中高亮了 $q_9$,暗示我们关注这个特定的重复点。
- 环路的大小: 环路可能只包含一个状态(自环),也可能包含多个状态。无论大小,只要有环路,就可以被“泵浦”。
本章通过详细阐述泵引理 (Pumping Lemma),为证明一个语言是否为非正则提供了强大的形式化工具。首先,定理被明确陈述:任何正则语言都存在一个泵浦长度 $p$,使得该语言中所有长度不小于 $p$ 的字符串 $s$ 都可以被拆分为三部分 $s=xyz$,并满足三个核心条件:
- 可泵性: $y$ 部分可以被重复或删除($xy^iz \in A$)。
- 非空性: $y$ 部分必须非空($|y|>0$)。
- 位置限制: $y$ 必须出现在字符串的初始部分($|xy| \le p$)。
接着,章节深入剖析了该引理的证明思路。证明的基石是:任何正则语言 A 都有一个对应的 DFA M。证明巧妙地将泵浦长度 $p$ 定义为 M 的状态数 $|Q|$。其核心逻辑在于,当 M 处理一个长度 $n \ge p$ 的字符串 $s$ 时,它会生成一个长度为 $n+1$ 的状态序列。根据鸽巢原理,这个长度超过状态总数的序列中,必然存在一个重复的状态,这意味着 M 的计算路径中形成了一个环路。这个环路的存在,正是字符串可以被“泵浦”的根本原因,从而严谨地推导出泵引理的三个条件。
这部分内容是计算理论的基石之一,其存在目的如下:
- 提供严格的判定工具:它提供了一种超越直觉的、形式化的方法来证明一个语言不是正则的。这是我们工具箱中第一个用于证明“不能性”的强大武器。
- 深化对正则语言本质的理解:通过理解泵引理的证明,我们能更深刻地认识到正则语言的本质特征——它们的“记忆”是有限的,这种有限性必然导致在处理长字符串时产生环路(状态重复)。一个语言之所以是正则的,正是因为它能容忍这种由环路带来的重复性。
- 为更高级的计算模型铺路:理解了正则语言的局限性,自然会引出“什么模型能克服这种局限性?”的问题。这为后续学习上下文无关语言和下推自动机等更强大的计算模型提供了动机和背景。
- DFA 酒店模型:
- 想象一个酒店,它只有有限多间客房(DFA的状态,数量为 $p$)。
- 一个长长的旅行团(长度 $\ge p$ 的字符串 $s$)按顺序入住,每人住一间房,第二天换到下一间指定的房间(状态转移)。旅行团有 $n+1$ 个“人-天”的住宿需求。
- 由于房间数量 $p$ 少于旅行团人数 $n$(实际上是$n+1$个节点),根据鸽巢原理,旅行团在住宿过程中,必然有至少两个人住进了同一间客房(状态重复)。
- 假设第 $j$ 天和第 $l$ 天的团员住进了同一间房(比如都住了 8 号房)。
- $x$ = 第 $j$ 天前的行程路线。
- $y$ = 第 $j$ 天到第 $l$ 天的行程路线(从8号房出发,最后又回到8号房,这是一个环路)。
- $z$ = 第 $l$ 天之后的行程路线。
- 泵浦:既然从第 $j$ 天到第 $l$ 天的行程是一个从8号房回到8号房的圈,那么这个圈可以走任意多次($y^i$),或者一次也不走($y^0$)。无论怎样,旅行团最终都能从8号房继续他们后面 $z$ 的行程,并到达终点。如果原来的行程是“成功的”(字符串被接受),那么经过泵浦后的新行程也必然是“成功的”。
- 绕圈的火车:
- 一个DFA就像一个有限的火车轨道系统,它有 $p$ 个车站(状态)。
- 一列很长的火车(字符串 $s$,长度 $\ge p$)在这个轨道上行驶,每节车厢经过一个车站(读取一个字符,进行一次状态转移)。
- 因为车站的数量是有限的,而火车的长度是无限的(或足够长),火车在行驶过程中必然会重复经过某个车站。
- 假设火车在时刻 $j$ 和时刻 $l$ 都经过了“中心站”。
- $x$ 部分:火车从“起始站”开到第一次到达“中心站”所驶过的轨道和经过的车厢。
- $y$ 部分:火车从第一次到达“中心站”到第二次到达“中心站”所驶过的一个环形轨道和对应的车厢。
- $z$ 部分:火车从第二次到达“中心站”后,继续行驶直到车尾离开系统所驶过的轨道和车厢。
- 泵浦的意义:
- “泵入”($i > 1$):意味着让火车在这个环形轨道 $y$ 上多绕几圈。既然绕一圈能回到“中心站”,那么多绕几圈也同样能回到“中心站”,然后再继续 $z$ 的旅程。
- “泵出”($i = 0$):意味着火车第一次到达“中心站”后,选择不走那个环形轨道 $y$,直接从“中心站”开始走 $z$ 的旅程。这是可能的,因为 $y$ 路径的起点和终点都是“中心站”。
- 如果原来的完整旅程是“成功的”(被DFA接受),那么所有这些绕圈或不绕圈的变种旅程,也必须是“成功的”。
33. 泵引理的证明与应用
3.1 拆分字符串s为xyz
📜 [原文14]
图 1.71
这部分内容实际上是上一节的延续,它缺失了文本,只有一个标题 "图 1.71"。根据上下文,这个标题指向的是随后的图片和描述,即如何根据找到的重复状态来具体地拆分字符串 $s$。我们将结合接下来的内容进行解释。
无。
无。
无。
3.2 拆分字符串的依据
📜 [原文15]
示例显示 $M$ 读取 $s$ 时状态 $q_{9}$ 重复
现在我们将 $s$ 分成 $x, y$ 和 $z$ 三部分。部分 $x$ 是 $s$ 中出现在 $q_{9}$ 之前的部分,部分 $y$ 是两个 $q_{9}$ 之间出现的部分,
部分 $z$ 是 $s$ 的剩余部分,出现在第二个 $q_{9}$ 之后。因此 $x$ 将 $M$ 从状态 $q_{1}$ 带到 $q_{9}$,$y$ 将 $M$ 从 $q_{9}$ 带回到 $q_{9}$,而 $z$ 将 $M$ 从 $q_{9}$ 带到接受状态 $q_{13}$,如下图所示。
这段话解释了如何利用上一步发现的重复状态,来指导我们将字符串 $s$ 分解成满足泵引理的 $x, y, z$ 三部分。
- 确定分解点: 分解的关键在于找到的那个重复状态,在例子中是 $q_9$。这个状态在DFA的状态序列中至少出现了两次。我们关注的是第一次出现和第二次出现的位置。
- 定义 $x$:
- $x$ 是输入字符串 $s$ 的前缀部分。
- 它的作用是驱动DFA从起始状态 $q_1$ 走到第一次出现重复状态 $q_9$ 的位置。
- 在状态序列图上,它对应于从起点到环路入口的路径所消耗的输入。
- 定义 $y$:
- $y$ 是紧跟在 $x$ 后面的那部分字符串。
- 它的作用是驱动DFA从第一次出现 $q_9$ 的位置,恰好走完一个环路,回到第二次出现 $q_9$ 的位置。
- $y$ 就是形成状态图中那个环路 (loop) 所消耗的输入子串。
- 定义 $z$:
- $z$ 是字符串 $s$ 剩下的后缀部分。
- 它的作用是驱动DFA从第二次出现 $q_9$ 的位置(也就是环路的终点)走到最终的接受状态 $q_{13}$。
- 在状态序列图上,它对应于从环路出口到终点的路径所消耗的输入。
通过这种方式,$s=xyz$ 的分解就和DFA的运行轨迹完美地对应起来了:$x$ (进环) -> $y$ (绕环) -> $z$ (出环到终点)。
- 设状态序列为 $r_0, r_1, \dots, r_n$。
- 设 $s = s_1s_2\dots s_n$。
- 我们找到了第一个重复状态,即存在 $j < l$,使得 $r_j = r_l$。
- $x = s_1s_2\dots s_{j}$: 驱动DFA从 $r_0$ 到 $r_j$ 的子串。
(注:严格来说,如果 $r_j$ 是读完第j个字符后的状态,那么 $x=s_1...s_j$。原文的图示和后面的严谨证明在下标上略有出入,但思想一致。我们以严谨证明为准,这里先按直觉理解)
- $y = s_{j+1}\dots s_{l}$: 驱动DFA从 $r_j$ 绕一圈回到 $r_l$ ($=r_j$) 的子串。
- $z = s_{l+1}\dots s_{n}$: 驱动DFA从 $r_l$ 到最终接受状态 $r_n$ 的子串。
- 语言: $L = a^*b$, $p=2$。
- 字符串: $s = aaab$ (长度为4)。
- 状态序列: $r_0=q_1 \xrightarrow{a} r_1=q_1 \xrightarrow{a} r_2=q_2 \xrightarrow{a} r_3=q_3$。
(修正一下DFA和例子,使其更清晰地展示xyz)
- 语言: $(ab)^*$ (ababab...)。DFA: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0$。$p=2$。
- 字符串: $s = abab$ (长度为4, $|s| \ge p=2$)。
- 状态序列: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0$。
- 重复状态: $q_0$ 在 $r_0, r_2, r_4$ 出现。我们选第一对重复: $r_0$ 和 $r_2$。
- 拆分:
- $j=0, l=2$。
- $x = s_1 \dots s_0 = \varepsilon$ (空字符串,因为循环从起点开始)。
- $y = s_1 \dots s_2 = ab$。
- $z = s_3 \dots s_4 = ab$。
- 验证拆分:
- $x$ (即 $\varepsilon$) 将DFA从 $q_0$ 带到 $q_0$。
- $y$ (即 ab) 将DFA从 $q_0$ 带回到 $q_0$。
- $z$ (即 ab) 将DFA从 $q_0$ 带到接受状态 $q_0$。
- 这个拆分是 $s = \varepsilon \cdot (ab) \cdot (ab)$,符合要求。
- 下标的精确性: 在非正式描述中,"之前"和"之间"可能有点模糊。在后面的正式证明中,下标 $j$ 和 $l$ 的精确定义将消除这种模糊性。
- 环路的位置: 这个环路不一定在字符串的中间,它完全可以从起始状态就开始,此时 $x=\varepsilon$。
3.3 可视化拆分后的DFA路径
📜 [原文16]
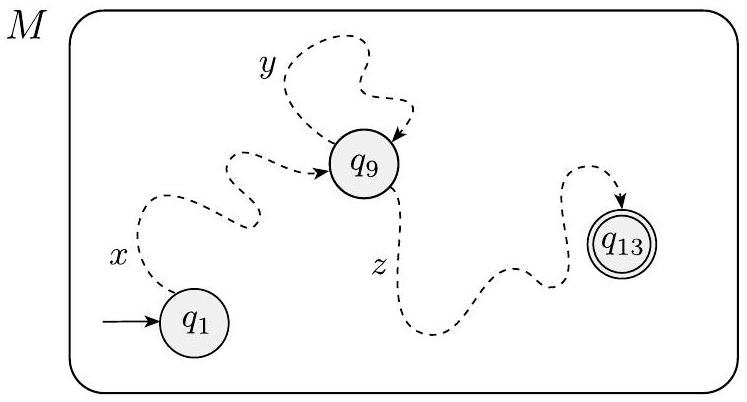
图 1.72
示例显示字符串 $x, y$ 和 $z$ 如何影响 $M$
这张图是对上一段文字描述的DFA路径的最终可视化,它清晰地展示了 $x, y, z$ 三个子串如何分别驱动DFA完成三段不同的旅程。
- 路径 $x$:
- 左上方的箭头路径代表了DFA读取子串 $x$ 的过程。
- 它使得DFA从起始状态 $q_1$ 转移到了环路点 $q_9$。
- 路径 $y$ (环路):
- 中间那个指向自身的循环箭头,代表了DFA读取子串 $y$ 的过程。
- 这个过程的起点和终点都是状态 $q_9$。
- 这直观地显示了 $y$ 的作用就是让DFA在状态图上“绕了一圈又回到了原点”。
- 路径 $z$:
- 右下方的箭头路径代表了DFA读取子串 $z$ 的过程。
- 它使得DFA从环路点 $q_9$ 转移到了最终的接受状态 $q_{13}$。
这张图的核心洞见在于,中间的 $y$ 环路是一个“可选”或“可重复”的模块。
- 我们可以选择走 $x$ 路径,然后跳过 $y$ 环路,直接走 $z$ 路径 ($x \to z$)。
- 我们可以选择走 $x$ 路径,然后走一次 $y$ 环路,再走 $z$ 路径 ($x \to y \to z$),这是原始字符串 $s$ 的路径。
- 我们也可以选择走 $x$ 路径,然后走两次 $y$ 环路,再走 $z$ 路径 ($x \to y \to y \to z$)。
- ...以此类推。
因为 $z$ 路径的起点 ($q_9$) 和 $y$ 环路的终点 ($q_9$) 是同一个状态,所以无论我们在环路上绕多少圈,总能顺利地与 $z$ 路径衔接上,并最终到达接受状态 $q_{13}$。这就为泵引理的条件1 ($xy^iz \in A$) 提供了最直观的证明。
这张图可以用扩展转移函数 $\hat{\delta}$ 来形式化描述:
- $\hat{\delta}(q, w)$: 表示从状态 $q$ 开始,读取字符串 $w$ 后到达的状态。
- 路径 $x$: $\hat{\delta}(q_1, x) = q_9$
- 路径 $y$: $\hat{\delta}(q_9, y) = q_9$
- 路径 $z$: $\hat{\delta}(q_9, z) = q_{13}$,并且 $q_{13} \in F$ (接受状态集合)。
- 推导 $xyyz \in A$:
- $\hat{\delta}(q_1, xyyz) = \hat{\delta}(\hat{\delta}(q_1, x), yyz)$
- $= \hat{\delta}(q_9, yyz)$ (根据 $x$ 的定义)
- $= \hat{\delta}(\hat{\delta}(q_9, y), yz)$
- $= \hat{\delta}(q_9, yz)$ (根据 $y$ 的定义)
- $= \hat{\delta}(\hat{\delta}(q_9, y), z)$
- $= \hat{\delta}(q_9, z)$ (再次根据 $y$ 的定义)
- $= q_{13}$ (根据 $z$ 的定义)
- 因为 $q_{13}$ 是接受状态,所以字符串 $xyyz$ 被DFA接受,即 $xyyz \in A$。
- 语言: $(ab)^*$。DFA: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0$。$p=2$。
- 字符串: $s = abab$。
- 拆分: $x=\varepsilon, y=ab, z=ab$。
- 环路点: $q_0$。
- 可视化:
- 路径 x: $\varepsilon$ (空串) 使DFA停留在 $q_0$。
- 路径 y: ab 使DFA从 $q_0$ 绕了一圈 ($q_0 \to q_1 \to q_0$) 回到 $q_0$。
- 路径 z: ab 使DFA从 $q_0$ 又绕了一圈,最终停在接受状态 $q_0$。
- 泵浦:
- $xy^0z = \varepsilon \cdot \varepsilon \cdot ab = ab$: DFA路径是 $q_0 \xrightarrow{ab} q_0$ (接受)。
- $xy^2z = \varepsilon \cdot (ab)^2 \cdot ab = ababab$: DFA路径是 $q_0 \xrightarrow{ab} q_0 \xrightarrow{ab} q_0 \xrightarrow{ab} q_0$ (接受)。
- 不要混淆字符串和状态: $x,y,z$ 是字符串(输入),而 $q_1, q_9, q_{13}$ 是状态(机器的内部配置)。$x,y,z$ 驱动着状态的变化。
- 图的通用性: 这张图描绘的是一般情况。在某些DFA中,环路可能更复杂,或者 $x, z$ 路径本身也可能包含其他环路,但这不影响核心论证:只要在处理 $s$ 的过程中存在至少一个由 $y$ 驱动的环路,泵浦性质就成立。
3.4 验证泵引理的三个条件
📜 [原文17]
让我们看看为什么这种对 $s$ 的划分满足这三个条件。假设我们运行 $M$ 在输入 $x y y z$ 上。我们知道 $x$ 将 $M$ 从 $q_{1}$ 带到 $q_{9}$,然后第一个 $y$ 将它从 $q_{9}$ 带回到 $q_{9}$,第二个 $y$ 也是如此,然后 $z$ 将它带到 $q_{13}$。由于 $q_{13}$ 是一个接受状态,$M$ 接受输入 $x y y z$。同样,它将接受任何 $i>0$ 的 $x y^{i} z$。对于 $i=0$ 的情况,$x y^{i} z=x z$,它也因类似原因被接受。这确立了条件 1。
这段文字开始逐一验证我们基于DFA环路所做的 $xyz$ 拆分,确实满足泵引理陈述中的全部三个条件。这里首先验证最重要的条件1。
- 验证 $i=2$ 的情况 ($xyyz$):
- 第一步 (输入x): 机器从 $q_1$ 开始,读完 $x$ 后到达 $q_9$。
- 第二步 (输入第一个y): 接着从 $q_9$ 开始,读完第一个 $y$ 后,由于 $y$ 是环路,机器回到 $q_9$。
- 第三步 (输入第二个y): 接着又从 $q_9$ 开始,读完第二个 $y$ 后,机器再次回到 $q_9$。
- 第四步 (输入z): 最后从 $q_9$ 开始,读完 $z$ 后,机器到达 $q_{13}$。
- 结论: 由于 $q_{13}$ 是原始字符串 $s$ 的接受状态,所以它是一个接受状态。因此,整个输入 $xyyz$ 被机器接受,即 $xyyz \in A$。
- 推广到任意 $i > 0$ 的情况 ($xy^iz$):
- 上述逻辑可以无限推广。无论中间的 $y$ 部分重复多少次 ($i$ 次),机器都只是在 $q_9$ 这个状态上“绕了 $i$ 圈”。
- 绕完 $i$ 圈后,机器仍然停在 $q_9$。
- 然后,它继续读取 $z$ 部分,最终的路径和结果与原始字符串完全相同,都会到达接受状态 $q_{13}$。
- 因此,对于任何 $i > 0$,$xy^iz \in A$。
- 验证 $i=0$ 的情况 ($xz$):
- 这种情况被称为“向下泵浦”。
- 第一步 (输入x): 机器从 $q_1$ 开始,读完 $x$ 后到达 $q_9$。
- 第二步 (输入z): 接着直接从 $q_9$ 开始读取 $z$ (因为 $y$ 部分被删除了)。读完 $z$ 后,机器将到达 $q_{13}$。
- 结论: 由于 $q_{13}$ 是接受状态,输入 $xz$ 也被机器接受,即 $xz \in A$。
综合以上所有情况,我们证明了对于所有 $i \ge 0$,都有 $xy^iz \in A$。泵引理的条件1成立。
这里是上一节用扩展转移函数 $\hat{\delta}$ 进行推导的文字化描述。
- 证明 $xy^iz \in A$ for $i \ge 0$:
- 我们已知:
- $\hat{\delta}(q_1, x) = q_9$
- $\hat{\delta}(q_9, y) = q_9$
- $\hat{\delta}(q_9, z) = q_{13}$ 且 $q_{13} \in F$
- 当 $i>0$ 时:
- $\hat{\delta}(q_1, xy^iz) = \hat{\delta}(\hat{\delta}(q_1, x), y^iz) = \hat{\delta}(q_9, y^iz)$
- $= \hat{\delta}(\hat{\delta}(q_9, y^{i-1}), yz) = \dots = \hat{\delta}(\hat{\delta}(q_9, y), z)$ (通过 $i-1$ 次归纳)
- $= \hat{\delta}(q_9, z) = q_{13} \in F$。
- 当 $i=0$ 时:
- $\hat{\delta}(q_1, xz) = \hat{\delta}(\hat{\delta}(q_1, x), z) = \hat{\delta}(q_9, z) = q_{13} \in F$。
- 结论: 在所有非负整数 $i$ 的情况下,$xy^iz$ 都能使DFA到达接受状态 $q_{13}$,因此都属于语言 $A$。
- 语言: $(ab)^*$。DFA: $q_0 \xrightarrow{a} q_1 \xrightarrow{b} q_0$。
- 字符串: $s = abab$。
- 拆分: $x=\varepsilon, y=ab, z=ab$。
- 验证条件1:
- $i=2$: $xy^2z = (ab)^2ab = ababab$。
- 路径: $q_0 \xrightarrow{ab} q_0 \xrightarrow{ab} q_0 \xrightarrow{ab} q_0$。终点 $q_0$ 是接受状态。所以 $ababab \in (ab)^*$。成立。
- $i=0$: $xy^0z = \varepsilon \cdot \varepsilon \cdot ab = ab$。
- 路径: $q_0 \xrightarrow{ab} q_0$。终点 $q_0$ 是接受状态。所以 $ab \in (ab)^*$。成立。
- $i=0$ 的重要性: "向下泵" 和 "向上泵" ($i \ge 2$) 同样重要。在某些非正则语言的证明中,“向下泵”是导出矛盾的关键。例如语言 $E=\{0^i1^j \mid i>j\}$,通过向下泵减少0的数量,可以使其不再满足 $i>j$ 的条件。
- $y$ 的选择: 证明中,我们是根据DFA的运行轨迹来确定 $y$ 的。而在使用泵引理进行反证时,我们是假设存在一个满足条件的 $y$,然后证明这个假设不成立。角色的转换是理解的关键。
3.5 验证条件2和条件3
📜 [原文18]
检查条件 2,我们看到 $|y|>0$,因为它是 $s$ 中在状态 $q_{9}$ 的两次不同出现之间发生的部分。
为了得到条件 3,我们确保 $q_{9}$ 是序列中第一次重复。根据鸽巢原理,序列中前 $p+1$ 个状态必须包含一个重复。因此,$|x y| \\leq p$。
这段话接着验证我们所做的 $xyz$ 拆分同样满足泵引理的条件2和条件3。
- 验证条件2: $|y| > 0$
- 回顾 $y$ 的定义: $y$ 是驱动DFA从第一次出现 $q_9$ 到第二次出现 $q_9$ 所消耗的输入子串。
- 逻辑: “第一次出现”和“第二次出现”是序列中两个不同的位置。假设第一次出现在位置 $j$,第二次出现在位置 $l$。根据定义,$l > j$。
- $y$ 是由输入字符串中第 $j+1$ 到第 $l$ 个字符组成的。
- 因为 $l > j$,所以 $l-(j+1)+1 = l-j \ge 1$。这意味着子串 $y$ 至少包含一个字符。
- 因此,$y$ 的长度必然大于0,即 $|y|>0$。条件2成立。
- 验证条件3: $|xy| \leq p$
- 回顾 $p$ 的定义: $p$ 是DFA的状态总数。
- 回顾鸽巢原理的应用: 我们是通过考察DFA状态序列的前 $p+1$ 个状态(即 $r_0, r_1, \dots, r_p$,这是读取字符串前 $p$ 个字符所产生的序列)来保证状态重复的。
- 选择第一个重复: 为了确保 $|xy|$ 尽可能小,我们在构造证明时,选择在这前 $p+1$ 个状态中找到的第一对重复状态。设为 $r_j = r_l$,其中 $0 \le j < l \le p$。
- 分析长度:
- $x$ 是从字符串开头到第 $j$ 个字符的子串。$|x|=j$。
- $y$ 是从第 $j+1$ 个字符到第 $l$ 个字符的子串。$|y|=l-j$。
- $xy$ 是从字符串开头到第 $l$ 个字符的子串。它的长度是 $|xy| = l$。
- 因为我们保证了第二次出现重复状态的位置 $l$ 是在前 $p+1$ 个状态序列之内找到的,所以必然有 $l \le p$。
- 因此,我们得到 $|xy| \le p$。条件3成立。
至此,我们已经证明了,对于任何正则语言A及其DFA,任何足够长的字符串 $s$ 都可以被拆分成满足泵引理全部三个条件的 $x, y, z$。泵引理得证。
- 证明条件2 ($|y|>0$):
- 我们找到的重复状态 $r_j = r_l$ 满足 $j < l$。
- $y = s_{j+1} \dots s_l$。
- $|y| = l - (j+1) + 1 = l-j$。
- 因为 $j < l$,所以 $l-j \ge 1$。
- 因此 $|y| > 0$。
- 证明条件3 ($|xy| \le p$):
- 重复状态 $r_j = r_l$ 是在状态序列的前 $p+1$ 个位置 ($r_0, \dots, r_p$) 中找到的。
- 这意味着第二次出现的位置 $l$ 的下标最大为 $p$。即 $l \le p$。
- $x = s_1 \dots s_j$。
- $y = s_{j+1} \dots s_l$。
- $xy = s_1 \dots s_l$。
- $|xy| = l$。
- 因为 $l \le p$,所以 $|xy| \le p$。
- DFA: 10个状态 ($p=10$)。
- 字符串 $s$: 长度 $n=12$。
- 状态序列: $r_0, r_1, \dots, r_{12}$。
- 鸽巢原理: 在 $r_0, \dots, r_{10}$ 中必有重复。
- 找到第一个重复: 假设我们检查序列,发现 $r_2$ 是第一个在后面有重复的状态,并且它的第一次重复出现在 $r_9$,即 $r_2=r_9$。
- 此时 $j=2, l=9$。
- 拆分:
- $x = s_1s_2$。$|x|=2$。
- $y = s_3s_4s_5s_6s_7s_8s_9$。$|y|=9-2=7$。
- $z = s_{10}s_{11}s_{12}$。
- 验证条件:
- 条件2: $|y|=7>0$。成立。
- 条件3: $|xy| = |x|+|y| = 2+7 = 9$。因为 $9 \le p=10$,所以 $|xy| \le p$。成立。
- (条件1已在之前证明)。
- “第一次重复”的精确含义: 严谨地说,我们是在序列 $r_0, r_1, \dots, r_p$ 中,从后往前看,找到第一个重复其前面某个状态的状态。例如,如果序列是 A, B, C, D, B, ... 那么 $r_4=r_1=B$ 是我们要找的第一对。这样能保证 $l$ 尽可能小。更简单的策略是,在 $r_0, ..., r_p$ 中找到任意一对重复 $r_j=r_l$,证明都成立。选择"第一个"重复是为了让证明更紧凑,并确保 $l \le p$。
3.6 泵引理的严谨证明
📜 [原文19]
证明 设 $M=\\left(Q, \\Sigma, \\delta, q_{1}, F\\right)$ 是一个识别 $A$ 的 DFA,且 $p$ 是 $M$ 的状态数。
设 $s=s_{1} s_{2} \\cdots s_{n}$ 是 $A$ 中的一个长度为 $n$ 的字符串,其中 $n \\geq p$。设 $r_{1}, \\ldots, r_{n+1}$ 是 $M$ 在处理 $s$ 时进入的状态序列,因此对于 $1 \\leq i \\leq n$,有 $r_{i+1}=\\delta\\left(r_{i}, s_{i}\\right)$。这个序列的长度为 $n+1$,至少为 $p+1$。根据鸽巢原理,序列中前 $p+1$ 个元素中必然有两个是相同的状态。我们称第一个为 $r_{j}$,第二个为 $r_{l}$。因为 $r_{l}$ 出现在从 $r_{1}$ 开始的序列中前 $p+1$ 个位置之内,所以 $l \\leq p+1$。现在设 $x=s_{1} \\cdots s_{j-1}, y=s_{j} \\cdots s_{l-1}$, 且 $z=s_{l} \\cdots s_{n}$。
由于 $x$ 将 $M$ 从 $r_{1}$ 带到 $r_{j}$,$y$ 将 $M$ 从 $r_{j}$ 带到 $r_{j}$,而 $z$ 将 $M$ 从 $r_{j}$ 带到接受状态 $r_{n+1}$,所以 $M$ 必须接受 $x y^{i} z$(对于 $i \\geq 0$)。我们知道 $j \\neq l$,所以 $|y|>0$;并且 $l \\leq p+1$,所以 $|x y| \\leq p$。因此我们满足了泵引理的所有条件。
这是对前面“证明思想”的形式化和紧凑化的总结。它将所有步骤串联起来,形成一个完整的、严谨的数学证明。
- 前提和设定 (Let...):
- 设 $M$ 是一个识别语言 $A$ 的DFA。
- 设 $p$ 是 $M$ 的状态数 ($p=|Q|$)。
- 设 $s$ 是 $A$ 中任意一个长度 $n \ge p$ 的字符串。
- 设 $r_1, \dots, r_{n+1}$ 是 $M$ 处理 $s$ 时的状态序列 (这里下标从1开始,与之前的 $r_0$ 略有不同,但不影响逻辑)。$r_1$ 是起始状态。
- 核心论证 (鸽巢原理):
- 状态序列的长度是 $n+1$,因为 $n \ge p$,所以 $n+1 \ge p+1$。
- 考察序列的前 $p+1$ 个状态 $r_1, \dots, r_{p+1}$。
- 我们有 $p+1$ 个状态(鸽子),但DFA只有 $p$ 个不同的状态(鸽巢)。
- 因此,在这 $p+1$ 个状态中,必有两个是相同的。
- 我们把第一次出现这种重复的两个状态记为 $r_j$ 和 $r_l$ (其中 $1 \le j < l \le p+1$)。
- 构造拆分 (Let...):
- 基于找到的重复位置 $j$ 和 $l$,将字符串 $s$ 拆分:
- $x = s_1 \dots s_{j-1}$ (空串如果 $j=1$)
- $y = s_j \dots s_{l-1}$
- $z = s_l \dots s_n$
- 验证三个条件:
- 条件1 ($xy^iz \in A$):
- $x$ 将DFA从起始状态 $r_1$ 带到 $r_j$。
- $y$ 将DFA从 $r_j$ 带回到 $r_j$ (因为 $r_j=r_l$)。
- $z$ 将DFA从 $r_j$ (= $r_l$) 带到最终的接受状态 $r_{n+1}$。
- 因此,无论 $y$ 部分重复多少次 (包括0次),DFA的路径都是 $r_1 \xrightarrow{x} r_j \xrightarrow{y^i} r_j \xrightarrow{z} r_{n+1}$。因为 $r_{n+1}$ 是接受状态,所以 $xy^iz$ 总被接受。条件1成立。
- 条件2 ($|y|>0$):
- 因为我们选择的 $j$ 和 $l$ 是不同的位置,即 $j < l$,所以 $j \ne l$。
- $y$ 是从 $s_j$到 $s_{l-1}$ 的子串,其长度为 $l-j$。
- 因为 $j < l$, 所以 $l-j \ge 1$。
- 所以 $|y|>0$。条件2成立。
- 条件3 ($|xy| \le p$):
- 我们是在序列的前 $p+1$ 个位置内找到了重复,所以 $l \le p+1$。
- $x=s_1\dots s_{j-1}, y=s_j\dots s_{l-1}$。
- $xy = s_1\dots s_{l-1}$。
- $|xy|$ 的长度是 $l-1$。
- 因为 $l \le p+1$,所以 $l-1 \le p$。
- 所以 $|xy| \le p$。条件3成立。
- 结论 (Therefore...):
- 我们已经证明,对于任意选择的长字符串 $s$,都存在一种满足所有三个条件的 $xyz$ 拆分。
- 因此,泵引理得证。
(注:原文证明中下标的处理有一些不严谨之处。例如,如果状态序列是 $r_1, ..., r_{n+1}$,长度为$n+1$,那么 $r_{i+1} = \delta(r_i, s_i)$,并且 $x=s_1..s_{j-1}, y=s_j..s_{l-1}$。则 $|xy| = l-1$。而 $l \le p+1$ 意味着 $l-1 \le p$。这与泵引理的 $|xy| \le p$ 一致。所以原文的逻辑是正确的,只是表达上可以更清晰)
本段是之前所有公式和推导的最终组合,形成一个完整的证明链。没有新的公式。
这个是纯理论证明的总结,不适合用新的数值示例来解释。之前的数值示例已经为这个证明的每一步提供了具体的感性认识。
- 下标的混乱: 证明中 $r_i$ 是第 $i$ 个状态,而 $s_i$ 是第 $i$ 个字符。$r_i$ 是处理完 $s_{i-1}$ 后的状态。这种下标的错位是理解时的一个小障碍。关键是理解其代表的逻辑关系,而不是纠结于具体的下标数字。
- 证明的结构: 这是一个标准的“直接证明”。它从“A是正则语言”这个前提出发,通过一系列逻辑构造和推导,直接得出了“A满足泵浦性质”的结论。
3.7 如何使用泵引理进行反证
📜 [原文20]
要使用泵引理证明语言 $B$ 不是正则的,首先假设 $B$ 是正则的以得到矛盾。然后使用泵引理保证存在一个泵浦长度 $p$,使得 $B$ 中所有长度大于或等于 $p$ 的字符串都可以被泵浦。接下来,找到 $B$ 中一个长度大于或等于 $p$ 但不能被泵浦的字符串 $s$。最后,通过考虑将 $s$ 分成 $x, y, z$ 的所有方式(如果方便,考虑泵引理的条件 3),并对于每种这样的划分,找到一个 $i$ 值使得 $x y^{i} z \\notin B$ 来证明 $s$ 不能被泵浦。这最后一步通常涉及将 $s$ 的各种划分方式分组为几种情况并单独分析它们。如果 $B$ 是正则的,那么 $s$ 的存在与泵引理相矛盾。因此 $B$ 不可能是正则的。
这段话给出了一个清晰的、按部就班的操作手册,指导我们如何应用泵引理来证明一个语言是非正则的。这是一个反证法 (proof by contradiction) 的标准流程,可以看作一个“游戏”。
游戏规则:
- 你的目标: 证明语言 $B$ 非正则。
- 对手的目标: 证明语言 $B$ 是正则的。
游戏步骤:
- 你的第一步:假设对手是对的。
- 你先说:“好吧,我们假设语言 $B$ 是正则的。” 这一步是为了引出矛盾。
- 对手的出招:给出泵浦长度 $p$。
- 因为你假设了 $B$ 是正则的,泵引理就生效了。泵引理说“存在一个泵浦长度 $p$”。
- 对手(或者说,定理本身)就会给你一个 $p$。你不知道 $p$ 具体是多少,但你知道它是一个存在且固定的正整数。
- 你的核心招式:选择一个“特殊”字符串 $s$。
- 现在轮到你。你需要在语言 $B$ 中,精心挑选一个字符串 $s$。
- 这个 $s$ 必须满足两个条件:
- 关键:你要选一个能够“体现”出语言 $B$ 非正则“本质”的字符串,一个让对手难以“泵浦”的字符串。这个 $s$ 通常会与 $p$ 相关,例如 $0^p1^p$。
- 对手的反击:拆分字符串 $s$。
- 现在球又到了对手那边。根据泵引理,对手声称 $s$ 可以被拆分成 $s=xyz$,并且这个拆分满足泵引理的三个条件:
- 你的制胜一击:证明对手是错的。
- 你的任务是证明对手的声称是不可能的。
- 你必须证明:无论对手怎么拆分 $s$ (只要拆分满足条件 $|y|>0$ 和 $|xy| \le p$),你总能找到一个整数 $i$ (可以是0, 2, 3, ...),使得泵浦后的新字符串 $xy^iz$ 不在语言 $B$ 中。
- 为了覆盖“所有拆分”,你通常需要按情况讨论。利用 $|xy| \le p$ 可以大大减少情况的数量。
- 宣布胜利:得出矛盾。
- 你已经证明了,你选择的那个字符串 $s$ 不可能被泵浦。
- 但这与泵引理(如果B是正则的,那么s必须可以被泵浦)相矛盾。
- 这个矛盾说明,你一开始的假设——“语言B是正则的”——是错误的。
- 因此,你最终得出结论:语言 $B$ 必须是非正则的。
这是一个逻辑流程,不涉及新的公式,但涉及逻辑符号的运用:
- 前提 (Assumption): $B$ is regular.
- 蕴含 (Implies): $\implies$
- $B \text{ is regular} \implies (\exists p > 0)(\forall s \in B, |s| \ge p)(\exists xyz=s, |y|>0, |xy|\le p)(\forall i \ge 0)(xy^iz \in B)$.
- 你的证明目标: Find one $s$ (dependent on $p$) such that for all possible $xyz$ decompositions (that satisfy $|y|>0, |xy|\le p$), you can find one $i$ where $xy^iz \notin B$.
- 形式化: $(\exists s \in B, |s|\ge p)(\forall xyz=s, |y|>0, |xy|\le p)(\exists i \ge 0)(xy^iz \notin B)$.
- 这恰好是上面泵引理结论的否定。证明了这个否定,就推翻了原结论,从而推翻了前提。
这个流程将在接下来的例1.73中被完整地演示,那会是最好的数值示例。
- 量词顺序是关键: 游戏步骤中的黑体字(你选择/对手选择)对应着逻辑量词($\exists$ 存在 / $\forall$ 所有)。顺序绝对不能错。是你先选 $s$,然后对手再拆分。你不能假设 $s$ 会被如何拆分。
- $p$ 是未知的: 你在选择 $s$ 的时候,不能假设 $p=5$ 或者任何具体数字。你的 $s$ 的构造必须对任何对手给出的 $p$ 都有效。这就是为什么 $s$ 通常用 $p$ 来表示,如 $s=0^p1^p$。
- 覆盖所有情况: 你的证明必须覆盖所有可能的拆分方式。如果遗漏了一种拆分情况,而那种情况恰好可以被泵浦,你的证明就失败了。
3.8 寻找关键字符串s的技巧
📜 [原文21]
找到 $s$ 有时需要一些创造性的思考。您可能需要在几个 $s$ 的候选字符串中进行尝试,才能找到一个有效的。尝试 $B$ 中那些似乎展现了 $B$ 的非正则性“本质”的成员。在下面的一些例子中,我们将进一步讨论寻找 $s$ 的任务。
这段话给出了使用泵引理证明中最具挑战性和创造性的一步——如何选择字符串 $s$——的一些实用建议。
- 创造性与试错: 作者承认,选择 $s$ 并非总是一目了然的,它需要创造性,甚至可能需要反复试错。你第一次想到的 $s$ 可能并不好用(它可能恰好可以被泵浦),这时候需要换一个再试。
- 核心技巧:寻找“本质”
- 你应该选择一个能够最典型地体现该语言“非正则”特性的字符串。
- 这个“本质”通常和语言定义中那种需要“无限记忆”的约束有关。
- 例如,对于 $B = \{0^n1^n\}$,其本质是“0和1的数量必须严格相等”。一个好的 $s$ 应该能让泵浦操作轻易地破坏这种相等关系。$s=0^p1^p$ 就是一个绝佳的选择,因为泵引理条件3限制了 $y$ 只能是0,泵浦 $y$ 就会直接改变0的数量,而1的数量不变,从而破坏了相等性。
- 对于 $F = \{ww \mid w \in \{0,1\}^*\}$ (一个串和它自身的重复),其本质是“前半部分和后半部分必须完全一样”。一个好的 $s$ 应该能让泵浦操作破坏这种“完全一样”的结构。
- 后续学习: 作者预告,在接下来的几个例子中,会通过实践进一步展示如何根据不同的语言来选择合适的 $s$。
简单来说,选择 $s$ 的艺术在于:选择一个字符串,利用泵引理的条件3 ($|xy| \le p$) 将可泵浦部分 $y$ “框”在一个特定的、结构单一的区域,使得对 $y$ 的任何泵浦操作(增加或删除字符)都会立刻、明显地破坏整个字符串赖以成立的核心结构。
本段是策略性建议,不含公式。
- 语言 $B = \{0^n1^n\}$:
- 好的选择: $s=0^p1^p$。因为 $|xy| \le p$,所以 $y$ 只能包含0。泵浦 $y$ 会改变0的数量,导致 $0$ 和 $1$ 的数量不再相等。
- 不好的选择: 可能没有“不好”的选择,但 $0^p1^p$ 是最直接的。
- 语言 $F = \{ww\}$:
- 好的选择: $s=0^p10^p1$。这里 $w=0^p1$。因为 $|xy| \le p$,所以 $y$ 只能是 $s$ 开头那段 $0^p$ 的一部分。泵浦 $y$ 会改变第一个 $w$ 中的0的数量,但不会改变第二个 $w$。这样,泵浦后的字符串就不再是 $w'w'$ 的形式了。
- 不好的选择: $s=0^{2p}$ (即 $w=0^p$)。这个字符串是 $0^{2p}$。我们可以拆分 $x=0^{p-1}, y=0, z=0^p$。那么 $xy^iz = 0^{p-1}0^i0^p = 0^{p+i-1}0^p$。这显然不是 $ww$ 的形式... 等一下,这个例子可以被泵浦!
- 重新分析不好的选择: 选 $s=0^{2p}$。对手可以这样拆分:$x=0^{2p-2}, y=00, z=\varepsilon$。那么 $xy^iz = 0^{2p-2}(00)^i$。这永远是偶数个0,总能写成 $w'w'$ 的形式(其中 $w'$ 是一半的0)。例如 $i=2$ 时,字符串是 $0^{2p+2}$,可以看作 $w'=0^{p+1}$ 的 $w'w'$。所以 $s=0^{2p}$ 可以被泵浦,无法导出矛盾!
- 这个试错过程完美地说明了本段的观点:选择 $s$ 需要仔细思考。
- 不要选择可以被泵浦的字符串: 如上例所示,即使一个语言是非正则的,它里面也可能存在某些可以被泵浦的长字符串。你的任务是找到那个“顽固不化”、不能被泵浦的字符串。
- 利用 $p$: 构造 $s$ 时,一定要用上 $p$。这保证了你的 $s$ 足够长,并且它的结构与泵浦长度 $p$ 产生了关联,便于利用条件3。
本章详细讲解了如何将泵引理的证明思想付诸实践。首先,通过将输入字符串 $s$ 与DFA的状态转移轨迹相关联,我们找到了拆分 $s$ 为 $xyz$ 的具体方法:$x$ 是进入状态环路前的部分,$y$ 是构成环路的部分,$z$ 是离开环路后的部分。这种基于DFA环路的拆分方法,被证明天然满足泵引理的三个条件:可泵性(环路可以绕任意圈)、非空性(环路有长度)和位置限制(环路在DFA处理长字符串的早期必然出现)。
随后,本章给出了使用泵引理进行反证法的清晰步骤,这是一个与试图证明语言正则的“对手”进行博弈的过程。核心策略是:假设语言正则,利用泵引理赋予的泵浦长度 $p$,精心构造一个长度与 $p$ 相关且能体现语言非正则本质的字符串 $s$。然后,通过分析所有可能的拆分方式(并利用 $|xy| \le p$ 大幅简化分析),证明 $s$ 无论如何都不能被泵浦,从而与泵引理产生矛盾,最终证明原语言非正则。选择合适的字符串 $s$ 是此过程中最具技巧性的一步。
这部分内容的存在,是为了将泵引理从一个抽象的理论定理,转化为一个可操作、可应用的实用工具。
- 完成理论闭环:提供了泵引理定理本身的严谨证明,使得整个理论体系是自洽和完备的。
- 提供操作指南:通过“如何使用泵引理”和“如何寻找s”的指导,为读者提供了清晰的路线图,解决了“学了定理不会用”的问题。
- 培养形式化证明思维:通过泵引理的应用实例,训练读者进行严格的、基于情况讨论的数学证明,这是计算机科学理论研究的核心技能。它教会我们如何与逻辑量词(“所有”、“存在”)打交道。
- “找茬”游戏:
- 游戏背景: 你的朋友声称他有一台“万能正则语言识别机”(一个DFA)。
- 你的任务: 证明他的机器有缺陷,无法识别某个你指定的非正则语言 $L$。
- 游戏开始:
- 你: “我们来试试语言 $L=\{0^n1^n\}$。我假设你的机器能识别它。”
- 朋友: “当然能!我的机器有 $p$ 个状态。根据泵引理,任何长度超过 $p$ 的字符串都能被我的机器‘泵浦’。” (他告诉你了他的机器状态数 $p$)。
- 你: “很好。那我给你一个测试字符串 $s=0^p1^p$。” (你精心构造了一个字符串,长度与他的机器状态数挂钩)。
- 朋友: “没问题。我的机器会把它分成 $xyz$,其中 $y$ 在前 $p$ 个字符内且非空,然后 $xy^iz$ 都能识别。”
- 你 (将军!): “根据你的规则 '$|xy| \le p$',你分的 $y$ 只能是 0...0 的形式。那么我选择泵浦两次,新字符串 $xyyz$ 的0会比1多。你的机器必须拒绝它,因为它不属于 $L$。但这又和你说的‘都能识别’矛盾了!所以,你的机器根本无法识别语言 $L$。”
- 破解密码系统:
- 一个正则语言就像一个设计有缺陷的密码系统。
- 泵引理就是这个系统的漏洞报告。报告上说:“任何长度超过 $p$ 的合法密文,其开头 $p$ 个字符内都含有一个‘循环节’($y$)。你可以把这个循环节重复任意次或删除,得到的新密文仍然是合法的。”
- 你的任务: 利用这个漏洞,证明某个语言(比如 $L=\{0^n1^n\}$)所生成的字符串不符合这个漏洞报告的描述,因此它不可能出自这个有缺陷的密码系统。
- 操作:
- 你拿到一个据称是该系统生成的长密文 $s=0^p1^p$。
- 漏洞报告说,循环节 $y$ 必须在前 $p$ 个字符(即全0部分)里找。
- 你尝试利用这个漏洞:把找到的循环节 $y$ (它肯定是几个0) 复制一遍。
- 你得到一个新密文 $s' = 0^{p+|y|}1^p$。
- 你发现,这个新密文 $s'$ 根本不属于语言 $L$ (因为0和1数量不等)。
- 结论: 语言 $L$ 的字符串不具备这个密码系统应有的“循环节”漏洞。因此,语言 $L$ 不可能是由这种有缺陷的密码系统(即任何DFA)生成的。所以 $L$ 是非正则的。
44. 泵引理的应用实例
4.1 示例 1.73: 证明 $B = \{0^n1^n \mid n \ge 0\}$ 非正则
📜 [原文22]
例 1.73
设 $B$ 为语言 $\left\\{0^{n} 1^{n} \mid n \geq 0\right\\}$。我们使用泵引理证明 $B$ 不是正则的。证明采用反证法。
这是应用泵引理的第一个完整示例。目标是证明语言 $B = \{0^n1^n \mid n \ge 0\}$ 是非正则的。
本段是引言,明确了要证明的目标和使用的方法。
- 目标语言 (Target Language): $B = \{0^n1^n \mid n \ge 0\}$。这个语言包含的字符串由若干个0后面跟着相同数量的1组成。例如:$\varepsilon, 01, 0011, 000111, \dots$。
- 证明工具 (Tool): 泵引理 (Pumping Lemma)。
- 证明方法 (Method): 反证法 (Proof by contradiction)。这是使用泵引理证明非正则性的标准方法。我们的整个论证将以“假设 B 是正则的”开始,并以导出矛盾结束。
- $B = \{0^n1^n \mid n \ge 0\}$:
- $B$: 语言的名称。
- $\{ \dots \mid \dots \}$: 集合构建符,花括号内描述集合元素的“形式”和“条件”。
- $0^n1^n$: 字符串的形式,表示 $n$ 个0后跟 $n$ 个1。
- $n \ge 0$: 变量 $n$ 的条件,表示 $n$ 是任意非负整数。
- 属于 $B$:
- $n=0$: $\varepsilon$ (空字符串)
- $n=1$: $01$
- $n=4$: $00001111$
- 不属于 $B$:
- $001$ (数量不匹配)
- $1010$ (顺序不匹配)
- 本段是引言,主要是设定场景。关键的易错点将在后续步骤中出现。读者需要牢记我们即将开始的是一个在“假设B是正则的”这个虚假前提下进行的逻辑推演。
4.2 示例 1.73: 选择字符串并应用引理
📜 [原文23]
假设 $B$ 是正则的,这与事实相反。设 $p$ 为泵引理给出的泵浦长度。选择 $s$ 为字符串 $0^{p} 1^{p}$。因为 $s$ 是 $B$ 的一个成员,并且 $s$ 的长度大于 $p$,所以泵引理保证 $s$ 可以被分成三部分,$s=x y z$,其中对于任何 $i \\geq 0$,字符串 $x y^{i} z$ 都在 $B$ 中。我们考虑三种情况来证明这个结果是不可能的。
这里是反证法游戏的前三步,完全按照我们之前总结的“操作手册”进行。
- 第一步:做出假设
- “假设 $B$ 是正则的”。这是反证法的起点。
- 第二步:获得泵浦长度 $p$
- 因为我们假设了 $B$ 是正则的,所以泵引理适用。
- 泵引理告诉我们,存在一个泵浦长度 $p$。我们不知道 $p$ 的具体值,但我们知道它是一个正整数常量。
- 第三步:选择关键字符串 $s$
- 我们选择了 $s = 0^p 1^p$。这个选择非常高明:
- $s$ 是否属于 $B$? 是的。它由 $p$ 个0后面跟着 $p$ 个1组成,符合 $0^n1^n$ 的形式 (这里 $n=p$)。
- $s$ 的长度是否 $\ge p$? 是的。$|s| = |0^p| + |1^p| = p + p = 2p$。因为 $p$ 是正整数,所以 $2p \ge p$。
- 这个 $s$ 的选择将 $p$ 这个抽象的数字嵌入到了字符串的具体结构中,为后续利用条件3 ($|xy| \le p$) 埋下了伏笔。
- 第四步:应用泵引理
- 既然 $s$ 是 $B$ 中一个足够长的字符串,那么根据泵引理,它必定可以被拆分成 $s=xyz$ 并满足所有泵浦条件。
- 特别是,对于任何 $i \ge 0$,$xy^iz$ 都必须还是 $B$ 的成员。
- 引出证明的下一步
- 我们的目标是证明上述结论是“不可能的”。
- 我们将通过分析所有可能的拆分方式来证明这一点。作者预告将分“三种情况”来讨论。
- $p$: 由泵引理保证存在的泵浦长度。
- $s = 0^p 1^p$: 我们选择的特定字符串。
- $|s| = 2p$
- $s = xyz$: 泵引理保证存在的拆分,必须满足:
- $|y| > 0$
- $|xy| \le p$
- $\forall i \ge 0, xy^iz \in B$
- 假设对手给出的泵浦长度是 $p=5$。
- 我们选择的字符串就是 $s = 0^5 1^5 = 0000011111$。
- $|s|=10$, 满足 $|s| \ge p=5$。
- 泵引理说,我们可以把 0000011111 拆分成 $xyz$。
- 并且,根据条件3 ($|xy| \le 5$),这个拆分中的 $x$ 和 $y$ 部分必须都位于字符串开头的 00000 之中。
- 例如,一种可能的拆分是 $x=00, y=000, z=11111$。
- 我们的任务就是要证明,所有这类可能的拆分(只要满足条件2和3)都无法通过泵浦测试。
- $p$ 不是你选的:要时刻记住 $p$ 是泵引理给定的,而不是你选择的。你的策略必须对任何 $p \ge 1$ 都有效。
- $s$ 是你选的:选择 $s$ 是整个证明中最关键的创造性步骤。$s=0^p1^p$ 是本题的标准答案,因为它能完美地利用上泵引理的所有条件。
4.3 示例 1.73: 情况讨论与导出矛盾
📜 [原文24]
- 字符串 $y$ 只由 0 组成。在这种情况下,字符串 $x y y z$ 的 0 的数量多于 1 的数量,因此不是 $B$ 的成员,违反了泵引理的条件 1。这种情况产生了矛盾。
- 字符串 $y$ 只由 1 组成。这种情况也产生了矛盾。
- 字符串 $y$ 由 0 和 1 组成。在这种情况下,字符串 $x y y z$ 可能有相同数量的 0 和 1,但是它们的顺序会错乱,一些 1 会在 0 之前。因此它不是 $B$ 的成员,这与事实矛盾。
这是反证法的最后一步:通过分析所有可能的 $xyz$ 拆分,证明每一种拆分都会在泵浦时产生矛盾。作者在这里提出了三种情况。
分析的基础:我们的字符串是 $s=0^p1^p$。泵引理保证 $s$ 可以被拆分为 $s=xyz$,满足 $|y|>0$ 和 $|xy| \le p$。
- 情况1: $y$ 只由 0 组成
- 为什么会出现这种情况? 这是最主要的情况。因为 $|xy| \le p$,而字符串 $s$ 的前 $p$ 个字符全是 '0',所以 $x$ 和 $y$ 都必须是 '0' 的子串。
- 泵浦会怎样? 让我们向上泵浦,考虑 $i=2$ 的情况,即新字符串 $s' = xyyz$。
- 原始字符串 $s$ 有 $p$ 个0和 $p$ 个1。
- 新字符串 $s'$ 比 $s$ 多了一个 $y$。因为 $y$ 只包含0,且 $|y|>0$,所以 $s'$ 的0的数量是 $p + |y|$,比 $p$ 要多。
- $s'$ 的1的数量没有变,仍然是 $p$。
- 因此,在 $s'$ 中,0的数量 ($p+|y|$) 不等于1的数量 ($p$)。
- 结论: $s' = xyyz$ 不符合语言 $B=\{0^n1^n\}$ 的定义,所以 $s' \notin B$。
- 矛盾: 这与泵引理的条件1“对于任何 $i \ge 0, xy^iz$ 都必须在 $B$ 中”相矛盾。
- 情况2: $y$ 只由 1 组成
- 为什么会出现这种情况? 要让 $y$ 只包含1,那么子串 $y$ 必须完全位于 $s$ 的后半部分 ($1^p$)。这意味着 $x$ 必须包含所有的 $p$ 个0,再加上可能的一些1。这样一来,$|x|$ 至少是 $p$。因为 $|y|>0$,所以 $|xy| = |x|+|y| > p$。
- 矛盾: 这直接与泵引理的条件3 ($|xy| \le p$) 相矛盾。因此,这种情况在泵引理的约束下是不可能发生的。
- 情况3: $y$ 由 0 和 1 组成
- 为什么会出现这种情况? 要让 $y$ 同时包含0和1,那么 $y$ 必须跨越 $s$ 中 $0^p$ 和 $1^p$ 的边界,形如 $0...01...1$。
- 矛盾1 (来自条件3): 同样地,因为 $s$ 的前 $p$ 个字符都是0,所以要让 $y$ 包含1,那么 $y$ 的结尾必须在第 $p+1$ 个字符或之后。这意味着 $|xy|$ 必然大于 $p$。这再次与条件3 ($|xy| \le p$) 相矛盾。所以这种情况也是不可能发生的。
- 矛盾2 (来自泵浦): 即使我们暂时忽略条件3,来分析泵浦 $y$ 的后果。如果 $y = 0...01...1$,那么 $xyyz$ 将会是 $x(0..1)(0..1)z$ 的形式。字符串中会出现 1 后面跟着 0 的情况,破坏了 $0^n1^n$ 的“所有0在所有1之前”的顺序规则。因此 $xyyz$ 也不在 $B$ 中。
综合来看,在泵引理的强约束(特别是条件3)下,唯一可能发生的只有情况1。而在情况1中,向上泵浦 ($i=2$) 或向下泵浦 ($i=0$) 都会导致0和1数量不相等,从而产生一个不在 $B$ 中的字符串,这与泵引理的条件1矛盾。
- $s = 0^p1^p = xyz$
- 约束: $|y|>0$, $|xy| \le p$
- 推论: 由于 $|xy| \le p$ 且 $s$ 的前 $p$ 个字符都是 '0',所以 $x$ 和 $y$ 字符串必须完全由 '0' 构成。
- $x = 0^a$
- $y = 0^b$
- $z = 0^{p-a-b}1^p$
- 其中 $a \ge 0, b > 0$ (因为 $|y|>0$), and $a+b \le p$ (因为 $|xy| \le p$)
- 分析泵浦 $xy^iz$:
- $xy^iz = (0^a)(0^b)^i(0^{p-a-b}1^p) = 0^a 0^{bi} 0^{p-a-b} 1^p = 0^{a+bi+p-a-b} 1^p = 0^{p+b(i-1)}1^p$。
- 选择 $i$ 制造矛盾:
- 选择 $i=2$: 新字符串是 $0^{p+b}1^p$。因为 $b>0$,所以 $p+b \ne p$。0和1数量不等,字符串 $\notin B$。矛盾。
- 选择 $i=0$: 新字符串是 $0^{p-b}1^p$。因为 $b>0$,所以 $p-b \ne p$。0和1数量不等,字符串 $\notin B$。矛盾。
- 由于我们找到了矛盾,所以最初的假设“B是正则的”不成立。
- 忽略条件3: 如果没有条件3 ($|xy| \le p$),我们就无法排除情况2和情况3,证明会变得复杂。对手可能会选择一个跨越中间的 $y$ 来泵浦,使得数量关系得以维持。条件3是简化证明的关键。
- “向下泵”($i=0$): 在这个例子中,向上泵 ($i=2$) 和向下泵 ($i=0$) 都能导出矛盾。在某些其他语言的证明中,可能只有一种方式能导出矛盾,需要灵活选择。
- 覆盖所有情况: 虽然利用条件3后我们发现只有情况1可能发生,但在完整的证明中,清晰地指出为什么情况2和3不可能发生,会使论证更加严谨和无懈可击。
4.4 示例 1.73: 结论与简化论证
📜 [原文25]
因此,如果我们假设 $B$ 是正则的,那么矛盾是不可避免的,所以 $B$ 不是正则的。请注意,我们可以通过应用泵引理的条件 3 来简化此论证,以消除情况 2 和 3。
在此例中,寻找字符串 $s$ 很容易,因为 $B$ 中任何长度为 $p$ 或更长的字符串都可以。在接下来的两个例子中,某些 $s$ 的选择不起作用,因此需要额外小心。
这部分是对例1.73的总结和反思。
- 最终结论:
- 我们从“假设B是正则的”出发。
- 通过应用泵引理,我们分析了所有可能性,并证明了在任何情况下都会导致矛盾。
- 因此,这个矛盾是“不可避免的”。
- 唯一的解释就是,我们最初的假设是错误的。
- 所以,最终结论是:$B$ 不是正则的。
- 简化论证的提示:
- 作者指出,前面分三种情况的讨论可以被简化。
- 简化的关键在于充分利用条件3 ($|xy| \le p$)。
- 正如我们在上一节分析的,条件3直接使得情况2($y$只含1)和情况3($y$含0和1)变得不可能。
- 因此,一个更简洁、更优雅的证明可以直接这样写:“根据泵引理条件3,因为 $|xy| \le p$,所以 $x$ 和 $y$ 必然只由0组成。又根据条件2, $|y|>0$。因此,当泵浦字符串 $xyyz$ 时,0的数量增加而1的数量不变,导致新字符串不属于 $B$。这与条件1矛盾。因此 $B$ 非正则。”
- 这个简化的版本实际上是标准证明的书写方式。
- 对选择 $s$ 的反思:
- 作者回顾了本例中选择字符串 $s=0^p1^p$ 的过程,并评价为“很容易”。
- 实际上,对于语言 $B$ 来说,任何形如 $0^k1^k$ (只要 $2k \ge p$) 的字符串都可以成功用于证明。
- 预警: 作者提醒我们,不要因此掉以轻心。在后续的例子中(如例1.74和1.75),选择哪个 $s$ 将会变得非常关键,有些看似合理的 $s$ 实际上是无法导出矛盾的“陷阱”。这需要我们更加深入地思考语言的结构和泵引理的约束。
本段为文字性总结,无新公式。
- 演示 $s$ 的其他选择:
- 假设 $p=5$。
- 我们可以选择 $s=0^51^5$ (如前所述)。
- 我们也可以选择 $s=0^61^6$。$|s|=12 \ge 5$。证明过程完全一样,因为 $|xy| \le 5$,所以 $y$ 还是只能由0组成。
- 我们甚至可以选择 $s=0^p1^p$ 之外的 $s=0^{p+k}1^{p+k}$。只要字符串足够长,且能利用条件3把 $y$ 限制在单一结构部分,证明就能成功。
- 证明的优雅性: 初学者可能会像原文第一遍那样罗列所有情况。而熟练的证明者会首先利用所有约束条件(特别是条件3)来排除不可能的情况,使证明主体只关注于唯一可能发生的情况。
- 不要路径依赖: 这个例子很“完美”,不代表所有泵引理的证明都这么直截了当。要为后续更复杂的挑战做好心理准备。
本章通过一个经典且完整的示例——证明语言 $B=\{0^n1^n \mid n \ge 0\}$ 是非正则的——详细演示了泵引理的实战应用。整个证明过程严格遵循了反证法的框架:
- 假设 $B$ 是正则的,从而获得一个未知的泵浦长度 $p$。
- 选择一个与 $p$ 相关的、能体现 $B$ 非正则本质的字符串 $s=0^p1^p$。
- 应用泵引理,断言 $s$ 必须可以被拆分为 $s=xyz$ 并满足三个泵浦条件。
- 分析所有可能的拆分。通过利用关键的条件3 ($|xy| \le p$),我们得出结论:可泵浦部分 $y$ 必然完全由 '0' 构成。
- 导出矛盾:对这个只含 '0' 的非空子串 $y$ 进行泵浦(例如,考虑 $xyyz$),会改变字符串中 '0' 的数量,而 '1' 的数量不变。这导致新字符串不再满足“0和1数量相等”的条件,即 $xyyz \notin B$。这与泵引理的条件1相矛盾。
- 得出结论:由于假设 $B$ 是正则的导致了不可避免的矛盾,因此该假设错误,$B$ 必定是非正则的。
最后,本章还强调了在此例中,巧妙利用条件3可以大大简化证明过程,并预示了在其他更复杂的语言中,选择合适的字符串 $s$ 将会更具挑战性。
这个例子的存在,具有极其重要的教学意义:
- 将理论付诸实践:它是泵引理理论教学后的第一个、也是最重要的实践环节。它手把手地展示了抽象的定理是如何应用到具体问题上的。
- 建立标准范式:例1.73的证明过程(尤其是简化后的版本)是使用泵引理进行非正则性证明的标准范本。学者可以通过模仿这个范式来解决其他类似的问题。
- 增强理解与信心:通过一个清晰、成功的证明,读者可以加深对泵引理三个条件(特别是条件3)威力的理解,并建立起使用这一工具解决问题的信心。
- 连接直觉与形式:我们在本章开头直觉地认为 $\{0^n1^n\}$ 需要无限记忆,而这个例子最终用严格的形式化语言证实了这个直觉。它展示了数学工具如何将模糊的直觉转化为坚实的证明。
- 拉伸橡皮筋:
- 想象字符串 $s=0^p1^p$ 是一根一半是黑色(0的部分)、一半是白色(1的部分)的橡皮筋。语言 $B$ 的规则是:黑色部分和白色部分的长度必须严格相等。
- 泵引理的条件3 ($|xy| \le p$) 告诉你:你只能在这根橡皮筋的黑色部分找到一小段可以拉伸或压缩的区域(即子串 $y$)。
- 泵浦 ($i=2$):你捏住 $y$ 这一小段黑色的区域,把它拉长了一倍。结果,整根橡皮筋的黑色部分变长了,而白色部分长度不变。
- 结果: 拉伸后的橡皮筋,黑色和白色不再等长。它违反了语言 $B$ 的规则。
- 矛盾: 泵引理说拉伸后也必须符合规则,但事实却违反了规则。这证明了语言 $B$ 的规则本身与“可拉伸性”(正则性)是根本不相容的。
- 天平称重:
- 语言 $B=\{0^n1^n\}$ 就像一个天平,要求左边托盘里的0砝码数量必须和右边托盘里的1砝码数量完全相等,天平才能平衡。
- 你放上了 $p$ 个0砝码和 $p$ 个1砝码,天平是平衡的($s=0^p1^p \in B$)。
- 泵引理的条件3 ($|xy| \le p$) 告诉你,你只能在左边的0砝码托盘里进行操作。
- 泵浦 ($i=2$):根据泵引理,你必须从左边的托盘里拿出至少一个0砝码(子串 $y$),然后再放回去两个同样重量的0砝码。
- 结果: 你这么做之后,左边托盘里的0砝码数量变成了 $p+|y|$,比右边的 $p$ 个1砝码要多。天平失衡了 ($xyyz \notin B$)。
- 矛盾: 泵引理保证操作后天平仍应平衡,但它却失衡了。这证明了语言 $B$ 的平衡要求太严格了,不允许这种“局部操作”,因此它不是正则的。
4.5 示例 1.74: 需要精细选择字符串的情况
📜 [原文26]
例 1.74
设 $C=\\{w \\mid w \\text { 包含相同数量的 } 0 \\text { 和 } 1\\}$。我们使用泵引理证明 $C$ 不是正则的。证明采用反证法。
这是第二个应用泵引理的例子。这次的目标语言是我们在导论中遇到的语言 $C$。
- 目标语言: $C = \{w \mid w \text{ 包含相同数量的0和1}\}$。这个语言与上一个例子 $B = \{0^n1^n\}$ 的关键区别在于,$C$ 不限制0和1的顺序。例如, $0101 \in C$ 但 $0101 \notin B$。
- 证明方法: 同样采用反证法。
- 挑战预告: 这个例子比上一个更微妙。我们在导论中凭直觉认为 $C$ 是非正则的,现在需要用泵引理来严格证明它。这个过程将揭示选择正确字符串 $s$ 的重要性。
- $C=\\{w \\mid w \\text { 包含相同数量的 } 0 \\text { 和 } 1\\}$
- 这个语言可以用一个更数学化的方式描述:$C = \{w \in \{0,1\}^* \mid \#_0(w) = \#_1(w) \}$。
- $\#_0(w)$: 字符串 $w$ 中符号 '0' 出现的次数。
- $\#_1(w)$: 字符串 $w$ 中符号 '1' 出现的次数。
- 属于 $C$:
- $\varepsilon$ (#0=0, #1=0)
- $01, 10$ (#0=1, #1=1)
- $0011, 0101, 1001, 1010, 0110, 1100$ (#0=2, #1=2)
- 不属于 $C$:
- $0, 1, 00, 11, 001, 110$ (数量不相等)
- 与B的区别: 必须时刻牢记 $C$ 对顺序没有要求。$B$ 是 $C$ 的一个真子集 ($B \subset C$)。
- 证明的难点: 正是因为 $C$ 对顺序没有要求,当我们泵浦一个字符串时,破坏顺序不再能作为导出矛盾的理由。我们唯一的武器就是破坏数量的相等性。
4.6 示例 1.74: 错误字符串选择的陷阱
📜 [原文27]
假设相反,$C$ 是正则的。设 $p$ 为泵浦引理给出的泵浦长度。与例 1.73 中一样,设 $s$ 为字符串 $0^{p} 1^{p}$。由于 $s$ 是 $C$ 的成员,且其长度大于 $p$,泵浦引理保证 $s$ 可以被分成三部分,$s=x y z$,其中对于任何 $i \\geq 0$,字符串 $x y^{i} z$ 都在 $C$ 中。我们希望证明这个结果是不可能的。但等等,它是可能的!如果我们将 $x$ 和 $z$ 设为空字符串,并将 $y$ 设为字符串 $0^{p} 1^{p}$,那么 $x y^{i} z$ 总是包含相同数量的 0 和 1,因此在 $C$ 中。所以看起来 $s$ 可以被泵浦。
这段话是一个戏剧性的转折,它展示了一个看似完美的计划是如何失败的,从而凸显了泵引理中一个经常被忽略的细节。
- 沿用旧策略: 作者一开始尝试完全照搬例1.73的成功策略。
- 假设: $C$ 是正则的。
- 获得: 泵浦长度 $p$。
- 选择: 和上次一样的字符串 $s = 0^p1^p$。这个字符串也属于 $C$ (有p个0, p个1),并且长度 $2p \ge p$。
- 出现意外:
- 我们希望证明 $s=0^p1^p$ 不能被泵浦。
- 但作者突然喊停:“但等等,它是可能的!” (But wait, it is possible!)
- “对手”的反击:
- 一个试图证明 $C$ 是正则的“对手”,可以提出这样一种拆分方式来反驳我们:
- $x = \varepsilon$ (空字符串)
- $y = 0^p1^p$ (整个字符串 $s$)
- $z = \varepsilon$ (空字符串)
- 让我们检查这种拆分:
- $s = xyz$? 是的, $\varepsilon \cdot (0^p1^p) \cdot \varepsilon = 0^p1^p$。
- $|y|>0$? 是的, $|y|=2p > 0$。
- 现在,让我们泵浦这种拆分:
- 新字符串是 $xy^iz = (0^p1^p)^i$。
- 在这个新字符串中,0的数量是 $p \times i$,1的数量也是 $p \times i$。
- 0和1的数量永远相等!
- 这意味着,对于所有 $i \ge 0$, $xy^iz$ 都属于 $C$。
- 证明失败:
- 我们找到了一种拆分 $s$ 的方法,使得 $s$ 可以被泵浦。
- 回顾一下我们的任务:我们需要证明“对于所有可能的拆分,$s$都不能被泵浦”。
- 既然我们已经找到了一种可以泵浦的拆分,我们就无法完成我们的证明任务了。
- 使用 $s=0^p1^p$ 的这个尝试失败了!
这段话是一个非常重要的教学环节,它告诉我们,在使用泵引理时,我们必须考虑到所有可能的拆分,而“对手”只需要找到一种能成功泵浦的拆分,就能挫败我们这一次的证明尝试。
- 语言: $C = \{w \mid \#_0(w) = \#_1(w)\}$
- 选择的字符串: $s = 0^p1^p$
- “对手”提出的拆分: $x=\varepsilon, y=0^p1^p, z=\varepsilon$
- 验证泵浦: $s' = xy^iz = (0^p1^p)^i$
- $\#_0(s') = p \times i$
- $\#_1(s') = p \times i$
- 因为 $\#_0(s') = \#_1(s')$,所以 $s' \in C$ 对所有 $i \ge 0$ 成立。
- 问题出在哪里?: “对手”的这个拆分 $x=\varepsilon, y=0^p1^p, z=\varepsilon$,导致 $|xy|=|0^p1^p|=2p$。如果 $p>1$,则 $2p>p$。这个拆分违反了泵引理的条件3 ($|xy| \le p$)。作者在这里是故意“忘记”条件3,来强调它的重要性。
- 设 $p=3$。我们选 $s=000111$。
- 对手拆分: $x=\varepsilon, y=000111, z=\varepsilon$。
- 泵浦:
- $i=2$: $xyyz = 000111000111$。 #0=6, #1=6。属于 $C$。
- $i=0$: $xz = \varepsilon$。 #0=0, #1=0。属于 $C$。
- 看起来 $s$ 可以被泵浦。但是,这个拆分中 $|xy|=|000111|=6$,而泵浦长度 $p=3$。$6 > 3$,所以这个拆分是无效的,因为它不满足 $|xy| \le p$。
- 忘记条件3: 这是本段的核心教训。如果不使用条件3,很多非正则语言看起来都可以被泵浦,导致证明失败。
- 逻辑角色的混淆: 我们(证明者)的任务是覆盖所有合法的拆分。对手(反驳者)只需要找到一个合法的拆分来击败我们。在这个失败的尝试中,我们没能堵死对手的所有路。
4.7 示例 1.74: 利用条件3完成证明
📜 [原文28]
这里,泵引理中的条件 3 是有用的。它规定当泵浦 $s$ 时,它必须被分割,使得 $|x y| \\leq p$。对 $s$ 可以被分割方式的这种限制使得更容易证明我们选择的字符串 $s=0^{p} 1^{p}$ 不能被泵浦。如果 $|x y| \\leq p$,那么 $y$ 必须只由 0 组成,所以 $x y y z \\notin C$。因此,$s$ 不能被泵浦。这给了我们所需的矛盾。
在经历了上一步的“失败”之后,这段话展示了如何利用被我们“遗忘”的条件3来力挽狂澜,完成证明。
- 引入救星:条件3
- 作者明确指出,条件3 ($|xy| \le p$) 是解决问题的关键。
- 这个条件极大地限制了 $s$ 可以被拆分的方式。
- 应用条件3到我们的选择上
- 我们选择的字符串是 $s = 0^p1^p$。
- 条件3说:$x$ 和 $y$ 两部分的组合长度不能超过 $p$。
- 因为 $s$ 的前 $p$ 个字符全部是 '0',所以 $x$ 和 $y$ 只能由 '0' 构成。
- 例如,如果 $p=5$, $s=0000011111$, $|xy| \le 5$ 意味着 $xy$ 必须是 00000 的一个前缀。
- 这样一来,上一段中对手提出的 $y=0^p1^p$ 的拆分就是不合法的了,因为它违反了条件3。
- 重新进行情况分析 (简化版)
- 在条件3的约束下,对于字符串 $s=0^p1^p$,任何合法的拆分 $xyz$ 都必须满足:
- $x$ 是若干个0组成的串 ($x=0^a$)。
- $y$ 是若干个0组成的串 ($y=0^b$)。
- $z$ 是剩下的0和所有的1 ($z=0^{p-a-b}1^p$)。
- 并且,根据条件2 ($|y|>0$),我们知道 $b \ge 1$。
- 泵浦并导出矛盾
- 现在我们再次泵浦,考虑 $i=2$ 的情况:$s' = xyyz$。
- $s'$ 比 $s$ 多了一个 $y$ 部分。
- 因为 $y$ 完全由0组成且非空,所以 $s'$ 的0的数量增加了 ($p+|y|$ 个),而1的数量保持不变 ($p$ 个)。
- 在新字符串 $s'$ 中,0和1的数量不再相等。
- 因此,$s' = xyyz \notin C$。
- 这与泵引理的条件1“$xy^iz$ 必须属于 $C$”产生了矛盾。
- 完成证明
- 我们证明了,对于我们选择的 $s=0^p1^p$,在满足泵引理所有约束(特别是条件3)的前提下,不存在任何一种能成功泵浦的拆分方式。
- 因此,$s$ 是一个“不可泵浦”的字符串。
- 这与“如果C是正则的,s就必须可泵浦”的结论相矛盾。
- 所以,最初的假设“$C$是正则的”是错误的。$C$是非正则的。
- 语言: $C=\{w \mid \#_0(w) = \#_1(w)\}$
- 假设: $C$ is regular.
- 获得: 泵浦长度 $p$.
- 选择: $s = 0^p1^p$.
- 拆分: $s=xyz$ 必须满足 $|y|>0$ 和 $|xy| \le p$.
- 推论: 从 $|xy| \le p$ 和 $s$ 的结构可知,y 必须是 $0^k$ 的形式,其中 $k \ge 1$ (因为 $|y|>0$)。
- 泵浦: 考虑 $s' = xy^2z$。
- $\#_0(s') = \#_0(s) + \#_0(y) = p + k$.
- $\#_1(s') = \#_1(s) = p$.
- 比较: 因为 $k \ge 1$, 所以 $p+k \ne p$. 因此 $\#_0(s') \ne \#_1(s')$.
- 结论: $s' \notin C$.
- 矛盾: 这与泵引理条件1矛盾。所以假设不成立,$C$ 非正则。
- 设 $p=3$。我们选 $s=000111$。
- 任何合法的拆分 $xyz$ 必须满足 $|xy| \le 3$。所以 $x,y$ 都在 000 内部。
- 可能拆分1: $x=0, y=0, z=0111$。
- 泵浦: $xyyz = 0000111$。#0=4, #1=3。不属于 $C$。
- 可能拆分2: $x=\varepsilon, y=00, z=0111$。
- 泵浦: $xyyz = 0000111$。#0=4, #1=3。不属于 $C$。
- ...等等。无论怎么在 000 里拆,y 总是非空的0串。泵浦后0的数量总会改变,导致与1的数量不再相等。
- 条件3是王牌:这个例子完美地展示了条件3的威力。它不是一个可有可无的“技术细节”,而是在很多证明中起决定性作用的核心工具。
- 证明的逻辑流程: 理解这个“差点失败但最终成功”的曲折过程,比单纯记住结论更重要。它揭示了泵引理证明中每一步的逻辑必要性。
4.8 示例 1.74: 关于字符串选择的进一步探讨
📜 [原文29]
在此例中选择字符串 $s$ 比在例 1.73 中需要更仔细。如果我们选择 $s=(01)^{p}$,我们就会遇到麻烦,因为我们需要一个不能被泵浦的字符串,而那个字符串可以被泵浦,即使考虑了条件 3。您能看出如何泵浦它吗?一种方法是设置 $x=\\varepsilon, y=01$ 和 $z=(01)^{p-1}$。那么对于每个 $i$ 值,$x y^{i} z \\in C$。如果您的第一次尝试未能找到不能被泵浦的字符串,请不要气馁。再试一个!
这段话进一步深化了“选择正确字符串 $s$”的重要性,通过一个具体的“坏”选择来说明问题。
- 提出一个“坏”选择:
- 作者建议我们尝试另一个看似合理的字符串 $s = (01)^p$。
- 这个字符串是 0101...01 ($p$ 次重复)。
- 检查 $s$ 的属性:
- $s$ 中有 $p$ 个0和 $p$ 个1,所以 $s \in C$。
- $|s| = 2p$,满足 $|s| \ge p$。
- 所以,$s=(01)^p$ 是一个合法的候选字符串。
- 证明这个“坏”选择是可泵浦的:
- 我们的目标是证明 $s=(01)^p$ 不能被泵浦,但作者指出,它恰恰可以被泵浦。
- “对手”可以提出如下拆分:
- $x = \varepsilon$
- $y = 01$
- $z = (01)^{p-1}$
- 检查这个拆分的合法性 (是否满足泵引理约束):
- $s=xyz$? 是的, $\varepsilon \cdot (01) \cdot (01)^{p-1} = (01)^p$。
- $|y|>0$? 是的, $|y|=2>0$。
- $|xy|\le p$? 是的, $|xy|=|\varepsilon \cdot 01|=2$。只要泵浦长度 $p \ge 2$(通常都是如此),这个条件就满足。
- 泵浦这个拆分:
- 新字符串 $s' = xy^iz = \varepsilon \cdot (01)^i \cdot (01)^{p-1} = (01)^{i+p-1}$。
- 在这个新字符串中,'0' 的数量是 $i+p-1$, '1' 的数量也是 $i+p-1$。
- 0和1的数量永远相等!
- 因此,对于所有 $i \ge 0$, $xy^iz \in C$。
- 再次失败与鼓励:
- 由于我们为 $s=(01)^p$ 找到了一个合法的、可以被成功泵浦的拆分方式,我们再次无法完成我们的反证。
- 这次的失败和上次不同。上次是因为我们忽略了条件3,而这次我们是在遵循了所有三个条件的情况下失败的。
- 失败的根本原因在于我们选错了 $s$。
- 作者最后鼓励读者:如果第一次选择的 $s$ 不起作用,不要灰心,再换一个试试。这强调了选择 $s$ 是一个需要探索和思考的过程。
- 失败的候选字符串: $s=(01)^p$
- 一个成功的拆分: $x=\varepsilon, y=01, z=(01)^{p-1}$
- 泵浦结果: $xy^iz = (01)^{i+p-1}$
- 验证: $\#_0((01)^{i+p-1}) = i+p-1$, $\#_1((01)^{i+p-1}) = i+p-1$。数量相等,恒属于 $C$。
- 为什么 $s=0^p1^p$ 好,而 $s=(01)^p$ 坏?
- $s=0^p1^p$ 的结构是同质的在前,异质的在后。条件3 ($|xy| \le p$) 能把 $y$ 牢牢地“锁”在同质的 $0^p$ 部分。泵浦一个纯0的串,必然破坏0和1的平衡。
- $s=(01)^p$ 的结构是交错的。条件3只能把 $y$ 锁在开头的 0101... 部分。对手可以选择一个结构上“平衡”的 $y$ (比如 01) 来泵浦,使得每次泵浦都是成对地增加0和1,无法破坏数量平衡。
- 设 $p=4$。
- 坏选择: $s=(01)^4 = 01010101$。
- 对手拆分: $x=\varepsilon, y=01, z=010101$。
- $|xy|=2 \le p=4$。合法。
- 泵浦:
- $i=2$: $xyyz = 0101010101 = (01)^5$。#0=5, #1=5。属于 $C$。
- $i=0$: $xz = 010101 = (01)^3$。#0=3, #1=3。属于 $C$。
- 好选择: $s=0^41^4 = 00001111$。
- 我们的证明: $|xy|\le 4$ 意味着 $y$ 只能由0组成。泵浦 $y$ 会破坏0和1的数量平衡。矛盾。
- 泵引理不是万能钥匙: 泵引理是一个强大的工具,但它不是一个自动化的算法。它需要使用者进行创造性的思考,特别是选择正确的 $s$。
- 换位思考: 在选择 $s$ 时,要像一个攻击者一样思考:我选择的这个 $s$,有没有可能被“对手”找到一个巧妙的拆分方式来化解掉我的攻击?如果能找到,就说明这个 $s$ 不够好。
4.9 示例 1.74: 利用正则语言封闭性的另一种证明
📜 [原文30]
证明 $C$ 非正则的另一种方法来自于我们已知 $B$ 非正则的事实。如果 $C$ 是正则的,那么 $C \\cap 0^{*} 1^{*}$ 也将是正则的。原因是语言 $0^{*} 1^{*}$ 是正则的,并且正则语言类在交集下是封闭的,这我们在脚注 3(第 46 页)中证明过。但是 $C \\cap 0^{*} 1^{*}$ 等于 $B$,并且我们从例 1.73 中知道 $B$ 是非正则的。
这段话提供了一种证明 $C$ 非正则的、完全不同的、更简洁的思路。这种方法不直接使用泵引理,而是利用正则语言的封闭性质。
- 核心思想: 这种方法的逻辑是“将未知问题转化为已知问题”。我们已经费力地用泵引理证明了 $B=\{0^n1^n\}$ 是非正则的 (这是一个已知事实)。现在我们想证明 $C$ 是非正则的 (这是一个未知问题)。如果我们能建立 $C$ 和 $B$ 之间的某种联系,也许就能从 $B$ 的非正则性推导出 $C$ 的非正则性。
- 反证法框架:
- 假设: $C$ 是正则的。
- 利用封闭性进行推演:
- 我们知道一个重要的定理:正则语言对交集运算是封闭的 (closed under intersection)。这意味着,如果 $L_1$ 是正则的,并且 $L_2$ 是正则的,那么它们的交集 $L_1 \cap L_2$ 也必须是正则的。
- 我们来构造一个交集:$C \cap 0^*1^*$。
- $C$: 我们假设它是正则的。
- $0^*1^*$: 这是一个正则表达式,它描述的语言是“任意多个0后面跟着任意多个1”。这显然是一个正则语言。
- 根据封闭性定理,如果我们的假设成立,那么 $C \cap 0^*1^*$ 这个新语言必须是正则的。
- 分析交集结果:
- $C = \{w \mid \#_0(w) = \#_1(w)\}$ (相同数量的0和1)。
- $0^*1^* = \{w \mid w \text{ 的形式是 } 0...01...1\}$ (所有0都在所有1之前)。
- $C \cap 0^*1^*$ 就是同时满足这两个条件的字符串集合:
- 这不正是语言 $B = \{0^n1^n \mid n \ge 0\}$ 的定义吗!
- 所以,我们得出结论:$C \cap 0^*1^* = B$。
- 导出矛盾:
- 我们的推演结果是:如果 $C$ 正则,那么 $B$ 也必须正则。
- 但是,我们在例1.73中已经严格证明了,$B$ 是非正则的!
- 这就产生了一个尖锐的矛盾。
- 最终结论:
- 矛盾的根源在于我们最初的假设。因此,假设“$C$是正则的”是错误的。
- $C$ 必须是非正则的。
这种证明方法非常优雅和强大,它避免了泵引理证明中繁琐的细节,而是从一个更高的、更结构化的层面来看待问题。
- 正则语言的封闭性 (Closure Properties):
- 如果 $L_1, L_2$ 是正则语言,那么:
- $L_1 \cup L_2$ (并集) 也是正则的。
- $L_1 \cdot L_2$ (连接) 也是正则的。
- $L_1^*$ (星号) 也是正则的。
- $L_1 \cap L_2$ (交集) 也是正则的。
- $\overline{L_1}$ (补集) 也是正则的。
- 证明逻辑:
- Assume $C$ is regular. (假设)
- $L_{reg} = 0^*1^*$ is regular. (已知)
- $C \cap L_{reg}$ must be regular. (根据交集封闭性)
- $C \cap L_{reg} = \{w \mid \#_0(w)=\#_1(w)\} \cap \{0^i1^j \mid i,j \ge 0\} = \{0^n1^n \mid n \ge 0\} = B$. (计算交集)
- So, $B$ must be regular. (由3,4得出)
- But we know $B$ is non-regular. (已知事实,来自例1.73)
- Contradiction. Therefore, the assumption in step 1 is false. $C$ is non-regular.
- 语言 $C$ 的成员: $\varepsilon, 01, 10, 0011, 1100, 0101, 1010, ...$
- 语言 $0^*1^*$ 的成员: $\varepsilon, 0, 1, 00, 11, 01, 001, 011, ...$
- 交集 $C \cap 0^*1^*$ 的成员: 我们在 $C$ 中寻找符合 $0^*1^*$ 形式的字符串。
- $\varepsilon$: 属于 $C$ 和 $0^*1^*$,所以属于交集。
- $01$: 属于 $C$ 和 $0^*1^*$,所以属于交集。
- $10$: 属于 $C$ 但不属于 $0^*1^*$。
- $0011$: 属于 $C$ 和 $0^*1^*$,所以属于交集。
- $1100$: 属于 $C$ 但不属于 $0^*1^*$。
- $0101$: 属于 $C$ 但不属于 $0^*1^*$。
- 交集中的成员是: $\varepsilon, 01, 0011, ...$ 这正是语言 $B$。
- 前提是“已知”: 这种方法依赖于你已经有了一个“非正则语言”的知识库。如果你连一个非正则语言都不知道,就无法使用这种归约的方法。通常 $\{0^n1^n\}$ 是我们学习的第一个非正则语言,是后续很多证明的基础。
- 选择正确的辅助语言: 这种方法的巧妙之处在于选择哪个已知的正则语言来进行运算(这里是 $0^*1^*$)。你需要选择一个能够通过运算“筛选”出你已知的非正则语言的辅助语言。
本章通过对语言 $C=\{w \mid w \text{ 包含相同数量的0和1}\}$ 的分析,深刻揭示了应用泵引理时的复杂性和技巧性。首先,文章展示了一个失败的尝试:如果直接套用上一个例子的字符串 $s=0^p1^p$ 却忽略了条件3 ($|xy| \le p$),那么对手可以提出一种看似可行的泵浦方案,导致证明失败。
接着,文章展示了正确的证明路径:通过严格应用条件3,将可泵浦部分 $y$ 牢牢锁定在字符串 $s=0^p1^p$ 开头的全'0'部分,从而确保任何泵浦操作都会破坏'0'和'1'的数量平衡,最终成功导出矛盾,证明了 $C$ 是非正则的。
此外,本章还探讨了选择字符串 $s$ 的重要性。通过反例 $s=(01)^p$ 说明,一个看似合理但结构交错的字符串,可能因为存在“平衡”的泵浦方式而导致证明失败。这强调了选择 $s$ 需要创造性思维和对语言结构的深刻洞察。
最后,文章还引入了一种不使用泵引理的、更为简洁的证明方法。该方法利用正则语言在交集运算下的封闭性。通过计算 $C \cap 0^*1^*$,我们得到了已知的非正则语言 $B=\{0^n1^n\}$。既然一个正则语言和一个正则语言的交集必须是正则的,而结果 $B$ 却是非正则的,那么唯一的解释就是我们最初的假设(“C是正则的”)是错误的。
这个例子的存在,其教学目的远比简单地证明 $C$ 非正则要丰富得多:
- 强调泵引理条件3的威力:通过“失败-成功”的对比,让读者亲身体会到条件3不是一个可有可无的附加项,而是在许多证明中起决定性作用的核心约束。
- 培养严谨的证明思维:展示了在进行数学证明时,必须考虑所有前提条件,任何一个条件的疏忽都可能导致错误的结论。
- 教授问题解决的策略:通过对“坏”字符串 $s=(01)^p$ 的分析,教会读者在遇到困难时如何反思和调整策略(即换一个更好的 $s$),培养了试错和探索的精神。
- 引入更高级的证明技巧:通过介绍利用“封闭性”的证明方法,为读者打开了一扇新的大门。这让读者了解到,解决一个问题可以有多种路径,有些路径可能比其他路径更为优雅和高效。这有助于建立一个更宏大、更结构化的形式语言知识体系。
- “审讯嫌疑人”模型:
- 嫌疑人: 语言 $C$。你怀疑他“不是一个正则的家伙”。
- 审讯手册: 泵引理。
- 第一次审讯(失败): 你问他:“如果你是正则的,我给你个物证 $s=0^p1^p$,你解释一下吧。” 你忘了用手册里的第三条规则(地点限制),结果嫌疑人狡猾地说:“我可以把整个物证作为‘可变部分y’,你看,无论怎么变,0和1的数量都成比例增加,我没问题!” 你被他绕进去了。
- 第二次审讯(成功): 你拿出审讯手册,指着第三条:“规则说,你的‘可变部分y’必须发生在物证的开头($|xy|\le p$)!” 嫌疑人哑口无言,因为物证开头全是0,他只能承认他的“可变部分y”是纯0的。你接着说:“那好,我把这个纯0的‘可变部分’复制一遍,物证里的0就比1多了,不符合你的身份(语言C)了!你还怎么解释?” 嫌疑人无法自圆其说,最终暴露。
- 高级侦探的方法(封闭性): 一个经验丰富的老侦探走过来说:“何必这么麻烦。” 他拿来一个已知的罪犯 $B$ (非正则)的档案,又拿来一个已知的良民 $0^*1^*$ (正则)的档案。他对你说:“你去查查你的嫌疑人 $C$ 和这个良民 $0^*1^*$ 有什么共同点(交集)。” 你一查,发现他们的共同点恰好就是罪犯 $B$!老侦探说:“一个好人(假设C是正则的)和一个良民的交集,怎么可能是个罪犯呢?所以你的嫌疑人 $C$ 根本就不是好人。”
- DNA突变检测:
- 正常基因(正则语言) 有个特点:它的基因序列中,任何长度超过 $p$ 的片段,其开头 $p$ 个碱基内都有一段“可重复序列”($y$)。你可以把这段序列复制几遍或删除,整个基因的功能不受影响(仍是正常基因)。
- 待检测基因(语言C) 的法则是:“A”碱基和“T”碱基的数量必须相等。
- 第一次检测(失败的s): 你选了一段交错的基因序列 $s=(\text{AT})^p$。你发现,如果你把“AT”作为“可重复序列”$y$来复制,每次都同时增加一个A和一个T,数量平衡没被破坏。你错误地认为这个基因是正常的。
- 第二次检测(成功的s): 你换了一段基因序列 $s=\text{A...A T...T}$ ($p$个A接$p$个T)。根据正常基因的特点,那个“可重复序列”$y$ 必须在前 $p$ 个A里面。它只能是纯A序列。当你把这个纯A序列复制一遍时,整个基因的A数量就比T多了。它的核心法则(A/T数量相等)被破坏了。
- 结论: 这个待检测基因不具备“正常基因”应有的“可重复特性”,因此它是一个异常基因(非正则语言)。
- 利用封闭性的想象: 你有一个数据库,知道基因B是“致病的”(非正则)。你发现,只要给你的待检测基因C带上一个“只看A开头T结尾”的滤镜(与$A^*T^*$求交集),显示出来的结果就和致病基因B一模一样。于是你立刻断定,你手上的基因C也是“致病的”。
4.10 示例 1.75: 证明 $F = \{ww \mid w \in \{0,1\}^*\}$ 非正则
📜 [原文31]
例 1.75
设 $F=\\left\\{w w \\mid w \\in\\{0,1\\}^{*}\\right\\}$。我们使用泵引理证明 $F$ 是非正则的。
这是第三个应用泵引理的例子,目标语言 $F$ 的结构与前两个都不同。
- 目标语言: $F = \{ww \mid w \in \{0,1\}^*\}$。
- 这个语言的构成方式是:取任意一个由0和1组成的字符串 $w$,然后将它自身复制一遍得到 $ww$。所有这样生成的字符串构成了语言 $F$。
- 换句话说, $F$ 中的字符串都有一个共同特征:它的前半部分和后半部分是完全相同的。
- 证明方法: 同样采用泵引理进行反证法。
- 挑战: 这个语言的“非正则性”本质在于前半部分和后半部分之间的精确对应关系。我们需要选择一个字符串 $s$,使得泵浦操作能够破坏这种对应关系。
- $F=\\left\\{w w \\mid w \\in\\{0,1\\}^{*}\\right\\}$
- $w \in \{0,1\}^*$: $w$ 是由0和1组成的任意有限长度的字符串(包括空字符串)。
- $ww$: 将字符串 $w$ 与它自身进行连接 (concatenation)。
- 语言的等价描述: $L = \{ s \mid s=ww \text{ for some } w \in \{0,1\}^* \}$。或者说, $L = \{ s \mid |s| \text{ is even and } s[1..\frac{|s|}{2}] = s[\frac{|s|}{2}+1..|s|] \}$。
- 属于 $F$:
- $w = \varepsilon \implies ww = \varepsilon$
- $w = 0 \implies ww = 00$
- $w = 1 \implies ww = 11$
- $w = 01 \implies ww = 0101$
- $w = 101 \implies ww = 101101$
- 不属于 $F$:
- $0, 1$ (长度为奇数,不可能写成 $ww$ 形式)
- $001$ (长度为奇数)
- $0110$ (前半部分01 $\neq$ 后半部分10)
- $0001$ (前半部分00 $\neq$ 后半部分01)
- 长度必须是偶数: 所有非空字符串 $s \in F$ 的长度 $|s|=2|w|$,必然是偶数。
- 不要与回文串混淆: 回文串是正读反读都一样,例如 101 是回文串但不在 $F$ 中。$F$ 要求的是前半段和后半段的直接复制。
4.11 示例 1.75: 选择正确的字符串并证明
📜 [原文32]
假设相反,$F$ 是正则的。设 $p$ 为泵引理给出的泵浦长度。设 $s$ 为字符串 $0^{p} 10^{p} 1$。因为 $s$ 是 $F$ 的成员,并且 $s$ 的长度大于 $p$,所以泵引理保证 $s$ 可以被分成三部分,$s=x y z$,满足引理的三个条件。我们证明这个结果是不可能的。
条件 3 再次至关重要,因为没有它,如果我们让 $x$ 和 $z$ 为空字符串,我们就可以泵浦 $s$。有了条件 3,证明成立,因为 $y$ 必须只由 0 组成,所以 $x y y z \\notin F$。
这段话直接给出了针对语言 $F$ 的证明核心。
- 标准开局:
- 假设: $F$ 是正则的。
- 获得: 泵浦长度 $p$。
- 选择关键字符串 $s$:
- 这里选择的字符串是 $s = 0^p 1 0^p 1$。
- 我们来检查这个 $s$:
- 它能否写成 $ww$ 的形式?是的,这里 $w = 0^p 1$。所以 $s=ww \in F$。
- 它的长度是否 $\ge p$?是的,$|s| = 2 \times (p+1) = 2p+2$,远大于 $p$。
- 这个选择非常巧妙。它构造了一个 $w$ 本身 ($0^p1$),使得 $w$ 的开头是单一重复的字符,便于利用条件3。同时,在两个 $w$ 之间没有明显的分界线。
- 应用条件3:
- 泵引理保证 $s$ 可以被拆分成 $s=xyz$,且满足 $|xy| \le p$。
- 我们的字符串 $s = 0^p 1 0^p 1$ 的前 $p$ 个字符全部是 '0'。
- 因此,条件3强制要求 $x$ 和 $y$ 都必须由开头的 $0^p$ 这一部分构成。
- 并且,根据条件2 ($|y|>0$),$y$ 必须是至少一个 '0' 组成的串。
- 泵浦并导出矛盾:
- 我们向上泵浦,考虑 $i=2$ 的情况,新字符串 $s' = xyyz$。
- 原字符串 $s = 0^p10^p1$。
- 由于 $y$ 是在第一段 $0^p$ 中增加的,所以新字符串 $s'$ 会变成 $0^{p+|y|}10^p1$。
- 现在我们来判断 $s'$ 是否还在 $F$ 中。
- $s'$ 的长度是 $2p+2+|y|$。
- 它的前半部分是 $0^{p+|y|/2}$ ... 这种方式很难判断。
- 我们换个角度:$s'$ 的前半部分 $w_1$ 和后半部分 $w_2$ 是否相等?
- $s' = \underbrace{0 \dots 0}_{p+|y|} 1 \underbrace{0 \dots 0}_{p} 1$。
- 第一部分 $w$ 被改变了(从 $0^p1$ 变成 $0^{p+|y|}1$ 的前缀),而第二部分 $w$ 完全没动 ($0^p1$)。
- 更具体地,新字符串的前半部分(长度为 $p+1+|y|/2$)和后半部分不再有 $w'w'$ 的关系了。
- 一个更清晰的看法:原来的 $s$ 是 $w$ 跟着 $w$。泵浦操作只在第一个 $w$ 内部增加了字符,而第二个 $w$ 保持原样。因此,修改后的第一个 $w$ 必然不等于未修改的第二个 $w$。
- 所以 $s'=xyyz$ 不再具有 $w'w'$ 的形式。$s' \notin F$。
- 这就产生了与泵引理条件1的矛盾。
- 对条件3重要性的再次强调:
- 作者提到,如果没有条件3,对手可以取 $x=\varepsilon, y=s, z=\varepsilon$。那么 $xy^iz = s^i = (ww)^i$。这不一定在 $F$ 中,例如 $(ww)^2 = wwww = (ww')(ww')$ 在F中。
- 作者的意思可能是,如果没有条件3,对手或许能找到某种巧妙的拆分,使得泵浦后仍满足 $w'w'$ 结构。但有了条件3,这种可能性就被彻底堵死了。
- 语言: $F=\{ww \mid w \in \{0,1\}^*\}$
- 选择: $s = 0^p10^p1$ (这里 $w=0^p1$)
- 拆分: $s=xyz$, 满足 $|y|>0, |xy| \le p$.
- 推论: $x = 0^a, y=0^b, z=0^{p-a-b}10^p1$, 其中 $b \ge 1, a+b \le p$.
- 泵浦: $s' = xy^2z = 0^a(0^b)^2 0^{p-a-b}10^p1 = 0^{p+b}10^p1$.
- 验证 $s' \in F$:
- $s'$ 的形式是 $w'w'$ 吗?即前半部分等于后半部分吗?
- $s'$ 的总长度是 $2p+2+b$。
- $s'$ 的前半部分 (长度 $(2p+2+b)/2$) 和后半部分显然不相等。例如,后半部分的结尾是'1',但前半部分很可能不是。
- 更简单的方法是:
- 原始的 $s = w_1w_2$, 其中 $w_1 = w_2 = 0^p1$。
- 泵浦后的 $s' = w'_1w_2$, 其中 $w'_1 = 0^{p+b}1$。
- 由于 $b \ge 1$, $w'_1 \ne w_1$, 所以 $w'_1 \ne w_2$。
- 因此 $s' \notin F$。
- 矛盾: 得出矛盾,所以 $F$ 非正则。
- 设 $p=3$。
- 选择 $s = 00010001$。这里 $w=0001$。$s \in F$。
- $|s|=8 \ge p=3$。
- 根据 $|xy| \le 3$, $x,y$ 必须在开头的 000 里。
- 设一种拆分:$x=0, y=00, z=10001$。
- 泵浦 $i=2$: $s' = xyyz = 0(00)^2 10001 = 0000010001$。
- 这个新字符串 $s'$,前半部分是 00000,后半部分是 10001。两者不相等,所以 $s' \notin F$。
- 矛盾产生。
- $s$ 的选择: 这是一个关键的易错点。如果选择 $s=0^{2p}$ (即 $w=0^p$),我们之前分析过,这个字符串可以被泵浦,无法导出矛盾。
- $s=(01)^p$ 也不行。可以拆成 $x=\varepsilon, y=01, z=(01)^{p-1}$。泵浦后 $xy^iz = (01)^{i+p-1}$。这依然是 $w'w'$ 的形式,其中 $w'=(01)^{(i+p-1)/2}$ (如果指数是偶数)。这个证明很复杂,但总之 $s=(01)^p$ 是个坏选择。
- $s=0^p10^p1$ 的精妙之处: 它在需要利用条件3的“同质”部分($0^p$)后面,紧跟了一个“标记”('1')。这个'1'使得我们能清晰地定位泵浦操作是在第一个 $w$ 中,还是第二个 $w$ 中,从而轻易地说明两个 $w$ 不再匹配。
4.12 示例 1.75: 对错误字符串选择的再次反思
📜 [原文33]
请注意,我们选择 $s=0^{p} 10^{p} 1$ 是为了展示 $F$ 的非正则性“本质”的字符串,而不是例如字符串 $0^{p} 0^{p}$。尽管 $0^{p} 0^{p}$ 是 $F$ 的成员,但它未能证明矛盾,因为它能被泵浦。
这段话是对上一个例子中“如何选择字符串 $s$”的进一步反思和总结。
- 重申好的选择: $s = 0^p 1 0^p 1$。
- 作者强调这个选择是成功的,因为它能有效地“展示”出语言 $F$ 的非正则性“本质”。
- 这个“本质”就是前半部分和后半部分的严格相等关系。
- $s=0^p10^p1$ 的结构(在纯0块中插入一个1作为分隔符)使得泵浦操作(必然发生在开头的纯0块)会轻易地破坏第一个 $0^p1$ 和第二个 $0^p1$ 之间的相等关系。
- 分析一个坏的选择: $s = 0^p 0^p = 0^{2p}$。
- 它是否是合法候选者? 是的。
- $s$ 可以看作 $w=0^p$ 的 $ww$ 形式,所以 $s \in F$。
- $|s| = 2p \ge p$。
- 为什么它失败了? 作者明确指出,它“未能证明矛盾,因为它能被泵浦”。
- 如何泵浦它?
- 对手可以找到一个合法的拆分方式来泵浦它。
- 设 $p \ge 2$。对手可以选择拆分 $x=0^{2p-2}, y=00, z=\varepsilon$。
- 这个拆分是否合法?
- $|y|=2>0$ (合法)。
- $|xy| = 2p$。这违反了 $|xy| \le p$。所以这个拆分不合法。
- 让我们重新找一个合法的拆分。根据 $|xy| \le p$, $x,y$ 必须在开头的 $0^p$ 中。
- 设 $x=0^{a}, y=0^{b}, z=0^{2p-a-b}$,其中 $b \ge 1, a+b \le p$。
- 泵浦 $i$ 次:$s' = xy^iz = 0^a(0^b)^i0^{2p-a-b} = 0^{2p+b(i-1)}$。
- 新字符串 $s'$ 的总长度是 $2p+b(i-1)$。
- 为了让 $s' \in F$,它的长度必须是偶数,并且前半部分等于后半部分。
- 如果 $b$ 是偶数,那么 $b(i-1)$ 也是偶数,总长度 $2p+b(i-1)$ 永远是偶数。新字符串可以写成 $w'w'$,其中 $w'=0^{p+b(i-1)/2}$。它可以被泵浦!
- 如果 $b$ 是奇数,那么当 $i$ 是偶数时,$i-1$是奇数, $b(i-1)$ 是奇数,总长度 $2p+b(i-1)$ 就是奇数。此时 $s' \notin F$。可以导出矛盾!
- 结论:使用 $s=0^{2p}$ 的证明变得非常复杂,你需要讨论 $y$ 的长度 $b$ 是奇数还是偶数。如果对手(拆分者)足够聪明,他总可以选择一个长度为偶数的 $y$ (只要 $p \ge 2$),比如 $y=00$,来挫败你的证明。因此,$s=0^{2p}$ 是一个非常糟糕、容易失败的选择。
这段话通过对比“好”与“坏”的 $s$ 选择,再次强调了创造性地构造 $s$ 以简化证明的重要性。
- 坏选择: $s = 0^{2p}$。
- 对手的策略: 假设 $p \ge 2$。对手总能找到一个拆分,使得 $y$ 的长度是偶数。例如,选择 $x=0^{k}, y=00, z=0^{2p-k-2}$,只要 $k+2 \le p$ 即可。
- 泵浦分析: 如果 $|y|$ 是偶数,设 $|y|=2k$ ($k\ge 1$)
- $s' = xy^iz$。$|s'| = |s| + (i-1)|y| = 2p + (i-1)2k = 2(p+(i-1)k)$。
- $|s'|$ 永远是偶数。
- $s'$ 是一个纯0串,任何长度为偶数的纯0串 $0^{2m}$ 都可以写成 $w'w'$ 的形式 ($w'=0^m$)。
- 因此,在这种情况下,$s'$ 永远在 $F$ 中。无法导出矛盾。
- 设 $p=4$。
- 坏选择: $s=0^8$。
- 对手的拆分: $x=0, y=00, z=0^5$。
- $|y|=2>0$。
- $|xy|=3 \le p=4$。这是一个合法的拆分。
- 泵浦:
- $i=2: xyyz = 0(00)^2 0^5 = 0^{10}$。$0^{10} = w'w'$ 其中 $w'=0^5$。所以 $0^{10} \in F$。
- $i=3: xyyyz = 0(00)^3 0^5 = 0^{12}$。$0^{12} = w'w'$ 其中 $w'=0^6$。所以 $0^{12} \in F$。
- $i=0: xz = 00^5 = 0^6$。$0^6 = w'w'$ 其中 $w'=0^3$。所以 $0^6 \in F$。
- 结论: 我们为 $s=0^8$ 找到了一个可以成功泵浦的合法拆分。所以 $s=0^8$ 不能用来证明 $F$ 非正则。
- 不要低估“对手”: 在使用泵引理时,你必须假设“对手”(即拆分方式的提出者)会尽一切可能找到一个让你无法导出矛盾的拆分。你的策略必须能应对最聪明的对手。
- 结构的单一性 vs. 复杂性: $s=0^{2p}$ 结构太单一了,给了对手可乘之机。而 $s=0^p10^p1$ 引入了'1'这个“杂质”,使得结构变得复杂,反而限制了对手的拆分选择,使我们的证明更容易成功。
本章通过对语言 $F = \{ww \mid w \in \{0,1\}^*\}$ 的非正则性证明,进一步深化了对泵引理应用技巧的探讨。核心挑战在于选择一个合适的字符串 $s$ 来进行反证。
文章首先展示了一个成功的选择:$s = 0^p10^p1$。这个字符串本身可以写作 $ww$ 的形式(其中 $w=0^p1$)。通过应用泵引理的条件3 ($|xy| \le p$),可泵浦部分 $y$ 被强制限制在字符串开头的 $0^p$ 部分。因此,对 $y$ 进行泵浦(如 $xyyz$)会改变第一个 $w$ 的内容,而第二个 $w$ 保持不变,从而破坏了前后两部分严格相等的“$ww$”结构,导致新字符串不属于 $F$,成功导出矛盾。
随后,文章通过分析一个失败的选择:$s = 0^{2p}$,来强调选择 $s$ 的重要性。尽管 $s=0^{2p}$ 也在 $F$ 中($w=0^p$),但由于其结构过于单一,证明者(“对手”)可以巧妙地选择一个长度为偶数的 $y$(如 $y=00$)进行拆分。在这种情况下,无论泵浦多少次,得到的字符串永远是偶数长度的全'0'串,总能写成 $w'w'$ 的形式,因此无法导出矛盾,导致证明失败。
这个对比鲜明地说明了,构造一个好的 $s$ 的关键在于:利用 $s$ 的内部结构和泵引理的条件3相配合,使得任何合法的泵浦操作都必然会破坏该语言的核心规则。
这个例子的主要教学目的在于:
- 展示泵引理应用的普遍性:通过一个与之前 $\{0^n1^n\}$ 和 $\{w \mid \#_0=\#_1\}$ 结构都不同的新语言 $F=\{ww\}$,展示了泵引理是一个可以广泛应用的工具,不仅仅局限于“计数”类问题。
- 深化对字符串选择策略的理解:这是本例的核心。它从正反两方面(成功和失败的 $s$ 选择)教育读者,选择 $s$ 不仅仅是满足长度要求,更是一种需要“精心设计”的艺术。一个好的 $s$ 能让证明势如破竹,一个坏的 $s$ 则可能让证明陷入僵局。
- 培养对抗性思维:在进行泵引理证明时,需要站在“对手”(即拆分者)的角度思考问题,预判对手可能的所有招数(所有合法的拆分),并选择一个能让对手无计可施的 $s$。这种换位思考和博弈思想是高级问题解决的关键能力。
- “连体双胞胎”模型:
- 语言 $F=\{ww\}$ 就像一个关于“完美连体双胞胎”的规则:录入系统的人必须是两个一模一样的人手拉手。
- 坏的测试案例($s=0^{2p}$): 你找来一对双胞胎,他们长得一模一样,而且都只穿纯黑色的衣服(全是0)。你试图通过“泵浦”(即在第一个人身上做点手脚)来证明他们不是完美双胞胎。但因为他们穿的衣服没有任何特征,你的手脚(比如在第一个人衣服上加长一截纯黑布料 $y$)很容易被掩盖。比如,加长后,他们仍然是两个穿着纯黑衣服的人,只是衣服变长了,看起来还是像一对(更长的)双胞胎。你的证明失败了。
- 好的测试案例($s=0^p10^p1$): 你找来另一对双胞胎,他们也一模一样,但他们的标准装扮是:一顶黑帽子($0^p$),加一件白衬衫('1')。泵引理规则说,你只能在第一个人戴的黑帽子上做手脚。你把他的黑帽子拉长了一点(泵浦了$y$)。现在,第一个人戴着一顶“加长黑帽”,穿着白衬衫;而第二个人还是戴着“标准黑帽”,穿着白衬衫。他们不再一模一样了!
- 结论: 这对双胞胎不符合“泵浦后仍然是完美双胞胎”的规则,说明“完美连体双胞胎”这个规则本身就不是“正则”的。
- 对称图形的拉伸:
- 语言 $F=\{ww\}$ 就像一个要求图形必须左右完全对称的规则(例如,【图A】【图A】)。
- 坏的图形($s=0^{2p}$): 你选择了一个非常简单的对称图形:一个纯色的长方形 【---】【---】。泵引理规则说,你只能在左半边图形的前半部分进行拉伸或压缩。你发现,如果你只拉伸纯色区域,无论怎么拉,左半边仍然是一个纯色长方形(只是变长了),而右半边还是原来的纯色长方形。它们不再对称了!等一下,这个比喻和我之前的分析结果不一致。
- 让我们重新思考这个比喻。关键在于 $s=0^{2p}$ 失败的原因是泵浦后依然是 $w'w'$ 的形式。
- $s=0^{2p}$ 是 0...0 | 0...0。
- 泵浦后 $s'=0^{2m}$ 是 0..0 | 0..0。
- 比喻:一个纯色长方形 【---】,左右对称就是 【---】【---】。对左边的长方形的一部分进行拉伸,得到 【----】【---】,这显然不对称了。
- 比喻的修正: 问题出在“如何判断对称”。对于纯色长方形,我们可能觉得 【----】 和 【---】 是“同类”的,而泵引理要求的是精确相等。所以 【----】 $\neq$ 【---】。那么为什么 $s=0^{2p}$ 证明会失败呢?因为我们必须覆盖所有合法的拆分。对手可以选择 $|y|$ 为偶数。
- 修正后的想象: 语言 F 是一台检测器,如果输入是 A A 它就亮绿灯。输入 $s=0^{2p}$ 就是 0^p 0^p。对手拆分使得 $y=00$。泵浦后输入变成 $s'=0^{p+k}0^{p-k}$... 不对,泵浦是在一个 $w$ 内部。 $s=ww$ 泵浦后是 $w'w$。
- 最终的、更准确的想象:
- 语言 $F$ 要求输入必须是两张一模一样的照片并排放在一起。
- 坏的测试照片($w=0^p$): 你选了两张纯白色的照片 [白][白]。泵引理的规则允许你在第一张照片的左侧区域(对应$|xy|\le p$)进行“像素复制”(泵浦)。对手很聪明,他选择复制的区域 $y$ 是偶数个白色像素。当你泵浦后,第一张照片虽然变宽了,但它仍然是一张纯白色的照片。所以新的输入 [更宽的白][原来的白]。这两张照片不一样!所以 $s=0^{2p}$ 应该是可以证明的。
- 重新审视原文分析: "...it fails to furnish a contradiction because it CAN be pumped." 这句话是关键。它认为 $s=0^{2p}$ 可以被泵浦。$xy^iz = 0^{2p+b(i-1)}$。这为什么可以被泵浦?因为 $F$ 的规则是“一个串和它自身的重复”。$0^{2m}$ 可以看作 $0^m$ 和 $0^m$ 的重复。所以 $0^{2p+b(i-1)}$ 如果其长度是偶数,它就属于 $F$。而对手可以通过选择一个 $|y|$ 为偶数的 $y$ 来保证泵浦后的长度始终为偶数!这就无法导出矛盾了。
- 好的测试照片($w=0^p1$): 你选了两张“上方是白色、底部有一条黑线”的照片 [白+线][白+线]。规则要求你只能在第一张照片的左侧白色区域进行像素复制。当你复制了任意白色像素后,第一张照片变成了 [更宽的白+线]。而第二张照片还是 [白+线]。这两张照片不再一样了。所以,新输入 [更宽的白+线][白+线] 会被拒绝。矛盾产生。
4.13 示例 1.76: 证明一元语言 $D = \{1^{n^2} \mid n \ge 0\}$ 非正则
📜 [原文34]
例 1.76
这里我们演示一个非正则的一元语言。设 $D=\\left\\{1^{n^{2}} \\mid n \\geq 0\\right\\}$。换句话说,$D$ 包含所有长度为完全平方数的 1 字符串。我们使用泵引理证明 $D$ 不是正则的。证明采用反证法。
这个例子引入了一种新的语言类型——一元语言 (unary language),并证明了其中一个典型例子是非正则的。
- 一元语言:
- 一元语言是指其字母表只包含一个符号的语言。在这里,字母表 $\Sigma = \{1\}$。
- 因此,一元语言中的所有字符串都形如 $1, 11, 111, \dots$,即 $1^k$。
- 一个一元语言完全由一个长度集合来定义。例如,语言 $D$ 就由集合 $\{0, 1, 4, 9, 16, \dots\}$ 来定义。
- 目标语言: $D = \{1^{n^2} \mid n \ge 0\}$。
- 这个语言包含的字符串,其长度必须是一个完全平方数。
- 例如:
- $n=0 \implies |s|=0^2=0 \implies s=\varepsilon$
- $n=1 \implies |s|=1^2=1 \implies s=1$
- $n=2 \implies |s|=2^2=4 \implies s=1111$
- $n=3 \implies |s|=3^2=9 \implies s=111111111$
- 证明方法: 依然是使用泵引理进行反证法。
- 挑战: 对于一元语言,泵浦操作的唯一效果就是改变字符串的长度。由于所有字符串结构都一样(都是一串'1'),我们不能像之前那样通过“破坏0和1的顺序或平衡”来制造矛盾。矛盾必须来自于泵浦后的字符串长度不再满足语言的规定(即不再是完全平方数)。
- $D=\\left\\{1^{n^{2}} \\mid n \\geq 0\\right\\}$
- $1^{n^2}$: 符号'1'重复 $n^2$ 次。
- $n \ge 0$: $n$ 是任意非负整数。
- 完全平方数序列: $0, 1, 4, 9, 16, 25, 36, \dots$
- 属于 $D$: $\varepsilon, 1, 1111, 111111111$
- 不属于 $D$: $11, 111, 11111$ (长度分别是 2, 3, 5,都不是完全平方数)。
- 一元语言的特殊性: 证明一元语言的非正则性,通常需要进行一些关于整数性质的数学分析,而不是像之前那样只做结构分析。
- 直觉: 直觉上,要判断一个数是不是完全平方数,需要进行计算,这似乎超出了有限自动机的能力。这个例子将严格证明这个直觉。
4.14 示例 1.76: 数学性质在证明中的应用
📜 [原文35]
假设相反,$D$ 是正则的。设 $p$ 为泵引理给出的泵浦长度。设 $s$ 为字符串 $1^{p^{2}}$。因为 $s$ 是 $D$ 的成员,且其长度至少为 $p$,泵引理保证 $s$ 可以被分成三部分,$s=x y z$,其中对于任何 $i \\geq 0$,字符串 $x y^{i} z$ 都在 $D$ 中。与前面例子一样,我们证明这个结果是不可能的。在这种情况下,这样做需要对完全平方数序列进行一些思考:
请注意此序列中连续成员之间不断增长的间隔。此序列中的大成员不能彼此靠近。
这是证明的前半部分,包括了假设、选择字符串,并指出了证明的核心洞察。
- 标准开局:
- 假设: $D$ 是正则的。
- 获得: 泵浦长度 $p$。
- 选择关键字符串 $s$:
- 选择了 $s = 1^{p^2}$。
- 检查 $s$:
- $s \in D$? 是的,因为它的长度 $p^2$ 是一个完全平方数 (当 $n=p$ 时)。
- $|s| \ge p$? 是的,$|s|=p^2$。只要 $p \ge 1$,$p^2 \ge p$。所以满足条件。
- 这个选择将泵浦长度 $p$ 和语言的平方数性质直接关联起来。
- 应用泵引理:
- 泵引理保证 $s=1^{p^2}$ 可以被拆分成 $s=xyz$,满足三个条件,特别是 $xy^iz \in D$ 对所有 $i \ge 0$ 成立。这意味着泵浦后的字符串长度必须仍然是完全平方数。
- 核心洞察:
- 作者引导我们观察完全平方数序列 $0, 1, 4, 9, 16, \dots$ 的一个关键性质。
- 这个性质是:连续完全平方数之间的间隔是不断增大的。
- $1-0=1$
- $4-1=3$
- $9-4=5$
- $16-9=7$
- ...
- $(n+1)^2 - n^2 = 2n+1$。
- 这个间隔 $(2n+1)$ 随着 $n$ 的增大而增大。
- 这意味着,大的完全平方数之间是稀疏的、彼此离得很远。
这个洞察是本证明的关键。我们将利用泵浦操作,构造出一个新字符串,其长度恰好落在两个相邻的、大的完全平方数之间的“无人区”,从而导出矛盾。
- 选择的 $s$: $s = 1^{p^2}$
- $s$ 的长度: $|s| = p^2$
- 关键性质: 连续完全平方数的差
- $(n+1)^2 - n^2 = (n^2+2n+1) - n^2 = 2n+1$
- 应用到我们的场景:
- 我们选的字符串长度是 $p^2$。
- 下一个更大的完全平方数是 $(p+1)^2$。
- 它们之间的差是 $(p+1)^2 - p^2 = 2p+1$。
- 这意味着,在 $p^2$ 和 $(p+1)^2$ 之间,没有任何一个数是完全平方数。任何长度 $L$ 满足 $p^2 < L < (p+1)^2$ 的字符串 $1^L$ 都不属于语言 $D$。
- 设 $p=10$。
- 我们选择的字符串 $s = 1^{10^2} = 1^{100}$。
- $s \in D$,且 $|s|=100 \ge p=10$。
- 下一个完全平方数是 $(10+1)^2 = 11^2 = 121$。
- 它们之间的间隔是 $121-100 = 21$。
- 任何长度在 101 到 120 之间的字符串 (如 $1^{101}, 1^{115}, 1^{120}$) 都不属于 $D$。
- 从结构证明到数值证明的转变: 理解这个证明的关键是认识到我们不再分析字符串的符号排列(因为只有'1'),而是分析其长度的算术性质。
- 间隔增长的重要性: 如果完全平方数之间的间隔是固定的,这个证明可能就不成立了。正是因为间隔 $(2n+1)$ 随 $n$ 增大,我们才能确保对于足够大的 $p$,泵浦 $y$ 所增加的长度不足以“跳”到下一个完全平方数。
4.15 示例 1.76: 利用长度限制导出矛盾
📜 [原文36]
现在考虑字符串 $xyz$ 和 $xy^{2}z$。这些字符串仅通过一个 $y$ 的重复而不同,因此它们的长度差异为 $y$ 的长度。根据泵引理的条件 3,$|xy| \\leq p$,因此 $|y| \\leq p$。我们有 $|xyz|=p^{2}$,因此 $|xy^{2}z| \\leq p^{2}+p$。但是 $p^{2}+p < p^{2}+2p+1=(p+1)^{2}$。此外,条件 2 意味着 $y$ 不是空字符串,因此 $|xy^{2}z|>p^{2}$。因此,$xy^{2}z$ 的长度严格介于连续的完全平方数 $p^{2}$ 和 $(p+1)^{2}$ 之间。因此,这个长度本身不可能是完全平方数。所以我们得到了矛盾 $xy^{2}z \\notin D$,并得出结论 $D$ 不是正则的。
这是证明的收尾部分,通过精确的数值分析导出最终的矛盾。
- 选择泵浦方式: 我们选择向上泵浦一次,即考虑 $i=2$ 的情况,得到新字符串 $s' = xy^2z$。
- 原字符串是 $s=xyz=1^{p^2}$,其长度 $|s|=p^2$。
- 新字符串 $s'$ 的长度 $|s'| = |x|+|y|+|y|+|z| = |xyz|+|y| = p^2 + |y|$。
- 分析新字符串的长度范围: 我们需要确定 $|s'| = p^2+|y|$ 的范围。
- 下界:
- 泵引理条件2说:$|y| > 0$。
- 所以,$|s'| = p^2 + |y| > p^2$。新字符串的长度严格大于 $p^2$。
- 上界:
- 泵引理条件3说:$|xy| \le p$。
- 因为 $x, y$ 都是由 '1' 组成的,所以 $|xy|=|x|+|y|$。
- 因此,我们有 $|y| \le |xy| \le p$。这意味着被泵浦的部分 $y$ 的长度不能超过泵浦长度 $p$。
- 所以,$|s'| = p^2 + |y| \le p^2+p$。新字符串的长度小于或等于 $p^2+p$。
- 将长度范围与完全平方数性质结合:
- 我们已经确定了新字符串的长度 $|s'|$ 满足不等式:$p^2 < |s'| \le p^2+p$。
- 我们再来看一下 $p^2$ 之后下一个完全平方数 $(p+1)^2$。
- $(p+1)^2 = p^2+2p+1$。
- 只要 $p \ge 1$,我们总有 $p^2+p < p^2+2p+1$。
- 所以,我们得到了一个关键的不等式链:
- 导出矛盾:
- 这个不等式链告诉我们,新字符串 $s'$ 的长度严格地介于两个连续的完全平方数 $p^2$ 和 $(p+1)^2$ 之间。
- 一个严格介于两个连续完全平方数之间的整数,其本身绝对不可能是一个完全平方数。
- 因此,$|s'|$ 不是一个完全平方数。
- 根据语言 $D$ 的定义,这意味着新字符串 $s' = xy^2z$ 不属于 $D$。
- 这与泵引理的条件1“$xy^iz$ 必须属于 $D$”产生了矛盾。
- 最终结论: 假设 $D$ 是正则的导致了矛盾,因此 $D$ 必须是非正则的。
- Let: $s=1^{p^2} = xyz$
- From Pumping Lemma conditions:
- (2) $|y| > 0$
- (3) $|xy| \le p \implies |y| \le p$
- Consider: $s' = xy^2z$
- Analyze length of $s'$:
- $|s'| = |xyz| + |y| = p^2 + |y|$
- Bounding $|s'|$:
- Lower bound: $|s'| = p^2 + |y| > p^2$ (using condition 2)
- Upper bound: $|s'| = p^2 + |y| \le p^2 + p$ (using condition 3)
- Combining bounds: $p^2 < |s'| \le p^2+p$
- Using property of squares: For $p \ge 1$, we know $p < 2p+1$, so $p^2+p < p^2+2p+1 = (p+1)^2$.
- Final inequality chain: $p^2 < |s'| < (p+1)^2$
- Conclusion: $|s'|$ is not a perfect square. Thus, $s' \notin D$.
- Contradiction: This contradicts condition 1 of the Pumping Lemma.
- Final result: $D$ is not regular.
- 设 $p=10$。
- $s=1^{100}$。$|s|=100=10^2$。
- $s$ 被拆分为 $xyz$。我们知道 $1 \le |y| \le 10$。
- 考虑 $s'=xy^2z$。它的长度是 $|s'| = 100 + |y|$。
- 由于 $1 \le |y| \le 10$,所以 $100+1 \le |s'| \le 100+10$,即 $101 \le |s'| \le 110$。
- 下一个完全平方数是 $(10+1)^2=121$。
- 我们看到,无论 $|y|$ 是1到10中的哪个值,新字符串的长度 $|s'|$ (在101到110之间) 都不可能是121,也大于100。
- 所以 $|s'|$ 必然不是一个完全平方数。$s' \notin D$。矛盾产生。
- 不等式的处理: 证明的关键在于不等式的推导 $p^2 < |s'| < (p+1)^2$。需要确保每一步都是严格的。例如, $p^2+p < (p+1)^2$ 在 $p=0$ 时不成立,但泵浦长度 $p$ 通常定义为DFA状态数,所以 $p \ge 1$,这个不等式是安全的。
- 选择 $i=2$: 在这个证明中,向上泵浦 ($i=2$) 是关键。如果向下泵浦 ($i=0$),新字符串长度是 $p^2-|y|$。这个长度小于 $p^2$,它有可能是另一个完全平方数(例如,如果 $p^2-|y|=(p-1)^2$)。要证明它不是会更复杂。而向上泵浦则能保证长度落在一个“安全”的非平方数区间内。
本章通过对一元语言 $D = \{1^{n^2} \mid n \ge 0\}$ 的分析,展示了如何将泵引理与数论性质相结合来完成非正则性的证明。一元语言的特殊性在于,泵浦操作只影响字符串的长度,因此证明的焦点从字符串结构转向了对其长度的数学分析。
证明过程遵循了标准的反证法流程:
- 假设 $D$ 是正则的,获得泵浦长度 $p$。
- 选择一个与 $p$ 和语言性质都相关的字符串 $s = 1^{p^2}$。
- 应用泵引理,断言 $s$ 可被拆分且泵浦后的字符串 $xy^iz$ 长度必须仍为完全平方数。
- 核心洞察:分析了完全平方数序列的性质,即连续的完全平方数 $(p^2, (p+1)^2)$ 之间的间隔 $(2p+1)$ 会随着 $p$ 的增大而增大。
- 导出矛盾:通过分析泵引理的条件2 ($|y|>0$) 和条件3 ($|xy| \le p \implies |y| \le p$),我们精确地界定了向上泵浦一次后得到的新字符串 $s' = xy^2z$ 的长度范围:$p^2 < |s'| \le p^2+p$。由于 $p^2+p < (p+1)^2$,这意味着新字符串的长度严格地位于两个连续的完全平方数之间,因此它本身不可能是完全平方数。这导致 $s' \notin D$,与泵引理的结论相矛盾。
- 结论:因此,$D$ 是非正则的。
这个例子体现了泵引理证明的灵活性,证明策略需要根据目标语言的特性来量身定制。
这个例子的存在,有几个重要的教学目的:
- 扩展泵引理的应用范围:将泵引理的应用从只关注符号排列和计数的语言,扩展到了只由长度性质定义的一元语言。这展示了泵引理的普适性。
- 引入数学分析工具:它教会读者,在计算机理论中,形式化证明有时需要借助其他数学领域的知识(如此处的数论和不等式分析)。这拓宽了问题解决的工具箱。
- 深化对泵引理条件的理解:这个证明再次巧妙地结合了条件2和条件3来精确地“夹”住新字符串的长度范围,让读者更深刻地体会到这两个条件如何协同工作以导出矛盾。特别是对 $|y|$ 上下界的分析,是很多泵引理证明中的常用技巧。
- 展示问题转化思想:将一个关于“语言正则性”的计算理论问题,成功地转化为了一个关于“整数平方数间隔”的纯数学问题来解决。
- “跳格子”游戏:
- 语言 $D$ 规定你只能站在标有完全平方数(1, 4, 9, 16, ...)的格子上。这些格子(特别是后面的)彼此相距很远。
- 你现在站在第 $p^2$ 号格子上。
- 泵引理规则告诉你:你可以向前“泵浦”一步。这一步的长度($|y|$)是受限制的:它大于0,但不能超过 $p$。
- 你向前跳了 $|y|$ 步,落在了第 $p^2+|y|$ 号格子上。
- 关键问题:你落下的这个新位置,还是一个“平方数”格子吗?
- 分析: 你知道下一个平方数格子在遥远的 $(p+1)^2 = p^2+2p+1$ 号位置。而你最多只能向前跳 $p$ 步。只要 $p \ge 1$,你的最大步长 $p$ 远小于到达下一个格子的所需距离 $2p+1$。
- 结论: 你的一跳,必然使你落在了 $p^2$ 和 $(p+1)^2$ 两个格子之间的“无人区”。这个位置不是平方数格子。
- 矛盾: 泵引理说你泵浦后也必须落在合法的格子上,但你却落在了外面。这证明了这个“游戏规则”(语言D)本身就不是“正则”的。
- 生长周期固定的植物:
- 有一种神奇的植物,它只在高度长到完全平方数(1cm, 4cm, 9cm, ...)时才会开花。
- 你有一株高度为 $p^2$ cm 的植物,它正在开花。
- 泵引理是一种“生长激素”,你可以给植物注射一次。这种激素有如下特点:
- 它一定会让植物长高一点($|y|>0$)。
- 它一次最多只能让植物长高 $p$ cm($|y| \le p$)。
- 你给这株 $p^2$ cm 高的植物注射了激素,它的新高度变成了 $p^2+|y|$ cm。
- 问题: 注射后,这株植物还会开花吗?也就是说,新高度 $p^2+|y|$ 还是一个完全平方数吗?
- 分析: 我们知道,下一次开花的高度是 $(p+1)^2 = p^2+2p+1$ cm。植物需要再长 $2p+1$ cm 才能再次开花。而我们的生长激素最多只能让它长高 $p$ cm。这个生长量不足以让它达到下一个开花高度。
- 结论: 新高度 $p^2+|y|$ 严格介于两个开花高度 $p^2$ 和 $(p+1)^2$ 之间。所以,植物不会开花。
- 矛盾: 泵引理(作为正则语言的普适规律)声称,这种操作后植物理应还处于开花状态(字符串仍在语言中)。但事实并非如此。因此,这种植物的生长规则(语言D)是不“正则”的。
4.16 示例 1.77: “向下泵浦”的应用
📜 [原文37]
例 1.77
有时“向下泵浦”在应用泵引理时很有用。我们使用泵引理证明 $E=\\left\\{0^{i} 1^{j} \\mid i>j\\right\\}$ 不是正则的。证明采用反证法。
这个例子将展示一种不同于以往的证明技巧——向下泵浦 (pumping down),即利用泵引理中 $i=0$ 的情况来导出矛盾。
- 目标语言: $E = \{0^i 1^j \mid i > j\}$。
- 该语言由一串0后跟一串1组成。
- 核心规则是:0的数量必须严格大于1的数量。
- 例如: $0, 00, 01, 001, 0001, 00011, \dots$
- 证明方法: 依然是使用泵引理进行反证法。
- 挑战: 之前我们都是通过“向上泵浦”($i=2$),增加某个符号的数量来破坏“数量相等”的规则。但对于语言 $E$,规则是“数量不等 ($i>j$)”。如果我们向上泵浦0,0的数量会变得更多,仍然满足 $i>j$,无法导出矛盾。这就需要我们转变思路。
- $E=\\left\\{0^{i} 1^{j} \mid i>j\\right\\}$:
- $0^i1^j$: 字符串的形式。
- $i > j$: 0和1数量必须满足的不等关系。$i, j$ 都是非负整数。
- 属于 $E$:
- $i=1, j=0$: $0$
- $i=2, j=1$: $001$
- $i=5, j=2$: $0000011$
- 不属于 $E$:
- $\varepsilon$ ($i=0, j=0$, 不满足 $i>j$)
- $01$ ($i=1, j=1$, 不满足 $i>j$)
- $011$ ($i=1, j=2$, 不满足 $i>j$)
- 严格大于: 规则是 $i > j$,而不是 $i \ge j$。这意味着 $i=j$ 的情况(如 $01, 0011$)不属于 $E$。
- $j=0$: 形如 $0^i (i>0)$ 的字符串都属于 $E$。
- $i$ 和 $j$ 的关系: $i$ 和 $j$ 是独立的变量,不像 $\{0^n1^n\}$ 那样被同一个 $n$ 绑定。
4.17 示例 1.77: 向上泵浦的失败与向下泵浦的成功
📜 [原文38]
假设 $E$ 是正则的。设 $p$ 为泵引理给出的 $E$ 的泵浦长度。设 $s=0^{p+1} 1^{p}$。那么 $s$ 可以分成 $x y z$,满足泵引理的条件。根据条件 3,$y$ 只包含 0。让我们检查字符串 $x y y z$ 以查看它是否可以在 $E$ 中。添加一个额外的 $y$ 副本会增加 0 的数量。但是,$E$ 包含所有 0 数量多于 1 数量的 $0^{*} 1^{*}$ 字符串,因此增加 0 的数量仍然会得到一个在 $E$ 中的字符串。没有发生矛盾。我们需要尝试其他方法。
泵引理指出,即使 $i=0$,也有 $x y^{i} z \\in E$,所以我们考虑字符串 $x y^{0} z=x z$。删除字符串 $y$ 会减少 $s$ 中 0 的数量。回想一下 $s$ 中 0 的数量只比 1 的数量多一个。因此,$x z$ 不可能比 1 包含更多 0,所以它不能是 $E$ 的成员。因此我们得到一个矛盾。
这段是本例证明的核心,清晰地展示了向上泵浦的失败和向下泵浦的成功。
- 标准开局与精妙的 $s$ 选择:
- 假设: $E$ 是正则的, 获得泵浦长度 $p$。
- 选择: $s = 0^{p+1}1^p$。
- 检查 $s$:
- $s \in E$? 是的。0的数量是 $p+1$,1的数量是 $p$。满足 $i>j$。
- $|s| \ge p$? 是的。$|s| = 2p+1 \ge p$。
- 这个选择非常精妙,它选择了恰好满足 $i>j$ 条件的“最小”字符串(0的数量只比1的数量多1)。这种“临界”状态最容易在泵浦时被破坏。
- 应用条件3:
- 根据 $|xy| \le p$,并且 $s$ 的开头是 $p+1$ 个0,我们推断出 $x$ 和 $y$ 必然只由0组成。
- 根据 $|y|>0$,我们知道 $y$ 至少包含一个0。
- 失败的尝试:向上泵浦 ($i=2$):
- 考虑新字符串 $s' = xyyz$。
- 原字符串 $s$ 中,$\#_0(s) = p+1$, $\#_1(s) = p$。
- 新字符串 $s'$ 中,$\#_0(s') = p+1+|y|$, $\#_1(s')=p$。
- 因为 $|y| \ge 1$,所以 $p+1+|y| > p+1$。
- 比较新字符串中0和1的数量:$p+1+|y| > p$。这个关系仍然满足语言 $E$ 的 $i>j$ 规则。
- 因此,$s'=xyyz \in E$。
- 结论: 向上泵浦无法导出矛盾。我们的证明陷入僵局。
- 成功的尝试:向下泵浦 ($i=0$):
- 作者提示我们“尝试其他方法”,并把目光投向了 $i=0$ 的情况。
- 考虑新字符串 $s'' = xy^0z = xz$。
- 这个操作相当于从原字符串 $s$ 中删除了子串 $y$。
- 分析数量变化:
- 原字符串 $s$ 中,$\#_0(s) = p+1$, $\#_1(s) = p$。
- 由于 $y$ 是由0组成的非空串 ($|y| \ge 1$), 删除 $y$ 会减少0的数量。
- 新字符串 $s''$ 中, $\#_0(s'') = (p+1) - |y|$, $\#_1(s'') = p$。
- 比较新数量:
- 因为我们知道 $1 \le |y| \le p$ (由 $|xy|\le p$ 可知)。
- 所以 $(p+1) - |y| \le (p+1)-1 = p$。
- 这意味着,在新字符串 $s''$ 中,0的数量最多是 $p$,而1的数量仍然是 $p$。
- 所以,$\#_0(s'') \le \#_1(s'')$。这违反了语言 $E$ 的核心规则 $i>j$。
- 结论: 新字符串 $s''=xz$ 不属于 $E$。
- 矛盾: 这与泵引理的条件1“$xy^iz$ 必须属于 $E$”相矛盾。
- 最终结论: 假设 $E$ 是正则的导致了矛盾,因此 $E$ 必须是非正则的。
- 语言: $E=\{0^i1^j \mid i>j\}$
- 选择: $s=0^{p+1}1^p$
- 拆分: $s=xyz$, 满足 $|y|>0$ 且 $|xy| \le p$。
- 推论: $x=0^a, y=0^b, z=0^{p+1-a-b}1^p$, 其中 $b \ge 1, a+b \le p$。
- 分析向上泵浦 ($i=2$):
- $s' = xy^2z = 0^{p+1+b}1^p$。
- $\#_0(s') = p+1+b$, $\#_1(s')=p$。
- $p+1+b > p$。所以 $s' \in E$。无矛盾。
- 分析向下泵浦 ($i=0$):
- $s'' = xz = 0^{p+1-b}1^p$。
- $\#_0(s'') = p+1-b$, $\#_1(s'')=p$。
- 因为 $b \ge 1$, 所以 $p+1-b \le p$。
- 所以 $\#_0(s'') \le \#_1(s'')$。这违反了 $i>j$ 的规则。
- $s'' \notin E$。
- 矛盾: 与泵引理条件1矛盾。$E$ 非正则。
- 设 $p=5$。
- 选择 $s = 0^6 1^5 = 00000011111$。
- $|xy| \le 5$, 所以 $y$ 是开头的 $0^6$ 的一部分,且 $1 \le |y| \le 5$。
- 向上泵浦 ($i=2$):
- 假设拆分为 $x=00, y=000, z=011111$。$|y|=3$。
- $s'=xyyz = 00(000)^2 011111 = 0^9 1^5$。
- $9>5$, 所以 $s' \in E$。无法得出矛盾。
- 向下泵浦 ($i=0$):
- 使用同样的拆分 $x=00, y=000, z=011111$。
- $s'' = xz = 00011111$。
- 这个字符串是 $0^31^5$。
- $3 \le 5$, 不满足 $i>j$。所以 $s'' \notin E$。
- 矛盾产生。
- 泵浦方向的选择: 这个例子是最好的说明,证明者需要灵活选择泵浦的“方向”($i$的值)。如果向上泵浦不行,要立刻想到尝试向下泵浦。
- $s$ 的“临界”选择: 选择 $s=0^{p+1}1^p$ 是成功的关键。如果选择 $s=0^{2p}1^p$,那么向下泵浦一次后,0的数量是 $2p-|y|$。因为 $|y| \le p$,所以 $2p-|y| \ge p$。我们仍然能保证新字符串的0数量大于等于1的数量。如果 $|y|$ 恰好是 $p$,则新数量相等,刚好不在E中,也能导出矛盾。但如果 $|y|<p$,则 $2p-|y|>p$,无法导出矛盾。所以 $s=0^{p+1}1^p$ 是一个更“安全”、更鲁棒的选择。
本章通过对语言 $E = \{0^i 1^j \mid i>j\}$ 的研究,重点演示了泵引理中“向下泵浦” ($i=0$) 技巧的应用。
证明首先遵循标准流程,选择了一个体现语言“临界”特性的字符串 $s=0^{p+1}1^p$,其中0的数量只比1的数量多一个。在应用泵引理的条件3 ($|xy| \le p$) 后,我们确定了可泵浦部分 $y$ 必然是开头的全'0'串的一部分。
接着,文章展示了常规的“向上泵浦”($i=2$) 在此例中是无效的。因为增加'0'的数量只会使字符串更符合 $i>j$ 的规则,无法导出矛盾。
证明的突破口在于转向向下泵浦 ($i=0
”的技巧,成功导出了矛盾。这个例子强调了在应用泵引理时,需要根据语言的具体性质,灵活地选择泵浦方向(向上或向下)和构造“临界”的测试字符串。
这个例子的教学目的非常明确:
- 引入“向下泵浦”的概念:它打破了之前例子中只使用“向上泵浦”($i \ge 2$)的思维定式,展示了泵引理条件1中 $i=0$ 的情况同样是导出矛盾的有力武器。
- 教授问题解决的灵活性:它告诉我们,当一条路走不通时(向上泵浦失败),应该立刻反思并尝试其他路径(向下泵浦)。这种灵活变通的思维在科学研究和工程实践中都至关重要。
- 强化对“临界”字符串选择的理解:选择 $s=0^{p+1}1^p$ 而不是 $s=0^{2p}1^p$ 或其他字符串,体现了选择一个恰好在规则边缘(0的数量只比1多一)的字符串,最容易在微小的扰动(泵浦)下“跌出”规则的边界。这是构造泵引理证明时一个非常高级的技巧。
- “勉强及格”的学生模型:
- 语言 $E$ 的规则是“分数必须及格”,但这里“及格线”不是固定的,而是要求“语文分($i$) > 数学分($j$)”。
- 你找到了一个学生,他的档案 $s$ 是“语文 $p+1$ 分,数学 $p$ 分”。他刚好及格,只高出了一分。
- 泵引理规则说,你可以对他的档案进行“泵浦”操作,而且操作必须在他的“语文分”档案部分进行(因为 $|xy|\le p$)。
- 向上泵浦(失败的尝试): 你给他增加了几分语文分。他的新分数变成“语文 $p+1+|y|$ 分,数学 $p$ 分”。他的语文分更高了,更满足“语文>数学”的规则了。你无法证明他不及格。
- 向下泵浦(成功的尝试): 你给他扣掉了几分语文分($|y| \ge 1$)。他的新分数变成“语文 $p+1-|y|$ 分,数学 $p$ 分”。因为他本来就只高出1分,你至少扣掉了1分,所以他的新语文分不会再比数学分高了(最多相等)。他不及格了!
- 矛盾: 泵引理说泵浦后学生应该仍然是及格的,但你通过向下泵浦让他不及格了。这证明了“语文>数学”这个规则本身就不是“正则”的,它无法容忍这种泵浦操作。
- 跷跷板模型:
- 语言 $E$ 的规则就像一个跷跷板,要求坐着'0'的那一端必须比坐着'1'的那一端更低(即0的数量 > 1的数量)。
- 你设置了一个场景 $s=0^{p+1}1^p$:在'0'那端放了 $p+1$ 公斤的重物,在'1'那端放了 $p$ 公斤的重物。'0'那端刚好比'1'那端重一点点,跷跷板倾斜了,满足了规则。
- 泵引理规则说,你只能在'0'那一端的重物上做手脚($|xy|\le p$)。
- 向上泵浦(失败): 你往'0'那端又加了一些重物($y$)。'0'那端变得更重了,跷跷板倾斜得更厉害,仍然满足规则。
- 向下泵浦(成功): 你从'0'那端拿走了一些重物($y$,且 $|y| \ge 1$)。因为'0'那端本来就只比'1'那端重1公斤,你至少拿走了1公斤。现在'0'那端的重量小于或等于'1'那端的重量了。跷跷板要么平衡了,要么向另一边倾斜了! 它不再满足“'0'那端必须更低”的规则。
- 矛盾: 泵引理的内在稳定性要求操作后跷跷板应保持原有状态,但它却改变了状态。因此,这个跷跷板的规则(语言E)是不“正则”的。
55. 章节练习
5.1 练习 1.1:DFA基础分析
📜 [原文39]
$^{\text {A }}$ 1.1 以下是两个 DFA $M_{1}$ 和 $M_{2}$ 的状态图。回答关于每个机器的以下问题。
$M_{1}$
$M_{2}$
a. 起始状态是什么?
b. 接受状态集是什么?
c. 机器在输入 aabb 时经过的状态序列是什么?
d. 机器是否接受字符串 aabb?
e. 机器是否接受字符串 $\varepsilon$?
这个练习旨在考察对确定性有限自动机 (DFA) 状态图的基本解读能力。
对于机器 $M_1$:
- a. 起始状态是什么?
- 起始状态是图中有一个“无源”箭头指向的状态。在 $M_1$ 中,这个状态是 $q_1$。
- b. 接受状态集是什么?
- 接受状态是在图中用双层圆圈表示的状态。在 $M_1$ 中,只有一个这样的状态:$q_2$。所以接受状态集是 $\{q_2\}$。
- c. 机器在输入 aabb 时经过的状态序列是什么?
- 从起始状态 $q_1$ 开始:
- 读入 a:从 $q_1$ 出发的 a 箭头指向 $q_2$。当前状态 $q_2$。
- 读入 a:从 $q_2$ 出发的 a 箭头指向 $q_1$。当前状态 $q_1$。
- 读入 b:从 $q_1$ 出发的 b 箭头指向 $q_1$。当前状态 $q_1$。
- 读入 b:从 $q_1$ 出发的 b 箭头指向 $q_1$。当前状态 $q_1$。
- 状态序列包括起始状态和每次读入后的状态,所以序列是:$q_1, q_2, q_1, q_1, q_1$。
- d. 机器是否接受字符串 aabb?
- 在读完整个字符串 aabb 后,机器停在了状态 $q_1$。因为 $q_1$ 不是接受状态,所以机器不接受该字符串。
- e. 机器是否接受字符串 $\varepsilon$?
- 输入为空字符串 $\varepsilon$ 意味着机器不读取任何符号,停留在起始状态 $q_1$。因为 $q_1$ 不是接受状态,所以机器不接受空字符串。
对于机器 $M_2$:
- a. 起始状态是什么?
- 起始状态是 $q_1$。
- b. 接受状态集是什么?
- $M_2$ 中有三个接受状态(双层圆圈):$q_1, q_2, q_4$。所以接受状态集是 $\{q_1, q_2, q_4\}$。
- c. 机器在输入 aabb 时经过的状态序列是什么?
- 从起始状态 $q_1$ 开始:
- 读入 a:从 $q_1$ 到 $q_2$。
- 读入 a:从 $q_2$ 到 $q_3$。
- 读入 b:从 $q_3$ 到 $q_4$。
- 读入 b:从 $q_4$ 到 $q_2$。
- 状态序列是:$q_1, q_2, q_3, q_4, q_2$。
- d. 机器是否接受字符串 aabb?
- 读完 aabb 后,机器停在状态 $q_2$。因为 $q_2$ 是一个接受状态,所以机器接受该字符串。
- e. 机器是否接受字符串 $\varepsilon$?
- 输入为空字符串时,机器停留在起始状态 $q_1$。因为 $q_1$ 本身就是一个接受状态,所以机器接受空字符串。
本练习不涉及复杂的公式推导,主要是对DFA状态图符号的解读:
- 状态 (State): 图中的圆圈 ($q_1, q_2, \dots$)。
- 起始状态 (Start State): 有一个起始箭头指向的圆圈。
- 接受状态 (Accept State): 用双层圆圈表示的状态。
- 转移 (Transition): 带标签的箭头,表示在当前状态下读入某个符号后将转移到哪个状态。
已在[逐步解释]中通过追踪字符串 aabb 和 ε 的路径给出了具体示例。
- 状态序列的长度: 状态序列的长度总是比输入字符串的长度多1,因为它包含了起始状态。
- 空字符串 $\varepsilon$ 的处理: 判断是否接受 $\varepsilon$ 非常简单,只需要看起始状态是否同时也是一个接受状态。
- DFA的确定性: 每个状态对于每个输入字母表中的符号,都必须有且仅有一条出边。这是DFA与NFA的关键区别之一。
5.2 练习 1.2 - 1.30: 综合练习
📜 [原文40]
(练习1.2至1.30的题目原文)
这部分包含了从1.2到1.30的一系列练习题。这些题目覆盖了本章介绍的关于正则语言的全部核心概念,包括:
- DFA 和 NFA:
- 形式化描述: 将状态图转换为五元组表示(状态集、字母表、转移函数、起始状态、接受状态集)。
- 状态图构建: 从语言描述或形式化描述出发,画出DFA或NFA。
- 语言识别: 判断给定的DFA/NFA识别什么样的语言。
- 正则运算:
- 并集、连接、星号: 如何通过构造NFA来实现这些运算。
- 交集、补集: 如何通过对DFA进行操作来实现这些运算(例如,乘积构造法求交集,交换接受与非接受状态求补集)。
- 正则表达式:
- 书写: 为给定语言编写正则表达式。
- 转换: 实现正则表达式与有限自动机之间的相互转换(例如,使用GNFA法或状态消除法将DFA/NFA转为正则表达式,使用汤普森构造法将正则表达式转为NFA)。
- 非正则语言与泵引理:
- 应用泵引理: 使用泵引理证明某些语言(如$\{0^n1^n2^n\}$, $\{www\}$, $\{a^{2^n}\}$)不是正则的。
- 逻辑辨析: 找出对泵引理的错误应用(如练习1.30)。
- 扩展模型:
- 有限状态传感器 (FST): 理解这种带输出的有限自动机模型。
这些练习的目的是巩固理论知识,并通过实践加深对算法和构造方法的理解。解决这些问题需要综合运用本章所学的各种定义、定理和构造技巧。由于题目数量众多,这里对每个题目类型进行概述性解释,而不是逐一解答。
解题策略概述:
- 对于构造DFA/NFA的题目,通常从分析语言的“记忆”需求入手。需要记住什么信息来区分应接受和应拒绝的字符串?每个信息点可以对应一个状态。
- 对于正则运算的题目,严格遵循课本中给出的构造性证明算法(如并集的NFA构造,交集的DFA乘积构造)。
- 对于正则表达式的题目,可以先尝试构建自动机,再将自动机转换为表达式,有时会更简单。
- 对于泵引理的证明,严格遵循“假设-选s-分析拆分-导出矛盾”的反证法框架。关键是选择一个能体现语言非正则本质且能利用条件3的字符串s。
- 对于辨析错误的题目,需要回到最基本的定义和定理,逐一检查证明的每一步是否符合逻辑,特别是量词(所有、存在)的使用是否正确。
这部分练习会大量运用到以下核心公式与表示法:
- DFA五元组: $M = (Q, \Sigma, \delta, q_0, F)$
- NFA五元组: $N = (Q, \Sigma, \delta, q_0, F)$,其中NFA的转移函数 $\delta: Q \times \Sigma_\varepsilon \to \mathcal{P}(Q)$。
- 正则表达式元字符: * (星号), | 或 ∪ (并集/或), () (分组), + (正闭包)。
- 泵引理的三个条件:
- $\forall i \ge 0, xy^iz \in A$
- $|y| > 0$
- $|xy| \le p$
- 语言运算符号: $\cap$ (交集), $\overline{L}$ (补集)。
- 练习1.4.a: 构造识别“至少有三个a和至少两个b”的DFA。可以构造两个简单的DFA:一个计数a(状态0, 1, 2, >=3),一个计数b(状态0, 1, >=2)。然后使用乘积构造法将这两个DFA组合起来,得到一个拥有 $4 \times 3 = 12$ 个状态的DFA。
- 练习1.29.A: 证明 $A_1 = \{0^n1^n2^n\}$ 非正则。选择 $s = 0^p1^p2^p$。根据 $|xy| \le p$,$y$ 只能由0组成。泵浦后 $xyyz$ 的0变多,而1和2不变,破坏了三者数量相等的关系,产生矛盾。
- NFA转DFA: 注意状态爆炸的可能性,子集构造法可能产生 $2^{|Q|}$ 个状态。
- DFA转正则表达式: 状态消除法过程繁琐,容易计算出错。
- 封闭性: 要记清DFA和NFA的封闭性质。例如,DFA类在补集下封闭,但NFA类不是(交换NFA的接受/非接受状态不一定得到补集)。
- 泵引理的对手思维: 在证明非正则时,必须假设对手会选择最有利的拆分方式来反驳你,你的证明必须能应对所有合法的拆分。
本节内容为一系列综合性练习题,旨在全面检验和巩固读者对第一章(或相关章节)关于正则语言理论的掌握程度。这些练习题覆盖了从基本概念到高级应用的所有知识点,包括有限自动机(DFA/NFA)的分析、设计与转换,正则运算(并、交、补、连接、星号)的构造性实现,正则表达式与有限自动机之间的等价转换,以及利用泵引理证明特定语言为非正则的技巧。此外,还涉及了一些如有限状态传感器(FST)等扩展模型,和对常见逻辑谬误的辨析。完成这些练习是深入理解正则语言理论、提升形式化建模与证明能力的关键环节。
练习题在教材或课程中扮演着至关重要的角色,其存在目的如下:
- 知识内化: 将被动接收的理论知识,通过主动解决问题的方式,转化为学习者自己掌握的技能。
- 技能训练: 许多理论(如子集构造法、状态消除法、泵引理应用)本质上是一种算法或过程性知识,需要通过反复练习才能熟练掌握并避免出错。
- 概念深化: 许多练习题(特别是那些有陷阱或需要巧妙思路的题目)旨在暴露学习者对概念理解的模糊之处,迫使他们重新审视定义和定理,从而达到更深层次的理解。
- 能力评估: 练习题是检验学习成果的标尺,可以帮助学习者和教学者评估对知识点的掌握情况。
- 培养严谨性: 形式语言的练习,特别是证明题,极大地训练了学生的逻辑思维、符号操纵和书写严谨数学证明的能力。
- “工具箱”模型: 整个章节的学习就像是往你的“理论工具箱”里添加各种工具(DFA、NFA、正则表达式、泵引理、封闭性定理等)。练习题就是各式各样的“修理任务”或“制造任务”。你需要在面对一个具体问题时,判断应该从工具箱里拿出哪一个或哪几个工具,并正确地使用它们来完成任务。例如,证明非正则性就拿出“泵引理”锤子;构造两个语言的交集就拿出“乘积构造”扳手。
- “侦探推理”模型: 每一道证明题都像一个案件。你有几条线索(语言的定义)和几条法则(定理)。你的任务是运用逻辑推理,从线索和法则出发,一步步构建证据链,最终要么找到罪证(导出矛盾),要么为嫌疑人脱罪(构造出相应的自动机或表达式)。
- “乐高积木”搭建: 将DFA/NFA的状态看作不同形状的乐高积木块,转移弧线看作连接件。
- 构造DFA/NFA: 就像根据一个设计蓝图(语言描述),用积木块搭建出一个能实现特定功能的模型。
- 正则运算: 就像学习如何将两个独立的乐高模型(两个自动机)通过特定的拼接规则(如并集、交集的构造算法)组合成一个更大、功能更复杂的模型。
- 自动机转表达式: 就像看着一个已经搭好的复杂乐高模型,反向工程出它的搭建说明书。
- “代码调试”: 将泵引理证明看作一次对“语言代码”的“压力测试”。
- 语言: 一段声称自己“性能稳定”(正则)的代码。
- 泵引理: 一个自动化测试工具,它会找到代码中的“循环”(可泵浦的y)。
- 测试过程: 该工具对这个“循环”进行各种操作(重复、删除),然后检查代码是否还能正常运行(字符串是否还在语言中)。
- 发现bug: 如果在某个操作下,代码崩溃了(字符串跑到了语言之外),你就找到了一个bug,证明了这段代码并非“性能稳定”(该语言非正则)。练习1.30就像是分析一个错误的bug报告,指出为什么测试员的操作不符合测试工具的规范。
6行间公式索引
- 语言C和语言D的定义:
- 完全平方数序列示例:
- 为构造NFA星号操作而定义的扩展转移函数δ,该构造存在缺陷,是练习1.15中的一个反例:
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。