2_上下文无关语言2.1.ZH

12

上下文无关语言

在第 1 章中，我们介绍了两种不同但等效的语言描述方法：有限自动机和正则表达式。我们展示了许多语言可以用这种方式描述，但某些简单的语言，例如 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ ，则不能。

在本章中，我们将介绍上下文无关文法，这是一种更强大的语言描述方法。这类文法可以描述具有递归结构的某些特征，这使其在各种应用中都很有用。

上下文无关文法最初用于研究人类语言。理解名词、动词、介词等术语及其各自短语之间关系的一种方法，自然会导致一种递归，因为名词短语可能出现在动词短语中，反之亦然。上下文无关文法帮助我们组织和理解这些关系。

上下文无关文法的一个重要应用是编程语言的规范和编译。编程语言的文法通常作为人们学习语言语法时的参考。编程语言的编译器和解释器设计者通常从获取语言的文法开始。大多数编译器和解释器都包含一个称为解析器的组件，它在生成编译代码或执行解释之前提取程序的意义。一旦有了上下文无关文法，许多方法都能促进解析器的构建。有些工具甚至可以根据文法自动生成解析器。

与上下文无关文法相关的语言集合称为上下文无关语言。它们包括所有正则语言以及许多额外的语言。在本章中，我们给出上下文无关文法的形式化定义，并研究上下文无关语言的性质。我们还将介绍下推自动机，这是一类识别上下文无关语言的机器。下推自动机很有用，因为它们使我们能够更深入地了解上下文无关文法的力量。

2.1 上下文无关文法

以下是上下文无关文法的一个示例，我们称之为 $G_{1}$ 。

\begin{aligned} & A \rightarrow 0 A 1 \\ & A \rightarrow B \\ & B \rightarrow \# \end{aligned}

文法由一系列替换规则组成，也称为产生式。每条规则都以文法中的一行出现，包含一个符号和一个由箭头分隔的字符串。该符号称为变量。该字符串由变量和称为终结符的其他符号组成。变量符号通常用大写字母表示。终结符类似于输入字母表，通常用小写字母、数字或特殊符号表示。其中一个变量被指定为开始变量。它通常出现在最顶层规则的左侧。例如，文法 $G_{1}$ 包含三条规则。 $G_{1}$ 的变量是 $A$ 和 $B$ ，其中 $A$ 是开始变量。它的终结符是 0, 1 和 \#。

你通过以下方式生成该语言的每个字符串来使用文法描述语言。

写下开始变量。它是顶层规则左侧的变量，除非另有说明。
找到一个已写下的变量以及一个以该变量开头的规则。用该规则的右侧替换已写下的变量。
重复步骤 2，直到没有变量为止。

例如，文法 $G_{1}$ 生成字符串 000\#111。获取字符串的替换序列称为推导。文法 $G_{1}$ 中字符串 000\#111 的推导是

A \Rightarrow 0 A 1 \Rightarrow 00 A 11 \Rightarrow 000 A 111 \Rightarrow 000 B 111 \Rightarrow 000 \# 111 .

你也可以用分析树以图形方式表示相同的信息。分析树的一个示例如图 2.1 所示。

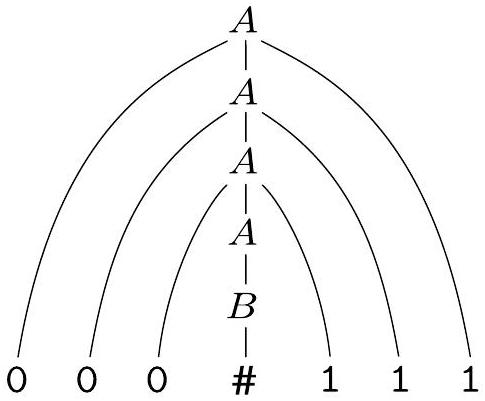
图 2.1

文法 $G_{1}$ 中 000\#111 的分析树

以这种方式生成的所有字符串构成文法的语言。我们将文法 $G_{1}$ 的语言表示为 $L\left(G_{1}\right)$ 。对文法 $G_{1}$ 进行一些实验，我们发现 $L\left(G_{1}\right)$ 是 $\left\{0^{n} \# 1^{n} \mid n \geq 0\right\}$ 。任何可以通过某些上下文无关文法生成的语言都称为上下文无关语言 (CFL)。为方便起见，在呈现上下文无关文法时，我们将几个具有相同左侧变量的规则（例如 $A \rightarrow 0 A 1$ 和 $A \rightarrow B$ ）缩写为一行 $A \rightarrow 0 A 1 \mid B$ ，其中符号 " $\mid$ " 表示 "或"。

以下是上下文无关文法的第二个示例，称为 $G_{2}$ ，它描述了英语的一个片段。

```

$\langle$ SENTENCE $\rangle \rightarrow\langle$ NOUN-PHRASE $\rangle\langle$ VERB-PHRASE $\rangle$

$\langle$ NOUN-PHRASE $\rangle \rightarrow\langle$ CMPLX-NOUN $\rangle \mid\langle$ CMPLX-NOUN $\rangle\langle$ PREP-PHRASE $\rangle$

$\langle$ VERB-PHRASE $\rangle \rightarrow\langle$ CMPLX-VERB $\rangle \mid\langle$ CMPLX-VERB $\rangle\langle$ PREP-PHRASE $\rangle$

$\langle$ PREP-PHRASE $\rangle \rightarrow\langle$ PREP $\rangle\langle$ CMPLX-NOUN $\rangle$

$\langle$ CMPLX-NOUN $\rangle \rightarrow\langle$ ARTICLE $\rangle\langle$ NOUN $\rangle$

$\langle$ CMPLX-VERB $\rangle \rightarrow\langle$ VERB $\rangle \mid\langle$ VERB $\rangle\langle$ NOUN-PHRASE $\rangle$

$\langle$ ARTICLE $\rangle \rightarrow \mathrm{a} \mid$ the

〈NOUN〉 → boy | girl | flower

|VERB → touches | likes | sees

$\langle$ PREP $\rangle \rightarrow$ with

```

文法 $G_{2}$ 有 10 个变量（括号内大写的语法术语）；27 个终结符（标准英文字母加上一个空格字符）；以及 18 条规则。 $L\left(G_{2}\right)$ 中的字符串包括：

```

a boy sees

the boy sees a flower

a girl with a flower likes the boy

```

这些字符串中的每一个在文法 $G_{2}$ 中都有推导。以下是此列表中第一个字符串的推导。

\begin{aligned} \langle\text { SENTENCE }\rangle & \Rightarrow\langle\text { NOUN-PHRASE }\rangle\langle\text { VERB-PHRASE }\rangle \\ & \Rightarrow\langle\text { CMPLX-NOUN }\rangle\langle\text { VERB-PHRASE }\rangle \\ & \Rightarrow\langle\text { ARTICLE }\rangle\langle\text { NOUN }\rangle\langle\text { VERB-PHRASE }\rangle \\ & \Rightarrow \mathrm{a}\langle\text { NOUN }\rangle\langle\text { VERB-PHRASE }\rangle \\ & \Rightarrow \mathrm{a} \text { boy }\langle\text { VERB-PHRASE } \\ & \Rightarrow \mathrm{a} \text { boy }\langle\text { CMPLX-VERB }\rangle \\ & \Rightarrow \mathrm{a} \text { boy }\langle\text { VERB }\rangle \\ & \Rightarrow \mathrm{a} \text { boy sees } \end{aligned}

上下文无关文法的形式化定义

让我们将上下文无关文法 (CFG) 的概念形式化。

定义 2.2

上下文无关文法是一个四元组 ( $V, \Sigma, R, S$ )，其中

$V$ 是一个有限集合，称为变量，
$\Sigma$ 是一个有限集合，与 $V$ 不相交，称为终结符，
$R$ 是一个有限的规则集合，每条规则都是一个变量和一个变量与终结符的字符串，并且
$S \in V$ 是开始变量。

如果 $u, v$ 和 $w$ 是变量和终结符的字符串，并且 $A \rightarrow w$ 是文法的一条规则，我们说 $u A v$ 导出 $u w v$ ，记作 $u A v \Rightarrow u w v$ 。如果 $u=v$ 或存在一个序列 $u_{1}, u_{2}, \ldots, u_{k}$ ，其中 $k \geq 0$ 且

u \Rightarrow u_{1} \Rightarrow u_{2} \Rightarrow \ldots \Rightarrow u_{k} \Rightarrow v .

我们说 $u$ 推导 $v$ ，记作 $u \stackrel{*}{\Rightarrow} v$ 。

文法的语言是 $\left\{w \in \Sigma^{*} \mid S \stackrel{*}{\Rightarrow} w\right\}$ 。

在文法 $G_{1}$ 中， $V=\{A, B\}$ ， $\Sigma=\{0,1, \#\}$ ， $S=A$ ，且 $R$ 是第 102 页上出现的三条规则的集合。在文法 $G_{2}$ 中，

\begin{aligned} V=\{ & \langle\text { SENTENCE }\rangle,\langle\text { NOUN-PHRASE }\rangle,\langle\text { VERB-PHRASE }\rangle, \\ & \langle\text { PREP-PHRASE }\rangle,\langle\text { CMPLX-NOUN }\rangle,\langle\text { CMPLX-VERB }\rangle, \\ & \langle\text { ARTICLE }\rangle,\langle\text { NOUN }\rangle,\langle\text { VERB }\rangle,\langle\text { PREP }\rangle\}, \end{aligned}

$\Sigma=\{\mathrm{a}, \mathrm{b}, \mathrm{c}, \ldots, \mathrm{z}$ , " " $\}$ 。符号 " " 是空格符号，不可见地放在每个单词（a, boy 等）之后，这样单词就不会连在一起。

我们通常只通过写下文法的规则来指定文法。我们可以将变量识别为出现在规则左侧的符号，并将终结符识别为其余的符号。按照惯例，开始变量是第一条规则左侧的变量。

上下文无关文法的例子

例子 2.3

考虑文法 $G_{3}=(\{S\},\{\mathrm{a}, \mathrm{b}\}, R, S)$ 。规则集 $R$ 是

S \rightarrow \mathrm{a} S \mathrm{~b}|S S| \varepsilon .

这个文法生成像 abab、aaabbb 和 aababb 这样的字符串。如果你将 a 视为左括号 "("，b 视为右括号 ")"，你就能更容易地看出这种语言是什么。从这个角度看， $L\left(G_{3}\right)$ 是所有正确嵌套括号的字符串的语言。请注意，规则的右侧可以是空串 $\varepsilon$ 。

例子 2.4

考虑文法 $G_{4}=(V, \Sigma, R,\langle\mathrm{EXPR}\rangle)$ 。

$V$ 是 $\{\langle \text{EXPR} \rangle,\langle \text{TERM} \rangle,\langle \text{FACTOR} \rangle\}$ ， $\Sigma$ 是 $\{\mathrm{a},+, \times,(), \ \}$ 。规则是

\begin{aligned} \langle\mathrm{EXPR}\rangle & \rightarrow\langle\mathrm{EXPR}\rangle+\langle\mathrm{TERM}\rangle \mid\langle\mathrm{TERM}\rangle \\ \langle\mathrm{TERM}\rangle & \rightarrow\langle\mathrm{TERM}\rangle \times\langle\mathrm{FACTOR}\rangle \mid\langle\mathrm{FACTOR}\rangle \\ \langle\mathrm{FACTOR}\rangle & \rightarrow(\langle\mathrm{EXPR}\rangle) \mid \mathrm{a} \end{aligned}

字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 和 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 可以用文法 $G_{4}$ 生成。分析树如下图所示。

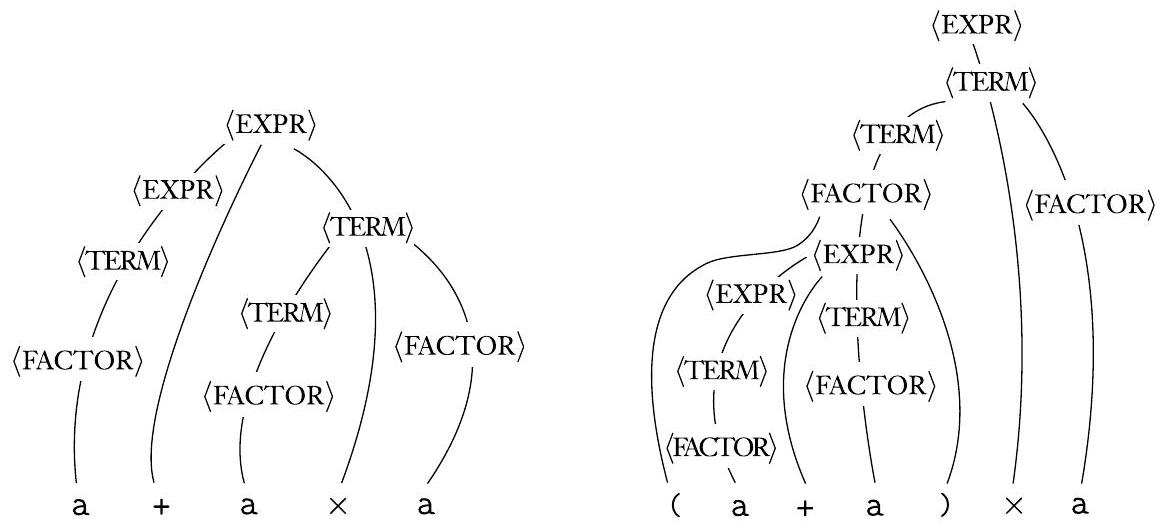
图 2.5

字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 和 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 的分析树

编译器将用编程语言编写的代码转换为另一种形式，通常是更适合执行的形式。为此，编译器在称为解析的过程中提取待编译代码的含义。这种含义的一种表示是代码的分析树，它位于编程语言的上下文无关文法中。我们将在定理 7.16 和问题 7.22 中讨论一种解析上下文无关语言的算法。

文法 $G_{4}$ 描述了与算术表达式相关的编程语言片段。请注意图 2.5 中的分析树如何“分组”操作。字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的树将 $\times$ 运算符及其操作数（后两个 a）分组为 + 运算符的一个操作数。在字符串 $(\mathrm{a}+\mathrm{a}) \times \mathrm{a}$ 的树中，分组顺序颠倒。这些分组符合乘法先于加法的标准优先级，以及使用括号覆盖标准优先级。文法 $G_{4}$ 旨在捕获这些优先级关系。

设计上下文无关文法

正如 1.1 节（第 41 页）讨论的有限自动机设计一样，上下文无关文法的设计也需要创造力。事实上，上下文无关文法比有限自动机更难构建，因为我们更习惯于为特定任务编写机器程序，而不是用文法描述语言。当面临构建 CFG 的问题时，以下技术（单独或组合使用）会很有帮助。

首先，许多 CFL 是更简单 CFL 的并集。如果你必须为可以分解为更简单部分的 CFL 构建 CFG，那么这样做，然后为每个部分构建单独的文法。这些单独的文法可以很容易地合并为原始语言的文法，方法是组合它们的规则，然后添加新规则 $S \rightarrow S_{1}\left|S_{2}\right| \cdots \mid S_{k}$ ，其中变量 $S_{i}$ 是各个文法的开始变量。解决几个更简单的问题通常比解决一个复杂的问题更容易。

例如，为了获得语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\} \cup\left\{1^{n} 0^{n} \mid n \geq 0\right\}$ 的文法，首先构建语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 的文法

S_{1} \rightarrow 0 S_{1} 1 \mid \varepsilon

以及语言 $\left\{1^{n} 0^{n} \mid n \geq 0\right\}$ 的文法

S_{2} \rightarrow 1 S_{2} 0 \mid \varepsilon

然后添加规则 $S \rightarrow S_{1} \mid S_{2}$ ，得到文法

\begin{aligned} S & \rightarrow S_{1} \mid S_{2} \\ S_{1} & \rightarrow 0 S_{1} 1 \mid \varepsilon \\ S_{2} & \rightarrow 1 S_{2} 0 \mid \varepsilon . \end{aligned}

其次，如果一种语言恰好是正则的，那么构建它的 CFG 就很容易，如果你能先为该语言构建一个 DFA。你可以将任何 DFA 转换为等效的 CFG，如下所示。为 DFA 的每个状态 $q_{i}$ 创建一个变量 $R_{i}$ 。如果 $\delta\left(q_{i}, a\right)=q_{j}$ 是 DFA 中的一个转移，则将规则 $R_{i} \rightarrow a R_{j}$ 添加到 CFG 中。如果 $q_{i}$ 是 DFA 的接受状态，则添加规则 $R_{i} \rightarrow \varepsilon$ 。将 $R_{0}$ 作为文法的开始变量，其中 $q_{0}$ 是机器的开始状态。请自行验证，由此产生的 CFG 生成的语言与 DFA 识别的语言相同。

第三，某些上下文无关语言包含带有两个子串的字符串，这两个子串是“关联”的，这意味着针对此类语言的机器需要记住有关其中一个子串的无限量信息，以验证它是否与另一个子串正确对应。这种情况发生在语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 中，因为机器需要记住 0 的数量，以验证它是否等于 1 的数量。你可以通过使用 $R \rightarrow u R v$ 形式的规则来构建 CFG 以处理这种情况，该规则生成字符串，其中包含 $u$ 的部分对应于包含 $v$ 的部分。

最后，在更复杂的语言中，字符串可能包含递归地作为其他（或相同）结构的一部分出现的某些结构。这种情况发生在例子 2.4 中生成算术表达式的文法中。每当出现符号 a 时，一个完整的括号表达式可能会递归地出现。为了实现这种效果，将生成结构的变量符号放置在规则中对应于该结构可能递归出现的位置。

二义性

有时，一个文法可以用几种不同的方式生成同一个字符串。这样的字符串将有几个不同的分析树，因此有几个不同的含义。这对于某些应用（例如编程语言）可能是不希望的，因为程序应该具有唯一的解释。

如果一个文法以几种不同的方式生成同一个字符串，我们说该字符串在该文法中是二义性地推导的。如果一个文法二义性地生成了某个字符串，我们说该文法是二义性的。

例如，考虑文法 $G_{5}$ ：

\langle\mathrm{EXPR}\rangle \rightarrow\langle\mathrm{EXPR}\rangle+\langle\mathrm{EXPR}\rangle|\langle\mathrm{EXPR}\rangle \times\langle\mathrm{EXPR}\rangle|(\langle\mathrm{EXPR}\rangle) \mid \mathrm{a}

这个文法二义性地生成了字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 。下图显示了两个不同的分析树。

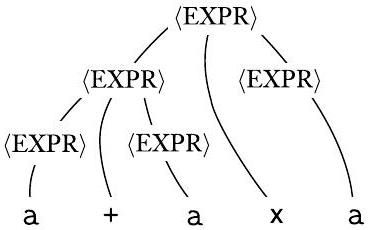
图 2.6

文法 $G_{5}$ 中字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的两个分析树

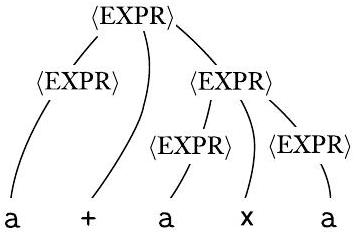
图 2.6

文法 $G_{5}$ 中字符串 $\mathrm{a}+\mathrm{a} \times \mathrm{a}$ 的两个分析树

这个文法没有捕捉到通常的优先级关系，因此它可能先分组 + 运算符，后分组 × 运算符，反之亦然。相比之下，文法 $G_{4}$ 生成完全相同的语言，但每个生成的字符串都有唯一的分析树。因此 $G_{4}$ 是无二义性的，而 $G_{5}$ 是二义性的。

文法 $G_{2}$ （第 103 页）是二义性文法的另一个例子。句子 the girl touches the boy with the flower 有两种不同的推导。在练习 2.8 中，你将被要求给出两个分析树，并观察它们与阅读该句子的两种不同方式的对应关系。

现在我们形式化二义性的概念。当我们说一个文法二义性地生成一个字符串时，我们指的是该字符串有两个或多个不同的分析树，而不是两个不同的推导。两个推导可能仅仅因为替换变量的顺序不同而不同，但它们的整体结构是相同的。为了专注于结构，我们定义一种以固定顺序替换变量的推导类型。如果每一步都替换最左边的剩余变量，那么文法 $G$ 中字符串 $w$ 的推导就是最左推导。定义 2.2（第 104 页）之前的推导就是最左推导。

定义 2.7

如果字符串 $w$ 具有两个或多个不同的最左推导，则称其在上下文无关文法 $G$ 中二义性地推导。如果文法 $G$ 二义性地生成了某个字符串，则称该文法是二义性的。

有时，当我们有一个二义性文法时，我们可以找到一个生成相同语言的无二义性文法。然而，有些上下文无关语言只能由二义性文法生成。这类语言被称为固有二义性语言。问题 2.41 要求你证明语言 $\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i=j \text{ 或 } j=k\right\}$ 是固有二义性的。

乔姆斯基范式

在使用上下文无关文法时，通常将它们简化形式会很方便。最简单且最有用的形式之一被称为乔姆斯基范式。乔姆斯基范式在给出处理上下文无关文法的算法时很有用，正如我们在第 4 章和第 7 章中所做的那样。

定义 2.8

上下文无关文法是乔姆斯基范式，如果每条规则都采用以下形式

\begin{aligned} & A \rightarrow B C \\ & A \rightarrow a \end{aligned}

其中 $a$ 是任何终结符， $A, B$ 和 $C$ 是任何变量——但 $B$ 和 $C$ 不能是开始变量。此外，我们允许规则 $S \rightarrow \varepsilon$ ，其中 $S$ 是开始变量。

定理 2.9

任何上下文无关语言都由乔姆斯基范式中的上下文无关文法生成。

证明思路 我们可以将任何文法 $G$ 转换为乔姆斯基范式。这种转换有几个阶段，其中违反条件的规则被替换为等效的令人满意的规则。首先，我们添加一个新的开始变量。然后，我们消除所有 $A \rightarrow \varepsilon$ 形式的 $\varepsilon$ 规则。我们还消除所有 $A \rightarrow B$ 形式的单元规则。在这两种情况下，我们都会修补文法，以确保它仍然生成相同的语言。最后，我们将剩余的规则转换为正确的形式。

证明首先，我们添加一个新的开始变量 $S_{0}$ 和规则 $S_{0} \rightarrow S$ ，其中 $S$ 是原始的开始变量。此更改保证开始变量不会出现在规则的右侧。

其次，我们处理所有 $\varepsilon$ 规则。我们删除 $\varepsilon$ 规则 $A \rightarrow \varepsilon$ ，其中 $A$ 不是开始变量。然后对于规则右侧出现的每个 $A$ ，我们添加一条删除该出现的新规则。换句话说，如果 $R \rightarrow u A v$ 是一条规则，其中 $u$ 和 $v$ 是变量和终结符的字符串，我们添加规则 $R \rightarrow u v$ 。我们对每个 $A$ 的出现都这样做，因此规则 $R \rightarrow u A v A w$ 会导致我们添加 $R \rightarrow u v A w, R \rightarrow u A v w$ 和 $R \rightarrow u v w$ 。如果存在规则 $R \rightarrow A$ ，我们添加 $R \rightarrow \varepsilon$ ，除非我们之前已经删除了规则 $R \rightarrow \varepsilon$ 。我们重复这些步骤，直到消除所有不涉及开始变量的 $\varepsilon$ 规则。

第三，我们处理所有单元规则。我们删除单元规则 $A \rightarrow B$ 。然后，每当出现规则 $B \rightarrow u$ 时，我们添加规则 $A \rightarrow u$ ，除非这是之前删除的单元规则。与之前一样， $u$ 是变量和终结符的字符串。我们重复这些步骤，直到消除所有单元规则。

最后，我们将所有剩余的规则转换为正确的形式。我们将每条规则 $A \rightarrow u_{1} u_{2} \cdots u_{k}$ （其中 $k \geq 3$ 且每个 $u_{i}$ 是变量或终结符符号）替换为规则 $A \rightarrow u_{1} A_{1}, A_{1} \rightarrow u_{2} A_{2}, A_{2} \rightarrow u_{3} A_{3} \ldots$ 和 $A_{k-2} \rightarrow u_{k-1} u_{k}$ 。 $A_{i}$ 是新变量。我们将上述规则中的任何终结符 $u_{i}$ 替换为新变量 $U_{i}$ ，并添加规则 $U_{i} \rightarrow u_{i}$ 。

例子 2.10

令 $G_{6}$ 为以下 CFG，并使用刚刚给出的转换过程将其转换为乔姆斯基范式。所呈现的文法系列说明了转换中的步骤。粗体显示的规则是刚添加的。灰色显示的规则是刚删除的。

原始 CFG $G_{6}$ 显示在左侧。应用第一步创建新开始变量的结果显示在右侧。

\begin{aligned} & S \rightarrow A S A \mid \mathrm{a} B \\ & A \rightarrow B \mid S \\ & B \rightarrow \mathrm{b} \mid \varepsilon \end{aligned}

\begin{aligned} \boldsymbol{S}_{\mathbf{0}} & \rightarrow \boldsymbol{S} \\ S & \rightarrow A S A \mid \mathrm{a} B \\ A & \rightarrow B \mid S \\ B & \rightarrow \mathrm{b} \mid \varepsilon \end{aligned}

删除 $\varepsilon$ 规则 $B \rightarrow \varepsilon$ （左侧显示）和 $A \rightarrow \varepsilon$ （右侧显示）。

\begin{array}{rlrl} S_{0} & \rightarrow S & S_{0} & \rightarrow S \\ S & \rightarrow A S A|\mathrm{a} B| \mathbf{a} & S & \rightarrow A S A|\mathrm{a} B| \mathrm{a}|\boldsymbol{S} \boldsymbol{A}| \boldsymbol{A} \boldsymbol{S} \mid \boldsymbol{S} \\ A & \rightarrow B|S| \boldsymbol{\varepsilon} & A & \rightarrow B|S| \varepsilon \\ B & \rightarrow \mathrm{b} \mid \varepsilon & B & \rightarrow \mathrm{b} \end{array}

3a. 删除单元规则 $S \rightarrow S$ （左侧显示）和 $S_{0} \rightarrow S$ （右侧显示）。

\begin{array}{rlrl} S_{0} & \rightarrow S & S_{0} & \rightarrow S|\boldsymbol{A} \boldsymbol{S} \boldsymbol{A}| \mathbf{a} \boldsymbol{B}|\mathbf{a}| \boldsymbol{S} \boldsymbol{A} \mid \boldsymbol{A} \boldsymbol{S} \\ S & \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S \mid S & S & \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S \\ A & \rightarrow B \mid S & & A \rightarrow B \mid S \\ B & \rightarrow \mathrm{b} & & B \rightarrow \mathrm{b} \end{array}

3b. 删除单元规则 $A \rightarrow B$ 和 $A \rightarrow S$ 。

\begin{aligned} S_{0} \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S & & S_{0} \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S \\ S \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S & & S \rightarrow A S A|\mathrm{a} B| \mathrm{a}|S A| A S \\ A \rightarrow B|S| \mathrm{b} & & A \rightarrow S|\mathrm{~b}| \boldsymbol{A} \boldsymbol{S} \boldsymbol{A}|\mathbf{a} \boldsymbol{B}| \mathbf{a}|\boldsymbol{S} \boldsymbol{A}| \boldsymbol{A} \boldsymbol{S} \\ B \rightarrow \mathrm{b} & & B \rightarrow \mathrm{b} \end{aligned}

通过添加额外的变量和规则将剩余的规则转换为正确的形式。最终的乔姆斯基范式文法等效于 $G_{6}$ 。（实际上，定理 2.9 中给出的过程会生成多个变量 $U_{i}$ 和多个规则 $U_{i} \rightarrow \text{a}$ 。我们通过使用单个变量 $U$ 和规则 $U \rightarrow \text{a}$ 来简化结果文法。）

\begin{aligned} S_{0} & \rightarrow A A_{1}|U B| \mathrm{a}|S A| A S \\ S & \rightarrow A A_{1}|U B| \mathrm{a}|S A| A S \\ A & \rightarrow \mathrm{b}\left|A A_{1}\right| U B|\mathrm{a}| S A \mid A S \\ A_{1} & \rightarrow S A \\ U & \rightarrow \mathrm{a} \\ B & \rightarrow \mathrm{b} \end{aligned}

📝 我的笔记

12