12.2
下推自动机
在本节中,我们介绍了一种新型的计算模型,称为下推自动机。这些自动机类似于非确定性有限自动机,但它们有一个额外的组件,称为栈。栈提供了超越控制中可用有限内存的额外内存。栈允许下推自动机识别某些非正则语言。
下推自动机在能力上与上下文无关文法等价。这种等价性非常有用,因为它为我们证明一种语言是上下文无关的提供了两种选择。我们可以提供生成它的上下文无关文法,也可以提供识别它的下推自动机。某些语言更容易用生成器来描述,而另一些则更容易用识别器来描述。
下图是有限自动机的示意图。控制表示状态和转移函数,纸带包含输入字符串,箭头表示输入磁头,指向要读取的下一个输入符号。
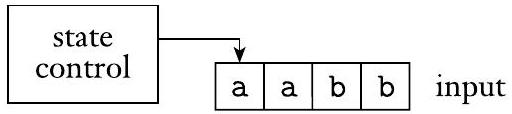
图 2.11
有限自动机示意图
通过添加栈组件,我们获得了下推自动机的示意图,如下图所示。
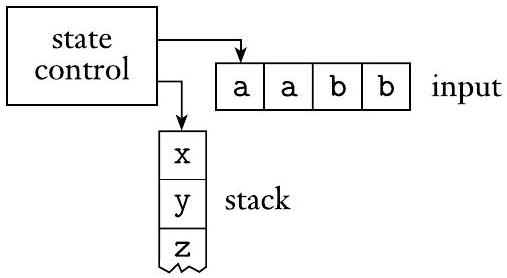
图 2.12
下推自动机示意图
下推自动机(PDA)可以在栈上写入符号,并在稍后读回它们。写入一个符号会“向下推”栈上的所有其他符号。在任何时候,都可以读取并移除栈顶的符号。然后,剩余的符号会向上移动。在栈上写入符号通常被称为压栈(pushing the symbol),而移除符号则被称为弹栈(popping it)。请注意,对栈的所有访问,无论是读取还是写入,都只能在顶部进行。换句话说,栈是一种“后进先出”的存储设备。如果某些信息被写入栈,然后又写入了额外的信息,那么较早的信息在较晚的信息被移除之前是不可访问的。
自助餐厅餐具柜上的盘子说明了栈。这叠盘子放在一个弹簧上,因此当一个新盘子放在栈顶时,下面的盘子会向下移动。下推自动机上的栈就像一叠盘子,每个盘子上都写有一个符号。
栈之所以有价值,是因为它可以存储无限量的信息。回想一下,有限自动机无法识别语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$,因为它无法在其有限内存中存储非常大的数字。PDA能够识别这种语言,因为它可以使用其栈来存储它所看到的 0 的数量。因此,栈的无限性允许 PDA 存储无限大的数字。下面的非正式描述展示了这种语言的自动机是如何工作的。
从输入中读取符号。每读取一个 0,就将其压栈。一旦看到 1,每读取一个 1 就从栈中弹栈一个 0。如果输入读取完成时栈恰好清空了 0,则接受输入。如果栈在 1 仍然存在时清空,或者 1 读取完成时栈仍然包含 0,或者在 1 之后输入中出现任何 0,则拒绝输入。
如前所述,下推自动机可能具有非确定性。确定性下推自动机和非确定性下推自动机在能力上并不等价。
非确定性下推自动机识别某些语言,这是任何确定性下推自动机都无法识别的,我们将在 2.4 节中看到。我们在示例 2.16 和 2.18 中给出了需要非确定性的语言。回想一下,确定性和非确定性有限自动机确实识别同一类语言,因此下推自动机的情况是不同的。我们关注非确定性下推自动机,因为这些自动机在能力上与上下文无关文法等价。
下推自动机的形式定义
下推自动机的形式定义类似于有限自动机,除了栈。栈是一种包含从某个字母表中提取的符号的设备。机器可以使用不同的字母表作为其输入字母表和栈字母表,因此现在我们指定输入字母表 $\Sigma$ 和栈字母表 $\Gamma$。
任何自动机的形式定义的核心是转移函数,它描述了其行为。回想一下,$\Sigma_{\varepsilon}=\Sigma \cup\{\varepsilon\}$ 和 $\Gamma_{\varepsilon}=\Gamma \cup\{\varepsilon\}$。转移函数的域是 $Q \times \Sigma_{\varepsilon} \times \Gamma_{\varepsilon}$。因此,当前状态、读取的下一个输入符号和栈顶符号决定了下推自动机的下一个动作。任一符号都可以是 $\varepsilon$,导致机器在不读取输入符号或不读取栈符号的情况下移动。
对于转移函数的范围,我们需要考虑当自动机处于特定情况时允许它做什么。它可能会进入某个新状态,并可能在栈顶写入一个符号。函数 $\delta$ 可以通过返回 $Q$ 的一个成员和 $\Gamma_{\varepsilon}$ 的一个成员来指示此操作,即 $Q \times \Gamma_{\varepsilon}$ 的一个成员。因为我们允许此模型中的非确定性,所以一种情况可能有几个合法的下一步动作。转移函数以通常的方式结合了非确定性,通过返回 $Q \times \Gamma_{\varepsilon}$ 的成员集,即 $\mathcal{P}\left(Q \times \Gamma_{\varepsilon}\right)$ 的成员。总而言之,我们的转移函数 $\delta$ 的形式为 $\delta: Q \times \Sigma_{\varepsilon} \times \Gamma_{\varepsilon} \longrightarrow \mathcal{P}\left(Q \times \Gamma_{\varepsilon}\right)$。
定义 2.13
下推自动机是一个 6 元组 ( $Q, \Sigma, \Gamma, \delta, q_{0}, F$ ),其中 $Q, \Sigma$,$\Gamma$ 和 $F$ 都是有限集,并且
- $Q$ 是状态集,
- $\Sigma$ 是输入字母表,
- $\Gamma$ 是栈字母表,
- $\delta: Q \times \Sigma_{\varepsilon} \times \Gamma_{\varepsilon} \longrightarrow \mathcal{P}\left(Q \times \Gamma_{\varepsilon}\right)$ 是转移函数,
- $q_{0} \in Q$ 是开始状态,并且
- $F \subseteq Q$ 是接受状态集。
下推自动机 $M=\left(Q, \Sigma, \Gamma, \delta, q_{0}, F\right)$ 的计算方式如下。如果 $w$ 可以写成 $w=w_{1} w_{2} \cdots w_{m}$,其中每个 $w_{i} \in \Sigma_{\varepsilon}$,并且存在状态序列 $r_{0}, r_{1}, \ldots, r_{m} \in Q$ 和字符串 $s_{0}, s_{1}, \ldots, s_{m} \in \Gamma^{*}$ 满足以下三个条件,则它接受输入 $w$。字符串 $s_{i}$ 表示 $M$ 在计算的接受分支上具有的栈内容序列。
- $r_{0}=q_{0}$ 且 $s_{0}=\varepsilon$。此条件表示 $M$ 以开始状态和空栈正确启动。
- 对于 $i=0, \ldots, m-1$,我们有 $\left(r_{i+1}, b\right) \in \delta\left(r_{i}, w_{i+1}, a\right)$,其中 $s_{i}=a t$ 和 $s_{i+1}=b t$ 对于某些 $a, b \in \Gamma_{\varepsilon}$ 和 $t \in \Gamma^{*}$。此条件表示 $M$ 根据状态、栈和下一个输入符号正确移动。
- $r_{m} \in F$。此条件表示在输入结束时出现接受状态。
下推自动机的例子
例子 2.14
以下是识别语言 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 的 PDA(第 112 页)的形式描述。设 $M_{1}$ 是 ( $Q, \Sigma, \Gamma, \delta, q_{1}, F$ ),其中
$\delta$ 由下表给出,其中空白条目表示 $\emptyset$。
| 输入: 栈: | 0 | | | 1 | | | $\varepsilon$ | | |
| :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
| | 0 | \$ | $\varepsilon$ | 0 | \$ | $\varepsilon$ | 0 | \$ | $\varepsilon$ |
| $q_{1}$ | $\left\{\left(q_{2}, \$\right)\right\}$ | | | | | | | | |
| $q_{2}$ | $\left\{\left(q_{2}, 0\right)\right\}$
$\left\{\left(q_{3}, \boldsymbol{\varepsilon}\right)\right\}$ | | | | | | | | |
| $q_{3}$ | | | | $\left\{\left(q_{3}, \varepsilon\right)\right\}$ | | | $\left\{\left(q_{4}, \boldsymbol{\varepsilon}\right)\right\}$ | | |
| $q_{4}$ | | | | | | | | | |
我们还可以使用状态图来描述 PDA,如图 2.15、2.17 和 2.19 所示。这些图类似于用于描述有限自动机的状态图,并进行了修改以显示 PDA 在状态之间转换时如何使用其栈。我们写“ $a, b \rightarrow c$ ”表示当机器正在从输入中读取 $a$ 时,它可以将栈顶的符号 $b$ 替换为 $c$。$a, b$ 和 $c$ 中的任何一个都可以是 $\varepsilon$。如果 $a$ 是 $\varepsilon$,机器可以在不读取任何输入符号的情况下进行此转移。如果 $b$ 是 $\varepsilon$,机器可以在不读取和弹栈任何符号的情况下进行此转移。如果 $c$ 是 $\varepsilon$,机器在沿着此转移时不会在栈上写入任何符号。
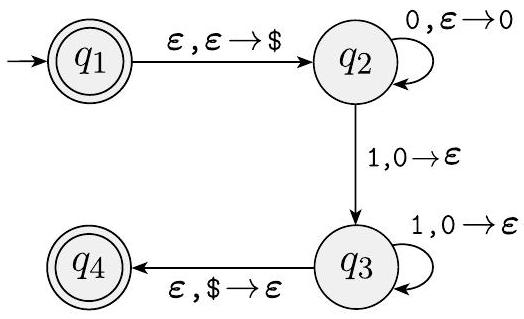
图 2.15
识别 $\left\{0^{n} 1^{n} \mid n \geq 0\right\}$ 的 PDA $M_{1}$ 的状态图
PDA 的形式定义没有明确的机制允许 PDA 测试空栈。这个 PDA 能够通过最初在栈上放置一个特殊符号 $\
类似地,PDA 无法明确测试是否已到达输入字符串的末尾。这个 PDA 能够达到这种效果,因为接受状态仅在机器位于输入末尾时才生效。因此,从现在开始,我们假设 PDA 可以测试输入的末尾,并且我们知道我们可以以相同的方式实现它。
例子 2.16
此示例说明了一个识别语言的下推自动机
非正式地,这种语言的 PDA 首先读取并压栈 a。当 a 结束时,机器将所有 a 放在栈上,这样它就可以将它们与 b 或 c 匹配。这个操作有点棘手,因为机器事先不知道是与 b 还是与 c 匹配 a。非确定性在这里派上了用场。
PDA 利用其非确定性,可以猜测是与 b 还是与 c 匹配 a,如图 2.17 所示。可以把机器想象成它的非确定性有两个分支,每个分支对应一个可能的猜测。如果其中任何一个匹配,该分支接受,并且整个机器接受。问题 2.27 要求您证明非确定性对于 PDA 识别这种语言至关重要。
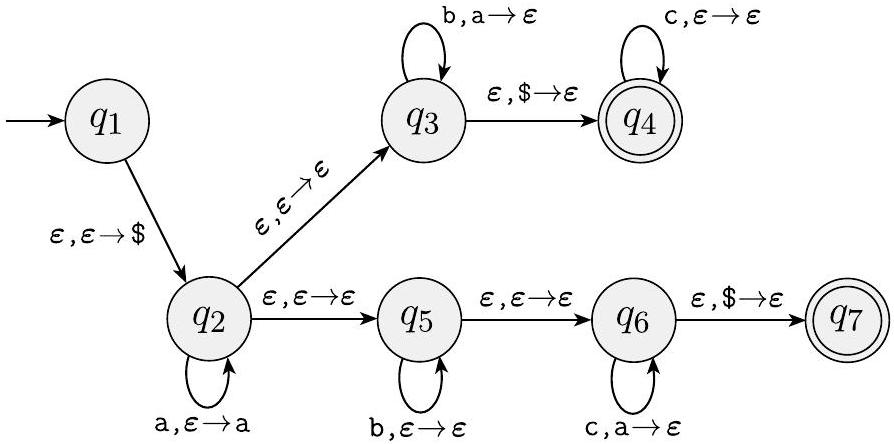
图 2.17
识别 $\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i, j, k \geq 0 \text { 且 } i=j \text { 或 } i=k\right\}$ 的 PDA $M_{2}$ 的状态图
例子 2.18
在此示例中,我们给出一个识别语言 $\left\{w w^{\mathcal{R}} \mid w \in\{0,1\}^{*}\right\}$ 的 PDA $M_{3}$。回想一下,$w^{\mathcal{R}}$ 表示 $w$ 的反向。PDA 的非正式描述和状态图如下。
首先将读取的符号压栈。在每一点,非确定性地猜测已到达字符串的中间,然后切换到每读取一个符号就弹栈,检查它们是否相同。如果它们总是相同的符号,并且栈在输入完成时同时清空,则接受;否则拒绝。
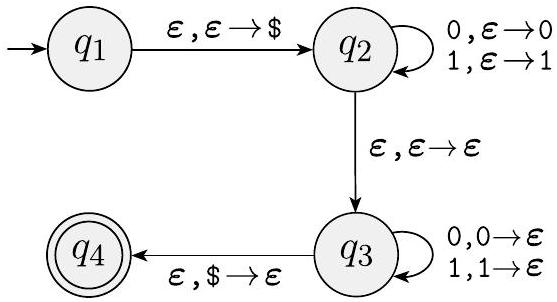
图 2.19
识别 $\left\{w w^{\mathcal{R}} \mid w \in\{0,1\}^{*}\right\}$ 的 PDA $M_{3}$ 的状态图
问题 2.28 表明这种语言需要一个非确定性 PDA。$\square$
与上下文无关文法的等价性
在本节中,我们展示了上下文无关文法和下推自动机在能力上是等价的。两者都能够描述上下文无关语言的类。我们展示了如何将任何上下文无关文法转换为识别相同语言的下推自动机,反之亦然。回想一下,我们将上下文无关语言定义为可以用上下文无关文法描述的任何语言,我们的目标是以下定理。
定理 2.20
一种语言是上下文无关语言当且仅当某些下推自动机识别它。
像往常一样,对于“当且仅当”定理,我们需要证明两个方向。在这个定理中,两个方向都很有趣。首先,我们做更容易的前向。
引理 2.21
如果一种语言是上下文无关语言,那么某些下推自动机识别它。
证明思路 设 $A$ 为一个 CFL。根据定义,我们知道 $A$ 有一个生成它的 CFG,$G$。我们展示如何将 $G$ 转换为等价的 PDA,我们称之为 $P$。
我们现在描述的 PDA $P$ 将通过接受其输入 $w$ 来工作,如果 $G$ 生成该输入,则通过确定是否存在 $w$ 的推导。回想一下,推导只是文法生成字符串时所做的一系列替换。推导的每一步都产生一个变量和终结符的中间字符串。我们设计 $P$ 来确定使用 $G$ 的规则进行的一系列替换是否可以从开始变量导向 $w$。
测试是否存在 $w$ 的推导的困难之一是确定要进行哪些替换。PDA 的非确定性允许它猜测正确替换的序列。在推导的每一步,都会非确定性地选择一个特定变量的规则,并用于替换该变量。
PDA $P$ 首先将开始变量写入其栈。它通过一系列中间字符串,一个接一个地进行替换。最终,它可能会到达一个只包含终结符的字符串,这意味着它已经使用文法推导了一个字符串。然后,如果这个字符串与它收到的输入字符串相同,则 $P$ 接受。
在 PDA 上实现此策略需要一个额外的想法。我们需要了解 PDA 在从一个中间字符串到另一个中间字符串时如何存储它们。简单地使用栈来存储每个中间字符串很诱人。然而,这不太奏效,因为 PDA 需要在中间字符串中找到变量并进行替换。PDA 只能访问栈顶部的符号,而这可能是一个终结符而不是一个变量。解决此问题的方法是只将中间字符串的一部分保留在栈上:从中间字符串中第一个变量开始的符号。在第一个变量之前出现的任何终结符都会立即与输入字符串中的符号匹配。下图显示了 PDA $P$。
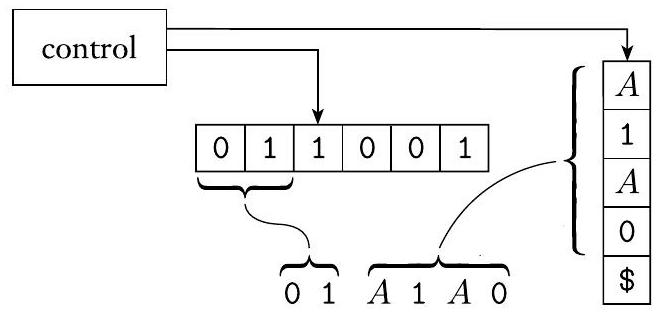
图 2.22
表示中间字符串 01A1A0 的 $P$
以下是 $P$ 的非正式描述。
- 将标记符号 $\$$ 和开始变量放在栈上。
- 永远重复以下步骤。
a. 如果栈顶是变量符号 $A$,则非确定性地选择 $A$ 的规则之一,并用规则右侧的字符串替换 $A$。
b. 如果栈顶是终结符 $a$,则从输入中读取下一个符号并将其与 $a$ 比较。如果它们匹配,则重复。如果它们不匹配,则在此非确定性分支上拒绝。
c. 如果栈顶是符号 $\$$,则进入接受状态。如果输入已全部读取,则接受输入。
证明 我们现在给出下推自动机 $P=\left(Q, \Sigma, \Gamma, \delta, q_{\text {start }}, F\right)$ 构造的形式细节。为了使构造更清晰,我们使用转移函数的简写表示法。这种表示法提供了一种在机器的一个步骤中将整个字符串写入栈的方法。我们可以通过引入额外的状态来模拟此操作,以便一次写入一个符号,如下面的形式构造所示。
设 $q$ 和 $r$ 是 PDA 的状态,设 $a$ 在 $\Sigma_{\varepsilon}$ 中,设 $s$ 在 $\Gamma_{\varepsilon}$ 中。假设我们希望 PDA 在读取 $a$ 并弹栈 $s$ 时从 $q$ 转移到 $r$。此外,我们希望它同时将整个字符串 $u=u_{1} \cdots u_{l}$ 压栈。我们可以通过引入新状态 $q_{1}, \ldots, q_{l-1}$ 并按如下方式设置转移函数来实施此操作:
我们使用符号 $(r, u) \in \delta(q, a, s)$ 来表示当 $q$ 是自动机的状态,$a$ 是下一个输入符号,$s$ 是栈顶符号时,PDA 可以读取 $a$ 并弹栈 $s$,然后将字符串 $u$ 压栈并进入状态 $r$。下图显示了此实现。
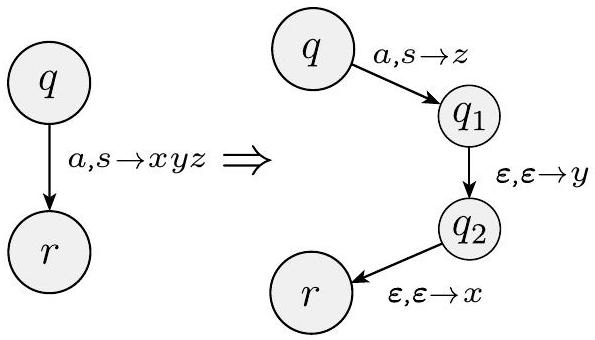
图 2.23
实现简写 $(r, x y z) \in \delta(q, a, s)$
$P$ 的状态是 $Q=\left\{q_{\text {start }}, q_{\text {loop }}, q_{\text {accept }}\right\} \cup E$,其中 $E$ 是我们为实现刚刚描述的简写而需要的状态集。开始状态是 $q_{\text {start}}$。唯一的接受状态是 $q_{\text {accept}}$。
转移函数定义如下。我们首先将栈初始化为包含符号 $\$$ 和 $S$,实现非正式描述中的步骤 1:$\delta\left(q_{\text {start }}, \boldsymbol{\varepsilon}, \boldsymbol{\varepsilon}\right)=\left\{\left(q_{\text {loop }}, S \$\right)\right\}$。然后我们为步骤 2 的主循环放入转移。
首先,我们处理情况 (a),其中栈顶包含一个变量。设 $\delta\left(q_{\text {loop }}, \boldsymbol{\varepsilon}, A\right)=\left\{\left(q_{\text {loop }}, w\right) \mid \text { 其中 } A \rightarrow w \text { 是 } R \text { 中的一条**规则** }\right\}$。
其次,我们处理情况 (b),其中栈顶包含一个终结符。设 $\delta\left(q_{\text {loop }}, a, a\right)=\left\{\left(q_{\text {loop }}, \varepsilon\right)\right\}$。
最后,我们处理情况 (c),其中空栈标记 $\$$ 在栈顶。设 $\delta\left(q_{\text {loop }}, \boldsymbol{\varepsilon}, \$\right)=\left\{\left(q_{\text {accept }}, \boldsymbol{\varepsilon}\right)\right\}$。
状态图如图 2.24 所示。
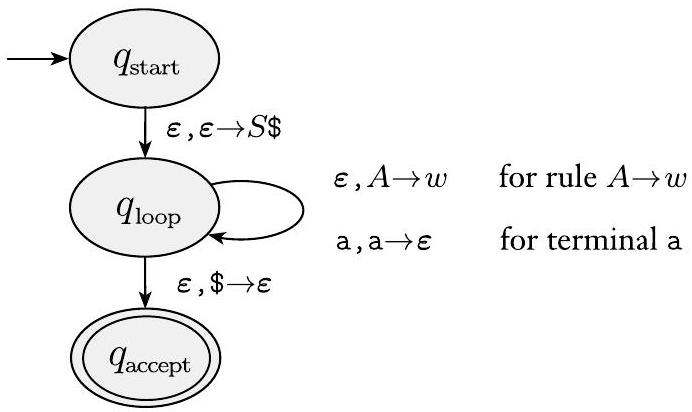
图 2.24
$P$ 的状态图
这完成了引理 2.21 的证明。
例子 2.25
我们使用引理 2.21 中开发的程序从以下 CFG $G$ 构造一个 PDA $P_{1}$。
转移函数如下图所示。
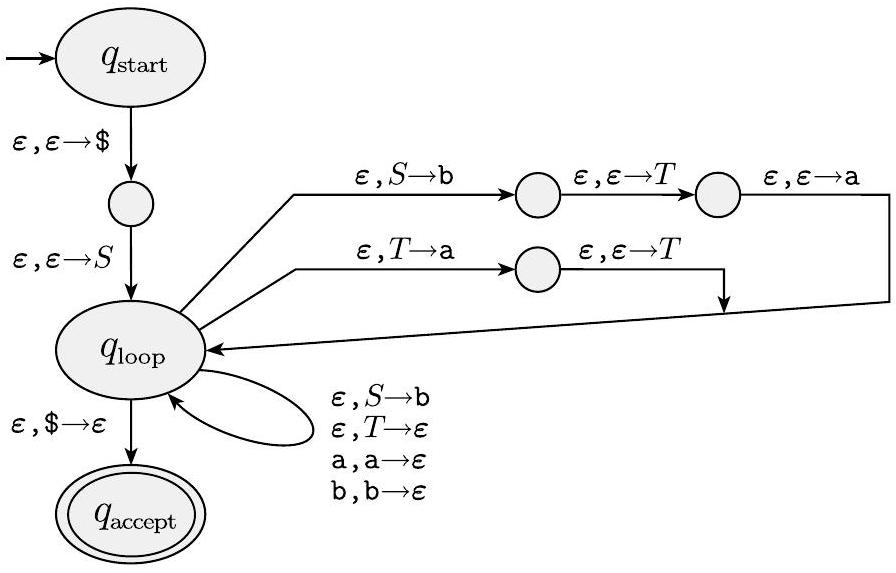
图 2.26
$P_{1}$ 的状态图
现在我们证明定理 2.20 的反向。对于前向,我们给出了将 CFG 转换为 PDA 的过程。主要思想是设计自动机以模拟文法。现在我们想提供一个相反方向的过程:将 PDA 转换为 CFG。我们设计文法以模拟自动机。这项任务具有挑战性,因为“编程”自动机比“编程”文法更容易。
引理 2.27
如果下推自动机识别某种语言,那么它是上下文无关语言。
证明思路 我们有一个 PDA $P$,我们想创建一个 CFG $G$,它生成所有 $P$ 接受的字符串。换句话说,$G$ 应该生成一个字符串,如果该字符串导致 PDA 从其开始状态转移到接受状态。
为了达到这个结果,我们设计了一个做更多事情的文法。对于 $P$ 中每对状态 $p$ 和 $q$,文法将有一个变量 $A_{p q}$。这个变量生成所有可以将 $P$ 从 $p$(空栈)带到 $q$(空栈)的字符串。请注意,这样的字符串也可以将 $P$ 从 $p$ 带到 $q$,无论 $p$ 处的栈内容如何,并在 $q$ 处使栈与 $p$ 处的状态相同。
首先,我们通过稍微修改 $P$ 来简化我们的任务,使其具有以下三个特征。
- 它有一个单一的接受状态,$q_{\text {accept}}$。
- 它在接受前清空其栈。
- 每个转移要么将符号压栈(压栈操作),要么从栈中弹栈(弹栈操作),但不同时进行两者。
赋予 $P$ 特征 1 和 2 很容易。为了赋予它特征 3,我们用一个通过新状态的两个转移序列替换每个同时弹栈和压栈的转移,并且我们用一个压栈然后弹栈任意栈符号的两个转移序列替换每个既不弹栈也不压栈的转移。
为了设计 $G$ 以使 $A_{p q}$ 生成所有以空栈从 $p$ 到 $q$ 的字符串,我们必须了解 $P$ 如何对这些字符串进行操作。对于任何这样的字符串 $x$, $P$ 在 $x$ 上的第一个动作必须是压栈,因为每个动作要么是压栈要么是弹栈,并且 $P$ 不能弹栈一个空栈。同样,在 $x$ 上的最后一个动作必须是弹栈,因为栈最终会变空。
在 $P$ 对 $x$ 的计算过程中会出现两种可能性。要么最后弹栈的符号与最初压栈的符号相同,要么不同。如果是这样,栈可能只在 $P$ 对 $x$ 的计算的开始和结束时为空。如果不是,最初压栈的符号必须在 $x$ 结束之前的某个点被弹栈,因此栈在此点变空。我们用规则 $A_{p q} \rightarrow a A_{r s} b$ 模拟前一种可能性,其中 $a$ 是第一个动作读取的输入,$b$ 是最后一个动作读取的输入,$r$ 是 $p$ 之后的状态,$s$ 是 $q$ 之前的状态。我们用规则 $A_{p q} \rightarrow A_{p r} A_{r q}$ 模拟后一种可能性,其中 $r$ 是栈变空时的状态。
证明 设 $P=\left(Q, \Sigma, \Gamma, \delta, q_{0},\left\{q_{\text {accept }}\right\}\right)$ 并构造 $G$。$G$ 的变量是 $\left\{A_{p q} \mid p, q \in Q\right\}$。开始变量是 $A_{q_{0}, q_{\text {accept}}}$。现在我们分三部分描述 $G$ 的规则。
- 对于每个 $p, q, r, s \in Q, u \in \Gamma$,以及 $a, b \in \Sigma_{\varepsilon}$,如果 $\delta(p, a, \varepsilon)$ 包含 ( $r, u$ ) 并且 $\delta(s, b, u)$ 包含 $(q, \varepsilon)$,则将规则 $A_{p q} \rightarrow a A_{r s} b$ 放入 $G$ 中。
- 对于每个 $p, q, r \in Q$,将规则 $A_{p q} \rightarrow A_{p r} A_{r q}$ 放入 $G$ 中。
- 最后,对于每个 $p \in Q$,将规则 $A_{p p} \rightarrow \varepsilon$ 放入 $G$ 中。
您可以通过以下数字获得此构造的一些见解。
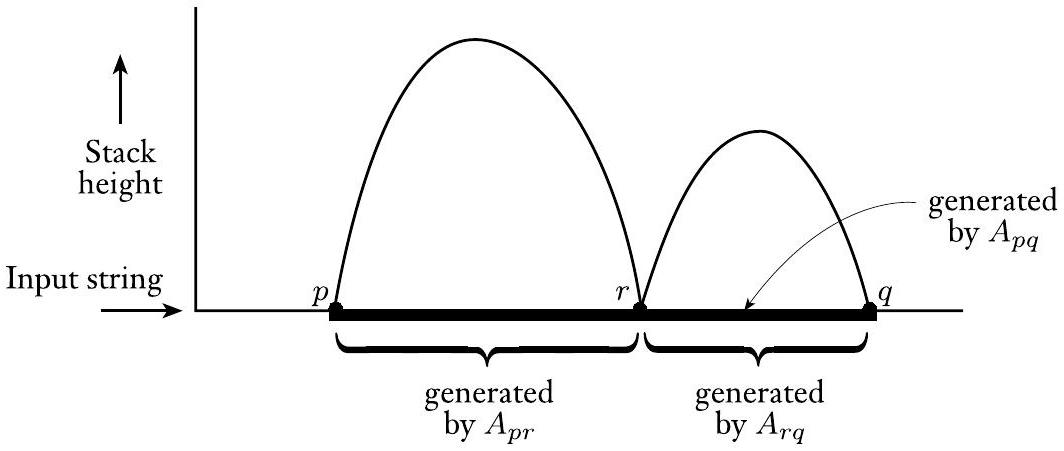
图 2.28
与规则 $A_{p q} \rightarrow A_{p r} A_{r q}$ 对应的 PDA 计算
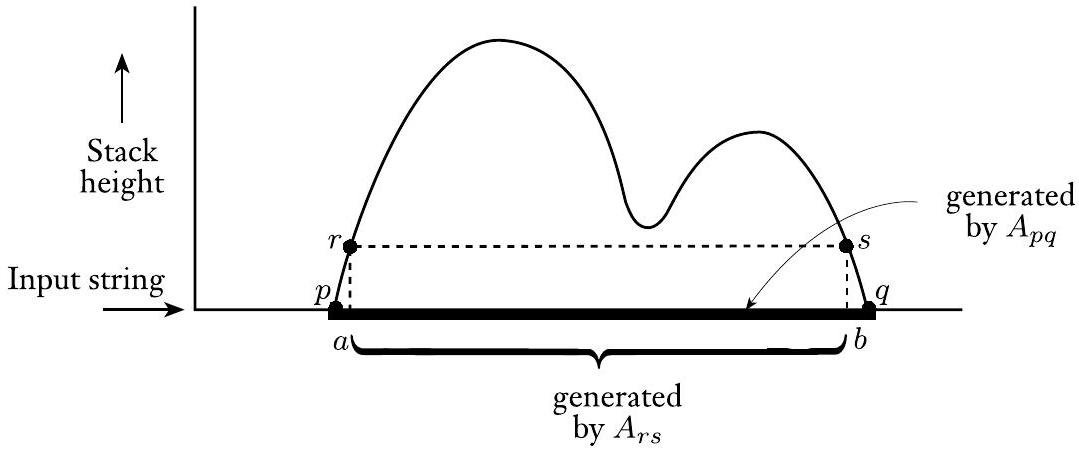
图 2.29
与规则 $A_{p q} \rightarrow a A_{r s} b$ 对应的 PDA 计算
现在我们通过证明 $A_{p q}$ 生成 $x$ 当且仅当 $x$ 可以将 $P$ 从 $p$(空栈)带到 $q$(空栈)来证明此构造有效。我们将“当且仅当”的每个方向视为一个单独的断言。
断言 2.30
如果 $A_{p q}$ 生成 $x$,那么 $x$ 可以将 $P$ 从 $p$(空栈)带到 $q$(空栈)。
我们通过对 $x$ 从 $A_{p q}$ 推导的步骤数进行归纳来证明此断言。
基础:推导有 1 步。
只有一步的推导必须使用右侧不包含变量的规则。在 $G$ 中,右侧不出现变量的唯一规则是 $A_{p p} \rightarrow \varepsilon$。显然,输入 $\varepsilon$ 将 $P$ 从 $p$(空栈)带到 $p$(空栈),因此基础得证。
归纳步骤:假设对于长度至多为 $k$ 的推导(其中 $k \geq 1$)成立,并证明对于长度为 $k+1$ 的推导成立。
假设 $A_{p q} \stackrel{*}{\Rightarrow} x$ 有 $k+1$ 步。此推导的第一步要么是 $A_{p q} \Rightarrow a A_{r s} b$,要么是 $A_{p q} \Rightarrow A_{p r} A_{r q}$。我们分别处理这两种情况。
在第一种情况下,考虑 $x$ 中由 $A_{r s}$ 生成的部分 $y$,因此 $x=a y b$。因为 $A_{r s} \xrightarrow{*} y$ 有 $k$ 步,归纳假设告诉我们 $P$ 可以从 $r$(空栈)到 $s$(空栈)。因为 $A_{p q} \rightarrow a A_{r s} b$ 是 $G$ 的一条规则,$\delta(p, a, \boldsymbol{\varepsilon})$ 包含 $(r, u)$ 并且 $\delta(s, b, u)$ 包含 $(q, \boldsymbol{\varepsilon})$,对于某些栈符号 $u$。因此,如果 $P$ 从 $p$(空栈)开始,读取 $a$ 后可以进入状态 $r$ 并将 $u$ 压栈。然后读取字符串 $y$ 可以将其带到 $s$ 并将 $u$ 保留在栈上。然后读取 $b$ 后可以进入状态 $q$ 并从栈中弹栈 $u$。因此,$x$ 可以将其从 $p$(空栈)带到 $q$(空栈)。
在第二种情况下,考虑 $x$ 中由 $A_{p r}$ 和 $A_{r q}$ 分别生成的部分 $y$ 和 $z$,因此 $x=y z$。因为 $A_{p r} \stackrel{*}{\Rightarrow} y$ 在至多 $k$ 步内,并且 $A_{r q} \stackrel{*}{\Rightarrow} z$ 在至多 $k$ 步内,归纳假设告诉我们 $y$ 可以将 $P$ 从 $p$ 带到 $r$,并且 $z$ 可以将 $P$ 从 $r$ 带到 $q$,并在开始和结束时清空栈。因此 $x$ 可以将其从 $p$(空栈)带到 $q$(空栈)。这完成了归纳步骤。
断言 2.31
如果 $x$ 可以将 $P$ 从 $p$(空栈)带到 $q$(空栈),那么 $A_{p q}$ 生成 $x$。
我们通过对 $P$ 从 $p$ 到 $q$ 的计算步骤数进行归纳来证明此断言,在输入 $x$ 上栈为空。
基础:计算有 0 步。
如果计算有 0 步,它在同一状态开始和结束——比如 $p$。所以我们必须证明 $A_{p p} \xrightarrow{*} x$。在 0 步内,$P$ 无法读取任何字符,所以 $x=\varepsilon$。根据构造,$G$ 有规则 $A_{p p} \rightarrow \varepsilon$,因此基础得证。
归纳步骤:假设对于长度至多为 $k$ 的计算(其中 $k \geq 0$)成立,并证明对于长度为 $k+1$ 的计算成立。
假设 $P$ 有一个计算,其中 $x$ 在 $k+1$ 步内将 $p$ 带到 $q$(空栈)。要么栈仅在此计算的开始和结束时为空,要么在其他地方也变空。
在第一种情况下,第一个动作中压栈的符号必须与最后一个动作中弹栈的符号相同。称此符号为 $u$。设 $a$ 为第一个动作中读取的输入,$b$ 为最后一个动作中读取的输入,$r$ 为第一个动作后的状态,$s$ 为最后一个动作前的状态。则 $\delta(p, a, \varepsilon)$ 包含 $(r, u)$ 并且 $\delta(s, b, u)$ 包含 $(q, \varepsilon)$,因此规则 $A_{p q} \rightarrow a A_{r s} b$ 在 $G$ 中。
设 $y$ 是 $x$ 中不包含 $a$ 和 $b$ 的部分,所以 $x=a y b$。输入 $y$ 可以将 $P$ 从 $r$ 带到 $s$,而不会触及栈上的符号 $u$,因此 $P$ 可以在输入 $y$ 上从 $r$(空栈)到 $s$(空栈)。我们已经移除了 $x$ 上的原始计算中 $k+1$ 步的第一步和最后一步,因此 $y$ 上的计算有 $(k+1)-2=k-1$ 步。因此,归纳假设告诉我们 $A_{r s} \xrightarrow{*} y$。因此 $A_{p q} \xrightarrow{*} x$。
在第二种情况下,设 $r$ 是栈变空的状态,而不是在对 $x$ 的计算的开始或结束时。则从 $p$ 到 $r$ 以及从 $r$ 到 $q$ 的计算部分各自包含至多 $k$ 步。设 $y$ 是第一部分计算期间读取的输入,$z$ 是第二部分计算期间读取的输入。归纳假设告诉我们 $A_{p r} \stackrel{*}{\Rightarrow} y$ 和 $A_{r q} \stackrel{*}{\Rightarrow} z$。因为规则 $A_{p q} \rightarrow A_{p r} A_{r q}$ 在 $G$ 中,$A_{p q} \stackrel{*}{\Rightarrow} x$,证明完成。
这完成了引理 2.27 和定理 2.20 的证明。
我们刚刚证明了下推自动机识别上下文无关语言的类。这个证明使我们能够建立正则语言和上下文无关语言之间的关系。因为每个正则语言都由一个有限自动机识别,并且每个有限自动机都是一个简单地忽略其栈的下推自动机,所以我们现在知道每个正则语言也是一个上下文无关语言。
推论 2.32
每个正则语言都是上下文无关语言。
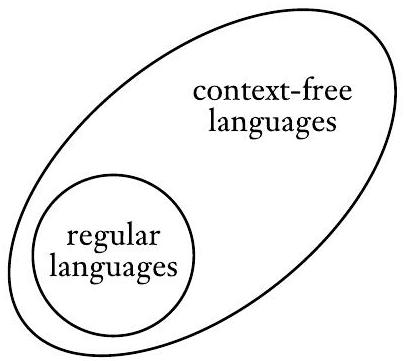
图 2.33
正则语言和上下文无关语言的关系