📝 我的笔记

还没有笔记

选中页面文字后点击「高亮」按钮添加

3_丘奇-图灵论题3.1.ZH

📜 原文
📖 逐步解释
∑ 公式拆解
💡 数值示例
⚠️ 易错点
📝 总结
🎯 存在目的
🧠 直觉心智模型
💭 直观想象

1\section*{3}
.

丘奇-图灵论题

到目前为止，在我们计算理论的发展中，我们已经提出了几种计算设备模型。有限自动机是具有少量内存的设备的良好模型。下推自动机是具有无限内存但只能以栈的后进先出方式使用的设备的良好模型。我们已经证明，一些非常简单的任务超出了这些模型的能力。因此，它们过于受限，无法作为通用计算机的模型。

3.1

图灵机

现在我们转向一个更强大的模型，它由艾伦·图灵于1936年首次提出，称为图灵机。与有限自动机类似，但具有无限且不受限制的内存，图灵机是通用计算机的更精确模型。图灵机可以做所有真实计算机能做的事情。尽管如此，即使是图灵机也无法解决某些问题。从非常真实的意义上讲，这些问题超出了计算的理论极限。

图灵机模型使用无限磁带作为其无限内存。它有一个磁头，可以读取和写入符号并在磁带上移动。

最初，磁带只包含输入字符串，其他地方都是空白。如果机器需要存储信息，它可以在磁带上写入这些信息。为了读取它所写入的信息，机器可以将其磁头移回它上面。机器持续计算，直到它决定产生一个输出。通过进入指定的接受状态和拒绝状态来获得接受和拒绝输出。如果它不进入接受状态或拒绝状态，它将永远运行，永不停止。

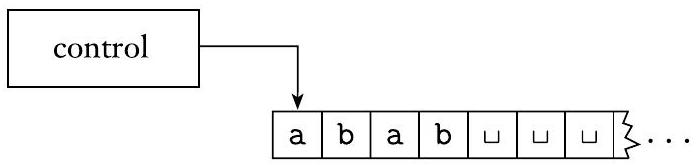
图 3.1

图灵机示意图

以下列表总结了有限自动机和图灵机之间的区别。

  1. 图灵机既可以在磁带上写入，也可以从磁带上读取。
  2. 读写头可以向左和向右移动。
  3. 磁带是无限的。
  4. 拒绝和接受的特殊状态立即生效。

让我们介绍一个图灵机 $M_{1}$，用于测试语言 $B=\left\{w \# w \mid w \in\{0,1\}^{*}\right\}$ 的成员资格。我们希望 $M_{1}$ 在其输入是 $B$ 的成员时接受，否则拒绝。为了更好地理解 $M_{1}$，想象一下你置身其中，站在由数百万个字符组成的一英里长的输入上。你的目标是确定输入是否是 $B$ 的成员——也就是说，输入是否包含两个由 # 符号分隔的相同字符串。输入太长，你无法记住所有内容，但允许你在输入上前后移动并做标记。显而易见的策略是之字形地移动到 # 两侧的对应位置，并确定它们是否匹配。在磁带上做标记以跟踪哪些位置对应。

我们设计 $M_{1}$ 以这种方式工作。它用读写头在输入字符串上进行多次遍历。每次遍历都会匹配 # 符号两侧的一个字符。为了跟踪已经检查过的符号，$M_{1}$ 会在检查完每个符号后将其划掉。如果它划掉了所有符号，这意味着所有内容都成功匹配，并且 $M_{1}$ 进入接受状态。如果它发现不匹配，它会进入拒绝状态。总而言之，$M_{1}$ 的算法如下。

$M_{1}=$ “在输入字符串 $w$ 上：

  1. 之字形地遍历磁带，在 # 符号两侧的对应位置之间检查这些位置是否包含相同的符号。如果不包含，或者没有找到 #，则拒绝。在检查完符号后将其划掉，以跟踪哪些符号对应。
  2. 当 # 左侧的所有符号都被划掉时，检查 # 右侧是否还有剩余符号。如果还有剩余符号，则拒绝；否则，接受。”

下图包含 $M_{1}$ 在输入 011000#011000 上启动后磁带的几个不连续的快照。

图 3.2

图灵机 $M_{1}$ 在输入 011000#011000 上计算的快照

对图灵机 $M_{1}$ 的这种描述草图式地说明了它的功能，但并未提供所有细节。我们可以通过提供类似于为有限自动机和下推自动机引入的形式化描述来详细描述图灵机。形式化描述指定了图灵机模型形式化定义的每个部分，该模型即将呈现。实际上，我们几乎从不提供图灵机的形式化描述，因为它们往往非常庞大。

图灵机的形式化定义

图灵机定义的核心是转移函数 $\delta$，因为它告诉我们机器如何从一个步骤到下一个步骤。对于图灵机，$\delta$ 采取以下形式：$Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}$。也就是说，当机器处于某个状态 $q$ 并且磁头位于包含符号 $a$ 的磁带方格上时，如果 $\delta(q, a)=(r, b, \mathrm{~L})$，机器会写入符号 $b$ 替换 $a$，并进入状态 $r$。第三个分量是 L 或 R，表示写入后磁头是向左还是向右移动。在这种情况下，L 表示向左移动。

定义 3.3

图灵机是一个 7 元组 $\left(Q, \Sigma, \Gamma, \delta, q_{0}, q_{\text {accept }}, q_{\text {reject }}\right)$，其中 $Q, \Sigma, \Gamma$ 都是有限集，并且

  1. $Q$ 是状态集，
  2. $\Sigma$ 是不包含空白符号 $\sqcup$ 的输入字母表，
  3. $\Gamma$ 是磁带字母表，其中 $\sqcup \in \Gamma$ 且 $\Sigma \subseteq \Gamma$，
  4. $\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}$ 是转移函数，
  5. $q_{0} \in Q$ 是起始状态，
  6. $q_{\text {accept }} \in Q$ 是接受状态，
  7. $q_{\text {reject }} \in Q$ 是拒绝状态，其中 $q_{\text {reject }} \neq q_{\text {accept }}$。

图灵机 $M=\left(Q, \Sigma, \Gamma, \delta, q_{0}, q_{\text {accept }}, q_{\text {reject }}\right)$ 的计算方式如下。最初，$M$ 接收其输入 $w=w_{1} w_{2} \ldots w_{n} \in \Sigma^{*}$ 在磁带最左侧的 $n$ 个方格上，磁带的其余部分是空白的（即，填充了空白符号）。磁头从磁带最左侧的方格开始。请注意，$\Sigma$ 不包含空白符号，因此磁带上出现的第一个空白标志着输入的结束。一旦 $M$ 启动，计算根据转移函数描述的规则进行。如果 $M$ 试图将其磁头向左移出磁带的左端，则即使转移函数指示 L，磁头也会在该次移动中停留在原位。计算继续进行，直到它进入接受状态或拒绝状态，此时它停止。如果两者都没有发生，$M$ 将永远运行。

当图灵机计算时，当前状态、当前磁带内容和当前磁头位置都会发生变化。这三个项目的一种设置称为图灵机的格局。格局通常以特殊的方式表示。对于状态 $q$ 和磁带字母表 $\Gamma$ 上的两个字符串 $u$ 和 $v$，我们用 $u q v$ 表示当前状态为 $q$，当前磁带内容为 $u v$，并且当前磁头位置在 $v$ 的第一个符号上的格局。磁带在 $v$ 的最后一个符号之后只包含空白。例如，$1011 q_{7} 01111$ 表示磁带为 101101111，当前状态为 $q_{7}$，并且磁头当前位于第二个 0 上的格局。图 3.4 描绘了一个具有该格局的图灵机。

图 3.4

具有格局 $1011 q_{7} 01111$ 的图灵机

在这里，我们形式化了我们对图灵机计算方式的直观理解。如果图灵机可以在一步内合法地从格局 $C_{1}$ 转移到格局 $C_{2}$，则称格局 $C_{1}$ 产生格局 $C_{2}$。我们通过以下方式正式定义这个概念。

假设我们有 $\Gamma$ 中的 $a, b$ 和 $c$，以及 $\Gamma^{*}$ 中的 $u$ 和 $v$，以及状态 $q_{i}$ 和 $q_{j}$。在这种情况下，$u a q_{i} b v$ 和 $u q_{j} a c v$ 是两个格局。如果转移函数 $\delta\left(q_{i}, b\right)=\left(q_{j}, c, \mathrm{~L}\right)$，则称

$$ u a q_{i} b v \quad \text { 产生 } \quad u q_{j} a c v $$

这处理了图灵机向左移动的情况。对于向右移动，如果 $\delta\left(q_{i}, b\right)=\left(q_{j}, c, \mathrm{R}\right)$，则称

$$ u a q_{i} b v \quad \text { 产生 } \quad u a c q_{j} v $$

当磁头位于格局的某一端时，会出现特殊情况。对于左端，格局 $q_{i} b v$ 产生 $q_{j} c v$ 如果转移是向左移动的（因为我们阻止机器移出磁带的左端），并且它产生 $c q_{j} v$ 对于向右移动的转移。对于右端，格局 $u a q_{i}$ 等同于 $u a q_{i} \sqcup$，因为我们假设空白跟在格局中表示的磁带部分后面。因此，我们可以像以前一样处理这种情况，磁头不再位于右端。

$M$ 在输入 $w$ 上的起始格局是格局 $q_{0} w$，表示机器处于起始状态 $q_{0}$，其磁头位于磁带最左侧的位置。在接受格局中，格局的状态是 $q_{\text {accept }}$。在拒绝格局中，格局的状态是 $q_{\text {reject }}$。接受格局和拒绝格局是停机格局，不再产生进一步的格局。因为机器被定义为在 $q_{\text {accept }}$ 和 $q_{\text {reject }}$ 状态时停机，所以我们也可以等效地将转移函数定义为更复杂的形式 $\delta: Q^{\prime} \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}$，其中 $Q^{\prime}$ 是 $Q$ 不包含 $q_{\text {accept }}$ 和 $q_{\text {reject }}$。如果存在一系列格局 $C_{1}, C_{2}, \ldots, C_{k}$，则图灵机 $M$ 接受输入 $w$，其中

  1. $C_{1}$ 是 $M$ 在输入 $w$ 上的起始格局，
  2. 每个 $C_{i}$ 产生 $C_{i+1}$，并且
  3. $C_{k}$ 是一个接受格局。

$M$ 接受的字符串集合是语言 $M$，或由 $M$ 识别的语言，表示为 $L(M)$。

定义 3.5
如果某个图灵机识别一种语言，则称该语言是图灵可识别的。 ${ }^{1}$

当我们启动图灵机处理输入时，可能会出现三种结果。机器可能接受、拒绝或循环。循环是指机器根本不停止。循环可能涉及任何简单或复杂的行为，但永不导致停机状态。

图灵机 $M$ 可能通过进入 $q_{\text {reject }}$ 状态并拒绝，或者通过循环来拒绝接受输入。有时很难区分一个正在循环的机器和一个仅仅运行了很长时间的机器。因此，我们更喜欢在所有输入上都停止的图灵机；此类机器永不循环。这些机器称为判决机，因为它们总是做出接受或拒绝的决定。识别某种语言的判决机也被称为判决该语言。

定义 3.6

如果某个图灵机能判定一种语言，则称该语言是图灵可判定的，或简称为可判定的。 ${ }^{2}$

接下来，我们给出可判定语言的例子。每种可判定语言都是图灵可识别的。我们将在第 4 章开发一种证明不可判定性的技术后，提供图灵可识别但不可判定的语言的例子。

图灵机示例

就像我们对有限自动机和下推自动机所做的那样，我们可以通过指定其七个部分来形式化描述一个特定的图灵机。然而，除了微小的图灵机之外，达到这种详细程度可能会很麻烦。因此，我们不会花太多时间提供此类描述。我们主要

[^0]只提供更高级别的描述，因为它们对我们的目的来说足够精确，并且更容易理解。然而，重要的是要记住，每个更高级别的描述实际上都只是其形式化对应物的简写。只要有耐心和细心，我们就可以详细地形式化描述本书中的任何图灵机。

为了帮助您理解形式化描述和高级描述之间的联系，我们在接下来的两个示例中给出状态图。如果您已经对这种联系感到满意，可以跳过它们。

示例 3.7

在这里，我们描述一个图灵机 (TM) $M_{2}$，它判定语言 $A=\left\{0^{2^{n}} \mid n \geq 0\right\}$，该语言由所有长度为 2 的幂的 0 字符串组成。

$M_{2}=$ “在输入字符串 $w$ 上：

  1. 从左到右遍历磁带，划掉每隔一个 0。
  2. 如果在阶段 1 中磁带包含一个 0，则接受。
  3. 如果在阶段 1 中磁带包含多于一个 0 且 0 的数量是奇数，则拒绝。
  4. 将磁头返回到磁带的左端。
  5. 转到阶段 1。”

阶段 1 的每次迭代都会将 0 的数量减半。当机器在阶段 1 中遍历磁带时，它会跟踪所看到的 0 的数量是偶数还是奇数。如果该数量是奇数且大于 1，则输入中原始的 0 的数量不可能是 2 的幂。因此，机器在这种情况下拒绝。但是，如果所看到的 0 的数量是 1，则原始数量一定是 2 的幂。因此，在这种情况下，机器接受。

现在我们给出 $M_{2}=\left(Q, \Sigma, \Gamma, \delta, q_{1}, q_{\text {accept }}, q_{\text {reject }}\right)$ 的形式化描述：

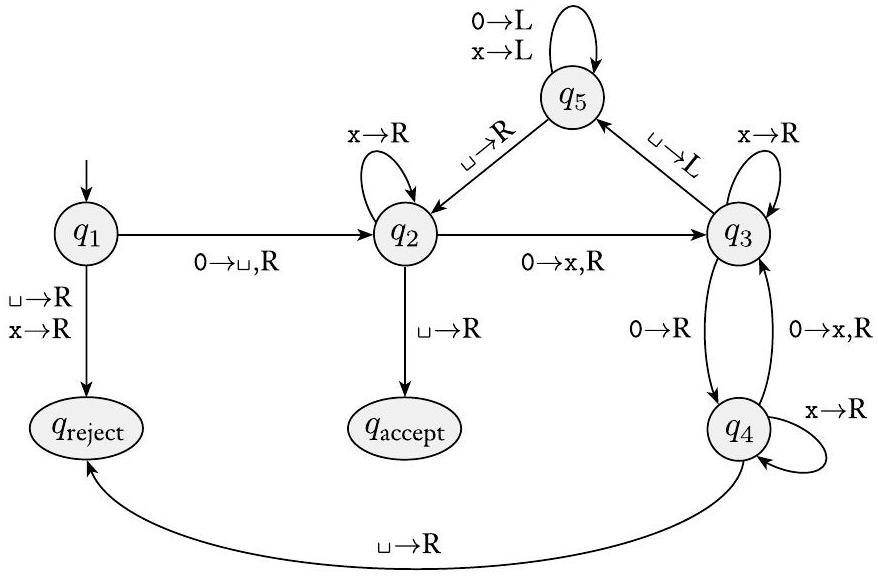
图 3.8

图灵机 $M_{2}$ 的状态图

在此状态图中，标签 $0 \rightarrow \sqcup, \mathrm{R}$ 出现在从 $q_{1}$ 到 $q_{2}$ 的转移上。此标签表示当处于状态 $q_{1}$ 且磁头读取 0 时，机器进入状态 $q_{2}$，写入 $\sqcup$，并将磁头向右移动。换句话说，$\delta\left(q_{1}, 0\right)=\left(q_{2}, \sqcup, \mathrm{R}\right)$。为清晰起见，我们在从 $q_{3}$ 到 $q_{4}$ 的转移中使用了简写 $0 \rightarrow \mathrm{R}$，表示机器在状态 $q_{3}$ 读取 0 时向右移动但不改变磁带，因此 $\delta\left(q_{3}, 0\right)=\left(q_{4}, 0, \mathrm{R}\right)$。

这台机器首先在磁带上最左边的 0 上方写入一个空白符号，以便它可以在阶段 4 中找到磁带的左端。虽然我们通常会使用更具指示性的符号，例如 # 作为左端分隔符，但我们在这里使用空白以保持磁带字母表以及状态图的小巧。示例 3.11 提供了另一种查找磁带左端的方法。

接下来，我们给出这台机器在输入 0000 上的一个示例运行。起始格局是 $q_{1} 0000$。机器进入的格局序列如下所示；按列向下和从左到右阅读。

| $q_{1} 0000$ | $\sqcup q_{5} \times 0 \times \sqcup$ | $\left\llcorner\mathrm{x} q_{5} \mathrm{xx} \sqcup\right.$ |

| :--- | :--- | :--- |

| $\pm q_{2} 000$ | $q_{5} \sqcup \mathrm{x} 0 \mathrm{x} \sqcup$ | $\sqcup q_{5} \mathrm{xxx} \sqcup$ |

| பx $q_{3} 00$ | $\sqcup q_{2} \times 0 \times \sqcup$ | $q_{5} \sqcup \mathrm{xxx} \sqcup$ |

| $\sqcup \times 0 q_{4} 0$ | $\left\llcorner\mathrm{x} q_{2} 0 \mathrm{x} \sqcup\right.$ | $\sqcup q_{2} \mathrm{xxx} \sqcup$ |

| $\sqcup \times 0 \times q_{3} \sqcup$ | $\sqcup \mathrm{xx} q_{3} \mathrm{x} \sqcup$ | $\sqcup \mathrm{x} q_{2} \mathrm{xx} \sqcup$ |

| $\sqcup \times 0 q_{5} \mathrm{x} \sqcup$ | $\sqcup \mathrm{xxx} q_{3} \sqcup$ | $\sqcup \mathrm{xx} q_{2} \mathrm{x} \sqcup$ |

| $\sqcup \mathrm{x} q_{5} 0 \mathrm{x} \sqcup$ | $\sqcup \mathrm{xx} q_{5} \mathrm{x} \sqcup$ | $\sqcup \times \mathrm{xx} q_{2} \sqcup$ |

| | | $\left\llcorner\mathrm{xxx} \sqcup q_{\text {accept }}\right.$ | $\square$

示例 3.9

以下是对 $M_{1}=\left(Q, \Sigma, \Gamma, \delta, q_{1}, q_{\text {accept }}, q_{\text {reject }}\right)$ 的形式化描述，该图灵机是我们非正式描述（第 167 页）的，用于判定语言 $B=\left\{w \# w \mid w \in\{0,1\}^{*}\right\}$。

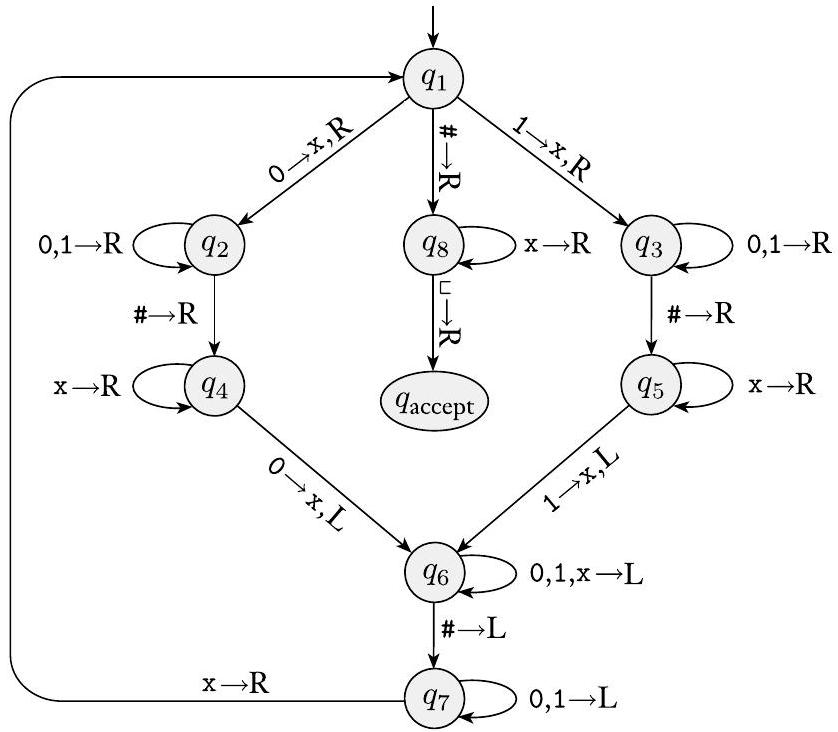
图 3.10

图灵机 $M_{1}$ 的状态图

在图 3.10 描绘了 TM $M_{1}$ 的状态图，您会发现从 $q_{3}$ 到自身的转移上有标签 $0,1 \rightarrow \mathrm{R}$。该标签表示当机器在状态 $q_{3}$ 中读取 0 或 1 时，它会保持在 $q_{3}$ 并向右移动。它不会改变磁带上的符号。

阶段 1 由状态 $q_{1}$ 到 $q_{7}$ 实现，阶段 2 由剩余状态实现。为了简化图，我们没有显示拒绝状态或指向拒绝状态的转移。每当一个状态缺少针对特定符号的出向转移时，这些转移就会隐式发生。因此，因为在状态 $q_{5}$ 中没有带有 # 的出向箭头，如果机器在状态 $q_{5}$ 中时磁头下方出现 #，它就会进入 $q_{\text {reject }}$ 状态。为了完整性，我们说磁头在每个这样的转移到拒绝状态时向右移动。

示例 3.11

在这里，一个 TM $M_{3}$ 正在做一些基本的算术。它判定语言 $C=\left\{\mathrm{a}^{i} \mathrm{~b}^{j} \mathrm{c}^{k} \mid i \times j=k \text{ 且 } i, j, k \geq 1\right\}$。

$M_{3}=$ “在输入字符串 $w$ 上：

  1. 从左到右扫描输入，以确定它是否是 $\mathrm{a}^{+} \mathrm{b}^{+} \mathrm{c}^{+}$ 的成员；如果不是，则拒绝。
  2. 将磁头返回到磁带的左端。
  3. 划掉一个 a 并向右扫描直到出现一个 b。在 b 和 c 之间来回穿梭，划掉一个 b 和一个 c，直到所有的 b 都消失。如果所有的 c 都已被划掉而一些 b 仍留下，则拒绝。
  4. 恢复被划掉的 b，如果有另一个 a 可划掉，则重复阶段 3。如果所有的 a 都已被划掉，则确定所有的 c 是否也已被划掉。如果是，则接受；否则，拒绝。”

让我们更仔细地检查 $M_{3}$ 的四个阶段。在阶段 1 中，机器像有限自动机一样运行。由于磁头从左到右移动，无需写入，它通过使用其状态来跟踪输入是否具有正确的形式。

阶段 2 看起来同样简单，但包含一个微妙之处。TM 如何找到输入磁带的左端？找到输入磁带的右端很容易，因为它以空白符号终止。但左端最初没有终止符。让机器找到磁带左端的一种技术是，当机器启动时磁头位于该符号上，它以某种方式标记最左边的符号。然后机器可以在需要将磁头重置到左端时向左扫描，直到找到该标记。示例 3.7 说明了这种技术；一个空白符号标记左端。

一种更巧妙的查找磁带左端的方法利用了我们定义图灵机模型的方式。回想一下，如果机器试图将其磁头移出磁带的左端，它会停留在原地。我们可以利用此功能来制造一个左端检测器。为了检测磁头是否位于左端，机器可以在当前位置上方写入一个特殊符号，同时在控制器中记录它替换的符号。然后它可以尝试向左移动磁头。如果它仍然位于特殊符号上方，则向左移动未成功，因此磁头一定位于左端。如果它位于不同的符号上方，则该位置左侧的磁带上仍然有一些符号。在继续之前，机器必须确保将更改的符号恢复到原始状态。

阶段 3 和 4 的实现很简单，并且每个阶段都使用几个状态。

示例 3.12

在这里，一个 TM $M_{4}$ 正在解决所谓的元素互异性问题。它给定一个由 # 分隔的 $\{0,1\}$ 上的字符串列表，其任务是当所有字符串都不同时接受。语言是

$$ E=\left\{\# x_{1} \# x_{2} \# \cdots \# x_{l} \mid \text { 每个 } x_{i} \in\{0,1\}^{*} \text{ 且 } x_{i} \neq x_{j} \text{ 对于每个 } i \neq j\right\} 。 $$

机器 $M_{4}$ 通过比较 $x_{1}$ 与 $x_{2}$ 到 $x_{l}$，然后比较 $x_{2}$ 与 $x_{3}$ 到 $x_{l}$，依此类推来工作。下面是非正式描述该语言的 TM $M_{4}$。

$M_{4}=$ “在输入 $w$ 上：

  1. 在最左边的磁带符号上方放置一个标记。如果该符号是空白，则接受。如果该符号是 #，则继续下一阶段。否则，拒绝。
  2. 向右扫描到下一个 # 并在其上方放置第二个标记。如果在遇到空白符号之前没有遇到 #，则只存在 $x_{1}$，因此接受。
  3. 通过之字形移动，比较标记的 # 右侧的两个字符串。如果它们相等，则拒绝。
  4. 将两个标记中最右边的标记移动到右侧的下一个 # 符号。如果在遇到空白符号之前没有遇到 # 符号，则将最左边的标记移动到其右侧的下一个 #，并将最右边的标记移动到其后的 #。这次，如果最右边的标记没有可用的 #，则所有字符串都已比较完毕，因此接受。
  5. 转到阶段 3。”

这台机器说明了标记磁带符号的技术。在阶段 2 中，机器在符号（在本例中为 #）上方放置一个标记。在实际实现中，机器在其磁带字母表中有两个不同的符号：# 和 \#。机器在 # 上方放置标记意味着机器在该位置写入符号 \#。移除标记意味着机器写入没有点的符号。通常，我们可能希望在磁带上的各种符号上方放置标记。为此，我们只需在磁带字母表中包含所有这些符号的带有点的版本。

我们从前面的例子中得出结论，所描述的语言 $A, B, C$ 和 $E$ 是可判定的。所有可判定语言都是图灵可识别的，因此这些语言也是图灵可识别的。证明一种语言是图灵可识别但不可判定则更为困难。我们将在第 4 章中进行。