📝 我的笔记

还没有笔记

选中页面文字后点击「高亮」按钮添加

3_丘奇-图灵论题3.2.ZH解释

📜 原文
📖 逐步解释
∑ 公式拆解
💡 数值示例
⚠️ 易错点
📝 总结
🎯 存在目的
🧠 直觉心智模型
💭 直观想象

11. 图灵机的变体

1.1 图灵机的变体介绍

📜 [原文1]

图灵机的替代定义比比皆是，包括带有多条磁带或带有非确定性的版本。它们被称为图灵机模型的变体。原始模型及其合理的变体都具有相同的能力——它们识别相同类的语言。在本节中，我们将描述其中一些变体以及它们在能力上等价的证明。我们将这种对定义中某些改变的不变性称为鲁棒性。有限自动机和下推自动机都是具有一定鲁棒性的模型，但图灵机具有惊人的鲁棒性。

📖 [逐步解释]

这段引言的核心思想是，图灵机这个计算模型不是一成不变的，我们可以对它的定义进行各种修改，但神奇的是，这些修改（在合理范围内）并不会增强或削弱它的计算能力。

  1. 替代定义比比皆是：想象一下，我们定义的图灵机是一辆“标准版”的汽车。现在，我们可以给这辆车增加各种“配件”，比如增加更多的轮子（多条磁带），或者让它在每个路口都有分身去探索所有可能的路径（非确定性）。这些带有新配件的汽车就是图灵机的“变体”。
  2. 相同的能力：尽管这些变体看起来更高级、更强大，但它们能到达的目的地（能识别的语言集合）和那辆“标准版”汽车是完全一样的。一个变体能解决的问题，标准版图灵机也能解决（可能慢一些），反之亦然。这种“能力相同”在计算理论中被称为“等价”。
  3. 不变性与鲁棒性：当一个模型的定义在发生改变后，其核心能力（比如能识别的语言类别）却保持不变，我们就说这个模型是“鲁棒的”（Robust）。“鲁棒性”这个词在工程和科学中很常见，意思就是“坚固”、“稳定”、“抗干扰能力强”。图灵机的鲁棒性非常惊人，意味着它的计算能力等级非常稳固，不容易因为一些定义的微调而改变。
  4. 与其他模型对比：
    • 有限自动机 (FA)：它也有一定的鲁棒性。例如，一个非确定性有限自动机（NFA）和一个确定性有限自动机（DFA）在计算能力上是等价的。
    • 下推自动机 (PDA)：它的鲁棒性就差一些。一个非确定性下推自动机比一个确定性下推自动机要强大，前者能识别所有的上下文无关语言，而后者只能识别确定性上下文无关语言这个子集。
    • 图灵机 (TM)：它的鲁棒性是“惊人的”。无论是多磁带、非确定性，还是我们后面会看到的其他各种变体，都无法超越标准图灵机的能力范围。这暗示了图灵机可能已经触及了“可计算”这个概念的本质边界。
💡 [数值示例]

这个部分是概念介绍，不涉及具体计算，我们用类比来举例：

  • 模型：交通工具
  • 能力：能到达的所有地点集合
  • 标准图灵机：一辆自行车。
  • 多带图灵机 (变体1)：一辆可以同时在几条平行小路上行驶的改装自行车。看起来效率高，但任何它能去的地方，普通自行车多花点时间来回骑几次也能到。
  • 非确定性图灵机 (变体2)：一辆在每个路口都能分身的魔法自行车。它能同时探索所有岔路。但一个普通骑手（确定性模拟）可以通过制定一个“路口编号探索计划”（比如先探索所有路口的第一个岔路，再回来探索所有路口的第二个岔路），确保最终也能找到魔法自行车能找到的任何地方。
  • 下推自动机：一辆只能在有特殊“下坡”标记的路上行驶的滑板车。给它加上“魔法分身”能力（非确定性），它就能去一些以前去不了的地方（因为有些决策需要预知未来，分身相当于试探）。这说明它的鲁棒性不强。
⚠️ [易错点]
  1. 误区：认为“变体”一定更强大。变体通常在“效率”上可能更高，或者“描述问题”时更方便，但在“计算能力”（能解决什么问题，不能解决什么问题）的层面上，它们与标准图灵机是等价的。不要混淆“效率”和“能力”。
  2. 边界：什么是不“合理”的变体？如果我们给图灵机增加一个“神谕”（Oracle），这个神谕可以直接告诉我们某个无法解决的问题（如停机问题）的答案，那么这个变体就超越了图灵机的能力。这种变体就不属于我们这里讨论的“等价”范畴了，它是一个更强大的模型。本节讨论的都是不引入“超自然”外部力量的内部结构性修改。
📝 [总结]

本段的核心是引入图灵机的“鲁棒性”概念。它告诉我们，图灵机的定义不是脆弱的，我们可以对其进行多种修改（如增加磁带、引入非确定性），但这些变体在计算能力上都与最基础的单带确定性图灵机等价。这为图灵机作为计算的通用模型奠定了坚实的基础。

🎯 [存在目的]

本段的目的是建立一个重要的认知：图灵机所定义的“可计算性”是一个非常稳定和普适的概念。在后续章节（尤其是丘奇-图灵论题）中，我们会论证任何我们直觉中“能被算法解决”的问题，都能被图灵机解决。本段通过展示图灵机模型自身的稳定性，为这个更宏大的论题提供了第一个有力的证据。

🧠 [直觉心智模型]

想象一个瑞士军刀。基础版可能只有一把主刀（标准图灵机）。你可以给它增加剪刀、螺丝刀、开瓶器等各种工具（变体）。这些新工具让它在处理特定任务时更方便快捷（效率提升），但它能做的所有事情（切割、拧螺丝等），你最终都可以只用那把主刀，通过更复杂的技巧和更多的时间来完成。这把军刀的“核心能力”并没有因为增加了工具而发生本质的飞跃。图灵机的鲁棒性也是如此。

💭 [直观想象]

你有一个非常聪明的机器人，它在一个无限长的仓库里工作，仓库地面上画着格子（磁带）。它的标准工作模式是：看一眼当前格子的货物，根据自己的程序手册，换掉这个货物，然后向左或向右移动一格。

现在你对它进行升级：

  1. 多带变体：你给它开了几个平行的无限仓库，让它同时在几个仓库里操作。
  2. 非确定性变体：你给它的程序手册在某些指令下写着“你可以选择做法A，也可以选择做法B”。

本节的结论是：无论你怎么升级，只要这个机器人能完成一项复杂的搬运任务，那个最原始的、只有一个仓库、每步都严格按指令执行的机器人，也能完成同样的任务，只是可能需要在一个仓库里来回跑动，用更复杂的步骤来模拟多仓库操作或模拟所有选择。

1.2 "停留"能力的等价性证明

📜 [原文2]

为了说明图灵机模型的鲁棒性，我们来改变允许的转移函数类型。在我们的定义中，转移函数强制磁头在每一步之后向左或向右移动；磁头不能仅仅停留在原地。假设我们允许图灵机具有停留在原地的能力。那么转移函数的形式将是 $\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$。这个特性是否会使图灵机能够识别额外的语言，从而增加模型的威力呢？当然不会，因为我们可以将任何具有“停留在原地”功能的图灵机转换为没有该功能的图灵机。我们通过将每个“停留在原地”的转移替换为两个转移来实现：一个向右移动，第二个再向左移动。

这个小例子包含了证明图灵机变体等价性的关键。要证明两个模型是等价的，我们只需要证明一个可以模拟另一个。

📖 [逐步解释]

这部分通过一个最简单的例子，展示了如何证明一个变体与标准模型是等价的。这个技术被称为“模拟”（Simulation）。

  1. 提出变体：标准的图灵机，磁头在每个步骤后必须移动（L或R）。现在我们提出一个变体，允许磁头“停留在原地”（S，Stay put）。
  2. 分析变体的转移函数：这个变体的转移函数的输出就多了一个选项。标准的是 $\{\mathrm{L}, \mathrm{R}\}$，现在是 $\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$。
    • 原函数：$\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}$
    • 新函数：$\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$
  3. 提出问题：这个新增的S选项，会不会让图灵机变得更强大？
  4. 给出否定回答和证明思路：答案是“不会”。证明方法是“模拟”：我们可以用一台没有S移动的标准图灵机，来完整地模仿一台有S移动的变体图灵机的行为。
  5. 模拟的具体实现：
    • 对于变体图灵机中所有L和R的转移，标准图リング机直接照搬。
    • 对于变体图灵机中任何一个S的转移，比如 (q, a) -> (q', b, S)，意思是“在q状态读到a，就转换到q'状态，把a改成b，然后磁头不动”。
    • 标准图灵机要模拟这个“不动”，可以用两步操作来代替：
  6. 第一步：向右移动。例如，定义一个新状态q'_R，增加一条转移 (q, a) -> (q'_R, b, R)。这样，状态变成了q'_R，格子内容写好了b，磁头向右移动了一格。
  7. 第二步：再向左移动。对于这个新状态q'_R，无论它右边读到什么符号（比如c），都立即无条件地向左移动，并进入最终的目标状态q'。即 (q'_R, c) -> (q', c, L) 对所有可能的c都成立。
    • 最终效果：经过“先右再左”这两步，磁头回到了原来的位置，格子内容也变成了b，状态变成了q'。这就完美地模拟了S移动的效果。
  8. 总结证明思想：这个小例子揭示了证明两个计算模型等价的通用方法：双向模拟。要证明模型A和模型B等价，需要：
    • 证明A可以模拟B（说明B的能力不超过A）。
    • 证明B可以模拟A（说明A的能力不超过B）。
    • 在这个例子中，由于标准图灵机本身就是“停留”变体的一种特殊情况（只是从未使用S移动），所以B模拟A是天然成立的。我们只需要证明A可以模拟B即可。
∑ [公式拆解]
  • 公式：$\delta: Q \times \Gamma \longrightarrow Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$
  • $\delta$ (delta)：这是转移函数的名字。
  • $Q$：所有可能状态的有限集合。
  • $\Gamma$ (Gamma)：磁带字母表，包含所有可以在磁带上读写的符号。
  • $Q \times \Gamma$：这是函数的输入，一个序对 (状态, 磁带符号)，代表了图灵机当前所处的局面。
  • $\longrightarrow$：表示映射关系，将输入映射到输出。
  • $Q \times \Gamma \times \{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$：这是函数的输出，一个三元组 (新状态, 要写入的符号, 磁头移动方向)。
  • $\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$：磁头移动方向的集合，L代表左移 (Left)，R代表右移 (Right)，S代表停留 (Stay)。
💡 [数值示例]

假设一台带S移动的变体图灵机 $M_S$ 有一条转移规则：

  • 规则：当处于状态 $q_1$，读到符号 0 时，它应该进入状态 $q_2$，将 0 改写为 1，并且磁头停留在原地。形式化为：$\delta_S(q_1, 0) = (q_2, 1, S)$。

现在我们构建一台标准图灵机 $M_{std}$ 来模拟这个行为。

  1. $M_{std}$ 没有 $q_2$ 状态，但我们会引入一个临时的中间状态，叫 $q_{1 \to 2, \text{move R}}$。
  2. $M_{std}$ 的转移函数 $\delta_{std}$ 包含以下两条规则来模拟 $M_S$ 的那一条规则：
    • 第一步 (写和右移)：$\delta_{std}(q_1, 0) = (q_{1 \to 2, \text{move R}}, 1, R)$
    • 解释：当 $M_{std}$ 处于 $q_1$ 并读到 0，它会先把 0 改成 1，然后进入临时状态 $q_{1 \to 2, \text{move R}}$，并把磁头向右移动一格。
    • 第二步 (左移回原位)：对于磁带上的任何一个可能的符号 $x \in \Gamma$ (例如 $x$ 可以是 0, 1, sqcup 等)，我们都添加一条规则：
    • 解释：一旦进入了临时状态 $q_{1 \to 2, \text{move R}}$，无论它右边读到什么符号 x，它都会立即进入最终的目标状态 $q_2$，保持符号 x 不变，并把磁头向左移动一格。
  3. 结果：执行完这两步后，$M_{std}$ 的磁带内容、磁头位置和当前状态，与 $M_S$ 执行完一步S移动后完全相同。我们用两步的代价，模拟了一步“停留”。
⚠️ [易错点]
  1. 临时状态的必要性：必须引入新的临时状态。如果试图重用 $q_1$ 或 $q_2$，会导致逻辑混乱。例如，如果第二步写成 (q1, x) -> (q2, x, L)，这会改变原有 $q_1$ 状态的行为。
  2. 第二步的通用性：模拟“向左返回”的规则必须对磁头上所有可能的符号都有效。因为我们不知道原磁头右边是什么，所以必须保证无论是什么，都能正确地移回来。
  3. 效率损失：模拟是有代价的。原来的一步操作，现在变成了两步。这再次印证了变体可能在效率上占优，但在计算能力上等价。
📝 [总结]

本段用一个简单的“磁头停留”变体作为例子，清晰地展示了“模拟”是证明计算模型等价性的核心技术。通过将变体模型的一个复杂操作分解为标准模型的多个简单操作的组合，我们可以证明标准模型有能力完成变体模型能做的任何事情。

🎯 [存在目的]

本段的目的是为后续更复杂的等价性证明（如多带图灵机和非确定性图灵机）提供一个简单的入门示例和“思想模板”。它让读者熟悉“模拟”这一证明策略，并直观感受到图灵机模型设计的灵活性和鲁棒性。

🧠 [直觉心智模型]

你是一个厨师，你的菜谱（转移函数）上只写了“向前一步”或“向后一步”。现在有人给了你一个新菜谱，上面有些步骤是“原地不动”。你怎么用旧菜谱完成新菜谱的任务？很简单，每当看到“原地不动”这条指令时，你就自己“向前一步，再立刻向后一步”，效果完全一样，只是多动弹了一下。

💭 [直观想象]

想象你在玩一个棋盘游戏，你的棋子每回合必须向左或向右移动一格。现在游戏规则更新，允许棋子“停在原地”一回合。如果你想用旧规则来玩这个新游戏，怎么办？很简单，当轮到你，而你选择“停在原地”时，你可以先把棋子向右移动一格，然后在下一瞬间（作为同一回合的一部分），再把它移回左边那一格。对于旁观者来说，你的棋子最终没有移动位置，你成功地用“一右一左”模拟了“停留”。

22. 多带图灵机

2.1 多带图灵机的定义

📜 [原文3]

一个多带图灵机就像一个普通的图灵机，但有几条磁带。每条磁带都有自己的磁头用于读写。最初，输入出现在磁带 1 上，其他磁带则为空白。转移函数被修改以允许同时在部分或所有磁带上进行读、写和磁头移动。形式上，它是

$$ \delta: Q \times \Gamma^{k} \longrightarrow Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{~S}\}^{k}, $$

其中 $k$ 是磁带的数量。表达式

$$ \delta\left(q_{i}, a_{1}, \ldots, a_{k}\right)=\left(q_{j}, b_{1}, \ldots, b_{k}, \mathrm{~L}, \mathrm{R}, \ldots, \mathrm{~L}\right) $$

表示如果机器处于状态 $q_{i}$ 并且磁头 1 到 $k$ 正在读取符号 $a_{1}$ 到 $a_{k}$，则机器进入状态 $q_{j}$，写入符号 $b_{1}$ 到 $b_{k}$，并根据规定指示每个磁头向左或向右移动，或停留在原地。

多带图灵机似乎比普通图灵机更强大，但我们可以证明它们在能力上是等价的。回想一下，如果两台机器识别相同的语言，则它们是等价的。

📖 [逐步解释]

这部分定义了一种看起来比标准图灵机强大很多的变体：多带图灵机。

  1. 结构：
    • 它不是一条磁带，而是有多条（比如 $k$ 条）无限长的磁带。
    • 每条磁带都配有自己独立的读写磁头。
    • 它仍然只有一个中央状态控制器（一个有限的 $Q$ 集合）。
  2. 初始状态：
    • 和标准图灵机一样，输入字符串 $w$ 被放置在第一条磁带上。
    • 所有其他的磁带（磁带2, 3, ..., k）开始时都是完全空白的。
  3. 转移函数的变化：这是核心区别。
    • 输入：单带图灵机的决策依据是 (当前状态, 当前磁头下的符号)。而多带图灵机的决策依据是 (当前状态, k个磁头下对应的k个符号)。它能同时看到所有磁带上磁头所在位置的信息。
    • 输出：单带图灵机的动作是 (新状态, 要写入的1个符号, 1个磁头的移动)。而多带图灵机的动作是 (新状态, 要写入的k个符号, k个磁头的独立移动)。它能在一个步骤里，同时在所有磁带上进行读写和移动操作。
  4. 形式化定义：对转移函数 $\delta$ 的解释。
    • $\delta: Q \times \Gamma^{k} \longrightarrow Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{~S}\}^{k}$
    • $Q \times \Gamma^k$：输入。当前状态，以及来自 $k$ 条磁带的 $k$ 个符号组成的元组。$\Gamma^k$ 表示 $\Gamma$ 的 $k$ 次笛卡尔积，即 $k$ 个符号的有序列表 $(\gamma_1, \gamma_2, \ldots, \gamma_k)$。
    • $Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{~S}\}^{k}$：输出。新状态，要写回 $k$ 条磁带的 $k$ 个新符号，以及 $k$ 个磁头各自的移动方向（L, R, 或 S）。
    • $\delta\left(q_{i}, a_{1}, \ldots, a_{k}\right)=\left(q_{j}, b_{1}, \ldots, b_{k}, \mathrm{~L}, \mathrm{R}, \ldots, \mathrm{~L}\right)$
    • 这是一个具体的例子，说明如果当前状态是 $q_i$，并且第1个磁头读到 $a_1$，第2个磁头读到 $a_2$，...，第 $k$ 个磁头读到 $a_k$，那么机器将：
  5. 状态变为 $q_j$。
  6. 第1个磁头把 $a_1$ 改写成 $b_1$，第2个磁头把 $a_2$ 改写成 $b_2$，...
  7. 第1个磁头左移，第2个磁头右移，...，第 $k$ 个磁头左移。每个磁头的移动是独立的。
  8. 直观感受与核心问题：多带图灵机看起来非常强大。例如，它可以把一条磁带上的内容复制到另一条上，而不需要在一条磁带上长距离来回移动。它还可以用一条磁带存储数据，另一条磁带做草稿计算，这非常像真实计算机的内存和寄存器的工作方式。所以一个很自然的问题是：它是不是真的比单带图灵机更强大（能识别更多语言）？本节的结论是“不”，它们能力等价。
∑ [公式拆解]
  • 公式1: $\delta: Q \times \Gamma^{k} \longrightarrow Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{~S}\}^{k}$
  • $\delta$: 转移函数。
  • $Q$: 状态的有限集合。
  • $\Gamma$: 磁带字母表。
  • $k$: 磁带的数量，是一个正整数。
  • $\Gamma^k$: $k$ 个磁带符号的有序元组 $(s_1, s_2, \ldots, s_k)$，其中每个 $s_i \in \Gamma$。这是 $k$ 个磁头同时读取到的信息。
  • $Q \times \Gamma^k$: 转移函数的输入，一个元组，如 (当前状态, (符号1, 符号2, ..., 符号k))。
  • $\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$: 磁头移动方向集合。
  • $\{\mathrm{L}, \mathrm{R}, \mathrm{S}\}^k$: $k$ 个移动方向的有序元组 $(m_1, m_2, \ldots, m_k)$，其中每个 $m_i \in \{\mathrm{L}, \mathrm{R}, \mathrm{S}\}$。
  • $Q \times \Gamma^k \times \{\mathrm{L}, \mathrm{R}, \mathrm{S}\}^k$: 转移函数的输出，一个元组，如 (新状态, (新符号1, ..., 新符号k), (移动1, ..., 移动k))。
  • 公式2: $\delta\left(q_{i}, a_{1}, \ldots, a_{k}\right)=\left(q_{j}, b_{1}, \ldots, b_{k}, \mathrm{~L}, \mathrm{R}, \ldots, \mathrm{~L}\right)$
  • 这是一个函数应用的实例。
  • 输入是状态 $q_i$ 和 $k$ 个磁头分别读到的符号 $a_1, \ldots, a_k$。
  • 输出是新的状态 $q_j$，$k$ 个要写入的新符号 $b_1, \ldots, b_k$，以及 $k$ 个磁头各自的移动方向。这个例子中给出的移动方向是 (L, R, ..., L)。
💡 [数值示例]

假设我们有一个 $k=2$ 的双带图灵机，它想实现一个功能：将磁带1上的 011 复制到磁带2。初始时磁带1为 011，磁带2为空白。

  • 初始配置：
  • 状态: $q_{start}$
  • 磁带1: ...sqcup |> 0 1 1 scup ... (|>表示起始，|表示磁头位置)
  • 磁带2: ...sqcup |> scup scup scup ...
  • 我们可能需要这样一条转移规则：
  • 规则1: $\delta(q_{start}, 0, \sqcup) = (q_{copy}, 0, 0, R, R)$
  • 解释: 在起始状态 $q_{start}$，如果磁带1读到0，磁带2读到空白sqcup，那么：
  1. 进入“复制”状态 $q_{copy}$。
  2. 磁带1的0保持不变。
  3. 磁带2的sqcup被改写成0。
  4. 两个磁头都向右移动一格。
    • 执行规则1后的配置：
    • 状态: $q_{copy}$
    • 磁带1: ...sqcup > 0 | 1 1 scup ...
    • 磁带2: ...sqcup > 0 | scup scup ...
    • 接下来可能需要另一条规则：
    • 规则2: $\delta(q_{copy}, 1, \sqcup) = (q_{copy}, 1, 1, R, R)$
    • 执行规则2两次后，最终磁带2上就会有011。这个过程比单带图灵机高效得多，后者需要来回移动很长的距离来搬运信息。
⚠️ [易错点]
  1. 混淆磁头：要记住每个磁头是独立的，它们的移动也是独立的。一个向左，一个向右是完全允许的。
  2. 忘记初始条件：除了磁带1有输入外，其余所有磁带必须是空白的。这是标准定义的一部分。
  3. 错误的强大感：虽然它看起来很方便、很强大，但这是一种“编程便利性”上的强大，而不是“计算理论能力”上的强大。任何多带图灵机能计算的语言，单带图灵机也都能计算，只是过程会笨拙得多。
📝 [总结]

本段引入了多带图灵机的定义，它通过拥有多条磁带和多个协同工作的磁头，提供了一个更灵活、更接近现代计算机架构的计算模型。其核心特征是转移函数能够根据所有磁头的信息，同时对所有磁带进行操作。虽然它看起来更强大，但接下来的部分将证明其计算能力与单带图灵机等价。

🎯 [存在目的]

引入多带图灵机有两个主要目的：

  1. 作为证明图灵机模型鲁棒性的一个重要和有说服力的例子。
  2. 在后续的算法复杂性理论中，多带图灵机是一个更方便的分析模型。很多算法在多带模型上描述起来更自然、更简洁。例如，后续证明非确定性图灵机等价性时，就是用一个三带的确定性图灵机来模拟，这比用单带机描述要清晰得多。
🧠 [直觉心智模型]

标准的单带图灵机就像一个只有一个工作台（磁带）的工匠。他所有的原材料、半成品、成品和工具都得放在这一个台子上。如果他想比较两个零件，他得先把一个拿到眼前，记住样子，再跑去台子另一头拿起另一个来比较。

多带图灵机就像一个拥有多个独立工作台的工匠。他可以把原材料放在一个台子，用另一个台子做草稿和切割，再用第三个台子进行组装。他可以同时在几个台子上操作，效率大大提高。但他能最终制造出来的东西的“种类”，和那个只有一个工作台的勤奋工匠是一样的。

💭 [直观想象]

想象你在写一篇大论文（进行一次计算）。

  1. 单带图灵机：你只有一张无限长的稿纸。你既要在这上面写正文，又要打草稿，还要查阅资料（假设资料也写在纸的远处）。你需要不断地在纸上翻来翻去，非常麻烦。
  2. 多带图灵机：你有好几张无限长的稿纸。一张用来写最终的正文，一张用来打草稿，一张贴满了参考资料。你可以同时看几张纸上的内容，并在它们上面书写，思路会清晰很多，速度也快得多。

33. 定理 3.13：多带与单带图灵机的等价性

3.1 定理内容与证明思路

📜 [原文4]

定理 3.13

每个多带图灵机都具有一个等价的单带图灵机。

证明 我们展示如何将多带图灵机 $M$ 转换为等价的单带图灵机 $S$。关键思想是展示如何用 $S$ 模拟 $M$。

假设 $M$ 有 $k$ 条磁带。那么 $S$ 通过将其信息存储在其单条磁带上来模拟 $k$ 条磁带的效果。它使用新符号 \# 作为分隔符来分隔不同磁带的内容。除了这些磁带的内容之外，$S$ 还必须跟踪磁头的位置。它通过写入一个带有圆点的磁带符号来标记该磁带上的磁头所在的位置。将这些视为“虚拟”磁带和磁头。像以前一样，“带点”的磁带符号只是添加到磁带字母表中的新符号。下图说明了如何使用一条磁带表示三条磁带。

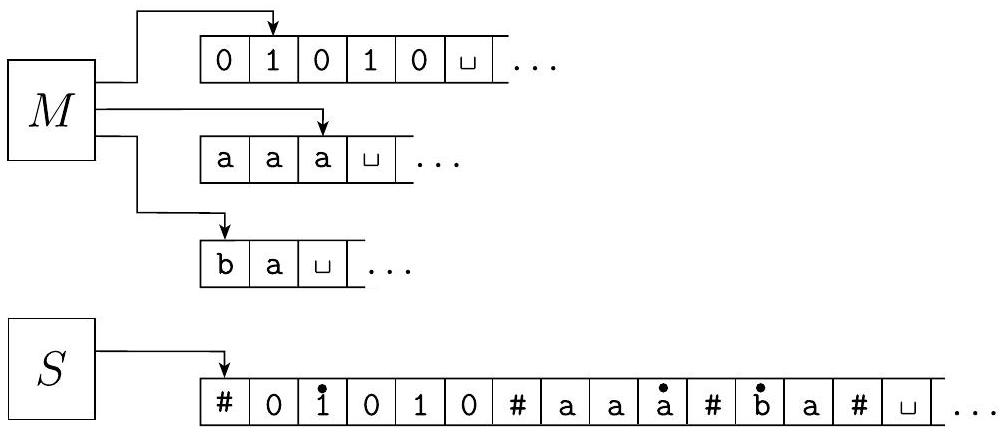
图 3.14

用一条磁带表示三条磁带

📖 [逐步解释]

这部分阐述了证明的核心：用一台单带图灵机 $S$ 来模拟一台多带图灵机 $M$。

  1. 定理陈述：明确指出，任何一个多带图灵机，都有一个与之能力等价的单带图灵机。这意味着多带并没有增加计算的“能力范围”。
  2. 证明策略：模拟：证明是构造性的。我们将具体说明如何一步步构建这台单带图灵机 $S$，使其行为能完全复制多带图灵机 $M$ 的一举一动。
  3. 核心思想：信息整合：单带图灵机 $S$ 只有一个存储空间（一条磁带），它必须把多带图灵机 $M$ 的所有信息都编码到这条磁带上。$M$ 的信息包括两部分：
    • 所有 $k$ 条磁带上存储的内容。
    • 所有 $k$ 个磁头在各自磁带上的位置。
  4. 编码方案：
    • 分隔符：$S$ 的磁带上使用一个特殊的符号 # (sharp/hashtag)，这个符号不在 $M$ 的原始字母表中。这个 # 就像书架上的隔板，用来区分存储的不同磁带的内容。
    • 磁带内容存储：$S$ 的磁带上会依次存放 $M$ 的磁带1的内容，然后是 #，然后是磁带2的内容，然后是 #，以此类推。整个结构看起来像：# tape1_content # tape2_content # ... # tapek_content #。
    • 磁头位置跟踪：如何表示 $M$ 的每个磁头在哪？$S$ 使用一种“加点”的符号。例如，如果 $M$ 的磁带1上，磁头正指着符号 a，那么在 $S$ 的磁带上，对应位置存储的就不是 a，而是一个新的、带点的符号 ȧ。这个 ȧ 是一种复合符号，意思是“这里的原始符号是a，并且有一个虚拟磁头指着它”。
    • 扩展字母表：为了实现上述方案，$S$ 的磁带字母表 $\Gamma_S$ 必须比 $M$ 的字母表 $\Gamma_M$ 更大。它需要包含 $\Gamma_M$ 中所有符号，所有符号的“带点”版本（例如 ȧ, ḃ, ...），以及分隔符 #。即 $\Gamma_S = \Gamma_M \cup \{\dot{\gamma} | \gamma \in \Gamma_M\} \cup \{\#\}$。
  5. 图示解释：图3.14直观地展示了这个编码方案。
    • $M$ 有三条磁带。
    • 磁带1内容是 011，磁头在 1 上。
    • 磁带2内容是 0，磁头在 0 上。
    • 磁带3内容是 10，磁头在 1 上。
    • $S$ 的单条磁带上就存储着：# 0 ṗ 1 # ȯ # ṗ 0 # (这里用 ṗ 代表带点的1，ȯ代表带点的0)。这一个长字符串完整地表达了 $M$ 当时的整个配置。
∑ [公式拆解]
  • 公式：
    $$ \# \stackrel{\bullet}{w}_{1} w_{2} \cdots w_{n} \# \stackrel{\bullet}{\sqcup} \# \cdots \# \stackrel{\bullet}{\sqcup} \# . $$
  • 这个公式在原文的步骤1中出现，我们提前在这里解释。它展示了 $S$ 初始化后磁带的样子。
  • $\#$: 分隔符。
  • $\stackrel{\bullet}{w}_{1}$: 这是 $w_1$ 的带点版本，表示 $M$ 的第一个磁头在输入字符串的第一个符号 $w_1$ 上。
  • $w_2 \cdots w_n$: 输入字符串的其余部分。
  • $\# \stackrel{\bullet}{\sqcup} \#$: 这代表了 $M$ 的第二条磁带。它初始为空白，磁头在起始的空白格 sqcup 上。所以用带点的空白符号 $\stackrel{\bullet}{\sqcup}$ 表示。
  • $\cdots$: 省略号表示类似地表示 $M$ 的第3到第 $k-1$ 条磁带。
  • $\# \stackrel{\bullet}{\sqcup} \#$: 代表 $M$ 的第 $k$ 条磁带。
  • .: 句号是文本结束的标点，不是磁带内容。
💡 [数值示例]

假设一个双带图灵机 $M$ ($k=2$)，输入为 ab。

  • $M$ 的初始配置:
  • 磁带1: |> a b scup ... (磁头在 a 上)
  • 磁带2: |> scup scup ... (磁头在 sqcup 上)
  • $S$ 模拟的初始磁带内容:
  • $S$ 的磁带: ... # ȧ b # ப̇ # ...
  • # 是分隔符。
  • ȧ b 代表磁带1的内容，ȧ 表示磁头在 a 上。
  • 第二个 # 分隔。
  • ப̇ 代表磁带2的内容，它的磁头在第一个空白格上。（这里用 ப 的带点形式 ப̇ 表示带点的空白符）。
  • 最后一个 # 结束。

现在假设 $M$ 有一条指令：$\delta(q_1, a, \sqcup) = (q_2, x, y, R, L)$。这意味着在 $q_1$ 状态，磁带1读到a，磁带2读到sqcup，则状态变为 $q_2$，磁带1写x并右移，磁带2写y并左移。

$S$ 要模拟这个过程，会非常繁琐，大致如下（详细步骤见下一节）：

  1. $S$ 的磁头从最左边的 # 开始，向右扫描，寻找带点的符号。它找到了 ȧ 和 ப̇。
  2. $S$ 在自己的状态中记下：“哦，虚拟磁头1在a上，虚拟磁头2在sqcup上”。
  3. $S$ 根据 $M$ 的转移规则 $\delta(q_1, a, \sqcup) = (q_2, x, y, R, L)$，在自己的状态中记下：“好的，接下来我要把a改成x并右移，把sqcup改成y并左移”。
  4. $S$ 的磁头回到最左边，开始第二次扫描，执行修改：
    • 找到 ȧ，把它改成 x，然后把旁边的 b 改成 ḃ (因为磁头1右移了)。
    • 找到 ப̇，把它改成 y。因为磁头2要左移，这可能会导致需要“挪动”整个磁带的内容，这是最复杂的部分（下一节会讲）。
  5. 经过这一系列复杂操作， $S$ 的磁带最终会变成反映 $M$ 新配置的样子。
⚠️ [易错点]
  1. 字母表问题：必须清醒地认识到，模拟图灵机 $S$ 的字母表比被模拟的 $M$ 的字母表要大得多。这是模拟能够实现的基础。
  2. 一个物理磁头 vs. k个虚拟磁头：$S$ 只有一个物理磁头，它在单条磁带上来回移动，以收集信息和更新状态。不要把它和 $M$ 的 $k$ 个（被$S$用带点符号模拟的）虚拟磁头搞混。
  3. 空间开销：$S$ 的磁带不仅存储了 $M$ 所有磁带的内容，还增加了分隔符，所以空间利用率较低。但因为磁带是无限的，这不成问题。
📝 [总结]

本段提出了用单带图灵机 $S$ 模拟多带图灵机 $M$ 的核心构造思想：将 $M$ 的多条磁带和多个磁头位置的所有信息，通过一种精巧的编码方案（使用分隔符#和带点符号），全部压缩到 $S$ 的单条磁带上。这为接下来的具体模拟步骤铺平了道路。

🎯 [存在目的]

本段的目的是介绍证明等价性的“蓝图”。在给出繁琐的具体执行步骤之前，先让读者理解信息是如何被表示和转换的。这种“表示法先行”的策略使得后续对复杂过程的描述变得更容易理解。

🧠 [直觉心智模型]

你有一堆乱七八糟的便签纸（多条磁带），每张上都用一个回形针（磁头）标记了看到哪里。现在要求你把所有信息都抄到一本笔记本（单条磁带）里，并且还要能随时知道每张便签纸的回形针位置。

你的做法是：在笔记本里，抄一页便签纸的内容，然后画一个大大的星号（分隔符#）隔开。再抄下一张便签纸的内容，再画星号... 为了记住回形针的位置，你在抄写时，如果某个字是回形针夹住的，你就用红笔写这个字（带点符号）。这样，一本笔记本就完整地记录了所有便签纸和回形针的信息。

💭 [直观想象]

想象一个电影剪辑师。

  1. 多带图灵机：他有多个屏幕，每个屏幕播放一段视频素材（多条磁带）。他可以同时观看所有屏幕的当前帧（多个磁头），然后决定每个屏幕是暂停、快进还是倒退。
  2. 单带图灵机模拟：现在他只有一个屏幕了。为了完成同样的工作，他把所有视频素材拼接成一个超长的视频，并在两段素材之间插入一段黑屏（分隔符#）。为了知道原来每个屏幕播放到哪了，他在那个长视频的对应帧上贴一个“当前播放”的透明贴纸（带点符号）。当他要模拟一次剪辑时，他需要：1. 先快速拖动这个长视频，找到所有贴纸的位置，把画面记在脑子里。2. 根据脑子里的信息做出决定。3. 再一次拖动长视频，找到每个贴纸，撕掉旧的，在新的位置（快进或倒退后的帧）贴上新的贴纸，并可能修改那一帧的画面。这个过程虽然笨重，但能完成同样的工作。

3.2 模拟步骤

📜 [原文5]

$S=$ “在输入 $w=w_{1} \cdots w_{n}$ 上：

  1. 首先，$S$ 将其磁带格式化，以表示 $M$ 的所有 $k$ 条磁带。格式化后的磁带包含

$$ \# \stackrel{\bullet}{w}_{1} w_{2} \cdots w_{n} \# \stackrel{\bullet}{\sqcup} \# \cdots \# \stackrel{\bullet}{\sqcup} \# . $$

  1. 为了模拟单个移动，$S$ 扫描其磁带，从第一个 \#（标记左端）到第 $(k+1)$ 个 \#（标记右端），以确定虚拟磁头下的符号。然后 $S$ 进行第二次扫描，根据 $M$ 的转移函数的规定更新磁带。
  2. 如果在任何时候 $S$ 将其中一个虚拟磁头向右移动到 \# 上，这个动作表示 $M$ 已将相应的磁头移动到该磁带先前未读取的空白部分。因此，$S$ 在该磁带单元格上写入一个空白符号，并将磁带内容从该单元格向右移动一位，直到最右边的 \#。然后它像以前一样继续模拟。”
📖 [逐步解释]

这部分详细描述了单带图灵机 $S$ 如何具体地执行模拟过程。整个过程可以分为初始化和循环模拟两个阶段。

阶段一：初始化 (步骤 1)

  1. 输入：$S$ 接收输入字符串 $w$。
  2. 格式化：$S$ 不会直接在 $w$ 上工作。它首先要清空磁带，并创建出我们在上一节讨论的那个格式。
    • 它写入 #。
    • 然后把输入 $w$ 抄写上去，但第一个符号 $w_1$ 要写成它的“带点”版本 $\dot{w}_1$，表示 $M$ 的磁带1的磁头在这里。
    • 然后，对于 $M$ 的其余 $k-1$ 条磁带，因为它们都是空的，所以 $S$ 会依次写入 #，一个带点的空白符 $\dot{\sqcup}$。
    • 最后，用一个 # 结尾。
    • 这样，初始的磁带布局就建立好了，完全反映了 $M$ 的初始状态。

阶段二：循环模拟 (步骤 2 和 3)

$S$ 进入一个大循环，这个循环的每一步都完整地模拟了 $M$ 的一步转移。模拟 $M$ 的一步又分为几个子步骤：

  • 子步骤 2.1 (信息收集扫描):
  • $S$ 的物理磁头移动到最左边的第一个 # 处。
  • 然后它开始向右扫描整个磁带，直到遇到第 $k+1$ 个 #（即最右边的#）。
  • 在扫描过程中，每当它看到一个“带点”的符号（比如 ċ 或 ė），它就会把这个符号的“不带点”版本（c 或 e）记录在自己的状态里。例如，它的状态可以设计成一个元组 (q_M, s_1, s_2, ..., s_k)，其中 q_M 是 $M$ 的当前状态，$s_i$ 是从第 $i$ 个虚拟磁带收集到的符号。
  • 当扫描完成时，$S$ 就知道了 $M$ 的当前状态和所有 $k$ 个虚拟磁头下的符号，这正是 $M$ 做出下一步决策所需的所有信息。
  • 子步骤 2.2 (执行更新扫描):
  • 现在 $S$ 知道了 $M$ 的当前局面 (q_M, s_1, ..., s_k)。$S$ 内部有一个 $M$ 的转移函数 $\delta_M$ 的副本。它查询 $\delta_M((q_M, s_1, ..., s_k))$，得到结果 (q'_M, b_1, ..., b_k, move_1, ..., move_k)。
  • $S$ 将自己的状态更新，以记住 $M$ 的新状态 q'_M。
  • 然后 $S$ 的物理磁头再次回到最左端，开始第二次从左到右的扫描。
  • 这次扫描的目的是执行更新操作。当它找到第 $i$ 个带点的符号时，它会：
  1. 将该符号的不带点版本改写为新的符号 $b_i$。
  2. 根据移动指令 move_i 来更新虚拟磁头的位置。这很关键：
    • 如果 move_i 是 L (左移)，它就把当前格子的点去掉，并在左边一个格子的符号上加上点。
    • 如果 move_i 是 R (右移)，它就把当前格子的点去掉，并在右边一个格子的符号上加上点。
    • 如果 move_i 是 S (停留)，它就不改变点的位置，只更新符号。
  • 子步骤 3 (处理磁带扩展):
  • 这是一个特殊情况处理。在子步骤2.2中，当 $S$ 试图将一个点向右移动，但发现右边紧邻的是一个 # 分隔符时，会发生什么？
  • 含义: 这意味着在 $M$ 中，对应的那个磁头移动到了一个之前从未使用过的空白区域。$M$ 的磁带是无限的，所以这很正常。
  • $S$ 的操作: $S$ 必须在自己的单条磁带上“创造”出新的空间。它的做法是：
  1. 在那个 # 的位置，写入一个空白符号 sqcup。
  2. 然后，将从这个 # 开始到磁带最右端的所有内容（包括其他磁带的内容和它们的分隔符）整体向右移动一格。这是一个非常耗时的操作。
  3. 移动完成后，新的空白格就插入成功了。现在 $S$ 就可以把那个“点”移动到这个新的空白格上。
    • 之后，$S$ 完成了对 $M$ 一步的模拟，准备回到子步骤2.1，开始模拟 $M$ 的下一步。
💡 [数值示例]

让我们继续之前双带图灵机 $M$ 的例子。

  • $M$ 的配置: 状态 $q_1$, 磁带1 |>a b, 磁带2 |>sqcup。
  • $S$ 的磁带: ... # ȧ b # ப̇ # ...
  • $M$ 的指令: $\delta(q_1, a, \sqcup) = (q_2, x, y, R, L)$

$S$ 模拟这一步：

  1. 信息收集扫描:
    • $S$ 的磁头从左到右扫过 # ȧ b # ப̇ #。
    • 它发现第一个带点符号是 ȧ，于是记下“磁带1读到a”。
    • 它发现第二个带点符号是 ப̇，于是记下“磁带2读到sqcup”。
    • 现在 $S$ 知道 $M$ 的输入是 (q_1, a, scup)。
  2. 查询与决策:
    • $S$ 查询 $M$ 的转移表，得到输出是 (q_2, x, y, R, L)。
    • $S$ 更新自己的状态，记住 $M$ 的新状态将是 $q_2$，并且记下要执行的操作：
    • 对磁带1: 写x，点右移。
    • 对磁带2: 写y，点左移。
  3. 执行更新扫描:
    • $S$ 的磁头回到最左边，再次从左到右扫描。
    • 处理磁带1: 找到 ȧ。
    • 将 ȧ 改成 x（去掉点，内容换成x）。磁带变为: # x b # ப̇ #
    • 因为要右移，把 b 改成 ḃ。磁带变为: # x ḃ # ப̇ #
    • 处理磁带2: 找到 ப̇。
    • 将 ப̇ 改成 y。磁带变为: # x ḃ # y #
    • 因为要左移，需要把点移到 y 左边的符号上。但左边是 #！这就触发了步骤3的特殊情况。
  4. 处理磁带扩展 (磁带2左移):
    • $S$ 发现要将磁带2的虚拟磁头移到#上。这意味着 $M$ 的磁带2磁头向左移入了一个新的空白区域。
    • $S$ 需要在 # 和 y 之间插入一个新的空白格。
    • 它将 y 和它右边的所有内容（在这里就是最后的#）都向右移动一格。
    • 磁带变为: # x ḃ # y # (这里用空格表示新插入的空白格)
    • 然后把这个新插入的空白格写成 sqcup : # x ḃ # scup y #
    • 最后，把点放在这个新插入的 sqcup 上：# x ḃ # ப̇ y #
  5. 模拟结束:
    • $S$ 的磁带最终变为 # x ḃ # ப̇ y #。
    • 这正好对应 $M$ 的新配置：状态 $q_2$, 磁带1 x |>b, 磁带2 |>sqcup y。
    • $S$ 完成了一次完整的模拟，准备开始下一次循环。
⚠️ [易错点]
  1. 磁带扩展的复杂性: 步骤3是整个模拟中最复杂和最耗时的部分。每次需要扩展磁带时，单带图灵机 $S$ 可能需要移动磁带上大量的数据。这导致了模拟的效率非常低，但并不影响其最终能够完成任务的“能力”。
  2. 磁头向左移出边界: 与向右扩展类似，如果虚拟磁头向左移动，超出了当前已记录内容的左边界（即移动到了分隔符#的左边），也需要执行类似的数据搬移操作，在左边插入新的空白格。
  3. 状态的复杂性: 模拟器 $S$ 的状态集需要足够大，以存储 $M$ 的当前状态以及从磁带上读取到的 $k$ 个符号。
📝 [总结]

本段详细描述了单带图灵机 $S$ 模拟多带图灵机 $M$ 的具体算法。该算法通过一个“扫描-更新”的循环来模拟 $M$ 的每一步。虽然这个过程，特别是当需要扩展磁带时，在单带机上显得非常笨拙和低效，但它在逻辑上是完全可行的。这证明了单带图灵机拥有完成任何多带图灵机任务的根本能力。

🎯 [存在目的]

这部分是整个定理证明的核心，它将上一节的“表示法”蓝图转化为了一个可执行的“算法”。通过给出具体的步骤，它无可辩驳地证明了模拟的可行性，从而完成了从多带图灵机到单带图灵机的能力等价性证明。

🧠 [直觉心智模型]

继续那个笔记本和便签纸的例子。你（单带机的磁头）要模拟便签纸上的一次更新。

  1. 信息收集: 你从笔记本第一页开始翻，找到所有用红笔写的字（带点符号），把这些字抄在手心上。
  2. 决策: 你看着手心里的字，查阅你的总规则书（$M$的转移函数），知道接下来每个红字要改成什么，以及每个回形针要怎么移动。
  3. 执行: 你再次从笔记本第一页开始翻。
    • 找到第一个红字，擦掉，写上新字。然后根据规则，把左边或右边的下一个字用红笔写。
    • 如果规则说要移到“画了星号”的地方（移出边界），你就得停下来，把星号后面的所有内容都往后挪一页，空出一页来，在上面写个“空白”，然后把这个“空白”用红笔写。这是个大工程。
    • 对所有红字都这么做一遍。
💭 [直观想象]

继续电影剪辑师的例子。他要模拟一次剪辑操作。

  1. 扫描: 他拖动进度条，把整个超长视频看一遍，记下所有贴着“当前播放”贴纸的帧的画面。
  2. 决策: 根据这些画面和剪辑规则，他知道接下来每个片段要怎么处理。
  3. 执行: 他再次从头拖动进度条。
    • 找到第一个贴纸，把它撕下来。根据规则，可能要修改这一帧的画面（比如加个滤镜），然后把贴纸贴到前面或后面的某一帧上。
    • 如果规则要求把贴纸贴到“黑屏”（#）上，他就必须把这段黑屏之后的所有视频内容都往后“推”，以插入一个新的空白帧，再把贴纸贴上去。这会导致整个长视频的时间码都要重新计算，非常耗时。
    • 他对所有贴纸都这样做。

3.3 推论 3.15

📜 [原文6]

推论 3.15

当且仅当某些多带图灵机识别该语言时，该语言才是图灵可识别的。

证明 图灵可识别语言由普通（单带）图灵机识别，而普通（单带）图灵机是多带图灵机的一种特殊情况。这证明了这个推论的一个方向。另一个方向则由定理 3.13 得出。

📖 [逐步解释]

这个推论是定理 3.13 的直接结果，它正式地将“多带图灵机可识别的语言”和“图灵可识别语言”（由标准单带图灵机定义的）这两个概念划上了等号。

这是一个“当且仅当”的命题，所以需要双向证明。

  1. 方向一：如果一个语言是图灵可识别的，那么它也是多带图灵机可识别的。
    • 证明：根据定义，“图灵可识别”意味着存在一个普通的、单带的图灵机 $M_1$ 来识别它。
    • 一个单带图灵机可以被看作是一个 $k=1$ 的多带图灵机。
    • 或者，我们可以构建一个 $k>1$ 的多带图灵机 $M_k$，让它只使用它的第一条磁带，完全模仿 $M_1$ 的行为，而忽略其他所有磁带。
    • 因此，任何单带图灵机能识别的语言，显然都有一个多带图灵机能识别它。这个方向的证明是平凡的（trivially true）。
  2. 方向二：如果一个语言是多带图灵机可识别的，那么它也是图灵可识别的。
    • 证明：假设一个语言 $L$ 被一个多带图灵机 $M_k$ 识别。
    • 根据我们刚刚证明的定理 3.13，对于这个 $M_k$，必然存在一个与之等价的单带图灵机 $S$。
    • “等价”意味着 $S$ 和 $M_k$ 识别完全相同的语言。所以，$S$ 也识别语言 $L$。
    • 根据定义，一个能被单带图灵机（即 $S$）识别的语言，就是“图灵可识别”的。
    • 所以，这个方向的证明直接由定理 3.13 保证。
📝 [总结]

推论 3.15 基于定理 3.13，正式确立了多带图灵机和单带图灵机在定义语言类别方面的能力是完全相同的。从此，当我们谈论一种语言是否是“图灵可识别”的，我们既可以用单带图灵机来证明，也可以方便地使用多带图灵机来证明，因为它们是等价的。

🎯 [存在目的]

这个推论的目的是将前面繁琐的技术证明（定理 3.13）转化为一个简洁而有力的结论。它授权我们在未来的讨论和证明中，可以自由地使用多带图灵机作为分析工具，而不用担心它的能力超出了标准的“图灵可识别”范畴。这极大地简化了后续许多复杂算法的描述和分析。

🧠 [直觉心智模型]
  1. 定理 3.13 是在说：“我能教你如何用一把锤子（单带机）造出任何用一整套工具箱（多带机）能造出的家具。”
  2. 推论 3.15 是在说：“所以，‘能被锤子造出的家具集合’和‘能被工具箱造出的家具集合’是完全一样的。”

44. 非确定性图灵机

4.1 非确定性图灵机的定义

📜 [原文7]

非确定性图灵机

非确定性图灵机以预期的方式定义。在计算中的任何一点，机器都可以根据几种可能性进行。非确定性图灵机的转移函数形式为

$$ \delta: Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}) . $$

非确定性图灵机的计算是一棵树，其分支对应于机器的不同可能性。如果计算的某个分支导致接受状态，则机器接受其输入。如果您觉得需要复习非确定性，请参阅第 1.2 节（第 47 页）。现在我们证明非确定性不影响图灵机模型的能力。

📖 [逐步解释]

这部分引入了另一个重要的图灵机变体：非确定性图灵机 (Nondeterministic Turing Machine, NTM)。

  1. 核心概念：选择的可能性
    • 与确定性图灵机（DTM）在任何情况下只有唯一一条路可走不同，非确定性图灵机在某些情况下，面对 (当前状态, 当前符号)，可能会有多个可供选择的下一步动作。
    • 这种“选择”不是随机的，而是并行的。可以想象成，机器在这一刻“分身”了，每个分身去执行一个可能的动作。
  2. 转移函数的形式化
    • $\delta: Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\})$
    • 这里的关键是输出部分 $\mathcal{P}(\dots)$，$\mathcal{P}$ 代表“幂集”（Power Set），即所有子集的集合。
    • 对于一个输入 (q, a)，转移函数不再返回一个单一的动作三元组 (q', b, L/R)，而是返回一个包含零个、一个或多个这种三元组的集合。
    • 如果集合是空的，意味着这条路走到了尽头（没有下一步），这个计算分支终止并拒绝。
    • 如果集合包含一个元素，它的行为就像一个确定性图灵机。
    • 如果集合包含多个元素，例如 { (q_1, b_1, L), (q_2, b_2, R) }，这意味着机器可以任选其一：要么进入 $q_1$，写 $b_1$，左移；要么进入 $q_2$，写 $b_2$，右移。
  3. 计算模型：树
    • 由于存在选择，NTM的整个计算过程不再是一条线性的配置序列，而是一棵“计算树”。
    • 树根：是起始配置。
    • 节点：树中的每个节点都是一个配置（状态、磁带内容、磁头位置）。
    • 分支：从一个节点延伸出的每条边，都对应转移函数返回的集合中的一个选择。
    • 路径/分支：从根节点到某个叶子节点的一条完整路径，代表一种可能的计算过程。
  4. 接受条件
    • DTM的接受条件是：线性的计算过程最终进入了接受状态。
    • NTM的接受条件是：在整棵计算树中，只要有至少一个分支（一条路径）最终到达了一个接受配置（即进入了 $q_{accept}$ 状态），那么这台NTM就接受它的输入。
    • 即使树上有一千条路径都陷入了死循环或拒绝了，但只要有一条路径成功，就算成功。
    • 如果所有路径都最终停止并且拒绝，或者所有路径都陷入死循环，那么NTM就不接受该输入。
  5. 核心问题：这种“分身乏术”、“预知未来”般的非确定性能力，是否让图灵机变得更强大了？（我们知道它使得下推自动机更强大了）。本节将证明，对于图灵机来说，答案仍然是“不”。
∑ [公式拆解]
  • 公式: $\delta: Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\})$
  • $\delta$: 非确定性转移函数。
  • $Q \times \Gamma$: 输入，和DTM一样，是 (当前状态, 当前磁带符号)。
  • $\mathcal{P}$: 幂集符号。$\mathcal{P}(S)$ 表示集合 $S$ 的所有子集的集合。
  • $Q \times \Gamma \times \{\mathrm{L}, \mathrm{R}\}$: 这是一个所有可能的“下一步动作”三元组 (新状态, 新符号, 移动方向) 的集合。
  • $\mathcal{P}(Q \times \Gamma \times \{\mathrm{L}, \mathrm{R}\})$: 转移函数的输出。它是一个集合，这个集合的元素是“下一步动作”三元组。
  • 例如，一个可能的输出可以是：$\{(q_2, 1, L), (q_3, 0, R)\}$。这表示机器有两个选择。
  • 另一个可能的输出是：$\{(q_5, 1, R)\}$。这表示只有一个选择，行为是确定性的。
  • 还一个可能的输出是：$\emptyset$（空集）。这表示没有选择，计算终止。
💡 [数值示例]

假设一个NTM要判断一个二进制串中是否包含11。

  • 输入: 010110
  • 一个可能的NTM设计思路:
  • 在状态 $q_0$ 时，如果读到0，保持 $q_0$ 右移。如果读到1，非确定性地选择：
  1. 继续保持 $q_0$ 右移（忽略这个1）。
  2. 进入“检查”状态 $q_1$ 并右移，去看看下一个是不是也是1。
    • 在状态 $q_1$ 时，如果读到1，就进入接受状态 $q_{accept}$。如果读到0或空白，就进入拒绝状态。
  • 计算树的某几条分支:
  • 分支A (聪明的选择):
  1. $q_0$, |010110 -> $q_0$, 0|10110 (读0，右移)
  2. $q_0$, 0|10110 -> $q_0$, 01|0110 (读1，选择忽略，继续右移)
  3. ... 一直忽略 ...
  4. $q_0$, 010|110 -> (读到第2个1，选择进入检查状态) -> $q_1$, 0101|10
  5. $q_1$, 0101|10 -> (读到1) -> $q_{accept}$！
    • 因为这条分支接受了，所以整个机器就接受输入010110。
  • 分支B (愚蠢的选择):
  1. $q_0$, |010110 -> $q_0$, 0|10110
  2. $q_0$, 0|10110 -> (读到第1个1，选择进入检查状态) -> $q_1$, 01|0110
  3. $q_1$, 01|0110 -> (读到0) -> $q_{reject}$ (这条分支失败了)
  • 分支C (一直忽略):
  • 始终选择忽略所有1，一直右移，直到磁带末尾，最终停机并拒绝。

尽管有分支B和C的失败，但因为分支A成功了，所以整个NTM成功识别出输入包含11。

⚠️ [易错点]
  1. 非确定性 vs. 随机性: 非确定性不是随机选择一条路走。它是“所有路都同时走”的模型。只要有一条路通向罗马，它就算能到罗马。
  2. 拒绝条件: NTM拒绝一个输入，当且仅当所有计算分支都最终停机并拒绝。如果哪怕只有一个分支在无限循环，而其他分支都拒绝了，那么整个NTM既不接受也不拒绝，它只是在那个输入上“不停止”。
  3. 计算树的无限分支: 某些NTM的计算树可能有无限深的分支（即陷入死循环的计算路径）。这是图灵机与有限自动机的非确定性的一个关键区别（NFA的计算树深度受输入长度限制）。
📝 [总结]

本段定义了非确定性图灵机 (NTM)。其核心是通过一个输出为“动作集合”的转移函数，允许机器在一步中探索多个可能性。其计算过程形成一棵树，只要树上存在任何一个接受分支，机器就接受其输入。这是一种强大的并行计算的抽象模型。

🎯 [存在目的]

引入NTM是为了探讨非确定性这一强大的计算资源是否会改变“可计算性”的边界。在P vs NP问题中，NTM扮演着核心角色，它是定义“NP”类问题的基础。在这里，我们的目标更基础：证明NTM和DTM在“可识别”语言的类别上是等价的，从而再次彰显图灵机模型的鲁棒性。

🧠 [直觉心智模型]

你是一个侦探，在破解一个迷宫般的案件。

  1. 确定性侦探 (DTM): 你在每个线索点，只能选择一条看起来最靠谱的路追下去。如果走错了，可能要退回来，再试另一条。
  2. 非确定性侦探 (NTM): 在每个出现多条可能线索的分岔口，你都能派出无数个分身，每个分身去追查一条线索。只要有一个分身最终破案了（到达接受状态），你就立刻宣布案件告破。
💭 [直观想象]

想象你在走一个巨大的迷宫。

  1. 确定性走法: 你用“右手扶墙”法，保证能走遍所有路径，但可能非常耗时。
  2. 非确定性走法: 在每个岔路口，你都“分裂”成几个人，每个人走一条路。如果迷宫有出口，那么必然有一个“你”会最先找到它。非确定性就像是拥有了这种无限分身的能力。

55. 定理 3.16：非确定性与确定性图灵机的等价性

5.1 证明思想

📜 [原文8]

定理 3.16

每个非确定性图灵机都具有一个等价的确定性图灵机。

证明思想 我们可以用确定性图灵机 $D$ 模拟任何非确定性图灵机 $N$。模拟背后的思想是让 $D$ 尝试 $N$ 的非确定性计算的所有可能分支。如果 $D$ 在这些分支中的一个上找到了接受状态，则 $D$ 接受。否则，$D$ 的模拟将不会终止。

我们将 $N$ 在输入 $w$ 上的计算视为一棵树。树的每个分支代表非确定性的一个分支。树的每个节点是 $N$ 的一个配置。树的根是开始配置。图灵机 $D$ 在这棵树中搜索一个接受配置。仔细进行此搜索至关重要，以免 $D$ 未能访问整个树。一个诱人的，但糟糕的想法是让 $D$ 使用深度优先搜索来探索树。深度优先搜索策略会一直向下遍历一个分支，然后再回溯探索其他分支。如果 $D$ 以这种方式探索树，则 $D$ 可能会永远沿着一个无限分支向下，并错过其他分支上的接受配置。因此，我们设计 $D$ 改用广度优先搜索来探索树。该策略会探索所有深度相同的分支，然后再继续探索下一个深度的任何分支。这种方法保证 $D$ 将访问树中的每个节点，直到遇到接受配置。

📖 [逐步解释]

这部分阐述了用确定性图灵机 $D$ 模拟非确定性图灵机 $N$ 的核心证明思路。

  1. 定理陈述：明确指出，任何NTM，都有一个与之能力等价的DTM。这意味着非确定性没有增加图灵机的计算能力范围。
  2. 核心思想：系统性地搜索计算树
    • $N$ 的计算是一棵庞大的树，DTM $D$ 的任务就是当一个“勤奋的园丁”，把这棵树彻底搜查一遍，看看有没有“接受”的果实。
    • 如果 $D$ 找到了一个接受配置，它就停下来并接受。
    • 如果 $N$ 的计算树上没有任何接受配置（所有分支要么拒绝，要么无限循环），那么 $D$ 的搜索过程也可能永远不会停止（因为它会不断地探索更深、更广的树枝），这正好符合“图灵可识别”的定义：在接受时停机，在不接受时可以不停机。
  3. 搜索策略的选择：BFS vs. DFS
    • 计算树：这棵树的节点是配置，边是NTM的一步转移。
    • 深度优先搜索 (Depth-First Search, DFS)：这是一个很自然但错误的想法。DFS会沿着一条计算路径一直走到底。
    • 问题所在：如果这条路径恰好是一个无限循环，那么 $D$ 就会永远陷在这个分支里，永远没有机会去检查其他分支。而可能在另一条很短的分支上，就有一个接受状态。这会导致 $D$ 无法找到本应找到的解。
    • 类比：一个愚蠢的侦探，选择了一条线索就死追到底，结果发现这条线索是别人伪造的，让他一直在原地兜圈子，而真正的破案线索就在他出发点的旁边，他却再也回不去了。
    • 广度优先搜索 (Breadth-First Search, BFS)：这是正确的策略。BFS会一层一层地探索树。
    • 过程：先检查所有深度为1的节点（即 $N$ 计算1步能到达的所有配置）。然后检查所有深度为2的节点，然后是深度3，以此类推。
    • 优势：这种策略保证了如果树的任何位置存在一个接受配置，BFS搜索最终必然会到达它。因为接受配置在某个有限的深度 $d$ 上，BFS在检查完所有深度小于 $d$ 的层之后，一定会开始检查第 $d$ 层，从而找到它。它不会被任何无限分支所困。
    • 类比：一个聪明的侦探，他先把所有离他一步之遥的线索都查一遍，再把所有两步之遥的线索查一遍... 这样，无论真正的线索藏在哪个角落，只要它存在，就一定会被按部就班地找到。
💡 [数值示例]

假设NTM $N$ 的计算树如下：

```

A (根)

/|\

B C D

/| \

E F G (接受状态)

|

H (无限循环的开始)

|

...

```

  • DFS策略: 如果 $D$ 采用DFS，它可能会选择 A -> B -> E -> H -> ... 这条路。它会陷入无限循环，永远也发现不了在另一条分支上的接受状态 G。因此 $D$ 会在应该接受的时候没有接受。
  • BFS策略: $D$ 会按以下顺序探索节点：
  1. 第0层: A
  2. 第1层: B, C, D
  3. 第2层: E, F, G <-- 在这里，D发现了接受状态G！
    • $D$ 立即停机并接受。它成功地模拟了 $N$。
⚠️ [易错点]
  1. 必须是BFS：在模拟NTM时，使用BFS而非DFS是证明等价性的关键，这是本证明思想中最核心的知识点。
  2. 模拟的效率：BFS搜索的代价非常高。树的宽度可能随深度指数级增长。因此，用DTM模拟NTM通常会导致运行时间从多项式时间爆炸到指数时间。这正是P vs NP问题的核心：非确定性虽然不改变“能算什么”（可计算性），但它可能极大地改变“算得多快”（复杂性）。
  3. 无限树：即使整棵计算树是无限的（即 $N$ 在该输入上不保证停机），BFS策略依然有效。只要树上存在一个接受节点，它就会在有限时间内被找到。如果不存在，搜索就会无限进行下去。
📝 [总结]

本段的证明思想是，通过让一个确定性图灵机 $D$ 对非确定性图灵机 $N$ 的计算树进行广度优先搜索 (BFS)，来系统性地检查所有可能的计算路径。BFS保证了只要存在接受路径，就一定能在有限时间内找到，从而完美地模拟了NTM的接受行为，而避免了被无限循环分支困住的风险。

🎯 [存在目的]

这段“证明思想”是在给出具体的技术实现（三条磁带如何工作）之前，先阐明整个模拟策略的逻辑和正确性。它强调了算法选择（BFS vs. DFS）对于处理无限搜索空间的重要性，这是计算理论中一个反复出现的主题。

🧠 [直觉心智模型]

想象一下你在一个巨大的图书馆里找一本特定的书（接受状态）。

  1. DFS：你选定一个书架，从第一本书看到最后一本。看完这个书架，再看下一个... 如果某个书架是魔法的，可以无限延伸，你就永远困在那里了。
  2. BFS：你先检查所有书架的第一本书。然后回来，检查所有书架的第二本书。然后是所有书架的第三本书... 这种方法虽然来回跑动很累，但保证了只要那本书在图书馆里，你迟早会摸到它。
💭 [直观想象]

你在看一段非确定性的“互动电影”，在每个节点你都可以选择剧情走向。

  1. DFS：你选择了一条剧情线，然后一直看了下去。结果这是一条无聊的、永远没有结局的剧情线。你错过了其他分支里精彩的“完美结局”。
  2. BFS：你先看完所有剧情线的第一分钟。然后倒带，把所有剧情线的第二分钟看完。再倒带... 这个过程很折磨人，但你保证不会错过任何一个分支里出现的“完美结局”。这个“倒带再播放”的笨拙过程，就是确定性图灵机在用BFS模拟非确定性。

5.2 证明细节：三带图灵机模拟

📜 [原文9]

证明 模拟确定性图灵机 $D$ 有三条磁带。根据定理 3.13，这种安排等同于拥有一条单条磁带。机器 $D$ 以特殊方式使用其三条磁带，如下图所示。磁带 1 始终包含输入字符串，并且从不改变。磁带 2 维护 $N$ 在其非确定性计算的某个分支上的磁带副本。磁带 3 跟踪 $D$ 在 $N$ 的非确定性计算树中的位置。

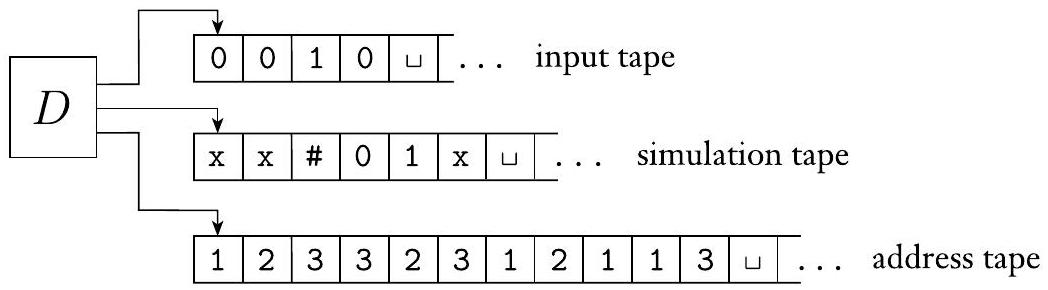
图 3.17

确定性图灵机 $D$ 模拟非确定性图灵机 $N$

首先，我们考虑磁带 3 上的数据表示。树中的每个节点最多可以有 $b$ 个子节点，其中 $b$ 是由 $N$ 的转移函数给出的可能选择的最大集合的大小。我们给树中的每个节点分配一个地址，该地址是字母表 $\Gamma_{b}=\{1,2, \ldots, b\}$ 上的字符串。我们将地址 231 分配给通过从根开始，转到其第 2 个子节点，再转到该节点的第 3 个子节点，最后转到该节点的第 1 个子节点而到达的节点。字符串中的每个符号告诉我们在模拟 $N$ 的非确定性计算中一个分支的一个步骤时接下来要做出的选择。有时，如果一个配置的选择太少，一个符号可能不对应任何选择。在这种情况下，地址无效，并且不对应任何节点。磁带 3 包含一个 $\Gamma_{b}$ 上的字符串。它表示 $N$ 的计算从根到由该字符串寻址的节点的分支，除非地址无效。空字符串是树根的地址。现在我们准备描述 $D$。

  1. 最初，磁带 1 包含输入 $w$，磁带 2 和 3 为空。
  2. 将磁带 1 复制到磁带 2，并将磁带 3 上的字符串初始化为 $\varepsilon$。
  3. 使用磁带 2 模拟 $N$ 在其非确定性计算的一个分支上输入 $w$。在 $N$ 的每一步之前，查阅磁带 3 上的下一个符号，以确定在 $N$ 的转移函数所允许的选择中做出哪个选择。如果磁带 3 上没有更多符号，或者此非确定性选择无效，则通过转到第 4 阶段来中止此分支。如果遇到拒绝配置，也转到第 4 阶段。如果遇到接受配置，则接受输入。
  4. 将磁带 3 上的字符串替换为字符串排序中的下一个字符串。通过转到第 2 阶段来模拟 $N$ 计算的下一个分支。
📖 [逐步解释]

这部分给出了模拟NTM $N$ 的DTM $D$ 的具体构造。为了清晰，我们使用一个三带的DTM $D$。（根据定理 3.13，这和一个单带DTM是等价的，所以不失一般性）。

三条磁带的分工：

  • 磁带 1 (输入带): 存储原始输入字符串 $w$。它从头到尾都不被修改。像一个只读的参考资料。
  • 磁带 2 (模拟带/工作带): 这是 $D$ 用来模拟 $N$ 的某一条特定计算分支的地方。它的内容会不断变化，完全复制 $N$ 在那条分支上磁带的样子。
  • 磁带 3 (地址带/路径带): 这是实现BFS的关键。它存储一个字符串，这个字符串代表了在 $N$ 的计算树中要探索的路径。

地址带（磁带 3）的工作原理：

  1. 分支编号: 首先，我们需要一个方法来唯一标识计算树中的每个节点。我们先找出 $N$ 的转移函数中，单个 (状态, 符号) 对可能产生的最大选择数，记为 $b$。例如，如果 $\delta(q,a)$ 的最大返回集合大小是3，那么 $b=3$。
  2. 地址字母表: 我们创建一个地址字母表 $\Sigma_b = \{1, 2, ..., b\}$。
  3. 节点地址: 树中任何一个节点都可以用 $\Sigma_b$ 上的一个字符串来表示它的路径。
    • 根节点: 地址是空字符串 $\varepsilon$。
    • 子节点: 如果一个节点的地址是 s，它的第 $i$ 个子节点的地址就是 s 后面拼接上字符 i，即 si。
    • 示例: 地址 231 表示从根节点出发，走第2个分支，到达新节点后，再走新节点的第3个分支，再走下一个节点的第1个分支。
  4. 地址的有效性: 不是所有地址都对应一个真实节点。例如，如果地址是231，但在走第2个分支到达的节点上，只有2个选择，那么23这个前缀是有效的，但第3个选择不存在，所以231这个地址就是无效的。
  5. BFS的实现: $D$ 通过按字符串顺序（字典序或长度优先的字典序）生成地址字符串，来达到BFS的效果。例如：$\varepsilon, 1, 2, ..., b, 11, 12, ...$。这保证了 $D$ 会先探索所有长度为1的路径，再探索所有长度为2的路径，以此类推，这正是BFS。

DTM $D$ 的完整算法：

  • 步骤 1 (初始化): 磁带1放上输入 $w$。磁带2和3清空。
  • 大循环开始 (这个循环会不断地模拟新的分支)
  • 步骤 4 (选择下一个分支):
  • 在磁带3上生成下一个地址字符串。例如，如果上次模拟的是地址21，这次就生成22。
  • 这个生成顺序必须是BFS的顺序（例如，按长度，同长度按字典序）。
  • 步骤 2 (准备模拟):
  • 将磁带1上的原始输入 $w$ 完整地复制到磁带2上。这确保每次模拟新分支都是从一个干净的初始状态开始。
  • 步骤 3 (执行模拟):
  • $D$ 开始在磁带2上模拟 $N$ 的计算。
  • 在模拟 $N$ 的第 $i$ 步时，$D$ 会读取磁带3上的第 $i$ 个地址符号。假设是j。
  • $D$ 查看 $N$ 在当前配置下的转移函数，并选择第 j 个可能的动作来执行。
  • 中止条件:
  1. 磁带3的地址字符串用完了（这意味着模拟完了这条有限路径）。
  2. 地址无效（例如，地址要求走第3个分支，但当前只有2个选择）。
  3. 模拟过程中 $N$ 进入了拒绝状态 $q_{reject}$。
    • 如果发生以上任一情况，$D$ 就中止对当前分支的模拟，并跳转回步骤 4，去尝试下一个地址。
    • 接受条件:
  4. 如果在模拟的任何时候，$N$ 进入了接受状态 $q_{accept}$。
    • $D$ 立即停止整个程序，并接受输入。模拟成功！
  • 如果大循环永不结束：这意味着 $D$ 永远在生成新的地址、模拟新的分支，但从未找到一个接受状态。在这种情况下，$D$ 就不会停机，也就不会接受输入。这与 $N$ 的行为一致。
💡 [数值示例]
  • NTM $N$: 输入 a，在 $q_0$ 状态读到a，有两个选择：
  1. (q_1, b, R)
  2. (q_{accept}, c, L)
    • 最大分支数 $b=2$。地址字母表是 $\{1, 2\}$。
    • DTM $D$ 开始模拟:
  3. 循环 1:
    • 步骤 4: 生成第一个地址 $\varepsilon$ (模拟0步)。
    • 步骤 2: 磁带2变为 |>a。
    • 步骤 3: 模拟路径 $\varepsilon$。路径长度为0，直接中止。跳到步骤4。
  4. 循环 2:
    • 步骤 4: 生成下一个地址 1。
    • 步骤 2: 磁带2重置为 |>a。
    • 步骤 3: 模拟路径 1。
    • 在 $q_0$ 读a，地址是1，选择第一个动作 (q_1, b, R)。
    • 磁带2变为 b |>sqcup，状态变为 $q_1$。
    • 地址1用完了，模拟中止。跳到步骤4。
  5. 循环 3:
    • 步骤 4: 生成下一个地址 2。
    • 步骤 2: 磁带2再次重置为 |>a。
    • 步骤 3: 模拟路径 2。
    • 在 $q_0$ 读a，地址是2，选择第二个动作 (q_{accept}, c, L)。
    • $D$ 模拟 $N$ 进入了 $q_{accept}$！
    • $D$ 立即停机并接受输入 a。
⚠️ [易错点]
  1. 地址生成顺序: 必须严格遵循BFS顺序。如果按字典序 1, 11, 111, ..., 2, ...，那又变回DFS了。正确的顺序是 1, 2, 11, 12, 21, 22, ... (按长度排序，同长度按字典序)。
  2. 重置工作带: 每次模拟新分支前，必须将磁带2恢复到初始状态（即从磁带1复制）。否则上一次模拟的“脏数据”会干扰下一次模拟。
  3. 无限循环: 这个算法正确地处理了NTM中的无限循环。如果路径 1 导向一个无限循环，DTM $D$ 在模拟它时，会因为地址串 1 用完而中止，然后继续去尝试路径 2。如果地址串是 111... 这样无限长，DTM也只会在模拟有限步后因为地址用完而停下，它永远在模拟有限深度的路径。
📝 [总结]

本段给出了一个确定性的、三磁带的图灵机 $D$ 的完整算法，该算法能够通过模拟非确定性图灵机 $N$ 的所有计算分支来确定其是否接受一个输入。它巧妙地使用一条“地址带”来系统地、以广度优先的顺序探索 $N$ 的计算树，从而保证了只要存在接受路径就一定能找到，同时避免了陷入无限循环的分支。这最终证明了NTM的计算能力并不比DTM强。

🎯 [存在目的]

本段是定理 3.16 的技术核心。它提供了一个构造性的证明，展示了如何将一个充满“魔法般选择”的非确定性计算过程，转化为一个按部就班、完全确定性的、虽然可能极其缓慢的搜索过程。这为计算理论中一个基石性的结论——确定性与非确定性在可计算性层面的等价——提供了坚实的依据。

🧠 [直觉心智模型]

你是一个项目经理（DTM $D$），手下有一个想象中的、可以无限分身的员工团队（NTM $N$）。你要检查这个团队是否能完成一个项目（接受输入）。

  1. 磁带1 (项目需求): 贴在墙上的项目需求书，永不改变。
  2. 磁带3 (任务清单): 你的任务板。上面列着所有要尝试的“工作路径”，按“1天能完成的”、“2天能完成的”... 这样的顺序排列。路径名就是地址，如 路径-2-1。
  3. 磁带2 (沙盒): 一个模拟环境。

你的工作流程是：

  1. 从任务板上取下一个任务，比如 路径-2-1。
  2. 重置沙盒环境（把项目需求抄进去）。
  3. 在沙盒里，严格按照 路径-2-1 指示的步骤（先走第2个选项，再走第1个选项）去模拟。
  4. 如果模拟成功（项目完成），你立刻向老板汇报成功。
  5. 如果模拟失败或路径走完了还没成功，你就擦掉沙盒，回到任务板，取下一个任务，周而复始。
💭 [直观想象]

你有一个游戏《命运之路》，里面充满了选择。你想知道是否存在一种通关路线。你只有一台普通的电脑（DTM $D$）来帮你。

  1. 磁带1: 游戏的安装文件，只读。
  2. 磁带3: 一个文本文件，里面是你自己写的“攻略路线图”，一行一个路线，如 Up, Down, Left。你按路线长度排序，确保先尝试所有短路线。
  3. 磁带2: 一个游戏存档。

你的操作：

  1. 从攻略路线图里复制第一行 Up。
  2. 新建一个游戏存档。
  3. 加载存档，在第一个选择点选择 Up。游戏没结束。
  4. 删掉存档。
  5. 从攻略图里复制下一行 Down。
  6. 新建存档，在第一个选择点选 Down。假设游戏通关了（进入接受状态）。
  7. 你立刻停止所有操作，大喊一声“能通关！”。

这个过程虽然笨拙（不停地删档、新建、重玩），但它保证了能用一台普通电脑，找出《命运之路》是否存在通关路线。

5.3 推论 3.18 与 3.19

📜 [原文10]

推论 3.18

当且仅当某些非确定性图リング机识别该语言时，该语言才是图灵可识别的。

证明 任何确定性图リング机自动也是非确定性图リング机，因此这个推论的一个方向立即得出。另一个方向则由定理 3.16 得出。

我们可以修改定理 3.16 的证明，以便如果 $N$ 总是终止其计算的所有分支，则 $D$ 也将总是终止。如果非确定性图灵机的所有分支在所有输入上都终止，我们称之为判定器。练习 3.3 要求您以这种方式修改证明，以获得定理 3.16 的以下推论。

推论 3.19

当且仅当某些非确定性图灵机判定该语言时，该语言才是可判定的。

📖 [逐步解释]

这两个推论分别将定理 3.16 的结论应用到了“图灵可识别”和“图灵可判定”这两个核心概念上。

推论 3.18: 对“图灵可识别”的等价性

  • 命题: “一个语言是图灵可识别的” 等价于 “存在一个NTM识别该语言”。
  • 双向证明:
  1. 方向一 (DTM -> NTM): 如果一个语言是图灵可识别的，那么根据定义，存在一个DTM $M$ 识别它。一个DTM可以被看作是一个特殊的NTM，只是它的转移函数返回的集合里永远只有一个元素。所以，这个DTM $M$ 本身就是一个能识别该语言的NTM。这个方向是自包含的。
  2. 方向二 (NTM -> DTM): 如果一个语言被某个NTM $N$ 识别。根据我们刚刚证明的定理 3.16，必然存在一个等价的DTM $D$。等价意味着 $D$ 也识别这个语言。根据定义，能被DTM识别的语言就是图灵可识别的。这个方向由定理 3.16 保证。

推论 3.19: 对“可判定”的等价性

  • 背景: 首先需要定义什么是“非确定性判定器”（Nondeterministic Decider）。一个NTM被称为判定器，如果它对于任何输入，其所有的计算分支都最终会停机（即进入接受或拒绝状态，没有无限循环）。
  • 命题: “一个语言是可判定的” 等价于 “存在一个NTM判定该语言”。
  • 证明思路: 这需要对定理 3.16 的证明过程进行一点修改和分析。
  • 方向一 (DTM判定器 -> NTM判定器): 同理，一个DTM判定器本身就是一个行为特殊的NTM判定器。
  • 方向二 (NTM判定器 -> DTM判定器): 我们需要证明，如果被模拟的NTM $N$ 是一个判定器，那么模拟它的DTM $D$ 也必然会停机。
  • 回顾 $D$ 的模拟过程：$D$ 在其地址带上按BFS顺序生成路径，并逐一模拟。
  • 因为 $N$ 是一个判定器，它的计算树中没有无限深的分支。这意味着整棵树是有限的（虽然可能非常巨大）。
  • DTM $D$ 的工作就是遍历这棵有限的树。当 $D$ 尝试了树上所有的节点（所有可能的有限地址）之后，如果还没找到接受状态，它就知道整棵树上都没有接受状态了。
  • 此时，$D$ 可以停下来并进入拒绝状态，而不是无限地去尝试更长的地址（因为更长的地址必然是无效的）。
  • 因此，如果 $N$ 总能停机，那么模拟它的 $D$ 也总能停机。这就证明了 $D$ 也是一个判定器。
📝 [总结]
  1. 推论 3.18 确立了非确定性不改变“图灵可识别”语言的范围。
  2. 推论 3.19 确立了非确定性也不改变“可判定”语言的范围。

这两个推论合在一起，完全说明了在“可计算性”和“可判定性”这两个核心层级上，非确定性这种计算资源没有带来质的飞跃。从此，在讨论一个语言是否可识别或可判定时，我们可以自由选择使用更方便的NTM模型来构建我们的论证。

🎯 [存在目的]

这两个推论的目的是将技术性的定理 3.16 的结论，清晰地应用和联系到计算理论的两个核心语言类别（图灵可识别和可判定）上。它们是定理 3.16 的“官方结论”，使得这个定理的意义和用途变得一目了然。

🧠 [直觉心智模型]
  1. 推论 3.18 (可识别): 如果我的“无限分身侦探团”（NTM）能通过找到一条线索来破案，那么我这个“按部就班的笨侦探”（DTM）通过系统排查也一定能找到那条线索来破案。反之亦然。所以我们能破的案件类型是一样的。
  2. 推论 3.19 (可判定): 现在，假设案件保证了所有线索要么通向“破案”，要么通向“死胡同”，绝不会无限延伸。那么，当我的“分身侦探团”（NTM判定器）能保证总给出“破了”或“破不了”的结论时，我这个“笨侦探”（DTM判定器）在系统排查完所有有限的线索后，也一定能给出“破了”或“破不了”的结论。

66. 枚举器

6.1 枚举器的定义

📜 [原文11]

枚举器

正如我们之前提到的，有些人用递归可枚举语言来指代图灵可识别语言。这个术语起源于一种称为枚举器的图灵机变体。广义地讲，枚举器是一种带有打印机的图灵机。图灵机可以使用该打印机作为输出设备来打印字符串。每当图灵机想要将一个字符串添加到列表中时，它就会将该字符串发送到打印机。练习 3.4 要求您给出枚举器的正式定义。下图描绘了此模型的示意图。

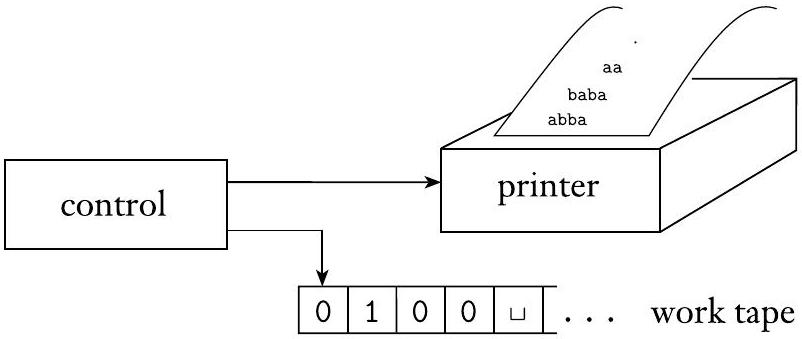
图 3.20

枚举器示意图

一个枚举器 $E$ 在其工作磁带上以空白输入开始。如果枚举器不停止，它可能会打印一个无限的字符串列表。由 $E$ 枚举的语言是它最终打印出的所有字符串的集合。此外，$E$ 可以按任何顺序生成语言的字符串，可能带有重复。现在我们准备阐述枚举器和图灵可识别语言之间的联系。

📖 [逐步解释]

这部分介绍了另一种看待图灵机能力的方式，不是作为“识别器”，而是作为“生成器”。

  1. 别名来源: “图灵可识别语言”有一个常见的别名叫做“递归可枚举语言”（Recursively Enumerable Language）。本节就是要解释“枚举”（Enumerate）这个词的由来。它来自一个叫做“枚举器”（Enumerator）的计算模型。
  2. 枚举器的结构:
    • 它本质上是一台图灵机。
    • 但它附加了一个特殊的输出设备：一台“打印机”。
    • 这台打印机可以打印出字符串。
  3. 枚举器的工作方式:
    • 无输入: 与作为识别器的图灵机不同，枚举器开始工作时，它的输入磁带是空的。它不需要外界给它一个问题来回答。它自己启动，自己开始计算。
    • 打印: 在计算过程中，枚举器可以随时决定“打印”一个字符串。它会把某个计算出的字符串发送给打印机。
    • 持续工作: 枚举器可以一直运行下去，永不停止。如果它不停止，它就可能打印出一个无限长的字符串列表。
  4. 枚举的语言 (Language Enumerated by E):
    • 一个枚举器 $E$ 所枚举的语言，就是它在其整个（可能是无限的）运行生命周期中，打印出来的所有字符串的集合。
  5. 枚举的特性:
    • 无序性: 枚举器打印字符串的顺序是任意的。它不需要按字典序或任何特定顺序打印。
    • 重复性: 枚举器可能会多次打印同一个字符串。但在最终的语言集合中，重复的元素只算一个。
  6. 核心联系: 本节的最终目的是要证明，“一个语言能被枚举器枚举出来” 和 “一个语言是图灵可识别的” 是两个完全等价的说法。
💡 [数值示例]

假设一个语言 $L = \{a, aa, aaa, \dots\}$，即所有由a组成的非空字符串。

一个枚举器 $E$ 来枚举这个语言 $L$ 可以这样工作：

  1. 开始时，工作磁带为空。
  2. 在磁带上写一个 a。
  3. 将磁带上的 a 发送到打印机。
  4. 在磁带上的 a 后面再追加一个 a，变为 aa。
  5. 将磁带上的 aa 发送到打印机。
  6. 在磁带上的 aa 后面再追加一个 a，变为 aaa。
  7. 将磁带上的 aaa 发送到打印机。
  8. ...无限重复下去...

这个枚举器 $E$ 打印出的列表是 a, aa, aaa, ...。这个列表所构成的集合就是语言 $L$。

另一个同样可以枚举 $L$ 的枚举器 $E'$ 可能工作方式很奇怪：

  1. 打印 aaa。
  2. 打印 a。
  3. 打印 aaaaa。
  4. 打印 aa。
  5. 打印 a (重复打印)。
  6. ...

只要它最终能保证所有 $a^n$ ($n \ge 1$) 都会被打印出来至少一次，那么它枚举的语言也同样是 $L$。

⚠️ [易错点]
  1. 枚举器 vs. 判定器: 不要混淆。识别器/判定器是“回答问题”的，你给它一个字符串，它回答“是”或“否”（或不回答）。枚举器是“列出答案”的，它不接收问题，而是主动地、不停地把属于某个集合的所有成员都吐出来。
  2. 停机问题: 如果语言是有限的，枚举器可以打印完所有字符串后停机。如果语言是无限的，枚举器必须永不停机，才能保证所有字符串都被打印出来。
  3. 顺序和重复不重要: 在判断一个枚举器枚举了什么语言时，我们只关心它打印出的字符串的“集合”，完全不在乎它打印的先后顺序和重复次数。
📝 [总结]

枚举器是一种带打印机的、无输入的图灵机变体。它通过不断运行并打印字符串的方式，来“生成”或“列出”一个语言的全部成员。它所生成的语言是其打印的所有字符串的集合，顺序和重复无关紧要。这个模型提供了从“生成”角度看计算问题的一个新视角。

🎯 [存在目的]

本段的目的是引入枚举器模型，并为“递归可枚举语言”这个术语提供一个直观的解释。更重要的是，它为定理 3.21 铺平了道路，该定理将揭示“识别”和“枚举”这两个看似不同的计算任务，在图灵机的层面上是等价的，从而再次强有力地证明了图灵机模型的鲁棒性和计算概念的统一性。

🧠 [直觉心智模型]
  1. 图灵识别器: 像一个海关官员。你拿一个物品（字符串）给他，他检查一番后盖上“准入”（接受）或“不准入”（拒绝）的章。
  2. 枚举器: 像一个诗人或作家。他不需要别人提问，自己关在房间里，灵感来了就写一首诗（一个字符串）扔出门外。他可能会一直写下去。外面的人收集他所有扔出来的诗，就得到了他的“作品集”（枚举的语言）。
💭 [直观想象]

想象一个神奇的喷泉。

  1. 图灵识别器: 你把一个球扔进喷泉，如果球是金色的，喷泉就把球染成红色喷出来（接受）；如果不是，就吞掉（拒绝）。
  2. 枚举器: 这个喷泉自己启动，不需要你扔球。它会源源不断地自己产生并喷出各种金色的球（语言中的字符串）。它可能会按大小喷，也可能随机喷，有时还会喷出重复的。你只要在下面用个大筐接着，最终会收集到所有可能的金色球。

77. 定理 3.21：识别与枚举的等价性

📜 [原文12]

定理 3.21

当且仅当某个枚举器枚举该语言时，该语言才是图灵可识别的。

证明 首先我们证明，如果我们有一个枚举器 $E$ 枚举语言 $A$，则图灵机 $M$ 识别 $A$。图灵机 $M$ 按以下方式工作。

$M=$ “在输入 $w$ 上：

  1. 运行 $E$。每次 $E$ 输出一个字符串时，将其与 $w$ 进行比较。
  2. 如果 $w$ 曾出现在 $E$ 的输出中，则接受。”

显然，$M$ 接受出现在 $E$ 列表中的那些字符串。

现在我们做另一个方向的证明。如果图灵机 $M$ 识别语言 $A$，我们可以为 $A$ 构建以下枚举器 $E$。假设 $s_{1}, s_{2}, s_{3}, \ldots$ 是 $\Sigma^{*}$ 中所有可能字符串的列表。

$E=$ “忽略输入。

  1. 对 $i=1,2,3, \ldots$ 重复以下操作。
  2. 对每个输入 $s_{1}, s_{2}, \ldots, s_{i}$，运行 $M$ $i$ 步。
  3. 如果任何计算接受，则打印出相应的 $s_{j}$。”

如果 $M$ 接受一个特定的字符串 $s$，它最终会出现在 $E$ 生成的列表中。事实上，它会无限次地出现在列表中，因为 $M$ 在步骤 1 的每次重复中都会从头开始在每个字符串上运行。这个过程产生了在所有可能的输入字符串上并行运行 $M$ 的效果。

📖 [逐步解释]

这个定理是连接“识别”和“枚举”两个概念的桥梁。它包含两个方向的证明。

方向一：如果语言 $A$ 可被枚举，则 $A$ 是图灵可识别的。

  • 前提: 我们有一个枚举器 $E$，它能打印出语言 $A$ 的所有字符串。
  • 目标: 我们需要构建一个图灵机 $M$，这个 $M$ 能识别语言 $A$。即，输入一个字符串 $w$，如果 $w \in A$，$M$ 就接受；如果 $w \notin A$，$M$ 就不接受（可以拒绝或无限循环）。
  • 构造 $M$:
  • $M$ 的输入是字符串 $w$。
  • $M$ 的内部包含一个模拟器，可以运行枚举器 $E$。
  • $M$ 启动 $E$ 的模拟。
  • $E$ 会开始打印字符串。每当 $E$ 打印出一个字符串 $s$ 时，$M$ 就立刻将 $s$ 与自己的输入 $w$ 进行比较。
  • 如果 $s = w$: 匹配成功！$M$ 立即停机并接受。
  • 如果 $s \neq w$: $M$ 就继续等待 $E$ 打印下一个字符串。
  • 正确性分析:
  • 如果 $w \in A$：因为 $E$ 能枚举 $A$ 的所有成员，所以 $w$ 最终一定会被 $E$ 打印出来。当它被打印出来的那一刻，$M$ 就会发现匹配并接受。
  • 如果 $w \notin A$：$E$ 永远不会打印出 $w$。因此，$M$ 将永远在等待和比较，它会无限循环下去。这符合图灵可识别的定义（接受时停机，不接受时可不停机）。

方向二：如果语言 $A$ 是图灵可识别的，则 $A$ 可被枚举。

  • 前提: 我们有一个图灵机 $M$，它能识别语言 $A$。
  • 目标: 我们需要构建一个枚举器 $E$，它能打印出语言 $A$ 的所有字符串。
  • 构造 $E$ (这个构造非常巧妙，被称为“Dovetailing”或“燕尾榫”法):
  • 首先，我们需要一个系统的方法来列出所有可能的输入字符串。假设我们能按某种顺序（如长度优先的字典序）生成 $\Sigma^*$ 中的所有字符串：$s_1, s_2, s_3, \ldots$。
  • 一个错误的想法: 依次对 $s_1, s_2, s_3, \ldots$ 运行 $M$。如果 $M(s_1)$ 接受，就打印 $s_1$；然后对 $s_2$ 运行 $M$ ... 这个想法的问题在于，如果 $M$ 在某个不属于 $A$ 的输入 $s_k$ 上无限循环，那么 $E$ 就会卡在 $s_k$ 上，永远没有机会去测试和打印后面的字符串了。
  • 正确的构造 (Dovetailing): $E$ 通过一个双重循环来模拟 $M$：
  • 外层循环 i: $i$ 从 1 到无穷大，代表“模拟步数上限”。
  • 内层循环 j: $j$ 从 1 到 $i$，代表“被测试的字符串索引”。
  • 算法:
  1. for i = 1, 2, 3, ...
  2. for j = 1, 2, ..., i
  3. 模拟图灵机 $M$ 在输入字符串 $s_j$ 上运行 $i$ 步。
  4. 如果这 $i$ 步之内，$M$ 停机并接受了 $s_j$，那么就打印 $s_j$。
    • 正确性分析:
    • 如果某个字符串 $s_k \in A$：那么识别器 $M$ 会在有限步（比如 $N$ 步）内接受 $s_k$。
    • 在我们的枚举器 $E$ 中，当外层循环的 i 增长到足够大（即 $i \ge k$ 且 $i \ge N$）时，内层循环就一定会执行到“在输入 $s_k$ 上模拟 $M$ $i$ 步”这个任务。
    • 因为 $i \ge N$，所以在这次模拟中，$M$ 必然会接受 $s_k$。于是，$E$ 就会打印出 $s_k$。
    • 这就保证了所有属于 $A$ 的字符串最终都会被 $E$ 打印出来。
    • 并行效果: 这个巧妙的双循环，其效果等同于“并行”地运行 $M$ 在所有可能的输入上。第一轮，所有字符串都只跑1步；第二轮，前两个字符串跑2步；第三轮，前三个字符串跑3步... 这种方法避免了被任何单个无限循环的计算卡住，保证了所有有限时间内能完成的计算最终都会被完成。
💡 [数值示例]

方向一示例:

  • 语言 $A = \{ "cat", "dog", "pig" \}$
  • 枚举器 $E$ 按顺序打印: dog, pig, cat。
  • 识别器 $M$ 输入 w = "cat":
  1. $M$ 启动 $E$。
  2. $E$ 打印 dog。$M$ 比较 "cat" == "dog"? 否。
  3. $E$ 打印 pig。$M$ 比较 "cat" == "pig"? 否。
  4. $E$ 打印 cat。$M$ 比较 "cat" == "cat"? 是！$M$ 接受。
    • 如果 $M$ 输入 w = "bird"，它会永远等下去，因为 $E$ 永远不会打印 bird。

方向二示例 (Dovetailing):

  • 语言 $A$ 被图灵机 $M$ 识别。
  • 所有可能的字符串列表: $s_1="", s_2="a", s_3="b", s_4="aa", ...$
  • 枚举器 $E$ 的工作流程:
  • i=1: 模拟 $M(s_1)$ 1步。假设不接受。
  • i=2:
  • 模拟 $M(s_1)$ 2步。假设不接受。
  • 模拟 $M(s_2)$ 2步。假设 $M$ 在第2步接受了 $s_2$ ("a")。打印 "a"。
  • i=3:
  • 模拟 $M(s_1)$ 3步。假设 $M$ 在第3步就无限循环了，但我们只模拟3步，所以没关系。
  • 模拟 $M(s_2)$ 3步。它在第2步就接受了，所以这次模拟也会发现它接受。再次打印 "a" (重复是允许的)。
  • 模拟 $M(s_3)$ 3步。假设不接受。
  • i=4:
  • ...
  • 模拟 $M(s_4)$ 4步。假设 $M$ 在第4步接受了 $s_4$ ("aa")。打印 "aa"。
  • 这个过程会一直持续下去，确保任何被 $M$ 接受的字符串，无论需要多少步，都会在 $E$ 的外循环 i 达到那个步数时被发现并打印出来。
⚠️ [易错点]
  1. 方向二证明的关键: 核心是Dovetailing技巧。如果不能理解为什么简单的串行模拟行不通，以及Dovetailing如何通过步数限制实现“并行”，就无法理解这个证明。
  2. 重复打印: 在方向二的构造中，一个被接受的字符串会被无限次地打印出来。例如，只要 $i$ 足够大，$M(s_2)$ 就会被一次又一次地模拟并成功，导致"a"被反复打印。但这没关系，因为枚举器的定义允许重复。
  3. 可识别 vs. 可判定: 如果 $M$ 是一个判定器（总能停机），那么方向二的构造会更简单些，但Dovetailing方法对于更一般的识别器（可能不停机）也同样有效，所以它是一个更强大的证明技巧。
📝 [总结]

定理 3.21 雄辩地证明了计算的两种基本模式——“识别”（回答是非题）和“枚举”（列出所有答案）——在图灵机的计算能力下是等价的。证明的关键在于两个方向的巧妙构造：用枚举器作为“答案生成器”来构建识别器，以及用“Dovetailing”并行模拟技巧，利用识别器来构建一个不会被卡住的枚举器。

🎯 [存在目的]

这个定理为“图灵可识别语言”提供了“递归可枚举”这个等价且更具描述性的名称。它从一个全新的角度揭示了这类语言的本质：它们是那些其成员可以被某个机械化过程逐一列举出来的集合。这个观点在高级计算理论，特别是与逻辑和递归函数论的联系中，非常重要。

🧠 [直觉心智模型]

想象一个神秘的俱乐部 $A$。

  1. 识别器 M: 是俱乐部门口的守卫。你报上一个名字 $w$，他查一下花名册，如果名字在上面，就让你进去（接受）。
  2. 枚举器 E: 是俱乐部内部的广播员。他会不停地、随机地念出花名册上的名字。
  3. 定理 3.21证明:
  4. 方向一: 如果你有广播员E，怎么当一个守卫M？很简单，你听着广播。有人报名字 $w$，你就一直听广播，直到广播念出 $w$，你就让他进。
  5. 方向二: 如果你只有守卫M，怎么当一个广播员E？你不能一个个问守卫“张三在吗？李四在吗？”因为问到某个不在的人，守卫可能会永远埋头查下去（无限循环）。你的做法（Dovetailing）是：你准备一个所有可能人名的列表。第一天，你把列表上第一个名字拿去问守卫，但只给他1秒钟查。第二天，你把前两个名字拿去问，每个给2秒钟... 这样，无论哪个名字在花名册上，无论守卫要查多久，总有一天，你会给他足够的时间让他查出来，那时你就可以把这个名字广播出去。

88. 与其他模型的等价性

📜 [原文13]

与其他模型的等价性

到目前为止，我们已经介绍了图灵机模型的几种变体，并证明它们在能力上是等价的。许多其他通用计算模型也已被提出。其中一些模型非常像图灵机，但另一些则大相径庭。它们都共享图灵机的基本特征——即不受限制地访问无限内存——这使它们区别于有限自动机和下推自动机等较弱的模型。值得注意的是，所有具有该特征的模型，只要满足合理的要求，最终都被证明在能力上是等价的。 ${ }^{3}$

[^1]为了理解这种现象，请考虑编程语言的类似情况。许多编程语言，例如 Pascal 和 LISP，在风格和结构上彼此看起来非常不同。是否可以在其中一种编程语言中编程某个算法而不能在其他编程语言中编程呢？当然不是——我们可以将 LISP 编译成 Pascal，将 Pascal 编译成 LISP，这意味着这两种语言描述了完全相同一类的算法。所有其他合理的编程语言也是如此。计算模型的普遍等价性正是出于相同的原因。任何满足某些合理要求的两个计算模型都可以相互模拟，因此在能力上是等价的。

这种等价现象具有重要的哲学推论。尽管我们可以想象许多不同的计算模型，但它们所描述的算法类别保持不变。虽然每个单独的计算模型在其定义上都具有一定的任意性，但它所描述的算法的底层类别是自然的，因为其他模型也达到了相同且独特的类别。这种现象对数学产生了深远的影响，我们将在下一节中展示。

📖 [逐步解释]

这部分是对本章内容进行一个拔高和总结，并引出其深远的哲学意义，为下一节的“丘奇-图灵论题”做铺垫。

  1. 回顾与总结: 到目前为止，我们已经证明了图灵机的几个变体（带“停留”选项的、多带的、非确定性的、枚举器模型）都与标准的、单带确定性图灵机在计算能力上等价。这显示了图灵机模型的鲁棒性。
  2. 扩展到其他模型: 作者指出，历史上除了图リング机，还出现过许多其他的、试图定义“什么是算法/计算”的模型。
    • 有些模型和图灵机很像。
    • 有些则完全不同，比如：
    • Lambda演算 ( Alonzo Church, 1930s)：基于函数抽象和应用的符号系统。
    • 递归函数 (Kurt Gödel, Jacques Herbrand, 1930s)：基于一组初始函数和构造规则来定义可计算函数。
    • Post对应问题 (Emil Post, 1940s)：一种基于字符串重写的系统。
  3. 共同特征与关键区别:
    • 共同特征: 所有这些“通用”计算模型，尽管形式各异，但都有一个共同的核心特征：可以不受限制地访问无限的内存。对于图灵机是无限磁带，对于函数式模型则体现在可以处理任意复杂的递归深度。
    • 与弱模型的区别: 这个特征正是它们与有限自动机（内存有限，即状态数有限）和下推自动机（内存是受限的栈）的根本区别。
  4. 惊人的结论：普遍等价性: 历史上一个惊人的发现是，所有这些满足“无限内存”和“基本合理操作”的计算模型，最终都被证明是相互等价的。即，任何一个模型能计算的函数/识别的语言，其他所有模型也都能。
  5. 编程语言的类比 (脚注):
    • 为了帮助理解这种普遍等价性，作者用现代编程语言做类比。
    • Pascal, C++, Python, LISP, Java... 这些语言在语法、风格、设计哲学上千差万别。
    • 但有没有一个算法，是只能用Python写，而绝对无法用C++实现的呢？没有。因为我们可以编写一个“编译器”或“解释器”，将一种语言翻译成另一种语言。
    • 这种“可编译性”或“可模拟性”意味着所有这些“图灵完备”的编程语言在计算能力上是等价的。它们描述的是同一个“算法”的集合。
    • 计算模型的等价性也是同理，模型之间可以相互“模拟”。
  6. 哲学推论与自然性:
    • 任意性 vs. 自然性: 任何一个具体的计算模型（如图灵机）的定义，都带有一些“人为”或“任意”的成分（比如为什么是磁带而不是别的？为什么是左右移动？）。
    • 然而，既然这么多形式迥异的模型最终都殊途同归，指向了同一个计算能力的等级，这强烈地暗示了它们所共同描述的那个“算法类别”或“可计算性”本身，不是一个随意的、人为的构造，而是一个自然的、根本的、独立于具体模型而存在的数学/逻辑概念。
    • 独特性: 这个类别是独特的，我们似乎找不到一个“半路”的模型，它的能力介于下推自动机和图灵机之间，并且同样“自然”和“鲁棒”。
  7. 预告: 这种“自然性”和“独特性”的现象，对数学基础产生了深远影响，并直接导向了计算理论的基石——丘奇-图灵论题。
⚠️ [易错点]
  1. “合理的要求”: 这个短语很重要。一个计算模型要被认为是“合理的”，它通常需要满足一些基本条件，比如它的操作必须是有限可描述的、每一步操作是机械的和确定的（即使模型本身是非确定性的，其选择集合也是确定的）。如果允许模型拥有“神谕”等超计算能力，那它就不在这个等价类里了。
  2. 效率不是重点: 再次强调，这里的“等价”是指“能算什么”的能力等价，而不是“算得多快”的效率等价。用图灵机模拟Lambda演算可能会非常慢，反之亦然，但这不影响它们的可计算性范围相同。
📝 [总结]

本段将前面关于图灵机变体等价性的讨论，提升到了一个更宏大的层面。它指出，历史上所有“合理”的通用计算模型，尽管形式各不相同，但最终都被证明在计算能力上是等价的。这种“普遍等价性”现象暗示了“可计算性”是一个独立于具体模型而存在的、深刻而自然的数学概念。这为下一节提出的丘奇-图灵论题——即图灵机的计算能力恰好就等于我们直觉中的“算法”能力——提供了强有力的哲学和历史支持。

🎯 [存在目的]

本段的目的是完成从具体技术证明到宏大哲学论断的过渡。它将前面所有关于鲁棒性的讨论汇集起来，赋予其深刻的意义，并为全书最重要的核心论题——丘奇-图灵论题——的登场搭好舞台。它告诉读者，我们之所以花了这么大力气研究图灵机的各种变体，不仅仅是为了技术练习，更是为了揭示一个关于计算本质的深刻真理。

🧠 [直觉心智模型]

想象一下不同国家古代的数学家都在研究“面积”。

  1. 中国的数学家可能用“割圆术”或“出入相补”原理。
  2. 古希腊的数学家可能用“穷竭法”。
  3. 印度的数学家可能有自己的一套代数方法。

他们使用的方法、符号、语言都完全不同（不同的计算模型）。但最终，他们对于同一个图形计算出的面积值都是一样的，他们能解决的“可求面积”的图形种类也是一样的（等价性）。这说明，“面积”这个概念是独立于具体求算方法而存在的、一个客观的几何属性（自然的数学概念）。“可计算性”也是如此。

💭 [直观想象]

全世界的人都想爬一座名为“计算之巅”的山。

  1. 图灵：设计了一条从北坡攀登的路线，需要绳索和冰镐（图灵机）。
  2. 丘奇：设计了一条从南坡的路线，需要高超的徒手攀岩技巧（Lambda演算）。
  3. 哥德尔：设计了一条从东坡的路线，需要解一系列复杂的逻辑谜题（递归函数）。

一开始，大家以为这三条路线能到达的高度不一样。但后来发现，任何一条路能到达的地方，另外两条路也都能到达。最终，他们都在同一个顶峰相遇了。这说明，这座山的“顶点”（可计算性的边界）是确定的，不因为你选择哪条攀登路线而改变。

9行间公式索引

  1. $$ \delta: Q \times \Gamma^{k} \longrightarrow Q \times \Gamma^{k} \times\{\mathrm{L}, \mathrm{R}, \mathrm{~S}\}^{k}, $$

解释: 这是多带图灵机的转移函数的通用形式，它根据当前状态和所有 $k$ 个磁头下的符号，决定新的状态、要在 $k$ 条磁带上写入的新符号以及 $k$ 个磁头各自的移动方向。

  1. $$ \delta\left(q_{i}, a_{1}, \ldots, a_{k}\right)=\left(q_{j}, b_{1}, \ldots, b_{k}, \mathrm{~L}, \mathrm{R}, \ldots, \mathrm{~L}\right) $$

解释: 这是一个多带图灵机转移函数的具体应用实例，展示了当机器在状态 $q_i$ 并读到符号序列 $a_1, \ldots, a_k$ 时，如何转移到新状态 $q_j$，写入新符号并移动磁头。

  1. $$ \# \stackrel{\bullet}{w}_{1} w_{2} \cdots w_{n} \# \stackrel{\bullet}{\sqcup} \# \cdots \# \stackrel{\bullet}{\sqcup} \# . $$

解释: 这展示了模拟多带图灵机的单带图灵机在初始化后，其磁带内容的格式，它通过分隔符#和带点符号来编码所有虚拟磁带的内容和磁头位置。

  1. $$ \delta: Q \times \Gamma \longrightarrow \mathcal{P}(Q \times \Gamma \times\{\mathrm{L}, \mathrm{R}\}) . $$

解释: 这是非确定性图灵机的转移函数的形式，其输出是一个包含多个可能动作的集合（由幂集符号 $\mathcal{P}$ 表示），体现了非确定性的选择。

109. 丘奇-图灵论题

📜 [原文14]

3.3 丘奇-图灵论题

到目前为止，我们已经提出了三种不同类型的计算模型：有限自动机、下推自动机和图灵机。它们的能力各不相同。有限自动机能识别正则语言，下推自动机能识别上下文无关语言，而图灵机能识别图灵可识别语言。在本节中，我们将考察图灵机模型与算法概念之间的关系。

在前面的章节中，我们非正式地引入了“算法”的概念。例如，在第 1 章中，我们将一个算法描述为处理某些数据的分步过程。这个定义是非正式的，而不是数学上精确的。对于有限自动机和下推自动机，我们有信心理解它们的能力，并且能够凭直觉判断某些问题是否超出了它们的能力范围。例如，我们知道 $a^{n} b^{n}$ 不是正则的，而 $a^{n} b^{n} c^{n}$ 不是上下文无关的。但是，要凭直觉判断一个问题是否“有算法”，即是否能被图灵机解决，就困难得多了。

在 20 世纪上半叶，在现代计算机出现之前，数学家们试图澄清“算法”的含义。他们面临的挑战是给出一个对“算法”的精确定义，这个定义要与我们对算法的直观概念相对应。一些数学家提出了各种各样的定义，但它们最终都被证明是等价的。阿隆佐·丘奇（Alonzo Church）

使用了我们现在所称的图灵机。这两个定义被证明是等价的。这一发现引出了丘奇-图灵论题，它为算法的直观概念提供了一个精确的定义。

9.1 丘奇-图灵论题的提出与内容

📜 [原文15]

在 20 世纪上半叶，在现代计算机出现之前，数学家们试图澄清“算法”的含义。他们面临的挑战是给出一个对“算法”的精确定义，这个定义要与我们对算法的直观概念相对应。一些数学家提出了各种各样的定义，但它们最终都被证明是等价的。阿隆佐·丘奇（Alonzo Church）使用了一种称为 $\lambda$-演算的技术，而艾伦·图灵（Alan Turing）则使用了我们现在所称的图灵机。这两个定义被证明是等价的。这一发现引出了丘奇-图灵论题，它为算法的直观概念提供了一个精确的定义。

丘奇-图灵论题

直观意义上的算法，等同于图灵机算法。

这个论题之所以没有被证明，是因为它将一个非形式化的直观概念（算法）与一个形式化的数学定义（图灵机）联系起来。论题并没有一个可以被数学证明的定理的地位。然而，它得到了大量的证据支持，并被普遍接受。

例如，考虑一个具体的问题，比如对整数列表进行排序。你可能已经学习了好几种算法，比如冒泡排序、插入排序或归并排序。这些都是我们直观理解的算法。对于这些算法中的每一种，我们都可以构造一个图灵机来实现它。此外，迄今为止，还没有人能够提出一个被普遍认为是算法，但不能用图灵机来模拟的例子。

📖 [逐步解释]

这部分正式提出了计算理论的基石——丘奇-图灵论题。

  1. 历史背景: 在计算机诞生之前，数学家们（如希尔伯特）就在讨论“算法”或“机械化过程”了，但这个概念非常模糊，是停留在直觉和哲学层面的。为了能严格地讨论“什么问题是可计算的”，他们迫切需要一个精确的、数学化的“算法”定义。
  2. 两大模型的提出:
    • 阿隆佐·丘奇: 提出了 $\lambda$-演算 (Lambda Calculus)，这是一个基于函数定义、应用和递归的符号系统。它是现代函数式编程语言（如LISP, Haskell）的理论鼻祖。
    • 艾伦·图灵: 提出了图灵机 (Turing Machine)，这是一个基于模拟人类计算过程的、机械化的读写符号模型。
  3. 等价性的发现: 一个令人震惊的发现是，这两个看起来风马牛不及的模型，在计算能力上竟然是等价的。任何能用 $\lambda$-演算表达的计算，都能用图灵机模拟，反之亦然。这暗示它们可能共同触及了“计算”这一概念的本质。
  4. 论题的正式陈述: 基于这种等价性和其他证据，丘奇和图灵共同提出了这个论题（虽然他们是独立提出的）：
    • 丘奇-图灵论题 (Church-Turing Thesis): 我们在直觉上认为的任何“算法”或“有效计算过程”，都可以由一台图灵机来执行。反之，任何图灵机执行的过程，也符合我们对“算法”的直观理解。
    • 简而言之：算法 = 图灵机。
  5. 为什么是“论题”而不是“定理”:
    • 定理 (Theorem) 是在形式系统内部，可以通过逻辑推导来证明其为真的陈述。
    • 论题 (Thesis) 或称“假说” (Hypothesis)，是连接一个非形式化概念和一个形式化定义的桥梁。
    • “直观意义上的算法”是一个模糊的、心理学上的、非形式化的概念，它无法被写进一个数学证明里。
    • 因此，我们永远无法“证明”图灵机就等于这个模糊的概念。我们只能不断地寻找证据来支持或反驳它。
  6. 支持论题的证据:
    • 证据一 (普遍等价性): 历史上所有被提出的、合理的、试图定义算法的计算模型（$\lambda$-演算, 递归函数, Post系统等）最终都被证明与图灵机等价。
    • 证据二 (缺乏反例): 至今为止，还没有人能找到一个例子，说“这是一个清晰的、一步步的、机械化的算法，但它无法用图灵机来实现”。
    • 证据三 (实践检验): 所有我们现实世界中的计算机（无论多么复杂），其计算能力都被认为是与图灵机等价的（在忽略物理限制如内存大小和时间的情况下）。任何能在你的电脑上运行的程序，理论上都能在图灵机上模拟。
∑ [公式拆解]
  • $\lambda$-演算: 这是一个数学符号系统，不是本课程的重点，但可以简单理解一下。它有三个基本操作：
  • 变量: x
  • 抽象 (定义函数): λx. t 表示一个匿名函数，它接受参数 x 并返回表达式 t 的值。例如 λx. x+1 就是一个加一函数。
  • 应用 (调用函数): t s 表示将函数 t 应用于参数 s。例如 (λx. x+1) 2 的结果就是 3。

通过这三种简单的操作，可以构建出所有可计算的函数。

💡 [数值示例]
  • 问题: 判断一个给定的正整数 $n$ 是否为素数。
  • 直观算法 (试除法):
  1. 如果 $n \le 1$，它不是素数。
  2. 从 $i=2$ 开始，到 $\sqrt{n}$ 结束。
  3. 检查 $n$ 能否被 $i$ 整除。
  4. 如果能，则 $n$ 不是素数，算法结束。
  5. 如果循环结束都没有找到能整除的 $i$，则 $n$ 是素数。
    • 丘奇-图灵论题说: 上面这个我们凭直觉写出来的“试除法”算法，一定可以被转化成一台（可能非常复杂的）图灵机。这台图灵机的输入是 $n$ 的二进制或一元表示，它会在有限步内停机，如果 $n$ 是素数则进入接受状态，否则进入拒绝状态。虽然我们不在这里构造它，但论题断言了它的存在性。
⚠️ [易错点]
  1. 不要试图去“证明”这个论题: 必须理解它的本质是一个连接直觉与形式的“桥梁”，是一个被广泛接受的“信念”或“公理”，而不是一个数学定理。
  2. 论题不关心效率: 论题只关心“能不能算”，不关心“算得快不快”。用图灵机模拟一个现代算法可能会慢到无法想象，但这不影响论题的正确性。
  3. 物理世界 vs. 数学世界: 论题是关于数学和算法的，不是关于物理现实的。量子计算等模型可能会在效率上超越经典计算机，但它们是否能解决图灵机无法解决的“不可判定”问题，仍然是一个开放和有争议的前沿领域。在经典计算理论的框架下，丘奇-图灵论题是基石。
📝 [总结]

丘奇-图灵论题是一个深刻的论断，它声称图灵机这个精确的数学模型，完整地捕捉了我们对“算法”这个模糊概念的全部直观内涵。这个论题虽然无法被证明，但由于大量的证据支持和缺乏任何反例，它已被普遍接受为计算理论的 foundational principle。它授权我们使用图灵机作为“算法”的正式代言人。

🎯 [存在目的]

这个论题的存在，为整个计算理论提供了坚实的地基。

  1. 它使“不可计算性”的证明成为可能: 在此之前，说一个问题“没有算法”是无意义的，因为“算法”的定义不清晰。有了这个论题，我们就可以通过证明“不存在能解决此问题的图灵机”，来雄辩地证明“不存在任何形式的算法能解决此问题”。
  2. 它统一了计算模型: 它告诉我们不必再苦苦寻找“更强大”的计算模型了（在经典框架内），图灵机已经达到了“算法”所能做的一切的极限。
  3. 它连接了数学与计算机科学: 它为计算机科学的核心概念——算法——提供了数学上的严谨性。
🧠 [直觉心智模型]

想象一下，古代人对“生命”有一个直观但模糊的概念。后来，生物学家发现了DNA，并提出了一个“DNA论题”：“任何我们直观上认为是‘生命’的东西，其核心机制都可以用DNA和相关的分子生物学来描述。”

  1. 这个“DNA论题”也无法被绝对“证明”，因为“生命”的直观定义是模糊的（比如病毒算不算生命？）。
  2. 但所有已知的生物都符合DNA理论，我们也没有找到反例。
  3. 这个论题使得生物学从描述性的科学，变成了一门可以进行精确分析和预测的科学。

丘奇-图灵论题在计算领域扮演了和“DNA论题”在生物学领域类似的角色。

💭 [直观想象]

你面前有一个号称“万能菜谱”的书（图灵机）。丘奇-图灵论题就是这样一个论断：“宇宙中任何一道你可以想象出来的、可以通过一步步明确指令做出来的菜（任何算法），其菜谱都能在这本‘万能菜谱’里找到一个等价的版本。” 你无法证明它，因为“可以想象出来的菜”这个概念太模糊了。但你发现，无论是法餐、中餐还是分子料理，似乎都能在这本书里找到做法。而且，从未有人能做出一样新菜，并有说服力地证明其做法绝对无法被这本“万能菜谱”所描述。于是，你接受了这个论题，并把这本“万能菜谱”作为定义所有“可烹饪菜肴”的标准。

9.2 论题的应用：希尔伯特的第十个问题

📜 [原文16]

一个重要的应用是，它允许我们通过证明不存在能解决某个问题的图灵机，来证明不存在解决该问题的“算法”。一个著名的例子是希尔伯特的第十个问题。

希尔伯特的第十个问题

在1900年，数学家大卫·希尔伯特提出了23个挑战性的数学问题。第十个问题是要求设计一个“算法”，该算法能够判断任意一个给定的丢番图方程（即系数为整数的多项式方程）是否存在整数解。例如，方程 $3x^2 - 2xy - y^2z - 7 = 0$ 是一个丢番图方程。而方程 $x^2+y^2=3$ 则没有整数解。几十年来，这个问题一直悬而未决。

直到1970年，尤里·马季亚谢维奇（Yuri Matiyasevich）基于朱莉娅·罗宾逊、马丁·戴维斯和希拉里·普特南的工作，证明了这样一个通用的算法是不存在的。他通过证明这个问题等价于停机问题来实现这一点，我们知道停机问题是不可判定的。根据丘奇-图灵论题，既然不存在图灵机来判定这个问题，那么就不存在任何我们直观意义上的“算法”来解决它。这个问题是“算法上不可解的”。

📖 [逐步解释]

这部分通过一个著名的历史问题，展示了丘奇-图灵论题的巨大威力。

  1. 论题的威力: 丘奇-图灵论题最大的作用，就是给了我们一个证明“某个问题无法用任何算法解决”的工具。证明策略是：
  2. 将问题形式化为一个语言。
  3. 证明这个语言不是图灵可判定的（即，不存在一个总能停机的图灵机来识别它）。
  4. 援引丘奇-图灵论题，得出结论：既然连图灵机都无法解决，那么就没有任何“算法”能解决它。
  5. 希尔伯特的第十个问题:
    • 提出: 1900年，大卫·希尔伯特，一位世纪之交的顶尖数学家，提出了23个他认为将指引20世纪数学发展方向的核心问题。
    • 问题陈述 (第十个): 是否存在一个“算法”，对于任何一个给定的丢番图方程，该算法都能在有限时间内给出答案：“是”（有整数解）或“否”（没有整数解）。
    • 丢番图方程 (Diophantine Equation): 一个变量和系数都限制为整数的多项式方程。例如 $ax+by=c$, $x^2+y^2=z^2$ 等。
  6. 问题的核心: 注意，希尔伯特不是要求去“解”任何一个方程，而是要求一个通用的“判断”程序。这个程序就像一个黑盒子，你把任何丢番图方程的描述丢进去，它就要能告诉你这个方程到底有没有整数解。
  7. 漫长的解决之路: 这个问题困扰了数学界70年。人们找不到这样一个算法，但也无法证明它不存在。证明它不存在的困难在于：你怎么能证明在所有可能想到的、无穷多种“算法”里，没有一个是可行的呢？
  8. 最终的解决:
    • 关键人物: 马丁·戴维斯 (Martin Davis), 希拉里·普特南 (Hilary Putnam), 朱莉娅·罗宾逊 (Julia Robinson) 做出了奠基性的工作。他们一步步地建立了丢番图方程解的集合与图灵机计算之间的联系。
    • 临门一脚: 1970年，苏联数学家尤里·马季亚谢维奇 (Yuri Matiyasevich) 证明了最后一个关键的引理（马季亚谢维奇定理），从而完成了整个证明链条。
    • 证明的本质: 他们的工作最终表明，一个语言 $L_D = \{ p | p \text{是一个有整数解的丢番图方程的编码} \}$ 是图灵可识别的，但不是图灵可判定的。（具体来说，他们证明了所有图灵可识别的语言都可以归约到这个问题上，而有些图灵可识别语言是不可判定的，例如停机问题的语言 $A_{TM}$）。
  9. 与丘奇-图灵论题的结合:
    • 马季亚谢维奇等人的工作给出了一个纯数学的、关于图灵机的结论：不存在一个总能停机的图灵机来判定丢番图方程是否有解。
    • 现在，丘奇-图灵论题登场了。它说：图灵机 = 算法。
    • 因此，既然不存在图灵机算法，就意味着不存在任何我们能想象的、任何形式的“算法”来解决这个问题。
    • 希尔伯特的第十个问题得到了一个否定的回答：不存在这样的算法。这个问题是“算法上不可解的”(algorithmically unsolvable)。
∑ [公式拆解]
  • 丢番图方程的例子:
  • $3x^2 - 2xy - y^2z - 7 = 0$
  • 这是一个三元（x, y, z）丢番图方程。我们要找的是是否存在一组整数 (x, y, z) 使得等式成立。
  • $x^2 + y^2 = 3$
  • 这是一个二元丢番图方程。我们可以轻易验证它没有整数解。因为整数的平方只能是 0, 1, 4, 9, ... 任意两个这样的数相加都不可能等于3。
  • $x^2 + y^2 = z^2$ (著名的勾股定理方程)
  • 它有无穷多组整数解，被称为勾股数，例如 (3, 4, 5), (5, 12, 13) 等。
💡 [数值示例]
  • 输入给“想象中的算法”: 一个方程的编码，比如 P(x,y,z) = x^3 + y^3 - z^3。
  • 算法的期望输出: "有解" (因为例如 $x=1, y=2, z$ 不是整数；但 $x=3, y=4, z$ 也不是整数... 费马大定理指出 n>2 时 $x^n+y^n=z^n$ 无正整数解，但这里允许负数和0。例如 $1^3+(-1)^3=0^3$，所以有解)。
  • 另一个输入: P(x,y,z) = 3xyz - x^3 - y^3 - z^3 - 1
  • 算法的期望输出: "有解" 或 "无解"。
  • 希尔伯特第十问题的结论: 这样一个能对任意输入的方程编码进行判断的通用“算法”盒子，是不可能被制造出来的。
⚠️ [易错点]
  1. 不可解 vs. 还没解出来: “不可解”是一个非常强的数学结论。它不是说我们“目前还不够聪明，没找到算法”，而是说我们已经用数学方法证明了这样的算法永远不可能存在，无论未来的数学或计算机如何发展（在经典计算框架内）。
  2. 特定方程的可解性: 结论并不是说我们无法判断任何一个特定丢番图方程的可解性。对于很多具体的方程（如上面举的例子），我们当然可以通过各种数学技巧来判断。结论是关于通用算法的不存在性。
📝 [总结]

希尔伯特的第十个问题是丘奇-图灵论题威力的最佳展示。数学家们通过将这个问题与图灵机的停机问题联系起来，证明了不存在一个能判定所有丢番图方程是否有整数解的图灵机。然后，借助丘奇-图灵论题这座桥梁，这个关于图灵机的数学结论被“翻译”为了一个关于“算法”的、更具普遍意义的结论：希尔伯特所寻求的通用算法是根本不存在的。

🎯 [存在目的]

本段的目的是用一个深刻而真实的历史案例，让学生具体地感受到丘奇-图灵论题不是一个空洞的哲学思辨，而是一个强大的、可以用来解决重要数学问题的工具。它展示了计算理论如何为数学的其他领域（在这里是数论）提供决定性的、甚至是革命性的答案。

🧠 [直觉心智模型]

你是一个药剂师，你想发明一种“万能诊断试纸”（通用算法）。这种试纸遇到任何一种“有解药的毒药”（有解的方程）就变蓝，遇到“无解药的毒药”（无解的方程）就变红。

  1. 马季亚谢维奇等人：他们通过几十年的研究，最终证明了，在化学原理（图灵机理论）层面，不可能制造出一种化合物（图灵机程序），能对所有毒药都产生正确的颜色反应。
  2. 丘奇-图灵论题：这个论题说“任何你能想象的诊断方法（算法），本质上都是一种化学反应（图灵机程序）”。
  3. 结论: 因此，你梦想中的那种“万能诊断试纸”是绝对不可能被发明出来的。
💭 [直观想象]

想象一个巨大的、无限的图书馆，里面放着所有可能的丢番图方程（每本书是一个方程）。有些书的封面上有一个隐藏的标记，表示“这本书里描述的方程有整数解”。

  1. 希尔伯特的梦想: 雇佣一个图书管理员（算法），给他任何一本书，他都能在有限时间内告诉你封面上到底有没有那个隐藏标记。
  2. 马季亚谢维奇的证明: 证明了这个图书管理员（如果他只是一个遵循机械化规则的机器人，即图灵机）是不存在的。因为要确定某些书上有没有标记，需要这个机器人去解决一个他自己无法解决的悖论（停机问题）。
  3. 丘奇-图灵论题的应用: 我们相信，任何一个“人类图书管理员”能遵循的明确步骤，这个“机器人图书管理员”也能学。既然机器人不存在，那么人类图书管理员也不可能拥有这样一套通用的判断方法。这个图书馆的秘密，无法通过一个统一的“算法”来完全揭示。

[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。