13.3
算法的定义
通俗地说,算法(algorithm)是执行某个任务的一系列简单指令的集合。算法在日常生活中司空见惯,有时被称为程序(procedure)或食谱(recipe)。算法在数学中也扮演着重要的角色。古代数学文献中包含了各种任务的算法描述,例如寻找素数和最大公约数。在当代数学中,算法比比皆是。
尽管算法在数学中有着悠久的历史,但算法本身的概念直到二十世纪才被精确定义。在此之前,数学家们对算法有着直观的认识,并在使用和描述它们时依赖于这种认识。但这种直观认识不足以对算法获得更深入的理解。以下故事讲述了算法的精确定义对于解决一个重要数学问题的重要性。
希尔伯特问题
1900年,数学家大卫·希尔伯特在巴黎举行的国际数学家大会上发表了一个现已闻名的演讲。在他的演讲中,他提出了23个数学问题,并将它们作为对未来一个世纪的挑战。他清单上的第十个问题涉及算法。
在描述该问题之前,让我们简要讨论一下多项式(polynomials)。多项式是项的和,其中每一项都是某些变量与一个常数(constant)(称为系数(coefficient))的乘积。例如,
是一个系数为6的项,而
是一个在变量 $x, y$ 和 $z$ 上有四项的多项式。对于此讨论,我们只考虑整数系数。多项式的根(root)是为其变量赋值,使得多项式的值为0。此多项式在 $x=5, y=3$ 和 $z=0$ 处有一个根。这个根是整数根,因为所有变量都被赋予了整数值。有些多项式有整数根,有些则没有。
希尔伯特的第十个问题是设计一种算法,用于测试多项式是否有整数根。他没有使用“算法”一词,而是使用了“一个过程,通过该过程,可以在有限数量的操作中确定”。[^4]有趣的是,在他提出这个问题的方式中,希尔伯特明确要求“设计”一种算法。因此,他显然假定这种算法必然存在——只需要有人找到它。
正如我们现在所知,对于这项任务,不存在任何算法;它是算法上不可解的。对于那个时期的数学家来说,要凭借他们对算法的直观概念得出这个结论几乎是不可能的。直观概念可能足以为某些任务提供算法,但对于证明特定任务不存在算法来说,它是无用的。证明算法不存在需要对算法有清晰的定义。第十个问题的进展必须等待这个定义。
这个定义出现在阿隆佐·丘奇(Alonzo Church)和艾伦·图灵(Alan Turing)1936年的论文中。丘奇使用一种称为 $\lambda$-演算的符号系统来定义算法。图灵则通过他的“机器”来定义。这两个定义被证明是等价的。这种算法的非形式化概念与精确定义之间的联系被称为丘奇-图灵论题(Church-Turing thesis)。
丘奇-图灵论题提供了解决希尔伯特第十个问题所必需的算法定义。1970年,尤里·马蒂亚塞维奇(Yuri Matijasevič)在马丁·戴维斯(Martin Davis)、希拉里·普特南(Hilary Putnam)和茱莉亚·罗宾逊(Julia Robinson)的工作基础上,证明了不存在算法来测试多项式是否有整数根。在第4章中,我们将开发形成证明这个问题和其他问题在算法上不可解的基础的技术。
| 算法的直观概念 | 等于 | 图灵机
算法 |
| :---: | :---: | :---: |
图 3.22
丘奇-图灵论题
[^2]让我们用我们的术语来阐述希尔伯特第十个问题。这样做有助于引入我们在第4章和第5章中探讨的一些主题。设
希尔伯特第十个问题本质上是问集合 $D$ 是否可判定。答案是否定的。相比之下,我们可以证明 $D$ 是图灵可识别的。在此之前,让我们考虑一个更简单的问题。这是希尔伯特第十个问题的一个类比,针对只有单个变量的多项式,例如 $4 x^{3}- 2 x^{2}+x-7$。设
这是一个识别 $D_{1}$ 的 TM $M_{1}$:
$M_{1}=$“在输入 $\langle p\rangle$ 上:其中 $p$ 是关于变量 $x$ 的多项式。
- 依次将 $x$ 设为 $0,1,-1,2,-2,3,-3, \ldots$ 等值,评估 $p$。如果在任何时候多项式评估为0,则接受。”
如果 $p$ 有一个整数根,$M_{1}$ 最终会找到它并接受。如果 $p$ 没有整数根,$M_{1}$ 将永远运行。对于多变量情况,我们可以提出一个类似的 TM $M$ 来识别 $D$。在这里,$M$ 遍历其变量的所有可能整数赋值。
$M_{1}$ 和 $M$ 都是识别器,但不是判定器。我们可以将 $M_{1}$ 转换为 $D_{1}$ 的判定器,因为我们可以计算单个变量多项式的根必须位于的界限,并将搜索限制在这些界限内。在问题 3.10 中,要求您证明此类多项式的根必须位于以下值之间
其中 $k$ 是多项式中的项数,$c_{\text {max }}$ 是具有最大绝对值的系数,而 $c_{1}$ 是最高阶项的系数。如果在此界限内未找到根,则机器拒绝。马蒂亚塞维奇的定理表明,计算多变量多项式的此类界限是不可能的。
描述图灵机的术语
我们已经来到了计算理论研究的一个转折点。我们仍然谈论图灵机,但我们从现在起真正的重点是算法。也就是说,图灵机仅仅作为算法定义的精确模型。我们跳过了图灵机本身的广泛理论,并且不会花费太多时间在图灵机的低级编程上。我们只需要对图灵机有足够的熟悉度,以相信它们能够捕捉所有算法。
考虑到这一点,让我们标准化描述图灵机算法的方式。首先,我们问:在描述此类算法时,应该提供何种程度的细节?学生们通常会问这个问题,尤其是在准备练习和问题的解决方案时。让我们考虑三种可能性。第一种是形式化描述,它完整地阐明了图灵机的状态、转移函数等等。这是最低、最详细的描述级别。第二种是更高级别的描述,称为实现描述,我们用英语散文描述图灵机移动其磁头以及它如何在磁带上存储数据的方式。在这个级别,我们不提供状态或转移函数的细节。第三种是高级描述,我们用英语散文描述算法,忽略实现细节。在这个级别,我们不需要提及机器如何管理其磁带或磁头。
在本章中,我们已经给出了图灵机的各种示例的形式化和实现级描述。练习较低级别的图灵机描述有助于您理解图灵机并获得使用它们的信心。一旦您感到自信,高级描述就足够了。
我们现在为描述图灵机设置一种格式和符号。图灵机的输入始终是一个字符串。如果我们要提供一个字符串以外的对象作为输入,我们必须首先将该对象表示为字符串。字符串可以很容易地表示多项式、图、文法、自动机以及这些对象的任何组合。图灵机可以被编程来解码该表示,以便它可以按我们预期的方式进行解释。我们将对象 $O$ 编码为字符串的表示法表示为 $\langle O\rangle$。如果我们有几个对象 $O_{1}, O_{2}, \ldots, O_{k}$,我们将其编码为单个字符串表示为 $\left\langle O_{1}, O_{2}, \ldots, O_{k}\right\rangle$。编码本身可以用许多合理的方式完成。我们选择哪种方式并不重要,因为图灵机总是可以将一种此类编码转换为另一种。
在我们的格式中,我们用带引号的缩进文本段来描述图灵机算法。我们将算法分解为多个阶段,每个阶段通常涉及图灵机计算的许多单独步骤。我们用进一步的缩进来表示算法的块结构。算法的第一行描述了机器的输入。如果输入描述只是 $w$,则输入被视为一个字符串。如果输入描述是对象的编码,如 $\langle A\rangle$,则图灵机首先隐式测试输入是否正确编码了所需形式的对象,如果不是,则拒绝它。
示例 3.23
设 $A$ 是由所有表示连通无向图的字符串组成的语言。回想一下,如果图中的每个节点都可以通过沿着图的边到达其他所有节点,则该图是连通的。我们写
以下是决定 $A$ 的 TM $M$ 的高级描述。
$M=$“在输入 $\langle G\rangle$ 上,一个图 $G$ 的编码:
- 选择 $G$ 的第一个节点并标记它。
- 重复以下阶段,直到没有新节点被标记:
- 对于 $G$ 中的每个节点,如果它通过一条边连接到一个已被标记的节点,则标记它。
- 扫描 $G$ 的所有节点以确定它们是否都被标记。如果是,则接受;否则,拒绝。”
为了进一步练习,让我们检查图灵机 $M$ 的一些实现级细节。通常我们将来不会提供这种程度的细节,您也不需要,除非在练习中明确要求。首先,我们必须理解 $\langle G\rangle$ 如何将图 $G$ 编码为字符串。考虑一种编码,它是 $G$ 的节点列表,后跟 $G$ 的边列表。每个节点都是一个十进制数,每条边是表示该边两端节点的十进制数对。下图描绘了这样一个图及其编码。
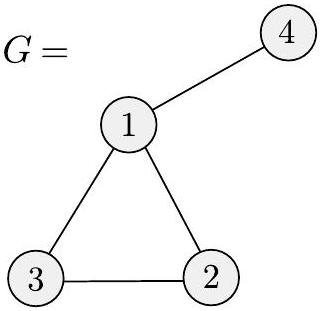
图 3.24
一个图 $G$ 及其编码 $\langle G\rangle$
当 $M$ 收到输入 $\langle G\rangle$ 时,它首先检查输入是否是某个图的正确编码。为此,$M$ 扫描磁带以确保有两个列表并且它们采用正确的形式。第一个列表应该是一个不同的十进制数列表,第二个列表应该是一个十进制数对列表。然后 $M$ 检查几件事。首先,节点列表不应包含重复;其次,边列表上出现的每个节点也应出现在节点列表上。对于第一点,我们可以使用示例 3.12 中 TM $M_{4}$ 中给出的用于检查元素唯一性的程序。类似的方法适用于第二次检查。如果输入通过这些检查,它就是某个图 $G$ 的编码。此验证完成输入检查,然后 $M$ 进入阶段1。
对于阶段1,$M$ 在最左边的数字上用一个点标记第一个节点。
对于阶段2,$M$ 扫描节点列表以找到一个未打点的节点 $n_{1}$ 并通过以不同的方式标记它(例如,下划线第一个符号)来标记它。然后 $M$ 再次扫描列表以找到一个打点的节点 $n_{2}$ 并也给它加上下划线。
现在 $M$ 扫描边列表。对于每条边,$M$ 测试两个带下划线的节点 $n_{1}$ 和 $n_{2}$ 是否是出现在该边中的节点。如果是,$M$ 给 $n_{1}$ 打点,移除下划线,并从阶段2的开始处继续。如果不是,$M$ 检查列表中的下一条边。如果没有更多的边,则 $\{n_{1}, n_{2}\}$ 不是 $G$ 的一条边。然后 $M$ 将 $n_{2}$ 上的下划线移动到下一个打点的节点,现在称此节点为 $n_{2}$。它重复本段中的步骤,像以前一样检查新对 $\{n_{1}, n_{2}\}$ 是否是一条边。如果没有更多的打点节点,$n_{1}$ 没有连接到任何打点的节点。然后 $M$ 设置下划线,使得 $n_{1}$ 是下一个未打点的节点,$n_{2}$ 是第一个打点的节点,并重复本段中的步骤。如果没有更多的未打点节点,$M$ 无法找到任何新节点来打点,因此它进入阶段4。
对于阶段4,$M$ 扫描节点列表以确定是否所有节点都被打点。如果是,它进入接受状态;否则,它进入拒绝状态。这完成了 TM $M$ 的描述。
练习
3.1 本练习涉及 TM $M_{2}$,其描述和状态图出现在示例 3.7 中。在每个部分中,给出 $M_{2}$ 在给定输入字符串上启动时进入的配置序列。
a. 0 。
${ }^{\mathrm{A}}$ b. 00 。
c. 000 。
d. 000000 。
3.2 本练习涉及 TM $M_{1}$,其描述和状态图出现在示例 3.9 中。在每个部分中,给出 $M_{1}$ 在给定输入字符串上启动时进入的配置序列。
${ }^{\mathrm{A}}$ a. 11.
b. 1\#1.
c. 1\#\#1.
d. $10 \# 11$.
e. $10 \# 10$.
${ }^{\text {A }}$ 3.3 修改定理 3.16 的证明以获得推论 3.19,证明当且仅当某些非确定性图灵机决定一种语言时,该语言是可判定的。(您可以假设以下关于树的定理。如果树中的每个节点都有有限数量的子节点,并且树的每个分支都有有限数量的节点,则树本身有有限数量的节点。)
3.4 给出枚举器的形式化定义。将其视为一种两磁带图灵机,它使用其第二个磁带作为打印机。包括枚举语言的定义。
${ }^{\text {A }}$ 3.5 检查图灵机的形式化定义以回答以下问题,并解释您的推理。
a. 图灵机能否在其磁带上写入空白符号 $\sqcup$?
b. 磁带字母表 $\Gamma$ 能否与输入字母表 $\Sigma$ 相同?
c. 图灵机的磁头能否在两个连续的步骤中处于相同位置?
d. 图灵机能否只包含一个状态?
3.6 在定理 3.21 中,我们证明了当且仅当某些枚举器枚举一种语言时,该语言是图灵可识别的。为什么我们没有使用以下更简单的算法来证明的前向方向?如前所述,$s_{1}, s_{2}, \ldots$ 是 $\Sigma^{*}$ 中所有字符串的列表。
$E=$“忽略输入。
- 对 $i=1,2,3, \ldots$ 重复以下操作。
- 在 $s_{i}$ 上运行 $M$。
- 如果它接受,则打印出 $s_{i}$。”
3.7 解释为什么以下不是合法图灵机的描述。
$M_{\text {bad }}=$“在输入 $\langle p\rangle$ 上,一个关于变量 $x_{1}, \ldots, x_{k}$ 的多项式:
- 尝试将 $x_{1}, \ldots, x_{k}$ 设置为所有可能的整数值。
- 在所有这些设置上评估 $p$。
- 如果其中任何一个设置评估为0,则接受;否则,拒绝。”
3.8 给出以下在字母表 $\{0,1\}$ 上的语言的图灵机的实现级描述。
${ }^{\mathrm{A}}$ a. $\{w \mid w \text { 包含相同数量的 0 和 1}\}$
b. $\{w \mid w \text { 包含两倍数量的 0,是 1 的两倍}\}$
c. $\{w \mid w \text { 不包含两倍数量的 0,是 1 的两倍}\}$