11. 可归约性
📜 [原文1]
在第4章中,我们将图灵机确立为通用计算机的模型。我们展示了几个可以在图灵机上解决的问题示例,并给出了一个计算上不可解的问题示例,$A_{\mathrm{TM}}$。在本章中,我们将研究一些额外的不可解问题。在此过程中,我们引入了证明问题计算上不可解的主要方法。它被称为可归约性。
这段话是本章的引言,起到了承上启下的作用。
- 承上:它首先回顾了第4章的核心内容。在计算理论中,我们需要一个精确的、数学化的模型来定义什么是“计算机”以及“计算”这个过程。第4章确立了图灵机 (Turing Machine) 就是这样一个标准模型。它虽然看起来简单(一条无限长的带子、一个读写头、一组状态),但其计算能力强大到可以模拟任何现代计算机能执行的算法。这被称为丘奇-图灵论题。同时,第4章不仅展示了图灵机能“做什么”(解决一些问题),更重要的是揭示了它的“不能做什么”。它通过“对角线法”证明了存在一个图灵机无法解决的问题,即 $A_{\mathrm{TM}}$ 问题。$A_{\mathrm{TM}}$ 问题问的是:“任意给定的图灵机 $M$ 是否接受任意给定的输入字符串 $w$?”。这个问题是不可判定的,意味着不存在一个图灵机(也就是不存在任何算法),能在有限时间内对所有可能的输入 $\langle M, w \rangle$ 都给出“是”或“否”的正确答案。
- 启下:本段接着预告了本章(第5章)的主要内容。既然我们已经有了一个已知的不可判定问题 $A_{\mathrm{TM}}$,我们能否利用它来发现更多不可判定问题呢?答案是肯定的。本章将介绍一种强大的技术——可归约性 (Reducibility),它将成为我们证明其他问题也是不可判定的主要工具。
- “不可解”不等于“目前还没解出来”:初学者容易将“不可解”或“不可判定”理解为“我们人类目前能力有限,还没找到算法”。这是错误的。计算理论中的“不可解”是一个绝对的、数学上的证明,它意味着永远不可能存在这样的通用算法,无论计算机多快,科技多发达。
- $A_{\mathrm{TM}}$ 的重要性:$A_{\mathrm{TM}}$ 问题在计算理论中的地位,类似于物理学中的“光速不变”或数学中的“1+1=2”,它是一个基石。它是我们后续证明其他问题不可解的“困难源头”。
本段作为开篇,回顾了图灵机作为通用计算模型以及第一个不可判定问题 $A_{\mathrm{TM}}$ 的发现,并引出了本章的核心工具——可归约性,预示着我们将用它来从 $A_{\mathrm{TM}}$ 出发,证明更多问题的不可解性。
本段的目的是为读者建立一个清晰的知识脉络。它告诉读者,我们不是凭空开始研究新问题,而是在已有的“图灵机”和“$A_{\mathrm{TM}}$ 不可判定”这两个坚实基础上,学习一种系统性的方法(可归约性)来扩展我们对计算边界的认知。
你可以把 $A_{\mathrm{TM}}$ 想象成是“万恶之源”或“困难的根源”。可归约性就像是一种“传染”机制。如果我们能证明解决问题 B 的难度“不亚于”解决 $A_{\mathrm{TM}}$,那么 $A_{\mathrm{TM}}$ 的“不可解”这种“病”就会通过可归约性“传染”给问题 B,从而证明问题 B 也是不可解的。
想象你站在一座名为“计算理论”的山脚下。第4章,你通过艰苦的“对角线法”攀爬,终于登上了第一座高峰,峰顶插着一面旗,写着“$A_{\mathrm{TM}}$ 不可判定”。现在,你站在这个高峰上,环顾四周,发现还有很多其他的山峰(其他问题)。本章要教你的可归约性,就像是给你一副望远镜和一套测量工具,让你不必再从山脚重新攀爬每一座山峰,而是可以通过在“$A_{\mathrm{TM}}$”峰顶的观察和比较,直接判断出远处的那些山峰是否也同样高不可攀(不可判定)。
📜 [原文2]
归约是将一个问题转换为另一个问题的方法,使得第二个问题的解决方案可以用来解决第一个问题。这种可归约性在日常生活中经常出现,即使我们通常不这样称呼它们。
这一段用通俗的语言定义了“归约”(Reduction)的核心思想。
归约的本质是一个“问题转换”和“方案利用”的过程。它包含两个问题,我们称之为问题 A 和问题 B。归约做了这样一件事:它提供了一个通用的方法(一个算法),可以把任何一个“问题 A 的实例”转换成一个“问题 B 的实例”。这个转换必须满足一个关键特性:转换后得到的“问题 B 的实例”的答案,可以直接或经过简单变换后,作为原来“问题 A 的实例”的答案。
换句话说,如果我们有了一个能解决问题 B 的“黑盒子”(一个能解答所有B类问题的解决方案),那么通过归约,我们就能造出一个解决问题 A 的“黑盒子”。我们把问题 A 的输入扔进我们的转换器,转换器输出一个问题 B 的输入,然后把这个新的输入扔进解决 B 的“黑盒子”,拿到答案,这个答案就是我们想要的 A 的答案。
“使得第二个问题的解决方案可以用来解决第一个问题” 这句话是关键。它建立了一种“依赖关系”:A 的解决可以依赖于 B 的解决。
这个概念并不局限于计算机科学,日常生活中比比皆是。段落中提到的例子就是为了让我们更好地理解这一点。
- 示例1:求解一元二次方程归约到使用计算器开平方根
- 问题 A:求解方程 $ax^2 + bx + c = 0$。
- 问题 B:计算一个非负数的平方根。
- 归约过程:我们知道求根公式是 $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$。这个公式本身就是归约。它把“求解一元二次方程”的任何实例(比如 $a=1, b=-3, c=2$),转换成了“计算平方根”的一个实例(计算 $\sqrt{(-3)^2 - 4 \cdot 1 \cdot 2} = \sqrt{1}$)。
- 方案利用:假设你有一个能解决问题 B 的“黑盒子”——一个计算器。你输入 1,它告诉你平方根是 1。你利用这个答案,就能算出 $x = \frac{3 \pm 1}{2}$,得到 $x_1=2, x_2=1$,从而解决了问题 A。
- 示例2:网上购物归约到有足够的钱
- 问题 A:在网上成功购买一部新手机。
- 问题 B:银行账户里有足够的余额。
- 归约过程:你想买手机,首先会查看价格,这就是将“买手机”问题转换成“需要多少钱”的问题。
- 方案利用:如果你有一个解决方案B(你账户里有足够的钱),那么你就可以点击“支付”按钮,从而解决问题A(成功买到手机)。如果你没有解决方案B,问题A就无法解决。
- 归约是单向的:A 归约到 B,意味着 B 的解决方案可以用来解决 A。但这并不意味着 A 的解决方案可以用来解决 B。例如,知道如何开车(解决“从家到公司”的问题),并不意味着你知道如何制造一辆汽车(解决“造车”的问题)。
- 归约本身需要是可计算的:将问题 A 转换为问题 B 的过程,本身必须是一个算法,是一个图灵机可以完成的工作。如果转换过程本身就是个不可解的问题,那这个归约就毫无意义。
本段用大白话解释了归约的定义:它是一种问题转换技术,通过它,我们可以利用问题B的解法来解决问题A。这个概念在日常生活中很常见。
本段的目的是在引入严格的数学定义之前,先给读者一个关于归约的直观、非形式化的理解。通过生活中的例子,降低学习门槛,让读者明白这并非一个全新的、凭空出现的抽象概念。
归约就像是“外包”。假设你是老板(问题 A),你需要完成一个任务。但你发现这个任务中的某个关键步骤(问题 B)你不会做,但你的下属小王会。于是你把整个任务重新打包,把需要小王做的那部分整理成他能看懂的格式,然后交给他。小王做完后把结果给你,你再用他的结果完成剩下的收尾工作。你就把解决 A 的问题,“归约”到了解决 B 的问题。
想象一个厨房里的场景。
- 问题 A:做一道番茄炒蛋。
- 问题 B:把鸡蛋打散并搅匀。
归约的过程就是你的菜谱告诉你:“第一步,取鸡蛋;第二步,将鸡蛋打入碗中搅匀;第三步...”。这个菜谱就把“做番茄炒蛋”这个复杂问题,归约到了“打鸡蛋”、“切番茄”、“开火”等一系列更简单的问题。如果你知道如何解决“打鸡蛋”这个问题,你就可以完成菜谱中的一步。
📜 [原文3]
例如,假设你想在一个新城市里找到路。你知道如果有一张地图,这样做会很容易。因此,你可以将找路的问题归约到获得城市地图的问题。
这是对归约概念的第一个具体例子。
- 问题 A:在一个新城市里找到路。这是一个比较复杂和宽泛的任务。
- 问题 B:获得一张这个城市的地图。这是一个更具体、更明确的目标。
这里的归约逻辑是:
- 识别依赖关系:你意识到,如果你拥有了“地图”(问题 B 的解决方案),那么“找路”(问题 A)就会变得非常简单,甚至是水到渠成。
- 转换问题焦点:因此,你不再直接去思考“我该怎么走?”,而是将你的精力全部投入到解决“我该去哪里搞到一张地图?”这个问题上。你把解决 A 的任务,成功地转换(归约)为解决 B 的任务。
- 利用解决方案:一旦你通过问路、去书店购买、或用手机App下载等方式解决了问题 B(获得了地图),你就可以利用这个地图,轻松地规划路线,从而解决问题 A。
这个例子清晰地展示了归约的核心:将一个问题的求解过程,转化为对另一个问题的求解过程的调用。
- 示例1:
- 问题 A 实例: “如何从北京市的‘天安门’走到‘故宫博物院’?”
- 问题 B 实例: “获得一张包含‘天安门’和‘故宫博物院’的北京市地图。”
- 归约实现: 你将注意力从“出门左转还是右转?”转移到“去哪里买地图或打开手机地图App?”
- 方案利用: 你打开了手机地图App(解决了B),在地图上清楚地看到了故宫就在天安门北面,步行即可。于是你解决了A。
- 示例2:
- 问题 A 实例: “如何从上海市‘人民广场’坐地铁到‘东方明珠’?”
- 问题 B 实例: “获得一张上海地铁线路图。”
- 归约实现: 你不去盲目地进地铁站,而是先在站内寻找地铁图(解决B)。
- 方案利用: 你在图上发现,可以从人民广场站乘坐2号线到陆家嘴站下车。问题A得以解决。
- 归约的有效性:这个归约是有效的,因为“获得地图”这个问题通常比“在一个陌生城市里凭感觉找路”要容易解决得多。如果获得地图本身比找路还难(比如在一个没有地图卖、没有网络、语言不通的地方),那这个归约虽然理论上成立,但实践中没有帮助。
- 归约与问题等价:找路归约到有地图,但有地图不一定归约到找路。你拿到地图后,可能只是想看看城市布局,并不想去某个具体地方。
本段通过“找路与地图”的生动例子,阐明了归约就是将一个困难问题(找路)转化为一个前提性问题(获取地图)的过程。
这个例子的目的是进一步巩固读者对归约的直观理解,使其生活化、形象化,为后面引入更抽象的数学和计算机问题的归约做铺垫。
归约就像是“解锁前置科技”。在策略游戏(如《星际争霸》或《文明》)里,你想造高级兵种(问题 A),但科技树告诉你必须先研究某个基础科技(问题 B)。于是你的目标就从“立刻暴兵”归约为“先研发那个科技”。一旦科技研发完成(问题 B 解决),造高级兵种的选项就解锁了(问题 A 可解)。
想象你是个侦探,要破解一个复杂的谋杀案(问题 A)。你发现案发现场有一串加密的数字。你意识到,如果你能破译这串数字(问题 B),很可能就能找到凶手的线索。于是,你的工作重心从漫无目的地寻找目击证人,归约到了集中精力破解密码上。一旦密码破解(B解决),案件就迎刃而解(A解决)。
📜 [原文4]
可归约性总是涉及两个问题,我们称之为$A$和$B$。如果$A$归约到$B$,我们可以使用$B$的解决方案来解决$A$。所以在我们的例子中,$A$是找路的问题,$B$是获得地图的问题。请注意,可归约性并没有说明单独解决$A$或$B$的问题,而只是说明在有$B$的解决方案的情况下,$A$的可解性。
这段话是对前面例子的总结,并提炼出可归约性的几个关键属性,开始向形式化定义过渡。
- “总是涉及两个问题,我们称之为$A$和$B$”: 明确了归约关系的基本结构,它是一个二元关系,作用于两个问题之间。
- “如果$A$归约到$B$,我们可以使用$B$的解决方案来解决$A$”: 这是归约的功能性定义。写作 $A \le_m B$ (m代表多一归约,一种常见的归约类型)。这句话的核心意思是:解决B的难度 >= 解决A的难度。因为如果你能解决B,A也就迎刃而解了。反过来说,解决A不会比解决B更难。
- “所以在我们的例子中,$A$是找路的问题,$B$是获得地图的问题”: 将抽象的A和B对应回具体的例子,加深理解。
- “请注意,可归约性并没有说明单独解决$A$或$B$的问题,而只是说明在有$B$的解决方案的情况下,$A$的可解性”: 这是非常关键的一点,揭示了归约的相对性。
- 归约不告诉你B是否可解。B可能是个很简单的问题(比如1+1=?),也可能是个极难的问题,甚至可能是不可解的问题。归约本身不关心这个。
- 归约只建立了一个“如果...那么...”的逻辑链条:如果 B可解,那么 A也可解。
- 这个逻辑链条的逆否命题同样至关重要:如果 A不可解,那么 B也必不可少。这正是我们将要用来证明问题不可解的核心武器。
- 示例1: 利用逆否命题
- 问题 A: 永生(已知不可解)。
- 问题 B: 制造出能治愈所有疾病的万能药。
- 归约: 我们可以说“永生问题”A归约到“制造万能药问题”B。因为如果能造出万能药(B可解),那么人就不会生病老死,永生问题A就解决了。
- 结论: 既然我们知道A(永生)是不可解的,那么根据逆否命题,我们推断B(制造万能药)也一定是不可解的。我们不需要去研究医学细节,仅通过逻辑归约就得出了结论。
- 示例2: 归约到一个已知可解问题
- 问题 A: 计算一个圆的面积。
- 问题 B: 测量圆的半径,并进行乘法和平方运算。
- 归约: A归约到B,因为面积 $S = \pi r^2$。
- 结论: 我们知道B是可解的(测量和乘法都是基本的可计算操作)。因此,我们可以断定A也是可解的。
- 混淆归约方向和难易度:$A$ 归约到 $B$ ($A \le_m B$) 意味着 $A$ 的难度小于等于 $B$。很多人会直觉上搞反,认为 $A$ 依赖 $B$,所以 $A$ 更难。这是错误的。正确的理解是,解决 $B$ 的能力是一种“更强大的能力”,拥有它就能顺便解决 $A$。
- 忽略归约本身的成本:在计算理论中,我们要求归约过程本身是可计算的,并且通常要求其计算复杂度要低于我们正在研究的问题的复杂度。例如,在P与NP问题中,我们谈论的是多项式时间归约,即转换过程本身必须在多项式时间内完成。
本段总结了可归约性的核心:它是一种表明“问题A的可解性依赖于问题B的可解性”的逻辑关系。它本身不判定任一问题的可解性,但它建立的这种依赖关系,尤其是其逆否命题,是证明问题不可解的关键。
本段的目的是从非形式化的例子中提炼出可归约性的逻辑本质,强调其“相对性”和“条件性”,为下一段将其应用于数学和计算问题做最后的铺垫。
可归约性就像一个“难度比较器”。$A \le_m B$ 告诉你,“从A到B这条路是通的,B是A的‘上位’问题”。它不告诉你A或B本身在绝对难度坐标系(可解/不可解)的哪个位置,但它给出了它们相对的难度关系。一旦你知道了其中一个的绝对位置,另一个的(部分)信息也就知道了。
- 如果B在“可解区”,A也一定在“可解区”。
- 如果A在“不可解区”,B也一定在“不可解区”。
想象有两个待办事项清单:
- 清单 A: “跑一次马拉松”。
- 清单 B: “拥有健康的身体和良好的体能”。
你可以说,完成清单A归约到完成清单B。这并不意味着拥有健康身体就等于跑了马拉SON,也不意味着跑马拉松就一定健康。它只是说,如果你能做到B,那么做到A的可能性就大大增加,甚至成为可能。反之,如果你连A(跑马拉松)都做不到,那几乎可以肯定你的B(身体健康和体能)没有达标。
📜 [原文5]
以下是可归约性的更多例子。从波士顿到巴黎旅行的问题归约到购买两城市之间机票的问题。而购买机票的问题又归约到赚取机票钱的问题。而赚取机票钱的问题又归约到找工作的问题。
这一段通过一个“归约链”的例子,来展示归约关系是可以传递的。
这个例子建立了一个任务依赖链条:
- 问题 A: 从波士顿到巴黎旅行。
- 问题 B: 购买一张波士顿到巴黎的机票。
- 问题 C: 赚到足够买机票的钱。
- 问题 D: 找到一份能赚钱的工作。
这个链条可以表示为: $A \le B \le C \le D$。
- A 归约到 B ($A \le B$): 要完成旅行,一个关键步骤是获得交通工具的凭证。因此,旅行问题归约到买票问题。如果你解决了B(买到了票),A就有了前提保障。
- B 归约到 C ($B \le C$): 要买到票,你需要支付费用。因此,买票问题归约到赚钱问题。如果你解决了C(有足够的钱),B就可以解决。
- C 归约到 D ($C \le D$): 在多数情况下,赚钱需要有工作。因此,赚钱问题归约到找工作问题。如果你解决了D(找到了工作),C就有了来源。
这个链条展示了归约的传递性:如果 $A \le B$ 且 $B \le C$,那么 $A \le C$。在这个例子里,最终“从波士顿到巴黎旅行”这个问题,被归约到了“找到一份工作”这个问题。
- 示例1:数值化归约链
- 问题 A: 成功从波士顿飞到巴黎。
- 问题 B: 获得一张价值$1000美元的机票。
- 问题 C: 账户里有$1000美元。
- 问题 D: 找到一份时薪$20美元的工作。
- 归约链的计算:
- 要解决C,你需要工作 $1000 / 20 = 50$ 小时。
- 所以,解决A最终归约到了“工作50小时”这个问题。如果你能解决“工作50小时”的问题,那么整个链条就都能解决。
- 示例2:学术领域的归约链
- 问题 A: 发表一篇关于“深度学习在蛋白质折叠中的应用”的博士论文。
- 问题 B: 获得支持论文结论的有效实验数据。
- 问题 C: 设计并成功运行一个深度学习模型进行模拟实验。
- 问题 D: 掌握深度学习、生物信息学和编程的知识。
- 归约链: $A \le B \le C \le D$。最终,写论文这个大目标被归约到了最基础的学习和掌握知识。
- 归约并非唯一路径:从波士顿到巴黎不一定非要买机票,也可以坐船,或者自己造火箭。归约只是展示了一条可行的依赖路径。在数学证明中,我们只需要找到任何一条有效的归约路径即可。
- 归约的终点:这个链条最终归约到一个我们假设可以解决或已知其性质的问题(比如“找工作”在现实中是可解的,尽管可能困难)。在计算理论中,我们会把未知问题归约到一个已知不可解或已知可解的问题上。
本段通过一个连锁的生活实例,说明了归约关系具有传递性,一个复杂问题可以被分解并归约为一系列更基础的问题。
本段的目的是引入归约的传递性这一重要性质。这个性质非常有用,因为它允许我们不必总是从最困难的根源问题(如 $A_{\mathrm{TM}}$)出发,我们可以从任何一个已知的不可判定问题出发进行归约。比如,如果我们后面证明了B是不可判定的,而C又可以归约到B,我们就能立刻知道C也是不可判定的。
归约链就像是“任务依赖图”。在项目管理中,一个大任务(里程碑)会被分解成许多子任务,这些子任务之间有先后依赖关系。你必须先完成前置任务,才能开始下一个。整个项目的完成,最终归约到了那些最基础、没有任何前置依赖的初始任务的完成。
想象多米诺骨牌。
- 第一块牌 (D): 找到工作
- 第二块牌 (C): 赚到钱
- 第三块牌 (B): 买到机票
- 第四块牌 (A): 去巴黎旅行
你推倒第一块牌(解决了D),它会撞倒第二块(解决了C),然后是第三块(解决了B),最终第四块倒下(解决了A)。“推倒第n块牌”的问题,归约到了“推倒第n-1块牌”的问题。整个序列的成功,归约到了推倒第一块牌的成功。
📜 [原文6]
可归约性也出现在数学问题中。例如,测量矩形面积的问题归约到测量其长度和宽度的问题。求解线性方程组的问题归约到求矩阵逆的问题。
这一段将可归约性的概念从生活实例过渡到更精确的数学问题领域,为进入计算理论的严格证明做准备。
- “测量矩形面积的问题归约到测量其长度和宽度的问题”
- 问题 A: 测量矩形面积。
- 问题 B: 测量其长度和宽度。
- 归约: 这是通过公式 面积 = 长 × 宽 实现的。这个公式告诉我们,只要我们能解决问题B(获得长度和宽度的值),我们就能通过一次乘法运算解决问题A。
- 难度关系: 测量长度和宽度是更基本的操作。计算面积的难度不超过测量长度、宽度再加一次乘法。
- “求解线性方程组的问题归约到求矩阵逆的问题”
- 问题 A: 求解线性方程组。
- 问题 B: 求一个矩阵的逆。
- 背景: 一个线性方程组可以写成矩阵形式 $A\mathbf{x} = \mathbf{b}$。其中,$A$ 是系数矩阵,$\mathbf{x}$ 是未知数向量,$\mathbf{b}$ 是常数向量。我们的目标是解出 $\mathbf{x}$。
- 归约: 如果矩阵 $A$ 的逆矩阵 $A^{-1}$ 存在(即B可解),我们可以通过在方程两边同时左乘 $A^{-1}$ 来求解 $\mathbf{x}$:
- 方案利用: 如果你有一个能解决问题B的算法或工具(比如MATLAB里的 inv() 函数),你就可以用它来解决问题A。
- 示例1: 矩形面积
- 问题 A 实例: 求一个长5米、宽3米的矩形面积。
- 归约: 将问题归约到测量长(得到5米)和宽(得到3米)。
- 方案利用: 计算 $5 \times 3 = 15$ 平方米。问题A解决。
- 示例2: 线性方程组
- 问题 A 实例: 求解方程组:
$2x + 3y = 8$
$x + y = 3$
- 矩阵形式: $\begin{pmatrix} 2 & 3 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 8 \\ 3 \end{pmatrix}$
- 归约: 问题归约到求矩阵 $A = \begin{pmatrix} 2 & 3 \\ 1 & 1 \end{pmatrix}$ 的逆。
- 方案利用: 我们(或者一个工具)计算出逆矩阵 $A^{-1} = \begin{pmatrix} -1 & 3 \\ 1 & -2 \end{pmatrix}$。(这是问题B的解)
- 然后我们计算 $\mathbf{x} = A^{-1}\mathbf{b} = \begin{pmatrix} -1 & 3 \\ 1 & -2 \end{pmatrix} \begin{pmatrix} 8 \\ 3 \end{pmatrix} = \begin{pmatrix} (-1)(8) + (3)(3) \\ (1)(8) + (-2)(3) \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}$。
- 所以解是 $x=1, y=2$。问题A解决。
- 矩阵不可逆的情况:对于第二个例子,如果矩阵 $A$ 是奇异的(行列式为0),它就没有逆矩阵。在这种情况下,问题B(求逆)无解。但这并不意味着问题A(解方程组)一定无解,它可能无解,也可能有无穷多解。这说明归约有时会把问题转换到一个更特定或有前提条件的领域。严谨的归约需要处理所有这些情况。
本段使用两个经典的数学例子(面积计算和线性代数)来强化归约的概念,表明它是一种在数学和科学中普遍存在的解决问题的思维模式。
此段的目的是提升归约概念的“严肃性”和“普适性”。从生活常识转向数学领域,能让读者意识到这不仅仅是一个比喻,而是一种可以被严格定义的、强大的数学工具,为最终应用到计算理论的证明上做好心理和知识上的准备。
归约是“调用函数/子程序”。在编程时,你写一个主函数(解决问题A),在主函数里,你会调用一个已经写好的、功能明确的子函数(解决问题B)。比如,主函数是calculateAndDisplayResults(),它会调用子函数invertMatrix()。主函数的正确执行,依赖于子函数的正确执行。
想象你是一位大厨(问题A:做一桌盛宴),你的厨房里有各种各样的现代化厨具(问题B:打蛋器,问题C:烤箱,问题D:微波炉...)。当你需要打发奶油时,你不会用手打半小时,而是把这个问题归约到“使用打蛋器”上。你只需要按一下按钮(调用解决方案),奶油就打好了。整个做盛宴的过程,就是不断地把一个个烹饪步骤归约到使用特定厨具上。
📜 [原文7]
可归约性在根据可判定性对问题进行分类中扮演着重要角色,在随后的复杂性理论中也同样重要。当$A$可归约到$B$时,解决$A$不会比解决$B$更难,因为$B$的解决方案也给出了$A$的解决方案。就可计算性理论而言,如果$A$可归约到$B$且$B$是可判定的,那么$A$也是可判定的。同理,如果$A$是不可判定的且可归约到$B$,那么$B$是不可判定的。这最后一个版本是证明各种问题不可判定性的关键。
这一段是本章乃至整个计算理论后半部分的核心思想的高度概括。它明确指出了可归约性最重要的两个应用。
- 应用领域:
- 可判定性分类 (Computability Theory): 即本章内容,用归约来划分问题是可判定的(有算法能解)还是不可判定的(没有算法能解)。
- 复杂性理论 (Complexity Theory): 后续章节内容(如P vs NP),用归约来对可判定问题内部进行更精细的难度划分,比如哪些是“容易解”的(P类问题),哪些是“可能很难解”的(NP完全问题)。
- 核心逻辑: “当$A$可归约到$B$时,解决$A$不会比解决$B$更难”。这是对 $A \le_m B$ 背后难度关系的再次强调。可以理解为:$Difficulty(A) \le Difficulty(B)$。
- 两个主要推论 (Rules of Inference):
- 推论1 (用于证明可判定性):
- 前提1: $A$ 可归约到 $B$ ($A \le_m B$)。
- 前提2: $B$ 是可判定的 (B is decidable)。
- 结论: $A$ 也是可判定的 (A is decidable)。
- 逻辑: 既然解决B的算法存在(前提2),并且我们有一个算法能把A转换成B(归约本身是可计算的),那么我们就可以组合出一个解决A的算法:先将A的实例转换成B的实例,再用B的算法去解,最后得到A的答案。整个过程是算法化的,所以A可判定。
- 推论2 (用于证明不可判定性):
- 这是推论1的逆否命题,也是本章的“核武器”。
- 前提1: $A$ 是不可判定的 (A is undecidable)。
- 前提2: $A$ 可归约到 $B$ ($A \le_m B$)。
- 结论: $B$ 也是不可判定的 (B is undecidable)。
- 逻辑(反证法): 假设B是可判定的。根据推论1,既然 $A \le_m B$ 且 B 可判定,那么 A 也应该是可判定的。但这与前提1“A是不可判定的”相矛盾。因此,最初的假设“B是可判定的”必须是错误的。所以,B一定是不可判定的。
- “这最后一个版本是证明各种问题不可判定性的关键”: 明确点出,本书接下来将反复使用推论2。我们会拿一个已知的、坚不可摧的不可判定问题(比如 $A_{\mathrm{TM}}$)作为我们的A,然后想办法把它归约到一个我们想证明其不可判定性的新问题B上。一旦归约成功,B的“死刑”就判了。
- 推论1示例:
- 问题 A: “判断一个数n是否能被6整除”。
- 问题 B: “判断一个数n是否能被2整除” 和 “判断一个数n是否能被3整除”。
- 归约: A 归约到 B,因为“n能被6整除”等价于“n能被2整除 AND n能被3整除”。
- 应用: 我们知道B中的两个子问题都是可判定的(有简单的除法算法)。因此,根据推论1,A也是可判定的。
- 推论2示例:
- 问题 A: $A_{\mathrm{TM}}$(“图灵机M是否接受w?”),已知不可判定。
- 问题 B: $HALT_{\mathrm{TM}}$(“图灵机M是否在输入w上停机?”),性质未知。
- 归约: 我们将要证明 $A_{\mathrm{TM}} \le_m HALT_{\mathrm{TM}}$。
- 应用: 一旦这个归约被证明,根据推论2,因为A($A_{\mathrm{TM}}$)是不可判定的,我们立刻得出结论:B($HALT_{\mathrm{TM}}$)也必须是不可判定的。
- 归约方向的再次强调: 为了证明 B 是不可判定的,必须证明 $A_{\mathrm{TM}} \le_m B$,而不是 $B \le_m A_{\mathrm{TM}}$。搞反方向,证明就完全无效。$B \le_m A_{\mathrm{TM}}$ 只能说明 B 的难度不超过 $A_{\mathrm{TM}}$,B 可能是可判定的,也可能是不可判定的,无法得出任何确定性结论。
本段是可归约性方法论的精髓。它阐明了归约如何根据已知问题的性质(可判定或不可判定)来推断未知问题的性质。特别是,它确立了通过将一个已知的不可判定问题归约到一个新问题来证明该新问题也是不可判定的核心策略。
本段的目的是将之前所有的直观铺垫,升华为一套清晰、可操作的证明逻辑和方法论。它为读者提供了“菜谱”,告诉他们接下来要进行的证明将遵循怎样的固定模式。
把所有问题想象成在一个“难度宇宙”中。可归约性就像是连接这些问题的“虫洞”或“传送门”,并且是单向的 ($A \to B$)。
- 推论1: 如果你知道B在一个叫“可解”的安全星球上,那么通过虫洞从A能到B,说明A也在这个安全星球上。
- 推论2: 如果你知道A在一个叫“不可解”的黑洞里,那么通过虫洞从A能到B,说明B也一定被困在同一个黑洞里,否则A就能通过B逃出黑洞了,这与A在黑洞里的事实矛盾。
想象一场法庭辩论。
- 推论2的逻辑:
- 检察官: 我要证明被告B犯了“不可判定罪”。
- 检察官: 我们已经知道,罪犯A是一个板上钉钉的“不可判定罪”犯人(这是已知事实,$A_{\mathrm{TM}}$)。
- 检察官: 现在我向法庭呈上证据(归约证明过程),证明“如果B是无辜的(可判定的),那么A也必然是无辜的(可判定的)”。
- 检察官: 但我们知道A是有罪的!这产生了矛盾。所以,唯一的解释就是,最初的假设“B是无辜的”是错的。
- 法官: 裁定!被告B“不可判定罪”罪名成立。
📜 [原文8]
简而言之,我们证明一个问题不可判定的方法是,证明某个已知不可判定的问题可以归约到它。
这句话是对上一段核心思想的最终总结,也是对接下来所有证明的“一句话攻略”。
- “我们证明一个问题不可判定的方法”: 指明了我们的目标——证明某个新问题是不可判定的。
- “是”: 引出具体的方法。
- “证明”: 强调这个过程需要严格的数学论证。
- “某个已知不可判定的问题”: 这是我们的出发点和武器。在本书的这个阶段,这个“已知不可判定问题”主要就是 $A_{\mathrm{TM}}$。我们把它当作“困难的黄金标准”。
- “可以归约到它”: “它”指的是我们想要证明其不可判定性的那个新问题。
所以,整个流程是:
已知不可判定问题 ($A_{known}$) $\le_m$ 新问题 ($B_{new}$) $\implies$ $B_{new}$ 是不可判定的
- 示例1:
- 目标: 证明“问题X”不可判定。
- 方法: 构造一个算法,该算法能将任何一个 $A_{\mathrm{TM}}$ 问题的实例 $\langle M, w \rangle$ 转化为一个“问题X”的实例 $x$。并且,这个转化必须保证:$M$ 接受 $w$ 当且仅当 $x$ 的答案是“是”。
- 完成上述构造,即完成了证明 $A_{\mathrm{TM}} \le_m X$。于是,X被证明是不可判定的。
- 示例2(本书即将展示的):
- 目标: 证明停机问题 $HALT_{\mathrm{TM}}$ 不可判定。
- 方法: 我们将展示如何将 $A_{\mathrm{TM}}$ 归约到 $HALT_{\mathrm{TM}}$。
- 结论: 一旦归约成功,$HALT_{\mathrm{TM}}$ 就被证明是不可判定的。
- 这几乎是唯一的通用方法:除了第一个不可判定问题 $A_{\mathrm{TM}}$ 是通过对角线法直接证明的,几乎所有其他在标准计算理论课程中遇到的不可判定性问题,都是通过归约来证明的。这凸显了归约这一工具的核心地位。
本句言简意赅地概括了证明问题不可判定的标准操作流程:找到一个已知的不可判定问题,并证明它可以归约到目标新问题。
本段的目的是给读者一个极其清晰和可记忆的“行动纲领”。在深入到复杂的技术细节之前,先让读者牢牢记住这个最高层级的策略,这样在后续的学习中就不会迷失方向。
这就像是困难的传递。如果你想证明一块新材料B和钻石一样硬(硬到无法被切割,即“不可判定”),你不需要重新发明所有测量硬度的仪器。你只需要证明,你可以用这块新材料B造出一把能划伤钻石A的工具。如果B能划伤A,说明B至少和A一样硬。既然A(钻石)已知是“无法被切割”的,那么B也一定是“无法被切割”的。这里,“用B造工具划伤A”的过程就是归约。
想象一个“不可解问题俱乐部”。
- 这个俱乐部有一个创始成员,名叫 $A_{\mathrm{TM}}$,它的会员资格是经过了最严格的“对角线法”认证的。
- 现在有一个新问题B想加入俱乐部。
- 入会规则是:必须由一位老会员(比如 $A_{\mathrm{TM}}$)为你做担保。
- 担保的方式就是归约:$A_{\mathrm{TM}}$ 必须能够证明,“如果B不是我们俱乐部成员(即可判定的),那我也就不可能是了”。
- 既然 $A_{\mathrm{TM}}$ 的会员资格是铁打的,那么这个担保就意味着B也必须是会员。
- 于是,B成功入会,成为不可判定问题俱乐部的新成员。
1.1 5.1
11.1 语言理论中的不可判定问题
📜 [原文9]
我们已经确立了$A_{\mathrm{TM}}$的不可判定性,即判断图灵机是否接受给定输入的问题。让我们考虑一个相关的问题,$H A L T_{\mathrm{TM}}$,即判断图灵机是否在给定输入上停机(通过接受或拒绝)的问题。这个问题广为人知为停机问题。我们利用$A_{\mathrm{TM}}$的不可判定性,通过将$A_{\text {TM }}$归约到$H A L T_{\text {TM }}$来证明停机问题的不可判定性。设
这一段正式开始了第一个使用归约方法的证明。它介绍了即将被证明为不可判定的新问题——停机问题 ($HALT_{\mathrm{TM}}$)。
- 回顾已知: 首先,再次强调我们的出发点和“武器”——$A_{\mathrm{TM}}$ 的不可判定性。
- $A_{\mathrm{TM}} = \{\langle M, w\rangle \mid M \text{ 是一个图灵机且 } M \text{ 接受 } w\}$。
- 这个问题问的是“是否接受?”。
- 引入新问题: 介绍停机问题 $HALT_{\mathrm{TM}}$。
- 这个问题问的是“是否停机?”。
- 停机包含两种情况:接受 (accept) 并停机,或者拒绝 (reject) 并停机。不停机的情况被称为循环 (loop)。
- 所以,$HALT_{\mathrm{TM}}$ 关心的是机器最终会不会给出一个明确的答复(无论是接受还是拒绝),而不是陷入无限循环。
- 两者的关系:
- 如果一个图灵机 $M$ 在输入 $w$ 上接受了,那么它一定停机了。
- 如果一个图灵机 $M$ 在输入 $w$ 上停机了,它可能是接受了,也可能是拒绝了。
- 从集合关系上看,$A_{\mathrm{TM}}$ 中的每个元素 $\langle M, w\rangle$ 也都属于 $HALT_{\mathrm{TM}}$ (只要 $M$ 接受 $w$)。但反之不成立。
- 声明证明策略: 明确指出我们将要使用的证明方法,完全符合上一节总结的“一句话攻略”。
- 目标: 证明 $HALT_{\mathrm{TM}}$ 是不可判定的。
- 方法: 将 $A_{\mathrm{TM}}$ 归约到 $HALT_{\mathrm{TM}}$ (证明 $A_{\mathrm{TM}} \le_m HALT_{\mathrm{TM}}$)。
- 逻辑: 一旦归约成功,由于 $A_{\mathrm{TM}}$ 是不可判定的,根据推论2,$HALT_{\mathrm{TM}}$ 也必须是不可判定的。
- 形式化定义: 给出了 $HALT_{\mathrm{TM}}$ 的严格集合定义。
- $HALT_{\mathrm{TM}}$: 这是我们为这个语言(或问题)起的名字。TM代表图灵机。
- $\{$ ... $\}$: 表示这是一个集合。在计算理论中,一个“问题”通常被形式化地定义为一个“语言”,而一个语言就是一个字符串的集合。
- $\langle M, w\rangle$: 这是集合中的元素,表示一个字符串。这个字符串是图灵机 $M$ 的编码和输入字符串 $w$ 的编码的组合。尖括号 $\langle \rangle$ 表示这是一个配对的编码。
- |: 读作“使得(such that)”,它后面的内容是对集合中元素必须满足的条件的描述。
- $M \text { is a TM and } M \text { halts on input } w$: 这就是成员资格的条件。一个字符串 $\langle M, w\rangle$ 属于 $HALT_{\mathrm{TM}}$ 这个集合,当且仅当它所代表的图灵机 $M$ 在输入它所代表的字符串 $w$ 时,最终会停机(即进入接受状态或拒绝状态)。
- 示例1 (属于 $HALT_{\mathrm{TM}}$):
- 设 $M_1$ 是一个图灵机,它的功能是:检查输入字符串 $w$ 是否包含子串 "aba"。如果包含,就接受;如果不包含,就拒绝。
- 设输入 $w_1 = $ "babab"。
- $M_1$ 在 $w_1$ 上运行时,会扫描字符串,找到 "aba",进入接受状态并停机。
- 因此,$\langle M_1, w_1 \rangle \in HALT_{\mathrm{TM}}$。
- 示例2 (属于 $HALT_{\mathrm{TM}}$):
- 使用上面同样的 $M_1$。
- 设输入 $w_2 = $ "bbbaaa"。
- $M_1$ 在 $w_2$ 上运行时,会扫描整个字符串,找不到 "aba",最终进入拒绝状态并停机。
- 因此,$\langle M_1, w_2 \rangle \in HALT_{\mathrm{TM}}$。
- 示例3 (不属于 $HALT_{\mathrm{TM}}$):
- 设 $M_2$ 是一个图灵机,它的功能是:如果输入是'a',就向右移动带头,永不停止。
- 设输入 $w_3 = $ "a"。
- $M_2$ 在 $w_3$ 上运行时,会进入一个无限循环,永远不会停机。
- 因此,$\langle M_2, w_3 \rangle \notin HALT_{\mathrm{TM}}$。
- 停机问题 vs $A_{\mathrm{TM}}$: 一定要分清这两个问题的区别。$A_{\mathrm{TM}}$ 只关心“接受”这一种结果。而 $HALT_{\mathrm{TM}}$ 关心“接受”和“拒绝”两种结果,只要不停机就不行。一个在所有输入上都拒绝并停机的机器,所有对应的 $\langle M, w \rangle$ 都不在 $A_{\mathrm{TM}}$ 中,但都在 $HALT_{\mathrm{TM}}$ 中。
本段引入了著名的停机问题 ($HALT_{\mathrm{TM}}$),给出了其形式化定义,并清晰地阐述了即将采用的证明策略:通过将 $A_{\mathrm{TM}}$ 归约到 $HALT_{\mathrm{TM}}$,来证明停机问题是不可判定的。
本段的目的是设定舞台。它挑选了计算理论中除了 $A_{\mathrm{TM}}$ 之外最著名的不可判定问题——停机问题——作为第一个通过归约来证明的目标。这既展示了归约方法的威力,也建立起了第二个“不可判定”的基石,为后续更复杂的归约提供了一个新的、可能更方便的出发点。
如果说 $A_{\mathrm{TM}}$ 问题是问:“这个程序最终会成功退出并返回‘成功’码吗?”,那么 $HALT_{\mathrm{TM}}$ 问题就是问:“这个程序最终会退出吗(无论返回‘成功’码还是‘失败’码)?”。直觉上,后者似乎是一个更“基础”或“简单”的问题,因为我们放宽了对输出的要求。然而,证明将告诉我们,它们在“可判定性”这个层面是同样困难的。
想象你在调试一个复杂的程序。
- 问 $A_{\mathrm{TM}}$ 问题,就像是在问:“程序运行后,最终会不会在屏幕上打印出‘耶!成功了!’?”
- 问 $HALT_{\mathrm{TM}}$ 问题,就像是在问:“这个程序会不会死机或者卡在一个无限循环里?它最终会结束运行吗?”
我们马上要证明,不存在一个通用的“死机检测器”能对所有程序和所有输入都给出正确判断。
11.2 定理 5.1:$H A L T_{\mathrm{TM}}$是不可判定的。
📜 [原文10]
证明思路 这个证明是通过反证法进行的。我们假设$H A L T_{\mathrm{TM}}$是可判定的,并利用这个假设来证明$A_{\mathrm{TM}}$是可判定的,这与定理4.11相矛盾。关键思想是证明$A_{\text {TM }}$可以归约到$H A L T_{\text {TM }}$。
假设我们有一个图灵机$R$来判定$H A L T_{\text {TM }}$。然后我们使用$R$来构造$S$,一个判定$A_{\text {TM }}$的图灵机。为了感受一下构造$S$的方法,假设你就是$S$。你的任务是判定$A_{\text {TM }}$。你得到一个$\langle M, w\rangle$形式的输入。如果$M$接受$w$,你必须输出接受;如果$M$循环或拒绝$w$,你必须输出拒绝。尝试模拟$M$在$w$上的运行。如果它接受或拒绝,你也这样做。但你可能无法确定$M$是否正在循环,在这种情况下,你的模拟将不会终止。这很糟糕,因为你是一个判决器,因此绝不允许循环。所以这个想法本身是行不通的。
相反,使用你拥有判定$H A L T_{\mathrm{TM}}$的图灵机$R$的假设。有了$R$,你可以测试$M$是否在$w$上停机。如果$R$指示$M$不在$w$上停机,则拒绝,因为$\langle M, w\rangle$不在$A_{\mathrm{TM}}$中。但是,如果$R$指示$M$在$w$上停机,你可以进行模拟而没有任何循环的危险。
因此,如果图灵机$R$存在,我们可以判定$A_{\text {TM }}$,但我们知道$A_{\text {TM }}$是不可判定的。根据这个矛盾,我们可以得出结论,$R$不存在。因此,$H A L T_{\text {TM }}$是不可判定的。
这部分是定理5.1的“证明思路”,它用非形式化的语言,引导读者理解整个证明的核心逻辑。这是一种非常好的教学方法,先讲故事,再给代码。
- 设定证明框架——反证法 (Proof by Contradiction):
- 第一步:假设。我们假设结论的反面是正确的,即假设“$HALT_{\mathrm{TM}}$ 是可判定的”。
- 第二步:推导。从这个假设出发,进行一系列逻辑上无懈可击的推导。
- 第三步:导出矛盾。我们的推导最终会得出一个与已知事实(公理或已证定理)相违背的结论。
- 第四步:下结论。由于推导过程无误,那一定是最初的假设出了问题。因此,假设是错误的,其反面(我们想证明的结论)才是正确的。
- 具体化假设:
- 假设“$HALT_{\mathrm{TM}}$ 是可判定的”,这意味着存在一个图灵机,我们称之为 $R$,它能判定 $HALT_{\mathrm{TM}}$。
- $R$ 的功能:输入 $\langle M, w \rangle$,如果 $M$ 在 $w$ 上停机,$R$ 就接受并停机;如果 $M$ 在 $w$ 上循环,$R$ 就拒绝并停机。重要的是,$R$ 自己永远不会循环。$R$ 就是我们幻想中存在的那个完美的“死机检测器”。
- 构建归约: 我们的目标是利用这个虚构的机器 $R$,来构造另一个机器 $S$,让 $S$ 能够判定 $A_{\mathrm{TM}}$。这就完成了 $A_{\mathrm{TM}} \le_m HALT_{\mathrm{TM}}$ 的归约。
- 第一人称体验(角色扮演 S): 为了让思路更清晰,作者让我们想象自己就是机器 $S$。
- 你的任务: 判定 $A_{\mathrm{TM}}$。输入是 $\langle M, w \rangle$。你需要判断 $M$ 是否接受 $w$。
- 一个失败的尝试: 最直接的想法是“直接模拟 $M$ 在 $w$ 上的运行”。
- 如果 $M$ 接受了 $w$,你($S$)也接受。这没问题。
- 如果 $M$ 拒绝了 $w$,你($S$)也拒绝。这也行。
- 问题在于:如果 $M$ 在 $w$ 上循环了,你的模拟也会跟着一起循环下去,永不停止。但你的身份是“判定器”(Decider),判定器绝不允许循环。所以,直接模拟的方案失败了。
- 正确的方案(使用“外挂”R): 现在,你($S$)被赋予了一个超能力——可以调用机器 $R$(那个完美的“死机检测器”)。
- 第一步: 拿到输入 $\langle M, w \rangle$ 后,你不要直接去模拟 $M$。而是先把 $\langle M, w \rangle$ 作为输入,去问你的“外挂” $R$。
- 第二步: 分析 $R$ 的回答。
- 情况1: $R$ 回答“拒绝”。这意味着 $R$ 判断出 $M$ 在 $w$ 上会循环。如果 $M$ 循环,它肯定不会接受 $w$。所以,$\langle M, w \rangle$ 不属于 $A_{\mathrm{TM}}$。在这种情况下,你($S$)就可以放心地直接拒绝。
- 情况2: $R$ 回答“接受”。这意味着 $R$ 判断出 $M$ 在 $w$ 上最终会停机。这太棒了!因为现在你知道了模拟 $M$ 在 $w$ 上的运行绝对不会导致无限循环。
- 第三步: 在 $R$ 告诉你 $M$ 会停机之后,你($S$)现在可以安全地去模拟 $M$ 在 $w$ 上的运行了。
- 模拟的结果只会有两种:$M$ 接受 $w$,或者 $M$ 拒绝 $w$。
- 如果模拟结果是 $M$ 接受,你($S$)就接受。
- 如果模拟结果是 $M$ 拒绝,你($S$)就拒绝。
- 导出矛盾:
- 通过上述步骤,我们设计出了一个完整的、在任何输入 $\langle M, w \rangle$ 上都能正确判断 $M$ 是否接受 $w$ 并且自身永不循环的图灵机 $S$。
- 换句话说,我们证明了:如果 $HALT_{\mathrm{TM}}$ 是可判定的(即 $R$ 存在),那么 $A_{\mathrm{TM}}$ 也是可判定的(即 $S$ 存在)。
- 但是,我们在定理4.11中已经铁证如山地证明了 $A_{\mathrm{TM}}$ 是不可判定的!
- 这就产生了矛盾。
- 最终结论:
- 矛盾的根源在于我们最初的假设——“$HALT_{\mathrm{TM}}$ 是可判定的”。
- 因此,这个假设必须是错误的。
- 结论:$HALT_{\mathrm{TM}}$ 是不可判定的。
- R和S的角色:一定要分清 $R$ 和 $S$ 的作用。$R$ 是我们假设存在的、用来解决 $HALT_{\mathrm{TM}}$ 的机器。$S$ 是我们利用R构造出来的、用来解决 $A_{\mathrm{TM}}$ 的机器。整个证明的核心就是这个构造过程。
- 模拟的安全性:$S$ 并不是在所有情况下都去模拟 $M$。它只有在通过 $R$ 确认模拟是“安全”(不会循环)的时候,才去执行模拟。这是整个设计的精髓。
证明思路的核心是:假设存在一个能判断程序是否停机(不死机)的完美工具 $R$。然后,我们可以利用这个工具 $R$ 来构建另一个工具 $S$,这个 $S$ 能完美地判断任何程序是否会“接受”某个输入。具体方法是, $S$ 先用 $R$ 检查程序会不会死机。如果会,那就肯定不会“接受”。如果不会,$S$ 就安全地运行它,看它最后是“接受”还是“拒绝”。这样一来,我们就造出了一个能判定 $A_{\mathrm{TM}}$ 的工具 $S$,但这与已知的“$A_{\mathrm{TM}}$ 不可判定”相矛盾。因此,我们最初假设的完美工具 $R$ 根本不可能存在。
“证明思路”部分的存在是为了让读者在接触严格的形式化证明之前,能够完全理解其背后的逻辑脉络和巧妙之处。它通过更易于理解的语言和类比,降低了认知负荷,使得后续的形式化证明部分更像是对已有思路的“翻译”而不是全新的创造。
这就像一个两步验证过程。
- 你想解决的问题 (A_TM): 判断一份收到的可执行文件 program.exe 在输入 input.txt 时,是否会输出“成功”。
- 你遇到的困难: 直接运行 program.exe,它可能会死机,你就永远等不到结果。
- 你幻想的工具 (R): 一个叫 AntiCrash.exe 的神奇软件,你给它 program.exe 和 input.txt,它立刻告诉你 program.exe 在这个输入上会不会死机。
- 你的解决方案 (S):
- 运行 AntiCrash.exe program.exe input.txt。
- 如果 AntiCrash.exe 说“会死机”,你直接断定 program.exe 不会输出“成功”。
- 如果 AntiCrash.exe 说“不会死机”,你才放心地去运行 program.exe,然后看它的输出是不是“成功”。
- 矛盾: 你这个解决方案如此完美,可以解决所有程序的“是否成功”问题。但我们已经知道这是不可能的。所以,那个神奇的 AntiCrash.exe 根本就不可能存在。
想象你是一位炸弹处理专家。
- 任务 ($A_{\mathrm{TM}}$):判断一个未知的炸弹装置($M$)在收到一个特定的无线电信号($w$)后,是否会“安全解除”($M$ 接受 $w$)。
- 危险:直接发送信号,装置可能会爆炸,也可能进入一个未知的倒计时循环($M$ 循环)。
- 假设的“神之探测器” ($R$): 你有一个设备,能隔着墙扫描炸弹,并立刻告诉你“发送这个信号后,装置会有反应(停机,无论是解除还是爆炸)”还是“发送这个信号后,装置会没反应(进入无限循环)”。
- 你的拆弹策略 ($S$):
- 用“神之探测器”扫描。
- 如果探测器显示“没反应”(循环),那它肯定不会“安全解除”,你报告任务失败。
- 如果探测器显示“有反应”(停机),你就知道发送信号后肯定会有个结果。你就可以大胆地发送信号,然后观察它到底是“安全解除”了还是“爆炸”了。
- 矛盾: 这个策略让你成为了一个能100%安全判断任何炸弹是否会“安全解除”的“神”。但我们已经从理论上知道(定理4.11),这样的“神”是不存在的。因此,那个“神之探测器”也必然只是幻想。
📜 [原文11]
证明 为了获得矛盾,我们假设图灵机$R$判定$H A L T_{\mathrm{TM}}$。我们构造图灵机$S$来判定$A_{\mathrm{TM}}$,其操作如下。
$S=$"在输入$\langle M, w\rangle$上,其中$M$是图灵机和$w$是字符串的编码:
- 在输入$\langle M, w\rangle$上运行图灵机$R$。
- 如果$R$拒绝,则拒绝。
- 如果$R$接受,则模拟$M$在$w$上的运行直到停机。
- 如果$M$接受了,则接受;如果$M$拒绝了,则拒绝。"
显然,如果$R$判定$H A L T_{\text {TM }}$,那么$S$判定$A_{\text {TM }}$。因为$A_{\text {TM }}$是不可判定的,$H A L T_{\text {TM }}$也必须是不可判定的。
这部分是定理5.1的严格形式化证明。它将刚才“证明思路”中的描述,翻译成了图灵机伪代码的形式。
“为了获得矛盾,我们假设图灵机$R$判定$H A L T_{\mathrm{TM}}$。”
这再次重申了反证法的起点。我们假设存在这样一个判定器 $R$。
- $R(\langle M, w \rangle)$ 接受 $\iff M$ 在 $w$ 上停机。
- $R(\langle M, w \rangle)$ 拒绝 $\iff M$ 在 $w$ 上循环。
- $R$ 自身总是停机的。
“我们构造图灵机$S$来判定$A_{\mathrm{TM}}$,其操作如下。”
这是归约的核心步骤:构建一个新机器 $S$,并利用 $R$ 作为其子程序。我们的目标是让 $S$ 成为 $A_{\mathrm{TM}}$ 的判定器。
$S$ 的算法描述:
$S$ 被设计为一个接受输入 $\langle M, w \rangle$ 的图灵机。
- “1. 在输入$\langle M, w\rangle$上运行图灵机$R$。”
- 这是 $S$ 的第一步。$S$ 将自己的输入原封不动地传给子程序 $R$。
- $S$ 会等待 $R$ 完成计算并给出结果(“接受”或“拒绝”)。因为 $R$ 是个判定器,所以 $S$ 在这一步的等待过程保证是有限的。
- “2. 如果$R$拒绝,则拒绝。”
- $R$ 拒绝意味着什么?根据 $R$ 的定义,这意味着 $M$ 在输入 $w$ 上会无限循环。
- 如果 $M$ 会循环,它肯定永远不会进入接受状态。
- 因此,$M$ 不接受 $w$,$\langle M, w \rangle$ 不属于 $A_{\mathrm{TM}}$。
- 在这种情况下,$S$ 做出拒绝的决定是完全正确的。并且 $S$ 在这一步就停机了。
- “3. 如果$R$接受,则模拟$M$在$w$上的运行直到停机。”
- $R$ 接受意味着什么?根据 $R$ 的定义,这意味着 $M$ 在输入 $w$ 上保证会停机。
- 这个保证是至关重要的,它使得 $S$ 接下来可以安全地进行模拟,而不用担心自己会陷入无限循环。
- $S$ 启动一个标准的通用图灵机模拟程序,来执行 $M$ 在 $w$ 上的指令。
- 因为已经知道 $M$ 会停机,所以这个模拟过程也保证是有限的。
- “4. 如果$M$接受了,则接受;如果$M$拒绝了,则拒绝。”
- 这是模拟结束后的处理。模拟的结果只有两种:$M$ 停机并接受,或者 $M$ 停机并拒绝。
- 如果 $M$ 接受 $w$,那么 $\langle M, w \rangle$ 属于 $A_{\mathrm{TM}}$。$S$ 此时做出接受的决定是正确的。
- 如果 $M$ 拒绝 $w$,那么 $\langle M, w \rangle$ 不属于 $A_{\mathrm{TM}}$。$S$ 此时做出拒绝的决定是正确的。
- 在这两种情况下,$S$ 都停机了。
“显然,如果$R$判定$H A L T_{\text {TM }}$,那么$S$判定$A_{\text {TM }}$。”
这是一个总结性陈述。我们来验证 $S$ 是否真的是 $A_{\mathrm{TM}}$ 的判定器。
- 正确性: 对于任何输入 $\langle M, w \rangle$:
- 如果 $\langle M, w \rangle \in A_{\mathrm{TM}}$ (即 $M$ 接受 $w$),那么 $M$ 必定会停机。$R$ 会接受,然后 $S$ 模拟 $M$ 也会得到接受的结果,所以 $S$ 接受。正确。
- 如果 $\langle M, w \rangle \notin A_{\mathrm{TM}}$ (即 $M$ 拒绝或循环),分两种情况:
- $M$ 拒绝 $w$:那么 $M$ 会停机。$R$ 会接受,然后 $S$ 模拟 $M$ 会得到拒绝的结果,所以 $S$ 拒绝。正确。
- $M$ 循环于 $w$:那么 $M$ 不会停机。$R$ 会拒绝,根据第2步,$S$ 直接拒绝。正确。
- 结论:$S$ 总能给出正确的答案。
- 停机性: $S$ 的每一步都是保证停机的。第1步因为 $R$ 是判定器。第2步直接停机。第3步因为 $R$ 保证了 $M$ 会停机。第4步是模拟结束后的操作,自然也停机。所以 $S$ 自身永远不会循环。
- 综上,$S$ 确实是一个 $A_{\mathrm{TM}}$ 的判定器。
“因为$A_{\text {TM }}$是不可判定的,$H A L T_{\text {TM }}$也必须是不可判定的。”
这是反证法的最后一步。
- 我们成功地从“$H A L T_{\mathrm{TM}}$ 是可判定的”这个假设,推导出了“$A_{\mathrm{TM}}$ 是可判定的”这个结论。
- 这个结论与定理4.11($A_{\mathrm{TM}}$ 不可判定)直接矛盾。
- 因此,我们的初始假设是错误的。
- 所以,$H A L T_{\mathrm{TM}}$ 必须是不可判定的。证明完毕。
这段形式化证明精确地执行了“证明思路”中的蓝图。它假设存在一个能判定停机问题的图灵机 $R$,然后利用 $R$ 作为子程序,一步步构建了一个能判定 $A_{\mathrm{TM}}$ 的图灵机 $S$。由于我们已知 $A_{\mathrm{TM}}$ 是不可判定的,这导致了逻辑矛盾,从而证明了最初的假设是错误的,即停机问题 $HALT_{\mathrm{TM}}$ 是不可判定的。
本段的目的是提供一个严谨、无歧义的数学证明,它是对前面非形式化讨论的最终确认。在计算机科学中,伪代码或算法描述是表达计算过程的标准方式,这种形式化的证明是不可或缺的。
将 $R$ 看作一个可以被调用的函数 doesItHalt(M, w),它返回 true 或 false。那么 $S$ 的逻辑就可以被写成一段(想象中的)代码:
```python
2S 的逻辑
def decide_A_TM(M, w):
3第1步:调用我们假设存在的“神仙函数”R
if doesItHalt(M, w) == false:
4第2步:R说M会循环,那肯定不接受
return "拒绝"
else: # R说M会停机
5第3步:安全地模拟M
result = simulate(M, w)
6第4步:根据模拟结果返回
return result # result会是“接受”或“拒绝”
```
这段代码 decide_A_TM 本身是完美无缺的,它总能给出正确答案且不会崩溃。但我们知道这样的完美函数是不可能存在的,所以,它所依赖的那个“神仙函数” doesItHalt 也必定不存在。
这好比一个逻辑谜题:
- 已知事实: 超人是无敌的。
- 假设: 世界上存在一种叫做“氪石”的物质,它可以让超人失去所有能力。
- 构造: 我现在设计一个计划 $S$ 来打败超人:
- 我先用一个“氪石探测器” $R$ 扫描超人。
- 如果探测器响了(有氪石),说明超人现在不是无敌的,我就可以用普通武器攻击他。
- 如果探测器没响(没氪石),我就放弃攻击。
- 推论: 如果“氪石探测器”$R$ 存在,那么我的计划 $S$ 就能找到打败超人的方法。
- 矛盾: 这与“超人是无敌的”这个已知事实相矛盾。
- 结论: 矛盾的根源在于假设。因此,那种能让超人失去能力的“氪石”物质,在逻辑上是不可能存在的。这里的“超人无敌”就是 $A_{\mathrm{TM}}$ 不可判定,“氪石”就是 $HALT_{\mathrm{TM}}$ 可判定。
📜 [原文12]
定理5.1阐明了我们证明一个问题不可判定的策略。这种策略是大多数不可判定性证明所共有的,除了$A_{\text {TM }}$本身的不可判定性,它是通过对角线法直接证明的。
这段话是对刚刚完成的证明进行方法论上的总结,并指出其普遍性。
- “定理5.1阐明了我们证明一个问题不可判定的策略”: 刚才证明 $HALT_{\mathrm{TM}}$ 的过程,不仅仅是解决了一个问题,更重要的是,它为我们提供了一个可重复使用的“模板”或“蓝图”。
- “这种策略是大多数不可判定性证明所共有的”: 这个模板(即归约法)是证明不可判定性的标准工具。接下来的许多证明都会遵循几乎完全相同的模式:
- 第一步: 宣称要用反证法,通过归约来证明新问题 B 是不可判定的。
- 第二步: 假设 B 是可判定的,即存在一个判定器 $R_B$。
- 第三步: 利用 $R_B$ 构造一个判定器 $S_A$ 来解决某个已知不可判定的问题 A (通常是 $A_{\mathrm{TM}}$)。
- 第四步: 指出 $S_A$ 的存在与“A是不可判定的”这个事实相矛盾。
- 第五步: 宣布假设错误,因此 B 必须是不可判定的。
- “除了$A_{\text {TM }}$本身的不可判定性,它是通过对角线法直接证明的”: 这是一个非常重要的区分。归约法本身需要一个“困难的源头”作为起点。这个最初的、最根本的不可判定问题,不能通过归约来证明(因为当时还没有更早的已知不可判定问题可以归约过来)。
- $A_{\mathrm{TM}}$ 的不可判定性,是通过一种完全不同的、更根本的证明技巧——对角线法 (Diagonalization) ——来直接确立的。
- 对角线法由康托尔在研究无穷集合时首创,图灵巧妙地将其应用于计算理论,构造出一个任何图灵机都无法正确判断的“悖论式”输入。
- 证明方法的层级:要理解证明方法是有层级的。
- 第0层: 对角线法,它“从无到有”地创造了第一个不可判定问题 $A_{\mathrm{TM}}$。
- 第1层: 归约法,它“从有到多”,利用 $A_{\mathrm{TM}}$ 作为种子,孵化出更多的不可判定问题(如 $HALT_{\mathrm{TM}}$, $E_{\mathrm{TM}}$ 等)。
- 不要混淆两种方法:问你 $A_{\mathrm{TM}}$ 如何证明不可判定,答案是对角线法。问你 $HALT_{\mathrm{TM}}$ 如何证明不可判定,答案是归约法(从 $A_{\mathrm{TM}}$ 归约)。
本段指出了刚刚演示的“通过归约进行反证”是证明不可判定性的一个通用策略,几乎所有此类证明都采用此法。同时,它也强调了这个策略的“起点”——$A_{\mathrm{TM}}$——其本身的不可判定性是通过独特的“对角线法”直接证明的。
本段的目的是进行方法论的梳理和总结,让读者从一个具体的证明案例中抽取出普适的规律。这有助于读者在后续学习中,能够更快地识别和理解证明的结构,抓住主要矛盾,而不是迷失在每个证明独特的构造细节中。
这就像是在生物学中追溯物种起源。
- 对角线法 就像是发现了地球上的“第一个生命细胞”(LUCA - Last Universal Common Ancestor)。它的出现是一个独特的、根本性的事件。
- 归约法 就像是研究“物种演化”。一旦有了第一个细胞,我们就可以通过演化和遗传(归约的传递性)来解释成千上万不同物种的出现。所有后来的物种,都可以追溯到那个最初的祖先。
- $A_{\mathrm{TM}}$ 就是计算理论里的“LUCA”,而 $HALT_{\mathrm{TM}}$, $E_{\mathrm{TM}}$ 等都是它的“后代”。
想象一场瘟疫的爆发。
- 对角线法是找到“零号病人”的过程,需要深入的流行病学调查和基因测序,过程非常独特和根本。这个“零号病人”就是 $A_{\mathrm{TM}}$。
- 归约法是追踪病毒传播链的过程。一旦找到了“零号病人”,我们就可以通过接触史追踪(归约),来确定张三、李四、王五($HALT_{\mathrm{TM}}$, $E_{\mathrm{TM}}$...)是不是也被感染了。我们不需要对每个人都进行复杂的基因测序,只需要证明他/她和已知病人有过“有效接触”(归约)即可。
11.3 定理 5.2:$E_{\mathrm{TM}}$是不可判定的。
📜 [原文13]
我们现在提出其他几个定理及其证明,作为使用归约方法证明不可判定性的进一步例子。设
这一段引入了本节要讨论的第二个不可判定问题:图灵机语言为空问题 ($E_{\mathrm{TM}}$)。
- “我们现在提出其他几个定理及其证明,作为使用归约方法证明不可判定性的进一步例子”: 开宗明义,接下来的内容是实践和巩固上一节学到的归约策略。
- “设...”: 开始形式化定义新问题。
- $E_{\mathrm{TM}}$ 的定义: 这个问题问的是:给定的图灵机 $M$ 所接受的语言是否为空集 $\emptyset$。
- 语言 (Language): 一个图灵机 $M$ 的语言,记作 $L(M)$,是指它所接受的所有字符串的集合。$L(M) = \{w \mid M \text{ 接受 } w\}$。
- 空集 (Empty Set, $\emptyset$): 不包含任何元素的集合。
- $L(M)=\emptyset$ 意味着,对于任何可能的输入字符串 $w$,图灵机 $M$ 都不会接受。它可能会在所有输入上都拒绝,或者在所有输入上都循环,或者在某些输入上拒绝、另一些上循环,但绝不会进入接受状态。
- $E$ 代表 "Empty"。
- $E_{\mathrm{TM}}$: 问题的名称,代表图灵机的空语言问题。
- $\{\langle M\rangle \mid ... \}$: 这是一个语言(问题的形式化定义),它的成员是图灵机的编码 $\langle M \rangle$。
- 注意: 这里的输入与 $A_{\mathrm{TM}}$ 和 $HALT_{\mathrm{TM}}$ 不同。$A_{\mathrm{TM}}$ 和 $HALT_{\mathrm{TM}}$ 的输入是一个对 $\langle M, w \rangle$,既包括机器也包括特定的输入。而 $E_{\mathrm{TM}}$ 的输入仅仅是机器的编码 $\langle M \rangle$。
- $L(M)=\emptyset$: 这是成员资格的判断条件。一个图灵机 $M$ 的编码 $\langle M \rangle$ 属于 $E_{\mathrm{TM}}$ 这个集合,当且仅当 $M$ 的语言是空集,即 $M$ 不接受任何字符串。
- 示例1 (属于 $E_{\mathrm{TM}}$):
- 设 $M_1$ 是一个图灵机,它的设计是:无论输入是什么,它都立刻进入拒绝状态并停机。
- 那么 $L(M_1) = \emptyset$,因为它不接受任何字符串。
- 因此,$\langle M_1 \rangle \in E_{\mathrm{TM}}$。
- 示例2 (属于 $E_{\mathrm{TM}}$):
- 设 $M_2$ 是一个图灵机,它的设计是:无论输入是什么,它都进入一个向右移动的无限循环。
- 那么 $L(M_2) = \emptyset$,因为它也不接受任何字符串。
- 因此,$\langle M_2 \rangle \in E_{\mathrm{TM}}$。
- 示例3 (不属于 $E_{\mathrm{TM}}$):
- 设 $M_3$ 是一个图灵机,它的功能是:接受所有以 'a' 开头的字符串。
- 它的语言 $L(M_3) = \{w \mid w \text{ 以 'a' 开头}\}$。这个语言显然不是空的,比如它包含 "a", "ab", "abc" 等。
- 因此,$L(M_3) \neq \emptyset$。
- 所以,$\langle M_3 \rangle \notin E_{\mathrm{TM}}$。
- 输入形式的差异: 必须牢记 $E_{\mathrm{TM}}$ 的输入只是 $\langle M \rangle$,而 $A_{\mathrm{TM}}$ 的输入是 $\langle M, w \rangle$。这个差异在构造归约时至关重要。这意味着,当我们从 $A_{\mathrm{TM}}$ 归约到 $E_{\mathrm{TM}}$ 时,我们需要把 $A_{\mathrm{TM}}$ 的输入 $\langle M, w \rangle$ 中的两个部分 ($M$ 和 $w$) 都巧妙地“塞”进一个新的图灵机 $M'$ 的设计里,然后把 $\langle M' \rangle$ 作为 $E_{\mathrm{TM}}$ 判定器的输入。
本段引入了另一个重要的判定问题——图灵机空语言问题 $E_{\mathrm{TM}}$,并给出了其严格的形式化定义。这个问题询问的是一个给定的图灵机是否不接受任何输入字符串。
引入 $E_{\mathrm{TM}}$ 的目的是展示归约技巧的多样性。证明 $E_{\mathrm{TM}}$ 的归约构造会比证明 $HALT_{\mathrm{TM}}$ 时更巧妙一些,因为它需要处理输入形式不匹配的问题。这能加深读者对归约核心——“信息编码与传递”——的理解。
$E_{\mathrm{TM}}$ 问题就像是在问:“一个程序 P.exe 是不是一个‘永远不会输出成功’的程序?”。它不关心具体某个输入,而是对程序的所有可能行为做一个整体的判断。这就像是在对一个产品做质检,判断它是不是一个“废品”(永不成功),而不是测试它在某个特定场景下能否工作。
想象你是一个游乐园的安全检查员。
- $A_{\mathrm{TM}}(\langle M, w \rangle)$ 像是问:“身高1米8的游客 (w) 去玩这个过山车 (M),能安全坐完吗?” 这是一个针对特定游客和特定项目的问题。
- $E_{\mathrm{TM}}(\langle M \rangle)$ 像是问:“这个新的过山车项目 (M),是不是设计上有缺陷,导致没有任何一个游客(无论身高体重)能安全坐完?” 这是一个针对整个项目的普遍性问题。
我们要证明,不存在一个通用的检测算法,能对所有游乐园项目都准确判断出它是不是“对所有人都危险”。
📜 [原文14]
证明思路 我们遵循定理5.1中采用的模式。我们假设$E_{\mathrm{TM}}$是可判定的,然后证明$A_{\mathrm{TM}}$是可判定的——这会产生矛盾。设$R$是判定$E_{\mathrm{TM}}$的图灵机。我们使用$R$来构造判定$A_{\mathrm{TM}}$的图灵机$S$。当$S$接收输入$\langle M, w\rangle$时,它将如何工作呢?
一个想法是让$S$在输入$\langle M\rangle$上运行$R$,看它是否接受。如果接受,我们知道$L(M)$是空的,因此$M$不接受$w$。但如果$R$拒绝$\langle M\rangle$,我们只知道$L(M)$不是空的,因此$M$接受某个字符串——但我们仍然不知道$M$是否接受特定的字符串$w$。所以我们需要使用一个不同的想法。
我们不在$\langle M\rangle$上运行$R$,而是在$\langle M\rangle$的修改版上运行$R$。我们修改$\langle M\rangle$以确保$M$拒绝除了$w$之外的所有字符串,但在输入$w$上它像往常一样工作。然后我们使用$R$来确定修改后的机器是否识别空语言。现在机器唯一能接受的字符串是$w$,所以它的语言非空当且仅当它接受$w$。如果$R$在输入修改后的机器描述时接受,我们知道修改后的机器不接受任何东西,并且$M$不接受$w$。
这是定理5.2的“证明思路”。它再次使用了“角色扮演”和“排除错误选项”的方式,引导我们找到正确的归约构造。
- 重申证明模式: 和定理5.1一样,采用反证法,通过将 $A_{\mathrm{TM}}$ 归约到 $E_{\mathrm{TM}}$ 来制造矛盾。
- 假设: $E_{\mathrm{TM}}$ 可判定,即存在一个判定器 $R$。$R$ 的功能是:输入 $\langle M \rangle$,如果 $L(M)=\emptyset$ 则接受,否则拒绝。$R$ 自身永不循环。
- 目标: 利用 $R$ 构造一个 $A_{\mathrm{TM}}$ 的判定器 $S$。$S$ 的输入是 $\langle M, w \rangle$。
- 一个失败的尝试:
- 想法: $S$ 拿到输入 $\langle M, w \rangle$后,直接把 $\langle M \rangle$ 扔给 $R$。
- 分析:
- 如果 $R$ 接受 $\langle M \rangle$,说明 $L(M)$ 是空的。既然 $M$ 不接受任何字符串,那它自然也不接受 $w$。此时 $S$ 可以安全地拒绝。这部分逻辑是对的。
- 问题在于: 如果 $R$ 拒绝 $\langle M \rangle$,说明 $L(M)$ 不是空的。这意味着 $M$ 至少接受一个字符串。但这个字符串是哪个?是 "abc"?是 "10101"?还是恰好就是我们关心的那个 $w$?我们完全不知道。仅仅知道 $M$ 会接受“某个”字符串,对于判断它是否接受“特定”的 $w$ 毫无帮助。
- 结论: 这个简单的想法失败了。
- 正确的方案(精巧的构造):
- 核心思想: 我们不能直接问关于 $M$ 的问题,因为 $R$ 给的信息太宽泛了。我们必须构造一个新的、特制的图灵机,我们叫它 $M_1$,然后把 $M_1$ 的描述 $\langle M_1 \rangle$ 喂给 $R$。这个 $M_1$ 的设计必须非常巧妙,使得 $R$ 对 $M_1$ 的回答能够间接地告诉我们关于“$M$ 是否接受 $w$”的信息。
- $M_1$ 的设计蓝图:
- $S$ 在拿到输入 $\langle M, w \rangle$ 后,它的工作不是去运行什么,而是“在内部”动态地生成一台新的图灵机 $M_1$ 的设计图(编码)。
- $M_1$ 的行为逻辑被设定为:
- 对于任何不等于 $w$ 的输入 $x$ (即 $x \neq w$),$M_1$ 直接拒绝。
- 对于等于 $w$ 的输入 $x$ (即 $x = w$),$M_1$ 不自己做决定,而是完全模仿 $M$ 在 $w$ 上的行为。也就是说,$M_1$ 在内部运行一个对 $M$ 在 $w$ 上的模拟。如果 $M$ 接受 $w$,$M_1$ 就接受;如果 $M$ 拒绝或循环于 $w$,$M_1$ 也跟着拒绝或循环。
- 分析这个构造:
- $M_1$ 能接受的唯一可能的字符串就是 $w$。所有其他字符串都被它直接过滤掉了。
- 因此,$M_1$ 的语言 $L(M_1)$ 只有两种可能性:
- 情况A: 如果 $M$ 接受 $w$,那么 $M_1$ 也会接受 $w$。此时 $L(M_1) = \{w\}$,这是一个非空语言。
- 情况B: 如果 $M$ 不接受 $w$ (拒绝或循环),那么 $M_1$ 也不会接受 $w$。由于 $M_1$ 已经拒绝了所有其他字符串,所以 $M_1$ 不接受任何字符串。此时 $L(M_1) = \emptyset$,这是一个空语言。
- 如何利用 $R$: 现在,$S$ 把构造好的 $\langle M_1 \rangle$ 交给 $R$。
- 如果 $R$ 接受 $\langle M_1 \rangle$,根据 $R$ 的定义,这意味着 $L(M_1) = \emptyset$。这对应我们分析的情况B,说明 $M$ 不接受 $w$。于是 $S$ 就可以拒绝。
- 如果 $R$ 拒绝 $\langle M_1 \rangle$,这意味着 $L(M_1) \neq \emptyset$。这对应我们分析的情况A,说明 $M$ 接受 $w$。于是 $S$ 就可以接受。
- 归约成功: 通过这个构造,$S$ 完美地将判断“$M$ 是否接受 $w$”的问题,转换成了判断“$M_1$ 的语言是否为空”的问题。$S$ 只需要执行这个构造,调用 $R$,然后根据 $R$ 的结果给出相反的答案,就能成为 $A_{\mathrm{TM}}$ 的判定器。这就产生了我们想要的矛盾。
- $M_1$ 是被创造的,不是被运行的: 一个常见的困惑是,如果 $M$ 在 $w$ 上循环,$M_1$ 在输入 $w$ 时不也会循环吗?那 $S$ 怎么构造 $M_1$?关键在于,$S$ 从未真正运行过 $M_1$。$S$ 的工作只是像一个编译器一样,把 $M$ 的代码和字符串 $w$ “拼接”成一段新的代码($M_1$ 的描述),然后把这段新代码交给 $R$ 去“静态分析”。$R$ 是否需要运行 $M_1$ 是 $R$ 的事(我们假设它有神奇的方法可以不运行就知道结果),$S$ 的任务只是生成描述。
- 信息的编码: 整个归约的精髓在于,我们把 $A_{\mathrm{TM}}$ 的输入 $\langle M, w \rangle$ 中的两部分信息,都成功地“硬编码”进了 $M_1$ 的结构里。$w$ 被用作 $M_1$ 内部的比较基准,而 $M$ 的行为则被 $M_1$ 在特定条件下进行模拟。
证明思路的核心是构造一个“代理”图灵机 $M_1$。这个 $M_1$ 的行为完全取决于我们想研究的原始图灵机 $M$ 是否接受特定的字符串 $w$。具体来说,$M_1$ 被设计成:它的语言要么只包含 $w$ 这一个字符串(如果 $M$ 接受 $w$),要么是空集(如果 $M$ 不接受 $w$)。这样,通过使用假想的“空语言判定器” $R$ 来检测 $M_1$ 的语言是否为空,我们就能反推出 $M$ 是否接受 $w$。这成功地将 $A_{\mathrm{TM}}$ 归约到了 $E_{\mathrm{TM}}$,从而导出矛盾。
本段的目的是展示一个更复杂的归约构造。与定理5.1中 $S$ 直接调用 $R$ 不同,这里的 $S$ 扮演了一个“创造者”的角色,它需要先“设计”并“建造”一个新的机器,才能去调用 $R$。这训练了读者一种更强大、更具创造性的归约思维。
这就像是“钓鱼执法”。
- 你的目标 ($A_{\mathrm{TM}}$): 查明嫌疑人张三($M$)是否会接受一笔特定赃款($w$)。
- 困难: 你不能直接把钱给张三看他收不收,因为这可能会打草惊蛇,或者他永远不给你答复(循环)。
- 假设的工具 ($R$): 你有一个神奇的审计工具,可以审计任何一个新成立的公司(图灵机),并告诉你这家公司的账本上是否会有任何收入(语言是否为空)。
- 你的策略 (构造 $M_1$): 你成立一家新的空壳公司,叫“唯w独尊”公司($M_1$)。你在公司章程里写下两条规则:
- 任何人想给本公司投钱($x$),如果钱的来源不是那笔特定的赃款($w$),一概拒绝。
- 如果有人想用那笔赃款($w$)来投资,本公司的决策将完全授权给张三($M$)来决定。
- 使用工具: 你现在用神奇审计工具 $R$ 来审计你新成立的“唯w独尊”公司($M_1$)。
- 如果工具报告“该公司账本将永远是空的”($L(M_1)=\emptyset$),你就能断定,张三($M$)肯定没有接受那笔赃款($w$)。
- 如果工具报告“该公司账本将会有收入”($L(M_1)\neq\emptyset$),那这笔唯一的收入来源只能是那笔赃款($w$),你就能断定,张三($M$)接受了赃款($w$)。
- 矛盾: 通过这种方式,你利用审计公司账本的工具,完美地解决了“判断张三是否受贿”的问题。但我们知道后者($A_{\mathrm{TM}}$)是无法被完美解决的。因此,那个神奇的审计工具($R$)不可能存在。
想象你是一个剧院的经理,你想知道一位著名的、行为古怪的演员($M$)是否愿意出演一部特定的剧本($w$)。
- 你的问题 ($A_{\mathrm{TM}}$): 演员 $M$ 是否会接下剧本 $w$?
- 假设的工具 ($R$): 你有一个神奇的票房预测机,你可以输入任何一部未来戏剧的完整策划案(一个新图灵机的描述),它能立刻告诉你这部剧的最终总门票销量是否为“零”(语言是否为空)。
- 你的策略 (构造 $M_1$): 你创建了一个新的戏剧策划案 $M_1$,名叫《只为w而演的戏》。策划案规定:
- 任何不是剧本 $w$ 的剧本,我们一律不演,直接拒绝。
- 如果拿来的是剧本 $w$,是否出演,全权由演员 $M$ 决定。
- 使用工具: 你把《只为w而演的戏》这份策划案输入票房预测机 $R$。
- 如果 $R$ 预测“总销量为零”,说明这部剧永远不会上演,这意味着演员 $M$ 拒绝了剧本 $w$。
- 如果 $R$ 预测“总销量不为零”,说明这部剧会上演,唯一的可能就是演员 $M$ 接下了剧本 $w$。
- 矛盾: 你利用票房预测机,解决了判断演员是否接剧本这个无解问题。因此,票房预测机不可能存在。
📜 [原文15]
证明 让我们用我们的标准符号来表示证明思路中描述的修改后的机器。我们称之为$M_{1}$。
$M_{1}=$"在输入$x$上:
- 如果$x \neq w$,则拒绝。
- 如果$x=w$,则在输入$w$上运行$M$,如果$M$接受,则接受。"
这台机器的描述中包含字符串$w$。它通过扫描输入并逐个字符地与$w$进行比较,以确定它们是否相同,从而以显而易见的方式进行$x=w$的测试。
综上所述,我们假设图灵机$R$判定$E_{\mathrm{TM}}$,并构造图灵机$S$来判定$A_{\text {TM }}$,如下所示。
$S=$"在输入$\langle M, w\rangle$上,其中$M$是图灵机和$w$是字符串的编码:
- 使用$M$和$w$的描述构造刚刚描述的图灵机$M_{1}$。
- 在输入$\left\langle M_{1}\right\rangle$上运行$R$。
- 如果$R$接受,则拒绝;如果$R$拒绝,则接受。"
如果$R$是$E_{\mathrm{TM}}$的判决器,$S$将是$A_{\mathrm{TM}}$的判决器。$A_{\mathrm{TM}}$的判决器不能存在,所以我们知道$E_{\mathrm{TM}}$必须是不可判定的。
这部分是定理5.2的严格形式化证明,它把“证明思路”中的构造方案用伪代码清晰地表达出来。
第一部分:$M_1$ 的形式化描述
- “让我们用我们的标准符号来表示证明思路中描述的修改后的机器。我们称之为$M_{1}$。”
- 这里开始给出 $M_1$ 的精确算法。这个 $M_1$ 是由 $S$ 根据自己的输入 $\langle M, w \rangle$ 动态构造出来的。
- $M_1$ 的算法:
- “在输入 $x$ 上:”: 这是 $M_1$ 自己运行时所遵循的规则。$x$ 是未来可能给 $M_1$ 的任何输入。
- “1. 如果$x \neq w$,则拒绝。”: $M_1$ 的第一道关卡。它把自己接收到的输入 $x$ 和它“内心”里存着的那个从 $S$ 那里继承来的字符串 $w$ 进行比较。如果不一样,就立刻拒绝并停机。
- “它通过扫描输入并逐个字符地与$w$进行比较...从而以显而易见的方式进行$x=w$的测试。”: 这句话解释了“如何实现 $x \neq w$ 的判断”,这是一个非常基本和标准的图灵机操作,是可计算的。
- “2. 如果$x=w$,则在输入$w$上运行$M$,如果$M$接受,则接受。”: 只有当输入 $x$ 精确地等于 $w$ 时,才进入第二步。在这一步,$M_1$ 启动一个内部模拟器,去运行它同样继承自 $S$ 的图灵机 $M$ 在输入 $w$ 上的过程。然后,$M_1$ 的行为完全复制 $M$ 的行为:如果 $M$ 接受,$M_1$ 就接受;如果 $M$ 拒绝或循环,$M_1$ 也会跟着拒绝或循环。
- $M_1$ 的语言分析: 正如“证明思路”中分析的,这个构造确保了 $L(M_1)$ 要么是 $\{w\}$ (当 $M$ 接受 $w$ 时),要么是 $\emptyset$ (当 $M$ 不接受 $w$ 时)。
第二部分:$S$ 的形式化描述
- “综上所述,我们假设图灵机$R$判定$E_{\mathrm{TM}}$,并构造图灵机$S$来判定$A_{\text {TM }}$,如下所示。”: 重申反证法的框架,并开始描述 $S$ 的算法。
- $S$ 的算法:
- “在输入$\langle M, w\rangle$上...”: $S$ 接收一个图灵机 $M$ 和一个字符串 $w$ 的编码。
- “1. 使用$M$和$w$的描述构造刚刚描述的图灵机$M_{1}$。”: 这是 $S$ 的核心创造性工作。$S$ 作为一个“机器制造机”,它读取 $M$ 的指令集和字符串 $w$,然后输出一台新的图灵机 $M_1$ 的描述(编码)。这个构造过程本身是一个算法,是可计算的。
- “2. 在输入$\left\langle M_{1}\right\rangle$上运行$R$。”: $S$ 将其“作品” $\langle M_1 \rangle$ 作为输入,去调用它假设存在的“空语言判定器” $R$。$S$ 等待 $R$ 的判决结果。
- “3. 如果$R$接受,则拒绝;如果$R$拒绝,则接受。”: 这是 $S$ 做出最终裁决的步骤,它采取了与 $R$ 相反的逻辑。
- $R$ 接受 $\langle M_1 \rangle$: 意味着 $L(M_1) = \emptyset$。根据我们对 $M_1$ 的分析,这等价于 $M$ 不接受 $w$。所以 $S$ 应该拒绝。
- $R$ 拒绝 $\langle M_1 \rangle$: 意味着 $L(M_1) \neq \emptyset$。根据我们对 $M_1$ 的分析,这等价于 $M$ 接受 $w$。所以 $S$ 应该接受。
- 注意这里有一个小小的逻辑跳跃:当 $R$ 拒绝时,$S$ 就接受。这实际上是颠倒了 $R$ 的输出。
第三部分:得出结论
- “如果$R$是$E_{\mathrm{TM}}$的判决器,$S$将是$A_{\mathrm{TM}}$的判决器。”: 这个构造是成功的。我们已经证明了,借助判定器 $R$,$S$ 可以正确且总能停机地判定 $A_{\mathrm{TM}}$。
- “$A_{\mathrm{TM}}$的判决器不能存在,所以我们知道$E_{\mathrm{TM}}$必须是不可判定的。”: 这再次应用了反证法的最终逻辑。既然我们从“$E_{\mathrm{TM}}$ 可判定”的假设推出了“$A_{\mathrm{TM}}$ 可判定”这个谬论,那么最初的假设必然是错误的。因此,$E_{\mathrm{TM}}$ 是不可判定的。
该证明通过一个精巧的构造,将判定 $A_{\mathrm{TM}}$ 的问题 $\langle M, w \rangle$ 归约到了判定 $E_{\mathrm{TM}}$ 的问题。其核心是构造一个“代理”机器 $M_1$,这个机器的语言是否为空,完全取决于 $M$ 是否接受 $w$。通过假设存在的 $E_{\mathrm{TM}}$ 判定器 $R$ 来检测 $M_1$,我们就能反推出关于 $\langle M, w \rangle$ 的答案。这与 $A_{\mathrm{TM}}$ 的不可判定性相矛盾,故 $E_{\mathrm{TM}}$ 也是不可判定的。
本段将“证明思路”中富有启发性但略显口语化的描述,转化为严谨、简洁、形式化的算法步骤。这是数学和计算机科学证明的标准格式,确保了逻辑的清晰无误和可复现性。
$S$ 的工作流程可以看作:
- 接收订单: 客户给你一个程序 $M$ 和输入 $w$,问你“M在w上会成功吗?”
- 定制一个“测试探针”: 你编写一个新的小程序 $M_1$。这个小程序 $M_1$ 的逻辑是:“我只对输入 $w$ 感兴趣。当输入是 $w$ 时,我的行为就完全看老大哥 $M$ 的脸色行事。”
- 发送给“质检部门”: 你把这个新的小程序 $M_1$ 发送给你假设存在的、能检测任何程序是否“永不成功”的质检部门 $R$。
- 解读报告并反向操作:
- 质检报告说 $M_1$ “永不成功”。你推断出:那肯定是老大哥 $M$ 对 $w$ 没给好脸色。你回复客户:“不会成功”。
- 质检报告说 $M_1$ “可能会成功”。你推断出:那唯一的成功机会就是老大哥 $M$ 对 $w$ 点头了。你回复客户:“会成功!”
- 暴露问题: 你发现你的这套流程可以完美回答所有客户的问题,但理论上这是不可能的。唯一的解释是,那个“质检部门” $R$ 根本就不存在。
想象一个基因工程师 $S$ 想知道某种特定的基因序列 $M$ 是否对一种特定的药物 $w$ 有“接受”反应 ($A_{\mathrm{TM}}$)。
- 构造病毒 $M_1$: 工程师 $S$ 设计一种新的、高度特化的病毒 $M_1$。这种病毒的外壳被设计成只能识别人类细胞 $x$ 中含有药物 $w$ 的情况。
- 如果细胞 $x$ 中没有药物 $w$ ($x \neq w$),病毒 $M_1$ 无法感染,直接失活(拒绝)。
- 如果细胞 $x$ 中有药物 $w$ ($x = w$),病毒 $M_1$ 就会将基因序列 $M$ 注入细胞,并让 $M$ 的表达来决定细胞的命运(模拟 $M$ 在 $w$ 上的行为)。如果 $M$ “接受” $w$,细胞就会裂解并释放更多病毒(接受)。
- 使用“万能检测仪” $R$: 工程师有一个假设存在的检测仪 $R$,可以检测任何一种病毒,并判断这种病毒是否“绝对无法感染任何细胞”(语言为空)。
- 进行检测: 工程师将新设计的病毒 $M_1$ 放入检测仪 $R$。
- 解读结果:
- 如果 $R$ 显示 $M_1$ “绝对无法感染”,工程师就知道是基因序列 $M$ 对药物 $w$ 没有“接受”反应。
- 如果 $R$ 显示 $M_1$ “可以感染”,那唯一的感染途径就是 $M$ 对 $w$ 有“接受”反应。
- 得出矛盾: 工程师发现他可以利用这个检测仪来解决所有“基因-药物”反应的判定问题,这在生物学上被证明是不可能的。因此,那个“万能检测仪” $R$ 必定不存在。
11.4 定理 5.3:$R E G U L A R_{\mathrm{TM}}$是不可判定的。
📜 [原文16]
关于图灵机的另一个有趣的计算问题是确定给定图灵机识别的语言是否也可以被更简单的计算模型识别。例如,我们让$R E G U L A R_{\mathrm{TM}}$成为判断给定图灵机是否具有等价的有限自动机的问题。这个问题等同于判断图灵机是否识别正则语言。设
定理 5.3
$R E G U L A R_{\text {TM }}$是不可判定的。
这一段引入了本节要讨论的第三个不可判定问题:图灵机语言为正则语言问题 ($REGULAR_{\mathrm{TM}}$)。
- 问题背景: 这一段从一个更广阔的视角来提出问题。我们知道图灵机是计算能力最强的模型之一。比它计算能力弱的模型有很多,比如有限自动机 (Finite Automata, FA) 和 下推自动机 (Pushdown Automata, PDA)。它们分别对应识别正则语言 (Regular Languages) 和上下文无关语言 (Context-Free Languages, CFL)。
- 一个自然而然的问题是:我们拿出一个图灵机 $M$,它可能非常复杂,但它所接受的语言 $L(M)$,有没有可能恰好是一个比较简单的语言,比如一个正则语言?如果是这样,就意味着我们可以用一个能力更弱、结构更简单的有限自动机来完成和这个复杂图灵机同样的工作(接受同样的语言)。
- 这个问题在编译器优化、程序验证等领域有实际意义。如果我们能判定一个复杂的程序实际上只在实现一个正则逻辑,我们就可以用更高效、更易于分析的方法来替代它。
- 定义新问题 $REGULAR_{\mathrm{TM}}$:
- “判断给定图灵机是否具有等价的有限自动机的问题”: 这是问题的非形式化描述。
- “这个问题等同于判断图灵机是否识别正则语言”: 这是根据计算理论的基本知识(乔姆斯基谱系)得到的等价描述。有限自动机能且仅能识别正则语言。
- 形式化定义: 给出了问题的集合表示。
- $REGULAR_{\mathrm{TM}}$: 问题的名称,代表图灵机的正则语言问题。
- $\{\langle M\rangle \mid ... \}$: 该问题的输入同样只是图灵机的编码 $\langle M \rangle$,和 $E_{\mathrm{TM}}$ 类似。
- $L(M) \text { is a regular language}$: 这是成员资格的判断条件。一个图灵机 $M$ 的编码 $\langle M \rangle$ 属于 $REGULAR_{\mathrm{TM}}$,当且仅当 $M$ 所接受的语言 $L(M)$ 是一个正则语言。
- 示例1 (属于 $REGULAR_{\mathrm{TM}}$):
- 设 $M_1$ 是一个图灵机,它接受所有由'a'和'b'组成的、以'a'结尾的字符串。
- $L(M_1) = \{w \in \{a,b\}^* \mid w \text{ ends with 'a'}\}$。
- 我们知道这个语言可以用一个简单的两状态有限自动机来识别,因此它是一个正则语言。
- 所以,$\langle M_1 \rangle \in REGULAR_{\mathrm{TM}}$。
- 示例2 (属于 $REGULAR_{\mathrm{TM}}$):
- 设 $M_2$ 是一个图灵机,它不接受任何字符串(即 $L(M_2) = \emptyset$)。
- 空语言 $\emptyset$ 是一个正则语言。(可以由一个没有接受状态的有限自动机识别)。
- 所以,$\langle M_2 \rangle \in REGULAR_{\mathrm{TM}}$。
- 示例3 (属于 $REGULAR_{\mathrm{TM}}$):
- 设 $M_3$ 是一个图灵机,它接受所有可能的输入字符串(即 $L(M_3) = \Sigma^*$,其中 $\Sigma$ 是字母表)。
- 全语言 $\Sigma^*$ 是一个正则语言。(可以由一个单一的、既是开始又是接受的状态的有限自动机识别)。
- 所以,$\langle M_3 \rangle \in REGULAR_{\mathrm{TM}}$。
- 示例4 (不属于 $REGULAR_{\mathrm{TM}}$):
- 设 $M_4$ 是一个图灵机,它接受语言 $\{0^n1^n \mid n \ge 0\}$ (n个0后面跟着n个1)。
- 我们从泵引理知道,这个语言不是正则语言,它是一个经典的上下文无关语言。因为它需要计数,而有限自动机没有记忆能力。
- 所以,$L(M_4)$ 不是正则语言。
- 因此,$\langle M_4 \rangle \notin REGULAR_{\mathrm{TM}}$。
- 图灵机本身 vs 图灵机识别的语言: 一定要区分图灵机这个“机器”和它识别的语言这个“字符串集合”。一个非常复杂的图灵机完全可能只识别一个非常简单的正则语言。我们判断的是语言的性质,而不是机器的复杂性。
- 正则语言是可判定语言的子集: 所有的正则语言都是可判定的,但反之不成立。$REGULAR_{\mathrm{TM}}$ 问的是语言是否属于“正则”这个更小的集合内。
本段引入了一个新的判定问题 $REGULAR_{\mathrm{TM}}$,它询问的是一个给定的图灵机所识别的语言是否是一个正则语言。并预告了即将证明它也是不可判定的。
引入 $REGULAR_{\mathrm{TM}}$ 的目的在于展示归约证明的更高阶技巧。这次的归约构造将比 $E_{\mathrm{TM}}$ 的更具创造性。它不再是简单地让新机器的语言变成“空”或“非空”,而是要让新机器的语言在“正则”和“非正则”之间切换。这需要我们找到一个经典的、我们熟知的“非正则语言”作为“毒药”嵌入到构造中。
这个问题就像是在问一个软件工程师:“你写的这个无比复杂的、上万行代码的程序 P.exe,它所实现的逻辑,是不是本质上就等价于一个简单的正则表达式?” 如果答案是“是”,那么原来的复杂代码就可以被极大地简化和优化。我们要证明的是,不存在一个通用的工具,能对所有程序都自动完成这样的判断。
想象你是一位文学评论家。
- 图灵机 $M$:一部长达百万字、结构复杂、意识流的小说。
- 正则语言:一首格式严谨的十四行诗。
- $REGULAR_{\mathrm{TM}}$ 问题: 你要判断这部百万字的小说,其所能表达的“核心主题集合”(它所接受的语言),是否和一个小小的十四行诗所能表达的“核心主题集合”是等价的。
- 我们要证明,不存在一个通用的文学分析算法,能够对所有小说都做出这样“降维打击”式的判断。
📜 [原文17]
证明思路 与不可判定性定理通常一样,这个证明是通过从$A_{\mathrm{TM}}$进行归约。我们假设$R E G U L A R_{\mathrm{TM}}$可以被图灵机$R$判定,并使用这个假设来构造一个判定$A_{\text {TM }}$的图灵机$S$。现在不那么明显的是如何利用$R$的能力来帮助$S$完成任务。尽管如此,我们还是可以做到。
其思路是,$S$接收其输入$\langle M, w\rangle$,然后修改$M$,使得生成的图灵机当且仅当$M$接受$w$时才识别正则语言。我们称修改后的机器为$M_{2}$。我们设计$M_{2}$,使其在$M$不接受$w$时识别非正则语言$\left\{0^{n} 1^{n} \mid n \geq 0\right\}$,在$M$接受$w$时识别正则语言$\Sigma^{*}$。我们必须说明$S$如何从$M$和$w$构造这样的$M_{2}$。在这里,$M_{2}$通过自动接受$\left\{0^{n} 1^{n} \mid n \geq 0\right\}$中的所有字符串来工作。此外,如果$M$接受$w$,则$M_{2}$接受所有其他字符串。
请注意,图灵机$M_{2}$的构造并非是为了实际在某些输入上运行它——这是一个常见的误解。我们构造$M_{2}$仅仅是为了将其描述输入到我们假设存在的$R E G U L A R_{\mathrm{TM}}$判决器中。一旦该判决器返回其答案,我们就可以使用它来获得$M$是否接受$w$的答案。因此,我们可以判定$A_{\mathrm{TM}}$,这是一个矛盾。
这是定理5.3的“证明思路”,揭示了一个非常精妙的归约构造。
- 确定基本框架:
- 方法: 从 $A_{\mathrm{TM}}$ 进行归约的反证法。
- 假设: $REGULAR_{\mathrm{TM}}$ 是可判定的,即存在一个判定器 $R$。$R$ 的功能是:输入 $\langle M \rangle$,如果 $L(M)$ 是正则语言则接受,否则拒绝。
- 目标: 利用 $R$ 构造一个 $A_{\mathrm{TM}}$ 的判定器 $S$。
- 点出难点:
- “现在不那么明显的是如何利用$R$的能力来帮助$S$完成任务”: 与 $E_{\mathrm{TM}}$ 不同,这里的 $R$ 提供的不是“是/否”这种简单的二元信息,而是“正则/非正则”这种更抽象的属性。如何把“$M$ 是否接受 $w$”这个具体事件,和一个语言的“正则性”这种全局属性联系起来,是本证明的难点和亮点。
- 核心构造思想:
- 和证明 $E_{\mathrm{TM}}$ 时一样,$S$ 在收到输入 $\langle M, w \rangle$ 后,需要动态地构造一台新的图灵机 $M_2$。
- $M_2$ 的设计目标是:它的语言 $L(M_2)$ 的正则性,要完全依赖于“$M$ 是否接受 $w$”这一事件。
- 具体设计蓝图: 我们需要找到两种语言,一种是确定正则的,另一种是确定非正则的。然后让 $M_2$ 的行为在这两种语言之间切换。
- 选定的非正则语言: $\{0^n1^n \mid n \ge 0\}$。这是我们最熟悉的非正则语言,它需要无限的记忆来匹配0和1的数量。我们用它来充当“毒药”。
- 选定的正则语言: $\Sigma^*$,即包含所有可能字符串的语言。这是一个非常简单的正则语言。我们用它来充当“解药”。
- $M_2$ 的行为逻辑:
- $S$ 收到 $\langle M, w \rangle$ 后,构造出的 $M_2$ 运行在自己的输入 $x$上,逻辑如下:
- 第一步: $M_2$ 首先检查自己的输入 $x$ 是否符合 $\{0^n1^n\}$ 的形式。
- 如果 $x$ 的形式是 $0^n1^n$: $M_2$ 立刻接受 $x$。
- 这意味着 $\{0^n1^n\}$ 这个非正则语言,永远是 $L(M_2)$ 的一个子集。
- 第二步: 如果 $x$ 的形式不是 $0^n1^n$:
- 在这种情况下,$M_2$ 不立即做决定。它会“暂停”对 $x$ 的处理,转而在内部模拟 $M$ 在 $w$ 上的运行。
- 如果 $M$ 接受了 $w$: 那么 $M_2$ 就接受当前的输入 $x$。
- 如果 $M$ 不接受 $w$ (拒绝或循环): 那么 $M_2$ 就拒绝当前的输入 $x$。
- 分析 $M_2$ 的语言 $L(M_2)$:
- 情况A: 如果 $M$ 接受 $w$。
- 对于形如 $0^n1^n$ 的字符串 $x$,$M_2$ 接受它们(根据第一步)。
- 对于不形如 $0^n1^n$ 的字符串 $x$,$M_2$ 也接受它们(因为 $M$ 接受 $w$,第二步的条件满足了)。
- 因此,在这种情况下,$M_2$ 接受了所有的字符串。$L(M_2) = \Sigma^*$。而 $\Sigma^*$ 是一个正则语言。
- 情况B: 如果 $M$ 不接受 $w$。
- 对于形如 $0^n1^n$ 的字符串 $x$,$M_2$ 接受它们(根据第一步)。
- 对于不形如 $0^n1^n$ 的字符串 $x$,$M_2$ 会拒绝它们(因为 $M$ 不接受 $w$,第二步的条件不满足)。
- 因此,在这种情况下,$M_2$ 只接受形如 $0^n1^n$ 的字符串。$L(M_2) = \{0^n1^n \mid n \ge 0\}$。这是一个经典的非正则语言。
- 如何利用 $R$:
- $S$ 将构造好的 $\langle M_2 \rangle$ 交给判定器 $R$。
- 如果 $R$ 接受 $\langle M_2 \rangle$,说明 $L(M_2)$ 是正则语言。这对应我们的情况A,即 $M$ 接受 $w$。于是 $S$ 就可以接受。
- 如果 $R$ 拒绝 $\langle M_2 \rangle$,说明 $L(M_2)$ 是非正则语言。这对应我们的情况B,即 $M$ 不接受 $w$。于是 $S$ 就可以拒绝。
- 点明易错点:
- “请注意,图灵机$M_{2}$的构造并非是为了实际在某些输入上运行它”: 再次强调!$S$ 只是一个“设计师”和“建筑师”,它建造了 $M_2$ 的蓝图 $\langle M_2 \rangle$。$S$ 自己从不运行 $M_2$。$S$ 建造 $M_2$ 的唯一目的,就是把这份蓝图交给 $R$ 去“审查”。审查过程是 $R$ 的事,我们假设的 $R$ 有能力审查蓝图并判断其最终产品的性质(语言是否正则)。
证明思路是通过构造一个“变色龙”般的图灵机 $M_2$。这个 $M_2$ 的语言 $L(M_2)$ 的“颜色”(语言性质)会根据“$M$ 是否接受 $w$”这个外部事件而改变:如果 $M$ 接受 $w$,$L(M_2)$ 就变成“正则”色($\Sigma^*$);如果 $M$ 不接受 $w$,$L(M_2)$ 就变成“非正则”色($\{0^n1^n\}$)。通过使用假想的“正则语言判定器” $R$ 来检测 $M_2$ 的“颜色”,我们就能反推出 $M$ 是否接受 $w$。这成功地将 $A_{\mathrm{TM}}$ 归约到了 $REGULAR_{\mathrm{TM}}$,从而导出矛盾。
这段“证明思路”的目的是为了展示一种更为强大和抽象的归约技巧。它告诉我们,归约不仅仅是关于“存在性”(空/非空),也可以是关于“结构性”(正则/非正则)。这种将一个问题的解(是/否)映射到另一个问题的某个数学属性上的思想,是计算理论中非常核心和深刻的。
这就像一个“化学试纸”实验。
- 你要检测的 ($A_{\mathrm{TM}}$): 一杯未知的透明液体($w$)是否含有某种特定的化学物质($M$接受)。
- 你假设的工具 ($R$): 一个神奇的仪器,可以分析任何一种混合溶液($M_2$),并告诉你这种溶液最终会形成“晶体”(正则语言)还是“胶体”(非正则语言)。
- 你的实验方案 (构造 $M_2$):
- 你先在烧杯里放入一种你知道肯定会形成胶体的物质A(比如 $\{0^n1^n\}$)。
- 然后你加入一种遇水会变色的指示剂B。
- 最后,你加入那杯待测液体($w$)。你设计的实验是:如果液体中含有特定化学物质($M$接受),那么指示剂B会中和掉物质A的胶体特性,并让整个溶液倾向于结晶,最终形成晶体($\Sigma^*$)。如果液体中没有特定化学物质,那么物质A将主导整个体系,最终形成胶体($\{0^n1^n\}$)。
- 使用工具: 你把这杯混合好的溶液($M_2$)放入神奇仪器($R$)中。
- 仪器报告“晶体” $\implies$ 液体中含有该物质。
- 仪器报告“胶体” $\implies$ 液体中不含该物质。
- 矛盾: 你利用这个仪器,完美地解决了化学成分检测问题。但这是不可能的。所以,那个能区分晶体和胶体的神奇仪器不可能存在。
想象你是一位编剧 $S$,你想知道一位大牌导演 $M$ 是否愿意执导一部特定的高风险剧本 $w$。
- 你的问题 ($A_{\mathrm{TM}}$): 导演 $M$ 是否接受剧本 $w$?
- 假设的工具 ($R$): 一个神奇的影评AI,能分析任何一部新电影的剧本($M_2$),并预测这部电影最终会是一部“爆米花商业片”(正则语言)还是一部“晦涩艺术片”(非正则语言)。
- 你的策略 (构造 $M_2$): 你写了一个新的剧本 $M_2$,名叫《导演的选择》。剧本内容如下:
- 电影的前半部分,固定是一段非常晦涩难懂的、关于数学的艺术片段(这部分对应 $\{0^n1^n\}$,确保了电影有“艺术片”的底子)。
- 电影的后半部分,情节走向取决于导演 $M$ 是否愿意执导剧本 $w$。如果 $M$ 愿意,后半部分就变成一场盛大的、所有人都皆大欢喜的追车和爆炸场面,把整部电影变成一部超级商业片(对应 $\Sigma^*$)。如果 $M$ 不愿意,后半部分就不拍了,电影就以那段晦涩的艺术片段结束。
- 使用工具: 你把《导演的选择》这个剧本输入影评AI $R$。
- 如果AI预测“爆米花商业片”,你知道是导演 $M$ 同意了,加入了商业元素。
- 如果AI预测“晦涩艺术片”,你知道是导演 $M$ 拒绝了,电影只保留了艺术片底子。
- 矛盾: 你利用这个影评AI,完美地解决了“判断导演意图”这个无解问题。因此,这个神奇的影评AI不可能存在。
📜 [原文18]
证明 我们设$R$是判定$R E G U L A R_{\mathrm{TM}}$的图灵机,并构造图灵机$S$来判定$A_{\text {TM }}$。那么$S$按以下方式工作。
$S=$"在输入$\langle M, w\rangle$上,其中$M$是图灵机,$w$是字符串:
- 构造以下图灵机$M_{2}$。
$M_{2}=$"在输入$x$上:
- 如果$x$具有$0^{n} 1^{n}$的形式,则接受。
- 如果$x$不具有此形式,则在输入$w$上运行$M$,如果$M$接受$w$,则接受。"
- 在输入$\left\langle M_{2}\right\rangle$上运行$R$。
- 如果$R$接受,则接受;如果$R$拒绝,则拒绝。"
这部分是定理5.3的严格形式化证明。
第一部分:$S$ 和 $M_2$ 的形式化描述
- “我们设$R$是判定$R E G U L A R_{\mathrm{TM}}$的图灵机,并构造图灵机$S$来判定$A_{\text {TM }}$。”: 再次设立反证法框架。假设存在判定器 $R$,我们要用它构造 $A_{\mathrm{TM}}$ 的判定器 $S$。
- $S$ 的算法:
- “在输入$\langle M, w\rangle$上...”: $S$ 接收 $M$ 和 $w$。
- “1. 构造以下图灵机$M_{2}$。”: $S$ 的核心工作是构建 $M_2$ 的描述。
- $M_{2}=$"在输入$x$上:”: 这是被构造出来的 $M_2$ 的行为规范。
- “2. 如果$x$具有$0^{n} 1^{n}$的形式,则接受。”: $M_2$ 做的第一件事是检查自己的输入 $x$。如果 $x$ 是一串0后面跟着相同数量的1(比如 "0011", "000111"),$M_2$ 就接受它。这是一个可以由图灵机完成的检查(例如,来回划掉0和1)。
- “3. 如果$x$不具有此形式,则在输入$w$上运行$M$,如果$M$接受$w$,则接受。”: 如果 $x$ 的形式不是 $0^n1^n$,$M_2$ 就转而执行一个内部任务:模拟 $M$ 在 $w$ 上的运行。注意,$M_2$ 此时完全忽略了它自己的输入 $x$。它唯一的行为动机来自于 $M$ 对 $w$ 的反应。如果内部模拟显示 $M$ 接受了 $w$,$M_2$ 就接受它当前的输入 $x$。否则(如果 $M$ 拒绝或循环),$M_2$ 就在这里拒绝或循环,从而不接受 $x$。
- “4. 在输入$\left\langle M_{2}\right\rangle$上运行$R$。”: $S$ 将构造好的 $M_2$ 的描述 $\langle M_2 \rangle$ 喂给判定器 $R$。
- “5. 如果$R$接受,则接受;如果$R$拒绝,则拒绝。”: $S$ 的最终决定直接复制 $R$ 的决定。我们来分析这一步的逻辑。
第二部分:逻辑分析
- $S$ 的决策逻辑:
- 如果 $R$ 接受 $\langle M_2 \rangle$,意味着 $R$ 判断 $L(M_2)$ 是一个正则语言。根据我们对 $M_2$ 的分析,这只发生在 $M$ 接受 $w$ 的情况(此时 $L(M_2) = \Sigma^*$)。$A_{\mathrm{TM}}$ 问题的答案是“是”,所以 $S$ 接受是正确的。
- 如果 $R$ 拒绝 $\langle M_2 \rangle$,意味着 $R$ 判断 $L(M_2)$ 是一个非正则语言。根据我们对 $M_2$ 的分析,这只发生在 $M$ 不接受 $w$ 的情况(此时 $L(M_2) = \{0^n1^n\}$)。$A_{\mathrm{TM}}$ 问题的答案是“否”,所以 $S$ 拒绝是正确的。
- 构造的有效性:
- 这个构造成功地将“$M$ 是否接受 $w$”这个问题映射到了“$L(M_2)$ 是否为正则语言”这个问题上。
- $M$ 接受 $w \iff L(M_2)$ 是正则语言 ($\Sigma^*$)
- $M$ 不接受 $w \iff L(M_2)$ 是非正则语言 ($\{0^n1^n\}$)
- 因此,$S$ 通过调用 $R$ 并采纳其结果,成为了 $A_{\mathrm{TM}}$ 的一个完美判定器。
第三部分:得出矛盾
- 我们从“$REGULAR_{\mathrm{TM}}$ 可判定”的假设,导出了“$A_{\mathrm{TM}}$ 可判定”的结论。
- 这与 $A_{\mathrm{TM}}$ 的不可判定性相矛盾。
- 因此,假设错误,$REGULAR_{\mathrm{TM}}$ 是不可判定的。
- $S$ 的输出为何与 $R$ 相同? 在上一个 $E_{\mathrm{TM}}$ 的证明中,$S$ 的输出与 $R$ 相反。而这里是相同的。初学者容易混淆。关键在于理解归约的映射关系:
- 在 $E_{\mathrm{TM}}$ 证明中:$M$ 接受 $w \iff L(M_1)$ 非空 $\iff R$ 拒绝。所以 $S$ 要和 $R$ 反着来。
- 在 $REGULAR_{\mathrm{TM}}$ 证明中:$M$ 接受 $w \iff L(M_2)$ 正则 $\iff R$ 接受。所以 $S$ 要和 $R$ 保持一致。
- 核心是理解映射,而不是死记硬背是“相同”还是“相反”。
该形式化证明通过构造图灵机 $M_2$ 来实施归约。$M_2$ 的语言 $L(M_2)$ 被设计为:如果 $M$ 接受 $w$,则 $L(M_2) = \Sigma^*$(正则);如果 $M$ 不接受 $w$,则 $L(M_2) = \{0^n1^n\}$(非正则)。因此,一个假设存在的 $REGULAR_{\mathrm{TM}}$ 判定器 $R$ 对 $\langle M_2 \rangle$ 的判断结果,直接就对应了 $A_{\mathrm{TM}}$ 问题 $\langle M, w \rangle$ 的答案。这使得我们可以构造一个 $A_{\mathrm{TM}}$ 的判定器 $S$,从而引出矛盾,证明 $REGULAR_{\mathrm{TM}}$ 不可判定。
本段以严谨的算法形式,固化了“证明思路”中的巧妙设计,是完成数学证明所必需的步骤。它展示了如何通过组合已知的语言(正则的 $\Sigma^*$ 和非正则的 $\{0^n1^n\}$)来构造一个“测试探针”,这是归约技术中一种非常强大和常用的模式。
$S$ 的流程如下:
- 接到任务: 判断 $M$ 是否接受 $w$。
- 写一个“混合体”程序 $M_2$:
- 这个程序首先检查输入是不是像 "$000111$" 这种形式,如果是就接受。
- 如果不是,它就去执行一个子任务:判断 $M$ 是否接受 $w$。如果接受,那么 $M_2$ 也接受;否则不接受。
- 分析 $M_2$ 的性质:
- 如果 $M$ 接受 $w$,那么 $M_2$ 实际上接受所有输入(无论是 $0^n1^n$ 形式还是其他形式),它的行为等价于一个非常简单的“万能接受器”,其逻辑是正则的。
- 如果 $M$ 不接受 $w$,那么 $M_2$ 只接受 $0^n1^n$ 形式的输入,它的行为需要“计数”,其逻辑是非正则的。
- 调用“专家” $R$: 把 $M_2$ 的代码交给能区分“正则逻辑”和“非正则逻辑”的专家 $R$。
- 听取专家的结论:
- $R$ 说:“这是正则逻辑”。$S$ 就知道 $M$ 接受了 $w$。
- $R$ 说:“这是非正则逻辑”。$S$ 就知道 $M$ 没有接受 $w$。
- 发现矛盾: $S$ 通过这个流程总能完成任务,但这是不可能的,所以专家 $R$ 不存在。
想象你是一个药剂师 $S$,你想知道一种神秘的草药 $M$ 是否能治愈一种特定的疾病 $w$。
- 假设的仪器 $R$: 你有一个仪器,能分析任何一种药剂 $M_2$ 的化学结构,并告诉你它的分子结构是“简单的链状结构”(正则)还是“复杂的空间网状结构”(非正则)。
- 配制新药剂 $M_2$: 你配制了一种新的药剂 $M_2$,配方如下:
- 基础成分是一种你知道的、具有“复杂空间网状结构”的稳定物质(比如 $\{0^n1^n\}$)。
- 你还加入了一种催化剂。这种催化剂的行为取决于草药 $M$ 能否治愈疾病 $w$。如果能治愈,催化剂就会被激活,它会打断基础成分的复杂结构,并使其与溶剂中的所有其他分子结合,形成一种非常“简单的链状结构”(比如 $\Sigma^*$)。如果不能治愈,催化剂就不起作用。
- 进行分析: 你将新药剂 $M_2$ 放入仪器 $R$。
- 解读报告:
- 报告显示“简单的链状结构” $\implies$ 草药有效。
- 报告显示“复杂的空间网状结构” $\implies$ 草药无效。
- 矛盾: 你发现这个方法可以准确测试所有草药的药效,但我们已知这是个无解难题。所以,那个能区分分子结构的仪器 $R$ 不可能存在。
📜 [原文19]
同样,可以通过类似的证明来表明,测试图灵机的语言是否是上下文无关语言、可判定语言,甚至是有限语言的问题都是不可判定的。实际上,一个称为赖斯定理的通用结果指出,判断图灵机识别的语言的任何属性都是不可判定的。我们在问题5.16中给出赖斯定理。
这一段是对刚刚完成的证明进行扩展和泛化,并引出一个极为重要的通用定理——赖斯定理 (Rice's Theorem)。
- 证明方法的可扩展性:
- “同样,可以通过类似的证明来表明...”: 这句话指出,我们刚才用来证明 $REGULAR_{\mathrm{TM}}$ 的那套方法论,并非只能用一次,它是一个强大的“模板”,可以被广泛应用。
- 可证明的其他问题:
- 上下文无关语言问题: 判断 $L(M)$ 是否是一个上下文无关语言 (CFL)。我们可以把 $M_2$ 的非正则部分换成一个“非上下文无关”的语言(比如 $\{a^nb^nc^n \mid n \ge 0\}$),而正则部分换成一个上下文无关语言(比如 $\Sigma^*$ 或 $\{0^n1^n\}$)来进行类似的构造。
- 可判定语言问题: 判断 $L(M)$ 是否是一个可判定语言。
- 有限语言问题: 判断 $L(M)$ 是否是一个有限集。我们可以构造 $M_2$,使其在 $M$ 接受 $w$ 时语言为 $\Sigma^*$ (无限),在 $M$ 不接受 $w$ 时语言为 $\{0^n1^n \text{ for } n < 100\}$ (有限)。
- 引入通用结果——赖斯定理:
- “实际上,一个称为赖斯定理的通用结果指出...”: 与其一个一个地证明,数学家们发现这些证明都有共同的模式,于是他们将这个模式抽象出来,形成了一个一劳永逸的、非常强大的定理。
- 赖斯定理的核心内容: “判断图灵机识别的语言的任何非平凡属性都是不可判定的。”
- 属性 (Property): 指的是语言的某种性质。比如,“是正则的”、“是有限的”、“包含字符串'aba'”、“是空集”等等,这些都是语言的属性。
- 非平凡属性 (Nontrivial Property): “非平凡”意味着这个属性不是对所有语言都成立,也不是对所有语言都不成立。换句话说,至少存在一个语言具有该属性,也至少存在一个语言不具有该属性。
- 平凡属性的例子: “是一个语言”(所有图灵机语言都是语言,这是平凡的)、“可以被图灵机识别”(根据定义,所有 $L(M)$ 都可以被图灵机 $M$ 识别,这也是平凡的)。
- 非平凡属性的例子: 我们上面提到的所有问题(空、正则、CFL、有限、包含'aba'等)都是非平凡的。例如,对于“是空语言”这个属性,$\emptyset$ 满足它,而 $\{a\}$ 不满足它。
- 赖斯定理的威力: 有了赖斯定理,我们再遇到类似问题时,就不需要重新做复杂的归约构造了。我们只需要检查两点:
- 这个问题是不是关于图灵机语言的属性的?(而不是关于图灵机本身,比如“这个图灵机有超过50个状态吗?”这种问题赖斯定理不管)。
- 这个属性是不是非平凡的?
- 如果两点都满足,我们就可以直接“引用赖斯定理”,宣布该问题是不可判定的。
- 预告: “我们在问题5.16中给出赖斯定理。” 这表明本书将在习题部分对赖斯定理进行更详细的阐述和证明。
- 赖斯定理的适用范围: 赖斯定理只适用于对语言本身性质的判断,而不适用于对图灵机实现细节的判断。
- 适用赖斯定理的例子 (语言属性):
- $L(M)$ 是否包含回文串?(不可判定)
- $L(M)$ 是否有无穷多个元素?(不可判定)
- 不适用赖斯定理的例子 (机器属性):
- $M$ 是否有超过10个状态?(可判定,直接数就行)
- $M$ 在输入 "aba" 时,带头是否会向左移动超过3次?(可判定,模拟有限步即可)
- $M$ 是否会在某个输入上停机?(不可判定,但这不是一个语言属性,而是关于机器行为和输入对的属性,所以不能直接用赖斯定理,需要用 $HALT_{\mathrm{TM}}$ 的证明)
本段将前面具体的归约证明,提升到了一个更普适的层面。它指出,我们证明 $REGULAR_{\mathrm{TM}}$ 的方法可以被用来证明其他许多关于语言性质的问题的不可判定性。最终,它引出了一个“终极定理”——赖斯定理,该定理指出,任何关于图灵机语言的非平凡属性都是不可判定的。
本段的目的是进行知识的抽象和升华。它向读者展示了数学和科学追求的共同目标:从具体的例子中发现普适的规律,并将其形式化为强大的定理。引入赖斯定理,极大地简化了后续对同类问题的判断,展现了理论的力量。
赖斯定理就像是给“代码静态分析”判了死刑。它告诉你,你不可能写出一个通用的程序 CodeAnalyzer.exe,这个程序能够读取任何其他程序 P.exe 的源代码,并回答关于 P.exe 最终行为的任何有趣问题。
- “这个程序最终会不会打印出‘Hello World’?”(不可判定)
- “这个程序接受的合法输入集合是不是有限的?”(不可判定)
- “这个程序的输出结果是否总是素数?”(不可判定)
基本上,只要问题是关于程序“做什么”(语言属性),而不是关于程序“长什么样”(机器属性),并且这个问题不是那么无聊(非平凡),那么它就是不可判定的。
想象你有一个“万能小说鉴赏器”。
- 赖斯定理说: 这个鉴赏器不可能回答关于小说内涵(语言属性)的任何非平凡问题。
- 你可以问的平凡问题 (可判定):
- “这本小说是不是用中文写的?”(是)
- “这本书是不是一本小说?”(是)
- 你不能问的非平凡问题 (不可判定):
- “这本小说的主题是不是关于爱情的?”
- “这本小说是不是一部悲剧?”
- “这本小说是否包含任何一个比喻手法?”
- 为什么?因为任何一个关于内涵的判断,我们都可以像之前那样构造一个“薛定谔式”的小说(比如《导演的选择》),它的内涵(是商业片还是艺术片)取决于某个外部的、不可判定的事件。如果你能判断这本小说的内涵,你就能解决那个不可判定的事件,从而产生矛盾。
11.5 定理 5.4:$E Q_{\mathrm{TM}}$是不可判定的。
📜 [原文20]
到目前为止,我们证明语言不可判定的策略涉及从$A_{\text {TM }}$进行归约。有时,当我们需要证明某些语言不可判定时,从其他不可判定语言(例如$E_{\mathrm{TM}}$)进行归约会更方便。定理5.4表明,测试两台图灵机的等价性是一个不可判定的问题。我们可以通过从$A_{\mathrm{TM}}$进行归约来证明它,但我们借此机会提供一个通过从$E_{\mathrm{TM}}$进行归约来证明不可判定性的示例。设
定理 5.4
$E Q_{\text {TM }}$是不可判定的。
这一段引入了本节的第四个不可判定问题:图灵机等价性问题 ($EQ_{\mathrm{TM}}$),并特别指出,这次的证明将采用一个新的策略。
- 回顾与展望:
- “到目前为止,我们证明语言不可判定的策略涉及从$A_{\text {TM }}$进行归约。”: 总结了前面的所有证明 ($HALT_{\mathrm{TM}}$, $E_{\mathrm{TM}}$, $REGULAR_{\mathrm{TM}}$) 都是直接或间接地把“万恶之源” $A_{\mathrm{TM}}$ 归约过来。
- “有时...从其他不可判定语言...进行归约会更方便。”: 提出了一个新的思路。既然我们已经证明了 $HALT_{\mathrm{TM}}$ 和 $E_{\mathrm{TM}}$ 也是不可判定的,它们也加入了“不可判定问题俱乐部”,成为了新的“困难源头”。现在,我们可以不必每次都回到最初的 $A_{\mathrm{TM}}$,而是可以从任何一个已知的不可判定问题出发。这体现了归约的传递性。如果 $A \le_m B$ 且 $B \le_m C$,则 $A \le_m C$。
- “借此机会提供一个通过从$E_{\mathrm{TM}}$进行归约来证明不可判定性的示例。”: 明确了本节证明的教学目的——演示如何利用一个“中途”的不可判定问题 ($E_{\mathrm{TM}}$) 来进行归约。
- 引入新问题 $EQ_{\mathrm{TM}}$:
- 问题描述: “测试两台图灵机的等价性”。
- “等价”的定义: 在这里,“等价”指的是它们识别(接受)完全相同的语言。即 $L(M_1) = L(M_2)$。两个图灵机内部的实现逻辑、状态数、运行时间可以完全不同,但只要它们最终接受的字符串集合一模一样,我们就说它们是等价的。
- 问题的重要性: 这个问题在程序验证、编译器优化等领域至关重要。例如,我想用一个更优化的程序 $M_2$ 去替换一个旧的程序 $M_1$,我必须保证 $M_2$ 和 $M_1$ 在功能上是完全等价的,即 $L(M_1) = L(M_2)$。这个定理告诉我们,不存在一个通用的算法来自动完成这种等价性检查。
- 形式化定义:
- 给出了 $EQ_{\mathrm{TM}}$ 的集合表示。
- $EQ_{\mathrm{TM}}$: 问题的名称,代表图灵机的等价性问题。
- $\{\left\langle M_{1}, M_{2}\right\rangle \mid ... \}$: 该问题的输入是一个图灵机对的编码 $\langle M_1, M_2 \rangle$。
- $L\left(M_{1}\right)=L\left(M_{2}\right)$: 这是成员资格的判断条件。一对图灵机 $\langle M_1, M_2 \rangle$ 的编码属于 $EQ_{\mathrm{TM}}$,当且仅当它们所接受的语言是完全相同的。
- 示例1 (属于 $EQ_{\mathrm{TM}}$):
- $M_1$: 接受所有偶数长度的二进制串。
- $M_2$: 先检查输入串长度是否为偶数,如果是,则接受;否则拒绝。
- $L(M_1) = L(M_2)$,尽管它们的算法描述可能不同。因此 $\langle M_1, M_2 \rangle \in EQ_{\mathrm{TM}}$。
- 示例2 (不属于 $EQ_{\mathrm{TM}}$):
- $M_1$: 接受语言 $\{a, ab\}$。
- $M_2$: 接受语言 $\{a, ba\}$。
- $L(M_1) \neq L(M_2)$,因为 $M_1$ 接受 "ab" 而 $M_2$ 不接受,$M_2$ 接受 "ba" 而 $M_1$ 不接受。
- 因此 $\langle M_1, M_2 \rangle \notin EQ_{\mathrm{TM}}$。
- 赖斯定理的应用: 也可以用赖斯定理来理解 $EQ_{\mathrm{TM}}$ 的不可判定性。固定一个图灵机 $M_2$(比如一个识别空语言的机器 $M_\emptyset$),那么 $EQ_{\mathrm{TM}}$ 就变成了判断“$L(M_1) = L(M_\emptyset) = \emptyset$”的问题,这正是 $E_{\mathrm{TM}}$ 问题。我们已经知道 $E_{\mathrm{TM}}$ 是判断语言的非平凡属性,因此不可判定。$EQ_{\mathrm{TM}}$ 是 $E_{\mathrm{TM}}$ 的一个更普遍的形式,所以它也必然是不可判定的。这个证明将要展示的,就是这个思路的严格化。
本段引入了图灵机等价性问题 $EQ_{\mathrm{TM}}$,并宣布将使用一种新的归约策略来证明其不可判定性:不再从最源头的 $A_{\mathrm{TM}}$ 出发,而是从一个我们刚刚证明为不可判定的问题 $E_{\mathrm{TM}}$ 出发,展示归约方法的灵活性和传递性。
本段的主要目的是教学。它通过一个精心选择的例子,向读者传授一个重要的技能:如何选择最“方便”的已知不可判定问题来进行归约。有时候,从 $E_{\mathrm{TM}}$ 或 $HALT_{\mathrm{TM}}$ 出发,会让归约的构造变得异常简单,而硬要从 $A_{\mathrm{TM}}$ 出发则会非常繁琐。这培养了读者在解决问题时的策略性思维。
这就像是在证明一个数学难题。你当然可以每次都从最基本的公理(如皮亚诺公理,相当于 $A_{\mathrm{TM}}$)开始推导,但这会非常漫长和痛苦。更聰明的方法是,利用已经证明过的、更高级的定理(比如勾股定理,相当于 $E_{\mathrm{TM}}$ 或 $HALT_{\mathrm{TM}}$)作为你的出发点。这会让你的证明更简洁、更优雅。
想象你要去一个很高的大楼的顶层。
- 从 $A_{\mathrm{TM}}$ 归约: 相当于每次都坚持从1楼开始爬楼梯。
- 从 $E_{\mathrm{TM}}$ 归约: 相当于你知道电梯可以把你带到50楼($E_{\mathrm{TM}}$ 被证明不可判定),而你的目的地在55楼。你就可以先坐电梯到50楼,再从50楼开始往上爬,这比从1楼开始爬要快得多。
我们要证明的 $EQ_{\mathrm{TM}}$ 问题,就像是51楼,从50楼的 $E_{\mathrm{TM}}$ 出发去证明它,会比从1楼的 $A_{\mathrm{TM}}$ 出发容易得多。
📜 [原文21]
证明思路 证明如果$E Q_{\mathrm{TM}}$是可判定的,那么$E_{\mathrm{TM}}$也将是可判定的,方法是从$E_{\mathrm{TM}}$到$E Q_{\mathrm{TM}}$进行归约。这个想法很简单。$E_{\mathrm{TM}}$是判断图灵机的语言是否为空的问题。$E Q_{\mathrm{TM}}$是判断两台图灵机的语言是否相同的问题。如果其中一种语言恰好是$\emptyset$,我们最终的问题是判断另一台机器的语言是否为空——即$E_{\mathrm{TM}}$问题。因此,从某种意义上说,$E_{\text {TM }}$问题是$E Q_{\text {TM }}$问题的一个特例,其中一台机器被固定为识别空语言。这个想法使得归约变得容易。
这是定理5.4的“证明思路”。它揭示了这次归约构造为何如此简单和直观。
- 确定归约方向和框架:
- 框架: 依然是反证法。假设 $EQ_{\mathrm{TM}}$ 可判定。
- 目标: 利用这个假设,证明 $E_{\mathrm{TM}}$ 可判定,从而导出矛盾。
- 归约方向: $E_{\mathrm{TM}} \le_m EQ_{\mathrm{TM}}$。
- 核心思想——特例化 (Specialization):
- 分析两个问题:
- $E_{\mathrm{TM}}$ 问题:输入 $\langle M \rangle$,问 $L(M) = \emptyset$ ?
- $EQ_{\mathrm{TM}}$ 问题:输入 $\langle M_1, M_2 \rangle$,问 $L(M_1) = L(M_2)$ ?
- 发现关系: 仔细观察,你会发现 $E_{\mathrm{TM}}$ 问题看起来就像是 $EQ_{\mathrm{TM}}$ 问题的一个“特殊情况”。
- 如何特殊化: 如果在 $EQ_{\mathrm{TM}}$ 问题中,我们把其中一台机器,比如说 $M_2$,固定成一台我们已知的、其语言就是空集 $\emptyset$ 的机器,那么 $EQ_{\mathrm{TM}}$ 问题就变成了:
- 归约的构造蓝图:
- 假设我们有一个能判定 $EQ_{\mathrm{TM}}$ 的“黑盒子” $R$。
- 我们要构造一个能判定 $E_{\mathrm{TM}}$ 的机器 $S$。
- $S$ 的工作流程如下:
- $S$ 接收输入 $\langle M \rangle$。它的任务是判断 $L(M)$ 是否为空。
- $S$ 不直接处理 $M$,而是先构造一个非常简单的、固定的图灵机 $M_\emptyset$,这个 $M_\emptyset$ 的功能就是拒绝所有输入,所以我们确切地知道 $L(M_\emptyset) = \emptyset$。
- 然后,$S$ 把 $\langle M, M_\emptyset \rangle$ 这一对图灵机的编码,作为输入喂给“黑盒子” $R$。
- $S$ 等待 $R$ 的回答。$R$ 会告诉我们 $L(M)$ 是否等于 $L(M_\emptyset)$。
- 如果 $R$ 回答“是”(接受),那就意味着 $L(M) = L(M_\emptyset) = \emptyset$。这正是 $S$ 想要知道的!于是 $S$ 就可以接受。
- 如果 $R$ 回答“否”(拒绝),那就意味着 $L(M) \neq L(M_\emptyset) = \emptyset$。于是 $S$ 就可以拒绝。
- 这个构造非常直接,几乎没有复杂的逻辑。
- 归约方向: 这里是 $E_{\mathrm{TM}} \le_m EQ_{\mathrm{TM}}$。我们用解决 $EQ_{\mathrm{TM}}$ 的能力来解决 $E_{\mathrm{TM}}$。因为 $E_{\mathrm{TM}}$ 已知不可判定,所以 $EQ_{\mathrm{TM}}$ 必须也不可判定。方向正确。
- 为何这次更简单: 这次归约之所以简单,是因为我们归约的“源头” $E_{\mathrm{TM}}$ 和“目标” $EQ_{\mathrm{TM}}$ 在结构上非常相似。$EQ_{\mathrm{TM}}$ 就像是 $E_{\mathrm{TM}}$ 的一个“双输入版本”。我们只需要把其中一个输入固定为一个常量,就能把它“降维”成 $E_{\mathrm{TM}}$。
证明思路的核心是,将空语言问题 $E_{\mathrm{TM}}$ 视为等价性问题 $EQ_{\mathrm{TM}}$ 的一个特例。通过将待测图灵机 $M$ 与一个已知的、语言为空的图灵机 $M_\emptyset$ 进行比较,就可以利用假想的 $EQ_{\mathrm{TM}}$ 判定器来解决 $E_{\mathrm{TM}}$ 问题。由于 $E_{\mathrm{TM}}$ 已知不可判定,这自然导致了矛盾。
本段的目的是展示最简单、最直观的一类归约:通过特例化进行的归约。它告诉我们,在寻找归约方法时,可以先思考“我的新问题 B 是否包含了某个已知不可解问题 A 作为其特例?” 如果是,那么归约构造通常会非常简单。
这就像你有一个可以比较任意两个数是否相等的工具,但你想知道某一个数是否等于零。
- 问题 A ($E_{\mathrm{TM}}$): 判断 $x$ 是否等于 0?
- 假设的工具 R ($EQ_{\mathrm{TM}}$): 一个函数 areTheyEqual(a, b),可以比较任意 a 和 b 是否相等。
- 你的解决方案 S: 你想写一个函数 isItZero(x)。你的实现是:
return areTheyEqual(x, 0);
- 逻辑: 你把判断“是否为零”这个单输入问题,归约到了“是否相等”这个双输入问题,方法是把第二个输入固定为0。
- 结论: 如果 isItZero 是个无解问题,那么 areTheyEqual 也必然是无解问题。
想象你是一位法官 $S$,你的任务是判断“被告 $M$ 是否一句话都没说(语言为空)”。
- 你的问题 ($E_{\mathrm{TM}}$): 判断 $M$ 是否沉默。
- 假设的助手 $R$ ($EQ_{\mathrm{TM}}$): 你有一个助手,他有特异功能,可以比较任意两个人 $M_1$ 和 $M_2$ 的全部言论,并告诉你他们的言论记录是否完全一样。
- 你的办案策略:
- 你找来一个众所周知的、从不说话的哑巴 $M_\emptyset$。
- 你让助手 $R$ 去比较被告 $M$ 和哑巴 $M_\emptyset$ 的言论记录。
- 如果助手报告“两人言论完全一样”,你就知道被告 $M$ 也是个哑巴(一句话没说)。
- 如果助手报告“两人言论不一样”,你就知道被告 $M$ 至少说过一句话。
- 矛盾: 你利用这个助手,完美解决了“判断是否沉默”的问题。但我们已知这是个无解问题 ($E_{\mathrm{TM}}$ 不可判定)。所以,你的特异功能助手 $R$ 不可能存在。
📜 [原文22]
证明 我们设图灵机$R$判定$E Q_{\text {TM }}$,并构造图灵机$S$来判定$E_{\text {TM }}$,如下所示。
$S=$"在输入$\langle M\rangle$上,其中$M$是图灵机:
- 在输入$\left\langle M, M_{1}\right\rangle$上运行$R$,其中$M_{1}$是拒绝所有输入的图灵机。
- 如果$R$接受,则接受;如果$R$拒绝,则拒绝。"
如果$R$判定$E Q_{\mathrm{TM}}$,则$S$判定$E_{\mathrm{TM}}$。但根据定理5.2,$E_{\mathrm{TM}}$是不可判定的,因此$E Q_{\mathrm{TM}}$也必须是不可判定的。
这部分是定理5.4的严格形式化证明,其简洁性体现了证明思路的巧妙。
第一部分:$S$ 的形式化描述
- “我们设图灵机$R$判定$E Q_{\text {TM }}$,并构造图灵机$S$来判定$E_{\text {TM }}$,如下所示。”: 设立反证法框架。假设存在 $EQ_{\mathrm{TM}}$ 判定器 $R$,用它构造 $E_{\mathrm{TM}}$ 判定器 $S$。
- $S$ 的算法:
- “在输入$\langle M\rangle$上,其中$M$是图灵机:”: $S$ 接收一个图灵机 $M$ 的编码。它的目标是判断 $L(M)$ 是否为空。
- “1. 在输入$\left\langle M, M_{1}\right\rangle$上运行$R$,其中$M_{1}$是拒绝所有输入的图灵机。”: 这是整个归约的核心。
- $S$ 首先需要一个“参照物”——一个我们确定其语言为空的图灵机。这里选择了 $M_1$,一个非常简单的、对任何输入都直接拒绝的图灵机。我们可以轻易地写出 $M_1$ 的描述,它只有一个状态,无论读到什么符号都进入拒绝状态。因此,我们确切地知道 $L(M_1) = \emptyset$。
- $S$ 将它自己的输入 $\langle M \rangle$ 和这个固定的参照物 $\langle M_1 \rangle$ 配对,形成一个新的输入 $\langle M, M_1 \rangle$。
- $S$ 将这个配对的输入交给假想的 $EQ_{\mathrm{TM}}$ 判定器 $R$ 去处理。
- “2. 如果$R$接受,则接受;如果$R$拒绝,则拒绝。”: $S$ 的最终决定完全复制 $R$ 的决定。
第二部分:逻辑分析
- $S$ 的决策逻辑:
- 如果 $R$ 接受 $\langle M, M_1 \rangle$,根据 $R$ 的定义,这意味着 $L(M) = L(M_1)$。既然我们知道 $L(M_1) = \emptyset$,这就等价于 $L(M) = \emptyset$。这正是 $E_{\mathrm{TM}}$ 问题所要判断的“是”的情况。所以 $S$ 接受是正确的。
- 如果 $R$ 拒绝 $\langle M, M_1 \rangle$,根据 $R$ 的定义,这意味着 $L(M) \neq L(M_1)$。既然 $L(M_1) = \emptyset$,这就等价于 $L(M) \neq \emptyset$。这正是 $E_{\mathrm{TM}}$ 问题所要判断的“否”的情况。所以 $S$ 拒绝是正确的。
- 构造的有效性:
- 这个构造成功地将 $E_{\mathrm{TM}}$ 判定问题 $\langle M \rangle$ 转换成了 $EQ_{\mathrm{TM}}$ 判定问题 $\langle M, M_1 \rangle$。
- $L(M) = \emptyset \iff L(M) = L(M_1) \iff R \text{ 接受 } \langle M, M_1 \rangle$
- 因此,$S$ 成为了 $E_{\mathrm{TM}}$ 的一个完美判定器。
第三部分:得出矛盾
- “如果$R$判定$E Q_{\mathrm{TM}}$,则$S$判定$E_{\mathrm{TM}}$。”: 总结我们构造的成功。
- “但根据定理5.2,$E_{\mathrm{TM}}$是不可判定的,”: 引用我们之前已经证明的事实。我们已经有了一个“不可判定俱乐部”的成员 $E_{\mathrm{TM}}$。
- “因此$E Q_{\mathrm{TM}}$也必须是不可判定的。”: 反证法得出结论。既然从“$EQ_{\mathrm{TM}}$ 可判定”的假设推出了“$E_{\mathrm{TM}}$ 可判定”的谬论,那么假设错误,$EQ_{\mathrm{TM}}$ 必须是不可判定的。
该形式化证明通过一个极其简洁的归约,证明了图灵机等价性问题 $EQ_{\mathrm{TM}}$ 的不可判定性。它将待判断的空语言问题 $E_{\mathrm{TM}}(\langle M \rangle)$,转化为判断 $M$ 是否与一个已知的、语言为空的图灵机 $M_1$ 等价的问题,即 $EQ_{\mathrm{TM}}(\langle M, M_1 \rangle)$。由于我们已经知道 $E_{\mathrm{TM}}$ 是不可判定的,那么能解决更一般问题的 $EQ_{\mathrm{TM}}$ 也必然是不可判定的。
本段的目的是用一个清晰、简短的范例,来巩固“从一个已知的、非 $A_{\mathrm{TM}}$ 的不可判定问题出发进行归约”的策略。它展示了当归约的源问题和目标问题结构相似时,证明可以变得何等优雅和直观。
$S$ 的代码实现:
```python
2一个已知的、拒绝所有输入的图灵机M1的描述
M1_description = "..."
3S 的逻辑
def decide_E_TM(M_description):
4构造EQ_TM的输入
input_for_R = (M_description, M1_description)
5调用假设存在的、判定EQ_TM的“神仙函数”R
6R返回true当且仅当两个TM的语言相等
if are_languages_equal(input_for_R) == true:
return "接受" # M的语言等于M1的空语言
else:
return "拒绝" # M的语言不等于M1的空语言
```
这段代码 decide_E_TM 完美地解决了 $E_{\mathrm{TM}}$ 问题。但我们已知 $E_{\mathrm{TM}}$ 无解,所以,它所依赖的那个“神仙函数” are_languages_equal 必然不存在。
你是一个珠宝鉴定师 $S$,你的任务是判断“一颗钻石 $M$ 是否完美无瑕(语言为空)”。
- 假设的仪器 $R$: 你有一台高科技对比仪 $R$,可以扫描任意两颗钻石 $M_1, M_2$,并判断它们的内部瑕疵分布是否完全一样。
- 你的鉴定策略:
- 你先拿出一颗官方认证的、绝对的标准完美钻石 $M_1$ (语言为空的图灵机)。
- 你把待测钻石 $M$ 和这颗标准完美钻石 $M_1$ 一起放入对比仪 $R$。
- 如果仪器显示“两颗完全一样”,你就知道待测钻石 $M$ 也是完美无瑕的。
- 如果仪器显示“不一样”,你就知道待测钻石 $M$ 内部有瑕疵。
- 矛盾: 你发现这个方法可以准确鉴定任何钻石是否完美无瑕。但我们已知“判断钻石是否完美无瑕”($E_{\mathrm{TM}}$)是一个无法用通用仪器解决的问题。因此,那台能对比任意两颗钻石的仪器 $R$ 必然不存在。
1.2 通过计算历史进行归约
12.1 定义 5.5:计算历史
📜 [原文23]
计算历史方法是证明$A_{\text {TM }}$可归约到某些语言的重要技术。当要证明不可判定的问题涉及测试某事物是否存在时,此方法通常很有用。例如,此方法用于证明希尔伯特第十问题(测试多项式是否存在整数根)的不可判定性。
图灵机在输入上的计算历史仅仅是机器处理输入时所经历的配置序列。它是这台机器计算的完整记录。
定义 5.5
设$M$是一个图灵机,$w$是一个输入字符串。$M$在$w$上的接受计算历史是配置序列$C_{1}, C_{2}, \ldots, C_{l}$,其中$C_{1}$是$M$在$w$上的起始配置,$C_{l}$是$M$的接受配置,并且每个$C_{i}$根据$M$的规则合法地跟随$C_{i-1}$。$M$在$w$上的拒绝计算历史定义类似,只是$C_{l}$是拒绝配置。
这一部分引入了一个全新的、非常强大的归约技术——计算历史法 (Computation History Method),并给出了核心概念计算历史的定义。
- 引入新技术:
- “计算历史方法是证明$A_{\text {TM }}$可归约到某些语言的重要技术”: 开宗明义,我们正在学习一种新的、用于构造归约的“套路”。
- 适用场景: “当要证明不可判定的问题涉及测试某事物是否存在时,此方法通常很有用”。这里的“某事物”通常指的就是一个“合法的计算过程”。
- 举例: 提到了一个非常著名的例子——希尔伯特第十问题。这个问题问的是:给定一个多项式方程,判断它是否存在整数解。马季亚谢维奇在1970年证明了这个问题是不可判定的,其证明的核心思想就是将图灵机的计算历史编码成一个多项式方程,使得“图灵机停机”等价于“多项式有整数解”。这展示了计算历史法的强大威力。
- 计算历史的非形式化定义:
- “图灵机在输入上的计算历史仅仅是机器处理输入时所经历的配置序列”: 这句话给出了一个直观的定义。
- 配置 (Configuration/Instantaneous Description, ID): 指的是图灵机在某个瞬间的“快照”。一个快照需要包含三个信息:
- 当前机器处于哪个状态 ($q_i$)。
- 当前磁带上的全部内容。
- 当前读写磁头的位置。
- 通常,我们将这三者合在一起表示,例如 u q v,表示当前状态是 q,磁带上是字符串 uv,且磁头指向 v 的第一个符号。
- 配置序列: 计算历史就是一连串这样的“快照”,从开始到结束,记录了计算的每一步。
- “它是这台机器计算的完整记录”: 就像飞机的“黑匣子”,或者一段程序的“log文件”,它包含了重现整个计算过程所需的所有信息。
- 计算历史的形式化定义 (定义 5.5):
- 接受计算历史 (Accepting Computation History):
- 它是一个有限的配置序列 $C_1, C_2, \ldots, C_l$。
- 它必须满足三个条件:
- 起始正确: $C_1$ 必须是 $M$ 在输入 $w$ 上的起始配置。通常是 $q_0w_1w_2...w_n$,其中 $q_0$ 是起始状态,磁头在 $w$ 的第一个字符上。
- 过程合法: 序列中的每一步转换都必须是合法的。即对于任意 $i > 1$,$C_i$ 必须是根据 $M$ 的转移函数 $\delta$ 从 $C_{i-1}$ 推导出的下一个配置。
- 结局正确: $C_l$ (最后一个配置) 必须是一个接受配置,即 $C_l$ 中包含接受状态 $q_{\text{accept}}$。
- 拒绝计算历史 (Rejecting Computation History): 定义类似,唯一的区别是最后一个配置 $C_l$ 是一个拒绝配置(包含拒绝状态 $q_{\text{reject}}$)。
- 如果 $M$ 在 $w$ 上循环: 那么它永远不会进入接受或拒绝状态,因此它在 $w$ 上既没有接受计算历史,也没有拒绝计算历史。
- 示例:
- 图灵机 M:
- 状态: {$q_0, q_1, q_{\text{accept}}$}
- 字母表: {0, sqcup} (sqcup代表空白符)
- 转移函数: $\delta(q_0, 0) = (q_1, \sqcup, R)$ (状态从 $q_0$ 变 $q_1$,把0改成空白,磁头右移)
$\delta(q_1, \sqcup) = (q_{\text{accept}}, \sqcup, R)$ (状态从 $q_1$ 变 $q_{\text{accept}}$,磁头右移)
- 输入 w: "0"
- 计算过程:
- 起始配置 $C_1$: $q_0 0$
- 根据 $\delta(q_0, 0) = (q_1, \sqcup, R)$,机器进入下一配置。磁带变成 $\sqcup$,状态是 $q_1$,磁头在 $\sqcup$ 的右边(可以认为是新的空白符)。配置 $C_2$ 为: $\sqcup q_1 \sqcup$
- 根据 $\delta(q_1, \sqcup) = (q_{\text{accept}}, \sqcup, R)$,机器进入下一配置。状态是 $q_{\text{accept}}$。配置 $C_3$ 为: $\sqcup \sqcup q_{\text{accept}}$
- 接受计算历史: 这个序列 $C_1, C_2, C_3$ 就是一个接受计算历史。
- $C_1 = q_0 0$ (起始正确)
- $C_2 = \sqcup q_1 \sqcup$ (从 $C_1$ 合法转移而来)
- $C_3 = \sqcup \sqcup q_{\text{accept}}$ (从 $C_2$ 合法转移而来,且是接受配置)
- 计算历史是有限的: 只有当图灵机停机时,才存在计算历史。循环的计算过程没有计算历史。
- 计算历史是唯一的(对于确定性图灵机): 一个确定性图灵机(DTM)在给定的输入上,其计算路径是唯一的,因此它最多只有一个计算历史(接受或拒绝)。非确定性图灵机(NTM)在同一个输入上可能有多个计算历史,对应不同的计算分支。
本节引入了计算历史的概念,它是一个图灵机在特定输入上从开始到结束所经历的所有“快照”(配置)的序列。一个“接受计算历史”是导致接受状态的合法配置序列。这个概念是后续归约证明中的一个关键工具,它将一个动态的“计算过程”物化成了一个静态的、可以被检查的“字符串”。
本节的目的是为了引入一种新的归约“媒介”。在之前的证明中,我们通过构造一个新机器的“行为”来编码信息。现在,我们学习如何将信息编码到一个“数据结构”——计算历史字符串——中。这种方法的巧妙之处在于,一个动态的、可能无限的计算过程,其“是否存在一个成功路径”的问题,被转化为了“是否存在一个满足特定语法规则的字符串”的问题。后者更容易被其他类型的机器(如下文的LBA或PDA)来检查。
计算历史就像是一盘棋的棋谱。
- 配置: 棋盘在某一回合的布局。
- 转移函数: 棋规(马走日,象走田)。
- 计算历史: 从开局到一方将军(接受)或被将(拒绝)的完整走法记录。
- 检查一个计算历史是否合法: 就相当于检查一步棋谱,看每一步是否都符合棋规。
- 计算历史法的思想: 我想知道“白方能否赢下这盘棋?”($A_{\mathrm{TM}}$),我把这个问题转化为“是否存在一个合法的、最终白方将军的棋谱?”。然后我设计一个“棋谱检查器”,用它的能力来回答我的问题。
想象一部法庭审判的完整录像带。
- 配置: 录像带的每一帧画面。
- 转移函数: 物理定律和法律程序。
- 接受计算历史: 一段完整的、从开庭到法官宣判“被告无罪”(接受)的录像,并且录像中的每一帧都必须是连续的、符合逻辑的。
- 计算历史法的思想: 我想知道“被告最终是否会被判无罪?”($A_{\mathrm{TM}}$),我把问题转化为“是否存在这样一段‘无罪判决’的合法录像带?”。然后我造一个“录像带鉴定仪”,让它去鉴定是否存在这样的录像带。
12.2 定义 5.6:线性有界自动机 (LBA)
📜 [原文24]
计算历史是有限序列。如果$M$在$w$上不停机,则$M$在$w$上不存在接受或拒绝计算历史。确定性机器在任何给定输入上最多有一个计算历史。非确定性机器在单个输入上可能有多个计算历史,对应于各种计算分支。目前,我们继续关注确定性机器。我们第一个使用计算历史方法证明不可判定性的证明涉及一种称为线性有界自动机的机器。
定义 5.6
线性有界自动机是一种受限制的图灵机,其中磁头不允许移出包含输入的磁带部分。如果机器试图将磁头移出输入的两端,则磁头会停留在原地——就像普通图灵机的磁头不会移出磁带的左端一样。
这一部分首先对计算历史做了补充说明,然后引入了我们将要研究的第一个与计算历史法相关的计算模型——线性有界自动机 (Linear Bounded Automaton, LBA)。
第一部分:计算历史的补充
- “计算历史是有限序列”: 再次强调,只有停机的计算才有计算历史。
- “确定性机器...最多有一个计算历史”: 对于DTM,路径是唯一的。
- “非确定性机器...可能有多个计算历史”: 对于NTM,一个输入可能对应多条并行的计算路径,其中一些可能接受,一些可能拒绝,一些可能循环。只要有一条路径接受,NTM就接受该输入。
- “目前,我们继续关注确定性机器”: 明确了当前讨论的范围,以简化问题。
第二部分:引入 LBA
- “我们第一个使用计算历史方法...涉及一种称为线性有界自动机的机器”: 预告了 LBA 即将扮演的角色。LBA 将作为我们构造的“计算历史检查器”。
第三部分:LBA 的定义 (定义 5.6)
- “线性有界自动机是一种受限制的图灵机”: LBA 不是一个全新的模型,它是图灵机的一个变种,其能力受到了限制。
- 核心限制: “磁头不允许移出包含输入的磁带部分”。
- 假设输入字符串是 $w$,其长度为 $n$。那么 LBA 的读写头只能在为 $w$ 分配的这 $n$ 个格子内移动。
- 这与标准图灵机形成鲜明对比,后者的磁头可以无限制地向右移动,使用无限的存储空间。
- 边界行为: “如果机器试图将磁头移出输入的两端,则磁头会停留在原地”。
- 这定义了当磁头试图“越界”时会发生什么。它不会像某些模型那样导致崩溃,而是像撞到一堵无形的墙,保持在边界单元格不动。
- 这类似于标准图灵机在最左端不能再向左移动。LBA 相当于在输入的右端也设置了这样一个“墙”。
- 示例1:
- 输入 w: "hello" (长度为5)
- LBA 的工作空间: 磁带上只有5个格子,分别写着 'h', 'e', 'l', 'l', 'o'。LBA 的磁头可以在这5个格子之间来回移动和读写,但它永远不能移动到第1个格子 'h' 的左边,也不能移动到第5个格子 'o' 的右边。
- 图灵机的工作空间: 如果这是一个标准图灵机,输入 "hello" 后,磁带是 ...sqcup, h, e, l, l, o, sqcup, sqcup, ...。磁头可以向右走到天荒地老。
- 示例2:
- LBA M: 假设它在位置5,状态q,读到'o'。转移函数是 $\delta(q, 'o') = (q', 'p', R)$ (向右移动)。
- 行为: 磁头会尝试向右移动,但由于到达了右边界,它会停在位置5不动。磁带上的 'o' 仍然会被改成 'p',状态也会变成 $q'$。最终配置的变化只是状态和磁带内容,磁头位置不变。
- “线性”的含义: 名字中的“线性”指的是 LBA 可用的存储空间与输入长度 $n$ 是线性关系。虽然严格说它不能移出输入的 $n$ 个格子,但通过使用更大的磁带字母表,它可以将每个格子中的信息密度提高一个常数倍,总存储量仍然是 $O(n)$。
- LBA 不是有限自动机: LBA 仍然是一个强大的模型。它不是FA,因为它可以在输入上来回读写。FA只能从左到右读一遍。LBA 也不是 PDA,因为它没有栈的后进先出限制,它的 $n$ 个格子是可随机访问的。
本节定义了线性有界自动机 (LBA),它是一种特殊的图灵机,其工作空间被严格限制在输入字符串本身所占的磁带区域内。这个空间限制是 LBA 的核心特征。
引入 LBA 的目的是为了后续的归约证明服务。LBA 的空间限制特性,使得它在给定输入长度下,总的可能配置数是有限的。这个关键性质将使得与 LBA 相关的某些问题(如 $A_{\mathrm{LBA}}$)是可判定的,但另一些问题(如 $E_{\mathrm{LBA}}$)却是不可判定的。这种“部分可解,部分不可解”的特性使它成为一个非常有趣的理论研究对象,并且是连接 $A_{\mathrm{TM}}$ 和上下文有关语言的桥梁。在接下来的证明中,LBA 将被用来扮演“计算历史检查器”的角色。
LBA 就像是一个在固定大小的沙盒里玩耍的孩子。
- 标准图灵机: 拥有一个无限大的沙滩,可以随意奔跑和堆沙子。
- LBA: 只能在自家的、由栅栏围起来的小沙盒里玩。沙盒的大小就是最初放入的玩具(输入)所占的大小。他不能跑到沙盒外面去。
- 这种限制使得他的总玩法(配置数)是有限的,尽管可能非常非常多。
想象一个在一行字上进行编辑的文本编辑器光标。
- 标准图灵机: 像 Word 或 VS Code,你可以不断地打字,文档可以无限长。
- LBA: 像一个古老的、固定长度显示的终端。你只能在屏幕上显示的那一行内移动光标和修改字符,光标无法移出这一行。
1.2.2.1 图 5.7 线性有界自动机示意图
📜 [原文25]
线性有界自动机是一种内存受限的图灵机,如下图所示。它只能解决需要适应输入所用磁带的内存问题。使用比输入字母表更大的磁带字母表可以使可用内存增加一个常数因子。因此,我们说对于长度为$n$的输入,可用内存量与$n$成线性关系——因此得名。
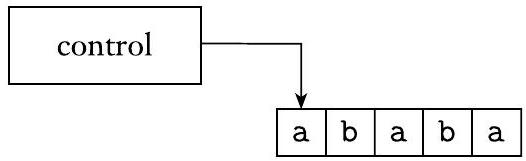
图 5.7
线性有界自动机示意图
这部分是对 LBA 定义的进一步解释,并配上了一张示意图来加深理解。
- “内存受限的图灵机”: 再次强调 LBA 的核心特征是其有限的工作空间。
- 示意图解读:
- 图中的磁带: 图中画出了一条磁带,但两端被明确地标记为“左端”和“右端”,并用竖线表示边界。这与标准图灵机两端用省略号表示无限延伸的画法截然不同。
- 输入: 输入字符串被放置在这段有界的磁带上。
- 读写头: 读写头被画在了磁带的中间,箭头指向下方,表示它只能在这个有界区域内活动。
- 有限自动机控制器: 和标准图灵机一样,它有一个有限状态的控制器来决定下一步的行为。
- 整体感觉: 整个图示传达出一种“被框住”、“受限制”的感觉。
- “它只能解决需要适应输入所用磁带的内存问题”: 这句话说明了 LBA 的能力边界。它能解决的问题,其算法所需的内存空间不能超过输入本身长度的常数倍。例如,判断一个字符串是否是回文串 ($w = w^R$),LBA可以做到(来回比较两端的字符并做标记)。但是,如果一个问题需要 $n^2$ 或 $2^n$ 的空间($n$是输入长度),LBA就无能为力了。
- “使用比输入字母表更大的磁带字母表可以使可用内存增加一个常数因子”: 这是一个技术细节,解释了为什么内存是“线性”的,而不完全等于输入长度 $n$。
- 输入字母表 $\Sigma$: 原始输入字符串中允许出现的字符集合。
- 磁带字母表 $\Gamma$: LBA 在计算过程中允许在磁带上读写的字符集合。$\Sigma \subseteq \Gamma$。
- 增加内存的技巧: 我们可以让 $\Gamma$ 更丰富。例如,除了原始字符 'a', 'b',我们还可以在 $\Gamma$ 中加入带标记的字符,如 'a_dot' (表示这个a下面做了个点标记), 'b_checked' (表示这个b已经被检查过)。甚至可以用一个磁带符号表示一对或多元组,如 $\langle a, 1, \text{checked} \rangle$。如果 $\Gamma$ 的大小是 $|\Sigma|$ 的 $k$ 倍,我们相当于把每个格子的信息容量扩大了 $k$ 倍,总内存就是 $k \times n$,仍然是线性的。
- “因此,我们说对于长度为$n$的输入,可用内存量与$n$成线性关系——因此得名。”: 总结了“线性有界”这个名字的由来。
- LBA 和 上下文有关语言 (Context-Sensitive Languages, CSLs): LBA 精确地识别上下文有关语言这一类语言(除空串外)。这是乔姆斯基谱系中介于上下文无关语言和递归可枚举语言之间的重要一环。虽然本书可能不深入探讨,但这是 LBA 在理论中地位的体现。
- 内存大小: LBA的内存是 $O(n)$,而不是严格的 $n$。这个常数因子的存在很重要,它给予了 LBA 在有限空间内进行复杂计算的灵活性。
本节通过示意图和文字解释,进一步阐明了线性有界自动机 (LBA) 的概念。LBA 是一个内存受限的图灵机,其可用内存与输入长度成线性关系,这是其名称的由来,也是其计算能力的核心特征。
图示和补充说明的目的是为了让 LBA 这个抽象概念更加具体化和形象化。通过视觉辅助和对“线性”一词来源的解释,帮助读者建立一个准确、牢固的心智模型,为理解后续基于 LBA 配置数量的证明(引理5.8)打下基础。
LBA就像一个只有一块固定大小白板的数学家。
- 输入: 别人在白板上写下的一道题。
- 计算: 他只能在这块白板上进行草稿、计算、标记和修改。他不能拿出额外的草稿纸。
- 聪明的做法: 为了在有限空间里记录更多信息,他可能会发明一些复合符号,或者用不同颜色的笔来做标记(对应更大的磁带字母表)。但无论如何,白板的大小是固定不变的,他能记录的信息总量有一个明确的上限。
想象一个在非常狭窄的厨房里做饭的厨师。
- 厨房台面 (磁带): 只有一米长。
- 食材 (输入): 所有的食材都必须在这一米长的台面上摆开。
- 厨师 (控制器+磁头): 只能在台面前来回走动,拿取和处理台面上的食材。他不能把东西放到地上或旁边的桌子上。
- 更大的磁带字母表: 相当于他可以使用“堆叠”技术,在一个盘子上放多种食材,或者使用多层置物架,在有限的台面面积上增加了存储容量。但总的来说,他能处理的食材总量还是受限于这个台面的线性尺寸。
12.3 引理 5.8:LBA 的配置数量
📜 [原文26]
尽管有内存限制,线性有界自动机(LBA)的功能相当强大。例如,$A_{\mathrm{DFA}}、A_{\mathrm{CFG}}、E_{\mathrm{DFA}}$和$E_{\mathrm{CFG}}$的判决器都是LBA。每个CFL都可以由LBA判决。事实上,要找到一个不能由LBA判决的可判定语言需要一些功夫。我们将在第9章中发展这样做的技术。
在这里,$A_{\mathrm{LBA}}$是确定LBA是否接受其输入的问题。尽管$A_{\text {LBA }}$与不可判定问题$A_{\text {TM }}$相同,其中图灵机被限制为LBA,但我们可以证明$A_{\text {LBA }}$是可判定的。设
在证明$A_{\mathrm{LBA}}$的可判定性之前,我们发现以下引理很有用。它指出,当长度为$n$的字符串作为输入时,LBA只能有有限数量的配置。
引理 5.8
设$M$是一个LBA,它有$q$个状态和磁带字母表中的$g$个符号。对于长度为$n$的磁带,$M$恰好有$q n g^{n}$个不同的配置。
这一部分分为两个层次:首先介绍 LBA 的强大能力和它自己的接受问题 $A_{\mathrm{LBA}}$,然后给出一个关键的引理,计算 LBA 可能配置的总数。
第一部分:LBA 的能力和 $A_{\mathrm{LBA}}$ 问题
- “尽管有内存限制,线性有界自动机(LBA)的功能相当强大”: 作者先给我们一个“惊喜”。虽然 LBA 看起来受限,但它的计算能力远超我们的想象。
- LBA能解决的问题:
- $A_{\mathrm{DFA}}$: 判断一个 DFA 是否接受某个字符串。
- $A_{\mathrm{CFG}}$: 判断一个 CFG 是否能生成某个字符串 (CYK算法)。
- $E_{\mathrm{DFA}}$: 判断一个 DFA 的语言是否为空。
- $E_{\mathrm{CFG}}$: 判断一个 CFG 的语言是否为空。
- “每个CFL都可以由LBA判决”: 接受一个上下文无关语言的问题,LBA 都能解决。
- LBA 不能解决的可判定语言: “要找到一个不能由LBA判决的可判定语言需要一些功夫”。这暗示了 LBA 的能力上限,但指出找到这样的例子并不容易。这部分内容将在第9章(空间复杂性)中讨论。
- 引入 $A_{\mathrm{LBA}}$ 问题: 这是 LBA 版本的“接受问题”。
- 与 $A_{\mathrm{TM}}$ 的对比: 它的定义形式和 $A_{\mathrm{TM}}$ 一模一样,只是把“TM”换成了“LBA”。
- 核心区别: $A_{\mathrm{TM}}$ 是不可判定的,而我们马上要证明 $A_{\mathrm{LBA}}$ 是可判定的。这是图灵机和线性有界自动机一个根本性的区别。
第二部分:引理 5.8
- 引理的作用: “在证明$A_{\mathrm{LBA}}$的可判定性之前,我们发现以下引理很有用”。这个引理是证明 $A_{\mathrm{LBA}}$ 可判定性的基石。
- 引理内容: “LBA只能有有限数量的配置”。这是由其有限的内存决定的。引理给出了这个有限数量的精确计算公式。
- 形式化陈述:
- 给定参数:
- $q$: LBA 的状态总数。
- $g$: LBA 的磁带字母表 $\Gamma$ 中的符号总数。
- $n$: 输入字符串的长度,也就是磁带的长度。
- 结论: LBA 在此设置下,总共有 $q \times n \times g^n$ 个不同的配置。
公式: LBA配置总数 = $q \times n \times g^n$
- 推导思路: 一个配置由三个独立部分组成:当前状态、磁头位置、磁带内容。根据组合数学的乘法原理,总配置数就是这三个部分可能性的乘积。
- 当前状态的可能性: 机器可以处于 $q$ 个状态中的任何一个。所以有 $q$ 种可能性。
- 磁头位置的可能性: 磁带长度为 $n$,磁头可以指向从第1个到第 $n$ 个的任何一个格子。所以有 $n$ 种可能性。
- 磁带内容的可能性: 磁带共有 $n$ 个格子。每个格子都可以写入 $g$ 个磁带符号中的任何一个。根据乘法原理, $n$ 个格子的内容组合起来,总共有 $g \times g \times \ldots \times g$ ($n$次) = $g^n$ 种可能性。
- 三者相乘: 将这三部分的可能数相乘,就得到了总的配置数:$q \times n \times g^n$。
- 示例1: 一个简单的 LBA
- $q = 3$ 个状态 ({$q_0, q_1, q_a$})
- $n = 2$ (输入为 "ab")
- $g = 4$ 个磁带符号 ({'a', 'b', 'x', 'y'})
- 总配置数: $3 \times 2 \times 4^2 = 6 \times 16 = 96$ 个。
- 这意味着这个 LBA 在输入 "ab" 上运行时,它最多只会经历96个不同的配置。如果它运行了97步还没有停机,那么根据鸽巢原理,它必定已经重复了至少一个配置,从而进入了无限循环。
- 示例2: 另一个 LBA
- $q = 10$ 个状态
- $n = 5$ (输入长度为5)
- $g = 2$ 个磁带符号 ({0, 1})
- 总配置数: $10 \times 5 \times 2^5 = 50 \times 32 = 1600$ 个。
- 这个 LBA 在长度为5的输入上,最多运行1600步就会停机或进入循环。
本节首先铺垫了 LBA 的强大能力,并提出了 LBA 自身的接受问题 $A_{\mathrm{LBA}}$,指明它与 $A_{\mathrm{TM}}$ 不同,是可判定的。为了证明这一点,本节给出了关键的引理5.8,它通过简单的组合学原理,精确计算出 LBA 在给定长度为 $n$ 的输入时,其不同配置的总数是有限的,具体为 $qng^n$。
引入这个引理的目的是为了量化 LBA 的“有限性”。虽然 LBA 的状态空间比有限自动机大得多,但它终究是有限的。这个“有限性”是证明 $A_{\mathrm{LBA}}$ 可判定的关键。有了这个确切的数字,我们就可以设计一个“带计时器”的模拟器:我们让 LBA 运行这么多次,如果还没停,就一定是死循环了。这就把不可判定的“循环”问题,转化为了可判定的“超时”问题。
这个引理就像是在计算魔方有多少种不同的状态。
- 魔方:一个 LBA
- 小方块位置和朝向:磁带内容
- 你正在拧的那个面:状态
- 你关注的那个块:磁头位置
- 虽然魔方的变化非常多($4.3 \times 10^{19}$ 种),但它终究是一个有限的数字。这意味着,如果你不停地随机转动魔方,你必然会在有限步内回到一个你之前见过的状态。LBA 也是同理。
想象一个只有88个键的钢琴。
- $q$: 你弹琴的力度(比如10种)。
- $n$: 钢琴的键数 (88)。
- $g$: 每个键能发出的音色(比如5种,钢琴、风琴、吉他...)。
- 一个配置: 在某个瞬间,你用某种力度,按下了88个键中的某一个,同时整个键盘设定为某种音色组合。
- 引理5.8: 计算了所有这些可能瞬间的总和。这个总和虽然巨大,但是有限的。你不可能永远弹奏出“全新”的音乐瞬间,总会在某一刻重复。
📜 [原文27]
证明 回想一下,$M$的配置就像其计算过程中的快照。配置由控制状态、磁头位置和磁带内容组成。在这里,$M$有$q$个状态。其磁带长度为$n$,因此磁头可以位于$n$个位置之一,并且磁带上可以出现$g^{n}$种可能的磁带符号串。这三个量的乘积是$M$在长度为$n$的磁带上不同配置的总数。
这部分是引理5.8的详细证明,它解释了公式 $qng^n$ 是如何通过基本计数原理推导出来的。
- “回想一下,$M$的配置就像其计算过程中的快照。”: 再次使用“快照”这个直观的比喻来定义配置。
- “配置由控制状态、磁头位置和磁带内容组成。”: 明确指出构成一个配置的三个独立要素。这是应用乘法原理的前提。
- 逐项分析可能性的数量:
- 控制状态: “$M$有$q$个状态。” 所以,状态部分有 $q$ 种可能性。
- 磁头位置: “其磁带长度为$n$,因此磁头可以位于$n$个位置之一。” 所以,磁头位置部分有 $n$ 种可能性。
- 磁带内容: “并且磁带上可以出现$g^{n}$种可能的磁带符号串。”
- 磁带有 $n$ 个格子。
- 每个格子可以填入 $g$ 个不同符号中的任意一个。
- 第1个格子有 $g$ 种选择。
- 第2个格子有 $g$ 种选择。
- ...
- 第 $n$ 个格子有 $g$ 种选择。
- 根据乘法原理,总的磁带内容组合数是 $g \times g \times \ldots \times g$ ($n$次),即 $g^n$。
- “这三个量的乘积是$M$在长度为$n$的磁带上不同配置的总数。”:
- 将三个独立要素的可能性数量相乘,得到最终结果。
- 总数 = (状态的可能性) $\times$ (磁头位置的可能性) $\times$ (磁带内容的可能性)
- 总数 = $q \times n \times g^n$
本段通过将 LBA 的配置分解为状态、磁头位置和磁带内容三个独立部分,并分别计算每个部分的可能性数量,最后运用乘法原理,清晰地推导出了 LBA 在长度为 n 的磁带上总配置数的公式为 $qng^n$。
本段的目的是提供引理5.8的严谨推导过程。在数学和理论计算机科学中,仅仅给出公式是不够的,必须清晰地展示其来源,确保逻辑的完备性和正确性。这个证明虽然简单,但它是一个很好的范例,展示了如何将一个复杂的计算模型对象(配置)分解为简单的、可计数的组件。
这就像是在计算一个网站的用户个人资料有多少种可能的组合。
- 状态 ($q$): 用户的会员等级(比如:普通、白银、黄金,共3种)。
- 磁头位置 ($n$): 用户的头像框样式(比如:10种)。
- 磁带内容 ($g^n$): 用户的昵称。假设昵称长度固定为5个字符($n=5$),每个字符可以是26个小写字母中的一个($g=26$)。那么昵称的可能性是 $26^5$ 种。
- 总配置数: 总的用户个人资料组合数 = $3 \times 10 \times 26^5$。
想象你在为一个角色扮演游戏设计角色。
- 状态 ($q$): 角色的职业(战士、法师、盗贼,共3种)。
- 磁头位置 ($n$): 角色的发型(长发、短发、光头、双马尾,共4种)。
- 磁带内容 ($g^n$): 角色的装备。假设有6个装备槽(头、胸、手、腿、脚、武器,$n=6$),每个槽位都有10种不同的装备可选($g=10$)。那么总的装备组合是 $10^6$ 种。
- 总的角色配置数: $3 \times 4 \times 10^6 = 12,000,000$ 种。
12.4 定理 5.9:$A_{\text {LBA }}$是可判定的。
📜 [原文28]
定理 5.9
$A_{\text {LBA }}$是可判定的。
证明思路 为了判断LBA $M$是否接受输入$w$,我们模拟$M$在$w$上的运行。在模拟过程中,如果$M$停机并接受或拒绝,我们相应地接受或拒绝。如果$M$在$w$上循环,就会出现困难。我们需要能够检测循环,以便我们可以停机并拒绝。
检测$M$何时循环的想法是,当$M$在$w$上计算时,它会从一个配置转移到另一个配置。如果$M$重复某个配置,它将一遍又一遍地重复这个配置,从而进入循环。因为$M$是LBA,它可用的磁带量是有限的。根据引理5.8,$M$在这样数量的磁带上只能处于有限数量的配置。因此,$M$在进入它以前进入过的某个配置之前,只有有限的时间可用。通过模拟$M$引理5.8给出的步数,可以检测$M$是否正在循环。如果$M$在那之前还没有停机,它一定是在循环。
这是定理5.9的“证明思路”,解释了为什么 $A_{\mathrm{LBA}}$ 是可判定的,这与 $A_{\mathrm{TM}}$ 形成了鲜明对比。
- 目标: 构造一个判定器来解决 $A_{\mathrm{LBA}}$。这个判定器在任何输入 $\langle M, w \rangle$ (其中 M 是 LBA) 上,都能在有限时间内给出“接受”或“拒绝”的答案。
- 基本策略: 模拟。最直接的方法就是模拟 LBA $M$ 在输入 $w$ 上的运行。
- 遇到的困难: 和之前分析 $A_{\mathrm{TM}}$ 时一样,直接模拟的最大障碍是无限循环。如果 $M$ 在 $w$ 上循环,我们的模拟器也会跟着循环,这就无法成为一个判定器。
- 解决困难的关键——检测循环:
- 循环的本质: 一个确定性计算模型(如 LBA 或 DTM)如果进入了它曾经到达过的同一个配置,那么由于其后续行为是完全由当前配置决定的,它必然会重复从那个配置开始的整个计算序列,从而陷入无限循环。
- LBA 的特殊性: 与标准图灵机不同,LBA 的配置总数是有限的!引理5.8给了我们这个定心丸,并算出了确切的上限:$qng^n$。
- 鸽巢原理 (Pigeonhole Principle): 想象有 $k = qng^n$ 个“鸽巢”(代表所有可能的配置),而 LBA 的计算过程是不断放出“鸽子”(代表当前的配置)。如果 LBA 运行了 $k+1$ 步,它就放出了 $k+1$ 只鸽子。由于只有 $k$ 个鸽巢,必然至少有一只鸽子飞进了它之前飞过的巢,即配置发生了重复。
- 检测方法: 因此,我们不需要在模拟时存储所有见过的配置并进行比较(虽然这也是一种方法)。一个更简单的方法是设置一个“计时器”。我们让模拟最多运行 $qng^n$ 步。
- 如果在这 $qng^n$ 步之内,$M$ 停机了(接受或拒绝),那很好,我们得到了答案。
- 如果运行了 $qng^n$ 步之后,$M$ 仍然没有停机,我们就可以百分之百地确定它已经进入了一个无限循环。因为它已经经历了 $qng^n+1$ 个配置,必然有重复。
- 完整的判定策略:
- 给定输入 $\langle M, w \rangle$。
- 首先从 $M$ 的描述中提取状态数 $q$,从磁带字母表中得到符号数 $g$,并测量输入 $w$ 的长度 $n$。
- 计算出配置数上限 $k = qng^n$。
- 开始模拟 $M$ 在 $w$ 上的运行,并同时启动一个步数计数器,从0开始。
- 在每一步模拟后,计数器加1。
- 如果在模拟过程中,$M$ 进入接受状态,则我们的判定器接受并停机。
- 如果在模拟过程中,$M$ 进入拒绝状态,则我们的判定器拒绝并停机。
- 如果计数器的值达到了 $qng^n$,而模拟仍未结束,我们的判定器就强行停止模拟,并直接拒绝(因为我们断定它已经循环了)。
这个策略覆盖了所有可能性,并且保证在有限步内(最多 $qng^n$ 步)结束。因此,它是一个有效的判定器。
- 为什么这个方法对标准图灵机无效?: 因为标准图灵机可以在无限的磁带上工作,它的配置总数是无限的。我们无法给出一个通用的配置数上限。因此,我们永远无法通过“超时”来确定一个标准图灵机是否进入了循环。这正是 $A_{\mathrm{TM}}$ 不可判定的根本原因之一。
- 步数上限: 理论上,步数上限可以是 $qng^n$。实际中,任何大于等于这个值的数都可以。这个数字可能非常巨大,但关键在于它是有限和可计算的。在可判定性理论中,我们不关心效率,只关心是否存在一个能在有限时间内完成的算法。
证明思路的核心在于利用 LBA 的内存限制。由于 LBA 的总配置数是有限的(由引理5.8给出),我们可以通过模拟 LBA 有限的步数来检测它是否会进入无限循环。如果在达到配置总数上限的步数后 LBA 仍未停机,我们就可以断定它已陷入循环。这使得我们可以构造一个总能停机的模拟器,从而证明 $A_{\mathrm{LBA}}$ 是可判定的。
本段的目的是清晰地解释 $A_{\mathrm{LBA}}$ 可判定性的根源,并将其与 $A_{\mathrm{TM}}$ 的不可判定性进行对比,从而深化读者对“有限配置空间”与“无限配置空间”这一本质区别的理解。它展示了模型的一个微小改动(内存有界 vs 无界)如何导致其核心性质(可判定性)发生根本性的改变。
这就像是在一个有限大小的迷宫里找出口。
- LBA: 在一个墙壁都已建好的、有限大小的迷宫里行走。
- 配置: 你在迷宫中的位置和朝向。
- 可判定性: 你可以通过一个简单的算法来判断能否走出迷宫:在迷宫里随意行走,并在走过的路上做标记。由于迷宫大小有限,你最终要么找到出口,要么会回到一个你已经做过标记的地方。一旦回到标记点,你就知道你在这个圈子里打转,永远也出不去了。因为总有办法在有限时间内知道结果,所以这个问题是“可判定”的。
- 标准图灵机: 在一个可以无限延伸的迷宫里行走。你永远无法通过“走遍所有地方”或“回到原点”来判断是否被困住了,因为迷宫本身是无限的。
想象你在玩一个电子游戏。
- LBA: 游戏运行在一台内存有限的老式游戏机上(比如红白机)。游戏中的所有变量(玩家位置、敌人状态、得分等)的总和构成了一个巨大的、但有限的状态空间。理论上,游戏如果运行足够长的时间,必然会重复某个一模一样的游戏画面。
- $A_{\mathrm{LBA}}$ 的判定器: 一个“游戏测试员”。他启动游戏,然后盯着屏幕。如果他发现游戏进入了一个死循环(比如某个动画不停地重复),或者游戏正常结束了,他都能在有限时间内发现。他可以带一个“秒表”,如果游戏运行了太长时间(超过了理论上所有可能画面的总数)还没结束,他就知道这游戏死机了。
- 标准图灵机: 一个在拥有无限内存的超级计算机上运行的程序。你无法通过“超时”来判断它是否死循环,因为它可能正在进行一个合法但非常漫长的计算。
📜 [原文29]
证明 判定$A_{\mathrm{LBA}}$的算法如下。
$L=$"在输入$\langle M, w\rangle$上,其中$M$是LBA,$w$是字符串:
- 模拟$M$在$w$上的运行,持续$q n g^{n}$步或直到停机。
- 如果$M$已停机,如果它接受了,则接受;如果它拒绝了,则拒绝。如果它没有停机,则拒绝。"
如果$M$在$w$上在$q n g^{n}$步内没有停机,它必然根据引理5.8重复了一个配置,因此正在循环。这就是为什么我们的算法在这种情况下拒绝的原因。
这部分是定理5.9的严格形式化证明,它将“证明思路”中的策略描述成一个具体的算法。
第一部分:算法 L 的描述
- “判定$A_{\mathrm{LBA}}$的算法如下。$L=$”: 我们将要构造的这个判定器命名为 $L$。
- “在输入$\langle M, w\rangle$上,其中$M$是LBA,$w$是字符串:”: 算法 $L$ 的输入。
- “1. 模拟$M$在$w$上的运行,持续$q n g^{n}$步或直到停机。”: 这是算法的核心步骤。
- 准备工作 (隐含): 在开始模拟前,判定器 $L$ 首先需要从输入 $\langle M, w \rangle$ 中解析出三个关键参数:
- $q$: $M$ 的状态数。
- $g$: $M$ 的磁带字母表大小。
- $n$: $w$ 的长度。
- 然后计算出步数上限 $k = qng^n$。
- 模拟过程: $L$ 启动一个通用 LBA 模拟器,并设置一个计数器。
- 停止条件: 这个模拟过程有两个停止条件,哪个先满足就按哪个来:
- $M$ 自己停机了(进入接受或拒绝状态)。
- 模拟的步数达到了上限 $k = qng^n$。
- 由于 $k$ 是一个有限的可计算的数,这个模拟步骤保证会在有限时间内结束。
- “2. 如果$M$已停机,如果它接受了,则接受;如果它拒绝了,则拒绝。如果它没有停机,则拒绝。”: 这是模拟结束后,$L$ 如何做出最终判决的规则。
- 情况1: $M$ 自己停机了: 这意味着模拟是因为第一个停止条件而结束的。
- 如果 $M$ 的停机状态是接受,那么 $\langle M, w \rangle \in A_{\mathrm{LBA}}$,所以 $L$ 也接受。正确。
- 如果 $M$ 的停机状态是拒绝,那么 $\langle M, w \rangle \notin A_{\mathrm{LBA}}$,所以 $L$ 也拒绝。正确。
- 情况2: $M$ 没有停机: 这意味着模拟是因为第二个停止条件(超时)而结束的。
- “如果它没有停机,则拒绝。”: 此时 $L$ 直接拒绝。
- 理由: 正如“证明思路”中分析的,运行了 $qng^n$ 步还没停,意味着 LBA $M$ 必定已经重复了至少一个配置,陷入了无限循环。既然 $M$ 循环了,它就不会接受 $w$,所以 $\langle M, w \rangle \notin A_{\mathrm{LBA}}$。因此 $L$ 拒绝是正确的。
第二部分:证明总结
- “如果$M$在$w$上在$q n g^{n}$步内没有停机,它必然根据引理5.8重复了一个配置,因此正在循环。”: 对算法第2步中“超时则拒绝”的合理性进行了再次说明,强调了其理论基础是引理5.8和鸽巢原理。
- “这就是为什么我们的算法在这种情况下拒绝的原因。”: 总结陈词。
该形式化证明给出了一个判定 $A_{\mathrm{LBA}}$ 的具体算法 $L$。该算法通过模拟 LBA 最多 $qng^n$ 步(其中 $q, n, g$ 分别是状态数、输入长度和磁带符号数)来工作。如果在这些步骤内 LBA 接受或拒绝,算法 $L$ 就相应地接受或拒绝。如果达到了步数上限 LBA 仍未停机,算法 $L$ 就断定其已进入循环并拒绝。由于该算法总能在有限步内对任何输入给出正确的“接受”或“拒绝”的答案,因此它是一个有效的判定器,从而证明了 $A_{\mathrm{LBA}}$ 是可判定的。
本段的目的是将定理5.9的证明以清晰、无歧义的算法形式呈现出来,完成一个完整的数学证明。它展示了如何将一个理论上的洞察(有限配置数)转化为一个具体的、可执行的算法步骤(带步数上限的模拟)。
算法 $L$ 就像是一个带“熔断机制”的测试脚本。
- 启动测试: run_test(M, w)。
- 设置超时: timeout = calculate_max_configs(M, w)。
- 执行: simulate(M, w, steps_limit=timeout)。
- 分析结果:
- if simulate_result == "accepted": return "PASS"。
- if simulate_result == "rejected": return "FAIL"。
- if simulate_result == "timeout": return "FAIL (due to infinite loop)"。
你是一个裁判,在看两个机器人下棋。
- 棋局 ($M$在$w$上运行): 两个机器人对弈。
- 棋局状态 (配置): 棋盘上所有棋子的位置。
- 可判定性: 你需要判断“白方最终能否赢棋?”
- 你的裁判算法 $L$:
- 你查阅规则手册,知道这个棋盘大小有限,总的合法棋局状态数是有限的,比如是 $N$ ($qng^n$)。(引理5.8)
- 你规定,一盘棋最多只能下 $N$ 步。(设置超时)
- 你开始观战。
- 如果在 $N$ 步内,白方将死了黑方,你宣布“白方赢”。
- 如果在 $N$ 步内,黑方将死了白方,或者和棋了,你宣布“白方没赢”。
- 如果双方下了 $N$ 步棋还没分出胜负,根据规则,你强行终止比赛,并判定“白方没赢”(因为他们陷入了循环,比如长将)。
- 结论: 你的这套裁判方法,总能在有限时间内对“白方能否赢棋”给出一个明确的裁决,因此这个问题是“可判定”的。
12.5 定理 5.10:$E_{\mathrm{LBA}}$是不可判定的。
📜 [原文30]
定理5.9表明LBA和TM在一个基本方面有所不同:对于LBA,接受问题是可判定的,但对于TM则不然。然而,某些涉及LBA的其他问题仍然是不可判定的。其中之一是空性问题$E_{\mathrm{LBA}}=\{\langle M\rangle \mid M$是一个LBA且$L(M)=\emptyset\}$。为了证明$E_{\mathrm{LBA}}$是不可判定的,我们给出一个使用计算历史方法的归约。
定理 5.10
$E_{\mathrm{LBA}}$是不可判定的。
这一段是一个重要的转折。它在刚刚证明了 LBA 的一个“好消息” ($A_{\mathrm{LBA}}$ 可判定) 之后,立刻要给我们一个“坏消息”,即 LBA 的空语言问题 $E_{\mathrm{LBA}}$ 依然是不可判定的。
- 承上启下:
- 回顾不同点: “定理5.9表明LBA和TM在一个基本方面有所不同:对于LBA,接受问题是可判定的,但对于TM则不然。” 这是对 $A_{\mathrm{LBA}}$ 和 $A_{\mathrm{TM}}$ 性质差异的总结。这个差异的根源在于内存是否有限。
- 引入相似点: “然而,某些涉及LBA的其他问题仍然是不可判定的。” 这句话告诉我们,不要因为 $A_{\mathrm{LBA}}$ 可判定就认为 LBA 是一个“简单”的模型。在其他方面,它和标准图灵机一样,能够引发不可判定性。
- 引入新问题 $E_{\mathrm{LBA}}$:
- 问题名称: 空性问题 $E_{\mathrm{LBA}}$。
- 形式化定义: $E_{\mathrm{LBA}}=\{\langle M\rangle \mid M \text{ 是一个LBA且 } L(M)=\emptyset\}$。
- 问题描述: 给定一个 LBA 的编码 $\langle M \rangle$,判断它所接受的语言是否为空集。即,是否存在任何一个字符串 $w$,使得 $M$ 接受 $w$?如果不存在这样的 $w$,则 $L(M)=\emptyset$。
- 与 $E_{\mathrm{TM}}$ 的关系: 这个问题的定义与 $E_{\mathrm{TM}}$ 完全一样,只是把“TM”换成了“LBA”。
- 声明证明策略:
- “为了证明$E_{\mathrm{LBA}}$是不可判定的,我们给出一个使用计算历史方法的归约。”:
- 目标: 证明 $E_{\mathrm{LBA}}$ 不可判定。
- 工具: 计算历史方法。
- 手段: 归约。具体来说,我们将从一个已知的不可判定问题($A_{\mathrm{TM}}$)归约到 $E_{\mathrm{LBA}}$。即证明 $A_{\mathrm{TM}} \le_m E_{\mathrm{LBA}}$。
- $A_{\mathrm{LBA}}$ vs $E_{\mathrm{LBA}}$: 一定要区分这两个问题。
- $A_{\mathrm{LBA}}$: 输入 $\langle M, w \rangle$,问“M是否接受w?” (可判定)
- $E_{\mathrm{LBA}}$: 输入 $\langle M \rangle$,问“M是否不接受任何东西?” (不可判定)
- 为什么会有这种差异?:
- $A_{\mathrm{LBA}}$ 可判定是因为我们有一个特定的输入 $w$,它的长度 $n$ 是固定的。这使得我们可以计算出配置总数的上限 $qng^n$,从而通过“超时”来解决循环问题。
- $E_{\mathrm{LBA}}$ 不可判定是因为我们没有一个特定的输入 $w$。我们需要判断 LBA $M$ 在所有无限多个可能输入上的行为。对于一个很长的输入 $w'$,其配置上限会变得非常大。我们无法通过模拟 $M$ 在所有输入上的运行来判断其语言是否为空,因为输入本身是无限多的。这就为不可判定性留下了“后门”。
本段在LBA的“接受问题”$A_{\mathrm{LBA}}$可判定的背景下,引入了LBA的“空语言问题”$E_{\mathrm{LBA}}$,并指出后者是不可判定的。本段还明确了将要使用的证明策略:利用新学的“计算历史方法”,将$A_{\mathrm{TM}}$归约到$E_{\mathrm{LBA}}$。
本段的目的是制造一个认知上的“张力”,加深读者对计算理论复杂性的理解。它表明,一个计算模型的性质不是单一的,“可判定”或“不可判定”的标签往往是针对特定问题而言的。通过证明 $E_{\mathrm{LBA}}$ 的不可判定性,它将首次正式地、完整地展示计算历史归约法这一强大技巧。
LBA就像一个“有固定任期的官员”。
- $A_{\mathrm{LBA}}$ (可判定): 问“这位官员($M$)在处理某一件特定的案件($w$)时,最终是否会给出‘批准’的批示?”。因为案件是特定的,我们可以预估出处理它所需的最长时间(配置上限)。如果超过这个时间他还没批,我们就知道他是在“打太极”(循环),相当于不批准。所以这个问题总能得到答案。
- $E_{\mathrm{LBA}}$ (不可判定): 问“这位官员($M$)在他的整个任期内,是不是一个‘万年不批’的官员,即他永远不会批准任何案件?”。要回答这个问题,你需要审查他可能遇到的所有无限多种案件。你无法通过模拟来完成这个任务。这个问题就变得不可判定了。
想象一个“配方检查机器人”。
- LBA: 这个机器人被设计用来检查食谱。它的内存大小取决于食谱的长度。
- $A_{\mathrm{LBA}}$ (可判定): 给定一个机器人($M$)和一个特定的食谱($w$),问“机器人检查完这个食谱后,会不会亮起‘通过’的绿灯?”。我们可以通过模拟机器人的工作来判定,因为食谱长度固定,机器人的总工作状态有限,我们可以通过超时来检测死循环。
- $E_{\mathrm{LBA}}$ (不可判定): 给定一个机器人($M$),问“这个机器人是不是一个‘极度挑剔的机器人’,以至于它不会给任何食谱亮绿灯?”。我们无法测试所有可能的无限多种食谱来回答这个问题。我们要证明,不存在一个更高阶的“机器人分析仪”,能自动判断任何一个配方检查机器人是否“极度挑剔”。
📜 [原文31]
证明思路 这个证明是通过从$A_{\mathrm{TM}}$进行归约。我们证明如果$E_{\mathrm{LBA}}$是可判定的,那么$A_{\text {TM }}$也将是可判定的。假设$E_{\mathrm{LBA}}$是可判定的。我们如何利用这个假设来判定$A_{\text {TM }}$?
对于一个图灵机$M$和一个输入$w$,我们可以通过构造一个特定的LBA $B$然后测试$L(B)$是否为空来确定$M$是否接受$w$。$B$识别的语言包含$M$在$w$上的所有接受计算历史。如果$M$接受$w$,这个语言包含一个字符串,因此是非空的。如果$M$不接受$w$,这个语言是空的。如果我们可以确定$B$的语言是否为空,显然我们可以确定$M$是否接受$w$。
现在我们描述如何从$M$和$w$构造$B$。请注意,我们不仅需要展示$B$的存在,还需要展示图灵机如何在给定$M$和$w$的描述的情况下获得$B$的描述。
正如我们为证明不可判定性而给出的先前的归约一样,我们构造$B$只是为了将其描述输入到假定的$E_{\mathrm{LBA}}$判决器中,而不是为了在某些输入上运行$B$。
这是定理5.10“计算历史归约法”的证明思路。它描绘了如何将一个“动态的计算过程”问题 ($A_{\mathrm{TM}}$) 转化为一个“静态的语言属性”问题 ($E_{\mathrm{LBA}}$)。
- 确定框架:
- 方法: 从 $A_{\mathrm{TM}}$ 归约的反证法。
- 假设: $E_{\mathrm{LBA}}$ 可判定,即存在一个判定器 $R_{ELBA}$。
- 目标: 利用 $R_{ELBA}$ 构造 $A_{\mathrm{TM}}$ 的判定器 $S_{ATM}$。
- 核心构造思想:
- $S_{ATM}$ 接收输入 $\langle M, w \rangle$。它的目标是判断 $M$ 是否接受 $w$。
- $S_{ATM}$ 会根据 $M$ 和 $w$ 构造一个特定的 LBA,我们称之为 $B$。
- 这个 LBA $B$ 被设计成一个“计算历史验证器”。
- $B$ 的语言 $L(B)$ 被设计为:包含且仅包含 $M$ 在 $w$ 上的接受计算历史的字符串表示。
- 分析 $L(B)$ 的性质:
- 情况1: 如果 $M$ 接受 $w$。
- 那么根据定义,必然存在一个接受计算历史 (一个配置序列 $C_1, \ldots, C_l$)。
- 我们将这个序列编码成一个单一的字符串(例如,用 # 分隔每个配置:#C1#C2#...#Cl#)。这个字符串就是 $M$ 在 $w$ 上的接受计算历史的表示。
- LBA $B$ 被设计成会接受这个特定的字符串。
- 因此,在这种情况下,$L(B)$ 至少包含一个元素,所以 $L(B)$ 非空。
- 情况2: 如果 $M$ 不接受 $w$ (拒绝或循环)。
- 那么根据定义,不存在接受计算历史。
- 因此,没有任何一个字符串是“$M$在$w$上的接受计算历史”。
- LBA $B$ 被设计成只接受这种字符串,所以它将不接受任何输入。
- 因此,在这种情况下,$L(B)$ 为空 ($L(B) = \emptyset$)。
- 如何利用假想的判定器 $R_{ELBA}$:
- $S_{ATM}$ 将构造好的 $\langle B \rangle$ 输入给 $R_{ELBA}$。
- 如果 $R_{ELBA}$ 接受 $\langle B \rangle$,说明它判断 $L(B)$ 是空的。这对应情况2,意味着 $M$ 不接受 $w$。所以 $S_{ATM}$ 应该拒绝。
- 如果 $R_{ELBA}$ 拒绝 $\langle B \rangle$,说明它判断 $L(B)$ 是非空的。这对应情况1,意味着 $M$ 接受 $w$。所以 $S_{ATM}$ 应该接受。
- 通过这种方式,$S_{ATM}$ 利用 $R_{ELBA}$ 完美地判定了 $A_{\mathrm{TM}}$。
- 对构造过程的要求:
- “我们不仅需要展示$B$的存在,还需要展示图灵机如何在给定$M$和$w$的描述的情况下获得$B$的描述”: 这是一个关键的技术要点。归约本身必须是一个可计算的过程。我们的 $S_{ATM}$ 必须是一个图灵机,它执行的“构造 LBA $B$”这个动作,必须是一个算法。我们必须能说清楚 $S_{ATM}$ 是如何一步步生成 $B$ 的编码的。
- 再次强调“构造不运行”:
- “我们构造$B$只是为了将其描述输入到假定的$E_{\mathrm{LBA}}$判决器中,而不是为了在某些输入上运行$B$”: 和之前的证明一样,$S_{ATM}$ 只是 $B$ 的“设计师”,它从不运行 $B$。$S_{ATM}$ 的工作是创造出一个“艺术品”($B$ 的描述),然后把它交给“鉴定师”($R_{ELBA}$)去评判。
证明思路的核心是设计一个 LBA $B$,使其语言 $L(B)$ 恰好是“$M$ 在 $w$ 上的接受计算历史”的集合。这样一来,“$M$ 是否接受 $w$” 这个问题就等价于 “$L(B)$ 是否为空” 这个问题。通过利用一个假想的 $E_{\mathrm{LBA}}$ 判定器来判断后者,我们就能解决前者,从而将 $A_{\mathrm{TM}}$ 归约到 $E_{\mathrm{LBA}}$ 并导出矛盾。
本段的目的是勾勒出“计算历史归约法”的宏观蓝图。它清晰地阐述了如何将一个关于“动态过程”($M$ 是否接受 $w$)的问题,转化为一个关于“静态集合属性”($L(B)$ 是否为空)的问题。这种动静转换的思想是本方法最深刻和最强大的地方。
这就像一个“犯罪现场调查”的逻辑。
- $A_{\mathrm{TM}}$ 问题: 判断“嫌疑人 $M$ 是否成功完成了那次银行抢劫 ($w$)?”
- 计算历史: 银行内部的全部监控录像。
- 接受计算历史: 一段完整的、清晰地记录了嫌疑人 $M$ 从进入银行到带着钱成功逃离 ($w$) 的合法监控录像。
- 构造 LBA B: 你构造了一个高度智能的“录像分析机器人” $B$。这个机器人的唯一功能是:给它一段录像,它能判断出这段录像“是不是嫌疑人M成功抢劫银行w的合法录像”。
- L(B) 的含义: 这个机器人 $B$ 会“亮绿灯”(接受)的录像集合,就是所有可能的“嫌疑人M成功抢劫银行w的合法录像”的集合。
- $E_{\mathrm{LBA}}$ 问题: 问“机器人B的语言是否为空”,就等价于问“这个世界上是否存在任何一段录像,能够作为M成功抢劫w的证据?”
- 归约逻辑:
- 如果嫌疑人 $M$ 真的成功抢劫了,那么至少存在一段真实的录像记录了此事。因此 $L(B)$ 非空。
- 如果嫌疑人 $M$ 没有成功抢劫,那么任何录像都不可能记录下他成功的过程。因此 $L(B)$ 为空。
- 矛盾: 如果你有一个能判断“证据是否存在”($E_{\mathrm{LBA}}$)的工具,你就能解决“嫌疑人是否犯罪”($A_{\mathrm{TM}}$)的问题。但后者无解,所以前者也无解。
想象你是一个游戏开发者 $S_{ATM}$,你想知道你设计的某个极其复杂的AI Boss ($M$) 在面对玩家的某个特定走位 ($w$) 时,是否会被击败(接受)。
- 构造游戏录像分析器 (LBA B): 你编写了一个新的工具 $B$。这个工具的功能是分析游戏录像文件。它只对一种录像文件感兴趣:记录了玩家使用走位 $w$ 最终击败 Boss $M$ 的全程战斗录像。任何其他的录像(比如玩家输了,或者用了其他走位),它都会判定为“无效”。
- $L(B)$: $B$ 能识别的语言,就是所有“玩家用走位w击败Boss M”的合法录像文件的集合。
- 使用假想的工具 ($R_{ELBA}$): 你有一个假想的云服务 $R_{ELBA}$,你可以上传任何一个“录像分析器”程序,它会告诉你这个分析器是不是一个“永远找不到有效录像”的程序(语言为空)。
- 进行归约:
- 你把新写的分析器 $B$ 上传到云服务 $R_{ELBA}$。
- 如果服务返回“是,这个分析器永远找不到有效录像”,你就知道是 AI Boss $M$ 在走位 $w$ 下不会被击败。
- 如果服务返回“否,这个分析器能找到有效录像”,你就知道 AI Boss $M$ 在走位 $w$ 下能被击败。
- 矛盾: 你利用这个云服务解决了判定Boss行为的无解问题。因此,这个云服务不可能存在。
1.2.5.1 图 5.11 B 的一个可能的输入
📜 [原文32]
现在我们描述如何从$M$和$w$构造$B$。请注意,我们不仅需要展示$B$的存在,还需要展示图灵机如何在给定$M$和$w$的描述的情况下获得$B$的描述。
正如我们为证明不可判定性而给出的先前的归约一样,我们构造$B$只是为了将其描述输入到假定的$E_{\mathrm{LBA}}$判决器中,而不是为了在某些输入上运行$B$。
我们构造$B$来接受其输入$x$,如果$x$是$M$在$w$上的接受计算历史。回想一下,接受计算历史是配置序列$C_{1}, C_{2}, \ldots, C_{l}$,这是$M$接受某个字符串$w$时所经历的。出于本证明的目的,我们假设接受计算历史表示为单个字符串,配置之间用#符号分隔,如图5.11所示。
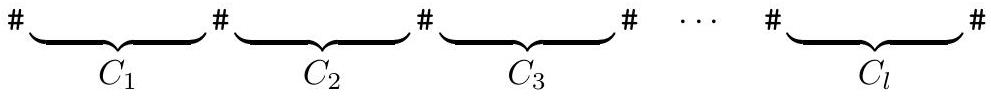
图 5.11
$B$的一个可能的输入
LBA $B$ 的工作方式如下。当它接收到输入$x$时,$B$应该在$x$是$M$在$w$上的接受计算历史时接受。首先,$B$根据分隔符将$x$分解为字符串$C_{1}, C_{2}, \ldots, C_{l}$。然后$B$确定$C_{i}$们是否满足接受计算历史的三个条件。
- $C_{1}$是$M$在$w$上的起始配置。
- 每个$C_{i+1}$合法地跟随$C_{i}$。
- $C_{l}$是$M$的接受配置。
这一部分开始深入到 LBA $B$ 的具体构造细节。$B$ 是一个“计算历史验证器”。这里描述了 $B$ 的输入格式和它要执行的验证任务。
- 输入格式:
- LBA $B$ 的输入,我们称之为 $x$,是一个字符串。
- 这个字符串 $x$ 声称自己是一个“$M$在$w$上的接受计算历史”。
- 为了让机器能够处理,我们将这个计算历史的配置序列 $C_1, C_2, \ldots, C_l$ 编码成一个单一字符串。
- 编码方式: 使用一个特殊的分隔符 # (假设它不在 $M$ 的字母表中) 来隔开每个配置。
- 图5.11的解释:
- 图中展示了一个长条,代表字符串 $x$。
- # C1 # C2 # ... # Cl #: 这就是 $x$ 的格式。它以 # 开头,以 # 结尾,中间是用 # 分隔的各个配置 $C_i$。
- 这个字符串 $x$ 就是 LBA $B$ 要分析的对象。
- LBA $B$ 的工作流程 (高层描述):
- $B$ 接收一个输入字符串 $x$。
- 它的目标是:如果 $x$ 确实是 $M$ 在 $w$ 上的一个合法的接受计算历史,那么 $B$ 就接受 $x$;否则,$B$ 拒绝 $x$。
- 为了做到这一点,$B$ 需要像一个裁判一样,检查 $x$ 是否满足成为“接受计算历史”的所有条件。
- 验证的三个核心条件:
- $B$ 首先会解析字符串 $x$,利用 # 分隔符把它切分成一个个的配置字符串 $C_1, C_2, \ldots, C_l$。然后,它依次检查以下三件事:
- 条件1: 起点是否正确?
- $B$ 需要验证 $C_1$ 是否等于 $M$ 在 $w$ 上的起始配置。
- 起始配置是由 $M$ 的起始状态 $q_0$ 和输入 $w$ 唯一决定的,通常是 $q_0w$。
- 由于 $S_{ATM}$ 在构造 $B$ 的时候,是知道 $M$ 和 $w$ 的,所以它可以把“正确的起始配置 $q_0w$”这个字符串硬编码到 $B$ 的逻辑里。$B$ 只需要比较它的第一个配置 $C_1$ 和它内心存着的那个标准答案是否一致即可。
- 条件2: 每一步转换是否合法?
- 这是最核心、最复杂的检查。$B$ 需要遍历所有相邻的配置对 $(C_i, C_{i+1})$,检查从 $C_i$ 到 $C_{i+1}$ 的转换是否符合 $M$ 的转移函数 $\delta$。
- 一次合法的转换,只会改变磁头周围很小一片区域。$C_i$ 和 $C_{i+1}$ 在大部分位置上应该是完全相同的。$B$ 需要验证:
- 远离磁头的地方,内容不变。
- 磁头下的符号、状态、磁头的新位置,这三者的变化是否与 $\delta$ 的某条规则匹配。
- 条件3: 终点是否正确?
- $B$ 需要验证最后一个配置 $C_l$ 是否是一个接受配置。
- 这很简单, $B$ 只需要扫描 $C_l$ 这个字符串,看看里面是否包含 $M$ 的接受状态 $q_{\text{accept}}$ 即可。
- LBA 的角色: 整个过程,LBA $B$ 都在自己的输入磁带(即字符串 $x$)上来回移动、比较、做标记,来完成这三项检查。由于 $x$ 的长度是有限的,LBA 的有限内存是足够的。
- 示例:
- $A_{\mathrm{TM}}$ 的输入: $\langle M, w \rangle$,其中 $M$ 是上一节定义的简单图灵机, $w = "0"$。
- 正确的接受计算历史字符串 $x_{accept}$: "#q00#sqcupq1sqcup#sqcupsqcupqaccept#"
- LBA $B$ 的行为:
- 输入: $x_{accept}$
- 检查1: $B$ 提取出 $C_1 = $ q00。$B$ 内部硬编码了 $M$ 在 $w="0"$ 上的起始配置也是 q00。两者匹配,通过。
- 检查3: $B$ 提取出 $C_l = $ sqcupsqcupqaccept。$B$ 扫描发现其中包含 $q_{\text{accept}}$。通过。
- 检查2:
- 比较 $C_1=$ q00 和 $C_2=$ sqcupq1sqcup。$B$ 需要根据 $M$ 的转移函数 $\delta(q_0, 0) = (q_1, \sqcup, R)$ 来验证这个转换是合法的。它会检查状态从 $q_0$ 变 $q_1$,0 变 $\sqcup$,磁头右移一位,这些都符合规则。通过。
- 比较 $C_2=$ sqcupq1sqcup 和 $C_3=$ sqcupsqcupqaccept。$B$ 需要根据 $\delta(q_1, \sqcup) = (q_{\text{accept}}, \sqcup, R)$ 来验证。通过。
- 最终: 所有检查都通过,$B$ 接受 $x_{accept}$。
- 一个错误的计算历史字符串 $x_{wrong}$: "#q00#q1sqcup#sqcupsqcupqaccept#"
- LBA $B$ 的行为:
- 当 $B$ 检查 $C_1$到 $C_2$ 的转换时,它发现 $C_1$ 是 q00,而 $C_2$ 是 q1sqcup。根据转移函数 $\delta(q_0, 0) = (q_1, \sqcup, R)$,磁带内容应该从 0 变成 sqcup,而磁头应该右移。在 q1sqcup 中,磁头没有右移,依然在第一个位置。这违反了规则。
- 因此,$B$ 拒绝 $x_{wrong}$。
本节详细描述了 LBA $B$ 作为“计算历史验证器”的工作原理。它接收一个声称是计算历史的字符串 $x$,并将其拆分成配置序列,然后严格地按顺序检查三个条件:起始配置是否正确、每一步转换是否合法、结束配置是否是接受配置。只有当所有条件都满足时,$B$ 才会接受 $x$。
本段的目的是将“计算历史归约法”的抽象思路,转化为一个具体、可执行的验证算法。它定义了“证据”(计算历史字符串)的格式,并明确了“验证证据”(LBA 的工作)需要做的三件事。这为下一段描述 LBA 如何在有限磁带上完成这些检查铺平了道路。
LBA $B$ 就像一个极其严格的论文审稿人。
- 输入 $x$: 一篇声称解决了某个数学难题的论文手稿。手稿由一系列的推导步骤组成。
- 审稿人的工作 (B 的工作):
- 检查引理: 检查论文的“第一步”($C_1$)是否基于一个公认的、正确的初始条件(起始配置)。
- 检查逻辑推导: 逐行逐句地检查论文的每一步推导($C_i \to C_{i+1}$),看是否严格遵守了数学逻辑(转移函数)。
- 检查结论: 检查论文的最终结论($C_l$)是否真的是它声称要证明的那个“定理已证”(接受配置)。
- 审稿人的决定: 只有当以上所有检查都完美无缺时,审稿人才会给出“接受发表”的意见。任何一个微小的逻辑瑕疵都会导致“拒稿”。
想象 LBA $B$ 是一个电影事实核查员。
- 输入 $x$: 一部号称是“历史纪录片”的电影胶片,内容是关于某场战役的。
- 核查员的工作:
- 核查开端: 检查电影的第一幕 ($C_1$),是否与史实记载的战役爆发时间、地点、双方兵力(起始配置)相符。
- 核查过程: 逐帧检查电影内容 ($C_i \to C_{i+1}$)。比如,电影中一个士兵中枪倒地,核查员要确认开枪的方向、子弹的型号、士兵的物理反应是否都符合当时的战场环境和物理学定律(转移函数)。
- 核查结局: 检查电影的最后一幕 ($C_l$),战役的结果是否与史实(接受配置)相符。
- 核查员的结论: 只有当电影从头到尾都完美符合史实时,核查员才会给这部电影贴上“真实纪录片”的标签(接受)。
📜 [原文33]
$M$在$w$上的起始配置$C_{1}$是字符串$q_{0} w_{1} w_{2} \cdots w_{n}$,其中$q_{0}$是$M$在$w$上的起始状态。在这里,$B$直接内置了这个字符串,因此它能够检查第一个条件。接受配置是包含$q_{\text {accept }}$状态的配置,因此$B$可以通过扫描$C_{l}$寻找$q_{\text {accept }}$来检查第三个条件。第二个条件最难检查。对于每对相邻配置,$B$检查$C_{i+1}$是否合法地跟随$C_{i}$。此步骤涉及验证$C_{i}$和$C_{i+1}$除了磁头下方和相邻位置外是否相同。这些位置必须根据$M$的转移函数进行更新。然后$B$通过在$C_{i}$和$C
i+1}$的相应位置之间进行之字形移动来验证更新是否正确完成。为了在之字形移动时跟踪当前位置,$B$用点标记磁带上的当前位置。最后,如果满足条件1、2和3,$B$接受其输入。
这一段详细描述了 LBA $B$ 是如何执行之前提到的三项检查的,特别是最难的第二项。
- 检查条件1 (起始配置):
- “$M$在$w$上的起始配置$C_{1}$是字符串$q_{0} w_{1} w_{2} \cdots w_{n}$...$B$直接内置了这个字符串,因此它能够检查第一个条件。”
- 这是说,在构造 LBA $B$ 的时候,我们的构造算法 $S$ 会把正确的起始配置(例如 q0abc)作为一个常量字符串“写死”在 $B$ 的程序逻辑里。
- 当 $B$ 运行时,它只需要读取输入 $x$ 的第一部分(直到第一个 #),然后和它内置的这个“标准答案”进行逐字符比较。如果完全一样,检查通过。
- 检查条件3 (接受配置):
- “接受配置是包含$q_{\text {accept }}$状态的配置,因此$B$可以通过扫描$C_{l}$寻找$q_{\text {accept }}$来检查第三个条件。”
- 这个检查也很简单。$B$ 移动到输入 $x$ 的末尾,找到最后一个配置 $C_l$。然后,它在 $C_l$ 这个子字符串上从头到尾扫描一遍,寻找是否存在 $q_{\text{accept}}$ 这个子串。如果找到了,检查通过。
- 检查条件2 (合法转移):
- “第二个条件最难检查。”: 这是整个验证过程的技术核心。
- “对于每对相邻配置,$B$检查$C_{i+1}$是否合法地跟随$C_{i}$。”: $B$ 需要做一个循环,依次处理 $(C_1, C_2), (C_2, C_3), \ldots, (C_{l-1}, C_l)$。
- “此步骤涉及验证$C_{i}$和$C_{i+1}$除了磁头下方和相邻位置外是否相同。”: 一步图灵机转移只会影响局部。比如,如果转移函数是 $\delta(q, a) = (p, b, R)$,那么在配置串中,只有状态 q 会变成 p,q 右边的符号 a 会变成 b,并且状态 p 会出现在 b 的右边。其他远离这三个位置(状态、磁头原位置、磁头新位置)的符号都应该保持不变。
- “然后$B$通过在$C_{i}$和$C_{i+1}$的相应位置之间进行之字形移动来验证更新是否正确完成。”: 这是 LBA 在有限内存上进行比较的经典技巧。
- 想象 LBA 的磁带上写着 ...#Ci#Ci+1#...。
- $B$ 的磁头先定位到 $C_i$ 的第一个字符。
- 它需要比较 $C_i$ 的第 $k$ 个字符和 $C_{i+1}$ 的第 $k$ 个字符是否相同(对于远离磁头的位置)。
- 为了实现这一点,$B$ 会:
- 读取 $C_i$ 的第 $k$ 个字符,并用一个特殊的“已读”标记(比如在字符下面加个点)来改写它,以记住自己读了什么以及读到了哪里。
- 然后磁头向右长途跋涉,越过 #,到达 $C_{i+1}$ 的第 $k$ 个字符。
- 比较这里的字符是否和它刚才记住的一样。如果不一样(并且这里不是合法的磁头活动区域),则验证失败,B拒绝。
- 如果一样,它也在这里做一个标记,然后回头,长途跋涉回到 $C_i$ 中刚刚标记过的位置的右边一个,即第 $k+1$ 个字符。
- 重复这个“之”字形或“Z”字形的来回比较过程,直到 $C_i$ 和 $C_{i+1}$ 都被比较完毕。
- “为了在之字形移动时跟踪当前位置,$B$用点标记磁带上的当前位置。”: 这就是刚才描述的技巧。LBA 利用它可写的磁带,在输入上做标记,充当“指针”或“书签”,来辅助自己完成复杂的比较任务。这正是 LBA 虽然内存有限但功能强大的原因。
- “最后,如果满足条件1、2和3,$B$接受其输入。”: 只有当所有检查都成功通过后,$B$ 才会进入接受状态。任何一步检查失败,都会导致 $B$ 立刻进入拒绝状态。
本段具体阐述了 LBA $B$ 作为验证器,如何利用其有限的读写磁带完成三项核心检查。对于简单的条件1和3,它通过内置字符串比较和子串扫描来完成。对于最复杂的条件2(合法转移),它使用了一种经典的“之字形”移动和“打点标记”的策略,在两个相邻的配置字符串之间来回穿梭,逐字符地进行比较和验证。
本段的目的是打消读者对于“LBA是否真的有能力完成这么复杂的验证任务”的疑虑。通过描述具体的算法思想(特别是“之字形”比较法),它雄辩地证明了,尽管 LBA 内存受限,但它完全有能力在其输入磁带上执行这种结构化的语法检查,从而证明了 LBA $B$ 的可构造性和有效性。
LBA $B$ 的“之字形”比较法,就像你用两根手指来核对两份并排摆放的名单。
- 左手食指指向第一份名单的第一个名字,右手食指指向第二份名单的第一个名字。你比较两个名字是否相同。
- 然后,两根手指同时下移,比较第二个名字。
- 这个过程一直持续下去。
- LBA 没有两根手指,它只有一个磁头。所以它必须通过来回移动和做标记来模拟这个过程。它先把左手指该指的地方用笔画个点,然后移动磁头(眼睛)去看右手指该指的地方,比较完了,再移动回头,找到刚才画的点,然后看下一个位置。
想象一个裁缝在检查一件衣服的两条袖子是否对称。
- 两条袖子: 相邻的两个配置 $C_i$ 和 $C_{i+1}$。
- 裁缝 (LBA B):
- 他先把左边袖子的袖口对齐(检查对齐和长度)。
- 然后他从袖口开始,用手一点一点地捏着两条袖子的对应位置,向上移动,检查每一处的宽度是否都一样(“之字形”比较远离磁头的部分)。
- 当他检查到袖子和肩膀连接处(磁头活动区域)时,他会根据设计图纸(转移函数),检查这里的缝线、褶皱是否符合要求。
- 整个过程中,他可能会用粉笔在袖子上做一些临时标记(打点)。
1.2.5.2 LBA B 的形式化证明与图 5.12
📜 [原文34]
通过反转判决器的答案,我们得到$M$是否接受$w$的答案。因此我们可以判定$A_{\mathrm{TM}}$,这是一个矛盾。
证明 现在我们准备陈述$A_{\text {TM }}$到$E_{\text {LBA }}$的归约。假设图灵机$R$判定$E_{\mathrm{LBA}}$。构造图灵机$S$来判定$A_{\mathrm{TM}}$,如下所示。
$S=$"在输入$\langle M, w\rangle$上,其中$M$是图灵机,$w$是字符串:
- 根据证明思路中的描述,从$M$和$w$构造LBA $B$。
- 在输入$\langle B\rangle$上运行$R$。
- 如果$R$拒绝,则接受;如果$R$接受,则拒绝。"
如果$R$接受$\langle B\rangle$,则$L(B)=\emptyset$。因此,$M$在$w$上没有接受计算历史,并且$M$不接受$w$。因此,$S$拒绝$\langle M, w\rangle$。同样,如果$R$拒绝$\langle B\rangle$,则$B$的语言是非空的。$B$唯一能接受的字符串是$M$在$w$上的接受计算历史。因此,$M$必须接受$w$。因此,$S$接受$\langle M, w\rangle$。图5.12展示了LBA $B$。
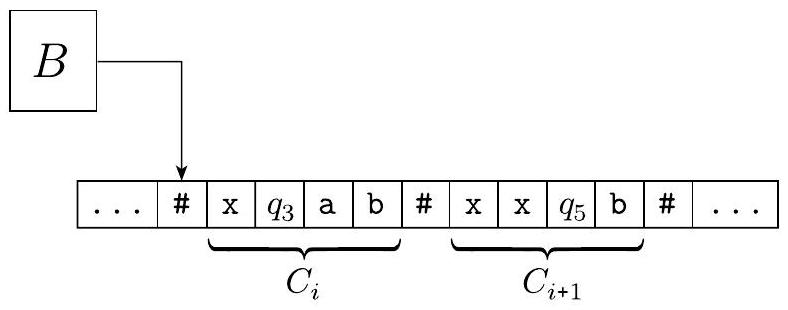
图 5.12
LBA $B$检查图灵机计算历史
这部分是定理5.10的最终形式化证明,并附上了 LBA $B$ 的工作流程图。
第一部分:$S$ 的形式化描述
- “通过反转判决器的答案...”: 这是对“证明思路”的总结,预示了 $S$ 的决策逻辑。
- $S$ 的算法:
- “在输入$\langle M, w\rangle$上...”: $S$ 接收 $A_{\mathrm{TM}}$ 的一个实例。
- “1. 根据证明思路中的描述,从$M$和$w$构造LBA $B$。”:
- 这是 $S$ 的核心构造步骤。$S$ 作为一个“编译器”,读取 $M$ 的转移函数和字符串 $w$,然后生成 LBA $B$ 的完整描述。$B$ 的逻辑就是我们刚刚详细讨论过的“计算历史验证器”。这个构造过程是纯算法的,是可计算的。
- “2. 在输入$\langle B\rangle$上运行$R$。”: $S$ 调用假设存在的 $E_{\mathrm{LBA}}$ 判定器 $R$,并将它刚刚的“作品” $\langle B \rangle$ 作为输入。
- “3. 如果$R$拒绝,则接受;如果$R$接受,则拒绝。”: $S$ 的最终判决与 $R$ 的判决相反。
- 为什么相反?
- $R$ 接受 $\iff L(B) = \emptyset \iff M$ 不接受 $w$。所以 $S$ 应该拒绝。
- $R$ 拒绝 $\iff L(B) \neq \emptyset \iff M$ 接受 $w$。所以 $S$ 应该接受。
- 这个逻辑是正确的。
第二部分:逻辑分析与矛盾
- “如果$R$接受$\langle B\rangle$...”: 这段话详细地重申了上一条的逻辑,确保读者完全理解为什么 $S$ 的判决是正确的,以及为什么它要和 $R$ 反着来。
- 这个构造成功地用 $R$ (判定 $E_{\mathrm{LBA}}$) 造出了 $S$ (判定 $A_{\mathrm{TM}}$)。
- 这与 $A_{\mathrm{TM}}$ 不可判定相矛盾。
- 因此,最初的假设($R$ 存在)是错误的。$E_{\mathrm{LBA}}$ 是不可判定的。
第三部分:图 5.12 解读
- 图的标题: “LBA $B$检查图灵机计算历史”。
- 图的整体结构: 这是一个流程图,描述了 LBA $B$ 在接收其输入 $x$(即计算历史字符串)后所做的事情。
- 起点: “输入x (计算历史)”
- 第一步: “把x分解成C1, ..., Cl”: 对应解析输入字符串。
- 第二步: “C1是M在w上的起始配置吗?”: 对应检查条件1。
- 如果是“否”,则“拒绝”。
- 如果是“是”,则进入下一步。
- 第三步: “Cl是接受配置吗?”: 对应检查条件3。
- 如果是“否”,则“拒绝”。
- 如果是“是”,则进入下一步。
- 第四步 (循环): “对于每个i从1到l-1”: 这是一个循环结构,对应检查条件2。
- 循环体: “Ci+1合法地跟随Ci吗?”
- 如果对于任何一个 $i$,“否”,则“拒绝”。
- 只有当所有的 $i$ 都检查通过(“是”)后,才能退出循环。
- 终点: 如果所有检查都通过了,流程最终指向“接受”。
- 图的意义: 这张图以一种非常直观的方式,总结了 LBA $B$ 的内部工作逻辑。它清晰地表明,$B$ 本身就是一个复杂的算法,而这个算法的目标就是验证一个字符串的语法和语义。
本节给出了定理5.10的最终形式化证明和流程图。证明的核心是构造一个 $A_{\mathrm{TM}}$ 判定器 $S$,它通过生成一个 LBA $B$(一个计算历史验证器),并利用假想的 $E_{\mathrm{LBA}}$ 判定器 $R$ 来检测 $L(B)$ 是否为空,来推断 $M$ 是否接受 $w$。图5.12直观地展示了 LBA $B$ 作为验证器时,其内部检查计算历史合法性的详细步骤。
提供最终的、严谨的证明文本是数学证明的必要环节。附上流程图(图5.12)则是为了通过视觉化手段,帮助读者更好地理解和记忆 LBA $B$ 内部复杂的验证逻辑,使得抽象的算法描述变得更加具体和易于掌握。
整个归约证明可以看作一个三层结构:
- 顶层 (S): $A_{\mathrm{TM}}$ 的判定器 $S$。它的工作是接收 $\langle M, w \rangle$,并给出“接受/拒绝”的最终答案。
- 中层 (B): LBA $B$。它是一个由 $S$ 创造出来的工具,一个“历史学家”。它的工作是接收一个字符串,并判断它是不是一段“合法的、成功的历史”。
- 底层 (R): $E_{\mathrm{LBA}}$ 的判定器 $R$。它是一个假设存在的“神谕”。它的工作是接收任何一个“历史学家”,并判断这个历史学家是不是一个“永远也找不到任何成功历史”的悲观主义者。
- 流程: $S$ 为了回答自己的问题,创造了历史学家 $B$。然后 $S$ 去问神谕 $R$:“我创造的这个历史学家 $B$ 是不是个悲观主义者?”。神谕的回答,经过 $S$ 的反向解读,就成了 $S$ 想要的答案。
想象一个大型的、自动化的法医鉴定实验室。
- 实验室总管 S: 接到任务,要判断“嫌疑人 M 是否真的完成了犯罪 W?” ($A_{\mathrm{TM}}$)。
- DNA序列分析仪 B (LBA): 总管 S 根据 M 和 W 的信息,配置了一台DNA分析仪 B。这台分析仪的唯一功能是:给它一段DNA序列,它能判断出“这是否是从犯罪现场 W 提取到的、属于嫌疑人 M 的、并且能证明其犯罪成功的DNA证据链?”。
- 质量检测部门 R (假想的): 实验室有一个假想的、万能的质检部门 R,你可以把任何一台分析仪送过去,它能告诉你“这台分析仪是不是一个永远也检测不出阳性结果的、有缺陷的机器?” ($E_{\mathrm{LBA}}$)。
- 总管 S 的操作:
- 配置好 DNA 分析仪 B。
- 把 B 送到质检部门 R。
- 如果 R 回报“机器有缺陷(永远测不出阳性)”,总管 S 就知道现场不可能找到嫌疑人的证据,即嫌疑人没有犯罪。
- 如果 R 回报“机器没缺陷(可能测出阳性)”,总管 S 就知道现场一定能找到证据,即嫌疑人犯罪了。
- 矛盾: 总管 S 通过这个流程完美破案,但这是不可能的。所以,那个万能的质检部门 R 不存在。
12.6 定理 5.13:$A L L_{\mathrm{CFG}}$是不可判定的。
📜 [原文35]
我们也可以使用通过计算历史进行归约的技术来建立与上下文无关文法和下推自动机相关的某些问题的不可判定性。回想一下,在定理4.8中,我们提出了一个算法来判断上下文无关文法是否生成任何字符串——也就是说,是否$L(G)=\emptyset$。现在我们证明一个相关的问题是不可判定的。这就是判断上下文无关文法是否生成所有可能字符串的问题。证明这个问题是不可判定的,是证明上下文无关文法等价性问题不可判定的主要步骤。设
定理 5.13
$A L L_{\text {CFG }}$是不可判定的。
这一段将我们的战场从图灵机和LBA,转移到了更简单的计算模型——上下文无关文法 (Context-Free Grammar, CFG) 和 下推自动机 (Pushdown Automaton, PDA),并引入了本节的新主角:$ALL_{\mathrm{CFG}}$ 问题。
- 应用领域的扩展:
- “我们也可以使用通过计算历史进行归约的技术来建立...不可判定性”: 指出“计算历史法”这个工具非常强大,不仅能用于证明关于 TM 和 LBA 的问题,还能“降维打击”,用来证明关于 CFG 和 PDA 的问题。
- 回顾与对比:
- 回顾: “回想一下...定理4.8中...判断上下文无关文法是否生成任何字符串——也就是说,是否$L(G)=\emptyset$。”
- 在第4章,我们证明了 CFG的空语言问题 $E_{\mathrm{CFG}}$ 是可判定的。我们可以通过一个算法,检查一个文法 G 是否能生成任何字符串。
- 对比: “现在我们证明一个相关的问题是不可判定的。”
- 这里形成了一个鲜明的对比,类似于 $A_{\mathrm{LBA}}$ (可判定) vs $E_{\mathrm{LBA}}$ (不可判定)。对于 CFG,空语言问题 $E_{\mathrm{CFG}}$ 是可判定的,但我们将要证明的全语言问题 $ALL_{\mathrm{CFG}}$ 是不可判定的。
- 这种“对称”问题的性质差异,是计算理论中一个非常迷人的主题。
- 引入新问题 $ALL_{\mathrm{CFG}}$:
- 问题描述: “判断上下文无关文法是否生成所有可能字符串的问题。”
- 动机: “证明这个问题是不可判定的,是证明上下文无关文法等价性问题不可判定的主要步骤。” 这句话指出了研究 $ALL_{\mathrm{CFG}}$ 的一个重要目的,它是证明 $EQ_{\mathrm{CFG}}$ (判断两个CFG是否等价) 不可判定的垫脚石。
- 形式化定义:
- 给出了 $ALL_{\mathrm{CFG}}$ 的集合表示。
- $ALL_{\mathrm{CFG}}$: 问题的名称,代表上下文无关文法的全语言问题。
- $\{\langle G\rangle \mid ... \}$: 该问题的输入是上下文无关文法 G 的编码。
- $L(G)=\Sigma^{*}$: 这是成员资格的判断条件。
- $L(G)$: 文法 G 所能生成的所有字符串的集合。
- $\Sigma^*$: 由字母表 $\Sigma$ 中的符号组成的所有可能的、有限长度的字符串的集合(包括空串)。这被称为“全语言”。
- 该条件要求 G 能够生成每一个可能的字符串。
- 示例1 (属于 $ALL_{\mathrm{CFG}}$):
- 字母表 $\Sigma = \{a, b\}$
- 文法 G: $S \to aS \mid bS \mid \epsilon$
- 这个文法可以生成任何由 a 和 b 组成的字符串,包括空串。因此 $L(G) = \{a, b\}^* = \Sigma^*$。
- 所以 $\langle G \rangle \in ALL_{\mathrm{CFG}}$。
- 示例2 (不属于 $ALL_{\mathrm{CFG}}$):
- 字母表 $\Sigma = \{0, 1\}$
- 文法 G: $S \to 0S1 \mid \epsilon$
- 这个文法生成语言 $\{0^n1^n \mid n \ge 0\}$。它不能生成字符串 "011", "10" 等。
- 所以 $L(G) \neq \Sigma^*$。
- 因此 $\langle G \rangle \notin ALL_{\mathrm{CFG}}$。
本段引入了上下文无关文法的全语言问题 $ALL_{\mathrm{CFG}}$,即判断一个给定的CFG是否能生成字母表上的所有字符串。作者通过与已知的、可判定的 $E_{\mathrm{CFG}}$ 问题进行对比,突出了这个新问题的特殊性,并预告了将使用计算历史归约法来证明其不可判定性。
本段的目的是将不可判定性的研究领域,从强大的图灵机模型,扩展到能力较弱的上下文无关文法。这表明不可判定性现象不仅仅存在于计算能力的顶端,在较低的层级也同样存在。证明 $ALL_{\mathrm{CFG}}$ 不可判定,也为后续证明一系列与程序语言(很多语言的语法是上下文无关的)相关的问题的不可判定性打开了大门。
$ALL_{\mathrm{CFG}}$ 问题就像是在问一个“随机字符串生成器”的设计师。
- CFG G: 你设计的随机字符串生成器的规则。
- $ALL_{\mathrm{CFG}}$ 问题: “你设计的这个生成器,是否有可能生成出所有可能的字符串组合?”
- 我们要证明,不存在一个通用的“规则分析器”,能对所有生成器规则都回答这个问题。
想象你是一个锁匠。
- CFG G: 一把锁的设计图纸(代表生成规则)。
- 语言 L(G): 这把锁能被哪些钥匙打开(生成的字符串)。
- $\Sigma^*$: 世界上所有可能的钥匙。
- $E_{\mathrm{CFG}}$ 问题 (可判定): 判断“这把锁是不是一把废锁,没有任何钥匙能打开它?”。锁匠可以通过分析图纸结构来判定。
- $ALL_{\mathrm{CFG}}$ 问题 (不可判定): 判断“这把锁是不是一把万能锁,世界上所有的钥匙都能打开它?”。我们将要证明,锁匠无法通过一个通用算法来分析所有图纸并回答这个问题。
📜 [原文36]
证明 这个证明是通过反证法进行的。为了得到矛盾,我们假设$A L L_{\text {CFG }}$是可判定的,并利用这个假设来证明$A_{\text {TM }}$是可判定的。这个证明类似于定理5.10的证明,但有一个小的额外转折:它是一个从$A_{\text {TM }}$通过计算历史进行的归约,但我们为了一个技术原因稍微修改了计算历史的表示方式,我们将在后面解释。
我们现在描述如何使用$A L L_{\text {CFG }}$的判决过程来判定$A_{\text {TM }}$。对于图灵机$M$和输入$w$,我们构造一个CFG $G$,当且仅当$M$不接受$w$时,它生成所有字符串。因此,如果$M$接受$w$,则$G$不会生成某些特定字符串。这个字符串是——你猜对了——$M$在$w$上的接受计算历史。也就是说,$G$被设计为生成所有不是$M$在$w$上的接受计算历史的字符串。
这是定理5.13的“证明思路”的第一部分,它设定了归约的总体策略,这个策略非常巧妙,与之前的证明有所不同。
- 确定框架:
- 方法: 从 $A_{\mathrm{TM}}$ 归约的反证法。
- 假设: $ALL_{\mathrm{CFG}}$ 可判定,即存在一个判定器 $R_{ALL}$。
- 目标: 利用 $R_{ALL}$ 构造 $A_{\mathrm{TM}}$ 的判定器 $S_{ATM}$。
- 预告“转折”:
- “这个证明类似于定理5.10的证明”: 说明我们仍然会使用计算历史这个核心工具。
- “但有一个小的额外转折...稍微修改了计算历史的表示方式”: 这是一个重要的提醒。直接使用 #C1#C2#... 这种格式的计算历史,对于 CFG (或 PDA) 来说,验证起来有困难。我们需要对这个“证据”的格式做一些手脚,让 PDA 能更方便地处理。
- 核心构造思想 (反向逻辑):
- 之前的证明 $E_{\mathrm{LBA}}$ 时,我们构造的 LBA $B$ 的语言是接受计算历史的集合。所以 $L(B)$ 非空 $\iff M$ 接受 $w$。
- 这次,我们的目标是使用 $ALL_{\mathrm{CFG}}$ 判定器。这个判定器关心的是语言是否为 $\Sigma^*$。
- 因此,我们的构造策略是反过来的:
- 我们要构造一个 CFG $G$。
- 这个 $G$ 的语言 $L(G)$ 被设计为:所有不是 $M$ 在 $w$ 上的接受计算历史的字符串的集合。
- 即,$L(G) = \Sigma^* - \{ \text{x} \mid \text{x 是 M 在 w 上的接受计算历史} \}$ (这里用集合减法表示)。
- 分析 $L(G)$ 的性质:
- 情况1: 如果 $M$ 不接受 $w$。
- 那么,不存在接受计算历史。
- 这意味着“$M$在$w$上的接受计算历史”的集合是空集。
- 所以 $L(G) = \Sigma^* - \emptyset = \Sigma^*$。在这种情况下,文法 $G$ 生成全语言。
- 情况2: 如果 $M$ 接受 $w$。
- 那么,存在一个(对于确定性TM)或多个(对于NTM)接受计算历史。
- 假设 $x_{accept}$ 是那个唯一的接受计算历史字符串。
- 那么 $L(G) = \Sigma^* - \{x_{accept}\}$。
- 在这种情况下,文法 $G$ 生成了除了 $x_{accept}$ 之外的所有字符串。它的语言不是全语言。
- 如何利用假想的判定器 $R_{ALL}$:
- $S_{ATM}$ 在收到 $\langle M, w \rangle$ 后,构造出这个特殊的文法 $G$。
- $S_{ATM}$ 将 $\langle G \rangle$ 输入给 $R_{ALL}$。
- 如果 $R_{ALL}$ 接受 $\langle G \rangle$,说明它判断 $L(G) = \Sigma^*$。这对应情况1,意味着 $M$ 不接受 $w$。所以 $S_{ATM}$ 应该拒绝。
- 如果 $R_{ALL}$ 拒绝 $\langle G \rangle$,说明它判断 $L(G) \neq \Sigma^*$。这对应情况2,意味着 $M$ 接受 $w$。所以 $S_{ATM}$ 应该接受。
- 再次地,通过这种巧妙的构造和反向逻辑,$S_{ATM}$ 完美地判定了 $A_{\mathrm{TM}}$。
证明思路的核心是构造一个上下文无关文法 $G$,让它生成所有“无效”的计算历史字符串。这里的“无效”指的是任何不符合“$M$在$w$上接受的计算历史”这个标准的字符串。通过这种设计,如果 $M$ 不接受 $w$,那么就没有有效的接受历史,于是所有字符串都是“无效”的,G的语言就是全语言 $\Sigma^*$。反之,如果 $M$ 接受 $w$,那么至少有一个字符串(那个正确的接受历史)是“有效”的,G就不会生成它,于是G的语言就不等于 $\Sigma^*$。这样,利用一个假想的 $ALL_{\mathrm{CFG}}$ 判定器,就能反推出 $M$ 是否接受 $w$。
本段展示了一种更为间接和巧妙的归约逻辑。它不再是去“识别正确”,而是去“识别所有不正确”。这种“补集思想”是证明中一个非常强大的技巧。同时,预告“计算历史表示法的修改”,为下文的技术难点埋下伏笔,引导读者思考为什么需要这样做,以及如何做。
这就像一个“大家来找茬”的游戏。
- 正确的接受计算历史: 一张完美无瑕的原画。
- $A_{\mathrm{TM}}$ 问题: 判断“是否存在这样一张完美的原画?”
- 构造 CFG G: 你设计了一个程序 $G$,它的功能是生成所有“找茬”图片。任何与原画有丝毫差异的图片(比如颜色不对、多一个东西、少一个东西),你的程序都能生成出来。
- $L(G)$ 的含义: 你的程序 $G$ 生成的图片集合,就是“所有非完美图片”的集合。
- $ALL_{\mathrm{CFG}}$ 问题: 问“你的程序G是否能生成出宇宙中所有的图片?”
- 逻辑:
- 如果不存在完美原画 ($M$不接受$w$),那么所有图片都是“找茬”图片,你的程序 $G$ 就能生成所有图片 ($L(G)=\Sigma^*$)。
- 如果存在一张完美原画 ($M$接受$w$),那么你的程序 $G$ 唯独生成不了这一张完美的,所以 $L(G) \neq \Sigma^*$。
- 矛盾: 如果你能判断程序 $G$ 是否能生成所有图片,你就能知道是否存在完美原画。但这无解,所以你的判断工具不存在。
想象一个国家要颁发“全国良民证”。
- 接受计算历史: 一个人的从出生到现在的、完全清白、没有任何违法乱纪行为的档案。
- $A_{\mathrm{TM}}$ 问题: 判断“公民 M 在 W 事件中,其档案是否清白?”
- 构造 CFG G: 政府设计了一个系统 $G$,专门用来生成和打印所有“有污点”的档案。任何人的档案,只要有一点点不合规矩的地方,这个系统都能把它打印出来。
- $L(G)$: 系统 $G$ 能打印出的所有“有污点档案”的集合。
- $ALL_{\mathrm{CFG}}$ 问题: 问“这个系统 $G$ 是否能打印出全国所有公民的档案?”
- 逻辑:
- 如果公民 M 在 W 事件中档案不清白 ($M$ 不接受 $w$),那么他的档案就是“有污点”的。但这个逻辑不对,让我们重新思考。
让我们回到“补集思想”:
- $A_{\mathrm{TM}}$ 问题: 判断“是否存在一个‘M在w上的接受历史’?”
- CFG G: 生成所有不是“M在w上的接受历史”的字符串。
- 逻辑:
- 如果不存在“M在w上的接受历史”,那么所有字符串都满足“不是接受历史”这个条件。所以 $L(G) = \Sigma^*$。
- 如果存在一个“M在w上的接受历史”(我们叫它 $x_a$),那么字符串 $x_a$ 不满足“不是接受历史”这个条件,所以 $G$ 生成不了 $x_a$。所以 $L(G) = \Sigma^* - \{x_a\} \neq \Sigma^*$。
- 矛盾: 利用 $ALL_{\mathrm{CFG}}$ 判定器判断 $L(G)$ 是否为 $\Sigma^*$,就可以知道“M在w上的接受历史”是否存在,即 $M$ 是否接受 $w$。这解决了 $A_{\mathrm{TM}}$,产生矛盾。
📜 [原文37]
为了使CFG $G$生成所有不能成为$M$在$w$上接受计算历史的字符串,我们利用以下策略。一个字符串可能由于几个原因而不能成为接受计算历史。$M$在$w$上的接受计算历史形式为$\# C_{1} \# C_{2} \# \cdots \# C_{l} \#$,其中$C_{i}$是$M$在$w$上计算的第$i$步的配置。那么,$G$生成所有符合以下条件的字符串:
- 不以$C_{1}$开头,
- 不以接受配置结尾,或者
- 某些$C_{i}$根据$M$的规则不能正确地生成$C_{i+1}$。
如果$M$不接受$w$,则不存在接受计算历史,因此所有字符串都以某种方式失败。因此,$G$将生成所有字符串,正如所期望的。
这一段深入到 CFG $G$ 的构造细节。$G$ 的目标是生成所有“无效”的计算历史。这里将“无效”这个概念分解成了三个具体的、可操作的子条件。
- “一个字符串可能由于几个原因而不能成为接受计算历史”: 这是一个关键的分解思想。一个字符串要想成为一个“合法的接受计算历史”,必须同时满足我们之前讨论的三个条件(起点正确、过程合法、终点正确)。反过来说,一个字符串只要违反了这三个条件中的任何一个,它就不是一个合法的接受计算历史。
- 利用“或”关系: 我们的文法 $G$ 就要利用这个“或”关系。$G$ 将由三个子文法 $G_1, G_2, G_3$ 组合而成(通过一个初始规则 $S \to S_1 | S_2 | S_3$)。
- $G_1$ 负责生成所有违反条件1的字符串。
- $G_2$ 负责生成所有违反条件3的字符串。
- $G_3$ 负责生成所有违反条件2的字符串。
- 因此,总的语言 $L(G) = L(G_1) \cup L(G_2) \cup L(G_3)$。这个并集就包含了所有“无效”的计算历史字符串。
- 三个“失败”条件:
- “1. 不以$C_{1}$开头”: $C_1$ 是 $M$ 在 $w$ 上的唯一正确的起始配置。任何一个字符串,如果它的格式不是 #C1#...,那它肯定不是一个合法的接受历史。例如,它的第一个配置不是 $C_1$,或者格式就不对(比如开头不是#)。生成所有这样的字符串对于 CFG 是可能的。
- “2. 不以接受配置结尾”: 合法的接受历史必须以一个包含 $q_{\text{accept}}$ 的配置 $C_l$ 结尾。任何一个字符串,如果它的最后一个配置 $C_l$ 中不包含 $q_{\text{accept}}$,那它就不是。生成所有这样的字符串对于 CFG 也是可能的。
- “3. 某些$C_{i}$根据$M$的规则不能正确地生成$C_{i+1}$”: 这是最核心的部分。一个字符串可能起点和终点都“看起来”对,但中间的某一步转换是“作弊”的。例如,从 $C_i$ 到 $C_{i+1}$ 的转换不符合 $M$ 的转移函数。$G$ 的任务就是捕捉到这种“作弊”行为。
- 对整体逻辑的再次确认:
- “如果$M$不接受$w$,则不存在接受计算历史”: 在这种情况下,任何一个字符串 $x$ 都会至少违反上述三个条件中的一个。(如果一个字符串 $x$ 碰巧同时满足了这三个条件,那它本身就构成了一个接受计算历史,与“不存在接受计算历史”的前提矛盾)。
- “因此所有字符串都以某种方式失败。因此,$G$将生成所有字符串,正如所期望的。”: 既然所有字符串都是“无效”的,而 $G$ 的设计目标就是生成所有“无效”的字符串,那么在这种情况下,$L(G)$ 自然就是 $\Sigma^*$。这与我们上一节的分析完全吻合。
本段将构造“生成所有无效计算历史的CFG $G$”这一宏大目标,分解为三个子任务:分别生成违反“正确起点”、“正确终点”、“合法过程”这三个条件的字符串。$G$ 的语言是这三类“失败”字符串的并集。通过这种“分而治之”的策略,复杂的设计问题变得更加清晰和可管理。
本段的目的是展示如何将一个复杂的语言定义 ($L(G) = \Sigma^* - \{x_{accept}\}$) 分解为几个更简单的、更容易用文法来描述的语言的并集 ($L(G_1) \cup L(G_2) \cup L(G_3)$)。这是形式语言理论和编译器设计中常用的技巧(例如,并集操作在上下文无关文法下是封闭的)。它为下一段具体讨论如何设计这几个子文法(特别是最难的 $G_3$)做好了铺垫。
这就像是建立一个“假新闻过滤器”。
- 目标: 设计一个系统 $G$,能识别并生成所有类型的假新闻。
- 分解任务: 你发现假新闻有几类:
- 来源造假: 新闻开头声称来自“联合国”,但实际上是个人杜撰的。(对应“不以 $C_1$ 开头”)
- 结论夸大: 新闻结尾得出了一个耸人听闻但毫无根据的结论。(对应“不以接受配置结尾”)
- 过程杜撰: 新闻的中间论证过程,引用了不存在的数据,或者逻辑推导错误。(对应“$C_i \to C_{i+1}$ 不合法”)
- 系统 G: 由三个子系统组成,分别负责生成上述三类假新闻。最终,系统 $G$ 能产出所有可能的假新闻。
- 逻辑: 如果这个世界上不存在“绝对真实完美的新闻”($M$ 不接受 $w$),那么所有的新闻都或多或少是“假新闻”,你的系统 $G$ 就能生成所有新闻。
想象一个自动化的游戏Bug查找器 $G$。
- 合法的接受计算历史: 一次完美无瑕的、从头玩到通关的游戏过程。
- 查找器 $G$ 的任务: 找到并记录所有导致游戏出错或无法通关的玩法。
- $G$ 的子模块:
- 模块1: 专门寻找“开局就错”的玩法,比如游戏还没加载完就按开始键导致崩溃。(违反起点)
- 模块2: 专门寻找“结局不对”的玩法,比如打败了最终Boss却没有触发通关动画。(违反终点)
- 模块3: 专门寻找“过程中出错”的玩法,比如角色穿墙、掉出地图、数值溢出等。(违反过程)
- $L(G)$: 所有这些“Bug玩法”记录的集合。
- 逻辑: 如果这个游戏本身就不可能被打通关($M$ 不接受 $w$),那么任何一种玩法最终都会走向失败或死循环,都是一种“Bug玩法”。因此,在这种情况下,Bug查找器 $G$ 能够记录下所有可能的玩法,其“语言”就是所有可能操作的集合 $\Sigma^*$。
1.2.6.1 PDA D 的构造与图 5.14
📜 [原文38]
现在我们来具体构造$G$。我们不直接构造$G$,而是构造一个PDA $D$。我们知道可以使用定理2.20(第117页)中给出的构造将$D$转换为CFG。我们这样做是因为,出于我们的目的,设计一个PDA比设计一个CFG更容易。在这种情况下,$D$将首先非确定性地分支,猜测要检查前面三个条件中的哪一个。一个分支检查输入字符串的开头是否是$C_{1}$,如果不是则接受。另一个分支检查输入字符串是否以包含接受状态$q_{\text {accept }}$的配置结尾,如果不是则接受。
第三个分支应该在某个$C_{i}$不能正确生成$C_{i+1}$时接受。它通过扫描输入直到非确定性地决定它已经到达$C_{i}$来工作。接下来,它将$C_{i}$压入堆栈直到到达由#符号标记的末尾。然后$D$弹出堆栈以与$C_{i+1}$进行比较。它们应该匹配,除了磁头位置附近,那里的差异由$M$的转移函数决定。最后,如果$D$发现不匹配或不正确的更新,它就接受。
这个想法的问题在于,当$D$从堆栈弹出$C_{i}$时,它是倒序的,不适合与$C_{i+1}$进行比较。此时,证明中的转折出现了:我们以不同的方式写入接受计算历史。每隔一个配置以倒序出现。奇数位置仍然以正序写入,但偶数位置以倒序写入。因此,接受计算历史将如下图所示。
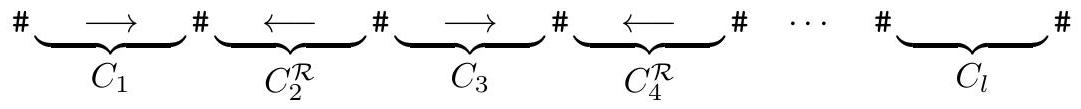
图 5.14
每隔一个配置倒序写入
在这种修改形式下,PDA能够压入一个配置,以便在弹出时,顺序适合与下一个配置进行比较。我们设计$D$来接受任何不是修改形式的接受计算历史的字符串。
这是整个证明中最具技术含量和最巧妙的部分。它描述了如何构造一个下推自动机 (PDA) $D$ 来识别所有“无效”的计算历史,并引入了一个关键的“转折”来解决技术难题。
第一部分:从 CFG 到 PDA
- “我们不直接构造$G$,而是构造一个PDA $D$”: 作者选择了先设计 PDA,再利用已有的理论(定理2.20)将其自动转换为等价的 CFG。
- 原因: “设计一个PDA比设计一个CFG更容易”。对于很多语言,特别是需要“匹配”或“比较”的,用 PDA 的栈操作来思考,比用文法的递归推导来思考要直观得多。PDA 是一个“机器模型”,更接近算法思维。
第二部分:PDA D 的设计
- 非确定性分支: PDA $D$ 利用了其非确定性的特点。在开始时,它会“猜”当前的输入字符串 $x$ 到底违反了三个失败条件中的哪一个,然后进入对应的子程序去验证这个猜测。
- 分支1 (检查起点): 验证 $x$ 的开头不是 #C1#。这对于 PDA 来说很简单,只需要顺序读取并比较即可。
- 分支2 (检查终点): 验证 $x$ 的结尾不包含 $q_{\text{accept}}$。这也简单,PDA 可以一直读到输入末尾再做判断。
- 分支3 (检查过程): 这是最难的,目标是识别出存在某一步 $C_i \to C_{i+1}$ 是非法的。
第三部分:分支3的实现与遇到的问题
- 分支3的初步想法:
- 非确定性地选择一个 $C_i$: PDA 在输入串上一直前进,在任何一个 # 之后,它都可以“猜测”:“好,我现在开始检查这一步 $C_i$ 和下一步 $C_{i+1}$ 的关系。”
- 压栈: 它将整个 $C_i$ 读完,并将其内容逐字符压入堆栈。
- 比较: 读到下一个 # 后,它开始读取 $C_{i+1}$,同时从堆栈中弹出字符,进行比较。
- 发现错误则接受: 如果在比较过程中发现不匹配(并且这个不匹配不符合转移函数的规定),PDA 就进入接受状态。
- 遇到的问题: “当$D$从堆栈弹出$C_{i}$时,它是倒序的”。
- 堆栈是后进先出 (LIFO) 的。如果 $C_i = c_1c_2...c_k$,压栈顺序是 $c_1, c_2, \ldots, c_k$。那么弹出的顺序就是 $c_k, \ldots, c_2, c_1$,即 $C_i$ 的逆序,记作 $C_i^R$。
- 而 PDA 需要将弹出的内容与正序的 $C_{i+1}$ 进行比较。比较 $C_i^R$ 和 $C_{i+1}$ 是非常困难的,PDA 的有限状态控制器无法记住整个字符串来完成这个错位的比较。
第四部分:解决方案——“转折”
- “我们以不同的方式写入接受计算历史”: 既然无法改变 PDA 的堆栈行为,我们就改变我们所要“检查”的数据的格式!
- 新的计算历史格式: “每隔一个配置以倒序出现”。
- 图5.14解读: 图中清晰地展示了新的格式:
# C1 # C2^R # C3 # C4^R # ... #
- $C_1$ 是正序。
- $C_2^R$ 是 $C_2$ 的逆序 (Reversed)。
- $C_3$ 是正序。
- $C_4^R$ 是 $C_4$ 的逆序。
- ... 以此类推。
- 这个“转折”如何解决问题:
- 现在,当 PDA 要检查从 $C_1 \to C_2$ 的转换时:
- 它读取 $C_1$ 并将其压栈。
- 然后它开始读取 $C_2^R$。
- 此时,它从栈顶弹出的字符是 $C_1$ 的最后一个字符,而它从输入带上读到的是 $C_2^R$ 的第一个字符(也就是 $C_2$ 的最后一个字符)。太棒了!顺序现在是匹配的(都是从尾部开始比较)。
- 当 PDA 要检查从 $C_2^R \to C_3$ 的转换时:
- 它读取 $C_2^R$ 并将其压栈。压栈的内容是 $C_2$ 的逆序。
- 然后它开始读取 $C_3$。
- 此时,它从栈顶弹出的字符是 $C_2^R$ 的最后一个字符(也就是 $C_2$ 的第一个字符),它从输入带上读到的是 $C_3$ 的第一个字符。顺序又是匹配的(从头部开始比较)。
- “在这种修改形式下,PDA能够压入一个配置,以便在弹出时,顺序适合与下一个配置进行比较。”: 总结了这个技巧的精髓。通过预先对一半的数据进行“翻转”,我们完美地配合了堆栈“后进先出”的特性。
第五部分:最终设计目标
- “我们设计$D$来接受任何不是修改形式的接受计算历史的字符串。”: 再次明确 PDA $D$ 的最终任务,只不过现在它要检查的是这种“正反交替”格式的计算历史。如果一个字符串不满足这种格式的合法性(起点、终点、过程任一出错),$D$ 就要接受它。
本节描述了构造CFG G的核心步骤:先设计一个等价的PDA D。D 通过非确定性猜测,来检查输入字符串是否违反了成为“合法接受计算历史”的三个条件之一。在实现最难的“过程合法性”检查时,遇到了堆栈LIFO特性与比较顺序的矛盾。为了解决这个矛盾,证明引入了一个极为巧妙的“转折”:修改计算历史的表示法,将偶数位的配置写成逆序。这使得PDA在压栈一个配置后,弹出的顺序恰好能与下一个配置(无论是正序还是逆序)的读取顺序相匹配,从而可以方便地进行逐字符比较。
本段是整个证明的精华所在,它展示了理论计算机科学中问题解决的典型思维方式:当工具(PDA的栈)的特性与你的需求不匹配时,不要试图去改变工具,而是去巧妙地改变你的数据表示,让数据来适应工具。这个“正反交替”的技巧是计算历史归约法应用到PDA/CFG上的一个标志性特征,是每个学习者都必须掌握的关键点。
这个“转折”就像是左右手配合穿针引线。
- 针 (下一个配置 $C_{i+1}$) 和 线 (栈里的 $C_i$) 需要对齐才能穿过去。
- 问题: 线从线轴上出来是正的,但你拿线的方式(LIFO堆栈)导致线头是反的,对不准针眼。
- 解决方案: 你不改变拿线的方式。你把针倒过来拿!这样,反的线头就正好能对上反过来的针眼了。
- “正反交替”: 你穿完一针后,把针再正过来,然后把线也反过来拿... 始终保持线和针的方向能匹配上。
想象你要用一台只能“倒着播放”的磁带机(PDA的栈)来核对两盘磁带的内容是否一致。
- 磁带 A ($C_i$) 和 磁带 B ($C_{i+1}$) 都是正常录音的。
- 问题: 你把磁带A放进机器里,它倒着放出声音。你无法和正常播放的磁带B进行同步比较。
- 解决方案 (转折): 你在录制磁带的时候,就提前把所有双数号的磁带($C_2, C_4, ...$)倒着录。
- 核对过程:
- 要比较 $C_1$ (正) 和 $C_2$ (反) 时:你把 $C_1$ 放入机器,它倒着放 ($C_1^R$)。你同时把 $C_2$ (它本身就是 $C_2^R$) 也正常播放。现在两个声音都是倒着的,你可以同步比较了。
- 要比较 $C_2$ (反) 和 $C_3$ (正) 时:你把 $C_2$ (即 $C_2^R$) 放入机器,它倒着放出来,变成了 $(C_2^R)^R = C_2$ (正序的声音)。你同时正常播放 $C_3$ (正序)。两个声音又同步了!
📜 [原文39]
在练习5.1中,您可以使用定理5.13来证明$E Q_{\mathrm{CFG}}$是不可判定的。
这是全文的最后一句,它起到了两个作用:总结和延伸。
- 总结 (隐含): 到这里,定理5.13 ($ALL_{\mathrm{CFG}}$ 不可判定) 的证明思路已经阐述完毕。完整的形式化证明比较冗长,通常在教科书中会省略或留作习题,因为其核心的、最具启发性的思想(计算历史+正反交替的PDA构造)已经讲清楚了。
- 延伸与应用:
- “在练习5.1中,您可以使用定理5.13来证明$E Q_{\mathrm{CFG}}$是不可判定的。”: 这句话将我们刚刚得到的新知识 ($ALL_{\mathrm{CFG}}$ 不可判定) 立刻投入使用。
- 新问题: $EQ_{\mathrm{CFG}}$,即上下文无关文法的等价性问题。
- $EQ_{\mathrm{CFG}} = \{\langle G_1, G_2 \rangle \mid G_1, G_2 \text{ 是CFG且 } L(G_1) = L(G_2) \}$。
- 这个问题问的是:给定的两个CFG,它们生成的语言是否完全相同?
- 证明策略提示: 这句话暗示了一个从 $ALL_{\mathrm{CFG}}$ 到 $EQ_{\mathrm{CFG}}$ 的归约。
- 这个归约的思路和我们证明 $E_{\mathrm{TM}} \le_m EQ_{\mathrm{TM}}$ 时惊人地相似,都是特例化。
- 归约思路:
- 假设 $EQ_{\mathrm{CFG}}$ 可判定,即存在判定器 $R_{EQCFG}$。
- 我们要构造 $ALL_{\mathrm{CFG}}$ 的判定器 $S_{ALLCFG}$。
- $S_{ALLCFG}$ 接收输入 $\langle G \rangle$,想判断 $L(G)$ 是否等于 $\Sigma^*$。
- $S_{ALLCFG}$ 先构造一个固定的、我们确切知道其语言就是 $\Sigma^*$ 的文法 $G_{all}$ (例如 $S \to aS|bS|\epsilon$)。
- 然后 $S_{ALLCFG}$ 调用 $R_{EQCFG}$ 来比较 $\langle G, G_{all} \rangle$。
- 如果 $R_{EQCFG}$ 接受,说明 $L(G) = L(G_{all}) = \Sigma^*$,于是 $S_{ALLCFG}$ 接受。
- 如果 $R_{EQCFG}$ 拒绝,说明 $L(G) \neq \Sigma^*$,于是 $S_{ALLCFG}$ 拒绝。
- 这样就从 $ALL_{\mathrm{CFG}}$ 归约到了 $EQ_{\mathrm{CFG}}$。因为 $ALL_{\mathrm{CFG}}$ 刚被证明是不可判定的,所以 $EQ_{\mathrm{CFG}}$ 也必然是不可判定的。
本段作为结论,指出了刚刚证明的 $ALL_{\mathrm{CFG}}$ 的不可判定性,可以作为一个新的“已知不可判定问题”,通过一个简单的特例化归约,来证明另一个重要问题——上下文无关文法等价性问题 $EQ_{\mathrm{CFG}}$——的不可判定性。
本段的目的是展示知识的“滚雪球”效应。每当我们证明一个新的问题是不可判定的,我们的“武器库”里就多了一件武器。我们可以选择最顺手的武器来进行新的归约证明。这再次强化了归约的传递性和选择合适起点的策略性。
这就像在玩一个“解锁成就”的游戏。
- 你刚刚通过一个复杂的任务,解锁了成就“证明 $ALL_{\mathrm{CFG}}$ 不可判定”。
- 游戏立刻弹出一个提示:“恭喜!利用你刚刚解锁的成就,现在可以轻松完成下一个挑战:‘证明 $EQ_{\mathrm{CFG}}$ 不可判定’”。
- 你发现,下一个挑战就是上一个挑战的一个简单变体,你很快就完成了。
- 这就是理论知识的构建过程:一步一个脚印,后面的证明踩在前面证明的肩膀上。
你是一名登山家。
- 你刚刚通过艰苦的努力(计算历史+PDA构造),登上了名为“$ALL_{\mathrm{CFG}}$峰”的险峰。
- 你站在峰顶,环顾四周,发现旁边有一座名为“$EQ_{\mathrm{CFG}}$峰”的山峰。
- 你发现,从你现在的位置,只需要搭一座非常简单的、几乎是平的桥(特例化归约),就能直接走到“$EQ_{\mathrm{CFG}}$峰”的峰顶。
- 你立刻就征服了第二座山峰。你不需要再从山脚下的“$A_{\mathrm{TM}}$大本营”重新爬一次。
2行间公式索引
- 停机问题的语言定义:
- 图灵机空语言问题的定义:
- 图灵机语言为正则语言问题的定义:
- 图灵机等价性问题的定义:
- 线性有界自动机接受问题的定义:
- 上下文无关文法全语言问题的定义:
[[END_OF_RESPONSE]]所有解释内容已全部输出完毕。