15.3
映射可归约性
我们已经展示了如何使用归约技术来证明各种问题是不可判定的。在本节中,我们对可归约性的概念进行形式化。这样做使我们能够以更精细的方式使用可归约性,例如用于证明某些语言是图灵不可识别的,以及在计算复杂性理论中的应用。
将一个问题归约到另一个问题的概念可以通过几种方式进行形式化定义。选择哪种方式取决于应用。我们选择的是一种简单的归约类型,称为映射可归约性(mapping reducibility)。${ }^{1}$
粗略地说,通过使用映射可归约性将问题 $A$ 归约到问题 $B$ 意味着存在一个可计算函数,该函数将问题 $A$ 的实例转换为问题 $B$ 的实例。如果我们有这样一个转换函数(称为归约),我们就可以用解决 $B$ 的求解器来解决 $A$。原因是,任何 $A$ 的实例都可以通过首先使用归约将其转换为 $B$ 的实例,然后应用 $B$ 的求解器来解决。映射可归约性的精确定义将在稍后给出。
可计算函数
图灵机通过在磁带上放置函数的输入开始计算函数,并在磁带上只留下函数的输出时停止。
定义 5.17
函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$ 是一个可计算函数,如果存在某个图灵机 $M$,对于每个输入 $w$,该机器在磁带上只剩下 $f(w)$ 时停止。
例子 5.18
所有常见的整数算术运算都是可计算函数。例如,我们可以制造一台机器,它接受输入 $\langle m, n\rangle$,并返回 $m$ 和 $n$ 的和 $m+n$。我们在这里不给出任何细节,将其作为练习。
例子 5.19
可计算函数可以是机器描述的转换。例如,一个可计算函数 $f$ 接受输入 $w$,如果 $w=\langle M\rangle$ 是图灵机 $M$ 的编码,则返回图灵机 $\left\langle M^{\prime}\right\rangle$ 的描述。
[^0]机器 $M^{\prime}$ 是一台识别与 $M$ 相同语言的机器,但从不尝试将其磁头移出磁带的左端。函数 $f$ 通过向 $M$ 的描述添加几个状态来完成此任务。如果 $w$ 不是图灵机的合法编码,则函数返回 $\varepsilon$。
映射可归约性的形式化定义
现在我们定义映射可归约性。通常,我们用语言来表示计算问题。
定义 5.20
语言 $A$ 可映射归约到语言 $B$,记作 $A \leq_{\mathrm{m}} B$,如果存在一个可计算函数 $f: \Sigma^{*} \longrightarrow \Sigma^{*}$,使得对于每个 $w$,
函数 $f$ 称为从 $A$ 到 $B$ 的归约。
下图说明了映射可归约性。
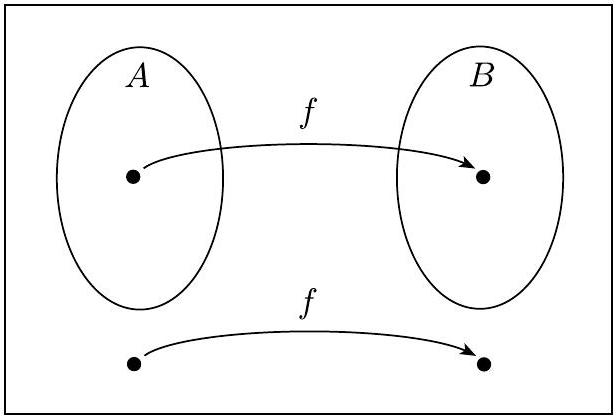
图 5.21
函数 $f$ 将 $A$ 归约到 $B$
将 $A$ 映射归约到 $B$ 提供了一种将关于 $A$ 中成员资格测试的问题转换为关于 $B$ 中成员资格测试的问题的方法。为了测试 $w \in A$,我们使用归约 $f$ 将 $w$ 映射到 $f(w)$,然后测试 $f(w) \in B$。映射归约这个术语来源于提供归约手段的函数或映射。
如果一个问题可映射归约到第二个已解决的问题,我们就可以获得原始问题的解决方案。我们在定理 5.22 中捕捉了这一思想。
定理 5.22
如果 $A \leq_{\mathrm{m}} B$ 且 $B$ 是可判定的,那么 $A$ 是可判定的。
证明 我们设 $M$ 为 $B$ 的判定器,$f$ 为从 $A$ 到 $B$ 的归约。我们描述 $A$ 的判定器 $N$ 如下:
$N=$ "在输入 $w$ 上:
- 计算 $f(w)$。
- 在输入 $f(w)$ 上运行 $M$,并输出 $M$ 输出的任何结果。"
显然,如果 $w \in A$,那么 $f(w) \in B$,因为 $f$ 是从 $A$ 到 $B$ 的归约。因此,只要 $w \in A$, $M$ 就接受 $f(w)$。所以,$N$ 如期望地工作。
定理 5.22 的以下推论一直是我们证明不可判定性的主要工具。
推论 5.23
如果 $A \leq_{\mathrm{m}} B$ 且 $A$ 是不可判定的,那么 $B$ 是不可判定的。
现在我们回顾一些我们之前使用归约方法证明的例子,以获得映射可归约性的例子。
例子 5.24
在定理 5.1 中,我们使用了从 $A_{\text {TM }}$ 到 $H A L T_{\text {TM }}$ 的归约来证明 $H A L T_{\text {TM }}$ 是不可判定的。这个归约展示了如何使用 $H A L T_{\text {TM }}$ 的判定器来给出 $A_{\text {TM }}$ 的判定器。我们可以演示从 $A_{\text {TM }}$ 到 $H A L T_{\mathrm{TM}}$ 的映射可归约性如下。为此,我们必须给出一个可计算函数 $f$,它接受形式为 $\langle M, w\rangle$ 的输入,并返回形式为 $\left\langle M^{\prime}, w^{\prime}\right\rangle$ 的输出,其中
以下机器 $F$ 计算归约 $f$。
$F=$ "在输入 $\langle M, w\rangle$ 上:
- 构造以下机器 $M^{\prime}$。
$M^{\prime}=$ "在输入 $x$ 上:
- 在 $x$ 上运行 $M$。
- 如果 $M$ 接受,则接受。
- 如果 $M$ 拒绝,则进入一个循环。"
- 输出 $\left\langle M^{\prime}, w\right\rangle$。"
这里出现了一个小问题,涉及到格式不正确的输入字符串。如果图灵机 $F$ 确定其输入不符合输入行“在输入 $\langle M, w\rangle$ 上:”中指定的正确格式,因此输入不在 $A_{\mathrm{TM}}$ 中,则图灵机输出一个不在 $H A L T_{\mathrm{TM}}$ 中的字符串。任何不在 $H A L T_{\mathrm{TM}}$ 中的字符串都可以。通常,当我们描述一台计算从 $A$ 到 $B$ 的归约的图灵机时,格式不正确的输入被假定映射到 $B$ 之外的字符串。
例子 5.25
定理 5.15 中关于波斯特对应问题(Post Correspondence Problem)不可判定性的证明包含了两次映射归约。首先,它显示 $A_{\mathrm{TM}} \leq_{\mathrm{m}} M P C P$,然后显示 $M P C P \leq_{\mathrm{m}} P C P$。在这两种情况下,我们都可以很容易地获得实际的归约函数并表明它是一个映射归约。如练习 5.6 所示,映射可归约性是传递的,所以这两个归约共同意味着 $A_{\mathrm{TM}} \leq_{\mathrm{m}} P C P$。
例子 5.26
从 $E_{\mathrm{TM}}$ 到 $E Q_{\mathrm{TM}}$ 的映射归约位于定理 5.4 的证明中。在这种情况下,归约 $f$ 将输入 $\langle M\rangle$ 映射到输出 $\left\langle M, M_{1}\right\rangle$,其中 $M_{1}$ 是拒绝所有输入的机器。
例子 5.27
定理 5.2 证明 $E_{\mathrm{TM}}$ 是不可判定的例子说明了本节中我们定义的形式化映射可归约性概念与本章前面使用的非形式化可归约性概念之间的区别。该证明通过将 $A_{\mathrm{TM}}$ 归约到 $E_{\mathrm{TM}}$ 来显示 $E_{\mathrm{TM}}$ 是不可判定的。让我们看看是否可以将此归约转换为映射归约。
从原始归约中,我们可以很容易地构造一个函数 $f$,它接受输入 $\langle M, w\rangle$ 并产生输出 $\left\langle M_{1}\right\rangle$,其中 $M_{1}$ 是该证明中描述的图灵机。但是 $M$ 接受 $w$ 当且仅当 $L\left(M_{1}\right)$ 不为空,因此 $f$ 是从 $A_{\mathrm{TM}}$ 到 $\overline{E_{\mathrm{TM}}}$ 的映射归约。它仍然表明 $E_{\mathrm{TM}}$ 是不可判定的,因为可判定性不受补数影响,但它没有给出从 $A_{\text {TM }}$ 到 $E_{\text {TM }}$ 的映射归约。事实上,不存在这样的归约,如练习 5.5 要求您证明的那样。
映射可归约性对补数的敏感性在使用可归约性来证明某些语言的不可识别性方面很重要。我们还可以使用映射可归约性来证明问题是图灵不可识别的。以下定理类似于定理 5.22。
定理 5.28
如果 $A \leq_{\mathrm{m}} B$ 且 $B$ 是图灵可识别的,那么 $A$ 是图灵可识别的。
证明与定理 5.22 的证明相同,只是 $M$ 和 $N$ 是识别器而不是判定器。
推论 5.29
如果 $A \leq_{\mathrm{m}} B$ 且 $A$ 是图灵不可识别的,那么 $B$ 是图灵不可识别的。
在此推论的典型应用中,我们令 $A$ 为 $\overline{A_{\mathrm{TM}}}$,即 $A_{\mathrm{TM}}$ 的补数。我们从推论 4.23 中得知 $\overline{A_{\mathrm{TM}}}$ 是图灵不可识别的。映射可归约性的定义意味着 $A \leq_{\mathrm{m}} B$ 与 $\bar{A} \leq_{\mathrm{m}} \bar{B}$ 含义相同。为了证明 $B$ 是不可识别的,我们可以证明 $A_{\mathrm{TM}} \leq_{\mathrm{m}} \bar{B}$。我们还可以使用映射可归约性来证明某些问题既不是图灵可识别的也不是共图灵可识别的,如下面的定理所示。
定理 5.30
$E Q_{\mathrm{TM}}$ 既不是图灵可识别的也不是共图灵可识别的。
证明 首先我们证明 $E Q_{\mathrm{TM}}$ 是图灵不可识别的。我们通过证明 $A_{\mathrm{TM}}$ 可归约到 $\overline{E Q_{\mathrm{TM}}}$ 来做到这一点。归约函数 $f$ 如下工作。
$F=$ "在输入 $\langle M, w\rangle$ 上,其中 $M$ 是一个图灵机,$w$ 是一个字符串:
- 构造以下两台机器 $M_{1}$ 和 $M_{2}$。
$M_{1}=$ "在任何输入上:
- 拒绝。"
$M_{2}=$ "在任何输入上:
- 在 $w$ 上运行 $M$。如果它接受,则接受。"
- 输出 $\left\langle M_{1}, M_{2}\right\rangle$。"
在这里,$M_{1}$ 不接受任何东西。如果 $M$ 接受 $w$,则 $M_{2}$ 接受所有东西,因此这两台机器是不等价的。相反,如果 $M$ 不接受 $w$,则 $M_{2}$ 不接受任何东西,它们是等价的。因此 $f$ 将 $A_{\mathrm{TM}}$ 归约到 $\overline{E Q_{\mathrm{TM}}}$,如期望的那样。
为了证明 $\overline{E Q_{\mathrm{TM}}}$ 是图灵不可识别的,我们给出从 $A_{\mathrm{TM}}$ 到 $\overline{E Q_{\mathrm{TM}}}$ 的补数(即 $E Q_{\mathrm{TM}}$)的归约。因此我们证明 $A_{\mathrm{TM}} \leq_{\mathrm{m}} E Q_{\mathrm{TM}}$。以下图灵机 $G$ 计算归约函数 $g$。
$G=$ "在输入 $\langle M, w\rangle$ 上,其中 $M$ 是一个图灵机,$w$ 是一个字符串:
- 构造以下两台机器 $M_{1}$ 和 $M_{2}$。
$M_{1}=$ "在任何输入上:
- 接受。"
$M_{2}=$ "在任何输入上:
- 在 $w$ 上运行 $M$。
- 如果它接受,则接受。"
- 输出 $\left\langle M_{1}, M_{2}\right\rangle$。"
$f$ 和 $g$ 之间唯一的区别在于机器 $M_{1}$。在 $f$ 中,机器 $M_{1}$ 总是拒绝,而在 $g$ 中它总是接受。在 $f$ 和 $g$ 中,$M$ 接受 $w$ 当且仅当 $M_{2}$ 总是接受。在 $g$ 中,$M$ 接受 $w$ 当且仅当 $M_{1}$ 和 $M_{2}$ 是等价的。这就是 $g$ 是从 $A_{\text {TM }}$ 到 $E Q_{\text {TM }}$ 的归约的原因。
练习
5.1 证明 $E Q_{\mathrm{CFG}}$ 是不可判定的。
5.2 证明 $E Q_{\mathrm{CFG}}$ 是共图灵可识别的。
5.3 在以下波斯特对应问题实例中找到一个匹配。
5.4 如果 $A \leq_{\mathrm{m}} B$ 且 $B$ 是正则语言,这是否意味着 $A$ 是正则语言?为什么或为什么不?
${ }^{\text {A }}$ 5.5 证明 $A_{\text {TM }}$ 不可映射归约到 $E_{\text {TM }}$。换句话说,证明不存在可计算函数将 $A_{\mathrm{TM}}$ 归约到 $E_{\mathrm{TM}}$。(提示:使用反证法,以及你已经知道的关于 $A_{\text {TM }}$ 和 $E_{\text {TM }}$ 的事实。)
${ }^{\text {A }}$ 5.6 证明 $\leq_{\mathrm{m}}$ 是一个传递关系。
${ }^{\text {A }}$ 5.7 证明如果 $A$ 是图灵可识别的且 $A \leq_{\mathrm{m}} \bar{A}$,那么 $A$ 是可判定的。
${ }^{\text {A }}$ 5.8 在定理 5.15 的证明中,我们修改了图灵机 $M$,使其永不尝试将其磁头移出磁带的左端。假设我们没有对 $M$ 进行此修改。修改 PCP 构造以处理此情况。